插值法计算实际利率
插值法怎么估利率计算公式

插值法怎么估利率计算公式插值法是一种常用的数值分析方法,用于在已知数据点之间估计未知数据点的数值。
在金融领域中,利率是一个非常重要的指标,对于投资和贷款都有着重要的影响。
因此,利率的估计和预测对于金融市场的参与者来说至关重要。
在本文中,我们将介绍如何使用插值法来估计利率,并给出相应的计算公式。
首先,让我们简要回顾一下插值法的基本原理。
插值法是一种利用已知数据点来估计未知数据点的数值的方法。
在金融领域中,我们通常会遇到一些已知的利率数据点,比如一年期、两年期、五年期等不同期限的利率。
我们可以使用这些已知的利率数据点来估计其他期限的利率,从而得到一个完整的利率曲线。
在金融市场中,利率曲线通常是非线性的,并且在不同期限上可能有着不同的形状。
因此,我们需要使用一种灵活的插值方法来估计利率曲线上任意期限的利率。
在这里,我们将介绍一种常用的插值方法——样条插值法。
样条插值法是一种利用分段低次多项式来逼近已知数据点的方法。
在利率曲线的估计中,我们可以使用样条插值法来逼近不同期限上的利率数据点,从而得到一个平滑的利率曲线。
具体来说,我们可以将利率曲线分成若干段,并在每一段上使用低次多项式来逼近已知的利率数据点。
通过这种方法,我们可以得到一个连续且光滑的利率曲线,从而可以方便地估计任意期限上的利率。
接下来,让我们来介绍如何使用样条插值法来估计利率曲线。
假设我们已经有了一些已知的利率数据点,比如一年期、两年期、五年期等不同期限的利率。
我们可以先将这些数据点按照期限的大小进行排序,并将它们分成若干段。
然后,在每一段上使用低次多项式来逼近已知的利率数据点,从而得到一个平滑的利率曲线。
在实际计算中,我们可以使用一些常见的低次多项式来进行插值,比如线性插值、二次插值、三次插值等。
这些插值方法都有各自的优缺点,我们可以根据实际情况来选择合适的插值方法。
在金融市场中,通常会使用三次样条插值来估计利率曲线,因为它可以得到一个光滑且具有良好数学性质的曲线。
插值法计算实际利率

因此 , 9 %现 值 利 率 , 1 0 3 5 . 6 1 7 9 %, 1 0 0 0 r 9 2 1 . 9 3 3 2
1 2 %, ( 1 0 3 5 . 6 1 7 — 1 0 0 0 ) /( 1 0 3 5 . 6 1 7 — 9 2 1 . 9 3 3 2 ) =( 9 %一 r ) /
2014 年 3 月 第 1 3期
教 育 教 学 论 坛
EDU C ATI ON TE ACH I N G FO RU M
Ma t " . 2 O1 4 N O. 13
插值法计算实 际利率
杨 丽霞 , 黄斯 婷
( 辽宁省阜新市细河职教 中心 , 辽宁 阜新 1 2 3 0 0 0 )
摘要 : 插值 法计算 实际利率 , 其原理是根据比例 关 系建立一个方程 , 然后 解方程 , 计算得 出所要 求的数据。插值 法是 函数逼近 的一种重要方法 , 是数值计算的基本课题 。 关键词 : 插值 法; 计算实际利率 ; 数值计算 中图分类号 : G 7 1 2 文献标 志码 : A
一
文章编号 : 1 6 7 4 — 9 3 2 4 ( 2 0 1 4 ) 1 3 — 0 1 0 5 — 0 2
、
插 值 法
( 3 ) 还需要注意的ቤተ መጻሕፍቲ ባይዱ个问题是 : 如果对A 1 和A 2 的数值 进行交换 , 则必须 同时对B l 和B 2 的数值也交换 , 否则 , 计算 得 出 的结 果一 定不正 确 。
( B 1 一 B 2 ) 计算得 出A的数值 。 ( 2 ) 仔 细 观察 一 下这 个方 程会 看 出一 个 特点 , 即相 对 应 的数据在等式两方的位置相同。例如 : A 1 位于等式左方表
求实际利率是要用内插法

求实际利率是要用内插法(又叫插值法)计算的。
“内插法”的原理是根据比例关系建立一个方程,然后,解方程计算得出所要求的数据。
例如:假设与A1对应的数据是B1,与A2对应的数据是B2,现在已知与A对应的数据是B,A介于A1和A2之间,则可以按照(A1-A)/(A1-A2)=(B1-B)/(B1-B2)计算得出A的数值,会计考试时如用到年金现值系数及其他系数时,会给出相关的系数表,再直接用内插法求出实际利率。
建议你学习一下财务成本管理的相关内容。
以教材35页的例题2-5为例:
59×(1+r)^-1+59×(1+r)^-2+59×(1+r)^-3+59×(1+r)^-4+(59+1250)×(1+r)^-5=1000(元)这个计算式可以转变为59×(P/A,r,5)+1250×(P/F,r,5)=1000
当r=9%时,59×3.8897+1250×0.6499=229.4923+812.375=1041.8673>1 000元当r=12%时,59×3.6048+1250×0.5674=212.6832+709.25=921.9332<1000元因此,
现值利率
1041.8673 9%
1000 r
921.9332 12%
(1041.8673-1000)/(1041.8673-921.9332)=(9%-r)/(9%-12%)
解之得,r=10%。
插值法例题计算过程

插值法例题计算过程(实用版)目录一、插值法简介二、插值法例题计算过程1.公式变形2.计算过程3.结论正文一、插值法简介插值法是一种求解未知数值的方法,通常用于预测和推断。
在财务管理中,插值法常用于计算实际利率、股票价格和债券价格等。
插值法的核心思想是根据已知的数据点,通过数学模型估算出未知数据点的值。
二、插值法例题计算过程假设有一个财务问题,需要计算一个项目的净现值(NPV)。
已知该项目在不同折现率下的净现值如下:- 当折现率为 12% 时,净现值为 116530- 当折现率为 i 时,净现值为 120000- 当折现率为 10% 时,净现值为 121765为了计算项目的实际利率,我们可以使用插值法。
首先,我们需要将公式进行变形,以便于理解和计算。
变形后的公式如下:(i-12%) / (10%-12%) = (120000-116530) / (121765-116530)接下来,我们可以按照以下步骤进行计算:1.将已知的数值代入公式中,得到:(i-12%) / (10%-12%) = 3470 / 52352.对公式进行化简,得到:(i-12%) / (10%-12%) = 0.66023.解方程,得到:i = 12% + 0.6602 * (10%-12%)i = 12% + 0.6602 * (-2%)i = 12% - 1.3204%i = 10.68%因此,该项目的实际利率为 10.68%。
通过以上计算过程,我们可以看到插值法在计算实际利率方面的应用。
在实际应用中,插值法还可以用于计算其他财务指标,如股票价格、债券价格等。
插值法计算实际利率

插值法计算实际利率“插值法”计算实际利率。
在08年考题中涉及到了实际利率的计算,其原理是根据比例关系建立一个方程,然后,解方程计算得出所要求的数据。
例如:假设与A1对应的数据是B1,与A2对应的数据是B2,现在已知与A对应的数据是B,A介于A1和A2之间,即下对应关系:A1 B1A(?) BA2 B2则可以按照(A1-A)/(A1-A2)=(B1-B)/(B1-B2)计算得出A的数值,其中A1、A2、B1、B2、B都是已知数据。
根本不必记忆教材中的公式,也没有任何规定必须B1>B2验证如下:根据:(A1-A)/(A1-A2)=(B1-B)/(B1-B2)可知:(A1-A)=(B1-B)/(B1-B2)×(A1- A2)A=A1-(B1-B)/(B1-B2)×(A1-A2)=A1+(B1-B)/(B1- B2)×(A2-A1)考生需理解和掌握相应的计算。
例如:某人向银行存入5000元,在利率为多少时才能保证在未来10年中每年末收到750元?5000/750=6.667 或 750*m=5000查年金现值表,期数为10,利率i=8%时,系数为6.710;利率i=9%,系数为6.418。
说明利率在8-9%之间,设为x%8% 6.710x% 6.6679% 6.418(x%-8%)/(9%-8%)= (6.667-6.71)/(6.418-6.71)计算得出 x=8.147。
二、经典例题2000年1月1日,ABC公司支付价款120000元(含交易费用),从活跃市场上购入某公司5年期债券,面值180000元,票面利率5%,按年支付利息(即每年9000元),本金最后一次支付。
合同约定,该债券的发行方在遇到特定情况时可以将债券赎回,且不需要为提前赎回支付额外款项。
XYZ公司在购买该债券时,预计发行方不会提前赎回。
ABC公司将购入的该公司债券划分为持有至到期投资,且不考虑所得税、减值损失等因素。
插值法计算实际利率

插值法计算实际利率20×0年1月1日,XYZ公司支付价款l 000元(含交易费用)从活跃市场上购入某公司5年期债券,面值1 250元,票面利率4.72%,按年支付利息(即每年59元),本金最后一次支付。
合同约定,该债券的发行方在遇到特定情况时可以将债券赎回,且不需要为提前赎回支付额外款项。
XYZ公司在购买该债券时,预计发行方不会提前赎回。
XYZ公司将购入的该公司债券划分为持有至到期投资,且不考虑所得税、减值损失等因素。
XYZ公司在初始确认时首先应计算确定该债券的实际利率,设该债券的实际利率为r,则可列出如下等式:59×(1+r)-1+59×(1+r)-2+59×(1+r)-3+59×(1+r)-4+(59+1250)×(1+r)-5=1000(元)(1)上式变形为:59×(1+r)-1+59×(1+r)-2+59×(1+r)-3+59×(1+r)-4+59×(1+r)-5+1250×(1+r)-5=1000(元)(2)2式写作:59×(P/A,r,5)+1250×(P/F,r,5)=1000 (3)(P/A,r,5)是利率为r,期限为5的年金现值系数;(P/F,r,5)是利率为r,期限为5的复利现值系数。
现值系数可通过查表求得。
当r=9%时,(P/A,9%,5)=3.8897,(P/F,9%,5)=0.6499代入3式得到59×3.8897+1250×0.6499=229.4923+812.375=1041.8673>1 000当r=12%时,(P/A,12%,5)=3.6048,(P/F,12%,5)=0.5674代入3式得到59×3.6048+1250×0.5674=212.6832+709.25=921.9332<1000采用插值法,计算r按比例法原理: 1041.8673 9%1000.0000 r921.9332 12%(1041.8673-1000)/(1041.8673-921.9332)=(9%-r)/(9%-12%)解之得,r=10%备注:此处要用到两个表:《年金现值系数表》、《复利现值系数表》题中的3.8897和3.6048是查《年金现值系数表》得来的,i=9%和12%,n=5;0.6499和0.5674是查《复利现值系数表》得来的,i=9%和12%,n=5假设两个实际利率的目的在于,确定现值1000在两个利率对应现值的范围内。
什么叫插值法通俗易懂

什么叫插值法通俗易懂
什么叫插值法通俗易懂:计算实际利率的一种方法
又称插值法。
根据未知函数f(x)在某区间内若干点的函数值,作出在该若干点的函数值与f(x)值相等的特定函数来近似原函数f(x),进而可用此特定函数算出该区间内其他各点的原函数f(x)的近似值,这种方法,称为内插法。
按特定函数的性质分,有线性内插、非线性内插等;按引数(自变量)个数分,有单内插、双内插和三内插等。
我国古代早就发明了内插法,当时称为招差术,如公元前1世纪左右的《九章算术》中的“盈不足术”即相当于一次差内插(线性内插);隋朝作《皇极历》的刘焯发明了二次差内插(抛物线内插);唐朝作《太衍历》的僧一行又发明了不等间距的二次差内插法;元朝作《授时历》的郭守敬进一步发明了三次差内插法。
在刘焯1000年后,郭守敬400年后,英国牛顿才提出内插法的一般公式。
内插法,一般是指数学上的直线内插,利用等比关系,是用一组已知的未知函数的自变量的值和与它对应的函数值来求一种未知函
数其它值的近似计算方法,是一种求未知函数,数值逼近求法,天文学上和农历计算中经常用的是白塞尔内插法,可参考《中国天文年历》的附录。
另外还有其他非线性内插法:如二次抛物线法和三次抛物线法。
因为是用别的线代替原线,所以存在误差。
可以根据计算结果比较误差值,如果误差在可以接受的范围内,才可以用相应的曲线代替。
一般查表法用直线内插法计算。
插值法计算实际利率

20×0年1月1日,XYZ公司支付价款l 000元(含交易费用)从活跃市场上购入某公司5年期债券,面值1 250元,票面利率%,按年支付利息(即每年59元),本金最后一次支付。
合同约定,该债券的发行方在遇到特定情况时可以将债券赎回,且不需要为提前赎回支付额外款项。
XYZ公司在购买该债券时,预计发行方不会提前赎回。
XYZ公司将购入的该公司债券划分为持有至到期投资,且不考虑所得税、减值损失等因素。
XYZ公司在初始确认时首先应计算确定该债券的实际利率,设该债券的实际利率为r,则可列出如下等式:59×(1+r)-1+59×(1+r)-2+59×(1+r)-3+59×(1+r)-4+(59+1250)×(1+r)-5=1000(元)(1)上式变形为:59×(1+r)-1+59×(1+r)-2+59×(1+r)-3+59×(1+r)-4+59×(1+r)-5+1250×(1+r)-5=1000(元)(2)2式写作:59×(P/A,r,5)+1250×(P/F,r,5)=1000 (3)(P/A,r,5)是利率为r,期限为5的年金现值系数;(P/F,r,5)是利率为r,期限为5的复利现值系数。
现值系数可通过查表求得。
当r=9%时,(P/A,9%,5)=,(P/F,9%,5)=代入3式得到59×+1250×=+=>1 000当r=12%时,(P/A,12%,5)=,(P/F,12%,5)=代入3式得到59×+1250×=+=<1000采用插值法,计算r按比例法原理:9%r12% /解之得,r=10%备注:此处要用到两个表:《年金现值系数表》、《复利现值系数表》题中的和是查《年金现值系数表》得来的,i=9%和12%,n=5;和是查《复利现值系数表》得来的,i=9%和12%,n=5假设两个实际利率的目的在于,确定现值1000在两个利率对应现值的范围内。
实际利率的核算方法和原理

关于内插法求实际利率,做出以下总结:(1)“内插法”的原理是根据等比关系建立一个方程,然后解方程计算得出所要求的数据。
例如:假设与A1对应的数据是B1,与A2对应的数据是B2,A介于A1和A2之间,已知与A对应的数据是B,则可以按照(A1-A)/(A1-A2)=(B1-B)/(B1-B2)计算得出A的数值。
(2)仔细观察一下这个方程会看出一个特点,即相对应的数据在等式两方的位置相同。
例如:A1位于等式左方表达式的分子和分母的左侧,与其对应的数字B1位于等式右方的表达式的分子和分母的左侧。
(3)还需要注意的一个问题是:如果对A1和A2的数值进行交换,则必须同时对B1和B2的数值也交换,否则,计算得出的结果一定不正确。
59×(1+r)^-1+59×(1+r)^-2+59×(1+r)^-3+59×(1+r)^-4+(59+1250)×(1+r)^-5=1000(元)这个计算式可以转变为59×(P/A,r,5)+1250×(P/F,r,5)=1000该式子采用的是复利现值系数的思路做的,如果改为年金现值系数,每年的利息其实就是年金,要收取5年,所以说是5年期的,59*(P/A,R,5)+1250×(P/F,R,5)=1000当r=9%时,59×3.8897+1250×0.6449=229.4923+806.125=1035.617>1 000元当r=12%时,59×3.6048+1250×0.5674=212.6832+709.25=921.9332<1000元因此,9%现值利率1035.6179%1000r921.933212%(1035.617-1000)/(1035.617-921.9332)=(9%-r)/(9%-12%)解之得,r=10%.9%是估计出来的。
在计算9%和12%之前,会有很多次预测,最终估算确定出9%和12%来推算r。
实际利率插值法计算公式

我们要探讨实际利率插值法的计算公式。
首先,我们需要了解什么是实际利率插值法。
实际利率插值法是一种用于估算实际利率的方法,特别是在金融和投资领域。
当我们知道一个投资或贷款的近似利率,但需要更精确的实际利率时,我们可以使用这种方法。
假设我们有一个已知的近似利率r_approx 和一个已知的误差范围Δr。
我们的目标是找到一个更精确的实际利率r_actual。
实际利率插值法的计算公式如下:
r_actual = r_approx + Δr × (近似利率与实际利率之间的差值)
这个公式可以帮助我们估算更精确的实际利率。
通过实际利率插值法,我们可以更准确地估算实际利率,这对于金融和投资决策非常重要。
例如,如果我们知道一个贷款的近似年利率为5%,但需要更精确的数值,我们可以使用实际利率插值法来找到更准确的数值。
这种方法可以帮助我们更好地理解投资或贷款的成本,并做出更明智的决策。
插值法计算实际利率

插值法计算实际利率20 X)年1月1日,XYZ公司支付价款I 000元(含交易费用)从活跃市场上购入某公司5年期债券,面值1 250元,票面利率4.72%,按年支付利息(即每年59元),本金最后一次支付。
合同约定,该债券的发行方在遇到特定情况时可以将债券赎回,且不需要为提前赎回支付额外款项。
XYZ公司在购买该债券时,预计发行方不会提前赎回。
XYZ公司将购入的该公司债券划分为持有至到期投资,且不考虑所得税、减值损失等因素。
XYZ公司在初始确认时首先应计算确定该债券的实际利率,设该债券的实际利率为r, 则可列出如下等式:59 X (1+ r)—1 + 59 X (1+ r)—2 + 59 X (1 + r)—3+ 59 X (1 + r)—4+( 59+ 1250) X (1 + r)—5= 1000 (元)(1)上式变形为:59 X (1+ r)—1 + 59 X (1+ r)—2 + 59 X (1 + r)—3+ 59 X (1 + r)—4+ 59 X (1 + r)—5 + 1250X (1 + r)—5= 1000 (元)(2)2 式写作:59 X ( P/A, r, 5)+ 1250 X( P/F, r, 5) =1000 (3)(P/A , r, 5)是利率为r,期限为5的年金现值系数;(P/F, r, 5)是利率为r,期限为5的复利现值系数。
现值系数可通过查表求得。
当r=9% 时,(P/A , 9%, 5)=3.8897 ,( P/F, 9% , 5)=0.6499代入 3 式得到59X3.8897+1250X0.6499 = 229.4923+812.375 = 1041.8673>1 000当r=12% 时,(P/A , 12%, 5)=3.6048 , ( P/F , 12% , 5)=0.5674代入 3 式得到59X3.6048+1250X0.5674 = 212.6832+709.25 = 921.9332<1000采用插值法,计算r按比例法原理:1041.8673 9%1000.0000 r921.9332 12%(1041.8673-1000)/(1041.8673-921.9332)=(9%-r)/(9%-12%)解之得,r=10%备注:此处要用到两个表:《年金现值系数表》、《复利现值系数表》题中的3.8897和3.6048是查《年金现值系数表》得来的,i=9%和12% , n=5; 0.6499和0.5674是查《复利现值系数表》得来的,i=9%和12% , n=5假设两个实际利率的目的在于,确定现值1000在两个利率对应现值的范围内。
插值法计算实际利率的原理

插值法计算实际利率的原理插值法计算实际利率的原理,听起来有点高深对吧?但其实它就像你在超市挑水果,想选个又大又甜的西瓜,得先瞅瞅价格和质量,才能做出最佳选择。
实际利率,就像那西瓜的真实口感,得经过一番“计算”,才能知道到底值不值得买。
简单来说,插值法就像是在找两个已知数据之间的桥梁,帮助我们猜测那些未知的东西。
想象一下,你在街上溜达,突然看到两家店。
一家卖冰淇淋,价格是五块钱,一家卖奶茶,价格十块。
你心想,冰淇淋太贵了,奶茶又便宜,那中间的六块钱的冰淇淋该是个什么味儿呢?插值法就可以帮你推测那中间的价格和品质。
通过两个已知的点,我们可以算出一个合理的“中间价”,这样就能省下不少“冤屈”的钱。
在金融领域,实际利率就是咱们在投资时最关心的事儿。
你想呀,银行给你存款利率是2%,可是通货膨胀率可能达到了3%。
听起来就像是你掏出一百块,结果只剩九十七块,真是心痛不已。
插值法就好比一根神奇的棒子,帮我们把这些利率数字串起来,让我们一目了然。
说到插值法,这个技术其实用得很广泛,不光是金融。
就像做菜,找不到调料怎么办?咱们可以根据现有的调料,来估算出缺少的味道。
插值法的核心思想就是通过已知的值来推测未知的值。
就像调味料的搭配,得有个分寸,太咸或太淡都不好,只有恰到好处,才能让菜肴美味可口。
再说实际利率的计算,通常咱们会看到一些公式,那些公式就像是复杂的菜谱,乍一看让人头大。
不过别担心,最终目的还是为了让你吃到美味的“利息”!看似复杂的计算其实只是把已知的利率和通货膨胀率进行“搭配”,用插值法来给出一个实际的利率,简单明了,通俗易懂。
别以为插值法只是在书本上见过。
生活中我们随处可见。
比如说,你参加聚会,朋友们问你这个那个人的身高。
你身边有两个人,一个180cm,一个160cm。
你心里就会想,“嘿,那我推测一下,那个家伙可能在170cm左右吧!”这就是一种非正式的插值法,简单又有效。
实际利率和插值法的结合,也不是说完全没有风险。
债券实际利率插值法的计算过程

债券实际利率插值法的计算过程
假设发行票面价值是600000 ,票面利率是8%,期限3年,到期还本付息的债券,初始确认成本为620000
先对实际利率的范围进行判断:
由于初始确认成本大于票面,则实际利率小于8%
先按3期,7%的年金现值系数和福利限制系数分别是2.624和0.816
计算债券每年应付利息=600000*8%=480000
利息和本金现值=48000*2.624+600000*0.816=615552
此时的现值小于面值,意味着实际利率小于7%
再按3期,6%的年金现值系数和复利现值系数分别是2.673和0.840
利息和本金现值=48000*2.673+600000*0.840=632304>620000
则实际利率在7%、6%之间
6% 632304
A% 620000 (A为实际利率)
7% 615552
设X%=6%-A,则
(6%-A%)/(632304-620000)=(6%-7%)/(632304-615552)
则X%=-0.73%
从而得到实际利率A=6%-(-0.73%)=6.73% 上述的就是插值法。
利率插值法计算公式

利率插值法计算公式
利率插值法是一种常用的金融计算方法,用于计算在不同时间点上的利率。
该方法依赖于已知的利率数据和时间点,通过插值计算出未知时间点的利率。
利率插值法的计算公式如下所示:
IR = IR1 + [(IR2 - IR1) / (T2 - T1)] * (T - T1) 其中,IR为所求时间点的利率,IR1和IR2分别为已知时间点的利率,T1和T2分别为已知时间点,T为所求时间点。
利率插值法的精度与已知利率数据的质量有关,因此在使用该方法时需要注意数据的准确性和完整性。
此外,利率插值法也存在一定的局限性,不适用于所有情况,需要根据具体情况进行选择。
- 1 -。
债券实际利率插值法的计算过程

债券实际利率插值法的计算过程第一步:收集市场数据首先,我们需要收集到期时间相似的债券的市场利率。
这些债券通常被称为基准债券或参考债券。
我们需要至少收集两个基准债券的市场利率,但最好收集三个或更多的债券,以确保计算结果的准确性。
第二步:计算每个基准债券的价格将每个基准债券的市场利率和到期时间带入债券定价模型,计算出每个基准债券的价格。
债券定价模型的具体选择可以根据实际情况而定,通常使用的模型包括贴现现金流模型和折现债券模型。
第三步:确定待估计债券价格计算待估计债券的市场利率对应的价格。
同样,我们可以使用债券定价模型来计算待估计债券的价格。
第四步:建立价格与利率之间的关系以基准债券的收益率为横坐标,基准债券的价格为纵坐标,建立一个价格与利率之间的关系图表。
可以绘制一条或多条拟合曲线,以观察价格与利率之间的趋势关系。
第五步:插值计算实际利率在建立的价格与利率关系的图表中,根据待估计债券的价格,找到对应的点。
然后,根据该点在图表中所处的位置,使用插值方法计算出待估计债券的实际利率。
常用的插值方法包括线性插值和二次插值。
线性插值将待估计点与其前后两个已知点之间进行直线插值。
二次插值则会根据待估计点附近的三个已知点计算出二次曲线,再根据二次曲线插值计算待估计点的实际利率。
第六步:检验计算结果计算得出待估计债券的实际利率后,可以将其代入债券定价模型中,计算出该利率对应的债券价格。
与实际市场价格进行对比,检验计算结果的准确性。
注意事项:1.在选择基准债券时,应选择到期时间与待估计债券相似的债券,以确保插值结果的准确性。
2.绘制价格与利率之间的关系时,应将基准债券的到期时间作为横坐标,以保持一致。
3.在进行插值计算时,要注意选择适当的插值方法以及控制误差范围,以确保计算结果的可靠性。
债券实际利率插值法是一种常用的债券定价方法,可以帮助投资者评估债券的实际收益率。
通过收集市场数据、建立价格与利率之间的关系,以及进行插值计算,投资者可以更准确地了解债券的收益情况,并做出相应的投资决策。
年金现值插值法求利率计算过程

年金现值插值法求利率计算过程
年金现值插值法是一种用于计算年金利率的方法,其计算步骤如下:
1. 首先确定年金的现值PV(Present Value)和年金的期数n (Number of Periods)。
2. 根据已知的年金现值PV、年金期数n和预估的利率r,计算出年金的未来值FV(Future Value),公式为FV = PV * (1 + r)^n。
3. 如果计算得到的年金未来值FV大于0,则说明预估的利率r过低;如果计算得到的年金未来值FV小于0,则说明预估的利率r过高。
4. 使用二分法逐步调整预估的利率r,直到计算得到的年金未来值FV接近0。
5. 不断重复步骤4,直到计算得到的年金未来值FV的绝对值小于一个可接受的误差范围。
6. 最后得到的利率r即为所求的年金利率。
需要注意的是,年金现值插值法是一种近似计算方法,结果可能存在一定的误差。
为了提高计算准确性,可以根据需要进行迭代次数的调整,并设置一个合理的误差范围。
资金时间价值、内插法计算实际利率

资金时间价值、内插法计算实际利率[本章前言]这是2010年的时候,写过的一篇专题,原贴在这里:/viewtopic.php?sand=reload(5591)&vforumoffset=0&offset=0&boardid=2&to picid=1000477不过,我现在又重新把冷了的菜拿出来炒一炒,加点小佐料,呵呵,味道也应该还行。
我基本没有更改原贴的核心内容,只是做了一些局部的修改,以适应2012年的考试要求,另外,也是为了让我的2012年财务管理总结的各章节得以完整的体现,所以,就把这贴子复制过来,丰富一下内容,再次发表。
同时,小鱼也希望大家要重视和掌握本章内容,本章是学好财管的基础知识,这是一定的!这一章我把它放在了总论之后来学习,其实,本来这就应该提前掌握的,学好了时间价值,财管后面的内容就相对容易理解得多了。
我不知道为何教材不按这样的顺序来安排,可能,我的想法和编教材的高师们想法有所不同。
如果苟同于小鱼的学友,就跟着我的思路先学好这一章吧。
呵呵。
时间就是我们的生命,这一点,没人能够怀疑。
我们的一生,也就是几十年,没人能够逃得出自然的规律,但,我们该如何把握自己的一生?让有限的生命,绽放无限的光彩?对于每一个人自己来说,他的生命就是有价值的,是否就可以这样理解为生命时间价值?我在第一章总论里面,聊了聊“暗时间”的一些话题,现在,我又想起了这个词,有些人,庸庸碌碌的过着日子,做每一件事都很“专注”,比如,闭目养神的时候,就真的很认真的闭目养神,大脑真的处于一种空闲状态。
在坐地铁的时候,就直勾勾的盯着对面排的美女,脑子里也就真专注的想着某些不良行为。
可是,把自己的生命活出价值的人,他在闭目养神的时候,坐地铁的时候,他的大脑,一定是在高速运转着的。
[学习要求]1、彻底理解时间价值的理念,明白什么叫资金时间价值。
2、学会画时间轴,能够做到在解每一个计算题之前,先把时间轴画出来,用时间轴来辅助解题,这样会让您一目了然,以防低级错误。
财务管理插值法公式是什么

财务管理插值法公式是什么学习财务管理的同学对于插值法应该不陌生,这插值法是有什么公式的呢?小编为你带来了“财务管理插值法”的相关知识,这其中也许就有你需要的。
什么是插值法插值法又称“内插法”,是利用函数f (x)在某区间中已知的若干点的函数值,作出适当的特定函数,在区间的其他点上用这特定函数的值作为函数f (x)的近似值,这种方法称为插值法。
如果这特定函数是多项式,就称它为插值多项式。
插值法计算实际利率20×0年1月1日,XYZ公司支付价款l 000元(含交易费用)从活跃市场上购入某公司5年期债券,面值1 250元,票面利率4.72%,按年支付利息(即每年59元),本金最后一次支付。
合同约定,该债券的发行方在遇到特定情况时可以将债券赎回,且不需要为提前赎回支付额外款项。
XYZ公司在购买该债券时,预计发行方不会提前赎回。
XYZ公司将购入的该公司债券划分为持有至到期投资,且不考虑所得税、减值损失等因素。
XYZ公司在初始确认时首先应计算确定该债券的实际利率,设该债券的实际利率为r,则可列出如下等式:59×(1+r)^1+59×(1+r)^2+59×(1+r)^3+59×(1+r)^4+(59+1 250)×(1+r)^5=1000(元)(1)上式变形为:59×(1+r)^1+59×(1+r)^2+59×(1+r)^3+59×(1+r)^4+59×(1 +r)^5+1250×(1+r)^5=1000(元)(2)2式写作:59×(P/A,r,5)+1250×(P/F,r,5)=1000 (3)(P/A,r,5)是利率为r,期限为5的年金现值系数;(P/F,r,5)是利率为r,期限为5的复利现值系数。
现值系数可通过查表求得。
当r=9%时,(P/A,9%,5)=3.8897,(P/F,9%,5)=0.6499 代入3式得到59×3.8897+1250×0.6499=229.4923+812.375=1041.8673>1 000当r=12%时,(P/A,12%,5)=3.6048,(P/F,12%,5)=0.5674代入3式得到59×3.6048+1250×0.5674=212.6832+709.25=921.9332<1000 采用插值法,计算r按比例法原理: 1041.8673 9%1000.0000 r921.9332 12%(1041.8673-1000)/(1041.8673-921.9332)=(9%-r)/(9%-12%)解之得,r=10%Lagrange插值Lagrange插值是n次多项式插值,其成功地用构造插值基函数的方法解决了求n次多项式插值函数问题。
【资产评估师学霸笔记】资产评估方法(下)
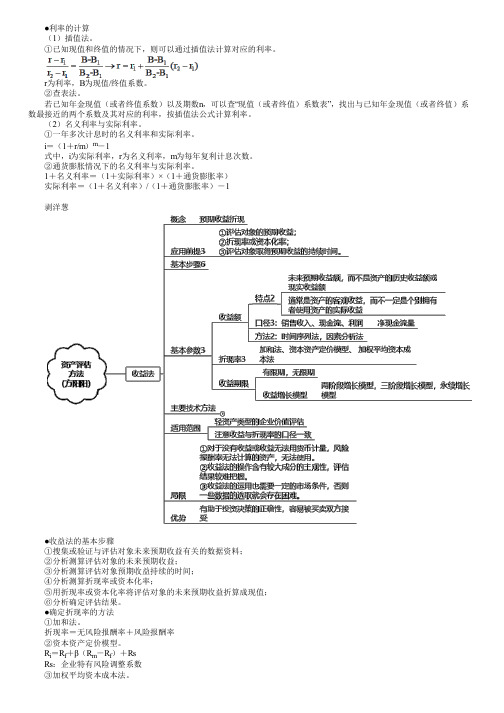
●利率的计算 (1)插值法。
①已知现值和终值的情况下,则可以通过插值法计算对应的利率。
r为利率,B为现值/终值系数。
②查表法。
若已知年金现值(或者终值系数)以及期数n,可以查“现值(或者终值)系数表”,找出与已知年金现值(或者终值)系数最接近的两个系数及其对应的利率,按插值法公式计算利率。
(2)名义利率与实际利率。
①一年多次计息时的名义利率和实际利率。
i=(1+r/m)m-1 式中,i为实际利率,r为名义利率,m为每年复利计息次数。
②通货膨胀情况下的名义利率与实际利率。
1+名义利率=(1+实际利率)×(1+通货膨胀率) 实际利率=(1+名义利率)/(1+通货膨胀率)-1 剥洋葱 ●收益法的基本步骤 ①搜集或验证与评估对象未来预期收益有关的数据资料; ②分析测算评估对象的未来预期收益; ③分析测算评估对象预期收益持续的时间; ④分析测算折现率或资本化率; ⑤用折现率或资本化率将评估对象的未来预期收益折算成现值; ⑥分析确定评估结果。
●确定折现率的方法 ①加和法。
折现率=无风险报酬率+风险报酬率 ②资本资产定价模型。
R i=R f+β(R m-R f)+Rs Rs:企业特有风险调整系数 ③加权平均资本成本法。
折现率=长期负债占资产总额的比重×长期负债利息率×(1-所得税率)+所有者权益占资产总额的比重×投资报酬率 剥洋葱 ●成本法的基本步骤 1.确定评估对象,并估算重置成本; 2.确定评估对象的使用年限; 3.测算评估对象的各项损耗或贬值额; 4.测算评估对象的价值。
参数含义方法公式重置成本现行再取得成本,社会一般生产力水平的客观必要成本重置核算法价格指数法功能价值类比法统计分析法复原重置成本:相同的全新资产更新重置成本:具有同等功能的全新资产实体性贬值有形损耗,使用及自然力的作用观察法使用年限法修复费用法功能性贬值技术进步引起的资产功能相对落后超额投资成本超额运营成本净超额运营成本折现经济性贬值外部条件的变化引起的资产闲置、收益下降间接计算法直接计算法综合成新率 年限成新率勘查成新率加权平均重置成本含义公式重置核算法购买型:购置价自建型:料、工、费及必要的资金成本和开发者的合理收益需要安装:购置价、运杂费、安装调试费以及其他必要费用不需要安装:购置价价格指数法历史成本(账面价值)=资产的历史成本×价格指数=资产的历史成本×(1+价格变动指数)功能价值类比法生产能力比例法规模经济效益指数法统计分析法 =∑某类资产账面历史成本×K 实体性贬值含义公式观察法判断成新率=重置成本×资产实体性贬值率=重置成本×(1-资产实体性成新率)使用年限法=重置成本×资产实体性贬值率实际已使用年限=名义已使用年限×资产利用率修复费用法恢复到其全新状态的修复费用 ●功能性贬值 超额运营成本=评估对象运营成本-比较案例运营成本 净超额运营成本=超额运营成本×(1-所得税税率) 被评估资产功能性贬值额=∑(被评估资产年净超额运营成本x折现系数) ●经济性贬值 ①间接计算法:资产利用率下降 经济性贬值额=资产的重置成本×资产的经济性贬值率 ②直接计算法:收益额减少 经济性贬值额=资产年收益损失额×(1-所得税税率)×(P/A,r,n) 剥洋葱 三种评估方法对比: 1.方法适用范围市场法用于评估具有活跃公开市场且具有可比成交案例的资产。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
插值法计算实际利率
20×0年1月1日,XYZ公司支付价款l 000元(含交易费用)从活跃市场上购入某公司5
年期债券,面值1 250元,票面利率4.72%,按年支付利息(即每年59元),本金最后一次支付。
合同约定,该债券的发行方在遇到特定情况时可以将债券赎回,且不需要为提前赎回支付额外款项。
XYZ公司在购买该债券时,预计发行方不会提前赎回。
XYZ公司将购入的该公司债券划分为持有至到期投资,且不考虑所得税、减值损失等因素。
XYZ公司在初始确认时首先应计算确定该债券的实际利率,设该债券的实际利率为r,则可列出如下等式:
59×(1+r)-1+59×(1+r)-2+59×(1+r)-3+59×(1+r)-4+(59+1250)×(1+r)-5=1000(元)(1)
上式变形为:
59×(1+r)-1+59×(1+r)-2+59×(1+r)-3+59×(1+r)-4+59×(1+r)-5+1250×(1+r)-5=1000(元)(2)
2式写作:59×(P/A,r,5)+1250×(P/F,r,5)=1000 (3)
(P/A,r,5)是利率为r,期限为5的年金现值系数;(P/F,r,5)是利率为r,期限为5的复利现值系数。
现值系数可通过查表求得。
当r=9%时,(P/A,9%,5)=3.8897,(P/F,9%,5)=0.6499
代入3式得到59×3.8897+1250×0.6499=229.4923+812.375=1041.8673>1 000
当r=12%时,(P/A,12%,5)=3.6048,(P/F,12%,5)=0.5674
代入3式得到59×3.6048+1250×0.5674=212.6832+709.25=921.9332<1000
采用插值法,计算r
按比例法原理: 1041.8673 9%
1000.0000 r
921.9332 12%
(1041.8673-1000)/(1041.8673-921.9332)=(9%-r)/(9%-12%)
解之得,r=10%
备注:
此处要用到两个表:《年金现值系数表》、《复利现值系数表》
题中的3.8897和3.6048是查《年金现值系数表》得来的,i=9%和12%,n=5;0.6499和0.5674是查《复利现值系数表》得来的,i=9%和12%,n=5
假设两个实际利率的目的在于,确定现值1000在两个利率对应现值的范围内。
开始会疑惑如何确定这两个假设的利率,后来发现这是一个估值,在确定9%和12%之前可能会有很多次的预估。
另外,现值的范围越小,计算出来的实际利率越精确。
对于这个值的预估,某网友给出这样的方法(还不是特别能理解那个原理,但是自己列了一个表,当然考试的时候是不可能这样列表的):一般考试会给出你大致的范围,比如注会考试就不会让你去慢慢试!一般情况下运用大升小降的原理去应付它就行,就是代入的利率求出的值大于需计算的利率的值,比如带入9%计算大于给定值,你就升高利率,升高到带入
能小于需计算的利率的值时就行。
比如带入11%小于给定值了,那么这个要求的利率就位于9%-11%之间。
“插值法”计算实际利率。
在08年考题中涉及到了实际利率的计算,其原理是根据比例关系建立一个方程,然后,解方程计算得出所要求的数据,
例如:假设与A1对应的数据是B1,与A2对应的数据是B2,现在已知与A对应的数据是B,A介于A1和A2之间,即下对应关系:
A1B1
A(?) B
A2B2
则可以按照(A1-A)/(A1-A2)=(B1-B)/(B1-B2)计算得出A的数值,其中A1、A2、B1、B2、B都是已知数据。
根本不必记忆教材中的公式,也没有任何规定必须B1>B2
验证如下:根据:(A1-A)/(A1-A2)=(B1-B)/(B1-B2)可知:
(A1-A)=(B1-B)/(B1-B2)×(A1-A2)
A=A1-(B1-B)/(B1-B2)×(A1-A2)
=A1+(B1-B)/(B1-B2)×(A2-A1)。
