圆形谐振腔
机械原理 谐振腔

机械原理谐振腔谐振腔是一种利用机械原理实现的谐振现象的装置。
它是由一个空腔和一些固定或可移动的结构组成的。
在这个腔中,声波或电磁波的能量可以在一定频率下被放大。
谐振腔在许多领域都有应用,如电子学、物理学、化学和生物学等。
谐振腔的结构可以是圆形、方形、长方形、椭圆形等形状。
在这些形状中,圆形是最常用的,因为它具有均匀的电场和磁场分布,这有利于谐振腔的稳定性。
谐振腔中主要的结构是反射镜和谐振腔体。
反射镜是一种反射能量的结构,通常是由两个金属板组成的,它们之间有一定的距离。
当电磁波或声波穿过谐振腔时,这些波会在反射镜之间来回反弹,形成谐振。
反射镜的位置和形状会影响谐振频率和模式。
谐振腔的谐振频率是由谐振腔的尺寸和形状决定的。
当电磁波或声波在谐振腔内传播时,它们会与谐振腔的边界发生反射,这种反射会导致电磁波或声波的相位发生变化。
当电磁波或声波的相位发生变化时,它们会在谐振腔内形成驻波。
驻波的频率与谐振腔的尺寸和形状有关。
谐振腔的谐振频率和谐振模式对于许多应用都非常重要。
例如,在微波炉中,谐振腔被用来产生微波,并使其在炉内形成谐振,从而加热食物。
在激光器中,谐振腔被用来放大光波,并使其与激光介质共振,从而产生激光束。
谐振腔的稳定性也是一个重要的问题。
由于谐振腔中存在许多不同频率的模式,因此必须采取一些措施来保持谐振频率的稳定性。
例如,在激光器中,通常使用一个反馈回路来控制谐振腔的频率。
这个反馈回路会监测激光器输出的频率,并根据需要调整谐振腔的尺寸或形状,以保持输出的频率稳定。
谐振腔是一种利用机械原理实现的谐振现象的装置,它在许多领域都有应用。
谐振腔的结构和谐振频率对于其应用非常重要,因此必须采取一些措施来保持其稳定性。
环形光学谐振腔

环形光学谐振腔环形光学谐振腔是一种可用于实现非线性光学效应的重要器件。
它允许光在环形光路中多次反射,并在中间介质和介质之间来回传播。
这种腔体可以增加光的光程长度,从而增强非线性效应。
本文将介绍环形光学谐振腔的基本原理、应用、制备和优化方法。
1.基本原理环形光学谐振腔是由一段光纤弯曲成圆环形状制成的,两个端面上包含高反射率和低反射率衬底的半反射镜。
当光从光纤传到环形腔中,它将多次自我匹配,形成一个纵向模式。
该谐振腔的光学腔长与波长比是整数倍。
因此,当光线在腔中传播时,它将被放大和稳定,从而导致许多有趣的非线性光学效应。
2.应用环形光学谐振腔广泛应用于光学传感器、光频梳、量子计算等领域。
例如,在光学传感器中,通过改变腔长来改变环形光学谐振腔周围介质的折射率可以确定环境中的折射率,从而实现对气体、液体或固体的检测。
此外,该谐振腔还可以用于测量非线性光学介质中的精细结构、制备光量子态、增强非线性光学效应和产生新颖的非线性光学现象。
3.制备在制备环形光学谐振腔时,首先要从一个通常为光纤的单模光纤制备出间断环的光纤构架。
为了使制备的环形光学谐振腔具有足够的机械强度和耐用性,通常先要在光纤弯曲区域施加一层保护套管。
接下来,使用微切割器和腐蚀剂在光纤的表面上制作微小凸台和凹槽。
最后,通过双面刻蚀技术在光纤末端制作半反射镜,将其形成环形光学谐振腔。
这种方法可以制备出Miniaturized和高度集成的环形光学谐振腔,具有较高的革新性和灵活性。
4.优化方法为了优化环形光学谐振腔的性能,一些非常有效的方法已经被提出。
其中的一个方法是通过使用二分频技术和最佳化二分频晶体的尺寸来增加谐振腔的带宽,从而使它更适用于广域非线性效应。
另一个优化方法包括使用波导耦合全反射和自动相位控制系统来优化谐振腔的耦合和微调。
此外,通过使用具有较高对称性的环形光学谐振腔,也可以优化非线性光学效应的表现,这是因为具有足够高的对称性可以减少过渡辐射流,从而增强非线性光学过程发生的可能性。
HFSS谐振腔体实例分析分解

内容概述柱体腔体谐振器简介MpUk" M 於5门5] 54.血--e 恻柱形腔休谐振器简介•:•微波腔休谐振器是由导体制成的封闭的空腔,电破波在其中连续反射,如果模式和頻率合适.就会产生驻波.即发生谐振现象。
❖微波谐振器迪主要参数有两个:谐振頻妄或谐振波长和品庾因数(.儿•:•今天我们将要使用HFSS分析的如下图m所示的圆形腔休谐舷由理论分析可知,当/ = “时,TN如提最低次模,孚小是罗氐次模*g三者的谐振波长分另欣仏。
=2®❖ TMow模的谐振波长与腔体长度无关,无法利用调节谐振腔长度的方法进行调遂但在園柱轴线方向引入一段细圆柱形导体或细圆柱形理质,可以使TM JW模的场分布发生变化, 通过改变细圆柱形导休介质的长度,可以实现谐振腔的调(°山呱:m畑仃珂$诃8<J3:46f I • »:HFSS设计概述HFSS设计概述❖今天使用HFSS分析设计一个圆形腔体谐振器,腔体的磁和截面主径都为丘忒腔体的外壁材质是厚度为mun的金恳铝(ahumnmn〉。
根据前面的公式可以计算岀该谐振腔TM她模WTEm模波长和頻率的理论值分别为:z TMI)iri = 39.3111111 心mio = 634GHz冷川=25.鮒皿】A EDI = n,92GHz❖首先我们在HFSS中创建该腔休模型,仿真计算岀TM血模和TEm模i皆振频率的实际值和品质因辿5,井查看TA缶模和TEm模的场分布^❖然后在圜形谐振腔体内部添加一个半径为5山】的介质圆柱,使用HFSS的参数扫描功能,分析介质圆柱的高度对口応模和正小楔谐振頻率的影的HFSS设计步骤和设计流程1•改名:工程名:Resonator ;设计名:Cavity剎 审鈕 bff 删HBHgggEEBn 由口 Definitions寸・由••(5-2•修改模式:本征模求解模式內9如fjj\[25X5] UH--a ;: x臥 Annoft SPSS RcsonAtorCavity 30 lodelerIRcsonAtor Cavity - lodclerjZ] E>1« (da1 Y««¥ 2/*ojael Qri#&,<!•】”Ioalk lir»l<niW P-o' x11 Saqy oT. g,Ej 的厂 4 lotion Onck .|v>cuai•次「QG«Jit* O&nxitiwcftwnes • xM M A 83:丄•selatig typ 已Q&xndtrte% E scitatiana V««h Opacklicck Ar.ilytn Stt-cp Optir^triec toAlyrtc giddsfiesoltsficxn^kry DiRL© CS^Lw yi" C»j0rt TY<o.sfQr EX t«r 济m O«ai0. £rc7«rla«a...v*#-«ci9top.co«n TASolution Type; Resonator - Cavity DrivenC Modal厂 T erminalT ransientC Composite Excitation 怡Network Analysis总 EigenmodeOK Cancel3•修改单位:mm::h Q P■ ![•P»rt Prort Clipt -54X'l烛!j g --冬Z ObjQHz By V«t«ri<il • 10ft SPSS攻・SurBce fiodeealroj»ri Qr *r B Si% ■Zb F *|3IRcsonfttor CAVxty 3D Kodeler (Resonator Cavity lodclcrJ ]・ 1 •:* Cwrjty (-!«)••DftClXKl^JK8』雾蹟澤i讶R>tp<4^«r * 沁PV251 msOOQO:S6・•OVax i ・bl ・・・:;:・,、•DjVifetXl YOlQ Gl PlsRil*... B«r Object Type Casdi“t ・ Syntar! UctMd ・l AftUrcpU归Matico $ett )r<5wmwjoiVMW4<i3tCp.C0m4.创建谐振腔模型4.1创建圆柱体E 夕CyiinderlO CwSeCylind"i 匕Coardirt^te System54.2 修改属性:Cavity, 0.8Properties: Resonator - Cavity • ModelerAttribute |Nome I Wlue4.3 修改参数:顶点(0,0,0), H=15, i-15O CrejteCyinder »- k. CoordinateS”t0E t 49 Mar -iM G 令 lirt?NomeC&^ity Meterifil Sojurn'SoK^ InsideOrientabori Glob 创ModelDisplay XVir.,.Colorn&pjr'^scuurr/厂厂厂厂厂厂厂厂 Shor/ HiddenUnit lE^ludted ^6」 De^cfiption ‘ Rc^d-onF/::夕巾亦f B ■ veojjmProprw20 (mm)5•设置边界条件:有限导体边界条件Finite Conductivity Boundary X Name: |FiniteCond1U$e DefaultsCancel庐冷於旅a.*屮亠・$今如塚勺6.添加求解设置项汕如r v M f2R25) 54."够• noft HPSS - Rcsoufttor - Cavity 30 lodeler (Rcson*tor - CavxtylodclcrJZ2T 石】. 咖 Irojert Orw d ・dJ«r KFSS Z M I* 力宀 X^PI D Of Q 、昂 xq »| U) I 3a xr•□00<=>|±1!©6©60'©恥 j 3 1 oI 府 二1 丽!G 选护4VMCUOB=^Ktr5 柝-Cf 39Q»A»£3 «3 tf F&At£udl & IJCClt«itl»M & ・esl Qjerdtiom p [JJJpWI 倉 Opm ! 口久・2 %?>a. ♦ 2J ou^xitiFrvj«c^ Accedesx ・ ・X A £x a :i-夕沁也-yeani 0 C^vny@ CVecteCyLiri'• Z Coirdinwt» Sr«i»si * 49 ritxu^ !» Q foils■ !v**-«ctotop.cofn TAEigen Solution Setup AcK/anced | Defaults | Expression Cache |Adaptive SolutionsMaximum Number of Passes:Maximum Delta Frequency Per Pa厂 Converge on Real Frequency OnlyUse DefaultsHPC and Anal/sis Options...确定取消Setup Name:[7 Ena bledMinimum Frequency:Number of Medes:General | Options7・设计检查Validation Check; Resonator - CavityValidation Check completed. Errors: 1 Warnings :: 0See Message Window For details.7.1有错误,査看之Mc5<jge Man agerR] A Cavity (Eiscmodc)Fixdu Condnctivity bogday TinitaCc&dl nzaz tbic^nass. This is n«t oxpatibLa with Ei^axri&da probls. (9.2^:43 下 牛 4月 C6, 2016)OCavity| 代 EH |Finite Conductivity BoundaryFinite Conductivity Boundary DefaultsName: FiniteCondlAdvancedSurface Roughness Model: C Hu raySurface Roughness: 「Set DC Thickness 0H^ll-Huray Surface Ratio;mmUse Defaults旳 Design Settings& 3D Model幻 Boundaries and ExcitationsMesh Operations& Analysis Setup 护 Optimetrics : 刃 Radiation7.2再检査AboN | Clo^e&运行分析Validation Check; Resonator - CavityCavityValidation Check completed9・查看谐振频率和品质因数Eigenmode DaU Ih/esh Statistics |Sok^d Mod^Eg&nrnocfe Fiequ=ricy (GHa)QModel 7.76031 0.000489英5 791925 Mode 211.6293 *i 0.00K430£S 904Z34Close10.查看模式1的中心平面的电场和磁场的分布 10.1创建中心平面:顶点:(0,0,7・5) 9法线方向(0AD• Solutions: Revori^tor - CsvitySirrulstbn| S CtuplDesign Vtfi^on [|Lm&drphM jJJ &卩XProfile I Cowergen回Q瓦蔽□ Cr«tcC><ind«r♦匕Coo-dr»4tc e O Plir-iM ::QOfabJ^• a GbMI竝i CT GhbJiYZPUnel♦的Urts10.2查看电场分布Create Field PlotFields Calculator...Category: | StandardQuantity In Volumerr ;.■...- :■;-ComplexMag_EV GC I OL EMagtHComplexMag_HVector^HMag_Jsurf ComplewMagJsurf VectoNsurf Mag_JvolCompleKMagjYol VectoNvol VectoR ealPo^ntingLocalJS ARAveragers ARS urface_Lo $s_D ensi tj Volume^Loss^D ensity vCavityAllObjects厂Plot on surface onlyCancel厂Streamlineyi Kt uJoadoicpyiwiLSV »At2 号 x>G 与 np^po 2卫痞艺-Q2・A !上 &!迪hE ■死518飞 ZfXh^lL TE ■讹rw->99-C9iaa»z^xr] p.*<H"«PQ 细!八・s avs • •■>n»T ia P3•m mmrJ 'TO口 pSCQ• uttf *•*!•"円ga* “u Qww >^u 心嗣口 s ,g ;匕cee ■邨 < tee-^siz yc€e -«9we ,9 recmt, 9 reo ■补 g* ree-^es-d reG-Hiair & tee ■钩曲£ % rcos-'occ-fc •■MWmz a3【押訂nU WW Q 21 CH°E> Q H M陀Q-■ i«XS •tvutpjtoj 叩伽“P Q 033 0 —. S ”A .- 吃(列夕弓【陀呵 ■^ru 2“__________ ! >""Af£EBd■ Wl □»p»x> ・・说。
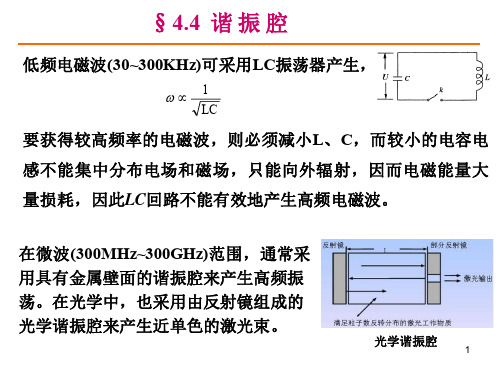
电动力学课件 4.4 谐振腔
k B 0
B
k E
2.有界空间中的电磁波
金属一般为良导体,电磁波几乎全部被反射。因此,若空间中 的良导体构成电磁波存在的边界,金属边界制约管内电磁波的存 在形式。在这种情况下, Helmholtz方程的解不再是平面波解而 受到导体界面边界条件的束缚。
3
二.理想导体边界条件
实际导体虽然不是理想导体,但是象银或铜等金属导体,对无线 电波来说,透入其内而损耗的电磁能量一般很小,接近于理想导体。 在一定频率的电磁波情形,两不同介质(包括导体)界面上的 边值关系可以归结为
E z A 3 s in k x x s in k y y c o11 sk z z
表明 A1、 A2、 A3中只有两个是独立的
3.谐振波型
( 1)电场强度
E x , t E x e i t
E x E y E z m L1
m n A1 cos x sin y sin L1 L2 m n A2 sin x cos y sin L1 L2 m n A3 sin x sin y cos L1 L2 n p A1 A2 A3 0 L2 L3
0
C3 0
C
z
O
因此
E x A1 co s k x x sin k y y sin k z z
A1 C 1 D 2 D 3
L3
B
Ex
D
( 2)考虑 x L 1 E x 有 x L1 0 x
sin k x L 1 0
L2
A
k x A1 sin k x x sin k y y sin k z z
光学谐振腔
1
谐振腔是在微波频率下工作的谐振元件,它是一个任意形状的 由导电壁包围的,并能在其中形成电磁振荡的介质区域,它具 有储存电磁能及选择一定频率信号的特性. 根据不同用途,微波谐振腔的种类是多种多样的:矩形腔、圆 柱形腔、球形腔。
微波谐振腔的原理及设计

微波谐振腔的原理及设计微波谐振腔是一种用于产生或探测微波信号的装置,它是微波技术中非常重要的组成部分。
本文将从原理和设计两个方面介绍微波谐振腔。
一、原理微波谐振腔的原理基于谐振现象,即当微波信号的频率与腔体的固有频率相等时,能量在腔体内部得到最大的传输和储存。
谐振腔通常采用金属腔体,其内部光滑的金属壁面能够反射微波信号,使其在腔内来回传播,形成驻波。
当微波信号的波长等于腔体的长度的整数倍时,驻波达到最大值,这就是谐振现象。
微波谐振腔的固有频率取决于腔体的几何形状和尺寸,通常用谐振模式的编号来表示。
常见的谐振模式包括长方形腔、圆柱腔和球形腔等。
不同的谐振模式有不同的场分布和能量分布特性,可以根据具体需求选择合适的谐振模式。
二、设计微波谐振腔的设计是为了满足特定的工作频率和谐振模式。
设计时需要考虑以下几个因素:1. 腔体的几何形状和尺寸:腔体的形状和尺寸直接影响谐振腔的固有频率和谐振模式。
设计时需要根据工作频率和谐振模式选择合适的腔体形状和尺寸。
2. 材料的选择:腔体通常采用导电材料制作,如铜、铝等。
导电材料能够有效地反射微波信号,提高能量的传输效率。
3. 耦合装置:为了将微波信号引入或从腔体中提取出来,需要设计合适的耦合装置。
常用的耦合装置包括波导耦合和同轴耦合等。
4. 电磁屏蔽和泄漏控制:微波谐振腔中的微波信号很强,容易对周围环境产生干扰。
因此,设计时需要考虑电磁屏蔽和泄漏控制,以减小对周围设备和系统的干扰。
5. 调谐和调制:为了满足不同应用需求,有时需要对微波谐振腔进行调谐和调制。
常用的调谐和调制方法包括机械调谐、电子调谐和压控调制等。
微波谐振腔的设计需要综合考虑上述因素,以实现对微波信号的高效产生和探测。
设计合理的微波谐振腔可以提高微波系统的性能和稳定性,广泛应用于通信、雷达、卫星导航等领域。
总结起来,微波谐振腔是一种基于谐振现象的装置,通过选择合适的谐振模式和设计合理的腔体结构,可以实现对微波信号的高效产生和探测。
激光谐振腔设计

激光谐振腔设计
激光谐振腔是激光器中的重要组成部分,它可以提高激光的输出功率和光束质量。
激光谐振腔的设计需要考虑多种因素,如腔体形状、镜面反射率、激光波长等。
在腔体形状的选择上,一般可以采用圆形、椭圆形、矩形等形状,不同形状的腔体对激光束的传输和聚焦效果不同。
在镜面反射率的选择上,需要根据激光器的波长和功率来确定,一般可以采用高反射镜和半反射镜组合的方式。
对于高功率激光器,还需要考虑谐振腔的散热问题。
为了避免谐振腔过热,一般会在腔体外部设置冷却系统,如水冷系统、气冷系统等。
此外,还需要考虑激光波长的匹配问题,以确保谐振腔的性能和输出功率。
总的来说,激光谐振腔的设计需要综合考虑多种因素,以获得最佳的激光输出效果。
- 1 -。
环形谐振腔

图37. 生物传感器示意图
图38. 圆盘波导的光场分布
39
参考文献
1. D.G.Rabus, Integrated Ring Resonators, Springer-Verlag Berlin Heidelberg, 2007, P.130-220 2. 韩秀友, 庞拂飞, 蔡海文, 《环形波导谐振腔集成光学器件》, 激光与光电子学进展, 41(8), 2004 3. 郭丽君, 石邦任,赵猛, 《集成光学陀螺环形谐振腔的优化设计与制备》, 光电工程,36 (8),2009 4. 郭丽君,石邦任,厉宝增, 《微型光学陀螺用光波导环形谐振腔的优化设计与制备》, 兵工 学报,31(11),2010 5. 张红星,潘炜,刘新开, 《光子晶体环形谐振器特性研究》, 光通信研究,第167期,2011 6. 姜立国,《环形谐振腔半导体激光器》,长春理工大学硕士论文,2005 7. 邹长铃,董春华,崔金明,《回音壁模式光学微腔:基础与应用》, 中国科学:物理学 力学 天文学,12(11),2012
图2. 简化模型示意图
4
•
5
•
6
传输矩阵法:
图3.简化模型示意图(一个输入、输出波导)
7
(8)
(10)
(9) (11)
(12)
(13) (14)
8
(15)
谐振中(m代表整数),
(17) (18)
(16)
9图4. 集Biblioteka 光学环形谐振腔的谐振曲线10
图5.简化模型示意图(两个输入、输出波导)
图15. 内部耦合多谐振腔(interring coupling)
20
7.
图16. “ 串联”多谐振腔示意图
21
第四章2-波导和空腔(矩、圆形波导、谐振腔)

xa
H0z (x, y) 0
y
y0
H0z (x, y) 0
y
yb
H0z (s) H0z (x, y) X (x)Y ( y)
Hz H0 cos kxx cos ky y expikzz
m
n
kx
, a
ky b ,
m, n
0, 1, 2, ...
TE波 边界条件:电磁场切向分量连续
z
s
zˆ
z
s
对偶性Es
1 2
kz2
s
Ez z
is
Hz
Hs
1 2 kz2
s
H z z
is
Ez
用纵向分量表示横向场
可区分TE和TM波
s
zˆ
z
Ez x
Hx
i ky 2 kz2
E0 sin kx x cos ky y exp ikz z
H y
i kx
2
k
2 z
E0 cos kx x sin ky y exp ikz z
其中kz
2
Ez x
i
H z y
TM波,H z 0
Ey
2
1
k
2 z
ikz
Ez y
i
H z x
高等数学1 谐振腔

高等数学1 谐振腔高等数学1 谐振腔什么是谐振腔?•谐振腔是一种能够通过反射将电磁波在内部来回传播的空间结构。
它通常由两个镜子或者反射面组成。
•在谐振腔中,当电磁波频率与腔内的固有频率匹配时,波将得到增强,形成共振。
谐振腔的数学模型1.谐振腔中电磁波满足的波动方程是二维的亥姆霍兹方程。
2.在某一方向上的电磁波传播可以用定态波函数(或称驻波函数)描述。
3.谐振腔最常见的模式是长方形谐振腔的驻波模式,也称为长方形谐振腔的本征模式(或基模)。
4.长方形谐振腔的本征模式是由两个方向上的驻波模式的乘积组合而成。
谐振腔中的本征频率与模式•长方形谐振腔中,每个模式都对应一个特定的本征频率。
•不同模式的本征频率是不同的,由于边界条件的限制,只有特定频率的波能够在谐振腔中得到增强,形成共振。
谐振腔中的波函数表示•谐振腔中的驻波模式可以通过波函数表示。
•波函数的形式与谐振腔的几何形状和边界条件有关。
•通过数学求解电磁场分布的波动方程,可以得到不同模式下的波函数表达式。
谐振腔的应用•谐振腔在光学器件中的应用十分广泛。
•谐振腔可以用于激光器、光纤通信系统以及光学谐振仪等设备。
•通过设计不同形状和尺寸的谐振腔,可以实现对特定频率的波的选择性增强。
总结•高等数学1中的谐振腔是一种能够通过反射将电磁波在内部来回传播的空间结构。
•谐振腔的数学模型可以用亥姆霍兹方程和本征模式来描述。
•谐振腔的本征频率与模式取决于谐振腔的几何形状和边界条件。
•谐振腔在光学器件中有广泛应用,可以实现对特定频率波的选择性增强。
以上是关于高等数学1中谐振腔的一些基础介绍和简要说明,希望能够帮助读者对该主题有更全面的了解。
谐振腔的数学模型谐振腔的数学模型主要利用了亥姆霍兹方程,该方程描述了电磁波在空间中的传播情况。
亥姆霍兹方程可以写作:[equation](其中,[equation]( 为电磁波的电场,[equation]( 为波矢。
在某一方向上的电磁波传播可以用定态波函数(或驻波函数)表示,定态波函数的形式为:[equation](其中,[equation]( 和 [equation]( 分别为波矢在 x 和 y 方向上的分量。
谐振腔的谐振条件(一)

谐振腔的谐振条件(一)谐振腔的谐振条件什么是谐振腔?谐振腔是一种用来放大特定频率的电磁波的装置。
在谐振腔中,电磁波可以在一定时间内来回反射,形成驻波。
驻波的特定频率称为谐振频率,而谐振条件描述了在谐振腔中形成谐振的条件。
谐振条件的定义谐振条件是指在谐振腔中,电磁波的频率必须满足特定的条件,才能形成驻波并达到谐振状态。
具体而言,谐振条件可以通过以下几个要点来描述:•腔长的整数倍:谐振腔的腔长必须是电磁波波长的整数倍。
换句话说,电磁波在谐振腔内来回反射所需的时间必须是一个完整的波长周期。
•极简交相位条件:在谐振腔的两个相邻反射面上,电磁波的相位必须有一个整数倍的差值。
这意味着电磁波在谐振腔中来回反射时,相位必须连续,以形成驻波。
•衰减足够小:谐振腔的材料和结构应具有足够小的损耗,以保持电磁波在谐振腔中持续反射,而不被过多衰减。
这样才能实现能量的积累和驻波的形成。
常见的谐振腔类型在电磁波学中,常见的谐振腔类型包括:1.矩形谐振腔:由四个边长相等的矩形金属板构成,是一种常见的研究对象。
谐振腔中的电磁波可以在长边和短边之间来回反射。
2.圆柱谐振腔:由一个圆柱体和两个圆盖构成,也是一种常见的谐振腔类型。
电磁波可在圆柱体内壁之间来回反射,并形成驻波。
3.球形谐振腔:由一个球形容器构成,是一种用于高频电磁波研究的谐振腔。
电磁波可以在球内壁上来回反射,形成驻波。
应用领域谐振腔在许多领域都有重要的应用,例如:•激光器:谐振腔用于激光的产生和放大,可以选择特定频率的激光输出。
•无线电通信:天线的谐振腔可以增强特定频率的信号,提高通信效果。
•数据存储:硬盘驻波谐振腔可用于增强特定频率的读写信号,提高存储密度。
总之,了解谐振腔的谐振条件是理解谐振腔工作原理和应用的关键。
掌握谐振条件可以帮助我们设计和优化谐振腔,提高电磁波的放大和利用效率。
基础乐理与视唱 谐振腔

基础乐理与视唱谐振腔什么是谐振腔谐振腔是指能够在特定频率下放大声音的空间或器材。
它通常由一个具有特定大小和形状的腔体和进、出口组成。
当声波进入谐振腔时,会发生共振现象,使得特定频率的声音在腔内得到放大,从而增强了声音的能量和音质。
谐振腔的工作原理谐振腔的工作原理基于共振的现象。
当一个物体受到外力作用时,它会以自身的固有频率振动。
当外界的激励频率等于物体的固有频率时,共振就会发生。
在谐振腔中,一般会有一个特定频率的声源,当声波进入腔内时,谐振腔的形状和尺寸会决定共振的频率,从而放大相应的声音。
谐振腔的类型谐振腔可以分为气体谐振腔和固体谐振腔两种类型。
气体谐振腔气体谐振腔通常是封闭的空间,例如气球、汽车的车厢等。
气体谐振腔的共振频率取决于腔体的体积和形状,以及气体内部的声速。
当声波进入气体谐振腔时,会引发共振现象,使得特定频率的声音在腔内得到放大。
固体谐振腔固体谐振腔通常是由坚硬的材料构成,例如空洞的乐器如吉他、小提琴等。
固体谐振腔的共振频率取决于腔体的尺寸、形状和材料的弹性模量。
当声波进入固体谐振腔时,会激发腔体内部的共振,从而放大特定频率的声音。
谐振腔在音乐中的应用谐振腔在音乐领域具有广泛的应用。
许多乐器本身就是谐振腔,它们的形状和尺寸决定了各自独特的音质。
以下是一些常见乐器中的谐振腔应用:管乐器管乐器如长笛、单簧管和号角等都是气体谐振腔。
它们的共振腔形状和长度可以通过键盘或簧片的开合来调节,从而改变演奏的音高。
弦乐器弦乐器如小提琴、大提琴和钢琴等都是固体谐振腔。
弦乐器的共振腔是由琴体和琴弦共同构成的。
琴体的形状和尺寸影响了乐器的共振特性,而琴弦的拉紧程度决定了音高。
打击乐器打击乐器如鼓和锣等也可以被视为谐振腔。
鼓的共振腔是由鼓面和鼓身组成的,它们的形状和材料决定了演奏出的声音。
在演奏鼓的时候,击打鼓面会激发鼓的共振,从而放大声音。
人声乐器人的声音发声过程中也涉及到谐振腔的作用。
口腔和喉咙可以被视为人声的谐振腔,它们的形状和大小会影响声音的音色和音量。
第5章谐振腔

r2=r1+L1 2= 1
(2)球面反射镜
1 T 2 R
0 1
R:球面镜曲率半径(凹为+,凸为-) 证
2 2 o ii 1 r,r2 1
=i+2 1=+i 2=-2
2-=-1 2=2-1
r1 R
R
r2 r1 2 2 R r1 1
注
R
或
F
1 0 T 0 1
r2 r1 2 1
即平面镜的反射定律
1
2 1
2、非稳定腔
(1)g1g2>1(2)g1g2<0(3)g1=0或g2=0(4)g1g2=1 如g1=g2=1, 即R1=R2=∞,平行平面腔,则
A 2 g2 1 1
B 2Lg2 2L
D 4 g1 g 2 2 g2 1 1
2 C ( g1 g 2 2 g1 g 2 ) 0 L
1 2L T 0 1
2
1 2L 1 2L 1 4L T 0 1 0 1 0 1
∵R1+R2>L
∴g1g2>0
L L L2 1 L R 2 R 1 R 1R 2
(1
L L L2 1 1 R 2 R1 R1R 2
L L )(1 ) 1 R1 R2
∴g1g2<1
(2)凹凸
R1
R1<0,R2>L
R<0
g>1
2g2 1 2 Lg 2 T 2 ( g1 g 2 2 g1 g 2 ) 4 g1 g 2 2 g 2 1 L
§2.1 谐振腔与模式.ppt

特殊形状的谐振腔: 折叠腔、环形腔、复合腔、分布式反馈腔等等
(a) 折叠腔 (c) 复合腔
(b) 环形腔 (d) 分布式反馈腔
第二章 开放式光腔与高斯光束/§2.1 谐振腔与模式
二、腔和模的联系
Δy
电磁场的解
Vxyz
处于有限范围的电磁场
分立的本征态(离散的矢量) kx xm , ky yn, kz zq
激光谐振腔构成原理
第二章 开放式光腔与高斯光束/§2.1 谐振腔与模式
一、谐振腔的构成与分类
固体激光棒
(a) 闭腔 (典型:半导体激光器)
(b) 开腔 (典型:气体激光器)
波导管
(c) 气体波导腔 (典型:HeNe波导激光器)
(开腔又可分为:稳定腔、非稳腔、临界腔)
第二章 开放式光腔与高斯光束/§2.1 谐振腔与模式
六、横模-具有相同的横向场分布的模式(不同的光斑花样)
(1) x, y 轴对称 TEMmnq (2) 旋转对称 TEMmnq 轴对称和旋转对称分布取决于腔的几何形状 基(横)模 TEM00
圆形谐振腔
方形谐振腔
第二章 开放式光腔与高斯光束/§2.1 谐振腔与模式
横模光斑花样:
(1) x, y 轴对称 :m-X向暗区数 n-Y向暗区数 (2) 旋转对称 :m-暗直径数 n-暗环数(半径方向)
基于有限元的圆形谐振腔分析

天津工业大学毕业论文基于有限元的圆形金属谐振腔的分析姓名:刘永超院(系)别:电子与信息工程学院专业:通信工程班级:通信094指导教师:夏靖2013年 6 月7 日天津工业大学毕业论文任务书院长教研室主任指导教师毕业论文开题报告表天津工业大学毕业论文进度检查记录摘要微波谐振腔其内部的电磁场分布在空间三个坐标方向上都将受到限制,均成驻波分布。
微波谐振腔在微波电路中起着与低频LC振荡回路相同的作用,是一种具有储能和选频特性的谐振器件。
本文主要研究圆形谐振腔的特性参数的计算和仿真,以及谐振腔内部的电磁场分布和变化规律。
研究方法主要是利用有限元分析法,有限元方法是求解偏微分方程的数值方法之一,广泛应用于各种工业领域。
有限元方法是求解电磁场问题的重要工具之一。
仿真所用软件为HFSS,对圆形谐振腔进行仿真,然后与理论结果进行比较。
本文首先介绍了有限元和圆形谐振腔的理论基础知识。
然后用HFSS对圆形金属谐振腔的特性参数和其内部的电磁场分布进行仿真。
仿真结果有:圆形金属谐振腔中各种不同TEM模式的谐振频率、品质因数和收敛性;圆形金属谐振腔内横截面和垂直截面上的电磁场分布与变化;腔体内介质高度对特性参数的影响。
关键词:圆形金属谐振腔;有限元法;HFSS仿真;电磁场ABSTRACTMicrowave resonant cavity of internal electromagnetic field distribution in space three coordinate direction will be limited, all into standing wave distribution. Microwave resonator in microwave circuits plays and low frequency oscillation loop of the same role LC, and it is one kind of devices which has the energy storage and choose the resonance frequency characteristics. In this paper, we study the properties of the circular cavity parameters calculation and simulation, and the change regularity and the electromagnetic field distribution within the cavity. Research methods mainly using finite element analysis, finite element method (fem) is one of the numerical methods for solving partial differential equations, is widely used in various industrial fields. The finite element method is one of the important tool for solving electromagnetic field problems. Simulation software HFSS, used for circular cavity are simulated, and compared with theoretical results.Firstly,this paper introduces the finite element theory of circular cavity basics. Then use HFSS to circular metal characteristics of the resonator parameters and its internal distribution of the electromagnetic field simulation. Simulation results are: the circular metal cavity in various different TEM mode's resonant frequency, quality factor and convergence; Circular metal inside the cavity of the electromagnetic field distribution on cross section and vertical section and change;Cavity medium height on the influence of the characteristic parameters in the body.Key words:Circular metal resonator; finite element method; HFSS simulation;electromagnetic waves目录第一章绪论 (1)1.1研究背景以及概况 (1)1.2谐振腔的发展和应用 (2)1.3本文的主要工作 (3)第二章有限元分析方法 (4)2.1有限元方法简介 (4)2.1.1有限元方法由来 (4)2.1.2有限元方法基本特点 (4)2.1.3有限元方法的基本步骤 (5)2.1.4应用领域 (6)2.2有限元分析示例 (6)2.3有限元方程组的求解 (9)2.3.1确定性问题矩阵方程求解的直接法 (9)2.3.2确定性问题矩阵方程求解的迭代法 (10)2.3.3本征值问题的解 (11)第三章圆形金属谐振腔理论 (12)3.1引言 (12)3.2谐振频率f0的概念与计算方法 (13)3.3品质因数Q0的概念与计算方法 (15)3.4圆形金属谐振腔 (17)3.4.1圆形金属谐振腔基本原理 (17)3.4.2圆柱腔中的三种常用振荡模 (18)3.5圆形金属谐振腔的激励与耦合 (23)3.5.1直接耦合 (23)3.5.2环耦合与探针耦合 (24)3.5.3孔耦合 (24)第四章微波谐振腔的仿真 (25)4.1电磁仿真软件ANSOFT HFSS (25)4.2圆形金属谐振腔的的仿真步骤 (26)4.2.1圆柱谐振腔的品质因数和谐振频率仿真 (26)4.2.2圆柱谐振腔内部电磁场分布仿真 (30)结束语 (42)参考文献 (43)附录 (44)外文资料 (44)中文翻译 (47)谢辞 (49)第一章绪论1.1研究背景以及概况目前,随着移动通信、卫星通信的迅速发展和通讯设备进一步向多功能、便携化、全数字化和高集成化方向发展,极大地推动了电子元器件的小型化、片式化和低成本化,以及其间组合化、功能集成化的发展进程。
谐振腔介绍资料

dW PL dt
0W
Q
另外,根据式(31-17),导出
(31-18) (31-19)
dW 2 0Wdt
比较(31-18)和(31-19)很清楚
二、品质因数Q0
1 2Q
(31-20)
这样,引入复频率,可以把谐振频率和值包含 在一个公式之中
1 ~ 0 1 j 2Q
讨论谐振腔的主要指标是谐振频率0、品质因数 Q 和电导 G。谐振腔的讨论思路是 : 理想腔 — 耦合腔 — 非理想腔,如图(31-2)所示。 在研究谐振频率 f0时,采用不计及腔损耗,即腔 壁由理想导体构成。但是,当研究 Q 时 , 则必须考虑 损耗的因素。 耦合腔和实际腔反映了谐振腔的具体应用。
0
i
y
Ey
j
z
0
k
E x E0 0 x 1 E y z z Hx j j 0 sin cos = j sin cos 0 z 0 l a l 2l a l E0 E0 0 1 E y x z x z Hz j j cos cos sin j sin x a a l 2a a l
2
2 E0 0 2 l 2 x 2 z 0 E0 a + 2 cos sin dxdz 0 0 2a a l 8 2 l a
2 1 1 l b a 2 2 2 1 E dv E0 sin x sin z dxdydz ablE02 a l 2 V 2 0 0 0 8
第5章谐振腔资料.

r22
1
1 F
0 1
r1 0
r1 r1
F
平行于光轴的光线过焦点
(3)若 r1 F1
r22
1
1 F
0 1
F1 1
F1
0
过焦点的光线平行于光轴
过光心的 2 光线不改
变方向
r1,r2
-2 2
F
F 1
r1,r2
例1 入射光线的坐标为r1=5cm,1=0.02弧度,求 通过曲率半径分别为R=0.4m、R=2.5m的凹面反射
g
2
2
g
2
1
R1、R2:两反射镜面曲率半径 L:谐振腔长度
证
①
②
R1
R2
④
③
L
r22 T1r11 r33 T2 r22 T2T1r11 r44 T3r33 T3T2T1r11 r55 T4 r44 T4T3T2T1r11
T T4T3T2T1
1 L
T1 T3 0 1
非稳 非稳 稳定
3、平凹腔: L<R时稳定
非稳 非稳
稳定
4、双凸腔、双平腔、平凸腔为非稳腔
§4 谐振腔衍射理论
推导思路:
出发点:菲涅尔基尔霍夫积分公式
应用
于谐振腔 利用自再现模概念,引进复常数
因子
衍射积分方程(一般表达式)
§4 谐振腔衍射理论
一、谐振腔模型——孔阑传输线 二、自再现模
1、概念光在腔内往返传播后,可以再现的一种稳定横向光场分布
ik
4
M
'
uq
(x'
,
y'
)
e
ik
(1 cos )ds'
4.12环形共振腔

A1 1 B 1 12
* 1 11 A2 A2 S12 B2 11 1 B2
(4.8-24)
S12 定义为耦合器的散射矩阵,由式(4.8-13)、
环形共振腔的一种特殊的情形
2 =0且t2 1
式(4.8-18)就变为
式中, 是共振腔内一次往返传输对应的相移,且
(4.8-19)
强度透射率(前向)
(4.8-20)
这里,不失一般性,取t是实数,t的常数相位总是可汇集于 ( 相位 中。当处共振态 m2 m为整数)前向强度透射 率则为 (4.8-21)
(4.8-26)
P 式中, m是第m个环形共振器中的一次往返ቤተ መጻሕፍቲ ባይዱ相移,m 定义为传 输矩阵。复数形式的相移记入了传输损耗和倾斜损耗。在第m 个和第m+1个光纤之间的耦合器,按照式(4.8-24),模式振 幅之间关系式为
(4.8-27)
Sm,m1 为耦合器(m,m+1)的散射矩阵(m>0)
利用式(4.8-24)、(4.8-26)和(4.8-27)结合图4.24, 从光纤1到光纤5的模式振幅间的关系表示为
11 12 1
2 2
(4.8-46)
The end
谢谢!
按照式(4.8-13) ,可以知道耦合常数 12 的 量级总小于(或等于)1.那么按照式(4.8-44)在某些特殊 的状态下布洛赫波数可能为复数。具有复数形式波数的布洛 赫波不能在周期性介质中传播。按照式(4.8-42)场振幅在布 洛赫波数为复数的这些特殊状态下呈指数衰减。这就是光子 带隙。如果用式(4.8-44)作出色散关系图,我们就会发现 光子带隙出现在一次往返对应的相移是2 的整数倍的特殊 状态下,光子带隙的中心正好落在 =2m (m 1, 2,3...). 光子带隙的中心侧的布洛赫波数可表示为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的概念。 只需做两个工作:
1)用叠加法将行波合成驻波; 2)两端利用边界条件。
第四章 微波谐振器
§4.4 圆柱形谐振腔
行波状态下圆波导TEmn模的纵向磁场分量
Hz
H0
J
m
Kc
r
cos m
sin m
e j z
两个传播方向相反的行波叠加时,场的表达式为
Hz
H
0
J
m
Kcr
cos
sin
m m
e
j
z
H 0
J
m
Kcr
cos
sin
m m
e
j
z
若z=0处放一短路板,则有边界条件 H z z0 0
带入上式可得
H0 H0
第四章 微波谐振器
§4.4 圆柱形谐振腔
故
Hz
H
0
J
m
Kcr
cos
sin
m m
e j z
e j z
j2H
0
J
m
Kcr
cos
sin
m m
sin
z
令 则有
Hm j2H0
H
z
HmJm
第四章 微波谐振器
§4.4 圆柱形谐振腔
4.4.1 场分量的表示式
1. TEmnp模
Ez 0 Hz 0
方法与讨论圆波导方法相似:
• 先求出纵向场
l
• 利用纵向场和横向场的关系求横向场
r
• 利用谐振腔两端的边界条件求待定常数
2R
谐振腔可看作是两端用短路板封起来的一段圆波导,
所以利用圆波导中两个传播方向相反的行波叠加形成纯驻波
t H z
Et ZTE zˆ Ht
j ZTE
t
rˆ
r
ˆ
1 r
E
j H z
Kc2 r
Hr
1 Kc2
2Hz zr
H
1 Kc2
1 2Hz
r z
Ez 0
求偏 导来
第四章 微波谐振器
§4.4 圆柱形谐振腔
具体各个场量可以写成
Er
j
mK
Kc2r
HmJm
Kcr
sin m
cos m
sin
p
l
z
Kcr
cos m
sin m
sin
z
(4-43)
第四章 微波谐振器
§4.4 圆柱形谐振腔
在z=l处有边界条件 H z zl 0
带入纵向磁场的表达式(5.2-2) ,可得
l p 或 p ( p 1,2,3 )
l
则腔体内纵向磁场的表达式可写为
Hz
H
m
J
m
Kcr
cos m
sin m
sin
p
l
z
n=1,2, …Beseel函数的导函数的根的序号;场量沿半径分 布的半个驻波的个数;即出现极大值的数目。
p=1,2,….场量沿纵向z分布的半个驻波的个数,即出现极 大值的数目。
第四章 微波谐振器
§4.4 圆柱形谐振腔
2. TMmnp模
Hz 0
Ez 0
行波状态下圆波导TMmn模的纵向电场分量
Ez
K 2 /
第四章 微波谐振器
§4.4 圆柱形谐振腔
此关系式成立
K 2 Kc2 2
K2
Kc2
p
l
2
mn
R
2
p
l
2
(4-48)
不同的m,n,p对应不同的TEmnp模,当腔体尺寸给定时, 腔内可以存在无穷多个谐振模式,即多谐性。
m=0,1,2 …Beseel函数的导函数的阶数;场量沿圆周分布 的整驻波的个数;
与TEmnp模一样, 工作于TMmnp模的谐振腔也具有多谐性。
第四章 微波谐振器
§4.4 圆柱形谐振腔
4.4.2 圆柱腔的基本参量
谐振频率 知道了波数K,则可以计算谐振频率和谐振波长.
谐振频率和波数K的关系为 谐振波长和波数K的关系为
fr
Kv
2
r
v fr
2
K
第四章 微波谐振器
§4.4 圆柱形谐振腔
j
Ez r
H
jEm
K Kc
J
' m
Kcr
cos m
sin m
cos
p l
z
Hz 0
Hz 0
第四章 微波谐振器
§4.4 圆柱形谐振腔
式中 /
Kc vmn/ R
vmn m阶贝塞尔函数的第n个根值
R
腔体内半径
K 2 /
且有
K2
Kc2
p
l
2
vmn R
2
p
l
2
(4-50)
2Ez rzr
将纵向电场带入,得
Er
j
Kc2
E0
J m'
Kcr
cos m
sin m
e
j
z
E0
J m'
Kcr
cos m
sin m
e
j z
若z=0处放一短路板,则有边界条件
Er z0 0
E0 E0
第四章 微波谐振器
§4.4 圆柱形谐振腔
横向电场Er可写成
Er
jE0
Kc
J
' m
Kcr
cos m
sin m
e j z
e j z
2E0
Kc
J
' m
Kcr
cos m
sin m
sin
z
令
Em 2E0
则
Er
Em
Kc
J m'
Kcr
cos m
sin m
sin
z
第四章 微波谐振器
§4.4 圆柱形谐振腔
或者
在与z=0相距l处再放一短路板,形成腔体
则有边界条件
Er zl 0
则有
l p 或 p ( p 1,2,3 )
l
则腔体内TMmnp模的纵向电场为
Ez
EmJm Kcr
cos m
sin m
cos
p
l
z
而腔体内TMmnp模的横向磁场为
Ht
j
zˆ
Et
1 Z TM
zˆ Et
Ht
1 Kc2
j zˆ t Ez
ZTM j
第四章 微波谐振器
§4.4 圆柱形谐振腔
腔体内TMmnp模的其它场分量为
Er
1 Kc2
公式 (4-5、4-6):
fr
Kv
2
r
v fr
2
K
对于TEmnp模,
K 2 Kc2
• 谐振腔在三个方向都呈纯驻波状态
• 相移常数满足 l p , ( p 1,2, )
(4-44) (4-45)
第四章 微波谐振器
§4.4 圆柱形谐振腔
不同
Ht
K
2 c
t H z
横向场量可以用纵向场量求出来
Ht
1 Kc2
z
t H z
Er
j
Kc2r
H z
由 e-γz 因子
或者
Et
K1c2
jzˆ
E
j K
Kc
H
m
J
' m
K
c
r
cos m
sin m
sin
p
l
z
Hr
Hm Kc
p
l
J
' m
Kcr
cos m
sin m
cos
p
l
z
(4-46)
H
Hm Kc2r
mp
l
Jm
Kcr
sin m
cos m
cos
p
l
z
Ez 0
/
Kc mn/ R
mn m阶贝塞尔函
数的导函数的 第n个根值.
R 腔体内半径
E0
J
m
Kcr
cos m
sin m
e
j z
两个传播方向相反的行波叠加时,场的表达式为
Ez
E0
J
m
Kc
r
cos m
sin m
e
j
z
E0
J
m
Kcr
cos m
sin m
e
j
z
横向电场为
Et
1 Kc2
z
t Ez
第四章 微波谐振器
§4.4 圆柱形谐振腔
横向电场分量为
Er
1 Kc2
2Ez zr
E
1 Kc2
2Ez zr
E
1 Kc2
2Ez rzr
HrLeabharlann 1Kc2j
r
Ez
Er
Em Kc
p l
J
' m
Kc
r
cos m
sin m
sin
p l
z
E
Emm Kc2r
p
l
Jm
Kcr
sin m
cos m
sin
p
l
z
Hr
jEm
mK
Kc2r
Jm
Kcr
sin m
cos m
cos
p
l
z
(4-49)
H
1 Kc2
