新疆第二师华山中学2018-2019学年高二上学期期末考试数学(文)试题 Word版含答案
2018-2019学年新疆第二师华山中学高二上学期期末考试语文试题 Word版

华山中学2018-2019学年第一学期高二年级期末考试语文试卷(考试时间:150分钟,满分:150分)一、课内知识单选题(共4小题,每题3分,共计12分)1.对下列加点词意义解释错误的一项()(3分)A.袜刬..金钗溜,袜刬:这里指跑掉鞋子以袜着地B.关河梦断..何处梦断:指梦中C.予买田其间,因往相.田相:观察D. 漏断..人初静漏:指更漏,古人计时用的漏壶。
这里“漏断”即指深夜。
2.方山子的一生可用“侠”“隐”两字来归纳,下面各句编为四组,均能表现其“侠”的一组是()(3分)①闾里之侠皆宗之②弃车马,毁冠服,徒步往来山中③从两骑,挟二矢,游西山④怒马独出,一发得之⑤精悍之色犹见于眉间⑥皆弃不取,独来穷山中A.①③④⑤B.②③④⑥C.①④⑤⑥D.②③⑤⑥3.下列有关文学常识的表述,不正确的一项是()(3分)A.苏轼,北宋文学家、书画家。
字子瞻,号东坡居士。
其文汪洋恣肆,明白畅达;其诗清新豪健,善用夸张比喻。
B.李清照,号易安居士,她的词分前期和后期。
前期多写其悠闲生活,多描写爱情生活、自然景物,韵调优美。
后期多慨叹身世,怀乡忆旧,情调悲伤。
C.陆游,字务观,号放翁,越州山阴人,陆游作品的鲜明特色是爱国主义精神。
不管遭受多少打击,他恢复神州的爱国信念始终不移。
D.辛弃疾,字幼安,号稼轩,南宋豪放派词人、将领。
与苏轼合称“苏辛”,与李清照并称“济南二安”。
其词题材广阔又善运用比喻入词,抒写力图恢复国家统一的爱国热情,倾诉壮志难酬的悲愤。
4.下列对陆游六十二岁时写的《临安春雨初霁》赏析有误的一项是()(3分)A.首联开口就言“世味”之“薄”,并惊问“谁令骑马客京华”。
写出了这位长期宦海沉浮,命途坎坷的老人的悲叹,说出了对世态炎凉的内心感受。
B.颔联点出“诗眼”,写诗人听了一夜的春雨,并未入眠。
那远远传来的如断如续的卖花声,带给他抚慰,写出了诗人此时内心的闲适与愉悦。
C.颈联写陆游客居京华,无事而作草书,晴窗下品着清茗,在作书品茶中消磨时光.。
新疆兵团第二师华山中学高二数学上学期期末考试试题 文 新人教B版

数学(文) 试卷命题人:李娟考生注意:本试题满分为150分,考试时间为120分钟。
一.选择题(本大题共12道小题,每小题5分,共60分,在每小题给出的选项中只有一项是符合要求的) 1.下列方程中表示圆的是 ( ) A . 223470x y x y ++++= B .2222590x y x y +-++= C .22223450x y x y +---= D .224250x y x y ---+=2.数据123,,,...,n a a a a 的方差为2σ,则数据1232,2,2,...,2n a a a a 的方差为( )A .22σB .2σC .22σD .24σ3. 从1,2,3,4中任取2个不相等的数,则取出的2个数之差的绝对值为2的概率( )A.12B. 13C. 14 D. 164.已知直线b x y +=,]3,2[-∈b ,则直线在y 轴上的截距大于1的概率是 ( ) A.15B.25C.35D.455.双曲线121022=-y x 的焦距为 ( ) A .22 B .24 C .32 D .34 6. 若抛物线22y px =的焦点与椭圆22162x y +=的右焦点重合,则p 的值为( ) A .2- B .2 C .4- D .47.抛物线px y 22=上一点Q ),6(0y 到焦点的距离为10,则焦点到准线的距离是( )A .4B .8C .12D .168.函数()f x 的定义域为开区间(),a b ,导函数'()f x 在区间(),a b 内的图像如图所示,则函数()f x 在开区间(),a b 内的极小值点有( ) 个。
A .1 B .2 C .3D .49.函数3223125y x x x =--+在[0,3]上的最大值和最小值依次是( )A .5,-15B .12,-15C .5,-4D .-4,-1510.已知函数32(6)1y x ax a x =+++-有极大值和极小值,则a 的取值范围是( ) A .-1<a <2 B .-3<a <6C .a <-3或a >6D .a <-1或a >211.设双曲线的一个焦点为F ,虚轴的一个端点为B ,如果直线FB 与该双曲线的一条渐近线垂直,那么此双曲线的离心率为 ( ) A. 2 B. 3 C.3+12D.5+1212.设A 是圆22(1)9x y ++=上的动点,,PA 是圆的切线, 且PA =4,则点P 到点Q(5,8)距离的最小值为( )A .5B .4C .6D .15二、填空题 (每小题5分,共20分)13.执行下边程序框图,输出的T= 。
新疆兵团农二师华山中学高二数学上学期期末考试试题

2015-2016学年第一学期高二年级期末考试数学 试卷(考试时间 :120分钟 满分:150分)第I 卷(选择题)一.选择题(每小题5分,共60分)1.设,x y R ∈,则“22x y ≥≥且”是“224x y +≥”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件2.抛掷一枚质地均匀的硬币,如果连续抛掷1000次,那么第999次出现反面朝上的概率是 ( )A .9991B .10001C .21D .10009993.直线y kx b =+与曲线31y x ax =++相切于点(2,3),则b 的值为 ( )A .-3B .9C .-15D .-74.圆M 的圆心在直线x y 2-=上,经过点)1,2(-A ,且与直线 1=+y x 相切, 则圆M 的方程为 ( )A.22(1)(2)2x y ++-=B.22(1)(2)2x y +++= C.22(1)(2)2x y -++= D.22(1)(2)2x y -+-= 5.若焦点在x 轴上的椭圆22x +m y 2=1的离心率a c =21,则m 等于( )A.3B.23C.38D.326.若向量),1,1(x a =→, )1,2,1(=→b , )1,1,1(=→c ,满足条件2)2()(-=⋅-→→→b a c ,则x =( )A .21 B .2 C .21- D .―2 7.若='=)2(,cos )(πf x x f 则( )A .1-B .23C .0D .18.在长为6cm 的线段上任取一点P ,使点P 到线段两段点的距离都大于2cm 的概率是( )A. 14B.31C. 12D. 329.命题“0x R ∃∈,3210x x -+>”的否定是 ( ) A .0x R ∃∈,3210x x -+< B .0x R ∃∈,3210x x -+≤ C .x R ∀∈,3210x x -+≤ D .不存在x R ∈,3210x x -+>10.直线AB 过抛物线x y =2的焦点F ,与抛物线相交于A 、B 两点,且|AB|=3,则线段AB 的中点到y 轴的距离为( ) A .21 B .1 C .89 D .45 11.如果直线0x y m ++=与圆222x y +=交于相异两点,A B O 、是坐标原点,OA OB OA OB +>-u u u r u u u r u u u r u u u r,那么实数m 的取值范围是( ).(2,2)A .(2,2)B .(2,2)2,2)C -U .(2,2)D -12.已知双曲线)0,0(12222>>=-b a by a x 上一点C ,过双曲线中心的直线交双曲线于B A ,两点,记直线BCAC ,的斜率分别为21,k k ,当||ln ||ln 22121k k k k ++最小时,双曲线离心率为( ) A .2 B .3 C 12.+ D 2.第II 卷(非选择题)二.填空题:(每小题5分,共20分)13.已知函数⎪⎩⎪⎨⎧<-≥.2,)1(,2,23x x x x 若关于x 的方程k x f =)(有两个不同的实根,则实数k 的取值范围是________。
新疆兵团第二师华山中学2018_2019学年高二数学下学期第一次调研试题文
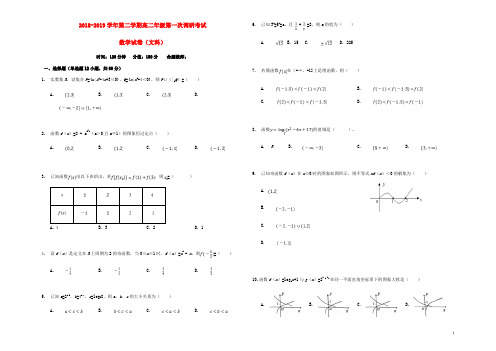
2018-2019学年第二学期高二年级第一次调研考试数学试卷(文科)时间:120分钟分值:150分命题教师:一、选择题(单选题12小题,共60分)1.实数集R,设集合P={x|x2-4x+3≤0},Q={x|x2-4<0},则P∪(∁R Q)=()A. B. C.D.2.函数f(x)=2 - a x+1(a>0且a≠1)的图象恒过定点()A. B. C. D.3.已知函数由以下表给出,若,则=()A.4B. 3C. 2D. 14.设f(x )是定义在R上周期为2的奇函数,当0≤x≤1时,f(x)=x2 - x,则=()A. B. C. D.5.已知a=21.3,b=40.7,c=log 38,则a,b,c的大小关系为()A. B. C. D. 6.已知3x=5y=a ,且+=2,则a的值为()A. B. 15 C. D. 2257.若偶函数在(-∞,-1]上是增函数,则()A. B.C. D.8.函数的值域是().A.RB.C.D.9.已知奇函数f(x)在x≥0时的图象如图所示,则不等式xf(x)<0的解集为()A.B.C.D.10.函数f(x)=log2x+1与g(x)=2- x -1在同一平面直角坐标系下的图象大致是()A. B. C. D.11.已知函数,若,则实数的取值范围是()A. B. C. D.12.函数y =,x∈(m,n]最小值为0,则m的取值范围是()A. B. C. D.二、填空题(本题共4小题,共20分)13.已知集合A={x|x2-4x+k=0}中只有一个元素,则实数k的值为______ .14.不等式的解集是_________.15.若幂函数f(x )的图象过点,则f(9)= ______ .16.对任意实数x均有e2x -(a-3)e x+4 -3a>0,则实数a的取值范围为______.三、解答题(本大题共6小题,共70分)17.(本题满分12分)已知命题p :“方程有两个不相等的实根”,命题p是真命题。
2017-2018学年新疆兵团第二师华山中学高二上学期期末考试数学(文)试题 解析版

2017-2018学年新疆兵团第二师华山中学高二上学期期末考试数学(文)试题解析版一、选择题:(12小题,每题5分,共60分)1. 已知复数z满足iz=2+3i,则z对应的点位于A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】D【解析】对应的点位于第四象限,选D2. 设命题p:∀x>0,x-lnx>0,则¬p为A. ∃x0>0,x0-lnx0>0B. ∃x0>0,x0-lnx0≤0C. ∀x>0,x-lnx<0D. ∀x>0,x-l nx≤0【答案】B【解析】由于全称命题的否定为特称命题,所以命题p:∀x>0,x-lnx>0,则¬p为∃x0>0,x0-lnx0≤0.故选B.3. 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.下图是源于其思想的一个程序框图,若输入的a,b 分别为5,2,则输出的n=A. 2B. 3C. 4D. 5【答案】C【解析】由程序框图可得,时,,继续循环;时,,继续循环;时,,继续循环;结束输出.点睛:循环结构的考查是高考热点,有时会问输出结果,或是判断框的条件是什么,这类问题容易错在审题不清,计数变量加错了,没有理解计数变量是在计算结果之前还是计算结果之后,最后循环进来的数是什么等问题,防止出错的最好的办法是按顺序结构写出每一个循环,这样就会很好的防止出错.4. 若a,b∈R,则“a>0,b>0”是“a+b>0”的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A【解析】当“a>0,b>0”时,由不等式的性质可知“a+b>0”,则“a>0,b>0”是“a+b>0”的充分不必要条件,故选A.5. 已知双曲线的一条渐近线为,则实数a的值为A. B. 2 C. D. 4【答案】D【解析】∵双曲线的渐近线为,∴,解得a=4,故选D.6. 下列说法错误的是A. 对分类变量X与Y,随机变量K2的观测值k越大,则判断“X与Y有关系”的把握程度越小B. 在回归直线方程=0.2x+0.8中,当解释变量x每增加1个单位时,预报变量平均增加0.2个单位C. 两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1D. 回归直线过样本点的中心(,)【答案】A【解析】A.对分类变量X与Y的随机变量K2的观测值k来说,k越大,“X与Y有关系”可信程度越大,因此不正确;B.在线性回归方程=0.2x+0.8中,当x每增加1个单位时,预报量平均增加0.2个单位,正确;C.两个随机变量相关性越强,则相关系数的绝对值越接近1,因此正确;D.回归直线过样本点的中心(,),正确.综上可知:只有A不正确.故选:A.7. 函数f(x)=2x2-4lnx的单调减区间为A. (-1,1)B. (1,+∞)C. (0,1)D. [-1,0)【答案】C【解析】f(x)的定义域是(0,+∞),,令f′(x)<0,解得:0<x<1,故选:C.8. 椭圆的焦点为F1,F2,点P在椭圆上,若|PF1|=4,则∠F1PF2的余弦值为A. B. C. D.【答案】B【解析】根据题意,椭圆的标准方程为,其中则,则cos∠F1PF2==.故选:B.9. 若a>0,b>0,且函数f(x)=4x3-ax2-2bx在x=1处有极值,则的最小值为A. B. C. D.【答案】C【解析】试题分析:因为函数在处有极值,所以,即,则(当且仅当且,即时取“=”);故选C.考点:1.函数的极值;2.基本不等式.10. 《论语》云:“名不正,则言不顺;言不顺,则事不成;事不成,则礼乐不兴;礼乐不兴,则刑罚不中;刑罚不中,则民无所措手足;所以名不正,则民无所措手足.”上述推理用的是A. 合情推理B. 归纳推理C. 类比推理D. 演绎推理【答案】A【解析】试题分析:因推理的格式符合三段论的形式,故是演绎推理,故应选D.考点:推理的形式.11. 已知点P在抛物线y2=4x上,点A(5,3),F为该抛物线的焦点,则△PAF周长的最小值为A. 12B. 11C. 10D. 9【答案】B【解析】抛物线y2=4x的焦点F(1,0),准线l:x=-1,点A(5,3)在抛物线内部,.P是抛物线上的动点,PD⊥l交l于D,由抛物线的定义可知|PF|=|PD|.∴要求|P A|+|PF|取得最小值,即求|P A|+|PD|取得最小,当D,P,A三点共线时|P A|+|PD|最小,为5-(-1)=6,则(|P A|+|PF|)min=6.△P AF周长的最小值为:6+5=11.故选B.点睛:求抛物线上一点到抛物线内一点的距离与到焦点的距离的和,应利用抛物线的定义转化为抛物线上的点到已知点的距离与到准线距离的和,当垂足、抛物线内的点、抛物线上的点三点共线时,距离和最小,即为抛物线内的点到准线的距离.12. 函数f(x)的定义域为R,f(1)=3,对任意x∈R,都有f(x)+f'(x)<2,则不等式e x•f(x)>2e x+e的解集为A. {x|x<1}B. {x|x>1}C. {x|x<-1或x>1}D. {x|x<-1或0<x<1}【答案】A【解析】令g(x)=e x f(x)-2e x-e,则g′(x)=e x f(x)+e x f′(x)-2e x=e x[f(x)+f′(x)-2],∵f(x)+f′(x)<2,∴f(x)+f′(x)-2<0,∴g′(x)<0,即g(x)在R上单调递减,又f(1)=3,∴g(1)=ef(1)-2e-e=0,故当x<1时,g(x)>g(1),即e x f(x)-2e x-e>0,整理得e x f(x)>2e x+e,∴e x f(x)>2e x+e的解集为{x|x<1}.故选:A.点睛:本题主要考查抽象函数的单调性以及函数的求导法则,属于难题.求解这类问题一定要耐心读题、读懂题,通过对问题的条件和结论进行类比、联想、抽象、概括,准确构造出符合题意的函数是解题的关键;解这类不等式的关键点也是难点就是构造合适的函数,构造函数时往往从两方面着手:①根据导函数的“形状”变换不等式“形状”;②若是选择题,可根据选项的共性归纳构造恰当的函数.本题通过观察四个选项,联想到函数g(x)=e x f(x)-2e x-e,再结合条件判断出其单调性,进而得出正确结论.二、填空题:(4小题,每题5分,共20分)13. 原始社会时期,人们通过在绳子上打结来计算数量,即“结绳计数”.当时有位父亲,为了准确记录孩子的成长天数,在粗细不同的绳子上打结,由细到粗,满七进一,那么孩子已经出生______天.【答案】510【解析】由题意满七进一,可得该图示为七进制数,化为十进制数为1×73+3×72+2×71+6×70=510.故答案为:510.14. 统计某产品的广告费用x与销售额y的一组数据如表:若根据如表提供的数据用最小二乘法可求得y对x的回归直线方程是=1.1x+4.6,则数据中的m的值应该是______.【答案】8【解析】由题意,,,∵y对x的回归直线方程是=1.1x+4.6,∴7+=4.4+4.6,∴m=8.故答案为:8.点睛:求解回归方程问题的三个易误点:① 易混淆相关关系与函数关系,两者的区别是函数关系是一种确定的关系,而相关关系是一种非确定的关系,函数关系是一种因果关系,而相关关系不一定是因果关系,也可能是伴随关系.② 回归分析中易误认为样本数据必在回归直线上,实质上回归直线必过点,可能所有的样本数据点都不在直线上.③ 利用回归方程分析问题时,所得的数据易误认为准确值,而实质上是预测值(期望值).15. 点P是双曲线(b>0)上一点,F1、F2是双曲线的左、右焦点,|PF1|+|PF2|=6,PF1⊥PF2,则双曲线的离心率为_______________【答案】【解析】根据题意,点P是双曲线(b>0)上一点,则有||PF1|-|PF2||=2a=2,设|PF1|>|PF2|,则有|PF1|-|PF2|=2,又由|PF1|+|PF2|=6,解可得:|PF1|=4,|PF2|=2,又由PF1⊥PF2,则有|PF1|2+|PF2|2=4c2=20,则c=,又由a=1,则双曲线的离心率e==故答案为:.16. 若函数y=e x+ax有大于零的极值点,则实数a的取值范围是()A. B. C. D.【答案】C【解析】∵y=e x+ax,∴y'=e x+a.由题意知e x+a=0有大于0的实根,由e x=-a,得a=-e x,∵x>0,∴e x>1.∴a<-1.故选C.三、解答题:(6小题,共70分)17. 设命题p:实数x满足(x-a)(x-3a)<0,其中a>0,命题q:实数x满足(x-3)(x-2)≤0.(1)若a=1,且p∧q为真,求实数x的取值范围.(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.【答案】(1);(2)【解析】试题分析:(1)由p∧q为真,即为p,q均为真命题,解两个不等式求交集即可;(2)若¬p是¬q的充分不必要条件,可得q是p的充分不必要条件,由题意可得P={x|a<x<3a},Q={x|2≤x≤3},由Q⊊P即可得解.试题解析:(1)由(x-1)(x-3)<0,得P={x|1<x<3},由(x-3)(x-2)≤0,可得Q={x|2≤x≤3},由p∧q为真,即为p,q均为真命题,可得x的取值范围是2≤x<3;(2)若¬p是¬q的充分不必要条件,可得q是p的充分不必要条件,由题意可得P={x|a<x<3a},Q={x|2≤x≤3},由Q⊊P,可得a<2且3<3a,解得1<a<2.18. 已知集合A={(x,y)︱x∈[0,2],y∈[-1,1]}.(1)若x,y∈Z,求x+y≥0的概率;(2)若x,y∈R,求x+y≥0的概率.【答案】(1);(2)【解析】试题分析:(1)因为x,y∈Z,且x∈[0,2],y∈[-1,1],基本事件是有限的,所以为古典概型,这样求得总的基本事件的个数,再求得满足x,y∈Z,x+y≥0的基本事件的个数,然后求比值即为所求的概率;(2)因为x,y∈R,且围成面积,则为几何概型中的面积类型,先求x,y∈Z,求x+y≥0表示的区域的面积,然后求比值即为所求的概率试题解析:(1)设“x+y≥0,x,y∈Z”为事件A,x,y∈Z,x∈[0,2],即x=0,1,2;y∈[-1,1],即y=-1,0,1.则基本事件有:(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1),(2,-1),(2,0),(2,1)共9个.其中满足“x+y≥0”的基本事件有8个,∴P(A)=.故x,y∈Z,x+y≥0的概率为.(2)设“x+y≥0,x,y∈R”为事件B,∵x∈[0,2],y∈[-1,1],则基本事件为如图四边形ABCD区域,事件B包括的区域为其中的阴影部分.∴P(B)====,故x,y∈R,x+y≥0的概率为.考点:几何概型中的面积类型和古典概型19. 某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.(1)根据茎叶图中的数据完成2×2列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?(2)从购买意愿弱的市民中按年龄进行分层抽样,共抽取5人,从这5人中随机抽取2人进行采访,求这2人都是年龄大于40岁的概率.附:.【答案】(1)见解析;(2)【解析】试题分析:(Ⅰ)根据茎叶图可填表格,再由公式计算,并且和比较大小,即可得出结论;(Ⅱ)根据层比为,分别得到年龄在20~40岁的抽取了2人,年龄大于40岁的抽取了3人,分别对这人分类标号,并通过列举法计算所有5人中随机抽取2人的所有可能情况,并计算其概率.试题解析:(Ⅰ)由茎叶图可得:由列联表可得:.所以,没有95%的把握认为市民是否购买该款手机与年龄有关.(Ⅱ)购买意愿弱的市民共有20人,抽样比例为,所以年龄在20~40岁的抽取了2人,记为a,b,年龄大于40岁的抽取了3人,记为A,B,C,从这5人中随机抽取2人,所有可能的情况为(a,b),(a,A),(a,B),(a,C),(b,A),(b,B),(b,C),(A,B),(A,C),(B,C),共10种,其中2人都是年龄大于40岁的有3种情况,所以概率为.20. 正方体ABCD-A1B1C1D1中,E为AB中点,F为CD1中点.(1)求证:EF∥平面ADD1A1;(2)求直线EF和平面CDD1C1所成角的正弦值.【答案】(1)见解析;(2)(1)取DD1中点M,连接MA,MF,易得AEFM是平行四边形,有EF∥AM,【解析】试题分析:从而得证;(2)因为EF∥AM,AD⊥平面CDD1C1,所以∠AMD与直线EF和平面CDD1C1所成角相等,在Rt△AMD中求解即可.试题解析:(1)证明:取DD1中点M,连接MA,MF,有,所以AEFM是平行四边形,所以EF∥AM,又AM⊂平面ADD1A1,EF⊄平面ADD1A1,所以EF∥平面ADD1A1,得证.(2)因为EF∥AM,AD⊥平面CDD1C1,所以∠AMD与直线EF和平面CDD1C1所成角相等,又在Rt△AMD中,有,所以直线EF和平面CDD1C1所成角的正弦值为.点睛:求直线和平面所成角的关键是作出这个平面的垂线进而斜线和射影所成角即为所求,有时当垂线较为难找时也可以借助于三棱锥的等体积法求得垂线长,进而用垂线长比上斜线长可求得所成角的正弦值,当空间关系较为复杂时也可以建立空间直角坐标系,利用向量求解.21. 已知点P(0,-2),椭圆E:的离心率为,F是椭圆E的右焦点,直线PF的斜率为2,O为坐标原点.(1)求椭圆E的方程;(2)直线l被圆O:x2+y2=3截得的弦长为3,且与椭圆E交于A、B两点,求△AOB面积的最大值.【答案】(1);(2)【解析】试题分析:(1)由直线PF的斜率和离心率列方程组求解即可;(2)当直线l与y轴平行时,易得△AOB面积为,当直线l与y轴不平行时,设直线l 的方程为y=kx+m,A(x1,y1),B(x2,y2),由直线与椭圆联立得(2k2+1)x2+4kmx+2(m2-1)=0,用弦长公式和点到直线距离公式求解面积即可.试题解析:(1)设F(c,0),由已知得,直线PF的斜率k=,得c=1,又,则,b=1,故椭圆E的方程为(2)记点O到直线l的距离为d,则,①当直线l与y轴平行时,直线l的方程为,易求,∴,②当直线l与y轴不平行时,设直线l的方程为y=kx+m,A(x1,y1),B(x2,y2),由已知得,∴,由得(2k2+1)x2+4kmx+2(m2-1)=0,又△=10k2+2>0,∴,,∴,,,当且仅当k=±1时取等号,综上当k=±1时,△AOB面积的最大值为22. 已知函数f(x)=a--lnx,g(x)=e x-ex+1.(1)若a=2,求函数f(x)在点(1,f(1))处的切线方程;(2)若f(x)=0恰有一个解,求a的值;(3)若g(x)≥f(x)恒成立,求实数a的取值范围.【答案】(1)1;(2)【解析】试题分析:(1)由f'(1)=0得切线斜率为1,进而得切线方程;(2)令m(x)=+ln x,求导得函数单调性和最值,进而得解;(3)由(Ⅱ)知函数的最大值为f(1)=a-1,g(x)=e x-ex+1,求导可得函数g(x)的最小值为g(1)=1,得1≥a-1,进而得解.试题解析:(1)∵a=2,∴,f'(x)=,∴f'(1)=0,∴切线方程为y=1;(2)令m(x)=+ln x,∴m'(x)=-+,∴当x在(0,1)时,m'(x)>0,m(x)递增,当x在(1,+∞)是,m'(x)<0,m(x)递减,故m(x)的最大值为m(1)=1,f(x)=0恰有一个解,即y=a,与m(x)只有一个交点,∴a=1;(Ⅲ)由(Ⅱ)知函数的最大值为f(1)=a-1,g(x)=e x-ex+1.g'(x)=e x-e,∴当x在(0,1)时,g'(x)<0,g(x)递减,当x在(1,+∞)时,g'(x)>0,g(x)递增,∴函数g(x)的最小值为g(1)=1,g(x)≥f(x)恒成立,∴1≥a-1,∴a≤2.点睛:导数问题经常会遇见恒成立的问题:(1)根据参变分离,转化为不含参数的函数的最值问题;(2)若就可讨论参数不同取值下的函数的单调性和极值以及最值,最终转化为,若恒成立;(3)若恒成立,可转化为(需在同一处取得最值).。
中学高二数学上学期期末考试试卷文

新疆兵团第二师华山中学 高二数学上学期期末考试试卷 文选择题(此题共12小题,每题5分,共60分)1. 设集合M ={1,2},N ={a 2},那么“1a =”是“N ⊆M”的 ( )A. 充分没必要要条件B. 必要不充分条件C. 充分必要条件D. 既不充分又没必要要条件2. 某校参加舞蹈社团的学生中,高一年级有40名,高二年级有30名,现用分层抽样的方式在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了8名,那么在高二年级的学生中应抽取的人数为( )A. 12B. 10C. 8D. 6 3. 以下有关命题的表达错误的选项是( )A. 关于命题:p ,R x ∈∃001020<++x x ,那么p ⌝为:,R x ∈∀012≥++x xB. 假设q p ∧为假命题,那么q p ,均为假命题C. 命题“若0232=+-x x ,那么1=x ”的逆否命题为:“若1≠x ,那么0232≠+-x x ” D 2=+-x x 是2=x 的必要不充分条件4. 双曲线122=-y x 的极点到其渐近线的距离等于( ) A .22 B .1 C .21 D .25. 已知函数1)6()(23++++=x a ax x x f 有极大值和极小值,那么实数a 的取值范围是 ( )A .(-1,2)B .(-∞,-3)∪(6,+∞)C .(-3,6)D .(-∞,-1)∪(2,+∞) 6. 假设抛物线2y ax =的准线的方程是2-=y ,那么实数a 的值是( ) A. 18 B. 18- C. 8 D. 8-7. 用秦九韶算法计算多项式1049732)(2345-+-+-=x x x x x x f 在2=x 时的值时,3V 的值为( )A .34B .22C .9D .18. 某车间为了规定工时定额,需要确信加工零件所花费的时刻,为此进行了5次实验,依照搜集到的数据(如下表),由最小二乘法求得回归直线方程为6.5468.0ˆ+=x y零件数x 个 10 20 30 40 50加工时间y (min ) 6275 81 89 但此刻表中有一个数据已模糊不清,请你推断出该数据的值为( ) A .68 B .68.2 C .69 D .759. 假设下面的程序框图输出的S 是62,那么①应为( )(第9题图) (第10题图)A. 7≤n B .6≤n C .5≤n D .4≤n10. 在正方体1111D C B A ABCD -中,F E 、别离为BC AB 、中点,那么异面直线EF 与1AB 所成角的余弦值为(A .23 B .33C .22D .2111. 甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为a ,再由乙猜甲适才所想的数字,把乙猜的数字记为b ,其中{},1,2,3,4,5,6a b ∈,若1a b -≤,就称甲乙“心相近”.现任意找两人玩那个游戏,那么他们“心相近”的概率为( )A.91 B. 92 C. 187 D. 9412. )(x f '是概念在非零实数集上的函数,)(x f '为其导函数,且0>x 时,0)()(<-'x f x f x ,记5log )5(log ,2.0)2.0(,2)2(22222.02.0f c f b f a ===,那么 ( ) A .b a c << B .c a b << C .c b a << D .a b c <<二.填空题(本大题共4小题,每题5分,共20分)13. 假设曲线x ax y ln 22-=在点),1(a 处的切线平行于x 轴,那么=a ___________.14. 从等腰直角△ABC 的底边BC 上任取一点D ,那么△ABD 为锐角三角形的概率为___________.15. 已知抛物线22(0)y px p =>,过其核心且斜率为-1的直线交抛物线于A 、B 两 点,假设线段AB 的中点的纵坐标为-2,那么该抛物线的准线方程为___________.ABCA 1 C 1 16. 方程11422=-+-t y t x 表示曲线C ,给出以下命题:①曲线C 不可能为圆; ②假设曲线C 为双曲线,那么1<t 或4>t ; ③若41<<t ,那么曲线C 为椭圆; ④假设曲线C 为核心在x 轴上的椭圆,那么1<t<52. 其中真命题的序号是____________(写出所有正确命题的序号).三.解答题(本大题共6小题,第17题10分,其余每题12分,共70分,解许诺写出文字说明,证明进程或演算步骤.) 17. 设p :实数x 知足03422<+-a ax x (其中0>a ),q :实数x 知足0)2)(3(<--x x (1)若1=a ,且p ∧q 为真,求实数x 的取值范围;(2)假设p 是q 的必要不充分条件,求实数a 的取值范围.18.高二某班50名学生在一次百米测试中,成绩全数都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18],如图是按上述分组方式取得的频率散布直方图.(1)假设成绩大于等于14秒且小于16秒规定为良好,求该班在这次百米测试中成绩为良好的人数; (2)请依照频率散布直方图,估量样本数据的众数和中位数(精准到);(3)设n m ,表示该班两个学生的百米测试成绩,已知[)[]18,1714,13, ∈n m ,求事件2||>-n m 的概率.19. 在平面直角坐标系中,已知一个双曲线的中心在原点,左核心为)0,2(-F ,且过点)0,3(D .(1)求该双曲线的标准方程;(2)假设P 是双曲线上的动点,点(1,0)A ,求线段PA 中点M 的轨迹方程.20. 如图,三棱柱111C B A ABC -中,侧棱ABC AA 底面⊥1,且侧棱和底面边长均为2,D 是BC 的中点. (1)求证:11//ADC B A 平面; (2)求三棱锥11ADB C -的体积.21. 已知椭圆22221(0)x y a b a b +=>>的右核心为2(30)F ,,离心率为e .(1)若e =,求椭圆的方程;(2)若直线0)y kx k =>(与椭圆相交于A B ,两点,假设220AF BF ⋅=,求2428118k a a +-的值.22. 已知函数x mx x f ln )(-=,(0>m ). (1)若1=m ,求函数)(x f 的极值;(2)求函数f(x)在区间[1,e]上的最小值; (3)若0)(≤x f 恒成立,求m 的取值范围.第一学期高二年级期末考试 文科数学 答案13. 1 14. 2115. 1-=x 16. ②④17. (1)当1=a ,解得1<x <3,即p 为真时实数x 的取值范围是1<x <3.q 为真时实数x 的取值范围是2<x <3.假设p ∧q 为真,那么p 真且q 真,∴实数x 的取值范围是(2,3).…………5分 (2)设A ={x|p (x )},B ={x|q (x )} =(2,3),p 是q 的必要不充分条件,那么A B ≠⊂由03422<+-a ax x 得0))(3(<--a x a x , 因为0>a ,A =)3,(a a ,因此有⎩⎨⎧≥≤332a a ,解得21≤≤a ; ∴实数a 的取值范围是21≤≤a . …………10分18.(1)依照直方图可知成绩在[)16,14内的人数:2838.05018.050=⨯+⨯人 (4)分(2)由图可知众数落在第三组[)16,15是5.1521615=+ 因为数据落在第一、二组的频率5.022.008.0104.01<=⨯+⨯=数据落在第一、二、三组的频率5.06.038.0108.0104.01>=⨯+⨯+⨯= 因其中位数必然落在第三组[)16,15中.假设中位数是x ,因此()5.038.01522.0=⨯-+x解得中位数74.157368.1519299≈≈=x…………8分(3)成绩在[)14,13的人数有:204.050=⨯人,设为b a ,成绩在[)18,17的人数有:306.050=⨯人,设为C B A ,,[)14,13,∈n m 时有ab 一种情形,[)18,17,∈n m 时有BC AC AB ,,三种情形n m ,散布在[)14,13和[)18,17时有bC bB bA aC aB aA ,,,,,六种情形,大体事件的总数为10事件6>-n m 由6个大体事件组成.因此()531066==>-n m P . …………12分 19. (1)双曲线的标准方程为1322=-y x …………6分 (2)设线段PA 的中点为(,)M x y ,点P 的坐标是00(,)x y ,由00122x x y y +⎧=⎪⎪⎨⎪=⎪⎩,得00212x x y y =-⎧⎨=⎩ …………9分因为点P 在双曲线上,得1)2(3)12(22=--y x∴线段PA 中点M 的轨迹方程是312)12(22=--y x . …………12分20.(1)证明:连接C A 1交1AC 于点O ,连接OD由题得四边形11A ACC 为矩形,O 为C A 1的中点, 又D 为BC 的中点, 因此OD B A ∥11ADC OD 平面⊂,11ADC B A 平面⊄因此11ADC B A 平面∥ …………5分21.(1)由题意得33c c a=⎧⎪⎨=⎪⎩,因此3a =.又由222a b c =+,解得23b =.因此椭圆的方程为221123x y +=. …………4分 (2)由22221y kx x y ab =⎧⎪⎨+=⎪⎩得222222()0b a k x a b +-=.设1122()()A x y B x y ,,,,由根与系数的关系可知,120x x +=,且2212222a b x x b a k =-+. ……6分 又211222(3)(3)AF x y BF x y =--=--,,,. 因此222121212(3)(3)(1)90AF BF x x y y k x x ⋅=--+=++=. ……8分 即222222(9)(1)90(9)a a k a k a --++=+-. ……9分整理得422424218818111818a a k a a a a -+==---+-.∴24281118k a a +=--. ……12分22.(1))0(,111)(>-=-='x xx x x f , 令0)(='x f 得x=1,令0)(>'x f 得x>1,令0)(<'x f 得0<x<1, 因此)(x f 在)1,0(上单调递减,在),1(+∞上单调递增,∴)(x f 的极小值为11ln 1)1(=-=f ,)(x f 无极大值 ……4分(2))0,0(,11)(>>-=-='m x x mx x m x f 令0)(='x f 得x=m 1,令0)(>'x f 得x>m 1,令0)(<'x f 得0<x<m 1,因此)(x f 在)1,0(m 上单调递减,在),1(+∞m 上单调递增,],1[e x ∈ ,① 当1110≥≤<m m即时,f(x)在],1[e 单调递增,f(x)的最小值为f(1)=m ②。
新疆维吾尔自治区第二师华山中学2018-2019学年高二上学期期末考试化学试题(解析版)

华山中学2018-2019学年第一学期高二年级期末考试化学试卷(考试时间:90分钟,满分:100分)可能用到的相对原子质量:H 1 C 12 N 14 O 16 Na 23 Mg 24 Al 27 Cl 35.5 Cr 52 Fe 56 Cu 64 Ag 108一、选择题(每小题只有一个答案符合题意,共15小题,每小题2分)1.下列物质中,其主要成分不属于烃的是()A. 汽油B. 甘油C. 煤油D. 柴油【答案】B【解析】试题分析:甘油为丙三醇,属于多元醇类,不是烃,其余各项都是混合物,其主要成分为烃类。
答案选B。
【考点定位】本题主要是考查烃的概念及常见有机物的组成【名师点睛】汽油、煤油、柴油均来自于石油的分馏,也有部分来自于石油的裂化。
根据沸点的不同,分别截取不同沸点的馏分,就得到汽油、煤油、柴油。
汽油馏分(<170℃),煤油馏分(170~230℃),轻柴油馏分(230~270℃),重柴油馏分(270~350℃)。
一般说来,汽油为C4-C12烃类混合物,煤油为C12-C15烃类混合物,柴油为C10-C22烃类混合物。
都属于烃类。
本题属于基础题,引导学生回归教材,主要基础知识的积累。
【此处有视频,请去附件查看】2.下列生活用品中主要由合成纤维制造的是( )A. 尼龙绳B. 宣纸C. 羊绒衫D. 棉衬衣【答案】A【解析】【详解】合成纤维是化学纤维的一种,是用合成高分子化合物做原料而制得的化学纤维的统称。
它以小分子的有机化合物为原料,经加聚反应或缩聚反应合成的线型有机高分子化合物,如聚丙烯腈、聚酯、聚酰胺等。
A、尼龙绳的主要成分是聚酯类合成纤维,故A正确;B、宣纸的的主要成分是纤维素,故B错误;C、羊绒衫的主要成分是蛋白质,故C错误;D、棉衬衫的主要成分是纤维素,故D错误。
【点睛】掌握常见物质的组成以及合成纤维的含义是解答本题的关键,题目难度不大,注意羊绒衫和棉衬衣的区别。
3.下列说法错误的是( )A. 糖类化合物也可称为碳水化合物B. 维生素D可促进人体对钙的吸收C. 蛋白质是仅由碳、氢、氧元素组成的物质D. 硒是人体必需的微量元素,但不宜摄入过多【答案】C【解析】A.糖类化合物符合通式C n(H2O)m,故称为碳水化合物,故A正确;B.维生素D可促进人体对钙的吸收,故B正确;C.蛋白质的基本组成元素是C、H、O、N四中元素,故仅由碳、氢、氧元素不正确,故C错误;D.硒是人体必需的微量元素,但不宜摄入过多,故D正确,故选C。
新疆维吾尔自治区第二师华山中学2018.doc

新疆维吾尔自治区第二师华山中学2018华山中学2018-2019学年第一学期高二年级期末考试语文试卷(考试时间150分钟,满分150分)一、课内知识单选题(共4小题,每题3分,共计12分)1.对下列加点词意义解释错误的一项A. 袜刬金钗溜,袜刬这里指跑掉鞋子以袜着地 B. 关河梦断何处梦断指梦中 C. 予买田其间,因往相田相观察 D. 漏断人初静漏指更漏,古人计时用的漏壶。
这里“漏断”即指深夜。
【答案】B 【解析】【详解】本题考查理解常见文言实词在文中的含义。
解答此类题目时,首先应审题,明确选择的要求,如本题“对下列加点词意义解释错误的一项”,然后应结合具体的语境,运用语法知识进行辨析。
B项,“梦断指梦中”解释是错的,“ 关河梦断何处”可以理解为“如今防守边疆要塞的从军生活只能在梦中出现,梦一醒不知身在何处”,“梦断”应该解释为“梦醒”。
故选B。
2.方山子的一生可用“侠”“隐”两字来归纳,下面各句编为四组,均能表现其“侠”的一组是①闾里之侠皆宗之②弃车马,毁冠服,徒步往来山中③从两骑,挟二矢,游西山④怒马独出,一发得之⑤精悍之色犹见于眉间⑥皆弃不取,独来穷山中 A. ①③④⑤B. ②③④⑥C. ①④⑤⑥D. ②③⑤⑥【答案】A 【解析】【详解】本题考查考生文言文的分析综合能力,属于主观概括性信息筛选。
解答此类题目时,要求考生认真审题,提干要求“均能表现其‘侠’的一组”,是组合类型的答案选项,考生在读懂原句的基础上,结合原文,能够对筛选的内容进行分析归纳,再用排除法选出正确答案。
本题中②⑥是在说“隐”,“毁冠服”理解为“毁坏书生衣帽”,可以看出他不在意功名仕途了;原文中写到“方山子世有勋阀”,“而其家在洛阳,园宅壮丽与公侯等。
河北有田,岁得帛千匹,亦足以富乐”,而方山子“皆弃不取”,可见方山子把这些功名利禄全都抛弃了,“独来穷山中”,可见他“隐”的性格特点。
选项中有②⑥的排除,故选A。
3.下列有关文学常识的表述,不正确的一项是A. 苏轼,北宋文学家、书画家。
新疆兵团第二师华山中学2017-2018学年第二学期高二年级期末考试文科数学试卷(含详细答案)

新疆兵团第二师华山中学2017-2018学年第二学期高二年级期末考试数学(文科) 试卷(考试时间:120分钟,满分:150分)一、选择题(每题5分,共计60分。
)1.设集合{}{}{}1,2,3,4,5,1,2,3,2,3,4U A B ===,则=)(B A C U ( ) A.{}2,3 B.{}1,4,5 C.{}4,5 D.{}1,5 2.下列函数中,既是奇函数又是增函数的为( ) A. 1y x =+ B. 2y x =- C. 1y x= D. ||y x x = 3.设命题p :2,2nn N n ∃∈>,则p ⌝为( ) A.2,2nn N n ∀∈> B.2,2nn N n ∃∈≤ C.2,2nn N n ∀∈≤D.2,=2n n N n ∃∈4.命题:p 所有有理数都是实数,命题:q 正数的对数都是负数,则下列为真命题的是( ) A .()p q ⌝∨ B .p q ∧ C .()()p q ⌝∧⌝D .()()p q ⌝∨⌝5. “sin α=21”是“212cos =α”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件6.已知432a =,254b =,1325c =,则( )A.b a c <<B.a b c <<C.b c a <<D.c a b <<7.把函数sin y x =(x R ∈)的图象上所有点向左平行移动3π个单位长度,再把所得图象上所有点的横坐标缩短到原来的12倍(纵坐标不变),得到的图象所表示的函数是( ) A.sin(2)3y x π=-,x R ∈ B. sin()26x y π=+,x R ∈C.sin(2)3y x π=+,x R ∈D.sin(2)32y x π=+,x R ∈ 8.函数f(x)=xcos2x 在区间[0,2π]上的零点个数为( ) A. 2 B. 3 C.4 D.59.定义在R 上的函数f (x )满足f (x+6)=f (x ),当-3≤x <-1时,f (x )=-(x+2)2,当-1≤x <3时,f (x )=x,则f (1)+f (2)+f (3)+…+f (2012)=( ) A.335 B.338 C.1678 D.2012 10. 如图,长方形ABCD 的边2AB =,1BC =,O 是AB 的中点,点P 沿着边,BC CD 与DA 运动,记BOP x ∠=.将动点P 到,A B 两点距离之和表示为x 的函数()f x ,则()y f x =的图像大致为( )。
新疆高二上学期期末考试数学试题(解析版)

一、单选题1.点关于y 轴的对称点的坐标为( ) (2,0,22)A A . B . (2,0,22)-(2,0,22)-C . D .(2,0,22)--(2,0,22)【答案】C【分析】根据给定条件,利用空间直角坐标系关于坐标轴对称点的坐标意义求解作答. 【详解】点关于y 轴的对称点的坐标. (2,0,22)A (2,0,22)--故选:C2.已知直线的方向向量为,平面的法向量为,则( ) l (1,1,2)a =r α(2,2,4)n =rA .//B .C .D .与相交l αl α⊥l α⊂l α【答案】B【分析】根据与平行,即可判断直线和平面的位置关系.a n【详解】因为,,故可得,即//,则直线. (2,2,4)n =r (1,1,2)a =r 2n a =n a l α⊥故选:B.3.若向量,,则( ) ()1,1,0a =()1,0,2b =- 3a b +=A B .4C .5D【答案】D【分析】由空间向量坐标的加减运算,和模长公式计算即可.【详解】解析:由题意,得, ()32,3,2a b +=3a b ∴+==故选:D.4.已知直线l 过、两点,则直线l 的倾斜角的大小为( ) ()1,1A -()1,3B A .B .C .D .4π3π23π34π【答案】A【分析】由两点坐标求出斜率,即可得出倾斜角【详解】直线过、两点,则直线的斜率,∴直线的倾斜角为.l ()1,1A -()1,3B l ()31111k -==--4π故选:A .5.如图,在斜四棱柱ABCD ﹣A 1B 1C 1D 1中,底面ABCD 是平行四边形,M 为A 1C 1与B 1D 1的交点.若,,,则=( )11A B a = 11A D b = 1A A c = BMA .B . 1122a b c -++ 1122a b c -+-C .D .1122--+ a b c 1122-+ a b c 【答案】B【分析】利用向量三角形法则、平行四边形法则即可得出. 【详解】因为斜四棱柱ABCD ﹣A 1B 1C 1D 1的底面是平行四边形, 又M 为A 1C 1,B 1D 1的交点,所以.1111111111()()222MB D B A B A D a b ==-=-所以. 11111()()222BM MB MB B B a b c a b c ⎡⎤=-=-+=--+=-+-⎢⎥⎣⎦故选:B6.以点为圆心,且与直线相切的圆的方程是( ) ()3,2-310x y --=A . B . 22(3)(2)1x y -++=22(3)(2)1x y ++-=C . D .22(3)(2)10x y ++-=22(3)(2)10x y -++=【答案】D【分析】设出圆的方程,由圆心到直线距离等于半径,得到答案. 【详解】设圆的方程为, 222(3)(2)x y r -++=故r 故圆的方程为. 22(3)(2)10x y -++=故选:D7.椭圆的焦点坐标是( )221516x y +=A .B .C .D .()11,0±(0,()0,11±()【答案】B【分析】由已知可得,椭圆的焦点在轴上,进而求出的值,即可解出. y 2c 【详解】由题意可知,椭圆的焦点在轴上,,,所以,y 25b =216a =22211c a b =-=所以椭圆的焦点坐标是.221516x y +=(0,故选:B.8.已知等比数列的首项和公比均为2,则的值为( ) {}n a 3a A . B .2 C .4 D .82-【答案】D【分析】根据等比数列的性质即可求解.【详解】由于等比数列的首项和公比均为2,{}n a 所以,233128a a q ===故选:D9.准线方程为的抛物线的标准方程为( ) 2x =A . B . C . D .28y x =28y x =-28x y =28x y =-【答案】B【分析】结合抛物线的定义求得正确答案. 【详解】由于抛物线的准线方程是,2x =所以抛物线的开口向左,设抛物线的方程为,()220y px p =->则,所以抛物线的标准方程为. 2,282pp ==28y x =-故选:B10.已知数列的前项和,则( ){}n a n 2n S n =2a =A .1 B .2 C .3 D .4【答案】C【分析】根据关系解决即可.,n n a S 【详解】由题知,数列的前项和,{}n a n 2n S n =所以, 122413a S S =-=-=故选:C11.双曲线的渐近线方程是( )22132x y -=A .B . 23y x =±32y x =±C .D . y =y =【答案】D【分析】根据焦点在横轴上双曲线的渐近线方程直接求解即可.【详解】由题得双曲线的方程为,所以22132x y -=a b ==所以渐近线方程为. b y x a =±=故选:D12.已知数列满足,且,则( ){}n a 211n n a a n +=++11a =4a =A .18 B .10 C .8 D .5【答案】A【分析】根据递推公式及可求出结果.1a 【详解】因为,,211n n a a n +=++11a =所以,21113a a =++=, 32418a a =++=. 439118a a =++=故选:A二、填空题13.已知,,则向量的坐标为________. ()0,2,1A ()5,2,2B -AB【答案】()5,4,1-【分析】根据空间向量的坐标表示方法即可求解. 【详解】因为,, ()0,2,1A ()5,2,2B -所以. ()()50,22,215,4,1AB =----=-故答案为:.()5,4,1-14.3与7的等差中项为___________. 【答案】5【分析】由等差中项的定义,若成等差数列,则即可求得. A G B ,,2A BG +=【详解】设3与7的等差中项为,则由等差中项的定义得. x 3752x +==故答案为:515.过点且与直线平行的直线方程为__________. ()1,2A -2310x y -+=【答案】2380.x y -+=【分析】两直线平行则它们的斜率相等,然后再将数据代入直线的点斜式方程可得.【详解】22310,,3x y k -+=∴=化简得: ()221,3y x ∴-=+2380.x y -+=故答案为:2380.x y -+=16.已知抛物线的焦点坐标为,则的值为___________. 22(0)y px p =>()2,0p 【答案】4【分析】利用抛物线的标准方程得到焦点坐标,从而求得值. p 【详解】因为抛物线,22(0)y px p =>所以抛物线的焦点坐标为,,02p ⎛⎫⎪⎝⎭又因为抛物线的焦点坐标为, 22(0)y px p =>()2,0所以,则. 22p=4p =故答案为:.4三、解答题17.已知,.()1,4,2a =- ()2,2,4b =-(1)若,求的值;12c b = cos ,a c <> (2)若,求实数的值.()()3ka b a b +-∥k【答案】(1) (2)13-【分析】(1)利用空间向量夹角公式的坐标运算直接求解;(2)根据两向量的共线定理,利用坐标运算求解.【详解】(1)由已知可得,,()11,1,22c b ==-()1,4,2a =- ∴cos ,a c a c a c⋅<>====(2),,()2,42,24ka b k k k +=-+-+ ()37,2,14a b -=--∵,∴存在实数使得, ()()3ka b a b +-∥m ()3ka b m a b +=- ∴,,,联立解得.27k m -=422k m +=-2414k m -+=-13k =-18.等差数列满足a 5=14,a 7=20,其前n 项和为Sn . {}n a (1)求数列的通项公式; {}n a (2)求该数列的前10项和. 10S 【答案】(1) 31n a n =-(2) 10155S =【分析】(1)由等差数列的通项公式求解即可; (2)由等差数列的求和公式求解即可. 【详解】(1)因为,5714,20a a ==所以,11414620a d a d +=⎧⎨+=⎩解得,123a d =⎧⎨=⎩所以; ()()1123131n a a n d n n =+-=+-=-(2). 101109101024531552S a d ⨯=+=⨯+⨯=19.(1)已知数列的前n 项和Sn =n 2+n ,求数列的通项公式; {}n a {}n a (2)设数列的首项为a 1=1,递推公式为an=1+,写出这个数列的前5项 {}n a 11n a -(2)n ≥【答案】(1);(2)=,. =2n a n 1=1a ,2a 2345358,,235a a a ===【分析】(1)Sn =n 2+n ,,两式相减即得解;21(2)n S n n n -=-≥(2)利用递推公式直接求解.【详解】解:(1)由题得Sn =n 2+n ,,221(1)1(2)n S n n n n n -=-+-=-≥所以两式相减得,又,=2n a n 11=2a S =所以适合.所以数列的通项公式为. =2n a n 1n ={}n a =2n a n (2)由题得=1+,. 1=1a ,2a 11=2a 3451325381,1,1223355a a a =+==+==+=所以数列的前5项为=,. 1=1a ,2a 2345358,,235a a a ===20.如图,在三棱柱中,侧面为矩形,平面平面,111ABC A B C -11ABB A 11ABB A ⊥11ACC A 分别是的中点.12,4,,AB AA D E ==11,BC A B(1)求证:平面;//DE 11ACC A (2)若侧面是正方形,求直线与平面所成角的正弦值. 11ACCA 11A C ADE 【答案】(1)详见解析;【分析】(1)取中点为,由题可得,然后利用线面平行的判定定理即得; AC F //DE 1A F (2)利用坐标法,求出平面的法向量,然后根据线面角的向量求法即得. ADE 【详解】(1)取中点为,连接,AC F 1,DF A F因为点分别为的中点, ,D F ,CB CA 故,, DF //AB 12DF AB =又点为的中点,且四边形为矩形, E 11A B 11ABB A 故,, 1A E //AB 112A E AB =故,, //DF 1A E 1DF A E =故四边形为平行四边形,1DFA E 则,又平面平面, //DE 1A F DE ⊄111,ACC A A F ⊂11ACC A 所以平面;//DE 11ACC A (2)因为为正方形,故可得,11ACC A 1AC AA ⊥又因为平面平面,且平面平面, 11ABB A ⊥11ACC A 11ABB A 111ACC A AA =又平面, AC ⊂11ACC A 所以平面, AC ⊥11ABB A 又平面,AB ⊂11ABB A 所以,又,,AC AB ⊥1AB AA ⊥1AC AA ⊥如图建立空间直角坐标系,则,()()()()0,0,0,2,0,1,0,4,1,4,0,0A D E C 所以,()()()112,0,1,0,4,1,4,0,0AD AE A C AC ====设平面的法向量为,则,ADE (),,n x y z =r 2040n AD x z n AE y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩令,则,1y =()2,1,4n =-设与平面所成角为,则11A C ADE θ111111,sin cos n A C n A C n A C θ⋅===⋅=故直线与平面11A C ADE 21.已知椭圆的中心为坐标原点O ,左右焦点分别为,,短轴长为2,离心率,过右焦1F 2F e =点的直线交椭圆于P ,Q 两点. 2F l (1)求椭圆的标准方程. (2)当直线的倾斜角为时,求的面积. l 4π1PFQ △【答案】(1).22121x y +=(2). 43【分析】(1)根据条件列出关于的式子,利用待定系数法求椭圆方程; ,,a b c (2)直线方程与椭圆方程联立,利用韦达定理表示三角形的面积.【详解】(1),解得:,∴.22222b c e a a b c =⎧⎪⎪==⎨⎪=+⎪⎩11a b c ⎧=⎪=⎨⎪=⎩22121x y +=(2)倾斜角为,,14k π⇒=()21,0F ∴:,l 1y x =-()112121212PQF PF F QF F P Q S S S F F y y =+=⨯⨯+△△△P Q P Q y y y y =+=-=,得, 22112y x x y =-⎧⎪⎨+=⎪⎩23210y y +-=, ,44310∆=+⨯⨯>23P Q y y +=-13P Q y y ⋅=-∴. 43S ==22.已知抛物线:,坐标原点为,焦点为,直线:. C 24y x =O F l 1y kx =+(1)若与只有一个公共点,求的值;l C k (2)过点作斜率为的直线交抛物线于两点,求的面积. F 2C ,A B OAB A 【答案】(1)1或0【分析】(1)将直线方程与抛物线方程联立,由或即可得解;0k =Δ0=(2)由抛物线的标准方程得到焦点坐标,从而得到直线方程,联立直线与抛物线方程,根据韦达定理及即可得解. 121||||2OAB S OF y y =⋅-A 【详解】(1)依题意,联立,消去,得,即,214y kx y x =+⎧⎨=⎩x 2114y ky =+2440ky y -+=①当时,显然方程只有一个解,满足条件; 0k =440y -+=②当时,,解得; 0k ≠2(4)440k ∆=--⨯=1k =综上:当或时直线与抛物线只有一个交点. 1k =0k =(2)因为抛物线:,所以焦点,C 24y x =(1,0)F 所以直线方程为,设,,()2122y x x =-=-11(,)A x y 22(,)B x y 联立,消去得,所以,,2224y x y x =-⎧⎨=⎩x 2240y y --=122y y +=124y y =-所以 12||y y -===所以1211||||122OAB S OF y y =⋅-=⨯⨯=A。
新疆兵团第二师华山中学高二数学上学期期末考试试题文(2021年整理)

新疆兵团第二师华山中学2017-2018学年高二数学上学期期末考试试题文编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(新疆兵团第二师华山中学2017-2018学年高二数学上学期期末考试试题文)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为新疆兵团第二师华山中学2017-2018学年高二数学上学期期末考试试题文的全部内容。
2017—2018学年第一学期高二年级期末考试数学(文科)试卷(考试时间:120分钟,满分:150分)一、选择题:(12小题,每题5分,共60分)1、已知复数z满足iz=2+3i,则z对应的点位于A。
第一象限 B. 第二象限C。
第三象限D。
第四象限2、设命题p:∀x>0,x-ln x>0,则¬p为A。
∃x0>0,x0-ln x0>0 B。
∃x0>0,x0-ln x0≤0C。
∀x>0,x-ln x<0 D. ∀x>0,x—ln x≤03、宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.下图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的n=A. 2B. 3C。
4 D。
54、若a,b∈R,则“a>0,b>0”是“a+b>0”的A. 充分不必要条件B。
必要不充分条件C。
充要条件D。
既不充分也不必要条件5、已知双曲线的一条渐近线为,则实数a的值为A。
B. 2 C。
D. 46、下列说法错误的是A. 对分类变量X与Y,随机变量K2的观测值k越大,则判断“X与Y有关系”的把握程度越小B. 在回归直线方程=0.2x+0。
8中,当解释变量x每增加1个单位时,预报变量平均增加0.2个单位C。
新疆第二师华山中学2018_2019学年高二物理上学期期末考试试题2019041603103

华山中学2018-2019学年第一学期高二年级期末考试物 理 试 卷考试时间:100分钟 分值:110分 Ⅰ卷(选择题,共48分)一、选择题(本题共12小题,每小题4分,共48分,其中1-8题为单选,9-12题为多选) 1.在如图所示的四个图中,标出了匀强磁场的磁感应强度B 的方向、通电直导线中电流I 的方向以及通电直导线所受安培力F 的方向,其中正确表示三者方向关系的图是( )A B C D2.如图所示电路,电源电动势为E ,内阻为r 。
当开关S 闭合后,小型直流电动机M 和指示灯L 都恰能正常工作。
已知指示灯L 的电阻为R 0,额定电流为I ,电动机M 的线圈电阻为R ,则下列说法中正确的是( ) A .电动机的额定电压为IR B .电动机的输出功率为I 2R C .电源的输出功率为IE -I 2rD .整个电路的热功率为I 2(R 0 + r )3.如下图所示,条形磁铁放在桌子上,一根通电直导线由S 极的上端平移到N 极的上端的过程中,导线保持与磁铁垂直,导线的通电方向如图,则在这个过程中磁铁受到的摩擦力(保持静止)( ) A .为零. B .方向由左变为向右. C .方向保持不变. D .方向由右变为向左.4.如图所示,质子(11H )和α粒子(42He )以相同的初动能垂直射入偏转电场(粒子不计重力),则这两个粒子射出电场时的侧位移y 之比为( ) A .1∶1B .1∶2C . 2∶1D .1∶4BvI5、如图所示,在两根平行长直导线M 、N 中,通入同方向同大小的电流,导线框abcd 和两导线在同一平面内,线框沿着与两导线垂直的方向,自右向左在两导线间匀速移动,在移动过程中,线框中感应电流的方向为( )A .沿abcda 不变B .沿adcba 不变C .由abcda 变成adcbaD .由adcba 变成abcda6.如图所示,有两个固定的、电量相等、电性相反的点电荷1Q 、2Q ,a 、b 是它们连线的中垂线上的两个点,c 是它们产生的电场中的另一点,以无穷远处为电势的零点,则下列说法中正确的是( ) A .a 、b 两点场强相同 B .a 点场强一定小于b 点场强 C .b 点的电势一定比a 点的电势高 D .c 点的电势一定比b 点的电势高7.如图所示,在坐标系xOy 中,有边长为a 的正方形金属线框abcd ,其一条对角线ac 和y 轴重合、顶点a 位于坐标原点O 处。
新疆第二师华山中学2018-2019学年高二上学期期中考试 (理科)数学试卷及答案

华山中学2018-2019学年第一学期高二年级期中考试理科数学 试卷(考试时间:120分钟,满分:150分) 命题教师:陈学阳一、选择题:(单选题,每题5分,共60分) 1、抛物线y = 22x 的准线方程是( )A. x =-12 B. x =12 C. y =-18 D. y =182、设平面α与平面β相交于直线m ,直线a 在平面α内,直线b 在平面β内,且m b ⊥,则""βα⊥是""b a ⊥的( )条件A.充分不必要B.必要不充分C.充要D.既不充分也不必要3、如果方程11222=+++m y m x 表示双曲线,则实数m 的取值范围是( ) A .)2,3(-- B .),1()2,(+∞---∞Y C .)1,1(- D .)1,2(-- 4、已知直线 y = x +1与曲线y =ln (x +a )相切,则a 的值为( )A. 1B. 2C. -1D. -2 5、 函数f (x )=的图象大致为( )A B C D6、过点M (1,1)作斜率为k 的直线与椭圆C :4222=+y x 相交于点A ,B ,若M 是线段AB 的中点,则k =( ) A . 2- B .2-C .21-D 22-7、 如图,已知棱长为1的正方体ABCD -A 1B 1C 1D 1中,E 是A 1B 1的中点,则直线AE 与平面ABC 1D 1所成的角的正弦值是( )A. B. C.D.8、已知命题p :“0],2,1[2≥-∈∀a x x ”,命题q :“022,2=-++∈∃a ax x R x ”.若命题“p 且q ”是真命题,则实数a 的取值范围为( )A .2-≤a 或1=aB .2-≤a 或21≤≤aC .1≥aD .12≤≤-a9、设双曲线的一条渐近线与抛物线y =2x + 1只有一个公共点,则双曲线的离心率为( )A .B .5C .D .10、若函数2)(3-+=ax x x f 在区间),1(+∞内是增函数,则实数a 的取值范围是( )A .),3(+∞B . ),3[+∞-C . ),3(+∞-D .)3,(--∞ 11、已知直线x =my -1与抛物线C :y 2=4x 相交于A ,B 两点,F 为C 的焦点.若|FA |=2|FB |,则m 等于( ) A.±3B. C. D.12、如图,在三棱锥中,平面平面与均为等腰直角三角形,且,点P 是线段AB 上的动点,若线段CD 上存在点Q ,使得异面直线PQ 与AC 成的角,则线段PA 长的取值范围是( )A. ]22,0( B.)36,0( C.]322,22[D. ]322,36(二、填空题(每题5分,共20分) 13、函数f (x )=的单调递减区间是______.14、已知双曲线2215x y m -=的右焦点与抛物线212y x =的焦点相同,则此双曲线的渐近线方程为15、函数f (x )= 221x - + x ln 在 [ ,e ]上的最大值是______16、已知抛物线C :24x y =的焦点为F ,点(22,0)A .若射线FA 与抛物线C 相交于点M ,与抛物线C 的准线相交于点N ,则MNFM=三、解答题(10+12+12+12+12+12=70分)17、(本题满分10分)甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次.得到甲、乙两位学生成绩的茎叶图.(Ⅰ)现要从中选派一人参加数学竞赛,对预赛成绩的平均值和方差进行分析,你认为哪位学生的成绩更稳定?请说明理由;(Ⅱ)在甲同学的8次预赛成绩中,从不小于80分的成绩中随机抽取2个成绩,列出所有结果,并求抽出的2个成绩均大于85分的概率.18、(本题满分12分)如图,在直三棱柱ABC -A 1B 1C 1中,点D 是BC 的中点. (1)求证:A 1B ∥平面ADC 1(2)若AB ⊥AC ,AB =AC =1,AA 1=2,求平面ADC 1与ABA 1所成二面角的正弦值.19、(本题满分12分)已知动点P 到定直线l :x =-4的距离比到定点F (2,0)的距离大2. (1)求动点P 的轨迹C 的方程; (2)A 、B 是轨迹C 上两个不同的点,O 是坐标原点,OA ⊥OB, 求证:直线AB 经过一定点,并求出这个定点的坐标。
新疆第二师华山中学2018_2019学年高二物理上学期期末考试试题

华山中学2018-2019学年第一学期高二年级期末考试物 理 试 卷考试时间:100分钟 分值:110分 Ⅰ卷(选择题,共48分)一、选择题(本题共12小题,每小题4分,共48分,其中1-8题为单选,9-12题为多选) 1.在如图所示的四个图中,标出了匀强磁场的磁感应强度B 的方向、通电直导线中电流I 的方向以及通电直导线所受安培力F 的方向,其中正确表示三者方向关系的图是( )A B C D2.如图所示电路,电源电动势为E ,内阻为r 。
当开关S 闭合后,小型直流电动机M 和指示灯L 都恰能正常工作。
已知指示灯L 的电阻为R 0,额定电流为I ,电动机M 的线圈电阻为R ,则下列说法中正确的是( ) A .电动机的额定电压为IR B .电动机的输出功率为I 2R C .电源的输出功率为IE -I 2rD .整个电路的热功率为I 2(R 0 + r )3.如下图所示,条形磁铁放在桌子上,一根通电直导线由S 极的上端平移到N 极的上端的过程中,导线保持与磁铁垂直,导线的通电方向如图,则在这个过程中磁铁受到的摩擦力(保持静止)( ) A .为零. B .方向由左变为向右. C .方向保持不变. D .方向由右变为向左.4.如图所示,质子(11H )和α粒子(42He )以相同的初动能垂直射入偏转电场(粒子不计重力),则这两个粒子射出电场时的侧位移y 之比为( ) A .1∶1B .1∶2C . 2∶1D .1∶4BFIFBIF ISNvIMSEr L5、如图所示,在两根平行长直导线M 、N 中,通入同方向同大小的电流,导线框abcd 和两导线在同一平面内,线框沿着与两导线垂直的方向,自右向左在两导线间匀速移动,在移动过程中,线框中感应电流的方向为( )A .沿abcda 不变B .沿adcba 不变C .由abcda 变成adcbaD .由adcba 变成abcda6.如图所示,有两个固定的、电量相等、电性相反的点电荷1Q 、2Q ,a 、b 是它们连线的中垂线上的两个点,c 是它们产生的电场中的另一点,以无穷远处为电势的零点,则下列说法中正确的是( ) A .a 、b 两点场强相同 B .a 点场强一定小于b 点场强 C .b 点的电势一定比a 点的电势高 D .c 点的电势一定比b 点的电势高7.如图所示,在坐标系xOy 中,有边长为a 的正方形金属线框abcd ,其一条对角线ac 和y 轴重合、顶点a 位于坐标原点O 处。
新疆兵团第二师华山中学高二数学上学期第一次调研考试试题 理

2018-2019学年高二年级第一次调研考试数学 试卷(考试时间:120分钟,满分:150分)一、选择题(每题5分,共60 分)1.命题“∀x ∈R ,|x|+x 2≥0”的否定是( )A .∀x ∈R ,|x|+x 2<0 B .∀x ∈R ,|x|+x 2≤0 C .∃x 0∈R ,|x 0|+x 02<0 D .∃x 0∈R ,|x 0|+x 02≥02.已知函数f(x)=x 2+bx ,则“b<0”是“f(f(x))的最小值与f(x)的最小值相等”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件3.下列关于命题的说法正确的是( )A .命题“若x 2=1,则x =1”的否命题为“若x 2=1,则x≠1” B .“x =-1”是“x 2-5x -6=0”的必要不充分条件C .命题“a,b 都是有理数”的否定是“a、b 都不是有理数”D .命题“若x =y ,则sinx =siny ”的逆否命题为真命题 4.用辗转相除法求840和1764的最大公约数是( ) A .84 B .12 C .168 D .252 5.执行如图所示的程序框图,则输出的结果是( )A .5 040B .4 850C .2 450D .2 5506.若椭圆x 2+my 2=1的焦点在y 轴上,且长轴长是短轴长的两倍.则m 的值为( ) A.12 B.14C .2D .47.到两定点A(0,0),B(3,4)距离之和为5的点的轨迹是( ) A .椭圆 B .AB 所在的直线C .线段ABD .无轨迹 8.已知P 是椭圆 x 225+y 2b 2=1(0<b<5)上除顶点外一点,F 1是椭圆的左焦点,若|OP →+OF 1→|=8,则点P 到该椭圆左焦点的距离为( ) A .6 B .4 C .52D.29.中央电视台为了调查近三年的春晚节目中各类节目的受欢迎程度,用分层抽样的方法,从2014年至2016年春晚的50个歌舞类节目,40个戏曲类节目,30个小品类节目中抽取样本进行调查,若样本中的歌舞类和戏曲类节目共有27个,则样本容量为( ) A .30 B .35 C .32 D .3610.如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分). 已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x ,y 的值分别为( ) A .2,5 B .5,8 C .5,5 D .8,811.从2名男生和2名女生中任意选择两人在星期六、星期日参加某公益活动,每天一人,则星期六安排一名男生、星期日安排一名女生的概率为( ) A.13 B.512 C.12D.71212.如图,已知椭圆C: x 2a 2+y2b 2=1(a>b>0),其中左焦点为F(-25,0),P 为C 上一点,满足|OP|=|OF|,且|PF|=4,则椭圆C 的方程为( )A.x 225+y 25=1 B.x 236+y 210=1 C.x 236+y 216=1 D.x 245+y225=1二、填空题(每题5分,共20分)13.已知焦点在x 轴上的椭圆, = 12,且它的长轴长等于圆C :x 2+y 2-2x -15=0的半径,则椭圆的标准方程是________ 14.某产品的广告费用x 与销售额y 的统计数据如下表:54根据上表可得回归方程 中的为9.4,据此模型预报广告费用为6万元时销售额约为________元. 15.下列四个命题中①“k =1”是“函数y =cos 2kx -sin 2kx的最小正周期为π”的充要条件;②“a =3”是“直线ax +2y +3a =0与直线3x +(a -1)y =a -7相互垂直”的充要条件;③函数y =x 2+4x 2+3的最小值为2.其中是假命题的为________(将你认为是假命题的序号都填上)a xb yˆˆˆ+=b ˆac16.已知O 为坐标原点, F 是椭圆C :x 2a 2+y2b 2=1(a>b>0)的左焦点,A ,B 分别为C 的左、右顶点.P 为C 上一点,且PF⊥x 轴.过点A 的直线 与线段PF 交于点M ,与y 轴交于点E.若直线BM 经过OE 的中点,则椭圆C 中 为________三、解答题(18题10分,其余每题12分)17.命题P :函数 有意义,命题q :实数 满足当 且 p ∧q 为真,求实数 的取值范围;若 是 的充分不必要条件,求实数a 的取值范围.18.已知a>0,设命题p :函数y =a x在R 上单调递增;命题q :不等式ax 2-ax +1>0对∀ x ∈R 恒成立.若p 且q 为假,p 或q 为真,求实数a 的取值范围.19.如图,已知椭圆 x 2a 2+y2b 2=1(a>b>0),F 1,F 2分别为椭圆的左、右焦点,A 为椭圆的上顶点,直线AF 2交椭圆于另一点B.(1)若∠F 1AB =90°,求椭圆中 的值;(2)若椭圆的焦距为2,且AF 2→=2F 2B →,求椭圆的方程.20.已知F 1,F 2为椭圆C : (a >b >0)的左右焦点,椭圆上的点到F 2的最近距离为2,且为13. )0)(34lg(22>-+-=a a ax x y 023<--x x 1=a p ⌝q⌝12222=+b y a x xx l a ca c ac(1)椭圆C 的方程;(2)设点A (-1,2),若P 是椭圆C 上的动点,求线段PA 中点M 的轨迹方程;(3)若E 是椭圆C 上的动点,求 的最大值和最小值.21.2018年“双节”期间,高速公路车辆较多.库尔勒市某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t )分成六段:(60,65),[65,70),[70,75),[75,80),[80,85),[85,90)后得到如图的频率分布直方图. (1)某调查公司在采样中,用到的是什么抽样方法? (2)求这40辆小型车辆车速的众数和中位数的估计值. (3)若从车速在[60,70)的车辆中任抽取2辆,求车 速在[65,70)的车辆至少有一辆的概率.22.某研究机构对高二学生的记忆力x 和判断力y 进行统计分析,得下表数据: (1)请在图中画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程; (3)试根据(2)求出的线性回归方程,预测记忆力为9的同学的判断力.相关公式:21.EF EF →→a x b y ˆˆˆ+=x b y ax n xy x n yx bni ini iiˆˆ,ˆ1221-=--=∑∑==高二第一次调研考试数学参考答案一.选择题1-5 CADAC 6-10 BCDDB 11-12 AC 二.填空题13.x 24+y 23=1 14. 65.5 15. ①②③ 16.13三.解答题17.解:(1)由-x 2+4ax-3a 2>0得x 2-4ax+3a 2<0, 即(x-a )(x-3a )<0,其中a >0, 得a <x <3a ,a >0,则p :a <x <3a ,a >0. 若a=1,则p :1<x <3, 由解得2<x <3. 即q :2<x <3.若p ∧q 为真,则p ,q 同时为真,即,解得2<x <3, ∴实数x的取值范围(2,3)..........................................................................................(6分)(2)若¬p 是¬q 的充分不必要条件,即q 是p 的充分不必要条件, ∴即(2,3)是(a ,3a )的真子集.所以,解得1≤a ≤2.实数a 的取值范围为[1,2]. .........................................(12分)18.解:∵y=ax在R 上单调递增,∴p :a>1.....................................................................(2分)又不等式ax 2-ax +1>0对∀x ∈R 恒成立,∴Δ<0,即a 2-4a<0,∴0<a<4.∴q :0<a<4........(4分)而命题p 且q 为假,p 或q 为真,那么p ,q 中有且只有一个为真,一个为假.. (1)若p真,q假,则a ≥4;(2)若p假,q真,则0<a ≤1...........................................................(8分)所以a的取值范围为(0,1]∪[4,+∞)......................................................................................(10分)19.(1)若∠F 1AB =90°,则△AOF 2为等腰直角三角形. 所以有|OA|=|OF 2|,即b = c.所以a =2c ,c a=22.....................................(6分)(2)由题知 A(0,b),F 2(1,0),设B(x ,y),由题意得x =32,y =-b2.代入x 2a 2+y 2b 2=1,得94a 2+b24b 2=1..即94a 2+14=1,解得a 2=3.所以椭圆方程为 x 23+y 22=1.................(12分)20.解:(1)由条件知,解得c=1,a=3.则b 2=a 2-c 2=8. 所以椭圆C :;............................................................................................................(4分) (2)设M (x ,y ),因为M 为PA 的中点,所以P (2x+1,2y-2). 又因为点P 在椭圆上,所以即为所求点M 的轨迹方程;..............(8分)(3)设E (x 0,y 0),则有. 因为F1(-1,0),F2(1,0).所以=.因为点E 在椭圆上,所以0. 所以.所以当时,所求最小值为7,当时,所求最大值为8...............................................(12分)21.解:(1)由题意知这个抽样是按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,是一个具有相同间隔的抽样,并且总体的个数比较多,这是一个系统抽样.故调查公司在采样中,用到的是系统抽样.............................................................................. ...................(2分)(2)众数的估计值为最高的矩形的中点,即众数的估计值等于77.5...........................................(4分)设图中虚线所对应的车速为x,则中位数的估计值为:0.01×5+0.02×5+0.04×5+0.06×(x-75)=0.5,解得x=77.5,即中位数的估计值为77.5............................................................................ ......(6分)(3)从图中可知,车速在[60,65)的车辆数为:m1=0.01×5×40=2(辆),车速在[65,70)的车辆数为:m2=0.02×5×40=4(辆).......................................................................... ...............................(8分)设车速在[60,65)的车辆设为a,b,车速在[65,70)的车辆设为c,d,e,f,则所有基本事件有:(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f)共15种....................... ..........(10分)其中车速在[65,70)的车辆至少有一辆的事件有:(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f)共14种,所以车速在[65,70)的车辆至少有一辆的概率为............................................(12分)22解:(1)把所给的四对数据写成对应的点的坐标,在坐标系中描出来,得到散点图.如图所示:......(3分)(2)x i y i =6×2+8×3+10×5+12×6=158,==9,==4,=62+82+102+122=344, ===0.7=-=4-0.7×9=-2.3,故线性回归方程为=0.7x-2.3...............................................(10分)当x=9时, =0.7×9-2.3=6.3-2.3=4,所以预测记忆力为9的同学的判断力约为4...........(12分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
华山中学2018-2019学年第一学期高二年级期末考试文科数学试卷(考试时间:120分钟,满分:150分)1 . i为虚数单位,则2016 11⎪⎭⎫⎝⎛-+iiA. B. C. i D. 12.从一堆产品(其中正品与次品都多于2件)中任取2件,下列事件是互斥事件但不是对立事件的是()A.恰好有1件次品和恰好有2件次品B.至少有1件次品和全是次品C.至少有1件正品和至少有1件次品D.至少有1件次品和全是正品3.下列有关命题的说法错误的是A. 若“”为假命题,则p,q均为假命题B. “”是“”的充分不必要条件C. “”的必要不充分条件是“”D. 若命题p:,,则命题:,4. 若曲线4xy=的一条切线l与直线x+2y﹣8=0平行,则l的方程为()A.8x+16y+3=0B.8x﹣16y+3=0C.16x+8y+3=0D.16x﹣8y+3=05.若抛物线y2=2px上一点P(2,y0)到其准线的距离为4,则抛物线的标准方程为() A.y2=4x B.y2=6x C.y2=8x D.y2=10x6. 小赵、小钱、小孙、小李四位同学被问到谁去过长城时,小赵说:我没去过;小钱说:小李去过;小孙说;小钱去过;小李说:我没去过.假定四人中只有一人说的是假话,由此可判断一定去过长城的是A. 小赵B. 小李C. 小孙D. 小钱7.2017世界特色魅力城市200强新鲜出炉,包括黄山市在内的28个中国城市入选,美丽的黄山风景和人文景观迎来众多宾客.现在很多人喜欢“自助游”,某调查机构为了了解“自助游”是否与性别有关,在黄山旅游节期间,随机抽取了100人,得如下所示的列联表:参照公式,得到的正确结论是( )A .有99.5%以上的把握认为“赞成‘自助游’与性别无关”B .有99.5%以上的把握认为“赞成‘自助游’与性别有关”C .在犯错误的概率不超过0.1的前提下,认为“赞成‘自助游’与性别无关”D .在犯错误的概率不超过0.1的前提下,认为“赞成‘自助游’与性别有关”参考公式:K 2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d ),其中n =a +b +c +d.8.如图是甲、乙两位同学高二上学期历史成绩的茎叶图,有一个数字被污损,用a(3≤a ≤8且a ∈N )表示被污损的数字.则甲同学的历史平均成绩不低于乙同学的历史平均成绩的概率为( )A.13B. 23C.16D.569. 已知:命题p :若函数||)(2a x x x f -+=是偶函数,则0=a .命题q :),0(+∞∈∀m ,关于x 的方程0122=+-x mx 有解.在①q p ∨;②q p ∧;③q p ∧⌝)(;④)()(q p ⌝∨⌝中为真命题的是( ) A .②③ B .①④ C .③④ D .②④10.《九章算术》是我国古代数学名著,也是古代数学的代表作.书中有如下问题:“今有勾八步,股一十五步,问勾中容圆,径几何?”其意思为:“已知直角三角形两直角边长分别为8步和15步,问其内切圆的“径为多少步?”现若向此三角形内投豆子,则豆子落在其内切圆内的概率是( )A.3π20B.π20C.3π10D.π1011.设双曲线C :x 2a 2-y 2b 2=1(a>0,b>0)的左、右焦点分别为F 1,F 2,以F 1F 2为直径的圆与双曲线左支的一个交点为P.若以OF 1(O 为坐标原点)为直径的圆与PF 2相切,则双曲线C 的离心率为( )A. 2B.-3+624C. 3D.3+62712.已知函数)(x f 是定义在R 上的奇函数,且当0>x 时,0)3()(=++-x f x f ;当)3,0(∈x 时,xxe xf ln )(=,其中e 是自然对数的底数,且72.2≈e ,则方程0)(6=-x x f 在]9,9[-上的解的个数为( )A .4B .5C .6D .7二、填空题(本大题共4小题,共20分)13.观察下列各式:a +b =1,a 2+b 2=3,a 3+b 3=4,a 4+b 4=7,a 5+b 5=11,…,则a 10+b 10=________.14.小明每天上学都需要经过一个有交通信号灯的十字路口,已知十字路口的交通信号灯绿灯亮灯的时间为40秒,红灯50秒,如果小明每天到路口的时间是随机的,则小明上学时到十字路口需要等待的时间不少于20秒的概率为________. 15.已知函数x m x x f ln )(2-=在),2[+∞上单调递增,则实数m 的取值范围为 .16.一个底面半径为2的圆柱被与底面所成角是60°的平面所截,截面是一个椭圆,则该椭圆的焦距等于________.三、解答题(本大题共6小题,共70分)17.(本小题满分10分)设函数()()1f x x x R =-∈.(1)求不等式()()15f x f x -+≤的解集;(2)若不等式()()2412f x f x a a +--≤-的解集是R ,求正整数a 的最小值.18.(本小题满分12分)在“新零售”模式的背景下,某大型零售公司为推广线下分店,计划在S市的A区开设分店为了确定在该区开设分店的个数,该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格记x表示在各区开设分店的个数,y表示这x个分店的年收入之和.Ⅰ该公司已经过初步判断,可用线性回归模型拟合y与x的关系,求y关于x的线性回归方程;Ⅱ假设该公司在A区获得的总年利润单位:百万元与x,y之间的关系为,请结合Ⅰ中的线性回归方程,估算该公司应在A区开设多少个分店时,才能使A区平均每个分店的年利润最大?参考公式:,,19.(本题满分12分)设抛物线24:的焦点为F,过F且斜率为(0)C y x=k k>的直线l与C交于A,B两点,AB=.||8(1)求l的方程;(2)求过点A,B且与C的准线相切的圆的方程.20.(本小题满分12分)如图,在四棱锥中,平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,,,M是PD的中点.Ⅰ平面平面PAC;Ⅱ当三棱锥的体积等于时,求PA的长;21.(本小题满分12分)已知为椭圆的右焦点,点在上,且轴. (1)求的方程(2)过的直线交于两点,交直线于点.证明:直线的斜率成等差数列.22.(本题满分12分)已知函数()1ln f x x a x =--. (1)若()0f x ≥,求a 的值; (2)设m 为整数,且对于任意正整数n ,2111111222n m ⎛⎫⎛⎫⎛⎫+++< ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭,求m 的最小值.高二期末文科答案一、选择题:本大题共12小题,每小题5分,共60分.二、填空题:本大题共4小题,每小题5分,共20分. 13.123; 14.31; 15.]8,(-∞; 16. 4 3 三、解答题(本大题共6小题,共70分) 17.(1) []1,4-; (2)4.试题解析:(1)不等式()()1215f x f x x x -+=-+-≤,解得14x -≤≤,所以解集是[]1,4-.————————————————————————————————————— 5分(2)()()4132f x f x x x +--=+-- 325x x ≤+-+=,所以225a a -≥恒成立,得()216a -≥,满足此不等式的正整数a 的最小值为4.——10分18.解:Ⅰ,,,,关于x 的线性回归方程.————————————————————6分 Ⅱ,A 区平均每个分店的年利润, 时,t 取得最大值,故该公司应在A 区开设4个分店时,才能使A 区平均每个分店的年利润最大——————12分19. 【答案】解:(1)由题意得(1,0)F ,l 的方程为(1)(0)y k x k =->.设1221(,),(,)A y x y x B ,由2(1),4y k x y x=-⎧⎨=⎩得2222(24)0k x k x k -++=.216160k ∆=+>,故122224k x k x ++=.所以122244||||||(1)(1)x k AB AF BF kx +=+=+++=. 由题设知22448k k+=,解得1k =-(舍去),1k =.因此l 的方程为1y x =-. (2)由(1)得AB 的中点坐标为(3,2),所以AB 的垂直平分线方程为2(3)y x -=--,即5y x =-+.设所求圆的圆心坐标为00(,)x y ,则00220005,(1)(1)16.2y x y x x =-+⎧⎪⎨-++=+⎪⎩解得003,2x y =⎧⎨=⎩或0011,6.x y =⎧⎨=-⎩ 因此所求圆的方程为22(3)(2)16x y -+-=或22(11)(6)144x y -++=.20.Ⅱ证明:因为底面ABCD 是菱形,所以. 因为平面ABCD ,平面ABCD , 所以又, 所以平面PAC . 又平面PBD ,所以平面平面PAC .——————————————————————————6分 Ⅲ解:因为底面ABCD 是菱形,且,, 所以.又,三棱锥的高为PA , 所以,解得.—————————————————————————————————12分21.解:(1) 因为点在上,且轴,所以, 设椭圆左焦点为,则,, 中,,所以. 所以,,又,故椭圆的方程为;(2)证明:由题意可设直线的方程为,令得,的坐标为, 由得,, 设,,,, 则有,①.记直线,,的斜率分别为,,, 从而,,.因为直线的方程为,所以,, 所以 ②.①代入②得, 又,所以,故直线,,的斜率成等差数列. 22. (1)()f x 的定义域为()0∞,+. ①若0a ≤,因为11ln 2022f a ⎛⎫<⎪⎝⎭=-+,所以不满足题意; ②若a >0,由()1a x af'x x x-=-=知,当()0x ,a ∈时,()f 'x <0;当(),+x a ∈∞时,()f 'x >0,所以()f x 在()0,a 单调递减,在(),+a ∞单调递增,故x =a 是()f x 在()0∞,+的唯一最小值点.由于()10f =,所以当且仅当a =1时,()0f x ≥.故a =1. (2)由(1)知当()1,x ∈+∞时,1ln 0x x -->. 令112n x =+得11ln 122n n ⎛⎫+< ⎪⎝⎭.从而 221111111ln 1ln 1ln 1112222222n n n ⎛⎫⎛⎫⎛⎫++++++<+++=-< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故2111111e 222n ⎛⎫⎛⎫⎛⎫+++< ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭. 而231111112222⎛⎫⎛⎫⎛⎫+++> ⎪⎪⎪⎝⎭⎝⎭⎝⎭,所以m 的最小值为3。
