十年高考真题分类汇编(2010-2019) 数学 专题17 复数
十年高考真题分类汇编(2010-2019) 数学 专题17 复数 Word版无答案原卷版

十年高考真题分类汇编(2010—2019)数学专题17复数1.(2019·全国1·文T1)设z=3-i1+2i,则|z|= ()A.2B.√3C.√2D.12.(2019·全国3·理T2文T2)若z(1+i)=2i,则z=( )A.-1-iB.-1+iC.1-iD.1+i3.(2019·北京·理T1文T2)已知复数z=2+i,则z·z=()A.√3B.√5C.3D.54.(2019·全国2·文T2)设z=i(2+i),则z=( )A.1+2iB.-1+2iC.1-2iD.-1-2i5.(2019·全国1·理T2)设复数z满足|z-i|=1,z在复平面内对应的点为(x,y),则( )A.(x+1)2+y2=1B.(x-1)2+y2=1C.x2+(y-1)2=1D.x2+(y+1)2=16.(2019·全国2·理T2)设z=-3+2i,则在复平面内对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限7.(2018·全国1·理T1文T2)设z=1-i1+i+2i,则|z|=()A.0B.12C.1D.√28.(2018·全国2·理T1)1+2i1-2i=()A.-45−35i B.-45+35iC.-35−45i D.-35+45i9.(2018·全国2·文T1)i(2+3i)=( )A.3-2iB.3+2i10.(2018·全国3·理T2文T2)(1+i)(2-i)=( )A.-3-iB.-3+iC.3-iD.3+i的共轭复数对应的点位于( ) 11.(2018·北京·理T2文T2)在复平面内,复数11-iA.第一象限B.第二象限C.第三象限D.第四象限12.(2018·浙江·4)复数2(i为虚数单位)的共轭复数是( )1-iA.1+iB.1-iC.-1+iD.-1-i13.(2017·全国1·理T3)设有下面四个命题p1:若复数z满足1∈R,则z∈R;p2:若复数z满足z2∈R,则z∈R;p3:若复数z1,z2满足z1z2∈R,则z1=z2;p4:若复数z∈R,则z∈R.其中的真命题为( )A.p1,p3B.p1,p4C.p2,p3D.p2,p4=( )14.(2017·全国2·理T1)3+i1+iA.1+2iB.1-2iC.2+iD.2-i15.(2017·全国2·文T2)(1+i)(2+i)= ( )A.1-iB.1+3iC.3+iD.3+3i16.(2017·山东·文T2)已知i是虚数单位,若复数z满足zi=1+i,则z2=( )A.-2iB.2iC.-2D.217.(2017·全国3·理T2)设复数z满足(1+i)z=2i,则|z|=( )A.1B.√2C.√2D.218.(2017·全国1·文T3)下列各式的运算结果为纯虚数的是( )A.i(1+i)2B.i2(1-i)19.(2017·山东·理T2)已知a∈R,i是虚数单位.若z=a+√3i,z·z=4,则a=()A.1或-1B.√7或-√7C.-√3D.√320.(2017·全国3·文T2)复平面内表示复数z=i(-2+i)的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限21.(2017·北京·理T2)若复数(1-i)(a+i)在复平面内对应的点在第二象限,则实数a的取值范围是( )A.(-∞,1)B.(-∞,-1)C.(1,+∞)D.(-1,+∞)22.(2016·全国2·理T1)已知z=(m+3)+(m-1)i在复平面内对应的点在第四象限,则实数m的取值范围是( )A.(-3,1)B.(-1,3)C.(1,+∞)D.(-∞,-3)=()23.(2016·全国3·理T2)若z=1+2i,则zz-1A.1B.-1C.iD.-I=()24.(2016·北京·文T2)复数1+2i2-iA.iB.1+iC.-iD.1-I25.(2016·全国1·理T2)设(1+i)x=1+yi,其中x,y是实数,则|x+yi|=( )A.1B.√2C.√3D.226.(2016·全国1·文T2)设(1+2i)(a+i)的实部与虚部相等,其中a为实数,则a=( )A.-3B.-2C.2D.327.(2016·全国2·文T2)设复数z满足z+i=3-i,则z=( )A.-1+2iB.1-2iC.3+2iD.3-2i28.(2016·全国3·文T2)若z=4+3i,则z|z|= ()A.1B.-1C.45+35i D.45−35i29.(2016·山东·理T1)若复数z满足2z+z=3-2i,其中i为虚数单位,则z=( )A.1+2iB.1-2iC.-1+2iD.-1-2i30.(2015·全国2·理T2)若a为实数,且(2+ai)·(a-2i)=-4i,则a=( )A.-1B.0C.1D.231.(2015·全国·文T3)已知复数z满足(z-1)i=1+i,则z=( )A.-2-iB.-2+iC.2-iD.2+i32.(2015·全国2·文T2)若a为实数,且2+ai1+i=3+i,则a=( )A.-4B.-3C.3D.433.(2015·安徽·文T1)设i是虚数单位,则复数(1-i)(1+2i)=( )A.3+3iB.-1+3iC.3+iD.-1+i34.(2015·湖南·文T1)已知(1-i)2z=1+i(i为虚数单位),则复数z=( ) A.1+i B.1-iC.-1+iD.-1-i35.(2015·全国1·理T1)设复数z满足1+z1-z=i,则|z|=()A.1B.√2C.√3D.236.(2015·湖北·理T1)i为虚数单位,i607的共轭复数....为( )A.iB.-iC.1D.-137.(2015·安徽·理T1)设i是虚数单位,则复数2i1-i在复平面内所对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限38.(2014·全国2·理T2)设复数z1,z2在复平面内的对应点关于虚轴对称,z1=2+i,则z1z2=( )A.-5B.5C.-4+iD.-4-i39.(2014·重庆·理T1)复平面内表示复数i(1-2i)的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限40.(2014·全国1·理T2)(1+i)3(1-i)2=()A.1+iB.1-iC.-1+iD.-1-I41.(2014·全国2·文T2)1+3i1-i=()A.1+2iB.-1+2iC.1-2iD.-1-2i42.(2014·全国1·文T3)设z=11+i+i,则|z|=()A.12B.√22C.√32D.243.(2013·全国1·理T2)若复数z满足(3-4i)z=|4+3i|,则z的虚部为( )A.-4B.-45C.4 D.4544.(2013·全国2·文T2)|2|=()A.2√2B.2C.√2D.145.(2013·全国2·理T2)设复数z 满足(1-i)z=2i,则z=( )A.-1+iB.-1-iC.1+iD.1-i46.(2013·全国1·文T2)1+2i(1-i )2=( ) A.-1-12iB.-1+12iC.1+12iD.1-12i47.(2012·全国·理T3)下面是关于复数z=2-1+i 的四个命题: p1:|z|=2, p2:z2=2i,p3:z 的共轭复数为1+i, p4:z 的虚部为-1,其中的真命题为( )A.p2,p3B.p1,p2C.p2,p4D.p3,p4 48.(2012·全国·文T2)复数z=-3+i 2+i 的共轭复数是( )A.2+iB.2-iC.-1+iD.-1-i49.(2011·全国·文T2)复数5i 1-2i =( )A.2-iB.1-2iC.-2+iD.-1+2i50.(2010·全国·理T2)已知复数z=√3+i (1-√3i )2,z 是z 的共轭复数,则z ·z =( ) A.14 B.12 C.1D.251.(2010·全国·文T3)已知复数z=√3+i (1-√3i )2,则|z|等于( ) A.14 B.12 C.1 D.252.(2018·天津·理T9文T9)i 是虚数单位,复数6+7i 1+2i =.53.(2019·天津·理T9文T9)i 是虚数单位,则|5-i 1+i |的值为___________.54.(2019·江苏·T 2)已知复数(a+2i)(1+i)的实部为0,其中i 为虚数单位,则实数a 的值是____ .55.(2018·上海·5)已知复数z 满足(1+i)z=1-7i(i 是虚数单位),则|z|= .56.(2017·浙江·12)已知a,b ∈R,(a+bi)2=3+4i(i 是虚数单位),则a2+b2=_____,ab=________.57.(2017·江苏·T 2)已知复数z=(1+i)(1+2i),其中i是虚数单位,则z的模是.58.(2017·天津·理T9文T9)已知a∈R,i为虚数单位,若a-i为实数,则a的值为.2+i59.(2016·江苏·T 2)复数z=(1+2i)(3-i),其中i为虚数单位,则z的实部是.的值为.60.(2016·天津·理T9)已知a,b∈R,i是虚数单位,若(1+i)(1-bi)=a,则ab61.(2016·北京·理T9)设a∈R,若复数(1+i)(a+i)在复平面内对应的点位于实轴上,则a= .62.(2015·天津·理T9)i是虚数单位,若复数(1-2i)(a+i)是纯虚数,则实数a的值为.63.(2015·江苏·T 3)设复数z满足z2=3+4i(i是虚数单位),则z的模为.64.(2015·重庆·理T11)设复数a+bi(a,b∈R)的模为√3 ,则(a+bi)(a-bi)= .。
高中数学—复数的历届高考试题解析

2010年高考复数1.【2010·浙江理数】对任意复数()i ,R z x y x y =+∈,i 为虚数单位,则下列结论正确的是( )A.2z z y -= B.222z x y =+ C.2z z x -≥ D.z x y ≤+2.【2010·全国卷2理数】复数231i i -⎛⎫= ⎪+⎝⎭( ) A.34i -- B.34i -+ C.34i - D.34i +3.【2010·陕西文数】复数z =1i i+在复平面上对应的点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 4.【2010·辽宁理数】设a,b 为实数,若复数11+2i i a bi=++,则( ) A.31,22a b == B.3,1a b == C.13,22a b == D.1,3a b == 5.【2010·江西理数】已知(x+i )(1-i )=y ,则实数x ,y 分别为( )A.x=-1,y=1B. x=-1,y=2C. x=1,y=1D. x=1,y=26.【2010·安徽文数】已知21i =-,则i(1)=( )i i C.i D.i7.【2010·浙江文数】设i 为虚数单位,则51i i -=+( ) A.-2-3i B.-2+3i C.2-3i D.2+3i8.【2010·山东文数】已知()2,a i b i a b R i+=+∈,其中i 为虚数单位,则a b +=( ) A. 1- B. 1 C. 2 D. 39.【2010·北京文数】在复平面内,复数6+5i, -2+3i 对应的点分别为A,B.若C 为线段AB 的中点,则点C 对应的复数是( )A.4+8iB.8+2iC.2+4iD.4+i10.【2010·四川理数】i 是虚数单位,计算i +i 2+i 3=( )A.-1B.1C.i -D.i11.【2010·天津文数】i 是虚数单位,复数31i i+-=( ) A.1+2i B.2+4i C.-1-2i D.2-i 12.【2010·天津理数】i 是虚数单位,复数1312i i -+=+( ) A.1+i B.5+5i C.-5-5i D.-1-i13.【2010·广东理数】若复数z 1=1+i ,z 2=3-i ,则z 1·z 2=( )A .4+2i B. 2+i C. 2+2i D.314.【2010·福建文数】i 是虚数单位,41i ()1-i +等于 ( ) A .iB .-iC .1D .-1高中数学高考总复习充分必要条件习题及详解一、选择题1.(文)已知a 、b 都是实数,那么“a 2>b 2”是“a >b ”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件2. (理)“|x -1|<2成立”是“x (x -3)<0成立”的( )A 充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件2.(2010·福建文)若向量a =(x,3)(x ∈R ),则“x =4”是“|a |=5”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分又不必要条件3.(文)已知数列{a n },“对任意的n ∈N *,点P n (n ,a n )都在直线y =3x +2上”是“{a n }为等差数列”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件 (理)(2010·南充市)等比数列{a n }中,“a 1<a 3”是“a 5<a 7”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分与不必要条件4.(09·陕西)“m >n >0”是“方程mx 2+ny 2=1表示焦点在y 轴上的椭圆”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件5.(文)设集合A ={x |x x -1<0},B ={x |0<x <3},那么“m ∈A ”是“m ∈B ”的( ) A .充分而不必要条件 B .必要而不充分条件C .充要条件 D .既不充分也不必要条件 (理)(2010·杭州学军中学)已知m ,n ∈R ,则“m ≠0或n ≠0”是“mn ≠0”的( )A .必要不充分条件B .充分不必要条件C .充要条件D .既不充分也不必要条件6.(文)(2010·北京东城区)“x =π4”是“函数y =sin2x 取得最大值”的( ) A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件(理)“θ=2π3”是“tan θ=2cos ⎝⎛⎭⎫π2+θ”的( ) A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件7.“m =12”是“直线(m +2)x +3my +1=0与直线(m -2)x +(m +2)y -3=0相互垂直”的( )A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件8.(2010·浙江宁波统考)设m ,n 是平面α内的两条不同直线,l 1,l 2是平面β内两条相交直线,则α⊥β的一个充分不必要条件是( )A .l 1⊥m ,l 1⊥nB .m ⊥l 1,m ⊥l 2C .m ⊥l 1,n ⊥l 2D .m ∥n ,l 1⊥n复数历届高考试题荟萃2010年高考复数1.【2010·浙江理数】对任意复数()i ,R z x y x y =+∈,i 为虚数单位,则下列结论正确的是( )A.2z z y -= B.222z x y =+ C.2z z x -≥ D.z x y ≤+【答案】D【解析】可对选项逐个检查,A 项,y z z 2≥-,故A 错;B 项,xyi y x z 2222+-=,故B 错;C 项,y z z 2≥-,故C 错;D 项正确.本题主要考察了复数的四则运算、共轭复数及其几何意义,属中档题.2.【2010·全国卷2理数】复数231i i -⎛⎫= ⎪+⎝⎭( ) A.34i -- B.34i -+ C.34i - D.34i +【答案】A【解析】本试题主要考查复数的运算. 231i i -⎛⎫= ⎪+⎝⎭22(3)(1)(12)342i i i i --⎡⎤=-=--⎢⎥⎣⎦. 3.【2010·陕西文数】复数z =1i i+在复平面上对应的点位于( ) A.第一象限 B.第二象限 C.第三象限D.第四象限 【答案】A 【解析】本题考查复数的运算及几何意义. 1i i +i i i 21212)1(+=-=,所以点()21,21位于第一象限 4.【2010·辽宁理数】设a,b 为实数,若复数11+2i i a bi=++,则( ) A.31,22a b == B.3,1a b == C.13,22a b == D.1,3a b == 【答案】A 【解析】本题考查了复数相等的概念及有关运算,考查了同学们的计算能力. 由121i i a bi +=++可得12()()i a b a b i +=-++,所以12a b a b -=⎧⎨+=⎩,解得32a =,12b =选A. 5.【2010·江西理数】已知(x+i )(1-i )=y ,则实数x ,y 分别为( )A.x=-1,y=1B. x=-1,y=2C. x=1,y=1D. x=1,y=2【答案】D【解析】考查复数的乘法运算.可采用展开计算的方法,得2()(1)x i x i y -+-=,没有虚部,x=1,y=2.6.【2010·安徽文数】已知21i =-,则i(1)=( )iiC.iD.i【答案】B【解析】直接乘开,用21i =-代换即可.(1)i i =+选B. 7.【2010·浙江文数】设i 为虚数单位,则51i i-=+( ) A.-2-3i B.-2+3i C.2-3i D.2+3i【答案】C 【解析】本题主要考察了复数代数形式的四则运算,属容易题.8.【2010·山东文数】已知()2,a i b i a b R i+=+∈,其中i 为虚数单位,则a b +=( ) A. 1- B. 1 C. 2 D. 3 【答案】B9.【2010·北京文数】在复平面内,复数6+5i, -2+3i 对应的点分别为A,B.若C 为线段AB 的中点,则点C 对应的复数是( )A.4+8iB.8+2iC.2+4iD.4+i 【答案】C10.【2010·四川理数】i 是虚数单位,计算i +i 2+i 3=( )A.-1B.1C.i -D.i 【答案】A【解析】由复数性质知:i 2=-1,故i +i 2+i 3=i +(-1)+(-i )=-1.11.【2010·天津文数】i 是虚数单位,复数31i i+-=( ) A.1+2i B.2+4i C.-1-2i D.2-i 【答案】A【解析】本题主要考查复数代数形式的基本运算,属于容易题.进行复数的除法的运算需要份子、分母同时乘以分母的共轭复数,同时将i 2改为-1. 331+24121-(1-)(1+)2i i i i i i i i +++===+()() 12.【2010·天津理数】i 是虚数单位,复数1312i i-+=+( ) A.1+i B.5+5i C.-5-5i D.-1-i 【答案】A【解析】本题主要考查复数代数形式的基本运算,属于容易题。
(2010-2019)高考数学真题分类汇编 复数 文(含解析)

专题复数历年高考真题汇编1.【2019年新课标1文科01】设z,则|z|=()A.2 B.C.D.1【解答】解:由z,得|z|=||.故选:C.2.【2018年新课标1文科02】设z2i,则|z|=()A.0 B.C.1 D.【解答】解:z2i2i=﹣i+2i=i,则|z|=1.故选:C.3.【2017年新课标1文科03】下列各式的运算结果为纯虚数的是()A.i(1+i)2B.i2(1﹣i)C.(1+i)2D.i(1+i)【解答】解:A.i(1+i)2=i•2i=﹣2,是实数.B.i2(1﹣i)=﹣1+i,不是纯虚数.C.(1+i)2=2i为纯虚数.D.i(1+i)=i﹣1不是纯虚数.故选:C.4.【2016年新课标1文科02】设(1+2i)(a+i)的实部与虚部相等,其中a为实数,则a等于()A.﹣3 B.﹣2 C.2 D.3【解答】解:(1+2i)(a+i)=a﹣2+(2a+1)i的实部与虚部相等,可得:a﹣2=2a+1,解得a=﹣3.故选:A.5.【2015年新课标1文科03】已知复数z满足(z﹣1)i=1+i,则z=()A.﹣2﹣i B.﹣2+i C.2﹣i D.2+i【解答】解:由(z﹣1)i=1+i,得z﹣1,∴z=2﹣i.故选:C.6.【2014年新课标1文科03】设z i,则|z|=()A.B.C.D.2【解答】解:z i i.故|z|.故选:B.7.【2013年新课标1文科02】()A.﹣1i B.﹣1i C.1i D.1i【解答】解: 1i.故选:B.8.【2012年新课标1文科02】复数z的共轭复数是()A.2+i B.2﹣i C.﹣1+i D.﹣1﹣i【解答】解:复数z1+i.所以复数的共轭复数为:﹣1﹣i.故选:D.9.【2011年新课标1文科02】复数()A.2﹣i B.1﹣2i C.﹣2+i D.﹣1+2i【解答】解: 2+i故选:C.10.【2010年新课标1文科03】已知复数Z,则|z|=()A.B.C.1 D.2【解答】解:化简得Z•••,故|z|,故选:B.考题分析与复习建议本专题考查的知识点为:复数的基本概念(复数的实部、虚部、共轭复数、复数的模等),复数相等的充要条件,考查复数的代数形式的四则运算,重点考查复数的除法运算,与向量结合考查复数及其加法、减法的几何意义等,历年考题主要以选择题题型出现,重点考查的知识点为复数的基本概念(复数的实部、虚部、共轭复数、复数的模等),复数相等的充要条件,考查复数的代数形式的四则运算,重点考查复数的除法运算等,预测明年本考点题目会比较稳定,备考方向以知识点复数的基本概念(复数的实部、虚部、共轭复数、复数的模等),复数相等的充要条件,考查复数的代数形式的四则运算为重点较佳.最新高考模拟试题1.复数52iz =-在复平面上的对应点位于( ) A .第一象限 B .第二象限C .第三象限D .第四象限【答案】A 【解析】,在复平面上的对应点为()2,1,位于第一象限. 故选A.2.设i z a b =+(a ,b ∈R ,i 是虚数单位),且22i z =-,则有( ) A .1a b +=- B .1a b -=- C .0a b -= D .0a b +=【答案】D 【解析】 因为,所以220a b -=,22ab =-, 解得11a b =⎧⎨=-⎩或11a b =-⎧⎨=⎩,所以0a b +=,故选D.3.若复数1i1ia z +=+为纯虚数,则实数a 的值为( ) A .1 B .1-C .0D .2【答案】B 【解析】故,解1a =-故选:B4.复数i (1+i )的虚部为( ) A .2 B .1C .0D .1-【答案】B 【解析】∵i (1+i )=-1+i , ∴i (1+i )的虚部为1.故选:B .5.已知复数11z i =-+,复数2z 满足122z z =-,则2z = ( ) A .2 B .2C .10D .10【答案】B 【解析】 由题得,所以.故选:B6.已知复数312i z i=+,则复数z 的实部为( )A .25-B .25i -C .15-D .15i -【答案】A 【解析】 解:∵,∴复数z 的实部为25-. 故选A . 7.复数122ii-=+( ) A .1i - B .i -C .iD .1i +【答案】B 【解析】.故选B8.已知i 为虚数单位,复数z 满足:,则在复平面上复数z 对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限【答案】D 【解析】 因为,所以复平面上复数z 对应的点为13(,)22-,位于第四象限, 故选D .9.设复数z a i =+,z 是其共轭复数,若3455z i z =+,则实数a =( ) A .4 B .3C .2D .1【答案】C 【解析】 解:z a i =+z a i ∴=-10.已知i 是虚数单位,复数z 满足,则z =( )A .2B .2C .1D .5【答案】A 【解析】,所以,故本题选A.11.复数,其中i 为虚数单位,则z 的实部是( ) A .-1 B .1C .2D .3【答案】D 【解析】解:∴,∴z的实部是3故选:D.12.已知复数,则复数z=()A.2i+B.2i-C.i D.i-【答案】C【解析】由题意,复数,则,故选C. 13.已知i为虚数单位,若,则b a=()A.1 B.2C .2D.2 【答案】C【解析】i为虚数单位,若,根据复数相等得到1212 ab⎧=⎪⎪⎨⎪=⎪⎩.故答案为:C.14.已知复数z满足,则||z=()A.2B.5 C.52D.8【答案】C【解析】∵,∴,∴.故选C .15.已知i 是虚数单位,则复数11i i -+在复平面上所对应的点的坐标为( ) A .()0,1 B .()1,0-C .()1,0D .()0,1-【答案】A 【解析】 ∵,∴该复数在复平面上对应的点的坐标为()0,1.故选A.16.若复数z 满足,则在复平面内z 的共轭复数对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限【答案】A 【解析】 由题得,所以1z i =+,所以在复平面内z 的共轭复数对应的点为(1,1),在第一象限. 故选:A17.已知复数z 满足12iz i =+,则z 的虚部是( ) A .1- B .i -C .2D .2i【答案】A 【解析】 因为12iz i =+所以所以虚部为1-所以选A18.已知31i zi-=-(其中i为虚数单位),则z的虚部为( )A.i-B.1-C.1D.2【答案】B【解析】因为,所以2z i=-,故z的虚部为1-,故选B.19.复数的虚部为()A.1-B.3-C.1 D.2【答案】B【解析】所以z的虚部为3-故选B项.20.已知复数,212z i=+(i为虚数单位),若12zz为纯虚数,则a=()A.2-B.2 C.12-D.12【答案】C【解析】∵,∴,∵12z z 为纯虚数, ∴12020a a +=⎧⎨-≠⎩,解得12a =-.故选:C . 21.设复数z 满足2ii z+=,则z =( ) A .1 B .5C .3D .5【答案】B 【解析】2ii z+=,,,故选B.22.已知复数1i z i=-,则2z +在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限【答案】A 【解析】 ∵,∴,∴2z +在复平面内对应的点的坐标为211,2⎛⎫- ⎪ ⎪⎝⎭,位于第一象限. 故选:A .23.复数z 满足(1)2z i i -=,则复数z =( )A .1i -B .12iC .1i +D .1i --【答案】D【解析】由题意得: 1z i ∴=--本题正确选项:D24.若复数是纯虚数,其中m 是实数,则1z =( ) A .i B .i - C .2i D .2i -【答案】B【解析】复数z =m (m +1)+(m +1)i 是纯虚数,故m (m +1)=0且(m +1)≠0,解得m =0,故z =i ,故i .故选:B .25.设i 为虚数单位,则复数22iz i -=+的共扼复数z =( )A .3455i + B .3455i -C .3455i -+D .3455i --【答案】A【解析】解:,故选:A .26.已知复数1z 、2z 在复平面内对应的点关于虚轴对称,113z i =+,则12z z =( )A .2B .3C .2D .1【答案】D【解析】由题意,复数1z 、2z 在复平面内对应的点关于虚轴对称,113z i =+, 则,所以,故选 D. 27.已知复数z 1=1+2i ,z 2=l ﹣i ,则12z z =( ) A .13i 22-- B .13i 22-+ C .13i 22- D .13i 22+ 【答案】B【解析】∵,∴.故选:B . 28.在复平面内,复数(2i)z -对应的点位于第二象限,则复数z 可取( )A .2B .-1C .iD .2i +【答案】B【解析】不妨设,则, 结合题意可知:,逐一考查所给的选项: 对于选项A :,不合题意; 对于选项B :,符合题意; 对于选项C :,不合题意; 对于选项D :,不合题意; 故选:B .29.已知i 为虚数单位,则复数3(1)i z i i +=-的虚部为( )A .1B .2C .1-D .2-【答案】C【解析】因为,所以z 的虚部为1-.30.已知复数(i 为虚数单位)在复平面内对应的点在直线2y x =上,则实数a 的值为() A .0 B .1- C .1 D .13-【答案】D【解析】因为,对应的点为(1,1)a a +-,因为点在直线2y x =上,所以,解得13a =-. 故选D.。
专题17 复数-高考题专项练习(解析版)

专题17 复数-高考题专项练习一、单选题1.(2018·全国高考真题(文)) A . B . C .D .【答案】D【分析】根据公式,可直接计算得(23)32i i i +=-+ 【解析】 ,故选D .【名师点睛】复数题是每年高考的必考内容,一般以选择或填空形式出现,属简单得分题,高考中复数主要考查的内容有:复数的分类、复数的几何意义、共轭复数,复数的模及复数的乘除运算,在解决此类问题时,注意避免忽略中的负号导致出错. 2.(2018·全国高考真题(理)) A . B . C .D .【答案】D 【解析】 故选D .3.(2019·全国高考真题(文))设,则= A .2 B . C .D .1【答案】C【分析】先由复数的除法运算(分母实数化),求得,再求. 【解析】因为,所以,所以,故选C .【名师点睛】本题主要考查复数的乘法运算,复数模的计算.本题也可以运用复数模的运算性质直接求解.4.(2019·全国高考真题(理))设复数z 满足,z 在复平面内对应的点为(x ,y ),则 A .22+11()x y += B .22(1)1x y -+= C .22(1)1y x +-= D .22(+1)1y x +=【答案】C【分析】本题考点为复数的运算,为基础题目,难度偏易.此题可采用几何法,根据点(x ,y )和点(0,1)之间的距离为1,可选正确答案C .【解析】,(1),z x yi z i x y i =+-=+-1,z i -=则22(1)1y x +-=.故选C .【名师点睛】本题考查复数的几何意义和模的运算,渗透了直观想象和数学运算素养.采取公式法或几何法,利用方程思想解题.5.(2020·浙江高考真题)已知a ∈R ,若a –1+(a –2)i (i 为虚数单位)是实数,则a = A .1 B .–1 C .2D .–2【答案】C【解析】因为(1)(2)a a i -+-为实数,所以202a a -=∴=,,故选C 6.(2020·全国高考真题(理))复数的虚部是 A . B . C .D .【答案】D【分析】利用复数的除法运算求出z 即可. 【解析】因为1131313(13)(13)1010i z i i i i +===+--+, 所以复数的虚部为.故选D .【点晴】本题主要考查复数的除法运算,涉及到复数的虚部的定义,是一道基础题. 7.(2020·全国高考真题(文))(1–i )4= A .–4 B .4 C .–4i D .4i【答案】A【分析】根据指数幂的运算性质,结合复数的乘方运算性质进行求解即可. 【解析】.故选A .【名师点睛】本题考查了复数的乘方运算性质,考查了数学运算能力,属于基础题. 8.(2020·全国高考真题(理))若z=1+i ,则|z 2–2z |= A .0B .1【答案】D【分析】由题意首先求得的值,然后计算其模即可. 【解析】由题意可得()2212z i i =+=,则()222212z z i i -=-+=-.故.故选D .【名师点睛】本题主要考查复数的运算法则和复数的模的求解等知识,属于基础题. 9.(2020·全国高考真题(文))若312i i z =++,则 A .0 B .1 C . D .2【答案】C【分析】先根据将化简,再根据向量的模的计算公式即可求出. 【解析】因为31+21+21z i i i i i =+=-=+,所以.故选C . 【名师点睛】本题主要考查向量的模的计算公式的应用,属于容易题. 10.(2017·山东高考真题(文))已知i 是虚数单位,若复数z 满足,则= A .-2i B .2i C .-2D .2【答案】A【解析】由得22(i)(1i)z =+,即,所以,故选A .【名师点睛】复数代数形式的加减乘除运算的法则是进行复数运算的理论依据,加减运算类似于多项式的合并同类项,乘法法则类似于多项式乘法法则,除法运算则先将除式写成分式的形式,再将分母实数化.注意下面结论的灵活运用:(1)(1±i)2=±2i ;(2)=i ,=-i .11.(2017·全国高考真题(理))设有下面四个命题 :若复数满足,则; :若复数满足,则; :若复数满足,则; :若复数,则. 其中的真命题为 A .B .【答案】B【解析】令i(,)z a b a b R =+∈,则由2211i i a b z a b a b-==∈++R 得,所以,故正确;当时,因为22i 1z ==-∈R ,而知,故不正确; 当时,满足,但,故不正确;对于,因为实数的共轭复数是它本身,也属于实数,故正确,故选B .【名师点睛】分式形式的复数,分子、分母同乘以分母的共轭复数,化简成i(,)z a b a b R =+∈的形式进行判断,共轭复数只需实部不变,虚部变为原来的相反数即可.12.(2017·北京高考真题(文))若复数(1–i )(a +i )在复平面内对应的点在第二象限,则实数a 的取值范围是 A .(–∞,1) B .(–∞,–1) C .(1,+∞) D .(–1,+∞)【答案】B【解析】设()()()()1i i 11i z a a a =-+=++-,因为复数对应的点在第二象限,所以,解得,故选B .【名师点睛】复数的分类及对应点的位置问题都可以转化为复数的实部与虚部应该满足的条件问题,只需把复数化为代数形式,列出实部和虚部满足的方程(不等式)组即可.复数z =a +b i 复平面内的点Z (a ,b )(a ,b ∈R).复数z =a +b i(a ,b ∈R) 平面向量. 13.(2018·全国高考真题(文))设,则 A . B . C .D .【答案】C【分析】利用复数的除法运算法则:分子、分母同乘以分母的共轭复数,化简复数,然后求解复数的模. 【解析】()()()()1i 1i 1i2i 2i 1i 1i 1i z ---=+=++-+,则,故选C . 【名师点睛】复数是高考中的必考知识,主要考查复数的概念及复数的运算.要注意对实部、虚部的理解,掌握纯虚数、共轭复数这些重要概念,复数的运算主要考查除法运算,通过分母实数化转化为复数的乘法,运算时特别要注意多项式相乘后的化简,防止简单问题出错,造成不必要的失分.14.(2019·北京高考真题(理))已知复数z=2+i,则A.B.C.3D.5【答案】D【分析】题先求得,然后根据复数的乘法运算法则即得.【解析】因为z2i,z z(2i)(2i)5=+⋅=+-=故选D.【名师点睛】本题主要考查复数的运算法则,共轭复数的定义等知识,属于基础题..15.(2018·浙江高考真题)若复数,其中i为虚数单位,则 =A.1+i B.1−iC.−1+i D.−1−i【答案】B【解析】22(1i)1i,1i1i(1i)(1i)z z+===+∴=---+,选B.【名师点睛】本题主要考查复数的运算及复数的概念,是一道基础题目.从历年高考题目看,复数题目往往不难,一般考查复数运算与概念或复数的几何意义,也是考生必定得分的题目之一.16.(2019·全国高考真题(理))设z=-3+2i,则在复平面内对应的点位于A.第一象限B.第二象限C.第三象限D.第四象限【答案】C【分析】先求出共轭复数再判断结果.【解析】由得则对应点(-3,-2)位于第三象限.故选C.17.(2019·全国高考真题(文))设z=i(2+i),则=A.1+2i B.–1+2iC.1–2i D.–1–2i【答案】D【分析】本题根据复数的乘法运算法则先求得,然后根据共轭复数的概念,写出.【解析】2i(2i)2i i 12i z =+=+=-+,所以,选D .【名师点睛】本题主要考查复数的运算及共轭复数,容易题,注重了基础知识、基本计算能力的考查.理解概念,准确计算,是解答此类问题的基本要求.部分考生易出现理解性错误.18.(2020·北京高考真题)在复平面内,复数对应的点的坐标是,则. A . B . C .D .【答案】B【分析】先根据复数几何意义得,再根据复数乘法法则得结果. 【解析】由题意得,.故选B .【名师点睛】本题考查复数几何意义以及复数乘法法则,考查基本分析求解能力,属基础题.19.(2020·海南高考真题)= A . B . C .D .【答案】B【解析】2(12)(2)2425i i i i i i ++=+++=,故选B. 20.(2020·海南高考真题) A .1 B .−1 C .i D .−i【答案】D【分析】根据复数除法法则进行计算. 【解析】,故选D.【名师点睛】本题考查复数除法,考查基本分析求解能力,属基础题. 21.(2017·全国高考真题(理))复数等于 A . B . C .D . 【答案】D【解析】=2-i .故选D .【名师点睛】这个题目考查了复数的除法运算,复数常考的还有几何意义,z =a +bi(a ,b ∈R)与复平面上的点Z(a ,b)、平面向量都可建立一一对应的关系(其中O 是坐标原点);复平面内,实轴上的点都表示实数;虚轴上的点除原点外都表示纯虚数.涉及到共轭复数的概念,一般地,当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数,复数z 的共轭复数记作.22.(2017·山东高考真题(理))已知,是虚数单位,若,,则 A .1或 B .或 C .D .【答案】A【解析】由,4z a z z =+⋅=得,所以,故选A .【名师点睛】复数(,)a bi a b R +∈的共轭复数是i(,)a b a b -∈R ,据此结合已知条件,求得的方程即可.23.(2017·全国高考真题(文))(2017新课标全国卷II (文)) A . B . C . D .【答案】B【解析】由题意,故选B .【名师点睛】首先对于复数的四则运算,要切实掌握其运算技巧和常规思路,如(+)i(,,,)ad bc a b c d R ∈. 其次要熟悉复数相关基本概念,如复数+i(,)a b a b R ∈的实部为、虚部为、模为、对应点为、共轭复数为.24.(2017·全国高考真题(文))复平面内表示复数z=i(–2+i)的点位于 A .第一象限 B .第二象限 C .第三象限D .第四象限【答案】C【解析】i(2i)12i z =-+=--,则表示复数i(2i)z =-+的点位于第三象限. 所以选C .【名师点睛】对于复数的四则运算,首先要切实掌握其运算技巧和常规思路,如.其次要熟悉复数的相关基本概念,如复数i(,)a b a b +∈R 的实部为、虚部为、模为、对应的点为、共轭复数为25.(2017·全国高考真题(理))(2017高考新课标III ,理3)设复数z 满足(1+i)z =2i ,则∣z ∣= A . B . C . D .2【答案】C【解析】由题意可得,由复数求模的法则可得,则.故选C . 【名师点睛】共轭与模是复数的重要性质,运算性质有: (1)1212z z z z ±=±;(2)1212z z z z ⨯=⨯;(3); (4);(5);(6).26.(2018·全国高考真题(理)) A . B . C .D . 【答案】D【分析】根据复数除法法则化简复数,即得结果.【解析】212(12)341255i i ii ++-+==∴-选D .【名师点睛】本题考查复数除法法则,考查学生基本运算能力. 二、填空题1.(2017·天津高考真题(文))已知,为虚数单位,若为实数,则的值为________. 【答案】-2 【解析】为实数, 则.【名师点睛】复数的分类及对应点的位置问题都可以转化为复数的实部与虚部应该满足的条件问题,只需把复数化为代数形式,列出实部和虚部满足的方程(不等式)组即可. 复数(,)z a bi a b R =+∈,当时,为虚数,当时,为实数,当0,0a b =≠时,为纯虚数. 2.(2019·江苏高考真题)已知复数的实部为0,其中为虚数单位,则实数a 的值是________. 【答案】2【分析】本题根据复数的乘法运算法则先求得,然后根据复数的概念,令实部为0即得a 的值. 【解析】, 令得.【名师点睛】本题主要考查复数的运算法则,虚部的定义等知识,意在考查学生的转化能力和计算求解能力.3.(2017·上海高考真题)已知复数满足,则________. 【答案】【分析】设(,)z a bi a b R =+∈,代入,由复数相等的条件列式求得的值得答案. 【解析】由,得,设(,)z a bi a b R =+∈, 由得,即,解得, 所以,则.【名师点睛】本题考查复数代数形式的乘除运算,考查了复数相等的条件以及复数模的求法,是基础题,着重考查了考生的推理与运算能力.4.(2019·浙江高考真题)复数(为虚数单位),则________. 【答案】【分析】本题先计算,而后求其模.或直接利用模的性质计算. 容易题,注重基础知识、运算求解能力的考查.【解析】1|||1|2z i ===+. 5.(2018·天津高考真题(理))i 是虚数单位,复数________. 【答案】4–i【分析】由题意结合复数的运算法则整理计算即可求得最终结果. 【解析】由复数的运算法则得.【名师点睛】本题主要考查复数的运算法则及其应用,意在考查学生的转化能力和计算求解能力.6.(2019·上海高考真题)设为虚数单位,,则的值为________. 【答案】【分析】把已知等式变形得,再由,结合复数模的计算公式求解即可.【解析】由365z i i -=+,得366z i =+,即 ,本题正确结果:【名师点睛】本题考查复数代数形式的乘除运算,考查复数模的求法,属于基础题. 7.(2019·天津高考真题(文))是虚数单位,则的值为________. 【答案】【分析】先化简复数,再利用复数模的定义求所给复数的模.【解析】5(5)(1)231(1)(1)i i i i i i i ---==-=++-. 8.(2018·上海高考真题)已知复数满足()117i z i +=-(是虚数单位),则________. 【答案】5【分析】把已知等式变形,然后利用复数代数形式的乘除运算化简,再由复数求模公式计算得答案.【解析】由(1+i )z=1﹣7i ,得()()()()1711768341112i i i iz i i i i -----====--++-,则|z|=5=.故答案为5.【名师点睛】本题考查了复数代数形式的乘除运算,考查了复数模的求法,是基础题. 9.(2020·江苏高考真题)已知是虚数单位,则复数(1i)(2i)z =+-的实部是________. 【答案】3【分析】根据复数的运算法则,化简即可求得实部的值. 【解析】因为复数,所以2223z i i i i =-+-=+, 所以复数的实部为3.故答案为3.10.(2020·天津高考真题)是虚数单位,复数________. 【答案】【分析】将分子分母同乘以分母的共轭复数,然后利用运算化简可得结果.【解析】()()()()8281510322225i i i ii i i i ----===-++-.故答案为. 11.(2020·全国高考真题(理))设复数,满足,,则=________. 【答案】【分析】方法一:令1,(,)z a bi a R b R =+∈∈,2,(,)z c di c R d R =+∈∈,根据复数的相等可求得2ac bd +=-,代入复数模长的公式中即可得到结果.方法二:设复数所对应的点为,12OP OZ OZ =+, 根据复数的几何意义及复数的模,判定平行四边形为菱形,,进而根据复数的减法的几何意义用几何方法计算.【解析】方法一:设1,(,)z a bi a R b R =+∈∈,2,(,)z c di c R d R =+∈∈,12()z z a c b d i i ∴+=+++=,,又,所以,,,2ac bd ∴+=-12()()z z a c b d i ∴-=-+-==.故答案为.方法二:如图所示,设复数所对应的点为,12OP OZ OZ =+,由已知,所以平行四边形为菱形,且都是正三角形,所以12Z 120OZ ∠=︒,222221212121||||||2||||cos12022222()122Z Z OZ OZ OZ OZ =+-︒=+-⋅⋅⋅-= 所以.【名师点睛】方法一:本题考查复数模长的求解,涉及到复数相等的应用;考查学生的数学运算求解能力,是一道中档题.方法二:关键是利用复数及其运算的几何意义,转化为几何问题求解12.(2017·江苏高考真题)已知复数z=(1+i )(1+2i ),其中i 是虚数单位,则z 的模是________.【答案】【分析】利用复数的运算法则、模的计算公式即可得出.【解析】复数z =(1+i )(1+2i )=1﹣2+3i =﹣1+3i ,所以|z |==【名师点睛】对于复数的四则运算,要切实掌握其运算技巧和常规思路,如()()a bi c di ++=.其次要熟悉复数相关概念,如复数(,)a bi a b R +∈的实部为、虚部为、模为、对应点为、共轭复数为.13.(2018·江苏高考真题)若复数满足,其中i 是虚数单位,则的实部为________.【答案】2【分析】先根据复数的除法运算进行化简,再根据复数实部概念求结果. 【解析】因为,则12i 2i iz +==-,则的实部为. 【名师点睛】本题重点考查复数相关基本概念,如复数+i(,)a b a b ∈R 的实部为、虚部为、模为、对应点为、共轭复数为.三、双空题1.(2017·浙江高考真题)已知a ,b ∈R ,2i 34i a b +=+()(i 是虚数单位)则________,ab =________.【答案】5, 2【解析】由题意可得,则,解得,则225,2a b ab +==.【名师点睛】本题重点考查复数的基本运算和复数的概念,属于基本题.首先对于复数的四则运算,要切实掌握其运算技巧和常规思路,如. 其次要熟悉复数相关基本概念,如复数(,)a bi a b R +∈的实部为、虚部为、模为、对应点为(,)、共轭为等.。
十年(2010-2019年)高考数学真题分类汇编:专题17 复数 (含答案解析)

十年(2010-2019年)高考数学真题分类汇编专题17复数1.(2019·全国1·文T1)设z=3-i1+2i ,则|z|= ( ) A.2 B.√3 C.√2 D.1【答案】C 【解析】∵z=3-i1+2i , ∴z=(3-i )(1-2i )(1+2i )(1-2i )=15−75i,∴|z|=√(15)2+(-75)2=√2.故选C.2.(2019·全国3·理T2文T2)若z(1+i)=2i,则z=( ) A.-1-i B.-1+i C.1-i D.1+i【答案】D 【解析】z=2i 1+i=2i (1-i )(1+i )(1-i )=2+2i2=1+i.故选D.3.(2019·北京·理T1文T2)已知复数z=2+i,则z ·z =( ) A.√3 B.√5 C.3 D.5【答案】D【解析】∵z=2+i,∴z =2-i. ∴z ·z =(2+i)(2-i)=5. 故选D.4.(2019·全国2·文T2)设z=i(2+i),则z =( ) A.1+2i B.-1+2i C.1-2i D.-1-2i【答案】D【解析】z=2i+i 2=-1+2i,则z =-1-2i.故选D.5.(2019·全国1·理T2)设复数z 满足|z-i|=1,z 在复平面内对应的点为(x,y),则( ) A.(x+1)2+y2=1 B.(x-1)2+y2=1C.x2+(y-1)2=1D.x2+(y+1)2=1 【答案】C【解析】设z=x+yi(x,y ∈R). 因为z-i=x+(y-1)i, 所以|z-i|=√x 2+(y -1)2=1, 则x2+(y-1)2=1.故选C.6.(2019·全国2·理T2)设z=-3+2i,则在复平面内 对应的点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限【答案】C【解析】由z=-3+2i,得z =-3-2i,则在复平面内z 对应的点(-3,-2)位于第三象限,故选C. 7.(2018·全国1·理T1文T2)设z=1-i1+i +2i,则|z|=( ) A.0 B.12C.1D.√2【答案】C 【解析】因为z=(1-i )2(1+i )(1-i )+2i=-2i2+2i=i,所以|z|=1.8.(2018·全国2·理T1)1+2i1-2i =( ) A.-45−35i B.-45+35iC.-35−45i D.-35+45i【答案】D 【解析】1+2i 1-2i=(1+2i )(1+2i )(1-2i )(1+2i )=1-4+4i 5=-35+45i. 9.(2018·全国2·文T1)i(2+3i)=( ) A.3-2i B.3+2iC.-3-2iD.-3+2i【答案】D【解析】i(2+3i)=2i+3i2=-3+2i.10.(2018·全国3·理T2文T2)(1+i)(2-i)=( )A.-3-iB.-3+iC.3-iD.3+i【答案】D【解析】(1+i)(2-i)=2+i-i2=3+i.11.(2018·北京·理T2文T2)在复平面内,复数11-i的共轭复数对应的点位于( ) A.第一象限 B.第二象限C.第三象限D.第四象限【答案】D【解析】∵11-i =1+i(1-i)(1+i)=1+i2=12+12i,∴12+12i的共轭复数为12−12i,而12−12i对应的点的坐标为(12,-12),点(12,-12)位于第四象限,故选D.12.(2018·浙江·4)复数21-i(i为虚数单位)的共轭复数是( ) A.1+i B.1-iC.-1+iD.-1-i【答案】B【解析】∵21-i =2(1+i)(1-i)(1+i)=2(1+i)2=1+i,∴复数21-i的共轭复数为1-i.13.(2017·全国1·理T3)设有下面四个命题p1:若复数z满足1z∈R,则z∈R;p2:若复数z满足z2∈R,则z∈R;p3:若复数z1,z2满足z1z2∈R,则z1=z2;p4:若复数z∈R,则z∈R.其中的真命题为( )A.p1,p3B.p1,p4C.p2,p3D.p2,p4 【答案】B【解析】p1:设z=a+bi(a,b∈R),则1z =1a+bi=a-bia2+b2∈R,所以b=0,所以z∈R.故p1正确;p2:因为i2=-1∈R,而z=i∉R,故p2不正确;p3:若z1=1,z2=2,则z1z2=2,满足z1z2∈R,而它们实部不相等,不是共轭复数,故p3不正确;p4:实数的虚部为0,它的共轭复数是它本身,也属于实数,故p4正确.14.(2017·全国2·理T1)3+i1+i=( )A.1+2iB.1-2iC.2+iD.2-i【答案】D【解析】3+i1+i =(3+i)(1-i)(1+i)(1-i)=4-2i2=2-i,故选D.15.(2017·全国2·文T2)(1+i)(2+i)= ( )A.1-iB.1+3iC.3+iD.3+3i【答案】B【解析】(1+i)(2+i)=2+3i+i2=1+3i,故选B.16.(2017·山东·文T2)已知i是虚数单位,若复数z满足zi=1+i,则z2=( )A.-2iB.2iC.-2D.2【答案】A【解析】(方法一)∵z=1+ii =1+1i=1-i,∴z2=(1-i)2=1-2i+i2=-2i.(方法二)由zi=1+i,得(zi)2=(1+i)2,即-z2=2i.所以z2=-2i.17.(2017·全国3·理T2)设复数z满足(1+i)z=2i,则|z|=( )A.12B.√22C.√2D.2【答案】C【解析】由题意,得z=2i=1+i,故|z|=√12+12=√2.18.(2017·全国1·文T3)下列各式的运算结果为纯虚数的是( )A.i(1+i)2B.i2(1-i)C.(1+i)2D.i(1+i)【答案】C【解析】∵i(1+i)2=2i2=-2,i2(1-i)=-1+i,(1+i)2=2i,i(1+i)=-1+i,∴(1+i)2=2i为纯虚数,故选C.19.(2017·山东·理T2)已知a∈R,i是虚数单位.若z=a+√3i,z·z=4,则a=()A.1或-1B.√7或-√7C.-√3D.√3 【答案】A【解析】由z=a+√3i,得z ·z =|z|2=a 2+3=4,所以a 2=1,a=±1,选A. 20.(2017·全国3·文T2)复平面内表示复数z=i(-2+i)的点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限【答案】C【解析】由题意可得z=-1-2i,在复平面内对应点(-1,-2),则该点位于第三象限.故选C.21.(2017·北京·理T2)若复数(1-i)(a+i)在复平面内对应的点在第二象限,则实数a 的取值范围是( ) A.(-∞,1)B.(-∞,-1)C.(1,+∞)D.(-1,+∞) 【答案】B【解析】设z=(1-i)(a+i)=(a+1)+(1-a)i,因为复数z 在复平面内对应的点 (a+1,1-a)在第二象限,所以{a +1<0,1-a >0,解得a<-1.故选B.22.(2016·全国2·理T1)已知z=(m+3)+(m-1)i 在复平面内对应的点在第四象限,则实数m 的取值范围是( ) A.(-3,1)B.(-1,3)C.(1,+∞)D.(-∞,-3) 【答案】A【解析】要使复数z 在复平面内对应的点在第四象限,应满足{m +3>0,m -1<0,解得-3<m<1,故选A.23.(2016·全国3·理T2)若z=1+2i,则zz -1=( ) A.1 B.-1C.iD.-I【答案】C【解析】由题意知z=1-2i,则zz-1=4i(1+2i)(1-2i)-1=4i5-1=i,故选C.24.(2016·北京·文T2)复数1+2i2-i=() A.i B.1+iC.-iD.1-I【答案】A【解析】1+2i2-i =(1+2i)(2+i)(2-i)(2+i)=2+i+4i-25=i,故选A.25.(2016·全国1·理T2)设(1+i)x=1+yi,其中x,y是实数,则|x+yi|=( )A.1B.√2C.√3D.2【答案】B【解析】(定义、性质)因为(1+i)x=1+yi,x,y∈R,所以x=1,y=x=1.所以|x+yi|=|1+i|=√2,故选B.26.(2016·全国1·文T2)设(1+2i)(a+i)的实部与虚部相等,其中a为实数,则a=( )A.-3B.-2C.2D.3【答案】A【解析】由已知(1+2i)(a+i)=a-2+(2a+1)i.∵(1+2i)(a+i)的实部与虚部相等,∴a-2=2a+1,解得a=-3,故选A.27.(2016·全国2·文T2)设复数z满足z+i=3-i,则z=( )A.-1+2iB.1-2iC.3+2iD.3-2i【答案】C【解析】由z+i=3-i,得z=3-2i,所以z=3+2i,故选C.28.(2016·全国3·文T2)若z=4+3i,则z|z|= ()A.1B.-1C.45+35i D.45−35i【答案】D【解析】因为z=4+3i,所以它的模为|z|=|4+3i|=√42+32=5,共轭复数为z =4-3i.故z |z |=4−3i,选D.29.(2016·山东·理T1)若复数z 满足2z+z =3-2i,其中i 为虚数单位,则z=( ) A.1+2i B.1-2i C.-1+2i D.-1-2i【答案】B【解析】设z=a+bi(a,b ∈R),则2z+z =3a+bi=3-2i,故a=1,b=-2,则z=1-2i,选B. 30.(2015·全国2·理T2)若a 为实数,且(2+ai)·(a-2i)=-4i,则a=( ) A.-1 B.0 C.1 D.2【答案】B【解析】∵(2+ai)(a-2i)=4a+(a 2-4)i=-4i, ∴{4a =0,a 2-4=-4,解之,得a=0. 31.(2015·全国·文T3)已知复数z 满足(z-1)i=1+i,则z=( ) A.-2-i B.-2+i C.2-i D.2+i【答案】C【解析】∵(z-1)i=1+i, ∴z=1+ii +1=(1+i )(-i )-i 2+1=1-i+1=2-i.32.(2015·全国2·文T2)若a 为实数,且2+ai1+i=3+i,则a=( )A.-4B.-3C.3D.4【答案】D【解析】由题意,得2+ai=(3+i)(1+i)=2+4i,则a=4.33.(2015·安徽·文T1)设i 是虚数单位,则复数(1-i)(1+2i)=( ) A.3+3i B.-1+3i C.3+i D.-1+i【答案】C【解析】由复数的乘法运算法则,得(1-i)(1+2i)=1-i+2i-2i2=1+i+2=3+i,因此选C. 34.(2015·湖南·文T1)已知(1-i )2z=1+i(i 为虚数单位),则复数z=( )A.1+iB.1-iC.-1+iD.-1-i【答案】D【解析】由已知得z=(1-i )21+i=-2i 1+i =-2i (1-i )(1+i )(1-i )=-2-2i2=-1-i. 35.(2015·全国1·理T1)设复数z 满足1+z1-z =i,则|z|=( ) A.1 B.√2 C.√3 D.2【答案】A 【解析】∵1+z =i,∴z=i -1=(i -1)(-i+1)(i+1)(-i+1)=i,∴|z|=1.36.(2015·湖北·理T1)i 为虚数单位,i 607的共轭复数....为( ) A.i B.-i C.1 D.-1【答案】A【解析】∵i607=i151×4+3=i3=-i,∴i607的共轭复数为i.37.(2015·安徽·理T1)设i 是虚数单位,则复数2i1-i 在复平面内所对应的点位于( ) A.第一象限B.第二象限C.第三象限D.第四象限 【答案】B【解析】由复数除法的运算法则可得,2i1-i =2i (1+i )(1-i )(1+i )=2i -22=-1+i,对应点为(-1,1)在第二象限.故选B. 38.(2014·全国2·理T2)设复数z1,z2在复平面内的对应点关于虚轴对称,z1=2+i,则z1z2=( ) A.-5 B.5 C.-4+i D.-4-i【答案】A【解析】由题意知:z2=-2+i.又z1=2+i,所以z1z2=(2+i)(-2+i)=i2-4=-5.故选A.39.(2014·重庆·理T1)复平面内表示复数i(1-2i)的点位于( ) A.第一象限B.第二象限C.第三象限D.第四象限 【答案】A【解析】因为i(1-2i)=i+2,其在复平面内对应的点为(2,1),位于第一象限.故选A. 40.(2014·全国1·理T2)(1+i )3(1-i )2=()A.1+iB.1-iC.-1+iD.-1-I【答案】D 【解析】(1+i )3(1-i )2=(1+i )2(1+i )(1-i )2=2i (1+i )-2i=-1-i.故选D.41.(2014·全国2·文T2)1+3i1-i =( ) A.1+2i B.-1+2i C.1-2i D.-1-2i【答案】B 【解析】1+3i1-i=(1+3i )(1+i )(1-i )(1+i )=-2+4i2=-1+2i,故选B.42.(2014·全国1·文T3)设z=11+i +i,则|z|=( ) A.12B.√22C.√32D.2【答案】B 【解析】因为z=11+i +i=1-i (1+i )(1-i )+i=1-i 2+i=12+12i,所以|z|=|12+12i|=√(12)2+(12)2=√22,故选B.43.(2013·全国1·理T2)若复数z 满足(3-4i)z=|4+3i|,则z 的虚部为( ) A.-4 B.-45C.4D.45【答案】D【解析】∵(3-4i)z=|4+3i|, ∴z=53-4i =5(3+4i )(3-4i )(3+4i )=35+45i. 故z 的虚部为45,选D.44.(2013·全国2·文T2)|21+i |=( )A.2√2B.2C.√2D.1【答案】C 【解析】∵21+i =1-i,∴|21+i|=|1-i|=√2. 45.(2013·全国2·理T2)设复数z 满足(1-i)z=2i,则z=( ) A.-1+i B.-1-i C.1+i D.1-i【答案】A【解析】z=2i 1-i =2i (1+i )(1-i )(1+i )=-2+2i2=-1+i. 46.(2013·全国1·文T2)1+2i(1-i )2=()A.-1-12i B.-1+12i C.1+12i D.1-12i【答案】B 【解析】1+2i (1-i )2=1+2i-2i =(1+2i )i 2=-2+i 2=-1+12i.47.(2012·全国·理T3)下面是关于复数z=2-1+i 的四个命题: p1:|z|=2, p2:z2=2i, p3:z 的共轭复数为1+i, p4:z 的虚部为-1, 其中的真命题为( ) A.p2,p3 B.p1,p2C.p2,p4 D.p3,p4【答案】C 【解析】z=2(-1-i )(-1+i )(-1-i )=-1-i,故|z|=√2,p 1错误;z 2=(-1-i)2=(1+i)2=2i,p 2正确;z 的共轭复数为-1+i,p 3错误;p 4正确.48.(2012·全国·文T2)复数z=-3+i2+i的共轭复数是( )A.2+iB.2-iC.-1+iD.-1-i【答案】D【解析】z=-3+i 2+i =(-3+i )(2-i )(2+i )(2-i )=-5+5i5=-1+i,故z 的共轭复数为-1-i.49.(2011·全国·文T2)复数5i1-2i =( )A.2-iB.1-2iC.-2+iD.-1+2i【答案】C【解析】5i 1-2i =5i (1+2i )(1-2i )(1+2i )=-10+5i5=-2+i.50.(2010·全国·理T2)已知复数z=√3+i(1-√3i )2,z 是z 的共轭复数,则z ·z =() A.1 B.1C.1D.2【答案】A【解析】∵z=√3+i (1-√3i )2=√3+i1-2√3i+3i 2 =√3+i -2-23i =√3+i √3i (-2-23i )(-2+23i )=-√34+i 4, ∴z =-√34−i 4.∴z ·z =(-√34-i 4)(-√34+i 4)=316+116=14.51.(2010·全国·文T3)已知复数z=√3+i(1-√3i )2,则|z|等于( ) A.14 B.12 C.1 D.2【答案】B【解析】z=√3+i 1+3i 2-23i =-√3+i 2+2√3i =-12×2√3-2i 4=i -√34,|z|=14×2=12.52.(2018·天津·理T9文T9)i 是虚数单位,复数6+7i1+2i = .【答案】4-i【解析】6+7i 1+2i =(6+7i )(1-2i )(1+2i )(1-2i )=6-12i+7i+145=20-5i5=4-i.53.(2019·天津·理T9文T9)i 是虚数单位,则|5-i 1+i |的值为___________.【答案】√13【解析】5-i 1+i =(5-i )(1-i )2=4-6i2=2-3i.|5-i 1+i |=√4+9=√13.54.(2019·江苏·T 2)已知复数(a+2i)(1+i)的实部为0,其中i 为虚数单位,则实数a 的值是____ .【答案】2【解析】∵(a+2i)(1+i)=a+ai+2i+2i2=a-2+(a+2)i,∴a-2=0,∴a=2.55.(2018·上海·5)已知复数z 满足(1+i)z=1-7i(i 是虚数单位),则|z|= .【答案】5【解析】因为(1+i)z=1-7i,所以|1+i||z|=|1-7i|,即√2|z|=5√2,解得|z|=5.56.(2017·浙江·12)已知a,b ∈R,(a+bi)2=3+4i(i 是虚数单位),则a2+b2=_____,ab=________.【答案】5 2【解析】由题意可得a2-b2+2abi=3+4i,则{a 2-b 2=3,ab =2,解得{a 2=4,b 2=1,则a 2+b 2=5,ab=2. 57.(2017·江苏·T 2)已知复数z=(1+i)(1+2i),其中i 是虚数单位,则z 的模是 .【答案】√10【解析】由已知得z=(1+i)(1+2i)=-1+3i,故|z|=√(-1)2+32=√10,答案为√10.58.(2017·天津·理T9文T9)已知a ∈R,i 为虚数单位,若a -i 为实数,则a 的值为 .【答案】-2【解析】∵a -i 2+i =(a -i )(2-i )(2+i )(2-i )=2a -15−a+25i 为实数,∴-a+25=0,即a=-2. 59.(2016·江苏·T 2)复数z=(1+2i)(3-i),其中i 为虚数单位,则z 的实部是 .【答案】5【解析】因为z=(1+2i)(3-i)=5+5i,所以z 的实部是5.60.(2016·天津·理T9)已知a,b ∈R,i 是虚数单位,若(1+i)(1-bi)=a,则ab 的值为 .【答案】2【解析】(1+i)(1-bi)=1+b+(1-b)i=a,则{1+b =a ,1-b =0,所以{a =2,b =1,即a b =2.故答案为2. 61.(2016·北京·理T9)设a ∈R,若复数(1+i)(a+i)在复平面内对应的点位于实轴上,则a= .【答案】-1【解析】∵(1+i)(a+i)=a-1+(a+1)i∈R,∴a+1=0,即a=-1.62.(2015·天津·理T9)i是虚数单位,若复数(1-2i)(a+i)是纯虚数,则实数a的值为. 【答案】-2【解析】(1-2i)(a+i)=a+2+(1-2a)i.∵(1-2i)(a+i)是纯虚数,∴a+2=0,且1-2a≠0,∴a=-2.63.(2015·江苏·T 3)设复数z满足z2=3+4i(i是虚数单位),则z的模为.【答案】√5【解析】因为z2=3+4i,所以|z2|=√32+42=5,所以|z|=√5.64.(2015·重庆·理T11)设复数a+bi(a,b∈R)的模为√3 ,则(a+bi)(a-bi)= .【答案】3【解析】因为复数a+bi的模为√3,所以2+b2=√3,即a2+b2=3.于是(a+bi)(a-bi)=a2-(bi)2=a2+b2=3.。
十年(2010-2019)高考数学真题分类汇编(试卷版+解析版):常用逻辑用

A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
28.(2014•陕西•理 T8)原命题为“若 z1,z2 互为共轭复数,则|z1|=|z2|”,关于其逆命题,否命题,逆否命题真
假性的判断依次如下,正确的是( )
A.真,假,真 B.假,假,真
C.真,真,假 D.假,假,假
的( )
A.充要条件
B.充分而不必要条件
C.必要而不充分条件 D.既不充分也不必要条件
3
18.(2016•山东•理 T6)已知直线 a,b 分别在两个不同的平面 α,β 内.则“直线 a 和直线 b 相交”是“平面
α 和平面 β 相交”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
13.(2017•天津•理 T4)设 θ∈R,则“
π
- 12
<
π
12”是“sin
1
θ<2”的(
)
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
14.(2017•浙江•理 T6)已知等差数列{an}的公差为 d,前 n 项和为 Sn,则“d>0”是“S4+S6>2S5”的 ( )
+ ≥ 6, 1.(2019•全国 3•文 T11)记不等式组 2 - ≥ 0 表示的平面区域为 D.命题 p:∃(x,y)∈D,2x+y≥9;命题 q:∀(x,y)∈D,2x+y≤12.下面给出了四个命题 ①p∨q ②¬p∨q ③p∧¬q ④¬p∧¬q 这四个命题中,所有真命题的编号是( ) A.①③ B.①② C.②③ D.③④
10年高考题之复数锦集

总题数:22 题第1题(2010年普通高等学校夏季招生考试数学文史类(北京卷))题目在复平面内,复数6+5i,-2+3i对应的点分别为A,B.若C为线段AB的中点,则点C对应的复数是( ) A.4+8i B.8+2iC.2+4i D.4+i答案C 由题意知A(6,5),B(-2,3),故C(2,4),则点C对应的复数为2+4i.第2题(2010年普通高等学校夏季招生考试数学文史类(天津卷))题目i是虚数单位,复数=( )A.1+2i B.2+4i C.-1-2i D.2-i 答案A =1+2i.第3题(2010年普通高等学校夏季招生考试数学理工农医类(天津卷))题目i是虚数单位,复数=( )A.1+i B.5+5i C.-5-5i D.-1-i答案A=1+i.第4题(2010年普通高等学校夏季招生考试数学文史类(辽宁卷))题目设a,b为实数,若复数=1+i,则( )A.a=,b= B.a=3,b=1C.a=,b= D.a=1,b=3答案A 由题意a+b i==∴a=,b=,选A项.第5题(2010年普通高等学校夏季招生考试数学理工农医类学(辽宁卷)) 题目设a,b为实数,若复数=1+i,则( )A.a=,b= B.a=3,b=1C.a=,b= D.a=1,b=3答案A 由题意a+b i==∴a=,b=,选A项.第6题(2010年普通高等学校夏季招生考试数学文史类(浙江卷))题目设i为虚数单位,则=( )A.-2-3i B.-2+3i C.2-3i D.2+3i 答案C =2-3i.第7题(2010年普通高等学校夏季招生考试数学理工农医类(浙江卷))题目对任意复数z=x+y i(x,y∈R),i为虚数单位,则下列结论正确的是( )A.|z-|=2y B.z2=x2+y2C.|z-|≥2x D.|z|≤|x|+|y|答案D 对于A:|z-|=|2y i|=2|y|≠2y,对于B:z2=x2-y2+2xy i≠x2+y2,对于C:|z-|=2|y|≥2x 不一定成立,对于 D:|z|==|x|+|y|成立.第8题(2010年普通高等学校夏季招生考试数学文史类(湖南卷))题目复数等于( )A.1+i B.1-iC.-1+i D.-1-i答案A =1+i.第9题(2010年普通高等学校夏季招生考试数学理工农医类(广东卷))题目若复数z1=1+i,z2=3-i,则z1·z2=( )A.4+2i B.2+i C.2+2i D.3+i答案A z1·z2=(1+i)(3-i)=3-i2+2i=4+2i.第10题(2010年普通高等学校夏季招生考试数学文史类(安徽卷))题目已知i2=-1,则i(1-i)=( )A. -iB. +iC.--i D.-+i答案B i(1-i)=i-i2=+i.第11题(2010年普通高等学校夏季招生考试数学理工农医类(安徽卷))题目i是虚数单位,=( )A. B.C. D.答案B . 第12题(2010年普通高等学校夏季招生考试数学文史类(山东卷))题目已知=b+i(a,b∈R),其中i为虚数单位,则a+b等于 ( ) A.-1 B.1 C.2 D.3答案B ∵=b+i,∴a+2i=-1+b i.∴a=-1,b=2.∴a+b=1.第13题(2010年普通高等学校夏季招生考试数学理工农医类(山东卷))题目已知=b+i(a,b∈R),其中i为虚数单位,则a+b等于 ( ) A.-1 B.1 C.2 D.3答案B ∵=b+i,∴a+2i=-1+b i.∴a=-1,b=2.∴a+b=1.第14题(2010年普通高等学校夏季招生考试数学理工农医类(江西卷))题目已知(x+i)(1-i)=y,则实数x,y分别为( )A.x=-1,y=1 B.x=-1,y=2C.x=1,y=1 D.x=1,y=2答案D 由(x+i)(1-i)=y,得x+1+(1-x)i=y,∴∴x=1,y=2.第15题(2010年普通高等学校夏季招生考试数学文史类(陕西卷))题目复数z=在复平面上对应的点位于( )A.第一象限 B.第二象限C.第三象限 D.第四象限答案A =(1-i)=+,对应点坐标为(,),该点位于第一象限.第16题(2010年普通高等学校夏季招生考试数学理工农医类(陕西卷))题目复数z=在复平面上对应的点位于( )A.第一象限 B.第二象限C.第三象限 D.第四象限答案A =(1-i)=+,对应点坐标为(,),该点位于第一象限.第17题(2010年普通高等学校夏季招生考试数学文史类(福建卷))题目i是虚数单位,()4等于( )A.i B.-iC.1 D.-1答案C =i,∴()4=i4=1.故选C.第18题(2010年普通高等学校夏季招生考试数学理工农医类(福建卷))题目对于复数a,b,c,d,若集合S={a,b,c,d}具有性质“对任意x,y∈S,必有xy∈S”,则当时,b+c+d等于( )A.1 B.-1 C.0 D.i答案B 因为集合中的元素是互异的,解方程组,得,∵x,y∈S,xy∈S,∴当c=i时,d=-i,b+c+d=-1;当c=-i时,d=i,b+c+d=-1,故b+c+d=-1.第19题(2010年普通高等学校夏季招生考试数学文史类(全国卷新课标))题目已知复数z=,则|z|等于( )A. B. C.1 D.2 答案B |z|====.第20题(2010年普通高等学校夏季招生考试数学理工农医类(全国卷新课标))题目已知复数z=,是z的共轭复数,则z·=( )A. B. C.1 D.2答案A z·=|z|2而|z|====,∴|z|2=,∴z·=.第21题(2009年普通高等学校夏季招生考试数学理工农医类(全国Ⅰ卷)) 题目已知,则复数z=()A.-1+3iB.1-3iC.3+iD.3-i答案B解析:∵,∴=(2+i)(1+i)=2+3i+i2=1+3i.∴z=1-3i.第22题(2009年普通高等学校夏季招生考试数学理工农医类(全国Ⅱ卷))题目=( )A.-2+4iB.-2-4iC.2+4iD.2-4i答案A解析:.故选A.总题数:22 题第23题(2009年普通高等学校夏季招生考试数学理工农医类(北京卷))题目在复平面内,复数z=i(1+2i)对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限答案B解析:∵z=i(1+2i)=-2+i,∴其对应点为(-2,1).故选B.第24题(2009年普通高等学校夏季招生考试数学文史类(天津卷))题目i是虚数单位,等于( )A.1+2iB.-1-2iC.1-2iD.-1+2i 答案D解析:因为.第25题(2009年普通高等学校夏季招生考试数学理工农医类(天津卷))题目i是虚数单位,等于()A.1+2iB.-1-2iC.1-2iD.-1+2i答案D解析:因为.第26题(2009年普通高等学校夏季招生考试数学文史类(辽宁卷))题目已知复数z=1-2i,那么等于…( )A. B.C. D.答案C解析: .第27题(2009年普通高等学校夏季招生考试数学理工农医类(辽宁卷))题目已知复数z=1-2i,那么等于…( )A. B. C. D.答案D解析:=1+2i,∴.第28题(2009年普通高等学校夏季招生考试数学文史类(浙江卷))题目设z=1+i(i是虚数单位),则( )A.1+iB.-1+iC.1-iD.-1-i 答案A解析:z=1+i,则,z2=2i,故,故选A. 第29题(2009年普通高等学校夏季招生考试数学理工农医类(浙江卷)) 题目设z=1+i(i是虚数单位),则=( )A.-1-iB.-1+iC.1-iD.1+i答案D解析:z=1+i,则,z2=2i,故=1+i,故选D.第30题(2009年普通高等学校夏季招生考试数学文史类(安徽卷))题目i是虚数单位,i(1+i)等于…( )A.1+iB.-1-iC.1-iD.-1+i 答案D解析:i(1+i)=i+i2=-1+i.第31题(2009年普通高等学校夏季招生考试数学理工农医类(安徽卷)) 题目i是虚数单位,若(a,b∈R),则乘积ab的值是()A.-15 B.-3 C.3 D.15答案B解析:==,∴ab=-3.第32题(2009年普通高等学校夏季招生考试数学文史类(山东卷)) 题目复数等于( )A.1+2iB.1-2iC.2+iD.2-i答案C解析:.第33题(2009年普通高等学校夏季招生考试数学理工农医类(山东卷)) 题目复数等于( )A.1+2iB.1-2iC.2+ID.2-i 答案C解析:.第34题(2009年普通高等学校夏季招生考试数学理工农医类(江西卷)) 题目若复数z=(x2-1)+(x-1)i为纯虚数,则实数x的值为( )A.-1B.0C.1D.-1或1答案A解析:由题意知∴x=-1.第35题(2009年普通高等学校夏季招生考试数学理工农医类(四川卷))复数的值是( )A.-1B.1C.-iD.i答案A解析:.第36题(2009年普通高等学校夏季招生考试数学理工农医类(重庆卷)) 题目已知复数z的实部为-1,虚部为2,则=()A.2-iB.2+iC.-2-iD.-2+i答案A解析:.第37题(2009年普通高等学校夏季招生考试数学理工农医类(陕西卷)) 题目已知z是纯虚数,是实数,那么z等于( )A.2iB.iC.-iD.-2iD解析:设z=bi(b≠0),则∈R,则b+2=0,∴b=-2.故选D.第38题(2009年普通高等学校夏季招生考试数学文史类(海南、宁夏卷))题目复数等于( )A.1B.-1C.iD.-i答案C解析: .故选C.第39题(2009年普通高等学校夏季招生考试数学理工农医类(海南、宁夏卷)) 题目复数等于……( )A.0B.2C.-2iD.2iD解析:原式.故选D.第40题(2009年普通高等学校夏季招生考试数学文史类(广东卷))题目下列n的取值中,使i n=1(i是虚数单位)的是( )A.n=2B.n=3C.n=4D.n=5答案C解析:∵i4=1,故选C.第41题(2009年普通高等学校夏季招生考试数学理工农医类(广东卷))题目设z是复数,α(z)表示满足z n=1的最小正整数n,则对虚数单位i,α(i)等于… ( ) A.8 B.6 C.4 D.2答案C解析:∵i4=1,∴α(i)=4.第42题(2008年普通高等学校夏季招生考试数学理工农医类(全国Ⅰ))题目设,且为正实数,则()A.2 B.1 C.0 D.答案D 解析: (a+i)2i=(a2-1+2ai)i=-2a+(a2-1)i.∵(a+i)2i为正实数,∴∴a=-1.第43题(2008年普通高等学校夏季招生考试数学理工农医类(全国Ⅱ)) 题目设且,若复数是实数,则()A. B. C. D.答案A 解析: (a+bi)3=a3+3a2·bi+3a(bi)2+(bi)3=a3+3a2bi-3ab2-b3i=(a3-3ab2)+(3a2b-b3)i为实数3a2b-b3=0,又∵b≠0,∴3a2-b2=0.∴b2=3a2.选A.第44题(2008年普通高等学校夏季招生考试数学理工农医类(天津卷)) 题目i是虚数单位,等于( )A.-1B.1C.-iD.i答案答案:A解析:==-1,故选A.总题数:22 题第45题(2008年普通高等学校夏季招生考试数学理工农医类(辽宁卷))题目复数的虚部是( )A.iB.C.iD.答案答案:B解析:+=(-2-i)+(1+2i)=-+i,故虚部为.第46题(2008年普通高等学校夏季招生考试数学理工农医类(浙江卷))题目已知是实数,是纯虚数,则=(A)1 (B)-1 (C)(D)-答案A 解析:==,∴=0.∴a=1.第47题(2008年普通高等学校夏季招生考试数学理工农医类(福建卷)) 题目若复数(是纯虚数,则实数a的值为A.1 B.2 C.1或2 D.-1、答案B 解析:∵(a2-3a+2)+(a-1)i是纯虚数,因此解得a=2.第48题(2008年普通高等学校夏季招生考试数学理工农医类(湖南卷)) 题目复数(1+)3等于A.8B.-8C.8iD.-8i答案D解析:(i)3=()3===-8i.第49题(2008年普通高等学校夏季招生考试数学文史类(广东卷))题目已知0<a<2,复数z=a+i(i是虚数单位),则|z|的取值范围是( )A.(1,5)B.(1,3)C.(1,)D.(1,)答案答案:C |z|=,∵0<a<2,∴1<<.|z|=,∵0<a<2,∴1<<.第50题(2008年普通高等学校夏季招生考试数学理工农医类(广东卷))题目已知0<a<2,复数z的实部为a,虚部为1,则|z|的取值范围是( )A.(1,5)B.(1,3)C.(1,)D.(1,) 答案答案:C解析:|z|=,∵0<a<2,∴1<<.第51题(2008年普通高等学校夏季招生考试数学理工农医类(安徽卷)) 题目复数()A.2 B.-2 C. D.答案A解析:i3(1+i)2=-i(2i)=-2i2=2.第52题(2008年普通高等学校夏季招生考试数学理工农医类(江西卷)) 题目在复平面内,复数对应的点位于A.第一象限 B.第二象限 C.第三象限 D.第四象限答案D解析:∵<2<π,∴角的终边落在第二象限,则sin2>0,cos2<0, 故该复数对应点位于第四象限.第53题(2008年普通高等学校夏季招生考试数学理工农医类(四川卷)) 题目复数2i(1+ i)2=(A)-4 (B)4 (C)-4i (D)4i答案A解析:2i(1+i)2=2i·(1+2i-1)=2i·2i=-4.第54题(2008年普通高等学校夏季招生考试数学理工农医类(四川卷延考))题目已知复数,则(A)(B)(C)(D)答案答案:D解析:,. 第55题(2008年普通高等学校夏季招生考试数学理工农医类(重庆卷))题目复数1+等于( )A.1+2iB.1-2iC.-1D.3答案答案:A解析:1+=1=1+2i.第56题(2008年普通高等学校夏季招生考试数学文史类(山东卷))题目设z的共轭复数是,若z+=4,z·=8,则等于(A)i (B)-i (C) 1 (D) i 答案D设z=a+bi,则=a-bi(a,b∈R),∵z+=4,z·=8,∴a=2,a2+b2=8.∴b=±2.当b=2时,=i,当b=-2时,=-i.故选D.第57题(2008年普通高等学校夏季招生考试数学理工农医类(山东卷))题目设z的共轭复数是,或z+=4,z·=8,则等于(A)1 (B)-i (C)±1 (D) ±i答案D 解析:设z=a+bi,则=a-bi(a,b∈R),∵z+=4,z·=8,∴a=2,a2+b2=8.∴b=±2.当b=2时,=i,当b=-2时,=-i.故选D.第58题(2008年普通高等学校夏季招生考试数学文史类(海南、宁夏卷))题目已知复数,则()A. 2B. -2C. 2iD. -2i答案A=2.第59题(2008年普通高等学校夏季招生考试数学理工农医类(海南、宁夏卷)) 题目已知复数,则()A. 2 iB. -2 iC. 2D. -2答案B 解析:z=1-i得z2=-2i,代入=-2i.∴选B.第60题(2007年普通高等学校夏季招生考试数学理工农医类(全国Ⅰ))题目2.设a是实数,且是实数,则A. B.1 C. D.2答案答案:B解析:∈R,∴=0.∴a=1.第61题(2007年普通高等学校夏季招生考试数学理工农医类(全国Ⅱ))题目3.设复数z满足=i,则z =(A) -2+i (B) -2-i (C) 2-i (D) 2+i 答案答案:C解析:z==2-.第62题(2007年普通高等学校夏季招生考试数学理工农医类(天津卷))题目1.是虚数单位,()A.B. C.D.答案C第63题(2007年普通高等学校夏季招生考试数学理工农医类(辽宁卷))题目5.若,则复数在复平面内所对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限答案答案:B解析:∵θ∈(,),∴cosθ<0,sinθ可正可负,且|cosθ|>|sinθ|.∴cosθ+sinθ<0.∴sinθ-cosθ>0.∴此复数在复平面内所对应的点在第二象限.第64题(2007年普通高等学校夏季招生考试数学理工农医类(福建卷))题目(1)复数等于A B - C i D -i答案答案:D解析: ==-i.第65题(2007年普通高等学校夏季招生考试数学理工农医类(湖南卷)) 题目1.复数等于()A. B. C. D.答案答案:C解析:()2==2i.第66题(2007年普通高等学校夏季招生考试数学文史类(广东卷新课标)) 题目2.若复数(1+b i)(2+i)是纯虚数(i是虚数单位,b是实数),则b=A.-2B.C.D.2答案D解析:(1+b i)(2+i)=2+i+2b i-b=(2-b)+(1+2b)i.∵是纯虚数,∴2-b=0且1+2b≠0.∴b=2.总题数:22 题第67题(2007年普通高等学校夏季招生考试数学理工农医类(广东卷新课标))题目2.若复数是纯虚数(是虚数单位,是实数)则=A.2B.C.D.-2 答案答案:A解析:(1+b i)(2+i)=2+i+2b i-b=(2-b)+(1+2b)i.∵是纯虚数,∴2-b=0且1+2b≠0.∴b=2.第68题(2007年普通高等学校夏季招生考试数学理工农医类(安徽卷))题目4.若a为实数,=-i,则a等于(A)(B)-(C)2(D)-2答案答案:B解析:化简=-i,得=-i,=-i,∴∴a=-.第69题(2007年普通高等学校夏季招生考试数学理工农医类(江西卷)) 题目1.化简的结果是A.2+iB.-2+iC.2-iD.-2-i答案答案:C解析:=2-i.第70题(2007年普通高等学校夏季招生考试数学理工农医类(四川卷)) 题目(1)复数的值是(A)0 (B)1 (C)-1 (D)1答案答案:A解析:原式=+i3=i-i=0.第71题(2007年普通高等学校夏季招生考试数学文史类(山东卷新课标))题目1.复数的实部是(A)-2 (B)2 (C)3 (D)4 答案B解析: ====2-i,∴实部为2.第72题(2007年普通高等学校夏季招生考试数学理工农医类(山东卷新课标))题目(1)若z=cosθ+isinθ(i为虚数单位),则使z2= -1的θ值可能是A. B. C. D.答案答案:D解析:z2=cos2θ-sin2θ+i2sinθcosθ=cos2θ+isin2θ=-1,∴∴2θ=2kπ+π.∴θ=.第73题(2007年普通高等学校夏季招生考试数学理工农医类(陕西卷))题目1.在复平面内,复数z=对应的点位于( )(A)第一象限(B)第二象限(C)第三象限(D )第四象限答案答案:D解析:z=,故选D.第74题(2006年普通高等学校夏季招生考试数学(理工农医类)全国卷Ⅰ(新课程))题目(4)如果复数(m2+i)(1+mi)是实数,则实数(A)1 (B)-1 (C)(D)-答案B解析:(m2+i)(1+mi)=(m2-m)+(1+m3)i∵复数(m2+i)(1+mi)是实数∴1+m3=0∴m=-1第75题(2006年普通高等学校夏季招生考试数学(理工农医类)全国卷Ⅱ(新课程)) 题目(3)(A)(B)(C)(D)答案A解析:∴选A第76题(2006年普通高等学校夏季招生考试数学(理工农医类)北京卷(新课程)) 题目(1)在复平面内,复数对应的点位于(A)第一象限 (B)第二象限(C)第三象限 (D)第四象限答案D解析:,虚部为负∴第四象限第77题(2006年普通高等学校夏季招生考试数学(理工农医类)天津卷(新课程))题目(1)i是虚数单位,=(A) (B) (C) (D)答案A解析:故选A.第78题(2006年普通高等学校夏季招生考试数学(理工农医类)浙江卷(新课程))题目(2)已知,其中m,n是实数,i是虚数单位,则m+ni=(A)1+2i (B)1-2i (C)2+i (D)2-i答案C解析:∵∴∴∴m+ni=2+i第79题(2006年普通高等学校夏季招生考试数学(理工农医类)福建卷(新课程)) 题目(1)设则复数为实数的充要条件是(A)(B)(C)(D)答案D∵(a+bi)(c+di)为实数∴虚部为0(a+bi)(c+di)=(ac-bd)+(ad+bc)i∴ad+bc=0第80题(2006年普通高等学校夏季招生考试数学(文理合卷)广东卷(新课程)) 题目2.若复数z满足方程z2+2=0,则z3=A. B. C.±2i D.+2答案C解析:设z=a+bi则 z2+2=0(a+bi)2+2=0a2+2abi-b2+2=0∴z=±i∴z3=(±i)3=±2i第81题(2006年普通高等学校夏季招生考试数学(理工农医类)安徽卷(新课程)) 题目(1)复数等于()(A)i (B)-i (C)(D)答案A解析:原式=第82题(2006年普通高等学校夏季招生考试数学(理工农医类)江西卷(新课程))题目2.已知复数z满足(+3i)z=3i,则z等于A.i B. i C. D.i 答案D解析:设z=a+bi,代入方程()(a+bi)=3i,化简,得(a-3b)+(3a+b)i=3i∴解得故选D另解:由题得z=第83题(2006年普通高等学校夏季招生考试数学(理工农医类)四川卷(新课程)) 题目(2)复数(1-i)3的虚部为(A)(B)(C)(D)答案D解析:(1-i)3=-2-2i∴虚部为-2.第84题(2006年普通高等学校夏季招生考试数学(理工农医类)陕西卷(新课程)) 题目2.复数等于(A)(B)(C)(D)答案D解析:原式=第85题(2005年普通高等学校夏季招生考试数学(理工农医类)全国卷Ⅰ(新课程)) 题目1.复数=(A)(B)(C)(D)答案A解法一:原式==== =i.解法二:原式====i.第86题(2005年普通高等学校夏季招生考试数学(理工农医类)全国卷Ⅱ(新课程)) 题目5.设a、b、c、d∈R,若为实例,则(A)bc+ad≠0 (B)bc-ad≠0(C)bc-ad=0 (D)bc+ad=0答案C解析:==∈R,∴bc-ad=0.第87题(2005年普通高等学校夏季招生考试数学(理工农医类)天津卷(新课程))题目若复数(a∈R,i为虚数单位)是纯虚数,则实数a的值为()A.-2 B.4 C.-6 D.6 答案C解析:==+i是纯虚数,∴=0.∴a=-6.故选C. 第88题(2005年普通高等学校夏季招生考试数学(文理合卷)辽宁卷(新课程))题目复数在复平面内,z所对应的点在A.第一象限 B.第二象限C.第三象限 D.第四象限答案B解析:z=-1==-1+i ,∴z对应点为(-1 ,1),在第二象限.总题数:22 题第89题(2005年普通高等学校夏季招生考试数学(理工农医类)浙江卷(新课程))题目在复平面内,复数+(1+i)2对应的点位于( )(A) 第一象限 (B) 第二象限 (C) 第三象限 (D)第四象限答案B解析:+(1+i)3=+[-2()]3=-8=-+i.故对应的点位于第二象限.第90题(2005年普通高等学校夏季招生考试数学(理工农医类)福建卷(新课程))题目复数z=的共轭复数是A.B.C.D.答案B解析:z====+i,∴z的共轭复数为-i.第91题(2005年普通高等学校夏季招生考试数学(理工农医类)湖北卷(新课程)) 题目()A. B.C. D.答案C解析:===-i(1+2i)=2-i. 第92题(2005年普通高等学校夏季招生考试数学(理工农医类)湖南卷(新课程))题目复数z=i+i2+i3+i4的值是A、-1B、0C、1D、i答案B解析:z=i+i2+i3+i4=i-1-i+1=0.第93题(2005年普通高等学校夏季招生考试数学(文理合卷)广东卷(新课程))题目若,其中、,是虚数单位,则(A)0 (B)2 (C)(D)5答案D解析:(a-2i)i=b-i,即2+a i=b-i,∴故a2+b2=1+4=5.第94题(2005年普通高等学校夏季招生考试数学(理工农医类)江西卷(新课程))题目设复数:为实数,则x=()A.-2 B.-1 C.1 D.2 答案A解:z1·z2=(1+i)·(x+2i)=(x-2)+(2+x)i,z1·z2∈R.∴2+x=0,∴x=-2.第95题(2005年普通高等学校夏季招生考试数学(理工农医类)重庆卷(新课程))题目()A. B.-C. D.-答案A解析:()2 005=[]2 005=()2 005=i2 005=i.第96题(2005年普通高等学校夏季招生考试数学(理工农医类)山东卷(新课程)) 题目()(A);(B);(C)1;(D)答案D解析:+=+=---=-1.第97题(2005年普通高等学校春季招生考试数学(文史类)北京卷(新课程))题目-2+i的共轭复数是………………………………………………()A.2+iB.2-iC.-2+iD.-2-i答案D第98题(2005年普通高等学校春季招生考试数学(理工农医类)北京卷(新课程))题目i-2的共轭复数是…………………………………………………()A.2+iB.2-iC.-2+iD.-2-i答案D第99题(2004年普通高等学校夏季招生考试数学(理工农医类)全国卷Ⅱ(新课程))题目(1-i)2·i等于……………………………………………………………………………()A.2-2iB.2+2iC.-2D.2答案D第100题(2004年普通高等学校夏季招生考试数学(理工农医类)全国卷Ⅲ(新课程)) 题目设复数ω=-+i,则1+ω等于……………………………………()A.-ωB.ω2C.-D.答案C第101题(2004年普通高等学校夏季招生考试数学(理工农医类)全国卷Ⅳ(新课程)) 题目()2等于…………………………………………………………()A.+iB.--iC.-iD.-+i答案D第102题(2004年普通高等学校夏季招生考试数学(理工农医类)天津卷(新课程)) 题目i是虚数单位,等于…………………………………()A.1+iB.-1-iC.1+3iD.-1-3i答案D第103题(2004年普通高等学校夏季招生考试数学(文理合卷)辽宁卷(新课程)) 题目设复数z满足=i,则|1+z|等于……………………………()。
(北京卷)十年真题(2010_2019)高考数学真题分类汇编专题02复数文(含解析)

专题02复数历年考题细目表题型年份考点试题位置单选题2019 复数的四则运算2019年北京文科02 单选题2018 复数的四则运算2018年北京文科02 单选题2017 复数的四则运算2017年北京文科02 单选题2016 复数的四则运算2016年北京文科02 单选题2013 复数的四则运算2013年北京文科04 单选题2012 复数的四则运算2012年北京文科02 单选题2011 复数的四则运算2011年北京文科02单选题2010 数系的扩充与复数的定义2010年北京文科02填空题2015 复数的四则运算2015年北京文科09填空题2014 数系的扩充与复数的定义2014年北京文科09历年高考真题汇编1.【2019年北京文科02】已知复数z=2+i,则z•()A.B.C.3 D.5【解答】解:∵z=2+i,∴z•.故选:D.2.【2018年北京文科02】在复平面内,复数的共轭复数对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:复数,共轭复数对应点的坐标(,)在第四象限.故选:D.3.【2017年北京文科02】若复数(1﹣i)(a+i)在复平面内对应的点在第二象限,则实数a的取值范围是()A.(﹣∞,1)B.(﹣∞,﹣1)C.(1,+∞)D.(﹣1,+∞)【解答】解:复数(1﹣i)(a+i)=a+1+(1﹣a)i在复平面内对应的点在第二象限,∴,解得a<﹣1.则实数a的取值范围是(﹣∞,﹣1).故选:B.4.【2016年北京文科02】复数()A.i B.1+i C.﹣i D.1﹣i【解答】解:i,故选:A.5.【2013年北京文科04】在复平面内,复数i(2﹣i)对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:∵复数z=i(2﹣i)=﹣i2+2i=1+2i∴复数对应的点的坐标是(1,2)这个点在第一象限,故选:A.6.【2012年北京文科02】在复平面内,复数对应的点的坐标为()A.(1,3)B.(3,1)C.(﹣1,3)D.(3,﹣1)【解答】解:∵1+3i,∴在复平面内,复数对应的点的坐标为(1,3),故选:A.7.【2011年北京文科02】复数()A.i B.﹣i C.D.【解答】解:i故选:A.8.【2010年北京文科02】在复平面内,复数6+5i,﹣2+3i对应的点分别为A,B.若C为线段AB的中点,则点C对应的复数是()A.4+8i B.8+2i C.2+4i D.4+i【解答】解:两个复数对应的点的坐标分别为A(6,5),B(﹣2,3),则其中点的坐标为C(2,4),故其对应的复数为2+4i.故选:C.9.【2015年北京文科09】复数i(1+i)的实部为.【解答】解:复数i(1+i)=﹣1+i,所求复数的实部为:﹣1.故答案为:﹣1.10.【2014年北京文科09】若(x+i)i=﹣1+2i(x∈R),则x=.【解答】解:∵(x+i)i=﹣1+2i,∴﹣1+xi=﹣1+2i,由复数相等可得x=2故答案为:2考题分析与复习建议本专题考查的知识点为:复数的基本概念(复数的实部、虚部、共轭复数、复数的模等),复数相等的充要条件,考查复数的代数形式的四则运算,重点考查复数的除法运算,与向量结合考查复数及其加法、减法的几何意义等,历年考题主要以选择填空题题型出现,重点考查的知识点为复数的基本概念(复数的实部、虚部、共轭复数、复数的模等),复数相等的充要条件,考查复数的代数形式的四则运算,重点考查复数的除法运算等,预测明年本考点题目会比较稳定,备考方向以知识点复数的基本概念(复数的实部、虚部、共轭复数、复数的模等),复数相等的充要条件,考查复数的代数形式的四则运算为重点较佳.最新高考模拟试题1.复数52iz =-在复平面上的对应点位于( ) A .第一象限 B .第二象限C .第三象限D .第四象限【答案】A 【解析】()()()52i 52i 2i 2i 2i z +===+--+,在复平面上的对应点为()2,1,位于第一象限. 故选A. 2.设i z a b =+(a ,b ∈R ,i 是虚数单位),且22i z =-,则有( ) A .1a b +=- B .1a b -=- C .0a b -= D .0a b +=【答案】D 【解析】因为2222()()22z a bi a b abi i =+=-+=-,所以220a b -=,22ab =-,解得11a b =⎧⎨=-⎩或11a b =-⎧⎨=⎩,所以0a b +=,故选D.3.若复数1i1ia z +=+为纯虚数,则实数a 的值为( ) A .1 B .1-C .0D .2【答案】B 【解析】()()()()()11111i 1i 112ai i a a ia z i i +-++-+===++- 故10,10a a +=-≠ ,解1a =- 故选:B4.复数i (1+i )的虚部为( )A B .1 C .0 D .1-【答案】B 【解析】∵i (1+i )=-1+i , ∴i (1+i )的虚部为1.5.已知复数11z i =-+,复数2z 满足122z z =-,则2z = ( )A .2 BCD .10【答案】B 【解析】 由题得222(1)2(1)11(1)(1)2i i z i i i i -------====+-+-+--,所以2z 故选:B6.已知复数312i z i=+,则复数z 的实部为( )A .25-B .25i -C .15-D .15i -【答案】A 【解析】解:∵3(12)2112(12)(12)55i i i z i i i i --===--++-, ∴复数z 的实部为25-. 故选A . 7.复数122ii-=+( ) A .1i - B .i -C .iD .1i +【答案】B 【解析】12(12)(2)2422(2)(2)5i i i i i i i i i ------===-++-. 故选B8.已知i 为虚数单位,复数z 满足:()z 12i i +=-,则在复平面上复数z 对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限【解析】因为2(2)(1)131312222i i i i z i i ----====-+, 所以复平面上复数z 对应的点为13(,)22-,位于第四象限,故选D .9.设复数z a i =+,z 是其共轭复数,若3455z i z =+,则实数a =( ) A .4 B .3C .2D .1【答案】C 【解析】 解: z a i =+Qz a i ∴=- 343443++2555555z a a i a i i a z ⎛⎫∴=+⇒+=-⇒= ⎪⎝⎭10.已知i 是虚数单位,复数z 满足2(1)1i i z-=+,则z =( )A B .2 C .1D 【答案】A 【解析】22(1)(1)22(1)1(1)111(1)(1)i i i i i i z i i i z i i i i ----⋅-=+⇒====--=--+++⋅-,所以1z i =--==A.11.复数()()21z i i =+-,其中i 为虚数单位,则z 的实部是( ) A .-1 B .1 C .2 D .3【答案】D 【解析】解:∴()()212213z i i i i i =+-=-++=-, ∴z 的实部是312.已知复数(1)1z i i -=+,则复数z =( ) A .2i + B .2i -C .iD .i -【答案】C 【解析】由题意,复数(1)1z i i -=+,则()()()()11121112i i i iz i i i i +++====--+,故选C. 13.已知i 为虚数单位,若1(,)1a bi a b R i=+∈-,则b a =( ) A .1 BCD .2【答案】C 【解析】 i 为虚数单位,若1(,)1a bi a b R i =+∈-,1112i a bi i +==+- 根据复数相等得到1212a b ⎧=⎪⎪⎨⎪=⎪⎩.121()22b a ==故答案为:C.14.已知复数z 满足2(1i)(3i)z +=+,则||z =( ) ABC.D .8【答案】C 【解析】∵2(1)(3)z i i +=+,∴2(3)86(86)(1)(43)(1)711(1)(1)i i i i z i i i i i i i +++-====+-=-+++-,∴||z === 故选C .15.已知i 是虚数单位,则复数11i i -+在复平面上所对应的点的坐标为( ) A .()0,1 B .()1,0-C .()1,0D .()0,1-【答案】A 【解析】 ∵()()()()111111i i i i i i i ---==++-,∴该复数在复平面上对应的点的坐标为()0,1. 故选A.16.若复数z 满足(1i)|1|z +=+,则在复平面内z 的共轭复数对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限【答案】A 【解析】 由题得22(1)1(1)(1)(1i)i z i i i -===-++-, 所以1z i =+,所以在复平面内z 的共轭复数对应的点为(1,1),在第一象限. 故选:A17.已知复数z 满足12iz i =+,则z 的虚部是( ) A .1- B .i -C .2D .2i【答案】A 【解析】 因为12iz i =+所以221222i i i z i i i++===-所以虚部为1- 所以选A 18.已知31iz i-=-(其中i 为虚数单位),则z 的虚部为( ) A .i -B .1-C .1D .2【答案】B 【解析】 因为3(3)(1)4221(1)(1)2i i i iz i i i i --++====+--+, 所以2z i =-,故z 的虚部为1-,故选B.19.复数2(1)41i z i -+=+的虚部为( )A .1-B .3-C .1D .2【答案】B 【解析】()()2421(1)44213112i i i i z i i i ---+-====-++ 所以z 的虚部为3- 故选B 项.20.已知复数()11z ai a R =+∈,212z i =+(i 为虚数单位),若12z z 为纯虚数,则a =( ) A .2- B .2C .12-D .12【答案】C 【解析】∵()12112z ai a R z i =+∈=+,,∴121(1)(12)12212(12)(12)55z ai ai i a a i z i i i ++-+-===+++-, ∵12z z 为纯虚数, ∴12020a a +=⎧⎨-≠⎩,解得12a =-.故选:C . 21.设复数z 满足2ii z+=,则z =( )A .1BC .3D .5【答案】B 【解析】2ii z+=Q, 221i z i i +∴==+22112ii i=+=-,z ∴== B.22.已知复数1i z i=-,则z 在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限【答案】A 【解析】∵ ()()()11111122i i i z i i i i +===-+--+,∴ 12z i =+,∴2z +在复平面内对应的点的坐标为12⎫⎪⎪⎝⎭,位于第一象限. 故选:A .23.复数z 满足(1)2z i i -=,则复数z =( ) A .1i - B .12i +C .1i +D .1i --【答案】D 【解析】 由题意得:()()()2121111i i iz i i i i +===-+--+ 1z i ∴=-- 本题正确选项:D24.若复数2(1)z m m m i =+++是纯虚数,其中m 是实数,则1z=( ) A .i B .i - C .2iD .2i -【答案】B 【解析】复数z =m (m +1)+(m +1)i 是纯虚数,故m (m +1)=0且(m +1)≠0,解得m =0,故z =i ,故111iz i i i ⋅===-⋅i .故选:B .25.设i 为虚数单位,则复数22iz i -=+的共扼复数z =( )A .3455i + B .3455i -C .3455i -+ D .3455i --【答案】A【解析】 解:22i (2i)34i 2i (2i)(2i)55z --===-++-Q ,3455z i ∴=+故选:A .26.已知复数1z 、2z在复平面内对应的点关于虚轴对称,11z =,则12z z =( )A .2 BCD .1【答案】D【解析】由题意,复数1z 、2z在复平面内对应的点关于虚轴对称,11z =,则21z =-,所以12212z z ====,故选D.27.已知复数z 1=1+2i ,z 2=l ﹣i ,则12z z =( )A .13i 22-- B .13i 22-+ C .13i 22- D .13i 22+【答案】B【解析】∵1212,1z i z i =+=-,∴1212(12)(1)131(1)(1)22z i i i i z i i i +++===-+--+. 故选:B .28.在复平面内,复数(2i)z -对应的点位于第二象限,则复数z 可取( )A .2B .-1C .iD .2i + 【答案】B【解析】不妨设(),z a bi a b R =+∈,则()()()()()2222i z i a bi a b b a i -=-+=++-,结合题意可知:20,20a b b a +<->,逐一考查所给的选项:对于选项A :24,22a b b a +=-=-,不合题意;对于选项B :22,21a b b a +=--=,符合题意;对于选项C :21,22a b b a +=-=,不合题意;对于选项D :25,20a b b a +=-=,不合题意;故选:B .29.已知i 为虚数单位,则复数3(1)i z i i +=-的虚部为( ) A .1B .2C .1-D .2- 【答案】C【解析】 因为3(3)(1)122(1)2i i i i i i i i i++++===--,所以z 的虚部为1-. 30.已知复数(i)(1i)z a =+-(i 为虚数单位)在复平面内对应的点在直线2y x =上,则实数a 的值为( )A .0B .1-C .1D .13- 【答案】D【解析】因为(i)(1i)1(1)z a a a i =+-=++-,对应的点为(1,1)a a +-,因为点在直线2y x =上,所以12(1)a a -=+,解得13a =-. 故选D.。
复数十年高考题(带详细解析)

复数十年高考题(带详细解析)1.设复数 $z_1=-1+i$,$z_2=z_1^3i$,则$arg(z_1)+\frac{arg(z_2)}{2}$ 等于()。
A。
$-\frac{7\pi}{12}$ B。
$\pi$ C。
$\frac{\pi}{2}$ D。
$\frac{\pi}{4}$2.复数 $z=m-2i$($m\in R$,$i$ 为虚数单位)在复平面上对应的点不可能位于()。
A。
第一象限 B。
第二象限 C。
第三象限 D。
第四象限3.如果 $\theta\in(\frac{\pi}{2},\pi)$,那么复数$(1+i)(\cos\theta+i\sin\theta)$ 的辐角的主值是()。
A。
$\theta+\frac{9\pi}{4}$ B。
$\theta+\frac{\pi}{4}$ C。
$\theta-\frac{\pi}{4}$ D。
$\theta+\frac{7\pi}{4}$4.复数 $\frac{1}{3}+i$ 的值是()。
A。
$-\frac{1}{3}+i$ B。
$i$ C。
$-\frac{1}{2}$ D。
$-\frac{1}{3}-i$5.如图 12-1,与复平面中的阴影部分(含边界)对应的复数集合是()。
图略]6.已知复数 $z=\frac{1}{2}+6i$,则 $arg(z)$ 是()。
A。
$\frac{11\pi}{6}$ B。
$\frac{6\pi}{7}$ C。
$\frac{3\pi}{5}$ D。
$\frac{5\pi}{3}$7.设复数 $z_1=-1-i$ 在复平面上对应向量 $OZ_1$,将$OZ_1$ 按顺时针方向旋转 $\frac{5\pi}{6}$ 后得到向量$OZ_2$,令 $OZ_2$ 对应的复数 $z_2$ 的辐角主值为 $\theta$,则 $\tan\theta$ 等于()。
A。
$2+\sqrt{3}$ B。
$-2+\sqrt{3}$ C。
十年真题(2010_2019)高考数学真题分类汇编专题17不等式选讲(理)(含解析)
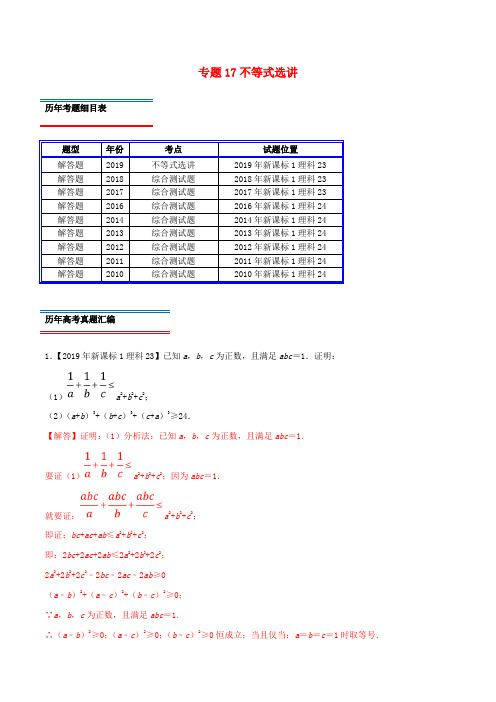
专题17不等式选讲历年考题细目表题型年份考点试题位置解答题2019 不等式选讲2019年新课标1理科23解答题2018 综合测试题2018年新课标1理科23解答题2017 综合测试题2017年新课标1理科23解答题2016 综合测试题2016年新课标1理科24解答题2014 综合测试题2014年新课标1理科24解答题2013 综合测试题2013年新课标1理科24解答题2012 综合测试题2012年新课标1理科24解答题2011 综合测试题2011年新课标1理科24解答题2010 综合测试题2010年新课标1理科24历年高考真题汇编1.【2019年新课标1理科23】已知a,b,c为正数,且满足abc=1.证明:(1)a2+b2+c2;(2)(a+b)3+(b+c)3+(c+a)3≥24.【解答】证明:(1)分析法:已知a,b,c为正数,且满足abc=1.要证(1)a2+b2+c2;因为abc=1.就要证:a2+b2+c2;即证:bc+ac+ab≤a2+b2+c2;即:2bc+2ac+2ab≤2a2+2b2+2c2;2a2+2b2+2c2﹣2bc﹣2ac﹣2ab≥0(a﹣b)2+(a﹣c)2+(b﹣c)2≥0;∵a,b,c为正数,且满足abc=1.∴(a﹣b)2≥0;(a﹣c)2≥0;(b﹣c)2≥0恒成立;当且仅当:a=b=c=1时取等号.即(a﹣b)2+(a﹣c)2+(b﹣c)2≥0得证.故a2+b2+c2得证.(2)证(a+b)3+(b+c)3+(c+a)3≥24成立;即:已知a,b,c为正数,且满足abc=1.(a+b)为正数;(b+c)为正数;(c+a)为正数;(a+b)3+(b+c)3+(c+a)3≥3(a+b)•(b+c)•(c+a);当且仅当(a+b)=(b+c)=(c+a)时取等号;即:a=b=c=1时取等号;∵a,b,c为正数,且满足abc=1.(a+b)≥2;(b+c)≥2;(c+a)≥2;当且仅当a=b,b=c;c=a时取等号;即:a=b=c=1时取等号;∴(a+b)3+(b+c)3+(c+a)3≥3(a+b)•(b+c)•(c+a)≥3×8••24abc=24;当且仅当a=b=c=1时取等号;故(a+b)3+(b+c)3+(c+a)3≥24.得证.故得证.2.【2018年新课标1理科23】已知f(x)=|x+1|﹣|ax﹣1|.(1)当a=1时,求不等式f(x)>1的解集;(2)若x∈(0,1)时不等式f(x)>x成立,求a的取值范围.【解答】解:(1)当a=1时,f(x)=|x+1|﹣|x﹣1|,由f(x)>1,∴或,解得x,故不等式f(x)>1的解集为(,+∞),(2)当x∈(0,1)时不等式f(x)>x成立,∴|x+1|﹣|ax﹣1|﹣x>0,即x+1﹣|ax﹣1|﹣x>0,即|ax﹣1|<1,∴﹣1<ax﹣1<1,∴0<ax<2,∵x∈(0,1),∴a>0,∴0<x,∴a∵2,∴0<a≤2,故a的取值范围为(0,2].3.【2017年新课标1理科23】已知函数f(x)=﹣x2+ax+4,g(x)=|x+1|+|x﹣1|.(1)当a=1时,求不等式f(x)≥g(x)的解集;(2)若不等式f(x)≥g(x)的解集包含[﹣1,1],求a的取值范围.【解答】解:(1)当a=1时,f(x)=﹣x2+x+4,是开口向下,对称轴为x的二次函数,g(x)=|x+1|+|x﹣1|,当x∈(1,+∞)时,令﹣x2+x+4=2x,解得x,g(x)在(1,+∞)上单调递增,f(x)在(1,+∞)上单调递减,∴此时f(x)≥g(x)的解集为(1,];当x∈[﹣1,1]时,g(x)=2,f(x)≥f(﹣1)=2.当x∈(﹣∞,﹣1)时,g(x)单调递减,f(x)单调递增,且g(﹣1)=f(﹣1)=2.综上所述,f(x)≥g(x)的解集为[﹣1,];(2)依题意得:﹣x2+ax+4≥2在[﹣1,1]恒成立,即x2﹣ax﹣2≤0在[﹣1,1]恒成立,则只需,解得﹣1≤a≤1,故a的取值范围是[﹣1,1].4.【2016年新课标1理科24】已知函数f(x)=|x+1|﹣|2x﹣3|.(Ⅰ)在图中画出y=f(x)的图象;(Ⅱ)求不等式|f(x)|>1的解集.【解答】解:(Ⅰ)f(x),由分段函数的图象画法,可得f(x)的图象,如右:(Ⅱ)由|f(x)|>1,可得当x≤﹣1时,|x﹣4|>1,解得x>5或x<3,即有x≤﹣1;当﹣1<x时,|3x﹣2|>1,解得x>1或x,即有﹣1<x或1<x;当x时,|4﹣x|>1,解得x>5或x<3,即有x>5或x<3.综上可得,x或1<x<3或x>5.则|f(x)|>1的解集为(﹣∞,)∪(1,3)∪(5,+∞).5.【2014年新课标1理科24】若a>0,b>0,且.(Ⅰ)求a3+b3的最小值;(Ⅱ)是否存在a,b,使得2a+3b=6?并说明理由.【解答】解:(Ⅰ)∵a>0,b>0,且,∴2,∴ab≥2,当且仅当a=b时取等号.∵a3+b3 ≥224,当且仅当a=b时取等号,∴a3+b3的最小值为4.(Ⅱ)∵2a+3b≥22,当且仅当2a=3b时,取等号.而由(1)可知,2246,故不存在a,b,使得2a+3b=6成立.6.【2013年新课标1理科24】已知函数f(x)=|2x﹣1|+|2x+a|,g(x)=x+3.(Ⅰ)当a=﹣2时,求不等式f(x)<g(x)的解集;(Ⅱ)设a>﹣1,且当x∈[,]时,f(x)≤g(x),求a的取值范围.【解答】解:(Ⅰ)当a=﹣2时,求不等式f(x)<g(x)化为|2x﹣1|+|2x﹣2|﹣x﹣3<0.设y=|2x﹣1|+|2x﹣2|﹣x﹣3,则y,它的图象如图所示:结合图象可得,y<0的解集为(0,2),故原不等式的解集为(0,2).(Ⅱ)设a>﹣1,且当x∈[,]时,f(x)=1+a,不等式化为1+a≤x+3,故x≥a﹣2对x∈[,]都成立.故a﹣2,解得a,故a的取值范围为(﹣1,].7.【2012年新课标1理科24】已知函数f(x)=|x+a|+|x﹣2|①当a=﹣3时,求不等式f(x)≥3的解集;②f(x)≤|x﹣4|若的解集包含[1,2],求a的取值范围.【解答】解:(1)当a=﹣3时,f(x)≥3 即|x﹣3|+|x﹣2|≥3,即,可得x≤1;,可得x∈∅;,可得x≥4.取并集可得不等式的解集为 {x|x≤1或x≥4}.(2)原命题即f(x)≤|x﹣4|在[1,2]上恒成立,等价于|x+a|+2﹣x≤4﹣x在[1,2]上恒成立,等价于|x+a|≤2,等价于﹣2≤x+a≤2,﹣2﹣x≤a≤2﹣x在[1,2]上恒成立.故当 1≤x≤2时,﹣2﹣x的最大值为﹣2﹣1=﹣3,2﹣x的最小值为0,故a的取值范围为[﹣3,0].8.【2011年新课标1理科24】设函数f(x)=|x﹣a|+3x,其中a>0.(Ⅰ)当a=1时,求不等式f(x)≥3x+2的解集(Ⅱ)若不等式f(x)≤0的解集为{x|x≤﹣1},求a的值.【解答】解:(Ⅰ)当a=1时,f(x)≥3x+2可化为|x﹣1|≥2.由此可得x≥3或x≤﹣1.故不等式f(x)≥3x+2的解集为{x|x≥3或x≤﹣1}.(Ⅱ)由f(x)≤0得|x﹣a|+3x≤0此不等式化为不等式组或即或因为a>0,所以不等式组的解集为{x|x}由题设可得1,故a=29.【2010年新课标1理科24】设函数f(x)=|2x﹣4|+1.(Ⅰ)画出函数y=f(x)的图象:(Ⅱ)若不等式f (x )≤ax 的解集非空,求a 的取值范围. 【解答】解:(Ⅰ)由于f (x ),函数y =f (x )的图象如图所示.(Ⅱ)由函数y =f (x )与函数y =ax 的图象可知,极小值在点(2,1)当且仅当a <﹣2或a 时,函数y =f (x )与函数y =ax 的图象有交点.故不等式f (x )≤ax 的解集非空时,a 的取值范围为(﹣∞,﹣2)∪[,+∞).考题分析与复习建议本专题考查的知识点为:解绝对值不等式、证明不等式、利用不等式恒成立求参数的值或范围,求含有绝对值的函数最值也是考查的热点.求解的一般方法是去掉绝对值,也可以借助数形结合求解.历年考题主要以解答题题型出现,重点考查的知识点为解绝对值不等式、证明不等式、利用不等式恒成立求参数的值或范围,求含有绝对值的函数最值也是考查的热点.预测明年本考点题目会比较稳定,备考方向以知识点解绝对值不等式、利用不等式恒成立求参数的值或范围,证明不等式为重点较佳.最新高考模拟试题1.已知函数()22()f x x a x a R =-+-∈. (1)当2a =时,求不等式()2f x >的解集;(2)若[2,1]x ∈-时不等式()32f x x ≤-成立,求实数a 的取值范围. 【答案】(1)2{|3x x <或()4cos(2)6f x x π=-;(2)空集. 【解析】解:(1)不等式()2f x >,即2222x x -+->.可得22222x x x ≥⎧⎨-+->⎩,或122222x x x <<⎧⎨-+->⎩或12222x x x ≤⎧⎨--+>⎩,解得23x <或2x >,所以不等式的解集为2{|2}3x x x <>或.(2)当[2,1]x ∈-时,220x -<,所以()22f x x a x =-+-, 由()32f x x ≤-得1x a -≤,即11a x a -≤≤+,则1211a a -≤-⎧⎨+≥⎩,该不等式无解,所以实数a 的取值范围是空集(或者∅). 2.已知()221f x x x =-++. (1)求不等式()6f x <的解集;(2)设m 、n 、p 为正实数,且()3m n p f ++=,求证:12mn np pm ++≤. 【答案】(1) ()1,3- (2)见证明 【解析】(1)①2x ≥时,()24133f x x x x =-++=-, 由()6f x <,∴336x -<,∴3x <,即23x ≤<,②12x -<<时,()4215f x x x x =-++=-,由()6f x <,∴56x -<,∴1x >-,即12x -<<, ③1x ≤-时,()42133f x x x x =---=-,由()6f x <,∴336x -<,∴1x >-,可知无解, 综上,不等式()6f x <的解集为()1,3-; (2)∵()221f x x x =-++,∴()36f =,∴()36m n p f ++==,且,,m n p 为正实数∴()222222236m n p m n p mn mp np ++=+++++=, ∵222m n mn +≥,222m p mp +≥,222n p np +≥, ∴222m n p mn mp np ++≥++,∴()()2222222363m n p m n p mn mp np mn mp np ++=+++++=≥++ 又,,m n p 为正实数,∴可以解得12mn np pm ++≤. 3.[选修4—5:不等式选讲]已知函数()|||2|(0)f x x m x m m =--+>. (1)当1m =,求不等式()1f x ≥的解集;(2)对于任意实数,x t ,不等式()21f x t t <++-恒成立,求实数m 的取值范围. 【答案】(1)113x x ⎧⎫-≤≤-⎨⎬⎩⎭;(2)()0,2 【解析】(1)当1m =时,()1f x ≥为:1211x x --+≥当1x ≥时,不等式为:1211x x ---≥,解得:3x ≤-,无解当112x -≤<时,不等式为:1211x x -+--≥,解得:13x ≤-,此时1123x -≤≤- 当12x <-时,不等式为:1211x x -+++≥,解得:1x -≥,此时112x -≤<-综上所述,不等式的解集为113x x ⎧⎫-≤≤-⎨⎬⎩⎭(2)对于任意实数x ,t ,不等式()21f x t t <++-恒成立等价于()()max min |2||1|f x t t <++- 因为|2||1||(2)(1)|3t t t t ++-≥+--=,当且仅当(2)(1)0t t +-≤时等号成立 所以()min |2||1|3t t ++-=因为0m >时,()2f x x m x m =--+=2,23,22,m x m x m x x m x m x m ⎧+<-⎪⎪⎪--≤≤⎨⎪-->⎪⎪⎩,函数()f x 单调递增区间为(,)2m -∞-,单调递减区间为(,)2m-+∞ ∴当2m x =-时,()max 322m mf x f ⎛⎫=-= ⎪⎝⎭332m∴<,又0m >,解得:02m << ∴实数m 的取值范围()0,24.选修4-5不等式选讲已知关于x 的不等式20x m x -+≤的解集为{|2}x x ≤-,其中0m >. (1)求m 的值;(2)若正数a ,b ,c 满足a b c m ++=,求证:2222b c aa b c++≥.【答案】(1)2m =(2)见证明 【解析】(1)由题意知:20x m x -+≤即20x m x m x ≥⎧⎨-+≤⎩或20x mm x x ≤⎧⎨-+≤⎩化简得:3x mm x ≥⎧⎪⎨≤⎪⎩或x m x m ≤⎧⎨≤-⎩ 0m >Q ∴不等式组的解集为{}x x m ≤- 2m ∴-=-,解得:2m =(2)由(1)可知,2a b c ++=由基本不等式有:22b a b a +≥,22c b c b+≥,22a c a c +≥三式相加可得:222222b c a a b c b c a a b c +++++≥++222b c a a b c a b c ∴++≥++,即:2222b c a a b c++≥ 5.选修4-5:不等式选讲 已知函数()13f x x x a =+++ (1)当1a =-时,解不等式()2f x ≥;(2)若存在0x 满足00()211f x x ++<,求实数a 的取值范围. 【答案】(1) 1|02x x x ⎧⎫≤≥⎨⎬⎩⎭或 (2) 24a << 【解析】(1)当1a =-时,()|1||31|f x x x =++-,当13x ≥时,不等式等价于1312x x ++-≥,解得12x ≥,12x ∴≥; 当113x -<<时,不等式等价于1312x x +-+≥,解得0x ≤,10x ∴-<≤;当1x ≤-时,不等式等价于1312x x ---+≥,解得12x ≤-,1x -∴≤.综上所述,原不等式的解集为1|02x x x ⎧⎫≤≥⎨⎬⎩⎭或. (2)由()00211f x x ++<,得003131x x a +++<,而()()000000313333333|3|x x a x x a x x a a +++=+++≥+-+=-, (当且仅当()()003330x x a ++≤时等号成立) 由题可知min (()2|1|)1f x x ++<,即31a -<, 解得实数a 的取值范围是24a <<. 6.已知函数()|2|f x ax =-.(Ⅰ)当4a =时,求不等式()|42|8f x x ++≥的解集;(Ⅱ)若[2,4]x ∈时,不等式()|3|3f x x x +-≤+成立,求a 的取值范围.【答案】(I )(,1][1,)-∞-+∞U ;(II )[1,2]- 【解析】(I )当4a =时,原不等式即|42||42|8x x -++≥,即|21||21|4x x -++≥.当12x ≥时,21214x x -++≥,解得1x ≥,∴1x ≥; 当1122x -≤≤时,12214x x -++≥,无解;当12x ≤-时,12214x x ---≥,解得1x ≤-,∴1x ≤-;综上,原不等式的解集为(,1][1,)-∞-+∞U(II )由()|3|3f x x x +-≤+得|2||3|3ax x x -+-≤+(*) 当[2,3]x ∈时,(*)等价于|2|33|2|2ax x x ax x -+-≤+⇔-≤即22a x -≤,所以2222a x x -+≤≤+恒成立,所以813a -≤≤ 当(3,4]x ∈时,(*)等价于|2|33|2|6ax x x ax -+-≤+⇔-≤ 即48ax -≤≤,所以48a x x-≤≤恒成立,所以12a -≤≤ 综上,a 的取值范围是[1,2]-7.已知函数()21f x x x a =-++,()2g x x =+. (1)当1a =-时,求不等式()()f x g x <的解集;(2)设12a >-,且当1,2x a ⎡⎫∈-⎪⎢⎣⎭,()()f x g x ≤,求a 的取值范围.【答案】(1)()0,2;(2)11,23⎛⎤- ⎥⎝⎦ 【解析】(1)当1a =-时,不等式()()f x g x <化为:21120x x x -+---<当12x ≤时,不等式化为12120x x x -+---<,解得:102x <≤当112x <≤时,不等式化为21120x x x -+---<,解得:112x <≤当1x >时,不等式化为21120x x x -+---<,解得:12x << 综上,原不等式的解集为()0,2 (2)由12a x -≤<,得221a x -≤<,21210a x --≤-< 又102x a a ≤+<+ 则()()211f x x x a x a =--++=-++∴不等式()()f x g x ≤化为:12x a x -++≤+得21a x ≤+对1,2x a ⎡⎫∈-⎪⎢⎣⎭都成立 21a a ∴≤-+,解得:13a ≤又12a >-,故a 的取值范围是11,23⎛⎤- ⎥⎝⎦8.已知函数()|2|f x x =-.(Ⅰ)求不等式()|1|f x x x <++的解集;(Ⅱ)若函数5log [(3)()3]y f x f x a =++-的定义域为R ,求实数a 的取值范围.【答案】(I )1,3⎛⎫+∞ ⎪⎝⎭(II )(,1)-∞【解析】解:(I )由已知不等式()|1|f x x x <++,得|2||1|x x x -<++, 当2x ≥时,不等式为21x x x -<++,解得3x >-,所以2x ≥; 当12x -<<时,不等式为21x x x -<++,解得13x >,所以123x <<; 当1x ≤-时,不等式为21x x x -<--,解得3x >,此时无解. 综上:不等式的解集为1,3⎛⎫+∞ ⎪⎝⎭.(II )若5log [(3)()3]y f x f x a =++-的定义域为R ,则(3)()30f x f x a ++->恒成立. ∵|1||2|3|12|333x x a x x a a ++--≥+-+-=-,当且仅当[1,2]x ∈-时取等号. ∴330a ->,即1a <.所以实数a 的取值范围是(,1)-∞. 9.已知函数()123f x x x =-+-. (Ⅰ)解关于x 的不等式()4f x ≤;(Ⅱ)若()20f x m m -->恒成立,求实数m 的取值范围.【答案】(Ⅰ)111,3⎡⎤⎢⎥⎣⎦;(Ⅱ)()2,1-.【解析】解:(I )当1x ≤时,不等式为:()1234x x -+-≤,解得1x ≥,故1x =. 当13x <<时,不等式为:()1234x x -+-≤,解得1x ≥,故13x <<1<x <3, 当3x ≥时,不等式为:()1234x x -+-≤,解得113x ≤,故1133x ≤≤. 综上,不等式()4f x ≤的解集为111,3⎡⎤⎢⎥⎣⎦.(II )由()20f x m m -->恒成立可得()2m m f x +<恒成立.又()37,35,1337,1x x f x x x x x -≥⎧⎪=-+<<⎨⎪-+≤⎩,故()f x 在(],1-∞上单调递减,在()1,3上单调递减,在[)3,+∞上单调递增,∴()f x 的最小值为()32f =. ∴22m m +<,解得21m -<<. 即m 的最值范围是()2,1-.10.已知函数()211f x x x =-++. (Ⅰ)解不等式()3f x ≥;(Ⅱ)记函数()f x 的最小值为m ,若,,a b c 均为正实数,且232a b c m ++=,求222a b c ++的最小值. 【答案】(Ⅰ){}11x x x ≤-≥或;(Ⅱ)914. 【解析】(Ⅰ)由题意, 3,11()2,1213,2x x f x x x x x ⎧⎪-≤-⎪⎪=--<<⎨⎪⎪≥⎪⎩,所以()3f x ≥等价于133x x ≤-⎧⎨-≥⎩或11223x x ⎧-<<⎪⎨⎪-≥⎩或1233x x ⎧≥⎪⎨⎪≥⎩.解得:1x ≤-或1x ≥,所以不等式的解集为{}11x x x ≤-≥或; (Ⅱ)由(1)可知,当12x =时, ()f x 取得最小值32,所以32m =,即233a b c ++=, 由柯西不等式得2222222()(123)(23)9a b c a b c ++++≥++=, 整理得222914a b c ++≥, 当且仅当123a b c ==时, 即369,,141414a b c ===时等号成立.所以222a b c ++的最小值为914.11.已知函数()12f x x a x =+++. (Ⅰ)求1a =时,()3f x ≤的解集;(Ⅱ)若()f x 有最小值,求a 的取值范围,并写出相应的最小值. 【答案】(Ⅰ)[3,0]-; (Ⅱ)见解析. 【解析】(Ⅰ)当1a =时,232()12121231x x f x x x x x x --≤-⎧⎪=+++=-<<-⎨⎪+≥-⎩∵()3f x ≤当2x -≤时()233f x x =--≤解得32x -≤≤-当21x -<<-时()13f x =≤恒成立当1x -≥时()233f x x =+≤解得10x -≤≤ 综上可得解集[3,0]-.(Ⅱ)(1)212()12(1)2121(1)211a x a x f x x a x a x a x a x a x -+--≤-⎧⎪=+++=-+--<<-⎨⎪+++≥-⎩当(1)0a -+>,即1a <-时,()f x 无最小值; 当(1)0a -+=,即1a =-时,()f x 有最小值1-;当(1)0a -+<且10a -≤,即11a -<≤时, min ()(1)f x f a =-= 当(1)0a -+<且10a ->,即1a >时, min ()(2)1f x f =-= 综上:当1a <-时,()f x 无最小值; 当1a =-时,()f x 有最小值1-;当11a -<≤时, min ()(1)f x f a =-= ; 当1a >时, min ()(2)1f x f =-=; 12.选修4-5:不等式选讲 已知函数()|23||1|f x x x =--+. (1)求不等式()6f x ≤的解集;(2)设集合M 满足:当且仅当x M ∈时,()|32|f x x =-,若,a b M ∈,求证:228223a b a b -++≤. 【答案】(1) {}210x x -≤≤;(2)见解析. 【解析】(1)()4,1323132,1234,2x x f x x x x x x x ⎧⎪-+<-⎪⎪=--+=-+-≤≤⎨⎪⎪->⎪⎩当1x <- 时,46x -+≤ ,得2x -≥ ,故21x -≤<-; 当312x -≤≤时,326x -+≤ ,得43x ≥- ,故312x -≤<;当32x >时,46x -≤ ,得10x ≤ ,故3102x <≤; 综上,不等式()6f x ≤的解集为{}210x x -≤≤(2)由绝对值不等式的性质可知()231(23)(1)32f x x x x x x =--+≤-++=- 等价于23(1)32x x x -≤-++-,当且仅当(23)(1)0x x -+≤,即213x -≤≤时等号成立,故21,3M ⎡⎤=-⎢⎥⎣⎦所以221,133a b -≤≤-≤≤, 所以222510(1),4(1)99a b ≤-≤-≤--≤-, 即228(1)(1)3a b ---≤.13.[选修4—5:不等式选讲] 已知函数()31f x x m x m =---- (1)若1m =,求不等式()1f x <的解集.(2)对任意的x R ∈,有()(2)f x f ≤,求实数m 的取值范围. 【答案】(1)(,3)-∞;(2)1123m -≤≤ 【解析】(1)()141f x x x =---<,所以11441(4)11(4)1141x x x x x x x x x <≤≤>⎧⎧⎧⎨⎨⎨---<---<--+<⎩⎩⎩或或解之得不等式()1f x <的解集为(,3)-∞. (2)当131,2m m m +>>-时,由题得2必须在3m+1的右边或者与3m+1重合, 所以1231,3m m ≥+∴≤,所以1123m -<≤,当131,2m m m +==-时,不等式恒成立,当131,2m m m +<<-时,由题得2必须在3m+1的左边或者与3m+1重合,由题得1231,3m m ≤+≥,所以m 没有解.综上,1123m -≤≤. 14.已知()21f x x x =+-. (1)证明()1f x x +≥; (2)若,,a b c +∈R ,记33311134abc a b c +++的最小值为m ,解关于x 的不等式()f x m <. 【答案】(1)见证明;(2) 2433x x ⎧⎫-<<⎨⎬⎩⎭【解析】(1)()2212211f x x x x x x +=+-≥-+=.当且仅当()2x 2x 10-≤,等号成立(2)∵333333311131333333234444abc abc abc abc m a b c a b c abc abc +++≥+=+≥⋅==,当且仅当a=b=c 等号成立由不等式()3f x <即()213f x x x =+-<.由()31,01211,02131,2x x f x x x x x x x ⎧⎪-+≤⎪⎪=+-=-<<⎨⎪⎪-≥⎪⎩得:不等式()3f x <的解集为2433x x ⎧⎫-<<⎨⎬⎩⎭.15.选修4—5:不等式选讲已知函数()11f x x mx =++-,m R ∈。
(整理)全国各地高考数学真题分章节分类汇编之复数

2010年全国各地高考数学真题分章节分类汇编之复数一、选择题:1.(2010年高考山东卷理科2)已知(a,b∈R),其中i为虚数单位,则a+b=(A)-1 (B)1 (C)2 (D)3【答案】B【解析】由得,所以由复数相等的意义知:,所以1,故选B.【命题意图】本题考查复数相等的意义、复数的基本运算,属保分题。
2.(2010年高考全国卷I理科1)复数(A)i(B) (C)12-13 (D) 12+13【答案】A【解析】.【命题意图】本小题主要考查复数的基本运算,重点考查分母实数化的转化技巧. 3.(2010年高考湖北卷理科1)若为虚数单位,图中复平面内点z表示复数z,则表示复数的点是A.EB.FC.GD.H【答案】D【解析】由图知z=,所以,故选D。
4.(2010年高考福建卷理科9)对于复数,若集合具有性质“对任意,必有”,则当时,等于( )A.1B.-1C.0D.【答案】B【解析】由题意,可取,所以,选B。
【命题意图】本题属创新题,考查复数与集合的基础知识。
5.(2010年高考安徽卷理科1)是虚数单位,A、B、C、D、1.B【解析】,选B.【规律总结】为分式形式的复数问题,化简时通常分子与分母同时乘以分母的共轭复数,然后利用复数的代数运算,结合得结论.6.(2010年高考天津卷理科1)i是虚数单位,复数=(A)1+i (B)5+5i (C)-5-5i (D)-1-i【答案】A【解析】,故选A。
【命题意图】本小题考查复数的基本运算,属保分题。
7.(2010年高考广东卷理科2)若复数z1=1+i,z2=3-i,则z1·z2=()A.4+2 i B. 2+ i C. 2+2 i D.3【答案】A【解析】。
8.(2010年高考四川卷理科1)i是虚数单位,计算i+i2+i3=(A)-1(B)1(C)(D)解析:由复数性质知:i2=-1故i+i2+i3=i+(-1)+(-i)=-1答案:A9. (2) (2010年全国高考宁夏卷2)已知复数,是z的共轭复数,则=A. B. C.1 D.2【答案】A解析:,所以.另解:,下略.10.(2010年高考陕西卷理科2)复数在复平面上对应的点位于(A)(A)第一象限(B)第二象限(C)第三象限(D)第四象限【答案】A【解析】∵,∴复数在复平面上对应的点位于第一象限.故选.11.(2010年高考江西卷理科1)已知,则实数,分别为A., B.,C.,D.,【答案】D12.(2010年高考浙江卷5)对任意复数z=x+yi (x,y∈R),i为虚数单位,则下列结论正确的是【答案】D13.(2010年高考辽宁卷理科2)设a,b为实数,若复数,则(A)(B)(C) (D)【答案】A14.(2010年高考全国2卷理数1)复数(A)(B)(C)(D)【答案】A【命题意图】本试题主要考查复数的运算.【解析】.二、填空题:1.(2010年高考江苏卷试题2)设复数z满足z(2-3i)=6+4i(其中i为虚数单位),则z的模为______▲_____.【答案】2[解析] 考查复数运算、模的性质。
2010—2019“十年高考”数学真题分类汇总 复数部分 理数(附参考答案)

17.(2016 年全国 I)设 (1 i)x 1 yi ,其中 x, y 是实数,则 x yi =
A.1
B. 2
C. 3
D.2
【答案】B. 18.(2016 年全国 II)已知 z (m 3) (m 1)i 在复平面内对应的点在第四象限,则实数 m
的取值范围是
A. 3,1
B.第二象限
C.第三象限
D.第四象限
【答案】B.
23.(2015
山东)若复数
z
z
满足
1i
i
,其中 i
为虚数单位,则
z
=
A.1 i
B.1 i
C. 1 i
D. 1 i
【答案】A.
24.(2015 四川)设 i 是虚数单位,则复数 i3 2 = i
A. i
B. 3i
C. i
D. 3i
57.(2011 山东)复数 z = 2 i ( i 为虚数单位)在复平面内对应的点所在象限为 2i
A.第一象限
B.第二象限
C.第三象限
D.第四象限
【答案】D.
58.(2011 安徽)设 i 是虚数单位,复数 ai 为纯虚数,则实数 a 为 i
A.2
B. 2
C.
D.
B. 1,3
C. 1 , +
D. - , 3
【答案】A.
19.(2016 年全国 III)若 z 1 2i ,则 4i zz 1
A.1
B. 1
C.i
D. i
【答案】C.
20.(2015
新课标
1)设复数
z
1
满足
2010-2019年十年高考数学真题分类汇编.docx

A.1
B.2
C.3
D.4
31(. 2017Ⅲ理 1)已知集合 A = (x, y) x2 + y2 = 1 ,B = (x, y) y = x ,则 A I B 中元素的个数为( )
A.3
B.2
C.1
D.0
32.(2018Ⅰ文 1)已知集合 A = 0,2 , B = -2,-1,0,1,2 ,则 A I B = ( )
A.(-14,16)
B.(-14,20)
C.(-12,18)
D.(-12,20)
x-3 2.(2010Ⅱ文 2)不等式 0 的解集为( )
x+2
A.{x|-2< x<3} B.{ x|x<-2}
C.{ x|x<-2,或 x>3} D.{ x∣x>3}
x -1
3.(2010Ⅱ文
5
理
3)若变量
x,y
1.集合
1.(2010Ⅰ文理 1)已知集合 A = x | x 2,x R,B = x | x 4,x Z ,则 A I B =( )
A.(0,2)
B.[0,2]
C.{0,2}
D.{0,1,2}
2.(2010Ⅱ文 1)设全集 U= x N * | x 6 ,集合 A={1,3},B={3,5},则 CU A U B =( )
A.{-1,0}
B.{0,1}
C.{-1,0,1}
D.{0,1,2}
20.(2016Ⅰ文 1)设集合 A={1,3,5,7},B={x| 2 x 5},则 A∩B=( )
A.{1,3}
B.{3,5}
C.{5,7}
D.{1,7}
21.(2016Ⅰ理 1)设集合 A={x|x2-4x+3<0},B={x|2x-3>0},则 A I B = ( )
十年高考真题分类汇编(2010—2019)数学(20210417120444)

十年高考真题分类汇编(2010—2019)数学专题空间向量1. (2014 •全国2 •理T11)直三棱柱ABC-A6C 、中,N%4R00 ,MN 分别是A £, A6的中 点,则6y 与4V 所成角的余弦值为() r 同 u.— 102. (2013 •北京•文T8)如图,在正方体被〃中,尸为对角线做的三等分点,尸到各顶点的距离的不同取值有()3. (2012 •陕西•理T5)如图,在空间直角坐标系中有直三棱柱板。
1二8与纸则直线与直线必夹角的余弦值为(4. (2010 •大纲全国•文T6)直三棱柱ABC-ABQ 中,若NBAC =90° ,AB=AC=AA1,则异面直线BA : 与AQ 所成的角等于()A. 30°B. 45°C. 60°D. 90°5. (2019 •天津•理 T17)如图,AE,平面 ABCD, CF 〃AE , AD 〃BC, AD_LAB, AB=AD=1, AE=BC 二2.(1)求证:BF 〃平面ADE;B -l B. 4个C 5个 D.6个A.3个 C.这⑵求直线CE与平面BDE所成角的正弦值;⑶若二面角E-BD-F的余弦值为京求线段CF的长.EB6.(2019 •浙江• T 19)如图,已知三棱柱ABC-A&C,平面 4月平面ABC, ZABC^0° , Z 区灰>30° ,4月引。
泡尸分别是〃;43的中点.(1)证明:年J_6C;⑵求直线房与平面46。
所成角的余弦值.7.(2019 •全国1•理T18)如图,直四棱柱极〃的底面是菱形,例=1,止2, N 员切40° ,EM,V分别是比破,4。
的中点.⑴证明:/V〃平面C、DE;(2)求二面角力T4M的正弦值.8.(2019 •全国2 •理T17)如图,长方体力用a-4£4〃的底面月颜是正方形,点£在棱前[上,龙LEG.⑴证明:麻山平面微a;⑵若AE=A^求二面角B-EC-C的正弦值.9.(2019 •全国3 •理T19)图1是由矩形ADEB,Rt^ABC和菱形BFGC组成的一个平面图形,其中AB=1, BE=BF=2, ZFBC=60° .将其沿AB, BC折起使得BE与BF重合,连接DG,如图2.(1)证明:图2中的A, C, G, D四点共面,且平面ABC_L平面BCGE;(2)求图2中的二面角B-CG-A的大小.10.(2018 •浙江• T 8)已知四棱锥S-ABCD的底面是正方形,侧棱长均相等,E是线段AB 上的点(不含端点).设SE与BC所成的角为01,SE与平面ABCD所成的角为82,二面角S-AB-C的平面角为83,则()A.01<02<03B.03<02<61C.01<O3<02D.92<03<0111.(2018 •全国3 •理T19)如图,边长为2的正方形4加9所在的平面与半圆弧曲所在平面垂直,"是曲上异于的点.(1)证明:平面AMD_L平面BMC;⑵当三棱锥M-ABC体积最大时,求面MAB与面MCD所成二面角的正弦值.12.(2018 •北京•理T16)如图,在三棱柱ABC-A瓜&中,CC_L平面ABCM & F, G分别为44:, AQ 4Q 能的中点,AB二BC二遍,AC=AA尸2.⑴求证:AC_L平面BEF;(2)求二面角B-CD-G的余弦值;16.(2018 •浙江• T9)如图,已知多面体ABCA瓜心, 44 £5 均垂直于平面ABC, Z板=120° , A.A^ GC=1, AB=BC=B-.B=^.(1)证明:四_L平面4A4;⑵求直线月a与平面月期所成的角的正弦值.17.(2018 •上海,T17)已知圆锥的顶点为P,底面圆心为0,半径为2.(1)设圆锥的母线长为4,求圆锥的体积;(2)设P0=4, 0A, 0B是底面半径,且NA0B=90° , M为线段AB的中点,如图,求异面直线PM与0B 所成的角的大小.18.(2017 •北京•理T16)如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD,平面ABCD, 点M在线段PB上,PD〃平面MAC, PA=PD二遍,AB=4.⑴求证:M为PB的中点;(2)求二面角B-PD-A的大小;⑶求直线MC与平面BDP所成角的正弦值.19.(2017 •全国 1 •理 T18)如图,在四棱锥 P-ABCD 中,AB〃CD,且NBAP=NCDP=90。
2010-2019年全国各地高考数学真题汇编-专题17 复数(含解析)(可编辑)

2010-2019年全国各地高考数学真题汇编专题17复数1.(2019·全国1·文T1)设z=3-i1+2i,则|z|= ()A.2B.√3C.√2D.12.(2019·全国3·理T2文T2)若z(1+i)=2i,则z=( )A.-1-iB.-1+iC.1-iD.1+i3.(2019·北京·理T1文T2)已知复数z=2+i,则z·z=()A.√3B.√5C.3D.54.(2019·全国2·文T2)设z=i(2+i),则z=( )A.1+2iB.-1+2iC.1-2iD.-1-2i5.(2019·全国1·理T2)设复数z满足|z-i|=1,z在复平面内对应的点为(x,y),则( )A.(x+1)2+y2=1B.(x-1)2+y2=1C.x2+(y-1)2=1D.x2+(y+1)2=16.(2019·全国2·理T2)设z=-3+2i,则在复平面内对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限7.(2018·全国1·理T1文T2)设z=1-i1+i+2i,则|z|=()A.0B.12C.1D.√28.(2018·全国2·理T1)1+2i1-2i=()A.-45−35i B.-45+35iC.-35−45i D.-35+45i9.(2018·全国2·文T1)i(2+3i)=( )A.3-2iB.3+2i10.(2018·全国3·理T2文T2)(1+i)(2-i)=( )A.-3-iB.-3+iC.3-iD.3+i的共轭复数对应的点位于( ) 11.(2018·北京·理T2文T2)在复平面内,复数11-iA.第一象限B.第二象限C.第三象限D.第四象限12.(2018·浙江·4)复数2(i为虚数单位)的共轭复数是( )1-iA.1+iB.1-iC.-1+iD.-1-i13.(2017·全国1·理T3)设有下面四个命题p1:若复数z满足1∈R,则z∈R;p2:若复数z满足z2∈R,则z∈R;p3:若复数z1,z2满足z1z2∈R,则z1=z2;p4:若复数z∈R,则z∈R.其中的真命题为( )A.p1,p3B.p1,p4C.p2,p3D.p2,p4=( )14.(2017·全国2·理T1)3+i1+iA.1+2iB.1-2iC.2+iD.2-i15.(2017·全国2·文T2)(1+i)(2+i)= ( )A.1-iB.1+3iC.3+iD.3+3i16.(2017·山东·文T2)已知i是虚数单位,若复数z满足zi=1+i,则z2=( )A.-2iB.2iC.-2D.217.(2017·全国3·理T2)设复数z满足(1+i)z=2i,则|z|=( )A.1B.√2C.√2D.218.(2017·全国1·文T3)下列各式的运算结果为纯虚数的是( )A.i(1+i)2B.i2(1-i)19.(2017·山东·理T2)已知a∈R,i是虚数单位.若z=a+√3i,z·z=4,则a=()A.1或-1B.√7或-√7C.-√3D.√320.(2017·全国3·文T2)复平面内表示复数z=i(-2+i)的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限21.(2017·北京·理T2)若复数(1-i)(a+i)在复平面内对应的点在第二象限,则实数a的取值范围是( )A.(-∞,1)B.(-∞,-1)C.(1,+∞)D.(-1,+∞)22.(2016·全国2·理T1)已知z=(m+3)+(m-1)i在复平面内对应的点在第四象限,则实数m的取值范围是( )A.(-3,1)B.(-1,3)C.(1,+∞)D.(-∞,-3)=()23.(2016·全国3·理T2)若z=1+2i,则zz-1A.1B.-1C.iD.-I=()24.(2016·北京·文T2)复数1+2i2-iA.iB.1+iC.-iD.1-I25.(2016·全国1·理T2)设(1+i)x=1+yi,其中x,y是实数,则|x+yi|=( )A.1B.√2C.√3D.226.(2016·全国1·文T2)设(1+2i)(a+i)的实部与虚部相等,其中a为实数,则a=( )A.-3B.-2C.2D.327.(2016·全国2·文T2)设复数z满足z+i=3-i,则z=( )A.-1+2iB.1-2iC.3+2iD.3-2i28.(2016·全国3·文T2)若z=4+3i,则z|z|= ()A.1B.-1C.45+35i D.45−35i29.(2016·山东·理T1)若复数z满足2z+z=3-2i,其中i为虚数单位,则z=( )A.1+2iB.1-2iC.-1+2iD.-1-2i30.(2015·全国2·理T2)若a为实数,且(2+ai)·(a-2i)=-4i,则a=( )A.-1B.0C.1D.231.(2015·全国·文T3)已知复数z满足(z-1)i=1+i,则z=( )A.-2-iB.-2+iC.2-iD.2+i32.(2015·全国2·文T2)若a为实数,且2+ai1+i=3+i,则a=( )A.-4B.-3C.3D.433.(2015·安徽·文T1)设i是虚数单位,则复数(1-i)(1+2i)=( )A.3+3iB.-1+3iC.3+iD.-1+i34.(2015·湖南·文T1)已知(1-i)2z=1+i(i为虚数单位),则复数z=( ) A.1+i B.1-iC.-1+iD.-1-i35.(2015·全国1·理T1)设复数z满足1+z1-z=i,则|z|=()A.1B.√2C.√3D.236.(2015·湖北·理T1)i为虚数单位,i607的共轭复数....为( )。
(2017-2019)高考理数真题分类汇编专题17 数系的扩充与复数的引入(教师版)

专题17 数系的扩充与复数的引入1.【2019年高考北京卷理数】已知复数2i z =+,则z z ⋅=A B C .3D .5【答案】D【解析】由题2i z =+,则(2i)(2i)5z z ⋅=+-=,故选D .2.【2019年高考全国Ⅰ卷理数】设复数满足=1i z -,在复平面内对应的点为(,y ),则 A .22+11()x y += B .221(1)x y +=- C .22(1)1y x +-=D .22(+1)1y x +=【分析】本题考点为复数的运算,为基础题目,难度偏易.此题可采用几何法,根据点(,y )和点(0,1)之间的距离为1,可选正确答案为C . 【答案】C【解析】由题可得i,i (1)i,z x y z x y =+-=+-i 1,z -==则22(1)1x y +-=.故选C . 3.【2019年高考全国Ⅱ卷理数】设=–3+2i ,则在复平面内z 对应的点位于 A .第一象限 B .第二象限 C .第三象限D .第四象限【答案】C【解析】由32i,z =-+得32i,z =--则32i z =--对应的点(-3,-2)位于第三象限.故选C . 4.【2019年高考全国Ⅲ卷理数】若(1i)2i z +=,则= A .1i -- B .1i -+ C .1i -D .1i + 【答案】D 【解析】()(2i 2i 1i 1i 1i 1i 1i )()z -===+++-.故选D . 【名师点睛】本题考查复数的除法的运算,渗透了数学运算素养.采取运算法则法,利用方程思想解题. 5.【2018年高考浙江卷】复数21i-(i 为虚数单位)的共轭复数是A .1+iB .1−iC .−1+iD .−1−i【答案】B【解析】22(1i)1i 1i 2+==+-Q ,∴共轭复数为1i -,故选B . 6.【2018年高考全国Ⅰ卷理数】设1i2i 1iz -=++,则||z = A .0 B .12C .1D【答案】C【解析】因为21i (1i)2i2i +2i 2i i 1i (1i)(1i)2z ---=+==+=++-,所以1||z ==,故选C . 7.【2018年高考全国Ⅱ卷理数】12i12i+=- A .43i 55-- B .43i 55-+ C .34i 55--D .34i 55-+【答案】D【解析】由题可得212i (12i)34i12i 55++-+==-,故选D . 8.【2018年高考全国Ⅲ卷理数】(1i)(2i)+-= A .3i -- B .3i -+ C .3i -D .3i +【答案】D【解析】2(1i)(2i)2i 2i i 3i +-==-+-=+,故选D . 9.【2018年高考北京卷理数】在复平面内,复数11i-的共轭复数对应的点位于 A .第一象限 B .第二象限 C .第三象限D .第四象限【答案】D【解析】11i 11i 1i (1i)(1i)22+==+--+的共轭复数为11i 22-, 对应点为11(,)22-,在第四象限.故选D .【名师点睛】此题考查复数的四则运算,属于送分题,解题时注意审清题意,切勿不可因简单导致马虎丢分.将复数化为最简形式,求其共轭复数,找到共轭复数在复平面的对应点,判断其所在象限. 10.【2017年高考全国Ⅰ卷理数】设有下面四个命题1p :若复数满足1z ∈R ,则z ∈R ;2p :若复数满足2z ∈R ,则z ∈R ;3p :若复数12,z z 满足12z z ∈R ,则12z z =; 4p :若复数z ∈R ,则z ∈R .其中的真命题为 A .13,p p B .14,p p C .23,p pD .24,p p【答案】B【解析】令i(,)z a b a b =+∈R , 则由2211i i a b z a b a b-==∈++R 得0b =,所以z ∈R ,故1p 正确; 当i z =时,因为22i 1z ==-∈R ,而i z =∉R 知,故2p 不正确; 当12i z z ==时,满足121z z ⋅=-∈R ,但12z z ≠,故3p 不正确; 对于4p ,因为实数的共轭复数是它本身,也属于实数,故4p 正确. 故选B .【名师点睛】分式形式的复数,分子、分母同乘以分母的共轭复数,化简成i(,)z a b a b =+∈R 的形式进行判断,共轭复数只需实部不变,虚部变为原的相反数即可. 11.【2017年高考全国Ⅱ卷理数】3i1i+=+ A .12i + B .12i - C .2i +D .2i -【答案】D【解析】由复数除法的运算法则有:3i (3i)(1i)2i 1i 2++-==-+,故选D . 【名师点睛】复数的代数形式的运算主要有加、减、乘、除.除法实际上是分母实数化的过程.在做复数的除法时,要注意利用共轭复数的性质:若1,2互为共轭复数,则1·2=|1|2=|2|2,通过分子、分母同乘以分母的共轭复数将分母实数化.12.【2017年高考全国Ⅲ卷理数】设复数满足(1+i)=2i ,则∣∣=A .12B .2C D .2【答案】C【解析】由题意可得2i1iz =+,由复数求模的法则可得1121||z z z z =,则2i1i z ===+C . 【名师点睛】共轭与模是复数的重要性质,运算性质有:(1)1212z z z z ±=±;(2)1212z z z z ⨯=⨯;(3)22z z z z ⋅==; (4)121212z z z z z z -≤±≤+;(5)1212z z z z =⨯;(6)1121||z z z z =. 13.【2017年高考北京卷理数】若复数(1i)(i)a -+在复平面内对应的点在第二象限,则实数a 的取值范围是 A .(,1)-∞ B .(,1)-∞- C .(1,)+∞D .(1,)-+∞【答案】B【解析】(1i)(i)(1)(1)i z a a a =-+=++-,因为对应的点在第二象限,所以1010a a +<⎧⎨->⎩,解得1a <-,故实数a 的取值范围是(,1)-∞-,故选B . 14.【2019年高考天津卷理数】i 是虚数单位,则5|ii|1-+的值为______________. 【分析】先化简复数,再利用复数模的定义求所给复数的模.【解析】5i (5i)(1i)|||||23i |1i (1i)(1i)---==-=++-. 15.【2019年高考浙江卷】复数11iz =+(i 为虚数单位),则||z =______________. 【分析】本题先计算,而后求其模.或直接利用模的性质计算. 容易题,注重基础知识、运算求解能力的考查.【答案】2【解析】由题可得1|||1i |2z ===+. 16.【2019年高考江苏卷】已知复数(2i)(1i)a ++的实部为0,其中i 为虚数单位,则实数a 的值是______________.【分析】本题根据复数的乘法运算法则先求得,然后根据复数的概念,令实部为0即得a 的值. 【答案】2【解析】2(2i)(1i)i 2i 2i 2(2)i a a a a a ++=+++=-++Q , 令20a -=,解得2a =.【名师点睛】本题主要考查复数的运算法则,虚部的定义等知识,意在考查学生的转化能力和计算求解能力.17.【2018年高考天津卷理数】i 是虚数单位,复数67i12i+=+______________. 【答案】4–i【解析】由复数的运算法则得:67i (67i)(12i)205i4i 12i (12i)(12i)5++--===-++-. 【名师点睛】本题主要考查复数的运算法则及其应用,意在考查学生的转化能力和计算求解能力.由题意结合复数的运算法则整理计算即可求得最终结果.18.【2018年高考江苏卷】若复数满足i 12i z ⋅=+,其中i 是虚数单位,则的实部为______________.【答案】2【解析】因为i 12i z ⋅=+,则12i2i iz +==-,则的实部为2. 19.【2017年高考天津卷理数】已知a ∈R ,i 为虚数单位,若i2ia -+为实数,则a 的值为______________.【答案】2- 【解析】因为i (i)(2i)(21)(2)i 212i 2i (2i)(2i)555a a a a a a -----+-+===-++-为实数, 所以205a +=,解得2a =-. 20.【2017年高考浙江卷】已知,ab ∈R ,2(i)34i a b +=+(i 是虚数单位),则22a b +=______________,ab =______________.【答案】5 2【解析】由题意可得222i 34i a b ab -+=+,则2232a b ab ⎧-=⎨=⎩,解得2241a b ⎧=⎨=⎩, 则225,2a b ab +==.21.【2017年高考江苏卷】已知复数(1i)(12i)z =++,其中i 是虚数单位,则的模是______________.【解析】(1i)(12i)1i 12i z =++=++==【名师点睛】(1)对于复数的四则运算,要切实掌握其运算技巧和常规思路,如(i)(i)a+b c+d =()()i(,)ac bd +ad +bc a,b,c d -∈R .(2)其次要熟悉复数相关概念,如复数i(,)a+b a b ∈R 的实部为a 、虚部为b 点为(,)a b 、共轭复数为i a b -.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【答案】A
【解析】(方法一)∵z= =1+ =1-i,
∴z2=(1-i)2=1-2i+i2=-2i.
(方法二)由zi=1+i,得(zi)2=(1+i)2,即-z2=2i.所以z2=-2i.
17.(2017·全国3·理T2)设复数z满足(1+i)z=2i,则|z|=( )
C.1-2iD.-1-2i
【答案】D
【解析】z=2i+i2=-1+2i,则 =-1-2i.故选D.
5.(2019·全国1·理T2)设复数z满足|z-i|=1,z在复平面内对应的点为(x,y),则( )
A.(x+1)2+y2=1
B.(x-1)2+y2=1
C.x2+(y-1)2=1
D.x2+(y+1)2=1
A.第一象限B.第二象限
C.第三象限D.第四象限
【答案】D
【解析】∵ i,∴ i的共轭复数为 i,而 i对应的点的坐标为 ,点 位于第四象限,故选D.
12.(2018·浙江·4)复数 (i为虚数单位)的共轭复数是( )
A.1+iB.1-i
C.-1+iD.-1-i
【答案】B
【解析】∵ =1+i,
∴复数 的共轭复数为1-i.
【答案】D
【解析】z= =1+i.故选D.
3.(2019·北京·理T1文T2)已知复数z=2+i,则z· =()
A. B. C.3D.5
【答案】D
【解析】∵z=2+i,∴ =2-i.
∴z· =(2+i)(2-i)=5. 故选D.
4.(2019·全国2·文T2)设z=i(2+i),则 =( )
A.1+2iB.-1+2i
p2:因为i2=-1∈R,而z=i∉R,故p2不正确;
p3:若z1=1,z2=2,则z1z2=2,满足z1z2∈R,而它们实部不相等,不是共轭复数,故p3不正确;
p4:实数的虚部为0,它的共轭复数是它本身,也属于实数,故p4正确.
14.(2017·全国2·理T1) =( )
A.1+2iB.1-2iC.2+iD.2-i
C.(1,+∞)
D.(-1,+∞)
【答案】B
【解析】设z=(1-i)(a+i)=(a+1)+(1-a)i,因为复数z在复平面内பைடு நூலகம்应的点
(a+1,1-a)在第二象限,所以 解得a<-1.故选B.
22.(2016·全国2·理T1)已知z=(m+3)+(m-1)i在复平面内对应的点在第四象限,则实数m的取值范围是( )
A.(-3,1)
B.(-1,3)
C.(1,+∞)
D.(-∞,-3)
13.(2017·全国1·理T3)设有下面四个命题
p1:若复数z满足 ∈R,则z∈R;
p2:若复数z满足z2∈R,则z∈R;
p3:若复数z1,z2满足z1z2∈R,则z1= ;
p4:若复数z∈R,则 ∈R.
其中的真命题为( )
A.p1,p3B.p1,p4C.p2,p3D.p2,p4
【答案】B
【解析】p1:设z=a+bi(a,b∈R),则 ∈R,所以b=0,所以z∈R.故p1正确;
【答案】C
【解析】设z=x+yi(x,y∈R).
因为z-i=x+(y-1)i,
所以|z-i|= =1,
则x2+(y-1)2=1.故选C.
6.(2019·全国2·理T2)设z=-3+2i,则在复平面内 对应的点位于( )
A.第一象限B.第二象限
C.第三象限D.第四象限
【答案】C
【解析】由z=-3+2i,得 =-3-2i,则在复平面内 对应的点(-3,-2)位于第三象限,故选C.
7.(2018·全国1·理T1文T2)设z= +2i,则|z|=()
A.0B. C.1D.
【答案】C
【解析】因为z= +2i= +2i=i,所以|z|=1.
8.(2018·全国2·理T1) =()
A.- iB.- i
C.- iD.- i
【答案】D
【解析】 =- i.
9.(2018·全国2·文T1)i(2+3i)=( )
19.(2017·山东·理T2)已知a∈R,i是虚数单位.若z=a+ i,z· =4,则a=()
A.1或-1
B. 或-
C.-
D.
【答案】A
【解析】由z=a+ i,得z· =|z|2=a2+3=4,所以a2=1,a=±1,选A.
20.(2017·全国3·文T2)复平面内表示复数z=i(-2+i)的点位于( )
【答案】D
【解析】 =2-i,故选D.
15.(2017·全国2·文T2)(1+i)(2+i)= ( )
A.1-iB.1+3iC.3+iD.3+3i
【答案】B
【解析】(1+i)(2+i)=2+3i+i2=1+3i,故选B.
16.(2017·山东·文T2)已知i是虚数单位,若复数z满足zi=1+i,则z2=( )
A.3-2iB.3+2i
C.-3-2iD.-3+2i
【答案】D
【解析】i(2+3i)=2i+3i2=-3+2i.
10.(2018·全国3·理T2文T2)(1+i)(2-i)=( )
A.-3-iB.-3+i
C.3-iD.3+i
【答案】D
【解析】(1+i)(2-i)=2+i-i2=3+i.
11.(2018·北京·理T2文T2)在复平面内,复数 的共轭复数对应的点位于( )
A.第一象限B.第二象限
C.第三象限D.第四象限
【答案】C
【解析】由题意可得z=-1-2i,在复平面内对应点(-1,-2),则该点位于第三象限.故选C.
21.(2017·北京·理T2)若复数(1-i)(a+i)在复平面内对应的点在第二象限,则实数a的取值范围是( )
A.(-∞,1)
B.(-∞,-1)
A. B.
C. D.2
【答案】C
【解析】由题意,得z= =1+i,故|z|= .
18.(2017·全国1·文T3)下列各式的运算结果为纯虚数的是( )
A.i(1+i)2B.i2(1-i)
C.(1+i)2D.i(1+i)
【答案】C
【解析】∵i(1+i)2=2i2=-2,i2(1-i)=-1+i,(1+i)2=2i,i(1+i)=-1+i,∴(1+i)2=2i为纯虚数,故选C.
十年高考真题分类汇编(2010—2019)数学
专题17复数
1.(2019·全国1·文T1)设z= ,则|z|= ()
A.2B. C. D.1
【答案】C
【解析】∵z= ,
∴z= i,
∴|z|= .
故选C.
2.(2019·全国3·理T2文T2)若z(1+i)=2i,则z=( )
A.-1-iB.-1+i
C.1-iD.1+i
