最短距离问题
线外一点到直线的最短距离

线外一点到直线的最短距离全文共四篇示例,供读者参考第一篇示例:在几何学中,我们经常会遇到这样一个问题:给定一个点和一条直线,求点到直线的最短距离。
这个问题在很多实际应用中都是非常常见的,比如在工程设计中需要确定某个点到直线的距离,或者在航海中需要确定飞行器到航线的距离。
要计算点到直线的最短距离,我们首先需要了解直线的方程以及点到直线的垂直距离的定义。
一条直线可以用方程Ax+By+C=0来表示,其中A、B、C是常数。
假设我们有一个点(x_0,y_0),我们想计算这个点到直线Ax+By+C=0的最短距离。
为了计算这个最短距离,我们可以利用点到直线的垂直距离公式。
点(x_0,y_0)到直线Ax+By+C=0的垂直距离可以表示为:d = \frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}这个公式的推导过程可以通过向量的方法来进行,但是为了简化,我们这里不展开具体的推导细节。
这个公式给出了点到直线的最短距离,我们可以通过这个公式来解决这个问题。
举例来说,假设我们有点(2,3)和直线2x+3y-6=0,我们想计算点(2,3)到直线2x+3y-6=0的最短距离。
根据上面的公式,我们可以将点的坐标和直线的系数代入公式中计算出最短距离d。
d = \frac{|2*2+3*3-6|}{\sqrt{2^2+3^2}} = \frac{1}{\sqrt{13}}通过上面的计算,我们可以得出点(2,3)到直线2x+3y-6=0的最短距离为\frac{1}{\sqrt{13}}。
这个计算过程可以很方便地通过计算机程序实现,从而解决大量点到直线距离计算的需求。
除了点到直线的最短距离,我们还可以考虑更一般的问题:线外一点到直线的最短距离。
这个问题稍微复杂一些,但是我们同样可以通过基本的几何知识和计算方法来解决。
我们可以通过直线的方程Ax+By+C=0计算直线的斜率k=-\frac{A}{B}。
然后,我们可以得到直线的法线方程y=kx+\frac{C}{B},这个方程表示直线的法线的斜率为-\frac{1}{k}且经过点(x_0,y_0)。
最短距离专题(答案部分)

1 / 13
基本应用
1.如图,∠AOB=30°,内有一点 P 且 OP=5,若 M、N 为边 OA、OB 上两动点, 那么△PMN 的周长最小为 5 .
【分析】根据题意画出符合条件的图形,求出 OD=OE=OP,∠DOE=60°,得出等 边三角形 DOE,求出 DE=5,求出△PMN 的周长=DE,即可求出答案. 【解答】解:作 P 关于 OA 的对称点 D,作 P 关于 OB 的对称点 E,连接 DE 交 OA 于 M,交 OB 于 N,连接 PM,PN,则此时△PMN 的周长最小, 连接 OD,OE, ∵P、D 关于 OA 对称,∴OD=OP,PM=DM, 同理 OE=OP,PN=EN,∴OD=OE=OP=5, ∵P、D 关于 OA 对称,∴OA⊥PD, ∵OD=OP,∴∠DOA=∠POA, 同理∠POB=∠EOB,∴∠DOE=2∠AOB2×30°═60°, ∵OD=OE=5,∴△DOE 是等边三角形, ∴DE=5 即△PMN 的周长是 PM+MN+PN=DM+MN+EN=DE=5,
【分析】(1)首先作出∠AOB 角平分线,再作出 MN 的垂直平分线,交点即为 P; (2)先作出 M 点关于 AB 的对称点 G,连接 NG 交 AB 于 Q,则 Q 就是所求. 【解答】解:(1)如图所示:
∴点 P 是所求做的点; (2)由题意,得 ∴点 Q 是所求作的点. 【点评】本题考查了角平分线的性质的运用,线段的垂直平分线的性质的运用, 轴对称最短路径问题的运用,解答时熟练掌握基本作图的方法是关键.
4 / 13
作 B 点关于 l 的对称点 B′,连接 AB′交E⊥AE,
有关最短距离问题

有关最短距离问题
例1.在河的同旁有A、B两个村庄,现在要在河边修一个供水站给A、B两村供水,问在那个位置修能使到A、B两村距离最短。
P B
A
这是课本中的一道题,做法相信大家都知道。
其实,这种方法还可以和其他知识合起来变形应用。
例2.要在一条河上修一座垂直于河岸的桥,河岸两旁有A、B两村,要使从A到B的距离最短,桥应该修在那个位置。
A
解:过点B做河岸的垂线,并截取BC,使BC等于河岸的宽度,连接AC交下边河岸于点P,则P点为所求的点。
做法如上图。
例3.在锐角三角形中求一点P,使P到此三角形三个顶点的距离和最短,求点P的位置。
E
D
P
C
B
A
解:假设P点在上图位置,连接PA、PB、PC,将⊿PAB逆时针方向旋转0
60.
在⊿PBD 中PB=DB ,∠PBD=060.所以⊿PBD 为正三角形。
所以PB=BD=PD.
由旋转性质知:PA=DE 。
所以PA+PB+PC=PC+PD+DE
由两点之间线段最短知,当E 、D 、P 、C 在同一直线上时,PA 、PB 、PC 距离之和最短。
所以∠EDB=∠BPC=0120 即∠BPA=∠BPC=∠APC=0120
因此,点P 在使∠BPA=∠BPC=∠APC=0120的位置时,到三角形三顶点的距离之和最短。
点到直线的距离最短 生活例子

点到直线的距离最短生活例子一、引言生活中,我们经常会遇到一些与点到直线距离相关的问题,比如在找寻最短路径、设计建筑物或者进行测量时。
点到直线的距离是一种重要的数学概念,它在现实生活中有着广泛的应用。
本文将通过一些生活例子来解释点到直线的距离。
二、点到直线的定义点到直线的距离是指空间中一点到一条直线的距离。
在数学上,我们可以通过垂直距离或者投影距离来计算点到直线的距离。
三、生活例子一:最短路径在日常生活中,我们经常需要选择最短路径来节省时间和精力。
我们去某个地方旅行,需要选择一条最短的路线;在购物时,我们想要找到离家最近的商店等。
这些都涉及到点到直线的距离的概念。
通过计算点到直线的距离,我们可以找到一条最短路径,从而节省时间和成本。
四、生活例子二:建筑设计在建筑设计中,点到直线的距离也是一个重要的概念。
设计师需要考虑到建筑物与基准线之间的距离,以确保建筑物的稳定性和美观性。
通过计算点到直线的距离,设计师可以确定建筑物与基准线的最佳位置,从而确保建筑物的稳固性和美感。
五、生活例子三:测量在工程测量中,点到直线的距离也是一个重要的概念。
工程师需要通过测量来确定物体与基准线之间的距离,以便进行建筑、施工和维护工作。
通过计算点到直线的距离,工程师可以准确地测量物体与基准线之间的距离,从而确保工程的准确性和安全性。
六、结论点到直线的距禮是一个重要的数学概念,在生活中有着广泛的应用。
通过生活例子的解释,我们可以更加直观地理解点到直线的距离的概念,并了解它在日常生活中的实际应用。
希望大家能够通过本文的介绍,对点到直线的距离有一个更加深入的了解。
七、生活例子四:交通规划交通规划是现代城市发展中不可或缺的一部分。
在设计城市道路和交通系统时,需要考虑点到直线的距离来确定最佳的道路布局和交通流线。
通过计算点到直线的距离,交通规划师可以更好地规划交通设施的位置和道路的走向,以便提高交通效率和减少交通拥堵。
八、生活例子五:地图制作在制作地图的过程中,点到直线的距离也是一个重要的因素。
【初二】最短距离问题总结

【初二】最短距离问题总结在初二数学课程中,最短距离问题是一个常见的问题类型。
本文将对最短距离问题进行总结和简要解析。
最短距离问题定义最短距离问题是指在给定的条件下,求解两个点之间最短路径的问题。
该问题常见于几何、图论和最优化等领域,在实践中具有广泛的应用。
最短距离问题解决方法1. 直线距离计算最简单的情况是直线距离计算。
当两个点在平面直角坐标系中给出时,可以使用勾股定理(即直角三角形斜边长度公式)计算两点之间的直线距离。
2. 曼哈顿距离计算曼哈顿距离是指在矩形网格中,从一个点到达另一个点所需要的最小移动次数(只能上下左右移动,不能斜向移动)。
曼哈顿距离计算可以通过两点横纵坐标的差值相加得到。
3. 最短路径算法对于复杂的情况,如图论中求解两点之间的最短路径,可以使用最短路径算法。
常见的最短路径算法包括迪杰斯特拉算法(Dijkstra Algorithm)和弗洛伊德算法(Floyd Algorithm)等。
这些算法可以在给定网络、权重或距离信息的情况下,计算出两点之间最短路径的长度和路径。
最短距离问题应用举例最短距离问题在实际生活中有广泛的应用,下面列举几个例子:1. 导航系统:导航系统通过计算起点和终点之间的最短路径,为驾驶员提供最优的导航路线。
2. 物流配送:物流公司需要计算货物从起点到终点的最短路径,以最大程度地减少运输成本和时间。
3. 网络通信:计算机网络中的路由算法使用最短路径算法来确定数据包传输的最佳路径。
4. 旅行规划:旅行者可以使用最短路径算法规划旅游路线,使得行程更加紧凑和高效。
总结最短距离问题是初二数学课程中的一个重要内容。
通过不同计算方法和最短路径算法,可以有效地解决两点之间最短路径的问题。
最短距离问题在实际中有许多应用场景,涉及导航、物流、网络通信和旅行规划等领域。
(完整版)勾股定理--最短距离问题
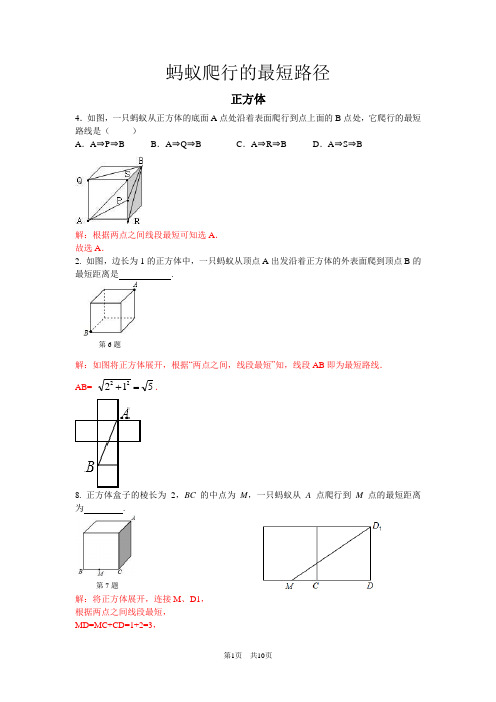
蚂蚁爬行的最短路径正方体4.如图,一只蚂蚁从正方体的底面A 点处沿着表面爬行到点上面的B 点处,它爬行的最短路线是( )A .A ⇒P ⇒B B .A ⇒Q ⇒BC .A ⇒R ⇒BD .A ⇒S ⇒ B解:根据两点之间线段最短可知选A . 故选A .2. 如图,边长为1的正方体中,一只蚂蚁从顶点A 出发沿着正方体的外表面爬到顶点B 的最短距离是 .解:如图将正方体展开,根据“两点之间,线段最短”知,线段AB 即为最短路线. AB=51222=+.8. 正方体盒子的棱长为2,BC 的中点为M ,一只蚂蚁从A 点爬行到M 点的最短距离为 .解:将正方体展开,连接M 、D1, 根据两点之间线段最短, MD=MC+CD=1+2=3,第6题第7题AB121MD 1=132322212=+=+DD MD .5.如图,点A 的正方体左侧面的中心,点B 是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A 沿其表面爬到点B 的最短路程是( )解:如图,AB= ()1012122=++.故选C .9.如图所示一棱长为3cm 的正方体,把所有的面均分成3×3个小正方形.其边长都为1cm ,假设一只蚂蚁每秒爬行2cm ,则它从下底面点A 沿表面爬行至侧面的B 点,最少要用 2.5秒钟.解:因为爬行路径不唯一,故分情况分别计算,进行大、小比较,再从各个路线中确定最短的路线.(1)展开前面右面由勾股定理得AB= = cm ;(2)展开底面右面由勾股定理得AB==5cm ;所以最短路径长为5cm ,用时最少:5÷2=2.5秒.长方体10.(2009•恩施州)如图,长方体的长为15,宽为10,高为20,点B 离点C 的距离为5,一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ,需要爬行的最短距离是 。
解:将长方体展开,连接A 、B ,根据两点之间线段最短,AB==25.A B A 1B 1D CD 1C 121411. 如图,一只蚂蚁从实心长方体的顶点A 出发,沿长方体的表面爬到对角顶点C 1处(三条棱长如图所示),问怎样走路线最短?最短路线长为 .解:正面和上面沿A 1B 1展开如图,连接AC 1,△ABC 1是直角三角形, ∴AC 1=()5342142222212=+=++=+BC AB18.(2011•荆州)如图,长方体的底面边长分别为2cm 和4cm ,高为5cm .若一只蚂蚁从P 点开始经过4个侧面爬行一圈到达Q 点,则蚂奴爬行的最短路径长为 cm .解:∵PA=2×(4+2)=12,QA=5 ∴PQ=13.故答案为:13.19.如图,一块长方体砖宽AN=5cm ,长ND=10cm ,CD 上的点B 距地面的高BD=8cm ,地面上A 处的一只蚂蚁到B 处吃食,需要爬行的最短路径是多少?解:如图1,在砖的侧面展开图2上,连接AB , 则AB 的长即为A 处到B 处的最短路程.解:在Rt △ABD 中,因为AD=AN+ND=5+10=15,BD=8, 所以AB 2=AD 2+BD 2=152+82=289=172. 所以AB=17cm .故蚂蚁爬行的最短路径为17cm .49、如图,长方体盒子(无盖)的长、宽、高分别12cm ,8cm,30cm.(1)在AB 中点C 处有一滴蜜糖,一只小虫从D 处爬到C 处去吃,有无数种走法,则最短路程是多少?(2)此长方体盒子(有盖)能放入木棒的最大长度是多少?12.如图所示:有一个长、宽都是2米,高为3米的长方体纸盒,一只小蚂蚁从A 点爬到B 点,那么这只蚂蚁爬行的最短路径为 米。
立体图形线路最短问题(最全)
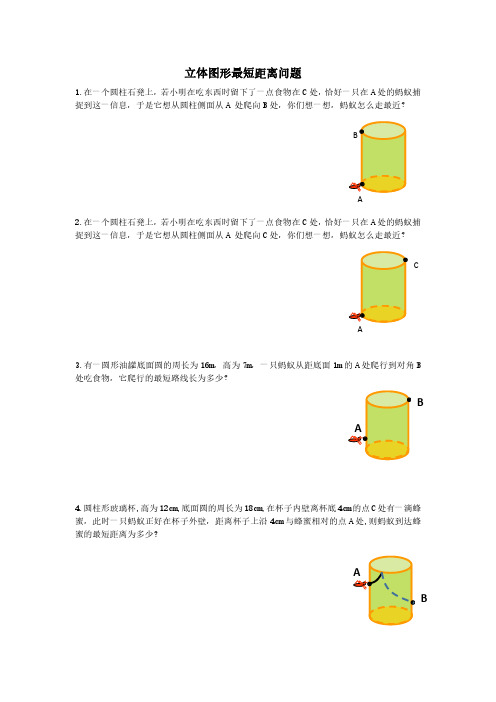
立体图形最短距离问题1.在一个圆柱石凳上,若小明在吃东西时留下了一点食物在C 处,恰好一只在A 处的蚂蚁捕捉到这一信息,于是它想从圆柱侧面从A 处爬向B 处,你们想一想,蚂蚁怎么走最近?2.在一个圆柱石凳上,若小明在吃东西时留下了一点食物在C 处,恰好一只在A 处的蚂蚁捕捉到这一信息,于是它想从圆柱侧面从A 处爬向C 处,你们想一想,蚂蚁怎么走最近?3.有一圆形油罐底面圆的周长为16m,高为7m,一只蚂蚁从距底面1m 的A 处爬行到对角B 处吃食物,它爬行的最短路线长为多少?4.圆柱形玻璃杯,高为12cm,底面圆的周长为18cm,在杯子内壁离杯底4cm 的点C 处有一滴蜂蜜,此时一只蚂蚁正好在杯子外壁,距离杯子上沿4cm 与蜂蜜相对的点A 处,则蚂蚁到达蜂蜜的最短距离为多少?C A ABBAB A CACA5.如图,在棱长为10厘米的正方体的一个顶点A 处有一只蚂蚁,现要向顶点B 处爬行,已知蚂蚁爬行的速度是1厘米/秒,且速度保持不变,问蚂蚁能否在20秒内从A 爬到B?6.已知长方体的长为AC=2cm,宽BC=1cm,高AA′=4.一只蚂蚁如果沿长方体的表面从A 点爬到B′点,那么沿哪条路最近?最短路程是多少?7..如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A 和B 是这个台阶两个相对的端点,A 点有一只蚂蚁,想到B 点去吃可口的食物,则蚂蚁沿着台阶面爬到B 点最短路程是多少?8.有一个如图示的长方体的透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深为AE=40cm,在水面上紧贴内壁G 处有一鱼饵,G 在水面线EF 上,且EG=60cm;一小虫想从鱼缸外的A 点沿壁爬进鱼缸内G 处吃鱼饵.(1)小动物应该走怎样的路线才使爬的路线最短呢?请你在图中画出它爬行的路线,并用箭头标注.(2)求小动物爬行的最短路线长?AB。
点到线段最短距离公式

点到线段最短距离公式全文共四篇示例,供读者参考第一篇示例:在几何学中,我们经常会遇到点到线段的最短距离问题。
这种问题在实际生活中也是非常常见的,比如我们在行驶时需要保持与前车的安全距离,或者在设计建筑物时需要计算两个设施之间的最短距离等等。
解决这类问题需要运用数学知识,特别是点到线段最短距离公式。
要计算点到线段的最短距离,我们首先需要了解什么是点、线段以及它们之间的关系。
点是空间中的一个位置,没有大小和形状;而线段是由两个端点确定的有限长度的线段。
点和线段之间的最短距离就是从点到线段上的某个点的距离,这个距离是垂直于线段的距离。
根据数学知识,我们可以得出点到线段最短距离的公式如下:设点P(x0, y0)到线段AB的端点A(x1, y1)和B(x2, y2)的距离公式为d,其计算步骤如下:1.计算线段AB的长度:AB=sqrt((x2-x1)^2 + (y2-y1)^2)3.如果d=0,则点P在线段AB上,距离为0;否则,计算点P到线段AB的最短距离:d = |(x2-x1)*(y1-y0)-(x1-x0)*(y2-y1)| / sqrt((x2-x1)^2 + (y2-y1)^2)4.点P到线段AB的最短距离即为d。
这个公式的推导过程可以通过几何方法或者向量方法来解释,但无论是哪种方法,最终的结果都是一样的。
这个公式在实际中的应用非常广泛,比如在计算机图形学中,就需要大量地使用到点到线段的最短距离公式来进行计算。
除了点到线段的最短距离公式,我们还可以推广到点到直线的最短距离问题。
点到直线的最短距离的计算方法与点到线段的方法很类似,只是直线是无限延伸的,所以我们只需要计算垂直于直线的距离即可。
点到线段的最短距离公式是一种非常重要的数学工具,在解决实际问题中有着广泛的应用。
通过掌握这个公式,我们可以更加准确地计算出点到线段的最短距离,从而更好地解决实际问题。
希望通过这篇文章的介绍,能够帮助大家更好地了解点到线段最短距离的计算方法,提高数学应用能力。
数学考点---最短距离问题(带答案)

数学考点---最短距离问题1.我们常利用“两点之间线段最短”解决两条线段和最小的相关问题,下面是熟悉的一道习题:如图1,已知,A,B在直线l的同一侧,在l上求作一点,使得PA+PB最小.我们只要作点B关于l的对称点B′,(如图2所示)根据对称性可知,PB=PB'.因此,求AP+BP最小就相当于求AP+PB′最小,显然当A、P、B′在一条直线上时AP+PB′最小,因此连接AB',与直线l的交点就是要求的点P.有很多问题都可用类似的方法去思考解决.探究:(1)如图3,正方形ABCD的边长为2,E为BC的中点,P是BD上一动点.连接EP,CP,则EP+CP的最小值是;运用:(2)如图4,平面直角坐标系中有三点A(6,4)、B(4,6)、C(0,2),在x轴上找一点D,使得四边形ABCD的周长最小,则点D的坐标应该是;操作:(3)如图5,A是锐角MON内部任意一点,在∠MON的两边OM,ON上各求作一点B,C,组成△ABC,使△ABC周长最小.(不写作法,保留作图痕迹)2.作图题(不写作法,保留作图痕迹):(1)如图①,点A、B在直线l的两侧,在l上求一点P,使得PA+PB最小;(2)如图②,点A、B在直线l的同一侧,在l上求一点P,使得PA+PB最小;(3)如图③,点A是锐角三角形MON内部任意一点,在∠MON的两边OM,ON上各取一点B、C,与点A组成三角形,使三角形周长最小;(4)如图④,AB是锐角三角形MON内部一条线段,在∠MON的两边OM,ON上各取一点C、D组成四边形,使四边形周长最小;(5)如图,连结M、N与直线l相交于点O,当两直线的夹角等于450,且OM=6,MN=2时,PM+PN的最小值是3.(1)如图,点A、B、C在直线l的同侧,在直线l上求作一点P,使得四边形APBC的周长最小,请写出作法(2)AB是锐角MON内部一条线段,在角MON的两边OM,ON上各取一点C,D组成四边形,使四边形周长最小.(如图所示)4.已知A(﹣3,8)和B(2,2),在x轴上有一点M,使得|AM|+|BM|为最短,那么点M的坐标为()A.(﹣1,0)B.(1,0)C.()D.()5.(1)如图,A、B两村位于一条河的两岸,假定河的两岸笔直且平行,现要在河上垂直于河岸建一座桥.问:应把桥建在什么位置,才能使A村经过这座桥到B村的路程最短?请画出草图,并简要说明作法及理由(2)A、B两村之间隔一条河,现在要在河上架一座桥.(1)要使这两村A、B之间的行程最短,桥应修在何处?请帮他们设计出来.(2)若两村A、B到河边的距离分别为50米和20米,河宽为30米,AC=40米,你能求出两村的最短路程吗?若能,请求出来6.在直角坐标系中,有四个点A(-8,3)、B(-4,5)、C(0,n)、D(m,0),当四边形ABCD的周长最短时,求m/n 的值7.如图,已知平面直角坐标系中,A、B两点的坐标分别为A(2,﹣3)、B(4,﹣1).(1)若P(x,0)是x轴上的一个动点,当△PAB的周长最短时,求x值;(2)若C(a,0)、D(a+3,0)是x轴上的两个动点,当四边形ABDC的周长最短时,求a的值;(3)设M、N分别为x轴、y轴上的动点,问:是否存在这样的点M(m,0)和(0,π),使四边形ABMV周长最短,若存在,求出m、n的值;若不存在,请说明理由8.在平面直角坐标系中,点A(2,1)、B(4,2),坐标原点为O点.(1)在y轴上有一动点C,求当AC+BC最小时,C点的坐标;(2)在直线y=x上有一动点D,求当AD+BD最小时,D点的坐标;(3)在x轴上有两个点E(m,0)、F(m+1,0),求当四边形CEFD周长最小时,m的值9.已知线段AB在x轴上(A在B的左边),且AB=3,点C(2,-4)、点D(4,-1),当AC+BD最小时,点A的坐标是() A(0,0) B(1,0) C(1.2,0) D(2,0)10.如图,圆柱形玻璃杯,高为11cm,底面周长为16cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为(结果保留根号)11.如图1,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,为了吃到蜂蜜,蚂蚁从外壁A处沿着最短路径到达内壁B 处.(1)如图2是杯子的侧面展开图,请在杯沿CD上确定一点P,使蚂蚁沿A-P-B路线爬行,距离最短.(2)结合图,求出蚂蚁爬行的最短路径长12.如图,长方体的长BE=5cm,宽AB=3cm,高BC=4cm,一只小蚂蚁从长方体表面由A点爬到D点去吃食物,则小蚂蚁走的最短路程是 cm13.如图,长方体的长BE=7,宽AB=5,高BC=5,一只小蚂蚁从A点爬到棱BC上,再爬到D点去吃糖,则小蚂蚁走的最短路程是14.如图,在边长为8的正方形ABCD中,E是AB边上的一点,且AE=6,点Q为对角线AC上的动点,则△BEQ周长的最小值为15.如图,AB是⊙O的直径,AB=8,=6,M是AB上一动点,则CM+DM的最小值()A.8 B.6 C.2+2D.416.在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(2,0),B(6,0)是x轴上的两点,则PA+PB 的最小值为17.如图,∠MON=90°,边长为4的等边△ABC的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,等边三角形的形状保持不变,运动过程中,点C到点O的最大距离为18.如图,∠MON=90°,矩形ABCD的顶点A,B分别在OM、ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=.运动过程中,当点D到点O的距离最大时,OA长度为()A. B.C.2 D.数学考点---最短距离问题答案1.解:(1)∵点A是点C关于BD的对称点,连接AE,则AE就是EP+CP的最小值,∴EP+CP的最小值=AE=;(2)作点C关于x轴的对称点C',连接AC',则AC'与x轴的交点即为点D的位置,∵点C'坐标为(0,﹣2),点A坐标为(6,4),∴直线C'A的解析式为:y=x﹣2,故点D的坐标为(2,0);(3)分别作点A关于OM的对称点A'、关于ON的对称点A'',连接A'A'',则A'A''与OM交点为点B的位置,与ON交点为C的位置;如图所示:点B、C即为所求作的点.2.解:(1)如图①,连接两点与直线的交点即为所求作的点P,则点P即为所求;(2)如图②,过A作直线l的垂线,在垂线上取点A′,使直线l是AA′的垂直平分线,连接BA′交直线l于P点,则点P即为所求;(3)作A关于OM的对称点A',关于ON的A对称点A'',与OM、ON相交于B、C,连接AB,BC,AC,则△ABC即为所求三角形;(4)作A关于OM的对称点E,再作B关于ON的对称点F,连接EF交OM于C,交ON于D,连接AC,CD,BD,则四边形ABCD即为所求;(5)作出点M关于直线l的对称点M′,连结M′N交直线l于点P;∵两直线的夹角等于45°,且OM=6,MN=2,∴∠MOP=45°,OM=OM′=6,NO=8,∴∠NOM′=90°,∴M′N==10,故答案为:103.解:(1)作点A关于直线l的对称点A′,②连接A′B于直线l交于P,则点P就是所求作的点.(2)解:如图,作A关于OM的对称点E,再作B关于ON的对称点F,连接EF即可.如图.ABCD便是周长最小的.4.解:找出点B关于x轴的对称点B′,连接AB′,与x轴的交于M点,连接BM,此时|AM|+|BM|为最短,由B 与B′关于x轴对称,B(2,2),所以B′(2,﹣2),又A(﹣3,8),则直线AB′的方程为y+2=(x﹣2)化简得:y=﹣2x+2,令y=0,解得x=1,所以M(1,0)故选:B5.(1)先确定AA′与河等宽,且AA′⊥河岸,连接BA′,与河岸的交点就是点C,过点C作CD垂直河岸,交另一河岸于点D,CD就是所求的桥的位置.理由:由作图过程可知,四边形ADCA′为平行四边形,AD平移至A′C即可得到线段A′B,两点之间,线段最短,由于河宽不变,CD即为桥.(2)解:(1)桥应该建在如图所示MN处,四边形AMKN是平行四边形.(2)作MH⊥BC垂足为H.两村A、B之间的最短路程=AN+KN+BK,∵四边形AMKN是平行四边形,∴AN=MK,在RT△BMH中,∵BH=70,MH=40,∴BM==10,∴AN+KN+BK=BM+KN=10+30,∴两村的最短路程为(10+30)米6.解:根据题意,作出如图所示的图象,过点B作B关于y轴的对称点B′、过点A关于x轴的对称点A′,连接A′B′,直线A′B′与坐标轴交点即为所求.设过A′与B′两点的直线的函数解析式为y=kx+b.∵A(﹣8,3),B(﹣4,5),∴A′(﹣8,﹣3),B′(4,5),依题意得:,解得,所以,C(0,n)为(0,).D(m,0)为(﹣,0)所以,=﹣.故答案为﹣7.解:(1)设点B(4,﹣1)关于x轴的对称点是B',其坐标为(4,1),设直线AB'的解析式为y=kx+b,把A (2,﹣3),B'(4,1)代入得:,解得,∴y=2x﹣7,令y=0,得x=,即当△PAB的周长最短时,x=.(2)过A点作AE⊥x轴于点E,且延长AE,取A'E=AE.做点F(1,﹣1),连接A'F.那么A'(2,3).直线A'F 的解析式为y﹣1=•(x﹣1),即y=4x﹣5,∵C点的坐标为(a,0),且在直线A'F上,∴0=4a﹣5,解得a=.∴当四边形ABDC的周长最短时,a=.(3)存在使四边形ABMN周长最短的点M、N,作A关于y轴的对称点A′,作B关于x轴的对称点B′,连接A′B′,与x轴、y轴的交点即为点M、N,∴A′(﹣2,﹣3),B′(4,1),∴直线A′B′的解析式为:y=x﹣,∴M(,0),N(0,﹣).∴m=,n=﹣8.解:(1)如图1,作A点关于y轴的对称点A′,连接A′B,交y轴于C,∴AC=A′C,∴AC+BC=A′C+BC=A′B,根据两点之间线段最短可知A′B就是AC+BC的最小值,∵点A(2,1),∴A′(﹣2,1),∵B(4,2),设直线A′B的解析式为y=kx+b,∴-2k+b=1,4k+b=2,解得k=1/6,b=4/3.∴直线A′B的解析式为y=x+,∴C (0,);(2)如图2,作A点关于直线y=x的对称点A″,连接A″B,交直线y=x于D,∴AD=DA″,∴AD+BD=DA″+BD=A″B,根据两点之间线段最短可知A″B就是AD+BD的最小值,∵点A(2,1),∴A″(1,2),∵B(4,2),∴直线BA″∥x轴,∴y=2,代入y=x中得x=2,∴D(2,2);(3)作点C关于x轴的对称点C′,则C′的坐标为(0,﹣),把C′向右平移1个单位得到点D'(1,﹣),连接DD′,与x轴交于点F,如图3,∴C′E=CE,又∵点E(m,0)、F(m+1,0),∴EF=1,∴C′D′∥EF,∴四边形C′D′FE为平行四边形,∴C′E=D′F,∴CE=D′F,∴CE+DF=DD′,此时CE+DF最小,而CD与EF的长一定,∴此时四边形CEFD周长最短.设直线DD′的解析式为y=k′x+n,把D(2,2)、D′(1,﹣)分别代入得2k′+n=2,k′+n= -4/3,解得k′=,n=﹣,∴直线DD′的解析式为y=x﹣,令y=0,则x ﹣=0,解得x=,∴D点坐标为(,0),∴m+1=,∴m=10.解:如图,将杯子侧面展开,作A关于EF的对称点A′,连接A′C,则A′C即为最短距离,A′C2=A′D2+CD2=82+122=208,∴CA′=4cm答:蚂蚁到达蜂蜜的最短距离的是4cm12.解:(1)如图(1),AD==;(2)如图(2),AD==;(3)如图(3),AD===4.可见,AD的最小值为.故选C.13.解:AE=AB+BE=5+7=12.DE=BC=5.AD===13.蚂蚁爬的最短路径长为1314.解:连接BD,DE,∵四边形ABCD是正方形,∴点B与点D关于直线AC对称,∴DE的长即为BQ+QE的最小值,∵AB=8,AE=6,∴DE=BQ+QE==10,∵AB=8,AE=6,∴BE=2,∴△BEQ周长的最小值=DE+BE=10+2=1215.解:如图,作点C关于AB的对称点C′,连接C′D与AB相交于点M,此时,点M为CM+DM的最小值时的位置,连接OC交C′D于N,连接OD,∵AB是⊙O的直径,=6,∴,∵,∴,∴OC⊥C′D,C′D=2DN,∴∠COD=60°,∴∠D=30°,∵AB=8,∴OD=4,∴DN=OD•sin60°=2,∴C′D=4.∴CM+DM的最小值=4.故选:D16.解:如图所示:作A点关于直线y=x的对称点A′,连接A′B,交直线y=x于点P,此时PA+PB最小,∵OA′=2,BO=6,∴PA+PB=A′B==2.故答案为:217.解:如图,取AB的中点D,连接OD、CD,∵△ABC是等边三角形,∴CD==2,∵∠MON=900,∴OD=AB==2,由图可知,当点O、C、D三点共线时点C到点O的距离最大,最大值为2+2.故答案为:2+218.解:如图,取AB的中点,连接OE、DE,∵∠MON=90°,∴OE=AE=AB=×2=1,∵四边形ABCD是矩形,∴AD=BC=,在Rt△ADE中,由勾股定理得,DE===2,由三角形的三边关系得,O、E、D三点共线时点D到点O的距离最大,此时,OD=OE+DE=1+2=3,过点A作AF⊥OD于F,则cos∠ADE==,即=,解得DF=,∵OD=3,∴点F是OD的中点,∴AF垂直平分OD,∴OA=AD=.故选:B.。
最短距离求解题技巧

最短距离求解题技巧最短距离求解问题是在计算机科学和运筹学中非常重要的一个问题。
它在许多领域中都有广泛的应用,包括路径规划、网络优化、数据挖掘等。
在本文中,我将介绍一些求解最短距离问题的常用技巧。
1. Dijkstra算法Dijkstra算法是求解单源最短路径问题的一种经典算法。
它通过逐步确定从源点到其他节点的最短路径,并使用一个优先级队列来选择下一个最近的节点。
Dijkstra算法的时间复杂度为O((V+E)logV),其中V是节点数,E是边数。
2. Bellman-Ford算法Bellman-Ford算法是求解单源最短路径问题的另一种经典算法。
与Dijkstra算法不同的是,Bellman-Ford算法可以处理图中存在负权边的情况。
Bellman-Ford算法通过对所有边进行V-1轮的松弛操作来逐步确定最短路径。
Bellman-Ford算法的时间复杂度为O(VE),其中V是节点数,E是边数。
3. Floyd-Warshall算法Floyd-Warshall算法是求解全源最短路径问题的一种经典算法。
它通过动态规划的方式计算从任意两个节点之间的最短路径。
Floyd-Warshall算法的时间复杂度为O(V^3),其中V是节点数。
Floyd-Warshall算法的优势是可以处理有向图或无向图中存在负权边的情况。
4. A*算法A*算法是一种启发式搜索算法,用于求解从起点到终点的最短路径。
它综合使用节点距离和启发式函数来评估节点的优先级,以选择下一个节点进行扩展。
A*算法通常在路径规划和游戏AI中使用。
A*算法的时间复杂度取决于启发函数的复杂度。
5. 最小生成树算法最小生成树算法是一种用于求解无向图的最短路径问题的算法。
它通过选择边来构建一个连通的生成树,使得树的权重和最小。
常见的最小生成树算法包括Prim算法和Kruskal算法。
Prim算法的时间复杂度为O(ElogV),Kruskal算法的时间复杂度为O(ElogE)。
点到圆的最小距离问题

点到圆的最小距离问题
在几何学中,点到圆的最小距离问题是一个常见的数学问题。
该问题的目标是
确定一个给定点与一个给定圆之间的最短距离。
我们需要明确一些基本概念和公式。
一个圆由圆心和半径定义。
给定圆的圆心
坐标为(x₀, y₀),半径为r。
而点的坐标为(x, y)。
我们需要找到点到圆的最小距离,即 d。
对于点到圆的最小距离问题,我们可以利用以下公式来计算:
d = |√((x - x₀)² + (y - y₀)²) - r|
其中,(x - x₀)²表示点横坐标与圆心横坐标的差的平方,(y - y₀)²表示点纵坐标与圆心纵坐标的差的平方,√表示开方运算,|…|表示绝对值运算。
我们可以通过计算上述公式,找到给定点与给定圆之间的最小距离。
但需要注
意的是,如果点位于圆内部,这个最小距离则为负数,表示点到圆的距离为负,即点在圆内。
通过求解点到圆的最小距离问题,我们可以在几何学、物理学和工程学等领域
中应用。
例如,在导航系统中,我们可以利用这个问题来确定两个点之间的最短路径,或者在建筑设计中,可以使用这个问题来确定物体与圆形结构之间的最小间隙。
点到圆的最小距离问题是一个基本且常见的数学问题。
通过利用相关公式,我
们可以准确计算出给定点与给定圆之间的最短距离,并在不同领域中应用这个问题的解决方法。
最短距离问题

第三讲最短距离问题一、知识梳理几何模型1条件:如图,、是直线同旁的两个定点.问题:在直线上确定一点,使的值最小.方法:作点关于直线的对称点,连结交于点,则的值最小几何模型2条件:如图,、是直线异侧的两个定点.且A、B到距离不相等问题:在直线上确定一点,使的值最大方法:作点关于直线的对称点,连结交于点,则的值最小二、方法归纳对于几何模型1,近年来,除了常见的“一个动点”外,出现了“两个动点”、“三个动点”等变式问题的问题,而解决此类问题的关键在于:找点关于线的对称点,实现“折”转“直”。
对于几何模型2,近年出现的中考题都是直接应用。
三、课堂精讲例题(一)、题中出现一个动点。
例1、在正方形ABCD中,点E为BC上一定点,且BE=10,CE=14,P为BD上一动点,求PE+PC 最小值。
【难度分级】A类〖试题来源〗经典例题〖选题意图〗使学生掌握几何模型1的应用〖解题思路〗作关于对称点,可以证明在上,易求解:作关于对称点四边形ABCD是正方形在上,且即是的最小值【搭配课堂训练题】1、已知:抛物线的对称轴为x=-1与轴交于两点,与轴交于点其中、(1)求这条抛物线的函数表达式.(2)已知在对称轴上存在一点P,使得的周长最小.请求出点P的坐标【难度分级】A类〖试题来源〗2009年山东济南中考真题。
〖答案〗解:(1)由题意得解得∴此抛物线的解析式为(2)连结、.因为的长度一定,所以周长最小,就是使最小.点关于对称轴的对称点是点,与对称轴的交点即为所求的点.设直线的表达式为则解得∴此直线的表达式为把代入得∴点的坐标为例2:已知:直线与轴交于A,与轴交于D,抛物线与直线交于A、E两点,与轴交于B、C 两点,且B点坐标为(1,0).(1)求抛物线的解析式;(2)在抛物线的对称轴上找一点M,使的值最大,求出点M的坐标.【难度分级】A类〖试题来源〗2009眉山中考数学真题〖选题意图〗使学生掌握几何模型2的应用〖解题思路〗直接应用几何模型2,由于B是C关于对称轴的对称点,所以连接AB,则AB 与对称轴的交点M即为所求。
圆锥曲线最短距离

圆锥曲线最短距离
圆锥曲线最短距离的问题,可以通过以下两种思路进行解答:
第一种,对于从该平面上的定点出发到椭圆上一点的最短距离的问题,可以采用仿射变换。
通过仿射变换将椭圆仿射为圆,并将仿射后的定点与圆心连线,再减去半径,即得到了该点到圆心的距离。
再将此距离按照仿射的规则转化为原来xOy坐标系的距离,即为所求。
第二种,对于从椭圆上的动点出发到定点最短距离的问题,可以将该点的坐标进行三角换元,得到P(acosθ,bsinθ),再利用两点间的距离公式求得最短距离。
如果该椭圆的焦点在坐标轴上,可以使用单独将椭圆方程中的x或y
配成完全平方,再使用三角换元的方式求解。
如果仍对圆锥曲线最短距离问题有疑问,可以请教数学老师或查阅相关数学书籍。
最短距离问题

球面上最短航线
在地球表面上,两地之间的最短距离是通过这两点的大圆的劣弧段。
其中赤道、经线圈、晨昏线都是大圆。
1、若两点在赤道上,则两点间最短航线应是沿着赤道朝两点间的劣弧方向运动,即向东或向西。
2、若两点在同一条经线上,则两点间最短航线应是沿着经线朝两点间的劣弧方向运动,即向北或向南。
3、若两地的经度差等于180,则经过这两点大圆是经线圈。
这两点间的最短距离是经过极点。
①同在北半球,最短航线必须经过北极点,其航行方向一定是先向正北,过北极点后再向正南。
②同在南半球,最短航线必须经过南极点,其航行方向一定是先向正南,过南极点后再向正北。
③两地位于不同半球,这时需要考虑经过北极点为劣弧,还是经过南极点为劣弧,然后确定最短航线的走向和航程。
4、若两地的经度差不等于180,则经过这两点大圆不是经线圈,而是与经线圈斜交,其最短航线不经过极点,具体分为两种情况:
①甲地位于乙地的东方,从甲到乙最短航程为:同在北半球,先向西北,再向西,最后向西南;同在南半球,先向西南,再向西,最后向西北;位于不同半球时,需要讨论哪一段为劣弧段。
②甲地位于乙地的西方,从甲到乙最短航程为:同在北半球,先向东北,再向东,最后向东南;同在南半球,先向东南,再向东,最后向东北;位于不同半球时,需要讨论哪一段
为劣弧段。
5、俯视图,经过两点的大圆的劣弧部分形状可视为两点间的直线(如图)。
间)。
初中最短距离问题的几种

初中最短距离问题的几种好嘞,今天咱们聊聊初中里的最短距离问题。
这可是个很有意思的话题,听起来好像很高深,但其实它就藏在咱们的日常生活中,嘿嘿。
想象一下,咱们要从家里到学校,得走多远?这个问题可是值得思考的。
别看这事儿简单,里面可是藏着不少学问呢。
谁都知道,走路不可能像飞一样直接,但如果你想省点力气,那就得好好琢磨一下最短的路线了。
最短距离问题,简单说就是找出两点之间最省事的路径。
比如说,咱们要从客厅到厨房,直接穿过去就好了。
可要是有个沙发挡着,嘿,那就得绕一下。
这样一来,大家都开始捉摸起这个问题的解决方案。
有些人可能会说,直接就走最短的路呗,没啥好考虑的。
可实际情况可复杂得多,走这条路的时候,可能会遇到大大的麻烦,比如小狗在那儿趴着,或者有个玩具挡路。
真是让人又想笑又想哭。
再比如,咱们要去个商场,前面堵车堵得严严实实,咋办呢?你肯定不会傻傻坐在车里等,肯定会想,换条路试试。
走得越多,咱们就越聪明。
就像我有个朋友,他每次去学校都爱换路线,老是找新路。
第一次我还以为他是在逗我,结果一问,发现他早就把那些小巷子都摸得一清二楚。
人家就是这么机灵,心里想的可不是单纯的走,而是找出那条省时又省力的路。
说到这里,大家可能会想,这个最短距离问题跟学习有什么关系呢?嘿,关系可大了去了。
就像咱们学习知识一样,不是所有的知识都得像书本上那样逐字逐句地啃。
有些捷径能让你事半功倍。
你可能会想,学数学的路上,有时候绕来绕去,最终发现直接用公式就能解决问题,这就是最短距离的另一种体现。
其实在生活中,最短距离的问题无处不在。
你有没有想过,咱们每天做的决定,也是在寻找最短路径?比如说,今天想吃什么,往往一开始脑海里会蹦出好多种选择。
可是等你想了半天,最后还是回到了最爱的那个地方。
就是那种感觉,绕来绕去,最后还是回到了起点。
这就是生活给我们的小调皮,让我们在最短的时间内做出最好的选择。
最短距离问题在团队协作中也同样重要。
想象一下,几个同学一起做项目,大家都在忙着各自的部分,但如果没人理清楚路线,最后的成果可就得打折扣。
最短距离问题

第三讲最短距离问题一、知识梳理几何模型1条件:如图,A、B是直线l同旁的两个定点.+的值最小.问题:在直线l上确定一点P,使PA PB几何模型2条件:如图,A、B是直线l异侧的两个定点.且A、B到l距离不相等-的值最大问题:在直线l上确定一点M,使MA MB二、方法归纳对于几何模型1,解决此类问题的关键在于:找点关于线的对称点,实现“折”转“直”。
对于几何模型2,近年出现的中考题都是直接应用。
三、课堂精讲例题(一)、题中出现一个动点。
例1、在正方形ABCD中,点E为BC上一定点,且BE=10,CE=14,P为BD上一动点,求PE+PC最小值。
2、(1)如图22,等腰直角三角形ABC的直角边长为2,E是斜边AB的中点,P是AC边上的一动点,则PB+PE的最小值为;(2)几何拓展:如图23, △ABC中,AB=2,∠BAC=300,若在AC、AB上各取一点M、N使BM+MN的值最小,这个最小值为;正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从A点爬行到M点的最短距离为多少?10、如图,正方形ABCD,AB边上有一点E,AE=3,EB=1,在AC上有一点P,使EP+BP为最短.求:最短距离EP+BP.如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC和BD,且AC=BD,若点A到河岸CD的中点的距离为500米,则牧童从A处把牛牵到河边饮水再回家,最短距离是()例1.(2007湖北潜江)如图1,小河边有两个村庄A、B.要在河边建一自来水厂向A村与B村供水.(1)若要使厂部到A、B村的距离相等,则应选择在哪建厂?(2)若要使厂部到A、B村的水管最省料,应建在什么地方?例2.两条公路OA、OB相交,在两条公路的中间有一个油库,设为点P,如在两条公路上各设置一个加油站,,请你设计一个方案,把两个加油站设在何处,可使运油车从油库出发,经过一个加油站,再到另一个加油站,最后回到油库所走的路程最短.。
曲线外一点到曲线的最短距离

曲线外一点到曲线的最短距离首先,我们来简单了解一下什么是曲线外一点到曲线的最短距离。
在二维平面上,一个点到一条曲线的最短距离是指,从该点到曲线上的某一个点所经过的路径长度最短。
这个问题可以用数学语言表述为:已知曲线上的点满足某一个函数的方程,求曲线外一点到曲线上某一点的最短距离。
首先,我们先来考虑一种简单的情况:直线外一点到直线的最短距离。
设直线的方程为y=f(x),我们要求点P(x0,y0)到直线的最短距离。
我们可以通过几何直观地得到结论,即点 P 到直线的最短距离就是点 P 到直线上的某一点Q(x,f(x))的距离,即d = sqrt((x0-x)^2 + (y0-f(x))^2)为了使d最小,我们需要对x求导,找到极值点。
通过求导计算可以得到:f'(x) = (x-x0) / (f(x)-y0)解出x之后,带入直线方程,可以求出点Q的坐标,从而求出最短距离。
接下来,我们再考虑一种稍微复杂一点的情况:曲线外一点到曲线的最短距离。
设曲线的方程为 y=f(x),我们要求点 P(x0,y0)到曲线的最短距离。
这个问题要比直线外一点到直线的最短距离要复杂一些,因为曲线上的点不再满足简单的线性关系。
首先,我们可以借助一种非常直观的方法来解决这个问题,即将曲线进行平移、旋转和缩放,转化为直线外一点到直线的最短距离的问题。
这个方法在实际问题中有着广泛的应用,特别是在工程设计和机械制造领域。
通过这种方法,我们可以将曲线几何图形变换成更容易求解的直线几何图形,从而求解出最短距离。
如果不能直接转化为直线外一点到直线的最短距离的问题,我们可以利用微积分的方法来解决。
具体来说,我们可以将曲线上的某一点Q(x,f(x))看作函数f(x)的导数的图像在点x处的切线,从而可以利用导数的定义来求出最短距离。
我们可以通过求导数f'(x),找到曲线上点Q的切线的斜率,然后利用点P和曲线上的某一点Q来构成切线的方程,从而求出最短距离。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
-最短距离问题
————————————————————————————————作者: ————————————————————————————————日期:
第三讲 最短距离问题 一.考情分析 中考分值 近五年杭州中考中,有一年考察此知识点,分值为6分,占全卷的5% 考查方式 此知识点在各种题型中都可以进行考察,虽然杭州中考考察的不多,但在平时的月考、
期中考试中,考察次数很频繁,在浙江其它城市的中考中,考察的次数也很多。
相信在以后的杭州中考中,此知识点必将重点考察。
二.知识回顾
几何模型1
条件:如图,A 、B 是直线l 同旁的两个定点.
问题:在直线l 上确定一点P ,使PA PB +的值最小.
方法:作点A 关于直线l 的对称点A ',连结A B '交l 于点P ,
则PA PB A B '+=的值最小
几何模型2
条件:如图,A 、B 是直线l 异侧的两个定点.且A 、B 到l 距
离不相等
问题:在直线l 上确定一点M ,使MA MB -的值最大
方法:作点B 关于直线l 的对称点B ',连结AB '交l 于点
0M ,则MA MB MA MB AB ''-=-=的值最小
三.重点突破
类型一:题中出现一个动点
(A )【典型例题1】在正方形ABCD 中,点E为BC 上一定点,且BE=10,CE=14,P 为BD 上一动点,求PE+PC 最小值。
(A)【典型例题2】已知:直线112y x =+与y 轴交于A ,与x 轴交于D,抛物线212
y x bx c =++与直线交于A 、E两点,与x 轴交于B、C 两点,且B 点坐标为 (1,0).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上找一点M ,使||AM MC -的值最大,求出点M的坐标.
〖搭配练习〗
(A )1.已知:抛物线的对称轴为x=-1与x 轴交于A B ,两点,与y 轴交于点C ,
其中()30A -,、()02C -,.
(1)求这条抛物线的函数表达式.
(2)已知在对称轴上存在一点P,使得PBC △的周长最小.请求出点P 的坐标
类型二:题中出现两个动点
(B )【典型例题3】如图:
在△AB C中,20A ∠=,10AB AC ==,M 、N 分别AB,AC 上动点,求BN+MN+MC 最小
值
(B)【典型例题4】如图,矩形ABC D中,AB=20,BC=10,若AC,A
B是各有一个动点M,N ,求BM+MN 最小值.
〖搭配练习〗
(B)1.恩施州自然风光无限,特别是以“雄、奇、秀、幽、险”著称于世.著名的恩施大峡谷()A 和世界级自然保护区星斗山()B 位于笔直的沪渝高速公路X 同侧,50km AB A =,、B 到直线X 的距离分别为10km 和40km ,要在沪渝高速公路旁修建一服务区P ,向A 、B 两景区运送游客.小民设计了两种方案,图8是方案一的示意图(AP 与直线X 垂直,垂足为P ),P 到A 、B 的距离之和1S PA PB =+,图9是方案二的示意图(点A 关于直线X 的对称点是A ',连接BA '交直线X 于点P ),P 到A 、B 的距离之和2S PA PB =+.
(1)求1S 、2S ,并比较它们的大小;
(2)请你说明2S PA PB =+的值为最小;
(3)拟建的恩施到张家界高速公路Y 与沪渝高速公路垂直,建立如图10所示的直角坐标系,B 到直线Y 的距离为30km ,请你在X 旁和Y 旁各修建一服务区P 、Q ,使P 、A 、B 、Q 组成的四边形的周长最小.并求出这个最小值.
(B)2.如图,在锐角ABC △中,4245AB BAC =∠=,°,BAC ∠的平分线
交BC 于点D M N ,、分别是AD 和AB 上的动点,则BM MN +的最小值是
________.
类型三:题中出现三个动点时
(B )【典型例题5】如图,在菱形ABCD 中,A B=2,∠BA D=60°,E,F,
P分别为AB,BC,AC 上动点,求PE+PF 最小值
〖搭配练习〗
(B)如图,∠AOB=45°,角内有一动点P ,PO=10,在AO ,BO 上有两动点Q,
R ,求△PQ R周长的最小值
类型四:综合压轴
(C )【典型例题6】如图,四边形ABCD 是正方形,△ABE 是等边三角形,M 为对角线BD(不含B 点)上任意一点,将BM 绕点B 逆时针旋转60°得到BN ,连接EN 、AM 、C M.
⑴ 求证:△AMB≌△E NB ;
⑵ ①当M 点在何处时,A M+CM 的值最小;
②当M 点在何处时,A M+BM+CM 的值最小,并说明理由;
⑶ 当AM+BM+CM的最小值为13+时,求正方形的边长.
〖搭配练习〗
(C)如图,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为
()
6,0
A-,()
6,0
B,()
0,43
C,延长AC到点D,使CD=1
2
AC,过点D作DE
∥AB交BC的延长线于点E.
(1)求D点的坐标;
(2)作C点关于直线DE的对称点F,分别连结DF、EF,若过B点的直线
y kx b
=+将四边形CDFE分成周长相等的两个四边形,确定此直线的解析
式;
(3)设G为y轴上一点,点P从直线y kx b
=+与y轴的交点出发,先沿y轴到达G点,再沿GA到达A点,若P点在y轴上运动的速度是它在直线GA上运动速度的2倍,试确定G点的位置,使P点按照上述要求到达A点所用的时间最短。
(要求:简述确定G点位置的方法,但不要求证明)
课后作业
基础训练题(A类)
1、如图,AC、BD为正方形ABCD对角线,相交于点O,点E为BC边的中点,正方形边长为2cm,在BD上找点P,使EP+CP之和最小,且最小值为________。
2、(1)如图17,等腰直角三角形ABC的直角边长为2,E是斜边AB的中点,P是AC边上的一动点,则PB+PE的最小值为;
(2)几何拓展:如图18, △ABC中,AB=2,∠BAC=300,若在AC、AB上各取一点M、N使BM+MN的值最小,这个最小值为 ;
3、如图19所示,正方形ABCD 的面积为12,ABE △是等边三角形,点E 在正方形
ABCD 内,在对角线AC 上有一点P ,使PD PE +的值最小,则这个最小值为
( )
A .23
B .26 C.3 D.6
4、如图20,已知直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD =2,BC =DC=5,点P 在BC 上移
动,则当PA +PD 取最小值时,△AP D中边AP 上的高为( )
A 、17172
B 、17174
C 、 17178
D 、3 提高训练(B 类)
1、如图,在直角坐标系中,点A的坐标为(-2,0),连结OA ,将线段OA 绕原点O 顺时针旋转120°,得到线段OB.(1)求点B 的坐标;
(2)求经过A 、O、B 三点的抛物线的解析式;
(3)在(2)中抛物线的对称轴上是否存在点C ,使△BOC 的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.(注意:本题中的结果均保留根号)
2、如图,抛物线2y ax bx c =++的顶点P 的坐标为4313⎛
⎫- ⎪ ⎪⎝⎭
,,交x 轴于A 、B两点,交y轴于点(03)C -,
. (1)求抛物线的表达式.
(2)把△ABC 绕AB 的中点E旋转180°,得到四边形ADBC .判断四
边形AD BC 的形状,并说明理由.
(3)试问在线段AC 上是否存在一点F ,使得△FBD 的周长最小,若存在,请写出点F 的坐标;若不存在,请说明理由.
综合迁移(C类)
1、如图,已知点A (-4,8)和点B (2,n )在抛物线2y ax =上.
(1) 求a 的值及点B 关于x 轴对称点P 的坐标,并在x 轴上找一点Q ,使得AQ +Q B最短,求出点Q 的坐标;
(2) 平移抛物线2y ax =,记平移后点A 的对应点为A′,点B 的对应点为B ′,点C (-2,0)和点D (-4,0)是x 轴上的两个定点.
① 当抛物线向左平移到某个位置时,A ′C+C B′ 最短,求此时抛物线的函数解析式;
② 当抛物线向左或向右平移时,是否存在某个位置,使四边形A ′B′CD 的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.
ﻬ2、定义一种变换:平移抛物线1F 得到抛物线2F ,使2F 经过1F 的顶点
A .设2F 的对称轴分别交12F F ,于点D
B ,,点
C 是点A 关于直线B
D 的对称点.
(1)如图24,若1F :2
y x =,经过变换后,得到2F :2y x bx =+,点C 的坐标为(20),,则 ①b 的值等于______________;②四边形ABCD 为( )
A .平行四边形
B .矩形
C .菱形
D .正方形
(2)如图25,若1F :2y ax c =+,经过变换后,点B 的坐标为(21)c -,,求ABD △的面积;
(3)如图26,若1F :2127333
y x x =-+,经过变换后,23AC =,点P 是直线AC 上的动点,求点P 到点D 的距离和到直线AD 的距离之和的最小值.。
