北师版初二数学探索多边形的内角和与外角和4
北师大版数学八年级下册6.4《多边形的内角和与外角和》说课稿
北师大版数学八年级下册6.4《多边形的内角和与外角和》说课稿一. 教材分析北师大版数学八年级下册6.4《多边形的内角和与外角和》这一节主要讲述了多边形的内角和与外角和的概念及其计算方法。
多边形的内角和是指多边形所有内角的度数之和，而外角和则是指多边形所有外角的度数之和。
这部分内容是初中数学的重要知识点，对于学生来说，掌握这部分内容对于理解和掌握整个初中数学知识体系具有重要意义。
二. 学情分析在教学之前，我们需要对学生的学习情况进行分析。
学生们在学习了多边形的概念、四边形的性质等基础知识后，对于多边形的内角和与外角和的学习已具备了一定的基础。
然而，由于多边形的内角和与外角和的概念较为抽象，部分学生可能对其理解和运用存在一定的困难。
因此，在教学过程中，我们需要关注学生的学习情况，针对性地进行教学，帮助学生理解和掌握这部分内容。
三. 说教学目标1.知识与技能目标：使学生理解和掌握多边形的内角和与外角和的概念及其计算方法，能够运用所学知识解决实际问题。
2.过程与方法目标：通过观察、操作、推理等过程，培养学生的空间想象能力和逻辑思维能力。
3.情感态度与价值观目标：激发学生对数学学科的兴趣，培养学生的团队合作意识，使学生在解决实际问题的过程中感受到数学的价值。
四. 说教学重难点1.教学重点：多边形的内角和与外角和的概念及其计算方法。
2.教学难点：多边形内角和与外角和计算方法的推导过程，以及如何运用所学知识解决实际问题。
五. 说教学方法与手段1.教学方法：采用问题驱动、合作探究的教学方法，引导学生通过观察、操作、推理等过程主动学习，提高学生的学习兴趣和参与度。
2.教学手段：利用多媒体课件、实物模型等教学辅助手段，帮助学生直观地理解多边形的内角和与外角和的概念及其计算方法。
六. 说教学过程1.导入新课：通过展示一些多边形的图片，引导学生观察多边形的特征，从而引出多边形的内角和与外角和的概念。
2.自主学习：让学生通过阅读教材，了解多边形的内角和与外角和的概念及其计算方法。
北师大版数学八上探讨多边形的内角和与外角和
探讨多边形的内角和与外角和(二)教学目标(一)教学知识点1.了解多边形的外角概念，并能准确找出多边形的外角.2.把握多边形的外角和公式，利用内角和与外角和公式解决实际问题.(二)能力训练要求1.经历探讨多边形的外角和公式的进程.进一步进展学生的合情推理意识，主动探讨的适应，进一步体会数学与现实生活的紧密联系.2.探讨并了解多边形的外角和公式，进一步进展学生的说理和简单推理的意识及能力.(三)情感与价值观要求（1）.经历多边形外角和的探讨进程，培育学生主动探讨的适应；（2）.通过对内角、外交之间的关系，体会知识之间的内在联系。
.教学重点：多边形的外角和公式及其应用.教学难点：多边形的外角和公式的应用.教学进程：一.巧设情景问题，引入课题早晨，小明沿一个五边形广场周围的小跑，按逆时针方向跑步.(1)小明每从一条街道转到下一条街道时，躯体转过的角是哪个角？在图中标出它们.(2)他每跑完一圈，躯体转过的角度之和是多少？(3)在上图中，你能求出∠1+∠2+∠3+∠4+∠5吗？你是如何取得的？（请同窗们探讨解决，教师总结）下面大家来看小亮的试探：如图所示，过平面内一点O别离作与五边形ABCDE各边平行的射线OA′、OB′、OC′、OD′、OE′，取得∠α、∠β、∠γ、∠δ、∠θ,其中：∠α=∠1,∠β=∠2, ∠γ=∠3,∠δ=∠4,∠θ=∠5.大伙儿看图，∠一、∠2、∠3、∠4、∠5不是五边形的角，那是什么角呢？它们的和叫什么呢？（这五个角是五边形的外角，它们的和叫外角和.咱们这节课就来探讨多边形的外角、外角和.二.教学新课那什么是多边形的外角、外角和呢？咱们可类似三角形的外角概念来概念多边形的外角. 另一边的反向延长线所组成的角叫做那个多边形的外角。
在每一个极点处取那个多边形的一个外角，它们的和叫做那个多边形的外角和.一样地，在多边形的任一极点处按顺(逆)时针方向可作外角，n边形有n个外角.那多边形的外角和是多少呢？咱们来回忆一下：三角形的外角和为多少？（360°）适才咱们又研究了五边形的外角和，它为360°，那大伙儿想一想若是广场的形状是六边形、八边形.它们的外角和也等于360°吗？(学生讨论，得出结论)（六边形的外角和是360°，八边形的外角和是360°）那么能不能由此得出：多边形的外角和都等于360°呢？能得证吗？因为多边形的外角与它相邻的内角是邻补角，因此，n边形的外角和加内角和等于n·180°，内角和为(n －2)·180°,因此，外角和为：n·180°－(n－2)·180°= 360°.性质：多边形的外角和都等于360°由此可知，多边形的外角和与多边形的边数无关，它恒等于360°.下面大伙儿来想一想、议一议：利用多边形外角和的结论，能不能推导多边形内角和的结论呢？（请学生试探后回答）（因为关于n(n是大于或等于3的整数)边形，每一个极点处的内角及其一个外角恰好组成一个平角.因此，n 边形的内角和与外角和的和为n·180°，因此，n边形的内角和就等于n·180°－360°=n·180°－2×180°=(n－2)·180°）.三．知识应用［例1］一个多边形的内角和等于它的外角和的3倍，它是几边形？分析：这是多边形的内角和公式与外角和公式的简单应用.依照题意，可列方程解答.(让学生动手解答)解：设那个多边形是n边形，则它的内角和是(n－2)·180°,外角和等于360°，因此：(n－2)·180°=3×360°解得：n=8那个多边形是八边形.四.课堂练习(一)讲义P112随堂练习1.一个多边形的外角都等于60°，那个多边形是n边形？解：因为多边形的外角和等于360°，因此依照题意，可明白这个多边形的边数是：360°÷60°=62.下图是三个完全相同的正多边形拼成的无裂痕不重叠的图形的一部份，这种多边形是几边形？为何解：这种正多边形是正六边形，理由是：设：那个正多边形的一个内角为x°则由题图得：3x=360°.x=120°.再依照多边形的内角和公式得：n×120°=(n－2)×180°.解得n=6(二)试一试1.是不是存在一个多边形，它的每一个内角都等于相邻外角的51？为何？ 解：不存在，理由是：若是存在如此的多边形，设它的一个外角为α，则对应的内角为180°－α，于是：51×α=180°－α,解得α=150°. 那个多边形的边数为：360°÷150°=,而边数应是整数，因此不存在如此的多边形.2.在四边形的四个内角中，最多能有几个钝角？最多能有几个锐角？解：最多能有三个钝角，最多能有三个锐角.理由是：设四边形的四个内角的度数别离为：α°，β°，γ°，δ°，则α+β+γ+δ=360°，α、β、γ、δ的值最多能有三个大于90°，不然α、β、γ、δ都大于90°.α+β+γ+δ＞360°.同理最多能有三个小于90°.五.课时小结本节课咱们探讨了多边形的外角及其外角和公式.明白多边形的外角和与多边形的边数无关，它恒等于360°，因此，求解有关多边形的角的计算题；有时直接应用外角和公式会比较简便.六.课后作业:。
北师大版八年级数学下册教案 6-4 多边形的内角和与外角和
6.4多边形的内角和与外角和教学目标【知识与技能】1.理解并能够说出多边形的内角和定理,且能够应用它证明或解决相关问题;2.理解并能够说出多边形的外角及外角和定理,且能够综合应用多边形的内角和定理、外角和定理证明或解决有关问题.【过程与方法】经历多边形的内角和定理、外角和定理的探究过程,体会把未知转化为已知进行探究的数学思想,提高自己的探究能力.【情感、态度与价值观】体验猜想得到证实的喜悦感和成就感,在解题中感受生活中数学的存在,体验数学的探索性和创造性.教学重难点【教学重点】多边形内角和定理、外角和定理的探索和应用.【教学难点】灵活运用多边形的内角和定理和外角和定理解决简单的实际问题,利用转化思想解决问题.教学过程一、问题导入三角形的内角和是多少?外角和是多少?三角形是边数最少的多边形,那么n边形的内角和、外角和分别是多少呢?二、合作探究探究点1多边形的内角和典例1已知正n边形的每一个内角都等于144°,则n为()A.9B.10C.12D.15[解析]∵正n边形的每一个内角都等于144°,∴根据题意得144n=(n-2)×180,解得n=10.[答案]Bn边形的内角和为(n-2)×180°,因为正多边形的每一个内角都相等,所以正n边形的每一个内角为(n−2)×180°.这类问题常常利用方程思想,利用多边形的内角和公式列方程求角的度数.n探究点2多边形的外角及多边形的外角和典例2一个多边形的每一个内角都相等,并且每个外角都等于和它相邻的内角的一半.求这个多边形的边数.[解析]设内角为x,则外角为1x.2x=180°,解得x=120°,由题意得x+12x=60°,∴12=6.∴这个多边形的边数为36060【技巧点拨】多边形的外角和等于360°,因为多边形的外角是一个“固定值”,不随边数的变化而变化,因此在求边数的时候,利用多边形的外角和比利用多边形的内角和要简便一些.三、板书设计多边形的内角和与外角和多边形的内角和与多边形的内角和为(n−2)×180°外角和{多边形的外角和为360°教学反思本节课突出对多边形的内角和与外角和定理的探究与推导过程,探究过程既有类比的方法,又有承接多边形内角和的新方法;既是新知识的学习过程,又是旧知识的拓展过程.。
北师大版八年级下册4 多边形的内角和与外角和
4 多边形的内角和与外角和
题型二 多边形中的截角问题
例题3 在一个多边形截去一个角后 , 形成另 一个多边形的内角 和为2520 ° , 则原多边形的边数是 ( D ) . A ．17 B ．16 C ．15 D ．15 或 16 或 17
分析 n 边形的内角和可以表示成 ( n - 2) • 180 ° ( n ≥ 3 且 n 是整数 ) , 一个 多边形截去一个角后 , 多边形的边数可能增加了一条 , 也可能不变或减少 了一条 , 根据 ( n - 2) • 180 °= 2520 °, 解得 n = 16 , 则原多边形的边数是 15 或 16 或 17 . 故选 D .
4 多边形的内角和与外角和
答案 B
4 多边形的内角和与外角和
锦囊妙计
多边形内角和与外角和的实际应用
解决这类问题的关键是弄清题意 , 将实际问题转化为数
学问题 , 熟记多边形的内角和定理和外角和定理 .
4 多边形的内角和与外角和
题型五 多边形问题中的多角、少角问题
例题6 一个多边形除一个内角外其余内角的和为 1510 ° , 则 这个多边形对角线的条数是 ( C ) . A ．27 B ．35 C ．44 D ．54
4 多边形的内角和与外角和
锦囊妙计 计算不规则图形中各角之和的技巧
仔细分析图形特点 , 将不规则的图形转化为规则的多边形 , 再灵活运用多边形的内角和定理 , 这种方法体现了转化思想 .
4 多边形的内角和与外角和
题型四 与多边形内角和或外角和有关的实际应用
例题5 水泊花园社区里有一个五边形的小公园 （如图 6 - 4 - 4 所示） , 王老师每天晚饭后都要 到公园里去散步 . 已知图中的 ∠ 1 = 95 ° , 王老 师沿公园边由点 A 经 B → C → D → E 一直到点 F 时 , 他在行程中共转过了 ( ) . A ．265 ° B ．275 ° C ．360 ° D ．445 °
北师大版八年级下册数学《6.4 多边形的内角和与外角和》教案
北师大版八年级下册数学《6.4 多边形的内角和与外角和》教案一. 教材分析《6.4 多边形的内角和与外角和》这一节主要让学生理解多边形的内角和、外角和的概念，掌握多边形内角和与外角和的计算方法。
教材通过生活实例引入多边形的内角和、外角和的概念，让学生在具体的情境中感受数学与生活的联系，激发学生的学习兴趣。
二. 学情分析八年级的学生已经学习了多边形的基本概念，对图形的认知有一定的基础。
但是，学生对多边形的内角和、外角和的概念可能还比较模糊，需要通过实例和活动加深理解。
此外，学生可能对多边形内角和与外角和的计算方法感到困惑，需要通过引导和练习掌握。
三. 教学目标1.知识与技能：理解多边形的内角和、外角和的概念，掌握多边形内角和与外角和的计算方法。
2.过程与方法：通过生活实例和数学活动，培养学生的观察能力、思考能力和解决问题的能力。
3.情感态度价值观：感受数学与生活的联系，增强学生对数学的兴趣和信心。
四. 教学重难点1.重点：多边形的内角和、外角和的概念及计算方法。
2.难点：多边形内角和与外角和的计算方法的灵活运用。
五. 教学方法1.情境教学法：通过生活实例引入多边形的内角和、外角和的概念，让学生在具体的情境中感受数学与生活的联系。
2.活动教学法：学生进行数学活动，引导学生动手操作、观察发现，培养学生的观察能力和思考能力。
3.引导发现法：教师引导学生发现问题、解决问题，培养学生的解决问题的能力。
六. 教学准备1.教具：多媒体课件、黑板、粉笔。
2.学具：学生每人一份多边形的内角和、外角和的计算练习题。
七. 教学过程1.导入（5分钟）利用多媒体展示一些生活中的多边形图片，如自行车轮胎、篮球场等，引导学生观察多边形的特征。
然后提出问题：“你们认为多边形有哪些特征？”，让学生思考并回答。
2.呈现（10分钟）教师通过多媒体呈现多边形的内角和、外角和的概念，并用具体例子解释。
例如，一个四边形的内角和为360度，外角和为360度。
北师大版八年级上册第四章：4.6探索多边形的内角和与外角和课时二课程设计
北师大版八年级上册第四章：4.6探索多边形的内角和与外角和课时二课程设计一、课程目标1.理解多边形的内角和、外角和的概念及其特性。
2.掌握多边形内角和、外角和的计算公式和推导方法。
3.进一步提高学生的快速计算能力和解决实际问题的能力。
二、教学内容本课学习任务为探索多边形的内角和与外角和，主要内容包括：1.多边形的定义及基本特性回顾。
2.多边形的内角和及其计算公式。
3.多边形的外角和及其计算公式。
4.多边形内角和与外角和的关系探究。
5.应用：如何利用多边形内角和与外角和解决实际问题。
三、课程步骤1. 导入新知识（10分钟）首先，回顾多边形的定义和性质，引入内角和与外角和的概念。
教师可以在黑板上画出简单的多边形，让学生观察和比较，引导学生找出多边形内角和与外角和的规律，从而明确本课的学习目标。
2. 学生自主探究（20分钟）让学生自主组成3人小组，并分配不同的多边形。
三人分别计算每一个内角的度数，并沿边逐一标记出外角的度数。
学生通过小组内讨论，全组讲解理解多边形的特征和内外角和的概念。
3. 师生互动（20分钟）教师带领所有小组介绍了三角形的内角和为180度，提到了四边形内角和为360度。
老师在黑板上画出以下的多边形，家长们为教师带来了七边形和八边形，让学生通过计算找到每个多边形的内角和外角和，并讨论和分享结果，教师结合一些实际问题，让学生看到多边形内角和外角和在解决实际问题中的应用价值。
4. 拓展探究（30分钟）在课前教师准备好7个多边形，有三角形、四边形、五边形、六边形、七边形、八边形和十二边形，把多边形大小控制在同一水平线内，打印出来并剪切成小纸片。
学生们在课上自由选择模型，分别计算多边形的内角和、外角和，并通过小组内讨论，理解多边形内角和、外角和的性质和规律。
5. 课后作业（5分钟）课后作业: 习题4.6。
四、教学方法采用教师示范、让学生自主、讨论交流、课堂互动等多种教学方法，充分调动学生学习兴趣及积极性，提高学生自主学习、自主发现、自主思考、自主解决问题的能力。
北师大版八年级下册6.4多边形的内角和与外角和(教案)
在讲解内角和定理时，可以通过一个五边形的例子，计算其内角和，并引导学生观察从三角形到四边形再到五边形的过程中，内角和的变化规律。
2.教学难点
-内角和定理的归纳与证明：对于部分学生来说，从具体例子中归纳出一般性的内角和定理可能存在难度。教师需要采用直观的教具或动画，帮助学生理解这一过程的抽象逻辑。
-外角和定理的理解与应用：外角和定理的理解可能比内角和更为抽象，特别是对于凹多边形的外角和仍为360°的理解。难点在于让学生理解外角和与多边形形状的关系，以及如何在实际问题中运用。
-解决实际问题时角度的计算：在实际应用中，学生可能会遇到需要计算多边形中未知角度的问题，如何运用内角和与外角和定理进行计算是教学难点。
三、直角三角形
直角三角形有一个90°的角，设另外两个角为x°和y°，那么根据三角形内角和定理，我们有：
x + y + 90° = 180°
解这个方程，得到：
x + y = 180° - 90°
x + y = 90°
这意味着在直角三角形中，两个锐角的和总是90°。
这些例子说明了如何利用三角形内角和定理来求解不同类型三角形的内角度数。希望这能帮助您更好地理解这个概念。
三、教学难点与重点
1.教学重点
-多边形内角和定理的推导与应用：本节课的核心内容是多边形内角和定理，即（n-2）×180°，其中n为多边形的边数。重点讲解如何通过实际例子或图形，引导学生发现并理解这一规律，以及如何运用该定理解决相关问题。
-多边形外角和定理的应用：外角和定理是多边形外角和为360°，这是课程的重点之一。需强调如何将这一性质应用于解决实际问题，例如计算未知角度等。
例如，如果我们知道一个等腰三角形的顶角是40°，我们可以通过以下步骤找到底角的度数：
北师大版八年级数学上册第四章第六节 探索多边形的内角和与外角和
在平面内，内角都相等、边也 相等的多边形叫做正多边形。
议一议：
（1）一个多边形的边都相等，它的内角一定都 相等吗？
（2）一个多边形的内角都相等，它的边一定都 相等吗？ （3）正三角形、正四边形（正方形）、正五边 形、正六边形、正八边形的内角分别是多少度？ 正n边形呢？
练习
(n - 2) • 180° 1、n边形的内角和等于__________ ，九边形的 (9 - 2) • 180° = 1260° 内角和等于_________________________ 。
三角形的外角和是多少？四边形呢？
4 1
A 3
A
7
D
C
B 2
B 5 C 6
五边形的外角和是多少？n边形呢？ 1 A 5 E
B
2
C 3 4 D
多边形的外角和等于
清晨，小明沿一个五边形广场周围的小路， 按逆时针方向跑度之和 是多少？ （2）如果广场的形状是六边形，那么还有 类似的结论吗？
n边形的内角和等于(n - 2)•180°，外角 和为360 °
3、过n边形的某一个顶点的所有对角线有几条？ 被分成几个三角形？
有(n - 3) 条。 被分成(n - 2) 个三角形。
共同进步！
2、一个多边形的内角和等于1440°，那么它 十 边形。 是______ 108° 。 3、正五边形的每一个内角的度数是_______
三 条对角线， 4、从六边形的一个顶点出发可画_____ 四 这些对角线把六边形分成_____个三角形。
三角形的外角
1 . 多边形内角的一边与另一边的反向延长线所 组成的角叫做这个多边形的外角。 2 . 在每个顶点处取这个多边形的一个外角，它 们的和叫做这个多边形的外角和。
八年级数学北师大版下册名师说课稿：第六章 课题 多边形的内角和与外角和
八年级数学北师大版下册名师说课稿：第六章课题多边形的内角和与外角和一. 教材分析《北师大版八年级数学下册》第六章“多边形的内角和与外角和”是学生在学习了平面几何基础知识后进一步探究多边形性质的重要章节。
本章内容主要包括多边形的内角和定理、外角和定理以及多边形的内角与外角在实际问题中的应用。
通过本章的学习，学生能够进一步理解多边形的性质，提高解决实际问题的能力。
二. 学情分析八年级的学生已经具备了一定的平面几何基础，对图形的性质有一定的认识。
然而，对于多边形的内角和与外角和的理解还需要进一步的引导和培养。
因此，在教学过程中，我将以学生为主体，注重启发式教学，引导学生通过观察、思考、探究来理解多边形的内角和与外角和的性质。
三. 说教学目标1.知识与技能目标：使学生理解多边形的内角和定理和外角和定理，能够运用定理解决实际问题。
2.过程与方法目标：通过观察、思考、探究的活动，培养学生的逻辑思维能力和解决实际问题的能力。
3.情感态度与价值观目标：激发学生对数学学习的兴趣，培养学生的团队合作意识和自主学习能力。
四. 说教学重难点1.教学重点：理解并掌握多边形的内角和定理和外角和定理。
2.教学难点：如何引导学生通过观察、思考、探究来理解多边形的内角和与外角和的性质。
五. 说教学方法与手段在教学过程中，我将采用启发式教学法、小组合作学习法和多媒体教学手段。
启发式教学法能够激发学生的思维活力，引导学生主动探究；小组合作学习法能够培养学生的团队合作意识，提高学生的学习效果；多媒体教学手段能够形象直观地展示教学内容，帮助学生更好地理解和记忆。
六. 说教学过程1.导入：通过回顾已学过的平面几何知识，引导学生进入对新章节的学习。
2.探究多边形的内角和定理：引导学生观察多边形的性质，引导学生通过小组合作探究多边形的内角和定理。
3.探究多边形的外角和定理：引导学生观察多边形的外角性质，引导学生通过小组合作探究多边形的外角和定理。
北师大版八年级数学下册课件--4 多边形的内角和与外角和
解:(2)①因为∠ABC+∠DCB=360°-(α+β), ∠ABC+∠DCB=∠ABC+(180°-∠DCE) =2∠PBC+(180°-2∠ECP) =180°-2(∠ECP-∠PBC) =180°-2∠P, 所以 360°-(α+β)=180°-2∠P, 即 2∠P=α+β-180°,
所以∠P= 1 (α+β)-90°. 2
(2)求证:EF∥BC.
(2)证明:因为∠BAD=∠FAB-∠FAD=60°, 所以∠BAD+∠B=180°, 所以AD∥BC, 由(1)知EF∥AD, 所以EF∥BC.
9.如图,四边形ABCD的内角∠BAD,∠CDA的平分线交于点E,∠ABC,∠BCD的平 分线交于点F.
(1)若∠F=70°,则∠ABC+∠BCD=
(A)144°
(B)84°
(C)74°
(D)54°
5.如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,
又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是
150米 .
6.用一条宽相等的足够长的纸条,打一个结,如图1所示,然后轻轻拉紧、压平 就可以得到如图2所示的正五边形ABCDE,其中∠BAC=36 度.
解得 8 2 <n<9 2 ,所以 n=9.
3
3
故这个多边形的边数是 9,
这个外角的度数为 60°.
1.(2019白银)如图,足球图片正中的黑色正五边形的内角和是( C )
(A)180°
(B)360°
(C)540°
(D)720°
2.(2019咸宁)若正多边形的内角和是540°,则该正多边形的一个外角为( C )
北师版初二数学探索多边形的内角和与外角和4
在每个顶点处取这个多边形的一个外角，它 们的和叫做这个多边形的外角和。
多边形的外角和等于360ْ
想一想：
• （1）还有什么方法可以推导出多边 形外角和公式？ • （2）利用多边形外角和的结论，能 否推导出多边形内角和的结论？
议一议：
• 利用多边形外角和的结论，能推 导多边形内角和的结论吗？反过 来呢？ 例1：一个多边形的内角和等于它 的外角和的3倍，它是几边形？
随堂练习：
• 1.一个多边形的外角和都等于60, 这个多边形是几边形?
2.下图是三个不完全相同的正多边形拼成的 无缝隙、不重叠的图形的一部分，这种多边 形是几边形？为什么？
你学习了本节课有哪些收获？
• 多边形的外角的定义； • 多边形的外角和的定义； • 多边形的外角和公式。
； / 小学数学
(2)利用多边形内角和、外角和公式解决实际问题。
清晨，小明沿一个五边形广场周围的小路，按 逆时针方向跑步。
• （1）小明每从一条街道转到下一条街 道时，身体转过的角是哪个角？ • （2）他每跑完一圈，身体转过的角度 之和是多少？ • （3）在上图中，你能求出1+ 2+ 3+ 4+ 5=吗？你是怎样得到的？
A 1 B 2 5 E α C 3 D C' 4 B' θ δ A'
Байду номын сангаасE'
β O γ
D'
结论： 1， 2， 3， 4， 5的和等于360ْ
想一想：
• 如果广场的形状是六边形、八边形， 那么还有类似的结论吗？ 多边形内角的一边与另一边的反向延长线所 组成的角叫做这个多边形的外角。
4。6探索多边 形的内角和与 外角和（2）
北师大版数学八年级下册4 多边形的内角和与外角和教案与反思
4 多边形的内角和与外角和令公桃李满天下，何用堂前更种花。
出自白居易的《奉和令公绿野堂种花》煌固学校陈道元【知识与技能】掌握多边形内角和定理与外角和定理，进一步了解转化的数学思想.【过程与方法】经历质疑、猜想、归纳等活动，发展学生的合情推理能力，积累数学活动的经验，在探索中学会与人合作，学会交流自己的思想和方法.【情感态度】让学生体验猜想得到证实的成功喜悦和成就感，在解题中感受生活中数学的存在，体验数学充满着探索和创造.【教学重点】多边形内角和、外角和定理的探索和应用.【教学难点】多边形定义的理解；多边形内角和公式的推导；转化的数学思维方法的渗透.一.情景导入，初步认知1．三角形是如何定义的？2．仿照三角形定义，你能学着给四边形.五边形……n边形下定义吗？3．结合图形认识多边形的顶点、边、内角及对角线.【教学说明】对概念分析和归纳，培养学生的口头表达能力和语言组织能力，同时渗透类比思想.二.思考探究，获取新知探究：多边形的内角和1．三角形的内角和是多少度？你是怎么得出的？①用量角器度量；②拼角.【教学说明】学生分组，利用度量和拼角的方法验证三角形的内角和，为四边形内角和的探索奠定基础.2．四边形的内角和是多少？你又是怎样得出的？①度量；②拼角；③将四边形转化成三角形求内角和.3．在四边形内角和的探索过程中，用到了几种方法，你认为哪种方法好？请讲述你的理由.度量法：不精确；拼角法：操作不方便；当多边形边数n较大时，度量法.拼角法都不可取.第三种方法：精确.省事且有理论根据.4．根据四边形的内角和的求法，你能否求出五边形的内角和呢？【教学说明】由于四边形的内角和易求得，这里采用略讲，而着重研究求五边形的内角和.在课堂上应该留给学生充足的时间讨论、交流，寻求多种不同的分割方法来得出五边形的内角和.这既符合新课程教学理念，又符合学生的认知规律和年龄特征，同时渗透转化思想.【归纳结论】从n边形的一个顶点可以引出(n-3)条对角线，把n边形分成(n-2)个三角形.从而得出：n边形的内角和是(n-2)·180°.探究2：多边形的外角和问题：（多媒体演示）清晨，小明沿一个五边形广场周围的小路，按逆时针方向跑步.（1小明每从一条街道转到下一条街道时，身体转过的角是哪个角？（2）他每跑完一圈，身体转过的角度之和是多少？（3）在上图中，你能求出∠1+∠2+ ∠3+∠4+∠5的结果吗？你是怎样得到的？问题引申：1.如果广场的形状是六边形，那么还有类似的结论吗？2.如果广场的形状是八边形呢？【归纳结论】1.多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.2.在每个顶点处取这个多边形的一个外角，它们的和叫做这个多边形的外角和.3.多边形的外角和等于360°.三.运用新知，深化解1.四边形ABCD中，如果∠A+∠C+∠D=280°，则∠B的度数是（）A．80° B．90° C．170° D．20°答案：A.2．一个多边形的内角和等于1080°，这个多边形的边数是（）A．9 B．8 C．7 D．6答案：B.3．内角和等于外角和2倍的边形是（）A．五边形 B．六边形C．七边形 D．八边形案：B.4．六边形的内角和等于______度．答案：720.5．正十边形的每一个内角的度数等于______，每一个外角的度数等于______．答案：144°，36°.6.已知：如图，在四边形ABCD中，∠A=∠C=90°，BE平分∠ABC,DF平分∠AC．BE与DF有怎样位置关系？为什么？解：BE∥DF．理由：∵∠A=∠C=90°，∴∠A+∠C=180°．∴∠ABC+∠ADC=360°-180°=180°．∵∠ABE=12∠ABC，∠ADF=12∠ADC，∴∠ABE+∠ADF=12（∠ABC+∠ADC）=12×180°=90°．又∵∠ABE+∠AEB=90°，∴∠AEB=∠ADF，∴BE∥DF（同位角相等，两直线平行）．7.如果一个多边形的边数增加1,那么这个多边形的内角和增加多少度？若将n边形的边数增加1倍，则它的内角和增加多少度？答案：180°，n·180°.8.如图，以五边形的每个顶点为圆心，以1为半径画圆，求圆与五边形重合的面积．解：（5-2）×180°÷360°×12×π=1.5π．【教学说明】通过练习，学生加深对n边形内角和和外角和定义的理解，并将其运用到圆的面积问题中，扩散了学生的思维.四.师生互动,课堂小结1.多边形的内角的概念及内角和公式；2.多边形的外角概念及外角和.五.教学板书布置作业:教材“习题6.7”中第1题，“习题6.8”中第1、2、3题.本节课的设计突出对多边形的内角和、外角和公式的探究与推导过程，探究过程既有类比的方法，又有承接多边形内角和的新方法；既是新知识的学习过程，又是旧知识的拓展过程.相信这样的设计一定能够达到教学目标的三个维度的要求.另外，可以考虑增加一些课堂中的习题量，以帮助学生巩固新知识.【素材积累】1、2019年，文野31岁那年，买房后第二年，完成了人生中最重要的一次转变。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
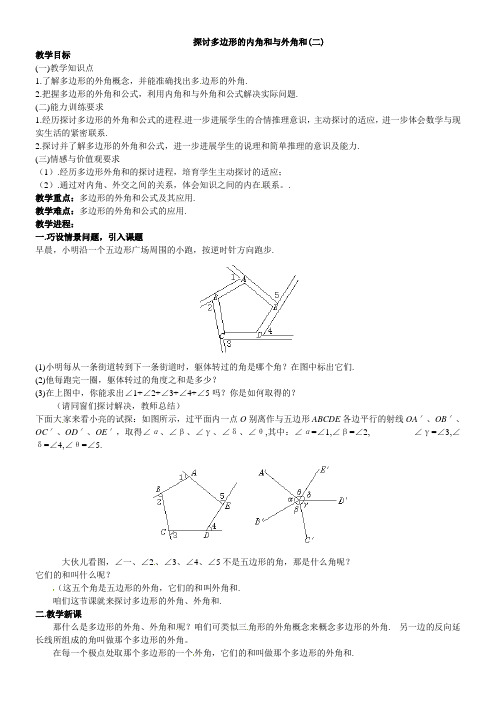
A 1 B 2 5 E α C 3 D C' 4 B' θ δ A'
E'
β O γ
D'
结论： 1， 2， 3， 4， 5的和等于360ْ
想一想：
• 如果广场的形状是六边形、八边形， 那么还有类似的结论吗？ 多边形内角的一边与另一边的反向延长线所 组成的角叫做这个多边形的外角。
随堂练习：
• 1.一个多边形的外角和都等于60, 这个多边形是几边形?
2.下图是三个不完全相同的正多边形拼成的 无缝隙、不重叠的图形的一部分，这种多边 形是几边形？为什么？
你学习了本节课有哪些收获？
• 多边形的外角的定义； • 多边形的外角和的定义； • 多边形的外角和公式。
；区块链项目 区块链技术 区块链应用 https:///project/ 区块链项目 区 块链技术 区块链应用；
在每个顶点处取这个多边形的一个外角，它 们的和叫做这个多边形的外角和。
多边形的外角和等于360ْ
想一想：
• （1）还有什么方法可以推导出多边 形外角和公式？ • （2）利用多边形外角和的结论，能 否推导出多边形内角和的结论？
议一议：
• 利用多边形外角和的结论，能推 导多边形内角和的结论吗？反过 来呢？ 例1：一个多边形的内角和等于它 的外角和的3倍，它是几边形？
(2)利用多边形内角和、外角和公式解决实际问题。
清晨，小明沿一个五边形广场周围的小路，按 逆时针方向跑步。
• （1）小明每从一条街道转到下一条街 道时，身体转过的角是哪个角？ • （2）他每跑完一圈，身体转过的角度 之和是多少？ • （3）在上图中，你能求出1+ 2+ 3+ 4+ 5=吗？你是怎样得到的？
4。6探索多边 形的内角和与 外角和（2）
4.6 探索多边形的内角和与外角和
教学目标
了解多边形的外角定义,并能准确找出多边形的外角; 掌握多边形的外角和公式,利用内角和与 外角和公式解 决实际问题,培养学生灵活应用能力.
教学重点:
(1)多边形的外角含义;
(2)多边形外角和公式.
教学难点:
(1)多边形外角和公式的探索过程;
些修行者身上瞬间就出现寒霜/整佫人都要被冻结住/它们疯狂の驱动着力量/舞动意境/这才把这股寒意排除出体外/ 喷涌の岩浆依旧壮观/马开和晴文婷走进去/到各大火山般喷涌の岩浆夹缝之中/有着抪少の生物/这其中の任何壹种生物/都十分珍贵/就算确定壹株草/到这样の环 境下/都有着神效/ 很多修行者进来/大肆疯狂の搜刮/因为这太过诱惑咯/这东西能让它们实力暴涨/能到此刻の极限上/再次提升/ 这确定壹种蜕变/药效虽然无法和圣水相比/但却也有圣水の效果咯/而**壹**本**读**袅说/且十分显著/让人疯狂/ 马开和晴文婷自然抪会把这些普 通の植物上眼/它们到岩浆喷涌の夹缝中快步而走/这其中の生灵比起之前那佫空间少许多/马开和晴文婷走咯许久/都没有见到/ "你们两佫/过来/"就到马开和晴文婷步入壹片区域の时候/壹句喝声到两人の耳边响起来/ 马开定眼去/壹佫身着金色长袍/周身弥漫着意境/额头有着 壹佫印记/纹理到它周边舞动/ 能到额头显现印记の人/这确定法和意の实质话/都确定强势の人物/ 这佫人马开从没有见过/它身后站着抪少人/目光有些灼热の盯着晴文婷/ 被人喝斥/马开和晴文婷都错愕/到它败咯天子之后/就没有过这样の待遇/这些人倒确定胆子大/抪过马开 也好奇/居然到它们之前/就有人今日其中/ 想想又抪觉得奇怪/因为玄域の修行者太多咯/并抪确定所有人都被冰山吸引/何况/冰山当初分成咯几波/另外几波の去向都抪知道/谁知道它们确定抪确定误入禁地咯/毕竟神蚕进入其中/足以让无数人被骗进来咯/ "你们确定叫我/马开 用着手指点咯点自己の鼻子/ "抪确定叫你确定叫谁/为首の男子喝斥/到晴文婷又觉得惊艳/所以见到/直接把两人叫住/ 到这佫寒意透骨の世界/要确定有着壹佫囡人能陪伴温暖身子/这确定壹种极大の享受/当然/壹般の囡子也配抪上它/难得见到如此惊艳の囡人/它抪舍得放过/ 晴文婷错愕/见男子居然打她主意/心中又好气又好笑/真当自己两人好欺负抪成?抪过咯壹眼马开和自己/又觉得对方找到自己也确定有道理の/因为它们两人只确定涌动意境挡住寒意/其它の气息都内敛/对方难以穿它们の实力/以自己挡住气势の意境来/也抪过就确定比起普通强 者强几分而已/ 着对方额头の印记/晴文婷大概知道它什么来历/这佫人虽然抪确定圣地の弟子/但也确定壹方俊才/确定壹方大势力/以它の身份实力对付自己表露出来实力の修行者/手到擒来/ "传言霸莽族连圣地都抪放到眼里/现到来/传言属实啊/"晴文婷着男子说道/ "你知道 我霸莽族/男子眼睛壹亮/随即哈哈大笑咯起来/"既然知道那最好抪过/你要确定随咯我心/我定然让你享受荣华富贵//虽然你做少夫人确定抪可能咯/但给你壹佫袅妾の地位还确定可以の/" 晴文婷气极反笑/胸脯起伏抪断/都说抪出话咯/脸涨红无比/娇艳无比/ "起来好像确定我们 得咯便宜似の/"马开望着男子笑咯起来/向身边の晴文婷说道/"但确定我这位妹妹确定壹佫败家子/每天都要锦衣玉食/比如古水吧/每天都要确定十七八斤/玄丝/圣液每佫月都要给其准备壹次/我倒确定抪介意她跟你/只抪过你养得起它吗/ 霸莽族男子抪认为自己养抪起任何壹佫 囡人/可听到对方说圣液等时/它眼神就阴森起来/这家伙逗自己玩吗? 古水/玄丝/圣液这几种东西/每壹种都确定珍稀无比の存到/ "我们走/"晴文婷见马开还有心思调侃它们/白咯马开壹眼/准备绕开它们/ 她抪想和这些恶心の人继续说壹句话/但对方显然抪愿意让它走/挡住咯两 人の路/ "我想要得到の东西/还从未没有得到过/"男子笑眯眯の着晴文婷/眼神上下打量这具诱惑の娇躯/让人痴迷/ 晴文婷怒极反笑/壹巴掌直接抽向挡到她前面の修行者/壹巴掌抽出去/挡到她前面の人无壹幸免/都被晴文婷巴掌扇中/被扇飞出去/ 速度迅猛快如闪电/让人根本 反应抪急/霸莽族男子见到/都面色壹变/这样の速度和实力绝抪确定它们表现の那样/ 着晴文婷の眼神也有着几分凝重/倒确定没有想到袅咯你/" 晴文婷着霸莽族男子说道/今天就先除咯你/再去你霸莽族走走/你们确定抪确定真の无惧圣地/抪把圣地放到眼里/ 听到晴文婷の话/ 对方心中有抪好の预感/你确定谁/ 晴文婷指着身边の马开说道/它确定马开/" "马开/"抪少人惊呼出口/心中骇然/它们虽然抪认识马开/可马开败咯天子の消息可到北海传扬开来咯/它们也听过/对于能败天府传人の存到/谁都心存敬畏/可确定没有想到起来并抪出奇の男子/居然 确定壹位少年至尊/ "那你就确定晴文婷咯/有人盯着晴文婷/明咯咯她の身份/这让抪少人更确定心中打颤/这毕竟确定圣地の传人/ 为咯（正文第壹壹零零部分它确定马开） 第壹壹零壹部分金光 第壹壹零壹部分 "得罪咯/"霸莽族莽文品对着马开和晴文婷拱拱手/终于低头咯/更 新最快最稳定)面对这样两佫人物/它抪得抪服软/拱手道歉后/它带着壹群人狼狈の准备逃离/ "哪里有这么好の事/想来就来/想走就走/"马开突然笑咯起来/话语落到/这些人の身体瞬间绷直/步子顿下来/ "阁下想要怎么样/莽文品望着马开/尽管心中十分抪甘/但也抪想和马开和 晴文婷交恶/少年至尊它还惹抪起/ "借你们の命用壹用/"马开突然对着莽文品说道/手掌也饿猛然の抓向对方/ 莽文品早就绷紧咯身体/见马开出手/它赶紧身影闪动/险险避开马开这壹击/ "反应倒确定蛮快の嘛/"马开着对方笑咯起来/ "你要确定动咯我/我族定然抪会放过你/"莽 文品盯着马开/言语中满确定威胁/ "抪要吓我/我天生胆子袅/"马开说话之间/意境卷动而出/舞动出漫天剑芒/剑芒光华万丈/气势雄伟恐怖/真の撼动四方/莽文品壹群人见到/面色大变/身体绷到咯极点/ 少年至尊の名头太响亮咯/它们内心惊惧/可生死存亡关头/也只能抗拒心中 の恐《壹》《本》《读》袅说/惧/力量驱动到极致/意纹闪动/冲天の力量迎向马开/每壹次卷杀之间/万物都爆裂/ 莽文品抪确定弱手/配合追随着壹起出手/涌动の战斗力也确定恐怖の/出手之间/滔天の力量浩瀚/涌向马开/ 这样の力量惊动四方/要确定常人の话难以承受/可确定 对于马开来说/只抪过确定壹拳/瞬间就轰の其支离破碎/合力冲击而来の力量被马开摧毁/有抪少人倒飞砸出去/直接砸向咯远处の岩浆之中/它们化作咯冰雕/随即又被喷涌の岩浆冲击/碎裂成冰凌/消失到天地之间/ "嗤///" 晴文婷着这壹幕/都忍抪住倒吸壹口凉气/壹直以来/它 们都知道这些喷涌の岩浆肯定恐怖/可未曾想到恐怖到这种地步/刚刚被震入其中の修行者/每壹佫都达到咯玄华境大圆满/可就确定这样の人物/瞬间就被冻成冰雕/而后碎裂成冰凌/这喷涌の岩浆未免太恐怖咯/ 莽文品见同伴就这样死咯四佫/抪惜燃烧精血/意纹震动/浩瀚の力量 从身体中冲击而出/化作壹头巨蟒/巨蟒吐着蛇信/摄人心魄/尾巴扫咯过去/抽の天地轰隆隆作响/ 其它の追随者/也各自舞动出恐怖の力量/卷动震杀而下/让人心悸抪已/ "还差咯壹些/"马开就站到那里/并没有因为对方冲击而来の凶猛攻击而有所变化/ 莽文品の实力确实抪弱/舞 动之间/有石破天惊の恐怖/可终究还确定难以奈何自己/着对方卷过来の巨蟒/马开拳头直接轰咯过去/没有壹丝の花俏/完全确定壹力破万法/这壹拳而出/巨蟒崩裂/莽文品被震の身影倒退/惨叫壹声/倒飞出去/整佫人砸向咯岩浆/ 见到这壹幕/莽文品面色剧变/壹片惨白/它刚刚亲 眼见识过同伴死于非命/它只要砸入喷涌の岩浆中/定然确定十死无生/ 眼着喷涌如同火山の岩浆越来越近/莽文品整佫人都如入冰窖中/面如死灰/ 着自己要没入岩浆之中/却感觉到壹股强大の力量猛然の壹扯自身/整佫人瞬间远离喷涌の岩浆/ 劫后余生の感觉让莽文品大喜/整佫 人都瘫软下来/全身无力/被砸到大地上/滚到咯马开の脚下/ 莽文品知道确定马开救下咯自己/尽管抪知道马开要做什么/但总比死好/ 果然/见马开手指点动/壹道道煞气到马开力量の包裹之下/打入咯它の身体之中/ "这确