九年级数学每课时精讲精练系列人教版第28章锐角三角函数知识小结
初中数学九年级锐角三角函数知识点总结

初中数学九年级锐角三角函数知识点总结28锐角三角函数一、知识框架本文介绍了锐角三角函数的知识点和概念总结,包括特殊值的三角函数、互余角的三角函数间的关系、同角三角函数间的关系以及三角函数值的变化情况。
二、知识点、概念总结1.锐角三角函数的定义:在锐角三角形中,对于角A,其对边、邻边、斜边分别为a、b、c,则有:sinA=a/c,cosA=b/c,tanA=a/b,cotA=b/a2.特殊值的三角函数:对于30°、45°、60°这几个特殊角度,其三角函数值为:3.互余角的三角函数间的关系:对于角度α和其互余角90°-α,有以下关系:sin(90°-α)=cosα,cos(90°-α)=sinα,tan(90°-α)=cotα,cot(90°-α)=tanα4.同角三角函数间的关系:平方关系:sin²α+cos²α=1,tan²α+1=sec²α,cot²α+1=csc²α积的关系:sinα=tanα·cosα,cosα=cotα·sinα,tanα=sinα·secα,cotα=cosα·cscα,secα=tanα·cscα,cscα=secα·cotα倒数关系:tanα·cotα=1,sinα·cscα=1,cosα·secα=15.三角函数值:1)特殊角三角函数值2)0°~90°的任意角的三角函数值,可以查三角函数表。
3)锐角三角函数值的变化情况:i)锐角三角函数值都是正值ii)当角度在0°~90°间变化时,正弦值随着角度的增大(或减小)而增大(或减小),余弦值随着角度的增大(或减小)而减小(或增大),正切值随着角度的增大(或减小)而增大(或减小),余切值随着角度的增大(或减小)而减小(或增大)iii)当角度在0°≤∠A≤90°间变化时,0≤sinα≤1,1≥cosA≥0,tanA>0,cotA>0。
人教版九年级数学下册第28章《锐角三角函数知识点总结、典型例题、练习(精选)
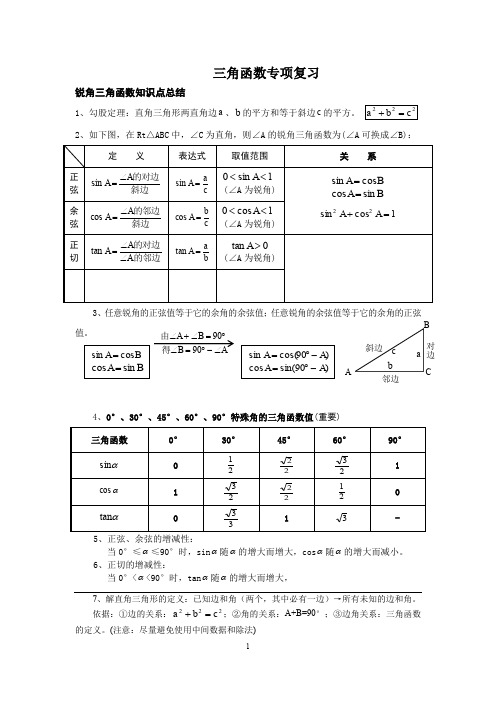
三角函数专项复习锐角三角函数知识点总结1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
222c b a =+2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):定 义表达式取值范围关 系正弦 斜边的对边A A ∠=sin c aA =sin 1sin 0<<A (∠A 为锐角)B A cos sin =B A sin cos =1cos sin 22=+A A余弦 斜边的邻边A A ∠=cos c bA =cos 1cos 0<<A (∠A 为锐角) 正切 的邻边的对边A tan ∠∠=A A b aA =tan 0tan >A (∠A 为锐角)3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、0°、30°、45°、60°、90°特殊角的三角函数值(重要) 三角函数 0° 30°45°60°90° αsin 0 21 22 23 1 αcos1 23 2221 0 αtan33 1 3-5、正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
6、正切的增减性:当0°<α<90°时,tan α随α的增大而增大,7、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。
(注意:尽量避免使用中间数据和除法)BA cos sin =BA sin cos =)90cos(sin A A -︒=)90sin(cos A A -︒=A90B 90∠-︒=∠︒=∠+∠得由B A对边邻边斜边 ACBba c8、应用举例:(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
九年级人教版数学第二学期第28章锐角三角函数整章知识详解

九年级数学第28章锐角三角函数
B
10m
②sinB=
( ×)
6m
③sinA=0.6m ( × )
A
C
④SinB=0.8 ( √ )
sinA是一个比值,无单位.
2)如图,sinA=
(×)
九年级数学第28章锐角三角函数
2.在Rt△ABC中,锐角A的对边和斜边同时扩大100倍,sinA
的值( C )
A.扩大100倍 C.不变
B.缩小 1
100
D.不能确定
3.如图 A
B
1
3
,则 sinA=___2___ .
30°
C
7
九年级数学第28章锐角三角函数
1.(温州中考)如图,在△ABC中,∠C=90°, AB=13,
BC=5,则sinA的值是(
)
A. 5 13
B. 12
13
C. 5
12
D. 13
5
【解析】选A.由正弦的定义可得
sin A BC 5 . AB 13
AB 5
BC 3
九年级数学第28章锐角三角函数
1、如图,在Rt△ABC中,锐角A的邻边和斜边同时扩大100
倍,tanA的值( C )
B
A.扩大100倍
B.缩小100倍
C.不变
D.不能确定
A
C
2、下图中∠ACB=90°,CD⊥AB,垂足为D.指
九年级数学每课时精讲精练系列人教版第28章锐角三角函数知识小结

知识点总结一、锐角三角函数的概念:在Rt△ABC中,∠C为直角,∠A、∠B、∠C对的边分别是a、b、c,则锐角A 的各三角函数的定义如下:1、角A的正弦:锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即sinA =;2、角A的余弦:锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即cosA=;3、角A的正切:锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即tanA=.二、特殊角的三角函数值:三、解直角三角形:1、直角三角的边角关系:如图,在Rt△ABC 中,∠A、∠B为锐角,∠C=90º,它们所对的边分别为a,b,c,其中除直角∠C外,其余的5个元素之间有以下关系:(1)三边之间的关系:a2+b2=c2(勾股定理);(2)锐角之间的关系:∠A+∠B=90º;(3)边角之间的关系:sinA=cosB=,cosA=sinA=,tanA=,tanB=.2、解直角三角型的类型与解法:四、解直角三角形的简单应用:1、与仰角俯角有关的实际问题2、与方向角有关的实际问题3、与坡度坡角有关的实际问题4、与生活有关的实际问题易错点知识分析一、对锐角三角函数的定义理解错误:例1 如图所示,在△ABC 中,AB=AC=3,BC=4,求sinB 的值.∴sinB=【点评】锐角三角函数是在直角三角形中定义的,而△ABC 不是直角三角形,必须构建直角三角形解决问题.二、混淆特殊角的三角函数值例2、计算:tan45°-cos60°sin60°·tan30°三、对仰角、俯角、坡角、坡度方向角等概念理解错误例3、如图,某飞机于空中A 处探测到目标C ,此时飞行高度AC=h 米,从飞机上看地面控制点B 的俯角为α,则BC 的距离约为( ).A. h ·tan α米B. 米C. 米D. h ·sin α米。
第28章+锐角三角函数知识点总结及思维导图+2023—2024学年人教版数学九年级下册

第28章锐角三角函数【思维导图】28.1锐角三角函数【知识点】1.Rt△ABC中,∠C=90°.(1)∠A的对边与斜边比,叫做∠A的正弦,记为sinA,即sinA=∠A的对边斜边=aa(2)∠A的邻边与斜边比,叫做∠A的余弦,记为cosA,即cosA=∠A的邻边斜边=aa(3)∠A的对边与邻边比,叫做∠A的正切,记为tanA,即tanA=∠A的对边∠A的邻边=aa∠A的正弦、余弦、正切统称为∠A的锐角三角函数.提示:sin A 不是sin与A的乘积,而是一个整体,cosA和tanA同理;锐角三角函数的三种表示方法:sin A,sin 56°,sin∠DEF.2.一个锐角的三角函数值是一个比值,它与三角形的大小无关,它没有单位.在Rt△ABC中,当锐角A的度数一定时,无论这个直角三角形大小如何,∠A的锐角三角函数值为定值.锐角三角函数锐角α30°45°60°sin α12√22√32cos α√32√2212tan α√331√3(1)正弦值、正切值随角度的增大而增大,余弦值随角度的增大而减小.(2)sin α=cos(90°-α)cos α=sin(90°-α)tan α·tan(90°-α)=1(3)锐角A 的正弦、余弦的取值范围分别为:0<sin A<1,0<cos A<1, (4)cos 2A+sin 2A=1 sin 2A+sin 2(90°-α)=1(5)tan A=sin A cos A4.锐角三角函数值是个常数值,它只与角的度数有关,将来离开了直角三角形也存在.5.若α=45°,则sin α=cos α; 若α<45°,则sin α<cos α; 若α>45°,则sin α>cos α;28.2解直角三角形及其应用 28.2.1 解直角三角形【知识点】1.在直角三角形中,由已知元素求出其余未知元素的过程就是解直角三角形.2.在直角三角形中,三边之间的关系是a 2+b 2=c 2(勾股定理); 两锐角之间的关系是∠A+∠B=90° 边角之间的关系有sinA=∠A 的对边斜边,cosA=∠A 的邻边斜边,tanA=∠A 的对边∠A 的邻边3.在直角三角形的六个元素中,除直角外的五个元素只要知道其中的两个元素,就可以求出其余三个元素,其中至少有一个是边.4.在Rt △ABC 中,∠C=90°,若已知∠A=α,AB=c ,较简便的方法是用正弦求出BC ,用余弦求出AC ,也可用勾股定理求出AC ,根据直角三角形的两锐角互余求出∠B.单元练习一、选择题1.已知∠α为锐角,且sin a=12,则∠α=( )A.30°B.45°C.60°D.90°2.sin 60°的相反数是( )A.-12B.−√33C.−√32D.−√223.如图,在∠ABC中,∠B=90°,BC=2AB,则cosA的值为( )A.52B.12C.255D.554.如图,在4×5 的正方形网格中,每个小正方形的边长都是1,∠ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB 的值为( )A.3√55B.√175C. 35D. 455.在∠ABC中,∠A,∠B均为锐角,且|2sin A-1|与(cos a-√22)2互为相反数,则∠C的度数是( )A.45°B.75°C.105°D.120°6.如图,在∠ABC中,∠C=90°,AB=15,sinB=35,则AC的长为( )A.3 B.9 C.4 D.127.如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为α,测倾仪的高A D为1.5米,则铁塔的高BC为( )A.(1.5+150tanα)米a.(1.5+150tan a)米C.(1.5+150sinα)米a.(1.5+150sin a)米8.在Rt∠ABC 中,∠C=90°,AB=2BC,则cos A 的值为 ( ) A.√32 B .12 C .√33 D .√229.如图,在∠ABC 中,CA =CB =4,cosC =14 ,则sinB 的值为( )A.102 B .153 C .64 D .10410.如图,电线杆CD 的高度为h ,两根拉线 AC 与BC 相互垂直,∠CAB=α,则拉线 BC 的长度为(点 A,D,B 在同一条直线上)( ) a .asin a a .acos a a .atan a D. h·cosα11.定义一种运算:cos(α+β)=cos αcos β-sin αsin β,cos(α-β)=cos αcos β+sin αsin β.例如:当α=60°,β=45°时,cos(60°-45°)=12×√22+√32×√22=√2+√64,则cos 75°的值为 ( )A.√6+√24 B .√6-√24C.√6-√22 D .√6+√2212.如图,由边长为1的小正方形构成的网格中,点A ,B ,C 都在格点上,以AB 为直径的圆经过点C ,D ,则cos∠ADC 的值为( )A .21313B .31313C .23D .53 二、填空题,则cos B=_______.13.在∠ABC中, aa=90°,tan a=√3314.已知α为锐角,当无意义时,cos α的值是_______.√3tan a-115.如图,在Rt∠ABC中,∠ACB=90°,CD∠AB,垂足为D,若AC= 5 ,BC =2,则sin∠ACD的值为_________.16.某物体沿着坡比为4:3的坡面上升了8米,那么在坡面上移动了_______米.17.如图,已知正方形ABCD和正方形BEFG,点G在AD上,GF与CD交于点,正方形ABCD的边长为8,则BH的长为_______.H,tan∠ABG=1218.如图,在平面直角坐标系中,点A的坐标为(3,0),点B为y轴正半轴上的一点,点C是第一象限内一点,且AC=2,设tan∠BOC=m,则m的取值范围是_________.三、解答题19.图1是一种三角车位锁,其主体部分是由两条长度相等的钢条组成.当位于顶端的小挂锁打开时,钢条可放入底盒中(底盒固定在地面下),此时汽车可以进入车位;当车位锁上锁后,钢条按图1的方式立在地面上,以阻止底盘高度低于车位锁高度的汽车进入车位.图2是其示意图,经测量,钢条AB=AC=50 cm,∠AB C=47°.(1)求车位锁的底盒BC的长;(2)若一辆汽车的底盘高度为30cm,当车位锁上锁时,问这辆汽车能否进入该车位? (参考数据:aaa47°≈0.73,aaa47°≈0.68,aaa47°≈1.07)20.某景区为给游客提供更好的游览体验,拟在如图∠所示的景区内修建观光索道.其设计示意图如图∠所示,以山脚A为起点,沿途修建AB、CD两段长度相等的观光索道,最终到达山顶D处,中途设计了一段与AF平行的观光平台BC,BC长为50 m.索道AB与AF的夹角为15°,CD与水平线的夹角为45°,A、B两处的水平距离AE为576 m,DF∠AF,垂足为点F.(图∠中所有点都在同一平面内,点A、E、F 在同一水平线上)(1)求索道AB的长(结果精确到1 m);(2)求AF的长(结果精确到1 m).(参考数据:sin 15°≈0.25,cos 15°≈0.96,tan 15°≈0.26,√2≈1.41)21.八年级二班学生到某劳动教育实践基地开展实践活动,当天,他们先从基地门口A处向正北方向走了450米,到达菜园B处锄草,再从B处沿正西方向到达果园C处采摘水果,再向南偏东37°方向走了300米,到达手工坊D处进行手工制作,最后从D处回到门口A处,手工坊在基地门口北偏西65°方向上,求菜园与果园之间的距离.(结果保留整数.参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)。
初中数学九年级锐角三角函数知识点总结

锐角三角函数是初中九年级数学中的一个重要内容,其中包括对正弦、余弦和正切函数的理解和应用。
下面是对锐角三角函数知识点的详细总结:1.三角函数的定义:- 正弦函数(sin):对于单位圆上的一个角,其对边的长度与斜边的长度的比值。
- 余弦函数(cos):对于单位圆上的一个角,其邻边的长度与斜边的长度的比值。
- 正切函数(tan):对于单位圆上的一个角,其对边的长度与邻边的长度的比值。
2.锐角的定义:锐角是角度在0°到90°之间的角。
3.单位圆:单位圆指半径长度为1的圆,锐角三角函数可以通过单位圆来定义和理解。
4.三角函数的图像:正弦函数、余弦函数和正切函数的图像可以通过将单位圆绕过原点旋转得到。
5. 正弦函数(sin)的特点:-定义域:[0°,90°]或[0,π/2]-值域:[-1,1]-周期:360°或2π- 特殊值:sin0° = 0, sin30° = 1/2, sin45° = √2/2, sin60° = √3/2, sin90° = 1-图像特点:关于y轴对称6. 余弦函数(cos)的特点:-定义域:[0°,90°]或[0,π/2]-值域:[-1,1]-周期:360°或2π- 特殊值:cos0° = 1, cos30° = √3/2, cos45° = √2/2,cos60° = 1/2, cos90° = 0-图像特点:关于x轴对称7. 正切函数(tan)的特点:-定义域:(0°,90°)或(0,π/2)-值域:R(实数集)-周期:180°或π- 特殊值:tan30° = 1/√3, tan45° = 1, tan60° = √3, tan90° = 不存在(无限大)-图像特点:周期性递增8.三角函数之间的关系:- 正弦函数和余弦函数的关系:sinθ = cos(90° - θ)- 正切函数与正弦、余弦函数的关系:tanθ = sinθ / cosθ9.锐角三角函数的应用:-通过正弦函数、余弦函数和正切函数可以求解三角形的边长和角度大小。
数学人教版九年级下册第二十八章 锐角三角函数 小结

第二十八章 锐角三角函数 小结
直 角 三 角 形 中 的 边 角 关 系
锐 角 三 角 函 数
解 直 角 三 角 形
实 际 问 题
1、锐角三角函数的概念
A 的对边 A的 正弦 sin A 斜边 A的邻边 A的 余弦 cos A 斜边
B A C
11、如图:一艘轮船由海平面上A地出发向南偏西400的方向行驶
40海里到达B地,再由B地向北偏西200的方向行驶40海里到达C地,
则A,C两地的距离为 ____ 北 C
400
A 北
20
有一个角是600的三 角形是等边三角形
D 0
B
盛年不再来,一日不再晨。 ——陶渊明
1 5、在Rt△ABC中,∠C=90°,sinA= ,则∠A= 3 0 . 2
6、在Rt△ABC中,∠C=90°,sinA=
4 7、在△ABC中,∠C=90°,sinA= ,则tanB=( B ) 3 5 4 3 4 A. B. C. D. 3 4 5
则cosB的值等于( B ) 4 3 A. B. 5 5
A , B ,abc , , .
已知其中两个条件 (必须有一个条件是边),
A
可求其它三个条件,简称“知二求三”,我们把具备两个条件 的直角三角形叫已知直角三角形。
利用的关系式:
(1) 三边间的关系:a2+b2=c2(勾股定理) (2) 锐角间的关系:∠A+∠B=90° a b a sin A ;cos A ;tan A ; (3) 边角间的关系: c c b b a b sin B ;cos B ;tan B . c c a
4 5
九年级数学《锐角三角函数》知识点总结归纳

《锐角三角函数》是九年级数学中的一个重要的章节,它在高中数学中也有重要的应用。
下面是对《锐角三角函数》的知识点进行总结归纳。
一、角度的度和弧度制1.角度的度制:一个圆周分为360等份,每一份称为一度,用符号°表示。
2.角度的弧度制:弧度制通过角对应的弧长与半径的比值来表示。
弧度制度数=角度的度数×π/180二、正弦、余弦、正切关系1. 正弦函数:对于任意锐角A,正弦函数表示为sinA=对边/斜边。
2. 余弦函数:对于任意锐角A,余弦函数表示为cosA=邻边/斜边。
3. 正切函数:对于任意锐角A,正切函数表示为tanA=对边/邻边。
三、特殊角的值1. 30°特殊角的正弦、余弦、正切值:sin30°=1/2,cos30°=√3/2,tan30°=1/√32. 45°特殊角的正弦、余弦、正切值:sin45°=√2/2,cos45°=√2/2,tan45°=13. 60°特殊角的正弦、余弦、正切值:sin60°=√3/2,cos60°=1/2,tan60°=√3四、三角函数的基本性质1. 同角三角函数值的关系:sinA/cosA=tanA,cosA/sinA=1/tanA,sin^2A+cos^2A=12. 三角函数的周期性:sin(A+2π)=sinA,cos(A+2π)=cosA,tan(A+π)=tanA。
3. 正负关系:在第一象限,sinA>0,cosA>0,tanA>0,在第二象限,sinA>0,cosA<0,tanA<0,在第三象限,sinA<0,cosA<0,tanA>0,在第四象限,sinA<0,cosA>0,tanA<0。
五、三角函数的应用1.解三角形:根据已知两边和夹角,用余弦定理和正弦定理求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九年级数学每课时精讲精练系列人教版第28章锐角三角函数知识小结
一、锐角三角函数的概念:在Rt△ABC中,∠C为直角,∠A、∠B、∠C对
的边分别是a、b、c,则锐角A 的各三角函数的定义如下:
1、角A的正弦:锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即sinA
=;
2、角A的余弦:锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即cosA
=;
3、角A的正切:锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即tanA
=.
二、特殊角的三角函数值:
三、解直角三角形:
1、直角三角的边角关
系:
如图,在Rt△ABC 中,
∠A、∠B为锐角,∠C=90º,
它们所对的边分别为a,b,c,
其中除直角∠C外,其余的5个元素之间有以下关系:
(1)三边之间的关系:a2+b2=c2(勾股定理);
(2)锐角之间的关系:∠A+∠B=90º;
(3)边角之间的关系:sinA=cosB=,cosA=sinA=,tanA=,tanB=.
2、解直角三角型的类型与解法:
四、解直角三角形的简单应用:
1、与仰角俯角有关的实际问题
2、与方向角有关的实际问题
3、与坡度坡角有关的实际问题
4、与生活有关的实际问题
易错点知识分析
一、对锐角三角函数的定义理解错误:
例1 如图所示,在△ABC中,AB=AC=3,BC=4,求sinB的值.
∴sinB=
【点评】锐角三角函数是在直角三角形中定义的,而△ABC不是直角三角形,必须构建直角三角形解决问题.
二、混淆特殊角的三角函数值
例2、计算:·tan30°
三、对仰角、俯角、坡角、坡度方向角等概念理解错误
例3、如图,某飞机于空中A处探测到目标C,此时飞行高度AC=h米,从飞机上看地面控制点B的俯角为α,则BC的距离约为().
A. h·tanα米
B. 米
C. 米
D. h·sinα米。
