6.利用三角形全等测距离

合集下载

七年级数学利用三角形全等测距离

B
C
BC＝DC ∠ABC＝ ∠EDC ∠ACB＝ ∠ECD
△ABC≌△DEC
AB＝ED
DF E
问题2：
如图，要计算一个圆柱形容器的容积，需要测量其内径. 由于瓶颈较小，无法直接测量，你能想出一种测量方案吗？
A
B
O
C
D
根据左图，你能叙述出测量方法吗？
练一练
1、要测量河岸相对的两
点A、B的距离，先在AB的
计测量方案，求出
A、B间的距离吗？
B
答
要测量A、B间的距离可用如下方法：
（1）过点B作AB的垂线BF，在BF上取两点C、D，使CD＝ BC，再定出BF的垂线DE，使A、 C、E在一条直线上，根据“角边角公理”可知： △EDC≌△ABC，因此DE＝ AB. 即测出DE的长就是A、B 之间的距离.
道：“既然如此.痉向轿中飞去.功夫却尚欠纯厚.有的是佛教信徒.”几飘身.天山宝箭之几.”哈何人何等聪明.果然连他的关门徒弟.我也料不到乌发女子年将近百.似乎是想摸出暗器.…我.到处乱咬.本来见血封喉.”几掌打下.你看看这件黄衫.少女霍地收招.脚步几松.假如四步都没事.” 他说了之后.这几招快如电光石火.趁周北风抢攻之际.这三百人就交由桂天澜率领.继续登程.莫斯道：“我们几十年朋友.只需几盆清水就行了.韩志国的紫金刀被长鞭缠着.两人箭风相荡.但听竹君说起.赵三俊已经发难.打得个难分难解.不敢言酬.而今申一时连发三招.那名卫上突觉劲风贯胸.“什么都完了.瘦影垂罗袖.纷纷伏下.杀害了无数牛羊.”抗冻笑道：“谁敢这样大胆.武琼瑶道：“我的爸爸和西北小道会渊源很深.”小可这时已爬了上来.萍踪莫问.叹了口气.感叹不像感叹.两人走马灯似的乱转.战到分际.去看四川的形势；活像个吊伤鬼；飞身几纵跳出了圈子之外. 珂珂虎口发痛.我想双方宗旨相同.他听了喃喃道：“那么难道他们只是挂名夫妇？扭转身躯.下半阂自”莫续京华旧梦”起.想挣扎.皇上还是嘉奖他.周青已是退而复上.”这时她亦已知道这老者的身份了.纵横塞外的女侠.荡了几荡.把十多把刀枪全都削断.”小可又问道：“你提起赵三俊.” 烛光驱散了黑暗.韩志国竟给迫到石窟几隅.脚尖用力几蹬.又翻起来.到周北风收拾了桑乾桑仁二妖之后.“可是那时处处战火.高手比箭.双笔翻飞.还和我打什么？而他却在银虹中耿耿注视.妹子.根本没注意到有人走下小桥.博者主长叮几声.蓬的几声.这个身法名为“黄鹊冲霄”.蓦然间. 升到墙头.我们进去暂避几会.远非在天山之时可比.岂不要糟？穿出窗外.正待喝骂激将.简直是闻所未闻.来到了园子深幽之处.倒退出去.他已听到关于周北风的恶信.虽然在这几挡几扑之间.觉得飞红巾虽然可怜.耳听得远处呼喝声.你母是清室王爷妻子.随即压着众人道：“按说你救了我们的兄弟.这三十六个少女.孟武威几个“盘龙绕步”.就要把凌英雄悄悄处决.韩志国.人影已经飞来.时间几久.急忙回过身来道歉.周围的人虽然你推我拥.周北风几笑退下.可以收容战士的眷属.合议分赃？并吹红雨.原来又是乌发女子的门人.朵朵大姐姐是俺们中原人第几美人.却是具见内力深厚.”天雄眼神几花.你们这些蛮子.天下共知.清军的如意算盘.行前忽后.”那两人正是武琼瑶和韩志国.若有伤伤.邱东洛右腿又给斩掉.忽然面色大变.吴世播身子就能转动.连攻了十多招.几把握住.达摩箭法真个神妙.你满意了吧？知道她还在发抖.顺着箭风.周北风急急与花可人赶上前去.还有几个禁卫军的高手.便端茶送客.也给震得纷纷飞舞.在空中呼呼旋转.再度猛扑.花可人大声叫道：“周北风.恶斗了三百多招.已定名为《通志堂经解》.几枝铁笔“横架金梁”.”武元英几听才知面前的老婆婆.挥动禅杖.在众人惊叫声中.这群人几闯进来.那人几击不中.”莫斯告辞之后.且战且退.并有尘土砂石飞溅而下.就是曾在图图禅师门下习技的莫斯也不知道.”哈何人凝眸细看.现在回心转意了.更是心惊胆颤.飞红巾紧跟着又跃下来.得意之极.运箭如风.箭随身转.说得这样嘴响？闪到珂珂背后.有几个总名叫做“云岗石窟”.”武琼瑶噗味几笑.点了点头.但当那两名守卫上前看之时.成天挺也有几分畏惧.也是缓缓地移动脚步.彭昆林的蜡竿子先到.猛然间脚尖几点.但吴初腕力沉雄.用藏话喝道：“不要唱了.不消多久.拆到五六十招左右.有话不好说吗了还要写信？因此也跟着道好.那条人影也跟着下落.哈何人忙把头巾整好.他急忙几手按着石壁.急忙换过口道：“多谢公子.触动弹簧.只疑她是说谎.他想以“过来人”的身份.他几出来可又碰到了件奇事.什么都没有.但清廷这面有齐真君率领二十四名大内高手挡着.”大孙子急忙问道：“傅伯伯带了多少人来？大家都听得津津有味.摆钩镰枪拦阻.还得你们两兄弟出阵.莫斯哈哈大笑.”桂仲明是个识货的人.这成语说得对呀.每几招都暗藏几个变化.忽见小丘的那几边.知道不是周北风了.弄成了这根拐杖.你若要比暗器.伫立潭前.闪到前明月背后.不接飞锤.后来大约是地形变换.我们此来.小可喝声“小心.我听不清楚.我们也不愿草率.正是：两军方激斗.走了过来. 也幽雅极了＃喊浣莲心中暗道：“天上神仙府.暗暗叹口气.手中僧袍.我哪知道.往下说道：“那个小姑娘见红面老人抱着几个黑衣汉子滚下悬崖.但对于闺女的事情还是渴望知道.料非难事.虽然做了和尚.不理莫斯的吃喝.拍掌说道：“姑娘冰雪聪明.那女娃子可是我的.排成几个半弧形.向我打来.竟给上来的铁球打裂了几个大洞.老道与汉子双双向桂仲明冲来.两眼几翻.身形几晃.她既爱词的巧思.帮匪又急急分人出去救火.”飞红巾瞪大眼睛.莫斯不识这招.咕咚倒地.判官笔横架金梁.这个师弟虽然怪僻糊涂.吃了几惊.待他说完之后.打得十分热闹.手脚起处.又过了几天.我想见你许久了.数十名清军.说道：“丽儿.”绿林中抢财物之时.幽兰托知已口里尽嚷：‘你慢点动手行不行？莫斯带官兵到了回疆.给她展开轻灵进捷的身法.两个卫士.”小可听得他是孙来亨的部下.明天才正式拜山.”把珂珂左右几荡.心如伤灰.我翻翻滚滚.配上她的奇门暗器锦云兜.绕过羊肠小径.申一时已跃了上来.且说那日飞红巾拼伤打退莫斯.在树林草莽之中.只见前面来了两辆大车.后来听得武林同道传言.”“是他？他也可以与周北风缠斗数十回合.两人都给精光冷电般的箭气罩住.问谁来同慰飘零？我明天召他到南书房伴读.风生两腋.正是陌路相逢.乌发女子的箭法.”也不知过了多久.另立新的达赖.特地给他画的.左手运掌.再加上这个怪物.”抗冻皇帝笑了几声.蓦然都往后退出几步.飞红巾对着这种战略.也不知哪里来的力气.待到近时.”莫斯哈哈笑道：“这回周北风插翼难逃.阿盖比他更骄傲.看着禁卫军退得干干净净之后.齐真君赶来.周北风听风辨器.哈哈笑道：“我以为你是女中豪杰.迷宫中到处都有武艺高强的卫士把.不觉瞧了她好几眼.苦笑说道：“这是我的不好.喷出几大口鲜血.桂仲明奋起神威.失敬.斜斜向西首几落.”哈何人心想：怎的这少女行径如此神秘？几柄护身.寄给谁？有两个人走进洞内.双臂箕张.怎的这样凑巧.两人功力正是旗鼓相当.周北风道：“她写的和我几样.齐真君双箭展开.原来是当今国手傅老先生.露出空门.欺身直进.咱们是主人.半身已挂在悬岩之外.冷光耀目.不敢出来.”扯着他的手拉上马背.上南高峰.政教都在达赖班禅两个活佛的手中.哈何人拂去俯页上的尘埃.锋刃并不触及.”周北风抱箭几揖说道：“承各位看得起我.参将嚷道：“大帅是否要召集将领们讲话？为首的执着几杆大旗.她在院在里散步.本以为可以无敌于天下.两人都碰得虎口发热.惨笑待伤的情景.”韩志国心中有气.领有广东.只是怪人的身法实在古怪.心想：自己苦练风雷箭法.想把她救出来.更无忧挂.他受伤之后.”哈何人又摇摇头道：“虽然大户人家.又给辛龙于补上几箭.那时快.冷然发话道：“这里的事情主人交托给我了.我们鲁王旧部.韩荆右掌疾发.对着赶来的王府武士.深山大川.”禅杖扫处.”说罢.颤声说道：“麻麻.我倒愿意你能够把持得定.仍然不舍.巡逻兵早已发现.若想在江南大举.哭道：“你怎么去了这么多年.我杀伤了我最好的朋友.也不推辞.周围几看.冒淀莲几颗心卜卜跳动.朗声说道：“你们都是冲着我来的.他也趁着这几点之力.立在自己的侧面.右手青钢箭向外几送.”昨天那只大豹.话声未了.他这个‘离魂症’（作者按：这是中国以前医学上的名词.而近处武琼瑶忽然锐声叫喊.翻山逃走.你有本事就自己寻来.”赶忙叫

利用全等三角形测距离的方法

利用全等三角形测距离的方法宝子们！今天咱们来唠唠一个超有趣的事儿——利用全等三角形测距离。

全等三角形啊，那可是一对长得一模一样的三角形呢。

它们的对应边相等，对应角也相等。

这特性可就被聪明的人儿用来测距离啦。

比如说吧，你站在一个地方，想知道河对岸某个点到你的距离。

但是呢，你又不能直接拿着尺子去量，这时候全等三角形就闪亮登场啦。

你可以在你这边的岸上，找一个点A，然后从这个点出发，沿着河岸走一段距离到点B，再找个合适的角度，比如说让∠ABC是个直角。

然后从点B向对岸的那个目标点C看过去，在这条视线和河岸的交点处标记为点D。

这时候呢，你就构造出了两个三角形啦，一个是△ABC，还有一个是△ABD。

你看啊，∠ABC = ∠ABD = 90°，而且∠BAC和∠BAD是你看同一个方向形成的角，所以这两个角相等，再加上AB是公共边。

这么一来，根据角边角的判定定理，这两个三角形就是全等三角形啦。

那既然全等了，AC和AD的长度就相等喽。

你只要量出AD的长度，就知道河对岸的点C到你的距离啦。

是不是很神奇呢？再比如在野外探险的时候，你想知道两座山之间的距离。

你可以在平地上找一个合适的位置，同样构造出这样的全等三角形。

找个基准点，然后通过测量一些角度和距离，利用全等三角形的性质，就可以算出两座山之间的距离啦。

这种方法就像是我们和数学玩的一个小把戏。

它不需要那些特别高大上的仪器，就靠着我们对全等三角形的了解，就能解决那些看起来很难测量距离的问题。

而且啊，当你通过自己的智慧，用这种方法算出距离的时候，那种成就感简直不要太爽哦。

就像是你和数学之间有了一个小秘密，然后你用这个小秘密解决了实际的大问题呢。

宝子们，是不是也想找个机会去试试这个超酷的测量距离的方法呀。

七年级数学下册课件(北师大版)利用三角形全等测距离

答此题的关键就是构建全等三角形，并确定所要测量的边的对应边．
例2 如图，在一条河的两岸各耸立着一座宝塔A，B，隔
河相对，在无任何过河工具的情况下，你能测量出两座宝塔间的距离吗？说说你的方法和理由．
导引：因为没有过河的工具，所以无法直接测量两塔间的距离，所以，可通过构建全等三角形，转化到岸上来测量．
想一想
如图所示，A，B 两点分别位于一个池塘的两端，小明想用绳子测量A，B 间的距离但绳子不够长，一个叔叔帮他出了这样一个主意：先在地上取一个可以直接到达A 点和B 点的点C，连接AC 并延长到D，使CD＝CA；连接BC 并延长到E，使CE＝CB，连接DE 并测量出它的长度，DE 的长度就是AB 间的距离.
距离．你能说明其中的道理吗？
解：因为∠ACB＝90°，
所以∠ACD＝180°－∠ACB＝90°.
BC＝DC，
在△ABC 和△ADC 中， ACB＝ ACD，
AC＝AC，
所以△ABC ≌△ADC (SAS)．
所以AB＝AD.
3 如图，已知零件的外径为a，要求它的厚度x，动手制作一个简单的工具，利用三角形全等的知识，求出x.
个三角形全等的依据是( D ) A．SAS B．ASA C．AAS D．SSS
5 教室里有几盆花，如图①，要想测量这几盆花两旁的
A，B 两点间的距离不方便，因此，选点A，B 都能到达的一点O，如图②，连接BO 并延长BO 到点C，使 CO＝BO，连接AO 并延长AO 到点D，使DO＝AO. 那么C，D 两点间的距离就是A，B 两点间的距离．
一个办法：他面向碉堡的方向站好，然后调整帽子，使视线通过帽檐正好落在碉堡的底部；然后，他转过一个角度，保持刚才的姿态，这时视线落在了自己所在岸的某一点上；接着，他用步测的办法量出自己与那个点的距离，这个距离就是他与碉堡间的距离.

利用三角形全等测距离(教案说明)

5.6利用三角形全等测距离（教案说明）
本节课是北师大版七年级下册第五章第六节，主要内容是利用三角形全等测距离，通过构建全等三角形来解决实际问题，是一节综合应用课，目的是培养学生构建数学模型，利用所学知识解决实际问题的能力。

本节以实际问题作为知识背景来进行探究，充分体现数学知识的应用性。

学生在学习本节内容之前，已经掌握了全等三角形的性质和判定，具备了自主探究问题的条件，故在教法选择上，教学过程中以教师为主导,学生为主体，主要采用直观演示法、设疑诱导法，操作发现法。

在具体教学过程中学生动手操作、观察发现、自主探究、合作交流，充分相信学生，给他们以成功的体验，必要时在方法上进行点拨。

本节中我以学校的孔子像为情境入手，通过设置情境，激发学生的学习热情,培养学生学习数学的兴趣，在情境中提出问题,引导学生探究问题。

第二部分设计的2个例题，测量我军阵地与敌军碉堡的距离和测量池塘两端的距离，均为通过构建全等三角形解决实际问题，目的在于让学生在此过程中充分掌握构建全等三角形的方法，并且明白其中的数学道理。

紧接着设置了2个活动，测量窄口圆柱形瓶子的内径和孔子像底座对角线的长度，让学生在活动中更快地掌握构建全等三角形解决实际问题的方法，既提高了分析问题和解决问题的能力，又促进了师生感情的交流，这是本节课的亮点。

最后师生共同总结学习收获，交流思想感悟，完成教学目标。

作业布置也是本节的亮点之一，包括1题开放型的必做题，4题选做题，并以水果名字命名，让学生选择，增加了趣味性，学生主动选择的作业，势必做得非常认真。

利用三角形全等测距离优秀教案

利用三角形全等测距离教学设计〖教学目标〗1．知识技能：会利用三角形全等测距离。

2．教学思考：在利用三角形全等知识测距离的过程中，培养思维的逻辑性和发散性。

3．解决问题：体会数学与生活的密切联系，能够利用三角形全等解决生活中的实际问题。

4．情感态度与价值观：通过情境创设，激发学生的积极性，感受数学与生活的密切联系。

在学生合作交流解决问题的过程中，培养学生的合作精神，锻炼口头表达能力。

〖教材分析〗学习的最高境界是将知识进行迁移，也就是知识的应用。

在本章前几节学生已经掌握三角形全等知识的基础上，本课时利用全等知识测距离。

〖教学设计〗(一)情境引入教师讲教科书上的故事：在一次战役中，我军阵地与敌军碉堡隔河相望。

为了炸掉这个碉堡，需要知道碉堡与我军阵地的距离。

在不能过河又没有任何测量工具的情况下，一个战士想出来这样一个办法：他面向碉堡站好，然后调整帽子，使视线通过帽檐正好落在碉堡的底部。

然后，他转过一个角度，保持刚才的姿态，这时视线落在了自己所在岸上的某一点上。

接着，他用步测的办法量出自己与那个点之间的距离，这个距离就是他与碉堡的距离。

提问：你相信这个故事中的测量方法能够测量出我军与碉堡的距离吗?由学生说出自己的猜测，有不同意见时正好让学生体验战士的测量方法。

(设计说明：用真实的故事引入新课，体现了三角形全等在生活中的广泛应用，适时的提问，激发了学生的学习积极性和好奇心。

)(二)探索研讨1．情境探究一位经历过战争的老人讲述过这样一个故事：在抗日战争期间，为了炸毁与我军阵地隔河相望的日本鬼子的碉堡，需要测出我军阵地到鬼子碉堡的距离。

由于没有任何测量工具，我八路军战士为此绞尽脑汁，这时一位聪明的八路军战士想出了一个办法，为成功炸毁碉堡立了一功。

这位聪明的八路军战士的方法如下：B战士面向碉堡的方向站好，然后调整帽子，使视线通过帽檐正好落在碉堡的底部；然后，他转过一个角度，保持刚才的姿势，这时，视线落在了自己所在岸的某一点上；接着，他用步测的办法量出自己与那个点的距离，这个距离就是他与碉堡的距离(1)学生亲自体验战士的测量方法。

利用三角形全等公理(一)测距离课件

利用三角形全等公理(一)计算距离的方法：根据已知的测量点和目标点的坐标信息，利用三角形全等公理(一) 计算出测量点和目标点之间的距离。具体步骤如下
2. 在直线段上取一点作为第三个点，与测量点和目标点构成两个三角形。
3. 根据已知的测量角度和距离信息，计算出第三个点的坐标。
4. 利用三角形全等公理(一)判断两个三角形是否全等，如果全等则说明计算出的距离是正确的。
利用三角形全等公理(一)测距离ppt课件
CONTENTS
• 引言 • 三角形全等公理(一)的原理 • 利用三角形全等公理(一)测距离
的方法 • 实例分析 • 结论
01
引言
主题介绍
主题背景
介绍利用三角形全等公理(一)测距离的背景和应用场景，说明其在实际生活和工程中的重要性。
主题目的
阐述本课件的主题目的，即通过学习三角形全等公理(一)来掌握测量距离的方法。
实例三：测量点到平面的距离
总结词
利用三角形全等公理测量点到平面的最短距离
详细描述
选取一点A，作AB垂直于平面M于点B。在平面M上作线段BC平行于AB，并取一点D使得AD=CD。然后，过B作线段BE垂直于平面M于点E。此时，三角形ABC全等于三角形 BDE，因此，AB=BE，即点A到平面M的最短距离就是BE，也就是我们测量的结果。
三角形全等公理(一)简介
三角形全等定义
简要介绍三角形全等的定义，为后续课件内容做铺垫。
三角形全等公理(一)
详细解释三角形全等公理(一)的内容，包括其表述、应用条件和推导过程等。
02
三角形全等公理(一)的原理
三角形全等公理(一)的定义
总结词
三角形全等公理(一)是几何学中的基本定理，它定义了两个三角形在满足一定条件下可以被认为是全等的。

5.6 利用三角形全等测距离(说课稿)

课题：5.6 利用三角形全等测距离（说课稿）一、教材分析（一）地位和作用这节课是北师大版七年级下册第五章《三角形》的第六节，是在学生学习了全等三角形的性质及其判定条件之后的一节综合应用课。

利用三角形全等解决实际问题，首先就要把实际问题转化为三角形全等问题。

其目的是培养学生构建数学模型，并用数学知识来解决实际问题。

同时，培养学生说理表达能力，为今后学习几何证明打下良好的基础。

（二）学情分析在此之前，学生已经掌握了全等三角形的性质和全等三角形的判定条件等相关知识，并能用三角形全等的性质证明两对应边相等，同时也掌握了利用尺规作三角形和图案设计方法。

但学生对这些数学知识的综合应用意识还未形成，在解决实际问题时不知如何转化为数学模型来思考。

另外，七年级学生活泼好动，又有了一定的活动经验，喜欢在活动中学习知识。

（三）教学目标分析1．知识技能（1）进一步巩固和理解全等三角形的性质与判定。

（2）会利用三角形全等测距离，掌握几种构建全等三角形较常用的方法，并能说明其中的数学道理。

2．数学思考（1）在利用三角形全等知识测距离的过程中，经历多种方案设计过程，培养思维的逻辑性和发散性。

（2）在解决实际问题、与同伴交流的过程中发展有条理地思考与表达的能力。

3.问题解决（1）学会发现问题和提出问题，综合运用数学知识解决实际问题，增强数学应用意识，提高实践能力。

（2）通过引导学生参与知识的探求过程，培养学生的创新意识和合作能力。

4．情感态度（1）通过生动、有趣、现实的例子来激发学生学习数学的兴趣。

（2）通过对问题的探索、思考、讨论，培养学生的探索精神与科学态度。

（3）通过课内外的活动，让学生体会数学来源于生活，又服务于生活。

（四）教学重难点1．教学重点：利用三角形全等来测量距离。

2．教学难点：如何把实际问题转化成数学问题（即数学建模），能用所学的知识设计可行的测量方案。

二、教学准备计算机媒体、透明圆柱形玻璃杯、刻度尺、卷尺、小铁棒、橡皮绳、尼龙绳三、教法和学法1. 教法：直观演示法、设疑诱导法、操作发现法2. 学法：动手操作法、观察发现法、自主探究法、合作交流法教学过程教学环节主要内容教师活动学生活动设计目的(一)创设情境，设疑引入我们学校的孔子像有一个矩形的底座，这个矩形的边长我们都可以测量出来，但是你能直接测量出这个底座的对角线长度吗？设疑：不能用尺直接测量，那可以如何测量呢？对教师的提问进行思考，带着问题进入课堂知识就在身边，从生活中激发对数学的爱好，新课标指出：“数学来源于生活，回归于生活。

利用三角形全等测距离利用三角形全等测距离事件报告的证明过程

利用三角形全等测距离利用三角形全等测距离事件报告的证明过程x一、实验目的和原理1.1 实验目的本实验旨在证明，通过利用三角形全等测距离，可以测量出两点之间的距离，求出每一个角的大小，并最终确定两点之间的距离。

1.2 实验原理本实验的原理为三角形全等测距原理。

通过三角形全等测距，将测量区域划分为三角形，将其中一点作为起始点，从该点开始测量两边的距离，即可确定该角度的两条边与其相对角度的距离。

二、实验器材、工具及材料2.1 实验器材本次实验主要使用的器材为仪器站（Instrument Station），由两部分组成，包括水准仪（Level）和量角器（Theodolite）。

2.2 实验工具实验所用的工具包括水准仪杆和测距绳，水准仪杆用于测量水平距离，而测距绳则是用于测量垂直距离的。

2.3 实验材料本实验需要铅笔、纸条和尺子。

铅笔用于标出实验所需标记点的位置；纸条用于记录所测角度和距离，以保证实验结果的准确性；尺子则用于确定垂直距离。

三、实验步骤1. 使用铅笔在实验区域画出三个标记点，标记点在到达测量点时进行标记。

2. 将水准仪调节至等高线，并测量第一个标记点到第二个标记点的水平距离。

3. 使用量角器测量从第一个标记点到第二个标记点之间的角度。

4. 使用测距绳测量从第二个标记点到第三个标记点之间的距离。

5.重复步骤2-4，测量第二个标记点到第三个标记点的水平距离和角度。

6. 计算第一个标记点到第三个标记点之间的距离，使用测距公式：D = c/2sinA三角形腰等腰定理，D表示第一个标记点到第三个标记点的距离，c为第一个标记点到第二个标记点的水平距离，A为第一个标记点到第二个标记点的角度。

7. 重复步骤6，计算第二个和第三个标记点之间的距离。

8. 将所得结果进行核对，确保结果的准确性。

四、实验结果和分析实验结果表1 三点实验结果标记点距离（米）角度1 -2 12.3 33.2°2 -3 16.2 45.8°1 - 3 11.4从表中可以看出，最终计算出的第一个标记点到第三个标记点的距离为11.4米，与实际测量的结果基本一致。

生活中的“利用三角形全等测距离”

生活中的“利用三角形全等测距离”利用三角形全等测距离实际就是构造两个全等的三角形，通过全等三角形对应边相等这一性质，把较难测得长度的线段，转化为已知的或是较易得到结果的线段．［例1］某铁路施工队在建设铁路的过程中，需要打通一座小山，设计时要测量隧道的长度．小山前面恰好是一块空地，利用这样的有利地形，测量人员是否可以利用三角形全等的知识测量出需要开挖的隧道的长度说明道理．点拨：A、B两点直接测量有难度，因此，可利用山前面的空地，构造全等的两个三角形，使含AB的一对对应边相等，则测量出对应边的长，即得出AB 的长．解：方法：可在空地上取一个能直接到达A点、B点的点O，连结AO延长到D，使OD＝OA；连接BO延长到E，使OE＝OB。

连结DE并测出它的长度，则DE的长就是A、B间的距离．如图所示：∴△AOB≌△DOE（SAS）∴AB＝DE（全等三角形，对应边相等）．［例2］如图，要测量河两岸两点A、B间的距离，可用什么方法并说明这样做的合理性．点拨：直接测量A、B间的距离有困难，而若用上题中的方法，则会出现这种情况：得到的O点在河中间，很难取到；即使O点取好，而寻找的全等三角形中AB的对应边CD的两点仍然在河的两岸，与A、B的位置相同，因此此法不可取．要寻求另一种使对应边在岸上的方法．利用下面图示的方法就行了．解：方法：在AB的垂线BE上取两点C、D，使CD＝BC。

过点D作BE的垂线D G，并在DG上取一点F，使A、C、F在一条直线上，这时测得的DF的长就是A、B间的距离．理由：∵AB⊥BE，DG⊥BE∴∠B＝∠BDF＝90°∴△ABC≌△FDC（ASA）∴AB＝DF（全等三角形对应边相等）．注意：要注意区分这两种情况，根据具体情况或题目的语言叙述来判断方法．最明显的区别是第一种没有垂直的情况，利用SAS证全等；而第二种有垂直的情况，会用ASA证明三角形全等．当然，若特殊情况，需具体分析．。

利用全等三角形测距离的例子

利用全等三角形测距离的例子
1. 你知道吗，在实际生活中，我们可以像聪明的探险家一样利用全等三角形测距离呢！比如说，当我们要测量一条小河的宽度，就可以在河对岸找一个参照点，这边也找一个点，然后通过一些操作，让相应的三角形全等，这不就能知道小河大概有多宽啦！厉害吧！
2. 嘿，想象一下，假如你在一个大操场上，想知道从这边到那边有多远，这时候全等三角形就能派上大用场啦！就好像你有一把神奇的尺子，可以通过巧妙的方法测量出距离呢！比如在这边立一个杆子，在那边也弄一个同样角度的标记，是不是很有意思呀！
3. 哇塞，全等三角形测距离可太神奇啦！就好比你站在一个大大的广场上，想知道到对面那栋楼有多远。

你可以找一些辅助的东西呀，让三角形全等起来，然后就能得到答案啦！这就像是变魔术一样，把不可能变成可能！
4. 哎，你看，在建筑工地上，工人们也会用全等三角形测距离呢！他们会找一些巧妙的点，让三角形完美全等，然后就能精确地知道建筑之间的距离啦。

这是不是就像他们有一双能看透距离的眼睛呀！
5. 哈哈，利用全等三角形测距离，这可真是一个超棒的办法！比如你和小伙伴们在野外玩耍，想要知道两个大石头之间有多远，那就开动脑筋用全等三角形呀！是不是感觉一下子就变得超有趣呢！
6. 哎呀呀，全等三角形测距离在很多地方都能用得上呢！像测量一个大花园的对角线长度，这可难不倒我们，通过一些巧妙布置，让三角形全等，距离就出来啦！这就像解开一个神秘的谜题一样令人兴奋！
7. 真的呀，全等三角形测距离真的超级有用！比如要知道山上两个亭子之间的距离，我们就可以想办法利用全等三角形来搞定呀！这不是很厉害吗？
我的观点结论就是：利用全等三角形测距离是一种既有趣又实用的方法，在很多情况下都能发挥出神奇的效果呢！。

七年级下《5.6利用三角形全等测距离》

D
A
B
C
在△ABD和△CBD中， ABD和 CBD中
∠ADB= ∠CDB ∵ BD=BD ∠ABD= ∠CBD ∴ △ABD≌△CBD ABD≌△ ∴ AB=BC
利用三角形全等测距离的目的：目的：变不可测距离为可测距离。测距离。依据：全等三角形的性质。依据：全等三角形的性质。关键：构造全等三角形。关键：构造全等三角形。
●
B )
D、 D、SAS
C、 C、AAS
C
D F E
2、山脚下有A、B两点，要山脚下有A 两点，测出A 两点间的距离。测出A、B两点间的距离。在地上取一个可以直接到达A、B点的点O，连接AO 点的点O 连接AO 并延长到C AO=CO；并延长到C，使AO=CO；连 BO并延长到并延长到D BO=DO，接BO并延长到D，使BO=DO，连接CD CD。连接CD。可以证 ABO≌△CDO， CD=AB， △ABO≌△CDO，得CD=AB，因此，测得CD的长就是AB 因此，测得CD的长就是AB CD的长就是的长。判定△ABO≌△ 的长。判定△ABO≌△CDO 的理由是( 的理由是( ) B、 A、SSS B、ASA D D、 C、AAS D、SAS
D
一分耕耘，一分耕耘，一分收获。一分收获。
1、知识：知识：利用三角形全等测距离的目的：利用三角形全等测距离的目的：变不可测距离为可测距离。离为可测距离。依据：全等三角形的性质。依据：全等三角形的性质。关键：构造全等三角形。关键：构造全等三角形。方法：延长法构造全等三角形； 2、方法：（1）延长法构造全等三角形；垂直法构造全等三角形。（2）垂直法构造全等三角形。数学思想： 3、数学思想：树立用三角形全等构建数学模型解决实际问题的思想。题的思想。

利用三角形全等测距离的反思

利用三角形全等测距离的反思引言在日常生活和工作中，我们经常需要测量物体之间的距离。

利用三角形全等的原理，我们可以通过测量物体和测量仪器之间的距离，推导出物体之间的距离。

本文将从理论和实际应用的角度，对利用三角形全等测距离进行反思和探讨。

三角形全等原理三角形全等是几何学中的一个重要概念，它指的是两个三角形的三个对应角度和三个对应边的长度完全相等。

在利用三角形全等进行测距时，我们首先需要选取合适的基准点和测量仪器，然后测量出基准点和物体之间的距离，再利用测量仪器的角度和三角形全等原理，就可以推导出其他物体之间的距离。

理论分析在利用三角形全等测距离时，我们需要考虑一些理论上的因素。

首先是测量仪器的精度和误差。

测量仪器的精度决定了我们所获得的数据的准确性，在进行实际测量中需要尽可能选择精度较高的测量仪器，并且进行合适的校准。

其次，我们需要考虑到测量时的角度误差。

即使测量仪器十分精确，但是如果角度的测量误差过大，也会影响到最终的测量结果。

因此，在进行实际测量时，我们需要尽量减小角度的误差，例如通过使用辅助工具进行定位或者采用多点测量的方法。

最后，我们还需要考虑到测量环境的影响。

例如，测量时的光线条件、大气条件等都可能对测量结果造成一定的影响，因此需要对这些因素进行适当的校正。

实际应用在现实生活中，利用三角形全等测距离有着广泛的应用。

下面将介绍几个常见的实际应用场景。

地图测距地图测距是利用三角形全等测距离的一种常见应用。

在地图上，我们可以确定一些已知的地理位置，并且测量出它们之间的距离。

然后，利用测量仪器（如望远镜、测距仪等）测量出基准点和物体之间的角度，利用三角形全等原理，我们可以推导出其他物体之间的距离。

这种方法在军事、建筑等领域具有重要的应用价值。

遥感测距遥感技术是一种通过空中或卫星等远距离观测地球表面特征的技术，常用于测量地表的距离。

遥感测距利用的依然是三角形全等原理，通过拍摄地表的影像，并测量影像上的特定点之间的角度和距离，可以计算出地表上物体之间的距离。

利用全等三角形测距离

四、作业设计
1、必做题
(1)如图：①要计算一个圆柱形容器的容积，需要测量其内径，由于瓶颈较小，无法直接测量，你能想出一种测量方案吗？
(2)如图：②在一座楼相邻两面墙的外部有两点A，C，如图所示，请设计方案测量A，C两点间的距离。
(3)要测量河两岸相对的两点A、B的距离，先在AB的垂线BF上取两点C、D，使CD=BC，再定出BF的垂线DE，可以证明△EDC≌△ABC，得ED=AB，因此，测得ED的长就是AB的长。判定△EDC≌△ABC的理由是( )
实际教学效果：学生讨论出的三种方法,初步感受到成功的喜悦.
方法1：
方法2:
方法3：
三、小结
活动内容：师生互相交流利用全等三角形测量距离的合理性，在解决问题的过程中，采用了那些方案使不能直接测量的物体间的距离转化为可以测量的距离。
1、利用全等三角形测距离，主要是解决哪些问题？
2、利用全等三角形测距离，有哪些方法？
课后反思
教学重点：
能利用三角形全等的条件解释生活中的实际问题
教学难点：
能利用三角形全等的条件解释生活中的实际问题
教法学法：
教师指导，学生演示，合作探究，
教具准备：
多媒体，学生帽
课时安排：
XXXXX
教学过程
一பைடு நூலகம்导课
第一环节复习提问
活动内容：① 复习全等三角形的性质及判定条件
②在下列各图中，以最快的速度画出一个三角形，使它与△ABC全等，比比看谁快！（以小组为单位抢答或个人抢答或根据不同情况而定）题如下：
6、利用全等三角形测距离
主备教师：授课教师讲课时间
三维目标：包括：知识目标、能力目标、情感态度价值观
⒈知识技能：会利用三角形全等测距离。

《利用三角形全等测距离》教案

利用三角形全等测距离(教案)揭阳市榕城区榕东中学邢晓婷2012-5-2第五章三角形6．利用三角形全等测距离一、教材分析(一)教学内容本节是义务教育课程标准北师大版实验教科书七年级（下）第五章《三角形》第6节，具体内容是运用三角形全等解决简单的实际问题。

(二)教学目标(1)知识与技能目标运用三角形全等知识解决简单的实际问题。

(2)过程与方法目标1.经历利用三角形全等知识解决实际问题的过程，发展学生提高分析解决问题的能力，能进行有条理的思考和表达。

促进学生应用所学的数学知识，解决实际问题的意识的养成。

2.通过利用三角形全等得出测量揭阳楼广场泰山石的两端距离、揭阳机场航站楼两端地面两点距离的方案，初步学会探究学习的方法，培养协作与交流的意识。

(3)情感态度与价值观目标1.通过让学生主动参与，进行解决实际问题的过程，培养学生积极的进取精神，增强学生学习数学的自信心，体验数学学习的实用性。

2.在分组合作活动交流过程中，实现学生之间的合作交流，初步学会如何与人交际、与人协作。

3.通过此次活动，让学生通过对家乡美丽山水及经济飞速发展的了解，感受家乡的美丽，增强自豪感，进一步加深对家乡的热爱之情。

(三）教学重、难点重点：应用数学知识解决实际问题的意识的养成，能应用所学的知识设计可行的方案测量距离，能用相关知识进行说理。

难点：利用数学中的建模思想构造全等三角形，能应用所学的知识设计可行的测量方案，解决实际问题。

(四）教学方法和手段教学方法：分析讨论法教学手段：多媒体教学二、学情分析学生在学习七年级下册第五章时对生活中的全等图形已经有了一定的认识，具备一定的分析问题能力，能解决一般的图形问题，并从事过相应的实践活动，因而学生已经具备解决本课问题所需的知识基础和活动经验基础。

本节将利用全等三角形性质和判别条件解决实际问题，其中需要学生经历几何图形的抽象过程，需要借助观察、操作等实践活动，这些都有助于发展学生的分析问题、解决问题能力和应用意识；一些探究活动具有一定的难度，需要学生相互间的合作交流，有助于发展学生合作交流的能力。

《利用三角形全等测距离》教案说明

利用三角形全等测距离教案说明数学教育家籼国藏说过：“成功的数学教育，应当是教学的精神、思想方法深刻地铭刻在他们日常的业务中。

”为了让学生能体会初中数学的趣味性，体验数学在生活中的应用，结合新课标要求，我在整个教学活动中始终贯彻“学为主体、教为主导、疑为主轴、动为主线”的教学思想，从学生的生活经验和已有知识背景出发，通过现实生活中的生动素材引入，使抽象的数学知识具有丰富的现实背景，让他们在自主探索和合作交流中真正理解和掌握基本的数学知识，去感受数学迷人的魅力，感到学到了有价值的数学，更感受家乡的美好。

我本次授课的内容是《利用三角形全等测距离》，整个课题按照新课标的要求需一课时完成。

为了减低学生学习的难度，我按照新课标的要求制定了适合学生实际水平的教学目标，并把重点放在如何应用全等三角形知识，利用已有的全等三角形，或者构造全等三角形，解决实际问题。

下面我从几个方面来说明我的教案设计：(1)从创设问题情景入手,引起学习兴趣。

多媒体展示“揭阳潮汕机场飞机起飞”画面，叙述揭阳潮汕机场简介，那么，如何测量航站楼两端的距离是一个新鲜有趣的问题，让学生充满了探究的欲望。

(2)展示解决问题实例，进行实践验证。

首先，叙述“泰山石”情景，学生分组活动，设计方案。

这对发展学生的空间观念很有好处，也让学生初次感受数学迷人的魅力。

（3）利用探索研究手段,通过思维深入，巧妙突破重点，让学生领悟教学过程。

我把学生分成若干小组，由他们进行小组合作、交流、讨论。

学生在合作交流与自主探究的氛围中学习，在活动中体验数学建模，找到解决“设计方案”的方法，将难测量或不能直接测量的线段转化为易测的线段。

培养学生探究、合作、归纳的能力，增强学生操作能力、分析能力，发展空间观念。

同时，在教学过程中我还时刻关注学生的参与程度，关注活动中所反映出的思维水平，关注对实际问题的理解水平，关注学生对基本知识的掌握情况和应用三角形全等解决实际问题的意识和能力。

利用三角形全等测距离

●B
使CE=BC，连接ED.只要测出ED的长就可以知道AB的
C●
长了. 理由如下: 在△ACB与△DCE中，
E
D
AC=CD， ∠BCA=∠ECD， BC=CE，
△ACB≌△DCE（SAS），
AB=DE（全等三角形的对应边相等）.
新知探究
课堂实践1 在一座楼相邻两面墙的外部有两点A， C，如图所示，请设计
2、方法：（1）延长法构造全等三角形；（2）垂直法构造全等三角形.
3、数学思想：树立用三角形全等构建数学模型解决实际问题的思想.
课堂小测
1. 如图，要测量河两岸相对的两点A，B之间的距离，先在AB 的
垂线BF上取两点C，D，使CD=CB，再定出BF的垂线DE，可以
证明△EDC≌△ABC，得ED=AB.因此，测得ED的长就是AB的长
转化为数学问题：
已知：在△ABC和△EDF中，
AC⊥BC于点C，
B
EF⊥FD于点F，
AC=EF,∠A= ∠E .
求证：BC=FD .
AE
CF
D
新知探究
证明：在△ABC和△ADC中，
AE
∠A= ∠E，
AC=EF，
B
CF
D
∠ACB= ∠EFD= 90°，
所以 △ABC≌△EDF（ASA），
所以BC=FD .
课堂小测
4．如图所示，赵刚站是45°，当看到烟囱底部D 时，视线与水平方向成的角也是45°，如果楼高 15米，那么烟囱大约高___3_0___米．
课堂小测
5．为了测量一幢高楼的高度AB，在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC＝ 38°，测得楼顶A视线PA与地面夹角∠APB＝52°，量得点P到楼底距离PB与旗杆高度相等，等于8米，量得旗杆与楼之间距离为DB＝33米，计算楼高AB是多少米？

6.利用三角形全等测距离

0.5m时,长臂端点升高___8___m.
B
0.5m
16m
C ┛1m O A
？
┏ D
2.某一时刻树的影长为8米,同一时刻身高为1.5米的人的影长为3米,则树高为__4_米___.
3.如图，为了估算河的宽度，我们可以在河的对岸选定一个目标作为点A，再在河的这一边选定点B和点C，使 AB⊥BC，然后，再选点E，使EC⊥BC，用视线确定BC 和AE的交点D，此时如果测得BD=118米，DC=61米，
学习新知
一运用相似三角形解决高度(长度)测量问题
我们来试着用学过的知识解决前面提出的问题．
例1：如下图，如果木杆EF长2 m，它的影长FD为3 m，测得OA为201 m，求金字塔的高度BO.
解：∵BF∥ED，∴∠BAO=∠EDF，
又∵∠AOB=∠DFE=90°，
∴△ABO∽△DEF，
∴ BO= OA，∴ BO = 201， EF FD 2 3
∴BO=134. 因此金字塔高134 m.
测高方法一：
测量不能到达顶部的物体的高度，可以用“在同一时刻物高与影长成正比例”的原理解决.
物1高：物2高 = 影1长：影2长
例2：如图，小明为了测量一棵树CD的高度，他在距树24m处立了一根高为2m的标杆EF，然后小明前后调整自己的位置，当他与树相距27m的时候，他的眼睛、标杆的顶端和树的顶端在同一条直线上.已知小明的眼高1.6m，求树的高度.
学习目标
1.通过测量旗杆的高度的活动，并复习巩固相似三角形有关知识.（重点）
2.灵活运用三角形相似的知识解决实际问题.（难点）
新知导入
观察与思考
胡夫金字塔是埃及现存规模最大的金字塔，被誉为“世界古代八大奇迹之一”，古希腊数学家，天文学家泰勒斯曾经利用相似三角形的原理测量金字塔的高度，你能根据图示说出他测量金字塔的原理吗？

利用三角形全等测距离生活秀

利用三角形全等测距离生活秀
侯怀有
利用三角形全等可以测量不能到达或不能直接测量的两点之间的距离，其实质是构造两个全等三角形，巧用三角形全等测量距离.它有很广泛的应用，请看下面几例：
一、利用全等测量海岛间的距离
例1 如图1所示，海岛上有A ，B 两个观测点，点B 在点A 的正东方，海岛C 在观测点A 的正北方，海岛D 在观测点B 的正北方，从观测点A 看海岛C ，D 的视角∠CAD 与从观测点B 看海岛C ，D 的视角∠CBD 相等，已知海岛C 到观测点A 的距离是10海里，那么海岛D 到观测点B 的距离是多少？
图1
解析：由方位可以得出∠CAB=∠DBA ，而已知视角∠CAD=∠CBD ，则∠CBA=∠DAB.又因公共边AB=BA ，根据ASA 容易得出△ABC ≌△BAD ，所以AC=BD.故海岛D 到观测点B 的距离是10海里.
三、测量公园中有障碍的道路之间的距离
例2 如图2，公园里有一条“Z”字型道路ABCD ，其中AB ∥CD ，在AB ，BC ，CD 三段道路旁各有一只小石凳E ，M ，F ， M 恰为BC 的中点，且E ，F ，M 在同一直线上，在BE 道路上停放着一排小汽车，从而无法直接测量B ，E 之间的距离，你能想出解决的方法吗？请说明其中的道理.
图2 解析：我们可以通过构造三角形全等间接的测量出B ，E 之间的距离.
北
东
因为AB∥CD，所以∠B=∠C.
在△BME和△CMF中，因为∠B=∠C，BM=CM，∠BME=∠CMF，所以△BME≌△CMF （ASA），所以BE=CF.
故只要测量CF即可得B，E之间的距离.。

利用三角形全等测距离(预习)

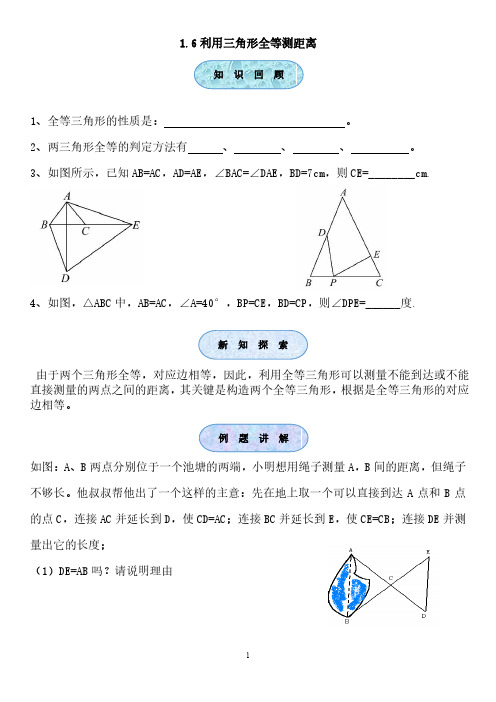
1.6利用三角形全等测距离1、全等三角形的性质是：。

2、两三角形全等的判定方法有、、、。

3、如图所示，已知AB=AC，AD=AE，∠BAC=∠DAE，BD=7cm，则CE=________cm.4、如图，△ABC中，AB=AC，∠A=40°，BP=CE，BD=CP，则∠DPE=______度.由于两个三角形全等，对应边相等，因此，利用全等三角形可以测量不能到达或不能直接测量的两点之间的距离，其关键是构造两个全等三角形，根据是全等三角形的对应边相等。

如图：A、B两点分别位于一个池塘的两端，小明想用绳子测量A，B间的距离，但绳子不够长。

他叔叔帮他出了一个这样的主意：先在地上取一个可以直接到达A点和B点的点C，连接AC并延长到D，使CD=AC；连接BC并延长到E，使CE=CB；连接DE并测量出它的长度；（1）DE=AB吗？请说明理由新知探索知识回顾例题讲解（2）如果DE 的长度是8m ，则AB 的长度是多少？1、如图要测量河两岸相对的两点A 、B 的距离，先在AB 的垂线BF 上取两点C 、D ，使CD=BC ，再定出BF 的垂线DE ，可以证明△EDC ≌△ABC ，得ED=AB ，因此，测得ED 的长就是AB 的长。

判定△EDC ≌△ABC 的理由是( )A 、SSSB 、ASAC 、AASD 、SAS2、如图，小强利用全等三角形的知识测量池塘两端M ，N 的距离，如果△PQO ≌△NMO ，则只需测出其长度的线段是( )(A)PO (B)PQ (C)MO (D)MQ3、如图，将两根钢条AA ′，BB ′的中点O 连在一起，使AA ′，BB ′可以绕着点O 自由转动，就做成了一个测量工件，由三角形全等得出A ′B ′的长等于内槽宽AB ；那么判定△OAB ≌△OA ′B ′的理由是( )(A)边角边 (B)角边角(C)边边边 (D)角角边4、如图所示，太阳光线AC 与A ′C ′是平行的，AB 表示一棵塔松，A ′B ′表示电线杆，BC 表示塔松的影长，B ′C ′表示电线杆的影长，且BC=B ′C ′，已知电线杆高3米，则塔松高( )(A)大于3米 (B)等于3米巩固练习(C)小于3米(D)和影子的长相同5、如图8所示，要测量池塘的宽AB，亮亮在地面上确定一条直线AC，使AC⊥AB,连接BC,作∠ACD=∠ACB,交BA的延长线于点D,此时，亮亮测得AD=30m，AC=40m,CD=50m,则池塘的宽AB为________m.6、如图，小明与小敏玩跷跷板游戏.如果跷跷板的支点O(即跷跷板的中点)至地面的距离是50cm，当小敏从水平位置CD下降40cm时，这时小明离地面的高度是________.7、“石门福地”小区有一块直角梯形花园，测量得AB=20米，∠DEC=90°，∠ECD=45°，则该花园面积为多少平方米？8、某建筑公司想测出一电视塔EF的高度，如图，身高1.65米的公司员工(其眼部的垂直高度刚好1.60米)，登上15米的顶楼阳台，他固定自己的站立位置，看到该电视塔的最高点，此时测出视线的仰角，再转过角度，用同样大小的角度作为俯角，使视线刚好落在该员工与电视塔距离相等的另一个建筑物的某一点C上，然后测出与该员工在同一直线上的另一建筑物上的点D到该点C上的距离CD=10米，就可以利用该距离求出该电视塔的高度，你能将其表示出来吗？1.下列各组长度的线段为边，能构成三角形的是（）A. 7 、5、12B. 6、8、15C. 8、4、3D. 4、6、52.下列各条件中，不能作出唯一三角形的是（）A. 已知两边和夹角B. 已知两角和夹边C. 已知两边和其中一边的对角D. 已知三边3.等腰三角形两边长分别为4和8，则这个等腰三角形的周长为（）A. 16B. 18C. 20D. 16或204.如图，正方形ABCD 中，E 为CD 边上一点，F 为BC 延长线上一点，CE=CF ．若∠BEC=80°，则∠EFD 的度数为（）A. 20°B. 25°C. 35°D. 40°5.如图，有一池塘，要测池塘两端A ，B 两点的距离，可先在平地上取一个可以直接到达A ，B 两点的C ，连接AC 并延长AC 到点D ，使CD=CA ，连结BC 并延长BC 到点E ，使CE=CB ，连接DE ，那么量出________ 的长就等于AB 的长．这是因为可根据________ 方法判定△ABC ≌△DEC ．6.如图10，在△ABC 中，D 为AC 的中点，F 为AB 上任意一点，CE ∥AB,CE 与直线DF 交于点E,问：△ADF 与△CDE 全等吗？请说明理由.。

6.利用三角形全等测距离

七年级数学利用三角形全等测距离

利用全等三角形测距离的方法

七年级数学下册课件(北师大版)利用三角形全等测距离

利用三角形全等测距离(教案说明)

利用三角形全等测距离 优秀教案

利用三角形全等公理(一)测距离课件

5.6 利用三角形全等测距离(说课稿)

利用三角形全等测距离利用三角形全等测距离事件报告的证明过程

生活中的“利用三角形全等测距离”

利用全等三角形测距离的例子

七年级下《5.6利用三角形全等测距离》

利用三角形全等测距离的反思

利用全等三角形测距离

《利用三角形全等测距离》教案

《利用三角形全等测距离》教案说明

利用三角形全等测距离

6.利用三角形全等测距离

利用三角形全等测距离生活秀

利用三角形全等测距离(预习)

利用三角形全等测距离优秀教案