2014年黄埔区初中数学教师解题比赛获奖情况公布
初中数学青年教师解题比赛及答案

初中数学青年教师解题比赛及答案近年来,随着数学教育的不断发展与普及,初中数学教师的教学水平成为提高学生数学能力的重要关键。
为了促进教师专业发展和提高解题能力,初中数学青年教师解题比赛应运而生。
本文将介绍该比赛的背景和目标,并提供部分解题答案作为参考。
一、比赛背景与目标初中数学青年教师解题比赛作为一项专业化竞赛活动,旨在提高青年教师的数学思维和解题能力,加强他们对数学知识的理解和应用。
该比赛通过精心设计的解题题目,考察参赛教师的数学知识储备、解题思路和创新能力,提升他们的教学实践能力和教育教学水平。
二、比赛筹备与参与初中数学青年教师解题比赛由当地教育行政部门、学校和专业团体共同筹备组织。
组织方根据不同年级和内容设置一系列题目,参赛教师需在规定时间内提交解答。
在比赛过程中,还可以结合教学实践和学生需求,设置一些案例分析和教学设计环节。
三、比赛题型与参赛要求初中数学青年教师解题比赛的题型多样,包括选择题、填空题、计算题、证明题等。
参赛教师需要熟练掌握各种数学知识,具备良好的数学分析和解题能力,灵活运用各类解题方法。
参赛教师需按照以下要求提交解答:1. 解题思路清晰、步骤完整:解题过程应该有条不紊,清晰地呈现出解决问题的思考过程和策略。
2. 结果准确、合理:答案应当准确无误,同时要注重解题的合理性和严谨性。
3. 简洁明了、易读易懂:解答应采用准确、简洁的语言表达,以便于阅读和理解。
四、答题示例以下是初中数学青年教师解题比赛的一道选择题和一道填空题的部分答案,供参考:1. 选择题:根据下列数据,判断A和B哪一个数大:A. 0.45B. 0.5解答:由于0.45小于0.5,所以B数大于A数。
2. 填空题:已知两个夹角的比是2:3,其中较小的夹角为40°,则另一个夹角度数为____°。
解答:设较小的夹角为2x,根据题意可得:2x/3x = 40°/x,解得x = 20°,所以另一个夹角度数为3x = 60°。
广州市中学数学优秀科组评选方案

姚瑶
校2009学年校优秀班主任
2010.7
陈景文
第十五届全国华罗庚金杯少年数学邀请赛优秀教练员
2010.4
林海
华罗庚金杯少年数学邀请赛优秀教练员奖
2009.4
唐琦
华罗庚金杯少年数学邀请赛优秀教练员奖
2011.4
邱传林
荣获第十六届全国华罗庚金杯少年数学邀请赛优秀教练员奖
2011.4
温晖
华罗庚金杯少年数学邀请赛优秀教练员奖
2011.6
陈颍
广州市中学数学青年教师“解题比赛”三等奖
2011.6
包承先
广州市中学数学青年教师“解题比赛”三等奖
2011.6
孙苏平
区“卡西欧”青年教师解题比赛一等奖
2011.1
唐琦
区“卡西欧”青年教师解题比赛一等奖
2011.1
姚瑶
区“卡西欧”青年教师解题比赛一等奖
2011.1
王革华
区“卡西欧”青年教师解题比赛一等奖
何方梅
区初中数学青年教师解题比赛二等奖
2011.1
邹芬
区初中数学青年教师解题比赛二等奖
2011.1
周珑
区初中数学青年教师解题比赛二等奖
2011.1
陈莫琼
区初中数学青年教师解题比赛二等奖
2011.1
陈家灿
区初中数学青年教师解题比赛二等奖
2011.1
刘颖斯
区初中数学青年教师解题比赛二等奖
2011.1
徐玲玲
2011.1
包承先
2011年广州市青年教师解题比赛萝岗区初赛二等奖
2011.1
张亚茹
2011年广州市青年教师解题比赛萝岗区初赛二等奖
广州市小学数学学科第二届教师解题比赛决赛获奖名单

广州市小学数学学科第二届教师解题比赛决赛获奖名单一等奖:(共53人)(排名不分先后,下同)【青年组】(32人)欧智毅越秀区朝天小学陈平忠天河区长湴小学陈智斌越秀区朝天小学尤学武天河区华景小学何伟雄越秀区东风西路小学周娟天河区龙口西小学郭睿越秀区东风西路小学陈伟天河区体育西路小学冼颂华越秀区教育发展中心胡敏天河区体育西路小学王武贵越秀区铁一小学黄浩荔湾区芦荻西小学黎美薇越秀区小北路小学曾仪荔湾区五眼桥小学巢亮白云区长红小学曾艳海珠区东风二小崔思敏白云区方圆小学赖敏贤海珠区海珠区第二实验小学刘冬青白云区广园实验小学冯良勇海珠区鹤鸣五巷小学喻宝贵白云区广园小学叶永标番禺区石碁镇沙涌小学李福仁白云区松溪小学陈慧番禺区市桥东兴小学曾迟灏黄埔区恒威实小黄海容南沙区横沥小学常珍花黄埔区怡园小学钟益鑫增城市水电二局小学李美红萝岗区萝峰小学张远生增城市中新镇中心小学王月霞花都区新华街横潭小学李武东从化市街口街中心小学【非青年组】(21人)黄卫群越秀区回民小学何燕天河区华康小学羊斌白云区广园小学杨跃天河区华美实验学校王四中白云区黄边小学洪同海天河区华师附小李长根白云区京溪小学杨海英天河区华阳小学周健图白云区民航广州子弟学校谭军辉天河区岭南中英文学校王朝阳白云区棠溪小学张凤红天河区先烈东小学周良平白云区贤丰小学欧阳亮萝岗区开发区一小蔡晓红荔湾区环西路小学杨志园增城市荔城街挂绿小学钟陈辉海珠区同福东路第二小学段新民增城市新塘镇凤凰城中英文学校郑祚彪番禺区石碁镇新英才中英文学校杨培琴增城市新塘镇汇美天恩小学刘宇帆南沙区万顷沙小学二等奖:(109人)【青年组】(65人)梁小燕越秀区大沙头小学钟国泉天河区昌乐小学梁冠殷越秀区回民小学陈伦鸿天河区华美实验学校林桦越秀区吉祥路小学陈经全天河区华师附小苏美珍越秀区人民北路小学陈继平天河区华阳小学谢怿越秀区五羊小学赖艳天河区华阳小学吴秋琳越秀区雅荷塘小学何小平天河区骏景小学范易荣荔湾区东沙小学崔瑞娟天河区棠东小学付绍琴荔湾区芳村小学吴迪海珠区海珠区第二实验小学卢镜生荔湾区合兴苑小学罗杰胜海珠区红棉小学李红斌荔湾区华侨小学欧卓莹海珠区江南新村第二小学杨绍彭荔湾区康有为纪念学校陆颖能海珠区瑞康路小学钟煜锋荔湾区康有为纪念学校陈瑞芬海珠区同福中路第一小学1香婉仪荔湾区龙津小学谢秀燕海珠区中大附小梁智丹荔湾区三元坊小学蔡敏珊白云区百事佳小学谭锋锋荔湾区西关培正邓伟生白云区大岭小学何素云荔湾区耀华小学李东海白云区金泉小学吴海文荔湾区耀华小学盛莉白云区民航广州子弟学校高云涛花都区赤坭镇白坭小学谢全维番禺区化龙镇化龙中心小学林国权花都区狮岭镇西头小学劳晓丹番禺区南村镇复中实验小学刘桂华花都区新华街莲塘小学郭荣波番禺区石碁镇傍西小学毕倩雯花都区新华街田美小学何绍成番禺区石碁镇东怡小学高艳群花都区新华街圆玄小学陈毅坚番禺区石碁镇海傍小学刘文涛黄埔区荔园小学江鲁华番禺区市桥实验小学黎德伦黄埔区文冲小学张锦荣南沙区庙南小学易彦黄埔区新港小学张桂锋南沙区麒麟小学林少群黄埔区怡园小学杨伟彬南沙区新同丰黄英平黄埔区中大实小齐胜萝岗区长平小学温淑珍增城市荔城街富鹏小学黄翠娣萝岗区福洞小学黎延毅增城市石滩镇金兰寺小学钟雪娴萝岗区香雪小学谷瑶斌增城市新塘镇凤凰城中英文学校欧阳东从化市河滨小学龚海文增城市新塘镇西洲小学欧阳桂锋从化市流溪小学李犹增城市中新天恩小学谢镜波从化市流溪小学郭文锋增城市中新镇育才小学【非青年组】(44人)徐文昌越秀区培正小学郭为民天河区华美实验学校陈国良越秀区署前路小学邝艳芬天河区华阳小学钟小杏越秀区文德路小学汤惠玲天河区天府路小学钟婉群荔湾区宝华培正小学古晓兰黄埔区荔园小学林丽琼荔湾区广船小学夏卫红黄埔区荔园小学黄丽青荔湾区华侨小学郭卫民黄埔区深井小学麦建文荔湾区沙面小学朱俊黄埔区怡园小学周少娴荔湾区詹天佑小学罗展朋萝岗区东区小学陈爱和白云区民航广州子弟学校朱活钊萝岗区东区小学李再华白云区三元里实验小学罗雨雄萝岗区禾丰小学叶中华海珠区海珠区第二实验小学黄锦洪番禺区石楼镇中心小学田锦红海珠区海珠区实验小学曾淑华番禺区石碁镇东怡小学王耀安花都区花东镇大塘小学蓝福强番禺区石碁镇仲元实验学校张建华花都区花东镇七星小学黄堪利番禺区石碁镇仲元实验学校高乐伦花都区花东镇杨荷小学招伟英番禺区市桥东兴小学庾洁妹花都区花东镇杨荷小学李启荣南沙区麒麟小学许丽妮花都区狮岭镇新民小学秦华南沙区一小曾洁雯花都区新华街第四小学林志明南沙区义沙小学龚本利增城市新蕾学校何桂荣南沙区义沙小学徐小军增城市新雅新世界实验学校黄少梅从化市城郊街黄场小学赖远方增城市正果镇龙潭埔小学钟少英从化市河滨小学黄共庆增城市中新镇福和小学黄光强从化市河滨小学注:三等奖共354人(其中青年组260人,非青年组94人),具体获奖名单由各区县教研室小数科公布。
2014数学竞赛获奖名单
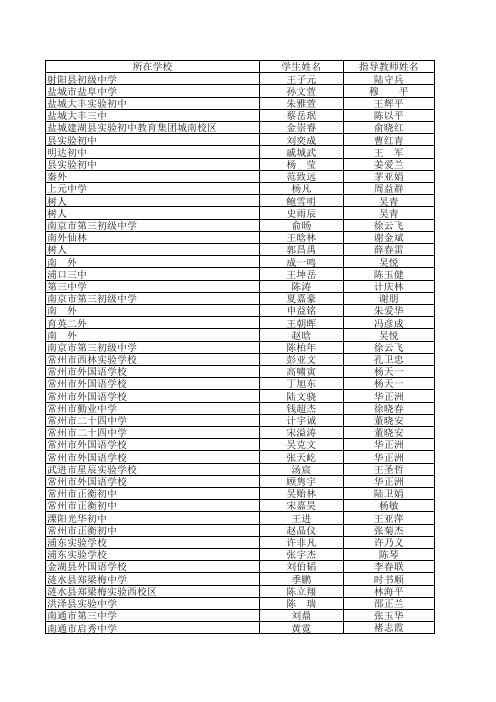
肖 强 许永祥 王辉平 王园娴 夏 云 徐 华 马海兵 蔡东明 魏左青 林升兰 羊为定 周文华 张长海 朱宝明 吴青 吴青 王超 茅亚娟 茅亚娟 吴悦 徐云飞 安惠琴 邢胜 马晓峰 蒋春玲 徐雁 王文宏 徐方方 蒋飞 周梅 王长松 蒋蕾 蒋春玲 石志会 叶彬彬 咸玉美 范文保 薛春雷 李家亮 何爱华 徐春芸 张方芳 徐云飞
严娟 蒋群锋 瞿锦华 朱靖江 陈秀 顾海艳 姜 涛 伞德硕 董妮 张东青 仲伟庆 李大信 高彩云 魏冰 杨正花 卢占武 翟洪卫 王其建 徐鑫 张桂英 张建婷 任婷婷 徐进侠 董作富 丰琴 赵庆波 赵 青 张同名 刘学宇 韩梅 封其瑞 熊卫庆 郭海强 李想 王斌 秦军战 侯立松 夏四应 施学年 王粉宝 王友峰 王友峰 周加锋 顾孝志 王春蕾 蔡海涛 刘芸
南通市第三中学 三厂初中 海南中学 能仁东校区 海南中学 东洲中学 外国语学校 外国语学校 华杰双语学校 华杰双语学校 海头二中 赣榆县实验中学 赣榆县实验中学 初级中学 东海县实验中学 东海县初级中学 东海县外国语学校 东海县培仁学校 东海县白塔初级中学 实验中学 实验中学 实验中学 海宁中学 板浦初级中学 东港中学新校区 苍梧校区 海州实验中学 市外国语学校 华侨双语 初级中学 初级中学 实验中学 宿迁市钟吾初中 宿豫实验初中 泗阳县实验初中 泗洪县育才实验学校 泗洪淮北中学 姜堰白米初中 泰州市民兴中学 姜堰溱潼二中 兴化市文正实验学校 兴化市文正实验学校 兴化市戴泽初级中学 兴化市楚水初级中学 兴化市板桥初级中学 泰兴市西城初级中学 靖江市实验学校
全国初中数学邀请赛获奖3等奖名单

2014年全国初中数学邀请赛获奖名单(三等奖146人) 学生姓名 安澜 白拉比 曹浩轩 曹紫昱 常亮 陈诗雨 陈天杨 陈奕洋 程尔聪 崔明轩 丁嘉琪 丁汐昂 丁语欣 董博豪 杜培昀 冯莉雅 冯恕 冯馨雨 冯梓轩 付文鼎 付逸弦 傅加豪 高溶 高天伟 高一帆 郭若荠 郭思琪 郭天傲 何文佶 何宇琦 贺思凯 就读学校 人大附中 北京二中分校 首师大附中 人大附中 人大附中 北京五中分校 人大附中 人大附中 北师大附中 北师大附属实验中学 西城外国语中学 北师大附属实验中学 清华附中 八十中 人大附中 汇文中学 人大附中 清华附中 人大附中 北师大附属实验中学 北师大朝阳附中 北京八十中 101中学 北京五中分校 人大附中 北京四中 西城外国语中学 北师大附属实验中学 北师大附属实验中学 北师大附属实验中学 人大附中 学生姓名 彭韵锦 齐嘉容 钱天翼 秦礼纳 宋九鹏 宋在 孙慈航 孙方圆 孙瑞阳 孙小淞 谭铭飞 谭欣雨 谭雅丹 谭智泉 汤昊华 屠镇海 汪泽西 王冬青 王汉寅 王皓元 王靖涵 王可萱 王陆辰 王镕祥 王文昊 王晓鸥 王子晗 王紫晨 危昊成 吴一非 吴漪澜 就读学校 北大附中 北师大附属实验中学 北师大附属实验中学 人大附中 北京四中 北师大附属实验中学 北师大附属实验中学 上地实验学校 人大附中分校 景山学校 北师大附属实验中学 人大附中 北京四中 北师大附属实验中学 北师大附属实验中学 人大附中 二十中 北师大附属实验中学 北师大附属实验中学 北师大附属实验中学 北师大附属实验中学 北师大附属实验中学 师达中学 北京五中分校 北京四中 三帆中学 北京八中 北师大附属实验中学 三帆中学 北师大附属实验中学 三帆学校
伍颉 武之圣 熊捷 徐浩轩 徐益泉 徐元熙 许进萱 薛司旸 杨诚远 杨富钧 杨名 杨雁娇 杨俣晟 于宸锴 于孟桐 原思聪 袁景昭 曾瑞彬 张博然 张弛 张恒睿 张家澍 张锦涵 张麒 张起帆 张沁 张赛哲 张天骏 张文佳 张一宁 张煜泽 张哲睿 章翼辰
初中数学教师解题比赛试题

初中数学教师解题比赛试题初中数学教师解题比赛试题一、比赛试题种类及要求本次解题比赛试题为初中数学教师专业能力测试,旨在考察参赛教师的数学解题能力、教学技能以及专业知识掌握程度。
试题将包括选择题、填空题、解答题等类型,全面考察教师的数学素养。
试题难度将按初中数学教学的实际需求和难度水平设置。
二、比赛试题内容1、选择题(1)在△ABC中,已知∠A=60°,∠B=45°,AB=2,则BC的长度为( )A. √3B. √6C. 2D. 2√3 答案:B(2)在实数范围内,方程x²+3x+2=0的解为( ) A. x=1 B. x=-1 C. x=2D. x=-2 答案:D2、填空题(1)已知一个圆的半径为5,那么它的内接正六边形的边长为____。
答案:5√3(2)若二次函数y=x²-4x+c的图像与x轴有交点,则c的取值范围是____。
答案:c≤43、解答题(1)求证:等腰三角形两底角的平分线相等。
证明:设△ABC为等腰三角形,底角∠B和∠C的平分线分别为BD和CE。
∵AB=AC,∴∠ABC=∠ACB。
又∵BD平分∠ABC,CE平分∠ACB,∴∠DBC=∠ECB。
在△DBC和△ECB中,∵DBC=ECB,BC=BC,∴△DBC ≌△ECB。
∴BD=CE,即等腰三角形两底角的平分线相等。
(2)已知一个二次函数y=ax²+bx+c的图像过点(1,2),且与x轴的两个交点的横坐标分别为x₁和x₂,其中x₁²+x₂²=9,求这个二次函数的解析式。
解:∵二次函数y=ax²+bx+c的图像过点(1,2),∴a+b+c=2 ①。
又∵该函数与x轴的两个交点的横坐标分别为x₁和x₂,其中x₁²+x₂²=9,∴x₁+x₂=-b/a,x₁x₂=c/a。
∴(x₁+x₂)²=(b/a)²,∴(b/a)²=(x₁²+x₂²)+2x ₁x₂=(9+2c/a)。
《广东省教育厅关于开展2014年度“一师一优课、一课一名师”活动的通知》

附件2广东省2014年度“一师一优课、一课一名师”活动方案一、活动目标落实《教育部办公厅关于开展2014年度“一师一优课、一课一名师”活动的通知》(教基二厅函〔2014〕13号)文件要求,通过活动,进一步增强教师对信息技术推进教学改革、提高教学质量重要性的认识,建设一支善用信息技术和优质数字教育资源开展教学活动的骨干教师队伍,推动信息技术和数字教育资源在中小学课堂教学中的合理有效应用和深度融合。
2014年度活动目标如下:(一)全省组织不少于20万名(约占全省中小学教师数的20%)教师在国家和省教育资源公共服务平台上“晒课”,促进信息技术在教学中的广泛应用,初步形成“人人用资源、课课有案例”的局面。
(二)形成一套覆盖义务教育阶段各年级各学科各版本的名师课程资源体系,小学和初中各学科30%以上的课程教材配有“同步名师课堂”,初步实现“一课一名师”。
(三)教育部“优质数字教育资源教学点全覆盖”项目学校至少有两名教师参加网上“晒课”,每所农村学校、教学点各学科第 1 页共8 页初中至少有一名骨干教师能够利用信息技术和优质数字教育资源优化教学,初步建设一支善用信息技术和优质数字教育资源开展教学活动的农村骨干教师队伍。
到2016年,参与网上“晒课”的教师比例达到60%,农村学校和教学点参与网上“晒课”的教师比例达到50%以上,小学和初中课程教材“同步名师课堂”资源覆盖率达100%。
二、活动方式(一)“优课”评选根据教育部的要求,“优课”评选的方式和要求如下:1.评选方式(1)网上“晒课”组织教师在规定的时间内进行实名注册,提交“晒课”相关材料,进行实名制网上“晒课”。
(2)“优课”评选在网上“晒课”的基础上,采取县(市、区)、地级市和省三级评选的方式,对年度各年级各学科各版本的资源开展逐级评选、推荐。
2014年,各地级以上市教育局推荐到参加省评审的“优课”数要不少于200节(其中农村、教学点推荐的“优课”数量不少于30%),经省评后择优推荐1500节报教育部,参加国家“优课”评比。
2013年全国初中数学竞赛黄埔区赛区获奖情况公布

广州市第86中学分校
吴素华
71
郭绮雯
广州市第86中学分校
王建锋
50
李孜成
广州市第86中学分校
吴素华
72
黄燕钰
广州石化中学
周健涛
51
方健喆
广州石化中学
焦展
73
孔德明
广州市第87中学
王星
52
徐俊文
广州市黄埔区双沙中学
陈丽萍
74
闫香港
广州市黄埔中大附属外国语实验中学
黄佳丽
53
邓晓玲
广州市黄埔区双沙中学
焦展
16欧阳效康广州来自第86中学分校吴素华28
陈运辉
广州市黄埔区港湾中学
吴玉湘
17
陈柏志
广州市黄埔区港湾中学
张祥富
29
徐葆霖
广州市黄埔区港湾中学
吴玉湘
18
张倩琪
广州石化中学
陈伟华
30
吴洪彬
广州市第84中学
高伟明
19
彭锐超
广州市黄埔区港湾中学
吴玉湘
31
梁梓豪
广州市第86中学分校
徐爱慧
三等奖(共43名)
黄佳丽
36
周力彬
广州市第123中学
杜鹃
58
李嘉
广州市第86中学分校
王建锋
37
蒲俏楠
广州市第123中学
杜鹃
59
陆智华
广州石化中学
焦展
38
杜哲宇
广州市第86中学分校
吴素华
60
彭伟涛
广州市第87中学
李小红
39
张艺慧
广州市第86中学分校
2014年全国初中数学联赛兰州市获奖

刘冠宇
男
九年级
吴彩霞
二等奖
149
10603
兰州树人中学
张宇鹏
男
九年级
吴彩霞
二等奖
150
10605
兰州树人中学
王晗晖
男
九年级
吴彩霞
二等奖
151
10611
兰州树人中学
腊炯桥
男
九年级
吴彩霞
二等奖
152
10619
兰州树人中学
王万有
男
九年级
吴彩霞
二等奖
153
10623
兰州树人中学
敏杰
男
九年级
吴彩霞
女
九年级
贾昀
二等奖
160
11221
兰州树人中学
魏宇棣
女
九年级
贾昀
二等奖
161
11243
兰州树人中学
刘江桐
男
九年级
贾昀
二等奖
162
11323
兰州树人中学
郑毅
男
九年级
贾昀
二等奖
163
11411
兰州树人中学
马灿
女
九年级
贾昀
二等奖
164
11725
兰州树人中学
李芝
女
九年级
田大富
二等奖
165
11739
兰州树人中学
30
35
兰州树人中学
宋一苇
女
九年级
贾昀
一等奖
31
11227
兰州树人中学
刘瑾哲
男
九年级
贾昀
一等奖
32
初中数学教师解题比赛试题及答案

青年教师基本功大赛试题一、选择题(10×2=20分,单选或多选)1.现实中传递着大量的数学信息,如反映人民生活水平的“恩格尔系数”、预测天气情况的“降雨概率”、表示空气污染程度的“空气指数”、表示儿童智能状况的“智商”等,这表明数学术语日趋()(A)人本化(B)生活化(C)科学化(D)社会化2. 导入新课应遵循()(A)导入新课的方法应能激发学生的学习兴趣、学习动机,造成悬念,达到激发情感,提出疑问的作用(B)要以生动的语言、有趣的问题或已学过的知识,引入新知识、新概念(C)导入时间应掌握得当,安排紧凑(D)要尽快呈现新的教学内容3.下列关于课堂教学的改进,理念正确的是()(A)把学生看作教育的主体,学习内容和学习方法由学生作主(B)促进学生的自主学习,激发学生的学习动机(C)教学方法的选用改为完全由教学目标来决定(D)尽可能多的提供学生有效参与的机会,让学生自己去发现规律,进而认识规律4.为了了解某地区初一年级7000名学生的体重情况,从中抽取了500名学生的体重,就这个问题来说,下面说法中正确的是()(A )7000名学生是总体(B)每个学生是个体(C )500名学生是所抽取的一个样本(D)样本容量是5005. 一个几何体的三视图如图2所示,则这个几何体是()主视图左视图俯视图图2 (A)(B)(C)(D)6.如图1,点A(m,n)是一次函数y=2x 的图象上的任意一点,AB 垂直于x 轴,垂足为B ,那么三角形ABO 的面积S关于m 的函数关系的图象大致为( )7.有三条绳子穿过一片木板,姊妹两人分别站在木板的左、右两边,各选该边的一条绳子。
若每边每条绳子被选中的机会相等,则两人选到同一条绳子的概率为( ) (A)21 (B) 31 (C) 61 (D) 918.一次数学课上,老师让大家在一张长12cm 、宽5cm 的矩形纸片内,折出一个菱形。
甲同学按照取两组对边中点的方法折出菱形EFGH (见方案一),乙同学沿矩形的对角线AC 折出∠CAE =∠DAC ,∠ACF =∠ACB 的方法得到菱形AECF (见方案二),请你通过计算,比较这两种折法中,菱形面积较大的是( )(A )甲 (B )乙 (C )甲乙相等 (D ) 无法判断9.迄今为止,人类已借助“网格计算”技术找到了630万位的最大质数。
2014年广州市高中数学教师解题比赛决赛试题与参考答案

2014年广州市高中数学教师解题比赛决 赛 试 题(2014年4月13日上午9∶00-11∶00)一、选择题:本大题共10小题,每小题5分,满分50分. 在每小题给出的四个选项中,有且只有一项是符合题目要求的.请将答案代号填在答题卷的相应位置上. 1.设集合{},,M a b c =,{}0,1N =,映射f :M N →满足()()()f a f b f c +=,则映射f :M N→的个数为A .1B .2C .3D .42.直角梯形ABCD 中,AB DC ,2AB CD =,45A ∠=,2AD =.以直线AB 为轴将梯形ABCD 旋转一周所得旋转体的体积为A .π328 B .π34 C .π3210 D .π243.已知()f x 是奇函数,定义域为{},0x x x ∈≠R ,又()f x 在区间()0,+∞上是增函数,且()10f -=,则满足()f x 0>的x 的取值范围是 A .()1,+∞B .()()1,01,-+∞C .()0,1D .()(),11,-∞-+∞4.已知虚数z =()2i x y -+,其中x 、y 均为实数,当1z =时,yx的取值范围是 A.⎡⎢⎣⎦B.⎡⎫⎛⎪ ⎢⎪ ⎣⎭⎝⎦ C.⎡⎣ D.)(⎡⎣5.设()2f x x ax b =++,且()112f ≤-≤,()214f ≤≤,则点(),a b 在aOb (O 为坐标原点)平面上的区域的面积是 A .12 B .1 C .2 D .926.已知向量OP ()2,1=,OA ()1,7=,OB ()5,1=,设X 是直线OP 上的一点(O 为坐标原点),那么XB XA ⋅的最小值是A .-16B .-8C .0D .47.等比数列{}n a 的公比为q ,则“10a >,且1q >”是“∀*n ∈N ,都有1n n a a +>”的A .充分非必要条件B .必要非充分条件C .充要条件D .既非充分又非必要条件8.若不论k 为何值,直线2y kx b k =+-与曲线221x y -=总有公共点,则b 的取值范围是A.(B.⎡⎣C .()2,2-D .[]2,2-9.已知集合A 、B 、C ,{}直线=A ,{}平面=B ,B A C =,若A a ∈,B b ∈,C c ∈,给出四个命题: ①c a bc b a //⇒⎩⎨⎧⊥⊥;②c a bc b a ⊥⇒⎩⎨⎧⊥//;③c a bc b a //////⇒⎩⎨⎧;④c a bc b a ⊥⇒⎩⎨⎧⊥//,则正确命题的个数为 A .0 B .1 C .2 D .310.在一次足球预选赛中,某小组共有5个球队进行双循环赛(每两队之间赛两场),已知胜一场得3分,平一场得1分,负一场得0分.积分多的前两名可出线(积分相等则要比净胜球数或进球总数).赛完后一个队的积分可出现的不同情况种数为 A .22 B .23 C .24 D .25 CD BA二、填空题:本大题共4小题,每小题5分,共20分. 请将答案填在答题卷的相应位置上. 11.已知x 是三角形的一个内角,满足231cos sin -=+x x ,则x = * . 12.已知正三棱锥S ABC -的高为3,底面边长为4,在正三棱锥内任取一点P ,使得P ABC V -12S ABC V -<的概率是 * .13.对于正整数n 和m ,其中n m <,定义!()(2)(3)()m n n m n m n m n km =----…,其中k 是满足km n >的最大整数,则=!20!1864 * . 14.有两个向量1(1,0)=e ,2(0,1)=e ,今有动点P ,从0(1,2)P -开始沿着与向量12+e e 相同的方向作匀速直线运动,速度为12+e e ;另一动点Q ,从0(2,1)Q --开始沿着与向量1232+e e 相同的方向作匀速直线运动,速度为1232+e e .设P 、Q 在时刻0t =秒时分别在0P 、0Q 处,则当00PQ P Q ⊥时,t = * 秒.三、解答题:本大题共6小题,共80分.解答应写出文字说明、演算步骤或推证过程. 15.(本小题满分12分)若函数21()sin sin cos (0)2f x ax ax ax a =-->的图象与直线y m =相切,若函数()f x 图象的两条相邻对称轴间的距离为4π.(1)求m 的值;(2)若点()0,0A x y 是()y f x =图象的对称中心,且00,2x π⎡⎤∈⎢⎥⎣⎦,求点A 的坐标.16.(本小题满分12分) 一个口袋中装有n 个红球(5n ≥且n ∈*N )和5个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.(1)试用n 表示一次摸奖中奖的概率p ;(2)若5n =,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;(3)记三次摸奖(每次摸奖后放回)恰有一次中奖的概率为P ,当n 取多少时,P 最大?如图所示,正四棱锥P ABCD -中,侧棱PA 与底面ABCD 所成角的正切值为26. (1)求侧面PAD 与底面ABCD 所成二面角的大小;(2)若E 是PB 中点,求异面直线PD 与AE 所成角的正切值;(3)在侧面PAD 上寻找一点F ,使EF ⊥侧面PBC . 试确定F 点的位置,并加以证明.18.(本小题满分14分)这是一个计算机程序的操作说明:(1)初始值1x =,1y =,0z =,0n =; (2)1n n =+(将当前1n +的值赋予新的n ); (3)2x x =+(将当前2x +的值赋予新的x ); (4)2y y =(将当前2y 的值赋予新的y ); (5)z z xy =+(将当前z xy +的值赋予新的z );(6)如果7000z >,则执行语句(7),否则回语句(2)继续进行; (7)打印n ,z ; (8)程序终止.由语句(7)打印出的数值为 , . 以下写出计算过程: PD E A C B如图,已知过点D (2,0)-的直线l 与椭圆2212x y +=交于不同的两点A 、B ,点M 是 弦AB 的中点.(1)若OP OA OB =+,求点P 的轨迹方程; (2)求||||MD MA 的取值范围. 20.(本小题满分14分)已知函数()e x f x x =-(e 为自然对数的底数). (1)求()f x 的最小值;(2)设不等式()f ax x >的解集为P ,且{}|02P x x ⊆≤≤,求实数a 的取值范围;(3)设n *∈N ,证明:1e e 1nnk k n =⎛⎫<⎪-⎝⎭∑.2014年广州市高中数学教师解题比赛 决赛试题参考答案一、选择题:本大题共10小题,每小题5分,满分50分.二、填空题:本大题共4小题,每小题5分,满分20分.11.56π 12.7813.21514. 2三、解答题,本大题共6小题,满分80分. 15.(本小题满分12分) 解:(1)2()sin sin cos f x ax ax ax =-12-1cos21sin 222ax ax -=-12-24ax π⎛⎫=+ ⎪⎝⎭. 由题意知,m 为()f x 的最大值或最小值,所以m =或m =. (2)由题设知,函数()f x 的周期为2π, 所以2a =. 所以()sin 44f x x π⎛⎫=+ ⎪⎝⎭. 令sin 404x π⎛⎫+= ⎪⎝⎭,得44x k ππ+=()k ∈Z ,即416k x ππ=-()k ∈Z .因为04162k πππ≤-≤()k ∈Z ,得1k =或2k =,因此点A 的坐标为3,016π⎛⎫ ⎪⎝⎭或7,016π⎛⎫⎪⎝⎭.16.(本小题满分12分)解:(1)一次摸奖从5n +个球中任选两个,有25n C +种,它们等可能,其中两球不同色有115n C C 种,所以一次摸奖中奖的概率1152510(5)(4)n n C C np C n n +==++.(2)若5n =,一次摸奖中奖的概率59p =,三次摸奖是独立重复试验,三次摸奖(每次摸奖后放回)恰有一次中奖的概率是123380(1)(1)243P C p p =⋅⋅-=. (3)设每次摸奖中奖的概率为p ,则三次摸奖(每次摸奖后放回)恰有一次中奖的概率为123233(1)(1)363P P C p p p p p ==⋅⋅-=-+,01p <<, 因为2'91233(1)(31)P p p p p =-+=--,所以在10,3⎛⎫ ⎪⎝⎭上P 为增函数,在1,13⎛⎫ ⎪⎝⎭上P 为减函数,当13p =时P 取得最大值. 所以101(5)(4)3n p n n ==++,解得20n =.故当20n =时,三次摸奖(每次摸奖后放回)恰有一次中奖的概率最大.17.(本小题满分14分)(1)解:连结AC ,BD 交于O ,连结PO .因为P —ABCD 为正四棱锥,所以PO ⊥底面ABCD .作PM ⊥AD 于M ,连结OM , 所以OM ⊥AD .所以∠PMO 为侧面P AD 与底面ABCD 所成二面角的平 面角.因为PO ⊥底面ABCD ,所以∠P AO 为P A 与底面ABCD 所成的角.所以tan PAO ∠=. 设AB a =,所以,.2a AO MO ==所以.PO =所以tan POPMO MO∠==60PMO ∠=︒.所以侧面P AD 与底面ABCD 所成的二面角为60°.(2)解:连结EO ,因为E 为PB 的中点,O 为BD 的中点,所以EO ∥PD .所以∠AEO 为异面直线AE 与PD 所成的角.在Rt ,,PAO AO PO ∆==中,所以PA =,12EO PD ==.由AO ⊥截面PDB ,可知AO ⊥EO . 在Rt △AOE 中,tan AO AEO EO ∠==即异面直线AE 与PD 所成角的正切值是1052.(3)证明:延长MO 交BC 于N ,连结PN ,取PN 中点G ,连结EG ,MG .因为P —ABCD 为正四棱锥且M 为AD 的中点,所以N 为BC 中点. 所以BC ⊥NM ,BC ⊥PN .因为NM PN N = ,所以BC ⊥平面PMN .因为BC ⊂平面PBC ,所以平面PMN ⊥平面PBC .因为PM =PN ,∠PMN =60°,所以△PMN 为正三角形. 所以MG ⊥PN . 所以MG ⊥平面PBC .取AM 中点为F ,连结FE ,则由EG ∥MF 且GE =MF ,得到MFEG 为平行四边形, 所以FE ∥MG .所以FE ⊥平面PBC .分 18.(本小题满分14分)依题意,01x =,12n n x x -=+, 所以{}n x 是等差数列,且21n x n =+. 因为011,2.n n y y y -==所以{}n y 是等比数列,且n n y 2=. 因为n n n n y x z z z +==-10,0, 所以1122n n n z x y x y x y =++⋅⋅⋅+即n z 23325272(21)2n n =⋅+⋅+⋅+⋅⋅⋅++⋅. ① 所以23412325272(21)2(21)2n n n z n n +=⋅+⋅+⋅+⋅⋅⋅+-⋅++⋅. ② ①—②得,1322)12(22222223+⋅++⋅-⋅⋅⋅-⋅-⋅-⋅-=n n n n z ()12122n n +=-+.依题意,程序终止时:7000n z >,17000n z -≤,即()()121227000,23227000.n nn n +⎧-+>⎪⎨-+≤⎪⎩ 解得8n =,进而7682z =.19.(本小题满分14分) 解法1:(1)①若直线l ∥x 轴,则点P 为(0,0).②设直线():2l y k x =+,并设点,,,A B M P 的坐标分别是112200(,),(,),(,),(,)A x y B x y M x y P x y , 由()222,22y k x x y ⎧=+⎨+=⎩消去x ,得 ()2222(21)82410k y k x k +++-=, (*)由直线l 与椭圆有两个不同的交点,可得()()222288(21)410k k k ∆=-+->,所以212k <. 由OP OA OB =+ 及方程(*),得2122821k x x x k =+=-+,()()1212242221ky y y k x k x k =+=+++=+,即2228,214.21k x k k y k ⎧=-⎪⎪+⎨⎪=⎪+⎩消去k ,并整理得,22240x y x ++=(20)x -<<.综上所述,点P 的轨迹方程为22240x y x ++=(20)x -<≤. (2)①当l ∥x 轴时,,A B 分别是椭圆长轴的两个端点,则点M 在原点O 处,所以,||2,||MD MA =||MD =②由方程(*),得212022,2x x kx+==-所以,|||DMD x x=-=01|||MA x x=-==所以||||MDMA=因为212k<()0,1,所以)||||MDMA∈+∞.综上所述,)||||MDMA∈+∞.解法2:(1)①若直线l∥x轴,则点P为(0,0).②设直线:2l x my=-,并设点,,,A B M P的坐标分别是112200(,),(,),(,),(,)A x yB x y M x y P x y,由222,22x myx y=-⎧⎨+=⎩消去x,得22(2)420m y my+-+=,(*)由直线l与椭圆有两个不同的交点,可得22(4)8(2)0m m∆=--+>,即28(2)0m->,所以22m>.由OP OA OB=+及方程(*),得12242my y ym=+=+,121228(2)(2)2x x x my mym=+=-+-=-+,即228,24.2xmmym⎧=-⎪⎪+⎨⎪=⎪+⎩由于0m≠(否则,直线l与椭圆无公共点),消去m,并整理得,22240x y x++=(20)x-<<.综上所述,点P的轨迹方程为22240x y x++=(20)x-<≤.(2)①当l∥x轴时,,A B分别是椭圆长轴的两个端点,则点M在原点O处,所以,||2,||MD MA=||||MDMA=②由方程(*),得12022,22y y mym+==+所以,|||DMD y y=-=01|||MA y y=-==,所以||||MDMA==因为22m >(0,1),所以)||||MD MA ∈+∞.综上所述,)||||MD MA ∈+∞. 20.(本小题满分14分)(1)解:因为()x f x e x =-,所以()1x f x e '=-.令()0f x '=,得0x =.所以当0x >时,()0f x '>,当0x <时,()0f x '<.所以函数()x f x e x =-在区间(),0-∞上单调递减,在区间()0,+∞上单调递增. 所以当0x =时,()f x 有最小值1.(2)解:因为不等式()f x ax >的解集为P ,且{}|02P x x ⊆≤≤,所以对任意[]0,2x ∈,不等式()f x ax >恒成立. 由()f x ax >,得()1e x a x +<,当0x =时,上述不等式显然成了,所以只需考虑(]0,2x ∈的情况.将()1e xa x +<变形为e 1xa x<-. 令()e 1xg x x =-,则()()21e x x -g x x '=. 当1x >时,()0g x '>,当1x <时,()0g x '<,所以()g x 在()0,1上单调递减,在()1,2上单调递增. 所以当1x =时,函数()g x 取得最小值e 1-. 故实数a 的取值范围为(),e 1-∞-.(3)证明:由(1)知,对任意实数x 均有1xe x -≥,即1xx e +≤.令k x n =-(*,1,2,,1n k n ∈=-N ),则01k n k e n-<-≤,所以1(1,2,,1)nnk kn k e e k n n --⎛⎫⎛⎫-≤==- ⎪ ⎪⎝⎭⎝⎭.即(1,2,,1)nkn k e k n n --⎛⎫≤=- ⎪⎝⎭. 所以(1)(2)211211nnnnn n n n e e e e n n n n -------⎛⎫⎛⎫⎛⎫⎛⎫++++≤+++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. 因为(1)(2)2111111111n n n e e e e e e e e e ----------+++++=<=--- ,所以 1211nnnnn n e n n n n e -⎛⎫⎛⎫⎛⎫⎛⎫++++< ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭.。
广州市中学数学青年教师解题竞赛

2011年广州市中学数学青年教师“解题比赛”获奖通知各区(县级市)教研室中数科,各中学数学科:2011年4月10日上午,广州市中学数学青年教师“解题比赛”决赛在广雅中学成功举行。
本次活动由广州市教育局教研室数学科和广州市中学数学教学研究会联合主办,共有619名(高中233名、初中386名)中学数学青年教师参加了本次“解题比赛”决赛。
参加决赛的青年教师都是直属中学和各区(县级市)“解题比赛”的优胜者。
广州市教育局教研室数学科和广州市中学数学教学研究会组织了部分教研会理事,市、区教研员和骨干教师及时评卷,并进行了复查,共评出初中一等奖40名,二等奖80名,三等奖119名,高中一等奖25名,二等奖44名,三等奖70名,获奖名单附后。
特此通知广州市教育局教研室数学科广州市中学数学教学研究会二〇一一年四月十一日附:2011年广州市中学数学青年教师“解题比赛”获奖名单初中组(排名不分先后)考号学校全称姓名等级7041石化中学王继承一等奖3021石化中学胡文龙一等奖3026广州市荔湾区广豪学校黄德华一等奖4022广州市天荣中学李发财一等奖9031蓝天中学余伟明一等奖6037广州市第二中学邱传林一等奖9007珠江中学严映峰一等奖2004广州市骏景中学程丹一等奖4032广州市第二中学李强一等奖7016广州市第2中学孙苏平一等奖3023花都区赤坭中学胡余华一等奖5040花都区金华中学刘巧英一等奖5016番禺区洛浦中学梁瑞芳一等奖7026广州市第2中学唐琦一等奖2022珠江中学丁瑞滨一等奖6019育才实验学校马亮一等奖1041广州市第113中学朱丛高一等奖4040同和中学李卫华一等奖9015广雅实验学校杨莹瑾一等奖7036广州市第二中学王碧莹一等奖6033广东省电力工业局第一工程局职工子弟学校彭青一等奖7033南武中学汪诗源一等奖8007广大附属实验学校王小丽一等奖1021广州市玉岩中学赵丰雪一等奖100467中边志强一等奖1039东环中学陈亚通一等奖6036番禺区华南碧桂园学校秦志农一等奖7010广大附属实验学校宋年胜一等奖7015江南中学孙莉娟一等奖7037广州外国语学校王福生一等奖1040广州市第47中学陈勇生一等奖4033花都区冯村中学李强军一等奖6001广东省实验中学附属天河学校刘玉清一等奖7008广州市第13中学施扬刚一等奖1033广州市第75中学周伟泽一等奖2045番禺区大岗中学郭浩荣一等奖4012番禺区石壁中学赖锦发一等奖6005广州市第89中学卢锐明一等奖6044第5中学任晶晶一等奖1031番禺区沙头中学周清华一等奖5007珠江中学李颖颐二等奖5018八一实验学校梁盈二等奖5037石井中学刘结开二等奖6020广铁一中马小飞二等奖7013广州大学附属中学苏青艳二等奖1009广大附属实验学校张书昌二等奖1020花都区圆玄中学章志光二等奖1045广州大学附属中学陈志娟二等奖2013南武实验邓广原二等奖3035第5中学黄丽君二等奖4010从化市从化中学康丽斯二等奖4024广州市第89中学李海英二等奖7011广州市荔湾区一中实验学校苏方方二等奖8027八一实验学校吴舜财二等奖8041增城二中徐建仁二等奖9002双桥实验学校许秀娜二等奖2041广州市第八十七中学顾星二等奖4006番禺区华南碧桂园学校蒋清庭二等奖5030荔景中学刘丽二等奖8002花都区芙蓉中学王梦婷二等奖8018广州市东圃中学温玉霖二等奖1018花都区北兴中学张育宁二等奖1025珠江中学陈立婷二等奖2021增城中学丁玲芬二等奖5024广州第四中学林洁英二等奖5028第52中学林艳丽二等奖5029龙涛中学凌涛二等奖8011广州市东圃中学王颖二等奖2005广州市第21中学程德松二等奖4002番禺区沙湾镇象达中学江俊华二等奖4027番禺区大岗中学李奎光二等奖4045广州市第75中学李晓丽二等奖5021珠江中学廖富有二等奖6015广东省实验中学附属天河学校罗贤龙二等奖6025广州市西关培英中学牛敏娜二等奖7004花都区长岗中学沈玲丹二等奖7005第97中学沈秋怡二等奖7006番禺区市桥桥兴中学沈晓欢二等奖9013庙头学校杨山二等奖1020广雅实验学校陈鸿二等奖5019荔湾中学梁远玲二等奖6012广州市第16中学罗洁茹二等奖7031广外附设外语学校汪春辉二等奖8001广州市第16中学王林丹二等奖8044广州大学附属中学徐佑军二等奖9006广园中学严克浩二等奖9044晓园中学曾伟东二等奖3020广州市陈嘉庚纪念中学胡妙婵二等奖4018增城中学李健二等奖5041番禺区潭山中学刘帅二等奖1006广州开发区中学张亮二等奖1034广州第四中学周文辉二等奖1008广州市第16中学蔡智雄二等奖1018番禺区钟村奥园学校陈迪银二等奖1021番禺区洛溪新城中学陈尖峰二等奖3017花都区九潭中学侯芳二等奖3024华附新世界学校胡振贵二等奖4019梓元岗中学李娟二等奖4039新市中学李松涛二等奖9028花都区芙蓉中学余建秦二等奖2001广州大学附属中学陈志勇二等奖4014荔城二中赖育章二等奖500867中李玉杰二等奖5036花都区培新中学刘红霞二等奖5044花都区芙蓉中学刘曦路二等奖6029华附新世界中学庞伟二等奖8036广园中学谢福耿二等奖1044广外附设外语学校邹炜玲二等奖1022真光实验学校陈建辉二等奖1027立贤中学陈龙彬二等奖2014广东省实验中学附属天河学校邓慧璇二等奖5009广州市第113中学李远清二等奖6035梅花中学齐美丽二等奖8008花都区雅瑶中学王雪莹二等奖8009广州市第一中学王亚萍二等奖8015培正中学魏振柱二等奖8035广州市黄埔区港湾中学谢春娥二等奖9026广东省实验中学于清二等奖9035第76中学袁慧敏二等奖1037第5中学周杨二等奖1023劬劳中学陈杰三等奖2003广州广雅实验学校程英三等奖3009广雅实验学校何健三等奖8012花都区新华二中王玉菊三等奖8021广州市第47中汇景实验学校吴杰泉三等奖8043珠江中学徐晓辉三等奖2015四中聚贤邓丽丽三等奖3007广州市泰安中学何惠平三等奖3011番禺区桥城中学何伟立三等奖5038第76中学刘金春三等奖1038花都区云山中学陈雪芬三等奖2037长堤真光中学高松发三等奖4005番禺区沙湾镇象达中学蒋鼎年三等奖4016广州市荔湾区一中实验学校黎乐锋三等奖5012广州市玉岩中学连明瑞三等奖6038广州市玉岩中学邱蓝青三等奖7029广大附属实验学校田茂清三等奖7039广州市第2中学王革华三等奖9045金沙中学詹小燕三等奖1023花都区秀全外国语学校赵柳三等奖1029从化市太平中学钟燕群三等奖2012广东省实验中学附属天河学校邓大艳三等奖2024中新中学方荣金三等奖2028番禺区鱼窝头第二中学冯海华三等奖7023广东省实验中学附属天河学校唐爱文三等奖7032花都区雅宝学校汪剑三等奖9005第5中学寻友利三等奖2017广州市第113中学邓敏民三等奖2019番禺区沙滘中学邓铁文三等奖2039华师附中番禺学校古敏锋三等奖3014番禺区大岗中学何远荣三等奖3027花都区金华中学黄凤梅三等奖5042广州市美华中学刘天亮三等奖9016番禺区沙头中学杨赵平三等奖1004广东省实验中学张捷三等奖1012萝岗区华峰中学张伟三等奖2026广东省实验中学附属天河学校费华菲三等奖2032广州市第16中学付娟三等奖3030花都区圆玄中学黄健楠三等奖5011番禺区桥城中学李志平三等奖7007珠江中学沈宇杰三等奖7012番禺区石碁第三中学苏金华三等奖7030花都区清布中学佟威三等奖8010广州外国语学校王艳艳三等奖8023番禺区东涌中学吴锐波三等奖1008中新中学张少华三等奖1036广州市南国学校陈秀丽三等奖2009同德南方崔亚叶三等奖3012花都区三和庄中学何秀平三等奖4041广州市玉岩中学李文力三等奖6016从化市河东中学骆活枢三等奖7001广州市第一中学尚思恩三等奖3001从化市第七中学郭嘉新三等奖4008广州市第一二三中学蒋叶莲三等奖4020广大附属实验学校李军三等奖7018华附新世界学校覃启艺三等奖7043广州市荔湾区广豪学校王锦风三等奖8031花都区云山中学伍建军三等奖8042南武中学徐小青三等奖9014广州市陈嘉庚纪念中学杨亚兴三等奖1001广州市荔湾区金道中学张创杰三等奖3032广州市荔湾区一中实验学校黄竻养三等奖3038番禺区南村中学黄清文三等奖3042第33中学贾晓燕三等奖6007广州7中陆曼丽三等奖9024从化市第七中学尹晓勇三等奖1025番禺区祈福英语实验学校郑小兵三等奖1026广州四中聚贤中学陈玲三等奖1032广州市第八十七中学陈婷三等奖1037广州市美华中学陈秀英三等奖1042培英实验中学陈玉莲三等奖2007南武实验崔波三等奖3028115中黄焕文三等奖4021广州市玉岩中学李定锋三等奖6017华附新世界学校骆健毅三等奖8034广大附属实验学校谢 雍三等奖8040番禺区石碁第三中学幸宇辉三等奖1032第5中学周琼三等奖1007同德南方蔡艺生三等奖1029广州四中聚贤中学陈倩婷三等奖4015番禺区新造中学兰建明三等奖5045第97中学刘颖三等奖8005广州市西关外国语学校王琦三等奖8024番禺区石碁第三中学吴润生三等奖8032南石中学肖建中三等奖1016广州大学附属中学陈丹波三等奖4007广州市第113中学蒋霞三等奖4036广州市第47中汇景实验学校李蓉三等奖4043广州市华颖中学李小红三等奖6008从化市从化中学陆慕萍三等奖6027第33中学欧阳嘉威三等奖6041广东省实验中学附属天河学校屈孝辉三等奖7021增城二中汤雪芬三等奖8003增城二中王鹏丙三等奖2027番禺区钟村中学冯桂平三等奖3015广州广雅实验学校贺福凯三等奖4004珠江中学姜红三等奖5043四中聚贤刘婷三等奖6002晓园中学刘智东三等奖6042广州市天河中学全文骊三等奖9041从化市河东中学曾莉萌三等奖1042绿翠中学朱其成三等奖2033番禺区新造中学付新三等奖3008番禺区大岗中学何嘉良三等奖5031广州市第九十三中学刘超然三等奖8045广东省实验中学附属天河学校许承丽三等奖1010番禺区祈福英语实验学校张婷三等奖1022真光实验学校赵庚昊三等奖4013三元里中学赖天奎三等奖4038广州广雅实验学校李淑瑜三等奖7035广州市长兴中学王比翼三等奖8022广州市第八十四中学吴丽敏三等奖9011珠江中学杨敏浩三等奖9019第5中学叶秋香三等奖1016花都区雅瑶中学张旭宏三等奖1019番禺区东涌镇鱼窝头中学章少荣三等奖1026114中郑仲娜三等奖1027广州市西关外国语学校钟敏健三等奖1045广州市第75中学邹务姣三等奖高中组(排名不分先后)考号学校全称姓名等级4028广州市天河中学王恒新一等奖1006广州市第六中学陈霞一等奖6030广州市第四十七中学周文超一等奖6037协和中学朱禹兰一等奖2015广州大学附属中学黄桂林一等奖3022广州市第六中学刘旭升一等奖4023广州市西关外国语学校万红珍一等奖3019广州市第7中学刘强一等奖4027增城高级中学王刚宝一等奖6021协和中学张欣一等奖5008永和中学吴新红一等奖2037番禺区象贤中学李伟一等奖3016协和中学刘伏英一等奖2023广州市广外附设外语学校姜海涛一等奖3030广东广雅中学罗文聪一等奖3032华南师范大学附属中学马腾冰一等奖6001广州市第65中学禹宇晨一等奖6034广州市第二中学朱建军一等奖2013增城中学黄娜一等奖2028广东广雅中学赖淑明一等奖4039广东广雅中学温丽一等奖6009广东广雅中学曾文达一等奖2010高级中学胡能其一等奖2029增城中学蓝留铺一等奖4008广州市第八十六中学宋君平一等奖5003广州大学附属中学吴坚二等奖5018广东广雅中学徐飞二等奖2026广州市第七十五中学邝菁华二等奖2039协和中学李雄杰二等奖3015从化市第六中学刘 容二等奖1024越秀外国语学校程传慧二等奖2038广东广雅中学李晓颖二等奖4019广东广雅中学唐艳群二等奖5024番禺区实验中学薛兴志二等奖2006广州市第80中学胡海波二等奖2011广州市第二中学胡守标二等奖5029广州市第二中学杨其武二等奖3005广东广雅中学梁辉二等奖1007番禺区象贤中学陈柏勇二等奖1017广州市第七十五中学陈文会二等奖2014广州市第六中学黄燕二等奖2019花都区秀全中学贾丽二等奖5025广东广雅中学阳建新二等奖5039广州市第二中学余广斌二等奖6004广州市第65中学袁红春二等奖6010广州市第65中学曾志斌二等奖6012广州市第八十六中学张科二等奖6028广州市第一中学周频二等奖1022协和中学陈永健二等奖2034广州市广大附属实验学校李科峰二等奖3008广州市天河中学林海滨二等奖4021广州市第八十九中学田鹰二等奖5007番禺区东涌中学吴素良二等奖5012广州市玉岩中学向良辉二等奖6014花都区实验中学张翠二等奖6020广东仲元中学张婷二等奖2003番禺区禺山高级中学何远清二等奖4012花都区邝维煜纪念中学汤国贤二等奖4025广铁一中王彪二等奖6031郑中钧中学周晓霞二等奖2041广州市玉岩中学于志华二等奖3025广州市第四中学刘殷二等奖5010广州市第四中学伍慧懿二等奖6038广州开发区外国语学校蔡军喜二等奖3014广州市第六中学刘涛二等奖3034广东番禺中学马志强二等奖4002广东番禺中学潘保伦二等奖4005广州市南沙中学石香二等奖6041广州市第二中学石岩二等奖5033广东仲元中学叶春风三等奖1030广州市玉岩中学邓四元三等奖3001广州市第四中学李雪芸三等奖3006花都区秀全中学梁振标三等奖3033育才中学马细惠三等奖4004番禺区二师附中彭玛生三等奖5014增城中学肖海英三等奖5028从化市第五中学杨健明三等奖2002广东番禺中学郭志锋三等奖2007广东广雅中学胡玲三等奖3003花都区邝维煜纪念中学李振华三等奖3021广州市东圃中学刘晓强三等奖3023花都区实验中学刘雅三等奖6011广州市第六中学张华三等奖6036花都区邝维煜纪念中学朱弢三等奖1016广州市第八十六中学陈石鑫三等奖1037番禺区象贤中学龚小风三等奖4038广州市第七十八中学温俊卿三等奖5009广州市真光中学伍海光三等奖5036广东番禺中学叶悦珍三等奖5037广州石化中学易欣三等奖6002广州市第80中学袁安三等奖1019花都区邝维煜纪念中学陈燕飞三等奖1028增城中学邓城三等奖1035广东广雅中学冯永先三等奖3035广州市第四十一中学麦燕仪三等奖4020广州市第一中学田畋三等奖4040广州市第九十七中学温效良三等奖2021广州市第八十九中学江娜萍三等奖2027郑中钧中学赖黎明三等奖3013广州市第五中学刘沙三等奖3028广州市第四中学刘运科三等奖5001执信中学文德良三等奖1026广东广雅中学代杰三等奖1034花都区秀全中学冯翠华三等奖4035广州市第65中学王小燕三等奖5031广州市第七十五中学杨月霞三等奖6005育才中学岳震三等奖1012广州市第七十六中学陈满林三等奖2009花都区秀全中学胡茂炉三等奖2036花都区新华中学李桃三等奖3012广州市第五中学刘玫三等奖4013花都区实验中学汤沛文三等奖5022协和中学许云勇三等奖6026培英中学赵玉香三等奖1011番禺区实验中学陈黎三等奖1015广州市第八十六中学陈少婉三等奖1041广州市第二中学唐国秋三等奖2024广东番禺中学金菲三等奖3010番禺区禺山高级中学林锦凌三等奖3020广州市第九十五中学刘喜云三等奖5011执信中学伍可亮三等奖6008花都区秀全中学曾绍信三等奖6029广东广雅中学周斌三等奖6035广州市南武中学朱双海三等奖1025花都区秀全中学崔高峰三等奖3002从化市第六中学李永雄三等奖3038广州市第二中学莫菊芳三等奖6039广州市第九十一中学王磊三等奖1021广州市第二中学陈颍三等奖1029番禺区南村中学邓华萍三等奖5017仙村中学徐甜三等奖1009广州市第八十九中学陈朝兵三等奖3039广州市第九十七中学莫爵敬三等奖1002广州市第二中学包承先三等奖1013番禺区二师附中陈敏贞三等奖1018广州市第80中学陈雪玲三等奖2005广州市真光中学贺育林三等奖4011番禺区石碁中学谭新远三等奖5004广州市第九十一中学吴乐宜三等奖。
全国初中数学邀请赛获奖1等奖名单

2014年全国初中数学邀请赛获奖名单(一等奖62人) 学生 …

2014年广州市初中教师解题决赛试题与参考答案

2014年广州市初中数学教师解题比赛决 赛 试 卷 2014-4-13本试卷共8页,第1-2页为选择题和填空题,第3-8页为解答题及答卷.请将选择题和填空题的答案做在第3页的答卷上.全卷共三大题23小题,满分150分,考试时间120分钟.第I 卷(选择题,共40分)一、选择题(本大题共10小题,每小题4分,满分40分,请将唯一正确的答案代号填在第3页的答题卷上.)1.已知集合{|A x x =是平行四边形},{|B x x =是矩形},{|C x x =是正方形},{|D x x =是菱形},则( ). A .A B ⊆ B .C B ⊆ C .D C ⊆ D .A D ⊆ 2.下列函数中,既是奇函数又是增函数的为( ). A . 1y x =+ B .2y x =- C .1y x =D .sin 22y x x ππ⎛⎫=-<< ⎪⎝⎭ 3.已知圆22:40C x y x +-=,l 过点(3,0)P 的直线,则( ). A .l 与C 相交 B .l 与C 相切 C .l 与C 相离 D .以上三个选项均有可能 4.如图1,在直角坐标系中,直线6y x =-与函数4(0)y x x=>的图象 相交于点A 、B ,设点A 的坐标为()11,x y ,那么长为1x ,宽为1y 的矩 形面积和周长分别为( ) .A .4,12B .8,12C .4,6D .8,6 5.如图2,在Rt △ABC 中,∠ACB =90°,∠A =α,将△ABC 绕点C 按顺时针方向旋转后得到△EDC ,此时点D 在AB 边上,则旋转角 的大小为( ).A .αB .2αC .90α-D .30α+ 6. 已知平面向量a ()2m =-,,b (1=,且()-⊥a b b ,则实数m 的值为( ). A.- B. C. D.图1图27.已知变量x y ,满足约束条件21110x y x y y ,,.⎧+≥⎪-≤⎨⎪-≤⎩则2z x y =-的最大值为( ). A .3- B .0 C .1 D .38.设x R ∈,则“12x >”是“2210x x +->”的( ).A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件 9. 如图3,ABC △与DEF △均为等边三角形,O 为BC 、EF 的中点,则AD ∶BE 的值为( ). A1 B1 C .5∶3 D .不确定 10.如图4,正方形ABCD 的边长为1,延长BA 至E ,使1AE =, 连接EC 、ED ,则sin CED ∠=( ). ABCD第II 卷(非选择题,共110分)二、填空题(本大题共6小题,每小题5分,共30分,将答案直接填在答题卷上.)11. 设集合A={3123|≤-≤-x x },集合B 为函数ln(1)y x =-的定义域,则A ⋂B= .12. 已知381P xy x =-+,22Q x xy =--,当0x ≠时,327P Q -=恒成立,则y 的值为__ __.13. 如图5,AB 是O 的直径,BC 是O 的切线,AC 与O 交于点D若3BC =,165AD =,则AB 的长为 .14. 下面的图形是由边长为l 的正方形按照某种规律排列而组成的:推测第n 个图形中,正方形的个数为__ ___,所有线段长的和为 _ _(用含n 的代数式表示).15. 正方形ABCD 、正方形BEFG 和正方形RKPF 的位置如图6所示,点G 在线段DK 上,正方形BEFG 的边长为4,则 DEK ∆的面积为__ ____. 16. 已知1x 、2x 是关于x 的一元二次方程 20(0)ax x a a +-=≠的两个根, 若124x x +=,则a 的值为____ __.A图4图2C图5 图6三、解答题(共7小题,满分8 0分.解答应写出必要的文字说明、演算步骤或证明过程.)17.(本小题满分8分)如图7,反比例函数(0)ky k x=<的图象经过点A (-3,m ),过 点A 作AB ⊥x 轴于点B ,△AOB 的面积为3.(1) 求k 和m 的值;(2) 若过A 点的直线y =ax +b 与x 轴交于C 点,且∠ACO =30°,求此直线的解析式. 18.(本小题满分8分)如图8,正△ABC 的边长为a , D 为AC 边上的一个动点, 延长AB 至E ,使BE =CD ,连结DE ,交BC 于点P . (1)求证:DP =PE ;(2)若D 为AC 的中点,求BP 的长. 19.(本小题满分12分)某果农在山地上种植同一种果树,收获时,该果农随机选取果树20株作为样本,测量它们每一株的果实产量(单位:kg ),获得的所有数据按照区 间(4045,,⎤⎦(((455050555560,,,,,⎤⎤⎤⎦⎦⎦进 行分组,得到频率分布直方图如图9.已知样本中 产量在区间(4550,⎤⎦上的果树株数是产量在区间(5060,⎤⎦上的果树株数的43倍. (1)求a ,b 的值;(2)从样本中产量在区间(5060,⎤⎦上的果树随机抽取两株,求产量在区间(5560,⎤⎦上的果树至少有一株被抽中的概率.图7图8图9图3a0.06b甲商店某种商品4月份(30天,4月1日为第一天)的销售价格P (元)与时间t (天)函数关系如图(一)所示,该商品日销售量Q (件)与时间t (天)函数关系如图(二)所示.(1)写出图(一)表示的销售价格与时间的函数关系式P f t =(),写出图(二)表示的日销售量与时间的函数关系式Q g t =(),及日销售金额M (元)与时间的函数关系M h t =(). (2)乙商店销售同一种商品,在4月份采用另一种销售策略,日销售金额N (元)与时间t (天)之间的函数关系为22102750N t t =--+,试比较4月份每天两商店销售金额的大小关系.21.(本小题满分12分)已知某个几何体的三视图如图10(主视图的弧线是半圆),根据图中标出的数据, (1)求这个组合体的体积;(2)若组合体的底部几何体记为1111D C B A ABCD -(如图11),其中BA B A 11为正方形.① 求证:D C AB B A 111平面⊥;② 若P 为棱11B A 上一点,求1PC AP +的最小值和达到最小值时1A P 的长度.图10图11如图一,在直角梯形ABCD 中,∠D =∠C =900,AB =4,BC =6,AD =8.点P 、Q 同时从A 点出发,分别作匀速运动,其中点P 沿AB 、BC 向终点C 运动,速度为每秒2个单位,点Q 沿AD 向终点D 运动,速度为每秒1个单位.当这两点中有一个点到达自己的终点时,另一个点也停止运动,设这两点从出发运动了t 秒. (1) 动点P 与Q 哪一点先到达自己的终点?此时t 为何值?(2) 当0<t <2时,求证:以PQ 为直径的圆与AD 相切(如图二);(3 )以PQ 为直径的圆能否与CD 相切?若有可能,求出t 的值或t 的取值范围;若不可 能,请说明理由.23.(本小题满分14分)已知R a ∈,函数()f x x x a =-,(1)当a =2时,写出函数)(x f y =的单调递增区间; (2)当a >2时,求函数)(x f y =在区间[]2,1上的最小值;(3)设0≠a ,函数)(x f 在),(n m 上既有最大值又有最小值,请分别求出n m 、的取值范围(用a 表示).图二图一2014年广州市初中数学青年教师解题决赛答案2014-4-1311.(]1,2 12.2 13.4 14.5n +3,15n +10 15.16 16.±63 三、解答题(共7小题,满分80分.解答应写出必要的文字说明、演算步骤或证明过程.)17.(本小题满分8分)解:(1)△AOB 的面积为3,AB =12AB BO =⨯, 解得2BO =,即2m =.()A ∴,将点()2A 代入(0)ky k x=<,解得k =-(2)当a =时,将点()2A 代入y x b =+,解得3b =,直线的解析式为0x +=;当a =时,将点()2A 代入y x b =+,解得1b =,直线的解析式为0x =;综上:直线的解析式为0x +=或0x =. 18.(本小题满分8分)(1)证明:过点D 作DF ∥AB ,交BC 于F .∵△ABC 为正三角形 , ∴∠CDF =∠A =60°. ∴△CDF 为正三角形 , ∴DF =CD , 又BE =CD ,∴BE =DF .又DF ∥AB ,∴ ∠PEB =∠PDF . 在△DFP 和△EBP 中,∠PEB =∠PDF∠BPE =∠FPD BE =FD∴△DFP ≌△EBP .∴DP =PE . (2)由(1)得△DFP ≌△EBP ,可得FP =BP , ∵D 为AC 中点,DF ∥AB ,∴BF =21BC =21a , ∴BP =21BF =41a .19.(本小题满分12分)(1)解:样本中产量在区间(4550,⎤⎦上的果树有520100a a ⨯⨯=(株), 样本中产量在区间(5060,⎤⎦上的果树有()()002520100002b b ..+⨯⨯=+(株), 依题意,有()41001000023a b .=⨯+,即()40023a b .=+.① 根据频率分布直方图可知()00200651b a ..+++⨯=, ② 解①②得:008004a b .,.==.(2)解:样本中产量在区间(5055,⎤⎦上的果树有0045204.⨯⨯=株,分别记为123A A A ,,,4A ,产量在区间(5560,⎤⎦上的果树有0025202.⨯⨯=株,分别记为12B B ,. 从这6株果树中随机抽取两株共有15种情况:()()1213A A A A ,,,,()14A A ,()()()()()()111223242122A B A B A A A A A B A B ,,,,,,,,,,,,()34A A ,,()31A B ,,()32A B ,,()()4142A B A B ,,,,()12B B ,.其中产量在(5560,⎤⎦上的果树至少有一株共有9种情况:()()1112A B A B ,,,,()()()()21223132A B A B A B A B ,,,,,,,,()()4142A B A B ,,,,()12B B ,.记“从样本中产量在区间(5060,⎤⎦上的果树随机抽取两株,产量在区间(5560,⎤⎦上的果树至少有一株被抽中”为事件M ,则()93155P M ==.解:(1)设价格函数是b kt y +=,过点(0,15)(30,30)则⎪⎩⎪⎨⎧==⇒⎩⎨⎧=+=2115303015k b b k b ∴),300(1521)(N t t t t f P ∈≤<+== 销售量函数m at y +=,过点)40,30(),160,0(,则⎩⎨⎧-==⇒⎩⎨⎧=+=41604030160a m m a m ∴),300(1604)(N t t t t g Q ∈≤<+-==则21(15)(4160)2202400(030,)2M t t t t t t N =+-+=-++<≤∈(2)22102750()N t t t N =--+∈⎩⎨⎧≤≤>≤<<-=-30120110035030t t t N M ()t N ∈ 即前11天甲商店销售额少,以后乙均比甲少21.(本小题满分12分) 解:(1)此组合体底部为长方体,上部为半个圆柱π+=⨯⨯π+⨯⨯=806401042110882V . (2) ①∵长方体1111D C B A ABCD - ,∴BA B A AD 11平面⊥.∵BA B A B A 111平面⊂,∴B A AD 1⊥.又∵BA B A 11是边长为8的正方形,∴11AB B A ⊥. ∵A AD AB =⋂1,∴D C AB B A 111平面⊥.②将上底面1111D C B A 展开,与平面BA B A 11共面时,连结A C 1交11B A 于点P ,即1AC 为最短距离.此时长度为97218822=+.111A PAB PC ,则1329A P =.解:(1) ∵当P 到C 时,t =5(秒);当Q 到D 时,t =8(秒).∴点P 先到达终点,此时t 为5秒; (2) 作BE ⊥DA 于点E ,则BE =23,∠A =60°,∠ABE =30°. 当0<t <2时,取AP 中点F ,连FQ ,则△AFQ 为等边三角形.∴FP =F A =FQ ,∴∠AQP =90°. ∴以PQ 为直径的圆与AD 相切. (3)当0<t<2时,以PQ 为直径的圆与CD 不可能相切. 当2≤t ≤5时,设以PQ 为直径的⊙O 与CD 相切于点K . 则有PC =10-2t ,DQ =8-t ,OK ⊥DC .∴OK 是梯形PCDQ 的中位线,∴PQ =2²OK =PC +DQ =18-3t . 在直角梯形PCDQ 中,PQ 2=CD 2+(DQ -PC )2,即(1 8-3t )2=(23)2+(t -2)2,2t 2-2 6 t +77=0.解之,得t =21513±, ∵21513+>5, 2<21513-≈ 4.56 <5, ∴当t =21513-时,以PQ 为直径的圆与CD 相切. 另解:设以PQ 为直径的⊙O 与CD 相切于点K .⊙O 交AD 于点Q 、H .则DK =3,DH =CP =10-2t ,DQ =8-t .由切割线定理,得DK 2=DH ·DQ .即(3)2 = (10 -2t ) (8 – t ).(以下与上面解法相同) 23.(本小题满分14分)(1)解:当2=a 时,=-=|2|)(x x x f ⎩⎨⎧<-≥-2),2(2),2(x x x x x x由图象可知,单调递增区间为(-∞,1],[2,+∞)(开区间不扣分)(2)因为2>a ,x ∈[1,2]时,所以f(x)=x(a-x)=-x 2+ax = 22()24a a x --+当1<2a ≤32,即32≤<a 时,42)2()(min -==a f x f当2a 32>,即3>a 时,1)1()(min -==a f x f min 24,23()1,3a a f x a a -<≤⎧=⎨->⎩ (3)⎩⎨⎧<-≥-=ax x a x ax a x x x f ),(),()(①当0>a 时,图象如右图所示由⎪⎩⎪⎨⎧-==)(42a x x y a y 得2)12(a x += ∴20a m <≤,a n a 212+≤< ②当0<a 时,图象如右图所示由⎪⎩⎪⎨⎧-=-=)(42x a x y a y 得a x 2)21(+= ∴a m a <≤+221, 02≤<n a。
中山市第三届初中数学教师解题比赛获奖通报

李厚友
华师中山附中
谢荣华
小榄华侨中学
刘俊健
古镇初级中学
王雪梅
西区中学
邢海秋
古镇初级中学
袁兰芳
坦洲中学
廖雪生
港口中学
段虎林
坦洲实验中学
关 莉
港口中学
杨启祥
石岐中学
邱啸林
港口中学
黄汉光
石岐中学
苏涌智
阜沙牛角中学
陈 敬
三乡桂山君里学校
谭小乐
东升旭日中学
袁 辉
三乡博爱中学
汤静中
东升初级中学
莫能博
中山市第三届初中数学教师解题比赛获奖通报
经学校选拔推荐,全市共202名教师参加了第三届初中数学教师解题比赛,根据竞赛成绩从高到低共评出一等奖22名,二等奖45名,三等奖42名,现将名单予以公布。
附件:中山市第三届初中数学教师解题比赛获奖名单
中山市教育局教研室
二○○九年十月二十二日
附件:
中山市第三届初中数学教师解题比赛获奖名单
徐 妍
坦洲第三初级中学
李施敏
黄圃镇中学
罗 琼
石岐启发中学
周 斌
华师中山附中
聂少林
神湾中学
皮雄亚
广东博文学校
汤 勇
沙溪溪角中学
李 锋
广东博文学校
潘 菁
三角镇沙栏中学
杨廷志
古镇初级中学
钟文明
三角镇沙栏中学
李建中
东升旭日中学
陈泽文
三角镇沙栏中学
赵 良
东升初级中学
余聪香
南头初级中学
王 群
板芙中学
向和林
南头初级中学
黄圃镇中学
万唤青
“十佳”中学数学青年教师 - 广州市中学数学之窗

广州市第三届高(初)中学数学“十佳青年教师”获奖通知
各中学:
由广州市教育局教研室数学科和广州市中学数学教学研究会主办的“广州市第三届高中(初中)数学十佳青年教师”的评选活动,得到各区(县级市)教育局教研室和各中学校长室、数学科组、数学教师的大力支持。
按评选要求,经过“解题比赛——论文评审——学校考核”程序决出了初中组、高中组各15名数学教师参加2008年12月16日的课堂教学评比活动。
最后综合评出初中组、高中组十佳青年数学教师各10名。
获奖名单附后。
特此通知。
广州市教育局教研室数学科
广州市中学数学教学研究会
2008年12月31日
附表1 广州市第三届高中“十佳青年数学教师”获奖名单
附表2 广州市第三届初中“十佳青年数学教师”获奖名单。
初中数学教师基本功比赛一等奖说题稿

目录
• 题目选择与背景分析 • 解题思路与方法探讨 • 题目变化与拓展应用 • 学生答题情况分析 • 教学反思与总结提升
题目选择与背景分析
01
选题依据及目的
依据数学课程标准, 强调核心概念和基本 技能的掌握。
引导学生运用所学知 识解决实际问题,提 高数学应用意识。
拓展题型
在原题基础上进行拓展,增加难度和复杂度,如引入参数、构造函数等,以此挑战 学生的解题能力和思维深度。
实际应用场景举例
几何应用
将几何知识与实际生活相结合,如 利用三角形稳定性原理设计建筑结 构、利用三角函数计算山峰高度等。
代数应用
将代数知识与实际问题相结合,如 利用方程解决年龄问题、利用不等 式优化资源分配等。
转化思想法
将复杂问题转化为简单问题,或者将未知问题转化为已知问题。这种方法需要 学生具备一定的数学素养和思维能力,能够灵活运用所学知识解决问题。
思路拓展与延伸
一题多解
鼓励学生尝试多种解法,培养发散思维和创新能力。通过比较 不同解法的优劣,可以帮助学生更好地理解数学问题的本质和 解题方法的多样性。
举一反三
通过解题过程,引导学生形成 正确的数学观念和思维方式。
题目难度及区分度
题目难度适中,既有一定的挑战 性,又不过于超出学生的认知水
平。
通过设置不同层次的题目,实现 对学生知识掌握情况的有效区分。
鼓励学生在解题过程中发挥创造 性和想象力,展现自己的数学才
能。
解题思路与方法探讨
02
常规解法展示
逐步推导法
02 03
增加限制条件
在原题基础上增加新的限制条件,如“在直角三角形中,已知一条直角 边长和斜边长,求另一条直角边长”,可变化为“在等腰直角三角形中, 已知一条直角边长,求斜边长”。
青年教师初中数学解题比赛决赛试卷及答案(广州市)

广州市青年教师初中数学解题比赛决赛试卷本试卷共8页,第1-2页为选择题和填空题,第3-8页为解答题及答卷。
请将选择题和填空题的答案做在第3页的答卷上。
全卷共三大题25小题,满分150分,考试时间120分钟。
题号 1 2 3 4 5 6 7 8 9 10 11 答案 D C D A A B B D C C A第I 卷(选择题,共44分)一、选择题(本大题共11小题,每小题4分,满分44分,请将唯一正确的答案代号填在第3页的答题卷上)1、a 是任意实数,下列判断一定正确的是( ). (A )a a -> (B )a a<2(C )23a a > (D )02≥a 2、已知集合},032|{},4|{22<--=<=x x x N x x M 则集合=⋂N M ( ). (A )}2|{-<x x (B )}3|{>x x (C )}21|{<<-x x (D )}32|{<<x x3、若二次函数2y ax bx c =++的图象如图所示,则点(a +b ,ac )在( ). (A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限(第3题)4、同圆的内接正十边形和外切正十边形的周长之比等于( ). (A )cos18°(B )sin18° (C )cos36°(D )sin36°5、用黑白两种颜色的正六边形地面砖按如下所示的规律,拼成若干个图案:则第8个图案中有白色地面砖( A )块.(A)34 (B)36 (C)38 (D)406、将正方形的四边四等分,包括顶点共有16个点,这16个点可得到的直线条数是( ). (A)120 (B)84 (C)82 (D)807、如图,⊙O 中,弦AD ∥BC ,DA =DC ,∠AOC =160°,则∠BCO 等于( ).(A )20° (B )30° (C )40° (D )50°(第7题) 8、如果y x ,为实数,且,0)1(22=-+-y x x 则x 的取值范围是( ).(A)任意实数 (B)负实数 (C)210≤<x (D)10≤≤x 9、方程012=-+x x 所有实数根的和等于( ).O C BAD Oxy(A)1- (B)1 (C)0 (D)510、将四个完全相同的矩形(长是宽的3倍),用不同的方式拼成一个大矩形,设拼得的大矩形面积是四个小矩形的面积和,则大矩形周长的值只可能是( ). (A)1种 (B)2种 (C)3种 (D)4种 11、一次函数b ax x f +=)((a 为整数)的图象经过点(98,19),它与x 轴的交点为(p,0),它与y 轴的交点为(0,q ),若p 是质数,q 为正整数,则满足条件的所有一次函数的个数为( ).(A)0 (B)1 (C)2 (D)大于2的整数第II 卷(非选择题,共106分)二、填空题(本大题共6小题,每小题5分,共30分,将答案直接填在第三页的答题卷上)12、函数x y lg =在定义域上是 OU 函数(填奇或偶);在区间 0—〉 上是增加的. 13、如图,有两个同心圆,大圆的弦AB 与小圆相切于点P , 大圆的弦CD 经过点P ,且CD =13,PD =4,两圆组成的圆环的面积是 36PI .P(第13题)14、已知t bac a c b c b a =+=+=+,那么直线t tx x f +=)(一定通过第 2、3 象限.T=2,-1 分析:利用和分比公式得a+b+c=0,t= -1,a+b+c ≠0,t=215、已知上的点,为上的点,为内一定点,为ON B OM A MON P MON ∠=∠,400则当PAB ∆的\周长取最小值时,的度数为APB ∠ 100° . 313-≤≤-t16、已知实数b a ,满足t b a ab t b ab a 那么且,,12222--==++的取值范围是 17、若c b a ,,为实数,且,2,0==++abc c b a 那么c b a ++的最小值可达到 4 . 三、解答题(共8小题,满分76分.解答应写出必要文字说明、演算步骤和证明过程) 18、(本题8分)若直线0=+-a y x 与圆122=+y x 相交,求实数a 的取值范围. 19、(本题8分)菱形ABCD 的边AB=5,对角线BD=6,且AC 与BD 相 交于点O ,沿BD 折叠得四面体ABCD ,已知该四面体的体积等于8, 求二面角A-BD-C 的大小.20、(本题8分)设,0,12≠=++a a x x x求1242++x x x 的值.21、(本题8分)某商场计划销售一批运动衣后可获总利润12000元. 在进行市场调查后, 为了促销降低了定价,使得每套运动衣少获利润10元,结果实际销售比计划增加了400 套,总利润比计划多了4000元,问实际销售运动衣多少套?每套运动衣实际利润多少元?.ABCDO22、(本题10分)已知任意三角形ABC,其面积为S. 作BC 的平行线与AB 、AC 分别交于D 、E . 设三角形BDE 的面积为M ,求证:M≤S 4123、(本题11分)已知:如图,在Rt △ABC 中,斜边AB =5厘米,BC =a 厘米,AC =b 厘米,a >b ,且a 、b 是方程2(1)40x m x m --++=的两根, ⑴求a 和b 的值;⑵△'''C B A 与△ABC 开始时完全重合,然后让△ABC 固定不动,将 △'''C B A 以1厘米/秒的速度沿BC 所在的直线向左移动.ⅰ)设x 秒后△'''C B A 与△ABC 的重叠部分的面积为y 平方厘米,求y 与x 之间的函数关系式,并写出x 的取值范围;ⅱ)几秒后重叠部分的面积等于38平方厘米?24、(本题11分)已知:如图,⊙O 与⊙P 相交于A 、B 两点,点P 在⊙O 上,⊙O 的弦AC 切⊙P 于点A ,CP 及其延长线交⊙P 于D 、E ,经过E 作EF ⊥CE 交CB 的延长线于F.⑴ 求证:BC 是⊙P 的切线;⑵ 若CD =2,CB =22,求EF 的长;⑶ 若设k =PE:CE,是否存在实数k,使△PBD 恰好是等边三角形?若存在,求出k 的值;若不 存在,请说明理由.25、(本题12分)如图,EFGH 是正方形ABCD 的内接四边形,两条对角线EG 和FH 相交于点O ,且它们所夹的AB CM A'B'C'锐角为θ,CFH BEG ∠∠与都是锐角,已知,,l FH k EG ==四边形EFGH 的面积为S ,(1) 求证:klS 2sin =θ (2) 试用S l k 、、来表示正方形ABCD 的面积.2005年广州市青年教师初中数学解题比赛决赛参考答案2005-3-20 一、选择题答案(每小题4分,共44分) 二、填空题答案(每小题5分,共30分)三、解答题(共8小题,满分76分.解答应写出必要文字说明、演算步骤和证明过程) 18、解:(代数方法)由题意,⎩⎨⎧=+-=+0122a y x y x⇒012222=-++a ax x直线与圆相交,∴0>∆即0)2(4)1(84222>--=--=∆a a a则022<-a ,即22<<-a 时,有0>∆直线与圆相交(此题可有几何方法,相应评分)19、解: AO=OC=435BO AB 2222=-=-,易得 θ = ∠ ⊥ ⊥AOC , BD OC , BD AO 为二面角A-BD-C 的平面角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年黄埔区初中数学教师解题比赛结果公布各中学:
黄埔区初中数学教师解题比赛已于2014年3月7日举行,获奖情况如下:
一等奖
曾小芹舒姝杨山吴江涛赵丽晓饶秋莎彭青顾星郭慰怀甄颖
二等奖
周晓岚李娜钟钦灵吴玉湘张启青钟武权罗香美
以上获一等奖的教师将被选送参加“广州市2014年广州市中学数学教师解题比赛”决赛,请通知选手做好参赛的准备。
决赛时间:2014年4月13日上午9:00时~11:00
决赛地点:广州市执信中学
黄埔区教育局教研室
二0一四年三月十日。
