20200405高一数学—等比数列(代证)
高中数学:专题2.4 等比数列-高中数学必修五课件

探 究
, 263
(2)
1 , 1 , 1 , 1 , …… 2 4 8 16
(3) 9,92,93,94,95,96, 97
(4) 36,36×0.9,36×0.92, 36×0.93,…
共同特点?从第2项起,每一项
与前一项的比都等于同一常数.
知识新授
1.等比数列定义
一般的,如果一个数列从第2项起,每一
定义式 公差(比)
an+1-an=d d 叫公差
通项公式
一般形式 等差(比)
中项
an= a1+(n-1)d an=am+(n-m)d
等比数列
an1 an q
q叫公比
an=a1qn-1 an=amqn-m
G ab
等比数列的定义; 等比中项; 等比数列的通式公式及其简单应用; 类比思想的运用;
课后作业: 1.课本 p53练习4, 2. p53习题2.4A组1
第二章 数列
2.4.1 等比 数列
渭源县第二中学 何华
学习目标
1.知识与技能:使学生掌握等比数列的定义及通项公式,发现等比数列 的一些简单性质,并能运用定义及通项公式解决一些实际问题。 2.过程与方法: (1)培养运用归纳类比的方法发现问题并解决问题的能力及运用方程的 思想的计算能力。 (2)采用观察、思考、类比、归纳、探究、得出结论的方法进行教学 (3)发挥学生的主体作用,作好探究性活动 3.情感态度与价值观:通过生活中的大量实例,鼓励学生积极思考,激发 学生对知识的探究精神和严肃认真的科学态度,培养学生的类比、归纳 的能力;
深
在等差数列 an 中
入
an am (n m)d
探
(n, m N* )
高一数学等比数列知识点总结

高一数学等比数列学问点总结等比数列是高一数学学习的内容,有哪些学问点需要重点把握呢?下面是学习啦我给大家带来的高一数学等比数列学问点,期望对你有关怀。
高一数学等比数列学问点1.等比中项假设在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项。
有关系:注:两个非零同号的实数的等比中项有两个,它们互为相反数,所以G=ab是a,G,b三数成等比数列的必要不充分条件。
2.等比数列通项公式an=a1*q(n-1)(其中首项是a1,公比是q)an=Sn-S(n-1)(n2)前n项和当q1时,等比数列的前n项和的公式为Sn=a1(1-qn)/(1-q)=(a1-a1*qn)/(1-q)(q1)当q=1时,等比数列的前n项和的公式为Sn=na13.等比数列前n项和与通项的关系an=a1=s1(n=1)an=sn-s(n-1)(n2)4.等比数列性质(1)假设m、n、p、qN*,且m+n=p+q,那么aman=apaq;(2)在等比数列中,依次每k项之和仍成等比数列。
(3)从等比数列的定义、通项公式、前n项和公式可以推出:a1an=a2an-1=a3an-2==akan-k+1,k{1,2,,n}(4)等比中项:q、r、p成等比数列,那么aqap=ar,ar那么为ap,aq等比中项。
记n=a1a2an,那么有2n-1=(an)2n-1,2n+1=(an+1)2n+1另外,一个各项均为正数的等比数列各项取同底指数幂后构成一个等差数列;反之,以任一个正数C为底,用一个等差数列的各项做指数构造幂Can,那么是等比数列。
在这个意义下,我们说:一个正项等比数列与等差数列是"同构'的。
(5)等比数列前n项之和Sn=a1(1-qn)/(1-q)(6)任意两项am,an的关系为an=amq(n-m)(7)在等比数列中,首项a1与公比q都不为零。
留意:上述公式中an表示a的n次方。
高一数学等比数列学问点1、acb2是a,b,c成等比数列的( )A.充分条件B.必要条件C.充要条件D.既不充分也不必要条件2ab2、a,b,c,d是公比为2的等比数列,那么等于( ) 2cd111A.1 B. C. D. 2483、{an}是等比数列,且an0,a2a42a3a5a4a625,那么a3a5 的值是( )A.5B.6C.7D.254、在等比数列{an}中,a1,a43,那么该数列前5项的积为( )9A.1B.3C.1D.35、ABC的三边a,b,c既成等比数列又成等差数列,那么三角形的样子是( )A.直角三角形B.等腰三角形C.等腰直角三角形D.等边三角形高一数学学习方法抓好根底是关键数学习题无非就是数学概念和数学思想的组合应用,弄清数学根本概念、根本定理、根本方法是推断题目类型、学问范围的前提,是正确把握解题方法的依据。
高一数学必修5等比数列知识点自己总结

高一数学必修5等比数列知识点自己总结等比数列是数学中常见的数列,其特点是每个数与前一个数的比例保持不变。
等比数列在高中数学中常用于解题和推导。
下面是关于高一数学必修5中等比数列的知识点总结。
一、等比数列的定义等比数列是一种数列,它的每一项与前一项之比都相等。
记作a1、a2、a3、...、an、...的等比数列,它的通项公式为an=a1*r^(n-1),其中a1是首项,r是公比,n是项数。
二、等比数列的性质1. 公比为0时,等比数列为常数列。
2. 公比大于1时,等比数列呈递增趋势。
3. 公比小于1但大于0时,等比数列呈递减趋势。
4. 公比小于-1但大于-1时,等比数列呈交替增减趋势。
5. 等比数列的首项与公比的正负关系决定了数列的增减趋势。
三、等比数列的通项公式等比数列的通项公式可以通过下述推导得出:设等比数列的首项是a1,公比是r,第n项是an,第n-1项是an-1。
an=a1*r^(n-1) (等比数列的通项公式)an-1=a1*r^(n-2) (等比数列的通项公式)将第一个式子除以第二个式子得:an/an-1=(a1*r^(n-1))/(a1*r^(n-2))=r即等比数列的两项之比恒等于公比r。
四、等比数列的和等比数列的前n项和可以通过以下公式计算得出:Sn=a1*(1-r^n)/(1-r) (等比数列的前n项和公式)其中Sn是前n项的和。
特殊情况下,当公比r=1时,等比数列的前n项和可以简化为Sn=n*a1。
五、等比中项等比数列中,若数列中的某个数是它前后两个数的几何平均数,则称该数为等比数列的等比中项。
设该数为x,前一项是a,后一项是b,根据等比数列的性质可得:a/x=x/b即x^2=ab,解得x=√(ab)。
六、等比数列的应用1. 判断一组数是否构成等比数列,可通过两项之比是否恒等于公比来判断。
2. 求等比数列的前n项和,可使用等比数列的前n项和公式Sn=a1*(1-r^n)/(1-r)。
(vip免费)高中数学必修五课件:2.4《等比数列(一)》(人教A版必修5)

3.已知三个数成等比数列,积为27,和为13,求 这三个解数:.设这三个数为aq,a,aq,则aqaq·+a·aa+ q=a2q=7,13,
整理得a3= q2-3,10q+3=0,
解得
a=3,q=3
或1, 3
∴这三个数为 1,3,9 或 9,3,1.
误区解密 忽视题中隐含条件而出错
【例 4】 已知数列-1,a1,a2,-4 成等差数列,
前言
高考状元是一个特殊的群体,在许多 人的眼中,他们就如浩瀚宇宙里璀璨夺目 的星星那样遥不可及。但实际上他们和我 们每一个同学都一样平凡而普通,但他们 有是不平凡不普通的,他们的不平凡之处 就是在学习方面有一些独到的个性,又有 着一些共性,而这些对在校的同学尤其是 将参加高考的同学都有一定的借鉴意义。
孙老师说,杨蕙心学习效率很高,认真执行老师 的复习要求,往往一个小时能完成别人两三个小 时的作业量,而且计划性强,善于自我调节。此 外,学校还有一群与她实力相当的同学,他们经 常在一起切磋、交流,形成一种良性的竞争氛围。
谈起自己的高考心得,杨蕙心说出了“听话” 两个字。她认为在高三冲刺阶段一定要跟随老师 的脚步。“老师介绍的都是多年积累的学习方法, 肯定是最有益的。”高三紧张的学习中,她常做 的事情就是告诫自己要坚持,不能因为一次考试 成绩就否定自己。高三的几次模拟考试中,她的 成绩一直稳定在年级前5名左右。
题型二 等比数列的判断
【例 2】
已知数列an
满足
a1=1,an+1=2an+1,
(1)求证:数列an+1是等比数列;
(2)求 an 的表达式.
(1)证明:因为 an+1=2an+1,所以 an+1+1=2(an+1),
由 a1=1,故 a1+1≠0,由上式易知 an+1≠0,所以aan+n+1+11
高一数学等比数列的性质

判断等比数列的方法
定义法:
an1 q(是与 n无关的数,或 且q式 0) 子 an
中项法:
an1•an1an2(0)
三个数a,b,c成等比数列
acb2
等比数列的性质例题1
例1 已知:b是a与c的等比中项,且a、b、c同号,
求证: abc, abbcca,3abc也成等比数列。
3
3
解:证明:由题设 得:
acb2
a b c 3 a b a b c c 3 b 3 a b b 2 b ( c a b b c c ) 2 a
3
3
3
3
∴ abc, abbcca,3abc也成等比数列
3
3
等比数列的性质例题2
例2 已知 an,bn是项数相同的等比数列, 求证 anbn是等比数列.
证明:设数列 an 的首项是 a 1 ,公比为 q 1
b bn 的首项为 1 ,公比为 q 2 ,那么数列 anbn
的第n项与第n+1项分别为:
a 1 q 1 n 1 b 1 q 2 n 1 与 a 1 q 1 n b 1 q 2 n
即 a 1 b 1 ( q 1 为 q 2 ) n 1 与 a 1 b 1 ( q 1 q 2 ) n
an a n 1b bn n 1a a 11 b b 11 ((q q 11 q q 22 ))nn 1q1q2. 它是一个与n无关的常数,
简记作: an
复习数列的有关概念2
如果数列 an 的第n项 a n 与n之间的关
系可以用一个公式来表示,这个公式就叫做 这个数列的通项公式。
S n a 1 a 2 a 3 a n 1 a n
叫做数列 an 的前n项和。
《高一数学等比数列》课件

等比数列具有很多特点和 常用公式,包括公比的取 值范围、前 n 项和的计算 公式等。
等比数列的性质
公比
公比是等比数列相邻 两项之比的常数,用 r 表示。
前 n 项和
计算等比数列前 n 项 的和的公式为 Sn = (A1 * (r^n - 1)) / (r - 1), 其中 Sn 表示前 n 项的 和。
• 数学相关教材 • 网络资源 • 其他相关参考资料
介绍等比数列的推广及其 在更广泛的领域中的应用, 例如指数函数和级数。
总结
重点知识点回顾
回顾等比数列的重要概念、公式和性质,并加深对它们的理解。
应用及其重要性
强调等比数列在各个领域中的广泛应用及其在问题求解中的重要性。
学习策略
分享一些学习等比数列的有效策略和技巧,帮助学生更好地掌握这一概念。
参考文献
物理学、经济学
等比数列在物理学和经济学 等领域也有广泛的应用,例 如物理学中的指数衰减和经 济学中的增长模型。
练习与拓展
1 例题练习
通过一系列的等比数列练 习题,巩固对等比数列的 理解和运用能力。
2 与其他数列的比较
将等比数列与等差数列和 斐波那契数列等其他数列 进行比较,了解它们之间 的异同。
3 拓展
《高一数学等比数列》 PPT课件
提供了全面且易于理解的高一数学等比数列PPT课件,帮助学生深入掌握等比 数列的概念、性质和应用,提升数学学习的效果。
什么是等比数列
1 定义
2 通项公式
3 性质和常用公式
等比数列是指数列的一种, 其中相邻两项之比是固定 的。
等比数列的通项公式为 An = A1 * r^(n-1) ,其中 An 表 示第 n 项,A1 表示首项, r 表示公比。
高中数学必修五-等比数列

等比数列知识集结知识元等比数列的通项公式知识讲解1.等比数列的通项公式【知识点的认识】1.等比数列的定义如果一个数列从第2项起,每一项与它的前一项的比值等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,通常用字母q表示(q≠0).从等比数列的定义看,等比数列的任意项都是非零的,公比q也是非零常数.2.等比数列的通项公式设等比数列{a n}的首项为a1,公比为q,则它的通项a n=a1•q n﹣13.等比中项:如果在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项.G2=a•b(ab≠0)4.等比数列的常用性质(1)通项公式的推广:a n=a m•q n﹣m,(n,m∈N*).(2)若{a n}为等比数列,且k+l=m+n,(k,l,m,n∈N*),则a k•a l=a m•a n(3)若{a n},{b n}(项数相同)是等比数列,则{λa n}(λ≠0),{a},{a n•b n},仍是等比数列.(4)单调性:或⇔{a n}是递增数列;或⇔{a n}是递减数列;q=1⇔{a n}是常数列;q<0⇔{a n}是摆动数列.例题精讲等比数列的通项公式例1.若公比为2的等比数列{a n}的各项都是正数,且a3a11=64,则a6等于()A.1B.2C.4D.8例2.已知等比数列{a n}前9项的积为512,且a8=32,则a2=()A.B.C.D.例3.在公比q为整数的等比数列{a n}中,S n是数列{a n}的前n项和,若a1∙a4=32,a2+a3=12,则下列说法错误的是()A.q=2B.数列{S n+2}是等比数列C.S8=510D.数列{lga n}是公差为2的等差数列等比数列的性质知识讲解1.等比数列的性质【等比数列】(又名几何数列),是一种特殊数列.如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,这个数列就叫做等比数列,因为第二项与第一项的比和第三项与第二项的比相等,这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0).注:q=1时,a n为常数列.等比数列和等差数列一样,也有一些通项公式:①第n项的通项公式,a n=a1q n﹣1,这里a1为首项,q为公比,我们发现这个通项公式其实就是指数函数上孤立的点.②求和公式,S n=,表示的是前面n项的和.③若m+n=q+p,且都为正整数,那么有a m•a n=a p•a q.例:2,x,y,z,18成等比数列,则y=.解:由2,x,y,z,18成等比数列,设其公比为q,则18=2q4,解得q2=3,∴y=2q2=2×3=6.故答案为:6.本题的解法主要是运用了等比数列第n项的通项公式,这也是一个常用的方法,即知道某两项的值然后求出公比,继而可以以已知项为首项,求出其余的项.关键是对公式的掌握,方法就是待定系数法.【等比数列的性质】(1)通项公式的推广:a n=a m•q n﹣m,(n,m∈N*).(2)若{a n}为等比数列,且k+l=m+n,(k,l,m,n∈N*),则a k•a l=a m•a n(3)若{a n},{b n}(项数相同)是等比数列,则{λa n}(λ≠0),{a},{a n•b n},仍是等比数列.(4)单调性:或⇔{a n}是递增数列;或⇔{a n}是递减数列;q=1⇔{a n}是常数列;q<0⇔{a n}是摆动数列.例题精讲等比数列的性质例1.已知等比数列{a n}中a5=1,若+++=5,则a2+a4+a6+a8=()A.4B.5C.16D.25例2.等比数列{a n}的各项均为正数,且a4a6+a3a7=18,则log3a1+log3a2+log3a3++log3a9=()A.12B.10C.9D.2+log35例3.已知数列{a n}为等比数列,且a2a3a4=-a72=-64,则tan=()A.B.C.D.当堂练习单选题练习1.已知等比数列{a n}的首项为1,且a6+a4=2(a3+a1),则a1a2a3…a7=()A.16B.64C.128D.256练习2.在等比数列{a n}中,a1=1,=8,则a6的值为()A.4B.8C.16D.32练习3.等比数列{a n}的各项均为正数,已知向量=(a4,a5),=(a7,a6),且∙=4,则log2a1+log2a2+…+log2a10=()A.12B.10C.5D.2+log25练习4.已知等比数列{a n}中,a3=2,a4a6=16,则=()A.2B.4C.8D.16练习5.设{a n}(n∈N*)是各项为正数的等比数列,q是其公比,K n是其前n项的积,且K5<K6,K6=K7>K8,则下列结论错误的是()A.0<q<1B.a7=1C.K9>K5D.K6与K7均为K n的最大值填空题练习1.已知数列{a n}的前n项和S n=3n-1,则首项a1=___,通项公式a n=________.练习2.已知等比数列a1,a2,a3,a4满足a1∈(0,1),a3∈(1,2),a4∈(2,4),则a6的取值范围为__.练习3.在等比数列{a n}中,已知a1+a2+a3=1,a2+a3+a4=2,则a8+a9+a10=_____.练习4.在等比数列{a n}中,a4,a8是关于x的方程x2+10x+4=0的两个实根,则a2a6a10=____.练习5.已知等比数列{a n}的首项为1,且a6+a4=2(a3+a1),则a1a2a3…a7=_____.练习6.已知无穷等比数列{a n}满足:对任意的n∈N*,sin a n=1,则数列{a n}公比q的取值集合为______________.解答题练习1.'(1)在等差数列{a n}中,已知a1=3,d=4,a n=59,求n;(2)在等比数列{a n}中,已知,求a1与q.'练习2.'已知等差数列{a n}中,a2+a3=14,a4-a1=6.(1)求数列{a n}的通项公式;(2)设等比数列{b n}满足b2=a1,b3=a3,若b6=a m,求实数m的值.'练习3.'已知数列{a n}满足:a1=1,a2=a(a>0).数列{b n}满足b n=a n a n+1(n∈N*).(1)若{a n}是等差数列,且b3=12,求a的值及{a n}的通项公式;(2)当{b n}是公比为a-1的等比数列时,{a n}能否为等比数列?若能,求出a的值;若不能,请说明理由.'。
高中数学必修5《等比数列的性质》PPT

在等比数列{an}中距首末两端等距离的两项的积相等, 即a1an=a2an-1=a3an-2=…
性质5 在等比数列{an}中,序号成等差数列的项仍成等比数列
工具
第二章 数列
栏目导引
已 知 各 项 均 为 正 数 的 等 比 数 列 {an} 中 , a1·a2·a3 = 5 , a7·a8·a9=10,则 a4·a5·a6=( )
A.5 2
B.7
C.6
D.4 2
工具
第二章 数列
栏目导引
工具
第二章 数列
栏目导引
[解题过程] a1·a2·a3=a23=5 a7·a8·a9=a83=10 a4·a5·a6=a53
3
又∵a52=a2·a8,∴a53=(a2·a8) 2
1
1
∴a4·a5·a6=(a23a83) 2 =(5×10) 2 =5 2.故选 A.
若{an}是等差数列,则ak,ak+m,ak+2m,…(k、 m∈N*)组成公差为md的等差数列
工具
第二章 数列
栏目导引
请把这些性质类比到等比数列
(小组合作交流)
工具
第二章 数列
栏目导引
等比数列的常用性质
性质1 性质2 性质3 性质4
通项公式的推广:an=am· qn-m (n,m∈N*) 若则{aak·n}a为l=等a比m·数an列,且k+l=m+n(k,l,m,n∈N*),
若{an}为等差数列,且k+l=m+n(k,l,m,n∈N*), 则ak+al=am+an
若{an}是等差数列,则2an=an-1+an+1,a1+an=a2 +an-1=a3+an-2=…
高一数学必修五第二章等比数列的概念课件

以此类推,每个格子里放的麦粒数都是前一个格子里麦粒
数的2倍,直到第64格,请给我足够的麦粒实现上述要求”。
国王觉得这个要求不高,就欣然同意了,假定千粒麦粒的
质量为40g,据查,目前世界年度小麦产量约为6亿吨,根
据以上数据,判断国王能否实现他的诺言?
一、导
• 等差数列前n项和:Sn= a1 + a2 +…+ an
多年才能产出所需小麦。
一、导
• (3)等比数列前n项和推导
乘以公比, 错位相减
• 等比数列首项a1,公比为q:
•
Sn= a1 + a2 +…+ an
①
•
qSn= a1q+…+an-1q + anq
•
qSn= a2 +…+ an + anq
②
• ①-②:(1-q)Sn=a1-anq=a1(1-qn)
• q=1
Sn=na1
• q≠1 Sn=a1(1-qn)/(1-q) (知3求2)
二、思
• (1)1/2,1/4,1/8,…,求S8; • (2)a1=27,a9=1/243,求S8; • (3)a1=3,q=2,n=6,求Sn; • (4)a1=27,q=-1/3,an=1/90,求Sn; • (5)在递增的等比数列{an}中,已知a1+an=34,a3*an-2=64,
且前n项和为Sn,则n= ( )。
三、议
• (1)a1=3,q=2,n=6,求Sn; • (2)a1=27,q=-1/3,an=1/90,求Sn; • (3)在递增的等比数列{an}中,已知a1+an=34,a3*an-2=64,
高一数学必修5等比数列知识点自己总结

高一数学必修5等比数列知识点自己总结高一数学必修5等比数列学问点自己总结等比数列一、基本概念与公式:1、等比数列的定义;2、等比数列的通项公式:(1)ana1qn1;(2)anamqnm.(其中a1为首项、am为第m项,an0;m,nN)3、等比数列的前n项和公式:当q=1时,Sn=na1(是关于n的正比例式);aanqa1(1qn)当q≠1时,Sn==KqnK,Sn=11q1q三、有关等比数列的几个特别结论1、等比数列an中,若mnpq(m,n,p,qN),则amanapaq留意:由Sn求an时应留意什么?n1时,a1S1;n2时,anSnSn1.2、等比数列an中的任意“等距离”的项构成的数列仍为等比数列.3、公比为q的等比数列an中的任意连续m项的和构成的数列Sm、S2m-Sm、S3m-S2m、S4m-S3m、(Sm≠0)仍为等比数列,公比为q.4、若an与bn为两等比数列,则数列kan、an(k0,k为常数)仍成等比数列.5、若an为等差数列,则cmkan、anbn、bn(c>0)是等比数列.an6、若bnbn0为等比数列,则logcbn(c>0且c1)是等差数列.7、在等比数列an中:(1)若项数为2n,则S偶S奇q(2)若项数为2n1,则S奇a1S偶qn8、数列an是公比不为1的等比数列数列an前n项和Sn=AqA,(q1,A0)定义递推公式通项公式中项等差数列an1andanan1d;anamnmdana1(n1)d 等比数列an1q(q0)ananan1q;anamqnmana1qn1(a1,q0)Aankank2Gankank(ankank0)(n,kN*,nk0)前n项和Snn(a1an)2(n,kN*,nk0)na1(q1)Sna11qna1anq(q2)1q1qn(n1)Snna1d2重要性质*amanapaq(m,n,p,qN,mnpq)amanapaq(m,n,p,qN*,mnpq)9、等比数列的判定方法(1)、an=an-1q(n≥2),q是不为零的常数,an-1≠0(2)、an=an -1an+1(n≥2,an-1,an,an+1≠0)(3)、an=cq(c,q均是不为零的常数)10、等比数列的前n项和的性质n2{an}是等比数列.{an}是等比数列.{an}是等比数列.(1)、若某数列前n项和公式为Sn=an-1(a≠0,±1),则{an}成等比数列.n(2)、若数列{an}是公比为q的等比数列,则Sn+m=Sn+qSm.(3)、在等比数列中,若项数为2n(n∈N*),则(4)、Sn,S2n-Sn,S3n -S2n成等比数列.扩展阅读:高一数学必修5等比数列学问点自己总结仔细等比数列一、基本概念与公式:1、等比数列的定义;2、等比数列的通项公式:(1)a(2)ana1qn1;amqnma为第m项,a.(其中a为首项、1mnn0;m,nN)3、等比数列的前n项和公式:当q=1时,Sn=na1(是关于n的正比例式);当q≠1a1(1qn)时,Sn==KqnK,1qSn=a1anq1q三、有关等比数列的几个特别结论1、等比数列a中,若nmnpq(m,n,p,qN),则amanapaq留意:由S求a时应留意什么?nnn1时,a1S1;n2时,anSnSn1.2、等比数列a中的任意“等距离”的项构成的数列n仍为等比数列.3、公比为q的等比数列a中的任意连续m项的和构成n的数列Sm、S2m-Sm、S3m-S2m、S4m-S3m、(Sm≠0)仍为等比数列,公比为qm.仔细4、若a与b为两等比数列,则数列ka、a、aknnnnnbn、anbn(k0,k为常数)仍成等比数列.5、若a为等差数列,则c(c>0)是等比数列.nan6、在等比数列a中:n(1)若项数为2n,则S偶S奇奇qa1(2)若项数为2n1,则SnS偶q8、数列a是公比不为1的等比数列数列a前n项n和Sn=Aq定义递推公式通项公式中项前AnA,(q1,A0)等差数列aadn1n等比数列an1q(q0)annnanan1d;aamnmdanan1q;aamqnmana1(n1)dana1qn1(a,q0)1ankank2*Gankank(ankank0)(n,kNnSn,nk0)(n,kN*,nk0)n(a1an)2项和n(n1)Snna1d2na1(q1)Sna11qna1anq(q2)1q1q重要amanapaq(m,n,p,qN*,mnpq)amanapaq(m,n,p,qN*,mnpq)仔细性质9、等比数列的判定方法(1)、an=an-1q(n≥2),q是不为零的常数,an-1≠0{an}是等比数列.(2)、an2=an-1an+1(n≥2,an-1,an,an+1≠0){an}是等比数列.(3)、an=cq(c,q均是不为零的常数){an}是等比数列.10、等比数列的前n项和的性质(1)、若某数列前n项和公式为Sn=an-1(a≠0,±1),则{an}成等比数列.(2)、在等比数列中,若项数为2n(n∈N*),则(3)、Sn,S2n-Sn,S3n -S2n成等比数列.n。
等比数列

高一数学-等比数列一、 考点、热点回顾1、数列的通项公式a n ,前n 项和记为S n ,则S n 与a n 的关系是:a n =⎩⎨⎧≥-=-2.1,11n S S n S n n。
2、等比数列(q =nn a a 1+ (n +∈N )或q =1-n n a a (n ≥2).);等比中项(如果G 是a 与b 的等比中项,那么a G =Gb ,即G 2= ab ,G =±ab );(t + k = m + n (两边的自然数个数相等),那么当{a n }为等比数列时,有:a t .a k = a m .a n );前n 项和公式是S n =⎪⎩⎪⎨⎧≠--=.1,1)1(,1,11时当时当q qq a q na n二、典型例题例1、设等比数列{a n }的前n 项和为S n ,S 4=1,S 8=17,则通项a n = .例2、若数列{a n }的前n 项和S n =3n -a ,数列{a n }为等比数列,则实数a 的值是 .例3、已知等比数列{a n }的各项均为正数,数列{b n }满足b n =lna n ,b 3=18,b 6=12,则数列{b n }前n 项和的最大值等于 .例4、设y=f(x )是一次函数,f(0)=1,且f(1),f(4),f(13)成等比数列,则f(2)+f(4)+…+f(2n)= .例5、已知{a n }为等比数列,a 3=2,a 2+a 4=320,求{a n }的通项公式.例6、已知数列{a n }的前n 项和为S n ,且对任意n ∈N *有a n +S n =n.(1)设b n =a n -1,求证:数列{b n }是等比数列;(2)设c 1=a 1且c n =a n -a n-1 (n ≥2),求{c n }的通项公式.例7、已知数列{a n }的前n 项和为S n ,且a 1=1,na n+1=(n+2)S n (n ∈N *).(1)求证:数列⎭⎬⎫⎩⎨⎧n S n 为等比数列;(2)求数列{a n }的通项公式及前n 项和S n ;例8、设数列{a n }的前n 项和S n =2a n -2n .(1)求a 3,a 4;(2)证明:{a n+1-2a n }是等比数列;(3)求{a n }的通项公式.例9、设数列{}n a 的前n 项和为n S ,已知()21nn n ba b S -=- (1)证明:当2b =时,{}12n n a n --⋅是等比数列;(2)求{}n a 的通项公式。
最新人教版高一数学知识(必修5)专题精讲附解答: 等比数列
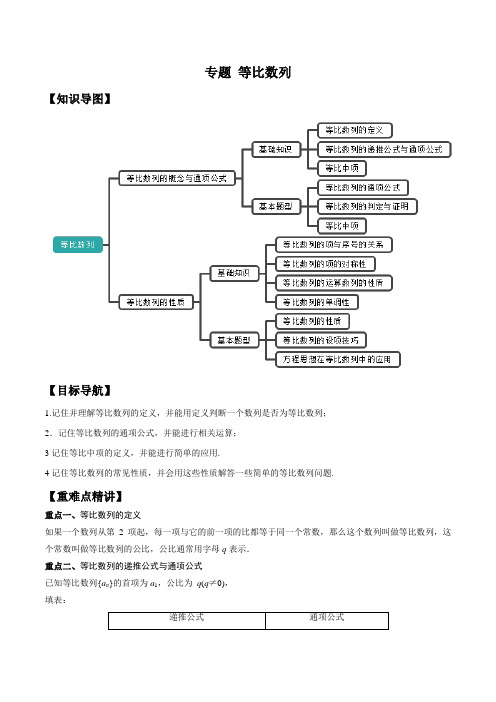
专题等比数列【知识导图】【目标导航】1.记住并理解等比数列的定义,并能用定义判断一个数列是否为等比数列;2.记住等比数列的通项公式,并能进行相关运算;3记住等比中项的定义,并能进行简单的应用.4记住等比数列的常见性质,并会用这些性质解答一些简单的等比数列问题.【重难点精讲】重点一、等比数列的定义如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示.重点二、等比数列的递推公式与通项公式已知等比数列{a n}的首项为a1,公比为q(q≠0),填表:递推公式通项公式a n=q(n≥2)a n=a1q n-1a n-1重点三、等比中项(1)如果三个数x,G,y组成等比数列,则G叫做x和y的等比中项.(2)如果G是x和y的等比中项,那么G2=xy,即G=±xy.重点四、等比数列的项与序号的关系(1)两项关系通项公式的推广:a n=a m·q n-m(m、n∈N*).(2)多项关系项的运算性质若m+n=p+q(m、n、p、q∈N*),则a m·a n=a p·a q.特别地,若m+n=2p(m、n、p∈N*),则a m·a n=a2p.重点五、等比数列的项的对称性有穷等比数列中,与首末两项“等距离”的两项之积等于首末两项的积(若有中间项则等于中间项的平方),(n为正奇数).即a1·a n=a2·a n-1=a k·a n-k+1=a2n-12重点六、等比数列的运算数列的性质(1)若{a n}是公比为q的等比数列,则①{c·a n}(c是非零常数)是公比为cq的等比数列;②{|a n|}是公比为|q|的等比数列.(2)若{a n}、{b n}分别是公比为q1、q2的等比数列,则数列{a n·b n}是公比为q1·q2的等比数列.重点七、等比数列的单调性(1)当a1>0,q>1或a1<0,0<q<1时,等比数列{a n}为递增数列;(2)当a1>0,0<q<1或a1<0,q>1时,等比数列{a n}为递减数列;(3)当q=1时,数列{a n}是常数列;(4)当q<0时,数列{a n}是摆动数列.【典题精练】考点1、等比数列的通项公式例1.【云南省中央民族大学附属中学芒市国际学校2017-2018学年高二下学期期中】数列{}n a满足111,43(2)n n a a a n -==+≥,则此数列的通项公式n a =________【答案】1241n n a -=⋅-.【解析】 ()1432n n a a n -=+≥Q ,()()11412n n a a n -∴+=+≥11a =Q ,则112a +=∴数列{}1n a +是以2为首项,4为公比的等比数列1124n n a -∴+=⋅,1241n n a -=⋅-故答案为1241n n a -=⋅-考点点睛:求等比数列的通项公式与求等差数列的通项公式一样,运用方程的思想,建立基本量的方程(或方程组)求解,在a 1,a n ,n ,q 四个量中,已知三个可求另一个. 考点2、等比数列的判定与证明例2.已知方程2110n n a x a x +-+=的两个根为,αβ,且6263ααββ-+=.(1)用n a 表示1n a +.(2)求证:23n a ⎧⎫-⎨⎬⎩⎭是等比数列.(3)若116a =,求数列{}n a 的通项公式. 【答案】(1)1326n n a a ++=;(2)证明见解析;(3)2132n n a ⎛⎫=- ⎪⎝⎭【解析】(1)由韦达定理,得11n n n a a a αβαβ+⎧+=⎪⎪⎨⎪=⎪⎩,,代入题设条件,得11623n n n a a a +⨯-⨯=,即1326n n a a ++=. (2)∵11232221233632222333n n n n n n a a a a a a +⎛⎫+--- ⎪⎝⎭===---, ∴23n a ⎧⎫-⎨⎬⎩⎭是公比为12的等比数列. (3)由(2)知,11221332n n a a -⎛⎫⎛⎫-=-⨯ ⎪ ⎪⎝⎭⎝⎭. ∵116a =,∴2132n n a ⎛⎫=- ⎪⎝⎭. 考点点睛:判定数列是等比数列的常用方法(1)定义法:a n +1a n =q (常数)或a n a n -1=q (常数)(n ≥2)⇔{a n }为等比数列. (2)等比中项法a 2n +1=a n ·a n +2(a n ≠0,n ∈N *)⇔{a n }为等比数列. (3)通项法:a n =a 1q n -1(其中a 1、q 为非零常数,n ∈N *)⇔{a n }为等比数列. 考点3、等比中项例3.【北京市东城二十二中2016-2017学年高一下学期期中】求23+与23-的等差中项为__________,等比中项为__________.【答案】2 ±1【解析】 23+和23-的等差中项为:232322++-=, 23+和23-的等比中项为(23)(23)1±+-=±.考点点睛:等比中项的应用主要有两点:①计算,与其它性质综合应用,起到简化计算、提高解题速度的作用.②用来判断或证明等比数列.考点4、等比数列的性质例4.若数列{}n a 是等比数列,下列命题正确的个数为( )① {}2n a 、{}2n a 均为等比数列; ②{}ln na 成等差数列; ③1n a ⎧⎫⎨⎬⎩⎭、{}n a 成等比数列; ④{}n ca 、{}n a k ±均为等比数列 A .4B .3C .2D .1 【答案】C【解析】若数列{a n }是等比数列,且首项为a 1,公比为q ,则a n =a 1•q n ﹣1, 则2n a =a 12•q 2(n ﹣1),这是一个以a 12为首项,以q 2为公比的等比数列,a 2n =a 1•q 2n ﹣1=a 1q•q 2(n ﹣1)=a 2•q 2(n ﹣1),这是一个以a 2为首项,以q 2为公比的等比数列,故①正确;当q <0时,数列{a n }存在负项,此时lga n 无意义,故②错误;1n a =11a •1q (n ﹣1),这是一个以11a 为首项,以1q为公比的等比数列,|a n |=|a 1|•|q|n ﹣1,这是一个以|a 1|为首项,以|q|为公比的等比数列,故③正确;当c=0时,ca n =0,此时数列{ca n }不是等比数列,当k=﹣a 1时,a 1+k=0,此时{a n +k}不是等比数列,当k=a 1时,a 1﹣k=0,此时{a n ﹣k}不是等比数列,故④错误故选:C .考点点睛:(1)若{a n }为等比数列,则{1a n},{|a n |},{a 2n },{pa n }(p ≠0),{a n a n +k }均为等比数列; (2)若{a n },{b n }均为等比数列,则{a n b n },{a n b n}都是等比数列. (3)若m +n =p +q (m ,n ,p ,q ∈N *),则a m ·a n =a p ·a q .(4)若等比数列的下标具有某种规律时,应考虑应用性质求解.考点5、等比数列的设项技巧例5.已知四个数前三个成等差,后三个成等比,中间两数之积为16,首尾两个数之积为-128,求这四个数.【答案】-4,2,8,32或4,-2,-8,-32.【解析】 设四个数为2a q -a 、a q、a 、aq , 则由题意得⎩⎨⎧ a 2q =162a q -a ·aq =-128,解得⎩⎪⎨⎪⎧ a =8q =4或⎩⎪⎨⎪⎧a =-8q =4. 因此所求的四个数为-4,2,8,32或4,-2,-8,-32. 考点点睛:等比数列中的设项方法与技巧(1)若三个数成等比数列,可设三个数为a ,aq ,aq 2或a q,a ,aq . (2)若四个数成等比数列,可设为a ,aq ,aq 2,aq 3;若四个数均为正(负)数,可设a q 3,a q,aq ,aq 3. 考点6、方程思想在等比数列中的应用例6.已知等比数列{a n }中,a 3+a 6=36,a 4+a 7=18,a n =12,求n . 【答案】9【解析】解法一:设等比数列{a n }的公比为q ,由题意,得⎩⎪⎨⎪⎧ a 1q 2+a 1q 5=36a 1q 3+a 1q 6=18,解得⎩⎪⎨⎪⎧ a 1=128q =12.∴a n =a 1q n -1=128×(12)n -1=12,∴(12)n -1=(12)8,∴n -1=8,∴n =9. 解法二:设等比数列{a n }的公比为q ,∵a 3+a 6=36,∴a n +a 7=a 3q +a 6q =q (a 3+a 6)=36q =18,∴q =12. ∴a 3+a 6=a 3+a 3q 3=a 3(1+q 3)=98a 3=36,∴a 3=32,∴a n =a 3q n -3=32×(12)n -3=12, ∴(12)n -3=(12)6,∴n -3=6,∴n =9.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等比数列
【知识巩固】
1.等比数列的基础知识
(1)定义:如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,那么这个数列叫做等比
数列,这个常数叫做等比数列的公比,通常用字母q 表示,即:1(0).n n a
q q a +=≠
(2)通项公式:11n n m n m a a q a q --=⋅=⋅
(3)前n 项和公式:111
(1)
,111,1n n n a a q a q q S q q
n a q ⎧-⋅-=≠⎪
=--⎨⎪⋅=⎩ 2.等比数列的性质
(1)若(,,,),m n p q m n p q Z +=+∈则,m n p q a a a a ⋅=⋅特别地2(,,),m n p m n p Z +=∈则2,m n p a a a ⋅=说明p a 是m a 和n a 的等比中项;
(2)等比数列{}n a 的公比为,q 前n 项和公式为,n S 前m 项和为,m S 则11n
n m
m S q S q -=- (3)等比数列{}n a 的前n 项和公式为,n S 则232,,,n n n n n S S S S S --仍是等比数列
特别注意:当n 为偶数时, 1.q ≠-
(4)若等比数列{}n a 的前n 项和公式为,n S 则,n n S A q B =⋅+且0.A B +=
(5)等比数列的单调性与公比q 和首项1a 有关,若等比数列单调递增,则1
100
;101a a q q ><⎧⎧⎨⎨><<⎩⎩或若等比数列单调递减,则1
100
.011a a q q ><⎧⎧⎨⎨<<>⎩⎩
或 3.等比数列的判断方法 (1)定义法:{}*1(,0)n n n
a
q n N q a a +=∈≠⇔是等比数列;
(2)中项法:2*
12()n n n a a a n N ++=⋅∈且{}0n n a a ≠⇔是等比数列
【课堂讲解】
1.等比数列的基本量
【例1】已知{}n a 为等比数列,262,162,a a ==则10____.a =
【练1】等比数列{}n a 中,若已知2348,a a ==和求该数列的通项公式及前5项和.
【练2】在等比数列{}n a 中,已知643524,64,a a a a -=⋅=求{}n a 的前8项和8.S
【练3】已知等比数列{}n a 满足:132410,4,a a a a +=⋅=且公比(0,1)q ∈ (1)求数列{}n a 的通项公式; (2)若数列前n 项和63
,4
n S =求n 的值.
【例2】35213333(n ++++⋯+= )
3
.(91)2n A - 13
.(91)2n B +- 3
.(91)8n C - 13
.(91)8
n D +-
【练4】设471031()22222()n f n n N +=++++⋯+∈,则()f n 等于( )
2
.(81)7n A - 2
.(81)7n B + 12
.(81)7n C +- 12
.(81)7
n D ++
【例3】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八 十一,请问尖头几盏灯?”意思是:“一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯多少?”现有类似问题:一座5层塔共挂了363盏灯,且相邻两层中的下一层灯数是上一层灯数的3倍,则塔的底层共有灯( ) A .81盏 B .112盏 C .162盏 D .243盏
【练5】我国古代数学著作《算法统宗》中有这样一个问题:“三百一十五里关,初步健步不为难,次日脚 痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还其大意为:“有一个人走315里路,第一天健步行走,从第二天起脚痛,每天走的路程为前一天的一半,走了6天后到达目的地.”则该人最后一天走
的路程为( ) A .20里 B .10里
C .5 里
D .2.5 里
2.等比数列的性质
【例4】已知数列{}n a 是递增的等比数列,149a a +=,238a a =,则6a 的值等于 .
【练6】设{}n a 是公差不为0的等差数列,12a =且1a ,3a ,6a 成等比数列,则{}n a 的前n 项和(n S = )
A .2744
n n +
B .2533n n +
C .2324
n n
+
D .2n n +
【练7】等比数列{}n a 满足:1611a a +=,3432
9
a a =,且公比(0,1)q ∈. (1)求数列{}n a 的通项公式;
(2)若该数列前n 项和21n S =,求n 的值.
【例5】设{}n a 是公比为q 的等比数列,则“1q >”是“{}n a 为递增数列”的( ) A .充分而不必要条件 B .必要而不充分条件
C .充分必要条件
D .既不充分也不必要条件
【练8】设{}n a 是等比数列,则“124a a a <<”是“数列{}n a 是递增数列”的( ) A .充分而不必要条件 B .必要而不充分条件
C .充分必要条件
D .既不充分也不必要条件
【例6】设等比数列{}n a 的前n 项和为n S ,若105:1:2S S =,则155:S S 等于( ) A .3:4 B .2:3 C .1:2 D .1:3
【练9】设等比数列{}n a 的前n 项和为n S ,若105:1:2S S =,则51015
105
(S S S S S ++=- )
A .72
B .72
-
C .
92 D .92
-
【例7】设等比数列{}n a 的前n 项和为n S ,若4
24S S =,则84
S S = .
【练10】已知等比数列{}n a 的前n 项和为n S ,若43S =,12812S S -=,则8S = .
【例8】等比数列{}n a 的前n 项和3n n S a =+,则a 的值为( ) A .3 B .1 C .3- D .1-
【练11】若等比数列{}n a 的前n 项和1
124,3n n S m -⎛⎫
=⋅+ ⎪
⎝⎭
则m 的值为_________.
3.等比数列的判断
【例9】在数列{}n a 中,已知12a =,1431n n a a n +=-+,n N ∈. (1)设n n b a n =-,求证:数列{}n b 是等比数列; (2)求数列{}n a 的前n 项和n S .
【练12】已知数列{}n a 的首项13
5
a =,1321n n n a a a +=+.
(1)求证:数列1
{
1}n
a -为等比数列. (2)求数列{}n a 的通项公式;。
