复变函数与积分变换第一章习题课
复变函数与积分变换第一章习题解答

。
n
2) R(
3) 事实上
罕 P(z) =X+iY=X- i Y; 可 = 霄芦 (因)
P(z)
立 +a,, P( 司=a。了"+a1 产+···+a,
4
l 3. 如果 z =e;r, 试证明
1 (1) z" +— = 2cosnt ; n z
II
·+anz n = 页 =a +a1 z+a产 +··
习题 一 解答
1. 求下列复数的实部与虚部 、 共辄复数 、 模与辐角 。
(l)
解 所以
(1)
3+2i
1
(2)
-:--—
1
3+2i
1
3�2i
言, 叫卢}飞, 2 =�(言) +(-卢『 = =卢
(3+2i), ImL : 2J
=-
1 =—(32i) (3+2iX3-2i) 13
3-2i
1
1- 1
3i
(2)
(1+i)6;
J�(2e一气 �32e一l坛"
( 3) 划 ;
1 一3
l I 、 i
=32[cos(-子 )+isin(-子)]=-16"3-16i
(2)
(I+i)'= [ �(i+i )J
=(高冗/4)6 = 8e31ri12 = -8i。 .J3
2
) 4 (
(3)
卢= (ei1t+2k于= eirr (2k+l)/6,k = 0,1,2,3,4,5 。
复变函数与积分变换习题答案

第一章 复数与复变函数1.1计算下列各式: (1) (1)(32);i i +--解: (1)(32)(1)322 3.i i i i i +--=+-+=-+ (2);(1)(2)ii i --解:2(13)3.(1)(2)2213101010i i i i i ii i i i i i +-====+----+-(3)1(1);1z z x iy z -=+≠-+ 解: 2222222211(1)(1)12.11(1)(1)(1)z x iy x iy x iy x y yi z x iy x y x y x y-+--++-+-===++++++++++ 1.3 将圆周方程22()0(0)a x y bx cy d a ++++=≠写成复数形式(即可z 与z 表示,其中z x iy =+).解: 把22,,22z z z z x y x y z z i+-==+=⋅代入圆周方程得: ()()0,222()()20,0.b caz z z z z z d iaz z b ic z b ic z d Az z Bz Bz C ⋅+++-+=⋅+-+++=⋅+++=故其中2,,2.A a B b ic C d ==+= 1.5 将下列各复数写成三角形式.(1) sin cos ;i αα+ 解: sin cos 1,i αα+= 故sin cos cos()sin().22i i ππαααα+=-+- (2) sincos.66i ππ--解: 2arg(sincos )arctan(cot ),666263i ππππππππ--=-=--=-s i n c o s 66i ππ--=2222cos()sin()cos()sin.3333i i ππππ-+-=- 1.7 指出满足下列各式的点z 的轨迹是什么曲线?(1) 1;z i +=解: 以(0,1)-为圆心,1为半径的圆周.(2) 0,zz az az b +++=其中a 为复数,为b 实常数;解: 由题设可知 2()()||0,z a z a b a +++-=即22||||,z a a b +=- 若2||,a b =则z 的轨迹为一点;a -若2||,a b >则z 的轨迹为圆,圆心在a -,若2||,a b <无意义.第二章 解析函数1.用导数定义,求下列函数的导数: (1) ()Re .f x z z = 解: 因0()()lim z f z z f z z∆→+∆-∆0()Re()Re lim z z z z z z zz∆→+∆+∆-=∆ 0Re Re Re limz z z z z z z z∆→∆+∆+∆∆=∆0Re lim(Re Re )z zz z z z∆→∆=+∆+∆ 000Re lim(Re )lim(Re ),z x y z xz zz z z x i y ∆→∆→∆→∆∆=+=+∆∆+∆ 当0z ≠时,上述极限不存在,故导数不存在;当0z =时,上述极限为0,故导数为0.3.确定下列函数的解析区域和奇点,并求出导数.(1)(,).az bc d cz d++至少有一不为零 解: 当0c ≠时,()az b f z cz d +=+除d z c =-外在复平面上处处解析, dz c=-为奇点,222()()()()()()()()().()()az bf z cz daz b cz d cz d az b cz d a cz d c az b ad cb cz d cz d +''=+''++-++=++-+-==++当0c =时,显然有0d ≠,故()az b f z d +=在复平面上处处解析,且()af z d'=. 5.设()f z 在区域D 内解析,试证: 222222()|()|4|()|.f z f z x y ∂∂'+=∂∂证: 设 222(),|()|,f z u i v f z u v =+=+ 222(),|()|()().u uu u f z i f z x y x y∂∂∂∂''=-=+∂∂∂∂ 而2222222222222222222222222()|()|()()2()()()(),f z u v u v x y x y u u v v u u v v u v uv xx x x y y y y∂∂∂∂+=+++∂∂∂∂⎡⎤∂∂∂∂∂∂∂∂=+++++++⎢⎥∂∂∂∂∂∂∂∂⎣⎦又()f z 解析,则实部u 及虚部v 均为调和函数.故222222220,0.u u v vu v x yx y∂∂∂∂=+==+=∂∂∂∂则22222222()|()|4(()())4|()|.u uf z f z x y x y∂∂∂∂'+=+=∂∂∂∂ 7.设sin ,px v e y =求p 的值使v 为调和函数,并求出解析函数().f z u iv =+ 解: 要使(,)v x y 为调和函数,则有0.xx yy v v v ∆=+=即2sin sin 0,px px p e y e y -=所以1p =±时,v 为调和函数,要使()f z 解析,则有,.x y y x u v u v ==-1(,)cos cos (),1sin ()sin .px pxx pxpx y u x y u dx e ydx e y y pu e y y pe y pφφ===+'=-+=-⎰⎰所以11()()sin ,()()cos .px px y p e y y p e y C p pφφ'=-=-+即(,)cos ,px u x y pe y C =+故(cos sin ),1,()(cos sin ),1.x z xze y i y C e C pf z e y i y C e C p -⎧++=+=⎪⎨--+=-+=-⎪⎩9.求下列各式的值。
第一章复变函数习题及解答

第⼀章复变函数习题及解答第⼀章复变函数习题及解答1.1 写出下列复数的实部、虚部;模和辐⾓以及辐⾓的主值;并分别写成代数形式,三⾓形式和指数形式.(其中,,R αθ为实常数)(1)1-;(2)ππ2(cosisin )33-;(3)1cos isin αα-+;(4)1ie +;(5)i sin R e θ;(6)i +答案(1)实部-1;虚部 2;辐⾓为 4π2π,0,1,2,3k k +=±±;主辐⾓为4π3;原题即为代数形式;三⾓形式为4π4π2(cosisin )33+;指数形式为4πi 32e .(2)略为5πi 35π5π2[cossin ], 233i e +(3)略为 i arctan[tan(/2)][2sin()]2c e αα(4)略为 i;(cos1isin1)ee e +(5)略为:cos(sin )isin(sin )R R θθ+(6)该复数取两个值θθθθθθ+=+=+1.2 计算下列复数 1)()103i 1+-;2)()31i 1+-;答案 1)3512i 512+-;2)()13π/42k πi632e0,1,2k +=;1.3计算下列复数(1 (2答案(1(2)(/62/3)i n eππ+1.4 已知x【解】令i ,(,)p q p q R =+∈,即,p q 为实数域(Real).平⽅得到2212()2i x p q xy +=-+,根据复数相等,所以1,(p q pq p x q x ?-=??=??=±==±+即实部为 ,x ±虚部为说明已考虑根式函数是两个值,即为±值.1.5 如果 ||1,z =试证明对于任何复常数,a b 有||1az bbz a +=+【证明】因为||1,11/z zz z z =∴=∴=,所以1()()1||||||||||||1()az b az b az b z az b az b z bz a bz a z z bzz az b az b az +++++=====+++++1.6 如果复数b a i +是实系数⽅程()01110=++++=--n n n n a z a z a z a z P 的根,则b a i -⼀定也是该⽅程的根.证因为0a ,1a ,… ,n a 均为实数,故00a a =,11a a =,… ,n n a a =.且()()kkz z =,故由共轭复数性质有:()()z P z P =.则由已知()0i ≡+b a P .两端取共轭得 ()()00i i =≡+=+b a P b a P 即()0i ≡-b a P .故b a i -也是()0=z P 之根.注此题仅通过共轭的运算的简单性质及实数的共轭为其本⾝即得证.此结论说明实系数多项式的复零点是成对出现的.这⼀点在代数学中早已被⼤家认识.特别地,奇次实系数多项式⾄少有⼀个实零点.1.7 证明:2222121212||||2(||||)z z z z z z ++-=+,并说明其⼏何意义. 1.8 若 (1)(1)n ni i +=-,试求n 的值.【解】因为 244444444(1)2(cos sin )2(cos sin )(1)2(cos sin )2(cos sin )n n nnnnn n n n n n i i i i i i ππππππππ+=+=+-=-=-所以 44sin sin n n ππ=- 即为4sin 0n π=所以4,4,(0,1,2,)n k n k k ππ===±±1.9将下列复数表为sin ,cos θθ的幂的形式(1) cos5θ;(2)sin5θ答案 53244235(1) cos 10cos sin 5cos sin (2) 5cos sin 10cos sin sin θθθθθθθθθθ-+-+1.10 证明:如果 w 是1的n 次⽅根中的⼀个复数根,但是1≠w 即不是主根,则必有2110n -++++=w w w1.11 对于复数,k k αβ,证明复数形式的柯西(Cauchy)不等式:22221111||(||||)||||n n nnk k k k k kk k k k αβαβαβ====≤≤∑∑∑∑ 成⽴。
复变函数与积分变换第一章习题课.

解:
1)(1 i 3)10 [2(cos2 i sin 2 )]10
3
3
210 (cos20 i sin 20 )
3
3
1024(cos2 i sin 2 )
3
3
512 i512 3.
2)3
27
2k i
3e 3 , k
0,1,2.
13
13
w0
3( 2
i
2
), w1
3,
w2
3( 2
x2
x
y2
i
x2
y
y2
u iv,
u2 v2 1 . 4
13.已知映射 z3,求: 2)区域0 arg z 在平面上的像。
3
解:
2)映射 z3将区域0 arg z 映成
3
0 arg z .
15.设f (z) 1 ( z z ),(z 0),试证:当 2i z z
22
2
2 22
z 34 , Argz arctan5 2k , k 0,1,.
2
3
2.当x, y等于什么实数时,等式
x 1 i( y 3) 1 i 5 3i
成立。
解:
原式等价于x 1 i( y 3) 2 8i, 根据复数
相等的概念,有
x y
1 3
28,即
x 1 .
y 11
13. 三角函数
1)定义:
sin z eiz eiz , cos z eiz eiz
2i
2
2)性质: 在复平面内是解析的,且 (sin z) cosz ,(cosz) sin z .
14. 对数函数
定义: 若 ew z ,则称 w 为复变函数 z 的对数 函数,记为 Lnz .
《复变函数与积分变换》习题册

《复变函数与积分变换》习题册合肥工业大学《复变函数与积分变换》校定平台课程建设项目资助2018年9月《复变函数与积分变换》第一章习题1.求下列各复数的实部、虚部、模、辐角和辐角主值:(1)122345i i i i +---; (2)312⎛⎫+ ⎪ ⎪⎝⎭.2. 将下列复数写成三角表达式和指数形式:(1)1; (2)21i i+.3. 利用复数的三角表示计算下列各式:(1; (2)103⎛⎫4. 解方程310z +=.5. 设12cos z zθ-+=(0,z θ≠是z 的辐角),求证:2cos n n z z n θ-+=.6.指出满足下列各式的点z 的轨迹或所在范围.(1)arg()4z i π-=;(2)0zz az az b +++=,其中a 为复数,b 为实常数. (选做)7.用复参数方程表示曲线:连接1i +与i 41--的直线段.8.画出下列不等式所确定的图形,指出它们是否为区域、闭区域,并指明它是有界的还是无界的?是单连通区域还是多连通区域?并标出区域边界的方向.(1) 11,Re 2z z <≤;(2) 0Re 1z <<;9.函数z w 1=把下列z 平面上的曲线映射成w 平面上怎么样的曲线? (1)224x y +=; (2)x y =; (3)1=x .10.试证:0Re limz z z→不存在.《复变函数与积分变换》第二章习题1.用导数定义求z z f Re )(=的导数.2.下列函数在何处可导,何处不可导?何处解析,何处不解析?(1)z z f 1)(=; (2))32233(3)(y y x i xy x z f -+-=;3.试讨论y ix xy z f 22)(+=的解析性,并由此回答:若复变函数),(),()(y x iv y x u z f +=中的),(y x u 和),(y x v 均可微,那么iv u z f +=)(一定可导吗?4.设3232()(f z my nx y i x lxy =+++)为解析函数,试确定,,l m n 的值.5.设()f z 在区域D 内解析,试证明在D 内下列条件是彼此等价的:(1)()f z =常数; (2)Re ()f z =常数; (3)()f z 解析.6.试解下列方程:(1)1ze =+; (2)0cos =z ; (3)0cos sin =+z z .7.求下列各式的值:(1)Ln(34)i -+; (2)i -33; (3)i e +2.8.等式33Ln 3Ln z z =是否正确?请给出理由.《复变函数与积分变换》第三章习题3.1复积分的概念与基本计算公式1. 计算积分dz ix y x C )(2⎰+-,其中C 为从原点到点1+i 的直线段.2.计算积分dz z zC ⎰的值,其中C 为2=z3.当积分路径是自i -沿虚轴到i ,利用积分性质证明:2)(22≤+⎰-dz iy x i i3.2柯西古萨基本定理1.计算积分dz z C ⎰1,其中C 为2=z2. 计算积分dz z e z C z)sin (⎰⋅-,其中C 为a z =.3.3基本定理的推广1. 计算积分dz z e Cz⎰,其中C 为正向圆周2=z 与负向圆周1=z 所组成。
复变函数与积分变换第一章复习资料

4
3
1i
6
2cos
4
2k 3
i sin
4
2k
3
(k 0,1,2).
10
三、函数的极限
1.函数极限的定义: 设函数 w f (z) 定义在 z0 的去心邻域
0 z z0 内, 如果有一确定的数 A 存在, 对于任意给定的 0, 相应地必有一正数 ( ) 使得当0 z z0 (0 )时,有 f (z) A
25
55
z1 7 1 i. z2 5 5
8
5. 复数的乘方
zn rn (cos n i sin n )
6. 复数的开方
w
n
z
r
1 n
cos
2kπ
i sin
2kπ
n
n
(k 0,1,2,,n 1)
9
例3 计算 3 1 i 的值.
解
1i
2
ห้องสมุดไป่ตู้1 2
1 2
i
2cos
4
i
sin
(4) z z 2Re(z), z z 2i Im(z).
7
例2
设
z1
5 5i,
z2
3
4i,
求 z1 z2
与
z1 z2
.
解 z1 5 5i (5 5i)(3 4i) z2 3 4i (3 4i)(3 4i)
(15 20) (15 20)i 7 1 i.
那末称 A 为 f (z)当 z 趋向于 z0 时的极限. 记作 lim f (z) A. (或 f (z) zz0 A)
zz0
注意: 定义中 z z0 的方式是任意的.
11
复变函数与积分变换习题册(含答案)

第1章 复数与复变函数 (作业1)一、填空题 1、ieπ2的值为 。
2、k 为任意整数,则34+k 的值为 。
3、复数i i (1)-的指数形式为 。
4、设b a ,为实数,当=a , b= 时,).35)(1()3()1(i i b i a ++=-++ 二、判断题(正确的划√,错误的划 ) 1、2121z z z z +=+ ( )2、()()())z Re(iz Im ;z Im iz Re =-= ( )3、()()i i i 125432+=++ ( ) 三、选择题1.当ii z -+=11时,5075100z z z ++的值等于( ) (A )i (B )i - (C )1 (D )1-2.复数)(tan πθπθ<<-=2i z 的三角表示式是( )(A ))]2sin()2[cos(secθπθπθ+++i (B ))]23sin()23[cos(sec θπθπθ+++i (C ))]23sin()23[cos(secθπθπθ+++-i (D ))]2sin()2[cos(sec θπθπθ+++-i 3.使得22z z =成立的复数z 是( )(A )不存在的 (B )唯一的 (C )纯虚数 (D )实数 4.若θi re i i=+--2)1(3,则( ) (A )πθ-==3arctan ,5r (B )πθ-==3arctan ,210r (C )3arctan ,210-==πθr (D )3arctan ,5-==πθr 5. 设复数z 位于第二象限,则z arg 等于( )。
(A) x y arctan 2+π (B) x y arctan +π (C) x y arctan 2-π (D) xy arctan +-π 四、计算与证明题 1、设ii i i z -+-=11,求.),Im(),Re(z z z z2、当x y ,等于什么实数时,等式()i iy i x +=+-++13531成立?3、求复数ii-+23的辐角。
复变函数与积分变换习题册(含答案)

第1章 复数与复变函数 (作业1)一、填空题 1、ieπ2的值为 。
2、k 为任意整数,则34+k 的值为 。
3、复数i i (1)-的指数形式为 。
4、设b a ,为实数,当=a , b= 时,).35)(1()3()1(i i b i a ++=-++ 二、判断题(正确的划√,错误的划 ) 1、2121z z z z +=+ ( )2、()()())z Re(iz Im ;z Im iz Re =-= ( )3、()()i i i 125432+=++ ( ) 三、选择题1.当ii z -+=11时,5075100z z z ++的值等于( ) (A )i (B )i - (C )1 (D )1-2.复数)(tan πθπθ<<-=2i z 的三角表示式是( )(A ))]2sin()2[cos(secθπθπθ+++i (B ))]23sin()23[cos(sec θπθπθ+++i (C ))]23sin()23[cos(secθπθπθ+++-i (D ))]2sin()2[cos(sec θπθπθ+++-i 3.使得22z z =成立的复数z 是( )(A )不存在的 (B )唯一的 (C )纯虚数 (D )实数 4.若θi re i i=+--2)1(3,则( ) (A )πθ-==3arctan ,5r (B )πθ-==3arctan ,210r (C )3arctan ,210-==πθr (D )3arctan ,5-==πθr 5. 设复数z 位于第二象限,则z arg 等于( )。
(A) x y arctan 2+π (B) x y arctan +π (C) x y arctan 2-π (D) xy arctan +-π 四、计算与证明题 1、设ii i i z -+-=11,求.),Im(),Re(z z z z2、当x y ,等于什么实数时,等式()i iy i x +=+-++13531成立?3、求复数ii-+23的辐角。
复变函数与积分第一章(2)答案
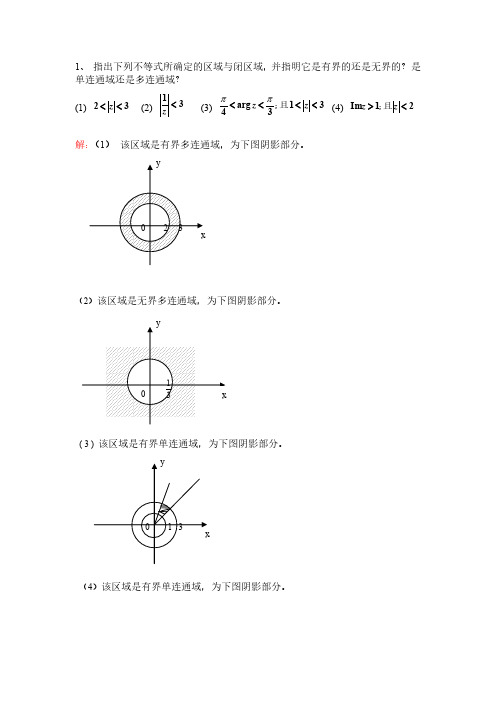
1、 指出下列不等式所确定的区域与闭区域,并指明它是有界的还是无界的?是单连通域还是多连通域? (1) 32<<z (2) 31<z (3) 313arg 4<<<<z z 且;
ππ (4) 21Im <>z z 且;
解:(1) 该区域是有界多连通域,为下图阴影部分。
(2)该区域是无界多连通域,为下图阴影部分。
( 3 ) 该区域是有界单连通域,为下图阴影部分。
(4)该区域是有界单连通域,为下图阴影部分。
2、 设
⎪⎩
⎪⎨⎧=≠+=,0,0,0,)(22z z y x y x z f 试证)(z f 在0=z 不连续。
证明: 若z 沿直线kx y =趋于0,则
()()()()()2
022220220,0,0,0,1lim lim lim lim k k x k x kx y x xy z f x x y x y x +=+=+=→→→→, 因该极限随k 的不同而不同,所以当()()0,0,→y x 时,()z f 的极限不存在。
而根据连续性的定义,只有当该极限存在并且极限值等于该函数在此处的函数值时,才认为函数在该点处连续,所以说)(z f 在0=z 不连续。
复变函数 第一章习题课

(3)
17
代入极坐标下拉普拉斯方程, 看是否满足.
∂ ∂v 1 ∂ 2 v ∂ sin ϕ 1 sin ϕ + = − + − ρ 2 ∂ρ ∂ρ ρ ∂ϕ ∂ρ ρ ρ ρ sin ϕ sin ϕ = 2 − 2 ≡ 0. (4)
ρ
ρ
可见, 前面假设的量函数v满足Laplace方程. 进一步, 应用C-R条件(求势函数u)
∂u 1 ∂v cosϕ ∂u ∂v sin ϕ = = 2 , = −ρ = . ∂ρ ρ ∂ϕ ∂ϕ ∂ρ ρ ρ
(5)
18
于是u的全微分为
cos ϕ ∂u ∂u cos ϕ sin ϕ du = dρ + dϕ = dρ + dϕ = d − . (6) 2 ∂ρ ∂ϕ ρ ρ ρ
9
消掉u的具体办法: Eq. (1a)左右对 左右对ϕ求偏导, 得到
1 ∂ 2v ∂ 2u = , 2 ∂ϕ∂ρ ρ ∂ϕ
接着Eq. (1b)左右乘ρ然后对ρ求偏导, 得到
∂ ∂v ∂ 2u =− , ρ ∂ρ ∂ρ ∂ρ∂ϕ
比较上面两式, 即可得到Eq. (3b).
两边同乘x2, 考虑到y/x=t, 所以得到
(1 + t 2 ) F ' ' (t ) + 2tF ' (t ) = 0.
(3)
F '' 2t 或者 F ' = − 1 + t 2 . 一次积分后, 得F ’(t)=C1/(1+t2). 再
次积分, 得到
F (t ) = C1arctg(t ) + C2 , (C1,2为积分常数)
复变函数习题解答(第1章)

复变函数习题解答(第1章)p44第一章习题(一)[ 13, 16, 17 , 20]13. 试证arg z ( -π arg z ≤π )在负实轴(包括原点)上不连续,除此而外在z平面上处处连续.记f(z) = arg z,D = \{ z∈ | Im(z) = 0,Re(z) ≤ 0},D1 = { z∈ | Re(z) 0},D2 = { z∈ | Im(z) 0},D3 = { z∈ | Im(z) 0}.(1) 首先,f(z)在原点无定义,故f(z)在原点处不连续.(2) 设a∈ ,且a 0.则f(a) = π.考察点列z n = | a | (cos(1/n-π)+ i sin(1/n-π)),n∈ +.显然,-π 1/n-π≤π,故f(z n) = 1/n-π.而lim n→∞z n = lim n→∞( | a | (cos(1/n-π)+ i sin(1/n-π)) ) = a,但lim n→∞f(z n) = lim n→∞(1/n-π) = -π≠f(a).故f(z)在a处不连续.(3) 下面证明f(z)在D1, D2, D3这三个区域上都连续.设z = x + i y,x, y∈ .(3.1) 在D1上,f(z) = arctan(y/x),因arctan(y/x)是{(x, y)∈ 2 | x 0 }上的二元连续函数,故f(z)是D1上的连续函数.(3.2) 在D2上,f(z) = arccot(x/y),因arccot(x/y)是{(x, y)∈ 2| y 0 }上的二元连续函数,故f(z)是D2上的连续函数.(3.3) 在D3上,f(z) = arccot(x/y) -π,因arccot(x/y) -π是{(x, y)∈ 2 | y 0 }上的二元连续函数,故f(z)是D3上的连续函数.(4) 最后证明f(z)是D = \{ z∈ | Im(z) = 0,Re(z) ≤ 0}上的连续函数.?a∈D,因为D = D1?D2?D3,故存在k (k = 1, 2, 3),使得a∈D k.因D k是开集故存在r 0,使得U r(a) = { z∈ | | z Ca | r } ?D k.根据(3),f(z)在D k上是连续的,故?ε 0,?η 0,使得?z∈D k,当| zCa | η时,| f(z) -f(a) | ε.设δ= min { r, η},则?z∈D,当| zCa | δ时,z∈U r(a) ?D k,又因| zCa | δ η,故必有| f(z) -f(a) | ε.所以,f在a处连续.由a的任意性,f(z)是上的连续函数.[连续性部分的证明可以用几何的方法,而且写起来会简单些.但我们之所以选择这个看起来很复杂的方法,是可以从这里看出θ(z) = arg(z)作为(x, y)的二元函数,在D1, D2, D3上都有很明显的可导的表达式,因此它在区域D上不仅是连续的,而且是连续可导二元函数:θx = y/(x2 + y2),θy = -x/(x2 + y2).证明中的第四部分并不是多余的,这是因为若f在两个集合A, B上都连续(即使它们有公共的部分),一般说来,并不能保证f在两个集合A?B上也连续.问题:若f在区域A, B上都连续,且A ?B ≠?,问f在A?B 上是否必连续?] 16. 试问函数f(z) = 1/(1 Cz )在单位圆| z | 1内是否连续?是否一致连续?(1) f(z)在单位圆| z | 1内连续.因为z在内连续,故f(z) = 1/(1 Cz )在\{1}内连续(连续函数的四则运算),因此f(z)在单位圆| z | 1内连续.(2) f(z)在单位圆| z | 1内不一致连续.令z n= 1 C 1/n,w n= 1 C 1/(n + 1),n∈ +.则z n, w n都在单位圆| z | 1内,| z n-w n | → 0,但| f(z n)-f(w n)| = | n - (n + 1) | = 1 0,故f(z)在单位圆| z | 1内不一致连续.[也可以直接用实函数f(x) = 1/(1 Cx )在(0, 1)不一致连续来说明,只要把这个实函数看成是f(z)在E = { z∈ | Im(z) = 0, 0 Re(z) 1 }上的限制即可.]17. 试证:复数列z n = x n + i y n以z0 = x0 + i y0为极限的充要条件是实数列{x n}及{y n}分别以x0及y0为极限.(?) 若复数列z n = x n + i y n以z0 = x0 + i y0为极限,则?ε 0,?N∈ +,使得?n N,有| z n -z0| ε.此时有| x n -x0| ≤ | z n -z0| ε;| y n -y0| ≤ | z n -z0| ε.故实数列{x n}及{y n}分别以x0及y0为极限.(?) 若实数列{x n}及{y n}分别以x0及y0为极限,则?ε 0,?N1∈ +,使得?n N1,有| x n -x0| ε/2;?N2∈ +,使得?n N2,有| y n -y0| ε/2.令N = max{N1, N2},则?n N,有n N1且n N2,故有| z n -z0| = | (x n -x0) + i (y n -y0)| ≤ | x n -x0| + | y n -y0| ε/2 + ε/2 = ε.所以,复数列z n = x n + i y n以z0 = x0 + i y0为极限.20. 如果复数列{z n}合于lim n→∞z n = z0≠∞,证明lim n→∞ (z1 + z2 + ... + z n)/n = z0.当z0≠∞时,结论是否正确?(1) ?ε 0,?K∈ +,使得?n K,有| z n -z0| ε/2.记M = | z1-z0 | + ... + | z K-z0 |,则当n K时,有| (z1 + z2 + ... + z n)/n-z0 | = | (z1-z0) + (z2-z0) + ... + (z n-z0) |/n≤ ( | z1-z0 | + | z2-z0 | + ... + | z n-z0 |)/n= ( | z1-z0 | + ... + | z K-z0 |)/n + ( | z K +1-z0 | + ... + | z n-z0 |)/n≤M/n + (n-K)/n (ε/2) ≤M/n + ε/2.因lim n→∞ (M/n) = 0,故?L∈ +,使得?n L,有M/n ε/2.令N = max{K, L},则当n K时,有23 | (z 1 + z 2 + ... + z n )/n - z 0 | ≤ M /n + ε /2 ε /2 + ε /2 = ε.所以,lim n →∞ (z 1 + z 2 + ... + z n )/n = z 0.(2) 当z 0 ≠ ∞时,结论不成立.这可由下面的反例看出.例:z n = (-1)n n ,n ∈ +.显然lim n →∞ z n = ∞.但?k ∈ +,有(z 1 + z 2 + ... + z 2k )/(2k ) = 1/2,因此数列{(z 1 + z 2 + ... + z n )/n }不趋向于∞.[这个结论的证明的方法与实数列的情况完全相同,甚至反例都是一样的.]p45第一章习题(二)[ 6, 8, 9, 11, 12 ]6. 设| z | = 1,试证:| (a z + b )/(b * z + a * ) | = 1.(z *表示复数z 的共轭)此题应该要求b * z + a * ≠ 0.| a z + b | = | (a z + b )* | = | a * z * + b * | = | a * z * + b * | | z | = | (a * z * + b *) z | = | a * z * z + b * z | = | a * | z |2 + b * z | = | b * z + a * |.故| (a z + b )/(b * z + a * ) | = 1.8. 试证:以z 1, z 2, z 3为顶点的三角形和以w 1, w 2, w 3为顶点的三角形同向相似的充要条件为1*****w z w z w z = 0.两个三角形同向相似是指其中一个三角形经过(一系列的)旋转、平移、位似这三种初等几何变换后可以变成另一个三角形(注意没有反射变换).例如z'z 312我们将采用下述的观点来证明:以z 1, z 2, z 3为顶点的三角形和以w 1, w 2, w 3为顶点的三角形同向相似的充要条件是:将它们的一对对应顶点都平移到原点后,它们只相差一个位似旋转.记f 1(z ) = z - z 1 (将z 1变到0的平移);f 3(z ) = z - w 1 (将0变到w 1的平移);那么,三角形z 1z 2z 3与三角形w 1w 2w 3同向相似4 ? 存在某个绕原点的旋转位似变换f 2(z ) = z 0 z ,使得f 2 ( f 1(z k )) = f 3(w k ),(k = 2, 3),其中z 0∈ \{0}? 存在z 0∈ \{0},使得z 0(z k - z 1) = w k - w 1,(k = 2, 3) ? (w 2 - w 1)/(z 2 - z 1) = (w 3 - w 1)/(z 3 - z 1)? 13131212w w z z w w z z ----= 0? 111***-*****12w w z z w w z z ----= 011*****w z w z w z = 0.[证完]9. 试证:四个相异点z 1, z 2, z 3, z 4共圆周或共直线的充要条件是(z 1 C z 4)/(z 1 C z 2) : (z 3 C z 4)/(z 3 C z 2)为实数.在平面几何中,共线的四个点A , B , C , D 的交比定义为(A , B ; C , D ) = (AC /CB ) : (AD /DB ).这是射影几何中的重要的不变量.类似地,在复平面上,(不一定共线的)四个点z 1, z 2, z 3, z 4的交比定义为[z 1z 2, z 3z 4] = (z 1 C z 3)/(z 2 C z 3) : (z 1 C z 4)/(z 2 C z 4).本题的结论是说:复平面上四个点共圆或共线的充要条件是其交比为实数.(?) 分两种情况讨论(1) 若(z 1 C z 4)/(z 1 C z 2)为实数,则(z 3 C z 4)/(z 3 C z 2)也是实数.设(z 1 C z 4)/(z 1 C z 2) = t ,t ∈ .则z 4 = (1 C t )z 1 + t z 2,故z 4在z 1, z 2所确定的直线上,即z 1, z 2, z 4共线.因此,同理,z 1, z 2, z 3也共线.所以,z 1, z 2, z 3, z 4是(2) 若(z 1 C z 4)/(z 1 C z 2)为虚数,则(z 3 C z 4)/(z 3 C z 2)也是虚数.故Arg ((z 1 C z 4)/(z 1 C z 2)) ≠ k π,Arg ((z 3 C z 4)/(z 3 C z 2)) ≠ k π.而Arg ((z 1 C z 4)/(z 1 C z 2)) C Arg ((z 3 C z 4)/(z 3 C z 2)) = Arg ((z 1 C z 4)/(z 1 C z 2) : (z 3 C z 4)/(z 3 C z 2)) = k π.注意到Arg ((z C z 4)/(z C z 2)) = Arg ((z 4 C z )/(z 2 C z ))是z 2 C z 到z 4 C z 的正向夹角,若Arg ((z 1 C z 4)/(z 1 C z 2)) = Arg ((z 3 C z 4)/(z 3 C z 2)),则z 1, z 3在z 2, z 4所确定的直线的同侧,且它们对z 2, z 4所张的角的大小相同,故z 1, z 2, z 3, z 4是共圆的.若Arg ((z 1 C z 4)/(z 1 C z 2)) = Arg ((z 3 C z 4)/(z 3 C z 2)) + π,则z 1, z 3在z 2, z 4所确定的直线的异侧,且它们对z 2, z 4所张的角的大小互补,故z 1, z 2, z 3, z 4也是共圆的.(?) 也分两种情况讨论(1) 若z1, z2, z3, z4是共线的,则存在s, t∈ \{0, 1},使得z4 = (1 Cs)z3 + s z2,z4 = (1 Ct)z1 + t z2,那么,z3Cz4 = s (z3 Cz2),即(z3Cz4)/(z3Cz2) = s;而z1Cz4 = t (z1 Cz2),即(z1Cz4)/(z1Cz2) = t,所以,(z1Cz4)/(z1Cz2) : (z3Cz4)/(z3Cz2) = t/s∈ .(2) 若z1, z2, z3, z4是共圆的,若z1, z3在z2, z4所确定的直线的同侧,那么,Arg ((z4Cz1)/(z2Cz1)) = Arg ((z4Cz3)/(z2Cz3))因此(z4Cz1)/(z2Cz1) : (z4Cz3)/(z2Cz3)是实数.也就是说(z1Cz4)/(z1Cz2) : (z3Cz4)/(z3Cz2)是实数.若z1, z3在z2, z4所确定的直线的异侧,则Arg ((z4Cz1)/(z2Cz1)) + Arg ((z2Cz3)/(z4Cz3)) = (2k + 1)π,故Arg ((z1Cz4)/(z1Cz2) : (z3Cz4)/(z3Cz2))= Arg ((z1Cz4)/(z1Cz2)) C Arg ((z3Cz4)/(z3Cz2))= Arg ((z1Cz4)/(z1Cz2)) + Arg ((z3Cz2)/(z3Cz4))= Arg ((z4Cz1)/(z2Cz1)) + Arg ((z2Cz3)/(z4Cz3)) = (2k + 1)π,所以,(z1Cz4)/(z1Cz2) : (z3Cz4)/(z3Cz2)仍为实数.[证完]这个题目写的很长,欢迎同学们给出更简单的解法.11. 试证:方程| z -z1 |/| z -z2 | = k ( 0 k ≠ 1,z1≠z2 )表示z平面的一个圆周,其圆心为z0,半径为ρ,且z0 = (z1 -k2 z2)/(1-k2),ρ = k | z1 -z2|/| 1-k2 |.到两定点距离成定比的点的轨迹是圆或直线.当比值不等于1时,轨迹是一个圆,这个圆就是平面几何中著名的Apollonius 圆.设0 k ≠ 1,z1≠z2,z0 = (z1 -k2 z2)/(1-k2),ρ = k | z1 -z2|/| 1-k2 |.?z∈ ,| z -z0 | = ρ?| z - (z1 -k2 z2)/(1-k2)| = k | z1 -z2|/| 1-k2 |?| z(1-k2)- (z1 -k2 z2) | = k | z1 -z2 |?| (z -z1) -k2 (z-z2)| = k | z1 -z2|?| (z -z1)/k-k (z-z2) | = | z1 -z2|?| (z -z1)/k-k (z-z2) | = | (z -z1)- (z-z2) |?| (z -z1)/k-k (z-z2) |2 = | (z -z1) - (z-z2) |2?| z -z1 |2/k2 + k2 | z-z2 |2 = | z -z1 |2 + | z-z2 |2?(1/k2 - 1)| z -z1 |2 = (1-k2 ) | z-z2 |2?| z -z1 |2/k2 = | z-z2 |2?| z -z1 |/| z-z2 | = k.[证完]直接地双向验证,可能需要下面的结论,其几何意义非常明显的.命题:若复数z, w≠ 0,则| | z | w /| w| - | w| z /| z| | = | w -z |.证明:我们用z*表示复数z的共轭.| | z | w /| w| - | w| z /| z| |2= | | z | w /| w| |2 + | | w| z /| z| |2- 2Re[( | z | w /| w|) (| w| z /| z|)* ]= | z |2 + | w|2- 2Re( w z* ) = | w -z |2.5或更直接地,| | z | w /| w| - | w| z /| z| |= | | z | w /| w| - | w| z /| z| | | z*/| z| | | w*/| w| |= | (| z | w /| w| - | w| z /| z|) (z*/| z|) (w*/| w|) |= | (| z | (z*/| z|) - | w| (w*/| w|)) | = | w -z |.12. 试证:Re(z) 0 ? | (1 -z)/(1 + z) | 1,并能从几何意义上来读本题.Re(z) 0 ?点z在y轴右侧?点z在点-1和点1为端点的线段的垂直平分线的右侧?点z在点-1和点1为端点的线段的垂直平分线的与1同侧的那一侧?点z到点-1的距离大于点z到点1的距离?|1 + z | | 1 -z | ?| (1 -z)/(1 + z) | 1.不用几何意义可以用下面的方法证明:设z = x + i y,x, y∈ .| (1 -z)/(1 + z) | 1 ?|1 + z | | 1 -z | ?|1 + z |2 | 1 -z |2? 1 + z2 + 2Re(z) 1 + z2- 2Re(z) ?Re(z) 0.[由本题结论,可知映射f(z) = (1 -z)/(1 + z)必然把右半平面中的点映射到单位圆内的点.并且容易看出,映射f(z)把虚轴上的点映射到单位圆周上的点.问题:f(z)在右半平面上的限制是不是到单位圆的双射?f(z)在虚轴上的限制是不是到单位圆周的双射?]???-?±≠≥?≤≡??αβχδεφγηι?κλμνοπθρστυ?ωξψζ∞????? ?∏∑? ⊥∠ √§ψ∈???????∠?????§ #?→←↑↓?∨∧??????∑ΓΦΛΩ??m∈ +,?m∈ +,★?α1, α2, ..., αn?lim n→∞,+n→∞?ε 0,∑u n,∑n≥ 1u n,m∈ ,?ε 0,?δ 0,?[0, 2π]l 2 dx,f(x) = (-∞, +∞)[-π, π]∑1 ≤k≤n u n,[0, 2π]。
(仅供参考)复变函数-第一章习题课

x2 + y2 x4
F ''(t) +
2y x3
F '(t)
=
0,
两边同乘x2, 考虑到y/x=t, 所以得到
(1+ t 2 )F ''(t) + 2tF '(t) = 0.
PlotPoints → 400, AspectRatio → 1,
TextStyle → 8FontSize → 20<E;
Show@u, vD
12
2
1
0
−1
y= -1
−2
−3
−4
−2
0
2
4
6
x=2
红线: u(x,y)=c1, 兰线: v(x,y)=c2, 分别是在点(2, -1)处 相切于直线x=2和y=-1的圆族. 两个切线本身也包含
偏导数:
∂v ∂x
= F '(t) ∂t ∂x
=
−
y x2
F '(t),
∂v ∂y
= F '(t) ∂t ∂y
= 1 F '(t), x
(2a)
∂2v ∂x 2
=
−
y x2
2 F ''(t)
+
2y x3
F '(t),
∂2v ∂y 2
=
1 x
2
F ''(t).
(2b)
14
将Eq.(2b)代入Laplace方程, 得
=
−
1
ρ
∂ 2u
∂ϕ 2
,
(2b)
比较Eqs. (2a)和(2b),自然得到
第1章复变函数习题答案习题详解

第一章习题详解1.求下列复数的实部与虚部,共轭复数、模与辐角:z 1)i231+解:()()()132349232323231231ii i i i i -=+-=-+-=+实部:133231=⎪⎭⎫⎝⎛+i Re 虚部:132231-=⎪⎭⎫⎝⎛+i Im 共轭复数:1323231ii +=⎪⎭⎫⎝⎛+模:1311323231222=+=+i 辐角:πππk arctg k arctg k i i Arg 23221331322231231+⎪⎭⎫ ⎝⎛-=+-=+⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+arg 2)ii i --131解:()()()2532332113311131312i i i i i i i i i i i i i i -=-+-=++---=+-+-=--实部:23131=⎪⎭⎫⎝⎛--i i i Re 虚部:25131-=⎪⎭⎫⎝⎛--i i i Im 共轭复数:253131i i i i +=⎪⎭⎫⎝⎛--模:234434253131222==+=--ii i 辐角:πππk arctg k arctg k i i i i i i Arg 235223252131131+⎪⎭⎫ ⎝⎛-=+⎪⎪⎪⎭⎫ ⎝⎛-=+⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛--arg3)()()ii i 25243-+解:()()()22672267272625243ii ii ii i --=-+=--=-+实部:()()2725243-=⎪⎭⎫⎝⎛-+i i i Re 虚部:()()1322625243-=-=⎪⎭⎫⎝⎛-+i i i Im 共轭复数:()()226725243ii i i +-=⎪⎭⎫⎝⎛-+模:()()2925226272524322=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=-+ii i 辐角:()()ππk arctg k arctg i i i Arg 272622722625243+⎪⎭⎫ ⎝⎛=+⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛-+4)ii i +-2184解:ii i i i i 31414218-=+-=+-实部:()14218=+-i i i Re 虚部:()34218-=+-i ii Im 共轭复数:()ii i i 314218+=+-模:1031422218=+=+-i ii 辐角:()()πππk arctg k arctg k i i i i ii Arg 23213244218218+-=+⎪⎭⎫⎝⎛-=++-=+-arg 2.当、等于什么实数时,等式成立?x y ()i iy i x +=+-++13531解:根据复数相等,即两个复数的实部和虚部分别相等。
复变函数与积分变换(修订版-复旦大学)课后的第一章习题答案

习题一1. 用复数的代数形式a +ib 表示下列复数.①解i4πππecos i sin 44-⎛⎫⎛⎫⎛⎫=-+-== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭②解:()()()()35i 17i 35i 1613i 7i 11+7i 17i 2525+-+==-++-③解: ()()2i 43i 834i 6i 510i ++=-++=+ ④解:()31i 1335=i i i 1i222-+-+=-+2.求下列各复数的实部和虚部(z =x +iy ) ① :∵设z =x +iy 则()()()()()()()22i i i i i i x a y x a y x y ax a y z a z ax y ax a yx a y-++-⎡⎤⎡⎤+--+-⎣⎦⎣⎦===+++++++ ∴()22222R e z a x a y z a x a y---⎛⎫= ⎪+⎝⎭++,()222Im z a xyz a x a y-⎛⎫=⎪+⎝⎭++.②解: 设z =x +iy∵()()()()()()()()323222222223223i i i 2i i 22i 33iz x y x y x y xy xy x y x x yxyy x y x y x xy x y y=+=++=-++⎡⎤=--+-+⎣⎦=-+- ∴()332Re 3zxxy=-,()323Im 3zxy y =-.③解:∵(()(){}33232111313188-+⎡⎤⎡⎤==--⋅-⋅+⋅-⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭()180i 18=+=∴R e 12=⎝⎭, Im 02=⎝⎭. ④解:∵()()(()2332313131i 28⎡⎤--⋅-⋅+⋅-⎢⎥⎣⎦=⎝⎭()180i 18=+=∴R e 12=⎝⎭, Im 02=⎝⎭.⑤解: ∵()()1,2i 211i,k n k n k k n k ⎧-=⎪=∈⎨=+-⋅⎪⎩.∴当2n k =时,()()R e i 1kn=-,()Im i 0n=;当21n k =+时,()R e i 0n =,()()Im i 1kn =-.3.求下列复数的模和共轭复数①解:2i -+==2i 2i -+=--②解:33-=33-=-③解:()()2i 32i 2i 32i ++=++==()()()()()()2i 32i 2i 32i 2i 32i 47i++=+⋅+=-⋅-=-④解:1i 1i 222++==()1i 11i 222i ++-⎛⎫== ⎪⎝⎭4、证明:当且仅当z z =时,z 才是实数.证明:若z z =,设i z x y =+,则有 i i x y x y +=-,从而有()2i 0y =,即y =0 ∴z =x 为实数.若z =x ,x ∈ ,则z x x ==. ∴z z =.命题成立.5、设z ,w ∈ ,证明: z w z w ++≤证明∵()()()()2z w z w z w z w z w +=+⋅+=++()()22222R e z z z w w z w wz z w z w w zwz w =⋅+⋅+⋅+⋅=++⋅+=++⋅()2222222zw z w z w z w z w++⋅=++⋅=+≤∴z wz w ++≤.6、设z ,w ∈ ,证明下列不等式. ()2222Re z w z z w w +=+⋅+ ()2222Re z wzz w w-=-⋅+()22222z wz w zw++-=+并给出最后一个等式的几何解释.证明:()2222Re z w z z w w +=+⋅+在上面第五题的证明已经证明了.下面证()2222Re z w z z w w -=-⋅+.∵()()()()222z w z w z w z w z w zz w w z w-=-⋅-=--=-⋅-⋅+()222Re zz w w=-⋅+.从而得证.∴()22222z w z w z w++-=+几何意义:平行四边形两对角线平方的和等于各边的平方的和. 7.将下列复数表示为指数形式或三角形式3352π2π;;1;8π(1);.cos sin 7199i i i i +⎛⎫--++ ⎪+⎝⎭ ①解:()()()()35i 17i 35i 7i 117i 17i +-+=++-3816i 198i e50255i θ⋅--===其中8πarctan19θ=-.②解:e i i θ⋅=其中π2θ=.π2ei i =③解:ππi i 1e e -==④解:()28π116ππ3θ-+==-.∴()2πi38π116πe--+=⋅⑤解:32π2πcos i sin 99⎛⎫+ ⎪⎝⎭解:∵32π2πcos i sin 199⎛⎫+= ⎪⎝⎭.∴322πi π.3i932π2πcos i sin 1e e 99⋅⎛⎫+=⋅= ⎪⎝⎭8.计算:(1)i 的三次根;(2)-1的三次根;(3)的平方根. ⑴i 的三次根.解:()13ππ2π2πππ22cos sin cosi sin0,1,22233++⎛⎫+=+= ⎪⎝⎭k k i k∴1ππ1cos i sini 6622=+=z . 2551cosπi sin πi6622=+=-z3991cosπi sinπi 6622=+=--z⑵-1的三次根解:()()132π+π2ππcos πi sin πcosi sin0,1,233k k k ++=+=∴1ππ1cosi sin3322=+=+z2cos πi sin π1=+=-z3551cosπi sinπ3322=+=--z⑶的平方根.πi4e 22⎫=⎪⎪⎝⎭)()1π12i44ππ2π2π44e 6cos i sin 0,122k k k ⎛⎫++ ⎪=⋅+= ⎪⎝⎭∴π11i 8441ππ6cos i sin 6e 88⎛⎫=⋅+=⋅ ⎪⎝⎭z911πi 8442996cos πi sin π6e 88⎛⎫=⋅+=⋅ ⎪⎝⎭z .9.设2πe,2inz n =≥. 证明:110n z z-+++=证明:∵2πi e nz ⋅= ∴1n z =,即10n z -=.∴()()1110n z z z --+++=又∵n ≥2. ∴z ≠1 从而211+0n z z z -+++=。
复变函数与积分变换第一章习题课概述

2.当x, y等于什么实数时,等式 x 1 i( y 3) 1 i 5 3i 成立。
2 2
3)为一直线: x 3;
1 12.函数 把下列 z平面上的曲线映射成 z 平面上怎样的曲线? 1 )x 2 y 2 4.
解: 1 x y 2 i 2 u iv, 2 2 z x y x y 1 2 2 u v . 4
13. 已知映射 z , 求:
函数,记为 Lnz .
w Lnz ln z iArgz
注 1.
Lnz
的主值支,记为lnz,即
ln z ln z i arg z
2.
Lnz
与lnz之间的关系是:
L n z ln z 2k i
k 1, 2,
15. 乘幂 z1 定义:
z2
z1
z2
e
z2 Lnz 1
u v v u f ( z ) i i x x y y
u u v v i i x y y x
11.解析与奇点 1)定义:如果函数 f ( z )在 z0 的某一邻域内处处 可导,则称f ( z ) 在 z0处解析;如果 f ( z )在区域 E 内每一点解析,则称 f ( z ) 在 E 内解析,或称 f ( z )是 E 内的一个解析函数. 不解析的点就称为是奇点。
3
2 k
3
i
, k 0,1,2.
1 3 1 3 w0 3( i ), w1 3, w2 3( i ). 2 2 2 2
复变函数与积分变换经典PPT—复变函数第一章小结与习题
z 2 r2 (cos 2 i sin 2) ,
则有
z2 z1
z2 z1
,
z2 Arg Arg z 2 Arg z 1 . z1
设复数 z 1 和 z 2的指数形式分别为
z 1 r1 e
z re
i
称为复数 z 的指数表示式.
4.复数的乘幂与方根 1) 乘积与商 两个复数乘积的模等于它们的模的乘积; 两个复数乘积的辐角等于它们的辐角的和.
若 z 1 r1 (cos 1 i sin 1) ,
z 2 r2 (cos 2 i sin 2) ,
则有
z1 z2 r1 r2 [cos( 1 2 ) i sin( 1 2 )] Arg( z1 z2 ) Argz1 A应的向量分别为 z 1 , z 2 ,
z
z1
y
先把 z 1 按逆时针方向 旋转一个角
所得向量
z 就表示积
z1 z 2 .
2 1
o
r2
复数相乘就是把模相乘, 辐角相加.
再把它的模扩大到
r2 倍 ,
r1
2,
r
z2
x
两个复数的商的模等于它们的模的商; 两个 复数的商的辐角等于被除数与除数的辐角之差.
设 G 是一个复数 个确定的法则存在 每一个复数 z x iy 的集合 . 如果有一 , 按这个法则 , 对于集合 G 中的
z , 就有一个或几个复数 w 是复变数
w u iv 与 z 的函数 ( 简称
之对应 , 那末称复变数 复变函数 ), 记作
复变函数与积分变换(练习题) (答案)

复变函数与积分变换第一章 练习题1. 计算(1)(2)i i i --;解:(1)103)31)(31()31(3123)2)(1(2i i i i i ii i i i i i i +-=+-+=-=+-=--;(2)10310)2)(1()2)(2(1)1)(1()2)(1()2)(1(i i i i i i i i i i i i i +-=---=----------=--。
2. 解方程组12122(1)43z z i i z iz i -=⎧⎨++=-⎩;解:消元法,)2()1(+⨯i 得:i z i 33)31(1-=+,解得:563)31)(31()31)(33(31331i i i i i ii z --=-+--=+-=,代入)1(得:517656322ii i z --=---⨯=。
3.求1i --、13i -+的模与辐角的主值;解:]arg arctan arctan,arctan arg ππππ,(,,三,二一,四-∈⎪⎪⎪⎩⎪⎪⎪⎨⎧-+=z x y x y xy z , ⎥⎦⎤⎢⎣⎡-+-=--)43s i n ()43c o s (21ππi i ;[])3a r c t a n s i n ()3a r c t a n c o s (1031-+-=+-ππi i 。
4.用复数的三角表示计算312⎛⎫- ⎪ ⎪⎝⎭、; 解:1)sin()cos()3cos()3cos(23133-=-+-=⎪⎭⎫ ⎝⎛-+-=⎪⎪⎭⎫⎝⎛-ππππi i i ; 3,2,1,0,4243s i n 4243c o s 2)43s i n43(c o s 228341=⎪⎪⎪⎪⎭⎫⎝⎛+++=⎥⎦⎤⎢⎣⎡+k k i k i ππππππ,⎪⎭⎫ ⎝⎛+=163sin 163cos 2830ππi z ,⎪⎭⎫ ⎝⎛+=1611sin 1611cos 2831ππi z ,⎪⎭⎫ ⎝⎛+=1619sin 1619cos 2832ππi z ,⎪⎭⎫ ⎝⎛+=1627sin 1627cos 2833ππi z 。
复变函数与积分变换练习册参考答案

分析:显然原方程可化简为一个典型的二项方程。
⎛ 1+ z ⎞ 解:由直接验证可知原方程的根 z ≠ 1 。所以原方程可改写为 ⎜ ⎟ = 1。 ⎝ 1− z ⎠
令
5
ω=
1+ z , ……………(1) 1− z
2π i 5
则 ω = 1 , ……………………(2)
5
方程(2)的根为 ω = 1, e
(5) lim
z →1
zz + 2 z − z − 2 3 = 。 2 z2 −1 zz + 2 z − z − 2 ( z + 2)( z − 1) z +2 3 = lim = lim = 。 2 z →1 ( z − 1)( z + 1) z →1 z + 1 2 z −1
提示: lim
z →1
(1 − cos α ) 2 + sin 2 α = 4sin 2
α
2
= 2sin
α
2
;因为当 0 < α < π 时,
sin α > 0 , 1 − cos α > 0 ,则 arg z = arctan
= arctan(tan +i sin
π −α
2
)=
π −α
2 e
π −α i 2
sin α α = arctan(cot ) 1 − cos α 2
。
6、 ( 2)
=e
2 ln 2 − 2kπ
7、方程 sinh z = i 的解为 三、计算和证明 1、试证函数
1 在复平面上任何点都不解析。 z
利用 C-R 条件,即用解析的充要条件判别,即 u =
复变函数与积分变换第一章习题课.ppt

x 0, y 0
3.令
zx iy
x z
z z z z 1 2 1 2
有如下一些常用的不等式:
y z
z z z z 1 2 1 2
4.表示
(3)三角表示: (4)指数表示:
z z (cos i sin ) r (cos i sin )
z2Lnz 1
注: 1.由于 Lnz 1 是多值的,因而一般来讲 z 1 也是多值的.定义中的 Lnz 1 如果取主值 z z ln z 2 1 z 所得结果 称为的 主值. ln z 1 1 e
2
z2
,
2 .当 z 2 是特 n
时, 就是我们所熟
第一章 习题课
u v v u f ( z ) i i x x y y
u u v v i i x y y x
11.解析与奇点 1)定义:如果函数 f ( z )在 z 0 的某一邻域内处处 可导,则称f ( z ) 在 z 0 处解析;如果 f ( z )在区域 E 内每一点解析,则称 f ( z ) 在 E内解析,或称 f ( z ) 是 E 内的一个解析函数. 不解析的点就称为是奇点。
7. 复变函数导数与微分
f(z )f(z ) 0 f (z )l i m 0 z z 0 z z 0
dw f ( z ) dz 0
8. C-R(Cauchy-Riemann)条件
u v , x y
v u . x y
( z ) u ( x , y ) iv ( x , y ) 9.可导的充要条件:函数 f 在 区域 E 内一点 zxiy 处可导的充分必要条 ( x ,y ), v ( x ,y ) 在点 ( x, y)处可微、 件是: u 且满足C-R条件. 10. f ( z) 可写成以下四种形式:
复变函数与积分变换学习指导(第一章)

复变函数与积分变换学习指导(第⼀章)第⼀章复数与复变函数本章⾸先引⼊复数域与复平⾯的概念,其次引⼊复平⾯上的点集、区域、Jordan曲线以及复变函数的极限与连续等概念。
第⼀节复数⼀.复数的表⽰1.2.欧拉公式3.虚数纯虚数且4.模辐⾓主辐⾓5. 与的关系当时,例1 求及解注意:⼀般有两种含义,⼀种是指⾮零复数⽆穷多辐⾓中的⼀⼆.复数的运算复数可以看作与复平⾯上的点对应,也可以看作是与平⾯上的向量相对应。
1.加法(遵循平⾏四边形法则)2.减法(遵循三⾓形法则)3.乘法设4.除法5.乘⽅注意:6.开⽅(即求的根)例2计算解故故例3 解⽅程解由有故三.共轭复数2.3.4.例P38.4证明并说明其⼏何意义。
证⼏何意义:平⾏四边形两条对⾓线长的平⽅和等于四条边长的平⽅和。
例P38.5设三点适合条件及试证是⼀个内接于单位圆周的正三⾓形的顶点。
证由知,位于单位圆周上,故只须证为正三⾓形的顶点即可。
由得⼜(由上题结论知),故即。
同理可得,故得证。
四.常⽤不等式1.2.1.过的直线的实⽅程为当时,表⽰之间的直线段,因此的直线段的复⽅程为过的直线的复⽅程为2. 三点共线3. 的中垂线⽅程为。
4.以为⼼,为半径的圆周⽅程为。
例P35.7证明:复平⾯上的直线⽅程可写成其中为⾮零复常数,为实常数。
证任给实直线⽅程令代⼊化简得令即得反之,设有⽅程令试证在负实轴上(包括原点)不连续,除此之外在复平⾯上处处连续。
证1)当时,⽆意义,故在原点不连续。
2)若为负实数,则,当由负实轴的下⽅趋于时,故在负实轴上任意⼀点上都不连续;3)对任意且不在负实轴上,,取中⼼在,不包含负实轴上的点,但整个包含在张⾓为的⾓形内的最⼤圆,半径当时,总有第⼆节复平⾯上的点集⼀.基本概念1.的的邻域。
2.的去⼼邻域——。
3.内点——若有⼀个邻域全含于,则为的内点。
4.外点——若且不是的聚点。
5.边界点——若的任意邻域内既有属于的点⼜有不属于的点,则为的边界点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.复数是指形如 z x iy 的数,实部记为 Re z x , 虚部 记为 Im z y . 2. 模: r z x2 y2 辐角: Argz arg z 2k 辐角主值: arg z
arctan y x arg z 2 y arctan x x0
6)方根运算:
z
n
i
2 k
n
wk (n z ) k n r e
k 0,1,2n 1
6. 实变复值函数 :
z (t ) x(t ) iy(t )
复变函数:
w f ( z ) u( x, y) iv( x, y)
7. 复变函数导数与微分
f ( z ) f ( z0 ) f ( z0 ) lim z z0 z z0
x 0, y 0 x 0, y 0
x 0, y 0
3.令
z x iy
xz
z1 z2 z1 z2
z1 z 2 z1 z 2
有如下一些常用的不等式:
yz
4.表示
(3)三角表示: (4)指数表示:
z z (cos i sin ) r(cos i sin )
10
解: 2 2 10 1 )( 1 i 3 ) [2(cos i sin )] 3 3 20 20 10 2 (cos i sin ) 3 3 2 2 1024 (cos i sin ) 3 3 512 i512 3.
10
2) 27 3e
2 2
3)为一直线: x 3;
1 12.函数 把下列 z平面上的曲线映射成 z 平面上怎样的曲线? 1 )x 2 y 2 4.
解: 1 x y 2 i 2 u iv, 2 2 z x y x y 1 2 2 u v . 4
13. 已知映射 z , 求:
注: 1.由于 Lnz1是多值的,因而一般来讲 z1 也是多值的.定义中的 Lnz1 如果取主值 z z ln z z 所得结果 称为的 主值. ln z1 1 e
2 1
2
z2
,
2 .当 z2 是特殊的 n 或 n z 悉的幂函数 或 n z .
1 n
时, 就是我们所熟
第一章 习题课
P55 1.求下列复数 z的实部与虚部、共轭复 数、 模与幅角: 1 3i 1 )z ; i 1 i
u v v u f ( z ) i i x x y y
u u v v i i x y y x
11.解析与奇点 1)定义:如果函数 f ( z )在 z0 的某一邻域内处处 可导,则称f ( z ) 在 z0处解析;如果 f ( z )在区域 E 内每一点解析,则称 f ( z ) 在 E 内解析,或称 f ( z )是 E 内的一个解析函数. 不解析的点就称为是奇点。
20.求下列函数的奇点: z 1 1 ) 2 ; z ( z 1)
解: 1 )函数的奇点是 z 0, z i.
24.计算: 1 ) Im{exp[exp (i)]}; 3) Re[sin( 1 i)];
ห้องสมุดไป่ตู้
解: 1 )e sin(sin 1); 3) sin 1 cosh 1;
cos1
3
2 )区域 0 arg z
解:
3
在平面上的像。
2 )映射 z 将区域 0 arg z
3
3
映成
0 arg z .
1 z z 15.设f ( z ) ( ), ( z 0), 试证:当 2i z z z 0时, f ( z )的极限不存在。
解: 2 xy f ( z) 2 , 令z沿着 y kx的方向趋近于 2 x y 2 xy 2kx 2 2k 0,则 lim 2 lim , 2 2 2 2 y kx, x 0 x y x 0 (1 k ) x 1 k 极限值与 k有关,即当 z 0时, f ( z )的 极限随 k的改变而改变,因此当 z 0时, f ( z )的极限不存在。
解: 1 )z 5[cos( ) i sin( )] 5e 2 2 3) z 2[cos( ) i sin( )] 2e ; 3 3
3
i 2
;
i
5) z cos( ) i sin( ) e 2 2
i 2
;
5.求下列各式的值: 1 )( 1 i 3 ) ; 2)3 27 ;
dw f ( z0 )dz
8. C-R(Cauchy-Riemann)条件
u v , x y
v u . x y
9.可导的充要条件:函数 f ( z) u( x, y) iv( x, y)在 区域 E 内一点 z x iy 处可导的充分必要条 件是: u ( x, y), v( x, y) 在点 ( x, y )处可微、 且满足C-R条件. 10. f ( z ) 可写成以下四种形式:
解: f ( z ) f (0) 考察 z 0时,极限 ,当z沿直线 y kx z 0 x 2 kx 0 2 2 f ( z ) f (0) x (1 k ) 趋于0时,有 lim lim z 0 x 0 z 0 x ikx
k , 极限随 k的改变而改变,从而 2 (1 k )(1 ki) f ( z ) f (0) 当z 0时,极限 不存在,则函数 z 0 在z 0点不可导,从而在 z 0点不解析。
函数,记为 Lnz .
w Lnz ln z iArgz
注 1.
Lnz
的主值支,记为lnz,即
ln z ln z i arg z
2.
Lnz
与lnz之间的关系是:
L n z ln z 2k i
k 1, 2,
15. 乘幂 z1 定义:
z2
z1
z2
e
z2 Lnz 1
解: 原式等价于 x 1 i ( y 3) 2 8i, 根据复数 x 1 2 x 1 相等的概念,有 , 即 . y 3 8 y 11
3.将下列复数化为三角式 和指数式: 1 i 1 ) 5i; 3)1 i 3; 5) ; 1 i
3
解: 1 )在整个复平面上解析 ,f ' ( z ) 3z 2i; 2z 3)除z 1点外处处解析, f ' ( z ) 2 ; 2 ( z 1)
2
18.下列复函数在 z 0点处是否解析? x2 y 2 , z 0; 2 D) f ( z ) x y z 0; 0,
解: 3 5 3 5 3 5 1 )z i, Re z , Im z , z i, 2 2 2 2 2 2 34 5 z , Argz arct an 2k , k 0,1,. 2 3
2.当x, y等于什么实数时,等式 x 1 i( y 3) 1 i 5 3i 成立。
13. 三角函数
1)定义:
eiz eiz eiz eiz sin z , cos z 2i 2
2)性质: 在复平面内是解析的,且 (sin z) cos z ,(cosz) sin z .
14. 对数函数
w e 定义: 若 z ,则称 w 为复变函数 z 的对数
25.求下列方程的全部解: 3 )e z 1;
解: 3 )z Ln(1) (2k 1)i, k 0,1,.
27.计算: 1 )Ln(3 4i), ln(3 4i); 3)(1 i)i ;
解: 4 1 )Ln(3 4i ) ln 5 i ( arctan 2k ), 3 4 ln(3 4i ) ln 5 i ( arctan ); 3
z re i
z x iy
(5)代数表示:
5.运算 1)相等; 2)四则运算,及运算规律; 3)共轭运算,及运算规律; 4) z z r r [cos( ) i sin( )]
1 2 1 2 1 2 1 2
5)
z1 r 1 [cos(1 2 ) i sin(1 2 )] z2 r2 r 1 ei (1 2 ). r2
3)(1 i) e
i
iLn (1i )
e
( 2 k ) i ln 2 4
;
2)函数在区域内解析与它在这一区域可导是等价 的. 3)解析一定可导,但可导不一定解析。
12. 指数函数
1) 定义: 2) 性质: 1. exp z ez 在复平面内处处解析; 2. (expz) exp z ; 3. e z 0 ;
exp z e z e x (cos y i sin y)
16.下列函数何处可导?何 处解析? 1 )f ( z ) x yi; 3) f ( z ) xy ix y;
2 2 2
解: 1 1 )f ( z )仅在直线 x 上可导,在复平面 2 上处处不解析。 3 )f ( z )仅在(0,0)上可导,在复平面上处 处 不解析。
17.指出下列函数的解析性 区域,并求其导数。 1 1 )z 2iz; 3) 2 ; z 1
3
2 k
3
i
, k 0,1,2.
1 3 1 3 w0 3( i ), w1 3, w2 3( i ). 2 2 2 2
9.指出下列各题中点 z的轨迹,并作图: 1 ) z 2 3i 5; 3) Re( z 2) 1;
