922135-理论力学之动力学-2平面运动加速度-zf

合集下载

理论力学：刚体平面运动的运动学 (2)

2020/12/9
3
理论力学
§7-1 刚体平面运动的运动学
三、平面图形上各点的加速度
y 动系：Ax’y’
y' aBt A
动点：刚体上的B点牵连运动：平移
B
A
aBnA x'
相对运动：圆周运动
o
aA x
aa ae arn art
ae aA,
an r
an BA
,
at r
at BA
aBt A AB ,
vA vB u AB 0
2、求加速度：研究AB 杆
aB
aA
aBnA
aBt A
a
t BA
aBt
aBn
上式在铅垂轴上投影： aBt A cos
aBn
u2 L
u
上式在水平轴上投影： aBt A sin aBt
AB
aBt A AB
u2
L2 cos
2020/12/9
BC
aBt BC
u2 L2
2020/12/9
vrB vrO vrBO vaB veB vrB vaB ve vrO vrBO
12
理论力学
§7-1 刚体平面运动的运动学
A
B
an rBO
vr O
at rBO
ar
a
3、求圆盘最高点B的加速度
arB
arO
at rBO
an rBO
aaB aeB arB
aaB
A
aA
ωOA O
C
Ca
vC
aB
B
aC
ω
aB
α
vC 2R aC vC 2R 2R

理论力学：刚体平面运动的动力学

§7-2 刚体平面运动的动力学
A
Mc
mg Mk
Fx O
Fy
常系数非齐次非线性微分方程
解：研究OA杆，进行受力分析
JO
d 2
dt 2
n i1
M O (Fi )
JO M mg M c M k
M mg
mg
L sin
2
M c c
Mk k( )
1 mL2 c k 1 mgLsin kbcos t
大小： a ar cos
2
2020/12/9
27
混沌（Chaos）：在确定的系统中出现类似随机的运动过程
2020/12/9
9
理论力学
§7-2 刚体平面运动的动力学
1963年美国科学家洛伦兹（Edward N. Lorenz) 从简化大气对流的动力学方程中得到一组三阶的非线性常微分方程。
即:
发现：该方程在一定参数下为周期解，在某些参数下为混沌解。
mR2
2R 2
2020/12/9
5
理论力学
§7-2 刚体平面运动的动力学
例：系统如图所示，设均质杆OA长为 L 质量为m，其阻力系数为 c，扭簧刚度系数为 k。当 OABC 时，扭簧无
变形，已知BC杆的转动： b cos t ,
试建立OA杆的运动微分方程。
A
mg
B
C
O
2020/12/9
6
理论力学
2020/12/9
F
B
B：滑块右侧与滑道接触
25
理论力学
§7-2 刚体平面运动的动力学
思考题：质量为m半径为R 的均质圆盘在倾角为θ 的固定
斜面上纯滚动，其上作用一主动力偶M，试定性分析作用在圆盘上的摩擦力的方向。

922136-理论力学之动力学-3平面动力学

3
2g 4l
,
FA
FB
3 8
mg
16
思考题：已知均质杆AB上的A点以匀速 u 铅垂运动，均质圆盘在地面上纯滚动。试确定当系统运动到图示位置时，地面作用在圆盘上的摩擦力的方向。（选择：A或B）
u
情况1 A
u
情况2 A
F
B
F
B
A：水平向右
B：水平向左
17
思考题：已知均质杆AB上的A点以匀速 u 铅垂运动，均质圆盘在地面上纯滚动。试确定当系统运动到图示位置时，滑块 A的哪一侧与墙面接触。（选择：A或B）
杆长为l，质量为m。求：此瞬时AB杆的角加速度,
地面约束力, 绳的拉力。
解：受力分析和运动分析
y Ca
O FB
aB
B
FA CaC mg
A
450
aA 0 x
应用刚体平面运动微分方程
macx FB
1m12 amcly2
FA mg (FA FB
)
l 2
sin
450
acx
acy
l
2
sin
450
Planar Motion of a Rigid Body)
设：刚体具有质量对
z
(xM , yM , zM )
称面 S，此平面在某一
固定平面内运动，作用
o
y
在刚体上的力系可简化
为S平面内的一个平面 x
力系。
M S
问题：用什么方法建立刚体的平面运动与力之间的关系？
12
§3-2、刚体定轴转动与平面运动微分方程
xc'
l2 f 12 xc'
g
sin

理论力学第2章平面任意力系

P
YAaPaM 0
a
MB(F)0:
X A 2 a Y A a P a M 0 A
联解上各式得：
XA P
XA
三力矩
YA
YA 2P
RB 2P
式
17
D
20
例14 自重为P=100KN的T字形刚架ABD，置于铅垂面内，载荷如图示。其中M=20KNm,F=400KN, q=20KN⁄m,l=1m。求固定端A的约束力。
x
dx
xc
l
根据合力矩定理
Fxc0 lq(x)xdx
xCF 10 lqx l2dxq3 l2
ql2l 23
11
小结
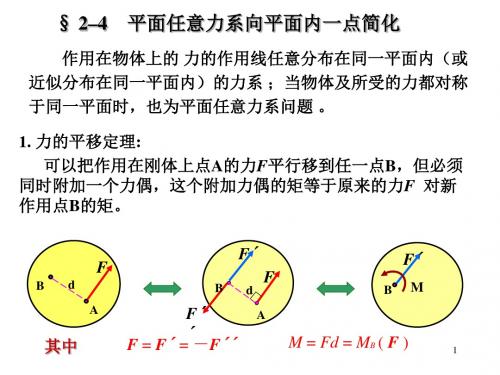
1. 力的平移定理:平移一力的同时必须附加一个力偶，附加力偶的矩等于原来的力对新作用点的矩。
2. 平面任意力系向平面内任选一点O简化:可得一个力和一个力偶。这个力等于该力系的主矢，作用线通过简化中心O。这个力偶的矩等于该力系的主矩。
F
Bd
F´
F
Bd
F´
BM
A
F´
A
其中
F = F´ =´－F´´
M = Fd = MB ( F )
1
2 .平面任意力系向作用面内一点简化 • 主矢和主矩
F2
F1
o Fn
F2´
M2
o
Mn
Fn´
F1´
M1
FR
´
M
o
任意点O 为简化中心
F1´ = F1 ， F2´ = F2 ，… ，Fn´ = Fn
Mi = Mo ( Fi ) (i = 1，2，…，n)
6m
解方程得:
W
P
12m

动力学基本概念及公式

动力学基本概念及公式动力学是力学的一个重要分支，研究物体受到力的作用下的运动规律及相应的数学描述。

本文将介绍动力学的基本概念和公式，以帮助读者更好地理解和应用动力学知识。

一、基本概念1. 位移（Displacement）：物体从初始位置到最终位置的位置变化。

通常用Δx表示，其大小和方向可以用矢量表示。

2. 速度（Velocity）：物体单位时间内位移的变化量。

速度的大小为位移变化量Δx除以时间变化量Δt。

速度也是矢量量值，可以用v表示。

3. 加速度（Acceleration）：物体单位时间内速度的变化量。

加速度的大小为速度变化量Δv除以时间变化量Δt。

加速度也是矢量量值，可以用a表示。

二、基本公式1. 平均速度公式（Average Velocity Formula）：v = Δx / Δt2. 平均加速度公式（Average Acceleration Formula）：a = Δv / Δt3. 速度和加速度之间的关系（Velocity and Acceleration Relationship）：v = v0 + at其中，v表示最终速度，v0表示初始速度，a表示加速度，t表示时间。

4. 运动学方程（Kinematic Equations）：（1）v = v0 + at（2）Δx = v0t + (1/2)at^2（3）v^2 = v0^2 + 2aΔx其中，v表示最终速度，v0表示初始速度，a表示加速度，t表示时间，Δx表示位移。

这些运动学方程是基于匀加速度运动的情况得出的，适用于只有加速度恒定的情况。

三、实例应用现以一个小球从静止开始下落，经过4秒钟的时间，求其在t=4s时的速度和位移。

根据运动学方程（1），代入已知条件：v = v0 + at由于小球从静止开始下落，初始速度v0为0，则方程变为：v = at根据方程中的加速度a，我们可以假设小球下落的加速度为9.8m/s^2（常见的自由落体加速度），则有：v = 9.8m/s^2 × 4s= 39.2m/s因此，小球在t=4s时的速度为39.2m/s。

理论力学第八章平面运动

vB vA vBA
刚性截面上任一点的速度等于基点的速度与该点随刚性截面
绕基点转动的速度的矢量和．这种求解速度的方法称为基点法，它是求解刚性截面内一点速度的基本方法．
2013年1月18日理论力学T 27
速度投影法由于A, B点是任意的，因此
vB vA vBA 表示了刚性截面上任意两点
21
曲柄连杆机构
AB杆平面运动的分解
2013年1月18日理论力学T
22
2013年1月18日理论力学T
23
2013年1月18日理论力学T
24
§7.2 平面运动刚体内各点的速度和加速度
1. 平面运动刚体内各点的速度刚性截面－S 基点－A 定系－O0 x0 y0 平移系－A x y
刚性截面的角速度－基点速度－ vA
2013年1月18日理论力学T
9
平面运动方程
x A x A( t ) yA yA( t )
φ φ( t )
对于每一瞬时 t ，都可以求出对应的 x A , y A , ，刚性截面S在该瞬时的位置也就确定了。
2013年1月18日理论力学T
10
已知：曲柄连杆机构中OA=r , AB=l;曲柄OA以 = t 绕O轴转动，为常数。求：连杆的平面运动方程。
y0
O
A B x0
解：确定连杆平面运动的3个独立变量与时间的关系
连杆的平面运动方程为
x A t rcosω t ,
2013年1月18日理论力学T
r y A t rsin ω t , φ t arcsin ( sin ω t) l
11
平面运动分解为平移和转动
当刚性截面Ｓ上Ａ点不动时，则刚体作定轴转动当刚性截面Ｓ上角不变时，则刚体作平移．

理论力学中的动力学分析与加速度的计算

理论力学中的动力学分析与加速度的计算动力学是理论力学中重要的一个分支，研究物体在受到力作用下的运动规律。

在动力学的分析中，计算加速度是非常重要的，它能揭示物体的速度变化情况以及力对物体运动的影响。

本文将介绍动力学分析中的基本概念以及计算加速度的方法。

一、运动物体的描述动力学研究的是物体在受力作用下的运动情况，为了描述运动物体的状态，我们需要引入一些基本概念。

1. 位移：物体在运动过程中，由于位置的变化而引起的变量称为位移。

通常用符号Δx表示。

2. 速度：速度是位移随时间的变化率，即单位时间内位移的大小。

用符号v表示。

3. 加速度：加速度是速度随时间的变化率，即单位时间内速度的变化量。

用符号a表示。

根据以上基本概念，我们可以推导出物体在匀变速运动的情况下，速度和加速度的计算方法。

二、匀变速运动中加速度的计算匀变速运动指的是物体的加速度保持恒定，速度按照一定规律变化的运动。

在这种情况下，我们可以通过已知的物理量来计算加速度。

假设一个物体的初速度为v0，末速度为v，时间为t，加速度为a。

根据物体运动的基本关系式可以得到以下等式：v = v0 + at （1）v = Δx / t （2）将式（1）代入式（2），可得：Δx / t = v0 + at通过变形，可以得到加速度a的计算公式：a = (v - v0) / t以上公式表明，当已知物体在运动过程中的初速度、末速度以及所用时间时，我们可以通过公式计算出加速度。

三、实际应用中的动力学分析与加速度计算动力学分析和加速度计算在实际应用中有着广泛的应用，下面以一个常见的例子来说明。

假设一个小球从高处自由落下，我们想要计算小球下落过程中的加速度。

首先，我们需要测量小球下落的时间，并记录为t。

同时，我们需要测量小球下落的距离，记录为Δx。

根据自由落体运动的特点，小球在自由落下过程中的加速度近似为地球的重力加速度g，约等于9.8 m/s^2。

根据公式a = Δx / t，我们可以计算出小球下落过程中的加速度。

5.1、平面运动速度、加速度分析(2-1)

平面运动速度加速度分析（2-1）刚体在运动过程中，如果其上各点的运动轨迹都是二维的平面曲线（或一维的直线），这种运动称为平面运动。

这时刚体上任意一点运动轨迹所在的平面都统称为刚体的运动平面。

概念：刚体作平面运动时可以不考虑它在运动平面法向上的厚度因素，而将平面运动图形上任意两点之间的速度关系)sin cos (θθj i AB r AB +=AB A B r r r +=AB A A B r v v ⨯+=ωBAB A r r r +=BA B B A r v v ⨯+=ω0 )( =⨯-AB B A r ωωB A ωω =⇒ r v v ⨯+=ω v v v +=r v ⨯=ωωr v = AB A B v v v +=ω =ABAB j i AB v ωθθ)cos sin ( +-= 0sin cos 00θθωAB AB k j iAB =A AB ωω =AB AB r ⨯=ωω 平面图形自身角速度：ABr ⨯ω平面运动图形上任意一点的速度，都等于随基点的平行移动速度加上绕基点的定轴转动速度。

AB t AB r a ⨯=ε2 ωAB n AB r a -=AB A B r v v ⨯+=ω)( AB AB A B r r a a ⨯⨯+⨯+=ωωε加速度关系平面运动图形上任意一点的加速度，都等于随基点的平行移动加速度加上绕基点的定轴转动加速度.n AB t AB B a a a +=定理5.1-1平面运动图形上任意一点的速度、加速度都等于随基点的平行移动速度、加速度,再加上绕基点的定轴转动速度、加速度.考虑到平面运动刚体在运动平面法向上的厚度因素时,则刚体的平面运动等于随基轴的平行移动加上绕基轴的定轴转动(基轴:经过基点且垂直于运动平面的直线).图1图2图3在图1中，若以圆轮轮缘上C点为基点，如何确定A、B、O、D 等各点的速度大小及方向？思考题讲述完毕！有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）。

理论力学—动力学PPT

10
工程动力学的研究模型
质点：质点是具有一定质量而几何形状和尺寸大小可以忽略不计的物体。广义的质点系统：系统内包含有限或无限个质点，这些质点都具有惯性，并占据一定的空间；质点之间，质点与边界之间，以不同的方式连接，或者附加以不同的约束与物理条件。
刚体：是质点系的一种特殊情形，其中任意两个质点间的距离保持不变。
如何确定地球同步卫星的轨道高度
F
？
O
R
1 1 1 2 2 2 2 gR vdv 2 gR dx v0 v ( )225 x R x
v v0 x R
例题 4
已知：m=15t, v0=20 m/min k=5.78MN/m。求：钢丝绳的最大拉力。 st 解：以弹簧在静载作用下变形后的平衡位置为原点建立 Ox坐标系 O l0 k
§11-2 质点的运动微分方程
d x m m 2 Fix x i dt d2y m m 2 Fiy y i dt d 2z m m 2 Fiz z i dt
2
ma Fi
i 1
n
直角坐标形式
n d r m 2 Fi i 1 dt
2
弧坐标形式
牛顿及其在力学发展中的贡献
★ 牛顿在光学上的主要贡献是发现了太阳光是由7种不同颜色的光合成的，他提出了光的微粒说。 ★ 牛顿在数学上的主要贡献是与莱布尼兹各自独立地发明了微积分，给出了二项式定理。
★ 牛顿在力学上最重要的贡献，也是牛顿对整个自然科学的最重要贡献是他的巨著《自然哲学的数学原理》。这本书出版于1687年，书中提出了万有引力理论并且系统总结了前人对动力学的研究成果，后人将这本书所总结的经典力学系统称为牛顿力学。 19

理论力学课件-动力学精选全文完整版

第一类问题-----已知质点的运动，求作用在质点上的力；第二类问题-----已知作用在质点上的力，求质点的运动规律。
26
总结 4.求解质点动力学问题的步骤：
（1）根据题意确定研究对象，选择恰当的坐标系；（2）分析研究对象的受力情况，作受力图；（3）分析研究对象的运动情况；（4）列出质点的动力学基本方程，然后求解；如是第二类问题，
（相对地面静止或作匀速直线平动的参考系）
(3)矢量性和瞬时性
二. 质点运动微分方程
F
ma
m
dv dt
m
d2r dt 2
6
利用合矢量投影定理 ,可以在直角坐标系, 自然坐标系及其他坐标系中建立投影方程.
1.质点运动微分方程在直角坐标系上的投影
d2x m dt 2 XFx
m
d2y dt 2
YFy
m
还需根据初始条件确定积分常数。
27
作业
• 9-2 • 9-12
28
例题：电梯以加速度a上升，在电梯地板上，放
有质量为m的重物。求重物对地板的压力。解：取重物为研究对象
进行受力分析与运动分析。
Fy= m ay
N - mg=m a
mg
N=mg+ma=N'
（静约束力；附加动约束力）
a
讨论：若加速度方向向下 N
b
l
FT
n
r
v
τ
z
mg
m
dv dt
F
t
0
m
v2 r
F
n
FT sin 600
0 F b mg FT cos 600
FT
mg cos 600
19.6N

理论力学第二篇运动学复习PPT学习教案

21vrB
2 5
0.03
5 0.06 5
52
m/s2
a B
aaB ( 0.365 5
2
0.06 5
5
2
)/2 55
0.15
2
m/s 2
第17页/共24页
[例5] 曲柄肘杆压床机构
已知:OA=0.15m,n=300 rpm,AB=0.76m,
求BC该=位BD置=0时.5的3m. B图D ，示A位B 及置时vD, AB水平.
解:OA定轴转动 ; AB, BC均作平面运动, 滑块B和C均作平动
①求 vc
对AB杆应用速度投影定理：
vB cos60 vA cos30 vB 3vA 3ro 对BC杆应用速度投影定理：vc vB sin 60
vc
3ro
3 2
3 2
r
o
()
第19页/共24页
②求 ac
以A为基点求B点加速度：
0.3
aen
s300
s300
m/ s
ae
1.5 ra
ac
d
O
300
/s
300
ac
1
O
aa
做加速度图。
A
ae
aen
ar
A
a取a aOeA方2 向0.投2影32， 1得.8：m/s2
, aa
ac sin
2O1B r 300 ae
2 ac
0.3
1.5
0.9m
/
s2
O1B第O1a41页eA/共2a4页a sinO310A0 ac 0
运动学dtdsdtdv点的合成运动牵连运动为平动时牵连运动为转动时其中平动可简化为一点的运动任一瞬时各点的轨迹形状相同各点的速度和加速度均相等定轴转动常量

理论力学刚体平面运动

rA
O
ω (rB rA ) ω b
2.3.3.刚体平面运动
刚体平面运动分解
B点运动方程
x B x A AB cos y B y A AB sin
AB ( x B x A ) 2 ( y B y A ) 2
轨迹
( x B x A ) ( y B y A ) AB
vCA ω rAC v A
取
ω
C
可知C点必存在。
rAC
vA
；
rAC v A
v CA
vA
A
C点称为速度瞬心
速度瞬心的特点：在每一个瞬时，平面运动刚体绕速度瞬心做定轴转动。
在不同的瞬时，瞬心位置C不同。
应用：当平面运动刚体上两点速度方向已知时，通过几何方法确定速度瞬心，则刚体上任意点速度方向已知。
2、图形的角速度、角加速度
t 0
t
（1 ）定义：角速度
角加速度

lim
t

t 0
B A
lim
、对平面运动图形而言是

标量，即只有大小、正负；但在公式推导时也可以表示成矢量：方向总垂直于纸面。
（2）、注意：根据、定义
定轴转动
曲线平动
刚体运动简化为平面运动
曲柄滑块机构平面运动
刚体平动
刚体曲线平动
机构运动演示
机构运动演示
机构运动演示
刚体定轴转动
2.2.2.平面图形的角位移、角速度角加速度
1、平面图形的角位移
任一有向线段AB的转角增量
(t t ) (t )

理论力学第九章刚体的平面运动2 (西安交大)

A ω O1 O2
B
ω O A B
练习题
vO O A B
找出下列平面运动刚体的速度瞬心。
B
O
vA
A
例：椭圆尺规的A端以速度vA沿x轴的负方向运动， AB=l 。试求B端的速度以及尺AB的角速度。 AB杆速度瞬心为C. 解：
y
vA vA AC l sin
vB
BC vB BC vA AC
凡涉及到平面运动图形相对转动的角速度和
角加速度时，不必指明基点和坐标系，只需说明平面图形的角速度和角加速度。相对基点(平动坐标系)的转动角速度(角加速度)就是相对于定系的绝对角速度(角加速度).
§9-2 平面运动的速度分析
1.基点法
设在平面运动刚体上取点 A为基点，已知其速度为 vA ，平面运动刚体的角速度为，分析图形上任一点B 的速度。 y´ y vBA B A O vA vA 动点－B点动系－平移系 Ax´y´
[v A ] AB [vB ] AB
v A v B cos 0 r 0 vB cos 0
应用速度投影定理无法求得连杆AB的角速度。
ω0
例如图平面铰链机构。已知杆O1A的角速度是ω1 ，杆
O2B的角速度是ω2，转向如图，且在图示瞬时，杆O1A
又O2B=b，O1A= b。试求在这瞬时 C 点的速度。 3
速度瞬心的特点瞬时性：不同的瞬时，有不同的速度瞬心；因此速度瞬心具有加速度。
唯一性：某一瞬时只有一个速度瞬心；
瞬时转动特性：平面图形在某一瞬时的运动都可以视为绕这一瞬时的速度瞬心作瞬时转动。注意瞬时平动与平动的区别：瞬时平动各点的速度相同，但是加速度不同。
练习题

922132-理论力学之动力学-1平面运动速度

16
例：已知OA杆的角速度，求：图示瞬时滑块B的速
度和 AB杆的角速度。
OA r, 600, AB 3r
vA A AB vA
O vB
2. 速度投影法
vB cos vA
解：研究连杆AB
1. 基点法
vB vA vBA
B
vB
vA
cos
vBA
AB
vBA AB
vA
tan
3r
vB
vA
cos
若选取若选取速度为零的点速度为零的点作为基点则求解速度问题作为基点则求解速度问题的计算会大大简化同时也能求出图形的角速度的计算会大大简化同时也能求出图形的角速度
第三章刚体动力学（一）
Dynamics of Rigid Bodies (Part One)
1
问题的引出
观察：车轮作什么运动？其运动有什么特点？
2
问题的引出
A O
B
连杆AB作什么运动？运动有什么特点？
•刚体的平面运动（plane motion of rigid bodies)：刚体在运动过程中，其上任意一点到某一固定平面的
距离保持不变。
3
§3-1、刚体平面运动的运动学
Kinematics of Planar Motion of Rigid Bodies
28
上任一点M 的速度
LL
AA vvAA
vvMMAA MM
v AA
vM vA vMA
M在AL上时速度大小为
CV
S LL
vM vA vMA vA AM
AL上必存在速度为零的一点CV
2)过A其它直线上的点
ACV
vA
vA和 vMA 不共线，速度均不为零

922134-理论力学之动力学-2平面运动加速度

x': aBx' aA sin aBnA y': aBy' aA cos aBt A
20
例：求系统在图示位置时，AB杆的角速度和角加速
度。
OA 2R,u R const.
1.求AB杆的角速度
B e
vr vCA R
30 o
uC
O
vA
A
动点：C 动系：AB杆绝动：直线相动：直线牵动：平面运动
vA AB CV A 2 3vO
aO OR
7
A
aAt B
y
aA aAn B
aBt O aO
x
B aBnO
aB aO aBt O aBnO
aA aB aAt B aAnB
大小: ?
方向:
4 ABR 4A2BR
aA aO aBt O aBnO aAt B aAnB
x：0
aO
2.加速度瞬心(Instant Center for acceleration)法
定义：某瞬时平面图形上加速度为零的点，称图形在该瞬时的加速度瞬心C a
定理：当平面图形的角速度与角加速度不同时为零，
必存在唯一的加速度瞬心
问题：过Ca的任一直线上各点的加速度分布有何特点？ —-- 与图形定轴转动时的加速度分布类似
aB
aA
aBt A
a
n BA
AB 0
B
a
n B
aB aA aBt A
aBn
a
t B
aA
aBt A
D y : aBn aA aBt A cos
aBt A 0
10
例：半径为R 的圆盘在水平板A上纯滚动，若该瞬时板的速度为u，加速度为a，轮心O相对板的速度为vr，相对加速度为ar。求圆盘的角速度和角加速度以及圆盘最高点B的速度和加速度

理论力学课件刚体平面运动的加速度分析

aBnA
=
AB
⋅
ω
2 AB
= 4m
s2
加速度矢量式投影到η轴上得
aB cos 45o = aBnA
aB = 5.66 m s2
αAB
an BA
at
y BA
aB aA B
加速度矢量式投影到y轴上得
0
= −a
aBt A
A cos
= 16
45° +
m s2
aBnA
cos
45°
+ aBt A
α AB
sin 45°
•结论：平面图形角速度不为零，任一瞬时，速度瞬心必存在且唯一。
6-2 刚体平面运动的速度分析
速度瞬心的特点
1、瞬时性：不同的瞬时，有不同的速度瞬心。 2、唯一性：某一瞬时只有一个速度瞬心。速度瞬心不是一个固定点。理解成“角色”
思考题：杆做什么运动？
vB
ω
vA
定轴转动
车轮在地面上纯滚动
6-2 刚体平面运动的速度分析
6-2 刚体平面运动的速度分析
平移
vvA = vvB
ωAB = 0
avA = avB α AB = 0
瞬时平移
vvA = vvB avA ≠ avB
ωAB = 0 α AB ≠ 0
vA A
ω
O
vB B
牢记！
6-2 刚体平面运动的速度分析
2、确定速度瞬心位置的方法
已知A、B两点的速度方向，
试确定速度瞬心的位置。
例6-5 图示机构，已知曲柄OA的角速度为ω，OA＝AB＝BO1＝ O1C＝r，角α = β = 60º，求滑块C的速度。
解：AB和BC作平面运动，其瞬心分别为P1和P2点，则

理论力学前三章总结

前三章总结第一章：质点运动学一．速度、加速度的分量表达式 1.直角坐标系k v j v i v k z j y i x dtrd v z y x ++=++== k a j a i a k z j y i x dtvd a z y x ++=++== 2.极坐标系rv r =径向速度θθ r v = 横向速度 j r i rv θ+=2θ r ra r -=径向加速度 ()θθθθ212r dt d rrr a =+=横向加速度 ()()()()j r dtd r i r r j r r i r r a θθθθθ22212+-=++-=3.自然坐标系i dtds i v v==dtdva t =切向加速度 ρ2v a n =法相加速度j v i dt dv a ρ2+=二．质点运动定律牛顿三大定律牛顿第一定律﹙惯性定律﹚牛顿第二定律﹙a m F=﹚ 牛顿第三定律﹙F F-=﹚三．质点运动微分方程 1.直角坐标系2.平面极坐标系3.自然坐标系⎪⎩⎪⎨⎧===),,,,,,(),,,,,,(),,,,,,(t z y x z y x F z m t z y x z y x F y m t z y x z y x F xm z y x ⎪⎩⎪⎨⎧=+=-),,,,()2(),,,,()(2t r r F rr m t r r F r r m r θθθθθθθθ ⎪⎪⎪⎩⎪⎪⎪⎨⎧===b n F F v m F dt dv m 02ρτ),,(t r r F r m =RF r m+=第二章质点动力学一．质点动力学的两类问题1、已知，求力2、已知力，求 1】从 2】从求轨道、轨道参数：ρ 、射程、射高3】从求周期T二：质点动力学的基本定理与基本守恒定律 1. 动量定理与动量守恒定律动量：动量定理：动量矩守恒定理： 2. 动量矩定理与动量矩守恒定律力矩：动量矩：动量矩定理：F r r m r dtd ⨯=⨯)( 即 M dtJd=⎰⋅=-2112t t dt M J J分量形式动量矩守恒定理：1.)(t r r=Fa m a→→)(t r r =)(t r r =)(t r r=)()()(r r r t r r t r r =→=→=pd dt F =⎰⎰-==⋅212112t t p p p p p d dt F=Fcv m =0=x F xx c mv =vm r p r J⨯=⨯=,F r M⨯=vm p=y z zF yF y z zy dt dm-=-)( z x xF zF z x x z dt dm -=-)( x y yF xF x y y x dt dm -=-)( 0=M 0=dtJdc J =cv m r =⨯2.3.动能定理与机械能守恒定律 a.功、力、位移b.功率c.势能1. 力场：如果空间每一点对质点都有一定的力作用着，而且此力的大小和方向只与该点的位置有关，这个空间就称为力场。

理论力学基础刚体的平面运动2

试求该瞬时滑块B的法向加速度。
（习题8－18）动画
OA r, O1B 2r
鞍山科技大学机械工程与自动化学院工程力学系
理论力学例四
刚体平面运动速度分析习题课
第八章
刚体的平面运动
vB
a
n B
vA
鞍山科技大学机械工程与自动化学院工程力学系
理论力学
刚体平面运动速度分析习题课
动画
鞍山科技大学机械工程与自动化学院工程力学系
理论力学例八
刚体平面运动速度分析习题课
第八章
刚体的平面运动
vCy
vCy
vCx
vCx
鞍山科技大学机械工程与自动化学院工程力学系
理论力学
刚体平面运动速度分析习题课
滑块B可沿水
第八章
刚体的平面运动
vr
va v
ve ODO B vD ODO D
vE
动点：滑块B 动系：固连在OC杆上
鞍山科技大学机械工程与自动化学院工程力学系
理论力学
刚体平面运动速度分析习题课
第八章
刚体的平面运动
例十一图示机构中曲柄OA长为2l ，以匀角速度ω0
绕轴O转动。在图示瞬时，AB=BO，∠OAD=90o。试求此时套筒D相对于杆BC的速度。
水平方向运动，并借套筒B带动杆OC转动。已知 AB和OE两平行线间的距离为b，图示位置，
600 , 300 , OD BD 试求此时杆OC的角速度，并求滑块E的速度。 (8—29)
动画
鞍山科技大学机械工程与自动化学院工程力学系