理论力学2平面力系资料
合集下载
理论力学 02平面汇交力系

5
第二节 平面汇交力系合成与平衡的解析法
一、力在直角坐标轴上的投影
y
Fy
Fy
F
B
Fx
Fx F cos Fy F cos
Fy Fx cos , cos F F F Fx 2 Fy 2
A
j
O i
Fx
x
力在坐标轴上的投影是代数量,而分力则是矢量。 在直角坐标系中,它们之间的关系可表达为:
21
用解析法求解平衡问题的基本步骤为: 1、选取研究对象 一般原则为: (1)有已知求未知; (2)由简单到复杂。 2、画受力图 受力图是计算的基础,不容许出现任何差错。
3、建立坐标轴,列平衡方程 在选择坐标轴时,应使尽可能多的未知力与 坐标轴垂直,同时还要便于投影。 4、求未知量 解方程,求出未知量。
F F ix i y FR y Fi y FR x Fi x cos , cos FR FR FR FR FR FR x FR y
2 2 2 2
10
例2-3 已知 F1 200N、 、 F2 300N、 F3 100N F4 250N , 各力方向如图所示, 试求该平面汇交力系的合力。
y
F
B A
F
C
B D
FAB
x
FBC
解:(1)先选取销钉 B为研究对象,画受力图。建立 图示坐标系Bxy ,相应的平衡方程为:
F 0, F 0,
x
y
FAB cos FBC cos 0
FAB sin FBC sin F 0
20
解得:
第二节 平面汇交力系合成与平衡的解析法
一、力在直角坐标轴上的投影
y
Fy
Fy
F
B
Fx
Fx F cos Fy F cos
Fy Fx cos , cos F F F Fx 2 Fy 2
A
j
O i
Fx
x
力在坐标轴上的投影是代数量,而分力则是矢量。 在直角坐标系中,它们之间的关系可表达为:
21
用解析法求解平衡问题的基本步骤为: 1、选取研究对象 一般原则为: (1)有已知求未知; (2)由简单到复杂。 2、画受力图 受力图是计算的基础,不容许出现任何差错。
3、建立坐标轴,列平衡方程 在选择坐标轴时,应使尽可能多的未知力与 坐标轴垂直,同时还要便于投影。 4、求未知量 解方程,求出未知量。
F F ix i y FR y Fi y FR x Fi x cos , cos FR FR FR FR FR FR x FR y
2 2 2 2
10
例2-3 已知 F1 200N、 、 F2 300N、 F3 100N F4 250N , 各力方向如图所示, 试求该平面汇交力系的合力。
y
F
B A
F
C
B D
FAB
x
FBC
解:(1)先选取销钉 B为研究对象,画受力图。建立 图示坐标系Bxy ,相应的平衡方程为:
F 0, F 0,
x
y
FAB cos FBC cos 0
FAB sin FBC sin F 0
20
解得:
理论力学第二章 平面力系

精品文档
§2-4 平面任意力系的平衡条件和平衡方程
一.平面任意力系的平衡方程
平面任意力系平衡的充要条件是: 力系的主矢和对任意点的主矩都等于零
FR 0
MO 0
因为 F R ( F x ) 2 ( F y ) 2 M O M O ( F i)
平面任意力系的平衡方程
Fx 0 Fy 0
求: 力系向 点O的简化结果;
合力与O的A交点到点 的距O离 ; x
合力作用线方程。
精品文档
解: (1)主矢:
F xF 1F 2cos232.9kN F yP 1P 2F 2sin670.1kN
F R '( F x)2 ( F y)2 7 0 9 .4 k N
c o s ( F R ',i) F R F 'x 0 .3 2 8 3 ,c o s ( F R ',j) F R F 'y 0 .9 4 4 6
例2-12
已知:A C C B l,F1k 0N
求: 铰链 A和 D杆C受力.
解: 取 A梁B,画受力图.
Fx 0 FAxFCcos450
Fy 0 FAy F Csi4n5F0
MA 0 F Cco 4s5 lF2l0
F C 2 .2 8 k8 ,精F N 品A 文 档x 2 k 0 ,F N A y 1 k 0 N
j)
Fiy FR
作用点为力的汇交点.
四、平面汇交力系的平衡方程
平衡条件
FR 0
平衡方程
Fx 0
精品文档
Fy 0
例2-1
已知: P 2k 0 R N 0m ,.h 6 0 , m .08
求:
1.水平拉力 F5时k,N碾子对地面及障碍物的压力?
§2-4 平面任意力系的平衡条件和平衡方程
一.平面任意力系的平衡方程
平面任意力系平衡的充要条件是: 力系的主矢和对任意点的主矩都等于零
FR 0
MO 0
因为 F R ( F x ) 2 ( F y ) 2 M O M O ( F i)
平面任意力系的平衡方程
Fx 0 Fy 0
求: 力系向 点O的简化结果;
合力与O的A交点到点 的距O离 ; x
合力作用线方程。
精品文档
解: (1)主矢:
F xF 1F 2cos232.9kN F yP 1P 2F 2sin670.1kN
F R '( F x)2 ( F y)2 7 0 9 .4 k N
c o s ( F R ',i) F R F 'x 0 .3 2 8 3 ,c o s ( F R ',j) F R F 'y 0 .9 4 4 6
例2-12
已知:A C C B l,F1k 0N
求: 铰链 A和 D杆C受力.
解: 取 A梁B,画受力图.
Fx 0 FAxFCcos450
Fy 0 FAy F Csi4n5F0
MA 0 F Cco 4s5 lF2l0
F C 2 .2 8 k8 ,精F N 品A 文 档x 2 k 0 ,F N A y 1 k 0 N
j)
Fiy FR
作用点为力的汇交点.
四、平面汇交力系的平衡方程
平衡条件
FR 0
平衡方程
Fx 0
精品文档
Fy 0
例2-1
已知: P 2k 0 R N 0m ,.h 6 0 , m .08
求:
1.水平拉力 F5时k,N碾子对地面及障碍物的压力?
理论力学2平面力系

4
i 1 4
合力大小:
FR
FR FR2x FR2y ( Fix ) 2 ( Fiy ) 2
θ
1.292 1.122 1.71kN
合力方向:
arctan
FRy FRx
arctan
1.12 41 1.29
(第象限)
14
六、平面汇交力系平衡的解析法
该力系平衡的必要和充分条件是: 该力系的合力FR 等于零。
6
二、平衡的几何法 F1 F2 F4
o
F2 F1 F3 FR=0
FRn 1
Fn
F3
F4
Fn 刚体平衡
结论:
力多边形自行封闭
平面汇交力系平衡的几何条件:该力系的力多边形自 行封闭。 7
例:门式刚架,在B点受一水平力F=20kN,不计刚架 自重。求支座 A、D 的约束力。
FD a F b
解法一: 1.取刚架为研究对象 2.画受力图 3.按比例作力三角形 4.量得
FD 10kN
FA 22.5kN
26.5
8
例:门式刚架,在B点受一水平力F=20kN,不计刚架 自重。求支座 A、D 的约束力。
FA
a
FD
b
F
1.取刚架为研究对象 AD 8m DC 4m CA 4 5m 解法二: F 2.画受力图 FA CA 22.4kN AD 3.作力三角形 F FD DC 10kN 4.由几何关系得 AD
16
解:1.取滑轮B为研究对象 2.画研究对象的受力图 3.列平衡方程
F 0 F 0
x
y
FBA F1 sin 30 F2 sin 60 0 FBC F1 cos 30 F2 cos 60 0
理论力学第二章平面力系

RA = RC = R, AC = a
B C
M1
A 60o
M2
60o D B
Mi = 0 C
a R - M1 = 0
RC
M1 = a R
(1)
M1
A
RA
取杆CD为研究对象。因C点约束方位
B
已定 , 则D点约束反力方位亦可确定,
C
画受力图。
RD = RC = R
M1
A 60o
M2
60o D
Mi = 0
力偶的表示方法
=
=
=
=
5.平面力偶系的合成和平衡条件
已知:M1, M2 ,Mn;
任选一段距离d
M1 d
F1
M2 d
F2
M1 F1d M2 F2d
Mn d
Fn
Mn Fnd
=
=
FR F1 F2 Fn
FR F1 F2 Fn
=
=
=
M FRd F1d F2d Fnd M1 M2 Mn
n
M Mi Mi
i 1
平面力偶系平衡的充要条件 M = 0,有如下平衡方程
Mi 0
平面力偶系平衡的必要和充分条件是:所有各力 偶矩的代数和等于零.
思考题1
刚体上A、B、C、D四点组成一个平行四边形,如在其 四个顶点作用有四个力,此四力沿四个边恰好组成封闭 的力多边形,如图所示。此刚体是否平衡?
F1 F2
y FR′
O
j
MO
Oi
x
Fn F1 F1 F2 F2
Fn Fn
y
F1′ M1
B C
M1
A 60o
M2
60o D B
Mi = 0 C
a R - M1 = 0
RC
M1 = a R
(1)
M1
A
RA
取杆CD为研究对象。因C点约束方位
B
已定 , 则D点约束反力方位亦可确定,
C
画受力图。
RD = RC = R
M1
A 60o
M2
60o D
Mi = 0
力偶的表示方法
=
=
=
=
5.平面力偶系的合成和平衡条件
已知:M1, M2 ,Mn;
任选一段距离d
M1 d
F1
M2 d
F2
M1 F1d M2 F2d
Mn d
Fn
Mn Fnd
=
=
FR F1 F2 Fn
FR F1 F2 Fn
=
=
=
M FRd F1d F2d Fnd M1 M2 Mn
n
M Mi Mi
i 1
平面力偶系平衡的充要条件 M = 0,有如下平衡方程
Mi 0
平面力偶系平衡的必要和充分条件是:所有各力 偶矩的代数和等于零.
思考题1
刚体上A、B、C、D四点组成一个平行四边形,如在其 四个顶点作用有四个力,此四力沿四个边恰好组成封闭 的力多边形,如图所示。此刚体是否平衡?
F1 F2
y FR′
O
j
MO
Oi
x
Fn F1 F1 F2 F2
Fn Fn
y
F1′ M1
理论力学第2章平面任意力系
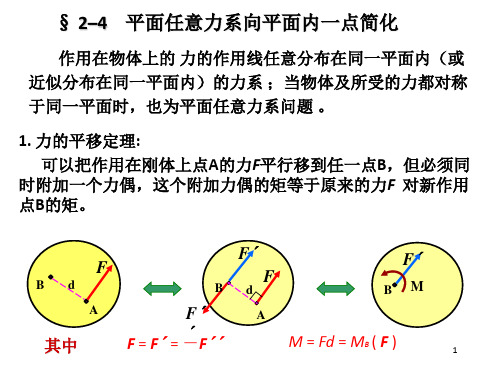
空载时轨道A 、 B的约束反力,并问此起重机在使用过程中有无翻
倒的危险。
解:
(1)起重机受力图如图
(2)列平衡方程 :
MA 0:
Q
Q(6 2) RB 4 W 2 P(12 2) 0
MB 0:
Q(6 2) W 2 P(12 2) RA 4 0
6m
解方程得:
W
P
12m
RA 170 2.5P
FR' Fi Fxi Fy j
MO MO (Fi )
3. 平面任意力系的简化结果
(1)FR´= 0,Mo ≠ 0, (2)FR´ ≠ 0,Mo = 0, (3)FR´≠ 0,Mo ≠ 0, (4)FR´= 0,Mo = 0,
合力偶,合力偶矩,MO MO (Fi )
合力,合力作用线通过简化中心O。
3
F2
j
F3
x
(437.6)2 (161.6)2
F1
1 1
100
Oi
1 2
466.5N
200
MO 21.44N m
y
合力及其与原点O的距离如图(c) 。 MO
x
y
d
x
O
FR FR′ 466.5N FR´
FR
O
d MO 45.96mm
(b)
(c)
FR
10
例11 水平梁AB受按三角形分布的载荷作用,如图示。载荷的
M
l
l
30
B
D
° F
3l
P
q
A
21
解:T字形刚架ABD的受力如图所示。
M
l
l
Fx 0
30
B
FAx 1 • q • 3a Fcos30 0
理论力学02平面力系的简化和平衡

即它就是作用线方程rxry例题2123平面力偶系作用在同一平面的多个力偶构成平面力偶系以其中任一力偶为基准通过移转改变力偶臂长度将其他力偶与该基准力偶叠合得到两个汇交力系再分别合成可以得到一个新力偶原力偶系的合力偶原力偶系的合力偶矩只受平面力偶系作用的刚体平衡充要条件
第二章
平面力系的简化和平衡
2.1力的合成与分解: 1.平行四边形法则: 作用于物体上同一点的两个力可合成 一个合力,此合力也作用于该点,合力的 大小和方向由以原两力矢为邻边所构成的 平行四边形的对角线来表示。
④ R ≠0, MO ≠0,为最一般的情况。此种情况还可以继续简 化为一个合力 R 。
合力R 的大小等于原力系的主矢 合力R 的作用线到简化中心的距离
MO d R
结论:
平面任意力系的简化结果 :①合力偶MO ; ②合力 合力矩定理:由于主矩 而合力对O点的矩
R
M O mO ( Fi )
主矩:
M O M O ( F ) 3F1 1.5P 1 3.9P 2 2355kN m
(2)求合力及其作用线位置:
d x 3.514m 0 0 cos 90 70.84
(3)求合力作用线方程:
MO MO
' ' FR x FRy y FRx x FRy y FRx
二、汇交力系的合成 由几何法知合力等于各分力的矢量和,即
R F Fn F i 1 F 2 F 3
又 由于
Fi X ii Yi j Zi k Fxii Fyi j Fzi k
代入上式得 R
F i F
xi
yi
j Fzi k
根据合矢量投影定理得合力在坐标轴的投影
第二章
平面力系的简化和平衡
2.1力的合成与分解: 1.平行四边形法则: 作用于物体上同一点的两个力可合成 一个合力,此合力也作用于该点,合力的 大小和方向由以原两力矢为邻边所构成的 平行四边形的对角线来表示。
④ R ≠0, MO ≠0,为最一般的情况。此种情况还可以继续简 化为一个合力 R 。
合力R 的大小等于原力系的主矢 合力R 的作用线到简化中心的距离
MO d R
结论:
平面任意力系的简化结果 :①合力偶MO ; ②合力 合力矩定理:由于主矩 而合力对O点的矩
R
M O mO ( Fi )
主矩:
M O M O ( F ) 3F1 1.5P 1 3.9P 2 2355kN m
(2)求合力及其作用线位置:
d x 3.514m 0 0 cos 90 70.84
(3)求合力作用线方程:
MO MO
' ' FR x FRy y FRx x FRy y FRx
二、汇交力系的合成 由几何法知合力等于各分力的矢量和,即
R F Fn F i 1 F 2 F 3
又 由于
Fi X ii Yi j Zi k Fxii Fyi j Fzi k
代入上式得 R
F i F
xi
yi
j Fzi k
根据合矢量投影定理得合力在坐标轴的投影
理论力学——2平面基本力系

27力偶系的合成与平衡1145cos30104145cos304874121527力偶系的合成与平衡1掌握共点力系合成与平衡的几何法与解析法3熟练运用平衡方程求解共点力系的平衡问题4理解力偶和力偶矩的概念并运用平衡条件求解力偶系的平衡问题2能正确地将力沿坐标轴分解并求力在坐标轴上的投影
第二章 基本力系
K
SB
(c)
§2–3 力的投影.力沿坐标轴的分解 3 力的投影.
y
一,力在坐标轴上的投影: 力在坐标轴上的投影:
Fx = F cos α
Fy = F cos β
b F a
y
B
β α
F Fx
O
a
b
x
结论:力在某轴上的投影,等于力的模乘以力与 结论:力在某轴上的投影, 该轴正向间夹角的余弦. 该轴正向间夹角的余弦. 夹角的余弦 反之, 已知时, 反之,当投影Fx ,Fy 已知时,则可求出 的大小和方向: 力 F 的大小和方向: Fy Fx 2 2 cos α = cos β = F = Fx + Fy F F
FB
D
(b)
x
P
又
= 14 °2' sin = 0.243 , cos = 0.969
联立求解, 联立求解,得
FB = 750 N
§2–4 4
共点力系合成与平衡的解析法
20kN的货物, 例题 2-4 利用铰车绕过定滑轮B的绳子吊起一重P=20kN的货物, ). 滑轮由两端铰链的水平刚杆AB 和斜刚杆BC 支持于点B (图(a) ). 所受的力. 不计铰车的自重, 不计铰车的自重,试求杆AB 和BC 所受的力.
§2–2 共点力系合成与平衡的几何法
例题2 图示是汽车制动机构的一部分. 例题2-2 图示是汽车制动机构的一部分.司机踩到制动蹬上 =212N, =45° 当平衡时, 水平, 的力P=212N,方向与水平面成α=45°角.当平衡时,BC水平, AD铅直,试求拉杆所受的力.已知EA=24cm,DE=6cm(点E在铅 铅直,试求拉杆所受的力. =24cm, =6cm( 都是光滑铰链,机构的自重不计 自重不计. 直线DA上),又B,C,D都是光滑铰链,机构的自重不计.
第二章 基本力系
K
SB
(c)
§2–3 力的投影.力沿坐标轴的分解 3 力的投影.
y
一,力在坐标轴上的投影: 力在坐标轴上的投影:
Fx = F cos α
Fy = F cos β
b F a
y
B
β α
F Fx
O
a
b
x
结论:力在某轴上的投影,等于力的模乘以力与 结论:力在某轴上的投影, 该轴正向间夹角的余弦. 该轴正向间夹角的余弦. 夹角的余弦 反之, 已知时, 反之,当投影Fx ,Fy 已知时,则可求出 的大小和方向: 力 F 的大小和方向: Fy Fx 2 2 cos α = cos β = F = Fx + Fy F F
FB
D
(b)
x
P
又
= 14 °2' sin = 0.243 , cos = 0.969
联立求解, 联立求解,得
FB = 750 N
§2–4 4
共点力系合成与平衡的解析法
20kN的货物, 例题 2-4 利用铰车绕过定滑轮B的绳子吊起一重P=20kN的货物, ). 滑轮由两端铰链的水平刚杆AB 和斜刚杆BC 支持于点B (图(a) ). 所受的力. 不计铰车的自重, 不计铰车的自重,试求杆AB 和BC 所受的力.
§2–2 共点力系合成与平衡的几何法
例题2 图示是汽车制动机构的一部分. 例题2-2 图示是汽车制动机构的一部分.司机踩到制动蹬上 =212N, =45° 当平衡时, 水平, 的力P=212N,方向与水平面成α=45°角.当平衡时,BC水平, AD铅直,试求拉杆所受的力.已知EA=24cm,DE=6cm(点E在铅 铅直,试求拉杆所受的力. =24cm, =6cm( 都是光滑铰链,机构的自重不计 自重不计. 直线DA上),又B,C,D都是光滑铰链,机构的自重不计.
第二章 理论力学平面力系

特殊时用 几 何法(解力三角形)比较简便。
2、一般对于受多个力作用的物体,且角度不特殊或 特殊,都用解析法。 3、投影轴常选择与未知力垂直,最好使每个方程中 只有一个未知数。
4、对力的方向判定不准的,一般用解析法。
5、解析法解题时,力的方向可以任意设,如果求出
负值,说明力方向与假设相反。对于二力构件,
力系分为:平面力系、空间力系 ①平面汇交力系 平面力系 ②平面平行力系(平面力偶系是其中的特殊情况 ) ③平面一般力系(平面任意力系) 平面汇交力系: 各力的作用线都在同一平面内且 汇交于一点的力系。 研究方法:几何法,解析法。
例:起重机的挂钩。
2.1 平面汇交力系的合成与平衡
2.1.1 平面汇交力系合成的几何法与平衡的几何条件 1、几何法
Y X
87.46 8.852, 83.55O 9.88
由于FRx为负,FRY为正,故 在第二象限,合力 FR的作用线通过汇交点O,如图2.12
【例2.5】
如图2.1 3所示为建筑工地使用的 井架把杆装置,杆AB的一端铰接在井架上, 另一端用钢索BC与井架连接。重物通过卷扬 机由绕过滑轮BC的钢索起吊。已知重物 Fw=2kN,把杆重量、滑轮的重量及滑轮的大 小不计,滑轮的轴承是光滑的。试求钢索BC 的拉力和把杆AB所受的力。
由图2.14(b)可知 DB CB cot l cot 30 0 tan 0.866 AB 2l 2l 40.90 将 40.90 代入方程并求解得 FA 13.2 KN FB 8.66 KN
解题技巧及说明: 1、一般地,对于只受三个力作用的物体,且角度
2、主矢和主矩
主矢:力系各力的矢量和,即 主矩:力系中各力对于任选简化中心O之矩的矢量和,即
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Fy FR
Fiy FR
15
???
❖ 例2-3如图2-11所示,作用
于吊环螺钉上的四个力F1, F2,F3,F4构成平面汇交
力系。已知各力的大小方
向F1 =360N,1=60°; F2 =550N,2 =0°; F3 =380N,3 =30°;F4 =300N, 4=70°。试用
解析法求合力的大小和方
Fy Fy1 Fy2 Fy3 Fy4 F1 sin a1 F2 sin a2 F3 sin a3 F4 sin a4 360sin 600 550sin 00 380sin 300 300sin 700 160
FR Fx2 Fy2 (1162)2 (160)2 1173N
FR F1 F2 Fn F
特
5
2.1.2 平面汇交力系平衡的几何条件
平面汇交力系平衡的必要与充分条件是: 该力系的合力等于零。用矢量式表示为:
Fi 0
平面汇交力系平衡的必要与充分条件是:该力系的 力多边形自行封闭,这是平衡的几何条件。
6
例 题 1 已知:P,a
PC
2a
D
a
求:A、B处约束反力。
第二章
平面力系
1
§2–1 平面汇交力系 §2–2 平面力对点之矩平面力偶 §2-3 平面任意力系的简化
§2–4 平面任意力系的平衡条件和平衡方程
§2–5 物体系统的平衡,静定和超静定问题
§2–6 平面简单桁架的内力计算
目录
2
§2–1 平面汇交力系
平面汇交力系:
❖ 力的作用线位于 同一平面内且汇
F2 F1
1 力在坐标轴上的投影
Fx F cos
Fy F cos
y
F
Fy
x O
Fx
力在坐标轴上的投影是代数量还是矢量?
11
力的解析表达式
F x Fx i
F y Fy j
y
Fy j Oi
F Fx x
解析表达式:F F x F y Fx i Fy j
F Fx2 F y2
cos(F,i) F x F
从(2)可得:FAB=FAC,代(1)得:FAC=F/(2 cos)
[点C] Fy=0; FD+FCAsin =0;
(3)(有:FCA=FAC)
F FD 2
tanα FL 2h
19
已知:F=60N 求:A,C点的作用力
FB a C
a 600 D
A
20
[例2-4]
21
2.2 平面力对点之矩,平面力偶
解: (1)取刚架为研究对象
A
B
(2)画受力图
FA
FB
(3)按比例作图求解
由图中的几何关系得
FB P tan 0.FB2
5P 2
7
[例2] 已知压路机碾子重P=20kN, r=60cm, 欲拉过h=8cm的障碍物。 求:在中心作用的水平力F的大小和碾子对障碍物的压力。
向。
各力的汇交点
解:
F1
F2
F3
F4
Fx F1cosα1 F2cosα2 F3cosα3 F4cosα4
Fy F1sinα1 F2sinα2 -F3sinα3 -F4sinα4
16
Fx Fx1 Fx2 Fx3 Fx4 F1 cos a1 F2 cos a2 F3 cos a3 F4 cos a4 360 cos 600 550 cos 00 380 cos 300 300 cos 700 360 0.5 550 380 0.866 300 0.342 1162N
FRx Fix i 1
n
FRy Fiy i 1
平面汇交力系的合力在某轴上的投影,等于力系
中各个分力在同一轴上投影的代数和。
14
4 平面汇交力系合成的解析法
FR
F F 2 Rx
2 Ry
( Fix )2 ( Fiy )2
cos(FR , i )
Fx FR
Fix FR
cos(FR ,
j)
2.2.1 力对点之矩(力矩)
矩心
F
力臂
力对点之矩是一个代数量
解: ①选碾子为研究对象 ②取分离体画受力图
∵当碾子刚离地面时NA=0,拉力F最大, 这时拉力F和自重及支反力NB构成一平衡力系。 由平衡的几何条件,力多边形封闭,故
8
③作力多边形或力三角形
F Ptg
NB
P
cos
又由几何关系: tg
r2 (rh)2 0.577
rh
所以
F=11.5kN , NB=23.1kN
cos(F, j) Fy F
12
2 合力的正交分解与力的解析表达式
F2 yF1
FRy
F3 FR
F4
j
A
Oi
FRx x
FR FRx FRy FRxi FRy j
FR FRx2 FRy2
cos(F , i ) FRx cos(F, j) FRy
F R
FR 13
3 合矢量投影定理
n
tga Fy 160 0.133 Fx 1162
可得a 7054'
因为Fx为正,Fy为负,故合力R在第四象限,指向如图所示
17
2.1.4 平面汇交力系的平衡方程
FR ( Fix )2 ( Fiy )2 0
Fix 0 Fiy 0
平面汇交力系平衡的必要和充分条件是:各力在
作用面内两个任选的坐标轴上投影的代数和等于零。 上式称为平面汇交力系的平衡方程。
由作用力和反作用力的关系,碾子对障碍物的压力等于23.1kN。
此题也可用力多边形方法用比例尺去量。
9
2.1.3 平面汇交力系合成与平衡的解析法
力在轴上的投影:
B F A
F
A
B
n
n
a
b
b
a
Fx ab
Fx ab
正负号的规定:
若 a到b的指向与n轴正向一致,取正号;
若 a到b的指向与n轴正向相反,取负号。 10
18
例2-4:图示压榨机,在A点作用水平力F、C块与光滑墙
接触,在F力作用使C块压紧物体D,求:物体D所受压力。
h
y
y
B
FAB
[C]
L
F
x
FCA x
L
F A
FAC [A]
FC
FD
C 解:[点A] Fx=0; – FABcos – FACcos – F=0 (1)
D
Fy=0; FABsin–FACsin =0 (2)
交于一点的力系。
A
F3 F4
3
平面汇交力系合成与平衡的几何法
2.1.1 平面汇交力系合成的几何法
F4
力的多边形:
F2 F1
F3
F3 F2 FR1
FR2 FR
F4
F2
F4
F3
A
F1
a
FR
用力多边形求合力的作图规则称为力的多边形F法1则。 a
4
结论:平面汇交力系可简化为一合力,其合力的大小 与方向等于各分力的矢量和(几何和),合力的作用线 通过汇交点。 用矢量式表示为:
