会面问题 利用概率论及MATLAB来求解
matlab在概率统计中的计算

4.1 计算组合数、验证概率的频率定义,计算古典概率
4.1.1 计算nk.
P
P
使用语句n^k
4
第4章 概率统计
例如计算 511
N=5^11 N=
48828125
如计算 5−2.8
N=5^(-2.8) N=
0.0110
4.1.2 计算组合数 Cnk
计算组合数 Cnk 时,使用语句nchoosek(n,k).
1
MATLAB6.0数学手册
光驱:8倍速以上; 内存:至少64MB,但推荐128MB以上; 硬盘:视安装方式不同要求不统一,但至少留1GB用于安装(安装后未必有1GB); 显卡:8位; MATLAB 6对软件的要求 Windows95 、Window98、Windows NT或Windows2000; Word97或word2000等,用于使用MATLAB Notebook; Adobe Acrobat Reader 用于阅读MATLAB的PDF的帮助信息。 MATLAB 6的安装和其它应用软件类似,可按照安装向导进行安装,这里不再赘述。 MATLAB的启动和退出 与常规的应用软件相同,MATLAB的启动也有多种方式,首先常用的方法就是双击桌面的 MATLAB图标,也可以在开始菜单的程序选项中选择MATLAB组件中的快捷方式,当然也可 以在MATLAB的安装路径的子目录中选择可执行文件“MATLAB.exe”。 启动MATLAB后,将打开一个MATLAB的欢迎界面,随后打开MATLAB的桌面系统(Desktop) 如图2-1所示。
在MATLAB命令行操作中,有一些键盘按键可以提供特殊而方便的编辑操作。比如:“↑” 可用于调出前一个命令行,“↓”可调出后一个命令行,避免了重新输入的麻烦。当然下 面即将讲到的历史窗口也具有此功能。 历史窗口(Command History) 历史命令窗口是MATLAB6新增添的一个用户界面窗口,默认设置下历史命令窗口会保留自 安装时起所有命令的历史记录,并标明使用时间,以方便使用者的查询。而且双击某一 行命令,即在命令窗口中执行该命令。 当前目录窗口(Current Directory )
Matlab在《概率论与数理统计》教学中的应用

Matlab在《概率论与数理统计》教学中的应用
Matlab提供了丰富的概率分布函数,可以帮助学生更好地理解不同的概率分布。
学生可以使用Matlab生成正态分布、二项分布、泊松分布等不同的概率分布,并画出相应的概率密度函数、累积分布函数等图形。
通过实际的计算和绘图,学生可以更直观地看到不同概率分布的特点,加深对概率分布的理解。
Matlab提供了各种统计函数,可以方便地进行数据的描述性统计和推断性统计。
学生可以使用Matlab计算样本的平均值、方差等描述性统计量,还可以使用Matlab进行假设检验、置信区间估计等推断性统计。
通过实际的计算和分析,学生可以更好地掌握统计学中的概念和方法。
Matlab还可以进行模拟实验,帮助学生理解概率和统计的原理。
学生可以使用Matlab 模拟抛硬币的实验,验证概率的定义和性质。
学生还可以使用Matlab模拟中心极限定理,观察样本均值的分布趋于正态分布的情况。
通过实际的模拟实验,学生可以更深入地理解抽样分布和极限定理等重要概念。
Matlab还可以用于数据的可视化。
学生可以使用Matlab绘制直方图、散点图、箱线图等图形,展示数据的分布和变化。
通过可视化的方式,学生可以更好地理解数据的特点和规律,并能够更直观地展示和解释统计分析的结果。
Matlab在《概率论与数理统计》教学中具有广泛的应用价值。
通过利用Matlab进行计算、模拟和可视化等任务,可以帮助学生更好地理解概率和统计的概念和方法,提高学习效果。
在教学中合理地使用Matlab可以有效地促进学生对概率论与数理统计的学习和理解。
概率论问题MATLAB仿真求解程序

clc; clear; close all; a=10; b=3; p=0.55; S=0; N=10000; m=6; %甲的赌本 %乙的赌本 %甲赢的概率 % 计数设置为0 % 模拟次数 %设定随机数状态值(1 2 3 4 5 6 ),改变这个值可以进行不同的实验
rand('state',m); %设置随机数状态 for k=1:N; at=a;%初始化甲的赌本 bt=b;%初始化乙的赌本 while at>0.5&bt>0.5;%模拟整个赌博过程 r=[(rand<p)-0.5]*2; % 算输赢 at=at+r;%交换赌本 bt=bt-r;%交换赌本 end S=S+(at<0.5); %如甲输,累加甲输的次娄 end P=S/N %计算甲输的概率值 g=p/[1-p]; Po=[1-g^b]/[1-g^(a+b)] %返回甲输光的概率理论值
%n 次中与平行线相交的次数的频率比,即相交的概率,vpa() 以任意精度(4 位小数点,默认值为 32 位)显示出来 pi_m=vpa((2*L*n)/(m*d),15) %利用投针频率估计圆周率 pi,vpa()以任意精度(15 位小数点,默认值为 32 位)显示出来
运行结果
p =.3207 pi_m =3.11817898347365
(A)
(B)
在图(A)中,当小球从顶部向下降落时,遇到第一层竖隔板,此时小球分别向左 右下落的概率各占一半(0.5);当小球继续下落遇到第二层竖隔板时,小球仍以 左右相同的概率往下落,以后每层均如此(如图(B)所示)。最后到了第 8 层底 部,小球将落入底部 9 个槽中的一个。但是小球落入每个槽内的概率是不一样的。 如查将这个 9 个槽编号为:1、2、3、45、6、7、8、9,计算小球落入第 9 个槽中 的概率。 理论分析:这是一个经典的二项分布概率模型。考虑在第 K 层小球运动方向有两种 可能,用 X k 表示,则 X k 服从两点分布。这里用 X k = 1 表示向右侧竖隔板方向运 动,用 X k = 0 表示向左侧竖隔板方向运动,它们发生的概率均为 0.5。最终位置 X 由 X = ∑ X k 决定,即二项分布决定,上述第 8 层即有 X ~ Binomial (8, 0.5) ,上述该
第8章 matlab 概率论与数理统计问题的求解

8.1.3 概率问题的求解
图4-9
• 例:
>> b=1; p1=raylcdf(0.2,b); p2=raylcdf(2,b); P1=p2-p1 P1 = 0.8449
>> p1=raylcdf(1,b); P2=1-p1 P2 = 0.6065
• 例:
>> syms x y; f=x^2+x*y/3; >> P=int(int(f,x,0,1/2),y,0,1/2) P= 5/192 >> syms x y; f=x^2+x*y/3; P=int(int(f,x,0,1),y,0,2) P= 1
8.1.2.3
பைடு நூலகம்
分布
• 例:
>> x=[-0.5:.02:5]‘; %x=[-eps:-0.02:-0.5,0:0.02:5]; x=sort(x’);替代 >> y1=[]; y2=[]; a1=[1,1,2,1,3]; lam1=[1,0.5,1,2,1]; >> for i=1:length(a1) y1=[y1,gampdf(x,a1(i),lam1(i))]; y2=[y2,gamcdf(x,a1(i),lam1(i))]; end >> plot(x,y1), figure; plot(x,y2)
8.1.2.2 正态分布
正态分布的概率密度函数为:
• 例:
>> x=[-5:.02:5]'; y1=[]; y2=[]; >> mu1=[-1,0,0,0,1]; sig1=[1,0.1,1,10,1]; sig1=sqrt(sig1); >> for i=1:length(mu1) y1=[y1,normpdf(x,mu1(i),sig1(i))]; y2=[y2,normcdf(x,mu1(i),sig1(i))]; end >> plot(x,y1), figure; plot(x,y2)
利用matlab辅助《概率论与数理统计》教学时需要注意的一个问题

助 其克服学 习和生活 中的 困难,极大 的带动和鼓舞 了苗 圃幼 高 自身的领导能力和组织能力, 实现 了预备党 员与入党积极分 苗 。例如 , 丁中有一个 叫别传杰 的学生 , 园 他在 2 1 0 0年“ 友 子 的 共 同 成 长 。 用 杯’ , 第六届全 国大学 生创 业设计暨沙盘模拟经营大赛总决赛 一 等奖, 作为会 计 5 8 班 的一名 园丁 , 03 在他 的鼓舞和带动下 , 班
先 争优 活 动 开 展 以来 , 丁 多 次 组 织 各 苗 圃理 论 学 习或 时事 讨 分 子 的 共 同 成长 。班 级联 系 人 在 实 施 《 色 苗 圃》 园 红 的过 程 中 需要
论 活动 , 学习 内容包 括朝核 问题 , 日关 系 , 中 社会主义新 农村 ,
自学入党 的基本知识、入党材 料的书写规范和政治学习 内容 ,
懂、 方法难以掌握 。 a 1 b是一种高性能的、 M 乞a 用于工程计 算的编 这篇论文抛砖 弓 玉, l 引起大家的共鸣 。 程 软件 , 它把科学 计算 、 结果 的可视化 和编程都集 中在一个 使 二、 数组地址和坐标系地址的微妙差异
圃活动使园丁从政 治 、 思想 、 习、 作、 学 工 生活纪律 、 考勤 、 动 会继续将这份“ 活 优秀 ’ 爱心 , , 和“ , 传承下去。例如 , 为苗 圃的会 作 参 与情况 、奖 惩情况等 8个方面 对入党积 极分子进 行综合考 计 5 8 0 1班 , 因学习 的校 区变 更、 导员老师 的调整 , 个班级 辅 整 察 。支部按照“ 成熟一个 , 发展一个 ” 的原则, 认真做好党 员发展 在很长一段 时间里凝聚力明显 下降。该班 的园丁王雯了解情况 工作。在‘ ‘ 创先争优 ” 动开展 以来 , 活 共发展党 员 1 0 , 2 人 预备党 后针对班 级同学 的情况 , 同学们进行 交流谈心 , 与 开展一些班 员转 正 3 人 , 中包括“ 0 2 ” 雄集 体成 员龚想 涛 和孟 亮 级活动 以增加班级凝聚力。通过相互的交流和学习下, 7 其 1・4英 班级凝 雨 支部党员在创 先争优活动开展 以来 , 在各类竞 赛活动 中, 获 聚 力 增 强 了 , 习 氛 围 也浓 厚 了 , 计 5 8 班 成 为全 院 英语 四 学 会 01 得国家级奖项 4人次 ,省级奖项 5 次,院级奖项 2 1人次 。 级一次性过级率最高 的班级,全班 4 人 4 9人 ,通过四级人数 达 4 6 () 2 党员教育得到 了加 强, 弥补 了“ 重发展 , 培养 ” 轻 的不足 。创 名 , 通过 六级人数达 2 7人。 () 4 促进 了班级联系人 与入党积极
matlab在概率论与数理统计课程教学过程中的应用

matlab在概率论与数理统计课程教学过程中的应用
Matlab在概率论与数理统计课程教学过程中的应用包括:
1. 使用Matlab处理、显示和分析概率分布。
可以使用Matlab 绘制直方图、折线图和其他可视化工具,表示不同类型的概率分布;
2. 使用Matlab进行统计模拟分析,包括随机变量的生成,抽样方法的分析,以及统计量的估计;
3. 使用Matlab进行统计推断,如检验统计假设、拟合概率分布并测试其相关性、以及定量比较等;
4. 利用Matlab进行多元统计分析,包括协方差和相关分析,多元回归分析等;
5. 利用Matlab进行数据处理测试,包括卡方检验、t检验、ANOVA等;
6. 使用Matlab进行非参数统计模型拟合,如Kolmogorov-Smirnov检验等;
7. 使用Matlab应用概率论方法,如随机事件分析、随机过程分析、以及马尔可夫链等;
8. 使用Matlab来计算和估计两个随机变量之间的各种统计函数,如相关系数、协方差等。
会面问题 利用概率论及MATLAB来求解
会面问题甲乙两人相约某天9:00-10:00在某地会面商谈生意,双方约定先到者必须等候另一人20分钟,过时如果另一人仍未到则可离去,试求两人能够会面的概率。
1用所学概率论知识建模并求解;2用Matlab 软件编程模拟实现这个过程,并与理论结果相比较。
解:用所学概率论知识建模并求解将9点到10点看成是0到60分钟,则甲乙两人到达的时间概率分布可看做是分布,此时不妨设甲到达的时间为t1,乙到达的时间为t2,(0<=t1,t2<=60) 当t1,t2满足|t1-t2|<=20时,两人则可碰面。
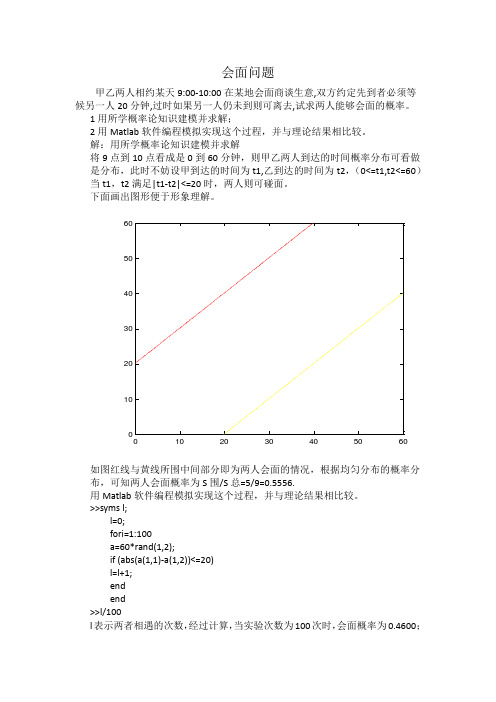
下面画出图形便于形象理解。
如图红线与黄线所围中间部分即为两人会面的情况,根据均匀分布的概率分布,可知两人会面概率为S 围/S 总=5/9=0.5556.用Matlab 软件编程模拟实现这个过程,并与理论结果相比较。
>>syms l;l=0;fori=1:100a=60*rand(1,2);if (abs(a(1,1)-a(1,2))<=20)l=l+1;endend>>l/100l 表示两者相遇的次数,经过计算,当实验次数为100次时,会面概率为0.4600; 01020304050600102030405060下面我们增大实验次数,实验次数为1000时,会面概率为0.5590;实验次数为10000时,会面概率为0.5525;实验次数为100000时,会面概率为0.5546;实验次数为1000000时,会面概率为0.5552;…从随机实验可以发现,当实验次数越来越大时,随机事件发生的概率就越来越稳定于一个值,而这个值与我们理论计算出来的值是一致的,因此从实验角度证明了概率论概率计算理论的正确性。
培养解决实际问题的能力,概率论与数理统计问题matlab实战

培养解决实际问题的能力,概率论与数理统计问题matlab实战
培养解决实际问题的能力,需要注重以下几点:
1. 提供真实的实际问题:了解实际问题,并且确保这些问题是切实存在的,而不仅仅是假设或者理论上的问题。
2. 培养综合运用知识的能力:让学生了解和掌握广泛的理论知识,并能够将这些知识应用到解决实际问题中。
这包括数学、统计学、编程等多个领域的知识。
3. 强调实践与动手能力:通过实际的操作和实践,学生能够掌握具体的解决问题的方法和技巧,培养他们的动手能力。
4. 提供合适的工具和资源:对于解决实际问题,合适的工具和资源是非常重要的,比如MATLAB等软件工具可以用来进行概率论和数理统计的实战练习。
5. 激发学生的兴趣和探索精神:鼓励学生主动探索和思考,培养他们对实际问题的兴趣,让他们通过解决实际问题来提升自己的能力。
至于概率论与数理统计问题的MATLAB实战,您可以通过以下几个步骤进行:
1. 确定问题和目标:选择一个与概率论和数理统计相关的实际问题,明确解决问题的目标和方法。
2. 收集数据:根据问题的要求,收集相应的数据,可以是实际观测数据或模拟生成的数据。
3. 数据预处理:对数据进行清洗、整理和转换,确保数据的质量和可用性。
4. 数据分析与建模:根据问题的要求,运用概率论和数理统计的相关方法,对数据进行分析和建模。
5. 结果可视化与解释:利用MATLAB等软件工具,将分析结果进行可视化展示,并对结果进行解释和讨论。
6. 结论总结与讨论:根据分析结果,总结结论,并进行讨论和推测,提出可能的解决方案或建议。
请注意,以上回答仅供参考,具体操作中需根据具体情况和问题的要求进行调整和完善。
实验5(1)-概率统计问题的Matlab求解.

参数估计
例2. 分别使用金球和铂球测定引力常数 (1)用金球测定观察值为:6.683 6.681 6.676 6.678 6.679 6.672 (2)用铂球测定观察值为:6.661 6.661 6.667 6.667 6.664 设测定值总体为 ,μ和σ为未知。对(1)、 (2)两种情况分别求μ和σ的置信度为0.9的置信区 间。
解:需要检验假设 H 0 : 1 2 0 H1 : 1 2 0 X=[78.1 72.4 76.2 74.3 77.4 78.4 76.0 75.5 76.7 77.3]; Y=[79.1 81.0 77.3 79.1 80.0 79.1 79.1 77.3 80.2 82.1]; [h,sig,ci]=ttest2(X,Y,0.05,-1) 结果显示为: h= 1 sig = 2.1759e-004 %说明两个总体均值相等的概率很小 ci = -Inf -1.9083 结果表明:h=1表示在 0.05 水平下,应该拒绝原假设,即 认为建议的新操作方法提高了产率,因此,比原方法好。
由上可知,金球测定的μ估计值为6.6782,置信 区间为[6.6750,6.6813]; σ的估计值为0.0039,置信区间为[0.0026, 0.0081]。 泊球测定的μ估计值为6.6640,置信区间为 [6.6611,6.6669]; σ的估计值为0.0030,置信区间为[0.0019, 0.0071]。
例 5 一道工序用自动化车床连续加工某种零件,由于刀具 损坏等会出现故障.故障是完全随机的,并假定生产任一零 件时出现故障机会均相同 .工作人员是通过检查零件来确定 工序是否出现故障的 . 现积累有 100 次故障纪录,故障出现 时该刀具完成的零件数如下:
459 612 926 527 775 402 699 447 621 764 362 452 653 552 859 960 634 654 724 558 624 434 164 513 755 885 555 564 531 378 542 982 487 781 49 610 570 339 512 765 509 640 734 474 697 292 84 280 577 666 584 742 608 388 515 837 416 246 496 763 433 565 428 824 628 473 606 687 468 217 748 706 1153 538 954 677 1062 539 499 715 815 593 593 862 771 358 484 790 544 310 505 680 844 659 609 638 120 581 645 851
Matlab在《概率论与数理统计》教学中的应用

Matlab在《概率论与数理统计》教学中的应用概率论是《概率论与数理统计》课程中的重要部分,Matlab可以帮助学生更好地理解和应用概率论。
1. 随机数生成与概率计算Matlab可以生成符合不同分布的随机数,如正态分布、均匀分布等,并进行概率计算和统计推断。
以正态分布为例,使用命令“normrnd(mu,sigma,m,n)”可以生成一个mu为均值,sigma为标准差的n行m列的正态分布随机数矩阵。
使用函数“normpdf(x,mu,sigma)”可以计算正态分布的概率密度函数在x处的取值,使用函数“normcdf(x,mu,sigma)”可以计算正态分布的累积分布函数在x处的取值。
这些功能可以帮助学生更好地理解正态分布的概念和相关理论。
2. 离散随机变量的概率分布1. 数据描述与可视化Matlab可以帮助学生更好地进行数据描述和可视化。
使用命令“mean(x)”可以计算数据的平均值,使用命令“std(x)”可以计算数据的标准差,使用命令“hist(x)”可以绘制数据的直方图。
这些功能可以帮助学生更好地理解数据的基本特征和数据分布情况。
2. 参数估计与假设检验Matlab可以帮助学生完成参数估计和假设检验。
以t检验为例,使用命令“ttest(x,y)”可以进行两样本t检验,使用命令“ttest(x,m)”可以进行单样本t检验。
这些功能可以帮助学生更好地进行参数估计和假设检验的计算和分析。
结语综上所述,Matlab是一款重要的数学软件工具,在《概率论与数理统计》课程教学中发挥着重要的作用。
通过Matlab,学生可以更好地理解和应用概率论和数理统计的理论知识,提高他们的数据分析和计算能力。
Matlab在《概率论与数理统计》教学中的应用

Matlab在《概率论与数理统计》教学中的应用概率论与数理统计是一门重要的数学学科,它主要研究随机事件发生的概率和随机变量的规律性。
Matlab是一种强大的科学计算软件,具有丰富的数学计算工具和图形绘制功能,因此在《概率论与数理统计》教学中,Matlab被广泛应用于概率论和数理统计的理论研究、统计分析和数据可视化等方面。
一、概率论的应用1. 概率计算:Matlab可以进行各种概率计算,包括事件的概率计算、条件概率计算、概率分布计算等。
通过编写相应的概率计算程序,可以方便地进行概率问题的求解和验证。
2. 模拟实验:概率论中常常需要进行大量的随机实验,通过模拟实验来验证概率理论的结论。
Matlab提供了丰富的随机数生成函数,可以生成各种分布的随机样本并进行相关的分析和验证。
3. 统计分布拟合:在概率论中,常常需要对实际观测数据进行统计分布的拟合。
Matlab提供了多种分布的函数和工具箱,可以帮助进行数据的拟合和参数估计。
二、数理统计的应用1. 描述统计分析:Matlab可以对数据进行基本的描述统计分析,包括数据的中心趋势、离散程度和分布状况的度量等。
通过编写相应的统计分析程序,可以方便地获取数据的平均值、方差、标准差等统计指标。
2. 参数估计与假设检验:在数理统计中,常常需要对总体参数进行估计和假设检验。
Matlab提供了多种参数估计和假设检验的函数和工具箱,可以进行参数的点估计、区间估计和假设检验等分析。
3. 数据可视化与分析:Matlab具有强大的数据可视化功能,可以绘制各种图表和图形,包括直方图、散点图、箱线图等。
通过对数据进行可视化分析,可以更直观地了解数据的分布特征和相关关系。
除了以上应用,Matlab还可以在概率论与数理统计的教学中进行实际案例分析和建模。
通过编写相应的程序和脚本,可以更具体地研究和解决实际问题,提高学生的应用能力和创新思维。
Matlab在《概率论与数理统计》教学中的应用范围广泛,包括概率计算、模拟实验、统计分布拟合、描述统计分析、参数估计与假设检验、数据可视化与分析等方面。
第3章 概率统计实例分析及MatlAb求解

第3章概率统计实例分析及MatlAb求解3.1 随机变量分布与数字特征实例及MATLAB求解3.1.1 MATLAB实现用mvnpdf和mvncdf函数可以计算二维正态分布随机变量在指定位置处的概率和累积分布函数值。
利用MATLAB统计工具箱提供函数,可以比较方便地计算随机变量的分布律(概率密度函数)、分布函数及其逆累加分布函数,见附录2-1,2-2,2-3。
MATLAB中矩阵元素求期望和方差的函数分别为mean和var,若要求整个矩阵所有元素的均方差,则要使用std2函数。
随机数生成函数:rand( )和randn( )两个函数伪随机数生成函数:A=gamrnd(a,lambda,n,m) % 生成n*m的 分布的伪随机矩阵B=raylrnd(b,n,m) %生成rayleigh的伪随机数3.1.2 相关实例求解例2-1计算服从二维正态分布的随机变量在指定范围内的累积分布函数值并绘图。
程序:%二维正态分布的随机变量在指定范围内的累积分布函数图形mu=[0 0];sigma=[0.25 0.3;0.3 1];%协方差阵x=-3:0.1:3;y=-3:0.2:3;[x1,y1]=meshgrid(x,y);%将平面区域网格化取值f=mvncdf([x1(:) y1(:)],mu,sigma);%计算累积分布函数值F=reshape(f,numel(y),numel(x));%矩阵重塑surf(x,y,F);caxis([min(F(:))-0.5*range(F(:)),max(F(:))]);%range(x)表示最大值与最小值的差,即极差。
axis([-3 3 -3 3 0 0.5]);xlabel('x'); ylabel('y');zlabel('Probability Density');图1 二维正太分布累积分布函数值图例2-2 设X 的概率密度为⎪⎪⎪⎩⎪⎪⎪⎨⎧<<-≤≤=其他。
8.7--概率统计问题的-MATLAB求解

输入命令 >> unifcdf(3,0,5)
ans = 0.6000
输出结果
输入命令 >> normcdf(90,80,6)-normcdf(69,80,6)
输出结果
ans = 0.9188
输入命令 >> 1-expcdf(100,2000)
ans = 0.9512
输出结果
8.7.2 随机变量的数字特征——数学期望与方差
输入命令 >> X=[0 1 2 3 4]; >> P=[0.1 0.2 0.3 0.2 0.2]; >> EX=sum(X.*P)
>> DX=sum(X.^2.*P)-(EX)^2
输出结果
EX = 2.2000
DX = 1.5600
输入命令 >> [E,D]=binostat(20,0.6)
E= 12 D= 4.8000
输出结果
EX = 1
DX = -1/4
输入命令 >> [E,D]=unifstat(0,10)
E= 5 D= 8.3333
输出结果
输入命令
E=
>> [E,D]=normstat(60,5)
60 D=
25
输出结果
输入命令 >> [E,D]=expstat(0.5)
E= 0.5000 D= 0.2500
第8章 MATLAB数学实验与数学建模
(四)
8.7 实验六 概率统计问题的MATLAB求解
8.7.1 几种常用的概率分布
1.离散型随机变量的概率 命令调用格式:
binopdf(k,n,p) 计算二项分布 B(n, p)中随机变量 k 的概率; binocdf(k,n,p) 计算二项分布 B(n, p)中随机变量 k 的概率; poisspdf(k, ) 计算泊松分布 P()中随机变量 k 的概率; poisscdf(k, ) 计算泊松分布 P()中随机变量 k 的概率.
概率学中MATLAB的基本使用

③ 数组的幂运算 在 MATLAB 中, 数组的幂运算与矩阵的幂运算完全不同. 数组的幂运算符号为“.^ ”(注意运算符中的小点号), 用来 表示元素对元素的幂运算. 而矩阵的幂运算符号为“^ ”. 例 1-12 进行数组与数的幂运算. 在命令窗口中输入: a = [1 3 4; 2 6 5; 3 2 4]; c = a.^2 回车后显示: c= 1 9 16 4 36 25 9 4 16 为了便于比较, 下面列出矩阵的幂运算.
二. 实验目的与要求
(1) 熟练掌握 MATLAB 软件的基本操作 软件的基本操作; (2) 熟练掌握 MATLAB 中数据输入的基本方法 中数据输入的基本方法; (3) 熟练掌握数据加、减、乘和除四则运算的基本方法; 熟练掌握数据加、 乘和除四则运算的基本方法 (4) 熟练掌握函数求导数、求微分和积分运算的基本方法 熟练掌握函数求导数、求微分和积分运算的基本方法; (5) 熟悉与排列、组合有关的操作命令. 熟悉与排列、组合有关的操作命令.
由于数组的除法运算有点特殊, 为了便于读者使用, 我们对数组的除法运算规则总结如下: (a) 数组间的除法运算为参与运算的数组中对应元 素相除, 结果数组与参与运算的数组大小相同. (b) 数组与标量的除法运算为数组中的每个元素与 标量相除, 结果数组与参与运算的数组大小相同. (c) 数组的除法运算符号有两个, 即左除号“./”与 右除号“.\”, 它们的关系是: a./b = b.\a .
3. 数组加、减、乘、除四则运算及其幂、开方、指数与对数 数组加、 除四则运算及其幂、开方、 运算 (1) 数组运算 ① 数组与标量的四则运算 数组与标量之间的四则运算是指数组中的每个元素与标量进 行加、 减、 乘、 除运算. 例 1-10 对数组进行乘、除与加、减一个数的运算. 在命令窗口中输入: x = [1 3 4; 2 6 5; 3 2 4]; a = 2*x-2 c = x/2
07概率统计的matlab求解

k}
C
k n
p
k
(1
p)nk
命令1:Fx=binocdf(x,n,p)
功能:计算二项分布的累积概率Fx=P{X≤x}=F(x)
命令2:x=binoinv(y, n,p)
功能:计算随机量x,使得y=P{X≤x}
命令3:X=binornd(n,p,M,N)
功能:产生M*N维符合二项分布的随机数矩阵X
命令4:Px=binopdf(x,n, p)
功能:计算试验中事件恰好发生x次的概率Px=P{X=x}
2019/11/4
10
泊松分布X~P(λ)
P{X k} e k
命令1:Fx=poisscdf(x,lambda)
k!
功能:计算累积概率Fx=P{X≤x}=F(x)
命令2:x=poissinv(p, lambda)
(3) specs=[1.5,1.9];
pp=normspec(specs,2,0.5)
2019/11/4
21
2019/11/4
Density
Probability Between Limits is 0.26209 0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
0
0.5
1
1.5
2
2.5
3
3.5
与此类似的有:求和(sum),最大(max),最小(min)等 2.离散型随机变量的期望----EX=sum(X.*P) 功能:计算随机值向量X与对应概率向量P的乘积之和 3.连续型随机变量的期望----EX=int(x*fx,x,a,b) 功能:用积分计算期望
概率统计在MATLAB中的实现方法解析

概率统计在MATLAB中的实现方法解析概率统计是一门研究随机现象的规律性和不确定性的学科,广泛应用于各个领域。
而MATLAB是一种强大的科学计算软件,可以在概率统计领域中提供很多实用的工具和方法。
本文将探讨概率统计在MATLAB中的实现方法,帮助读者更好地理解和应用于实践。
一、概率分布的生成和拟合在概率统计中,对于一些已知的概率分布,我们常常需要生成符合该分布的随机数,或者通过已有的样本数据对分布进行拟合。
在MATLAB中,可以使用一些函数来实现这些操作。
首先,对于已知的概率分布,例如正态分布(高斯分布),可以使用normrnd()函数生成符合该分布的随机数。
该函数的输入参数包括均值和标准差,输出为符合正态分布的随机数。
例如,我们可以生成100个符合均值为0,标准差为1的正态分布随机数:```MATLABx = normrnd(0, 1, 100, 1);```对于已有的样本数据,我们可以使用fitdist()函数对数据进行概率分布的拟合。
该函数可以自动选择合适的分布类型,并给出对应的参数估计值。
例如,我们有一组样本数据x,需要对其进行正态分布的拟合:```MATLABdist = fitdist(x, 'Normal');```通过fitdist()函数返回的dist对象,我们可以获取该分布的参数估计值、置信区间等信息。
二、假设检验和置信区间估计假设检验和置信区间估计是概率统计中常用的分析方法,用于判断样本数据是否符合某个假设、计算参数估计的可信度等。
在MATLAB中,可以使用一些函数来实现假设检验和置信区间估计。
对于假设检验,MATLAB提供了ttest2()和chi2gof()等函数,用于分别进行两样本t检验和卡方检验。
例如,我们有两组样本数据x和y,需要进行两样本t检验:```MATLAB[h, p] = ttest2(x, y);```通过ttest2()函数返回的h值可以判断是否拒绝原假设,p值则表示检验结果的显著性。
第10章 用MATLAB解决概率问题

连续型随机变量的期望
• 应用举例 • 例 17 已知随机变量X的概率
3x , 0 x 1 P( x) 0, 其它
2
求EX和E(4X-1)。
• • • • • • • • • •
程序: 解:在Matlab编辑器中建立M文件LX0817.m: syms x p_x=3*x^2; EX=int(x*p_x,0,1) EY=int((4*x-1)*p_x,0,1) 运行结果为: EX = 3/4 EY = 2
指数分布
正态分布 卡方分布 T分布 F分布
expcdf(x,lambda)
normcdf(x,mu,sigma) chi2cdf(x,n) tcdf(x,n) fcdf(x,n1,n2)
应用举例
• 例7 某公共汽车站从上午7:00起每15分钟来一班 车。若某乘客在7:00到7:30间任何时刻到达此站 是等可能的,试求他候车的时间不到5分钟的概率。
应用举例
• 例16 随机抽取6个滚珠测得直径(mm)如下: 11.70 12.21 11.90 11.91 12.32 12.32 试求样本平均值。 • 程序: >> X=[11.70 12.21 11.90 11.91 12.32 12.32];
>> mean(X)
• 则结果显示如下: ans=12.0600
(2) 方差
• 离散型随机变量的方差及样本方差 • 方差 设X的分布律为 由
PX xk Pk , k 1.2,...
D( X ) E[(X EX ) ] E( X ) E ( X )
2 2 2
则方差 DX=sum(X.^2*P)-(EX).^2
• 标准差:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
会面问题
甲乙两人相约某天9:00-10:00在某地会面商谈生意,双方约定先到者必须等候另一人20分钟,过时如果另一人仍未到则可离去,试求两人能够会面的概率。
1用所学概率论知识建模并求解;
2用Matlab 软件编程模拟实现这个过程,并与理论结果相比较。
解:用所学概率论知识建模并求解
将9点到10点看成是0到60分钟,则甲乙两人到达的时间概率分布可看做是分布,此时不妨设甲到达的时间为t1,乙到达的时间为t2,(0<=t1,t2<=60) 当t1,t2满足|t1-t2|<=20时,两人则可碰面。
下面画出图形便于形象理解。
如图红线与黄线所围中间部分即为两人会面的情况,根据均匀分布的概率分布,可知两人会面概率为S 围/S 总=5/9=0.5556.
用Matlab 软件编程模拟实现这个过程,并与理论结果相比较。
>>syms l;
l=0;
fori=1:100
a=60*rand(1,2);
if (abs(a(1,1)-a(1,2))<=20)
l=l+1;
end
end
>>l/100
l 表示两者相遇的次数,经过计算,当实验次数为100次时,会面概率为0.4600; 0102030405060
010
20
30
40
50
60
下面我们增大实验次数,
实验次数为1000时,会面概率为0.5590;
实验次数为10000时,会面概率为0.5525;
实验次数为100000时,会面概率为0.5546;
实验次数为1000000时,会面概率为0.5552;
…
从随机实验可以发现,当实验次数越来越大时,随机事件发生的概率就越来越稳定于一个值,而这个值与我们理论计算出来的值是一致的,因此从实验角度证明了概率论概率计算理论的正确性。
