【三维设计】高考数学一轮复习 课时跟踪检测(四十七)直线、平面垂直的判定与性质 理 新人教A版
高考数学一轮复习 直线、平面垂直的判定与性质课时跟踪检测 理 湘教版

高考数学一轮复习直线、平面垂直的判定与性质课时跟踪检测理湘教版(分Ⅰ、Ⅱ卷,共2页)第Ⅰ卷:夯基保分卷1.在空间中,给出下面四个命题:①过一点有且只有一个平面与已知直线垂直;②若平面外两点到平面的距离相等,则过两点的直线必平行于该平面;③垂直于同一条直线的两条直线互相平行;④若两个平面相互垂直,则一个平面内的任意一条直线必定垂直于另一个平面内的无数条直线.其中正确的命题是( )A.①②B.②③C.③④D.①④2.(2014·南昌模拟)设a,b是夹角为30°的异面直线,则满足条件“a⊂α,b⊂β,且α⊥β”的平面α,β( )A.不存在B.有且只有一对C.有且只有两对D.有无数对3.已知在空间四边形ABCD中,AD⊥BC,AD⊥BD,且△BCD是锐角三角形,则必有( ) A.平面ABD⊥平面ADC B.平面ABD⊥平面ABCC.平面ADC⊥平面BDC D.平面ABC⊥平面BDC4.如图,直三棱柱ABCA1B1C1中,侧棱长为2,AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的动点,AB1,DF交于点E.要使AB1⊥平面C1DF,则线段B1F的长为( )A.12B.1C.32D.25.如图所示,在四棱锥PABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足________时,平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)6.假设平面α∩平面β=EF,AB⊥α,CD⊥β,垂足分别为B,D,如果增加一个条件,就能推出BD⊥EF,现有下面四个条件:①AC⊥α;②AC与α,β所成的角相等;③AC与BD在β内的射影在同一条直线上;④AC∥EF.其中能成为增加条件的是________.(把你认为正确的条件序号都填上)7.(2013·辽宁高考)如图,AB 是圆O 的直径,PA 垂直圆O 所在的平面,C 是圆O 上的点.(1)求证:BC ⊥平面PAC ;(2)设Q 为PA 的中点,G 为△AOC 的重心.求证:QG ∥平面PBC .8.(2013·北京高考)如图,在四棱锥P ABCD 中,AB ∥CD ,AB⊥AD ,CD =2AB ,平面PAD ⊥底面ABCD ,PA ⊥AD ,E 和F 分别为CD 和PC 的中点.求证:(1)PA ⊥底面ABCD ;(2)BE ∥平面PAD ;(3)平面BEF ⊥平面PCD .第Ⅱ卷:提能增分卷1.如图1,在边长为1的等边三角形ABC 中,D ,E 分别是AB ,AC 上的点,AD =AE ,F 是BC 的中点,AF 与DE 交于点G .将△ABF 沿AF 折起,得到如图2所示的三棱锥A BCF ,其中BC =22.图1 图2(1)证明:DE ∥平面BCF ;(2)证明:CF ⊥平面ABF ;(3)当AD =23时,求三棱锥F DEG 的体积V F DEG .2.如图,在三棱锥A BOC 中,AO ⊥平面COB ,∠OAB =∠OAC =π6,AB =AC =2,BC =2,D 、E 分别为AB 、OB 的中点.(1)求证:CO ⊥平面AOB ;(2)在线段CB 上是否存在一点F ,使得平面DEF ∥平面AOC ,若存在,试确定F 的位置;若不存在,请说明理由.3.如图,在正三棱柱ABC A 1B 1C 1中,点D 在边BC 上,AD ⊥C 1D .(1)求证:AD ⊥平面BCC 1B 1;(2)设E 是B 1C 1上的一点,当B 1E EC 1的值为多少时,A 1E ∥平面ADC 1?请给出证明.答 案第Ⅰ卷:夯基保分卷1.选D 易知①④正确;对于②,过两点的直线可能与平面相交;对于③,垂直于同一条直线的两条直线可能平行,也可能相交或异面.故选D.2.选D 过直线a 的平面α有无数个,当平面α与直线b 平行时,两直线的公垂线与b 确定的平面β⊥α,当平面α与b 相交时,过交点作平面α的垂线与b 确定的平面β⊥α.故选D.3.选C ∵AD ⊥BC ,AD ⊥BD ,BC ∩BD =B ,∴AD ⊥平面BDC ,又AD ⊂平面ADC ,∴平面ADC ⊥平面BDC .故选C.4.选A 设B 1F =x ,因为AB 1⊥平面C 1DF ,DF ⊂平面C 1DF ,所以AB 1⊥DF .由已知可以得A 1B 1=2,设Rt△AA 1B 1斜边AB 1上的高为h ,则DE =12h .又2×2=h 22+22,所以h =233,DE =33.在Rt△DB 1E 中,B 1E =⎝ ⎛⎭⎪⎫222-⎝ ⎛⎭⎪⎫332=66.由面积相等得66×x 2+⎝ ⎛⎭⎪⎫222=22x ,得x =12. 5.解析:由定理可知,BD ⊥PC .∴当DM ⊥PC (或BM ⊥PC )时,即有PC ⊥平面MBD .而PC ⊂平面PCD ,∴平面MBD ⊥平面PCD .答案:DM ⊥PC (或BM ⊥PC 等)6.解析:如果AB 与CD 在一个平面内,可以推出EF 垂直于该平面,又BD 在该平面内,所以BD ⊥EF .故要证BD ⊥EF ,只需AB ,CD 在一个平面内即可,只有①③能保证这一条件.答案:①③7.证明:(1)证明:由AB 是圆O 的直径,得AC ⊥BC .由PA ⊥平面ABC ,BC ⊂平面ABC ,得PA ⊥BC .又PA ∩AC =A ,PA ⊂平面PAC ,AC ⊂平面PAC ,所以BC ⊥平面PAC .(2)连OG 并延长交AC 于M ,连接QM ,QO ,由G 为△AOC 的重心,得M 为AC 中点.由Q 为PA 中点,得QM ∥PC .又O 为AB 中点,得OM ∥BC .因为QM ∩MO =M ,QM ⊂平面QMO ,MO ⊂平面QMO ,BC ∩PC =C ,BC ⊂平面PBC ,PC ⊂平面PBC ,所以平面QMO ∥平面PBC .因为QG ⊂平面QMO ,所以QG ∥平面PBC .8.证明:(1)因为平面PAD ⊥底面ABCD ,且PA 垂直于这两个平面的交线AD ,所以PA ⊥底面ABCD .(2)因为AB ∥CD ,CD =2AB ,E 为CD 的中点,所以AB ∥DE ,且AB =DE .所以ABED 为平行四边形.所以BE ∥AD .又因为BE ⊄平面PAD ,AD ⊂平面PAD ,所以BE ∥平面PAD .(3)因为AB ⊥AD ,而且ABED 为平行四边形.所以BE ⊥CD ,AD ⊥CD ,由(1)知PA ⊥底面ABCD ,所以PA ⊥CD ,因为PA ∩AD =A ,所以CD ⊥平面PAD .所以CD ⊥PD .因为E 和F 分别是CD 和PC 的中点,所以PD ∥EF ,所以CD ⊥EF .又EF ∩BE =E ,所以CD ⊥平面BEF .所以平面BEF ⊥平面PCD .第Ⅱ卷:提能增分卷1.解:(1)证明:如图1,在等边三角形ABC 中,AB =AC .∵AD =AE ,∴AD DB =AE EC,∴DE ∥BC , ∴DG ∥BF ,如图2,DG ⊄平面BCF ,BF ⊂平面BCF ,∴DG ∥平面BCF .同理可证GE ∥平面BCF .∵DG ∩GE =G ,∴平面GDE ∥平面BCF ,∴DE ∥平面BCF .(2)证明:如图1,在等边三角形ABC 中,F 是BC 的中点,∴AF ⊥FC ,∴BF =FC =12BC =12. 在图2中,∵BC =22,∴BC 2=BF 2+FC 2, ∴∠BFC =90°,∴FC ⊥BF .∵BF ∩AF =F ,∴CF ⊥平面ABF .(3)∵AD =23,∴BD =13,AD ∶DB =2∶1, 在图2中,AF ⊥FC ,AF ⊥BF ,∴AF ⊥平面BCF ,由(1)知平面GDE ∥平面BCF , ∴AF ⊥平面GDE .在等边三角形ABC 中,AF =32AB =32, ∴FG =13AF =36,DG =23BF =23×12=13=GE ,∴S △DGE =12DG ·EG =118, ∴V F DEG =13S △DGE ·FG =3324. 2.解:(1)证明:因为AO ⊥平面COB ,所以AO ⊥CO ,AO ⊥BO .即△AOC 与△AOB 为直角三角形.又因为∠OAB =∠OAC =π6,AB =AC =2, 所以OB =OC =1.由OB 2+OC 2=1+1=2=BC 2,可知△BOC 为直角三角形.所以CO ⊥BO ,又因为AO ∩BO =O ,所以CO ⊥平面AOB .(2)在段线CB 上存在一点F ,使得平面DEF ∥平面AOC ,此时F 为线段CB 的中点. 如图,连接DF ,EF ,因为D 、E 分别为AB 、OB 的中点,所以DE ∥OA .又DE ⊄平面AOC 上,所以DE ∥平面AOC .因为E 、F 分别为OB 、BC 的中点,所以EF ∥OC .又EF ⊄平面AOC ,所以EF ∥平面AOC ,又EF ∩DE =E ,EF ⊂平面DEF ,DE ⊂平面DEF ,所以平面DEF ∥平面AOC .3.解:(1)证明:在正三棱柱中,CC 1⊥平面ABC ,AD ⊂平面ABC ,∴AD ⊥CC 1. 又∵AD ⊥C 1D ,CC 1∩C 1D =C 1,CC 1⊂平面BCC 1B 1,C 1D ⊂平面BCC 1B 1,∴AD ⊥平面BCC 1B 1.(2)由(1),得AD ⊥BC .在正三角形ABC 中,D 是BC 的中点.当B1EEC1=1,即E为B1C1的中点时,A1E∥平面ADC1.证明如下,作图如图所示.事实上,正三棱柱ABCA1B1C1中,四边形BCC1B1是矩形,且D,E分别是BC,B1C1的中点,所以B1B∥DE,B1B=DE.又∵B1B∥AA1,且B1B=AA1,∴DE∥AA1,且DE=AA1.∴四边形ADEA1为平行四边形,∴EA1∥AD.而A1E⊄平面ADC1,AD⊂平面ADC1,故A1E∥平面ADC1.。
【三维设计】高考数学一轮复习 (基础知识+高频考点+解题训练)直线、平面平行的判定及性质教学案

第四节直线、平面平行的判定及性质[知识能否忆起]一、直线与平面平行1.判定定理2.性质定理二、平面与平面平行1.判定定理2.两平面平行的性质定理[小题能否全取]1.(教材习题改编)下列条件中,能作为两平面平行的充分条件的是( )A.一个平面内的一条直线平行于另一个平面B.一个平面内的两条直线平行于另一个平面C.一个平面内有无数条直线平行于另一个平面D.一个平面内任何一条直线都平行于另一个平面解析:选D 由面面平行的定义可知,一平面内所有的直线都平行于另一个平面时,两平面才能平行,故D正确.2.已知直线a,b,平面α,则以下三个命题:①若a∥b,b⊂α,则a∥α;②若a∥b,a∥α,则b∥α;③若a∥α,b∥α,则a∥b.其中真命题的个数是( )A.0 B.1C.2 D.3解析:选A 对于命题①,若a∥b,b⊂α,则应有a∥α或a⊂α,所以①不正确;对于命题②,若a∥b,a∥α,则应有b∥α或b⊂α,因此②也不正确;对于命题③,若a∥α,b∥α,则应有a∥b或a与b相交或a与b异面,因此③也不正确.3.(教材习题改编)若一直线上有相异三个点A,B,C到平面α的距离相等,那么直线l与平面α的位置关系是( )A.l∥αB.l⊥αC.l与α相交且不垂直D.l∥α或l⊂α解析:选D 由于l上有三个相异点到平面α的距离相等,则l与α可以平行,l⊂α时也成立.4.平面α∥平面β,a⊂α,b⊂β,则直线a,b的位置关系是________.解析:由α∥β可知,a ,b 的位置关系是平行或异面. 答案:平行或异面5.(2012·衡阳质检)在正方体ABCD -A 1B 1C 1D 1中,E 是DD 1的中点,则BD 1与平面ACE 的位置关系为________.解析:如图.连接AC ,BD 交于O 点,连接OE ,因为OE ∥BD 1,而OE ⊂平面ACE ,BD 1⊄平面ACE ,所以BD 1∥平面ACE .答案:平行1.平行问题的转化关系: 线∥线判定判定性质线∥面――→判定性质面∥面性质 2.在解决线面、面面平行的判定时,一般遵循从“低维”到“高维”的转化,即从“线线平行”到“线面平行”,再到“面面平行”;而在性质定理的应用中,其顺序恰好相反,但也要注意,转化的方向总是由题目的具体条件而定,决不可过于“模式化”.3.辅助线(面)是求证平行问题的关键,注意平面几何中位线,平行四边形及相似中有关平行性质的应用.典题导入[例1] (2011·福建高考)如图,正方体ABCD -A 1B 1C 1D 1中,AB =2,点E 为AD 的中点,点F 在CD 上.若EF ∥平面AB 1C ,则线段EF 的长度等于________.[自主解答] 因为直线EF ∥平面AB 1C ,EF ⊂平面ABCD ,且平面AB 1C ∩平面ABCD =AC ,所以EF ∥AC .又因为点E 是DA 的中点,所以F 是DC 的中点,由中位线定理可得EF =12AC .又因为在正方体ABCD -A 1B 1C 1D 1中,AB =2,所以AC =2 2.所以EF = 2.[答案]2本例条件变为“E 是AD 中点,F ,G ,H ,N 分别是AA 1,A 1D 1,DD 1与D 1C 1的中点,若M 在四边形EFGH 及其内部运动”,则M 满足什么条件时,有MN ∥平面A 1C 1CA .解:如图,∵GN∥平面AA1C1C,EG∥平面AA1C1C,又GN∩EG=G,∴平面EGN∥平面AA1C1C.∴当M在线段EG上运动时,恒有MN∥平面AA1C1C.由题悟法解决有关线面平行、面面平行的基本问题要注意:(1)判定定理与性质定理中易忽视的条件,如线面平行的判定定理中条件线在面外易忽视.(2)结合题意构造或绘制图形,结合图形作出判断.(3)举反例否定结论或用反证法推断命题是否正确.以题试法1.(1)(2012·浙江高三调研)已知直线l∥平面α,P∈α,那么过点P且平行于直线l的直线( )A.只有一条,不在平面α内B.有无数条,不一定在平面α内C.只有一条,且在平面α内D.有无数条,一定在平面α内解析:选C 由直线l与点P可确定一个平面β,且平面α,β有公共点,因此它们有一条公共直线,设该公共直线为m,因为l∥α,所以l∥m,故过点P且平行于直线l的直线只有一条,且在平面α内.(2)(2012·潍坊模拟)已知m,n,l1,l2表示直线,α,β表示平面.若m⊂α,n⊂α,l1⊂β,l2⊂β,l1∩l2=M,则α∥β的一个充分条件是( )A.m∥β且l1∥αB.m∥β且n∥βC.m∥β且n∥l2D.m∥l1且n∥l2解析:选D 由定理“如果一个平面内有两条相交直线分别与另一个平面平行,那么这两个平面平行”可得,由选项D可推知α∥β.典题导入[例2] (2012·辽宁高考)如图,直三棱柱ABC -A ′B ′C ′,∠BAC =90°,AB =AC =2,AA ′=1,点M ,N 分别为A ′B 和B ′C ′的中点.(1)证明:MN ∥平面A ′ACC ′;(2)求三棱锥A ′-MNC 的体积.(锥体体积公式V =13Sh ,其中S 为底面面积,h 为高)[自主解答] (1)证明:法一:连接AB ′、AC ′,因为点M ,N分别是A ′B 和B ′C ′的中点,所以点M 为AB ′的中点. 又因为点N 为B ′C ′的中点, 所以MN ∥AC ′. 又MN ⊄平面A ′ACC ′,AC ′⊂平面A ′ACC ′,因此MN ∥平面A ′ACC ′.法二:取A ′B ′的中点P .连接MP .而点M ,N 分别为AB ′与B ′C ′的中点,所以MP ∥AA ′,PN ∥A ′C ′.所以MP ∥平面A ′ACC ′,PN ∥平面A ′ACC ′.又MP ∩PN =P , 因此平面MPN ∥平面A ′ACC ′.而MN ⊂平面MPN , 因此MN ∥平面A ′ACC ′.(2)法一:连接BN ,由题意得A ′N ⊥B ′C ′,平面A ′B ′C ′∩平面B ′BCC ′=B ′C ′,所以A ′N ⊥平面NBC .又A ′N =12B ′C ′=1,故V A ′-MNC =V N -A ′MC =12V N -A ′BC =12V A ′-NBC =16.法二:V A ′-MNC =V A ′-NBC -V M -NBC =12V A ′-NBC =16.由题悟法利用判定定理证明线面平行的关键是找平面内与已知直线平行的直线,可先直观判断平面内是否已有,若没有,则需作出该直线,常考虑三角形的中位线、平行四边形的对边或过已知直线作一平面找其交线.以题试法2.(2012·淄博模拟)如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是BD,BB1的中点.(1)求证:EF∥平面A1B1CD;(2)求证:EF⊥AD1.解:(1)在正方体ABCD-A1B1C1D1中,连接B1D,在平面BB1D内,E,F分别为BD,BB1的中点,∴EF∥B1D.又∵B1D⊂平面A1B1CD.EF⊄平面A1B1CD,∴EF∥平面A1B1CD.(2)∵ABCD-A1B1C1D1是正方体,∴AD1⊥A1D,AD1⊥A1B1.又A1D∩A1B1=A1,∴AD1⊥平面A1B1D.∴AD1⊥B1D.又由(1)知,EF∥B1D,∴EF⊥AD1.典题导入[例3] 如图,已知ABCD-A1B1C1D1是棱长为3的正方体,点E在AA1上,点F在CC1上,G在BB1上,且AE=FC1=B1G=1,H是B1C1的中点.(1)求证:E,B,F,D1四点共面;(2)求证:平面A1GH∥平面BED1F.[自主解答] (1)在正方形AA1B1B中,∵AE=B1G=1,∴BG=A1E=2,∴BG綊A1E.∴四边形A1GBE是平行四边形.∴A1G∥BE.又C1F綊B1G,∴四边形C1FGB1是平行四边形.∴FG綊C1B1綊D1A1.∴四边形A 1GFD 1是平行四边形. ∴A 1G 綊D 1F . ∴D 1F 綊EB .故E ,B ,F ,D 1四点共面. (2)∵H 是B 1C 1的中点,∴B 1H =32.又B 1G =1,∴B 1G B 1H =23. 又FC BC =23,且∠FCB =∠GB 1H =90°, ∴△B 1HG ∽△CBF . ∴∠B 1GH =∠CFB =∠FBG . ∴HG ∥FB .∵GH ⊄面FBED 1,FB ⊂面FBED 1,∴GH ∥面BED 1F . 由(1)知A 1G ∥BE ,A 1G ⊄面FBED 1,BE ⊂面FBED 1, ∴A 1G ∥面BED 1F . 且HG ∩A 1G =G , ∴平面A 1GH ∥平面BED 1F .由题悟法常用的判断面面平行的方法 (1)利用面面平行的判定定理;(2)面面平行的传递性(α∥β,β∥γ⇒α∥γ); (3)利用线面垂直的性质(l ⊥α,l ⊥β⇒α∥β).以题试法3.(2012·北京东城二模)如图,矩形AMND 所在的平面与直角梯形MBCN 所在的平面互相垂直,MB ∥NC ,MN ⊥MB .(1)求证:平面AMB ∥平面DNC ; (2)若MC ⊥CB ,求证:BC ⊥AC .证明:(1)因为MB ∥NC ,MB ⊄平面DNC ,NC ⊂平面DNC , 所以MB ∥平面DNC .又因为四边形AMND 为矩形,所以MA ∥DN . 又MA ⊄平面DNC ,DN ⊂平面DNC . 所以MA ∥平面DNC .又MA ∩MB =M ,且MA ,MB ⊂平面AMB , 所以平面AMB ∥平面DNC .(2)因为四边形AMND是矩形,所以AM⊥MN.因为平面AMND⊥平面MBCN,且平面AMND∩平面MBCN=MN,所以AM⊥平面MBCN.因为BC⊂平面MBCN,所以AM⊥BC.因为MC⊥BC,MC∩AM=M,所以BC⊥平面AMC.因为AC⊂平面AMC,所以BC⊥AC.1.(2013·浙江模拟)已知直线m⊥平面α,直线n⊂平面β,则下列命题正确的是( ) A.若n∥α,则α∥βB.若α⊥β,则m∥nC.若m⊥n,则α∥βD.若α∥β,则m⊥n解析:选D 由m⊥α,α∥β,n⊂β⇒m⊥n.2.平面α∥平面β的一个充分条件是( )A.存在一条直线a,a∥α,a∥βB.存在一条直线a,a⊂α,a∥βC.存在两条平行直线a,b,a⊂α,b⊂β,a∥β,b∥αD.存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α解析:选D 若α∩β=l,a∥l,a⊄α,a⊄β,a∥α,a∥β,故排除A.若α∩β=l,a⊂α,a∥l,则a∥β,故排除B.若α∩β=l,a⊂α,a∥l,b⊂β,b∥l,则α∥β,b∥α,故排除C.3.如图,正方体ABCD-A1B1C1D1中,E,F分别为棱AB,CC1的中点,在平面ADD1A1内且与平面D1EF平行的直线( )A.不存在B.有1条C.有2条D.有无数条解析:选D 由题设知平面ADD1A1与平面D1EF有公共点D1,由平面的基本性质中的公理知必有过该点的公共直线l,在平面ADD1A1内与l平行的线有无数条,且它们都不在平面D1EF内,由线面平行的判定定理知它们都与平面D1EF平行.4.(2012·浙江模拟)已知α,β,γ是三个不重合的平面,a,b是两条不重合的直线,有下列三个条件:①a ∥γ,b ⊂β;②a ∥γ,b ∥β;③b ∥β,a ⊂γ.如果命题“α∩β=a ,b ⊂γ,且________,则a ∥b ”为真命题,则可以在横线处填入的条件是( )A .①或②B .②或③C .①或③D .只有②解析:选C 由定理“一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行”可得,横线处可填入条件①或③,结合各选项知,选C.5.(2012·开封模拟)如图所示,在空间四边形ABCD 中,E ,F 分别为边AB ,AD 上的点,且AE ∶EB =AF ∶FD =1∶4,又H 、G 分别为BC ,CD 的中点,则( )A .BD ∥平面EFGH ,且四边形EFGH 是矩形B .EF ∥平面BCD ,且四边形EFGH 是梯形C .HG ∥平面ABD ,且四边形EFGH 是菱形 D .EH ∥平面ADC ,且四边形EFGH 是平行四边形解析:选B 由AE ∶EB =AF ∶FD =1∶4知EF 綊15BD ,∴EF ∥面BCD .又H ,G 分别为BC ,CD 的中点,∴HG 綊12BD ,∴EF ∥HG 且EF ≠HG .∴四边形EFGH 是梯形.6.(2012·山西四校联考)在空间内,设l ,m ,n 是三条不同的直线,α,β,γ是三个不同的平面,则下列命题中为假命题的是( )A .α⊥γ,β⊥γ,α∩β=l ,则l ⊥γB .l ∥α,l ∥β,α∩β=m ,则l ∥mC .α∩β=l ,β∩γ=m ,γ∩α=n ,l ∥m ,则l ∥nD .α⊥γ,β⊥γ,则α⊥β或α∥β解析:选D 对于A ,∵如果两个相交平面均垂直于第三个平面,那么它们的交线垂直于第三个平面,∴该命题是真命题;对于B ,∵如果一条直线平行于两个相交平面,那么该直线平行于它们的交线,∴该命题是真命题;对于C ,∵如果三个平面两两相交,有三条交线,那么这三条交线交于一点或相互平行,∴该命题是真命题;对于D ,当两个平面同时垂直于第三个平面时,这两个平面可能不垂直也不平行,∴D 不正确.7.设a ,b 为空间的两条直线,α,β为空间的两个平面,给出下列命题: ①若a ∥α,a ∥β,则α∥β;②若a ⊥α,a ⊥β,则α∥β; ③若a ∥α,b ∥α,则a ∥b ;④若a ⊥α,b ⊥α,则a ∥b . 上述命题中,所有真命题的序号是________.解析:①错误.因为α与β可能相交;③错误.因为直线a 与b 还可能异面、相交.答案:②④8.已知平面α∥β,P ∉α且P ∉β,过点P 的直线m 与α,β分别交于A .C ,过点P 的直线n 与α,β分别交于B ,D ,且PA =6,AC =9,PD =8则BD 的长为________.解析:如图1,∵AC ∩BD =P ,∴经过直线AC 与BD 可确定平面PCD .∵α∥β,α∩平面PCD =AB ,β∩平面PCD =CD , ∴AB ∥CD .∴PA AC =PB BD ,即69=8-BD BD. ∴BD =245.如图2,同理可证AB ∥CD .∴PA PC =PB PD ,即63=BD -88. ∴BD =24.综上所述,BD =245或24.答案:245或249.(2012·浙江模拟)下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,P 分别为其所在棱的中点,能得出直线AB ∥平面MNP 的图形的序号是________.(写出所有符合要求的图形序号)解析:对于①,注意到该正方体的经过直线AB 的侧面与平面MNP 平行,因此直线AB 平行于平面MNP ;对于②,注意到直线AB 和过点A 的一个与平面MNP 平行的平面相交,因此直线AB 与平面MNP 相交;对于③,注意到直线AB 与MP 平行,且直线AB 位于平面MNP 外,因此直线AB 与平面MNP 平行;对于④,易知此时AB 与平面MNP 相交.综上所述,能得出直线AB 平行于平面MNP 的图形的序号是①③.答案:①③10.(2013·西安模拟)如图,FD 垂直于矩形ABCD 所在平面,CE ∥DF ,∠DEF =90°.(1)求证:BE ∥平面ADF ;(2)若矩形ABCD 的一边AB =3,EF =23,则另一边BC 的长为何值时,三棱锥F -BDE 的体积为3?解:(1)证明:过点E 作CD 的平行线交DF 于点M ,连接AM .因为CE ∥DF ,所以四边形CEMD 是平行四边形.可得EM =CD 且EM ∥CD ,于是四边形BEMA 也是平行四边形,所以有BE ∥AM .而AM ⊂平面ADF ,BE ⊄平面ADF ,所以BE ∥平面ADF .(2)由EF =23,EM =AB =3,得FM =3且∠MFE =30°.由∠DEF =90°可得FD =4,从而得DE =2.因为BC ⊥CD ,BC ⊥FD ,所以BC ⊥平面CDFE .所以,V F -BDE =V B -DEF =13S △DEF ×BC . 因为S △DEF =12DE ×EF =23,V F -BDE =3, 所以BC =32. 综上当BC =32时,三棱锥F -BDE 的体积为 3. 11.如图,在直四棱柱ABCD -A1B 1C 1D 1中,底面ABCD 为等腰梯形,AB ∥CD ,且AB =2CD ,在棱AB 上是否存在一点F ,使平面C 1CF ∥平面ADD 1A 1?若存在,求点F 的位置;若不存在,请说明理由.解:存在这样的点F ,使平面C 1CF ∥平面ADD 1A 1,此时点F 为AB的中点,证明如下:∵AB ∥CD ,AB =2CD ,∴AF 綊CD ,∴四边形AFCD 是平行四边形,∴AD ∥CF .又AD ⊂平面ADD 1A 1,CF ⊄平面ADD 1A 1.∴CF ∥平面ADD 1A 1.又CC 1∥DD 1,CC 1⊄平面ADD 1A 1,DD 1⊂平面ADD 1A 1,∴CC 1∥平面ADD 1A 1,又CC 1,CF ⊂平面C 1CF ,CC 1∩CF =C ,∴平面C 1CF ∥平面ADD 1A 1.12.(2013·潍坊二模)如图,点C 是以AB 为直径的圆上一点,直角梯形BCDE 所在平面与圆O 所在平面垂直,且DE ∥BC ,DC ⊥BC ,DE=12BC =2,AC =CD =3. (1)证明:EO ∥平面ACD ;(2)证明:平面ACD ⊥平面BCDE ;(3)求三棱锥E -ABD 的体积.解:(1)证明:如图,取BC 的中点M ,连接OM ,ME .在△ABC 中,O 为AB 的中点,M 为BC 的中点,∴OM ∥AC .在直角梯形BCDE 中,DE ∥BC ,且DE =12BC =CM , ∴四边形MCDE 为平行四边形.∴EM ∥DC .∴平面EMO ∥平面ACD ,又∵EO ⊂平面EMO ,∴EO ∥平面ACD .(2)证明:∵C 在以AB 为直径的圆上,∴AC ⊥BC .又∵平面BCDE ⊥平面ABC ,平面BCDE ∩平面ABC =BC .∴AC ⊥平面BCDE .又∵AC ⊂平面ACD ,∴平面ACD ⊥平面BCDE .(3)由(2)知AC ⊥平面BCDE .又∵S △BDE =12×DE ×CD =12×2×3=3, ∴V E -ABD =V A -BDE =13×S △BDE ×AC =13×3×3=3.1.若平面α∥平面β,直线a ∥平面α,点B ∈β,则在平面β内与过B 点的所有直线中( )A .不一定存在与a 平行的直线B .只有两条与a 平行的直线C .存在无数条与a 平行的直线D .存在唯一与a 平行的直线解析:选A 当直线a 在平面β内且经过B 点时,可使a ∥平面α,但这时在平面β内过B 点的所有直线中,不存在与a 平行的直线,而在其他情况下,都可以存在与a 平行的直线.2.(2012·南宁二模)如图所示,在四面体ABCD 中,M ,N 分别是△ACD ,△BCD 的重心,则四面体的四个面中与MN 平行的是________________.解析:连接AM 并延长,交CD 于E ,连接BN ,并延长交CD 于F ,由重心性质可知,E ,F 重合为一点,且该点为CD 的中点E ,由EM MA =EN NB =12,得MN ∥AB .因此,MN ∥平面ABC 且MN ∥平面ABD . 答案:平面ABC ,平面ABD3.(2012·北京东城区模拟)一个多面体的直观图和三视图如图所示,其中M ,N 分别是AB ,AC 的中点,G 是DF 上的一动点.(1)求该多面体的体积与表面积;(2)求证:GN ⊥AC ;(3)当FG =GD 时,在棱AD 上确定一点P ,使得GP ∥平面FMC ,并给出证明.解:(1)由题中图可知该多面体为直三棱柱,在△ADF 中,AD ⊥DF ,DF =AD =DC =a ,所以该多面体的体积为12a 3. 表面积为12a 2×2+2a 2+a 2+a 2=(3+2)a 2.(2)连接DB ,FN ,由四边形ABCD 为正方形,且N 为AC 的中点知B ,N ,D 三点共线,且AC ⊥DN .又∵FD ⊥AD ,FD ⊥CD ,AD ∩CD =D ,∴FD ⊥平面ABCD .∵AC ⊂平面ABCD ,∴FD ⊥AC .又DN ∩FD =D ,∴AC ⊥平面FDN .又GN ⊂平面FDN ,∴GN ⊥AC .(3)点P 与点A 重合时,GP ∥平面FMC .取FC 的中点H ,连接GH ,GA ,MH .∵G 是DF 的中点,∴GH 綊12CD . 又M 是AB 的中点,∴AM 綊12CD . ∴GH ∥AM 且GH =AM .∴四边形GHMA 是平行四边形.∴GA ∥MH .∵MH ⊂平面FMC ,GA ⊄平面FMC ,∴GA ∥平面FMC ,即当点P 与点A 重合时,GP ∥平面FMC .1.已知m ,n ,l 为三条不同的直线,α,β为两个不同的平面,则下列命题中正确的是( )A .α∥β,m ⊂α,n ⊂β⇒m ∥nB .l ⊥β,α⊥β⇒l ∥αC .m ⊥α,m ⊥n ⇒n ∥αD .α∥β,l ⊥α⇒l ⊥β解析:选D 对于选项A ,m ,n 平行或异面;对于选项B ,可能出现l ⊂α这种情形;对于选项C ,可能出现n ⊂α这种情形.2.如图,三棱柱ABC -A1B 1C 1,底面为正三角形,侧棱A 1A ⊥底面ABC ,点E ,F 分别是棱CC 1,BB 1上的点,点M 是线段AC 上的动点,EC =2FB .当点M 在何位置时,BM ∥平面AEF?解:法一:如图,取AE 的中点O ,连接OF ,过点O 作OM ⊥AC 于点M .∵侧棱A 1A ⊥底面ABC ,∴侧面A 1ACC 1⊥底面ABC ,∴OM ⊥底面ABC .又∵EC=2FB,∴OM綊FB綊12 EC.∴四边形OMBF为矩形.∴BM∥OF.又∵OF⊂面AEF,BM⊄面AEF.故BM∥平面AEF,此时点M为AC的中点.法二:如图,取EC的中点P,AC的中点Q,连接PQ,PB,BQ,∴PQ∥AE.∵EC=2FB,∴PE綊BF,PB∥EF,∴PQ∥平面AEF,PB∥平面AEF.又PQ∩PB=P,∴平面PBQ∥平面AEF,又∵BQ⊂面PQB,∴BQ∥平面AEF.故点Q即为所求的点M,此时点M为AC的中点.3.(2012·蚌埠二中质检)如图1所示,在Rt△ABC中,AC=6,BC=3,∠ABC=90°,CD为∠ACB的角平分线,点E在线段AC上,CE=4.如图2所示,将△BCD沿CD折起,使得平面BCD⊥平面ACD,连接AB,设点F是AB的中点.(1)求证:DE⊥平面BCD;(2)若EF∥平面BDG,其中G为直线AC与平面BDG的交点,求三棱锥B-DEG的体积.解:(1)证明:∵AC=6,BC=3,∠ABC=90°,∴∠ACB=60°.∵CD为∠ACB的角平分线,∴∠BCD=∠ACD=30°.∴CD=2 3.∵CE=4,∠DCE=30°,∴DE=2.则CD2+DE2=EC2.∴∠CDE=90°,DE⊥DC.又∵平面BCD⊥平面ACD,平面BCD∩平面ACD=CD,DE⊂平面ACD,∴DE⊥平面BCD.(2)∵EF∥平面BDG,EF⊂平面ABC,平面ABC∩平面BDG=BG,∴EF∥BG.∵点E在线段AC上,CE=4,点F是AB的中点,∴AE=EG=CG=2.如图,作BH ⊥CD 于H .∵平面BCD ⊥平面ACD , ∴BH ⊥平面ACD .由条件得BH =32, S △DEG =13S △ACD =13×12AC ·CD ·sin 30°=3,∴三棱锥B -DEG 的体积V =13S △DEG ·BH =13×3×32=32.。
2012高三数学《三维设计》配套资料课件第7章第5节直线、平面垂直的判定与性质

因为∠APB=∠ADB=60° , 所以 PA=PB= 6,HD=HC=1.可得 PH= 3. 1 等腰梯形 ABCD 的面积为 S= AC×BD=2+ 3. 2 3+2 3 1 所以四棱锥的体积为 V= ×(2+ 3)× 3= . 3 3
[归纳领悟] 1.判定面面垂直的方法 (1)面面垂直的定义.
②OA⊂α,OB⊂β,
③OA⊥l,OB⊥l,
则∠AOB就叫做二面角αlβ的平面角.
2.平面与平面垂直的判定定理.
文字语言 一个平面过另一个 判定 平面的一条 垂线 , 定理 则这两个平面互相 垂直 图形语言 符号语言
3.平面与平面垂直的性质定理. 文字语言 性 两个平面互相垂直, 质 则一个平面内垂直 定 于 交线 的直线垂直 图形语言 符号语言
图形语言
符号语言
面的两条直线 定理 平行
二、平面与平面垂直 1.二面角 (1)二面角:从一条直线 出发的两个半平面 所组成的图 形叫做二面角.这条直线叫做 二面角的棱 .两个半 平面叫做二面角的面. 如图,记作:αlβ 或 αABβ或PABQ.
(2)二面角的平面角 如图,二面角αlβ,
若有①O∈l,
答案:C
3.如图,已知在四棱锥P-ABCD中,
底面ABCD是矩形,PA⊥平面ABCD, PA=AD=1,AB=2,E、F分别是 AB、PD的中点. (1)求证:AF∥平面PEC; (2)求PC与平面ABCD所成的角的正切值; (3)求二面角P-EC-D的正切值.
解:(1)证明:如图,取 PC 的中点 O, 连结 OF、OE,则 FO∥DC, 1 且 FO=2DC, ∴FO∥AE, 又 E 是 AB 的中点, 且 AB=DC, ∴FO=AE.
[归纳领悟]
解答此类问题时一要注意依据定理条件才能得出结
【三维设计】高考数学一轮复习 第七章第五节 直线 平面垂直的判定与性质 文 湘教版名师课件

由 PF=7FC,得三棱锥 F-BCD 的高为18PA,故
VF-BCD=13·S△ BCD·18PA=13×
1 3×8×2
3=14.
所以 VP-BDF=VP-BCD-VF-BCD=2-14=74.
[类题通法] 1.解答此类问题的关键在于熟练把握空间垂直关系的判定与 性质,注意平面图形中的一些线线垂直关系的灵活利用,这是证 明空间垂直关系的基础. 2.由于“线线垂直”“线面垂直”“面面垂直”之间可以相 互转化,因此整个证明过程围绕着线面垂直这个核心而展开,这 是化解空间垂直关系难点的技巧所在.
[典例] (2013·山东高考)如图,四棱锥 P-ABCD 中,AB⊥AC,
AB⊥PA,AB∥CD,AB=2CD,E,F,G,M,N 分别为 PB,
AB,BC,PD,PC 的中点. (1)求证:CE∥平面 PAD;
思考
证明线面平行的常用方法有哪些?
提示:一是判断定理;
二是转化证明面面平行.
(2)求证:平面 EFG⊥平面 EMN.
答案:B
2.若 m,n 是两条不同的直线,α,β 是两个不同的平面,则下
列命题不.正确的是 A.若 α∥β,m⊥α,则 m⊥β
()
B.若 m∥n,m⊥α,则 n⊥α
C.若 m∥α,m⊥β,则 α⊥β
D.若 α∩β=m,且 n 与 α,β 所成的角相等,则 m⊥n 解析:容易判定选项 A、B、C 都正确,对于选项 D,当直线
(1)求证:BD⊥平面 PAC;
证明线面垂直有哪些方法?
(2)若侧棱 PC 上的点 F 满足 PF=7FC, 求三棱锥 P-BDF 的体积. 求体积有哪些方法?
思考
[解] (1)证明:因为 BC=CD,所以△ BCD 为等腰三角形.
高考数学一轮复习专题训练—直线、平面垂直的判定与性质

直线、平面垂直的判定与性质考纲要求1.以立体几何的定义、公理和定理为出发点,认识和理解空间中线面垂直的有关性质与判定定理;2.能运用公理、定理和已获得的结论证明一些空间图形的垂直关系的简单命题.知识梳理1.直线与平面垂直 (1)直线和平面垂直的定义如果一条直线l 与平面α内的任意直线都垂直,就说直线l 与平面α互相垂直. (2)判定定理与性质定理文字语言图形表示符号表示判定定理一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直⎭⎪⎬⎪⎫l ⊥al ⊥b a ∩b =O a ⊂αb ⊂α⇒l ⊥α 性质定理两直线垂直于同一个平面,那么这两条直线平行⎭⎬⎫a ⊥αb ⊥α⇒a ∥b(1)定义:一条斜线和它在平面上的射影所成的锐角叫做这条直线和这个平面所成的角,一条直线垂直于平面,则它们所成的角是直角;一条直线和平面平行或在平面内,则它们所成的角是0°的角. (2)范围:⎣⎡⎦⎤0,π2. 3.二面角(1)定义:从一条直线出发的两个半平面所组成的图形叫做二面角;(2)二面角的平面角:在二面角的棱上任取一点,以该点为垂足,在两个半平面内分别作垂直于棱的两条射线,这两条射线所构成的角叫做二面角的平面角.(3)二面角的范围:[0,π]. 4.平面与平面垂直 (1)平面与平面垂直的定义两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直. (2)判定定理与性质定理文字语言图形表示符号表示判定定理一个平面经过另一个平面的一条垂线,则这两个平面互相垂直⎭⎬⎫l ⊥αl ⊂β⇒α⊥β 性质定理如果两个平面互相垂直,则在一个平面内垂直于它们交线的直线垂直于另一个平面⎭⎪⎬⎪⎫α⊥βα∩β=al ⊥a l ⊂β⇒l ⊥α1.三个重要结论(1)若两平行线中的一条垂直于一个平面,则另一条也垂直于这个平面.(2)若一条直线垂直于一个平面,则它垂直于这个平面内的任何一条直线(证明线线垂直的一个重要方法).(3)垂直于同一条直线的两个平面平行.2.使用线面垂直的定义和线面垂直的判定定理,不要误解为“如果一条直线垂直于平面内的无数条直线,就垂直于这个平面”. 3.三种垂直关系的转化线线垂直判定定理性质线面垂直判定定理性质定理面面垂直诊断自测1.判断下列结论正误(在括号内打“√”或“×”)(1)直线l 与平面α内的无数条直线都垂直,则l ⊥α.( )(2)垂直于同一个平面的两平面平行.()(3)若两平面垂直,则其中一个平面内的任意一条直线垂直于另一个平面.()(4)若平面α内的一条直线垂直于平面β内的无数条直线,则α⊥β.()答案(1)×(2)×(3)×(4)×解析(1)直线l与平面α内的无数条直线都垂直,则有l⊥α或l与α斜交或l⊂α或l∥α,故(1)错误.(2)垂直于同一个平面的两个平面平行或相交,故(2)错误.(3)若两个平面垂直,则其中一个平面内的直线可能垂直于另一平面,也可能与另一平面平行,也可能与另一平面相交,也可能在另一平面内,故(3)错误.(4)若平面α内的一条直线垂直于平面β内的所有直线,则α⊥β,故(4)错误.2.已知互相垂直的平面α,β交于直线l.若直线m,n满足m∥α,n⊥β,则()A.m∥l B.m∥n C.n⊥l D.m⊥n答案 C解析由题意知,α∩β=l,所以l⊂β,因为n⊥β,所以n⊥l.3.在三棱锥P-ABC中,点P在平面ABC中的射影为点O.(1)若P A=PB=PC,则点O是△ABC的________心.(2)若P A⊥PB,PB⊥PC,PC⊥P A,则点O是△ABC的________心.答案(1)外(2)垂解析(1)如图1,连接OA,OB,OC,OP,在Rt△POA,Rt△POB和Rt△POC中,P A=PB=PC,所以OA=OB=OC,即O为△ABC的外心.图1(2)如图2,延长AO,BO,CO分别交BC,AC,AB于H,D,G.因为PC⊥P A,PB⊥PC,P A∩PB=P,所以PC⊥平面P AB,又AB⊂平面P AB,所以PC⊥AB,因为PO⊥AB,PO∩PC =P,所以AB⊥平面PGC,又CG⊂平面PGC,所以AB⊥CG,即CG为△ABC边AB上的高.同理可证BD,AH分别为△ABC边AC,BC上的高,即O为△ABC的垂心.图24.(2021·日照检测)已知α,β表示两个不同的平面,m为平面α内的一条直线,则“α⊥β”是“m⊥β”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案 B解析m⊂α,m⊥β⇒α⊥β,反过来,若m⊂α,α⊥βD m⊥β(m∥β或m与β斜交),所以“α⊥β”是“m⊥β”的必要不充分条件.5.(2021·西安联考)已知AB是圆柱上底面的一条直径,C是上底面圆周上异于A,B的一点,D为下底面圆周上一点,且AD⊥圆柱的底面,则必有()A.平面ABC⊥平面BCD B.平面BCD⊥平面ACDC.平面ABD⊥平面ACD D.平面BCD⊥平面ABD答案 B解析因为AB是圆柱上底面的一条直径,所以AC⊥BC,又AD垂直于圆柱的底面,所以AD⊥BC,因为AC∩AD=A,所以BC⊥平面ACD.由于BC⊂平面BCD.所以平面BCD⊥平面ACD.6.(2018·全国Ⅰ卷)在长方体ABCD-A1B1C1D1中,AB=BC=2,AC1与平面BB1C1C所成的角为30°,则该长方体的体积为()A.8 B.6 2 C.8 2 D.8 3答案 C解析连接BC1,因为AB⊥平面BB1C1C,所以∠AC1B=30°,AB⊥BC1,所以△ABC1为直角三角形.又AB=2,所以BC1=2 3.又B1C1=2,所以BB1=232-22=22,故该长方体的体积V=2×2×22=8 2.考点一线面垂直的判定与性质【例1】(2019·全国Ⅱ卷)如图,长方体ABCD-A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.(1)证明:BE ⊥平面EB 1C 1;(2)若AE =A 1E ,AB =3,求四棱锥E -BB 1C 1C 的体积.(1)证明 由已知得B 1C 1⊥平面ABB 1A 1,BE ⊂平面ABB 1A 1,故B 1C 1⊥BE .又BE ⊥EC 1,B 1C 1∩EC 1=C 1,B 1C 1,EC 1⊂平面EB 1C 1,所以BE ⊥平面EB 1C 1. (2)解 由(1)知∠BEB 1=90°.由题设知Rt △ABE ≌Rt △A 1B 1E , 所以∠AEB =∠A 1EB 1=45°, 故AE =AB =3,AA 1=2AE =6.如图,作EF ⊥BB 1,垂足为F ,则EF ⊥平面BB 1C 1C ,且EF =AB =3. 所以四棱锥E -BB 1C 1C 的体积V =13×3×6×3=18.感悟升华 1.证明直线和平面垂直的常用方法有:(1)判定定理;(2)垂直于平面的传递性(a ∥b ,a ⊥α⇒b ⊥α);(3)面面平行的性质(a ⊥α,α∥β⇒a ⊥β);(4)面面垂直的性质(α⊥β,α∩β=a ,l ⊥a ,l ⊂β⇒l ⊥α).2.证明线面垂直的核心是证线线垂直,而证明线线垂直则需借助线面垂直的性质.因此,判定定理与性质定理的合理转化是证明线面垂直的基本思路.【训练1】 如图,在四棱锥P -ABCD 中,P A ⊥底面ABCD ,AB ⊥AD ,AC ⊥CD ,∠ABC =60°,P A =AB =BC ,E 是PC 的中点.证明:(1)CD⊥AE;(2)PD⊥平面ABE.证明(1)在四棱锥P-ABCD中,∵P A⊥底面ABCD,CD⊂平面ABCD,∴P A⊥CD,又∵AC⊥CD,且P A∩AC=A,∴CD⊥平面P AC.又AE⊂平面P AC,∴CD⊥AE.(2)由P A=AB=BC,∠ABC=60°,可得AC=P A.∵E是PC的中点,∴AE⊥PC.由(1)知AE⊥CD,且PC∩CD=C,∴AE⊥平面PCD.又PD⊂平面PCD,∴AE⊥PD.∵P A⊥底面ABCD,AB⊂平面ABCD,∴P A⊥AB.又∵AB⊥AD,且P A∩AD=A,∴AB⊥平面P AD,又PD⊂平面P AD,∴AB⊥PD.又∵AB∩AE=A,∴PD⊥平面ABE.考点二面面垂直的判定与性质【例2】(2020·全国Ⅰ卷)如图,D为圆锥的顶点,O是圆锥底面的圆心,△ABC是底面的内接正三角形,P为DO上一点,∠APC=90°.(1)证明:平面P AB⊥平面P AC;(2)设DO =2,圆锥的侧面积为3π,求三棱锥P -ABC 的体积. (1)证明 由题设可知,P A =PB =PC . 由△ABC 是正三角形,可得△P AC ≌△P AB ,△P AC ≌△PBC . 又∠APC =90°,故∠APB =90°,∠BPC =90°.从而PB ⊥P A ,PB ⊥PC ,又P A ,PC ⊂平面P AC ,P A ∩PC =P , 故PB ⊥平面P AC ,又PB ⊂平面P AB , 所以平面P AB ⊥平面P AC .(2)解 设圆锥的底面半径为r ,母线长为l , 由题设可得rl =3,l 2-r 2=2,解得r =1,l = 3. 从而AB = 3.由(1)可得P A 2+PB 2=AB 2,故P A =PB =PC =62. 所以三棱锥P -ABC 的体积为 13·12·P A ·PB ·PC =13×12×⎝⎛⎭⎫623=68. 感悟升华 1.判定面面垂直的方法主要是:(1)面面垂直的定义;(2)面面垂直的判定定理(a ⊥β,a ⊂α⇒α⊥β).2.已知平面垂直时,解题一般要用性质定理进行转化.在一个平面内作交线的垂线,将问题转化为线面垂直,然后进一步转化为线线垂直.【训练2】 (2021·安徽A10联盟检测)如图,在四棱锥A -BCDE 中,△ADE 是边长为2的等边三角形,平面ADE ⊥平面BCDE ,底面BCDE 是等腰梯形,DE ∥BC ,DE =12BC ,BE=DC =2,BD =23,点M 是DE 边的中点,点N 在BC 上,且BN =3.(1)证明:BD ⊥平面AMN ;(2)设BD ∩MN =G ,求三棱锥A -BGN 的体积. (1)证明 ∵△ADE 是等边三角形,M 是DE 的中点, ∴AM ⊥DE .又平面ADE ⊥平面BCDE ,平面ADE ∩平面BCDE =DE , ∴AM ⊥平面BCDE ,∵BD ⊂平面BCDE ,∴AM ⊥BD ,∵MD =ME =1,BN =3,DE ∥BC ,DE =12BC ,∴MD 綉CN ,∴四边形MNCD 是平行四边形, ∴MN ∥CD .又BD =23,BC =4,CD =2,∴BD 2+CD 2=BC 2, ∴BD ⊥CD ,∴BD ⊥MN .又AM ∩MN =M ,∴BD ⊥平面AMN . (2)解 由(1)知AM ⊥平面BCDE , ∴AM 为三棱锥A -BGN 的高. ∵△ADE 是边长为2的等边三角形, ∴AM = 3.易知GN =34CD =32,又由(1)知BD ⊥MN ,∴BG =BN 2-NG 2=332.∴S △BGN =12BG ·NG =12×332×32=938.∴V A -BGN =13S △BGN ·AM =13×938×3=98.考点三 平行与垂直的综合问题角度1 平行与垂直关系的证明【例3】 如图,在四棱锥P -ABCD 中,底面ABCD 为矩形,平面P AD ⊥平面ABCD ,P A ⊥PD ,P A =PD ,E ,F 分别为AD ,PB 的中点.求证:(1)PE ⊥BC ;(2)平面P AB ⊥平面PCD ; (3)EF ∥平面PCD .证明 (1)因为P A =PD ,E 为AD 的中点, 所以PE ⊥AD .因为底面ABCD 为矩形,所以BC ∥AD . 所以PE ⊥BC .(2)因为底面ABCD 为矩形,所以AB ⊥AD .又因为平面P AD ⊥平面ABCD ,平面P AD ∩平面ABCD =AD ,AB ⊂平面ABCD , 所以AB ⊥平面P AD .又PD ⊂平面P AD ,所以AB ⊥PD . 又因为P A ⊥PD ,且P A ∩AB =A , 所以PD ⊥平面P AB .又PD ⊂平面PCD , 所以平面P AB ⊥平面PCD .(3)如图,取PC 中点G ,连接FG ,DG . 因为F ,G 分别为PB ,PC 的中点, 所以FG ∥BC ,FG =12BC .因为ABCD 为矩形,且E 为AD 的中点, 所以DE ∥BC ,DE =12BC .所以DE ∥FG ,DE =FG .所以四边形DEFG 为平行四边形. 所以EF ∥DG .又因为EF ⊄平面PCD ,DG ⊂平面PCD , 所以EF ∥平面PCD .感悟升华 1.三种垂直的综合问题,一般通过作辅助线进行线线、线面、面面垂直间的转化. 2.垂直与平行的结合问题,求解时应注意平行、垂直的性质及判定的综合应用.如果有平面垂直时,一般要用性质定理,在一个平面内作交线的垂线,使之转化为线面垂直,然后进一步转化为线线垂直.角度2 平行垂直关系与几何体的度量【例4】 (2019·天津卷)如图,在四棱锥P -ABCD 中,底面ABCD 为平行四边形,△PCD 为等边三角形,平面P AC ⊥平面PCD ,P A ⊥CD ,CD =2,AD =3.(1)设G ,H 分别为PB ,AC 的中点,求证:GH ∥平面P AD ; (2)求证:P A ⊥平面PCD ;(3)求直线AD 与平面P AC 所成角的正弦值. (1)证明 连接BD ,易知AC ∩BD =H ,BH =DH .又由BG =PG ,故GH 为△PBD 的中位线,所以GH ∥PD . 又因为GH ⊄平面P AD ,PD ⊂平面P AD ,所以GH ∥平面P AD . (2)证明 取棱PC 的中点N ,连接DN .依题意,得DN ⊥PC .又因为平面P AC ⊥平面PCD ,平面P AC ∩平面PCD =PC ,DN ⊂平面PCD ,所以DN ⊥平面P AC .又P A ⊂平面P AC ,所以DN ⊥P A . 又已知P A ⊥CD ,CD ∩DN =D , 所以P A ⊥平面PCD .(3)解 连接AN ,由(2)中DN ⊥平面P AC ,可知∠DAN 为直线AD 与平面P AC 所成的角. 因为△PCD 为等边三角形,CD =2且N 为PC 的中点, 所以DN = 3.又DN ⊥AN ,在Rt △AND 中,sin ∠DAN =DN AD =33.所以直线AD 与平面P AC 所成角的正弦值为33. 感悟升华 1.平行垂直关系应用广泛,不仅可以证明判断空间线面、面面位置关系,而且常用以求空间角和空间距离、体积.2.综合法求直线与平面所成的角,主要是找出斜线在平面内的射影,其关键是作垂线,找垂足,把线面角转化到一个三角形中求解.【训练3】 如图,AB 是⊙O 的直径,P A 垂直于⊙O 所在的平面,C 是圆周上不同于A ,B 的一动点.(1)证明:△PBC是直角三角形;(2)若P A=AB=2,且当直线PC与平面ABC所成角的正切值为2时,求直线AB与平面PBC 所成角的正弦值.(1)证明∵AB是⊙O的直径,C是圆周上不同于A,B的一动点.∴BC⊥AC,∵P A⊥平面ABC,∴P A⊥BC,又P A∩AC=A,P A,AC⊂平面P AC,∴BC⊥平面P AC,∴BC⊥PC,∴△BPC是直角三角形.(2)解如图,过A作AH⊥PC于H,∵BC⊥平面P AC,∴BC⊥AH,又PC∩BC=C,PC,BC⊂平面PBC,∴AH⊥平面PBC,∴∠ABH是直线AB与平面PBC所成的角,∵P A⊥平面ABC,∴∠PCA是直线PC与平面ABC所成的角,∵tan∠PCA=P AAC=2,又P A=2,∴AC=2,∴在Rt △P AC 中,AH =P A ·AC P A 2+AC 2=233,∴在Rt △ABH 中,sin ∠ABH =AH AB =2332=33,故直线AB 与平面PBC 所成角的正弦值为33.与垂直平行相关的探索性问题立体几何中的探索性问题是近年高考的热点,题目主要涉及线面平行、垂直位置关系的探究,条件或结论不完备的开放性问题的探究,重点考查逻辑推理,直观想象与数学运算核心素养. 【典例】 如图所示,在四棱锥P -ABCD 中,底面ABCD 为直角梯形,∠ABC =∠BAD =90°,△PDC 和△BDC 均为等边三角形,且平面PDC ⊥平面BDC .(1)在棱PB 上是否存在点E ,使得AE ∥平面PDC ?若存在,试确定点E 的位置;若不存在,试说明理由. (2)若△PBC 的面积为152,求四棱锥P -ABCD 的体积. 解 (1)存在点E ,当点E 为棱PB 的中点时,使得AE ∥面PDC ,理由如下:如图所示,取PB 的中点E ,连接AE ,取PC 的中点F ,连接EF ,DF ,取BC 的中点G ,连接DG .因为△BCD 是等边三角形,所以∠DGB =90°. 因为∠ABC =∠BAD =90°,所以四边形ABGD 为矩形,所以AD =BG =12BC ,AD ∥BC .因为EF 为△BCP 的中位线,所以EF =12BC ,且EF ∥BC ,故AD =EF ,且AD ∥EF ,所以四边形ADFE 是平行四边形,从而AE ∥DF , 又AE ⊄平面PDC ,DF ⊂平面PDC , 所以AE ∥平面PDC .(2)取CD 的中点M ,连接PM ,过点P 作PN ⊥BC 交BC 于点N ,连接MN ,如图所示. 因为△PDC 为等边三角形,所以PM ⊥DC .因为PM ⊥DC ,平面PDC ⊥平面BDC ,平面PDC ∩平面BDC =DC . 所以PM ⊥平面BCD ,故PM 为四棱锥P -ABCD 的高. 又BC ⊂平面BCD ,所以PM ⊥BC .因为PN ⊥BC ,PN ∩PM =P ,PN ⊂平面PMN ,PM ⊂平面PMN ,所以BC ⊥平面PMN . 因为MN ⊂平面PMN ,所以BC ⊥MN . 由M 为DC 的中点,易知NC =14BC .设BC =x ,则△PBC 的面积为x 2·x 2-⎝⎛⎭⎫x 42=152,解得x =2,即BC =2, 所以AD =1,AB =DG =PM = 3.故四棱锥P -ABCD 的体积为V =13×S 梯形ABCD ×PM =13×1+2×32×3=32.素养升华 1.求条件探索性问题的主要途径:(1)先猜后证,即先观察与尝试给出条件再证明;(2)先通过命题成立的必要条件探索出命题成立的条件,再证明充分性.2.涉及点的位置探索性问题一般是先根据条件猜测点的位置再给出证明,探索点的存在问题,点多为中点或三等分点中某一个,也可以根据相似知识建点.平行或垂直关系入手,把所探究的结论转化为平面图形中线线关系,从而确定探究的结果. 【训练】 如图,三棱锥P -ABC 中,P A ⊥平面ABC ,P A =1,AB =1,AC =2,∠BAC =60°.(1)求三棱锥P -ABC 的体积;(2)在线段PC 上是否存在点M ,使得AC ⊥BM ,若存在点M ,求出PMMC 的值;若不存在,请说明理由.解 (1)由题知AB =1,AC =2,∠BAC =60°, 可得S △ABC =12·AB ·AC ·sin 60°=32,由P A ⊥平面ABC ,可知P A 是三棱锥P -ABC 的高. 又P A =1,所以三棱锥P -ABC 的体积V =13·S △ABC ·P A =36.(2)在平面ABC 内,过点B 作BN ⊥AC ,垂足为N .在平面P AC 内,过点N 作MN ∥P A 交PC 于点M ,连接BM .由P A ⊥平面ABC 知P A ⊥AC ,所以MN ⊥AC . 由于BN ∩MN =N ,故AC ⊥平面MBN . 又BM ⊂平面MBN ,所以AC ⊥BM .在Rt △BAN 中,AN =AB ·cos ∠BAC =12,从而NC =AC -AN =32.由MN ∥P A ,得PM MC =AN NC =13.A 级 基础巩固一、选择题1.(2021·淮北质检)已知平面α,直线m ,n ,若n ⊂α,则“m ⊥n ”是“m ⊥α”的( )A .充分不必要条件B .充分必要条件C .必要不充分条件D .既不充分也不必要条件答案 C解析 由n ⊂α,m ⊥n ,不一定得到m ⊥α;反之,由n ⊂α,m ⊥α,可得m ⊥n . ∴若n ⊂α,则“m ⊥n ”是“m ⊥α”的必要不充分条件.2.在正方体ABCD -A 1B 1C 1D 1中,E 为棱CD 的中点,则( ) A .A 1E ⊥DC 1 B .A 1E ⊥BD C .A 1E ⊥BC 1 D .A 1E ⊥AC 答案 C解析 如图,由题设知,A 1B 1⊥平面BCC 1B 1,且BC 1⊂平面BCC 1B 1,从而A 1B 1⊥BC 1. 又B 1C ⊥BC 1,且A 1B 1∩B 1C =B 1,所以BC 1⊥平面A 1B 1CD ,又A 1E ⊂平面A 1B 1CD ,所以A 1E ⊥BC 1.3.(2021·郑州调研)已知m ,l 是两条不同的直线,α,β是两个不同的平面,则下列可以推出α⊥β的是( ) A .m ⊥l ,m ⊂β,l ⊥α B .m ⊥l ,α∩β=l ,m ⊂α C .m ∥l ,m ⊥α,l ⊥β D .l ⊥α,m ∥l ,m ∥β答案 D解析 在A 中,m ⊥l ,m ⊂β,l ⊥α,则α与β相交或平行,故A 错误; 在B 中,m ⊥l ,α∩β=l ,m ⊂α,则α与β有可能相交但不垂直,故B 错误; 在C 中,m ∥l ,m ⊥α,l ⊥β,则α∥β,故C 错误;在D 中,l ⊥α,m ∥l ,则m ⊥α,又m ∥β,则α⊥β,故D 正确.4.已知三棱柱ABC -A 1B 1C 1的侧棱与底面垂直,体积为94,底面是边长为3的正三角形,若P 为底面A 1B 1C 1的中心,则P A 与平面ABC 所成角的大小为( ) A.5π12 B .π3C.π4 D .π6答案 B解析 如图,取正三角形ABC 的中心为O ,连接OP ,则∠P AO 是P A 与平面ABC 所成的角.因为底面边长为3, 所以AD =3×32=32,AO =23AD =23×32=1.三棱柱的体积为34×(3)2AA 1=94, 解得AA 1=3,即OP =AA 1=3, 所以tan ∠P AO =OPOA=3,因为直线与平面所成角的范围是⎣⎡⎦⎤0,π2, 所以∠P AO =π3.5. (2020·昆明诊断)如图,AC =2R 为圆O 的直径,∠PCA =45°,P A 垂直于圆O 所在的平面,B 为圆周上不与点A 、C 重合的点,AS ⊥PC 于S ,AN ⊥PB 于N ,则下列不正确的是( )A.平面ANS⊥平面PBCB.平面ANS⊥平面P ABC.平面P AB⊥平面PBCD.平面ABC⊥平面P AC答案 B解析∵P A⊥平面ABC,BC⊂平面ABC,∴P A⊥BC,又AC为圆O直径,所以AB⊥BC,又P A∩AB=A,∴BC⊥平面P AB,又AN⊂平面ABP,∴BC⊥AN,又AN⊥PB,BC∩PB=B,∴AN⊥平面PBC,又AN⊂平面ANS,∴平面ANS⊥平面PBC,∴A正确,C,D显然正确.6.(2020·衡水调研)如图,点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动,则下列四个结论:①三棱锥A-D1PC的体积不变;②A1P∥平面ACD1;③DP⊥BC1;④平面PDB1⊥平面ACD1.其中正确的结论的个数是()A.1个B.2个C.3个D.4个答案 C解析对于①,由题意知AD1∥BC1,从而BC1∥平面AD1C,故BC1上任意一点到平面AD1C 的距离均相等,所以以P为顶点,平面AD1C为底面,则三棱锥A-D1PC的体积不变,故①正确;对于②,连接A1B,A1C1,A1C1綉AC,由于①知:AD1∥BC1,所以面BA1C1∥面ACD1,从而由线面平行的定义可得,故②正确;对于③,由于DC⊥平面BCC1B1,所以DC⊥BC1,若DP⊥BC1,则BC1⊥平面DCP,所以BC1⊥PC,则P为中点,与P为动点矛盾,故③错误;对于④,连接DB1,由DB1⊥AC且DB1⊥AD1,可得DB1⊥面ACD1,从而由面面垂直的判定知,故④正确.二、填空题7.(2019·北京卷)已知l,m是平面α外的两条不同直线.给出下列三个论断:①l⊥m;②m∥α;③l⊥α.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:________. 答案若m∥α,l⊥α,则l⊥m(或若l⊥m,l⊥α,则m∥α,答案不唯一)解析已知l,m是平面α外的两条不同直线,由①l⊥m与②m∥α,不能推出③l⊥α,因为l可以与α平行,也可以相交不垂直;由①l⊥m与③l⊥α能推出②m∥α;由②m∥α与③l⊥α可以推出①l⊥m.故正确的命题是②③⇒①或①③⇒②.8.如图,在直三棱柱ABC -A 1B 1C 1中,侧棱长为2,AC =BC =1,∠ACB =90°,D 是A 1B 1的中点,F 是BB 1上的动点,AB 1,DF 交于点E ,要使AB 1⊥平面C 1DF ,则线段B 1F 的长为________.答案 12解析 设B 1F =x ,因为AB 1⊥平面C 1DF ,DF ⊂平面C 1DF , 所以AB 1⊥DF , 由已知可得A 1B 1=2,设Rt △AA 1B 1斜边AB 1上的高为h ,则DE =12h .又12×2×2=12×h 22+22,所以h =233,DE =33.在Rt △DB 1E 中,B 1E =⎝⎛⎭⎫222-⎝⎛⎭⎫332=66. 由面积相等得12×66×x 2+⎝⎛⎭⎫222=12×22x , 得x =12.9.如图所示,在四棱锥P -ABCD 中,P A ⊥底面ABCD ,且底面各边都相等,M 是PC 上的一动点,当点M 满足________时,平面MBD ⊥平面PCD (只要填写一个你认为是正确的条件即可).答案 DM ⊥PC (或BM ⊥PC ) 解析 连接AC ,BD ,则AC ⊥BD ,因为P A ⊥底面ABCD ,BD ⊂平面ABCD ,所以P A ⊥BD .又P A ∩AC =A ,所以BD ⊥平面P AC ,PC ⊂平面P AC ,所以BD ⊥PC . 所以当DM ⊥PC (或BM ⊥PC )时, 有PC ⊥平面MBD .PC ⊂平面PCD ,所以平面MBD ⊥平面PCD . 三、解答题10.如图,在三棱锥P -ABC 中,AB =BC =22,P A =PB =PC =AC =4,O 为AC 的中点.(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且MC =2MB ,求点C 到平面POM 的距离. (1)证明 因为AP =CP =AC =4,O 为AC 的中点, 所以OP ⊥AC ,且OP =2 3.连接OB ,因为AB =BC ,AB 2+BC 2=AC 2,所以△ABC 为等腰直角三角形,且OB ⊥AC ,OB =12AC =2.由OP 2+OB 2=PB 2知,OP ⊥OB .由OP ⊥OB ,OP ⊥AC 且OB ∩AC =O ,知PO ⊥平面ABC . (2)解 作CH ⊥OM ,垂足为H .又由(1)可得OP ⊥CH ,所以CH ⊥平面POM . 故CH 的长为点C 到平面POM 的距离. 由题设可知OC =12AC =2,CM =23BC =423,∠ACB =45°.所以OM =253,CH =OC ·MC ·sin ∠ACB OM =455.所以点C 到平面POM 的距离为455.11. (2021·昆明诊断)如图,在四棱锥P -ABCD 中,底面ABCD 是菱形,∠BAD =60°,△P AD 是正三角形,E 为线段AD 的中点.(1)求证:平面PBC ⊥平面PBE ;(2)是否存在满足PF →=λFC →(λ>0)的点F ,使得V B -P AE =34V D -PFB ?若存在,求出λ的值;若不存在,请说明理由.(1)证明 因为△P AD 是正三角形,E 为线段AD 的中点, 所以PE ⊥AD .因为底面ABCD 是菱形,所以AD =AB ,又∠BAD =60°, 所以△ABD 是正三角形, 所以BE ⊥AD . 又BE ∩PE =E , 所以AD ⊥平面PBE . 又AD ∥BC , 所以BC ⊥平面PBE . 又BC ⊂平面PBC , 所以平面PBC ⊥平面PBE .(2)解 由PF →=λFC →,知(λ+1)FC =PC , 所以V B -P AE =12V P -ADB =12V P -BCD =λ+12V F -BCD ,V D -PFB =V P -BDC -V F -BDC =λV F -BCD . 因此,λ+12=3λ4,得λ=2.故存在满足PF →=λFC →(λ>0)的点F , 使得V B -P AE =34V D -PFB ,此时λ=2.B 级 能力提升12.如图,正三角形ABC 的中线AF 与中位线DE 相交于点G ,已知△A ′DE 是△ADE 绕直线DE 翻折过程中的一个图形,现给出下列命题: ①恒有直线BC ∥平面A ′DE ; ②恒有直线DE ⊥平面A ′FG ;③恒有平面A ′FG ⊥平面A ′DE ,其中正确命题的个数为( )A.0 B.1 C.2 D.3答案 D解析对于①,∵DE为△ABC的中位线,∴DE∥BC,又知DE⊂平面A′DE,BC⊄平面A′DE,∴BC∥平面A′DE,故①正确;对于②,∵△ABC为等边三角形,AF为BC边上的中线,∴BC⊥AF,又知DE∥BC,∴DE⊥AF,∴DE⊥FG,根据翻折的性质可知,DE⊥A′G,又A′G∩FG=G,∴DE⊥平面A′FG,故②正确;对于③,由②知DE⊥平面A′FG,又知DE⊂平面A′DE,∴平面A′FG⊥平面A′DE,故③正确.综上,正确的命题为①②③. 13.(2019·全国Ⅰ卷)已知∠ACB=90°,P为平面ABC外一点,PC=2,点P到∠ACB两边AC,BC的距离均为3,那么P到平面ABC的距离为________.答案 2解析如图,过点P作PO⊥平面ABC于O,则PO为P到平面ABC的距离.再过O作OE⊥AC于E,OF⊥BC于F,连接PC,PE,PF,则PE⊥AC,PF⊥BC.所以PE=PF=3,所以OE=OF,所以CO为∠ACB的平分线,即∠ACO=45°.在Rt△PEC中,PC=2,PE=3,所以CE=1,所以OE=1,所以PO=PE2-OE2=32-12= 2.14.如图,在平行四边形ABCM中,AB=AC=3,∠ACM=90°.以AC为折痕将△ACM折起,使点M到达点D的位置,且AB⊥DA.(1)证明:平面ACD ⊥平面ABC ;(2)Q 为线段AD 上一点,P 为线段BC 上一点,且BP =DQ =23DA ,求三棱锥Q -ABP 的体积.(1)证明 由已知可得,∠BAC =90°,即BA ⊥AC .又BA ⊥AD ,AC ∩AD =A ,AC ,AD ⊂平面ACD ,所以AB ⊥平面ACD . 又AB ⊂平面ABC , 所以平面ACD ⊥平面ABC .(2)解 由已知可得, DC =CM =AB =3, DA =AM =3 2. 又BP =DQ =23DA ,所以BP =2 2.作QE ⊥AC ,垂足为E ,则QE 綉13DC .由已知及(1)可得DC ⊥平面ABC ,所以QE ⊥平面ABC ,QE =1. 因此,三棱锥Q -ABP 的体积为V Q -ABP =13×QE ×S △ABP =13×1×12×3×22sin 45°=1.。
高考数学一轮复习课时跟踪检测(四十三)直线、平面垂直的判定及其性质理(重点高中)

课时跟踪检测(四十三) 直线、平面垂直的判定及其性质 (二)重点高中适用作业A 级——保分题目巧做快做)(的中点,则CD 为棱E 中,1D 1C 1B 1A ABCD 在正方体)Ⅲ全国卷(2017·.1 1DC ⊥E 1A .ABD ⊥E 1A .B 1BC ⊥E 1A .C AC ⊥E 1A .D ,1B =C 1B ∩1B 1A ,1BC ⊥C 1B ,1BC ⊥1B 1A 法一:由正方体的性质,得 C 解析:选 .CD 1B 1A 平面⊥1BC 所以 ,CD 1B 1A 平面⊂E 1A 又 .1BC ⊥E 1A 所以 错;D 、B ∴垂直,BD ,AC 不与AE ,而AE 投影为上的ABCD 在平面E 1A ∵法二: ,1BC ⊥C 1B ,且C 1B 上的投影为1B 1BCC 在平面E 1A ∵ 正确;C ,故1BC ⊥E 1A ∴ ,CE ⊥1BC ,C 1B ⊥1BC 证明:由条件易知,( .1B 1CEA 平面⊥1BC ∴,C =C 1B ∩CE 又 .)1BC ⊥E 1A ∴,1B 1CEA 平面⊂E 1A 又 ,E 1D 上的投影为1D 1DCC 在平面E 1A ∵ 错.A 垂直,故1DC 不与E 1D 而 2.如图,在Rt △ABC 中,∠ABC =90°,P 为△ABC 所在平面外一点,PA ⊥平面ABC ,则四面体P ABC 中直角三角形的个数为( )A .4B .3C .2D .1 解析:选A 由PA ⊥平面ABC 可得△PAC ,△PAB 是直角三角形,且PA ⊥BC .又∠ABC =90°,所以△ABC 是直角三角形,且BC ⊥平面PAB ,所以BC ⊥PB ,即△PBC 为直角三角形,故四面体P ABC 中共有4个直角三角形.3.(2018·吉林实验中学测试)设a ,b ,c 是空间的三条直线,α,β是空间的两个平面,则下列命题中,逆命题不成立的是( )A .当c ⊥α时,若c ⊥β,则α∥βB .当b ⊂α时,若b ⊥β,则α⊥βC .当b ⊂α,且c 是a 在α内的射影时,若b ⊥c ,则a ⊥bD .当b ⊂α,且c ⊄α时,若c ∥α,则b ∥c解析:选B A 的逆命题为:当c ⊥α时,若α∥β,则c ⊥β,由线面垂直的性质知c ⊥β,故A 正确;B 的逆命题为:当b ⊂α时,若α⊥β,则b ⊥β,显然错误,故B 错误;C的逆命题为:当b⊂α,且c是a在α内的射影时,若a⊥b,则b⊥c.由三垂线逆定理知b⊥c,故C正确;D的逆命题为:当b⊂α,且c⊄α时,若b∥c,则c∥α.由线面平行判定定理可得c∥α,故D正确.4.(2018·贵阳监测考试)如图,在三棱锥PABC中,不能证明AP⊥BC的条件是( )A.AP⊥PB,AP⊥PCB.AP⊥PB,BC⊥PBC.平面BPC⊥平面APC,BC⊥PCD.AP⊥平面PBC解析:选B A中,因为AP⊥PB,AP⊥PC,PB∩PC=P,所以AP⊥平面PBC,又BC⊂平面PBC,所以AP⊥BC,故A能证明AP⊥BC;C中,因为平面BPC⊥平面APC,BC⊥PC,所以BC⊥平面APC,又AP⊂平面APC,所以AP⊥BC,故C能证明AP⊥BC;由A知D能证明AP⊥BC;B中条件不能判断出AP⊥BC,故选B. 5.(2018·唐山一模)如图,在正方形ABCD中,E,F分别是BC,CD的中点,G是EF的中点,现在沿AE,AF及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H,那么,在这个空间图形中必有( )B.AH⊥平面EFHA.AG⊥平面EFHD.HG⊥平面AEFC.HF⊥平面AEF解析:选B 根据折叠前、后AH⊥HE,AH⊥HF不变,得AH⊥平面EFH,B正确;∵过A只有一条直线与平面EFH垂直,∴A不正确;∵AG⊥EF,EF⊥GH,AG∩GH=G,∴EF⊥平面HAG,又EF⊂平面AEF,∴平面HAG⊥AEF,过H作直线垂直于平面AEF,一定在平面HAG内,∴C不正确;由条件证不出HG⊥平面AEF,∴D不正确.故选B.6.如图,PA⊥⊙O所在平面,AB是⊙O的直径,C是⊙O上一点,AE⊥PC,AF⊥PB,给出下列结论:①AE⊥BC;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC,其中真命题的序号是________.解析:①AE⊂平面PAC,BC⊥AC,BC⊥PA⇒AE⊥BC,故①正确,②AE⊥PC,AE⊥BC,PB⊂平面PBC⇒AE⊥PB,AF⊥PB,EF⊂平面AEF⇒EF⊥PB,故②正确,③若AF ⊥BC ⇒AF ⊥平面PBC ,则AF ∥AE 与已知矛盾,故③错误,由①可知④正确.答案:①②④7.(2018·兰州实战考试)α,β是两平面,AB ,CD 是两条线段,已知α∩β=EF ,AB ⊥α于B ,CD ⊥α于D ,若增加一个条件,就能得出BD ⊥EF .现有下列条件:①AC ⊥β;②AC 与α,β所成的角相等;③AC 与CD 在β内的射影在同一条直线上;④AC ∥EF .其中能成为增加条件的序号是________.解析:由题意得,AB ∥CD ,∴A ,B ,C ,D 四点共面.①中,∵AC ⊥β,EF ⊂β,∴AC ⊥EF ,又∵AB ⊥α,EF ⊂α,∴AB ⊥EF ,∵AB ∩AC =A ,∴EF ⊥平面ABCD ,又∵BD ⊂平面ABCD ,∴BD ⊥EF ,故①正确;②不能得到BD ⊥EF ,故②错误;③中,由AC 与CD 在β内的射影在同一条直线上可知平面ABCD ⊥β,又AB ⊥α,AB⊂平面ABCD ,∴平面ABCD ⊥α.∵平面ABCD ⊥α,平面ABCD ⊥β,α∩β=EF ,∴EF ⊥平面ABCD ,又BD ⊂平面ABCD ,∴BD ⊥EF ,故③正确;④中,由①知,若BD ⊥EF ,则EF ⊥平面ABCD ,则EF ⊥AC ,故④错误,故填①③.答案:①③ABCD ,将四边形CD ⊥BD ,2=BD ,1=CD =AD =AB 中,ABCD .如图所示,在四边形8沿对角线BD 折成四面体A ′BCD ,使平面A ′BD ⊥平面BCD ,则下列结论正确的是________..16的体积为BCD ′A 四面体③;90°=C ′BA ②∠;BD ⊥C ′A ①解析:∵BD ⊥CD ,平面A ′BD ⊥平面BCD ,平面A ′BD ∩平面BCD =BD ,CD ⊂平面BCD ,∴CD ⊥平面A ′BD ,∴CD ⊥A ′D .,2=BD ,1=CD =AD =AB ∵ ,2BC =2C ′A +2B ′A ∴,3=BC ,2=C ′A ∴ ∴A ′B ⊥A ′C ,即∠BA ′C =90°,.16=×12×112×13=V 的体积BCD ′A 四面体 答案:②③9.(2017·全国卷Ⅰ)如图,在四棱锥P ABCD 中,AB ∥CD ,且∠BAP =∠CDP =90°.(1)证明:平面PAB ⊥平面PAD ;(2)若PA =PD =AB =DC ,∠APD =90°,且四棱锥P ABCD 的体,求该四棱锥的侧面积.83积为 解:(1)证明:由∠BAP =∠CDP =90°, 得AB ⊥AP ,CD ⊥PD .因为AB ∥CD ,所以AB ⊥PD .又AP ∩PD =P ,所以AB ⊥平面PAD .又AB ⊂平面PAB ,所以平面PAB ⊥平面PAD .(2)如图所示,在平面PAD 内作PE ⊥AD ,垂足为E .由(1)知,AB ⊥平面PAD ,故AB ⊥PE ,可得PE ⊥平面ABCD ..x 22=PE ,x 2=AD ,则由已知可得x =AB 设 故四棱锥P ABCD 的体积.3x 13=PE ·AD ·AB 13=ABCD P V 2.=x ,故83=3x 13由题设得 .22=PC =PB ,22=BC =AD ,2=DC =AB =PD =PA 从而 可得四棱锥P ABCD 的侧面积为12.32+6=sin 60°2BC 12+DC ·PD 12+AB ·PA 12+PD ·PA 10.如图①,△ABC 为等腰直角三角形,∠B =90°,将△ABC 沿中位线DE 翻折,得到如图②所示的空间图形(∠ADB 为锐角).(1)求证:BC ⊥平面ABD ;的大小.ABD ∠时,求36的体积为BCE A ,当三棱锥2=BC 若(2)解:(1)证明:在等腰直角△ABC 中,AB ⊥BC ,又DE 为△ABC 的中位线,∴DE ∥BC ,∴DE ⊥AB .由翻折,可知DE ⊥AD ,DE ⊥DB ,又AD ∩DB =D ,∴DE ⊥平面ABD .又BC ∥DE ,∴BC ⊥平面ABD .(2)由(1)知,平面ABD ⊥平面BCED ,交线为BD ,如图,作AO ⊥BD 于点O ,则AO ⊥平面BCED ,则三棱锥A BCE 的高为AO ,,1=×2×112=DB ·BC ·12=BCE △S ,36=AO ×1×13=AO ×BCE △S ×13=BCE A V 由 .32=AO 可得 ,32=AO AD =ADO ∠sin 中,ADO △Rt 在∴ ∴∠ADO =∠ADB =60°,又AD =DB ,∴△ADB 是等边三角形,∴∠ABD =60°.B 级——拔高题目稳做准做1.如图,在三棱锥D ABC 中,若AB =CB ,AD =CD ,E 是AC 的中点,则下列命题中正确的是( )A .平面ABC ⊥平面ABDB .平面ABD ⊥平面BCDC .平面ABC ⊥平面BDE ,且平面ACD ⊥平面BDED .平面ABC ⊥平面ACD ,且平面ACD ⊥平面BDE解析:选C 因为AB =CB ,且E 是AC 的中点,所以BE ⊥AC ,同理,DE ⊥AC ,由于DE ∩BE =E ,于是AC ⊥平面BDE .因为AC ⊂平面ABC ,所以平面ABC ⊥平面BDE .又AC ⊂平面ACD ,所以平面ACD ⊥平面BDE .故选C.2.(2018·广州模拟)如图是一个几何体的平面展开图,其中四边形ABCD为正方形,E,F分别为PA,PD的中点,在此几何体中,给出下面四个结论:①直线BE与直线CF异面;②直线BE与直线AF异面;③直线EF∥平面PBC;④平面BCE⊥平面PAD.其中正确结论的个数是( )B.2A.1C.3D.4解析:选 B 画出该几何体,如图所示,①因为E,F分别是PA,PD的中点,所以EF∥AD,所以EF∥BC,直线BE与直线CF是共面直线,故①不正确;②直线BE与直线AF满足异面直线的定义,故②正确;③由E,F分别是PA,PD的中点,可知EF∥AD,所以EF∥BC,因为EF⊄平面PBC,BC⊂平面PBC,所以直线EF∥平面PBC,故③正确;④因为BE与PA的关系不能确定,所以不能判定平面BCE⊥平面PAD,故④不正确.所以正确结论的个数是2.3.如图所示,在四棱锥PABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足______时,平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)解析:连接AC,则AC⊥BD,∵PA⊥底面ABCD,∴PA⊥BD.又PA∩AC=A,∴BD⊥平面PAC,∴BD⊥PC.∴当DM⊥PC(或BM⊥PC)时,即有PC⊥平面MBD.而PC⊂平面PCD,∴平面MBD⊥平面PCD.答案:DM⊥PC(或BM⊥PC) 4.(2018·武汉调研)在矩形ABCD中,AB<BC,现将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折的过程中,给出下列结论:①存在某个位置,使得直线AC与直线BD垂直;②存在某个位置,使得直线AB与直线CD垂直;③存在某个位置,使得直线AD与直线BC垂直.其中正确结论的序号是________.BD⇒ ⎭⎪⎬⎪⎫AE⊥BDAC⊥BD AE∩AC=A 则.CE ,连接E 于BD ⊥AE 作A 垂直,过点BD 与AC 假设①解析:⊥平面AEC ⇒BD ⊥CE ,而在平面BCD 中,EC 与BD 不垂直,故假设不成立,①错误.②假设AB ⊥CD ,∵AB ⊥AD ,AD ∩CD =D ,∴AB ⊥平面ACD ,∴AB ⊥AC ,由AB <BC 可知,存在这样的等腰直角三角形,使AB ⊥CD ,故假设成立,②正确.③假设AD ⊥BC ,∵DC ⊥BC ,∴BC ⊥平面ADC ,∴BC ⊥AC ,即△ABC 为直角三角形,且AB 为斜边,而AB <BC ,故矛盾,假设不成立,③错误.答案:②5.(2018·湖北七市(州)联考)《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形的直棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵ABM DCP 与刍童13=V 台体体积公式:.1D 1A =1B 1A ,AD =AB 的组合体中,1D 1C 1B 1A ABCD h分别为台体上、下底面的面积,S ,′S ,其中h )S +S′S +′S (为台体的高.(1)证明:直线BD ⊥平面MAC ;,求该组合体的体233=′V 的体积1D 1B 1A A ,三棱锥3=MA ,2=1D 1A ,1=AB 若(2)积.解:(1)证明:由题意可知ABM DCP 是底面为直角三角形的直棱柱,∴AD ⊥平面MAB ,∴AD ⊥MA .又MA ⊥AB ,AD ∩AB =A ,AD ⊂平面ABCD ,AB ⊂平面ABCD ,∴MA ⊥平面ABCD ,∴MA ⊥BD ,又AB =AD ,∴四边形ABCD 为正方形,∴BD ⊥AC .又MA ∩AC =A ,MA ⊂平面MAC ,AC ⊂平面MAC ,∴BD ⊥平面MAC .,h 的高为1D 1C 1B 1A ABCD 设刍童(2),233=h ×2×2×12×13=′V 的体积1D 1B 1A A 则三棱锥 ,3=h ∴ =733+32=3)×12×22+22+2×(113+×13×1×12=V 故该组合体的体积.17366.(2018·山西重点中学联考)如图1,在梯形ABCD 中,AD ∥BC ,AD ⊥DC ,BC =2AD ,平面⊥1F 1ABE 的位置,使平面1F 1ABE 折起到四边形AB 沿ABEF 是矩形.将矩形ABEF 四边形 2.的中点,如图1AF 为M ,ABCD;DC ⊥1BE 求证:(1) ;1BCE 平面∥DM 求证:(2) 的位置关系,并说明理由.1ME 与CD 判断直线(3) .AB ⊥1BE 为矩形,所以1F 1ABE 证明:因为四边形(1)解: ,1F 1ABE 平面⊂1BE ,AB =1F 1ABE 平面∩ABCD ,且平面1F 1ABE 平面⊥ABCD 因为平面 .ABCD 平面⊥1BE 所以 .DC ⊥1BE ,所以ABCD 平面⊂DC 因为 为矩形,1F 1ABE 证明:因为四边形(2) .1BE ∥AM 所以 ,1BCE 平面⊂1BE ,1BCE 平面⊄AM 因为 .1BCE 平面∥AM 所以 ,1BCE 平面⊂BC ,1BCE 平面⊄AD ,BC ∥AD 因为 .1BCE 平面∥AD 所以 又AD ∩AM =A ,.1BCE 平面∥ADM 所以平面 因为DM ⊂平面ADM ,.1BCE 平面∥DM 所以 相交.1ME 与CD 线直(3)理由如下:,QM ,PQ ,AP ,连接Q 的中点1CE ,P 的中点BC 取 .1BE 12=PQ ,且1BE ∥PQ 所以 的中点,1AF 为M 中,1F 1ABE 在矩形 .1BE 12=AM ,且1BE ∥AM 所以 所以PQ ∥AM ,且PQ =AM .所以四边形APQM 为平行四边形.所以MQ ∥AP ,MQ =AP .因为四边形ABCD 为梯形,P 为BC 的中点,BC =2AD ,所以AD ∥PC ,且AD =PC .所以四边形ADCP 为平行四边形.所以CD ∥AP ,且CD =AP .所以CD ∥MQ ,且CD =MQ .所以四边形CDMQ 为平行四边形..1CE ∥DM ,即CQ ∥DM 所以 ,1CE ≠DM 因为 为底边的梯形.1CE ,DM 是以C 1DME 所以四边形 相交.1ME 与CD 所以直线。
2021年高考数学一轮复习 7.5直线、平面垂直的判定及其性质课时跟踪训练 文

2021年高考数学一轮复习 7.5直线、平面垂直的判定及其性质课时跟踪训练文一、选择题1.已知平面α及α外的一条直线l,下列命题中不正确的是( )A.若l垂直于α内的两条平行线,则l⊥αB.若l垂直于α内的所有直线,则l⊥αC.若l垂直于α内的两条相交直线,则l⊥αD.若l垂直于α内的任意一条直线,则l⊥α解析:选项B、D是直线与平面垂直的定义,选项C是直线和平面垂直的判定定理,而A中,直线l也可以是与平面α斜交或平行的直线,故选A.答案:A2.(xx·辽宁卷)已知m,n表示两条不同直线,α表示平面.下列说法正确的是( ) A.若m∥α,n∥α,则m∥nB.若m⊥α,n⊂α,则m⊥nC.若m⊥α,m⊥n,则n∥αD.若m∥α,m⊥n,则n⊥α解析:选项A中,平行于同一平面的两条直线可以平行、相交、异面,故选项A是错误的;选项B中,由线面垂直的性质知:直线垂直于平面,则直线垂直于平面内的任意一条直线,故选项B正确;选项C中,n可能在平面α内,故选项C错误;选项D中,两直线垂直,其中一条直线与一个平面平行,则另一条直线和这个平面可以平行、相交,也可以在平面内,故选项D错误.所以选B.答案:B3.(xx·唐山模拟)设l、m、n均为直线,其中m、n在平面α内,则“l⊥α”是“l ⊥m且l⊥n”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析:当l⊥α时,l⊥m且l⊥n.但当l⊥m,l⊥n时,若m、n不是相交直线,则得不到l⊥α.答案:A4.已知m、n是两条不同的直线,α、β、γ是三个不同的平面,则下列命题中正确的是( )A.若α⊥β,α∩β=m,且n⊥m,则n⊥α或n⊥βB.若m不垂直于α,则m不可能垂直于α内的无数条直线C.若α∩β=m,n∥m,且n⊄α,n⊄β,则n∥α且n∥βD.若α⊥β,m∥n,n⊥β,则m∥α解析:∵n∥m,m⊂α,n⊄α,∴n∥α;同理可知n∥β.故选C.答案:C5.(xx·新课标全国卷Ⅱ)正三棱柱ABC—A1B1C1的底面边长为2,侧棱长为3,D为BC 中点,则三棱锥A—B1DC1的体积为( )A.3 B.32C.1 D.32解析:由题意可知AD⊥BC,由面面垂直的性质定理可得AD⊥平面DB1C1,又AD=2·sin60°=3,所以VA—B1DC1=13AD·S△B1DC1=13×3×12×2×3=1,故选C.答案:C6.如图,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°.将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下列命题正确的是( )A.平面ABD⊥平面ABCB.平面ADC⊥平面BDCC.平面ABC⊥平面BDCD.平面ADC⊥平面ABC解析:∵在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,∴BD⊥CD.又平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD,故CD⊥平面ABD,则CD⊥AB.又AD⊥AB,CD∩AD=D,故AB⊥平面ADC.∴平面ABC⊥平面ADC.故选D.答案:D二、填空题7.已知平面α,β和直线m,给出条件:①m∥α;②m⊥α;③m⊂α;④α∥β.当满足条件________时,有m⊥β (填所选条件的序号).解析:若m⊥α,α∥β,则m⊥β.答案:②④8.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足__________时,平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)解析:由定理可知,BD⊥PC.∴当DM⊥PC(或BM⊥PC)时,就有PC⊥平面MBD,而PC⊂平面PCD,∴平面MBD⊥平面PCD.答案:DM⊥PC(或BM⊥PC等)9.如图,在三棱柱ABC—A1B1C1中,各棱长均为2,AA1⊥底面ABC,D为棱AB的中点,则点C1到平面A1DC的距离为__________.解析:如图所示,连接AC1交A1C于点O,连接DO、BC1,则DO∥BC1,故BC1∥平面A1DC,则点C1到平面A1DC的距离等于点B到平面A1DC的距离,设点B到平面A1DC的距离为h,由等体积法得VA1-BDC=VB-A1DC,即13×12×3×1×2=13×12×3×5×h,得h=255.答案:25 5三、解答题10.在几何体ABCDE中,∠BAC=90°,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB =AC=BE=2,CD=1.(1)求证:DC∥平面ABE;(2)求证:AF⊥平面BCDE;(3)求证:平面AFD⊥平面AFE.证明:(1)∵DC⊥平面ABC,EB⊥平面ABC∴DC∥EB,又∵DC⊄平面ABE,EB⊂平面ABE,∴DC∥平面ABE.(2)DC⊥平面ABC,∴DC⊥AF,又∵AB=AC,F为BC的中点∴AF⊥BC,∴AF⊥平面BCDE.(3)由(2)知AF⊥平面BCDE,∴AF⊥EF,在三角形DEF中,由计算知DF⊥EF,∴EF⊥平面AFD,又EF⊂平面AFE,∴平面AFD⊥平面AFE.11.(xx·太原调研)在菱形ABCD中,∠A=60°,线段AB的中点是E,现将△ADE沿DE折起到△FDE的位置,使平面FDE和平面EBCD垂直,线段FC的中点是G.(1)证明:BG ∥平面FDE ;(2)判断平面FEC 和平面EBCD 是否垂直,并证明你的结论.解:(1)证明:如图,设DE 和CB 的延长线交于点H ,连接FH .在菱形ABCD 中,∠A =60°,线段AB 的中点是E ,可得BE ∥CD ,且BE =12CD ,∴BE 是△HCD 的中位线,B 为HC 的中点. ∵线段FC 的中点是G ,∴BG 是△CFH 的中位线, ∴BG ∥FH ,而FH ⊂平面FDE ,BG ⊄平面FDE , ∴BG ∥平面FDE .(2)由菱形ABCD 中∠A =60°,得△ABD 为正三角形. ∵线段AB 的中点是E ,∴DE ⊥AE ,EF ⊥DE .又平面FDE 和平面EBCD 垂直,平面FDE ∩平面EBCD =DE , ∴EF ⊥平面EBCD ,平面FEC 和平面EBCD 垂直.12.(xx·北京卷)如图,在三棱柱ABC -A 1B 1C 1中,侧棱垂直于底面,AB ⊥BC ,AA 1=AC =2,BC =1,E ,F 分别是A 1C 1,BC 的中点.(1)求证:平面ABE ⊥平面B 1BCC 1; (2)求证:C 1F ∥平面ABE ;(3)求三棱锥E-ABC的体积.解:(1)证明:在三棱柱ABC-A1B1C1中,BB1⊥底面ABC.所以BB1⊥AB.又因为AB⊥BC,所以AB⊥平面B1BCC1.所以平面ABE⊥平面B1BCC1.(2)证明:取AB中点G,连接EG,FG.因为E,F分别是A1C1,BC的中点,所以FG∥AC,且FG=12 AC.因为AC∥A1C1,且AC=A1C1,所以FG∥EC1,且FG=EC1.所以四边形FGEC1为平行四边形.所以C1F∥EG.又因为EG⊂平面ABE,C1F⊄平面ABE,所以C1F∥平面ABE.(3)因为AA1=AC=2,BC=1,AB⊥BC,所以AB=AC2-BC2= 3.所以三棱锥E-ABC的体积V=13S△ABC·AA1=13×12×3×1×2=33.23790 5CEE 峮34784 87E0 蟠22366 575E 坞20665 50B9 傹p34060 850C 蔌v S38887 97E7 韧39695 9B0F 鬏24768 60C0 惀 22813 591D 夝24684 606C 恬。
1414_2023届高考数学一轮复习习题:直线平面垂直的判定及其性质(含解析)新人教B版.doc_0

直线、平面垂直的判定及其性质一、选择题1.已知m ,n ,l 是直线,α,β是平面,α⊥β,α∩β=l ,n ⊂β,n ⊥l ,m ⊥α,则直线m 与n 的位置关系是()A.异面B.相交但不垂直C.平行D.相交且垂直C[因为α⊥β,α∩β=l ,n ⊂β,n ⊥l ,所以n ⊥α.又m ⊥α,所以m ∥n .]2.(2021·白银市第十中学高三期末)设α,β,γ为不同的平面,m ,n ,l 为不同的直线,则下列条件一定能得到m ⊥β的是()A.α∩γ=m ,α⊥γ,β⊥γB.α⊥β,α∩β=l ,m ⊥l C.n ⊥α,n ⊥β,m ⊥αD.α⊥γ,β⊥γ,m ⊥αC[在A 中,因为α∩γ=m ,所以m ⊂α,m ⊂γ,而β⊥γ,m 并不垂直于β内的所有直线,所以β和m 可能不垂直,故A 错误;在B 中,m 只垂直于β内的一条直线,所以不能推出m ⊥β,故B 错误;在C 中,因为n ⊥α,n ⊥β,所以α∥β,又m ⊥α,所以m ⊥β,故C 正确;在D 中,由α⊥γ,β⊥γ,不能推出α∥β,所以由m ⊥α不能推出m ⊥β,故D 错误.]3.(2021·河南鹤壁高三二模)如图,在正四棱柱ABCD A 1B 1C 1D 1中,E ,F 分别是AB 1,BC 1的中点,则以下结论中不成立的是()A.EF 与BB 1垂直B.EF 与BD 垂直C.EF 与CD 异面D.EF 与A 1C 1异面D[如图所示,连接A 1B ,由几何关系可得点E 为A 1B 的中点,且BF =FC 1,由三角形中位线的性质可得:EF ∥A 1C 1,即EF 与A 1C 1不是异面直线,很明显,EF 与CD 异面,由几何关系可得:A 1C 1⊥BB 1,A 1C 1⊥BD ,则EF ⊥BB 1,EF ⊥BD ,综上可得,选项D 中的结论不成立.故选D.]4.(2021·南宁模拟)在四棱锥P ABCD 中,PA ⊥平面ABCD ,底面ABCD 是正方形,且PA =AB =2,则直线PB 与平面PAC 所成角为()A.π6B.π4C.π3D.π2A[连接BD ,交AC 于点O .因为PA ⊥平面ABCD ,底面ABCD 是正方形,所以BD ⊥AC ,BD ⊥PA .又因为PA ∩AC =A ,所以BD ⊥平面PAC ,故BO ⊥平面PAC .连接OP ,则∠BPO 即为直线PB 与平面PAC 所成角.又因为PA =AB =2,所以PB =22,BO =2.所以sin∠BPO =BO PB =12,所以∠BPO =π6.故选A.]5.在正方体ABCD A 1B 1C 1D 1中,E 为棱CD 的中点,则()A.A 1E ⊥DC 1B.A 1E ⊥BD C.A 1E ⊥BC 1D.A 1E ⊥ACC[如图,∵A 1E 在平面ABCD 上的投影为AE ,而AE 不与AC ,BD 垂直,∴选项B,D 错误;∵A 1E 在平面BCC 1B 1上的投影为B 1C ,且B 1C ⊥BC 1,∴A 1E ⊥BC 1,故选项C 正确;(证明:由条件易知,BC 1⊥B 1C ,BC 1⊥CE ,又CE ∩B 1C =C ,∴BC 1⊥平面CEA 1B 1.又A 1E ⊂平面CEA 1B 1,∴A 1E ⊥BC 1.)∵A 1E 在平面DCC 1D 1上的投影为D 1E ,而D 1E 不与DC 1垂直,故选项A 错误.故选C.]6.如图所示,在四边形ABCD 中,AD ∥BC ,AD =AB ,∠BCD =45°,∠BAD =90°.将△ADB 沿BD 折起,使平面ABD ⊥平面BCD ,构成三棱锥A BCD ,则在三棱锥A BCD 中,下列结论正确的是()A.平面ABD ⊥平面ABC B.平面ADC ⊥平面BDC C.平面ABC ⊥平面BDC D.平面ADC ⊥平面ABC D[∵在四边形ABCD 中,AD ∥BC ,AD =AB ,∠BCD =45°,∠BAD =90°,∴BD ⊥CD .又平面ABD ⊥平面BCD ,且平面ABD ∩平面BCD =BD ,故CD ⊥平面ABD ,则CD ⊥AB .又AD ⊥AB ,AD ∩CD =D ,AD ⊂平面ADC ,CD ⊂平面ADC ,故AB ⊥平面ADC .又AB ⊂平面ABC ,∴平面ADC ⊥平面ABC .]二、填空题7.已知四边形ABCD 为平行四边形,PA ⊥平面ABCD ,当平行四边形ABCD 满足条件时,有PC ⊥BD (填上你认为正确的一个条件即可).四边形ABCD 是菱形(答案不唯一)[四边形ABCD 为平行四边形,PA ⊥平面ABCD ,∴BD ⊥PA ,当四边形ABCD 是菱形时,BD ⊥AC ,又PA ∩AC =A ,∴BD ⊥平面PAC ,∴PC ⊥BD .故答案为四边形ABCD 是菱形.]8.已知a ,b 是两条不同的直线,α,β是两个不同的平面,在下列命题①α∥β∥α∥β;②α⊥β⊥α∥β;③a ∥b ∥a ∥b ;④a ⊥b ⊥a ∥b 中,正确的命题是(只填序号).②④[①:与同一条直线平行的两个平面不一定平行,在本题的条件下,两平面可能相交,所以①是假命题;②:根据直线与平面的位置关系可得:由a⊥α,a⊥β可得出α∥β,所以②是真命题.③:根据直线与平面的位置关系可得:a与b可以是任意的位置关系,所以③是假命题;④:垂直于同一个平面的两条直线平行,所以④是真命题;故答案为②④.]9.如图,在四棱锥PABCD中,侧面PAD为正三角形,底面ABCD为正方形,侧面PAD ⊥底面ABCD,M为底面ABCD内的一个动点,且满足MP=MC,则点M在正方形ABCD内的轨迹为.(填序号)①[符合条件的轨迹为线段PC的垂直平分面与平面AC的交线,③④不正确.根据题意可知PD=DC,则点D符合“M为底面ABCD内的一个动点,且满足MP=MC”,设AB的中点为N,连接PN、DN,取PC的中点E,连接NE、DE,所以DE⊥PC,因为平面PAD⊥底面ABCD,AB⊥AD,所以AB⊥平面PAD,所以AB⊥PA,因为PA=BC,AN=NB,∠PAB=∠CBN,所以△PAN≌△CBN,∴PN=CN,点N也符合“M为底面ABCD内的一个动点,且满足MP=MC”,且NE⊥PC,所以PC⊥平面EDN,当M点在线段DN上运动时,都有PC⊥ME,且E是中点,总有MP=MC,所以点M在正方形ABCD内的轨迹是线段DN,所以①正确②不正确.]三、解答题10.(2021·江苏徐州一中高三期中)如图,在四棱锥P ABCD 中,底面ABCD 是矩形,PA ⊥平面PCD ,M ,N 分别是AB ,PC 的中点.求证:(1)直线MN ∥平面PAD ;(2)直线CD ⊥平面PAD .[证明](1)根据题意,取PD 的中点G ,连接NG 、AG ,G 是PD 的中点,N 是PC 的中点,则NG ∥DC 且NG =12DC ,则四边形MNGA 是平行四边形,则有MN ∥AG ,又由MN ⊄平面PAD 中,而AG ⊂平面PAD 中,则有直线MN ∥平面PAD .(2)PA ⊥平面PCD ,CD ⊂平面PCD ,所以PA ⊥CD ,又由底面ABCD 是矩形,则CD ⊥AD ,而PA ∩AD =A ,PA ,AD ⊂平面PAD ,所以直线CD ⊥平面PAD .11.(2021·茂名一模)如图,在三棱柱ABC A 1B 1C 1中,AA 1⊥平面ABC ,点D 是AB 的中点,BC =AC ,AB =2DC =2,AA 1=3.(1)求证:平面A 1DC ⊥平面ABB 1A 1;(2)求点A 到平面A 1DC 的距离.[解](1)证明:∵在三棱柱ABC A 1B 1C 1中,AA 1⊥平面ABC ,点D 是AB 的中点,BC =AC ,CD ⊂平面ABC ,∴CD ⊥AB ,CD ⊥AA 1,∵AB ∩AA 1=A ,∴CD ⊥平面ABB 1A 1,∵CD ⊂平面A 1DC ,∴平面A 1DC ⊥平面ABB 1A 1.(2)点D 是AB 的中点,BC =AC ,AB =2DC =2,AA 1=3.设点A 到平面A 1DC 的距离为d ,∵VA 1ACD =VA A 1CD,∴13×S △ACD ×AA 1=13×S △DCA 1×d ,∴13×12×1×1×3=13×12×1×2×d ,解得d =32,∴点A 到平面A 1DC 的距离为32.1.(2021·武汉模拟)如图所示,在斜三棱柱ABC A 1B 1C 1中,∠BAC =90°,BC 1⊥AC ,则点C1在平面ABC 上的射影H 必在()A.直线AB 上B.直线BC 上C.直线AC 上D.△ABC 的内部A[连接AC 1(图略),因为AC ⊥AB ,AC ⊥BC 1,AB ∩BC 1=B ,所以AC ⊥平面ABC 1,又AC⊂平面ABC ,所以平面ABC 1⊥平面ABC ,所以点C 1在平面ABC 上的射影H 必在两平面的交线AB 上,故选A.]2.已知圆锥的顶点为P ,母线PA ,PB 所成角的余弦值为34,PA 与圆锥底面所成角为60°,若△PAB 的面积为7,则该圆锥的体积为.263π[作示意图如图所示,设底面半径为r ,PA 与圆锥底面所成角为60°,则∠PAO=60°,则PO =3r ,PA =PB =2r ,又PA ,PB 所成角的余弦值为34,则sin∠APB =74,则S △PAB =12PA ·PB ·sin∠APB=12·2r ·2r ·74=7,解得r =2,故圆锥的体积为13·π·(2)2·6=263π.]3.如图,在四棱锥P ABCD 中,底面四边形ABCD 是菱形,点E 在线段PC 上,PA ∥平面EBD .(1)证明:点E 为线段PC 中点;(2)已知PA ⊥平面ABCD ,∠ABC =60°,点P 到平面EBD 的距离为1,四棱锥P ABCD 的体积为23,求PA .[解](1)证明:连接AC ,与BD 相交于点O ,连接EO ,则经过PA 的平面PAC 与平面EBD 交线为EO .因为PA ∥平面EBD ,所以PA ∥EO .因为四边形ABCD 是菱形,所以O 为AC 的中点,所以EO 是△PAC 中位线,于是E 为线段PC 中点.(2)因为PA ∥平面EBD ,所以点A 到平面EBD 的距离等于点P 到平面EBD 的距离等于1.因为PA ⊥平面ABCD ,所以EO ⊥平面ABCD ,所以平面EBD ⊥平面ABCD ,平面EBD ∩平面ABCD =BD .因为AO ⊥BD ,所以AO ⊥面EBD ,因此AO =1.因为∠ABC =60°,所以四边形ABCD 是边长为2的菱形,面积为2×2×sin 60°=23,所以四棱锥P ABCD 的体积为V P ABCD =13·23·PA ,由13·23·PA =23,得PA =3.1.(2019·全国卷Ⅰ)已知∠ACB =90°,P 为平面ABC 外一点,PC =2,点P 到∠ACB 两边AC ,BC 的距离均为3,那么P 到平面ABC 的距离为.2[如图,过点P 作PO ⊥平面ABC 于O ,则PO 为P 到平面ABC 的距离.再过O 作OE ⊥AC 于E ,OF ⊥BC 于F ,连接PC ,PE ,PF ,则PE ⊥AC ,PF ⊥BC .又PE =PF =3,所以OE =OF ,所以CO 为∠ACB 的平分线,即∠ACO =45°.在Rt△PEC 中,PC =2,PE =3,所以CE =1,所以OE =1,所以PO =PE 2-OE 2=32-12=2.]2.《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P ABCD 中,侧棱PD ⊥底面ABCD ,且PD =CD ,过棱PC 的中点E ,作EF ⊥PB 交PB 于点F ,连接DE ,DF ,BD ,BE .(1)证明:PB ⊥平面DEF .试判断四面体DBEF 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;(2)若面DEF 与面ABCD 所成二面角的大小为π3,求DC BC的值.[解](1)证明:因为PD ⊥底面ABCD ,所以PD ⊥BC ,由底面ABCD 为长方形,有BC ⊥CD ,而PD ∩CD =D ,所以BC ⊥平面PCD .而DE ⊂平面PCD ,所以BC ⊥DE .又因为PD =CD ,点E 是PC 的中点,所以DE ⊥PC .而PC ∩BC =C ,所以DE ⊥平面PBC .而PB ⊂平面PBC ,所以PB ⊥DE .又PB ⊥EF ,DE ∩EF =E ,所以PB ⊥平面DEF .由DE ⊥平面PBC ,PB ⊥平面DEF ,可知四面体BDEF 的四个面都是直角三角形,即四面体BDEF 是一个鳖臑,其四个面的直角分别为∠DEB ,∠DEF ,∠EFB ,∠DFB .(2)如图,在面PBC 内,延长BC 与FE 交于点G ,则DG 是平面DEF 与平面ABCD 的交线.由(1)知,PB ⊥平面DEF ,所以PB ⊥DG .又因为PD ⊥底面ABCD ,所以PD ⊥DG .而PD ∩PB =P ,所以DG ⊥平面PBD .故∠BDF 是面DEF 与面ABCD 所成二面角的平面角,设PD =DC =1,BC =λ,有BD =1+λ2,在Rt△PDB 中,由DF ⊥PB,得∠DPF =∠FDB =π3,则tanπ3=tan∠DPF =BD PD=1+λ2=3,解得λ=2.所以DC BC =1λ=22.故当面DEF 与面ABCD 所成二面角的大小为π3时,DC BC =22.。
《三维设计》2014届高考数学一轮复习教学案(基础知识+高频考点+解题训练)直线、平面垂直的判定与性质
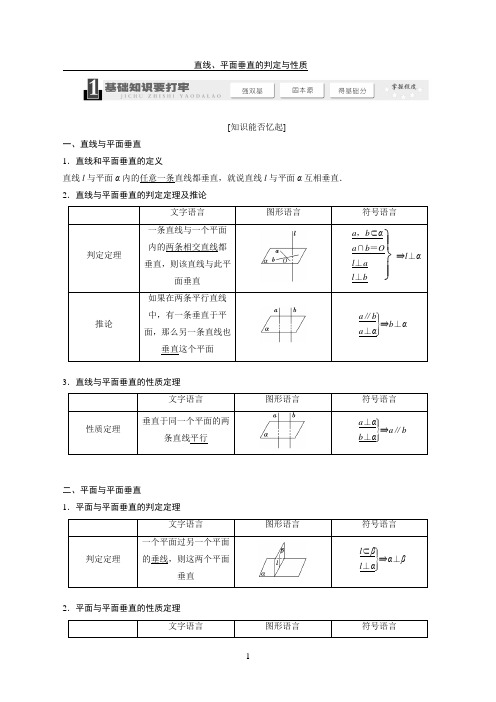
直线、平面垂直的判定与性质[知识能否忆起]一、直线与平面垂直1.直线和平面垂直的定义直线l与平面α内的任意一条直线都垂直,就说直线l与平面α互相垂直.2.直线与平面垂直的判定定理及推论3.直线与平面垂直的性质定理二、平面与平面垂直1.平面与平面垂直的判定定理2.平面与平面垂直的性质定理[小题能否全取]1.(教材习题改编)已知平面α,β,直线l,若α⊥β,α∩β=l,则()A.垂直于平面β的平面一定平行于平面αB.垂直于直线l的直线一定垂直于平面αC.垂直于平面β的平面一定平行于直线lD.垂直于直线l的平面一定与平面α、β都垂直2.(2012·厦门模拟)如图,O为正方体ABCD-A1B1C1D1的底面ABCD的中心,则下列直线中与B1O 垂直的是()A.A1D B.AA1C.A1D1D.A1C13.已知α,β是两个不同的平面,m,n是两条不重合的直线,则下列命题中正确的是() A.若m∥α,α∩β=n,则m∥nB.若m⊥α,m⊥n,则n∥αC.若m⊥α,n⊥β,α⊥β,则m⊥nD.若α⊥β,α∩β=n,m⊥n,则m⊥β.4.如图,已知P A⊥平面ABC,BC⊥AC,则图中直角三角形的个数为________.5.(教材习题改编)如图,已知六棱锥P -ABCDEF的底面是正六边形,PA⊥平面ABC,P A =2AB.则下列命题正确的有________.①P A⊥AD;②平面ABC⊥平面PBC;③直线BC∥平面P AE;④直线PD与平面ABC所成角为30°.1.在证明线面垂直、面面垂直时,一定要注意判定定理成立的条件.同时抓住线线、线面、面面垂直的转化关系,即:2.在证明两平面垂直时,一般先从现有的直线中寻找平面的垂线,若这样的直线图中不存在,则可通过作辅助线来解决,如有平面垂直时,一般要用性质定理.3.几个常用的结论:(1)过空间任一点有且只有一条直线与已知平面垂直.(2)过空间任一点有且只有一个平面与已知直线垂直.典题导入[例1](2012·襄州模拟)若m,n为两条不重合的直线,α,β为两个不重合的平面,给出下列命题:①若m,n都平行于平面α,则m,n一定不是相交直线;②若m 、n 都垂直于平面α,则m ,n 一定是平行直线;③已知α,β互相垂直,m ,n 互相垂直,若m ⊥α,则n ⊥β;④m ,n 在平面α内的射影互相垂直,则m ,n 互相垂直.其中的假命题的序号是________.由题悟法解决此类问题常用的方法有:①依据定理条件才能得出结论的,可结合符合题意的图形作出判断;②否定命题时只需举一个反例.③寻找恰当的特殊模型(如构造长方体)进行筛选.典题导入[例2] (2012·广东高考)如图所示,在四棱锥P -ABCD 中,AB ⊥平面P AD ,AB ∥CD ,PD =AD ,E 是PB 的中点,F 是DC 上的点且DF =12AB ,PH为△P AD 中AD 边上的高.(1)证明:PH ⊥平面ABCD ; (3)证明:EF ⊥平面PAB .由题悟法证明直线和平面垂直的常用方法有: (1)利用判定定理.(2)利用判定定理的推论(a ∥b ,a ⊥α⇒b ⊥α). (3)利用面面平行的性质(a⊥α,α∥β⇒a ⊥β).(4)利用面面垂直的性质.当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.以题试法2.(2012·启东模拟)如图所示,已知P A ⊥矩形ABCD 所在平面,M ,N 分别是AB ,PC 的中点. (1)求证:MN ⊥CD ;(2)若∠PDA =45°,求证:MN⊥平面PCD .典题导入[例3] (2012·江苏高考)如图,在直三棱柱ABC -A 1B 1C 1中,A 1B 1=A 1C 1,D ,E 分别是棱BC ,CC 1上的点(点D 不同于点C ),且AD ⊥DE ,F 为B 1C 1的中点.求证:(1)平面ADE ⊥平面BCC 1B 1; (2)直线A 1F ∥平面ADE ..由题悟法1.判定面面垂直的方法: (1)面面垂直的定义.(2)面面垂直的判定定理(a ⊥β,a ⊂α⇒α⊥β). 2.在已知平面垂直时,一般要用性质定理进行转化,转化为线面垂直或线线垂直.转化方法:在一个平面内作交线的垂线,转化为线面垂直,然后进一步转化为线线垂直.以题试法3.(2012·泸州一模)如图,在四棱锥P -ABCD 中,底面ABCD 为菱形,∠BAD =60°,Q 为AD 的中点.(1)若P A =PD ,求证:平面PQB ⊥平面P AD ; (2)若点M 在线段PC 上,且PM =tPC (t >0),试确定实数t 的值,使得P A ∥平面MQB .1.(2012·杭州模拟)设a ,b ,c 是三条不同的直线,α,β是两个不同的平面,则a⊥b的一个充分条件是()A.a⊥c,b⊥c B.α⊥β,a⊂α,b⊂βC.a⊥α,b∥αD.a⊥α,b⊥α.2.设α,β,γ是三个不重合的平面,l是直线,给出下列命题①若α⊥β,β⊥γ,则α⊥γ;②若l上两点到α的距离相等,则l∥α;③若l⊥α,l∥β,则α⊥β;④若α∥β,l⊄β,且l∥α,则l∥β.其中正确的命题是()A.①②B.②③C.②④D.③④3.给出命题:(1)在空间里,垂直于同一平面的两个平面平行;(2)设l,m是不同的直线,α是一个平面,若l ⊥α,l∥m,则m⊥α;(3)已知α,β表示两个不同平面,m为平面α内的一条直线,则“α⊥β”是“m⊥β”的充要条件;(4)a,b是两条异面直线,P为空间一点,过P 总可以作一个平面与a,b之一垂直,与另一个平行.其中正确命题个数是()A.0 B.1C.2 D.34.(2013·济南模拟)如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在底面ABC上的射影H必在()A.直线AB上B.直线BC上C.直线AC上D.△ABC内部.5.(2012·曲阜师大附中质检)如图所示,直线P A 垂直于⊙O所在的平面,△ABC内接于⊙O,且AB 为⊙O的直径,点M为线段PB的中点.现有结论:①BC⊥PC;②OM∥平面APC;③点B到平面P AC 的距离等于线段BC的长.其中正确的是()A.①②B.①②③C.①D.②③6.(2012·济南名校模拟)如图,在四边形ABCD 中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下面命题正确的是()A.平面ABD⊥平面ABC B.平面ADC⊥平面BDC C.平面ABC⊥平面BDC D.平面ADC⊥平面ABC 7.如图所示,在四棱锥P-ABCD中,P A⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足________时,平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)8.(2012·忻州一中月考)正四棱锥S-ABCD的底面边长为2,高为2,E是BC的中点,动点P在四棱锥的表面上运动,并且总保持PE⊥AC,则动点P的轨迹的长为________.10. 如图所示,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.(1)求证:DM∥平面APC;(2)求证:平面ABC⊥平面APC.11.(2012·北京海淀二模)如图所示,P A⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,P A=AB=2,点E为线段PB的中点,点M在AB上,且OM∥AC. (1)求证:平面MOE∥平面P AC;(2)求证:平面P AC⊥平面PCB.。
【三维设计】2014高考数学一轮复习 课时跟踪检测(四十七)直线、平面垂直的判定与性质 理 新人教A

课时跟踪检测(四十七) 直线、平面垂直的判定与性质1.(2012·某某模拟)设a,b,c是三条不同的直线,α,β是两个不同的平面,则a ⊥b的一个充分条件是( )A.a⊥c,b⊥c B.α⊥β,a⊂α,b⊂βC.a⊥α,b∥α D.a⊥α,b⊥α2.设α,β,γ是三个不重合的平面,l是直线,给出下列命题①若α⊥β,β⊥γ,则α⊥γ;②若l上两点到α的距离相等,则l∥α;③若l ⊥α,l∥β,则α⊥β;④若α∥β,l⊄β,且l∥α,则l∥β.其中正确的命题是( )A.①②B.②③C.②④D.③④3.给出命题:(1)在空间里,垂直于同一平面的两个平面平行;(2)设l,m是不同的直线,α是一个平面,若l⊥α,l∥m,则m⊥α;(3)已知α,β表示两个不同平面,m为平面α内的一条直线,则“α⊥β”是“m⊥β”的充要条件;(4)a,b是两条异面直线,P为空间一点,过P总可以作一个平面与a,b之一垂直,与另一个平行.其中正确命题个数是( )A.0 B.1 C.2 D.34.(2013·某某模拟)如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在底面ABC上的射影H必在( )A.直线AB上B.直线BC上C.直线AC上D.△ABC内部5.(2012·曲阜师大附中质检)如图所示,直线PA垂直于⊙O所在的平面,△ABC内接于⊙O,且AB为⊙O的直径,点M为线段PB的中点.现有结论:①BC⊥PC;②OM∥平面APC;③点B到平面PAC的距离等于线段BC的长.其中正确的是( )A.①②B.①②③C.① D.②③6.(2012·某某模拟)如图,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD =90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下面命题正确的是( )A.平面ABD⊥平面ABC B.平面ADC⊥平面BDCC.平面ABC⊥平面BDC D.平面ADC⊥平面ABC7.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足________时,平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)8.(2013·某某中学月考)正四棱锥S-ABCD的底面边长为2,高为2,E是BC的中点,动点P在四棱锥的表面上运动,并且总保持PE⊥AC,则动点P的轨迹的长为________.9.(2013·某某模拟)点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动,给出下列四个命题:①三棱锥A-D1PC的体积不变;②A1P∥平面ACD1;③DP⊥BC1;④平面PDB1⊥平面ACD1.其中正确的命题序号是________.10.如图所示,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB 为正三角形.(1)求证:DM ∥平面APC ; (2)求证:平面ABC ⊥平面APC .11.(2012·海淀二模)如图所示,PA ⊥平面ABC ,点C 在以AB 为直径的⊙O 上,∠CBA =30°,PA =AB =2,点E 为线段PB 的中点,点M 在AB 上,且OM ∥AC .(1)求证:平面MOE ∥平面PAC ; (2)求证:平面PAC ⊥平面PCB .12.(2012·某某摸底)如图,在多面体ABCDEF 中,四边形ABCD 是梯形,AB ∥CD ,四边形ACFE 是矩形,平面ACFE ⊥平面ABCD ,AD =DC =CB =AE =a ,∠ACB =π2.(1)求证:BC ⊥平面ACFE ;(2)若M 是棱EF 上一点,AM ∥平面BDF ,求EM 的长.1.如图,在三棱锥D -ABC 中,若AB =CB ,AD =CD ,E 是AC 的中点,则下列正确的是( )A.平面ABC⊥平面ABDB.平面ABD⊥平面BDCC.平面ABC⊥平面BDE,且平面ADC⊥平面BDED.平面ABC⊥平面ADC,且平面ADC⊥平面BDE2.(2012·某某高考)已知矩形ABCD,AB=1,BC= 2.将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中,( )A.存在某个位置,使得直线AC与直线BD垂直B.存在某个位置,使得直线AB与直线CD垂直C.存在某个位置,使得直线AD与直线BC垂直D.对任意位置,三对直线“AC与BD”,“AB与CD”,“AD与BC”均不垂直3.(2012·某某模拟)如图,在三棱锥P-ABC中,△PAC,△ABC分别是以A,B为直角顶点的等腰直角三角形,AB=1.(1)现给出三个条件:①PB=3;②PB⊥BC;③平面PAB⊥平面ABC.试从中任意选取一个作为已知条件,并证明:PA⊥平面ABC;(2)在(1)的条件下,求三棱锥P-ABC的体积.答案课时跟踪检测(四十七)A级1.选C 对于选项C,在平面α内存在c∥b,因为a⊥α,所以a⊥c,故a⊥b;A,B 选项中,直线a,b可能是平行直线,相交直线,也可能是异面直线;D选项中一定有a∥b.2.选D 对于①:若α⊥β,β⊥γ,则α⊥γ,前者不是后者的充分条件,比如当α∥γ时,也有α⊥β,β⊥γ.对于②:显然错误,当l⊥α,l∩α=A时,l上到A距离相等的两点到α的距离相等.③④显然正确.3.选B (1)错,也可能相交;(2)正确;(3)“α⊥β”是“m⊥β”的必要条件,命题错误;(4)当异面直线a,b垂直时才可以作出满足要求的平面,命题错误.4.选A 由AC⊥AB,AC⊥BC1,∴AC⊥平面ABC1.又∵AC⊂面ABC,∴平面ABC1⊥平面ABC.∴C1在面ABC上的射影H必在两平面交线AB 上.5.选B 对于①,∵PA⊥平面ABC,∴PA⊥BC.∵AB为⊙O的直径,∴BC⊥AC.∴BC⊥平面PAC.又PC⊂平面PAC,∴BC⊥PC;对于②,∵点M为线段PB的中点,∴OM∥PA.∵PA⊂平面PAC,∴OM∥平面PAC;对于③,由①知BC⊥平面PAC,∴线段BC的长即是点B到平面PAC 的距离,故①②③都正确.6.选D 在平面图形中CD⊥BD,折起后仍有CD⊥BD,由于平面ABD⊥平面BCD,故CD ⊥平面ABD,CD⊥AB,又AB⊥AD,故AB⊥平面ADC,所以平面ABC⊥平面ADC.7.解析:由定理可知,BD⊥PC.∴当DM⊥PC(或BM⊥PC)时,即有PC⊥平面MBD.而PC⊂平面PCD,∴平面MBD⊥平面PCD.答案:DM⊥PC(或BM⊥PC等)8.解析:如图,设AC∩BD=O,连接SO,取CD的中点F,SC的中点G,连接EF,EG,FG,设EF交AC于点H,连接GH,易知AC⊥EF,GH∥SO,∴GH⊥平面ABCD,∴AC⊥GH,∴AC⊥平面EFG,故动点P的轨迹是△EFG,由已知易得EF=2,GE=GF=62,∴△EFG的周长为2+6,故动点P的轨迹长为2+ 6.答案:2+ 69.解析:连接BD交AC于O,连接DC1交D1C于O1,连接OO1,则OO1∥BC1.∴BC1∥平面AD1C,动点P到平面AD1C的距离不变,∴三棱锥P-AD1C的体积不变.又VP-AD1C=VA-D1PC,∴①正确.∵平面A1C1B∥平面AD1C,A1P⊂平面A1C1B,∴A1P∥平面ACD1,②正确.由于DB不垂直于BC1显然③不正确;由于DB1⊥D1C,DB1⊥AD1,D1C∩AD1=D1,∴DB1⊥平面AD1C.DB1⊂平面PDB1,∴平面PDB1⊥平面ACD1,④正确.答案:①②④10.证明:(1)由已知,得MD是△ABP的中位线,所以MD∥AP.又MD⊄平面APC,AP⊂平面APC,故MD∥平面APC.(2)因为△PMB为正三角形,D为PB的中点,所以MD⊥PB.所以AP⊥PB.又AP⊥PC,PB∩PC=P,所以AP⊥平面PBC.因为BC⊂平面PBC,所以AP⊥BC.又BC⊥AC,AC∩AP=A,所以BC⊥平面APC.因为BC⊂平面ABC,所以平面ABC⊥平面APC.11.证明:(1)因为点E为线段PB的中点,点O为线段AB的中点,所以OE∥PA.因为PA⊂平面PAC,OE⊄平面PAC,所以OE∥平面PAC.因为OM∥AC,且AC⊂平面PAC,OM⊄平面PAC,所以OM∥平面PAC.因为OE⊂平面MOE,OM⊂平面MOE,OE∩OM=O,所以平面MOE∥平面PAC.(2)因为点C 在以AB 为直径的⊙O 上,所以∠ACB =90°,即BC ⊥AC . 因为PA ⊥平面ABC ,BC ⊂平面ABC ,所以PA ⊥BC . 因为AC ⊂平面PAC ,PA ⊂平面PAC ,PA ∩AC =A ,所以BC ⊥平面PAC . 因为BC ⊂平面PCB , 所以平面PAC ⊥平面PCB .12.解:(1)证明:因为∠ACB =π2,所以BC ⊥AC .又因为BC ⊂平面ABCD ,平面ACFE ∩平面ABCD =AC ,平面ACFE ⊥平面ABCD ,所以BC ⊥平面ACFE .(2)记AC ∩BD =O ,在梯形ABCD 中,因为AD =DC =CB =a ,AB ∥CD ,所以∠ACD =∠CAB =∠DAC .所以π=∠ABC +∠BCD =∠DAB +∠ACD +∠ACB =3∠DAC +π2,所以∠DAC =π6,即∠CBO =π6.又因为∠ACB =π2,CB =a ,所以CO =33a .连接FO ,由AM ∥平面BDF 得AM ∥FO ,因为四边形ACFE 是矩形,所以EM =CO =33a . B 级1.选C 要判断两个平面的垂直关系,就需固定其中一个平面,找另一个平面内的一条直线与第一个平面垂直.因为AB =CB ,且E 是AC 的中点,所以BE ⊥AC ,同理有DE ⊥AC ,于是AC ⊥平面BDE .因为AC 在平面ABC 内,所以平面ABC ⊥平面BDE .又由于AC ⊂平面ACD ,所以平面ACD ⊥平面BDE .2.选B 对于AB ⊥CD ,因为BC ⊥CD ,可得CD ⊥平面ACB ,因此有CD ⊥AC .因为AB =1,BC =2,CD =1,所以AC =1,所以存在某个位置,使得AB ⊥CD .3.解:法一:(1)选取条件① 在等腰直角三角形ABC 中, ∵AB =1, ∴BC =1,AC = 2. 又∵PA =AC ,∴PA = 2. ∴在△PAB 中,AB =1,PA = 2.又∵PB =3, ∴AB 2+PA 2=PB 2.∴∠PAB =90°,即PA ⊥AB . 又∵PA ⊥AC ,AB ∩AC =A , ∴PA ⊥平面ABC .(2)依题意得,由(1)可知PA ⊥平面ABC ,V 三棱锥P -ABC =13PA ·S △ABC =13×2×12×12=26. 法二:(1)选取条件② ∵PB ⊥BC ,又AB ⊥BC ,且PB ∩AB =B , ∴BC ⊥平面PAB . ∵PA ⊂平面PAB , ∴BC ⊥PA .又∵PA ⊥AC ,且BC ∩AC =C , ∴PA ⊥平面ABC .(2)依题意得,由(1)可知PA ⊥平面ABC . ∵AB =BC =1,AB ⊥BC , ∴AC =2, ∴PA =2,∴V 三棱锥P -ABC =13PA ·S △ABC =13×12AB ·BC ·PA =13×12×1×1×2=26.法三:(1)选取条件③ 若平面PAB ⊥平面ABC ,∵平面PAB ∩平面ABC =AB ,BC ⊂平面ABC ,BC ⊥AB , ∴BC ⊥平面PAB .∵PA ⊂平面PAB ,∴BC ⊥PA . ∵PA ⊥AC ,且BC ∩AC =C , ∴PA ⊥平面ABC . (2)同法二.。
【三维设计】高考数学一轮复习 教师备选作业 第七章 第五节 直线、平面垂直的判定及性质 理

第七章第五节直线、平面垂直的判定及性质一、选择题1.给出以下命题,其中错误的是 ( )A.如果一条直线垂直于一个平面内的无数条直线,则这条直线垂直于这个平面B.垂直于同一平面的两条直线互相平行C.垂直于同一直线的两个平面互相平行D.两条平行直线中的一条垂直于一个平面,则另一条也垂直于这个平面2.设l,m是两条不同的直线,α是一个平面,则下列命题正确的是 ( ) A.若l⊥m,m⊂α,则l⊥αB.若l⊥α,l∥m,则m⊥αC.若l∥α,m⊂α,则l∥mD.若l∥α,m∥α,则l∥m3.若m、n是两条不同的直线,α、β、γ是三个不同的平面,则下列命题中的真命题是( )A.若m⊂β,α⊥β,则m⊥αB.若α∩γ=m,β∩γ=n,m∥n,则α∥βC.若m⊥β,m∥α,则α⊥βD.若α⊥γ,α⊥β,则β⊥γ4.已知α,β,γ是三个不同的平面,命题“α∥β,且α⊥γ⇒β⊥γ”是真命题,如果把α,β,γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题有 ( ) A.0个B. 1个C.2个D.3个5.已知两条直线m,n,两个平面α,β,给出下面四个命题:①m∥n,m⊥α⇒n⊥α;②α∥β,m⊂α,n⊂β⇒m∥n;③m∥n,m∥α⇒n∥α;④α∥β,m∥n,m⊥α⇒n⊥β.其中正确命题的序号是 ( )A.①③B.②④C.①④D.②③6.如图,四边形ABCD中,AB=AD=CD=1,BD=2,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是( )A .A ′C ⊥BDB .∠BA ′C =90°C .CA ′与平面A ′BD 所成的角为30°D .四面体A ′-BCD 的体积为13二、填空题7.已知直线l ,m ,n ,平面α,m ⊂α,n ⊂α,则“l ⊥α”是“l ⊥m 且l ⊥n ”的________条件.(填“充分不必要”、“必要不充分”、“充要”“既不充分也不必要”)8.正四棱锥S -ABCD 的底面边长为2,高为2,E 是边BC 的中点,动点P 在表面上运动,并且总保持PE ⊥AC ,则动点P 的轨迹的周长为________.9.如图所示,在四棱锥P -ABCD 中,PA ⊥底面ABCD ,且底面各边都相等,M 是PC 上的一动点,当点M 满足__________时,平面MBD ⊥平面PCD .(只要填写个你认为是正确的条件即可)三、解答题10.三棱柱ABC -A1B 1C 1中,AA 1⊥平面ABC ,AC =BC =AA 1=2,∠ACB =90°,E 为BB 1的中点,∠A 1DE =90°,求证:CD ⊥平面A 1ABB 1.11.如图,三棱锥A -BCD 中,∠BCD =90°,BC =CD =1,AB ⊥平面BCD ,∠ADB =60°,E ,F 分别是AC ,AD 上的动点,且AE AC =AF AD=λ(0<λ<1). (1)求证:不论λ为何值,总有平面BEF ⊥平面ABC ;(2)当λ为何值时,平面BEF ⊥平面ACD .12. 如图,直角三角形BCD 所在的平面垂直于正三角形ABC 所在的平面,其中DC ⊥CB ,PA ⊥平面ABC ,DC =BC =2PA ,E 、F 分别为DB 、CB 的中点.(1)证明:AE ⊥BC ;(2)求直线PF与平面BCD所成的角.详解答案一、选择题1.解析:一条直线可以垂直于一个平面内的无数条平行直线,但这条直线不垂直这个平面.答案:A2.解析:根据定理:两条平行线中的一条垂直于一个平面,另一条也垂直于这个平面可知B正确.答案:B3.解析:对于A,由m⊂β,α⊥β显然不能得知m⊥α;对于B,由条件也不能确定α∥β;对于C,由m∥α得,在平面α上必存在直线l∥m.又m⊥β,因此l⊥β,且l⊂α,故α⊥β;对于D,垂直于同一平面的两个平面不一定垂直,因此D也不正确.答案:C4.解析:若α,β换为直线a,b,则命题化为“a∥b,且a⊥γ⇒b⊥γ”,此命题为真命题;若α,γ换为直线a,b,则命题化为“a∥β,且a⊥b⇒b⊥β”,此命题为假命题;若β,γ换为直线a,b,则命题化为“a∥α,且b⊥α⇒a⊥b”,此命题为真命题,故选C.答案:C5.解析:对于①,由于两条平行线中的一条直线与一个平面垂直,则另一条直线也与该平面垂直,因此①是正确的;对于②,分别位于两个平行平面内的两条直线必没有公共点,但它们不一定平行,因此②是错误的;对于③,直线n可能位于平面α内,此时结论显然不成立,因此③是错误的;对于④,由m⊥α且α∥β得m⊥β,又m∥n,故n⊥β,因此④是正确的.答案:C6.解析:取BD的中点O,∵A′B=A′D,∴A′O⊥BD,又平面A′BD⊥平面BCD,平面A′BD∩平面BCD=BD,∴A′O⊥平面BCD,∵CD⊥BD,∴OC不垂直于BD.假设A′C⊥BD,∵OC为A′C在平面BCD内的射影,∴OC⊥BD,矛盾,∴A′C不垂直于BD,A错误;∵CD⊥BD,平面A′BD⊥平面BCD,∴CD⊥平面A ′BD ,A ′C 在平面A ′BD 内的射影为A ′D ,∵A ′B =A ′D =1,BD =2,∴A ′B ⊥A ′D ,A ′B ⊥A ′C ,B 正确;∠CA ′D 为直线CA ′与平面A ′BD 所成的角,∠CA ′D =45°,C 错误;V A ′-BCD =13S △A ′BD ·CD =16,D 错误.答案:B二、填空题7.解析:若l ⊥α,则l 垂直于平面α内的任意直线,故l ⊥m 且l ⊥n ,但若l ⊥m 且l ⊥n ,不能得出l ⊥α.答案:充分不必要8.解析:如图,取CD 的中点F 、SC 的中点G ,连接EF ,EG ,FG ,设EF 交AC 于点H ,易知AC ⊥EF ,又GH ∥SO ,∴GH ⊥平面ABCD .∴AC ⊥GH .又GH ∩EF =H ,∴AC ⊥平面EFG .故点P 的轨迹是△EFG ,其周长为2+ 6. 答案:2+ 69.解析:由PA ⊥BD ,AC ⊥BD 可得BD ⊥平面PAC ,所以BD ⊥PC .所以当DM ⊥PC (或BM ⊥PC )时,即有PC ⊥平面MBD ,而PC ⊂平面PCD ,∴平面MBD ⊥平面PCD .答案:DM ⊥PC (或BM ⊥PC 等)三、解答题10. 证明:∵AC =BC =2,∠ACB =90°,∴AB =2 2.设AD =x ,则BD =22-x ,∴A 1D 2=4+x 2,DE 2=1+(22-x )2, A 1E 2=(22)2+1.∵∠A 1DE =90°,∴A 1D 2+DE 2=A 1E 2.∴x = 2.∴D 为AB 的中点.∴CD ⊥AB .又AA 1⊥CD 且AA 1∩AB =A ,∴CD ⊥平面A 1ABB 1.11. 解:(1)∵AB ⊥平面BCD ,∴AB ⊥CD .∵CD ⊥BC ,且AB ∩BC =B ,∴CD ⊥平面ABC . 又∵AE AC =AF AD =λ(0<λ<1),∴不论λ为何值,恒有EF ∥CD .∴EF ⊥平面ABC ,EF ⊂平面BEF .∴不论λ为何值恒有平面BEF ⊥平面ABC .(2)由(1)知,BE ⊥EF ,∵平面BEF ⊥平面ACD , ∴BE ⊥平面ACD .∴BE ⊥AC .∵BC =CD =1,∠BCD =90°,∠ADB =60°, ∴BD =2,AB =2tan 60°= 6.∴AC =AB 2+BC 2=7.由AB 2=AE ·AC ,得AE =67. ∴λ=AE AC =67.12.解:(1)证明:连接EF ,AF .因为E 、F 分别是BD 、BC 的中点,所以EF ∥DC . 又DC ⊥BC ,所以EF ⊥BC .因为△ABC 为等边三角形,所以BC ⊥AF .EF ∩AF =F 所以BC ⊥平面AEF ,又AE ⊂平面AEF ,故BC ⊥AE .(2)连接PE .因为平面BCD ⊥平面ABC ,DC ⊥BC ,AF ⊥BC ,所以DC ⊥平面ABC ,AF ⊥平面BCD .因为PA ⊥平面ABC ,PA =12DC , 所以PA 綊12DC . 又因为EF 綊12DC ,所以EF 綊PA ,故四边形APEF 为矩形. 所以PE 綊AF .所以PE ⊥平面BCD .则∠PFE 即为直线PF 与平面BCD 所成的角. 在Rt △PEF 中,因为PE =AF =32BC ,EF =12DC =12BC ,所以tan ∠PFE =PE EF =3, 故∠PFE =60°,即直线PF 与平面BCD 所成的角为60°.。
三维设计高考数学人教版理科一轮复习配套题库7.4直线、平面平行的判定与性质(含答案详析)

高考真题备选题库第7章立体几何第4节直线、平面平行的判定与性质考点平行关系1.(2010山东,5分)在空间,下列命题正确的是()A.平行直线的平行投影重合B.平行于同一直线的两个平面平行C.垂直于同一平面的两个平面平行D.垂直于同一平面的两条直线平行解析:A项中平行直线的平行投影不一定重合,有可能平行,B项中平行于同一条直线的两个平面可能平行、相交,C项中垂直于同一个平面的两个平面可能平行、相交,D项正确.答案:D2.(2009·福建,5分)设m,n是平面α内的两条不同直线;l1,l2是平面β内的两条相交直线,则α∥β的一个充分而不必要条件是()A.m∥β且l1∥αB.m∥l1且n∥l2C.m∥β且n∥βD.m∥β且n∥l2解析:∵m∥l1,且n∥l2,又l1与l2是平面β内的两条相交直线,∴α∥β,而当α∥β时不一定推出m∥l1且n∥l2.答案:B3.(2012山东,12分)如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.(1)求证:BE=DE;(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.解:(1)取BD的中点O,连接CO,EO.由于CB=CD,所以CO⊥BD,又EC⊥BD,EC∩CO=C,CO,EC⊂平面EOC,所以BD⊥平面EOC,因此BD⊥EO,又O为BD的中点,所以BE=DE.(2)法一:取AB的中点N,连接DM,DN,MN,因为M是AE的中点,所以MN∥BE.又MN⊄平面BEC,BE⊂平面BEC,所以MN∥平面BEC.又因为△ABD为正三角形.所以∠BDN=30°,又CB=CD,∠BCD=120°,因此∠CBD=30°,所以DN∥BC.又DN⊄平面BEC,BC⊂平面BEC,所以DN∥平面BEC.又MN∩DN=N,故平面DMN∥平面BEC.又DM⊂平面DMN,所以DM∥平面BEC.法二:延长AD,BC交于点F,连接EF.因为CB=CD,∠BCD=120°,所以∠CBD=30°.因为△ABD为正三角形,所以∠BAD=60°,∠ABC=90°,因此∠AFB =30°,所以AB =12AF . 又AB =AD ,所以D 为线段AF 的中点.连接DM ,由于点M 是线段AE 的中点, 因此DM ∥EF .又DM ⊄平面BEC ,EF ⊂平面BEC , 所以DM ∥平面BEC .。
2020届三维设计一轮复习第八章 立体几何第五节 直线、平面垂直的判定与性质

返回
(2)PD⊥平面ABE.
[证明] 由PA=AB=BC,∠ABC=60°,可得AC=PA. ∵E是PC的中点,∴AE⊥PC. 由(1)知AE⊥CD,且PC∩CD=C, ∴AE⊥平面PCD. ∵PD⊂平面PCD,∴AE⊥PD. ∵PA⊥底面ABCD,AB⊂底面ABCD,∴PA⊥AB. 又∵AB⊥AD,且PA∩AD=A, ∴AB⊥平面PAD, ∵PD⊂平面PAD, ∴AB⊥PD. 又∵AB∩AE=A,∴PD⊥平面ABE.
⊥m⇒/ l∥α,∵l⊥m时,l可能在α内.
故“l⊥m”是“l∥α”的必要不充分条件. 答案:B
返回
2.设α,β是两个不同的平面,l,m是两条不同的直线,且l
⊂α,m⊂β
()
A.若l⊥β,则α⊥β B.若α⊥β,则l⊥m
C.若l∥β,则α∥β D.若α∥β,则l∥m
解析:∵l⊥β,l⊂α,∴α⊥β(面面垂直的判定定理),故 A正确.
返回
2.平面与平面垂直的判定定理与性质定理
文字语言
图形语言
符号语言
判定 定理
一个平面过另一个平 面的垂线❷,则这两 个平面垂直
性质 定理
两个平面垂直,则一 个平面内垂直于_交__线_
的直线与另一个平面
垂直
_l_⊂_β___ _l_⊥__α___ ⇒α⊥β
_α_⊥__β___ αl___⊂∩l___⊥β___β___a=____a___ ⇒l⊥α
a_∩__b_=__O_ _l_⊥__a__
_l_⊥__b__
⇒l⊥α
性质 垂直于同一个平面 定理 的两条直线__平__行__
_a_⊥__α___ _b_⊥__α____
⇒a∥b
高考数学一轮复习课时跟踪检测直线、平面垂直的判定及其性质理

课时跟踪检测(四十三)直线、平面垂直的判定及其性质(一)普通高中适用作业A级一一基础小题练熟练快1 .设a,卩为两个不同的平面,直线I ? a ,则“ I丄卩”是“ a丄卩”成立的()A. 充分不必要条件B.必要不充分条件C.充要条件 D .既不充分也不必要条件解析:选A依题意,由I丄卩,I ? a可以推出a丄卩;反过来,由a丄卩,I ? a 不能推出I丄卩.因此“ I丄卩”是“ a丄卩”成立的充分不必要条件,故选 A.2. 设a为平面,a, b为两条不同的直线,则下列叙述正确的是()A.若a//a, b//a,贝U a// b B .若a 丄a, a// b,贝U b丄aC.若a丄a, a丄b,贝U b/ a D .若a/a, a丄b,贝U b丄a解析:选B若a// a , b// a,则a与b相交、平行或异面,故A错误;易知B正确;若a丄a , a 丄b,贝y b// a或b? a,故C错误;若a//a, a丄b,贝U b / a或b? a或b与a相交,故D错误.3. (2018 •广州一模)设m n是两条不同的直线, a ,卩是两个不同的平面,下列命题中正确的是()A. 若n? 3 , a丄卩,贝y mL aB. 若ml a , n/ n, n // 3 ,贝U a 丄3C. 若ml n, n? a , n? 3,贝U a丄3D. 若 a / 3 , m? a , n? 3 ,贝U m/ n解析:选B A中m与a的位置关系不能确定,故A错误;T mL a , m〃n,:n 丄a,又n// 3 ,「・a丄3,故B正确;若ml n, m? a , n? 3 ,则a与3的位置关系不确定,故C错误;若a// 3,m? a , n? 3,则m与n平行或异面,故D错误.选B.4.(2018 •天津模拟)设I是直线,a , 3是两个不同的平面,则下列说法正确的是()A.若I // a , I // 3 ,则 a / 3 B .若I // a , I 丄 3 ,贝a 丄3C.若 a L 3 ,I 丄a,贝U I // 3 D .若 a 丄3,I 〃a,则I 丄3解析:选B对于A,若I // a , I // 3 ,贝U a // 3或a与3相交,故A错;易知B 正确;对于C,若a L 3 , I丄a,贝U I //3或I? 3,故C错;对于D,若a丄3 , I // a , 则I与3的位置关系不确定,故D 错.选B.5. 如图,在三棱锥D-ABC中,若AB= CB AD= CD E是AC的中点,则下列命题中正确的是()/ '■*、A. 平面ABC平面ABDB. 平面ABD平面BCDC. 平面ABC平面BDE且平面ACD_平面BDED. 平面ABCL平面ACD且平面ACD_平面BDE解析:选C 因为AB= CB且E是AC的中点,所以BE! AC同理,DEI AC由于DEH BE=E,于是ACL平面BDE因为AC?平面ABC所以平面ABCL平面BDE又AC?平面ACD所以平面ACD_平面BDE故选C.6.(2018 •广州模拟)如图是一个几何体的平面展开图,其中四边形ABCD^正方形,E, F分别为PA PD的中点,在此几何体中,给出下面四个结论:①直线BE与直线CF异面;②直线BE与直线AF异面;③直线EF//平面PBC④平面BCEL平面PAD其中正确结论的个数是()A. 1C. 3解析:选B画出该几何体,如图所示,①因为E, F分别是PAPD的中点,所以EF// AD所以EF/ BC直线BE与直线CF是共面直线,故①不正确;②直线BE与直线AF满足异面直线的定义,故②正确;③ 由E, F分别是PA PD的中点,可知EF/ AD所以EF/ BC因为EF?平面PBC BC?平面PBC所以直线EF/平面PBC故③正确;④因为BE与PA的关系不能确定,所以不能判定平面BCEL平面PAD故④不正确•所以正确结论的个数是 2.7.如图,已知/ BAC= 90°,PC L平面ABC则在△ ABC △ PAC的边所在的直线中,与PC垂直的直线有_________________ ;与AP垂直的直线有解析:••• PC L平面ABC••• PC垂直于直线AB BC AC••• ABL AC,AB丄PC A8 PC= C,• ABL平面PAC又AF?平面PAC• ABLAP,与AP垂直的直线是AB答案:AB BC, ACAB&若a ,卩是两个相交平面,m为一条直线,则下列命题中,所有真命题的序号为①若mLa,则在②若mLa,则在③若m?a,则在④若m?a,则在解析: :对于①,若内一定不存在与m平行的直线;内一定存在无数条直线与m垂直;内不一定存在与m垂直的直线;内一定存在与m垂直的直线.mL a ,如果a ,卩互相垂直,则在平面卩内存在与m平行的直线,故①错误;对于②,若mi a ,则m垂直于平面a内的所有直线,故在平面卩内一定存在无数条直线与m垂直,故②正确;对于③④,若n? a ,则在平面卩内一定存在与m垂直的直线,故③错误,④正确.答案:②④9.在直三棱柱ABGABC中,平面a与棱AB AC, AC, AB分别交于点E, F, G H且直线AA//平面a .有下列三个命题:①四边形EFG是平行四边形;②平面 a // 平面BCCB;③平面a丄平面BCFE其中正确命题的序号是____________解析:如图所示,因为AA //平面a ,平面a门平面AABB= EH所以AA/ EH同理AA/ GF,所以EH// GF又ABGA B C是直三棱柱,易知EH= GF= AA,所以四边形EFGH是平行四边形,故①正确;若平面 a //平面BBCQ,由平面a门平面A B i C i = GH平面BCCB门平面A i B C = BC , 知GH/ B i C i ,而GH/ B C不一定成立,故②错误;由AA丄平面BCFE结合AA / EH知EHL平面BCFE又EH?平面a ,所以平面a丄平面BCFE故③正确.答案:①③1 0.(20 1直线进行翻折,在翻折的过程中,给出下列结论:①存在某个位置,使得直线AC与直线BD垂直;②存在某个位置,使得直线AB与直线CD垂直;③存在某个位置,使得直线AD与直线BC垂直.其中正确结论的序号是AEL BD 解析:①假设AC与BD垂直,过点A作AEL BD于E,连接CE则ACL BD ? BDAE n AC= A 丄平面AEC BDL CE而在平面BCD中 , EC与BD不垂直,故假设不成立,①错误.②假设AE L CD T A吐AD ADH CD= D,••• ABL 平面 ACD••• ABLAC 由 AB <BC 可知,存在这样的等腰直角三角形, 使ABL CD 故假设成立,②正确. ③假设AD L BC•/ DC L BC • BC L 平面 ADC• BC L AC 即厶ABC 为直角三角形,且 AB 为斜边, 而A 扌BC 故矛盾,假设不成立,③错误. 答案:②B 级一一中档题目练通抓牢ABGABC 中,/ BAC= 90°, BC L AC 贝U C 在)B.直线BC 上C. 直线AC 上D. A ABC 内 部解析:选 A 连接 AC (图略),由AC L AB ACL BC , ABA BC = B 得 ACL 平面 ABC vAC ?平面ABC 二平面ABC L 平面 ABC • C 在平面ABC 上的射影 H 必在两平面的交线 AB 上.2.如图所示,在四边形 ABCD 中 , AD// BC AD= AB / BCD= 45°, / BAD= 90° .将厶ADE 沿 BD 折起,使平面 ABDL 平面BCD 构成三棱锥 A BCD 则在三棱锥 A BCD 中,下列结论正确的是()ABCD 中 , AD// BC AD= AB / BCD= 45°, / BAD= 90° ,BD L CD又平面ABDL 平面BCD 且平面 ABD A 平面BCD= BD 故CDL 平面ABD 贝U CDL AB又 AD L AB AD A CD= D, AD ?平面 ADC CD ?平面 ADC 故 ABL 平面 ADC 又AB ?平面ABC •平面ADCL 平面ABC1.如图,在斜三棱柱 底面ABC 上的射影H 必在(A.直线AB 上A.平面 ABDL 平面 ABC B .平面ADCL 平面BDC C.平面 ABC L 平面BDCD .平面ADCL 平面 ABC解析:选D •••在四边形3.如图,在直二棱柱ABC - ABC中,侧棱长为2, AC= BC= 1,/ ACB=90°, D是AB的中点,F是BB上的动点,AB, DF交于点E要使AB丄平面CDF贝熾段BF的长为()1A.2C.2解析:选 A 设BF= x,因为AB丄平面CDF DF?平面CDF,所以AB丄DF.由已知可得AB =护,1设Rt△ AAB斜边AB上的高为h,贝U D吕尹又2X ,-'2= h ;22+—2一2,所以h=孚,Dm#.在Rt△ DBE 中,BE=寸¥ 2—芈2=罟.由面积相等得普x2+卑2=乌彳,解得x=2.4.如图所示,在四棱锥P-ABCD中,PAL底面ABCD且底面各边都要填写一个你认为是正确的条件即可)相等,M是PC上的一动点,当点M满足 _____ 时,平面MB L平面PCD只解析:连接AC则AC L BD•/ PAL底面ABCD 二PA! BD又PA O AC= A,「. BD丄平面PAC••• BDL PC•••当DML PC或BM L PC时,即有PC丄平面MBD而PC?平面PCD•平面MB!平面PCD答案:DM L PC(或BM L PC5. (2018 •兰州实战考试)a ,卩是两平面,AB CD是两条线段,已知 a O卩=EF, ABL a于B, CDL a于D,若增加一个条件,就能得出BDL EF.现有下列条件:① ACL卩;②AC与a ,卩所成的角相等;③ AC与CD在卩内的射影在同一条直线上;④ AC// EF其中能成为增加条件的序号是___________ .解析:由题意得,AB// CD • A, B, C, D四点共面.①中,••• AC L 3 , EF? 3 , • AC L EF,又T ABL a , EF? a ,••• ABL EF,T ABH AC= A,A EF丄平面ABCD又••• BD?平面ABCD:BD L EF,故①正确;②不能得到BD L EF,故②错误;ABC L 卩,又AE L a , AB③中,由AC与CD在卩内的射影在同一条直线上可知平面平面ABCD二平面ABC丄a . •平面ABC丄a ,平面ABC L卩,a H卩=EF, • EF丄平面ABCD又BD?平面ABCD •- BD L EF,故③正确;④中,由①知,若BD L EF,则EFL平面ABCD则EFL AC故④错误,故填①③答案:①③6. (2017 •全国卷I )如图,在四棱锥P-ABCD中 , AB// CD且/ BAF^Z CD2 90°.(1) 证明:平面PABL平面PAD(2) 若PA= PD= AB= DC Z APD= 90°,且四棱锥R ABCD勺体8积为3,求该四棱锥的侧面积.解:⑴证明:由Z BAP=Z CDP= 90° ,得ABL AP CDL PD因为AB// CD所以AB± PD又APH PD= P,所以ABL平面PAD又A田平面PAB所以平面PABL平面PAD⑵如图所示,在平面PAD内作PEL AD垂足为E由(1)知,AB L平面PAD故ABL PE可得PEL平面ABCD设AB= x,则由已知可得AD= :2X , PE=~22X.故四棱锥P-ABCD勺体积1 1 3V P-ABCD= A D・ PE= 3X3.1 8由题设得3X3= 3,故X = 2.3 3从而PA= PD= AB= DC= 2 , AD= BC= 2 2 , PB= PC= 2_:2.可得四棱锥P-ABC啲侧面积为2P A- PD^ 2P A- AB^ ^PD- DO *BC sin 60 ° = 6+ 2:3.7. (2017 •山东高考)由四棱柱 ABCDAiBCD 截去三棱锥 C -BCD 后得到的几何体如图⑵设M 是OD 的中点,证明:平面 AEML 平面BCD.因为ABCDA i B i CD 是四棱柱,所以 AO // OC A i O = OC因此四边形AOCC 为平行四边形,所以 AO// OC,因为OC ?平面BCD, AC ?平面BCD ,所以A i O//平面BCD .⑵ 因为E, M 分别为AD OD 的中点,所以EM/ AO因为AOL BD,所以EM L BD又AE 丄平面 ABCD BD ?平面ABCD所以A i E L BD因为 B i D // BD ,所以 EM L B i D , A i E L B i D ,又 A i E ?平面 A i EM EM ?平面 A i EM A i E H EM= E ,所以B i D 丄平面A EM又B i D ?平面B CD ,所以平面A i EM L 平面B CD .C 级一一重难题目自主选做i .(20 i 8 •湖北七市(州)联考)《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形的直棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵 ABMDCP 与刍童ABCDA i B i C D所示.四边形 ABC [为正方形, E 为AD 的中点, AE 丄平面ABCD(1)证明: AO//平面O 为AC 与 BD 的交点,证明:(1)取BD 的中点1 d_________的组合体中,AB= AD AB = AD.台体体积公式:V= g S'+{§飞+ S)h,其中S', S分别为台体上、下底面的面积,h为台体的高.⑴证明:直线BC L平面MAC(2)若AB= 1, AD = 2, MA=73,三棱锥A-ABD的体积V'= 辔,求该组合体的体积.解:⑴ 证明:由题意可知ABMDCP是底面为直角三角形的直棱柱,•••AC L平面MAB ••• AD丄MA又MA_ AB ADn AB- A, AD?平面ABCD AB?平面ABCD•MAL平面ABCD •- MAL BD又AB= AD •四边形ABC西正方形,• BD L AC又MA C AC=代 MA 平面MAC AC?平面MAC•BC丄平面MAC⑵设刍童ABCDABCD的高为h ,则三棱锥A-ABD的体积V'= 3x l x 2X 2X h=3 2• h= ;3 ,故该组合体的体积V= l x i x .:3X 1+ 3x(12+ 22+,讦X22)x .'3 = ¥ + 号=卫討.2.如图,已知三棱柱ABCA' B' C'的侧棱垂直于底面,AB= AC,/ BAC= 90°,点M N分别为A B和B C'的中点.(1) 证明:MN/平面AA C C;(2) 设AB=入AA ,当入为何值时,CNL平面A MN试证明你的结论.解:(1)证明:如图,取A B'的中点E,连接ME NE因为M, N分别为A B和B C的中点,所以NE/ A C , ME // AA'.又A ' C' ?平面AA C' C, AA' ?平面AA C C,所以M曰平面AA C C, NE//平面AA' C C,又因为M C NE=E,所以平面MN/平面AA' C' C,因为MN平面MNE所以M/平面AA C' C⑵连接BN设AA = a,贝U AB=入AA'=入a,由题意知BC=®a, CN k BN^、J a2+ ?入2a2,因为三棱柱ABCA' B' C的侧棱垂直于底面,所以平面A B C丄平面BB' C C.因为AB= AC,点N是B C的中点,所以A B = A C , A N丄B C ,所以A NX平面BB C C,所以CNL A N要使CNL平面A MN只需CNL BN即可,所以CN+ BN= BC,即卩2 a2+1 入2a2= 2 入2a2, 解得入=2,故当入=,2时,CNL平面A MN。
【三维设计】高考数学 第七章 第五节 直线、平面垂直的判定与性质课件 文

直线、平面垂直的判定与性质
2.两条相交直线 a⊥α 3.平行
a,b⊂ α a⊥α
a∩b= O l⊥ a b⊥α 4.(1)射影
a∥ b (3)0
∠PAO
二、1.(1)两个半平面 直线 AB 半平面 α 和 β (2)在半平面 α 和 β 二面角的平面角 ⊂β l⊥α (3)交线 α⊥ β 直角 2.(1)直二面角 (2)垂线 l
(2)连接PM, MC,∵∠ PDA= 45° ,PA⊥ AD,∴ AP= AD. ∵四边形 ABCD为矩形,∴ AD=BC,∴AP = BC. 又∵ M为 AB的中点,∴ AM= BM. 而∠PAM=∠ CBM=90° , ∴△PAM≌△ CBM. ∴ PM= CM. 又 N为 PC的中点,∴MN⊥PC. 由 (1)知,MN⊥CD, PC∩ CD=C,∴ MN⊥平面PCD.
[答案]
①③④
[以题试法1]
选D
对于①,由b不在平面α内知,直线b或
者平行于平面α,或者与平面α相交,若直线b与平面α相交, 则直线b与直线a不可能垂直,这与已知“a⊥b”相矛盾,因 此①正确.对于②,由a∥α知,在平面α内必存在直线 a1∥a,又a⊥β,所以有a1⊥β,所以α⊥β,②正确.对于
③,若直线a与平面α相交于点A,过点A作平面α、β的交线
l⊂β α∩β= a l⊥a
[小题能否全取] 1.选D 对于A中可与α平行或相交,不正确. 对于B中,可与α垂直或斜交,不正确.
对于C中,可与直线l平行或相交,不正确.
2.选D 易知AC⊥平面BB1D1D. ∵A1C1∥AC,∴A1C1⊥平面BB1D1D.
又B1O⊂平面BB1D1D,∴A1C1⊥B1O.
高考数学一轮复习课时跟踪检测直线、平面垂直的判定及其性质理

课时跟踪检测(四十三)直线、平面垂直的判定及其性质(一)普通高中适用作业A级——基础小题练熟练快1.设α,β为两个不同的平面,直线l⊂α,则“l⊥β”是“α⊥β”成立的( ) A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件解析:选A 依题意,由l⊥β,l⊂α可以推出α⊥β;反过来,由α⊥β,l⊂α不能推出l⊥β.因此“l⊥β”是“α⊥β”成立的充分不必要条件,故选A.2.设α为平面,a,b为两条不同的直线,则下列叙述正确的是( )A.若a∥α,b∥α,则a∥b B.若a⊥α,a∥b,则b⊥αC.若a⊥α,a⊥b,则b∥α D.若a∥α,a⊥b,则b⊥α解析:选B 若a∥α,b∥α,则a与b相交、平行或异面,故A错误;易知B正确;若a⊥α,a⊥b,则b∥α或b⊂α,故C错误;若a∥α,a⊥b,则b∥α或b⊂α或b与α相交,故D错误.3.(2018·广州一模)设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )A.若m⊂β,α⊥β,则m⊥αB.若m⊥α,m∥n,n∥β,则α⊥βC.若m⊥n,m⊂α,n⊂β,则α⊥βD.若α∥β,m⊂α,n⊂β,则m∥n解析:选B A中m与α的位置关系不能确定,故A错误;∵m⊥α,m∥n,∴n⊥α,又∵n∥β,∴α⊥β,故B正确;若m⊥n,m⊂α,n⊂β,则α与β的位置关系不确定,故C错误;若α∥β,m⊂α,n⊂β,则m与n平行或异面,故D错误.选B.4.(2018·天津模拟)设l是直线,α,β是两个不同的平面,则下列说法正确的是( ) A.若l∥α,l∥β,则α∥β B.若l∥α,l⊥β,则α⊥βC.若α⊥β,l⊥α,则l∥β D.若α⊥β,l∥α,则l⊥β解析:选B 对于A,若l∥α,l∥β,则α∥β或α与β相交,故A错;易知B 正确;对于C,若α⊥β,l⊥α,则l∥β或l⊂β,故C错;对于D,若α⊥β,l∥α,则l与β的位置关系不确定,故D错.选B.5.如图,在三棱锥DABC中,若AB=CB,AD=CD,E是AC的中点,则下列命题中正确的是( )A.平面ABC⊥平面ABDB.平面ABD⊥平面BCDC.平面ABC⊥平面BDE,且平面ACD⊥平面BDED.平面ABC⊥平面ACD,且平面ACD⊥平面BDE解析:选C 因为AB=CB,且E是AC的中点,所以BE⊥AC,同理,DE⊥AC,由于DE∩BE =E,于是AC⊥平面BDE.因为AC⊂平面ABC,所以平面ABC⊥平面BDE.又AC⊂平面ACD,所以平面ACD⊥平面BDE.故选C.6.(2018·广州模拟)如图是一个几何体的平面展开图,其中四边形ABCD为正方形,E,F分别为PA,PD的中点,在此几何体中,给出下面四个结论:①直线BE与直线CF异面;②直线BE与直线AF异面;③直线EF∥平面PBC;④平面BCE⊥平面PAD.其中正确结论的个数是( )A.1 B.2C.3 D.4解析:选B 画出该几何体,如图所示,①因为E,F分别是PA,PD的中点,所以EF∥AD,所以EF∥BC,直线BE与直线CF是共面直线,故①不正确;②直线BE与直线AF满足异面直线的定义,故②正确;③由E,F分别是PA,PD的中点,可知EF∥AD,所以EF∥BC,因为EF⊄平面PBC,BC⊂平面PBC,所以直线EF∥平面PBC,故③正确;④因为BE与PA的关系不能确定,所以不能判定平面BCE⊥平面PAD,故④不正确.所以正确结论的个数是2.7.如图,已知∠BAC=90°,PC⊥平面ABC,则在△ABC,△PAC的边所在的直线中,与PC垂直的直线有____________;与AP垂直的直线有________.解析:∵PC⊥平面ABC,∴PC垂直于直线AB,BC,AC.∵AB⊥AC,AB⊥PC,AC∩PC=C,∴AB⊥平面PAC,又∵AP⊂平面PAC,∴AB⊥AP,与AP垂直的直线是AB.答案:AB,BC,ACAB8.若α,β是两个相交平面,m 为一条直线,则下列命题中,所有真命题的序号为________.①若m ⊥α,则在β内一定不存在与m 平行的直线; ②若m ⊥α,则在β内一定存在无数条直线与m 垂直; ③若m ⊂α,则在β内不一定存在与m 垂直的直线; ④若m ⊂α,则在β内一定存在与m 垂直的直线.解析:对于①,若m ⊥α,如果α,β互相垂直,则在平面β内存在与m 平行的直线,故①错误;对于②,若m ⊥α,则m 垂直于平面α内的所有直线,故在平面β内一定存在无数条直线与m 垂直,故②正确;对于③④,若m ⊂α,则在平面β内一定存在与m 垂直的直线,故③错误,④正确.答案:②④9.在直三棱柱ABC A 1B 1C 1中,平面α与棱AB ,AC ,A 1C 1,A 1B 1分别交于点E ,F ,G ,H ,且直线AA 1∥平面α.有下列三个命题:①四边形EFGH 是平行四边形;②平面α∥平面BCC 1B 1;③平面α⊥平面BCFE .其中正确命题的序号是________.解析:如图所示,因为AA 1∥平面α,平面α∩平面AA 1B 1B =EH ,所以AA 1∥EH .同理AA 1∥GF ,所以EH ∥GF ,又ABC A 1B 1C 1是直三棱柱,易知EH =GF =AA 1,所以四边形EFGH 是平行四边形,故①正确;若平面α∥平面BB 1C 1C ,由平面α∩平面A 1B 1C 1=GH ,平面BCC 1B 1∩平面A 1B 1C 1=B 1C 1,知GH ∥B 1C 1,而GH ∥B 1C 1不一定成立,故②错误;由AA 1⊥平面BCFE ,结合AA 1∥EH 知EH ⊥平面BCFE ,又EH ⊂平面α,所以平面α⊥平面BCFE ,故③正确.答案:①③10.(2018·武汉调研)在矩形ABCD 中,AB <BC ,现将△ABD 沿矩形的对角线BD 所在的直线进行翻折,在翻折的过程中,给出下列结论:①存在某个位置,使得直线AC 与直线BD 垂直; ②存在某个位置,使得直线AB 与直线CD 垂直; ③存在某个位置,使得直线AD 与直线BC 垂直. 其中正确结论的序号是________.解析:①假设AC 与BD 垂直,过点A 作AE ⊥BD 于E ,连接CE .则⎭⎪⎬⎪⎫AE ⊥BDAC ⊥BD AE ∩AC =A ⇒BD ⊥平面AEC ⇒BD ⊥CE ,而在平面BCD 中,EC 与BD 不垂直,故假设不成立,①错误.②假设AB ⊥CD ,∵AB ⊥AD ,AD ∩CD =D ,∴AB⊥平面ACD,∴AB⊥AC,由AB<BC可知,存在这样的等腰直角三角形,使AB⊥CD,故假设成立,②正确.③假设AD⊥BC,∵DC⊥BC,∴BC⊥平面ADC,∴BC⊥AC,即△ABC为直角三角形,且AB为斜边,而AB<BC,故矛盾,假设不成立,③错误.答案:②B级——中档题目练通抓牢1.如图,在斜三棱柱ABCA1B1C1中,∠BAC=90°,BC1⊥AC,则C1在底面ABC上的射影H必在( )A.直线AB上B.直线BC上C.直线AC上D.△ABC内部解析:选A 连接AC1(图略),由AC⊥AB,AC⊥BC1,AB∩BC1=B,得AC⊥平面ABC1.∵AC⊂平面ABC,∴平面ABC1⊥平面ABC.∴C1在平面ABC上的射影H必在两平面的交线AB上.2.如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°.将△ADB沿BD折起,使平面ABD⊥平面BCD,构成三棱锥ABCD,则在三棱锥ABCD中,下列结论正确的是( )A.平面ABD⊥平面ABC B.平面ADC⊥平面BDCC.平面ABC⊥平面BDC D.平面ADC⊥平面ABC解析:选D ∵在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,∴BD⊥CD.又平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD,故CD⊥平面ABD,则CD⊥AB.又AD⊥AB,AD∩CD=D,AD⊂平面ADC,CD⊂平面ADC,故AB⊥平面ADC.又AB⊂平面ABC,∴平面ADC⊥平面ABC.3.如图,在直三棱柱ABC A 1B 1C 1中,侧棱长为2,AC =BC =1,∠ACB =90°,D 是A 1B 1的中点,F 是BB 1上的动点,AB 1,DF 交于点E .要使AB 1⊥平面C 1DF ,则线段B 1F 的长为( )A.12 B .1 C.32D .2解析:选A 设B 1F =x ,因为AB 1⊥平面C 1DF ,DF ⊂平面C 1DF ,所以AB 1⊥DF .由已知可得A 1B 1=2,设Rt △AA 1B 1斜边AB 1上的高为h ,则DE =12h .又2×2=h 22+22,所以h =233,DE =33.在Rt △DB 1E 中,B 1E =⎝ ⎛⎭⎪⎫222-⎝ ⎛⎭⎪⎫332=66. 由面积相等得66× x 2+⎝⎛⎭⎪⎫222=22x ,解得x =12. 4.如图所示,在四棱锥P ABCD 中,PA ⊥底面ABCD ,且底面各边都相等,M 是PC 上的一动点,当点M 满足______时,平面MBD ⊥平面PCD .(只要填写一个你认为是正确的条件即可)解析:连接AC ,则AC ⊥BD , ∵PA ⊥底面ABCD ,∴PA ⊥BD . 又PA ∩AC =A ,∴BD ⊥平面PAC , ∴BD ⊥PC .∴当DM ⊥PC (或BM ⊥PC )时,即有PC ⊥平面MBD . 而PC ⊂平面PCD , ∴平面MBD ⊥平面PCD . 答案:DM ⊥PC (或BM ⊥PC )5.(2018·兰州实战考试)α,β是两平面,AB ,CD 是两条线段,已知α∩β=EF ,AB ⊥α于B ,CD ⊥α于D ,若增加一个条件,就能得出BD ⊥EF .现有下列条件:①AC ⊥β;②AC 与α,β所成的角相等;③AC 与CD 在β内的射影在同一条直线上;④AC ∥EF .其中能成为增加条件的序号是________.解析:由题意得,AB ∥CD ,∴A ,B ,C ,D 四点共面. ①中,∵AC ⊥β,EF ⊂β,∴AC ⊥EF ,又∵AB ⊥α,EF ⊂α,∴AB ⊥EF ,∵AB ∩AC =A ,∴EF ⊥平面ABCD , 又∵BD ⊂平面ABCD ,∴BD ⊥EF ,故①正确; ②不能得到BD ⊥EF ,故②错误;③中,由AC 与CD 在β内的射影在同一条直线上可知平面ABCD ⊥β,又AB ⊥α,AB ⊂平面ABCD ,∴平面ABCD ⊥α.∵平面ABCD ⊥α,平面ABCD ⊥β,α∩β=EF ,∴EF ⊥平面ABCD ,又BD ⊂平面ABCD ,∴BD ⊥EF ,故③正确;④中,由①知,若BD ⊥EF ,则EF ⊥平面ABCD ,则EF ⊥AC ,故④错误,故填①③. 答案:①③6.(2017·全国卷Ⅰ)如图,在四棱锥P ABCD 中,AB ∥CD ,且∠BAP =∠CDP =90°.(1)证明:平面PAB ⊥平面PAD ;(2)若PA =PD =AB =DC ,∠APD =90°,且四棱锥P ABCD 的体积为83,求该四棱锥的侧面积.解:(1)证明:由∠BAP =∠CDP =90°, 得AB ⊥AP ,CD ⊥PD . 因为AB ∥CD ,所以AB ⊥PD . 又AP ∩PD =P , 所以AB ⊥平面PAD .又AB ⊂平面PAB ,所以平面PAB ⊥平面PAD . (2)如图所示,在平面PAD 内作PE ⊥AD ,垂足为E . 由(1)知,AB ⊥平面PAD , 故AB ⊥PE , 可得PE ⊥平面ABCD .设AB =x ,则由已知可得AD =2x ,PE =22x . 故四棱锥P ABCD 的体积V P ABCD =13AB ·AD ·PE =13x 3.由题设得13x 3=83,故x =2.从而PA =PD =AB =DC =2,AD =BC =22,PB =PC =2 2. 可得四棱锥P ABCD 的侧面积为12PA ·PD +12PA ·AB +12PD ·DC +12BC 2sin 60°=6+2 3.7.(2017·山东高考)由四棱柱ABCDA1B1C1D1截去三棱锥C1B1CD1后得到的几何体如图所示.四边形ABCD为正方形,O为AC与BD的交点,E为AD的中点,A1E⊥平面ABCD.(1)证明:A1O∥平面B1CD1;(2)设M是OD的中点,证明:平面A1EM⊥平面B1CD1.证明:(1)取B1D1的中点O1,连接CO1,A1O1,因为ABCDA1B1C1D1是四棱柱,所以A1O1∥OC,A1O1=OC,因此四边形A1OCO1为平行四边形,所以A1O∥O1C,因为O1C⊂平面B1CD1,A1O⊄平面B1CD1,所以A1O∥平面B1CD1.(2)因为E,M分别为AD,OD的中点,所以EM∥AO.因为AO⊥BD,所以EM⊥BD.又A1E⊥平面ABCD,BD⊂平面ABCD,所以A1E⊥BD,因为B1D1∥BD,所以EM⊥B1D1,A1E⊥B1D1,又A1E⊂平面A1EM,EM⊂平面A1EM,A1E∩EM=E,所以B1D1⊥平面A1EM,又B1D1⊂平面B1CD1,所以平面A1EM⊥平面B1CD1.C级——重难题目自主选做1.(2018·湖北七市(州)联考)《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形的直棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵ABMDCP与刍童ABCDA1B1C1D1的组合体中,AB =AD ,A 1B 1=A 1D 1.台体体积公式:V =13(S ′+S ′S +S )h ,其中S ′,S 分别为台体上、下底面的面积,h 为台体的高.(1)证明:直线BD ⊥平面MAC ;(2)若AB =1,A 1D 1=2,MA =3,三棱锥A A 1B 1D 1的体积V ′=233,求该组合体的体积.解:(1)证明:由题意可知ABM DCP 是底面为直角三角形的直棱柱,∴AD ⊥平面MAB ,∴AD ⊥MA .又MA ⊥AB ,AD ∩AB =A ,AD ⊂平面ABCD ,AB ⊂平面ABCD , ∴MA ⊥平面ABCD ,∴MA ⊥BD ,又AB =AD ,∴四边形ABCD 为正方形,∴BD ⊥AC . 又MA ∩AC =A ,MA ⊂平面MAC ,AC ⊂平面MAC , ∴BD ⊥平面MAC .(2)设刍童ABCD A 1B 1C 1D 1的高为h ,则三棱锥A A 1B 1D 1的体积V ′=13×12×2×2×h =233,∴h =3,故该组合体的体积V =12×1×3×1+13×(12+22+12×22)×3=32+733=1736.2.如图,已知三棱柱ABC A ′B ′C ′的侧棱垂直于底面,AB =AC ,∠BAC =90°,点M ,N 分别为A ′B 和B ′C ′的中点.(1)证明:MN ∥平面AA ′C ′C ;(2)设AB =λAA ′,当λ为何值时,CN ⊥平面A ′MN ,试证明你的结论.解:(1)证明:如图,取A ′B ′的中点E ,连接ME ,NE . 因为M ,N 分别为A ′B 和B ′C ′的中点,所以NE ∥A ′C ′,ME ∥AA ′.又A ′C ′⊂平面AA ′C ′C ,AA ′⊂平面AA ′C ′C ,所以ME ∥平面AA ′C ′C ,NE ∥平面AA ′C ′C ,又因为ME ∩NE =E ,所以平面MNE ∥平面AA ′C ′C , 因为MN ⊂平面MNE , 所以MN ∥平面AA ′C ′C .(2)连接BN ,设AA ′=a ,则AB =λAA ′=λa ,由题意知BC =2λa ,CN =BN = a 2+12λ2a 2,因为三棱柱ABC A ′B ′C ′的侧棱垂直于底面, 所以平面A ′B ′C ′⊥平面BB ′C ′C . 因为AB =AC ,点N 是B ′C ′的中点, 所以A ′B ′=A ′C ′,A ′N ⊥B ′C ′, 所以A ′N ⊥平面BB ′C ′C ,所以CN ⊥A ′N , 要使CN ⊥平面A ′MN ,只需CN ⊥BN 即可,所以CN 2+BN 2=BC 2,即2⎝ ⎛⎭⎪⎫a 2+12λ2a 2=2λ2a 2,解得λ=2,故当λ=2时,CN ⊥平面A ′MN .。
2025高考数学一轮复习-7.4-直线、平面垂直的判定与性质-专项训练【含答案】

2025高考数学一轮复习-7.4-直线、平面垂直的判定与性质-专项训练基础巩固练1.能保证直线a与平面α平行的条件是()A.b⊂α,a∥bB.b⊂α,c∥α,a∥b,a∥cC.b⊂α,A,B∈a,C,D∈b,且AC∥BDD.a⊄α,b⊂α,a∥b2.在三棱台ABC-A1B1C1中,直线AB与平面A1B1C1的位置关系是()A.相交B.平行C.在平面内D.不确定3.已知a,b,c为三条不重合的直线,α,β,γ为三个不重合的平面,现给出以下四个命题:① ∥ ∥ ⇒α∥β;② ∥ ∥ ⇒α∥β;③ ∥ ∥ ⇒a∥α;④ ∥ ∥ ⇒a∥β.其中为真命题的是()A.①②③B.①④C.②D.①③④4.(2023连云港质检)若过直线l外两点作与l平行的平面,则这样的平面()A.不存在B.只有一个C.有无数个D.不能确定5.(多选题)如图所示,P为矩形ABCD所在平面外一点,矩形对角线的交点为O,M为PB的中点,给出以下结论,其中正确的是()A.OM∥PDB.OM∥平面PCDC.OM∥平面PDAD.OM∥平面PBA6.(多选题)(2023无锡调研)设a,b是两条不同的直线,α,β,γ是三个不同的平面,则α∥β的一个充分条件是()A.存在一条直线a,a∥α,a∥βB.存在一条直线a,a⊂α,a∥βC.存在一个平面γ,满足α∥γ,β∥γD.存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α7.如图,E,F,G分别是四面体ABCD的棱BC,CD,DA的中点,则此四面体中与过点E,F,G的截面平行的棱是.8.如图所示,在正方体ABCD-A1B1C1D1中,M,E,F,N分别是A1B1,B1C1,C1D1,D1A1的中点,求证:(1)E,F,B,D四点共面;(2)平面MAN∥平面EFDB.9.如图所示,已知正方体ABCD-A1B1C1D1.(1)求证:平面A1BD∥平面B1D1C.(2)若E,F分别是AA1,CC1的中点,求证:平面EB1D1∥平面FBD.综合提升练10.(多选题)四棱锥的平面展开图如图所示,其中四边形ABCD为正方形,点E,F,G,H分别为PA,PD,PC,PB的中点,则在原四棱锥中()A.平面EFGH∥平面ABCDB.BC∥平面PADC.AB∥平面PCDD.平面PAD∥平面PAB11.如图,点A,B,C,M,N为正方体的顶点或所在棱的中点,则下列各图中,不满足直线MN∥平面ABC的是()A BC D12.(2023苏州月考)如图,在斜三棱柱ABC-A1B1C1中,点D1为A1C1上的点.当 1 1 1 1=时,BC1∥平面AB1D1.第12题图第13题图13.如图,在直三棱柱ABC-A1B1C1中,D为AA1的中点,点P在侧面BCC1B1上运动,当点P满足条件时,A1P∥平面BCD.(填一个满足题意的条件即可)14.如图,在四棱锥P-ABCD中,AB∥CD,AB=2CD,E为PB的中点.(1)求证:CE∥平面PAD.(2)在线段AB上是否存在一点F,使得平面PAD∥平面CEF?若存在,请证明你的结论;若不存在,请说明理由.创新应用练15.如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是棱BC,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面AEF,则线段A1P的长度的取值范围是()A.1,2 D.[2,3]参考答案1.D2.B3.C4.D5.ABC6.CD7.BD,AC8.证明(1)如图,连接B1D1.∵E,F分别是B1C1和C1D1的中点,∴EF∥B1D1.又BD∥B1D1,∴BD∥EF.∴E,F,B,D四点共面.(2)由题意知MN∥B1D1,B1D1∥BD,∴MN∥BD.又MN⊄平面EFDB,BD⊂平面EFDB,∴MN∥平面EFDB,如图,连接MF.∵点M,F分别是A1B1与C1D1的中点,∴MF AD.∴四边形ADFM是平行四边形.∴AM∥DF.∵AM⊄平面EFDB,DF⊂平面EFDB,∴AM∥平面EFDB.又AM∩MN=M,∴平面MAN∥平面EFDB.9.证明(1)因为B1B DD1,所以四边形BB1D1D是平行四边形,所以B1D1∥BD.又BD⊄平面B1D1C,B1D1⊂平面B1D1C,所以BD∥平面B1D1C.同理A1D∥平面B1D1C.又A1D∩BD=D,所以平面A1BD∥平面B1D1C.(2)由BD∥B1D1,B1D1⊂平面EB1D1,BD⊄平面EB1D1,得BD∥平面EB1D1.如图,取BB1的中点G,连接AG,GF,易得AE∥B1G,又因为AE=B1G,所以四边形AEB1G是平行四边形,所以B1E∥AG.易得GF∥AD,又因为GF=AD,所以四边形ADFG是平行四边形,所以AG∥DF,所以B1E ∥DF,又B1E⊂平面EB1D1,DF⊄平面EB1D1,所以DF∥平面EB1D1.又因为BD∩DF=D,所以平面EB1D1∥平面FBD.10.ABC11.D12.113.P是CC1的中点(答案不唯一)14.解(1)如图,取P A的中点H,连接EH,DH,因为E为PB的中点,所以EH∥AB,且EH=12AB,又AB∥CD,且CD=12AB,所以EH∥CD,且EH=CD,所以四边形DCEH为平行四边形,所以CE∥DH,又DH⊂平面PAD,CE⊄平面PAD,所以CE ∥平面PAD.(2)存在.当F为AB的中点时,平面P AD∥平面CEF.证明如下:如图,取AB的中点F,连接CF,EF,则AF=12AB,因为CD=12AB,所以AF=CD,又AF∥CD,所以四边形AFCD为平行四边形,所以CF∥AD.又AD⊂平面PAD,CF⊄平面PAD,所以CF∥平面PAD,由(1)知CE∥平面PAD,又CE∩CF=C,CE,CF⊂平面CEF,所以平面CEF∥平面PAD.故当F为AB的中点时,平面PAD∥平面CEF.15.B。
(江苏专版)高考数学一轮复习 第八章 立体几何 课时跟踪检测(三十七)直线、平面垂直的判定及其性质

课时跟踪检测(三十七) 直线、平面垂直的判定及其性质 一抓基础,多练小题做到眼疾手快1.设α,β为两个不同的平面,直线l ⊂α,则“l ⊥β”是“α⊥β”成立的________条件(填“充分不必要”“必要不充分”“充要”或“既不充分也不必要”).解析:依题意,由l ⊥β,l ⊂α可以推出α⊥β;反过来,由α⊥β,l ⊂α不能推出l ⊥β.因此“l ⊥β”是“α⊥β”成立的充分不必要条件.答案:充分不必要2.在空间四边形ABCD 中,平面ABD ⊥平面BCD ,且DA ⊥平面ABC ,则△ABC 的形状是________.解析:过A 作AH ⊥BD 于H ,由平面ABD ⊥平面BCD ,得AH ⊥平面BCD ,则AH ⊥BC ,又DA ⊥平面ABC ,所以BC ⊥DA ,所以BC ⊥平面ABD ,所以BC ⊥AB ,即△ABC 为直角三角形.答案:直角三角形3.已知平面α,β和直线m ,给出条件:①m ∥α;②m ⊥α;③m ⊂α;④α∥β.当满足条件________时,有m ⊥β.(填所选条件的序号)解析:若m ⊥α,α∥β,则m ⊥β.故填②④.答案:②④4.一平面垂直于另一平面的一条平行线,则这两个平面的位置关系是________. 解析:由线面平行的性质定理知,该面必有一直线与已知直线平行.再根据“两平行线中一条垂直于一平面,另一条也垂直于该平面”得出两个平面垂直.答案:垂直5.如图,在长方体ABCD A 1B 1C 1D 1中,AB =AD =3 cm ,则直线AA 1到平面BB 1D 1D 的距离为________ cm.解析:连结AC 交BD 于点O ,则AO ⊥BD .因为BB 1⊥平面ABCD ,AO⊂平面ABCD ,所以BB 1⊥AO .又BB 1∩BD =B ,所以AO ⊥平面BB 1D 1D .又AA 1∥BB 1,AA 1⊄平面BB 1D 1D ,BB 1⊂平面BB 1D 1D ,所以AA 1∥平面BB 1D 1D ,所以线段AO 的长就是直线AA 1到平面BB 1D 1D 的距离.因为AB =AD =3 cm ,AB ⊥AD ,AO ⊥BD ,所以AO =322,即直线AA 1到平面BB 1D 1D 的距离为322.答案:3226.如图,PA ⊥⊙O 所在平面,AB 是⊙O 的直径,C 是⊙O 上一点,AE⊥PC ,AF ⊥PB ,给出下列结论:①AE ⊥BC ;②EF ⊥PB ;③AF ⊥BC ;④AE⊥平面PBC ,其中真命题的序号是________.解析:①AE ⊂平面PAC ,BC ⊥AC ,BC ⊥PA ⇒AE ⊥BC ,故①正确,②AE ⊥PC ,AE ⊥BC ,PB ⊂平面PBC ⇒AE ⊥PB ,又AF ⊥PB ,EF ⊂平面AEF ⇒EF ⊥PB ,故②正确,③若AF ⊥BC ⇒AF ⊥平面PBC ,则AF ∥AE 与已知矛盾,故③错误,由①可知④正确.答案:①②④二保高考,全练题型做到高考达标1.(2018·某某中学测试)已知α,β,γ是三个不同的平面,命题“α∥β,且α⊥γ⇒β⊥γ”是真命题,如果把α,β,γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题的个数为________.解析:若α,β换为直线a ,b ,则命题化为“a ∥b ,且a ⊥γ⇒b ⊥γ”,此命题为真命题;若α,γ换为直线a ,b ,则命题化为“a ∥β,且a ⊥b ⇒b ⊥β”,此命题为假命题;若β,γ换为直线a ,b ,则命题化为“a ∥α,且b ⊥α⇒a ⊥b ”,此命题为真命题.答案:22.如图,在Rt △ABC 中,∠ABC =90°,P 为△ABC 所在平面外一点,PA ⊥平面ABC ,则四面体P ABC 中直角三角形的个数为________.解析:由PA ⊥平面ABC 可得△PAC ,△PAB 是直角三角形,且PA ⊥BC .又∠ABC =90°,所以△ABC 是直角三角形,且BC ⊥平面PAB ,所以BC ⊥PB ,即△PBC 为直角三角形,故四面体P ABC 中共有4个直角三角形.答案:43.已知正△ABC 的边长为2 cm ,PA ⊥平面ABC ,A 为垂足,且PA =2 cm ,那么点P 到BC 的距离为________cm.解析:如图,取BC 的中点D ,连结AD ,PD ,则BC ⊥AD ,又因为PA⊥平面ABC ,所以PA ⊥BC ,所以BC ⊥平面PAD ,所以PD ⊥BC ,则PD 的长度即为点P 到BC 的距离.在Rt △PAD 中,PA =2,AD =3,可得PD =22+32=7.答案:74.已知P为△ABC所在平面外一点,AC=2a,△PAB,△PBC都是边长为a的等边三角形,则平面ABC和平面PAC的位置关系为________.解析:如图所示,PA=PB=PC=AB=BC=a,取AC的中点D,连结PD,BD,则PD⊥AC,BD⊥AC.又AC=2a,所以PD=BD=22a,在△PBD中,PB2=BD2+PD2,所以∠PDB=90°,所以PD⊥BD,所以PD⊥平面ABC.又PD⊂平面PAC,所以平面PAC⊥平面ABC.答案:垂直5.已知直线a和两个不同的平面α,β,且a⊥α,a∥β,则α,β的位置关系是________.解析:记b⊂β且a∥b,因为a∥b,a⊥α,所以b⊥α,因为b⊂β,所以α⊥β.答案:垂直6.如图,已知∠BAC=90°,PC⊥平面ABC,则在△ABC,△PAC的边所在的直线中,与PC垂直的直线有____________;与AP垂直的直线有________.解析:因为PC⊥平面ABC,所以PC垂直于直线AB,BC,AC.因为AB⊥AC,AB⊥PC,AC∩PC=C,所以AB⊥平面PAC,又因为AP⊂平面PAC,所以AB⊥AP,与AP垂直的直线是AB.答案:AB,BC,ACAB7.如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:①BD⊥AC;②△BAC是等边三角形;③三棱锥DABC是正三棱锥;④平面ADC⊥平面ABC.其中正确的是________(填序号).解析:由题意知,BD ⊥平面ADC ,故BD ⊥AC ,①正确;AD 为等腰直角三角形斜边BC 上的高,平面ABD ⊥平面ACD ,所以AB =AC =BC ,△BAC 是等边三角形,②正确;易知DA =DB =DC ,又由②知③正确;由①知④错误.答案:①②③8.如图,直三棱柱ABC A 1B 1C 1中,侧棱长为2,AC =BC =1,∠ACB =90°,D 是A 1B 1的中点,F 是BB 1上的动点,AB 1,DF 交于点E .要使AB 1⊥平面C 1DF ,则线段B 1F 的长为________. 解析:设B 1F =x ,因为AB 1⊥平面C 1DF ,DF ⊂平面C 1DF ,所以AB 1⊥DF .由已知可以得A 1B 1=2,设Rt△AA 1B 1斜边AB 1上的高为h ,则DE =12h . 又2×2=h ×22+22, 所以h =233,DE =33. 在Rt△DB 1E 中,B 1E =⎝ ⎛⎭⎪⎫222-⎝ ⎛⎭⎪⎫332=66. 由面积相等得66× x 2+⎝ ⎛⎭⎪⎫222=22x ,得x =12. 即线段B 1F 的长为12. 答案:129.(2017·某某三模)如图,在四棱锥P ABCD 中,底面ABCD 是矩形,平面PAD ⊥平面ABCD ,AP =AD ,M ,N 分别为棱PD ,PC 的中点.求证:(1)MN ∥平面PAB ;(2)AM ⊥平面PCD .证明:(1)因为M ,N 分别为棱PD ,PC 的中点,所以MN ∥DC ,又因为底面ABCD 是矩形,所以AB ∥DC ,所以MN ∥AB .又AB ⊂平面PAB ,MN ⊄平面PAB ,所以MN∥平面PAB.(2)因为AP=AD,M为PD的中点,所以AM⊥PD.因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,CD⊥AD,CD⊂平面ABCD,所以CD⊥平面PAD.又AM⊂平面PAD,所以CD⊥AM.因为CD∩PD=D,CD⊂平面PCD,PD⊂平面PCD,所以AM⊥平面PCD.10.(2018·某某高三年级期中考试)如图,在三棱锥SABC中,SA=SC,AB⊥AC,D为BC的中点,E为AC上一点,且DE∥平面SAB.求证:(1)AB∥平面SDE;(2)平面ABC⊥平面SDE.证明:(1)因为DE∥平面SAB,DE⊂平面ABC,平面SAB∩平面ABC=AB,所以DE∥AB.因为DE⊂平面SDE,AB⊄平面SDE,所以AB∥平面SDE.(2)因为D为BC的中点,DE∥AB,所以E为AC的中点.又因为SA=SC,所以SE⊥AC,又AB⊥AC,DE∥AB,所以DE⊥AC.因为DE∩SE=E,DE⊂平面SDE,SE⊂平面SDE,所以AC⊥平面SDE.因为AC⊂平面ABC,所以平面ABC⊥平面SDE.三上台阶,自主选做志在冲刺名校1.(2018·某某实战考试)α,β是两平面,AB,CD是两条线段,已知α∩β=EF,AB⊥α于B,CD⊥α于D,若增加一个条件,就能得出BD⊥EF.现有下列条件:①AC⊥β;②AC与α,β所成的角相等;③AC与CD在β内的射影在同一条直线上;④AC∥EF.其中能成为增加条件的序号是________.解析:由题意得,AB∥CD,所以A,B,C,D四点共面,①:因为AC⊥β,EF⊂β,所以AC⊥EF,又因为AB⊥α,EF⊂α,所以AB⊥EF,因为AB∩AC=A,所以EF⊥平面ABCD,又因为BD⊂平面ABCD,所以BD⊥EF,故①正确;②不能得到BD⊥EF,故②错误;③:由AC与CD在β内的射影在同一条直线上可知平面ABCD⊥β,又AB⊥α,AB⊂平面ABCD,所以平面ABCD⊥α.因为平面ABCD⊥α,平面ABCD⊥β,α∩β=EF,所以EF⊥平面ABCD,又BD⊂平面ABCD,所以BD⊥EF,故③正确;④:由①知,若BD⊥EF,则EF⊥平面ABCD,则EF⊥AC,故④错误,故填①③.答案:①③2.如图,点P在正方体ABCDA1B1C1D1的面对角线BC1上运动,则下列四个命题:①三棱锥AD1PC的体积不变;②A1P∥平面ACD1;③DP⊥BC1;④平面PDB1⊥平面ACD1.其中正确的命题序号是________.解析:由题意可得BC1∥AD1,又AD1⊂平面AD1C,BC1⊄平面AD1C,所以BC1∥平面AD1C.所以点P到平面AD1C的距离不变,VAD1PC=VPAD1C,所以体积不变,故①正确;连结A1C1,A1B,可得平面ACD1∥平面A1C1B.又因为A1P⊂平面A1C1B,所以A1P ∥平面ACD1,故②正确;当点P运动到B点时,△DBC1是等边三角形,所以DP不垂直于BC1,故③不正确;因为AC⊥平面DD1B1B,DB1⊂平面DD1B1B,所以AC⊥DB1.同理可得AD1⊥DB1.所以DB1⊥平面ACD1.又因为DB1⊂平面PDB1.所以平面PDB1⊥平面ACD1.故④正确.综上,正确的序号为①②④.答案:①②④3.(2018·某某调研)在直三棱柱ABCA1B1C1中,AB=AC=AA1=3a,BC=2a,D是BC的中点,E,F分别是AA1,CC1上一点,且AE=CF=2a.(1)求证:B1F⊥平面ADF;(2)求三棱锥B1ADF的体积;(3)求证:BE∥平面ADF.解:(1)证明:因为AB =AC ,D 为BC 的中点, 所以AD ⊥BC .在直三棱柱ABC A 1B 1C 1中,因为B 1B ⊥底面ABC ,AD ⊂底面ABC , 所以AD ⊥B 1B .因为BC ∩B 1B =B ,所以AD ⊥平面B 1BCC 1, 因为B 1F ⊂平面B 1BCC 1,所以AD ⊥B 1F .在矩形B 1BCC 1中,因为C 1F =CD =a ,B 1C 1=CF =2a , 所以Rt △DCF ≌Rt △FC 1B 1,所以∠CFD =∠C 1B 1F , 所以∠B 1FD =90°,所以B 1F ⊥FD .因为AD ∩FD =D ,所以B 1F ⊥平面AFD .(2)因为B 1F ⊥平面AFD ,所以VB 1ADF =13·S △ADF ·B 1F =13×12×AD ×DF ×B 1F =52a 33.(3)证明:连结EF ,EC ,设EC ∩AF =M ,连结DM , 因为AE =CF =2a ,所以四边形AEFC 为矩形,所以M 为EC 中点,因为D 为BC 中点,所以MD ∥BE .因为MD ⊂平面ADF ,BE ⊄平面ADF ,所以BE ∥平面ADF .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时跟踪检测(四十七) 直线、平面垂直的判定与性质1.(2012·杭州模拟)设a,b,c是三条不同的直线,α,β是两个不同的平面,则a ⊥b的一个充分条件是( )A.a⊥c,b⊥c B.α⊥β,a⊂α,b⊂βC.a⊥α,b∥α D.a⊥α,b⊥α2.设α,β,γ是三个不重合的平面,l是直线,给出下列命题①若α⊥β,β⊥γ,则α⊥γ;②若l上两点到α的距离相等,则l∥α;③若l ⊥α,l∥β,则α⊥β;④若α∥β,l⊄β,且l∥α,则l∥β.其中正确的命题是( )A.①②B.②③C.②④D.③④3.给出命题:(1)在空间里,垂直于同一平面的两个平面平行;(2)设l,m是不同的直线,α是一个平面,若l⊥α,l∥m,则m⊥α;(3)已知α,β表示两个不同平面,m为平面α内的一条直线,则“α⊥β”是“m⊥β”的充要条件;(4)a,b是两条异面直线,P为空间一点,过P总可以作一个平面与a,b之一垂直,与另一个平行.其中正确命题个数是( )A.0 B.1 C.2 D.34.(2013·珠海模拟)如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在底面ABC上的射影H必在( )A.直线AB上B.直线BC上C.直线AC上 D.△ABC内部5.(2012·曲阜师大附中质检)如图所示,直线PA垂直于⊙O所在的平面,△ABC内接于⊙O,且AB为⊙O的直径,点M为线段PB的中点.现有结论:①BC⊥PC;②OM∥平面APC;③点B到平面PAC的距离等于线段BC的长.其中正确的是( )A.①② B.①②③ C.① D.②③6.(2012·惠州模拟)如图,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD =90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下面命题正确的是( )A.平面ABD⊥平面ABC B.平面ADC⊥平面BDCC.平面ABC⊥平面BDC D.平面ADC⊥平面ABC7.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足________时,平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)8.(2013·清远中学月考)正四棱锥S-ABCD的底面边长为2,高为2,E是BC的中点,动点P在四棱锥的表面上运动,并且总保持PE⊥AC,则动点P的轨迹的长为________.9.(2013·中山模拟)点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动,给出下列四个命题:①三棱锥A-D1PC的体积不变;②A1P∥平面ACD1;③DP⊥BC1;④平面PDB1⊥平面ACD1.其中正确的命题序号是________.10.如图所示,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB 为正三角形.(1)求证:DM ∥平面APC ; (2)求证:平面ABC ⊥平面APC .11.(2012·北京海淀二模)如图所示,PA ⊥平面ABC ,点C 在以AB 为直径的⊙O 上,∠CBA =30°,PA =AB =2,点E 为线段PB 的中点,点M 在AB 上,且OM ∥AC .(1)求证:平面MOE ∥平面PAC ; (2)求证:平面PAC ⊥平面PCB .12.(2012·珠海摸底)如图,在多面体ABCDEF 中,四边形ABCD 是梯形,AB ∥CD ,四边形ACFE 是矩形,平面ACFE ⊥平面ABCD ,AD =DC =CB =AE =a ,∠ACB =π2.(1)求证:BC ⊥平面ACFE ;(2)若M 是棱EF 上一点,AM ∥平面BDF ,求EM 的长.1.如图,在三棱锥D -ABC 中,若AB =CB ,AD =CD ,E 是AC 的中点,则下列正确的是( )A.平面ABC⊥平面ABDB.平面ABD⊥平面BDCC.平面ABC⊥平面BDE,且平面ADC⊥平面BDED.平面ABC⊥平面ADC,且平面ADC⊥平面BDE2.(2012·浙江高考)已知矩形ABCD,AB=1,BC= 2.将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中,( )A.存在某个位置,使得直线AC与直线BD垂直B.存在某个位置,使得直线AB与直线CD垂直C.存在某个位置,使得直线AD与直线BC垂直D.对任意位置,三对直线“AC与BD”,“AB与CD”,“AD与BC”均不垂直3.(2012·莆田模拟)如图,在三棱锥P-ABC中,△PAC,△ABC分别是以A,B为直角顶点的等腰直角三角形,AB=1.(1)现给出三个条件:①PB=3;②PB⊥BC;③平面PAB⊥平面ABC.试从中任意选取一个作为已知条件,并证明:PA⊥平面ABC;(2)在(1)的条件下,求三棱锥P-ABC的体积.答案课时跟踪检测(四十七)A级1.选C 对于选项C,在平面α内存在c∥b,因为a⊥α,所以a⊥c,故a⊥b;A,B 选项中,直线a,b可能是平行直线,相交直线,也可能是异面直线;D选项中一定有a∥b.2.选D 对于①:若α⊥β,β⊥γ,则α⊥γ,前者不是后者的充分条件,比如当α∥γ时,也有α⊥β,β⊥γ.对于②:显然错误,当l⊥α,l∩α=A时,l上到A距离相等的两点到α的距离相等.③④显然正确.3.选B (1)错,也可能相交;(2)正确;(3)“α⊥β”是“m⊥β”的必要条件,命题错误;(4)当异面直线a,b垂直时才可以作出满足要求的平面,命题错误.4.选A 由AC⊥AB,AC⊥BC1,∴AC⊥平面ABC1.又∵AC⊂面ABC,∴平面ABC1⊥平面ABC.∴C1在面ABC上的射影H必在两平面交线AB 上.5.选B 对于①,∵PA⊥平面ABC,∴PA⊥BC.∵AB为⊙O的直径,∴BC⊥AC.∴BC⊥平面PAC.又PC⊂平面PAC,∴BC⊥PC;对于②,∵点M为线段PB的中点,∴OM∥PA.∵PA⊂平面PAC,∴OM∥平面PAC;对于③,由①知BC⊥平面PAC,∴线段BC的长即是点B到平面PAC 的距离,故①②③都正确.6.选D 在平面图形中CD⊥BD,折起后仍有CD⊥BD,由于平面ABD⊥平面BCD,故CD ⊥平面ABD,CD⊥AB,又AB⊥AD,故AB⊥平面ADC,所以平面ABC⊥平面ADC.7.解析:由定理可知,BD⊥PC.∴当DM⊥PC(或BM⊥PC)时,即有PC⊥平面MBD.而PC⊂平面PCD,∴平面MBD⊥平面PCD.答案:DM⊥PC(或BM⊥PC等)8.解析:如图,设AC∩BD=O,连接SO,取CD的中点F,SC的中点G,连接EF,EG,FG,设EF交AC于点H,连接GH,易知AC⊥EF,GH∥SO,∴GH⊥平面ABCD,∴AC⊥GH,∴AC⊥平面EFG,故动点P的轨迹是△EFG,由已知易得EF=2,GE=GF=62,∴△EFG的周长为2+6,故动点P的轨迹长为2+ 6.答案:2+ 69.解析:连接BD交AC于O,连接DC1交D1C于O1,连接OO1,则OO1∥BC1.∴BC1∥平面AD1C,动点P到平面AD1C的距离不变,∴三棱锥P-AD1C的体积不变.又VP-AD1C=VA-D1PC,∴①正确.∵平面A1C1B∥平面AD1C,A1P⊂平面A1C1B,∴A1P∥平面ACD1,②正确.由于DB不垂直于BC1显然③不正确;由于DB1⊥D1C,DB1⊥AD1,D1C∩AD1=D1,∴DB1⊥平面AD1C.DB1⊂平面PDB1,∴平面PDB1⊥平面ACD1,④正确.答案:①②④10.证明:(1)由已知,得MD是△ABP的中位线,所以MD∥AP.又MD⊄平面APC,AP⊂平面APC,故MD∥平面APC.(2)因为△PMB为正三角形,D为PB的中点,所以MD⊥PB.所以AP⊥PB.又AP⊥PC,PB∩PC=P,所以AP⊥平面PBC.因为BC⊂平面PBC,所以AP⊥BC.又BC⊥AC,AC∩AP=A,所以BC⊥平面APC.因为BC⊂平面ABC,所以平面ABC⊥平面APC.11.证明:(1)因为点E为线段PB的中点,点O为线段AB的中点,所以OE∥PA.因为PA⊂平面PAC,OE⊄平面PAC,所以OE∥平面PAC.因为OM∥AC,且AC⊂平面PAC,OM⊄平面PAC,所以OM∥平面PAC.因为OE⊂平面MOE,OM⊂平面MOE,OE∩OM=O,所以平面MOE∥平面PAC.(2)因为点C 在以AB 为直径的⊙O 上,所以∠ACB =90°,即BC ⊥AC . 因为PA ⊥平面ABC ,BC ⊂平面ABC ,所以PA ⊥BC . 因为AC ⊂平面PAC ,PA ⊂平面PAC ,PA ∩AC =A ,所以BC ⊥平面PAC . 因为BC ⊂平面PCB , 所以平面PAC ⊥平面PCB .12.解:(1)证明:因为∠ACB =π2,所以BC ⊥AC .又因为BC ⊂平面ABCD ,平面ACFE ∩平面ABCD =AC ,平面ACFE ⊥平面ABCD ,所以BC ⊥平面ACFE .(2)记AC ∩BD =O ,在梯形ABCD 中,因为AD =DC =CB =a ,AB ∥CD ,所以∠ACD =∠CAB =∠DAC .所以π=∠ABC +∠BCD =∠DAB +∠ACD +∠ACB =3∠DAC +π2,所以∠DAC =π6,即∠CBO =π6.又因为∠ACB =π2,CB =a ,所以CO =33a .连接FO ,由AM ∥平面BDF 得AM ∥FO ,因为四边形ACFE 是矩形,所以EM =CO =33a . B 级1.选C 要判断两个平面的垂直关系,就需固定其中一个平面,找另一个平面内的一条直线与第一个平面垂直.因为AB =CB ,且E 是AC 的中点,所以BE ⊥AC ,同理有DE ⊥AC ,于是AC ⊥平面BDE .因为AC 在平面ABC 内,所以平面ABC ⊥平面BDE .又由于AC ⊂平面ACD ,所以平面ACD ⊥平面BDE .2.选B 对于AB ⊥CD ,因为BC ⊥CD ,可得CD ⊥平面ACB ,因此有CD ⊥AC .因为AB =1,BC =2,CD =1,所以AC =1,所以存在某个位置,使得AB ⊥CD .3.解:法一:(1)选取条件① 在等腰直角三角形ABC 中, ∵AB =1, ∴BC =1,AC = 2. 又∵PA =AC ,∴PA = 2. ∴在△PAB 中,AB =1,PA = 2.又∵PB =3, ∴AB 2+PA 2=PB 2.∴∠PAB =90°,即PA ⊥AB . 又∵PA ⊥AC ,AB ∩AC =A , ∴PA ⊥平面ABC .(2)依题意得,由(1)可知PA ⊥平面ABC ,V 三棱锥P -ABC =13PA ·S △ABC =13×2×12×12=26. 法二:(1)选取条件② ∵PB ⊥BC ,又AB ⊥BC ,且PB ∩AB =B , ∴BC ⊥平面PAB . ∵PA ⊂平面PAB , ∴BC ⊥PA .又∵PA ⊥AC ,且BC ∩AC =C , ∴PA ⊥平面ABC .(2)依题意得,由(1)可知PA ⊥平面ABC . ∵AB =BC =1,AB ⊥BC , ∴AC =2, ∴PA =2,∴V 三棱锥P -ABC =13PA ·S △ABC =13×12AB ·BC ·PA =13×12×1×1×2=26.法三:(1)选取条件③ 若平面PAB ⊥平面ABC ,∵平面PAB ∩平面ABC =AB ,BC ⊂平面ABC ,BC ⊥AB , ∴BC ⊥平面PAB .∵PA ⊂平面PAB ,∴BC ⊥PA . ∵PA ⊥AC ,且BC ∩AC =C , ∴PA ⊥平面ABC . (2)同法二.。
