[精品]2019学年高中数学第一章集合与函数概念1.1_1.1.3综合应用练习新人教版必修(1)

合集下载

高中数学第一章集合与函数概念1.1集合1.1.2集合间的基本关系练习新人教A版必修1

高中数学第一章集合与函数概念1.1集合1.1.2集合间的基本关系练习新人教A版必修1课时过关·能力提升基础巩固1.已知集合P={1},Q={0,1,4},下列式子不正确的是()A.P⫋QB.P⊆QC.1∈PD.1⊆Q解析:∵P={1},Q={0,1,4},∴P⊆Q,P⫋Q,1∈P均正确.答案:D2.如果集合A={x|x>-1},那么()A.0⊆AB.{0}∈AC.⌀∈AD.{0}⊆A解析:“∈”表示元素与集合的关系,“⊆”表示集合与集合的关系,从而可知D正确.答案:D3.集合A={0,1,2}的子集的个数是()A.16B.8C.7D.4解析:由于A中含有3个元素,则它有23=8个子集.答案:B4.设a,b∈R,集合{1,a+b,a}=,则b-a等于()A.1B.-1C.2D.-2答案:C5.已知集合A=,B=,则()A.A⊇BB.A⫌BC.A=BD.A⫋B解析:x=∈B,但∈B,∉A,故A⫋B.答案:D6.若集合A={-1,0},B={0,1,x+2},集合A,B的关系如图所示,则实数x的值为.解析:由题图知A⫋B,故-1=x+2,解得x=-3.答案:-37.已知集合A⫋{1,2,3},且A中至少含有一个奇数,则这样的集合A有个.解析:∵A⫋{1,2,3},∴A中至多含有2个元素.又A中至少有一个奇数,∴A可能为{1},{1,2},{1,3},{3},{2,3},共5个.答案:58.已知集合A={2,-1},B={m2-m,-1},且A=B,记由实数m的值构成的集合为C,则集合C的真子集个数为.解析:∵A=B,∴m2-m=2,解得m=-1或m=2.∴C={-1,2},∴集合C的真子集为⌀,{-1},{2},共3个.答案:39.已知集合A={x|1≤x≤2},B={x|1≤x≤a}.(1)若A是B的真子集,求a的取值范围;(2)若B是A的子集,求a的取值范围;(3)若A=B,求a的取值范围.解:(1)若A是B的真子集,即A⫋B,则a>2.(2)若B是A的子集,即B⊆A,则a≤2.(3)若A=B,则必有a=2.10.如图所示的Venn图中表示的是四边形、梯形、平行四边形、菱形、正方形这五种几何图形之间的关系,问集合A,B,C,D,E分别是哪种图形的集合?解:观察Venn图,得B,C,D,E均是A的子集,且有E⊆D,D⊆C.梯形、平行四边形、菱形、正方形都是四边形,故A={四边形};梯形不是平行四边形,而菱形、正方形是平行四边形,故B={梯形},C={平行四边形};又正方形是菱形,故D={菱形},E={正方形}.能力提升1.已知集合A⊆{1,2,3},且A中至少有两个元素,则满足条件的集合A共有()A.3个B.4个C.5个D.8个解析:满足条件的集合A有{1,2},{1,3},{2,3},{1,2,3},共4个.答案:B2.已知集合A={x|x≤-1,或x≥1},B={x|a<x<a+1},且B⊆A,则实数a的取值范围是()A.a≤-2B.a≥1C.-2≤a≤1D.a≤-2或a≥1解析:由题意知,B≠⌀.作出如图所示的数轴,由B⊆A可得a+1≤-1或a≥1,即实数a的取值范围是a≤-2或a≥1.答案:D3.已知集合A=,B={a2,a+b,0},若A=B,则a2 016+b2 017的值为()A.0B.2C.1D.-1解析:由题意知a≠0,否则无意义,故=0,b=0.此时集合A={a,0,1},B={a2,a,0}.由A=B,得a2=1,则a=±1(舍去正值).∴a2016+b2017=1.答案:C★4.已知集合M=,N=,则集合M,N的关系是() A.M=N B.M⫋NC.N⊆MD.N⫋M解析:明确集合M,N中的元素,依据有关概念来判断.(方法1)用列举法分别表示集合M,N.集合M=,集合N=,-,-,则有M⫋N.(方法2)设n=2m或2m+1,m∈Z,则有N==,故M⫋N.答案:B5.已知全集U=R,则正确表示集合M={-1,0,1}和N={x|x2+x=0}关系的Venn图是()解析:∵N={x|x2+x=0},∴N={-1,0}.又M={-1,0,1},∴N⫋M.故选B.答案:B6.已知集合A={x|x2-2x+a=0,a∈R},若集合A有且仅有2个子集,则a的值是.解析:因为集合A有且仅有2个子集,所以A仅含有一个元素,即关于x的方程x2-2x+a=0有两个相等的实数根.所以Δ=4-4a=0,解得a=1.答案:17.若集合A={x∈R|x2-5x+m=0},B={x∈R|x-3=0},且B⊆A,则实数m=,集合A=.解析:易得B={3}.∵B⊆A,∴3∈A,即9-15+m=0.∴m=6.解方程x2-5x+6=0,得x1=2,x2=3,∴A={2,3}.答案:6{2,3}★8.已知集合A={2,4,6,8,9},B={1,2,3,5,8},是否存在集合C,使C中每一个元素都加上2变成A 的一个子集,且C中每个元素都减去2就变成了B的一个子集?若存在,求出集合C;若不存在,请说明理由.解:假设存在满足条件的集合C.A中元素都减去2,得集合E={0,2,4,6,7}.B中元素都加上2,得集合F={3,4,5,7,10}.则集合C中的元素均在E,F中,因此满足条件的C为{4}或{7}或{4,7}.。

高中数学第一章集合与函数概念1.1集合1.1.3第1课时并集、交集练习新人教A版必修1(2021年

2018-2019学年高中数学第一章集合与函数概念1.1 集合1.1.3 第1课时并集、交集练习新人教A版必修1编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2018-2019学年高中数学第一章集合与函数概念1.1 集合1.1.3 第1课时并集、交集练习新人教A版必修1）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2018-2019学年高中数学第一章集合与函数概念1.1 集合1.1.3 第1课时并集、交集练习新人教A版必修1的全部内容。

第一章 1.1 1。

1。

3 第1课时并集、交集1．下列关系：Q∩R＝R∩Q；Z∪N＝N；Q∪R＝R∪Q;Q∩N＝N中，正确的个数是（）A．1 B．2C．3 D．4解析：只有Z∪N＝N是错误的，应是Z∪N＝Z.答案：C2．已知集合A＝｛1,2,3}，B＝｛1，3}，则A∩B＝（)A．｛2} B．{1，2}C．｛1，3} D．{1，2,3｝解析：∵1∈A，1∈B,3∈A，3∈B，∴A∩B＝{1,3}．答案：C3．若集合A＝｛x|－2＜x＜1}，B＝｛x｜0＜x＜2}，则集合A∪B＝（）A．{x|－1＜x＜1} B．{x|－2＜x＜2｝C．{x｜－2＜x＜1｝D．｛x|0＜x＜1｝解析：因为A＝｛x|－2＜x＜1}，B＝{x｜0＜x＜2｝，所以A∪B＝{x|－2＜x＜2}．答案：B4．已知集合A＝{1,2,4},B＝{2,4，6}，则A∪B＝________。

解析:由条件得A∪B＝{1，2，4，6｝．答案：{1，2,4,6}5．已知集合A＝｛(x，y)｜y＝x＋3｝，B＝{(x，y）|y＝3x－1}，则A∩B＝________。

高一数学练习册答案：第一章集合与函数概念

2019高一数学练习册答案：第一章集合与函数概念1.1集合1 1 1集合的含义与表示1.D.2.A.3.C.4.{1,-1}.5.{x|x=3n+1,n∈N}.6.{2,0,-2}.7.A={(1,5),(2,4),(3,3),(4,2),(5,1)}.8.1.9.1,2,3,6.10.列举法表示为{(-1,1),(2,4)},描述法的表示方法不唯一,如可表示为(x,y)|y=x+2,y=x2.11.-1,12,2.1 1 2集合间的基本关系1.D.2.A.3.D.4. ,{-1},{1},{-1,1}.5. .6.①③⑤.7.A=B.8.15,13.9.a≥4.10.A={ ,{1},{2},{1,2}},B∈A.11.a=b=1.1 1 3集合的基本运算(一)1.C.2.A.3.C.4.4.5.{x|-2≤x≤1}.6.4.7.{-3}.8.A∪B={x|x3,或x≥5}.9.A∪B={-8,-7,-4,4,9}.10.1.11.{a|a=3,或-221 1 3集合的基本运算(二)1.A.2.C.3.B.4.{x|x≥2,或x≤1}.5.2或8.6.x|x=n+12,n∈Z.7.{-2}.8.{x|x6,或x≤2}.9.A={2,3,5,7},B={2,4,6,8}.10.A,B的可能情形有:A={1,2,3},B={3,4};A={1,2,4},B={3,4};A={1,2,3,4},B={3,4}.11.a=4,b=2.提示:∵A∩ 綂UB={2}，∴2∈A，∴4+2a-12=0 a=4，∴A={x|x2+4x-12=0}={2,-6},∵A∩ 綂UB={2}，∴-6 綂UB，∴-6∈B，将x=-6代入B,得b2-6b+8=0 b=2,或b=4.①当b=2时,B={x|x2+2x-24=0}={-6,4},∴-6 綂UB，而2∈綂UB，满足条件A∩ 綂UB={2}.②当b=4时,B={x|x2+4x-12=0}={-6,2},∴2 綂UB，与条件A∩ 綂UB={2}矛盾.1.2函数及其表示1 2 1函数的概念(一)1.C.2.C.3.D.4.22.5.-2,32∪32,+∞.6.[1,+∞).7.(1)12,34.(2){x|x≠-1，且x≠-3}.8.-34.9.1.10.(1)略.(2)72.11.-12,234.1 2 1函数的概念(二)1.C.2.A.3.D.4.{x∈R|x≠0,且x≠-1}.5.[0，+∞).6.0.7.-15,-13,-12,13.8.(1)y|y≠25.(2)[-2,+∞).9.(0,1].10.A∩B=-2,12;A∪B=[-2,+∞).11.[-1,0).1 2 2函数的表示法(一)1.A.2.B.3.A.4.y=x100.5.y=x2-2x+2.6.1x.7.略.8.x1234y828589889.略.10.1.11.c=-3.1 2 2函数的表示法(二)1.C.2.D.3.B.4.1.5.3.6.6.7.略.8.f(x)=2x(-1≤x0),-2x+2(0≤x≤1).9.f(x)=x2-x+1.提示:设f(x)=ax2+bx+c，由f(0)=1,得c=1，又f(x+1)-f(x)=2x，即a(x+1)2+b(x+1)+c-(ax2+bx+c)=2x，展开得2ax+(a+b)=2x,所以2a=2,a+b=0,解得a=1，b=-1.10.y=1.2(02.4(203.6(404.8(601.3函数的基本性质1 3 1单调性与最大(小)值(一)1.C.2.D.3.C.4.[-2,0),[0,1),[1,2].5.-∞,32.6.k12.7.略.8.单调递减区间为(-∞,1),单调递增区间为[1,+∞).9.略.10.a≥-1. 11.设-10，∴(x1x2+1)(x2-x1)(x21-1)(x22-1)0，∴函数y=f(x)在(-1，1)上为减函数.1 3 1单调性与最大(小)值(二)1.D.2.B.3.B.4.-5,5.5.25.6.y=316(a+3x)(a-x)(011.日均利润最大，则总利润就最大.设定价为x元，日均利润为y元.要获利每桶定价必须在12元以上，即x12.且日均销售量应为440-(x-13)·400，即x23,总利润y=(x-12)[440-(x-13)·40]-600(121 3 2奇偶性1.D.2.D.3.C.4.0.5.0.6.答案不唯一,如y=x2.7.(1)奇函数.(2)偶函数.(3)既不是奇函数，又不是偶函数.(4)既是奇函数，又是偶函数.8.f(x)=x(1+3x)(x≥0),x(1-3x)(x0).9.略.10.当a=0时，f(x)是偶函数;当a≠0时，既不是奇函数，又不是偶函数.11.a=1，b=1，c=0.提示:由f(-x)=-f(x)，得c=0，∴f(x)=ax2+1bx,∴f(1)=a+1b=2 a=2b-1.∴f(x)=(2b-1)x2+1bx.∵f(2)3，∴4(2b-1)+12b3 2b-32b0 0单元练习1.C.2.D.3.D.4.D.5.D.6.B.7.B.8.C.9.A.10.D.11.{0,1,2}.12.-32.13.a=-1,b=3.14.[1,3)∪(3,5].15.f1217.T(h)=19-6h(0≤h≤11),-47(h11).18.{x|0≤x≤1}.19.f(x)=x只有唯一的实数解，即xax+b=x(*)只有唯一实数解，当ax2+(b-1)x=0有相等的实数根x0，且ax0+b≠0时，解得f(x)=2xx+2，当ax2+(b-1)x=0有不相等的实数根，且其中之一为方程(*)的增根时，解得f(x)=1.20.(1)x∈R,又f(-x)=(-x)2-2|-x|-3=x2-2|x|-3=f(x)，所以该函数是偶函数.(2)略.(3)单调递增区间是[-1,0],[1,+∞)，单调递减区间是(-∞,-1],[0,1].21.(1)f(4)=4×13=5.2,f(5.5)=5×1.3+0.5×3.9=8.45,f(6.5)=5×1.3+1×3.9+0.5×6 5=13.65.(2)f(x)=1.3x(0≤x≤5),3.9x-13(56.5x-28.6(622.(1)值域为[22,+∞).(2)若函数y=f(x)在定义域上是减函数，则任取x1,x2∈(0,1]且x1f(x2)成立，即(x1-x2)2+ax1x20，只要a-2x1x2即可，由于x1,x2∈(0,1]，故-2x1x2∈(-2,0)，a-2，即a的取值范围是(-∞,-2). 要练说，得练看。

高中数学第一章集合与函数概念1.1集合课后习题(A组.B组)

第一章集合与函数概念1．1集合1．1．1集合的含义与表示练习（第5页）1．用符号“∈”或“∉”填空：（1）设A 为所有亚洲国家组成的集合，则：中国_______A ，美国_______A ，印度_______A ，英国_______A ；（2）若2{|}A x x x ==，则1-_______A ；（3）若2{|60}B x x x =+-=，则3_______B ；（4）若{|110}C x N x =∈≤≤，则8_______C ，9.1_______C ．1．（1）中国∈A ，美国∉A ，印度∈A ，英国∉A ；中国和印度是属于亚洲的国家，美国在北美洲，英国在欧洲．（2）1-∉A 2{|}{0,1}A x x x ===．（3）3∉B 2{|60}{3,2}B x x x =+-==-．（4）8∈C ，9.1∉C 9.1N ∉．2．试选择适当的方法表示下列集合：（1）由方程290x -=的所有实数根组成的集合；（2）由小于8的所有素数组成的集合；（3）一次函数3y x =+与26y x =-+的图象的交点组成的集合；（4）不等式453x -<的解集．2．解：（1）因为方程290x -=的实数根为123,3x x =-=，所以由方程290x -=的所有实数根组成的集合为{3,3}-；（2）因为小于8的素数为2,3,5,7，所以由小于8的所有素数组成的集合为{2,3,5,7}；（3）由326y x y x =+⎧⎨=-+⎩，得14x y =⎧⎨=⎩，即一次函数3y x =+与26y x =-+的图象的交点为(1,4)，所以一次函数3y x =+与26y x =-+的图象的交点组成的集合为{(1,4)}；（4）由453x -<，得2x <，所以不等式453x -<的解集为{|2}x x <．1．1．2集合间的基本关系1．写出集合{,,}a b c 的所有子集．1．解：按子集元素个数来分类，不取任何元素，得∅；取一个元素，得{},{},{}a b c ；取两个元素，得{,},{,},{,}a b a c b c ；取三个元素，得{,,}a b c ，即集合{,,}a b c 的所有子集为,{},{},{},{,},{,},{,},{,,}a b c a b a c b c a b c ∅．2．用适当的符号填空：（1）a ______{,,}a b c ；（2）0______2{|0}x x =；（3）∅______2{|10}x R x ∈+=；（4）{0,1}______N ；（5）{0}______2{|}x x x =；（6）{2,1}______2{|320}x x x -+=．2．（1）{,,}a a b c ∈ a 是集合{,,}a b c 中的一个元素；（2）20{|0}x x ∈= 2{|0}{0}x x ==；（3）2{|10}x R x ∅=∈+= 方程210x +=无实数根，2{|10}x R x ∈+==∅；（4）{0,1}N （或{0,1}N ⊆） {0,1}是自然数集合N 的子集，也是真子集；（5）{0}2{|}x x x = （或2{0}{|}x x x ⊆=） 2{|}{0,1}x x x ==；（6）2{2,1}{|320}x x x =-+= 方程2320x x -+=两根为121,2x x ==．3．判断下列两个集合之间的关系：（1）{1,2,4}A =，{|8}B x x =是的约数；（2）{|3,}A x x k k N ==∈，{|6,}B x x z z N ==∈；（3）{|410}A x x x N +=∈是与的公倍数,，{|20,}B x x m m N +==∈．3．解：（1）因为{|8}{1,2,4,8}B x x ==是的约数，所以A B ；（2）当2k z =时，36k z =；当21k z =+时，363k z =+，即B 是A 的真子集，B A ；（3）因为4与10的最小公倍数是20，所以A B =．1．1．3集合的基本运算1．设{3,5,6,8},{4,5,7,8}A B ==，求,A B A B I U ．1．解：{3,5,6,8}{4,5,7,8}{5,8}A B ==I I ，{3,5,6,8}{4,5,7,8}{3,4,5,6,7,8}A B ==U U ．2．设22{|450},{|1}A x x x B x x =--===，求,A B A B I U ．2．解：方程2450x x --=的两根为121,5x x =-=，方程210x -=的两根为121,1x x =-=，得{1,5},{1,1}A B =-=-，即{1},{1,1,5}A B A B =-=-I U ．3．已知{|}A x x =是等腰三角形，{|}B x x =是直角三角形，求,A B A B I U ．3．解：{|}A B x x =I 是等腰直角三角形，{|}A B x x =U 是等腰三角形或直角三角形．4．已知全集{1,2,3,4,5,6,7}U =，{2,4,5},{1,3,5,7}A B ==，求(),()()U U U A B A B I I 痧?．4．解：显然{2,4,6}U B =ð，{1,3,6,7}U A =ð，则(){2,4}U A B =I ð，()(){6}U U A B =I 痧．1．1集合习题1．1 （第11页） A 组1．用符号“∈”或“∉”填空：（1）237_______Q ；（2）23______N ；（3）π_______Q ；（4_______R ；（5Z ；（6）2_______N ． 1．（1）237Q ∈ 237是有理数；（2）23N ∈ 239=是个自然数；（3）Q π∉ π是个无理数，不是有理数；（4R 是实数；（5Z 3=是个整数；（6）2N ∈ 25=是个自然数． 2．已知{|31,}A x x k k Z ==-∈，用 “∈”或“∉” 符号填空：（1）5_______A ；（2）7_______A ；（3）10-_______A ．2．（1）5A ∈；（2）7A ∉；（3）10A -∈．当2k =时，315k -=；当3k =-时，3110k -=-；3．用列举法表示下列给定的集合：（1）大于1且小于6的整数；（2）{|(1)(2)0}A x x x =-+=；（3）{|3213}B x Z x =∈-<-≤．3．解：（1）大于1且小于6的整数为2,3,4,5，即{2,3,4,5}为所求；（2）方程(1)(2)0x x -+=的两个实根为122,1x x =-=，即{2,1}-为所求；（3）由不等式3213x -<-≤，得12x -<≤，且x Z ∈，即{0,1,2}为所求．4．试选择适当的方法表示下列集合：（1）二次函数24y x =-的函数值组成的集合；（2）反比例函数2y x =的自变量的值组成的集合；（3）不等式342x x ≥-的解集． 4．解：（1）显然有20x ≥，得244x -≥-，即4y ≥-，得二次函数24y x =-的函数值组成的集合为{|4}y y ≥-；（2）显然有0x ≠，得反比例函数2y x=的自变量的值组成的集合为{|0}x x ≠；（3）由不等式342x x ≥-，得45x ≥，即不等式342x x ≥-的解集为4{|}5x x ≥． 5．选用适当的符号填空：（1）已知集合{|233},{|2}A x x x B x x =-<=≥，则有：4-_______B ； 3-_______A ； {2}_______B ； B _______A ；（2）已知集合2{|10}A x x =-=，则有：1_______A ； {1}-_______A ； ∅_______A ； {1,1}-_______A ；（3）{|}x x 是菱形_______{|}x x 是平行四边形；{|}x x 是等腰三角形_______{|}x x 是等边三角形．5．（1）4B -∉； 3A -∉； {2}B ； B A ；2333x x x -<⇒>-，即{|3},{|2}A x x B x x =>-=≥；（2）1A ∈； {1}-A ； ∅A ； {1,1}-=A ； 2{|10}{1,1}A x x =-==-；（3）{|}x x 是菱形{|}x x 是平行四边形；菱形一定是平行四边形，是特殊的平行四边形，但是平行四边形不一定是菱形；{|}x x 是等边三角形{|}x x 是等腰三角形．等边三角形一定是等腰三角形，但是等腰三角形不一定是等边三角形．6．设集合{|24},{|3782}A x x B x x x =≤<=-≥-，求,A B A B U I ．6．解：3782x x -≥-，即3x ≥，得{|24},{|3}A x x B x x =≤<=≥，则{|2}A B x x =≥U ，{|34}A B x x =≤<I ．7．设集合{|9}A x x =是小于的正整数，{1,2,3},{3,4,5,6}B C ==，求A B I ，A C I ，()ABC I U ，()A B C U I ．7．解：{|9}{1,2,3,4,5,6,7,8}A x x ==是小于的正整数，则{1,2,3}A B =I ，{3,4,5,6}A C =I ，而{1,2,3,4,5,6}B C =U ，{3}B C =I ，则(){1,2,3,4,5,6}A B C =I U ，(){1,2,3,4,5,6,7,8}A B C =U I ．8．学校里开运动会，设{|}A x x =是参加一百米跑的同学，{|}B x x =是参加二百米跑的同学，{|}C x x =是参加四百米跑的同学，学校规定，每个参加上述的同学最多只能参加两项，请你用集合的语言说明这项规定，并解释以下集合运算的含义：（1）A B U ；（2）A C I ．8．解：用集合的语言说明这项规定：每个参加上述的同学最多只能参加两项，即为()A B C =∅I I ．（1）{|}A B x x =U 是参加一百米跑或参加二百米跑的同学；（2）{|}A C x x =I 是既参加一百米跑又参加四百米跑的同学．9．设{|}S x x =是平行四边形或梯形，{|}A x x =是平行四边形，{|}B x x =是菱形， {|}C x x =是矩形，求B C I ，A B ð，S A ð．9．解：同时满足菱形和矩形特征的是正方形，即{|}B C x x =I 是正方形，平行四边形按照邻边是否相等可以分为两类，而邻边相等的平行四边形就是菱形，即{|}A B x x =是邻边不相等的平行四边形ð，{|}S A x x =是梯形ð．10．已知集合{|37},{|210}A x x B x x =≤<=<<，求()R A B U ð，()R A B I ð，()R A B I ð，()R A B U ð．10．解：{|210}A B x x =<<U ，{|37}A B x x =≤<I ，{|3,7}R A x x x =<≥或ð，{|2,10}R B x x x =≤≥或ð，得(){|2,10}R A B x x x =≤≥U 或ð，(){|3,7}R A B x x x =<≥I 或ð，(){|23,710}R A B x x x =<<≤<I 或ð，(){|2,3710}R A B x x x x =≤≤<≥U 或或ð．B 组1．已知集合{1,2}A =，集合B 满足{1,2}A B =U ，则集合B 有个．1．4 集合B 满足A B A =U ，则B A ⊆，即集合B 是集合A 的子集，得4个子集．2．在平面直角坐标系中，集合{(,)|}C x y y x ==表示直线y x =，从这个角度看，集合21(,)|45x y D x y x y ⎧-=⎫⎧=⎨⎨⎬+=⎩⎩⎭表示什么？集合,C D 之间有什么关系？2．解：集合21(,)|45x y D x y x y ⎧-=⎫⎧=⎨⎨⎬+=⎩⎩⎭表示两条直线21,45x y x y -=+=的交点的集合，即21(,)|{(1,1)}45x y D x y x y ⎧-=⎫⎧==⎨⎨⎬+=⎩⎩⎭，点(1,1)D 显然在直线y x =上，得D C ．3．设集合{|(3)()0,}A x x x a a R =--=∈，{|(4)(1)0}B x x x =--=，求,A B A B U I ．3．解：显然有集合{|(4)(1)0}{1,4}B x x x =--==，当3a =时，集合{3}A =，则{1,3,4},A B A B ==∅U I ；当1a =时，集合{1,3}A =，则{1,3,4},{1}A B A B ==U I ；当4a =时，集合{3,4}A =，则{1,3,4},{4}A B A B ==U I ；当1a ≠，且3a ≠，且4a ≠时，集合{3,}A a =，则{1,3,4,},A B a A B ==∅U I ．4．已知全集{|010}U A B x N x ==∈≤≤U ，(){1,3,5,7}U A B =I ð，试求集合B ． 4．解：显然{0,1,2,3,4,5,6,7,8,9,10}U =，由U A B =U ，得U B A ⊆ð，即()U U A B B =I 痧，而(){1,3,5,7}U A B =I ð，得{1,3,5,7}U B =ð，而()U U B B =痧，即{0,2,4,6,8.9,10}B =．第一章集合与函数概念1．2函数及其表示1．2．1函数的概念练习（第19页）1．求下列函数的定义域：（1）1()47f x x =+；（2）()1f x =+． 1．解：（1）要使原式有意义，则470x +≠，即74x ≠-，得该函数的定义域为7{|}4x x ≠-；（2）要使原式有意义，则1030x x -≥⎧⎨+≥⎩，即31x -≤≤，得该函数的定义域为{|31}x x -≤≤．2．已知函数2()32f x x x =+，（1）求(2),(2),(2)(2)f f f f -+-的值；（2）求(),(),()()f a f a f a f a -+-的值．2．解：（1）由2()32f x x x =+，得2(2)322218f =⨯+⨯=，同理得2(2)3(2)2(2)8f -=⨯-+⨯-=，则(2)(2)18826f f +-=+=，即(2)18,(2)8,(2)(2)26f f f f =-=+-=；（2）由2()32f x x x =+，得22()3232f a a a a a =⨯+⨯=+，同理得22()3()2()32f a a a a a -=⨯-+⨯-=-，则222()()(32)(32)6f a f a a a a a a +-=++-=，即222()32,()32,()()6f a a a f a a a f a f a a =+-=-+-=．3．判断下列各组中的函数是否相等，并说明理由：（1）表示炮弹飞行高度h 与时间t 关系的函数21305h t t =-和二次函数21305y x x =-；（2）()1f x =和0()g x x =．3．解：（1）不相等，因为定义域不同，时间0t >；（2）不相等，因为定义域不同，0()(0)g x x x =≠．1．2．2函数的表示法练习（第23页）1．如图，把截面半径为25cm 的圆形木头锯成矩形木料，如果矩形的一边长为xcm ，面积为2ycm ，把y 表示为x 的函数．1．解：显然矩形的另一边长为2250x cm -，222502500y x x x x =-=-，且050x <<，即22500(050)y x x x =-<<．2．下图中哪几个图象与下述三件事分别吻合得最好？请你为剩下的那个图象写出一件事．（1）我离开家不久，发现自己把作业本忘在家里了，于是返回家里找到了作业本再上学；（2）我骑着车一路匀速行驶，只是在途中遇到一次交通堵塞，耽搁了一些时间；（3）我出发后，心情轻松，缓缓行进，后来为了赶时间开始加速．2．解：图象（A ）对应事件（2），在途中遇到一次交通堵塞表示离开家的距离不发生变化；图象（B ）对应事件（3），刚刚开始缓缓行进，后来为了赶时间开始加速；图象（D ）对应事件（1），返回家里的时刻，离开家的距离又为零；图象（C ）我出发后，以为要迟到，赶时间开始加速，后来心情轻松，缓缓行进．3．画出函数|2|y x =-的图象． O 离开家的距离时间（A ） O 离开家的距离时间（B ） O 离开家的距离时间（C ） O 离开家的距离时间（D ）3．解：2,2|2|2,2x x y x x x -≥⎧=-=⎨-+<⎩，图象如下所示．{|},{0,1}A x x B ==是锐角，从A 到B 的映射是“求正弦”，4．设中元素60o相对应与A B 中的元素是什么？与B 中的元素22相对应的A 中元素是什的么？ 4．解：因为3sin 60=o ，所以与A 中元素60o 相对应的B 中的元素是3；因为2sin 452=o，所以与B 中的元素22相对应的A 中元素是45o ． 1．2函数及其表示习题1．2（第23页） 1．求下列函数的定义域：（1）3()4x f x x =-；（2）2()f x x =；（3）26()32f x x x =-+；（4）4()x f x -=． 1．解：（1）要使原式有意义，则40x -≠，即4x ≠，得该函数的定义域为{|4}x x ≠；（2）x R ∈，2()f x x =都有意义，即该函数的定义域为R ；（3）要使原式有意义，则2320x x -+≠，即1x ≠且2x ≠，得该函数的定义域为{|12}x x x ≠≠且；（4）要使原式有意义，则4010x x -≥⎧⎨-≠⎩，即4x ≤且1x ≠，得该函数的定义域为{|41}x x x ≤≠且．2．下列哪一组中的函数()f x 与()g x 相等？（1）2()1,()1x f x x g x x =-=-；（2）24(),()()f x x g x x ==；（3）326(),()f x x g x x ==．2．解：（1）()1f x x =-的定义域为R ，而2()1x g x x=-的定义域为{|0}x x ≠，即两函数的定义域不同，得函数()f x 与()g x 不相等；（2）2()f x x =的定义域为R ，而4()()g x x =的定义域为{|0}x x ≥，即两函数的定义域不同，得函数()f x 与()g x 不相等；（3）对于任何实数，都有362x x =，即这两函数的定义域相同，切对应法则相同，得函数()f x 与()g x 相等．3．画出下列函数的图象，并说出函数的定义域和值域．（1）3y x =；（2）8y x =；（3）45y x =-+；（4）267y x x =-+． 3．解：（1）定义域是(,)-∞+∞，值域是(,)-∞+∞；（2）定义域是(,0)(0,)-∞+∞U ，值域是(,0)(0,)-∞+∞U ；（3）定义域是(,)-∞+∞，值域是(,)-∞+∞；（4）定义域是(,)-∞+∞，值域是[2,)-+∞．4．已知函数2()352f x x x =-+，求(2)f -，()f a -，(3)f a +，()(3)f a f +．4．解：因为2()352f x x x =-+，所以2(2)3(2)5(2)2852f -=⨯--⨯-+=+，即(2)852f -=+；同理，22()3()5()2352f a a a a a -=⨯--⨯-+=++，即2()352f a a a -=++；22(3)3(3)5(3)231314f a a a a a +=⨯+-⨯++=++，即2(3)31314f a a a +=++；22()(3)352(3)3516f a f a a f a a +=-++=-+，即2()(3)3516f a f a a +=-+．5．已知函数2()6x f x x +=-，（1）点(3,14)在()f x 的图象上吗？（2）当4x =时，求()f x 的值；（3）当()2f x =时，求x 的值．5．解：（1）当3x =时，325(3)14363f +==-≠-，即点(3,14)不在()f x 的图象上；（2）当4x =时，42(4)346f +==--，即当4x =时，求()f x 的值为3-；（3）2()26x f x x +==-，得22(6)x x +=-，即14x =． 6．若2()f x x bx c =++，且(1)0,(3)0f f ==，求(1)f -的值．6．解：由(1)0,(3)0f f ==，得1,3是方程20x bx c ++=的两个实数根，即13,13b c +=-⨯=，得4,3b c =-=，即2()43f x x x =-+，得2(1)(1)4(1)38f -=--⨯-+=，即(1)f -的值为8．7．画出下列函数的图象：（1）0,0()1,0x F x x ≤⎧=⎨>⎩；（2）()31,{1,2,3}G n n n =+∈．7．图象如下：8．如图，矩形的面积为10，如果矩形的长为x ，宽为y ，对角线为d ，周长为l ，那么你能获得关于这些量的哪些函数？8．解：由矩形的面积为10，即10xy =，得10(0)y x x =>，10(0)x y y =>，由对角线为d ，即22d x y =+，得22100(0)d x x x =+>，由周长为l ，即22l x y =+，得202(0)l x x x =+>，另外2()l x y =+，而22210,xy d x y ==+，得22222()22220(0)l x y x y xy d d =+=++=+>，即2220(0)l d d =+>．9．一个圆柱形容器的底部直径是dcm ，高是hcm ，现在以3/vcm s 的速度向容器内注入某种溶液．求溶液内溶液的高度xcm 关于注入溶液的时间ts 的函数解析式，并写出函数的定义域和值域．9．解：依题意，有2()2dx vt π=，即24v x t dπ=，显然0x h ≤≤，即240v t h dπ≤≤，得204h d t v π≤≤，得函数的定义域为2[0,]4h d vπ和值域为[0,]h ． 10．设集合{,,},{0,1}A a b c B ==，试问：从A 到B 的映射共有几个？并将它们分别表示出来．10．解：从A 到B 的映射共有8个．分别是()0()0()0f a f b f c =⎧⎪=⎨⎪=⎩，()0()0()1f a f b f c =⎧⎪=⎨⎪=⎩，()0()1()0f a f b f c =⎧⎪=⎨⎪=⎩，()0()0()1f a f b f c =⎧⎪=⎨⎪=⎩，()1()0()0f a f b f c =⎧⎪=⎨⎪=⎩，()1()0()1f a f b f c =⎧⎪=⎨⎪=⎩，()1()1()0f a f b f c =⎧⎪=⎨⎪=⎩，()1()0()1f a f b f c =⎧⎪=⎨⎪=⎩．Ｂ组1．函数()r f p =的图象如图所示．（1）函数()r f p =的定义域是什么？（2）函数()r f p =的值域是什么？（3）r 取何值时，只有唯一的p 值与之对应？1．解：（1）函数()r f p =的定义域是[5,0][2,6)-U ；（2）函数()r f p =的值域是[0,)+∞；（3）当5r >，或02r ≤<时，只有唯一的p 值与之对应．2．画出定义域为{|38,5}x x x -≤≤≠且，值域为{|12,0}y y y -≤≤≠的一个函数的图象．（1）如果平面直角坐标系中点(,)P x y 的坐标满足38x -≤≤，12y -≤≤，那么其中哪些点不能在图象上？（2）将你的图象和其他同学的相比较，有什么差别吗？2．解：图象如下，（1）点(,0)x 和点(5,)y 不能在图象上；（2）省略．3．函数()[]f x x =的函数值表示不超过x 的最大整数，例如，[ 3.5]4-=-，[2.1]2=．当( 2.5,3]x ∈-时，写出函数()f x 的解析式，并作出函数的图象．3．解：3, 2.522,211,10()[]0,011,122,233,3x x x f x x x x x x --<<-⎧⎪--≤<-⎪⎪--≤<⎪==≤<⎨⎪≤<⎪≤<⎪⎪=⎩图象如下4．如图所示，一座小岛距离海岸线上最近的点P 的距离是2km ，从点P 沿海岸正东12km 处有一个城镇．（1）假设一个人驾驶的小船的平均速度为3/km h ，步行的速度是5/km h ，t （单位：h ）表示他从小岛到城镇的时间，x （单位：km ）表示此人将船停在海岸处距P 点的距离．请将t 表示为x 的函数．（2）如果将船停在距点P 4km 处，那么从小岛到城镇要多长时间（精确到1h ）？4．解：（1）驾驶小船的路程为222x +，步行的路程为12x -，得222125x x t +-=+，(012)x ≤≤，即24125x x t +-=+，(012)x ≤≤．（2）当4x =时，2441242583()3535t h +-=+=+≈．第一章集合与函数概念1．3函数的基本性质1．3．1单调性与最大（小）值练习（第32页）1．请根据下图描述某装配线的生产效率与生产线上工人数量间的关系．1．答：在一定的范围内，生产效率随着工人数量的增加而提高，当工人数量达到某个数量时，生产效率达到最大值，而超过这个数量时，生产效率随着工人数量的增加而降低．由此可见，并非是工人越多，生产效率就越高．2．整个上午(8:0012:00):天气越来越暖，中午时分(12:0013:00):一场暴风雨使天气骤然凉爽了许多.暴风雨过后，天气转暖，直到太阳落山(18:00)才又开始转凉.画出这一天8:0020:00:期间气温作为时间函数的一个可能的图象，并说出所画函数的单调区间.2．解：图象如下[8,12]是递增区间，[12,13]是递减区间，[13,18]是递增区间，[18,20]是递减区间．3．根据下图说出函数的单调区间，以及在每一单调区间上，函数是增函数还是减函数.3．解：该函数在[1,0]-上是减函数，在[0,2]上是增函数，在[2,4]上是减函数，在[4,5]上是增函数．4．证明函数()21f x x =-+在R 上是减函数.4．证明：设12,x x R ∈，且12x x <，因为121221()()2()2()0f x f x x x x x -=--=->，即12()()f x f x >，所以函数()21f x x =-+在R 上是减函数.5．设()f x 是定义在区间[6,11]-上的函数.如果()f x 在区间[6,2]--上递减，在区间[2,11]-上递增，画出()f x 的一个大致的图象，从图象上可以发现(2)f -是函数()f x 的一个 . 5．最小值． 1．3．2单调性与最大（小）值练习（第36页）1．判断下列函数的奇偶性：（1）42()23f x x x =+；（2）3()2f x x x =- （3）21()x f x x+=；（4）2()1f x x =+. 1．解：（1）对于函数42()23f x x x =+，其定义域为(,)-∞+∞，因为对定义域内每一个x 都有4242()2()3()23()f x x x x x f x -=-+-=+=，所以函数42()23f x x x =+为偶函数；（2）对于函数3()2f x x x =-，其定义域为(,)-∞+∞，因为对定义域内每一个x 都有33()()2()(2)()f x x x x x f x -=---=--=-，所以函数3()2f x x x =-为奇函数；（3）对于函数21()x f x x+=，其定义域为(,0)(0,)-∞+∞U ，因为对定义域内每一个x 都有22()11()()x x f x f x x x-++-==-=--，所以函数21()x f x x+=为奇函数；（4）对于函数2()1f x x =+，其定义域为(,)-∞+∞，因为对定义域内每一个x 都有22()()11()f x x x f x -=-+=+=，所以函数2()1f x x =+为偶函数.2.已知()f x 是偶函数，()g x 是奇函数，试将下图补充完整.2．解：()f x 是偶函数，其图象是关于y 轴对称的；()g x 是奇函数，其图象是关于原点对称的．习题1.3A 组1.画出下列函数的图象，并根据图象说出函数()y f x =的单调区间，以及在各单调区间上函数()y f x =是增函数还是减函数.（1）256y x x =--；（2）29y x =-. 1．解：（1）5(,)2-∞上递减；函数在5[,)2+∞上递增；函数在（2）函数在(,0)-∞上递增；函数在[0,)+∞上递减.2.证明：（1）函数2()1f x x =+在(,0)-∞上是减函数；（2）函数1()1f x x=-在(,0)-∞上是增函数. 2．证明：（1）设120x x <<，而2212121212()()()()f x f x x x x x x x -=-=+-，由12120,0x x x x +<-<，得12()()0f x f x ->，即12()()f x f x >，所以函数2()1f x x =+在(,0)-∞上是减函数；（2）设120x x <<，而1212211211()()x x f x f x x x x x --=-=，由12120,0x x x x >-<，得12()()0f x f x -<，即12()()f x f x <，所以函数1()1f x x=-在(,0)-∞上是增函数. 3.探究一次函数()y mx b x R =+∈的单调性，并证明你的结论.3．解：当0m >时，一次函数y mx b =+在(,)-∞+∞上是增函数；当0m <时，一次函数y mx b =+在(,)-∞+∞上是减函数，令()f x mx b =+，设12x x <，而1212()()()f x f x m x x -=-，当0m >时，12()0m x x -<，即12()()f x f x <，得一次函数y mx b =+在(,)-∞+∞上是增函数；当0m <时，12()0m x x ->，即12()()f x f x >，得一次函数y mx b =+在(,)-∞+∞上是减函数.4.一名心率过速患者服用某种药物后心率立刻明显减慢，之后随着药力的减退，心率再次慢慢升高.画出自服药那一刻起，心率关于时间的一个可能的图象（示意图）.4．解：自服药那一刻起，心率关于时间的一个可能的图象为5.某汽车租赁公司的月收益y 元与每辆车的月租金x 元间的关系为21622100050x y x =-+-，那么，每辆车的月租金多少元时，租赁公司的月收益最大？最大月收益是多少？5．解：对于函数21622100050x y x =-+-，当162405012()50x =-=⨯-时，max 307050y =（元），即每辆车的月租金为4050元时，租赁公司最大月收益为307050元．6.已知函数()f x 是定义在R 上的奇函数，当0x ≥时，()(1)f x x x =+.画出函数()f x的图象，并求出函数的解析式.6．解：当0x <时，0x ->，而当0x ≥时，()(1)f x x x =+，即()(1)f x x x -=--，而由已知函数是奇函数，得()()f x f x -=-，得()(1)f x x x -=--，即()(1)f x x x =-，所以函数的解析式为(1),0()(1),0x x x f x x x x +≥⎧=⎨-<⎩.B 组1.已知函数2()2f x x x =-，2()2([2,4])g x x x x =-∈.（1）求()f x ，()g x 的单调区间；（2）求()f x ，()g x 的最小值.1．解：（1）二次函数2()2f x x x =-的对称轴为1x =，则函数()f x 的单调区间为(,1),[1,)-∞+∞，且函数()f x 在(,1)-∞上为减函数，在[1,)+∞上为增函数，函数()g x 的单调区间为[2,4]，且函数()g x 在[2,4]上为增函数；（2）当1x =时，min ()1f x =-，因为函数()g x 在[2,4]上为增函数，所以2min ()(2)2220g x g ==-⨯=．2.如图所示，动物园要建造一面靠墙的2间面积相同的矩形熊猫居室，如果可供建造围墙的材料总长是30m ，那么宽x （单位：m ）为多少才能使建造的每间熊猫居室面积最大？每间熊猫居室的最大面积是多少？2．解：由矩形的宽为x m ，得矩形的长为3032x m -，设矩形的面积为S ，则23033(10)22x x x S x --==-，当5x =时，2max 37.5S m =，即宽5x =m 才能使建造的每间熊猫居室面积最大，且每间熊猫居室的最大面积是237.5m ．3.已知函数()f x 是偶函数，而且在(0,)+∞上是减函数，判断()f x 在(,0)-∞上是增函数还是减函数，并证明你的判断.3．判断()f x 在(,0)-∞上是增函数，证明如下：设120x x <<，则120x x ->->，因为函数()f x 在(0,)+∞上是减函数，得12()()f x f x -<-，又因为函数()f x 是偶函数，得12()()f x f x <，所以()f x 在(,0)-∞上是增函数．复习参考题A 组1．用列举法表示下列集合：（1）2{|9}A x x ==；（2）{|12}B x N x =∈≤≤；（3）2{|320}C x x x =-+=.1．解：（1）方程29x =的解为123,3x x =-=，即集合{3,3}A =-；（2）12x ≤≤，且x N ∈，则1,2x =，即集合{1,2}B =；（3）方程2320x x -+=的解为121,2x x ==，即集合{1,2}C =．2．设P 表示平面内的动点，属于下列集合的点组成什么图形？（1）{|}P PA PB =(,)A B 是两个定点；（2）{|3}P PO cm =()O 是定点.2．解：（1）由PA PB =，得点P 到线段AB 的两个端点的距离相等，即{|}P PA PB =表示的点组成线段AB 的垂直平分线；（2）{|3}P PO cm =表示的点组成以定点O 为圆心，半径为3cm 的圆．3.设平面内有ABC ∆，且P 表示这个平面内的动点，指出属于集合{|}{|}P PA PB P PA PC ==I 的点是什么.3．解：集合{|}P PA PB =表示的点组成线段AB 的垂直平分线，集合{|}P PA PC =表示的点组成线段AC 的垂直平分线，得{|}{|}P PA PB P PA PC ==I 的点是线段AB 的垂直平分线与线段AC 的垂直平分线的交点，即ABC ∆的外心．4.已知集合2{|1}A x x ==，{|1}B x ax ==.若B A ⊆，求实数a 的值.4．解：显然集合{1,1}A =-，对于集合{|1}B x ax ==，当0a =时，集合B =∅，满足B A ⊆，即0a =；当0a ≠时，集合1{}B a =，而B A ⊆，则11a =-，或11a =，得1a =-，或1a =，综上得：实数a 的值为1,0-，或1．5.已知集合{(,)|20}A x y x y =-=，{(,)|30}B x y x y =+=，{(,)|23}C x y x y =-=，求A B I ，A C I ，()()A B B C I U I .5．解：集合20(,)|{(0,0)}30x y A B x y x y ⎧-=⎫⎧==⎨⎨⎬+=⎩⎩⎭I ，即{(0,0)}A B =I ；集合20(,)|23x y A C x y x y ⎧-=⎫⎧==∅⎨⎨⎬-=⎩⎩⎭I ，即A C =∅I ；集合3039(,)|{(,)}2355x y B C x y x y ⎧+=⎫⎧==-⎨⎨⎬-=⎩⎩⎭I ；则39()(){(0,0),(,)}55A B B C =-I U I .6.求下列函数的定义域：（1）y =（2）||5y x =-. 6．解：（1）要使原式有意义，则2050x x -≥⎧⎨+≥⎩，即2x ≥，得函数的定义域为[2,)+∞；（2）要使原式有意义，则40||50x x -≥⎧⎨-≠⎩，即4x ≥，且5x ≠，得函数的定义域为[4,5)(5,)+∞U ．7.已知函数1()1x f x x-=+，求：（1）()1(1)f a a +≠-；（2）(1)(2)f a a +≠-.7．解：（1）因为1()1x f x x-=+，所以1()1a f a a -=+，得12()1111a f a a a-+=+=++，即2()11f a a+=+；（2）因为1()1x f x x-=+，所以1(1)(1)112a a f a a a -++==-+++，即(1)2a f a a +=-+． 8.设221()1x f x x +=-，求证：（1）()()f x f x -=；（2）1()()f f x x=-. 8．证明：（1）因为221()1x f x x +=-，所以22221()1()()1()1x x f x f x x x +-+-===---，即()()f x f x -=；（2）因为221()1x f x x +=-，所以222211()11()()111()x x f f x x x x++===---，即1()()f f x x=-. 9.已知函数2()48f x x kx =--在[5,20]上具有单调性，求实数k 的取值范围.9．解：该二次函数的对称轴为8k x =，函数2()48f x x kx =--在[5,20]上具有单调性，则208k ≥，或58k ≤，得160k ≥，或40k ≤，即实数k 的取值范围为160k ≥，或40k ≤． 10．已知函数2y x -=，（1）它是奇函数还是偶函数？（2）它的图象具有怎样的对称性？（3）它在(0,)+∞上是增函数还是减函数？（4）它在(,0)-∞上是增函数还是减函数？10．解：（1）令2()f x x -=，而22()()()f x x x f x ---=-==，即函数2y x -=是偶函数；（2）函数2y x -=的图象关于y 轴对称；（3）函数2y x -=在(0,)+∞上是减函数；（4）函数2y x -=在(,0)-∞上是增函数．B 组1.学校举办运动会时，高一（1）班共有28名同学参加比赛，有15人参加游泳比赛，有8人参加田径比赛，有14人参加球类比赛，同时参加游泳比赛和田径比赛的有3人，同时参加游泳比赛和球类比赛的有3人，没有人同时参加三项比赛.问同时参加田径和球类比赛的有多少人？只参加游泳一项比赛的有多少人？1．解：设同时参加田径和球类比赛的有x 人，则158143328x ++---=，得3x =，只参加游泳一项比赛的有15339--=（人），即同时参加田径和球类比赛的有3人，只参加游泳一项比赛的有9人．2.已知非空集合2{|}A x R x a =∈=，试求实数a 的取值范围.2．解：因为集合A ≠∅，且20x ≥，所以0a ≥． 3.设全集{1,2,3,4,5,6,7,8,9}U =，(){1,3}U A B =U ð，(){2,4}U A B =I ð，求集合B . 3．解：由(){1,3}U A B =U ð，得{2,4,5,6,7,8,9}A B =U ，集合A B U 里除去()U A B I ð，得集合B ，所以集合{5,6,7,8,9}B =.4.已知函数(4),0()(4),0x x x f x x x x +≥⎧=⎨-<⎩.求(1)f ，(3)f -，(1)f a +的值. 4．解：当0x ≥时，()(4)f x x x =+，得(1)1(14)5f =⨯+=；当0x <时，()(4)f x x x =-，得(3)3(34)21f -=-⨯--=；(1)(5),1(1)(1)(3),1a a a f a a a a ++≥-⎧+=⎨+-<-⎩． 5.证明：（1）若()f x ax b =+，则1212()()()22x x f x f x f ++=；（2）若2()g x x ax b =++，则1212()()()22x x g x g x g ++≤. 5．证明：（1）因为()f x ax b =+，得121212()()222x x x x a f a b x x b ++=+=++， 121212()()()222f x f x ax b ax b a x x b ++++==++，所以1212()()()22x x f x f x f ++=；（2）因为2()g x x ax b =++，得22121212121()(2)()242x x x x g x x x x a b ++=++++，22121122()()1[()()]22g x g x x ax b x ax b +=+++++ 2212121()()22x x x x a b +=+++，因为2222212121212111(2)()()0424x x x x x x x x ++-+=--≤，即222212121211(2)()42x x x x x x ++≤+，所以1212()()()22x x g x g x g ++≤. （1）已知奇函数()f x 在[,]a b 上是减函数，试问：6.[,]b a --上是增函数还是减函数？它在（2）已知偶函数()g x 在[,]a b 上是增函数，试问：[,]b a --上是增函数还是减函数？它在6．解：（1）函数()f x 在[,]b a --上也是减函数，证明如下：设12b x x a -<<<-，则21a x x b <-<-<，因为函数()f x 在[,]a b 上是减函数，则21()()f x f x ->-，又因为函数()f x 是奇函数，则21()()f x f x ->-，即12()()f x f x >，所以函数()f x 在[,]b a --上也是减函数；（2）函数()g x 在[,]b a --上是减函数，证明如下：设12b x x a -<<<-，则21a x x b <-<-<，因为函数()g x 在[,]a b 上是增函数，则21()()g x g x -<-，又因为函数()g x 是偶函数，则21()()g x g x <，即12()()g x g x >，所以函数()g x 在[,]b a --上是减函数．7.《中华人民共和国个人所得税》规定，公民全月工资、薪金所得不超过2000元的部分不必纳税，超过2000元的部分为全月应纳税所得额.此项税款按下表分段累计计算：某人一月份应交纳此项税款为26.78元，那么他当月的工资、薪金所得是多少？7．解：设某人的全月工资、薪金所得为x 元，应纳此项税款为y 元，则0,02000(2000)5%,2000250025(2500)10%,25004000175(4000)15%,40005000x x x y x x x x ≤≤⎧⎪-⨯<≤⎪=⎨+-⨯<≤⎪⎪+-⨯<≤⎩由该人一月份应交纳此项税款为26.78元，得25004000x <≤， 25(2500)10%26.78x +-⨯=，得2517.8x =，所以该人当月的工资、薪金所得是2517.8元．。

高中数学第一章集合与函数概念1.1.3.2补集及集合运算的综合应用aa高一数学

2021/12/13
第十六页，共四十四页。
【跟踪训练 1】 (1)设集合 U＝{1,2,3,4,5,6}，M＝
{1,3,5}，则∁UM＝( )
A．{2,4,6}
B．{1,3,5}
C．{1,2,4}
D．U
(2)若全集 U＝{x∈R|－2≤x≤2}，则集合 A＝{x∈R|－
2≤x≤0}的补集∁UA 为( )
2021/12/13
第十四页，共四十四页。
解法二：借助 Venn 图，如图所示．
由图可知 B＝{2,3,5,7}．
2021/12/13
第十五页，共四十四页。
拓展提升求集合补集的基本方法及处理技巧
(1)基本方法：定义法． (2)两种处理技巧 ①当集合用列举法表示时，可借助 Venn 图求解； ②当集合是用描述法表示的连续数集时，可借助数轴，利用数轴分析求解．
A．{x∈R|0<x<2} B．{x∈R|0≤x<2}
C．{x∈R|0<x≤2} D．{x∈R|0≤x≤2}
2021/12/13
第十七页，共四十四页。
解析 (1)因为集合 U＝{1,2,3,4,5,6}，M＝{1,3,5}，所以∁UM＝{2,4,6}．
(2)借助数轴(如图)易得∁UA＝{x∈R|0<x≤2}．
②若 A≠∅，则需满足2a－2≥1， a≤2，
解得32≤a<2，综上所述 a≥32.
2021/12/13
第二十五页，共四十四页。
拓展提升
利用补集求参数问题的方法
(1)解答本题的关键是利用 A ∁RB，对 A＝∅与 A≠∅进行分类讨论，转化为等价不等式(组)求解，同时要注意区域端点的问题．
(2)不等式中的等号在补集中能否取到，要引起重视，还要注意补集是全集的子集．

高中数学第一章集合与函数概念 1.1-1.1.3 集合的基本运算第2课时补集及集合运算的综合

集合的基本运算第2课时补集及集合运算的综合应用A级基础巩固一、选择题1．已知全集U＝R，集合A＝{x|1≤2x＋1<9}，则∁U A＝( )A．{x|x<0或x>4} B．{x|x≤0或x>4}C．{x|x≤0或x≥4} D．{x|x<0或x≥4}解析：因为U＝R，A＝{x|0≤x<4}，所以∁U A＝{x|x<0或x≥4}．答案：D2.已知全集U＝R，集合A＝{1，2，3，4，5}，B＝{x∈R|x≥2}，则右图中阴影部分所表示的集合为( )A．{1} B．{0，1}C．{1，2} D．{0，1，2}解析：图中阴影部分所表示的集合为A∩(∁R B)，因为A＝{1，2，3，4，5}，B＝{x∈R|x≥2}，所以∁R B＝{x|x<2}，所以A∩(∁R B)＝{1}．答案：A3．已知集合A＝{x∈R|－2<x<6}，B＝{x∈R|x<2}，则A∪(∁R B)＝( )A．{x|x<6} B．{x|－2<x<2}C．{x|x>－2} D．{x|2≤x<6}解析：由B＝{x∈R|x<2}，得∁R B＝{x|x≥2}．又A＝{x∈R|－2<x<6}，所以A∪(∁R B)＝{x|x>－2}．答案：C4．设全集是实数集R，M＝{x|－2≤x≤2}，N＝{x|x<1}，则(∁R M)∩N＝( )A．{x|x<－2} B．{x|－2<x<1}C．{x|x<1} D．{x|－2≤x<1}解析：由题可知∁R M＝{x|x<－2或x>2}，故(∁R M )∩N ＝{x |x <－2}．答案：A5．已知S ＝{x |x 是平行四边形或梯形}，A ＝{x |x 是平行四边形}，B ＝{x |x 是菱形}，C ＝{x |x 是矩形}．下列式子不成立的是( )A ．B ∩C ＝{x |x 是正方形}B ．∁A B ＝{x |x 是邻边不相等的平行四边形}C ．∁S A ＝{x |x 是梯形}D ．A ＝B ∪C解析：根据平行四边形和梯形的概念知，选项D 错误．答案：D二、填空题6．设集合U ＝{1，2，3，4，5}，A ＝{1，2，3}，B ＝{3，4，5}，则∁U (A ∩B )＝________．解析：因为A ＝{1，2，3}，B ＝{3，4，5}，所以A ∩B ＝{3}，故∁U (A ∩B )＝{1，2，4，5}．答案：{1，2，4，5}7．已知全集U ＝{1，2，3，4，5}，A ＝{1，2，3}，那么∁U A 的子集个数有________个．解析：∁U A ＝{4，5}，子集有∅，{4}，{5}，{4，5}，共4个．答案：48．已知全集U ＝{2，4，a 2－a ＋1}，A ＝{a ＋1，2}，∁U A ＝{7}，则a ＝________．解析：由∁U A ＝{7}，得4∈A ，故a ＋1＝4，即a ＝3，此时，U ＝{2，4，7}，满足A ⊆U ，故a ＝3.答案：3三、解答题9．设全集是数集U ＝{2，3，a 2＋2a －3}，已知A ＝{b ，2}，∁U A ＝{5}，某某数a ，b 的值．解：因为∁U A ＝{5}，所以5∈U 且5∉A .又b ∈A ，所以b ∈U ，由此得⎩⎪⎨⎪⎧a 2＋2a －3＝5，b ＝3，解得⎩⎪⎨⎪⎧a ＝2，b ＝3或⎩⎪⎨⎪⎧a ＝－4，b ＝3.经检验都符合题意．10．已知集合A ＝{x |3≤x <7}，B ＝{x |2<x <10}，C ＝{x |x <a }，全集为实数集R.(1)求A ∪B ，(∁R A )∩B ；(2)若A ∩C ≠∅，求a 的取值X 围．解：(1)因为A ＝{x |3≤x <7}，B ＝{x |2<x <10}，所以A ∪B ＝{x |2<x <10}．因为A ＝{x |3≤x <7}，所以∁R A ＝{x |x <3或x ≥7}，所以(∁R A )∩B ＝{x |x <3或x ≥7}∩{x |2<x <10}＝{x |2<x <3或7≤x <10}．(2)如图所示，当a >3时，A ∩C ≠∅.B 级能力提升1．已知全集U ＝{－1，1，3}，集合A ＝{a ＋2，a 2＋2}，且∁U A ＝{－1}，则a 的值是( )A ．－1B ．1C ．3D ．±1解析：因为U ＝{－1，1，3}，∁U A ＝{－1}，所以A ＝{1，3}，又因为a 2＋2≥2，所以a2＋2＝3且a ＋2＝1，得a ＝－1.答案：A2．已知集合A ＝{0，2，4，6}，∁U A ＝{－1，1，－3，3}，∁U B ＝{－1，0，2}，则集合B ＝______________．解析：∵∁U A ＝{－1，1，－3，3}，∴U ＝{－1，1，0，2，4，6，－3，3}，又∁U B ＝{－1，0，2}，∴B ＝{1，4，6，－3，3}．答案：{1，4，6，－3，3}3．设全集U ＝⎩⎨⎧⎭⎬⎫－13，5，－3，集合A ＝{x |3x 2＋px －5＝0}，B ＝{x |3x 2＋10x ＋q ＝0}，且A ∩B ＝⎩⎨⎧⎭⎬⎫－13.求∁U A ，∁U B . 解：因为A ∩B ＝⎩⎨⎧⎭⎬⎫－13，所以－13∈A 且－13∈B ，所以3⎝ ⎛⎭⎪⎫－132－13p －5＝0，3⎝ ⎛⎭⎪⎫－132－13×10＋q ＝0，解得p ＝－14，q ＝3.故A ＝{x |3x 2－14x －5＝0}＝⎩⎨⎧⎭⎬⎫－13，5， B ＝{x |3x 2＋10x ＋3＝0}＝⎩⎨⎧⎭⎬⎫－13，－3，所以∁U A ＝{－3}，∁U B ＝{5}．。

(精品)高中数学必修1全套同步练习册

第一章集合与函数概念1.1.1（1）集合的含义与表示1．下列几组对象可以构成集合的是( )．A．充分接近π的实数的全体B．善良的人C．某校高一所有聪明的同学D．某单位所有身高在1.7 m以上的人2．下面有四个语句：①集合N*中最小的数是0；②－a∉N，则a∈N；③a∈N，b∈N，则a＋b的最小值是2；④x2＋1＝2x的解集中含有2个元素．其中正确语句的个数是( )．A．0 B．1 C．2 D．33．下列所给关系正确的个数是( )．①π∈R；②3∉Q；③0∈N*；④|－4|∉N*.A．1 B．2 C．3 D．44．已知x、y、z为非零实数，代数式x|x|＋y|y|＋z|z|＋|xyz|xyz的值所组成的集合是M，则下列判断正确的是( )．A．0∉M B．2∈M C．－4∉M D．4∈M5．满足“a∈A且4－a∈A”，a∈N且4－a∈N的有且只有2个元素的集合A的个数是( )．A．0 B．1 C．2 D．36．设集合M中的元素为平行四边形，p表示某个矩形，q表示某个梯形，则p________M，q________M.7．已知集合A中只含有1，a2两个元素，则实数a不能取的值为________．8．集合A中的元素y满足y∈N且y＝－x2＋1，若t∈A，则t的值为________．9．以方程x2－5x＋6＝0和方程x2－x－2＝0的解为元素的集合中共有________个元素．10．设1,0，x三个元素构成集合A，若x2∈A，求实数x的值．11．已知集合M中含有三个元素2，a，b，集合N中含有三个元素2a,2，b2，且M＝N，求a，b的值．12．(能力提升)设P、Q为两个非空实数集合，P中含有0,2,5三个元素，Q中含有1,2,6三个元素，定义集合P＋Q中的元素是a＋b，其中a∈P，b∈Q，则P＋Q中元素的个数是多少？1.1.1（2）集合的含义与表示1．下列集合表示法正确的是( )．A ．{1,2,2}B ．{全体实数}C ．{有理数}D ．{祖国的大河} 2．集合M ＝{(x ，y )|xy >0，x ∈R ，y ∈R }是指( )．A ．第一象限内的点集B ．第三象限内的点集C ．第一、三象限内的点集D ．第二、四象限内的点集 3．下列语句：①0与{0}表示同一个集合；②由1,2,3组成的集合可表示为{1,2,3}或{3,2,1}；③方程(x －1)2(x －2)2＝0的所有解的集合可表示为{1,1,2}； ④集合{x |4<x <5}可以用列举法表示．正确的是( )．A ．只有①和④B ．只有②和③C ．只有②D ．以上语句都不对 4．直线y ＝2x ＋1与y 轴的交点所组成的集合为( )．A ．{0,1}B ．{(0,1)}C.⎩⎨⎧⎭⎬⎫－12，0 D.⎩⎨⎧⎭⎬⎫⎝ ⎛⎭⎪⎫－12，05．集合A ＝{y |y ＝x 2＋1}，集合B ＝{(x ，y )|y ＝x 2＋1}(A 、B 中x ∈R ，y ∈R )．选项中元素与集合的关系都正确的是( )．A ．2∈A ，且2∈B B ．(1,2)∈A ，且(1,2)∈BC ．2∈A ，且(3,10)∈BD ．(3,10)∈A ，且2∈B 6．集合A ＝{a ，b ，(a ，b )}含有________个元素．7．用列举法表示集合A ＝⎩⎨⎧⎭⎬⎫x |x ∈Z ，86－x ∈N ＝________.8．已知集合{－1,0,1}与集合{0，a ，b }相等，则a 2 010＋b 2 011的值等于________．9．设－5∈{x |x 2－ax －5＝0}，则集合{x |x 2＋ax ＋3＝0}中所有元素之和为________．10．用另一种方法表示下列集合．(1){绝对值不大于2的整数}；(2){能被3整除，且小于10的正数}；(3){x |x ＝|x |，x <5且x ∈Z }；(4){(x ，y )|x ＋y ＝6，x ∈N *，y ∈N *}；(5){－3，－1,1,3,5}．11．用适当的方法表示下列对象构成的集合． (1)绝对值不大于3的整数；(2)平面直角坐标系中不在第一、三象限内的点； (3)方程2x ＋1＋|y －2|＝0的解．12．(能力提升)已知集合M ＝{0,2,4}，定义集合P ＝{x |x ＝ab ，a ∈M ，b ∈M }，求集合P .1.1.2 集合间的基本关系1．下列说法：①空集没有子集；②任何集合至少有两个子集； ③空集是任何集合的真子集；④若∅A ，则A ≠∅. 其中正确的有( )．A ．0个B ．1个C ．2个D ．3个2．如果A ＝{x |x >－1}，那么正确的结论是( )．A ．0⊆AB ．{0}AC ．{0}∈AD ．∅∈A3．集合A ＝{x |0≤x <3且x ∈Z }的真子集的个数是( )．A ．5B ．6C ．7D ．84．下列关系中正确的是________．①∅∈{0}；②∅{0}；③{0,1}⊆{(0,1)}；④{(a ，b )}＝{(b ，a )}．5．集合U 、S 、T 、F 的关系如图所示，下列关系错误的有________．①S U ；②F T ；③S T ；④S F ；⑤S F ；⑥F U .6．已知集合A ＝{(x ，y )|x ＋y ＝2，x ，y ∈N }，试写出A 的所有子集．7．已知集合A ＝⎩⎨⎧⎭⎬⎫x |x ＝k3，k ∈Z ，B ＝⎩⎨⎧⎭⎬⎫x |x ＝k6，k ∈Z ，则( )．A ．AB B ．B AC ．A ＝BD ．A 与B 关系不确定8．满足{a }⊆M {a ，b ，c ，d }的集合M 共有( )．A ．6个B ．7个C ．8个D ．15个9．设A ＝{1,3，a }，B ＝{1，a 2－a ＋1}，若B A ，则a 的值为________．10．已知集合P ＝{x |x 2＝1}，集合Q ＝{x |ax ＝1}，若Q ⊆P ，那么a 的取值是________．11．已知M ＝{a －3,2a －1，a 2＋1}，N ＝{－2,4a －3,3a －1}，若M ＝N ，求实数a 的值．12．(能力提升)已知集合A ＝{x |－2≤x ≤5}，B ＝{x |m ＋1≤x ≤2m －1}． (1)若B ⊆A ，求实数m 的取值范围； (2)若x ∈Z ，求A 的非空真子集的个数；(3)当x ∈R 时，若没有元素使x ∈A 与x ∈B 同时成立，求实数m 的取值范围．1.1.3（1）集合的基本运算（交集与并集）1．已知集合M ＝{x |－3<x ≤5}，N ＝{x |x <－5或x >5}，则M ∪N 等于( )．A ．{x |x <－5或x >－3}B ．{x |－5<x <5}C ．{x |－3<x <5}D ．{x |x <－3或x >5}2．满足条件M ∪{1}＝{1,2,3}的集合M 的个数是( )．A ．1B ．2C ．3D ．43．设集合M＝{m∈Z|－3<m<2}，N＝{n∈Z|－1≤n≤3}，则M∩N等于( )．A．{0,1} B．{－1,0,1}C．{0,1,2} D．{－1,0,1,2}4．满足{1,3}∪A＝{1,3,5}的所有集合A的个数是( )．A．1 B．2 C．3 D．45．已知集合A＝{(x，y)|y＝2x＋1}，B＝{x|y＝x－1}，则A∩B＝()．A．{－2} B．{(－2，－3)}C．∅D．{－3}6．满足{0,1}∪A＝{0,1,2}的所有集合A是________．7．若集合P＝{x|x2＝1}，集合M＝{x|x2－2x－3＝0}，则P∩M＝________.8．设集合A＝{x|x>－1}，B＝{x|－2<x<2}，则A∪B＝________.9．集合A＝{0,2，a2}，B＝{1，a}，若A∩B＝{1}，则a＝________.10．已知集合A＝{1,3,5}，B＝{1,2，x2－1}，若A∪B＝{1,2,3,5}，求x及A∩B.11．若A∩B＝A，A∪C＝C，B＝{0,1,2}，C＝{0,2,4}，写出满足上述条件的所有集合A. 12．(能力提升)设U＝{1,2,3}，M，N是U的子集，若M∩N＝{1,3}，则称(M，N)为一个“理想配集”，求符合此条件的“理想配集”的个数(规定(M，N)与(N，M)不同)．1.1.3（2）集合的基本运算（补集及综合运算）1．设全集U＝R，A＝{x|0≤x≤6}，则∁R A＝( )．A．{0,1,2,3,4,5,6} B．{x|x<0或x>6}C．{x|0<x<6} D．{x|x≤0或x≥6}2．已知全集U＝{2,5,8}，且∁U A＝{2}，则集合A的真子集个数为( )．A．3 B．4 C．5 D．63．若A为全体正实数的集合，B＝{－2，－1,1,2}，则下列结论中正确的是( )．A．A∩B＝{－2，－1} B．(∁R A)∪B＝{－2，－1,1}C．A∪B＝{1,2} D．(∁R A)∩B＝{－2，－1}4．在如图中，用阴影表示出集合(∁U A)∩(∁U B)．5．已知U 为全集，集合M 、N 是U 的子集，若M ∩N ＝N ，则( )．A ．(∁U M )⊇(∁U N )B ．M ⊆(∁U N )C ．(∁U M )⊆(∁U N )D ．M ⊇(∁U N )6．已知集合A ＝{x |x <a }，B ＝{x |1<x <2}，且A ∪(∁R B )＝R ，则实数a 的取值范围是( )．A ．a ≤2 B．a <1 C ．a ≥2 D．a >27．已知集合A ＝{3,4，m }，集合B ＝{3,4}，若∁A B ＝{5}，则实数m ＝________.8．设全集U ＝A ∪B ＝{x ∈N *|0<x <10}，若A ∩(∁U B )＝{m |m ＝2n ＋1，n ＝0,1,2,3,4}，则集合B ＝________.9．设U ＝{0,1,2,3}，A ＝{x ∈U |x 2＋mx ＝0}，若∁U A ＝{1,2}，则实数m ＝________.10．设全集U ＝R ，集合A ＝{x |x ≥0}，B ＝{y |y ≥1}，则∁U A 与∁U B 的包含关系是________．11．已知全集U ＝R ，A ＝{x |－4≤x ≤2}，B ＝{x |－1<x ≤3}，P ＝{x |x ≤0或x ≥52}，(1)求A ∩B ；(2)求(∁U B )∪P ；(3)求(A ∩B )∩(∁U P )．12．(能力提升)已知全集U ＝R ，集合A ＝{x |－1≤x ≤2}，B ＝{x |4x ＋p <0}，且B ⊆∁U A ，求实数p 的取值范围．1.2.1函数的概念1．下列式子中不能表示函数y ＝f (x )的是( )．A ．x ＝y 2＋1B ．y ＝2x 2＋1 C ．x －2y ＝6 D ．x ＝y2．函数y ＝1－x ＋x 的定义域是( )．A ．{x |x ≥0} B．{x |x ≥1}C ．{x |x ≥1}∪{0}D ．{x |0≤x ≤1} 3．与y ＝|x |为相等函数的是( )．A ．y ＝(x )2B ．y ＝x 2C ．y ＝⎩⎪⎨⎪⎧x x >0－x x <0D ．y ＝3x 34．给出下列函数：①y ＝x 2－x ＋2，x >0；②y ＝x 2－x ，x ∈R ；③y ＝t 2－t ＋2，t ∈R ；④y ＝t 2－t ＋2，t >0.其中与函数y ＝x 2－x ＋2，x ∈R 是相等函数的是________．5．如果函数f ：A →B ，其中A ＝{－3，－2，－1,1,2,3,4}，对于任意a ∈A ，在B 中都有唯一确定的|a |和它对应，则函数的值域为________．6．已知函数f (x )＝x 2－4x ＋5，f (a )＝10，求a 的值．7．下列各组函数表示相等函数的是( )．A ．y ＝x 2－9x －3与y ＝x ＋3B ．y ＝x 2－1与y ＝x －1C ．y ＝x 0(x ≠0)与y ＝1(x ≠0)D．y ＝2x ＋1，x ∈Z 与y ＝2x －1，x ∈Z8．设f (x )＝x 2－1x 2＋1，则f 2f ⎝ ⎛⎭⎪⎫12＝( )．A ．1B ．－1 C.35 D ．－359．y ＝x ＋4x ＋2的定义域为________．10．集合{x |－1≤x <0或1<x ≤2}用区间表示为________．11．求函数y ＝x ＋26－2x －1的定义域，并用区间表示．12．(能力提升)若函数f (x )的定义域为[－2,1]，求g (x )＝f (x )＋f (－x )的定义域．1.2.2（1）函数的表示法1．若g (x ＋2)＝2x ＋3，g (3)的值是( )． A ．9 B ．7 C ．5 D ．32．已知正方形的周长为x ，它的外接圆的半径为y ，则y 关于x 的解析式为( )．A ．y ＝12xB ．y ＝24xC ．y ＝28xD ．y ＝216x3．下列图形中，不可能作为函数y ＝f (x )图象的是( )．4．已知f (2x ＋1)＝3x －2且f (a )＝4，则a 的值为________． 5．已知f (x )与g (x )分别由下表给出那么f (g (3))＝________.6．已知函数f (x )是二次函数，且它的图象过点(0,2)，f (3)＝14，f (－2)＝8＋52，求f (x )的解x 1 2 3 4 g (x ) 3 1 4 2x 1 2 3 4 f (x ) 4 3 2 1析式．7．下列表格中的x 与y 能构成函数的是( )． A.B.C.D.8．已知函数f (x ＋1)＝3x ＋2，则f (x )的解析式是( )．A ．f (x )＝3x ＋2B ．f (x )＝3x ＋1C ．f (x )＝3x －1D ．f (x )＝3x ＋4 9．下列图形中，可以是函数y ＝f (x )图象的是________．11．作出下列函数的图象：(1)f (x )＝x ＋x 0；(2)f (x )＝1－x (x ∈Z ，且－2≤x ≤2)．12．(能力提升)已知函数f (x )对任意实数a 、b ，都有f (ab )＝f (a )＋f (b )成立． (1)求f (0)与f (1)的值；(2)求证：f ⎝ ⎛⎭⎪⎫1x ＝－f (x )；(3)若f (2)＝p ，f (3)＝q (p ，q 均为常数)，求f (36)的值．1.2.2.（2）函数的表示法（分段函数及映射）1．下列对应不是映射的是( )．2．以下几个论断：①从映射角度看，函数是其定义域到值域的映射； ②函数y ＝x －1，x ∈Z 且x ∈(－3,3]的图象是一条线段； ③分段函数的定义域是各段定义域的并集，值域是各段值域的并集； ④若D 1、D 2分别是分段函数的两个不同对应关系的值域，则D 1∩D 2＝∅. 其中正确的论断有( )．A ．0个B ．1个C ．2个D ．3个3．若定义运算a ⊙b ＝⎩⎪⎨⎪⎧ba ≥b ，a a <b ，则函数f (x )＝x ⊙(2－x )的值域是( )．A ．(－∞，1]B ．(－∞，1)C ．(－∞，＋∞) D．(1，＋∞)4．设集合P ＝{x |0≤x ≤4}，Q ＝{y |0≤y ≤2}，则下列的对应不表示从P 到Q 的映射的是( )．A ．f ：x →y ＝12xB ．f ：x →y ＝13xC ．f ：x →y ＝23x D ．f ：x →y ＝xx 非负数非正数 y 1 －1 x 奇数 0 偶数y 1 0 －1 x 有理数无理数 y 1 －1 x 自然数整数有理数y 1 0 －15．下列图形是函数y ＝⎩⎪⎨⎪⎧x 2， x <0x －1，x ≥0的图象的是________．6．已知f (x )＝⎩⎪⎨⎪⎧2x ，x <0，x 2，x ≥0，若f (x )＝16，则x 的值为________．7．作出函数y ＝⎩⎪⎨⎪⎧1x0<x <1，xx ≥1的图象，并求其值域．8．函数f (x )＝|x －1|的图象是( )．9．设函数f (x )＝⎩⎪⎨⎪⎧x 2＋2 x ≤2，2x x >2，若f (x 0)＝8，则x 0＝________.10．设集合A ＝B ＝{(x ，y )|x ∈R ，y ∈R }，点(x ，y )在映射f ：A →B 的作用下对应的点是(x －y ，x ＋y )，则B 中点(3,2)对应的A 中点的坐标为________．11．已知f (x )＝⎩⎪⎨⎪⎧x x ＋4x ≥0，x x －4 x <0，若f (1)＋f (a ＋1)＝5，求a 的值．12．(能力提升)在交通拥挤及事故多发地段，为了确保交通安全，规定在此地段内，车距d 是车速v (公里/小时)的平方与车身长S (米)的积的正比例函数，且最小车距不得小于车身长的一半．现假定车速为50公里/小时，车距恰好等于车身长，试写出d 关于v 的函数关系式(其中S 为常数)．1.3.1（1）函数的单调性1．函数y ＝－x 2的单调减区间是( )．A ．[0，＋∞)B．(－∞，0]C ．(－∞，0) D ．(－∞，＋∞) 2．定义在R 上的函数f (x )对任意两个不相等的实数a ，b ，总有f a －f ba －b>0，则必有( )．A ．函数f (x )先增后减B ．函数f (x )先减后增C ．函数f (x )是R 上的增函数D ．函数f (x )是R 上的减函数 3．下列说法中正确的有( )．①若x 1，x 2∈I ，当x 1<x 2时，f (x 1)<f (x 2)，则y ＝f (x )在I 上是增函数；②函数y ＝x 2在R 上是增函数；③函数y ＝－1x在定义域上是增函数；④y ＝1x的单调区间是(－∞，0)∪(0，＋∞)．A ．0个B ．1个C ．2个D ．3个4．函数f (x )＝－2x 2＋mx ＋1在区间[1,4]上是单调函数，则实数m 的取值范围是________． 5．函数y ＝－(x －3)|x |的递增区间为________．6．已知f (x )是定义在[－1,1]上的增函数，且f (x －1)<f (1－3x )，求x 的取值范围．7．若函数y ＝f (x )在区间(a ，b )上是增函数，在区间(b ，c )上也是增函数，则函数y ＝f (x )在区间(a ，b )∪(b ，c )上( )．A ．必是增函数B ．必是减函数C ．是增函数或减函数D ．无法确定单调性8．函数y ＝f (x )在R 上为增函数，且f (2m )>f (－m ＋9)，则实数m 的取值范围是( )．A ．(－∞，－3)B ．(0，＋∞)C．(3，＋∞) D．(－∞，－3)∪(3，＋∞)9．已知函数f (x )为区间[－1,1]上的增函数，则满足f (x )<f ⎝ ⎛⎭⎪⎫12的实数x 的取值范围为________． 10．已知函数y ＝8x 2＋ax ＋5在[1，＋∞)上递增，那么a 的取值范围是________．11．已知函数f (x )＝x 2－2ax －3在区间[1,2]上单调，求实数a 的取值范围．12．(能力提升)若f (x )＝x 2＋bx ＋c ，且f (1)＝0，f (3)＝0. (1)求b 与c 的值；(2)试证明函数y ＝f (x )在区间(2，＋∞)上是增函数．1.3.1（2）函数的最大（小）值1．函数y ＝f (x )在[－2,2]上的图象如图所示，则此函数的最小值、最大值分别是( )．A ．f (－2)，0B ．0,2C ．f (－2)，2D ．f (2)，22．函数y ＝1x 2在区间⎣⎢⎡⎦⎥⎤12，2上的最大值是( )． A.14B ．－1C ．4D ．－4 3．函数f (x )＝x 2＋3x ＋2在区间(－5,5)上的最大、最小值分别为( )．A ．42,12B ．42，－14C ．12，－14D ．无最大值，最小值为－144．函数y ＝2x 2＋1，x ∈N *的最小值为________．5．若函数y ＝k x(k >0)在[2,4]上的最小值为5，则k 的值为________． 6．画出函数f (x )＝⎩⎪⎨⎪⎧－2x，x ∈－∞，0，x 2＋2x －1，x ∈[0，＋∞的图象，并写出函数的单调区间，函数最小值．7．函数y ＝2x在区间[2,4]上的最大值、最小值分别是( )．A ．1，12B.12，1 C.12，14D.14，128．函数f (x )＝11－x 1－x的最大值是( )．A.45B.54C.34D.439．已知函数y *f (x )是(0，＋∞)上的减函数，则f (a 2－a ＋1)与f ⎝ ⎛⎭⎪⎫34的大小关系是________．10．已知函数f (x )＝x 2－6x ＋8，x ∈[1，a ]，并且f (x )的最小值为f (a )，则实数a 的取值范围是________．11．某租车公司拥有汽车100辆，当每辆车的月租金为3 000元时，可全部租出，当每辆车的月租金每增加60元时，未租出的车将会增加一辆．租出的车每月需要维护费160元，未租出的车每月需要维护费60元．(1)当每辆车的月租金定为3 900元时，能租出多少辆车？(2)当每辆车的月租金为多少元时，租车公司的月收益最大？最大月收益是多少？12．(能力提升)已知函数f (x )＝x 2＋2ax ＋2，x ∈[－5,5]． (1)当a ＝－1时，求函数f (x )的最大值和最小值；(2)求实数a 的取值范围，使y ＝f (x )在区间[－5,5]上是单调函数．1.3.2函数的奇偶性1. 已知y ＝f (x )是偶函数，且f (4)＝5，那么f (4)＋f (－4)的值为( )． A ．5 B ．10 C ．8 D ．不确定2．对于定义域是R 的任意奇函数y ＝f (x )，都有( )．A ．f (x )－f (－x )>0B ．f (x )－f (－x )≤0C ．f (x )·f (－x )≤0 D．f (x )·f (－x )>03．已知函数f (x )＝1x2(x ≠0)，则这个函数( )．A ．是奇函数B ．既是奇函数又是偶函数C ．是偶函数D ．既不是奇函数又不是偶函数4．若函数f (x )＝(x ＋1)(x －a )为偶函数，则a 等于( )．A ．－2B ．－1C ．1D ．25．奇函数y ＝f (x )(x ∈R )的图象必定经过点( )．A ．(a ，f (－a ))B ．(－a ，f (a ))C ．(－a ，－f (a )) D.⎝⎛⎭⎪⎫a ，f ⎝ ⎛⎭⎪⎫1a6．已知函数y ＝f (x )为奇函数，若f (3)－f (2)＝1，则f (－2)－f (－3)＝________.7．如果定义在区间[2－a,4]上的函数y ＝f (x )为偶函数，那么a ＝________.8．已知函数f (x )＝ax 2＋bx ＋3a ＋b 为偶函数，其定义域为[a －1,2a ]，则a 的值为________．9．若f (x )＝(m －1)x 2＋6mx ＋2是偶函数，则f (0)、f (1)、f (－2)从小到大的顺序是________．10．如图是偶函数y ＝f (x )在x ≥0时的图象，请作出y ＝f (x )在x <0时的图象．11．判断下列函数的奇偶性：(1)f (x )＝2x －1＋1－2x ；(2)f (x )＝x 4＋x ；(3)f (x )＝⎩⎪⎨⎪⎧ x 2＋20－x 2－2x >0，x ＝0，x <0；(4)f (x )＝x 3－x 2x －1.12．(能力提升)已知定义在R 上的奇函数f (x )满足f (x ＋2)＝－f (x )，求f (6)的值．章末质量评估一、选择题1．如果集合A ＝{x |x ≤3}，a ＝2，那么( )．A ．a ∉AB ．{a }AC ．{a }∈AD ．a ⊆A2．函数y＝2x ＋1＋3－4x 的定义域为( )．A.⎝ ⎛⎭⎪⎫－12，34B.⎣⎢⎡⎦⎥⎤－12，34C.⎝⎛⎦⎥⎤－∞，12D.⎝ ⎛⎭⎪⎫－12，0∪(0，＋∞)3．已知全集U ＝R ，集合A ＝{x |－2≤x ≤3}，B ＝{x |x <－1或x >4}，那么集合A ∩(∁U B )等于 A ．{x |－2≤x <4} B ．{x |x ≤3或x ≥4}C．{x |－2≤x <－1} D ．{x |－1≤x ≤3} 4．若函数f (x )满足f (3x ＋2)＝9x ＋8，则f (x )的解析式是( )．A ．f (x )＝9x ＋8B ．f (x )＝3x ＋2C ．f (x )＝－3x －4D ．f (x )＝3x ＋2或f (x )＝－3x －4 5．设集合A ＝{x |1<x <2}，B ＝{x |x <a }，满足A B ，则实数a 的取值范围是( )．A ．{a |a ≥2} B．{a |a ≤1}C．{a |a ≥1} D．{a |a ≤2}6．如果奇函数y ＝f (x )在区间[1,5]上是减函数，且最小值为3，那么y ＝f (x )在区间 [－5，－1]上是( )．A ．增函数且最小值为3B ．增函数且最大值为3C ．减函数且最小值为－3D ．减函数且最大值为－37．设函数f (x )＝1＋x21－x2，则有( )．A ．f (x )是奇函数，f ⎝ ⎛⎭⎪⎫1x ＝－f (x )B ．f (x )是奇函数，f ⎝ ⎛⎭⎪⎫1x ＝f (x )C ．f (x )是偶函数，f ⎝ ⎛⎭⎪⎫1x ＝－f (x )D ．f (x )是偶函数，f ⎝ ⎛⎭⎪⎫1x ＝f (x ) 8．设f ，g 都是由A 到A 的映射，其对应法则如下表(从上到下)：表 1 映射f 的对应法则表2 映射g 的对应法则则与f [g (1)]相同的是( )．A ．g [f (1)]B ．g [f (2)]C ．g [f (3)]D ．g [f (4)]9．设集合A ＝{x |0≤x ≤2}，B ＝{y |1≤y ≤2}，若对于函数y ＝f (x )，其定义域为A ，值域为B ，则这个函数的图象可能是( )．10．若函数y ＝f (x )为偶函数，且在(0，＋∞)上是减函数，又f (3)＝0，则f x ＋f －x 2x<0的解集为( )．A ．(－3,3)B ．(－∞，－3)∪(3，＋∞)C ．(－3,0)∪(3，＋∞) D．(－∞，－3)∪(0,3) 二、填空题11．设集合A ＝{－1,1,3}，B ＝{a ＋2，a 2＋4}，A ∩B ＝{3}，则实数a 的值________．12．用列举法表示集合：A ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪2x ＋1∈Z ，x ∈Z ＝________. 13．函数y ＝f (x )是R 上的偶函数，且当x >0时，f (x )＝x 3＋1，则当x <0时，f (x )＝________.14．某城市出租车按如下方法收费：起步价8元，可行3 k m(含3 k m)，3 k m 后到10 k m(含10 k m)每走1 k m 加价1.5元，10 k m 后每走1 k m 加价0.8元，某人坐该城市的出租车走了20 k m ，他应交费________元．原象 1 2 3 4 象 3 4 2 1 原象 1 2 3 4 象 4 3 1 2三、解答题，（解答时应写出必要的文字说明、证明过程或演算步骤．)15．(10分)设A ＝{x |2x 2＋ax ＋2＝0}，B ＝{x |x 2＋3x ＋2a ＝0}，且A ∩B ＝{2}． (1)求a 的值及集合A ，B ；(2)设全集U ＝A ∪B ，求(∁U A )∪(∁U B )； (3)写出(∁U A )∪(∁U B )的所有子集．16．已知y ＝f (x )为二次函数，且f (x ＋1)＋f (x －1)＝2x 2－4x ，求f (x )的表达式．17．已知函数f (x )＝2x ＋1x ＋1.(1)判断函数在区间[1，＋∞)上的单调性，并用定义证明你的结论； (2)求该函数在区间[1,4]上的最大值与最小值．18．某工厂生产某种零件，每个零件的成本为40元，出厂价是60元，该厂为鼓励销售商订购，决定当一次订购量超过100个时，每多订购1个，订购的全部零件的出厂单价就降低0.02元，但实际出厂单价不能低于51元．(1)当一次订购量为多少时，零件的实际出厂单价降为51元？(2)设一次订购量为x 个，零件的实际出厂单价为p 元，写出函数p ＝f (x )的表达式．19已知函数f (x )对任意x 、y ∈R 都有f (x ＋y )＝f (x )＋f (y )，且x >0时，f (x )<0，f (1)＝－2. (1)判断函数f (x )的奇偶性．(2)当x ∈[－3,3]时，函数f (x )是否有最值？如果有，求出最值；如果没有，请说明理由．2.1.1指数与指数幂的运算（1）1. 若242x x =-，则x 的取值范围是（）A.0x >B.0x <C.0x ≥D.0x ≤ 2．计算20032004(32)(32)+⋅-的值是（）A.1B.32-C.32+D.23- 3．化简：()⎪⎭⎫ ⎝⎛<+-2391246322b a bab a 的结果是（）A.23a b -B.32b a -C. (23)a b ±-D.32ba - 4下列说法：①16的4次方根是2；②416的运算结果是±2； ③当n 为大于1的奇数时，n a 对任意a ∈R 有意义；④当n 为大于1的偶数时，na 只有当a ≥0时才有意义．其中正确的是( ) A ．①③④ B ．②③④ C ．②③ D ．③④5．求值（1）33(2)-=；（22(2)-=；（344(32)-=．6．当810x <<22(8)(10)x x --= ______． 70(52)9454552+-=-． 8726726+-．9化简：1212--+-+x x x x ） (12)x <<．10．化简：24334(1)(1)(1)x x x -+--1132343(1)(1)8x x ++ 12x y x y y x+++．2.1.1指数与指数幂的运算（2）１．下列运算中，正确的是（）A.5552a a a ⋅=B.56a a a +=C.5525a a a ⋅=D.5315()a a -=- ２．下列根式与分数指数幂的互化中．正确的是（）A.12()(0)x x =->13(0)y y =<C.340)xx -=>D.130)x x -=≠ 3．式子a ） A.111144a b B.111142a b C.114a D.114b4． 3216842111111(1)(1)(1)(1)(1)(1)222222++++++的值等于（） A.64112- B.63122- C.651122- D.32314(1)2-5．化简：（1）131121373222[()()()]ab ab b ---⋅⋅⋅=．（2）21131133344()()x y z x y z ---⋅⋅⋅⋅⋅=．（3)20a >=．6．若103,104x y ==，则10x y-=． 7.计算：π0＋2－2×21412⎪⎭⎫⎝⎛＝________.8.已知3a ＝2,3b ＝15，则32a －b ＝________.9．求值： 341681⎛⎫ ⎪⎝⎭， 12100-， 314-⎛⎫ ⎪⎝⎭10．已知0,0a b >>，化简：11112244()()a b a b -÷-11．化简求值： (1)()31064.0-－(－18)0＋4316＋2125.0；(2)a －1＋b －1(ab )－1(a ，b ≠0)．12．(能力提升)化简1111124242(1)(1)(1)x x x x x x -+++-+．13．(能力提升)已知a ＋a －1＝5，求下列各式的值： (1)a 2＋a －2；(2)2121--aa .2.1.2 指数函数及其性质（1）1．函数2(232)xy a a a =-+是指数函数，则a 的取值范围是（） A.0,1a a >≠ B.1a = C.12a = D.1a =或12a =2．函数y = ） A.(2,)-+∞ B.[1,)+∞ C.(,1]-∞- D.(,2)-∞-3．函数f (x )＝3x -3(1<x ≤5)的值域是( )A ．(0，＋∞) B．(0,9)C.⎝ ⎛⎦⎥⎤19，9D.⎝ ⎛⎭⎪⎫13，27 4．若函数y ＝(1－2a )x是实数集R 上的增函数，则实数a 的取值范围为( )A.⎝ ⎛⎭⎪⎫12，＋∞B ．(－∞，0)C.⎝⎛⎭⎪⎫－∞，12D.⎝ ⎛⎭⎪⎫－12，12 5．若221(2)(2)xxa a a a -++>++，则x 的范围为．6已知函数()f x 满足：对任意的12x x <，都有12()()f x f x <，且有1212()()()f x x f x f x +=⋅，则满足上述条件的一个函数是．7．将三个数10.20.7321.5,1.3,()3-按从小到大的顺序排列是8．（1）函数y =（2）函数y =的定义域是；值域是．9已知指数函数y ＝f (x )的图象过点M (3,8)，则f (4)＝________，f (－4)＝________.10．已知 2223422(),()(0,1)x x x x f x a g x a a a +-+-==>≠，确定x 的范围，使得()()f x g x >．11．实数,a b 满足11111212a b ++=--，则a b +=．12．(能力提升)若函数2121x xa ay ⋅--=-为奇函数，（1）确定a 的值；（2）讨论函数的单调性．2.1.2 指数函数及其性质（2）１．如图指数函数①x y a =②x y b =③x y c =④xy d =的图象，则（）A.01a b c d <<<<<B.01b a d c <<<<<C.1a b c d <<<<D.01a b d c <<<<<2．在同一坐标系中，函数xy a =与函数1y ax =+的图象只能是（）A B C D3．要得到函数122xy -=的图象，只要将函数1()4xy =的图象（）A.向左移1个单位B.向右移1个单位C.向左移0.5个单位D.向右移0.5个单位4．已知()|21|xf x =-，当a b c <<时，有()()()f a f c f b >>，则下列各式中正确的是 ( ) A.22a c > B.22a b > C.22ac -< D.222a c +<5函数y ＝2－x的图象是( )．6．若函数(1)(0,1)xy a b a a =-->≠图象不经过第二象限，则,a b 的满足的条件是_____________． 7．将函数21()3xy =图象的左移2个单位，再下移1个单位所得函数的解析式是； 8．函数21x y a+=-(0,1)a a >≠的图象过定点．9．函数22363xx y -+=的单调递减区间是．10．已知函数311()()212xf x x =+-，(1)求()f x 的定义域； 11．如果75+->x x a a (a >0，a ≠1)，(2)讨论()f x 的奇偶性； (3)证明：()0f x >．求x 的取值范围．12已知指数函数()(0,1)xf x a a a =>≠，根据它的图象判断121[()()]2f x f x +和12()2x x f +的大小（不必证明）．13．函数f (x )＝a x(a >0，且a ≠1)在区间[1,2]上的最大值比最小值大a2，求a 的值．2.1.2 指数函数及其性质（3）1．某种细菌在培养过程中，每20分钟分裂一次（一个分裂为两个），经过3小时，这种细菌由1个可繁殖成（）A.511个B.512个C.1023个D.1024个2．某商场进了A B 、两套服装，A 提价20%后以960元卖出，B 降价20%后以960元卖出，则这两套服装销售后（）A.赚不亏B. 赚了80元C.亏了80元D.赚了2000元 3.某商品降价20%后，欲恢复原价，则应提价（）A. 25%B.20%C.30%D.15%4.已知a ＝30.2，b ＝0.2－3，c ＝(－3)0.2，则a ，b ，c 的大小关系为( )．A.a >b >cB.b >a >cC.c >a >bD.b >c >a5．某新型电子产品2002年初投产，计划到2004年初使其成本降低36%，那么平均每年应降低成本.6. 据报道，1992年底世界人口达到54.8亿，若世界人口的年平均增长率为%x ，到2005年底全世界人口为y 亿，则y 与x 的函数关系是.7.某工厂的一种产品的年产量第二年比第一年增加21%，第三年比第二年增加44%，则这两年的平均增长率是.8．a ＝0.80.7，b ＝0.80.9，c ＝1.20.8，则a ，b ，c 的大小关系是________．9．函数y ＝a x在[0,1]上的最大值与最小值之和为3，则a ＝________.10.甲、乙两人于同一天分别携款1万元到银行储蓄。

高一数学集合知识点及练习题

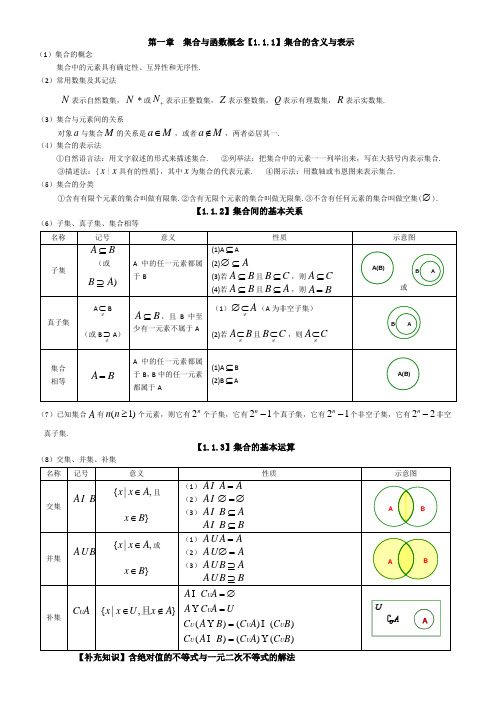
第一章集合与函数概念【1.1.1】集合的含义与表示（1）集合的概念集合中的元素具有确定性、互异性和无序性. （2）常用数集及其记法N 表示自然数集，N *或N +表示正整数集，Z 表示整数集，Q 表示有理数集，R 表示实数集.（3）集合与元素间的关系对象a 与集合M 的关系是a M ∈，或者a M ∉，两者必居其一. （4）集合的表示法①自然语言法：用文字叙述的形式来描述集合. ②列举法：把集合中的元素一一列举出来，写在大括号内表示集合.③描述法：{x |x 具有的性质}，其中x 为集合的代表元素. ④图示法：用数轴或韦恩图来表示集合. （5）集合的分类①含有有限个元素的集合叫做有限集.②含有无限个元素的集合叫做无限集.③不含有任何元素的集合叫做空集(∅).【1.1.2】集合间的基本关系（6）子集、真子集、集合相等（7）已知集合A 有(1)n n ≥个元素，则它有2n 个子集，它有21n -个真子集，它有21n -个非空子集，它有22n -非空真子集.【1.1.3】集合的基本运算（8）交集、并集、补集 B{x A A = ∅=∅ B A ⊆ B B ⊆ B{x A A = A ∅= B A ⊇ B B ⊇()A C B UA A U U U ==∅=【补充知识】含绝对值的不等式与一元二次不等式的解法（1）含绝对值的不等式的解法（2）一元二次不等式的解法0)例题讲解1.已知全集U R =，则正确表示集合{1,0,1}M =-和{}2|0N x x x =+=关系的韦恩（Venn ）图是 ( )答案 B解析由{}2|0N x x x =+=，得{1,0}N =-，则N M ⊂,选B.2.设U =R ，{|0}A x x =>，{|1}B x x =>，则U AB =ð( )A ．{|01}x x ≤<B ．{|01}x x <≤C ．{|0}x x <D ．{|1}x x > 答案 B解析对于{}1U C B x x =≤，因此U A B =ð{|01}x x <≤3.（北京文）设集合21{|2},{1}2A x xB x x =-<<=≤，则A B = （） A ．{12}x x -≤< B ．1{|1}2x x -<≤ C ．{|2}x x < D ．{|12}x x ≤<答案 A解析本题主要考查集合的基本运算以及简单的不等式的解法. 属于基础知识、基本运算的考查∵1{|2},2A x x =-<<{}2{1}|11B x x x x =≤=-≤≤， ∴{12}AB x x =-≤<，故选A.4.(山东卷理)集合{}0,2,A a =,{}21,B a =,若{}0,1,2,4,16AB =,则a 的值为 ( )A.0B.1C.2D.4 答案 D解析 ∵{}0,2,A a =,{}21,B a =,{}0,1,2,4,16A B =∴2164a a ⎧=⎨=⎩∴4a =,故选D.【命题立意】:本题考查了集合的并集运算,并用观察法得到相对应的元素,从而求得答案,本题属于容易题. 5.（全国卷Ⅱ文）已知全集U ={1，2，3，4，5，6，7，8}，M ={1，3，5，7}，N ={5，6，7}，则C u ( M N )=( ) A.{5，7} B.{2，4} C. {2.4.8} D. {1，3，5，6，7} 答案 C6.已知全集U R =，集合{212}M x x =-≤-≤和{21,1,2,}N x x k k ==-=的关系的韦恩（Venn ）图如图1所示，则阴影部分所示的集合的元素共有 ( )A. 3个B. 2个C. 1个D. 无穷多个答案 B解析由{212}M x x =-≤-≤得31≤≤-x ，则{}3,1=⋂N M ，有2个，选B. 7．设,a b R ∈，集合{1,,}{0,,}ba b a b a+=，则b a -= （） A ．1 B ．1- C ．2 D ．2-答案 C8．已知集合M ＝｛x |x ＜3｝，N ＝｛x |log 2x ＞1｝，则M ∩N ＝（）A ．∅B ．｛x |0＜x ＜3｝C ．｛x |1＜x ＜3｝D ．｛x |2＜x ＜3｝答案 D解析 {}{}2log 12N x x x x =>=>,用数轴表示可得答案D 。

高中数学第一章集合与函数的概念1.1集合1.1.3第二课时补集及综合应用aa高一数学

12/9/2021
第十六页，共二十五页。
【备用例1】已知集合(jíhé)A={x|2x-4<0},B={x|0<x<5},全集U=R,求:
(1)A∩B;
(2)(∁UA)∩B.
解:A={x|2x-4<0}={x|x<2},B={x|0<x<5}, (1)A∩B={x|0<x<2}. (2)因为(yīn wèi)A={x|x<2},全集U=R,
(C)A⊆U
(D)A=B
2.(补集运算)已知全集U={1,2,3,4,5,6,7},集合(jíhé)A={1,3,5,6},则∁UA等于(
)
(A){C1,3,5,6} (B){2,3,7}
(C){2,4,7}
(D){2,5,7}
解析(jiě xī):由题意知∁UA={2,4,7},选C.
12/9/2021
解
得
a=3,综上所述,所求
a
的取值范围为
{a|a≥3}.
12/9/2021Fra bibliotek第二十二页，共二十五页。
【备用(bèiyòng)例2】设全集是实数集R,A={x1 | ≤x≤3},B={x|x2+a<0}.
(1)当a=-4时,求A∩B和A∪B;
2
(2)若(∁RA)∩B=B,求实数a的取值范围.
解:(1)因为 A={x| 1 ≤x≤3},B={x|x2+a<0}, 2
12/9/2021
第十三页，共二十五页。
误区警示(jǐnɡ shì) (1)利用数轴求集合的交、并、补集运算时需注意点的虚实情况的变化. (2)通过改变原不等式的不等号方向取补集时,要防止漏解.如 A=｛x| 1 <0｝,∁RA≠

高中数学第一章集合与函数概念1.1集合1.1.3第2课时补集及集合运算的综合应用课件新人教A版必修1

2．已知集合A＝{x|x＜a}，B＝{x|x＜－1，或x＞ 0}，若A∩(∁RB)＝∅，求实数a的取值范围．
解：∵B＝{x|x＜－1，或x＞0}，
∴∁RB＝{x|－1≤x≤0}．因而要使A∩(∁RB)＝∅，结合数轴分析(如下图)，可得a≤－1.
1．全集与补集的互相依存关系 (1)全集并非是包罗万象，含有任何元素的集合，它是对于研究问题而言的一个相对概念，它仅含有所研究问题中涉及的所有元素，如研究整数，Z就是全集，研究方程的实数解，R 就是全集．因此，全集因研究问题而异． (2)补集是集合之间的一种运算．求集合A的补集的前提是 A是全集U的子集，随着所选全集的不同，得到的补集也是不同的，因此，它们是互相依存、不可分割的两个概念．
解：∁RB＝{x|x≤1 或 x≥2}≠∅. ∵A ∁RB，∴分 A＝∅和 A≠∅两种情况讨论． (1)若 A＝∅，此时有 2a－2≥a，∴a≥2； (2)若 A≠∅，则有2aa≤－1，2<a，或22aa－－22<≥a2，， ∴a≤1. 综上所述，a≤1 或 a≥2.
解答本题的关键是利用 A ∁RB，对 A＝∅与 A≠∅进行分类讨论，转化为等价不等式(组)求解，同时要注意区域端点的问题．
⑤ 搁置问题抓住老师的思路。碰到自己还没有完全理解老师所讲内容的时候，最好是做个记号，姑且先把这个问题放在一边，继续听老师讲后面的内容，以免顾此失彼。来自：学习方法网
⑥ 利用笔记抓住老师的思路。记笔记不仅有利于理解和记忆，而且有利于抓住老师的思路。
2019/5/25
最新中小学教学课件
25
谢谢欣赏！
求集合补集的基本方法及处理技巧
(1)基本方法：定义法．
(2)两种处理技巧：
①当集合用列举法表示时，直接套用定义或借助 Venn图求解．

精选推荐018-2019学年度高中数学第一章集合与函数的概念 1.1 集合 1.1.3 第一课时并集、交集练习新人教

第一课时并集、交集【选题明细表】1.设集合M={y|y=x2+1,x∈R},N={y|y=-x2+1,x∈R},则M∩N是( C )(A){0,1} (B){(0,1)}(C){1} (D)以上都不对解析:M∩N={y|y≥1}∩{y|y≤1}={1},选C.2.已知集合A={0,1,2,3,4,5},B={1,3,6,9},C={3,7,8},则(A∩B)∪C等于( C )(A){0,1,2,6,8} (B){3,7,8}(C){1,3,7,8} (D){1,3,6,7,8}解析:因为集合A={0,1,2,3,4,5},B={1,3,6,9},所以A∩B={1,3},因为C={3,7,8},所以(A∩B)∪C={1,3,7,8},故选C.3.满足{1,3}∪A={1,3,5}的所有集合A的个数是( D )(A)1 (B)2 (C)3 (D)4解析:因为{1,3}∪A={1,3,5},所以1和3可能是集合A的元素,5一定是集合A的元素,则集合A可能是{5},{1,5},{3,5},{1,5,3}共4个.故选D.4.(2018·重庆市第一中学高一月考)设集合A={(x,y)|x+y=1},B={(x,y)|2x-y=-4},则A∩B等于( D )(A){x=-1,y=2} (B)(-1,2)(C){-1,2} (D){(-1,2)}解析:由得所以A∩B={(-1,2)},故选D.5.已知集合A={1,3,m2},B={1,m},A∪B=A,则m等于( B )(A)3 (B)0或3 (C)1或0 (D)1或3解析:因为B∪A=A,所以B⊆A,因为集合A={1,3,m2},B={1,m},所以m=3,或m2=m,所以m=3或m=0.故选B.6.设集合A={x|x2-(a+3)x+3a=0},B={x|x2-5x+4=0},集合A∪B中所有元素之和为8,则实数a的取值集合为( D )(A){0} (B){0,3}(C){1,3,4} (D){0,1,3,4}解析:解方程x2-5x+4=0得x=4或1,所以B={1,4},解方程x2-(a+3)x+3a=0得x=3或a,所以A={3}或{3,a},因为1+4+3=8,所以A={3}或{3,0}或{3,1}或{3,4}.所以a=0或1或3或4.故选D.7.(2018·桂林一中高一期中)若集合A={x|2x+1>0},B={x|2x-1<2},则A∩B= .解析:由A中不等式解得x>-,即A={x|x>-},由B中不等式解得x<,即B={x|x<},则A∩B={x|-<x<}.答案:{x|-<x<|8.已知集合A={x|1≤x≤2},B={x|x<a},若A∩B=A,则实数a的取值范围是,若A∩B=∅,则a的范围为.解析:根据题意,集合A={x|1≤x≤2},若A∩B=A,则有A⊆B,必有a>2,若A∩B=∅,必有a≤1.答案:{a|a>2} {a|a≤1}9.集合A,B各有两个元素,A∩B中有一个元素,若集合C同时满足:(1)C⊆(A∪B),(2)C⊇(A∩B),则满足条件C的个数为( D )(A)1 (B)2 (C)3 (D)4解析:设A={a,b},B={b,c},由(1)知C⊆{a,b,c},由(2)知{b}⊆C,所以C中必有元素b,则C的个数为22=4,故选D.10.设A={x|2x2-px+q=0},B={x|6x2+(p+2)x+5+q=0},若A∩B={},则A∪B等于( A )(A){,,-4} (B){,-4}(C){,} (D){}解析:由A∩B={}知,∈A,∈B,所以⇒所以A={x|2x2+7x-4=0}={-4,},B={x|6x2-5x+1=0}={,}.显然,A∪B={,,-4}.故选A.11.已知集合A={4,5,2},B={4,m},若A∪B=A,则m= .解析:因为A∪B=A,所以B⊆A.又A={4,5,2},B={4,m}.所以m=5或m=2.由m=2知m=0或m=4.当m=4时与集合中元素的互异性矛盾,故m=0或5.答案:0或512.已知集合A={x|2a+1≤x≤3a-5},B={x|x<-1,或x>16},若A⊆(A∩B),求实数a的取值范围. 解:因为A⊆(A∩B),且(A∩B)⊆A,所以A∩B=A,即A⊆B.显然A=∅满足条件,此时a<6.若A≠∅,如图所示,则或由解得a∈∅;由解得a>.综上,满足条件A⊆(A∩B)的实数a的取值范围是{a|a<6,或a>}.13.已知集合A={x|2m-1<x<3m+2},B={x|x≤-2或x≥5},是否存在实数m,使A∩B≠∅?若存在,求实数m的取值范围;若不存在,请说明理由.解:若A∩B=∅,分A=∅和A≠∅讨论:(1)若A=∅,则2m-1≥3m+2,解得m≤-3,此时A∩B=∅;(2)若A≠∅,要使A∩B=∅,则应有即所以-≤m≤1.综上,当A∩B=∅时,m≤-3或-≤m≤1,所以当m取值范围为{m|-3<m<-或m>1}时,A∩B≠∅.。

必修一第一章集合与函数概念同步练习(含答案)

第一章集合与函数概念同步练习1.1.1 集合的含义与表示一. 选择题：1.下列对象不能组成集合的是（）A.小于100的自然数B.大熊猫自然保护区C.立方体内若干点的全体D.抛物线2x y =上所有的点 2.下列关系正确的是（）A.N 与+Z 里的元素都一样B.},,{},,{c a b c b a 与为两个不同的集合C.由方程0)1(2=-x x 的根构成的集合为}1,1,0{D.数集Q 为无限集 3.下列说法不正确的是（）A.*0N ∈B.Z ∉1.0C.N ∈0D.Q ∈24.方程⎩⎨⎧-=-=+3212y x y x 的解集是（）A.}1,1{-B.)1,1(-C.)}1,1{(-D.1,1-二.填空题：5.不大于6的自然数组成的集合用列举法表示______________.6.试用适当的方式表示被3除余2的自然数的集合____________.7.已知集合}7,3,2,0{=M ，由M 中任取两个元素相乘得到的积组成的集合为 ________. 8.已知集合}012{2=++∈=x ax R x M 只含有一个元素，则实数=a ______,若M 为空集,可a 的取值范围为_________.三.解答题：9.代数式}{)8(2x x x ∈-- ，求实数x 的值。

10.设集合A=},,2),{(N y x x y y x ∈+-=，试用列举法表示该集合。

11.已知}33,2{12+++∈x x x 试求实数x 的值。

1.1.2 集合的含义与表示一. 选择题：1.集合Φ与}0{的关系，下列表达正确的是（） A.φ=}0{ B.φ⊆}0{ C.}0{∈φ D.φ}0{⊇2.已知集合A=}3,2,1{，则下列可以作为A 的子集的是（）A.}4,1{B.}3,2{C.}4,2{D.}4,3,1{ 3.集合},,{c b a 的非空真子集个数是（）A.5B.6C.7D.8 4.已知集合M={正方形}，N={菱形}，则（）A.N M =B.N M ∈C.M ≠⊂ND.N ≠⊂M二.填空题5.用适当的符号填空①},2_____{0Z n n x x ∈=②}_____{1质数③},,_____{}{c b a a ④}0))((_____{},{=--b x a x x b a ⑤},12______{},14{++∈+=∈+=N k k x x N k k x x 6.写出集合}1{2=x x 的所有子集_______________________7.设集合}{},63{a x x B x x A <=≤<-=，且满足A ≠⊂,B 则实数a 的取值范围是_________三.解答题8.已知集合B 满足}2,1{≠⊂B ⊆}5,4,3,2,1{，试写出所有这样的集合 9.已知}5{>=x x A ，}3{x x B <=，试判断A 与B 的关系 10.已知A=}3,4,1{},2,1{a B a =+，且B A ⊆，求a 的值1.1.3集合的基本运算（一）一.选择题1.已知集合A=}4,3,2,1{，}6,4,1{=B ，则=B A I （） A.}4,2,1{ B.}6,4,3,2,1{ C.}4,1{ D.}4,3,1{2.设A=}2{->x x ，}21{<<-=x x B ，则=B A Y （） A.R B.}2{<x x C.}1{->x x D.}2{->x x3.设{=A 等腰三角形} ，B={等边三角形}，C={直角三角形}，=C B A I Y )(（） A.{等腰三角形} B.{直角三角形} C.φ D.{等腰直角三角形}4.已知集合}90{<<∈=x Z x M ，},2{+∈==N n n x x N ，则=N M I （）A.{}6,4,2B.{}8,6,4,2C.{}7,6,5,4,3,2D.{}8,7,6,5,4,3,2,1 二.填空题5.{偶数}I {奇数}=__________.6.已知集合}31{<≤-=x x A ，}13{≤<-=x x B ，则=B A I __________.7.若集合A B A =I ，则=B A Y ___________.8.已知集合}33{<≤-=x x A ，}2{≤=x x B ，则=B A Y ___________.三.解答题9.集合},,523),{(R y x y x y x A ∈=-=},,132),{(R y x y x y x B ∈-=+=，求 B A I 10.已知集合},3,1{a A =，}1,1{2+-=a a B ，且A B A =Y ，求a 的值 11.已知集合},02{2=+-∈=b ax x R x A }05)2(6{2=++++∈=b x a x R x B且}21{=B A I ，求B A Y1.1.3集合的基本运算（二）一.选择题1.已知全集R U =，集合}1{<=x x M ，则M C u 为（） A.}1{≥x x B.}1{>x x C.}1{<x x D.}1{≤x x2.设全集}4,3,2{=U ，}2,3{-=a A ，}3{=A C u ，则a 的值是（） A.7 B.1- C.17-或 D.71-或3.已知全集R U =，集合}32{<≤-=x x A ，则A C u =（）A.}32{≥-≤x x x 或B.}32{>-≤x x x 或C.}32{>-<x x x 或D.}32{≥-<x x x 或 4.已知全集}8,7,6,5,4,3,2,1{=U ，集合}5,4,3{=A ，}6,3,1{=B ，那么集合 C={2，7，8}可以表示为（）A.B C uB.B A IC.B C A C u u ID.B C A C u u Y二.填空题5.设全集R U =，}62{<≤=x x A ，}4{≤=x x B ，则B A I =__，__=B C A u I ,__=B A C u I .6.全集=U {三角形}，=A {直角三角形}，则A C u =____________.7.设全集}4,3,2,1,0{=U }3,2,1,0{=A ，}4,3,2{=B ，则=B A C u I ____8.已知全集},2,1,0{=U 且}2{=A C u ，则A 的真子集共有___个.三.解答题9.设全集R U =，集合},43{R x x x M ∈<≤-=，},51{R x x x N ∈≤<-=,求①N M Y ②N C M C u u I10.设全集=U {1，2，3，4，5，6，7，8，9}，集合}2{=B A I ，}9,1{=B C A C u u I ，}8,6,4{=B A C u I ，求B A ,11.已知}1,4,2{2+-=x x U ，}1,2{+=x B ，}7{=B C u ，求x 的值1.2.1函数的概念（一）一.选择题1.函数13)(+=x x f 的定义域为（）A.)31,(--∞B.),31(+∞- C.),31[+∞- D.]31,(--∞2.已知函数q px x x f ++=2)(满足0)2()1(==f f ，则)1(-f 的值为（） A.5 B.5- C.6 D.6-3.下列函数中)()(x g x f 与表示同一函数的是（）A.1)()(0==x g x x f 与 B.xx x g x x f 2)()(==与C.22)1()()(+==x x g x x f 与D.33)()(x x g x x f ==与 4.下列各图象中，哪一个不可能为)(x f y =的图象（）二.填空题5.已知x x x f 2)(2-=，则=)2(f ______________.6.已知12)1(2+=+x x f ,则=)(x f ______________.7.已知)(x f 的定义域为],4,2[则)23(-x f 的定义域为_______________. 8.函数11)(22---=x x x f 的定义域为______________.三.解答题9.设⎩⎨⎧≥+<-=)0(22)0(12)(2x x x x x f ，求)2(-f 和)3(f10.求下列函数的定义域（1）321)(+=x x f （2）x x x g -++=1)10()(011.已知)(x f 为一次函数，且34)]([+=x x f f ，求)(x fx(D)(B)(C) (A)x1.2.1函数的概念（二）一、选择题1.函数x x y 22-=的定义域为}3,2,1,0{，其值域为（） A.}3,0,1{- B.}3,2,1,0{ C.}31{≤≤-y y D.}30{≤≤y y2.函数)(11)(2R x xx f ∈+=的值域是（） A.)1,0( B.]1,0( C.)1,0[ D.]1,0[ 3.下列命题正确的有（） ①函数是从其定义域到值域的映射②x x x f -+-=23)(是函数③函数)(2N x x y ∈=的图象是一条直线④x x g xx x f ==)()(2与是同一函数 A.1个 B.2个 C.3个 D.4个 4.函数xx x y -+=)32(的定义域为（）A.⎭⎬⎫⎩⎨⎧-≠<230x x x 且B.{}0<x xC.{}0>x xD.⎭⎬⎫⎩⎨⎧-≠≠∈230x x R x 且二.填空题5.已知函数⎪⎩⎪⎨⎧≥<<--≤+=2,221,1,2)(2x x x x x x x f ，若3)(=x f ，则x 的值为__________.6.设函数33)(2+-=x x x f ，则)()(a f a f --等于____________.7.设函数x x x f --=1)(，则=)]1([f f ____________.8.函数[]3,1,322∈+-=x x x y 的值域是________________.三.解答题9.求函数242x x y --=的值域10.已知函数1122---=x x y ，求20072008y x +的值 11.已知函数bax xx f +=)(（a .0≠a ，b 且为常数）满足1)2(=f ，x x f =)(有唯一解，求函数)(x f y =的解析式和)]3([-f f 的值.1.2.2 函数表示法（一）一、选择题1.设集合{}c b a A ,,=，集合B=R ，以下对应关系中，一定能成建立A 到B 的映射的是（）A.对A 中的数开B.对A 中的数取倒数C.对A 中的数取算术平方D.对A 中的数开立方2.某人从甲村去乙村，一开始沿公路乘车，后来沿小路步行，图中横轴表示走的时间，纵轴表示某人与乙村的距离，则较符合该人走法的图是（）3.已知函数23)12(+=+x x f ，且2)(=a f ，则a 的值等于（）A.8B.1C.5D.1-4.若x xx f -=1)1(，则当10≠≠x x 且时，)(x f 等于（）A.x 1B.11-xC.x -11D.11-x二.填空题5.若[]36)(+=x x g f ，且12)(+=x x g ，则=)(x f ______________.6.二次函数的图象如图所示，则此函数的解析式为___________.ttt ABDC7.已知函数⎩⎨⎧<≥=0,0,)(2x x x x x f 则=-)2(f ________,)4(f =_______8.集合}5,3,1{-=B ，12)(-=x x f 是A 到B 的函数，则集合 A 可以表示为____________________三.解答题9.已知函数)(x f 是一次函数，且14)]([-=x x f f ，求)(x f 的解析式10.等腰三角形的周长为24，试写出底边长y 关于腰长x 的函数关系式，并画出它的图象 11.作出函数31--+=x x y 的图象，并求出相应的函数值域1.2.2 函数表示法（二）一、选择题1.已知集合{}{}20,40≤≤=≤≤=y y B x x A ，按对应关系f ，不能成为从A 至B 的映射的一个是（） A.x y x f 21:=→ B.2:-=→x y x f C.x y x f =→: D.2:-=→x y x f2.如图，函数1+=x y 的图象是（）y3.设}8,6,2,1,0,21{},4,2,1,0{==B A ，下列对应关系能构成A 到B 的映射的是（）A.1:3-→x x fB.2)1(:-→x x fC.12:-→x x fD.x x f 2:→4.已知函数⎩⎨⎧>+-≤+=1,31,1)(x x x x x f ，则⎥⎦⎤⎢⎣⎡)25(f f =（） A.21 B.23 C.25 D.29 二.填空题5.设函数⎪⎪⎩⎪⎪⎨⎧≥<≤-<≤-+=2,320,2101,22)(x x x x x x f ，则)43(-f 的值为______, )(x f 的定义域为_____.6.)(x f 的图象如图，则)(x f =____________.7.对于任意R x ∈都有)(2)1(x f x f =+，当10≤≤x 时，)5.1-的值是____________.8.23)1(+=+x x f ，且2)(=a f ，则a 的值等于____________.三.解答题9.作出下列函数的图象（1）x y -=1,)2(≤∈x Z x 且（2）3422--=x x y ,)30(<≤xA B CD10.已知函数⎩⎨⎧<+≥-=4),3(4,4)(x x f x x x f ，求)1(-f 的值11.求下列函数的解析式（1）已知)(x f 是二次函数，且1)()1(,2)0(-=-+=x x f x f f ，求)(x f （2）已知x x f x f 5)()(3=-+，求)(x f1.3.1 函数单调性与最大（小）值（一）一.选择题1.若),(b a 是函数)(x f y =的单调递增区间，()b a x x ,,21∈，且21x x <，（） A.)()(21x f x f < B.)()(21x f x f = C.)()(21x f x f > D.以上都不正确2.下列结论正确的是（）A.函数x y -=在R 上是增函数B.函数2x y =在R 上是增函数C.x y =在定义域内为减函数D.xy 1=在)0,(-∞上为减函数 3.函数111--=x y （） A.在),1(+∞-内单调递增 B.在),1(+∞-内单调递减 C.在),1(+∞内单调递增 D.在),1(+∞内单调递减 4.下列函数在区间),0(+∞上为单调增函数的是（） A.x y 21-= B.x x y 22+= C.2x y -= D.xy 2=二.填空题5.已知函数)(x f 在),0(+∞上为减函数，那么)1(2+-a a f 与)43(f 的大小关系是________.6.函数)(x f y =7.已知13)(22-+-=a ax ax x f )0(<a ，则3(f ______.8.函数342+--=x x y 的单调递增区间为_______,当=x _______时,y 有最______值为____.三.解答题9.已知)(x f y =在定义域)1,1(-上为减函数，且)1()1(2-<-a f a f 求a 的取值范围。

2018-2019学年高中数学第一章集合与函数概念 1.1 集合 1.1.3 第2课时补集及集合运算的综合应用练习新人

大道之行也，天下为公，选贤与能，讲信修睦。

故人不独亲其亲，不独子其子，使老有所终，壮有所用，幼有所长，矜、寡、孤、独、废疾者皆有所养，男有分，女有归。

货恶其弃于地也，不必藏于己；力恶其不出于身也，不必为己。

第一章 1.1 1.1.3 第2课时补集及集合运算的综合应用1．设全集U＝{1,2,3,4,5,6}，A＝{1,2}，B＝{2,3,4}，则A∩{∁U B}＝( )A．{1,2,5,6} B．{1}C．{2} D．{1,2,3,4}解析：因为∁U B＝{1,5,6}，所以A∩(∁U B)＝{1}，故选B.答案：B2．已知全集U＝R，A＝{x|x≤0}，B＝{x|x≥1}，则集合∁U(A∪B)＝( )A．{x|x≥0}B．{x|x≤1}C．{x|0≤x≤1}D．{x|0＜x＜1}解析：由题意可知，A∪B＝{x|x≤0或x≥1}，所以∁U(A∪B)＝{x|0＜x＜1}．答案：D3．设全集U＝R，集合A＝{x|x≥1}，B＝{x|0≤x≤2}，则∁U(A∩B)是( )A．{x|1≤x≤2}B．{x|0≤x≤1}C．{x|x＞2或x＜1} D．{x|0≤x＜1}解析：∵A∩B＝{x|1≤x≤2}，∴∁U(A∩B)＝{x|x＞2或x＜1}．答案：C4．设集合S＝{三角形}，A＝{直角三角形}，则∁S A＝____________________.答案：{锐角三角形或钝角三角形}5．设集合U＝{1,2,3,4,5}，A＝{2,4}，B＝{3,4,5}，C＝{3,4}，则(A∪B)∩(∁U C)＝________.解析：A∪B＝{2,3,4,5}，∁U C＝{1,2,5}，故(A∪B)∩(∁U C)＝{2,5}．答案：{2,5}6．设U＝R，A＝{x|a≤x≤b}，∁U A＝{x|x＜3或x＞4}，求a，b的值．解：∵A＝{x|a≤x≤b}，∴∁U A＝{x|x＜a或x＞b}．又∁U A＝{x|x＜3或x＞4}，∴a＝3，b＝4.1。