§15-3 康普顿效应
《康普顿效应》课件

实验中的注意事项与误差控制
01
注意事项
02
1. 确保X射线源的强度适中,避免对实验装置造成过 大的负荷。
03
2. 确保散射物质的纯度和厚度,以减小误差。
实验中的注意事项与误差控制
• 保持实验环境的温度和湿度恒定,以减小误差。
实验中的注意事项与误差控制
01
误差控制
02
03
04
1. 使用高精度的测量设备, 如单色仪和光谱仪,以提高测
通过研究不同材料对康普顿效应的影响,可以为材料科学 中的光子控制、光子与物质相互作用等领域提供新的思路 和方法。
要点二
与生物医学的交叉研究
康普顿效应在生物医学领域具有潜在的应用价值,如光子 医学、光子成像等,通过跨学科合作可以推动这些领域的 发展。
THANKS
感谢您的观看
量精度。
2. 对实验数据进行多次测量 和平均,以减小误差。
3. 对实验数据进行合理的统 计和分析,以得出正确的结论
。
04
康普顿效应的应用 领域
天文学观测
观测遥远天体
康普顿效应可用于观测遥远的天体,通过分析星光与大气分子的相互作用,了 解天体的性质和结构。
探测暗物质
通过观测宇宙射线与大气分子的相互作用,利用康普顿效应可以间接探测暗物 质的存在。
光子与电子的相互作用过程中,光子的能量传递给电子,导 致光子的能量降低,同时电子获得能量并可能从原子中逸出 。
康普顿散射的过程与结果
康普顿散射是指当高能光子(如X射线或伽马射 线)与物质中的电子相互作用时,光子能量降 低并改变运动方向的现象。
在康普顿散射过程中,光子的能量降低,运动 方向发生改变,同时产生一个或多个低能光子 。这一过程可以用量子力学来描述。
康普顿效应名词解释

康普顿效应名词解释在原子物理学中,康普顿散射,或称康普顿效应(英语:Compton effect),是指当X射线或伽马射线的光子跟物质相互作用,因失去能量而导致波长变长的现象。
相应的还存在逆康普顿效应——光子获得能量引起波长变短。
这一波长变化的幅度被称为康普顿偏移。
康普顿效应通常指物质电子云与光子的相互作用,但还有物质原子核与光子的相互作用——核康普顿效应存在。
康普顿效应首先在1923年由美国华盛顿大学物理学家康普顿观察到,并在随后的几年间由他的研究生吴有训进一步证实。
康普顿因发现此效应而获得1927年的诺贝尔物理学奖。
这个效应反映出光不仅仅具有波动性。
此前汤姆孙散射的经典波动理论并不能解释此处波长偏移的成因,必须引入光的粒子性。
这一实验说服了当时很多物理学家相信,光在某种情况下表现出粒子性,光束类似一串粒子流,而该粒子流的能量与光频率成正比。
在引入光子概念之后,康普顿散射可以得到如下解释:电子与光子发生弹性碰撞(弹性碰撞产生的非弹性散射),电子获得光子的一部分能量而反弹,失去部分能量的光子则从另一方向飞出,整个过程中总动量守恒,如果光子的剩余能量足够多的话,还会发生第二次甚至第三次弹性碰撞。
康普顿散射可以在任何物质中发生。
当光子从光子源发出,射入散射物质(一般指金属)时,主要是与电子发生作用。
如果光子的能量相当低(与电子束缚能同数量级),则主要产生光电效应,原子吸收光子而产生电离。
如果光子的能量相当大(远超过电子的束缚能)时,则我们可以认为光子对自由电子发生散射,而产生康普顿效应。
如果光子能量极其大(>1.022百万电子伏特)则足以轰击原子核而生成一对粒子:电子和正电子,这个现象被称为成对产生。
由于光子具有波粒二象性,因此,应该可以用波动理论诠释这效应。
埃尔温·薛定谔于1927年给出半经典理论。
这理论是用经典电动力学来描述光子,用量子力学来描述电子。
:28, 286康普顿效应对放射生物学十分重要,由于它是高能量X射线与生物中的原子核间,最有可能发生的相互作用,因此亦被应用于放射疗法。
15-3 康普顿效应
Il 较大 I l0
二、光子论对康普顿效应的解释
1. 经典物理遇到的困难 • 根据经典电磁波理论,当电磁波通过物质时,物 质中带电粒子将作受迫振动,其频率等于入射光 频率,所以它所发射的散射光频率应等于入射光 频率: l 0 o 在 • 电磁波为横波, j 90 方向无散射波 经典物理无法解释康普顿效应.
l 10.24nm
'
Ek 4.6610 J
17
44 18
o
'
在康普顿效应中,入射的 x 射线波长为 5.00×10-2nm, 求在散射角为60°方向上 散射 x 射线的波长和引起这种散射的反 冲电子所获得的动能。
h l l0 (1 cos ) m0c h 2.43 1012 m m0c
E p c E
2 2 2
2 0
E0 0 ,
E h h p c c l
E pc
“波粒二象性”
借用经典“波”和“粒子” 术语,但既不是经典波,又 不是经典粒子
描述光的 粒子性
IA IN
2
E h
p h
描述光的 波动性
l
N A2
振幅越大,表示光子数越多, 光子到达该处概率越大
—— 概率波
1.波长为0.710Ǻ的X射线投射到石墨上,在与入射方向 成45o角处,观察到康普顿散射的波长变化为多少Ǻ? A. √ 0.0071 B. 0.071 C. 0.036 D. 0.703 2.波长为=0.0708nm的x射线,在石蜡上受到康普顿散射, 则在方向上所散射的x射线的波长为 :
)m0c 2.0410 ( J )
2
14
Ek l0
hc
15 量子物理基础—康普顿效应及光子理论的解释

4.5 1023 kgms 1
h/
tan (h ) /( h 0 ) 0
0.20 arctan 42.3 0.22
视为黑体,则 1)太阳表面的温度; 2)太阳的辐射功率; 3)由于热辐射而使太阳质量耗损1%经历的时间。 (已知太阳半径 RS=6.96×108m, 质量Ms=2 ×1030kg)
解:
1)根据维恩位移定律 mT b
T
b m
2.897103 m K 49010 9 m
5.9 103 K
大学物理 第三次修订本
15
第15章 量子物理基础
实验规律
(1) 对于原子量较小的散射物质,康普顿散射 较强,反之较弱。 (2)波长的改变量 -0 随散射角θ的增加而增加。
(3)对不同的散射物质,只要在同一个散射角下, 波长的改变量 - 0 都相同。
大学物理 第三次修订本
16
第15章 量子物理基础
(3)电子的初速度
19
第15章 量子物理基础 例2 钾的光电效应红限为0= 6.210-7m。求(1)电子 的逸出功;(2)在波长为3.0 10-7m的紫外线照射下, 遏止电压为多少?(3)电子的初速度为多少? 解 (1)逸出功
2eU a 2 1.6 10 2.14 vm ms 1 8.67 105 ms 1 11 m 9.11031 大学物理 第三次修订本
0.01M s c 11 t 10 年 P
大学物理 第三次修订本
5
2
第15章 量子物理基础 1、光电效应的实验
饱和电流∝光强度I
存在截止频率: > 0
瞬时性
1 2 mVm ekν eU 0 最大初动能与入射频率成线性关系: 2
康普顿效应

康普顿效应康普顿效应是指X射线与物质相互作用时发生的散射现象。
这一现象是由美国物理学家康普顿于20世纪20年代首次发现和研究的,因此得名。
1. 康普顿效应的原理康普顿效应的原理可以通过经典的散射理论进行解释。
当X射线与物质发生散射时,X射线会和物质中的自由电子发生相互作用。
根据经典电磁理论,电磁波的能量与频率有关,而不受辐射源的改变。
因此,当X射线被散射时,其频率保持不变。
然而,康普顿发现当X射线与自由电子相互作用时,散射X射线的频率发生了变化。
他的实验表明,散射X射线的频率比入射X射线的频率低,且频率差与散射角度成正比。
这一发现违背了经典电磁理论的预期,为新的量子理论提供了重要的实验依据。
2. 康普顿散射公式康普顿散射公式描述了康普顿效应中散射X射线频率变化和散射角度之间的关系。
该公式可以用来计算散射角度和散射波长之间的关系。
康普顿散射公式的表达式如下:λ' - λ = (h / m_e) * (1 - cosθ)其中,λ’是散射X射线的波长,λ是入射X射线的波长,h是普朗克常数,m_e 是电子的质量,θ是散射角度。
康普顿散射公式的重要性在于它揭示了X射线的粒子性质。
通过实验测量散射角度和散射波长之间的关系,可以验证量子理论对X射线的正确性。
3. 康普顿效应的应用康普顿效应在物理学和医学领域有广泛的应用。
3.1 X射线散射的研究康普顿效应的发现为研究物质的结构和性质提供了新的手段。
通过测量散射X射线的频率和角度,可以获取有关物质中电子的信息。
这对于研究晶体结构、材料表面性质等具有重要意义。
3.2 医学影像学康普顿效应在医学影像学中的应用非常广泛。
通过X射线扫描,可以获取人体内部组织和骨骼的影像。
康普顿效应的散射X射线可以提供有关组织密度和成分的信息,进而帮助医生进行疾病诊断和治疗方案的制定。
3.3 安全检测康普顿效应也被应用于安全检测领域。
通过测量散射X射线的频率和散射角度,可以检测出携带危险物品或非法物品的人员。
康普顿效应ppt课件

当光线通过大气中的气溶胶时,会发生米氏散射。米氏散射的散射强度与波长 的二次方成反比。
相关诺贝尔奖得主介绍
康普顿
康普顿因发现康普顿效应而获得 1927年诺贝尔物理学奖。
德布罗意
德布罗意提出物质波理论,认为所 有微观粒子都具有波粒二象性,并 因此获得1929年诺贝尔物理学奖 。
戴维森和汤姆逊
光学仪器设计
在光学仪器设计中,利用康普顿效应可以更好地控制和调 整光的传播路径和聚焦,提高仪器的准确性和稳定性。
医学成像与诊断
康普顿效应在医学成像与诊断中发挥了重要作用,如X射 线和CT成像技术,通过探测光子与物质相互作用产生的散 射和能量变化来获取人体内部结构信息。
对未来科技发展的启示
1 2 3
偏转角的大小取决于入射光子的能量、物质的性质以及碰撞过程中的散射角。
通过测量偏转角,可以研究物质的结构和性质,以及光子与物质的相互作用机制。
03
康普顿效应的实验验证
实验设备与材料
康普顿散射实验装置 光电倍增管
X射线源 测量仪器
实验步骤与操作
将X射线源放置在实验装置的一端 ,将光电倍增管放置在另一端, 用于检测散射后的X射线。
康普顿散射的过程
入射光子与物质原子或分子的电子发 生碰撞,传递能量和动量给电子。
散射光子的能量低于入射光子的能量 ,这是由于部分能量传递给电子。
电子获得能量后,跃迁到更高能级, 并释放出一个与入射光子方向不同的 散射光子。
康普顿效应的定量描述
康普顿散射的偏转角是一个重要的物理量,它描述了散射光子与入射光子之间的夹 角。
康普顿效应PPT课件
contents
目录
• 康普顿效应概述 • 康普顿效应的物理原理 • 康普顿效应的实验验证 • 康普顿效应的意义与影响 • 康普顿效应的扩展知识
康普顿效应

康普顿效应科技名词定义中文名称:康普顿效应英文名称:Compton effect其他名称:康普顿散射(Compton scattering)定义:短波电磁辐射(如X射线,伽玛射线)射入物质而被散射后,除了出现与入射波同样波长的散射外,还出现波长向长波方向移动的散射现象。
所属学科:大气科学(一级学科);大气物理学(二级学科)本内容由全国科学技术名词审定委员会审定公布康普顿效应实验原理图1923年,美国物理学家康普顿在研究x射线通过实物物质发生散射的实验时,发现了一个新的现象,即散射光中除了有原波长l0的x光外,还产生了波长l>l0 的x光,其波长的增量随散射角的不同而变化。
这种现象称为康普顿效应(compton effect)。
用经典电磁理论来解释康普顿效应遇到了困难。
康普顿借助于爱因斯坦的光子理论,从光子与电子碰撞的角度对此实验现象进行了圆满地解释.我国物理学家吴有训也曾对康普顿散射实验作出了杰出的贡献。
目录康普顿效应 compton effect对康普顿散射现象的研究经历了一、二十年才得出正确结果。
康普顿效应第一次从实验上证实了爱因斯坦提出的关于光子具有动量的假设。
这在物理学发展史上占有重要的位置。
光子在介质中和物质微粒相互作用时,可能使得光向任何方向传播,这种现象叫光的散射.康普顿效应1922年,美国物理学家康普顿在研究石墨中的电子对X射线的散射时发现,有些散射波的波长比入射波的波长略大,他认为这是光子和电子碰撞时,光子的一些能量转移给了电子,康普顿假设光子和电子、质子这样的实物粒子一样,不仅具有能量,也具有动量,碰撞过程中能量守恒,动量也守恒.按照这个思想列出方程后求出了散射前后的波长差,结果跟实验数据完全符合,这样就证实了他的假设。
这种现象叫康普顿效应。
编辑本段发现1922~1923年康普顿研究了X射线被较轻物质(石墨、石蜡等)散射后光的成分,发现散射谱线中除了有波长与原波长相同的成分外,还有波长较长的成分。
15-3 康普顿效应
= 0
45
90
135
对不同散射元素 (在同一角下) 随原子序数 Z • I0 、 I
0
鞍山科技大学 姜丽娜
2
• 二、康普顿的理论解释 • • • •
•
· 经典电磁理论只能解释波长不变的散射光; · 康普顿用光子的概念解释了上述现象。 1.物理图象 · 假定:入射光由光子组成; 光子和散射物中的受原子束缚较
3
三、定量分析 康普顿散射效应
X射线光子与“静止”的“自由电子”弹性碰撞
碰撞过程中能量守恒
碰撞过程中动量守恒
m
波长偏移 ——与实验吻合
鞍山科技大学 姜丽娜 4
• 式中 •
c
h m0c
= 0.0242621Å
0.0243 Å = 24310-12米
•
c 称作 康普顿波长
鞍山科技大学 姜丽娜 5
• 四、讨论
• • • • • • • • • • • • • 1. 只和 有关, = 0 = 0,只有 0 的散射光; = 900 = c,有 0和 0 c 两种散射光; = 1800 = 2c,有 0和 0 2c 两种散射光。 2.为何只有X光才有康普顿散射现象? 由 0 ccos 第二项数量级约00243 A,只有0也很小时,才有明显的 3.为什么还有 0的散射光存在? 光子与束缚较紧的电子的碰撞,应看作是和整个原子相碰。 · 因 原子质量 >> 光子质量, 在弹性碰撞中散射光子的能量(波长)几乎不变。 · 或由 = (1 - cos )h/M0c很小而知。 (M0:原子静止质量)
可以直接求出普朗克常数。
O P
鞍山科技大学 姜丽娜
15-3 康普顿效应

Δ 0
在同一散射角下,对于所有的散射物质,波 长的改变量都相同。
相对原子质量小的物质,康普顿散射比较显著, 相对原子质量大的物质,康普顿散射较弱;
二、康普顿散射的解释 1. 经典理论遇到的困难 按经典理论是X射线的电场迫使散射物中的电子作受迫振动,而向周围辐射同频率的电磁波 的过程。
0.750
波长 λ
o (A)
不同侧面
(干涉、衍射)
粒子性 突出表现在与物质相互作用中
(光电效应、康普顿效应、)
光在传播过程中表现出波的特性,而在与物质相互作用的过程中表现出粒子的特 性。这就是说,光具有波和粒子两方面的特性,称为光的波粒二象性。
单纯用 波动 均不能完整地描述光的性质 粒子
光既是粒子,又是波。 光既不是经典观念中的粒子,也不是经典观念中的波。
射X射线。求:
(1) 散射X射线相对于入射线的波长改变量;
(2) 引起这种散射的反冲电子所获得的动能Ek。
解: (1) 波长的改变量为
Δ h (1 cos) 2.431012(1 cos90 )m
m0c = 2.4310- 12m.
(2) 反冲电子所获得的动能Ek等于X光子损失的能量
所以
Ek mc 2 m0c2 h0 h
碰撞后: 反冲电子:速度为u,与x轴正方向成θ角,质量m;
光子:频率为ν,能量hν,动量hν/c,与x轴正方向成φ角。
h
c
h 0
c
e
θ
x
e
mu
h 0 m0c2 h mc 2 p0 p1 p2
(mu)2 ( h 0 )2 ( h )2 2( h 0 )( h )cos
c
康普顿 效应

康普顿效应康普顿效应,也称为康普顿散射,是描述X射线通过物质时发生散射现象的一种物理现象。
这一现象是由于X射线与物质中的自由电子发生碰撞而发生的。
康普顿效应是近代物理学的重要发现之一,对现代物理学的发展产生了重要影响。
康普顿效应是由美国物理学家康普顿于1923年发现的。
他在实验中发现,当X射线入射到物质中时,会与物质中的自由电子发生碰撞,从而使X射线发生能量和波长的变化。
这一现象被称为康普顿效应。
康普顿效应证实了光的粒子性质,并为验证爱因斯坦的光量子假设提供了实验证据。
康普顿效应的实验装置通常包括一个X射线源、一个散射物体(通常是金属),以及一个能观测到散射后X射线的探测器。
实验过程中,X射线源会发射出一束高能量的X射线,入射到散射物体上。
与散射物体内的自由电子发生碰撞后,X射线的能量和波长会发生变化,并且出射角度也会发生改变。
观测到的散射射线的能量和角度分布可以用来研究康普顿效应。
康普顿效应可以用普朗克常数和电子质量来描述。
根据康普顿效应的理论,入射X射线和散射X射线的波长差值与散射角度有关,可以通过以下公式表示:Δλ = λ' - λ = h/mc * (1 - cosθ)其中,Δλ为散射射线的波长差值,λ'和λ分别为散射射线和入射射线的波长,h为普朗克常数,m为电子质量,c为光速,θ为散射角度。
这个公式成为康普顿公式,它对于解释X射线在物质中发生散射的现象起到了重要作用。
康普顿效应的发现对现代物理学的发展有着重要的意义。
首先,康普顿效应证实了光的粒子性质,支持了光的粒子-波动二象性,进一步验证了爱因斯坦的光量子假设。
其次,康普顿效应为核物理的发展打下了基础。
康普顿效应的发现表明,X射线是由高能量的光子组成的,提供了进一步研究核物理和相对论物理的线索。
此外,康普顿效应还在医学领域起到了重要作用,主要应用于X射线的成像和辐射治疗。
总之,康普顿效应的发现揭示了X射线在物质中发生散射的基本规律,证实了光的粒子性质,并为现代物理学的发展提供了重要线索。
《康普顿效应》课件

康普顿效应在高能散射 和极端条件下的研究仍 存在挑战,需要进一步 深入研究和探索。
参考文献
康普顿散射的理论与实验研究
XXX,XXX出版社,2010年
A p p licatio n o f C o m p to n Effect in N o n d estru ctive Testin g
XXX,YYY出版社,2013年
3
实验结果的观测与分析
实验结果可以通过绘制散射光强度与散射角的关系曲线来观察和分析康普顿效应。
第四部分:应用领域
X射线荧光光谱技术
非破坏性检测技术
X射线荧光光谱技术利用康普 顿效应测量样品中的元素含量, 广泛应用于材料分析和地质研 究等领域。
康普顿效应可用于非破坏性检 测技术,如检测工件的内部缺 陷和材料的组成。
康普顿效应的推导
康普顿效应的推导需要考虑 能量守恒和动量守恒的原理, 最终得出光子波长的变化公 式。
第三部分:实验装置和实验结果
1
康普顿效应的实验装置
康普顿效应实验装置包括源、散射介质和探测器,通过测量散射角和散射光的能 量变化来研究康普顿效应。
2ቤተ መጻሕፍቲ ባይዱ
实验过程和方法
实验过程主要包括调整散射角、测量散射光的能谱和分析实验数据等步骤。
《康普顿效应》PPT课件
康普顿效应是指入射光子与自由电子发生散射时,光子的波长发生变化的现 象。本课件将介绍康普顿效应的原理、实验装置和应用领域。
第一部分:介绍
什么是康普顿效应?
康普顿效应是入射光子与 自由电子散射时光子波长 发生变化的现象,揭示了 光子的波粒二象性。
康普顿效应的历史背 景
康普顿效应由美国物理学 家康普顿于1923年首次发 现,为该领域的重要里程 碑。
康普顿效应知识点

康普顿效应知识点康普顿效应是指光的散射现象中,入射光子与散射光子之间发生能量和动量转移的现象。
这一效应的发现对于量子力学的发展起到了重要的推动作用。
本文将介绍康普顿效应的基本原理、数学表达以及实验验证等知识点。
一、康普顿效应的基本原理康普顿效应是由美国物理学家康普顿于1923年首次发现的,他通过实验证实了光的颗粒性质,并提出了光子与电子发生碰撞后发生能量和动量转移的观念。
康普顿效应的基本原理可以用以下几点来概括:1. 光的颗粒性质:康普顿效应的实验证实了光具有颗粒性质,即光可以看作是由一系列具有能量和动量的光子组成的。
2. 光与物质的相互作用:康普顿发现,当光子与物质中的自由电子碰撞时,光子的能量和动量会发生改变。
这是因为在碰撞过程中,光子与电子之间发生能量和动量转移。
3. 能量和动量转移:康普顿效应说明了入射光子与散射光子之间发生了能量和动量的转移。
具体来说,入射光子的能量减小,而散射光子的能量增加;入射光子的动量改变,而散射光子的动量也发生了变化。
二、康普顿效应的数学表达康普顿效应可以用数学表达来描述。
假设光子的入射能量为E,波长为λ;入射角为θ,散射角为φ。
根据康普顿散射公式,可以得到散射光子的波长λ'的计算公式:λ' - λ = \frac{h}{m_e c}(1 - \cos{\theta})其中,h为普朗克常量,m_e为电子质量,c为光速。
该公式表明,散射光子的波长与入射光子的波长之差与散射角度的余弦值有关。
由此可见,散射光子的波长与散射角度相关,而与入射光子的波长无关。
这意味着,康普顿效应可以通过测量散射光子的波长变化来研究入射光子与物质的相互作用。
三、康普顿效应的实验验证康普顿效应的实验证实了光的颗粒性质,并提供了实验数据来支持上述理论。
实验通常采用散射仪器,可以测量入射光子和散射光子的能量以及散射角度,从而计算散射光子的波长差。
实验证明,散射光子的波长差与散射角度呈正比关系,而与入射光子的波长无关。
康普顿效应的产生原理

康普顿效应的产生原理
康普顿效应是指当高能光子与物质中的自由电子发生非弹性碰撞时,光子的能量和动量发生改变的现象。
康普顿效应的产生原理可以解释为:
1. 光子是一种电磁波,具有波粒二象性。
光子与电子的相互作用可以看作是光子粒子和电子粒子之间的散射过程。
2. 光子在与电子发生碰撞时,会向电子传递部分能量和动量。
根据能量和动量守恒定律,光子的能量和动量在散射后会发生变化。
3. 康普顿效应中,光子的能量增加,动量也发生了变化。
这是因为电子对光子施加了一个反冲力,使光子的能量和动量发生了改变。
4. 具体来说,康普顿效应的计算可以利用康普顿公式,即E' -
E = \frac{h}{m_e c}(1 - \cos\theta),其中E'为光子散射后的能量,E为光子散射前的能量,h为普朗克常数,m_e为电子质量,c为光速,θ为光子散射角度。
5. 康普顿效应的产生可以通过实验证实,当高能光子通过物质时,散射出来的光子能谱会发生能量偏移,即康普顿散射能谱。
根据康普顿效应的原理,可以解释为散射光子的能量增加。
总结起来,康普顿效应的产生是光子与物质中的电子发生非弹性碰撞时,能量和动量发生改变的结果。
这一效应为量子力学
提供了光粒子和物质粒子之间相互作用的实验依据,也验证了光的波粒二象性。
15-3 康普顿效应

第十五章
量子物理
14
物理学
第五版
1515-3
康普顿效应
解 (1) ∆λ = λC (1 − cos θ ) = λC (1 − cos 90 ) = λC )
= 2.43 × 10 −12 m
(2) 反冲电子的动能 )
λ0 Ek = mc − m0 c = − = (1 − ) = 295 eV λ0 λ λ0 λ
(2) λ ) ∆
第十五章
hν0 e0 c
hν y e c
e θ
e0
ϕ
x
mv
量子物理
11
物理学
第五版
1515-3
康普顿效应
思考: 思考:(1)为什么必须用X射线呢? 为什么必须用X射线呢?
第十五章
量子物理
12
(1)光电效应是电子对光子能量全部吸收, )光电效应是电子对光子能量全部吸收, (2)康普顿效应是电子对光子能量部分吸收。 )康普顿效应是电子对光子能量部分吸收。 为什么会出现选择性呢? 为什么会出现选择性呢? 不存在出现选择性的问题。 不存在出现选择性的问题。 光电效应中主要是光子的能量较低, 光电效应中主要是光子的能量较低,有的电子对光 子能量全部吸收了,但也有部分吸收的, 子能量全部吸收了,但也有部分吸收的,即发生了 康普顿效应,但很微弱。 康普顿效应,但很微弱。 举例说来, 埃的紫光(或说是紫外线 举例说来,以4000埃的紫光 或说是紫外线)为例 埃的紫光 或说是紫外线) 其散射的光子的波长的改变量约为十万之几, ,其散射的光子的波长的改变量约为十万之几,基 本无法测定; 本无法测定;伦琴射线的波长的改变量可达百分之 光电效应和康普顿效应都有了; 射线的波长 十,光电效应和康普顿效应都有了;γ射线的波长 的改变量可与本身波长同数量级——这就是明显的 的改变量可与本身波长同数量级 这就是明显的 康普顿效应了。 康普顿效应了。
153 康普顿效应

振动方程: xAcots()
稳定状态的受迫振动是一个与简谐驱动力同 频率的简谐振动。
散射线的频率等于入射线频率
2. 光子论对康普顿效应的解释:
康普顿散射是光与物质的相互作用:
Compton散射是光和离子实和核外价电子发生 弹性碰撞的结果
离子实
散射光中与入射光波长相 同的射线
核外价电子
0.700
应 (d)
普 顿 (c) 度
康强
对 (b)
石 (a) 墨相
效
的
石 (a) 墨相 的对
(b)
康强 普 顿 (c) 度 效 应 (d)
φ=135 O
o
波长λ(A)
φ=90 O
φ=0 O φ=45 O
0.750
... .. ..............................................................................
h hc
dh 2d chc2dh2d c
单色X射线
散射体
S1 S2
晶体 探测器
石 (a) 墨相 的对
(b)
康强 普 顿 (c) 度 效 应 (d)
... .. ..........
φ=0 O
o
0.700 0.750 波长 (A)
石 (a) 墨相 的对
(b)
康强 普 顿 (c) 度 效 应 (d)
§15-3 康普顿效应
爱因斯坦断言:光是由光子组成,但真正证 明光是由光子组成的还是康普顿实验。
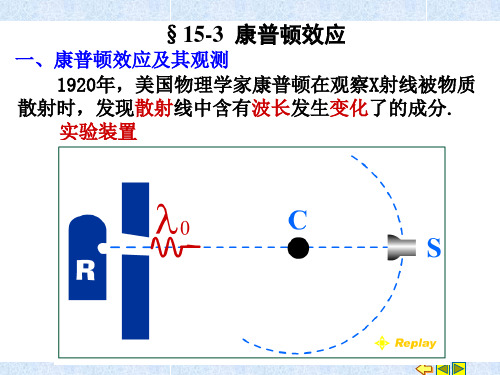
一、康普顿效应及其观测
实验装置示意图
晶体
单色X射线
散射体
S1 S2
探测器
第15章-2-康普顿效应

~ R( 1 1 ) 2 2 m n
mn
m 1,2,3,4,5 n m 1, m 2,
R 光谱项:T ( n) 2 n
结论:谱线的波数可以表示为两个光谱项之差。
15-4-2 原子的经典模型
1897年 J.J.汤姆孙发现电子
1903年,汤姆孙提出原子的“葡萄干蛋糕模型” 1.汤姆逊的面包夹葡萄干模型 整个原子呈胶冻状的球体, 正电荷均匀分布于球体上,而电 子镶嵌在原子球内,在各自的平 衡位置附近作简谐振动,并发射 同频率的电磁波。
En E1 n
2
基态 n 1
13.6
3. 氢原子光谱的理论解释:
(1)里德伯常数的理论值与 实验值符合得很好。
m e4 1 En 2 2 2 8 0 h n me4 1 1 ~ v ( 2 2 ), 2 3 8 0 h c n f ni m e4 1.097107 m 1 2 8 0 h3c
1
§15-4 氢原子光谱和玻尔理论
连续光谱
Na
H
线状光谱
Hg
Cu
钠的吸收光谱
太阳光谱
原子光谱——线状谱
§15-4-1 氢原子光谱
410.2 434.0 486.1 656.3
nm
H H
H
H
紫外区
可见光区
红外区 红外区
n2 (n 3,4,5,6) B 364.56nm 巴尔末发现: B 2 n 4 里德伯改写:~ 1 R( 1 1 ) ~ 1 22 n 2 波数: 1 里德伯常数 R 4 B 1 096776 107 m 实验值
34
h
光电效应实质:
大学物理15.3康普顿效应
光子能量: E h
E 2 p2c2 m02c4
光子的动量:
p E c
h
c
h
康普顿效应的定量分析
Y
h 0 m0
eX
Y h
mv
X
h
n
c
h 0
c
n0
X
mv
(1)碰撞前
(2)碰撞后 (3)动量守恒
碰撞前,电子平均动能(约百分之几eV),与入 射的X射线光子的能量(104~105eV)相比可忽略
物质散射时,波长 发生变化的现象
,电子可看作静止的。
由能量守恒: mc 2 h h 0 Байду номын сангаас0c2
由动量守恒:
h
c
n0
h 0
c
n
mv
n0 n cos
m m0
1
v2 c2
h
n
c
h 0
c
n0
X
mv
0
2h m0c
sin2
2
康普顿散射公式
c
h m0c
电子的康普顿波长 c 0.0243 Å
1927诺贝尔物理学奖
• A.H.康普顿 • 发现了X射线通过
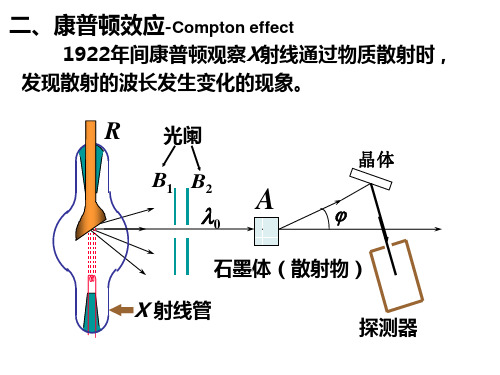
二、康普顿效应-Compton effect
1922年间康普顿观察X射线通过物质散射时,
发现散射的波长发生变化的现象。
R 光阑
B1 B2
0
A
晶体
石墨体(散射物)
X 射线管
探测器
(a)
石 墨 的 (b) 康 普 顿 (c) 效 应
(d)
0.700
... .. ..............................................................................
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2ϕ sin
ϕ= sin ≈ 0 .5832 2 2λ c
1 (λ − λ 0 ) 2
2
ϕ = 71.36
2011年3月2日星期三
理学院 物理系
大学物理
§15-3
康普顿效应
例15-5 波长为 1.0Å的 x 射线在碳块上作康普顿散射实 15的 验散射角 ϕ =60° ° 求(1)散射的 x 射线的波长 散射的 射线的波长; (2)反冲电子的动能 反冲电子的动能; 反冲电子的动能 (3)反冲电子的速度。 反冲电子的速度。 反冲电子的速度 解 (1) ∆ λ = λ − λ = 2λ sin 2 ϕ = 1.2 ×10 −12 m = 0.0012 nm 0 c 2
(c) (d)
2011年3月2日星期三
理学院 物理系
大学物理
§15-3
康普顿效应
二、对实验结果的分析 1、康普顿散射的实验结果与光的波动说相矛盾 康普顿散射的实验结果与光的波动说相矛盾 光是电磁波 带电粒子作受迫振动 与实验结果相矛盾
辐射频率不会发生变化
经典理论只能解释波长不变的散射, 经典理论只能解释波长不变的散射, 而不能说明康普顿散射
大学物理
§15-3
康普顿效应
§15-3 151、实验装置 、 x 射 线 源
A
康普顿效应
一、康普顿效应的实验及其规律
探测器
K
ϕ
石墨 晶体
光栏
1926年,康普顿观测了x射线沿各方向的散射光波 年 康普顿观测了 射线沿各方向的散射光波 射线沿各方向的散射光波, 并发现在散射光线中有波长大于入射光波长的现象 并发现在散射光线中有波长大于入射光波长的现象 ——康普顿效应 康普顿效应
2011年3月2日星期三
理学院 物理系
大学物理
§15-3
康普顿效应
2、光子理论解释 (1)X 射线由 的光子组成; ε = hν 的光子组成;
(2)光子与实物粒子一样, (2)光子与实物粒子一样,能与电子等粒子作弹性 光子与实物粒子一样 碰撞。 碰撞。
美国实验物理学家, 康普顿 美国实验物理学家,芝加 哥大学教授。 哥大学教授。因发现康普顿效应而获 1927年诺贝尔物理学奖 年诺贝尔物理学奖。 得1927年诺贝尔物理学奖。
理学院 物理系
=
h
cosϕ + mv cosθ
2011年3月2日星期三
大学物理
§15-3
康普顿效应
可得, 消去θ与v 可得 波长的改变量为
散射使
hν0 n0 c
hν n c
ϕ e θ
mv
h (1− cosϕ ) 2ϕ ∆λ =λ − λ 0 = = 2λc sin m0c
h −12 ≈ 2.4 ×10 m = 0.0024nm λc = m0c
∵E0 = m0c = 8.02×10 J 可见 Ek << E0 ∴v << c 相对论效应可以忽略
2
−14
1 电子的速度可由 E k ≈ m 0 v 2 2 2 Ek 6 −1 v= = 7 .20 × 10 m ⋅ s m0
m0v h/ λ mv = ≈ 由正弦定理 sin θ sin ϕ sin ϕ ϕ hsin ϕ θ sin θ = = 0.8650 m0λv
理学院 物理系
2011年3月2日星期三源自大学物理§15-3
康普顿效应
(2) 由入射光子的能量可得入射光的波长为
6.63×10 ×3×10 -12 = 2.49×10 m λ0 = = −19 6 ε0 0.5×10 ×1.6×10
hc
8
−34
由 ∆λ = λ − λ 0 = λc (1− cosϕ ) = 2λc
2
康普顿波长
2011年3月2日星期三
理学院 物理系
大学物理
§15-3
康普顿效应
四、康普顿散射实验的意义
1、进一步确认了光的粒子性; 进一步确认了光的粒子性; 2、确认了动量守恒定律与能量守恒定律在 微观粒子相互作用中的正确性。 微观粒子相互作用中的正确性。
2011年3月2日星期三
理学院 物理系
大学物理
2011年3月2日星期三
理学院 物理系
大学物理
§15-3
康普顿效应
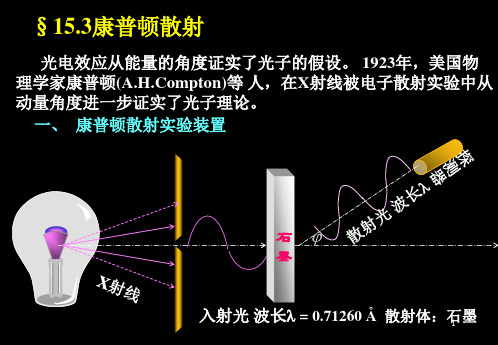
2、康普顿散射的实验规律 康普顿散射的实验规律
(a) (b)
ϕ = 00
(1)散射 (1)散射X 射线的波长中有 两个峰值
. ... ........ . ... .. .. ... ........ . ... ......... ........ ...... ... ....... ... .. . .... .. . ..... .. ...
hν0 + m0c = hν + mc
2
2 2
2
Ek = mc − m0c = hν0 − hν
ε = hν = hν0 − Ek
= 0.50 − 0.20 = 0.30MeV
2011年3月2日星期三
理学院 物理系
大学物理
§15-3
康普顿效应
散射光子的波长
由
ε=
hc
6.63×10 ×3×108 λ= = = 4.14×10-12 m ε 0.30×106 ×1.6×10−19 散射光子的动量 hc
λ = λ 0+ ∆λ = 0.1+ 0.0012= 0.1012nm
hc hc hc∆λ Ek = hν0 − hν = − =
(2)由碰撞过程中能量守恒 (2)由碰撞过程中能量守恒
= 2.36×10 J
2011年3月2日星期三
−17
λ0
λ
λ0λ
理学院 物理系
大学物理
§15-3
康普顿效应
(3)电子的静能量为 电子的静能量为
λ −34
6.63×10−34 -22 -1 p= = =1.60×10 kg ⋅ m⋅ s −12 λ 4.14×10 h
散射光子的质量 由
hν h m = 2 = 2 = φ c c cλ
−34
ε
ε = mφc
2
6.63×10 = 5.34×10−31kg = 3×108 ×4.14×10−12
ϕ
θ ≈ 59.88
2011年3月2日星期三
mv ≈ m0v
h/ λ
理学院 物理系
0.70 0.750
ϕ = 450
ϕ = 900
ϕ = 1350
λ (埃) 埃
(2)∆λ = λ − λ0 有关, 只与散射角ϕ有关,且随ϕ
的增大而增大; 的增大而增大; (3)不同散射物质, (3)不同散射物质,在同一 不同散射物质 散射角下波长的改变相同; 散射角下波长的改变相同; (4)波长为 (4)波长为λ的散射光强度 随散射物质原子序数的增 加而减小。 加而减小。
§15-3
康普顿效应
例15-4 15-
在康普顿实验中,当能量为 在康普顿实验中,当能量为0.50MeV的X射线 的 射线 的光子射中一个静止电子时, 的光子射中一个静止电子时,该电子获得的 动能为 0.20MeV (1)散射光子的波长 能量、动量与质量。 散射光子的波长、 求:(1)散射光子的波长、能量、动量与质量。 (2)散射光子与入射方向的夹角 散射光子与入射方向的夹角。 (2)散射光子与入射方向的夹角。 解: (1) 碰撞过程中能量守恒
2011年3月2日星期三
理学院 物理系
大学物理
§15-3
康普顿效应
三、康普顿效应的理论解释 X 射线光子与电子的碰撞 能量守恒
hν0 n0 c
hν n c
ϕ e θ
mv
hν0 + m0c = hν + mc
2
2
动量守恒
h
hν0 hν n0 = n + mv c c
λ0 λ h sin ϕ = mv sinθ λ
2011年3月2日星期三
理学院 物理系
大学物理
§15-3
康普顿效应
定 性 分 析
(1)在同一散射角下, (1)在同一散射角下,所有散射物质波长的改变 在同一散射角下 都是相同的。所以康普顿散射 康普顿散射只能是光子与所 ∆λ都是相同的。所以康普顿散射只能是光子与所 有物质原子中的共同成分相互作用的结果。 有物质原子中的共同成分相互作用的结果。这一 成分必是电子。 成分必是电子。康普顿散射是光子与电子碰撞的 结果; 结果; (2)光子在与电子碰撞中可能损失部分能量使波长 (2)光子在与电子碰撞中可能损失部分能量使波长 变长; 变长; (3)如果光子与原子中束缚很紧的电子发生碰撞 如果光子与原子中束缚很紧的电子发生碰撞, (3)如果光子与原子中束缚很紧的电子发生碰撞, 散射光线波长不变; 散射光线波长不变; (4)原子量较小的物质中的电子一般束缚较弱, (4)原子量较小的物质中的电子一般束缚较弱,康 原子量较小的物质中的电子一般束缚较弱 普顿散射较强;原子量较大的物质中的电子一般束 普顿散射较强;原子量较大的物质中的电子一般束 缚较强,所以康普顿散射就较弱 康普顿散射就较弱。 缚较强,所以康普顿散射就较弱。
