4-4-3-圆与扇形(三).教师版
第3章圆-圆的计算(教案)

(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“圆在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了圆的计算的基本概念、重要性和应用。同时,我们也通过实践活动和小组讨论加深了对圆的计算的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
举例:在讲解圆的面积公式时,可通过绘制正多边形逼近圆的方法,引导学生发现并理解面积公式A=πr²的推导过程。在解决弧长计算问题时,教师可引导学生将角度转换公式θ(弧度)=θ(度数)×π/180,以便于应用弧长公式进行计算。
四、教学流程
(一)导入新课(用时5分钟)
同学们,今天我们将要学习的是《圆的计算》这一章节。在开始之前,我想先问大家一个问题:“你们在日常生活中是否遇到过需要计算圆形物体周长或面积的情况?”(如计算自行车车轮的周长)这个问题与我们将要学习的内容密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索圆的计算的奥秘。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解圆的基本概念,包括圆周长、圆面积等。圆周长是圆周率π与直径的乘积,圆面积则是圆周率π与半径平方的乘积。它们在工程、设计等领域有着广泛的应用。
【教师版】小学奥数4-4-1 圆与扇形(一).专项练习及答案解析

研究圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,通过变动图形的位置或对图形进行分割、旋转、拼补,使它变成可以计算出面积的规则图形来计算它们的面积.圆的面积2πr =;扇形的面积2π360nr =⨯;圆的周长2πr =;扇形的弧长2π360nr =⨯.一、 跟曲线有关的图形元素: ①扇形:扇形由顶点在圆心的角的两边和这两边所截一段圆弧围成的图形,扇形是圆的一部分.我们经常说的12圆、14圆、16圆等等其实都是扇形,而这个几分之几表示的其实是这个扇形的圆心角占这个圆周角的几分之几.那么一般的求法是什么呢?关键是360n.比如:扇形的面积=所在圆的面积360n⨯;扇形中的弧长部分=所在圆的周长360n⨯扇形的周长=所在圆的周长+360n⨯2⨯半径(易错点是把扇形的周长等同于扇形的弧长)②弓形:弓形一般不要求周长,主要求面积.一般来说,弓形面积=扇形面积-三角形面积.(除了半圆)③”弯角”:如图:弯角的面积=正方形-扇形④”谷子”:如图:“谷子”的面积=弓形面积2⨯二、 常用的思想方法:①转化思想(复杂转化为简单,不熟悉的转化为熟悉的) ②等积变形(割补、平移、旋转等) ③借来还去(加减法)④外围入手(从会求的图形或者能求的图形入手,看与要求的部分之间的”关系”)板块一 平移、旋转、割补、对称在曲线型面积中的应用例题精讲圆与扇形【例 1】 如图,圆O 的直径AB 与CD 互相垂直,AB =10厘米,以C 为圆心,CA 为半径画弧。
求月牙形ADBEA (阴影部分)的面积。
D【考点】圆与扇形 【难度】3星 【题型】解答 【关键词】华杯赛,决赛,第9题,10分 【解析】 ①月牙形ADBEA (阴影部分)的面积=半圆的面积+△ABC 的面积-扇形CAEBC 的面积②月牙形ADBEA 的面积=211π525π502524⨯⨯+-⨯⨯=(平方厘米),所以月牙形ADBEA 的面积是25平方厘米。
六年级奥数第8次课:圆与扇形(教师版)

【我生命中最最最重要的朋友们,请你们仔细听老师讲而且随着老师的思想走。
学业的成功重在于考点的不停过滤,相信我赠予你们的是你们学业成功的过滤器。
感谢使用!!!】圆与扇形一、考点、热门回首五年级已经学习过三角形、矩形、平行四边形、梯形以及由它们形成的组合图形的有关问题,这一讲学习与圆有关的周长、面积等问题。
圆的周长、面积计算公式:c d 或 c 2 r s r 2半圆的周长、面积计算公式:c rd s 1 r 22扇形的周长、面积:c ad 2r s a r 2360 360如无特别说明,圆周率都取π=3.14 。
二、典型例题:例 1、以下列图所示,200 米赛跑的起点和终点都在直跑道上,中间的弯道是一个半圆。
已知每条跑道宽 1.22 米,那么外道的起点在内道起点前方多少米?(精准到0.01 米)剖析与解:半径越大,周长越长,因此外道的弯道比内道的弯道长,要保证内、外道的人跑的距离相等,外道的起点就要向前移,移的距离等于外道弯道与内道弯道的长度差。
固然弯道的各个半径都不知道,但是两条弯道的中心线的半径之差等于一条跑道之宽。
设外弯道中心线的半径为R,内弯道中心线的半径为r ,则两个弯道的长度之差为πR- π r =π( R-r )= 3.14 ×1.22 ≈ 3.83 (米)。
即外道的起点在内道起点前方 3.83 米。
例 2、有七根直径 5 厘米的塑料管,用一根橡皮筋把它们勒紧成一捆(如左下列图),此时橡皮筋的长度是多少厘米?剖析与解:由右上图知,绳长等于 6 个线段 AB 与 6 个 BC弧长之和。
将图中与BC弧近似的6 个弧所对的圆心角平移拼补,获得 6 个角的和是 360°,因此 BC弧所对的圆心角是 60°,6 个 BC弧等于直径 5 厘米的圆的周长。
而线段AB等于塑料管的直径,由此知绳长=5× 6+ 5×3.14 = 45.7 (厘米)。
例 3 、左下列图中四个圆的半径都是 5 厘米,求暗影部分的面积。
苏教版六年级(下)数学第1讲:扇形统计图(教师版)(有答案)

扇形统计图【教学目标】1.使学生认识扇形统计图,进一步明确扇形统计图的特点和作用;体会各种统计图的特点,初步学习选择合适的统计图表示数据信息。
2.使学生能根据绘制出的扇形统计图分析数据所反映的一些简单事实,能作出一些简单的推理与判断,进一步认识统计是解决实际问题的一种策略和方法。
3.使学生在学习统计知识的同时,感受数学与生活的联系及其在生活中的应用。
【趣味导入】【知识梳理】一、认识扇形统计图如右图就是一个扇形统计图。
扇形统计图是用整个圆代表总体,各个扇形分别代表组成总体的各个部分,扇形的大小反映部分占总体的百分比大小,因此,扇形统计图能清楚地表示出部分与整体的关系。
注意:扇形统计图只能看出各部分数量同总数的关系,而不能看出各部分数量的多少。
在不同的统计图中,不能简单地根据百分百的大小来比较部分量的大小。
二、统计图的选择条形统计图、扇形统计图与扇形统计图的特点条形统计图折线统计图扇形统计图特点用一定的单位长度表示一定的数量用整个圆面积表示总数,用圆内的扇形面积表示各部分占总数的百分比。
用直条的长短表示数量的多少。
用折线起伏表示数量的增减变化。
作用从图中能清楚地看出个数量的多少,便与相互比较。
从图中能清楚地看出数量增减变化的情况,也能看出数量的多少。
从图中能清楚地看出各部分与总数的百分比,以及部分与部分之间的关系。
总结:要想清楚的看出各部分数量与总数量之间的关系,可以选择扇形统计图。
要反映数量的增减变化情况,可以选择折现统计图。
要想直观的看出数量的多少,可以选择条形统计图。
【特色讲解】题目类型一:扇形统计图中的相关计算例题1.下面是李叔叔家上个月家庭开支情况:(1)食品开支占总开支的()%;服装开支占总开支的()%。
(2)在食品、服装、水电和文化四项开支中,()开支所占的比例最大,()开支所占的比例最小。
(3)如果李叔叔上个月的总开支是2000元,那么其他开支()元,结余()元,食品开支比服装开支多()元。
圆与扇形.题库教师版.doc

圆与扇形精选题【例 1】 图中的4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?【解析】 如下图所示:可以将每个圆内的阴影部分拼成一个正方形,每个正方形的面积为11240.542⨯÷⨯=⨯=()(平方厘米),所以阴影部分的总面积为248⨯=(平方厘米).【巩固】如图所示,四个全等的圆每个半径均为2m ,阴影部分的面积是 .或【解析】 我们虽没有学过圆或者圆弧的面积公式,但做一定的割补后我们发现其实我们并不需要知道这些公式也可以求出阴影部分面积.如图,割补后阴影部分的面积与正方形的面积相等,等于222216m ⨯=()().【例 2】 如图中三个圆的半径都是5cm ,三个圆两两相交于圆心.求阴影部分的面积和.(圆周率取3.14)【解析】 将原图割补成如图,阴影部分正好是一个半圆,面积为255 3.14239.25(cm )⨯⨯÷=【巩固】如图,大圆半径为小圆的直径,已知图中阴影部分面积为1S ,空白部分面积为2S ,那么这两个部分的面积之比是多少?(圆周率取3.14)【解析】 如图添加辅助线,小圆内部的阴影部分可以填到外侧来,这样,空白部分就是一个圆的内接正方形.设大圆半径为r ,则222S r =,221π2S r r =-,所以()12: 3.142:257:100S S =-=.移动图形是解这种题目的最好方法,一定要找出图形之间的关系. 【例 3】 请计算图中阴影部分的面积.【解析】 法一:为了求得阴影部分的面积,可以从下图的整体面积中扣掉一个圆的面积,就是要求的面积了.=-要扣掉圆的面积,如果按照下图把圆切成两半后,从两端去扣掉也是一样.如此一来,就会出现一个长方形的面积.O半圆半圆103-=因此,所求的面积为210330cm ⨯=(). 【例 4】 求如图中阴影部分的面积.(圆周率取3.14)44【解析】 可将左下橄榄型的阴影部分剖开,两部分分别顺逆时针90︒,则阴影部分转化为四分之一圆减去一个等腰直角三角形,所以阴影部分的面积为211π444 4.5642⨯⨯-⨯⨯=.【巩固】如图,四分之一大圆的半径为7,求阴影部分的面积,其中圆周率π取近似值227.【解析】 原题图中的左边部分可以割补至如右上图位置,这样只用先求出四分之一大圆的面积,再减去其内的等腰直角三角形面积即为所求.因为四分之一大圆的半径为7,所以其面积为:2211227π738.5447⨯⨯≈⨯⨯=.四分之一大圆内的等腰直角三角形ABC 的面积为17724.52⨯⨯=,所以阴影部分的面积为38.524.514-=. 【例 5】 (华校2005~2006年度第一学期期中测试第6题)大圆半径为R ,小圆半径为r ,两个同心圆构成一个环形.以圆心O 为顶点,半径R 为边长作一个正方形:再以O 为顶点,以r 为边长作一个小正方形.图中阴影部分的面积为50平方厘米,求环形面积.(圆周率取3.14)【解析】 环形的面积应该用大圆的面积减去小圆的面积,但分别求出两个圆的面积显然不可能.题中已知阴影部分的面积,也就是2250R r -=平方厘米,那么环形的面积为:2222πππ()π50=157R r R r -=-=⨯(平方厘米).【巩固】图中阴影部分的面积是225cm ,求圆环的面积.【解析】 设大圆半径为R ,小圆半径为r ,依题有222522R r -=,即2250R r -=.则圆环面积为:22222πππ()50π157(cm )R r R r -=-==.【例 6】 (2008年101中学考题)已知图中正方形的面积是20平方厘米,则图中里外两个圆的面积之和是 .(π取3.14)【解析】 设图中大圆的半径为r ,正方形的边长为a ,则小圆的直径等于正方形的边长,所以小圆的半径为2a ,大圆的直径2r 等于正方形的对角线长,即222(2)r a a =+,得222a r =.所以,大圆的面积与正方形的面积之比为:22π:π:2r a =,所以大圆面积为:202π10π÷⨯=;小圆的面积与正方形的面积之比为:22π():π:42aa =,所以小圆的面积为:204π5π÷⨯=;两个圆的面积之和为:10π5π15π15 3.1447.1+==⨯=(平方厘米).【巩固】图中小圆的面积是30平方厘米,则大圆的面积是 平方厘米.(π取3.14)【解析】 设图中大圆的半径为r ,正方形的边长为a ,则小圆的直径等于正方形的边长,所以小圆的半径为2a ,大圆的直径2r 等于正方形的对角线长,即222(2)r a a =+,得222a r =.所以,大圆的面积与小圆的面积之比为:222222π:π()::2:12424a a a a r r ===, 即大圆的面积是小圆面积的2倍,大圆的面积为30260⨯=(平方厘米).【巩固】(2008年四中考题)图中大正方形边长为a ,小正方形的面积是 .【解析】 设图中小正方形的边长为b ,由于圆的直径等于大正方形的边长,所以圆的直径为a ,而从图中可以看出,圆的直径等于小正方形的对角线长,所以22222a b b b =+=,故2212b a =,即小正方形的面积为212a .【例 1】 如图,两个正方形摆放在一起,其中大正方形边长为12,那么阴影部分面积是多少?(圆周率取3.14)AFEAFE【解析】 方法一:设小正方形的边长为a ,则三角形ABF 与梯形ABCD 的面积均为()122a a +⨯÷.阴影部分为:大正方形+梯形-三角形ABF -右上角不规则部分=大正方形-右上角不规则部分=14圆.因此阴影部分面积为:3.1412124113.04⨯⨯÷=. 方法二:连接AC 、DF ,设AF 与CD 的交点为M ,由于四边形ACDF 是梯形,根据梯形蝴蝶定理有ADM CMF S S =△△,所以DCF S S =阴影扇形 3.1412124113.04=⨯⨯÷=【巩固】如右图,两个正方形边长分别是10和6,求阴影部分的面积.(π取3)【解析】 (法1)观察可知阴影部分面积等于三角形ACD 的面积减去月牙BCD 的面积,那么求出月牙BCD 的面积就成了解题的关键.月牙BCD 的面积为正方形BCDE 的面积减去四分之一圆:166π6694⨯-⨯⨯⨯=; 则阴影部分的面积为三角形ACD 的面积减去月牙BCD 的面积,为:()110669392S =⨯+⨯-=阴影.(法2)观察可知AF 和BD 是平行的,于是连接AF 、BD 、DF .则ABD ∆与BDF ∆面积相等,那么阴影部分面积等于BDF ∆与小弓形的面积之和,也就等于DEF ∆与扇形BED 的面积之和,为:211(106)6π63924-⨯⨯+⨯⨯=.【例 2】 如图,ABC 是等腰直角三角形,D 是半圆周的中点,BC 是半圆的直径.已知10AB BC ==,那么阴影部分的面积是多少?(圆周率取3.14)DD【解析】 连接PD 、AP 、BD ,如图,PD 平行于AB ,则在梯形ABDP 中,对角线交于M 点,那么ABD ∆与ABP ∆面积相等,则阴影部分的面积转化为ABP ∆与圆内的小弓形的面积和.ABP ∆的面积为:()10102225⨯÷÷=;弓形面积: 3.145545527.125⨯⨯÷-⨯÷=; 阴影部分面积为:257.12532.125+=.【例 3】 图中给出了两个对齐摆放的正方形,并以小正方形中右上顶点为圆心,边长为半径作一个扇形,按图中所给长度阴影部分面积为 ;(π 3.14=)A【解析】 连接小正方形AC ,有图可见ACD ABC S S S S =+-△△阴影扇形∵211144222AC ⨯=⨯⨯ ∴232AC =同理272CE =,∴48AC CE ⨯= ∴148242ACD S =⨯=△290π412.56360S =⨯=扇形,14482ABC S =⨯⨯=△ ∴2412.56828.56S =+-=阴影【例 4】 如图,ABCD 是边长为a 的正方形,以AB 、BC 、CD 、DA 分别为直径画半圆,求这四个半圆弧所围成的阴影部分的面积.(π取3)DCBADCBA【解析】 这道题目是很常见的面积计算问题.阴影部分是一个花瓣状的不规则图形,不能直接通过面积公式求解,观察发现阴影部分是一个对称图形,我们只需要在阴影部分的对称轴上作两条辅助线就明了了.如图,这样阴影部分就划分成了4个半圆减去三角形,我们可以求得,()4S S S =⨯-阴影半圆三角形 21142222a a a π⎡⎤⎛⎫=⨯⨯⨯-⨯⨯⎢⎥ ⎪⎝⎭⎢⎥⎣⎦212a =【巩固】如图,正方形ABCD 的边长为4厘米,分别以B 、D 为圆心以4厘米为半径在正方形内画圆.求阴影部分面积.(π取3)DBADB【解析】 由题可知,图中阴影部分是两个扇形重叠的部分,我们可以利用容斥原理从图形整体上考虑来求阴影部分面积;同样,我们也可以通过作辅助线直接求阴影部分的面积. 解法一:把两个扇形放在一起得到1个正方形的同时还重叠了一块阴影部分. 则阴影部分的面积为=21π44482⋅⋅-⨯=; 解法二:连接AC ,我们发现阴影部分面积的一半就是扇形减去三角形的面积, 所以阴影部分面积=212π444284⨯⋅⋅-⨯÷=().【例 5】 (2008年四中考题)已知三角形ABC 是直角三角形,4cm AC =,2cm BC =,求阴影部分的面积.【解析】 从图中可以看出,阴影部分的面积等于两个半圆的面积和与直角三角形ABC 的面积之差,所以阴影部分的面积为:2214121ππ42 2.5π4 3.8522222⎛⎫⎛⎫⨯+⨯-⨯⨯=-= ⎪ ⎪⎝⎭⎝⎭(2cm ).【例 6】 如图,矩形ABCD 中,AB =6厘米,BC =4厘米,扇形ABE 半径AE =6厘米,扇形CBF 的半径CB =4厘米,求阴影部分的面积.(π取3)A【解析】 方法一:观察发现,阴影部分属于一个大的扇形,而这个扇形除了阴影部分之外,还有一个不规则的空白部分ABFD 在左上,求出这个不规则部分的面积就成了解决这个问题的关键.我们先确定ABFD 的面积,因为不规则部分ABFD 与扇形BCF 共同构成长方形ABCD ,所以不规则部分ABFD 的面积为2164π4124⨯-⨯⨯=(平方厘米), 再从扇形ABE 中考虑,让扇形ABE 减去ABFD 的面积, 则有阴影部分面积为21π612154⨯⨯-=(平方厘米).方法二:利用容斥原理2211π6π4461544EAB BCF ABCD S S S S =+-=⨯+⨯-⨯=阴影扇形扇形长方形(平方厘米)【巩固】求图中阴影部分的面积.【解析】 阴影部分面积=半圆面积+扇形面积-三角形面积22211211π()π121241.042282=⨯+⨯-⨯=.【巩固】如右图,正方形的边长为5厘米,则图中阴影部分的面积是 平方厘米,(π 3.14=)C【解析】 观察可知阴影部分是被以AD 为半径的扇形、以AB 为直径的半圆形和对角线BD 分割出来的,分头求各小块阴影部分面积明显不是很方便,我们发现如果能求出左下边空白部分的面积,就很容易求出阴影部分的面积了,我们再观察可以发现左下边空白部分的面积就等于三角形ABD 的面积减去扇形ADE 的面积,那么我们的思路就很清楚了.因为45ADB ∠=︒,所以扇形ADE 的面积为:224545π 3.1459.8125360360AD ⨯⨯=⨯⨯=(平方厘米), 那么左下边空白的面积为:1559.8125 2.68752⨯⨯-=(平方厘米),又因为半圆面积为:215π9.812522⎛⎫⨯⨯= ⎪⎝⎭(平方厘米),所以阴影部分面积为:9.8125 2.68757.125-=(平方厘米).【例 7】 已知半圆所在的圆的面积为62.8平方厘米,求阴影部分的面积.(π 3.14=)B【解析】 由于阴影部分是一个不规则图形,所以要设法把它转化成规则图形来计算.从图中可以看出,阴影部分的面积是一个45°的扇形与一个等腰直角三角形的面积差. 由于半圆的面积为62.8平方厘米,所以262.8 3.1420OA =÷=. 因此:22210AOB S OA OB OA =⨯÷=÷=△(平方厘米). 由于AOB ∆是等腰直角三角形,所以220240AB =⨯=. 因此:扇形ABC 的面积24545ππ4015.7360360AB =⨯⨯=⨯⨯=(平方厘米). 所以,阴影部分的面积等于:15.710 5.7-=(平方厘米).【例 8】 如图,等腰直角三角形ABC 的腰为10;以A 为圆心,EF 为圆弧,组成扇形AEF ;两个阴影部分的面积相等.求扇形所在的圆面积.【解析】 题目已经明确告诉我们ABC 是等腰直角三角形,AEF 是扇形,所以看似没有关系的两个阴影部分通过空白部分联系起来.等腰直角三角形的角A 为45度,则扇形所在圆的面积为扇形面积的8倍. 而扇形面积与等腰直角三角形面积相等,即11010502S =⨯⨯=扇形, 则圆的面积为508400⨯=【例 9】 如图,直角三角形ABC 中,AB 是圆的直径,且20AB =,阴影甲的面积比阴影乙的面积大7,求BC 长.(π 3.14=)【解析】 因为两块阴影部分都是不规则图形,单独对待它们无法运用面积公式进行处理,而解题的关键就是如何把它们联系起来,我们发现把两块阴影加上中间的一块,则变成1个半圆和1个直角三角形,这个时候我们就可以利用面积公式来求解了. 因为阴影甲比阴影乙面积大7,也就是半圆面积比直角三角形面积大7. 半圆面积为:21π101572⨯⨯=,则直角三角形的面积为157-7=150,可得BC =2⨯150÷20=15.【巩固】三角形ABC 是直角三角形,阴影I 的面积比阴影II 的面积小225cm ,8cm AB =,求BC 的长度.I IABCI【解析】 由于阴影I 的面积比阴影II 的面积小225cm ,根据差不变原理,直角三角形ABC 面积圆与扇形精选题11 减去半圆面积为225cm ,则直角三角形ABC 面积为218π258π2522⎛⎫⨯+=+ ⎪⎝⎭(2cm ), BC 的长度为()8π25282π 6.2512.53+⨯÷=+=(cm ).【巩固】 如图,三角形ABC 是直角三角形,阴影部分①比阴影部分②的面积小28平方厘米,AB 长40厘米.求BC 的长度?(π取3.14)【解析】 图中半圆的直径为AB ,所以其面积为2120π200 3.146282⨯⨯≈⨯=. 有空白部分③与①的面积和为628,又②-①28=,所以②、③部分的面积和62828656+=.有直角三角形ABC 的面积为12AB BC ⨯⨯=1406562BC ⨯⨯=.所以32.8BC =厘米.【例 10】 如图,求阴影部分的面积.(π取3)43【解析】 如图,图中阴影部分为月牙儿状,月牙儿形状与扇形和弓形都不相同,目前我们还不能直接求出 它们的面积,那么我们应该怎么来解决呢?首先,我们分析下月牙儿状是怎么产生的,观察发现月牙儿形是两条圆弧所夹部分,再分析可以知道,两条圆弧分别是不同圆的圆周的一部分,那么我们就找到了解决问题的方法了.阴影部分面积=12小圆面积+12中圆面积+三角形面积-12大圆面积=2221111π3π434π52222⋅⋅+⋅⋅+⨯⨯-⋅⋅ =6【例 11】 (2009年十三分入学测试题)图中的长方形的长与宽的比为8:3,求阴影部分的面积.204【解析】 如下图,设半圆的圆心为O ,连接OC .。
小学数学-有答案-沪教版六年级(上)小升初题单元试卷:第4章_圆和扇形(03)

沪教版六年级(上)小升初题单元试卷:第4章圆和扇形(03)一、选择题(共10小题)1. 如图,大圆的周长与两个小圆的周长和比较()A.大圆的周长长B.两个小圆的周长和长C.一样长D.无法判定2. 如图,大半圆的周长()两个小半圆的周长之和。
A.=B.>C.<3. 一个正方形的边长和圆的半径相等,已知正方形的面积是20平方米,圆的面积是()平方米。
A.无法解答B.62.8C.12.56D.15.74. 小圆和大圆的半径比是2:3,那么小圆和大圆的面积比是()A.2:3B.4:9C.无法判断5. 圆的半径扩大到原来的2倍,则它的面积扩大到原来的()倍。
A.2B.4C.6D.86. 小圆直径是3厘米,大圆半径是6厘米,小圆的面积是大圆面积的()A.14B.18C.1167. 小圆直径是3,大圆半径是6,小圆的面积是大圆面积的()A.12B.14C.18D.1168. 一个圆的半径扩大3倍,面积扩大()倍。
A.3B.6C.99. 设C为圆的周长,则Cπ×12=()A.圆的半径B.圆的直径C.圆的面积D.圆的周长10. 在长5厘米,宽3厘米的长方形中,画一个最大的半圆,这个半圆的周长是厘米。
()A.9.42B.18.84C.14.42D.12.85二、填空题(共16小题)在同一圆中,周长总是直径的π倍。
________.半径是2分米的圆,周长和面积相等。
________.(判断对错)在长为10厘米,宽为8厘米的长方形中画一个最大的圆,这个圆的半径是________,面积是________.在纸片上将圆规两脚间的距离定为4cm,画出的圆的面积是50.24cm2,如果把这个圆平均分成若干份。
剪拼成一个近似的长方形,这个近似长方形的长是12.56cm.要剪一个面积是9.42平方分米的圆形纸片,至少要面积是________平方分米的正方形纸片。
若两个圆的半径比是1:2,则它们的面积比是1:2________.(判断对错)大圆的直径是小圆直径的2倍,大圆的周长是小圆周长的________倍,小圆的面积是大圆的________.两圆相比,周长小的面积一定小。
全国通用六年级下册数学奥数:几何之圆与扇形(解析版)
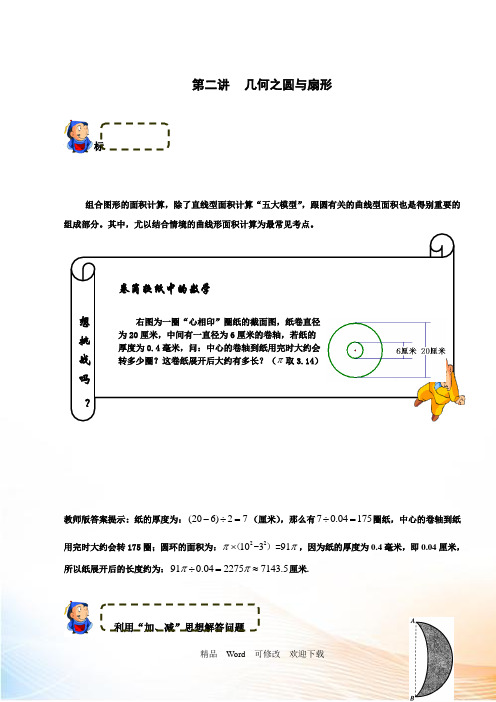
第二讲 几何之圆与扇形教学目标组合图形的面积计算,除了直线型面积计算“五大模型”,跟圆有关的曲线型面积也是得别重要的组成部分。
其中,尤以结合情境的曲线形面积计算为最常见考点。
教师版答案提示:纸的厚度为:(206)27-÷=(厘米),那么有70.04175÷=圈纸,中心的卷轴到纸用完时大约会转175圈;圆环的面积为:2210391ππ⨯(-)=,因为纸的厚度为0.4毫米,即0.04厘米,所以纸展开后的长度约为:910.0422757143.5ππ÷=≈厘米.利用“加、减”思想解答问题想挑 战 吗 ? 卷筒软纸中的数学右图为一圈“心相印”圈纸的截面图,纸卷直径 为20厘米,中间有一直径为6厘米的卷轴,若纸的 厚度为0.4毫米,问:中心的卷轴到纸用完时大约会 转多少圈?这卷纸展开后大约有多长?(π取3.14)【例1】 如图,一个“月牙”形屏幕在屏幕上随意平行移动(不许发生转动也不越过屏幕边界),已知线段AB 是月牙外半圆弧的直径,长为2厘米。
初始时,A 、B 两点在矩形屏幕的一条边上。
屏幕的长和宽分别为30厘米和20厘米。
问:屏幕上“月牙”擦不到的部分的面积是多少平方厘米?(π取3)分析:由于“月牙”形屏幕在屏幕上只能平行移动(不许发生转动也不越过屏幕边界),所以它擦不到的地方只是屏幕的右上角和右下角两部分,如右下图中斜线所示区域,其面积为0.5平方厘米。
[前铺]如右图所示,等腰直角三角形ABC 的高AD=4厘米,以AD 为直径作圆分别交AB 、AC 与E 、F ,求阴影部分的面积。
(π取3) 分析:连接EF ,那么有BED ABD EOD S S S =-阴影三角形扇形,计算可得阴影部分面积为6平方厘米。
[巩固]一个长方形的长为9,宽为6,一个半径为l 的圆在这个长方形内任意运动,在长方形内这圆无法运动到的部分,面积的和是多少?(π取3)分析:圆无法运动到的部分是右下图中角处的阴影部分面积的4倍,114111π⨯⨯-⨯⨯=[拓展]如右图所示,用一块面积为36平方厘米铝板下料,可裁出七个同样大小的圆铝板。
知识点全面梳理--04圆和扇形--师
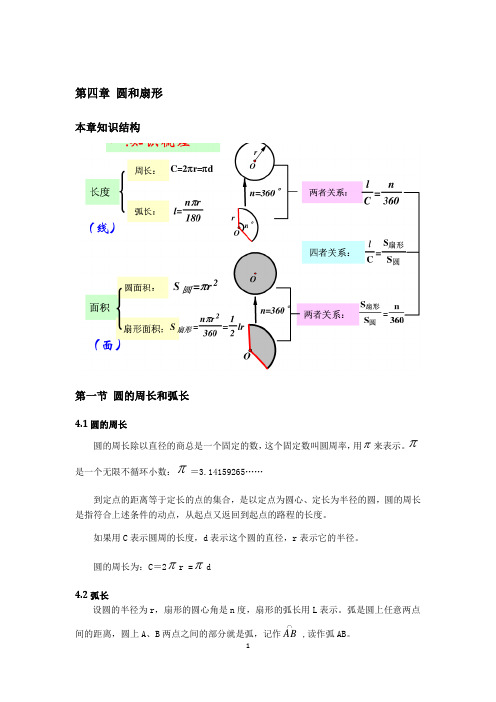
第四章圆和扇形本章知识结构第一节圆的周长和弧长4.1圆的周长圆的周长除以直径的商总是一个固定的数,这个固定数叫圆周率,用π来表示。
π是一个无限不循环小数:π=3.14159265……到定点的距离等于定长的点的集合,是以定点为圆心、定长为半径的圆,圆的周长是指符合上述条件的动点,从起点又返回到起点的路程的长度。
如果用C表示圆周的长度,d表示这个圆的直径,r表示它的半径。
圆的周长为:C=2πr =πd4.2弧长设圆的半径为r,扇形的圆心角是n度,扇形的弧长用L表示。
弧是圆上任意两点间的距离,圆上A、B两点之间的部分就是弧,记作⋂AB ,读作弧AB。
1802360110r r ππ=⨯=圆心角所对的弧长; 18023600rn r n L n ππ=⨯=圆心角所对的弧长。
第二节 圆和扇形的面积4.3圆的面积2r S π=圆的面积4.4扇形的面积由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形。
设组成扇形的半径为r ,圆心角为0n ,弧长为l ,扇形的面积:S =360n ×πr 2=21Lr本章最重点内容本章是圆与扇形,掌握圆的周长的计算公式和弧长的概念,会计算圆的面积及扇形的面积,是我们学习的重点。
1.圆的周长公式:r d C ⋅=⋅=ππ2. 2.弧长公式:180360rdl ⋅=⋅=ππ.3.圆的面积公式:2r S ⋅=π 4.扇形面积公式:lr r n S 213602=⋅=π扇. 5.特别地:360n C l =,360n S S =扇,即:SSC l 扇=. 本章错题集【结合个人平时作业具体情况总结、整理、添加】1.如图,一个半径为1厘米的小圆盘沿着一个半径为4厘米的大圆盘外侧做无滑动的滚动。
当小圆盘的中心围绕大圆盘中心转动90度后,小圆盘运动过程中扫过的面积是多少平方厘米?(3π=)【答案】:小圆盘运动过程中扫过的面积由两部分组成,即两半圆加四分之一环形。
2221(64)418S πππ=⨯+⨯-⨯÷=平方厘米。
【上海初中数学讲义】预初(上)第14讲:圆与扇形的面积 教师版

第14讲 圆与扇形的面积1. 圆的面积公式:设圆的半径长为r ,面积为S ,那么圆的面积2==S r r r ππ⨯ 2. 圆环面积圆环的计算公式(r 表示小圆半径,R 表示大圆半径)22=S R r ππ-圆环 3. 扇形面积公式:设组成扇形的半径为r ,圆心角为o n ,弧长为l ,那么21==3602n S r lr π扇形 特别地:360S nS=扇 4. 组合图形面积(1)计算图形面积时,经常用到割补法,要善于添加辅助线,把图形分割成几个基本图形,再分别求出它们的面积.(2)一些复杂的图形,要经常用到平移、翻转等方法,把复杂图形转化为基本图形,再分别计算它们的面积.【例题1】填空:1. 在一个正方形里面画一个最大的圆,这个圆的周长是6.28厘米,这正方形的面积是_________平方厘米.剩下的面积是__________平方厘米.2. 大圆半径是3分米,小圆半径是2分米,小圆面积是大圆面积的__________.3. 已知外圆的半径为2cm ,内圆半径为1cm ,圆环的面积为 .4.小圆的半径为2,大圆的直径为8,那么大圆的面积是小圆的__________倍.5. 甲圆的半径是乙圆的43,则甲圆与乙圆的周长之比为 面积之比为_______ 6. A B 两圆的周长之比为2:3,其中一个大圆的面积是18,另外一个圆的面积为:______ 7. 若两圆的周长和为87.92cm ,并且大圆的直径是小圆直径的3倍,则小圆的面积为______【例题2】(圆的面积)已知甲圆的半径长等于乙圆的直径长,且它们的面积之和是100平方厘米,那么甲圆的面积是多少?【例题3】(圆环面积)已知一个圆形花坛的直径是4米,沿它的外侧铺一条1米宽的小路,求这条小路的面积。
【例题4】(扇形面积)已知圆心角为60 ,OC=6厘米,AC=2厘米,求阴影部分的面积.【例题5】(组合图形问题)求图中阴影部分的面积.【例题6】如图,长方形ABCD的长AD=8cm,宽AB=6cm,求阴影部分的周长和面积.【例题7】有一只狗被拴在建筑物的墙角上,这个建筑物是边长600厘米的正方形,拴狗的绳子长20米,现在狗从A点出发,将绳子拉紧顺时针跑,求狗跑过的图形面积【练习1】填空:1. 有相同周长的长方形、正方形、圆,它们的面积从大到小是_________________________.2. 如果一个扇形所含圆弧的长是相同半径圆周长的51,那么这个扇形的面积是这个圆面积的 .3. 如图,三个同心圆的半径分别为2、6、10,则图中阴影部分占大圆面积的____________%.(第3题)(第4题)(第5题)4. 如图,大小两个圆重叠部分的面积是20平方厘米,是大圆面积的18,是小圆面积的16,则大圆面积比小圆面积多__________平方厘米.5. 如图所示,圆1O 、圆2O 、圆3O 的半径均为1厘米,则阴影部分的面积为_______平方厘米.【练习2】 两个圆的周长之比是3∶2,面积之差是10平方厘米,两个圆的面积之和是多少?【练习3】如图中两个相连的正方形的边长分别是8厘米、3厘米,求阴影部分的面积.【练习4】求阴影部分的面积.【练习5】某已知直角三角形三边长为12、16、20,求阴影部分的面积.【练习6】如图,已知AB=10cm,以AB为直径的半圆绕A点旋转了30 ,求阴影部分的面积.(结果保留π)【练习7】如图A与B两个圆(只有14)的圆心,那么两个阴影部分的面积相差多少平方厘米?【练习8】如图,小杨将自家宠物A栓在墙角,若绳长为3米,求小狗在地面活动的最大区域面积.【练习1】如图所示,Rt△ABC中,∶C=90°,AB=10,那么图中两个扇形(即阴影部分)的面积之和为___________.【练习2】已知正方形的边长为2,求右图中阴影部分的面积.A B【练习3】求下列阴影部分的面积.(1) (2)【练习4】已知小正方形的边长是2,大正方形的边长是4,求阴影部分的面积.【练习5】如图是以边长为40米的正方形ABCD 的顶点A 为圆心,AB 长为半径的弧与以CD 、BC 为直径的半圆构成的花坛(图中阴影部分).小杰沿着这个花坛边以相同的速度跑了6圈,用去了8分钟,求小杰平均每分钟跑多少米?A BCD【例题精讲】【例题1】(1)4、0.86 (2)49(3)3π (4)4 (5)3:4、9:16 (6)8 (7)494π 【例题2】280cm 【例题3】5π2m 【例题4】143π2cm 【例题5】(1)32 (2)816-π 【例题6】()10cm π+8、2(2648)cm -π 【例题7】166π2m【学习巩固】【练习1】(1)圆、正方形、长方形 (2)15(3)33 (4)40 (5)2π【练习2】26【练习3】9(214-π)2cm【练习4】()88-π 【练习5】96 【练习6】253π2cm 【练习7】()238cm -π 【练习8】52π2m【家庭作业】 【练习1】254π 【练习2】24-π【练习3】(1)8π (2)24-π 【练习4】2+π【练习5】()6030/min m +π。
初中数学沪教版(五四制)六年级上册第四章 圆和扇形第1节 圆的周长和弧长-章节测试习题(3)

章节测试题1.【答题】如图,将△ABC绕点C旋转60°,得到△A′B′C,已知AC=6,BC=4,则点A走过的路径长()A.B.C. 6πD. 2π【答案】D【分析】根据弧长的计算公式解答即可.【解答】∵将△ABC绕点C旋转60°,得到△A′B′C,AC=6,∴点A走过的路径为以AC长为半径,圆心角为60°的弧长,即,选D.2.【答题】已知圆锥的底面面积为9π cm2,母线长为6cm,则该圆锥的侧面积是()A. 18cm2B. 27cm2C. 18π cm2D. 27π cm2【答案】C【分析】根据圆锥侧面积的计算公式解答即可.【解答】设底面半径是r,=9,r=3,底面周长是6 ,侧面积是18π cm2,选C.3.【答题】如图,将半径为2,圆心角为的扇形OAB绕点A逆时针旋转,点的对应点分别为,连接,则图中阴影部分的面积是A.B.C.D.【答案】C【分析】本题考查了扇形面积的计算,等边三角形的判定和性质,旋转的性质,正确的作出辅助线是解题的关键.【解答】解:连接OO′,BO′.∵将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,∴∠OAO′=60°,∴△OAO′是等边三角形,∴∠AOO′=60°,OO′=OA,∴当O′中⊙O上.∵∠AOB=120°,∴∠O′OB=60°,∴△OO′B是等边三角形,∴∠AO′B=120°.∵∠AO′B′=120°,∴∠B′O′B=120°,∴∠O′B′B=∠O′BB′=30°,∴图中阴影部分的面积=S△B′O′B﹣(S扇形O′OB﹣S△OO′B)=×1×2﹣(﹣×2×)=2﹣.选C.4.【答题】如图,矩形ABCD,以A为圆心,AD为半径作弧交BC于点F,交AB的延长线于点E,已知 AD=4,AB=2,则阴影部分的面积为()A. 2π﹣4B.C.D.【答案】A【分析】本题考查了矩形的性质,勾股定理及扇形的面积公式,解决这类问题注意转化思想的运用.【解答】连接AF,由题意得,AF=AD=4,由勾股定理得,BF==2,∴∠BAF=45°,∴阴影部分的面积=,选A.5.【答题】如图,半径为2cm,圆心角为的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为()A.B.C.D.【答案】A【分析】本题考查了扇形的面积公式,解决这类问题注意转化思想的运用.【解答】解:连接AB,OD.∵扇形OAB的圆心角为90°,扇形半径为2,∴扇形面积为:=π(cm2),半圆面积为:×π×12=(cm2),∴S Q+S M=S M+S P=(cm2),∴S Q=S P.∵两半圆的直径相等,∴∠AOD=∠BOD=45°,∴S绿色=S△AOD=×2×1=1(cm2),∴阴影部分Q的面积为:S扇形AOB﹣S半圆﹣S绿色=π﹣﹣1=﹣1(cm2).选A.6.【答题】如图,正方形ABCD内接于半径为2的⊙O,则图中阴影部分的面积为()A. π+1B. π+2C. π﹣1D. π﹣2【答案】D【分析】本题考查了正方形的性质,扇形的面积公式,解决这类问题注意转化思想的运用.【解答】解:连接∵ABCD是正方形,∴圆内接正方形的边长为,所以阴影部分的面积为:选D.7.【答题】(2016·深圳中考)如图,在扇形OAB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF 的边长为2时,阴影部分的面积为()A. 2π-4B. 4π-8C. 2π-8D. 4π-4【答案】A【分析】本题考查了扇形的面积公式,解决这类问题注意转化思想的运用.【解答】如图,连接OC.∵∠AOB=90°,正方形CDEF的顶点C是的中点,∴∠COD=45°,在等腰直角△OCD中,由勾股定理得OC=4,∴S阴影=S扇形OBC-S△ODC=-×(2)²=2π-4,选A.8.【答题】如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕点A逆时针旋转30°后得到△ADE,点B经过的路径为弧BD,则图中阴影部分的面积为()A. πB. πC. πD. π【答案】A【分析】本题考查了扇形的面积公式,解决这类问题注意转化思想的运用.【解答】∵AB=5,AC=3,BC=4,∴△ABC为直角三角形.由题意得S△AED=S△ABC,由图形可知S阴影=S△AED+S扇形ADB-S△ABC,∴S阴影=S扇形ADB==π,选A.9.【答题】如图,Rt△ABC中,AB=AC=4,以AB为直径的圆交AC于D,则图中阴影部分的面积为()A. 2B. +1C. +2D. 4+【答案】C【分析】本题考查了扇形的面积公式,解决这类问题注意转化思想的运用.明确图中阴影部分的面积等于半圆的面积减去一个弓形的面积.依面积公式计算即可.【解答】解:半径OB=2,圆的面积为,半圆面积为连接AD,OD,根据直径对的圆周角是直角,∴AD⊥BC,∵点O是圆心,Rt△ABC是等腰直角三角形,∴OD⊥AB,∴扇形ODB的面积等于四分之一圆面积为△DOB的面积∴弓形DB的面积∴阴影部分的面积选C.10.【答题】(3分)如图,在△ABC中,AB=8cm,BC=4cm,∠ABC=30°,把△ABC以点B为中心按逆时针方向旋转,使点C旋转到AB边的延长线上的点C′处,那么AC边扫过的图形图中阴影部分)的面积是()A. 20πcm2B. (20π+8)cm2C. 16πcm2D. (16π+8)cm2【答案】A【分析】利用圆环的面积公式计算即可.【解答】因为△ABC≌△A′BC,所以AC边扫过的图形中阴影部分的面积是一个圆环的面积,即=20πcm²,选A.11.【答题】已知扇形的圆心角为 450,半径长为 12,则该扇形的弧长为()A. πB. 3πC. 2πD. π【答案】B【分析】根据扇形面积计算公式和弧长公式计算即可.【解答】解:=3π.选B.12.【答题】如图,在中,.,.是中线,点、同时从点出发,以相同的速度分别沿、方向移动,当点到达点时,运动停止,直线分别与、相交于、,则在点、移动过程中,点移动路线的长度为().A.B.C.D.【答案】D【分析】根据圆的性质和弧长公式解答即可.【解答】解:如图,∴CD⊥AB,∴∠ADE=∠CDF=,CD=AD=DB,在△ADE和△CDF中,∴△ADE≌△CDF(SAS),∴∠DAE=∠DCF,∵∠AED=∠CEG,∴∠ADE=∠CGE=,∴A、C、G、D四点共圆,∴点G的运动轨迹为弧CD,∵AB=4,∴∴∵DA=DC,OA=OC,∴DO⊥AC,∴∴点G的运动轨迹的长为选D.13.【答题】如图,等边三角形内接于⊙,若,则图中阴影部分的面积为().A.B.C.D.【答案】C【分析】本题考查了扇形的面积公式,解决这类问题注意转化思想的运用.【解答】解:连接OB、OC,过O作OD⊥BC于D,则∵是等边三角形,由勾股定理得:∴阴影部分的面积S=S扇形BOC−S△OBC选C.14.【答题】如图,扇形AOB中,OA=2,C为弧AB上的一点,连接AC,BC,如果四边形AOBC为菱形,则图中阴影部分的面积为()A.B.C.D.【答案】D【分析】本题考查了扇形的面积公式,解决这类问题注意转化思想的运用.【解答】连接OC,过点A作AD⊥CD于点D,四边形AOBC是菱形可知OA=AC=2,再由OA=OC可知△AOC是等边三角形,可得∠AOC=∠BOC=60°,故△ACO与△BOC为边长相等的两个等边三角形,再根据锐角三角函数的定义得出AD=OA•sin60°=2×=,因此可求得S阴影=S扇形AOB﹣2S△AOC=﹣2××2×=﹣2.选D.方法总结:本题考查的是扇形面积的计算,熟记扇形的面积公式及菱形的性质是解答此题的关键.15.【答题】圆锥的底面直径是80cm,母线长90cm,则它的侧面积是()A. 360πcm2B. 720πcm2C. 1800πcm2D. 3600πcm2【答案】D【分析】根据圆锥侧面积的计算公式解答即可.【解答】圆锥的侧面积=×80π×90=3600π(cm2) .选D.16.【答题】弧长等于半径的圆弧所对的圆心角为()A.B.C.D. 60°【答案】B【分析】本题考查了弧长公式的应用,注意:半径为r,圆心角为nº所对的弧的长度是.【解答】设半径为r,圆心角为nº,由题意得,,∴.选B.17.【答题】如图,⊙A与⊙B外切于点D,PC,PD,PE分别是圆的切线,C,D,E是切点,若∠CED=x°,∠ECD=y°,⊙B的半径为R,则弧DE的长度是()A.B.C.D.【答案】B【分析】根据切线长定理和弧长公式计算即可.【解答】根据题意,由切线长定理可知:PC=PD=PE,即点C,D,E在以P为圆心,PC长为半径的⊙P上,由圆周角定理得:∠DPE=2∠ECD=2y° ,连接BD,BE,则∠BDP=∠BEP=90°,在四边形BDPE中,∠B+∠BDP+∠DPE+∠BEP=360°,即:∠B+90°+2y°+90°=360°, 解得:∠B=180°-2y°.∴弧DE的长度是: 选B.18.【答题】如图,扇形折扇完全打开后,如果张开的角度(∠BAC)为120°,骨柄AB的长为30 cm,扇面的宽度BD的长为20 cm,那么这把折扇的扇面面积为()A. cm2B. cm2C. cm2D. 300πcm2【答案】C【分析】根据扇形的面积公式计算即可.【解答】解:∵AB=30cm,BD=20cm,∴AD=30﹣20=10(cm),∴S阴影=S扇形BAC ﹣S扇形DAE===cm2选C.19.【答题】在正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,则图中阴影部分的面积为()A. πa2﹣a2B. a2﹣πa2C. a2D. πa2【答案】A【分析】根据扇形的面积公式计算即可.【解答】由题意可得出:S阴影=2S扇形﹣S正方形=2×﹣a2= πa2﹣a2,选A.20.【答题】将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为()A. 8πcm2B. cm2C. cm2D. 4πcm2【答案】D【分析】根据扇形的面积公式计算即可.【解答】由图可得阴影部分面积为圆心角为120°,两个半径分别为4和2的圆环的面积的差.由∠BCA=90°,∠BAC=30°,AB=4cm,求得BC=2,AC=2,∠A′BA=120°,∠CBC′=120°,所以阴影部分面积=(S△A′BC′+S扇形BAA′)-S扇形BCC′-S△ABC=×(42-22)=4cm2故选:D。
小学奥数 4-4-1 圆与扇形(一).教师版

研究圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,通过变动图形的位置或对图形进行分割、旋转、拼补,使它变成可以计算出面积的规则图形来计算它们的面积.圆的面积2πr =;扇形的面积2π360nr =⨯;圆的周长2πr =;扇形的弧长2π360nr =⨯.一、跟曲线有关的图形元素:①扇形:扇形由顶点在圆心的角的两边和这两边所截一段圆弧围成的图形,扇形是圆的一部分.我们经常说的12圆、14圆、16圆等等其实都是扇形,而这个几分之几表示的其实是这个扇形的圆心角占这个圆周角的几分之几.那么一般的求法是什么呢?关键是360n.比如:扇形的面积=所在圆的面积360n⨯;扇形中的弧长部分=所在圆的周长360n⨯扇形的周长=所在圆的周长+360n⨯2⨯半径(易错点是把扇形的周长等同于扇形的弧长)②弓形:弓形一般不要求周长,主要求面积.一般来说,弓形面积=扇形面积-三角形面积.(除了半圆)③”弯角”:如图:弯角的面积=正方形-扇形④”谷子”:如图:“谷子”的面积=弓形面积2⨯二、常用的思想方法:①转化思想(复杂转化为简单,不熟悉的转化为熟悉的) ②等积变形(割补、平移、旋转等) ③借来还去(加减法)④外围入手(从会求的图形或者能求的图形入手,看与要求的部分之间的”关系”)板块一 平移、旋转、割补、对称在曲线型面积中的应用【例 1】 如图,圆O 的直径AB 与CD 互相垂直,AB =10厘米,以C 为圆心,CA 为半径画弧。
求月牙形ADBEA (阴影部分)的面积。
例题精讲圆与扇形D【考点】圆与扇形 【难度】3星 【题型】解答 【关键词】华杯赛,决赛,第9题,10分 【解析】 ①月牙形ADBEA (阴影部分)的面积=半圆的面积+△ABC 的面积-扇形CAEBC 的面积②月牙形ADBEA 的面积=211π525π502524⨯⨯+-⨯⨯=(平方厘米),所以月牙形ADBEA 的面积是25平方厘米。
【教师必备】小学奥数4-4-3 圆与扇形(三).专项检测及答案解析

研究圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,通过变动图形的位置或对图形进行分割、旋转、拼补,使它变成可以计算出面积的规则图形来计算它们的面积.圆的面积2πr =;扇形的面积2π360nr =⨯;圆的周长2πr =;扇形的弧长2π360nr =⨯.一、 跟曲线有关的图形元素: ①扇形:扇形由顶点在圆心的角的两边和这两边所截一段圆弧围成的图形,扇形是圆的一部分.我们经常说的12圆、14圆、16圆等等其实都是扇形,而这个几分之几表示的其实是这个扇形的圆心角占这个圆周角的几分之几.那么一般的求法是什么呢?关键是360n.比如:扇形的面积=所在圆的面积360n⨯;扇形中的弧长部分=所在圆的周长360n⨯扇形的周长=所在圆的周长360n⨯+2⨯半径(易错点是把扇形的周长等同于扇形的弧长) ②弓形:弓形一般不要求周长,主要求面积.一般来说,弓形面积=扇形面积-三角形面积.(除了半圆)③”弯角”:如图:弯角的面积=正方形-扇形④”谷子”:如图:“谷子”的面积=弓形面积2⨯二、 常用的思想方法:①转化思想(复杂转化为简单,不熟悉的转化为熟悉的) ②等积变形(割补、平移、旋转等) ③借来还去(加减法)④外围入手(从会求的图形或者能求的图形入手,看与要求的部分之间的”关系”)板块、曲线型旋转问题【例 1】 正三角形ABC 的边长是6厘米,在一条直线上将它翻滚几次,使A 点再次落在这条直线上,那么A 点在翻滚过程中经过的路线总长度是多少厘米?如果三角形例题精讲圆与扇形面积是15平方厘米,那么三角形在滚动过程中扫过的面积是多少平方厘米?(结果保留π)【考点】曲线型旋转问题 【难度】3星 【题型】解答 【解析】 如图所示,A 点在翻滚过程中经过的路线为两段120︒的圆弧,所以路线的总长度为:1202π628π360⨯⨯⨯=厘米;三角形在滚动过程中扫过的图形的为两个120︒的扇形加上一个与其相等的正三角形,面积为:2120π621524π15360⨯⨯⨯+=+平方厘米.【答案】24π15+【巩固】直角三角形ABC 放在一条直线上,斜边AC 长20厘米,直角边BC 长10厘米.如下图所示,三角形由位置Ⅰ绕A 点转动,到达位置Ⅱ,此时B ,C 点分别到达1B ,1C 点;再绕1B 点转动,到达位置Ⅲ,此时A ,1C 点分别到达2A ,2C 点.求C 点经1C 到2C 走过的路径的长.60︒30︒B 1C 1C 2A 2CB AⅢⅡⅠ【考点】曲线型旋转问题 【难度】3星 【题型】解答【解析】 由于BC 为AC 的一半,所以30CAB ∠=︒,则弧1CC 为大圆周长的18030536012︒-︒=︒,弧12C C 为小圆周长的14,而112C C CC +即为C 点经1C 到2C 的路径,所以C 点经1C 到2C 走过的路径的长为5150652π202π10π5ππ12433⨯⨯+⨯⨯=+=(厘米).【答案】65π3【巩固】如图,一条直线上放着一个长和宽分别为4cm 和3cm 的长方形Ⅰ.它的对角线长恰好是5cm .让这个长方形绕顶点B 顺时针旋转90°后到达长方形Ⅱ的位置,这样连续做三次,点A 到达点E 的位置.求点A 走过的路程的长.ⅣⅢⅡⅠEDCBA【考点】曲线型旋转问题 【难度】3星 【题型】解答 【解析】 因为长方形旋转了三次,所以A 点在整个运动过程中也走了三段路程(如右上图所示).这三段路程分别是:第1段是弧1AA ,它的长度是12π44⨯⨯⨯(cm );第2段是弧12A A ,它的长度是12π54⨯⨯⨯(cm );第3段是弧2A E ,它的长度是12π34⨯⨯⨯(cm );所以A 点走过的路程长为:1112π42π52π36π444⨯⨯⨯+⨯⨯⨯+⨯⨯⨯=(cm ).【答案】6π【例 2】 草场上有一个长20米、宽10米的关闭着的羊圈,在羊圈的一角用长30米的绳子拴着一只羊(见如图).问:这只羊能够活动的范围有多大?(圆周率取3.14)【考点】曲线型旋转问题 【难度】3星 【题型】解答【解析】 如图所示,羊活动的范围可以分为A ,B ,C 三部分,其中A 是半径30米的34个圆,B ,C 分别是半径为20米和10米的14个圆. 所以羊活动的范围是222311π30π20π10444⨯⨯+⨯⨯+⨯⨯222311π302010444⎛⎫=⨯⨯+⨯+⨯ ⎪⎝⎭2512=.【答案】2512【巩固】一只狗被拴在底座为边长3m 的等边三角形建筑物的墙角上(如图),绳长是4m ,求狗所能到的地方的总面积.(圆周率按3.14计算)3【考点】曲线型旋转问题 【难度】3星 【题型】解答 【解析】 如图所示,羊活动的范围是一个半径4m ,圆心角300°的扇形与两个半径1m ,圆心角120°的扇形之和.所以答案是243.96m .【答案】43.96【例 3】 如图是一个直径为3cm 的半圆,让这个半圆以A 点为轴沿逆时针方向旋转60︒,此时B 点移动到'B 点,求阴影部分的面积.(图中长度单位为cm ,圆周率按3计算).BA【考点】曲线型旋转问题 【难度】3星 【题型】解答 【解析】 面积=圆心角为60︒的扇形面积+半圆-空白部分面积(也是半圆)=圆心角为60︒的扇形面积22603π3π 4.5(cm )3602=⨯⨯==.【答案】4.5【例 4】 如图所示,直角三角形ABC 的斜边AB 长为10厘米,60ABC ∠=︒,此时BC 长5厘米.以点B 为中心,将ABC ∆顺时针旋转120︒,点A 、C 分别到达点E 、D 的位置.求AC 边扫过的图形即图中阴影部分的面积.(π取3)E【考点】曲线型旋转问题 【难度】3星 【题型】解答 【解析】 注意分割、平移、补齐.E DB A如图所示,将图形⑴移补到图形⑵的位置, 因为60EBD ∠=︒,那么120ABE ∠=︒,则阴影部分为一圆环的13.所以阴影部分面积为()221π753AB BC ⨯⨯-=(平方厘米).【答案】75【巩固】如右图,以OA 为斜边的直角三角形的面积是24平方厘米,斜边长10厘米,将它以O 点为中心旋转90︒,问:三角形扫过的面积是多少?(π取3)【考点】曲线型旋转问题 【难度】3星 【题型】解答 【解析】 从图中可以看出,直角三角形扫过的面积就是图中图形的总面积,等于一个三角形的面积与四分之一圆的面积之和.圆的半径就是直角三角形的斜边OA .因此可以求得,三角形扫过的面积为:124π10102425π994+⨯⨯⨯=+=(平方厘米).【答案】99【巩固】(“学而思杯”数学试题)如图,直角三角形ABC 中,B ∠为直角,且2BC =厘米,4AC = 厘米,则在将ABC ∆绕C 点顺时针旋转120︒的过程中,AB 边扫过图形的面积为 .(π 3.14=)C B AB'A'C B A【考点】曲线型旋转问题 【难度】3星 【题型】解答 【解析】 如右上图所示,假设ABC ∆旋转120︒到达''A B C ∆的位置.阴影部分为AB 边扫过的图形.从图中可以看出,阴影部分面积等于整个图形的总面积减去空白部分面积,而整个图形总面积等于扇形'ACA 的面积与ABC ∆的面积之和,空白部分面积等于扇形'BCB 的面积与''A B C ∆的面积,由于ABC ∆的面积与''A B C ∆的面积相等,所以阴影部分的面积等于扇形'ACA 与扇形'BCB 的面积之差,为22120120π4π24π12.56360360⨯⨯-⨯⨯==(平方厘米).【答案】12.56【例 5】 如下图,△ABC 是一个等腰直角三角形,直角边的长度是1米。
小学奥数—圆与扇形(三)

A
BC
DE
【例 2】 草场上有一个长 20 米、宽 10 米的关闭着的羊圈,在羊圈的一角用长 30 米的绳子拴着一只羊(见如 图).问:这只羊能够活动的范围有多大?(圆周率取 3.14 )
4-3-3 圆与扇形 题库
学生版
page 2 of 8
【巩固】一只狗被拴在底座为边长 3m 的等边三角形建筑物的墙角上(如图),绳长是 4m ,求狗所能到的地方 的总面积.(圆周率按 3.14 计算)
A
B
D
C
【例 8】 (华杯赛初赛)半径为 25 厘米的小铁环沿着半径为 50 厘米的大铁环的内侧作无滑动的滚动,当小 铁环沿大铁环滚动一周回到原位时,问小铁环自身转了几圈?
【巩固】如果半径为 25 厘米的小铁环沿着半径为 50 厘米的大铁环的外侧作无滑动的滚动,当小铁环沿大铁 环滚动一周回到原位时,问小铁环自身转了几圈?
360 扇形中的弧长部分 所在圆的周长 n
360 扇形的周长 所在圆的周长 n 2 半径(易错点是把扇形的周长等同于扇形的弧长)
360 ②弓形:弓形一般不要求周长,主要求面积.
一般来说,弓形面积 扇形面积-三角形面积.(除了半圆)
③”弯角”:如图:
弯角的面积 正方形-扇形
④”谷子”:如图:
正方形的边长为 10,那么阴影部分的面积是多少?( 取 3.14)
A
10 D
P
B QC
4-3-3 圆与扇形 题库
学生版
page 8 of 8
【巩固】如右图,以 OA 为斜边的直角三角形的面积是 24 平方厘米,斜边长 10 厘米,将它以 O 点为中心旋 转 90 ,问:三角形扫过的面积是多少?( π 取 3)
4-3-3 圆与扇形 题库
04-六年级秋季班-第18讲:圆和扇形章节复习-教师版

A BO圆和扇形章节复习内容分析圆和扇形是初中数学六年级第四章的内容,同学们需要学会用圆的周长、面积、弧长和扇形面积公式进行简单的计算,并体会近似与精确的数学思想.难点是圆的组合图形的面积计算,同学们需要灵活运用各个基本图形面积的计算方法,并能看出组合图形是由哪些基本图形组成,从而进行相关的计算. 知识精讲基本内容注意点4.1 圆的周长 1、圆的周长公式及应用. 4.2 弧长 1、弧长公式及应用. 4.3 圆的面积 1、圆的面积公式及应用. 4.4 扇形的面积1、扇形的面积公式及应用;2、*圆的组合图形的面积计算.圆一:圆的周长1、 圆的周长通过操作和计算,我们发现圆的周长都是直径的固定的倍数,我们把这个倍数叫做圆周率,用字母π表示,π读作“pai”;圆周率π是个无限不循环小数, 3.14π≈.圆的周长÷直径 = 圆周率.用字母C 表示圆的周长,d 表示直径,r 表示半径,那么:C d π=或2C r π=二:弧长1、弧和圆心角的概念如图,圆上A 、B 两点之间的部分就是弧,记作:AB ,读作:弧AB ;AOB ∠称为圆心角.ABO2、弧长公式设圆的半径长为r ,n °圆心角所对的弧长是l ,那么:180nl r π=. 三:圆的面积1、 圆的面积圆所占平面的大小叫做圆的面积.设圆的半径长为r ,面积为S ,那么:圆的面积2S r r r ππ=⨯=.四:扇形的面积1、 扇形的概念由组成圆心角的两条半径和圆心角所对的弧围成的图形,叫做扇形. 如图,空白部分记作扇形AOB . 2、 扇形的面积设组成扇形的半径为r ,圆心角为n °,弧长为l ,那么:213602n S r lr π==扇形.五:圆的组合图形1、三角形的面积 =2⨯底高. 2、等腰直角三角形的面积 =24=直角边的平方斜边的平方. 3、长方形的面积 =⨯长宽. 4、正方形的面积 = 边长的平方 = 2对角线的平方.5、菱形的面积 =2对角线之积.6、梯形的面积 =()2⨯上底+下底高.7、圆的面积 =π⨯半径的平方. 8、扇形的面积 =360π⨯⨯︒圆心角半径的平方.例题解析【例1】 圆的周长是这个圆半径的( )倍A .6B .2πC .3.14D .6.28【难度】★【答案】B 【解析】圆的周长公式2l r π=,所以周长是半径的2π倍. 【总结】考查圆的周长与半径的关系.【例2】 同一个圆里,直径与半径的比是______.【难度】★【答案】2:1.【解析】直径是半径的两倍,所以比是2:1. 【总结】考查同一个圆的直径与半径的关系.【例3】 要画一个周长为18.84厘米的圆,它的半径应取______厘米. 【难度】★【答案】3.【解析】18.84 3.1423÷÷=厘米. 【总结】考查圆的周长公式的应用.【例4】 如果圆的半径缩小到它的13,那么圆的周长缩小到原来的______.【难度】★【答案】13.【解析】由2l r π=可知圆的周长与半径成正比,所以周长也缩小到原来的13.【总结】考查圆的周长的计算.【例5】 如果圆上一条弧长占圆周长的15,那么这条弧所对的圆心角占圆的周角的______.【难度】★【答案】72︒.【解析】由180n r l π=可知,弧长与圆心角成正比,故圆心角为:1360725⨯=.【总结】考查弧长公式的运用.【例6】 圆心角为45°的扇形,如果拼成一个圆,需要这样的扇形至少____个. 【难度】★【答案】8.【解析】360458÷=. 【总结】考查扇形与圆的关系.【例7】 下列叙述中正确的个数是( ) (1)弧的长度只取决于弧所在圆的半径大小;(2)两条弧的长度相等,则它们所对的圆心角相等;(3)圆心角扩大3倍,而圆的半径缩小13,那么原来的弧长不变.A .0B .1C .2D .3【难度】★【答案】B【解析】由180n rl π=,可知弧长取决于圆心角和半径,所以(1)、(2)都错,弧长与半径和圆心角都成正比,所以(3)对.【总结】考查对弧长公式的理解及决定弧长的量.【例8】 一个扇形的面积是它所在圆面积的79,这个扇形的圆心角是______度. 【难度】★【答案】280.【解析】因为213602n S r lr π==扇形,所以°°73602809n =⨯=. 【总结】考查扇形的面积与圆心角的关系.【例9】 一个圆的周长为9.42厘米,那么这个圆的面积是______平方厘米. 【难度】★★ 【答案】27.065cm .【解析】9.42 3.142 1.5r cm =÷÷=半径,所以面积为:23.14 1.5 1.57.065cm ⨯⨯=. 【总结】考查圆的周长与面积的计算.【例10】 把一根长314厘米的细钢丝绕在一个圆筒上,正好绕10周,这个圆筒的半径是( )A .5B .10C .20D .3.14【难度】★★【答案】A 【解析】31410 3.1425÷÷÷=. 【总结】考查圆的周长在实际问题中的应用.【例11】 在一个边长为8厘米的正方形内画一个最大的圆,这个圆的周长是______厘米. 【难度】★★【答案】8π.【解析】圆的直径等于正方形的边长,所以周长是8d ππ=. 【总结】考查圆的周长的计算.【例12】 有一个直径是8厘米的半圆形铁片,这个铁片的周长是______厘米. 【难度】★★【答案】20.56cm .【解析】28 3.1482820.56d cm π÷+=⨯÷+=. 【总结】考查半圆的周长,半圆的周长等于半圆加上直径的长..【例13】 一个环形纸板,内圆半径是3厘米,外圆直径是10厘米,这个环形纸板的面积是3厘米______平方厘米.【难度】★★【答案】16π.【解析】外圆半径是5厘米,故圆环面积为:225316ππ-=()平方厘米. 【总结】考查圆环的面积的计算,大圆面积减去小圆面积.【例14】 下列说法正确的是( ) A .扇形是圆的一部分,圆的一部分是扇形 B .圆中任意画两条半径,一定能构成两个扇形 C .如果圆的面积扩大9倍,那么圆的直径扩大9倍D .在所有扇形中,圆半径大的面积大【难度】★★【答案】B【解析】圆的一部分不一定是扇形;圆的面积扩大9倍,直径扩大3倍;扇形的面积与圆心角和半径都有关.【总结】考查圆和扇形的关系及圆的面积与直径的关系.【例15】 已知大扇形的面积是小扇形面积的94倍,如果它们的圆心角相等,那么小扇形的半径是大扇形半径的______.【难度】★★【答案】23.【解析】扇形的面积与半径的平方成正比,所以小扇形的半径是大扇形半径的23. 【总结】考查扇形的面积与半径的关系.【例16】 已知扇形的弧长是9.42厘米,圆心角是270°,那么这个扇形的面积是______平方厘米【难度】★★【答案】237.68cm .【解析】扇形的半径为:9.42180270 3.142cm ⨯÷÷=, 故扇形的面积为:22703.1429.42360⨯⨯=2cm . 【总结】考查扇形的弧长与扇形的面积的计算,注意公式的准确运用.【例17】 图中的三角形是等边三角形,阴影部分是一个扇形,那么阴影部分的面积是______平方厘米.【难度】★★【答案】152π平方厘米. 【解析】23001533602S ππ=⨯⨯=阴影平方厘米. 【总结】考查扇形的面积,注意本题中圆心角度数为300°.【例18】 .下面两个图形中,其中正方形的面积相等,那么阴影部分面积大小关系是( ) A .甲 > 乙 B .甲 < 乙C .甲 = 乙D .无法比较【难度】★★【答案】C【解析】乙的四个扇形恰好组成一个圆. 【总结】本题主要考查对阴影部分的面积的计算.【例19】 要画一个面积是3.14平方厘米的圆,圆规两脚之间的距离要取______厘米. 【难度】★★【答案】1.【解析】圆规两脚间的距离就是圆的半径,2 3.14 3.1411r r =÷==,所以厘米. 【总结】考查利用圆的面积求圆的半径.【例20】 在周长为24厘米的正方形纸片上剪去一个最大的圆,则剩余部分的周长是______厘米,面积是______平方厘米.(结果保留π).【难度】★★【答案】42.84;7.74.【解析】剩余部分的周长是正方形的周长加上圆的周长,剩余部分的面积是正方形面积减去圆的面积,而最大圆的直径为正方形的边长,因为正方形的周长为24厘米,故边长为6厘米,即636d r C d ππ====圆,,故厘米,24C =正方形厘米, 所以剩余部分周长为:62418.842442.84π+=+=厘米,面积为226633697.74r πππ=⨯-⨯=-=平方厘米.【总结】考查圆的周长与面积的计算,注意正方形中剪出的最大圆的直径即为正方形的边长.【例21】 如图,阴影部分周长相同的有( ) A .1个 B .2个 C .3个 D .4个【难度】★★【答案】D【解析】阴影部分的周长都等于大半圆的长加小半圆的长,每个图中都只有一个大半圆, 所有的小半圆周长也相等,所以四个阴影部分周长都相等,故选D . 【总结】考查阴影部分的周长的计算.【例22】 如图,正方形中,分别以两个对角顶点为圆心,以正方形的边长6为半径画弧,形成树叶形的图案(阴影部分),求树叶形图案的周长.【难度】★★【答案】18.84.【解析】树叶形的周长是半径为6的半圆的周长,所以618.84C r ππ===.ABCD A B CD【总结】考查阴影部分的周长的计算,注意认真分析图形的特征.【例23】 扇形的面积是314平方厘米,扇形所在的圆的面积是1256平方厘米,这个扇形的圆心角是多少度?【难度】★★【答案】90︒.【解析】扇形的面积与圆心角成正比,所以314360901256⨯=︒.【总结】考查扇形的面积与圆心角的关系.【例24】 如图,AB = BC = CD = 2厘米,分别求出大、中、小圆的周长和面积. 【难度】★★【答案】642C C C πππ===小大中厘米,厘米,厘米;94S S S πππ===小大中平方厘米,平方厘米,平方厘米. 【解析】64C d C d ππππ====大大中中厘米,厘米, 2C d ππ==小小厘米,2r S ππ==小小平方厘米,22r 9r 4S S ππππ====大大中中平方厘米,平方厘米.【总结】考查圆的周长和面积的计算.【例25】 如图,四边形ABCD 是长方形,AB = 12 cm ,求图中阴影部分的面积. 【难度】★★ 【答案】28.26cm 2. 【解析】6AD BC cm ==, 212672cm S S =⨯==长半圆,226218cm ππ⨯÷=,()()211367218928.26cm 22ABD S S S S ππ=--=--==△阴影长半圆. 【总结】考查阴影部分面积的计算,注意用规则图形的面积去表示不规则图形的面积. 【例26】 一辆自行车轮胎的外直径是0.7米,如果车轮每分钟转90周,40分钟能行多远?通过一座567米的大桥需要多少分钟?(π取3)【难度】★★【答案】76503米,分.【解析】40分钟能行:30.790407560⨯⨯⨯=米,需要时间:5671893÷=分.【总结】考查圆的周长的在实际问题中的应用.【例27】 在长19厘米,宽9厘米的长方形纸片中,剪半径都是1.5厘米的小圆,共可剪出小圆多少个?剪去这些小圆后,剩下的边角料的总面积是多少?.【难度】★★【答案】43.83平方厘米. 【解析】9 1.523÷⨯=(), 19 1.5261÷⨯=(),所以可剪出3618⨯=个圆,剩下的面积是:219918 1.517140.543.83ππ⨯-⨯⨯=-=平方厘米. 【总结】考查长方形中剪出圆的问题,注意认真分析.【例28】 四个半径为2厘米的圆围成的图形中,求阴影部分的面积和周长.【难度】★★【答案】3.44平方厘米,12.56厘米.【解析】面积:2442164 3.44ππ⨯-⨯=-=平方厘米; 周长:222412.56r πππ=⨯⨯==厘米.【总结】考查阴影部分的周长与面积的计算,注意观察阴影部分图形的特征.【例29】 如图,圆的周长为6.28厘米,圆的面积与长方形的面积正好相等,图中阴影部分的周长是______厘米.【难度】★★★ 【答案】7.85厘米.【解析】圆的半径为:6.28 3.1421÷÷=厘米,则2r 3.14S S π===圆长方形平方厘米, 故长方形的长为:3.141 3.14÷=厘米,所以阴影部分的周长为:()3.1412 6.28427.85cm +⨯+÷-=厘米.【总结】考查阴影部分的周长的计算,注意此周长包含了四分之一的弧长和三条线段长. 【例30】 两个连在一起的皮带轮,其中一个轮子直径是3 dm ,当它旋转7周时,另一个轮子转了5周,则另一个轮子的半径是______dm .【难度】★★★【答案】4.2.【解析】由题意,可得另一个轮子的半径为:375 4.2⨯÷=dm . 【总结】本题中要找到两个轮子转动的距离的关系,然后再计算即可.【例31】 将一个圆沿半径剪开,再拼成一个近似长方形,已知这个长方形的周长是41.4厘米,那么,这个圆的周长和面积各是多少?【难度】★★★【答案】31.4厘米,78.5平方厘米.【解析】圆的半径为:41.42 3.1415÷÷+=()厘米,故圆的周长为:2 3.14531.4⨯⨯=厘米,圆的面积为:3.145578.5⨯⨯=平方厘米.【总结】考查圆的周长与面积的计算.拥有2台拥有1台20% 其他【例32】 在一次对某小区500户家庭拥有电视机的数量的调查中,调查结果如图所示,根据图中所给的信息回答问题:(1)家中拥有一台电视机的家庭有几户?(2)如果拥有一台电视机的家庭数正好是拥有2台电视机的家庭数的27,那么拥有2台电视机的家庭有几户?(3)图中的“其他”的扇形的圆心角是几度?【难度】★★★【答案】(1)100户;(2)350户;(3)36. 【解析】(1)()50020%100⨯=户; (2)21003507÷=(户); (3)()35050070%360120%70%36÷=⨯--=︒,. 【总结】考查有关扇形图的简单计算.课后作业【作业1】 若一弧的长是它所在圆的周长的15,则此弧所对的圆心角是______度.【难度】★【答案】72.【解析】弧长与圆心角成正比,1360725⨯=.【总结】考查弧长与圆心角的关系.【作业2】 如果一条弧所对的圆心角缩小为原来的14,所在圆的半径扩大为原来的3倍,那么所得的新弧长与原来的弧长之比是______.【难度】★【答案】3:4.【解析】180nl r π=,弧长与圆心角、半径成正比,所以比为3:4. 【总结】考查弧长与圆心角和半径的关系.【作业3】 甲圆与乙圆的半径之比是 2 : 3,则甲与乙的直径之比是______,周长之比是______,面积之比是______.【难度】★【答案】2:3,2:3,4:9.【解析】半径比等于直径比等于周长比,面积比等于半径比的平方. 【总结】考查圆中各个基本量之间的关系. 【作业4】 下列说法正确的个数是( ) (1)半径越大,圆的面积越大; (2)半径越大,所对的弧越长; (3)弧是圆上两点间的一条线段; (4)圆心角相等,它们所对的弧长也相等.A .1个B .2个C .3个D .4个【难度】★★【答案】A【解析】2S r π=,圆的面积只与半径有关,(1)√;180nl r π=弧长与半径和圆心角都有关系;(2)×; (3)×; (4)×,弧长与半径和圆心角都有关.【总结】考查弧长的影响因素. 【作业5】 求下列各圆的周长和面积: (1)r = 3,C =______,S =______; (2)d = 8,C =______,S =______;(3)l = 5,n = 72°,S =______.【难度】★★【答案】(1)C = 9.42,S = 28.26;(2)C = 25.12,S = 50.24; (3)S = 49.76.【解析】222360nC r S r S r πππ===,,.【总结】考查圆的周长与面积的计算.【作业6】 求下列弧的弧长:(1)r = 4,n = 90°,l =______;(2)d = 9,n = 120°l =______; (3)C = 20,n = 175°l =______.【难度】★★【答案】(1)6.28;(2)9.42;(3)9.72.【解析】(1)9042180180n l r πππ==⨯==6.28,(2)91209239.4221802r d l ππ=÷==⨯==,; (3)10175101759.72218018C r l ππππ===⨯=≈,.【总结】考查弧长的计算. 【作业7】 在长是6厘米,宽是4厘米的长方形内剪一个最大的圆,则圆的面积是______平方厘米【难度】★★【答案】12.56.【解析】圆的直径等于4厘米,2412.56S r ππ===平方厘米.【总结】考查圆的面积的计算.【作业8】 用一根长为37.68厘米的铅丝围成一个圆,圆的面积是______平方厘米.【难度】★★【答案】113.04平方厘米.【解析】237.68 3.142636113.04r S r ππ=÷÷====厘米,平方厘米.【总结】本题中铁丝的总长度就是所围成的圆的周长,从而算出半径和面积.【作业9】 一个圆环形纸片,外环半径6厘米,内环半径5厘米,这个圆环的面积是______平方厘米,周长是______厘米.【难度】★★【答案】34.54;69.08.【解析】221236251134.54S r r πππππ=-=-==圆环平方厘米;()1222269.08C r r ππ=+==圆环厘米.【总结】考查圆环的面积与周长的计算.【作业10】 已知一个扇形的半径是6厘米,圆心角是120°,则此扇形的周长是______厘米.【难度】★★【答案】24.56厘米. 【解析】1202261241224.56180180n C l r r r πππ=+=+=⨯+=+=扇厘米. 【总结】考查扇形周长的计算,注意扇形的周长还要包含两条半径的长.【作业11】 扇形的半径是6分米,扇形的弧长是4π分米,这段弧所对的圆心角是______度,这个扇形的面积是______平方分米.(结果保留π)【难度】★★【答案】120,12π. 【解析】180********l n r πππ⨯===,212012360S r ππ==平方分米. 【总结】考查扇形的圆心角和面积的计算.A B O A BCD B C D 【作业12】 一个时钟的时针长5厘米,它从上午8点到下午4点,时针针尖走过的距离是( ).A .203πB .103πC .60πD .30π【难度】★★【答案】203π.【解析】2402051801803n l r πππ==⨯=. 【总结】考查弧长在计算时针所走过的路程中的计算.【作业13】 已知一条弧长等于1,它的半径为R ,这条弧所对的圆心角增加1°,则它的弧长增加( )A .1nB .180Rπ C .180R π D .1360【难度】★★【答案】B【解析】由弧长公式1800n R l π=可知,当圆心角增加1°时,弧长则增加180R π. 【总结】考查对弧长公式中每个量的理解.【作业14】 如图,半径r = 12,60AOB ∠=︒,求这个图形的周长.【难度】★★【答案】86.8厘米. 【解析】30012122202486.8180C ππ=⨯+⨯=+=厘米. 【总结】此图的周长包含了弧长和两条半径的长.【作业15】 如图,正方形ABCD 的边长为4,求阴影部分的面积和周长.【难度】★★【答案】面积为16,周长为18.84.【解析】阴影部分的面积是正方形的面积加上圆的面积,再减去扇形的面积;阴影部分的周长则是三段弧的长的和.故2244441624S ππ⨯⎛⎫=⨯+⨯-= ⎪⎝⎭阴影, 12242618.844C r R πππππ=+⨯=+==阴影. 【总结】考查阴影部分的面积和周长的计算,认真分析阴影图形的特征.【作业16】 如图,四边形ABCD 是长方形,AB = 10 cm ,BC = 6 cm ,求阴影部分的周长.【难度】★★【答案】33.12厘米.【解析】()121026448833.124C πππ=⨯+⨯++=+=厘米. 【总结】考查阴影部分周长的计算,注意包含了每一段弧和线段的长.AB C A BCD 【作业17】 如图,一个边长是1厘米的等边三角形,将它沿直线作顺时针方向翻动,到达图示中最右边三角形的位置,点B 所经过的路程是______厘米.(结果保留π)【难度】★★★【答案】2π.【解析】分析整个运动过程,可知B 经过的路程恰好为一个圆周,所以B 所经过的路程 是22r ππ=.【总结】考查图形在翻转过程中,图形上每个一点的运动轨迹,综合性较强,教师要带领学 生共同分析.【作业18】 如图所示,已知正方形ABCD 的边长为3.2厘米,在这个正方形中有个半径为0.4厘米的圆沿着它的四条边滚动一周,求圆滚动时扫过的面积.(保留π)【难度】★★★【答案】7.040.16π+. 【解析】经过分析可知圆扫过的面积为,大正方形的面积减去中间空白处的小正方形的面积再减去四个弯角的面积.一个弯角的面积是:210.40.40.40.160.044ππ⨯-⨯⨯=-, 则4个弯角的面积是:(0.160.04)40.640.16ππ-⨯=-, 而中间空白部分的正方形的面积是:(3.20.80.8)(3.20.80.8) 1.6 1.6 2.56--⨯--=⨯=, 故圆扫过的面积为:3.2 3.2 2.56(0.640.16)7.040.16ππ⨯---=+.【总结】本题综合性较强,主要是要分析清楚圆在滚动时扫过的面积的状态.。
奥数:4-3-3圆与扇形题库

研究圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,通过变动图形的位置或对图形进行分割、旋转、拼补,使它变成可以计算出面积的规则图形来计算它们的面积.圆的面积2πr =;扇形的面积2π360nr =⨯;圆的周长2πr =;扇形的弧长2π360nr =⨯.一、跟曲线有关的图形元素:①扇形:扇形由顶点在圆心的角的两边和这两边所截一段圆弧围成的图形,扇形是圆的一部分.我们经常说的12圆、14圆、16圆等等其实都是扇形,而这个几分之几表示的其实是这个扇形的圆心角占这个圆周角的几分之几.那么一般的求法是什么呢?关键是360n.比如:扇形的面积=所在圆的面积360n⨯;扇形中的弧长部分=所在圆的周长360n⨯扇形的周长=所在圆的周长360n⨯+2⨯半径(易错点是把扇形的周长等同于扇形的弧长)②弓形:弓形一般不要求周长,主要求面积.一般来说,弓形面积=扇形面积-三角形面积.(除了半圆)③”弯角”:如图:弯角的面积=正方形-扇形④”谷子”:如图:“谷子”的面积=弓形面积2⨯二、常用的思想方法:①转化思想(复杂转化为简单,不熟悉的转化为熟悉的) ②等积变形(割补、平移、旋转等) ③借来还去(加减法)④外围入手(从会求的图形或者能求的图形入手,看与要求的部分之间的”关系”)板块一 平移、旋转、割补、对称在曲线型面积中的应用【例 1】 下图中每一个小正方形的面积是1平方厘米,那么格线部分的面积是多少平方厘米?例题精讲圆与扇形【解析】 割补法.如右图,格线部分的面积是36平方厘米.【巩固】下图中每一个小正方形的面积是1平方厘米,那么格线部分的面积是多少平方厘米?【解析】 割补法.如右图,格线部分的面积是36平方厘米.【例 2】 如图,在18⨯8的方格纸上,画有1,9,9,8四个数字.那么,图中的阴影面积占整个方格纸面积的几分之几?【解析】 我们数出阴影部分中完整的小正方形有8+15+15+16=54个,其中部分有6+6+8=20个,部分有6+6+8=20(个),而1个 和1个 正好组成一个完整的小正方形,所以阴影部分共包含54+20=74(个)完整小正方形,而整个方格纸包含8⨯18=144(个)完整小正方形.所以图中阴影面积占整个方格纸面积的74144,即3772.【巩固】在4×7的方格纸板上面有如阴影所示的”6”字,阴影边缘是线段或圆弧.问阴影面积占纸板面积的几分之几?【解析】 矩形纸板共28个小正方格,其中弧线都是14圆周,非阴影部分有3个完整的小正方形,其余部分可拼成6个小正方格.因此阴影部分共28-6-3=19个小正方格.所以,阴影面积占纸板面积的1928.【例 3】 (2019年西城实验考题)在一个边长为2厘米的正方形内,分别以它的三条边为直径向内作三个半圆,则图中阴影部分的面积为 平方厘米.【解析】 采用割补法.如果将阴影半圆中的2个弓形移到下面的等腰直角三角形中,那么就形成两个相同的等腰直角三角形,所以阴影部分的面积等于两个等腰直角三角形的面积和,即正方形面积的一半,所以阴影部分的面积等于21222⨯=平方厘米.【巩固】如图,在一个边长为4的正方形内,以正方形的三条边为直径向内作三个半圆.求阴影部分的面积.【解析】 阴影部分经过切割平移变成了一个面积为正方形一半的长方形,则阴影部分面积为 4428⨯÷=.【例 4】 (人大附中分班考试题)如图,正方形边长为1,正方形的4个顶点和4条边分别为4个圆的圆心和半径,求阴影部分面积.(π取3.14)【解析】 把中间正方形里面的4个小阴影向外平移,得到如右图所示的图形,可见,阴影部分的面积等于四个正方形面积与四个90︒的扇形的面积之和,所以,221444441π14π7.14S S S S S =⨯+⨯=⨯+=⨯+⨯=+=圆阴影圆.【例 5】 图中的4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?【解析】 如下图所示:可以将每个圆内的阴影部分拼成一个正方形,每个正方形的面积为11240.542⨯÷⨯=⨯=()(平方厘米),所以阴影部分的总面积为248⨯=(平方厘米).【巩固】如图所示,四个全等的圆每个半径均为2m,阴影部分的面积是.或【解析】我们虽没有学过圆或者圆弧的面积公式,但做一定的割补后我们发现其实我们并不需要知道这些公式也可以求出阴影部分面积.如图,割补后阴影部分的面积与正方形的面积相等,等于222216m⨯=()().【例6】如右图,有8个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心.则花瓣图形的面积是多少平方厘米? (π取3)【解析】本题直接计算不方便,可以利用分割移动凑成规则图形来求解.如右上图,连接顶角上的4个圆心,可得到一个边长为4的正方形.可以看出,与原图相比,正方形的每一条边上都多了一个半圆,所以可以把原花瓣图形的每个角上分割出一个半圆来补在这些地方,这样得到一个正方形,还剩下4个14圆,合起来恰好是一个圆,所以花瓣图形的面积为224π119+⨯=(平方厘米).【总结】在求不规则图形的面积时,我们一般要对原图进行切割、移动、补齐,使原图变成一个规则的图形,从而利用面积公式进行求解.这个切割、移动、补齐的过程实际上是整个解题过程的关键,我们需要多多练习,这样才能快速找到切割拼补的方法、【例7】如图中三个圆的半径都是5cm,三个圆两两相交于圆心.求阴影部分的面积和.(圆周率取3.14)【解析】将原图割补成如图,阴影部分正好是一个半圆,面积为255 3.14239.25(cm)⨯⨯÷=【巩固】如图,大圆半径为小圆的直径,已知图中阴影部分面积为1S,空白部分面积为2S,那么这两个部分的面积之比是多少?(圆周率取3.14)【解析】 如图添加辅助线,小圆内部的阴影部分可以填到外侧来,这样,空白部分就是一个圆的内接正方形.设大圆半径为r ,则222S r =,221π2S r r =-,所以()12: 3.142:257:100S S =-=.移动图形是解这种题目的最好方法,一定要找出图形之间的关系.【例 8】 计算图中阴影部分的面积(单位:分米).A A【解析】 将右边的扇形向左平移,如图所示.两个阴影部分拼成—个直角梯形. ()5105275237.5+⨯÷=÷=(平方分米).【巩固】如图,阴影部分的面积是多少?224【解析】 首先观察阴影部分,我们发现阴影部分形如一个号角,但是我们并没有学习过如何求号角的面积,那么我们要怎么办呢?阴影部分我们找不到出路,那么我们不妨考虑下除了阴影部分之外的部分吧!观察发现,阴影部分左侧是一个扇形,而阴影部分右边的空白部分恰好与左边的扇形构成一个边长为4的正方形,那么阴影部分的面积就等于大的矩形面积减去正方形面积.则阴影部分面积(222)4(22)48++⨯-+⨯=【例 9】 请计算图中阴影部分的面积.【解析】 法一:为了求得阴影部分的面积,可以从下图的整体面积中扣掉一个圆的面积,就是要求的面积了.=-要扣掉圆的面积,如果按照下图把圆切成两半后,从两端去扣掉也是一样.如此一来,就会出现一个长方形的面积.半圆半圆-=因此,所求的面积为210330cm ⨯=().法二:由于原来的月牙形很难直接计算,我们可以尝试构造下面的辅助图形:如左上图所示,我们也可以这样来思考,让图形往右侧平移3cm 就会得到右上图中的组合图形,而这个组合图形中右端的月牙形正是我们要求的面积.显然图中右侧延伸出了多少面积,左侧就会缩进多少面积.因此,所求的面积是210330cm ⨯=().【例 10】 求图中阴影部分的面积.12CB12CB【解析】 如图,连接BD ,可知阴影部分的面积与三角形BCD 的面积相等,即为1112123622⨯⨯⨯=.【例 11】 求如图中阴影部分的面积.(圆周率取3.14)【解析】 可将左下橄榄型的阴影部分剖开,两部分分别顺逆时针90︒,则阴影部分转化为四分之一圆减去一个等腰直角三角形,所以阴影部分的面积为211π444 4.5642⨯⨯-⨯⨯=.【巩固】如图,四分之一大圆的半径为7,求阴影部分的面积,其中圆周率π取近似值227.【解析】 原题图中的左边部分可以割补至如右上图位置,这样只用先求出四分之一大圆的面积,再减去其内的等腰直角三角形面积即为所求.因为四分之一大圆的半径为7,所以其面积为: 2211227π738.5447⨯⨯≈⨯⨯=. 四分之一大圆内的等腰直角三角形ABC 的面积为17724.52⨯⨯=,所以阴影部分的面积为38.524.514-=.【例 12】 求下列各图中阴影部分的面积.(1)1010(2)ba【解析】 在图(1)中,阴影部分经过切割平移变成了一个底为10,高为5的三角形,利用三角形面积公式可以求得110102522S =⨯⨯=阴影;在图(2)中,阴影部分经过切割平移变成了一个长为b ,宽为a 的长方形,利用长方形面积公式可以求得S a b ab =⨯=阴影.【巩固】求下列各图中阴影部分的面积(图中长度单位为cm ,圆周率按3计算):⑴3⑵4⑶111⑷2⑸2⑹【解析】 ⑴4.5 ⑵4 ⑶1 ⑷2 ⑸1.5 ⑹4.5【例 13】 如图,ABCD 是正方形,且1FA AD D E ===,求阴影部分的面积.(取π3=)【解析】 方法一:两个分割开的阴影部分给我们求面积造成了很大的麻烦,那么我们把它们通过切割、移动、补齐,使两块阴影部分连接在一起,这个时候我们再来考虑,可能会有新的发现. 由于对称性,我们可以发现,弓形BMF 的面积和弓形BND 的面积是相等的,因此,阴影部分面积就等于不规则图形BDWC 的面积.因为ABCD 是正方形,且F A =AD =DE =1,则有CD =DE .那么四边形BDEC 为平行四边形,且∠E =45°.我们再在平行四边形BDEC 中来讨论,可以发现不规则图形BDWC 和扇形WDE 共同构成这个平行四边形,由此,我们可以知道阴影部分面积=平行四边形BDEC -扇形DEW 245511π13608=⨯-⨯⨯=.方法二:先看总的面积为14的圆,加上一个正方形,加上一个等腰直角三角形,在则阴影面积为总面积扣除一个等腰直角三角形,一个14圆,一个45︒的扇形.那么最终效果等于一个正方形扣除一个45︒的扇形.面积为215113188⨯-⨯⨯=.【巩固】求图中阴影部分的面积(单位:cm ).2【解析】 从图中可以看出,两部分阴影的面积之和恰好是梯形的面积,所以阴影部分面积为21(24)39cm 2⨯+⨯=.【例 14】 如图,长方形ABCD 的长是8cm ,则阴影部分的面积是 2cm .(π 3.14=)【解析】 阴影部分的面积实际上是右上图阴影部分面积的一半,所以求出右上图中阴影部分面积再除以2即可.长方形的长等于两个圆直径,宽等于1个圆直径,所以右图的阴影部分的面积等于:()2882822π2 6.88⨯÷-÷÷⨯⨯=所以左图阴影部分的面积等于6.882 3.44÷=平方厘米.【例 15】 (2019年西城实验期末考试题)如图所示,在半径为4cm 的图中有两条互相垂直的线段,阴影部分面积A 与其它部分面积B 之差(大减小)是 2cm .【解析】 如图,将圆对称分割后,B 与A 中的部分区域能对应,B 仅比A 少了一块矩形,所以两部分的面积差为:()()222128cm ⨯⨯⨯=.【巩固】一块圆形稀有金属板平分给甲、乙二人.但此金属板事先已被两条互相垂直的弦切割成如图所示尺寸的四块.现甲取②、③两块,乙取①、④两块.如果这种金属板每平方厘米价值1000元,问:甲应偿付给乙多少元?5cm 7.5cm3cm 2cm ④③②①【解析】 如右上图所示,④的面积与Ⅰ的面积相等,①的面积等于②与Ⅱ的面积之和.可见甲比乙多拿的部分为中间的长方形,所以甲比乙多拿的面积为:2537.522 5.511cm -⨯-=⨯=()()(),而原本应是两人平分,所以甲应付给乙:11100055002⨯=(元).【例16】求右图中阴影部分的面积.(π取3)【解析】看到这道题,一下就会知道解决方法就是求出空白部分的面积,再通过作差来求出阴影部分面积,因为阴影部分非常不规则,无法入手.这样,平移和旋转就成了我们首选的方法.(法1)我们只用将两个半径为10厘米的四分之一圆减去空白的①、②部分面积之和即可,其中①、②面积相等.易知①、②部分均是等腰直角三角形,但是①部分的直角边AB的长度未知.单独求①部分面积不易,于是我们将①、②部分平移至一起,如右下图所示,则①、②部分变为一个以AC 为直角边的等腰直角三角形,而AC为四分之一圆的半径,所以有AC=10.两个四分之一圆的面积和为150,而①、②部分的面积和为11010502⨯⨯=,所以阴影部分的面积为15050100-=(平方厘米).(法2)欲求图①中阴影部分的面积,可将左半图形绕B点逆时针方向旋转180°,使A与C重合,从而构成如右图②的样子,此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.所以阴影部分面积为21110101010022π⨯⨯-⨯⨯=(平方厘米).A【例17】(第四届走美决赛试题)如图,边长为3的两个正方形BDKE、正方形DCFK并排放置,以BC 为边向内侧作等边三角形,分别以B、C为圆心,BK、CK为半径画弧.求阴影部分面积.(π 3.14=)EE【解析】 根据题意可知扇形的半径r 恰是正方形的对角线,所以223218r =⨯=,如右图将左边的阴影翻转右边阴影下部,S S S =-阴影扇形柳叶1118π2(18π33)34=⨯-⨯-⨯183π8.58=-=板块二 曲线型面积计算【例 18】 如图,已知扇形BAC 的面积是半圆ADB 面积的34倍,则角CAB 的度数是________. DCBA【解析】 设半圆ADB 的半径为1,则半圆面积为21ππ122⨯=,扇形BAC 的面积为π42π233⨯=.因为扇形BAC的面积为2π360n r ⨯,所以,22ππ23603n ⨯⨯=,得到60n =,即角CAB 的度数是60度.【例 19】 如下图,直角三角形ABC 的两条直角边分别长6和7,分别以,B C 为圆心,2为半径画圆,已知图中阴影部分的面积是17,那么角A 是多少度(π3=)【解析】 167212ABC S =⨯⨯=△,三角形ABC 内两扇形面积和为21174-=,根据扇形面积公式两扇形面积和为2π24360B C∠+∠⨯⨯=°,所以120B C ∠+∠=°,60A ∠=°.【例 20】 如图,大小两圆的相交部分(即阴影区域)的面积是大圆面积的415,是小圆面积的35.如果量得小圆的半径是5厘米,那么大圆半径是多少厘米?【解析】 小圆的面积为2π525π⨯=,则大小圆相交部分面积为325π15π5⨯=,那么大圆的面积为422515ππ154÷=,而2251515422=⨯,所以大圆半径为7.5厘米.【例 21】 有七根直径5厘米的塑料管,用一根橡皮筋把它们勒紧成一捆(如图),此时橡皮筋的长度是多少厘米?(π取3)CBA【解析】 由右图知,绳长等于6个线段AB 与6个BC 弧长之和.将图中与BC 弧相似的6个弧所对的圆心角平移拼补,可得到6个角的和是360︒, 所以BC 弧所对的圆心角是60︒,6个BC 弧合起来等于直径5厘米的圆的周长. 而线段AB 等于塑料管的直径,由此知绳长为:565π45⨯+=(厘米).【例 22】 如图,边长为12厘米的正五边形,分别以正五边形的5个顶点为圆心,12厘米为半径作圆弧,请问:中间阴影部分的周长是多少?(π 3.14=)【解析】 如图,点C 是在以B 为中心的扇形上,所以AB CB =,同理CB AC =,则ABC ∆是正三角形,同理,有CDE ∆是正三角形.有60ACB ECD ∠=∠=,正五边形的一个内角是1803605108-÷=,因此60210812ECA ∠=⨯-=,也就是说圆弧AE 的长度是半径为12厘米的圆周的一部分,这样相同的圆弧有5个,所以中间阴影部分的周长是()122 3.1412512.56cm 360⨯⨯⨯⨯=.【例 23】 如图是一个对称图形.比较黑色部分面积与灰色部分面积的大小,得:黑色部分面积________灰色部分面积.【解析】 图中四个小圆的半径为大圆半径的一半,所以每个小圆的面积等于大圆面积的14,则4个小圆的面积之和等于大圆的面积.而4个小圆重叠的部分为灰色部分,未覆盖的部分为黑色部分,所以这两部分面积相等,即灰色部分与黑色部分面积相等.【例 24】 如图,大圆半径为小圆的直径,已知图中阴影部分面积为1S ,空白部分面积为2S ,那么这两个部分的面积之比是多少?(圆周率取3.14)【解析】 如图添加辅助线,小圆内部的阴影部分可以填到外侧来,这样,空白部分就是一个圆的内接正方形.设大圆半径为r ,则222S r =,2212S r r π=-,所以()12: 3.142:257:100S S =-=.移动图形是解这种题目的最好方法,一定要找出图形之间的关系.【例 25】 用一块面积为36平方厘米的圆形铝板下料,从中裁出了7个同样大小的圆铝板.问:所余下的边角料的总面积是多少平方厘米?【解析】 大圆直径是小圆的3倍,半径也是3倍,小圆面积∶大圆面积22π:π1:9r R ==,小圆面积13649=⨯=,7个小圆总面积4728=⨯=,边角料面积36288=-=(平方厘米).【例 26】 如图,若图中的圆和半圆都两两相切,两个小圆和三个半圆的半径都是1.求阴影部分的面积.【解析】 由于直接求阴影部分面积太麻烦,所以考虑采用增加面积的方法来构造新图形.由右图可见,阴影部分面积等于16大圆面积减去一个小圆面积,再加上120︒的小扇形面积(即13小圆面积),所以相当于16大圆面积减去23小圆面积.而大圆的半径为小圆的3倍,所以其面积为小圆的239=倍,那么阴影部分面积为21259π1π 2.5636⎛⎫⨯-⨯⨯== ⎪⎝⎭.【例 27】 如图所示,求阴影面积,图中是一个正六边形,面积为1040平方厘米,空白部分是6个半径为10厘米的小扇形.(圆周率取3.14)CA【解析】 所要求的阴影面积是用正六边形的面积减去六个小扇形面积、正六边形的面积已知,现在关键是小扇形面积如何求,有扇形面积公式2π360n R S =扇.可求得,需要知道半径和扇形弧的度数,由已知正六边形每边所对圆心角为60°,那么120AOC ∠=︒,又知四边形A B C O 是平行四边形,所以120ABC ∠=︒,这样就可求出扇形的面积和为21206π10628360⨯⨯⨯=(平方厘米),阴影部分的面积1040628412=-=(平方厘米).【例 28】 (09年第十四届华杯赛初赛)如下图所示,AB 是半圆的直径,O 是圆心,AC CD DB ==,M 是CD 的中点,H 是弦CD 的中点.若N 是OB 上一点,半圆的面积等于12平方厘米,则图中阴影部分的面积是 平方厘米.【解析】 如下图所示,连接OC 、OD 、OH .本题中由于C 、D 是半圆的两个三等分点,M 是CD 的中点,H 是弦CD 的中点,可见这个图形是对称的,由对称性可知CD 与AB 平行.由此可得CHN ∆的面积与CHO ∆的面积相等,所以阴影部分面积等于扇形COD 面积的一半,而扇形COD 的面积又等于半圆面积的13,所以阴影部分面积等于半圆面积的16,为11226⨯=平方厘米.【巩固】如图,C 、D 是以AB 为直径的半圆的三等分点,O 是圆心,且半径为6.求图中阴影部分的面积.【解析】如图,连接OC、OD、CD.由于C、D是半圆的三等分点,所以AOC∆和COD∆都是正三角形,那么CD与AO是平行的.所以ACD∆的面积与OCD∆的面积相等,那么阴影部分的面积等于扇形OCD的面积,为21π618.846⨯⨯=.【例29】如图,两个半径为1的半圆垂直相交,横放的半圆直径通过竖放半圆的圆心,求图中两块阴影部分的面积之差.(π取3)O【解析】本题要求两块阴影部分的面积之差,可以先分别求出两块阴影部分的面积,再计算它们的差,但是这样较为繁琐.由于是要求面积之差,可以考虑先从面积较大的阴影中割去与面积较小的阴影相同的图形,再求剩余图形的面积.如右图所示,可知弓形BC或CD均与弓形AB相同,所以不妨割去弓形BC.剩下的图形中,容易看出来AB与CD是平行的,所以BCD∆与ACD∆的面积相等,所以剩余图形的面积与扇形ACD的面积相等,而扇形ACD的面积为260π10.5360⨯⨯=,所以图中两块阴影部分的面积之差为0.5.【例30】如图,两个正方形摆放在一起,其中大正方形边长为12,那么阴影部分面积是多少?(圆周率取3.14)AFEAFE【解析】方法一:设小正方形的边长为a,则三角形ABF与梯形ABCD的面积均为()122a a+⨯÷.阴影部分为:大正方形+梯形-三角形ABF-右上角不规则部分=大正方形-右上角不规则部分=14圆.因此阴影部分面积为:3.1412124113.04⨯⨯÷=.方法二:连接AC、DF,设AF与CD的交点为M,由于四边形ACDF是梯形,根据梯形蝴蝶定理有ADM CMFS S=△△,所以DCFS S=阴影扇形3.1412124113.04=⨯⨯÷=【巩固】如右图,两个正方形边长分别是10和6,求阴影部分的面积.(π取3)【解析】 (法1)观察可知阴影部分面积等于三角形ACD 的面积减去月牙BCD 的面积,那么求出月牙BCD 的面积就成了解题的关键.月牙BCD 的面积为正方形BCDE 的面积减去四分之一圆:166π6694⨯-⨯⨯⨯=;则阴影部分的面积为三角形ACD 的面积减去月牙BCD 的面积,为:()110669392S =⨯+⨯-=阴影.(法2)观察可知AF 和BD 是平行的,于是连接AF 、BD 、DF . 则ABD ∆与BDF ∆面积相等,那么阴影部分面积等于BDF ∆与小弓形的面积之和,也就等于DEF ∆与扇形BED 的面积之和,为:211(106)6π63924-⨯⨯+⨯⨯=.【例 31】 如图,ABC 是等腰直角三角形,D 是半圆周的中点,BC 是半圆的直径.已知10AB BC ==,那么阴影部分的面积是多少?(圆周率取3.14)DD【解析】 连接PD 、AP 、BD ,如图,PD 平行于AB ,则在梯形ABDP 中,对角线交于M 点,那么ABD ∆与ABP ∆面积相等,则阴影部分的面积转化为ABP ∆与圆内的小弓形的面积和. ABP ∆的面积为:()10102225⨯÷÷=;弓形面积: 3.145545527.125⨯⨯÷-⨯÷=; 阴影部分面积为:257.12532.125+=.【例 32】 图中给出了两个对齐摆放的正方形,并以小正方形中右上顶点为圆心,边长为半径作一个扇形,按图中所给长度阴影部分面积为 ;(π3.14=)A【解析】 连接小正方形AC ,有图可见 ACD ABC S S S S =+-△△阴影扇形∵211144222AC ⨯=⨯⨯ ∴232AC =同理272CE =,∴48AC CE ⨯=∴148242ACD S =⨯=△290π412.56360S =⨯=扇形,14482ABC S =⨯⨯=△ ∴2412.56828.56S =+-=阴影【例 33】 如图,图形中的曲线是用半径长度的比为2:1.5:0.5的6条半圆曲线连成的.问:涂有阴影的部分的面积与未涂有阴影的部分的面积的比是多少?【解析】 假设最小圆的半径为r ,则三种半圆曲线的半径分别为4r ,3r 和r .阴影部分的面积为:()()22222111π4π3ππ5π222r r r r r -++=,空白部分的面积为:()222π45π11πr r r -=,则阴影部分面积与空白部分面积的比为5:11.【例 34】 (2019年西城实验考题)奥运会的会徽是五环图,一个五环图是由内圆直径为6厘米,外圆直径为8厘米的五个环组成,其中两两相交的小曲边四边形(阴影部分)的面积都相等,已知五个圆环盖住的面积是77.1平方厘米,求每个小曲边四边形的面积.(π 3.14=)【解析】 ⑴每个圆环的面积为:22π4π37π21.98⨯-⨯==(平方厘米);⑵五个圆环的面积和为:21.985109.9⨯=(平方厘米); ⑶八个阴影的面积为:109.977.132.8-=(平方厘米); ⑷每个阴影的面积为:32.88 4.1÷=(平方厘米).【例 35】 已知正方形ABCD 的边长为10厘米,过它的四个顶点作一个大圆,过它的各边中点作一个小圆,再将对边中点用直线连擎起来得右图.那么,图中阴影部分的总面积等于______方厘米.(π 3.14=)【解析】39.25【例 36】 如图,ABCD 是边长为a 的正方形,以AB 、BC 、CD 、DA 分别为直径画半圆,求这四个半圆弧所围成的阴影部分的面积.(π取3)D CBAaDCBA a【解析】 这道题目是很常见的面积计算问题.阴影部分是一个花瓣状的不规则图形,不能直接通过面积公式求解,观察发现阴影部分是一个对称图形,我们只需要在阴影部分的对称轴上作两条辅助线就明了了.如图,这样阴影部分就划分成了4个半圆减去三角形,我们可以求得,()4S S S =⨯-阴影半圆三角形 21142222a a a π⎡⎤⎛⎫=⨯⨯⨯-⨯⨯⎢⎥ ⎪⎝⎭⎢⎥⎣⎦212a =【巩固】如图,正方形ABCD 的边长为4厘米,分别以B 、D 为圆心以4厘米为半径在正方形内画圆.求阴影部分面积.(π取3)D BA DB【解析】 由题可知,图中阴影部分是两个扇形重叠的部分,我们可以利用容斥原理从图形整体上考虑来求阴影部分面积;同样,我们也可以通过作辅助线直接求阴影部分的面积.解法一:把两个扇形放在一起得到1个正方形的同时还重叠了一块阴影部分.则阴影部分的面积为=21π44482⋅⋅-⨯=;解法二:连接AC ,我们发现阴影部分面积的一半就是扇形减去三角形的面积,所以阴影部分面积=212π444284⨯⋅⋅-⨯÷=().【例 37】 (2019年四中考题)已知三角形ABC 是直角三角形,4cm AC =,2cm BC =,求阴影部分的面积.【解析】 从图中可以看出,阴影部分的面积等于两个半圆的面积和与直角三角形ABC 的面积之差,所以阴影部分的面积为:2214121ππ42 2.5π4 3.8522222⎛⎫⎛⎫⨯+⨯-⨯⨯=-= ⎪ ⎪⎝⎭⎝⎭(2cm ).【例 38】 (奥林匹克决赛试题)在桌面上放置3个两两重叠、形状相同的圆形纸片.它们的面积都是100平方厘米,盖住桌面的总面积是144平方厘米,3张纸片共同重叠的面积是42平方厘米.那么图中3个阴影部分的面积的和 是平方厘米.【解析】 根据容斥原理得1003242144S ⨯--⨯=阴影,所以100314424272S =⨯--⨯=阴影(平方厘米)【例 39】 (2019年国际小学数学竞赛)如图所示,ABCD 是一边长为4cm 的正方形,E 是AD 的中点,而F 是BC 的中点.以C 为圆心、半径为4cm 的四分之一圆的圆弧交EF 于G ,以F 为圆心、半径为2cm 的四分之一圆的圆弧交EF 于H 点,若图中1S 和2S 两块面积之差为2π(cm )m n -(其中m 、n 为正整数),请问m n +之值为何?S 2S 1G HFE DCBAS图1S 2S 1G HF E DCB A【解析】 (法1)2248cm FCDES=⨯=,21π44π4BCD S =⨯⨯=扇形2(cm ),21π2π4BFH S =⨯⨯=扇形2(cm ),而124ππ8FCDE BCD BFH S S S S S -=--=--扇形扇形3π8=-2(cm ),所以3m =,8n =,3811m n +=+=.(法2)如右上图,1S S +=BFEA BFH S S -=扇形2422π48π⨯-⨯⨯÷=-2(cm ), 24444π4164πABCD BCD S S S S +=-=⨯-⨯⨯÷=-扇形2(cm ),所以,12(8π)(164π)3π8S S -=---=-2(cm ),故3811m n +=+=.【巩固】在图中,两个四分之一圆弧的半径分别是2和4,求两个阴影部分的面积差.(圆周率取3.14)【解析】 我们只要看清楚阴影部分如何构成则不难求解.左边的阴影是大扇形减去小扇形,再扣除一个长方形中的不规则白色部分,而右边的阴影是长方形扣除这块不规则白色部分,那么它们的差应为大扇形减去小扇形,再减去长方形.则为:ππ4422423 3.148 1.4244⨯⨯-⨯⨯-⨯=⨯-=.【例 40】 如图,矩形ABCD 中,AB =6厘米,BC =4厘米,扇形ABE 半径AE =6厘米,扇形CBF 的半径CB =4厘米,求阴影部分的面积.(π取3)。
初中数学.与圆有关的位置关系.教师版
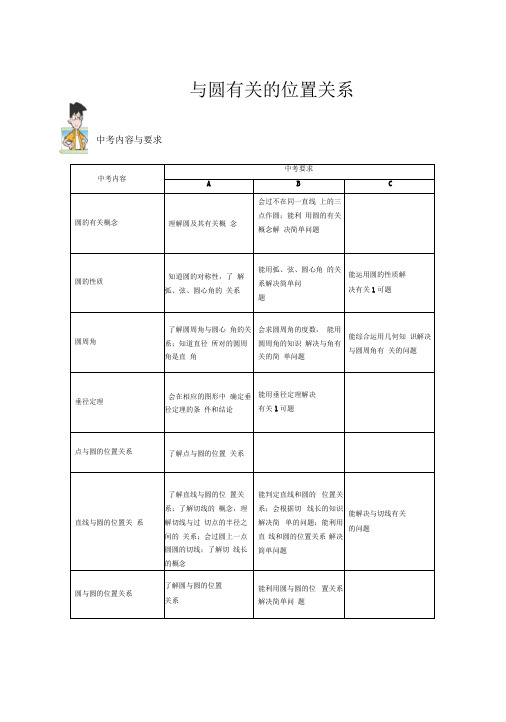
与圆有关的位置关系中考内容中考要求A B C圆的有关概念理解圆及其有关概念会过不在同一直线上的三点作圆;能利用圆的有关概念解决简单问题圆的性质知道圆的对称性,了解弧、弦、圆心角的关系能用弧、弦、圆心角的关系解决简单问题能运用圆的性质解决有关1可题圆周角了解圆周角与圆心角的关系;知道直径所对的圆周角是直角会求圆周角的度数,能用圆周角的知识解决与角有关的简单问题能综合运用几何知识解决与圆周角有关的问题垂径定理会在相应的图形中确定垂径定理的条件和结论能用垂径定理解决有关1可题点与圆的位置关系了解点与圆的位置关系直线与圆的位置关系了解直线与圆的位置关系;了解切线的概念,理解切线与过切点的半径之间的关系;会过圆上一点圆圆的切线;了解切线长的概念能判定直线和圆的位置关系;会根据切线长的知识解决简单的问题;能利用直线和圆的位置关系解决简单问题能解决与切线有关的问题圆与圆的位置关系了解圆与圆的位置关系能利用圆与圆的位置关系解决简单问题中考内容与要求,中考考点分析圆是北京中考的必考内容,主要考查圆的有关性质与圆的有关计算,每年的第20题都会考查,第1小题一般是切线的证明,第2小题运用圆与三角形相似、解直角三角形等知识求线段长度问题,有时也以阅读理解、条件开放、结论开放探索题作为新的题型。
要求同学们重点掌握圆的有关性质,掌握求线段、角的方法,理解概念之间的相互联系和知识之间的相互转化,理解直线和圆的三种位置关系,掌握切线的性质和判定方法,会根据条件解决圆中的动态问题。
与圆有关的位置关系点和圆的位置关系[直线利阅的位置关系点和国的位苫矢系的ft 质利判定 直技和剧的位宥关系的性质和判定确定留的条件~| @线的性质用判定TM 角形外接冏|园和圆的位置关系定义示例剖析点和圆的位置关系:点P 在圆外:点和圆的位置关系有:点在圆上、点在圆内、点在圆外三种,这三种关系由这个点到圆心的距 离与半径的大小关系决定.设。
O 的半径为r ,点P 到圆心O 的距离为 点P 在圆上:d ,则有:/VA点在圆外 d r ;点在圆上 d r ; 点在圆内 d r .点P 在圆内:确定圆的条件:1.圆的确定确、个圆有两个基本条件:①圆心(定点) ,确正圆的位置;②半径(正长),确正圆的大小.只 Qy C有当圆心和半径都确定时,圆才能确定.模块点和圆的位置关系知识导航 生【例1】1.已知△ ABC 中, ACB 90 , AC 2 , BC 3, AB 的中点为 M ,⑴ 以C 为圆心,2为半径作OC,则点A , B , M 与OC 的位置关系如何?⑵ 若以C 为圆心作。
五年级下册数学试题-培优专题训练:03圆与扇形(5年级培优)教师版

圆✧ 任意一个圆,它的周长除以直径的商总是一个固定的数,这个数叫圆周率。
如果用C 表示圆周的长度,d 表示这个圆的直径,r 表示它的半径,π表示圆周率,就有:d c =π或rc 2=。
π是一个无限不循环小数:Λ89793238461415926535.3=π, 我们在做题时,通常取14.3=π。
✧ 圆的周长:r C π2=或d C π= ✧ 圆的面积:2r S π=扇形✧ 扇形是圆的一部分,它是由圆心角的两条半径和圆心角所对弧围成的图形,扇形的大小由它的半径和弧所对的圆心角的大小决定,因为扇形是圆的一部分,所以扇形的弧长和面积的计算方法就是从圆周长和面积的计算方法中引申出来的。
✧ 如右图所示,设扇形的圆心角是n 度,利用圆的周长计算公式可知扇形的弧长计算公式是r n r n l ππ⨯=⨯=1802360 扇形的面积计算公式是lr r n S 213602=⨯=π ✧ 一些特殊角的扇形可以看作是ΛΛ43314161、、、的圆来计算。
重难点:圆和扇形的面积公式一个圆形的铁环,直径是40厘米,做这样一个铁环需要用多长的铁条?【答案】125.6厘米 【知识点】圆的周长 【难度】A 【出处】底稿 【分析】6.12514.340=⨯(厘米)小明在一条路上滚铁环,铁环的直径是50厘米,滚动了78.5米,求铁环滚动了几圈?【答案】50圈 【知识点】圆的周长 【难度】A 【出处】底稿 【分析】()5014.35.05.78=⨯÷(圈)有两根长188.4厘米的铁丝,分别围成一个正方形和一个圆,哪个面积大?大多少?【答案】圆的面积大 【知识点】圆的面积 【难度】B 【出处】底稿【分析】正方形的面积:1.4744.188=÷(厘米) 41.22181.471.47=⨯(平方厘米) 圆的面积:3014.324.188=÷÷(厘米) 2826303014.3=⨯⨯(平方厘米) 所以圆的面积大。
吉教版六年级上册《第4章_圆和扇形》小学数学-有答案-同步练习卷A(3)

吉教版六年级上册《第4章圆和扇形》同步练习卷A(3)一、填空题1. 半径为l米的圆的面积为________,一个面积为12.56平方厘米的圆的半径是________.2. 直径为l米的圆的面积为________.3. 一圆形杯盖周长为18.84厘米,则这个杯盖的面积是________.4. 如果已知圆的半径为r,那么半圆的面积公式为S半圆=________.5. 外滩海关大钟钟面的直径是5.8米,面积是________平方米(结果保留一位小数).6. 有大小两个圆,大圆直径是小圆直径的3倍,那么大圆周长是小圆周长的________倍;小圆面积是大圆面积的________.(填几分之几)二、选择题圆的半径扩大为原来的3倍,则()A.面积扩大为原来的9倍B.面积扩大为原来的6倍C.面积扩大为原来的3倍D.面积不变半径为l厘米的圆的面积与边长为1厘米的正方形的面积之比为()A.1:1B.2:1C.π:1D.π:4三、解答题一种麦田的自动旋转喷灌装置的射程15米。
它能喷灌的面积有多少平方米?一个雷达圆形屏幕的直径是40厘米,它的面积是多少平方米?在一个边长为20cm的正方形内画一个最大的圆,这个圆的面积是多少?一个直径为40厘米的圆形铝板上有4个半径为5厘米的小孔。
这块铝板的面积是多少平方厘米?如图中的曲线是用半径长度的比为4:3:1的7条半圆曲线连成的。
涂有阴影的部分与未涂阴影部分的面积比是多少?参考答案与试题解析吉教版六年级上册《第4章圆和扇形》同步练习卷A(3)一、填空题1.【答案】3.14平方米,2厘米【考点】圆、圆环的面积【解析】圆的面积=πr2,由此代入数据即可解答。
【解答】解:(1)3.14×12=3.14(平方米);(2)3.14×r2=12.56,则r2=4,又因2×2=4,所以这个圆的半径是2厘米。
故答案为:3.14平方米,2厘米。
2.【答案】0.785平方米【考点】圆、圆环的面积【解析】根据圆的面积公式:s=πr2,把数据代入它们的公式进行解答。
吉教版六年级上册《第4章_圆和扇形》小学数学-有答案-同步练习卷A(5)

吉教版六年级上册《第4章圆和扇形》同步练习卷A(5)一、填空题1. 已知扇形的圆心角为l20∘,半径为3,则这个扇形的面积是________.2. 如果圆的半径r=30cm,那么弧长为36cm的扇形的面积是________.3. 一扇形面积是所在圆面积的2,扇形的圆心角是________.34. 圆心角为60.的扇形面积为8.96平方厘米,它所在圆的面积是________.5. 一扇形的半径5厘米,面积15.7平方厘米,这个扇形的圆心角是________.6. 一个扇形的弧长是20π厘米,面积是240π平方厘米,则扇形的圆心角是________.二、选择题下列说法正确的是()A.扇形是圆的一部分,圆的一部分是扇形B.扇形的半径越大,面积就越大’C.在圆中任意画两条半径,一定能构成两个扇形D.两条半径和一条弧长就能组成一个扇形扇形的半径不变,圆心角扩大为原来的2倍,则()A.面积扩大为原来的4倍B.面积扩大为原来的2倍C.面积不变D.面积缩小为原来的一半三、解答题求图中扇形的周长和面积。
直径为l8cm的圆中,圆心角40∘.的扇形面积是多少?某海关大楼的大钟时针长1.8米,从上午11点到下午4点,时针扫过的面积是多少平方米?如图,求图中阴影部分的面积。
(单位:cm)⊙A,⊙B,⊙C两两不相交,且半径都是1cm,则图中的三个扇形的面积之和为多少?弧长的和为多少?⊙A,⊙B,⊙C,⊙D两两不相交,且半径都是1cm,则图中的四个扇形的面积之和为多少?弧长的和为多少?参考答案与试题解析吉教版六年级上册《第4章圆和扇形》同步练习卷A(5)一、填空题1.【答案】9.42【考点】圆、圆环的面积【解析】直接根据扇形的面积公式:S=nπr 2360,将数据代入计算即可求解。
【解答】解:S=nπr 2360=120×3.14×32360=9.42.答:这个扇形的面积是9.42.故答案为:9.42.2.【答案】540cm2【考点】圆、圆环的面积【解析】根据扇形的弧长公式和扇形的面积公式可知S扇形面积=nπr2360=12×nπr180×γ=12Lr,依此进行计算。
2021年上海市六年级数学期末复习-第4章《圆和扇形》考点分类复习导学案(教师版)

沪教版六年级上册第4章《圆和扇形》考点分类复习导学案【考点1:圆周率的概念】例题1.下列说法中错误的是( )A.圆周率π的值等于3.14B.圆周率π的值是圆周长与直径的比值C.圆周率π的值与元的大小无关D.圆周率π是一个无限不循环小数【答案】A【变式1】(金山2017期末15)下列说法正确的是( )(A )圆的周长÷圆的直径=圆周率; (B )两个奇数一定互素;(C )1,2,3,4 能组成比例; (D )因为42.18.4=÷,所以4.8能被1.2整除.【答案】A【考点2:圆的周长及半圆周长】例题1.如图1所示,已知半圆的半径为3厘米,那么半圆形的周长为多少厘米?分析:由题意知3厘米,所以. 反思: 封闭图形的四周长称为周长,求得半圆的长度与直径的长度之和即可.计算的时候不要忘了直径.图1=r 厘米)63(323r 2r 221C +π=⨯+⨯π=+π⨯=【变式1】.用一张边长为5分米的正方形纸片见一个最大的圆,求这个圆的周长.分析:由题意知d=5分米,所以.反思:要求出这个圆的周长应该知道这个圆与正方形的位置关系,从而找到圆的半径,再求出圆的周长.如图3所示,可知圆的直径是正方形的边长,即d=5分米.如果在长方形纸上剪一个最大的圆,直径即为长方形的宽.【变式2】.(闵行2018期末17)如图是由两个正方形和两个扇形组成的组合图形,那么阴影部分的周长为 cm .【答案】33.98【变式3】如果圆的周长为12.56厘米,那么这个圆的半径是 厘米.【答案】2【变式4】小丽家钟的分针长为5cm ,时针的长度是分针长度的35,从下午1点到下午5点,时针针尖走过 cm.【答案】6.28【变式4】(金山2017期末12)如果圆的直径是6米,那么这个圆的周长为___________米.【变式5】如图是由一个半径为r 的半圆和一条直径所组成的图形,那么这个图形的周长可表示为 (结果保留π)图3(分米)15.753.14d C =⨯=π=【答案】2r r π+【考点3:圆环】例题1.如图2所示,圆环的外圆周长C 1=250厘米,内周长C 2=150厘米,求圆环的宽度d (保留π).分析:设外圆的半径是R 1,内圆的半径是R 2,则d = R 1-R 2,因为,, 所以1257550d πππ=-=(厘米)反思:圆环的宽度就是两圆半径之差,利用两圆的周长可分别求得两圆半径.【变式1】.(普陀2017期末29)求图中阴影部分的周长和面积.(单位:cm )【答案】25.12cm ; 25.122cm ;(第20题图)π=π=1252250R 1π=π=752150R 2【考点4:扇形与圆之间的关系】例题1.求图1中扇形的周长和面积.分析: 26,(36060)300,360n R cm n S r π==-==扇,2300663094.2360S cm ππ=⨯⨯=≈扇. 反思:扇形面积公式2360n S r π=⋅扇中,圆心角n 指的是所求弧所对的圆心角,所以图中弧所对的圆心角应该是n =(360-60)=300°.例题2.求图中阴影部分的面积.分析:设∠A 、∠B 、∠C 所对的弧长分别为123l l l 、、,由题意知,∠A+∠B+∠C=180°,半径r=15毫米, 则1180A l r π=,2180B l r π=,3180C l r π=. 所以三段弧长之和为123()15180180180180A B C r l l l l r r r A B C r ππππππ=++=++=++==(毫米) 反思:本例涉及弧长计算,弧长与圆的半径和圆心角有关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
研究圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,通过变动图形的位置或对图形进行分割、旋转、拼补,使它变成可以计算出面积的规则图形来计算它们的面积.圆的面积2πr =;扇形的面积2π360nr =⨯;圆的周长2πr =;扇形的弧长2π360nr =⨯.一、跟曲线有关的图形元素:①扇形:扇形由顶点在圆心的角的两边和这两边所截一段圆弧围成的图形,扇形是圆的一部分.我们经常说的12圆、14圆、16圆等等其实都是扇形,而这个几分之几表示的其实是这个扇形的圆心角占这个圆周角的几分之几.那么一般的求法是什么呢?关键是360n.比如:扇形的面积=所在圆的面积360n⨯;扇形中的弧长部分=所在圆的周长360n⨯扇形的周长=所在圆的周长360n⨯+2⨯半径(易错点是把扇形的周长等同于扇形的弧长) ②弓形:弓形一般不要求周长,主要求面积.一般来说,弓形面积=扇形面积-三角形面积.(除了半圆)③”弯角”:如图: 弯角的面积=正方形-扇形④”谷子”:如图: “谷子”的面积=弓形面积2⨯二、常用的思想方法:①转化思想(复杂转化为简单,不熟悉的转化为熟悉的) ②等积变形(割补、平移、旋转等) ③借来还去(加减法)④外围入手(从会求的图形或者能求的图形入手,看与要求的部分之间的”关系”)板块、曲线型旋转问题【例 1】 正三角形ABC 的边长是6厘米,在一条直线上将它翻滚几次,使A 点再次落在这条直线上,那么A点在翻滚过程中经过的路线总长度是多少厘米?如果三角形面积是15平方厘米,那么三角形在滚例题精讲圆与扇形动过程中扫过的面积是多少平方厘米?(结果保留π)【考点】曲线型旋转问题 【难度】3星 【题型】解答【解析】 如图所示,A 点在翻滚过程中经过的路线为两段120︒的圆弧,所以路线的总长度为:1202π628π360⨯⨯⨯=厘米;三角形在滚动过程中扫过的图形的为两个120︒的扇形加上一个与其相等的正三角形,面积为:2120π621524π15360⨯⨯⨯+=+平方厘米.【答案】24π15+【巩固】直角三角形ABC 放在一条直线上,斜边AC 长20厘米,直角边BC 长10厘米.如下图所示,三角形由位置Ⅰ绕A 点转动,到达位置Ⅱ,此时B ,C 点分别到达1B ,1C 点;再绕1B 点转动,到达位置Ⅲ,此时A ,1C 点分别到达2A ,2C 点.求C 点经1C 到2C 走过的路径的长.60︒30︒B 1C 1C 2A 2CB AⅢⅡⅠ【考点】曲线型旋转问题 【难度】3星 【题型】解答【解析】 由于BC 为AC 的一半,所以30CAB ∠=︒,则弧1CC 为大圆周长的18030536012︒-︒=︒,弧12C C 为小圆周长的14,而112CC C C +即为C 点经1C 到2C 的路径,所以C 点经1C 到2C 走过的路径的长为5150652π202π10π5ππ12433⨯⨯+⨯⨯=+=(厘米).【答案】65π3【巩固】如图,一条直线上放着一个长和宽分别为4cm 和3cm 的长方形Ⅰ.它的对角线长恰好是5cm .让这个长方形绕顶点B 顺时针旋转90°后到达长方形Ⅱ的位置,这样连续做三次,点A 到达点E 的位置.求点A 走过的路程的长.ⅣⅢⅡⅠEDCBA【考点】曲线型旋转问题 【难度】3星 【题型】解答【解析】 因为长方形旋转了三次,所以A 点在整个运动过程中也走了三段路程(如右上图所示).这三段路程分别是:第1段是弧1AA ,它的长度是12π44⨯⨯⨯(cm );第2段是弧12A A ,它的长度是12π54⨯⨯⨯(cm );第3段是弧2A E ,它的长度是12π34⨯⨯⨯(cm );所以A 点走过的路程长为:1112π42π52π36π444⨯⨯⨯+⨯⨯⨯+⨯⨯⨯=(cm ).【答案】6π【例 2】 草场上有一个长20米、宽10米的关闭着的羊圈,在羊圈的一角用长30米的绳子拴着一只羊(见如图).问:这只羊能够活动的范围有多大?(圆周率取3.14)【考点】曲线型旋转问题 【难度】3星 【题型】解答【解析】 如图所示,羊活动的范围可以分为A ,B ,C 三部分,其中A 是半径30米的34个圆,B ,C 分别是半径为20米和10米的14个圆. 所以羊活动的范围是222311π30π20π10444⨯⨯+⨯⨯+⨯⨯222311π302010444⎛⎫=⨯⨯+⨯+⨯ ⎪⎝⎭2512=.【答案】2512【巩固】一只狗被拴在底座为边长3m 的等边三角形建筑物的墙角上(如图),绳长是4m ,求狗所能到的地方的总面积.(圆周率按3.14计算)3【考点】曲线型旋转问题 【难度】3星 【题型】解答【解析】 如图所示,羊活动的范围是一个半径4m ,圆心角300°的扇形与两个半径1m ,圆心角120°的扇形之和.所以答案是243.96m .【答案】43.96【例 3】 如图是一个直径为3cm 的半圆,让这个半圆以A 点为轴沿逆时针方向旋转60︒,此时B 点移动到'B点,求阴影部分的面积.(图中长度单位为cm ,圆周率按3计算).【考点】曲线型旋转问题 【难度】3星 【题型】解答【解析】 面积=圆心角为60︒的扇形面积+半圆-空白部分面积(也是半圆)=圆心角为60︒的扇形面积22603π3π 4.5(cm )3602=⨯⨯==. 【答案】4.5【例 4】 如图所示,直角三角形ABC 的斜边AB 长为10厘米,60ABC ∠=︒,此时BC 长5厘米.以点B 为中心,将ABC ∆顺时针旋转120︒,点A 、C 分别到达点E 、D 的位置.求AC 边扫过的图形即图中阴影部分的面积.(π取3)E【考点】曲线型旋转问题 【难度】3星 【题型】解答 【解析】 注意分割、平移、补齐.E DB A如图所示,将图形⑴移补到图形⑵的位置,因为60EBD ∠=︒,那么120ABE ∠=︒,则阴影部分为一圆环的13.所以阴影部分面积为()221π753AB BC ⨯⨯-=(平方厘米).【答案】75【巩固】如右图,以OA 为斜边的直角三角形的面积是24平方厘米,斜边长10厘米,将它以O 点为中心旋转90︒,问:三角形扫过的面积是多少?(π取3)A'AO【考点】曲线型旋转问题【难度】3星 【题型】解答【解析】 从图中可以看出,直角三角形扫过的面积就是图中图形的总面积,等于一个三角形的面积与四分之一圆的面积之和.圆的半径就是直角三角形的斜边OA .因此可以求得,三角形扫过的面积为:124π10102425π994+⨯⨯⨯=+=(平方厘米).【答案】99【巩固】(“学而思杯”数学试题)如图,直角三角形ABC 中,B ∠为直角,且2BC =厘米,4AC = 厘米,则在将ABC ∆绕C 点顺时针旋转120︒的过程中,AB 边扫过图形的面积为 .(π 3.14=)C B AB'A'C B A【考点】曲线型旋转问题 【难度】3星 【题型】解答【解析】 如右上图所示,假设ABC ∆旋转120︒到达''A B C ∆的位置.阴影部分为AB 边扫过的图形.从图中可以看出,阴影部分面积等于整个图形的总面积减去空白部分面积,而整个图形总面积等于扇形'ACA 的面积与ABC ∆的面积之和,空白部分面积等于扇形'BCB 的面积与''A B C ∆的面积,由于ABC ∆的面积与''A B C ∆的面积相等,所以阴影部分的面积等于扇形'ACA 与扇形'BCB 的面积之差,为22120120π4π24π12.56360360⨯⨯-⨯⨯==(平方厘米). 【答案】12.56【例 5】 如下图,△ABC 是一个等腰直角三角形,直角边的长度是1米。
现在以C 点为圆点,顺时针旋转90度,那么,A B边在旋转时所扫过的面积是平方米 。
(π=3.14)【考点】曲线型旋转问题【难度】3星【题型】解答【解析】边扫过的面积为左下图阴影部分,可分为右下图所示的两部分。
因为2221r r+=,所以212r=。
所求面积为()222211111110.6775424428rππππ⎛⎫-+--+=⎪⎝⎭⨯⨯⨯=(平方米)【答案】0.6775【例 6】如图30-14,将长方形ABCD绕顶点C顺时针旋转90度,若AB=4,BC=3,AC=5,求AD边扫过部分的面积.(π取3.14)DCBA【考点】曲线型旋转问题【难度】3星【题型】解答【解析】如下图所示,D\A\B\DCBA A\D\A如下图所示,端点A扫过的轨迹为AA A''',端点D扫过轨迹为DD D''',而AD之间的点,扫过的轨迹在以A、D轨迹,AD,A D''所形成的封闭图形内,且这个封闭图形的每一点都有线段AD上某点扫过,所以AD边扫过的图形为阴影部分.显然,有阴影部分面积为A D C ACA ACDS S S S''''∆∆+--直角扇形直角扇形CD D,而直角三角形A D C''、ACD面积相等.=A D C ACA ACD ACAS S S S S S''''''∆∆+---直角扇形直角扇形CD D扇形扇形CD D222290909=(54)7.065()36036044AC CDππππ-=-==平方厘米即AD边扫过部分的面积为7.065平方厘米.【答案】7.065【例 7】 (祖冲之杯竞赛试题)如图,ABCD 是一个长为4,宽为3,对角线长为5的正方形,它绕C 点按顺时针方向旋转90︒,分别求出四边扫过图形的面积.CBD A【考点】曲线型旋转问题 【难度】3星 【题型】解答【解析】 容易发现,DC 边和BC 边旋转后扫过的图形都是以线段长度为半径的圆的14,如图: B'A'DCBA因此D C边扫过图形的面积为4π,BC 边扫过图形的面积为9π4. 2、研究AB 边的情况.在整个AB 边上,距离C 点最近的点是B 点,最远的点是A 点,因此整条线段所扫过部分应该介于这两个点所扫过弧线之间,见如图中阴影部分:DB'A'A下面来求这部分的面积.观察图形可以发现,所求阴影部分的面积实际上是:扇形'ACA 面积+三角形''A B C 面积-三角形ABC 面积一扇形'BCB 面积=扇形'ACA 面积一扇形'BCB 面积225π3π44=-4π= 3、研究AD 边扫过的图形.由于在整条线段上距离C 点最远的点是A ,最近的点是D ,所以我们可以画出AD 边扫过的图形,如图阴影部分所示:AA'B'D用与前面同样的方法可以求出面积为:225π4π9π444-=旋转图形的关键,是先从整体把握一下”变化过程”,即它是通过什么样的基本图形经过怎样的加减次序得到的.先不去考虑具体数据,一定要把思路捋清楚.最后你会发现,所有数据要么直接告诉你,要么就”藏”在那儿,一定会有.可以进一步思考,比如平行四边形的旋转问题、一般三角形的旋转问题等等,此类问题的解决对提高解决几何图形问题的能力是非常有益的.【答案】(1)BC 边扫过图形的面积为9π4(2)AB 边扫过图形的面积为4π(3)AD 边扫过图形的面积为9π4(4)D C边扫过图形的面积为4π【例 8】 (华杯赛初赛)半径为25厘米的小铁环沿着半径为50厘米的大铁环的内侧作无滑动的滚动,当小铁环沿大铁环滚动一周回到原位时,问小铁环自身转了几圈? 【考点】曲线型旋转问题 【难度】3星 【题型】解答【解析】 对于这类问题,可以在初始时在小环上取一点A ,观察半径OA ,如图⑴,当小环沿大环内壁滚动到与初始相对的位置,即滚动半个大圆周时,如图⑵,半径OA 也运动到了与初始时相对的位置.这时OA 沿大环内壁才滚动了半圈.继续进行下半圈,直到OA 与初始位置重合,这时OA 自身转了1圈,因此小铁环自身也转了1圈.⑵⑴AO A O【总结】对于转动的圆来说,当圆心转动的距离为一个圆周长时,这个圆也恰好转了一圈.所以本题也可以考虑小铁环的圆心轨迹,发现是一个半径与小铁环相等的圆,所以小铁环的圆心转过的距离等于自己的圆周长,那么小铁环转动了1圈.【答案】1圈【巩固】如果半径为25厘米的小铁环沿着半径为50厘米的大铁环的外侧作无滑动的滚动,当小铁环沿大铁环滚动一周回到原位时,问小铁环自身转了几圈?【考点】曲线型旋转问题 【难度】3星 【题型】解答【解析】 如图,同样考虑小圆的一条半径OA ,当小圆在大圆的外侧滚动一周,即滚动了大圆的半周时,半径OA滚动了540︒,滚动了一圈半,所以当小圆沿大圆外侧滚动一周时,小圆自身转了3圈.⑴O A⑵OA也可以考虑小圆圆心转过的距离.小圆圆心转过的是一个圆周,半径是小圆的3倍,所以这个圆的周长也是小圆的3倍,由于小圆的圆心每转动一个自身的周长时,小圆也恰好转了一圈,所以本题中小圆自身转了3圈.【答案】3圈【巩固】如图所示,大圆周长是小圆周长的n (1n >)倍,当小圆在大圆内侧(外侧)作无滑动的滚动一圈后又回到原来的位置,小圆绕自己的圆心转动了几周?【考点】曲线型旋转问题 【难度】3星 【题型】解答 【解析】 为了确定圆绕圆心转动几周,首先要明确圆心转动的距离.设小圆的半径为“单位1”,则大圆的半径为“n ”.⑴在内测滚动时,如图⑴所示,因为圆心滚动的距离为2π(1)n ⨯-.所以小圆绕自己的圆心转动了:2π(1)12πn n ⨯-=-(圈).图(1)图(2)⑵在外侧滚动时,如图⑵所示. 因为圆心滚动的距离为2π(1)n ⨯+.所以小圆绕自己的圆心转动了:2π(1)12πn n ⨯+=+(圈). 【答案】n-1和n+1【例 9】 如图,15枚相同的硬币排成一个长方形,一个同样大小的硬币沿着外圈滚动一周,回到起始位置.问:这枚硬币自身转动了多少圈?【考点】曲线型旋转问题 【难度】3星 【题型】解答【解析】 当硬币在长方形的一条边之内滚动一次时,由于三个硬币的圆心构成一个等边三角形,所以这枚硬币的圆心相当于沿着半径为硬币2倍的圆旋转了180606060︒-︒-︒=︒.而硬币上的每一点都是半径等于硬币的圆旋转,所以硬币自身旋转了120°.当硬币从长方形的一条边滚动到另一条边时,这枚硬币的圆心相当于沿着半径为硬币2倍的圆旋转了360606090150︒-︒-︒-︒=︒.而硬币上的每一点都是半径等于硬币的圆旋转,所以硬币自身旋转了300º.长方形的外圈有12个硬币,其中有4个在角上,其余8个在边上,所以这枚硬币滚动一圈有8次是在长方形的一条边之内滚动,4次是从长方形的一条边滚动到另一条边.120830042160︒⨯+︒⨯=︒,所以这枚硬币转动了2160º,即自身转动了6圈.另解:通过计算圆心轨迹的长度,每走一个2π即滚动了一周.【答案】6圈【巩固】12个相同的硬币可以排成下面的4种正多边形(圆心的连线).用一个同样大小的硬币,分别沿着四个正多边形的外圈无滑动地滚动一周.问:在哪个图中这枚硬币自身转动的圈数最多,最多转动了多少圈?【考点】曲线型旋转问题 【难度】3星 【题型】解答【解析】 对于同样是12个硬币,所转动的圆心轨迹其实分为两部分,一是在”角”上的转动,一是在”边”上的滚动.抓住关键方法:圆心轨迹长度2π÷=自身转动圈数.结论:一样多;都是6圈.【答案】一样多;都是6圈【例 10】 一枚半径为1cm 的圆形硬币相互紧靠着平放在桌面上,让一枚硬币沿着它们的外轮廓滚过后回到原来的位置,那么与原A 点重合的点是______.硬币自己转动______,硬币圆心的运动轨迹周长为_______.【考点】曲线型旋转问题 【难度】3星 【题型】解答【解析】 先计算轨迹的长度:三个半径为2的半圆,1(22π)36π2⨯⨯⨯=,6π2π3÷=,即为3周,所以答案为A 点,3周,6π. 【答案】A 点,3周,6π【例 11】 先做一个边长为2cm 的等边三角形,再以三个顶点为圆心,2cm 为半径作弧,形成曲边三角形(如左图).再准备两个这样的图形,把一个固定住(右图中的阴影),另一个围绕着它滚动,如右图那样,从顶点相接的状态下开始滚动.请问此图形滚动时经过的面积是多少平方厘米?(π 3.14=)CBA 222【考点】曲线型旋转问题 【难度】3星 【题型】解答【解析】 在处理图形的运动问题时,描绘出物体的运动轨迹是解决问题的第一步,只有大的方向确定了,才能实施具体的计算.图⑴图⑵图⑶图⑷在数学中,本题所作出的这个曲边三角形叫“莱洛三角形”,“莱洛三角形”有一个重要的性质就是它在所有方向上的宽度都相同.为了求出“莱洛三角形”滚动时经过的面积,可以分2步来思考:第1步:如图⑵所示,当“莱洛三角形”从顶点A 的上方滚动到顶点A 的左边时,这时阴影“莱洛三角形”滚动的这部分面积是以A 为圆心、2cm 为半径、圆心角为60°的扇形.在顶点A 、B 、C 处各有这样的一个扇形;第2步:如图⑶所示,当“莱洛三角形”在边AB 上滚动时,这时可以把阴影“莱洛三角形”看作是以图⑶中D 点为圆心的圆的一部分,这个圆在以C 点为圆心的弧AB 上滚动,可知此时圆心D 运动的轨迹是图⑶中的弧'DD ,所以此时阴影“莱洛三角形”滚动的这部分面积是以C 为圆心、4cm 为半径、圆心角为60°的扇形减去半径为2cm 的60°的扇形;综上所述,去掉图⑷中阴影“莱洛三角形”后所形成的组合图形就是要求的面积. 滚动时经过的面积是:22226060603π23π4π28π25.12(cm )360360360⎛⎫⎛⎫⨯⨯⨯+⨯⨯⨯-⨯⨯== ⎪ ⎪⎝⎭⎝⎭.【答案】25.12【例 12】 下图为半径20厘米、圆心角为1440的扇形图.点C、D 、E 、F 、G 、H、J 是将扇形的B 、K弧线分为8等份的点.求阴影部分面积之和.【考点】曲线型旋转问题 【难度】3星 【题型】解答 【解析】 如下图,做出辅助线,△KMA 与△AN G形状相同(对应角相等),大小相等(对应边相等),有△KMA ≌△ANG ,KMAANGSS=,而△L MA是两个三角形的公共部分,所以上图中的阴影部分面积相等.所以,G NMK 与扇形KG A的面积相等,那么K GEB 的面积为2倍扇形KGA 的面积.扇形KGA 的圆心角为01448×3=540,所以扇形面积为05420360⨯60ππ⨯=平方厘米.那么KGE B的面积为602π⨯=120π平方厘米.如下图,做出另一组辅助线.B△JQA与△AR H形状相同(对应角相等),大小相等(对应边相等), 有△JQ A≌△ARH,JQAARHSS==5△A,而△PQA 是两个三角形的公共部分,所以右图中的阴影部分面积相等.所以,JHRQ 与扇形JH A的面积相等,那么JHDC 的面积为2倍扇形JHA 的面积.扇形JHA 的圆心角为001441808=,所以扇形面积为2182020360ππ⨯⨯=平方厘米. 那么JHDC 的面积为20240ππ⨯=平方厘米.所以,原题图中阴影部分面积为KGEB JHDC S S -=1204080πππ-=≈80×3.14=251.2平方厘米.【答案】251.2【例 13】 10个一样大的圆摆成如图所示的形状.过图中所示两个圆心A,B 作直线,那么直线右上方圆内图形面积总和与直线左下圆内图形面积总和的比是多少?BA【考点】曲线型旋转问题 【难度】3星 【题型】解答【解析】 直线AB 的右上方的有2个完整的圆,2个半圆,1个1个而1个1个正好组成一个完整的圆,即共有4个完整的圆,那么直线AB 的左下方有10-4=6个完整的圆,每个圆的面积相等,所以直线右上方圆内图形面积总和与直线左下圆内图形面积总和的比是4:6=2:3.【答案】2:3【例 14】 在图中,一个圆的圆心是0,半径r=9厘米,∠1=∠2=15°.那么阴影部分的面积是多少平方厘米?(π取3.14)21OCAB【考点】 【难度】2星 【题型】填空 【关键词】奥林匹克,初赛,11题【考点】曲线型旋转问题 【难度】3星 【题型】解答【解析】 有AO=O B,所以△A OB 为等腰三角形,AO =OC ,所以△AO C为等腰三角形.∠ABO=∠1=15°,∠A OB=180°-∠1-∠ABO=150°. ∠AC O=∠2=15°,∠A OC=180°-∠2-∠AC O=150°,所以 ∠BOC =360°-∠AOB-∠AOC=60°,所以扇形BOC 的面积为260942.39360π⨯⨯≈(平方厘米).【答案】42.39【例 15】 图是由正方形和半圆形组成的图形.其中P点为半圆周的中点,Q 点为正方形一边的中点.已知正方形的边长为10,那么阴影部分的面积是多少?(π取3.14)10DB【考点】曲线型旋转问题 【难度】3星 【题型】解答 【关键词】奥林匹克,初赛,11题【解析】 过P 做AD 平行线,交AB 于O 点,P 为半圆周的中点,所以0为AB 中点.O DPB有2ABCD DPC 101S 1010100S 12.522ππ=⨯==⨯⨯=半圆,(). AOP OPQB 101101S 510+37.5S 105550.2222∆⎡⎤⎛⎫=⨯⨯==++⨯⨯= ⎪⎢⎥⎝⎭⎣⎦梯形(), 阴影部分面积为ABCD AOP DPC OPQB S S S S 10012.537.55012.512.551.75.ππ∆+-=+--=+≈半圆梯形-【答案】51.75。
