表达与识读相贯体

合集下载

机械制图-轴套类零件的表达与识读

7.1轴套类零件的结构分析
7.1.1轴套类零件的结构特点
1．轴类零件轴类零件一般是由同轴线上不同直径的圆柱体（或
圆锥体）构成的。圆柱体的直径，由机械设计计算得到。轴零件作用之一是承载传动件，为满足装配要求，有时需在轴上加工键槽、凹坑（安装紧定螺钉）结构。有时由于使用要求，会在轴上加工螺纹，或在轴端加工出平面。
对称的移出断面可以配置在视图中断处，如下图所示，并且省略标柱。
7.2.2 局部放大图和与轴套类零件有关的简化画法
1.局部放大图用大于原图形所用的比例绘制出的图形，称为局部放大图。零件的细小结构在
视图中表达不清，或不便于标注尺寸和技术要求时，可采用局部放大图表达。局部放大图可画成视图、剖视图或断面图。
在不致引起误解时，图中的小圆角、45°小倒角或锐边的小倒圆可省略不画，但必须注明尺寸或在技术要求中加以说明。
滚花结构一般采用在轮廓线附近用细实线局部画出的方法表示。
零件上较小的结构及斜度已在一个图形中表达清楚时，在其他图形应当简化或省略。
7.3轴套类零件的尺寸及技术要求的标注
轴套类零件有轴向尺寸（沿轴线方向）和径向尺寸（沿直径方向）。轴向尺寸的尺寸基准，通常选在重要的端面、接触面上。径向尺寸的尺寸基准则采用轴套类零件的轴线。
中的径向尺寸如 95h6、 60H7、 93等，其基准是零件
的轴线。轴向尺寸如8、200.1、64、49、40、2940.2 等是定形尺寸，其尺寸基准为轴套的右端面。A—A、B—
B两个移出断面图主要标注孔槽的尺寸，其中16、 40、 78、36 36是定形尺寸。“A—A”中的85为定位尺寸；
227和142 0.1也是定位尺寸。
+0.021，下极限偏差为+ 0.002），公差等级为IT6；基本偏差代号为k；其公差带代号为k6。

任务2 绘制两正交圆柱三视图

项目四组合体的表达与识读
任务2 绘制两正交圆柱三视图
1、相贯线的定义
即两回转体相互贯穿时的表面交线。
两个回转体相交(或称相贯)，表面产生的交线称为相贯线。
圆柱与圆柱相交圆锥与圆柱相交圆柱与圆球相交
2、正交圆柱体相贯线的投影描点画法两个直径不等的圆柱正交，求作相贯线的投影。
相贯线的近似画法
(2)当两圆柱直径相等时，相贯线空间形状为两个相交的椭圆，在非圆视图上的投影为过两轴线交点的相交直线；在视图
上——“平分天下”。
两个同轴回转体的相贯线
圆柱轴线通过球心，相贯线为与圆柱直径相等的圆，主视图投影为直线。
圆柱穿孔后的相贯线
绘制两正交圆柱三视图
小结： 1、相贯线的概念和特性。 2、积聚性画法求作正交圆柱相贯线，以及相贯线的简易画
相贯线的特点是总是弯向大圆柱的轴线。当两圆柱垂直正交且直径有差异时，可采用圆弧相贯线的近似画法：在非圆视图上相贯线的投影以大圆弧的半径为半径、连接两端点，画圆弧即可。
两正交圆柱相贯线弯曲变化趋势
变化趋势
(1)在非圆视图上,相贯线的的投影曲线
始终由小圆柱向大圆柱轴线弯曲凸进(吃进)——以小“吃”大(小国侵略大国)。
法。 3、绘制两正交

机械制图《识读叠加类组合体》电子教案

【教学过程】第一课时：引入：前几章介绍了正投影的原理以及点、线、面和基本几何体的投影知识。

本章将进一步研究画、看组合体视图的方法以及有关尺寸标注等问题，今天将对组合体的概念和组合形式作分析。

讲授：任务1 绘制支架组合体的三视图一、组合体的组合形式1.叠加：由基本几何体叠加而成。

2.切割：在基本几何体上进行切割、钻孔、挖槽等形成的形体。

3.综合：既有叠加又有切割（a）叠加型（b）切割型（c）综合型二、组合体的表面连接关系（1）平齐或不平齐当两基本体表面平齐时，结合处不画分界线。

当两基本体表面不平齐时，结合处应画出分界线。

如下图所示：（a）表面平齐（b）表面不平齐（2）相切当两基本体表面相切时，在相切处不画分界线。

如下图所示：（a）正确画法（b）错误画法（3）相交当两基本体表面相交时，在相交处应画出分界线。

如下图所示：（a）正确画法（b）错误画法课堂练习：练习册P68先分析每道习题的组合形式（请学生回答），然后学生自行补画交线，教师巡视指导。

完成后，投影仪对照参考答案，讲解正确画法和应注意的事项。

课后作业：P69、70第二课时：讲授：三、形体分析法形体分析法——假想将组合体分解为若干基本体，分析各基本体的形状、组合形式和相对位置，弄清组合体的形体特征，这种分析方法称为形体分析法。

1.形体分析如图所示的支架可分解成三个部分（提问学生：每一部分可看作由几个基本体组成）。

（a）支座（b）分解图2.选择视图先选择主视图，主视图应选择较多地反映组合体的形体特征及其相互位置关系为投影方向。

主视图确定好后，俯、左视图也就随之确定了。

3.画三视图支架的三视图步骤如下：课堂练习：每人一张A4白纸，绘制支架三视图。

课堂小结：组合体视图的画法，注意三等关系，注意图线规范。

【教学过程】引入：前面已学习了平面切割几何体形成的截交线，现在开始学习两个几何体互相贯穿形成的相贯线。

讲授：一、相贯线概念：两个基本形体相交（或称相贯）时表面产生的交线称为相贯线。

《机械制图》识读绘制相贯体三视图

2 任务二识读绘制相贯体三视图
利用表面取点法，求两正交圆柱的相贯线
a'
b'
解题步骤
d'
e'
c'
①分析：相贯线的水平投影和侧面投影已知，可利用表面取点法求共有点；
②求出相贯线上的特殊点A、B、 C；
③求出若干个一般点D、E；
④光滑且顺次地连接各点，作出相贯线，
并且判别可见性； ⑤整理轮廓线。
a
b
子目录 SUB CONTENTS
项目三识读绘制组合体三视图
3
任务一识读绘制截断体三视图任务二识读绘制相贯体三视图任务三绘制复杂组合体三视图任务四识读复杂组合体三视图任务五组合体构形训练任务六第三角画法训练
2 任务二识读绘制相贯体三视图
绘制较复杂形体的投影图时，常常需要画出形体表面上的交线——平面与立体表面的交线或两立体表面的交线。掌握这些交线的性质和画法，将有助于准确地画出机件的投影，也有利于读图时对机件结构形状的分析。
相贯线的形状与弯曲方向
当两个直径不等的圆柱相交时，相贯线在同
C
时平行于两圆柱轴线的投影面上的投影，其弯曲
勾凸趋势总是“ ”向小圆柱，向大圆柱轴线；
B
而两个直径相等的圆柱相交时，相贯线为平面椭
A
圆曲线，在同时平行于两圆柱轴线的投影面上，
此相贯线的投影为直线。
D
18
2 任务二识读绘制相贯体三视图
d
ce
16
yy
a" (b")
d" (e")
c"
yy
A DC
2 任务二识读绘制相贯体三视图

任务三绘制与识读组合体三视图汇编

（3）连线。将正面投影1′、2′、3′、4′、5′依次光滑连接成曲线，即为所求截交线的正面投影，如图（c）所示。
任务三绘制与识读组合体三视图
学习资料
QV 1'
3' 2' 4'
5'
3" 2"(4")
1"(5")
12
PH
4
3
5
圆锥被正平面截切的三视图
任务三绘制与识读组合体三视图
实施任务一、识读
学习资料
截平面的位置
平行于任一素线
截交线的形状
轴测图
投影面
抛物线+直线
任务三绘制与识读组合体三视图
学习资料
截平面的位置
与轴线倾斜
截交线的形状
轴测图
投影面
椭圆或双曲线+直线
任务三绘制与识读组合体三视图
学习资料
截平面的位置
与轴线平行
截交线的形状
轴测图
投影面
双曲线+直线
（1）如图（a）所示，立体是由圆锥以及大小两圆柱同轴线组合成的组合回转体，且轴线垂直于 W面，其中大小圆柱面的侧面投影有积聚性，而圆锥的投影无积聚性。
（2）顶尖被水平面截切:截切圆锥表面得交线为双曲线，截切小圆柱、大圆柱表面得交线分别为平行于轴线的直素线。该截平面的正面投影和侧面投影积聚成一直线， H面投影反映实形。
任务三绘制与识读组合体三视图
学习资料
2.圆锥的截交线截平面与圆锥轴线位置不同，其截交线将有五种不同的形状，见表。
截平面的位置
轴测图
投影面
与轴线垂直

25相贯线的画法与识读——相贯线

两圆柱轴线相交、直径相等、共切于一球面
圆柱与圆锥轴线相交且共切于一球
积聚为相交两直线
投影为圆
投影为圆
投影为相交两椭圆
三、相贯线的特殊情况
3.轴线平行的两圆柱体相交圆柱面上的相贯线是两条平行轴线的直线。
平行轴线的直线
三、相贯线的特殊情况
例：补画图示相交立体的正投影 ① 圆柱与半球表面同轴线相交，相贯线为半圆。②圆柱与圆柱轴
CAD作图演示
二、相贯线的作图方法
2.辅助平面法假设作一辅助平面，与相贯的两回转体相交，先求出辅助平面
与两回转体的截交线，两截交线的交点必为相贯线上的点。选择辅助平面的原则：辅助平面应为特殊位置平面，并作在两
回转面的相交范围内。
作图步骤
1.作辅助平面 2.分别作出辅助平面与两回转面的截交线。
谢谢！
3.两回转面截交线的交点，即为所求相贯线的上点。
二、相贯线的作图方法
例：求轴线正交的圆柱与圆锥台的相贯线由于圆柱的侧面投影积聚为圆，所以相贯线的侧面投影与此圆重合，
要求的是相贯线的正面投影和水平投影。
y R
R
CAD作图演示
y
二、相贯线的作图方法
例：求圆锥台与半球的相贯线由于锥面、球面的各投影都无积聚性，所以相贯线的各面投影都
线正交，直径不等，其相贯线为空间曲线。
CAD作图演示
三、相贯线的特殊情况
例：求图示相交立体的侧面投影 1）两圆柱内、外表面相交，轴线正交且直径相等，相贯线为相
交的平面椭圆。 2）两圆柱相交，①内表面相交，其轴线正交、直径不等，相贯线
为空间曲线，②内外表面相交，其轴线平行，相贯线为直线。
CAD作图演示
需要通过选用合适的辅助平面求解。

20表达与识读常见组合体(四)22952

一、形体分析法看叠加型组合体视图，分部分想形状，综合起来，想象整体。
1．形体分析法看叠加型组合体视图（以轴承座为例）
一、形体分析法看叠加型组合体视图，分部分想形状，综合起来，想象整体。
1．形体分析法看叠加型组合体视图（以轴承座为例）
一、形体分析法看叠加型组合体视图，分部分想形状，综合起来，想象整体。
V形铁三视图识读
第一次切割
第二次切割
三、典型零件三视图识读方法
1 ．阶梯轴识读，主要分析主视图选择及线面对应关系。
三、典型零件三视图识读方法
2 ．轴套识读，主要分析主视图选择及放置方向。
三、典型零件三视图识读方法
3 ．法兰盘识读，主要分析主视图选择及放置方向，同时注意分布小圆孔中心线位置。
三、典型零件三视图识读方法
2．看叠加型组合体视图，进一步熟悉形体分析法。
一、形体分析法看叠加型组合体视图，分部分想形状，综合起来，想象整体。
2．看叠加型组合体视图，进一步熟悉形体分析法。
二、用分部切割法分析切割型组合体
分析切割面类型，分析线面对应关系。
二、用分部切割法分析切割型组合体
第ห้องสมุดไป่ตู้次切割
第二次切割
第三次切割
二、用分部切割法分析切割型组合体
4 ．呆扳手识读，主要分析主视图选择及表面相交、相切的画法。
相贯线
三、典型零件三视图识读方法
5 ．拨叉识读，主要分析主视图选择及表面相交、相切的画法。
相切
三、典型零件三视图识读方法
6 ．三通零件识读，主要结合相贯线画法识读三视图。主要分析主视图选择及表面相交、相切的画法。
相贯线
第四节表达与识读常见组合体
看组合体视图及应用与实践

试题(基本体识读100)

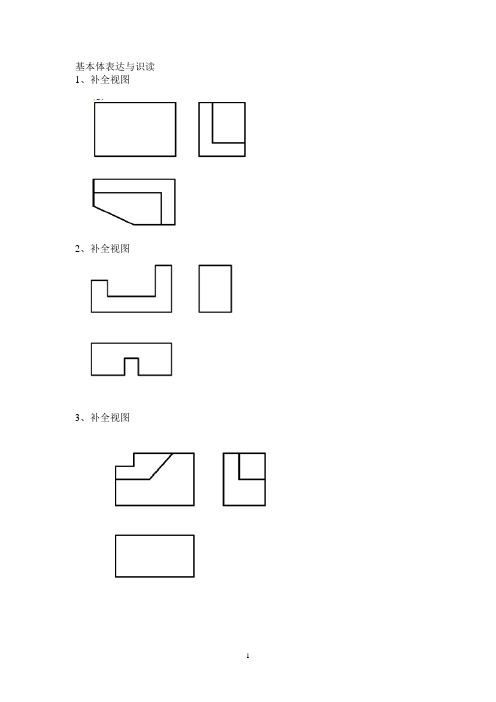
基本体表达与识读1、补全视图、补全视图23、补全视图4、补全视图5、已知立体的俯视图和左视图，画全主视图。

6、已知立体的主视图和左视图，画全俯视图。

7、已知立体的主视图和左视图，画全俯视图。

8、求作1／4圆球面上A点的侧面投影和水平投影。

9、求作圆柱体表面上A点的水平投影和侧面投影。

10、求作1/4圆球面上A点的正面投影和水平投影。

12、平面P 面，平面R 面，平面Q 面，平面S 面。

13、平面A 面，平面B 面，平面C 面，15、平面A 面，平面B 面，平面C 面，16、平面A 面，平面B 面，平面C 面，、18、已知立体的主视图和俯视图，画左视图20、已知立体的主视图和俯视图，画左视图21、已知立体的主视图和俯视图，画左视图23、已知立体的主视图和左视图，画俯视图24、已知立体的主视图和左视图，画俯视图25、已知立体的主视图和左视图，画俯视图27、已知立体的主视图和俯视图，画左视图28、已知立体的主视图和俯视图，画左视图30、已知立体的主视图和左视图，画俯视图31、已知立体的主视图和左视图，画俯视图32、已知立体的主视图和俯视图，画左视图34、已知立体的主视图和俯视图，画左视图35、已知立体的主视图，画出俯视图和左视图中截交线及轮廓线的投影。

36、已知立体的主视图和俯视图，画左视图37、已知立体的主视图和俯视图，画左视图38、已知立体的主视图和俯视图，画左视图39、绘制切割圆柱第三视图41、绘制切割圆柱第三视图43、绘制切割圆柱第三视图45、绘制切割圆柱第三视图47、绘制切割圆柱第三视图48、绘制切割圆柱第三视图50、已知立体的主视图，补画俯视图和左视图中相贯线及缺漏轮廓线的投影。

51、已知立体的主视图和左视图，画出俯视图中截交线及缺漏轮廓线的投影。

52、已知立体的主视图和俯视图，补画左视图中相贯线及缺漏轮廓线的投影。

53、已知立体的主视图和俯视图，画出左视图中截交线及缺漏轮廓线的投影。

54、已知立体的主视图和左视图，补画俯视图中相贯线及缺漏轮廓线的投影。

形体投影图的绘制和识读

平面立体—由平面多边形所围成的立体，如棱柱体和棱锥体等。

2.什么是曲面立体? 什么是母线、素线、回转曲面?曲面立体—由曲面或曲面与平面所围成的立体，如圆柱体和圆锥体等。

曲面立体的曲面是由运动的母线（直线或曲线），绕着固定的导线做运动形成的。

母线上任一点的运动轨迹形成的圆周称为纬圆。

母线在曲面上的任一位置称素线。

母线绕一定轴作旋转运动而形成的曲面，称为回转曲面。

3.什么是截交线、相贯线? 它们是怎么形成的?与立体相交的平面称为截平面，截平面与立体表面的交线称为截交线，平面与平面立体产生的截交线是由截交点连接而成。

截交点是截平面与平面立体棱线的交点或是截平面与截平面交线的端点。

两立体相交又称为两立体相贯。

相交的两立体成为一个整体称为相贯体。

它们表面的交线称为相贯线，相贯线是两立体表面的共有线，相贯线是由贯穿点连接而成。

4.平面与圆柱相交,产生哪几种截交线? 平面与圆锥相交,产生哪几种截交线?5.平面与圆柱相交，截平面与圆柱的轴线倾斜截交线是椭圆，截平面与圆柱的轴线垂直截交线是圆，截平面与圆柱的轴线平行截交线是直线。

平面与圆锥相交：截平面与圆锥的轴线垂直截交线是圆，截平面与圆锥的轴线倾斜且与圆锥的所有素线相交截交线是椭圆，截平面与圆锥的轴线倾斜且与圆锥的一条素线平行截交线是抛物线，截平面与圆锥的轴线平行截交线是双曲线，截平面通过圆锥的锥顶截交线是直线。

6.轴测投影图的基本分类有哪些?轴测投影按投射线与投影面相对位置的不同分为正轴测投影和斜轴测投影两类，每类按轴向变化率的不同又分为三种：（1）正（或斜）等测轴测投影：三个轴向变化率均相等，即p=q=r，称正（或斜）等测；（2）正（或斜）二测轴测投影：三个轴向变化率其中有两个相等，即p=q≠r，称正（或斜）二测；（3）正（或斜）三测轴测投影：三个轴向变化率均不相等，即p≠q≠r，称正（或斜）三测；6. 正等轴测投影图和斜二轴测投影图的绘制有哪些差别?正等轴测投影图和斜二轴测投影图的画法基本一样，只是画图时根据轴间角建立的坐标系不同，根据轴向变化系数的不同，量取尺寸时的比例不同。

相贯线的画法

相贯线的画法
作图步骤：（1）求特殊点：
直接定出相贯线的最左点 Ⅰ 和最右点Ⅲ的三面投影。
再求出出相贯线的最前点 Ⅱ和最后点Ⅳ的三面投影。
求正交两圆柱的相贯线
相贯线的画法
（2）求一般点：在已知相贯线的侧面投影图上任取一重影点 5″、6″，找出水平投影5、6，然后作出正面投影5′、6′。
(3) 光滑连相贯线：相贯线的正面投影左右、前后对称，后面的相贯线与前面的相贯线重影，只需按顺序光滑连接前面可见部分的各点的投影，即完成作图。
相贯线的画法
此课件下载可自行编辑修改，供参考！感谢你的支持，我们会努力做得更好！
用辅助平面法求相贯线时，要选择合适的辅助平面，以便简化作图。选择的原则是：辅助平面与两曲面立体的截交线投影是简单易画的图形—由直线或圆弧构成的图形。
相贯线的画法圆柱和Biblioteka 锥正交时的相贯线相贯线的画法
例求圆柱与圆锥正交时相贯线的投影。
1' 4'
3' 5' 2'
PV2
PV1 PV3
1"
4" PW2 PW1
相贯线的画法
当圆柱直径变化时，相贯线的变化趋势:
交线向大圆柱一侧弯
相贯线的画法
交线为两条平面曲线（椭圆）
圆柱与圆锥正交相贯线
想用一辅助平面截切相贯两立体，则辅助平面与两立体表面都产生截交线。截交线的交点既属于辅助平面，又属于两立体表面，是三面公有点，即相贯线上的点。利用这种方法求出相贯线上若干点，依次光滑连接起来，便是所求的相贯线。这种方法称为“三面共点辅助平面法”，简称辅助平面法。
相贯线的画法
例如图所示已知两圆柱的三面投影，求作它们的相贯线。

相贯线画法与识读说课示例

（）施目标三实
对于这个层次教学，分了六步进行。我第一步：在黑板上出示教模（图）出概念，后通过先出引然提问引导学员分析和讨论。是课堂教学中的关键环节。了这为达到教学目标，在分析相贯体时层层设疑，学员带着问题我让研习相贯体。然后用启发、拨指导等方法，学员在形体中点让寻找相贯线形式和部位。先通过实例讲解相贯线的概念、首定义、图的方法与步骤，作讲解相贯线的画法，过设疑把实体通相贯，向空贯。实例中得出结论：论是相贯还是穿孑，引在无Ｌ相贯线的形式是一样的．法也是一样的。求第二步：师生一起边画图边分析，作图过程中要强调学在员作图的准确性和美感。要求学员能够熟练找出相贯线的特
在复习导人新课时，设置了讲练结合的手法，过认定我通目标，施目标，习反馈，置作业，排双边活动，用启实练布安运发式和讨论相结合的教学方法，由浅人深、由易到难地在教学过程中展开。样的教学安排，仅有利于调动学员的学习积这不极参与性，且符合学员循序渐进的认识规律。而
一
、
说教材

机械制图课程标准

《机械制图》课程标准一 .课程的地位与任务机械制图是汽车维修专业学生必修的一门技术基础课，也是机械行业从事专业技术工作的人员必需掌握的一项职业技能。

本课程是研究机械图样的绘制与识读规律和方法的一门学科，通过投影理论的学习，培养和发展学生的空间分析问题能力、空间想象构形能力以及对空间几何问题的图解能力，使学生熟练掌握识读和绘制常见机械类专业图样的基本技能; 为学生后续专业课程的学习，以及课程设计、毕业设计打下坚实基础；为学生毕业后就业和从事专业技术工作培训职业实用技能。

二 .课程简述1.课程目标：（一）基本知识教学要求：1、掌握机械制图的基本概念和国家标准；2、掌握绘图方法和基本技能；3、具有一定的识图机械图样的能力和图示表达能力；（二）能力目标：能绘制中等复杂程度的三视图，包括想象该零件的结构形状；了解图样中有关技术要求，如表面粗糙度、极限与配合、形状和位置公差的符号、代号及其含义。

了解零件测绘的一般方法。

（三）思想教育目标：1、培养学生认真、细致、严谨的工作作风，形成良好的职业习惯和敬业精神；2、具备辩证思维的能力，具有求实创新的意识；3、培养学生遵纪守法的思想观念，加强职业道德意识，全面提高自身素质。

三,教学要求及时数分配第一章制图的基本知识与技能（1）教学内容第一节：制图的基本规定第二节：尺寸注法第三节：尺规绘图(2)教学要求1、明确本课程的性质、任务和重要性，树立正确的学习目的；2、了解本课程的主要内容、学习特点和学习方法；3、掌握国家标准中有关图幅、图线等制图基本规定及尺寸标注的规定；4、初步培养学生掌握使用绘图工具的能力，并使学生掌握平面图形的基本作图方法，为学习投影作图打下基础；5、掌握常用的圆周等分和正多边形的作法6、理解斜度和锥度的概念，掌握其画法和标注、了解椭圆的画法、掌握线段连接的作图方法7、通过尺寸标注的教学，使学生掌握在基本体视图上正确、齐全、清晰地标注尺寸的方法；(3)重点和难点重点：1、掌握国家标准中的有关图幅、图线、尺寸标注、基本作图方法2、培养学生空间想象能力；3、培养学生严谨的工作作风。

组合三视图的绘制和识读—双柱杯形基础剖面图的绘制与识读

任务资讯
4.3.1 视图表达方法的应用二、辅助视图 1.局部视图 2.镜像视图把镜面放在形体的下面，代替水平投影面，在镜面中反射得到的图像，称为镜像投影图
任务资讯
4.3.1 视图表达方法的应用二、辅助视图 3.旋转视图（又称展开视图）当形体的某一部分与基本投影面倾斜时，假想将形体的倾斜部分旋转到与某一选定的基本投影面平行，再向该基本投影面投影，所得的视图称为旋转视图（又称展开视图），其目的用于表达形体上倾斜部分的结构外形。
1.局部视图将形体的某一部分向基本投影
面投射所得到的视图称为局部视图，其目的是用于表达形体上局部结构的外形。
任务资讯
4.3.1 视图表达方法的应用二、辅助视图 1.局部视图局部视图一般按投影关系配置，必要时也可配置在其他适当位置。局部视图的范围应以视图轮廓线和波浪线的组合表示；当所表示的局部结构形状完整，且轮廓线成封闭时，波浪线可省略。
任务资讯
4.3.1 视图表达方法的应用一、基本视图画图时，可根据物体的形状和结构特点，选用其中必要的几个基本视图。每个视图一般均应标注图名，图名宜标注在视图的下方或一侧，并在图名下用粗实线绘一条横线，其长度应以图名所占长度为准。
任务资讯
4.3.1 视图表达方法的应用二、辅助视图
一、作图分析
作图前的基本分析过程与前述的组合体分析过程类似，主要区别是考虑选择何剖切平面、选择何剖面图表示其内外结构。
任务实施
动画演示：双柱杯形基础剖切过程
任务资讯
4.2.5 肋杯形基础三视图的绘制三、尺寸标注
巩固训练
按要求绘制图样 1．求作下图所示形体的W面投影，并将V、W面
投影改为合适的剖面。

任务1截断体和相贯体的三视图绘制与识读-习题答案(精)

任务1 截断体和相贯体的三视图绘制与识读-习题答案
【题一】判断题：
1. 截交线一定组成一个封闭的平面图形。

√
2. 平面截割球体时，不管截平面的位置如何，截交线的空间形状总是圆。

√
【题二】单选题：
1. 两立体相交称为立体相贯，其表面产生的交线被称为（ D ）。

A、棱线
B、交线
C、截交线
D、相贯线
2. 两圆柱体直径相等，当其正交时，相贯线是（ C ）。

A、双曲线
B、两闭合的空间曲线
C、两个椭圆
D、两直线
【题三】名词解释：
1.截交线
截平面与基本体表面交线称为截交线
2.截交线都具有下列两个基本性质
共有性截交线既在截平面上，又在基本体表面上。

截交线上的每一点都是截平面与基本体表面的共有点。

这些共有点的集合（即共有线）就是截交线。

封闭性任何基本体的截交线都是一个封闭的平面图形（平面折线、平面曲线或两者的组合）。

3.相贯线
两立体相交称为两立体相贯，两相交的物体称为相贯体。

4.相贯形式
两平面立体相贯；平面立体与回转体相贯；两回转体相贯
5.相贯线具有下列两个基本性质
相贯线是两相交基本体表面的共有线，相贯线上每个点都是两立体表面的共有点。

相贯线一般是封闭的空间曲线，特殊情况下可以是平面曲线或直线段。

6.同坡屋面
坡屋面是常见的一种屋面形式，最常见的是屋檐等高的同坡屋面，即屋檐高度相等、各屋面与水平面倾角相等的屋面。

怎样判断三视图上的形体特征

,
矛 ;喂弓召 ` 绍
、
、
不合格的不予聘任进行层层筛选理
,
工作进展有条有
点企业指导他们做好技师聘任制工作并在市汽车
配件厂召开了工人技师聘任制工作现场会
,
十分顺利
四
、
。
当场宣
搞好聘任
,
。
政策兑现
, ,
布
:
受聘技师享受每月技术津贴 2 0 元
图三的俯视图是三角形形的四分之一
, ,
,
柱
园锥
园环
园球 )
,
或是它们的切割体
,
, ,
图四的主视图是园
图三的形体特征是
和相贯体
。
当然具体情况还要具体分析尽
,
,
那么
,
这两个视图就是它们
,
管截交线和相贯线具有相当的难度但是如果判断出它们的形体特征
,
,
果
。
因此
,
我们在技师考评工作结束后
立即深入试
开展工人技师考评的试点工作
,
使我们对技师
3 1
聘任制的重大意义有了更现实的认识
。。
,
尽管这项工
、
度
,
有着强大的生命力
、、、
。
作刚刚开始但确实是一项顺乎民心的好政策好制
俯视图又有两个视图根本不是矩形线框如

【汽车机械与电气识图】2、任务2.5 识读轴承座的三视图

如图所示为轴承座的三视图，请根据三视图构想该轴承座的形状，并识读其尺寸。
一、组合体表面的连接关系
图2-5-2各视图中存在错误，请你构想其形体将其改正。
（1）
（2）
（3）
（4）
组合体表面连接关系有以下几种：
1、共面
两立体表面处于同一平面内，两相邻表面之间无分界线。
3、相切
相邻两
表面光
滑过渡
图中有哪些尺寸标注不恰当，请试着正确标注。参考答案：
（1）同心圆的直径标注在非圆视图上有什么好处？（2）尺寸标注在两视图之间有何好处？
看图步骤方法
【方法】①运用形体分析法从最能反映物体形状、位置特征的主视图入手，将复杂的视图按线框分成几个部分。 ②运用三视图的投影规律，找出各线框在其他视图上的投影，从而分析各组成部分的形状和它们之间的位置。 ③综合想象组合体的整体形状。
组合体是由若干几何体按一定的位置和方式组合而成的，因此在视图上除了要表明各几何体的大小外，还需要表示它们之间的相对位置和组合体本身的总体尺寸。通常，组合体的尺寸包括下列三种：（1）定形尺寸表示各几何体大小（长、宽、高）的尺寸；（2）定位尺寸表示各几何体之间相对位置（上下、左右、前后）的尺寸；（3）总体尺寸表示组合体总长、总宽、总高的尺寸。 3、尺寸基准
视图联系起来分析。
（3）先看整体形状，后看细小结构；
2、看图时要抓特征视图
（4）先看外部结构，后看内部形状。
四、组合体的尺寸标注
1、基本要求在组合体的视图上标注尺寸，应做到正确、完整、清晰。（1）正确尺寸标注必须符合国家标准的规定；（2）完整所注各类尺寸应齐全，到不遗漏、不多余；（3）清晰尺寸布置要整齐清晰，便于看图。 2、尺寸种类