微波技术第1章1
微波技术第1章 传输线理论1-电报方程

2r
假如导体的表面电阻为Rs,而导体间填充介质具 有的复数介电常数为
j
导磁率为: 试确定传输线参量。
0r
解 同轴线参量为
L ( 2 )2
2
0
b a
1 r2
rdrd
2
ln b
a
C
2 b 1 rdrd 2
(ln b a )2 0 a r 2
lnb a
ቤተ መጻሕፍቲ ባይዱ
R
Rs
(2 )2
(
2 0
1 a2
ad
2 0
1 b2
bd
)
RS
2
1 1 a b
G
(ln b a
)2
2
0
b a
1 r2
rdrd
2
lnb a
内外导体具有表面电阻R s的同轴线
y
,
a
x
b Rs
注意
表1.1 列出了同轴线、双线和平行板传输线的参量。 从下一章将看到,大部分传输线的传播常数,特性阻抗和衰 减是直接由场论解法导出的。 该例题先求等效电路参数(L,C,R,G)的方法,只适用于 相对较简单的传输线。虽然如此,它还是提供了一种有用的直 观概念,将传输线和它的等效电路联系起来。
《微波技术与天线》第二版刘学观 第1章

(1-1-5)
式中, Z=R+jωL, Y=G+jωC, 分别称为传输线单位长串联阻抗和 单位长并联导纳。
第1章 均匀传输线理论 2. 均匀传输线方程的解 将式(1- 1- 5)第1式两边微分并将第 2 式代入, 得
d 2U ( z ) ZYU ( z ) 0 2 dz
同理可得
d I ( z) ZYI ( z ) 0 2 dz
第1章 均匀传输线理论
图 1-1 各种微波传输线 (a) 双导体传输线; (b) 波导; (c) 介质传输线
第1章 均匀传输线理论 对均匀传输线的分析方法通常有两种: 一种是场分析法, 即
从麦克斯韦尔方程出发, 求出满足边界条件的波动解, 得出传输
线上电场和磁场的表达式, 进而分析传输特性; 第二种是等效电 路法, 即从传输线方程出发, 求出满足边界条件的电压、 电流波 动方程的解, 得出沿线等效电压、电流的表达式, 进而分析传输 特性。前一种方法较为严格, 但数学上比较繁琐, 后一种方法实
b Z0 ln r a
60
(1-1-17)
式中, εr为同轴线内、外导体间填充介质的相对介电常数。 常
用的同轴线的特性阻抗有50 Ω 和75Ω两种。
第1章 均匀传输线理论 2) 传播常数 γ 传播常数 γ 是描述传输线上导行波沿导波系统传播过程中 衰减和相移的参数, 通常为复数,由前面分析可知
1 2 1 2
。 对于 LC
R G j LC 1 jL 1 jC
1 ( RY0 GZ 0 ) j LC 2
于是小损耗传输线的衰减常数α和相移常数β分别为
(1-1-19)
1 α= (RY0+GZ0) 2 LC β=ω
微波技术 1章阻抗圆图

用Zc除以等式的两边就得到归一化输入阻抗和反射系数的关系
Zin 1 R jX Zc 1
(1.91)
式中R代表归一化电阻,X代表归一化电抗。反射系数为复数,可表示为
= e j ' j''
(1.92)
所以有
Zin R jX 1 (' j'' )
.44 .07
.07 .42
.08 .41
.09 .40
.10
.39 .11
.38 .12
等|Γ|圆
z
.5 1
.43 .08 .42 .09 .41 .40 .10 .39 .11
.38 .12
.37 .13
.36 .14
.35 .15 .16
.34 .17
.33 .18
.32 .19
.31 .20
实际上一般的圆图都会在上面指示出向源 及向负载方向移动时的转动方向。
向源移动
z2
z1
向负载移 动
z2
z
逆时针转动 .48 .47
.45
.46 .04
.03
.02
.44 .05
.49 .01
.00 .01 .02
.00 .49 .48
.03 .04
0
.47 .46
.05
.45
顺时针转动
.06
.43 .06
由已知点的参数去求另一点的参数时,沿等|Γ|圆向何方旋转,转多少角度就
成了解决问题的关键。
传输线上位置的移动
沿等|Γ|圆转动
.48 .47
.45
.46 .04
.03
.02
微波课件1-微波技术与微波器件-栾秀珍-清华大学出版社

2.集中参数(Lumped Parameters) 集中参数电路:电参数集中在一个小的空间的电路。
在低频电路中,电能量集中在电容器中,磁能量 集中在电感器中,只有电阻元件消耗能量,连接各元 件的导线是一个理想导线,不消耗能量,属于集中参 数电路。 特点:传输线上各点的电压(电流)处处相等,不随位 置变化。
Y1 = G1 + jC1
d2I dz 2
Z1Y1I
令 Z1Y1 (R1 jL1)(G1 jC1) j
——传播常数
d2V dz2
2V
0 ,(1)
——波动方程。 电压的通解
d2I dz2
2I
0
(2)
V(z) = Aez + Bez = Vi(z) + Vr(z)
dV dz
Z1I
dI dz
1 . 2 . 1 基本概念 1 . 2 . 2 传输线方程及其解
1 . 2 . 1 基本概念
1.TEM波传输线的结构特点
(1)双导体结构;
(2)电场可看成 是由一个导体的 正电荷指向另一 导体的负电荷;
结论1:传输线同 一横截面对应位 置的两导线上的 电流 等幅、反向。
(3)磁场可看 成是由导体上的 电流激发。
Y1V
V(z) = Aez + Bez = Vi(z) + Vr(z)
Z1Y1 (R1 jL1 )(G1 jC1 ) j
I (z) dV
Aez
Bez
Z1dz Z1 / Z1 /( )
A ez B ez
Z0
Z0
Ii(z) Ir(z)
Z0
Z1
Z1 Y1
微波技术和天线(第四版)刘学观 第1章

第一章均匀传输线理论第章传输1.1节均匀传输线方程及其解1.2节传输线的阻抗与状态参量1.3节无耗传输线的状态分析1.4节传输线的传输功率、效率与损耗1.5节阻抗匹配151.6节史密斯圆图及其应用1.7节同轴线的特性阻抗1.1 均匀传输线方程及其解 本节要点传输线分类均匀传输线等效及传输线方程传输线方程解及其分析传输线的特性参数1.微波传输线定义及分类微波传输线是用以传输微波信息和能量的各种形式的传输系统的总称,它的作用是引导电磁波沿一定方向传输因此又称为导波系统 第一类是双导体传输线,它由二根或二根以上平行传输,因此又称为导波系统。
第类是双导体传输线由根或根以平行导体构成,因其传输的电磁波是横电磁波(TEM 波)或准TEM 波,故又称为TEM 波传输线,主要包括平行双线同轴线带状线和微带线等行双线、同轴线、带状线和微带线等。
第二类是均匀填充介质的金属波导管,因电磁波在管内传播,故称为波导,主要包括矩形波导、圆波导、脊形波导和椭圆波导等。
第三类是介质传输线,因电磁波沿传输线表面传播,故称为表面波波导,主要包括介质波导、镜像线和单根表面波传输线等。
2. 均匀传输线方程当高频电流通过传输线时,在传输线上有:导线将产生热耗,这表明导线具有分布电阻;在周围产生磁场,即导线存在分布电感;由于导线间绝缘不完善而存在漏电流,表明沿线各处有分布电导;两导线间存在电压,其间有电场,导线间存在分布电容。
这四个分布元件分别用单位长分布电阻、漏电导、电感和电容描述。
设传输线始端接信号源,终端接负载,坐标如图所示。
Δz其上任意微分小段等效为由电阻R Δz 、电感L Δz 、电容C Δz z +Δz z z 0和漏电导G Δz 组成的网络。
i (z +Δz ,t )i (z ,t )R ΔzL Δz u (z +Δz ,t )u (z ,t )G Δz C Δz设时刻t 在离传输线终端z 处的电压和电流分别为u (z,t ) 和i (z,t ),+z +z +z z +Δz而在位置z Δz 处的电压和电流分别为u (z Δz,t )和i (z Δz,t )。
微波技术基础 ppt课件

由此两式消去 H t :
k2 z2 2 E vt z tE zja vz tH z ⑤
同理,由①、③可得:
k2 z2 2 H vt z tH zja vz tE z ⑥
k2 2 →无界媒质中电磁波的传播常数
★重要结论:规则导行系统中,导波场的横向分量可 由纵向分量完全确定。
再由③出发:
结构—两根平行导线; 缺点—随着信号频率升高,导线电阻损耗增大,不能有效引
导微波。
➢ 微波频段导波系统
米波频段结构—改进型双导线即平行双导体线; 分米波~厘米波频段结构—封闭式双导体导波系统即同轴线; 厘米波~毫米波频段结构—柱面金属波导;
毫米波~亚毫米波频段结构—柱面金属波导、介质波导。
导波系统的主要功能 1)、无辐射损耗地引导电磁波沿其轴向行进而将能
× H vjE v
× E vj H v
v H0
v E0
采用广义柱坐标系(u,υ,z),设导波沿z向(轴向)传播, 微分算符▽和电场Ε、磁场Η可以表示成:
E v ( u , v t, z ) a v z E /v t ( z u , v , z ) a r z E z ( u , v , z )
H v ( u , v , z ) H v t ( u , v , z ) a v z H z ( u , v , z )
展开后令方程两边的横向分量和纵向分量分别相等
两边乘以
jωμ
v
t× H t j
a v zE v z ①
ta v zH za v z H zt j
v E t②
两边作
★重要结论:规则导行系统中导波场的纵向分量满足标量亥 姆霍兹方程 。
色散关系式
纵向场分量可以表示成横向坐标r和纵向坐标z的函数,即
微波技术第1章-传输线理论1

电磁波传播问题概述
• 时域一般波动方程
r r r 2 r ∂E ∂ E 1 ∂J 2 ∇ E − µε − µε 2 = ∇ρ + µ ∂t ∂t ε ∂t r r 2 r r ∂H ∂ H 2 ∇ H − µε − µε 2 = −∇ × J ∂t ∂t
(9)
一阶时间偏导数代表损耗,二阶代表波动。 一阶时间偏导数代表损耗,二阶代表波动。
(5)
r r r r D = εE , B = µH
短路面(理想导体边界)
r r n×E = 0 S r r r n×H =α S r r n•D =σ S r r n•B =0
S
→
Et
S
= 0,
Hn S = 0 Ht
S
En S ≠ 0,
≠0
(6)
切向电场为零, 切向电场为零,切向磁场不为零的界 电壁)均可视为等效短路面 等效短路面。 面(电壁)均可视为等效短路面。
第1章 微波传输线
§1.1 引言
*传输系统:把微波能量从一处传到另一处的装置。 传输系统:把微波能量从一处传到另一处的装置。
传输系统也叫导波结构或导波系统。 传输系统也叫导波结构或导波系统。 微波中常用传输系统: 微波中常用传输系统: 传输线:由两根或两根以上平行导体构成。 *传输线:由两根或两根以上平行导体构成。 通常工作在其主模( 通常工作在其主模(TEM波或准TEM波) 。 故又称为TEM波传输线。(含平行双线、同轴线和微带线等) 波传输线。 含平行双线、同轴线和微带线等) 波导管:由单根封闭柱形导体空腔构成。 *波导管:由单根封闭柱形导体空腔构成。 电磁波在管内传播,简称波导。 电磁波在管内传播,简称波导。 表面波波导:由单根介质或敷介质层导体构成。 *表面波波导:由单根介质或敷介质层导体构成。 电磁波沿其表面传播。 电磁波沿其表面传播。
微波技术基础简答题整理

对于电场线,总是垂直于理想管壁,平行于理想管壁的分量为 对于磁场线,总是平行于理想管壁,垂直于理想管壁的分量为 ( P82)
0 或不存在; 0 或不存在。
2-10. 矩形波导的功率容量与哪些因素有关? 矩形波导的功率容量与波导横截面的尺寸、模式(或波形) 导中填充介质的击穿强度等因素有关。 (P90)
工作波长 λ,即电磁波在无界媒介中传输时的波长, λ与波导的形状与尺寸无关。 截止波数为传播常数 γ等于 0 时的波数,此时对应的频率称为截止频率,对应的 波长则称为截止波长。它们由波导横截面形状、尺寸,及一定波形等因素决定。 波长只有小于截止波长, 该模式才能在波导中以行波形式传输, 当波长大于截止 波长时,为迅衰场。
2-2. 试从多个方向定性说明为什么空心金属波导中不能传输 TEM模式。※
如果空心金属波导内存在 TEM 波,则要求磁场应完全在波导横截面内,而且是 闭合曲线。 由麦克斯韦第一方程, 闭合曲线上磁场的积分应等于与曲线相交链的 电流。由于空心金属波导中不存在沿波导轴向(即传播方向)的传到电流,所以 要求存在轴向位移电流,这就要求在轴向有电场存在,这与 TEM 波的定义相矛 盾,所以空心金属波导内不能传播 TEM 波。
按损耗特性分类: ( 1)分米波或米波传输线(双导线、同轴线) ( 2)厘米波或分米波传输线(空心金属波导管、带状线、微带线) ( 3)毫米波或亚毫米波传输线(空心金属波导管、介质波导、介质镜像线、微 带线) ( 4)光频波段传输线(介质光波导、光纤)
1-3. 什么是传输线的特性阻抗,它和哪些因素有关?阻抗匹配的物理实质是什 么?
4-5. 微波谐振器的两个主要功能是 储能 和选频 。
4-6. 无耗传输线谐振器串联谐振的条件是 Zin =0,并联谐振的条件是 Zin =∞。
01微波技术第1章传输线理论

传 输 线 理 论
二、分布参数的概念及传输线的 等效电路
• 电路理论的前提是集中参数,其条件为: •
ι<<λ ι:电器尺寸,λ:工作波长 传输线中工作波长和传输长度可比拟,沿 线的电压、电流不仅是时间的函数,还是 空间位置的函数,从而形成分布参数的概 念。
传 输 线 理 论
传输线上处处存在分布电阻、分布电 感,线间处处存在分布电容和漏电导。分 布参数为:R(Ω/m)、L(H/m) C(F/m)、 G(S/m) 如果分布参数沿线均匀,则为均匀传 输线,否则,为非均匀传输线。 传输线的等效电路如图1.1.1所示
EXP:双根传输线
传 输 线 理 论
Zc取决于传输线的几何尺寸和周围媒介, 与传输线的位置和工作频率无关。
传 输 线 理 论
⑶ 相速和波长 相速:某一等相面推进的速度 令α=0(无耗),由ωt-βz=常数,得
传 输 线 理 论
§1-3 反射系数、输入阻抗与 驻波系数
传输线上的电压、电流既然具有波
传 输 线 理 论
第一章 传输线理论
§1-1 传输线的种类及分布 参数的概念
传 输 线 理 论
• 定义:广义上讲,凡是能够导引电磁波
•
沿一定方向传输的导体、介质或由他们 共同组成的导波系统,都可以称为传输 线。 传输线是微波技术中最重要的基本元件 之一,原因有两点: ⑴ 完成把电磁波的能量从一处传到另一 处。 ⑵ 可构成各种用途的微波元件。 Exp:耦合器、匹配器、电容、电感等
传 输 线 理 论
1.3.2式的意义在于: ⑴ 无耗传输线上各点反射系数的大小相等, 均等于终端反射系数的大小。 ⑵ 只要求出|Γ|,若已知λ或β则可求出任意 点的反射系数Γz 随着ZL的性质不同,传输线上将会有 如下不同的工作状:
电磁场与微波技术第一章
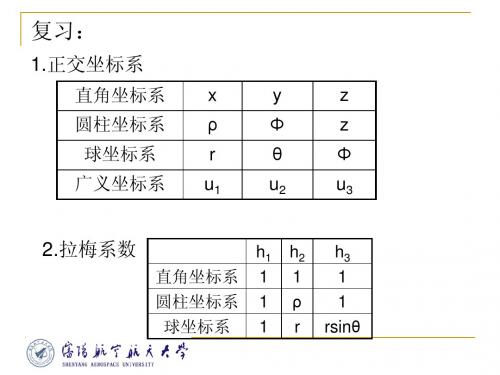
t t0时刻, 令f ( p, t0 ) f (u1 , u2 , u3 , t0 ) f 0
f0为常量,给f 一个微小增量df ,
面S
, u2 , u3 , t0 ) f 0 df f ( p, t0 ) f (u1
(3)方向导数最大值及对应方向; (4) 方向导数最小值及对应方向。
2 2 ˆ ˆ ˆz 在空间点 例3.求矢量场F x 4 x y 2 xy z p( , , z) p(2 2 ,
4
,3)处的散度。
r ˆ ˆA r , 试求在球体V:r a,0 , 例3. 已知A 2 r r 0 2 , 及其界面r a,0 ,0 2上验证 高斯定理。
t0),场值相等的点的集合称
导体等势面
为等值面。
温度场: 等温面
热源
2.由于空间任意点与场值是一一对应关系,故标量场的函
数是单值函数,各等值面是互不相交的。
3. 标量函数f(u1 ,u 2 ,u 3 ,t), 等值面方程为: f(u1 ,u 2 ,u 3 ,t0 ) f 0 ( f 0 为常量)。
, t0 ) f ( p1 , t0 ) df f ( p1
f (u1 du1 , u2 du2 , u3 du3 , t0 ) f (u1 , u2 , u3 , t0 )
3 f f f f du1 du2 du3 dui u1 u2 u3 i 1 ui
3 广义坐标系中,任意方向线元 dl u ˆi hi dui
3 f 3 1 f df dui u ˆi hi dui ˆi u i 1 i 1 hi ui i 1 ui
微波技术第1章_阻抗圆图

Z in = Z c
1+ Γ 1− Γ
用Zc除以等式的两边就得到归一化输入阻抗和反射系数的关系 Z in 1 + Γ (1.91) = = R + jX Zc 1− Γ 式中R代表归一化电阻 代表归一化电阻, 代表归一化电抗 反射系数为复数, 代表归一化电抗。 式中 代表归一化电阻,X代表归一化电抗。反射系数为复数,可表示为
1、等R线 、 线
将(1.93a)两边同加 )两边同加1 于是有 按的Γ’幂序排列 按的 幂序排列
( 等式两边各加上
1 − Γ ' 2 − Γ '' 2 R +1 = +1 ' 2 '' 2 (1 − Γ ) + Γ 2(1 − Γ ' ) R +1 = (1 − Γ ' ) 2 + Γ ''2
Γ’’
-1
32 0.
0. 43
阻抗圆图
阻抗圆图的构成 Γ’’
3、等|Γ|线、等ρ线、等k 线 、 Γ线 线
复平面上以(0,0)为圆心的一系列同心圆簇 在Γ’+jΓ’’复平面上以 复平面上以 为圆心的一系列同心圆簇 即是等|Γ|线 即是等 线 因为 ρ =
1+ Γ 1- Γ k= 1− Γ 1+ Γ
ρ=∞ ρ=5 ρ=2 ρ=1 Γ=0 |Γ|=1/3
θ=0 θ=-600
.34 .33
.38 .12 .37 .13 .36 .35 .14 .15 .16 .17
Γ’
.23
阻抗圆图 最后把以上的这些特殊点、 最后把以上的这些特殊点、线和面加以总结 ⑴开路点,短路点,匹配点 开路点,短路点, 坐标 参数 Γ’’ 电压波节
微波技术与天线——第1章

(1-7a) 根据双曲函数的表达式,上式整理后可得 (1-7c)
第一章、传输线理论 (2)已知传输线始条件 这时将坐标原点z=0选在始端较为适宜。将始端条件 U(0)=U1,I(O)=I1 ,代入式(1—4),同样可得沿线的 电压电流表达式为
(1-6b)
第一章、传输线理论 4、传输线的特性参量 传输线的特性参量主要包括:传播常数、特性阻抗、 相速和相波长 (1)、传播常数
反映波经过单位长度传输线后幅度和相位的变化 的物理量。
传播常数γ 一般为复数,可表示为 其中实部α称为衰减常数,表示行波每经过单位长度 后振幅的衰减,单位为分贝/米(dB/m)或奈培/米
第一章、传输线理论 (NP/m);虚部β称为相移常数,表示行波每经过单位长 度后相位滞后的弧度数,单位为弧度/米(rad/m)。 对于低耗传输线,一般满足 R0 L0 , G0 C0 , 所以有
第一章、传输线理论 由此可得
衰减常数是由传输线的导体电阻损耗αc和填充介质的漏 电损耗αd两部分组成。对于无耗传输线RO=0,G0=0
实际应用中,在微波频段内,总能满 足 R0 L0 , G0 C0 因此可把微波传输线当作无耗传输线来看待。
第一章、传输线理论 (2)特性阻抗 特性阻抗定义:传输线上入射波电压Ui(z)与入射波电流 Ii(z)之比。或反射波电压Ur(z)与反射波电流Ir(z)之比 的负值,即
图1-2
图1-3
第一章、传输线理论
电阻器
第一章、传输线理论 电容器
第一章、传输线理论 电感器
图1-9
图1-10
图1-11
第一章、传输线理论 在微波频率下传输线的分布参数效应
体现为分布参数电感,电容,电导和电阻
微波传输线的特点
第1章-射频微波工程基础介绍

第1章 射频/微波工程介绍 表1-1
第1章 射频/微波工程介绍
以上这些波段的划分并不是惟一的,还有其他许多 不同的划分方法,它们分别由不同的学术组织和政府机 构提出,甚至还在相同的名称代号下有不同的范围,因 此波段代号只是大致的频谱范围。其次,以上这些波段 的分界也并不严格,工作于分界线两边临近频率的系统 并没有质和量上的跃变,这些划分完全是人为的,仅是 一种助记符号。
电路,取得一个比较好的折中方案。
第1章 射频/微波工程介绍
1.3 射频/
1.3.1 由于频率、 阻抗和功率是贯穿射频/微波工程的
三大核心指标,故将其称为射频铁三角。它能够形象地 反映射频/微波工程的基本内容。这三方面既有独立特 性,又相互影响。三者的关系可以用图1-2表示。
第1章 射频/微波工程介绍
第1章 射频/微波工程介绍
1.2.2 射频/ 由上述基本特性可归纳出射频/微波与普通无线电相
比有以下优点: (1) 频带宽。可传输的信息量大。 (2) 分辨率高。连续波多普勒雷达的频偏大,成像更
清晰,反应更灵敏。 (3) 尺寸小。电路元件和天线体积小。 (4) 干扰小。不同设备相互干扰小。 (5) 速度快。数字系统的数据传输和信号处理速度
第1章 射频/微波工程介绍
(3) 导航系统: 微波着陆系统(MLS),GPS,无线信标,防撞系统, 航空、 航海自动驾驶等。 (4) 遥感: 地球监测,污染监测,森林、 农田、 鱼汛监测,矿 藏、 沙漠、 海洋、 水资源监测,风、 雪、 冰、 凌监 测,城市发展和规划等。
第1章 射频/微波工程介绍
4. 射频/微波频带比普通的中波、 短波和超短波的 频带要宽几千倍以上,这就意味着射频/微波可以携带 的信息量要比普通无线电波可能携带的信息量大的多。 因此,现代生活中的移动通信、 多路通信、 图像传输、 卫星通信等设备全都使用射频/微波作为传送手段。 射频/微波信号还可提供相位信息、 极化信息、 多普勒频移信息等。这些特性可以被广泛应用于目标 探测、 目标特征分析、 遥测遥控、 遥感等领域。
微波技术1章传输线方程及其解

02
传输线方程是描述电磁波在传输 线中传播特性的偏微分方程,包 含了电场和磁场分量以及时间和 空间变量。
传输线方程的形式
传输线方程的一般形式为:∂E/∂t=c^2*∂^2E/∂x^2+σE,其中E为电场强度,t为时间,x为空间变量,c 为光速,σ为电导率。
数值解的概念
数值解是通过数值计算方法求解方程的方法。数值解可以提供精确的结果,但需要使用 数值计算软件或算法。
数值解的求解过程
数值解通常采用迭代方法、有限差分法、有限元法等数值计算技术来求解方程。在传输 线方程中,数值解可以通过离散化传输线并使用数值算法来求解。
数值解的应用场景
数值解适用于大规模复杂系统和实际工程应用。通过数值计算软件或算法,可以高效地 处理复杂的传输线问题,并提供精确的结果。
05 结论
本章总结
传输线方程是描述微波传输线中电磁波传播的基本方 程,通过求解该方程可以得到微波信号在传输线中的
传播特性。
输标02入题
本章介绍了传输线方程的基本形式和求解方法,包括 时域和频域的求解方法。
01
03
传输线方程的求解方法在实际应用中具有广泛的应用, 如微波测量、微波通信、雷达系统等领域。
04 传输线的应用
微波传输系统
微波传输系统概述
微波传输系统是利用微波波段电磁波进行信息传输的系统,广泛 应用于通信、广播、电视等领域。
微波传输系统的组成
微波传输系统主要由发射机、传输线路、接收机三部分组成,其中 传输线路是实现信号传输的关键部分。
微波传输系统的特点
微波传输系统具有频带宽、容量大、抗干扰能力强等优点,但也存 在传输损耗大、传输距离短等局限性。
精品课件-微波技术基础(廖承恩)-第1章

开波导使电磁波能量约束在波导结构的周围(波导内和波 导表面附近)沿轴向传播,其导行波是表面波。
第1章 引论
● 导模(guided mode) 导行波的模式,又称传输模、 正规模,是能够沿导行系统独立存在的场型。其特点是: ①在 导行系统横截面上的电磁场呈驻波分布,且是完全确定的。这 一分布与频率无关,并与横截面在导行系统上的位置无关;② 导模是离散的,具有离散谱;当工作频率一定时,每个导模具 有唯一的传播常数;③导模之间相互正交,彼此独立,互不耦 合;④具有截止特性,截止条件和截止波长因导行系统和模式 而异。
第1章 引论
第1章 引论
从电子学和物理学的观点看,微波这段电磁谱具有不同于 其它波段的如下重要特点:
● 似光性和似声性 微波的波长很短,比地球上一般物 体(如飞机、舰船、汽车、坦克、火箭、导弹、建筑物等)的尺 寸相对要小得多,或在同一量级。这使微波的特点与几何光学 相似,即所谓似光性。因此,使用微波工作,能使电路元件尺 寸减小;使系统更加紧凑;可以设计制成体积小、波束很窄、 方向性很强、增益很高的天线系统,接收来自地面或宇宙空间 各种物体反射回来的微弱信号,从而确定物体的方位和距离, 分析目标的特征。
第1章 引论
第1章 引 论
1.1 微波及其特点 1.2 微波的应用 1.3 本书的内容框图 1.4 导行波及其一般传输特性 本章提要 习题
第1章 引论
1.1 微波及其特点 就现代微波理论和技术的研究和发展而论,微波 (microwave)是指频率从300 MHz至3 000 GHz范围内的电磁波, 其相应的波长从1 m至0.1 mm。这段电磁频谱包括分米波(频率 从300 MHz至3 000 MHz)、厘米波(频率从3 GHz至30 GHz)、 毫米波(频率从30 GHz至300 GHz)和亚毫米波(频率从300 GHz 至3 000 GHz)四个波段。 在雷达、通信及常规微波技术中,常用拉丁字母代号表示 微波的分波段。表1.1- 1(a)、(b)分别示出常用微波分波段代 号和家用电器的频段。
微波技术 1章三种传输状态

(1.73)
线上任意点的输入阻抗为
Z in
V (z) I (z)
jZ ctgz
(1.74)
|V| |I|
|V| |I|
φV
φI
φV φI
Zin
无耗传输线的三种工作状态
(2) 终端开路传输线
终端开路时电流IL =0, 得到线上电压电流分布为
V (z)=VL cos z 2V cos z
A e j(2 z) 2
所以
(z)
A2e j z A1e j z
A2 A1
e j(2 12 z) (z) e j
(1.58a)
由上式可知,反射系数的模|Γ(z)|是反射波电压振幅值与入射波电压振幅值之比:
(z) V (z) A2 V (z) A1
c
1 1
( (
z) z)
(1.63)
也可以写为
(z) Zin (z) Zc Yc Yin (z) Zin (z) Zc Yc Yin (z)
(1.64)
无耗传输线的三种工作状态
反射系数Γ及输入阻抗Zin
反射系数Γ(z)与负载阻抗ZL 间的关系
由式(1.64)
(z) Zin (z) Zc Zin ( z) Zc
(1.58b)
反射系数的幅角为反射波电压与入射波电压的相位差,即
(z) arg((z)) argV (z) argV (z)) 2 1 2 z
(1.58c)
无耗传输线的三种工作状态
反射系数Γ及输入阻抗Zin
反射系数Γ(z)是参考面位置z的函数,在z=0处的反射系数称为负载反射系数ΓL,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
R jL L 1 R 1 G 1 Z0 2 jL 1 2 jC G jC C L 1 R G L (1-1-15) 1 j 2 L C C C
可见, 损耗很小时的特性阻抗近似为实数。 对于直径为d、间距为D的平行双导线传输线, 其特性阻 抗为
u( z, t ) =Ri(z, t) L i ( z, t ) z t u( z, t ) i ( z , t ) =Gu(z, t) C z t
(1-1-3)
这就是均匀传输线方程, 也称电报方程。
对于时谐电压和电流, 可用复振幅表示为 u(z, t)=Re[U(z)e jωt] i(z, t)=Re[I(z)e jωt]
Z0
120
2D ln d r
(1-1-16)
式中, εr为导线周围填充介质的相对介电常数。 常用的平 行双导线传输线的特性阻抗有250Ω, 400Ω和600Ω三种。
第1章 均匀传输线理论 对于内、外导体半径分别为a、b的无耗同轴线, 其特性阻抗为
b Z0 ln r a
60
(1-1-17)
z z A1e cos(t z ) A2 e cos(t z ) i ( z , t ) i ( z , t ) i ( z , t ) 1 [ A1e z cos(t z ) A2 e z cos(t z )] Z0
(1-1-4)
第1章 均匀传输线理论 将上式代入(1- 1- 3)式, 即可得到时谐传输线方程
dU ( z ) ZI ( z ) dz dI ( z ) YU ( z ) dz
式中, Z=R+jωL, Y=G+jωC,
(1-1-5)
分别称为传输线单位长串联阻抗和单位长并联导纳。
第1章 均匀传输线理论
第1章 均匀传输线理论
1.1 均匀传输线方程及其解
1. 均匀传输线方程
均匀传输线组成的导波系统都可等效为的均匀平行双导线系统。
在均匀传输线上任意一点z处, 取一微分线元Δz(Δz<<λ), 该线元可视为集总参数电路, 其上有电阻 RΔz、电感LΔz 、 电容CΔz和漏电导GΔz(其中R, L, C, G分别为单位长电阻、 单位长电感、 单位长电容和单位长漏电导)。
在微波技术中, 常可把传输线看作是无损耗的, 下面着重介绍均匀无耗传输线。
第1章 均匀传输线理论
麦克斯韦方程 ( Maxwell Equations)
C
C
C
C
D H dl ( J ) dS ( 1 ) S t B E dl dS (2) S t B dS 0 (3) D dS q (4)
(1-1-1)
u(z, t)+RΔzi(z, t)+ Lz i ( z, t ) u(z+Δz, t)=0 t ) i(z, t)+GΔzu(z+Δz, t)+ CΔz u( z z, t-i(z+Δz, t)=0
(1-1-2)
t
第1章 均匀传输线理论 将式(1- 1- 1)代入式(1- 1- 2), 并忽略高阶小量, 可得
2. 均匀传输线方程的解
将式(1- 1- 5)第1式两边微分并将第 2 式代入, 得
d 2U ( z ) ZYU ( z ) 0 2 dz
同理可得
d 2 I ( z) ZYI ( z ) 0 2 dz
第1章 均匀传输线理论
齐次二阶微分方程
令 γ 2=ZY=(R+jωL)(G+jωC), 则上两式可写为
Z0 ( R jL) /(G jC)
(1- 1- 7a) (1- 1-7b)
式中, A1, A2为待定系数, 由边界条件确定。
第1章 均匀传输线理论 令γ=α+jβ, 则可得传输线上的电压和电流的瞬时值表达式为
入射波
反射波
u ( z, t ) u ( z, t ) u ( z, t )
d 2U ( z ) 2U ( z ) 0 dz 2 (1-1-6) d 2 I ( z) 2 I ( z) 0 dz 2 显然电压和电流均满足一维波动方程。 电压和电流的通解为
U(z)=U+(z)+U-(z)=A1e +γz+A2e –γz
1 I ( z) I ( z) I ( z) ( A1e z A2e z ) Z0
I1
(1-1-12)
可见, 只要已知终端负载电压Ul、电流 Il 及传输线特性参数γ 、Z0, 则传输线上任意一点的电压和电流就可由式(1-1-12)求得。
第1章 均匀传输线理论
3. 传输线的工作特性参数
1) 特性阻抗Z0 传输线上任一点的行波电压与行波电流之比,即入射波电压与 入射波电流之比,或反射波电压与反射波电流之比的负值。
第1章 均匀传输线理论
第1章 均匀传输线理论
1.1 均匀传输线方程及其解 1.2 传输线阻抗与状态参量 1.3 无耗传输线的状态分析 1.4 传输线的传输功率、 效率与损耗
1.5 阻抗匹配
1.6 同轴线的特性阻抗
习
题
第1章 均匀传输线理论
引言
微波传输线:
用以传输微波信息和能量的各种形式的传输系统(均匀传输线) 方向:导行波(电磁波)传播的方向为纵向, 垂直于导波传播的 方向为横向。 TEM波,TM波和TE波
第1章 均匀传输线理论 讨论第一种情况: 将边界条件 z=0 处U(0)=Ul、I(0)=Il 代入式(1- 1-7), 得
Ul=A1+A2 I l= 1 (A1-A2) Z0 由此解得 (1-1-9)
1 A1= (Ul+IlZ0) 2 1 A2= (Ul-IlZ0) 2
(1-1-10)
第1章 均匀传输线理论 将上式代入式(1- 1- 7), 则有
U(z)=Ul ch γ z+I1Z0 shγ z
U1 I(z)=I1 ch γ z+ shγ z Z0
写成矩阵形式为 U(z) I(z) = ch γ z
1 sh γ z Z0
(1-1-11)
Z0sh γ z
U1
ch γ z
(1-1-18)
α为衰减常数, 单位为dB/m(有时也用Np/m, 1Np/m=8.86 dB/m); β为相移常数, 单位为rad/m。
第1章 均匀传输线理论 对于无耗传输线,R=G=0, 则α=0, 此时 γ =jβ, β=ω 损耗很小的传输线, 即满足R<<ωL、G<<ωC时, 有
1 2 1 2
R jL Z0 G jC
说明:特性阻抗Z0通常是个复数, 且与工作频率有关,传输线 自身分布参数决定,与负载及信源无关。 对于均匀无耗传输线, R=G=0, 传输线的特性阻抗为
1 Z0 C
(1-1-14)
此时, 特性阻抗Z0为实数, 且与频率无关。
第1章 均匀传输线理论 当损耗很小, 即满足R<<ωL、 G<<ωC时,有
用Z0来表示, 其倒数称为特性导纳, 用Y0来表示。
由定义得
U ( z) U ( z) Z0 I ( z) I ( z)
由式(1- 1- 6)及(1- 1- 7)得特性阻抗的一般表达式为
R jL Z0 G jC
(1-1-13)
第1章 均匀传输线理论
(1-1-8)
由上式可见,:传输线上电压和电流以波的形式传播, 在任一点的电压或电流均由沿-z方向传播的行波(称为入射波) 和沿+z方向传播的行波(称为反射波)叠加而成。
第1章 均匀传输线理论
确定待定系数,
由图 1- 2(a)可知, 传输线的边界条件通常有以下三种: ① 已知终端电压Ul和终端电流Il; ② 已知始端电压Ui和始端电流Ii; ③ 已知信源电动势Eg和内阻Zg以及负载阻抗Zl。
式中, εr为同轴线内、外导体间填充介质的相对介电常数。 常
用的同轴线的特性阻抗有50 Ω 和75Ω两种。
第1章 均匀传输线理论 2) 传播常数 γ 传播常数 γ 是描述传输线上导行波沿导波系统传播过程中 衰减和相移的参数, 通常为复数,由前面分析可知
(R jwL)(G jwC) a j
(1-1-20)
第1章 均匀传输线理论 3) 相速p与波长 λ 传输线上的相速定义为电压、电流入射波(或反射波)等 相位面沿传输方向的传播速度, 用υp来表示。 由式(1- 1- 8) 得等相位面的运动方程为
ωt±βz=const(常数)
上式两边对t微分, 有
dz vp dt
(积分) 任意媒质
第1章 均匀传输线理论
图 1-2 均匀传输线及其等效电路 (a)均匀平行双导线系统; (b) 均匀平行双导线的等效电路 (c) 有耗传输线的等效电路; (d) 无耗传输线的等效电路
第1章 均匀传输线理论 设在时刻t, 位置z处的电压和电流分别为u(z, t)和i(z, t), 而 在位置z+Δz处的电压和电流分别为 u(z+Δz,t)和i(z+Δz, t), 对很小的Δz, 忽略高阶小量, 有 u ( z , t ) z u(z+Δz, t)-u(z, t)= z i ( z , t ) i(z+Δz, t)-i(z, t)= z z 对图 1- 2(b), 应用基尔霍夫定律可得
。 对于 LC
R G j LC 1 jL 1 jC
1 ( RY0 GZ 0 ) j LC 2
