自由度1习题分析
机械设计基础平面机构的运动简图及自由度

归纳起来, 在下述场合中常出现虚约束:
(1) 运动轨迹重叠时, 如图2-16所示。
(2) 两构件同步在几处接触而构成多种移动副,且各移动副 旳导路相互平行时,其中只有一种起约束作用,其他都是虚约 束,如图2-15。
(3) 两构件同步在几处配合而构成几种回转副,且各回转副 轴线相互重叠时,这时只有一种回转副起约束作用,其他都是 虚约束。例如回转轴一般都有两个或两个以上同心轴承支持, 但计算时只取一种。
F=3n-2pL-pH=3×3-2×4-0=1
此成果与实际情况一致。
图2-15 机构中旳虚约束(两构件同步在几处接触
而构成多种移动副,且各移动副旳导路相互平行)
图2-16(a)、(b)所示为机车车轮联动装置和机构运动简图。图 中旳构件长度为lAB=lCD=lEF, lBC=lAD, lCE=lDF。该机构旳自 由度为
假如一种平面机构有N个构件,其中必有一种构件是机架( 固定件),该构件受到三个约束而自由度自然为零。此时,机构 旳活动构件数为n=N-1。显然,这些活动构件在未连接构成 运动副之前总共应具有3n个自由度。而当这些构件用运动副联 接起来构成机构之后,其自由度数即随之降低。若机构中共有 pL个低副和pH个高副,则这些运动副引入旳约束总数为 2pL+pH。 所以,用活动构件总旳自由度数减去运动副引入旳约 束总数就是机构旳自由度数。机构旳自由度用F表达,即:
件作为机架,运动链相对机架旳自由度必须不小于零,且 原动件数目等于运动链旳自由度数。
图2-12 刚性桁架
对于图2-12所示旳构件组合, 其自由度为
F 2n 2 pL pH 3 2 2 3 0 0
计算成果F=0,阐明该构件组合中全部活动构件旳总自由度数 与运动副所引入旳约束总数相等,各构件间无任何相对运动旳 可能,它们与机架(固定件)构成了一种刚性桁架,因而也就不 称其为机构。但它在机构中,可作为一种构件处理。
工件组合定位和自由度分析详解

单个定位时:
V1 限制了: x z
V2 限制了:
V3 限制了:
x
y
z z
x 两次重复限制,z 叁次重复限制,
按上准则分析,实际V1、V2较V3先
参与,V1、V2参与分不出先后,假
z 设V1为首参限制了 x ,V2次 参 xz 限制了 ;V3最后限制了 y y 。
图2.29 三个V形块 组合定位分析
2、判断准则 (1)定位元件单个定位时,限制转动自由度的作用在组合 定位中不变; (2)组合定位中各定位元件单个定位时限制的移动自由度 ,相互间若无重复,则在组合定位中该元件限制该移动自 由度的作用不变;若有重复,其限制自由度的作用要重新 分析判断,方法如下:
1)在重复限制移动自由度的元件中,按各元件实际参与定 位的先后顺序,分首参和次参定位元件,若实际分不出,可 假设;
x z 固定顶尖1限制了:
y
活动顶尖2限制了:
yz
x z y 固定顶尖为首参,限制了:
活动顶尖 y z
例5 如图2.32工件以外圆柱在两V形块上定位,分析各元 件限制的自由度。
图2.32 V形块组合定位分析右-V1、左-V2
单个定位时:
V1 限制了:x y
}
V2 限制了: y
y 两次重复限制,V1 首参限制了
例3:如图2.30工件以内孔面、平面在圆柱销、支承平面上 定位,分析各元件限制的自由
单个定位时:
平销面 限限制制了了 ::xxxyy
z
y
}
综且合x 限y 重制复了限x制 x
y
y
z
例4:如图2.31工件以两顶尖孔在两顶尖上定位,分析各元件限制 自由度。
图2.31 两顶尖组合定位分析
1 平面机构运动简图和自由度 习题答案
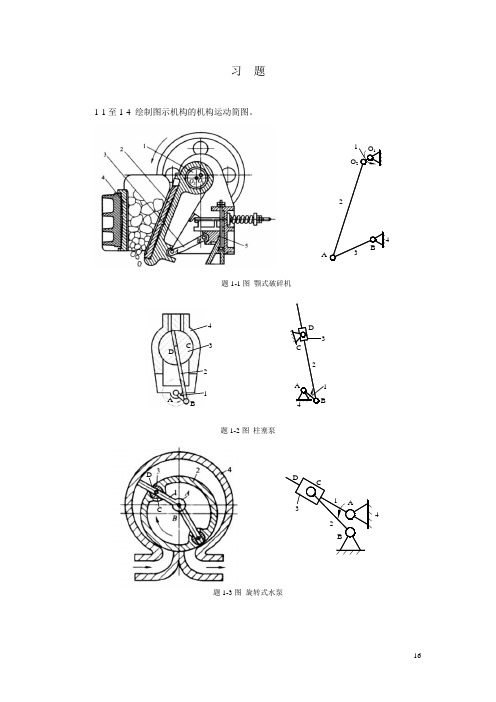
习 题1-1至1-4 绘制图示机构的机构运动简图。
题1-1图 颚式破碎机题1-2图 柱塞泵题1-3图 旋转式水泵O 1O 2AB1 234ABCD 1 2 3 4 A B CD1 234 AB CD1 2 34CD题1-4图 冲压机构1-5至1-10 指出机构运动简图中的复合铰链、局部自由度和虚约束,并计算各机构的自由度。
题1-6图解:构件3、4、5在D 处形成一个复合铰链,没有局部自由度和虚约束。
32352701L H F n P P =--=⨯-⨯-=解:没有复合铰链、局部自由度和虚约束。
323921301L H F n P P =--=⨯-⨯-= 题1-5图题1-5图56 ABCDEFO 1 O 2 D F1 2 345 6EGFEG题1-7图题1-8图题1-9图 题1-10图解:A 处为复合铰链,没有局部自由度和虚约束。
323721001L H F n P P =--=⨯-⨯-=解:A 处为复合铰链,没有局部自由度和虚约束。
323721001L H F n P P =--=⨯-⨯-=解:B 处为局部自由度,没有复合铰链和虚约束。
32352710L H F n P P =--=⨯-⨯-=解:C 处为复合铰链,E 处为局部自由度,没有虚约束。
32372912L H F n P P =--=⨯-⨯-=AB C DE IFG HADBECAEBCDGF1-11图示为一手动冲床机构,试绘制其机构运动简图,并计算自由度。
试分析该方案是否可行;如果不可行,给出修改方案。
题1-11图手动冲床答:此方案自由度为0,不可行。
改进方案如图所示:手动冲床运动简图手动冲床改进方案。
机械设计基础IA--第一章平面机构的自由度及速度分析--习题与答案

第1章 平面机构的自由度和速度分析本章要点:1、理解运动副及其分类,熟识各种平面运动副的一般表示方法;了解平面机构的组成。
2、熟练看懂教材中的平面机构的运动简图。
3、能够正确判断和处理平面机构运动简图中的复合铰链、局部自由度和常见的虚约束,综合运用公式F=3n-2P L -P H 计算平面机构的自由度并判断其运动是否确定。
第一节 平面机构的组成基本概念1、平面机构的定义:所有构件都在互相平行的平面内运动的机构2、自由度:构件所具有的独立运动个数3、运动副:两个构件直接接触组成的仍能产生某些相对运动的联接 第二节 平面机构的运动简图平时观察机构的组成及运动形式时,不可能将复杂的机构全部绘制下来观看,应该将不必要的零件去掉,用简单的线条表示机构的运动形式:机构的运动简图、机构简图 步 骤1、运转机械,搞清楚运动副的性质、数目和构件数目;2、测量各运动副之间的尺寸,选投影面(运动平面);3、按比例绘制运动简图;简图比例尺:μl =实际尺寸 m / 图上长度mm4、检验机构是否满足运动确定的条件。
第三节 平面机构的自由度 一、平面机构自由度计算公式机构的自由度保证机构具有确定运动,机构中各构件相对于机架的独立运动数目 一个原动件只能提供一个独立运动 机构具有确定运动的条件为 自由度=原动件的个数平面机构的每个活动构件在未用运动副联接之前,都有三个自由度 经运动副相联后,构件自由度会有变化:自由度的计算公式 F=3n -(2PL +Ph )二、计算平面机构自由度的注意事项活动构件 构件总自由度 3×n 低副约束数 2 × P高副约束数1 × P h n1、复合铰链:两个以上的构件在同一处以转动副相联2、局部自由度:与输出件运动无关的自由度出现在加装滚子的场合,计算时应去掉Fp3、虚约束:对机构的运动实际不起作用的约束计算自由度时应去掉虚约束第四节速度瞬心及在机构速度分析上的应用机构运动分析的任务、目的和方法(1)任务:在已知机构尺寸及原动件运动规律的情况下,确定机构中其他构件上某些点的轨迹、位移、速度及加速度和构件的角位移、角速度及角加速度。
自由度计算习题及答案

自由度计算习题及答案自由度计算习题及答案自由度是统计学中一个重要的概念,用于描述样本数据中可以自由变动的部分。
在统计学中,我们常常需要计算自由度来进行假设检验、方差分析等统计推断。
本文将给出一些自由度计算的习题及答案,帮助读者更好地理解和应用这一概念。
习题一:假设有一组样本数据,包含10个观测值。
我们希望进行一个t检验,假设总体均值为0。
请计算该t检验的自由度。
解答一:t检验的自由度由样本容量和样本数据的分布决定。
对于独立样本t检验,自由度等于两组样本的自由度之和再减去2。
在这个例子中,我们只有一组样本数据,因此自由度为10-1=9。
习题二:某公司想要比较两种不同的广告策略对销售额的影响。
他们随机选择了两组顾客,每组分别观看了不同的广告。
请计算用于比较两组销售额的独立样本t检验的自由度。
解答二:在独立样本t检验中,自由度等于两组样本的自由度之和再减去2。
假设第一组观测了n1个顾客,第二组观测了n2个顾客,那么自由度为n1+n2-2。
习题三:某研究人员想要比较三种不同的治疗方法对患者疼痛程度的影响。
他们随机将患者分为三组,每组接受不同的治疗。
请计算用于比较三组疼痛程度的方差分析的自由度。
解答三:方差分析的自由度由分子自由度和分母自由度组成。
对于一元方差分析,分子自由度为组数减1,即3-1=2。
分母自由度为总样本容量减去组数,即n-3。
在这个例子中,假设每组的样本容量为n,则分母自由度为3n-3。
习题四:某研究人员想要比较两种不同的教学方法对学生成绩的影响。
他们随机将学生分为两组,一组接受传统教学,另一组接受创新教学。
请计算用于比较两组学生成绩的配对样本t检验的自由度。
解答四:配对样本t检验的自由度等于配对观测值的数量减去1。
在这个例子中,假设有n对配对观测值,则自由度为n-1。
通过以上习题及答案的解析,我们可以看到自由度的计算对于统计推断是至关重要的。
正确计算自由度可以确保我们所做的统计分析具有可靠性和准确性。
机床夹具设计基础——例题解析

的限制。以避免重复
三爪卡盘夹持较短
X Y Z Y Z
Y Z
属于不完全定位, 如果只加工工件的外圆表面,而无轴向尺寸方面的要求,则定位是合理的, 如果工件有轴向尺寸要求时,则应该增加限制X方向移动的定位支撑点。
三爪卡盘夹持较短
X Y Z Y Z
Y Z
X
图示工件以底面及与其垂直的两圆柱孔为定位基准。若采用一个平面和两 个短圆柱销定位(如图a所示),则平面限制3个自由度 1限制2个自由度 ,短圆柱销2限制 2个自由度 ,短圆柱销 。其中自由度 被重
复限制,属过定位。此时,由于工件孔心距的误差和两定位销中心距的误差, 可能导致两定位销无法同时进入工件孔内。为解决这一过定位问题,可将两定 位销之一在定位干涉方向(Y向)上削边,做成菱形销(图b),以避免干涉。
已知:外径d为: 500 mm 0.03
0.05 内径D为: 300 mm
内外圆同轴度为0.02mm,
试计算用调整法加工这批工件时,
工序尺寸H的定位误差是多少?
解: 基准不重合误差: 基准位移误差:
同轴度误差:
w
c
0.05 0.025mm 2
TD 2 sin
2
0.03 0.021mm 90 2 sin 2
组合定位
1.几个定位元件组合起来定位时,限制的自由度是每个定位元件限 制的自由度数之和. 2.组合定位中的每个定位元件改变它单独定位所限制的自由度. 3.组合定位中,定位元件单独起限制移动自由度转为限制转动自由 度,不再起限制移动自由度,但是限制自由度数量不变. 消除组合定位中的过定位,把限制移动方向的自由度定位元件改 为能移动的定位元件. 消除组合定位中的过定位,也可以改变定位元件的结构.比如:一面 两孔中菱形销
统计学一元线性回归课后习题答案分析

(1)绘制运送距离和运送时间的散点图,判断二者之间的关系形 态 (2)计算线性相关系数,说明两个变量之间的关系强度。 (3)利用最小二乘法求出估计的回归方程,并解释回归系数的实 际意义。
运送时间(天)
(1)绘制运送距离和运送时间的散点图,判断二者之间的关系形态
(4)计算判定系数,并解释其意义。
= 81444968.68 =0.9963 81750763.71
人均GDP对人均消费的影响达到99.6%。
(5)检验回归方程线性关系的显著性(a=0.05)。
提出假设
H0:1=0 人均消费水平与人均GDP之间的
线性关系不显著 计算检验统计量F
F SSR 1 81444968.68 1 1331.6921 SSE (n 2) 305795.03 (7 2)
率
次数
1
81.1
21
2
76.6
58
3
76.6
85
4
75.7
68
5
73.8
74
6
72.2
93
7
71.2
72
8
70.8
122
9
91.4
18
10
68.5
125
1)绘制散点图,说明二者之间的股息形态
顾客投诉次数
140 120 100
80 60 40 20
0 0
20
40
60
航班正点率
二者之间为负的线性相关关系
1580.46315 E( y0 ) 2975.74999
人均GDP为5 000元时,人均消费水平95%的预 测区间为[1580.46315,2975.74999]。
机械设计基础习题及答案3平面连杆机构的自由度

平面机构的自由度和速度分析一、复习思考题1、什么是运动副?运动副的作用是什么?什么是高副?什么是低副?2、平面机构中的低副和高副各引入几个约束?3、机构自由度数和原动件数之间具有什么关系?4、用机构运动简图表示你家中的缝纫机的踏板机构。
5、计算平面机构自由度时,应注意什么问题?二、填空题1、运动副是指能使两构件之间既保持接触。
而又能产生一定形式相对运动的。
2、由于组成运动副中两构件之间的形式不同,运动副分为高副和低副。
3、运动副的两构件之间,接触形式有接触,接触和接触三种。
4、两构件之间作接触的运动副,叫低副。
5、两构件之间作或接触的运动副,叫高副。
6、回转副的两构件之间,在接触处只允许孔的轴心线作相对转动。
7、移动副的两构件之间,在接触处只允许按方向作相对移动。
8、带动其他构件的构件,叫原动件。
9、在原动件的带动下,作运动的构件,叫从动件。
10、低副的优点:制造和维修,单位面积压力,承载能力。
11、低副的缺点:由于是摩擦,摩擦损失比大,效率。
12、暖水瓶螺旋瓶盖的旋紧或旋开,是低副中的副在接触处的复合运动。
13、房门的开关运动,是副在接触处所允许的相对转动。
14、抽屉的拉出或推进运动,是副在接触处所允许的相对移动。
15、火车车轮在铁轨上的滚动,属于副。
三、判断题1、机器是构件之间具有确定的相对运动,并能完成有用的机械功或实现能量转换的构件的组合。
()2、凡两构件直接接触,而又相互联接的都叫运动副。
()3、运动副是联接,联接也是运动副。
()4、运动副的作用,是用来限制或约束构件的自由运动的。
()5、螺栓联接是螺旋副。
()6、两构件通过内表面和外表面直接接触而组成的低副,都是回转副。
()7、组成移动副的两构件之间的接触形式,只有平面接触。
()8、两构件通过内,外表面接触,可以组成回转副,也可以组成移动副。
()9、运动副中,两构件联接形式有点、线和面三种。
()10、由于两构件间的联接形式不同,运动副分为低副和高副。
杨可桢《机械设计基础》(第6版)复习笔记及课后习题详解(含考研真题)-平面机构的自由度和速度分析

第1章平面机构的自由度和速度分析1.1复习笔记【通关提要】本章是本书的基础章节之一,主要介绍了平面机构自由度的计算和平面机构的速度分析。
学习时需要掌握平面机构运动简图的绘制、自由度的计算和速度瞬心的应用等内容。
本章主要以选择题、填空题和计算题的形式考查,复习时需把握其具体内容,重点记忆。
【重点难点归纳】一、运动副及其分类(见表1-1-1)表1-1-1运动副及其分类二、平面机构运动简图机构运动简图指用简单线条和符号来表示构件和运动副,并按比例定出各运动副的位置,来表明机构间相对运动关系的简化图形。
1.机构中运动副表示方法机构运动简图中的运动副的表示方法如图1-1-1所示。
图1-1-1平面运动副的表示方法2.构件的表示方法构件的表示方法如图1-1-2所示。
图1-1-2构件的表示方法3.机构中构件的分类(见表1-1-2)表1-1-2机构中构件的分类三、平面机构的自由度活动构件的自由度总数减去运动副引入的约束总数称为机构自由度,以F表示。
1.平面机构自由度计算公式F=3n-2P L-P H式中,n为机构中活动构件的数目;P L为低副的个数;P H为高副的个数。
机构具有确定运动的条件是:机构的自由度F>0且F等于原动件数目。
2.计算平面机构自由度的注意事项(见表1-1-3)表1-1-3计算平面机构自由度的注意事项四、速度瞬心及其在机构速度分析上的应用(见表1-1-4)表1-1-4速度瞬心及其应用1.2课后习题详解1-1至1-4绘出图示(图1-2-1~图1-2-4)的机构运动简图。
图1-2-1唧筒机构图1-2-2回转柱塞泵图1-2-3缝纫机下针机构图1-2-4偏心轮机构答:机构运动简图分别如图1-2-5~图1-2-8所示。
1-5至1-13指出(图1-2-9~图1-2-17)机构运动简图中的复合铰链、局部自由度和虚约束,计算各机构的自由度。
解:(1)图1-2-9所示机构的自由度为F=3n-2P L-P H=3×7-2×10-0=1(2)图1-2-10中,滚子1处有一个局部自由度,则该机构的自由度为F=3n-2P L-P H=3×6-2×9-0=0(3)图1-2-11中,滚子1处有一个局部自由度,则该机构的自由度为F=3n-2P L-P H=3×8-2×11-1=1(4)图1-2-12所示机构的自由度为F=3n-2P L-P H=3×8-2×11-0=2(5)图1-2-13所示机构的自由度为F=3n-2P L-P H=3×6-2×8-1=1(6)图1-2-14中,滚子1处有一个局部自由度,则该机构的自由度为F=3n-2P L-P H=3×4-2×5-1=1(7)图1-2-15中,滚子1处有一个局部自由度,A处为三个构件汇交的复合铰链,移动副B、B′的其中之一为虚约束。
计量经济学习题解析

第一章1、下列假想模型是否属于揭示因果关系的计量经济学模型?为什么?(1)t S =+t R ,其中t S 为第t 年农村居民储蓄增加额(单位:亿元),t R 为第t 年城镇居民可支配收入总额(单位:亿元)。
(2)1t S -=+t R ,其中1t S -为第t-1年底农村居民储蓄余额(单位:亿元),t R 为第t 年农村居民纯收入总额(单位:亿元)。
2、 指出下列假想模型中的错误,并说明理由:其中,t RS 为第t 年社会消费品零售总额(单位:亿元),t RI 为第t 年居民收入总额(单位:亿元)(指城镇居民可支配收入总额与农村居民纯收入总额之和),t IV 为第t 年全社会固定资产投资总额(单位:亿元)。
3、 下列设定的精良经济模型是否合理?为什么?(1)301i i i GDP GDP ββμ==+⋅+∑ 其中,i GDP (i=1,2,3)是第一产业、第二产业、第三产业增加值,μ为随机干扰项。
(2)财政收入=f (财政支出)+ μ,μ为随机干扰项。
答案1、(1)不是。
因为农村居民储蓄增加额应与农村居民可支配收入总额有关,而与城镇居民可支配收入总额没有因果关系。
(2)不是。
第t 年农村居民的纯收入对当年及以后年份的农村居民储蓄有影响,但并不对第t-1的储蓄产生影响。
2、一是居民收入总额RI t 前参数符号有误,应是正号;二是全社会固定资产投资总额IV t 这一解释变量的选择有误,它对社会消费品零售总额应该没有直接的影响。
3、(1)不合理,因为作为解释变量的第一产业、第二产业和第三产业的增加值是GDP 的构成部分,三部分之和正为GDP 的值,因此三变量与GDP 之间的关系并非随机关系,也非因果关系。
(2)不合理,一般来说财政支出影响财政收入,而非相反,因此若建立两者之间的模型,解释变量应该为财政收入,被解释变量应为财政支出;另外,模型没有给出具体的数学形式,是不完整的。
第二章五、计算分析题1、令kids 表示一名妇女生育孩子的数目,educ 表示该妇女接受过教育的年数。
单自由度振动习题分析

振幅
A
Fp
令
11 Fp 12 FP 11
1
11
12 FP 11 12 FP 11
yst
m 2
Fp 11
(t ) m y
稳态解
11
y (t ) Fp sin t
仍是位移动力系数 是内力动力系数吗?
y (t )
5.阻尼系数
m k11 / 5190 (kg)
2
W mg 50.86(kN)
c 2m 3601 ( N s/m)
6.若质量增加800kg,体系的周期和阻尼比为多少
5 8 . 2 10 2 136.89(1 / s 2 ) 5190 800
11.70(1 / s)
例2: 对图示体系作自由振动试验.用钢 解: 1.阻尼比 丝绳将上端拉离平衡位置2cm,用 1 2 ln 0.0276 力16.4kN,降绳突然切断,开始作 2 4 1 自由振动.经4周期,用时2秒,振幅 降为1cm.求 1.阻尼比 2.刚度系数 2.刚度系数 2cm 3 16 . 4 10 3.无阻尼周期 k11 8.2 105 ( N / m) 16.4kN 4.重量 0.02 5.阻尼系数 6.若质量增加800kg体系 的周期和阻尼比为多少
FP m o
2 Ak 3
l
m A 2
k
A
1 mA 2 3
解:
M
o
0
1 2 2 2 Fp l mA l mA 3l Ak 2l 0 3 3
经整理后,解得:
3FP A 10 m 2 4k
阻尼对振动的影响
1、关于阻尼,有两种定义或理解: 2、在建筑物中产生阻尼、耗散能量的因素 1)结构在变形过程中材料内部有摩擦,称“内摩擦”,耗散能量; 2)建筑物基础的振动引起土壤发生振动,此振动以波的形式向周围扩散, 振动波在土壤中传播而耗散能量; 3)土体内摩擦、支座上的摩擦、结点上的摩擦和空气阻尼等等。 3、阻尼力的确定:总与质点速度反向;大小与质点速度有如下关系: 1)使振动衰减的作用; 2)使能量耗散。
《机械设计基础》复习题1解读
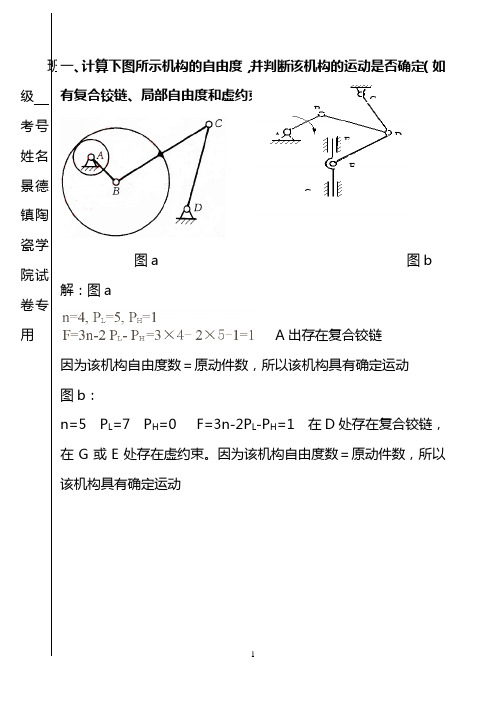
一、计算下图所示机构的自由度,并判断该机构的运动是否确定(如有复合铰链、局部自由度和虚约束需指出其所在位置:图a 图b 解:图aA 出存在复合铰链因为该机构自由度数=原动件数,所以该机构具有确定运动 图b :n=5 P L =7 P H =0 F=3n-2P L -P H =1 在D 处存在复合铰链,在G 或E 处存在虚约束。
因为该机构自由度数=原动件数,所以该机构具有确定运动班级 考号 姓名 景德镇陶瓷学院试卷专用ABC DEF G图c 图d 解:c)、机构中,n=6,p L=8,p H=1 F=3n-2p L-p H=1,B 处复合铰链,E处虚约束,D处局部自由度(8分)d)、机构中,n=7,p L=9,p H=1 F=3n-2p L-p H=2,D处复合铰链,A处虚约束,K处局部自由度(8分)二、画出下列图所示各机械的传动角和压力角。
图中标注箭头的构件为原动件解:三、计算题:1.根据图中各杆的尺寸,分别判断两种机构是何种类型,要求有分析计算过程。
第2题图 a第2题图b解:左图示:20+50≤45+30,满足杆长条件,最短杆为机架,所以是双曲柄机构右图示:50+60≥40+70,满足杆长条件,以最短杆的对边为机架,所以是曲柄摇杆机构2.图示a为一偏置直动从动件盘形凸轮机构。
已知AB段为凸轮的推程廓线,试在图上标注推程运动角Φ图a 图b解:如图a所示,以O为圆心作圆并与导路相切,此即为偏距圆。
过B点作偏距圆的下切线,此线为凸轮与从动件在B点接触时,导路的方向线。
推程运动角如下左图所示。
3.上图示b为一偏置直动从动件盘形凸轮机构。
已知凸轮是一个以C为圆心的圆盘,试求轮廓上D点与尖顶接触时的压力角,并作图表示解:如图b所示,以O为圆心作圆并与导路相切,此即为偏距圆。
过D点作偏距圆的下切线,此线为凸轮与从动件在D点接触时,导路的方向线。
凸轮与从动件在D点接触时的压力角如上右图所示。
4.试比较正常齿制渐开线标准直齿圆柱齿轮的基圆和齿根圆,在什么条件下基圆大于齿根圆?什么条件下基圆小于齿根圆?解:正常齿制渐开线标准直齿圆柱齿轮的齿根圆直径:基圆直径假定则解得故当齿数时,正常齿制渐开线标准直齿圆柱齿轮的基圆大于齿根圆;齿数,基圆小于齿根圆。
1平面机构运动简图和自由度习题答案
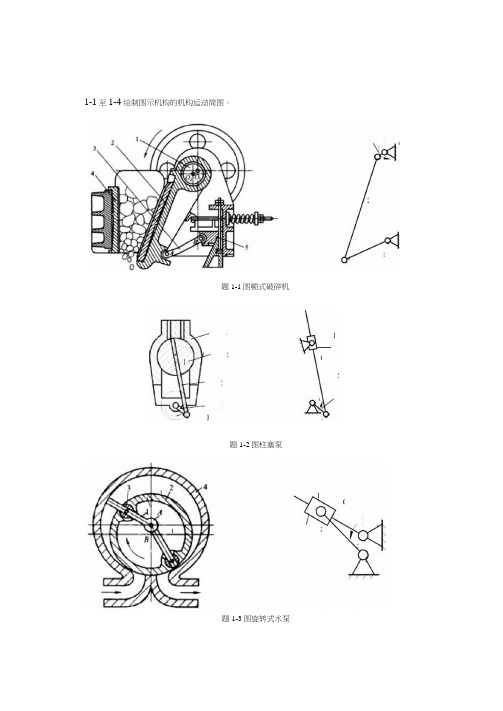
1-1至1-4绘制图示机构的机构运动简图。
题1-1图顿式破碎机
题1-2图柱塞泵
题1-3图旋转式水泵
I
題1-4图冲压机构
1-5至1-10指岀机构运动简图中的复合铁链、局部自由度和虚约束,并计算各机构的
自由度。
解:构件3、4、5在D处形成一个复合钱
链,没有局部自由度和虚约朿。
F=3H —2P L—P H=3X5-2X7-0=1
题1-5图
解:没有复合铁链、局部自由度和虚约束。
F = 3n-2P L-P H=3X9-2X13-0=1
题1-6图
1
1
解:A处为复合绞链,没有局部自由度和虚约
朿。
F = 3n-2R —P H=3X7-2X10-0=1
解:C处为复合较链,E处为局部自由度, 没有
虚约束。
F=3H_2P I_P H=3X7-2X9-1=2
题1-10图
题1-8图
1-11图示为一手动冲床机构,试绘制其机构运动简图,并计算自由度。
试分析该方案 是否可行;如果不可行,给出修改方案。
答:此方案自由度为0,不可行。
改进方案如图所示:
于•动冲床改进方
案。
《结构力学》习题解答(内含解答图)

解:杆AB由固定支撑与基础联结形成一体,此外,杆AB又用链杆1再与基础联结,故链杆1为多余约束;将此部分取为刚片,杆CD取为刚片,则两刚片用个BC、链杆2、链杆3三根不平行也不交于一点相连,组成几何不变体。所以,体系是具有一个多余约束的几何不变体系。
习题2-4试对图示体系进行几何组成分析。
习题2-8试对图示体系进行几何为了便于分析,对图中的链杆和刚片进行编号,分析过程见图2-21(b)。首先去掉二元体NMI、JNI,然后分析剩余部分。杆AD由固定支撑与基础联结形成一体,构成几何不变体,在此基础上增加二元体DEB、EFC、EHF形成刚片Ⅰ(注意固定铰支座与铰相同);铰结△GIJ为刚片Ⅱ;刚片I与刚片Ⅱ之间用不交于一点的杆DI、杆GI、杆HJ相连,组成几何不变体。
另外,该题也可用二元体概念求解,即杆AB由固定支撑与基础联结形成一体后,把杆BC和链杆1作为二元体,由规则三,组成几何不变体;再将杆CD和链杆2作为二元体,组成几何不变体,而链杆3为多余约束。
习题2-5试对图示体系进行几何组成分析。
习题2-5图习题2-5解答图
解:地基为刚片I,折杆BCD为刚片Ⅱ(注意曲杆BC与CD在C点刚性联结),刚片I与刚片Ⅱ之间用不交于一点的链杆1和杆AB、杆ED相连,组成几何不变体,而曲杆AB和ED的联结方式为图(b)中的虚线。
习题2-12图习题2-12解答图
习题2-13试对图示体系进行几何组成分析。
习题2-13图习题2-13解答图
解:将原图结点进行编号,并将支座6换为单铰,如图(b)。取基础为刚片Ⅰ,△134为刚片Ⅱ,△235为刚片Ⅲ,由规则一知,三刚片用三个不共线的铰联结组成几何不变体。在此基础上增加二元体674、785,而杆38看作多余约束。杆910由铰联结着链杆10,可看作二元体,则整个体系为有一个多余约束的几何不变体系。
机构的结构分析—习题答案
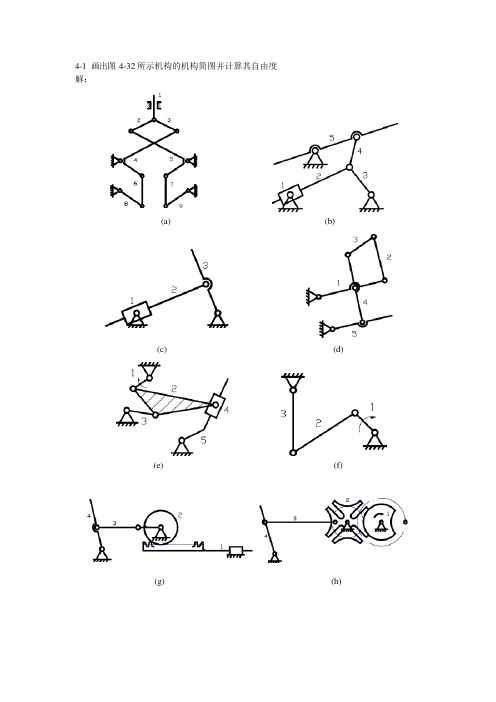
4-1画出图 4-32 所示机构的机构简图并计算其自由度解:(a)(b)(c) (d)(e) (f)(g)(h)(i)(j)(k) (l)(m) (n)(o) (p)计算各构件自由度:(q)(r)(a)(b) n = 9, P L = 13, P Hn = 5, P L = 7, P H = 0, F = 3n - 2P L - P H= 1= 0, F = 3n - 2P L - P H = 1(c)(d)(e)(f)n = 3, P L = 4, P H n = 5, P L = 7, P H n = 5, P L = 7, P H n = 3, P L= 4, P H= 0, F = 3n - 2P L - P H= 1 = 0, F = 3n - 2P L - P H= 1 = 0, F = 3n - 2P L - P H = 1= 0, F = 3n - 2P L- P H= 1(g) n = 4, P L= 5, P H= 1, F = 3n - 2P L- P H= 1(h) 间歇时, n = 4, P L= 5, P H= 1, F = 3n - 2P L- P H= 1;销进入槽轮时, n = 5, P L= 7, P H= 0, F = 3n - 2P L- P H= 1(i) (j) (k)(l) n = 4, P L= 5, P H= 1, F = 3n - 2P L- P H= 1n = 3, P L = 3, P H = 2, F = 3n - 2P L - P H = 1 n = 4, P L = 5, P H = 0, F = 3n - 2P L - P H = 2 n = 4, P L = 5, P H = 1, F = 3n - 2P L - P H = 1 (m) (n)(o) n = 5, P L= 6, P Hn = 5, P L = 6, P H n = 5, P L= 6, P H= 1, F = 3n - 2P L- P H= 2= 2, F = 3n - 2P L - P H = 1= 2, F = 3n - 2P L- P H= 1(p) n = 12, P L= 17, P H= 0, F = 3n - 2P L- P H= 25321 3421534214 5321(q)(r) n = 5, P L = 7, P Hn = 3, P L = 3, P H = 0, F = 3n - 2P L - P H= 1= 2, F = 3n - 2P L - P H = 14-2 图 4-33 所示为一简易冲床的初拟设计方案。
自由度计算习题

自由度计算习题一、自由度的概念在统计学中,自由度是指数据集中独立或可自由变化的变量的数量。
它在统计推断和假设检验中起着重要的作用,用于衡量数据集中的信息量。
计算自由度可以帮助我们确定合适的统计分布和进行正确的假设检验。
本文将介绍一些关于自由度计算的习题,以帮助读者更好地理解和应用自由度的概念。
二、习题一:独立样本 t 检验某研究人员对两组学生进行了一项实验,旨在比较两组学生的成绩是否存在显著差异。
数据如下表所示:组别样本数量平均值标准差A307510B308012现在,我们需要计算独立样本 t 检验时的自由度。
根据独立样本 t 检验的自由度公式,自由度为两组样本数量之和减去2:dd=d1+d2−2其中,d1和d2分别表示两组样本数量。
对于这个例子,在第一组和第二组样本数量均为30,因此自由度为:dd=30+30−2=58三、习题二:相关样本 t 检验某医院的研究人员对某种新药物的疗效进行了研究。
他们测试了同一组患者在服用该药物前后的血压,并记录了数据。
下表是服药前后每个患者的血压数据:患者服药前血压服药后血压11401302150135316015041351305145140现在,我们需要计算相关样本 t 检验时的自由度。
根据相关样本 t 检验的自由度公式,自由度为样本数量减去1:dd=d−1对于这个例子,样本数量为5,因此自由度为:dd=5−1=4四、习题三:卡方检验某调查机构随机抽取了100个人,调查了他们喜欢的颜色,并将结果列在下表中:颜色人数红色30黄色25蓝色20绿色25现在,我们需要计算卡方检验时的自由度。
根据卡方检验的自由度公式,自由度为 (行数-1) 乘以 (列数-1):$$ df = (r - 1) \\times (c - 1) $$其中,d表示行数,d表示列数。
对于这个例子,行数为4,列数为1,因此自由度为:$$ df = (4 - 1) \\times (1 - 1) = 3 \\times 0 = 0 $$五、习题四:方差分析某研究人员对三组学生进行了一项实验,旨在比较三个组别的成绩是否存在显著差异。
机械设计基础习题及答案
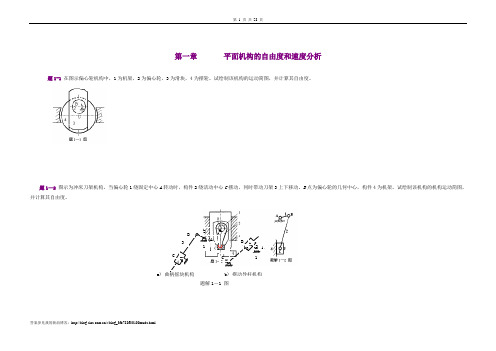
第一章平面机构的自由度和速度分析题1-1在图示偏心轮机构中,1为机架,2为偏心轮,3为滑块,4为摆轮。
试绘制该机构的运动简图,并计算其自由度。
题1—2图示为冲床刀架机构,当偏心轮1绕固定中心A转动时,构件2绕活动中心C摆动,同时带动刀架3上下移动。
B点为偏心轮的几何中心,构件4为机架。
试绘制该机构的机构运动简图,并计算其自由度。
题1—3计算题1-3图a)与图b)所示机构的自由度(若有复合铰链,局部自由度或虚约束应明确指出)。
题1-3图a)题1-3图b)题1—4计算题1—4图a、图b所示机构的自由度(若有复合铰链,局部自由度或虚约束应明确指出),并判断机构的运动是否确定,图中画有箭头的构件为原动件。
题1—5 计算题1—5图所示机构的自由度(若有复合铰链,局部自由度或虚约束应明确指出),并标出原动件。
题1—5图 题解1—5图题1-6 求出图示的各四杆机构在图示位置时的全部瞬心。
第二章 连杆机构题2-1在图示铰链四杆机构中,已知 l BC =100mm ,l CD =70mm ,l AD =60mm ,AD 为机架。
试问:(1)若此机构为曲柄摇杆机构,且AB 为曲柄,求l AB 的最大值;(2)若此机构为双曲柄机构,求l AB 最小值; (3)若此机构为双摇杆机构,求l AB 的取值范围。
题2-2 如图所示的曲柄滑块机构: (1)曲柄为主动件,滑块朝右运动为工作 行程,试确定曲柄的合理转向,并简述其理由;(2)当曲柄为主动件时,画出极位夹角θ,最小传动角g min ; (3)设滑块为主动件,试用作图法确定该机构的死点位置 。
D题2-1图题2-3图示为偏置曲柄滑块机构,当以曲柄为原动件时,在图中标出传动角的位置,并给出机构传动角的表达式,分析机构的各参数对最小传动角的影响。
题2-4设计一曲柄摇杆机构,已知机构的摇杆DC长度为150mm,摇杆的两极限位置的夹角为45°,行程速比系数K=1.5,机架长度取90mm。
机械设计基础习题答案

平面机构及其自由度1、如图a 所示为一简易冲床的初拟设计方案,设计者的思路是:动力由齿轮1输入,使轴A 连续回转;而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构将使冲头4上下运动以达到冲压的目的。
试绘出其机构运动简图(各尺寸由图上量取),分析其是否能实现设计意图?并提出修改方案。
解 1)取比例尺l μ绘制其机构运动简图(图b )。
图 b )2)分析其是否能实现设计意图。
由图b 可知,3=n ,4=l p ,1=h p ,0='p ,0='F故:00)0142(33)2(3=--+⨯-⨯='-'-+-=F p p p n F h l因此,此简单冲床根本不能运动(即由构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架),故需要增加机构的自由度。
3)提出修改方案(图c )。
为了使此机构能运动,应增加机构的自由度(其方法是:可以在机构的适当位置增加一个活动构件和一个低副,或者用一个高副去代替一个低副,其修改方案很多,图c 给出了其中两种方案)。
图 c 1) 图 c 2) 2、试画出图示平面机构的运动简图,并计算其自由度。
解:3=n ,4=l p ,0=h p ,123=--=h l p p n F解:4=n ,5=l p ,1=h p ,123=--=h l p p n F3、计算图示平面机构的自由度。
解:7=n ,10=l p ,0=h p ,123=--=h l p p n F解:8=n ,11=l p ,1=h p ,123=--=h l p p n F ,局部自由度解:9=n ,12=l p ,2=h p ,123=--=h l p p n F解: D,E,FG 与D ,H ,J ,I 为对称结构,去除左边或者右边部分,可得,活动构件总数为7,其中转动副总数为8,移动副总数为2,高副数为0,机构自由度为1。
(其中E 、D 及H 均为复合铰链)4、试求图示各机构在图示位置时全部瞬心的位置(用符号ij P 直接标注在图上)。
结构动力学习题解答

由
d (T + U ) = 0 得系统运动微分方程 dt
1 (m 2 ⎛ ̇̇ A + ⎜ K + m B )r A 2 ϕ ⎜ ⎝ + K
A
A
B
rA 2 ⎞ ⎟ϕ rB 2 ⎟ ⎠
A
= 0;
因此系统的固有频率为:
⎛ r 2 2⎜ K A + K B A 2 ⎜ rB ⎝ (m A + m B )rA 2 ⎞ ⎟ ⎟ ⎠ ⎛ r 2 2⎜ K A + K B A 2 ⎜ rB ⎝ (m A + m B ) ⎞ ⎟ ⎟ ⎠
(4) 由动量距定理 (
̇̇ 得: ∑ m (F ) = I θ
0 0
m
1 1 1 1 1 ̇̇ lθ ⋅ k1 ⋅ l + lθ ⋅ k1 ⋅ l )= ml 2θ 2 2 2 2 2
̇̇ + k1 θ = 0 , θ 2m
k1
k1
得:
则
ω=
k1 。 2m
图 1-33(d)
1.5 求下图所示系统的固有频率。图中匀质轮 A 半径 R,重物 B 的重量为 P/2,弹簧刚度为 k. 解:以 θ 为广义坐标,则 系统的动能为
d (T + U ) = 0 ,进一步得到系 dt
统的运动微分方程; (3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。 1.2 叙述用衰减法求单自由度系统阻尼比的方法和步骤。 用衰减法求单自由度系统阻尼比的方法有两个:衰减曲线法和共振法。 方法一:衰减曲线法。 求解步骤: (1)利用试验测得单自由度系统的衰减振动曲线,并测得周期和相邻波峰和波谷 的幅值 Ai 、 Ai +1 。 (2)由对数衰减率定义 δ = ln(
自由度计算习题答案

自由度计算习题答案自由度计算习题答案自由度是统计学中一个重要的概念,它用于衡量数据集中的独立信息的数量。
在统计分析中,我们经常需要计算自由度,以便正确地进行假设检验和推断。
本文将介绍一些常见的自由度计算习题,并给出详细的答案解析。
1. 一组有10个观测值的数据集,求其自由度。
答案:自由度的计算公式是n-1,其中n表示观测值的数量。
因此,这组数据集的自由度为10-1=9。
解析:自由度是衡量数据集中独立信息的数量,而在这个数据集中,我们已经知道了10个观测值。
当我们知道了n-1个观测值后,最后一个观测值就可以通过求和并减去前面n-1个观测值的平均值来确定。
因此,自由度为9。
2. 一个实验中,研究人员将两组参与者分为实验组和对照组,每组各有20人。
他们想要比较两组参与者的平均得分是否有显著差异。
求该实验的自由度。
答案:该实验的自由度为38。
解析:在这个实验中,我们有两组参与者,每组各有20人。
为了比较两组参与者的平均得分是否有显著差异,我们需要计算两组的自由度。
根据自由度的计算公式,实验组的自由度为20-1=19,对照组的自由度也为20-1=19。
然后,我们将两组的自由度相加,即可得到该实验的自由度,即19+19=38。
3. 一组有8个观测值的数据集,其中有3个缺失值。
求该数据集的有效自由度。
答案:该数据集的有效自由度为5。
解析:在这个数据集中,有8个观测值,但其中有3个缺失值。
缺失值表示我们无法获得这些观测值的具体数据,因此在计算自由度时,我们需要将缺失值排除在外。
有效自由度的计算公式是n-k,其中n表示观测值的数量,k表示缺失值的数量。
因此,这个数据集的有效自由度为8-3=5。
4. 一组有12个观测值的数据集,假设其总体方差为5。
现在我们想要对该数据集进行方差检验,求该检验的自由度。
答案:该检验的自由度为11。
解析:方差检验通常使用F分布进行,而F分布的自由度是根据分子自由度和分母自由度来确定的。
