第16章 方程预测
SPSS_16_实用教程习题答案

SPSS_16_实⽤教程习题答案第⼀章1-1答:SPSS的运⾏⽅式有三种,分别是批处理⽅式、完全窗⼝菜单运⾏⽅式、程序运⾏⽅式。
1-2 答:与⼀般电⼦表格处理软件相⽐,SPSS的“Data V iew”窗⼝还有以下⼀些特性:(1)⼀个列对应⼀个变量,即每⼀列代表⼀个变量(V ariable)或⼀个被观测量的特征;(2)⾏是观测,即每⼀⾏代表⼀个个体、⼀个观测、⼀个样品,在SPSS中称为事件(Case);(3)单元包含值,即每个单元包括⼀个观测中的单个变量值;(4)数据⽂件是⼀张长⽅形的⼆维表。
第⼆章2-1 答:SPSS中输⼊数据⼀般有以下三种⽅式:(1)通过⼿⼯录⼊数据;(2)可以将其他电⼦表格软件中的数据整列(⾏)的复制,然后粘贴到SPSS中;(3)通过读⼊其他格式⽂件数据的⽅式输⼊数据。
2-2 答:选择“Transform”菜单的Replace Missing V alues命令,弹出Replace Missing V alues 对话框。
先在变量名列中选择1个或多个存在缺失值的变量,使之添加到“New V ariable(s)”框中,这时系统⾃动产⽣⽤于替代缺失值的新变量。
最后选择合适的替代⽅式即可。
2-3 答:选择“Data”菜单中的Weight Cases命令,出现如图2-22所⽰的Weight Cases对话框。
其中,Do not weight cases项表⽰不做加权,这可⽤于取消加权;Weight cases by 项表⽰选择1个变量做加权。
2-4 答:变量的⾃动赋值可以将字符型、数字型数值转变成连续的整数,并将结果保存在⼀个新的变量中。
具体操作的过程如下:选择“Transform”菜单中的Automatic Recode命令,在出现的对话框中,从左边的变量列表中选择需要⾃动赋值的变量,将它添加到V ariable -> New Name框中,然后在下⾯New Name右边的⽂本框中输⼊新的变量名称,单击New Name按钮,将新的变量名添加到上⾯的框中。
16第十六章 中国古代的科学技术与五大发明

二、天文学
(二)天文理论 中国古代在宇宙理论方面留下了丰富的遗产。 盖天说 盖天说最为古老,第一次盖天说认为“天圆如张盖,地方如棋局”,意为天是圆形的,像一把张开的 大伞覆盖在地上;地是方形的,像一个棋盘;日月星辰则像爬虫一样过往天空。而第二次盖天说载于《周髀 算经》,认为天是半圆形的,地是拱形的,日、月、星辰附着天而平转,不能转到地的下面。它比第一次盖天 说有所进步,能解释一些天文现象;但理论的错误导致推算与天象不符,遂逐渐被浑天说取代。 浑天说 东汉张衡所著《浑天仪图注》是“浑天说”的代表作。他说:“浑天如鸡子,天体圆如弹丸,地如鸡 子中黄。孤居于天内,天大而地小。天表里有水,天之包地,犹壳之裹黄。天地各乘气而立,载水而浮……天 转如车毂之运也,周旋无端,其形浑浑,故曰浑天。”可见浑天说比盖天说进了一步,它认为天不是一个半球 形,而是一个圆球,地球在其中,就如鸡蛋黄在鸡蛋内部一样。浑天说以对天象的直观观察为基础,能较好地 解释一些天体的运动,在历法中有较大实用意义。这一说法在中国古代天文领域称雄了上千年。 宣夜说 宣夜说由东汉前期的郄萌作了系统的总结和明确的表达。他指出“天了无质,仰而瞻之,高远无极 ”,不存在一个“固体”的天球。他还指出:“日月众星,自然浮生虚空之中,其行其止皆须气焉。”(《晋 书·天文志》)他从正面提出了日、月、星辰悬浮于宇宙空间,并依靠气的作用而运动的观点。宣夜说描述 了一幅日、月、星辰在物质的无限空间运动的图景。这些见解比浑天说和托勒密的地心说都要高过一筹, 是中国古代一种朴素的无限宇宙观念。 中国古代天文学理论成就启发了现代天文理论,为世界天文学发展作出了重要贡献。
(一)《齐民要术》 北魏贾思勰所著的《齐 民要术》是中国现存最 早而又最完整的农学著 作,是中国古代农业体系 形成的标志。全书共十 卷,九十二篇。内容包括 农、林、牧、副、渔各 个方面,涉及范围极广, 总结了从西周到北魏一 千六百多年的农业生产 技术经验。《齐民要术 》是中国古代最重要的 农业科学著作,在世界农 学史、生物学史上占有 重要地位。
第17章《函数及其图象》集体备课文稿

长兴县实验初中教师集体备课文稿一. 授课内容和课时安排授课内容:八年级下册第17章《函数及其图象》§17. 1变量与函数、§17.2函数的图象、§17.3一次函数课时安排:第一课时:变量与函数(1) 第六课时:一次函数的认识 第二课时:变量与函数(2) 第七课时:一次函数的图象(1) 第三课时:平面直角坐标系(1) 第八课时:一次函数的图象(2) 第四课时:平面直角坐标系(2) 第九课时:一次函数的性质第五课时:函数的图象 第十课时:一次函数的图象及性质二.第16章《数的开方》授课存在的主要问题:1.对于平方根和立方根的概念,学生比较容易接受,但在做题时,对于正数的平方根经常出现漏解的情况;2.对于二次根式的三条性质,前两条比较容易接受,在具体的习题中也能很好的利用。
但 对于性质3:a a =2,很多同学经常容易搞错,特别是a 为负数时,2a 应该等于a 的 相反数容易出错,例如:()=-2)6(,有的同学会填-6;也有同学会写±6;3.对于二次根式的化简,部分同学还不过关,有待进一步加强和相关训练;4.在实数范围内的化简、计算以及因式分解、求方程的解等等,很多同学由于多种原因,解题正确率不高;5.刚接触无理数、实数这两个概念,在区分无理数、有理数、整数、分数时,部分学生容易混淆。
三.三节内容的教材分析【教学目标】本章前三节的主要内容是变量与函数的认识,以及函数图象的认识;另外主要是一次函数的图象及性质。
教学目标是:1.通过对实际问题中数量之间相互依存关系的探索,学会用函数思想去进行描述和研究其变化规律;通过结合丰富的实际问题,让学生了解常量和变量、自变量与函数的意义,初步理解对应的思想,逐步学会运用函数的观点观察、分析问题,预测实际问题中变量的变化趋势。
2.认识并会画平面直角坐标系,了解现实生活中数形结合思想的实例,体会平面直角坐标系在函数研究中的地位和作用。
基于神经网络和相似天数法的电价预测方法研究

系,加权因子 ω^ 需要考虑元素单位的差异,并且每个
使用的器件随其单元而变化。 从预测日前一天起的
过去 45 天以及上一年预测日前过去的 45 天,都被考
虑用于选择类似的日期。 根据算法,每个小时都有一
组单独的相似日,如果更改了预测日期,则会以相同
的方式选择类似的日期。
然后,假设它是实际价格,在 t + h 时间上相似的价格
日,使用这些数据,其中 h 表示小时。
2 神经网络体系结构
2. 1 神经网络训练
神经网络训练用于选择网络参数,以最小化采样集
的拟合误差。 对于给定的训练数据集,目标函数定义为:
1
E = ∑ ( ΔO - ΔO ∗ ) 2
(4)
2
其中, ΔO 和 ΔO ∗ 分别为网络输出和期望输出。
ïïΔL t - 1 = L t - 1 - L pt- 1
(3)
í
p
ïΔP t = P t - P t
ï
p
îΔP t - 1 = P t - 1 - P t - 1
其中, L t 和 P t 分别为预测日的负载和价格; L pt 和
2
P pt 分别为过去相似日期的负载和价格; ΔL t 为预测日
与相似日之间的负荷偏差; ΔP t 为预测日与相似日之
similar days method
Tian Qingliang
State Grid Yinan County Power Supply Company Linyi 276300 China
Abstract This article aims to demonstrate the superiority of neural networks and similar day method models using
第16 章 主成分分析和因子分析

qˆij = l 1qjij,i =1,L,n.
(2.11.2)
应该注意,向量 ci 和 qi (除坐标平移之外)可以从奇异值分解(singular value
decomposition, SVD)
XI 1ee = l1c1d1 +L+ l pcpd p n
(2.12)
( ) 一步得出。其中具有关系式 l1d1 :L:l pd p =(q1:L:qn)。
本文将提供某些最新理论成果和实际应用以全面考察 PCA 和 FA。
2.主成分
2.1.一般问题
主成分问题可以用如下非常一般的步骤进行阐述。令 x 是一个 p 维向量, y 是一个q 维 向量,其中 x 和 y 的一些分量可能是相同的。我们要用z = Ay代替 y ,其中 A是一个r×q
矩阵且r < q ,使得用z 代替 y 预测x 的损失尽可能小。如果
2.3.主成分解释
为了用原始测量指标的影响解释主成分,需要表 1 中列出的计算。
表1 原始变量
与主成分的相关系数
z1
K
zp
xi 对 z1,L,zr
的复相关系数
x1
cˆ11 / s11 L
cˆp1 / s11
s11
r 1
c
ˆ2
j1
=
R1
2
j=1
M
M
M
M
M
xp
cˆ1p / spp L
cˆpp / spp
2
p×n 矩阵表示
X =(x1 :L: xn)
11的估计量是
S =(n 1) 1XI e1eX
n
(2.7)
其中e是n 维 1 向量。 i 的估计l i 和Ci 的估计量ci 可以从谱分解中得出
第16章SWAT模型1

第16章SWA T模型16.1 概述SWA T(Soil and Water Assessment Tool)(Arnold et al., 1998; Neitsch et al., 2002)是由美国农业部农业研究中心(USDA-ARS)开发的流域尺度模型。
模型开发的目的是在具有多种土壤、土地利用和管理条件的复杂流域,预测长期土地管理措施对水、泥沙和农业污染物的影响。
SWA T模型经历了不断的改进,很快便在水资源和环境领域中得到广泛承认和普及。
Bera et al.(2003)称之为在农业和森林为主的流域具有连续模拟能力的最有前途的非点源模型。
模型主要组成部分包括气候、水文、土壤温度和属性、植被生长、营养物、杀虫剂和土地管理等。
本章首先介绍了SWA T模型的发展历史和基本结构,然后从水文评估、污染物流失、气候变化影响、洪水短期预报、敏感性分析、率定和不确定性分析、模拟关键影响因素及与其他模型的比较和耦合等方面详细介绍了SWA T模型的最新研究进展,进而分析了模型特点,并提出今后研究的展望,最后结合黄河河源区气候变化对水文循环影响的研究案例详细介绍了SWA T模型的具体应用。
16.2 模型发展历史16.2.1 模型的发展与改进SWA T主要基于SWRRB,并且吸取了CREAMS、GLEAMS、EPIC和ROTO的主要特征。
SWA T作为一种非点源模型已被并入BASINS(Better Assessment Science Integrating point and Nonpoint Sources)。
BASINS由美国环保局(USEPA)开发,其主要目的是在全国范围内分析和制定最大日负荷(Total Maximum Daily Loads, TMDL)的标准和指导方针。
SWA T模型自90s初开发以来,已经经历了不断的回顾和扩展。
模型主要的改进版本为:⑴ SWA T94.2:添加了水文响应单元(HRUs)。
计量经济学》第三版靳庭良章课后题答案

Rooms=4
房间数为4时,住房价格最低
(6)
ln(price) = 17.59 − 0.868 ln(nox) − 0.087 ln(dist) − 0.545rooms
+ 0.062rooms 2 − 0.044stratio
6.(1)Y = 0 + 1 + 2 +
(2) Y尖 = −50.01638 + 0.086450 + 52.37031
(3)0至少为0,负数不符合经济经济意义;1介于0和1之间,符合经济意义,
2至少为0,符合经济意义。
)F = 146.3 > 0.05(2,18)
原回归方程具有联合显著性。
(4)Y尖 = −50.01638 + 0.086450 ∗ 2500 + 52.37031 ∗ 16 = 1004.03358
《计量经济学》
(第三版)
——靳庭良
第一章练习题
一、1.D 2.C 3.A
二、1.计量经济学是是一门由统计学、理论经济学和数学结合形成的一门经济学
分支学科,其目的是揭示社会经济现象发展变化中的数量规律。
计量经济学与理论经济学:第 3 页第 2 段
计量经济学与经济统计学:第 3 页第 3 段
计量经济学与数理统计学:第 3 页第 4 段
取全微分得 = 0.86
dY = ∗ (0.86
+ 0.22dZ
20
+ 0.22dZ) = 1000 ∗ (0.86 ∗
+ 0.22 ∗ 1) = 228.6
2000
第二章练习题
穷举法

第16章 穷举算法与实验穷举方法是基于计算机特点而进行解题的思维方法。
一般是在一时找不出解决问题的更好途径(即从数学上找不到求解的公式或规则)时,可以根据问题中的的部分条件(约束条件)将所有可能解的情况列举出来,然后通过一一验证是否符合整个问题的求解要求,而得到问题的解。
这样解决问题的方法我们称之为穷举算法。
穷举算法特点是算法简单,但运行时所花费的时间量大。
因此,我们在用穷举方法解决问题时,应尽可能将明显的不符合条件的情况排除在外,以尽快取得问题的解。
虽然穷举法效率并不高,但是适应一些没有明显规律可循的问题的解决。
因为穷举算法就是从所有可能的情况中搜索正确的答案,所以一般可按如下步骤: 第1步: 对于一种可能的情况,列举出来并计算其结果;第2步:判断结果是否满足要求,如果不满足则执行第1步来搜索下一个可能的情况,如果满足要求,则表示寻找到一个正确的答案,执行下一步操作,如寻找其他正确(合适)的答案或者中断循环。
16.1三角形数问题16.1.1 问题描述将 ,F ,E ,D ,C ,B ,A 这六个变量排成如图所示的三角形,这六个变量分别取[1,6]上的整数,且均不相同。
求使三角形三条边上的变量之和相等的全部解。
如图就是一个解。
A 6B C 3 1D F 2 4E 516.1.2 问题分析程序引入变量123456,,,,,i i i i i i ,代表,F ,E ,D ,C ,B ,A 并让它们分别顺序取1至6的正整数,在它们互不相同的前提条件下,测试由它们排成的如图所示的三角形三条边上的变量之和是否相等,如相等即为一种满足要求的排列,把它们输出。
当这些变量取尽所有的组合后,程序就可得到全部可能的解。
细节见下面的程序。
【程序1】%穷举法解三角形数 for i1=1:6 for i2=1:6 if i1==i2 continue;endfor i3=1:6if i1==i3 || i2==i3continue;endfor i4=1:6if i1==i4 || i2==i4 || i3==i4continue;endfor i5=1:6if i1==i5 || i2==i5 || i3==i5 || i4==i5continue;endfor i6=1:6if i1==i6 || i2==i6 || i3==i6 || i4==i6 || i5==i6continue;endif i1+i2+i4==i1+i3+i6 && i1+i2+i4==i4+i5+i6fprintf ('%6d\n',i1) ;fprintf ('%4d%4d\n',i2,i3) ;fprintf ('%2d%4d%4d\n\n',i4,i5,i6) ;endendendendendendEnd16.1.3 问题讨论按穷举法编写的程序通常不能适应变化的情况。
尼科尔森《微观经济理论-基本原理与扩展》(第9版)课后习题详解(第16章 劳动市场)
尼科尔森《微观经济理论-基本原理与扩展》(第9版)第6篇要素市场定价第16章劳动市场课后习题详解跨考网独家整理最全经济学考研真题,经济学考研课后习题解析资料库,您可以在这里查阅历年经济学考研真题,经济学考研课后习题,经济学考研参考书等内容,更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验,从前辈中获得的经验对初学者来说是宝贵的财富,这或许能帮你少走弯路,躲开一些陷阱。
以下内容为跨考网独家整理,如您还需更多考研资料,可选择经济学一对一在线咨询进行咨询。
1.假定一年中有8000小时(实际上有8760小时),某人的潜在市场工资为5美元/小时。
(1)此人的最高临界收入是多少?如果他(或她)选择将75%的收入用于休闲,则他将工作多少小时?(2)假定此人的一个富有的叔叔去世了,留给了他(或她)一笔每年4000美元的收入。
如果他(或她)继续将其最高临界收入的75%用于休闲,则他将工作多少小时?(3)如果市场工资从5美元/小时提高至10美元/小时,则你对(2)的答案有何变化?(4)画出(2)和(3)所揭示的个人劳动供给曲线。
解:(1)此人全部收入为:8000540000⨯=(美元/年);其中,用于休闲的支出为:0.754000030000⨯=(美元/年);因而此人每年用于闲暇的时间为:30000/56000=(小时);用于工作的时间为:800060002000-=(小时)。
(2)在此人得到遗产后,他的全收入为:40000400044000+=(美元/年);其中,用于休闲的支出为:0.754400033000⨯=(美元/年);因而此人每年用于闲暇的时间为:33000/56600=(小时);用于工作的时间为:800066001400-=(小时)。
(3)如果市场工资提高后,他的全收入为:800010400084000⨯+=(美元/年);其中,用于休闲的支出为:0.758400063000⨯=(美元/年);因而此人每年用于闲暇的时间为:63000/106300=(小时);用于工作的时间为:800063001700-=(小时)。
第二章 等式与不等式 章节验收测评卷(解析版)-2024-2025学年高一数学单元速记巧练

即△=4a2-4(a+2)=0,解得a=2或a=-1.
故答案为:2或-1
2- 20的解集为 6.(24-25 高一上·上海·单元测试)不等式
【答案】3.)
{-×-2)?×-1)s?, 【分析】将分式不等式等价于
a=2023 当且仅当
时取等号,
2024b+20242024b20245=2.
b=2024 当且仅当
时取等号,
所以2023a+2024b+2023a+202424, 当且仅当a=2023b=2024时取等号,
即22023a+2024b+2023a+20245-4时,必有a-2023,b-2024’
所以 (2023a+20246(2023a2024)-4 成立,
的最小值,然后可得.
【详解】因为x<-3,所以x+3<0,-(x+3)>0,
所以-(x+3)+-(x+3)22-x+3)×-x+3)=22,
当且仅兰当-(x+3)=-(x+3) 即x=-3-√2时等号成立,
所以 (x+3)+(x+3<-2J2,,所以 x+x23s-3-2√2
.故答案为:-3-2√2
“2023a+2024b+2023a+2024b=4”是“(2023a+2024b)(2023a+2024b)=4 ”的( )
A.充分非必要条件
B.必要非充分条件
C.充要条件
D.既非充分又非必要条件
【答案】A
【分析】根据充分条件和必要条件的定义结合基本不等式分析判断即可.
【详解】因为
20230+2023a22)2023020230=2,
第二章 等式与不等式
章节验收测评卷
2022版新教材高考物理一轮复习第16章原子物理第1讲原子结构和波粒二象性课件鲁科版

【核心归纳】 1.与光电效应有关的五组易混概念对比 (1)光子与光电子:光子指光在空间传播时的每一份能量,光子 不带电;光电子是金属表面受到光照射时,发射出来的电子,其本 质是电子。光子是因,光电子是果。 (2)光电子的动能与光电子的最大初动能:只有金属表面的电子 直接向外飞出时,只需克服原子核的引力做功的情况,才具有最大 初动能。
4.光电管上加正向与反向电压的情况分析 (1)光电管加正向电压的情况(如图所示) ①P 右移时,参与导电的光电子数增加; ②P 移到某一位置时,所有逸出的光电子 恰好都参与了导电,光电流恰好达到最大值; ③P 再右移时,光电流不再增大。
(2)光电管加反向电压的情况(图中电源正、负极互换) ①P 右移时,参与导电的光电子数减少; ②P 移到某一位置时,所有逸出的光电子恰好都不参与导电,光 电流恰好为 0,此时光电管两端加的电压为遏止电压; ③P 再右移时,光电流始终为 0。
思考辨析 1.氢原子能级的量子化是氢原子光谱不连续的成因。
(√ )
2.玻尔理论能很好地解释氢原子光谱为什么是一些分立的亮线。
3.巴耳末公式是玻尔理论的一种特殊情况。
(√ ) (√ )
光谱分析。
线状谱和吸收光谱都对应某种元素,都可以用来进行
四、粒子的波动性和量子力学的建立 1.光的波粒二象性 (1)光的干涉、衍射、偏振现象证明光具有波动性。 (2)光电效应说明光具有粒子性。 (3)光既具有波动性,又具有粒子性,称为光的波粒二象性。
思考辨析
1.美国物理学家康普顿发现了康普顿效应,证实了光的粒子性。
2.光子数量越大,其粒子性越明显。
(√ ) (×)
3.光具有粒子性,但光子又不同于宏观概念的粒子。 ( √ )
02
关键能力·提升综合性
第16章 劳动力市场
第16章 劳动力市场1.假定一年中有8000小时(实际上有8760小时),并且一个人有一潜在的市场工资为每小时5美元。
a .这个人的最高收入是多少?如果他将这一收入的75%用来享受闲暇,则他将工作多少小时?b .假设一位富有的叔叔去世了,留给这个人每年4000美元的年金。
如果他继续将其最高收入的75%用来享受闲暇,则他将工作多少小时?c .如果市场工资由每小时5美元变为每小时10美元,则对b 的答案有何变化?d .画图说明由b 和c 所隐含的这个人的劳动供给曲线。
解:a .此人全部收入为:8000540000⨯=(美元/年)。
其中,用于休闲的支出为0.754000030000⨯=(美元/年),因而此人每年用于闲暇的时间为30000/56000=(小时),用于工作的时间为800060002000-=(小时)。
b .在此人得到遗产后,他的全收入为40000400044000+=(美元/年);其中,用于休闲的支出为0.754400033000⨯=(美元/年),因而此人每年用于闲暇的时间为33000/56600=(小时),于工作的时间为800066001400-=(小时)。
c .如果市场工资提高后,他的全收入为:800010400084000⨯+=(美元/年);其中,用于休闲的支出为0.758400063000⨯=(美元/年),因而此人每年用于闲暇的时间为63000/106300=(小时),用于工作的时间为:800063001700-=(小时)。
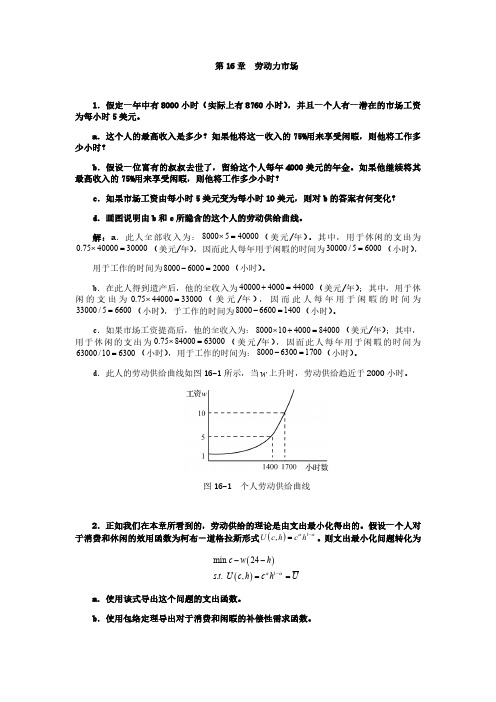
d .此人的劳动供给曲线如图16-1所示,当上升时,劳动供给趋近于2000小时。
w图16-1 个人劳动供给曲线2.正如我们在本章所看到的,劳动供给的理论是由支出最小化得出的。
假设一个人对于消费和休闲的效用函数为柯布-道格拉斯形式()1,U c h c h αα-=。
则支出最小化问题转化为()()1min 24..,c w h s t U c h c h Uαα---==a .使用该式导出这个问题的支出函数。
中考数学专题训练第16讲统计与概率(解析版)

统计与概率易错点梳理易错点01 调查方式的选择错误全面调查是对考查对象的全体调查.要求对考查范围内所有个体进行一个不漏的逐个准确统计.而抽样调查则只是对总体中的部分个体进行调查.以样本来估计总体的情况。
易错点02 对各种统计图的意义理解错误条形图能显示每组中的具体数据.注意各个小组不相连.扇形图能显示部分在总体中所占的百分比.注意不能直接判断具体数据的大小.折线图能显示数据的变化趋势.也能得到具体数据的大小.直方图能显示数据的分布情况.能得到每组数据的多少.注意各个小组无间隔。
易错点03 求中位数忘记排序求一组数据的中位数必须将数据按照由小到大(或由大到小)的顺序排列.然后再取中间一个数或中间两个数的平均数就是这组数据的中位数。
易错点04 不能正确计算方差方差是一组数据中各数据与它们的平均数的差的平方的平均数.即:ns 12=[21)(x x -+22)(x x -+……+2)(x x n -]。
易错点05 混淆确定性事件和随机事件的概念在一定条件下.有些事件必然会发生.这样的事件称为必然事件.有些事件必然不会发生.这样的事件称为不可能事件.必然事件与不可能事件统称确定事件.在一定条件下.可能发生也可能不发生的事件称为随机事件。
易错点06 混淆频率与概率频率和概率是两个不同的概念.事件的概率是一个确定的常数.而频率是不确定的.当试验次数较少时.频率的大小摇摆不定.当试验次数增大时.频率的大小波动变小.并逐渐稳定在概率附近。
易错点梳理考向01 数据的收集与整理例题1:(2021·辽宁凌海·九年级期中)如图①所示.一张纸片上有一个不规则的图案(图中画图部分).小雅想了解该图案的面积是多少.她采取了以下的办法:用一个长为5m.宽为3m 的长方形.将不规则图案围起来.然后在适当位置随机地向长方形区域扔小球.并记录小球在不规则图案上的次数(球扔在界线上或长方形区域外不计入试验结果).她将若干次有效试验的结果绘制成了图②所示的折线统计图.由此她估计此不规则图案的面积大约为( )A .6m 2B .5m 2C .4m 2D .3m 2【答案】A【思路分析】首先假设不规则图案面积为x .根据几何概率知识求解不规则图案占长方形的面积大小.继而根据折线图用频率估计概率.综合以上列方程求解. 【解析】解:假设不规则图案面积为x m 2. 由已知得:长方形面积为53⨯=15m 2.根据几何概率公式小球落在不规则图案的概率为:15x. 当事件A 试验次数足够多.即样本足够大时.其频率可作为事件A 发生的概率估计值.故由折线图可知.小球落在不规则图案的概率大约为0.4. 综上有:15x=0.4. 解得x =6. 故选:A .例题分析【点拨】本题考查几何概率以及用频率估计概率.并在此基础上进行了题目创新.解题关键在于清晰理解题意.能从复杂的题目背景当中找到考点化繁为简.创新题目对基础知识要求极高.例题2:(2021·内蒙古呼伦贝尔·中考真题)下列说法正确的是()A.在小明.小红.小月三人中抽2人参加比赛.小刚被轴中是随机事件B.要了解学校2000学生的体质健康情况.随机抽取100名学生进行调查.在该调查中样本容量是100名学生C.预防“新冠病毒”期间.有关部门对某商店在售口罩的合格情况进行抽检.抽检了20包口罩.其中18包合格.该商店共进货100包.估计合格的口罩约有90包D.了解某班学生的身高情况适宜抽样调查【答案】C【思路分析】根据随机事件的定义、样本容量的定义、用样本的率计算总体中该项的数量、全面调查的特点依次判断即可得到答案.【解析】解:在小明.小红.小月三人中抽2人参加比赛.小刚被轴中是不可能事件.故A选项不正确.要了解学校2000学生的体质健康情况.随机抽取100名学生进行调查.在该调查中样本容量是100.故B选项错误.预防“新冠病毒”期间.有关部门对某商店在售口罩的合格情况进行抽检.抽检了20包口罩.其中18包合格.故该口罩的合格率为90%.该商店共进货100包.估计合格的口罩约有90包.故C选项正确.了解某班学生的身高情况适宜全面调查.故D选项错误.故选:C.【点拨】此题考查语句判断.正确理解随机事件的定义、样本容量的定义、用样本的率计算总体中该项的数量、全面调查的特点是解题的关键.考向02 数据分析例题3:(2021·云南·昆明市第三中学模拟预测)垃圾分类是对垃圾进行有效处置的一种科学管理方式.是对垃圾收集处置传统方式的改革.甲乙两班各有40名同学参加了学校组织的2020年“生活垃圾分类回收”的考试.考试规定成绩大于等于96分为优异.两个班成绩的平均数、中位数、方差如表所示.则下列说法正确的是()参加人数平均数中位数方差甲40 95 93 5.1乙40 95 95 4.6AB.甲班成绩优异的人数比乙班多C.甲.乙两班竞褰成绩的众数相同D.小明得94分将排在甲班的前20名【答案】D【思路分析】分别根据方差的意义、中位数意义、众数的定义及平均数的意义逐一判断即可.【解析】A.乙班成绩的方差小于甲班成绩的方差.所以乙班成绩稳定.此选项错误.不符合题意.B.乙班成绩的中位数大于甲班.所以乙班成绩不低于95分的人数多于甲班.此选项错误.不符合题意.C.根据表中数据无法判断甲、乙两班成绩的众数.此选项错误.不符合题意.D.因为甲班共有40名同学.甲班的中位数是93分.所以小明得94分将排在甲班的前20名.此选项正确.符合题意.故选:D.【点拨】本题考查了平均数、中位数、方差及众数的概念.平均数、中位数及众数反映的是一组数据的平均趋势及水平.平均数与每个数据有关.方差反映的是一组数据的波动程度.在平均数相同的情况下.方差越小.说明数据的波动程度越小.也就是说这组数据更稳定.例题4:(2021·江苏洪泽·二模)实验中学选择10名青少年志愿者参加读书日活动.年龄如表所示:这10名志愿者年龄的众数和中位数分别是()年龄12 13 14 15人数 2 3 4 1【答案】C【思路分析】根据众数和中位数的意义求解.【解析】解:这10名志愿者年龄出现次数最多的是14.因此众数是14.将这10名志愿者年龄从小到大排列处在中间位置的两个数的平均数为13142=13.5.因此中位数是13.5.故选:C【点拨】本题考查众数和中位数的应用.熟练掌握众数和中位数的意义和计算方法是解题关键.考向03 概率例题5:(2021·云南省楚雄天人中学九年级期中)在一个不透明的纸箱中.共有15个蓝色、红色的玻璃球.它们除颜色外其他完全相同.小柯每次摸出一个球后放回.通过多次摸球试验后发现摸到蓝色球的频率稳定在20%.则纸箱中红色球很可能有()A.3个B.6个C.9个D.12个【答案】D【思路分析】根据利用频率估计概率得到摸到蓝色球的概率为20%.由此得到摸到红色球的概率=1-20%=80%.然后用80%乘以总球数即可得到红色球的个数.【解析】解:∵摸到蓝色球的频率稳定在20%.∴摸到红色球的概率=1-20%=80%.∵不透明的布袋中.有黄色、白色的玻璃球共有15个.∴纸箱中红球的个数有15×80%=12(个).故选:D.【点拨】本题考查了利用频率估计概率:大量重复实验时.事件发生的频率在某个固定位置左右摆动.并且摆动的幅度越来越小.根据这个频率稳定性定理.可以用频率的集中趋势来估计概率.这个固定的近似值就是这个事件的概率.例题6:(2021·福建省漳州第一中学九年级期中)我国古代有着辉煌的数学研究成果.其中《算经十书》是指汉、唐一千多年间的十部著名的数学著作.这些数学著作曾经是隋唐时代国子监算学科的教科书.十部书的名称是:《周髀算经》、《九章算术》、《海岛算经》、《张丘建算经》、《夏侯阳算经》、《五经算术》、《缉古算经》、《缀术》、《五曹算经》、《孙子算经》、《算经十书》标志着中国古代数学的高峰.《算经十书》这10部专著.有着十分丰富多彩的内容.是了解我国古代数学的重要文献.这10部专著中据说有6部成书于魏晋南北朝时期.其中《张丘建算经》、《夏侯阳算经》就成书于魏晋南北朝时期.某中学拟从《算经十书》专著中的魏晋南北朝时期的6部算经中任选2部作为“数学文化”进行推广学习.则所选2部专著恰好是《张丘建算经》、《夏侯阳算经》的概率为()A.13B.15C.115D.118【答案】C【思路分析】设六部成书于魏晋南北朝的算经分别用A、B、C、D、E、F表示.其中《张丘建算经》、《夏侯阳算经》分别用A、B表示,列树形图表示所有等可能性.根据概率公式即可求解.【解析】解:设六部成书于魏晋南北朝的算经分别用A、B、C、D、E、F表示.其中《张丘建算经》、《夏侯阳算经》分别用A、B表示.根据题意列树形图得由树形图得共有30种等可能性.其中两部专著恰好是A 、B 即《张丘建算经》、《夏侯阳算经》的有两种等可能性.∴所选2部专著恰好是《张丘建算经》、《夏侯阳算经》的概率为213015P ==. 故选:C【点拨】本题考查了列树形图求概率.根据题意分别用字母表示六种算经并正确列出树形图是解题关键.一、单选题1.在一个不透明的口袋中装有4个红球和若干个白球.他们除颜色外其他完全相同.通过多次摸球实验后发现.摸到红球的频率稳定在25%附近.则口袋中白球可能有( ) A .12个 B .14个 C .15个 D .16个【答案】A【解析】设白球有x 个.根据题意列出方程.4254100x =+. 解得x =12.经检验得x =12是原方程的解. 故选A .2.(2021·湖南·长沙市开福区青竹湖湘一外国语学校九年级期中)下列调查中.适合于采用普查方式的是( ) A .调查央视“五一晚会”的收视率 B .了解外地游客对兴城旅游景点的印象 C .了解一批新型节能灯的使用寿命 D .了解某航班上的乘客是否都持有“绿色健康码” 【答案】D【解析】A.调查央视“五一晚会”的收视率.适合抽样调查. B.了解外地游客对兴城旅游景点的印象.适合抽样调查. C.了解一批新型节能灯的使用寿命.适合抽样调查.微练习D.了解某航班上的乘客是否都持有“绿色健康码”.适合普查. 故选:D .3.(2021·江苏·连云港市新海实验中学二模)我校开展了“好书伴我成长”读书活动.为了解5月份九年级学生的读书情况.随机调查了九年级50名学生读书的册数.统计数据如下表所示.下列说法正确的是( )册数 0 1 2 3 4 人数 41216171A 【答案】B【解析】这组样本数据中.3出现了17次.出现的次数最多.∴这组数据的众数是3.将这组样本数据按从小到大的顺序排列.其中处于中间的两个数都是2.∴这组数据的中位数为2.观察表格.可知这组样本数据的平均数为: (0 × 4 + 1 × 12 + 2 × 16 + 3 × 17 + 4 ×1)÷50=9950. 这组数据的方差为:()()()()()22222140-1.98+121-1.98+162-1.98+173-1.98+4-1.9850⎡⎤⨯⨯⨯⨯⎣⎦ 2≠.故选:B .4.(2021·江苏新吴·二模)已知一组数据x 、y 、的平均数为3.方差为4.那么数据2x -.2y -.2z -的平均数和方差分别( )A .1.2B .1.4C .3.2D .3.4【答案】B【解析】由于数据x 、y 、z 的平均数为3.所以有x +y +z =9 则[]111(2)(2)(2)(6)31333x y z x y z -+-+-=++-=⨯= 由于数据x 、y 、z 的方差为4.即2221(3)(3)(3)43x y z ⎡⎤-+-+-=⎣⎦所以22222211(21)(21)(21)(3)(3)(3)433x y z x y z ⎡⎤⎡⎤--+--+--=-+-+-=⎣⎦⎣⎦即数据2x -.2y -.2z -的方差仍为4故数据2x -.2y -.2z -的平均数和方差分别为1和4 故选:B .5.(2021·黑龙江绥化·中考真题)近些年来.移动支付已成为人们的主要支付方式之一.某企业为了解员工某月,A B 两种移动支付方式的使用情况.从企业2000名员工中随机抽取了200人.发现样本中AB 、两种支付方式都不使用的有10人.样本中仅使用A 种支付方式和仅使用B 种支付方式的员工支付金额a (元)分布情况如下表: 支付金额a (元)01000a <≤ 10002000a <≤ 2000a >仅使用A 36人 18人 6人 仅使用B 20人28人2人①根据样本数据估计.企业2000名员工中.同时使用,A B 两种支付方式的为800人. ②本次调查抽取的样本容量为200人.③样本中仅使用A 种支付方式的员工.该月支付金额的中位数一定不超过1000元. ④样本中仅使用B 种支付方式的员工.该月支付金额的众数一定为1500元. 其中正确的是( ) A .①③ B .③④ C .①② D .②④【答案】A【解析】解:根据题目中的条件知:①从企业2000名员工中随机抽取了200人.同时使用,A B 两种支付方式的人为:20010(362018+28+6+2)=80--++(人).∴样本中同时使用,A B 两种支付方式的比例为:8022005=. ∴企业2000名员工中.同时使用,A B 两种支付方式的为:220008005⨯=(人).故①正确. ②本次调查抽取的样本容量为200.故②错误.③样本中仅使用A 种支付方式的员工共有:60人.其中支付金额在01000a <≤之间的有.36人.超过了仅使用A 种支付方式的员工数的一半.由中位数的定义知:中位数一定不超过1000元.故③是正确.④样本中仅使用B 种支付方式的员工.从表中知月支付金额在10002000a <≤之间的最多.但不能判断众数一定为1500元.故④错误.综上:①③正确.故选:A .6.为考察两名实习工人的工作情况.质检部将他们工作第一周每天生产合格产品的个数整理成甲.乙两组数据.如下表:甲 2 6 7 7 8 乙23488关于以上数据.下列说法正确的有()个.①甲、乙的众数相同.②甲、乙的中位数相同.③甲的平均数小于乙的平均数.④甲的方差小于乙的方差.A.1个B.2个C.3个D.4个【答案】A【解析】甲的众数为7.乙的众数为8.故①错误.甲的中位数为7.乙的中位数为4.故②错误.甲的平均数为15×(2+6+7+7+8)=6.乙的平均数为15×(2+3+4+8+8)=5.故③错误.甲的方差为15×[(2﹣6)2+(6﹣6)2+(7﹣6)2+(7﹣6)2+(8﹣6)2]=4.4.乙的方差为15×[(2﹣5)2+(3﹣5)2+(4﹣5)2+(8﹣5)2+(8﹣5)2]=6.4.甲的方差小于乙的方差.故④正确.故选:A.7.(2021·黑龙江松北·二模)两个不透明盒子里分别装有3个标有数字3.4.5的小球.它们除数字不同外其他均相同.甲、乙二人分别从两个盒子里摸球1次.二人摸到球上的数字之和为奇数的概率是()A.13B.23C.49D.59【答案】C【解析】解:画树状图如图:共有9种等可能的结果.甲、乙二人摸到球上的数字之和为奇数的结果有4种.∴甲、乙二人摸到球上的数字之和为奇数的概率为49.故选:C.8.有两把不同的锁和三把不同的钥匙.其中两把钥匙分别能打开这两把锁.第三把钥匙不能打开这两把锁.随机取出一把钥匙开任意一把锁.一次打开锁的概率是()A.12B.13C.14D.23【答案】B【解析】解:列表得:锁1 锁2钥匙1 (锁1.钥匙1)(锁2.钥匙1)钥匙2 (锁1.钥匙2)(锁2.钥匙2)钥匙3 (锁1.钥匙3)(锁2.钥匙3)由表可知.所有等可能的情况有6种.其中随机取出一把钥匙开任意一把锁.一次打开锁的2种.则P(一次打开锁)=21=63.故选:B.9.(2021·山东南区·二模)一个口袋中有3个黑球和若干个白球.在不允许将球倒出来数的前提下.小明为估计其中的白球数.采用了如下的方法:从口袋中随机摸出一球.记下颜色.然后把它放回口袋中.摇匀后再随机摸出一球.记下颜色.再放回.不断重复上述过程.小明共摸了100次.其中80次摸到白球.根据上述数据.小明可估计口袋中的白球大约有()A.18个B.15个C.12个D.10个【答案】C【解析】解:由题可得:31008080-÷=12(个).故答案为:12.10.广东省2021年的高考采用“312++”模式:“3”是指语文、数学、外语3科为必选科目.“1”是指在物理、历史2科中任选1科.“2”是指在化学、生物、思想政治、地理4科中任选2科.若小红在“1”中选择了历史.则她在“2”中选地理、生物的概率是()A.16B.13C.14D.12【答案】A【解析】解:用树状图表示所有可能出现的结果如下:共有12种等可能的结果数.其中选中“地理”“生物”的有2种.则P(地理、生物)=2÷12=16.故选A.二、填空题11.(2021·北京丰台·二模)某单位有10000名职工.想通过验血的方式筛查出某种病毒的携带者.如果对每个人的血样逐一化验.需要化验10000次.统计专家提出了一种化验方法:随机地按5人一组分组.然后将各组5个人的血样混合再化验.如果混合血样呈阴性.说明这5个人全部阴性.如果混合血样呈阳性.说明其中至少有一个人呈阳性.就需要对这组的每个人再分别化验一次.假设携带该病毒的人数占0.05%.回答下列问题:(1)按照这种化验方法是否能减少化验次数________(填“是”或“否”).(2)按照这种化验方法至多需要________次化验.就能筛查出这10000名职工中该种病毒的携带者.【答案】是2025【解析】解:(1)第一轮化验10000名÷5=2000次<10000次故按照这种化验方法是能减少化验次数故答案为:是(2)按照这种方法需要两轮化验.第一轮化验2000次携带该病毒的人数=10000×0.05%=5人最多有5组需要进行第二轮化验一一化验需要5×5=25次化验一共进行2000+25=2025次化验.按照这种化验方法至多需要2025次化验.就能筛查出这10000名职工中该种病毒的携带者.故答案为:2025.12.某校组织了一次初三科技小制作比赛.有A、B、C、D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%.其它几个班的参赛作品情况及获奖情况绘制在图1和图2两幅尚不完整的统计图中.则获奖率最高的班级是________.【答案】C班【解析】解:由统计图可得.A 班的获奖率为:1410035%100%()40%÷⨯⨯=.B 班的获奖率为:()11100135%20[]%20%100%44%÷⨯---⨯=.C 班的获奖率为50%.D 班的获奖率为:()810020%100%40%÷⨯⨯=.由上可得.获奖率最高的班级是C 班.故答案为:C 班. 13.(2021·内蒙古赛罕·二模)下列命题错误的序号是_________.①若1∠和2∠是同位角.则12∠=∠.②如果一个三角形的两条边和一个角与另一个三角形的两条边和一个角相等.那么这两个三角形全等.1x -.④某班投票选班长.小丽15票.小伟20票.小刚18票.这组数据的众数是20.⑤为排查肺炎疑似病人同机乘客的健康情况.应采用全面调查的方式进行. 【答案】①②③④【解析】解:①两直线平行时.同位角相等.不是所有互为同位角的两个角都相等.故此命题错误.②根据三角形全等的判定定理可知.当一个三角形的两个边和其夹角与另一个三角形的对应边角相等时.两个三角形才会全等.故此命题错误.③一般地.(0)a a ≥的式子叫作二次根式.需要10x -≥这个条件存在.题中没有.故此命题错误.④一组数据中出现次数最多的那个数据叫作这组数据的众数.故此命题错误.⑤排查所有同机乘客需要进行全面调查.故此命题正确.14.(2021·贵州铜仁·中考真题)若甲、乙两人射击比赛的成绩(单位:环)如下: 甲:6.7.8.9.10. 乙:7.8.8.8.9.则甲、乙两人射击成绩比较稳定的是______________(填甲或乙). 【答案】乙【解析】解:甲乙二人的平均成绩分别为:678910==85x ++++甲.78889==85x ++++乙.∴二人的方差分别为:()()()()()22222268788898108==25S -+-+-+-+-甲()()()()()22222278888888982==55S -+-+-+-+-乙. ∵22S S 乙甲>.乙的成绩比较稳定.故答案为:乙15.(2021·四川·成都绵实外国语学校九年级期中)小明为研究函数y =2x的图象.在﹣2、﹣1、1中任取一个数为横坐标.在﹣2、﹣1、2中任取一个数为纵坐标组成点P 的坐标.点P 在函数y =2x的图象上的概率是___.【答案】13【解析】解:列表如下:2-1-22- ()2,2--()2,1-- ()2,2-1-()1,2--()1,1--1,21()1,2-()1,1-1,2其中点P 在函数2y x=上的有()2,1--.()1,2--.1,2共3种. 所有点P 在函数y =2x 的图象上的概率是31=.93故答案为:1316.(2021·四川·成都嘉祥外国语学校九年级期中)有四张正面分别标有数字﹣4.﹣3.﹣2.1.的不透明卡片.它们除数字不同外其他全部相同.现将它们背面朝上.洗匀后从中抽取一张.将该卡片上的数字记为a .放回后洗匀.再从中抽取一张.将该卡片上的数字记为b .则a .b 使得二次函数y =x 2﹣(a +5)x +3当x ≤1时y 随x 的增大而减小.且一元二次方程(a +2)x 2+bx +1=0有解的概率为 ___. 【答案】516【解析】解:∵二次函数y =x 2﹣(a +5)x +3.二次项系数为1.大于0. ∴抛物线开口向上.对称轴为直线52a x +=. ∵要使得当x ≤1时.y 随x 的增大而减小. ∴应满足512a +≥. 解得:3a ≥-.∵一元二次方程(a +2)x 2+bx +1=0有解.∴20a +≠且()2420b a ∆=-+≥. ∴2a ≠-且()2420b a ∆=-+≥.∴由题意可知.a 仅能取-3或1.当3a =-时.()224324b b ∆=-⨯-+=+.∴b 取﹣4.﹣3.﹣2.1时.均满足0∆≥.当1a =时.()2241212b b ∆=-⨯+=-.∴仅有b 取﹣4时.满足0∆≥.综上分析.当3a =-时.b 取﹣4.﹣3.﹣2.1.满足题意.当1a =时.b 取﹣4满足题意.共有5种情况满足题意.∵由题意可得.两次抽取共有16种情况发生. ∴两次抽取后满足题意的概率为516P =. 故答案为:516. 三、解答题17.某校为了解本校初中学生体能情况.随机抽取部分学生进行了一次测试.并根据标准按测试成绩分成A .B .C .D 四个等级.绘制出以下两幅不完整的统计图.请根据图中信㿝解答下列问题:(1)本次抽取㐱加则试的学生为 人.扇形统计图中A 等级所对的圆心角是 度. (2)请补全条形统计图.(3)若该校初中学生有1200人.请估计该校学生体能情况成绩为C 等级的有多少人数? 【答案】(1)50.108.(2)画图见解析.(3)240人 【解析】解:(1)由B 类22人.占比44%.可得: 总人数为:2244%=50人.扇形统计图中A 等级所对的圆心角是30%360=108, 故答案为:50.108(2)C 类的人数有:501522310---=人. 补全图形如下:(3)该校初中学生有1200人.则该校学生体能情况成绩为C 等级的有:10120024050⨯=人. 答:该校初中学生有1200人.则该校学生体能情况成绩为C 等级的有240人. 18.甲、乙两名队员参加射击训练.每人射击10次.成绩分别如下:平均成绩 中位数 众数 方差甲 a 7 7 1.2 乙 7b8c根据以上信息.(1)填空:a = .b = .c = .(2)从平均数和中位数的角度来比较.成绩较好的是 .(填“甲”或“乙”) (3)若需从甲、乙两名队员中选择一人参加比赛.你认为选谁更加合适?请说明理由. 【答案】(1)7.7.5.4.2.(2)乙.(3)选择乙参加比赛.理由见解析 【解析】解:(1)甲的平均成绩为()()1115264728195122816971010a =⨯+⨯+⨯+⨯+⨯=++++= 乙的成绩从低到高排列为:3.4.6.7.7.8.8.8.9.10. 所以中位数()1787.52b =+= ()()()()()()()222222213747672773879710710c ⎡⎤=-+-+-+-+-+-+-⎣⎦=[]11691034910++++++ =4.2故答案为:7.7.5.4.2.(2)由表中数据可知.甲、乙平均成绩相等.乙的中位数7.5大于甲的中位数7.说明乙的成绩好于甲. 故答案为:乙.(3)选择乙参加比赛.理由:从平均数上看.甲、乙平均成绩相等.总分相等.从中位数上看乙的中位数和众数都大于甲.说明乙的成绩好于甲. 从方差上看乙的方差大于甲只说明乙的成绩没有甲稳定. 从众数看乙的众数是8.甲的众数是7.说明乙成绩要好些. 从折线图看.乙开始时发挥不好.后来乙的成绩呈上升趋势. 故应选乙队员参赛.19.(2021·四川达州·九年级期中)达州市红色旅游景点众多.例如罗江镇张爱萍故居.宣汉县红军公园、王维舟纪念馆.万源战史陈列馆等等.为了解初三学生对达州历史文化的了解程度.随机抽取了男、女各m 名学生进行问卷测试.问卷共30道选择题.现将得分情况统计.并绘制了如图不完整的统计图(数据分组为A 组:18x <.B 组:1822x ≤<.C 组:2226x ≤<.D 组:2630x ≤≤.x 表示问卷测试的分数).其中男生得分处于C 组的有14人.男生C 组得分情况分别为:22.22.22.22.22.23.23.23.24.24.24.25.25.25.男生、女生得分的平均数、中位数、众数(单位:分)如表所示:组别 平均数 中位数 众数 男 20 n22 女202320(1)求m .n 的值.(2)已知初三年级总人数为1800人.请估计参加问卷测试.成绩处于C 组的人数. (3)据了解男生中有两名同学得满分.女生中分数最高的两名同学分别是30分和29分.现从这四名同学中随机抽取两名参加全校总决赛.用树状图或列表的方法求恰好抽到两名男生的概率是多少?【答案】(1)50m =.25n =.见解析.(2)522人.(3)见解析.16【解析】解:(1)由题意得:1428%50m =÷=(人).男生成绩处在A 组的百分比=1-24%-46%-28%=2%.∴男生的中位数成绩为第25名与第26名成绩的平均成绩 ∵()502%24%12⨯+=(人). ∴男生中位数()2525225n =+÷=. 女生C 组人数502132015=---=(人). 条形图如图所示:(2)14151800522100+⨯=(人). 答:估计成绩处于C 组的人数约为522人. (3)如图所以恰好抽到两名男生的概率为:21126=. 20.现有两根长度分别为3cm 和4cm 的线段.同时.在一旁另有8根长度不等的线段.这些线段的长度分别与相应的卡片正面上标注的线段长一致.这8张卡片的背面完全相同.卡片正面上分别标注了2cm 3cm 3cm 4cm 4cm 5cm 6cm 6cm 、、、、、、、.把这8张卡片背面朝上.从中随机抽取一张卡片.以卡片上标注的数据对应的线段作为第三条线段的长度.回答以下问题:(1)“从中抽取的长度能够与3cm 和4cm 组成直角三角形”的概率为________. (2)求抽出的卡片上标注的数据对应的线段能够与3cm 和4cm 的线段组成等腰三角形的概率.(3)小红和小艺打算以取出一张卡片上标注的数据对应的线段能够与3cm 和4cm 组成三角形的周长的奇偶性作为游戏规则.若三角形周长为奇数.则小红胜.若三角形周长为偶数.则小艺胜.请问游戏公平吗?若公平.请说明理由.若不公平.请重新设计一个公平的游戏规则.【答案】(1)18.(2)12.(3)不公平.游戏规则改为:等腰三角形的周长为偶数.则小艺胜.等腰三角形周长为奇数.则小红胜【解析】解:(1)∵该三条线段组成的是直角三角形. ∴2234=5+22437-. ∴符合的卡片有标注5cm 的一张.∴“从中抽取的长度能够与3cm 和4cm 组成直角三角形”的概率为18.故答案为:18.(2)能构成等腰三角形的线段有3cm .3 cm .4 cm .4 cm 共四条.∴抽出的卡片上标注的数据对应的线段能够与3cm 和4cm 的线段组成等腰三角形的概率为4182=. (3)∵3+4=7.∴当抽到的线段为奇数即抽到3cm 、3cm 或5cm 时.三角形的周长为偶数.此时小艺胜的概率为38.当抽到的线段为偶数即抽到2cm 、4cm 、4cm 、6cm 或6cm 时.三角形的周长为奇数.此时小红胜的概率为58. ∴游戏不公平.游戏规则改为:等腰三角形的周长为偶数.则小艺胜.等腰三角形周长为奇数.则小红胜. 21.(2021·浙江·宁波市镇海蛟川书院九年级期中)A 、B 两人去九龙湖风景区游玩.已知每天某一时段开往风景区有三辆舒适程度不同的车.开过来的顺序也不确定.两人采取了。
伍德里奇计量经济学导论第5版笔记和课后习题详解

伍德里奇《计量经济学导论》(第5版)笔记和课后习题详解目录第1章计量经济学的性质与经济数据1.1复习笔记1.2课后习题详解第一篇横截面数据的回归分析第2章简单回归模型2.1复习笔记2.2课后习题详解第3章多元回归分析:估计3.1复习笔记3.2课后习题详解第4章多元回归分析:推断4.1复习笔记4.2课后习题详解第5章多元回归分析:OLS的渐近性5.1复习笔记5.2课后习题详解第6章多元回归分析:深入专题6.1复习笔记6.2课后习题详解第7章含有定性信息的多元回归分析:二值(或虚拟)变量7.1复习笔记7.2课后习题详解第8章异方差性8.1复习笔记8.2课后习题详解第9章模型设定和数据问题的深入探讨9.1复习笔记9.2课后习题详解第二篇时间序列数据的回归分析第10章时间序列数据的基本回归分析10.1复习笔记10.2课后习题详解第11章OLS用于时间序列数据的其他问题11.1复习笔记11.2课后习题详解第12章时间序列回归中的序列相关和异方差性12.1复习笔记12.2课后习题详解第三篇高级专题讨论第13章跨时横截面的混合:简单面板数据方法13.1复习笔记13.2课后习题详解第14章高级的面板数据方法14.2课后习题详解第15章工具变量估计与两阶段最小二乘法15.1复习笔记15.2课后习题详解第16章联立方程模型16.1复习笔记16.2课后习题详解第17章限值因变量模型和样本选择纠正17.1复习笔记17.2课后习题详解第18章时间序列高级专题18.1复习笔记18.2课后习题详解第19章一个经验项目的实施19.2课后习题详解本书是伍德里奇《计量经济学导论》(第5版)教材的学习辅导书,主要包括以下内容:(1)整理名校笔记,浓缩内容精华。
每章的复习笔记以伍德里奇所著的《计量经济学导论》(第5版)为主,并结合国内外其他计量经济学经典教材对各章的重难点进行了整理,因此,本书的内容几乎浓缩了经典教材的知识精华。
(2)解析课后习题,提供详尽答案。
计量经济学_电子科技大学中国大学mooc课后章节答案期末考试题库2023年

计量经济学_电子科技大学中国大学mooc课后章节答案期末考试题库2023年1.当存在序列相关时,广义最小二乘法的预测结果通常优于普通最小二乘法。
参考答案:正确2.若Park检验和White检验均未检验出异方差性,回归模型一定不存在异方差问题。
参考答案:错误3.时间序列模型预测中,动态预测的效果一定优于静态预测的效果。
参考答案:错误4.计量经济学可用于描述商品需求曲线,即需求量与价格的关系。
参考答案:正确5.通常情况下,Logit模型和Probit模型得到的参数估计值在符号和显著性上是相似的。
参考答案:正确6.多重共线性指的是解释变量与被解释变量之间存在的线性关系。
参考答案:错误7.调整的判定系数可精确度量线性概率模型的拟合优度。
参考答案:错误8.计量模型的预测既可以进行均值预测,又可以进行区间预测。
参考答案:正确9.计量经济学只能做定量研究,不能做定性研究,如个人的职业选择。
参考答案:错误10.若某解释变量在理论上对被解释变量没有影响,该解释变量的参数估计值一定为0.参考答案:错误11.研究大学毕业生是选择就业还是选择深造,可采用Logit模型或Probit模型。
参考答案:正确12.预测是对被解释变量样本外的观测值的估计。
参考答案:错误13.回归方程中,被解释变量等于其估计值与随机误差项之和。
参考答案:错误14.随机误差项的总体均值为0以及随机误差项与解释变量不相关保证了参数估计量的无偏性。
参考答案:正确15.多重共线性可能造成参数估计值的符号与预期不一致。
参考答案:正确16.异方差性产生的后果主要包括:参考答案:OLS估计的假设检验不可靠。
_OLS估计量不再是有效的。
_标准误的OLS 估计量是有偏的。
_OLS估计量仍是无偏的。
17.若回归模型修正了非纯异方差性问题后,无需检验纯异方差性问题。
参考答案:错误18.均方根误差RMSE指标越小,模型的预测能力越强。
参考答案:正确19.时间序列分析体现了“让数据自己说话”的思想。
时间序列分析试题

第九章 时间序列分析一、单项选择题1、乘法模型是分析时间序列最常用的理论模型。
这种模型将时间序列按构成分解为( ) 等四种成分,各种成分之间( ),要测定某种成分的变动,只须从原时间序列中( )。
A. 长期趋势、季节变动、循环波动和不规则波动;保持着相互依存的关系;减去其他影响成分的变动B. 长期趋势、季节变动、循环波动和不规则波动;缺少相互作用的影响力量;减去其他影响成分的变动C. 长期趋势、季节变动、循环波动和不规则波动;保持着相互依存的关系;除去其他影响成分的变动D.长期趋势、季节变动、循环波动和不规则波动;缺少相互作用的影响力量;除去其他影响成分的变动答案:C2、加法模型是分析时间序列的一种理论模型。
这种模型将时间序列按构成分解为( )等四种成分,各种成分之间( ),要测定某种成分的变动,只须从原时间序列中( )。
A. 长期趋势、季节变动、循环波动和不规则波动;保持着相互依存的关系;减去其他影响成分的变动B. 长期趋势、季节变动、循环波动和不规则波动;缺少相互作用的影响力量;减去其他影响成分的变动C. 长期趋势、季节变动、循环波动和不规则波动;保持着相互依存的关系;除去其他影响成分的变动D.. 长期趋势、季节变动、循环波动和不规则波动;缺少相互作用的影响力量;除去其他影响成分的变动答案:B3、利用最小二乘法求解趋势方程最基本的数学要求是( )。
A.∑=-任意值2)ˆ(t Y Y B. ∑=-min )ˆ(2t Y Y C. ∑=-max )ˆ(2t Y Y D. 0)ˆ(2∑=-t Y Y 答案:B4、从下列趋势方程t Y t86.0125ˆ-=可以得出( )。
A. 时间每增加一个单位,Y 增加0.86个单位B. 时间每增加一个单位,Y 减少0.86个单位C. 时间每增加一个单位,Y 平均增加0.86个单位D. 时间每增加一个单位,Y 平均减少0.86个单位答案:D.5、时间序列中的发展水平( )。
Python量化投资基础教程教学课件第十六章 股指期货期现套利策略

19. ContextInfo.cost = 0
#交易成本初值
20. ContextInfo.profit = 0
#持仓盈利初
21. ContextInfo.profit_acc = 0
#平仓累计盈利初值
22. ContextInfo.Portfolio =0
#套利组合标识初值
mmission)*IF_multiplier
#IF交易成本
组合价差为股指期货市值减去ETF的市值。
1. spread = IF_values - ETF_values
2. spread_now = IF_values[-1] - ETF_values[-1]
3. spread_change = spread[-1]/spread[-2]-1
#年月日时分
4. barday = timetag_to_datetime(bartimetag,'%Y%m%d')
#年月日
基本信息获取模块
查询合约乘数。不同的期货有不同的合约乘数,在程序中需先查询,后
使用。若不能查询,则需要自己根据交易所的规定设定。
1. #查询合约乘数tag,'%Y%m%d')
2. IF_multiplier = ContextInfo.get_contract_multiplier('IF00.IF')
基本信息获取模块
查询期货和现货品种k线收盘价格序列
可利用ContextInfo.get_market_data()分开查询每个品种的价格
1. IF_closes = ContextInfo.get_market_data(['close'], stock_code=code0,\ period = Cont
eviews做方程预测完整PPT学习教案

第17页/共38页
regression”表示)。残差不确定通常是预测误差的主要来源。 在动态预测中,因为滞后因变量和由滞后随机变量构成的ARMA项
的存在,使得新息不确定性更为复杂。EViews也将这些值设为它们的期 望值,这与实际值有随机偏差。含有滞后因变量和ARMA项的预测在后 面详细讨论。
第15页/共38页
16
2.系数不确定
et yt xtb
第14页/共38页
15
1.残差不确定
误差的第一种来源是由残差或新息(innovation) 的不确定引起的,
因为方程中的新息 在整个预测区间未知,被设为它 t 们的期望值。在残 差期望值为零时,单t 个残差值非零;单个误差的方差越大,预测中的总
体误差越大。 测 量 方 差 的 标 准 方 式 是 回 归 标 准 差 ( 在 输 出 方 程 中 用 “ S.E.of
1 Th yˆt yt
h 1tT1 yt
Theil Inequality Coefficient
h
1
1
T h
(
tT 1
yˆt
yt )2
泰尔不等系数
1
第19页/共38h页
1
T h
yˆt2
tT 1
ቤተ መጻሕፍቲ ባይዱ h
1
1
T h
yt2
tT 1
20
16 库埃特流动和泊肃叶流动

6. 直到y=D,检查u=ue?,否则,另假设τ 进行5步,反复直到u=ue
7. 用6步得到的τ,重新进行2-7,得到最终 收敛的τ(大循环)
时间相关有限差分法 二维非定常流N-S方程
能量方程
MacCormack法
网格划分 流入边界条件,x=0,用不可压流的解给 u,v,p,T 初始条件,t=0, u,v,p,T.用不可压流解或 均匀值
At y=D: u=ue , T=Te。 上界流体和与动平板间的摩擦剪力e 热传导qe 平行流线(Paralel streamline) At y=0: u=0 , T=Tw。
下界流体和与动平板间的摩擦剪力w 热传导qw
温度场: 1.平板上下温度一般不同,产生温度梯度 2. 动能由摩擦消耗变成内能,内能的变化由 温度升高显示出来(粘性耗散)
速度型影响小,温度型影响大
绝热壁 速度型影响和温度型影响比冷壁大
解析分析 一些量随温度的变化 Pr近似常数
能量方程——恢复因子
对于可压库埃特流,τ为常数
积分得h/Pr+u2/2-bu=c,积分时Pr为常数 按边界条件,y=0,h=hw,u=0
按边界条件,y=D,h=he,u=ue得 代入b,c则
2u/ y2=0. 积分得到u=ay+b
代入边界条件 At y=0,u=0; => b=0. At y=D,u=ue; => a=ue/D . 所以 u=ue(y/D).——x向速度线性分布
剪力e= du/dy. 代入 u/y=ue/D . 所以e= (ue/D)——剪应力在全场为常值
两个重要的趋势:
得到:x-momentum equation:
/y( u/y)=0
第16章变形分析与建模

节 回归平方和,同样选择的因子作为预选因子,作F检验,
若其影响显著时,则接纳该因子进入回归方程。在选入第
回 三个因子后,对原先已选入的因子重新进行检验,在检验
归 分
出不显著因子后,应将它剔除出回归方程,然后继续检验 已入选的回归方程因子的显著性。
析 •(4)在确认选入回归方程的因子均为显著因子后,则继
江 苏 海 洋 大 学 (测绘学院)
9
回归方程显著性检验(1)
第 1
1、离差平方和、残差平方各、回归平方和
节
n
n
S离 ( yt y)2 ( yt yˆt yˆt y)2
回
t 1 n
t 1 n
n
归 ( yt yˆt )2 ( yˆt y)2 2 ( yt yˆt )(yˆt y)
列 i (i 1,2,, m)称为滑动平均(Moving Average)参数;
分 at 为白噪声序列。
析 当i 0时,模型变为n阶自回归模型AR(n):
模
xt 1xt1 2 xt2 n xtn at
型 当i 0时,模型变为m阶滑动平均模型MA(m):
xt at 1t1 2t2 mtm
模
2020/9/29
江 苏 海 洋 大 学 (测绘学院)
2
第十六章 变形分析与建模
变
形
观
测
§1 回归分析法
与
变
形
分
析
2020/9/29
江 苏 海 洋 大 学 (测绘学院)
3
曲线拟合
第 •曲线拟合是趋势分析法中的一种,又称曲线
1 回归、趋势外推或趋势曲线分析。迄今为止, 节 它是一种研究最多、最为流行的定量预测方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十六章方程预测本章描述了对一个单方程进行预测或计算拟合值的过程。
这里描述的技术是利用通过回归方法估计得到的方程来进行预测。
§16.1EViews中的方程预测为说明一个被估计方程的预测过程,我们从一个简单的例子开始。
假设我们有1947:01—1995:01年美国国内生产总值(GDP)、消费(CS)和投资(INV),这些数据包含在工作区间为1946:01—1995:4的工作文件(16_1)中。
我们运用1947:01—1995:01这段时期的数据,估计GDP对常数、CS和INV的回归,并用AR(1)修正残差序列相关,用该模型预测GDP。
估计得到的方程结果由方程对象eq_gdp给出:注意该估计样本的观测值做了调整,以解释该模型在推导AR(1)估计时一、如何进行预测为预测该方程的GDP,在方程的工具栏中按Forecast按钮,或选择Procss/ Forecast …。
这时会出现下表:我们应提供如下信息:1、序列名预测后的序列名将所要预测的因变量名填入编辑框中。
EViews默认了一个名字,但可以将它变为任意别的有效序列名。
这个名字应不同于因变量名,因为预测过程会覆盖已给定的序列值。
S.E.(Optional)如果需要,可以为该序列的预测标准差提供一个名字。
如果省略该项,预测标准误差将不被保存。
GARCH(Optional)对用ARCH估计的模型,还可以保存条件方差的预测值(GARCH项)。
见16章对GARCH估计的讨论。
2、预测方法可以在如下方法中进行选择:动态(Dynamic)—从预测样本的第一期开始计算多步预测。
静态(Static)—利用滞后因变量的实际值而不是预测值计算一步向前(one-step-ahead)预测的结果。
还可以做如下的选项:结构(Structural)—预测时EViews将忽略方程中的任何ARMA项。
若不选此项,在方程中有ARMA项时,动态与静态方法都会对残差进行预测。
但如果选择了Structural,所有预测都会忽略残差项而只对模型的结构部分进行预测。
样本区间(Sample range)—必须指定用来做预测的样本。
如果缺选,EViews将该样本置为工作文件样本。
如果指定的样本超出估计方程所使用的样本区间(估计样本),那么会使EViews产生样本外预测。
注意:需要提供样本外预测期间的解释变量值。
对静态预测,还必须提供滞后因变量的数值。
3、输出可以选择以图表或数值,或者二者同时的形式来观察预测值。
只有当预测样本中包含因变量的观测值时,才可以得到预测估计值。
假设在样本区间1947:01—1995:01间对eq_gdp进行动态预测。
预测值放在序列GDPFD中,EViews将会显示预测曲线和加减两个标准差的带状域以及预测的估计值。
注意:预测值被保存在GDPFD序列中。
因为GDPFD序列是一个标准的EViews序列,所以可以利用序列对象的所有标准工具来检验预测结果。
我们可以通过绘出曲线图来检查实际值与拟合值。
这是从1947:02到1995:01整个时期上的动态预测。
对每个时期,前一个GDP(-1)的预测值在形成后期的GDP预测值时被使用。
注意,实际值与拟合值图形的细微差别:要对一个序列进行一步向前预测(静态预测),单击方程工具栏中的Forecast键,然后选择Static进行预测。
EViews将显示预测结果为:我们可以比较GDP的实际值和动态预测拟合值GDPFD、静态预测拟合值GDPFS,可以看出一步向前静态预测比动态预测要更为准确,因为对每个时期,在形成GDP的预测值时使用的是GDP(-1)的实际值。
§16.2 预测基础EViews将预测结果在Forecast name项命名并存储。
我们把该序列称为预测序列。
预测样本中指定了EViews将计算出的拟合值和预测值的结果期间。
如果出现不能预测的情况,将返还缺失值NA,在有些情况下,为了防止含有缺失值的预测,EViews会自动进行缺失值调整。
值得注意的是预测样本可能与估计方程所使用的样本观察值发生重叠,也可能没有重叠。
对于没有包含在预测样本中的数值,会有两种选择。
作为缺省,EViews 将用其因变量的实际值充填,另一种是不选择Insert actuals for out-of-sample,预测样本外的数值将都赋予“NA”。
于是,这些规则的结果是被预测序列中的所有数据在预测过程中将被覆盖,被预测序列的已存值将会丢失。
一、计算预测值对预测样本中的每一观察值,EViews 利用估计参数、等式右边的外生变量、以及滞后内生变量和残差的实际值或估计值来计算因变量的拟合值。
构造预测值的方法取决于估计模型和用户设定的环境。
为说明预测过程,我们从一个简单的线性回归模型开始,等式右边不含滞后内生变量和ARMA 项。
假设给出如下方程列表,并做出估计:y c x z选择Forecast ,给定预测期间,然后单击OK 。
对预测期内的每一观察值,EViews 将用估计出的参数和回归因子x ,z 的对应值计算y 的拟合值:t t t z c x c c y)3(ˆ)2(ˆ)1(ˆˆ++=对预测期内的所有观测值,应该确保等号右边外生变量的值有效。
如果外二、缺失值调整预测值被赋值为NA有两种情况:1、只要有一个解释变量有缺失值;2、只要有一个解释变量的样本超出了工作文件的范围,这还包括在AR 模型中的隐含误差项。
在公式中没有动态成分(如没有滞后内生变量或ARMA误差项)时,被预测序列中的缺失值并不影响随后的预测值。
如果有了动态成分,即使是被预测序列中的一个缺失值也将会影响到以后所有的预测值。
EViews将对方程中滞后变量的预测样本起始点进行调整,直到获得有效的预测值。
例如,假设利用下面的方程进行动态预测:y c y(-1)ar(-1),如果指定工作文件的起点为预测样本的起点,EViews将向后调整两个预测样本观测值,并且使用滞后变量前面的预测值。
三、预测误差与方差假设真实的模型由下式给定:这里是独立同分布,均值为零的随机扰动项,是未知参数向量。
下面我们放松是独立的限制。
生成y 的真实模型我们尚不知道,但我们得到了未知参数的估计值b 。
设误差项均值为零,可以得到y 的预测方程:ββb x yt t '=ˆ该预测的误差为实际值与预测值之差b x y e '-=tt t x y εβ+'=t εtε1.残差不确定误差的第一种来源是由残差或新息(innovation)的不确定引起的,因为方程中的新息在整个预测区间未知,被设为它们的期望值。
在残差期望值为零时,单个残差值非零;单个误差的方差越大,预测中的总体误差越大。
测量方差的标准方式是回归标准差(在输出方程中用“S.E.of regression ”表示)。
残差不确定通常是预测误差的主要来源。
在动态预测中,因为滞后因变量和由滞后随机变量构成的ARMA 项的存在,使得新息不确定性更为复杂。
EViews 也将这些值设为它们的期望值,这与实际值有随机偏差。
含有滞后因变量和ARMA 项的预测在后面详细讨论。
t εtε2.系数不确定预测误差的第二个来源是系数的不确定。
方程中系数b的估计值是由随机情况下的真实系数β导出的。
求出的回归方程中估计系数的标准差是用来衡量估计系数精确度的一个指标。
系数不确定的影响程度由外生变量决定。
因为在计算预测值时,要用估计系数乘以外生变量X,外生变量超出它们的均值越多,预测的不确定性越大。
3.预测可变性预测可变性由预测标准差来衡量。
对一个没有滞后因变量或ARMA 项的单方程,预测标准差由下式计算:tt x X X x s se forecast )(1''+=式中s 为回归标准差。
标准差可以说明随机误差项和系数的不确定性。
用最小二乘法估计的线性回归模型做出的点预测是最优的,因为在由线性无偏估计做出的预测中它的预测方差最小。
此外,如果随机误差项服从正态分布,则预测误差服从t-分布。
如果赋给预测标准差一个名字,EViews 将在工作文件中计算并保存一个预测标准差序列。
可以利用它形成预测的置信区间。
如果选择Do graph 项输出,EViews 将显示预测值及加减两个标准差的带状图。
这两个标准差带在95%的置四、预测效果评估假设我们利用1947:02~1995:01的样本数据估计出的GDP方程,然后分别进行1947:02~1995:01和1994:01~1995:01关于GDP的动态预测。
如果选中Forecast evaluation (预测效果评估),EViews将显示预测效果评估的统计结果表:§16.3 含有滞后因变量的预测在方程等号的右边出现滞后变量时,预测变得更为复杂。
例如,我们可以在原来的形式后面引入y的一阶滞后:y c x z y(-1)并且单击Forecast键,和前面一样在对话框中写入序列名。
不过我们还面临着对方程等号右边y的滞后值如何进行估计的问题。
这里提供了两种方法:动态预测与静态预测。
一、动态预测如果选择动态预测,EViews将从预测样本的起始日期开始,对y进行多步预测。
对如上只指定一个滞后变量的情况:二、静态预测静态预测对因变量进行一系列的一步向前预测:EViews 采用滞后内生变量的实际值,通过下式对k =0 , 1 , 2 , … ,h 计算每一个预测值:k T k T k T k T y c z c x c c y++++++++++=)4(ˆ)3(ˆ)2(ˆ)1(ˆˆ111静态预测要求外生变量和任何滞后内生变量在预测样本中的观测值可以获得。
如上,如果需要,EViews 将对预测样本进行调整以解释滞后变量的前期样本。
如果没有某期数据,对应该期的预测值为NA 。
它并不会对以后预测产生影响。
三、静态预测与动态预测的对比这两种方法在多期预测中生成的第一期结果相同。
因此,两个预测序列(一个静态的和一个动态的)在预测样本中的第一个值相同。
只有在存在滞后因变量或ARMA 项时,两种方法以后各期的值才不同。
§16.4含有ARMA误差项的预测用含有ARMA项的方程进行预测会更为复杂。
如果方程中包含AR或MA项,需要了解EViews是如何利用滞后残差进行预测的。
一、结构预测EViews以默认的方式利用估计出的ARMA结构预测残差值,如下所述:对有些类型的工作,可能希望ARMA误差项总为零。
如果选择Structural (ignore ARMA),选择结构预测,EViews在计算预测值时将假设误差总为零。
如果被估计方程没有ARMA项,该选项对预测没有影响。
二、含有AR误差项的预测对包含AR误差项的方程,EViews将把该方程的残差预测加到基于解释变量的结构模型预测中。
为计算残差的估计,EViews需要滞后残差值的估计或实际值。
