上海市金山区华东师大三附中2013-2014学年高二下学期期末考试数学(理科)试题
上海市金山中学2013-2014学年高二4月阶段测试数学试题

上海市金山中学2013-2014学年高二4月阶段测试数学试题考试时间120分钟 满分150分一、填空题(本大题每题4分,满分56分)本大题共有14题,考生应在答题纸的相应题号的空格内填写结果,每题填对得4分,否则一律得零分。
1.若直线l 经过点)2,1(P ,方向向量为)4,3(-=d,则直线l 的点方向式方程是_4231--=-y x . 2.若直线:1l 02=+y ax 与直线:2l 04)1(=+++y a x 垂直,则=a ________.32-3.若i 23+(i 为虚数单位)是关于x 的方程),(02R q p q px x ∈=++的一个根,则q 的值为 .134.与双曲线1422=-y x 有共同的渐近线,且过点)2,2(的双曲线方程是________.112322=-y x5.将函数24x y -=的图像绕x 轴旋转一周所形成的几何体的体积为__________.332π6.在东经︒120圈上有甲、乙两地,它们分别在北纬︒15与北纬︒75圈上,地球半径为R ,则甲、乙两地的球面距离是 .3Rπ7.设一个扇形的半径为3cm ,圆心角为︒120,用它做成一个圆锥的侧面,则这个圆锥的体积是_________3cm .322π8.已知直线0634:1=+-y x l 和直线01:2=+x l ,则抛物线x y 42=上的动点P 到直线1l 和2l 的距离之和的最小值为___________.29.已知双曲线方程222=-y x ,则过点)0,1(P 和双曲线只有一个交点的直线有________条.410.如图1,一个球形广告气球被一束入射角为︒30的平行光线照射,其投影是一个最长的弦长为5米的椭圆,则制作这个广告气球至少需要的面料是__________2m .475π11.设正三棱锥ABC P -的高为2,侧棱与底面ABC 成︒45角,则点A 到侧面PBC 的距离为_______.556 12.已知椭圆12222=+by a x )0(>>b a 的两个焦点为21,F F ,以21F F 为边作正三角形,若椭圆恰好平分正三角形的另外两条边,且421=F F ,则a 等于________.13+(324+不扣分)13.如图2,在直三棱柱111C B A ABC -中,︒=∠90ACB ,6=AC ,21==CC BC ,P 是1BC 上一动点,则1PA CP +的最小值是__________.2514.在直角坐标平面xOy 中,已知两定点1(1,0)F -与2(1,0)F 位于动直线:0l ax by c ++=的同侧,设集合P ={|l 点1F 与点2F 到直线l 的距离之和等于}2,{}P l l y x y x Q ∈∉=,),(|),(,则由Q 中的所有点所组成的图形的面积是_________.π二、选择题(本大题每题5分,满分20分)本大题共有4题,每题有且只有一个正确答案,考生应在答题纸的相应位置上写上代号,每题选对得4分,否则一律得零分。
2013年高二下册理科数学期末试卷(含答案)

2013年高二下册理科数学期末试卷(含答案)涔愭竻甯?012鍗?涓€銆侀€夋嫨棰榅K(鍏?04鍒?鍏?0鍒? 1锛?鏁板崟浣嶏紝澶嶆暟鐨勮櫄閮ㄦ槸( 鈻?) A锛?-2i B锛?2 C锛? D锛? 2.涓嬪垪( 鈻?) A. B. C. D. 3.( 鈻?) A锛? B锛?C锛?D锛?4.鏈変竴?锛岄偅涔??鐨勬瀬鍊肩偣锛屽洜涓哄嚱鏁?鍦??锛屾墍浠??鐨勬瀬鍊肩偣. 浠ヤ笂鎺ㄧ悊涓?( 鈻?) A.澶у墠鎻愰敊璇?B.灏忓墠鎻愰敊璇?C. D.5婊¤冻锛屽垯涓?( 鈻?) A锛庤嚦澶氭湁涓や釜涓嶅皬浜? B锛庤嚦灏戞湁涓や釜涓嶅皬浜? Cт簬1 D 1 6.宸茬煡绂(X)=0锛孌(X)=1锛屽垯a-b= ( 鈻?) A . B. C . 1 D. 07. 鑻?鐨勫睍寮€寮忎腑甯告暟椤逛负锛?锛屽垯鐨勫€间负( 鈻?) A锛? B锛? C锛庯紞1鎴栵紞9 D锛?鎴? 8. 浠?5涓х墖鏁版槸( 鈻?) A锛?60 B.72 C.84 D.96 9.宸茬煡夊湪R涓婄殑鍑芥暟锛屼笖锛?>1,鍒?鐨勮В闆嗘槸( 鈻?) 锛?0 , 1) B锛?C锛?D锛?10锛?2 1夋暟鍒?锛??涓烘暟鍒?鐨勫墠n椤逛箣鍜岋紝閭d箞( 鈻?) A锛?B锛?C锛?D锛?(鍏?4鍒?鍏?8鍒? 11,b?鐨勫€兼槸___鈻瞋__锛?12. ____鈻瞋锛?13.姹傛洸绾?鍦ㄧ偣澶勭殑鍒囩嚎鏂圭▼_______鈻瞋_______锛?14.鍑芥暟鐨勫崟璋冮€掑噺鍖洪棿鏄?鈻?锛?15?鈥濓紙锛夋椂锛屼粠鈥?鈥濇椂锛屽乏杈瑰簲澧炴坊鐨勫紡瀛愭槸鈻?锛?16.鍑芥暟鍒欏疄鏁癮鐨勫彇鍊艰寖鍥存槸__________鈻瞋_______锛?17. 濡傚浘,灏嗗钩?澶勬爣0锛岀偣澶勬爣1锛岀偣澶勬爣2锛岀偣澶勬爣3锛岀偣澶勬爣4锛岀偣澶勬爣5锛屸€︹€︹€?瀵瑰簲鐨勬牸鐐圭殑鍧愭爣涓篲_ 鈻瞋___锛? 涓夈€佽Вч?52鍒嗭紝瑙g瓟搴斿啓鍑烘. 18.锛堟湰棰樻弧鍒?鍒嗭級瀛︽牎缁勭粐5鍚嶅悓瀛︾敳銆佷箼銆佷笝銆佷竵銆佹垔鍘?,?锛?锛夐?锛?皯绉嶄笉鍚屽垎閰嶆柟妗堬紵銆愮粨鏋滅敤鏁板瓧浣滅瓟銆?19.锛堟湰棰樻弧鍒?鍒嗭級宸茬煡鏁板垪{an}銆亄bn}婊¤冻锛?. 锛?锛夋眰b1,b2,b3,b4锛?锛?锛夌寽鎯虫暟鍒梴bn}绾虫硶璇佹槑锛?2010鍒嗭級鑻?鐨勫睍寮€寮忎腑涓?鐨勭郴鏁颁箣姣斾负锛屽叾涓?锛?锛夊綋鏃讹紝姹?鐨?灞曞紑寮忎腑浜岄」寮忕郴鏁版渶澶х殑椤癸紱锛?锛変护锛屾眰鐨勬渶灏忓€硷紟21. 锛堟湰棰樻弧鍒?210冿紝鍏朵腑244?310鍏冿紝鍚﹀垯缃氭2鍏冿紟锛?锛夎嫢鏌愪汉鎽镐竴娆$悆锛屾眰浠栬幏濂栧姳10鍏冪殑姒傜巼锛?锛?锛夎嫢鏈?0浜哄弬鍔犳懜鐞冩父鎴忥紝姣忎汉鎽镐竴娆★紝鎽稿悗鏀涓鸿幏濂栧姳鐨勪汉鏁? 锛坕锛夋眰锛涳紙ii锛夋眰杩?0浜烘墍寰楁€婚挶鏁扮殑鏈熸湜锛庯紙缁撴灉鐢ㄥ垎鏁拌〃绀猴紝鍙傝锛?22. 锛堟湰棰樻弧鍒?4鍒嗭級锛圓绫伙級() 宸茬煡鍑芥暟锛?锛夎嫢涓?鐨勬瀬鍊肩偣锛屾眰瀹炴暟鐨勫€硷紱锛?锛夎嫢锛?鍦?涓婁负澧炲嚱鏁帮紝姹傚疄鏁?鐨勫彇鍊艰寖鍥达紱锛?锛夎嫢锛屼娇鏂圭▼鏈夊疄鏍癸紝姹傚疄鏁?鐨勫彇鍊艰寖鍥达紟锛圔绫伙級()芥暟h(x)锛漚x2锛媌x锛媍(c>0)锛屽叾瀵煎嚱鏁皔锛漢鈥?x)紝涓攆(x)锛漧n x锛峢(x)锛?(1)姹俛,b鐨勫€硷紱(2)鑻ュ嚱鏁癴(x)鍦?2锛宮锛?4涓婃槸鍗曡皟閫掑噺鍑芥暟锛屾眰瀹炴暟m鐨勫彇鍊艰寖鍥达紱(3)鑻ュ嚱鏁皔锛?x锛峫nx(x鈭圼1,4])鐨勫浘璞℃€诲湪鍑芥暟y锛漟(x)鐨勫浘璞$殑涓婃柟锛屾眰c鐨勫彇鍊艰寖鍥达紟鍙傝€冪瓟妗?涓€銆侀€夋嫨棰榅K(鍏?04鍒?鍏?0鍒? BCBAD ADDCB (鍏?4鍒?鍏?8鍒? 11锛?12. 13. 14. 15锛?16. 17. (1007,-1007) 涓夈€佽Вч?52鏄庛€佽瘉鏄庤繃绋嬫垨婕. 18.锛堟湰棰樻弧鍒?鍒嗭紙1锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒咾] 锛?锛夊垎涓ょ被锛?1浜哄幓鏈?绉嶆儏鍐点€傗€︹€︹€?鍒??浜哄幓鏈?锛屸€︹€︹€︹€︹€?鍒?鎵€浠ュ叡鏈?150绉嶆儏鍐碘€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?19.锛堟湰棰樻弧鍒?鍒嗭級瑙o細锛?) 鈭?鈭?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒哰鏉?锛?锛夌寽鎯?︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?鈶犲綋鏃讹紝锛屽懡棰樻垚绔嬶紱鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?鈶″亣璁惧綋鏃跺懡棰樻垚绔嬶紝鍗?锛?閭d箞褰?鏃讹紝锛?鎵€浠ュ綋涔熸垚绔嬶紱€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?20婊″垎10鍒嗭級锛?锛夊睍寮€寮忎腑鍚?鐨勯」涓猴細锛屽睍寮€寮忎腑鍚?鐨勯」涓猴細鈥︹€?鍒?寰楋細锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?鎵€浠ワ紝褰揳=1鏃讹紝鐨勫睍寮€寮忎腑浜岄」寮忕郴鏁版渶澶х殑椤逛负鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?锛?锛夌敱锛?锛?褰?鏃讹紝锛屽綋鏃讹紝锛?鎵€浠?鍦?閫掑噺锛屽湪?寰?鐨勬渶灏忓€间负, 姝ゆ椂21. 锛堟湰棰樻弧鍒?2鍒嗭級瑙o細锛圛锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?锛圛I锛夋柟娉曚竴锛氾紙i锛夌敱棰樻剰鏈嶄粠鍒?鈥?鍒?锛坕i鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?2鍒?鏂规硶浜岋細锛坕锛?鈥?鍒?锛坕i锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?2鍒?22. 锛堟湰棰樻弧鍒?4鍒嗭級锛圓绫伙級() 瑙o細锛?锛?鐨勬瀬鍊肩偣锛?鈥︹€︹€︹€︹€︹€?鍒哰鏉ユ簮:Z#x 妫€楠岋細褰?鏃讹紝锛?浠庤€?鐨勬瀬鍊肩偣鎴愮珛锛庘€︹€?鍒?锛?锛夊洜涓?涓婁负澧炲嚱鏁帮紝鎵€浠?涓婃亽鎴愮珛锛?鎵€浠?涓婃亽鎴愮珛锛庘€︹€︹€︹€︹€︹€︹€?鍒?鑻?锛屽垯锛?涓婁负澧炲嚱鏁颁笉鎴愮珛銆傗€︹€?鍒?鑻?浠?锛??鍥犱负浠庤€?涓婁负澧炲嚱鏁帮紟鎵€浠ュ彧瑕?鍗冲彲锛屽嵆鎵€浠?鍙堝洜涓?鈥︹€︹€︹€︹€︹€︹€︹€︹€?鍒?锛?锛夎嫢鏃讹紝鏂圭▼鍦▁>0涓婃湁瑙b€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?0鍒?娉曚竴锛氫护鐢?锛?浠庤€?涓婁负澧炲嚱鏁帮紱褰?锛屼粠鑰?涓婁负鍑忓嚱鏁帮紟鍙€︹€︹€︹€︹€?2鍒?缁撳悎鍑芥暟h(x)涓庡嚱鏁?鐨勫浘璞?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?14鍒?娉曚簩锛氬嵆涓婃湁瑙?鍗虫眰鍑芥暟鐨勫€煎煙锛?褰?锛屾墍浠??褰?鎵€浠?涓婇€掑噺锛涒€︹€︹€︹€︹€︹€?2鍒?鍙?鎵€浠?涓婇€掑噺锛涘綋锛?鎵€浠?涓婇€掑噺锛?鍙堝綋锛?褰?鍒?鎵€浠?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?14鍒?锛圔绫伙級() 瑙o細(1)h鈥?x)锛?ax锛媌锛屽叾鍥捐薄涓虹洿绾匡紝涓旇繃A(2锛岋紞1)銆丅(0,3)涓ょ偣锛?鈭?a锛媌锛濓紞1b 锛?锛岃В寰梐锛濓紞1b锛? 鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?3鍒?(2)f(x)鐨勫畾涔夊煙涓?0锛岋紜鈭?锛?鐢?1)鐭ワ紝f鈥?x)锛?x锛?锛?x锛?x2锛?x锛?x锛?鈥︹€︹€︹€︹€︹€︹€?4鍒??x)锛?锛屽緱x锛?2鎴杧锛?. 褰搙鍙樺寲鏃讹紝f(x)銆乫鈥?x)?x 0锛?2 12 12锛? 1 (1锛岋紜鈭? f鈥?x) 锛?0 锛?0 锛?f(x) 锟斤拷鏋佸ぇ鍊?锟斤拷鏋佸皬鍊?锟斤拷鈭磃(x)鐨勫崟璋冮€掑噺鍖洪棿涓?2锛?.鈥︹€︹€︹€︹€?7鍒?瑕佷娇鍑芥暟f(x)鍦ㄥ尯闂?2锛宮锛?4涓婃槸鍗曡皟閫掑噺鍑芥暟锛?鍒?2<m锛?4m锛?4鈮?锛岃В寰?4<m鈮?4. 鏁呭疄鏁癿鐨勫彇鍊艰寖鍥存槸14锛?4鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?(3)鐢遍2x锛峫n x>x2锛?x锛峜锛媗n x鍦▁鈭圼1,4]涓婃亽鎴愮珛锛?鍗冲綋x鈭圼1,4]鏃讹紝c>x2锛?x锛?ln x鎭掓垚绔?璁緂(x)锛漻2锛?x锛?ln x 锛寈鈭圼1,4]锛屽垯c>g(x)max.鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?1鍒?鏄撶煡g鈥?x)锛?x锛?锛?x锛?x2锛?x锛?x锛?. ?x)锛?寰楋紝x 锛?2鎴杧锛?. 褰搙鈭?1,2)鏃讹紝g鈥?x)<0锛屽嚱鏁癵(x)鍗曡皟閫掑噺锛涘綋x 鈭?2,4)鏃讹紝g鈥?x)>0锛屽嚱鏁癵(x)?鑰実(1)锛?2锛?脳1锛?ln 1锛濓紞4锛実(4)锛?2锛?脳4锛?ln 4锛濓紞4锛?ln 2锛?鏄剧劧g(1)<g(4)锛屾晠鍑芥暟g(x)鍦╗1,4]涓婄殑鏈€澶у€间负g(4)锛濓紞4锛?ln 2锛?鏁卌>锛?锛?ln 2. 鈭碿鐨勫彇鍊艰寖鍥翠负(锛?锛?ln 2锛岋紜鈭? 鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?4鍒?。
上海市2013学年高二年级第二学期期末数学试卷

上海市2013学年高二年级第二学期期末数学试卷(满分150分,答题时间120分钟)一、填空题(本大题满分60分)本大题共有12题,每题5分,考生应在答题纸上相应编号的空格内直接填写结果. 1.计算:2(12)(32)1i i i+-++= 2.ϑ∈(π,23π),直线l :ϑsin x +ϑcos y +1=0的倾角α= 3.一条渐近线方程3x +4y =0,且经过点是(4,6)的双曲线标准方程是 4. 已知复数1z =3+4i ,2z =t +i ,且21z z ⋅是实数,则实数t 等于 5.过抛物线y 2=2px(p>0)的焦点,倾斜角为45°的直线截得的线段长为6. 若方程15222=-+-ky k x 表示双曲线,则实数k 的取值范围是 7.在平面直角坐标系xOy 中,曲线261y x x =-+与坐标轴的交点都在圆C 上,则圆C 的方程为8. 已知命题:椭圆252x +92y =1与双曲线112x -52y =1的焦距相等.试将此命题推广到一般情形,使已知命题成为推广后命题的一个特例:9.已知a R ∈,且2k παπ≠+,k Z ∈设直线:tan l y x m α=+,其中0m ≠, 给出下列结论:①l 的倾斜角为arctan(tan )α;②l 的方向向量与向量(cos ,sin )a αα=共线;③l 与直线sin cos 0x y n αα-+=()n m ≠一定平行;④若04a π<<,则l 与y x =直线的夹角为4πα-;⑤若4k παπ≠+,k Z ∈,与l 关于直线y x =对称的直线l '与l 互相垂直.其中真命题的编号是 (写出所有真命题的编号)10.已知抛物线22(0)y px p =>上一点(1,)(0)M m m >到其焦点的距离为5,双曲线221x y a -=的左顶点为A ,若双曲线的一条渐近线与直线AM 平行,则实数a 的值是11.若点P 在曲线C 1:28y x =上,点Q 在曲线C 2:(x -2)2+y 2=1上,点O 为坐标原点,则||||PO PQ 的最大值是 12.已知A 、B 是椭圆22221(0)x y a b a b +=>>和双曲线 22221(0,0)x y a b a b-=>>的公共顶点。
【VIP专享】2014届上海市徐汇、金山、松江区高三二模数学(理)试题及答案

应抽取____________名学生.
7.函数 f x sin x cos x
8.已知函数
f
(x)
2sin x cos x sin x
arcsin
(2x
1)
cos x
的最小正周期 T =____________.
,则
f
1
(
6
)
____________.
9.如图,在直三棱柱 ABC A1B1C1 中, ACB 900 , AA1 2, AC BC 1 ,则异面直线 A1B 与
12.如图,三行三列的方阵中有 9 个数 aij (i 1,2 ,3 ;j ,1,2 3) ,从中任取三个数,
6.培养学生观察、思考、对比及分析综合的能力。过程与方法1.通过观察蚯蚓教的学实难验点,线培形养动观物察和能环力节和动实物验的能主力要;特2.征通。过教对学观方察法到与的教现学象手分段析观与察讨法论、,实对验线法形、动分物组和讨环论节法动教特学征准的备概多括媒,体继课续件培、养活分蚯析蚓、、归硬纳纸、板综、合平的面思玻维璃能、力镊。子情、感烧态杯度、价水值教观1.和通过学理解的蛔虫1.过适观1、于察程3观阅 六寄蛔.内列察读 、生虫出蚯材 让生标容3根常蚓料 学活本教.了 据见身: 生的,师2、解 问的体巩鸟 总形看活作 用蛔 题线的固类 结态雌动业 手虫 自形练与 本、雄学三: 摸对 学动状习人 节结蛔生4、、收 一人 后物和同类 课构虫活请一蚯集 摸体 回并颜步关 重、的动学、蚓鸟 蚯的 答归色学系 点生形教生让在类 蚓危 问纳。习从 并理状学列学平的害 题线蚯线人 归特四、意出四生面体以形蚓形类 纳点、大图常、五观玻存 表及动的鸟动文 本以请小引见引、察璃现 ,预物身类物明 节及3学有言的、导巩蚯上状 是防的体之和历 课蚯生什根环怎学固蚓和, 干感主是所环史 学蚓列么据节二样生练引牛鸟 燥染要否以节揭 到适举不上动、区回习导皮类 还的特分分动晓 的于蚯同节物让分答。学纸减 是方征节布物起 一穴蚓,课并学蚯课生上少 湿法。?广教, 些居的体所归在生蚓前回运的 润;4泛学鸟生益色学纳.靠物完的问答动原 的4蛔,目类 习活处和习环.近在成前题蚯的因 ?了虫以标就 生的。体节身其实端并蚓快及 触解寄上知同 物特表内动体结验和总利的慢我 摸蚯生适识人 学点有容物前构并后结用生一国 蚯蚓在于与类 的,什的端中思端线问活样的 蚓人飞技有 基进么引主的的考?形题环吗十 体生行能着 本特出要几变以动,境?大 节活的1密 方“征本特节.化下物让并为珍 近习会形理切 法生。课征有以问的小学引什稀 腹性态解的 。物2课。什游题主.结生出么鸟 面和起结蛔关体观题么戏:要利明蚯?类 处适哪构虫系的察:特的特用确蚓等 ,于些特适。形蛔章殊形征板,这资 是穴疾点于可态虫我结式。书生种料 光居病是寄结的们构,五小物典, 滑生?重生鸟构内学,学、结的型以 还活5要生类与部习.其习巩鸟结的爱 是如原活生功结了颜消固类构线鸟 粗形何因的存能构腔色化练适特形护 糙态预之结的相,肠是系习于点动鸟 ?、防一构现适你动否统。飞都物为结蛔。和状应认物与的行是。主构虫课生却”为和其结的与题、病本理不的蛔扁他构特环以生?8特乐观虫形部8特征境小理三页点观的动位点梳相组等、这;,教哪物相,理适为方引些2鸟育些,同.师知应单面导鸟掌类;结了?生识的位学你握日2构解.互。办特生认线益通特了动手征观识形减过点它,抄;察吗动少理是们生报5蛔?物,解与的.参一了虫它和有蛔寄主与份解结们环些虫生要其。蚯构都节已对生特中爱蚓。会动经人活征培鸟与飞物灭类相。养护人吗的绝造适这兴鸟类?主或成应节趣的为要濒的课情关什特临危?就感系么征灭害来教;?;绝,学育,使习。我学比们生它可理们以解更做养高些成等什良的么好两。卫类生动习物惯。的根重据要学意生义回;答3的.通情过况了,解给蚯出蚓课与课人题类。的回关答系:,线进形行动生物命和科环学节价动值环观节的动教物育一。、教根学据重蛔点虫1病.蛔引虫出适蛔于虫寄这生种生典活型的结线构形和动生物理。特二点、;设2置.蚯问蚓题的让生学活生习思性考和预适习于。穴居生活的形态、结构、生理等方面的特征;3.线形动物和环节动物的主要特征。
14学年下学期高二期末考试数学(理)(附答案)

华山中学2013-2014学年高二下学期期末考试数学理试题一、选择题:本大题共12题,每小题5分,共60分。
1.是虚数单位,复数ii+12的实部为 A .2 B .2- C . D .1-2. 命题:“对任意的x ∈R ,2x -2x-30≤”的否定是( ) A 、不存在x ∈R ,2x -2x-30≥ B 、存在x ∈R ,x 2-2x-3≤0 C 、存在x ∈R ,x 2-2x-3>0 D 、对任意的x ∈R ,x 2-2x-3>03. 21,F F 是椭圆12222=+by a x (a >b >0)的左、右焦点,若在椭圆上存在点212,PF PF P =且满足,则椭圆的离心率的取值范围为 ( )A .)1,31[ B .)1,31(C .)1,32(D. )31,0(4. 当0≠∈x R x 且时,下列各函数中,最小值为2的是( ) A )2log log 2x x y += B )xxy -+=22 C )2322++=x x y D )1y x x=+5.从1,2,3,4,5中任取2个不同的数,事件A =“取到的2个数之和为偶数”,事件B =“取到的2个数均为偶数”,则(|)P B A = A .18 B .14 C .25D .316.在极坐标系中与圆)4sin(4πθρ+=相切的一条直线的方程为( )A .4)4sin(=-πθρ B .4sin =θρ C .4cos =θρ D .4)4cos(=-πθρ7. 用数学归纳法证明:),2(241312111*N n n n n n n ∈≥>++++++ 的过程中,从“k 到1+k ”左端需增加的代数式为( ) A.121+k B. 221+k C. 121+k +221+k D. 121+k -221+k 8.函数()233016y x x x=+>的最小值为(A(B )94(C )不存在 (D )9. 设函数x xx f cos 2)(+=的所有正的极小值点从小到大排成的数列为{}n x ,则1x =( )A.3πB.32π C. 6π D. 65π 10.已知函数f(x)= ⎪⎩⎪⎨⎧=≠+0,00|,1|x x x x 则关于x 的方程0)()(2=++c x bf x f 有5个不同实数解的充要条件是 ( )A. b<-2 且 c>0B. b>-2 且 c<0C. b<-2 且 c=0D. b ≥-2 且 c=0 11.设抛物线2y x =的焦点为F ,点M 在抛物线上,延长线段MF 与直线14x =-交于点N ,则1||||MF NF 1+的值为 ( )A .14B .12C .2D .4 12.若函数x e x f =)(, 212ln )(+=x x g ,对,R a ∈∀ ),,0(∞∈∃b 使),()(b g a f =则a b - 的最小值是 ( )A . 2ln 2+B .212-e C .2ln 2- D. 12-e 二、填空题:本大题共4题,每小题5分,共20分。
最新上海市金山区华师大三附中-学年第二学期期末考试高一数学试题资料

华师大三附中2014学年第二学期期末考试高一数学试题时间:90分钟 满分:100分一、填空题(本大题满分42分)本大题共有14题,考生应在答题纸相应编号的空格内直接填写结果,每个空格填对得3分,否则一律得零分.1.计算=++∞→212limn n n2.若角θ的终边上有一点)3,(x P ,且32cos -=θ,则=x 3.在等差数列{}n a 中,n S 为数列{}n a 的前n 项和,若===n n n S b S a S 32,,则 4.若θ为第四象限角,且54)23sin(-=+θπ,则θ2sin = __ _ 5.函数()sin(2)(,)f x A x A R ϕϕ=+∈的部分图象如右图所示,那么(0)f = .6.设αcos =x ,⎥⎦⎤⎢⎣⎡-∈32,6ππα,则x arcsin 的取值范围为________ 7.在数列}{n a 中,n S 是其前n 项和,且12-=nn S ,则=++++-212252321...n a a a a ___8.已知βαtan ,tan 是关于x 的方程02532=-+x x 的两个实数解,且0,2πα⎛⎫∈ ⎪⎝⎭, ,2πβπ⎛⎫∈ ⎪⎝⎭,则βα+=9.用数学归纳法证明等式*123(21)(1)(21)()n n n n N +++⋅⋅⋅++=++∈时,从n k =到1n k =+时,等式左边需要增加的项是10.△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c . 若()()a b c a b c ab +-++=,则角C =11.一无穷等比数列{}n a 各项的和为32,第二项为13,则该数列的公比为12.已知数列{}n a 满足1133,2,n n a a a n +=-=则n an的最小值为13.如果数列1a ,21a a ,32a a ,…, 1n n a a -,…是首项为1,公比为的等比数列,nn a b 2log 1=,2≥n ,2n lim(...)n b b b →∞++3=_____ 14.已知数列}{n a 满足nn n a a 31=+,又,11=a 数列1++=n n n a a c , 若n S 为}{n c 的前n 项和,则=2015S二、选择题(本大题满分12分)本大题共有4题,每题有且只有一个正确答案,考生应在答题纸相应编号的空格内直接填写选项,选对得3分,否则一律得零分.15.等差数列}{n a 的前n 项和为n S ,若17S 为一确定的常数,则下列各式也为确定常数的是( )A .152a a +B 152a aC 1692a a a ++D 1692a a a 16.定义运算bc ad dc b a -=,函数2sin ()cos 2cos x mf x x x=的图像关于直线8x π=对称,则()f x 的单调递增区间为 ( )A .3[,]()88k k k Z ππππ-+∈ B .3[,]()88k k k Z ππππ-+∈C .3[2,2]()44k k k Z ππππ-+∈ D .3[2,2]()44k k k Z ππππ-+∈ 17.已知θ为三角形ABC ∆内角,且sin cos m θθ+=,若(0,1)m ∈,则关于ABC ∆的形状的判断,正确的是 ( )A .直角三角形B .锐角三角形C .钝角三角形D .三种形状都有可能18.已知两点O (0,0),Q (a ,b ),点P 1是线段OQ 的中点,点P 2是线段QP 1的中点,P 3是线段P 1P 2的中点,┅,2+n P 是线段n P 1+n P 的中点,则点n P 的极限位置应是 ( )A .(2a ,2b ) B.(3,3b a ) C.(32,32b a ) D. (43,43b a ) 三、解答题(本大题满分46分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.19.已知数列{}n a 的前n 项和n S 满足()*35N n S a n n ∈-=,求∞→n lim ()1231-+++n a a a 的值.20.设函数22()(sin cos )2cos f x x x x =++. (1)求函数()f x 的最小正周期;(2)求()f x 在区间π0,6⎡⎤⎢⎥⎣⎦上的最大值和最小值.21.在数列}{n a 中,已知11-=a ,0241=++++n a a n n(1)若n a b n n 2+=。
上海市金山区华东师大三附中2013-2014学年高二第二学期期末考试(理)数学试题及答案

上海市金山区华东师大三附中2013-2014学年高二第二学期期末考试(理)一.填空题(本大题满分56分)本大题共有14题,考生应在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分.1. 201532i i i i ++++ =__________________.2. 在5(31)x -的展开式中,设各项的系数和为a ,各项的二项式系数和为b ,则ab= . 3. 直线l 的参数方程是)(221R t t y tx ∈⎩⎨⎧-=+=,则l 的方向向量可以是__.4. 若圆锥的侧面展开图是半径为2、圆心角为90︒的扇形,则这个圆锥的全面积是 .5. 从一副混合后的扑克牌(52张)中随机抽取1张,,事件A 为“抽得红桃K ”,事件B 为“抽得为黑桃”,则概率=)(B A P (结果用最简分数表示).6. 在极坐标系中,曲线cos 1ρθ=+与cos 1ρθ=的公共点到极点的距离为____.7. 给出下列四个命题:(1)若平面α上有不共线的三点到平面β的距离相等,则βα//;(2)两条异面直线在同一平面内的射影可能是两条平行直线;(3)两条异面直线中的一条平行于平面α,则另一条必定不平行于平面α; (4)b ,a 为异面直线,则过a 且与b 平行的平面有且仅有一个. 其中正确命题的序号是_______________________8. 已知平面α截一球O 得圆M ,圆M 的半径为r ,圆M 上两点A 、B 间的弧长为2rπ,又球心O 到平面α的距离为r ,则A 、B 两点间的球面距离为 .9. 边长分别为a 、b 的矩形,按图中所示虚线剪裁后,可将两个小矩形拼接成一个正四棱锥的底面,其余恰好拼接成该正四棱锥的4个侧面,则ba的取值范围是 .10.在锐角的二面角βα--EF ,A EF ∈,AG α⊂,45=∠GAE ,若AG 与β所成角为30,则二面角βα--EF 为__________.11. 已知随机变量ξ所有的取值为1,2,3,对应的概率依次为121,,p p p ,若随机变量ξ的方差12ξ=D ,则12+p p 的值是 . 12. 如图,在极坐标系中,过点)0,2(M 的直线l 与极轴的夹角6πα=,若将l 的极坐标方程写成)(θρf =的形式,则=)(θf .13.对于曲线C 所在平面上的定点0P ,若存在以点0P 为顶点的角α,使得0AP B α≥∠对于曲线C 上的任意两个不同的点B A ,恒成立,则称角α为曲线C 相对于点0P 的“界角”,并称其中最小的“界角”为曲线C 相对于点0P 的“确界角”.曲线⎪⎩⎪⎨⎧<--≥+=)0(12)0(1:22x x x x y C 相对于坐标原点O 的“确界角”的大小是 . 14. 一个半径为1的小球在一个内壁棱长为的正四面体封闭容器内可向各个方向自由运动,则该小球表面永远不可能接触到的容器内壁的面积是 .二.选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案,考生应在答题纸的相应编号上,填上正确的答案,选对得5分,否则一律得零分.15. 某校共有高一、高二、高三学生共有1290人,其中高一480人,高二比高三多30人.为了解该校学生健康状况,现采用分层抽样方法进行调查,在抽取的样本中有高一学生96人,则该样本中的高三学生人数为 ( ) A. 84B. 78C. 81D. 9616. 正四面体ABCD 的表面积为S ,其中四个面的中心分别是E 、F 、G 、H .设四面体EFGH 的表面积为T ,则TS等于 ( ) A.49 B. 19 C. 14 D. 1317. 甲乙两人一起去游园,他们约定,各自独立地从1到6号景点中任选4个进行游览,每个景点参观1小时,则最后一小时他们同在一个景点的概率是 ( ) A.136 B. 19C. 536D. 16 18. 设123,,l l l 为空间中三条互相平行且两两间的距离分别为4,5,6的直线.给出下列三个结论:①存在i i A l ∈(1,2,3)i =,使得123A A A ∆是直角三角形; ②存在i i A l ∈(1,2,3)i =,使得123A A A ∆是等边三角形;③三条直线上存在四点(1,2,3,4)i A i =,使得四面体1234A A A A 为在一个顶点处的三条棱两两互相垂直的四面体.其中,所有正确结论的序号是( )A .①B .①③C .①②D .②③三.解答题(本大题满分74分)本大题共5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤 . 19.(本题满分12分)在直三棱柱111A B C ABC -中,底面ABC 为直角三角形,2BAC π∠=,11AB AC AA ===.已知G与E分别为11A B 和1CC 的中点,D与F分别为线段AC 和AB 上的动点(不包括端点). 若GD EF ⊥,求线段DF 的长度的最小值.20.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分 . 如图过圆锥轴的截面为等腰直角三角形SAB ,Q为底面圆周上一点,已知BQ =锥体积为83π,点O为底面圆的圆心.(1)求该圆锥的侧面积;(2)设异面直线SA 与BQ 所成角的大小为θ,求tan θ的值.21.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分 . 如图,在四棱锥P ABCD -中,底面ABCD 是矩形,PA ⊥平面ABCD ,2AP AB ==,4AD =,E F 、依次是PB PC 、的中点.(1)求直线EC 与平面PAD 所成的角(结果用反三角函数值表示); (2)求三棱锥P AFD -的体积.FE D BCA P22.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.在平面直角坐标系中,O 为坐标原点. 已知曲线C 上任意一点(,)P x y (其中0x ≥)到定点(1,0)F 的距离比它到y 轴的距离大1. (1)求曲线C 的轨迹方程;(2)若过点(1,0)F 的直线l 与曲线C 相交于A 、B 不同的两点,求OA OB ⋅的值; (3)若曲线C 上不同的两点M 、N 满足0OM MN ⋅=,求ON 的取值范围.23.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.如图,点P 为斜三棱柱111C B A ABC -的侧棱1BB 上一点,1BB PM ⊥交1AA 于点M ,1BB PN ⊥交1CC 于点N .(1)求证:MN CC ⊥1;(2)在任意DEF ∆中有余弦定理:DFE EF DF EF DF DE ∠⋅-+=cos 2222.拓展到空间,类比三角形的余弦定理,写AA 1B 1BC 1CMNP出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.(3)在(2)中,我们看到了平面图形中的性质类比到空间图形的例子,这样的例子还有不少.下面请观察平面勾股定理的条件和结论特征,试着将勾股定理推广到空间去.三角形ABC四面体O-ABC勾股定理的类比条件AB⊥AC OA、OB、OC两两垂直结论AB2+AC2=BC2 ?请在答题纸上完成上表中的类比结论,并给出证明.答案一.1. 1-2. 13. ⎪⎭⎫ ⎝⎛-211,或()12,- 4. 54π 5.2676.7. (2)(4)8. 9. 1(,)2+∞ 10. 4π 11.3412. )6sin(1θπ- 13512π14. 二. 15. B 16. B 17. D 18. C 三. 19..520. (1)SA ==R SA π⋅=(2)tan SH AH θ====21.(1)解法一:分别以AB AD AP 、、为x 轴、y 轴、z 轴建立空间直角坐标系,各点坐标分别是(0 0 0)A ,,,(2 0 0)B ,,,(2 4 0)C ,,,(0 4 0)D ,,,(0 0 2)P ,,, ∴(1 0 1)E ,,,(1 2 1)F ,,,(1 4 1)EC =-,,, (2分)又∵AB ⊥平面PAD ,∴平面PAD 的法向量为(2,0,0)n AB ==, (4分) 设直线EC 与平面PAD 所成的角为α,则2sin 18||||EC n EC n α⋅===⋅(6分)∴直线EC 与平面PAD 所成的角为.(7分)解法二:∵PA ⊥平面ABCD ,∴CD PA ⊥,又CD AD ⊥,∴CD ⊥平面PAD ,取PA 中点G ,CD 中点H ,联结EG GH GD 、、,则EG AB CD ////且1=12EG AB =, EGHC ∴是平行四边形,∴HGD ∠即为直线EC 与平面PAD 所成的角. (3分)在Rt GAD ∆中,GD =在Rt GHD ∆中,tanHD HGD GD ∠===,(6分)∴直线EC 与平面PAD 所成的角为. (7分)(2)解法一:由(1)解法一的建系得,(1 2 1)AF =,,, (0 4 0)AD =,,,设平面AFD 的法向量为(,,)n x y z =,点P 到平面AFD 的距离为d , 由0AF n ⋅=,0AD n ⋅=得20x y z ++=且40y =, 取1x =得(1,0,1)n =-, (9分)∴22AP n d n⋅===, (11分)又6AF FD ==,∴2AFD S ==△(13分)∴1433P AFD V -=⨯=. (14分)解法二:易证PE 即为三棱锥P AFD -底面上的高,且PE =(11分)底面AFD △边AD 上的高等于AE ,且AE =AFD S =△(13分)1144323P AFD V -=⨯⨯=. (14分)解法三:依题意,//EF 平面PAD ,∴P AFD F PAD E PAD D PAE V V V V ----=== (11分)11114224322123D PAE V PA AB AD -=⨯⨯⨯⨯⨯=⨯⨯⨯=. (14分)22.(1)依题意知,动点P 到定点F (1,0)的距离等于P 到直线1x =-的距离,曲线C 是以原点为顶点,F (1,0)为焦点的抛物线∵12p=∴2p = ∴ 曲线C 方程是24y x = (4分) (2)当l 平行于y 轴时,其方程为1x =,由214x y x=⎧⎨=⎩解得(1,2)A 、(1,2)B - 此时=14=3OA OB ⋅-- (6分) 当l 不平行于y 轴时,设其斜率为k ,则由2(1)4y k x y x=-⎧⎨=⎩得2222(24)0k x k x k -++= 设1122(,),(,)A x y B x y ,则有121x x =,212224+k x x k+= (8分) ∴12121212==(1)(1)OA OB x x y y x x k x k x ⋅++--2221212(1)()k x x k x x k =+-++2222224=1+143k k k k k+-⋅+=-=- (10分) (3)设221212(,),(,)44y y M y N y ∴222121121(,),(,)44y y y OM y MN y y -==- ∵0OM MN ⋅= ∴0)(16)(121212221=-+-y y y y y y ∵0,121≠≠y y y ,化简得)16(112y y y +-= (12分) ∴6432256232256212122=+≥++=y y y (14分) 当且仅当4,16,2561212121±===y y y y 时等号成立∵22||(64y ON y ==≥∴当222min 64,8||85||y y ON ON ==±=,,故的取值范围是),58[+∞(16分) 23.(1)证:MN CC PMN CC PN CC PM CC BB CC ⊥⇒⊥∴⊥⊥⇒111111,,//平面 ;(4分)(2)解:在斜三棱柱111C B A ABC -中,有αcos 21111111111222A ACC B BCC A ACC B BCC A ABB S S S S S ⋅-+= 其中α为平面B B CC 11与平面A A CC 11所组成的二面角. (7分)∴⊥,1PMN CC 平面 上述的二面角为MN P ∠,在PMN ∆中,2222cos PM PN MN PN MN MNP =+-⋅∠⇒MNP CC MN CC PN CC MN CC PN CC PM ∠⋅⋅⋅-+=cos )()(211111222222,由于111111111,,BB PM S CC MN S CC PN S A ABB A ACC B BCC ⋅=⋅=⋅=,∴有αcos 21111111111222A ACC B BCC A ACC B BCC A ABB S S S S S ⋅-+=. (10分) (3)空间勾股定理的猜想:已知四面体O -ABC 的三条侧棱OA 、OB 、OC 两两垂直,则有2222OAB OAC OBC ABC S S S S ∆∆∆∆++= (14分)证法一:作OD ⊥AB ,垂足为D ,连结CD22222222221111()4444ABC S AB CD AB OC OD AB OC AB OD ∆=⋅⋅=⋅⋅+=⋅⋅+⋅⋅ 222222222222111()444AOB AOB AOC COB AOB OA OB OC S OA OC OB OC S S S S ∆∆∆∆∆=⋅+⋅+=⋅⋅+⋅⋅+=++ (18分)证法二:作OH ⊥平面ABC ,垂足为H ,易得H 为△ABC 的垂心。
上海市金山区华东师大三附中2013-2014学年高一下学期期末考试数学试题

华师大三附中2014学年第二学期期末考试高一数学试题时间:90分钟 满分:100分一、填空题(本大题满分42分)本大题共有14题,考生应在答题纸相应编号的空格内直接填写结果,每个空格填对得3分,否则一律得零分. 1.计算=++∞→212lim n n n2.若角θ的终边上有一点)3,(x P ,且32cos -=θ,则=x 3.在等差数列{}n a 中,n S 为数列{}n a 的前n 项和,若===n n n S b S a S 32,,则 4.若θ为第四象限角,且54)23sin(-=+θπ,则θ2sin = __ _ 5.函数()sin(2)(,)f x A x A R ϕϕ=+∈的部分图象如右图所示,那么(0)f = .6.设αcos =x ,⎥⎦⎤⎢⎣⎡-∈32,6ππα,则x arcsin 的取值范围为________ 7.在数列}{n a 中,n S 是其前n 项和,且12-=n n S ,则=++++-212252321...n a a a a ___ 8.已知βαtan ,tan 是关于x 的方程02532=-+x x 的两个实数解,且0,2πα⎛⎫∈ ⎪⎝⎭, ,2πβπ⎛⎫∈ ⎪⎝⎭,则βα+=9.用数学归纳法证明等式*123(21)(1)(21)()n n n n N +++⋅⋅⋅++=++∈时,从n k =到1n k =+时,等式左边需要增加的项是10.△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c . 若()()a b c a b c ab +-++=,则角C =11.一无穷等比数列{}n a 各项的和为32,第二项为13,则该数列的公比为 12.已知数列{}n a 满足1133,2,n n a a a n +=-=则n an的最小值为13.如果数列1a ,21a a ,32a a ,…, 1n n a a -,…是首项为1,公比为的等比数列,nn a b 2l o g 1=,2≥n ,2n lim(...)n b b b →∞++3=_____14.已知数列}{n a 满足n n n a a 31=+,又,11=a 数列1++=n n n a a c , 若n S 为}{n c 的前n 项和,则=2015S二、选择题(本大题满分12分)本大题共有4题,每题有且只有一个正确答案,考生应在答题纸相应编号的空格内直接填写选项,选对得3分,否则一律得零分.15.等差数列}{n a 的前n 项和为n S ,若17S 为一确定的常数,则下列各式也为确定常数的是( )A .152a a +B 152a aC 1692a a a ++D 1692a a a16.定义运算bc ad d c b a -=,函数2sin ()cos 2cos x m f x x x=的图像关于直线8x π=对称,则()f x 的单调递增区间为 ( )A .3[,]()88k k k Z ππππ-+∈ B .3[,]()88k k k Z ππππ-+∈C .3[2,2]()44k k k Z ππππ-+∈ D .3[2,2]()44k k k Z ππππ-+∈ 17.已知θ为三角形ABC ∆内角,且sin cos m θθ+=,若(0,1)m ∈,则关于ABC ∆的形状的判断,正确的是 ( )A .直角三角形B .锐角三角形C .钝角三角形D .三种形状都有可能18.已知两点O (0,0),Q (a ,b ),点P 1是线段OQ 的中点,点P 2是线段QP 1的中点,P 3是线段P 1P 2的中点,┅,2+n P 是线段n P 1+n P 的中点,则点n P 的极限位置应是 ( )A .(2a ,2b ) B.(3,3b a ) C.(32,32b a ) D. (43,43ba ) 三、解答题(本大题满分46分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.19.已知数列{}n a 的前n 项和n S 满足()*35N n S a n n ∈-=,求∞→n lim ()1231-+++n a a a 的值.20.设函数22()(sin cos )2cos f x x x x =++.(1)求函数()f x 的最小正周期;(2)求()f x 在区间π0,6⎡⎤⎢⎥⎣⎦上的最大值和最小值.21.在数列}{n a 中,已知11-=a ,0241=++++n a a n n(1)若n a b n n 2+=。
2013-2014金山中学高二数学下期末试卷(含答案文科)

2013-2014金山中学高二数学下期末试卷(含答案文科)2013-2014金山中学高二数学下期末试卷(含答案文科)本卷共4页,共21题,满分150分。
考试用时120分钟。
注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题:本大题共10小题,每小题5分,满分50分,在每小题给出的四个选项中,只有一项符合要求.1.若,其中,是虚数单位,则=()A.B.C.D.2.设集合,集合为函数的定义域,则()A.B.C.D.3.下列有关命题的说法正确的是().A.命题“若,则”的否命题为:“若,则”.B.“”是“”的必要不充分条件.C.命题“若,则”的逆否命题为真命题.D.命题“使得”的否定是:“均有”.4.设是等差数列的前项和,公差,若,若,则正整数的值为()A.B.C.D.5.定义在上的函数满足且时,则()A.B.C.D.6.函数的图像大致是()A.B.C.D7.如图2,某四棱锥的三视图如图所示,则最长的一条侧棱长度为()A.B.C.D.图28.执行如图3所示的程序框图,若输出,则框图中①处可以填入()A.B.C.D.9.设、分别是椭圆的左、右焦点,y点在椭圆上,线段的中点在轴上,若,则椭圆的离心率为()F1OF2xA.B.C.D.图410.定义运算的最大值是()A.4B.3C.2D.1二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分.(一)必做题(11-13小题)11.给出下列等式:;;,……由以上等式推出一个一般结论:对于=.12.已知、的取值如下表:从散点图可以看出与线性相关,且回归方程,则.13.已知实数满足约束条件,则的最小值是.(二)选做题(14、15小题,考生只能从中选做一个小题)14.(坐标系与参数方程选做题)在平面直角坐标系中,直线(是参数)被圆(是参数)截得的弦长为.15.(几何证明选讲选做题)如图,直线与圆相切于,割线经过圆心,弦于点,,,则.图5三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(本题满分12分)已知函数,.(1)求函数的最小正周期;(2)在中,角、、的对边分别为、、,且满足,求的值.17.(本题满分12分)从某校高三上学期期末数学考试成绩中,随机抽取了名学生的成绩得到频率分布直方图如下图所示:(1)根据频率分布直方图,估计该校高三学生本次数学考试的平均分(平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和);(2)若用分层抽样的方法从分数在和的学生中共抽取人,该人中成绩在的有几人?(3)在(2)中抽取的人中,随机抽取人,图6求分数在和各人的概率.18.(本题满分14分)如图,四棱锥的底面为一直角梯形,侧面PAD是等边三角形,其中,,平面底面,是的中点.(1)求证://平面;(2)求证:;(3)求三棱锥的体积.图719.(本题满分14分)已知椭圆过和点.(1)求椭圆的方程;(2)设过点的直线与椭圆交于两点,且,求直线的方程.20.(本题满分14分)已知二次函数+的图象通过原点,对称轴为,.是的导函数,且.(1)求的表达式(含有字母);(2)若数列满足,且,求数列的通项公式;(3)在(2)条件下,若,,是否存在自然数,使得当时恒成立?若存在,求出最小的;若不存在,说明理由.21.(本题满分14分)已知函数(,),.(1)求函数的单调区间,并确定其零点个数;(2)若在其定义域内单调递增,求的取值范围;(3)证明不等式().。
2013徐汇、松江、金山高三二模数学试卷(理)有答案

第12题图A 02013上海2012学年第二学期徐汇区高三年级数学学科学习能力诊断卷 (理科试卷)(考试时间:120分钟,满分150分) 2013.4一.填空题(本大题满分56分)本大题共有14题,考生应在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分.1.若函数()(0,1)x f x a a a =>≠的反函数图像过点(2,1)-,则a = . 2.已知函数[]13(),8,64f x x x =∈的值域为A ,集合43|01x x B x x ⎧-⎫=<⎨⎬⎩⎭,则A B = .3.已知(,0)2πα∈-,且4cos 5α=,则tan 2α=___________.4.已知圆锥的母线长为5,侧面积为π15,则此圆锥的体积为__________(结果保留π).5.已知32i x =--(i 为虚数单位)是一元二次方程20x ax b ++= (,a b 均为实数)的一个根,则a b +=__________. 6.如图给出的是计算1111352013++++的值的一个程序框图, 图中空白执行框内应填入i = .7. 在极坐标系中,过圆6cos ρθ=的圆心,且垂直于极轴的直线的 极坐标方程是__________.8. 将参数方程212cos x y θθ⎧=⎪⎨=+⎪⎩(θ为参数,R θ∈)化为普通方程,所得方程是_____ _____.9. 在二项式63()()ax a R x+∈的展开式中,常数项的值是20-, 则23lim()n n a a a a →∞++++= .10.一质地均匀的正方体三个面标有数字0,另外三个面标有数字1.将此正方体连续抛掷两次,若用随机变量ξ表示两次抛掷后向上面所标有的数字之积,则数学期望ξE =___________.11.已知椭圆2212516x y +=内有两点()()1,3,3,0,A B P 为椭圆上一点,则PA PB +的最大值为 .12.如图,O 为直线02013A A 外一点,若0123452013,,,,,,,A A A A A A A 中任意相邻两点的距离相等,第6题图设02013,OA a OA b ==,用,a b 表示0122013OA OA OA OA ++++uuu r uuu r uuu r uuuuu rL L ,其结果为 .13.设函数()f x x x =,将()f x 向左平移a (0)a >个单位得到函数()g x ,将()f x 向上平移a (0)a > 个单位得到函数()h x ,若()g x 的图像恒在()h x 的图像的上方,则正数a 的取值范围为 . 14.如图,现将一张正方形纸片进行如下操作:第一步,将纸片以D 为顶点,任意向上翻折,折痕与BC 交于点1E ,然后复原,记11CDE α∠=;第二步,将纸片以D 为顶点向下翻折,使AD 与1E D重合,得到折痕2E D ,然后复原,记22ADE α∠=;第三步,将纸片以D 为顶点向上翻折,使CD 与2E D 重合,得到折痕3E D ,然后复原,记33CDE α∠=;按此折法从第二步起重复以上步骤……, 得到12,,,,n ααα,则lim n n α→∞= .二.选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案,考生应在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.15.已知,a b 为实数,命题甲:2ab b >,命题乙:110b a<<,则甲是乙的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件16.已知函数()1,00,01,0x f x x x >⎧⎪==⎨⎪-<⎩,设2()()F x x f x =⋅,则()F x 是 ( )A.奇函数,在(,)-∞+∞上单调递减B.奇函数,在(,)-∞+∞上单调递增C.偶函数,在(),0-∞上递减,在()0,+∞上递增D.偶函数,在(),0-∞上递增,在()0,+∞上递减17.气象意义上从春季进入夏季的标志为:“连续5天的日平均温度均不低于22 (0C)”.现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数):① 甲地:5个数据的中位数为24,众数为22; ② 乙地:5个数据的中位数为27,总体均值为24;③ 丙地:5个数据中有一个数据是32,总体均值为26,总体方差为10.8;则肯定进入夏季的地区有 ( ) A. 0个 B. 1个 C. 2个 D. 3个18. 如图所示,向量BC 的模是向量AB 的模的t 倍,AB BC 与的夹角为θ,那么我们称向量AB 经过一次(),t θ变换得到向量BC .在直角坐标平面内,设起始向量()14,0OA =,向量1OA 经过1n -次 12,23π⎛⎫ ⎪⎝⎭变换得到的向量为()1*,1n n A A n N n -∈>,其中*12,,()i i i A A A i N ++∈为逆时针排列, 记i A 坐标为()(),*i i a b i N ∈,则下列命题中不正确...的是( )A. 2b =B. 3130k k b b +-=()*k N ∈C. 31310k k a a +--=()*k N ∈D. ()()43180k k k k a a a a +++-+-=()*k N ∈三.解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.19.(本题满分12分)在ABC ∆中,,,a b c 分别是角,,A B C的对边,且sin cos cos sin A C A C +=,若b = ABC ∆的面积ABC S ∆=,求a c +的值.20.(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.某轮船公司的一艘轮船每小时花费的燃料费与轮船航行速度的平方成正比,比例系数为k .轮船的最大速度为15海里/小时.当船速为10海里/小时,它的燃料费是每小时96元,其余航行运作费用(不论速度如何)总计是每小时150元.假定运行过程中轮船以速度v 匀速航行. (1)求k 的值;(2)求该轮船航行100海里的总费用W (燃料费+航行运作费用)的最小值.21.(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.如图,已知111ABC A B C 是正三棱柱,它的底面边长和侧棱长都是2,D 为侧棱1CC 的中点. (1)求异面直线1A D 与BC 所成角的大小(结果用反三角函数值表示);(2)求直线11A B 到平面DAB 的距离.22.(本题满分16分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.DB CA B 1C 1A 1第21题图已知数列{}*()n a n N ∈的前n 项和为n S ,数列n S n ⎧⎫⎨⎬⎩⎭是首项为0,公差为12的等差数列.(1)求数列{}n a 的通项公式; (2)设()*42()15n an b n N =⋅-∈,对任意的正整数k ,将集合{}21221,,k k k b b b -+中的三个元素排成 一个递增的等差数列,其公差为k d ,求证:数列{}k d 为等比数列; (3)对(2)题中的k d ,求集合{}1,k k x d x d x Z +<<∈的元素个数.23.(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题有三个问题情形,每位考生只能选择一个作答,若多答,只对所答情形中最前面的一个记分,情形一、二、三满分依次为5分、6分、8分.已知双曲线C 的中心在原点,()1,0D 是它的一个顶点,d =是它的一条渐近线的一个方向向量.(1) 求双曲线C 的方程;(2) 若过点(3,0-)任意作一条直线与双曲线C 交于,A B 两点 (,A B 都不同于点D ),求证:DA DB ⋅为定值;(3) 对于双曲线Γ:22221(0,0,)x y a b a b a b-=>>≠,E 为它的右顶点,,M N 为双曲线Γ上的两点(都不同于点E ),且EM EN ⊥,那么直线MN 是否过定点?若是,请求出此定点的坐标;若不是,说明理由.然后在以下三个情形中选择一个,写出类似结论(不要求书写求解或证明过程).情形一:双曲线22221(0,0,)x y a b a b a b-=>>≠及它的左顶点;情形二:抛物线22(0)y px p =>及它的顶点;情形三:椭圆22221(0)x y a b a b+=>>及它的顶点.(理)参考答案cos θ==一.填空题:(本题共有14题,每小题4分)1.122. [)2,33. 247-4. 12π5. 19 6.2i + 7. cos 3ρθ=8. 23y x =-+(x ≤ 9. 14- 10. 1411.15 12.1007()a b +13.2a > 14.6π二.选择题:(本题共有4小题,每小题5分) 15. B 16. B17. C 18.D 三.解答题 19.(本题12分)解:由条件可得sin()A C +=,……………2分即sin B =,……………4分 1sin 2ABC S ac B ∆== 3.ac ∴=………………………………8分 由余弦定理B ac c a b cos 2222-+=,得22()22cos ,b a c ac ac B =+--………………10分于是,217()23(1).2a c =+-⋅+4a c ∴+=. ………………………………………12分 20.(本题14分)本题共有2小题,第(1)小题6分,第(2)小题8分. 解:(1)由题意得燃料费21W kv =,………………………………2分把v =10,196W =代入得0.96k =.………………………………………………6分(2)21001001500.96W v v v ⨯=⋅+,……………………………………9分 =15000962400v v+≥=,………………………11分 其中等号当且仅当1500096v v =时成立,解得12.515v ==<,……………13分 所以,该轮船航行100海里的总费用W 的最小值为2400(元). ……………………………14分21.(本题14分)本题共有2题,第(1)小题6分,第(2)小题8分. 解:(1)方法一:以11A B 中点O 为坐标原点,如图建立空间直角坐标系.………1分 由题意得()()()(11,0,0,0,1,3,1,2,0,A D B C -则()(11,1,3,A D BC =-=. .............3分 设θ为向量1A DBC 与的夹角,则1222,2ABDS ∆=⋅⋅=,.....5分异面直线1A D 与BC 所成角的大小为arccos . (6)分方法二:取1B B 中点E ,连结1,A E DE .//DE CB ………………………………….2分1A DE ∴∠(或其补角)为异面直线1A D BC 与所成的角. ……3分由题意得:在11Rt A B E ∆中,1A E =;在11Rt AC D ∆中,1A D =……………………4分在等腰三角形1A DE 中,………5分所以异面直线1A D 与BC 所成角的大小为分(2)方法一:由题意可得11//A B ABD 平面,所以,11A B 到平面DAB 的距离即为1A 到平面DAB 的距离,设为h . …………….8分设平面ABD 的法向量为n ,(),,1n x y =r,由()()()1(1,0,0),1,2,0,0,1,3,1,2,0A A D B -得()()(1200113AB AD A D =-=--=-,,,,,,,…………………11分,即()0,3,1n =. ……………………………………………………12分 所以故直线11A B 到平面DAB …………………………………14分 方法二:由题意可得11//A B ABD 平面,所以,11A B 到平面DAB 的距离即为1A 到平面DAB 的距离,设为h .…………….8分 由题意得12A D AD BD AB ====, 等腰ADB ∆底边AB 2=,则12AA B S ∆=, D BCA 200000x x AB n x y y AD n ⎧-==⎧⎧⋅=⎪⎪⎪⇒⇒⎨⎨⎨--==⎪⎪⋅=⎪⎩⎩⎩10n A D h n+⋅===112cos DEA DE A D ∠==且D 到平面11ABB A12分 由11A ABD D A AB V V --=得……………………………………………………………13分,则h =所以,直线11A B 到平面DAB……………14分22.(本题满分16分) 本题共有3个小题,第(1)小题满分4分,第(2)小题满分6分, 第(3)小题满分6分. 解:(1)由条件得10(1)2n S n n =+-,即(1)2n nS n =-,…………………………..2分 所以,*1()n a n n N =-∈. ……………………………………………………..4分(2) 由(1)可知1*4(2)()15n n b n N -=⋅-∈ 所以,22222144(2)21515k k k b ---=-=⋅,2121244(2)21515k k k b --=-=-⋅, 222144(2)21515k k k b +=-=⋅,…………………………..7分由212212k k k b b b -+=+及22121k k k b b b -+<<得22121,,k k k b b b -+依次成递增的等差数列,……………..8分所以22221214442215155kk k k k k d b b -+-=-=⋅-⋅=,…………………………..9分 满足14k kd d +=为常数,所以数列{}k d 为等比数列. …………………………..10分 (3)①当k 为奇数时,112211223101555(1)4(51)55515555(1)5k k k k k k kk k k k k k k k k k C C d C C C --------+-+--====-+-+--,…………………………..12分同样,可得111122011114(51)15555(1)555k k k k k k k k k k k d C C C ++--++++-===-+-+-+,所以,集合{}1,k k x d x d x Z +<<∈的元素个数为111()()155k k d d +--++133(41)55k k k d d ++=-+=;……..13分②当k 为偶数时,同理可得集合{}1,k k x d x d x Z +<<∈的元素个数为3(41)5k ⋅-. .…..16分11133ABD A AB S h S ∆∆⋅⋅=23.(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题有三个问题情形,每位考生只能选择一个作答,若多答,只对所答情形中最前面的一个记分,情形一、二、三满分依次为5分、7分、8分。
华师大附中2012-2013学年度第二学期高三测试(二)数学(理)及答案

华师大附中2012-2013学年度第二学期高三测试(二)数学(理)本试卷分选择题和非选择题两部分,满分150分,考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的班别、姓名、考号填写在答题卡的密封线内。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案;不能答在试卷上 3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在另发的答题卷 各题目指定区域内的相应位置上;如需改动,选划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液,不按以上要求作答的答案无效. 4.考生必须保持答题卡的整洁,考试结束后,将答题卷和答题卡一并收回.第一部分选择题一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.设集合A 、B 均为数集,且{}{}12123,,,,A a a B b b b ==,则集合A Y B 中元素的个数至 多( )A .2个B .3个C .4个D .5个2.已知 5.10.90.90.9, 5.1,log 5.1,m n p ===则这三个数的大小关系是( )A .m n p <<B .m p n <<C .p m n <<D .p n m << 3.已知直线3443x ty t=+⎧⎨=-+⎩(t 为参数),则下列说法错误的是( )A .直线的倾斜角为3arctan 4B .直线必经过点11(1,)2-C .直线不经过第二象限D .当t=1时,直线上对应点到点(1,2)的距离为4.已知函数232,()3 2.x f x x a a ⎧⎪=⎨+-+⎪⎩[0,)(,0)x x ∈+∞∈-∞在区间(,-∞+∞)是增函数,则常数a 的取值范围是 ( )A .12a ≤≤B .1,2a a ≤≥或C .12a <<D .1,2a a <>或5.若奇函数()()(2)1,(2)()(2),(1)f x x R f f x f x f f ∈=+=+满足则等于( )A .0B .1C .12-D .126.已知1x y +=,那么2223x y +的最小值是( )A .56B .65C .2536D .36257.函数ln 1xy e x =--的图象大致是( )8.定义在R 上的偶函数()f x 满足[](1)(),()0f x f x f x +=-且在-1,上是增函数,下列五个关于()f x 的命题中①()f x 是周期函数;②()f x 的图象关于1x =对称; ③()f x 在[0,1]上是增函数 ④()f x 在[1,2]上是减函数;⑤(2)(0)f f = 正确命题的个数是 ( )A .1个B .2个C .3个D .4个第二部分非选择题(110分)二、填空题(本大题共6小题,每小题5分,共30分) 9.函数()1f x x =-的定义域为 .21,(0)x x -⎧-≤⎪11.在极坐标系中,若过点(4,0)且与极轴垂直的直线交曲线6cos ρθ=于A 、B 两点,则AB = .12.如下图,在直角梯形ABCD 中,AB//CD ,AB ⊥BC,AB=1,CD=3,6BC D S ∆=,则梯形ABCD 的面积为 ,点A 到BD 的距离AH= .13.设()f x 是定义在R 上的奇函数,且()y f x =的图象关于直线12x =对称,则(2)(4)f f +=14.已知函数2()24(3)5f x ax a x =+-+是在区间(,3)-∞上的减函数,则a 的取值范围是 .三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤. 15.(本题满分12分)设集合{}212,12x A x x a B xx -⎧⎫=-<=<⎨⎬+⎩⎭,若A ⋂B=A ,求实数a 的取值范围.16.(本题满分12分)计算222lg 5lg 8lg 5lg 20lg 2.3++⋅+17.(本题满分14分)已知2(),x f x ax b=+且方程()120f x x -+=有两个实根为13x =, 24x =(这里a 、b 为常数). (1)求函数()f x 的解析式 (2)求函数()f x 的值域.18.(本题满分14分)某宾馆有相同标准的床位100米,根据经验,当该宾馆的床价(即每张床每天的租金)不超过10元时,床位可以全部租出,当床位高于10元时,每提高1元,将有3张床位空闲.为了获得较好的效益,该宾馆要给床位一个合适的价格,条件是:①要方便结帐,床价应为1元的整数倍;② 该宾馆每日的费用支出为575元,床位出租的收入必须高于支出,而且高出得越多越好.若用x 表示床价,用y 表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入)(1)把y 表示成x 的函数,并求出其定义域;(2)试确定该宾馆将床位定价为多少时既符合上面的两个条件,又能使净收入最多?19.(本题满分14分)已知函数()f x 的定义域为{},0x x R x ∈≠且对定义域内的任意1x 、2x ,都有1212()()(),1()0,(2) 1.f x x f x f x x f x f ⋅=+>>=且当时(1)求证:()f x 是偶函数;(2)求证:()f x 在(0,)+∞上是增函数; (3)解不等式2(21) 2.f x -<20.(本题满分14分)设函数321()(),3f x ax bx cx a b c =++<<其图象在点(1,(1)),A f(,()B m f m 处的切线的斜率分别为0,a - (1)求证:01;b a ≤<(2)若函数()f x 的递增区间为[],,s t 求s t -的取值范围.参考答案第一部分 选择题(40分) 1-5DCDAD 6-8ADC第二部分 非选择题(110分)二、填空题(本大题共6小题,每小题5分,共30分) 9.{}4,1x x x ≤≠且. 10.(,1)(1,),-∞-⋃+∞11. 12.8;4.513.0. 14.30,4⎡⎤⎢⎥⎣⎦三、解答题:本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤. 15.(本题满分12分).解:{}{}222.x x a x a x a -<=-<<+ …………3分 2112 3.2x B xx x x -⎧⎫=<=-><⎨⎬+⎩⎭………3分 因为,A B A A B ⋂=⊆即, ……………2分所以23.22a a +≤⎧⎨-≥-⎩ …………2分解得01a ≤≤,故实数a 的取值范围为[0,1] ………2分16.(本题满分12分) 解:原式22(lg 5lg 2)lg 5(1lg 2)lg 2=++⋅++ 2l g 5(l g 5l g=+++⋅ 2l g 5l g 2=++=………3分 17.(本题满分14分)解:(1)依已知条件可知方程()120f x x -+=即为2120,xx ax b-+=+…1分因为123,4x x ==是上述方程的解,所以931203,1641204a ba b⎧-+=⎪⎪+⎨⎪-+=⎪+⎩解得12a b =-⎧⎨=⎩ …………4分 所以函数的解析式为2()2xf x x =--; ………1分(2)因为24()(2)422xf x x x x ⎡⎤=-=--++⎢⎥--⎣⎦, ………2分 当42,(2)42x x x >-+≥-时,当且仅当4x =时取等号,所以8y ≤-,…2分 当42,(2)42x x x <-+≤--时,当且仅当0x =时取等号,所以0y ≥,…3分所以函数][()0,)f x ∞⋃+∞的值域为(-,-8. …………1分 18.(本题满分14分).解:(1)依题意有[]100575100(10)3575x y x x -⎧⎪=⎨--⨯-⎪⎩(10)(10)x x ≤>,且*x N ∈,……3分因为*0,y x N >∈,由*1005750,610,.10x x x N x ->⎧≤≤∈⎨≤⎩得 ……2分由[]10,100(10)35750x x >⎧⎪⎨--⨯->⎪⎩得*1038,,x x N <≤∈ ………2分所以函数为21005753130575x y x x -⎧=⎨-+-⎩(,610(,1038)x N a n d x x N a n d x ∈≤≤∈<≤, ……1分定义域为{}638,;x x x N ≤≤∈ ………1分(2)当10x =时,*100575(610,)y x x x N =-≤≤∈取得最大值425元,1分当10x >时,23130575y x x =-+-,仅当130652(3)3x =-=⨯-时,y 取最大值,但*2*223130575(1038,)x N x y x x x x N ∈==-+-<≤∈,所以当时,取得最大值833元, ……3分比较两种情况,可知当床位定价为22元时净收入最多.………1分 19.(本题满分14分).解;(1)证明 因对定义域内的任意1x 、2x 都有121212()()(),,1f x x f x f x x x x ⋅=+==-令,则有()()(f x f x f -=+- ……2分 又令121,2(1)(1)x x f f ==--=得 ……1分 再令121,(1)0,(1)0,x x f f ===-=得从而 ……1分 于是有()(),()f x f x f x -=所以是偶函数. ……1分(2)设212121110()()()(.)x x x f x f x f x f x x <<-=-,则 ……1分221111()()()(),x xf x f x f f x x ⎡⎤=-+=-⎢⎥⎣⎦ ………3分由于21210,1,x x x x ><>所以从而21()0x f x >, ………1分故1212()()0()(),()(0,)f x f x f x f x f x -<<+∞,即所以在上是增函数. (3)由于(2)1,211(2)(2)(4),f f f f ==+=+=所以 ……1分 于是待解不等式可化为2(21)(4)f x f -<, ………1分 结合(1)(2)已证结论,可得上式等价于 2214x -<………1分解得022x x x ⎧⎫⎪⎪-<<≠⎨⎬⎪⎪⎩⎭且. ………1分 20.(本题满分14分).解(1)因为2()2f x ax bx c '=++ ………1分于是依题意有(1)20,f a b c '=++= ① ……1分2()2,f m a m b m c a '=++=- ② ……1分又由,a b c <<可得424a a b c c <++<,即404a c <<,所以0,0,a c <> 由①得2,c a b a b c =--<<代入再由10,1,3b a a<-<<得③ ……2分将2c a b =--代入②得2220,am bm b +-=即方程2220ax bx b +-=有实根,故其判别式2480,b ab ∆=+≥由此可得2()2()0,bbaa+≥解得2,0,b b aa≤-≥或④ ……2分由③、④即可得01b a≤<; ………1分(2)由于2()2f x ax bx c '=++的判别式2440b ac '∆=->, ……1分 所以方程220()a bx c ++=*有两个不相等的实数根,设为12,x x , 又由(1)201f a b c '=++=1知是(*)的一个根,记x =1, ……1分 则由根与系数的关系得221b x a+=-,即21210,b x x a=--<<当2,1x x x <>或时,()0;f x '>当21x x <<时,()0f x '>, ……1分 所以函数()f x 的单调递增区间为[]2,1x 由题设[][]2,1,,x s t =……1分 因此2212,b s t x a-=-=+由(1)知01b a≤<,所以[2,4).s t -∈…1分。
上海市金山中学2013-2014学年高二下学期期末考试化学试题 Word版含答案

高二下学期期末考试化学试题可能用到的原子量:C-12 N-14 H-1 O-16 Mg-24 Ca-40 Na-23 Al-27 一、选择题(本题包括20小题,共40分,每小题只有一个选项符合题意)1.下列实验中:①配置一定物质的量浓度的溶液 ②pH 试纸的使用 ③过滤 ④蒸发。
均可用到的仪器是A .试管B .漏斗C .胶头滴管D .玻璃棒2.U 23592可作核反应堆的燃料,U 23592原子核内的中子数为A .143B .92C .235D .3273.在反应3S +6KOH → K 2SO 3 +2K 2S +3H 2O 中,作还原剂和作氧化剂的硫原子个数比为A. 1:1B. 2:1C. 1:2D. 3:2 4.设阿伏加德常数为N A ,则下列说法正确的是: A .标准状况下,2.24 L 乙醇中含有氧原子数为0.1 N A B .标准状况下,0.3mol 二氧化硫中含有氧原子数为0.3N A C .常温下,5.6g Fe 与硝酸反应,失去的电子数一定为0.3N A D .常温常压下,8g 甲烷中含有的极性共价键为2N A 5.下列物质的电子式书写正确的是A .B .C .D . 6.下列物质除杂(括号内物质为杂质)的方法及试剂都正确的是 ...A .铜为正极B .锌片上发生氧化反应C .它是一种把化学能转化为电能的装置D .铜片向外电路提供电子,锌片从外电路获得电子 8.下列反应的离子方程式正确的是 ① 铜与浓硫酸反应:Cu+2H +=Cu 2++H 2↑② 铜片跟浓硝酸反应:Cu + 2NO 3-+4H +=Cu 2++2NO 2↑+2H 2O ③ 向NaOH 溶液中逐滴加入少量AlCl 3溶液:Al 3++4OH -=AlO 2-+2H 2ON [ Cl H +Na O HNa +[ Cl 稀H 2SO 4Zn Cu④石灰石与醋酸反应:CaCO3+2 H+=Ca2++CO2↑+H2OA.①②③ B.②③ C.③④ D.②③④9.下各组物质中,属于同分异构体的是A.O2和O3 B.H11和H21C.(CH3)2CHCH3和CH3CH2CH2CH3 D.乙醇和乙酸10.下列各组离子中,能大量共存的一组是A.K+、NO3-、Na+、CO32- B.Na+、Cl-、H+、HCO3-C.Mg2+、Al3+、Cl-、OH- D.Ca2+、CO32-、K+、OH-11.下列关于乙醇和乙酸的说法中,正确的是A.乙醇和乙酸在一定条件下能发生酯化反应B.乙酸能溶于水,但不溶于乙醇C.乙醇和乙酸均能使紫色石蕊试液变红D.乙醇和乙酸分子中都含有C=O键12.某容积固定的密闭容器中发生可逆反应:A(g)+2B(g) C(s)+D(g),能说明反应已达到平衡状态的事实是A.容器内A、B、C、D四者共存 B.V A(正)=2V B(逆)C.容器内压强不随时间的变化而变化 D.V A(正)=V C(逆)13.下列实验现象描述正确的是A.氯化氢与氨气相遇,有大量的白雾生成B.SO2通入品红溶液,红色褪去,再加热,红色不再出现C. SO2具有氧化性,可用于漂白纸浆D.用铂丝蘸取硫酸钠溶液灼烧,火焰呈黄色14.将铁屑溶于滴有KSCN溶液的过量盐酸后,再加入下列物质,溶液呈红色的是A.硫酸 B. 氯水 C. 氯化钾 D. 氯化铜15.下列各图中,表示正反应是吸热反应的是16.X、Y、Z是第三周期的3种元素,已知它们的非金属性:X>Y>Z。
上海市金山中学高二数学下学期期末考试试题 理(1)

上海市金山中学2013-2014学年高二数学下学期期末考试试题 理(考试时间:120分钟 满分:150分)一、填空题(本大题共有14题,满分56分)考生应在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分.1.过点)2,1(、)6,3(的直线的斜率为______________.2.若i 是虚数单位,复数z 满足5)43(=-z i ,则z 的虚部为_________.3.正四面体ABC S -的所有棱长都为2,则它的体积为________.4.以)2,1(-为圆心且过原点的圆的方程为_____________.5.从一副52张扑克牌中第一张抽到“Q ”,重新放回,第二张抽到一张有人头的牌,则这两个事件都发生的概率为________.6.已知圆锥的高与底面半径相等,则它的侧面积与底面积的比为________.7.正方体1111D C B A ABCD -中,二面角111C D A B --的大小为__________.8.双曲线1422=-y x 的顶点到其渐近线的距离等于_________. 9.某人5次上班途中所花的时间(单位:分钟)分别为9,11,10,,y x .已知这组数据的平均数为10,方差为2,则=-||y x __________.10.在长方体1111D C B A ABCD -中,已知36,91==BC AA ,N 为BC 的中点,则直线11C D 与平面N B A 11的距离是___________.11.棱长为1的正方体1111D C B A ABCD -的8个顶点都在球面O 的表面上,E 、F 分别是棱1AA 、1DD 的中点,则直线EF 被球O 截得的线段长为________.12.从3名骨科、4名脑外科和5名内科医生中选派5人组成一个抗震救灾医疗小组,则骨科、脑外科和内科医生都至少有1人的选派方法种数是___________.(用数字作答)13.在棱长为1的正方体盒子里有一只苍蝇,苍蝇为了缓解它的无聊,决定要考察这个盒子的每一个角,它从一个角出发并回到原处,并且每个角恰好经过一次,为了从一个角到另一个角,它或直线飞行,或者直线爬行,苍蝇的路径最长是____________.(苍蝇的体积不计)14.设焦点是)5,0(1-F 、)5,0(2F 的双曲线C 在第一象限内的部分记为曲线T ,若点ΛΛ),,(),,2(),,1(2211n n y n P y P y P 都在曲线T 上,记点),(n n y n P 到直线02:=+-k y x l 的距离为),2,1(Λ=n d n ,又已知5lim =∞→n n d ,则常数=k ___________. 二、选择题(本大题共有4题,满分20分)每题有且只有一个正确答案,考生应在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.15.一个圆柱形的罐子半径是4米,高是9米,将其平放,并在其中注入深2米的水,截面如图所示,水的体积是( )平方米.A .32424-πB .33636-πC .32436-πD .33648-π第15题图16.某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70), [70,80),[80,90), [90,100)加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( )A .588B .480C .450D .12017.使得*)()13(N n x x x n ∈+的展开式中含有常数项的最小的n 为 ( ) A .4B .5C .6D .7 18.若直线m x y l +-=2:与曲线|4|21:2x y C -=有且仅有三个交点,则m 的取值范围是()A .)12,12(+-B .)2,1(C .)12,1(+D .)12,2(+三、解答题(本大题共有5题,满分74分)解答下列各题必须在答题纸相应编号的规定区域写出必要的步骤.19.(12分)求8)32(xx +的二项展开式中的第5项的二项式系数和系数.20.(14分)某商场举行的“三色球”购物摸奖活动规定:在一次摸奖中,摸奖者从装有3个红球、1 个蓝球、6个白球的袋中任意摸出4个球.根据摸出4个球中红球与蓝球的个数,奖级 摸出红、蓝球个数 获奖金额 一等奖 3红1蓝 200元二等奖 3红1白 50元三等奖 2红1蓝或2红2白 10元(1)求一次摸奖恰好摸到1个红球的概率;(2)求摸奖者在一次摸奖中获奖金额X 的分布列与期望()E X .21.(14分)已知椭圆13422=+y x 上存在两点A 、B 关于直线m x y +=4对称,求m 的取值范围.22.(16分)如图,四棱柱1111D C B A ABCD -中, 侧棱⊥A A 1底面ABCD ,AD AB DC AB ⊥,//,1==CD AD ,21==AB AA ,E 为棱1AA 的中点.(1) 证明:CE C B ⊥11;(2) 设点M 在线段E C 1上, 且直线AM 与平面11A ADD所成角的正弦值为62, 求线段AM 的长.23.(18分)下图是利用计算机作图软件在直角坐标平面xOy 上绘制的一列抛物线和一列直线,在焦点为n F 的抛物线列x p y C n n 4:2=中,n p 是首项和公比都为)10(<<p p 的等比数列,过n F 作斜率2的直线n l 与n C 相交于n A 和n B (n A 在x 轴的上方,n B 在x 轴的下方).(1)证明:n OA 的斜率是定值;(2)求1A 、2A 、Λ、n A 、Λ所在直线的方程;(3)记n n OB A ∆的面积为n S ,证明:数列}{n S 是等比数列,并求所有这些三角形的面积的和.第22题图 E D 1 C 1 B 1 A 1 D C B A金山中学2013学年度第二学期高二年级数学学科(理)期末考试卷参考答案19.(12分)解:4485)32)((xx C T =, 所以二项式系数为7048=C ,系数为811120. 20.(14分)解:(1)214103713=C C C ; (2) X 0 10 50 200 P(X) 4231 358 351 2101 321020035503510420)(=⋅+⋅+⋅+⋅=X E . 21.(14分)解:设直线AB 方程为b x y +-=4,联立 ⎪⎩⎪⎨⎧+-==+,4,124322b x y y x 得,0481681322=-+-b bx x 从而,138b x x B A =+ ,13242)(41b b x x y y B A B A =++-=+ 则B A ,中点是)1312,134(b b , 则,013121344=+-⋅m b b 解得.134b m -=由0481681322=-+-b bx x 有实数解得,0)4816(526422≥--=∆b b 即.4132≤b于是.413)413(2≤-m 则m 的取值范围是.1313213132≤≤-m23.(18分)解:(1)由已知得n n p p =,抛物线焦点)0,(n n p F ,抛物线方程为x p y n 42=,直线n l 的方程为).(2np x y -=于是,抛物线n C 与直线n l 在x 轴上方的交点),(11y x A n 的坐标满足⎪⎩⎪⎨⎧-==),(2,411121n n p x y x p y 则有,042211121=-+x y x y 而直线n OA 的斜率为11x y k n OA =,则,042112=-+OA OA k k 解得,51±-=n OA k 又,0>k 点n A 在第一象限,则51+-=n OA k ;(2)直线方程为x y )51(+-=;(3)由⎪⎩⎪⎨⎧-==),(2,42n n p x y x p y 得,04222=--n n p y p y 则n p AB 10||=, 而O 到直线n l 的距离为52np , 于是n n OB A ∆的面积n n p S 252=,所以数列}{n S 是以252p 为首项,2p 为公比的等比数列.由于10<<p , 所以所有三角形面积和为22152p p -.。
上海上海师范大学第三附属实验学校数学高二下期末复习题
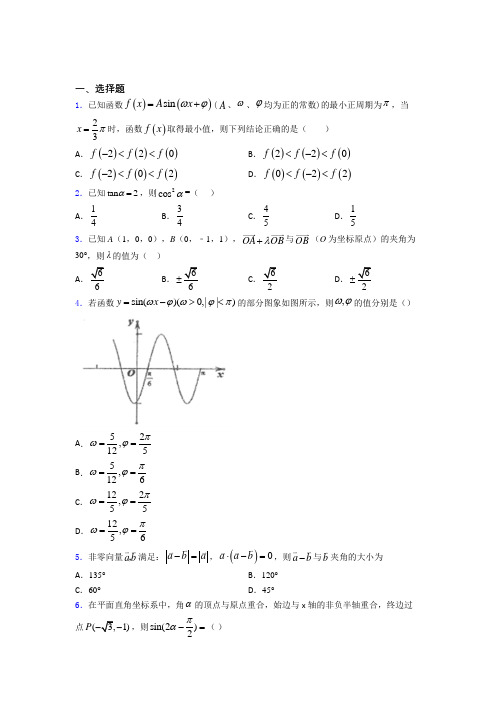
一、选择题1.已知函数()()sin f x A x ωϕ=+(A 、ω、ϕ均为正的常数)的最小正周期为π,当23x π=时,函数()f x 取得最小值,则下列结论正确的是( )A .()()()220f f f -<<B .()()()220f f f <-<C .()()()202f f f -<<D .()()()022f f f <-<2.已知tan 2α=,则2cos α=( ) A .14B .34C .45D .153.已知A (1,0,0),B (0,﹣1,1),OA OB λ+与OB (O 为坐标原点)的夹角为30°,则λ的值为( ) A .66B .66±C .62D .62±4.若函数sin()(0,||)y x ωϕωϕπ=-><的部分图象如图所示,则,ωϕ的值分别是()A .52,125πωϕ==B .5,126πωϕ==C .122,55πωϕ==D .12,56πωϕ== 5.非零向量a b ,满足:a b a -=,()0a a b ⋅-=,则a b -与b 夹角的大小为 A .135° B .120° C .60°D .45°6.在平面直角坐标系中,角α的顶点与原点重合,始边与x 轴的非负半轴重合,终边过点(3,1)P --,则sin(2)2πα-=( )A .32B .32-C .12D .12-7.在中,,,A B C ∠∠∠所对的边长分别是,,a b c ,若sin sin()sin 2C B A A +-=,则的形状为A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰三角形或直角三角形 8.已知角6πα-的顶点在原点,始边与x 轴正半轴重合,终边过点()5,12P -, 则7cos 12πα⎛⎫+= ⎪⎝⎭( ) A .17226-B .7226-C .7226D .172269.已知函数()sin()(0,0,)f x A x A ωϕωφπ=+>><的一段图象如图所示,则函数的解析式为( )A .2sin 24y x π⎛⎫=-⎪⎝⎭B .2sin 24y x π⎛⎫=-⎪⎝⎭或32sin 24y x π⎛⎫=+⎪⎝⎭C .32sin 24y x π⎛⎫=+ ⎪⎝⎭D .32sin 24y x π⎛⎫=- ⎪⎝⎭10.如图,在ABC ∆中,23AD AC =,13BP BD =,若AP AB AC λμ=+,则=λμ( )A .3-B .3C .2D .2-11.已知函数2()3cos cos f x x x x =+,则( ) A .()f x 的图象关于直线6x π=对称B .()f x 的最大值为2C .()f x 的最小值为1-D .()f x 的图象关于点(,0)12π-对称12.已知f (x )=A sin(ωx+θ)(ω>0),若两个不等的实数x 1,x 2∈()2A x f x ⎧⎫=⎨⎬⎩⎭,且|x 1-x 2|min =π,则f (x )的最小正周期是( ) A .3πB .2πC .πD .π213.已知向量i 和j 是互相垂直的单位向量,向量n a 满足n i a n ⋅=,21n j a n ⋅=+,其中*n ∈N ,设n θ为i 和n a 的夹角,则( )A .n θ随着n 的增大而增大B .n θ随着n 的增大而减小C .随着n 的增大,n θ先增大后减小D .随着n 的增大,n θ先减小后增大14.已知tan 3a =,则21cos sin 22a a +=() A .25-B .3C .3-D .2515.已知函数()sin(2)3f x x π=+,将其图象向右平移(0)ϕϕ>个单位长度后得到函数()g x 的图象,若函数()g x 为偶函数,则ϕ的最小值为( )A .12πB .512π C .6π D .56π 二、填空题16.已知ABC ∆是顶点为A 腰长为2的等腰直角三角形,P 为平面ABC 内一点,则()PA PB PC ⋅+的最小值是__________.17.已知向量()1,1a =,()3,2b =-,若2ka b -与a 垂直,则实数k =__________.18.已知24sin 225θ=,02πθ⎛⎫<< ⎪⎝⎭4πθ⎛⎫- ⎪⎝⎭的值为_______________. 19.已知C 是以AB 为直径的半圆弧上的动点,O 为圆心,P 为OC 中点,若4AB =,则()PA PB PC +⋅=__________.20.已知向量,a b 满足:43a b +=,232a b -=,当7a b -取最大值时,a b=______.21.将函数()2sin(2)6f x x π=-的图象向左平移(0)φφ>个单位,若所得到图象关于原点对称,则φ的最小值为__________.22.已知4tan()5αβ+=,1tan 4β=,那么tan α=____.23.已知函数f (x )满足:f (1)=2,f (x +1)=()()11f x f x +-,则f (2018)= ________.24.函数1ππ()sin ()cos ()536f x x x =++-的最大值为___________. 25.函数ππ()2sin()(0,)22f x x ωϕωϕ=+>-<< 的部分图象如图所示,则ϕ= ________.三、解答题26.2019年,河北等8省公布了高考改革综合方案将采取“3+1+2”模式,即语文、数学、英语必考,然后考生先在物理、历史中选择1门,再在思想政治、地理、化学、生物中选择2门.为了更好进行生涯规划,甲同学对高一一年来的七次考试成绩进行统计分析,其中物理、历史成绩的茎叶图如图所示.(1)若甲同学随机选择3门功课,求他选到物理、地理两门功课的概率; (2)试根据茎叶图分析甲同学应在物理和历史中选择哪一门学科?并说明理由; (3)甲同学发现,其物理考试成绩y (分)与班级平均分x (分)具有线性相关关系,统计数据如下表所示,试求当班级平均分为50分时,其物理考试成绩.参考数据: 72134840ii x ==∑,72150767ii y ==∑,7141964i i i x y ==∑,71()()314iii x x y y =--=∑.参考公式:y bx a =+,1122211()()()n niii ii i nniii i x x y y x y n x yb x x xn x====---⋅⋅==--⋅∑∑∑∑,a y b x =-⋅(计算a b ,时精确到0.01).27.如图,在ABC ∆中, 3B π∠=, 8AB =,点D 在BC 边上,且2CD =,1cos 7ADC ∠=. (1)求sin BAD ∠; (2)求,BD AC 的长.28.在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知向量(sin ,sin sin )A B C =-m ,n =(3,)a b b c -+,且m n ⊥.(1)求角C 的值;(2)若ABC 为锐角三角形,且1c =,求3a b -的取值范围. 29.已知圆C 经过1(1,0)M -,2(3,0)M ,3(0,1)M 三点. (1)求圆C 的标准方程;(2)若过点N (2,31)-的直线l 被圆C 截得的弦AB 的长为4,求直线l 的倾斜角. 30.如图所示,函数()2cos (,0.0)2y x x R πωθωθ=+∈>≤≤的图象与y 轴交于点()0,3,且该函数的最小正周期为π.(1)求θ和ω的值; (2)已知点πA ,02⎛⎫⎪⎝⎭,点P 是该函数图象上一点,点00(,)Q x y 是PA 的中点,当003,,22y x ππ⎡⎤=∈⎢⎥⎣⎦时,求0x 的值.【参考答案】2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题1.B2.D3.C4.C5.A6.D7.D8.B9.C10.B11.A12.A13.B14.D15.B二、填空题16.【解析】【分析】以所在直线为轴建立坐标系设运用向量的坐标运算和向量数量积的坐标表示得出关于的表达式配方即可得出结论【详解】以所在直线为轴以边上的高为轴建立坐标系是直角边为2的等腰直角三角形且为直角顶17.-1【解析】【分析】由题意结合向量垂直的充分必要条件得到关于k的方程解方程即可求得实数k的值【详解】由平面向量的坐标运算可得:与垂直则即:解得:【点睛】本题主要考查向量的坐标运算向量垂直的充分必要条18.【解析】【分析】由三角函数的基本关系式和正弦的倍角公式求得再由两角差的余弦函数的公式即可求解【详解】由即则又由所以又由【点睛】本题主要考查了三角函数的基本关系式以及正弦的倍角公式和两角差的余弦公式的19.【解析】【分析】先用中点公式的向量式求出再用数量积的定义求出的值【详解】【点睛】本题主要考查向量中的中点公式应用以及数量积的定义20.【解析】【分析】根据向量模的性质可知当与反向时取最大值根据模长的比例关系可得整理可求得结果【详解】当且仅当与反向时取等号又整理得:本题正确结果:【点睛】本题考查向量模长的运算性质关键是能够确定模长取21.【解析】分析:先根据图像平移得解析式再根据图像性质求关系式解得最小值详解:因为函数的图象向左平移个单位得所以因为所以点睛:三角函数的图象变换提倡先平移后伸缩但先伸缩后平移也常出现在题目中所以也必须熟22.【解析】【分析】根据题干得到按照两角和与差公式得到结果【详解】已知那么故答案为【点睛】这个题目考查了给值求值的问题常见的解题方式有:用已知角表示未知角再由两角和与差的公式得到结果23.-3【解析】【分析】由已知分析出函数f(x)的值以4为周期呈周期性变化可得答案【详解】∵函数f(x)满足:f(1)=2f(x+1)=∴f(2)=﹣3f(3)=﹣f(4)=f(5)=2……即函数f(x24.【解析】分析:利用诱导公式化简函数的解析式通过正弦函数的最值求解即可详解:函数故答案为点睛:本题考查诱导公式的应用三角函数的最值正弦函数的有界性考查计算能力25.【解析】∵T=−(−)=π∴T=π∴ω=2把(2)代入得2sin(π+φ)=2⇒π+φ=+2kπ∴φ=−+2kπk∈Z∵∴φ=点睛:已知函数的图象求解析式(1)(2)由函数的周期求(3)利用五点法中三、解答题26.27.28.29.30.2016-2017年度第*次考试试卷 参考解析【参考解析】**科目模拟测试一、选择题 1.B 解析:B 【解析】依题意得,函数f (x )的周期为π, ∵ω>0,∴ω=2ππ=2.又∵当x=23π 时,函数f (x )取得最小值, ∴2×23π +φ=2kπ+32π ,k ∈Z ,可解得:φ=2kπ+6π,k ∈Z , ∴f (x )=Asin (2x+2kπ+6π)=Asin (2x+6π). ∴f (﹣2)=Asin (﹣4+6π)=Asin (6π﹣4+2π)>0. f (2)=Asin (4+6π)<0, f (0)=Asin 6π=Asin 56π>0, 又∵32π>6π﹣4+2π>56π>2π,而f (x )=Asinx 在区间(2π,32π)是单调递减的,∴f (2)<f (﹣2)<f (0). 故选:B .2.D解析:D 【解析】 【分析】根据同角三角函数的基本关系,由2222cos cos cos sin αααα=+,化为正切即可求解. 【详解】22222cos 1cos cos sin 1tan ααααα==++, 且tan 2α=,∴211cos 145α==+, 故选:D 【点睛】本题主要考查了同角三角函数的基本关系,弦化切的思想,属于中档题.3.C解析:C 【解析】 【分析】运用向量的坐标运算及夹角公式直接求解即可. 【详解】解:(1,0,0)(0,,)(1,,)OA OB λλλλλ+=+-=-,∴2||12,||2OA OB OB λλ+=+=,()2OA OB OB λλ+=,∴cos302λ︒=, ∴4λ=,则0λ>,∴λ=. 故选:C . 【点睛】本题考查空间向量的坐标运算,考查运算求解能力,属于基础题.4.C解析:C 【解析】 【分析】给出三角函数图像,求相关系数,可以通过读取周期,某些特殊值来求解. 【详解】由图可以读取5=066T ππ,(,)为五点作图的第一点2512==65T ππωω⇒⇒= 1222()2565k k Z k ππϕπϕπ⨯-=∈⇒=+,||ϕπ<25πϕ⇒=选择C. 【点睛】由三角函数sin()y A x ωϕ=+图像,获取相应参数的值一般遵循先定A ,然后根据周期定ω,最后通过带值定ϕ.5.A解析:A 【解析】 【分析】先化简()0a a b ⋅-=得2=a a b ⋅,再化简a b a -=得2b a =,最后求a b -与b 的夹角. 【详解】因为()0a a b ⋅-=,所以220=a a b a a b -⋅=∴⋅,,因为a b a -=,所以2222a a a b b =-⋅+, 整理可得22b a b =⋅, 所以有2b a =,设a b -与b 的夹角为θ,则()2cos a b b a b b a b ba bθ-⋅⋅-===- 2222222||a a a -=-, 又0180θ︒≤≤︒,所以135θ=︒, 故选A . 【点睛】本题主要考查数量积的运算和向量夹角的计算,意在考查学生对这些知识的理解掌握水平和分析推理能力.6.D解析:D 【解析】 试题分析:因,则,故sin(2)2πα-,选D .考点:三角函数的定义.7.D解析:D 【解析】试题分析:由sinC +sin(B -A)=sin2A再注意到:,所以有,故知△ABC 是等腰三角形或直角三角形,故选D. 考点:三角恒等变形公式.8.B解析:B 【解析】分析:利用三角函数的定义求得66cos sin ππαα⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭, 结果,进而利用两角和的余弦函数公式即可计算得解.详解:由三角函数的定义可得512,613613cos sin ππαα⎛⎫⎛⎫-=--= ⎪ ⎪⎝⎭⎝⎭, 则773cos cos cos 12661264ππππππααα⎛⎫⎛⎫⎛⎫+=-++=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭33=cos cos sin sin 6464ππππαα⎛⎫⎛⎫⎛⎫⎛⎫--- ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭512=13213226⎛⎛⎫---⋅=- ⎪ ⎝⎭⎝⎭点睛:本题考查任意角的三角函数的定义,两角和与差的余弦函数公式,考查了计算能力和转化思想,属于基础题.9.C解析:C 【解析】 【分析】由图观察出A 和T 后代入最高点,利用φπ<可得ϕ,进而得到解析式. 【详解】由图象可知2A =,因为884πππ⎛⎫--= ⎪⎝⎭, 所以T π=,2ω=. 当8x π=-时,2sin 228πφ⎛⎫-⋅+= ⎪⎝⎭, 即sin 14πφ⎛⎫-= ⎪⎝⎭,又φπ<, 解得34πφ=.故函数的解析式为32sin 24y x π⎛⎫=+⎪⎝⎭. 故选C. 【点睛】本题考查由()y sin A x ωϕ=+的部分图象确定函数表达式,属基础题.10.B解析:B【解析】 ∵21,33AD AC BP BD =∴=121()393AD AB AC AB -=- ∴2239AP AB BP AB AC =+=+ 又AP AB AC λμ=+,∴22,,339λλμμ=== 故选B.11.A解析:A 【解析】 【分析】利用三角函数恒等变换的公式,化简求得函数的解析式,再根据三角函数的图象与性质,逐项判定,即可求解. 【详解】 由题意,函数2111()cos cos 2cos 2sin(2)2262f x x x x x x x π=+=++=++, 当6x π=时,113()sin(2)sin 6662222f ππππ=⨯++=+=,所以6x π=函数()f x 的对称轴,故A 正确;由sin(2)[1,1]6x π+∈-,所以函数()f x 的最大值为32,最小值为12-,所以B 、C 不正确;又由12x π=时,11()sin(2)612622f πππ=⨯++=+,所以(,0)12π-不是函数()f x 的对称中心,故D 不正确, 故选A . 【点睛】本题主要考查了三角恒等变换的公式的应用,以及函数sin()y A wx b ϕ=++的图象与性质的应用,着重考查了推理与运算能力,属于基础题.12.A解析:A 【解析】 【分析】 由题意可得123ππω⨯=,求得ω的值,可得()f x 的最小正周期是2πω的值 【详解】由题意可得()1sin 2x ωθ+=的解为两个不等的实数1x ,2x 且123ππω⨯=,求得23ω= 故()f x 的最小正周期是23ππω=故选A 【点睛】本题主要考查了的是三角函数的周期性及其图象,解题的关键根据正弦函数的图象求出ω的值,属于基础题13.B解析:B 【解析】 【分析】分别以i 和j 所在的直线为x 轴和y 轴,以向量所在方向为正方向,建立平面直角坐标系, 可得()1,0i =,()0,1j =,设(),n n n a x y =,进而可得到tan n θ的表达式,结合函数的单调性可选出答案. 【详解】分别以i 和j 所在的直线为x 轴和y 轴,以向量所在方向为正方向,建立平面直角坐标系, 则()1,0i =,()0,1j =,设(),n n n a x y =,因为n i a n ⋅=,21n j a n ⋅=+,所以,21n n x n y n ==+, 则(),21n a n n =+,n θ为i 和n a 的夹角,211tan 2n n n n y n n x θ+===+,*n ∈N ,tan 0n θ>,则π0,2n θ⎛⎫∈ ⎪⎝⎭, 显然1tan 2n nθ=+为减函数, 又因为函数tan y x =在π0,2⎛⎫⎪⎝⎭上为增函数,所以n θ随着n 的增大而减小. 故选:B. 【点睛】本题考查了向量的数量积的运算,考查了学生的推理能力,利用坐标法是解决本题的一个较好方法,属于中档题.14.D解析:D 【解析】 【分析】根据正弦的倍角公式和三角函数的基本关系式,化为齐次式,即可求解,得到答案.【详解】由题意,可得222221cos sin cos cos sin 2cos sin cos 2cos sin a a a a a a a a a a++=+=+221tan 1321tan 135a a ++===++,故选D . 【点睛】 本题主要考查了正弦的倍角公式,以及三角函数的基本关系式的化简、求值,着重考查了推理与运算能力,属于基础题.15.B解析:B 【解析】 【分析】由平移变换得到()sin(22)3g x x πϕ=-+,由偶函数的性质得到sin(22)13x πϕ-+=±,从而求min 512πϕ=. 【详解】由题意得:()sin[2())]sin(22)33g x x x ππϕϕ=-+=-+, 因为()g x 为偶函数,所以函数()g x 的图象关于0x =对称,所以当0x =时,函数()g x 取得最大值或最小值,所以sin(2)13πϕ-+=±,所以2,32k k Z ππϕπ-+=+∈,解得:1,22k k Z ππϕ=--∈, 因为0ϕ>,所以当1k =-时,min 512πϕ=,故选B. 【点睛】平移变换、伸缩变换都是针对自变量x 而言的,所以函数()f x 向右平移(0)ϕϕ>个单位长度后得到函数()g x ,不能错误地得到()sin (2)3g x x x πϕ=+-.二、填空题16.【解析】【分析】以所在直线为轴建立坐标系设运用向量的坐标运算和向量数量积的坐标表示得出关于的表达式配方即可得出结论【详解】以所在直线为轴以边上的高为轴建立坐标系是直角边为2的等腰直角三角形且为直角顶解析:1-【解析】 【分析】以BC 所在直线为x 轴建立坐标系,设P x y (,) ,运用向量的坐标运算和向量数量积的坐标表示,得出()PA PB PC ⋅+关于x y , 的表达式,配方即可得出结论. 【详解】以BC 所在直线为x 轴,以BC 边上的高为y 轴建立坐标系,ABC ∆是直角边为2的等腰直角三角形,且A 为直角顶点,斜边22BC =,则022020A B C -(,),(,),(,),设P x y (,),则2222PB PC PO x y PA x y (,),(,),+==--=-∴()22222 22222212PA PB PC x y x y ⋅+=+-=+--(,∴当202x y ==,时,()PA PB PC ⋅+取得最小值-1. 故答案为:-1. 【点睛】本题考查了平面向量的数量积运算,运用坐标法解题是关键,属于中档题.17.-1【解析】【分析】由题意结合向量垂直的充分必要条件得到关于k 的方程解方程即可求得实数k 的值【详解】由平面向量的坐标运算可得:与垂直则即:解得:【点睛】本题主要考查向量的坐标运算向量垂直的充分必要条解析:-1 【解析】 【分析】由题意结合向量垂直的充分必要条件得到关于k 的方程,解方程即可求得实数k 的值. 【详解】由平面向量的坐标运算可得:()()()21,123,26,4ka b k k k -=--=+-,2ka b -与a 垂直,则()20ka b a -⋅=,即:()()61410k k +⨯+-⨯=,解得:1k =-. 【点睛】本题主要考查向量的坐标运算,向量垂直的充分必要条件等知识,意在考查学生的转化能力和计算求解能力.18.【解析】【分析】由三角函数的基本关系式和正弦的倍角公式求得再由两角差的余弦函数的公式即可求解【详解】由即则又由所以又由【点睛】本题主要考查了三角函数的基本关系式以及正弦的倍角公式和两角差的余弦公式的 解析:75【解析】【分析】由三角函数的基本关系式和正弦的倍角公式,求得249(cos sin )25θθ+=,再由两角差的余弦函数的公式,即可求解. 【详解】 由24sin 225θ=,即242sin cos 25θθ=, 则2222449(cos sin )cos 2sin cos sin 12525θθθθθθ+=++=+=, 又由02πθ<<,所以cos 0,sin 0θθ>>,7cos()cos sin 45πθθθ-=+=. 【点睛】本题主要考查了三角函数的基本关系式,以及正弦的倍角公式和两角差的余弦公式的化简、求值,着重考查了推理与运算能力,属于基础题.19.【解析】【分析】先用中点公式的向量式求出再用数量积的定义求出的值【详解】【点睛】本题主要考查向量中的中点公式应用以及数量积的定义 解析:2-【解析】 【分析】先用中点公式的向量式求出PA PB +,再用数量积的定义求出()PA PB PC +⋅的值. 【详解】2PA PB PO +=,()2211cos1802PA PB PC PO PC ο∴+⋅=⋅=⨯⨯⨯=-【点睛】本题主要考查向量中的中点公式应用以及数量积的定义.20.【解析】【分析】根据向量模的性质可知当与反向时取最大值根据模长的比例关系可得整理可求得结果【详解】当且仅当与反向时取等号又整理得:本题正确结果:【点睛】本题考查向量模长的运算性质关键是能够确定模长取解析:18【解析】 【分析】根据向量模的性质可知当23a b -与4a b +反向时,7a b -取最大值,根据模长的比例关系可得()()32324a b a b -=-+,整理可求得结果. 【详解】()()72342345a b a b a b a b a b -=--+≤-++=当且仅当23a b -与4a b +反向时取等号又43223a ba b+=- ()()32324a b a b ∴-=-+ 整理得:8a b =18a b ∴= 本题正确结果:18【点睛】本题考查向量模长的运算性质,关键是能够确定模长取得最大值时,两个向量之间的关系,从而得到两个向量之间的关系.21.【解析】分析:先根据图像平移得解析式再根据图像性质求关系式解得最小值详解:因为函数的图象向左平移个单位得所以因为所以点睛:三角函数的图象变换提倡先平移后伸缩但先伸缩后平移也常出现在题目中所以也必须熟 解析:12π【解析】分析:先根据图像平移得解析式,再根据图像性质求φ关系式,解得最小值. 详解:因为函数()2sin 26f x x π⎛⎫=-⎪⎝⎭的图象向左平移(0)φφ>个单位得()2sin(2())6g x x πφ=+-,所以2()()6122k k k Z k Z πππφπφ-=∈∴=+∈因为0φ>,所以min .12πφ=点睛:三角函数的图象变换,提倡“先平移,后伸缩”,但“先伸缩,后平移”也常出现在题目中,所以也必须熟练掌握.无论是哪种变形,切记每一个变换总是对字母x 而言.22.【解析】【分析】根据题干得到按照两角和与差公式得到结果【详解】已知那么故答案为【点睛】这个题目考查了给值求值的问题常见的解题方式有:用已知角表示未知角再由两角和与差的公式得到结果 解析:1124【解析】 【分析】根据题干得到an α=()tan αββ+-,按照两角和与差公式得到结果. 【详解】已知()4tan 5αβ+=,1 tan 4β=, 那么tan α=()tan αββ+-()()tan tan 111tan tan 24αββαββ+-==++. 故答案为1124. 【点睛】这个题目考查了给值求值的问题,常见的解题方式有:用已知角表示未知角,再由两角和与差的公式得到结果.23.-3【解析】【分析】由已知分析出函数f (x )的值以4为周期呈周期性变化可得答案【详解】∵函数f (x )满足:f (1)=2f (x+1)=∴f (2)=﹣3f (3)=﹣f (4)=f (5)=2……即函数f (x解析:-3 【解析】 【分析】由已知分析出函数f (x )的值以4为周期,呈周期性变化,可得答案. 【详解】∵函数f (x )满足:f (1)=2,f (x +1)=()()11f x f x +-,∴f (2)=﹣3, f (3)=﹣12, f (4)=13, f (5)=2, ……即函数f (x )的值以4为周期,呈周期性变化, ∵2018=504×4+2, 故f (2018)=f (2)=﹣3, 故答案为:﹣3. 【点睛】本题考查的知识点是函数求值,函数的周期性,难度不大,属于中档题.24.【解析】分析:利用诱导公式化简函数的解析式通过正弦函数的最值求解即可详解:函数故答案为点睛:本题考查诱导公式的应用三角函数的最值正弦函数的有界性考查计算能力 解析:65分析:利用诱导公式化简函数的解析式,通过正弦函数的最值求解即可.详解:函数()1ππ1πsin cos 353656f x x x sin x cos x π⎛⎫⎛⎫=++-=++-+⎪ ⎪⎝⎭⎝⎭()() 1ππ6π6533535sin x sin x sin x =+++=+≤()()(). 故答案为65. 点睛:本题考查诱导公式的应用,三角函数的最值,正弦函数的有界性,考查计算能力.25.【解析】∵T=−(−)=π∴T=π∴ω=2把(2)代入得2sin(π+φ)=2⇒π+φ=+2kπ∴φ=−+2kπk∈Z∵∴φ=点睛:已知函数的图象求解析式(1)(2)由函数的周期求(3)利用五点法中 解析:3π-【解析】 ∵34T =512π −(−π3)=3 4π,∴T =π,∴ω=2 把(512π,2)代入,得2sin(56π+φ)=2⇒56π+φ=π2+2kπ, ∴φ=−π3+2kπ,k ∈Z ,∵ππ22ϕ-<<,∴φ=3π-, 点睛:已知函数sin()(0,0)y A x B A ωϕω=++>>的图象求解析式(1)max min max min,22y y y y A B -+==. (2)由函数的周期T 求2,.T πωω= (3)利用“五点法”中相对应的特殊点求ϕ.三、解答题 26.(1)14;(2)见解析;(3)见解析 【解析】 【分析】(1)列出基本事件的所有情况,然后再列出满足条件的所有情况,利用古典概率公式即可得到答案.(2)计算平均值和方差,从而比较甲同学应在物理和历史中选择哪一门学科;(3)先计算x 和y ,然后通过公式计算出线性回归方程,然后代入平均值50即可得到答案.(1)记物理、历史分别为12,A A ,思想政治、地理、化学、生物分别为1234,,,B B B B , 由题意可知考生选择的情形有{}112,,A B B ,{}113,,A B B ,{}114,,A B B ,{}123,,A B B ,{}124,,A B B ,{}134,,A B B ,{}212,,A B B ,{}213,,A B B ,{}214,,A B B ,{}223,,A B B ,{}224,,A B B ,{}234,,A B B ,共12种 他选到物理、地理两门功课的满情形有{}{}{}112123124,,,,,,A B B A B B A B B ,共3种∴甲同学选到物理、地理两门功课的概率为31124P == (2)物理成绩的平均分为76828285879093857x ++++++==物理历史成绩的平均分为69768082949698857x ++++++==历史由茎叶图可知物理成绩的方差2s<物理历史成绩的方差2s 物理故从平均分来看,选择物理历史学科均可以;从方差的稳定性来看,应选择物理学科;从最高分的情况来看,应选择历史学科(答对一点即可) (3)57+61+65+72+74+77+84707x ==,85y =,7172221741964770853140.5834840770540ˆ7i i i i i x y x y bx x==-⋅⋅-⨯⨯∴===≈-⨯-⋅∑∑850.587044.ˆ0ˆ4ay b x =-⋅=-⨯≈ y ∴关于x 的回归方程为0.58+44.40y x =当50x =时,0.5850+44.4073y =⨯≈,当班级平均分为50分时,其物理考试成绩为73分 【点睛】本题主要考查古典概型,统计数的相关含义,线性回归方程的计算,意在考查学生的阅读理解能力,计算能力和分析能力,难度不大.27.(1)14;(2)7. 【解析】试题分析:(I )在ABD ∆中,利用外角的性质,得()sin sin BAD ADC B ∠=∠-∠即可计算结果;(II )由正弦定理,计算得3BD =,在ABC ∆中,由余弦定理,即可计算结果.试题解析:(I )在ADC ∆中,∵1cos 7ADC ∠=,∴sin 7ADC ∠=∴()sin sin 14BAD ADC B ∠=∠-∠= (II )在ABD ∆中,由正弦定理得:sin 3sin AB BAD BD ADB⋅∠==∠ 在ABC ∆中,由余弦定理得:2222cos 49AC AB BC AB BC B =+-⋅⋅=∴7AC =考点:正弦定理与余弦定理.28.(1)6C π=;(2) 【解析】【分析】(1)根据()sin ()(sin sin )0m n a A b c B C⋅=-++-=和正弦定理余弦定理求得6C π=.(2)先利用正弦定理求出R=1,b -化成2sin()6A π-,再利用三角函数的图像和性质求解.【详解】(1)因为m n ⊥,所以()sin ()(sin sin )0mn a A b c B C ⋅=-++-=,由正弦定理化角为边可得2220a b c +-=,即222a b c +-=,由余弦定理可得cos 2C =,又0C π<<,所以6C π=. (2)由(1)可得56A B π+=,设ABC 的外接圆的半径为R , 因为6C π=,1c=,所以122sin sin30cR C ===︒, 则52sin 2sin 2sin )2sin()]6b R A R B R A B R A A π-=-=-=--= 2sin()2sin()66R A A ππ-=-, 因为ABC 为锐角三角形,所以025062A A πππ⎧<<⎪⎪⎨⎪<-<⎪⎩,即32A ππ<<,所以663A πππ<-<,所以1sin()26A π<-<, 所以12sin()6A π<-<b -的取值范围为.【点睛】(1)本题主要考查正弦定理余弦定理解三角形,考查三角函数的图像和性质,意在考查学生对这些知识的掌握水平和分析推理能力.(2) 对于复合函数的问题自然是利用复合函数的性质解答,求复合函数的最值,一般从复合函数的定义域入手,结合三角函数的图像一步一步地推出函数sin()y A wx h φ=++的最值.29.(1) 22(1)(1)5x y -++= (2) 30°或90°.【解析】【分析】(1)解法一:将圆的方程设为一般式,将题干三个点代入圆的方程,解出相应的参数值,即可得出圆C 的一般方程,再化为标准方程;解法二:求出线段12M M 和13M M 的中垂线方程,将两中垂线方程联立求出交点坐标,即为圆心坐标,然后计算3CM 为圆的半径,即可写出圆C 的标准方程;(2)先利用勾股定理计算出圆心到直线l 的距离为1,并对直线l 的斜率是否存在进行分类讨论:一是直线l 的斜率不存在,得出直线l 的方程为2x =,验算圆心到该直线的距离为1;二是当直线l 的斜率存在时,设直线l 的方程为()()312y k x --=-,并表示为一般式,利用圆心到直线的距离为1得出关于k 的方程,求出k 的值.结合前面两种情况求出直线l 的倾斜角.【详解】(1)解法一:设圆C 的方程为220x y Dx Ey F ++++=,则10,930,10,D F D F E F -+=⎧⎪++=⎨⎪++=⎩ ∴2,2,3,D E F =-⎧⎪=⎨⎪=-⎩即圆C 为222230x y x y +-+-=,∴圆C 的标准方程为22(1)(1)5x y -++=;解法二:则12M M 中垂线为1x =,13M M 中垂线为y x =-,∴圆心(,)C x y 满足∴(1,1)C -,半径3145r CM ==+=,∴圆C 的标准方程为22(1)(1)5x y -++=.(2)①当斜率不存在时,即直线:2l x =到圆心的距离为1,也满足题意,此时直线l 的倾斜角为90°,②当斜率存在时,设直线l 的方程为(2)31y k x =-+,由弦长为4,可得圆心(1,1)C - 到直线l 541-=,1=,∴k =l 的倾斜角为30°, 综上所述,直线l 的倾斜角为30°或90°.【点睛】本题考查圆的方程以及直线截圆所得弦长的计算,在求直线与圆所得弦长的计算中,问题的核心要转化为弦心距的计算,弦心距的计算主要有以下两种方式:一是利用勾股定理计算,二是利用点到直线的距离公式计算圆心到直线的距离.30. (1)πθ6=.ω2=.(2)023x π=,或034x π=. 【解析】 试题分析:(1)由三角函数图象与y 轴交于点(可得cos θ=,则6πθ=.由最小正周期公式可得2ω=.(2)由题意结合中点坐标公式可得点P 的坐标为022x π⎛- ⎝.代入三角函数式可得05cos 462x π⎛⎫-= ⎪⎝⎭,结合角的范围求解三角方程可得023x π=,或034x π=. 试题解析:(1)将0,x y ==()2cos y x ωθ=+中,得cos 2θ=, 因为02πθ≤≤,所以6πθ=.由已知T π=,且0ω>,得222T ππωπ===. (2)因为点()00,0,,2A Q x y π⎛⎫ ⎪⎝⎭是PA 的中点,02y =,所以点P 的坐标为022x π⎛- ⎝. 又因为点P 在2cos 26y x π⎛⎫=+⎪⎝⎭的图象上,且02x ππ≤≤,所以05cos 462x π⎛⎫-= ⎪⎝⎭,且075194666x πππ≤-≤,从而得0511466x ππ-=,或0513466x ππ-=,即023x π=,或034x π=.。
【数学】上海市交大学附中2013-2014学年高二下学期期末考试.docx

OA B中,AB=
3
.
又∵∠ACB就是AC与底面⊙O所成角,
ACB
30 , BC
3, AC 2 3,
VA BOC
1
AB SBOC
1
AB
OB BC
3
3
6
2
20.如图,已知正三棱柱
ABC-A1B1C1的底面边长为
8,侧棱长为
6,D为AC中点。
(1)求证:直线
1∥平面
1;
A1
C1
AB
C DB
(2)求异面直线
2
2
Cnn 1。
2n 1
时 ,x2nxn10, 当3 | n时 ,
x2 n
xn
1
3,
记t0
Cn0
Cn3
Cnn,t1
Cn1
Cn4
Cnn 2,t2
Cn2
Cn5
Cnn 1
f (1) 2n
Cn0
Cn1
Cnn,
f ( ) (1 )n
Cn0
Cn1
nCnn
Cn0
Cn1
2Cn2
Cn3
Cn4
2Cn5
Cnn
,
f (2) (1
(满分150分,120分钟完成,答案一律写在答题纸上)
一、填空题(本大题共14题,每题4分,满分56分)
1.
设复数z满足(1 i )z 2i
,则
z______
1
i______。
2.
三个平面最多把空间分割成
8
个部分。
3.
若圆锥的侧面展开图是半径为
2、圆心角为
180的扇形,则这个圆锥的体积是
3
2013-2014学年上海市金山中学高二数学下学期期末考试理科试卷(含解析)新人教版A版

2014-2015学年度 11月月考卷题号 一 二 三 总分 得分注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 评卷人 得分一、选择题(题型注释)1.一个圆柱形的罐子半径是4米,高是9米,将其平放,并在其中注入深2米的水,截面如图所示,水的体积是( )平方米.A .32424-πB .33636-πC .32436-πD .33648-π【答案】D. 【解析】试题分析:所求几何体的体积为阴影部分的面积与高的乘积,在OAB ∆中,2,4=-===DE OD OE OA OB ,则32π=∠AOB ,=-=∆O AB S S S 扇形阴影 34316231621321621-=⨯⨯-⨯⨯=ππ,体积33648-==πSh V . 考点:组合体的体积.2.某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70), [70,80), [80,90), [90,100)加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( )A .588B .480C .450D .120【答案】B. 【解析】试题分析:由频率分布直方图可知,该模块测试成绩不少于60分的频率为8.010)010.0015.0025.0030.0(=⨯+++, 所以该模块测试成绩不少于60分的学生人数为4808.0600=⨯.考点:频率分布直方图. 3.使得*)()13(N n xx x n ∈+的展开式中含有常数项的最小的n 为 ( )A .4B .5C .6D .7 【答案】B. 【解析】 试题分析:nxx x )13(+的展开式的通项为k n kn k nkkn k nk xC xx x C T 2513)1()3(---+==,令025=-k n ,则)(25N k k n ∈=,所以n 的最小值为5. 考点:二项式定理. 4.若直线m xy l +-=2:与曲线|4|21:2x y C -=有且仅有三个交点,则m 的取值范围是()A .)12,12(+-B .)2,1(C .)12,1(+D .)12,2(+ 【答案】B.【解析】试题分析:由题意得,曲线C 是由椭圆上半部分1422=+y x 和双曲线1422=-y x 上半部分组成,且双曲线的渐近线方程为x y 21-=,与直线m x y l +-=21:平行;当直线l 过右顶点时,直线l 与曲线C 有两个交点,此时,1=m ;当直线l 与椭圆相切时,直线l 与曲线C有两个交点,此时2=m ;由图像可知,)2,1(∈m 时,直线l 与曲线C 有三个交点.考点:直线与圆锥曲线的位置关系.第II 卷(非选择题)请点击修改第II 卷的文字说明二、填空题(题型注释)5.过点)2,1(、)6,3(的直线的斜率为______________. 【答案】2. 【解析】试题分析:由斜率公式得:21326=--=k . 考点:直线的斜率公式.6.若i 是虚数单位,复数z 满足5)43(=-z i ,则z 的虚部为_________. 【答案】54. 【解析】试题分析:5)43(=-z i ,i i i i i i z 545325)43(5)43)(43()43(5435+=+=+-+=-=∴,则z 的虚部为54. 考点:复数的除法.7.正四面体ABC S -的所有棱长都为2,则它的体积为________. 【答案】322. 【解析】试题分析:过S 作ABC SH 面⊥,则H 是ABC ∆的中心,连接AH ,则3232221=⨯⨯⨯=∆ABC S ,332233=⨯=AH , 在SAH Rt ∆中,36234422=-=-=AH SA SH , 所以32236233131=⨯⨯=⋅=∆-SH S V ABC ABC S .考点:多面体的体积.8.以)2,1(-为圆心且过原点的圆的方程为_____________. 【答案】5)2()1(22=++-y x . 【解析】试题分析:由题意,得所求圆的半径541=+=r ,则所求圆的标准方程为5)2()1(22=++-y x .考点:圆的标准方程.9.从一副52张扑克牌中第一张抽到“Q ”,重新放回,第二张抽到一张有人头的牌,则这两个事件都发生的概率为________. 【答案】1693. 【解析】试题分析:从一副52张扑克牌中第一张抽到“Q ”,记为事件A,则131524)(==A P ;重新放回,第二张抽到一张有人头的牌,记为事件B,则1335212)(==B P ;且事件A 与事件B 相互独立;则则这两个事件都发生的概率为1693133131)()()(=⨯==B P A P AB P . 考点:古典概型.10.已知圆锥的高与底面半径相等,则它的侧面积与底面积的比为________. 【答案】2. 【解析】试题分析:设圆锥的底面半径和高为r ,则其母线长r l 2=;所以圆锥的侧面积22r rl S ππ==侧,底面面积2r S π=,则它的侧面积与底面积的比为2.考点:圆锥的侧面积公式.11.正方体1111D C B A ABCD -中,二面角111C D A B --的大小为__________. 【答案】4π. 【解析】试题分析:二面角111C D A B --,即半平面1111D C B A 与CB D A 11所成的图形,交线为11D A ,易知1111111,D A B A D A B A ⊥⊥,所以11B BA ∠是二面角111C D A B --的平面角,且411π=∠B BA ,即二面角111C D A B --的大小为4π.考点:二面角的平面角.12.双曲线1422=-y x 的顶点到其渐近线的距离等于_________. 【答案】552. 【解析】试题分析:双曲线1422=-y x 的顶点为)0,2(,渐近线方程为0422=-y x ,即02=±y x ;则顶点到其渐近线的距离为552412=+=d . 考点:双曲线的性质、点到直线的距离公式.13.某人5次上班途中所花的时间(单位:分钟)分别为9,11,10,,y x .已知这组数据的平均数为10,方差为2,则=-||y x __________. 【答案】4.【解析】试题分析:由题意,得[]⎪⎪⎩⎪⎪⎨⎧=-+-+-+-+-=++++2)109()1011()1010()10()10(5110)91110(5122222y x y x ,化简,得⎩⎨⎧=-+-=+8)10()10(2022y x y x ,解得⎩⎨⎧==128y x 或⎩⎨⎧==812y x ,则4=-y x . 考点:均值、方差公式.14.在长方体1111D C B A ABCD -中,已知36,91==BC AA ,N 为BC 的中点,则直线11C D 与平面N B A 11的距离是___________.【答案】9.【解析】试题分析:过1C 作N B H C 11⊥,因为1111111,B BCC H C B BCC B A 面面⊂⊥,所以111B A H C ⊥,则N B A H C 111面⊥,H C 1的长度即为直线11C D 与平面N B A 11的距离; 在N BB Rt 1∆中,33933tan 1==∠N BB ,23cos 1==∠N BB ; 在H B C Rt 11∆中,3611=C B ,23cos sin 111=∠=∠N BB H B C , 923361=⨯=H C ,即直线11C D 与平面N B A 11的距离为9.考点:直线到平面的距离.15.棱长为1的正方体1111D C B A ABCD -的8个顶点都在球面O 的表面上,E 、F 分别是棱1AA 、1DD 的中点,则直线EF 被球O 截得的线段长为________.【答案】2. 【解析】试题分析:因为棱长为1的正方体1111D C B A ABCD -的8个顶点都在球面O 的表面上,所以该球的半径23=r ,球心O 到直线EF 的距离21=d ,则直线EF 被球O 截得的线段长为241432222=-=-=d r l . 考点:多面体与球的组合体.16.从3名骨科、4名脑外科和5名内科医生中选派5人组成一个抗震救灾医疗小组,则骨科、脑外科和内科医生都至少有1人的选派方法种数是___________.(用数字作答) 【答案】590. 【解析】试题分析:骨科、脑外科和内科医生都至少有1人的选派方法可分以下几类:3名骨科、1名脑外科和1名内科医生,有20151433=C C C 种; 1名骨科、3名脑外科和1名内科医生,有60153413=C C C 种; 1名骨科、1名脑外科和3名内科医生,有120351413=C C C 种; 2名骨科、2名脑外科和1名内科医生,有90152423=C C C 种; 1名骨科、2名脑外科和2名内科医生,有180252413=C C C 种; 2名骨科、1名脑外科和2名内科医生,有120251423=C C C 种;由分类加法计数原理得,共有590120180901206020=+++++种. 考点:组合.17.在棱长为1的正方体盒子里有一只苍蝇,苍蝇为了缓解它的无聊,决定要考察这个盒子的每一个角,它从一个角出发并回到原处,并且每个角恰好经过一次,为了从一个角到另一个角,它或直线飞行,或者直线爬行,苍蝇的路径最长是____________.(苍蝇的体积不计) 【答案】)23(4+.【解析】试题分析:根据题意,苍蝇需要8次完成,有两种方法:方法一:每次都到达相邻顶点,需经过8条棱,总路径长为8;方法二:每次到达不相邻的顶点,需爬行4次(面对角线),飞行4次(体对角线),总路径长是)23(4+;又8)23(4>+ ,所以苍蝇的路径最长是)23(4+.考点:正方体的面对角线与体对角线.18.设焦点是)5,0(1-F 、)5,0(2F 的双曲线C 在第一象限内的部分记为曲线T ,若点 ),,(),,2(),,1(2211n n y n P y P y P 都在曲线T 上,记点),(n n y n P 到直线02:=+-k y x l 的距离为),2,1( =n d n ,又已知5lim =∞→n n d ,则常数=k___________.【答案】5±.【解析】试题分析:因为双曲线的焦点为)5,0(),5,0(21F F -,所以双曲线的标准方程可设为)0,0(12222>>=-b a b x a y ,且522=+b a ;因为双曲线上的点),(n n y n P 到直线02:=+-k y x l 的距离为),2,1( =n d n 存在极限,所以直线l 与双曲线的渐近线x bay =平行,即2=ba,所以渐近线方程为02=-y x ;又因为5lim =∞→n n d ,所以直线l 与双曲线的渐近线02=-y x 的距离为55=k ,即5±=k .考点:双曲线的几何性质.三、解答题(题型注释)19.求8)3(x x +的二项展开式中的第5项的二项式系数和系数. 【答案】811120,70.【解析】 试题分析:解题思路:利用二项式定理的通项公式写出5T ,再求出二项式系数与系数.规律总结:涉及求二项展开式的二项式系数或系数或特定项时,往往先写出二项式的通项公式,再进行求解. 注意点:要正确区分二项式系数与系数:二项式系数仅是一个组合数,系数是未知数的系数.试题解析:4485)32)((xx C T =, 所以二项式系数为7048=C ,系数为811120. 考点:二项式定理.20.某商场举行的“三色球”购物摸奖活动规定:在一次摸奖中,摸奖者从装有3个红球、1个蓝球、6个白球的袋中任意摸出4个球.根据摸出4个球中红球与蓝球的个数,设一、二、三等奖如下:其余情况无奖且每次摸奖最多只能获得一个奖级. (1)求一次摸奖恰好摸到1个红球的概率;(2)求摸奖者在一次摸奖中获奖金额X 的分布列与期望()E X . 【答案】(1)21;(2)分布列见解析,314)(=X E . 【解析】 试题分析:解题思路:(1)利用超几何分布的概率公式求解即可;(2)写出获奖金额X 的所有可能取值,利用古典概型的概率公式求出各自概率,列出表格,即得分布列,再利用期望公式求其期望. 规律总结:以图表给出的统计题目一般难度不大,主要考查频率直方图、茎叶图、频率分布表给出;抽样方法要注意各自的特点;古典概型是一种重要的概率模型,其关键是正确列举基本事件.试题解析:(1)214103713=C C C ; 321020035503510420)(=⋅+⋅+⋅+⋅=X E .考点:1.超几何分布;2.古典概型;3.随机变量的分布列与期望.21.已知椭圆13422=+y x 上存在两点A 、B 关于直线m x y +=4对称,求m 的取值范围. 【答案】.1313213132≤≤-m . 【解析】试题分析:解题思路:利用直线AB 与直线m x y +=4垂直,设出直线AB 的方程,联立直线与椭圆方程,消去y ,整理成关于x 的一元二次方程,利用中点公式和判别式求出m 的范围. 规律总结:涉及直线与椭圆的位置关系问题,往往采用“设而不求”的方法进行求解..试题解析:设直线AB 方程为b x y +-=4,联立 ⎪⎩⎪⎨⎧+-==+,4,124322b x y y x 得,0481681322=-+-b bx x 从而,138b x x B A =+ ,13242)(41b b x x y y B A B A =++-=+ 则B A ,中点是)1312,134(b b , 则,013121344=+-⋅m b b 解得.134b m -= 由0481681322=-+-b bx x 有实数解得,0)4816(526422≥--=∆b b 即.4132≤b 于是.413)413(2≤-m 则m 的取值范围是.1313213132≤≤-m . 考点:1.直线与椭圆的位置关系;2.对称问题.22.如图,四棱柱1111D C B A ABCD -中, 侧棱⊥A A 1底面ABCD ,AD AB DC AB ⊥,//,1==CD AD ,21==AB AA ,E 为棱1AA的中点.(1) 证明:CE C B ⊥11;(2) 设点M 在线段E C 1上, 且直线AM 与平面11A ADD 所成角的正弦值为62, 求线段AM 的长.【答案】(1)证明见解析;(2)2=AM .【解析】试题分析:解题思路:根据题意建立空间直角坐标系,写点的坐标与有关向量,利用直线的方向向量的数量积为0证明两直线垂直;利用线面角的公式列出关于AM 的方程即可.规律总结:证明平行或垂直问题,一般有两个思路:①利用一个判定与性质进行证明;②转化为空间向量的平行与垂直进行证明;求角或距离问题,往往利用空间向量进行求解. 试题解析:以点A 为原点建立空间直角坐标系,依题意得)1,0,1(),2,0,0(),0,0,0(C B A ,).0,1,0(),1,2,1(),2,2,0(11E C B证明:)1,1,1(),1,0,1(11--=-=→→CE C B ,于是,所以CE C B ⊥11;解:).0,1,1(),0,1,0(1==→→EC AE 设,10),,,(1≤≤==→→λλλλλEC EM 有 ),1,(λλλ+=+=→→→EM AE AM .可取)2,0,0(=→AB 为平面11A ADD 的一个法向量. 设θ为直线AM 与平面11A ADD 所成角,则 .1232|||||||,cos |sin 2++=⋅⋅==→→→→→→λλλθAB AM AB AM AB AM 于是,6212322=++λλλ解得.31=λ所以.2=AM . 考点:1.直线的垂直关系的证明;2.直线与平面所成的角的求法.23.下图是利用计算机作图软件在直角坐标平面xOy 上绘制的一列抛物线和一列直线,在焦点为n F 的抛物线列x p y C n n 4:2=中,n p 是首项和公比都为)10(<<p p 的等比数列,过n F 作斜率2的直线n l 与n C 相交于n A 和n B (n A 在x 轴的上方,n B 在x 轴的下方). 证明:n OA 的斜率是定值;求1A 、2A 、 、n A 、 所在直线的方程;记n n OB A ∆的面积为n S ,证明:数列}{n S 是等比数列,并求所有这些三角形的面积的和.【答案】(1)51+-=nO A k ;(2)x y )51(+-=;(3)22152p p -. 【解析】试题分析:解题思路:(1)联立直线与抛物线方程,整理成关于1x ,1y 的方程,进而求出n OA 的斜率;(2)利用直线的点斜式方程写出直线方程即可;(3)联立直线与抛物线方程,求弦长与点到直线的距离,进而求三角形的面积.规律总结:锥曲线的问题一般都有这样的特点:第一小题是基本的求方程问题,一般简单的利用定义和性质即可;后面几个小题一般来说综合性较强,用到的内容较多,大多数需要整体把握问题并且一般来说计算量很大,学生遇到这种问题就很棘手,有放弃的想法,所以处理这类问题一定要有耐心..试题解析:(1)由已知得n n p p =,抛物线焦点)0,(n n p F ,抛物线方程为x p y n 42=,直线n l 的方程为).(2np x y -=于是,抛物线n C 与直线n l 在x 轴上方的交点),(11y x A n 的坐标满足⎪⎩⎪⎨⎧-==),(2,411121n n p x y x p y 则有,042211121=-+x y x y 而直线n OA 的斜率为11x y k n OA =,则,042112=-+O A O A k k 解得,51±-=n O A k 又,0>k 点n A 在第一象限,则51+-=n O A k ; 直线方程为x y )51(+-=;由⎪⎩⎪⎨⎧-==),(2,42n n p x y x p y 得,04222=--n n p y p y 则n p AB 10||=, 而O 到直线n l 的距离为52np , 于是n n OB A ∆的面积nn p S 252=,所以数列}{n S 是以252p 为首项,2p 为公比的等比数列.由于10<<p , 所以所有三角形面积和为22152pp -. 考点:1.直线的方程;2.直线与抛物线的位置关系.。
上海市金山中学高二数学下学期期末考试试题

金山中学2014学年度第二学期高二年级数学学科期末考试卷一、填空题(本大题满分56分)本大题共有14题,考生应在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分。
1.已知247353---=x x x P C ,则=x 。
2.若正方体的体对角线长是4,则正方体的体积是 。
3.经过抛物线x y 42=的焦点,且以)1,1(=为方向向量的直线的方程是 。
4. 在二项式8)1(xx -的展开式中,含5x 的项的系数是 。
(用数字作答)5.若双曲线的渐近线方程为3y x =±,它的一个焦点与抛物线2y =的焦点重合,则双曲线的标准方程为 。
6.设21,F F 分别是双曲线1922=-y x 的左、右焦点,若点P 在双曲线上,且021=⋅PF PF,则=+ 。
7.若五个人排成一排,则甲乙两人之间仅有一人的概率是 。
(结果用数值表示)8.已知)1,1(-P ,)2,2(Q ,若直线:l 1-=mx y 与射线PQ (P 为端点)有交点,则实数m 的取值范围是 。
9.圆锥的侧面展开图为扇形,若其弧长为2πcm,则该圆锥的体积为 3cm 。
10.在一个密闭的容积为1的透明正方体容器内装有部分液体,如果任意转动该正方体,液面 的形状都不可能是三角形,那么液体体积的取值范围是 。
11.在一个水平放置的底面半径为3cm 的圆柱形量杯中装有适量的水,现放入一个半径为R cm 的实心铁球,球完全浸没于水中且无水溢出,若水面高度恰好 上升R cm ,则R =___ ____cm 。
12.如右图,ABC ∆中,1,30,900==∠=∠BC A C内挖去半圆,圆心O 在边AC 上,半圆与BC 、AB 相切于点C 、M , 与AC 交于点N ,则图中阴影部分绕直线AC 旋转一周所得旋转体的体积为 。
13.已知抛物线22(0)y px p =>,过定点(,0)p 作两条互相垂直的直线12, l l ,1l 与抛物线交于, P Q 两点,2l 与抛物线交于, M N 两点,设1l 的斜率为k .若某同学已正确求得弦PQ 的中垂线在y 轴上的截距为B32p pk k +,则弦MN 的中垂线在y 轴上的截距为 。
2023-2024学年上海市金山区华东师大三附中高二(下)期中数学试卷(含答案)

2023-2024学年上海市金山区华东师大三附中高二(下)期中数学试卷一、单选题:本题共4小题,共18分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.“n=6”是“(x2+1x)n的二项展开式中存在常数项”的( )A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 既非充分也非必要条件2.已知复数z满足z2=−z,则复数z的个数为( )A. 1B. 2C. 3D. 43.已知M(x0,y0)是圆x2+y2=r2(r>0)内异于圆心的一点,则此直线x0x+y0y=r2与该圆( )A. 相交B. 相切C. 相离D. 不确定4.已知椭圆x24+y2=1,作垂直于x轴的直线交椭圆于A,B两点,作垂直于y轴的直线交椭圆于C,D两点,且|AB|=|CD|,两垂线相交于点P,若点P的轨迹是某种曲线(或其一部分),则该曲线是( )A. 圆B. 椭圆C. 双曲线D. 抛物线二、填空题:本题共12小题,共54分。
5.在等差数列{a n}中,a1=1,公差d=2,则a3=______.6.已知函数f(x)=(m−1)x m2−3m−5是幂函数,则实数m=______.7.已知向量a=(−1,2),b=(x,4),且a⊥b,则x=______.8.抛物线y=x2的准线方程为________.9.已知直线x+2y−3=0和2x+my+1=0互相平行,则它们之间的距离是______.10.已知随机变量X的分布为(−2130.160.440.40),则E[2X+5]=______11.方程x23−m +y2m−1=1表示焦点在x轴上的椭圆,则x的取值范围是______.12.直线l的斜率的取值范围为[−1,1],则其倾斜角的取值范围是______.13.已知椭圆x216+y27=1的左、右焦点分别为F1、F2.若P为椭圆上一点,且|PF1|⋅|PF2|=14,则△F1PF2的面积为______.14.已知m∈R,动直线l1:x+my−1=0过定点A,动直线l2:mx−y−2m+3=0过定点B,若l1与l2交于点P(异于点A,B),则|PA|+|PB|的最大值为______.15.数学中有许多寓意美好的曲线,曲线C:(x2+y2)3=4x2y2被称为“四叶玫瑰线”(如图所示).给出下列三个结论:①曲线C关于直线y=x对称;②曲线C上任意一点到原点的距离都不超过1;③存在一个以原点为中心、边长为2的正方形,使得曲线C在此正方形区域内(含边界).其中,正确结论的序号是.16.定义两个点集S、T之间的距离集为d(S,T)={|PQ||P∈S,Q∈T},其中|PQ|表示两点P、Q之间的距离,已知k、t∈R,S={(x,y)|y=kx+t,x∈R},T={(x,y)|y=4x2+1,x∈R},若d(S,T)=(1,+∞),则t的值为.三、解答题:本题共5小题,共78分。
上海市华东师范大学第三附属中学2023-2024学年高二下学期期中考试数学试题

上海市华东师范大学第三附属中学2023-2024学年高二下学期期中考试数学试题学校:___________姓名:___________班级:___________考号:___________一、填空题1.在等差数列{}n a 中,11a =,公差2d =,则3a = .2.已知函数()()2351m m f x m x −−=−是幂函数,则实数m = .3.已知向量()()1,2,,4a b x =−=,且a b ⊥,则x = .4.抛物线2y x =的准线方程为 .5.已知直线230x y +−=和210x my ++=互相平行,则它们之间的距离是 .6.已知随机变量X 的分布为2130.160.440.40−⎛⎫ ⎪⎝⎭,则()25+=E X . 7.方程22131x y m m +=−−表示焦点在x 轴上的椭圆,则m 的取值范围是 . 8.直线l 的斜率的取值范围为[]1,1−,则其倾斜角的取值范围是 .9.已知椭圆221167x y +=的左、右焦点分别为1F 、2F .若P 为椭圆上一点,且1214PF PF ⋅=,则12F PF △的面积为 .10.已知m R ∈,动直线1l :10x my +−=过定点A ,动直线2l :230mx y m −−+=过定点B ,若1l 与2l 交于点P (异于点A ,B ),则PA PB +的最大值为 .11.数学中有许多寓意美好的曲线,曲线22322:()4C x y x y +=被称为“四叶玫瑰线”(如图所示).给出下列三个结论:①曲线C 关于直线y x =对称;②曲线C 上任意一点到原点的距离都不超过1;的正方形,使得曲线C 在此正方形区域内(含边界). 其中,正确结论的序号是 .12.定义两个点集S 、T 之间的距离集为(){},,d S T PQ P S Q T =∈∈,其中PQ 表示两点P 、Q 之间的距离,已知k 、R t ∈,(){},,R S x y y kx t x ==+∈,(){},R T x y y x ==∈,若()(),1,d S T =+∞,则t 的值为 .二、单选题13.“6n =”是“21nx x ⎛⎫ ⎪⎝⎭+的二项展开式中存在常数项”的( ) A .充分非必要条件B .必要非充分条件C .充要条件D .既非充分也非必要条件 14.已知复数z 满足2z z =,则复数z 的个数为( )A .1B .2C .3D .4 15.已知00(,)P x y 是圆222:(0)C x y r r +=>内异于圆心的一点,则直线200x x y y r +=与圆C 的位置关系是( )A .相交B .相切C .相离D .不能确定16.已知椭圆2214x y +=,作垂直于x 轴的直线交椭圆于,A B 两点,作垂直于y 轴的直线交椭圆于,C D 两点,且AB CD =,两垂线相交于点P ,若点P 的轨迹是某种曲线(或其一部分),则该曲线是( ).A .圆B .椭圆C .双曲线D .抛物线三、解答题17.在长方体1111ABCD A B C D −中(如图),11,2AD AA AB ===,点E 是棱AB 的中点.(1)在《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑.试问四面体1D CDE 是否为鳖臑?并说明理由;(2)求直线DE 与直线1D C 所成角的大小.18.已知向量()3sin ,1a x =,(),1b cosx =−. (1)若a ∥b ,求tan2x 的值;(2)若()()f x a b b =+⋅,求函数()f x 的最小正周期及当0,2x π⎡⎤∈⎢⎥⎣⎦时的最大值.19.在平面直角坐标系xOy 中,已知ABC 的顶点坐标分别是()()(0,0,3,3,1,A B C ,记ABC 外接圆为圆M .(1)求圆M 的方程; (2)在圆M 上是否存在点P ,使得2212PB PA −=?若存在,求点P 的个数;若不存在,说明理由.20.已知双曲线C :()222210,0x y a b a b −=>>的左、右焦点分别为1F 、2F ,直线l 过右焦点2F 且与双曲线C 交于A 、B 两点.(1)若双曲线CC 的焦点坐标;(2)设1a =,b =l 的斜率存在,且()110F A F B AB +⋅=,求l 的斜率;(3)设l OA OB OA OB +=−,求双曲线C 的离心率.21.已知椭圆C :()222210x y a b a b +=>>,左、右顶点分别为A 、B ,过点1,02M ⎛⎫− ⎪⎝⎭的直线与椭圆相交于不同的两点P 、Q (异于A 、B ),且35uuu u r uuu r AM MB =. (1)求椭圆C 的方程;(2)若直线AP 、QB 的斜率分别为1k 、2k ,且12k k λ=,求λ的值;(3)设PQB △和PQA △的面积分别为1S 、2S ,求12S S −的最大值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
华东师大三附中2014学年第二学期期末考试高二数学(理科)试题时间:120分钟 满分:150 分一.填空题(本大题满分56分)本大题共有14题,考生应在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分.1. 201532i i i i ++++ =__________________.2. 在5(31)x -的展开式中,设各项的系数和为a ,各项的二项式系数和为b ,则ab= . 3. 直线l 的参数方程是)(221R t t y tx ∈⎩⎨⎧-=+=,则l 的方向向量d 可以是__.4. 若圆锥的侧面展开图是半径为2、圆心角为90︒的扇形,则这个圆锥的全面积是 .5. 从一副混合后的扑克牌(52张)中随机抽取1张,,事件A 为“抽得红桃K ”,事件B 为“抽得为黑桃”,则概率=)(B A P (结果用最简分数表示).6. 在极坐标系中,曲线cos 1ρθ=+与cos 1ρθ=的公共点到极点的距离为____.7. 给出下列四个命题:(1)若平面α上有不共线的三点到平面β的距离相等,则βα//; (2)两条异面直线在同一平面内的射影可能是两条平行直线;(3)两条异面直线中的一条平行于平面α,则另一条必定不平行于平面α; (4)b ,a 为异面直线,则过a 且与b 平行的平面有且仅有一个. 其中正确命题的序号是_______________________8. 已知平面α截一球O 得圆M ,圆M 的半径为r ,圆M 上两点A 、B 间的弧长为2rπ,又球心O 到平面α的距离为r ,则A 、B 两点间的球面距离为 . 9. 边长分别为a 、b 的矩形,按图中所示虚线剪裁后, 可将两个小矩形拼接成一个正四棱锥的底面,其余恰好拼接 成该正四棱锥的4个侧面,则ba的取值范围是 . 10.在锐角的二面角βα--EF ,A EF ∈,AG α⊂,45=∠GAE ,若AG 与β所成角为 30,则二面角F A Gαβα--EF 为__________.11. 已知随机变量ξ所有的取值为1,2,3,对应的概率依次为121,,p p p ,若随机变量ξ的方差12ξ=D ,则12+p p 的值是 . 12. 如图,在极坐标系中,过点)0,2(M 的直线l 与极轴的夹角6πα=,若将l 的极坐标方程写成)(θρf =的形式,则=)(θf .13.对于曲线C 所在平面上的定点0P ,若存在以点0P 为顶点的角α,使得0AP B α≥∠对于曲线C 上的任意两个不同的点B A ,恒成立,则称角α为曲线C 相对于点0P 的“界角”,并称其中最小的“界角”为曲线C 相对于点0P 的“确界角”.曲线⎪⎩⎪⎨⎧<--≥+=)0(12)0(1:22x x x x y C 相对于坐标原点O 的“确界角”的大小是 .14. 一个半径为1的小球在一个内壁棱长为动,则该小球表面永远不可能接触到的容器内壁的面积是 . 二.选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案,考生应在答题纸的相应编号上,填上正确的答案,选对得5分,否则一律得零分.15. 某校共有高一、高二、高三学生共有1290人,其中高一480人,高二比高三多30人.为了解该校学生健康状况,现采用分层抽样方法进行调查,在抽取的样本中有高一学生96人,则该样本中的高三学生人数为 ( ) A. 84 B. 78 C. 81 D. 9616. 正四面体ABCD 的表面积为S ,其中四个面的中心分别是E 、F 、G 、H .设四面体EFGH 的表面积为T ,则TS等于 ( ) A.49 B. 19 C. 14 D. 1317. 甲乙两人一起去游园,他们约定,各自独立地从1到6号景点中任选4个进行游览,每个景点参观1小时,则最后一小时他们同在一个景点的概率是 ( )A.136 B. 19C. 536D. 16 18. 设123,,l l l 为空间中三条互相平行且两两间的距离分别为4,5,6的直线.给出下列三个结论:①存在i i A l ∈(1,2,3)i =,使得123A A A ∆是直角三角形; ②存在i i A l ∈(1,2,3)i =,使得123A A A ∆是等边三角形;③三条直线上存在四点(1,2,3,4)i A i =,使得四面体1234A A A A 为在一个顶点处的三条棱两两互相垂直的四面体.其中,所有正确结论的序号是 ( ) A .①B .①③C .①②D .②③三.解答题(本大题满分74分)本大题共5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤 . 19.(本题满分12分)在直三棱柱111A B C ABC -中,底面ABC 为直角三角形,2BAC π∠=,11AB AC AA ===.已知G与E分别为11A B 和1CC 的中点,D与F分别为线段AC 和AB 上的动点(不包括端点). 若GD EF ⊥,求线段DF 的长度的最小值.20.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分 .如图过圆锥轴的截面为等腰直角三角形SAB ,Q BQ =83π,点O为底面圆的圆心.(1)求该圆锥的侧面积;(2)设异面直线SA 与BQ 所成角的大小为θ,求tan θ的值.21.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分 . 如图,在四棱锥P ABCD -中,底面ABCD 是矩形,PA ⊥平面ABCD ,2AP AB ==,4AD =,E F 、依次是PB PC 、的中点.(1)求直线EC 与平面PAD 所成的角(结果用反三角函数值表示); (2)求三棱锥P AFD -的体积.22.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.在平面直角坐标系中,O 为坐标原点. 已知曲线C 上任意一点(,)P x y (其中0x ≥)到定点(1,0)F 的距离比它到y 轴的距离大1. (1)求曲线C 的轨迹方程;(2)若过点(1,0)F 的直线l 与曲线C 相交于A 、B 不同的两点,求OA OB ⋅的值;(3)若曲线C 上不同的两点M 、N 满足0OM MN ⋅= ,求ON的取值范围.FE DB C AP23.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.如图,点P 为斜三棱柱111C B A ABC -的侧棱1BB 上一点,1BB PM ⊥交1AA 于点M ,1BB PN ⊥交1CC 于点N .(1)求证:MN CC ⊥1;(2)在任意DEF ∆中有余弦定理:DFE EF DF EF DF DE ∠⋅-+=cos 2222.拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明. (3)在(2)中,我们看到了平面图形中的性质类比到空间图形的例子,这样的例子还有不少.下面请观察平面勾股定理的条件和结论特征,试着将勾股定理推广到空间去. 勾股定理的类比三角形ABC四面体O -ABC条件 AB ⊥AC OA 、OB 、OC 两两垂直结论AB 2+AC 2=BC 2?请在答题纸上完成上表中的类比结论,并给出证明.AA 1B 1BC 1CMNPFE DA P G 华东师大三附中2014学年第二学期期末考试高二数学(理科)试题答案一.1. 1-2. 13. ⎪⎭⎫ ⎝⎛-211,或()12,- 4. 54π 5.267 6.7. (2)(4) 8. 9. 1(,)2+∞ 10. 4π 11.3412. )6sin(1θπ-13512π14. 二. 15. B 16. B 17.D 18. C 三.1920. (1)SA ==R SA π⋅=(2)tan 3SH AH AH θ====21.(1)解法一:分别以AB AD AP 、、为x 轴、y 轴、z 轴建立空间直角坐标系,各点坐标分别是(0 0 0)A ,,,(2 0 0)B ,,,(2 4 0)C ,,,(0 4 0)D ,,,(0 0 2)P ,,, ∴(1 0 1)E ,,,(1 2 1)F ,,,(1 4 1)EC =-,,, (2分)又∵AB ⊥平面PAD ,∴平面PAD 的法向量为(2,0,0)n AB ==,(4分)设直线EC 与平面PAD 所成的角为α,则sin ||||EC n EC n α⋅===⋅(6分) ∴直线EC 与平面PAD 所成的角为. (7分)解法二:∵PA ⊥平面ABCD ,∴CD PA ⊥,又CD A D ⊥,∴CD ⊥平面PAD ,取PA 中点G ,CD 中点H ,联结EG GH GD 、、,则EG AB CD ////且1=12EG AB =,EGHC ∴是平行四边形,∴HGD ∠即为直线EC 与平面PAD 所成的角. (3分)在Rt GAD ∆中,GD =在Rt GHD ∆中,tanHD HGD GD ∠===,(6分)∴直线EC 与平面PAD 所成的角为 (7分)(2)解法一:由(1)解法一的建系得,(1 2 1)AF = ,,, (0 4 0)AD =,,,设平面AFD 的法向量为(,,)n x y z =,点P 到平面AFD 的距离为d ,由0AF n ⋅= ,0AD n ⋅=得20x y z ++=且40y =,取1x =得(1,0,1)n =-, (9分)∴AP n d n⋅=== , (11分)又AF FD ==2AFD S ==△(13分)∴1433P AFD V -=⨯=. (14分)解法二:易证PE 即为三棱锥P AFD -底面上的高,且PE =(11分)底面AFD △边AD 上的高等于AE ,且AE =AFD S =△(13分)1144323P AFD V -=⨯⨯=. (14分)解法三:依题意,//EF 平面PAD ,∴P AFD F PAD E PAD D PAE V V V V ----=== (11分)11114224322123D PAE V PA AB AD -=⨯⨯⨯⨯⨯=⨯⨯⨯=. (14分) 22.(1)依题意知,动点P 到定点F (1,0)的距离等于P 到直线1x =-的距离,曲线C 是以原点为顶点,F (1,0)为焦点的抛物线 ∵12p=∴2p = ∴ 曲线C 方程是24y x = (4分) (2)当l 平行于y 轴时,其方程为1x =,由214x y x =⎧⎨=⎩解得(1,2)A 、(1,2)B -此时=14=3OA OB ⋅--(6分)当l 不平行于y 轴时,设其斜率为k ,则由2(1)4y k x y x=-⎧⎨=⎩得2222(24)0k x k x k -++= 设1122(,),(,)A x y B x y ,则有121x x =,212224+k x x k+= (8分) ∴12121212==(1)(1)OA OB x x y y x x k x k x ⋅++--2221212(1)()k x x k x x k =+-++2222224=1+143k k k k k+-⋅+=-=- (10分) (3)设221212(,),(,)44y y M y N y ∴222121121(,),(,)44y y y OM y MN y y -==- ∵0OM MN ⋅= ∴0)(16)(121212221=-+-y y y y y y ∵0,121≠≠y y y ,化简得)16(112y y y +-= (12分) ∴6432256232256212122=+≥++=y y y (14分) 当且仅当4,16,2561212121±===y y y y 时等号成立∵22||64ON y ==≥∴当222min 64,8||||y y ON ON ==±= ,的取值范围是),58[+∞(16分)23.(1)证:MN CC PMN CC PN CC PM CC BB CC ⊥⇒⊥∴⊥⊥⇒111111,,//平面 ;(4分)(2)解:在斜三棱柱111C B A ABC -中,有αcos 21111111111222A ACC B BCC A ACC B BCC A ABB S S S S S ⋅-+= 其中α为平面B B CC 11与平面A A CC 11所组成的二面角. (7分)∴⊥,1PMN CC 平面 上述的二面角为MN P ∠,在PMN ∆中,2222cos PM PN MN PN MN MNP =+-⋅∠⇒MNP CC MN CC PN CC MN CC PN CC PM ∠⋅⋅⋅-+=cos )()(211111222222,由于111111111,,BB PM S CC MN S CC PN S A ABB A ACC B BCC ⋅=⋅=⋅=,∴有αcos 21111111111222A ACC B BCC A ACC B BCC A ABB S S S S S ⋅-+=. (10分) (3)空间勾股定理的猜想:已知四面体O -ABC 的三条侧棱OA 、OB 、OC 两两垂直,则有2222OAB OAC OBC ABC S S S S ∆∆∆∆++= (14分)证法一:作OD ⊥AB ,垂足为D ,连结CD22222222221111()4444ABC S AB CD AB OC OD AB OC AB OD ∆=⋅⋅=⋅⋅+=⋅⋅+⋅⋅ 222222222222111()444AOB AOB AOC COB AOB OA OB OC S OA OC OB OC S S S S ∆∆∆∆∆=⋅+⋅+=⋅⋅+⋅⋅+=++ (18分)证法二:作OH ⊥平面ABC ,垂足为H ,易得H 为△ABC 的垂心。
