几何图形模型二--鸟头模型
4几何五大模型——鸟头模型

---------------------------------------------------------------最新资料推荐------------------------------------------------------4几何五大模型——鸟头模型几何五大模型鸟头模型一两点都在边上:鸟头定理:(现出鸟头模型。
然后按一下出现一个鸟头,勾勒出鸟头的轮廓,出现如图的鸟头几何模型。
最后真实的鸟头隐去,只留下几何模型。
最后按一下,出公式。
)△ADE△ABCS ADAE=S ABAC EDC BA 二一点在边上,一点在边的延长线上:△CDE△ABCS CDCE=S BCAC EDCBA 本讲要点如图,AD=DB ,AE=EF=FC ,已知阴影部分面积为 5 平方厘米,△ ABC 的面积是平方厘米.例例 2 (1 )如图在△ABC 中,D 、E 分别是AB ,AC 上的点,且AD:AB=2:5, AE:AC=4:7, △ABC 的面积是的面积是 16 平方厘米,求△ABC 的面积。
(2 )如图在△ABC 中,D 在 BA 的延长线上,E 在在 AC 上,且 AB:AD=5:2 ,AE:EC=3:2, △ADE 的面积是的面积是 12 平方厘米,求△ABC 的面积。
已知△DEF 的面积为12 平方厘米,BE=CE,AD=2BD,CF=3AF,求△ABC 的面积。
1 / 22例例 1 例例 2 例例 3 三角形 ABC 面积为 1,AB 边延长一倍到 D,BC 延长 2 倍到 E,CA 延长 3 倍到 F,问三角形 DEF 的面积为多少?三角形 ABC 面积为 1,AB 边延长一倍到 D,BC 延长 2 倍到 E,CA 延长 3 倍到 F,问三角形 DEF 的面积为多少? FEDCBA 例例 4 例例 5 长方形ABCD 面积为 120,EF 为 AD 上的三等分点,G、H、I 为 DC 上的四等分点,阴影面积是多大?长方形 ABCD 面积为 120,EF 为 AD 上的三等分点,G、H、I 为 DC 上的四等分点,阴影面积是多大?如图,过平行四边形 ABCD 内的一点 P 边作边 AD 、 BC 的平行线 EF 、 GH ,若PBD 为的面积为 8平方分米,求平行四边形 PHCF 的面积比平行四边形 PGAE 的面积大多少平方分米? AB CDEFGHP 例例 61. 如下左图,在ABC △ 中,D 、E 分别是 BC 、AB 的三等分点,且ABC △ 的面积是 54 ,求CDE △ 的面积。
平面几何常考五大模型---等积变换、鸟头、蝴蝶、相似、 燕尾
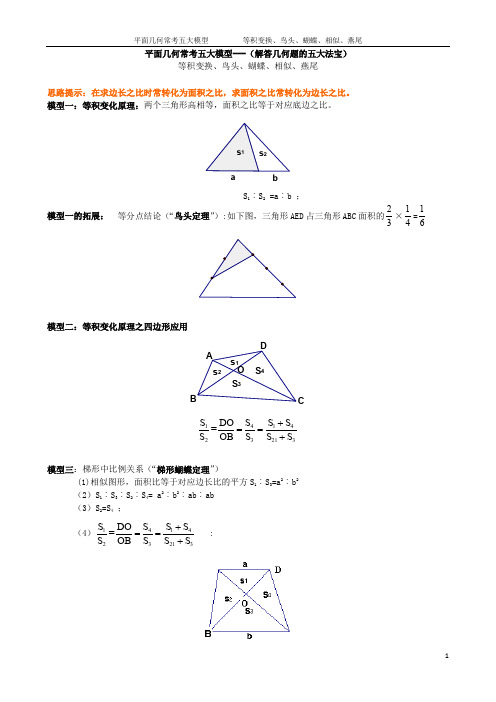
平面几何常考五大模型---(解答几何题的五大法宝)等积变换、鸟头、蝴蝶、相似、燕尾思路提示:在求边长之比时常转化为面积之比,求面积之比常转化为边长之比。
模型一:等积变化原理:两个三角形高相等,面积之比等于对应底边之比。
bS 1︰S 2 =a ︰b ;模型一的拓展: 等分点结论(“鸟头定理”):如下图,三角形AED 占三角形ABC 面积的23×14=16模型二:等积变化原理之四边形应用S 4S 3s 2s 1O DC BA141423213S S =S S S S DO OB S S +==+模型三:梯形中比例关系(“梯形蝴蝶定理”)(1)相似图形,面积比等于对应边长比的平方S 1︰S 3=a 2︰b2(2)S 1︰S 3︰S 2︰S 4= a 2︰b 2︰ab ︰ab (3)S 2=S 4 ;(4)141423213S S =S S S S DO OB S S +==+ :模型四:相似三角形性质①a b c hA B C H=== ; ②相似三角形面积之比等于对应连长之比的平方S 1︰S 2=a 2︰A 2hh H cb a CB Aac b HC B模型五:燕尾定理F ED CBAS △ABG :S △AGC =S △BGE :S △GEC =BE :EC ; S △BGA :S △BGC =S △AGF :S △GFC =AF :FC ; S △AGC :S △BCG =S △ADG :S △DGB =AD :DB ;【例1】:如右图,在△ABC 中,BE=3AE ,CD=2AD .若△ADE 的面积是1平方厘米,那么三角形ABC 的面积是多少?【解答】连接BD,S △ABD 和S △ AED 同高,面积比等于底边比,所以三角形ABD 的面积是4,S △ABD 和S △ABC 同高面积比等于底边比,三角形ABC 的面积是ABD 的3倍,是12. 【总结】要找准那两个三角形的高相同。
小学奥数_几何五大模型(鸟头模型)讲解学习

模型二 鸟头模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上如图 2), 则:():()ABC ADE S S AB AC AD AE =⨯⨯△△EDCBAEDCB A图⑴ 图⑵【例 1】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.EDCBAEDCBA【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△,::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△,所以:(24):(75)ADE ABC S S =⨯⨯△△,设8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 .【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那三角形等高模型与鸟头模型么三角形ABC 的面积是多少?EDC B AA B C DE【解析】 连接BE .∵3EC AE = ∴3ABC ABE S S =V V 又∵5AB AD =∴515ADE ABE ABC S S S =÷=÷V V V ,∴1515ABC ADE S S ==V V .【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍?乙甲E DCBAA BCDE甲乙【解析】 连接AD .∵3BE =,6AE =∴3AB BE =,3ABD BDE S S =V V 又∵4BD DC ==,∴2ABC ABD S S =V V ,∴6ABC BDE S S =V V ,5S S =乙甲.【例 2】 如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.EDCBA EDCBA【解析】 连接BE ,::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△,所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△,设6ADE S =△份,则25ABC S =△份,12ADE S =△平方厘米,所以1份是2平方厘米,25份就是50平方厘米,ABC △的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【例 3】 如图所示,在平行四边形ABCD 中,E 为AB 的中点,2AF CF =,三角形AFE (图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?【解析】 连接FB .三角形AFB 面积是三角形CFB 面积的2倍,而三角形AFB 面积是三角形AEF 面积的2倍,所以三角形ABC 面积是三角形AEF 面积的3倍;又因为平行四边形的面积是三角形ABC 面积的2倍,所以平行四边形的面积是三角形AFE 面积的326⨯=()倍.因此,平行四边形的面积为8648⨯=(平方厘米).【例 4】 已知DEF △的面积为7平方厘米,,2,3BE CE AD BD CF AF ===,求ABC △的面积.FED CBA【解析】 :():()(11):(23)1:6BDE ABCS S BD BE BA BC =⨯⨯=⨯⨯=△△,:():()(13):(24)3:8CEF ABC S S CE CF CB CA =⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =⨯⨯=⨯⨯=△△设24ABC S =△份,则4BDE S =△份,4ADF S =△份,9CEF S =△份,244497DEF S =---=△份,恰好是7平方厘米,所以24ABC S =△平方厘米【例 5】 如图,三角形ABC 的面积为3平方厘米,其中:2:5AB BE =,:3:2BC CD =,三角形BDE 的面积是多少?AB EC DDC EB A【解析】 由于180ABC DBE ︒∠+∠=,所以可以用共角定理,设2AB =份,3BC =份,则5BE =份,325BD =+=份,由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△,设6ABC S =△份,恰好是3平方厘米,所以1份是0.5平方厘米,25份就是250.512.5⨯=平方厘米,三角形BDE 的面积是12.5平方厘米【例 6】 (2007年”走美”五年级初赛试题)如图所示,正方形ABCD 边长为6厘米,13AE AC =,13CF BC =.三角形DEF 的面积为_______平方厘米.A【解析】 由题意知13AE AC =、13CF BC =,可得23CE AC =.根据”共角定理”可得,():():()12:(33)2:9CEF ABC S S CF CE CB AC =⨯⨯=⨯⨯=△△;而66218ABC S =⨯÷=△;所以4CEF S =△;同理得,:2:3CDE ACD S S =△△;,183212CDE S =÷⨯=△,6CDF S =△ 故412610DEF CEF DEC DFC S S S S =+-=+-=△△△△(平方厘米).【例 7】 如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =;延长CA 至F ,使3AF AC =,求三角形DEF 的面积.F EDCB AABCDEF【解析】 (法1)本题是性质的反复使用.连接AE 、CD . ∵11ABC DBC S S =V V ,1ABC S =V , ∴S 1DBC =V .同理可得其它,最后三角形DEF 的面积18=. (法2)用共角定理∵在ABC V 和CFE V 中,ACB ∠与FCE ∠互补, ∴111428ABC FCE S AC BC S FC CE ⋅⨯===⋅⨯V V . 又1ABC S =V ,所以8FCE S =V . 同理可得6ADF S =V ,3BDE S =V .所以186318DEF ABC FCE ADF BDE S S S S S =+++=+++=V V V V V .【例 8】 如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EFHGA B CD EF【解析】 连接AC 、BD .根据共角定理∵在ABC △和BFE △中,ABC ∠与FBE ∠互补,∴111133ABC FBE S AB BC S BE BF ⋅⨯===⋅⨯△△. 又1ABC S =△,所以3FBE S =△.同理可得8GCF S =△,15DHG S =△,8AEH S =△.所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△.所以213618ABCD EFGH S S ==.【例 9】 如图,四边形EFGH 的面积是66平方米,EA AB =,CB BF =,DC CG =,HD DA =,求四边形ABCD 的面积.H GFED CB AA B CDEFGH【解析】 连接BD .由共角定理得:():()1:2BCD CGF S S CD CB CG CF =⨯⨯=△△,即2CGF CDB S S =△△同理:1:2ABD AHE S S =△△,即2AHE ABD S S =△△所以2()2AHE CGF CBD ADB ABCD S S S S S +=+=△△△△四边形 连接AC ,同理可以得到2DHG BEF ABCD S S S +=△△四边形5AHE CGF HDG BEF EFGH ABCD ABCD S S S S S S S =++++=△△△△四边形四边形四边形所以66513.2ABCD S =÷=四边形平方米【例 10】 如图,将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ,若四边形ABCD 的面积为5,则四边形EFGH 的面积是 .A B CD E F GHA B CD EF GH【解析】 连接AC 、BD .由于2BE AB =,2BF BC =,于是4BEF ABC S S ∆∆=,同理4HDG ADC S S ∆∆=.于是444BEF HDG ABC ADC ABCD S S S S S ∆∆∆∆+=+=.再由于3AE AB =,3AH AD =,于是9AEH ABD S S ∆∆=,同理9CFG CBD S S ∆∆=. 于是999AEH CFG ABD CBD ABCD S S S S S ∆∆∆∆+=+=.那么491260EFGH BEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ∆∆∆∆=+++-=+-==.【例 11】如图,在ABC △中,延长AB 至D ,使BD AB =,延长BC 至E ,使12CE BC =,F 是AC 的中点,若ABC △的面积是2,则DEF △的面积是多少?A BCDEF【解析】 ∵在ABC △和CFE △中,ACB ∠与FCE ∠互补,∴224111ABC FCE S AC BC S FC CE ⋅⨯===⋅⨯△△. 又2ABC S =V ,所以0.5FCE S =V . 同理可得2ADF S =△,3BDE S =△.所以20.532 3.5DEF ABC CEF DEB ADF S S S S S =++-=++-=△△△△△【例 12】如图,1ABC S =△,5BC BD =,4AC EC =,DG GS SE ==,AF FG =.求FGS S V .SGF E DCBA【解析】 本题题目本身很简单,但它把本讲的两个重要知识点融合到一起,既可以看作是”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用,也可以看作是找点,最妙的是其中包含了找点的3种情况.最后求得FGS S △的面积为4321115432210FGS S =⨯⨯⨯⨯=△.【例 13】 如图所示,正方形ABCD 边长为8厘米,E 是AD 的中点,F 是CE 的中点,G 是BF 的中点,三角形ABG 的面积是多少平方厘米?ABCD EF GABCDEF G【解析】 连接AF 、EG .因为218164BCF CDE S S ==⨯=△△,根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”8AEF S =V ,8EFG S =V ,再根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”,得到16BFC S =V ,32ABFE S =,24ABF S =V ,所以12ABG S =V 平方厘米.【例 14】四个面积为1的正六边形如图摆放,求阴影三角形的面积.【解析】 如图,将原图扩展成一个大正三角形DEF ,则AGF ∆与CEH ∆都是正三角形.假设正六边形的边长为为a ,则AGF ∆与CEH ∆的边长都是4a ,所以大正三角形DEF 的边长为4217⨯-=,那么它的面积为单位小正三角形面积的49倍.而一个正六边形是由6个单位小正三角形组成的,所以一个单位小正三角形的面积为16,三角形DEF 的面积为496.由于4FA a =,3FB a =,所以AFB ∆与三角形DEF 的面积之比为43127749⨯=.同理可知BDC ∆、AEC ∆与三角形DEF 的面积之比都为1249,所以ABC ∆的面积占三角形DEF 面积的1213134949-⨯=,所以ABC ∆的面积的面积为4913136496⨯=.【巩固】已知图中每个正六边形的面积都是1,则图中虚线围成的五边形ABCDE 的面积是 .B DCEA【解析】 从图中可以看出,虚线AB 和虚线CD 外的图形都等于两个正六边形的一半,也就是都等于一个正六边形的面积;虚线BC 和虚线DE 外的图形都等于一个正六边形的一半,那么它们合起来等于一个正六边形的面积;虚线AE外的图形是两个三角形,从右图中可以看出,每个三角形都是一个正六边形面积的16,所以虚线外图形的面积等于11132363⨯+⨯=,所以五边形的面积是12103633-=.。
六年级奥数专题—几何五大模型—鸟头模型学习与巩固

几何五大模型——鸟头模型一 两点都在边上:鸟头定理:(现出“鸟头模型”。
然后按一下出现一个鸟头,勾勒出鸟头的轮廓,出现如图的鸟头几何模型。
最后真实的鸟头隐去,只留下几何模型。
最后按一下,出公式。
)△ADE △ABC S AD ×AE=S AB ×ACED C B A二 一点在边上,一点在边的延长线上:△CDE△ABC S CD ×CE =S BC ×AC例 1 如图,AD=DB ,AE=EF=FC ,已知阴影部分面积为5平方厘米,△ ABC的面积是平方厘米.例2 (1)如图在△ABC中,D、E分别是AB,AC上的点,且AD:AB=2:5, AE:AC=4:7,△ABC的面积是16平方厘米,求△ABC的面积。
(2)如图在△ABC中,D在BA的延长线上,E在AC上,且AB:AD=5:2,AE:EC=3:2,△ADE的面积是12平方厘米,求△ABC的面积。
例3 已知△DEF的面积为12平方厘米,BE=CE,AD=2BD,CF=3AF,求△ABC的面积。
例4 三角形ABC 面积为1,AB 边延长一倍到D ,BC 延长2倍到E ,CA 延长3倍到F ,问三角形DEF 的面积为多少?FEDC BA例5 长方形ABCD 面积为120,EF 为AD 上的三等分点,G 、H 、I 为DC 上的四等分点,阴影面积是多大?例6 如图,过平行四边形ABCD内的一点P作边AD、BC的平行线EF、GH,若PBD 的面积为8平方分米,求平行四边形PHCF的面积比平行四边形PGAE的面积大多少平方分米?作业:1. 如下左图,在ABC △中,D 、E 分别是BC 、AB 的三等分点,且ABC △的面积是54,求CDE △的面积。
2. 如图,长方形ABCD 的面积是1,M 是AD 边的中点,N 在AB 边上,且12AN BN.那么,阴影部分的面积等于 .AB CD M N 图13. 如图以ABC △的三边分别向外做三个正方形ABIH 、ACFG 、BCED ,连接HG 、EF 、BID ,又得到三个三角形,已知六边形DEFGHI 的面积是77平方厘米,三个正方形的面积分别是9、16、36平方厘米,则三角形ABC 的面积是多少?I HGFED CB A4. 如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =;延长CA 至F ,使3AF AC =,求三角形DEF 的面积。
平面几何五种模型

② AO : OC S1 S2 : S4 S3
【上下比】
=
=
=
【上上比】
=
=
=
由上述比例可以按数学运算原则推出很多规则:如
面积交叉相乘的乘积相等
=
= S1 S3 S2 S4
梯形蝴蝶定理( 梯蝴蝶 )
① S1 : S3 a2 : b2 →上:下 = a2 : b2
② S1 : S3 : S2 : S4 a2 : b2 : ab : ab →上:下:左:右 = a2 : b2 : ab : ab
+
+
=1
2
③ S 的对应份数为 a b →a2+2ab+b2=a2+b2+ab+ab 有木有↑
4 相似三角形 形状相同,大小不同的三角形,只要形状不变,无论大小怎么改变,他们都相似。 1 相似三角形的一切对应线段的长度成比例,并且 =它们的相似比 2 相似三角形的面积比 =相似比的平方
3 连接三角形两边中点的线段叫做三角形的中位线 三角形中位线定理:三角形的中位线长 =它所对应的底边长的一半 就是三角形任 2 边中点连出来的中位线就是第三边长的一半! 出题几率:多产生于 2 条平行线造成的相似三角形
等于浅紫色三角形是“嵌入”在大三角形 ABC里面,注意,鸟头定理用的是乘积比!不是
单独的线段比 ~
记忆上用 夹角 2 边
最好记,这里等于
E
D
A 对顶角
D E
A
B
C
B
C
D 互补角 A
E
D
A
E
B
CB
C
鸟头定理的证明,写出来是因为很多题目的解题过程,都需要补这么一条辅助线来过度连
小学几何五大模型

鸟头模型,是平面图形中常用的五个模型之一,其特点是通过边与面积的关系来解决问题。
对于初学者来说,最重要的是理解什么是鸟头模型并熟记它的特征。
一、鸟头模型的相关知识1.定义:两个三角形中有一个角相等或互补(相加等于180度),这两个三角形就叫共角三角形。
这个模型就叫鸟头模型。
其中存在的比例关系就叫做共角定理。
2.核心:比例模型有:二、鸟头模型的原理剖析三、鸟头模型的方法运用鸟头模型解题四部曲:第一步:观察:图中是否有鸟头模型第二步:构造:鸟头模型第三步:假设:线段长度或图形面积第四步:转化:将假设的未知数转化到鸟头模型中计算例1:如图,已知AD:BD=2:3 ,AE:EC=3:1,三角形ADE的面积是6平方厘米,求三角形ABC的面积?第一步:标条件第二步:确定等角位置 A小夹边AD×AE(小夹边指的是:小三角形夹着等角A的两边)大夹边AB×AC第三步:利用鸟头模型结论S△ADE:S△ABC=小夹边乘积:大夹边乘积=(2×3):(5×4)=6:20=3:103:10的意思是:三角形ADE的面积是3份,三角形ABC的面积是10份。
第四步:先除后乘算面积三角形ADE的面积是6平方厘米,对应3份,6÷3=2平方厘米/份;所求三角形 ABC的面积是10份,2×10=20 平方厘米。
例2:如图,已知BC:CD=5:2,AE:EC=1:1,三角形ABC的面积是20平方厘米,求三角形CDE的面积?第一步:标条件第二步:确定补角位置 C小夹边CD×CE(小夹边指的是:小三角形夹着补角C的两边)大夹边CA×CB第三步:利用鸟头模型结论S△CDE:S△ABC=小夹边乘积:大夹边乘积=(2×1):(2×5)=2:10=1:51:5的意思是:三角形CDE的面积是1份,三角形ABC的面积是5份。
第四步:先除后乘算面积三角形ABC的面积是20平方厘米,对应5份,20÷5=4 平方厘米/份;所求三角形 CDE的面积是1份,4×1=4平方厘米。
爱提分几何第02讲鸟头模型资料

精品文档鸟头模型讲_几何第02知识图谱-一、鸟头模型三角形中的鸟头四边形中的鸟头02讲_鸟头模型几何第一:鸟头模型知识精讲两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.共角三我们把这样的(相等角或互补角)两夹边的乘积之比.角形的面积比等于对应角.的面积是:ADE的面积比△ABC图形,称为鸟头模型.如图所示,△三点剖析进而利用鸟头模型的结论简单化复杂问题,:复杂图形如何构造鸟头模型,重难点进而解决它们.题模精讲三角形中的鸟头题模一、例1.1.1面积ABCADE,,那么三角形占三角形如图,.________的精品文档.精品文档答案:解析:.根据鸟头模型,1.1.2、例ABC,中,,已知已知三角形,ABC在三角形.的面积是,那么三角形24DEF_______面积是答案:7解析:精品文档.精品文档所占比例分别为根据鸟头模型,、、.因此,、、.1.1.3例、,求阴影部BD=2AD 中,,,AG=2CGABC如图,在△面积的几分之几?分的面积占△ABC答案:解析:,故BG;.,故连结,.同理,,即.面积的ABC,故阴影部分的面积占△精品文档.精品文档四边形中的鸟头题模二、例1.2.1.三角形48,,如图,长方形ABCD的面积是.__________CEF的面积是答案:10解析:面积是△.根据鸟头模型,△CEF是CE连接BD,是BC的,CF的CD.的面积是CEFBCD面积的.那么△、例1.2.2精品文档.精品文档边上,且的面积是如图,长方形ABCD1N,是AD边的中点,在AB..那么,阴影部分的面积为答案:解析:..连结例1.2.3、在边DC上,,ADABCD如图,正方形中,点E在边上,点F ._____的面积的比值是的面积与正方形,则ABCD精品文档.精品文档答案:解析:和、三块空白的面积分别占总面积的的面积的比值是,因此ABCD的面积与正方形.、例1.2.4,那60的面积是,E是CD边上的中点,ABCD 如图所示,长方形.__________的面积是么三角形AEF答案:精品文档.精品文档27解析:的面积ABF,ABCD△CEF的面积占长方形△面积的,连接BD面积的ABCD的面积占长方形ABCD面积的,△ADE占长方形面积的的面积占长方形ABCD.所以△AEF.,面积是例1.2.5、的面的面积相等.△AEFADFABCD如图在长方形中,△ABE、△、四边形AECF面积的几分之几?ABCD积是长方形答案:解析:精品文档.,同ABCD面积的,故与△ABE等底等高的长方形面积占面积的CEF面积占ABCD理.因此,,△.ABCD面积的,△AEF的面积是长方形1.2.6、例平方厘米,右上如图,长方形面积为35平方厘米,左边直角三角形的面积为5__________角直角三角形面积为7那么中间三角形平方厘米.面积是(阴影部分)平方厘米.答案:15.5解析:,由两个直角三角形面积可设,则.阴影得,所以.面积精品文档.精品文档、例1.2.7,DE,分别为,,为正六边形.如图,ABCDEFG,HI,JK,LAB,BCCD,.请问:小正六边形占大正EF,FA边上的三等分点,形成了正六边形GHIJKL六边形面积的几分之几?答案:解析:,根;,S设正六边形ABCDEF的面积为,则;小正六边形是,因此据鸟头模型,,一样的三角形得到的,面积为大正六边形减去六个和.小正六边形占大正六边形面积的精品文档.精品文档随堂练习随练1.1、三倍.倍,中,AD的长度是BD的3AC的长度是EC的3在三角形如图,ABC.角形AED的面积是10,那么三角形ABC的面积是__________答案:20解析:面面积是△ABC是AC.根据鸟头模型,有△的ADE是ADAB的,AE.的面积是ABC20.那么△积的随练1.2、,甲乙两个图形面积的,在右图的三角形ABC中,.比是_________精品文档.精品文档答案:解析:.根据鸟头模型,,所以甲、乙两个图形面积的比是随练1.3、,,,12的面积是.已知△DEF如图所示,的面积是多少?那么△ABC答案:36解析:精品文档.,同理的面积是△ABC面积的根据鸟头模型,△AEF ABCDEF的面积是△CDE的面积都是△ABC面积的.所以△和△可得△BDF.的面积是.所以△面积的ABC、随练1.4.请问:三角形,16如图,已知长方形ADEF的面积是,.__________BCE的面积是答案:3解析:.那么△DEF面积是△面积的BCEDF连接,根据鸟头模型,可知△.BCE的面积是精品文档.精品文档、1.5随练,如果阴影的面积是在长方形如图所示,ABCD6中,,,.的面积是__________ABCD那么长方形答案:18解析:.那么阴影部分的BCD根据鸟头模型,可知△CEF面积是△面积的.阴影的面积是△BCD面积的,是长方形ABCD面积的.ABCD,那么长方形的面积是6面积是1.6随练、精品文档.精品文档的面积是中,ABCD,长方形ABCD如图,在长方形.________AEF48,那么三角形的面积是答案:12解析:ADF的面积是长方形面积的根据一半模型和等高模型,△ABE,△的面积是长方形面积的,△CEF的面积是长方形面积的,面积AEF的面积是长方形面积的,所以△是.课后作业作业1、如图所示,已知,,而且△ABC的面积是60.那.么△__________的面积是ADE 精品文档.精品文档答案:12解析:的面积是,即△的面积是△ABCADE面积的ADE根据鸟头模型,△.、作业2倍.如果△ACBDAB的长度是的4倍,的长度是EC的3中,如图,在△ABC 的面积是多少平方厘米?20平方厘米,那么△ADE的面积为ABC答案:10解析:精品文档.精品文档.由鸟头模型可知,由题意知,,平方厘米.3、作业,上的一点,且中,如右图,在三角形为为的中点,.已知四边形的面积为的面积是35,则三角形_____答案:42解析:.,易知,,故4作业、的值?如图,已知,,试求,精品文档.精品文档答案:解析:,根据鸟头模型,,同理.,因此、5作业点的四等分AAC边上靠近EAB如图所示,D是边上靠近A点的三等分点,是,那么三C是FBC边上靠近点的五等分点.如果三角形ABC的面积是24点,.的面积是DEF__________角形答案:5.6精品文档.精品文档解析:,由鸟头模型可得,,,所以.、作业6是的三等分点,边靠近CF是是如图,三角形ABC中,DAB边的中点,EAC 的面积是多少?三角形ABC边靠近BCB的四等分点,三角形的面积为1.DEF答案:解析:,,同理根据鸟头模型,.的面积是:DEF,所以三角形精品文档.精品文档7、作业如CE中,AF的长度是FD的2倍,的长度等于ED.ABCD如图,在平行四边形的面积是多少平方厘果平行四边形ABCD的面积为FDE120平方厘米,那么△米?答案:10解析:.由鸟头模型可知,,由题意知,AC连接,平方厘米.8、作业点的三等分点,边上靠近DAD96长方形ABCD的面积是平方厘米,E是如图,平方厘米.__________CCDF是边上靠近点的四等分点.阴影部分的面积是精品文档.精品文档答案:平方厘米40解析:,分别求出它们的面积.,△考虑空白△AEB,△BFCEDF,AD的;它的高为AB首先求△AEB的面积.它的底为AE,是长方形的长与长方形的宽相等.的面积是长方形面积的,即AEB所以△平方厘米.,BF 同样可求得平方厘米的面积是长方形面积的平方厘米.,即△EDF的面积是长方形面积的,阴影部分的面积为所以空白部分的总面积为作业9、精品文档.精品文档ACF2,三角形ADBADEF如图,已知长方形的面积是16,三角形的面积是ABC的面积是4.请问:三角形的面积是多少?答案:7解析:,;;,;因此,;.精品文档.。
小学几何五大模型

鸟头模型,是平面图形中常用的五个模型之一,其特点是通过边与面积的关系来解决问题。
对于初学者来说,最重要的是理解什么是鸟头模型并熟记它的特征。
一、鸟头模型的相关知识1.定义:两个三角形中有一个角相等或互补(相加等于180度),这两个三角形就叫共角三角形。
这个模型就叫鸟头模型。
其中存在的比例关系就叫做共角定理。
2.核心:比例模型有:二、鸟头模型的原理剖析三、鸟头模型的方法运用鸟头模型解题四部曲:第一步:观察:图中是否有鸟头模型第二步:构造:鸟头模型第三步:假设:线段长度或图形面积第四步:转化:将假设的未知数转化到鸟头模型中计算例1:如图,已知AD:BD=2:3,AE:EC=3:1,三角形ADE的面积是6平方厘米,求三角形ABC的面积?第一步:标条件第二步:确定等角位置A小夹边AD×AE(小夹边指的是:小三角形夹着等角A的两边)大夹边AB×AC第三步:利用鸟头模型结论S△ADE:S△ABC=小夹边乘积:大夹边乘积=(2×3):(5×4)=6:20=3:103:10的意思是:三角形ADE的面积是3份,三角形ABC的面积是10份。
第四步:先除后乘算面积三角形ADE的面积是6平方厘米,对应3份,6÷3=2平方厘米/份;所求三角形ABC的面积是10份,2×10=20平方厘米。
例2:如图,已知BC:CD=5:2,AE:EC=1:1,三角形ABC的面积是20平方厘米,求三角形CDE的面积?第一步:标条件第二步:确定补角位置C小夹边CD×CE(小夹边指的是:小三角形夹着补角C的两边)大夹边CA×CB第三步:利用鸟头模型结论S△CDE:S△ABC=小夹边乘积:大夹边乘积=(2×1):(2×5)=2:10=1:51:5的意思是:三角形CDE的面积是1份,三角形ABC的面积是5份。
第四步:先除后乘算面积三角形ABC的面积是20平方厘米,对应5份,20÷5=4平方厘米/份;所求三角形CDE的面积是1份,4×1=4平方厘米。
4几何五大模型——鸟头模型

---------------------------------------------------------------最新资料推荐------------------------------------------------------4几何五大模型——鸟头模型几何五大模型鸟头模型一两点都在边上:鸟头定理:(现出鸟头模型。
然后按一下出现一个鸟头,勾勒出鸟头的轮廓,出现如图的鸟头几何模型。
最后真实的鸟头隐去,只留下几何模型。
最后按一下,出公式。
)△ADE△ABCS ADAE=S ABAC EDC BA 二一点在边上,一点在边的延长线上:△CDE△ABCS CDCE=S BCAC EDCBA 本讲要点如图,AD=DB ,AE=EF=FC ,已知阴影部分面积为 5 平方厘米,△ ABC 的面积是平方厘米.例例 2 (1 )如图在△ABC 中,D 、E 分别是AB ,AC 上的点,且AD:AB=2:5, AE:AC=4:7, △ABC 的面积是的面积是 16 平方厘米,求△ABC 的面积。
(2 )如图在△ABC 中,D 在 BA 的延长线上,E 在在 AC 上,且 AB:AD=5:2 ,AE:EC=3:2, △ADE 的面积是的面积是 12 平方厘米,求△ABC 的面积。
已知△DEF 的面积为12 平方厘米,BE=CE,AD=2BD,CF=3AF,求△ABC 的面积。
1 / 22例例 1 例例 2 例例 3 三角形 ABC 面积为 1,AB 边延长一倍到 D,BC 延长 2 倍到 E,CA 延长 3 倍到 F,问三角形 DEF 的面积为多少?三角形 ABC 面积为 1,AB 边延长一倍到 D,BC 延长 2 倍到 E,CA 延长 3 倍到 F,问三角形 DEF 的面积为多少? FEDCBA 例例 4 例例 5 长方形ABCD 面积为 120,EF 为 AD 上的三等分点,G、H、I 为 DC 上的四等分点,阴影面积是多大?长方形 ABCD 面积为 120,EF 为 AD 上的三等分点,G、H、I 为 DC 上的四等分点,阴影面积是多大?如图,过平行四边形 ABCD 内的一点 P 边作边 AD 、 BC 的平行线 EF 、 GH ,若PBD 为的面积为 8平方分米,求平行四边形 PHCF 的面积比平行四边形 PGAE 的面积大多少平方分米? AB CDEFGHP 例例 61. 如下左图,在ABC △ 中,D 、E 分别是 BC 、AB 的三等分点,且ABC △ 的面积是 54 ,求CDE △ 的面积。
小学奥数-几何五大模型(鸟头模型).

模型二 鸟头模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上如图 2),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△EDCBAEDCB A图⑴ 图⑵【例 1】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.三角形等高模型与鸟头模型EDCBAEDCBA【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△,::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△,所以:(24):(75)ADE ABC S S =⨯⨯△△,设8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 .【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少?EDCBAABCDE【解析】 连接BE .∵3EC AE =∴3ABC ABE S S = 又∵5AB AD =∴515ADE ABE ABC S S S =÷=÷,∴1515ABC ADE S S ==.【巩固】如图,三角形被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍?乙甲E DCBAABCDE甲乙【解析】 连接AD .∵3BE =,6AE =∴3AB BE =,3ABD BDE S S =又∵4BD DC ==,∴2ABC ABD S S =,∴6ABC BDE S S =,5S S =乙甲.【例 2】 如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.EDCBAEDCBA【解析】 连接BE ,::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△,所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△,设6ADE S =△份,则25ABC S =△份,12ADE S =△平方厘米,所以1份是2平方厘米,25份就是50平方厘米,ABC△的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【例 3】 如图所示,在平行四边形中,E为的中点,2AF CF =,三角形(图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?【解析】 连接.三角形面积是三角形面积的2倍,而三角形面积是三角形面积的2倍,所以三角形面积是三角形面积的3倍;又因为平行四边形的面积是三角形面积的2倍,所以平行四边形的面积是三角形面积的326⨯=()倍.因此,平行四边形的面积为8648⨯=(平方厘米).【例 4】 已知DEF △的面积为7平方厘米,,2,3BE CE AD BD CF AF ===,求ABC △的面积.FED CBA【解析】 :():()(11):(23)1:6BDE ABC S S BD BE BA BC =⨯⨯=⨯⨯=△△,:():()(13):(24)3:8CEF ABC S S CE CF CB CA =⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =⨯⨯=⨯⨯=△△设24ABC S =△份,则4BDE S =△份,4ADF S =△份,9CEF S =△份,244497DEF S =---=△份,恰好是7平方厘米,所以24ABC S =△平方厘米【例 5】 如图,三角形ABC 的面积为3平方厘米,其中:2:5AB BE =,:3:2BC CD =,三角形BDE 的面积是多少?AB ECDDC EB A【解析】 由于180ABC DBE ︒∠+∠=,所以可以用共角定理,设2AB =份,3BC =份,则5BE =份,325BD =+=份,由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△,设6ABC S =△份,恰好是3平方厘米,所以1份是0.5平方厘米,25份就是250.512.5⨯=平方厘米,三角形BDE 的面积是12.5平方厘米【例 6】 (2007年”走美”五年级初赛试题)如图所示,正方形ABCD 边长为6厘米,13AE AC =,13CF BC =.三角形DEF 的面积为平方厘米.A【解析】 由题意知13AE AC =、13CF BC =,可得23CE AC =.根据”共角定理”可得,():():()12:(33)2:9CEF ABC S S CF CE CB AC =⨯⨯=⨯⨯=△△;而66218ABC S =⨯÷=△;所以4CEF S =△;同理得,:2:3CDE ACD S S =△△;,183212CDE S =÷⨯=△,6CDF S =△故412610DEF CEF DEC DFC S S S S =+-=+-=△△△△(平方厘米).【例 7】 如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =;延长CA 至F ,使3AF AC =,求三角形DEF 的面积.FEDCBA AB CDEF【解析】 (法1)本题是性质的反复使用.连接AE 、CD .∵11ABC DBCS S=,1ABC S =,∴S 1DBC =.同理可得其它,最后三角形DEF 的面积18=.(法2)用共角定理∵在ABC 和CFE 中,ACB ∠与FCE ∠互补, ∴111428ABC FCES AC BC SFC CE ⋅⨯===⋅⨯.又1ABC S =,所以8FCE S =. 同理可得6ADF S =,3BDE S =.所以186318DEF ABC FCE ADF BDE S S S S S =+++=+++=.【例 8】 如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EFHGA B CD EF【解析】 连接AC 、BD .根据共角定理∵在ABC △和BFE △中,ABC ∠与FBE ∠互补,∴111133ABC FBES AB BC S BE BF⋅⨯===⋅⨯△△.又1ABC S =△,所以3FBE S =△.同理可得8GCF S =△,15DHG S =△,8AEH S =△.所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△.所以213618ABCDEFGHS S ==.【例 9】 如图,四边形EFGH 的面积是66平方米,EA AB =,CB BF =,DC CG =,HD DA =,求四边形ABCD 的面积.H GFED CB A A B CDEFGH 【解析】 连接BD .由共角定理得:():()1:2BCD CGF S S CD CB CG CF =⨯⨯=△△,即2CGF CDB S S =△△同理:1:2ABD AHE S S =△△,即2AHE ABD S S =△△ 所以2()2AHE CGF CBD ADB ABCD S S S S S +=+=△△△△四边形连接AC ,同理可以得到2DHG BEF ABCD S S S +=△△四边形5AHE CGF HDG BEF EFGH ABCD ABCD S S S S S S S =++++=△△△△四边形四边形四边形所以66513.2ABCD S =÷=四边形平方米【例 10】如图,将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ,若四边形ABCD 的面积为5,则四边形EFGH 的面积是 .A B CD EF GHA B CD EF GH【解析】 连接AC 、BD .由于2BE AB =,2BF BC =,于是4BEF ABC S S ∆∆=,同理4HDG ADC S S ∆∆=.于是444BEF HDG ABC ADC ABCD S S S S S ∆∆∆∆+=+=.再由于3AE AB =,3AH AD =,于是9AEH ABD S S ∆∆=,同理9CFG CBD S S ∆∆=. 于是999AEH CFG ABD CBD ABCD S S S S S ∆∆∆∆+=+=.那么491260EFGH BEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ∆∆∆∆=+++-=+-==.【例 11】如图,在ABC △中,延长AB 至D ,使BD AB =,延长BC 至E ,使12CE BC =,F 是AC 的中点,若ABC △的面积是2,则DEF △的面积是多少?A BCDEF【解析】 ∵在ABC △和CFE △中,ACB ∠与FCE ∠互补,∴224111ABC FCE S AC BC S FC CE ⋅⨯===⋅⨯△△. 又2ABC S =,所以0.5FCE S =. 同理可得2ADF S =△,3BDE S =△.所以20.532 3.5DEF ABC CEF DEB ADF S S S S S =++-=++-=△△△△△【例 12】如图,1ABC S =△,5BC BD =,4AC EC =,DG GS SE ==,AF FG =.求FGS S .SGF E DCBA【解析】 本题题目本身很简单,但它把本讲的两个重要知识点融合到一起,既可以看作是”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用,也可以看作是找点,最妙的是其中包含了找点的3种情况.最后求得FGS S △的面积为4321115432210FGS S =⨯⨯⨯⨯=△.【例 13】如图所示,正方形ABCD 边长为8厘米,E 是AD 的中点,F 是CE 的中点,G 是BF 的中点,三角形ABG 的面积是多少平方厘米?ABC DEF GABCDEF G【解析】 连接AF 、EG .因为218164BCF CDE S S ==⨯=△△,根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”8AEF S =,8EFG S =,再根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”,得到16BFC S =,32ABFE S =,24ABF S =,所以12ABG S =平方厘米.【例 14】四个面积为1的正六边形如图摆放,求阴影三角形的面积.【解析】 如图,将原图扩展成一个大正三角形DEF ,则AGF ∆与CEH ∆都是正三角形.假设正六边形的边长为为a ,则AGF ∆与CEH ∆的边长都是4a ,所以大正三角形DEF 的边长为4217⨯-=,那么它的面积为单位小正三角形面积的49倍.而一个正六边形是由6个单位小正三角形组成的,所以一个单位小正三角形的面积为16,三角形DEF 的面积为496.由于4FA a =,3FB a =,所以AFB ∆与三角形DEF 的面积之比为43127749⨯=.同理可知BDC ∆、AEC ∆与三角形DEF 的面积之比都为1249,所以ABC ∆的面积占三角形DEF 面积的1213134949-⨯=,所以ABC ∆的面积的面积为4913136496⨯=.【巩固】已知图中每个正六边形的面积都是1,则图中虚线围成的五边形ABCDE 的面积是 .B DCEA【解析】 从图中可以看出,虚线AB 和虚线CD 外的图形都等于两个正六边形的一半,也就是都等于一个正六边形的面积;虚线BC 和虚线DE 外的图形都等于一个正六边形的一半,那么它们合起来等于一个正六边形的面积;虚线AE 外的图形是两个三角形,从右图中可以看出,每个三角形都是一个正六边形面积的16,所以虚线外图形的面积等于11132363⨯+⨯=,所以五边形的面积是121036-=.33最新文件仅供参考已改成word文本。
小学奥数 几何五大模型(鸟头模型)学生版

模型二 鸟头模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上如图 2),则:():()ABCADES S AB AC AD AE =⨯⨯△△EDCBAEDCB A图⑴ 图⑵如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADES =△平方厘米,求ABC △的面积.EDCBAEDCBA三角形等高模型与鸟头模型【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少?EDCBAABCD E【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍?乙甲E DCBAABCDE甲乙如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADES=△平方厘米,求ABC △的面积. ED CBAEDCBA如图所示,在平行四边形ABCD 中,E 为AB 的中点,2AF CF =,三角形AFE (图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?。
鸟头模型的原理

鸟头模型的原理
嘿,朋友们!今天咱来聊聊鸟头模型。
这鸟头模型啊,就像是一把神奇的钥匙,能打开好多数学难题的大门呢!
你看啊,鸟头模型就好像是一只聪明的小鸟,它有着自己独特的本领。
想象一下,一只小鸟在天空中自由自在地飞翔,它能看到好多我们看不到的风景。
鸟头模型也是这样,它能让我们发现那些隐藏在图形中的奇妙关系。
比如说,在一些几何图形中,看似毫无头绪的几条边和几个角,通过鸟头模型就能找到它们之间的联系。
这就好比我们在一堆杂乱无章的拼图中,突然发现了关键的那几块,一下子就能把整个画面拼凑起来,是不是很神奇?
我们平时遇到的那些三角形啊、四边形啊,有时候真让人头疼。
但有了鸟头模型,就好像给我们配了一副超级眼镜,能让我们看清它们的真面目。
它能让那些复杂的图形变得简单易懂,就像给迷雾中的我们点亮了一盏明灯。
你说,这鸟头模型是不是很厉害?它就像一个隐藏在数学世界里的小秘密,等着我们去发现和探索。
而且啊,一旦你掌握了它,你就会发现解决问题变得轻而易举,就像武林高手找到了绝世秘籍一样。
我们在学习鸟头模型的时候,可不能马虎哦!要像对待宝贝一样仔细研究它。
多做几道题,多尝试几种方法,慢慢就会发现它的奇妙之处。
别小看这些题目,它们可都是我们提升能力的好机会呢!
你想想,如果我们能熟练运用鸟头模型,那在数学的海洋里岂不是可以畅游无阻?那些难题就不再是难题,而是我们展示自己能力的舞台啦!难道不是吗?
所以啊,朋友们,让我们一起好好研究鸟头模型,让它成为我们学习数学的得力助手。
让我们和这只神奇的“小鸟”一起在数学的天空中翱翔吧!相信我,你一定会爱上它的!。
小升初几何模型微课(3)——鸟头模型

几何模型突破——鸟头模型
两个三角形中有一个角相等或互补,
则这两个角叫做共角三角形。
所以
鸟头模型也叫做共角模型。
模型结论:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
相等角AC AB
AE AD S S ABC ADE ⨯⨯=∆∆
互补角AC AB
AE AD S S ABC ADE ⨯⨯=∆∆
例题如图,已知三角形A B C 面积为1,
延长A B 至D ,使B D =A B ,延长
B C 至E ,使C E =2B C ,延长C A
至F ,使A F =3A C ,求三角形
D E F 的面积。
1
1421
1231
131⨯⨯=⨯⨯=⨯⨯=⨯⨯=⨯⨯=⨯⨯=∆∆∆∆∆∆CA CB CF CE S S AB AC AD AF S S BC BA BE BD S S ABC CEF ABC AFD ABC BDE
如图,三角形A B C面积为1.延长B A至D,使得D A=A B,延长C A至E,使E A=2A C,延长
C B至F,使F B=3B C,求三角形
D
E F的面积
课后作业如图,四边形A B C D的面积是10平方米,E A=A B,F B=B C,G C=C D,H D=D A,求四边形E F G H的面积。
小学图形计算—鸟头模型

A
S∆ABE
S∆ABC
E
B
=
=
AE
AC
… … (2)
将等式(1)和等式(2)相乘:
C
S∆ADE
S∆ABE
×
S∆ABE
S∆ABC
=
AD
AB
×
AE
AC
=>
S∆ADE
S∆ABC
=
AD × AE
AB × A
六、练习题1
如图,已知AD ∶ BD = 2:3, A ∶ CE = 3:4,∆ABC的面积是70cm2,求∆ADE的面积?
A
2
D
3
B
解题点拨:
3
根据鸟头模型共角定理可知:
E
S∆ABC
S∆ADE
4
C
=
AB×AC (2+3)×(3+4)
=
AD×AE
2×3
5×7
=
2×3
由于∆ =70cm2,可得∆ADE =12cm2
=356来自六、练习题2如图,已知∆BC面积为1,延长AB到D,使得BD=AB,延长BC到E,使得CE=2BC,延
B
E
A
D
C
一、鸟头模型的由来
B
这个模型的形状酷似一只鸟的
E
头,人们将其称为鸟头模型。
其中,鸟嘴部分是∆ADE,鸟
嘴和鸟头部分构成∆ABC。鸟
A
头模型主要讨论∆ADE和∆ABC
D
的一些数学性质。
C
二、鸟头模型—共角定理
定理:如果两个三角形有一组对应角相等,则它们的面积之比等于对
应角两边乘积之比。 A
D
E
S∆ABE
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何图形基本模型鸟头模型姓名
概述:共角三角形(鸟头模型)
如果两个三角形有一个角相等或互补,这两个三角形叫共角三角形。
它们的面积比等于对应角两夹边的乘积比。
D
即有关系式
S ADE AD AE
S ABC AB AC
∆
∆
⨯
=
⨯
存在。
(图1)
证明:
那么:图2模型的比例关系式为:
【问题1】在三角形ABC中,D在BA的延长线上,E在AC上,并且有AB:AD=5:2,AE:EC=3:2,三角形ADE的面积为12,求三角形ABC的面积。
【练习】1、如下图,三角形ABC的面积为1,并且AE=3AB,BD=2BC,求三角形BDE的面积。
A B E
D
2、在三角形ABC中,DE分别是AB、AC上的点,并且有AD:AB=2:5,AE:AC=4:7,三角形ADE的面积为12,求三角形ABC的面积。
3、在三角形ABC中,DE分别是AB
、AC上的点,并且有AD:AB=2:3,
AE:AC=3:4,三角形
ADE的面积为60平方厘米,求四边形DEBC的面积。
【问题2】已知三角形DEF的面积为7,BE=CE,AD=2BD,CF=3AF, 求三角形ABC的面积。
A
B E C
【问题3】如下图,正方形的边长为6厘米,并且有AE=1
3
EC,CF=
1
3
BC,求三角形DEF的面积。
D
E
B F C
独立练习:
1、图中△AOB 的面积为15cm 2,线段OB 的长度为OD 的3倍,则梯形ABCD 的面积为______ .
2、图中,在长方形内画了一些线,已知边上三块面积分别为13,25,49。
那么图中阴影部分的面积是________________ S 2
S 11349
35F
E D
C B A
3、如图,在三角形ABC 中,D 为BC 的中点,E 为AB 上的一点,且13BE AB
,已知四边形EDAC 的面积是35,求三角形ABC 的面积。
4、如下图,在三角形ABC 中,BD=2AD ,AG=2CG ,BE=EF=FC ,求四边形DGFE 面积占三角形ABC 的 几分之几?
5、如下图,三角形ABC的面积为1,将AB延长至D,使AB=BD,将BC延长至E,使CE=2BC,将CA延长至F,使AF=3CA,求三角形DEF的面积。
A
B C E
D
5、如下图,长方形ABCD的面积为42平方厘米,并且有AE=1
3
EC,CF=
1
3
BC,
求阴影部分三角形DEF的面积。
A D
(注:文档可能无法思考全面,请浏览后下载,供参考。
可复制、编制,期待你的好评与关注)E。
