流体力学第四章流动阻力和能量损失

合集下载

《流体力学》第四章流动阻力和能量损失4.8-4.9

ζ：局部阻力系数
2
实验研究表明：局部损失和沿程损失一样，不同的流态遵循不同的规律。
如果流体以层流经过局部阻碍，而且受干扰后仍能保持层流的话,局部阻力系数为： B
z=
Re
要使局部阻碍处受边壁强烈干扰的流动仍能保持层流，只有当Re远小于2000才有可能。因此，以紊流的局部损失讨论为主。
局部阻碍的种类很多，但按其流动特性来分，主要是过流断面的扩大或收缩、流动方向的改变、流量的合入与分出三种基本形式以及这几种形式的不同组合。
2 a 1v12 a 2 v2 hm = 2g 2g v2 + (a 02 v2 - a 01v1 ) g
av a v v2 hm = + (a 02 v2 - a 01v1 ) 2g 2g g
(v1 - v2 ) hm = 2g
2
2 1 1
2 2 2
（取动能、动量修正系数均为1）
突然扩大的水头损失等于以平均流速差计算的流速水头。断面突然扩大时的水流图形
gQ p1 A2 - p2 A2 + g A2 ( Z1 - Z 2 ) = (a 02 v2 - a 01v1 ) g
Q = v2 A2 p1 p2 v2 ( Z1 + ) - ( Z 2 + ) = (a 02v2 - a 01v1 ) g g g
将上式代入能量方程
2 p1 a 1v12 p2 a 2 v2 hm = ( Z1 + + ) - (Z2 + + ) g 2g g 2g
Re=1000000时弯管的局部阻力系数
序号断面形状 R/d(R/b) 1 圆形方形 h/b=1.0 矩形 h/b=0.5 矩形 h/b=2.0

流体力学4流动阻力和能量损失

粘性切应力：各流层的时均流速不同，存在相对 du 运动。
1
惯性切应力：脉动引起的动量交换产生的切应力。

y
dy
管心线时均流速分布线 u f y
u u
y2

2 u ux u u ux y x y
u
A
A
l
y1
x

横向脉动产生的紊流惯性切应力
p1 A p2 A Al cos 0l 2 r0 0 p1 p2 2 0l Z1 Z 2 r0
2 0l hf r0

因而

令
2 0 r0 J 0 J l r0 2 hf

沿程水头损失与速度v的关系
1

Z1
p1

1v12
2g
Z2
2
p2

2 2v2
2g
hl
均匀流
1
p1 ) (Z 2
hl h f ( Z1
2
p2
) h
lg h f lg k m lg v h f kv m
层流：m=1，hf ~ v1 紊流：m=1.75~2，hf ~ v1.75~2
2、莫迪图

莫迪以柯氏公式为基础绘制出工业管道沿程阻力系数的曲线。
3、简化公式

莫迪公式

阿里特苏里公式
1 6 3 1 2000 K 10 0.0055 d Re 7 K 适于 Re 4000 ~ 10 , 0.01, 0.05 d
系列1
25 20

流体力学第四章：流体阻力及能量损失

减小摩擦阻力的方法
优化物体表面粗糙度、使用润滑剂、改变流体的流速和方向等。
形状阻力
形状阻力
由于物体形状的不同，流体在绕过物体时产生的阻力。
形状阻力公式
$F_s = frac{1}{2} rho u^2 A C_s$，其中$C_s$为形状阻力系数，与物体形状、流体性质和流速有关。
减小形状阻力的方法
详细描述
汽车设计中的流体阻力优化主要包括车身形状设计和空气动力学套件的应用。设计师会采用流线型设计来减小空气阻力，同时也会采用导流板、扰流板等空气动力学套件来调整汽车周围的空气流动，以提高汽车的行驶
稳定性、减小风噪，并降低燃油消耗。
THANKS FOR WATCHING
感谢您的观看
详细描述
船舶航行中的流体阻力主要来自船体与水之间的摩擦力以及水对船体的冲击力。为了减小流体阻力，船舶设计师通常会采用流线型设计，优化船体表面的光滑度，以及减少不必要的突出物，从而提高航行效率。
管道流动中的能量损失
总结词
管道中流体流动时，由于流体与管壁之间的摩擦以及流体内部的湍流等效应，会产生能量损失。
根据伯努利方程、欧拉方程等计算公式，结合物体的形状、速度和流体密度等参数进行计算。
02 流体阻力现象
摩擦阻力
摩擦阻力
由于流体与物体表面的相对运动产生摩擦而形成的阻力。
摩擦阻力公式
$F_f = frac{1}{2} rho u^2 A C_f$，其中$rho$为流体密度，$u$为流速，$A$为流体与物体接触的表面积，$C_f$ 为摩擦阻力系数。
流体力学第四章流体阻力及能量损失
目录
• 流体阻力的概念 • 流体阻力现象 • 能量损失原理 • 流体阻力的减小方法 • 实际应用案例

流体力学第四章流动阻力与管路水力计算

图4-7 水力光滑管和水力粗糙管
第四章流动阻力与管路水力计算
3.湍流阻力与流速分布 (1)湍流阻力在湍流中，流体内部不仅存在着因流层间的时均流速不同而产生的粘滞切应力τ１，而且还存在着由于脉动使流体质点之间发生动量交换而产生的惯性切应力τ２。
第四章流动阻力与管路水力计算
(2)湍流速度分布实验证明，流体在管道中作湍流运动时，过流断面上的速度分布如图4-8所示。
第四章流动阻力与管路水力计算
第四章流动阻力与管路水力计算
3.圆管层流运动时的沿程阻力系数
第四章流动阻力与管路水力计算
第四章流动阻力与管路水力计算
解：v=Q/A=4Q/π=4×75×/π×m/s=0.96m/s 二、圆管湍流的沿程损失计算实际工程中，除少数流动为层流外，绝大多数都属于湍流运动，因此湍流的特征和运动规律在解决工程实际问题中有重要的作用。 1.湍流脉动现象与时均法
第四章流动阻力与管路水力计算
均匀流动是指流速大小和方向均沿流程不变的流动。由于这种流动只能发生在壁面（截面形状、大小、表面粗糙度等）不发生任何变化的直管段上，所以在均匀流动时，只有沿程损失，没有局部损失。为了寻找沿程损失的变化规律，需要先建立沿程损失和沿程阻力之间的关系式，又称为均匀流动方程式。
第四章流动阻力与管路水力计算
图4-8 湍流速度分布
第四章流动阻力与管路水力计算
4.湍流沿程阻力系数的确定由于湍流的复杂性，至今还不能完全通过理论推导的方法确定湍流沿程阻力系数l，只能借助实验研究总结一些经验或半经验公式。 (1)尼古拉兹实验为了得到l的变化规律，尼古拉兹在类似图4-2所示的实验台上，采用人工粗糙管(管内壁上均匀敷有粒度相同的砂粒)进行了大量实验。

流体力学第4章流动阻力和能量损失

雷诺的实验装置如图 4.1 所示，水箱 A 内水位保持不变，阀门 C 用于调节流量，容器 D 内盛有容重与相近的颜色水，容器 E 水位也保持不变，经细管 E 流入玻璃管 B，用以演示水流流态，阀门 F 用于控制颜色水流量。
图 4.1 雷诺实验装置 ·73·
·74·
流体力学
当 B 管内流速较小时，管内颜色水成一股细直的流速，这表明各液层间毫不相混。这种分层有规则的流动状态称为层流。如图 4.1(a)所示。当阀门 C 逐渐开大流速增加到某一临界流速 vk 时，颜色水出现摆动，如图 4.1(b)所示。继续增大 B 管内流速，则颜色水迅速与周围清水相混，如图 4.1(c)所示。这表明液体质点的运动轨迹是极不规则的，各部分流体互相剧烈掺混，这种流动状态称为紊流或湍流。能量损失在不同的流动状态下规律如何呢？雷诺在上述装置的管道 B 的两个相距为 L 的断面处加设两根测压管，定量测定不同流速时两测压管液面之差。根据伯努利方程，测压管液面之差就是两断面管道的沿程损失，实验结果如图 4.2 所示。
流体力学
Z1 +
由均匀流的性质：
p1
γ
+
ห้องสมุดไป่ตู้
α 1v12
2g
=
= Z2 +
2 α 2 v2
p2
γ
+
2 α 2 v2
2g
+ hl1−2
α 1v12
2g
代入上式，得：
2g
hl = h f
⎛ p1 ⎞ ⎛ p2 ⎞ (4-11) ⎜ + Z1 ⎟ ⎟−⎜ ⎜ ⎟ + Z2 ⎟ hf = ⎜ ⎝γ ⎠ ⎝ γ ⎠ 上式说明，在均匀流条件下，两过流断面间的沿程水头损失等于两过流断面测压管水头的差值，即流体用于克服阻力所消耗的能量全部由势能提供。考虑所取流段在流向上的受力平衡条件。设两断面间的距离为 L，过流断面面积 A1=A2=A，在流向上，该流段所受的作用力有：重力分量 γ Alcosα、断面压力 p1A 和 p2A、管壁切力 τ0.l.2πr0(τ0 为管壁切应力， r0 为圆管半径)。

《流体力学》第四章流动阻力和能量损失4.8-4.9解析

Q = v2 A2 p1 p2 v2 ( Z1 + ) - ( Z 2 + ) = (a 02v2 - a 01v1 ) g g g
2 1 1
将上式代入能量方程
2 a 1v12 a 2 v2 hm = 2g 2g v2 + (a 02 v2 - a 01v1 ) g
p1 a v p2 a v hm = (Z1 + + ) - (Z2 + + ) g 2g g 2g
大量实验研究表明紊流的局部阻力系数取决于：局部阻碍的的几何形状固体壁面的相对粗糙度雷诺数其中，起主导作用的是：局部阻碍的的几何形状
相对粗糙的影响
Re的影响
沿程损失和局部损失本质上都是由紊流掺混作用引起的惯性阻力和粘性阻力造成的。
突然扩大的局部损失
2 p1 a 1v12 p2 a 2v2 hm = (Z1 + + ) - (Z2 + + ) g 2g g 2g
A2
A1
2
A1 2 v12 v12 hm = (1) = z1 A2 2 g 2g
2 2 A2 v v hm = ( - 1)2 2 = z 2 2 A1 2g 2g
A A 2 2 2 1 突然扩大的阻力系数为： z = ( 1) z1 = (1) 2 A1 A2
突然扩大前后有两个不同的平均流速，因而有两个相应的阻力系数，计算时必须注意使选用的阻力系数与流速水头相适应。当流体从管道进入无限大空间时，ζ1=1，这是突然扩大的特殊情况，称为出口阻力系数。
30°
0.120 0.058 0.066 0.120 0.054 0.051 0.120 0.058 0.062 0.120 0.042 0.042

空气流动的流体力学原理—流动阻力和能量损失

-1.12
-0.68
-0.27
-0.08
0.11
1.4
-2.55
-1.20
-0.75
-0.30
-0.10
0.10
1.5
-2.62
-1.25
-0.78
-0.32
-0.12
0.09
支
例题1：如下图所示，某三通支管道直径D=100mm,主管道D=150mm,夹角角度为
30°，主管道与支管道风速均为12m/s，求主管道局部阻力和支管道局部阻力。
1.弯头的曲率半径R；
2.转角α；
3.弯头管道参数：如圆形弯头
的直径D方形弯头的宽和高。
附表一、圆形截面弯头阻力系数（部分）
曲率半径
阻力系数
D
1.5D
2D
2.5D
3D
7.5
0.028
0.021
0.018
0.016
0.014
10
0.058
0.044
0.037
0.033
0.029
30
0.110
0.081

. × . × ×
=
= . ×
= . （）

× .
例题2：如下图所示，某矩形弯头参数如下：a=200mm,b=100mm，弯
曲半径R=400mm,弯曲角度为90°，风管内风速v=12m/s，求空气流过此弯
头的局部阻力。
解：1.先计算矩形风管的当量直径D当
L----管道的长度（m）
ρ---空气的密度（kg/m³）
v---空气的平均流速（m/s）
λ---沿程阻力系数，和雷诺数Re有关。

沿程阻力计算公式还可以表示为：Hm=RL

《流体力学》第四章流动阻力和能量损失4.6-4.7

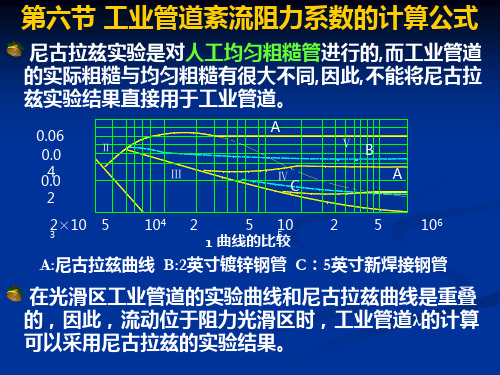
第七节
非圆管的沿程损失
怎么把非圆管折合成圆管? 水力半径当量直径 A R 水力半径:过流断面面积和湿周之比。
1 2 d d 对于圆管： R A 4 d 4
de = 4 R
2ab 对于矩形管： d e = a+ b
对于方形管：
de = a
非圆管流中的流态判断的临界雷诺
λ计算公式
紊流光滑区： 1 2 lg Re 2.51 (尼古拉兹光滑区公式)
紊流粗糙区： (尼古拉兹粗糙区公式)
0.3164 0.25 Re
(布拉修斯公式)
K 0.11 d
0.25
1
3.7d 2 lg K
(希弗林松公式)
半经验公式
纯经验公式
紊流过渡区
0.06 0.04 A
Ⅱ
Ⅴ Ⅲ Ⅳ
B A
0.02
2×103 5 104
C 2 5
2
l
曲线的比较
5
105
106
A:尼古拉兹曲线 B:2英寸镀锌钢管 C：5英寸新焊接钢管
在光滑区工业管道的实验曲线和尼古拉兹曲线是重叠的，因此，流动位于阻力光滑区时，工业管道λ的计算可以采用尼古拉兹的实验结果。
在粗糙区，工业管道和尼古拉兹的实验曲线都是与横坐标轴平行。这就存在用尼古拉兹粗糙区公式计算工业管道的可能性。问题在于如何确定工业管道的K值。当量糙粒高度:和工业管道粗糙区λ值相等的同直径尼古拉兹粗糙管的糙粒高度。
数仍为2000。应用当量直径计算非圆管的能量损失，并不适用于所有情况。
对矩形、方形、三角形结果接近，但对长缝形和星形断面差别较大。应用于层流时，误差较大。

土力学第四章流动阻力和水头损失

漩涡区中产生了较大的能量损失
漩涡区
C A C
D B
漩涡体形成、运转和分裂
漩涡区中产生了较大的能量损失
C A C
D B
流速分布急剧变化
漩涡区中产生了较大的能量损失
C A
D B
C 漩涡的形成，运转和分裂；流速分布急剧变化，都使液体产生较大的能量损失。这种能量损失产生在局部范围之内，叫做局部水头损失hj 。
颜色水
l
hf
Q
V t
下游阀门再打开一点，管道中流速增大
红色水开始颤动并弯曲，出现波形轮廓
颜色水
l
hf
下游阀门再打开一点，管中流速继续增大
红颜色水射出后，完全破裂，形成漩涡，扩散至全管，使管中水流变成红色水。这一现象表明：液体质点运动中会形成涡体，各涡体相互混掺。
Q
V t
颜色水
l
hf
Q
水流半径R
R A

粘性流体的两种流态
4.2.1 雷诺实验
雷诺：O.Osborne Reynolds (1842～1912) 英国力学家、物理学家和工程师，杰出实验科学家
1867年-剑桥大学王后学院毕业 1868年-曼彻斯特欧文学院工程学教授
1877年-皇家学会会员
1888年-获皇家勋章
1905年-因健康原因退休
两个过水断面的湿周相同，形状不同，过水断面面积一般不相同，水头损失也就不同。因此，仅靠湿周也不能表征断面几何形状的影响。
由于两个因素都不能完全反映横向边界对水头损失
的影响，因此，将过水断面的面积和湿周结合起来，全
面反映横向边界对水头损失影响。
水流半径R:
R
A

流体力学第四章

同的规律。因此，在计算管流水头损失时必须首先判别出流动状态。
大量的实验表明，流体的流动状态不仅由临界速度一个参数决定。
影响流体流动类型的因素：
①流体的流速ｕ；②管径ｄ；③流体密度 ρ；④流体的粘度 μ。
ｕ、ｄ、ρ越大，μ越小，就越容易从层流转变为湍流。上述中四个因素所组成的复合数群ｄｕρ／μ，是
差计，其液面高差△ｈ＝４ｃｍ，
求作用水头Ｈ。
考点二雷诺实验
实际流体的流动由于粘滞性的存在而具有两种不同的状态，英国物理学家雷诺（Ｒｅｙｎｏｌｄｓ）通过大量的实验研究发现，实际流体在管路中流动存在着两种不同的状态，并且测定了管路中的能量损失与不同的流动状态之间的关系，此即著名的雷诺实验。
试验过程（装置如下图）：实验过程中使水箱中的水位保持恒定。实验开始前水箱中颜色水的阀门以及玻璃管上的阀门都是关闭的。开始实验时，逐渐打开玻璃管出口端上的阀门，并开启颜色水的阀门，使颜色水能流人玻璃管中。 ①层流：流动状态主要表现为流体质点的摩擦和变形，这种流体质点互不干扰各自成层的流动称为层流。ａ．流体质点做直线运动；ｂ．流体分层流动，层间不相混合、不碰撞；ｃ．流动阻力来源于层间粘性摩擦力。
湿周较小———外部阻力较小
{ } 面积Ａ较小———内部阻力较小
水力半径小
综合阻力较大
湿周较大———外部阻力较大
水力半径与阻力特性
例题图中所示为一从水箱引水的水平直管。已知管径ｄ＝２０ｃｍ，
管长Ｌ＝４０ｍ，局部水头损失系数：进口 ζ１＝０．５，阀门 ζ２＝０．６。当通过流量Ｑ＝０．２ｍ３／ｓ时，在相距△Ｌ＝１０ｍ的１－１及２－２断面间装一水银压
试验方法：
在试验段上接出两根测压管。液体在等直径的水平管路中稳定流时，由伯努利方程可得：ｈｆ

《工程流体力学》第四章流动损失

1、运动参数的脉动：紊流特征：旋涡结构紊流运动：旋涡迁移掺混的随机运动
精密测速仪测定流场中M点瞬时速度：随机变化曲线运动参数的脉动（脉动现象）：在足够长时段T内，随机值具有围绕某一“平均值”而上下变动的现象
紊流脉动：各空间点的速度、压强等物理量，随时间围绕某一“平均值”作不规则变化的流动现象。
(b)继续开大阀门C：B管中流速增大，有色液体的流动并无变化，仍为层流。
当B管中平均流速达到某一值时，层流开始转变紊流 —— 临界状态(临界区)。
临界状态：流束发生动荡、分散、个别地方出现中断。
(c)再稍开大阀门C：B管中流速超过临界值VK’，则有色液体不再呈现流束动荡和分散中断，而破碎掺混变成一种紊乱的流动状态，有色流体质点布满B管中—紊流。
管中水流为紊流。
(2)保持层流的最大流速就是临界流速：
流态分析：
层流：各流层互不掺混，只有粘性引起的各流层间的滑动摩擦阻力。
紊流：许多大大小小的涡体动荡于各流层间，有粘性阻力，惯性阻力。（由质点掺混，互相碰撞所引起的）
紊流阻力>>层流阻力
层流到紊流的转变过程：
假设流体原来作直线层流运动，由于某种原因干扰，流层发生波动。
水力半径：截面面积A与流体湿周长c之比水力半径表征截面的流通能力： A增加，c变小，则流体流通能力增加。
几种断面的水力半径：
当量直径de：当非圆管的水力半径 = 圆管的水力半径时，这时圆管的直径就是非圆管的当量直径。如当非圆管的水力半径R = 圆管的水力半径d/4时，则圆管的直径d = 4R为非圆管的当量直径de。
上临界速度VK’不稳定：受试验设备，周围环境影响很大 (1)当管壁光滑，入口平滑，周围干扰较小时：VK’可达到较高值。即速度较大时，层流才转变为紊流 (2)当管壁粗糙，周围干扰较大时， VK’可达到的值较小。即速度较小时，层流就转变为紊流

流体力学_龙天渝_流动阻力和能量损失

（2）光滑黄铜管的沿程水头损失
在Re<105时可用布拉修斯公式:
由图4-11和莫迪图可得出一致的结果.
(3)K=0.15mm工业管道的水头损失根据Re=80000，K/d=0.15mm/100mm=0.0015，由莫迪图得 0.024。
第七节非圆管的沿程损失
非圆管的沿程损失一般用到当量直径计算。水力半径为过流断面面积A和湿周之比。
（ b）（ c）图4-2 由紊流变为层流的临界流速小于由层流转变为紊流的临界流速。称为上临界流速，为下临界流速。上临界流速不稳定,下临界流速稳定,一般的临界流速指的是下临界流速。
（ a）
流态的判别标准——临界雷诺数
பைடு நூலகம்
流动状态不仅和流速v有关，还和管径d、流体的动力黏度和密度有关，用一无因次数Re表示，称雷诺数：
式（4-30）和式（4-32）都是半经验公式，还有两个应用广泛的经验公式，光滑区的布拉休斯公式：
上式适用于Re<105的情况。还有粗糙区的希弗林松公式：
紊流过渡区和柯列勃洛克公式柯列勃洛克根据大量的工业管道试验资料，整理出工业管道过渡区曲线，并提出该曲线的方程：
K为工业管道的当量粗糙粒高度，可查4-1。该式为尼古拉兹光滑区公式和粗糙区公式的机械组合。为简化计算，莫迪以柯氏公式为基础绘制出反映Re、K/d和对应关系的莫迪图，在该图上可根据Re和K/d直接查出。此外，还有一些人为简化计算，在柯氏公式的基础上提出了
[例4-11]某钢板制风道，断面尺寸为400mm×200mm，管长 80m。管内平均流速v=10m/s。空气温度t=20℃，求压强损失 pf。 [解]（1）当量直径
（2）求Re。查表，t=20 ℃时， =15.7×10-6m2/s

流体力学-第四章-流动阻力和能量损失(章结)

K（mm) 管道材料 K（mm)
表面光滑砖风道
4.0
度锌钢管
0.15
矿渣混凝土板风道 1.5
钢管
0.046
钢丝网抹灰风道 10~15
铸铁管
0.25
胶合板风道
1.0
混凝土管
0.3~3.0
墙内砌砖风道
5~10 木条拼合圆管 0.18~0.9
确定沿程阻力系数的方法：
（1）经验公式（2）莫迪图（3）查相关手册
二、等效过程
（1）用实验方法对某种材料的管道进行沿程损失实验，测出和 hf ;
（2）再用达西公式计算出λ；
hf
l d
2
2g
（3）用尼古拉兹阻力平方区公式计算出绝对
粗糙度K。
1
(1.74 2 lg d )2
2K
此时的K值在阻力的效果上是与人工粗糙管的管道粗糙度相当的，故称其为当量粗糙度。
莫迪(Mood渐扩管 (d)减缩管
(e)折弯管
(f)圆弯管
(g)锐角合流三通
(h)圆角分流三通
在局部阻碍范围内损失的能量，只占局部损失中的一部分，另一部分是在局部阻碍下游一定长度的管段上损耗掉的，这段长度称为局部阻碍的影响长度。受局部阻碍干扰的流动，经过影响长度后，流速分布和紊流脉动才能达到均匀流动的正常状态。
核心问题2 水力半径、湿周、当量直径
以上讨论的都是圆管，圆管是最常用的断面形式。但工程上也常用到非圆管的情况。例如通风系统中的风道，有许多就是矩形的。如果设法把非圆管折合成圆管来计算，那么根据圆管制定的上述公式和图表，也就适用于非圆管了。这种由非圆管折合到圆管的方法是从水力半径的概念出发，通过建立非圆管的当量直径来实现的。

流体力学第四章-黏性流体的运动和阻力计算

Pgh qvpvq12 dL 4 8v 2 q
6、层流起始段长度——见课本74页
*4.4 圆管中的湍流流动
30
一、脉动现象与时均值
1、这种在定点上的瞬时运动参数随时间而发生波动的现象称为
脉动。
2、时均法分析湍流运动
u u u'
如取时间间隔T，瞬时速度在T时间内的平均值称为时间平均速度，简称时均速度，即
二局部阻力某段管道上流体产生的总的能量损失应该是这段管路上各种能量损失的迭加即等于所有沿程能量损失与所有局部能量损失的和用公式表示为三总能量损失能量损失的量纲为长度工程中也称其为水头损失221圆管层流时的运动微分方程牛顿力学分析法可参考课本71页的ns方程分析法取长为dx半径为r的圆柱体不计质量力和惯性力仅考虑压力和剪应力则有pdpdxdprdxdpdrdudxdpdrdu根据牛顿粘性定律再考虑到则有dr图41圆管层流的速度和剪应力分布25在过流断面的任一半径r处取一宽度为dr的圆环如图42所示
u1
Tudt1
T(uu')dt1
Tudt1
T
u'dt
T0
T0
T0
T0
u1
T
u'dt
T0
时均压强
p
1
T
pdt
T0
.
二、湍流的速度结构、水力光滑管和水力粗糙管
31
1．湍流的速度结构管中湍流的速度结构可以划分为以下三个区域：
（1）粘性底层区（层流底层）：在靠近管壁的薄层区域内，流体的粘性力起主要作用，速度分布呈线性，速度梯度很大，这一薄层叫粘性底层。如图所示。
湍流层流的临界速度 ——下临界流速
v c ——上临界速度
v c ——下临界速度

第一篇流体力学第四章阻力损失与管路计算

• 有了当量直径,只要用de 代替d,就可利用圆管的计算公式来进行非圆管沿程损失的计算,即
上一页
返回
第四节局部损失的计算
• 局部损失可按下式计算:
• 局部损失的计算可以转化为求局部阻力系数ζ 的问题.对于不同的局部阻碍,有不同的局部阻力系数ζ 值,其多数通过试验确定,并编制成专用计算图、表,供计算时查用.表４-１列出了各种常用管件的局部阻力系数ζ值.应当注意,表４-１中的ζ 值都是针对某一过流断面的平均流速而言的,查表时必须与指定的断面流速相对应,凡未注明的,均应采用局部阻碍以后断面的平均流速.
• 根据流体的边界情况,将流动阻力和能量损失分为两种形式:一种是沿程阻力与沿程能量损失;另一种是局部阻力与局部能量损失.
下一页返回
第一节流动阻力与能量损失
• 如图４-１所示,水箱侧壁上连接一根由三段不同直径的管段所组成的管路.在边壁沿程不变的管段上(１－２、２－３、３－４、４－５段), 阻碍流体流动的阻力沿程基本不变,这类阻力称为沿程阻力.为克服沿程阻力而产生的能量损失称为沿程能量损失.沿程损失以水柱高度表示时,称为沿程水头损失,用符号hf 表示.图中的hf１２、hf２３、hf３４、 hf４５就是相应１－２、２－３、３－４、４－５各管段的沿程水头损失.图中整个管路的沿程水头损失等于各管段的沿程水头损失之和, 即
• 人们很早以前就发现沿程损失与流速之间存在着某种关系,但直到１８８３年,英国物理学家雷诺在他做的试验中揭示了流体运动存在着两种流态,这才认识到沿程损失与流速的关系与流态密切相关.
• 雷诺试验的装置如图４-２所示,水箱A 中水位恒定,水流通过玻璃管B 恒定出流,阀门K 用来调节管内流量,容器D 中盛有颜色水,颜色水可以经过细管E 注入玻璃管B 中.

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2g
hf
均匀流中流体用于克服阻力所消耗的能量全部由势能提供。
1v12
2g
2v2 2
2g
h f ( z1
p1

) ( z2
p2

)
加速度为零， F 0
p1 A p2 A Al cos 2 l r 0
2 l hf r
r 均匀流基本方程 J 2
圆管层流的速度分布、沿程损失
du 牛顿内摩擦定律： dr
均匀流基本方程：
r J 2
边界条件：r=r0时，u=0
流速分布：
u um
J 2 2 u (r0 r ) 4
r=0时，u最大
τ
umax
J 2 J 2 r0 d 4 16
Q J 2 J 2 r0 d 平均流速：v A 8 32 1 v umax 2
一般工程计算中：
f (局部阻碍形状)
U2 p H0 z 2g g
(LT ) ML T L L LLL 2 3 2 LT (ML )( LT )
1 2
1
2
§4-1 沿程损失和局部损失
整个管道的能量损失等于各管段的沿程损失和局部损失的总和。
hl hf hm
l v hf d 2g
（3）第Ⅲ区，紊流光滑区，Re＞4000，
f3 (Re) （4）第Ⅳ区，紊流过渡区， f 4 (Re, K/ d) （5）第Ⅴ区，紊流粗糙区， f5 (K/ d)
f 2 (Re)
§4-6 管路中的局部阻力
局部水头损失：
v hm 2g
2
紊流局部阻力系数：
f (局部阻碍形状， Re, K/ d)
作业：U形水银压差计中，已知h1＝0.3m，h2＝ 0.2m，h3＝0.25m。A点的相对压力为pA＝24.5kPa，酒精的比重为0.8，试求B点空气的相对压力。
流动பைடு நூலகம்力和能量损失
量纲分析
量纲是各种类别物理量的标志。基本量纲：长度——L；质量——M；时间——T 导出量纲：
dl v dt dv a dt
32 vl h f Jl 2 d
32 vl hf 2 d 2 l v hf d 2g
Re vd
64 Re
圆管层流的沿程阻力系数仅与雷诺数有关，和管壁粗糙度无关

§4-4 圆管中的紊流运动
层流流速：
J 2 2 u (r0 r ) 4
紊流流速： 0 1 u ln y C k
2
v hm 2g
2
§4-2 层流、紊流和雷诺数
层流：分层有规则的流动状态紊流:液体质点的运动轨迹不规则，各部分流体互相剧烈掺混。
lg h f
m=1.75-2.0
m=1
hf Kv
临界流速 vk
m
过层流渡区
紊流
lg v
*流态的判别条件
流动状态不仅和流速v有关，还和管径d、流体的动力粘滞系数μ 和密度ρ 有关。
Re
Vd

Vd

临界雷诺数：（圆管）层流：
Rek Re Re
vk d

2000
vd

vd
2000 2000
紊流：

非圆管管道： Re
Vd

Vd

水力半径：
R
A

当量直径： d
de 4 R
例题1：有一矩形截面的小排水沟，水深15cm，底宽 20cm，流速0.15m/s，水温10℃，试判别流态。
§4-3 圆管中的层流运动
均匀流基本方程均匀流：位于同一流线上各质点的流速矢量沿流程不变。迁移加速度为零。均匀流只能发生在长直管道或渠道这一类断面形状和大小都沿程不变的流动中，因此，只有沿程损失，而没有局部损失。
均匀流能量方程
z1
p1

1v12
2g

z2
p2

2v2 2
dim v LT dima LT
1 2
F ma
dim F MLT
2
dP p dA
dimp ML T

1
2
对于任何物理量A： dim A
LM T

量纲和谐凡是正确反应客观规律的物理方程，其各项的量纲必须一致的性质，称为量纲和谐。不同类的量纲不能相加减。
§4-5 管路中的沿程阻力
层流：λ 仅与Re有关，与管壁粗糙度无关。
64 f (Re) Re
紊流：λ 取决于Re和管壁相对粗糙度两个因素。
f (Re, K/ d)
尼古拉兹实验曲线
尼古拉兹实验：（1）第Ⅰ区，层流区，Re＜2000， f (Re) 1 （2）第Ⅱ区，临界过渡区，Re=2000～4000，