有理数提高训练
有理数混合运算提高350题专项练习(附答案)
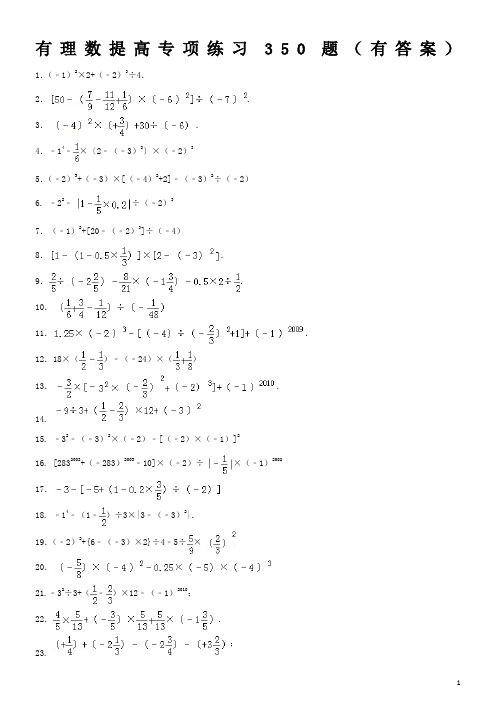
有理数提高专项练习350题(有答案)1.(﹣1)2×2+(﹣2)3÷4.2..3..4.﹣14﹣×〔2﹣(﹣3)2〕×(﹣2)35.(﹣2)3+(﹣3)×[(﹣4)2+2]﹣(﹣3)2÷(﹣2)6. ﹣22﹣÷(﹣2)37.(﹣1)2+[20﹣(﹣2)3]÷(﹣4)8..9..10.11..12.18×()﹣(﹣24)×()13..14.15. ﹣32﹣(﹣3)2×(﹣2)﹣[(﹣2)×(﹣1)]216. [2832003+(﹣283)2003﹣10]×(﹣2)÷×(﹣1)200217.18. ﹣14﹣(1﹣)÷3×|3﹣(﹣3)2|.19.(﹣2)2+{6﹣(﹣3)×2}÷4﹣5÷×20.21.﹣32÷3+(﹣)×12﹣(﹣1)2010;22..;23.;24.;25..26.27..;29.;30.31. .32..;33.﹣32+(﹣3)2+(﹣5)2×(﹣)﹣0.32÷|﹣0.9|.34.(﹣2×5)3﹣(﹣1)×(﹣)2﹣(﹣)2.35.1×﹣(﹣)×2+(﹣)÷136. ﹣22+(﹣2)4×()3﹣|0.28|÷(﹣)237.(﹣+)×18+3.95×6﹣1.45×6..38.39..40. [(﹣1)2005+(﹣﹣)×24]÷|﹣32+5|.41.[2﹣(+﹣)×24]÷5×(﹣1)200942. ﹣14﹣[﹣2+(1﹣0.2÷)×(﹣3)].43.44..45. ﹣5+[﹣﹣(1﹣0.2÷)×(﹣3)2]46. ﹣10+8÷(﹣2)2﹣(﹣4)×(﹣3);;47.48. 3×(﹣1)10+(﹣22)×|(﹣2)3|÷4÷2﹣|(﹣3)2|÷(﹣3)2×(﹣1)11;49. ;.50.51. [1]×24]÷(﹣5);52. (﹣10)+8×(﹣2)2﹣(﹣4)×(﹣3);53. ﹣0.252÷(﹣0.5)3+(﹣)×(﹣1)10;54. ﹣3×(﹣)2﹣4×(1﹣)﹣8÷()2;55.(﹣2)3﹣1×(﹣)﹣(﹣2)×(﹣1)×(﹣4).;56.;57.58. ﹣24+|6﹣10|﹣3×(﹣1)2009.59. |﹣1.3|+;60. (﹣13)+(+12)+(﹣7)+(+38);;61.62.(+163)﹣[(+63)+(﹣259)+(﹣41)].;63.;64..65.66.﹣22﹣(﹣22)+(﹣2)2+(﹣2)3﹣3267. 22+(﹣4)+(﹣2)+4;68.(﹣8)+(+0.25)﹣(﹣9)+(﹣);;69.70. (﹣)÷(﹣﹣);71. ﹣9÷;72. ﹣14﹣×[2﹣(﹣3)2].73.74.75.76.﹣14×[﹣32×﹣2]×(﹣).77.﹣32﹣(﹣3)2+32×(﹣1)2006;78..79..80. 33×(﹣2)2﹣(﹣3)3×(﹣2)383.84..85.(﹣3)÷(﹣1)×0.75×|﹣2|÷|﹣3|.86.﹣1+3﹣5+7﹣9+11﹣…﹣1997+1999;87. 11+12﹣13﹣14+15+16﹣17﹣18+…+99+100;88. 1991×1999﹣1990×2000;89. 4726342+472 6352﹣472 633×472 635﹣472 634×472 636;90. 1+4+7+ (244)1+91.92. 1.94.﹣22﹣(﹣1)2001×(﹣)÷+(﹣3)295.;96.97.98. ﹣5﹣22÷[(﹣)2+3×(﹣)]÷(﹣22)99.(﹣3)+(+2)﹣(+2)﹣(﹣7);100.﹣23÷×;101.[﹣+﹣﹣(﹣)]×(﹣36);102.(+)÷(﹣)﹣×(﹣1);103.﹣14﹣(1﹣0.5)××[2﹣(﹣3)2].104.(2﹣3+1)÷(﹣1).105.+++…+.106.﹣14+〔1﹣(1﹣0.5×)〕×|2﹣(﹣3)2|.107.108.﹣12008﹣[5×(﹣2)﹣(﹣4)2÷(﹣8)]109.110.;111.[2﹣(﹣3)2]×[(﹣1)2008﹣(1﹣0.5×)]112.113. 0﹣21116.﹣23÷×(﹣)2+(﹣0.8)×5×(﹣)117.﹣32+5×(﹣)﹣(﹣4)2÷(﹣8)118.;119..120.﹣16;﹣121.122.﹣0.252÷÷(﹣1)100+(1+2﹣3.75)×12 123. 2﹣3﹣5+(﹣3)25﹣(﹣+﹣)÷124.127. ﹣22+(﹣3)×[(﹣4)2+(﹣2)3]﹣(﹣3)2÷(﹣2)128.(﹣5)﹣(+3)+(﹣9)﹣(﹣7)+;129. 10﹣23+32﹣17﹣21+45;130.(﹣3)+(+2)﹣(+2)﹣(﹣7);131.﹣9.2﹣(7.1)﹣(﹣3)+6+(+2.9);132. 3.6+41.8﹣12﹣11﹣51;133..134. [212﹣(38+16﹣34)×24]÷5×(﹣1)2001135.136.;137.()×(﹣36).138.(﹣20)+(+3)﹣(﹣5)﹣(+7);139.(+6)+(﹣5)﹣(﹣4)+(+2)+(﹣1)﹣(+1);140.﹣13×﹣0.34×+×(﹣13)﹣×0.34;141.(﹣)×(﹣0.25)×(﹣5)×(﹣4)3;142.(﹣3)3÷2×+4﹣2×(﹣);143.﹣16﹣(0.5﹣)÷×[﹣2﹣(﹣3)3]﹣|﹣0.52|.144.0﹣14﹣(﹣1)+(﹣1.95)3×0.5×0﹣|﹣5|+5.145..146.1+.147.;148..149.150. [53﹣4×(﹣5)2﹣(﹣1)10]÷(﹣24﹣24+24).151.﹣32+27÷(﹣3)2﹣(﹣)2×|﹣22|﹣(﹣1)2007152.;153..154. [47﹣(18.75﹣1÷)×2]÷0.46156.(﹣105)×﹣178×6.67﹣7.67×(﹣178)157.﹣(﹣23)﹣(+59)+(﹣35)+|﹣5﹣32|;158. 1﹣[(﹣5)2×﹣0.8]÷2×(﹣1+).159.﹣÷×(﹣0.6)×+(﹣2)3160. 4﹣(﹣2)2﹣32÷(﹣1)2009+0×(﹣2)5.161.162.(﹣5)×(﹣0.75)﹣(﹣5)×0.125+(﹣5)×(﹣0.125).163.﹣20+(﹣18)﹣12+10;164.;165.;166.﹣2.5×17×(﹣4)×(﹣0.1);167. 33.1﹣10.7﹣(﹣22.9)﹣;168.(﹣36)÷4﹣5×(﹣1.2);169.;170..171.172..173..176. [﹣21×(﹣1)3+6÷×3﹣52]×.177.178.﹣32﹣50÷(﹣5)2﹣1;179..180. 0﹣3+(﹣)﹣(﹣22)﹣5÷(﹣);181. 10÷[﹣(﹣1+1)]×6;182. 18+32÷(﹣2)3﹣(﹣4)2×5;183.﹣7×(﹣)+19×(﹣)﹣5×(﹣).184. 8﹣2×(﹣3)2+[(﹣2)×3]2185.186. 3×(﹣4)+28÷(﹣7);187.﹣14+×[32﹣(﹣3)2];188. (﹣10)+8×(﹣3)2﹣(﹣4)×(﹣3).189.(﹣2)3﹣2×(﹣3)+|2﹣5|﹣(﹣1)2010190. 48×(﹣+﹣)191. (+7)+(﹣8)﹣(+3)﹣(﹣4);192.﹣1﹣2÷(﹣)×(﹣3);193.﹣36×(﹣﹣);194.﹣13﹣(1﹣0.5)××[2﹣(﹣3)2];195.(﹣0.25)×1.25×(﹣4)×(﹣8);196.(﹣1)10×2+(﹣2)3÷4.197. ﹣(﹣3)2﹣[3+0.4×(﹣1)]÷(﹣2).198. ;199. ;200.;201. 3﹣(﹣2)×(﹣1)﹣8÷(﹣)2×|3+1|.202.﹣24÷42﹣(﹣2)3×(﹣0.5)2+(﹣)2×(﹣32)203.﹣32+×(﹣3)3÷(﹣1)25.204.205.﹣14﹣(1﹣)÷3×|3﹣(﹣3)2|;206. ﹣1100﹣(1﹣0.5)×[3﹣(﹣3)2].207.(﹣2)3﹣|﹣9|﹣()÷(﹣).208.﹣22+(﹣3)÷﹣(﹣3)2÷(﹣2)209.[15.25﹣13﹣(﹣14.75)]×(﹣0.125)÷210.()÷211.212.﹣12+[+8×(﹣3)]×0﹣(﹣5)2213. +6÷(﹣2)+(﹣4)×214.216.217.﹣9+5×(﹣6)﹣(﹣4)2÷(﹣8);218. .219.(﹣10)2﹣5×(﹣2×3)2+23×10.221. ﹣22﹣32÷[(﹣2)3﹣(﹣1)2]222.(+10)+(﹣11.5)+(﹣10)﹣(+4.5);223.(﹣81)÷×÷(﹣16);224.﹣32﹣[﹣5﹣0.2÷×(﹣2)2];225. 24×(﹣﹣)+(﹣)2÷(﹣).226..227.228.[(﹣3)2÷×﹣6]÷[﹣(﹣1)2006].229. ﹣14﹣(﹣2)3×5+0.25÷(﹣)2.230.(﹣20)+(+3)﹣(﹣5)﹣(+7);231. |﹣|+|﹣|+|﹣|﹣|﹣|;232.(﹣5)×6+(﹣125)÷(﹣5);233.+(﹣)﹣(﹣)+;234.(﹣﹣+)×4;235.﹣18÷(﹣3)2+5×(﹣)3﹣(﹣15)÷5.236..238. ﹣22﹣(1﹣×0.2)÷(﹣2)3239.(﹣2)2+(﹣1﹣3)÷(﹣)+|﹣|×(﹣24)241. (﹣1)2009+(﹣5)×|(﹣2)3+2|﹣(﹣4)2÷(﹣).242.(﹣÷.243.﹣4﹣28﹣(﹣29)+(﹣24)249.(﹣2)4×(﹣5)+[(﹣3)3+(﹣2)4×(﹣1)9]250. (﹣)+(﹣);251. 5﹣(8﹣9);252.﹣9×0.375﹣9×0.625;253. 9×(﹣)÷9×(﹣);254.﹣72+2×(﹣3)2﹣(﹣6)÷(﹣)2;255.﹣32﹣[32﹣(﹣2)2]×[2﹣(1﹣)].256.﹣16+23+(﹣17)﹣(﹣7);257.(﹣)+(﹣)﹣(﹣)﹣(+)﹣(﹣)258.(﹣+﹣)×(﹣16)259.﹣14+(1﹣0.5)××〔2﹣(﹣3)2〕260.﹣20+(﹣14)﹣(﹣18)+|﹣13|;261. ﹣32×[(1﹣7)÷6]3+75÷(﹣5)2;262.﹣3×23﹣(﹣3×2)2+(﹣23×3);263.÷(﹣2)﹣÷(﹣1)﹣0.5÷2×;264. (﹣10)2+[(﹣2)2﹣(3+32)×2];265. [÷(﹣)+0.4×(﹣)2]×(﹣1)5.266.(1﹣+)×(﹣48)267.﹣12﹣(﹣10)÷×2+(﹣4)3268. |﹣|÷|﹣|﹣×(﹣4)2269. ﹣1﹣[2﹣(1﹣×0.5)]×[32﹣(﹣2)2]270272. 0274.275.﹣32﹣[(﹣2)2﹣(1﹣×)÷(﹣2)].276.278.(﹣8)÷[(﹣)×(﹣)÷(﹣2)];279.(﹣36)×(﹣+﹣);285.(﹣)2÷(﹣)2÷|﹣6|2×(﹣)2286. |﹣1|+|﹣|+|﹣|+…+|| 287.20﹣3×[23﹣2×(﹣3)]﹣(﹣1)2007288. 25﹣3×[32+2×(﹣3)]+5;289..290.×(﹣1)+×(﹣2)+×(﹣50)﹣×(﹣20)291. .292. ﹣23﹣(﹣3)2×(﹣1)2﹣(﹣1)3293.294. (﹣3)2÷3﹣12×(﹣+﹣)295. (+﹣)×12+12÷(+);296. 5÷(﹣2﹣2)×6.297.(﹣++)×(﹣12);298.(﹣2)2+(﹣2)÷(﹣)+|﹣|×(﹣24).299.(+﹣)÷(﹣)300.﹣42÷(﹣2)2+12÷(﹣)×3301.﹣0.52+(﹣)2﹣|﹣22﹣4|﹣(﹣1)3×()3÷(﹣)4 302. {[3÷(﹣)+0.4×(﹣)2]÷(﹣)﹣20}×(﹣1)2005 303.(﹣32)﹣[5﹣(+3)+(﹣5)+(﹣2)]304. 25×﹣(﹣25)×+25×(﹣)305.306. (﹣2)2﹣|﹣7|+3﹣2×(﹣);307. ﹣36×(﹣﹣);308. ﹣16﹣(1﹣0.5)××[2﹣(﹣3)2];309.(﹣3)2008×﹣12008﹣(﹣1)2008.310.311. 0.25×(﹣2)3﹣[4÷(﹣)2+1].;312.313. .314. ..315.316. 5×(﹣6)﹣(﹣4)2÷(﹣8);317. (3.9﹣1.45)2÷(﹣0.125)+49.34;318. (﹣1)5﹣[﹣3×(﹣)2﹣(﹣1)÷(﹣2)2].319.(﹣3)3﹣[(2﹣1.5)3÷2×(﹣8)2+×(﹣)2﹣()3].320. 20+(﹣12)﹣(﹣18)321. 23×10+(﹣2)×(﹣5)2322.323.324.325. .326.﹣0.5+(﹣15)﹣(﹣17)﹣|﹣12|;327.[﹣22+(﹣2)3]﹣(﹣2)×(﹣3);328.()÷();329.;330.﹣14+[1﹣(1﹣0.5×2)]÷|2﹣(﹣3)2|;331. [(﹣3)2﹣22﹣(﹣5)2]××(﹣2)4.332. 4×(﹣3)2﹣13+(﹣)﹣|﹣43|;333. ﹣32﹣[(﹣2)2﹣(1﹣×)÷(﹣2)].334. (﹣11)×+(+5)×+(﹣137)÷5+(+113)÷5;335. ﹣8﹣[﹣7+(1﹣×0.6)÷(﹣3)].;336.337.﹣(﹣1)2005+4÷(﹣2)﹣|﹣12|.338. (﹣4)2×(﹣2)÷[(﹣2)3﹣(﹣4)].339.340. ;341. ﹣(﹣0.75)+;342. (﹣1)3×103×;343. 0÷.344.345. ﹣0.252÷+(+﹣3.75)×24347.348.;349.(﹣1)2006+;350.;351.﹣4.037×12+7.537×12﹣36×().参考答案(供参考):1.原式=1×2+(﹣8)÷4=2+(﹣2)=0.2.原式=[50﹣(﹣+)×36]÷49=[50﹣(×36﹣×36+×36)]÷49=[50﹣(28﹣33+6)]÷49 =(50﹣1)÷49=49÷49=1.3.原式=16×=12+(﹣5)=74.原式=﹣1﹣×(2﹣9)×(﹣8)=﹣1﹣=﹣.5.原式=﹣8+(﹣3)×18﹣9÷(﹣2)=﹣8﹣54﹣9÷(﹣2)=﹣62+4.5=﹣57.5.6. 原式=﹣4﹣÷(﹣8)=﹣4+=﹣37. (﹣1)2+[20﹣(﹣2)3]÷(﹣4)=1+[20﹣(﹣8)]÷(﹣4)=1+28×(﹣)=1﹣7=﹣6.8.原式=[1﹣(1﹣)]×[2﹣9]=[1﹣]×(﹣7)=×(﹣7)=﹣.9.原式=×(﹣)﹣×(﹣)﹣2=﹣+﹣2=﹣2=﹣1.10.原式=(+﹣)×(﹣48)=﹣(×48+×48﹣×48)=﹣(8+36﹣4)=﹣40.11.原式=1.25×(﹣8)﹣[(﹣4)÷()+1]﹣1=﹣10﹣[(﹣4)×+1]﹣1=﹣10+8﹣1=﹣3.12.原式=[18×﹣18×]﹣[(﹣24)×+(﹣24)×]=(9﹣6)﹣[(﹣8)+(﹣3)]=3﹣(﹣11)=14.13.原式=﹣×[﹣9×﹣8]+1=﹣×(﹣12)+1=18+1=19.14.原式=﹣3+6﹣8+9=4;15. 原式=﹣9﹣9×(﹣2)﹣[(﹣2)×1]²=﹣9+18-4=5 16.原式=﹣10×(﹣2)×5×1=100.17.原式=﹣3﹣[﹣5+(1﹣)×(﹣)=﹣3﹣[﹣5﹣]=﹣3+5+=18. ﹣14﹣(1﹣)÷3×|3﹣(﹣3)2|=﹣1﹣÷3×|3﹣9|=﹣1﹣××6=﹣1﹣1=﹣2. 19.原式=4+[6+6]÷4﹣5××=4+3﹣4=3.20.原式=21.原式=﹣9÷3+(﹣)×12﹣1=﹣6;22.原式===﹣.23.原式=﹣+﹣=3﹣6=﹣3;24.原式=﹣×﹣8×=﹣2﹣4=﹣6;25.原式=×(﹣36)=﹣1; 26.原式=﹣9×﹣[25×(﹣)+60×﹣2]=﹣3﹣(﹣15+15﹣2)=﹣3+2=﹣1 27.原式=8﹣8÷(﹣4)×(﹣2)+0=8﹣4=4.28.原式=[﹣×4×6]÷5×(﹣1)=[﹣(﹣5)]÷5×(﹣1)=.29. 原式=﹣++﹣=﹣++﹣=﹣2;30.原式=﹣×(﹣36)=718;31.原式={1﹣[﹣(﹣)]×16}÷[﹣﹣﹣]=[1﹣(+)×16]÷[﹣﹣﹣]=[1﹣1-41]÷(﹣2)=-41×(﹣)=81. 32.原式=;33.原式=﹣9+9+25×()﹣0.09÷0.9=﹣9+9+(﹣20)﹣0.1=﹣20﹣0.1=﹣20.134.原式=﹣1000﹣(﹣)×﹣100=﹣1099.35.原式=×+×﹣×=×(+﹣)=×()=. 36. 原式=﹣4+16×﹣0.28=﹣4+2﹣28=﹣3037.原式=(﹣+)×18+(3.95﹣1.45)×6=17.38.原式=.39.原式=﹣16×(﹣2)÷(﹣1)+(+﹣)×24=﹣32+×24+×24﹣×24=﹣32+27+32﹣18=9. 40. [(﹣1)2005+(﹣﹣)×24]÷|﹣32+5|=[﹣1+×24]÷|﹣4|=4÷4=141.原式==××(﹣1)=﹣.42. 原式=﹣1﹣[﹣2+×(﹣3)]=﹣1﹣[﹣2﹣2]=﹣1+4=3.43. 原式=21×23×32×34×43×45×54×56×65×67=44.=﹣﹣8×=﹣﹣=﹣545. 原式=﹣5﹣﹣(1﹣×)×9=﹣5﹣(1﹣)×9=﹣5﹣6=﹣11. 46. 原式=﹣10+8÷4﹣12=﹣10+2﹣12=﹣20.47.原式=(﹣﹣)×(﹣)=(﹣)×(﹣)=3.48. 原式=3+(﹣4)×8÷4÷2﹣9÷9×(﹣1)=3﹣4+1=0. 49. 原式=64﹣{81﹣[﹣+×(﹣4)]÷(﹣3)}=64﹣{81﹣3}=64﹣77=﹣13.50.原式=×(﹣)﹣×(﹣)﹣××=﹣+﹣=.51. 原式=(1315﹣15+4﹣14)×(﹣)=(1315﹣25)×(﹣)=41310; 52. 原式=﹣10+32﹣12=10;53. 原式=﹣÷(﹣)+()=﹣=;54. 原式=﹣3×﹣4×﹣8×=﹣﹣18=﹣20; 55.原式=﹣8+×+8=﹣8++8=.56.原式=﹣++××1=﹣++=; 57.原式=﹣27×4﹣4×()=﹣=0;58. 原式=﹣16+4﹣3×(﹣1)=﹣12+3=﹣9. 59. 原式=1.3+0=1.3;60. 原式=﹣13+12﹣7+38=﹣20+50=30;61.原式=[﹣3+3.5]+[﹣2﹣]=0﹣3=﹣3; 62. 原式=163﹣[63﹣259﹣41]=163+237=400.63.原式=﹣(﹣0.04+0.04)+(8﹣9×1)×=﹣1×=﹣;64.原式=(﹣3×﹣4×+1×)÷|2×﹣|×2=(﹣﹣+)÷||×2=﹣×4×2=﹣4;65.原式=×16×1﹣()=1﹣(﹣9+56﹣90)=1+9﹣56+90=44.66.原式=﹣4+4+4﹣8﹣9=﹣13. 67.原式=22﹣4﹣2+4=20; 68.原式=(﹣8)++9﹣=1;69. 原式=(+﹣)×(﹣24)﹣8=(﹣32)﹣3+66﹣8=23;70. 原式=(﹣)÷(﹣﹣)=1;71. 原式=(﹣9)××(﹣)×(﹣4)=﹣;72. 原式=(﹣1)﹣×(2﹣9)=.73.原式=﹣÷(﹣+)=﹣÷=﹣74.原式=(﹣2)÷(×)×+5=(﹣2)÷×+5=﹣2×32×+5=﹣48+5=﹣43.75.原式=(﹣2)×9×(﹣1)﹣12÷[3﹣1]=18﹣12÷2=18﹣6=12.76.原式=﹣1×[﹣9×﹣2]×(﹣)=﹣1×(﹣4﹣2)×(﹣)=﹣6×=﹣9. 77. 原式=﹣9﹣9+9×1=﹣9; 78. 原式=﹣24×+(﹣8)=﹣1﹣8=﹣9.79.原式=﹣8×8﹣8×+64=﹣1.80. 原式=×36﹣×36+×36=28﹣30+27=25. 81. 原式=﹣5﹣4=﹣9.82. 原式=27×4﹣(﹣27)×(﹣8)=27×(4﹣8)=﹣108.83. 原式=(1﹣)×(2﹣9)=×(﹣7)=.84.=1+2(﹣+﹣…﹣)=1+2(﹣)=.85.原式=3××××=1.86.原式=(﹣1+3)+(﹣5+7)+(﹣9+11)+…+(﹣1997+1999)=2××=1000;87.原式=(11﹣13)+(12﹣14)+(15﹣17)+…+(95﹣97)+(96﹣98)+(99+100)=﹣2×+199=﹣88+199=111;88.原式=(1990+1)(2000﹣1)﹣1990×2000=1990×2000﹣1990+2000﹣1﹣1990×2000=10﹣1=9;89.原式=4726342+4726352﹣(472634﹣1)×(472634+1)﹣(472635﹣1)(472635+1)=4726342+4726352﹣4726342+1﹣4726352+1=2;90.原式=×(1﹣+﹣+…+﹣)=×(1﹣)=×=;91.根据题意可知第n项就是a n=1+3(n﹣1),即有244=1+3(n﹣1),∴n=82,∴一共有82个数,又∵1+244=245,4+241=245…,∴原式=(1+244)×82÷2=10045;92. 设原式=m,那么3m=3+m﹣,∴2m=3﹣,∴m=;93. 原式=﹣+﹣+﹣=(1+)﹣(+)+(+)﹣(+)+(+)﹣(+)=1+﹣﹣+…﹣﹣=1﹣=.94.原式=﹣4﹣(﹣1)×(﹣)×6+9=﹣4﹣1+9=4.95. 原式=+﹣﹣=﹣=96. 原式=﹣+﹣(﹣8﹣1)=﹣+﹣×(﹣9)=+3=97.原式=5×+7×﹣12×=(5+7﹣12)×=0.98. 原式=﹣5﹣4÷[﹣]÷(﹣4)=﹣5﹣4÷(﹣2)÷(﹣4)=﹣5﹣(﹣2)÷(﹣4)=﹣5﹣=﹣5.99.原式=﹣3+2﹣2+7=(﹣3﹣2)+(2+7)=﹣6+10=4;100.原式=﹣8××=﹣8;101.原式=(﹣)×(﹣36)+×(﹣36)﹣×(﹣36)﹣(﹣)×(﹣36)=21﹣27+30﹣10=14;102.原式=÷(﹣)﹣×(﹣)=﹣1+1=0;103.原式=﹣1﹣0.5××[2﹣9]=﹣1+=.104.(2﹣3+1)÷(﹣1)=(﹣+)×(﹣)=×(﹣)+(﹣)×(﹣)+×(﹣)=﹣2+3﹣.105.∵,∴原式=1﹣+﹣+﹣+…+﹣=1﹣=.106.原式=﹣1+[1﹣]×7=﹣1+=107.原式=[1+(﹣)×16]÷=[1+(﹣)×16]×=﹣7×=108.原式=﹣1﹣[5×(﹣2)﹣16÷(﹣8)]=﹣1﹣[﹣10+2]=﹣1+8=7.109.原式=-1-[2-(1-61)]×6=-1-7=-8110. 原式==30.111.原式=(2﹣9)×[1﹣(1﹣)]=﹣7×(1﹣)=﹣7×=﹣.112.原式=﹣16×(﹣4)+(5﹣5)﹣2+(﹣1)=64+0﹣2﹣1=61.113.原式===;114.==27+20﹣21=26;115.=(﹣1﹣4)×===.116.原式=﹣8××+(﹣)×5×(﹣)=﹣8+1=﹣7.117.﹣32+5×(﹣)﹣(﹣4)2÷(﹣8)=﹣9﹣8﹣16÷(﹣8)=﹣9﹣8+2=﹣15.118. 原式=(﹣9﹣4+18)÷5=(+5)÷5=+5÷5==;119. 原式=﹣8×1﹣12÷(﹣)=﹣8+48=40120. 原式=﹣16×+×(﹣)=﹣6﹣=﹣;121. 原式=﹣16×(﹣4)+[5﹣5]﹣2﹣1=64﹣2﹣1=61.122.原式=﹣×(﹣8)×1+×12+×12﹣×12=++28﹣45=17+28﹣45=0.123.原式=﹣×××=;124. 原式=﹣24×1﹣24×(﹣)﹣24×﹣24×(﹣)=﹣24+18﹣4+15=5.125. 原式=(=﹣1﹣9=﹣10;126 原式=32﹣(﹣8+4﹣2)=32+8﹣4+2=38;127. 原式=﹣4+(﹣3)×(16﹣8)+9÷2=﹣4﹣24+4.5=﹣23.5128.原式=﹣5﹣3﹣9+7+=﹣9;129.原式=26;130.原式=﹣+﹣+=﹣6+10=4;131.原式=﹣9.2﹣7.1+3+6.2+2.9=﹣4.2=﹣4;132.原式=3.6+41.8﹣12.6﹣51.8=﹣19;133.原式=﹣+﹣﹣﹣﹣=﹣2=.134. 原式=(212﹣480)÷5×(﹣1)=268÷5=.135.原式=﹣16+16﹣1××=﹣.136. =×(﹣8)﹣[4×+1]+1=﹣2﹣[9+1]+1=﹣2﹣10+1=﹣12+1=﹣11;137.()×(﹣36)=×(﹣36)﹣×(﹣36)+×(﹣36)﹣×(﹣36)=﹣28+30﹣27+14=﹣55+44=﹣11.138. 原式=﹣20+3+5﹣7=﹣19;139. 原式=(+6+4)+(+2﹣1)﹣5﹣1=11+1﹣5﹣1=5;140. 原式=﹣13×(+)﹣0.34×(+)=﹣13﹣0.34=﹣13.34;141. 原式=××5×64=50;142. 原式=﹣27××+4+=﹣++4=﹣;143. 原式=﹣1﹣(﹣)×3×(﹣2+27)﹣|﹣|=﹣1+×75﹣=﹣1+12﹣=11.144. 0﹣14﹣(﹣1)+(﹣1.95)3×0.5×0﹣|﹣5|+5=0﹣1+1+0﹣5+5=0.145.原式=﹣9××[25×(﹣)﹣(﹣60)×]=﹣3×[﹣15+15]=﹣3×0=0.146.原式=1+++…+=1+++…+=2×(++…+)=2×(1﹣+﹣+…+﹣)=2×(1﹣)=.147. =4+(﹣2)=2;148. =﹣1+[1﹣×24﹣×24+×24]÷5=﹣1+[1﹣9﹣4+18]÷5=﹣1+×=﹣1+=.149.原式=﹣1﹣(﹣﹣)×(﹣)=﹣1﹣(﹣﹣)×(﹣)=﹣1﹣×(﹣)=﹣1+= 150. 原式=(125﹣4×25﹣1)÷(﹣16﹣24+16)=24÷(﹣24)=﹣1.151.原式=﹣9+27÷9﹣×4﹣(﹣1)=﹣9+3﹣1+1=﹣6.152. 原式=4+3﹣1=6;153. 原式=[﹣3.5﹣1.5﹣1.4+0.4]÷9=(﹣6)÷9=.154. 原式=[47﹣(18﹣)×]÷0.46=[47﹣×]×=×=20;155. 原式===.156.原式=﹣105×+105×﹣105×﹣178×6.67+7.67×178=﹣21×3+15×4﹣35×5+178×(7.67﹣6.67)=﹣63+60﹣175+178=0157.原式=23﹣59﹣35+37=﹣34;158.原式=﹣()××()=﹣=.159.原式=﹣××(﹣)×+(﹣8)=+(﹣8)=﹣.160. 原式=4﹣4﹣9÷(﹣1)+0=4﹣4+9+0=9.161.原式==﹣2﹣9+5=﹣6.162.原式=(﹣5)×(﹣0.75﹣0.125﹣0.125)=(﹣5)×(﹣1)=5.163.原式=﹣20﹣18﹣12+10=﹣40;164.原式=﹣﹣﹣3=﹣4;165.原式=﹣×48=﹣24;166.原式=﹣2.5×17×4×0.1=﹣×17×4×=﹣17;167.原式=33.1﹣10.7+22.9﹣2.3=43;168.原式=﹣36÷4+5×1.2=﹣9+6=﹣3;169.原式=﹣×(﹣9×+0.8)÷=××=;170.原式=﹣4﹣6+2+3×=﹣4﹣6+2+1=﹣7171.=﹣1﹣0.5××6+1=﹣1. 172.=﹣÷﹣4×3=﹣14.173. 原式=﹣1﹣(﹣)××(﹣6)=﹣1+1=0;174. 原式=﹣25﹣[﹣8+÷(﹣4)×(﹣2)]=﹣25﹣(﹣8+)=﹣25+=﹣17;175. 原式=××(﹣)+×﹣=﹣+××=﹣﹣=(或).176. 原式=(21+6×3×3﹣25)×=50×=177.原式=×(﹣)﹣﹣÷(﹣)=﹣﹣+=﹣.178.原式=﹣9﹣50÷25﹣1=﹣12;179.原式=﹣1﹣[2﹣(1﹣)]×(9﹣4)=.180. 0﹣3+(﹣)﹣(﹣22)﹣5÷(﹣)=﹣3﹣+4+20=21﹣=20;181. 10÷[﹣(﹣1+1)]×6=10÷(﹣)×6=10÷×6=10×6×6=360;182. 18+32÷(﹣2)3﹣(﹣4)2×5=18+32÷(﹣8)﹣16×5=18﹣4﹣80=18﹣84=﹣66;183. ﹣7×(﹣)+19×(﹣)﹣5×(﹣)=(﹣7+19﹣5)×(﹣)=(﹣12+19)×(﹣)=7×(﹣)=﹣22.184. 原式=8﹣2×9+36=8﹣18+36=26.185. 原式=4+(﹣4)÷(﹣)+×(﹣16)=4+6﹣1=9.186. 原式=﹣12﹣4=﹣16;187. 原式=﹣1+×[9﹣9]=﹣1;188. 原式=﹣10+8×9﹣12=﹣10+72﹣12=50189. 原式=﹣8﹣2×(﹣3)+3﹣1=﹣8+6+3﹣1=0190. 原式=48×(﹣)+48×+48×(﹣)=﹣8+36﹣4=24.191. (+7)+(﹣8)﹣(+3)﹣(﹣4)=7﹣8﹣3+4=11﹣11=0;192.﹣1﹣2÷(﹣)×(﹣3)=﹣1﹣×(﹣)×(﹣3)=﹣1﹣4=﹣6;193.﹣36×(﹣﹣)=(﹣36)×+(﹣36)×(﹣)+(﹣36)×(﹣)=﹣4+6+2=﹣4+8=4;194.﹣13﹣(1﹣0.5)××[2﹣(﹣3)2]=﹣1﹣××(2﹣9)=﹣1+=;195.(﹣0.25)×1.25×(﹣4)×(﹣8)=(﹣0.25)×(﹣4)×[1.25×(﹣8)]=1×(﹣10)=﹣10;196.(﹣1)10×2+(﹣2)3÷4=1×2+(﹣8)÷4=2﹣2=0.197. 原式=﹣9﹣(3﹣×)×(﹣)=﹣9+×=﹣.198. 原式=﹣﹣﹣=(﹣1)﹣1=﹣2;199.原式=﹣1﹣(﹣+﹣)×(﹣36)=﹣1+11=10;200.原式=4÷9×(﹣)=×(﹣)=﹣1;201. 原式=3﹣2﹣8÷×4=﹣127.202.原式=﹣1+8×﹣4=﹣3.203.原式=﹣9+×(﹣27)÷(﹣1)=﹣9+3=﹣6204.原式===205. 原式=﹣1﹣××6=﹣2;206. 原式=﹣1﹣0.5××(﹣6)=﹣1﹣0.5×(﹣2)=0.207.原式=﹣8﹣9﹣(﹣)×(﹣)=﹣8﹣9+6﹣1=﹣12.208.﹣22+(﹣3)÷﹣(﹣3)2÷(﹣2)=﹣4+(﹣9)﹣9÷(﹣2)=﹣8.5.209.原式==210. 原式=(30﹣13)×(﹣0.125)÷=﹣17;211. 原式=×=;212. 原式=﹣1﹣25=﹣26;213. 原式=3﹣3﹣10=214.原式=﹣×3×4÷(﹣)×=.215. 原式=﹣1÷25×(﹣)+0.2=+=.216. 原式=×(﹣9×﹣0.8)×(﹣)=×(﹣)×(﹣)=217. 原式=﹣9+5×(﹣6)﹣16÷(﹣8)=﹣9﹣30+2=﹣37;218. 原式=9﹣×﹣6×=9﹣﹣9=.219.原式=100﹣5×36+8×10=100﹣180+80=0.220. 原式=﹣×[﹣9×﹣8]=﹣×[﹣4﹣8]=﹣×(﹣12)=18.221.原式=﹣4﹣9÷[﹣8﹣1]=﹣4﹣9÷(﹣9)=﹣4+1=﹣3.222. (+10)+(﹣11.5)+(﹣10)﹣(+4.5)=10﹣11.5﹣10﹣4.5=10﹣10﹣11.5﹣4.5=﹣16;223.(﹣81)÷×÷(﹣16)=(﹣81)××÷(﹣16)=﹣16÷(﹣16)=1;224.﹣32﹣[﹣5﹣0.2÷×(﹣2)2]=﹣9﹣[﹣5﹣××4]=﹣9﹣[﹣5﹣1]=﹣9+6=﹣3;225. 24×(﹣﹣)+(﹣)2÷(﹣)=24×﹣24×﹣24×+×(﹣72)=4﹣18﹣15﹣8=4﹣41=﹣37.226. 原式=[(﹣×)﹣×]×=[(﹣)﹣]×=(﹣)×=×=2原式=﹣1÷25×(﹣)﹣1=﹣227.228. 原式=[9××﹣6]÷(﹣)=(4﹣6)×(﹣2)=4229. 原式=﹣1﹣(﹣8)×5+÷=﹣1﹣(﹣40)+1=40230.原式=(﹣20)+(+3)+(+5)+(﹣7)=[(+3)+(+5)]+[(﹣20)+(﹣7)]=8+(﹣27)=﹣19;231. 原式===()+[(﹣)+(﹣)]=+(﹣)=;232.原式=﹣30+25=﹣5;233.原式=3+(﹣)++2=3+3=6;234.原式=×4﹣×4﹣×4+×4=﹣1﹣+=1;235. 原式=﹣18÷9﹣+3=﹣2+3﹣=.236.原式==﹣11﹣1=﹣12237. =﹣1+1.5××=;238. ﹣22﹣(1﹣×0.2)÷(﹣2)3=﹣4+(1﹣0.04)÷8=﹣3.88239. 原式=﹣4﹣3=﹣7;240. 原式=4+4×﹣×16=4+6﹣1=9.241. 原式=﹣1+(﹣5)×|﹣8+2|﹣16×(﹣2)=﹣1+(﹣5)×6+32=﹣1﹣30+32=1.242..243.原式=﹣4﹣28+29﹣24=﹣27;244.原式=﹣2×(5﹣4+8)=﹣;245.原式=﹣4+1=﹣3;246.原式=(﹣9×﹣0.8)××=;247. 原式=(﹣+﹣)×36=﹣27+60﹣21=12;248.原式=﹣1﹣0=﹣1249. 原式=(﹣2)4×{﹣5+(﹣1)9}+(﹣3)3=16×(﹣6)+(﹣27)=﹣96﹣27=﹣123.250.原式=﹣1.251.原式=5﹣(﹣1)=6.252.原式=﹣9×(0.375+0.625)=﹣9.253.原式=9×××=.254.原式=﹣49+2×9﹣(﹣6)×9=﹣49+18+54=23.255.原式=﹣9﹣(9﹣4)×(2﹣)=﹣9﹣5×=﹣15256.﹣16+23+(﹣17)﹣(﹣7)=﹣16+23﹣17+7=﹣33+30=﹣3;257.(﹣)+(﹣)﹣(﹣)﹣(+)﹣(﹣)=﹣+﹣+﹣=(﹣+)﹣+﹣=﹣=;258.(﹣+﹣)×(﹣16)=(﹣)×(﹣16)+×(﹣16)﹣×(﹣16)=8﹣12+10=18﹣12=6;259.﹣14+(1﹣0.5)××〔2﹣(﹣3)2〕=﹣1+××(2﹣9)=﹣1+=.260. 原式=﹣20﹣14+18+13=﹣3.261. 原式=﹣9×(﹣1)+75÷25=12.262. 原式=﹣3×8﹣36﹣8×3=﹣84;263. 原式=÷(﹣)﹣÷(﹣)﹣××=×(﹣)﹣×(﹣)﹣××=﹣+﹣=;264. 原式=100+4﹣(3+9)×2=104﹣24=80;265. 原式=(﹣×4+×)×(﹣1)=(﹣15+2.5)×(﹣1)=12.5.266.原式=1×(﹣48)﹣×(﹣48)+×(﹣48)=﹣48+8﹣36=﹣76;267.原式=﹣1+40﹣64=﹣25;268. 原式=÷﹣=×﹣=;269. 原式=﹣1﹣(2﹣)×5=﹣1﹣10+=270 .原式=﹣×24﹣×24+×24+1=32.271. 原式=(﹣3.5﹣1.5﹣1.4+0.4)÷9=(﹣6)÷9=﹣;272. 原式=﹣+﹣﹣=﹣.273. 原式=0.75+3.25+0.125﹣0.125=4;274. 原式=﹣1﹣1×()×3﹣2=.275.﹣32﹣[(﹣2)2﹣(1﹣×)÷(﹣2)]=﹣9﹣[4﹣(1﹣)÷(﹣2)]=﹣9﹣[4﹣×(﹣)] =﹣9﹣(4+)=﹣13.2.276.原式=﹣×[﹣+++]+6=﹣25+6=(或﹣18).277. 原式=﹣+﹣+﹣=﹣;278. 原式=﹣+﹣+=;279. 原式=11+10×(﹣)=﹣11;280. 原式=××()=﹣;281. 原式=﹣1﹣×52=﹣;282. 原式=9+12×(﹣)+4×=9.283. 原式=﹣8÷[(﹣)×(﹣)×(﹣)]=﹣8÷(﹣)=﹣8×(﹣16)=128.284. 原式=(﹣36)×(﹣)+(﹣36)×+(﹣36)×(﹣)=16﹣30+21=7.285. 原式=÷()2÷36×=×=.286. 原式=1﹣+﹣+﹣+…+﹣=1﹣=.287.原式=20﹣3×(8+6)+1=20﹣42+1=﹣21.288. 原式=25﹣3×(9﹣6)+5=25﹣9+5=21;289. 原式=﹣÷+×24+×24﹣×24=﹣1+33+56﹣90=﹣91+89=﹣2290.原式=×(﹣1﹣2﹣50+20)=×(﹣33)=﹣7.291. =(1﹣+﹣…+﹣)=(1+﹣﹣)=×=.292. 原式=﹣8﹣9×1+1=﹣8﹣9+1=﹣16;293. 原式=×(+)﹣15×(2)=×﹣15×3=1.4﹣45=﹣43.6.294. 原式=9÷3﹣12×(﹣)﹣12×﹣12×(﹣)=3+4﹣3+2=6.295. 原式=3+4﹣6+12×=1+16=17;296. 原式=5÷(﹣)×6=﹣5××6=﹣.297. 原式=()×(﹣12)﹣×(﹣12)+×(﹣12)+×(﹣12)=﹣3+10﹣4﹣18=﹣15;298. 原式=4+(﹣2)×(﹣1.5)+×(﹣16)=4+3﹣1=6.299.原式=(+﹣)×(﹣36)=×(﹣36)+×(﹣36)﹣×(﹣36)=﹣28﹣30+33=﹣25;300.原式=﹣16÷4+12×(﹣3)×3=﹣4﹣108=﹣112.301.原式=﹣0.25+﹣|﹣4|﹣(﹣)×÷=﹣.025+﹣4+÷=﹣0.25+﹣4+2=﹣0.25+0.25﹣4+2=﹣2.302.原式={[÷(﹣)+0.4×]÷(﹣)﹣20}×(﹣1)={[﹣15+]÷(﹣)﹣20}×(﹣1)=[﹣÷(﹣)﹣20]×(﹣1)=12.303. 原式=(﹣32)﹣(5﹣3﹣5﹣2)=﹣32﹣5+3+5+2=﹣32+(5﹣5)+(3+2)=﹣26;304. 原式=25×+25×+25×(﹣)=25×[++(﹣)]=25.305.原式=﹣1+×﹣8÷|﹣9+1|=1﹣8÷8=0.306. (﹣2)2﹣|﹣7|+3﹣2×(﹣)=4﹣7+3+1=8﹣7=1;307. ﹣36×(﹣﹣)=×(﹣36)﹣×(﹣36)﹣×(﹣36)=﹣4+6+2=﹣4+8=4;308. ﹣16﹣(1﹣0.5)××[2﹣(﹣3)2]=﹣1﹣××(2﹣9)=﹣1+=;309. (﹣3)2008×﹣12008﹣(﹣1)2008=(﹣3)2008××﹣1﹣1=×﹣2 =﹣2=﹣.310.,=×××…××××…×=(×)×(×)×(×)×(×)×=.311. 原式=0.25×(﹣8)﹣[4×+1]=﹣2﹣10=﹣12.312. 原式=﹣×(﹣48)+×(﹣48)﹣×(﹣48)=8﹣36+4=﹣24;313. 原式=﹣4﹣(1﹣2)2×(﹣)=.314.原式=[﹣3.5﹣1.5﹣1.4+0.4]÷9=(﹣6)÷9=.315.原式=====316. 原式=﹣30﹣16÷(﹣8)=﹣30+2=﹣28;317.原式=()2÷(﹣)+49=﹣+=;318.原式=﹣1﹣[﹣3×﹣(﹣)÷4]=﹣1﹣(﹣+)=﹣1+1=0;319.原式=﹣27﹣[××64+×﹣]=﹣27﹣(3+﹣)=﹣33.320. 原式=20﹣12+18=38﹣12=26.321. 原式=8×10﹣2×25=80﹣50=30.322. 原式==﹣3+2=﹣1.323. 原式==﹣27﹣20+21=﹣26.324. 原式=====325. 原式=====﹣1+20+8=27.326. 原式=﹣0.5﹣15+17﹣12=﹣27.5+17=﹣10.5;327. 原式=(﹣4﹣8)﹣6=﹣12﹣6=﹣18;328. 原式=﹣18+108﹣30+21=81;329. 原式=﹣1.6÷[×(﹣27)﹣4]=﹣1.6÷(﹣16)=0.1;330. 原式=﹣1+[1﹣(1﹣1)]÷7=﹣1+=﹣;331. 原式=(9﹣4﹣25)×××16=(﹣20)×××16=﹣600.332. 原式=4×9﹣13﹣﹣64=;333. 原式=(﹣9)﹣[4﹣(1﹣)×(﹣)]=(﹣9)﹣(4+)=.334.(﹣11)×+(+5)×+(﹣137)÷5+(+113)÷5=(﹣11)×+(+5)×+(﹣137)×+(+113)×=×[(﹣11)+(+5)+(﹣137)+(+113)]=×[﹣6+(﹣24)]=×(﹣30)=﹣6.335. ﹣8﹣[﹣7+(1﹣×0.6)÷(﹣3)]=﹣8﹣[﹣7+(1﹣×)×(﹣)]=﹣8﹣[﹣7+(1﹣)×(﹣)]=﹣8﹣[﹣7+×(﹣)]=﹣8﹣(﹣7﹣)=﹣8+7=﹣336.原式=(﹣2)÷×+5=﹣64×+5=﹣400+5=﹣395;337.原式=1+(﹣2)﹣1=﹣2.338. 原式=16×(﹣2)÷(﹣8+4)=﹣32÷(﹣4)=8.原式=(﹣2.5)2×(﹣1)÷×0.5=6.25×(﹣1)×8×0.5=﹣25339.340. 原式=25×(++)=25×=30;341. 原式=++﹣=1+﹣==﹣;342. 原式=﹣1×(﹣)÷÷=××10=;343. 原式=0344.=[]×÷[(0.125×8)9×0.125]==[]×8=(﹣2﹣3)×8=﹣40.345. 原式==﹣1+33+56﹣90=﹣2.347. 原式=×(+×3.2)÷=﹣+××=﹣+=﹣1.348. 原式=[(﹣9)×﹣0.8]÷(﹣)=(﹣)×(﹣)=;349. 原式=1﹣24×(+﹣)=0;350. 原式=(+﹣)×(﹣60)=×(﹣60)=﹣30;351. 原式=(7.537﹣4.037)×12﹣36×(﹣+)=42﹣12=30.。
专题2-35 《有理数及其运算》计算题综合训练(提高篇)(专项练

专题2.35 《有理数及其运算》计算题综合训练(提高篇)(专项练习)一、解答题 1.(1)3233(10)43434⎛⎫⎛⎫÷-⨯-÷-- ⎪ ⎪⎝⎭⎝⎭(2)()22012201121(0.25)4522--⨯+-÷-(3)1111864126⎛⎫-⨯-++÷ ⎪⎝⎭(4)()2222114(32)333⎡⎤⎛⎫⎛⎫-÷---⨯-+-⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦(5)22222411.35 1.057.7393⎛⎫⎛⎫⎛⎫⨯-+⨯--⨯- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(6)2432151|2|(3)(2)62⎛⎫⎡⎤-+⨯-----÷- ⎪⎣⎦⎝⎭(7)222311513543⎡⎤⎛⎫⎛⎫⎛⎫-⨯÷---÷-+⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦(8)111112123123100+++++++++++2.(1)421211(1)0.52368⎛⎫⎛⎫---÷----⎪ ⎪⎝⎭⎝⎭(2)21211312144335⎛⎫⎛⎫--⨯--++÷- ⎪ ⎪⎝⎭⎝⎭3.计算:(1)(+16)﹣(+11)﹣(﹣18)+(﹣15);(2)﹣12﹣(1﹣0.5)÷212(2)5⎡⎤⨯--⎣⎦;(3)4341(72)()98253-⨯-+-;(4)22222211()19()6()777-⨯-+⨯-+⨯-4.计算:(1)()()()7935------;(2) 4.2 5.78.410-+-+;(3)15214632-++-.5.计算:(1)3583927⎛⎫-⨯-+ ⎪⎝⎭; (2)23121111113382⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫---÷-⨯-⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦.6.计算(能简算的要简算):(1)(4)8( 2.5)(125)-⨯⨯-⨯-; (2)1111(24)46812⎛⎫-+-+⨯- ⎪⎝⎭;(3)121321334⎛⎫⎛⎫÷-÷- ⎪ ⎪⎝⎭⎝⎭; (4)14(81)2(16)49-÷⨯⨯-.7.计算:32531(4)(1)42⎡⎤⎛⎫-⨯-++-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦; (2)153(30)265⎛⎫-⨯-- ⎪⎝⎭.8.计算:(1)45(8)()( 1.25)34-⨯-⨯-⨯; (2)1138()842-⨯+-;(3) 3311.83(11.8) 1.711.811.8(0.3)44⨯--⨯-⨯-⨯-.9.计算:(l)243(1)()( 2.5)()3925+⨯-⨯-⨯-; (2)5183()(2)()()115134-⨯-⨯-⨯-.10.计算:(1)2304124()(2)3-⨯+---;(2)422311(1){[()0.4(1)](2)}532---+⨯-÷-.11.计算下列各题: (1)1112-134-114+412; (2)(-22.84)-(+38.57)+(-37.16)-(-32.57); (3)112-56+234+38-423; (4)(-36)-(-28)+(+125)+(-4)-(+53)-(-40).11.计算:(1)20173(1)(6)(2)⨯-+-÷-; (2)42232[1(3)]()(15)35-÷--+-⨯-.13. 计算: (1)131123-2 1.25848⎛⎫⎛⎫+-+- ⎪ ⎪⎝⎭⎝⎭; (2)()32018112122⎛⎫-+-⨯---- ⎪⎝⎭;(3)11112-342⎛⎫-⨯+ ⎪⎝⎭.14.计算:(1)2–12×(13–14+12); (2)–12018+24÷(–2)2–32×(13)2.15.计算:(1)-13-5+8; (2)123()45935-+⨯;(3)201921(1)(1)33(3)2---÷⨯--.16.计算:(1)0﹣(﹣2) (2)(+10)+(﹣14)(3)5.6+(﹣0.9)+4.4+(﹣8.1) (4)1﹣47+15﹣37+95(5)(﹣0.5)﹣(﹣314)+2.75﹣(+712). 17.计算(1)﹣5+3﹣2 (2)﹣20﹣(﹣18)+(﹣14)+13(3)5.6+(﹣0.9)+4.4+(﹣8.1)(4)(+ 32)﹣512﹣52+(﹣712)18.计算(1)36﹣76+(﹣23)﹣(﹣10)(2)﹣6﹣9(4)(﹣134)﹣(+613)﹣2.25+103(4)11+(﹣35)﹣(﹣41)+(﹣16)(5)(﹣323)﹣(﹣234)﹣(﹣123)﹣(+1.75)(6)(﹣478)﹣(﹣512)+(﹣414)﹣(+318).19.计算(1)(﹣9.8)﹣(+6);(2)4.7﹣(﹣8.9)﹣7.5+(﹣6);(3)1﹣3+5﹣7+9﹣11+…+97﹣99 (4)1.75+(﹣612)+338+(﹣134)+(+258).20.计算:(1)45+(﹣20);(2)(﹣8)﹣(﹣1);(4)|﹣10|+|+8|;(4)(﹣12)﹣5+(﹣14)﹣(﹣39);(5)0.47﹣456﹣(﹣1.53)﹣116;(6)36﹣76+(﹣23)﹣105;(7)﹣20+|﹣14|﹣(﹣18)﹣13;(8)(8)(+1.75)+(﹣13)+(+45)+(+1.05)+(﹣23)+(+2.2).21.计算:(1)-∣-3∣×123-12÷(-6)﹙2)25×﹙-0.125﹚×﹙-4﹚×﹙-45) ×﹙-8﹚×114(3)1-2-3+4+5-6-7+8+…-2007+2008+2009-2010(5)(13-14-16)×(-48)22.计算:(1)3(4)8(3)(3)-+-+--- (2)357244612⎛⎫-⨯-+ ⎪⎝⎭(3)223(3)3(2)4-÷-+⨯-+- (4)()()3116-2---48⎛⎫÷⨯ ⎪⎝⎭23.计算:(1)12-17+3-5; (2)3()(4)24-⨯--;(4)3777(1)48128--÷; (4)20112(1)6[3(3)]--⨯--; 24.计算(1)﹣22+(﹣3)×[(﹣4)2+2] (2)﹣16×34﹣(﹣16)×12+16×(﹣14)25.先阅读第(1)题的计算过程,再根据第(1)题的解题方法完成第(2)题: (1)计算5231591736342⎛⎫⎛⎫⎛⎫-+-++- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 解:5231591736342⎛⎫⎛⎫⎛⎫-+-++- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=()()()()5231591736342⎡⎤⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-+-+-+-+++++-+- ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎣⎦⎣⎦=[(–5)+(–9)+(+17)+(–3)]+52316342⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-+-+++- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦=1101144⎛⎫+-=- ⎪⎝⎭.上面这种解题方法叫做拆项法.(2)计算:∣522120092013402216332⎛⎫⎛⎫⎛⎫-+-++- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭; ∣()35917424816++++-.26.计算:(1)2150--÷256-+() (2)20111222.7524(1)83⎛⎫+-⨯+- ⎪⎝⎭(3)311312122⎛⎫-÷⨯--÷- ⎪⎝⎭27.计算:(1) -13×23-0.34×27+13×(-13)-57×0.34;(2) 3113×4112-1113×4112×2-9.5×1113.28.观察下列等式111122=-⨯,1112323=-⨯,1113434=-⨯, 将以上三个等式两边分别相加得:1111111113111223342233444++=-+-+-=-=⨯⨯⨯. (1)猜想并写出:()11n n =+_____________. (2)直接写出下列各式的计算结果: ∣1111 (12233420162017)+++++=⨯⨯⨯⨯______________; ∣()11111223341n n ++++=⨯⨯⨯+______________.(3)探究并计算:1111 (13355720152017)+++++⨯⨯⨯⨯.29.计算:(1)2125824(3)3-+-+÷-⨯;(2)20171313[2()24]5(1)2864-+-⨯÷⨯-.30.计算: (1)514-(-223)+(-314)-(+423); (2)(-3594812-+)×(-24);(4)(-3)÷34×43×(-15);(4)-14+|(-2)3-10|-(-3)÷(-1)2017.31.运用运算律作较简便的计算:(1)-1.25×(-5)×3×(-8);(2)(5231234+-)×(-12);(3)113(19)19(19) 424-⨯--⨯-⨯-.32.计算(1)146842213⎛⎫-⨯-÷-+⎪⎝⎭(2)422112250.25326-÷-+⨯--()()()33.计算:(1)135()(12)6412-+-⨯-;(2)2215(1)4()2--⨯--÷-.34.计算题:(1)23+17+(-7)+(-16);(2)(-514)+(-3.5);(4)(+23)+(-34);(4)23+(-15)+(-1)+13.35.解答下列各题:(1)(﹣3.6)+(+2.5) (2)-37﹣(﹣312)﹣247+12(3)(﹣49)﹣(+91)﹣(﹣5)+(﹣9) (4)﹣5﹣(﹣11)+213﹣(﹣23)(5)312﹣(﹣13)+223+(﹣12) (6)25﹣|﹣112|﹣(+214)﹣(﹣2.75)(7)(﹣7)﹣(﹣11)+(﹣9)﹣(+2) (8)(﹣414)﹣(+513)﹣(﹣414) 36.计算:(1)()()()()910283+-++---+; (2)()1212237⎛⎫⎛⎫-⨯-⨯-⎪ ⎪⎝⎭⎝⎭;(3)6663210111111⎛⎫⎛⎫⨯⨯-+⨯- ⎪ ⎪⎝⎭⎝⎭--; (4)()()0.5151712-+-----; (4)3416401373⎛⎫⎛⎫-⨯-⨯⨯ ⎪ ⎪⎝⎭⎝⎭; (6)()157362612⎛⎫+-⨯- ⎪⎝⎭;(6)()()15144⎛⎫⨯⨯- ⎪⎝⎭---; (8)18(19)1519-⨯.37.请阅读下列材料: 计算:121123031065⎛⎫÷-+- ⎪⎝⎭. 方法一:121123031065⎛⎫÷-+- ⎪⎝⎭121123036105⎡⎤⎛⎫⎛⎫=÷+-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦1513062⎛⎫=÷- ⎪⎝⎭1133010=⨯=. 方法二:计算原数的倒数 211213106530⎛⎫-+-÷⎪⎝⎭ 21123031065⎛⎫=-+-⨯ ⎪⎝⎭20351210=-+-=,所以原式110=. 请依照上题用两种方法计:113224261437⎛⎫÷-+- ⎪⎝⎭.38.计算:42991310.25(1)12 3.7524283⎛⎫⎛⎫-÷-⨯-++-⨯ ⎪ ⎪⎝⎭⎝⎭.39.计算下列各题: (1)()157482812⎡⎤⎛⎫-⨯--+ ⎪⎢⎥⎝⎭⎣⎦(2)()()222211432333⎡⎤⎛⎫⎛⎫-÷---⨯-+-⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦(3)()()232415123262⎛⎫⎡⎤-+⨯-----÷- ⎪⎣⎦⎝⎭(4)666433363777⎛⎫⎛⎫⨯--⨯--⨯ ⎪ ⎪⎝⎭⎝⎭40.计算与化简:(1)12﹣(﹣6)+(﹣9); (2)(﹣48)×(﹣1572812-+);(3) ﹣32÷(﹣2)2×|﹣113|×6+(﹣2)3.(1)-5-(-3)+(-4)-[-(-2)]; (2)-14+13712812⎛⎫--+ ⎪⎝⎭×(-24);(3)-62×2112⎛⎫- ⎪⎝⎭-32÷3112⎛⎫- ⎪⎝⎭×3;(4)22539⎛⎫⎛⎫--+- ⎪ ⎪⎝⎭⎝⎭-(-1)1000-2.45×8+2.55×(-8).42.计算:(1)(213−13+16)×(−78); (2)−24×(−1)4−|−12|÷[−(12)2];(3)−18÷(−3)2+5×(−12)3−(−15)÷5.43.计算: (1)12(13)(17)33⎛⎫--++--- ⎪⎝⎭; (2)()()1352119+----;(3)()()()743410--+---+-; (4)67( 3.2)(1)5⎛⎫----+- ⎪⎝⎭.(1)22452(3)(1)(1)---⨯---; (2)24103(2)554⎛⎫⎛⎫-+----÷- ⎪ ⎪⎝⎭⎝⎭;(4)11124834⎛⎫-⨯-+ ⎪⎝⎭.45.计算:(1)32821142⎛⎫-++- ⎪⎝⎭; (2)242113(1)326⎛⎫---⨯-÷ ⎪⎝⎭.46.计算:(1)8214(3)(6)(3)|4|-+⨯-+-÷-+-; (2)22019342(1)5293⎛⎫-⨯-÷⨯- ⎪⎝⎭.47.计算: (1)23×(2﹣5)+(﹣6)÷(﹣4); (2)133()(48)6412-+-⨯-;(3)﹣13+(﹣12)+3×[12﹣(﹣1)6]﹣0.12.48.计算:(1)215482()14+÷⨯--; (2)2213(2)0.254[()]4028-⨯-÷--.49.计算: (1) 316+(157-)+(126-)+(647-); (2) 25.7+(-7.3)+(-13.7)+7.3;(3)(-2.125)+(135+)+(158+)+(-3.2); (4) (-0.8)+6.4+(-9.2)+3.6+(-1).50.计算: (1)| -2|÷(-12)+(-5)×(-2); (2) (23-12+56)×(-24);(3) 15÷(-32+56); (4) (-2)2-|-7|-3÷(-14)+(-3)3×(-13)2.参考答案1.(1)13-;(2)174-;(3)-8;(4)496;(5)8;(6)13-;(7)161;(8)200101 【分析】根据有理数的混合运算法则分别计算. 【详解】 解:(1)3233(10)43434⎛⎫⎛⎫÷-⨯-÷-- ⎪ ⎪⎝⎭⎝⎭=3112123124451034⎛⎫⎛⎫⎛⎫⨯-⨯-÷-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=110441015153-⨯⨯⨯ =13-;(2)()22012201121(0.25)4522--⨯+-÷-=()2012220111422554⎛⎫--⨯+-÷- ⎪⎝⎭ =2012201151424254⎛⎫-⨯-⨯⎪⎝⎭=2011411444⎛⎫-⨯⨯- ⎪⎝⎭=174-; (3)1111864126⎛⎫-⨯-++÷ ⎪⎝⎭ =111866412⎛⎫⨯--⨯⎪⎝⎭ =1114848486412⨯-⨯-⨯ =8124--=-8;(4)()2222114(32)333⎡⎤⎛⎫⎛⎫-÷---⨯-+-⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦=()91116(32)349⎡⎤-÷--⨯--⎢⎥⎣⎦=111423⎛⎫--- ⎪⎝⎭=12323+ =496; (5)22222411.35 1.057.7393⎛⎫⎛⎫⎛⎫⨯-+⨯--⨯- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=44411.35 1.057.7999⨯-⨯+⨯ =()411.35 1.057.79-+⨯=4189⨯=8;(6)2432151|2|(3)(2)62⎛⎫⎡⎤-+⨯-----÷- ⎪⎣⎦⎝⎭=()5112246274-+⨯+-⨯ =14125625-+⨯⨯=213-+=13-;(7)222311513543⎡⎤⎛⎫⎛⎫⎛⎫-⨯÷---÷-+⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦=3531345254⎛⎫⨯⨯+⨯+ ⎪⎝⎭=35141254⎛⎫⨯++⎪⎝⎭=511284⨯+ =160+1 =161;(8)111112123123100+++++++++++ =()()()11111221331100100222+++++⨯+⨯+⨯=2222122334100101++++⨯⨯⨯⨯ =11112122334100101⎛⎫⨯++++⎪⨯⨯⨯⨯⎝⎭=11111112122334100101⎛⎫⨯-+-+-++- ⎪⎝⎭=200101【点睛】本题考查了有理数的混合运算,解题的关键是掌握运算法则和运算顺序,以及一些常用的简便运算方法.2.(1)38-;(2)20. 【分析】(1)先计算有理数的乘方与减法、将有理数的除法转化为乘法,再计算绝对值运算、有理数的乘法与减法即可得;(2)先计算有理数的乘方、有理数的乘法与减法,再计算有理数的除法与加减法即可得. 【详解】(1)原式()11116684⎛⎫=--⨯---- ⎪⎝⎭, 3118=---, 38=-;(2)原式1212121214415329⎡⎤⎛⎫=--⨯--⨯+⨯+÷ ⎪⎢⎥⎝⎭⎣⎦, ()381542219=----++⨯, 1093=--+,20=.【点睛】本题考查了含乘方的有理数混合运算,熟记有理数的运算法则和运算律是解题关键. 3.(1)8;(2)4;(3)71225;(4)﹣44. 【分析】(1)根据有理数的加减法可以解答本题;(2)根据有理数的乘方、有理数的乘除法和减法可以解答本题; (3)根据乘法分配律可以解答本题; (4)根据乘法分配律可以解答本题. 【详解】解:(1)(+16)﹣(+11)﹣(﹣18)+(﹣15) =16+(﹣11)+18+(﹣15) =(16+18)+[(﹣11)+(﹣15)] =34+(﹣26) =8;(2)﹣12﹣(1﹣0.5)÷212(2)5⎡⎤⨯--⎣⎦ =﹣1﹣12×5×(2﹣4) =﹣1﹣12×5×(﹣2)=﹣1+5 =4; (3)4341(72)()98253-⨯-+-=(﹣72)×49﹣(﹣72)×38+(﹣72)×425﹣(﹣72)×13=﹣32+27+(﹣111325)+24 =71225; (4)22222211()19()6()777-⨯-+⨯-+⨯- =[(﹣11)+19+6]×(﹣227) =14×(﹣227) =﹣44.【点睛】本题主要考查的是含有乘方的有理数的混合运算,掌握有理数的运算法则是解题的关键. 4.(1)-8;(2)3.1;(3)34. 【分析】根据有理数的加、减混合运算的相关法则进行计算即可.【详解】(1)()()()()()()793579351688⎡⎤------=-+-++=-+=-⎣⎦ ;(2)()()4.2 5.78.410 4.28.4 5.71012.615.7 3.1-+-+=--++=-+=; (3)15214632-++-=11523334263424⎛⎫⎛⎫--++=-+= ⎪ ⎪⎝⎭⎝⎭. 【点睛】熟悉“有理数加减混合运算的相关运算法则,能灵活的使用运算律把符号相同的数结合到一起先相加”是解答本题的关键.5.(1)7 ; (2) 132【分析】(1) 先运算乘方,再利用乘法分配率进行解答.(2) 根据有理数混合运算的解题步骤进行解答.【详解】解:(1)35858327271587927927⎛⎫⎛⎫-⨯-+=-⨯--⨯=-= ⎪ ⎪⎝⎭⎝⎭; (2)2312111-1-1-1338-2-⎡⎤⎛⎫⎛⎫⎛⎫÷⨯⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦⎛⎫ ⎪⎝⎭ 459279388⎡⎤⎛⎫⎛⎫=+÷-⨯- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 458279398⎛⎫⎛⎫=-⨯⨯- ⎪ ⎪⎝⎭⎝⎭ 427582798398⎛⎫⎛⎫=⨯--⨯⨯- ⎪ ⎪⎝⎭⎝⎭ 352=-+ 132=. 【点睛】进行含乘方的混合运算时,先计算乘方,再根据有理数混合运算的解题步骤进行解答,解题过程中可灵活运用运算律.6.(1)-10000;(2)3;(3)1;(4)256【解析】【分析】(1)根据乘法交换律和结合律计算即可;(2)利用乘法分配率计算即可;(3)利用除法法则计算即可;(4)利用乘除法混合运算法则计算即可.【详解】(1)原式()()()()[]4 2.5812510100010000=-⨯-⨯⨯-=⨯-=-.(2)原式1111(24)(24)(24)(24)6432346812⎛⎫=-⨯-+⨯--⨯-+⨯-=-+-= ⎪⎝⎭. (3)原式108510341334385⎛⎫⎛⎫=÷-÷-=⨯⨯= ⎪ ⎪⎝⎭⎝⎭.(4)原式9444(81)(16)(81)(16)16162564999=-÷⨯⨯-=-⨯⨯⨯-=⨯=. 【点睛】 本题考查了有理数的混合运算,有理数的混合运算首先弄清运算顺序,先乘方,再乘除,最后算加减,有括号先算括号里边的,同级运算从左到右依次计算,然后利用各种运算法则计算,有时可以利用运算律来简化运算.7.(1)-6;(2)28【解析】【分析】(1)先算乘方,再用乘法分配律进行计算;(2)利用乘法分配律进行计算.【详解】解(1)32531(4)(1)42⎡⎤⎛⎫-⨯-++-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦ 3116148⎡⎤⎛⎫=⨯-++- ⎪⎢⎥⎝⎭⎣⎦ 3116(1)161648⎛⎫=⨯-+⨯+⨯- ⎪⎝⎭1612(2)6=-++-=-(2)153(30)265⎛⎫-⨯-- ⎪⎝⎭ 15330(30)(30)265⎛⎫⎛⎫=-⨯+-⨯-+-⨯- ⎪ ⎪⎝⎭⎝⎭15251828=-++=.【点睛】本题考查了有理数的含有乘方的混合运算,注意运用运算定律使计算更简便.8.(1)-503;(2)9;(3)59 【解析】【分析】(1)利用乘法的交换,结合律进行计算即可(2)利用乘法分配律进行计算即可(3)利用逆乘法分配律计算即可【详解】(1)原式=10×(-53 )=-503(2)原式=-1-2+12=9(3)原式=11.8 ×333+1.7-+0.344⎛⎫ ⎪⎝⎭=11.8×5=59 【点睛】此题考查有理数的乘法,解题关键在于掌握运算法则9.(1)2-9 ;(2)613【解析】【分析】原式各项根据负因式个数确定出正负,再利用乘法法则计算即可得到结果.【详解】(1)54532-=-392259⨯⨯⨯ (2)511836=11513413⨯⨯⨯ 【点睛】此题考查有理数的乘法,解题关键在于掌握运算法则10.(1)1;(2)518. 【解析】【分析】(1)结合负整数指数幂、零指数幂的概念进行求解即可(2)先算乘方,再算乘除,最后算加减,有括号,要先做括号内的运算.【详解】(1)2304124()(2)3-⨯+--- =3141164⨯+-24116=+-16116=+-1=.(2)422311(1){[()0.4(1)](2)}532---+⨯-÷- 3121{[()]4}59523=--+⨯-÷ 31311[()]5954=---⨯ 32211()5454=-+⨯ 5411=1()9090-+ 65190=- 13118=- 518=. 【点睛】此题考查有理数的混合运算,解题关键在于掌握负整数指数幂,零指数幂的运算法则 11.(1)13;(2)-66;(3)-78;(4)100. 【解析】【分析】(1)利用加法的交换律和结合律把分母相同的项合在一起分别计算,即可得结果; (2)利用加法的交换律和结合律把能凑整的小数合在一起分别计算,即可得结果;(3)先把带分数拆分成整数与分数的和,然后利用加法的交换律和结合律把整数、分数(分母为2、4、8与3、6的分别计算)分别合在一起计算,最后再通分计算,即可得结果; (4)先去括号,利用加法的交换律和结合律分别把正数、负数合在一起分别计算,即可得结果;【详解】(1)原式=1131114112244⎛⎫⎛⎫++-- ⎪ ⎪⎝⎭⎝⎭ =16-3=13.(2)原式=(-22.84-37.16)+(-38.57+32.57)=-(22.84+37.16)-(38.57-32.57)=-60-6=-66.(3)原式=1533212426483+-+++--=()1335212424863⎛⎫⎛⎫+-+++-+ ⎪ ⎪⎝⎭⎝⎭=46354188866⎛⎫⎛⎫-+++-+ ⎪ ⎪⎝⎭⎝⎭=133182-+-=1312188-+-=78- (4)原式=362812545340-++--+=(2812540)(45336)++-++=193-93=100【点睛】本题考查了加法运算律在加减混合运算中的应用,灵活运用加法交换律和结合律能达到简便计算的目的。
有理数提高训练

有理数的有关概念1、写出比3小的非负整数 ,比-3大的非正整数 ,绝对值不大于3的非正整数 ,绝对值大于2不小于4的整数 。
最大的负整数 ,最小的正整数 ,最小的非负整数 ,最大的非正整数 ,绝对值最小的有理数 。
2、如果a 、b 互为相反数,则 ,如果a 、b 互为倒数,则 。
3、如果|x|=5,则x= ,如果|-x|=|-5|,则x= ,如果|a|=|b|,则 。
4、如果|x+4|+|y-3|=0,则x 3+y 3= 。
5、如果a >-a ,则a 0,如果a=-a ,则a 0,如果a <-a ,则a 0。
6、如果|a|=a ,则a ,如果|a|=-a ,则a ,如果1=aa ,则a ,如果1-=aa ,则a ,如果2<|x|≤5,则整数x= 。
7、当x= 时,|x+2|有最小值 。
8、某数的绝对值是5,那么这个数是 。
134756≈ (保留四个有效数字) 9、( )2=16,(-32)3= 。
10、计算:(-2)100+(-2)101的是( )A.2100B.-1C.-2D.-210011、下列代数式中值一定是正数的是( )A .x 2B.|-x+1|C.(-x)2+2 D.-x 2+112、相反数等于它本身的数是 ;绝对值等于它本身的数是 ; 13、倒数等于它本身的数是 ;平方等于它本身的数是 ; 13、若a 、b 互为相反数,则-a-b= ;14、若2(x+3)与3(1-x )互为相反数,则x 的值为 ;15、-[+〔-3〕]的相反数是 ,-1.5的相反数的倒数是 ,倒数的绝对值 是 ;16、若x<0,且2|x|+3x=m ,则m 0,若|x|=3,则x= ,若|-x|=6,则x= 17、若|a|+|b|=|a+b|,则a 、b 的关系是( ) A 、a 、b 绝对值相等 B 、a 、b 异号C 、a+b 的和是非负数D 、a 、b 同号或其中一个为0 18、|a|=3,|b|=2,则|a+b|等于( ) A 、5 B 、1 C 、5或1 D 、±5或±119、|a+5|=|a|+|-5|,则a 为 ;13、绝对值小于2013的所有整数之和是 ;20、在正整数中,前50个偶数的和减去前50个奇数的和,差是( ) A 、50 B 、-50 C 、100 D 、-10021、两个有理数的商为正数,和为负数,这两个数的符号( ) A 、一正一负 B 、都是负 C 、都是正 D 、不确定 22、已知a 、b 为整数,且ab=4,则a-b= 。
有理数提高训练题

有理数及其运算全章拔高训练题一、学科内综合题(每题4分,共40分)1.计算:2242226(1)(3)(1)33-⨯+-÷-.2.如图所示,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度.从上图可以看出,终点表示的数是-2.请参照上图,完成填空:已知A 、B 是数轴上的点,(1)如果点A 表示的数是-3,•将A•向右平移7•个单位长度,那么终点表示的数是______;(2)如果点B 表示的数是3,将B 向左移动7个单位长度,再向左移动5个单位长度,•那么终点表示的数是________.3.计算:1234562001200220032004-+-+-++-+-.4.1月10日下午,出租车司机小王在东西走向的人民大道上运营.•如果规定向东为正,向西为负,出租车的行车里程如下(单位:千米):+15,-4,+13,-10,-12,+3,-17.将最后一名乘客送到目的地时,小王距出车地点的距离是多少千米?5.已知:21(1)0a b -++=,那么201320132013()a b a b +++的值是多少?6.计算:111111112233445566778++++++⨯⨯⨯⨯⨯⨯⨯.7.计算12+14+18+116+132+164.8.将-2,-1,0,1,2,3,4,5,6这9个数分别填入右图的9个空格中,使得横、竖、斜对角的3对数相加的和为6.9.计算:2399100(1)(1)(1)(1)(1)-⋅-⋅-⋅⋅-⋅-.10.若0ab <,求||a a +||b b +||ab ab 的值.二、学科间综合题(每题10分,共20分)11.已知a 、b 互为相反数,c 、d 互为倒数,且x 的绝对值是5, 试求()()43x a b cd a b cd -+-++-+-的值.12.一口水井,水面比井口低3米,一只蜗牛从水面沿着井壁往井口爬,第一次往上爬了0.5米后又往下滑了0.1米;第二次往上爬了0.42米,却又下滑了0.15米;第三次往上爬了0.7米,却下滑了0.15米;第四次往上爬了0.75米,却下滑了0.1米;第五次往上爬了0.55米,没有下滑;第六次蜗牛又往上爬了0.48米,问蜗牛有没有爬出井口?三、应用题(10分)13.某自行车厂本周计划每日生产400辆自行车,由于人数和操作原因,每日实际生产量分别为405辆,393辆,397辆,410辆,391辆,385辆,405辆.(1)用正负数表示每日实际生产量与计划量的增减情况;(2)该车厂本周实际生产多少辆自行车?平均每日实际生产多少辆自行车?四、创新题(每题10分,共20分)14.已知:13=1=14×12×22; 13+23=9=14×22×32; 13+23+33=36=14×32×42; 13+23+33+43=100=14×42×52. (1)猜想填空:13+23+33+…+(n -1)3+n 3=______;(n 为正整数)(2)计算:23+43+63+…+983+1003.15.已知m 、n 、p 满足20m m +=,n n =,1p p ⋅=, 化简121n m p p n n ---++-+.答案:1.-7021252.解:(1)+4 (2)-9.3.分析:-1002.4.分析:这是一道实际问题,在理解题意之后,•不难发现我们只需对所给的数据进行加法运算,所得的结果就是本题的结论.解:∵+15+(-4)+(+13)+(-10)+(-12)+3+(-17)=15-4+13-10-12+3-17=-12.∴小王距出车地点的距离是偏西12千米.5.解:由题意易知a=1,b=-1,代入原式=02003+12003+(-1)2003=0.6.解:原式=(1-12)+(12-13)+(13-14)+…+(17-18)=78. 7.分析:该式的特点是后一项为前一项的一半,因此如果我们把后一项加上它本身,就可以得到前一项的值.解:原式=12+14+18+116+132+(164+164)-164=12+14+18+116+(132+132)-164=12+14+18+(116+116)-164=(12+12)-164=1-164=6364. 点拨:在运算过程中,巧用运算规律和其他运算方法和技巧,可以使运算简捷方便.8.解:第一行:5 -2 3 第二行:0 2 4第三行:1 6 -19.分析:由乘方的符号法则,易知对于一个有理数a ,有(-a )2n =a 2n ,(-a )2n+1=-a 2n+1(n 为整数).解:原式=(-1)×1×(-1)×…×(-1)×1=50(1)(1)(1)-⨯-⨯⨯-个×1=1.点拨:注意(-1)2n =1,(-1)2n+1=-1(n 为整数).10.解:分两种情况考虑:①a>0,b<0,原式=a b ab a b ab ++--=1-1-1=-1.②a<0,b>0,原式=a b ab a b ab++--=-•1+1-1=-1. 二、11.解:当x=5时,原式=5-(0-1)+│0-4│+│3-1│=12;当x=-5时,原式=-5-(0-1)+│0-4│+│3-1│=2.12.分析:把往上爬的距离记为“+”,下滑的距离记为“-”,可表示出每次上爬和下滑的情况,转化为有理数的加法运算.解:+(0.5)+(-0.1)+(+0.42)+(-0.15)+(+0.7)+(-0.15)+(+0.75)+(-0.1)+(+•0.55)+0+(+0.48)=2.9<3,所以蜗牛没有爬出井口.三、13.解:(1)把超过计划量的车辆数用正数表示,把低于计划量的车辆数用负数表示,可得(2)本周总增减量为(+5)+(-7)+(-3)+(+10)+(-9)+(-15)+(+5)=-14.因此,本周实际总生产量为400×7+(-14)=2786(辆),平均每日实际生产2786÷7=398(辆).点拨:本题在计算本周总的产量时,也可将每日的产量直接相加,但由于这些数较大,所以较繁.四、14.解:(1)13+23+33+…+(n-1)3+n3=14n2(n+1)2.(2)23+43+63+…+983+1003=(1×2)3+(2×2)3+(2×3)3+…+(2×49)3+(2×50)3=23×(13+23+33+…+493+503)=23×14×502×512=13 005 000.点拨:很多数学题的结论不直接给出,需要去寻找和发现合理运用猜想,就能较快地找到结论或结果.15.-2 点拨:根据已知条件先分别求出m、n、p的值或其范围再化简.五、16.3 17.C。
(完整版)有理数提高题(有答案)

2有理数基础训练题一、填空:1、 在数轴上表示一2的点到原点的距离等于( )。
2、 若 I a I =— a,则 a () 0.3、 任何有理数的绝对值都是( )。
4、 如果a+b=O,那么a 、b 一定是()。
5、 将0.1毫米的厚度的纸对折20次,列式表示厚度是( )。
6 已知 |a| 3,| b| 2,| a b| a b ,则 a b ( )7、 |x 2| |x 3|的最小值是()。
1 18、 在数轴上,点A 、B 分别表示 -,则线段AB 的中点所表示的数是()4 2a b20109、 若a,b 互为相反数,m, n 互为倒数,P 的绝对值为3,则 ------- mn p 2 p ()。
10、若 abc ^0,则 |a| |b|a b|c|的值是( c).11、下列有规律排列的一列数:.32531、 一、 一、一、 一、•…,其中从左到右第100个数是( ) 二、解答问题:1、已知x+3=0,|y+5|+4的值是4, z 对应的点到-2对应的点的距离是7, 求 x 、y 、 z 这三个数两两之积的和。
3、若2x |4 5x| |1 3x| 4的值恒为常数,求x 满足的条件及此时常数的值4、若 a,b,c 为整数,且 |a b |2010 |c a |2010 1,试求 |c a| |a b| |b c| 的值5 7 9 11 13 15 171 5、计算:一—+ _ 一----- 1 --- ——-- 1 --- — ----- 1--- 66 12 20 30 42 56 720 1能力培训题知识点一:数轴例1:已知有理数a 在数轴上原点的右方,有理数 b 在原点的左方,那么()2、利用数轴能直观地解释相反数;例2:如果数轴上点 A 到原点的距离为 3,点B 到原点的距离为 5,那么A 、B 两点的距离 为 ________________ 。
拓广训练:1、 在数轴上表示数a 的点到原点的距离为 3,则a 3__________ .2、 已知数轴上有 A 、B 两点,A 、B 之间的距离为1,点A 与原点O 的距离为3,那么所有满 足条件的点 B 与原点O 的距离之和等于 _____________________ 。
有理数提高训练

第一章有理数提高训练题一、选择题1、在0,()()221,3,3,3------,234- ,2a 中,正数的个数为( )A .1个 B.2个 C.3个 D.4个2、下列说法中,正确的是( )A 负整数和负分数统称为有理数B 正分数、0、负分数统称为分数C 正整数、负整数、正分数、负分数统称为有理数D 0不是有理数3、如右图,数轴上一动点A 向左移动2个单位长度到达点B ,再向右移动5个单位长度到达点C ,若点C 表示的数为1,则点A 表示的数为( )A 7B 3C -3D -24、下列说法正确的是( )A 、倒数等于它本身的数只有1B 、平方等于它本身的数只有1C 、立方等于它本身的数只有1D 、正数的绝对值是它本身5、-4的倒数的相反数是( ) A .-4 B .4 C .-41 D .416、已知一个数的倒数的相反数为135,则这个数为 ( )。
A 、165B 、516C 、165- D 、516-7、如果一个有理数的绝对值是8,那么这个数一定是( )。
A 、-8 B 、-8或8 C 、8 D 、以上都不对 8、如果a a =-,下列成立的是( )A 、0a >B 、0a <C 、0a >或0a =D 、0a <或0a = 9.若x 是-3的相反数,y =5,则x y +的值为( ) A .-8 B .2 C .8或-2 D .-8或210、红星队在4场足球赛中战绩是:第一场3︰1胜,第二场2︰3负,第三场0︰0平, 第四场2︰5负,则红星队在这次比赛中总的净胜球数是( )球A .+1B .-1C .+2D .-2 11、下列各组数中相等的是( )A 、-2与)2(--B 、-2与2-C 、2-与2--D 、2-与212. 据宁波市统计局公布的第六次人口普查数据,本市常住人口760.57万人,其中760.57 万人用科学记数法表示为 ( )A .7.6057×105人B .7.6057×106人C .7.6057×107人D .0.76057×107人 13.第六次人口普查公布的数据表明,登记的全国人口数量约为1340 000 000人,这个数据用 科学记数法表示为( )A.134×107人B.13.4×108 人C.1.34×109人D.1.34×1010人· · · B A C 0 15 214.从《中华人民共和国2011年国民经济和社会发展统计报告》中获悉,去年我国国内生产 总值达397983亿元.请你以亿元..为单位用科学计数法表示去年我国的国内生产总值(结果 保留两个有效数字)( ) A. 3.9×1013B.4.0×1013C.3.9×l05D. 4.0×l0515. 今年5月,我市第六次人口普查办公室发布了全市常住人口为578.99万人,用科学 记数法(保留2个有效数字)可以表示为( )A .58×105人B .5.8×105人C . 5.8×106人D .0.58×107人16.某市在一次扶贫助残活动中,共捐款3185800元,将3185800元用科学记数法表示(保留两个有效数字)为( )A .3.1×610元B .3.1×510元C .3.2×610元D .3.18×610元 17. 已知地球距离月球表面约为383900千米,那么这个距离用科学记数法表示为 (保留三个有效数字)( )A .3.84×104千米B .3.84×105千米C .3.84×106千米D .38.4×104千米18. 由四舍五入法得到的近似数8.8×103,下列说法中正确的是( ).A .精确到十分位,有2个有效数字B .精确到个位,有2个有效数字C .精确到百位,有2个有效数字D .精确到千位,有4个有效数字 19、下列说法正确的是( )A .近似数4.0精确到十分位,有两个有效数字B .近似数41030.2⨯精确到百分位 C .用科学记数法表示250000为41025⨯ D .近似数2.120有三个有效数字 20、按括号内的要求用四舍五入法对1022.0099的近似值,其中错误..的是( )。
初一有理数提高练习题及答案

有理数提高训练一、选择题1、已知|a|=2 , |b|=3,且在数轴上表示有理数b的点在a的左边,贝0 a - b的值为()A . -1B . -5 C. -1 或- 5 D. 1或52、下列说法正确的是()3、如果a和2b互为相反数,且b^ 0,那么a的倒数是()1 1 2■ ■—A.丄B. 2-C. ■-D.4、如下图,数轴的单位长度为 1.如果点A, B表示的数的绝对值相等,那么点A表示的数是()I 丨A BA.—4 B 2 C . 0 D . 45、如果与1互为相反数,则丨迄+习等于()A. 2 B . _ C . 1 D . 16、已知a,b是有理数,若a在数轴上的对应点的位置如图所示,「:■ L -」,有以下结论:①-I.;②「「: . ■」:③; ' _ :;④一;. 山:“则所有正确的结论是()A.①,④B. ①,③C. ②,③D. ②,④7、下列说法正确的是()①0是绝对值最小的有理数②相反数大于本身的数是负数③数轴上原点两侧的数互为相反数④两个数比较,绝对值大的反而小A ①②B ①③C ①②③D ①②③④8、下列说法中,正确的是( )。
9、下面的说法中,正确的个数是( )值最小的有理数,请问: ...、一:、]三数之和为多少?”你能回答主持人的问题吗?其和应为(A 、一 1B 、0 11、若 -l<a<0 ,则的大小关系是12、有理数a 、b 、c 、d 在数轴上的位置如图 1所示,下列结论中错误的是 ()图1A.a+b<0B.c+d>0C.|a+c|=a+cD.|b+d|=b+d13、如图,一八1在数轴上的位置如图所示,A . T 是正数 B. — a 是负数 C. 也是负数 D. 一尬不是负数①若 a + b=0,则 |a|=|b| ③若 |a|=|b|,则 a=b A.1个 B.2 个 ②若 |a|=a,贝U a > 0④若a 为有理数,则a 2=(-a )C.3 个D.4 个10、在一次智力竞赛中,主持人问了这样的一道题目: 」是最小的正整数,-是最大的负整数的相反数,I 是绝对D、2则-:----:--■ - -■ - L'-14、对于有理数、_:,如果,- J :' ! ' 11 ,则下列各式成立的是(:A' <0-且」」* D .「;』■川且・」a,b 是有理数,它们在数轴上的对应点的位置如下图所示:把a,-a,b,-b 按照从小到大的顺序排列二、填空题16、如果 |a-2|=0 ,|b|=3 , 求a+b 的值17、绝对值不大于 10的所有整数的和等于 ,绝对值小于5的所有负整数的和为18、在数轴上,若 A 点表示数:,点B 表示数一5,A 、B 两点之间的距离为 7,则::- 19、 已知:J71-120、如果,Hr 21、设一;> 0, : v 0,且 22、=0,则「V 的值为,用“v”号把...、—」、:、—一:连接起来小明在写作业时不慎将一滴墨水滴在数轴上,根据图的数值,判断墨迹盖住的整数共有个.15、A -b v -a v av bB -a v -b v av bC -b v av -a v bD -b v bv -a v a23、用“ 一”与“ 一”表示一种法则:(a — b ) = - b ,( a — b )=-玄,如(2一 3) = -3 , 则:「UM . I" . 丁厂-124、 右0v a v 1,则a , a ,二的大小关系是25、 水位上升用正数表示,水位下降用负数表示,如图,水面从原来的位置到第二次变化后的位置,其变化值是三、简答题26、已知 |a-3 | + | b-4 | =0,求; 的值.27、如图所示,一个点从数轴上的原点开始,先向右移动 3个单位长度,再向左移动 5个单位长度,可以看到终点表 示的数是-匚,已知点A ,B 是数轴上的点,请参照下图并思考。
有理数的加法与减法(提升训练) (1)

2.5 有理数的加法与减法【提升训练】一、单选题1.若三个有理数a 、b 、c 满足0a b c ++=,且a b c >>,则一定有( )A .0a >,0b =,0c <B .0a >,0b >,0c <C .0a >,0b <,0c <D .0a >,0c <2.在某航展上,一架“20J -”飞机在某一高度开始进行10min 的特技表演,然后每隔2min 记录一次该飞机高度变化,5次记录数据如下:(注:正号表示比前一次记录高,负号表示比前一次记录低) 1.5, 3.2,0.5,2,4km km km km km +-+-+.在上述5次记录时,飞机的实际高度最低是哪次( ) A .第2次 B .第3次 C .第4次 D .第5次3.将5-(+3)-(-4)+(-2)写成省略加号和的形式是( )A .-5-3+4-2B .5-3-4-2C .5-3+4-2D .5+3-4-24.设a 是最大的负整数,b 是绝对值最小的数,c 是倒数等于自身的有理数,则a -b +c 的值为( ) A .0 B .-2 C .0或3 D .0或-25.若m 是任意的有理数,则||2m --一定是( )A .零B .非负数C .正数D .负数6.3-,4+,7-的和比它们绝对值的和小( )A .8-B .14-C .20D .20-7.设两个有理数的和为a ,差为b ,则a 与b 的大小关系是( )A .a b >B .a b =C .a b <D .不能确定8.下列说法正确的是( )A .两数之和必大于任何一个加数B .同号两数相加,符号不变,并把绝对值相加C .两负数相加和为负数,并把绝对值相减D .异号两数相加,取绝对值较大的加数的符号,并把绝对值相加9.数轴上点A 表示-3,从A 出发,沿数轴向右移动4个单位到达点B,点B 表示的数是( ) A .7 B .—7或-1 C .1 D .—7或110.下列说法中,正确的是( )A .互为相反数的两数之和为零B .若|a|=|b|,则a =bC .0是最小的整数D .数轴上两个有理数,较大的数离原点较远 11.如果a =14-,b =-2,c =324-,那么︱a ︱+︱b ︱-︱c ︱等于( ) A .-12 B .112 C .12 D .-11212.若b<0,刚a ,a+b ,a -b 的大小关系是( )A .a<a <+b -b aB .<a<a-b a+bC .a<<a-b a+bD .<a<a+b a-b13.已知|a|=1,|b|=2,且a>b ,则a -b 的值为( )A .1或3B .-1或-3C .1D .314.如图,数轴上A ,B 两点分别对应有理数a ,b ,则下列结论:①a>0,b<0;①a -b<0;①a+b>0;①|a|-|b|>0,其中正确的有( )A .1B .2C .3D .015.已知a ,b 两数在数轴上对应点的位置如图,设M a b =+,N a b =-+,H a b =-,则下列各式正确的是( )A .M N H >>B .H N M >>C .H M N >>D .M H N >>16.式子﹣2①①①1①+3①①+2)省略括号后的形式是( )A .2+1①3+2B .①2+1+3①2C .2①1+3①2D .2①1①3①217.有理数,a b 在数轴上的位置如图所示,下列结论正确的是( )A .0a b -<B .0a b --<C .0()a b -->D .()0a b ---<18.在数轴上,与表示数-5的点距离3个单位长度的点表示的数是( )A .-2B .-8C .-2或-8D .3±19.|x |=8,|y |=4,x <y ,则x -y 的值是( )A .-12B .-4C .4或12D .-4或 -1220.绝对值大于1且小于4的所有整数的和是( )A .6B .–6C .0D .421.一天早晨气温为﹣4①,中午上升了7①,半夜又下降了8①,则半夜的气温是( )A .﹣16①B .﹣4①C .4①D .﹣5①22.冬季某天我国三个城市的最高气温分别是-13①,1①,-3①,它们任意两城市中最大的温差是( ) A .12① B .16① C .10① D .14①23.“九宫图”传说是远古时代洛河中的一个神龟背上的图案,故又称“龟背图”,就是把 1,2,3,4,5,6,7,8,9 九个数字,分别填入九个方格中,使得每行、每列、每条对角线上的三个数之和都相等,现在小刚模仿九宫图,将 -3,-2,-1 ,0,1,2,3,4,5这九个数字分别填如图的九个方格中,其中a 、b 、c 分别表示其中的一个数,则a -b +c 的值为( )A .-1B .0C .1D .3 24.如果a ,b ,c 为非零有理数且a + b + c = 0,那么a b c abc a b c abc+++的所有可能的值为( A .0 B .1或- 1 C .2或- 2 D .0或- 225.已知3,1,0a b a b ==+>,则-a b 的值是( )A .4-或2B .4或2-C .4-或2-D .4或226.若120a b -++=,则+a b 的值是( )A .-1B .1C .0D .327.下列说法正确的有( )①所有的有理数都能用数轴上的点表示;①符号不同的两个数互为相反数;①有理数分为正数和负数;①两数相减,差一定小于被减数;①两数相加,和一定大于任何一个加数.A .4个B .2个C .1个D .3个28.一名粗心的同学在进行加法运算时,将“①5”错写成“①5”进行运算,这样他得到的结果比正确答案① ①A .少5B .少10C .多5D .多1029.已知|a|=1,|b|=2,|c|=4,且a >b >c ,则a -b+c= ( )A .-1或-3B .7C .-3或7D .-1 30.已知a 、b 为有理数,且b >0,则||||||a b ab a b ab ++的值是( ) A .3 B .﹣1 C .﹣3 D .3 或﹣131.下列说法正确的有( )①两个有理数的和为负数,则这两个数中至少有一个是负数;①若a b <,则a b <;①a 为任何有理数,则2a --必为负数;①若0a a +=,则a 为非正数;A .1个B .2个C .3个D .4个32.下列四种说法:①减去一个数,等于加上这个数的相反数;①两个互为相反数的数和为0;①两数相减,差一定小于被减数;①如果两个数的绝对值相等,那么这两个数的和或差等于零.其中正确的说法有( )A .4个B .3个C .2个D .1个33.若|x|=7|y|=5x+y>0,,且,那么x-y 的值是 ( )A .2或12B .2或-12C .-2或12D .-2或-1234.计算-3-1的结果是( )A .2B .-2C .4D .-435.下列运算错误的是( ①A .13÷①-3①=3×(①3)B .-5÷①-12①=①5×(①2)C .8-①-2①=8+2D .0÷3=0 36.2019年某市一月份的平均气温为-3 ①,三月份的平均气温为9 ①,则三月份的平均气温比一月份的平均气温高( )A .6 ①B .-6 ①C .12 ①D .-12 ①37.如果a ,b ,c 是非零有理数,那么a b c abc a b c abc+++的所有可能的值为( ). A .4-,2-,0,2,4B .4-,2-,2,4C .0D .4-,0,4 38.计算123456782017201820192020+--++--+++--值为( ) A .0 B .﹣1 C .2020 D .-202039.如图,在一个由六个圆圈组成的三角形里,把-1,-2,-3,-4,-5,-6这6个数分别填入图中圆圈里,要求三角形每条边上的三个数的和S 都相等,那么S 的最大值是( )A .-9B .-10C .-12D .-1340.有理数a 、b 在数轴上的位置如图所示,且|a |<|b |,下列各式中正确的个数是( )①a +b <0;①b ﹣a >0;①11b a>- ;①3a ﹣b >0;①﹣a ﹣b >0.A .2个B .3个C .4个D .5个 二、填空题41.计算:111111201820172017201620182016-+---=______. 42.如果240x y -++=,那么代数式y -x 的值是____________.43.绝对值大于﹣12且小于13的所有整数的和是_______.44.已知|x |=1,|y |=3,若||x y x y +=+,则x -y =____45.已知数轴上A 、B 两点所对应的数分别是1和3,P 为数轴上任意一点,对应的数为x .(1)则A 、B 两点之间的距离为________;(2)式子|1||3||2017||2019|x x x x -+-++-+-的最小值为________.三、解答题46.某仓库原有某种货物库存200千克,现规定运入为正,运出为负;一天中七次出入如下(单位:千克)(1)在第________次纪录时库存最多.(2)求最终这一天库存增加或减少了多少?(3)若货物装卸费用为每千克0.3元,问这一天需装卸费用多少元?47.某一出租车一天下午以鼓楼为出发地在东四方向营运,向东为正,向西为负,行车里程(单位:km )依先后次序记录如下:9+,3-,8-,6+,6-,4-,10+.(1)将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?(2)若每千米的价格为2.4元,司机一个下午的营运额是多少?48.某食品厂计划平均每天生产200袋食品,但是由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超过计划量记为正):(1)根据记录的数据,求产量最多的一天比产量最少的一天多生产食品多少袋?(2)根据记录的数据,求该厂本周实际共生产食品多少袋?49.某路公交车从起点经过A ,B ,C ,D 站到达终点,各站上下乘客的人数如下(上车为正,下车为负):起点(20,0),(12,4),(8,9),(6,4),(2,7)A B C D ----,终点()0,____.(1)在横线上填写适当的数,并说明该数的实际意义;(2)行驶在哪两站之间时,车上的乘客最多?(3)若乘坐该车的票价为每人2元,则这一趟公交车能收入多少钱? 50.庐江某出租车司机,在东西方向的周瑜大道上连续接送5批客人,行驶路程记录如下表(规定向东为正,向西为负,单位:km ):(1)接送完第5批客人后,该驾驶员在起始出发地的什么方向,距离起始出发地多少千米?(2)若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?(3)若该出租车的计价标准为:行驶路程不超过2.5km 收费6元,超过2.5km 的部分按每千米1.6元收费,在这过程中该驾驶员共收到车费多少元?51.从数轴上看: a 表示数a 的点到原点之间的距离,类似地4a -表示数a 的点到表示数4的点之间的距离.一般地a b -表示数a 的点到表示数b 的点之间的距离.(1)在数轴上,若表示数x 的点与表示数2-的点之间的距离为5个单位长度,则 x =________;. (2)对于任何有理数x ,式子 16x x ++- 有最_____(大或小)值,该值为________.(3)利用数轴,求方程 549x x -++= 的所有整数解的和;52.一电子跳蚤落在数轴上的某点k 0处,第一次从k 0向左跳1个单位到k 1,第二次从k 1向右跳2个单位到k 2,第三次由k 2处向左跳3个单位到k 3,第四次由k 3向右跳4个单位k 4…,按以上规律:(1)若k 0处为原点,那第10次时,跳蚤落在数轴上的点表示的数是多少?第2019次呢?(2)若跳了100次后,电子跳蚤落在数轴上的点表示的数是0,则k 0表示的数是多少?53.在2020年抗洪抢险中,解放军战士的冲锋舟加满汽油后沿东西方向的河流抢救灾民,早晨从A 地出发,晚上到达B 地,约定向东为正方向,当天的航行路程记录如下(单位:千米):+15,﹣8,+9,﹣6,+14,﹣5,+13,﹣10.(1)B 地位于A 地的什么方向?距离A 地多少千米?(2)若冲锋舟每千米耗油0.6升,油箱容量为30升,求冲锋舟当天救灾过程中至少还需补充多少升油? (3)救灾过程中,冲锋舟离出发点A 最远时,距A 地多少千米?54.“学雷锋活动月”活动中,对某小组做好事情况进行统计如下表(1)完成上表.(2)谁做的好事最多,谁最少?(3)最多的比最少的多多少?55.已知6x =,3y =(1)若x 、y 异号,直接写出x 和y 的差为_____(2)若x y <,直接写出x 与y 的和为_____56.学校为了备战校园足球联赛,利用体育课让学生进行足球训练,为了训练学生快速抢断转身,体育老师设计了折返跑训练.老师在东西方向的足球场上画了一条直线插上不同的折返旗帜,如果约定向西为正,向东为负,练习一组的行驶记录如下(单位:米):+40,﹣30,+45,﹣25,+25,﹣35,+15,﹣28,+16,﹣18.(1)学生最后到达的地方在出发点的哪个方向?距出发点多远?(2)学生训练过程中,最远处离出发点多远?(3)学生在一组练习过程中,跑了多少米?57.新华文具用品店最近购进了一批钢笔,进价为每支6元,为了合理定价,在销售前五天试行机动价格,卖出时每支以10元为标准,超过10元的部分记为正,不足10元的部分记为负.文具店记录了这五天该钢笔的售价情况和售出情况,如下表所示:(1)填空:这五天中赚钱最多的是第几天?这天赚了多少钱?(2)求新华文具用品店这五天出售这种钢笔一共赚了多少钱;(3)新华文具用品店准备用这五天赚的钱全部购进这种钢笔,进价仍为每支6元为了促销这种钢笔,每只钢笔的售价在10元的基础上打九折,本次购进的这种钢笔全部售出后共赚了多少钱?58.2018年10月,团委号召各校组织开展捐赠衣物的“暖冬行动”.某校七年级6个班参加了这次捐赠活动,若每班捐赠衣物以100件为基准,超过的件数用正数表示,不足的件数用负数表示,记录如下:(1)捐赠衣物最多的班比最少的班多多少件?(2)该校七年级学生共捐赠多少件衣物?该校七年级学生平均每人捐赠多少件衣物?59.2019年中秋、国庆两大节日喜相逢,全国放假八日,高速公路免费通行,各地风景区游人如织.其中,闻名于世的黄山风景区,在9月30日的游客人数为0.9万人,接下来的七天中,每天的游客人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数).(1)10月3日的人数为______万人.(2)八天假期里,游客人数最多的是10月______日,达到______万人;游客人数最少的是10月_____日,达到_______万人.(3)请问黄山风景区在这八天内一共接待了多少游客?(结果精确到万位)(4)如果你也打算在下一个国庆节出游黄山,对出行的日期有何建议?60.某天,一辆货车从货场A出发,向东走了2千米到达批发部B,继续向东走1.5千米到达商场C,接着向西走了5.5千米到达超市D,最后回到货场A.(1)用1厘米表示1千米,以东为正方向,以货场为原点,画出数轴并在数轴上标明货场A,批发部B,商场C,超市D的位置;(2)超市D距离货场A千米;(3)若货车行驶1千米耗油a升,该天共耗油多少升?(用含a的式子表示)61.大学生小王把自家的石榴放到了网上实行包邮销售,他原计划每天卖100斤石榴,但实际每天的销售量与计划量相比有出入,下表是某周的销售情况(超额记为正,不足记为负:单位:斤)(1)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售______斤;(2)若石榴每斤按5元出售,每斤石榴的运费平均2元,那么小王本周一共收入多少元?。
专项一_有理数_数轴_相反数_绝对值提高题

专项一 有理数提高训练:1.6,2005,212,0,—3,+1,41-,—6.8中,正整数和负分数共有( ) A .3个 B .4个 C .5个 D .6个2.1- 不是( ) A.自然数. B.负数. C.整数. D.有理数.3.下列说法正确的是( )A.0是表示没有. B。
非负有理数就是正有理数.C。
整数和分数统称为有理数. D.正整数和负整数统称为整数.4.下列说法错误的是( )A.零是整数 B.零是非负数. C.零是最小的整数.D.零是偶数.5.最小的整数是( ) A.1- B.0 C。
1 D。
不存在.6.下列说法不正确的是( ) A.有理数可分为正整数.正分数.0。
负整数.负分数. B.一个有理数不是分数就是整数.C.一个有理数不是正数就是负数. D.若一个数是整数,则这个数一定是有理数.7.在数2005,1.10,32,6.0,,4.6--π中 ( ) A.有理数有6个 B。
π-是负数 C.非正数有3个 D.以上都不对.8。
下列各数中一定是有理数的是( ) A 。
π B 。
a C 。
13D.a-3 9.最小的有理数是( )A 。
0 B 。
1 C.0,1 D.没有10.下列说法正确的是( )A 。
有最大的负数,没有最小的正数;B 。
没有最大的有理数,也没有最小的有理数C.有最大的非负数,没有最小的非负数; D 。
有最大的负整数,没有最小的正整数11.某年度某国家有外债10亿美元,有内债10亿美元,应用数学知识来解释说明,下列说法合理的是( )A.如果记外债为—10亿美元,则内债为+10亿美元B.这个国家的内债。
外债互相抵消C 。
这个国家欠债共20亿美元 D.这个国家没有钱12. 在 —3 ,+ 3,21—,—4。
7,—0.1,0,2中,最大的数是( ) A 、—0。
1 B 、0 C 、—4。
7 D 、313。
下列互为相反数的有( )对 ①-1与+(—1), ②+(+1)与-1, ③—(-2)与+(-2), ④+[-(+1)与—[+(—1)],⑤—(—2)与-(+2) ⑥(A)6 (B )5 (C )4 (D )314。
(完整版)有理数专题训练

有理数专题训练专题一 有理数的概念及其应用例1. 已知a,b 互为相反数,c,d 互为倒数,x 的绝对值是2,求cd m cd b a -++)(的值。
练习: 已知a 、b 互为相反数,c 、d 互为倒数,│x │=3,求代数式a+b -cdx+3x .的值。
巩固:已知a 、b 互为相反数,c 、d 互为倒数,x 的平方等于4,试求()()()200920102d c b a x d c x ⨯-+++⨯⨯- 的值。
专题二 非负数的性质例2. 若0)2(12=-++y x ,求y x 的值练习:已知有理数满足01331=-+++-c b a ,求()2011c b a ⨯⨯的值.巩固:若1-x 与2)2(+y 互为相反数,求32015y x +的值专题三 绝对值的化简例3. 有理数a 、b 、c 在数轴上的位置如图,试化简:||||||23a b b c c a -+---。
练习1. 数,a b 在数轴上对应的点如右图所示,试化简a b b a b a a ++-+--巩固。
实数a b c ,,在数轴上的对应点如图,化简a c b a b a c +--++-专题四 有理数的实际应用例4. 一辆汽车沿着一条南北方向的公路来回行驶。
某一天早晨从A 地出发,晚上到达B 地。
约定向北为正,向南为负,当天记录如下:(单位:千米)-18.3, -9.5, +7.1, -14, -6.2, +13, -6.8, -8.5(1)问B 地在A 地何处,相距多少千米?(2)若汽车行驶每千米耗油0.2升,那么这一天共耗油多少升?练习:某检修工人检修电话线路,乘车时设定前进为正,后退为负,某天自A 的出发到收工时,所行路程为(单位:千米):4+,3-,22+,8-,2-,17+,3-,2-,12+,5-,7+,问收工时距A 地多远?若每千米耗油4升,问从A 地出发到收工共耗油多少升?巩固:李老师在学校西面的南北路上从某点A 出发来回检查学生的植树情况,设定向南的路程记为正数.向北的路程记为负数,那么李老师所行路程依次为(单位:百米):+12,-l0,+10,-8,-6,-5,-3.(1)求李老师最后是否回到出发点A ?(2)李老师离开出发点A 最远时有多少千米? (3)李老师共走了多少千米?专题五 有理数的混合运算例5.计算(1)()⎪⎭⎫ ⎝⎛-⨯--⨯-253112232 (2)()()⎭⎬⎫⎩⎨⎧-÷⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-⨯+----22114.031132练习:(1) 32322)4(3213-⨯--⎪⎭⎫ ⎝⎛-⨯- (2) []24)3(2611--⨯--巩固:(1)20152322)1()31()3.0(2.13-÷-+-÷⨯- (2)⎥⎦⎤⎢⎣⎡----⨯-31)32()2()43(3专题六 分类讨论思想例6. 已知3,4a b ==且b<a ,求a 、b 的值.练习:已知7,5==n m 且n m n m +=+,求m-n 的值.巩固:已知9,42==n m 且m n n m -=-,求m+n 的值.专题七 有理数的运算(裂项相消)例7.计算: 201520141 (4)31321211⨯++⨯+⨯+⨯练习:201520132.........752532312⨯++⨯+⨯+⨯巩固:201520131.........751531311⨯++⨯+⨯+⨯专题八 乘方的应用(错位相减)例8.2015322...........2221+++++=S练习:2015323...........3331+++++=S巩固:2015325...........5551+++++=S定时练习1. 已知a 、b 互为相反数,c 、d 互为倒数,x 2=9,求代数式a+b -cdx+3x .的值2. 若0)3(252=++-y x ,求2015)2(y x +的值3、如果有理数a 、b 、c 在数轴上的位置如图所示,求a b a c b c ++--+的值.4、 某一出租车一天下午以鼓楼为出发地在东西方向营运,向东为正,向西为负,行车里程(单位:km )依先后次序记录如下:+9、 ?3、 ?5、 +4、 ?8、 +6、 ?3、?6、 ?4、 +10。
有理数提高训练

b c a 10 有理数概念复习提高篇教学目标: 通过复习,熟练掌握数轴,相反数,绝对值等概念和意义教学重点。
基本概念及意义的理解教学难点:绝对值的意义典例精析例1:化简 |a -|-a || 例2:已知|a|=2,|b|=3,求a+b 的值。
例3:有理数a,b,c 在数轴上的位置如图所示:试化简:│a+b │-│b-1│-│a-c │-│1-c │例4:已知x 2=(-2)2,y 3=-1,求(1)x ·y2012的值。
(2)x 3/y 2012的值。
例5:用“*”代表一种运算,若a*b=(a+b )-(a-b ),求(-3)*4的值。
例6:求|110-111|+|111-112|+…|149-150|的值综合训练1、 |若|a |=3,则a 的值是2、 -5|的相反数是 。
-0.125的倒数的相反数是 。
-0.875的相反数的倒数是 。
3、 |3-π|= 。
4、 如果|b|=-b ,则b 的取值范围是 。
5、 绝对值不大于1的整数是 。
6、 若a >0,b <0,则a+b 0;若a <0,b <0,|a|<|b|,则a+b 0.7、 b b ||a |a |+的值可能是 。
化简=|a ||a |a- 。
8、 把6800用科学记数法表示为6.8 ×10n ,则n 的值是( )A. ④B. ③C. ②D. ①9、 若a 和2b 互为相反数,则a 的负倒数是( ) A. -2b B. 2b C. b D. b2 10、 如果a 是负数,那么-a, 2a , a + |a| ,a a 这四个数中,负数的个数是( ) A. 1 B. 2 C.3 D. 411、 设x 是有理数,那么下列各式中一定表示正数的是( )A. 2008xB. x + 2008C. |2008x|D. |x| + 200812、 如果a,b 都是有理数,且有b < 0,那么下列不等关系中,正确的是( )A. a < a + b < a - bB. a < a - b < a + bC. a + b < a < a - bD. a - b < a + b < a13、 如果a 是有理数,那么下列说法中正确的是() A. 2)21(+a 是正数 B. a 2 +1 的值大于1C. 2)21(--a 的值是负数 D. 2)21(--a +1 的值不大于1 14、若a+b=0,|a|=6,则|a-b|值是 。
人教版七年级上册同步提高训练一(有理数)

人教版七年级上册同步提高训练一(有理数)姓名__________________________日期�_______________________一、单项选择题1.某种药品说明书上标明保管温度是〔20±3〕0C ,那么该药品在〔 〕范围内保管最适宜.A . 170C~200CB . 200C ~230C C . 170C ~230CD . 170C ~240C 2.以下四个数中,在−2和−1之间的是〔 〕. A . −110B . −910C . −1110D . −23103.如图是加工零件的尺寸要求,现有以下直径尺寸的产品(单位: mm ),其中不合格的是〔 〕A . 45.02∅B . 45.01∅C . 44.98∅D . 44.9∅4.一种面粉的质量标识为〝25±0.25千克〞,那么以下面粉中合格的是〔 〕 A . 24.70千克 B . 25.30千克 C . 24.80千克 D . 25.51千克 5.在数﹣〔﹣3〕,0,〔﹣3〕2,|﹣9|,﹣14中,正数的有〔 〕个. A . 2 B . 3 C . 4 D . 5 6.以下说法不正确的选项是〔 〕A . 最小的非负整数是0B . 1是相对值最小的正数C . 倒数等于它自身的数是±1D . 一个有理数不是整数就是分数 二、填空题7.一列数:1,-3,9,-27,81,-243,…,其中某三个相邻数的和是-1701,那么这三个数中最大的数是_____.8.假设浪费20元钱,记作〝20+〞元,那么糜费12元钱,记作____________元. 9.在以下各数. ① π ② 0 ③ -3.14 ④ -101 ⑤-13 ⑥111 ⑦1.11 ⑧ π5 ⑨ 37中,正分数是__________(只填写序号) 三、解答题10.把以下各数填入相应的大括号内:23-, 12,﹣0.01, 125,7,1,﹣〔﹣4〕,+〔﹣1〕 正数集合{ } 正数集合{ } 非负整数集合{ } 分数集合{ }.11.某检修小组从A 地动身,在东西向的马路上检修线路,假设规则向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:km)〔1〕在第次纪录时距A地最远.〔2〕求收工时距A地何处多远?〔3〕假定每千米耗油0.15升,每升汽油需6.8元,问这天检修小组任务一天回到出车地时需汽油费多少元?12.李强靠勤工俭学的支出维持上大学的费用.下面是他某一周的收支状况表〔支出为正,支出为负,单位为元〕〔1〕到这个周末,李强有多少节余?〔2〕照这样,李强一个月〔按30天计算〕能有多少节余?〔3〕按以上的支出水平,李强一个月〔按30天计算〕至少有多少支出才干维持正常开支?13.唐山质量监视局从某食品厂消费的袋装食品中抽出样品20袋,检测每袋的质量能否契合规范,把超越或缺乏的局部区分用正、正数来表示,记载如下表:〔1〕假定每袋食品的规范质量为450克,那么抽样检测的20袋食品的总质量是多少克?〔2〕假定该种食品的合格规范为450±5克,求该种食品抽样检测的合格率?14.如图,半径..为1个单位长度的圆片上有一点A与数轴上的原点重合,AB是圆片的直径〔注:计算结果保管π〕.〔1〕把圆片沿数轴向右滚动半周..,点B抵达数轴上点C的位置,点C表示的数是数〔填〝在理〞或〝有理〞〕,这个数是 .〔2〕圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为正数,依次运动状况记载如下:+2,﹣1,,+4,﹣3,.①第3次滚动周后,A点回到原点.②在①的条件下,第6次滚动周后,A点距离原点4π.③在②的条件下,当圆片完毕运动时,A点运动的路程是多少?参考答案1.C 2.C 3.D 4.C 5.B 6.B 7.729 8.-12 9.⑥、⑦、⑨10.答案见地析.11.〔1〕四;〔2〕收工时距A地2km;〔3〕检修小组任务一天需汽油费约为48.96元.12.〔1〕7元;〔2〕30元;〔3〕330元.13.〔1〕总质量为9017克;〔2〕食品的合格率为95%.14.〔1〕在理, 〔2〕①-1 ;②1或-3;③24π或28π。
1-2 有理数(提升训练)(原卷版)

1.2 有理数【提升训练】一、单选题1.实数a ,b 在数轴上的对应点的位置如图所示,下列式子成立的是( )A .b a b a <-<-<B .b a a b <-<<-C .b b a a <-<-<D .a b b a -<-<< 2.9-的绝对值是( )A .9B .9-C .19D .19- 3.数轴上表示数m 和2m +的点到原点的距离相等,则m 为( )A .2-B .2C .1D .1-4.以下各数中,比1-小的数是( )A .2B .0C .12-D .2-5.如图,数轴上的A ,B ,C 三点所表示的数分别为a ,b ,c ,且原点为O ,根据图中各点位置,下列数值最大的是( )A .aB .bC .cD .b -6.下列四个数中,比1-大的数是( )A .2-B .1-C .0D .π-7.下列四个数中,最小的数是( )A .3-B .0C .1-D .78.20211-的相反数是( )A .2021B .2021-C .1D .1-9.﹣|﹣2021|等于( )A .﹣2021B .2021C .﹣12021D .1202110.平面直角坐标系中,点O 是坐标原点,过点A (1,2)的直线y =kx +b 与x 轴交于点B ,且S △AOB =4,则k 的值是( )A .25 B .23- C .25或23- D .25-或2311.在数轴上表示﹣2.1和3.3两点之间的整数有( )A .4个B .5个C .6个D .7个12.如图,数轴上有A 、B 、C 、D 四个点,其中绝对值小于2的数对应的点是( )A .点AB .点BC .点CD .点D13.实数a 、b 在数轴上的位置如图所示,且这两个点到原点的距离相等,下列结论中,正确的是()A .0a b +=B .0a b -=C .||||a b <D .0ab >14.如图,在数轴上,注明了四段的范围,若某段上有两个整数,则这段是( )A .段△B .段△C .段△D .段△15.已知0a <,0ab <,且a b >,那么将a ,b ,a -,b -按照由大到小的顺序排列正确的是( )A .a b b a ->->>B .b a a b >>->-C .b a a b >->>-D .a b b a ->>->161的相反数是( )A 1B 1C .1-D .117.实数a ,b ,c 在数轴上的对应点的位置如图所示,则不正确的结论是( )A .3a >B .0b a -<C .0ab <D .a c >-18.实数a ,b ,c ,d 在数轴上的对应点的位置如图所示,则正确的结论是( )A .a >﹣4B .bd >0C .|a|>|d|D .b+c >019.3的绝对值是( )A .3-B .3CD .1320.下列各数中最小非负数是( )A .-2B .-1C .0D .121.下列比较大小正确的是( )A .5(5)--<+-B .1334->-C .22()33--=-- D .10(5)3--< 22.有理数a ,b 在数轴上的对应点的位置如下图所示,则下列结论正确的是( )A .b a <-B .0ab >C .a b >D .02b a -< 23.如果2a +和()21b -互为相反数,那么()2019a b +的值是( ) A .2019- B .2019 C .1 D .1-24.如图,一个动点从原点O 开始向左运动,每秒运动1个单位长度,并且规定:每向左运动3秒就向右运动2秒,则该动点运动到第2021秒时所对应的数是( )A .-406B .-405C .-2020D .-202125.有理数比较大小错误的是( )A .21-<B .1123-<-C .2|6|(2)->-D .1033->- 26.如图,数轴上A ,B ,C 三点所表示的数分别为a ,b ,c ,且AB BC =.如果有0,0,0a b b c a c +<+>+<,那么该数轴原点0的位置应该在( )A .点A 的左边B .点A 与B 之间C .点B 与C 之间D .点C 的右边27.若a ,b ,c ,m 都是不为零的有理数,且23++=a b c m ,2a b c m ++=,则b 与c 的关系是( ) A .互为相反数 B .互为倒数 C .相等 D .无法确定28.如图,在数轴上,点A 表示数1,现将点A 沿数轴作如下移动,第一次将点A 向左移动3个单位长度到达点1A ,第二次将点1A 向右移动6个单位长度到达点2A ,第三次将点2A 向左移动9个单位长度到达点3A ,…,按照这种移动规律进行下去,第2021次移动到点2021A ,那么点2021A 所表示的数为( )A .3029-B .3032-C .3035-D .3038-29.已知有理数,,a b c 在数轴上的位置如图所示,且满足a c b <<.则下列各式:△b a c ->->-;△0ab ac ab ac-=;△+=+a b a b ;△0a b c b a c ---+-=.其中正确的有( )A .4个B .3个C .2个D .1个30.中国人最早使用负数,可追溯到两千多年前的秦汉时期,2021-的相反数是( )A .2021-B .2021C .12021D .12021- 31.已知a ,b ,c ,三个数在数轴上,对应点的位置如图所示,下列各式错误的是( )A .b a c <<B .a b -<C .0a b +<D .0c a ->32.数轴上有O ,A ,B ,C ,D 五个点,各点的位置与所表示的数如图所示,且35d <<.若数轴上有一点M ,M 所表示的数为m ,且3m d m -=-,则关于点M 的位置,下列叙述正确的是( )A .M 在O ,B 之间B .M 在O ,C 之间 C .M 在C ,D 之间 D .M 在A ,D 之间33.点M ,N ,P 和原点O 在数轴上的位置如图所示,点M ,N ,P 表示的有理数为a ,b ,c (对应顺序暂不确定).如果0bc <,0b c +>,ab ac >,那么表示数c 的点为( ).A .点MB .点NC .点PD .点O34.如图,数轴上有A ,B ,C ,D 四个点,其中所对应的数的绝对值最小的点是( )A .点AB .点BC .点CD .点D35.在以A 为原点的数轴上,存在点B ,C ,满足2AB BC =,若点B 表示的数为8,则点C 表示的( ) A .4 B .12 C .4或12 D .4-或12-36.在数轴上从左到右有,,A B C 三点,其中1AB =,2BC =,如图所示,设点,,A B C 所对应数的和是x ,则下列说法错误的是( )A .若以点A 为原点,则x 的值是4B .若以点B 为原点,则x 的值是1C .若以点C 为原点,则x 的值是4-D .若以BC 的中点为原点,则x 的值是2-37.有理数a ,b 在数轴上的对应点的位置如图所示,则下列式子中正确的是( )△0a b <<;△a b <;△0ab >;△a b a b ->+A .△△B .△△C .△△D .△△38.下列计算中,结果等于5的是( )A .()()94---B .()()94-+-C .94-+-D .9+4-+ 39.已知有理数,a b 满足:2|2|(2)0a b b -+-=.如图,在数轴上,点O 是原点,点A 所对应的数是a ,线段BC 在直线OA 上运动(点B 在点C 的左侧),BC b =,下列结论△4,2a b ==;△当点B 与点O 重合时,3AC =;△当点C 与点A 重合时,若点P 是线段BC 延长线上的点,则2PO PA PB +=;△在线段BC 运动过程中,若M 为线段OB 的中点,N 为线段AC 的中点,则线段MN 的长度不变. 其中正确的是( )A .△△B .△△C .△△△△D .△△△40.设有理数a 、b 、c 满足(0)a b c ac >><,且c b a <<,则222a b b c a c xx x ++++++﹣﹣的最小值是( )A .2a c -B .22a b c ++C .22a b c ++D .22a b c +- 二、填空题41.数轴上表示3的点到原点的距离是_________ .42.若()2210a b -++=,则3a b +=_________.43.写出一个负数,使这个数的绝对值小于4______.44.等边ABC 在数轴上的位置如图所示,点A 、C 对应的数分别为0和﹣1,若ABC 绕顶点按顺时针方向在数轴上连续翻转,翻转1次后,点B 所对应的数为1,则连续翻转2020次后,点B 对应的数是__.45.在数轴上表示,,a b c 三个数的点的位置如图所示,化简式子:a c b c +--结果为__________.三、解答题46.如图一根木棒放在数轴上,数轴的1个单位长度为1cm ,木棒的左端与数轴上的点A 重合,右端与点B 重合.(1)若将木棒沿数轴向右水平移动,则当它的左端移动到点B 时,它的右端在数轴上所对应的数为16;若将木棒沿数轴向左水平移动,则当它的右端移动到A 点时,则它的左端在数轴上所对应的数为4,由此可得到木棒长为 cm .(2)图中点A 所表示的数是 ,点B 所表示的数是 .(3)由题(1)(2)的启发,请你能借助“数轴”这个工具帮助小红解决以下问题:一天,小红去问曾当过数学老师现在退休在家的爷爷的年龄,爷爷说:“我若是你现在这么大,你还要25年才出生;你若是我现在这么大,我已经125岁,是老寿星了,哈哈!”,请求出爷爷现在多少岁了?47.如图,已知线段AB m =(m 为常数),点C 为直线AB 上一点(不与A 、B 重合),点P 、 Q 分别在线段BC 、AC 上,且满足2CQ AQ =,2CP BP =.(1)如图1,点C 在线段AB 上,求PQ 的长;(用含m 的代数式表示)(2)如图2,若点C 在点A 左侧,同时点Р在线段AB 上(不与端点重合),求22AP CQ PQ +-的值. 48.已知,,a b c 在数轴上的对应点如图所示,且a b =;(1)根据数轴判断:+a b _________0,c b -__________0.(填>,<,=)(2)1c a c b a b c ---+++-.49.已知下列各数:5-,13,4,0, 1.5-,5,133,12-.把上述各数填在相应的集合里: 正有理数集合:{ }负有理数集合:{ }分数集合:{ }50.在一张长方形纸条上画一条数轴,并在两处虚线处,将纸条进行折叠,产生的两条折痕中,左侧折痕与数轴的交点记为A ,右侧折痕与数轴的交点记为B .(1)若数轴上一点P (异于点B ),且P A =AB ,则P 点表示的数为 ;(2)若数轴上有一点Q ,使QA =3QB ,求Q 点表示的数;(3)若将此纸条沿两条折痕处剪开,将中间的一段纸条对折,使其左右两端重合,这样连续对折(n ≥2)次后,再将其展开,请直接写出最左端的折痕和最右端的折痕之间的距离(用含n 的式子表示,可以不用化简) .51.如图,已知数轴上A 、B 两点所表示的数分别为﹣2和6(1)求线段AB 的长;(2)已知点P 为数轴上点A 左侧的一个动点,且M 为PA 的中点,N 为PB 的中点.请你画出图形,并探究MN 的长度是否发生改变?若不变,求出线段MN 的长;若改变,请说明理由.52.点A 、B 在数轴上所表示的数如图所示,回答下列问题:(1)将A 在数轴上向左移动1个单位长度,再向右移动9个单位长度,得到点C ,求出B 、C 两点间的距离是多少个单位长度?(2)若点B 在数轴上移动了m 个单位长度到点D ,且A 、D 两点间的距离是3,求m 的值.53.如图,数轴上A ,B 两点之间的距离为30,有一根木棒MN ,设MN 的长度为x .MN 数轴上移动,M 始终在左,N 在右.当点N 移动到与点A ,B 中的一个重合时,点M 所对应的数为9,当点N 移动到线段AB 的中点时,点M 所对应的数是多少?54.阅读下面材料:在数轴上6与1-所对的两点之间的距离:6(1)7--=;在数轴上2-与3所对的两点之间的距离:235--=;在数轴上8-与4-所对的两点之间的距离:(8)(4)4---=;在数轴上点A 、B 分别表示数a 、b ,则A 、B 两点之间的距离AB a b b a =-=-.回答下列问题:(1)数轴上表示2-和5-的两点之间的距离是_______;数轴上表示数x 和3的两点之间的距离表示为_______;数轴上表示数_______和_______的两点之间的距离表示为2x +;(2)七年级研究性学习小组在数学老师指导下,对式子23x x ++-进行探究:△请你在草稿纸上画出数轴,当表示数x 的点在2-与3之间移动时,32x x -++的值总是一个固定的值为:_______.△请你在草稿纸上画出数轴,要使327x x -++=,数轴上表示点的数x =_______.55.把4-,4.5,0,12-四个数在数轴上分别表示出来,再用“<”把它们连接起来.56.在数轴上表示下列各数:14, 1.5,3,0,2.5,52----,并将它们按从小到大的顺序排列.57.以1厘米为1个单位长度用直尺画数轴时,数轴上互为相反数的点A 和点B 刚好对着直尺上的刻度2和刻度8.(1)写出点A 和点B 表示的数;(2)写出在点B 左侧,并与点B 距离为9.5厘米的直尺左端点C 表示的数;(3)若直尺长度为a 厘米,移动直尺,使得直尺的长边CD 的中点与数轴上的点A 重合,求此时左端点C 表示的数.58.将下列各数在数轴上表示出来,并比较它们的大小(用“<”连接).()4--, 3.5--,112⎛⎫+- ⎪⎝⎭,0,()2.5++59.已知数轴上三点A ,O ,B 对应的数分别为﹣6,0,1,点M 为数轴上任意一点,其对应的数为x .(1)A 、B 两点间的距离是 ,若点M 到点A 、点B 的距离相等,那么x 的值是 ;(2)数轴上是否存在点M ,使点M 到点A ,点B 的距离之和是59?若存在,请直接写出x 的值;若不存在,请说明理由.(3)如果点M 以每秒2个单位长度的速度从点O 向左运动时,点A 和点B 分别以每秒5个单位长度和每秒1个单位长度的速度也向右运动,且三点同时出发,那么几秒种后点M 运动到点A 、点B 之间,且点M 到点A 、点B 的距离相等?60.如图,直径为1个单位的圆片上有一点A 与数轴上的原点重合,AB 是圆片的直径.(1)把圆片沿数轴向右滚动1周,点A 到达数轴上点C 的位置,点C 表示的数是 ;(2)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:2+,1-,3+,4-,3-.△第几次滚动后,A 点距离原点最近?△当圆片结束运动时,A 点运动的路程共有多少?此时点A 所表示的数是多少?61.如图,一个点从数轴上的原点开始,先向左移动2cm 到达A 点,再向左移动3cm 到达B 点,然后向右移动9cm 到达C 点,数轴上一个单位长度表示1cm .(1)请你在数轴上表示出A ,B ,C 三点的位置;(2)把点C 到点A 的距离记为CA ,则CA = cm .(3)若点B 沿数轴以每秒3cm 匀速向右运动,经过 秒后点B 到点C 的距离为3cm .(4)若点B 以每秒2cm 的速度匀速向左移动,同时A 、C 点分别以每秒1cm 、4cm 的速度匀速向右移动.设移动时间为t 秒,试探索:CA AB -的值是否会随着t 的变化而改变?请说明理由.62.在下列空格里打“√”,表示该数属于哪种类型的数:63.已知数轴上点A 、B 、C 所表示的数分别是3-,7+,x . (1)求线段AB 的长;(2)若4AC =,△求x 的值;△若点M 、N 分别是AB 、AC 的中点,求线段MN 的长度. 64.点A 、B 、C 、O 是数轴上的四个点,它们分别表示数4-、1-、3、0.(1)在数轴上表示这四个数,并求BC 的长;(2)若2AD BC =,点P 是DC 的中点,试求点P 表示的数. 65.在数轴上,已知在纸面上有一数轴(如图),折叠纸面.(1)若1表示的点与1-表示的点重合,则4表示的点与数______表示的点重合; (2)若-1表示的点与3表示的点重合,-3表示的点与数______表示的点重合; (3)若数p 表示的点与原点重合,此时折线与数轴的交点表示的有理数是______;(3)若数轴上A 、B 两点之间的距离为m 个单位长度,点A 表示的有理数是a ,并且A 、B 两点经折叠后重合,请写出此时折线与数轴的交点表示的有理数是______.66.把下列各数在数轴上表示出来,并按从小到大的顺序用“<”连接起来.()11.5,0,3,2.5,1,42------67.定义:关于x 的两个一次二项式,其中任意一个式子的一次项系数都是另一个式子的常数,则称这两个式子互为“对称二项式”.例如,式子34+x 与43x +互为“对称二项式”. (1)判断式子52x -+ 与25x -+ (填“是”或“不是”)互为“对称二项式”(2)已知式子ax b +的“对称二项式”是34x -且数a b 、在数轴上所对应的点为AB 、.△若数轴上有一点P到A B 、两点的距离的和 11PA PB +=,则点P 在数轴上的数是 ,△若 218a b x -+-+=,求 x的值.68.我们知道数轴上点A ,B 分别表示数a ,b ,那么点A ,B 之间的距离AB =|a ﹣b |. 回答下列问题:(1)数轴上,表示3的点与表示5的点距离是 ;表示﹣2的点与表示﹣6的点距离是 . (2)若数轴上的点A 表示的数为x ,点B 表示的数为﹣1,则A ,B 两点的距离可以表示为 . (3)若数轴上的点A 表示的数为x ,点B 表示的数为3,A ,B 的距离是5,则x = . (4)已知数轴上A ,B 两点之间的距离为1,点A 到原点的距离为3,则点B 表示的数是 . (5)当代数式|x +1|+|x ﹣2|取最小值时,相应的x 的取值范围是 . 69.有理数a 、b 、c 在数轴上的位置如图.(1)判断正负,用“<”或“>”填空:a -b___________0; a+c_____________0 ;c -b___________0 (2)化简:2a b a c c b -++--70.数轴上表示数a 的点与原点的距离叫做数a 的绝对值,记作a .数轴上表示数a 的点与表示数b 的点的距离记作a b -,如35-表示数轴上表示数3的点与表示数5的点的距离,()3535+=--表示数轴上表示数3的点与表示数-5的点的距离,3a -表示数轴上表示数a 的点与表示数3的点的距离.根据以上材料回答下列问题:(将结果直接填写在答题卡相应位置,不写过程) (1)若22x x -=+,则x =_______,若31x x -=+,则x =_______; (2)若314x x -++=,则x 能取到的最小值是_______;最大值是_______; (3)若314x x --+=,则x 能取到的最大值是_______; (4)关于x 的式子21x x -++的取值范围是_______.。
有理数与无理数(提升训练) (3)

2.2 有理数与无理数【基础训练】 一、单选题1.下列四个数中,无理数是( )A .13B .0.5757C D .π2.下列实数中是无理数的是( )A .-2BCD .43117、0.57527522752227、2π中,无理数是( )A B .117 C .0.57527522752227 D .2π4.在实数11,,0,27π- )个.A .1个B .2个C .3个D .4个5.下列各数中,为无理数的是( )A .0.3B .227C D6 ) A .负数B .无理数C .有理数D .整数7.下列各数中,是无理数的是( )A .227B .3πC .0.3010010001D8.约公元前5世纪的古希腊时期,由于“他”第一次数学危机,这个“他”指的是( ) A .毕达哥拉斯B .希帕索斯C .笛卡儿D .苏格拉底9.下列各数中是有理数的是( )A B C .13-D .π10.在17-,2π,0,3.14,0.326,133-中,无理数的个数有( ) A .1个B .2个C .3个D .4个11.在下列各数中是无理数的是( )A .0.12B .13 C D 12.下列实数是无理数的是( )A B .13C .3.1415D .﹣513.在实数:3.14159,1.010010001…(相邻两个1之间依次多一个0),0,5π,449中,无理数有( ) A .1个 B .2个C .3个D .4个14.在311-,0.223,2π,0.243456中,无理数有( )个. A .2B .3C .4D .515.下列四个数中,无理数是( ) A .237B .0C .0.12D .π16.下列各数无理数有( )0,-3.14227,0.101001……,π,2.35858⋅⋅A .1个B .2个C .3个D .4个17.零一定是( ) A .整数B .负数C .正数D .奇数18.下列各数中,属于正有理数的是( ) A .-0.1B .0C .-1D .219.在下列各数中,正数的个数有______个.( ) -6,0.1234,152-,0.3,0,19,15A .2B .3C .4D .520.下列各数中,既不是正数又不是负数的是( ) A .2 B .1C .3-D .021.在22-,115,0,19,6-,3这五个数中,正数的个数是( ) A .1B .2C .3D .422.下列各数属于负整数的是( ). A .2B .2-C .12-D .023.下列四个数中,属于无理数的是( )A .BC D .0.171771777124.在6+,13, 3.1415-,0中,表示正数的有( ). A .1个B .2个C .3个D .4个25.下列各数中,为无理数的是( )A B C .14D26.下列各数是无理数的是( )A .3π-B C .52-D .6-27.|1|-的相反数是( ) A .1- B .1C .0D .228.在-5,-12,-1,0这四个数中,最小的数是( ). A .-5B .-12C .-1D .029.下列选项是无理数的为( )A .13-B C .3.1415926D .π-30.下列实数中,是无理数的是( )AB .C .16D .0.06006000631.下列各数中,是无理数的为( ) A .0 B .3.14C .-πD .71132.在实数13-,0,7 )A .13-B .0C .7D 33.在实数﹣2、﹣1、0、1中,最小的实数是( ) A .﹣2B .﹣1C .0D .134.在0,1,-1,2这四个数中,是负数的是( ) A .0B .1C .-1D .235.下列各数中3,7-,23-,5.6,0,π-,15,19,非正整数有( ) A .1个B .2个C .3个D .4个36.在一组数-2,0.4,0,π,227-,1.3,3.2121121112…(相邻的两个2之间依次多一个1)中,有理数的个数是( ) A .3B .4C .5D .637.下列几种说法中不正确的个数有( )①正整数和负整数的全体组成整数集合 ①带“-”的数是负数 ①0是最小的自然数 ①10.555.5-⋯是有理数 ①0.26-是负分数 A .2个B .3个C .4个D .5个38.下列关于“0”的说法中,正确的是( ) A .0是最小的数 B .0是最小的非负数 C .0的倒数是0D .0除以任何数都得039 1.212212221…,227,π, ) A .1个B .2个C .3个D .4个40.下面四个选项中,根据阴影部分与整个图形所反映出的部分与整体的数量关系来看,和下图一致的是( )A .B .C .D .二、填空题41.在数0、π、﹣0.1010010001,5.6,227中,无理数有_____个. 42.在数3.16,﹣10,2π,227-,1.3,1.2121121112…(每两个2之间依次多1个1)中有__个无理数.43.给出下列各数:32,﹣(+6),﹣1.5,0,﹣|﹣3|,4,π,在这些数中,整数是_______________,非负数是_______________,互为相反数的是_______________,绝对值最小的数是__________,分数是_________,无理数是_________.44.请把下列各数填入相应的集合中1 2,5.2,0,2π,227,﹣22,53-,2005,﹣0.030030003…正数集合:{________________…};分数集合:{________________…};非负整数集合:{________________…};有理数集合:{________________…}.45.比较大小:34-________-0.8(填“>”、“=”或“<”)三、解答题46.把下列各数填入它所属的括号内:15,−19,-5,512,0,-5.32,37%(1)分数集合{…};(2)整数集合{…}.47.把下列个数分别填入相应集合内:-10,6,-173,0,3101,-2.25,10%,-18整数集合:;负分数集合:;正分数集合;;非负数集合:;48.请把下列各数填入相应的集合中:8,﹣2,5.6﹣,0,﹣910,5,﹣712,31.25,﹣3%.负分数集合:{…};正整数集合:{…}.49.把下列各数填入相应的大括号内23-、12、0.01-、125、1、(4)--、(1)+-、279、0正数集合{ …};负数集合{ …}.分数集合{ …};正整数集合{ …}.50.把下列各数填入相应的括号内:-2.5,10,0.22,0,1213-,-20,+9.78,+68,0.45,47+,2π,0.33…正整数{ ……}负整数{ ……} 正分数{ ……} 负分数{ ……}51.把下列各数的序号填在相应的大括号里:①0;①3.1415926;①200%;①2020-;①π;① 6.143-;①108+;①227-;①111整数:{ …}; 正数:{ …}; 正分数:{ …}; 负有理数:{ …} 52.把下列各数填在表示集合的相应大括号中: +6,-8,-0.4,25,0,-23,9.15,145正整数集合﹛ ﹜ 负分数集合﹛ ﹜ 非负数集合﹛ ﹜53.如图,每个椭圆表示一个数集,请在每个椭圆内填上6个数,其中三个写在重叠部分,54.把下列各数分别填在相应的横线上: -0.2,135,-(-5),-7,0,13-,0.618,200%,-2π,-0.1010010001…. 分数有:__________________________________________________; 自然数有:________________________________________________; 负有理数有:______________________________________________. 55.请把下列各数填入相应的集合中: ﹣(+4),|﹣3.5|,0,3π,10%,2018,+(﹣5),﹣2.030030003…(每两个3之间逐次加一个0).正分数集合:{ …}; 负有理数集合:{ …};非负整数集合:{ …};无理数集合:{ …}.。
人教版数学七年级上册第1章 有理数 能力提升训练(二)

七年级上册第1章能力提升训练(二)一.选择题1.下列四个数中,最小的数是()A.0B.﹣C.5D.﹣12.计算4+(﹣8)÷(﹣4)﹣(﹣1)的结果是()A.2B.3C.7D.3.截至北京时间2020年4月14日7时30分,全球新冠肺炎确诊病例已超200万例,达2019320例.将数字“2019320“用科学记数法表示为()A.0.201932×107B.2.01932×106C.20.1932×105D.201.932×1044.如图,数轴上的A、B两点所表示的数分别为a、b,则下列各数中,最大的是()A.B.a+b C.a+b2D.a﹣b5.数轴上,点A、B分别表示﹣1、7,则线段AB的中点C表示的数是()A.2B.3C.4D.56.下列4个三角形中,底和高的比是3:2的是()A.B.C.D.7.北京市居民用水实行阶梯水价,实施细则如下表:分档水量年用水量(立方米)水价(元/立方米)第一阶梯0﹣180(含180) 5.00第二阶梯180﹣260(含260)7.00第三阶梯260以上9.00若某户2019年共用水230立方米,则应交水费为()A.1150元B.1250元C.1610元D.2070元8.下列说法中,正确的有()①0是最小的整数;②若|a|=|b|,则a=b;③互为相反数的两数之和为零;④数轴上表示两个有理数的点,较大的数表示的点离原点较远.A.0个B.1个C.2个D.3个9.如图所示的是图纸上一个零件的标注,Φ30±表示这个零件直径的标准尺寸是30mm,实际合格产品的直径最小可以是29.98mm,最大可以是()A.30mm B.30.03mm C.30.3mm D.30.04mm10.定义运算a★b=|ab﹣2a﹣b|,如1★3=|1×3﹣2×1﹣3|=2.若a=2,且a★b=3,则b的值为()A.7B.1C.1或7D.3或﹣3二.填空题11.2020的绝对值是.12.如果ab=﹣1,则称a、b互为“负倒数”.那么﹣2的“负倒数”等于.13.已知a与b的和为2,b与c互为相反数,若|c|=1,则a=.14.对于两个非零整数x,y,如果满足这两个数的积等于它们的和的6倍,称这样的x,y 为友好整数组,记作<x,y>,<x,y>与<y,x>视为相同的友好整数组.请写出一个友好整数组,这样的友好整数组一共有组.15.定义一种新运算:a※b=,则2※3﹣4※3的值.三.解答题16.计算:(1)(2)17.已知两个方程3x+2=﹣4与3y﹣3=2m﹣1的解x、y互为相反数,求m的值.18.有一个填写运算符号的游戏:在“1□3□6□9”中的每个□内,填入+,﹣,×,÷中的某一个(可重复使用),然后计算结果.(1)计算:1+3﹣6﹣9;(2)若1÷3×6□9=﹣7,请推算□内的符号;(3)在“1□3□6﹣9”的□内填入符号后,使计算所得数最小,直接写出这个最小数.19.农历新年来临之际,某公益团体购买了10箱苹果赠送给敬老院,苹果每箱以15千克为标准,称重记录如下(超过标准的千克数为正数)(单位:千克)1.2,﹣1,0.2,0,0.5,﹣0.2,1,﹣0.8,﹣0.5,0.3这10箱苹果一共多少千克?20.对于任意四个有理数a、b、c、d,可以组成两个有理数对(a,b)与(c,d).我们规定:(a,b)⋆(c,d)=bc﹣ad.例如:(1,2)⋆(3,4)=2×3﹣1×4=2.根据上述规定解决下列问题:(1)有理数对(3,﹣5)⋆(4,﹣2)=;(2)若有理数对(﹣4,3x﹣1)⋆(2,1﹣x)=8,求x的值;(3)当满足等式(﹣2,3x﹣1)⋆(k,x+k)=5+k的x是整数时,求整数k的值.参考答案一.选择题1.解:∵|﹣|<|﹣1|,∴﹣>﹣1,∴5>0>﹣>﹣1,因此最小的数是﹣1,故选:D.2.解:原式=4+2+1=7,故选:C.3.解:将2019320用科学记数法表示为2.01932×106.故选:B.4.解:方法一:由数轴可得:b<0<a,取a=0.2,b=﹣0.8,则==﹣0.25,a+b=0.2+(﹣0.8)=0.6,a+b2=0.2+(﹣0.8)2=0.2+0.64=0.84,a﹣b=0.2﹣(﹣0.8)=0.2+0.8=1,最大的是1,故选项D正确,方法二:由数轴可得:b<0<a,因为<0,a+b<0,a+b2>0,a﹣b>0,而a﹣b>a+b2,所以a﹣b最大,故选:D.5.解:线段AB的中点C表示的数为:=3,故选:B.6.解:A、三角形的高不知道,无法得出底和高的比,故此选项错误;B、三角形的高为1.5,底为2,底和高的比为:2:1.5=4:3,故此选项错误;C、三角形的高为3,底为2,底和高的比为:2:3,故此选项错误;D、三角形的高为3,底为4.5,底和高的比为:4.5:3=3:2,故此选项正确.故选:D.7.解:由题意可得:180×5+(230﹣180)×7=1250(元).故选:B.8.解:①0是最小的整数,错误,没有最小的整数;②若|a|=|b|,则a=±b,故此选项错误;③互为相反数的两数之和为零,正确;④数轴上表示两个有理数的点,较大的数表示的点离原点较远,只有都是正数时较大的数表示的点离原点较远,故此选项错误.故选:B.9.解:由零件标注φ30可知,零件的直径范围最大30+0.03mm,最小30﹣0.02mm,∴最大可以是30+0.03=30.03(mm).故选:B.10.解:∵a★b=3,且a=2,∴|2b﹣4﹣b|=3,∴2b﹣4﹣b=3或2b﹣4﹣b=﹣3,解得b=7或b=1,故选:C.二.填空题11.解:根据绝对值的概念可知:|2020|=2020,故答案为:2020.12.解:根据题意,得﹣2的负倒数等于.故答案为:.13.解:∵|c|=1,∴c=±1,∵b与c互为相反数,∴b+c=0,∴b=﹣1或1,∵a与b的和为2,∴a+b=2,∴a=3或1.故答案为:3或1.14.解:由已知可得若为为友好整数组,则xy≠0,且xy=6(x+y)∴(x﹣6)y=6x,显然当x=6时该等式不成立,∴x≠6∴y===6+∵y是整数∴是整数∴当x﹣6=1,即x=7时,y=42,故<7,42>是一个友好整数组.∵x,y是整数∴是整数,且x﹣6是整数∵xy≠0,且<x,y>与<y,x>视为相同的友好整数组.∴x﹣6=±1或±2或±3或±4或﹣6,∴这样的友好整数组一共有2+2+2+2+1=9(组).故答案为:<7,42>;9.15.解:∵a※b=,∴2※3﹣4※3=3×3﹣(4﹣3)=9﹣1=8,三.解答题16.解:(1)=﹣36+16+(﹣18)=﹣38;(2)=﹣16﹣56÷4×(﹣)﹣1=﹣16﹣14×(﹣)﹣1=﹣16+2﹣1=﹣15.17.解:方程3x+2=﹣4,解得:x=﹣2,因为x、y互为相反数,所以y=2,把y=2代入第二个方程得:6﹣3=2m﹣1,解得:m=2.18.解:(1)1+3﹣6﹣9=4﹣6﹣9=﹣2﹣9﹣11;(2)∵1÷3×6□9=﹣7,∴1×□9=﹣7,∴2□9=﹣7,∵2﹣9=﹣7,∴□内的符号为“﹣”;(3)这个最小数是﹣26,理由:∵在“1□3□6﹣9”的□内填入符号后,使计算所得数最小,∴1□3□6的结果是负数即可,∵1□3□6的最小值是1﹣3×6=﹣17,∴1□3□6﹣9的最小值时﹣17﹣9=﹣26,∴这个最小数是﹣26.19.解:(1.2﹣1+0.2+0+0.5﹣0.2+1﹣0.8﹣0.5+0.3)+15×10=150.7(千克),答:这10箱苹果一共重150.7千克.20.解:(1)根据题意得:原式=﹣20+6=﹣14;故答案为:﹣14;(2)根据题意得:2(3x﹣1)+4(1﹣x)=8去括号得,6x﹣2+4﹣4x=8,移项合并得:2x=6,解得:x=3(3)∵等式(﹣2,3x﹣1)⋆(k,x+k)=5+k的x是整数,∴(3x﹣1)k﹣(﹣2)(x+k)=5+k,∴(3k+2)x=5,∴x=,∵k是整数,∴3k+2=±1或±5,∵k为整数,∴k=﹣1,1.。
2-2 有理数与无理数(提升训练)(原卷版)

2.2 有理数与无理数【提升训练】 一、单选题1.在0.51525354…0.2、1π13111 )A .2B .3C .4D .52.下列说法中:①0是最小的整数;①有理数不是正数就是负数;①非负数就是正数;①整数和分数统称有理数,其中正确的是( ) A .①B .①C .①D .①3.下面的说法中,正确的个数是( )①0是整数;①2-是负分数;①3.2不是正数;①自然数一定是非负数;①负数一定是负有理数. A .1个B .2个C .3个D .4个4.下列说法正确的是( ) A .整数分为正整数和负整数B .正分数、负分数统称有理数C .零既可以是正整数,也可以是负分数D .所有的分数都是有理数5.对于 3.271-,下列说法不正确的是( ) A .是负数,不是整数 B .是分数,不是自然数 C .是有理数,不是分数 D .是负有理数,且是负分数6.下列结论正确的是( ) A .0既是正数,又是负数 B .0是最小的正数C .0是最小的整数D .0既不是正数也不是负数 7.在数0,117-,π3,0.13,0.01010101,2.3%中,有理数有( ) A .5个 B .4个C .3个D .2个8.在数12-,﹣|﹣2|,+[﹣(+0.5)],﹣(﹣1)中负数的个数是( ) A .4个B .3个C .2个D .1个9.下列各数中,不是分数的是( ) A .12B .30%-C .63-D .0.101510.在 ()8--,7--∣∣,0-,223⎛⎫- ⎪⎝⎭这四个数中,负数有( ) A .1 个B .2 个C .3 个D .4 个11.下列说法正确的是( ) A .所有的整数都是正数 B .不是正数的数一定是负数 C .0 是最小的有理数 D .整数和分数统称有理数12.在下列各数:56,+1,6.7,-(-3),0,722,-5,25%中,属于整数的有( ) A .2个B .3个C .4个D .5个13.下列四个数中,是负分数的是( ) A .32B .4C .-5D .13-14.在()2--,7--,202010-⨯,()31--,52⎛⎫-+ ⎪⎝⎭,42-中,非正数有( ) A .1个 B .2个C .3个D .4个15.在31,7π,0,0.6四个数中,有理数有( ) A .1个B .2个C .3个D .4个16.下列说法不正确的是( ) A .0既不是正数,也不是负数 B .0的绝对值是0C .立方根等于本身的数是1D .一个有理数不是整数就是分数17.下列各数中,既是分数又是负数的是( ) A .31-.B .4-C .0D .2.818.在有理数()3--,()22--,0,2--,22-,13-中,负数的个数是( ) A .1个B .2个C .3个D .4个19.在数12⎛⎫-- ⎪⎝⎭,-42,9--,227,(-1)2004,0中,非负数的个数是( ) A .3B .4C .5D .620.在有理数1, 0,-5, -12,(-5.23)2,37-中,负数的个数有( ) A .2个 B .3个C .4个D .5个21.在﹣4,227,0,3.14159,﹣5.2,2中正有理数的个数有( ) A .1个B .2个C .3个D .4个22.下列各数中:+5、-2.5、43-、2、75、-(-7)、0、3-+,负有理数有( )A .2个B .3个C .4个D .5个23.下列说法中正确的是( ) A .在有理数中,零的意义仅表示没有 B .一个数不是负数就是正数C .正有理数和负有理数组成全体有理数D .零是整数24.小强在笔记上整理了以下结论,其中错误的是( ) A .有理数可分为正数、零、负数三类 B .一个有理数不是整数就是分数 C .正有理数分为正整数和正分数D .负整数、负分数统称为负有理数25.在3.14159,4,1.1010010001…,4.21,π,132中,有理数有( ) A .1个B .2个C .3个D .4个26.下列说法错误..的是( ) A .-3是负有理数B .0不是整数C .25是正有理数 D .-0.3是负分数27.在下列数:3+,()2.1+-,12-, 5.5-,0,9--中,正数有( ) A .1个B .2个C .3个D .4个28.下列说法中:①0是最小的整数;①有理数不是正数就是负数;①非负数就是正数;①2π-不仅是有理数,而且是分数;①237是无限循环小数,所以不是有理数;①绝对值等于本身的数是正数;①正数中没有最小的数,负数中没有最大的数.其中错误的说法的个数为( ) A .7个B .6个C .5个D .4个29.下列六个数中:3.14227,0.21,0.1212212221……(每两个1之间增加一个2),其中无理数的个数是( ). A .2B .3C .4D .53076、2π) A .1个B .2个C .3个D .4个31.在下列各数中,你认为是无理数的是( )A .227B .2π C D .0.3⋅32.下列说法中正确的是( ) A .a -表示的数一定是负数 B .a -表示的数一定是正数 C .a -表示的数一定是正数或负数 D .a -可以表示任何有理数33.实数122,0.020********π-,……(每两个2之间依次增加1个零)中无理数的个数是( ) A .4B .3C .2D .134.下列实数中,属于无理数的是① ①A .47-B .0C .3D .0.313113111335.下列说法不正确的是( ) A±3 B .12-是14的平方根 C .带根号的数不一定是无理数 D .a 2的算术平方根是a36.下面的说法中,正确的个数是( ) ①0是整数;①223-是负分数; 3.2③不是正数;④自然数一定是非负数;⑤负数一定是负有理数. A .1个B .2个C .3个D .4个37.下列说法中错误的有( ) ①133-是负分数;①4.2不是正数;①自然数一定是正数;①非负有理数不包括0. A .1个 B .2个 C .3个 D .4个38.在实数﹣2270 3.14,2π中无理数有( )A .2个B .3个C .4个D .5个39.下列分数不能化成有限小数的是( ) A .625B .324C .412 D .11640.下列各数中的无理数是( )A B .3.14C .113D .π二、填空题41.与3-相距6个单位长度的点所对应的有理数是_________.42.在实数π,870中,无理数的个数是________个. 43.把下列各数填入相应的集合里: ﹣3,|﹣5|,+(13-),﹣3.14,0,﹣1.2121121112…,﹣(﹣2.5),34,﹣|45-|,3π 正数集合:{_____________…}; 整数集合:{_____________…}; 负分数集合:{_____________…}; 无理数集合:{_____________…}.44.把下列各数分别填在相应的集合内:-11,4.8,73,-2.7,16,3.1415926,-34,73,0. 正数集合:{ …}; 负分数集合:{ …}; 整数集合:{ …}; 非负整数集合:{ …}. 45.在4-,112-,0,3.2-,0.5-,5,1-,2.4中,若负数共有M 个,正数共有N 个,则M N -=______.三、解答题46.把下列数按照要求填入相应的集合内:+8.5,﹣325,0.35,0,3.14,12,0.3,π,10%,﹣2.626626662… 无理数集合:{ …}; 负数集合:{ …}.47.下列各数填入它所在的数集中:18-,227,3.1416,0,2001,35,0.142-,95%,π.正数集:{ …};整数集:{ …};自然数集:{ …};分数集:{ …}.48.把以下各数填在相应的括号里:5-,13+,0.62,0, 6.4-,173-,7.正整数:{};负整数:{};分数:{};整数:{}.49.请把下列各数填入相应的集合中:-1.5,7.4,-2,+72,-0.6,53,27-,0,-0.101,-19.正数集合:{…}负数集合:{…}分数集合:{…}负整数集合:{…}50.把下列各数填入表示它所在的数集的大括号:2.4-,3,2.008,103-,114,0.15-,0,()2.28--,3.14,4--正数集合:{…}负分数集合:{…}51.把下列有理数填入它属于的集合的内:3,12-,-2020,-3.1416,0,113-负数集合{}整数集合{}52.把下列各数填入相应的大括号里.-0.78,3,14+,-10,0,-4.正数:{ }; 分数:{ }; 非负整数:{ };53.把下列各数填在相应的括号里: 8-,0.275,227,0,104-,(3)--,13-,2- 正数集合{}; 负整数集合{} ; 分数集合{} ; 负数集合{}54.把下列各数分别填入相应的大括号里:7.1-,3,5--,45+,34-,0,()0.25-+,12 非负数集合{ ……}; 整数集合 { ……}; 分数集合 { ……} 55.根据给出的下列数①-9.3;①6;①0;①173-;①-100;①134+;①-2.25;①0.01;①+65;①27-,从中找出对应的数并填空(填序号):整数集合:{ …}; 分数集合:{ …}; 负数集合:{ …}; 56.把下列各数填在相应的表示集合的括号内()1221,,3,0,,0.3,1.7,237-------(1)整数:{}(2)非负整数:{} (3)非正数:{} (4)有理数:{}57.把下列各数分别填入相应的集合中 0, -54,3.14, -|-2|, 2π , 0.130********…, 0.13 (1)整数集合:{________________________…} (2)分数集合:{________________________…} (3)负有理数集合:{____________________…} (4)无理数集合:{______________________…}58.把下列各数分别填入相应的集合里:()2+-,0,0.314-, 5.0101001-(两个1间的0的个数依次多1个),()11--,227,143-,0.33333,325-. 正有理数集合:{ } 无理数集合: { } 整数集合: { } 分数集合: { } 59.把下列各数按要求分类:①4-,①25%-,①1-,①12,①10.2--,①2,①1.5,①0,① 0.123,① 4.1010010001...(填序号) 整数集合:{ }. 分数集合:{ }. 正数集合:{ }. 非负有理数集合:{ }.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有理数
一.选择题:
1. 已知数轴上的三点A 、B 、C 分别表示有理数,1,1a -,那么|1|a +表示( )
A . A 、
B 两点的距离 B .A 、
C 两点的距离
C .A 、B 两点到原点的距离之和
D .A 、C 两点到原点的距离之和
2. 若||5,||3,0a b a b ==+>,那么a b -的值是( )
A .2或8
B .2或-2
C .8或-8
D .-2或-8
3. 定义运算符号“*”的意义为:ab b
a b a +=*(其中a 、b 均不为0)。
下面有两个结论(1)
运算“*”满足交换律;(2)运算“*”满足结合律。
其中( )
A .只有(1)正确
B .只有(2)正确
C .(1)和(2)都正确
D .(1)和(2)都不正确
4. 如果,,a b c 为非零有理数,则||||||
a b c a b c ++的值有( )
A .1个
B .2个
C .3个
D .4个
5. 设0a b c ++=,0abc >,则||||||b c a c a b a b c +++++的值是( )
A .-3
B .1
C . 3或-1
D .-3或1
6. 有理数a 等于它的倒数,有理数b 等于它的相反数,则20102011a b +等于( )
A .0
B .1
C .-1
D .2
7. 若||1m m =+,则()201041m +=( )
A .-1
B .1
C .12-
D .12
8.在2-、3、4、5-这四个数中,任意取两个数相乘,所得乘积最大的是:
A 、20
B 、-20
C 12
D 、10
9.1米长的小棒,第一次截去一半,第二次截去剩下的一半。
如此下去,第六次后剩下的小棒长为(
) A 、121
B 、321
C 、641
D 、1281
10.不超过3
23⎪⎭⎫
⎝⎛-的最大整数是: A 、-4 B 、-3 C 、3 D 、4
11.如果两个数的和比每个加数都小,那么这两个数( )
A 、均为正数
B 、均为负数
C 、一正一负
D 、一个为零
12.如果两个有理数的积为正数,和为负数,那么这两个数( )
A 、都是负数
B 、都是正数
C 、异号且正数的绝对值大
D 、异号且负数的绝对值大
13.数()21
1⨯-、()22211⎪⎭⎫ ⎝⎛⨯-、()33211⎪⎭⎫ ⎝⎛⨯-、()4
4211⎪⎭⎫
⎝⎛⨯-中,最小的是( )
A 、()22211⎪⎭⎫ ⎝⎛⨯-
B 、()3
3211⎪⎭⎫ ⎝⎛⨯- C 、()211⨯- D 、()4
4211⎪⎭⎫
⎝⎛⨯-
14.a 为有理数,下列说法中正确的是( )
A 、()21+a 的值是正数
B 、12+a 的值是正数
C 、()21+-a 的值是负数
D 、12
+-a 的值小于1 15.如果两个有理数的和是正数,那么这两个数( )
A 、一定都是正数
B 、一定都是负数
C 、一定都是非负数
D 、至少有一个是正数
二.填空题:
1、计算:()=⎪⎭⎫ ⎝⎛-+--÷322
2113537 ; 2、1003的个位数是 ;
3、小华写出四个有理数,其中每三个数之和分别为2,17,-1,-3。
那么小华写出的四个数的和等于 ;
4、一个数的平方等于它的相反数,这个数一定是 ;
5、计算:()()=-+-2003200422 ;
6、一个有理数与它的倒数相等,这样的有理数有 。
7、有一种“二十四点”的游戏,其游戏的规则是这样的:任取四个1至10之间的自然数,将这四个数(每个数用且只用一次)进行加减乘除四则运算,使其结果等于24,现有四个有理数3,4,-6,10,运用上述规则的算法,使其结果等于24,运算式可以是 。
8、计算:=-++-+-+-10099654321 。
9、平方数小于20的整数有 个。
10、若()0122
12=++-y x ,则22y x +的值是 。
11. 初一“数学晚会”上,有10个同学藏在10个大盾牌后面。
男同学的盾牌前面写的是一个正数,女同
学的盾牌前面写的是一个负数。
这10个盾牌如下所示:30
30)(-、255--、12+a 、200912009)(-、97198-、8-、2--、333)
(-,)(24-⨯、15-⨯。
则盾牌后面的同学中,男同学有 个,女同学有 个。
12.已知|4||1|0x y -++=,则32011x y 的值为_________;
13. 数轴上有A 、B 两点,如果点A 对应的数是-2,且A 、B 两点的距离为3,则点B 对应的数是_________;
14.已知数轴上有A 、B 两点,A 、B 之间的距离为2,点A 与原点O 的距离为6,则所有满足条件的点B 与
原点O 的距离的和为_________;
15.在数轴上,点A 、B 分别表示2
141,-,则线段AB 的中点所表示的数是_________; 16.若,a b 互为相反数,,m n 互为倒数,P 的绝对值为3,则()20102a b mn p p ++-=_________;
17.如果a+b >0,a-b <0,ab <0,则a 0,b 0,
(填“=”或“<”或“>”)
18.若0 abc ,0=++c b a ,则=+++++c
b a b a
c a c b
三.解答题:
1.若||5,||3x y ==,且||x y y x -=-,求()
||x y x y ++的值。
2.已知|2|ab -与|1|b -互为相反数,试求代数式: ()()
()()()()111112*********a b a b a b +++++++++的值。
规律探索 1、 观察算式:
(13)2(15)3(17)4(19)513,135,1357=,13579,,2222+⨯+⨯+⨯+⨯+=++=+++++++= 按规律填空:1+3+5+…+99= ?,1+3+5+7+…+(21)n -= ?
2、如图是某同学在沙滩上用石子摆成的小房子。
观察图
形的变化规律,写出第n 个小房子用了多少块石子?
3、 用黑、白两种颜色的正六边形地面砖(如图所示)的规律,
拼成若干个图案:(1)第3个图案中有白色地面砖多少块?(2)
第n 个图案中有白色地面砖多少块?
4、 观察下列一组图形,如图,根据其变化规律,可得第10个图形中三角形的个数为多少?第n 个图形中三角形的个数为多少?
5、 观察右图,回答下列问题:
(1)图中的点被线段隔开分成四层,则第一层有1个点,第二层有3个点,第
三层有多少个点,第四层有多少个点?
(2)如果要你继续画下去,那第五层应该画多少个点,第n 层有多少个点?
(3)某一层上有77个点,这是第几层?
(4)第一层与第二层的和是多少?前三层的和呢?前4层的和呢?你有没有发现什么规律?根据你的推测,前12层的和是多少?
6.有一列数1234,,,,n a a a a a 其中:1a =6×2+1,2a =6×3+2,3a =6×4+3,4a =6×5+4;…则第n 个数n a = ,当n a =2001时,n = 。
7.通过计算探索规律:
152=225可写成100×1×(1+1)+25
252=625可写成100×2×(2+1)+25
352=1225可写成100×3×(3+1)+25
452=2025可写成100×4×(4+1)+25
…………
752=5625可写成
归纳、猜想得:(10n+5)2=
根据猜想计算:19952=。
