中考中关于折叠和旋转问题测试题

合集下载

2023年九年级中考数学一轮专题练习图形的平移、折叠和旋转(含解析)

2023年中考数学一轮专题练习 ——图形的平移、折叠和旋转5一、单选题（本大题共12小题）1. （重庆市2022年）下列北京冬奥会运动标识图案是轴对称图形的是（） A ． B ．C ．D ．2. （浙江省台州市2022年）如图是战机在空中展示的轴对称队形．以飞机B ，C 所在直线为x 轴、队形的对称轴为y 轴，建立平面直角坐标系．若飞机E 的坐标为(40，a )，则飞机D 的坐标为（）A ．(40,)a -B ．(40,)a -C ．(40,)a --D ．(,40)a - 3. （浙江省嘉兴市2022年）“方胜”是中国古代妇女的一种发饰，其图案由两个全等正方形相叠组成，寓意是同心吉祥．如图，将边长为2cm 的正方形ABCD 沿对角线BD 方向平移1cm 得到正方形A B C D ''''，形成一个“方胜”图案，则点D ，B ′之间的距离为（）A ．1cmB ．2cmC ．－1)cmD ．(2－1)cm4. （浙江省杭州市2022年）如图，在平面直角坐标系中，已知点P(0，2)，点A(4，2)．以点P为旋转中心，把点A按逆时针方向旋转60°，得点B．在1M⎛⎫⎪⎪⎝⎭，()21M-，()31,4M，4112,2M⎛⎫⎪⎝⎭四个点中，直线PB经过的点是（）A．1M B．2M C．3M D．4M5. （四川省德阳市2022年）下列图形中，既是中心对称图形又是轴对称图形的是（）A．B．C．D．6. （四川省广安市2022年）如图，菱形ABCD的边长为2，点P是对角线AC上的一个动点，点E、F分别为边AD、DC的中点，则PE + PF的最小值是（）A．2 B．C．1.5 D7. （黑龙江省省龙东地区2022年）下列图形是汽车的标识，其中是中心对称图形但不是轴对称图形的是（）A ．B ．C ．D ．8. （北京市2022年）图中的图形为轴对称图形，该图形的对称轴的条数为（）A ．1B ．2C ．3D ．59. （福建省2022年）如图，现有一把直尺和一块三角尺，其中90ABC ∠=︒，60CAB ∠=︒，AB ＝8，点A 对应直尺的刻度为12.将该三角尺沿着直尺边缘平移，使得△ABC 移动到A B C '''，点A '对应直尺的刻度为0，则四边形ACC A ''的面积是（）A ．96B ．C ．192D ． 10. （广东省2022年）在平面直角坐标系中，将点()1,1向右平移2个单位后，得到的点的坐标是（）A ．()3,1B ．()1,1-C ．()1,3D ．()1,1- 11. （广西百色市2022年）如图，在△ABC 中，点A （3，1），B （1，2），将△ABC 向左平移2个单位，再向上平移1个单位，则点B 的对应点B ′的坐标为（）A ．（3，-3）B ．（3，3）C ．（－1，1）D ．（－1，3） 12. （浙江省金华市2022年）如图是一张矩形纸片ABCD ，点E 为AD 中点，点F 在BC 上，把该纸片沿EF 折叠，点A ，B 的对应点分别为A B A E '''，，与BC 相交于点G ，B A ''的延长线过点C ．若23BF GC =，则AD AB的值为（）A ．B ．C ．207D ．83二、填空题（本大题共6小题）13. （浙江省丽水市2022年）三个能够重合的正六边形的位置如图．已知B 点的坐标是(，则A 点的坐标是．14. （浙江省台州市2022年）如图，△ABC的边BC长为4cm．将△ABC平移2cm得到△A′B′C′，且BB′⊥BC，则阴影部分的面积为2cm．15. （山东省潍坊市2022年）如图，在直角坐标系中，边长为2个单位长度的正方形ABCO绕原点O逆时针旋转75︒，再沿y轴方向向上平移1个单位长度，则点B''的坐标为．16. （浙江省台州市2022年）如图，在菱形ABCD中，∠A=60°，AB=6．折叠该菱形，使点A落在边BC上的点M处，折痕分别与边AB，AD交于点E，F．当点M与点B 重合时，EF的长为；当点M的位置变化时，DF长的最大值为．17. （浙江省丽水市2022年）一副三角板按图1放置，O 是边()BC DF 的中点，12cm BC =．如图2，将ABC 绕点O 顺时针旋转60︒，AC 与EF 相交于点G ，则FG 的长是 cm ．18. （山东省潍坊市2022年）小莹按照如图所示的步骤折叠A 4纸，折完后，发现折痕AB ′与A 4纸的长边AB 恰好重合，那么A 4纸的长AB 与宽AD 的比值为．三、解答题（本大题共9小题）19. （浙江省丽水市2022年）如图，将矩形纸片折叠，使点B 与点D 重合，点A 落在点P 处，折痕为．(1)求证：PDE CDF △≌△；(2)若4cm,5cm CD EF ==，求BC 的长．20. （浙江省丽水市2022年）如图，在66⨯的方格纸中，点A ，B ，C 均在格点上，试按要求画出相应格点图形．ABCDEF(1)如图1，作一条线段，使它是AB 向右平移一格后的图形；(2)如图2，作一个轴对称图形，使AB 和AC 是它的两条边；(3)如图3，作一个与ABC 相似的三角形，相似比不等于1．21. （黑龙江省省龙东地区2022年）如图，在正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，ABC 的三个顶点坐标分别为()1,1A -，()2,5B -，()5,4C -．(1)将ABC 先向左平移6个单位，再向上平移4个单位，得到111A B C △，画出两次平移后的111A B C △，并写出点1A 的坐标；(2)画出111A B C △绕点1C 顺时针旋转90°后得到221A B C △，并写出点2A 的坐标；(3)在（2）的条件下，求点1A 旋转到点2A 的过程中所经过的路径长（结果保留π）． 22. （四川省广安市2022年）数学活动课上，张老师组织同学们设计多姿多彩的几何图形，下图都是由边长为1的小等边三角形构成的网格，每个网格图中有3个小等边三角形已涂上阴影，请同学们在余下的空白小等边三角形中选取一个涂上阴影，使得4个阴影小等边三角形组成一个轴对称图形或中心对称图形，请画出4种不同的设计图形．规定：凡通过旋转能重合的图形视为同一种图形）23. （黑龙江省2022年）如图，在边长为1个单位长度的小正方形组成的网格中，△ABC与△DEF关于点O成中心对称，△ABC与△DEF的顶点均在格点上，请按要求完成下列各题．（1）在图中画出点O的位置；（2）将△ABC先向右平移4个单位长度，再向下平移2个单位长度，得到△A1B1C1，请画出△A1B1C1；（3）在网格中画出格点M，使A1M平分∠B1A1C124. （黑龙江省齐齐哈尔市2022年）综合与实践数学是以数量关系和空间形式为主要研究对象的科学．数学实践活动有利于我们在图形运动变化的过程中去发现其中的位置关系和数量关系，让我们在学习与探索中发现数学的美，体会数学实践活动带给我们的乐趣．如图①，在矩形ABCD中，点E、F、G分别为边BC、AB、AD的中点，连接EF、DF，H为DF的中点，连接GH．将△BEF绕点B旋转，线段DF、GH和CE的位置和长度也随之变化．当△BEF绕点B顺时针旋转90°时，请解决下列问题：(1)图②中，AB=BC，此时点E落在AB的延长线上，点F落在线段BC上，连接AF，猜想GH与CE之间的数量关系，并证明你的猜想；(2)图③中，AB=2，BC=3，则GHCE=；(3)当AB=m , BC=n时．GHCE=．(4)在（2）的条件下，连接图③中矩形的对角线AC，并沿对角线AC剪开，得△ABC （如图④)．点M、N分别在AC、BC上，连接MN，将△CMN沿MN翻折，使点C的对应点P落在AB的延长线上，若PM平分∠APN，则CM长为．25. （黑龙江省省龙东地区2022年）ABC和ADE都是等边三角形．(1)将ADE绕点A旋转到图①的位置时，连接BD，CE并延长相交于点P（点P与点A重合），有PA PB PC+=（或PA PC PB+=）成立；请证明．(2)将ADE绕点A旋转到图②的位置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？并加以证明；(3)将ADE 绕点A 旋转到图③的位置时，连接BD ，CE 相交于点P ，连接PA ，猜想线段PA 、PB 、PC 之间有怎样的数量关系？直接写出结论，不需要证明．26. （北京市2022年）在平面直角坐标系xOy 中，已知点(,),.M a b N 对于点P 给出如下定义：将点P 向右(0)a ≥或向左(0)a <平移a 个单位长度，再向上(0)b ≥或向下(0)b <平移b 个单位长度，得到点P'，点P'关于点N 的对称点为Q ，称点Q 为点P 的“对应点”．(1)如图，点(1,1),M 点N 在线段OM 的延长线上，若点(2,0),P -点Q 为点P 的“对应点”．①在图中画出点Q ；②连接,PQ 交线段ON 于点.T 求证：1;2NT OM = (2)O 的半径为1，M 是O 上一点，点N 在线段OM 上，且1(1)2ON t t =<<，若P 为O 外一点，点Q 为点P 的“对应点”，连接.PQ 当点M 在O 上运动时直接写出PQ 长的最大值与最小值的差（用含t 的式子表示）27. （河南省2022年）综合与实践综合与实践课上，老师让同学们以“矩形的折叠”为主题开展数学活动．(1)操作判断操作一：对折矩形纸片ABCD ，使AD 与BC 重合，得到折痕EF ，把纸片展平；操作二：在AD 上选一点P ，沿BP 折叠，使点A 落在矩形内部点M 处，把纸片展平，连接PM ，BM ．根据以上操作，当点M 在EF 上时，写出图1中一个30°的角：．(2)迁移探究小华将矩形纸片换成正方形纸片，继续探究，过程如下：将正方形纸片ABCD按照（1）中的方式操作，并延长PM交CD于点Q，连接BQ．①如图2，当点M在EF上时，∠MBQ＝ °，∠CBQ＝ °；②改变点P在AD上的位置（点P不与点A，D重合），如图3，判断∠MBQ与∠CBQ的数量关系，并说明理由．(3)拓展应用在（2）的探究中，已知正方形纸片ABCD的边长为8cm，当FQ＝1cm时，直接写出AP的长．参考答案1. 【答案】C【分析】根据轴对称图形的定义进行逐一判断即可．【详解】A.不是轴对称图形，故A错误；B.不是轴对称图形，故B错误；C.是轴对称图形，故C正确；D.不是轴对称图形，故D错误．故选：C．2. 【答案】B【分析】直接利用关于y轴对称，纵坐标相同，横坐标互为相反数，进而得出答案．【详解】解：根据题意，点E与点D关于y轴对称，∵飞机E的坐标为(40，a)，∴飞机D的坐标为(-40，a)，故选：B．3. 【答案】D【分析】-′求解即可．先求出BD，再根据平移性质求得BB'=1cm，然后由BD BB【详解】解：由题意，BD=，由平移性质得BB'=1cm，∴点D，B′之间的距离为DB'=BD BB-′=（1）cm，故选：D．4. 【答案】B【分析】根据含30°角的直角三角形的性质可得B（2，PB的解析式，依次将M1，M2，M3，M4四个点的一个坐标代入y+2中可解答．【详解】解：∵点A（4，2），点P（0，2），∴PA ⊥y 轴，PA =4，由旋转得：∠APB =60°，AP =PB =4，如图，过点B 作BC ⊥y 轴于C ，∴∠BPC =30°，∴BC =2，PC∴B （2，2+2设直线PB 的解析式为：y =kx +b ，则222k b b ⎧+=+⎪⎨=⎪⎩∴2k b ⎧=⎪⎨=⎪⎩∴直线PB 的解析式为：y =x +2，当y =0+2=0，x∴点M 1（-0）不在直线PB 上，当x y =-3+2=1，∴M 2（-1）在直线PB 上，当x =1时，y =+2，∴M 3（1，4）不在直线PB 上，当x =2时，y ，∴M 4（2，112）不在直线PB 上．故选：B ．5. 【答案】A【分析】根据轴对称和中心对称的定义逐项判断即可．轴对称图形是把一个图形沿一条直线折叠，直线两旁的部分能够互相重合；中心对称图形是把一个图形绕某一点旋转180°，旋转后的图形能够与原来的图形重合．【详解】A 、既是中心对称图形，又是轴对称图形，符合题意；B 、是轴对称图形，但不是中心对称图形，不符合题意；C 、是轴对称图形，但不是中心对称图形，不符合题意；D 、是中心对称图形，但不是轴对称图形，不符合题意；故选：A ．6. 【答案】A【分析】取AB 中点G 点，根据菱形的性质可知E 点、G 点关于对角线AC 对称，即有PE =PG ，则当G 、P 、F 三点共线时，PE +PF =PG +PF 最小，再证明四边形AGFD 是平行四边形，即可求得FG =AD ．【详解】解：取AB 中点G 点，连接PG ，如图，∵四边形ABCD 是菱形，且边长为2，∴AD =DC =AB =BC =2，∵E 点、G 点分别为AD 、AB 的中点，∴根据菱形的性质可知点E 、点G 关于对角线AC 轴对称，∴PE =PG ，∴PE +PF =PG +PF ，即可知当G 、P 、F 三点共线时，PE +PF =PG +PF 最小，且为线段FG ，如下图，G 、P 、F 三点共线，连接FG ，∵F 点是DC 中点，G 点为AB 中点，∴， 1122DF DC AB AG ===∵在菱形ABCD 中，，∴，∴四边形AGFD 是平行四边形，∴FG =AD =2，故PE +PF 的最小值为2，故选：A ．7. 【答案】C【分析】根据中心对称图形的定义判断即可．【详解】解：∵是轴对称图形，也是中心对称图形， ∴不符合题意；∵是轴对称图形，不是中心对称图形∴不符合题意；∵不是轴对称图形，是中心对称图形∴符合题意；∵是轴对称图形，不是中心对称图形∴不符合题意；故选C ．8. 【答案】D【分析】根据题意，画出该图形的对称轴，即可求解．【详解】解∶如图，DC AB ∥DF AG ∥一共有5条对称轴．故选：D9. 【答案】B【分析】根据直尺与三角尺的夹角为60°，根据四边形ACC A ''的面积为sin602sin60AA AC AB AA ⋅'︒︒⋅'=，即可求解．【详解】解：依题意ACC A ''为平行四边形，∵90ABC ∠=︒，60CAB ∠=︒，AB ＝8，12AA '=．2AC AB ∴=∴平行四边形ACC A ''的面积=sin602sin60AA AC AB AA ''⋅︒=︒⋅2812=⨯⨯=故选B10. 【答案】A【分析】把点()1,1的横坐标加2，纵坐标不变，得到()3,1，就是平移后的对应点的坐标．【详解】解：点()1,1向右平移2个单位长度后得到的点的坐标为()3,1．故选A ．11. 【答案】D【分析】根据图形的平移性质求解．【详解】解：根据图形平移的性质，B ′（1-2，2+1），即B ′（-1，3）；故选：D ．12. 【答案】A【分析】令BF =2x ，CG =3x ，FG =y ，易证CGA CFB ''△∽△，得出CG A G CF B F'='，进而得出y =3x ，则AE =4x ，AD =8x ，过点E 作EH ⊥BC 于点H ，根据勾股定理得出EH =，最后求出AD AB的值．【详解】解：过点E 作EH ⊥BC 于点H ，又四边形ABCD 为矩形，∴∠A =∠B =∠D =∠BCD =90°，AD =BC ，∴四边形ABHE 和四边形CDEH 为矩形，∴AB =EH ，ED =CH ， ∵23BF GC =， ∴令BF =2x ，CG =3x ，FG =y ，则CF =3x +y ，2B F x '=，，由题意，得==90CA G CB F ''︒∠∠，又GCA '∠为公共角，∴CGA CFB ''△∽△， ∴CG A GCF B F '='，则53232x yx x y x-=+，整理，得()()30x y x y +-=，解得x =-y （舍去），y =3x ，∴AD =BC =5x +y =8x ，EG =3x ，HG =x ，在Rt △EGH 中EH 2+HG 2=EG 2，则EH 2+x 2=(3x )2，解得EH=， EH=-(舍)，∴AB=，∴ADAB ==．故选：A ．13.【答案】3A【分析】 52x y A G -'=如图，延长正六边形的边BM 与x 轴交于点E ，过A 作AN x ⊥轴于N ，连接AO ，BO ，证明,BOE AON 可得,,A O B 三点共线，可得,A B 关于O 对称，从而可得答案．【详解】解：如图，延长正六边形的边BM 与x 轴交于点E ，过A 作AN x ⊥轴于N ，连接AO ，BO ，∴ 三个正六边形，O 为原点，,120,BM MO OH AH BMO OHA,BMO OHA ≌,OB OA 11209030,18012030,2MOE BMO MOB60,90,BOE BEO同理：120303060,906030,AON OAN,BOE AON,,A O B ∴三点共线，,A B ∴关于O 对称，3,3.A故答案为：3.A14. 【答案】8【分析】根据平移的性质即可求解．【详解】解：由平移的性质S △A ′B ′C ′=S △ABC ，BC =B ′C ′，BC ∥B ′C ′，∴四边形B ′C ′CB 为平行四边形，∵BB ′⊥BC ，∴四边形B ′C ′CB 为矩形，∵阴影部分的面积=S △A ′B ′C ′+S 矩形B ′C ′CB -S △ABC=S 矩形B ′C ′CB=4×2=8(cm 2)．故答案为：8．15.【答案】(1)【分析】连接OB ，OB '由题意可得∠BOB '=75°，可得出∠COB '=30°，可求出B '的坐标，即可得出点B ''的坐标．【详解】解：如图：连接OB ，OB '，作B M '⊥y 轴∵ABCO 是正方形，OA =2∴∠COB =45°，OB=∵绕原点O 逆时针旋转75︒∴∠BOB '=75°∴∠COB '=30°∵=OB =∴，∴∵沿y 轴方向向上平移1个单位长度∴故答案为：16. 【答案】6-【分析】当点M 与点B 重合时，EF垂直平分AB ，利用三角函数即可求得EF的长；【详解】解：当点M 与点B 重合时，由折叠的性质知EF 垂直平分AB ，∴AE =EB =12AB =3， OB 'MB 'MO =B '(B ''(1)(1)在Rt △AEF 中，∠A =60°，AE =3，tan60°=EF AB， ∴EF =3当AF 长取得最小值时，DF 长取得最大值，由折叠的性质知EF 垂直平分AM ，则AF =FM ，∴FM ⊥BC 时，FM 长取得最小值，此时DF 长取得最大值，过点D 作DG ⊥BC 于点C ，则四边形DGMF 为矩形，∴FM =DG ，在Rt △DGC 中，∠C =∠A =60°，DC =AB =6，∴DG =DC sin60°∴DF 长的最大值为AD -AF =AD -FM =AD -DG =6-3故答案为：36-317. 【答案】3【分析】BC 交EF 于点N ，由题意得，=90EDF BAC ∠=∠︒，60DEF ∠=︒，30DFE ∠=︒，=45ABC ACB ∠=∠︒，BC =DF =12，根据锐角三角函数即可得DE ，FE ，根据旋转的性质得ONF △是直角三角形，根据直角三角形的性质得3ON =，即3NC =，根据角之间的关系得CNG △是等腰直角三角形，即3NG NC ==cm ，根据90FNO FED ∠=∠=︒，30NFO DFE ∠=∠=︒得FON FED △∽△，即ON FN DE DF=，解得FN = 【详解】解：如图所示，BC 交EF 于点N ，由题意得，=90EDF BAC ∠=∠︒，60DEF ∠=︒，30DFE ∠=︒，=45ABC ACB ∠=∠︒，BC =DF =12，在Rt EDF 中，12tan tan 60DF DE EDF ===∠︒12sin sin 60DF EF EDF ===∠︒∵△ABC 绕点O 顺时针旋转60°，∴60BOD NOF ∠=∠=︒，∴90NOF F ∠+∠=︒，∴18090FNO NOF F ∠=︒-∠-∠=︒，∴ONF △是直角三角形， ∴132ON OF ==（cm ）， ∴3NC OC ON =-=（cm ），∵90FNO ∠=︒，∴18090GNC FNO ∠=︒-∠=︒，∴NGC 是直角三角形，∴18045NGC GNC ACB ∠=-∠-∠=︒，∴CNG △是等腰直角三角形，∴3NG NC ==cm ，∵90FNO FED ∠=∠=︒，30NFO DFE ∠=∠=︒，∴FON FED △∽△，即ON FN DE DF=，12FN =，FN =∴3FG FN NG =-=（cm ），故答案为：3．18. 1【分析】判定△AB ′D ′是等腰直角三角形，即可得出AB ′=AD ，再根据AB ′= AB ，再计算即可得到结论．【详解】解：∵四边形ABCD 是矩形，∴∠D =∠B =∠DAB =90°，由操作一可知：∠DAB ′=∠D ′AB ′=45°，∠AD ′B ′=∠D =90°，AD =AD ′，∴△AB ′D ′是等腰直角三角形，∴AD =AD ′= B ′D ′，由勾股定理得AB ′=，又由操作二可知：AB ′=AB ，∴=AB ，∴AB AD=， ∴A 4纸的长AB 与宽AD：1．故答案为：：1．19. 【答案】(1)证明见解析 (2)163cm 【分析】（1）利用ASA 证明即可；（2）过点E 作EG ⊥BC 交于点G ，求出FG 的长，设AE =x ，用x 表示出DE 的长，在Rt △PED 中，由勾股定理求得答案．(1)∵四边形ABCD 是矩形，∴AB =CD ，∠A =∠B =∠ADC =∠C =90°，由折叠知，AB =PD ，∠A =∠P ，∠B =∠PDF =90°，∴PD =CD ，∠P =∠C ，∠PDF =∠ADC ，∴∠PDF -∠EDF =∠ADC -∠EDF ,∴∠PDE =∠CDF ，在△PDE 和△CDF 中，P C PD CDPDE CDF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴PDE CDF △≌△（ASA ）；(2)如图，过点E 作EG ⊥BC 交于点G ，∵四边形ABCD 是矩形,∴AB =CD =EG =4cm ，又∵EF =5cm ，∴3GF =,设AE =x ，∴EP =x ，由PDE CDF △≌△知，EP =CF =x ，∴DE =GC =GF +FC =3+x ，在Rt △PED 中，222PE PD DE +=,即()22243x x +=+，解得，76x =， ∴BC =BG +GC = 77163663++=cm ． 20. 【答案】(1)画图见解析(2)画图见解析(3)画图见解析【分析】（1）分别确定A ，B 平移后的对应点C ，D ，从而可得答案；（2）确定线段AB ，AC 关于直线BC 对称的线段即可；（3）分别计算ABC 的三边长度，再利用相似三角形的对应边成比例确定DEF 的三边长度，再画出DEF 即可．(1)解：如图，线段CD 即为所求作的线段，(2)如图，四边形ABDC 是所求作的轴对称图形，(3)如图，如图，DEF 即为所求作的三角形，由勾股定理可得：221310,2,ABAC 而2,BC = 同理：2226210,22,DF DE 而4,EF 1,2AB AC BC DF DE EF .ABC DFE ∽21. 【答案】(1)见解析；()15,3A -(2)见解析；()22,4A(3)点1A 旋转到点2A 所经过的路径长为5π2【分析】（1）根据题目中的平移方式进行平移，然后读出点的坐标即可；（2）先找出旋转后的对应点，然后顺次连接即可；（3）根据旋转可得点1A 旋转到点2A 为弧长，利用勾股定理确定圆弧半径，然后根据弧长公式求解即可．(1)解：如图所示△A 1B 1C 1即为所求，()15,3A -；(2)如图所示△A 2B 2C 2即为所求，；(3)∵ ∴点旋转到点所经过的路径长为． 22. 【答案】见解析【分析】根据轴对称图形的定义、中心对称图形的定义画出图形即可 ()22,4A 115AC 1A 2A 90π55π1802⨯=【详解】解：如下图所示：23. 【答案】（1）作图见解析；（2）作图见解析；（3）作图见解析；【分析】（1）连接对应点B 、F ，对应点C 、E ，其交点即为旋转中心的位置；（2）利用网格结构找出平移后的点的位置，然后顺次连接即可；（3）根据网格结构的特点作出即可．【详解】解：（1）如图所示，连接BF ，CE 交于点O ，点O 即为所求．（2）如图所示，△A 1B 1C 1为所求；（3）如图所示，点M 即为所求．理由：连接11,B M C M ，根据题意得：111111A B AC B M C M ====∴四边形111A B MC 菱形，∴A 1M 平分∠B 1A 1C 1．24. 【答案】(1)12GH CE =，证明见解析 (2)13GH CE = (3)2GH m CE n =(4)【分析】（1）先证明△ABF ≌△CBE ，得AF =CE ，再根据中位线性质得GH =12AF ，等量代换即可；（2）连接AF ，先证明△ABF ∽△CBE ，得到AF ：CE 的比值，再根据中位线性质得GH =12AF ，等量代换即可；（3）连接AF ，先证明△ABF ∽△CBE ，用含m 、n 的代数式表达出AF ：CE 的比值，再根据中位线性质得GH =12AF ，等量代换即可；（4）过M 作MH ⊥AB 于H ，根据折叠性质得∠C =∠MPN ，根据角平分线证明出∠C =∠PMH ，设CM =PM =x ，HM =y ，根据三角函数定义找到x 、y 之间的关系，再利用△AHM ∽△ABC ，得到CM BC H AM A =，代入解方程即可． (1) 解：12GH CE =，理由如下： ∵AB =BC ，四边形ABCD 为矩形，∴四边形ABCD 为正方形，∴∠ABC =∠CBE =90°，∵E 、F 为BC ，AB 中点，∴BE =BF ，∴△ABF ≌△CBE ，∴AF =CE ，∵H 为DF 中点，G 为AD 中点，∴GH =12AF ， ∴12GH CE =． (2) 解：13GH CE =，连接AF ，如图所示，由题意知，BF =12AB =1，BE =12BC =32， ∴，由矩形ABCD 性质及旋转知，∠ABC =∠CBE =90°，∴△ABF ∽△CBE ，∴AF ：CE =2:3，∵G 为AD 中点，H 为DF 中点，∴GH =， ∴．故答案为：． (3)解：，连接AF ，如图所示，23AB BF BC BE ==12AF 13GH CE =132GH m CE n=由题意知，BF ==，BE ==， ∴，由矩形ABCD 性质及旋转知，∠ABC =∠CBE =90°，∴△ABF ∽△CBE ，∴AF ：CE =m ：n ，∵G 为AD 中点，H 为DF 中点，∴GH =， ∴．故答案为：． (4)解：过M 作MH ⊥AB 于H ，如图所示，由折叠知，CM =PM ，∠C =∠MPN ，12AB 2m 12BC 2n AB BF m BC BE n==12AF 2GH m CE n =2mn∵PM 平分∠APN ，∴∠APM =∠MPN ，∴∠C =∠APM ，∵AB =2，BC =3，∴AC设CM =PM =x ，HM =y ，由知，，即，∵HM ∥BC ，∴△AHM ∽△ABC ，∴，即，， ∴，解得：x，故答案为：． 25. 【答案】(1)证明见解析(2)图②结论：PB PA PC =+，证明见解析(3)图③结论：PA PB PC +=【分析】（1）由△ABC 是等边三角形，得AB =AC ，再因为点P 与点A 重合，所以PB =AB ，PC =AC ，PA =0，即可得出结论；（2）在BP 上截取BF CP =，连接AF ，证明BAD CAE ≌（SAS ），得ABD ACE ∠=∠，再证明CAP BAF ≌△△（SAS ），得CAP BAF ∠=∠，AF AP =，然后证明AFP 是等边三角形，得PF AP =，即可得出结论；（3）在CP 上截取CF BP =，连接AF ，证明BAD CAE ≌（SAS ），得ABD ACE ∠=∠，再证明BAP CAF ≌△△（SAS ），得出CAF BAP ∠=∠，AP AF =，然后证明AFP 是等边三角形，得PF AP =，即可得出结论：PA PB PF CF PC +=+=．(1)证明：∵△ABC 是等边三角形，∴AB =AC ，∵点P 与点A 重合，∴PB =AB ，PC =AC ，PA =0，sin sin C APM ∠=∠AB HM AC PM =y x =y =C M BC H AM A =3y =3y =3=∴PA PB PC +=或PA PC PB +=；(2)解：图②结论：PB PA PC =+证明：在BP 上截取BF CP =，连接AF ，∵ABC 和ADE 都是等边三角形， ∴AB AC =，AD AE =，60BAC DAE ∠=∠=︒ ∴BAC CAD DAE CAD ∠+∠=∠+∠， ∴BAD CAE ∠=∠，∴BAD CAE ≌（SAS ），∴ABD ACE ∠=∠，∵AC =AB ，CP =BF ，∴CAP BAF ≌△△（SAS ），∴CAP BAF ∠=∠，AF AP =， ∴CAP CAF BAF CAF ∠+∠=∠+∠， ∴60FAP BAC ∠=∠=︒，∴AFP 是等边三角形，∴PF AP =，∴PA PC PF BF PB +=+=；(3)解：图③结论：PA PB PC +=，理由：在CP 上截取CF BP =，连接AF ，∵ABC 和ADE 都是等边三角形，∴AB AC =，AD AE =，60BAC DAE ∠=∠=︒∴BAC BAE DAE BAE ∠+∠=∠+∠，∴BAD CAE ∠=∠，∴BAD CAE ≌（SAS ），∴ABD ACE ∠=∠，∵AB =AC ，BP =CF ，∴BAP CAF ≌△△（SAS ），∴CAF BAP ∠=∠，AP AF =，∴BAF BAP BAF CAF ∠+∠=∠+∠，∴60FAP BAC ∠=∠=︒，∴AFP 是等边三角形，∴PF AP =，∴PA PB PF CF PC +=+=，即PA PB PC +=．26. 【答案】(1)见解析(2)42t -【分析】（1）①先根据定义和(1,1)M 求出点P'的坐标，再根据点P'关于点N 的对称点为Q 求出点Q 的坐标；②延长ON 至点()3,3A ，连接AQ ，利用AAS 证明ΔΔAQT OPT ≅，得到12TA TO OA ==，再计算出OA ，OM ，ON ，即可求出12NT ON OT OM =-==；（2）连接PO 并延长至S ，使OP OS =，延长SQ 至T ，使ST OM =，结合对称的性质得出NM 为Δ'P QT 的中位线，推出1=2NM QT ，得出()12221SQ ST TQ t t =-=--=-，则()()max min 2PQ PQ PS QS PS QS QS -=+--=．(1)解：①点Q 如下图所示．∵点(1,1)M ，∴点(2,0)P -向右平移1个单位长度，再向上平移1个单位长度，得到点P'， ∴()'1,1P -，∵点P'关于点N 的对称点为Q ，()2,2N ，∴点Q 的横坐标为：()2215⨯--=，纵坐标为：2213⨯-=，∴点()5,3Q ，在坐标系内找出该点即可；②证明：如图延长ON 至点()3,3A ，连接AQ ，∵ //AQ OP ，∴AQT OPT ∠=∠，在ΔAQT 与ΔOPT ∠中，AQT OPT ATQ OTP AQ OP ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()ΔΔAQT OPT AAS ≅， ∴12TA TO OA ==， ∵ ()3,3A ，(1,1)M ，(2,2)N ，∴OA ==OMON =∴12TO OA ==∴NT ON OT =-= ∴12NT OM =； (2)解：如图所示，连接PO 并延长至S ，使OP OS =，延长SQ 至T ，使ST OM =，∵(,)M a b ，点P 向右(0)a ≥或向左(0)a <平移a 个单位长度，再向上(0)b ≥或向下(0)b <平移b 个单位长度，得到点P'，∴'1PP OM ==，∵点P'关于点N 的对称点为Q ，∴'NP NQ =，又∵OP OS =，∴OM ∥ST ，∴NM 为Δ'P QT 的中位线，∴//NM QT ，1=2NM QT ， ∵1NM OM ON t =-=-，∴222TQ NM t ==-，∴()12221SQ ST TQ t t =-=--=-，在ΔPQS 中，PS QS PQ PS QS -<<+，结合题意，max PQ PS QS =+，min PQ PS QS =-，∴()()max min 242PQ PQ PS QS PS QS QS t -=+--==-，即PQ 长的最大值与最小值的差为42t -．27. 【答案】(1)BME ∠或ABP ∠或PBM ∠或MBC ∠(2)①15，15；②MBQ CBQ ∠=∠，理由见解析 (3)4011AP =cm 或24cm 13【分析】（1）根据折叠的性质，得12BE BM =，结合矩形的性质得30BME ∠=︒，进而可得30ABP PBM MBC ∠=∠=∠=︒；（2）根据折叠的性质，可证()Rt Rt HL BQM BQC ∆≅∆，即可求解；（3）由（2）可得QM QC =，分两种情况：当点Q 在点F 的下方时，当点Q 在点F 的上方时，设AP PM x ==，分别表示出PD ，DQ ，PQ ，由勾股定理即可求解．(1) 解：12AE BE AB AB BM ===， 12BE BM =∴ 90BEM ∠=︒∵30BME ∠=︒∴60MBE ∠=︒∴ABP PBM ∠=∠∵30ABP PBM MBC ∠=∠=∠=︒∴(2)∵四边形ABCD 是正方形∴AB =BC ，∠A =∠ABC =∠C =90°由折叠性质得：AB =BM ，∠PMB =∠BMQ =∠A =90°∴BM =BC①BM BC BQ BQ ==∵，∴()Rt Rt HL BQM BQC ∆≅∆MBQ CBQ ∠=∠∴30MBC15MBQ CBQ ∠=∠=︒∴②BM BC BQ BQ ==∵，()Rt Rt HL BQM BQC ∆≅∆∴MBQ CBQ ∠=∠∴(3)当点Q 在点F 的下方时，如图，1cm 4cm 8cm FQ DF FC AB ====∵，，8413(cm)QC CD DF FQ =--=--=∴，DQ =DF +FQ =4+1=5(cm) 由（2）可知，QM QC =设8AP PM x PD x ===-，，222PD DQ PQ +=∴，即()()222853x x -+=+ 解得：4011x =∴40cm 11AP =；当当点Q 在点F 的上方时，如图，1cm 4cm 8cm FQ DF FC AB ====∵，， 5QC =∴cm ，DQ =3cm ，由（2）可知，QM QC =设8AP PM x PD x ===-，，222PD DQ PQ +=∴，即()()222835x x -+=+ 解得：2413x =∴24cm 13AP =．。

2020届中考数学专题复习演练：折叠问题(有答案)

折叠问题一、选择题1.如图，菱形纸片ABCD中，∠A=60°，折叠菱形纸片ABCD，使点C落在DP（P为AB中点）所在的直线上，得到经过点D的折痕DE．则∠DEC的大小为（）A. 78°B. 7 5°C. 60°D. 45°2.如图，在矩形纸片ABCD中，AB＝4，AD＝3，折叠纸片使DA与对角线DB重合，点A落在点A′处，折痕为DE，则A′G的长是A. 1B.C.D. 23.如图，在矩形ABCD中，AB＜AD，E为AD边上一点，且AE= AB，连结BE，将△ABE沿BE翻折，若点A 恰好落在CE上点F处，则∠CBF的余弦值为（）A. B.C.D.4.如图，在矩形纸片ABCD中，AB=6，AD=8，折叠该纸片，使得AB边落在对角线AC上，点B落在点F处，折痕为AE，则线段EF的长为（）A. 3B. 4C. 5D. 65.如图，在Rt△ABC中，∠C=90°，BD平分∠ABC交AC于D，沿DE所在直线折叠，使点B恰好与点A重合，若CD=2，则AB的值为（）A. B.4 C.D. 8二、填空题6.如图，在Rt△ACB中，∠ACB=90°，AB=10，BC=6，点N是线段BC上的一个动点，将△ACN沿AN折叠，使点C落在点C'处，当△NC'B是直角三角形时，CN的长为________．7.如图，在△ABC中，∠C=90°，AC=BC=2 ，D是AB的中点，点E、F分别在AC、BC边上运动（点E不与点A、C重合），且保持AE=CF，连接DE、DF、EF．在此运动变化的过程中，下列结论：①△DFE是等腰直角三角形；②四边形CEDF的周长不变；③点C到线段EF的最大距离为1．其中正确的结论有________．（填写所有正确结论的序号）8.如图，在Rt△ABC中，∠C=90°，BC=2 ，AC=2，点D是BC的中点，点E是边AB上一动点，沿DE所在直线把△BDE翻折到△B′DE的位置，B′D交AB于点F．若△AB′F为直角三角形，则AE的长为________．9.如图，矩形ABCD中，AD=5，AB=6，点E为DC上一个动点，把△ADE沿AE折叠，点F为CD上一个动点，把△BCF沿BF折叠，当点D的对应点和点C的对应点都落在点D′处时，EF的长为________．10.矩形纸片ABCD中，AD=4cm，AB=10cm，按如图方式折叠，使点B与点D重合，折痕为EF，则DE=________ cm．11.如图，在▱ABCD中，AB=，AD=4，将▱ABCD沿AE翻折后，点B恰好与点C重合，则折痕AE的长为________.12.如图，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置．若∠EFB＝65°，则∠AED′的度数为________.13.已知等边△ABC中，点D，E分别在边AB，BC上，把△BDE沿直线DE翻折，使点B落在点Bˊ处，DBˊ，EBˊ分别交边AC于点F，G，若∠ADF=80°，则∠EGC的度数为________14.如图，在矩形ABCD中，AB=5，BC=3，点E为射线BC上一动点，将△ABE沿AE折叠，得到△AB′E．若B′恰好落在射线CD上，则BE的长为________．15.如图，在矩形中，将绕点按逆时针方向旋转一定角度后，的对应边交边于点．连接、，若，，，则________（结果保留根号）．三、综合题16.已知将一矩形纸片ABCD折叠，使顶点A与C重合，折痕为EF．（1）求证：CE=CF；（2）若AB =8 cm，BC=16 cm，连接AF，写出求四边形AFCE面积的思路．17.如图，矩形纸片ABCD中，AB=6，BC=8．折叠纸片使点B落在AD上，落点为B′．点B′从点A开始沿AD移动，折痕所在直线l的位置也随之改变，当直线l经过点A时，点B′停止移动，连接BB′．设直线l与AB相交于点E，与CD所在直线相交于点F，点B′的移动距离为x，点F与点C的距离为y．（1）求证：∠BEF=∠AB′B；（2）求y与x的函数关系式，并直接写出x的取值范围．参考答案一、选择题1. B2. C3.B4.A5. C二、填空题6.或7.①③8.3或9. 10.5.811.3 12.50° 13.80° 14.或15 15.三、综合题16.（1）证明：∵矩形纸片ABCD折叠，顶点A与C重合，折痕为EF，∴∠1=∠2，AD∥BC，∴∠1=∠3，∴∠2=∠3，∴CE=CF．（2）解：思路：连接AF① 由矩形纸片ABCD折叠，易证四边形AFCE为平行四边形；② Rt△CED中，设DE为x，则CE为16-x，CD=8，根据勾股定理列方程可求得DE，CE的长；③由CF=CE，可得CF的长；运用平行四边形面积公式计算CF×CD可得四边形AFCE的面积．17.（1）证明：如图，由四边形ABCD是矩形和折叠的性质可知，BE=B′E，∠BEF=∠B′EF，∴在等腰△BEB′中，EF是角平分线，∴EF⊥BB′，∠BOE=90°，∴∠ABB′+∠BEF=90°，∵∠ABB′+∠AB′B=90°，∴∠BEF=∠AB′B；（2）解：①当点F在CD之间时，如图1，作FM⊥AB交AB于点M，∵AB=6，BE=EB′，AB′=x，BM=FC=y，∴在Rt△EAB′中，EB′2=AE2+AB′2，∴（6﹣AE）2=AE2+x2解得AE=，tan∠AB′B==，tan∠BEF==，∵由（1）知∠BEF=∠AB′B，∴=，化简，得y=x2﹣x+3，（0＜x≤8﹣2）②当点F在点C下方时，如图2所示．设直线EF与BC交于点K设∠ABB′=∠BKE=∠CKF=θ，则tanθ==．BK=，CK=BC﹣BK=8﹣．∴CF=CK•tanθ=（8﹣）•tanθ=8tanθ﹣BE=x﹣BE．在Rt△EAB′中，EB′2=AE2+AB′2，∴（6﹣BE）2+x2=BE2解得BE=．∴CF=x﹣BE=x﹣=﹣x2+x﹣3 ∴y=﹣x2+x﹣3（8﹣2＜x≤6）综上所述，y=．。

中考数学《旋转》专题练习含答案解析

旋转一、选择题（共6小题，每小题4分，满分24分）1．下列图形中，你认为既是中心对称图形又是轴对称图形的是（）A．B．C．D．2．如图，所给的图案由△ABC绕点O顺时针旋转（）前后的图形组成的．A．45°、90°、135°B．90°、135°、180°C．45°、90°、135°、180°、225° D．45°、180°、225°3．如图，边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′，图中阴影部分的面积为（）A．B．C．1﹣D．1﹣4．如图，P是等边三角形ABC内一点，∠APB，∠BPC，∠CPA的大小之比为5：6：7，则以PA，PB，PC为边的三角形三内角大小之比（从小到大）是（）A．2：3：4 B．3：4：5C．4：5：6 D．以上结果都不对5．下列图形中，是中心对称图形的是（）A．菱形B．等腰梯形C．等边三角形D．等腰直角三角形6．在平面直角坐标系中，点P（2，﹣3）关于原点对称的点的坐标是（）A．（2，3）B．（﹣2，3）C．（﹣2，﹣3）D．（﹣3，2）二、填空题（共6小题，每小题5分，满分30分）7．在平面直角坐标系中，已知点P0的坐标为（1，0），将点P0绕着原点O按逆时针方向旋转60°得点P1，延长OP1到点P2，使OP2=2OP1再将点P2绕着原点O按逆时针方向旋转60°得点P3，则点P3的坐标是．8．如图所示，△ABC中，∠BAC=90°，AB=AC=5，△ABC按逆时针方向旋转一个角度后，成为△ACD，则旋转中心是点、旋转角是．9．如图，设P是等边三角形ABC内任意一点，△ACP′是由△ABP旋转得到的，则PA PB+PC（选填“＞”、“=”、“＜”）10．如图，E、F分别是正方形ABCD的边BC、CD上一点，且BE+DF=EF，则∠EAF=度．11．如图，O是等边△ABC内一点，将△AOB绕A点逆时针旋转，使得B，O两点的对应分别为C，D，则旋转角为度，图中除△ABC外，还有等边三形是△．12．如图，Rt△ABC中，P是斜边BC上一点，以P为中心，把这个三角形按逆时针方向旋转90°得到△DEF，图中通过旋转得到的三角形还有．三、解答题13．已知：正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N．当∠MAN绕点A旋转到BM=DN时（如图1），易证BM+DN=MN．（1）当∠MAN绕点A旋转到BM≠DN时（如图2），线段BM、DN和MN之间有怎样的数量关系？写出猜想，并加以证明；（2）当∠MAN绕点A旋转到如图3的位置时，线段BM、DN和MN之间又有怎样的数量关系？请直接写出你的猜想．14．如图，正方形ABCD的边长为1，AB，AD上各有一点P，Q，如果△APQ的周长为2，求∠PCQ的度数．15．有两张完全重合的矩形纸片，小亮同学将其中一张绕点A顺时针旋转90°后得到矩形AMEF（如图1），连接BD、MF，若此时他测得BD=8cm，∠ADB=30°．（1）请直接写出AF的长；（2）小红同学用剪刀将△BCD与△MEF剪去，与小亮同学继续探究．他们将△ABD绕点A顺时针旋转得△AB1D1，AD1交FM于点K（如图2），设旋转角为β（0°＜β＜90°），当△AFK为等腰三角形时，求△AFK的面积（保留根号）．旋转参考答案与试题解析一、选择题（共6小题，每小题4分，满分24分）1．下列图形中，你认为既是中心对称图形又是轴对称图形的是（）A．B．C．D．【考点】中心对称图形；轴对称图形．【分析】根据轴对称图形与中心对称图形的概念求解．【解答】解：既是中心对称图形又是轴对称图形的只有A．故选A．【点评】掌握好中心对称与轴对称的概念．轴对称的关键是寻找对称轴，两边图象沿对称轴折叠后可重合，中心对称是要寻找对称中心，图形旋转180度后与原图重合．2．如图，所给的图案由△ABC绕点O顺时针旋转（）前后的图形组成的．A．45°、90°、135°B．90°、135°、180°C．45°、90°、135°、180°、225° D．45°、180°、225°【考点】旋转的性质．【专题】计算题．【分析】根据旋转的性质，把旋转后的图形看作为正八边形，依次得到旋转的角度．【解答】解：把△ABC绕点O顺时针旋转45°，得到△HEF；顺时针旋转180°，得到△ADC；顺时针旋转225°，得到△HGF；故选D．【点评】本题考查了旋转的性质：旋转前后的两个图形全等，对应点与旋转中心的连线段的夹角等于旋转角，对应点到旋转中心的距离相等．3．如图，边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′，图中阴影部分的面积为（）A．B．C．1﹣D．1﹣【考点】旋转的性质；正方形的性质．【分析】设B′C′与CD的交点为E，连接AE，利用“HL”证明Rt△AB′E和Rt△ADE全等，根据全等三角形对应角相等∠DAE=∠B′AE，再根据旋转角求出∠DAB′=60°，然后求出∠DAE=30°，再解直角三角形求出DE，然后根据阴影部分的面积=正方形ABCD的面积﹣四边形ADEB′的面积，列式计算即可得解．【解答】解：如图，设B′C′与CD的交点为E，连接AE，在Rt△AB′E和Rt△ADE中，，∴Rt△AB′E≌Rt△ADE（HL），∴∠DAE=∠B′AE，∵旋转角为30°，∴∠DAB′=60°，∴∠DAE=×60°=30°，∴DE=1×=，∴阴影部分的面积=1×1﹣2×（×1×）=1﹣．故选：C．【点评】本题考查了旋转的性质，正方形的性质，全等三角形判定与性质，解直角三角形，利用全等三角形求出∠DAE=∠B′AE，从而求出∠DAE=30°是解题的关键，也是本题的难点．4．如图，P是等边三角形ABC内一点，∠APB，∠BPC，∠CPA的大小之比为5：6：7，则以PA，PB，PC为边的三角形三内角大小之比（从小到大）是（）A．2：3：4 B．3：4：5C．4：5：6 D．以上结果都不对【考点】旋转的性质；三角形内角和定理；等边三角形的性质．【专题】计算题．【分析】将△APB绕A点逆时针旋转60°得△AP′C，显然有△AP′C≌△APB，连PP′，则AP′=AP，∠P′AP=60°，得到△AP′P是等边三角形，PP′=AP，所以△P′CP的三边长分别为PA，PB，PC；再由∠APB+∠BPC+∠CPA=360°，∠APB：∠BPC：∠CPA=5：6：7，得到∠APB=100°，∠BPC=120°，∠CPA=140°，这样可分别求出∠PP′C=∠AP′C﹣∠AP′P=∠APB ﹣∠AP′P=100°﹣60°=40°，∠P′PC=∠APC﹣∠APP′=140°﹣60°=80°，∠PCP′=180°﹣（40°+80°）=60°，即可得到答案．【解答】解：如图，将△APB绕A点逆时针旋转60°得△AP′C，显然有△AP′C≌△APB，连PP′，∵AP′=AP，∠P′AP=60°，∴△AP′P是等边三角形，∴PP′=AP，∵P′C=PB，∴△P′CP的三边长分别为PA，PB，PC，∵∠APB+∠BPC+∠CPA=360°，∠APB：∠BPC：∠CPA=5：6：7，∴∠APB=100°，∠BPC=120°，∠CPA=140°，∴∠PP′C=∠AP′C﹣∠AP′P=∠APB﹣∠AP′P=100°﹣60°=40°，∠P′PC=∠APC﹣∠APP′=140°﹣60°=80°，∠PCP′=180°﹣（40°+80°）=60°，∴∠PP′C：∠PCP′：∠P′PC=2：3：4．故选A．【点评】本题考查了旋转的性质：旋转前后的两个图形全等，对应点与旋转中心的连线段的夹角等于旋转角，对应点到旋转中心的距离相等．也考查了等边三角形的性质．5．下列图形中，是中心对称图形的是（）A．菱形B．等腰梯形C．等边三角形D．等腰直角三角形【考点】中心对称图形．【分析】旋转180°后与原图重合的图形是中心对称图形．【解答】解：菱形，等腰梯形，等边三角形，等腰直角三角形都是轴对称图形；菱形既是轴对称图形，又是中心对称图形．故选A．【点评】运用轴对称和中心对称图形概念，找出符合条件的图形．【链接】如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．如果一个图形绕某一点旋转180°后能够与自身重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．6．在平面直角坐标系中，点P（2，﹣3）关于原点对称的点的坐标是（）A．（2，3）B．（﹣2，3）C．（﹣2，﹣3）D．（﹣3，2）【考点】关于原点对称的点的坐标．【分析】根据“平面直角坐标系中任意一点P（x，y），关于原点的对称点是（﹣x，﹣y）”解答．【解答】解：根据中心对称的性质，得点P（2，﹣3）关于原点对称的点的坐标是（﹣2，3）．故选B．【点评】关于原点对称的点坐标的关系，是需要识记的基本问题．记忆方法是结合平面直角坐标系的图形记忆．二、填空题（共6小题，每小题5分，满分30分）7．在平面直角坐标系中，已知点P0的坐标为（1，0），将点P0绕着原点O按逆时针方向旋转60°得点P1，延长OP1到点P2，使OP2=2OP1再将点P2绕着原点O按逆时针方向旋转60°得点P3，则点P3的坐标是（﹣1，）．【考点】坐标与图形变化﹣旋转．【专题】压轴题．【分析】已知将点P0绕着原点O按逆时针方向旋转60°得点P1，则OP1=1，P1点的坐标是（．则P2的坐标是；再将点P2绕着原点O按逆时针方向旋转60°得点P3，则点P3与P2关于y轴对称，因而点P3的坐标就很容易求出．【解答】解：∵点P0绕着原点O按逆时针方向旋转60°得点P1，∴P1点的坐标是（，∴P2的坐标是，又∵点P3与P2关于y轴对称，∴点P3的坐标是（﹣1，）．【点评】解决本题的关键是正确理解题目，按题目的叙述一定要把各点的大致位置确定，正确地作出图形．8．如图所示，△ABC中，∠BAC=90°，AB=AC=5，△ABC按逆时针方向旋转一个角度后，成为△ACD，则旋转中心是点A、旋转角是∠CAD，是90°．【考点】旋转的性质．【分析】确定图形的旋转时首先要确定旋转前后的对应点，即可确定旋转中心．【解答】解：旋转中心是点A、旋转角是∠CAD，是90°．【点评】本题主要考查了旋转的定义，正确确定旋转中的对应点，是确定旋转中心，旋转角的前提．9．如图，设P是等边三角形ABC内任意一点，△ACP′是由△ABP旋转得到的，则PA＜PB+PC（选填“＞”、“=”、“＜”）【考点】旋转的性质；三角形三边关系；等边三角形的判定．【分析】此题只需根据三角形的任意两边之和大于第三边和等边三角形的性质，进行分析即可．【解答】解：根据三角形的三边关系，得：BC＜PB+PC．又AB=BC＞PA，∴PA＜PB+PC．【点评】本题结合旋转主要考查了三角形的三边关系：两边之和大于第三边，两边之差小于第三边．10．如图，E、F分别是正方形ABCD的边BC、CD上一点，且BE+DF=EF，则∠EAF=45度．【考点】旋转的性质；正方形的性质．【分析】根据BE+DF=EF，则延长FD到G，使DG=BE，则FG=EF，可以认为是把△ABE 绕点A逆时针旋转90度，得到△ADG，根据旋转的定义即可求解．【解答】解：如图：延长FD到G，使DG=BE，则FG=EF，在△ABE和△ADG中，，∴△ABE≌△ADG（SAS），∴AE=AG又∴AF=AF，GF=EF∴△AGF≌△AEF∴∠EAF=∠GAF=×90°=45°．【点评】本题考查旋转的性质．旋转变化前后，对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等．要注意旋转的三要素：①定点﹣旋转中心；②旋转方向；③旋转角度．11．如图，O是等边△ABC内一点，将△AOB绕A点逆时针旋转，使得B，O两点的对应分别为C，D，则旋转角为60度，图中除△ABC外，还有等边三形是△AOD．【考点】旋转的性质；等边三角形的性质；等边三角形的判定．【分析】根据旋转的性质及全等三角形的性质作答．【解答】解：∵将△AOB绕A点逆时针旋转，使得B，O两点的对应分别为C，D，∴△AOB≌△ADC，∴OA=AD，∠BAO=∠DAC，∴∠BAO+∠OAC=∠DAC+∠OAC=∠BAC=60°，即∠OAD=60°，所以旋转角为60°．∵OA=AD，∠OAD=60°，∴△AOD为等边三角形．【点评】此题主要考查了图形旋转的性质：旋转变化前后，对应线段、对应角分别相等，图形的大小、形状都不改变．12．如图，Rt△ABC中，P是斜边BC上一点，以P为中心，把这个三角形按逆时针方向旋转90°得到△DEF，图中通过旋转得到的三角形还有△EPQ．【考点】旋转的性质．【分析】旋转中心是P，旋转方向为逆时针，旋转角是90度，已确定，再通过观察发现全等三角形，判断是否符合本题的旋转规律．【解答】解：根据旋转的性质可知，旋转中心是P，旋转角是90度，图中通过旋转得到的三角形还有△EPQ．【点评】本题考查旋转两相等的性质，即对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等．三、解答题13．已知：正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N．当∠MAN绕点A旋转到BM=DN时（如图1），易证BM+DN=MN．（1）当∠MAN绕点A旋转到BM≠DN时（如图2），线段BM、DN和MN之间有怎样的数量关系？写出猜想，并加以证明；（2）当∠MAN绕点A旋转到如图3的位置时，线段BM、DN和MN之间又有怎样的数量关系？请直接写出你的猜想．【考点】旋转的性质；全等三角形的判定与性质；正方形的性质．【专题】计算题；压轴题．【分析】（1）BM+DN=MN成立，证得B、E、M三点共线即可得到△AEM≌△ANM，从而证得ME=MN．（2）DN﹣BM=MN．证明方法与（1）类似．【解答】解：（1）BM+DN=MN成立．证明：如图，把△ADN绕点A顺时针旋转90°，得到△ABE，则可证得E、B、M三点共线（图形画正确）．∴∠EAM=90°﹣∠NAM=90°﹣45°=45°，又∵∠NAM=45°，∴在△AEM与△ANM中，∴△AEM≌△ANM（SAS），∴ME=MN，∵ME=BE+BM=DN+BM，∴DN+BM=MN；（2）DN﹣BM=MN．在线段DN上截取DQ=BM，在△ADQ与△ABM中，∵，∴△ADQ≌△ABM（SAS），∴∠DAQ=∠BAM，∴∠QAN=∠MAN．在△AMN和△AQN中，∴△AMN≌△AQN（SAS），∴MN=QN，∴DN﹣BM=MN．【点评】本题考查了旋转的性质，解决此类问题的关键是正确的利用旋转不变量．14．如图，正方形ABCD的边长为1，AB，AD上各有一点P，Q，如果△APQ的周长为2，求∠PCQ的度数．【考点】正方形的性质；全等三角形的判定与性质．【专题】计算题．【分析】简单的求正方形内一个角的大小，首先从△APQ的周长入手求出PQ=DQ+BP，然后将△CDQ逆时针旋转90°，使得CD、CB重合，然后利用全等来解．【解答】解：如图所示，△APQ的周长为2，即AP+AQ+PQ=2①，正方形ABCD的边长是1，即AQ+QD=1，AP+PB=1，∴AP+AQ+QD+PB=2②，①﹣②得，PQ﹣QD﹣PB=0，∴PQ=PB+QD．延长AB至M，使BM=DQ．连接CM，△CBM≌△CDQ（SAS），∴∠BCM=∠DCQ，CM=CQ，∵∠DCQ+∠QCB=90°，∴∠BCM+∠QCB=90°，即∠QCM=90°，PM=PB+BM=PB+DQ=PQ．在△CPQ与△CPM中，CP=CP，PQ=PM，CQ=CM，∴△CPQ≌△CPM（SSS），∴∠PCQ=∠PCM=∠QCM=45°．【点评】熟练掌握正方形的性质，会运用正方形的性质进行一些简单的运算．15．有两张完全重合的矩形纸片，小亮同学将其中一张绕点A顺时针旋转90°后得到矩形AMEF（如图1），连接BD、MF，若此时他测得BD=8cm，∠ADB=30°．（1）请直接写出AF的长；（2）小红同学用剪刀将△BCD与△MEF剪去，与小亮同学继续探究．他们将△ABD绕点A顺时针旋转得△AB1D1，AD1交FM于点K（如图2），设旋转角为β（0°＜β＜90°），当△AFK为等腰三角形时，求△AFK的面积（保留根号）．【考点】锐角三角函数的定义；旋转的性质．【专题】操作型．【分析】（1）根据旋转的性质可知△AFM≌△ADB，则AF=AD=BD•cos∠ADB=8×=4cm；（2）当△AFK为等腰三角形时，由于AM＜AF，那么A不能是等腰△AFK的顶点，则分两种情况：①K为顶点，即AK=FK时；②F为顶点，即AF=FK．针对每一种情况，利用三角形的面积公式，可分别求出△AFK的面积．【解答】解：（1）AF=；（2）△AFK为等腰三角形时，分两种情况：①当AK=FK时，如图．过点K作KN⊥AF于N，则KN⊥AF，AN=NF=AF=2cm．在直角△NFK中，∠KNF=90°，∠F=30°，∴KN=NF•tan∠F=2cm．∴△AFK的面积=×AF×KN=；②当AF=FK时，如图．过点K作KP⊥AF于P．在直角△PFK中，∠KPF=90°，∠F=30°，∴KP=KF=2cm．∴△AFK的面积=×AF×KP=12cm2．【点评】本题考查旋转的性质，旋转变化前后，对应线段、对应角分别相等，图形的大小、形状都不改变．注意（2）中需分情况讨论△AFK为等腰三角形时的不同分类，不要漏解．。

中考数学压轴题之旋转(中考题型整理,突破提升)及详细答案

【答案】解：（1）CG=EG （2）（1）中结论没有发生变化，即 EG=CG．证明：连接 AG，过 G 点作 MN⊥AD 于 M，与 EF 的延长线交于 N 点．
在△ DAG 与△ DCG 中， ∵ AD=CD，∠ ADG=∠ CDG，DG=DG， ∴ △ DAG≌ △ DCG． ∴ AG=CG．在△ DMG 与△ FNG 中， ∵ ∠ DGM=∠ FGN，FG=DG，∠ MDG=∠ NFG， ∴ △ DMG≌ △ FNG． ∴ MG=NG 在矩形 AENM 中，AM=EN．在 Rt△ AMG 与 Rt△ ENG 中， ∵ AM=EN， MG=NG， ∴ △ AMG≌ △ ENG． ∴ AG=EG ∴ EG=CG．（3）（1）中的结论仍然成立．
4．如图（1）所示，将一个腰长为 2 等腰直角△ BCD 和直角边长为 2、宽为 1 的直角△ CED 拼在一起．现将△ CED 绕点 C 顺时针旋转至△ CE’D’，旋转角为 a．（1）如图（2），旋转角 a=30°时，点 D′到 CD 边的距离 D’A=______．求证：四边形 ACED′ 为矩形；（2）如图（1），△ CED 绕点 C 顺时针旋转一周的过程中，在 BC 上如何取点 G，使得 GD’=E’D；并说明理由．
【答案】（1）详见解析；（2）FE·sin( －90°) 【解析】【分析】 (1)由四边形 ABCD 是平行四边形得 AF∥ BE，所以∠ FAE=∠ BEA，由折叠的性质得 ∠ BAE=∠ FAE，∠ BEA=∠ FEA,所以∠ BAE=∠ FEA，故有 AB∥ FE，因此四边形 ABEF 是平行四边形，又 BE=EF,因此可得结论； (2)根据点 M 在线段 BE 上和 EC 上两种情况证明∠ ENG＝90°－，利用菱形的性质得到

2019-2020年中考数学专题复习题型九折叠旋转问题含解析(最新整理)

2019-2020 年中考数学专题复习题型九折叠旋转问题含解析1.（xx 贵州安顺第7 题）如图，矩形纸片ABCD 中，AD=4cm，把纸片沿直线AC 折叠，点B 落在E 处，AE 交DC 于点O，若AO=5cm，则AB 的长为（）A．6cm B．7cm C．8cm D．9cm【答案】C．2.（xx 湖南张家界第 14 题）如图，在正方形ABCD 中，AD=，把边BC 绕点B 逆时针旋转30°得到线段BP，连接AP 并延长交CD 于点E，连接P C，则三角形PCE 的面积为．【答案】．3.（xx·湖北荆门·3分）两个全等的三角尺重叠放在△ACB 的位置，将其中一个三角尺绕着点C 按逆时针方向旋转至△DCE 的位置，使点A 恰好落在边DE 上，AB 与CE 相交于点F．已知∠ACB=∠DCE=90°，∠B=30°，AB=8cm，则CF= 2 cm．4.（xx 甘肃兰州第 14 题）如图，在正方形和正方形中，点在上，，将正方形绕点顺时针旋转，得到正方形，此时点在上，连接，则( )A. B. C. D.【答案】AA5.（xx 浙江嘉兴第16 题）一副含和角的三角板和叠合在一起，边与重合，（如图1），点为边的中点，边与相交于点，此时线段的长是．现将三角板绕点按顺时针方向旋转（如图2），在从到的变化过程中，点相应移动的路径长共为．（结果保留根号）【答案】12－12．12－18．6.(xx 辽宁沈阳第16 题)如图，在矩形中，,将矩形绕点按顺时针方向旋转得到矩形，点落在矩形的边上，连接，则的长是.【答案】.7.（xx 年重庆A4 分）如图，矩形ABCD 中，连接BD，∠DBC 的角平分线BE 交DC 于点E，现把△BCE 绕点B 逆时针旋转，记旋转后的△BCE 为，当射线和射线都与线段AD 相交时，设交点分别F，G，若△BFD 为等腰三角形，则线段DG 长为▲ .【答案】.8.（xx 年上海4 分）已知在△ABC 中，．将△ABC 绕点A 旋转，使点B 落在原△ABC 的点C 处，此时点C 落在点D处．延长线段AD，交原△ABC 的边BC 的延长线于点E，那么线段DE 的长等于▲．【答案】.9.（xx 年福建福州4 分）如图，在中，=90°，，将绕点C逆时针转60°，得到△MNC，则BM的长是▲．【答案】.10.（xx 江苏无锡第10 题）如图，△ABC 中，∠BAC=90°，AB=3，AC=4，点D 是BC 的中点，将△ABD 沿AD 翻折得到△AED，连CE，则线段CE 的长等于（ D ）A．2 B． C． D．11.（xx 新疆乌鲁木齐第 9 题）如图，在矩形中，点在上，点在上，把这个矩形沿折叠后，使点恰好落在边上的点处，若矩形面积为且，则折痕的长为（ C ）A．B． C. D．12.（xx 重庆A 卷第18 题）如图，正方形ABCD 中，AD=4，点E 是对角线AC 上一点，连接DE，过点E 作EF⊥ED，交AB 于点F，连接DF，交AC 于点G，将△EFG 沿EF 翻折，得到△EFM，连接DM，交EF 于点N，若点F 是AB 的中点，则△EMN 的周长是．13.(xx 河南第 15 题)如图，在中，，，点，分别是边，上的动点，沿所在的直线折叠，使点的对应点始终落在边上. 若为直角三角形，则的长为．【答案】1 或.14.（xx 江苏苏州第18 题）如图，在矩形中，将绕点按逆时针方向旋转一定角度后，的对应边交边于点．连接、，若，，则（结果保留根号）．【答案】.15.（xx 海南第 17 题）如图，在矩形ABCD 中，AB=3，AD=5，点E 在DC 上，将矩形ABCD 沿AE 折叠，点D 恰好落在BC 边上的点F 处，那么cos∠EFC 的值是．【答案】.16.（xx·黑龙江齐齐哈尔·3分）如图，在边长为2 的菱形ABCD 中，∠A=60°，点M 是AD 边的中点，连接MC，将菱形ABCD 翻折，使点A 落在线段CM 上的点E 处，折痕交AB 于点N，则线段EC 的长为﹣1 ．17.（xx·吉林·3分）在三角形纸片ABC 中，∠C=90°，∠B=30°，点D（不与B，C 重合）是BC 上任意一点，将此三角形纸片按下列方式折叠，若EF的长度为a，则△DEF的周长为 3a（用含a的式子表示）．18.（xx 河南）如图，已知AD∥BC，AB⊥BC，AB=3，点E 为射线BC 上一个动点，连接AE，将△ABE 沿AE 折叠，点B 落在点B′处，过点B′作AD 的垂线，分别交AD，BC 于点M，N．当点B′为线段MN 的三等分点时，BE 的长为或．19.（xx 年河南3 分）如图，正方形ABCD 的边长是16，点E 在边AB 上，AE=3，点F 是边BC 上不与点B、C 重合的一个动点，把△EBF 沿EF 折叠，点B 落在B′处，若△CDB′恰为等腰三角形，则DB′的长为▲．【答案】16 或.20.（xx 年江苏泰州3 分）如图，矩形中，AB=8，BC=6，P 为AD 上一点，将△ABP 沿BP 翻折至△EBP，PE 与CD 相交于点O，且OE=OD，则AP 的长为▲．【答案】.21.（xx 湖北鄂州第8 题3 分）如图，在矩形ABCD 中，AB=8，BC=12，点E 是BC 的中点，连接AE，将△ABE 沿AE 折叠，点B 落在点F 处，连接FC，则sin∠ECF =（）A.B．C．D．【答案】D.22.（xx•四川自贡,第10 题4 分）如图，在矩形中，,是边的中点，是线段边上的动点，将△沿所在直线折叠得到△, 连接,则的最小值是（ A ）B'A DEB F CA.B.6 C. D.423.（xx•绵阳第 12 题，3 分）如图，D 是等边△ABC 边AB 上的一点，且AD：DB=1：2，现将△ABC 折叠，使点C 与D 重合，折痕为E F，点E，F 分别在A C 和B C 上，则C E：CF=（B ）A.B．C．D．24.（xx•四川省内江市，第 14 题，5分）如图，在四边形ABCD 中，AD∥BC，∠C=90°，E 为CD 上一点，分别以EA，EB 为折痕将两个角（∠D，∠C）向内折叠，点C，D 恰好落在AB 边的点F 处．若AD=2，BC=3，则EF 的长为．25.（xx•浙江滨州,第17 题4 分）如图，在平面直角坐标系中，将矩形AOCD沿直线AE折叠（点E在边DC上），折叠后顶点D恰好落在边OC上的点F处.若点D的坐标为(10,8），则点E的坐标为.【答案】（10,3）“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。

中考数学折叠,旋转问题专题含答案

【经典例题1】如图，CD是⊙O的直径，AB是⊙O的弦，AB⊥CD，垂足为G，OG：OC＝3：5，AB＝8．（1）求⊙O的半径；（2）点E为圆上一点，∠ECD＝15°，将沿弦CE翻折，交CD于点F，求图中阴影部分的面积．【解析】（1）连接AO，如右图1所示，∵CD为⊙O的直径，AB⊥CD，AB＝8，∴AG＝＝4，∵OG：OC＝3：5，AB⊥CD，垂足为G，∴设⊙O的半径为5k，则OG＝3k，∴（3k）2+42＝（5k）2，解得，k＝1或k＝﹣1（舍去），∴5k＝5，即⊙O的半径是5；（2）如图2所示，将阴影部分沿CE翻折，点F的对应点为M，∵∠ECD＝15°，由对称性可知，∠DCM＝30°，S阴影＝S弓形CBM，连接OM，则∠MOD＝60°，∴∠MOC＝120°，过点M作MN⊥CD于点N，∴MN＝MO•sin60°＝5×，∴S阴影＝S扇形OMC﹣S△OMC＝＝，即图中阴影部分的面积是：．练习1-1如图，在⊙O中，点C在优弧上，将弧沿BC折叠后刚好经过AB 的中点D，连接AC，CD．则下列结论中错误的是（）A．AC＝CD B．+＝C．OD⊥AB D．CD平分∠ACB 【解析】A、过D作DD'⊥BC，交⊙O于D'，连接CD'、BD'，由折叠得：CD＝CD'，∠ABC＝∠CBD'，∴AC＝CD'＝CD，故①正确；B、∵AC＝CD'，∴，由折叠得：，∴＝，故②正确；C、∵D为AB的中点，∴OD⊥AB，故③正确；D、延长OD交⊙O于E，连接CE，∵OD⊥AB，∴∠ACE＝∠BCE，∴CD不平分∠ACB，故④错误；故选：D．练习1-2如图，AB是⊙O的弦，点C在上，点D是AB的中点．将在沿AC 折叠后恰好经过点D，若⊙O的半径为2，AB＝8．则AC的长是（）A．6B．C．2D．4【解析】如图，延长BO交⊙O于E，连接AE，OA，OD，OC，BC，作CH⊥AB 于H．∵AD＝DB，∴OD⊥AB，∴∠ADO＝90°，∵OA＝2，AD＝DB＝4，∴OD＝＝2，∵BE是直径，∴∠BAE＝90°，∵AD＝DB，EO＝OB，∴OD∥AE，AE＝2OD＝4，∴AE＝AD，∴＝，∴＝，∴∠CAE＝∠CAH＝45°，∴∠BOC＝2∠CAB＝90°，∴BC＝OC＝2，∵CH⊥AB，∴∠CAH＝∠ACH＝45°，∴AH＝CH，设AH＝CH＝x，则BH＝8﹣x，在Rt△BCH中，∵CH2+BH2＝BC2，∴x2+（8﹣x）2＝（2）2，∴x＝6或2（舍弃），在Rt△ACH中，∵AC＝，∴AC＝6．故选：A．练习1-3在扇形AOB中，∠AOB＝75°，半径OA＝12，点P为AO上任一点（不与A、O重合）．（1）如图1，Q是OB上一点，若OP＝OQ，求证：BP＝AQ．（2）如图2，将扇形沿BP折叠，得到O的对称点O'．①若点O'落在上，求的长．②当BO'与扇形AOB所在的圆相切时，求折痕的长．（注：本题结果不取近似值）【解析】（1）证明：∵BO＝AO，∠O＝∠O，OP＝OQ，∴△BOP≌△AOQ（SAS）．∴BP＝AQ．（2）解：①如图1，点O'落在上，连接OO'，∵将扇形沿BP折叠，得到O的对称点O'，∴OB＝O'B，∵OB＝OO'，∴△BOO'是等边三角形，∴∠O'OB＝60°．∵∠AOB＝75°，∴∠AOO'＝15°．∴的长为．②BO'与扇形AOB所在的圆相切时，如图2所示，∴∠OBO'＝90°．∴∠OBP＝45°．过点O作OC⊥BP于点C，∵OA＝OB＝12，∠COB＝∠OBP＝45°，∴．又∵∠AOB＝75°，∠COB＝45°，∴∠POC＝30°，∴．∴．∴折痕的长为．旋转类【经典例题2】如图1，在锐角△ABC中，AB=5，AC=42，∠ACB=45∘. 计算：求BC的长；操作：将图1中的△ABC绕点B按逆时针方向旋转，得到△A1BC1.如图2，当点C1在线段CA的延长线上时。

中考数学专题旋转练习题(8套)含答案

旋转基础练习一一、选择题1．在26个英文大写字母中，通过旋转180°后能与原字母重合的有（）A．6个B．7个C．8个D．9个2．从5点15分到5点20分，分针旋转的度数为（）A．20°B．26°C．30°D．36°3．如图1，在Rt△ABC中，∠ACB=90°，∠A=40°，以直角顶点C为旋转中心，将△ABC 旋转到△A′B′C的位置，其中A′、B′分别是A、B的对应点，且点B在斜边A′B′上，直角边CA′交AB于D，则旋转角等于（）A．70°B．80°C．60°D．50°(图1) (图2) (图3)二、填空题．1．在平面内，将一个图形绕一个定点沿着某个方向转动一个角度，这样的图形运动称为________，这个定点称为________，转动的角为________．2．如图2，△ABC与△ADE都是等腰直角三角形，∠C和∠AED都是直角，点E在AB 上，如果△ABC经旋转后能与△ADE重合，那么旋转中心是点_________；旋转的度数是__________．3．如图3，△ABC为等边三角形，D为△ABC内一点，△ABD经过旋转后到达△ACP的位置，则，（1）旋转中心是________；（2）旋转角度是________；（3）△ADP是________三角形．三、解答题．1．阅读下面材料：如图4，把△ABC沿直线BC平行移动线段BC的长度，可以变到△ECD的位置．如图5，以BC为轴把△ABC翻折180°，可以变到△DBC的位置．(图4) (图5) (图6) (图7) 如图6，以A点为中心，把△ABC旋转90°，可以变到△AED的位置，像这样，其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的，这种只改变位置，不改变形状和大小的图形变换，叫做三角形的全等变换．回答下列问题如图7，在正方形ABCD 中，E 是AD 的中点，F 是BA 延长线上一点，AF=21AB ．（1）在如图7所示，可以通过平行移动、翻折、旋转中的哪一种方法，使△ABE 移到△ADF 的位置？（2）指出如图7所示中的线段BE 与DF 之间的关系．2．一块等边三角形木块，边长为1，如图，现将木块沿水平线翻滚五个三角形，那么B 点从开始至结束所走过的路径长是多少？答案:一、1．B 2．C 3．B二、1．旋转旋转中心旋转角 2．A 45° 3．点A 60° 等边三、1．（1）通过旋转，即以点A 为旋转中心，将△ABE 逆时针旋转90°．（2）BE=DF ，BE ⊥DF2．翻滚一次滚120° 翻滚五个三角形，正好翻滚一个圆，所以所走路径是2．旋转基础练习二一、选择题1．△ABC 绕着A 点旋转后得到△AB′C′，若∠BAC′=130°，∠BAC=80°，则旋转角等于（） A ．50° B ．210° C ．50°或210° D ．130° 2．在图形旋转中，下列说法错误的是（）A ．在图形上的每一点到旋转中心的距离相等B ．图形上每一点转动的角度相同C ．图形上可能存在不动的点D ．图形上任意两点的连线与其对应两点的连线长度相等3．如图，下面的四个图案中，既包含图形的旋转，又包含图形的轴对称的是（）二、填空题1．在作旋转图形中，各对应点与旋转中心的距离________．2．如图，△ABC和△ADE均是顶角为42°的等腰三角形，BC、DE分别是底边，图中的△ABD绕A旋转42°后得到的图形是________，它们之间的关系是______，其中BD CE（填“>”,“<”或“=”）．3．如图，自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F，∠EAF=45°，在保持∠EAF=45°的前提下，当点E、F分别在边BC、CD上移动时，BE+DF与EF的关系是________．三、解答题1．如图，正方形ABCD的中心为O，M为边上任意一点，过OM随意连一条曲线，将所画的曲线绕O点按同一方向连续旋转3次，每次旋转角度都是90°，这四个部分之间有何关系？2．如图，以△ABC的三顶点为圆心，半径为1，作两两不相交的扇形，则图中三个扇形面积之和是多少？3．如图，已知正方形ABCD的对角线交于O点，若点E在AC的延长线上，AG⊥EB，交EB的延长线于点G，AG的延长线交DB的延长线于点F，则△OAF与△OBE重合吗？如果重合给予证明，如果不重合请说明理由？答案:一、1．C 2．A3．D二、1．相等2．△ACE 图形全等= 3．相等三、1．这四个部分是全等图形2．∵∠A+∠B+∠C=180°，∴绕AB、AC的中点旋转180°，可以得到一个半圆，∴面积之和=21． 3．重合：证明：∵EG ⊥AF ∴∠2+∠3=90° ∵∠3+∠1+90°=180° ∵∠1+∠3=90° ∴∠1=∠2同理∠E=∠F ，∵四边形ABCD 是正方形，∴AB=BC ∴△ABF ≌△BCE ，∴BF=CE ，∴OE=OF ，∵OA=OB ∴△OBE 绕O 点旋转90°便可和△OAF 重合．旋转基础练习三一、选择题1．如图，摆放有五杂梅花，下列说法错误的是（以中心梅花为初始位置）（） A ．左上角的梅花只需沿对角线平移即可B ．右上角的梅花需先沿对角线平移后，再顺时针旋转45°C ．右下角的梅花需先沿对角线平移后，再顺时针旋转180D ．左下角的梅花需先沿对角线平移后，再顺时针旋转90° 2．同学们曾玩过万花筒吧，它是由三块等宽等长的玻璃镜片围成的，如图是看到的万花筒的一个图案，图中所有三角形均是等边三角形，其中的菱形AEFG 可以看成把菱形ABCD 以 A 为中心（）A ．顺时针旋转60°得到的B ．顺时针旋转120°得到的C ．逆时针旋转60°得到的D ．逆时针旋转120°得到的3．下面的图形中，绕着一个点旋转120°后，能与原来的位置重合的是（）A ．（1），（4）B ．（1），（3）C ．（1），（2）D ．（3），（4）二、填空题1．如图，五角星也可以看作是一个三角形绕中心点旋转_______次得到的，每次旋转的角度是________．2．图形之间的变换关系包括平移、_______、轴对称以及它们的组合变换．3．如图，过圆心O和图上一点A连一条曲线，将OA绕O点按同一方向连续旋转三次，每次旋转90°，把圆分成四部分，这四部分面积_________．三、解答题．1．请你利用线段、三角形、菱形、正方形、圆作为“基本图案”绘制一幅以“校运动会”为主题的徽标．2．如图，是某设计师设计的方桌布图案的一部分，请你运用旋转的方法，将该图案绕原点O顺时针依次旋转90°、180°、270°，并画出图形，你来试一试吧！但是涂阴影时，要注意利用旋转变换的特点，不要涂错了位置，否则你将得不到理想的效果，并且还要扣分的噢！3．如图，△ABC的直角三角形，BC是斜边，将△ABP绕点A逆时针旋转后，能与△AC P′重合，如果AP=3，求PP′的长．答案:一、1．D 2．D 3．C二、1．4 72°2．旋转3．相等三、1．答案不唯一，学生设计的只要符合题目的要求，都应给予鼓励．2．略3．∵△ABP绕点A逆时针旋转后，能与△ACP′重合，∴AP′=AP，∠CAP′=∠BAP，∴∠PAP′=∠PAC+∠CAP′=∠PAC+∠BAP=∠BAC=90°，△PAP′为等腰直角三角形，PP′为斜边，∴旋转基础练习四一、选择题1．在英文字母VWXYZ中，是中心对称的英文字母的个数有（）A．1个B．2个C．3个D．4个2．下面的图案中，是中心对称图形的个数有（）A．1个B．2个C．3个D．4个3．如图，把一张长方形ABCD的纸片，沿EF折叠后，ED′与BC的交点为G，点D、C分别落在D′、C′的位置上，若∠EFG=55°，则∠1=（）A．55°B．125°C．70°D．110°二、填空题1．关于某一点成中心对称的两个图形，对称点连线必通过_________．2．把一个图形绕着某一个点旋转180°，如果它能够与另一个图形重合，那么就说这两个图形是_________图形．3．用两个全等的直角非等腰三角形可以拼成下面图形中的哪几种：_______（填序号）（1）长方形；（2）菱形；（3）正方形；（4）一般的平行四边形；（5）等腰三角形；（6）梯形．三、解答题1．仔细观察所列的26个英文字母，将相应的字母填入下表中适当的空格内．A2．如图，在正方形ABCD中，作出关于P点的中心对称图形，并写出作法．3．如图，是由两个半圆组成的图形，已知点B是AC的中点，画出此图形关于点B成中心对称的图形．答案:一、1．B 2．D 3．D二、1．这一点（对称中心）2．中心对称3．（1）（4）（5）三、1．略2．作法：（1）延长CB且BC′=BC；（2）延长DB且BD′=DB，延长AB且使BA′=BA；（3）连结A′D′、D′C′、C′B则四边形A′BC′D′即为所求作的中心对称图形，如图所示．3.略.旋转基础练习五一、选择题1．下面图形中既是轴对称图形又是中心对称图形的是（）A．直角B．等边三角形C．直角梯形D．两条相交直线2．下列命题中真命题是（）A．两个等腰三角形一定全等B．正多边形的每一个内角的度数随边数增多而减少C．菱形既是中心对称图形，又是轴对称图形D．两直线平行，同旁内角相等3．将矩形ABCD沿AE折叠，得到如图的所示的图形，已知∠CED′=60°，则∠AED的大小是（）A．60°B．50°C．75°D．55°二、填空题1．关于中心对称的两个图形，对称点所连线段都经过__________，而且被对称中心所________．2．关于中心对称的两个图形是_________图形．3．线段既是轴对称图形又是中心对称图形，它的对称轴是_________，它的对称中心是__________．三、解答题1．分别画出与已知四边形ABCD成中心对称的四边形，使它们满足以下条件：21085（1）以顶点A 为对称中心，（2）以BC 边的中点K 为对称中心．2．如图，已知一个圆和点O ，画一个圆，使它与已知圆关于点O 成中心对称．3．如图，A 、B 、C 是新建的三个居民小区，我们已经在到三个小区距离相等的地方修建了一所学校M ，现计划修建居民小区D ，其要求：（1）到学校的距离与其它小区到学校的距离相等；（2）控制人口密度，有利于生态环境建设，试写居民小区D 的位置．答案:一、1．D 2．C 3．A二、1．对称中心平分 2．全等 3．线段中垂线，线段中点．三、1．略 2．作出已知圆圆心关于O 点的对称点O′，以O′为圆心，已知圆的半径为半径作圆．3．连结AB 、AC ，分别作AB 、AC 的中垂线PQ 、GH 相交于M ，学校M 所在位置，就是△ABC 外接圆的圆心，小区D 是在劣弧BC 的中点即满足题意．旋转基础练习六一、选择题1．下列图形中，既是轴对称图形，又是中心对称图形的是（） A ．等边三角形 B ．等腰梯形 C ．平行四边形 D ．正六边形2．下列图形中，是中心对称图形，但不是轴对称图形的是（）A ．正方形B ．矩形C ．菱形D ．平行四边形3．如图所示，平放在正立镜子前的桌面上的数码“21085”在镜子中的像是（）A ．21085B ．28015C ．58012D ．51082二、填空题1．把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做__________．2．请你写出你所熟悉的三个中心对称图形_________．3．中心对称图形具有什么特点（至少写出两个）_____________．三、解答题1．在平面内，如果一个图形绕一个定点旋转一定的角度后能与自身重合，那么就称这个图形是旋转对称图形，转动的这个角称为这个图形的一个旋转角，例如：正方形绕着它的对角线的交点旋转90°后能与自身重合，所以正方形是旋转对称图形，应有一个旋转角为90°．（1）判断下列命题的真假（在相应括号内填上“真”或“假”） ①等腰梯形是旋转对称图形，它有一个旋转角为180°；（） ②矩形是旋转对称图形，它有一个旋转角为180°；（）（2）填空：下列图形中是旋转对称图形，且有一个旋转角为120°是_____．（写出所有正确结论的序号）①正三角形；②正方形；③正六边形；④正八边形．（3）写出两个多边形，它们都是旋转对称图形，却有一个旋转角为72°，并且分别满足下列条件：①是轴对称图形，但不是中心对称图形；②既是轴对称图形，又是中心对称图形．2．如图，将矩形A 1B 1C 1D 1沿EF 折叠，使B 1点落在A 1D 1边上的B 处；沿BG 折叠，使D 1点落在D 处且BD 过F 点．（1）求证：四边形BEFG 是平行四边形；（2）连接BB ，判断△B 1BG 的形状，并写出判断过程．FG DECA B1A 1B 1C 1D3．如图，直线y=2x+2与x 轴、y 轴分别交于A 、B 两点，将△AOB 绕点O 顺时针旋转90°得到△A 1OB 1．（1）在图中画出△A 1OB 1；（2）设过A 、A 1、B 三点的函数解析式为y=ax 2+bx+c ，求这个解析式．答案：一、1．D 2．D 3．D二、1．中心对称图形 2．答案不唯一 3．答案不唯一三、1．（1）①假 ②真（2）①③（3）①例如正五边形正十五边形 •②例如正十边正二十边形2．（1）证明：∵A 1D 1∥B 1C 1，∴∠A 1BD=∠C 1FB 又∵四边形ABEF 是由四边形A 1B 1EF 翻折的，∴∠B 1FE=∠EFB ，同理可得：∠FBG=∠D 1BG ， ∴∠EFB=90°-21∠C 1FB ，∠FBG=90°-21∠A 1BD ， ∴∠EFB=∠FBG∴EF ∥BG ，∵EB ∥FG ∴四边形BEFG 是平行四边形．（2）直角三角形，理由：连结BB ，∵BD 1∥FC 1，∴∠BGF=∠D 1BG ，∴∠FGB=∠FBG 同理可得：∠B 1BF=∠FB 1B ． ∴∠B 1BG=90°，∴△B 1BG 是直角三角形 3．解：（1）如右图所示（2）由题意知A 、A 1、B 1三点的坐标分别是（-1，0），（0，1），（2，0）∴⎩=++⎪⎨=⎪⎧=-+a b cc a b c 04210 解这个方程组得⎩⎪⎪=⎪⎨=⎪⎪⎪=-⎧c b a 12121∴所求五数解析式为y=-21x 2+21x+1．旋转基础练习七一、选择题1．下列函数中，图象一定关于原点对称的图象是（） A ．y=x1B ．y=2x+1C ．y=-2x+1D ．以上三种都不可能2．如图，已知矩形ABCD 周长为56cm ，O 是对称线交点，点O 到矩形两条邻边的距离之差等于8cm ，则矩形边长中较长的一边等于（）A ．8cmB ．22cmC ．24cmD ．11cm 二、填空题1．如果点P （-3，1），那么点P （-3，1）关于原点的对称点P′的坐标是P′_______． 2．写出函数y=-x 3与y=x3具有的一个共同性质________（用对称的观点写）． DCAB O三、解答题1．如图，在平面直角坐标系中，A （-3，1），B （-2，3），C （0，2），画出△ABC 关于x 轴对称的△A′B′C′，再画出△A′B′C′关于y 轴对称的△A″B″C″，那么△A″B″C″与△ABC 有什么关系，请说明理由．2．如图，直线AB 与x 轴、y 轴分别相交于A 、B 两点，且A （0，3），B （3，0），现将直线AB 绕点O 顺时针旋转90°得到直线A 1B 1．（1）在图中画出直线A 1B 1；（2）求出过线段A 1B 1中点的反比例函数解析式；（3）是否存在另一条与直线A 1B 1平行的直线y=kx+b （我们发现互相平行的两条直线斜率k 相等）它与双曲线只有一个交点，若存在，求此直线的解析式；若不存在，请说明不存在的理由．答案:一、1．A 2．B 二、1．（3，-1） 2．答案不唯一参考答案：关于原点的中心对称图形．三、1．画图略，△A″B″C″与△ABC 的关系是关于原点对称． 2．（1）如右图所示，连结A 1B 1；（2）A 1B 1中点P （1.5，-1.5），设反比例函数解析式为y=x k ，则y=-x2.25．（3）A 1B 1：设y=k 1x+b 1 ⎩=-⎨⎧=-k b 033311⎩=-⎨⎧=b k 3111∴y=x+3∵与A 1B 1直线平行且与y=x2.25相切的直线是A 1B 1•旋转而得到的． ∴所求的直线是y=x+3，下面证明y=x+3与y=-x2.25相切， ⎩⎪=-⎨⎪⎧=+x y y x 2.253 ⇒x 2+3x+2.25=0，b 2-4ac=9-4×1×2.25=0，∴y=x+3与y=-x2.25相切．旋转基础练习八一、选择题1．在图所示的4个图案中既包含图形的旋转，还有图形轴对称是（）2．将三角形绕直线L 旋转一周，可以得到如图所示的立体图形的是（）二、填空题1．基本图案在轴对称、平移、旋转变化的过程中，图形的______和______都保持不变．2．如上右图，是由________关系得到的图形．三、解答题 1．（1）图案设计人员在进行图设计时，常常用一个模具板来设计一幅幅美丽漂亮的图案，你能说出用同一模具板设计出的两个图案之间是什么关系吗？（2）现利用同一模具板经过平移、旋转、轴对称设计一个图案，并说明你所表达的意义．2．如图，你能利用平移、旋转或轴对称这样的变化过程来分析它的形成过程吗？答案:一、1．D 2．B二、1．形状大小2．旋转三、1．（1）用同一块模块设计出的两个图案之间可能是由平移、旋转、•轴对称变化得到的，或者是由这三种变化的组合而成的；（2）略2．略。

2021年中考真题精选5——翻折、旋转

2021年中考真题精选5 ——翻折、旋转1.（2021•宿迁）如图，折叠矩形纸片ABCD，使点B落在点D处，折痕为MN，已知AB＝8，AD＝4，则MN的长是（）A．B．2C．D．42.（2021•苏州）如图，在平行四边形ABCD中，将△ABC沿着AC所在的直线折叠得到△AB′C，B′C交AD于点E，连接B′D，若∠B＝60°，∠ACB＝45°，AC＝，则B′D的长是（）A．1B．C．D．3.（2021•扬州）如图，一次函数y＝x+的图象与x轴、y轴分别交于点A，B，把直线AB绕点B顺时针旋转30°交x轴于点C，则线段AC长为（）A．+B．3C．2+D．+4.（2021•河南）如图，▱OABC的顶点O（0，0），A（1，2），点C在x轴的正半轴上，延长BA交y轴于点D．将△ODA绕点O顺时针旋转得到△OD′A′，当点D的对应点D′落在OA上时，D′A′的延长线恰好经过点C，则点C的坐标为（）A．（2，0）B．（2，0）C．（2+1，0）D．（2+1，0）5.（2021•衡阳）如图，矩形纸片ABCD，AB＝4，BC＝8，点M、N分别在矩形的边AD、BC上，将矩形纸片沿直线MN折叠，使点C落在矩形的边AD上，记为点P，点D落在G处，连接PC，交MN于点Q，连接CM．下列结论：①四边形CMPN是菱形；②点P与点A重合时，MN＝5；③△PQM的面积S的取值范围是4≤S≤5．其中所有正确结论的序号是（）A．①②③B．①②C．①③D．②③6.（2021•武汉）如图，AB是⊙O的直径，BC是⊙O的弦，先将沿BC翻折交AB于点D，再将沿AB翻折交BC于点E．若＝，设∠ABC＝α，则α所在的范围是（）A．21.9°＜α＜22.3°B．22.3°＜α＜22.7°C．22.7°＜α＜23.1°D．23.1°＜α＜23.5°7.（2021•广西）如图，矩形纸片ABCD，AD：AB＝：1，点E，F分别在AD，BC上，把纸片如图沿EF折叠，点A，B的对应点分别为A′，B′，连接AA′并延长交线段CD于点G，则的值为（）A．B．C．D．8.（2021•台州）如图，将长、宽分别为12cm，3cm的长方形纸片分别沿AB，AC折叠，点M，N恰好重合于点P．若∠α＝60°，则折叠后的图案（阴影部分）面积为（）A．（36）cm2B．（36）cm2C．24cm2D．36cm29.（2021•丽水）如图，在Rt△ABC纸片中，∠ACB＝90°，AC＝4，BC＝3，点D，E分别在AB，AC上，连结DE，将△ADE沿DE翻折，使点A的对应点F落在BC的延长线上，若FD平分∠EFB，则AD的长为（）A．B．C．D．10.（2021•通辽）如图，已知AD∥BC，AB⊥BC，AB＝3，点E为射线BC上一个动点，连接AE，将△ABE沿AE折叠，点B落在点B′处，过点B′作AD的垂线，分别交AD，BC于M，N两点，当B′为线段MN的三等分点时，BE的长为（）A．B．C．或D．或11.（2021•自贡）如图，在正方形ABCD中，AB＝6，M是AD边上的一点，AM：MD＝1：2．将△BMA沿BM对折至△BMN，连接DN，则DN的长是（）A．B．C．3D．12.（2021•自贡）如图，直线y＝﹣2x+2与坐标轴交于A、B两点，点P是线段AB上的一个动点，过点P作y轴的平行线交直线y＝﹣x+3于点Q，△OPQ绕点O顺时针旋转45°，边PQ扫过区域（阴影部分）面积的最大值是（）A．πB．πC．πD．π13.（2021•宜宾）如图，在矩形纸片ABCD中，点E、F分别在矩形的边AB、AD上，将矩形纸片沿CE、CF折叠，点B落在H处，点D落在G处，点C、H、G恰好在同一直线上，若AB＝6，AD＝4，BE＝2，则DF的长是（）A．2B．C．D．314.（2021•南充）如图，在矩形ABCD中，AB＝15，BC＝20，把边AB沿对角线BD平移，点A′，B′分别对应点A，B给出下列结论：①顺次连接点A′，B′，C，D的图形是平行四边形；②点C到它关于直线AA′的对称点的距离为48；③A′C﹣B′C的最大值为15；④A′C+B′C的最小值为9．其中正确结论的个数是（）A．1个B．2个C．3个D．4个15.（2021•鄂尔多斯）如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，将边BC沿CN折叠，使点B落在AB上的点B′处，再将边AC沿CM折叠，使点A落在CB′的延长线上的点A′处，两条折痕与斜边AB分别交于点N、M，则线段A′M的长为（）A．B．C．D．16.（2021•阜新）如图，弧长为半圆的弓形在坐标系中，圆心在（0，2）．将弓形沿x轴正方向无滑动滚动，当圆心经过的路径长为2021π时，圆心的横坐标是（）A．2020πB．1010π+2020C．2021πD．1011π+2020 17.（2021•桂林）如图，正方形OABC的边长为2，将正方形OABC绕点O逆时针旋转角α（0°＜α＜180°）得到正方形OA′B′C′，连接BC′，当点A′恰好落在线段BC′上时，线段BC′的长度是．18.（2021•东营）如图，正方形纸片ABCD的边长为12，点F是AD上一点，将△CDF沿CF折叠，点D落在点G处，连接DG并延长交AB于点E．若AE＝5，则GE的长为．19.（2021•大连）如图，在菱形ABCD中，∠BAD＝60°，点E在边BC上，将△ABE沿直线AE翻折180°，得到△AB′E，点B的对应点是点B′．若AB′⊥BD，BE＝2，则BB′的长是．20.（2021•无锡）如图，在Rt△ABC中，∠BAC＝90°，AB＝2，AC＝6，点E在线段AC上，且AE＝1，D是线段BC上的一点，连接DE，将四边形ABDE沿直线DE翻折，得到四边形FGDE，当点G恰好落在线段AC上时，AF＝．21.（2021•盐城）如图，在矩形ABCD中，AB＝3，AD＝4，E、F分别是边BC、CD上一点，EF⊥AE，将△ECF沿EF翻折得△EC′F，连接AC′，当BE＝__________时，△AEC′是以AE为腰的等腰三角形．22.（2021•南京）如图，将▱ABCD绕点A逆时针旋转到▱A′B′C′D′的位置，使点B′落在BC上，B′C′与CD交于点E．若AB＝3，BC＝4，BB′＝1，则CE的长为．23.（2021•江西）如图，将▱ABCD沿对角线AC翻折，点B落在点E处，CE交AD于点F，若∠B＝80°，∠ACE＝2∠ECD，FC＝a，FD＝b，则▱ABCD的周长为．24.（2021•河南）小华用一张直角三角形纸片玩折纸游戏，如图1，在Rt△ABC中，∠ACB＝90°，∠B＝30°，AC＝1．第一步，在AB边上找一点D，将纸片沿CD折叠，点A 落在A'处，如图2；第二步，将纸片沿CA'折叠，点D落在D′处，如图3．当点D′恰好落在原直角三角形纸片的边上时，线段A′D′的长为．25.（2021•杭州）如图是一张矩形纸片ABCD，点M是对角线AC的中点，点E在BC边上，把△DCE沿直线DE折叠，使点C落在对角线AC上的点F处，连接DF，EF．若MF＝AB，则∠DAF＝度．26.（2021•达州）如图，在边长为6的等边△ABC中，点E，F分别是边AC，BC上的动点，且AE＝CF，连接BE，AF交于点P，连接CP，则CP的最小值为．27.（2021•资阳）将一张圆形纸片（圆心为点O）沿直径MN对折后，按图1分成六等份折叠得到图2，将图2沿虚线AB剪开，再将△AOB展开得到如图3的一个六角星．若∠CDE＝75°，则∠OBA的度数为．28.（2021•成都）如图，在矩形ABCD中，AB＝4，AD＝8，点E，F分别在边AD，BC上，且AE＝3，按以下步骤操作：第一步，沿直线EF翻折，点A的对应点A′恰好落在对角线AC上，点B的对应点为B′，则线段BF的长为；第二步，分别在EF，A′B′上取点M，N，沿直线MN继续翻折，使点F与点E重合，则线段MN的长为．29.（2021•凉山州）如图，将△ABC绕点C顺时针旋转120°得到△A'B'C，已知AC＝3，BC＝2，则线段AB扫过的图形（阴影部分）的面积为．30.（2021•威海）如图，先将矩形纸片ABCD沿EF折叠（AB边与DE在CF的异侧），AE交CF于点G；再将纸片折叠，使CG与AE在同一条直线上，折痕为GH．若∠AEF＝α，纸片宽AB＝2cm，则HE＝cm．31.（2021•泰安）如图，将矩形纸片ABCD折叠（AD＞AB），使AB落在AD上，AE为折痕，然后将矩形纸片展开铺在一个平面上，E点不动，将BE边折起，使点B落在AE 上的点G处，连接DE，若DE＝EF，CE＝2，则AD的长为．32.（2021•海南）如图，在矩形ABCD中，AB＝6，AD＝8，将此矩形折叠，使点C与点A重合，点D落在点D′处，折痕为EF，则AD′的长为，DD′的长为．33.（2021•本溪）如图，将正方形纸片ABCD沿PQ折叠，使点C的对称点E落在边AB上，点D的对称点为点F，EF交AD于点G，连接CG交PQ于点H，连接CE．下列四个结论中：①△PBE～△QFG；②S△CEG＝S△CBE+S四边形CDQH；③EC平分∠BEG；④EG2﹣CH2＝GQ•GD，正确的是（填序号即可）．34.（2021•广东）如图，边长为1的正方形ABCD中，点E为AD的中点．连接BE，将△ABE沿BE折叠得到△FBE，BF交AC于点G，求CG的长．35.（2021•乐山）在等腰△ABC中，AB＝AC，点D是BC边上一点（不与点B、C重合），连结AD．（1）如图1，若∠C＝60°，点D关于直线AB的对称点为点E，连结AE，DE，则∠BDE ＝；（2）若∠C＝60°，将线段AD绕点A顺时针旋转60°得到线段AE，连结BE．①在图2中补全图形；②探究CD与BE的数量关系，并证明；（3）如图3，若＝k，且∠ADE＝∠C．试探究BE、BD、AC之间满足的数量关系，并证明．36.（2021•临沂）如图，已知正方形ABCD，点E是BC边上一点，将△ABE沿直线AE折叠，点B落在F处，连接BF并延长，与∠DAF的平分线相交于点H，与AE，CD分别相交于点G，M，连接HC．（1）求证：AG＝GH；（2）若AB＝3，BE＝1，求点D到直线BH的距离；（3）当点E在BC边上（端点除外）运动时，∠BHC的大小是否变化？为什么？37.（2021•菏泽）在矩形ABCD中，BC＝CD，点E、F分别是边AD、BC上的动点，且AE＝CF，连接EF，将矩形ABCD沿EF折叠，点C落在点G处，点D落在点H 处．（1）如图1，当EH与线段BC交于点P时，求证：PE＝PF；（2）如图2，当点P在线段CB的延长线上时，GH交AB于点M，求证：点M在线段EF的垂直平分线上；（3）当AB＝5时，在点E由点A移动到AD中点的过程中，计算出点G运动的路线长．38.（2021•重庆）在等边△ABC中，AB＝6，BD⊥AC，垂足为D，点E为AB边上一点，点F为直线BD上一点，连接EF．（1）将线段EF绕点E逆时针旋转60°得到线段EG，连接FG．①如图1，当点E与点B重合，且GF的延长线过点C时，连接DG，求线段DG的长；②如图2，点E不与点A，B重合，GF的延长线交BC边于点H，连接EH，求证：BE+BH＝BF；（2）如图3，当点E为AB中点时，点M为BE中点，点N在边AC上，且DN＝2NC，点F从BD中点Q沿射线QD运动，将线段EF绕点E顺时针旋转60°得到线段EP，连接FP，当NP+MP最小时，直接写出△DPN的面积．39.（2021•贵港）已知在△ABC中，O为BC边的中点，连接AO，将△AOC绕点O顺时针方向旋转（旋转角为钝角），得到△EOF，连接AE，CF．（1）如图1，当∠BAC＝90°且AB＝AC时，则AE与CF满足的数量关系是；（2）如图2，当∠BAC＝90°且AB≠AC时，（1）中的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由．（3）如图3，延长AO到点D，使OD＝OA，连接DE，当AO＝CF＝5，BC＝6时，求DE的长．40.（2021•本溪）在▱ABCD中，∠BAD＝α，DE平分∠ADC，交对角线AC于点G，交射线AB于点E，将线段EB绕点E顺时针旋转α得线段EP．（1）如图1，当α＝120°时，连接AP，请直接写出线段AP和线段AC的数量关系；（2）如图2，当α＝90°时，过点B作BF⊥EP于点，连接AF，请写出线段AF，AB，AD之间的数量关系，并说明理由；（3）当α＝120°时，连接AP，若BE＝AB，请直接写出△APE与△CDG面积的比值．41.（2021•吉林）如图①，在Rt△ABC中，∠ACB＝90°，∠A＝60°，CD是斜边AB上的中线，点E为射线BC上一点，将△BDE沿DE折叠，点B的对应点为点F．（1）若AB＝a．直接写出CD的长（用含a的代数式表示）；（2）若DF⊥BC，垂足为G，点F与点D在直线CE的异侧，连接CF，如②，判断四边形ADFC的形状，并说明理由；（3）若DF⊥AB，直接写出∠BDE的度数．42.（2021•北京）如图，在△ABC中，AB＝AC，∠BAC＝α，M为BC的中点，点D在MC上，以点A为中心，将线段AD顺时针旋转α得到线段AE，连接BE，DE．（1）比较∠BAE与∠CAD的大小；用等式表示线段BE，BM，MD之间的数量关系，并证明；（2）过点M作AB的垂线，交DE于点N，用等式表示线段NE与ND的数量关系，并证明．43.（2021•鄂尔多斯）旋转是一种重要的图形变换，当图形中有一组邻边相等时往往可以通过旋转解决问题．（1）尝试解决：如图①，在等腰Rt△ABC中，∠BAC＝90°，AB＝AC，点M是BC上的一点，BM＝1cm，CM＝2cm，将△ABM绕点A旋转后得到△ACN，连接MN，则AM ＝cm．（2）类比探究：如图②，在“筝形”四边形ABCD中，AB＝AD＝a，CB＝CD，AB⊥BC 于点B，AD⊥CD于点D，点P、Q分别是AB、AD上的点，且∠PCB+∠QCD＝∠PCQ，求△APQ的周长．（结果用a表示）（3）拓展应用：如图③，已知四边形ABCD，AD＝CD，∠ADC＝60°，∠ABC＝75°，AB＝2，BC＝2，求四边形ABCD的面积．44.（2021•徐州）如图1，正方形ABCD的边长为4，点P在边AD上（P不与A、D重合），连接PB、PC．将线段PB绕点P顺时针旋转90°得到PE，将线段PC绕点P逆时针旋转90°得到PF，连接EF、EA、FD．（1）求证：①△PDF的面积S＝PD2；②EA＝FD；（2）如图2，EA、FD的延长线交于点M，取EF的中点N，连接MN，求MN的取值范围．45.（2021•毕节市）如图1，在Rt△ABC中，∠BAC＝90°，AB＝AC，D为△ABC内一点，将线段AD绕点A逆时针旋转90°得到AE，连接CE，BD的延长线与CE交于点F．（1）求证：BD＝CE，BD⊥CE；（2）如图2，连接AF，DC，已知∠BDC＝135°，判断AF与DC的位置关系，并说明理由．。

专题18 折叠问题-中考数学压轴题精品专题练(第二期)

一、选择题1．（2017四川省乐山市，第10题，3分）如图，平面直角坐标系xOy 中，矩形OABC 的边OA 、OC 分别落在x 、y 轴上，点B 坐标为（6，4），反比例函数x y 6=的图象与AB 边交于点D ，与BC 边交于点E ，连结DE ，将△BDE 沿DE 翻折至△B 'DE 处，点B '恰好落在正比例函数y =kx 图象上，则k 的值是（）A ．52-B ．211-C ．51-D ．241- 2．（2017四川省内江市，第11题，3分）如图，在矩形AOBC 中，O 为坐标原点，OA 、OB 分别在x 轴、y 轴上，点B 的坐标为（0，33），∠ABO =30°，将△ABC 沿AB 所在直线对折后，点C 落在点D 处，则点D 的坐标为（）A ．（32，332）B ．（2，332）C ．（332，32）D ．（32，3﹣332） 3．（2017江苏省无锡市，第10题，3分）如图，△ABC 中，∠BAC =90°，AB =3，AC =4，点D 是BC 的中点，将△ABD 沿AD 翻折得到△AED ，连CE ，则线段CE 的长等于（）A ．2B ．54C ．53D ．754．（2017浙江省台州市，第10题，4分）如图，矩形EFGH 的四个顶点分别在菱形ABCD 的四条边上，BE =BF ，将△AEH ，△CFG 分别沿边EH ，FG 折叠，当重叠部分为菱形且面积是菱形ABCD 面积的116时，则AE EB为（）A ． 53B ．2C ． 52D ．4 5．（2017衢州，第9题，3分）如图，矩形纸片ABCD 中，AB =4，BC =6，将△ABC 沿AC 折叠，使点B 落在点E 处，CE 交AD 于点F ，则DF 的长等于（）A ． 53B ． 35C ． 37D ． 45 6．（2017湖南省长沙市，第12题，3分）如图，将正方形ABCD 折叠，使顶点A 与CD 边上的一点H 重合（H 不与端点C ，D 重合），折痕交AD 于点E ，交BC 于点F ，边AB 折叠后与边BC 交于点G ．设正方形ABCD 的周长为m ，△CHG 的周长为n ，则mn 的值为（）A ．22B ．21 C ．215 D ．随H 点位置的变化而变化7．（2016内蒙古包头市）如图，直线243y x=+与x轴、y轴分别交于点A和点B，点C、D分别为线段AB、OB的中点，点P为OA上一动点，PC+PD值最小时点P的坐标为（）A．（﹣3，0）B．（﹣6，0）C．（32-，0）D．（52-，0）8．（2016内蒙古呼伦贝尔市，第6题，3分）将点A（3，2）向左平移4个单位长度得点A′，则点A′关于y轴对称的点的坐标是（）A．（﹣3，2）B．（﹣1，2）C．（1，﹣2）D．（1，2）9．（2016内蒙古呼伦贝尔市，第12题，3分）如图，Rt△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为PQ，则线段BQ的长度为（）A．53B．52C．4D．510．（2016天津市）如图，把一张矩形纸片ABCD沿对角线AC折叠，点B的对应点为B′，AB′与DC相交于点E，则下列结论一定正确的是（）A．∠DAB′=∠CAB′B．∠ACD=∠B′CD C．AD=AE D．AE=CE 11．（2016四川省南充市）如图，对折矩形纸片ABCD，使AB与DC重合得到折痕EF，将纸片展平；再一次折叠，使点D落到EF上点G处，并使折痕经过点A，展平纸片后∠DAG的大小为（）A．30°B．45°C．60°D．75°12．（2016四川省资阳市）如图，矩形ABCD与菱形EFGH的对角线均交于点O，且EG∥BC，将矩形折叠，使点C与点O重合，折痕M N恰好过点G若AB=6，EF=2，∠H=120°，则DN的长为（）A．32B．632+C．63-D．236-13．（2016四川省雅安市）如图，在矩形ABCD中，AD=6，AE⊥BD，垂足为E，ED=3BE，点P、Q分别在BD，AD上，则AP+PQ的最小值为（）A．22B．2C．23D．3314．（2016山东省威海市）如图，在矩形ABCD中，AB=4，BC=6，点E为BC的中点，将△ABE沿AE折叠，使点B落在矩形内点F处，连接CF，则CF的长为（）A．95B．125C．165D．18515．（2016山东省枣庄市）如图，△ABC的面积为6，AC=3，现将△ABC沿AB所在直线翻折，使点C落在直线AD上的C′处，P为直线AD上的一点，则线段BP的长不可能是（）A．3B．4C．5.5D．1016．（2016山东省济宁市）如图，在4×4正方形网格中，黑色部分的图形构成一个轴对称图形，现在任意选取一个白色的小正方形并涂黑，使黑色部分的图形仍然构成一个轴对称图形的概率是（）A．613B．513C．413D．31317．（2016山东省聊城市）如图，把一张矩形纸片ABCD沿EF折叠后，点A落在CD边上的点A′处，点B落在点B′处，若∠2=40°，则图中∠1的度数为（）A．115°B．120°C．130°D．140°18．（2016广西百色市）如图，正△ABC的边长为2，过点B的直线l⊥AB，且△ABC与△A′BC′关于直线l对称，D为线段BC′上一动点，则AD+CD的最小值是（）A．4B．32C．23D．2319．（2016广西钦州市）如图，把矩形纸片ABCD沿EF翻折，点A恰好落在BC边的A′处，若AB3，∠EF A=60°，则四边形A′B′EF的周长是（）A ．133+B ．33+C ．43+D ．53+20．（2016江苏省南通市）平面直角坐标系xOy 中，已知A （﹣1，0）、B （3，0）、C （0，﹣1）三点，D （1，m ）是一个动点，当△ACD 的周长最小时，△ABD 的面积为（）A ．13B ．23C ．43D ．8321．（2016江苏省宿迁市）如图，把正方形纸片ABCD 沿对边中点所在的直线对折后展开，折痕为M N ，再过点B 折叠纸片，使点A 落在M N 上的点F 处，折痕为BE ．若AB 的长为2，则F M 的长为（）A ．2B ．3C ．2D ．122．（2016江苏省苏州市）矩形OABC 在平面直角坐标系中的位置如图所示，点B 的坐标为（3，4），D 是OA 的中点，点E 在AB 上，当△CDE 的周长最小时，点E 的坐标为（）A ．（3，1）B ．（3，43）C ．（3，53） D ．（3，2） 23．（2016江苏省镇江市）如图，在平面直角坐标系中，坐标原点O 是正方形OABC 的一个顶点，已知点B 坐标为（1，7），过点P （a ，0）（a ＞0）作PE ⊥x 轴，与边OA 交于点E （异于点O 、A ），将四边形ABCE 沿CE 翻折，点A ′、B ′分别是点A 、B 的对应点，若点A ′恰好落在直线PE 上，则a 的值等于（）A．54B．43C．2D．324．（2016海南省）如图，AD是△ABC的中线，∠ADC=45°，把△ADC沿着直线AD对折，点C落在点E的位置．如果BC=6，那么线段BE的长度为（）A．6B．62C．23D．3225．（2016浙江省台州市）小红用次数最少的对折方法验证了一条四边形丝巾的形状是正方形，她对折了（）A．1次B．2次C．3次D．4次26．（2016浙江省温州市）如图，一张三角形纸片ABC，其中∠C=90°，AC=4，BC=3．现小林将纸片做三次折叠：第一次使点A落在C处；将纸片展平做第二次折叠，使点B落在C处；再将纸片展平做第三次折叠，使点A落在B处．这三次折叠的折痕长依次记为a，b，c，则a，b，c的大小关系是（）A．c＞a＞b B．b＞a＞c C．c＞b＞a D．b＞c＞a27．（2016浙江省湖州市）如图1，在等腰三角形ABC中，AB=AC=4，BC=7．如图2，在底边BC上取一点D，连结AD，使得∠DAC=∠ACD．如图3，将△ACD沿着AD所在直线折叠，使得点C落在点E处，连结BE，得到四边形ABED．则BE的长是（）A．4B．174C．32D．2528．（2016浙江省舟山市）把一张圆形纸片按如图所示方式折叠两次后展开，图中的虚线表示折痕，则BC 的度数是（）A．120°B．135°C．150°D．165°29．（2016湖北省咸宁市）已知菱形OABC在平面直角坐标系的位置如图所示，顶点A（5，0），OB=45，点P是对角线OB上的一个动点，D（0，1），当CP+DP最短时，点P的坐标为（）A．（0，0）B．（1，12）C．（65，35）D．（107，57）30．（2016福建省莆田市）如图，在△ABC中，∠ACB=90°，AC=BC=4，将△ABC折叠，使点A落在BC 边上的点D处，EF为折痕，若AE=3，则sin∠BFD的值为（）A．13B．223C．24D．3531．（2016贵州省遵义市）如图，正方形ABCD的边长为3，E、F分别是AB、CD上的点，且∠CFE=60°，将四边形BCFE沿EF翻折，得到B′C′FE，C′恰好落在AD边上，B′C′交AB于点G，则GE的长是（）A ．334-B ．425-C ．423-D ．523-32．（2016湖北省鄂州市）如图，菱形ABCD 的边AB =8，∠B =60°，P 是AB 上一点，BP =3，Q 是CD 边上一动点，将梯形APQD 沿直线PQ 折叠，A 的对应点A ′．当CA ′的长度最小时，CQ 的长为（）A ．5B ．7C ．8D ．13233．（2016福建省龙岩市）如图，在周长为12的菱形ABCD 中，AE =1，AF =2，若P 为对角线BD 上一动点，则EP +FP 的最小值为（）A ．1B ．2C ．3D ．434．（2016贵州省毕节市）如图，正方形ABCD 的边长为9，将正方形折叠，使顶点D 落在BC 边上的点E 处，折痕为GH ．若BE ：EC =2：1，则线段CH 的长是（）A ．3B ．4C ．5D ．635．（2016黑龙江省牡丹江市）如图，在平面直角坐标系中，A （﹣8，﹣1），B （﹣6，﹣9），C （﹣2．﹣9），D （﹣4，﹣1）．先将四边形ABCD 沿x 轴翻折，再向右平移8个单位长度，向下平移1个单位长度后，得到四边形A 1B 1C 1D 1，最后将四边形A 1B 1C 1D 1，绕着点A 1旋转，使旋转后的四边形对角线的交点落在x 轴上，则旋转后的四边形对角线的交点坐标为（）A ．（4，0）B ．（5，0）C ．（4，0）或（﹣4，0）D ．（5，0）或（﹣5，0）36．（2015常州）将一张宽为4cm 的长方形纸片（足够长）折叠成如图所示图形，重叠部分是一个三角形，则这个三角形面积的最小值是（）A ．338cm 2B ．8cm 2C ．3316cm 2 D ．16cm 2 37．（2015贵港）在平面直角坐标系中，若点P （m ，m ﹣n ）与点Q （﹣2，3）关于原点对称，则点M （m ，n ）在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限38．（2015庆阳）在如图所示的平面直角坐标系中，△OA 1B 1是边长为2的等边三角形，作△B 2A 2B 1与△OA 1B 1关于点B 1成中心对称，再作△B 2A 3B 3与△B 2A 2B 1关于点B 2成中心对称，如此作下去，则△B 2n A 2n +1B 2n +1（n 是正整数）的顶点A 2n +1的坐标是（）A ．（4n ﹣13）B ．（2n ﹣13）C ．（4n +13D ．（2n +13）39．（2015桂林）如图，在△ABC中，AB=10，AC=8，BC=12，AD⊥BC于D，点E、F分别在AB、AC边上，把△ABC沿EF折叠，使点A与点D恰好重合，则△DEF的周长是（）A．14B．15C．16D．1740．（2015南宁）如图，AB是⊙O的直径，AB=8，点M在⊙O上，∠MA B=20°，N是弧M B的中点，P 是直径AB上的一动点．若M N=1，则△P M N周长的最小值为（）A．4B．5C．6D．741．（2015北海）如图，在矩形OABC中，OA=8，OC=4，沿对角线OB折叠后，点A与点D重合，OD与BC交于点E，则点D的坐标是（）A．（4，8）B．（5，8）C．（245，325）D．（225，365）42．（2015攀枝花）如图，在边长为2的等边△ABC中，D为BC的中点，E是AC边上一点，则BE+DE 的最小值为．二、填空题43．（2017四川省成都市，第25题，4分）如图1，把一张正方形纸片对折得到长方形ABCD，再沿∠ADC 的平分线DE折叠，如图2，点C落在点C′处，最后按图3所示方式折叠，使点A落在DE的中点A′处，折痕是FG，若原正方形纸片的边长为6cm，则FG= cm．44．（2017四川省达州市，第16题，3分）如图，矩形ABCD中，E是BC上一点，连接AE，将矩形沿AE 翻折，使点B落在CD边F处，连接AF，在AF上取点O，以O为圆心，OF长为半径作⊙O与AD相切于点P．若AB=6，BC=33，则下列结论：①F是CD的中点；②⊙O的半径是2；③AE=92CE；④32S阴影．其中正确结论的序号是．45．（2017山东省潍坊市，第18题，3分）如图，将一张矩形纸片ABCD的边BC斜着向AD边对折，使点B落在AD边上，记为B′，折痕为CE，再将CD边斜向下对折，使点D落在B′C边上，记为D′，折痕为CG，B′D′=2，BE=13BC．则矩形纸片ABCD的面积为．46．（2017广东省，第16题，4分）如图，矩形纸片ABCD中，AB=5，BC=3，先按图（2）操作：将矩形纸片ABCD沿过点A的直线折叠，使点D落在边AB上的点E处，折痕为AF；再按图（3）操作，沿过点F的直线折叠，使点C落在EF上的点H处，折痕为FG，则A、H两点间的距离为．47．（2017南宁，第16题，3分）如图，菱形ABCD的对角线相交于点O，AC=2，BD=23，将菱形按如图方式折叠，使点B与点O重合，折痕为EF，则五边形AEFCD的周长为．48．（2017江苏省连云港市，第16题，3分）如图，已知等边三角形OAB与反比例函数kyx（k＞0，x＞0）的图象交于A、B两点，将△OAB沿直线OB翻折，得到△OCB，点A的对应点为点C，线段CB交x轴于点D，则BDDC的值为．（已知sin15°=62）49．（2017江西省，第12题，3分）已知点A（0，4），B（7，0），C（7，4），连接AC，BC得到矩形AOBC，点D的边AC上，将边OA沿OD折叠，点A的对应边为A'．若点A'到矩形较长两对边的距离之比为1：3，则点A'的坐标为．50．（2017河南省，第15题，3分）如图，在Rt△ABC中，∠A=90°，AB=AC，BC2+1，点M，N分别是边BC，AB上的动点，沿MN所在的直线折叠∠B，使点B的对应点B′始终落在边AC上，若△MB′C 为直角三角形，则BM的长为．51．（2017浙江省宁波市，第18题，4分）如图，在菱形纸片ABCD中，AB=2，∠A=60°，将菱形纸片翻折，使点A落在CD的中点E处，折痕为FG，点F，G分别在边AB，AD上，则cos∠EFG的值为．52．（2017湖北省武汉市，第15题，3分）如图，在△ABC中，AB=AC=23，∠BAC=120°，点D、E都在边BC上，∠DAE=60°．若BD=2CE，则DE的长为．53．（2017湖北省襄阳市，第16题，3分）如图，在△ABC中，∠ACB=90°，点D，E分别在AC，BC上，且∠CDE=∠B，将△CDE沿DE折叠，点C恰好落在AB边上的点F处．若AC=8，AB=10，则CD的长为．54．（2017贵州省贵阳市，第15题，4分）如图，在矩形纸片ABCD中，AB=2，AD=3，点E是AB的中点，点F是AD边上的一个动点，将△AEF沿EF所在直线翻折，得到△A′EF，则A′C的长的最小值是．55．（2017辽宁省营口市，第17题，3分）在矩形纸片ABCD中，AD=8，AB=6，E是边BC上的点，将纸片沿AE折叠，使点B落在点F处，连接FC，当△EFC为直角三角形时，BE的长为．56．（2017辽宁省锦州市，第15题，3分）如图，正方形ABCD中，AB=2，E是CD中点，将正方形ABCD 沿AM折叠，使点B的对应点F落在AE上，延长MF交CD于点N，则DN的长为．57．（2017重庆，第18题，4分）如图，正方形ABCD中，AD=4，点E是对角线AC上一点，连接DE，过点E作EF⊥ED，交AB于点F，连接DF，交AC于点G，将△EFG沿EF翻折，得到△EFM，连接DM，交EF于点N，若点F是AB的中点，则△EMN的周长是．58．（2017重庆B，第18题，4分）如图，正方形ABCD中，AD=4，点E是对角线AC上一点，连接DE，过点E作EF⊥ED，交AB于点F，连接DF，交AC于点G，将△EFG沿EF翻折，得到△EFM，连接DM，交EF于点N，若点F是AB的中点，则△EMN的周长是．59．（2017青海省西宁市，第20题，2分）如图，将▱ABCD沿EF对折，使点A落在点C处，若∠A=60°，AD=4，AB=6，则AE的长为．60．（2016云南省曲靖市）如图，在矩形ABCD中，AD=10，CD=6，E是CD边上一点，沿AE折叠△ADE，使点D恰好落在BC边上的F处，M是AF的中点，连接B M，则sin∠AB M= ．61．（2016吉林省）在三角形纸片ABC中，∠C=90°，∠B=30°，点D（不与B，C重合）是BC上任意一点，将此三角形纸片按下列方式折叠，若EF的长度为a，则△DEF的周长为（用含a的式子表示）．62．（2016宁夏）如图，Rt△AOB中，∠AOB=90°，OA在x轴上，OB在y轴上，点A，B的坐标分别为（3，0），（0，1），把Rt△AOB沿着AB对折得到Rt△AO′B，则点O′的坐标为63．（2016四川省内江市）如图所示，已知点C（1，0），直线y=﹣x+7与两坐标轴分别交于A，B两点，D，E分别是AB，OA上的动点，则△CDE周长的最小值是．64．（2016山东省东营市）如图，折叠矩形ABCD的一边AD，使点D落在BC边的点F处，已知折痕AE=55cm，且tan∠EFC=34，那么矩形ABCD的周长为cm．65．（2016山东省临沂市）如图，将一矩形纸片ABCD折叠，使两个顶点A，C重合，折痕为FG．若AB=4，BC=8，则△ABF的面积为．66．（2016山东省德州市）如图，半径为1的半圆形纸片，按如图方式折叠，使对折后半圆弧的中点M与圆心O重合，则图中阴影部分的面积是．67．（2016山东省日照市）如图，△ABC是一张直角三角形纸片，∠C=90°，两直角边AC=6cm、BC=8cm，现将△ABC折叠，使点B与点A重合，折痕为EF，则tan∠CAE= ．68．（2016山东省济南市）如图1，在矩形纸片ABCD中，AB=83AD=10，点E是CD中点，将这张纸片依次折叠两次；第一次折叠纸片使点A与点E重合，如图2，折痕为M N，连接M E/NE；第二次折叠纸片使点N与点E重合，如图3，点B落到B′处，折痕为HG，连接HE，则tan∠EHG= ．69．（2016山东省青岛市）如图，以边长为20cm的正三角形纸板的各顶点为端点，在各边上分别截取4cm 长的六条线段，过截得的六个端点作所在边的垂线，形成三个有两个直角的四边形．把它们沿图中虛线剪掉，用剩下的纸板折成一个底为正三角形的无盖柱形盒子，则它的容积为cm3．70．（2016广东省）如图，矩形ABCD中，对角线AC=23，E为BC边上一点，BC=3BE，将矩形ABCD 沿AE所在的直线折叠，B点恰好落在对角线AC上的B′处，则AB= ．71．（2016广西南宁市）如图，在4×4正方形网格中，有3个小正方形已经涂黑，若再涂黑任意一个白色的小正方形（每一个白色的小正方形被涂黑的可能性相同），使新构成的黑色部分的图形是轴对称图形的概率是．72．（2016广西河池市）如图的三角形纸片中，AB=AC，BC=12cm，∠C=30°，折叠这个三角形，使点B 落在AC的中点D处，折痕为EF，那么BF的长为cm．73．（2016江苏省淮安市）如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，点F在边AC上，并且CF=2，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是．74．（2016江苏省盐城市）如图，已知菱形ABCD的边长2，∠A=60°，点E、F分别在边AB、AD上，若将△AEF沿直线EF折叠，使得点A恰好落在CD边的中点G处，则EF= ．75．（2016河北省）如图，已知∠AOB=7°，一条光线从点A出发后射向OB边．若光线与OB边垂直，则光线沿原路返回到点A，此时∠A=90°-7°=83°．当∠A＜83°时，光线射到OB边上的点A1后，经OB反射到线段AO上的点A2，易知∠1=∠2．若A1A2⊥AO，光线又会沿A2→A1→A原路返回到点A，此时∠A=__ ___°．……若光线从点A发出后，经若干次反射能沿原路返回到点A，则锐角∠A的最小值=___ ____°．76．（2016江苏省苏州市）如图，在△ABC中，AB=10，∠B=60°，点D、E分别在AB、BC上，且BD=BE=4，将△BDE沿DE所在直线折叠得到△B′DE（点B′在四边形ADEC内），连接AB′，则AB′的长为．77．（2016江苏省连云港市）如图1，将正方形纸片ABCD对折，使AB与CD重合，折痕为EF．如图2，展开后再折叠一次，使点C与点E重合，折痕为GH，点B的对应点为点M，E M交AB于N．若AD=2，则M N= ．78．（2016河南省）如图，已知AD∥BC，AB⊥BC，AB=3，点E为射线BC上一个动点，连接AE，将△ABE 沿AE折叠，点B落在点B′处，过点B′作AD的垂线，分别交AD，BC于点M，N．当点B′为线段M N 的三等分点时，BE的长为．79．（2016浙江省绍兴市）如图，矩形ABCD中，AB=4，BC=2，E是AB的中点，直线l平行于直线EC，且直线l与直线EC之间的距离为2，点F在矩形ABCD边上，将矩形ABCD沿直线EF折叠，使点A恰好落在直线l上，则DF的长为．80．（2016浙江省金华市）如图，Rt△ABC纸片中，∠C=90°，AC=6，BC=8，点D在边BC上，以AD为折痕△ABD折叠得到△AB′D，AB′与边BC交于点E．若△DEB′为直角三角形，则BD的长是．81．（2016湖北省黄冈市）如图，在矩形ABCD中，点E、F分别在边CD、BC上，且DC=3DE=3a．将矩形沿直线EF折叠，使点C恰好落在AD边上的点P处，则FP= ．82．（2016贵州省黔东南州）如图，在平面直角坐标系xOy中，矩形OABC的边OA、OC分别在x轴和y 轴上，OC=3，OA=26，D是BC的中点，将△OCD沿直线OD折叠后得到△OGD，延长OG交AB于点E，连接DE，则点G的坐标为．83．（2016湖北省随州市）如图，直线y=x+4与双曲线kyx（k≠0）相交于A（﹣1，a）、B两点，在y轴上找一点P，当PA+PB的值最小时，点P的坐标为．84．（2016湖南省张家界市）如图，将矩形ABCD沿GH对折，点C落在Q处，点D落在E处，EQ与BC相交于F．若AD=8cm，AB=6cm，AE=4cm．则△EBF的周长是cm．85．（2016甘肃省天水市）如图，把矩形纸片OABC放入平面直角坐标系中，使OA、OC分别落在x轴、y轴上，连接OB，将纸片OABC沿OB折叠，使点A落在点A′的位置，若OB=5，tan∠BOC=12，则点A′的坐标为．86．（2016重庆市）正方形ABCD中，对角线AC，BD相交于点O，DE平分∠ADO交AC于点E，把△ADE 沿AD翻折，得到△ADE′，点F是DE的中点，连接AF，BF，E′F．若AE=2．则四边形ABFE′的面积是．87．（2016重庆市）如图，在正方形ABCD中，AB=6，点E在边CD上，DE=13DC，连接AE，将△ADE沿AE翻折，点D落在点F处，点O是对角线BD的中点，连接OF并延长OF交CD于点G，连接BF，BG，则△BFG的周长是．88．（2016黑龙江省齐齐哈尔市）如图，在边长为2的菱形ABCD 中，∠A =60°，点M 是AD 边的中点，连接M C ，将菱形ABCD 翻折，使点A 落在线段CM 上的点E 处，折痕交AB 于点N ，则线段EC 的长为．89．（2016黑龙江省龙东地区）如图，M N 是⊙O 的直径，M N =4，∠A M N =40°，点B 为弧AN 的中点，点P 是直径M N 上的一个动点，则PA +PB 的最小值为．90．（2015宜宾）如图，一次函数的图象与x 轴、y 轴分别相交于点A 、B ，将△AOB 沿直线AB 翻折，得△ACB ．若C （32，32），则该一次函数的解析式为．91．（2015达州）如图，将矩形ABCD 沿EF 折叠，使顶点C 恰好落在AB 边的中点C ′上，点D 落在D ′处，C ′D ′交AE 于点M ．若AB =6，BC =9，则A M 的长为．三、解答题92．（2017吉林省，第26题，10分）《函数的图象与性质》拓展学习片段展示：【问题】如图①，在平面直角坐标系中，抛物线24(2)3y a x =--经过原点O ，与x 轴的另一个交点为A ，则a = ．【操作】将图①中抛物线在x 轴下方的部分沿x 轴折叠到x 轴上方，将这部分图象与原抛物线剩余部分的图象组成的新图象记为G ，如图②．直接写出图象G 对应的函数解析式．【探究】在图②中，过点B （0，1）作直线l 平行于x 轴，与图象G 的交点从左至右依次为点C ，D ，E ，F ，如图③．求图象G 在直线l 上方的部分对应的函数y 随x 增大而增大时x 的取值范围．【应用】P 是图③中图象G 上一点，其横坐标为m ，连接PD ，PE ．直接写出△PDE 的面积不小于1时m 的取值范围．93．（2017四川省达州市，第25题，12分）如图1，点A 坐标为（2，0），以OA 为边在第一象限内作等边△OAB ，点C 为x 轴上一动点，且在点A 右侧，连接BC ，以BC 为边在第一象限内作等边△BCD ，连接AD 交BC 于E ．（1）①直接回答：△OBC 与△ABD 全等吗？②试说明：无论点C 如何移动，AD 始终与OB 平行；（2）当点C 运动到使AC 2=AE •AD 时，如图2，经过O 、B 、C 三点的抛物线为y 1．试问：y 1上是否存在动点P ，使△BEP 为直角三角形且BE 为直角边？若存在，求出点P 坐标；若不存在，说明理由；（3）在（2）的条件下，将y 1沿x 轴翻折得y 2，设y 1与y 2组成的图形为M ，函数33y x m =+的图象l与M 有公共点．试写出：l 与M 的公共点为3个时，m 的取值．94．（2017德州，第23题，10分）如图1，在矩形纸片ABCD 中，AB =3cm ，AD =5cm ，折叠纸片使B 点落在边AD 上的E 处，折痕为PQ ，过点E 作EF ∥AB 交PQ 于F ，连接BF ．（1）求证：四边形BFEP 为菱形；（2）当点E在AD边上移动时，折痕的端点P、Q也随之移动；①当点Q与点C重合时（如图2），求菱形BFEP的边长；②若限定P、Q分别在边BA、BC上移动，求出点E在边AD上移动的最大距离．95．（2017山东省淄博市，第23题，9分）如图，将矩形纸片ABCD沿直线MN折叠，顶点B恰好与CD 边上的动点P重合（点P不与点C，D重合），折痕为MN，点M，N分别在边AD，BC上，连接MB，MP，BP，BP与MN相交于点F．（1）求证：△BFN∽△BCP；（2）①在图2中，作出经过M，D，P三点的⊙O（要求保留作图痕迹，不写做法）；②设AB=4，随着点P在CD上的运动，若①中的⊙O恰好与BM，BC同时相切，求此时DP的长．96．（2017山西省，第22题，12分）综合与实践背景阅读早在三千多年前，我国周朝数学家商高就提出：将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三，股四，弦五”．它被记载于我国古代著名数学著作《周髀算经》中．为了方便，在本题中，我们把三边的比为3：4：5的三角形称为（3，4，5）型三角形．例如：三边长分别为9，12，15或32,42,523，4，5）型三角形．用矩形纸片按下面的操作方法可以折出这种类型的三角形．实践操作如图1，在矩形纸片ABCD中，AD=8cm，AB=12cm．第一步：如图2，将图1中的矩形纸片ABCD沿过点A的直线折叠，使点D落在AB上的点E处，折痕为AF，再沿EF折叠，然后把纸片展平．第二步：如图3，将图2中的矩形纸片再次折叠，使点D与点F重合，折痕为GH，然后展平，隐去AF．第三步：如图4，将图3中的矩形纸片沿AH折叠，得到△AD′H，再沿AD′折叠，折痕为AM，AM与折痕EF 交于点N ，然后展平．问题解决（1）请在图2中证明四边形AEFD 是正方形．（2）请在图4中判断NF 与ND ′的数量关系，并加以证明．（3）请在图4中证明△AEN 是（3，4，5）型三角形．探索发现（4）在不添加字母的情况下，图4中还有哪些三角形是（3，4，5）型三角形？请找出并直接写出它们的名称．97．（2017广西桂林市，第26题，12分）已知抛物线214y ax bx =+-（a ≠0）与x 轴交于点A （﹣1，0）和点B （4，0）．（1）求抛物线1y 的函数解析式；（2）如图①，将抛物线1y 沿x 轴翻折得到抛物线2y ，抛物线2y 与y 轴交于点C ，点D 是线段BC 上的一个动点，过点D 作DE ∥y 轴交抛物线1y 于点E ，求线段DE 的长度的最大值；（2）在（2）的条件下，当线段DE 处于长度最大值位置时，作线段BC 的垂直平分线交DE 于点F ，垂足为H ，点P 是抛物线2y 上一动点，⊙P 与直线BC 相切，且S ⊙P ：S △DFH =2π，求满足条件的所有点P 的坐标．98．（2017广西贵港市，第26题，10分）已知，在Rt △ABC 中，∠ACB =90°，AC =4，BC =2，D 是AC 边上的一个动点，将△ABD 沿BD 所在直线折叠，使点A 落在点P 处．（1）如图1，若点D 是AC 中点，连接PC ．①写出BP ，BD 的长；②求证：四边形BCPD 是平行四边形．（2）如图2，若BD =AD ，过点P 作PH ⊥BC 交BC 的延长线于点H ，求PH 的长．99．（2017江苏省宿迁市，第25题，10分）如图，在平面直角坐标系xOy 中，抛物线223y x x =--交x 轴于A ，B 两点（点A 在点B 的左侧），将该抛物线位于x 轴上方曲线记作M ，将该抛物线位于x 轴下方部分沿x 轴翻折，翻折后所得曲线记作N ，曲线N 交y 轴于点C ，连接AC 、BC ．（1）求曲线N 所在抛物线相应的函数表达式；（2）求△ABC 外接圆的半径；（3）点P 为曲线M 或曲线N 上的一动点，点Q 为x 轴上的一个动点，若以点B ，C ，P ，Q 为顶点的四边形是平行四边形，求点Q 的坐标．100．（2017江苏省宿迁市，第26题，10分）如图，在矩形纸片ABCD 中，已知AB =1，BC =3，点E 在边CD 上移动，连接AE ，将多边形ABCE 沿直线AE 翻折，得到多边形AB ′C ′E ，点B 、C 的对应点分别为点B ′、C ′．（1）当B ′C ′恰好经过点D 时（如图1），求线段CE 的长；（2）若B ′C ′分别交边AD ，CD 于点F ，G ，且∠DAE =22.5°（如图2），求△DFG 的面积；（3）在点E 从点C 移动到点D 的过程中，求点C ′运动的路径长．101．（2017浙江省绍兴市，第24题，14分）如图1，已知□ABCD ，AB ∥x 轴，AB =6，点A 的坐标为（1，-4），点D 的坐标为（-3，4），点B 在第四象限，点P 是□ABCD 边上一个动点．（1）若点P 在边BC 上，PD =CD ，求点P 的坐标．（2）若点P 在边AB 、AD 上，点P 关于坐标轴对称的点Q ，落在直线1y x =-上，求点P 的坐标．（3）若点P 在边AB ，AD ，CD 上，点G 是AD 与y 轴的交点，如图2，过点P 作y 轴的平行线PM ，过点G 作x 轴的平行线GM ，它们相交于点M ，将△PGM 沿直线PG 翻折，当点M 的对应点落在坐标轴上时，求点P 的坐标（直接写出答案）．102．（2017金华，第23题，10分）如图1，将△ABC 纸片沿中位线EH 折叠，使点A 对称点D 落在BC 边上，再将纸片分别沿等腰△BED 和等腰△DHC 的底边上的高线EF ，HG 折叠，折叠后的三个三角形拼合形成一个矩形，类似地，对多边形进行折叠，若翻折后的图形恰能合成一个无缝隙，无重叠的矩形，这样的矩形称为叠合矩形．（1）将▱ABCD 纸片按图2的方式折叠成一个叠合矩形AEFG ，则操作形成的折痕分别是线段，；S 矩形AE S ▱ABCD = ．（2）如图4，四边形ABCD 纸片满足AD ∥BC ，AD ＜BC ，AB ⊥BC ，AB =8，CD =10，小明把该纸片折叠，得到叠合正方形，请你帮助画出叠合正方形的示意图，并求出AD 、BC 的长．103．（2017辽宁省盘锦市，第26题，14分）如图，直线y =﹣2x +4交y 轴于点A ，交抛物线212y x bx c =++ 于点B （3，﹣2），抛物线经过点C （﹣1，0），交y 轴于点D ，点P 是抛物线上的动点，作PE ⊥DB 交DB 所在直线于点E ．（1）求抛物线的解析式；（2）当△PDE 为等腰直角三角形时，求出PE 的长及P 点坐标；（3）在（2）的条件下，连接PB ，将△PBE 沿直线AB 翻折，直接写出翻折点后E 的对称点坐标．104．（2017辽宁省葫芦岛市，第26题，14分）如图，抛物线22y ax x c =-+（a ≠0）与x 轴、y 轴分别交于点A ，B ，C 三点，已知点A （﹣2，0），点C （0，﹣8），点D 是抛物线的顶点．（1）求抛物线的解析式及顶点D 的坐标；（2）如图1，抛物线的对称轴与x 轴交于点E ，第四象限的抛物线上有一点P ，将△EBP 沿直线EP 折叠，使点B 的对应点B '落在抛物线的对称轴上，求点P 的坐标；（3）如图2，设BC 交抛物线的对称轴于点F ，作直线CD ，点M 是直线CD 上的动点，点N 是平面内一点，当以点B ，F ，M ，N 为顶点的四边形是菱形时，请直接写出点M 的坐标．105．（2017辽宁省辽阳市，第26题，14分）如图1，抛物线213y x bx c =++经过A （3-0）、B （0，﹣2）两点，点C 在y 轴上，△ABC 为等边三角形，点D 从点A 出发，沿AB 方向以每秒2个单位长度的速度向终点B 运动，设运动时间为t 秒（t ＞0），过点D 作DE ⊥AC 于点E ，以DE 为边作矩形DEGF ，使点F 在x 轴上，点G 在AC 或AC 的延长线上．（1）求抛物线的解析式；（2）将矩形DEGF 沿GF 所在直线翻折，得矩形D 'E 'GF ，当点D 的对称点D '落在抛物线上时，求此时点D '的坐标；（3）如图2，在x 轴上有一点M （23，0），连接BM 、CM ，在点D 的运动过程中，设矩形DEGF 与四边形ABMC 重叠部分的面积为S ，直接写出S 与t 之间的函数关系式，并写出自变量t 的取值范围． 106．（2017黑龙江省龙东地区，第28题，10分）如图，矩形AOCB 的顶点A 、C 分别位于x 轴和y 轴的正半轴上，线段OA 、OC 的长度满足方程15130x y -+-=（OA ＞OC ），直线y =kx +b 分别与x 轴、y 轴交于M 、N 两点，将△BCN 沿直线BN 折叠，点C 恰好落在直线MN 上的点D 处，且tan ∠CBD =34．（1）求点B 的坐标；（2）求直线BN 的解析式；（3）将直线BN 以每秒1个单位长度的速度沿y 轴向下平移，求直线BN 扫过矩形AOCB 的面积S 关于运动的时间t （0＜t ≤13）的函数关系式．107．（2017黑龙江省龙东地区，第28题，10分）如图，矩形AOCB 的顶点A 、C 分别位于x 轴和y 轴的正半轴上，线段OA 、OC 的长度满足方程15130x y --=（OA ＞OC ），直线y =kx +b 分别与x 轴、y 轴交于M 、N 两点，将△BCN 沿直线BN 折叠，点C 恰好落在直线MN 上的点D 处，且tan ∠CBD =34．（1）求点B 的坐标；（2）求直线BN 的解析式；（3）将直线BN 以每秒1个单位长度的速度沿y 轴向下平移，求直线BN 扫过矩形AOCB 的面积S 关于运动的时间t （0＜t ≤13）的函数关系式．108．（2017湖南省娄底市，第26题，10分）如图，抛物线2y ax bx c =++与x 轴交于两点A （﹣4，0）和B （1，0），与y 轴交于点C （0，2），动点D 沿△ABC 的边AB 以每秒2个单位长度的速度由起点A 向终点B 运动，过点D 作x 轴的垂线，交△ABC 的另一边于点E ，将△ADE 沿DE 折叠，使点A 落在点F 处，设点D 的运动时间为t 秒．（1）求抛物线的解析式和对称轴；（2）是否存在某一时刻t ，使得△EFC 为直角三角形？若存在，求出t 的值；若不存在，请说明理由；（3）设四边形DECO 的面积为s ，求s 关于t 的函数表达式．109．（2016新疆）如图，▱ABCD 中，AB =2，AD =1，∠ADC =60°，将▱ABCD 沿过点A 的直线l 折叠，使点D 落到AB 边上的点D ′处，折痕交CD 边于点E ．（1）求证：四边形BCED ′是菱形；（2）若点P 时直线l 上的一个动点，请计算PD ′+PB 的最小值．。

2023年中考数学一轮专题练习 ——图形的平移、折叠和旋转(含解析)

2023年中考数学一轮专题练习——图形的平移、折叠和旋转1一、单选题（本大题共10小题）1. （湖南省永州市2022年）剪纸是我国具有独特艺术风格的民间艺术，反映了劳动人民对现实生活的深刻感悟.下列剪纸图形中，是中心对称图形的有（）①②③④A．①②③B．①②④C．①③④D．②③④2. （湖南省湘西州2022年）下面4个汉字中，可以看作是轴对称图形的是（）A．B．C．D．3. （湖南省益阳市2022年）如图，已知△ABC中，∠CAB＝20°，∠ABC＝30°，将△ABC绕A点逆时针旋转50°得到△AB′C′，以下结论：①BC＝B′C′，②AC∥C′B′，③C′B′⊥BB′，④∠ABB′＝∠ACC′，正确的有（）A．①②③B．①②④C．①③④D．②③④4. （2022年西藏）如图，在菱形纸片ABCD中，E是BC边上一点，将△ABE沿直线AE翻折，使点B落在B'上，连接DB'．已知∠C＝120°，∠BAE＝50°，则ADB'∠的度数为（）A．50°B．60°C．80°D．90°5. （2022年西藏）下列图形中是轴对称图形的是（）A ．B ．C ．D ． 6. （黑龙江省大庆市2022年）如图，将平行四边形ABCD 沿对角线BD 折叠，使点A 落在E 处．若156∠=︒，242∠=︒，则A ∠的度数为( )A ．108︒B ．109︒C ．110︒D ．111︒7. （广东省河源市2021）下列图形中，既是轴对称图形又是中心对称图形的是（） A ． B ． C ． D ． 8. （辽宁省抚顺本溪辽阳市2022年）下列图形中，既是轴对称图形又是中心对称图形的是（）A ．B ．C ．D ．9. （江苏省无锡市2022年）雪花、风车…．展示着中心对称的美，利用中心对称，可以探索并证明图形的性质，请思考在下列图形中，是中心对称图形但不一定是轴对称图形的为（）A ．扇形B ．平行四边形C ．等边三角形D ．矩形10. （江苏省扬州市2022年）如图，在ABC ∆中，AB AC <，将ABC 以点A 为中心逆时针旋转得到ADE ，点D 在BC 边上，DE 交AC 于点F ．下列结论：①；②平分；③，其中所有正确结论的序号是（）AFE DFC △△DA BDE ∠CDF BAD ∠=∠A．①②B．②③C．①③D．①②③二、填空题（本大题共6小题）11. （湖南省湘西州2022年）在平面直角坐标系中，已知点P（﹣3，5）与点Q（3，m ﹣2）关于原点对称，则m＝_____．12. （湖南省益阳市2022年）如图，将边长为3的正方形ABCD沿其对角线AC平移，使A的对应点A′满足AA′＝13AC，则所得正方形与原正方形重叠部分的面积是_____．13. （湖北省仙桃2021）在平面直角坐标系中，点A（a，2）与点B（6，b）关于原点对称，则ab= ．14. （湖南省永州市2022年）如图，图中网格由边长为1的小正方形组成，点A为网格线的交点.若线段OA绕原点O顺时针旋转90°后，端点A的坐标变为______．15. （辽宁省盘锦市2022年）如图，四边形ABCD为矩形，3AB AD==，点E为边BC上一点，将DCE沿DE翻折，点C的对应点为点F，过点F作DE的平行线交AD 于点G，交直线BC于点H．若点G是边AD的三等分点，则FG的长是．16. （黑龙江省大庆市2022年）如图，正方形ABCD 中，点E ，F 分别是边,AB BC 上的两个动点，且正方形ABCD 的周长是周长的2倍，连接分别与对角线交于点M ，N ．给出如下几个结论：①若，则；②；③若，则；④若，则．其中正确结论的序号为．三、解答题（本大题共7小题）17. （湖南省湘潭市2022年）如图，在平面直角坐标系中，已知ABC 的三个顶点的坐标分别为()1,1A -，()4,0B -，()2,2C -．将ABC 绕原点O 顺时针旋转90︒后得到111A B C △．BEF ,DE DF AC 2,3AE CF ==4EF =180EFN EMN ∠+∠=︒2,3AM CN ==4MN =2,3MN BE AM==4EF=(1)请写出1A 、1B 、1C 三点的坐标：1A ，1B ，1C(2)求点B 旋转到点1B 的弧长．18. （江苏省无锡市2022年）如图，已知四边形ABCD 为矩形AB =4BC =，点E 在BC 上，CE AE =，将△ABC 沿AC 翻折到△AFC ，连接EF ．(1)求EF 的长；(2)求sin ∠CEF 的值．19. （江苏省常州市2022年）如图，点A 在射线OX 上，OA a =．如果OA 绕点O 按逆时针方向旋转(0360)<≤︒n n 到OA '，那么点A '的位置可以用(),︒a n 表示．(1)按上述表示方法，若3a =，37n =，则点A '的位置可以表示为；(2)在（1）的条件下，已知点B 的位置用()3,74︒表示，连接A A '、A B '．求证：A A A B ''=．20. （吉林省2022年）图①，图②均是44⨯的正方形网格，每个小正方形的顶点称为格点．其中点A ，B ，C 均在格点上．请在给定的网格中按要求画四边形．(1)在图①中，找一格点D ，使以点A ，B ，C ，D 为顶点的四边形是轴对称图形；(2)在图②中，找一格点E ，使以点A ，B ，C ，E 为顶点的四边形是中心对称图形． 21. （辽宁省抚顺本溪辽阳市2022年）在ABC 中，90,BAC AB AC ∠=︒=，线段AB 绕点A 逆时针旋转至AD （AD 不与AC 重合），旋转角记为α，DAC ∠的平分线AE 与射线BD 相交于点E ，连接EC ．(1)如图①，当20α=︒时，AEB ∠的度数是；(2)如图②，当090α︒<<︒时，求证：2BD CE +=；(3)当0180,2AE CE α︒<<︒=时，请直接写出BD ED的值． 22. （湖北省荆州市2022年）如图1，在矩形ABCD 中，AB ＝4，AD ＝3，点O 是边AB 上一个动点（不与点A 重合），连接OD ，将△OAD 沿OD 折叠，得到△OED ；再以O 为圆心，OA 的长为半径作半圆，交射线AB 于G ，连接AE 并延长交射线BC 于F ，连接EG ，设OA ＝x ．(1)求证：DE 是半圆O 的切线；(2)当点E 落在BD 上时，求x 的值；(3)当点E 落在BD 下方时，设△AGE 与△AFB 面积的比值为y ，确定y 与x 之间的函数关系式；(4)直接写出．．．．：当半圆O 与△BCD 的边有两个交点时，x 的取值范围． 23. （江西省2022年）问题提出：某兴趣小组在一次综合与实践活动中提出这样一个问题：将足够大的直角三角板()90,60PEF P F ∠=︒∠=︒的一个顶点放在正方形中心O 处，并绕点O 逆时针旋转，探究直角三角板PEF 与正方形ABCD 重叠部分的面积变化情况（已知正方形边长为2）．(1)操作发现：如图1，若将三角板的顶点P 放在点O 处，在旋转过程中，当OF 与OB 重合时，重叠部分的面积为；当OF 与BC 垂直时，重叠部分的面积为；一般地，若正方形面积为S ，在旋转过程中，重叠部分的面积1S 与S 的关系为；(2)类比探究：若将三角板的顶点F 放在点O 处，在旋转过程中，,OE OP 分别与正方形的边相交于点M ，N ．①如图2，当BM CN =时，试判断重叠部分OMN 的形状，并说明理由；②如图3，当CM CN =时，求重叠部分四边形OMCN 的面积（结果保留根号）；(3)拓展应用：若将任意一个锐角的顶点放在正方形中心O 处，该锐角记为GOH ∠（设GOH α∠=），将GOH ∠绕点O 逆时针旋转，在旋转过程中，GOH ∠的两边与正方形ABCD 的边所围成的图形的面积为2S ，请直接写出2S 的最小值与最大值（分别用含α的式子表示），（参考数据：sin15tan152︒=︒=︒=参考答案1. 【答案】A【分析】根据中心对称图形的定义判断即可；【详解】解：在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形；∴是中心对称图形的是：①②③；故选：A．【点睛】本题主要考查中心对称图形的定义，掌握中心对称图形的定义是解题的关键．2. 【答案】C【分析】利用轴对称图形的定义进行解答即可．【详解】解：A、不是轴对称图形，故此选项不合题意；B、不是轴对称图形，故此选项不合题意；C、是轴对称图形，故此选项符合题意；D、不是轴对称图形，故此选项不合题意；故选：C．【点睛】此题主要考查了轴对称图形，关键是掌握如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴．3. 【答案】B【分析】根据旋转的性质可得，BC＝B′C′，∠C′AB′＝∠CAB＝20°，∠AB′C′＝∠ABC ＝30°，再根据旋转角的度数为50°，通过推理证明对①②③④四个结论进行判断即可．【详解】解：①∵△ABC绕A点逆时针旋转50°得到△AB′C′，∴BC＝B′C′．故①正确；②∵△ABC绕A点逆时针旋转50°，∴∠BAB′＝50°．∵∠CAB＝20°，∴∠B′AC＝∠BAB′﹣∠CAB＝30°．∵∠AB′C′＝∠ABC＝30°，∴∠AB′C′＝∠B′AC．∴AC∥C′B′．故②正确；③在△BAB′中，AB＝AB′，∠BAB′＝50°，∴∠AB′B＝∠ABB′＝1（180°﹣50°）＝65°．2∴∠BB′C′＝∠AB′B+∠AB′C′＝65°+30°＝95°．∴CB′与BB′不垂直．故③不正确；④在△ACC′中，AC ＝AC ′，∠CAC ′＝50°，∴∠ACC ′＝12（180°﹣50°）＝65°．∴∠ABB ′＝∠ACC ′．故④正确．∴①②④这三个结论正确．故选：B ．【点睛】此题考查了旋转性质的应用，图形的旋转只改变图形的位置，不改变图形的形状与大小，还考查了等腰三角形的判定和性质、平行线的判定等知识．熟练掌握旋转的性质是解题的关键．4. 【答案】C【分析】由翻折的性质知∠BAE =B AE '∠=50°，AB '=AB ，再由菱形的性质得∠BAD =120°，AB '=AD ，最后利用三角形内角和定理可得答案．【详解】解：∵四边形ABCD 是菱形，∠C =120°，∴∠BAD =∠C =120°，AB =AD ，∵将△ABE 沿直线AE 翻折，使点B 落在B '上，∴∠BAE =B AE '∠=50°，AB '=AB ，∴BAB ∠'=100°，AB '=AD ，∴DAB '∠=20°，∴AB D '∠=ADB '∠=（180°-20°）÷2=80°，故选：C ．【点睛】本题主要考查了菱形的性质，翻折的性质，三角形内角和定理等知识，求出DAB '∠=20°是解题的关键． 5. 【答案】B【分析】直接利用轴对称图形的定义进行判断．如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形．【详解】解：A ，C ，D 选项中的图形都不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形；B 选项中的图形能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形；故选：B ．【点睛】此题主要考查了轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．6. 【答案】C【分析】先根据平行四边形的性质，得出AB CD ，根据平行线的性质，得出156ABE ∠=∠=︒，根据折叠得出1282ABD ABE ∠=∠=︒，根据三角形内角和得出∠A 的度数即可．【详解】解：∵四边形ABCD 为平行四边形，∴AB CD ，156ABE ∴∠=∠=︒，根据折叠可知，ABD EBD ∠=∠， ∴11562822ABD ABE ∠=∠=⨯︒=︒， 242∠=︒，∴1802110A ABD ∠=︒-∠-∠=︒，故C 正确．故选：C ．7. 【答案】D【分析】根据中心对称图形和轴对称图形的定义，即可求解．在平面内，如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形；在平面内，如果把一个图形绕某个点旋转180°后，能与原图形重合，那么就说这个图形是中心对称图形．【详解】解：A 、既不是中心对称图形，又不是轴对称图形，故本选项不符合题意； B 、是轴对称图形，不是中心对称图形，故本选项不符合题意；C 、既不是中心对称图形，又不是轴对称图形，故本选项不符合题意；D 、既是轴对称图形又是中心对称图形，故本选项符合题意；故选：D ．8. 【答案】D【分析】根据轴对称图形与中心对称图形的概念逐项判断即可．【详解】A ．既不是轴对称图形，也不是中心对称图形，故本选项不符合题意；B ．是轴对称图形，不是中心对称图形，故本选项符合题意；C ．不是轴对称图形，是中心对称图形，故本选项不符合题意；D ．既是轴对称图形，也是中心对称图形，故本选项不符合题意；故选：D ．9. 【答案】B【分析】根据轴对称图形与中心对称图形的概念求解．【详解】解：A 、扇形是轴对称图形，不是中心对称图形，故此选项不合题意；B 、平行四边形不一定是轴对称图形，是中心对称图形，故此选项符合题意；C 、等边三角形是轴对称图形，不是中心对称图形，故此选项不合题意；D、矩形既是轴对称图形，又是中心对称图形，故此选项不合题意；故选：B．10. 【答案】D【分析】根据旋转的性质可得对应角相等，对应边相等，进而逐项分析判断即可求解．【详解】解：∵将以点为中心逆时针旋转得到，∴，，，，故①正确；，，，，，∴DA平分BDE∠，故②正确；ADE ABC≌，BAC DAE∴∠=∠，，AFE DFC△△，CAE CDF∴∠=∠，CDF BAD∠=∠∴，故③正确故选D11. 【答案】【分析】平面直角坐标系中任意一点P（x，y），关于原点的对称点是（﹣x，﹣y），即求关于原点的对称点时，横、纵坐标都变成原数的相反数．【详解】解：根据、两点关于原点对称，则横、纵坐标均互为相反数，，，故答案为：3-．【点睛】本题主要考查了平面直角坐标系内两点关于原点对称时横、纵坐标均互为相反数这一特征，熟练掌握该特征是解题的关键．12. 【答案】4【分析】由正方形边长为3，可求AC＝，则AA′＝AC，由平移可得重叠部分是正方形，根据正方形的面积公式可求重叠部分面积．【详解】解：∵正方形ABCD的边长为3，ABC A ADEADE ABC≌E C∴∠=∠AFE DFC∠=∠∴AFE DFC△△ADE ABC≌AB AD∴=ABD ADB∴∠=∠ADE ABC∠=∠ADB ADE∴∠=∠BAD CAE∴∠=∠3-P Q25m∴-=-3m∴=-13∴AC＝，∴AA′＝13 AC∴A′C＝2由题意可得重叠部分是正方形，∴重叠部分的正方形的边长为，∴S重叠部分＝4．故答案为：4．【点睛】本题考查了正方形的性质，平移的性质，关键是灵活运用这些性质解决问题．13. 【答案】12【分析】根据关于原点对称的两点坐标关系：横、纵坐标均互为相反数，即可求出a和b的值，从而求出结论．【详解】解：∵点A（a，2）与点B（6，b）关于原点对称，∴a=-6，b=-2∴ab=12故答案为：12．14. 【答案】()2,2-【分析】根据题意作出旋转后的图形，然后读出坐标系中点的坐标即可．【详解】解：线段OA绕原点O顺时针旋转90°后的位置如图所示，∴旋转后的点A的坐标为（2，-2），故答案为：（2，-2）．【点睛】题目主要考查图形的旋转，点的坐标，理解题意，作出旋转后的图形读出点的坐标是解题关键．15. 【分析】过点E 作EM GH ⊥于点M ，根据题意可得四边形HEDG 是平行四边形，证明HE FE =，等面积法求得ME ，勾股定理求得HM ，可得HF 的长，进而即可求解．【详解】①如图，过点E 作EM GH ⊥于点M ，DE GH ∥，AD BC ∥∴四边形HEDG 是平行四边形113HE GD AD ∴=== 折叠 ∴FED CED ∠=∠90MED ∠=︒即90FEM FED ∠+∠=︒90CED HEM ∴∠+∠=︒HEM FEM ∴∠=∠90,EMF EMH ME ME ∠=∠=︒=HEM FEM ∴≌HM MF ∴=，1EF HE ==1EF EC ∴==四边形ABCD 是矩形90,C DC AB ∴∠=︒==Rt EDC 中，DE =GH DE ∴==ME HG ⊥，HG DE ∥ 1122DEF DEC S ME DE S DC EC ∴=⨯==⨯DC EC ME DE ⨯∴===Rt HME中，HM =2FG HG HF HG HM ∴=-=-==②如图，当113AG AD ==时，同理可得312HE GD AD AG ==-=-=，2EC EF HE ===，DE ∴=DC EC ME DE ⨯∴==RtHME中，HM ===2FG HF HG HM HG ∴=-=-=故答案为：16. 【答案】②【分析】根据已知条件可得，即可判断①，进而推出，导角可得②正确，作于点，连接，证明是直角三角形，勾股定理验证③，证明，即可判断④求解．【详解】解：∵正方形的周长是周长的2倍，∴，，①若，则，故①不正确；如图，在的延长线上取点，使得，=+EF AE FC 45EDF ∠=︒DG EF ⊥G ,GM GN GMN 30BEF MNG ∠=∠=︒ABCD BEF BE BF EF AB BC ++=+∴=+EF AE FC 2,3AE CF ==5EF =BA H AH CF =四边形是正方形，，，，，，，，，，，，，，，，，即，故②正确；如图，作于点，连接，则，，，，同理可得，ABCD 90DAH DAE DCF ∴∠=∠=∠=︒AD CD =ADH CDF ∴≌CDF ADH ∴∠=∠HD DF =H DFC ∠=∠EF AE CF AE AH EH =+=+=DE DE =DHE DFE ∴≌()SSS HDE FDE ∴∠=∠H EFD ∠=∠HED FED ∠=∠90CDF ADF ADH ADF HDF ∠+∠=∠+∠=∠=︒45EDF HDE ∴∠=∠=︒H DFC DFE ∠=∠=∠45EMN HED EAM DEF ∠=∠+∠=︒+∠41805DE EFN EMN F DF EDF DEF C DFC ∴∠+∠=∠+∠︒+∠=∠+∠=+︒180EFN EMN ∠+∠=︒DG EF ⊥G ,GM GN 90DGE DAE ∠=∠=︒AED GED ∠=∠DE DE =AED GED ∴≌GDF CDF ≌，关于对称轴，关于对称，,GM AM GN CN ∴==，45,45EGM EAM NGF NCF ∠=∠=︒∠=∠=︒，180454590MGN ∴∠=︒-︒-︒=︒，是直角三角形，③若，，，故③不正确，，若，即，，，，又CFN EFN ∠=∠，AME CFN ∴∠=∠，22AEM CFN ∴∠=∠，即AMG CFG ∠=∠，GMN BFE ∴∠=∠，30BEF MNG ∴∠=∠=︒，cos cos cos30BE BEF GNM EF ∴∠==∠=︒= 3BE =，EF ∴== 故④不正确．故答案为：②．17. 【答案】(1)（1，1）；（0，4）；（2，2）(2)2π【分析】（1）将△ABC 绕着点O 按顺时针方向旋转90°得到△A 1B 1C 1，点A 1，B 1，C 1的坐标即为点A ，B ，C 绕着点O 按顺时针方向旋转90°得到的点，由此可得出结果．（2）由图知点B 旋转到点1B 的弧长所对的圆心角是90º，OB =4，根据弧长公式即可计算求出．(1),AG DG CF ADE GDE GDF CDF ∴==∠=∠∠=∠，,A G ∴DE ,C G DF GMN ∴2,3AM CN ==∴2,3GM GN ==4MN ∴≠MG AM =2,3MN BE AM==sin MNG ∠=12MG MN =30MNG ∴∠=︒180EFN EMN ∠+∠=︒180EMN AME ∠+∠=︒解：将△ABC 绕着点O 按顺时针方向旋转90°得到△A 1B 1C 1，点A 1，B 1，C 1的坐标即为点A ，B ，C 绕着点O 按顺时针方向旋转90°得到的点，所以A 1（1，1）；B 1（0，4）；C 1（2，2）(2)解：由图知点B 旋转到点1B 的弧长所对的圆心角是90度，OB =4，∴点B 旋转到点1B 的弧长=904180π⨯⨯=2π 18. 【答案】(2)【分析】(1)先由Rt ABE ∆可求得AE 的长度，再由角度关系可得90FAE ∠=，即可求得EF 的长;(2)过F 作FM CE ⊥于M ，利用勾股定理列方程，即可求出EM 的长度，同时求出FM 的长度，得出答案.(1)设BE x =，则4EC x =-，∴4AE EC x ==-，在Rt ABE ∆中，222AB BE AE +=，∴(()2224x x +=-， ∴1x =，∴1BE =，3AE CE ==，∵AE EC =，∴12∠=∠，∵90ABC ∠=，∴902CAB ∠=-∠，∴901CAB ∠=-∠，由折叠可知，∴，∴，∴，在中，.FAC BAC ∆≅∆901FAC CAB ∠=∠=-∠AF AB ==190FAC ∠+∠=90FAE ∠=Rt FAE ∆EF =(2)过F 作FM ⊥BC 于M ，∴∠FME =∠FMC =90°，设EM =a ,则EC =3-a ，在中，，在中，，∴，∴， ∴， ∴， ∴， ∴19. 【答案】(1)(3,37°)Rt FME222FM FE EM =-Rt FMC 222FM FC MC =-2222FE EM FC MC -=-()222243a a -=--53a =53EM =FM sin FM CEF EF ∠===(2)见解析【分析】（1）根据点的位置定义，即可得出答案；（2）画出图形，证明△AOA ′≌△BOA ′（SAS ），即可由全等三角形的性质，得出结论．(1)解：由题意，得A ′(a ,n °)， ∵a=3,n=37，∴A′(3,37°)，故答案为：(3,37°)； (2)证明：如图，∵()3,37A '︒，B (3,74°)，∴∠AOA ′=37°，∠AOB =74°，OA = OB =3，∴∠A ′OB =∠AOB -∠AOA ′=74°-37°=37°，∵OA ′=OA ′，∴△AOA ′≌△BOA ′（SAS ），∴A ′A =A ′B ．20. 【答案】(1)图见解析(2)图见解析【分析】（1）以所在直线为对称轴，找出点的对称点即为点，再顺次连接点即可得；（2）根据点平移至点的方式，将点进行平移即可得点，再顺次连接点即可得．(1)解：如图①，四边形ABCD 是轴对称图形．AC B D ,,,A B C D B A C E ,,,A B C E(2)解：先将点B 向左平移2格，再向上平移1个可得到点A ，则将点C 按照同样的平移方式可得到点E ，如图②，平行四边形ABCE 是中心对称图形．21. 【答案】(1)45︒(2)见解析(3)2或2【分析】（1）根据旋转的性质可知AB AD =，当20α=︒时可根据等腰三角形的性质计算ADB ∠的角度，再由90BAC ∠=︒，AE 是DAC ∠的平分线可知35DAE ∠=︒，由三角形外角的性质，通过AEB ADB DAE ∠=∠-∠即可得出答案；（2）延长DB 到F ，使BF CE =，连接AF ，先证明ADE ACE △≌△，可推导DEA CEA ∠=∠、ADE ACE ∠=∠、DE CE ∠=，再由已知条件及等腰三角形的性质推导45DEA CEA ∠=∠=︒，然后证明ABF ACE ≌△△，推导90=︒∠FAE ，在Rt AFE 中，由三角函数可计算EF ，即可证明2BD CE +=；（3）分两种情况讨论：①当090α︒<<︒时，借助（2）可知2)BD CE =，再求BD ED的值即可；②当90180α︒≤<︒时，在线段BD 上取点F ，使得BF CE =，结合（2）中ADE ACE △≌△，可知DE CE =、ADE ACE ∠=∠，易证明ABF ACE ≌△△，可推导BAF CAE ∠=∠、AE AF =、90EAF ∠=︒， 45AEF AFE ∠=∠=︒，在Rt AFE 中，由三角函数可计算EF =，即可推导2)BD CE =，再求BD ED 的值即可． (1)解：由旋转可知，AB AD =，当20α=︒时，可知180180208022ABD ADB α︒-︒-︒∠=∠===︒， ∵90BAC ∠=︒，AE 是DAC ∠的平分线，∴90203522BAC DAE α∠-︒-︒∠===︒， ∴803545AEB ADB DAE ∠=∠-∠=︒-︒=︒．故答案为：45︒；(2)证明：延长DB 到F ，使BF CE =，连接AF ．∵AB AC =，AD AB =，∴AD AC =，∵AE 平分DAC ∠，∴DAE CAE ∠=∠，∵AE AE =，∴ADE ACE △≌△，∴DEA CEA ∠=∠，ADE ACE ∠=∠，DE CE ∠=，∵AB AD =，∴ABD ADB ∠=∠，∵180ADE ADB ∠+∠=︒，∴180ACE ABD ∠+∠=︒，∵90BAC ∠=︒，∴360()3601809090BEC ACE ABD BAC ∠=︒-∠+∠-∠=︒-︒-︒=︒，∵DEA CEA ∠=∠ ∴190452DEA CEA ∠=∠=⨯︒=︒， ∵180ABF ABD ∠+∠=︒，180ACE ABD ∠+∠=︒，∴ABF ACE ∠=∠，∵AB AC =，BF CE =，∴ABF ACE ≌△△，∴AF AE =，45AFB AEC ∠=∠=︒，∴180180454590FAE AFB DEA ∠=︒-∠-∠=︒-︒-︒=︒，在Rt AFE 中，90=︒∠FAE ， ∵cos AE AEF EF ∠=，∴cos cos 45AE AE EF AEF ===∠︒，∵2EF BF BD DE CE BD CE BD CE =++=++=+，∴2BD CE +=；(3)①当090α︒<<︒时，由（2）可知，DE CE =，2BD CE +，∴2BD CE =-，当2AE CE =时，可知222)BD CE CE CE =-=，∴2BD ED ===； ②当90180α︒≤<︒时，如下图，在线段BD 上取点F ，使得BF CE =，由（2）可知，ADE ACE △≌△，∴DE CE =，ADE ACE ∠=∠，∵AB AC =，∴ABF ADE =∠∠，∴ABF ACE ∠=∠，∵BF CE =，∴()ABF ACE SAS △≌△，∴BAF CAE ∠=∠，AE AF =，∴90EAF CAF CAE CAF BAF BAC ∠=∠+∠=∠+∠=∠=︒， ∴180452EAF AEF AFE ︒-∠∠=∠==︒，在Rt AFE 中，cos AE AEF EF ∠=，∴cos cos 45AE AE EF AEF ===∠︒，∴2BD BF EF DE CE CE CE =++=++，当2AE CE =时，可知222)BD CE CE CE =+=，∴2BD ED ==．综上所述，当0180,2AE CE α︒<<︒=时，2BD ED =或2BD ED=． 22. 【答案】(1)见详解(2)32(3)2293(0)4362x y x x =<<+ (4)332x <≤或2548x <≤ 【分析】（1）根据切线的判定定理求解即可；（2）如图，在Rt OEB ∆，根据勾股定理列方程求解即可；（3）先证DAO AEG ∆∆∽，求出AE ，然后证明AEG ABF ∆∆∽，根据相似三角形面积比等于相似比的平方即可求解；（4）结合图形，分情况讨论即可求出x 的取值范围．(1)证明：在矩形ABCD 中，90DAB ∠=︒，△OED 是△OAD 沿OD 折叠得到的，90OED DAB ∴∠=∠=︒，即OE DE ⊥，∴ DE 是半圆O 的切线；(2) 解：△OED 是△OAD 沿OD 折叠得到的，3,DE AD OA OE x ∴====，4OB AB OA x ∴=-=-，在Rt DAB ∆中，5DB =，532EB DB DE ∴=-=-=，在Rt OEB ∆中，222OE EB OB +=，()22224x x ∴+=-，解得32x =，答：x 的值为32．(3)解：在Rt DAO ∆中，DO△OED 是△OAD 沿OD 折叠得到的，AE OD ∴⊥，AG 是O 的直径，90AEG ∴∠=︒，即AE EG ⊥，OD EG ∴∥，90DAO AEG ∠=∠=︒AOD EGA ∴∠=∠，DAO AEG ∴∆∆∽，DO DA AG AE∴= ，3,AE AE ==， 90,AEG ABC EAG BAF ∠=∠=︒∠=∠，AEG ABF ∴∆∆∽，2AGEAFB S AE S AB ∆∆⎛⎫∴= ⎪⎝⎭，即()222949x y x ==+ ⎪ ⎪⎝⎭， 229436x y x ∴=+ （302x <<）(4)解：由（2）知，当E 在DB 上时， 32x =，如图，当点E 在DC 上时， 3x = ，∴当332x <≤时，半圆O 与△BCD 的边有两个交点；当半圆O 经过点C 时，半圆O 与△BCD 的边有两个交点，连接OC ，在Rt OBC ∆中，4,,3OB x OC x BC =-==，222OB BC OC +=，()22243x x ∴-+= ，解得258x =， ∴当2548x ≤≤时，半圆O 与△BCD 的边有两个交点；综上所述，当半圆O 与△BCD 的边有两个交点时，x 的取值范围为：332x <≤或2548x <≤． 23. 【答案】(1)1,1， (2)①OMN 是等边三角形，理由见解析；1 (3)tan ,1tan 4522αα⎛⎫-︒- ⎪⎝⎭ 【分析】（1）如图1，若将三角板的顶点P 放在点O 处，在旋转过程中，当OF 与OB 重合时，OE 与OC 重合，此时重叠部分的面积=△OBC 的面积=14正方形ABCD 的面积=1；当OF 与BC 垂直时，OE ⊥BC ，重叠部分的面积=14正方形ABCD 的面积=1；一般地，若正方形面积为S ，在旋转过程中，重叠部分的面积S 1与S 的关系为S 1=14S ．利用全等三角形的性质证明即可；（2）①结论：△OMN 是等边三角形．证明OM =ON ，可得结论；②如图3中，连接OC ，过点O 作OJ ⊥BC 于点J ．证明△OCM ≌△OCN （SAS ），推出∠COM =∠CON =30°，解直角三角形求出OJ ，即可解决问题；（3）如图4-1中，过点O 作OQ ⊥BC 于点Q ，当BM =CN 时，△OMN 的面积最小，即S 2最小．如图4-2中，当CM =CN 时，S 2最大．分别求解即可．(1)如图1，若将三角板的顶点P 放在点O 处，在旋转过程中，当OF 与OB 重合时，OE 与OC 重合，此时重叠部分的面积=△OBC 的面积=14正方形ABCD 的面积=1；当OF 与BC 垂直时，OE ⊥BC ，重叠部分的面积=14正方形ABCD 的面积=1；一般地，若正方形面积为S ，在旋转过程中，重叠部分的面积S 1与S 的关系为S 1=14S ．114S S =理由：如图1中，设OF交AB于点J，OE交BC于点K，过点O作OM⊥AB于点M，ON⊥BC于点N．∵O是正方形ABCD的中心，∴OM=ON，∵∠OMB=∠ONB=∠B=90°，∴四边形OMBN是矩形，∵OM=ON，∴四边形OMBN是正方形，∴∠MON=∠EOF=90°，∴∠MOJ=∠NOK，∵∠OMJ=∠ONK=90°，∴△OMJ≌△ONK（AAS），∴S△PMJ=S△ONK，∴S四边形OKBJ=S正方形OMBN=14S正方形ABCD，∴S1=14 S．故答案为：1，1，S1=14 S．(2)①如图2中，结论：△OMN是等边三角形．理由：过点O作OT⊥BC，∵O是正方形ABCD的中心，∴BT=CT，∵BM=CN，∴MT=TN，∵OT⊥MN，∴OM=ON，∵∠MON=60°，∴△MON是等边三角形；②如图3中，连接OC，过点O作OJ⊥BC于点J．∵CM=CN，∠OCM=∠OCN，OC=OC，∴△OCM≌△OCN（SAS），∴∠COM=∠CON=30°，∴∠OMJ=∠COM+∠OCM=75°，∵OJ⊥CB，∴∠JOM=90°-75°=15°，∵BJ=JC=OJ=1，∴JM=OJ•tan15°=2∴CM=CJ-MJ=1-（2-，∴S四边形OMCN=2×12×CM×OJ=．(3)如图4，将HOG∠沿翻折得到，则，此时则当在上时，比四边形的面积小，设，则当最大时，最小，，即时，最大，此时垂直平分，即，则OM ON=如图5中，过点O作OQ⊥BC于点Q，OM ON=，OQ MN⊥∴BM=CN∴当BM=CN时，△OMN的面积最小，即S2最小．在Rt△MOQ中，MQ=OQ•tan2α=tan2α，∴MN=2MQ=2tan2α，∴S2=S△OMN=12×MN×OQ=tan2α．如图6中，同理可得，当CM=CN时，S2最大．OH HOG'∠MON M ON'≌,M N BC 2S NOM C',=M C a CN b'=MNMS'2SMNMS'211222a bab+⎛⎫=≤ ⎪⎝⎭M C NC'=MNMS'OC M N'ON OM'=,,OC OC OCN OCM CN CM =∠=∠=则△COM ≌△CON ，∴∠COM =2α， ∵∠COQ =45°，∴∠MOQ =45°-2α， QM =OQ •tan （45°-2α）=tan （45°-2α）， ∴MC =CQ -MQ =1-tan （45°-2α）， ∴S 2=2S △CMO =2×12×CM ×OQ =1-tan （45°-2α）．。

2022年中考数学复习之挑战压轴题(填空题)：图像的平移、折叠、旋转(含答案)

2022年中考数学复习之挑战压轴题（填空题）：图像的平移、折叠、旋转一．填空题（共10小题）1．（2021秋•鼓楼区校级期末）如图，在△ABC中，AB＝AC，BC＝6，tan∠ACB＝2，点P在边AC上运动（可与点A，C重合），将线段BP绕点P逆时针旋转120°，得到线段DP，连接BD，CD，则CD长的最小值为．2．（2021秋•历城区期末）如图，在矩形ABCD中，AB＝3，AD＝9，点E，F分别在边AD，BC上，且AE＝2，沿直线EF翻折，点A的对应点A′恰好落在对角线AC上，点B的对应点为B′，分别在线段EF，A′B′上取点M，N，沿直线MN二次翻折，使点F与点E重合，则线段MN的长为．3．（2021•綦江区校级三模）如图，在矩形ABCD中，E为AB边上的一点，将△ADE沿DE 翻折，得到△DEF，且F在BC边上，G为AD边上的一点，过点G作AD的垂线交DF 于点H，连接AH交DE于点P，连接AF，若AB＝7，BF＝3，HA平分∠GHF，则AG 的长度为．4．（2021•马鞍山模拟）如图，将边长为4的正方形ABCD纸片沿EF折叠，点C落在AB边上的点G处，点D与点H重合，CG与EF交于点P，取GH的中点Q连接PQ，则△GPQ的周长最小值是．5．（2020•海安市模拟）如图，矩形ABCD中，AB＝3，BC＝4，点E是AB边上一点，且AE＝，点F是边BC上的任意一点，把△BEF沿EF翻折，点B的对应点为G，连接AG，CG，则四边形AGCD的面积的最小值为．6．（2021春•东阳市期末）在综合实践课上，小明把边长为2cm的正方形纸片沿着对角线AC剪开，如图1所示．然后固定纸片△ABC，把纸片△ADC沿AC的方向平移得到△A′D′C′，连A′B，D′B，D′C，在平移过程中：（1）四边形A′BCD′的形状始终是；（2）A′B+D′B的最小值为．7．（2021•路北区一模）如图，边长为1的正方形ABCD在等边长的正六边形外部做顺时针滚动，滚动一周回到初始位置时停止．第一次滚动时正方形旋转了°，点A在滚动过程中到出发点的最大距离是．8．（2021•河北区模拟）如图，四边形ABCD是边长为2的正方形，E是BC边的中点，F 是直线DE上的动点．连接CF，将线段CF逆时针旋转90°得到CG，连接EG，则EG 的最小值是．9．在正方形ABCD中，点P是对角线AC上一点，连接DP，将DP绕点D逆时针旋转90°后得到线段DE，连接PE，点C关于直线PE的对称点是C′，连接C′E、C′P、C′A．若四边形AC′ED是平行四边形，PC＝2，则平行四边形AC′ED的面积是．10．（2020•衢州二模）如图，在矩形ABCD中，AD＝8，AB＝6，点E是CD的中点，过点E作EF∥BC，交对角线BD于点F．将△DEF绕点D逆时针方向旋转得到△DE1F1，连接CE1，BF1，设旋转角度为α（0°＜α＜180°），则＝；连接CF1，当△DF1B 为直角三角形时，CF1＝．2022年中考数学复习之挑战压轴题（填空题）：图像的平移、折叠、旋转（10题）参考答案与试题解析一．填空题（共10小题）1．（2021秋•鼓楼区校级期末）如图，在△ABC中，AB＝AC，BC＝6，tan∠ACB＝2，点P在边AC上运动（可与点A，C重合），将线段BP绕点P逆时针旋转120°，得到线段DP，连接BD，CD，则CD长的最小值为．【考点】轴对称﹣最短路线问题；旋转的性质；解直角三角形；等腰三角形的性质．【专题】图形的相似；推理能力．【分析】以BC为边构建出和△BPD相似的三角形，通过将CD边转化为其他边来求值．【解答】解：如图所示，以BC为底边向上作三等腰△BQC，连接BP．由题意可得△BQC和△BPQ均为顶角为120°的等腰三角形，可得，∠QBC＝∠PBD＝30°，∴∠QBC﹣∠QBD＝∠PBD﹣∠QBD，∴∠PBQ＝∠DBC，∴△PBQ∽△DBC，∴，∴当PQ⊥AC时，有PQ最小，即此时CD最小，如图所示，设OP′⊥AC，延长AQ与BC交K，此时QP'为QP的最小值，可得AK⊥BC，∵△BQC中，∠BQC＝120°，BC＝6，∴BK＝3，∠QBK＝30°，∴QK＝＝，∵tan∠ACB＝＝，KC＝3，∴AK＝＝，∴AQ＝AK﹣QK＝，AC＝＝，∵∠AP'Q＝∠AKC＝90°，∠QAP'＝∠CAK，∴△AQP'∽△ACK，∴，∴，∴QP'＝，∴CD＝＝．【点评】本题考查的是瓜豆原理的知识点，重难点在于构造相似三角形的手拉手模型，属于难题．2．（2021秋•历城区期末）如图，在矩形ABCD中，AB＝3，AD＝9，点E，F分别在边AD，BC上，且AE＝2，沿直线EF翻折，点A的对应点A′恰好落在对角线AC上，点B的对应点为B′，分别在线段EF，A′B′上取点M，N，沿直线MN二次翻折，使点F与点E重合，则线段MN的长为．【考点】翻折变换（折叠问题）；相似三角形的判定与性质；矩形的性质．【专题】几何综合题；压轴题；推理能力．【分析】如图，过点F作FT⊥AD于T，则四边形ABFT是矩形，连接FN，EN，设AC 交EF于J．证明△FTE∽△ADC，求出ET＝1，EF＝，设A′N＝x，根据NF＝NE，可得12+（3﹣x）2＝22+x2，解方程求出x，可得结论．【解答】解：如图，过点F作FT⊥AD于T，则四边形ABFT是矩形，连接FN，EN，设AC交EF于J．∵四边形ABFT是矩形，∴AB＝FT＝3，BF＝AT，∵四边形ABCD是矩形，∴AB＝CD＝3，AD＝BC＝9，∠B＝∠D＝90°∴AC＝＝＝3，∵∠TFE+∠AEJ＝90°，∠DAC+∠AEJ＝90°，∴∠TFE＝∠DAC，∵∠FTE＝∠D＝90°，∴△FTE∽△ADC，∴＝＝，∴＝＝，∴TE＝1，EF＝，∴BF＝AT＝AE﹣ET＝2﹣1＝1，设A′N＝x，∵NM垂直平分线段EF，∴NF＝NE，∴12+（3﹣x）2＝22+x2，∴x＝1，∴FN＝＝＝，∴MN＝＝＝，故答案为：．【点评】本题属于几何综合题，考查矩形的性质，翻折变换，相似三角形的判定和性质，勾股定理等知识，解题的关键是正确寻找相似三角形解决问题，学会利用参数构建方程解决问题，属于中考填空题中的压轴题．3．（2021•綦江区校级三模）如图，在矩形ABCD中，E为AB边上的一点，将△ADE沿DE 翻折，得到△DEF，且F在BC边上，G为AD边上的一点，过点G作AD的垂线交DF 于点H，连接AH交DE于点P，连接AF，若AB＝7，BF＝3，HA平分∠GHF，则AG 的长度为7．【考点】翻折变换（折叠问题）；相似三角形的判定与性质；角平分线的性质；矩形的性质．【专题】推理填空题；矩形菱形正方形；推理能力．【分析】过点A作AN⊥DF于点N，延长AB，DF交于点M，设AE＝x，AD＝y，由翻折可知：EF＝AE＝x，DF＝AD＝BC＝y，则BE＝AB﹣AE＝7﹣x，CF＝BC﹣BF＝y﹣3，在Rt△BEF和Rt△DFC中，根据勾股定理得x＝，y＝，证明△BFM∽△ADM，可得BM＝，证明△EFM∽△ANM，可得AN＝7，然后根据角平分线的性质可以解决问题．【解答】解：如图，过点A作AN⊥DF于点N，延长AB，DF交于点M，设AE＝x，AD＝y，由翻折可知：EF＝AE＝x，DF＝AD＝BC＝y，则BE＝AB﹣AE＝7﹣x，CF＝BC﹣BF＝y﹣3，在Rt△BEF和Rt△DFC中，根据勾股定理，得：BE2+BF2＝EF2，DC2+CF2＝DF2，∴（7﹣x）2+32＝x2，72+（y﹣3）2＝y2，解得x＝，y＝，∴EF＝，AD＝，∴BE＝7﹣x＝，CF＝y﹣3＝，∵BF∥AD，∴△BFM∽△ADM，∴＝，∴＝，∴BM＝，∴EM＝BM+BE＝+＝，∴AM＝AB+BM＝7+＝，由翻折可知：∠EFD＝∠EAD＝90°，∵AN⊥DF，∴∠EFM＝∠ANM＝90°，∴EF∥AN，∴△EFM∽△ANM，∴＝，∴＝，∴AN＝7，∵HA平分∠GHF，AN⊥DF，HG⊥AD，∴AG＝AN＝7．故答案为：7．【点评】本题考查了矩形的相关证明与计算，相似三角形的判定与性质，熟练掌握矩形的性质与相似三角形的性质与判定是解题的关键．4．（2021•马鞍山模拟）如图，将边长为4的正方形ABCD纸片沿EF折叠，点C落在AB 边上的点G处，点D与点H重合，CG与EF交于点P，取GH的中点Q连接PQ，则△GPQ的周长最小值是2+2．【考点】翻折变换（折叠问题）；正方形的性质；轴对称﹣最短路线问题．【专题】平移、旋转与对称．【分析】如图，取CD的中点N，连接PN，PB，BN．首先证明PQ＝PN，PB＝PG，推出PQ+PG＝PN+PB≥BN，求出BN即可解决问题．【解答】解：如图，取CD的中点N，连接PN，PB，BN．由翻折的性质以及对称性可知；PQ＝PN，PG＝PC，HG＝CD＝4，∵QH＝QG，∴QG＝2，在Rt△BCN中，BN＝＝2，∵∠CBG＝90°，PC＝PG，∴PB＝PG＝PC，∴PQ+PG＝PN+PB≥BN＝2，∴PQ+PG的最小值为2，∴△GPQ的周长的最小值为2+2，故答案为2+2．【点评】本题考查翻折变换，正方形的性质，直角三角形斜边中线的性质，勾股定理等知识，解题的关键是学会添加常用辅助线，学会用转化的思想思考问题，属于中考填空题中的压轴题．5．（2020•海安市模拟）如图，矩形ABCD中，AB＝3，BC＝4，点E是AB边上一点，且AE＝，点F是边BC上的任意一点，把△BEF沿EF翻折，点B的对应点为G，连接AG，CG，则四边形AGCD的面积的最小值为．【考点】翻折变换（折叠问题）；三角形的面积；矩形的性质．【专题】推理填空题；平移、旋转与对称；几何直观；运算能力；推理能力．【分析】根据矩形ABCD中，AB＝3，BC＝4，可得AC＝5，由AE＝可得点F是边BC上的任意位置时，点C始终在AC的下方，设点G到AC的距离为h，要使四边形AGCD 的面积的最小，即h最小．所以点G在以点E为圆心，BE为半径的圆上，且在矩形ABCD 的内部．过点E作EH⊥AC，交圆E于点G，此时h最小．根据锐角三角函数先求得h 的值，再分别求得三角形ACD和三角形ACG的面积即可得结论．【解答】解：如图，在矩形ABCD中，AB＝3，BC＝4，∠B＝∠D＝90°，连接AC，∴AC＝5，∵AB＝3，AE＝，∴点F是边BC上的任意位置时，点G始终在AC的下方，设点G到AC的距离为h，S四边形AGCD＝S△ACD+S△ACG＝3×4+×5h，＝6+h．要使四边形AGCD的面积最小，即h最小．∵点G在以点E为圆心，BE为半径的圆上，且在矩形ABCD的内部．过点E作EH⊥AC，交圆E于点G，此时h最小．在Rt△ABC中，sin∠BAC＝＝，在Rt△AEH中，AE＝，sin∠BAC＝＝，解得EH＝AE＝，EG＝BE＝AB﹣AE＝3﹣，∴h＝EH﹣EG＝﹣（3﹣）＝﹣3．∴S四边形AGCD＝6+×（﹣3）＝﹣＝．故答案为：．【点评】本题考查了翻折变换，解决本题的关键是确定满足条件的点G的位置，运用相似、锐角三角函数等知识解决问题．6．（2021春•东阳市期末）在综合实践课上，小明把边长为2cm的正方形纸片沿着对角线AC剪开，如图1所示．然后固定纸片△ABC，把纸片△ADC沿AC的方向平移得到△A′D′C′，连A′B，D′B，D′C，在平移过程中：（1）四边形A′BCD′的形状始终是平行四边形；（2）A′B+D′B的最小值为2．【考点】作图﹣平移变换；正方形的性质；轴对称﹣最短路线问题．【专题】作图题；推理能力．【分析】（1）利用平移的性质证明即可．（2）如图2中，作直线DD′，作点C关于直线DD′的对称点C″，连接D′C″，BC″，过点B作BH⊥CC″于H．求出BC″，证明A′B+BD′＝BD′+CD′＝BD′+D′C″≥BC″，可得结论．【解答】解：（1）如图2中，∵A′D′＝BC，A′D′∥BC，∴四边形A′BCD′是平行四边形，故答案为：平行四边形．（2）如图2中，作直线DD′，作点C关于直线DD′的对称点C″，连接D′C″，BC″，过点B作BH⊥CC″于H．∵四边形ABCD是正方形，∴AB＝BC＝2，∠ABC＝90°，∴AC＝AB＝2，∵BJ⊥AC，∴AJ＝JC，∴BJ＝AC＝，∵∠BJC＝∠JCH＝∠H＝90°，∴四边形BHCJ是矩形，∵BJ＝CJ，∴四边形BHCJ是正方形，∴BH＝CH＝，在Rt△BHC″中，BH＝，HC″＝3，∴BC″＝＝＝2，∵四边形A′BCD′是平行四边形，∴A′B＝CD′，∴A′B+BD′＝BD′+CD′＝BD′+D′C″≥BC″，∴A′B+BD′≥2，∴A′B+D′B的最小值为2，故答案为：2【点评】本题考查作图﹣平移变换，轴对称最短问题，勾股定理等知识，解题的关键是学会利用轴对称解决最短问题，属于中考常考题型．7．（2021•路北区一模）如图，边长为1的正方形ABCD在等边长的正六边形外部做顺时针滚动，滚动一周回到初始位置时停止．第一次滚动时正方形旋转了150°，点A在滚动过程中到出发点的最大距离是+．【考点】旋转的性质；正多边形和圆；轨迹．【专题】平移、旋转与对称；解直角三角形及其应用．【分析】如图，点A的运动轨迹是图中红线．延长AE交红线于H，线段AH的长，即为点A在滚动过程中到出发点的最大距离．【解答】解：第一次滚动正方形旋转了240°﹣90°＝150°．如图，点A的运动轨迹是图中红线．延长AE交红线于H，线段AH的长，即为点A在滚动过程中到出发点的最大距离．易知EH＝EA2＝＝，在△AEF中，∵AF＝EF＝1，∠AFE＝120°，∴AE＝，∴AH＝AE+EH＝+．∴点A在滚动过程中到出发点的最大距离为+．故答案为：150，+【点评】本题考查旋转变换，正方形的性质，正六边形的性质，解直角三角形等知识，解题的关键是理解题意，学会正确寻找点A的运动轨迹，属于中考填空题中的压轴题．8．（2021•河北区模拟）如图，四边形ABCD是边长为2的正方形，E是BC边的中点，F 是直线DE上的动点．连接CF，将线段CF逆时针旋转90°得到CG，连接EG，则EG的最小值是．【考点】旋转的性质；正方形的性质．【专题】矩形菱形正方形．【分析】如图，作直线BG．由△CBG≌△CDF，推出∠CBG＝∠CDF，因为∠CDF是定值，推出点G在直线BG上运动，且tan∠CBG＝tan∠CDF＝＝，根据垂线段最短可知，当EG⊥BG时，EG的长最短．【解答】解：如图，作直线BG．∵四边形ABCD是正方形，∴CB＝CD，∠BCD＝90°，∵∠FCG＝∠DCB＝90°，∴∠BCG＝∠DCF，∵CG＝CF，∴△CBG≌△CDF，∴∠CBG＝∠CDF，∵∠CDF是定值，∴点G在直线BG上运动，且tan∠CBG＝tan∠CDF＝＝，根据垂线段最短可知，当EG⊥BG时，EG的长最短，此时tan∠EBG＝＝，设EG＝m，则BG＝2m，在Rt△BEG中，∵BE2＝BG2+EG2，∴1＝m2+4m2，∴m＝（负根已经舍弃），∴EG的最小值为，故答案为．【点评】本题考查旋转变换、正方形的性质、全等三角形的判定和性质、垂线段最短、解直角三角形等知识，解题的关键是准确寻找全等三角形解决问题，学会利用垂线段最短解决最值问题，属于中考填空题中的压轴题．9．在正方形ABCD中，点P是对角线AC上一点，连接DP，将DP绕点D逆时针旋转90°后得到线段DE，连接PE，点C关于直线PE的对称点是C′，连接C′E、C′P、C′A．若四边形AC′ED是平行四边形，PC＝2，则平行四边形AC′ED的面积是2+4．【考点】旋转的性质；平行四边形的性质；正方形的性质；轴对称的性质．【专题】矩形菱形正方形．【分析】如图，连接DC′，作PH⊥CD于H，设CD交EC′于K．只要证明△ADC′≌△CDP，△DKC′，△PCH是等腰直角三角形即可解决问题；【解答】解：如图，连接DC′，作PH⊥CD于H，设CD交EC′于K．∵四边形ABCD是正方形，∴AD＝CD，∵四边形ADEC′是平行四边形，∴DE＝AC′＝DP，∠DAC′＝∠DEK，∵AD⊥CD，AD∥EC′，∴CD⊥EC′，∵∠PDE＝90°，∴∠PDC+∠CDE＝90°，∠CDE+∠DEK＝90°，∴∠CDP＝∠DAC′，∴△ADC′≌△CDP，∴DC′＝PC＝2，∠ADC′＝∠DCP＝45°，∵∠ADC＝∠PHC＝90°，∴∠KDC′＝45°，∴△DKC′，△PCH是等腰直角三角形，∴DK＝KC′＝CH＝PH＝，∴C′K＝PH，CK′∥PH，∴四边形PHKC′是平行四边形，∵∠PHK＝90°，∴四边形PHKC′是矩形，∴PH＝PC′＝PC＝2，∴AD＝CD＝2+2，∴四边形AC′ED的面积＝（2+2）＝2+4．故答案为2+4．【点评】本题考查旋转变换、正方形的性质、平行四边形的性质、等腰直角三角形的判定和性质、全等三角形的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考填空题中的压轴题．10．（2020•衢州二模）如图，在矩形ABCD中，AD＝8，AB＝6，点E是CD的中点，过点E作EF∥BC，交对角线BD于点F．将△DEF绕点D逆时针方向旋转得到△DE1F1，连接CE1，BF1，设旋转角度为α（0°＜α＜180°），则＝；连接CF1，当△DF1B 为直角三角形时，CF1＝或．【考点】旋转的性质；勾股定理；矩形的性质．【专题】平移、旋转与对称；图形的相似；解直角三角形及其应用；运算能力；推理能力．【分析】由△BDF1∽△CDE1可得＝；分为∠BDF1＝90°，∠DF1B＝90°两种情形，分别解斜△CDF1即可得．【解答】解：如图1，∵△DEF绕点D逆时针方向旋转得到△DE1F1，∴∠EDF＝∠E1DF1，∴∠EDF﹣∠EDF1＝∠E1DF1﹣∠EDF1，∴∠F1DB＝∠E1DC，∵＝＝，＝＝，∴＝，∴△BDF1∽△CDE1，∴＝＝＝，故答案是；如图2，当∠BDF1＝90°时，在△CDF1中，CD＝6，DF1＝5，∠CDF1＝90°﹣∠BDC，作F1G⊥CD于G，在Rt△AGF1中，DF1＝5，∠AF1G＝∠BDC，∴F1G＝DF1•cos∠AF1G＝5•cos∠BDC＝5•＝5×＝3，DG＝5•sin∠BDC＝4，∴CG＝CD﹣DG＝2，∴CF＝＝，如图3，当∠DF1B＝90°时（图中F1′），∵，∴∠DCF1′＝∠DBF1′＝30°，作F1′H⊥CD于H，∴设F1′H＝a，则CH＝a，∴DH＝6﹣，在Rt△DHF1′中，由勾股定理得，（6﹣）2+a2＝52，∴，（舍去），\∴CF1′＝2a＝3﹣4，故答案是或3﹣4．【点评】本题以旋转为背景，考查了三角形相似和解直角三角形，解决问题的关键是正确分类和数量熟练掌握基本图形．考点卡片1．三角形的面积（1）三角形的面积等于底边长与高线乘积的一半，即S△＝×底×高．（2）三角形的中线将三角形分成面积相等的两部分．2．角平分线的性质角平分线的性质：角的平分线上的点到角的两边的距离相等．注意：①这里的距离是指点到角的两边垂线段的长；②该性质可以独立作为证明两条线段相等的依据，有时不必证明全等；③使用该结论的前提条件是图中有角平分线，有垂直角平分线的性质语言：如图，∵C在∠AOB的平分线上，CD⊥OA，CE⊥OB∴CD＝CE3．等腰三角形的性质（1）等腰三角形的概念有两条边相等的三角形叫做等腰三角形．（2）等腰三角形的性质①等腰三角形的两腰相等②等腰三角形的两个底角相等．【简称：等边对等角】③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合．【三线合一】（3）在①等腰；②底边上的高；③底边上的中线；④顶角平分线．以上四个元素中，从中任意取出两个元素当成条件，就可以得到另外两个元素为结论．4．勾股定理（1）勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2＝c2．（2）勾股定理应用的前提条件是在直角三角形中．（3）勾股定理公式a2+b2＝c2的变形有：a＝，b＝及c＝．（4）由于a2+b2＝c2＞a2，所以c＞a，同理c＞b，即直角三角形的斜边大于该直角三角形中的每一条直角边．5．平行四边形的性质（1）平行四边形的概念：有两组对边分别平行的四边形叫做平行四边形．（2）平行四边形的性质：①边：平行四边形的对边相等．②角：平行四边形的对角相等．③对角线：平行四边形的对角线互相平分．（3）平行线间的距离处处相等．（4）平行四边形的面积：①平行四边形的面积等于它的底和这个底上的高的积．②同底（等底）同高（等高）的平行四边形面积相等．6．矩形的性质（1）矩形的定义：有一个角是直角的平行四边形是矩形．（2）矩形的性质①平行四边形的性质矩形都具有；②角：矩形的四个角都是直角；③边：邻边垂直；④对角线：矩形的对角线相等；⑤矩形是轴对称图形，又是中心对称图形．它有2条对称轴，分别是每组对边中点连线所在的直线；对称中心是两条对角线的交点．（3）由矩形的性质，可以得到直角三角形的一个重要性质，直角三角形斜边上的中线等于斜边的一半．7．正方形的性质（1）正方形的定义：有一组邻边相等并且有一个角是直角的平行四边形叫做正方形．（2）正方形的性质①正方形的四条边都相等，四个角都是直角；②正方形的两条对角线相等，互相垂直平分，并且每条对角线平分一组对角；③正方形具有四边形、平行四边形、矩形、菱形的一切性质．④两条对角线将正方形分成四个全等的等腰直角三角形，同时，正方形又是轴对称图形，有四条对称轴．8．正多边形和圆（1）正多边形与圆的关系把一个圆分成n（n是大于2的自然数）等份，依次连接各分点所得的多边形是这个圆的内接正多边形，这个圆叫做这个正多边形的外接圆．（2）正多边形的有关概念①中心：正多边形的外接圆的圆心叫做正多边形的中心．②正多边形的半径：外接圆的半径叫做正多边形的半径．③中心角：正多边形每一边所对的圆心角叫做正多边形的中心角．④边心距：中心到正多边形的一边的距离叫做正多边形的边心距．9．轨迹10．轴对称的性质（1）如果两个图形关于某直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线．由轴对称的性质得到一下结论：①如果两个图形的对应点的连线被同一条直线垂直平分，那么这两个图形关于这条直线对称；②如果两个图形成轴对称，我们只要找到一对对应点，作出连接它们的线段的垂直平分线，就可以得到这两个图形的对称轴．（2）轴对称图形的对称轴也是任何一对对应点所连线段的垂直平分线．11．轴对称-最短路线问题1、最短路线问题在直线L上的同侧有两个点A、B，在直线L上有到A、B的距离之和最短的点存在，可以通过轴对称来确定，即作出其中一点关于直线L的对称点，对称点与另一点的连线与直线L 的交点就是所要找的点．2、凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合本节所学轴对称变换来解决，多数情况要作点关于某直线的对称点．12．翻折变换（折叠问题）1、翻折变换（折叠问题）实质上就是轴对称变换．2、折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．3、在解决实际问题时，对于折叠较为复杂的问题可以实际操作图形的折叠，这样便于找到图形间的关系．首先清楚折叠和轴对称能够提供给我们隐含的并且可利用的条件．解题时，我们常常设要求的线段长为x，然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案．我们运用方程解决时，应认真审题，设出正确的未知数．13．作图-平移变换（1）确定平移后图形的基本要素有两个：平移方向、平移距离．（2）作图时要先找到图形的关键点，分别把这几个关键点按照平移的方向和距离确定对应点后，再顺次连接对应点即可得到平移后的图形．14．旋转的性质（1）旋转的性质：①对应点到旋转中心的距离相等．②对应点与旋转中心所连线段的夹角等于旋转角．③旋转前、后的图形全等．（2）旋转三要素：①旋转中心；②旋转方向；③旋转角度．注意：三要素中只要任意改变一个，图形就会不一样．15．相似三角形的判定与性质（1）相似三角形相似多边形的特殊情形，它沿袭相似多边形的定义，从对应边的比相等和对应角相等两方面下定义；反过来，两个三角形相似也有对应角相等，对应边的比相等．（2）三角形相似的判定一直是中考考查的热点之一，在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形；或依据基本图形对图形进行分解、组合；或作辅助线构造相似三角形，判定三角形相似的方法有事可单独使用，有时需要综合运用，无论是单独使用还是综合运用，都要具备应有的条件方可．16．解直角三角形（1）解直角三角形的定义在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．（2）解直角三角形要用到的关系①锐角、直角之间的关系：∠A+∠B＝90°；②三边之间的关系：a2+b2＝c2；③边角之间的关系：sin A＝＝，cos A＝＝，tan A＝＝．（a，b，c分别是∠A、∠B、∠C的对边）。

中考数学中考最后压轴题训练---折叠旋转问题

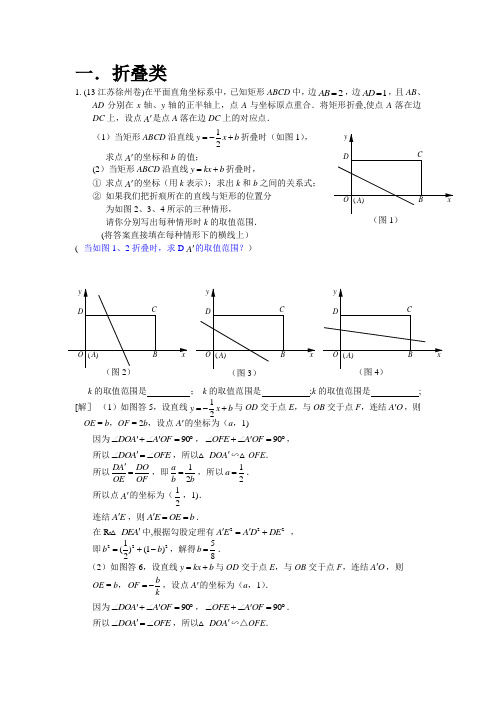
一．折叠类1. (13江苏徐州卷)在平面直角坐标系中，已知矩形ABCD 中，边2AB =，边1AD =，且AB 、AD 分别在x 轴、y 轴的正半轴上，点A 与坐标原点重合．将矩形折叠,使点A 落在边DC 上，设点A '是点A 落在边DC 上的对应点．（1）当矩形ABCD 沿直线12y x b =-+折叠时（如图1），求点A '的坐标和b 的值；(2）当矩形ABCD 沿直线y kx b =+折叠时，① 求点A '的坐标（用k 表示）；求出k 和b 之间的关系式； ② 如果我们把折痕所在的直线与矩形的位置分为如图2、3、4所示的三种情形，请你分别写出每种情形时k 的取值范围．(将答案直接填在每种情形下的横线上） (--当如图1、2折叠时，求D A '的取值范围？）k 的取值范围是； k 的取值范围是 ;k 的取值范围是 ;[解］（1）如图答5，设直线12y x b =-+与OD 交于点E ，与OB 交于点F ，连结A O '，则OE = b ，OF = 2b ，设点A '的坐标为（a ，1)因为90DOA A OF ''∠+∠=︒，90OFE A OF '∠+∠=︒，所以DOA OFE '∠=∠，所以△DOA '∽△OFE ．所以DA DO OE OF '=，即12a b b=，所以12a =．所以点A '的坐标为（12，1)．连结A E '，则A E OE b '==．在R t △DEA '中,根据勾股定理有222A E A D DE ''=+ ，即2221()(1)2b b =+-，解得58b =．（2）如图答6，设直线y kx b =+与OD 交于点E ，与OB 交于点F ，连结A O '，则OE = b ，bOF k =-，设点A '的坐标为（a ，1）．因为90DOA A OF ''∠+∠=︒，90OFE A OF '∠+∠=︒．所以DOA OFE '∠=∠，所以△DOA '∽△OFE ．（图1）所以DA DOOE OF'=，即1a b b k=-，所以a k =-．所以A '点的坐标为（k -，1）．连结A E '，在Rt △DEA '中，DA k '=-，1DE b =-,A E b '=．因为222A E A D DE ''=+，所以222()(1)b k b =-+-．所以212k b +=．在图答6和图答7中求解参照给分．（3)图13﹣2中：21k -≤≤-; 图13﹣3中：1-≤k≤2-+ 图13﹣4中：20k -≤［点评]这是一道有关折叠的问题，主要考查一次函数、四边形、相似形等知识,试题中贯穿了方程思想和数形结合的思想,请注意体会。

2022年九年级数学复习专题---图形的变换(平移、翻折、旋转)综合问题题

2022年中考数学复习专题---图形的变换（平移、翻折、旋转）综合题班级：___________姓名：___________学号：___________1．综合与实践问题情境：综合与实践课上，同学们以“三角形纸片的折叠与旋转“为主题展开数学活动，探究有关的数学问题．动手操作：已知：三角形纸片ABC 中，6120AB AC BC BAC ==∠=︒，，.将三角形纸片ABC 按如下步骤进行操作：第一步：如图1，折叠三角形纸片ABC ，使点C 与点A 重合，然后展开铺平，折痕分别交BC AC ，于点D E ，，连接AD ，易知AD CD =．第二步：在图1的基础上，将三角形纸片ABC 沿AD 剪开，得到ABD ∆和ACD ∆.保持ABD ∆的位置不变，将ACD ∆绕点D 逆时针旋转得到FDG ∆(点F G ，分别是A C ，的对应点)，旋转角为()0360αα︒<<︒问题解决：（1）如图2，小彬画出了旋转角0120α︒<<︒时的图形，设线段FG AC ，交于点P ，连接AG DP ，.小彬发现DP 所在直线始终垂直平分线段AG .请证明这一结论；（2）如图3，小颖画出了旋转角90α=︒时的图形，设直线AF 与直线CG 相交于点O ，连接CF 判断此时COF ∆的形状，说明理由；（3）在ACD ∆绕点D 逆时针旋转过程中，当FG BC ⊥时，请直接写出B F ，两点间的距离．2．如图，△ABC 中，已知∠C=90°，∠B=60°，点D 在边BC 上，过D 作DE ⊥AB 于E ．（1）连接AD ，取AD 的中点F ，连接CF ，EF ，判断△CEF 的形状，并说明理由（2）若．把△BED 绕着点D 逆时针旋转m （0＜m ＜180）度后，如果点B 恰好落在初始Rt △ABC 的边上，那么m=3．问题背景：如图1，在矩形ABCD 中，30AB ABD =∠=︒，点E 是边AB 的中点，过点E 作EF AB ⊥交BD 于点F ．实验探究：（1）在一次数学活动中，小明在图1中发现AEDF=_________．将图1中的BEF 绕点B 按逆时针方向旋转90︒，连接,AE DF ，如图2所示，发现AEDF=_________．（2）小亮同学继续将BEF 绕点B 按逆时针方向旋转，连接,AE DF ，旋转至如图3所示位置，请问探究（1）中的结论是否仍然成立?并说明理由．拓展延伸：（3）在以上探究中，当BEF 旋转至D 、E 、F 三点共线时，AE 的长为____________．4．如图，在Rt ABC 中，90ACB ∠=︒，CD 平分ACB ∠．P 为边BC 上一动点，将DPB 沿着直线DP 翻折到DPE ，点E 恰好落在CDP 的外接圆O 上．（1）求证：D 是AB 的中点．（2）当60BDE ∠=︒，BP =DC 的长．（3）设线段DB 与O 交于点Q ，连结QC ，当QC 垂直于DPE 的一边时，求满足条件的所有QCB ∠的度数．5．如图1，O 为正方形ABCD 的中心，分别延长OA 、OD 到点,F E ，使OF=2OA ，OE 2OD =，连接EF ，将FOE ∆绕点O 按逆时针方向旋转角α得到F OE ''∆，连接,AE BF ''（如图2）．（1）探究AE '与BF '的数量关系，并给予证明；（2）当30α=︒时，求证：AOE '为直角三角形．6．如图，在△ABC 中，AB =∠B =45°，∠C =60°．（1）求BC 边上的高线长．（2）点E 为线段AB 的中点，点F 在边AC 上，连结EF ，沿EF 将△AEF 折叠得到△PEF ． ①如图2，当点P 落在BC 上时，求∠AEP 的度数． ②如图3，连结AP ，当PF ⊥AC 时，求AP 的长．7．如图1，点C 在线段AB 上，分别以AC 、BC 为边在线段AB 的同侧作正方形ACDE 和正方形BCMN ，连结AM 、BD ．（1）AM与BD的关系是：________．（2）如果将正方形BCMN绕点C顺时针旋转锐角α(如图2)．(1) 中所得的结论是否仍然成立？请说明理由．（3）在(2)的条件下，连接AB、DM，若AC=4，BC=2，求AB2+DM2的值．8．已知正方形ABCD，一等腰直角三角板的一个锐角顶点与A重合，将此三角板绕A点旋转时，两边分别交直线BC、CD于M、N．（1）当M、N分别在边BC、CD上时（如图1），求证：BM+DN=MN；（2）当M、N分别在边BC、CD所在的直线上时（如图2），线段BM、DN、MN之间又有怎样的数量关系，请直接写出结论；（不用证明）（3）当M、N分别在边BC、CD所在的直线上时（如图3），线段BM、DN、MN之间又有怎样的数量关系，请写出结论并写出证明过程．9．如图，已知∠ABC=90°，△ABE是等边三角形，点P为射线BC上任意一点（点P与点B不重合），连接AP，将线段AP绕点A逆时针旋转60°得到线段AQ，连接QE并延长交射线BC于点F．(1)如图，当BP=BA时，∠EBF=______°，猜想∠QFC =______°；(2)如图，当点P为射线BC上任意一点时，猜想∠QFC的度数，并加以证明．(3)已知线段AB＝BP＝x，点Q到射线BC的距离为y，求y关于x的函数关系式．10．我们知道，直角坐标系是研究“数形结合”的重要工具．请探索研究下列问题：（1）如图1，点A 的坐标为（-5，1），将点A 绕坐标原点（0，0）按顺时针方向旋转90°，得对应点A '，若反比例函数(0)k y x x=>的图像经过点A '，求k 的值．（2）将（1）中的(0)ky x x =>的图像绕坐标原点（0，0）按顺时针方向旋转45°，如图2，旋转后的图像与x 轴相交于点B ，若直线x =C 与点D ，求△BCD 的面积．（3）在（2）的情况下，半径为6的M 的圆心M 在x 轴上，如图3，若要使△BCD 完全在M 的内部，求M 的圆心M 横坐标xm 的范围（直接写出结果，不必写详细的解答过程）．11．对于平面直角坐标系xOy 中的点A 和点P ，若将点P 绕点A 逆时针旋转90︒后得到点Q ，则称点Q 为点P 关于点A 的“垂链点”，图1为点P 关于点A 的“垂链点”Q 的示意图．（1）已知点A 的坐标为(0,0)，点P 关于点A 的“垂链点”为点Q ；①若点P 的坐标为(2,0)，则点Q 的坐标为________； ②若点Q 的坐标为(2,1)-，则点P 的坐标为________；（2）如图2，已知点C 的坐标为(1,0)，点D 在直线113y x =+上，若点D 关于点C 的“垂链点”在坐标轴上，试求出点D 的坐标；（3）如图3，已知图形G 是端点为(1,0)和(0,2)-的线段，图形H 是以点O 为中心，各边分别与坐标轴平行的边长为6的正方形，点M 为图形G 上的动点，点N 为图形H 上的动点，若存在点(0,)T t ，使得点M 关于点T 的“垂链点”恰为点N ，请直接写出t 的取值范围．12．如图，正比例函数y ＝12x 与反比例函数()0k y x x =>的图象交于点A ，将正比例函数y ＝12x 向上平移6个单位，交y 轴于点C ，交反比例函数图象于点B ，已知AO ＝2BC ．（1）求反比例函数解析式；（2）作直线AB ，将直线AB 向下平移p 个单位，恰与反比例函数图象有唯一交点，求p 的值．13．综合与实践：问题情境：（1）如图，点E 是正方形ABCD 边CD 上的一点，连接BD 、BE ，将DBE ∠绕点B 顺针旋转90︒，旋转后角的两边分别与射线DA 交于点F 和点G ．①线段BE 和BF 的数量关系是______．②写出线段DE 、DF 和BD 之间的数量关系．并说明理由；操作探究：（2）在菱形ABCD 中，60ADC ∠=︒，点E 是菱形ABCD 边CD 所在直线上的－点，连接BD 、BE ，将DBE ∠绕点B 顺时针旋转120︒，旋转后角的两边分别与射线DA 交于点F 和点G ．①如图，点E 在线段DC 上时，请探究线段DE 、DF 和BD 之间的数量关系，写出结论并给出证明；②如图，点E在线段CD的延长线上时，BE交射线DA于点M，若2==，直接写出线段FM和AGDE DC a的长度．14．两个全等的直角三角形ABC和DEF重叠在一起，其中∠A＝60°，AC＝4．固定△ABC不动，将△DEF 进行如下操作：(1)操作发现如图①，△DEF沿线段AB向右平移(即D点在线段AB内移动)，连接DC，CF，FB，四边形CDBF的形状在不断的变化，那么它的面积大小是否变化呢?如果不变化，请求出其面积．(2)猜想论证如图②，当D点移到AB的中点时，请你猜想四边形CDBF的形状，并说明理由．(3)拓展探究如图③，△DEF的D点固定在AB的中点，然后绕D点按顺时针方向旋转△DEF，使DF落在AB边上，此时F点恰好与B点重合，连接AE，求sinα翻折问题姓名：___________班级：___________学号：___________1．如图将矩形纸片ABCD 沿AE 翻折，使点B 落在线段DC 上，对应的点为F ．（1）求证：EFC DAF ∠=∠；（2）若3tan 4AE EFC =∠=，求AB 的长．2．如图，在Rt△ABC 中，∠C=90°，AC=BC=2,AD 是BC 边上的中线，将A 点翻折与点D 重合，得到折痕EF ，求:CE AE 的值.3．如图，点A ，M ，N 在O 上，将MN 沿MN 折叠后，与AM 交于点B ．（1）若70MAN ∠=︒，则ANB ∠=________°；（2）如图1，点B 恰好是翻折所得MN 的中点， ①若MA MN =，求AMN ∠的度数；②若tan MAN ∠=tan AMN ∠的值；（3）如图2，若222AB BN MN +=，求MBAB的值．4．已知矩形ABCD 中，AB ＝2，BC ＝m ，点E 是边BC 上一点，BE ＝1，连接AE ，沿AE 翻折△ABE 使点B 落在点F 处．（1）连接CF ，若CF ∥AE ，求m 的值；（2）连接DF ，若65≤DF ，求m 的取值范围．5．如图1，一张矩形纸ABCD ，ABa AD=，点,E F 分别在边,CD AB 上，且AE EF =，把ADE 沿AE 翻折得到AGE ．（1）如图1，若1AD =．（Ⅰ）当AD DE =时，AFE ∠=_____度；（Ⅱ）当//AG EF 时，求AF 的长度．（2）若直线EG 与边AB 交于点H ，当2AH FH =时，求a 的最小值．6．如图，在折纸游戏中，正方形ABCD 沿着BE ，BF 将BC ，AB 翻折，使A ，C 两点恰好落在点P ．（1）求证：45EBF ∠=︒．（2）如图，过点P 作//MN BC ，交BF 于点Q ． ①若5BM =，且10MP PN ⋅=，求正方形折纸的面积． ②若12QP BC =，求AM BM的值．7．如图，在ABC 中，12,120AC BC ACB ==∠=︒，点D 是AB 边上一点，连接CD ，以CD 为边作等边CDE △．（1）如图1，若45CDB ∠=︒，求等边CDE △的边长；（2）如图2，点D 在AB 边上移动过程中，连接BE ，取BE 的中点F ，连接,CF DF ，过点D 作DG AC ⊥于点G ． ①求证：CFDF ．②如图3，将CFD 沿CF 翻折得CFD '，连接BD '，求出BD '的最小值．8．在矩形ABCD 中，1AB =，BC a =，点E 是边BC 上一动点，连接AE ，将ABE △沿AE 翻折，点B 的对应点为点B '．（1）如图，设BE x =，BC =E 从B 点运动到C 点的过程中． ①AB CB ''+最小值是______，此时x =______； ②点B '的运动路径长为．（2）如图，设35BE a =，当点B 的对应点B '落在矩形ABCD 的边上时，求a 的值．9．如图1，平行四边形ABCD 的对角线AC ，BD 相交于点O ，CD 边的垂直平分线EH 交BD 于点E ，连接AE ，CE ．（1）过点A 作//AF EC 交BD 于点F ，求证：AF BF =；（2）如图2，将ABE △沿AB 翻折得到'ABE △．①求证：'//BE CE ；②若'//AE BC ，1OE =，求CE 的长度．10．如图，矩形ABCD 中，已知6AB =．8BC =，点E 是射线BC 上的一个动点，连接AE 并延长，交射线DC 于点F ．将ABE △沿直线AE 翻折，点B 的对应点为点B '，延长AB '交直线CD 于点M ．（1）如图1，若点B '恰好落在对角线AC 上，求BE CE的值．（2）如图2．当点E 为BC 的中点时，求DM 之长．（3）若32BE CE =，求sin DAB '∠．11．【基础巩固】（1）如图①，ABC ACD CED α∠=∠=∠=，求证：ABC CED ∽△△．【尝试应用】（2）如图②，在菱形ABCD 中，60A ∠=︒，点E ，F 分别为边,AD AB 上两点，将菱形ABCD 沿EF 翻折，点A 恰好落在对角线DB 上的点P 处，若2PD PB =，求AE AF的值．【拓展提高】（3）如图③，在矩形ABCD 中，点P 是AD 边上一点，连接,PB PC ，若2,4,120PA PD BPC ==∠=︒，求AB 的长．12．如图，在ABC 中，60B ∠=︒，AD BC ⊥于点D ，CE AB ⊥于点E ，AB CE =．（1）如图1，将ABD △沿AD 翻折到AFD ，AF 交CE 于点G ，探索线段AB 、AG 、CG 之间有何等量关系，并加以证明；（2）如图2，H 为直线BC 上任意一点，连接AH ，将AH 绕点A 逆时针旋转60°到AH '，连接CH '，若BD =，求CH '的最小值．13．如图，在矩形ABCD 中，12BC AB =，F 、G 分别为AB 、DC 边上的动点，连接GF ，沿GF 将四边形AFGD 翻折至四边形EFGP ，点E 落在BC 上，EP 交CD 于点H ，连接AE 交GF 于点O（1）GF 与AE 之间的位置关系是：______，GF AE 的值是：______，请证明你的结论；（2）连接CP ，若3tan 4CGP ∠=，GF =CP 的长14．如图，在矩形ABCD 中，8AB =，10BC =，点P 在矩形的边CD 上由点D 向点C 运动.沿直线AP 翻折ADP ∆，形成如下四种情形，设DP x =，ADP ∆和矩形重叠部分（阴影）的面积为y .（1）如图4，当点P 运动到与点C 重合时，求重叠部分的面积y ；（2）如图2，当点P 运动到何处时，翻折ADP ∆后，点D 恰好落在BC 边上？这时重叠部分的面积y 等于多少？15．如图1，ABC 中，AB AC =，点D 在BA 的延长线上，点E 在BC 上，连接DE 、DC ，DE 交AC 于点G ，且DE DC =．（1）找出一个与BDE ∠相等的角；（2）若AB =mAD ，求DG GE的值（用含m 的式子表示）；（3）如图2，将ABC 沿BC 翻折，若点A 的对应点A '恰好落在DE 的延长线上，求BE EC的值．16．在等腰直角三角形ABC中，∠BAC=90°，AB=AC，D是斜边BC的中点，连接AD．（1）如图1，E是AC的中点，连接DE，将△CDE沿CD翻折到△CDE′，连接AE′，当时，求AE的值．（2）如图2，在AC上取一点E，使得CE=13AC，连接DE，将△CDE沿CD翻折到△CDE′，连接AE′交BC于点F，求证：DF=CF．。

中考一轮复习数学专题15 图形的旋转、翻折(对称)与平移(学生版)

专题15 图形的旋转、翻折（对称）与平移一、单选题1．（2022·广东）在平面直角坐标系中，将点()1,1向右平移2个单位后，得到的点的坐标是（） A ．()3,1 B ．()1,1- C ．()1,3 D ．()1,1-2．（2022·广西）如图，在△ABC 中，点A （3，1），B （1，2），将△ABC 向左平移2个单位，再向上平移1个单位，则点B 的对应点B ′的坐标为（）A ．（3，-3）B ．（3，3）C ．（－1，1）D ．（－1，3）3．（2020·山东菏泽）在平面直角坐标系中，将点()3,2P -向右平移3个单位得到点P '，则点P '关于x 轴的对称点的坐标为（）A ．()0,2-B ．()0,2C ．()6,2-D ．()6,2--4．（2020·四川自贡）在平面直角坐标系中，将点()2,1向下平移3个单位长度，所得点的坐标是（） A ．(),-11 B ．(),51 C ．(),24 D ．(),-225．（2021·四川雅安）如图，将ABC 沿BC 边向右平移得到DEF ，DE 交AC 于点G ．若:3:1BC EC =．16ADG S =△．则CEG S △的值为（）A ．2B ．4C ．6D ．86．（2021·浙江丽水）四盏灯笼的位置如图．已知A ，B ，C ，D 的坐标分别是 (−1，b )，(1，b )，(2，b )，(3.5，b )，平移y 轴右侧的一盏灯笼，使得y 轴两侧的灯笼对称，则平移的方法可以是（）A ．将B 向左平移4.5个单位B ．将C 向左平移4个单位 C ．将D 向左平移5.5个单位 D ．将C 向左平移3.5个单位7．（2022·四川南充）如图，将直角三角板ABC 绕顶点A 顺时针旋转到AB C ''△，点B '恰好落在CA 的延长线上，3090∠=︒∠=︒，B C ，则BAC '∠为（）A ．90︒B ．60︒C ．45︒D ．308．（2022·山东青岛）如图，将ABC 先向右平移3个单位，再绕原点O 旋转180︒，得到A B C '''，则点A 的对应点A '的坐标是（）A ．(2,0)B ．(2,3)--C ．(1,3)--D ．(3,1)--9．（2022·内蒙古呼和浩特）如图，ABC 中，90ACB ∠=︒，将ABC 绕点C 顺时针旋转得到EDC △，使点B 的对应点D 恰好落在AB 边上，AC 、ED 交于点F ．若BCD α∠=，则EFC ∠的度数是（用含α的代数式表示）（）A ．1902α︒+B ．1902α︒-C ．31802α︒-D ．32α 10．（2022·四川内江）如图，在平面直角坐标系中，点B 、C 、E 在y 轴上，点C 的坐标为（0，1），AC ＝2，Rt△ODE 是Rt△ABC 经过某些变换得到的，则正确的变换是（）* 本号资料皆来源于微信：数学A ．△ABC 绕点C 逆时针旋转90°，再向下平移1个单位B ．△ABC 绕点C 顺时针旋转90°，再向下平移1个单位C ．△ABC 绕点C 逆时针旋转90°，再向下平移3个单位D ．△ABC 绕点C 顺时针旋转90°，再向下平移3个单位11．（2022·黑龙江绥化）如图，线段OA 在平面直角坐标系内，A 点坐标为()2,5，线段OA 绕原点O 逆时针旋转90°，得到线段OA '，则点A '的坐标为（）A ．()5,2-B ．()5,2C ．()2,5-D ．()5,2-12．（2021·四川广安）如图，将ABC 绕点A 逆时针旋转55︒得到ADE ，若70E ∠=︒且AD BC ⊥于点F ，则BAC ∠的度数为（）A ．65︒B ．70︒C ．75︒D ．80︒13．（2020·湖北黄石）在平面直角坐标系中，点G 的坐标是()2,1-，连接OG ，将线段OG 绕原点O 旋转180︒，得到对应线段OG '，则点G '的坐标为（）A ．()2,1-B ．()2,1C ．()1,2-D ．()2,1--14．（2020·四川攀枝花）如图，直径6AB =的半圆，绕B 点顺时针旋转30︒，此时点A 到了点A '，则图中阴影部分的面积是（）．A ．2πB ．34πC ．πD ．3π15．（2022·天津）如图，在△ABC 中，AB =AC ，若M 是BC 边上任意一点，将△ABM 绕点A 逆时针旋转得到△ACN ，点M 的对应点为点N ，连接MN ，则下列结论一定正确的是（）A ．AB AN = B ．AB NC ∥ C ．AMN ACN ∠=∠D ．MN AC ⊥16．（2022·江苏扬州）如图，在ABC ∆中，AB AC <，将ABC 以点A 为中心逆时针旋转得到ADE ，点D 在BC 边上，DE 交AC 于点F ．下列结论：△AFE DFC △△；△DA 平分BDE ∠；△CDF BAD ∠=∠，其中所有正确结论的序号是（）A ．△△B ．△△C ．△△D ．△△△17．（2021·黑龙江牡丹江）如图，△AOB 中，OA ＝4，OB ＝6，AB ＝，将△AOB 绕原点O 旋转90°，则旋转后点A 的对应点A ′的坐标是（）A ．（4，2）或（﹣4，2）B ．（4）或（﹣4） C ．（﹣2）或（2） D ．（2，﹣2，18．（2021·广东广州）如图，在Rt ABC 中，90C ∠=︒，6AC =，8BC =，将ABC 绕点A 逆时针旋转得到A B C '''，使点C '落在AB 边上，连结BB '，则sin BB C ''∠的值为（）A ．35B ．45CD 19．（2021·河南）如图，OABC 的顶点(0,0)O ，(1,2)A ，点C 在x 轴的正半轴上，延长BA 交y 轴于点D ．将ODA 绕点O 顺时针旋转得到OD A ''△，当点D 的对应点D 落在OA 上时，D A ''的延长线恰好经过点C ，则点C 的坐标为（）A ．0)B ．C ．1,0)D ．1,0)20．（2020·海南）如图，在Rt ABC 中， 90,30,1,C ABC AC cm ∠=︒∠=︒=将Rt ABC 绕点A 逆时针旋转得到Rt AB C ''△，使点C '落在AB 边上，连接BB '，则BB '的长度是（）A ．1cmB ．2cmCD ．21．（2020·山东菏泽）如图，将ABC 绕点A 顺时针旋转角α，得到ADE ，若点E 恰好在CB 的延长线上，则BED ∠等于（）A ．2α B ．23α C ．α D ．180α︒-22．（2020·山东聊城）如图，在Rt ABC △中，2AB =，30C ∠=︒，将Rt ABC △绕点A 旋转得到Rt A B C '''∆，使点B 的对应点B '落在AC 上，在B C ''上取点D ，使2B D '=，那么点D 到BC 的距离等于（）．A ．21⎫+⎪⎪⎝⎭B 1C 1D 123．（2020·山东枣庄）如图，平面直角坐标系中，点B 在第一象限，点A 在x 轴的正半轴上，30AOB B ∠=∠=︒，2OA =，将AOB 绕点O 逆时针旋转90︒，点B 的对应点B '的坐标是（）A ．(1,2-+B ．()C ．(2+D ．(- 二、填空题 24．（2022·山东临沂）如图，在平面直角坐标系中，ABC 的顶点A ，B 的坐标分别是()0,2A ，()2,1B -．平移ABC 得到A B C '''，若点A 的对应点A '的坐标为()1,0-，则点B 的对应点B '的坐标是_____________．25．（2021·辽宁鞍山）如图，△ABC 沿BC 所在直线向右平移得到△DEF ，若EC ＝2，BF ＝8，则BE ＝___．26．（2021·湖南湘潭）在平面直角坐标系中，把点()2,1A -向右平移5个单位得到点A '，则点A '的坐标为____． 27．（2021·吉林长春）如图，在平面直角坐标系中，等腰直角三角形AOB 的斜边OA 在y 轴上，2OA =，点B 在第一象限．标记点B 的位置后，将AOB 沿x 轴正方向平移至111AO B 的位置，使11A O 经过点B ，再标记点1B 的位置，继续平移至222A O B △的位置，使22A O 经过点1B ，此时点2B 的坐标为__________．28．（2021·湖南怀化）如图，在平面直角坐标系中，已知(2,1)A -，(1,4)B -，(1,1)C -，将ABC 先向右平移3个单位长度得到111A B C △，再绕1C 顺时针方向旋转90︒得到221A B C △，则2A 的坐标是____________．29．（2022·山东潍坊）如图，在直角坐标系中，边长为2个单位长度的正方形ABCO 绕原点O 逆时针旋转75︒，再沿y 轴方向向上平移1个单位长度，则点B ''的坐标为___________．30．（2020·江苏镇江）如图，在△ABC 中，BC ＝3，将△ABC 平移5个单位长度得到△A 1B 1C 1，点P 、Q 分别是AB 、A 1C 1的中点，PQ 的最小值等于_____．31．（2020·广东广州）如图，点A 的坐标为()1,3，点B 在x 轴上，把OAB ∆沿x 轴向右平移到ECD ∆，若四边形ABDC 的面积为9，则点C 的坐标为_______．32．（2020·湖南湘西）在平面直角坐标系中，O 为原点，点(6,0)A ，点B 在y 轴的正半轴上，30ABO ∠=︒．矩形CODE 的顶点D ，E ，C 分别在,,OA AB OB 上，2OD =．将矩形CODE 沿x 轴向右平移，当矩形CODE 与ABO重叠部分的面积为CODE 向右平移的距离为___________．33．（2022·湖南永州）如图，图中网格由边长为1的小正方形组成，点A 为网格线的交点.若线段OA 绕原点O 顺时针旋转90°后，端点A 的坐标变为______．34．（2021·湖北随州）如图，在Rt ABC 中，90C ∠=︒，30ABC ∠=︒，BC =ABC 绕点A 逆时针旋转角α（0180α︒<<︒）得到AB C ''△，并使点C '落在AB 边上，则点B 所经过的路径长为______．（结果保留π）35．（2020·广西）以原点为中心，把()3,4M 逆时针旋转90°得到点N ，则点N 的坐标为______． 36．（2022·广西贺州）如图，在平面直角坐标系中，OAB 为等腰三角形，5OA AB ==，点B 到x 轴的距离为4，若将OAB 绕点O 逆时针旋转90︒，得到OA B ''△，则点B '的坐标为__________．37．（2022·湖北随州）如图1，在矩形ABCD 中，8AB =，6AD =，E ，F 分别为AB ，AD 的中点，连接EF ．如图2，将△AEF 绕点A 逆时针旋转角()090θθ<<︒，使EF AD ⊥，连接BE 并延长交DF 于点H ，则△BHD 的度数为______，DH 的长为______．本@号资料皆来源于微信*：数学38．（2021·四川巴中）如图，把边长为3的正方形OABC 绕点O 逆时针旋转n °（0＜n ＜90）得到正方形ODEF ，DE 与BC 交于点P ，ED 的延长线交AB 于点Q ，交OA 的延长线于点M ．若BQ ：AQ ＝3：1，则AM ＝__________．9(0)0αα︒<<︒得到AB C ''△，连接BB '，CC '，则CAC '△与BAB '△的面积之比等于_______．40．（2020·四川眉山）如图，在Rt ABC 中，90BAC ∠=︒，2AB =．将ABC 绕点A 按顺时针方向旋转至11AB C △的位置，点1B 恰好落在边BC 的中点处，则1CC 的长为________．41．（2020·山东烟台）如图，已知点A (2，0)，B (0，4)，C (2，4)，D (6，6)，连接AB ，CD ，将线段AB 绕着某一点旋转一定角度，使其与线段CD 重合（点A 与点C 重合，点B 与点D 重合），则这个旋转中心的坐标为_____．42．（2020·甘肃天水）如图，在边长为6的正方形ABCD 内作45EAF ∠=︒，AE 交BC 于点E ，AF 交CD 于点F ，连接EF ，将ADF ∆绕点A 顺时针旋转90︒得到ABG ，若3DF =，则BE 的长为__________．三、解答题43．（2022·安徽）如图，在由边长为1个单位长度的小正方形组成的网格中，△ABC 的顶点均为格点（网格线的交点）．(1)将△ABC 向上平移6个单位，再向右平移2个单位，得到111A B C △，请画出111A B C △﹔(2)以边AC 的中点O 为旋转中心，将△ABC 按逆时针方向旋转180°，得到222A B C △，请画出222A B C △．44．（2022·黑龙江牡丹江）如图，在边长为1个单位长度的小正方形组成的网格中，△ABC 与△DEF 关于点O 成中心对称，△ABC 与△DEF 的顶点均在格点上，请按要求完成下列各题．（1）在图中画出点O 的位置；（2）将△ABC 先向右平移4个单位长度，再向下平移2个单位长度，得到△A 1B 1C 1，请画出△A 1B 1C 1；（3）在网格中画出格点M ，使A 1M 平分△B 1A 1C 145．（2021·黑龙江哈尔滨）如图，方格纸中每个小正方形的边长均为1个单位长度，ABC ∆的顶点和线段DE 的端点均在小正方形的顶点上．（1）在方格纸中将ABC ∆向上平移1个单位长度，再向右平移2个单位长度后得到MNP ∆；（点A 的对应点是点M ，点B 的对应点是点N ，点C 的对应点是点P ），请画出MNP ∆；（2）在方格纸中画出以DE 为斜边的等腰直角三角形DEF （点F 在小正方形的顶点上）．连接FP ，请直接写出线段FP 的长．46．（2021·安徽）图，在每个小正方形的边长为1个单位的网格中，ABC 的顶点均在格点（网格线的交点）上．（1）将ABC 向右平移5个单位得到111A B C △，画出111A B C △；（2）将（1）中的111A B C △绕点C 1逆时针旋转90︒得到221A B C △，画出221A B C △．47．（2022·湖南）如图所示的方格纸(1格长为一个单位长度）中，AOB ∆的顶点坐标分别为(3,0)A ，(0,0)O ，(3,4)B ．(1)将AOB ∆沿x 轴向左平移5个单位，画出平移后的△111AO B （不写作法，但要标出顶点字母）； (2)将AOB ∆绕点O 顺时针旋转90︒，画出旋转后的△222A O B （不写作法，但要标出顶点字母）； (3)在（2）的条件下，求点B 绕点O 旋转到点2B 所经过的路径长（结果保留)π．48．（2022·黑龙江）如图，在正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，ABC 的三个顶点坐标分别为()1,1A -，()2,5B -，()5,4C -．(1)将ABC 先向左平移6个单位，再向上平移4个单位，得到111A B C △，画出两次平移后的111A B C △，并写出点1A 的坐标；(2)画出111A B C △绕点1C 顺时针旋转90°后得到221A B C △，并写出点2A 的坐标； (3)在（2）的条件下，求点1A 旋转到点2A 的过程中所经过的路径长（结果保留π）．49．（2020·四川巴中）如图所示，ABC 在边长为1cm 的小正方形组成的网格中．（1）将ABC 沿y 轴正方向向上平移5个单位长度后，得到111A B C △，请作出111A B C △，并求出11A B 的长度；（2）再将111A B C △绕坐标原点O 顺时针旋转180°，得到222A B C △，请作出222A B C △，并直接写出点2B 的坐标；（3）在（1）（2）的条件下，求线段AB 在变换过程中扫过图形的面积和．50．（2022·江苏常州）如图，点A 在射线OX 上，OA a =．如果OA 绕点O 按逆时针方向旋转(0360)<≤︒n n 到OA '，那么点A '的位置可以用(),︒a n 表示．(1)按上述表示方法，若3a =，37n =，则点A '的位置可以表示为______；(2)在（1）的条件下，已知点B 的位置用()3,74︒表示，连接A A '、A B '．求证：A A A B ''=．51．（2021·黑龙江）如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系内，ABO 的三个顶点坐标分别为()()()1,3,4,3,00,0A B --．（1）画出ABO 关于x 轴对称的11A B O ，并写出点1A 的坐标；（2）画出ABO 绕点O 顺时针旋转90︒后得到的22A B O ，并写出点2A 的坐标；（3）在（2）的条件下，求点A 旋转到点2A 所经过的路径长（结果保留π）．52．（2021·青海西宁）如图，正比例函数12y x =与反比例函数(0)ky x x =>的图象交于点A ，AB x ⊥轴于点B ，延长AB 至点C ，连接OC ．若2cos 3BOC ∠=，3OC =．（1）求OB的长和反比例函数的解析式；（2）将AOB绕点О旋转90°，请直接写出旋转后点A的对应点A'的坐标．53．（2021·江苏淮安）如图，方格纸上每个小正方形的边长均为1个单位长度，△ABC的顶点A、B、C都在格点上（两条网格线的交点叫格点）．请仅用无刻度的直尺按下列要求画图，并保留画图痕迹（不要求写画法）．（1）将△ABC绕点A按顺时针方向旋转90°，点B的对应点为B1，点C的对应点为C1，画出△AB1C1；（2）连接CC1，△ACC1的面积为；*本号资料皆来源于微信：数学第*六感（3）在线段CC1上画一点D，使得△ACD的面积是△ACC1面积的15．54．（2021·辽宁阜新）下面是小明关于“对称与旋转的关系”的探究过程，请你补充完整．（1）三角形在平面直角坐标系中的位置如图1所示，简称G ，G 关于y 轴的对称图形为1G ，关于x 轴的对称图形为2G ．则将图形1G 绕____点顺时针旋转____度，可以得到图形2G ．（2）在图2中分别画出．．．．G 关于 y 轴和直线1y x =+的对称图形1G ，2G ．将图形1G 绕____点（用坐标表示）顺时针旋转______度，可以得到图形2G ．（3）综上，如图3，直线1:22l y x =-+和2:l y x =所夹锐角为α，如果图形G 关于直线1l 的对称图形为1G ，关于直线2l 的对称图形为2G ，那么将图形1G 绕____点（用坐标表示）顺时针旋转_____度（用α表示），可以得到图形2G ．55．（2021·贵州毕节）如图1，在Rt ABC 中，90BAC ∠=︒，AB AC =，D 为ABC 内一点，将线段AD 绕点A 逆时针旋转90°得到AE ，连接CE ，BD 的延长线与CE 交于点F ．（1）求证：BD CE =，BD CE ⊥；（2）如图2．连接AF ，DC ，已知135BDC ∠=︒，判断AF 与DC 的位置关系，并说明理由．56．（2021·内蒙古通辽）已知AOB 和MON △都是等腰直角三角形OM OA ⎫<<⎪⎪⎝⎭，90AOB MON ∠=∠=︒．（1）如图1，连接AM ，BN ，求证：AM BN =；（2）将MON △绕点O 顺时针旋转．△如图2，当点M 恰好在AB 边上时，求证：2222AM BM OM +=；△当点A ，M ，N 在同一条直线上时，若4OA =，3OM =，请直接写出线段AM 的长．57．（2021·湖南衡阳）如图，点E 为正方形ABCD 外一点，90AEB =︒∠，将Rt ABE △绕A 点逆时针方向旋转90︒得到,ADF DF 的延长线交BE 于H 点．（1）试判定四边形AFHE 的形状，并说明理由；（2）已知7,13BH BC ==，求DH 的长．58．（2021·北京）如图，在ABC 中，,,AB AC BAC M α=∠=为BC 的中点，点D 在MC 上，以点A 为中心，将线段AD 顺时针旋转α得到线段AE ，连接,BE DE ．（1）比较BAE ∠与CAD ∠的大小；用等式表示线段,,BE BM MD 之间的数量关系，并证明；（2）过点M 作AB 的垂线，交DE 于点N ，用等式表示线段NE 与ND 的数量关系，并证明．59．（2021·浙江嘉兴）小王在学习浙教版九上课本第72页例2后，进一步开展探究活动：将一个矩形ABCD 绕点A 顺时针旋转()090αα︒<≤︒，得到矩形'''AB C D[探究1]如图1，当90α=︒时，点'C 恰好在DB 延长线上．若1AB =，求BC 的长．[探究2]如图2，连结'AC ，过点'D 作'//'D M AC 交BD 于点M ．线段'D M 与DM 相等吗？请说明理由．[探究3]在探究2的条件下，射线DB 分别交'AD ，'AC 于点P ，N （如图3），MN ，PN 存在一定的数量关系，并加以证明．60．（2021·四川阿坝）如图，Rt ABC 中，90ACB ∠=︒，将ABC 绕点C 顺时针旋转得到DEC ，点D 落在线段AB 上，连接BE ．（1）求证：DC 平分ADE ∠；（2）试判断BE 与AB 的位置关系，并说明理由：（3）若BE BD =，求tan ABC ∠的值．61．（2020·湖南邵阳）已知：如图△，将一块45°角的直角三角板DEF 与正方形ABCD 的一角重合，连接,AF CE ，点M 是CE 的中点，连接DM ．（1）请你猜想AF 与DM 的数量关系是__________．（2）如图△，把正方形ABCD 绕着点D 顺时针旋转α角（090a ︒<<︒）．△AF 与DM 的数量关系是否仍成立，若成立，请证明；若不成立，请说明理由；（温馨提示：延长DM 到点N ，使MN DM =，连接CN ）△求证：AF DM ⊥；△若旋转角45α=︒，且2EDM MDC ∠=∠，求AD ED 的值．（可不写过程，直接写出结果）62．（2020·江苏常州）如图1，点B 在线段CE 上，Rt△ABC △Rt△CEF ，90ABC CEF ∠=∠=︒，30BAC ∠=︒，1BC =．（1）点F 到直线CA 的距离是_________；（2）固定△ABC ，将△CEF 绕点C 按顺时针方向旋转30°，使得CF 与CA 重合，并停止旋转． △请你在图1中用直尺和圆规画出线段EF 经旋转运动所形成的平面图形（用阴影表示，保留画图痕迹，不要求写画法）该图形的面积为_________；△如图2，在旋转过程中，线段CF 与AB 交于点O ，当OE OB =时，求OF 的长．63．（2020·福建）如图，ADE ∆由ABC ∆绕点A 按逆时针方向旋转90︒得到，且点B 的对应点D 恰好落在BC 的延长线上，AD ，EC 相交于点P ．（1）求BDE ∠的度数；（2）F 是EC 延长线上的点，且∠=∠CDF DAC ．△判断DF 和PF 的数量关系，并证明；△求证：=EP PC PF CF．64．（2020·甘肃金昌）如图，点M ，N 分别在正方形ABCD 的边BC ，CD 上，且45MAN ∠=︒，把ADN △绕点A 顺时针旋转90︒得到ABE △．（1）求证：AEM △△ANM ．（2）若3BM =，2DN =，求正方形ABCD 的边长．。

2022年中考数学复习之挑战压轴题(选择题)：图像的平移、折叠、旋转(含答案)

2022年中考数学复习之挑战压轴题（选择题）：图像的平移、折叠、旋转一．选择题（共10小题）1．（2021•绵阳模拟）如图，在△ABC中，D是AC边上的中点，连接BD，把△BDC沿BD 翻折，得到△BDC′，DC'与AB交于点E，连接AC′，若AD＝AC′＝2，BD＝3，则点D到BC的距离为（）A．B．C．D．2．（2021•佳木斯二模）如图，在正方形ABCD中，M是AB上一动点，E是CM的中点，AE绕点E顺时针旋转90°得EF，连接DE，DF，CF．下列结论：①DE＝EF；②∠CDF＝45°；③∠AEM＝∠FEC；④∠BCM+∠DCF＝45°．其中结论正确的序号是（）A．①②③ B．①③④ C．②③④ D．①②④3．（2018•乐清市模拟）如图，一张三角形纸片ABC，其中∠BAC＝60°，BC＝6，点D是BC边上一动点，将BD，CD翻折使得B′，C′分别落在AB，AC边上，（B与B′，C 与C′分别对应），点D从点B运动运动至点C，△B′C′D面积的大小变化情况是（）A．一直减小B．一直不变C．先减小后增大D．先增大后减小4．（2020•卧龙区一模）如图，已知点A1（1，1），将点A1向上平移1个单位长度，再向右平移2个单位长度得到点A2；将点A2向上平移2个单位长度，再向右平移4个单位长度得到点A3；将点A3向上平移4个单位长度，再向右平移8个单位长度得到点A4，…按这个规律平移下去得到点A n（n为正整数），则点A n的坐标是（）A．（2n，2n﹣1）B．（2n﹣1，2n）C．（2n﹣1，2n+1）D．（2n﹣1，2n﹣1）5．（2021•宜兴市校级二模）如图，四边形ABCD为矩形，点E为边AB一点，将△ADE沿DE折叠，点A落在矩形ABCD内的点F处，连接BF，且BE＝EF，∠BEF的正弦值为，则的值为（）A．B．C．D．6．（2021•雷州市模拟）如图，菱形ABCD的边长为4，∠A＝60°，M是AD的中点，N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A′MN，连接A′C，则当A′C取得最小值时，tan∠DCA′的值为（）A．B．C．D．7．（2021•滨城区二模）如图，四边形ABCD是矩形纸片，AB＝2，对折矩形片ABCD，使AD与BC重合，折痕为EF，展平后再过点B折叠矩形纸片，使点A落在EF上的点N 处，折痕BM与EF交于点Q；再次展平，连接BN，MN，延长MN交BC于点G；P为线段BM上一动点，有如下结论：①∠ABN＝60°；②AM＝1；③△BMG是等边三角形；④QN＝BG；⑤若H是BN的中点，则PN+PH的最小值是，其中正确结论的序号是（）A．①②③④⑤ B．①②③ C．②③④ D．①③④⑤8．（2012•十堰）如图，O是正△ABC内一点，OA＝3，OB＝4，OC＝5，将线段BO以点B 为旋转中心逆时针旋转60°得到线段BO′，下列结论：①△BO′A可以由△BOC绕点B逆时针旋转60°得到；②点O与O′的距离为4；③∠AOB＝150°；④S四边形AOBO′＝6+3；⑤S△AOC+S△AOB＝6+．其中正确的结论是（）A．①②③⑤ B．①②③④ C．①②③④⑤ D．①②③9．（2020秋•乌兰察布期末）如图，边长为24的等边三角形ABC中，M是高CH所在直线上的一个动点，连接MB，将线段BM绕点B逆时针旋转60°得到BN，连接HN．则在点M运动过程中，线段HN长度的最小值是（）A．12B．6C．3D．110．（2021•伊金霍洛旗一模）如图，菱形ABCD的形状和大小保持不变，将菱形ABCD绕点B旋转适当角度得到菱形A'BC'D'，边A'D'与AD，DC交于E，F（D，E，F不重合），连接EB，FB．在旋转过程中，下列判断错误的是（）A．EB平分∠AED'B．FB平分∠A'FCC．△DEF的周长是一个定值D．S△DEF+2S△BEF＝S菱形ABCD2022年中考数学复习之挑战压轴题（选择题）：图像的平移、折叠、旋转（10题）参考答案与试题解析一．选择题（共10小题）1．（2021•绵阳模拟）如图，在△ABC中，D是AC边上的中点，连接BD，把△BDC沿BD 翻折，得到△BDC′，DC'与AB交于点E，连接AC′，若AD＝AC′＝2，BD＝3，则点D到BC的距离为（）A．B．C．D．【考点】翻折变换（折叠问题）；点到直线的距离．【专题】平移、旋转与对称；推理能力．【分析】连接CC'，交BD于点M，过点D作DH⊥BC'于点H，由翻折知，△BDC≌△BDC'，BD垂直平分CC'，证△ADC'为等边三角形，利用解直角三角形求出DM＝1，C'M ＝DM＝，BM＝2，在Rt△BMC'中，利用勾股定理求出BC'的长，在△BDC'中利用面积法求出DH的长，则可得出答案．【解答】解：如图，连接CC'，交BD于点M，过点D作DH⊥BC'于点H，∵AD＝AC′＝2，D是AC边上的中点，∴DC＝AD＝2，由翻折知，△BDC≌△BDC'，BD垂直平分CC'，∴DC＝DC'＝2，BC＝BC'，CM＝C'M，∴AD＝AC′＝DC'＝2，∴△ADC'为等边三角形，∴∠ADC'＝∠AC'D＝∠C'AC＝60°，∵DC＝DC'，∴∠DCC'＝∠DC'C＝×60°＝30°，在Rt△C'DM中，∠DC'C＝30°，DC'＝2，∴DM＝1，C'M＝DM＝，∴BM＝BD﹣DM＝3﹣1＝2，在Rt△BMC'中，BC'＝＝＝，∵S△BDC'＝BC'•DH＝BD•CM，∴DH＝3×，∴DH＝，∵∠DCB＝∠DBC'，∴点D到BC的距离为，故选：C．【点评】本题考查了轴对称的性质，解直角三角形，勾股定理等，解题关键是会通过面积法求线段的长度．2．（2021•佳木斯二模）如图，在正方形ABCD中，M是AB上一动点，E是CM的中点，AE绕点E顺时针旋转90°得EF，连接DE，DF，CF．下列结论：①DE＝EF；②∠CDF＝45°；③∠AEM＝∠FEC；④∠BCM+∠DCF＝45°．其中结论正确的序号是（）A．①②③ B．①③④ C．②③④ D．①②④【考点】旋转的性质；全等三角形的判定与性质；正方形的性质．【专题】图形的全等；矩形菱形正方形；平移、旋转与对称；图形的相似；推理能力；应用意识．【分析】延长AE交DC的延长线于点H，由“AAS”可证△AME≌△HCE，可得AE＝EH，由直角三角形的性质可得AE＝EF＝EH，可判断①；由四边形内角和定理可求2∠ADE+2∠EDF＝270°，可得∠ADF＝135°，可判断②；由连接AC，过点E作EP⊥AD 于点P，过点F作FN⊥EP于N，交CD于G，由梯形中位线定理可求PE＝（AM+CD），由“AAS”可证△APE≌△ENF，可得AP＝NE＝AD，即可求AM＝2DG＝2×＝DF，从而证明△MAC∽△FDC，得∠MCA＝∠DCF，即可得∠BCM+∠DCF＝45°，故可判定④；由条件不能证明△AEM与△FEC全等，可判断③，即可得到答案．【解答】解：如图，延长AE交DC的延长线于点H，如图：∵点E是CM的中点，∴ME＝EC，∵AB∥CD，∴∠MAE＝∠H，∠AME＝∠HCE，∴△AME≌△HCE（AAS），∴AE＝EH，又∵∠ADH＝90°，∴DE＝AE＝EH，∵AE绕点E顺时针旋转90°得到EF，∴AE＝EF，∠AEF＝90°，∴AE＝DE＝EF，故①正确；∵AE＝DE＝EF，∴∠DAE＝∠ADE，∠EDF＝∠EFD，∵∠AEF+∠DAE+∠ADE+∠EDF+∠EFD＝360°，∴2∠ADE+2∠EDF＝270°，∴∠ADF＝135°，∴∠CDF＝∠ADF﹣∠ADC＝135°﹣90°＝45°，故②正确；连接AC，过点E作EP⊥AD于点P，过点F作FN⊥EP于N，交CD于G，如图：∵EP⊥AD，FN⊥EP，∠ADC＝90°，∴四边形PDGN是矩形，∴PN＝DG，∠DGN＝90°，∵EP⊥AD，AM⊥AD，CD⊥AD，∴AM∥PE∥CD，∴＝＝1，∴AP＝PD，∴PE是梯形AMCD的中位线，∴PE＝（AM+CD），∵∠FDC＝45°，FN⊥CD，∴∠DFG＝∠FDC＝45°，∴DG＝GF，DF＝DG，∵∠AEP+∠FEN＝90°，∠AEP+∠EAP＝90°，∴∠FEN＝∠EAP，又∵AE＝EF，∠APE＝∠ENF＝90°，∴△APE≌△ENF（AAS），∴AP＝NE＝AD，∵PE＝（AM+CD）＝NE+NP＝AD+NP，∴AM＝NP＝DG，∴AM＝2DG＝2×＝DF，又∵AC＝CD，∴＝＝，∵∠MAC＝∠FDC＝45°，∴△MAC∽△FDC，∴∠MCA＝∠DCF，∵∠BCM+∠MCA＝45°，∴∠BCM+∠DCF＝45°，故④正确；由条件不能证明△AEM与△FEC全等，故不能证明∠AEM＝∠FEC，故③错误，∴正确的有①②④，故选：D．【点评】本题考查了正方形的性质，全等三角形的判定和性质，矩形的判定和性质，旋转的性质，平行线分线段成比例，梯形中位线的定理等知识，灵活运用这些性质解决问题是本题的关键．3．（2018•乐清市模拟）如图，一张三角形纸片ABC，其中∠BAC＝60°，BC＝6，点D是BC边上一动点，将BD，CD翻折使得B′，C′分别落在AB，AC边上，（B与B′，C 与C′分别对应），点D从点B运动运动至点C，△B′C′D面积的大小变化情况是（）A．一直减小B．一直不变C．先减小后增大D．先增大后减小【考点】翻折变换（折叠问题）．【专题】三角形．【分析】如图，作B′H⊥DC′于H．设BD＝DB′＝x，则CD＝DC′＝6﹣x．构建二次函数，利用二次函数的性质即可判断．【解答】解：如图，作B′H⊥DC′于H．设BD＝DB′＝x，则CD＝DC′＝6﹣x．∵∠A＝60°，∴∠B+∠C＝120°，由翻折不变性可知：∠B＝∠DB′B，∠C＝∠DC′C，∴∠BDB′+∠CDC′＝120°，∴∠B′DC′＝60°，∴B′H＝x，∴S△DB′C′＝（6﹣x）＝﹣（x﹣3）2+，∴S△DB′C′的值先增大后减小，故选：D．【点评】本题考查翻折变换、二次函数的性质等知识，解题的关键是学会构建二次函数，利用二次函数的性质解决问题，属于中考选择题中的压轴题．4．（2020•卧龙区一模）如图，已知点A1（1，1），将点A1向上平移1个单位长度，再向右平移2个单位长度得到点A2；将点A2向上平移2个单位长度，再向右平移4个单位长度得到点A3；将点A3向上平移4个单位长度，再向右平移8个单位长度得到点A4，…按这个规律平移下去得到点A n（n为正整数），则点A n的坐标是（）A．（2n，2n﹣1）B．（2n﹣1，2n）C．（2n﹣1，2n+1）D．（2n﹣1，2n﹣1）【考点】坐标与图形变化﹣平移；规律型：点的坐标．【专题】作图题；应用意识．【分析】探究规律，利用根据解决问题即可．【解答】解：由题意知，A1（1，1），A2（3，2），A3（7，4），A4（15，8），…A n（2n﹣1，2n﹣1）．故选：D．【点评】本题考查坐标与图形变化﹣平移，解题的关键是学会探究规律的方法，属于中考常考题型．5．（2021•宜兴市校级二模）如图，四边形ABCD为矩形，点E为边AB一点，将△ADE沿DE折叠，点A落在矩形ABCD内的点F处，连接BF，且BE＝EF，∠BEF的正弦值为，则的值为（）A．B．C．D．【考点】翻折变换（折叠问题）；解直角三角形；矩形的性质．【专题】平移、旋转与对称；几何直观．【分析】过点E作EM⊥BF于点M，作点F作FN⊥AB于点N．设NF＝24k，EF＝25k，则NE＝7k，则BE＝EF＝25k，NB＝BE﹣NE＝25k﹣7k＝18k，所以BF＝，根据∠AED+∠FED+∠BEF＝∠EBF+∠EFB+∠BEF＝180°，推出∠AED＝∠FED＝∠EBF＝∠EFB，所以tan∠AED＝tan∠NBF＝＝＝，则＝，因此AD＝AE＝×25k＝k，即可解决问题．【解答】解：如图．过点E作EM⊥BF于点M，作点F作FN⊥AB于点N．∵∠BEF的正弦值为，∴设NF＝24k，EF＝25k，则NE＝7k，∴BE＝EF＝25k，NB＝BE﹣NE＝25k﹣7k＝18k，∴BF＝＝，由折叠可知，∠AED＝∠FED，AE＝25k，∴AB＝AE+EB＝25k+25k＝50k，∵BE＝EF，∴∠EBF＝∠EFB，∵∠AED+∠FED+∠BEF＝∠EBF+∠EFB+∠BEF＝180°，∴∠AED＝∠FED＝∠EBF＝∠EFB，∴tan∠AED＝tan∠NBF＝＝＝，∴＝，∴AD＝AE＝×25k＝k，∴＝＝．故选：A．【点评】本题属于四边形综合题，考查了矩形的性质，翻折变换，解直角三角形等知识，解题的关键是学会利用参数解决问题，属于中考压轴题．6．（2021•雷州市模拟）如图，菱形ABCD的边长为4，∠A＝60°，M是AD的中点，N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A′MN，连接A′C，则当A′C取得最小值时，tan∠DCA′的值为（）A．B．C．D．【考点】翻折变换（折叠问题）；解直角三角形；等边三角形的判定与性质；菱形的性质．【专题】矩形菱形正方形；平移、旋转与对称；运算能力；推理能力．【分析】根据题意得出A′的位置，过点M作MH⊥DC于点H，进而利用锐角三角函数关系即可解决问题．【解答】解：如图所示：∵MA′是定值，当A′C长度取最小值时，即A′在MC上时，过点M作MH⊥DC于点H，在边长为4的菱形ABCD中，∠A＝60°，∵M为AD中点，∴2MD＝AD＝CD＝4，∠HDM＝60°，∴∠HMD＝30°，∴HD＝MD＝1，∴HM＝DM×cos30°＝，∴CH＝HD+CD＝5，∴tan∠DCA′＝＝，∴tan∠DCA′的值为．故选：B．【点评】本题考查翻折变换、菱形的性质、勾股定理、两点之间线段最短等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，本题的突破点是正确寻找点A′的位置．7．（2021•滨城区二模）如图，四边形ABCD是矩形纸片，AB＝2，对折矩形片ABCD，使AD与BC重合，折痕为EF，展平后再过点B折叠矩形纸片，使点A落在EF上的点N 处，折痕BM与EF交于点Q；再次展平，连接BN，MN，延长MN交BC于点G；P为线段BM上一动点，有如下结论：①∠ABN＝60°；②AM＝1；③△BMG是等边三角形；④QN＝BG；⑤若H是BN的中点，则PN+PH的最小值是，其中正确结论的序号是（）A．①②③④⑤ B．①②③ C．②③④ D．①③④⑤【考点】翻折变换（折叠问题）；解直角三角形；等边三角形的性质；矩形的性质；轴对称﹣最短路线问题．【专题】矩形菱形正方形；平移、旋转与对称；推理能力．【分析】先证明BN＝2BE，推出∠ENB＝30°，再利用翻折不变性以及直角三角形、等边三角形的性质一一判断即可．【解答】解：在Rt△BEN中，∵BN＝AB＝2BE，∴∠ENB＝30°，∴∠ABN＝60°，故①正确，∴∠ABM＝∠NBM＝∠NBG＝30°，∴AM＝AB•tan30°＝，故②错误，∵∠AMB＝∠BMN＝60°，∵AD∥BC，∴∠GBM＝∠AMB＝60°，∴∠MBG＝∠BMG＝∠BGM＝60°，∴△BMG为等边三角形，故③正确．∴BG＝BM＝2AM＝，∵EF∥BC∥AD，AE＝BE，∴BQ＝QM，MN＝NG，∴QN是△BMG的中位线，∴QN＝BG，故④正确．连接PE．∵BH＝BE＝1，∠MBH＝∠MBE，∴E、H关于BM对称，∴PE＝PH，∴PH+PN＝PE+PN，∴E、P、N共线时，PH+PN的值最小，最小值＝EN＝，故⑤正确，故选：D．【点评】本题考查翻折变换、等边三角形的判定和性质、矩形的性质、三角形中位线定理、直角三角形的性质、轴对称最短问题等知识，熟练掌握翻折变换得性质是解题的关键．8．（2012•十堰）如图，O是正△ABC内一点，OA＝3，OB＝4，OC＝5，将线段BO以点B 为旋转中心逆时针旋转60°得到线段BO′，下列结论：①△BO′A可以由△BOC绕点B逆时针旋转60°得到；②点O与O′的距离为4；③∠AOB＝150°；④S四边形AOBO′＝6+3；⑤S△AOC+S△AOB＝6+．其中正确的结论是（）A．①②③⑤ B．①②③④ C．①②③④⑤ D．①②③【考点】旋转的性质；全等三角形的判定与性质；等边三角形的判定与性质；勾股定理的逆定理．【专题】压轴题．【分析】证明△BO′A≌△BOC，又∠OBO′＝60°，所以△BO′A可以由△BOC绕点B逆时针旋转60°得到，故结论①正确；由△OBO′是等边三角形，可知结论②正确；在△AOO′中，三边长为3，4，5，这是一组勾股数，故△AOO′是直角三角形；进而求得∠AOB＝150°，故结论③正确；S四边形AOBO′＝S△AOO′+S△OBO′＝6+4，故结论④错误；如图②，将△AOB绕点A逆时针旋转60°，使得AB与AC重合，点O旋转至O″点．利用旋转变换构造等边三角形与直角三角形，将S△AOC+S△AOB转化为S△COO″+S△AOO″，计算可得结论⑤正确．【解答】解：由题意可知，∠1+∠2＝∠3+∠2＝60°，∴∠1＝∠3，又∵OB＝O′B，AB＝BC，∴△BO′A≌△BOC，又∵∠OBO′＝60°，∴△BO′A可以由△BOC绕点B逆时针旋转60°得到，故结论①正确；如图①，连接OO′，∵OB＝O′B，且∠OBO′＝60°，∴△OBO′是等边三角形，∴OO′＝OB＝4．故结论②正确；∵△BO′A≌△BOC，∴O′A＝5．在△AOO′中，三边长为3，4，5，这是一组勾股数，∴△AOO′是直角三角形，∠AOO′＝90°，∴∠AOB＝∠AOO′+∠BOO′＝90°+60°＝150°，故结论③正确；S四边形AOBO′＝S△AOO′+S△OBO′＝×3×4+×42＝6+4，故结论④错误；如图②所示，将△AOB绕点A逆时针旋转60°，使得AB与AC重合，点O旋转至O″点．易知△AOO″是边长为3的等边三角形，△COO″是边长为3、4、5的直角三角形，则S△AOC+S△AOB＝S四边形AOCO″＝S△COO″+S△AOO″＝×3×4+×32＝6+，故结论⑤正确．综上所述，正确的结论为：①②③⑤．故选：A．【点评】本题考查了旋转变换中等边三角形，直角三角形的性质．利用勾股定理的逆定理，判定勾股数3、4、5所构成的三角形是直角三角形，这是本题的要点．在判定结论⑤时，将△AOB向不同方向旋转，体现了结论①﹣结论④解题思路的拓展应用．9．（2020秋•乌兰察布期末）如图，边长为24的等边三角形ABC中，M是高CH所在直线上的一个动点，连接MB，将线段BM绕点B逆时针旋转60°得到BN，连接HN．则在点M运动过程中，线段HN长度的最小值是（）A．12B．6C．3D．1【考点】旋转的性质；全等三角形的判定与性质；等边三角形的性质．【专题】等腰三角形与直角三角形．【分析】取CB的中点G，连接MG，根据等边三角形的性质可得BH＝BG，再求出∠HBN ＝∠MBG，根据旋转的性质可得MB＝NB，然后利用“边角边”证明△MBG≌△NBH，再根据全等三角形对应边相等可得HN＝MG，然后根据垂线段最短可得MG⊥CH时最短，再根据∠BCH＝30°求解即可．【解答】解：如图，取BC的中点G，连接MG，∵旋转角为60°，∴∠MBH+∠HBN＝60°，又∵∠MBH+∠MBC＝∠ABC＝60°，∴∠HBN＝∠GBM，∵CH是等边△ABC的对称轴，∴HB＝AB，∴HB＝BG，又∵MB旋转到BN，∴BM＝BN，在△MBG和△NBH中，，∴△MBG≌△NBH（SAS），∴MG＝NH，根据垂线段最短，当MG⊥CH时，MG最短，即HN最短，此时∠BCH＝×60°＝30°，CG＝AB＝×24＝12，∴MG＝CG＝×12＝6，∴HN＝6，故选：B．【点评】本题考查了旋转的性质，等边三角形的性质，全等三角形的判定与性质，垂线段最短的性质，作辅助线构造出全等三角形是解题的关键，也是本题的难点．10．（2021•伊金霍洛旗一模）如图，菱形ABCD的形状和大小保持不变，将菱形ABCD绕点B旋转适当角度得到菱形A'BC'D'，边A'D'与AD，DC交于E，F（D，E，F不重合），连接EB，FB．在旋转过程中，下列判断错误的是（）A．EB平分∠AED'B．FB平分∠A'FCC．△DEF的周长是一个定值D．S△DEF+2S△BEF＝S菱形ABCD【考点】旋转的性质；三角形的面积；菱形的性质．【专题】矩形菱形正方形；应用意识．【分析】如图，过点B作BH⊥A′D′于H，BM⊥AD于M，BN⊥CD于N．利用角平分线的判定定理证明选项A，B正确，再利用全等三角形的性质证明△DEF的周长＝2DM ＝定值，即可判断．【解答】解：如图，过点B作BH⊥A′D′于H，BM⊥AD于M，BN⊥CD于N．∵菱形BA′D′C′是由菱形ABCD旋转得到，菱形的每条边上的高相等，∴BM＝BH＝BN，∵BH⊥A′D′于H，BM⊥AD于M，BN⊥CD于N，∴BE平分∠AED′，BF平分∠A′FC，故选项A，B不符合题意，∵∠BME＝∠NHE＝90°，BE＝BE，BM＝BH，∴Rt△BEM≌Rt△BEH（HL），∴EH＝EM，同法可证，FH＝FN，∴△DEF的周长＝DE+EF+DF＝DE+EM+DF+FN＝DM+DN，∵∠BMA＝∠BNC＝90°，BM＝BN，BA＝BC，∴Rt△BMA≌Rt△BNC（HL），∴AM＝CN，∵DA＝DC，∴DM＝DN，∴△DEF的周长＝2DM＝定值，故选项C不符合题意，故选：D．【点评】本题考查旋转变换的性质，菱形的性质，角平分线的判定定理，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考选择题中的压轴题．考点卡片1．规律型：点的坐标规律型：点的坐标．2．点到直线的距离（1）点到直线的距离：直线外一点到直线的垂线段的长度，叫做点到直线的距离．（2）点到直线的距离是一个长度，而不是一个图形，也就是垂线段的长度，而不是垂线段．它只能量出或求出，而不能说画出，画出的是垂线段这个图形．3．三角形的面积（1）三角形的面积等于底边长与高线乘积的一半，即S△＝×底×高．（2）三角形的中线将三角形分成面积相等的两部分．4．全等三角形的判定与性质（1）全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．（2）在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．5．等边三角形的性质（1）等边三角形的定义：三条边都相等的三角形叫做等边三角形，等边三角形是特殊的等腰三角形．①它可以作为判定一个三角形是否为等边三角形的方法；②可以得到它与等腰三角形的关系：等边三角形是等腰三角形的特殊情况．在等边三角形中，腰和底、顶角和底角是相对而言的．（2）等边三角形的性质：等边三角形的三个内角都相等，且都等于60°．等边三角形是轴对称图形，它有三条对称轴；它的任意一角的平分线都垂直平分对边，三边的垂直平分线是对称轴．6．等边三角形的判定与性质（1）等边三角形是一个非常特殊的几何图形，它的角的特殊性给有关角的计算奠定了基础，它的边角性质为证明线段、角相等提供了便利条件．同是等边三角形又是特殊的等腰三角形，同样具备三线合一的性质，解题时要善于挖掘图形中的隐含条件广泛应用．（2）等边三角形的特性如：三边相等、有三条对称轴、一边上的高可以把等边三角形分成含有30°角的直角三角形、连接三边中点可以把等边三角形分成四个全等的小等边三角形等．（3）等边三角形判定最复杂，在应用时要抓住已知条件的特点，选取恰当的判定方法，一般地，若从一般三角形出发可以通过三条边相等判定、通过三个角相等判定；若从等腰三角形出发，则想法获取一个60°的角判定．7．勾股定理的逆定理（1）勾股定理的逆定理：如果三角形的三边长a，b，c满足a2+b2＝c2，那么这个三角形就是直角三角形．说明：①勾股定理的逆定理验证利用了三角形的全等．②勾股定理的逆定理将数转化为形，作用是判断一个三角形是不是直角三角形．必须满足较小两边平方的和等于最大边的平方才能做出判断．（2）运用勾股定理的逆定理解决问题的实质就是判断一个角是不是直角．然后进一步结合其他已知条件来解决问题．注意：要判断一个角是不是直角，先要构造出三角形，然后知道三条边的大小，用较小的两条边的平方和与最大的边的平方比较，如果相等，则三角形为直角三角形；否则不是．8．菱形的性质（1）菱形的定义：有一组邻边相等的平行四边形叫做菱形．（2）菱形的性质①菱形具有平行四边形的一切性质；②菱形的四条边都相等；③菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；④菱形是轴对称图形，它有2条对称轴，分别是两条对角线所在直线．（3）菱形的面积计算①利用平行四边形的面积公式．②菱形面积＝ab．（a、b是两条对角线的长度）9．矩形的性质（1）矩形的定义：有一个角是直角的平行四边形是矩形．（2）矩形的性质①平行四边形的性质矩形都具有；②角：矩形的四个角都是直角；③边：邻边垂直；④对角线：矩形的对角线相等；⑤矩形是轴对称图形，又是中心对称图形．它有2条对称轴，分别是每组对边中点连线所在的直线；对称中心是两条对角线的交点．（3）由矩形的性质，可以得到直角三角形的一个重要性质，直角三角形斜边上的中线等于斜边的一半．10．正方形的性质（1）正方形的定义：有一组邻边相等并且有一个角是直角的平行四边形叫做正方形．（2）正方形的性质①正方形的四条边都相等，四个角都是直角；②正方形的两条对角线相等，互相垂直平分，并且每条对角线平分一组对角；③正方形具有四边形、平行四边形、矩形、菱形的一切性质．④两条对角线将正方形分成四个全等的等腰直角三角形，同时，正方形又是轴对称图形，有四条对称轴．11．轴对称-最短路线问题1、最短路线问题在直线L上的同侧有两个点A、B，在直线L上有到A、B的距离之和最短的点存在，可以通过轴对称来确定，即作出其中一点关于直线L的对称点，对称点与另一点的连线与直线L 的交点就是所要找的点．2、凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合本节所学轴对称变换来解决，多数情况要作点关于某直线的对称点．12．翻折变换（折叠问题）1、翻折变换（折叠问题）实质上就是轴对称变换．2、折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．3、在解决实际问题时，对于折叠较为复杂的问题可以实际操作图形的折叠，这样便于找到图形间的关系．首先清楚折叠和轴对称能够提供给我们隐含的并且可利用的条件．解题时，我们常常设要求的线段长为x，然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案．我们运用方程解决时，应认真审题，设出正确的未知数．13．坐标与图形变化-平移（1）平移变换与坐标变化①向右平移a个单位，坐标P（x，y）⇒P（x+a，y）①向左平移a个单位，坐标P（x，y）⇒P（x﹣a，y）①向上平移b个单位，坐标P（x，y）⇒P（x，y+b）①向下平移b个单位，坐标P（x，y）⇒P（x，y﹣b）（2）在平面直角坐标系内，把一个图形各个点的横坐标都加上（或减去）一个整数a，相应的新图形就是把原图形向右（或向左）平移a个单位长度；如果把它各个点的纵坐标都加（或减去）一个整数a，相应的新图形就是把原图形向上（或向下）平移a个单位长度．（即：横坐标，右移加，左移减；纵坐标，上移加，下移减．）14．旋转的性质（1）旋转的性质：①对应点到旋转中心的距离相等．②对应点与旋转中心所连线段的夹角等于旋转角．③旋转前、后的图形全等．（2）旋转三要素：①旋转中心；②旋转方向；③旋转角度．注意：三要素中只要任意改变一个，图形就会不一样．15．解直角三角形（1）解直角三角形的定义在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．（2）解直角三角形要用到的关系①锐角、直角之间的关系：∠A+∠B＝90°；②三边之间的关系：a2+b2＝c2；③边角之间的关系：sin A＝＝，cos A＝＝，tan A＝＝．（a，b，c分别是∠A、∠B、∠C的对边）。

中考数学压轴题第四部分图形的平移翻折与旋转

4.1 图形的平移、翻折与旋转1.如图，在平面直角坐标系中，正三角形OAB的顶点B的坐标为（2, 0），点A在第一象限内，将△OAB沿直线OA 的方向平移至△O′B′A′的位置，此时点A′的横坐标为3，则点B′的坐标为（）．A．（4，B．（3，C．（4，D．（3，2.如图，在平面直角坐标系中，点A的坐标为(0, 6)，将△OAB沿x轴向左平移得到△O′A′B′，点A的对应点A′落在直线34y x=-上，则点B与其对应点B′间的距离为______．3.已知直线y＝2x＋(3－a)与x轴的交点在A(2, 0)，B(3, 0)之间（包括A、B两点）则a的取值范围是_____________．4.如图，在矩形ABCD中，AD＝15，点E在边DC上，连结AE，△ADE沿直线AE翻折后点D落到点F，过点F作FG⊥AD，垂足为G．如果AD＝3GD，那么DE＝_____．5.如图，在△ABC中，CA＝CB，∠C＝90°，点D是BC的中点，将△ABC沿着直线EF折叠，使点A与点D重合，折痕交AB于点E，交AC于点F，那么sin∠BED的值为____________．6.如图，在矩形ABCD中，AB＝6，AD＝8，把矩形ABCD沿直线MN翻折，点B落在边AD上的E点处，若AE＝2AM，那么EN的长等于．7.如图，已知在Rt△ABC中，∠C＝90°，AC＝BC＝1，点D在边BC上，将△ABC沿直线AD翻折，使点C落在点C′处，连结AC′．直线AC′与CB的延长线相交于点F．如果∠DAB＝∠BAF，那么BF＝______________．8.如图，已知Rt△ABC中，D是斜边AB的中点，AC＝4，BC＝2，将△ACD沿直线CD折叠，点A落在点E处，连结AE，那么线段AE的长度等于__________．9.如图，在矩形纸片ABCD中，AB＜BC，点M、N分别在AD、BC上，沿直线MN将四边形DMNC翻折，点C恰好与点A重合．如果此时在原图中△CDM与△MNC的面积比是1∶3，那么MNDM的值等于___________．10.如图，△ABC中，AB＝AC＝5cm，BC＝6cm，BD平分∠ABC，BD交AC于点D．如果将△ABD沿BD翻折，点A 落在点A′处，那么△DA′C的面积为_______．11.如图，在Rt△ABC中，∠ACB＝90°．将△ABC沿BD折叠，点C恰好落在AB边上的点C′处，折痕为BD．再将其沿DE折叠，使点A落在DC′的延长线上的点A′处，若△BED与△ABC相似，则相似比BDAC＝___________．12.如图，已知扇形OAB的半径为6，圆心角为90°，E是半径OA上一点，F是AB上一点．将扇形AOB沿着EF 对折，使得折叠后的'A F恰好与半径OB相切于点G，若OE＝5，则O到折痕EF的距离为__________．13.如图，正方形ABCD的边长为4，E为BC上的一点，BE＝1，F为AB上的一点，AF＝2，P为AC上一个动点，则PF＋PE的最小值为．14.如图，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD＋PE最小，则这个最小值为（）．A B．C．D15.如图，将正方形ABCD沿MN折叠，使点D落在AB边上，对应点为D′，点C落在C′处．若AB＝6，AD′＝2，则折痕MN的长为_________．16.如图，矩形ABCD中，AB＝8，BC＝6，点P为AD边上一点，将△ABP沿BP翻折至△EBP，PE与CD相交于点O，且OE＝OD，则AP的长为_______．17.如图，∠AOB＝30°，点M、N分别在边OA、OB上，且OM＝1，ON＝3，点P、Q分别在边OB、OA上，则MP＋PQ＋QN的最小值是_________．18.如图，正方形ABCD的边长为3，点E在AB边上且BE＝1，点P、Q分别是边BC、CD上的动点（均不与顶点重合），当四边形AEPQ的周长取得最小值时，四边形AEPQ的面积是____________．19.如图，已知钝角三角形ABC，∠A＝35°，OC为AB边的中线．将△AOC绕着点O顺时针旋转，点C落在BC 边上的点C′处，点A落在点A′处，连结BA′，如果A、C、A′在同一条直线上，那么∠BA′C′的度数为__________．20.如图，在Rt△ABC中，∠C＝90°，AC＝BC ABC绕着点A顺时针旋转60°得到△AB′C′，连结C′B，则C′B的长为___________．21.如图，△ABC中，∠ABC＞90°，tan∠BAC＝34，BC＝4，将三角形绕着点A旋转，点C落在直线AB上的点C′处，点B落在点B′处，若C、B、B′恰好在一直线上，则AB的长为______________．22.如图，在正方形ABCD中，E、F分别在BC、AB边上，如果AF＝BE，那么∠AOD的度数是__________．23.如图，△ABC、△EFG均是边长为2的等边三角形，点D是边BC、EF的中点，直线AG、FC相交于点M．当△EFG绕点D旋转时，线段BM长的最小值是（）A．2B1C D124.如图，已知Rt△ACB中，∠ACB＝90°，AC＝6，BC＝4，将△ABC绕直角顶点C顺时针旋转90°得到△DEC，若点F是DE的中点，连结AF，则AF= ．25.如图，在△ABC中，∠ABC＝90°，AB＝BC ABC绕点C逆时针旋转60°，得到△MNC，则BM的长是___________．26.如图，在△ABC中，∠CAB＝65°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′//AB，则旋转角的度数为（）．A．35°B．40°C．50°D．65°27.已知在△ABC中，AB＝AC＝8，∠BAC＝30°，将△ABC绕点A旋转，使点B落在原△ABC的点C处，此时点C落在点D处．延长线段AD，交原△ABC的边BC的延长线于点E，那么线段DE的长等于．28.如图，△ABC≌△DEF（点A、B分别与点D、E对应），AB＝AC＝5，BC＝6．△ABC固定不动，△DEF运动，并满足点E在BC边从B向C移动（点E不与B、C重合），DE始终经过点A，EF与AC边交于点M，当△AEM是等腰三角形时，BE＝_________．29.如图，在四边形ABCD中，∠A＝90°，AB＝AD＝3，点M、N分别是线段BC、AB上的动点（含端点，但点M不与点B重合），点E、F分别是DM、MN的中点，则EF长度的最大值为．30.如图，正方形ABCD的边长为16，点E在边AB上，AE＝3，点F是边BC上不与B、C重合的一个动点，把△EBF 沿EF折叠，点B落在B′处．若△CDB′恰为等腰三角形，则DB′的长为_______________．31.如图，在△ABC中，AB＝BC＝4，AO＝BO，P是射线CO上的一个动点，∠AOC＝60°，则当△PAB为直角三角形时，AP的长为．32.在平面直角坐标系中，点A，B，动点C在x轴上，若以A、B、C三点为顶点的三角形是等腰三角形，则点C的个数为（）．A.2B.3C.4D.533.在平行四边形ABCD中，AB＜BC，已知∠B＝30°，AB＝ABC沿AC翻折至△AB′C，使点B′落在平行四边形ABCD所在的平面内，连结B′D．若△AB′D是直角三角形，则BC的长为_____________．34.如图，AC是矩形ABCD的对角线，AB＝2，BC＝E、F分别是线段AB、AD上的点，连结CE、CF，当∠BCE＝∠ACF且CE＝CF时，AE＋AF＝______．35.如图，矩形ABCD中，AB＝8，BC＝4．点E在边AB上，点F在边CD上，点G、H在对角线AC上．若四边形EGFH是菱形，则AE的长是（）．A．B．C．5 D．636.如图，过平行四边形ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH，那么图中的平行四边形AEMG 的面积S 1与平行四边形HCFM 的面积S 2的大小关系是（）．A ．S 1＞S 2B ．S 1＜S 2C ．S 1＝S 2D ．2S 1＝S 237.如图，小贤为了体验四边形的不稳定性，将四根木条用钉子钉成一个矩形框架ABCD ，B 与D 两点之间用一根橡皮筋．．．拉直固定，然后向右扭动框架，观察所得四边形的变化．下面判断错误．．的是（）． A ．四边形ABCD 由矩形变为平行四边形； B ．BD 的长度增大；C ．四边形ABCD 的面积不变； D ．四边形ABCD 的周长不变．38.如图，C 是以AB 为直径的半圆O 上一点，连结AC 、BC ，分别以AC 、BC 为边向外作正方形ACDE 和正方形BCFG ，DE 、FG 、AC 、BC 的中点分别是M 、N 、P 、Q ．若MP ＋NQ ＝14，AC ＋BC ＝18，则AB 的长是（）． A. 29 B. 790 C. 13 D. 16 39.如图1，点P 是以r 为半径的⊙O 外一点，点P ′在线段OP 上，若满足OP ·OP ′＝r 2，则称点P ′是点P 关于⊙O的反演点．如图2，在Rt △ABO 中，∠B ＝90°，AB ＝2，BO ＝4，⊙O 的半径为2，如果点A ′、B ′分别是点A 、B 关于⊙O 的反演点，那么A ′B ′的长是____．40.如图，已知⊙O 1的半径为1，⊙O 2的半径为2，O 1O 2＝5，⊙O 分别与⊙O 1外切，与⊙O 2内切，那么⊙O 半径r 的取值范围是__________．41.如图，在边长为4的正方形ABCD 中，先以点A 为圆心，AD 为半径画弧，再以AB 边的中点为圆心，AB 的一半为半径画弧，则两弧之间的阴影部分的面积是_________（结果保留π）．42.如图，半圆O 的直径AE ＝4，点B 、C 、D 均在半圆上，若AB ＝BC ，CD ＝DE ，连结OB 、OD ，则图中阴影部分的面积为_________．43.如图1，菱形ABCD 的边长为2，∠A ＝60°，以点B 为圆心的圆与AD ，DC 相切，与AB 、CB 的延长线分别相交于点E 、F ，则图中阴影部分的面积为（）．A 2πB πC 2πD ．2π+44.如图，半径为5的半圆的初始状态是直径平行于桌面上的直线b ，然后把半圆沿直线b 进行无滑动滚动，使半圆的直径与直线b 重合为止，则圆心O 运动路径的长度等于_____．45.如图，⊙O 的半径为2，AB ，CD 是互相垂直的两条直径，点P 是⊙O 上任意一点（P 与A ，B ，C ，D 不重合），过点P 作PM ⊥AB 于点M ，PN ⊥CD 于点N ，点Q 是MN 的中点，当点P 沿着圆周转过45°时，点Q 走过的路径长为_________． A. 4π B. 2π C. 6π D. 3π 46.如图，在平面直角坐标系中，已知点A (0, 1)，点P 在线段OA 上，以AP 为半径的⊙P 的周长为1．点M 从点A 开始沿⊙P 按照逆时针方向转动，射线AM 交x 轴于点N (n , 0) ，设点M 转过的路程为m （0＜m ＜1）．随着点M 的转动，当m 从13变化到23时，点N 相应移动的路程长为____________．47.已知⊙P 的半径为2，圆心在函数y=8x的图象上运动，当⊙P 与坐标轴相切于点D 时，则符合条件的点D 的个数为（）．A ．0B ．1C ．2D ．448.如图，AB 是⊙O 的弦，AB ＝6，点C 是⊙O 上的一个动点，且∠ACB ＝45°．若M 、N 分别是AB 、BC 的中点，那么MN 长的最大值是__________．49.如图，正方形ABCD 的边长为1，中心为点O ，有一边长大小不定的正六边形EFGHIJ 绕点O 可任意旋转，在旋转过程中，这个正六边形始终在正方形ABCD 内（包括正方形的边），当这个六边形的边长最大时，AE 的最小值为． 50.如图，正比例函数11y k x =的图象与反比例函数22k y x=的图象相交于A 、B 两点，其中点A 的横坐标为2，当y 1＞y 2时，x 的取值范围是（）． A ．x ＜－2或x ＞2 B ． x ＜－2或0＜x ＜2 C ．－2＜x ＜0或0＜x ＜2 D ．－2＜x ＜0或x ＞251.正比例函数y 1＝mx （m ＞0）的图象与反比例函数2k y x=（k ≠0）的图象交于A (n , 4)、B 两点，AM ⊥y 轴，垂足为M ，若△AMB 的面积为8，则满足y 1＞y 2的实数x 的取值范围是___________．52.如图，在平面直角坐标系中，四边形ODEF 和四边形ABCD 都是正方形，点F 在x 轴的正半轴上，点C 在边DE 上，反比例函数k y x=（k ≠0，x ＞0）的图象过点B 、E ．若AB ＝2，则k 的值为________．53.如图，点A 1、A 2依次在y =（x ＞0）的图象上，点B 1、B 2依次在x 轴的正半轴上，若△A 1OB 1、△A 2B 1B 2均为等边三角形，则点B 2的坐标为________．54.如图，在平面直角坐标系中，直线y ＝k 1x ＋2与x 轴交于点A ，与y 轴交于点C ，与反比例函数2k y x =在第一象限内的图象交于点B ，连结BO ，若S △OBC ＝1，tan ∠BOC ＝13，则k 2的值是（）．A ．－3B ．1C ．2D ．3 55.如图，在平面直角坐标系的第一象限内，边长为1的正方形ABCD 的边均平行于坐标轴，点A 的坐标为(a , a )．若曲线3y x=（x ＞0）与此正方形的边有交点，则a 的取值范围是_____________． 56.如图，已知点A 在反比例函数k y x =（x ＜0）上，作Rt △ABC ，点D 为斜边AC 的中点，连结DB 并延长交y 轴于点E ，若△BCE 的面积为8，则k ＝．57.如图，已知∠AOB ＝90°，在∠AOB 的平分线ON 上依次取点C 、F 、M ，过点C 作DE ⊥OC ，分别交OA 、OB 于点D 、E ，以FM 为对角线作菱形FGMH ，已知∠DFE ＝∠GFH ＝120°，FG ＝FE ．设OC ＝x ，图中阴影部分的面积为y ，则y 与x 之间的函数关系式是（）． A. 223x y = B. 23x y = C. 232x y = D. 233x y = 58.如图1，正方形ABCD 的边长为3，动点P 从点B 出发以每秒3个单位长度的速度沿着BC -CD -DA 运动，到达点A 停止运动；另一动点Q 同时从点B 出发以每秒1个单位长度的速度沿着BA 边向点A 运动，到达点A 停止运动．设点P 运动时间为x 秒，△BPQ 的面积为y ，则y 关于x 的函数图象是（）．A ．B ．C ．D ．59.如图1，在平面直角坐标系中，点A 的坐标为(2, 2)，点P (m , n )在直线y ＝－x ＋2上运动．设△APO 的面积为S ，则下面能够反映S 与m 的函数关系的图象是（）．60.如图1，在Rt△ABC中，∠C＝90°，∠BAC＝30°，AB＝8．以DEFG的一边在直线AB上，且点D与点A重合．现将正方形DEFG沿A→B的方向以每秒1个单位的速度匀速运动，当点D与点B重合时停止，则在这个运动过程中，正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是（）．61.如图，已知正△ABC的边长为2，E，F，G分别是AB，BC，CA上的点，且AE=BF=CG，设△EFG的面积为y，AE的长为x，则y关于x的函数图象大致是（）．图1 A．B．C．D．62.如图1，矩形ABCD中，AB＝3，BC＝5，点P是BC边上的一个动点（点P与点B、C不重合），现将△PCD沿直线PD折叠，使点C落到点F处；过点P作∠BPF的角平分线交AB于点E．设BP＝x，BE＝y，则下列图像中，能表示y 与x的函数关系的图象大致是（）．63.函数x xx y2 2+=的图象为（）．A．B．C．D．。

备考2023年中考数学二轮复习-图形的变换_轴对称变换_翻折变换(折叠问题)-综合题专训及答案

备考2023年中考数学二轮复习-图形的变换_轴对称变换_翻折变换（折叠问题）-综合题专训及答案翻折变换（折叠问题）综合题专训1、(2016连云港.中考真卷) 我们知道：光反射时，反射光线、入射光线和法线在同一平面内，反射光线、入射光线分别在法线两侧，反射角等于入射角．如右图，AO为入射光线，入射点为O，ON为法线（过入射点O且垂直于镜面的直线），OB为反射光线，此时反射角∠BON等于入射角∠AON．问题思考：（1）如图1，一束光线从点A处入射到平面镜上，反射后恰好过点B，请在图中确定平面镜上的入射点P，保留作图痕迹，并简要说明理由；（2）如图2，两平面镜OM、ON相交于点O，且OM⊥ON，一束光线从点A出发，经过平面镜反射后，恰好经过点B．小昕说，光线可以只经过平面镜OM反射后过点B，也可以只经过平面镜ON反射后过点B．除了小昕的两种做法外，你还有其它做法吗？如果有，请在图中画出光线的行进路线，保留作图痕迹，并简要说明理由；问题拓展：（3）如图3，两平面镜OM、ON相交于点O，且∠MON=30°，一束光线从点S出发，且平行于平面镜OM，第一次在点A处反射，经过若干次反射后又回到了点S，如果SA和AO的长均为1m，求这束光线经过的路程；（4）如图4，两平面镜OM、ON相交于点O，且∠MON=15°，一束光线从点P出发，经过若干次反射后，最后反射出去时，光线平行于平面镜OM．设光线出发时与射线PM的夹角为θ（0°＜θ＜180°），请直接写出满足条件的所有θ的度数（注：OM、ON足够长）2、(2017磴口.中考模拟) 如图，把一张矩形的纸ABCD沿对角线BD折叠，使点C 落在点E处，BE与AD交于点F．（1）求证：△ABF≌△EDF；（2）若将折叠的图形恢复原状，点F与BC边上的点M正好重合，连接DM，试判断四边形BMDF的形状，并说明理由．3、(2017吉林.中考模拟) 如图，在矩形ABCD中，E是边AB的中点，连接DE，△ADE 沿DE折叠后得到△FDE，点F在矩形ABCD的内部，延长DF交于BC于点G．（1）求证：FG=BG；（2）若AB=6，BC=4，求DG的长．4、(2019吴兴.中考模拟) 定义：长宽比为：为正整数的矩形称为矩形下面，我们通过折叠的方式折出一个矩形，如图a所示．操作1：将正方形ABEF沿过点A的直线折叠，使折叠后的点B落在对角线AE上的点G处，折痕为AH．操作2：过点G作CD∥AB，使点D、点C分别落在边AF，BE上.则四边形ABCD 为矩形．（1）证明：四边形ABCD为矩形；（2）点M是边AB上一动点．如图b，O是对角线AC的中点，若点N在边BC上，，连接求的值；连结AC，CM，当△AMC为等腰三角形时，将△CBM沿着CM翻折，点B的对称点为B’,连结AB’求的值.5、(2018龙湾.中考模拟) 如图，以AB为直径作⊙O，点C为⊙O上一点，劣弧CB 沿BC翻折，交AB于点D，过A作⊙O的切线交DC的延长线于点E．（1）求证：AC=CD；（2）已知tanE= ，AC=2，求⊙O的半径．6、(2016江西.中考真卷) 解方程组与证明（1）解方程组：．（2）如图，Rt△ABC中，∠ACB=90°，将Rt△ABC向下翻折，使点A与点C重合，折痕为DE．求证：DE∥BC．7、(2016郓城.中考模拟) 如图，将矩形纸片ABCD沿对角线BD折叠，使点A落在平面上的F点处，DF交BC于点E．（1）求证：△DCE≌△BFE；（2）若CD=2，∠ADB=30°，求BE的长．8、(2018荆州.中考真卷) 如图，对折矩形纸片ABCD，使AB与DC重合，得到折痕MN，将纸片展平；再一次折叠，使点D落到MN上的点F处，折痕AP交MN于E；延长PF交AB于G．（1）求证：△AFG≌△AFP；（2）△APG为等边三角形．9、(2018柳州.中考模拟) 如图，把长方形纸片ABCD沿EF折叠后．点D与点B重合，点C落在点C′的位置上．若∠1=60°，AE=1．（1）求∠2、∠3的度数；（2）求长方形纸片ABCD的面积S．10、(2019仁寿.中考模拟) （本小题满分9分）如图1，在矩形ABCD中，P为CD边上一点（DP＜CP），∠APB=90°．将△ADP 沿AP翻折得到△AD′P，PD′的延长线交边AB于点M，过点B作BN∥MP交DC 于点N．（1）求证：AD2=DP•PC；（2）请判断四边形PMBN的形状，并说明理由；（3）如图2，连接AC，分别交PM，PB于点E，F．若，求的值．11、(2016贵阳.中考模拟) 如图，矩形ABCD中，AB=6，BC=8，点E是射线CB上的一个动点，把△DCE沿DE折叠，点C的对应点为C′．（1）若点C′刚好落在对角线BD上时，BC′=；（2）若点C′刚好落在线段AB的垂直平分线上时，求CE的长；（3）若点C′刚好落在线段AD的垂直平分线上时，求CE的长．12、(2011遵义.中考真卷) 把一张矩形ABCD纸片按如图方式折叠，使点A与点E重合，点C与点F重合（E、F两点均在BD上），折痕分别为BH、DG．（1）求证：△BHE≌△DGF；（2）若AB=6cm，BC=8cm，求线段FG的长．13、(2020拱墅.中考模拟) 如图1，折叠矩形纸片ABCD，具体操作：①点E为AD边上一点（不与点A，D重合），把△ABE沿BE所在的直线折叠，A点的对称点为F点；②过点E对折∠DEF，折痕EG所在的直线交DC于点G，D点的对称点为H 点．（1）求证：△ABE∽△DEG．（2）若AB=3，BC=5①点E在移动的过程中，求DG的最大值②如图2，若点C恰在直线EF上，连接DH，求线段DH的长．14、(2020.中考真卷) 如图，在平面直角坐标系中，点O为坐标原点，抛物线y=ax2+bx+c的顶点是A（1，3），将OA绕点O顺时针旋转90°后得到OB，点B 恰好在抛物线上，OB与抛物线的对称轴交于点C.（1）求抛物线的解析式；（2） P是线段AC上一动点，且不与点A，C重合，过点P作平行于x轴的直线，与△OAB的边分别交于M，N两点，将△AMN以直线MN为对称轴翻折，得到△A′MN，设点P的纵坐标为m.①当△A′MN在△OAB内部时，求m的取值范围；②是否存在点P，使S△A′MN = S△OA′B，若存在，求出满足条件m的值；若不存在，请说明理由.15、(2020湖州.中考真卷) 已知在△ABC中，AC＝BC＝m，D是AB边上的一点，将∠B 沿着过点D的直线折叠，使点B落在AC边的点P处（不与点A，C重合），折痕交BC边于点E.（1）特例感知：如图1，若∠C＝60°，D是AB的中点，求证：AP＝AC；（2）变式求异：如图2，若∠C＝90°，m＝，AD＝7，过点D作DH⊥AC 于点H，求DH和AP的长；（3）化归探究：如图3，若m＝10，AB＝12，且当AD＝a时，存在两次不同的折叠，使点B落在AC边上两个不同的位置，请直接写出a的取值范围.翻折变换（折叠问题）综合题答案1.答案：2.答案：3.答案：4.答案：5.答案：6.答案：7.答案：8.答案：9.答案：10.答案：11.答案：12.答案：13.答案：14.答案：15.答案：。

2020年江苏省中考数学试题分类汇编(8)——图形的变化(含答案)

2020年江苏省中考数学试题分类（8）——图形的变化一．翻折变换（折叠问题）（共3小题） 1．（2020•无锡）如图，在四边形ABCD 中（AB ＞CD ），∠ABC ＝∠BCD ＝90°，AB ＝3，BC =√3，把Rt △ABC 沿着AC 翻折得到Rt △AEC ，若tan ∠AED =√32，则线段DE 的长度（）A ．√63B ．√73C ．√32D ．2√752．（2020•南通）矩形ABCD 中，AB ＝8，AD ＝12．将矩形折叠，使点A 落在点P 处，折痕为DE ．（1）如图①，若点P 恰好在边BC 上，连接AP ，求AA AA的值；（2）如图②，若E 是AB 的中点，EP 的延长线交BC 于点F ，求BF 的长．3．（2020•无锡）如图，在矩形ABCD 中，AB ＝2，AD ＝1，点E 为边CD 上的一点（与C 、D 不重合），四边形ABCE 关于直线AE 的对称图形为四边形ANME ，延长ME 交AB 于点P ，记四边形P ADE 的面积为S ．（1）若DE =√33，求S 的值；（2）设DE ＝x ，求S 关于x 的函数表达式．二．平移的性质（共1小题） 4．（2020•镇江）如图，在△ABC 中，BC ＝3，将△ABC 平移5个单位长度得到△A 1B 1C 1，点P 、Q 分别是AB 、A 1C 1的中点，PQ 的最小值等于．三．旋转的性质（共1小题）5．（2020•苏州）如图，在△ABC中，∠BAC＝108°，将△ABC绕点A按逆时针方向旋转得到△AB'C'．若点B'恰好落在BC边上，且AB'＝CB'，则∠C'的度数为（）A．18°B．20°C．24°D．28°四．旋转对称图形（共1小题）6．（2020•镇江）点O是正五边形ABCDE的中心，分别以各边为直径向正五边形的外部作半圆，组成了一幅美丽的图案（如图）．这个图案绕点O至少旋转°后能与原来的图案互相重合．五．中心对称图形（共1小题）7．（2020•徐州）下列垃圾分类标识的图案既是轴对称图形，又是中心对称图形的是（）A．B．C．D．六．关于原点对称的点的坐标（共1小题）8．（2020•淮安）在平面直角坐标系中，点（3，2）关于原点对称的点的坐标是（）A．（2，3）B．（﹣3，2）C．（﹣3，﹣2）D．（﹣2，﹣3）七．坐标与图形变化-旋转（共1小题）9．（2020•南通）以原点为中心，将点P（4，5）按逆时针方向旋转90°，得到的点Q所在的象限为（）A．第一象限B．第二象限C．第三象限D．第四象限八．作图-旋转变换（共1小题） 10．（2020•常州）如图1，点B 在线段CE 上，Rt △ABC ≌Rt △CEF ，∠ABC ＝∠CEF ＝90°，∠BAC ＝30°，BC ＝1．（1）点F 到直线CA 的距离是；（2）固定△ABC ，将△CEF 绕点C 按顺时针方向旋转30°，使得CF 与CA 重合，并停止旋转． ①请你在图1中用直尺和圆规画出线段EF 经旋转运动所形成的平面图形（用阴影表示，保留画图痕迹，不要求写画法）．该图形的面积为；②如图2，在旋转过程中，线段CF 与AB 交于点O ，当OE ＝OB 时，求OF 的长．九．几何变换综合题（共1小题） 11．（2020•淮安）[初步尝试]（1）如图①，在三角形纸片ABC 中，∠ACB ＝90°，将△ABC 折叠，使点B 与点C 重合，折痕为MN ，则AM 与BM 的数量关系为； [思考说理]（2）如图②，在三角形纸片ABC 中，AC ＝BC ＝6，AB ＝10，将△ABC 折叠，使点B 与点C 重合，折痕为MN ，求AA AA的值；[拓展延伸]（3）如图③，在三角形纸片ABC 中，AB ＝9，BC ＝6，∠ACB ＝2∠A ，将△ABC 沿过顶点C 的直线折叠，使点B 落在边AC 上的点B ′处，折痕为CM ． ①求线段AC 的长；②若点O 是边AC 的中点，点P 为线段OB ′上的一个动点，将△APM 沿PM 折叠得到△A ′PM ，点A 的对应点为点A ′，A ′M 与CP 交于点F ，求AA AA的取值范围．一十．平行线分线段成比例（共1小题） 12．（2020•无锡）如图，在Rt △ABC 中，∠ACB ＝90°，AB ＝4，点D ，E 分别在边AB ，AC 上，且DB ＝2AD ，AE ＝3EC ，连接BE ，CD ，相交于点O ，则△ABO 面积最大值为．一十一．相似三角形的判定（共1小题）13．（2020•南京）如图，在△ABC 和△A 'B 'C '中，D 、D '分别是AB 、A 'B '上一点，AA AA=A′A′A′A′．（1）当AAA′A′=AA A′A′=AAA′A′时，求证△ABC ∽△A 'B 'C '．证明的途径可以用下面的框图表示，请填写其中的空格．（2）当AAA′A′=AA A′A′=AAA′A′时，判断△ABC 与△A 'B 'C ′是否相似，并说明理由．一十二．相似三角形的判定与性质（共6小题）14．（2020•无锡）如图，等边△ABC 的边长为3，点D 在边AC 上，AD =12，线段PQ 在边BA 上运动，PQ =12，有下列结论： ①CP 与QD 可能相等；②△AQD 与△BCP 可能相似； ③四边形PCDQ 面积的最大值为31√316；④四边形PCDQ 周长的最小值为3+√372．其中，正确结论的序号为（）A ．①④B ．②④C ．①③D ．②③ 15．（2020•南通）如图，在正方形网格中，每个小正方形的边长均为1，△ABC 和△DEF 的顶点都在网格线的交点上．设△ABC 的周长为C 1，△DEF 的周长为C 2，则A 1A 2的值等于．16．（2020•盐城）如图，BC∥DE，且BC＜DE，AD＝BC＝4，AB+DE＝10．则AAAA的值为．17．（2020•泰州）如图，在△ABC中，∠C＝90°，AC＝3，BC＝4，P为BC边上的动点（与B、C不重合），PD∥AB，交AC于点D，连接AP，设CP＝x，△ADP的面积为S．（1）用含x的代数式表示AD的长；（2）求S与x的函数表达式，并求当S随x增大而减小时x的取值范围．18．（2020•苏州）如图，在矩形ABCD中，E是BC的中点，DF⊥AE，垂足为F．（1）求证：△ABE∽△DF A；（2）若AB＝6，BC＝4，求DF的长．19．（2020•无锡）如图，DB过⊙O的圆心，交⊙O于点A、B，DC是⊙O的切线，点C是切点，已知∠D ＝30°，DC=√3．（1）求证：△BOC∽△BCD；（2）求△BCD的周长．一十三．相似形综合题（共2小题）20．（2020•宿迁）【感知】如图①，在四边形ABCD中，∠C＝∠D＝90°，点E在边CD上，∠AEB＝90°，求证：AA AA=AA AA．【探究】如图②，在四边形ABCD 中，∠C ＝∠ADC ＝90°，点E 在边CD 上，点F 在边AD 的延长线上，∠FEG ＝∠AEB ＝90°，且AA AA=AA AA，连接BG 交CD 于点H ．求证：BH ＝GH ．【拓展】如图③，点E 在四边形ABCD 内，∠AEB 十∠DEC ＝180°，且AA AA=AA AA，过E 作EF 交AD于点F ，若∠EF A ＝∠AEB ，延长FE 交BC 于点G ．求证：BG ＝CG ．21．（2020•徐州）我们知道：如图①，点B 把线段AC 分成两部分，如果AA AA=AA AA，那么称点B 为线段AC的黄金分割点．它们的比值为√5−12．（1）在图①中，若AC ＝20cm ，则AB 的长为 cm ；（2）如图②，用边长为20cm 的正方形纸片进行如下操作：对折正方形ABCD 得折痕EF ，连接CE ，将CB 折叠到CE 上，点B 对应点H ，得折痕CG ．试说明：G 是AB 的黄金分割点；（3）如图③，小明进一步探究：在边长为a 的正方形ABCD 的边AD 上任取点E （AE ＞DE ），连接BE ，作CF ⊥BE ，交AB 于点F ，延长EF 、CB 交于点P ．他发现当PB 与BC 满足某种关系时，E 、F 恰好分别是AD 、AB 的黄金分割点．请猜想小明的发现，并说明理由．一十四．解直角三角形的应用（共3小题） 22．（2020•南通）如图，测角仪CD 竖直放在距建筑物AB 底部5m 的位置，在D 处测得建筑物顶端A 的仰角为50°．若测角仪的高度是1.5m ，则建筑物AB 的高度约为 m ．（结果保留小数点后一位，参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19）23．（2020•淮安）如图，三条笔直公路两两相交，交点分别为A 、B 、C ，测得∠CAB ＝30°，∠ABC ＝45°，AC ＝8千米，求A 、B 两点间的距离．（参考数据：√2≈1.4，√3≈1.7，结果精确到1千米）．24．（2020•连云港）筒车是我国古代利用水力驱动的灌溉工具，唐代陈廷章在《水轮赋》中写道：“水能利物，轮乃曲成”．如图，半径为3m 的筒车⊙O 按逆时针方向每分钟转56圈，筒车与水面分别交于点A 、B ，筒车的轴心O 距离水面的高度OC 长为2.2m ，筒车上均匀分布着若干个盛水筒．若以某个盛水筒P 刚浮出水面时开始计算时间．（1）经过多长时间，盛水筒P 首次到达最高点？（2）浮出水面3.4秒后，盛水筒P 距离水面多高？（3）若接水槽MN 所在直线是⊙O 的切线，且与直线AB 交于点M ，MO ＝8m ．求盛水筒P 从最高点开始，至少经过多长时间恰好在直线MN 上．（参考数据：cos43°＝sin47°≈1115，sin16°＝cos74°≈1140，sin22°＝cos68°≈38）一十五．解直角三角形的应用-仰角俯角问题（共3小题）25．（2020•苏州）如图，小明想要测量学校操场上旗杆AB 的高度，他作了如下操作：（1）在点C 处放置测角仪，测得旗杆顶的仰角∠ACE ＝α；（2）量得测角仪的高度CD ＝a ；（3）量得测角仪到旗杆的水平距离DB ＝b ．利用锐角三角函数解直角三角形的知识，旗杆的高度可表示为（）A ．a +b tan αB ．a +b sin αC ．a +A AAAAD ．a +AAAAA26．（2020•镇江）如图，点E 与树AB 的根部点A 、建筑物CD 的底部点C 在一条直线上，AC ＝10m ．小明站在点E 处观测树顶B 的仰角为30°，他从点E 出发沿EC 方向前进6m 到点G 时，观测树顶B 的仰角为45°，此时恰好看不到建筑物CD 的顶部D （H 、B 、D 三点在一条直线上）．已知小明的眼睛离地面1.6m ，求建筑物CD 的高度（结果精确到0.1m ）．（参考数据：√2≈1.41，√3≈1.73．）27．（2020•泰州）我市在凤城河风景区举办了端午节赛龙舟活动，小亮在河畔的一幢楼上看到一艘龙舟迎面驶来，他在高出水面15m的A处测得在C处的龙舟俯角为23°；他登高6m到正上方的B处测得驶至D处的龙舟俯角为50°，问两次观测期间龙舟前进了多少？（结果精确到1m，参考数据：tan23°≈0.42，tan40°≈0.84，tan50°≈1.19，tan67°≈2.36）一十六．解直角三角形的应用-方向角问题（共3小题）28．（2020•宿迁）如图，在一笔直的海岸线上有A，B两个观测站，A在B的正西方向，AB＝2km，从观测站A测得船C在北偏东45°的方向，从观测站B测得船C在北偏西30°的方向．求船C离观测站A的距离．29．（2020•徐州）小红和爸爸绕着小区广场锻炼．如图，在矩形广场ABCD边AB的中点M处有一座雕塑．在某一时刻，小红到达点P处，爸爸到达点Q处，此时雕塑在小红的南偏东45°方向，爸爸在小红的北偏东60°方向，若小红到雕塑的距离PM＝30m，求小红与爸爸的距离PQ．（结果精确到1m，参考数据：√2≈1.41，√3≈1.73，√6≈2.45）30．（2020•南京）如图，在港口A处的正东方向有两个相距6km的观测点B、C．一艘轮船从A处出发，沿北偏东26°方向航行至D处，在B、C处分别测得∠ABD＝45°、∠C＝37°．求轮船航行的距离AD．（参考数据：sin26°≈0.44，cos26°≈0.90，tan26°≈0.49，sin37°≈0.60，cos37°≈0.80，tan37°≈0.75．）一十七．简单几何体的三视图（共1小题）31．（2020•淮安）下列几何体中，主视图为圆的是（）A．B．C．D．一十八．简单组合体的三视图（共3小题）32．（2020•镇江）如图，将棱长为6的正方体截去一个棱长为3的正方体后，得到一个新的几何体，这个几何体的主视图是（）A．B．C．D．33．（2020•盐城）如图是由4个小正方体组合成的几何体，该几何体的俯视图是（）A．B．C．D．34．（2020•苏州）如图，一个几何体由5个相同的小正方体搭成，该几何体的俯视图是（）A．B．C．D．一十九．由三视图判断几何体（共1小题）35．（2020•常州）如图是某几何体的三视图，该几何体是（）A．圆柱B．三棱柱C．四棱柱D．四棱锥2020年江苏省中考数学试题分类（8）——图形的变化参考答案与试题解析一．翻折变换（折叠问题）（共3小题） 1．【解答】解：方法一：如图，延长ED 交AC 于点M ，过点M 作MN ⊥AE 于点N ，设MN =√3x ， ∵tan ∠AED =√32， ∴AA AA=√32， ∴NE ＝2x ，∵∠ABC ＝90°，AB ＝3，BC =√3， ∴∠CAB ＝30°， ∴AC ＝2√3，由翻折可知： ∠EAC ＝30°，∴AM ＝2MN ＝2√3x ， ∴AN =√3MN ＝3x ， ∵AE ＝AB ＝3， ∴5x ＝3， ∴x =35，∴AN =95，MN =3√35，AM =6√35， ∵AC ＝2√3，∴CM ＝AC ﹣AM =4√35， ∵MN =3√35，NE ＝2x =65， ∴EM =√AA 2+AA 2=3√75，∵∠ABC ＝∠BCD ＝90°， ∴CD ∥AB ，∴∠DCA ＝30°，由翻折可知：∠ECA ＝∠BCA ＝60°， ∴∠ECD ＝30°，∴CD 是∠ECM 的角平分线， ∴A △AAA A △AAA =AAAA=AA AA，∴√34√35=3√75−AA ，解得，ED =√73．方法二：如图，过点D 作DM ⊥CE ，由折叠可知：∠AEC ＝∠B ＝90°， ∴AE ∥DM ，∴∠AED ＝∠EDM ， ∴tan ∠AED ＝tan ∠EDM =√32，∵∠ACB ＝60°，∠ECD ＝30°，设EM =√3m ，由折叠性质可知，EC ＝CB =√3， ∴CM =√3−√3m ，∴tan ∠ECD =AA AA =√33， ∴DM ＝（√3−√3m ）×√33=1﹣m ，∴tan ∠EDM =AA AA =√32，即√3A 1−A=√32解得，m =13，∴DM =23，EM =√33，在直角三角形EDM 中，DE 2＝DM 2+EM 2，解得，DE =√73．故选：B ． 2．【解答】解：（1）如图①中，取DE 的中点M ，连接PM ．∵四边形ABCD 是矩形， ∴∠BAD ＝∠C ＝90°，由翻折可知，AO ＝OP ，AP ⊥DE ，∠2＝∠3，∠DAE ＝∠DPE ＝90°，在Rt △EPD 中，∵EM ＝MD ， ∴PM ＝EM ＝DM ， ∴∠3＝∠MPD ，∴∠1＝∠3+∠MPD ＝2∠3， ∵∠ADP ＝2∠3， ∴∠1＝∠ADP ， ∵AD ∥BC ，∴∠ADP ＝∠DPC ， ∴∠1＝∠DPC ，∵∠MOP ＝∠C ＝90°， ∴△POM ∽△DCP ， ∴AA AA =AAAA =812=23，∴AA AA=2AA 2AA=23．解法二：证明△ABP 和△DAE 相似，AA AA=AA AA=23．（2）如图②中，过点P 作GH ∥BC 交AB 于G ，交CD 于H ．则四边形AGHD 是矩形，设EG ＝x ，则BG ＝4﹣x∵∠A ＝∠EPD ＝90°，∠EGP ＝∠DHP ＝90°， ∴∠EPG +∠DPH ＝90°，∠DPH +∠PDH ＝90°， ∴∠EPG ＝∠PDH ， ∴△EGP ∽△PHD ， ∴AA AA=AA AA=AA AA=412=13，∴PH ＝3EG ＝3x ，DH ＝AG ＝4+x ，在Rt △PHD 中，∵PH 2+DH 2＝PD 2， ∴（3x ）2+（4+x ）2＝122，解得x =165（负值已经舍弃）， ∴BG ＝4−165=45，在Rt △EGP 中，GP =√AA 2−AA 2=125， ∵GH ∥BC ，∴△EGP ∽△EBF ， ∴AA AA=AA AA，∴1654=125AA，∴BF ＝3．3．【解答】解：（1）∵在矩形ABCD 中，∠D ＝90°，AD ＝1，DE =√33，∴AE =√AA 2+AA 2=2√33，∴tan ∠AED =AAAA =√3，∴∠AED ＝60°， ∵AB ∥CD ，∴∠BAE ＝60°，∵四边形ABCE 关于直线AE 的对称图形为四边形ANME ， ∴∠AEC ＝∠AEM ， ∵∠PEC ＝∠DEM ，∴∠AEP ＝∠AED ＝60°， ∴△APE 为等边三角形， ∴S =12×（2√33+√33）×1=√32；（2）过E 作EF ⊥AB 于F ，由（1）可知，∠AEP ＝∠AED ＝∠P AE ， ∴AP ＝PE ，设AP ＝PE ＝a ，AF ＝ED ＝x ，则PF ＝a ﹣x ，EF ＝AD ＝1，在Rt △PEF 中，（a ﹣x ）2+1＝a 2，解得：a =A 2+12A ，∴S =12⋅A ×1+12×A 2+12A ×1=12A +A 2+14A =3A 2+14A ．二．平移的性质（共1小题） 4．【解答】解：取AC 的中点M ，A 1B 1的中点N ，连接PM ，MQ ，NQ ，PN ， ∵将△ABC 平移5个单位长度得到△A 1B 1C 1， ∴B 1C 1＝BC ＝3，PN ＝5，∵点P 、Q 分别是AB 、A 1C 1的中点， ∴NQ =12B 1C 1=32， ∴5−32≤PQ ≤5+32，即72≤PQ ≤132， ∴PQ 的最小值等于72，故答案为：72．三．旋转的性质（共1小题） 5．【解答】解：∵AB '＝CB '， ∴∠C ＝∠CAB '，∴∠AB 'B ＝∠C +∠CAB '＝2∠C ，∵将△ABC 绕点A 按逆时针方向旋转得到△AB 'C '， ∴∠C ＝∠C '，AB ＝AB '， ∴∠B ＝∠AB 'B ＝2∠C ，∵∠B +∠C +∠CAB ＝180°， ∴3∠C ＝180°﹣108°， ∴∠C ＝24°，∴∠C '＝∠C ＝24°，故选：C ．四．旋转对称图形（共1小题） 6．【解答】解：连接OA ，OE ，则这个图形至少旋转∠AOE 才能与原图象重合， ∠AOE =360°5=72°．故答案为：72．五．中心对称图形（共1小题） 7．【解答】解：A 、不是中心对称图形，不是轴对称图形，故此选项不合题意； B 、不是中心对称图形，是轴对称图形，故此选项不合题意； C 、既是中心对称图形，也是轴对称图形，故此选项符合题意； D 、不是中心对称图形，不是轴对称图形，故此选项不合题意；故选：C ．六．关于原点对称的点的坐标（共1小题） 8．【解答】解：点（3，2）关于原点对称的点的坐标是：（﹣3，﹣2）．故选：C ．七．坐标与图形变化-旋转（共1小题） 9．【解答】解：如图，∵点P （4，5）按逆时针方向旋转90°，得点Q 所在的象限为第二象限．故选：B ．八．作图-旋转变换（共1小题） 10．【解答】解：（1）如图1中，作FD ⊥AC 于D ，∵Rt △ABC ≌Rt △CEF ，∠ABC ＝∠CEF ＝90°，∠BAC ＝30°，BC ＝1． ∴∠ACB ＝60°，∠FCE ＝∠BAC ＝30°，AC ＝CF ， ∴∠ACF ＝30°， ∴∠BAC ＝∠FCD ，在△ABC 和△CDF 中，{∠AAA =∠AAAAAAA =AAAA AA =AA， ∴△ABC ≌△CDF （AAS ）， ∴FD ＝BC ＝1，法二：∵∠ECF ＝∠FCD ＝30°，FD ⊥CD ，FE ⊥CE ， ∴DF ＝EF ， ∵EF ＝BC ＝1，∴DF ＝1．故答案为1；（2）线段EF 经旋转运动所形成的平面图形如图所示，此时点E 落在CF 上的点H 处．S 阴＝S △EFC +S 扇形ACF ﹣S 扇形CEH ﹣S △AHC ＝S 扇形ACF ﹣S 扇形ECH =30⋅A ⋅22360−30⋅A ⋅(√3)2360=A12．故答案为A12．（3）如图2中，过点E 作EH ⊥CF 于H ．设OB ＝OE ＝x ．在Rt △ECF 中，∵EF ＝1，∠ECF ＝30°，EH ⊥CF ， ∴EC =√3EF =√3，EH =√32，CH =√3EH =32，在Rt △BOC 中，OC =√AA 2+AA 2=√1+A 2， ∴OH ＝CH ﹣OC =32−√1+A 2，在Rt △EOH 中，则有x 2＝（√32）2+（32−√1+A 2）2，解得x =√73或−√73（不合题意舍弃），∴OC =1+(√73)2=43，∵CF ＝2EF ＝2，∴OF ＝CF ﹣OC ＝2−43=23．九．几何变换综合题（共1小题）11．【解答】解：（1）如图①中，∵△ABC 折叠，使点B 与点C 重合，折痕为MN ， ∴MN 垂直平分线段BC ， ∴CN ＝BN ，∵∠MNB ＝∠ACB ＝90°， ∴MN ∥AC ， ∵CN ＝BN ， ∴AM ＝BM ．故答案为AM ＝BM ．（2）如图②中，∵CA ＝CB ＝6， ∴∠A ＝∠B ，由题意MN 垂直平分线段BC ， ∴BM ＝CM ， ∴∠B ＝∠MCB ， ∴∠BCM ＝∠A ， ∵∠B ＝∠B ，∴△BCM ∽△BAC ， ∴AA AA =AAAA ，∴610=AA6，∴BM =185， ∴AM ＝AB ﹣BM ＝10−185=325， ∴AA AA=325185=169．（3）①如图③中，由折叠的性质可知，CB ＝CB ′＝6，∠BCM ＝∠ACM ， ∵∠ACB ＝2∠A ， ∴∠BCM ＝∠A ， ∵∠B ＝∠B ，∴△BCM ∽△BAC ， ∴AA AA =AAAA =AA AA∴69=AA 6，∴BM ＝4，∴AM ＝CM ＝5， ∴69=5AA ，∴AC =152．②如图③﹣1中，∵∠A ＝∠A ′＝∠MCF ，∠PF A ′＝∠MFC ，P A ＝P A ′， ∴△PF A ′∽△MFC ， ∴AA AA =AA′AA，∵CM ＝5， ∴AA AA =AA′5，∵点P 在线段OB 上运动，OA ＝OC =154，AB ′=152−6=32， ∴32≤P A ′≤154， ∴310≤AA AA≤34．一十．平行线分线段成比例（共1小题） 12．【解答】解：如图，过点D 作DF ∥AE ，则AA AA =AA AA =23，∵AA AA=13，∴DF ＝2EC ， ∴DO ＝2OC ， ∴DO =23DC ，∴S △ADO =23S △ADC ，S △BDO =23S △BDC ， ∴S △ABO =23S △ABC ，∵∠ACB ＝90°，∴C 在以AB 为直径的圆上，设圆心为G ，当CG ⊥AB 时，△ABC 的面积最大为：12×4×2＝4，此时△ABO 的面积最大为：23×4=83．故答案为：83．一十一．相似三角形的判定（共1小题） 13．【解答】（1）证明：∵AA AA=A′A′A′A′，∴AA A′A′=AAA′A′， ∵AA A′A′=AA A′A′=AA A′A′， ∴AA A′A′=AA A′A′=AA A′A′，∴△ADC ∽△A ′D ′C '， ∴∠A ＝∠A ′， ∵AA A′A′=AAA′A′， ∴△ABC ∽△A ′B ′C ′．故答案为：AAA′A′=AA A′A′=AAA′A′，∠A ＝∠A ′．（2）如图，过点D ，D ′分别作DE ∥BC ，D ′E ′∥B ′C ′，DE 交AC 于E ，D ′E ′交A ′C ′于E ′．∵DE ∥BC ，∴△ADE ∽△ABC ， ∴AA AA=AA AA=AA AA，同理，A′A′A′A′=A′A′A′A′=A′A′A′A′，∵AA AA =A′A′A′A′， ∴AA AA =A′A′A′A′，∴AAA′A′=AAA′A′，同理，AA AA =A′A′A′A′，∴AA −AA AA =A′A′−A′A′A′A′，即AA AA=A′A′A′A′，∴AA A′A′=AAA′A′， ∵AA A′A′=AA A′A′=AA A′A′， ∴AA A′A′=AA A′A′=AA A′A′，∴△DCE ∽△D ′C ′E ′， ∴∠CED ＝∠C ′E ′D ′， ∵DE ∥BC ，∴∠CED +∠ACB ＝180°，同理，∠C ′E ′D ′+∠A ′C ′B ′＝180°， ∴∠ACB ＝∠A ′C ′B ′， ∵AA A′A′=AAA′A′，∴△ABC ∽△A ′B ′C ′．一十二．相似三角形的判定与性质（共6小题）14．【解答】解：①利用图象法可知PC ＞DQ ，或通过计算可知DQ 的最大值为√212，PC 的最小值为3√32，所以PC ＞DQ ，故①错误．②设AQ ＝x ，则BP ＝AB ﹣AQ ﹣PQ ＝3﹣x −12=52−x ， ∵∠A ＝∠B ＝60°， ∴当AA AA=AA AA 或AA AA=AA AA时，△ADQ 与△BPC 相似，即1252−A=A3或123=A52−A ，解得x ＝1或32或514，∴当AQ ＝1或32或514时，两三角形相似，故②正确③设AQ ＝x ，则四边形PCDQ 的面积＝S △ABC ﹣S △ADQ ﹣S △BCP =√34×32−12×x ×√32×12−12×3×（3﹣x −12）×√32=3√38+5√38x ，∵x 的最大值为3−12=52，∴x =52时，四边形PCDQ 的面积最大，最大值=31√316，故③正确，如图，作点D 关于AB 的对称点D ′，作D ′F ∥PQ ，使得D ′F ＝PQ ，连接CF 交AB 于点P ′，在射线P ′A 上取P ′Q ′＝PQ ，此时四边形P ′CDQ ′的周长最小．过点C 作CH ⊥D ′F 交D ′F 的延长线于H ，交AB 于J ．由题意，DD ′＝2AD •sin60°=√32，HJ =12DD ′=√34，CJ =3√32，FH =32−12−14=34， ∴CH ＝CJ +HJ =7√34，∴CF =√AA 2+AA 2=(34)2+(7√34)2=√392， ∴四边形P ′CDQ ′的周长的最小值＝3+√392，故④错误，故选：D ．15．【解答】解：∵AA AA =√22=√2， AAAA=√22+222=√2， AA AA =√22√22=√2，∴AA AA =AA AA =AA AA =√2， ∴△ABC ∽△DEF ，∴A 1A 2=AA AA=√22，故答案为：√22． 16．【解答】解：∵BC ∥DE ， ∴△ADE ∽△ABC ， ∴AA AA =AA AA =AAAA ，即4AA =AA 4=AA AA ， ∴AB •DE ＝16，∵AB +DE ＝10， ∴AB ＝2，DE ＝8，∴AAAA=AA AA =84=2，故答案为：2． 17．【解答】解：（1）∵PD ∥AB ， ∴AAAA=AA AA ， ∵AC ＝3，BC ＝4，CP ＝x ， ∴A4=AA 3，∴CD =34A ， ∴AD ＝AC ﹣CD ＝3−34A ，即AD =−34A +3；（2）根据题意得，S =12AA ⋅AA =12A (−34A +3)=−38(A −2)2+32，∴当x ≥2时，S 随x 的增大而减小，∵0＜x ＜4，∴当S 随x 增大而减小时x 的取值范围为2≤x ＜4．18．【解答】解：（1）∵四边形ABCD 是矩形，∴AD ∥BC ，∠B ＝90°，∴∠DAF ＝∠AEB ，∵DF ⊥AE ，∴∠AFD ＝∠B ＝90°，∴△ABE ∽△DF A ；（2）∵E 是BC 的中点，BC ＝4，∴BE ＝2，∵AB ＝6，∴AE =√AA 2+AA 2=√62+22=2√10，∵四边形ABCD 是矩形，∴AD ＝BC ＝4，∵△ABE ∽△DF A ，∴AA AA =AA AA ，∴AA =AA ⋅AA AA =2√10=65√10． 19．【解答】证明：（1）∵DC 是⊙O 的切线，∴∠OCD ＝90°，∵∠D ＝30°，∴∠BOC ＝∠D +∠OCD ＝30°+90°＝120°，∵OB ＝OC ，∴∠B ＝∠OCB ＝30°，∴∠DCB ＝120°＝∠BOC ，又∵∠B ＝∠B ＝30°，∴△BOC ∽△BCD ；（2）∵∠D ＝30°，DC =√3，∠OCD ＝90°，∴DC =√3OC =√3，DO ＝2OC ，∴OC ＝1＝OB ，DO ＝2，∵∠B ＝∠D ＝30°， ∴DC ＝BC =√3，∴△BCD 的周长＝CD +BC +DB =√3+√3+2+1＝3+2√3．一十三．相似形综合题（共2小题）20．【解答】【感知】证明：∵∠C ＝∠D ＝∠AEB ＝90°，∴∠BEC +∠AED ＝∠AED +∠EAD ＝90°，∴∠BEC ＝∠EAD ，∴Rt △AED ∽Rt △EBC ，∴AA AA =AA AA ．【探究】证明：如图1，过点G 作GM ⊥CD 于点M ，由（1）可知AA AA =AA AA ，∵AA AA =AA AA ，AA AA =AA AA ， ∴AA AA =AA AA ，∴BC ＝GM ，又∵∠C ＝∠GMH ＝90°，∠CHB ＝∠MHG ，∴△BCH ≌△GMH （AAS ），∴BH ＝GH ，【拓展】证明：如图2，在EG 上取点M ，使∠BME ＝∠AFE ，过点C 作CN ∥BM ，交EG 的延长线于点N ，则∠N ＝∠BMG ，∵∠EAF +∠AFE +∠AEF ＝∠AEF +∠AEB +∠BEM ＝180°，∠EF A ＝∠AEB ，∴∠EAF ＝∠BEM ，∴△AEF ∽△EBM ，∴AA AA =AA AA ，∵∠AEB +∠DEC ＝180°，∠EF A +∠DFE ＝180°，而∠EF A ＝∠AEB ，∴∠CED ＝∠EFD ，∵∠BMG +∠BME ＝180°，∴∠N ＝∠EFD ，∵∠EFD +∠EDF +∠FED ＝∠FED +∠DEC +∠CEN ＝180°，∴∠EDF ＝∠CEN ，∴△DEF ∽△ECN ，∴AA AA =AA AA ，又∵AA AA =AA AA ， ∴AA AA =AA AA ，∴BM ＝CN ，又∵∠N ＝∠BMG ，∠BGM ＝∠CGN ，∴△BGM ≌△CGN （AAS ），∴BG ＝CG ．21．【解答】解：（1）∵点B 为线段AC 的黄金分割点，AC ＝20cm ，∴AB =√5−12×20＝（10√5−10）cm ．故答案为：（10√5−10）．（2）延长EA ，CG 交于点M ，∵四边形ABCD 为正方形，∴DM ∥BC ，∴∠EMC ＝∠BCG ，由折叠的性质可知，∠ECM ＝∠BCG ，∴∠EMC ＝∠ECM ，∴EM ＝EC ，∵DE ＝10，DC ＝20，∴EC =√AA 2+AA 2=√102+202=10√5，∴EM ＝10√5，∴DM ＝10√5+10，∴tan ∠DMC =AA AA =10√5+10=√5+1=√5−12． ∴tan ∠BCG =√5−12，即AA AA =√5−12， ∵AB ＝BC ， ∴AAAA =√5−12， ∴G 是AB 的黄金分割点；（3）当BP ＝BC 时，满足题意．理由如下：∵四边形ABCD 是正方形，∴AB ＝BC ，∠BAE ＝∠CBF ＝90°，∵BE ⊥CF ，∴∠ABE +∠CFB ＝90°，又∵∠BCF +∠BFC ＝90°，∴∠BCF ＝∠ABE ，∴△ABE ≌△BCF （ASA ），∴BF ＝AE ，∵AD ∥CP ，∴△AEF ∽△BPF ， ∴AAAA=AA AA ，当E 、F 恰好分别是AD 、AB 的黄金分割点时， ∵AE ＞DE ， ∴AAAA =AA AA ，∵BF ＝AE ，AB ＝BC ，∴AA AA =AA AA =AA AA ， ∴AA AA =AA AA ，∴BP ＝BC ．一十四．解直角三角形的应用（共3小题）22．【解答】解：如图，过点D 作DE ⊥AB ，垂足为点E ，则DE ＝BC ＝5，DC ＝BE ＝1.5，在Rt △ADE 中，∵tan ∠ADE =AA AA ，∴AE ＝tan ∠ADE •DE ＝tan50°×5≈1.19×5＝5.95（米），∴AB ＝AE +BE ＝5.95+1.5≈7.5（米），故答案为：7.5．23．【解答】解：过点C 作CD ⊥AB 于点D ，如图所示．在Rt △ACD 中，AC ＝8（千米），∠CAD ＝30°，∠CDA ＝90°，∴CD ＝AC •sin ∠CAD ＝4（千米），AD ＝AC •cos ∠CAD ＝4√3（千米）≈6.8（千米）．在Rt △BCD 中，CD ＝4（千米），∠BDC ＝90°，∠CBD ＝45°，∴∠BCD ＝45°，∴BD ＝CD ＝4（千米），∴AB ＝AD +BD ＝6.8+4≈11（千米）．答：A 、B 两点间的距离约为11千米．24．【解答】解：（1）如图1中，连接OA ．由题意，筒车每秒旋转360°×56÷60＝5°，在Rt △ACO 中，cos ∠AOC =AA AA =2.23=1115． ∴∠AOC ＝43°，∴180−435=27.4（秒）．答：经过27.4秒时间，盛水筒P 首次到达最高点．（2）如图2中，盛水筒P 浮出水面3.4秒后，此时∠AOP ＝3.4×5°＝17°，∴∠POC ＝∠AOC +∠AOP ＝43°+17°＝60°，过点P 作PD ⊥OC 于D ，在Rt △POD 中，OD ＝OP •cos60°＝3×12=1.5（m ），2.2﹣1.5＝0.7（m ），答：浮出水面3.4秒后，盛水筒P 距离水面0.7m ．（3）如图3中，∵点P 在⊙O 上，且MN 与⊙O 相切，∴当点P 在MN 上时，此时点P 是切点，连接OP ，则OP ⊥MN ，在Rt △OPM 中，cos ∠POM =AA AA =38，∴∠POM ＝68°，在Rt △COM 中，cos ∠COM =AA AA =2.28=1140，∴∠COM ＝74°，∴∠POH ＝180°﹣∠POM ﹣∠COM ＝180°﹣68°﹣74°＝38°，∴需要的时间为385=7.6（秒），答：盛水筒P 从最高点开始，至少经过7.6秒恰好在直线MN 上．一十五．解直角三角形的应用-仰角俯角问题（共3小题）25．【解答】解：过C 作CF ⊥AB 于F ，则四边形BFCD 是矩形，∴BF ＝CD ＝a ，CF ＝BD ＝b ，∵∠ACF ＝α，∴tan α=AA AA =AA A ， ∴AF ＝b •tan α，∴AB ＝AF +BF ＝a +b tan α，故选：A ．26．【解答】解：如图，延长FH，交CD于点M，交AB于点N，∵∠BHN＝45°，BA⊥MH，则BN＝NH，设BN＝NH＝x，∵HF＝6，∠BFN＝30°，∴tan∠BFN=AAAA=AAAA+AA，即tan30°=AA+6，解得x＝8.19，根据题意可知：DM＝MH＝MN+NH，∵MN＝AC＝10，则DM＝10+8.19＝18.19，∴CD＝DM+MC＝DM+EF＝18.19+1.6≈19.8（m）．答：建筑物CD的高度约为19.8m．27．【解答】解：如图，根据题意得，∠C＝23°，∠BDE＝50°，AE＝15m，BE＝21m，在Rt△ACE中，tan C＝tan23°=AAAA=15AA≈0.42，解得：CE≈35.7，在Rt△BDE中，tan∠BDE＝tan50°=AAAA=21AA≈1.19，解得：DE≈17.6，∴CD＝CE﹣DE＝35.7﹣17.6＝18.1≈18m，答：两次观测期间龙舟前进了18m．一十六．解直角三角形的应用-方向角问题（共3小题）28．【解答】解：如图，过点C作CD⊥AB于点D，则∠CAD＝∠ACD＝45°，∴AD＝CD，设AD＝x，则AC=√2x，∴BD＝AB﹣AD＝2﹣x，∵∠CBD＝60°，在Rt△BCD中，∵tan∠CBD=AA AA，∴A2−A=√3，解得x＝3−√3．经检验，x＝3−√3是原方程的根．∴AC=√2x=√2（3−√3）＝（3√2−√6）km．答：船C离观测站A的距离为（3√2−√6）km．29．【解答】解：过点P作PN⊥BC于N，如图，则四边形ABNP是矩形，∴PN＝AB，∵四边形ABCD是矩形，∴∠A＝90°，∵∠APM＝45°，∴△APM是等腰直角三角形，∴AM=√22PM=√22×30＝15√2（m），∵M是AB的中点，∴PN＝AB＝2AM＝30√2m，在Rt△PNQ中，∠NPQ＝90°﹣∠DPQ＝90°﹣60°＝30°，∴NQ=√33PN＝10√6m，PQ＝2NQ＝20√6≈49（m）；答：小红与爸爸的距离PQ约为49m．30．【解答】解：如图，过点D作DH⊥AC于点H，在Rt△DCH中，∠C＝37°，∴CH=AA AAA37°，在Rt△DBH中，∠DBH＝45°，∴BH=AA AAA45°，∵BC＝CH﹣BH，∴AAAAA37°−AAAAA45°=6，解得DH≈18km，在Rt△DAH中，∠ADH＝26°，∴AD=AAAAA26°≈20km．答：轮船航行的距离AD约为20km．一十七．简单几何体的三视图（共1小题）31．【解答】解：正方体的主视图为正方形，球的主视图为圆，圆柱的主视图是矩形，圆锥的主视图是等腰三角形，故选：B．一十八．简单组合体的三视图（共3小题）32．【解答】解：从正面看是一个正方形，正方形的右上角是一个小正方形，故选：A．33．【解答】解：观察图形可知，该几何体的俯视图是．故选：A．34．【解答】解：从上面看，是一行三个小正方形．故选：C．一十九．由三视图判断几何体（共1小题）35．【解答】解：该几何体的主视图为矩形，左视图为矩形，俯视图是一个正方形，则可得出该几何体是四棱柱．故选：C．。

2023年中考数学一轮专题练习图形的平移、折叠和旋转(含解析)

2023年中考数学一轮专题练习 ——图形的平移、折叠和旋转2一、单选题（本大题共10小题）1. （天津市2022年）在一些美术字中，有的汉字是轴对称图形．下面4个汉字中，可以看作是轴对称图形的是（） A ．B ．C ．D ．2. （湖南省娄底市2022年）下列与2022年冬奥会相关的图案中，是中心对称图形的是（）A ．B ．C ．D ．3. （湖南省郴州市2022年）下列图形既是轴对称图形又是中心对称图形的是（）A ．B ．C ．D ．4. （江苏省常州市2022年）在平面直角坐标系xOy 中，点A 与点1A 关于x 轴对称，点A 与点2A 关于y 轴对称．已知点1(1,2)A ，则点2A 的坐标是（） A ．(2,1)- B ．(2,1)--C ．(1,2)-D ．(1,2)--5. （湖南省长沙市2022年）在平面直角坐标系中，点(5,1)关于原点对称的点的坐标是（） A ．(5,1)- B ．(5,1)- C ．(1,5) D ．(5,1)-- 6. （湖南省邵阳市2022年）下列四种图形中，对称轴条数最多的是（） A ．等边三角形B ．圆C ．长方形D ．正方形7. （湖南省怀化市2022年）如图，△ABC 沿BC 方向平移后的像为△DEF ，已知BC =5，EC =2，则平移的距离是（）A ．1B ．2C ．3D ．48. （湖南省衡阳市2022年）下列图形中既是中心对称又是轴对称的是（）A ．可回收垃圾B ．其他垃圾C ．有害垃圾D ．厨余垃圾9. （四川省雅安市2022年）在平面直角坐标系中，点（a +2，2）关于原点的对称点为（4，﹣b ），则ab 的值为（） A ．﹣4B ．4C ．12D ．﹣1210. （天津市2022年）如图，在△ABC 中，AB =AC ，若M 是BC 边上任意一点，将△ABM 绕点A 逆时针旋转得到△ACN ，点M 的对应点为点N ，连接MN ，则下列结论一定正确的是（）A ．AB AN = B ．AB NC ∥ C ．AMN ACN ∠=∠D ．MN AC ⊥二、填空题（本大题共8小题）11. （辽宁省抚顺本溪辽阳市2022年）在平面直角坐标系中，线段AB 的端点(3,2),(5,2)A B ，将线段AB 平移得到线段CD ，点A 的对应点C 的坐标是(1,2)-，则点B 的对应点D 的坐标是．12. （吉林省2022年）第二十四届北京冬奥会入场式引导牌上的图案融入了中国结和雪花两种元素．如图，这个图案绕着它的中心旋转角()0360αα︒<<︒后能够与它本身重合，则角α可以为度．（写出一个即可）13. （辽宁省抚顺本溪辽阳市2022年）如图，正方形ABCD 的边长为10，点G 是边CD 的中点，点E 是边AD 上一动点，连接BE ，将ABE △沿BE 翻折得到FBE ，连接GF ．当GF 最小时，AE 的长是．14. （辽宁省大连市2022年）如图，对折矩形纸片ABCD ，使得AD 与BC 重合，得到折痕EF ，把纸片展平，再一次折叠纸片，使点A 的对应点A '落在EF 上，并使折痕经过点B ，得到折痕BM ．连接，若，，则的长是．15. （辽宁省大连市2022年）如图，在平面直角坐标系中，点A 的坐标是1,2，将线段OA 向右平移4个单位长度，得到线段BC ，点A 的对应点C 的坐标是．16. （江苏省扬州市2022年）“做数学”可以帮助我们积累数学活动经验．如图，已知三角形纸片ABC ，第1次折叠使点B 落在BC 边上的点B '处，折痕AD 交BC 于点D；第MF MF BM ⊥6cm AB =ADcm2次折叠使点A 落在点D 处，折痕MN 交AB '于点P ．若12BC =，则MP MN += ．17. （江苏省无锡市2022年）△ABC 是边长为5的等边三角形，△DCE 是边长为3的等边三角形，直线BD 与直线AE 交于点F ．如图，若点D 在△ABC 内，∠DBC =20°，则∠BAF ＝ °；现将△DCE 绕点C 旋转1周，在这个旋转过程中，线段AF 长度的最小值是．18. （湖北省荆州市2022年）规定：两个函数，的图象关于y 轴对称，则称这两个函数互为“Y 函数”．例如：函数与的图象关于y 轴对称，则这两个函数互为“Y 函数”．若函数（k 为常数）的“Y 函数”图象与x轴只有一个交点，则其“Y 函数”的解析式为．三、解答题（本大题共5小题）19. （四川省自贡市2022年）如图，用四根木条钉成矩形框ABCD ，把边BC 固定在地面上，向右推动矩形框，矩形框的形状会发生改变（四边形具有不稳定性）．1y 2y 122y x =+222y x =-+()2213y kx k x k =+-+-(1)通过观察分析，我们发现图中线段存在等量关系，如线段EB 由AB 旋转得到，所以EB AB =．我们还可以得到FC ＝， EF ＝；(2)进一步观察，我们还会发现EF ∥AD ，请证明这一结论；(3)已知BC 30,DC 80==cm cm ，若BE 恰好经过原矩形DC 边的中点H ，求EF 与BC 之间的距离．20. （湖北省十堰市2022年）已知90ABN ∠=︒，在ABN ∠内部作等腰ABC ，AB AC =，()090BAC αα∠=︒<≤︒．点D 为射线BN 上任意一点（与点B 不重合），连接AD ，将线段AD 绕点A 逆时针旋转α得到线段AE ，连接EC 并延长交射线BN 于点F ．(1)如图1，当90α=︒时，线段BF 与CF 的数量关系是；(2)如图2，当090α︒<<︒时，（1）中的结论是否还成立？若成立，请给予证明；若不成立，请说明理由；(3)若60α=︒，AB =BD m =，过点E 作EP BN ⊥，垂足为P ，请直接写出PD 的长（用含有m 的式子表示）．21. （黑龙江省绥化市2022年）我们可以通过面积运算的方法，得到等腰三角形底边上的任意一点到两腰的距离之和与一腰上的高之间的数量关系，并利用这个关系解决相关问题．(1)如图一，在等腰ABC 中，AB AC =，BC 边上有一点D ，过点D 作DE AB ⊥于E ，DF AC ⊥于F ，过点C 作CG AB ⊥于G .利用面积证明：DE DF CG +=．(2)如图二，将矩形ABCD 沿着EF 折叠，使点A 与点C 重合，点B 落在B ′处，点G 为折痕EF 上一点，过点G 作GM FC ⊥于M ，GN BC ⊥于N .若8BC =，3BE =，求GM GN +的长．(3)如图三，在四边形ABCD 中，E 为线段BC 上的一点，EA AB ⊥，ED CD ⊥，连接BD ，且AB AECD DE=，BC =3CD =，6BD =，求ED EA +的长． 22. （天津市2022年）将一个矩形纸片OABC 放置在平面直角坐标系中，点(0,0)O ，点(3,0)A ，点(0,6)C ，点P 在边OC 上（点P 不与点O ，C 重合），折叠该纸片，使折痕所在的直线经过点P ，并与x 轴的正半轴相交于点Q ，且30OPQ ∠=︒，点O 的对应点O '落在第一象限．设OQ t =．(1)如图①，当1t =时，求O QA ∠'的大小和点O '的坐标；(2)如图②，若折叠后重合部分为四边形，,O Q O P ''分别与边AB 相交于点E ，F ，试用含有t 的式子表示O E '的长，并直接写出t 的取值范围；(3)若折叠后重合部分的面积为t 的值可以是（请直接写出两个不同．．．．的值即可）．23. （湖北省鄂州市2022年）如图1，在平面直角坐标系中，Rt △OAB 的直角边OA 在y 轴的正半轴上，且OA =6，斜边OB =10，点P 为线段AB 上一动点．(1)请直接写出点B 的坐标；(2)若动点P满足∠POB=45°，求此时点P的坐标；(3)如图2，若点E为线段OB的中点，连接PE，以PE为折痕，在平面内将△APE折叠，点A的对应点为A'，当PA'⊥OB时，求此时点P的坐标；(4)如图3，若F为线段AO上一点，且AF=2，连接FP，将线段FP绕点F顺时针方向旋转60°得线段FG，连接OG，当OG取最小值时，请直接写出OG的最小值和此时线段FP扫过的面积．参考答案1. 【答案】D【分析】根据轴对称图形的概念对各项分析判断即可得解．【详解】A．不是轴对称图形，故本选项错误；B．不是轴对称图形，故本选项错误；C．不是轴对称图形，故本选项错误；D．是轴对称图形，故本选项正确．故选：D．2. 【答案】D【分析】中心对称图形定义：如果一个图形绕某一点旋转180度，旋转后的图形能和原图形回完全重合，那么这个答图形叫做中心对称图形，根据中心对称图形定义逐项判定即可．【详解】解：根据中心对称图形定义，可知D符合题意，故选：D．3. 【答案】B【分析】根据轴对称图形和中心对称图形的定义判断即可．【详解】解：A、该图形是轴对称图形，不是中心对称图形，故A选项错误；B、该图形既是轴对称图形，也是中心对称图形，故B选项正确；C、该图形不是轴对称图形，是中心对称图形，故C选项错误；D、该图形既不是轴对称图形，也不是中心对称图形，故D选项错误．故答案为B．4. 【答案】D【分析】直接利用关于x，y轴对称点的性质分别得出A，A点坐标，即可得出答案．2【详解】解：∵点1A的坐标为（1，2），点A与点1A关于x轴对称，∴点A的坐标为（1，-2），∵点A与点A关于y轴对称，2∴点A的坐标是（-1，﹣2）．2故选：D．5. 【答案】D【分析】根据关于原点对称的两个点，横坐标、纵坐标分别互为相反数，即可求解．【详解】--．解：点(5,1)关于原点对称的点的坐标是(5,1)故选D．6. 【答案】B【分析】分别求出各个图形的对称轴的条数，再进行比较即可．【详解】解：因为等边三角形有3条对称轴；圆有无数条对称轴；长方形有2条对称轴；正方形有4条对称轴；经比较知，圆的对称轴最多．故选：B．7. 【答案】C【分析】根据题意判断BE的长就是平移的距离，利用已知条件求出BE即可．【详解】因为ABC沿BC方向平移，点E是点B移动后的对应点，所以BE的长等于平移的距离，由图可知，点B、E、C在同一直线上，BC=5，EC=2，所以BE=BC-ED=5-2=3,故选 C．8. 【答案】C【分析】根据中心对称图形和轴对称图形的定义，逐一判断各个选项，即可得到答案．【详解】解：A．既不是中心对称图形也不是轴对称图形，B．既不是中心对称图形也不是轴对称图形，C．既是中心对称又是轴对称图形，D．是轴对称图形但不是中心对称图形，故选C．9. 【答案】D【分析】a b，可得a，b的值，再首先根据关于原点对称的点的坐标特点可得240,20代入求解即可得到答案．【详解】解：点（a+2，2）关于原点的对称点为（4，﹣b），∴240,20a b，a b解得：6,2,ab12,故选D10. 【答案】C【分析】根据旋转的性质，对每个选项逐一判断即可．【详解】解：∵将△ABM绕点A逆时针旋转得到△ACN，∴△ABM≌△ACN，∴AB=AC，AM=AN，∴AB不一定等于AN，故选项A不符合题意；∵△ABM≌△ACN，∴∠ACN=∠B，而∠CAB不一定等于∠B，∴∠ACN不一定等于∠CAB，∴AB与CN不一定平行，故选项B不符合题意；∵△ABM≌△ACN，∴∠BAM=∠CAN，∠ACN=∠B，∴∠BAC=∠MAN，∵AM=AN，AB=AC，∴△ABC和△AMN都是等腰三角形，且顶角相等，∴∠B=∠AMN，∴∠AMN=∠ACN，故选项C符合题意；∵AM=AN，而AC不一定平分∠MAN，∴AC与MN不一定垂直，故选项D不符合题意；故选：C．11. 【答案】(1,2)【分析】根据点的平移法则：横坐标，右移加，左移减；纵坐标，上移加，下移减解答即可．【详解】解：点A（3，2），点A的对应点C（-1，2），将点A（3，2）向左平移4个单位，所得到的C（-1，2），∴B（5，2）的对应点D的坐标为（1，2），故答案为：(1,2)．12. 【答案】60或120或180或240或300（写出一个即可）【分析】如图（见解析），求出图中正六边形的中心角，再根据旋转的定义即可得．【详解】解：这个图案对应着如图所示的一个正六边形，它的中心角3601606︒∠==︒， 0360α︒<<︒， ∴角α可以为60︒或120︒或180︒或240︒或300︒，故答案为：60或120或180或240或300（写出一个即可）．13. 【答案】5【分析】根据动点最值问题的求解步骤：①分析所求线段端点（谁动谁定）；②动点轨迹；③最值模型（比如将军饮马模型）；④定线段；⑤求线段长（勾股定理、相似或三角函数），结合题意求解即可得到结论．【详解】解：①分析所求线段GF 端点：G 是定点、F 是动点；②动点F 的轨迹：正方形ABCD 的边长为10，点E 是边AD 上一动点，连接BE ，将ABE △沿BE 翻折得到FBE ，连接GF ，则10BF BA ==，因此动点轨迹是以B 为圆心，10BA =为半径的圆周上，如图所示：③最值模型为点圆模型；④GF 最小值对应的线段为10GB -；⑤求线段长，连接GB ，如图所示：在Rt BCG ∆中，90C ∠=︒，正方形ABCD 的边长为10，点G 是边CD 的中点，则5,10CG BC ==，根据勾股定理可得BG =当G F B 、、三点共线时，GF最小为10，接下来，求AE 的长：连接EG ，如图所示根据翻折可知,90EF EA EFB EAB =∠=∠=︒，设AE x =，则根据等面积法可知EDG BCG BAE BEG S S S S S ∆∆∆∆=+++正方形，即()111111005105101022222DE DG BC CG AB AE BG EF x x ⎡⎤=⋅+⋅+⋅+⋅=-+⨯++⎣⎦整理得)120x =，解得2015x AE====，故答案为：5．14. 【答案】【分析】根据直角三角形的中线定理，先证明四边形是平行四边形，再证明是等边三角形，分别根据直角三角形中的三角函数求出AM 和DM ，从而得到答案．【详解】解：如下图所示，设A E '交BM 于点O ，连接AO ，∵点E 是中点，∴在Rt ABM 和 Rt A BM '中，,AO OM OB OA OB OM '====,∴,OAE OBE OBA OA B ''∠=∠∠=∠ ，∵OBE OBA '∠=∠，AOA M 'AOM∴OAE OA B '∠=∠ ，∵90,90OAE AOE OA B OA M ︒︒''∠+∠=∠+∠=，∴AOE OA M '∠=∠，∴//AO A M '，∵//AM OA '∴四边形AOA M '是平行四边形，∴AM OA '=∴AM AO OM ==,∴是等边三角形，∴∴ ∴∵，，∴，∴，∵， ∴∴故答案为：15. 【答案】()5,2【分析】由将线段OA 向右平移4个单位长度，可得点A 1,2向右边平移了4个单位与C 对应，再利用“右移加”即可得到答案．【详解】解：∵将线段OA 向右平移4个单位长度，∴点A 1,2向右边平移了4个单位与C 对应，∴14,2,C 即5,2,C故答案为：5,2.16. 【答案】6【分析】根据第一次折叠的性质求得12BD DB BB ''==和AD BC ⊥，由第二次折叠得到AM DM =，MN AD ⊥，进而得到MN BC ，易得MN 是ADC 的中位线，最后由三角形的中位线求解．【详解】AOM 60AMO OMA ︒'∠=∠=tan tan 60AB AMO AM ︒∠==AM =MF BM ⊥60OMA ︒'∠=30A MF ︒'∠=18015030DMF ︒︒︒∠=-=132DF AB ==tan 30DF MD ==︒AD AM MD =+=解：∵已知三角形纸片ABC ，第1次折叠使点B 落在BC 边上的点B '处，折痕AD 交BC 于点D ， ∴12BD DB BB ''==，AD BC ⊥． ∵第2次折叠使点A 落在点D 处，折痕MN 交AB '于点P ，∴AM DM =，AN ND =，∴MN AD ⊥，∴MN BC ．∵AM DM =，∴MN 是ADC 的中位线， ∴12MP DB '=，12MN DC =． ∵12BC =，2BD DC CB BD BC +=+'=， ∴()111162222MP MN DB DC DB DB B C BC +=+=+='+''='．故答案为：6．17. 【答案】80 4##4【分析】利用SAS 证明△BDC ≌△AEC ，得到∠DBC =∠EAC =20°，据此可求得∠BAF 的度数；利用全等三角形的性质可求得∠AFB =60°，推出A 、B 、C 、F 四个点在同一个圆上，当BF 是圆C 的切线时，即当CD ⊥BF 时，∠FBC 最大，则∠FBA 最小，此时线段AF 长度有最小值，据此求解即可．【详解】解：∵△ABC 和△DCE 都是等边三角形，∴AC =BC ，DC =EC ，∠BAC =∠ACB =∠DCE =60°，∴∠DCB +∠ACD =∠ECA +∠ACD =60°，即∠DCB =∠ECA ，在△BCD 和△ACE 中，CD CE BCD ACE BC AC =⎧⎪∠=∠⎨⎪=⎩，∴△ACE ≌△BCD （ SAS ），∴∠EAC =∠DBC ，∵∠DBC =20°，∴∠EAC =20°，∴∠BAF =∠BAC +∠EAC =80°；设BF 与AC 相交于点H ，如图：∵△ACE ≌△BCD∴AE =BD ，∠EAC =∠DBC ，且∠AHF =∠BHC ，∴∠AFB =∠ACB =60°，∴A 、B 、C 、F 四个点在同一个圆上，∵点D 在以C 为圆心，3为半径的圆上，当BF 是圆C 的切线时，即当CD ⊥BF 时，∠FBC 最大，则∠FBA 最小，∴此时线段AF 长度有最小值，在Rt △BCD 中，BC =5，CD =3，∴BD4，即AE =4，∴∠FDE =180°-90°-60°=30°，∵∠AFB =60°，∴∠FDE =∠FED =30°，∴FD =FE ，过点F 作FG ⊥DE 于点G ，∴DG =GE =32， ∴FE =DF =cos30DG ︒∴AF =AE -FE故答案为：80；18. 【答案】或【分析】分两种情况，根据关于y 轴对称的图形的对称点的坐标特点，即可求得．【详解】解：函数（k 为常数）的“Y 函数”图象与x 轴只有一个交点，函数（k 为常数）的图象与x 轴也只有一个交点，当k =0时，函数解析为，它的“Y 函数”解析式为，它们的图象与x 轴只有一个交点，23y x =-244y x x =-+-()2213y kx k x k =+-+-∴()2213y kx k x k =+-+-23y x =--23y x =-当时，此函数是二次函数，它们的图象与x 轴都只有一个交点，它们的顶点分别在x 轴上，，得，故k +1=0，解得k =-1，故原函数的解析式为，故它的“Y 函数”解析式为，故答案为：或．19. 【答案】(1)CD ，AD ；(2)见解析；(3)EF 于BC 之间的距离为64cm ．【分析】（1）由推动矩形框时，矩形ABCD 的各边的长度没有改变，可求解；（2）通过证明四边形BEFC 是平行四边形，可得结论；（3）由勾股定理可求BH 的长，再证明△BCH ∽△BGE ，得到BH CH BE EG=，代入数值求解EG ，即可得到答案．(1)解：∵ 把边BC 固定在地面上，向右推动矩形框，矩形框的形状会发生改变（四边形具有不稳定性）．∴由旋转的性质可知矩形ABCD 的各边的长度没有改变，∴AB ＝BE ，EF ＝AD ，CF ＝CD ，故答案为：CD ，AD ；(2)解：∵四边形ABCD 是矩形，∴AD BC ，AB ＝CD ，AD ＝BC ，∵AB ＝BE ，EF ＝AD ，CF ＝CD ，∴BE ＝CF ，EF ＝BC ，∴四边形BEFC 是平行四边形，∴EF BC ，∴EF AD ；(3)解：如图，过点E 作EG ⊥BC 于点G ， 0k≠∴()()2432104k k k k ---⎡⎤⎣⎦∴=10k k+=244y x x =---244y x x =-+-23y x =-244y x x =-+-∵DC ＝AB ＝BE ＝80cm ，点H 是CD 的中点，∴ CH ＝DH ＝40cm ，在Rt △BHC 中，∠BCH ＝90°，BH50=（cm ），∵ EG ⊥BC ，∴∠EGB ＝∠BCH ＝90°，∴CH EG ，∴ △BCH ∽△BGE ， ∴BH CH BE EG =， ∴， ∴EG ＝64，∵ EF BC ，∴EF 与BC 之间的距离为64cm ．20. 【答案】(1)BF =CF(2)成立；理由见解析 (3)62m PD =-或PD =0或62m PD =- 【分析】（1）连接AF ，先根据“SAS”证明ACE ABD ∆∆≌，得出90ACE ABD ∠=∠=︒，再证明Rt Rt ABF ACF ≌，即可得出结论；（2）连接AF ，先说明EAC BAD ∠=∠，然后根据“SAS”证明ACE ABD ∆∆≌，得出90ACE ABD ∠=∠=︒，再证明Rt Rt ABF ACF ≌，即可得出结论；（3）先根据60α=︒，AB =AC ，得出△ABC 为等边三角形，再按照60BAD ∠︒＜，60BAD ∠=︒，60BAD ∠︒＞三种情况进行讨论，得出结果即可．(1)解：BF =CF ；理由如下：连接AF ，如图所示：504080EG=根据旋转可知，90DAE α∠==︒，AE =AD ， ∵∠BAC =90°，∴90EAC CAD ∠+∠=︒，90BAD CAD ∠+∠=︒， ∴EAC BAD ∠=∠，∵AC =AB ，∴ACE ABD ∆∆≌（SAS ），∴90ACE ABD ∠=∠=︒，∴1809090∠=︒-︒=︒ACF ，∵在Rt △ABF 与Rt △ACF 中AB AC AF AF =⎧⎨=⎩， ∴Rt Rt ABF ACF ≌（HL ），∴BF =CF ．故答案为：BF =CF ．(2)成立；理由如下：连接AF ，如图所示：根据旋转可知，DAE α∠=，AE =AD ， ∵BAC α∠=，∴EAC CAD α∠-∠=，BAD CAD α∠-∠=， ∴EAC BAD ∠=∠，∵AC =AB ，∴ACE ABD ∆∆≌，∴90ACE ABD ∠=∠=︒，∴1809090∠=︒-︒=︒ACF ，∵在Rt △ABF 与Rt △ACF 中AB AC AF AF =⎧⎨=⎩， ∴Rt Rt ABF ACF ≌（HL ），∴BF =CF ．(3)∵60α=︒，AB =AC ，∴△ABC 为等边三角形，∴60ABC ACB BAC ∠=∠=∠=︒，AB AC BC === 当60BAD ∠︒＜时，连接AF ，如图所示：根据解析（2）可知，Rt Rt ABF ACF ≌， ∴1302BAF CAF BAC ∠=∠=∠=︒，∵AB = tan tan30BF BAF AB∴∠=︒=，即tan304BF AB =⨯︒==， 4CF BF ∴==，根据解析（2）可知，ACE ABD ∆∆≌， ∴CE BD m ==，∴4EF CF CE m =+=+，906030FBC FCB ∠=∠=︒-︒=︒， 60EFP FBC FCB ∴∠=∠+∠=︒， ∵90EPF ∠=︒，∴906030FEP ∠=︒-︒=︒， ∴()1142222m PF EF m ==+=+， 42622m m BP BF PF ∴=+=++=+，∴6622m m PD BP BD m =-=+-=-；当60BAD ∠=︒时，AD 与AC 重合，如图所示：∵60DAE ∠=︒，AE AD =，∴△ADE 为等边三角形，∴∠ADE =60°，∵9030ADB BAC ∠=︒-∠=︒，∴603090ADE ∠=︒+︒=︒，∴此时点P 与点D 重合，0PD =；当60BAD ∠︒＞时，连接AF ，如图所示：根据解析（2）可知，Rt Rt ABF ACF ≌， ∴1302BAF CAF BAC ∠=∠=∠=︒，∵AB = tan tan30BF BAF AB∴∠=︒=，即tan304BF AB =⨯︒==， 4CF BF ∴==，根据解析（2）可知，ACE ABD ∆∆≌， ∴CE BD m ==，∴4EF CF CE m =+=+，∵906030FBC FCB ∠=∠=︒-︒=︒，60EFP FBC FCB ∴∠=∠+∠=︒，∵90EPF ∠=︒，∴906030FEP ∠=︒-︒=︒， ∴()1142222m PF EF m ==+=+， 42622m m BP BF PF ∴=+=++=+， ∴6622m m PD BD BF m ⎛⎫=-=-+=- ⎪⎝⎭；综上分析可知，62m PD =-或PD =0或62m PD =-． 21. 【答案】(1)证明见解析(2)4(3)【分析】（1）根据题意，利用等面积法ABC ABD ACD S S S ∆∆∆=+，根据等腰ABC 中，AB AC =，即可得到结论；（2）根据题中条件，利用折叠性质得到AFE CFE ∠=∠，结合矩形ABCD 中AD BC ∥得到AFE FEC ∠=∠，从而有CFE FEC ∠=∠，从而确定EFC ∆是等腰三角形，从而利用（1）中的结论得到=GM GN FH +，结合勾股定理及矩形性质即可得到结论；（3）延长BA CD 、交于F ，连接EF ，过点B 作BG FC ⊥于G ，根据AB AE CD DE =，EA AB ⊥，ED CD ⊥，得到ABC ∆是等腰三角形，从而由（1）知ED EA BG +=，在Rt BCG ∆中，BG ==Rt BDG ∆中，6BD =，BG =BG =1x =，从而得到结论．(1)证明：连接AD ，如图所示：在等腰ABC 中，AB AC =，BC 边上有一点D ，过点D 作DE AB ⊥于E ，DF AC ⊥于F ，过点C 作CG AB ⊥于G ，∴由ABC ABD ACD S S S ∆∆∆=+得111222AB CG AB ED AC FD ⋅=⋅+⋅， ∴DE DF CG +=；(2)解：连接CG ，过点F 作FH BC ⊥于H ，如图所示：根据折叠可知AFE CFE ∠=∠，在矩形ABCD 中，AD BC ∥，则AFE FEC ∠=∠，CFE FEC ∴∠=∠，即EFC ∆是等腰三角形，在等腰EFC ∆中，FC EC =，EF 边上有一点G ，过点G 作GM FC ⊥于M ，GN BC ⊥于N ，过点F 作FH BC ⊥于H ，由（1）可得=GM GN FH +，在Rt ABE ∆中，90B ∠=︒，3,835BE AE EC BC BE ===-=-=，则4AB =，在四边形ABHF 中，90B BAF FHB ∠=∠=∠=︒，则四边形ABHF 为矩形，4FH AB ∴==，即4GM GN FH AB +===；(3)解：延长BA CD 、交于F ，连接EF ，过点B 作BG FC ⊥于G ，在四边形中，E 为线段上的一点，，，则，又，，，即是等腰三角形，由（1）可得，设，，，在中，在中，，，22. 【答案】(1)60O QA ∠='︒，点O '的坐标为32⎛ ⎝⎭ (2)36O E t '=-，其中t 的取值范围是23t <<(3)3，103．（答案不唯一，满足3t ≤< 【分析】（1）先根据折叠的性质得60O QA ∠='︒，即可得出30∠=︒'QO H ，作O H OA '⊥，然后求出O H '和OH ，可得答案；（2）根据题意先表示3=-QA t ，再根据12QA QE =，表示QE ，然后根据O E O Q QE =''-表示即可，再求出取值范围；ABCD BC EA AB ⊥ED CD ⊥90BAE CDE ∠=∠=︒AB AE CD DE=∴ABE DCE ∆∆ABE C ∴∠=∠ABC ∆∴ED EA BG +==GD x 90EDC BGC ∠=∠=︒BC =3CD =Rt BCG ∆BG Rt BDG ∆6BD =BG ∴BG =1x =BG ∴=ED EA BG +==（3）求出t =3时的重合部分的面积，可得从t =3之后重合部分的面积始终是求出P 与C 重合时t 的值可得t 的取值范围，问题得解．(1)在Rt POQ △中，由30OPQ ∠=︒，得9060OQP OPQ ∠=-∠=︒︒．根据折叠，知PO Q POQ '△≌△，∴O Q OQ '=，60︒∠=∠='O QP OQP ．∵180O QA O QP OQP ∠=︒--∠'∠'，∴60O QA ∠='︒．如图，过点O′作O H OA '⊥，垂足为H ，则90O HQ ∠='︒．∴在Rt O HQ '中，得9030QO H O QA ∠=︒-'∠='︒．由1t =，得1OQ =，则1O Q '=．由1122'==QH O Q ，222'+='O H QH O Q得32=+=OH OQ QH ，'=O H∴点O '的坐标为32⎛ ⎝⎭．(2)∵点(3,0)A ，∴3OA =．又OQ t =，∴3QA OA OQ t =-=-．同（1）知，'=O Q t ，60O QA ∠='︒．∵四边形OABC 是矩形，∴90OAB ∠=︒．在Rt EAQ △中，9030QEA EQA ∠=-∠=︒︒，得12QA QE =． ∴22(3)62QE QA t t ==-=-．又O E O Q QE =''-，∴36O E t '=-.如图，当点O ′与AB 重合时，OQ O Q t '==，60AQO '∠=︒，则30AO Q ∠='︒， ∴12AQ t =， ∴132t t +=，解得t =2，∴t 的取值范围是23t <<；(3)3，103．（答案不唯一，满足3t ≤< 当点Q 与点A 重合时，3AO '=，30DAO '∠=︒，∴cos 30AO AD '==︒则132ADP S =⨯⨯=∴t =3时，重合部分的面积是从t =3之后重合部分的面积始终是当P 与C 重合时，OP ＝6，∠OPQ ＝30°，此时t ＝OP ·tan30°＝由于P 不能与C 重合，故t <所以3t ≤<23. 【答案】(1)（8，6）(2)（67，6） (3)（112，6） (4)OG 的最小值为4，线段FP 扫过的面积为83π 【分析】（1）由勾股定理即可求解；（2）连接OP ，过点P 作PQ ⊥OB 于点Q ，因为∠POB =45°，所以PQ =OQ ，设PQ =OQ =x ，则BQ =10-x ，根据tan B 的值，即可求得x 的值，再利用勾股定理，即可求解；（3）令PA '交OB 于点D ，由点E 为线段OB 的中点，可得152A E AE OB '===，152BE OB ==，利用折叠的性质、正切函数、勾股定理，即可求解；（4）当以点F 为圆心，OF 的长为半径画圆，与AB 的交点即为点P ，再将线段FP 绕点F 顺时针方向旋转60°得线段FG ，此时OG 最小，利用三角函数、等边三角形的判定与性质、扇形的面积公式，即可求解．(1)解：在Rt △OAB 中，8AB ===，∴点B 的坐标为（8，6）；(2)解：连接OP ，过点P 作PQ ⊥OB 于点Q ，如图，∵∠POB=45°，∴∠OPQ=45°，∴∠POB=∠OPQ，∴PQ=OQ，设PQ=OQ=x，则BQ=10-x，在Rt△OAB中，6384 tanOABAB===，在Rt△BPQ中，3104 tanPQ xBBQ x===-，解得307x=，∴307 OQ PQ==，在Rt△POQ中，7OP==，在Rt△AOP中，67 AP==，∴点P的坐标为（67，6）；(3)解：令PA'交OB于点D，如图，∵点E为线段OB的中点，∴152AE OB==，152BE OB==，∵6384tan PD OA B BD AB ====，设3PD a =，则4BD a =，∴5BP a ==，54DE BE BD a =-=-∴85AP AB BP a =-=-，由折叠的性质，可得5A E AE '==，85A P AP a '==-，∴88A D A P PD a ''=-=-，在Rt △A DE 中，222A D DE A E ''+=，即22288545()()a a -+-=，解得121825，a a ==， ∵BD BE <，即45a <， ∴54a <， ∴12a =， ∴1118522A P '=-⨯=， ∴点P 的坐标为（112，6）； (4) 解：以点F 为圆心，OF 的长为半径画圆，与AB 的交点即为点P ，再将线段FP 绕点F 顺时针方向旋转60°得线段FG ，连接OG ，此时OG 最小，如图，由题可知，624FP FG FO OA AF ===-=-=，在Rt APF 中，2142cos AF AFP FP ∠===， ∴60AFP ∠=︒，∵60PFG ∠=︒，∴60OFG ∠=︒，∴OFG △是等边三角形，∴4OG FO ==，∴OG的最小值为4，∴线段FP扫过的面积=26048 3603ππ⨯=．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

折叠与旋转问题
1、如图，把矩形ABCD 沿EF 对折，若150∠=
，则AEF ∠等于（） A ．115
B ．130
C ．120
D ．65
2、如图，折叠矩形纸片ABCD ，先折出折痕（对角线）BD ，再折叠使AD 边与对角线BD 重合，得折痕DG ，如果
AB=2，BC=1，那么AG 的长为（） 3、把长方形ABCD 沿AE 翻折使点D 落在BC 边上的点
F 处，
（1）如果∠BAF=60°，则∠DAE 为多少度？
（2）如果AB=8cm ，AD=10cm ，则AE 长是多少？ 4、如图，将边长为8cm 的正方形纸片ABCD 折叠，使
点D 落在BC 边中点E 处，点A 落在点F 处，折痕为MN ，则线段CN 的长是（）．（A ）3cm （B ）4cm （C ）5cm （D ）6cm
5、如图，把矩形纸片ABCD 沿EF 折叠，使点B 落在边AD 上的点B '处，点A 落在点A '处；
（1）求证：B E BF '=；
（2）设A E a A B b B F c ===，，，试猜想a b c ，，之间的
一种关系，并给予证明．
6、如图，把一张矩形的纸ABCD 沿对角线BD 折叠，使点C 落在点E 处，BE 与AD 交于点F ． ⑴求证：ΔABF ≌ΔEDF ；
⑵若将折叠的图形恢复原状，点F 与BC 边上的点M 正好重
合，连接DM ，试判断四边形BMDF 的形状，并说明理由．
旋转问题
1、在ABC △中，2AB AC ==，90A ∠=°，取一块含45°角的直角三角尺，将直角顶点放在斜边BC 边的中点O 处（如图1），绕O 点顺时针方向旋转，使90°角的两边与Rt ABC △的两边AB AC ，分别相交于点E F ，（如图2）
．设BE x =，CF y =．（1）探究：在图2中，线段AE 与CF 之间有怎样的大小关系？试证明你的结论；（2）若将直角三角尺45°角的顶点放在斜边BC 边的中点O 处（如图3），绕O 点顺时针方向旋转，其他条件不变． A
B
C
D E
F 1
A
B
C
D
F
E
A
B
C
D
F
A '
B '
E
C D
B A M 第22题图
F E
①试写出y 与x 的函数解析式，以及x 的取值范围；
②将三角尺绕O 点旋转（如图4）的过程中，OEF △是否能成为等腰三角形？若能，直接写出OEF △为等腰三角形时x 的值；若不能，请说明理由．
5、如图所示，在平面直角坐标系中，矩形ABOC 的边BO 在x 轴的负半轴上，边OC 在
y 轴的正半轴上，且1AB =，3OB =，矩形ABOC 绕
点O 按顺时针方向旋转60
后得到矩形EFOD ．点A 的对应点为点E ，点B 的对应点为点F ，点C 的对应点为点
D ，抛物线2y ax bx c =++过点A
E D ，，．
（1）判断点E 是否在y 轴上，并说明理由；（2）求抛物线的函数表达式；
（3）在x 轴的上方是否存在点P ，点Q ，使以点O B P Q ，，，为顶点的平行四边形的面积是矩形ABOC 面积的2倍，且点P 在抛物线上，若存在，请求出点P ，点Q 的坐标；若不存在，请说明理由．
A
O C B
A
O C
B
O C B
A (F )
A
O C
B
F
E
E
E
F 图1
图2
图3
图4 第25题图
y x y x
O
D
E
C F
A B
方法一方法二
6、如图，阴影部分是由5个小正方形组成的一个直角图形，请用二种方法分别在下图方格内添涂黑二个小正方形，使它们成为轴对称图形．
8. 如图，边长为
2的正方形ABCO 中，点F 为x 轴上一点，CF=1，过点B 作BF 的垂线，交y 轴于点E ．
（1）求过点E 、B 、F 的抛物线的解析式；
（2）将∠EBF 绕点B 顺时针旋转，角的一边交y 轴正半轴于点M ，另一边交x 轴于点N ，设BM 与（1）中抛物线的另一个交点为点G ，且点G
的横坐标为56
，EM 与NO 有怎样的数量关系？请说明
你的结论．
（3）点P 在（1）中的抛物线上，且PE 与y 轴所成锐角的正切值为2
3，求点P 的坐标．
9.已知如图，抛物线n mx x y ++=
2
2
1与x 轴交于A 、
B 两点，与y 轴交于
C 点，四边形OBHC 为矩形，CH 的延长线交抛物线于点
D （5，2），连结BC 、AD . (1)求C 点的坐标及抛物线的解析式；
(2)将△BCH 绕点B 按顺时针旋转90°后再沿x 轴对折得到△BEF （点C 与点E 对应），判断点E 是否落在抛物线上，并说明理由；
(3)设过点E 的直线交AB 边于点P ，交CD 边于点Q . 问是否存在点P ，使直线PQ 分梯形ABCD 的面积为1∶3两部分？若存在，求出P 点坐标；若不存在，请说明理由.。