第2章电阻电路的等效变换
合集下载
第二章 电阻电路的等效变换
＋
i
＋
… i
＋ －
u
－
K=1，2 ， i
＋ －
u
Reg
u
G1
in Gn
u
－
Geg
分流公式： 分流公式：ik=Gku=Gk/Geg i n=2时，Reg=R1R2/（R1+R2） 时 （ i1=R2/（R1+R2）， 2=R1/（R1+R2）×i ），i （ （ *混联：有串，又有并 混联：有串， 混联 1 R1 R2 R3 R4
对于△ 对于△形，各电阻中电流为：i12=u12/R12 i23=u23/R23 i31=u31/R31 各电阻中电流为：
i ′ =i12-i31=u12/R12-u31/R31 1
i ′2 =u23/R23-u12/R12
i ′3 =u31/R31-u23/R23
i1 + i 2 + i 3 = 0
③
2
2 i31 1 i12
④
2
⑤
i′2
1
1
R2
3
自已补充:R 自已补充 4与1串,R3与2串,然 串 串然 后再并 i2
R4 R3 2
3
i3 2
1
1
2-5
电压源和电流源的串联和并联
＋
1、n个电压源串联：us=∑usk--------等效电压源 、 个电压源串联： 等效电压源 个电压源串联 ＋ － ＋ ○ ○ －○ us1 us2 usn。 。 注：正、负号取 。 。 。 2、n个电流源的并联： 个电流源的并联： 、 个电流源的并联 is1 is=is1+is2+…is=∑isk 。 。
αi
＋ uS － i ＋
i
＋
… i
＋ －
u
－
K=1，2 ， i
＋ －
u
Reg
u
G1
in Gn
u
－
Geg
分流公式： 分流公式：ik=Gku=Gk/Geg i n=2时，Reg=R1R2/（R1+R2） 时 （ i1=R2/（R1+R2）， 2=R1/（R1+R2）×i ），i （ （ *混联：有串，又有并 混联：有串， 混联 1 R1 R2 R3 R4
对于△ 对于△形，各电阻中电流为：i12=u12/R12 i23=u23/R23 i31=u31/R31 各电阻中电流为：
i ′ =i12-i31=u12/R12-u31/R31 1
i ′2 =u23/R23-u12/R12
i ′3 =u31/R31-u23/R23
i1 + i 2 + i 3 = 0
③
2
2 i31 1 i12
④
2
⑤
i′2
1
1
R2
3
自已补充:R 自已补充 4与1串,R3与2串,然 串 串然 后再并 i2
R4 R3 2
3
i3 2
1
1
2-5
电压源和电流源的串联和并联
＋
1、n个电压源串联：us=∑usk--------等效电压源 、 个电压源串联： 等效电压源 个电压源串联 ＋ － ＋ ○ ○ －○ us1 us2 usn。 。 注：正、负号取 。 。 。 2、n个电流源的并联： 个电流源的并联： 、 个电流源的并联 is1 is=is1+is2+…is=∑isk 。 。
αi
＋ uS － i ＋
第二章电阻电路的等效变换
ab
20 100 60
120 60
ab 20 100
100 Rab＝70
ab
20 100 60
40
例2 求: Rab
5
15 6
a 20
b
缩短无
电阻支路
7
6
Rab＝10
4 a b
15
10
20
5
a
15 b
7 6 6 4 a
b
15 7
3
例6
求: Rab c
对称电路 c、d等电位
R
R
R
c R
a R
断路 a
+a
2 +
U
6V –
(a)
b
3 9V +
(b)
解: a
+
+a U b
a +
3A 2 U
3A 3 U
b
(a)
b
(b)
例1: 求下列各电源等效变换
+a
3A 1 U
解:
(c)
b
a
+
1 +
U
3V –
(c)
b
+a
2A 5 U
(d) b
a
+
5 -
U
10V +
(d)
b
例2: 试用电压源与电流源等效变换的方法，计算2
2.1 概述
1 一些概念
1）电阻电路 仅由电源和线性电阻构成的电路。
2）等效的概念：
若结构、元件参数不相同的两部分电路N1、N2，具 有相同的电压、电流关系，则称它们彼此等效。
i
高等教育出版社第六版《电路》第2章_电阻电路的等效变换课件
k 1
n
顺之者正，逆之者负。
2、串联： is1 is2
isn
is = is1= is2 = isn is
(1)电流相同的电流源能串联，但每个电源中的电压不确定。 (2)电流不相等，则不能串联，否则，违背KCL。 3、电流源is 和R、 us的串联： us is + – + u1 – R 注意：电压变化了。
第二章 电阻电路的等效变换
§2-1 引言
线性电路：由线性无源元件（R、L、C·）、线性受控 · · 源和独立电源组成。 线性电阻电路：由线性电阻、线性受控源和独立电源组成。 直流电路：独立电源为直流电源的线性电阻电路。
§2-2 电路的等效变换
一、等效的概念：
R R R1 §2-2 电路的等效变换 1 1 R2 i + R4 u R _ 3 ,
解：用电源变换法。受控源和独立源一样可以进行电源转换。 R i R _ + uR_ i R + uR + + ic + uc _ uS R _uS _
uc Ric 2 2 uR 4uR
Ri + Ri + uc = us
2uR 4uR us us uR 2V 6 在进行电源变换时，为避免出错控制量一般不要转换掉!
i2
i3
i3
u31 u23 R31 R23
R1u23 R3u12 R1R2 R2 R3 R3 R1 R1R2 R2 R3 R3 R1
R2u31 R1u23 R1R2 R2 R3 R3 R1 R1R2 R2 R3 R3 R1
由Y : R R R2 R3 R3 R1 R12 1 2 R3 R1R2 R2 R3 R3 R1 R23 R1 R R R2 R3 R3 R1 R31 1 2 R2
n
顺之者正，逆之者负。
2、串联： is1 is2
isn
is = is1= is2 = isn is
(1)电流相同的电流源能串联，但每个电源中的电压不确定。 (2)电流不相等，则不能串联，否则，违背KCL。 3、电流源is 和R、 us的串联： us is + – + u1 – R 注意：电压变化了。
第二章 电阻电路的等效变换
§2-1 引言
线性电路：由线性无源元件（R、L、C·）、线性受控 · · 源和独立电源组成。 线性电阻电路：由线性电阻、线性受控源和独立电源组成。 直流电路：独立电源为直流电源的线性电阻电路。
§2-2 电路的等效变换
一、等效的概念：
R R R1 §2-2 电路的等效变换 1 1 R2 i + R4 u R _ 3 ,
解：用电源变换法。受控源和独立源一样可以进行电源转换。 R i R _ + uR_ i R + uR + + ic + uc _ uS R _uS _
uc Ric 2 2 uR 4uR
Ri + Ri + uc = us
2uR 4uR us us uR 2V 6 在进行电源变换时，为避免出错控制量一般不要转换掉!
i2
i3
i3
u31 u23 R31 R23
R1u23 R3u12 R1R2 R2 R3 R3 R1 R1R2 R2 R3 R3 R1
R2u31 R1u23 R1R2 R2 R3 R3 R1 R1R2 R2 R3 R3 R1
由Y : R R R2 R3 R3 R1 R12 1 2 R3 R1R2 R2 R3 R3 R1 R23 R1 R R R2 R3 R3 R1 R31 1 2 R2
第02章电阻电路的等效变换(丘关源)
（1-29）
(6)恒压源并联任何元件其两端电压不变；
恒流源串联任何元件其流出电流不变；
a a
+ us
－
+ +
－
对外等效
us
－
b
c
b c
对外等效
is
+
－
d
is
d
（1-30）
例1 用电源等效变换法求i R5
R1 u1 + R2 R3 i
+
i=?
解：
-u3
R4
is
R5 u3 — R3 i
应 用 举 例
一、理想电压源的串联和并联
1、串联 + uS1_ _ uS2 +
+ 注意参考方向
º uS＝＋uS1 …－uS2 i + uS _ º
等效
+
uS _
º +
_ º
2、并联
条件：uS＝uS1＝uS2 方向相同 º 恒压源中的电流由外电路决定。相同的恒压源才能并联 。
（1-21）
uS1_
u S2
+ _
i
º
3、恒压源与任意支路(非恒压源)并联的等效 i i + + + + 任意 uS 对外等效 uS _ u _ u 元件 _ _ 4、实际电压源的串联等效
+ i +
uS1 _
R1
_ uS2 + u
R2 _
等效
uS _ R + i +
u
_
uS＝＋uS1－uS2
R＝R1 ＋ R2
（1-22）
二、理想电流源的串联和并联
(6)恒压源并联任何元件其两端电压不变；
恒流源串联任何元件其流出电流不变；
a a
+ us
－
+ +
－
对外等效
us
－
b
c
b c
对外等效
is
+
－
d
is
d
（1-30）
例1 用电源等效变换法求i R5
R1 u1 + R2 R3 i
+
i=?
解：
-u3
R4
is
R5 u3 — R3 i
应 用 举 例
一、理想电压源的串联和并联
1、串联 + uS1_ _ uS2 +
+ 注意参考方向
º uS＝＋uS1 …－uS2 i + uS _ º
等效
+
uS _
º +
_ º
2、并联
条件：uS＝uS1＝uS2 方向相同 º 恒压源中的电流由外电路决定。相同的恒压源才能并联 。
（1-21）
uS1_
u S2
+ _
i
º
3、恒压源与任意支路(非恒压源)并联的等效 i i + + + + 任意 uS 对外等效 uS _ u _ u 元件 _ _ 4、实际电压源的串联等效
+ i +
uS1 _
R1
_ uS2 + u
R2 _
等效
uS _ R + i +
u
_
uS＝＋uS1－uS2
R＝R1 ＋ R2
（1-22）
二、理想电流源的串联和并联
电路理论基础第二章电阻电路的等效变换.
■ _________________________________________________秦二五五阻竜賂鬲看效交鎭5 MT\ 2-2『WL略g*j»c凭. r -「电m 的■!»"井JBi 1-「削血的、知联结*>^洒联结的帶玻^^换'2-5 f 电压■、电汶4K的*税加井联11 2-6「4&际他sRftdKjn.st及如nat. 72-7r«r入电》1•重点:1.电路等效的概念2.电阻的串、并联3.电阻的Y・A变换4.电压源和电流源的等效变换2-1引言•电阻电路仅由电源和线性电阻构成的电路。
①欧姆定律和基尔霍夫定律是分析电•分析方法阻电路的依据.②等效变换的方法，也称化简的方法・IW回，『Wk I下賈***yuj^" ...... .... . 一組由从旨•麦以2-2电路的等效变换1 •二端电路（网络）任何一个复杂的电路，向外引出两个端钮，且从一个端子流入的电流等于从另一个端子流出的电流，则称这一电路为二端网络（或一端口网络）。
・回「王廣r下V2-3电阻的串联和并联1.电阻串联R\①电路特点+ HI - + W & - + 冷(a)各电阻顺序连接，流过同一电流(KCL)。
(b)总电压等于各串联电阻的电压之和(KVL)。
以=叫+••• + '" --- + 叫t 回，：上贡「下IT.. ....2. 电阻并联(a)各电阻两端为同一电压(KVL)。
(b)总电流等于流过各并联电阻的电流之和(KCL).i =八 + 02+ + L+「込回，：上贡「下IT② 等效电阻■：~I/. RH 血人dij KCL: / = /1 +，2+ …+ S+ ' * +/…= U/R\ +M /7?2 + 十 M /R n=M (1//?]+ 1/7?2—H '/RJ=uG 門na = G + G ----------- <7 =牙 G > aoq12nk k①电路特点HiIO — +ftU迟回，上黃丨下帀《隽捡 等效电导等于并联的各电导之和.例3-2两电阻的分流.R 显心1冬_叽 刊 \R +1/ RjR\ + RjlR\ .二 RJ1//?+1做，一 R\+Rjz, = —―~~—— i = -----1 R + \ K 、 & +&------- 1 --------- 1 -------- hR' RRfI ③并联电阻的分流 IL u/R,kk_一 一/ ~ u! R eq上黃丨下帀1/尺2即 <老II --------- ---- ------- ——亠“ • 亠亠J 亠亠A 亠亠—亠■亠▲ »■■■■•亠令午+亠▲亠▲▲亠▲▲“ 亠亠.亠亠 S 亠亠1 从以上例题可得求解串、并联电路的一般步骤：①求出等效电阻或等效电导.②应用欧姆定律求出总电压或总电流.③应用欧姆定律或分压.分流公式求各电阻上的削流和电压《以上的关键在于识别各电阻的串联.并联关系！求"Rah，Red o(5 + 5)x 15 +(y (5 + 5)+ 15(15 • 5)X 5uh —例3・6求：。
第2章电阻电路的等效变换
总电流
U S 18 I= = A = 6A R 3
由分流公式得
6 I1 = I = × 6A = 4A 4× 4 9 6 + (1 + ) 4+4
再分流得
6
1 I x = I 1 = 2A 2
返回
电路分析基础
第2章 电阻电路的等效变换
2.2.4 Y形电路和Δ形电路之间 的等效变换
返回
电路分析基础
如何等效化简电桥测温电路? 如何等效化简电桥测温电路?
返回
电路分析基础
第2章 电阻电路的等效变换
2.1 等效变换
电阻电路
线性电阻电路
非线性电阻电路
简化线性电阻电路的主要依据是等效变换
返回
电路分析基础
第2章 电阻电路的等效变换
2.1.1 一端口网络的定义
二端网络
一端口网络
流入一个端子的电流必定等于流出另一端子的电流
Ig =
Rp Rg + R p
× 10 × 10 −3 = 1 × 10 −3 mA
解之得应并联的电阻为
0.1RG 2 × 10 3 Rp = = Ω ≈ 222.22Ω 0.9 9
返回
电路分析基础
第2章 电阻电路的等效变换
2.2.3 电阻的混联
判别电路的串并联关系根据以下原则： 判别电路的串并联关系根据以下原则： （1）看电路的结构特点。 看电路的结构特点。 （2）看电压、电流关系。 看电压、电流关系。 （3）对电路作变形等效。 对电路作变形等效。 （4）找出等电位点。 找出等电位点。
R4 R5 R2(R3 + ) R4+R5 R = R1 + R4 R5 R2 + (R3 + ) R4 + R5
第二章电阻电路的等效变换
（2）R1增大，Uis增大，对其它元件均无影响
26
$2-5 电压源及电流源串联和并联（39）
1、电压源串联（如图）： 1 + 等效电压源符号： 1 + Us 2 +Us1+ Us2 Us 2 +Usn -
Us=Us1+Us2+….+Usn Usk与Us方向一致取“+”，否则，取“-”
27
2、电流源并联（如图）
22
R 23 R 31
R23
2
2、 △ 型连接等效变换为Y型连接
1
23
R13
R23
R12 2
R R
1
R R R
3
12
R 1 2 R 31 R 23 R R 12 R 23 R 23 R R 31 R 23 R 23 R
31
2
1 R1 R3 3 R2 2
12
31
R
3
• 端口施加电压法求Rin： 端口施加电压源U，则有端口电流I， 求出端口伏安特性表达式：U=IR 则Rin=R=U/I
C）若端口内部有独立电源 先将电压源短路，电流源开路， 求输入电阻归结为 a）b）情况 34
二、实例： 例2-5（ 44页）（自学）
练习题 2-12 ：试求图（a）图（b）中的Rab
则： I Req=U 等效电路： 结论：串联电阻，等效电阻为各电阻之和。
例2-3-1 电路如图，求U1
I + U1 R1 R2 -
+
Us -
KVL：IR IR U 1 2 S + US I U2 R1 R2 R 1 U R *I Us 1 1 R R 1 2
第二章电阻电路的等效变
第二章-电阻电路的等效变第二章 电阻电路的等效变换2.1 学习要点1. 电阻的等效变换：电阻的串并联， Y 与△的等效变换。
2. 电源的串联、并联及等效变换。
3. “实际电源”的等效变换。
4. 输入电阻的求法。
2.2 内容提要 2.2.1 电阻的等效变换1. 电阻的串联：等效电阻： R eq ＝∑1=k nk R ；分压公式：u k ＝eqkeq ×R R u ； 2. 电阻的并联：等效电导：G eq ＝∑1=k nk G ；分流公式：qe G G i i keqk ×=；2.2.2. 电阻的Y 与△的等效变换1. △→Y ：一般公式：Y 形电阻＝形电阻之和形相邻电阻的乘积∆∆；即31232331*********231231212311++=++=++R R R R R R R R R R R R R R R R R R 2312＝2. Y →△：一般公式：形不相邻电阻形电阻两两乘积之和形电阻＝Y Y ∆；即：213322131113322123313322112++=++=++=R R R R R R R RR R R R R R R R R R R R R R R R2.2.3 电源的串联、并联等效变换 电源的串联、并联等效变换见表2.1。
表2.1 电源的串联、并联等效变换图2.2.4 “实际电源”的等效变换 1. “实际电压源”→“实际电流源” R i ＝R u 或 G i ＝1/R u i s ＝u s /R u 2. “实际电流源”→“实际电压源”R u ＝R i ＝1/G i u s ＝i s R i ＝i s /G i两者等效互换的原则是保持其端口的V AR 不变。
2.2.5 输入电阻的求法一端口无源网络输入电阻的定义（见图2.2）：R in ＝u/ i1. 当一端口无源网络由纯电阻构成时，可用电阻的 串并联、Y 形与△形等效变换化简求得。
2. 当一端口无源网络内含有受控源时，可采用外加电压法或外加电流法求得： 即输入电阻R in ＝u s /i 或 R in ＝u/ i s方法是：在端口处加一电压源u s （或电流源i s ）, 再求比值u s /i 或u/ i s ，该比值即是一端口无源网络的输入电阻。
第二章电阻电路等效变换
3、在同样的条件下，等效电路的形式也不是唯 一的。
4、电路进行等效变换的目的是为了简化电路以 方便地求解未知量。
3
§2-2 电阻的串联、并联和混联
一、电阻的串联 （Series connection of resistors）
1、电阻的串联 特点：在串联电路中，各元件流过的电流相同。
由欧姆定律及KVL得： i u = u 1 + u 2 + + u n a =R1i+R2i+ +Rni + u =（R1+R2+ +Rn）i 令R eq=R1+R2+…+Rn=Rk b 则有 u= R eqi
27
电压源： u U s Rs i 电流源： u i Is Rs I s Rs i u Rs
电源模型等效的条件为： 电压源 I RS + US a Uab b
Is
US
RS
Is
电流源 I' a
RS ' RS
Uab' RS'
b
U s I s Rs' Rs Rs'
即形电阻 电阻两两乘积之和 Rmn i' 接在与 Rmn相对端钮的电阻 31
R31
i3'
i'1 2
R23
i'2 3
21
2）形等效为Y形，有：
i1'
R12
i2'
R31 R12 R1 R12 R23 R31 R12 R23 R2 R12 R23 R31 R23 R31 R3 R R R 12 23 31
第二章 电阻电路的等效变换
4
Rab＝10
15 10
a b
a b
7
20
15
3
返 回
上 页
下 页
例 2-8 求图 2-5电路 a b 端的等效电阻。
Req (2 // 2 (4 // 4 2) // 4) // 3 (1 4 // 4) // 3 1.5
21
复习
1、电阻的串联 等效电阻、分压
23
例2－4 图2－7所示电路每个电阻都是2Ω, 求a, b两端的等效电阻
解：
c
d
e
根据电路的对称性, 可知 c, d, e三点等电位, 故可用导线短接。
8 2 8 2 16 3 3 2 Req [(2//1) 2]// 2//1 2 // 2 8 2 3 3 15 3 3
26
R12 ( R23 + R31 ) R12 + R23 + R31
i1
i1
i3
i2
i3
i2
R12 R31 R12 + R23 + R31 R23 R12 R12 + R23 + R31 R31 R23 R12 + R23 + R31
27
同理,令i1=0, 可得: R23 ( R12 + R31 ) R2 + R3 = R12 + R23 + R31 同理,令i2=0, 可得:
25
二、 等效变换：保证伏安特性相同
对应端口电压、电流分别相等
i1
u12 = f1 ( i1 , i2 , i3 ) u23 = f 2 ( i1 , i2 , i3 ) u31 = f3 (i1 , i2 , i3 )
第2章 电阻电路的等效变换
方法2：加流看压法
原理图：
R in
+
u
-
i 列u、iS为变量的方程
S
u
⇒ Rin = iS
练习1：求端口的最简等效形式
R i1
i
+
βi1
_uS
Rin
判断：是无源网络吗？ 最简形式是什么？
由KCL（设流入为正）： i + i1 − βi1 = 0
由VCR：i1
=
−
uS R
得：
R in
=
uS i
=R
1− β
王馨梅
第二章 电阻电路的等效变换
“电阻电路”：由电阻、独立源、受控源组成 (不含L或C) 等效变换的目的：为了化简电路！
课件符号： ★ 重要 * 大纲之外的知识扩展
§§22--11、、§§22--22 等等效效概概念念
2Ω 1Ω 2Ω
i
+
u
i
+
2Ω
u
-
-
N1
N2
★概念：两个网络的端口伏安特性曲线完全相同，则 称这两个网络对外等效。
但等效电导好求：
n
∑ G eq =
Gk
k =1
i k = G k u = G k × ( R eq ⋅ i ) ⇒
并联分流公式： i k
=
Gk G eq
i
并联电导越大 则分流越大
思考：电阻除了串并联关系之外，还有其它连接方式吗？
三、Δ⎯Y之间的等效变换
引例：
A
B
A
B
A
B
R1
R2
R3
1
R12
2
R31
第二章 电阻电路的等效变换
最后求得
10 10 i= = = 4A R 2.5
§ 2.5 电压源、电流源的串联和并联
一、理想电压源的串并联
+ uS1 _ + uSn _ º I + 5V _ + 5V _ º I º + 5V _ º º + uS _ º º
1.串联:
可等效成一个理想电压源uS
uS=us1+us2+…+usn=∑ uSk ( 注意参考方向) 2.并联:
§ 2. 3 电阻的串联、并联和串并联
一、电阻串联(Series Connection of Resistors) 1.电路特点:
R1 i + Rk Rn + un _ _
+ u1 _ + u k _ u
(a)各电阻顺序连接，流过同一电流(KCL)； (b)总电压等于各串联电阻的电压之和 (KVL)。
§ 2.1 引言
时不变线性电路：由时不变线性无源元件、线性受 控源和独立电源组成的电路，简称线性电路。本书 大部分是线性电路。 线性电阻电路：电路的无源元件均为线性电阻构成 的电路，简称电阻电路。本书2、3、4章介绍电阻 电路分析。 直流电路：电路中的独立电源都是直流电源。
§ 2.2 电路的等效变换
3× 5 R1 = = 1.5Ω 3+ 2+ 5 3× 2 R2 = = 0.6Ω 3+ 2+ 5 2× 5 R3 = = 1Ω 3+ 2+5
再 用电阻串联和并联公式，求 出连 接到电压源两 端单口的等效电阻
(0.6 + 1.4)(1 + 1) R = 1.5 + = 2.5Ω 0.6 + 1.4 + 1 + 1
第02章 电阻电路的等效变换
u i is R0
i
R0=R , is=us/R
u us Ri
u is R0 R0 i
i
i
i' Ru 0 O
u
is
i
R=R0, us=Ris
所以，如果令
R R0
us R is
电压源、电阻的串联组合与电流源、电阻的并联组合 可以相互等效变换。 i R + + u i +
1
1
R3
3
R1
R2
2 3
R31
R12
R23
2
星接（Y接）
三角接（△接）
R1 R2 R2 R3 R3 R1 R12 R3 R1 R2 R2 R3 R3 R1 R23 R1 R1 R2 R2 R3 R3 R1 R31 R2
三式相加后通分可 得，Δ形连接变Y形 连接的电阻等效变 换关系式为(下页)
例2－2 求电流i 和 i5
④
i5
② ①
③
i5
②
④
① i1
③
等效电阻 R = 1.5Ω
i5
②
④ ③
i = 2A
i1
①
×
i5
-
i1 1A
2 1 - 6 2 1 1
1 A 3
②
*电阻的混联
电阻串并联的组合称为电阻混联。处理混联电路问 题的方法是：利用电阻串联或并联的公式对电路进 行等效变换，将复杂的混联电路转化成简单的电路 。 〖例1-6〗 求图1-19所示电路的等效电阻Rab， 已知图中各电阻的阻值均为20Ω 。
R2
2
3
R31
R12
R23
i
R0=R , is=us/R
u us Ri
u is R0 R0 i
i
i
i' Ru 0 O
u
is
i
R=R0, us=Ris
所以，如果令
R R0
us R is
电压源、电阻的串联组合与电流源、电阻的并联组合 可以相互等效变换。 i R + + u i +
1
1
R3
3
R1
R2
2 3
R31
R12
R23
2
星接（Y接）
三角接（△接）
R1 R2 R2 R3 R3 R1 R12 R3 R1 R2 R2 R3 R3 R1 R23 R1 R1 R2 R2 R3 R3 R1 R31 R2
三式相加后通分可 得，Δ形连接变Y形 连接的电阻等效变 换关系式为(下页)
例2－2 求电流i 和 i5
④
i5
② ①
③
i5
②
④
① i1
③
等效电阻 R = 1.5Ω
i5
②
④ ③
i = 2A
i1
①
×
i5
-
i1 1A
2 1 - 6 2 1 1
1 A 3
②
*电阻的混联
电阻串并联的组合称为电阻混联。处理混联电路问 题的方法是：利用电阻串联或并联的公式对电路进 行等效变换，将复杂的混联电路转化成简单的电路 。 〖例1-6〗 求图1-19所示电路的等效电阻Rab， 已知图中各电阻的阻值均为20Ω 。
R2
2
3
R31
R12
R23
第2章 电阻电路的等效变换
结论 串联电路的等效电阻等于各分电阻之和。
等效：对外部电路(端钮以外)效果相同。
2.串联电阻上电压的分配
R1
Rk
Rn
i + u1 _ + uk_ + un _
+
u
_
表明
uk
Rk i
Rk
u Req
Rk u Req
u
电压与电阻成正比，因此串联电阻电路可作分压电路。
两个电阻的分压：
i
+ u
u-+__1
等效的目的：化简电路
电阻的串联： Req= Rk
电 阻 电
2.2 电阻的等效变换 ( ，★ )
电阻的并联：Geq= Gk 电阻的Y- 等效变换
uk
ik
Rk GRk eqi
Geq
u
路
电压源串联：uS= uSk
的 等 效
2.3 独立源的等效变换 (，★)
电流源并联: iS= iSk 实际电源两种模型间的等效： uS=iSRS
(3)等效电导等于并联的各电导之和。
Geq=G1+G2+ ... +Gk+ ... +Gn= Gk = 1/Rk
3. 并联电阻的分流： 由 ik u/Rk Gk i u/Req Geq
ik
Gk i Geq
电流分配与
电导成正比
对于两电阻并联，有：
i
+ i1
i2
u_ R1
R2
1 Req
思考与练习
1.等效变换的概 念是什么？“电 路等效就是相等” 这句话对吗？为 什么？
2.电路等效变 换的目的是 什么？
第二章电阻电路的等效
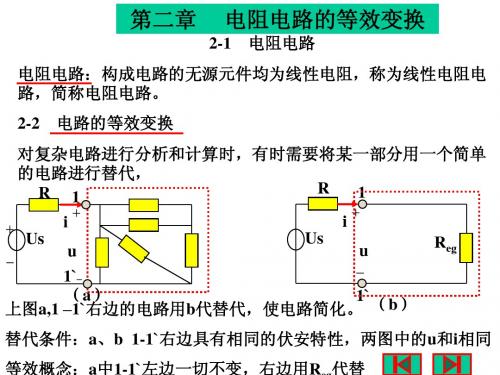
电路的等效变换就是用一个较为简单的电路
替代原电路；其替代条件为：替代（简化）的电路
与原电路具有相同的伏安特性。
如图所示：
R1
1-1'以左的
RS i 1 R2
电路未被替换，uS+_
+u -
R4 R3
R5
1' 原电路
RS i 1
+
+
uS -
u_ Req
1' 替代电路
而1-1' 以右的电路用等效电阻Req 替代。 两个电路的u,i相同，
? u12 ? R1i1 ? R2i2 ?
联立以上几式：
? ?
u
23
?
R2i2
?
R3i
? ?
? ?
i1
?
i2
?
i3
?
0
? ?
?
可解 ? i1 ?
?
R 3 u 12
Δ 型联结
? ? ?
ab..对流应入的对端应子端之子间的具电有 流相分同别的相电等压；；???
则两种联接方式可以相互等效变换。
3.Y—Δ 变换公式
i1 - 1+
如图Y形联结时有 u31 R1 u12
两两端子之间的电压：+ 3
? u 12 ? R1i1 ? R 2 i2 ?
? ?
u
23
?
R2i2 ?
=(R1+R2+······Rn)i=Reqi
u Req ? i ? R1 ? R2 ?
n
? ? Rn ? Rk k?1
若n个相同的电阻R串联时则有Req=nR
由此可得：电阻串联时的等效电阻等于各电阻之和；
二章电阻电路等效变换
2、理想电流源
（1）并联： 所连接的各电流源端为同一电压。
保持端口电流、电 压相同的条件下，图
(a)等效为图(b)。等效 is1
变换式：
i
is2
is
is = is1 - is2
(a)
(b)
（2）串联：只有电流数值、方向完全相同的理想电流 源才可串联。
1
二、实际电源模型：
1、实际电压源模型
（1）伏安关系：
i=1.5A Uab=6(i-1)=3V R=Uab/1=3Ω
13
四、三个电阻的星形、三角形连接及等效变换 1、电阻的星形、三角形连接
(a) 星形连接（T形、Y形）
(b) 三角形连接（形、形）
14
2、从星形连接变换为三角形连接
R1
R3
R2
R31 R12 R23
变换式：R12
R1
R2
R1R2 R3
∴i3=i2/3 KCL: i2+i3=I
∴i3=i/4 ∴u=3i+2i = 5i
- 2i0 +
i0
i1 i2
i3
R= u/I=5Ω
21
二、含受控源简单电路的分析：
基本分析思想：运用等效概念将含受控源电路化简、 变换为只有一个单回路或一个独立节点的最简形式， 然后进行分析计算。 例1：求电压u、电流i。
R23
R2
R3
R2 R3 R1
15
3、从三角形连接变换为星形连接
R1
R3
R2
变换式：R1
R12
R12 R31 R23
R31
R31 R12 R23
R2
R12
R23 R23
R31
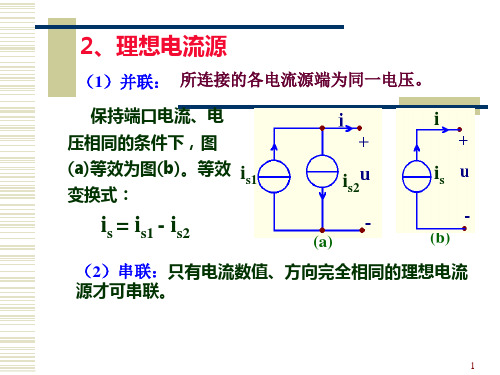
（1）并联： 所连接的各电流源端为同一电压。
保持端口电流、电 压相同的条件下，图
(a)等效为图(b)。等效 is1
变换式：
i
is2
is
is = is1 - is2
(a)
(b)
（2）串联：只有电流数值、方向完全相同的理想电流 源才可串联。
1
二、实际电源模型：
1、实际电压源模型
（1）伏安关系：
i=1.5A Uab=6(i-1)=3V R=Uab/1=3Ω
13
四、三个电阻的星形、三角形连接及等效变换 1、电阻的星形、三角形连接
(a) 星形连接（T形、Y形）
(b) 三角形连接（形、形）
14
2、从星形连接变换为三角形连接
R1
R3
R2
R31 R12 R23
变换式：R12
R1
R2
R1R2 R3
∴i3=i2/3 KCL: i2+i3=I
∴i3=i/4 ∴u=3i+2i = 5i
- 2i0 +
i0
i1 i2
i3
R= u/I=5Ω
21
二、含受控源简单电路的分析：
基本分析思想：运用等效概念将含受控源电路化简、 变换为只有一个单回路或一个独立节点的最简形式， 然后进行分析计算。 例1：求电压u、电流i。
R23
R2
R3
R2 R3 R1
15
3、从三角形连接变换为星形连接
R1
R3
R2
变换式：R1
R12
R12 R31 R23
R31
R31 R12 R23
R2
R12
R23 R23
R31
[工学]第2章 电阻电路的等效变化
![[工学]第2章 电阻电路的等效变化](https://img.taocdn.com/s3/m/e885ad12f111f18583d05a67.png)
2、电压源、电流源 、受控源
US 3、KCL—— IS ∑ i=0 或 ∑ i入= ∑ i出 推广到闭合面
KVL——
∑ u=0
或 ∑u压降= ∑ u压升
沿不同路径两点间的压降相同
二、电阻电路的等效变换
1、电阻串并联： Req、分压、分流 2、Y—△ :
R Δ相邻电阻乘积 R GΔ Y相邻电导乘积 GY
Rn + un _ _ 等效 i
Req
u
Req=( R1+ R2 +…+Rn) = Rk 结论： 串联电路的总电阻等于各分电阻之和。 3. 串联电阻上电压的分配 º + + u1 u u2 _ + º
例：两个电阻分压, 如下图 i
R1
R1 u1 u R1 R2
R2 u2 u R1 R2
即 R IS R 2R R 2R RL + UL _
I S RRL UL 4 R RL
P44例2-4.
求UR 2
受控源和独立源一样可以进行电源转换,但要 注意保存控制量。
12V
+ _
+u _
R
i
2 uR 12V
2
2
+
_
+u _
R
i
2 + 4 uR _
U R 2i 4U R 2i 2i 8i 12V
i = i1+ i2+ …+ ik+ …+in
2. 等效电阻Req
i
i i2 Rk ik Rn in 等效 + u _
+ u _ R1
i1 R2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
u2 6i1 6 15 90V u3 6i3 6 10 60V u4 3i3 30V
i5 10 7.5 2.5 A
例 a
20
求: Rab b
100 60 80 10
a
20
b
100 60 120 60
40
50
a
20
b
100
a
（1） 电路特点
R1
Rk
Rn
+ un _ _
i
+
+ u1 _ + u k _
u
(a) 各电阻顺序连接，流过同一电流 (KCL)； (b) 总电压等于各串联电阻的电压之和 (KVL)。
u u1 uk un
(2) 等效电阻
R1 Rk Rn 等效
R eq
i
+
+ u1
包含
1
R12
a
R3 1
d
R4
b
R31
R2
R1
R3 3 Y型网络
三端 网络
2
R23 型网络
3
2
2. —Y 变换的等效条件
R1 R2 R12 R1 R2 R3 R2 R3 R23 R2 R3 R1 R3 R1 R31 R3 R1 R2
简记方法：
R12 R31 R1 R12 R23 R31 R23 R12 R2 R12 R23 R31 R3 R31 R23 R12 R23 R31
R1 +
R3
R2
+
US _
US _ + _
i1
ri1/R3
R2//R3
i1
ri1
R2 R3 R R1 R2 R3
注:
+
US _
i1
R
+
(R2//R3)ri1/R3 _
Ri1 ( R2 // R3 )ri1 / R3 U S US 受控源和独立源一样可以进行电 i1 R ( R2 // R3 )r / R3 源转换；转换过程中注意不要丢 失控制量。
1/3k
1/3k 1/3k
E
R 1k
E
1k 3k i E 3k 3k R
例
1
+ 20V 1
计算90电阻吸收的功率
4
9 90 1 4 3 3 3 9 9 9
1
i
+
i1
20V
90 10
-
10 90 Req 1 10 10 90
+
20V 90 1
+
转换
u _
us
is Gi
, Ri 1
Gi
i + uS _ Ri
注意 (1) 变换关系 数值关系: 方向：电流源电流方向与电压源电压方向相反。 (2) 等效是对外部电路等效，对内部电路是不等效的。 开路的电压源中无电流流过 Ri； 表 开路的电流源可以有电流流过并联电导Gi 。 现 电压源短路时，电阻中Ri有电流； 在 电流源短路时, 并联电导Gi中无电流。 (3) 理想电压源与理想电流源不能相互转换。
第2章 电阻电路的等效变换
重点： 1. 电路等效的概念； 2. 电阻的串、并联； 3. Y— 变换; 4. 电压源和电流源的等效变换；
2.1
电阻电路 分析方法
引言
仅由电源和线性电阻构成的电路
（1）欧姆定律和基尔霍夫定律是分 析电阻电路的依据；
（2）等效变换的方法,也称化简的方法
2.2
等效电路
+
uS _
º +
_ º
并联 +
º
uS1_
u S2
+ _ º
us us1 us 2
相同的电压 源才能并联, 电源中的电 流不确定。
电压源支路的串、并联及其等效
+ i +
uS1 _
R1
+
uS2 _ R2 _
uS _ R + i +
u
u
_
u us1 R1i us 2 R2 i (uS1 uS 2 ) ( R1 R2 )i uS Ri
i = i1+ i2+ …+ ik+ …+in
(2) 等效电阻
i + u _ R1 i1 R2 i2 Rk ik Rn in
等效
i
+ u _
Req
由KCL:
i = i1+ i2+ …+ ik+ …+in =u/R1 +u/R2 + …+u/Rn=u(1/R1+1/R2+…+1/Rn)=uGeq
Geq G1 G2 Gn Gk Gk
例5.
求电流i1 R1
R3 +
R3
US/R1 R2
R2//R1
+
US _
ri1
_
i1
ri1
+
_ + R US(R2//R1)/R1 _
i
+ ri1 _
i1
R1 US/R1
R3 + R2
ri1
_
R2 R1 R R3 R2 R1
Ri ri1 U S ( R2 // R1 ) / R1
相同的理想电流源才能串联, 每个电流源的端电压不能确定
2.6
电压源和电流源的等效变换
实际电压源、实际电流源两种模型可以进行等效变换， 所谓的等效是指端口的电压、电流在转换过程中保持不变。
i
+ uS _
Ri
端口特性
+
u _
实 际 电 压 源
iS Gi i =iS – Giu
i + u _
实 际 电 流 源
p1=G1u2， p2=G2u2，， pn=Gnu2 p1: p2 : : pn= G1 : G2 : :Gn
总功率
p=Gequ2 = (G1+ G2+ …+Gn ) u2
=G1u2+G2u2+ +Gnu2
=p1+ p2++ pn 表明
（1） 电阻并联时，各电阻消耗的功率与电阻大小成反比 （2） 等效电阻消耗的功率等于各串联电阻消耗功率的总和
例6. 把电路转换成一个电压源和一个电阻的串连。
1k
1k I 2k º + U _ º 10V
500I - I +
0.5I 10V
º
+ U _ º
U 500I 2000I 10 1500I 10
10V
1.5k
I
º
+ U _ º
2.７ 输入电阻
1. 定义 无 源
i
+ u -
Rk u uk Rk i Rk uu Req Req
说明电压与电阻成正比，因此串连电阻电路可作分压电路
例 i
两个电阻的分压：
º + + u1 R1 u u2 R2 _ + º
R1 u1 u R1 R2 R2 u2 u R1 R2
注意方向 !
(4) 功率
p1=R1i2， p2=R2i2，， pn=Rni2 p1: p2 : : pn= R1 : R2 : :Rn 总功率 p=Reqi2 = (R1+ R2+ …+Rn ) i2 =R1i2+R2i2+ +Rni2 表明 =p1+ p2++ pn
3. 电阻的串并联
例
电路中有电阻的串联，又有电阻的并联， 这种连接方式称电阻的串并联。
6
计算各支路的电压和电流。
i1
+
165V
5
i1 5
i2
6
i3 i4 i5
12
+
165V
i2
18 9
i3
-
18
4
-
i1 165 11 15 A i2 90 18 5 A i3 15 5 10 A i4 30 4 7.5 A
10
+ 10V _
6A
10
+
70V
_
+ 6V _
10
2A 6A
10
+
66V
_
例4.
10 6
6
I=?
4
2A 10
2A
10 4
I=? +
+
40V
+
40V
+
2A
30V
_
_
30V
_ I=?
_
30 60 I 1.5 A 20
10 10
+
60V
+
30V
_
_
例5.
求电流i1 R1
电路的等效变换
1. 二端电路（网络）
任何一个复杂的电路, 向外引出两个端钮，且从一个 端子流入的电流等于从另一端子流出的电流，则称这一电 路为二端络网(或一端口网络)。 无 源 i 无 一 i 源 端 口
2. 二端电路等效的概念
两个二端电路，端口具有相同的电压、电流关系,则 称它们是等效的电路。
B
1 R1 1 R2 R1 R2 Req 1 R1 1 R2 R1 R2