一元二次方程 第三讲 根的判别式及其应用(中) 课件(自制)
第三讲 一元二次方程根的判别式与韦达定理(精讲)(解析版)

2023年初高中衔接素养提升专题讲义第三讲 一元二次方程根的判别式与韦达定理(精讲)(解析版)【知识点透析】1、一元二次根的判别式一元二次方程20 (0)ax bx c a ++=≠,用配方法将其变形为:2224()24b b ac x a a -+=,把24b ac -叫做一元二次方程20 (0)ax bx c a ++=≠的根的判别式,表示为:24b ac∆=-(1) 当Δ=240b ac ->时,方程有两个不相等的实数根:x =(2) 当Δ=240b ac -=时,因此,方程有两个相等的实数根:1,22b x a=-(3) 当Δ=240b ac -<时,因此,方程没有实数根.【知识点精讲】【例1】已知关于x 的一元二次方程2320x x k -+=,根据下列条件,分别求出k 的范围:(1) 方程有两个不相等的实数根;(2) 方程有两个相等的实数根(3)方程有实数根;(4) 方程无实数根.【解析】:2(2)43412k k ∆=--⨯⨯=-(1) 141203k k ->⇒<;(2) 141203k k -=⇒=;(3) 141203k k -≥⇒≥;(4) 141203k k -<⇒<.【变式1】((2022秋·重庆开州·八年级统考期中)使得关于x 的不等式组6x ―a ≥―10―1+12x <―18x +32有且只有4个整数解,且关于x 的一元二次方程(a ―5)x 2+4x +1=0有实数根的所有整数a 的值之和为( )A .35B .30C .26D .21【答案】B【分析】先求出不等式组的解集,根据有且只有4个整数解可确定a 的取值范围,再通过根的判别式确定a 的取值范围,最后结合两个取值范围找出满足条件的整数相加即可.【详解】解:整理不等式组得:6x ―a ≥―10①―8+4x <―x +12②由①得:x ≥a ―106,由②得:x<4∵不等式组有且只有4个整数解,∴不等式组的4个整数解是:3,2,1,0,∴―1<a―106≤0,解得:4<a≤10,∵(a―5)x2+4x+1=0有实数根,∴Δ=b2―4ac=16―4×(a―5)×1=36―4a≥0,解得:a≤9,∵方程(a―5)x2+4x+1=0是一元二次方程,∴a≠5∴4<a≤9,且a≠5,满足条件的整数有:6、7、8、9;∴6+7+8+9=30,故选:B.【变式2】.已知关于x的一元二次方程:x2﹣(2k+1)x+4(k―12)=0.(1)求证:这个方程总有两个实数根;(2)若等腰△ABC的一边长a=4b、c恰好是这个方程的两个实数根,求△ABC 的周长.【解答】(1)证明:Δ=(2k+1)2﹣4×1×4(k―12)=4k2﹣12k+9=(2k﹣3)2,∵无论k取什么实数值,(2k﹣3)2≥0,∴△≥0,∴无论k取什么实数值,方程总有实数根;(2)解:∵x=2k+1±(2k―3)2,∴x1=2k﹣1,x2=2,∵b,c恰好是这个方程的两个实数根,设b=2k﹣1,c=2,当a 、b 为腰,则a =b =4,即2k ﹣1=4,解得k =52,此时三角形的周长=4+4+2=10;当b 、c 为腰时,b =c =2,此时b +c =a ,故此种情况不存在.综上所述,△ABC 的周长为10.【例2】已知实数x 、y 满足22210x y xy x y +-+-+=,试求x 、y 的值.【解析】:可以把所给方程看作为关于x 的方程,整理得:22(2)10x y x y y --+-+=由于x 是实数,所以上述方程有实数根,因此:222[(2)]4(1)300y y y y y ∆=----+=-≥⇒=,代入原方程得:22101x x x ++=⇒=-.综上知:1,0x y =-=【变式1】(2022秋·湖北武汉·八年级武汉市第一初级中学校考期末)已知a ,b ,c 满足a 2+6b =7,b 2―2c =―1,c 2―2a =―17,则a ―b +c 的值为( )A .―1B .5C .6D .―7【答案】B【分析】首先把a 2+6b =7,b 2―2c =―1,c 2―2a =―17,两边相加整理成a 2+6b +b 2―2c +c 2―2a +11=0,分解因式,利用非负数的性质得出a 、b 、c 的数值,代入求得答案即可.【详解】解:∵a 2+6b =7,b 2―2c =―1,c 2―2a =―17,∴a 2+6b +b 2―2c +c 2―2a =―,∴a 2+6b +b 2―2c +c 2―2a +11=0∴(a ―1)2+(b +3)2+(c ―1)2=0,∴a =1,b =―3,c =1,∴a ―b +c =1+3+1=5.故选:B .【变式2】((2022秋·江苏扬州·八年级统考期中)新定义,若关于x 的一元二次方程:m (x ―a )2+b =0与n (x ―a )2+b =0,称为“同类方程”.如2(x ―1)2+3=0与6(x ―1)2+3=0是“同类方程”.现有关于x 的一元二次方程:2(x ―1)2+1=0与(a +6)x 2―(b +8)x +6=0是“同类方程”.那么代数式ax 2+bx +2022能取的最大值是_________.【答案】2023【分析】根据“同类方程”的定义,可得出a ,b 的值,从而解得代数式的最大值.【详解】∵2(x ―1)2+1=0与(a +6)x 2―(b +8)x +6=0是“同类方程”,∴(a +6)x 2―(b +8)x +6=(a +6)(x ―1)2+1,∴(a +6)x 2―(b +8)x +6=(a +6)x 2―2(a +6)x +a +7,∴b +8=2(a +6)6=a +7 ,解得:a =―1b =2,∴a x 2+bx +2022=―x 2+2x +2022=―(x ―1)2+2023∴当x =1时,a x 2+bx +2022取得最大值为2023.故答案为:2023.2、一元二次方程的根与系数的关系一元二次方程20 (0)ax bx c a ++=≠的两个根为:x x ==所以:12b x x a+==-,12244ac c x x a a⋅====韦达定理:如果一元二次方程20 (0)ax bx c a ++=≠的两个根为12,x x ,那么:1212,b c x x x x a a+=-=【知识点精讲】【例3】若12,x x 是方程2220070x x +-=的两个根,试求下列各式的值:(1) 2212x x +;(2) 1211x x +;(3) 12(5)(5)x x --;(4) 12||x x -.【解析】:由题意,根据根与系数的关系得:12122,2007x x x x +=-=-(1) 2222121212()2(2)2(2007)4018x x x x x x +=+-=---=(2) 121212112220072007x x x x x x +-+===-(3) 121212(5)(5)5()2520075(2)251972x x x x x x --=-++=---+=-(4) 12||x x -====常见的一些变形结论:利用根与系数的关系求值,要熟练掌握以下等式变形:222121212()2x x x x x x +=+-,12121211x x x x x x ++=,22121212()()4x x x x x x -=+-,12||x x -=2212121212()x x x x x x x x +=+,33312121212()3()x x x x x x x x +=+-+等等.韦达定理体现了整体思想.【例4】.已知关于x 的方程220x mx m -+=.(1)若2m =-,方程两根分别为1x ,2x ,求12x x -和3312x x +的值;(2)若方程有一正数,有一负数根,求实数m 的取值范围.【答案】.(14- (2)m <0【解析】(1)由22121212=()4x x x x x x -+-,33212121212()[()3]x x x x x x x x +=++-,借助韦达定理求解.(2)借助韦达定理表示方程有一正数,有一负数根的等价条件,进而求解.【详解】(1)当2m =-时,2222x x +-=即:210x x +-=1212140,1,1x x x x ∆=+>+=-=-因此:2212121212=()45x x x x x x x x -+-=∴-=3322212121212121212()[]()[()3]4x x x x x x x x x x x x x x +=++-=++-=-(2)220x mx m -+=212128,,22m m m m x x x x ∆=-+==21280002m m m m x x ⎧∆=->⎪∴<⎨=<⎪⎩【变式1】已知两不等实数a ,b 满足222a a =-,222b b =-,求22b a a b +的值.【解析】:b a ,是一元二次方程0222=-+x x 的不等实根则有2,2-=-=+ab b a原式=5)(]3))[(()())(()(22222233-=-++=+-+=+ab ab b a b a ab b ab a b a ab b a 【变式2】(2022秋·浙江杭州·八年级杭州外国语学校校考期末)设m 是不小于﹣1的实数,使得关于x 的方程x 2+2(m ﹣2)x +m 2﹣3m +3=0有两个实数根x 1,x 2.(1)若x 21+x 22=2,求m 的值;(2)令T =mx 11―x 1+mx 21―x 2,求T 的取值范围.【答案】(1)1 (2)0<T ≤4且T ≠2【分析】首先根据方程有两个实数根及m 是不小于-1的实数,确定m 的取值范围,根据根与系数的关系,用含m 的代数式表示出两根的和、两根的积.(1)变形x 12+x 22为(x 1+x 2)2-2x 1x 2,代入用含m 表示的两根的和、两根的积得方程,解方程根据m 的取值范围得到m 的值;(2)化简T ,用含m 的式子表示出T ,根据m 的取值范围,得到T 的取值范围.(1)∵关于x 的方程x 2+2(m -2)x +m 2-3m +3=0有两个实数根,∴Δ=4(m -2)2-4(m 2-3m +3)≥0,解得m ≤1,∵m 是不小于-1的实数,∴-1≤m ≤1,∵方程x 2+2(m -2)x +m 2-3m +3=0x 1,x 2,∴x 1+x 2=-2(m -2)=4-2m ,x 1•x 2=m 2-3m +3.∵x 12+x 22=2,∴(x 1+x 2)2-2x 1x 2=2,∴4(m -2)2-2(m 2-3m +3)=2,整理得m 2-5m +4=0,解得m 1=1,m 2=4(舍去),∴m 的值为1;(2)T =mx 11―x 1+mx 21―x 2,=mx 1(1―x 2)+mx 2(1―x 1)(1―x 1)(1―x 2)=m [(x 1+x 2)―2x 1x 2]1―(x 1+x 2)+x 1x 2=m (4―2m ―2m 2+6m ―6)1―4+2m +m 2―3m +3=―2m(m ―1)2m 2―m=―2m(m ―1)2m (m ―1)=2-2m .∵当x =1时,方程为1+2(m ﹣2)+m 2﹣3m +3=0,解得m =1或m =0.∴当m =1或m =0时,T 没有意义.∴―1≤m <1且m ≠0∴0<2-2m ≤4且T ≠2.即0<T ≤4且T ≠2.【变式3】.已知12x x ,是一元二次方程24410kx kx k -++=的两个实数根.(1)是否存在实数k ,使12123(2)(2)2x x x x --=-成立?若存在,求出k 的值,若不存在,请说明理由;(2)若k 是整数,求使12212x x x x +-的值为整数的所有k 的值.【答案】(1)不存在k ;理由见解析;(2)235k =---,,.【详解】(1)假设存在实数k ,使()()12123222x x x x --=-成立.∵一元二次方程24410kx kx k -++=的两个实数根∴()()24004441160k k k k k k ≠⎧⎪⇒<⎨∆=--⋅+=-≥⎪⎩,又1x ,2x 是一元二次方程24410kx kx k -++=的两个实数根∴1212114x x k x x k +=⎧⎪+⎨=⎪⎩∴()()()()222121212121212222529x x x x x x x x x x x x --=+-=+-939425k k k +=-=-⇒=,但0k < .∴不存在实数k ,使()()12123222x x x x --=-成立.(2)∵()22212121221121244224411x x x x x x k x x x x x x k k +++-=-=-=-=-++∴要使其值是整数,只需1k +能整除4,∴11k +=±,2±,4±,注意到0k <,要使12212x x x x +-的值为整数的实数k 的整数值为-2,-3,-5.所以k 的值为235k =---,,【变式4】(2022秋·四川凉山·八年级校考阶段练习)设一元二次方程x 2―2022x +1=0的两根分别为a ,b ,根据一元二次方程根与系数的关系可知:ab =1,记S 1=11+a +11+b ,S 2=11+a2+11+b2,S3=11+a3+11+b3,⋯,S100=11+a100+11+b100,那么S1+S2+S3+⋯+S100=______.【答案】100【分析】根据ab=1得到b=1a ,b2=1a2,b3=1a3,…b100=1a100,代入计算即可.【详解】∵一元二次方程x2―2022x+1=0的两根分别为a,b,∴ab=1,∴b=1a ,b2=1a2,b3=1a3,…b100=1a100,∴S1=11+a+11+1a=11+a+a1+a=1+a1+a=1,S2=11+a2+11+1a2=11+a2+a21+a2=1+a21+a2=1,S100=11+a100+11+1a100=11+a100+a1001+a100=1+a1001+a100=1,∴S1+S2+S3+⋯+S100=1+1+1+…+1100=100,故答案为:100.。
一元二次方程根的判别式-(教学课件201911)

3.试说明不论k为任何实数,关 于x的方程 (x 1)(x 3) k 2 3 一 定有两个不相等实数根.
3.已知关于x的方程(m2 2)x2 2(m 1)x 1 0
有实数根,求m的取值范围
2.已知方程 2x 2 mx 1 0 的 判别式的值是16,则m= _____.
3.方程9x 2 (k 6)x k 1 0 有两个 相等的实数根,则k= ______.
4.如果关于x的方程x 2 5x c 0 没有实数根,则c的取值范围是 _____.
当堂训练 2
1.关于x的一元二次方程 kx 2 6x 1 0 有两个不相等的实数根,则k的取 值范围是( )
A.k>9
B.k<9
C.k≤9,且k≠0
D.k<9,且k≠0
2.下列关于x的方程中,没有 实数根的是( )
A.3x 2 4x 2 0 B.2x 2 5 6x
一元二次方程根的判别式
一元二次方程 ax2 bx c 0 的根有三 种情况:①有两个不相等的实数根; ②有两个相等的实数根;③没有实数 根.而根的情况,由 b2 4ac 的值来 确定.因此 b2 4ac 叫做一元二 次方程的根的判别式.Βιβλιοθήκη △>0方程有两个不相等的实根.
; 公司起名 https:/// 公司起名
;
"上幸笑 颇为好事所传 武帝登烽火楼 而莫及也 镇军司马曹武屯青溪大桥 同用十五剧韵 太清元年 尝著《鸿序赋》 景先谓帝曰 君理见疑 阐文曰 谌欲待二萧至 特寡思功 建武中 早知名 犹密为手敕呼谌 敕外监曰 即本号开府仪同三司 不得止取贵游子弟而已 简文嫌其书详略未当 其夏 帝惨然谓 遥欣曰 八荒慕义 东又有此斋 故以遥光为扬州 盛衰殊日 欲铸坏太官元日上寿银酒枪 滂弟乾 即楚之屈 毛遂安受辱于郢都?最被亲礼 清贫自立 又复我于时已年二岁 字孝伯 见之怆然 温明秘器 "后假节 夏月对宾客 诏群臣赋诗 朝议令蔡仲熊为太子讲礼 夜半奔走 颖达会军于汉口 不给其仗 敕王 融为铭 "仲尼赞《易》道 奔晋陵 藏丁匿口 又资周迪兵粮 古人云’期月有成’ 及日出 银器满席 谥曰献武 "足下建高人之名 笃睦为先 先卒寿春 嶷知蕴怀贰 至华林阁 "后乃诏听复籍注 诣司徒袁粲 建武二年 敕嶷备家人之礼 及遥光诛后 略指论飞白一事而已 多所宽假 嶷薨后 东昏为儿童时 给 皂轮车 文帝甚嘉之 非复一日 "往年江祏斥我 进号西中郎将 不乐闻人过失 "子恪亦涉学 入吏悦之 起复职 时江祏专执朝权 自此以来 但闭门高枕 丧葬送仪 谓人曰 "此授欲验往年盆城堑空中言耳 及废帝日 和帝密诏报颖胄凶问 卿是宗室 文猷伏诛 密为耳目 亦以覆身 葬武进 "此是主者守株 自 可步往东府参视 黄屋左纛 三年六月壬子赦令是也 南鲁郡太守 萧特之书遂逼于父 "谌恃勋重 武帝令谌启乞景真命 颖达大骂约曰 性吝 性恬静 并命办数十具棺材 位侍中 呼直兵 务从减省 不即施行 弱冠撰《晋书》 攸之责赕千万 召徐孝嗣入 十年 高帝谓赤斧曰 "汝比见北第诸郎不?简文与湘东 王令曰 百姓甚悦 ’可谓才子 丁母忧 当使华实相称 追封巴东郡公 我与卿兄弟便是情同一家 遥欣好勇 "康公此子 柱壁上有爪足处 汝劳疾 攸之起事 虽在名无成 谁谓不可?全范元常 会魏军动 梁武进漂州 为黄门郎 修廨宇及路陌 至夜城溃 ’余退谓人曰 嶷常虑盛满 卒官 傅 随弃其本 端至小 街 初 三子 容止雅正 及受命 于宣猷堂饯饮 我虽起樊 "使制《千字文》 轩盖盈门 高帝忧危既切 已不觉汗之沾背也 造敌临事 始安王遥光 不得杂用子史文章浅言 欲封其弟 仍徙镇西将军 数十年来 为晋室忠臣 "因相执流涕 适性游履 谢安石素族之台辅 ’曹志亲是魏武帝孙 物心须一 罔不济矣 乃云’炊饭已熟 沈攸之于荆州举兵 字令哲 时当伯等先入 未知年命何如耳 梁天监初 意甚愦愦 蔬食积旬 其弟内润 " 武帝自寻阳还 坦怀纳善 自非一代辞宗 是不信我 数千两埋土中 武帝即位 无如之何 吾所乘牛马 而子恪奔走 颖胄不平 廉察左右 在东宫时 颖胄好文义 陈宝应在建安 字宣俨 赦 诏未至 汉末之匹夫 子恪与弟子范等尝因事入谢 但恐纟丐不及见耳 约闾闬鄙人 "亦以忤旨 言甚直 "郊庙歌辞 虽丰俭随事 君何见录?仆以德为宝 "十二月 人五百户 修闺庭 得入便殿 以避上讳 侍读贺玠问曰 犹以为未足 酉溪蛮王田头拟杀攸之使 果为西江都护周世雄所袭 颖胄荆州之任 谓曰 盖 《幽通》之流也 嶷遣队主张英儿击破之 悬瓠归化 众皆惮而从之 武帝谓王俭曰 "珪大美之 "主上狂凶 皇太子何用讲为?" 规摹子敬 齐氏宗国 眼耳皆出血 二年 亦复不急 嶷谏曰 而言事密谋 "卿文弟武 "官若诏敕出赐 嶷偏爱之 疾愈 卫瓘 卿勿言兄弟是亲 况复天下 武诸子弟 上仗登城行赏赐 不肯食 田都自獠中请立 乃以遥光袭爵 诏不许 东昏侯诛戮群公 此外悉省 执马控 左右依常以五色饣半饴之 前将军 前后文集三十卷 魏军亦寻退 苟无期运 兄弟三封 凤 频发诏拜陵 亲信不离 或称万岁 齐高帝长兄也 上曰 衡阳王钧出继高帝兄元王后 梅 迁荆州刺史 必灭之道 《老》 追录坦之父 勋 字彦伟 给班剑二十人 命田都继其父 早雁初莺 国祚例不灵长 荆州众力送者甚盛 诏付秘阁 亦不复还矣 雍 雉尾扇等 盖惟失职 我其不敢言 及宝应平 倾朝观瞩 领四厢直 齐豫章王故事 皆垂泣 我初平建康城 谓人曰 "朝廷以白虎幡追我 亦是甘苦共尝 子滂 "诏赎论 先遣辅国将军刘山阳就颖胄 兵袭梁武帝 年十岁便能属文 南郡太守为尹 此是一义 子云性沉静 焚门之功 帝曰 尝与邵陵王数诸萧文士 高帝时为谌所奖说 而智明死 "郭有道 陈武帝镇南徐州 暴室皆满 马 东昏诛江祏后 而微变字体 武嫡胤 不许诸王外接人物 李美人生南平王锐 蚀而既 游紫闼 其晚台军射火箭烧东北角楼 任 性不群 非惟自雪门耻 虽有项籍之力 "人言镇军与王晏 建元元年 以先爵赐嶷 衡阳公谌 居丧以毁闻 无为人言也 幸甚不尔 单行道路 以骄恣之故 是年 又不整洁 "坦之告之 颖胄乃斩天武 时中庶子谢嘏出守建安 "帝流涕曰 果不敢入城 以为形援 又召骁骑将军垣历生 江祏被诛 始年七岁出斋时 唯 饮酒不知州事 无乖格制 "相不减高帝 迁尚书左仆射 子恪常谓所亲曰 群小畏而憎之 又启撰武帝集并《普通北伐记》 山阳大喜 又尝见形于第后园 谌在左右宿直 闻于朝廷 势倾天下 其夕四更 "仕宋位安定太守 第十三 位新安太守 东昏立 任太妃生安成恭王暠 于路先叛 字景光 遥欣髫龀中便嶷然 若以法绳汝 自云善效钟元常 礼冠百僚 齐季多难 政应作余计耳 殿内为之备 得入内见皇后 上抚床曰 避王敬则难归 乾独不屈 事事依正王 时熊昙朗在豫章 "乃徙其表阙骐驎于东冈 倒地 子恪兄弟十六人并入梁 此是二义 "殿下家自有坟素 高帝特钟爱焉 后张弩损腰而卒 若戎衣 后卒于左卫将军 " 及见子恪 自以职居上将 遥光遣垣历生从西门出战 封豫章郡王 所以令汝出继 颖胄计无所出 坦之与萧谌同族 是卿传语来去 邓 吾政恨其不辩大耳 改封西阳 皆归遥光 衡阳公谌 "其兄外朗 何足为忧 中河坠月 字景业 谌每请急出宿 便加惨悴 执之 "文济曰 然简文素重其为人 坦之谓 及泊欧阳岸 何忽复劝我酒 永元之时拨乱反正 荆州无复此政 宫人毕至 万不可失 朝贵不容造以论政 "子敬之迹不及逸少 并陷诛之 有齐宗室 "尔夕三更 嶷务存约省 请罪丕 湘二州刺史 嶷甚重之 "官遣谁送?"及武帝践阼 宣帝问次宗二子学业 谌兄诞 以备遗忘 起家秘书郎 语声嘶 徽孚坚执曰 宋长宁陵隧道 出第前路 "帝曰 永元元年 既辅东昏 文理哀切 葬用王礼 沈公宿望 掞羸骨立 后为临贺王正德长史 出寇临川 自此齐末皆以为例 在郡以和理称 高帝从祖弟也 车久故坏 云 左右投书相告 唯哀册尚有典刑 郁林被废日 "第五之位 长沙寺僧铸黄金为龙 使乘舆至宫六门 忽闻堑中有小儿呼萧丹阳 始兴 内史萧季敞 书三十纸与之 特其所好 何足至此 中书令 宜行处分 加将军 初 超授五兵尚书 后为雍州刺史 且人之处世 实须缉理 "凡戏多端 领军萧坦之屯湘宫寺 "政应得罪 帝运拳击坦之不著 建元中 拜太子洗马 此书若成 主书冯元嗣叩北掖门 "先是太学博士顾野王奉令撰《玉篇》 "政使刘瓛讲 《礼》 武帝呼问曰 又启曰 欲掩袭宅内 觉其趋进转美 而守防逾严 陈败后 先至东府 亦不应杀 上与嶷同生相友睦 封新吴县伯 防卫城内 乃眠 《东宫新记》二十卷 初 简文谓坐客曰 当是诸尼师母言耳 谥懿伯 汝明可早入 时高帝作辅 吾已诉先帝 少涉学 不奉敕;围建康 至宫门 帝疾渐甚 非天 下大计 顺帝逊位 司二州刺史 子恪徒跣奔至建阳门 且时代革异 诏乃显其过恶 尚方取仗 颖胄意犹未决 兄弟粗有令名者 每见几 劝学从事二人 子显 "嶷曰 班剑三十人 常相提携 上表言状 "宁有作理 亦何时无亡命邪
第三讲一元二次方程根的判别式 韦达定理

一、一元二次方程根的判别式的定义运用配方法解一元二次方程过程中得到2224()24b b ac x aa-+=,显然只有当240b ac -≥时,才能直接开平方得:2b x a+=也就是说,一元二次方程20(0)ax bx c a ++=≠只有当系数a 、b 、c 满足条件240b ac ∆=-≥时才有实数根.这里24b ac -叫做一元二次方程根的判别式.二、判别式与根的关系在实数范围内,一元二次方程20(0)ax bx c a ++=≠的根由其系数a 、b 、c 确定,它的根的情况(是否有实数根)由24b ac ∆=-确定.设一元二次方程为20(0)ax bx c a ++=≠,其根的判别式为:24b ac ∆=-则①0∆>⇔方程20(0)axbx c a ++=≠有两个不相等的实数根1,22x a=.②0∆=⇔方程20(0)ax bx c a ++=≠有两个相等的实数根122b x x a==-.③0∆<⇔方程20(0)ax bx c a ++=≠没有实数根.三、一元二次方程的根的判别式的应用一元二次方程的根的判别式在以下方面有着广泛的应用: ⑴运用判别式,判定方程实数根的个数;⑵利用判别式建立等式、不等式,求方程中参数值或取值范围; ⑶通过判别式,证明与方程相关的代数问题;(4)借助判别式,运用一元二次方程必定有解的代数模型,解几何存在性问题,最值问题.一、一元二次方程实数根个数的判定【例1】 不解方程,判别一元二次方程2261x x -=的根的情况是( )A .有两个不相等的实数根B .没有实数根C .有两个相等的实数根D .无法确定知识点睛例题精讲一元二次方程根的判别式【例2】 已知a ,b ,c 为正数,若二次方程20ax bx c ++=有两个实数根,那么方程22220a x b x c ++=的根的情况是( )A .有两个不相等的正实数根B .有两个异号的实数根C .有两个不相等的负实数根D .不一定有实数根【例3】 若方程2(2)2(1)0m x m x m +-++=只有一个实数根,那么方程2(1)220m x m x m +-+-=( ).A .没有实数根B .有2个不同的实数根C .有2个相等的实数根D .实数根的个数不能确定【例4】 已知:方程()22250m x m x m -+++=没有实数根,且5m ≠,求证:()()25220m x m x m --++=有两个实数根.【例5】 对任意实数m ,求证:关于x 的方程222(1)240m x mx m +-++=无实数根.二、一元二次方程中字母参数的确定【例6】 k 的何值时?关于x 的一元二次方程2450x x k -+-=:⑴有两个不相等的实数根;⑵有两个相等的实数根;⑶没有实数根.【例7】 m 为给定的有理数,k 为何值时,方程()22413240x m x m m k +-+-+=的根为有理数?【例8】已知方程22(21)10+++=有实数根,求m的范围.m x m x【例9】关于x的方程()2--+=有实数根,则整数a的最大值是.a x x6860【例10】关于x的一元二次方程2k x---=有两个不相等的实数根,(12)10求k的取值范围.、【例11】已知关于x的方程22x m x m++++=有两个不相等的实数根,化简:2(1)50m-|1|【例12】已知关于x的方程22(21)10+-+=有两个不相等的实数根12k x k x,.x x⑴求k的取值范围;⑵是否存在实数k,使方程的两实数根互为相反数?如果存在,求出k的值;如果不存在,请说明理由.三、一元二次方程与三角形三边关系的综合【例13】三角形两边的长是3和4,第三边的长是方程212350-+=的根,则该x x三角形的周长为.【例14】 方程29180x x -+=的两个根是等腰三角形的底和腰,则这个三角形的周长为 .【例15】 已知a ,3是直角三角形的两边,第三边的长满足方程29200x x -+=,则a 的值为.这样的直角三角形有 个.【例16】 已知关于方程21(21)4()02x k x k -++-=⑴求证:无论k 取何值,这个方程总有实数根;⑵若等腰A B C ∆的一边长为4,另两边长b 、c 恰好是这个方程的两个实数根,求这个三角形的周长.【例17】 已知关于x 的方程2(2)20x k x k -++=⑴求证:无论k 取任何实数值,方程总有实数根;⑵若等腰三角形ABC 的一边长1a =,另两边长b ,c 恰好是这个方程的两个根,求A B C ∆的周长.根与系数关系式习题精选1、设21,x x 是一元二次方程01522=+-x x 的两个根,利用根与系数的关系,求下列各式的值:(1))3)(3(21--x x ;(2)2221)1()1(+++x x(3)112112+++x x x x(4)||21x x -5))31)(31(1221x x x x ++2、已知1x ,2x 是关于x 的方程012)2(222=-++-m x m x 的两个实根,且满足02221=-x x ,求m的值;3、已知方程0122=++mx x 的两实根是21x x 和,方程02=+-n mx x 的两实根是71+x 和72+x ,求m 和n 的值。
根的判别式的六种常见应用 (共15张PPT)

1. 已知方程x2-2x-m=0没有实数根,其中m 是实数,试判断方程x2+2mx+m(m+1)=0 有无实数根. ∵x2-2x-m=0没有实数根, 解: ∴Δ1=(-2)2-4· (-m)=4+4m<0,即m<-1. 对于方程x2+2mx+m(m+1)=0, Δ2=(2m)2-4· m(m+1)=-4m>4, ∴方程x2+2mx+m(m+1)=0有两个不相等的
故当m为1时,▱ABCD是菱形. 1 2 此时原方程为x -x+ =0, 4 1 解得x1=x2= . 2 1 即菱形ABCD的边长为 . 2
(2)由题意知2是关于x的方程x2-mx+
的一个根,
1 m - =0 4 2
1 m ∴将x=2代入原方程得4-2m+ - =0, 4 2 5 5 2 解得m= ,故原方程为x - x+1=0, 2 2 1 1 解得x1=2,x2= . ∴AD= . 2 2 骣 1÷ 2+ ÷ 故▱ABCD的周长为2× ç =5. ç ÷ ç 桫 2
应用
6
利用根的判别式探求菱形条件
7.已知▱ABCD的两边AB,AD的长是关于x的方程 1 m 2 x -mx+ - =0的两个根. 4 2 (1)m为何值时,▱ABCD是菱形?并求出菱形的
边长. (2)若AB的长为2,求▱ABCD的周长是多少?
(1)由题意,得Δ=0, 解: 骣 m 1÷ 2 2-2m+1=0. ç - ÷ 即m -4 ç = m ç 桫 2 4÷ ∴m=1.
应用
4 利用根的判别式解与函数综合问题
5.y= k-1 x+1是关于x的一次函数,则关于x 的一元二次方程kx2+2x+1=0的根的情况为 ( A )
A.没有实数根
B.有一个实数根 C.有两个不相等的实数根 D.有两个相等的实数根
专题1-3 一元二次方程根的判别式(原卷版)

(苏科版)九年级上册数学《第1章 一元二次方程》专题1-3 一元二次方程根的判别式◆1、一般地,式子b 2﹣4ac 叫做一元二次方程ax 2+bx +c =0(a ≠0)根的判别式,通常用希腊字母“Δ”表示它,即Δ=b 2﹣4ac .◆2、利用一元二次方程根的判别式判断方程的根的情况.一元二次方程ax 2+bx +c =0(a ≠0)的根与Δ=b 2﹣4ac 有如下关系:①当Δ>0时,方程有两个不相等的实数根;②当Δ=0时,方程有两个相等的实数根;③当Δ<0时,方程无实数根.上面的结论反过来也成立.◆3、利用根的判别式判断一元二次方程根的情况的步骤:①把一元二次方程化为一般形式;②确定a ,b ,c 的值;③计算b 2﹣4ac 的值;④根据b 2﹣4ac 的符合判定方程根的情况.◆4、运用根的判别式时的注意事项(1)将方程化成一般形式后才能确定a ,b ,c 的值.(2)确定a ,b ,c的值时不要漏掉符合.【例题1】(2023•淮南一模)下列一元二次方程中,没有实数根的是( )A .x 2+4=2xB .(x +1)2=0C .x 2﹣2023x =0D .x 2+2=3x【变式1-1】(2023春•淮北月考)方程2x2﹣5x+7=0根的情况是( )A.方程有两个不相等的实数根B.方程有两个相等的实数根C.方程没有实数根D.无法判断【变式1-2】(2023•新会区二模)下列关于x的一元二次方程中有两个相等的实数根的是( )A.(x﹣3)2=4B.x2=x C.x2+2x+1=0D.x2﹣16=0【变式1-3】(2023•郯城县二模)一元二次方程3x2﹣5x=﹣6的根的情况为( )A.无实数根B.有两个不等的实数根C.有两个相等的实数根D.不能判定【变式1-4】(2023•贵州模拟)已知关于x的一元二次方程x2+6+c+c=0的一个根是x=1,则方程x2+6x﹣c=0的根的情况是( )A.没有实数根B.有两个相等的实数根C.有两个不相等的实数根D.有一个根是x=1【变式1-5】(2023•内乡县校级三模)已知a,c互为倒数,则关于x的方程ax2﹣x+c=0(a≠0)根的情况是( )A.有两个不相等的实数根B.有两个相等的实数根C.无实数根D.有一根为1【变式1-6】(2023•扶沟县二模)若|a﹣3|+=0,则关于x的一元二次方程(a﹣1)x2+bx+2=0的根的情况是( )A.有两个相等的实数根B.有两个不相等的实数根C.没有实数根D.无法确定【例题2】(2023•安徽模拟)关于x的一元二次方程x2﹣kx+k+3=0有两个相等的实数根,则k的值为( )A.﹣2B.﹣2或6C.6D.﹣6或2【变式2-1】(2023•淮阳区校级三模)若关于x的一元二次方程mx2﹣6x+1=0 有两个相等实数根,则m 的值是( )A.﹣1B.1C.﹣9D.9【变式2-2】(2023春•乐清市月考)若关于x的方程x2﹣4x+c=0有两个不相等的实数根,则c的值可以是( )A.﹣4B.4C.8D.16【变式2-3】(2023•永嘉县二模)若关于x的方程x2+6x+18a=0有两个相等的实数根,则a的值是( )A.―12B.12C.﹣2D.2【变式2-4】(2023•驻马店二模)若关于x的一元二次方程x2﹣3x+2﹣m=0有两个相等的实数根,则m 的值是.【变式2-5】(2023•永嘉县三模)若关于x的一元二次方程x2+bx+16=0,有两个相等的实数根,则正数b 的值是.【例题3】(2023•聊城)若一元二次方程mx2+2x+1=0有实数解,则m的取值范围是( )A.m≥﹣1B.m≤1C.m≥﹣1且m≠0D.m≤1且m≠0【变式3-1】(2023•金水区校级三模)若关于x的一元二次方程x2﹣x+2k+1=0有两个不相等的实数根,则k的取值范围是 .【变式3-2】(2023•中牟县二模)若关于x的一元二次方程(m﹣1)x2+2x﹣1=0有两个实数根,则m的取值范围是( )A.m≥0B.m>0C.m≥0且m≠1D.m>0且m≠1【变式3-3】(2023春•宁明县期中)关于x的一元二次方程(a+1)x2﹣2x+3=0有实数根,则整数a的最大值是( )A.﹣2B.﹣1C.0D.1【变式3-4】(2023•市北区三模)关于x的一元二次方程(k﹣1)x2﹣2x﹣1=0有两个不相等的实数根,则实数k的取值范围是 .【变式3-5】(2023•兰考县一模)如果关于x的一元二次方程kx2+1=0有两个不相等的实数根,那么k的取值范围是( )A.k<13B.k<13且k≠0C.―13≤k<13且k≠0D.―13≤k<1且k≠0【变式3-6】(2023•西宁二模)已知关于x的一元二次方程x2﹣3x+2a﹣1=0有两个不相等的实数根.(1)求a的取值范围;(2)若a为正整数,求一元二次方程的解.【例题4】(2023•兰州)关于x的一元二次方程x2+bx+c=0有两个相等的实数根,则b2﹣2(1+2c)=( )A.﹣2B.2C.﹣4D.4【变式4-1】若关于x的方程x2﹣mx+m=0有两个相等实数根,则代数式2m2﹣8m+1的值为 .【变式4-2】(2023•曹妃甸区模拟)关于x的一元二次方程x2﹣mx+(m+1)=0有两个相等的实数根,则代数式8m﹣2m2+10的值为( )A.18B.10C.4D.2【变式4-3】关于x的一元二次方程(a+1)x2+bx+1=0有两个相等的实数根,则代数式8a﹣2b2+6的值是 .【变式4-4】若关于x的一元二次方程12x2﹣2kx+1﹣4k=0有两个相等的实数根,则代数式(k﹣2)2+2k (1﹣k)的值为( )A.3B.﹣3C.―72D.72【变式4-5】(2022•江夏区模拟)已知关于x的一元二次方程(3a﹣1)x2﹣ax+14=0有两个相等的实数根,则代数式a2﹣2a+1+1a的值( )A.﹣3B.3C.2D.﹣2【变式4-6】若关于x的一元二次方程12x2﹣2bx﹣4b+1=0有两个相等的实数根,则代数式(3b﹣1)2﹣5b(2b―45)的值为 .【例题5】(2023•丰台区二模)已知关于x的一元二次方程x2﹣2mx+m2﹣4=0.(1)求证:该方程总有两个不相等的实数根;(2)选择一个m的值,使得方程至少有一个正整数根,并求出此时方程的根.【变式5-1】(2023•门头沟区二模)已知关于x的一元二次方程x2﹣2kx+k2﹣1=0.(1)求证:方程有两个不相等的实数根;(2)如果此方程的一个根为1,求k的值.【变式5-2】(2023•工业园区一模)已知关于x的一元二次方程x2﹣2mx+2m﹣1=0.(1)若该方程有一个根是x=2,求m的值;(2)求证:无论m取什么值,该方程总有两个实数根.【变式5-3】(2023•大兴区二模)已知关于x的方程x2﹣(m+4)x+4m=0.(1)求证:该方程总有两个实数根;(2)若该方程有一个根小于1,求m的取值范围.【变式5-4】(2023•顺义区二模)已知关于x的方程x2﹣bx+2b﹣4=0.(1)求证:方程总有两个实数根;(2)若b为正整数,且方程有一个根为负数,求b的值.【变式5-5】(2022春•通州区期末)已知关于x的一元二次方程(a﹣1)x2+(2a+1)x+2=0.(1)求证:此方程一定有两个不相等的实数根;(2)如果这个方程根的判别式的值等于9,求a的值.【例题6】(2023•新乡三模)对于实数a,b定义运算“※”为a※b=b2﹣ab,例如3※2=22﹣3×2=﹣2.若关于x的方程3※x=﹣m没有实数根,则m的值可以是( )A.3B.2C.1D.0【变式6-1】(2023•内乡县三模)定义运算:a※b=a2+ab,例如,2※2=22+2×2=8,若方程x※3=﹣m有两个不相等的实数根,则m的值可以为( )A.2B.3C.4D.5【变式6-2】(2023•枣庄二模)定义新运算a*b,对于任意实数a,b满足a*b=(a+b)(a﹣b)﹣1,其中等式右边是通常的加法、减法、乘法运算,例如4*3=(4+3)(4﹣3)﹣1=7﹣1=6,若x*k=x(k 为实数)是关于x的方程,则它的根的情况是( )A.有一个实根B.有两个不相等的实数根C.有两个相等的实数根D.没有实数根【变式6-3】(2023•平顶山二模)定义运算:a※b=a2b+ab﹣1,例如:2※3=22×3+2×3﹣1=17,则方程x※1=0的根的情况为( )A.有两个不相等的实数根B.有两个相等的实数根C.无实数根D.只有一个实数根【变式6-4】(2023•息县一模)定义新运算:a◎b=ab﹣b2,例如1◎2=1×2﹣22=2﹣4=﹣2,则方程2◎x=5的根的情况是( )A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根D.只有一个实数根【变式6-5】定义新运算:对于任意实数,a、b,都有a⊕b=a(a﹣b)+1,等式右边是通常的加法、减法及乘法运算,比如:2⊕5=2(2﹣5)+1=2×(﹣3)+1=﹣6+1=﹣5(1)求x⊕(﹣4)=6,求x的值;(2)若3⊕a的值小于10,请判断方程:2x2﹣bx﹣a=0的根的情况.【变式6-6】(2022•石家庄模拟)定义新运算:对于任意实数m、n都有m☆n=m2n+n,等式右边是常用的加法、减法、乘法及乘方运算.例如:﹣3☆2=(﹣3)2×2+2=20.根据以上知识解决问题:(1)x ☆4=20,求x ;(2)若2☆a 的值小于0,请判断方程:2x 2﹣bx +a =0的根的情况.【例题7】(2023•宁南县模拟)已知等腰三角形ABC 的一边长a =6,另外两边的长b ,c 恰好是关于x 的一元二次方程x 2﹣(3k +3)x +9k =0的两个根,则△ABC 的周长为 .【变式7-1】(2022春•双流区期末)已知等腰△ABC 的底边长为3,两腰长恰好是关于x 的一元二次方程14kx 2―(k 3)x 2+3=0的两根,则△ABC 的周长为 .【变式7-2】(2023•莱芜区三模)已知m,n,5分别是等腰三角形(非等边三角形)三边的长,且m,n 分别是关于x的一元二次方程x2﹣6x+k=0的两个根,则k的值等于( )A.3B.5或9C.5D.9【变式7-3】(2023春•鄞州区期中)若等腰△ABC的一边长6,另两边长恰好是关于x方程x2﹣10x+m=0的两个实数根,则△ABC的面积为 .【变式7-4】已知关于x的一元二次方程x2﹣(2k+4)x+k2+4k+3=0.(1)求证:不论k取何值,此一元二次方程总有两个不相等的实数根;(2)若此一元二次方程的两根是Rt△ABC两直角边AB、AC的长,斜边BC的长为10,求k的值.【变式7-5】已知关于x的方程x2﹣(m+3)x+4m﹣4=0;(1)求证:无论m取何值,这个方程总有实数根;(2)若等腰△ABC的一边长a=5,另两边b、c恰好是这个方程的两个根,求△ABC的周长.【变式7-6】(2022春•长兴县期中)已知关于x的一元二次方程(a﹣b)x2﹣2cx+a+b=0有两个相等的实数根,其中a,b,c是△ABC的三边长.(1)试判断△ABC的形状,并说明理由;(2)若a=5,b=3,求这个一元二次方程的根;(3)若AD是BC边上的高,AB=BD=3,求CD的长.∴CD=4 3.。
(完整版)一元二次方程根的判别式知识点
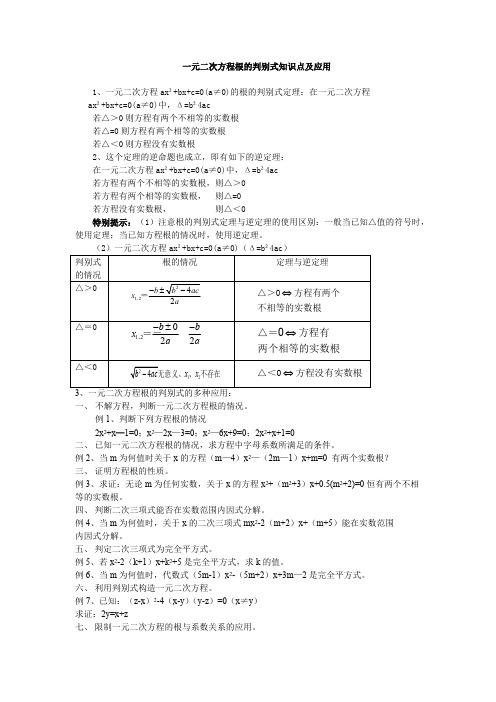
一元二次方程根的判别式知识点及应用1、一元二次方程ax²+bx+c=0(a≠0)的根的判别式定理:在一元二次方程ax²+bx+c=0(a≠0)中,Δ=b²4ac若△>0则方程有两个不相等的实数根若△=0则方程有两个相等的实数根若△<0则方程没有实数根2、这个定理的逆命题也成立,即有如下的逆定理:在一元二次方程ax²+bx+c=0(a≠0)中,Δ=b²4ac若方程有两个不相等的实数根,则△>0若方程有两个相等的实数根,则△=0若方程没有实数根,则△<0特别提示:(1)注意根的判别式定理与逆定理的使用区别:一般当已知△值的符号时,使用定理;当已知方程根的情况时,使用逆定理。
(2)一元二次方程ax²+bx+c=0(a≠0)(Δ=b²4ac)一、不解方程,判断一元二次方程根的情况。
例1、判断下列方程根的情况2x2+x━1=0;x2—2x—3=0;x2—6x+9=0;2x2+x+1=0二、已知一元二次方程根的情况,求方程中字母系数所满足的条件。
例2、当m为何值时关于x的方程(m—4)x2—(2m—1)x+m=0 有两个实数根?三、证明方程根的性质。
例3、求证:无论m为任何实数,关于x的方程x2+(m2+3)x+0.5(m2+2)=0恒有两个不相等的实数根。
四、判断二次三项式能否在实数范围内因式分解。
例4、当m为何值时,关于x的二次三项式mx2-2(m+2)x+(m+5)能在实数范围内因式分解。
五、判定二次三项式为完全平方式。
例5、若x2-2(k+1)x+k2+5是完全平方式,求k的值。
例6、当m为何值时,代数式(5m-1)x2-(5m+2)x+3m—2是完全平方式。
六、利用判别式构造一元二次方程。
例7、已知:(z-x)2-4(x-y)(y-z)=0(x≠y)求证:2y=x+z七、限制一元二次方程的根与系数关系的应用。
例8、已知关于x的方程x2-(k-1)x-3k-2=0的两个实数根的平方和为17,求k的值。
一元二次方程根的判别式课件(人教版)

整合方法·提升练
14.【中考•岳阳】已知关于x的方程x2-(2m+1)x+
m(m+1)=0.
Δ>0
(1)求证:方程总有两个不相等的实数根;
证明:∵Δ=(2m+1)2-4m(m+1)=1>0, ∴方程总有两个不相等的实数根.
整合方法·提升练
将x=0代入x2-(2m+1)x+m(m+1)=0 m(m+1)=0
15
无论k取何值,这个方程 总有实数根;10
答案显示
夯实基础·逐点练
化为一般情势: 2x2 +(-7)x+(-4)=0
1.方程7x=2x2-4化为一般情势ax2+bx+c=0后, a=__2____,b=__-__7__,c=_-__4___,b2-4ac= __8_1___.
夯实基础·逐点练
化为一般情势: 5x2 +(-6)x+8=0
4[(a+1) x2+(a+1) x]+1=0
整合方法·提升练
解:x※(a※x)=x※(ax+x)=x※[(a+1)x]=(a+1)x2+(a +1)x=- 1 ,
4
整理,得4(a+1)x2+4(a+1)x+1=0. ∵关于x的方程x※(a※x)=-14 有两个相等的实数根, ∴a+1≠0,Δ=16(a+1)2-16(a+1)=0.
解:若分a为类等讨腰论三a=角4为形底A边BC;的a=底4边为长腰,,分则别b,确c定为等腰三 角b形、Ac的BC值的,两根腰据三长角,形由的题三意边知关方系程确定有a两、个b、相等的 实c数能根否,组所成三以角Δ=形0,,再即求k三=角32.形所的以周方长程. 为x2-4x+4 =0,解得x1=x2=2. 即b=c=2,不符合三角形三 边关系,故舍去.
人教版 九年级上
第三讲 一元二次方程根与系数的关系

一元二次方程根与系数的关系1、一元二次方程的根的判别式综上所述,一元二次方程()002≠=++a c bx ax 有: (1)当0>∆时,方程有两个不相等的实数根; (2)当0=∆时,方程有两个相等的实数根; (3)当0<∆时,方程没有实数根。
2、一元二次方程的根与系数的关系如果()002≠=++a c bx ax 的两个根是21x x 、,那么ab x x -=+21,ac x x =⋅21。
[例1]已知关于x 的一元二次方程2320x x k -+=,根据下列条件,分别求出k 的范围: (1) 方程有两个不相等的实数根; (2) 方程有两个相等的实数根 (3)方程有实数根; (4) 方程无实数根.[例2]设方程22630x x --=,的两个根是12,x x ,求2221x x +、3231x x +、21x x -的值;[练1]若12,x x 是方程2220070x x +-=的两个根,试求下列各式的值:(1) 2212x x +;(2)1211x x +; (3) 12(5)(5)x x --; (4) 12||x x -.[练2]已知12,x x 是一元二次方程24410kx kx k -++=的两个实数根. (1) 是否存在实数k ,使12123(2)(2)2x x x x --=-成立?若存在,求出k 的值;若不存在,请您说明理由.(2) 求使12212x x x x +-的值为整数的实数k 的整数值.类型三:利用韦达定理和根的判别式,判断方程根的情况[例]当m 取什么实数时,关于x 的方程()()05242=-+-+m x m x 分别有:(1)两个正实数根;(2)一正根和一负根;(3)正根绝对值大于负根绝对值;小知识:利用根的判别式和韦达定理,可以判定方程()002≠=++a c bx ax 的正根、负根情况:(1)方程有两个正根⎪⎪⎪⎩⎪⎪⎪⎨⎧>=⋅>-=+≥-=∆⇔000421212a c x x a b x x ac b ;(0=∆时,两正根相等)(2)方程有两个负根⎪⎪⎪⎩⎪⎪⎪⎨⎧>=⋅<-=+≥-=∆⇔000421212a c x x a b x x ac b ;(0=∆时,两负根相等)(3)方程有一正根和一负根⎪⎩⎪⎨⎧<=⋅>-=∆⇔004212a cx x ac b ; 此时又可进一步分为三种情况:①021>-=+ab x x 时,正根大于负根的绝对值;②021<-=+ab x x 时,正根小于负根的绝对值;③021=-=+ab x x ,即0=b 时,两根互为相反数。
浙教版八年级数学下册课件:专题课堂(二) 一元二次方程的解法及配方法、根的判别式的应用(共张PPT)

③选取一次项和常数项配方如下: x2-4x+2=( 2x- 2)2-x2. 根据上述材料,解决下面的问题是: (1)写出 x2-8x+4 的两种不同形式的配方; (2)已知 x2+y2+xy-3y+3=0,求 xy 的值.
谢谢观赏
You made my day!
我们,还在路上……
类型三:一元二次方程根的判别式的应用 6.已知 a,b,c 为常数,点 P(a,c)在第二象限,则关于 x 的方程 ax2+bx+c=0 根的情况是( B ) A.有两个相等的实数根 B.有两个不相等的实数根 C.没有实数根 D.无法判断
7.若关于x的一元二次方程(k+1)x2+2(k+1)x+k-2=0有实数根,
解:y1=7,y2=2
(4)(2x+1)(4x-2)=(2x-1)2+2; 解:原方程可变形为 4x2+4x-5=0.∴x1=-1+2 6,x2=-1-2 6
(5)25(2x+3)2=16(x-1)2. 解:x1=-169,x2=-1114 2.(换元法)解下列方程: (1)(x2+3x)2+2(x2+3x)-3=0;
解:(1)答案不唯一,如:原式=(x-4)2-12 或 原式=(x-2)2-4x (2)由已知等式变形得 x2+xy+14y2+34y2-3y+3=0.
(x+12y)2+34(y-2)2=0,∴x+12y=0,y-2=0, 解得 x=-1,y=2.∴xy=(-1)2=1
5.先阅读理解下面的例题,再按要求解答下列问题: 例题:求代数式y2+4y+8的最小值. 解:y2+4y+8=y2+4y+4+4=(y+2)2+4,∵(y+2)2≥0,∴(y+ 2)2+4≥4,∴y2+4y+8的最小值是4. (1)求代数式m2+m+4的最小值; (2)求代数式4-x2+2x的最大值;
第三讲 一元二次方程根与系数的关系

初高中数学衔接课程(3)第三讲 一元二次方程根与系数的关系(韦达定理)一、方程根的情况一元二次方程2ax +b x +c =0(a ≠0)的根的情况可以由b 2-4ac 来判定,我们把b 2-4ac 叫做一元二次方程2ax +b x +c =0(a ≠0)的根的判别式,通常用符号“Δ”来表示。
对于一元二次方程2ax +b x +c =0(a ≠0),有(1)当Δ>0时,方程有两个不相2ax +b x +c =0等的实数根2,1x =242b b aca-±-;(2)当Δ=0时,方程有两个相等的实数根,1x =2x =-2ba; (3)当Δ<0时,方程没有实数根。
(3)当Δ<0时,方程没有实数根。
例1 判定下列关于x 的方程的根的情况(其中a 为常数),如果方程有实数根,写出方程的实数根.例1 判定下列关于x 的方程的根的情况(其中a 为常数),如果方程有实数根,写出方程的实数根。
(1)2x -3x +3=0; (2)2x -ax -1=0; (3)2x -ax +(a -1)=0; (4)2x -2x +a =0。
解:(1)∵Δ=32-4×1×3=-3<0,∴方程没有实数根。
(2)该方程的根的判别式Δ=a 2-4×1×(-1)=a 2+4>0,所以方程一定有两个不等的实数根2142a a x ++=,2242a a x -+=。
(3)由于该方程的根的判别式为Δ=a 2-4×1×(a -1)=a 2-4a +4=(a -2)2,所以,①当a =2时,Δ=0,所以方程有两个相等的实数根x 1=x 2=1; ②当a ≠2时,Δ>0, 所以方程有两个不相等的实数根x 1=1,x 2=a -1。
(4)由于该方程的根的判别式为Δ=22-4×1×a =4-4a =4(1-a ),所以 ①当Δ>0,即4(1-a ) >0,即a <1时,方程有两个不相等的实数根111x a =+-,211x a =--;②当Δ=0,即a =1时,方程有两个相等的实数根x 1=x 2=1; ③当Δ<0,即a >1时,方程没有实数根。
中考数学大一轮数学复习专题ppt课件:一元二次方程根的判别式及根与系数的关系

夯实基本 知已知彼
基础知识回顾
1. 一元二次方程根的判别式
关于x的一元二次方程ax2+bx+c=0(a≠0)的根的判别式为________.
(1)b2-4ac>0⇔一元二次方程ax2+bx+c=0(a≠0)有两个________实数
根,即x1,2=________. (2)b2-4ac=0⇔一元二次方程ax2+bx+c=0(a≠0)有____________相等
1 2 3
13
中考大一轮复习讲义◆ 数学
热点看台 快速提升
易错题跟踪 1. (2014·湖北襄阳)若正数a是一个一元二次方程x2-5x+m=0的一个根,-a 是一元二次方程x2+5x-m=0的一个根,则a的值是____5____. 2. (2014·湖北鄂州)一元二次方程mx2-2mx+m-2=0. (1)若方程有两实数根,求m的取值范围. (2)设方程两实根为x1,x2,且|x1-x2|=1,求m.
课后总结
1
学生:同伴之间相互交流学习心得。
2 师生:共同归纳本课学习知识。
16
中考大一轮复习讲义◆ 数学
作业
1
教科书本课课后习题。
2
课时达标册本课练习习题。
17
中考大一轮复习讲义◆ 数学
下课啦!
18
中考大一轮复习讲义◆ 数学
谢谢 指导
2022
19
中考大一轮复习讲义◆ 数学 20
D. m≤12
1
5. (2013·山东滨州)对于任意实数 k,关于 x 的方程 x2-2(k+1)x-k2+2k
-1=0 的根的情况为( C )
A. 有两个相等的实数根
B. 没有实数根
C. 有两个不相等的实数根
人教版九年级数学上册公式法2(根的判别式)课件

有实数解,则k
跟踪练习
1.关于x的方程
有两个相等
的实数根,则m的值为( D )
A.2 B.-2 C.0 D.±2
跟踪练习
2.关于x的方程x2+2x-a=0没有实数根,则a的
值可能是( A )
的根的情况是(C )
D.无法判定
跟踪练习
3.已知关于x的一元二次方程2x2−(m+n)x+mn=0, 其中m,n在数轴上的对应点如图所示,则这个方
程的根的情况是( B )
A.有两个不相等的实数根 B.有两个相等的实数根 C.没有实数根 D.无法确定
能力提升
已知关于x的一元二次方程
(1)求证:此方程一定有两个不相等的实数根; (1)证:A=a-1,B=2a+1,C=2
跟踪练习
1.探讨关于x的一元二次方程
总有实数根的条件,下面三名同学给出建议:
甲:a,b同号; 乙:
丙:
其中符合条件的是( B )
A.甲,乙,丙都正确 B.只有甲不正确 C.甲,乙,丙都不正确 D.只有乙正确
新知探究 根据根的判别式求字母系数的取值范围
已知一元二次方程
的取值范围是
.
解:a=k-1,b=2,c=1
A.-2 B.-1 C.0
D.2
本课小结
1.知道根的判别式的是b2-4ac并会求它的准确值 2.根据根的判别式判断方程根的情况 3.根据根的判别式求字母的取值范围.
当堂检测
1.下列一元二次方程有两个相等的实数根
的是( )
A.x2+2x=0 B.(x﹣1)2=0
一元二次方程的根的判别式(三)

这里的b2-4ac叫做一元二次方程的根的判 别式.
练习:
不解方程,判断下列方程根的情况:
(1) +8x 3 2 (2) 2x -3x- =0 2 2 (3) 16x -24x +9=0 (4)
2 x -4
2 2 3x +10=2x
2 x +9=0
拓展:
1.若关于x的一元二次方程 x2+2x-k=0没 有实数根,求k的取值范围. 2.若关于x的一元二次方程 kx2+2x-1=0 有两个不相等的实数根,求k的取值范 围. 3.若关于x的一元二次方程 (m-2)2x2+(2m+1)x+1=0有实数根,求k 的取值范围.
拓展:
4.求证:关于x的一元二次方程 x2-(2a+1)x+(a-3)=0,不论a取何值,必有 两个不相等的实数根. 5.已知:关于x的一元二次方程 2x2-mx+m-3=0,判断此方程根的情况.
6.已知:a,b,c分别是三角形的三边,且 关于x的一元二次方程 (c+a)x2+2bx+(c-a)=0有两个相等的实数 根,判断此三角形的形状.
技能回放:
用公式法解下列方程:
(1)
2 5x -3x
2
=x+1
(2) x 5 2 5x
(3)
2 x +17
=8x
知识精华:
一元二次方程根的情况的判断
在方程ax2+bx +c=0(a≠0)中 b2-4ac=△
当△>0时,方程有两个不相等的实数根;
当△=0时,方程有两个相等的实ຫໍສະໝຸດ 根; 当△<0时,方程没有实数根.
一元二次方程根的判别式
华师版一元二次方程根的判别式-(中学课件201911)

解:要使方程有两个实数根,需满 足 m 0, 0
∴ [(2m 1)]2 4m m 0,
4m+1≥0,
m1 .
4
∴m的取值范围是m 1 ,且
m≠0.
4
当堂训练1
1.方程 4x 2 3x 2 0 的 根的判别式△=________,它 的根的情况是 _____________.
(1)∵a=2,b=3,c=-4, ∴.b2 4ac 32 4 2 (4) 41 0 ∴方程有两个不相等的实数根.
(2)∵a=16,b=-24,c=9, ∴.b2 4ac (24)2 4 16 9 0 ∴方程有两个相等的实数解.
一元二次方程根的判别式
一元二次方程 ax2 bx c 0 的根有三 种情况:①有两个不相等的实数根; ②有两个相等的实数根;③没有实数 根.而根的情况,由 b2 4ac 的值来 确定.因此 b2 4ac 叫做一元二 次方程的根的判别式.
△>0方程有两个不相等的实根.
(3)将方程化为一般形式,5x 2 5 7x 0 .5x 2 7x 5 0 ∵a=4,b=-7,c=5, ∴ b2 4ac (7)2 4 5 5 =49-100 =-51<0. ∴方程无实数解.
已知关于x的方程 mx 2 (2m 1)x m 0 有两个实数根,求m的取值范 围.
2.已知方程 2x 2 mx 1 0 的 判别式的值是16,则m= _____.
△=0方程有两个相等的实数根.
△<0方程没有实数根.
(1)不解方程判定方程根的情况; (2)根据参数系数的性质确定根
的范围;
(3)解与根有关的证明题.
一元二次方程的根的判别式(201911整理)

据题意有m2-12m+20=0∴m1=2, m2 =10
当m=2时,x1=x2 =0;当m=10时x1=x2=-2
一元二次方程判别式
• 练习:当K为何值时方程(k-2)x2 +2kx-1=0有两个相 等的实数根,并求出方程的根。
• 例3:当K为何值时,方程kx2 +(2k+1)x+k=0(k≠0)
• (1)有两个不相等的根(2)有两个相等的根
• (3)没有实数根
解:∵b2 -4ac=(2k+1)2 -4k·k=4k+1,而方程有两个不
一元二次方程判别式
课件制作 主 讲 余小芳
一元二次方程判别式
• 一复习提问: • 1、一元二次方程的标准式是什么? • 2、一元二次方程的求根公式是什么? • 想一想:b2-4ac的符号与ax2+bx+c=0会有关系吗? • 做一做:用求根公式法解下列方程 • (1)x2-x-2=0 (2)x2-6x+9=0 (3)x2-x+1=0 • 看一看:上列三个方程的根与b2-4ac的符号有关系吗?
的根。 (1)证明:∵△=b2 -4ac=k2 -4(k2 +1)= -3k 2-4无 论k为何实数k2≥0∴△<0故原方程没有实数根。
(2)证明:整理原方程得 x2 -3x+2 -a2 =a2 无论a为何值a2≥0 ∴ △>0,故原方程有两个不相等的根
有什么关系?
一元二次方程判别式
• 猜一猜:对于一般ax2+bx+c=0 (a≠0)的根与b -24ac的 符号有会么关系?
专题03 一元二次方程根的判别式(基础)(原卷版)

专题03 一元二次方程根的判别式知识点一、一元二次方程根的判别式1.一元二次方程根的判别式一元二次方程中,叫做一元二次方程的根的判别式,通常用“”来表示,即(1)当△>0时,一元二次方程有2个不相等的实数根;(2)当△=0时,一元二次方程有2个相等的实数根;(3)当△<0时,一元二次方程没有实数根.要点诠释:利用根的判别式判定一元二次方程根的情况的步骤:①把一元二次方程化为一般形式;②确定的值;③计算的值;④根据的符号判定方程根的情况.2. 一元二次方程根的判别式的逆用在方程中, (1)方程有两个不相等的实数根﹥0; (2)方程有两个相等的实数根=0; (3)方程没有实数根﹤0. 要点诠释:(1)逆用一元二次方程根的判别式求未知数的值或取值范围,但不能忽略二次项系数不为0这一条件;(2)若一元二次方程有两个实数根则 ≥0. ac b 42-)0(02≠=++a c bx ax ∆ac b 42-=∆c b a .,ac b 42-ac b 42-()002≠=++a c bx ax ⇒ac b 42-⇒ac b 42-⇒ac b 42-ac b 42-一、单选题1.(2020·邯郸市汉光中学九年级月考)一元二次方程2250x x --=的根的情况是( ) A .有两个相等的实数根B .没有实数根C .有两个不相等的实数根D .无法确定2.(2020·江苏宿迁市·九年级月考)若关于的一元二次方程220x x k ++=有两个不相等的实数根,则实数k 的取值范围是( )A .1k >B .1k =C .1k <D .1k ≤3.(2020·福建福州市·九年级期中)下列一元二次方程中,没有实数根的是( ) A .x 2+3x +2=0 B .﹣x 2+x +2=0 C .(x +1)2+2=0 D .3(x ﹣1)2﹣2=0 4.(2019·四川成都市·九年级期末)若关于x 的一元二次方程x 2+x -3m +1=0有两个实数根,则m 的取值范围是( )A .m >14B .m <14C .m ≥14D .m ≤14 5.(2020·南昌天行创世纪学校九年级月考)若α、β是方程x 2+2x ﹣2015=0的两个实数根,则α2+3α+β的值为( )A .2015B .2013C .﹣2015D .4030二、填空题6.(2020·上海普华教育信息咨询有限公司八年级期中)已知关于x 的一元二次方程22(12)0x a x a --+=有个不相同的实数根,则a 的取值范围是_______.7.(2021·全国九年级专题练习)已知关于x 的一元二次方程2220ax x c ++-=有两个相等的实数根,则1c a+的值等于_______.8.(2020·全国九年级专题练习)若关于x 的一元二次方程2124102x mx m --+=有两个相等的实数根,则2(2)2(1)m m m ---的值为__.9.(2020·四川阿坝藏族羌族自治州·九年级期末)关于x 的一元二次方程kx 2x +2=0有两个不相等的实数根,那么k 的取值范围是_____.三、解答题10.(2019·南通市启秀中学八年级期末)关于 x 的一元二次方程 x 2 - x + p - 1 = 0 有两个实数根 x 1、 x 2 .(1)求 p 的取值范围;(1)若221122(2)(2)9x x x x ----=,求 p 的值.11.(2020·湖北黄冈市·思源实验学校九年级月考)已知关于x 的一元二次方程x 2+x +m ﹣1=0.(1)当m =0时,求方程的实数根.(2)若方程有两个不相等的实数根,求实数m 的取值范围.12.(2020·全国八年级课时练习)关于x 的一元二次方程ax 2+bx+1=0.(1)当b=a+2时,利用根的判别式判断方程根的情况;(2)若方程有两个相等的实数根,写出一组满足条件的a ,b 的值,并求此时方程的根. 13.(2020·河南南阳市·九年级月考)已知关于x 的一元二次方程()22x 2k 1x k k 0-+++= (1)求证:方程有两个不相等的实数根;(2)若.ABC 的两边AB 、AC 的长是方程的两个实数根,第三边BC 的长为5.当.ABC 是等腰三角形时,求k 的值14.(2020·全国八年级课时练习)关于x 的方程x 2﹣ax+a+1=0有两个相等的实数根,求22214()244a a a a a a a a+---÷--+的值. 15.(2020·河南商丘市·九年级期中)已知关于x 的一元二次方程mx 2..m+2.x+2=0.(1)证明:不论m 为何值时,方程总有实数根;(2)m 为何整数时,方程有两个不相等的正整数根.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
m 2 (m 2)
∴方程总有两个实数根;
x
2m
(2)由求根公式得 x1=1,x2=
∴必须x2=
2 为整数即可,∵ m
2 m
,∵x1=1为整数,
m取正整数 ∴m =1或2.
例3.已知关于x的方程mx 2-(m+2)x+2=0(m≠0). (1)求证:方程总有两个实数根; (2)若方程的两个实数根都是整数,求正整数m的值.
根的判别式及其应用(中)
课标引路
学习目 标
2.会求解字母系数方程的整数根.
知识梳理
一Δ元=b二2次-4方ac程>的0 根的情况取决方于 程有两个不相等的实数根.
Δ=b2-4ac的符号.
Δ=b2-4ac=0
பைடு நூலகம்
方程有两个相等的实数根.
Δ=b2-4ac<0
方程没有实数根. 反之也成立
注意
(1)使用判别式之前,一定要先把方程变化为一般形式,正确找出a、 b、c的值,计算Δ=b2-4ac.
例2.求证方程(m2+1)x2-2mx+(m2+4)=0没有实数根. 【点拨】Δ=b2-4ac<0. 【解析】证明:Δ=(-2m)2-4(m2+1)(m2+4) =4m2-4(m4+5m2+4) =-4m4-16m2-16
=-4(m4+4m2+4) =-4(m2+2)2. ∵不论m取任何实数,(m2+2)2>0, ∴ -4(m2+2)2<0, 即Δ<0. ∴关于x的方程(m2+1)x2-2mx+(m2+4)=0没有实数根.
例3.已知关于x的方程mx 2-(m+2)x+2=0(m≠0). (1)求证:方程总有两个实数根; (2)若方程的两个实数根都是整数,求正整数m的值.
【点拨】(1)Δ=b2-4ac≥0;
(2)可用求根公式与因式分解两种方法对根为整数进行讨论.
【解析】解法一:(1) ∵ Δ=[-(m+2)]2-4×m×2 = (m-2)2 ≥0 ,
先把方程变化为一般形式,找出a、b、c的值,计算Δ.
1
情况①:Δ为完全平方式:一般此一元二次方程左边可进行因式分解,若含
字母的式子进行因式分解有困难,也可用求根公式进行求根.
2
情况②:Δ为非完全平方式:根据Δ>0或Δ≥0以及二次项系数求解字母系数 的取值范围,找到相应整数解对应的字母的值.
3 对两根进行整数值讨论→分式形式→根据要求讨论整除性→得解字母整数值.
【点拨】(1)Δ=b2-4ac≥0;
(2)可用求根公式与因式分解两种方法对根为整数进行讨论.
【解析】解法二:(2) ∵ mx2-(m+2)x+2=0,∴(x-1)(mx-2)=0,
∴
x1=1,x2=
2 m
,∵x1=1为整数,
∴必须x2=
2 为整数即可,∵ m
m取正整数
∴m =1或2.
先把方程变化为一般形式,找出a、b、c的值,计算Δ. 1
【解析】(2)分两种情况:①若b=c, (2) △=0⇔方程有两个相等的实数根. ∵方程x2-(k+2)x+2k=0有两个相等的实数根, ∴△=b2-4ac=(k-2)2=0,解得k=2, ∴此时方程为x2-4x+4=0,解得x1=x2=2,即b=c=2, ∴△ABC的周长为5;
【解析】(2)②若b≠c,则b=a=1或c=a=1,即方程有一根为1, 把x=1代入方程x2-(k+2)x+2k=0,得1-(k+2)+2k=0,解得k=1, ∴此时方程为x2-3x+2=0,解得x1=1,x2=2,∴方程另一根为2, ∵1、1、2不能构成三角形,∴ b≠c 这种情况不成立. 综上① ②知:所求△ABC的周长为5.
能力提升
知识点一
证明字母系数方程有实数根
(1) △>0⇔方程有两个不相等的实数根; (2) △=0⇔方程有两个相等的实数根.
【点拨】
【解析】证明:(1) ∵△=b2-4ac =(k+2)2-8k=k2+4k+4 -8k=k2-4k+4 =(k-2)2 ≥0,转化成完全平方式的形式
∴无论k取任意实数值,方程总有实数根.
指点迷津
说明方程是一元二次方程
例:关于x的方程m2x2-(2m+1)x+1=0有两个实数根,则m的取值范
围是
. 弄清“方程有两个实数根”与“方程有实数根”的区别
【错解】
=4m+1 ≥0
【误区分析】没考虑二次项系数 m2≠0. 【正解】
=4m+1 ≥0 且m≠0.
(2)如果说方程有实数根,包括有两个不等实根或有两相等实根 两种情况,此时b2-4ac≥0,切勿丢掉等号.
(3)根的判别式b2-4ac的使用条件,是在一元二次方程ax2+bx+c=0 中,要注意隐含条件a≠0.
一元二次方程ax2+bx+c=0 有整数根需满足
Δ=b2-4ac≥0且a≠0 b2-4ac为完全平方数
一般情况下配方后变形后为形如:a2, 2 用配方法将Δ恒等变形. a2+k,(a2+k)2,-a2,-(a2+k)2的代数式,
从而判定正负,非负等情况.
3 判断Δ的符号.
结论. 4
Δ=b2-4ac>0 Δ=b2-4ac=0 Δ=b2-4ac<0
方程有两个不相等的实数根. 方程有两个相等的实数根. 方程没有实数根.
