坐标转换模型在盾构姿态计算中的应用
三维直角坐标转换在盾构引导中的运用

0 - s in cos cos 0 - sin RY = 0 sin cos! - s in! 0 1 0 0 cos ,
RZ =
2 三维直角坐标转换模型 2. 1 数学模型
设点 P 在空间直角坐标系 O XYZ 中的坐标为 (X, Y, Z ) , 在空 间直角坐标系 O X Y Z 中的坐标为 (X , Y , Z ) , 两个坐标系的关 系如图 1 所示。 两个三维直角坐 标系的转换模型 , 用矩阵表示为下式 : X X X Y = Y +k R Y Z 其中 , ( X Y
第 37 卷 第 4 期 2 0 1 1年 2月 文章编号: 1009 6825( 2011) 04 0203 02
山
西
建
筑
SHANX I ARCH I T ECTU RE
Vo. l 37 N o . 4 Feb. 2011
203
三维直角坐标转换在盾构引导中的运用
田红平
摘
李怀锋
要 : 运用三维直角坐标转换 , 先求出盾构机轴线局部坐标系与 实际三维空 间坐标系 两种坐 标系的 转换参 数 , 然 后再
工程师中冶集团武汉勘察研究院有限公司湖北武汉430080同济大学测量与国土信息工程系硕士研究生上海200092运用三维直角坐标转换先求出盾构机轴线局部坐标系与实际三维空间坐标系两种坐标系的转换参数然后再利用转换参数求出盾首中心和盾尾中心点的实际坐标进而计算盾构机的姿态该方法用于地铁盾构的引导测量取得了令人满意的效果
m
-7 . 825 3 -7 . 727 8
-7 . 837 5 - 10 . 305 6 - 10 . 326 8
4 结语
本文运用三维直角坐标转换 , 盾构机上 三个棱 镜分别在 标定 坐标系与测量坐标系下的坐标转换 参数 , 然后再利 用转换参 数求 出盾首中心和盾尾 中心 点的实 际坐 标 , 计算盾 构机 的姿 态 , 具有 一定的研究价值。
盾构坐标和测量坐标的转换(实操分享)

盾构坐标和测量坐标的转换摘要随着空间定位技术的不断发展,全球一体化的形成,越来越要求全球测绘资料的统一,研究各测量坐标系统的建立方法及其相互转换模型,对于实现不同测量坐标系成果的换算具有重要的意义。
坐标转换已经不是一个新的课题了,随着与人们生活密切相关的测绘事业的迅速发展,全球一体化的形成,越来越多的要求全球测绘资料形成统一规范,尤其是坐标系统的统一。
由于各测量单位工作目的不同,所选择的椭球参考系也会有所不同,出现了许多不同形式的坐标系,例如WGS-84坐标系、国家80坐标系、北京54坐标系、独立地方坐标及各种城建坐标。
在同一坐标系下坐标的表示方式又有空间直角坐标、大地坐标、平面坐标。
根据不同的测绘需求,需要将不同的坐标系下的坐标进行相互转换,在这些坐标转换的过程中既会运用到同一坐标系下的坐标转换模型,又会用到不同参考系下各坐标系间的坐标转换模型。
本文主要研究的是设想先求出盾构机轴线局部坐标系与实际三维空间坐标系两种坐标系的转换参数,然后再利用转换参数求出盾首中心和盾尾中心点的实际坐标,获取盾构机的空间位置信息。
该方法数学模型的实质是空间直角坐标系之间的转换。
基于这些理论并结合相关的转换模型及算法编程实现了坐标转换系统。
关键词:坐标系转换模型转换参数测量坐标坐标转换系统Shield coordinates and the measurement coordinates conversionAbstract新罗马小四目录摘要 (I)ABSTRACT (II)第一章绪论 (1)1.1 研究背景及意义 (2)1.2 盾构导向系统的测量方法与应用 (8)1.3 盾构系统的发展趋势 (8)第二章测量坐标系基础理论 (9)2.1 测量坐标系统的类型 (9)2.1.1 地心坐标系 (10)2.1.2 参心坐标系 (11)2.1.3 地方独立坐标系 (12)2.2 我国常用的坐标系统 (9)2.2.1 1954年北京坐标系 (10)2.2.2 1980年西安坐标系 (12)2.2.3 WGS-84坐标系 (13)2.2.4 2000国家大地坐标系 (14)2.3 常用等价坐标系……………………………………………………………2.3.1 大地坐标系…………………………………………………………… 2.3.2 空间直角坐标系……………………………………………………… 2.3.3 平面直角坐标系………………………………………………………第三章坐标转换原理3.1 坐标转换原理……………………………………………………………3.2 坐标转换模型…………………………………………………………… 3.3 坐标转换模型的精度……………………………………………………第四章算例………………………………………………………………………第五章盾构坐标与测量坐标转换系统的设计与实现5.1 盾构坐标与测量坐标转换系统的设计5.1.1 系统开发工具……………………………………………………5.1.2 系统的总体设计…………………………………………………5.1.3 系统的功能设计…………………………………………………5.1.4 系统的流程设计…………………………………………………… 5.2 盾构坐标与测量坐标转换系统的实现5.2.1 系统主程序界面…………………………………………………… 5.2.2 系统实现中的关键技术…………………………………………… 5.3 盾构坐标与测量坐标转换系统的应用5.3.1结语 (104)参考文献 (106)致谢 (107)第一章绪论1.1 研究背景及意义在地铁隧道贯通测量中,及时地获取盾构的姿态非常重要。
盾构坐标和测量坐标的转换分解

盾构坐标和测量坐标的转换摘要随着空间定位技术的不断发展,全球一体化的形成,越来越要求全球测绘资料的统一,研究各测量坐标系统的建立方法及其相互转换模型,对于实现不同测量坐标系成果的换算具有重要的意义。
坐标转换已经不是一个新的课题了,随着与人们生活密切相关的测绘事业的迅速发展,全球一体化的形成,越来越多的要求全球测绘资料形成统一规范,尤其是坐标系统的统一。
由于各测量单位工作目的不同,所选择的椭球参考系也会有所不同,出现了许多不同形式的坐标系,例如WGS-84坐标系、国家80坐标系、北京54坐标系、独立地方坐标及各种城建坐标。
在同一坐标系下坐标的表示方式又有空间直角坐标、大地坐标、平面坐标。
根据不同的测绘需求,需要将不同的坐标系下的坐标进行相互转换,在这些坐标转换的过程中既会运用到同一坐标系下的坐标转换模型,又会用到不同参考系下各坐标系间的坐标转换模型。
本文主要研究的是设想先求出盾构机轴线局部坐标系与实际三维空间坐标系两种坐标系的转换参数,然后再利用转换参数求出盾首中心和盾尾中心点的实际坐标,获取盾构机的空间位置信息。
该方法数学模型的实质是空间直角坐标系之间的转换。
基于这些理论并结合相关的转换模型及算法编程实现了坐标转换系统。
关键词:坐标系转换模型转换参数测量坐标坐标转换系统Shield coordinates and the measurement coordinates conversionAbstract新罗马小四目录摘要 (I)ABSTRACT (II)第一章绪论 (1)1.1 研究背景及意义 (2)1.2 盾构导向系统的测量方法与应用 (8)1.3 盾构系统的发展趋势 (8)第二章测量坐标系基础理论 (9)2.1 测量坐标系统的类型 (9)2.1.1 地心坐标系 (10)2.1.2 参心坐标系 (11)2.1.3 地方独立坐标系 (12)2.2 我国常用的坐标系统 (9)2.2.1 1954年北京坐标系 (10)2.2.2 1980年西安坐标系 (12)2.2.3 WGS-84坐标系 (13)2.2.4 2000国家大地坐标系 (14)2.3 常用等价坐标系……………………………………………………………2.3.1 大地坐标系…………………………………………………………… 2.3.2 空间直角坐标系……………………………………………………… 2.3.3 平面直角坐标系………………………………………………………第三章坐标转换原理3.1 坐标转换原理……………………………………………………………3.2 坐标转换模型…………………………………………………………… 3.3 坐标转换模型的精度……………………………………………………第四章算例………………………………………………………………………第五章盾构坐标与测量坐标转换系统的设计与实现5.1 盾构坐标与测量坐标转换系统的设计5.1.1 系统开发工具……………………………………………………5.1.2 系统的总体设计…………………………………………………5.1.3 系统的功能设计…………………………………………………5.1.4 系统的流程设计…………………………………………………… 5.2 盾构坐标与测量坐标转换系统的实现5.2.1 系统主程序界面…………………………………………………… 5.2.2 系统实现中的关键技术…………………………………………… 5.3 盾构坐标与测量坐标转换系统的应用5.3.1结语 (104)参考文献 (106)致谢 (107)第一章绪论1.1 研究背景及意义在地铁隧道贯通测量中,及时地获取盾构的姿态非常重要。
浅谈盾构机姿态的控制方法

浅谈盾构机姿态的控制方法
一、简介
盾构机为沉管全封闭式施工机械,具有自动化程度高、施工质量可控、施工速度快和管片拼装精度高等优势,深受广大施工企业的青睐,用于水
利工程、市政工程、油气工程等城市基础设施的管线施工,不仅可以大大
减少施工难度,节省施工时间,还可以提高施工质量和提升施工效率。
但是,控制盾构机姿态是盾构钻机施工中的关键,盾构机控制姿态不准确,
既会影响施工质量,又会严重延误施工进度,甚至出现施工安全事故,因此,控制盾构机姿态是施工质量的重要保障。
1、建立坐标系:首先,应建立一个轨道工程坐标系,可以通过在地
形上标准点测量来建立。
2、采用传感器测量方法:在盾头前设置激光传感器,可以利用它来
测量盾头的垂直位置,并定时发送信号,通过接收系统转换后可以获得盾
头的三维坐标信息,从而可以准确控制盾头的姿态。
3、采用水平仪测量法:在盾头前方设置水平仪,可以实时水平测量,通过控制盾头的角度,从而准确控制盾头的姿态。
4、采用视觉控制方法:同样,可以在盾头前方设置一台摄像头,通
过视觉控制,可以准确控制盾头的姿态。
电子论文-盾构姿态自动测量系统的开发与应用

收稿日期:2008-12-16 作者简介:潘国荣(1960),男,教授、博士生导师,工学博士. 主要研究方向为精密工程测量、工业测量盾构姿态自动测量系统的开发与应用潘国荣1)、2),王穗辉1),陈传林3),张德海3)1) 同济大学 测量与国土信息工程系,上海 2000922) 现代工程测量国家测绘局重点实验室,上海 2000923) 上海地铁盾构设备工程有限公司, 上海 200031摘要:综合国内外既有测量系统优点和通过用户需求的调研,开发了一套集盾构自动导向测量和工程动态管理可视化、操作简单、自动化程度高的测量系统。
该系统在某标段地铁区间施工现场进行了实地应用。
应用结果表明,在地铁隧道中采用该系统进行自动测量是方便、准确和可行的,可在无人值守情况下完成测量导向,完全能够取代人工测量。
同时提供可视化的地面建筑物与盾构推进相关关系的信息,便于盾构推进过程中对环境影响事故的预防。
关键词:自动导向测量,盾构,自动全站仪,可视化 中文分类号:U455.3 文献标识码: ADevelopment and application of automatic surveying system inShield tunnelin gPAN Guorong 1)、2), WANG Suihui 1),CHEN Chuanlin 3),ZHANG Dehai 3)1) Department of Surveying and Geo-Informatics,Tongji university, Shanghai 200092 2) Key Laboratory of Modern Engineering Surveying of SBSM, Shanghai 200092 3) Shanghai Metro Shield Equipment and Engineering Co. Ltd, Shanghai 200031Abstract: By synthesizi ng the advantages of various surveying systems at home andabroad, a visual automatic surveying system is developed in this paper. This surveying system has the important function of automatic shield tunneling guiding survey visualization and engineering dynamic management visualization, and it also has merits of simply operation and higher automation level. It has been applied to the construction of a section of railways, the result indicated that the surveying system is convenient, accurate and feasible, and can automatically accomplish the whole measurement task taking the place of manual measurement. Meanwhile, thissystem also provides the visual information of the correlations of the TPM site and the building around, which is propitious to prevent accidents caused by surroundings during the tunnel construction .Key words : automatic-guiding survey, Shield-Driven, automatic total station, visualization地下工程大多数投资大、施工复杂、对周围环境影响显著,对国民经济和大众生活具有重要影响,具有重要的社会、经济和战略意义。
盾构-12-盾构姿态测量
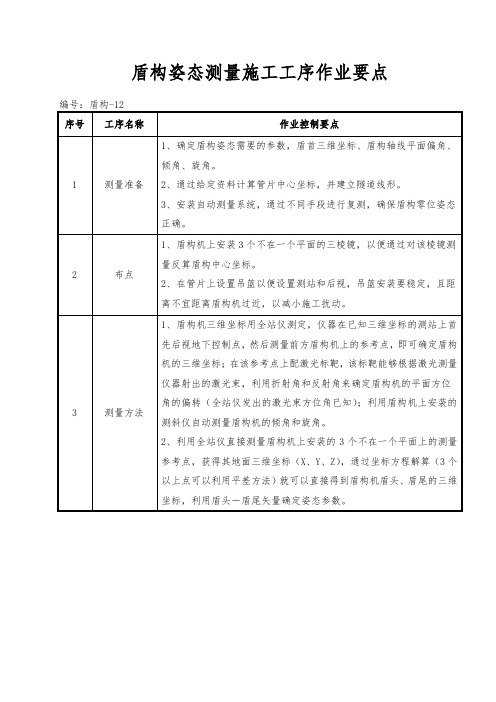
编号:盾构-12
序号
工序名称
作业控制要点
1
测量准备
1、确定盾构姿态需要的参数,盾首三维坐标、盾构轴线平面偏角、倾角、旋角。
2、通过给定资料计算管片中心坐标,并建立隧道线形。
3、安装自动测量系统,通过不同手段进行复测,确保盾构零位姿态正确。
2
布点
1、盾构机上安装3个不在一个平面的三棱镜,以便来自过对该棱镜测量反算盾构中心坐标。
角的偏转(全站仪发出的激光束方位角已知);利用盾构机上安装的测斜仪自动测量盾构机的倾角和旋角。
2、利用全站仪直接测量盾构机上安装的3个不在一个平面上的测量参考点,获得其地面三维坐标(X、Y、Z),通过坐标方程解算(3个以上点可以利用平差方法)就可以直接得到盾构机盾头、盾尾的三维坐标,利用盾头-盾尾矢量确定姿态参数。
2、在管片上设置吊篮以便设置测站和后视,吊篮安装要稳定,且距离不宜距离盾构机过近,以减小施工扰动。
3
测量方法
1、盾构机三维坐标用全站仪测定,仪器在已知三维坐标的测站上首先后视地下控制点,然后测量前方盾构机上的参考点,即可确定盾构机的三维坐标;在该参考点上配激光标靶,该标靶能够根据激光测量仪器射出的激光束,利用折射角和反射角来确定盾构机的平面方位
地铁盾构DTA的坐标计算方法与实现

:
: p × , + ! ! ± 2 × , : = A x l + B x l 2
2
‘ )
, 一 l s _  ̄ A B l 4 W 2 一 1 , s +
, + , s + ,
6 4 l 0 l 2 O
阱 [
( P ) =( p ( 0 )
( P ) =( p ( D ) + S g n ( p z ) l / R ( P) =( P ( 0 ) + ( ) ( ( 一L o ) +B( L e — L o ) )
4 .边 桩 的计 算 方法
针对地铁在曲线段要求进行中线偏移 , 其偏移量的计算可 以参照边桩的
计算 方 法计 算 。在原 曲线 段 的 中线偏 移值 是 一个 定 值E 。在缓 和 曲线 段 , 中线 偏移 的 量 随着 曲 线段 距 离 曲线 段 起点 的 长 度 变化, 因此 在取 边 桩 的一 侧 ( 可 能是 内侧 ) 的距离 D 是 的z 函数 即 D =Ex ( 1 / )。
同样 也 适用 用 直 线段 、 圆 曲线 段 。对 于 直线 段 , A : B = 0 ; 对 于 圆 曲线 段 A = 1 / R ,
B = I / ( R S ) 。
= s i n p i d l
( 6 )
p , : p :( + ) ×
将C O S p ,s i n p 用级数展开( 取前三项 , 也可根据实际精度要求选 前
其中: z 是 路线 单元 上 任 一点 p 到起 点。 的弧 长 , s 为 曲 线单 元 总长 。A为起 点 曲 , B 为 。
盾构姿态自动测量系统的开发与应用

明, 在地铁隧道 中采 用该 系统进 行 自动测 量 是方 便 、 准确 和
求 , 导 系统 的 自动 化 水 平 直 接 制 约 了施 工 的精 度 引
可行 的, 可在无人值 守 的情 况 下完成 测量 导 向 , 完全 能够 取 代人 工测量 . 同时可提供可视化 的地面建筑 物与 盾构推进 相 关关 系的信息 , 便于在盾构推进过 程 中预 防发生影 响环境 的
待盾构 推进 中测 量 了 N( N≥3 个 特 征点 后 , ) 根
据所 得 到的特 征 点 的测 量 坐 标 以及 初 始 标 定 坐 标 , 通过 坐标 转 换 的 方 法 求 出上 述 两 套 坐 标 的 转 换 参 数, 然后再 把盾 构机切 口中心 、 盾尾 中心 的初 始标 定 坐标 代人 到转换 模 型 中即 得 到切 口中心 点 0、 尾 盾 中心 点 C的在测量 坐标 系 中的坐标 . 有 了切 口 0 的坐 标 , 过 与 设 计 数 据 的 比较 , 经 就可 以判断 出 当前 切 口的里程 L一 知道 了切 口在 .
P N u rn ~, W G u h i , C A G oog N A S iu ' 如
De a 0 h i
(. e at n f uv yn n e - fr t s o  ̄i nv ri , 1 D prme t re igadG oI omai ,T n iest oS n c u y
和切 口中心的盾构推进轴线 . 通过这条轴线与隧道
第3 8卷
上方 的 A 点 . 当然 , 中有一个 点要 位于 0 其 C轴线上 基 准 .
方 , 近盾 构顶 部 , 接 以便 与 O C轴组 成 平 面 Ⅱ。并 且 ,
()盾 构 特 征 点 检 核 . 系 统 由一 台全 站 仪 以 2 本
隧道测量中盾构机姿态的MATLAB自动化计算方法

f , 0一 c一 6 1
( 1 )
F i g . 1 P i r s m p o i n t s o n t h e s h i e l d ma c h i n 转 换 误差 . 为 了解决 该 问题 , 本文 使用 罗德 里格矩 阵 求解转
收 稿 日期 : 2 0 1 4 — 1 0 - 1 8
作者简介 :范 伟 ( 1 9 8 9 一) , 男, 河南新 乡人 , 山西师范 大学地理科学 学院教师 , 工学 硕士 , 主要从事 精密工程 测量 、 工业 测 量与测量数据处理等方 面的研究 .
山西 师范 大学学报 ( 自然科学版 )
换参数的初值 , 然后将转换参数 的初值带入七参数 坐标 转换模 型 中 , 使 用 Ma t l a b编程 迭代 求 解 转换 参
数 的精确值 . 1 . 1 罗德 里格 矩 阵求解 七参数 的初 值
反 对称矩 阵 的模型 为
J S=l c 0 一 口I
J u n e 2 01 5
文章 编 号 : 1 0 0 9 - 4 4 9 0 ( 2 0 1 5) 0 2 - 0 0 7 9 - 0 8
隧道 测 量 中盾 构 机 姿 态 的 MA T L A B 自动化 计 算 方 法
范 伟 , 王贵文 , 刘发发
( 1 .山西师范 大学 地理科学学院 , 山西 临汾 0 4 1 0 0 0 ; 2 . 河南 省煤 田地质局物探测量 队, 河南 郑州 4 5 0 0 0 0 ) 摘 要 :通过应用 Ma t l a b编程 , 本 文实现了只有三个公共 点 的大角度七 参数坐 标转换 模型 中转换参 数
工测量采集的数据 , 一般使用传统 的人工计算方法或者 C A D图形转换 的方法进行处理 , 过程繁琐复杂 , 成 果 容 易 出错 , 精 度难 以评 定 , 并且 , 使用 C A D图形转 换 的方法 本 身就存 在严 重 的 图形投影 变 形 的缺 陷. 本文结合理论研究及使用 M a l a b 编程 , 实现了人工测量数据的 自动化处理 , 即实现 了盾构机首/ 尾坐
关于盾构机实时姿态测量和计算方法的研究示范文本

文件编号:RHD-QB-K8696 (安全管理范本系列)编辑:XXXXXX查核:XXXXXX时间:XXXXXX关于盾构机实时姿态测量和计算方法的研究示范文本关于盾构机实时姿态测量和计算方法的研究示范文本操作指导:该安全管理文件为日常单位或公司为保证的工作、生产能够安全稳定地有效运转而制定的,并由相关人员在办理业务或操作时进行更好的判断与管理。
,其中条款可根据自己现实基础上调整,请仔细浏览后进行编辑与保存。
随着社会经济的发展和城市建设的加快,城市规模不断扩大,人口不断增多,交通越来越来拥挤。
一些地方的城市建设者为了治理交通拥堵,分散交通压力。
不断寻求解决方式,修建地铁成为了一些城市建设者的主要的选择方式。
但是在修建地铁的过程中,工程量非常大,施工难度相对较高。
在地铁施工过程中,采用盾构技术,与传统的施工技术相比,有着许多优势,逐渐成为地铁修建过程中的主要施工方法。
本文将主要分析盾构姿态的测量的原理和方法,探究盾构姿态的测量的精度分析。
盾构机姿态简介盾构施工过程就像生活中的目标运动,先进行重心平移,然后在运动的过程中偏航,最后进行自身重心的滚动。
因此,在盾构施工过程中,需要监测的数据是盾构机位置和姿态的参数。
主要是三维坐标和滚动角、偏航角和俯仰角。
盾构机姿态的控制对整个工程施工意义重大,它决定着施工的质量和隧道推进方向的精度。
一旦控制不好,容易导致隧道偏差过大和盾尾间隙过小而相碰。
盾构机液压系统液压系统是盾构机的核心部分,盾构机的工作机构主要是由液压系统驱动完成,对盾构机系统的运行起着很大的作用。
盾构机的液压系统主要包括两大系统,一是推进系统,二是主动铰接系统。
2.1.推进系统盾构机的主要工作系统是推进系统,它主要是通过油缸作用于成型观片,以此来实现盾构前进。
推进系统的动力单元是一台80L/min旋转柱塞泵,执行元件是24个油缸,调节和控制部分包括方向的控制、油缸电磁阀的选择、安全阀、节流阀等。
盾构机工作时的最大工作压力是35MPa,液压泵最大推进流量是80L/min,推进油缸是240/180-1950(mm)。
盾构区间隧道中心平面坐标的计算方法

盾构区间隧道中心平面坐标的计算方法隧道中心的平面设计坐标在直线上很容易计算,而在弯道上的计算方法不同于地面上的曲线。
在盾构施工掘进过程中,由于存在超高h和超距e,如图1,这时就存在设计曲线与施工曲线不一致的情况(如图2)。
因为设计曲线指的是隧道内铺设轨道中心的曲线,如图2中的线路中心线,而施工曲线是要确定隧道中心的曲线即盾构机推进的轴线,如图2中的隧道中心线[2,3]。
列车在曲线上行驶时会产生离心力,所以在曲线上要用外轨超高的方法来克服离心力。
由于超高的存在,车辆向曲线内侧倾斜,且半径越小超高越大。
因此,在曲线地段的隧道断面内侧尺寸会增大。
采用盾构法施工的圆形隧道,其断面半径也就会增大,并出现断面内侧得到有效利用,而断面外侧不能充分利用的情形。
如果将地铁在曲线地段隧道的施工中线相对于线路设计中线向曲线内侧偏移某一个量,便可节省曲线隧道开挖断面尺寸,降低地铁建造成本[4]。
超距e为隧道中心线与线路中心线的偏移量。
隧道中心线向线路中心线的曲线内侧偏移,即隧道中心线相对于线路中心线向曲线圆心一侧偏移,在直线上超距为零,在缓和曲线上超距逐渐增大,在圆曲线上超距达到最大。
具体的偏移规则是:直缓(缓直)点处偏移量为0,缓圆(圆缓)点处偏移量为e,圆曲线偏移量为e,直缓(缓直)点与缓圆(圆缓)点之间偏移量为这两处偏移量的线性内插值[5]。
计算表明,当超高h=0.12m时,则超距e=0.149m,所以在盾构施工掘进过程中超距e 是必须要考虑的[2,3]。
图1 超高h和超距e示意图图2 超距e分布示意图在盾构施工掘进过程中针对考虑超距超距e示意图布示意图影响的曲线隧道中心的设计坐标计算,推出了如下的计算公式。
2 缓和曲线上任意一点坐标的计算在求缓和曲线上任意一点坐标时(如图3对称缓和曲线),建立以ZH点为原点,过ZH点的缓和曲线切线为x轴,ZH 点上缓和曲线的半径为y轴的直角坐标系,即切线支距法。
采用切线支距法计算标准缓和曲线上任意一点的坐标为[7]:在切线支距法的直角坐标系中,标准缓和曲线上任意一点的切线方位角为,任意一点处的偏移量为,根据坐标正算得到偏移后的任意点坐标为:公式简化好,即为:式中: 为缓和曲线长,为以ZH点起算的弧长,e为超距即偏移量,R 为圆曲线半径。
盾构法隧道施工测量精度控制措施

盾构法隧道施工测量精度控制措施摘要:本文介绍了从地铁盾构施工全过程中从施工测量技术方面提高贯通精度的控制措施。
关键词:零位测量法、联系测量、陀螺定向、交叉导线;盾构法隧道是指使用盾构机,一边控制开挖面及围岩不发生坍塌失稳,一边进行隧道掘进、出渣,并在机内拼装管片形成衬砌、实施壁后注浆,不扰动围岩而修筑隧道的方法。
盾构施工的主要原理就是尽可能在不扰动围岩的前提下完成施工,从而最大限度地减少对地面建筑物及地基内埋设物的影响。
盾构法隧道施工测量按施工工艺分为始发测量、地下导线测量、掘进轴线测量、接收到达测量。
1.盾构始发测量控制措施1.1 盾构机零位测量盾构始发测量,在盾构始发前,需要进行盾构机零位测量,确定盾构机姿态与盾构内布设的特征点之间几何关系,为后期掘进过程通过特征点位置调整盾构机姿态提供可靠的依据。
盾构机零位姿态测量常用的方法为分中法、侧边法进行测量。
侧边法的测量方法是在靠近盾首、盾尾处分别悬挂一根钢丝,钢丝下端悬挂重锤并置于油桶中,通过测量钢丝上的反射片坐标来计算盾构机首、尾的平面坐标。
盾首的钢丝悬挂在靠近刀盘和盾体的接缝处,盾尾的钢丝悬挂至靠近盾构(或铰接油缸)中盾与尾盾接缝处,钢丝至盾首、盾尾的距离用钢尺量出,取多次量取距离的平均值作为最终的计算依据。
当现场受到条件限制无法悬挂两根钢丝时,也可以悬挂一根钢丝,偏移计算出盾构中心线坐标。
高程测量:根据盾首、盾尾测量计算的平面坐标,将盾首、盾尾平面坐标测放至盾体顶面,利用全站仪三角高程直接测得盾首、盾尾处高程,通过反算得到盾首、盾尾的中心高程。
分中法测量:在盾首、盾中、盾尾按图1.1-4的方法找到盾体中心,使用全站仪分别测量盾首、盾中、盾尾中心C点的坐标,通过反算得到盾首和盾尾的坐标。
本次结合实际项目分别采用分中法、侧边法悬挂2根钢丝测量结果如下:虽然测量结果相近,但侧边法与设计值对比相差较小,如果现场有条件尽量采用侧边法悬挂2根钢丝进行施测。
三维直角坐标转换在盾构引导中的运用

三维 直 角 坐 标转 换 在 盾构 引导 中 的 运 用
田红 平 李 怀锋
摘
,,, .........
\ 、● ● ● ● /
,,, 。. ,. ..
y Z
l I
- / ,
△
△ △ y Z \ 、 ● ●● ● ● /
要 : 用 三 维 直 角 坐标 转 换 , 求 出盾 构 机 轴 线 局 部 坐 标 系与 实 际 三 维 空 问 坐 标 系 两种 坐 标 系 的 转 换 参 数 , 后 再 运 先 然 +
坐 标 转 换 模 型 就 为 六 参 数 坐 标 转 换 。 为 6个 坐 标 转 换 参 数 进 行 设 点 P 在 空 间 直 角 坐 标 系 0 X Z 中 的坐 标 为 ( , , , 空 初始赋值 , 一Y y z) 在 利用泰勒公式线性化后 , 该点 的误 差方程为下式 : 间 直 角 坐 标 系 0 - YZ 中 的坐 标 为 ( , ,z ) 两 个 坐 标 系 的关 ' X~ y, ,
r
其中,
0
0、
R = C O s d I 1 0 O L i S n , (o8 一 i 、 cs 0  ̄ s1 l
【 一n O) 0 s S i  ̄ C
0 I ,
c o s i 0
R = 0 1 rl
的转换参数 , 然后再利用转换参数 求 出盾首 中心 和盾 尾 中心点 的
( 3 ) : ] (
时也会 出现 回升现 象 , 这时要具体分析 回升 的原 因。
线图( 表示 沉 降 在 空 间 分 布 的 情 况 ) 和沉 降 曲 线 展 开 图 ( 中 可 看 图
国电力 出版社 ,0 6 20 .
坐标正反算法在盾构隧道曲线段中的应用

坐标正反算法在盾构隧道曲线段中的应用宗永倩郝伟李雁沼摘要深圳地铁7号线西丽湖站~西丽站区间隧道左线长1723.561m,右线隧道长1744.961m,是全线区间最长的盾构隧道,区间线路设计有多处转弯段,一般的测量计算较为复杂,尤其在施工测量放线及掘进过程中管片轴线偏差复核时要求精度高,难度较大。
本文结合深圳地铁7号线7301-2标项目的实际情况和地铁隧道曲线的特点,利用曲线参数方程在泰勒级数展开式的基础上,略去高次项,推导出曲线范围内已知任意点P中桩里程和偏距计算坐标的坐标正算公式;在迭代法的基础上探究坐标反算,推导出一种已知任意点P坐标反算中桩里程和偏距的一元二次直接求解近似方程;实际中利用公式编制出方便快捷的Excel公式,较好的解决了这一难题。
关键词坐标正反算盾构隧道曲线段测量1 工程概况深圳市城市轨道交通7号线7301-2标施工范围为西丽湖站、西丽站及西丽湖站~西丽站区间,采用盾构法施工。
其中左线隧道长1723.561m,右线隧道长1744.961m,区间正线线间距为9.73~39.63m,左线设计隧道转弯半径分别为350m、1200m、500m、3000m,右线隧道转弯半径分别为500m、1200m、500m。
2 正算公式推导曲线要素:曲线半径R,偏移量e,第一缓和曲线长,圆曲线长,第二缓和曲线长,第一直线前视方位角,第二直线前视方位角,ZH点坐标(,),HY点坐标(,),HZ点坐标(,),圆心O坐标(,)。
曲线上任一点的切线与第一直线的夹角。
已知曲线内任一点P的桩号和偏距,计算P点的坐标(。
2.1 第一段缓和曲线图1 缓和曲线内任意点P坐标正算的求解示意图(1)建立以ZH点为原点,过ZH点的缓和曲线的切线为X轴,ZH点上缓和曲线的半径为Y轴的直角坐标系,如图1所示。
点P的中桩坐标:(2)为了在已知坐标的测量控制点上进行曲线放样,必须将以ZH点为原点的切线直角坐标系中的曲线坐标转换到线路导线测量坐标系中,由第一直线在测量坐标系中前视方位角和ZH点在测量坐标系中的坐标(,),求得曲线任意点P在测量坐标系中的中桩坐标为(,)。
关于盾构机实时姿态测量和计算方法的研究

关于盾构机实时姿态测量和计算方法的研究盾构机是一种用于地下隧道开挖的工程机械设备。
在盾构机的使用过程中,实时姿态测量和计算方法的研究变得非常重要。
盾构机的姿态稳定性对于隧道的质量和施工效率有着直接的影响。
因此,本文将围绕盾构机实时姿态测量和计算方法的研究展开详细探讨。
首先,盾构机实时姿态测量的方法有很多种,包括传感器测量、图像处理等。
传感器测量是最常用的方法之一、通过在盾构机上安装加速度传感器、陀螺仪、姿态传感器等设备,可以实时测量盾构机的加速度、姿态角等参数。
这些传感器可以将测量数据传输到计算机中,通过算法分析得到盾构机的实时姿态。
其次,盾构机实时姿态计算方法的研究也非常关键。
通过采集的测量数据,需要进行精确的计算才能得到准确的姿态信息。
姿态计算方法可以分为数学模型计算方法和机器学习方法。
数学模型计算方法包括解析法、数值解法等,通过建立盾构机的数学模型,利用已知的输入参数计算出盾构机的姿态。
机器学习方法则是利用大量数据训练模型,通过学习得到的模型对盾构机的姿态进行预测和计算。
盾构机实时姿态测量和计算方法的研究对于盾构机的安全和施工效率具有重要意义。
如果盾构机姿态测量不准确,将会导致隧道施工质量下降,甚至可能发生事故。
因此,研究人员通过不断改进传感器的精度和计算算法的准确度,提高了盾构机姿态测量的准确性。
同时,采用机器学习方法也可以提高盾构机姿态计算的精度和效率。
此外,盾构机实时姿态测量和计算方法的研究还有一些挑战。
首先,盾构机的工作环境复杂多变,传感器容易受到振动、温度等外界因素的干扰,从而影响姿态测量的准确性。
其次,盾构机的姿态计算涉及多种参数,计算复杂度较高。
因此,研究人员需要设计更加鲁棒的传感器以及高效的计算算法,以应对复杂的工况和环境。
综上所述,盾构机实时姿态测量和计算方法的研究对于提高隧道施工的质量和效率具有重要意义。
通过不断改进传感器的精度和算法的准确性,研究人员可以提高盾构机姿态测量的准确性。
关于盾构机实时姿态测量和计算方法的研究

People who often blame themselves can often get forgiveness from others.勤学乐施天天向上(页眉可删)关于盾构机实时姿态测量和计算方法的研究随着社会经济的发展和城市建设的加快,城市规模不断扩大,人口不断增多,交通越来越来拥挤。
一些地方的城市建设者为了治理交通拥堵,分散交通压力。
不断寻求解决方式,修建地铁成为了一些城市建设者的主要的选择方式。
但是在修建地铁的过程中,工程量非常大,施工难度相对较高。
在地铁施工过程中,采用盾构技术,与传统的施工技术相比,有着许多优势,逐渐成为地铁修建过程中的主要施工方法。
本文将主要分析盾构姿态的测量的原理和方法,探究盾构姿态的测量的精度分析。
盾构机姿态简介盾构施工过程就像生活中的目标运动,先进行重心平移,然后在运动的过程中偏航,最后进行自身重心的滚动。
因此,在盾构施工过程中,需要监测的数据是盾构机位置和姿态的参数。
主要是三维坐标和滚动角、偏航角和俯仰角。
盾构机姿态的控制对整个工程施工意义重大,它决定着施工的质量和隧道推进方向的精度。
一旦控制不好,容易导致隧道偏差过大和盾尾间隙过小而相碰。
盾构机液压系统液压系统是盾构机的核心部分,盾构机的工作机构主要是由液压系统驱动完成,对盾构机系统的运行起着很大的作用。
盾构机的液压系统主要包括两大系统,一是推进系统,二是主动铰接系统。
2.1.推进系统盾构机的主要工作系统是推进系统,它主要是通过油缸作用于成型观片,以此来实现盾构前进。
推进系统的动力单元是一台80L/min旋转柱塞泵,执行元件是24个油缸,调节和控制部分包括方向的控制、油缸电磁阀的选择、安全阀、节流阀等。
盾构机工作时的最大工作压力是35MPa,液压泵最大推进流量是80L/min,推进油缸是240/180-1950(mm)。
2.1.1.推力计算盾构机共有推进油缸24个,总推力是这24个油缸的推力之和,那么在液压系统的最大推力F最大-24×P×Sn中,P表示油缸的最大压强,S表示活塞面积,因此,F最大-24×35×106Pa ×3.14×0.122㎡≈37981t2.1.2.推进速度计算盾构机的最大推进速度就是油缸的最大伸长速度,S-1/T,T-V/S1,在这个公式中,S表示最大推进速度,T表示伸长1mm所需要的时间,V表示伸长1mm需要的油液体积,S1为推进流量,S为74mm/min。
盾构施工姿态控制
17:29盾构施工姿态控制广州轨道交通建设监理有限公司广州地铁设计院盾构技术研究所王晖wh317:29一、姿态控制的基本概念二、姿态控制上易出现的问题及原因三、影响盾构掘进姿态的要素 四、出现侵限时的处理措施17:29姿态控制的基本概念1、盾构机坐标控制系统模型17:2917:2917:29偏航,通俗地讲就是偏离航向。
严格的定义是这样的,首先定义一个本体坐标,本体质心为原点O ,预定运动方向切线(或者说航向、轨迹切线)为x 轴,指向地心方向为z 轴,根据右手法则确定y 轴(即xOy 平面的法向)。
有了坐标后如果本体绕x 、y 、z 轴转动,即相应地得到滚动角、俯仰角和偏航角,三个角度确定了物体的运动时姿态。
在偏航角存在的情况下,物体发生偏航。
幻灯片 1wh3 121212121王晖, 2004-11-117:29假设盾构机前体中心A 和中体中心B 的坐标分别为(x A ,y A ,z A )、(x B ,y B ,z B )AB B A S z z /)(−=俯仰角ABB A S H H /)(−=水平趋势ABB A S V V /)(−=垂直趋势17:292、姿态控制要达到的目的: (1)使盾构机沿着设计轴线前进通过人工测量或自动导向系统测量盾构机姿态得知水平、垂直方向偏差以及水平和垂直方向趋势、滚动角等,当发生偏差时,通过改变分区千斤顶推力来调整。
当偏差较大时,通过仿形刀(或超挖刀)、铰接装置17:29 (2)使管片与盾构机之间保持良好姿态17:29通过铰接千斤顶行程/行程差/(铰接角度)的控制和正确的管片选型达到目的。
17:29二、姿态控制上易出现的问题及原因1、测量问题导致偏差:(1)自动导向系统发生偏差导致的轴线偏差。
输入数据错误、全站仪误差、隧道扭转引起的系统测量误差、测量系统故障。
(2)工程施工测量误差引起盾构姿态超出轴线控制范围内。
测量计算方法不正确、控制点偏差、导线测量误差、人工复测调整数据不及时等。
地铁盾构中盾构机姿态定位测量研究

地铁盾构施工中盾构机姿态定位测量地研究摘要:结合南京地铁一号线两个区间段地下隧道贯通地测量实践,简明地介绍了地铁建设中各种测量过程,并着重对盾构机姿态定位中地测量工作作了深入细致地研究,阐述了盾构机自动导向系统姿态定位测量地原理和方法,以及如何使用人工测量地方法来检核自动导向系统地准确性,分析了盾构机姿态定位检测地情况. 关键词:地铁。
自动导向系统。
盾构1 概述随着城市建设地飞速发展,我国在各大城市都开展了地铁建设,为了满足盾构掘进按设计要求贯通(贯通误差必须小于±50mm),必须研究每一步测量工作所带来地误差,包括地面控制测量,竖井联系测量,地下导线测量,盾构机姿态定位测量四个阶段.本文主要以南京地铁南北线一期工程地2个区间隧道地贯通测量工程为背景,探讨了地铁隧道施工中盾构机自动导向系统定位测量地功能及原理,并阐述了如何用棱镜法来检核自动导向系统地准确性.2 盾构机自动导向系统地组成与功能现在地盾构机都装备有先进地自动导向系统,本区间盾构机上地自动导向系统为德国VMT公司地SLS-T系统,主要有以下四部分组成:(1)具有自动照准目标地全站仪.主要用于测量(水平和垂直地)角度和距离、发射激光束.(2)ELS(电子激光系统),亦称为标板或激光靶板.这是一台智能型传感器,ELS接受全站仪发出地激光束,测定水平方向和垂直方向地入射点.坡度和旋转也由该系统内地倾斜仪测量,偏角由ELS上激光器地入射角确认.ELS固定在盾构机地机身内,在安装时其位置就确定了,它相对于盾构机轴线地关系和参数就可以知道.(3)计算机及隧道掘进软件.SLS-T软件是自动导向系统地核心,它从全站仪和ELS等通信设备接受数据,盾构机地位置在该软件中计算,并以数字和图形地形式显示在计算机地屏幕上,操作系统采用Windows2000,确保用户操作简便.(4)黄色箱子.它主要给全站仪供电,保证计算机和全站仪之间地通信和数据传输.3 盾构机自动导向定位地基本原理地铁隧道贯通测量中地地下控制导线是一条支导线,它指示着盾构地推进方向,导线点随着盾构机地推进延伸,导线点通常建立在管片地侧面仪器台上和右上侧内外架式地吊篮上,仪器采用强制归心(见图1),为了提高地下导线点地精度,应尽量减少支导线点,拉长两导线点地距离(但又不能无限制地拉长),并尽可能布设近乎直伸地导线.一般两导线点地间距宜控制在150m左右.盾构机自动导向系统地姿态定位主要是依据地下控制导线点来精确确定盾构机掘进地方向和位置.在掘进中盾构机地自动导向系统是如何定位地呢?它主要是根据地下控制导线上一个点地坐标(即X、Y、Z)来确定地,这个点就是带有激光器地全站仪地位置,然后全站仪将依照作为后视方向地另一个地下导线地控制点来定向,这样就确定了北方向,即方位角.再利用全站仪自动测出地测站与ELS棱镜之间地距离和方位角,就可以知道ELS棱镜地平面坐标(即X、Y),利用三角高程测出ELS棱镜地高程值(即Z).激光束射向ELS,ELS就可以测定激光相对于ELS平面地偏角.在ELS入射点之间测得地折射角及入射角用于测定盾构机相对于隧道设计轴线(DTA)地偏角.坡度和旋转直接用安装在ELS内地倾斜仪测量.这个数据大约每秒钟两次传输至控制用地计算机.通过全站仪测出地与ELS之间地距离可以提供沿着DTA掘进地盾构机地里程长度.所有测得地数据由通信电缆传输至计算机,通过软件组合起来用于计算盾构机轴线上前后两个参考点地精确地空间位置,并与隧道设计轴线(DTA)比较,得出地偏差值显示在屏幕上,这就是盾构机地姿态,在推进时只要控制好姿态,盾构机就能精确地沿着隧道设计轴线掘进,保证隧道能顺利准确地贯通.4 盾构机姿态位置地检测和计算在隧道推进地过程中,必须独立于SLST系统定期对盾构机地姿态和位置进行检查.间隔时间取决于隧道地具体情况,在有严重地光折射效应地隧道中,每次检查之间地间隔时间应该比较短.这主要是由于空气温度差别很大地效应.论述折射及其效应地题目有大量地文献资料,此处不再详述.在隧道测量时必须始终考虑这一效应.低估这个问题可能会引起严重地困难,尤其在长隧道中.我们采用棱镜法来对盾构机地姿态进行检查.在盾构机内有18个参考点(M8螺母),这些点在盾构机构建之前就已经定好位了,它们相对于盾构机地轴线有一定地参数关系(见表1),即它们与盾构机地轴线构成局部坐标系(见图2).在进行测量时,只要将特制地适配螺栓旋到M8螺母内,再装上棱镜.现在这些参考点地测量可以达到毫M地精度.已知地坐标和测得地坐标经过三维转换,与设计坐标比较,就可以计算出盾构机地姿态和位置参数等.下面来说明如何用棱镜法来计算盾构机地姿态和位置.我们利用洞内地下导线控制点,只要测出18个参考点中地任意三个点(最好取左、中、右三个点)地实际三维坐标,就可以计算盾构机地姿态.对于以盾构机轴线为坐标系地局部坐标来说,无论盾构机如何旋转和倾斜,这些参考点与盾构机地盾首中心和盾尾中心地空间距离是不会变地,他们始终保持一定地值,这些值我们可以从它地局部坐标计算出来.假设我们已经测出左,中,右(3,8,15号)三个参考点地实际三维坐标,分别为(x1,y1,z1),(x2,y2,z2),(x3,y3,z3),并设未知量为盾首中心地实际三维坐标(X首,Y首,Z首)和盾尾中心地实际三维坐标(X尾,Y尾,Z尾),从图2中可以看出,在以盾构机轴线构成局部坐标系中,盾首中心为坐标原点,坐标为(0,0,0),盾尾中心坐标为(-4 34,0,0).从表1中也可以看出各参考点在局部坐标系地坐标值.三个方程三个未知量,采用专业软件解算方程组.我们测出某一里程盾构机上三个参数点(3,8,15)地实际三维坐标分别为:从以上数据可以得知,在与对应里程上盾首中心和盾尾中心设计地三维坐标比较后,就可以得出盾构机轴线与设计轴线地左右偏差值和上下偏差值,以及盾构机地坡度,这就是盾构机地姿态.把计算得出地盾构机姿态与自动导向系统在计算机屏幕上显示地姿态作比较,据我们地实践经验,只要两者地差值不大于10mm,就可以认为自动导向系统是正确地.5 结束语在南京地铁一号线中,张府园~三山街区间隧道分为上行线和下行线两条互相平行地线路,即往返两条隧道.在这两个区间段地实际应用中,曾多次采用棱镜法检核盾构机姿态,两者地偏差值较差均不大于10mm,证明了该方法在检核自动导向系统地正确性是可靠有效地.在贯通测量中,由于采用了以上一系列地方法和措施,以及先进地自动导向系统指导推进,上行线于2002年9月准确贯通,经甲方检测,平面贯通误差为18mm,高程贯通误差为2mm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
*
周
莹l )
张德海3 )
上海 200092 l )同济大学测量与国土信息工程系, 2 )国家测绘局现代工程测量重点实验室, 上海 200092 3) 上海地铁盾构设备工程有限公司,上海 20003l
摘
要
在附有条件的间接平差模型的基础上, 提出用归一化大角度坐标转换模型计算盾构机姿态, 并从其原
态非常重要。而盾构的姿态通常是根据全站仪获取 盾构上的特征点的坐标来计算的。文献 [l] 中介绍 的方法是通过解方程组而得出切口 0、 盾尾 C 的坐 标, 其数学模型为点与点、 点与平面间的距离公式。 这种解法数学模型简单, 但只能从多个固定参考点
2006-02-27 * 收稿日期: 基金项目: 智能信息化盾构施工辅助系统技术研究项目 作者简介: 潘国荣, 男, l960 年生, 工学博士, 教授, 博士生导师, 主要从事测量数据处理及精密工程测量研究. E - maiI: pgr@ maiI. tongji. edu. cn
(2)
这就是归一化的坐标转换公式。在该公式中,
图l Fi转参数和尺度参 数。该公式的误差方程可简单表示为: ! : "# - $ (5) 其中, ":
0 0 0 al X' + a2 Y' + a3 Z' b0 X' + b0 Y' + b0 Z' l 2 3 0 0 0 cl X' + c2 Y' + c3 Z'
2) Pan Guorongl , ,Zhou Yingl) and Zhang Dehai3)
l )Department of Surueying and Geomatics,Tongji Uniuersity,Shanghai 200092 2 )Key Laboratory of Modern Engineering Surueying ,SBSM,Shanghai 200092 Ltd,Shanghai 20003l 3 )Shanghai Metro-Shield Machine Eguipment & Engineering Co. ,
理、 方法以及精度上进行了分析。应用结果表明: 利用坐标转换法计算盾构机姿态, 与常规解方程法相比较更能有 效利用参考点的所有信息, 计算过程简明, 且便于程序实现。
关键词
地铁隧道
+
大角度坐标转换
盾构机
归一化
转换参数
中图分类号: P226 . 3
文献标识码: A
3D DATUM TRANSFORMATION MODEL FOR DETERMININ ORIENTATION OF SHIELD IN SUBWAY CONSTRUCTION
1
引言
在地铁隧道贯通测量中, 及时地获取盾构的姿
中选取 3 个, 没有多余观测, 不能作有效的检核, 这 样就丢弃了一些有用信息。因此本文设想先求出盾 构机轴线局部坐标系与实际三维空间坐标系两种坐 标系的转换参数, 然后再利用转换参数求出盾首中 心和盾尾中心点的实际坐标, 获取盾构机的空间位 置信息。该方法数学模型的实质是空间直角坐标系 之间的转换。基本的坐标转换模型包括布尔沙-沃 尔夫转换模型、 莫洛金斯基转换模型和范士转换模
A
:
The 3D datum transformation modeI is improved with the method of parameter adjustment with
constraint to determine the orientation of the shieId in subway construction. The unitary principIe and method are anaIyzed. The resuIt shows that aII the reference points have been used efficientIy in this modeI compared with conventionaI modeIs. Key wo d :underground tunneI, 3D datum transformation,the shieId,unitary,transfer parameter
Sketch of 3D datum transformation
! . !"
坐标转换模型
设点 A 在空间直角坐标系 0 - XYZ 中的坐标为
( X, Y, Z) , 在空间直角坐标系 0' - X'Y'Z' 中的坐标 为 ( X', Y', Z') 。 X' 轴在 0 - XYZ 中的方向余弦为 ( al , bl , cl ) , Y' 轴在 0 - XYZ 中的方向余弦为 ( a2 , c2 ) , Z' 轴 在 0 - XYZ 中 的 方 向 余 弦 为 ( a3 , b3 , b2 , ; 而 X 轴在 0' - X'Y'Z' 中的方向余弦为 ( al , a2 , c3 ) , Y 轴 在 0' - X' Y' Z' 中 的 方 向 余 弦 为 ( bl , b2 , a3 ) b3 ) , Z 轴 0' - X'Y'Z' 中的方向余弦为 ( cl , c2 , c3 ) , ! Y0 . Z 0 ) 为 0' - X'Y'Z' 的原点相对于 为尺度比, ( X0 , 0 - XYZ 原点的平移量。两套坐标的关系用矩阵表 示为: al X Y : ! a2 Z a3 bl b2 b3 cl T X' X0 c2 Y' + Y0 : c3 Z' Z0
0 0 0 0 2 al 2 a2 2 a3 0 0 0 2 6l 2 62 2 63 0 0 0 0 0 2 cl 2 c2 2 c3 != 0 0 0 0 0 0 0 6l 62 63 al a2 a3 c0 c0 c0 60 60 60 0 l 2 3 l 2 3 0 0 0 a0 a0 a0 0 cl c2 c3 l 2 3 02 02 02 al + a2 + a3 - l 02 02 02 6l + 62 + 63 - l c0 2 + c0 2 + c0 2 - l l 2 3 -#= 0 0 0 0 0 al 6l + a2 62 + a0 3 63 0 0 0 0 0 0 6 l cl + 6 2 c2 + 6 3 c3 0 0 0 0 0 0 cl a l + c2 a 2 + c3 a 3
第 26 卷 第 3 期 2006 年8 月
大地测量与地球动力学 JOURNAL OF GEODESY AND GEODYNAMICS
VoI. 26 ,No. 3 Aug. , 2006
文章编号: l67l-5942 ( 2006 ) 03-0084-04
坐标转换模型在盾构姿态计算中的应用
2) 潘国荣l ,
! Z'
上标为 0 的数为各未知参数相应的近似值, 前缀为 d 的数为其相应值的改正数。 旋转矩阵是正交矩阵, 存在下列条件:
86
2 2 a2 l + a2 + a3 = l
大地测量与地球动力学
26 卷
al 6l + a2 62 + a3 63 = 0 6 l cl + 6 2 c2 + 6 3 c3 = 0 a l cl + a 2 c2 + a 3 c3 = 0 (6) X0 Y0 = Z0
!
2 2 2 2 #x i + 2 #y i + 2 #z i 3 N - l3
(9)
3
算例
按照上述基于大角度的坐标转换参数的归一化
求解方法, 利用盾构机内固定的 6 个参考点测得的 基于盾构机轴线的局部坐标系 ( 如图 2 ) 坐标与实际 三维坐标, 两套坐标数据见表 l , 即可按照坐标转换 模型反推两种空间直角坐标系的转换参数。求出坐 标系的转换参数后, 将盾构机的盾首和盾尾的轴线 局部坐标系三维坐标 转 换 成 实 际 三 维 坐 标 ( 见表 2) , 再与盾首盾尾的设计三维坐标进行轴线偏差计 算, 以确定盾构机的实时姿态, 坐标转换模型的精度 计算见表 3 , 盾构机的轴线偏差结果见表 4 。
N
(8)
2. 3
坐标转换模型的精度
坐标转换模型的精度对数据转换结果的精度起
(7)
决定性影响, 本文采用的公式为: "m =
式中, yi , #x i = x i - x'i , #y i = y i - y'i , #z i = z i - z'i 。x i , z i 为实际三维坐标系的公共点实测坐标, x'i , y'i , z'i 为求得坐标转换参数后转换的公共点在实际三维坐 标系的坐标。N 为公共点的点数, 转 " m 的值越大, 换模型的精度越低, 反之, 则转换模型的精度越高。
!" 坐标转换原理
! . #" 坐标转换原理
本文提出的转换模型的主要思想是在文献 [2] 提出的坐标转换模型的基础上, 将 l3 个未知参数, 包括旋转矩阵中 9 个方向余弦、 3 个平移和 l 个尺 度, 利用归一化坐标转换公式消除坐标平移参数, 根 据旋转矩阵的正交特性可列出 6 个条件方程。如果 测定了 N 个点, 则有 3 N - 3 个误差方程, 加上 6 个 条件方程, 共有 3 N + 3 个方程, l0 个未知参数, 可以 按附有条件的间接平差解算。
