奇异值分解
奇异值分解与特征值分解的比较分析(六)

奇异值分解与特征值分解是线性代数中非常重要的两个概念,它们在数据分析、图像处理、信号处理等领域都有着广泛的应用。
在本文中,我们将对这两种分解方法进行比较分析,探讨它们的优势和局限性。
奇异值分解(Singular Value Decomposition,简称SVD)是一种将一个矩阵分解成三个矩阵的操作,通常用于降维和矩阵逆的计算。
给定一个矩阵A,它的奇异值分解可以写成A=UΣV^T,其中U和V是正交矩阵,Σ是对角矩阵,对角线上的元素称为奇异值。
特征值分解(Eigenvalue Decomposition)则是将一个方阵分解成特征向量和特征值的操作。
给定一个方阵A,它的特征值分解可以写成A=QΛQ^T,其中Q是特征向量矩阵,Λ是特征值对角矩阵。
首先,我们来比较两种分解方法的适用范围。
特征值分解只适用于方阵,而奇异值分解则可适用于任意形状的矩阵。
这使得SVD在实际应用中更加灵活,能够处理各种形状的数据。
另一方面,特征值分解在对称矩阵上有更好的性能,因为对称矩阵的特征向量是正交的,从而使得特征值分解更加简洁和高效。
其次,我们来比较两种分解方法的稳定性和数值计算的复杂度。
在数值计算中,特征值分解的计算复杂度通常高于奇异值分解,特别是在矩阵规模较大时。
此外,特征值分解对矩阵的条件数非常敏感,如果矩阵的条件数较大,计算结果可能会出现较大误差。
相比之下,奇异值分解对矩阵的条件数不太敏感,因此更加稳定。
另外,我们还可以从几何的角度来比较奇异值分解和特征值分解。
特征值分解实质上是将一个线性变换表示成一组基向量的缩放变换,而奇异值分解则是将一个线性变换表示成两个正交变换的叠加。
因此,奇异值分解能够提供更加直观的几何解释,对于理解数据的结构和特征更加有帮助。
最后,我们来谈谈两种分解方法在数据降维和信息提取方面的应用。
奇异值分解在图像压缩、信号处理等领域有着广泛的应用,能够帮助我们去除数据中的噪音和冗余信息,从而实现数据的降维和信息的提取。
奇异值分解法

奇异值分解法奇异值分解是一种基于数学的计算技术,有助于研究者在处理非结构化数据时,对数据中的模式和特征进行识别和分析。
主要的应用以及计算机视觉领域,如图像压缩,图像识别,网络指纹识别,特征识别,图像融合,图像检索,脸部识别,图像分类等。
它可以有效地提取结构信息,从而改善数值分析误差和结果准确度。
奇异值分解算法最早由犹太数学家图良克提出,用于解决高维数据的维度问题。
它的核心是利用奇异向量的分解,将原始数据矩阵分解为有限个相对低维的部分,然后在每个部分内求出最佳的拟合系数,最后将拟合系数合并,即可得出整个原始矩阵。
奇异值分解法的主要步骤是:首先,计算原始数据矩阵的奇异值和奇异向量,然后,根据固有值确定奇异值和奇异向量,确定压缩程度,综合利用奇异值分解和奇异向量,进行特征提取和矩阵重建,从而将复杂的原始矩阵压缩成有限的低维数据,增加模型的处理速度,提高预测准确度。
除了图像处理外,奇异值分解在信号处理,数据挖掘,社交网络分析,自然语言处理,机器学习等领域也都有广泛应用。
它可以用来识别微弱的特征,筛选出重要变量,减少数据维度,提高预测准确度,快速处理大型数据集,提高模型效率。
奇异值分解是一种高效的数据分析技术,可以提取原始数据中的有用信息,增强模型的精确性。
它的应用非常广泛,可以改善各种计算机视觉任务的性能,为商业,科学和技术发展带来重大的突破和改进。
然而,奇异值分解也有一些缺点。
例如,它要求原矩阵具有有限的解,但是很多实际数据集中存在大量的噪声,它可能会对奇异值分解造成影响,导致分析结果不准确。
另外,它也有较高的计算复杂度,不能有效地处理大型数据集。
总而言之,奇异值分解是一种有效的数学分析方法,它可以有效地提取原始数据中的有用信息,为计算机视觉和大数据分析研究提供有益的参考。
然而,由于它的计算复杂度较高,要求原矩阵具有有限解,它也存在一定的局限性,需要采取灵活的处理方法以获取更准确有效的分析结果。
奇异值分解

奇异值分解奇异值分解是线性代数中一种重要的矩阵分解,在信号处理、统计学等领域有重要应用。
定义:设A为m*n阶矩阵,AHA的n个特征值的非负平方根叫作A的奇异值。
记为σi(A)。
如果把AHA的特征值记为λi(A),则σi(A)=λi(AHA)^(1/2)。
定理:(奇异值分解)设A为m*n阶复矩阵,则存在m阶酉阵U和n阶酉阵V,使得:A = U*S*V’其中S=diag(σi,σ2,……,σr),σi>0 (i=1,…,r),r=rank(A)。
推论:设A为m*n阶实矩阵,则存在m阶正交阵U和n阶正交阵V,使得A = U*S*V’其中S=diag(σi,σ2,……,σr),σi>0 (i=1,…,r),r=rank(A)。
说明:1、奇异值分解非常有用,对于矩阵A(m*n),存在U(m*m),V(n*n),S(m*n),满足A = U*S*V’。
U和V中分别是A的奇异向量,而S是A的奇异值。
AA'的正交单位特征向量组成U,特征值组成S'S,A'A的正交单位特征向量组成V,特征值(与AA'相同)组成SS'。
因此,奇异值分解和特征值问题紧密联系。
2、奇异值分解提供了一些关于A的信息,例如非零奇异值的数目(S的阶数)和A的秩相同,一旦秩r确定,那么U的前r列构成了A的列向量空间的正交基。
关于奇异值分解中当考虑的对象是实矩阵时: S对角元的平方恰为A'A特征值的说明. (对复矩阵类似可得)从上面我们知道矩阵的奇异值分解为: A=USV, 其中U,V是正交阵(所谓B为正交阵是指B'=B-1, 即B'B=I), S为对角阵.A'A=V'S'U'USV=V'S'SV=V-1S2V上式中, 一方面因为S是对角阵, S'S=S2, 且S2对角元就是S的对角元的平方. 另一方面注意到A'A是相似与S2的, 因此与S2有相同特征值.注:下面的符号和上面的有差异,注意区分SVD步骤:1、求AHA或AAH2、求AHA或AAH的特征值及特征向量x1,x2,...xr, r个特征值组成3、U=(x1,x2,...xr)地4、V1=AU1Δr-1,取V2与其正交,则V=(V1,V2)则n阶复方阵U的n个列向量是U空间的一个标准正交基,则U是U距阵.一个简单的充分必要判别准则是方阵U的转置共扼距阵乘以U 等于单位阵,则U是U距阵正交向量组的性质定义1Euclid空间V的一组两两正交的非零向量叫做V的一个正交向量组.若正交向量组的每一个向量都是单位向量,这个正交组就叫做一个标准正交向量组.设V是一个n维Euclid空间.若V中n个向量α1,α2,…,αn构成一个正交组,则由定理9.2.1知道这n个向量构成V的一个基.这样的一个基叫做V的一个正交基.若V的一个正交基还是一个标准正交向量组,则称这个基是V的一个标准正交基。
矩阵的奇异值分解

非对称矩阵分解
非对称矩阵的特征值分解
对于非对称矩阵,其特征值可能是复数,因此不能直接进行实数域上的特征值分 解。但是,可以通过引入复数域上的特征向量和特征值,将非对称矩阵分解为复 数域上的特征向量矩阵和特征值矩阵的乘积。
非对称矩阵的奇异值分解
对于任意实非对称矩阵,都可以进行奇异值分解,即$A = USigma V^T$,其中 $U$和$V$是正交矩阵,$Sigma$是对角矩阵,对角线上的元素是$A$的奇异值。 非对称矩阵的奇异值分解在数据降维、图像处理等领域有广泛应用。
通信信道均衡策略
信道均衡原理
在通信系统中,信道均衡是一种用于补偿信道失真、提高通信质量的技术。奇异值分解可用于信道均衡中的信道 矩阵分解,从而实现对信道特性的准确估计和补偿。
基于奇异值分解的信道均衡算法
利用奇异值分解对信道矩阵进行分解,根据得到的奇异值和左右奇异向量设计均衡器,实现对信道失真的有效补 偿。
3
个性化推荐
结合用户历史行为数据和相似度计算结果,为用 户推荐与其兴趣相似的物品或服务。
05 奇异值分解在信号处理和 通信中应用
信号降噪与重构技术
基于奇异值分解的信号降噪
利用奇异值分解能够将信号分解为多个独立成分的特点,对含噪信号进行降噪处理,提高信号质量。
信号重构技术
通过保留奇异值分解得到的主要成分,对信号进行重构,实现信号的压缩和恢复。
特殊类型矩阵分解
正定矩阵的Cholesky分解
对于正定矩阵,可以进行Cholesky分解,即$A = LL^T$,其中$L$是下三角 矩阵。Cholesky分解在求解线性方程组、最优化问题等场景中具有重要作用。
稀疏矩阵的分解
对于稀疏矩阵,可以采用特定的分解方法,如LU分解、QR分解等,以便更有效 地进行存储和计算。这些分解方法在数值计算、科学计算等领域有广泛应用。
奇异值分解
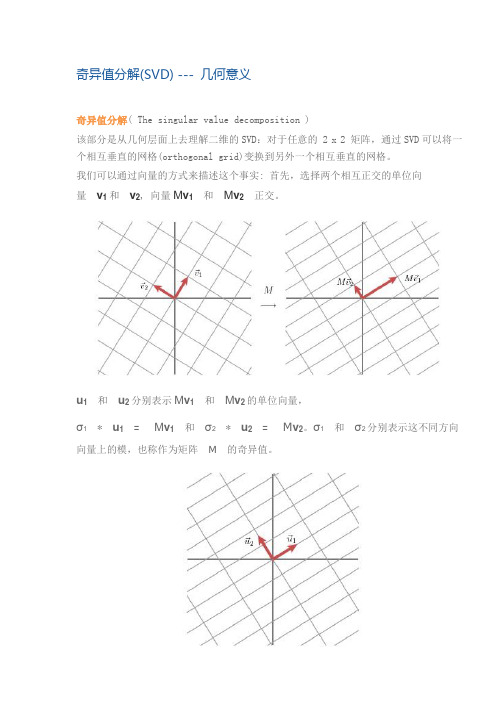
奇异值分解(SVD) --- 几何意义奇异值分解( The singular value decomposition )该部分是从几何层面上去理解二维的SVD:对于任意的 2 x 2 矩阵,通过SVD可以将一个相互垂直的网格(orthogonal grid)变换到另外一个相互垂直的网格。
我们可以通过向量的方式来描述这个事实: 首先,选择两个相互正交的单位向量v1 和v2, 向量M v1和M v2正交。
u1和u2分别表示M v1和M v2的单位向量,σ1* u1= M v1和σ2* u2= M v2。
σ1和σ2分别表示这不同方向向量上的模,也称作为矩阵M的奇异值。
这样我们就有了如下关系式M v1= σ1u1M v2= σ2u2我们现在可以简单描述下经过M线性变换后的向量x 的表达形式。
由于向量v1和v2是正交的单位向量,我们可以得到如下式子:x = (v1x) v1 + (v2x) v2这就意味着:M x = (v1x) M v1 + (v2x) M v2M x = (v1x) σ1u1 + (v2x) σ2u2向量内积可以用向量的转置来表示,如下所示v x = v T x最终的式子为M x = u1σ1v1T x + u2σ2v2T xM = u1σ1v1T + u2σ2v2T上述的式子经常表示成M = UΣV Tu 矩阵的列向量分别是u1,u2 ,Σ是一个对角矩阵,对角元素分别是对应的σ1和σ2,V 矩阵的列向量分别是v1,v2。
上角标T表示矩阵V 的转置。
这就表明任意的矩阵M是可以分解成三个矩阵。
V 表示了原始域的标准正交基,u 表示经过M 变换后的co-domain的标准正交基,Σ表示了V 中的向量与u 中相对应向量之间的关系。
(V describes an orthonormal basis in the domain, and U describes an orthonormal basis in the co-domain, and Σ describes how much the vectors in V are stretched to give the vectors in U.)如何获得奇异值分解?( How do we find the singular decomposition? ) 事实上我们可以找到任何矩阵的奇异值分解,那么我们是如何做到的呢?假设在原始域中有一个单位圆,如下图所示。
奇异值分解定理

奇异值分解定理奇异值分解(Singular Value Decomposition,简称SVD)是线性代数中一种重要的矩阵分解方法,常用于数据分析、信号处理、图像压缩等领域。
SVD的定理表明,任何矩阵都可以分解成三个矩阵的乘积,其中一个矩阵是正交矩阵,另外两个矩阵是对角矩阵,且对角线上的元素称为奇异值。
奇异值分解定理的数学概念比较复杂,需要一定的线性代数基础。
下面将对奇异值分解定理进行详细解释。
给定一个m行n列的实数矩阵A,假设rank(A)为r.那么存在两个实数方阵U(m×r)和V(n×r),使得:A = UΣV^T其中,U的每一列是A^TA的特征向量,V的每一列是AA^T的特征向量,Σ是一个对角矩阵,对角线上的元素称为奇异值。
奇异值分解定理的证明比较复杂,这里只给出一个简要的证明思路。
假设A的列向量为{a1, a2, ..., an},它们构成了一个n维向量空间的一组基。
我们可以将这组基转化为标准正交基,得到一组正交矩阵U和V。
然后我们可以通过对U和V进行一些数学操作,得到UΣV^T形式的矩阵。
最后,我们可以证明这个矩阵确实满足奇异值分解定理的要求。
奇异值分解定理在数据分析中有广泛的应用。
例如,在推荐系统中,我们可以通过SVD将用户对物品的评分矩阵分解,得到用户和物品的特征矩阵,从而进行个性化推荐。
在语音识别中,我们可以通过SVD将语音信号分解成一组基本声音的叠加,从而实现语音信号的降噪和特征提取。
在图像压缩中,我们可以通过SVD将图像分解成一组基本的图像模式,从而实现图像的降噪和压缩。
奇异值分解定理的应用不仅局限于上述领域,还可以应用于信号处理、图像处理、文本处理等其他领域。
通过奇异值分解,我们可以将复杂的问题转化为简单的线性代数运算,从而大大简化问题的求解过程。
然而,奇异值分解也有一些限制。
首先,奇异值分解是一种数值方法,对计算精度要求较高。
其次,奇异值分解的计算复杂度较高,对于大规模矩阵的分解可能会很耗时。
第15章 奇异值分解

• 实际应用中提到矩阵的奇异值分解时,通常指截断奇异值分解。
截断奇异值分解
例
• 矩阵A的秩为3,
• 若取k=2,则其截断奇异值分解是
几何解释
• 从线性变换的角度理解奇异值分解, m x n 矩阵A表示从n维空间Rn到 m维空间Rm的一个线性变换,
坐标系的旋转或反射变换U,得到向量
。
• 原始空间的标准正交基,
经过坐标系的旋转变换VT、 坐标轴的缩放变换刃、 坐标系的旋转变换U, 得到和经过线性变换A等价的结果。
例
• 给定一个2阶矩阵
• 其奇异值分解为
例
• 观察基于矩阵A的奇异值分解将R2的标准正交基
• 进行线性转换的情况 • 首先,VT表示一个旋转变换,将标准正交基e1, e2旋转,得到向
• 的奇异值分解
例
• (1)求ATA的特征值和特征向量
• 得到齐次线性方程组
例
• 该方程有非零解的充要条件是
• 解此方程,得矩阵ATA的特征值
和
。
• 将特征值代入线性方程组,得到对应的单位特征向量
例
• (2)求正交矩阵V • 构造正交矩阵V
• (3)求对角矩阵
• 奇异值为
和
• 构造对角矩阵
例
• (3)求 m x n 对角矩阵
• 计算A的奇异值
• 构造 m x n 矩形对角矩阵 ,主对角线元素是奇异值,其余 元素是零
奇异值分解的计算
• (4) 求m阶正交矩阵U • 对A的前r个正奇异值,令 • 得到 • 求AT的零空间的一组标准正交基
奇异值分解滤波原理

奇异值分解滤波原理奇异值分解将一个矩阵分解为三个矩阵的乘积:A=UΣV^T。
其中,A 为待分解的矩阵,U和V是两个正交矩阵,Σ是一个对角矩阵,对角线上的元素称为奇异值。
奇异值按照从大到小的顺序排列,代表了矩阵中每个特征的重要性。
在滤波原理中,SVD将待处理的矩阵A分解为U、Σ和V三个矩阵,然后根据奇异值的大小选择保留哪些特征。
奇异值较大的特征表示了数据中的主要信息,而奇异值较小的特征则代表了噪声或不重要的信息。
通过保留较大的奇异值与其对应的特征向量,可以获得近似于原始矩阵的重建矩阵。
这个重建矩阵保留了原始矩阵中最重要的特征,同时去除了噪声和冗余信息,从而实现了滤波的效果。
SVD滤波可以应用于多种领域。
在图像处理中,可以通过SVD分解图像矩阵,保留重要的奇异值和特征向量,然后重建图像。
这样可以减少图像中的噪声和压缩图像的大小。
在文本处理中,可以利用SVD对文档-词矩阵进行分解,从而找到文档和词语之间的关联性,并进行文本聚类、关键词提取等任务。
在机器学习中,SVD可以用于矩阵降维。
通过选择适当数量的重要奇异值和对应的特征向量,可以将高维数据降低到低维空间,从而减小计算复杂度和存储空间,并提升机器学习算法的效果。
需要注意的是,SVD滤波在实际应用中需要根据具体问题进行调整。
选择需要保留的奇异值个数是一个关键的步骤,过多或过少都可能导致结果不准确或信息丢失。
此外,SVD的计算过程较为复杂,计算量也较大,因此在实际应用中需要进行优化和加速。
综上所述,奇异值分解滤波原理是通过对矩阵进行分解,选择保留重要的奇异值和对应的特征向量,从而实现减少噪声和降低维度的目的。
这一原理被广泛应用于图像处理、文本处理和机器学习等领域,具有重要的实际价值和理论意义。
奇异值分解及其在数据处理中的应用

奇异值分解及其在数据处理中的应用奇异值分解(Singular Value Decomposition, SVD)是一种常见的矩阵分解方法,其广泛应用于信号和数据处理、图像和语音处理等领域。
在本文中,我们将介绍奇异值分解的基本原理以及其在数据处理中的应用。
一、奇异值分解的基本原理奇异值分解是一种将一个矩阵分解成三个矩阵的方法,具体而言,SVD将一个m×n的矩阵A分解为下列三个矩阵的乘积形式:A=UΣV^T其中,U是一个m×m的正交矩阵,Σ是一个m×n的对角矩阵,V是一个n×n的正交矩阵,而T表示转置。
特别的,由于Σ是个对角矩阵,因此其对角线上的元素称为奇异值,它是由矩阵A的奇异向量计算得到的。
此外,由于U和V是正交矩阵,因此它们各自的列向量是标准正交基。
SVD的基本原理是矩阵的右奇异向量和左奇异向量描述了矩阵在某种意义下的特性。
在图像和语音处理等领域,SVD被广泛应用于图像去噪、信号压缩等处理过程中。
二、奇异值分解在数据处理中的应用1. 矩阵的降维SVD主要应用于数据的降维,在大规模高维数据处理中,使用SVD技术将高维数据降维,有助于减少数据存储量,加快数据处理速度以及提高数据分析、建模效率。
2. 图像压缩和去噪在图像处理领域中,人们常常使用SVD来对图像进行压缩和去噪处理,其中奇异值的数量是决定图像质量和图像处理速度的关键因素。
当奇异值数量比较少时,图像质量较差,图像处理速度较快;当奇异值数量比较多时,图像质量较好,图像处理速度较慢。
3. 自然语言处理在自然语言处理领域中,SVD也被广泛应用。
例如,使用SVD对文本进行分解,可以减少文本的维度,提高文本分类的效率。
此外,使用SVD也可以对词向量进行降噪,提高词向量的准确度,从而增强机器学习算法在自然语言处理中的应用。
4. 推荐系统在推荐系统中,SVD可以用来构建用户-物品矩阵,并通过分解该矩阵得到用户和物品的隐藏特征,进而实现基于矩阵分解的推荐算法。
奇异值分解的几何解释

奇异值分解的几何解释奇异值分解的几何解释1. 引言奇异值分解(Singular Value Decomposition, SVD)是线性代数中一种重要的矩阵分解方法,广泛应用于信号处理、数据压缩、模式识别等领域。
本文将从几何的角度解释奇异值分解,并探讨其在理解数据集结构、特征提取以及降维等方面的重要性。
2. 奇异值分解的定义与基本概念我们定义奇异值分解为:对于一个m×n的矩阵A,存在一个分解形式A = UΣV^T,其中U是m×m的正交矩阵,Σ是m×n的对角矩阵,V是n×n的正交矩阵。
Σ的对角元素称为奇异值,通常按照降序排列。
这个分解将矩阵A映射为三个矩阵的乘积。
3. 奇异值分解的几何解释在几何角度上看,我们可以将奇异值分解理解为一个线性变换的过程。
对于一个m维的向量空间中的向量x,矩阵A将这个向量映射到了一个n维的向量空间中的向量Ax。
而奇异值分解就是将这个映射过程拆解为以下三个步骤:1. 矩阵V^T对向量x进行旋转操作。
这个矩阵的列向量是标准正交基,它将向量x映射到了一个新的坐标系。
2. 矩阵Σ对向量在新坐标系中的坐标进行拉伸操作。
对于每个坐标轴上的坐标值,通过奇异值的大小决定了拉伸的程度。
3. 矩阵U将拉伸后的向量映射回原始的向量空间中。
它也是一个标准正交基,它保持了向量的方向。
整个过程可以看作是一次从原始向量空间到新向量空间的映射。
4. 奇异值分解的几何意义奇异值分解在数据分析中具有重要的几何意义。
通过奇异值分解,我们可以理解数据集的结构。
奇异值的大小代表了数据集中各个方向上的重要性,越大的奇异值对应的方向在数据集中的方差越大,也就是数据集中的主要特征方向。
而奇异值较小的方向则表示对数据集的解释程度较低,可以看作是噪音或次要特征。
通过分解得到的U和V矩阵,我们可以直观地观察数据集的主要特征以及它们在空间中的分布。
奇异值分解还可以用于特征提取。
通过保留较大的奇异值,我们可以选择其中最重要的特征,从而实现对数据集的降维处理。
奇异值分解及其应用

奇异值分解及其应用奇异值分解(Singular Value Decomposition, SVD)是一种在线性代数中非常重要的分解方式,它将矩阵分解为三个矩阵的乘积,即U、Σ和V。
其中U和V都是正交矩阵,Σ则是一个对角矩阵。
奇异值分解最早是由Eckart和Young在1936年提出,它最初是为了在矩阵近似问题中得到最优的解决方案。
随着计算机技术的不断发展,奇异值分解也被广泛应用于许多领域,例如图像处理、声音处理和推荐系统等领域。
在图像处理中,奇异值分解可以用来对图像进行降噪处理和压缩。
将一张高清晰度的图片进行奇异值分解,可以得到三个矩阵U、Σ和V。
我们可以将这些矩阵中较小的奇异值减小或者设为0,来降低图像文件的大小。
这样做的好处是不影响图像的可识别度,并且可以加快图像的传输速度。
在声音处理以及语音识别领域,奇异值分解也被广泛应用。
Famous speech recognition系统使用的就是奇异值分解。
语音识别是将一个声音样本转化成一个数字信号的过程。
语音信号通常是高密度的,并且采样率非常高,如果不将其进行压缩,则无法进行存储和处理。
通过分解声音样本,同样可以降低信号的噪音,并且为声音处理系统提供更高的性能和更好的准确性。
推荐系统也是奇异值分解可应用的领域之一。
推荐系统有时候需要根据一些相似度的标准来对项目进行排序。
对于大量的用户和项目,推荐系统需要维护一个巨大的数据矩阵。
计算相似性等复杂的算法会对计算机造成巨大的负担,因此通常需要进行矩阵分解以降低数据维度。
总之,奇异值分解是一种十分有用的数学工具,它可以较好地解决许多实际问题中的数学问题,并被广泛应用于许多领域。
另外,在进行奇异值分解时,我们需要注意矩阵是否满足特定的数学条件,如奇异值和转置矩阵的奇异值相同等。
在实际操作过程中,需要仔细考虑这些因素,以获得更加准确和稳定的结果。
奇异值分解的标准正交基

奇异值分解的标准正交基1. 引言1.1 奇异值分解简介奇异值分解(Singular Value Decomposition,简称SVD)是一种广泛应用于数据分析和处理中的线性代数技术。
它将一个矩阵分解为三个矩阵的乘积,其中一个矩阵是一个正交矩阵,另一个矩阵是一个对角矩阵,而最后一个矩阵是另一个正交矩阵的转置。
SVD的应用涵盖了很多领域,例如图像压缩、推荐系统、语音识别等。
在SVD中,矩阵的奇异值代表了矩阵的重要性和方向性。
通过SVD可以对矩阵进行降维和信息提取,从而减少数据的冗余性和提高数据的可解释性。
SVD还可以用于矩阵的逆矩阵计算和矩阵的伪逆计算,从而在求解方程组和优化问题时起到重要作用。
SVD是一种非常强大的工具,能够对数据进行深入的分析和处理,为数据科学和机器学习提供了重要的支持。
在接下来的正文中,我们将详细介绍SVD的数学原理、计算方法、应用领域以及与标准正交基的关系,以及SVD的优缺点。
2. 正文2.1 奇异值分解的数学原理奇异值分解(Singular Value Decomposition,简称SVD)是一种常用的矩阵分解方法,可以将一个矩阵分解为三个矩阵的乘积,即A = UΣV^T。
U和V是正交矩阵,Σ是对角矩阵,对角线上的元素称为奇异值。
奇异值分解的数学原理可以通过以下几个步骤来解释:1. 对于任意一个矩阵A,我们可以将其转置后与自身相乘得到一个方阵A^TA。
然后,我们可以求解该方阵的特征值和特征向量。
2. 接下来,将A^TA的特征向量组成一个正交矩阵V,矩阵V的列向量就是矩阵A的右奇异向量。
5. 将A的奇异值按照降序排列在对角线上得到对角矩阵Σ,这样就完成了矩阵A的奇异值分解。
奇异值分解的数学原理从特征值和特征向量出发,通过对矩阵进行分解,将其表示为正交矩阵的乘积形式,为后续的计算和应用提供了基础。
2.2 奇异值分解的计算方法奇异值分解的计算方法通常涉及到矩阵的特征值分解和奇异值分解的联系。
矩阵的奇异值分解

矩阵的奇异值分解(singular value decomposition, SVD)是线性代数中的一种重要的矩阵分解方法,它在很多领域中都具有广泛应用,包括图像处理、数据压缩、信号处理等。
奇异值分解不仅是矩阵的一种表达形式,还可以帮助我们理解矩阵的结构,从而更好地应用于实际问题中。
奇异值分解的基本思想是将一个矩阵分解成三个矩阵的乘积。
对于一个m×n的矩阵A,它的奇异值分解可以表示为A=UΣV^T,其中U和V是m×m和n×n维的酉矩阵,Σ是一个m×n的对角矩阵,对角线上的元素称为奇异值。
通常情况下,奇异值按照从大到小的顺序排列。
奇异值分解的一个重要应用是矩阵的降维。
对于一个m×n的矩阵A,我们可以选择保留其中最大的k个奇异值,然后将矩阵A分解为UkΣkVk^T,其中Uk、Σk和Vk分别是U、Σ和V的前k列构成的矩阵。
这样得到的矩阵Ak=UkΣkVk^T可以近似地表示原始矩阵A,且Ak是一个更低维度的矩阵。
通过选择合适的k值,可以在保留较高精度的情况下大大降低矩阵的存储和计算复杂度。
奇异值分解还可以用来解决线性方程组的最小二乘解问题。
对于一个m×n的矩阵A和一个m维的向量b,我们可以将矩阵A分解为A=UΣV^T,然后将方程组Ax=b转化为Σy=Ub,其中y=V^Tx。
求解线性方程组Σy=Ub相对简单,通过计算得到向量y后,再通过y=V^Tx计算得到向量x,就得到了原始线性方程组的最小二乘解。
此外,奇异值分解还可以用于计算矩阵的伪逆。
对于一个m×n的矩阵A,它的伪逆A^+可以通过奇异值分解得到。
具体地,如果A的奇异值分解为A=UΣV^T,那么A^+可以表示为A^+=VΣ^+U^T,其中Σ^+是Σ的逆矩阵的转置。
伪逆矩阵在很多问题中都有重要应用,比如在解决过约束线性方程组和最小二乘解的问题中。
总之,矩阵的奇异值分解是线性代数中的一种重要的矩阵分解方法,它具有广泛的应用价值。
奇异值分解和最小二乘法

奇异值分解和最小二乘法引言奇异值分解(Singular Value Decomposition,简称SVD)和最小二乘法(Least Squares Method)是数学和统计学领域中常用的技术和方法。
SVD是一种矩阵分解方法,可以将一个矩阵分解成三个矩阵的乘积,而最小二乘法是一种用于拟合数据和求解最优参数的方法。
本文将深入探讨奇异值分解和最小二乘法的原理、应用以及优缺点。
奇异值分解(SVD)奇异值分解是一种重要的矩阵分解技术,可以将一个任意形状的矩阵分解为三个矩阵的乘积。
设矩阵A是一个m×n的实数矩阵,那么SVD将A分解为以下形式:A=UΣV T其中,U是一个m×m的正交矩阵,其中的列向量称为左奇异向量;Σ是一个m×n 的对角矩阵,对角线上的元素称为奇异值;V是一个n×n的正交矩阵,其中的列向量称为右奇异向量。
SVD的特点是奇异值按照从大到小的顺序排列,最后一些奇异值较小的可以被忽略。
SVD的应用1.降维:在机器学习和数据分析中,经常需要对高维数据进行降维处理。
SVD可以帮助我们找到原始数据中的主要特征,从而达到降维的效果。
2.图像压缩:SVD可以将图像分解为奇异值和特征向量的乘积,对奇异值进行截断可以实现图像的压缩。
3.矩阵逆和伪逆:SVD可以用于求解矩阵的逆和伪逆,特别是当矩阵不可逆或接近奇异时,SVD仍然可以提供一个合理的解。
SVD的优缺点SVD的优点包括: - 可以处理任意形状的矩阵,对矩阵没有限制。
- SVD分解后的矩阵可逆,方便逆向操作。
- 可以提供数据的主要特征,对于降维处理有较好的效果。
而SVD的缺点包括: - 计算量大:SVD的计算复杂度为O(min(m^2n, mn^2)),对于大规模矩阵计算会很慢。
- 空间消耗大:SVD需要存储三个矩阵,存储空间消耗较大。
最小二乘法最小二乘法是一种用来拟合数据和求解最优参数的方法,可以处理带有误差的数据集,常用于回归分析和数据拟合。
奇异值分解(SVD)与主成分分析(PCA)

奇异值分解(SVD)与主成分分析(PCA)奇异值分解(SVD)与主成分分析(PCA)1 算法简介奇异值分解(Singular Value Decomposition),简称SVD,是线性代数中矩阵分解的⽅法。
假如有⼀个矩阵A,对它进⾏奇异值分解,可以得到三个矩阵相乘的形式,最左边为m维的正交矩阵,中间为m*n 的对⾓阵,右边为n维的正交矩阵:A = U Σ V T A=U\Sigma V^{T} A=UΣV T这三个矩阵的⼤⼩如下图所⽰:矩阵Σ \Sigma Σ除了对⾓元素其他元素都为0,并且对⾓元素是从⼤到⼩排列的,前⾯的元素⽐较⼤,后⾯的很多元素接近0。
这些对⾓元素就是奇异值。
( u i u_i ui为m维⾏向量, v i v_i vi为n维⾏向量)Σ \Sigma Σ中有n个奇异值,但是由于排在后⾯的很多接近0,所以我们可以仅保留⽐较⼤的前r个奇异值,同时对三个矩阵过滤后⾯的n-r个奇异值,奇异值过滤之后,得到新的矩阵:在新的矩阵中,Σ \Sigma Σ只保留了前r个较⼤的特征值:实际应⽤中,我们仅需保留三个⽐较⼩的矩阵,就能表⽰A,不仅节省存储量,在计算的时候更是减少了计算量。
SVD在信息检索(隐性语义索引)、图像压缩、推荐系统、⾦融等领域都有应⽤。
主成分分析(Principal Components Analysis),简称PCA,是⼀种数据降维技术,⽤于数据预处理。
⼀般我们获取的原始数据维度都很⾼,⽐如1000个特征,在这1000个特征中可能包含了很多⽆⽤的信息或者噪声,真正有⽤的特征才100个,那么我们可以运⽤PCA算法将1000个特征降到100个特征。
这样不仅可以去除⽆⽤的噪声,还能减少很⼤的计算量。
简单来说,就是将数据从原始的空间中转换到新的特征空间中,例如原始的空间是三维的(x,y,z),x、y、z分别是原始空间的三个基,我们可以通过某种⽅法,⽤新的坐标系(a,b,c)来表⽰原始的数据,那么a、b、c就是新的基,它们组成新的特征空间。
使用奇异值分解进行矩阵分解的数值计算方法

奇异值分解(Singular Value Decomposition,简称SVD)是一种常用的矩阵分解方法,它在数据挖掘、图像处理、自然语言处理等领域都有着广泛的应用。
本文将通过数值计算的角度来探讨奇异值分解的原理和方法。
1. 奇异值分解的基本概念奇异值分解是将一个矩阵分解为三个矩阵的乘积,其数学表示形式为:A=UΣV^T,其中A是一个m×n的矩阵,U是一个m×m的正交矩阵,Σ是一个m×n的对角矩阵,V^T是一个n×n的正交矩阵。
在实际应用中,我们通常将矩阵A分解为U、Σ和V^T三个矩阵,其中U和V^T为正交矩阵,Σ为对角矩阵,对角线上的元素称为奇异值。
奇异值分解可以将原始矩阵A的信息进行压缩和提取,为后续的数据分析和处理提供了基础。
2. 奇异值分解的数值计算方法奇异值分解的数值计算方法主要包括基于幂法的迭代算法和基于分解的直接计算方法。
在实际应用中,由于幂法的收敛速度较慢,所以更多的是采用基于分解的直接计算方法,如Jacobi方法、分治法等。
这些方法通过特征值分解、QR分解等数值计算技术来实现奇异值分解,从而得到矩阵A的奇异值和相关的正交矩阵。
3. 奇异值分解在数据压缩和降维中的应用奇异值分解在数据挖掘和图像处理中有着重要的应用,其中最典型的应用就是数据压缩和降维。
通过奇异值分解,我们可以将高维的数据进行压缩和降维,从而减少数据的存储空间和计算复杂度。
同时,奇异值分解还可以提取数据的主要特征,帮助我们理解和分析数据的结构和规律。
4. 奇异值分解在推荐系统中的应用奇异值分解在推荐系统中也有着重要的应用,尤其是在协同过滤推荐算法中。
通过对用户-物品评分矩阵进行奇异值分解,我们可以得到用户和物品的隐含特征,从而实现对用户的个性化推荐。
基于奇异值分解的推荐算法在Netflix奖金赛等推荐系统比赛中取得了很好的成绩,证明了其在实际应用中的有效性和可行性。
5. 奇异值分解的局限性和改进虽然奇异值分解在各个领域都有着重要的应用,但是它也存在一些局限性。
如何使用奇异值分解进行信号处理(七)

奇异值分解(Singular Value Decomposition,简称SVD)是一种重要的矩阵分解方法,在信号处理中有着广泛的应用。
本文将探讨如何使用奇异值分解进行信号处理,并对其原理和应用进行详细介绍。
1. 奇异值分解的基本原理奇异值分解是将一个任意形状的矩阵分解为三个矩阵的乘积的过程。
给定一个矩阵A,其奇异值分解可以表示为:A=UΣV^T,其中U和V是正交矩阵,Σ是对角矩阵。
这里的U和V表示A的左奇异向量和右奇异向量,Σ的对角元素是A的奇异值。
2. 奇异值分解在信号处理中的应用在信号处理中,奇异值分解可以用来进行信号去噪、信号压缩和信号恢复等操作。
具体地说,可以将信号表示为一个矩阵,然后对该矩阵进行奇异值分解,利用奇异值的大小和奇异向量的性质来进行信号处理。
3. 信号去噪在信号处理中,信号往往会受到各种噪声的影响,导致信号质量下降。
奇异值分解可以通过去除奇异值较小的部分来实现信号的去噪。
具体地说,可以对信号的奇异值进行阈值处理,将较小的奇异值置为0,然后利用剩下的奇异值和奇异向量恢复原始信号。
这样可以有效地去除噪声,提高信号的质量。
4. 信号压缩奇异值分解还可以用来对信号进行压缩。
在奇异值分解的过程中,奇异值通常是按照大小递减的顺序排列的,因此可以只保留前几个奇异值和对应的奇异向量,然后舍弃后面的奇异值和奇异向量。
这样可以实现对信号的压缩,减少信号的存储空间,并且在一定程度上保留了原始信号的信息。
5. 信号恢复除了进行信号去噪和信号压缩外,奇异值分解还可以用来对信号进行恢复。
通过对信号的奇异值和奇异向量进行处理,可以实现对原始信号的恢复,还原出原始信号的信息。
6. 实际应用奇异值分解在信号处理中有着广泛的应用。
例如,在图像处理中,可以利用奇异值分解对图像进行压缩和去噪;在通信系统中,可以利用奇异值分解对信号进行编码和解码。
此外,奇异值分解还在语音处理、音频处理等领域有着重要的应用。
7. 总结奇异值分解是一种重要的矩阵分解方法,在信号处理中有着广泛的应用。
奇异值分解公式

奇异值分解公式
奇异值分解(Singular Value Decomposition,简称SVD)是一种矩阵分解的方法,用于将一个矩阵分解成三个矩阵的乘积。
其公式如下:
假设有一个 m × n 的实数矩阵 A,则它的奇异值分解可以表示为:A = UΣV^T
其中,U 是一个 m × m 的正交矩阵,Σ是一个 m × n 的对角矩阵,V 是一个 n × n 的正交矩阵。
^T 表示矩阵的转置。
对角矩阵Σ的对角线上的元素称为奇异值(singular values),按照从大到小的顺序排列。
U 的列向量称为左奇异向量(left singular vectors),V 的列向量称为右奇异向量(right singular vectors)。
奇异值分解在数据压缩、降维、推荐系统等领域具有广泛应用,可以帮助我们提取出矩阵的主要特征,并且能够有效地减少数据的维度。
奇异值分解原理

奇异值分解原理
奇异值分解(Singular Value Decomposition,SVD)是一种矩阵分解技术,它可以将一个矩阵分解为三个矩阵的乘积,这三个矩阵分别是左奇异矩阵,奇异值矩阵和右奇异矩阵。
奇异值分解的主要应用之一是矩阵的减少,这种减少可以用来减少矩阵的计算复杂度,以及减少需要存储的内存大小。
奇异值分解的另一个主要应用是降维,它可以将原始数据集中的特征映射到较低维度的特征空间,从而能够去除噪声和保留最重要的特征。
这样做的好处是减少计算量和节省内存,同时还能提高计算机的运行效率。
此外,奇异值分解还可以用于机器学习中的特征提取和特征抽取,它可以将原始数据的高维特征映射到较低维特征空间,从而提取出最重要的特征,并减少噪声的影响。
总之,奇异值分解是一种非常有用的数学工具,可以用于减少矩阵计算复杂度,减少内存大小,降维,特征提取以及特征抽取等任务。
它可以有效地帮助我们解决许多数据分析问题,因此被广泛应用于许多机器学习领域。
矩阵分离问题

矩阵分离问题
矩阵分离问题是指给定一个矩阵,如何将其分解为两个矩阵的乘积。
矩阵分离问题的解决方法有多种,其中比较常用的方法有QR分
解和奇异值分解。
1. QR分解:
QR分解是将一个矩阵分解为一个正交矩阵和一个上三角矩阵的
乘积。
该方法可以通过Gram-Schmidt正交化过程实现。
具体步骤如下:
- 对于一个矩阵A,找到一个正交矩阵Q,使得Q的列向量构成
了A的列空间的一组正交基。
- 将A表示为两个矩阵的乘积:A = QR,其中Q是正交矩阵,R
是上三角矩阵。
2. 奇异值分解:
奇异值分解是将一个矩阵分解为三个矩阵的乘积。
具体步骤如下: - 对于一个矩阵A,找到两个正交矩阵U和V,使得A可以表示
为三个矩阵的乘积:A = UΣV^T。
- U和V是A的左奇异向量和右奇异向量构成的矩阵,Σ是一个对角矩阵,其对角线上的元素是A的奇异值。
矩阵分离问题在很多应用中都有重要作用,比如图像处理、数据压缩和信号处理等领域。
通过将矩阵分解为两个或多个矩阵的乘积,可以简化复杂的运算和处理过程,并提高计算效率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
奇异值分解
奇异值分解(Singular Value Decomposition,以下简称SVD)是在机器学习领域广泛应用的算法,它不光可以用于降维算法中的特征分解,还可以用于推荐系统,以及自然语言处理等领域。
是很多机器学习算法的基石。
本文就对SVD的原理做一个总结,并讨论在在PCA 降维算法中是如何运用运用SVD的。
奇异值分解(SVD)
特征值分解仅适用于提取方阵特征,但在实际应用中,大部分数据对应的矩阵都不是方阵;
矩阵可能是有很多0的稀疏矩阵,存储量大且浪费空间,这时就需要提取主要特征;
奇异值分解是将任意较复杂的矩阵用更小、更简单的 3个子矩阵的相乘表示,用这3个小矩阵来描述大矩阵重要的特性。
应用:在使用线性代数的地方,基本上都要使用 SVD。
SVD 不仅仅应用在 PCA 、图像压缩、数字水印、推荐系统和文章分类、 LSA (隐性语义分析)、特征压缩(或数据降维)中,在信号分解、信号重构、信号降噪、数据融合、同标识别、目标跟踪、故障检测和神经网络等方面也有很好的应用,是很多机器学习算法的基石。
