会根据二次函数的图像判断abc符号

合集下载

二次函数图像与abc符号关系课件

二次函数图像与abc符号关系课件
目录
• 二次函数的基本概念 • 二次函数的图像分析 • 二次函数的abc符号变化对图像的影响 • 实际应用举例 • 总结与思考
01
二次函数的基本概念
二次函数的一般形式
总结词
二次函数的一般形式是$f(x) = ax^2 + bx + c$，其中$a, b, c$是常数，且$a neq 0$。
于负半轴。
对二次函数图像与abc符号关系的深入思考
a符号与开口大小的关系
虽然a决定了开口方向，但a的绝对值大小也会影响开口的大小。当|a|越大，开口越宽；当|a|越小，开口越窄。
b符号与对称性的关系
b的符号和大小决定了抛物线的对称性。当b=0时，抛物线关于y轴对称；当b≠0时，抛物线关于x=−b/2a对称。
详细描述
在二次函数的一般形式$f(x) = ax^2 + bx + c$中，$a, b, c$分别被称为二次项系数、一次项系数和常数项。它们的符号决定了函数的开口方向、顶点位置等性质。例如，当$a > 0$时，函数图像开口向上；当$a < 0$时，函数图像开口向下。
二次函数的开口方向与abc符号的关系
04
实际应用举例
利用二次函数解决实际问题
总结词
通过理解二次函数的图像和abc符号关系，可以解决一些实际问题。
详细描述
二次函数图像的开口方向、顶点位置和对称轴等特性，可以帮助我们解决一些实际问题，例如最值问题、面积问题等。
二次函数在数学建模中的应用
总结词
二次函数是数学建模中常用的函数之一，可以用来描述一些实际问题中的数量关系。
05
总结与思考

二次函数中的abc

课题由二次函数y=ax2+bx+c的图像判断a、b、c的符号授课类型微课教材分析二次函数y=ax2+bx+c（a,b,c是常数,a≠0）的系数a,b,c的符号和它的图像之间有着相辅相成的关系.由二次函数的图像位置可以得到a,b,c（或者含有的a,b,c的代数式）的符号;反之,由a,b,c（或者含有的a,b,c的代数式）的符号也可以确定图像的位置.这是一种由形到数、由数到形的转换,是数形结合思想的很好的诠释.也是一种等价、同一的关系。

学情分析学生已经学习了二次函数的概念图像和简单性质，能够简单运用函数知识解决方程和不等式问题。

从中考命题要求和课程标准的角度来看，关于二次函数的a、b、c的试题主要包括：简单结论型、结论综合型、结论组合导出型。

要学好二次函数内容、从容应对二次函数中考题，熟悉二次函数的a、b、c与图像的关系，必须深刻领会数形结合思想，能够用函数的观点看方程与不等式（组）。

教学目标知识与技能1.会根据二次函数的图像判断a,b,c的符号以及与a,b,c有关的代数式的符号；2.能够根据a,b,c的符号，判断二次函数的图像.过程与方法1.利用几何画板演示，让学生感受函数图像与系数a,b,c的关系，体会数形结合的思想方法.情感态度与价值 1.在学习过程中，培养学生的探究精神，合作能力.教学重点探究二次函数的图像与系数a,b,c的关系.教学难点根据二次函数的图像判断与a,b,c有关的代数式的符号.教学方法几何画板演示教学法、引导分析法、合作探究法.教学过程教学环节教师活动学生活动设计意图（一）问题引入教师提出思考问题已知二次函数y=ax2+bx+c的图像如图所示，则a 0 ， b 0 ， c 0（填>、<、=）.学生思考问题.通过问题提出，引发学生思考，进入学习状态.。

九年级数学二次函数中a,b,c符号的确定

九年级数学二次函数中a ，b ，c 符号的确定珠海市第四中学（519015）邱金龙二次函数)0(2≠++=a c bx ax y 的图象是抛物线，利用图象来确定a ，b ，c 的符号，是常见的问题，解决的关键是对二次函数的图象和性质的正确理解。

一、a ，b ，c 符号的确定（1）a 符号的确定。

抛物线的开口向上，a ＞0，抛物线的开口向下，a ＜0。

（2）c 符号的确定。

因为x=0时，由c bx ax y ++=2得，y ＝c ，故抛物线与y 轴交点在y 轴的正半轴，c ＞0，抛物线与y 轴交点在y 轴的负半轴，c ＜0，抛物线经过原点，c ＝0。

（3）b 符号的确定。

b 的符号要看对称轴ab x 2-=，再结合a 的符号来确定。

二、应用举例1、二次函数c bx ax y ++=2的图象分别如图所示，试分别判断（A ）（B ）（C ）（D ）图中a ，b ，c 的符号。

分析：（A ）图中，抛物线的开口向上，故a ＞0；抛物线与y 轴的交点P 在y 轴的负半轴，故c ＜0。

对称轴ab x 2-=＞0，而a ＞0，故b ＜0。

（B ）图中，抛物线的开口向下，故a ＜0；抛物线与y 轴的交点P 在y 轴的正半轴，故c ＞0。

对称轴ab x 2-=＜0，而a ＜0，故b ＜0。

（C ）图中（过程略），a ＞0，c ＞0 ，b ＞0。

（D ）图中（过程略），a ＜0， c ＜0 ，b ＞0。

2、（2004重庆中考题）二次函数c bx ax y ++=2的图象如图，则点M （b ，ac ）在（） A 、第一象限 B 、第二象限C 、第三象限D 、第四象限分析：抛物线的开口向下，故a ＜0；抛物线与y 轴的交点在y 轴的正半轴，故c ＞0。

对称轴ab x 2-=＞0，而a ＜0，故b ＞0。

因此，点M （b ，ac ）的横坐标为正，纵坐标为负，在第四象限，选（D ）。

3、（2004陕西中考题）二次函数y =ax 2+bx+c 的图象如图所示，则下列关于a 、b 、c 间的关系判断正确的是（）A 、ab ＜0B 、bc ＜0C 、.a+b+c ＞0D 、a －b+c ＜0分析：抛物线的开口向下，故a ＜0；抛物线与y 轴的交点在y 轴的负半轴，故c ＜0。

二次函数系数abc与图像的关系

二次函数系数a 、b 、c 与图像的关系一、首先就y=ax 2+bx+c （a≠0）中的a ，b ，c 对图像的作用归纳如下：1 a 的作用：决定开口方向：a > 0开口向上；a < 0开口向下；决定张口的大小：∣a ∣越大，抛物线的张口越小．2 b 的作用：b 和a 与抛物线图像的对称轴、顶点横坐标有关．b 与a 同号，说明02<-a b ，则对称轴在y 轴的左边；b 与a 异号，说明，则对称轴在y 轴的右边；特别的，b = 0，对称轴为y 轴．3 c 的作用：c 决定了抛物线与y 轴的交点纵坐标．抛物线与y 轴的交点（0，c ） c > 0 抛物线与y 轴的交点在y 轴的正半轴；c < 0 抛物线与y 轴的交点在y 轴的负半轴；特别的，c = 0，抛物线过原点．4 a,b,c 共同决定判别式的符号进而决定图象与x 轴的交点与x 轴两个交点与x 轴一个交点与x 轴没有交点5 几种特殊情况：x=1时，y=a + b + c ；x= -1时，y=a - b + c ．当x = 1时，① 若y > 0，则a + b + c >0；② 若y < 时0，则a + b + c < 0当x = -1时，① 若y > 0，则a - b + c >0；② 若y < 0，则a - b + c < 0．扩：x=2, y=4a + 2b + c ；x= -2, y=4a -2b + c ； x=3, y=9a +3 b + c ；x= -3, y=9a -3b + c 。

反之，给我们相应的二次函数图象，我们可以得到其系数a,b,c 以及它们组合成的一些关系结构（例如对称轴; 判别式 ……等等）的符号二、经典例题讲解例1 已知二次函数()02≠++=a c b a χχγ的图像如图，则a 、b 、c 满足（） A ．a < 0，b < 0，c > 0 ；B ．a < 0，b < 0，c < 0 ；C ． a < 0，b > 0，c > 0 ；D ．a > 0，b < 0，c > 0 ；例2（2015呼和浩特）如图，四个二次函数的图像中分别对应的是： ①2χγa =②2χγb =③2χγc =④2χγd =，则a ， b ， c ， d 的大小关系是．A ．a > b > c > dB ．a > b > d > cC ．b > a > c > dD ．b > a > d > c例3已知二次函数y=ax 2+bx+c的图象如图，其对称轴x=-1，给出下列结果①b 2＞4ac ；②abc ＞0；③2a+b=0；④a+b+c ＞0；⑤4a-2b+c ＜0，则正确的结论是（）A 、①②③④B 、②④⑤C 、②③④D 、①④⑤练习1. （2015•重庆）已知抛物线y=ax 2+bx+c （a ≠0）在平面直角坐标系中的位置如图所示，则下列结论中，正确的是（）A 、a ＞0B 、b ＜0C 、c ＜0D 、a+b+c ＞02.（2015•文山州）已知二次函数y=ax 2+bx+c 的图象如图所示，则a ，b ，c 满足（）A 、a ＜0，b ＜0，c ＞0，b 2- 4ac ＞0B 、a ＜0，b ＜0，c ＜0，b 2- 4ac ＞0C 、a ＜0，b ＞0，c ＞0，b 2- 4ac ＜0D 、a ＞0，b ＜0，c ＞0，b 2- 4ac ＞03.（2015•泸州）已知二次函数y=ax 2+bx+c （a ，b ，c 为常数，a ≠0）的图象如图所示，有下列结论：①abc ＞0，②b 2- 4ac ＜0，③a-b+c ＞0，④a+b+c ＜0，其中正确结论的个数是（）A 、1B 、2C 、3D 、44.（2015•仙游县二模）已知二次函数y=ax 2+bx+c （a ≠0）的图象如图所示，给出以下结论： ①a+b+c ＜0； ②a ﹣b+c ＜0； ③b+2a ＜0； ④abc ＞0．5.（2011•雅安）已知二次函数y=ax2+bx+c的图象如图，其对称轴x=-1，给出下列结果①b2＞4ac；②abc＞0；③2a+b=0；④a+b+c＞0；⑤a-b+c＜0，则正确的结论是（）A、①②③④B、②④⑤C、②③④D、①④⑤6.（2015•黔南州）如图所示为二次函数y=ax2+bx+c（a≠0）的图象，在下列选项中错误的是（）A、ac＜0B、x＞1时，y随x的增大而增大C、a+b+c＞0D、方程ax2+bx+c=0的根是=-1，=3能力提升1.已知二次函数y=ax2+bx+c（a≠0）的图象如下图所示，有下列5个结论：①abc＜0；②a-b+c＞0；③2a+b=0；④b2- 4ac＞0；⑤a+b+c＞m（am+b）+c（m＞1的实数），其中正确的结论有（）A．1个B．2个C．3个D．4个2.（2015•天津）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列结论：①b2- 4ac＞0；②abc＞0；③8a+c＞0；④9a+3b+c＜0其中，正确结论的个数是（）A、1B、2C、3D、43．（2014•玉林一模）如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：①b2＞4ac；②2a+b=0；③3a+c=0；④a+b+c=0．其中正确结论的个数是（）4. 如图所示，二次函数y=ax2+bx+c（a≠0）的图象经过点（-1，2），且与x轴交点的横坐标为x1、x2，其中-2＜x1＜-1，0＜x2＜1，下列结论：①abc＞0；②4a-2b+c＜0；③2a-b ＞0；④b2+8a＞4ac，正确的结论是。

二次函数图象与系数a、b、c的关系

模块三函数第五讲二次函数图象与a 、b 、c 的关系知识梳理夯实基础二次函数图象的特征与a ，b ，c 的关系字母的符号图象的特征a >0开口向上aa <0开口向下b =0对称轴为y 轴ab >0（a 与b 同号）对称轴在y 轴左侧bab <0（a 与b 异号）对称轴在y 轴右侧c =0经过原点c >0与y 轴正半轴相交cc <0与y 轴负半轴相交b 2–4ac =0与x 轴有唯一交点（顶点）b 2–4ac >0与x 轴有两个交点b 2–4acb 2–4ac <0与x 轴没有交点常用公式及方法：（1）二次函数三种表达式：表达式顶点坐标对称轴一般式c bx ax y ++=2⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22abx 2-=顶点式()kh x a y +-=2()k h ,hx =交点式()()12y a x x x x =--()⎪⎪⎭⎫ ⎝⎛--+4,222121x x a x x 221x x x +=（2）韦达定理：若二次函数c bx ax y ++=2图象与x 轴有两个交点且交点坐标为（1x ，0）和（2x ，0），则a b x x -=+21，acx x =⋅21。

（3）赋值法：在二次函数c bx ax y ++=2中，令1=x ，则c b a y ++=；令1-=x ，则c b a y +-=；令2=x ，则c b a y ++=24；令2-=x ，则c b a y +-=24；利用图象上对应点的位置来判断含有a 、b 、c 的关系式的正确性。

直击中考胜券在握1．（2021·山东日照中考）抛物线()20y ax bx c a =++¹的对称轴是直线1x =-，其图象如图所示．下列结论：①0abc <；②()()2242a c b +<；③若()11,x y 和()22,x y 是抛物线上的两点，则当1211x x +>+时，12y y <；④抛物线的顶点坐标为()1,m -，则关于x 的方程21ax bx c m ++=-无实数根．其中正确结论的个数是（）A ．4B ．3C ．2D ．1【答案】B 【分析】①由图象开口方向，对称轴位置，与y 轴交点位置判断a ，b ，c 符号．②把2x =±分别代入函数解析式，结合图象可得22(4)(2)a c b +-的结果符号为负．③由抛物线开口向上，距离对称轴距离越远的点y 值越大．④由抛物线顶点纵坐标为m 可得2ax bx c m ++…，从而进行判断21ax bx c m ++=-无实数根．【详解】解：①Q 抛物线图象开口向上，0a \>，Q 对称轴在直线y 轴左侧，a \，b 同号，0b >，Q 抛物线与y 轴交点在x 轴下方，0c \<，0abc \<，故①正确．②22(4)(2)(42)(42)a c b a c b a c b +-=+++-，当2x =时242ax bx c a c b ++=++，由图象可得420a c b ++>，当2x =-时，242ax bx c a c b ++=+-，由图象可得420a c b +-<，22(4)(2)0a c b \+-<，即22(4)(2)a c b +<，故②正确．③11|1||(1)|x x +=--，22|1||(1)|x x +=--，12|1||1|x x +>+Q ，\点1(x ，1)y 到对称轴的距离大于点2(x ，2)y 到对称轴的距离，12|y y \>，故③错误．④Q 抛物线的顶点坐标为(1,)m -，y m \…，2ax bx c m \++…，21ax bx c m \++=-无实数根．故④正确，综上所述，①②④正确，故选：B ．【点睛】本题考查二次函数的图象的性质，解题关键是熟练掌握二次函数2(0)y ax bx c a =++¹中a ，b ，c 与函数图象的关系．2．（2021·四川巴中中考）已知二次函数y ＝ax 2+bx +c 的自变量x 与函数y 的部分对应值见表格，则下列结论：①c ＝2；②b 2﹣4ac ＞0；③方程ax 2+bx ＝0的两根为x 1＝﹣2，x 2＝0；④7a +c ＜0．其中正确的有（）x…﹣3﹣2﹣112…y … 1.8753m 1.8750…A ．①④B ．②③C ．③④D ．②④【答案】B 【分析】由表格可以得到二次函数图象经过点点（-3，1.875）和点（1，1.875），这两点关于对称轴对称，由此得到对称轴直线，设出二次函数顶点式，代入两点，求解出二次函数解析式，得到a ，b ，c 的值，依次代入到①②③④中进行判断即可解决．【详解】解：由表格可以得到，二次函数图象经过点(3,1.875)-和点(1,1.875)，Q 点(3,1.875)-与点(1,1.875)是关于二次函数对称轴对称的，\二次函数的对称轴为直线3112x -+==-，\设二次函数解析式为2(1)y a x h =++，代入点(2,3)-，(2,0)得，390a h a h +=ìí+=î，解得38278a h ì=-ïïíï=ïî，\二次函数的解析式为：2327(1)88y x =-++，Q 233384y x x =--+，3c \=，\①是错误的，2934430168b ac -=+´´>Q ，\②是正确的，方程20ax bx +=为233084x x --=，即为220x x +=，12x \=-，20x =，\③是正确的，3377()3088a c +=´-+=>Q ，\④是错误的，\②③是正确的，故选：B ．【点睛】本题考查了二次函数系数特征和二次函数解析式求法，利用待定系数法求解函数解析式是通法，由表格提炼出对称轴的信息，是解题的突破口，此题，也可以通过二次函数系数特征来解决．3．（2021·牡丹江中考）如图，抛物线y ＝ax 2＋bx ＋c （a ≠0）的顶点为（1，n ），与x 轴的一个交点B （3，0），与y 轴的交点在（0，﹣3）和（0，﹣2）之间．下列结论中：①ab c>0；②﹣2＜b 53<-；③（a ＋c ）2﹣b 2＝0；④2c ﹣a ＜2n ，则正确的个数为（）A ．1B ．2C ．3D ．4【答案】B 【分析】根据二次函数的图象和性质逐一进行判断即可【详解】解：∵抛物线y ＝ax 2＋bx ＋c （a ≠0）的开口向上， ∴a ＞0，∵抛物线线y ＝ax 2＋bx ＋c （a ≠0）的顶点坐标为（1，n ），∴对称轴x =12ba-=，∴b =-2a ＜0，∵抛物线与y 轴的交点在（0，﹣3）和（0，﹣2）之间∴-3＜c ＜-2＜0，∴abc>0；故①正确；∵抛物线线x 轴的一个交点B （3，0），∴9a +3b +c =0，抛物线线x 轴的一个交点（-1，0），∵b =-2a ∴c =32b，∴-3＜32b＜-2，∴﹣2＜b 43<-，故②错误；∵抛物线线x 轴的一个交点（-1，0），∴a -b +c =0，∴（a ＋c ）2﹣b 2＝（a +b +c ）（a -b +c ）=0，故③正确；∵a ＞0，∴-a ＜0∵b =-2a ∴3a +2b =-a ＜0∴2c ﹣a ＞2（a +b +c ），∵抛物线y ＝ax 2＋bx ＋c （a ≠0）的顶点为（1，n ），∴a +b +c =n ，∴2c ﹣a ＞2n ；故④错误；故选：B 【点睛】本题考查了二次函数图象与系数的关系：对于二次函数y =ax 2+bx +c （a ≠0），明确以下几点：①二次项系数a 决定抛物线的开口方向和大小：当a ＞0时，抛物线向上开口；当a ＜0时，抛物线向下开口；②一次项系数b 和二次项系数a 共同决定对称轴的位置：当a 与b 同号时（即ab ＞0），对称轴在y 轴左；当a 与b 异号时（即ab ＜0），对称轴在y 轴右；③常数项c 决定抛物线与y 轴交点位置：抛物线与y 轴交于（0，c ）．4．（2021·湖北荆门中考）抛物线2y ax bx c =++（a ，b ，c 为常数）开口向下且过点(1,0)A ，(,0)B m （21m -<<-），下列结论：①20b c +>；②20a c +<；③ (1)0a m b c +-+>；④若方程()(1)10a x m x ---=有两个不相等的实数根，则244ac b a -<．其中正确结论的个数是（）A ．4B ．3C ．2D ．1【答案】A 【分析】根据已知条件可判断0c >，0a b <<，据此逐项分析解题即可．【详解】解：Q 抛物线开口向下a \<把(1,0)A ，(,0)B m 代入2y ax bx c =++得200a b c am bm c ++=ìí++=î2am bm a b\+=+20am bm a b \+--=(1)()0m am a b -++=21m -<<-Q 0am a b \++=,(1)am c a m b\=+=-0c \>110m \-<+<10m +<Q 11022m +\-<<1022b a\-<-<10b a\>>0a b \<<①220b c b a b b a +=--=->，故①正确；②220a c a a b a b +=--=-<，故②正确；③ (1)2230a m b c b c b a b b a +-+=-+=---=-->，故③正确；；④若方程()(1)10a x m x ---=有两个不相等的实数根，即2(1)10ax a m x am -++-=22(1)4(1)a m a am D =+--222(1)44a m a m a=+-+2244a bb a a a--=-⋅+22444b a ab a=+++24()4b a a b a=+++2440b ac a =-+>244ac b a \-<，故④正确，即正确结论的个数是4，故选：A ．【点睛】本题考查二次函数的图象与性质、二次函数与系数a 、b 、c 关系，涉及一元二次方程根的判别式，是重要考点，有难度，掌握相关知识是解题关键．5．（2021·辽宁丹东中考）已知抛物线2(0)y ax bx c a =++>，且13,22a b c a b c ++=--+=-．判断下列结论：①0abc <；②220a b c ++>；③抛物线与x 轴正半轴必有一个交点；④当23x ££时，3y a =最小；⑤该抛物线与直线y x c =-有两个交点，其中正确结论的个数（）A ．2B ．3C ．4D ．5【答案】D 【分析】由题意易得1,12b c a ==--，则有0c <，进而可判定①②，当x =1时，则12y a b c =++=-，当x =-1时，则有32y a b c =-+=-，然后可判定③，由题意可知抛物线的对称轴为直线104x a =-<，则有当23x ££时，y 随x 的增大而增大，故可得④；联立抛物线及直线解析式即可判断⑤．【详解】解：∵13,22a b c a b c ++=--+=-，∴两式相减得12b =，两式相加得1c a =--，∴0c <，∵0,0,0a b c >><，∴0abc <，故①正确；∴12222102a b c a a a ++=+´--=>，故②正确；∵当x =1时，则12y a b c =++=-，当x =-1时，则有32y a b c =-+=-，∴当0y =时，则方程20ax bx c =++的两个根一个小于-1，一个根大于1，∴抛物线与x 轴正半轴必有一个交点，故③正确；由题意可知抛物线的对称轴为直线1024b x a a=-=-<，∴当23x ££时，y 随x 的增大而增大，∴当2x =时，有最小值，即为424113y a b c a a a =++=+--=，故④正确；联立抛物线2y ax bx c =++及直线y x c =-可得：2x c ax bx c -=++，整理得：22012ax x c -+=，∴1804ac D =->，∴该抛物线与直线y x c =-有两个交点，故⑤正确；∴正确的个数有5个；故选D ．【点睛】本题主要考查二次函数的综合，熟练掌握二次函数的图象与性质是解题的关键．6．（2021·山东枣庄中考）二次函数()20y ax bx c a =++¹的部分图象如图所示，对称轴为12x =，且经过点()2,0．下列说法：①0abc <；②20b c -+=；③420a b c ++<；④若11,2y ⎛⎫-⎪⎝⎭，25,2y ⎛⎫⎪⎝⎭是抛物线上的两点，则12y y <；⑤()14b c m am b c +>++（其中12m ¹）．正确的结论有（）A ．2个B ．3个C ．4个D ．5个【答案】B 【分析】先根据抛物线开口向下、与y 轴的交点位于y 轴正半轴0,0a c <>，再根据对称轴可得0b a =->，由此可判断结论①；将点()2,0代入二次函数的解析式可判断结论②③；根据二次函数的对称轴可得其增减性，由此可判断结论④；利用二次函数的性质可求出其最大值，由此即可得判断结论⑤．【详解】解：Q 抛物线的开口向下，与y 轴的交点位于y 轴正半轴，0,0a c \<>，Q 抛物线的对称轴为122b x a =-=，0b a \=->，0abc \<，则结论①正确；将点()2,0代入二次函数的解析式得：420a b c ++=，则结论③错误；将a b =-代入得：20b c -+=，则结论②正确；Q 抛物线的对称轴为12x =，32x \=和12x =-时的函数值相等，即都为1y ，又Q 当12x ³时，y 随x 的增大而减小，且3522<，12y y \>，则结论④错误；由函数图象可知，当12x =时，y 取得最大值，最大值为1111142424a b c b b c b c ++=-++=+，12m ¹Q ，214b c am bm c +>++\，即1()4b c m am b c +>++，结论⑤正确；综上，正确的结论有①②⑤，共3个，故选：B ．【点睛】本题考查了二次函数的图象与性质，熟练掌握二次函数的图象与性质是解题关键．7．（2021·四川广安中考）二次函数()20y ax bx c a =++¹的图象如图所示，有下列结论：①0abc >，②420a b c -+<，③()a b x ax b -³+，④30a c +<，正确的有（）A ．1个B ．2个C ．3个D ．4个【答案】C【分析】根据抛物线的开口方向，对称轴，与y 轴交点可得a ，b ，c 的符号，从而判断①；再根据二次函数的对称性，与x 轴的交点可得当x =-2时，y ＞0，可判断②；再根据x =-1时，y 取最大值可得a -b +c ≥ax 2+bx +c ，从而判断③；最后根据x =1时，y =a +b +c ，结合b =2a ，可判断④．【详解】解：∵抛物线开口向下，∴a ＜0，∵对称轴为直线x =-1，即12b a-=-，∴b =2a ，则b ＜0，∵抛物线与y 轴交于正半轴，∴c ＞0，∴abc ＞0，故①正确；∵抛物线对称轴为直线x =-1，与x 轴的一个交点横坐标在0和1之间，则与x 轴的另一个交点在-2和-3之间，∴当x =-2时，y =4a -2b +c ＞0，故②错误；∵x =-1时，y =ax 2+bx +c 的最大值是a -b +c ，∴a -b +c ≥ax 2+bx +c ，∴a -b ≥ax 2+bx ，即a -b ≥x （ax +b ），故③正确；∵当x =1时，y =a +b +c ＜0，b =2a ，∴a +2a +c =3a +c ＜0，故④正确；故选：C ．【点睛】此题主要考查了二次函数的图象与系数的关系，要熟练掌握，解答此题的关键是要明确：①二次项系数a 决定抛物线的开口方向和大小：当a ＞0时，抛物线向上开口；当a ＜0时，抛物线向下开口；②一次项系数b 和二次项系数a 共同决定对称轴的位置：当a 与b 同号时（即ab ＞0），对称轴在y 轴左；当a 与b 异号时（即ab ＜0），对称轴在y 轴右．（简称：左同右异）③常数项c 决定抛物线与y 轴交点．抛物线与y 轴交于（0，c ）．8．（2021·湖南株洲中考）二次函数()20y ax bx c a =++¹的图像如图所示，点 P 在x 轴的正半轴上，且1OP =，设()M ac a b c =++，则 M 的取值范围为（）A ．1M <-B ．10M -<<C ．0M <D ．0M >【答案】D【分析】由图像可得0a <，0c >，当1x =，y a b c =++，并与x 轴交于OP 之间，得0a b c ++<，据悉可得()0M ac a b c =++>，据此求解即可．【详解】解：由图像可知，图像开口向下，并与y 轴相交于正半轴，∴0a <，0c >，当1x =，211y a b c a b c =++=++g g ，∵1OP =，并由图像可得，二次函数2y ax bx c =++与x 轴交于OP 之间，∴0a b c ++<∴()0M ac a b c =++>，故选：D ．【点睛】本题考查二次函数图象及性质，熟悉相关性质是解题的关键．9．（2021·齐齐哈尔中考）如图，二次函数2(0)y ax bx c a =++¹图象的一部分与x 轴的一个交点坐标为()1,0，对称轴为1x =-，结合图象给出下列结论：①0a b c ++=；②20a b c -+<；③关于x 的一元二次方程20(a 0)++=¹ax bx c 的两根分别为-3和1；④若点()14,y -，()22,y -，()33,y 均在二次函数图象上，则123y y y <<；⑤()a b m am b -<+（m 为任意实数）．其中正确的结论有（）A ．1个B ．2个C ．3个D ．4个【答案】C 【分析】根据二次函数的图像及性质逐项分析即可判断．【详解】解：∵二次函数2(0)y ax bx c a =++¹图象的一部分与x 轴的一个交点坐标为()1,0，∴当x =1时，0a b c ++=，故结论①正确；根据函数图像可知，当10x y =-<，，即0a b c -+<，对称轴为1x =-，即12b a-=-，根据抛物线开口向上，得0a ＞，∴20b a =＞，∴0a b c b -+-<，即20a b c -+<，故结论②正确；根据抛物线与x 轴的一个交点为()1,0，对称轴为1x =-可知：抛物线与x 轴的另一个交点为(-3，0)，∴关于x 的一元二次方程20(a 0)++=¹ax bx c 的两根分别为-3和1，故结论③正确；根据函数图像可知：213y y y <<，故结论④错误；当x m =时，2()y am bm c m am b c =++=++，∴当1m =-时，()a b c m am b c -+=++，即()a b m am b -=+，故结论⑤错误，综上：①②③正确，故选：C ．【点睛】本题主要考查二次函数图像与系数的关系，解题的关键是熟练掌握二次函数的性质，正确理解二次函数与方程的关系．10．（2021·湖北鄂州中考）二次函数()20y ax bx c a =++¹的图象的一部分如图所示．已知图象经过点()1,0-，其对称轴为直线1x =．下列结论：①0abc <；②420a b c ++<；③80a c +<；④若抛物线经过点()3,n -，则关于x 的一元二次方程()200ax bx c n a ++-=¹的两根分别为3-，5，上述结论中正确结论的个数为（）A ．1个B ．2个C ．3个D ．4个【答案】C【分析】根据二次函数的图象与性质进行逐项判断即可求解．【详解】解：①由图象可知，a ＜0，b ＞0，c ＞0，∴abc ＜0，故①正确；②∵对称轴为直线x = 2b a-=1，且图象与x 轴交于点（﹣1，0），∴图象与x 轴的另一个交点坐标为（3，0），b=﹣2a ，∴根据图象，当x =2时，y =4a +2b +c ＞0，故②错误；③根据图象，当x =﹣2时，y =4a ﹣2b +c =4a +4a +c =8a +c ＜0，故③正确；④∵抛物线经过点()3,n -，∴根据抛物线的对称性，抛物线也经过点()5,n ，∴抛物线2y ax bx c =++与直线y =n 的交点坐标为（﹣3，n ）和（5，n ），∴一元二次方程()200ax bx c n a ++-=¹的两根分别为3-，5，故④正确，综上，上述结论中正确结论有①③④，故选：C ．本题考查二次函数的图象与性质，熟练掌握二次函数的图象与系数之间的关系是解答的关键．11．（2021·江苏宿迁·中考真题）已知二次函数2y ax bx c =++的图像如图所示，有下列结论：①0a ＞；②24b ac -＞0；③40a b +=；④不等式21ax b x c +-+（）＜0的解集为1≤x ＜3，正确的结论个数是（）A ．1B ．2C ．3D ．4【答案】A【分析】根据抛物线的开口方向、于x 轴的交点情况、对称轴的知识可判①②③的正误，再根据函数图象的特征确定出函数的解析式，进而确定不等式，最后求解不等式即可判定④．【详解】解：∵抛物线的开口向上，∴a ＞0，故①正确；∵抛物线与x 轴没有交点∴24b ac -＜0，故②错误∵由抛物线可知图象过（1,1），且过点（3,3）1933a b c a b c ++=ìí++=î∴8a+2b=2∴4a +b =1，故③错误；由抛物线可知顶点坐标为（1,1），且过点（3,3）则抛物线与直线y=x 交于这两点∴()21ax b x c +-+＜0可化为2ax bx c x ++<，根据图象，解得：1＜x ＜3故选A ．【点睛】本题主要考查了二次函数图象的特征以及解不等式的相关知识，灵活运用二次函数图象的特征成为解答本题的关键．12．（2021·四川达州中考）如图，已知抛物线2y ax bx c =++（a ，b ，c 为常数，0a ¹）经过点()2,0，且对称轴为直线12x =，有下列结论：①0abc >；②0a b +>；③4230a b c ++<；④无论a ，b ，c 取何值，抛物线一定经过,02c a ⎛⎫ ⎪⎝⎭；⑤2440am bm b +-≥．其中正确结论有（）A ．1个B ．2个C ．3个D ．4个【答案】D【分析】①根据图像开口向上，对称轴位置，与y 轴交点分别判断出a ,b ,c 的正负②根据对称轴公式2b x a =-，12x =判断,a b 的大小关系③根据2x =时，0y =，比较423a b c ++与0的大小；④根据抛物线的对称性，得到2x =与1x =-时的函数值相等结合②的结论判断即可⑤根据抛物线对称轴找到顶点坐标的纵坐标，比较任意一点与顶点的纵坐标值，即比较函数值的大小即可判断结论．【详解】①图像开口朝上，故0a > ，根据对称轴“左同右异”可知0b <，图像与y 轴交点位于x 轴下方，可知c <0abc \>故①正确；②122b x a =-=得=-a b 0a b \+=③2y ax bx c =++Q 经过()2,0420a b c \++=又由①得c <04230a b c \++<故③正确；④根据抛物线的对称性，得到2x =与1x =-时的函数值相等\ 当1x =-时0y =，即0a b c -+=a b=-Q 20a c \+=即12c a=- \ 2y ax bx c =++经过,02c a ⎛⎫⎪⎝⎭，即经过(1,0)- 故④正确；⑤当12x =时,1142y a b c =++, 当x m =时,2y am bm c =++0a >Q\ 函数有最小值1142a b c ++\ 21142am bm c a b c ++³++化简得2440am bm b +-≥，故⑤正确．综上所述：①③④⑤正确．故选D ．【点睛】本题考查二次函数图象与性质，二次函数解析式中系数与图像的关系，结合图像逐项分析,结已知条件得出结论是解题的关键．13．（2021·湖北随州中考）如图，已知抛物线2y ax bx c =++的对称轴在y 轴右侧，抛物线与x 轴交于点()2,0A -和点B ，与y 轴的负半轴交于点C ，且2OB OC =，则下列结论：①0a b c ->；②241b ac -=；③14a =；④当10b -<<时，在x 轴下方的抛物线上一定存在关于对称轴对称的两点M ，N （点M 在点N 左边），使得AN BM ^．其中正确的有（）A ．1个B ．2个C ．3个D ．4个【答案】B【分析】依据抛物线的图像和性质，根据题意结合二次函数图象与系数的关系，逐条分析结论进行判断即可【详解】①从图像观察，开口朝上，所以0a >，对称轴在y 轴右侧，所以0b <，图像与y 轴交点在x 轴下方，所以0c <0,0a b a b c--><\，所以①不正确；②点()2,0A -和点B ，与y 轴的负半轴交于点(0,)C c ，且2OB OC=设(2,0)B c -代入2y ax bx c =++,得：2420ac bc c -+=0c ¹Q \241b ac -=，所以②正确；③Q ()2,0A -，(2,0)B c -设抛物线解析式为：(2)(2)y a x x c =++过(0,)C c 4c ac \= 14a \=，所以③正确；④如图：设,AN BM 交点为P ，对称轴与x 轴交点为Q ，顶点为D ，根据抛物线的对称性，APB △ 是等腰直角三角形，()2,0A -Q ，(2,0)B c -22AB c \=-，112PQ AB c ==- 又对称轴2(2)12c x c -+-==+ (1,1)P c c \+- 由顶点坐标公式可知24(1,)4ac b D c a-+ 14a =Q 2(1,)D c cb \+- 由题意21c b c -<-，解得1b > 或者1b <-由①知0b <\1b <-，所以④不正确．综上所述：②③正确共2个故选B ．【点睛】本题考查了二次函数图象与系数的关系，利用了数形结合的思想，二次函数2y ax bx c =++（a ≠0），a 的符号由抛物线的开口决定；b 的符号由a 及对称轴的位置确定；c 的符号由抛物线与y 轴交点的位置确定，此外还有注意利用特殊点1，-1及2对应函数值的正负来解决是解题的关键．14．（2021·天津中考）已知抛物线2y ax bx c =++（,,a b c 是常数，0a ¹）经过点(1,1),(0,1)--，当2x =-时，与其对应的函数值1y >．有下列结论：①0abc >；②关于x 的方程230ax bx c ++-=有两个不等的实数根；③7a b c ++>．其中，正确结论的个数是（）A ．0B ．1C ．2D ．3【答案】D【分析】根据函数与点的关系,一元二次方程根的判别式,不等式的性质，逐一计算判断即可【详解】∵抛物线2y ax bx c =++（,,a b c 是常数，0a ¹）经过点(1,1),(0,1)--，当2x =-时，与其对应的函数值1y >．∴c =1＞0，a -b +c = -1,4a -2b +c ＞1，∴a -b = -2,2a -b ＞0，∴2a -a -2＞0，∴a ＞2＞0，∴b =a +2＞0，∴abc ＞0，∵230ax bx c ++-=,∴△=24(3)b a c --=28b a +＞0,∴230ax bx c ++-=有两个不等的实数根；∵b =a +2，a ＞2，c =1，∴a +b +c =a +a +2+1=2a +3，∵a ＞2，∴2a ＞4，∴2a +3＞4+3＞7，故选D ．【点睛】本题考查了二次函数的性质，一元二次方程根的判别式，不等式的基本性质，熟练掌握二次函数的性质，灵活使用根的判别式，准确掌握不等式的基本性质是解题的关键．15．（2021·四川遂宁中考）已知二次函数2(0)y ax bx c a =++¹的图象如图所示，有下列5个结论：①0abc >；②24b ac <；③23c b <；④2()a b m am b +>+（1m ¹）；⑤若方程2ax bx c ++＝1有四个根，则这四个根的和为2，其中正确的结论有（）A ．2个B ．3个C ．4个D ．5个【答案】A【分析】根据抛物线的开口向下，对称轴方程以及图象与y 轴的交点得到a ，b ，c 的取值，于是可对①进行判断；根据抛物线与x 轴的交点的个数可对②进行判断；根据对称轴可得12b a-=，则12a b =-，根据1x =-可得0a b c -+<，代入变形可对③进行判断；当1x =时，y a b c =++的值最大，即当(1)x m m =¹时，即a b c ++>2am bm c ++，则可对④进行判断；由于方程ax 2+bx +c =1有2个根，方程ax 2+bx +c =-1有2个根，则利用根与系数的关系可对⑤进行判断．【详解】解：①∵抛物线开口方向向下，∴a ＜0，∵抛物线与y 轴交于正半轴，∴c ＞0，∵对称轴在y 轴右侧，∴b ＞0，∴abc ＜0，①错误；②∵抛物线与x 轴有两个交点∴24b ac ->0∴24b ac >，故②错误；③∵抛物线的对称轴为直线x =1，∴12b a-=，∴12a b =-由图象得，当1x =-时，0y a b c =-+<，∴102b bc --+<∴23c b <，故③正确；④当1x =时，y a b c =++的值最大，∴当(1)x m m =¹时，a b c ++>2am bm c ++，∴()a b m am b +>+（1m ¹），∵b ＞0，∴2()a b m am b +>+（1m ¹），故④正确；⑤∵方程|ax 2+bx +c |=1有四个根，∴方程ax 2+bx +c =1有2个根，方程ax 2+bx +c =-1有2个根，∴所有根之和为2×（-b a）=2×2a a =4，所以⑤错误．∴正确的结论是③④，故选：A【点睛】本题考查了二次函数图象与系数的关系：对于二次函数y =ax 2+bx +c （a ≠0），二次项系数a 决定抛物线的开口方向和大小．当a ＞0时，抛物线向上开口；当a ＜0时，抛物线向下开口；一次项系数b 和二次项系数a 共同决定对称轴的位置．当a 与b 同号时（即ab ＞0），对称轴在y 轴左；当a 与b 异号时（即ab ＜0），对称轴在y 轴右．常数项c 决定抛物线与y 轴交点位置：抛物线与y 轴交于（0，c ）．抛物线与x 轴交点个数由△决定：△=b 2-4ac ＞0时，抛物线与x 轴有2个交点；△=b 2-4ac =0时，抛物线与x 轴有1个交点；△=b 2-4ac ＜0时，抛物线与x 轴没有交点．16．（2013·山东德州中考）函数y=x 2+bx+c 与y=x 的图象如图所示，有以下结论：①b 2﹣4c ＞0；②b+c+1=0；③3b+c+6=0；④当1＜x ＜3时，x 2+（b ﹣1）x+c ＜0．其中正确的个数为A ．1B ．2C ．3D ．4【答案】B【详解】分析：∵函数y=x2+bx+c与x轴无交点，∴b2﹣4c＜0；故①错误．当x=1时，y=1+b+c=1，故②错误．∵当x=3时，y=9+3b+c=3，∴3b+c+6=0．故③正确．∵当1＜x＜3时，二次函数值小于一次函数值，∴x2+bx+c＜x，∴x2+（b﹣1）x+c＜0．故④正确．综上所述，正确的结论有③④两个，故选B．。

确定abc的符号

教法、学法指导
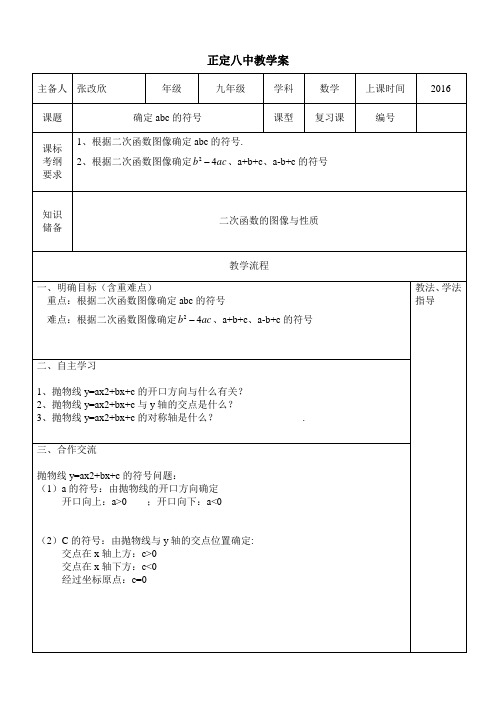
2、自主学习
1、抛物线y=ax2+bx+c的开口方向与什么有关？
2、抛物线y=ax2+bx+c与y轴的交点是什么？
3、抛物线y=ax2+bx+c的对称轴是什么？.
3、合作交流
抛物线y=ax2+bx+c的符号问题：
（1）a的符号：由抛物线的开口方向确定
开口向上：a>0；开口向下：a<0
（2）C的符号：由抛物线与y轴的交点位置确定:
交点在x轴上方：c>0
交点在x轴下方：c<0
经过坐标原点：c=0
4、展示评价
（3）b的符号：由对称轴的位置确定：
对称轴在y轴左侧：a、b同号
对称轴在y轴右侧：பைடு நூலகம்、b异号
对称轴是y轴：b=0
简记为：左同右异
（4）b -4ac的符号：由抛物线与x轴的交点个数确定:
与x轴有两个交点：b -4ac>0
与x轴有一个交点：b -4ac=0
与x轴无交点：b -4ac<0
5、质疑解难
抛物线y=ax2+bx+c的符号问题：
（5）a+b+c的符号：由x=1时抛物线上的点的位置确定
（6）a-b+c的符号：由x=-1时抛物线上的点的位置确定
6、巩固延伸
已知：二次函数y=ax2+bx+c的图象如图所示，下列结论中：①abc＞0；②b=2a；③a+b+c＜0；④a+b-c＞0;⑤a-b+c＞0正确的个数是（）
A、2个B、3个
C、4个D、5个
板书设计：
课后反思：
正定八中教学案

2.二次函数有关符号的判断

练一练：
1、已知：二次函数y=ax2+bx+c的图象如图所示，下列结论中：①abc＞0；②b=2a；③a+b+c＜0； ④a+b-c＞0; ⑤a-b+c＞0正确的个数是（ C ） y A、2个 B、3个
C、4个
D、5个
-1 o
1
x
练一练：
2、已知：二次函数y=ax2+bx+c的图象如图所示，下列结论中不正确的是（ D ） y A、abc＞0 B、b2-4ac＞0
C、2a+b＞0
D、4a-2b
3、已知：二次函数y=ax2+bx+c的图象如图所示，下列结论中：①b＞0；②c<0；③4a+2b+c ＞ 0； ④（a+c）2＜b2，其中正确的个数是（ B ） A、4个 B、3个
C、2个
D、1个
y
o
x=1
x
谈谈你的收获? 1 a、b、c、△等符号性质 2 a+b+c的符号 3 a-b+c的符号 4 解信息题技巧`
a>0 b<0 c>0 △>0
o
x
做一做
抛物线y=ax2+bx+c如图所示，试确定a、b、c、△ 的符号： y
a>0 b>0 c=0 △>0
x
o
练一练
抛物线y=ax2+bx+c如图所示，试确定a、b、c、△ 的符号： y
o
a<0 b<0 c>0 △>0
x
你行的!
抛物线y=ax2+bx+c如图所示，试确定a、b、c、△ 的符号： y

二次函数的图象中abc式子的正负判断

《根据二次函数的图象判定abc式子的正负》专项练习
1.二次函数y=ax2+bx+c（a≠0）的图象如图如图所示，若M=a+b﹣c，N=4a﹣2b+c，P=2a ﹣b．则M，N，P中，值小于0的数有（）
A：3个 B：2个 C：1个 D：0个
2.如图为二次函数y=ax2+bx+c（a≠0）的图象，则下列说法：①a＞0；②2a+b=0；③a+b+c ＞0；④△＞0；⑤4a﹣2b+c＜0，其中正确的个数为（）
A：1 B：2 C：3 D：4
3.如图，抛物线y=ax2+bx+c经过点（﹣1，0），对称轴l如图所示，则下列结论：①abc ＞0；②a﹣b+c=0；③2a+c＜0；④a+b＜0，其中所有正确的结论是（）
A：①③ B：②③ C：②④ D：②③④
（第3题图）
4、二次函数y=ax2+bx+c（a≠0）的图象如图，给出下列四个结论：①4ac-b2＜0；②4a+c ＜2b；③3b+2c＜0；④m（am+b）+b＜a（m≠-1），
其中正确结论的是
5、二次函数y=ax2+bx+c（a≠0）的图象如图，给出下列四个结论：①4ac﹣b 2 ＜0；
②4a+c＜2b；③3b+2c＜0；④m（am+b）+b＜a（m≠﹣1），其中正确结论的个数是（）
6、二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列说法：①2a+b=0②当-1≤x≤3时，y＜0③若（x1，y1）、（x2，y2）在函数图象上，当x1＜x2时，y1＜y2④9a+3b+c=0。

其中正确的是（）
A:①②④ B:①④ C:①②③ D:③④。

二次函数一般式的图像与性质与abc符号

对于二次函数y=ax²+bx+c （ a≠0 ）的图
象及图象的形状、开口方向、位置又是怎样的？
通过变形能否将 y=ax²+bx+c转化为 y = a(x+m)2 +k的形式？
二次函数一般式的图像与性质与 abc符号
y=ax²+bx+c
=a（x2+
b a
x）+c
=a〔x2+ b
x+
b
2
–
b
2
2、抛物线y=2（x-2）2 - 3是由抛物线y=2(x-2)2
向下___平移_3__单位而得到的，也可由抛物线y=2x2 先向__右_平移_2__单位，再而得向__下__平移___3_单位得到的。
二次函数一般式的图像与性质与 abc符号
二次函数y=ax² y = a(x+m)2 y = a(x+m)2 +k
二次函数一般式的图像与性质与 abc符号
做一做:
2.说出下列抛物线的开口方向、顶点坐标和对称轴：
(1 )y 5 x 2 5 x 3 (2 )y 2 x 2 22 x 3 4 24
(3) y 2(x 1)(x 2)
(4) y 2x(1 x) 3 2
3. 说出上面函数的图象可由怎样的抛物线
26.1 二次函数的图象与性质（5）
二次函数一般式的图像与性质与 abc符号
知识回顾:
二次函数y=ax² y = a(x-m)2
y = a(x-m)2 +k
时，图象将发生怎样的变化？
1、顶点坐标？
（0，0）
（m，0）
（ m，k ）
2、对称轴？
（ y轴或直线x=0）（直线x= m ）

二次函数中的系数abc符号

B. a<0, b > 0, c<0, b２ <4ac
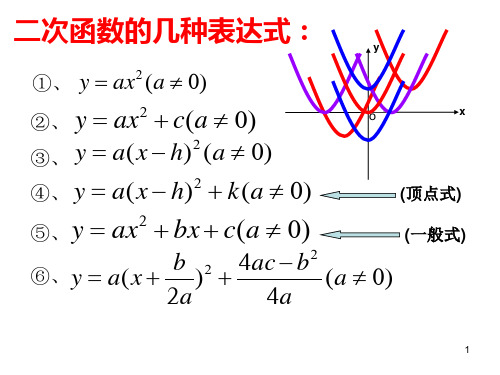
C. a<0, b>0, c>0, b２ > 4ac
D. a>0, b<0, c<0, b２ > 4ac
26
训练2：如图所示抛物线y=ax２+bx+c，则有：
A. a+b+c<0 B. a+b+c=0 C. a+b+c>0 D. a+b+c符号不定
c>0
交点在x轴下方
c<0
经过坐标原点
c=0
7
归纳知识点：
（3）b的符号：由对称轴的位置确定：
对称轴在y轴左侧
a、b同号
对称轴在y轴右侧
a、b异号
对称轴是y轴（4）b2-4ac的符号：
b=0 简记为：左同右异
由抛物线与x轴的交点个数确定:
与x轴有两个交点与x轴有一个交点与x轴无交点
b2-4ac>0 b2-4ac=0
注意：图象的递增性，以及利用图象求自变量x或函数值y的取值范围
（2）a，b，c，Δ的正负与图象的位置关系注意：图象与轴有两个交点A（x1，0），B（x2，0）时
√Δ AB=|x2-x1|= √(x1+x2)2+4x1 x2= ——|a| 这一结论及推导过程。
返回 35
分析： a> 0，b< 0，c< 0
隐含：a－b＋c <0
∴ c －b <－ a c －b < 0
c <b
30
训练6:如图已知二次函数y=ax２+bx+c,如果 a>b>c,且a+b+c=0,则它的图像可能是

二次函数图像与abc的关系ppt课件

练习1：二次函数
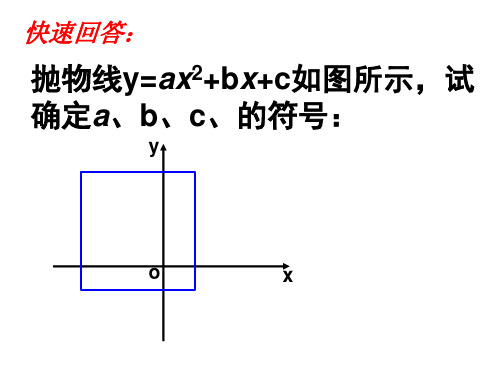
y=ax2+bx+c(a≠0)的图象
如上图所示，那么下列判断
y
正确的有（填序号）
.③ ⑦ ①、abc>0,
●
x
-2 -1 o 1 2
②、b2-4ac<0,
③、2a+b>0,
④、a+b+c<0,
⑤、a-b+c>0,
⑥、4a+2b+c<0,
⑦、4a-2b+c<0.
为了规范事业单位聘用关系，建立和完善适应社会主义市场经济体制的事业单位工作人员聘用制度，保障用人单位和职工的合法权益
判断b的符号
(2)因为对称轴在y轴右侧，所以
b 2a
0பைடு நூலகம்
，而a＜0，故b＞0；
为了规范事业单位聘用关系，建立和完善适应社会主义市场经济体制的事业单位工作人员聘用制度，保障用人单位和职工的合法权益
判断c的符号
(3)因为x＝0时，y＝c，即图象与y轴交点的坐标是(0，c)，而图中这一点在y轴正半轴，即c＞0；
为了规范事业单位聘用关系，建立和完善适应社会主义市场经济体制的事业单位工作人员聘用制度，保障用人单位和职工的合法权益
判断b2－4ac的符号
(4)因为顶点在第一象限，其纵坐标
4ac b2 0 ，且a＜0，所以4acb2 0，故
4a
b2 4ac0 。
为了规范事业单位聘用关系，建立和完善适应社会主义市场经济体制的事业单位工作人员聘用制度，保障用人单位和职工的合法权益
分析：已知的是几何关系(图形的位置、形状)，需要求出的是数量关系，所以应发挥数形结合的作用．

6.3.2二次函数的图象与abc符号的关系

6.3.3二次函数的图象与c b a 、、的符号设计：孙祥审核：孙良付班级：姓名：备课时间：2011年月日上课时间：2011年月日【学习目标】1.经历根据二次函数的图象确定c b a 、、和ac b 42-的符号的过程，体会函数图象与关系式之间的联系；2.渗透数形结合的数学思想。

【课前自学】222. 抛物线()312-+-=x y 的图象开口向，顶点坐标是，说明当x = 时，y 有最值是；对称轴是，当x 时，y 随x 的增大而增大. 3. 抛物线342+-=x x y 与x 轴的交点坐标是，与y 轴的交点坐标是；把它转化为顶点式是：，则顶点坐标是 .【课堂学习】一、自主探索：1.观察c bx ax y ++=2的图象，你能得到关于c b a 、、的哪些信息？ 2.归纳：⑴a 的符号由决定：①开口方向向 ⇔ a 0；②开口方向向 ⇔ a 0⑵b 的符号由决定； ① 在y 轴的左侧 ⇔b a 、；② 在y 轴的右侧 ⇔b a 、； ③ 是y 轴 ⇔b 0.⑶c 的符号由决定： ①点（0，c ）在y 轴正半轴 ⇔c 0； ②点（0，c ）在原点 ⇔c 0； ③点（0，c ）在y 轴负半轴 ⇔c 0.⑷ac b 42-的符号由决定：①抛物线与x 轴有交点⇔ b 2-4ac 0 ⇔方程有实数根； ②抛物线与x 轴有交点⇔ b 2-4ac 0 ⇔方程有实数根； ③抛物线与x 轴有交点⇔ b 2-4ac 0 ⇔方程实数根； ④特别的，当抛物线与x 轴只有一个交点时，这个交点就是抛物线的点. ⑸特别的，当x =1时，y = ，对应的点的坐标记为：；当x =-1时，y = ，对应的点的坐标记为： .【课堂练习】二次函数的图象与性质具体如下图所示：【典型例题】例1、已知二次函数y=ax 2+bx+c （a ≠0）的图象如图所示，则下列4个结论中：①abc>0；②b<a+c ；③4a+2b+c>0；④b 2-4ac>0； ⑤b=2a.正确的是（填序号）【拓展提升】如图抛物线c bx ax y ++=2与x 轴交与点(-3,0)、(1,0),与y 轴交与点（0,-3）.结合图象回答：⑴当0>x 时，y 的取值范围是；当0<x 时，y 的取值范围是 . ⑵当0<y 时，x 的取值范围是；当0>y 时，x 的取值范围是 . ⑶>++c bx ax 20的解集是；c bx ax++2≤0的解集是 .归纳观察图像的方法：①当0>x 时⇔观察的函数图象；当0<x 时⇔观察的函数图象. ②当0>y 时⇔观察的函数图象；当0<y 时⇔观察的函数图象.【课后作业】1.根据图象填空，并说明理由：⑴a 0 ⇔ ；b 0 ⇔；c0 ⇔ ；abc 0.⑵b 2-4ac 0 ⇔ .⑶c b a ++ 0；c b a +- 0；⑷当0>x 时，y 的取值范围是；当0>y 时，x 的取值范围是 .2.（2009年齐齐哈尔市）已知二次函数2(0)y ax bx c a =++≠的图象如下图所示，则下列结论：0ac >①；②方程20ax bx c ++=的两根之和大于0y ③随x 的增大而增大；④0a b c -+<，其中正确的个数（ A ．4个 B ．3个 C ．2个 D ．1个3.（2009年兰州）二次函数c bx ax y ++=2的图象如图所示，则下列关系式不正确的是A ．a ＜0B.abc ＞0C.c b a ++＞0D.ac b 42-＞04.若直线y=ax+b 不经过一、三象限，则抛物线c bx ax y ++=2（）. (A)开口向上，对称轴是y 轴; (B) 开口向下，对称轴是y 轴; (C)开口向上, 对称轴是直线x=1;(D) 开口向下，对称轴是直线x=-1;5. 抛物线()()312-+=x x y 的顶点坐标是( ).(A)(-1,-3); (B)(1,3); (C)(-1,8); (D)(1,-8);6. 若二次函数c bx ax y ++=2的图象的开口向下，顶点在第一象限，抛物线交于y 轴的正半轴; 则点⎪⎭⎫⎝⎛b c a P ,在（）. (A)第一象限; (B) 第二象限; (C) 第三象限; (D) 第四象限;7. 关于二次函数y=ax 2＋bx ＋c 的图象有下列命题：①当c=0时，函数的图象经过原点；②当c ＞0且函数图象开口向下时，方程ax 2＋bx ＋c=0必有两个不等实根；③当a ＜0，函数的图象最高点的纵坐标是ab ac 442-；④当b=0时，函数的图象关于y 轴对称．其中正确命题的个数有（） A ．1个 B ．2个 C ．3个D ．4个8．已知直线y=x+m 与抛物线2x y =相交于两点，则实数m 的取值范围是( ). (A)m ﹥41-; (B)m ﹤41-; (C)m ﹥41; (D) m ﹤41.9.若一条抛物线c bx ax y ++=2的顶点在第二象限，交于y 轴的正半轴，与x 轴有两个交点，则下列结论正确的是（）.(A)a ﹥0,bc ﹥0; (B)a ﹤0,bc ﹤0; (C) a ﹤0, bc ﹥0; (D) a ﹥0, bc ﹤0 10. 抛物线232+-=x x y 不经过（）.（A ）第一象限; (B) 第二象限; (C) 第三象限; (D) 第四象限11. 在同一直角坐标系中，抛物线542-+=x x y 与直线y=2x-6的交点个数是( ). (A)0个 (B)1个 (C)2个 (D)3个 12．已知反比例函数xk y =的图象在二、四象限，则二次函数222k x kx y +-=的图象大致为（）A ．B ．C ．D ．。

二次函数的图像与字母abc的关系

课次教学计划一、知识要点二次函数y=ａx２+bx+c系数符号得确定:ﻫ(１)ａ由抛物线开口方向确定:开口方向向上,则a>０;否则ａ<0。

ﻫ(２)ｂ由对称轴与a得符号确定:由对称轴公式x＝判断符号、ﻫ(３)c由抛物线与y轴得交点确定:交点在y轴正半轴,则c〉0;否则ｃ＜０、ﻫ(4)b2－４ac得符号由抛物线与ｘ轴交点得个数确定:2个交点,b2—４ac>0;1个交点,b ２—4ａｃ=0;没有交点,b２—4ac<0。

ﻫ(5)当ｘ＝1时,可确定a+b+c得符号,当x=-1时,可确定ａ-ｂ+c得符号。

ﻫ(6)由对称轴公式x=,可确定2a+b得符号.二、基础练习１、已知抛物线y＝ax２+bｘ+c(a≠0)在平面直角坐标系中得位置如图所示,则下列结论中,正确得就是( D )A、ａ>0B、b〈0Ｃ、c〈0 Ｄ、ａ+ｂ+ｃ〉02、已知二次函数ｙ=ax2+bｘ+ｃ得图象如图,其对称轴ｘ=-1,给出下列结果①b2>4ac;②ａｂc〉0;③2a+b=0; ④a+b+c〉0;⑤a—b+c＜０,则正确得结论就是( D)A、①②③④Ｂ、②④⑤Ｃ、②③④D、①④⑤３、如图,二次函数ｙ＝ax2+bx+c得图象与y轴正半轴相交,其顶点坐标为( ,1),下列结论:①ac〈０;②a＋b=0;③4ａc—b2=４a;④a+b+ｃ<0。

其中正确结论得个数就是( C )1\2\3A、1B、2Ｃ、3Ｄ、4４、已知二次函数ｙ=ax2＋bｘ+c得图象如图所示,对称轴为直线x=1,则下列结论正确得就是(B)Ａ、ac＞0 B、方程ａｘ２+ｂx＋ｃ=0得两根就是x1＝-1,x2=3C、２ａ-ｂ=0D、当ｘ＞0时,y随ｘ得增大而减小5、已知二次函数y=ax２+bx+c(a,b,c为常数,ａ≠0)得图象如图所示,有下列结论:①abc>0,②-4ac＜0,③a—b+c〉0,④4ａ－2b+c〈０,其中正确结论得个数就是(Ａ4)A、1B、2C、3 Ｄ、４6、(如图所示得二次函数y=ax2+bx+c得图象中,刘星同学观察得出了下面四条信息:(1)b2—4ａc>0;(2)c＞１;(3)2a—b<0;(4)a+b＋c＜０。

二次函数的图像与字母a、b、c的关系

课次教学计划教学过程：一、知识要点二次函数y=ax 2+bx+c 系数符号的确定：（1）a 由抛物线开口方向确定：开口方向向上，则a ＞0；否则a ＜0．（2）b 由对称轴和a 的符号确定：由对称轴公式x=判断符号．（3）c 由抛物线与y 轴的交点确定：交点在y 轴正半轴，则c ＞0；否则c ＜0．（4）b 2-4ac 的符号由抛物线与x 轴交点的个数确定：2个交点，b 2-4ac ＞0；1个交点，b 2-4ac=0；没有交点，b 2-4ac ＜0．（5）当x=1时，可确定a+b+c 的符号，当x=-1时，可确定a-b+c 的符号．（6）由对称轴公式x=，可确定2a+b 的符号．二、基础练习1、已知抛物线y=ax 2+bx+c （a ≠0）在平面直角坐标系中的位置如图所示，则下列结论中，正确的是（ D ） A 、a ＞0 B 、b ＜0 C 、c ＜0 D 、a+b+c ＞02、已知二次函数y=ax 2+bx+c 的图象如图，其对称轴x=-1，给出下列结果①b 2＞4ac ； ②abc ＞0；③2a+b=0； ④a+b+c ＞0；⑤a-b+c ＜0，则正确的结论是（ D ） A 、①②③④ B 、②④⑤ C 、②③④ D 、①④⑤3、如图，二次函数y=ax 2+bx+c 的图象与y 轴正半轴相交，其顶点坐标为（21，1），下列结论：①ac ＜0；②a+b=0；③4ac-b 2=4a ；④a+b+c ＜0．其中正确结论的个数是（ C ）1\2\3A 、1B 、2C 、3D 、4任课教师学科版本年段辅导类型上课时间学生签名数学北师大初三课题二次函数y=a 2x +bx+c 系数符号的确定方法课次教学目标掌握二次函数中字母 a 、b 、c 三者与图象之间的关系。

教学策略教学重点、难点：利用图形的性质与特殊性来确定字母a 、b 、c 三者之间的关系。

4、已知二次函数y=ax 2+bx+c 的图象如图所示，对称轴为直线x=1，则下列结论正确的是（B ）A 、ac ＞0B 、方程ax 2+bx+c=0的两根是x 1=-1，x 2=3 C 、2a-b=0 D 、当x ＞0时，y 随x 的增大而减小5、已知二次函数y=ax 2+bx+c （a ，b ，c 为常数，a ≠0）的图象如图所示，有下列结论： ①abc ＞0，②2b -4ac ＜0，③a-b+c ＞0，④4a-2b+c ＜0，其中正确结论的个数是（A4 ） A 、1 B 、2 C 、3 D 、46、（如图所示的二次函数y=ax 2+bx+c 的图象中，刘星同学观察得出了下面四条信息：（1）b 2-4ac ＞0；（2）c ＞1；（3）2a-b ＜0；（4）a+b+c ＜0．你认为其中错误的有（D2） A 、2个 B 、3个 C 、4个 D 、1个7、抛物线y=ax 2+bx+c （a ≠0）的图象如图所示，则下列说法正确的是（C ） A 、b 2-4ac ＜0 B 、abc ＜0 C 、 -a2b＜-1 D 、a-b+c ＜08、已知二次函数y=ax 2+bx+c （a ≠0）的图象如图所示，现有下列结论：①b 2-4ac ＞0 ②a ＞0 ③b ＞0 ④c ＞0 ⑤9a+3b+c ＜0，则其中结论正确的个数是（B ）1/2/5 A 、2个 B 、3个 C 、4个 D 、5个9、已知二次函数y=ax 2的图象开口向上，则直线y=ax-1经过的象限是（D ） A 、第一、二、三象限 B 、第二、三、四象限 C 、第一、二、四象限 D 、第一、三、四象限10、二次函数y=ax 2+bx+c 的图象如图所示，则下列结论正确的是（D ）A 、a ＜0，b ＜0，c ＞0，b 2-4ac ＞0B 、a ＞0，b ＜0，c ＞0，b 2-4ac ＜0C 、a ＜0，b ＞0，c ＜0，b 2-4ac ＞0D 、a ＜0，b ＞0，c ＞0，b 2-4ac ＞011、已知二次函数y=ax 2+bx+c 的图象如图所示，那么下列判断不正确的是（B ） A 、ac ＜0 B 、a-b+c ＞0C 、b=-4aD 、关于x 的方程a 2x +bx+c=0的根是x 1=-1，x 2=512、已知二次函数y=ax 2+bx+c 的图象如图所示，则a ，b ，c 满足（A ）A 、a ＜0，b ＜0，c ＞0，2b -4ac ＞0 B 、a ＜0，b ＜0，c ＜0，2b -4ac ＞0C 、a ＜0，b ＞0，c ＞0，2b -4ac ＜0D 、a ＞0，b ＜0，c ＞0，2b -4ac ＞013、已知二次函数y=2ax +bx+c （a ≠0）的图象如图所示，有下列4个结论，其中正确的结论是（B ） A 、abc ＞0 B 、b ＞a+c C 、2a-b=0 D 、2b -4ac ＜014、已知二次函数y=2ax +bx+c （a ≠0）的图象如图所示，则下列结论： ①ac ＞0；②a-b+c ＜0；③当x ＜0时，y ＜0；④方程2ax +bx+c=0（a ≠0）有两个大于-1的实数根．其中错误的结论有（C ） A 、②③ B 、②④ C 、①③ D 、①④15、如图所示为二次函数y=ax 2+bx+c （a ≠0）的图象，在下列选项中错误的是（C ） A 、ac ＜0 B 、x ＞1时，y 随x 的增大而增大C 、a+b+c ＞0D 、方程ax 2+bx+c=0的根是1x =-1，2x =316、二次函数y=ax 2+bx+c 的图象如图所示，下列结论错误的是（B ） A 、ab ＜0 B 、ac ＜0C 、当x ＜2时，函数值随x 增大而增大；当x ＞2时，函数值随x 增大而减小D 、二次函数y=2ax +bx+c 的图象与x 轴交点的横坐标就是方程2ax +bx+c=0的根17、已知二次函数y=ax 2+bx+c 的图象如图所示，则下列结论正确的是（D ）A 、a ＞0B 、c ＜0C 、b 2-4ac ＜0 D 、a+b+c ＞018、二次函数y=ax 2+bx+c （a ≠0）的图象如图所示，下列结论①a ，b 异号；②当x=1和x=3时，函数值相等； ③4a+b=0；④当y=4时，x 的取值只能为0，结论正确的个数有（ C ）个．1/2/3A 、1B 、2C 、3D 、4三、能力练习1.已知二次函数c bx ax y ++=2的图象如图 l －2－2所示，则a 、b 、c 满足（） A ．a ＜0，b ＜0，c ＞0 B ．a ＜0，b ＜0，c ＜0C ．a ＜0，b ＞0，c ＞0D ．a ＞0，b ＜0，c ＞0 2.已知二次函数c bx ax y ++=2(a ≠0）且a ＜0，a －b+c ＞0，则一定有（）A ．b 2－4ac ＞0B ．b 2－4ac ＝0C ．b 2－4ac ＜0D ．b 2－4ac ≤03.二次函数c bx ax y ++=2的图象如图1－2－10，则点（b ，ca）在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限4．若二次函数c bx ax y ++=2的图象如图，则ac_____0（“＜”“＞”或“=”）第4题图 5．二次函数c bx ax y ++=2的图象如图 1－2－14所示，则下列关于a 、b 、c 间的关系判断正确的是（） A ．ab ＜0 B 、bc ＜0 C ．a+b ＋c ＞0 D ．a －b 十c ＜0四、知识小结：函数二次函数)0,,(2≠++=a c b a c bx ax y 是常数，图像 a>0a<0y0 xy0 x性质（1）抛物线开口向上，并向上无限延伸；（2）对称轴是x=ab2-，顶点坐标是（a b 2-，ab ac 442-）；（3）在对称轴的左侧，即当x<a b2-时，y 随x 的增大而减小；在对称轴的右侧，即当x>ab2-时，y 随x 的增大而增大，简记左减右增；（4）抛物线有最低点，当x=ab2-时，y 有最小值，（1）抛物线开口向下，并向下无限延伸；（2）对称轴是x=ab2-，顶点坐标是（a b 2-，ab ac 442-）；（3）在对称轴的左侧，即当x<ab2-时，y 随x 的增大而增大；在对称轴的右侧，即当x>ab2-时，y 随x的增大而减小，简记左增右减；（4）抛物线有最高点，当x=ab2-时，y 有最大值，例题．已知抛物线c bx ax y ++=2过三点（－1，－1）、（0，－2）、（1，l ）．（1）求抛物线所对应的二次函数的表达式；（2）写出它的开口方向、对称轴和顶点坐标；（3）这个函数有最大值还是最小值？这个值是多少？五、中考真题回顾：（09佛山）19．（1）请在坐标系中画出二次函数22y x x =-+的大致图象；（2）在同一个坐标系中画出22y x x =-+的图象向上平移两个单位后的图象；（3）直接写出平移后的图象的解析式.注：图中小正方形网格的边长为1.（1）画图（略）注：基本反映图形的特征（如顶点、对称性、变化趋势、平滑）给2分，满足其中的两至三项给1分，满足一项以下给0分；（2）画图、写解析式（略）注：画图满分2分，同（1）的标准；写解析式2分（无过程不扣分）．（11·佛山）21.如图，已知二次函数y ＝ax 2＋bx ＋c 的图像经过A （－1，－1）、B （0，2）、C （1，3）；（1）求二次函数的解析式；（2）画出二次函数的图像；【答案】解：（1）根据题意，得⎩⎪⎨⎪⎧a －b ＋c ＝－1c ＝2a ＋b ＋c ＝3 ………………2分解得a ＝－1，b ＝2，c ＝2………………4分ab ac y 442-=最小值ab ac y 442-=最大值xy O第19题图xyoABC1所以二次函数的解析式为y ＝－x 2＋2x ＋2………………5分（2）二次函数的图象如图………………8分给分要点：顶点、对称、光滑（各1分）（12佛山）22.(1)任选以下三个条件中的一个，求二次函数c bx ax y ++=2的解析式； ①y 随x 变化的部分数值规律如下表：②有序数对()0,1-、()4,1、()0,3满足c bx ax y ++=2； ③已知函数c bx ax y ++=2的图象的一部分（如图）． (2)直接写出二次函数c bx ax y ++=2的三个性质．解析：（1）方法一：由可得：C=3，0=+-c b a ，4=++c b a ，所以1-=a ，2=b ，C=3，所以二次函数解析式为：322++-=x x y方法二：由②可得：0=+-c b a ，4=++c b a ，039=++c b a ，解之得：1-=a ，2=b ，C=3，所以二次函数解析式为：322++-=x x y 方法三：由③可得：C=3，0=+-c b a ，12=-ab，解之得：1-=a ，2=b ，C=3，所以二次函数解析式为：322++-=x x y （三种选其一即可）（2）1、对称轴为1=x ， 2、开口向下 3、与x 轴有2个交点x -1 0 1 2 3 y343xyoABC14、交y轴正半轴考察知识：待定系数法求二次函数解析式、二次函数的性质及图像（2013•佛山）24．如图①，已知抛物线y=ax2+bx+c经过点A（0，3），B（3，0），C（4，3）．（1）求抛物线的函数表达式；（2）求抛物线的顶点坐标和对称轴；（3）把抛物线向上平移，使得顶点落在x轴上，直接写出两条抛物线、对称轴和y轴围成的图形的面积S（图②中阴影部分）．分析：（1）把点A、B、C代入抛物线解析式y=ax2+bx+c利用待定系数法求解即可；（2）把抛物线解析式整理成顶点式形式，然后写出顶点坐标与对称轴即可；（3）根据顶点坐标求出向上平移的距离，再根据阴影部分的面积等于平行四边形的面积，列式进行计算即可得解．解：（1）∵抛物线y=ax2+bx+c经过点A（0，3），B（3，0），C（4，3），∴，解得，所以抛物线的函数表达式为y=x2﹣4x+3；（2）∵y=x2﹣4x+3=（x﹣2）2﹣1，∴抛物线的顶点坐标为（2，﹣1），对称轴为直线x=2；（3）如图，∵抛物线的顶点坐标为（2，﹣1），∴PP′=1，阴影部分的面积等于平行四边形A′APP′的面积，平行四边形A′APP′的面积=1×2=2，∴阴影部分的面积=2．点评：本题考查了待定系数法求二次函数解析式，二次函数的性质，二次函数图象与几何变换，（3）根据平移的性质，把阴影部分的面积转化为平行四边形的面积是解题的关键．。

二次函数与abc的关系

几种特殊情况：x=1时,y=a + b + c；x= -1时,y=a - b + c．当x = 1时,①若y > 0,则a + b + c >0；②若y < 时0,则a + b + c < 0当x = -1时,①若y > 0,则a - b + c >0；②若y < 0,则a - b + c < 0．扩：x=2, y=4a + 2b + c ；x= -2, y=4a -2b + c ； x=3, y=9a +3 b + c ；x= -3, y=9a -3b + c ;反之,给我们相应的二次函数图象,我们可以得到其系数a,b,c以及它们组合成的一; 判别式b2−4ac ;y=a+b+c……等等的符号些关系结构例如对称轴−b2a4．2017四川省广安市如图所示,抛物线c=2的顶点为B﹣1,3,与x轴的交+y+axbx点A 在点﹣3,0和﹣2,0之间,以下结论：①042=-ac b ；②a +b +c ＞0；③2a ﹣b =0；④c ﹣a =3其中正确的有A ．1B ．2C ．3D ．45．2017四川省眉山市若一次函数y =a +1x +a 的图象过第一、三、四象限,则二次函数2y ax ax =-A ．有最大值4aB ．有最大值﹣4aC ．有最小值4aD ．有最小值﹣4a1. 2017贵州遵义第11题如图,抛物线y =ax 2+bx +c 经过点﹣1,0,对称轴l 如图所示,则下列结论：①abc ＞0；②a ﹣b +c =0；③2a +c ＜0；④a +b ＜0,其中所有正确的结论是A ．①③B ．②③C ．②④D ．②③④9. 2017黑龙江齐齐哈尔第10题如图,抛物线2y ax bx c =++0a ≠的对称轴为直线2x =-,与x 轴的一个交点在(3,0)-和(4,0)-之间,其部分图象如图所示,则下列结论：①40a b -=；②0c <；③30a c -+>；④242a b at bt ->+t 为实数；⑤点19(,)2y -,25(,)2y -,31(,)2y -是该抛物线上的点,则123y y y <<,正确的个数有 A ．4个 B ．3个 C ．2个 D ．1个6．2017四川省绵阳市将二次函数2x y =的图象先向下平移1个单位,再向右平移3个单位,得到的图象与一次函数y =2x +b 的图象有公共点,则实数b 的取值范围是A ．b ＞8B ．b ＞﹣8C ．b ≥8D ．b ≥﹣82．2017四川省南充市二次函数2y ax bx c =++a 、b 、c 是常数,且a ≠0的图象如图所示,下列结论错误的是A ．4ac ＜b 2B ．abc ＜0C ．b +c ＞3aD ．a ＜b23. 2017浙江金华第6题对于二次函数()212y x =--+是图象与性质,下列说法正确的是A ．对称轴是直线1x =,最小值是2B ．对称轴是直线1x =,最大值是2C . 对称轴是直线1x =-,最小值是2D ．对称轴是直线1x =-,最大值是226. 2017新疆乌鲁木齐第15题如图,抛物线2y ax bx c =++过点()1,0-,且对称轴为直线1x =,有下列结论：①0abc <；②1030a b c ++>；③抛物线经过点()14,y 与点()23,y -,则12y y >；④无论,,a b c 取何值,抛物线都经过同一个点,0c a ⎛⎫- ⎪⎝⎭；⑤20am bm a ++≥,其中所有正确的结论是．15.2017贵州黔东南州第9题如图,抛物线y =ax 2+bx +ca ≠0的对称轴为直线x =﹣1,给出下列结论：①b 2=4ac ；②abc ＞0；③a ＞c ；④4a ﹣2b +c ＞0,其中正确的个数有A ．1个B ．2个C ．3个D ．4个16.2017山东烟台第11题二次函数)0(2≠++=a c bx ax y 的图象如图所示,对称轴是直线1=x ,下列结论：①0<ab ；②ac b 42>；③0<++c b a ；④03<+c a .其中正确的是A ．①④ B．②④ C. ①②③ D ．①②③④17.2017四川泸州第8题下列曲线中不能表示y 与x 的函数的是A ．B ．C ．D ． 16. 2017山东日照第12题已知抛物线y =ax 2+bx +ca ≠0的对称轴为直线x =2,与x 轴的一个交点坐标为4,0,其部分图象如图所示,下列结论：①抛物线过原点；②4a +b +c =0；③a ﹣b +c ＜0；④抛物线的顶点坐标为2,b ；⑤当x ＜2时,y 随x 增大而增大．其中结论正确的是A．①②③B．③④⑤C．①②④D．①④⑤12.2017江苏盐城第6题如图,将函数y=12x－22+1的图象沿y轴向上平移得到一条新函数的图象,其中点A1,m,B4,n平移后的对应点分别为点A'、B'．若曲线段AB扫过的面积为9图中的阴影部分,则新图象的函数表达式是A．y＝12x222 B．y＝12x22+7 C．y＝12x225 D．y＝12x22+47.2017广西贵港第10题将如图所示的抛物线向右平移1个单位长度,再向上平移3个单位长度后,得到的抛物线解析式是A．()211y x=-+ B．()211y x=++C.()2211y x=-+ D．()2211y x=++8.2017贵州安顺第10题二次函数y=ax2+bx+c≠0的图象如图,给出下列四个结论：①4ac﹣b2＜0；②3b+2c＜0；③4a+c＜2b；④mam+b+b＜am≠1,其中结论正确的个数是A．1 B．2 C．3 D．44.2017浙江宁波第10题抛物线2222y x x m m是常数的顶点在A.第一象限B.第二象限C.第三象限D.第四象限1．2016·山东省滨州市·3分抛物线y=2x2﹣2x+1与坐标轴的交点个数是A．0 B．1 C．2 D．32．2016·山东省滨州市·3分在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点选择180°得到抛物线y=x2+5x+6,则原抛物线的解析式是A．y=﹣x﹣2﹣B．y=﹣x+2﹣ C．y=﹣x﹣2﹣D．y=﹣x+2+点评本题考查的是二次函数的图象与几何变换,熟知二次函数的图象旋转及平移的法则是解答此题的关键．3．2016广西南宁3分二次函数y=ax2+bx+ca≠0和正比例函数y=x的图象如图所示,则方程ax2+b﹣x+c=0a≠0的两根之和A．大于0 B．等于0 C．小于0 D．不能确定4．2016贵州毕节3分一次函数y=ax+ba≠0与二次函数y=ax2+bx+ca≠0在同一平面直角坐标系中的图象可能是A． B． C．D．5.2016·福建龙岩·4分已知抛物线y=ax2+bx+c的图象如图所示,则|a﹣b+c|+|2a+b|=A．a+b B．a﹣2b C．a﹣b D．3a 10．2016贵州毕节3分一次函数y=ax+ba≠0与二次函数y=ax2+bx+ca≠0在同一平面直角坐标系中的图象可能是A． B． C．D．11. 2016·浙江省绍兴市·4分抛物线y=x2+bx+c其中b,c是常数过点A2,6,且抛物线的对称轴与线段y=01≤x≤3有交点,则c的值不可能是A．4 B．6 C．8 D．1012. 2016·湖北随州·3分二次函数y=ax2+bx+ca≠0的部分图象如图所示,图象过点﹣1,0,对称轴为直线x=2,下列结论：14a+b=0；29a+c＞3b；38a+7b+2c＞0；4若点A﹣3,y1、点B﹣,y2、点C,y3在该函数图象上,则y1＜y3＜y2；5若方程ax+1x﹣5=﹣3的两根为x1和x2,且x1＜x2,则x1＜﹣1＜5＜x2．其中正确的结论有A．2个 B．3个 C．4个 D．5个13.2016·四川南充抛物线y=x2+2x+3的对称轴是A．直线x=1 B．直线x=﹣1 C．直线x=﹣2 D．直线x=2 14．2016·四川泸州已知二次函数y=ax2﹣bx﹣2a≠0的图象的顶点在第四象限,且过点﹣1,0,当a﹣b为整数时,ab的值为A．或1 B．或1 C．或D．或15．2016·四川攀枝花如图,二次函数y=ax2+bx+ca＞0图象的顶点为D,其图象与x 轴的交点A、B的横坐标分别为﹣1和3,则下列结论正确的是A．2a﹣b=0B．a+b+c＞0C．3a﹣c=0D．当a=时,△ABD是等腰直角三角形16.2016·黑龙江齐齐哈尔·3分如图,抛物线y=ax2+bx+ca≠0的对称轴为直线x=1,与x轴的一个交点坐标为﹣1,0,其部分图象如图所示,下列结论：①4ac＜b2；②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3；③3a+c＞0④当y＞0时,x的取值范围是﹣1≤x＜3⑤当x＜0时,y随x增大而增大其中结论正确的个数是A．4个 B．3个 C．2个 D．1个17．2016·湖北黄石·3分以x为自变量的二次函数y=x2﹣2b﹣2x+b2﹣1的图象不经过第三象限,则实数b的取值范围是A．b≥B．b≥1或b≤﹣1 C．b≥2D．1≤b≤218．2016·湖北荆门·3分若二次函数y=x2+mx的对称轴是x=3,则关于x的方程x2+mx=7的解为A．x1=0,x2=6 B．x1=1,x2=7 C．x1=1,x2=﹣7 D．x1=﹣1,x2=719.2016·青海西宁·3分如图,在△ABC中,∠B=90°,tan∠C=,AB=6cm．动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动．若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是A．18cm2 B．12cm2 C．9cm2 D．3cm221. 2016·四川眉山·3分若抛物线y=x2﹣2x+3不动,将平面直角坐标系xOy先沿水平方向向右平移一个单位,再沿铅直方向向上平移三个单位,则原抛物线图象的解析式应变为A．y=x﹣22+3 B．y=x﹣22+5 C．y=x2﹣1 D．y=x2+44．2016·四川南充已知抛物线y=ax2+bx+c开口向上且经过点1,1,双曲线y=经过点a,bc,给出下列结论：①bc＞0；②b+c＞0；③b,c是关于x的一元二次方程x2+a﹣1x+=0的两个实数根；④a﹣b﹣c≥3．其中正确结论是填写序号5．2016·四川泸州若二次函数y=2x2﹣4x﹣1的图象与x轴交于Ax1,0、Bx2,0两点,则+的值为7.2016·湖北荆州·3分若函数y=a﹣1x2﹣4x+2a的图象与x轴有且只有一个交点,则a的值为8. 2016·辽宁丹东·10分某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低．若该果园每棵果树产果y千克,增种果树x棵,它们之间的函数关系如图所示．1求y与x之间的函数关系式；2在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克3当增种果树多少棵时,果园的总产量w千克最大最大产量是多少12．2016·四川内江12分某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成．已知墙长为18米如图14所示,设这个苗圃园垂直于墙的一边长为x米．1若苗圃园的面积为72平方米,求x；2若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗如果有,求出最大值和最小值；如果没有,请说明理由；3当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围．16.2016·黑龙江龙东·6分如图,二次函数y=x+22+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A﹣1,0及点B．1求二次函数与一次函数的解析式；2根据图象,写出满足x+22+m≥kx+b的x的取值范围．21.2016·内蒙古包头一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3：2．设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2．1求y与x之间的函数关系式；2若图案中三条彩条所占面积是图案面积的,求横、竖彩条的宽度．24. 2016·山东潍坊旅游公司在景区内配置了50辆观光车共游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x元是5的倍数．发现每天的营运规律如下：当x不超过100元时,观光车能全部租出；当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆．已知所有观光车每天的管理费是1100元．1优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元注：净收入=租车收入﹣管理费2当每辆车的日租金为多少元时,每天的净收入最多。

二次函数abc组合的符号判断

二次函数abc组合的符号判断对于二次函数中abc组合的符号判断套路掌握情况，分为三个层次，首先根据函数图象确定a，b，c符号以及对称轴信息，其次是找特殊点的函数值，获取等式和不等式，最后在判断残缺型符号时，将等式代入不等式。

过程中考查学生读图，数形结合以及逻辑分析能力。

单选题(本大题共7小题，共100分)1.(本小题12分)如图，二次函数的图象开口向上，对称轴为直线x=1，且图象经过点（3，0），则下列结论正确的是( )∙ A.∙ B.∙ C.∙ D.核心考点: 二次函数图象与系数的关系 abc组合的符号判断2.(本小题12分)已知二次函数的图象如图所示，下列结论：①；②；③；④b+2a=0；⑤．其中正确的有( )∙ A. 1个∙ B. 2个∙ C. 3个∙ D. 4个核心考点: 二次函数图象与系数的关系abc组合的符号判断3.(本小题12分)已知二次函数的图象如图所示，下列结论：①；②；③；④．其中正确的是( )∙ A. ②③∙ B. ③④∙ C. ②④∙ D. ①④核心考点: 二次函数图象与系数的关系 abc组合的符号判断4.(本小题16分)如图所示，二次函数的图象中，王刚同学观察得出了下面四条结论：①；②；③；④．其中错误的有( )∙ A. 1个∙ B. 2个∙ C. 3个∙ D. 4个核心考点: 二次函数图象与系数的关系abc组合的符号判断5.(本小题16分)已知二次函数的图象如图所示，其对称轴为直线，则下列结论正确的是( )∙ A.∙ B. a+b=0∙ C.∙ D.核心考点: 二次函数图象与系数的关系 abc组合的符号判断6.(本小题16分)如图，二次函数图象的顶点在第一象限，且过点（0，1）和（-1，0）．下列结论：①；②；③；④当时，．其中正确的有( )∙ A. 1个∙ B. 4个∙ C. 3个∙ D. 2个核心考点: 二次函数图象与系数的关系abc组合的符号判断7.(本小题16分)已知二次函数的图象如图所示，下列结论：①；②b+2a=0；③抛物线与x轴的另一个交点为（4，0）；④；⑤．其中正确的是( )∙ A. ②③⑤∙ B. ①②③⑤∙ C. ①②④⑤∙ D. ①③④⑤核心考点: 二次函数图象与系数的关系 abc组合的符号判断单选题(本大题共6小题，共100分)1.(本小题15分)二次函数图象的一部分如图所示，其对称轴为直线x=-1，且过点（-3，0）．下列说法：①；②2a-b=0；③；④若，是抛物线上的两点，则．其中正确的是( )∙ A. ①②∙ B. ②③∙ C. ①②④∙ D. ②③④核心考点: 二次函数图象与系数的关系 abc组合的符号判断2.(本小题15分)二次函数的图象如图所示，下列结论：①；②；③；④．其中正确的是( )∙ A. ①②∙ B. ②③∙ C. ③④∙ D. ①④核心考点: 二次函数图象与系数的关系abc组合的符号判断3.(本小题15分)如图所示，二次函数的图象中，小轩同学观察得出了如下四条结论：①；②；③；④．其中正确的是( )∙ A. ①②∙ B. ②③∙ C. ①②③∙ D. ①②③④核心考点: 二次函数图象与系数的关系 abc组合的符号判断4.(本小题15分)已知二次函数的图象如图所示，有下列结论：①；②2a+b=0；③；④．其中正确的有( )个．∙ A. 1 ∙ B. 2 ∙ C. 3 ∙D. 4核心考点: 二次函数图象与系数的关系 abc 组合的符号判断5.(本小题20分) 已知二次函数的图象如图所示，它与x 轴的两个交点分别为（-1，0），（3，0）．下列结论：①；②b-2a=0；③；④．其中正确的是( )∙A. ③ ∙B. ②③ ∙C. ③④ ∙D. ①②核心考点: 二次函数图象与系数的关系 abc 组合的符号判断6.(本小题20分)已知二次函数的图象经过，（2，0）两点，且，图象与y轴正半轴的交点在（0，2）的下方，则下列结论：①；②；③；④．其中正确的是( )∙ A. ①②∙ B. ②③∙ C. ①②④∙ D. ①②③④核心考点: 二次函数图象与系数的关系abc组合的符号判断。