交换排序和归并排序
数据排序的方法

数据排序的方法
1. 冒泡排序:通过多次遍历数组,依次比较相邻的两个元素并交换位置,将最大(或最小)的元素逐渐冒泡至数组的一端。
2. 插入排序:将数组分为已排序和未排序两部分,依次将未排序部分的元素插入到
已排序部分的合适位置,使得已排序部分一直保持有序。
3. 选择排序:每次从未排序部分选出最大(或最小)的元素,放到已排序部分的末尾,直到未排序部分为空。
4. 归并排序:将数组分为若干个小部分,对每个小部分进行排序,然后再合并这些
有序小部分,直至整个数组有序。
5. 快速排序:通过选择一个基准元素,将数组分为小于基准和大于基准的两部分,
然后递归对这两部分进行排序。
6. 堆排序:将数组看作是一个完全二叉树,通过调整树的结构使得每个节点的值都
大于等于其子节点(大顶堆)或小于等于其子节点(小顶堆),然后逐个取出根节点得到
排序结果。
7. 希尔排序:对数组进行间隔分组,对每个分组进行插入排序,然后逐渐缩小间隔
直至1,最终进行一次插入排序。
8. 计数排序:统计数组中每个元素出现的次数,然后根据元素值的顺序将元素依次
放入结果数组。
9. 桶排序:将数组划分为若干个桶,根据元素的大小把元素放入相应的桶中,然后
再对每个桶中的元素进行排序,最后将所有桶中的元素依次放入结果数组。
10. 基数排序:按照元素的每一位进行排序,从低位到高位逐步稳定。
这些排序方法有各自的优缺点,适用于不同的数据特点和应用场景。
在实际应用中需
要根据具体情况选择合适的排序方法。
数字的大小排序

数字的大小排序数字的大小排序在我们的日常生活中经常会用到,不论是在数学领域,还是在实际应用中,都需要对数字按照大小进行排序。
本文将介绍几种常用的数字排序方法,以帮助读者更好地理解和应用数字排序算法。
一、冒泡排序冒泡排序是一种简单直观的排序算法,基本思想是通过比较相邻的两个数字,如果前一个数字大于后一个数字,则交换它们的位置,这样一轮比较下来,最大的数字会“冒泡”到数组的末尾。
重复这个过程,直到所有数字按照从小到大的顺序排列。
举个例子来说明冒泡排序的过程,假设我们有一个包含6个数字的数组:[5, 2, 8, 3, 1, 9]。
经过一轮冒泡比较后,数组变为[2, 5, 3, 1, 8, 9]。
接着再进行一轮冒泡比较,数组变为[2, 3, 1, 5, 8, 9]。
继续进行比较和交换,最终得到按照从小到大排序的数组:[1, 2, 3, 5, 8, 9]。
二、选择排序选择排序是一种简单但不稳定的排序算法,它的基本思想是每次从待排序的数字中选出最小的数字,放到已排序数字的末尾,直到所有数字按照从小到大的顺序排列。
以同样的例子来说明选择排序的过程,假设我们有一个包含6个数字的数组:[5, 2, 8, 3, 1, 9]。
首先,找到数组中最小的数字1,并将其与数组的第一个数字5交换位置,此时数组变为[1, 2, 8, 3, 5, 9]。
接着,在剩下的数字中,找到最小的数字2,并将其与数组的第二个数字8交换位置,此时数组变为[1, 2, 8, 3, 5, 9]。
继续进行比较和交换,最终得到按照从小到大排序的数组:[1, 2, 3, 5, 8, 9]。
三、插入排序插入排序是一种简单且稳定的排序算法,适用于小规模的数字排序。
它的基本思想是从待排序的数字中逐个取出数字,并将其插入到已排序数字的合适位置,直到所有数字按照从小到大的顺序排列。
继续以同样的例子来说明插入排序的过程,假设我们有一个包含6个数字的数组:[5, 2, 8, 3, 1, 9]。
C语言八大排序算法
C语⾔⼋⼤排序算法C语⾔⼋⼤排序算法,附动图和详细代码解释!来源:C语⾔与程序设计、⽵⾬听闲等⼀前⾔如果说各种编程语⾔是程序员的招式,那么数据结构和算法就相当于程序员的内功。
想写出精炼、优秀的代码,不通过不断的锤炼,是很难做到的。
⼆⼋⼤排序算法排序算法作为数据结构的重要部分,系统地学习⼀下是很有必要的。
1、排序的概念排序是计算机内经常进⾏的⼀种操作,其⽬的是将⼀组“⽆序”的记录序列调整为“有序”的记录序列。
排序分为内部排序和外部排序。
若整个排序过程不需要访问外存便能完成,则称此类排序问题为内部排序。
反之,若参加排序的记录数量很⼤,整个序列的排序过程不可能在内存中完成,则称此类排序问题为外部排序。
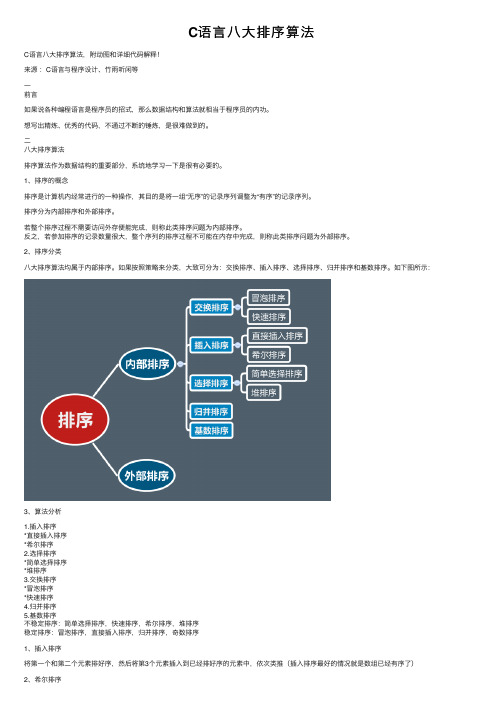
2、排序分类⼋⼤排序算法均属于内部排序。
如果按照策略来分类,⼤致可分为:交换排序、插⼊排序、选择排序、归并排序和基数排序。
如下图所⽰:3、算法分析1.插⼊排序*直接插⼊排序*希尔排序2.选择排序*简单选择排序*堆排序3.交换排序*冒泡排序*快速排序4.归并排序5.基数排序不稳定排序:简单选择排序,快速排序,希尔排序,堆排序稳定排序:冒泡排序,直接插⼊排序,归并排序,奇数排序1、插⼊排序将第⼀个和第⼆个元素排好序,然后将第3个元素插⼊到已经排好序的元素中,依次类推(插⼊排序最好的情况就是数组已经有序了)因为插⼊排序每次只能操作⼀个元素,效率低。
元素个数N,取奇数k=N/2,将下标差值为k的数分为⼀组(⼀组元素个数看总元素个数决定),在组内构成有序序列,再取k=k/2,将下标差值为k的数分为⼀组,构成有序序列,直到k=1,然后再进⾏直接插⼊排序。
3、简单选择排序选出最⼩的数和第⼀个数交换,再在剩余的数中⼜选择最⼩的和第⼆个数交换,依次类推4、堆排序以升序排序为例,利⽤⼩根堆的性质(堆顶元素最⼩)不断输出最⼩元素,直到堆中没有元素1.构建⼩根堆2.输出堆顶元素3.将堆低元素放⼀个到堆顶,再重新构造成⼩根堆,再输出堆顶元素,以此类推5、冒泡排序改进1:如果某次冒泡不存在数据交换,则说明已经排序好了,可以直接退出排序改进2:头尾进⾏冒泡,每次把最⼤的沉底,最⼩的浮上去,两边往中间靠16、快速排序选择⼀个基准元素,⽐基准元素⼩的放基准元素的前⾯,⽐基准元素⼤的放基准元素的后⾯,这种动作叫分区,每次分区都把⼀个数列分成了两部分,每次分区都使得⼀个数字有序,然后将基准元素前⾯部分和后⾯部分继续分区,⼀直分区直到分区的区间中只有⼀个元素的时候,⼀个元素的序列肯定是有序的嘛,所以最后⼀个升序的序列就完成啦。
排序有哪几种方法

排序有哪几种方法排序是计算机科学中非常重要的概念之一,它指的是将一组元素按照某种规则进行重新排列的过程。
排序算法可以分为多种类型,包括插入排序、交换排序、选择排序、归并排序、快速排序、堆排序、计数排序、桶排序、基数排序等。
下面我将详细介绍每种排序方法的原理、特点和应用场景。
1. 插入排序(Insertion Sort)插入排序是一种简单且直观的排序算法。
它的原理是将一个未排序的元素逐个地插入到已排序的部分中,最终形成一个完全有序的序列。
具体操作是从第二个元素开始,将其与前面已排序的元素逐个比较并插入到正确的位置。
插入排序的时间复杂度为O(n^2),适用于小规模或部分有序的序列。
2. 交换排序(Exchange Sort)交换排序包括冒泡排序和快速排序。
冒泡排序(Bubble Sort)的原理是从头到尾依次比较相邻的两个元素,如果顺序不对则交换位置,一轮下来可以将最大的元素移动到末尾。
快速排序(Quick Sort)使用了分治的思想,通过选择一个基准元素将序列分成左右两部分,左边的元素都小于该基准值,右边的元素都大于该基准值,然后递归地对左右两部分进行快速排序。
交换排序的平均时间复杂度为O(nlogn),适合用于排序大规模随机数据。
3. 选择排序(Selection Sort)选择排序的原理很简单:每一次从未排序的部分中选择最小(或最大)的元素,放到已排序部分的末尾。
具体操作是通过不断找到最小元素的索引,然后将其与第一个未排序元素交换,如此循环直到所有元素都被排序。
选择排序的时间复杂度为O(n^2),适用于简单的排序需求。
4. 归并排序(Merge Sort)归并排序采用了分治的思想,将一个序列递归地分成两个子序列,直到每个子序列只有一个元素,然后将两个有序的子序列合并成一个有序的序列。
具体操作是比较两个子序列的第一个元素,将较小的元素放入结果序列,然后再比较较小元素所在子序列的下一个元素与另一个子序列的第一个元素,直到所有元素都被放入结果序列。
数据结构专科电子教案九

49
25
16
08
0
21 08
21
1
2
3
4 piv5ot
pivot 08 16
21 25 25 49
划分的层数等于对应二叉搜
索树的高度减1
25
区间数等于对应二叉搜索树
25 的分支结点数
49
快速排序示例所对应的二叉搜索树
31085 13586 1380 36 1356 45 4488 953 72 593
分析
快速排序中,若把每次划分所用的基 准元素看作根结点,把划分得到的左区 间和右区间看作为根结点的左子树和右 子树。那么整个排序过程就对应一棵具 有n个元素的二叉搜索树,所需划分的层 数就等于对应二叉搜索树的高度减 1 , 所需划分的所有区间数等于对应二叉搜 索树中分支结点数。
pivot
21
25
if ( k!= i-1 ) { x=A[i-1] ; A[i-1]=A[k] ; A[k]=x ; }
} }
直接选择 i =2 时选择排序的过程
08
25
49
25
16
21
5
i -1 k
j 49 25
08
25
49
i -1 k
08
25
49
i -1
25 16 21 25 25
j
25 16 21 k j 16 < 25
堆排序是不稳定的
9.3 交 换 排 序
一、气泡排序 二、快速排序
9.3.1 气 泡 排 序
Bubble Sorting
基本思想:通过相邻元素之间的比较和 交换使排序码较小的元素逐渐从底部移向 顶部,即从下标较大的单元移向下标较小 的单元。(当然,随着排序码较小的元素 逐渐上移,排序码较大的元素逐渐下移)
三个数怎么比较排序的方法

三个数怎么比较排序的方法三个数的比较排序方法有许多,下面我会详细介绍其中一些常用的方法,包括冒泡排序、选择排序、插入排序、快速排序、归并排序和堆排序。
1. 冒泡排序:冒泡排序是最简单的排序算法之一。
它通过多次比较并交换相邻的两个元素来进行排序。
具体步骤如下:- 从第一个数开始,依次与后面的数进行比较,如果当前数比后面的数大,则交换它们的位置。
- 每完成一次遍历,最大的数就会“冒泡”到最后的位置。
- 重复上述步骤,但是每次比较的范围减一,直到所有数都被排序。
2. 选择排序:选择排序思路简单,每次通过找出最小的数,并将其与未排序部分的第一个数交换位置来进行排序。
具体步骤如下:- 遍历未排序部分,找到最小的数,并记录其下标。
- 将最小的数与未排序部分的第一个数交换位置。
- 重复上述步骤,但是每次比较的范围减一,直到所有数都被排序。
3. 插入排序:插入排序将待排序的数插入到已排序部分的合适位置。
具体步骤如下:- 从第二个数开始,与前面的已排序部分进行比较,找到合适的位置。
- 如果当前数比前面的数小,则将前面的数后移一位,直到找到合适的位置。
- 将当前数插入到找到的位置。
- 重复上述步骤,直到所有数都被排序。
4. 快速排序:快速排序是一种高效的排序算法。
它通过把数组分成两部分,并对这两部分分别进行排序来实现排序的目的。
具体步骤如下:- 选择一个基准数,可以是数组中的任意一个数。
- 将数组分成小于基准数的部分和大于基准数的部分。
- 递归地对两部分分别进行排序。
- 合并两部分,得到最终排序结果。
5. 归并排序:归并排序是一种稳定的排序算法,它使用分治的思想,将数组分成多个子数组,然后合并这些子数组以获得排序结果。
具体步骤如下:- 将数组分成两个部分,分别对这两个部分进行排序。
- 合并两个排序好的部分,得到一个排序好的数组。
- 对合并后的数组重复上述步骤,直到所有子数组都被合并。
6. 堆排序:堆排序是一种基于完全二叉堆的排序算法。
排序的基本操作

排序的基本操作
排序的基本操作包括:
1. 比较:将两个元素进行比较,确定它们的相对顺序。
2. 交换:如果两个元素的顺序不符合要求,则交换它们的位置。
3. 插入:将一个元素插入到已排序的部分中,使得整个序列仍然保持有序。
4. 移动:移动元素的位置,以腾出空间来插入新的元素。
5. 归并:将两个有序的序列合并为一个有序的序列,通常用于归并排序。
6. 分割:将一个序列分割为较小的序列,进行递归排序,通常用于快速排序。
7. 选择:从未排序的序列中选择最小(或最大)的元素,并放到已排序的序列末尾(或开头)。
8. 冒泡:依次比较相邻的两个元素,将较大(或较小)的元素向后(或向前)冒泡至正确的位置。
9. 堆化:将一个无序的序列转换为最大(或最小)堆的形式,通常用于堆排序。
10. 递归:将一个问题拆分为更小规模的子问题,并通过递归
求解子问题来解决原问题,用于归并排序和快速排序等等。
这些基本操作可以用于实现各种排序算法,如冒泡排序、插入排序、选择排序、归并排序、快速排序、堆排序等。
不同的排序算法之间主要就是这些基本操作的顺序和组合方式的不同。
概述插入排序交换排序选择排序归并排序基数排序外部排序小结

Type getKey ( ) { return key; } //提取关键字 void setKey ( const Type x ) { key = x; } //修改 Element<Type> & operator = //赋值 ( Element<Type> & x ) { this = x; } int operator == ( Type & x ) //判this == x { return ! ( this->key >x || x < this->key ); } int operator != ( Type & x ) //判this != x { return this->key < x || x < this->key ; } int operator <= ( Type & x ) //判this x { return ! (this->key > x ); } int operator >= ( Type & x ) //判this x { return ! (this->key < x ); } int operator < ( Type & x ) //判this < x { return this->key > x; }
KCN i n(n 1) / 2 n / 2,
2 i 1 n 1
RMN (i 2) (n 4)(n 1) / 2 n / 2
2 i 1
n 1
若待排序对象序列中出现各种可能排列的概 率相同,则可取上述最好情况和最坏情况的 平均情况。在平均情况下的关键字比较次数 和对象移动次数约为 n2/4。因此,直接插入 排序的时间复杂度为 o(n2)。 直接插入排序是一种稳定的排序方法。
五种常见的排序方法

五种常见的排序方法在计算机科学中,排序是一种非常重要的操作,它可以将一组数据按照一定的顺序排列。
排序算法是计算机科学中最基本的算法之一,它的应用范围非常广泛,例如数据库查询、数据压缩、图像处理等。
本文将介绍五种常见的排序算法,包括冒泡排序、选择排序、插入排序、快速排序和归并排序。
一、冒泡排序冒泡排序是一种简单的排序算法,它的基本思想是将相邻的元素两两比较,如果前面的元素大于后面的元素,则交换它们的位置,一遍下来可以将最大的元素放在最后面。
重复这个过程,每次都可以确定一个最大的元素,直到所有的元素都排好序为止。
冒泡排序的时间复杂度为O(n^2),空间复杂度为O(1)。
二、选择排序选择排序是一种简单的排序算法,它的基本思想是每次从未排序的元素中选择最小的元素,将它放到已排序的元素的末尾。
重复这个过程,直到所有的元素都排好序为止。
选择排序的时间复杂度为O(n^2),空间复杂度为O(1)。
三、插入排序插入排序是一种简单的排序算法,它的基本思想是将一个元素插入到已排序的元素中,使得插入后的序列仍然有序。
重复这个过程,直到所有的元素都排好序为止。
插入排序的时间复杂度为O(n^2),空间复杂度为O(1)。
四、快速排序快速排序是一种高效的排序算法,它的基本思想是选择一个基准元素,将序列分成两个子序列,其中一个子序列的所有元素都小于基准元素,另一个子序列的所有元素都大于基准元素。
然后递归地对这两个子序列进行排序。
快速排序的时间复杂度为O(nlogn),空间复杂度为O(logn)。
五、归并排序归并排序是一种高效的排序算法,它的基本思想是将序列分成两个子序列,然后递归地对这两个子序列进行排序,最后将这两个有序的子序列合并成一个有序的序列。
归并排序的时间复杂度为O(nlogn),空间复杂度为O(n)。
总结在实际的应用中,选择合适的排序算法非常重要,不同的排序算法有不同的优劣势。
冒泡排序、选择排序和插入排序是三种简单的排序算法,它们的时间复杂度都为O(n^2),在处理小规模的数据时比较适用。
排序(sort)或分类排序

排序(sort)或分类所谓排序,就是要整理文件中的记录,使之按关键字递增(或递减)次序排列起来。
其确切定义如下:输入:n个记录R1,R2,…,R n,其相应的关键字分别为K1,K2,…,K n。
输出:R il,R i2,…,R in,使得K i1≤K i2≤…≤K in。
(或K i1≥K i2≥…≥K in)。
1.被排序对象--文件被排序的对象--文件由一组记录组成。
记录则由若干个数据项(或域)组成。
其中有一项可用来标识一个记录,称为关键字项。
该数据项的值称为关键字(Key)。
注意:在不易产生混淆时,将关键字项简称为关键字。
2.排序运算的依据--关键字用来作排序运算依据的关键字,可以是数字类型,也可以是字符类型。
关键字的选取应根据问题的要求而定。
【例】在高考成绩统计中将每个考生作为一个记录。
每条记录包含准考证号、姓名、各科的分数和总分数等项内容。
若要惟一地标识一个考生的记录,则必须用"准考证号"作为关键字。
若要按照考生的总分数排名次,则需用"总分数"作为关键字。
排序的稳定性当待排序记录的关键字均不相同时,排序结果是惟一的,否则排序结果不唯一。
在待排序的文件中,若存在多个关键字相同的记录,经过排序后这些具有相同关键字的记录之间的相对次序保持不变,该排序方法是稳定的;若具有相同关键字的记录之间的相对次序发生变化,则称这种排序方法是不稳定的。
注意:排序算法的稳定性是针对所有输入实例而言的。
即在所有可能的输入实例中,只要有一个实例使得算法不满足稳定性要求,则该排序算法就是不稳定的。
排序方法的分类1.按是否涉及数据的内、外存交换分在排序过程中,若整个文件都是放在内存中处理,排序时不涉及数据的内、外存交换,则称之为内部排序(简称内排序);反之,若排序过程中要进行数据的内、外存交换,则称之为外部排序。
注意:①内排序适用于记录个数不很多的小文件②外排序则适用于记录个数太多,不能一次将其全部记录放人内存的大文件。
常见排序算法及其对应的时间复杂度和空间复杂度

常见排序算法及其对应的时间复杂度和空间复杂度排序算法经过长时间演变,⼤体可以分为两类:内排序和外排序。
在排序过程中,全部记录存放在内存,则成为内排序;如果排序过程中需要使⽤外存,则称为外排序,本⽂讲的都属于内排序。
内排序有可以分为以下⼏类:(1)插⼊排序:直接插⼊排序、⼆分法插⼊排序、希尔排序(2)选择排序:直接选择排序、堆排序(3)交换排序:冒泡排序、快速排序(4)归并排序(5)基数排序排序⽅法时间复杂度(平均)时间复杂度(最坏)时间复杂度(最好)空间复杂度稳定性复杂性直接插⼊排序O(n2)O(n2)O(n)O(1)稳定简单希尔排序O(nlog2n)O(n2)O(n1.3)O(1)不稳定较复杂直接选择排序O(n2)O(n2)O(n2)O(1)不稳定简单堆排序O(nlog2n)O(nlog2n)O(nlog2n)O(1)不稳定较复杂冒泡排序O(n2)O(n2)O(n)O(1)稳定简单快速排序O(nlog2n)O(n2)O(nlog2n)O(nlog2n)不稳定较复杂归并排序O(nlog2n)O(nlog2n)O(nlog2n)O(n)稳定较复杂基数排序O(d(n+r))O(d(n+r))O(d(n+r))O(n+r)稳定较复杂⼀、插⼊排序•思想:每步将⼀个待排序的记录,按其顺序码⼤⼩插⼊到前⾯已经排序的字序列的合适位置,直到全部插⼊排序完为⽌。
•关键问题:在前⾯已经排好序的序列中找到合适的插⼊位置。
•⽅法:直接插⼊排序插⼊排序的最好情况是数组已经有序,此时只需要进⾏n-1次⽐较,时间复杂度为O(n)最坏情况是数组逆序排序,此时需要进⾏n(n-1)/2次⽐较以及n-1次赋值操作(插⼊)平均来说插⼊排序算法的复杂度为O(n2)空间复杂度上,直接插⼊法是就地排序,空间复杂度为(O(1))⼆分插⼊排序最坏情况:每次都在有序序列的起始位置插⼊,则整个有序序列的元素需要后移,时间复杂度为O(n2)最好情况:待排序数组本⾝就是正序的,每个元素所在位置即为它的插⼊位置,此时时间复杂度仅为⽐较时的时间复杂度,为O(log2n)平均情况:O(n2)空间复杂度上,⼆分插⼊也是就地排序,空间复杂度为(O(1))。
数据结构——排序——8种常用排序算法稳定性分析

数据结构——排序——8种常⽤排序算法稳定性分析⾸先,排序算法的稳定性⼤家应该都知道,通俗地讲就是能保证排序前2个相等的数其在序列的前后位置顺序和排序后它们两个的前后位置顺序相同。
在简单形式化⼀下,如果Ai = Aj, Ai原来在位置前,排序后Ai还是要在Aj位置前。
其次,说⼀下稳定性的好处。
排序算法如果是稳定的,那么从⼀个键上排序,然后再从另⼀个键上排序,第⼀个键排序的结果可以为第⼆个键排序所⽤。
基数排序就是这样,先按低位排序,逐次按⾼位排序,低位相同的元素其顺序再⾼位也相同时是不会改变的。
另外,如果排序算法稳定,对基于⽐较的排序算法⽽⾔,元素交换的次数可能会少⼀些(个⼈感觉,没有证实)。
回到主题,现在分析⼀下常见的排序算法的稳定性,每个都给出简单的理由。
(1)冒泡排序冒泡排序就是把⼩的元素往前调或者把⼤的元素往后调。
⽐较是相邻的两个元素⽐较,交换也发⽣在这两个元素之间。
所以,如果两个元素相等,我想你是不会再⽆聊地把他们俩交换⼀下的;如果两个相等的元素没有相邻,那么即使通过前⾯的两两交换把两个相邻起来,这时候也不会交换,所以相同元素的前后顺序并没有改变,所以冒泡排序是⼀种稳定排序算法。
(2)选择排序选择排序是给每个位置选择当前元素最⼩的,⽐如给第⼀个位置选择最⼩的,在剩余元素⾥⾯给第⼆个元素选择第⼆⼩的,依次类推,直到第n-1个元素,第n个元素不⽤选择了,因为只剩下它⼀个最⼤的元素了。
那么,在⼀趟选择,如果当前元素⽐⼀个元素⼩,⽽该⼩的元素⼜出现在⼀个和当前元素相等的元素后⾯,那么交换后稳定性就被破坏了。
⽐较拗⼝,举个例⼦,序列5 8 5 2 9,我们知道第⼀遍选择第1个元素5会和2交换,那么原序列中2个5的相对前后顺序就被破坏了,所以选择排序不是⼀个稳定的排序算法。
(3)插⼊排序插⼊排序是在⼀个已经有序的⼩序列的基础上,⼀次插⼊⼀个元素。
当然,刚开始这个有序的⼩序列只有1个元素,就是第⼀个元素。
Sorting

:桶排序、计数排序、基数排序
简单选择排序
相对于冒泡排序: 交换次数相当少
例如: { 2, 2, 1}, 第一次选的时候变成 { 1, 2, 2 }, 两个2的次序就变了
不稳定排序
时间复杂度分析
最好 O(n^2) 最坏 O(n^2) 平均 O(n^2)
1.交换排序: 冒泡排序、快速排序
2.插入排序: 直接插入排序、希尔排序
4.归并排序
非基于比较的排序
:桶排序、计数排序、基数排序
3.基数排序(又叫鸽巢排序)
在计数排序中,当k很大时,时间和空间的开销都会增大(可以想一下对 序列{8888,1234,9999}用计数排序,此时不但浪费很多空间,而且时间 方面还不如比较排序.
基数排序时间T(n)=d*(2k+3n),其中d是记录值的位数, (2k+3n)是每一趟计数排序时间,上文分析过了,k不超 过9,d的值一般也很小,k、d都可以看成是一个很小的 常数,所以时间复杂度o(n)。最坏最佳情况并不改变 时间复杂度。基数排序是稳定的。辅助空间同计数排序 k+n.
维护一个k大小的堆 时间复杂度: O(n * log k)
1.交换排序: 冒泡排序、快速排序
2.插入排序: 直接插入排序、希尔排序
基于比较的排序
O ( N * log N )
3.选择排序: 简单选择排序、堆排序
4.归并排序
非基于比较的排序
:桶排序、计数排序、基数排序
每一趟归并都需要扫描一遍所有记录,耗时 O(n)
最好 O(n)
最坏 O(n^2)
平均 O(n^2)
1. 求冒泡排序总共需要交换的次数 50, 40, 95, 20, 15, 70, 60, 45,
数组各种排序算法和复杂度分析

数组各种排序算法和复杂度分析Java排序算法1)分类:插⼊排序(直接插⼊排序、希尔排序)交换排序(冒泡排序、快速排序)选择排序(直接选择排序、堆排序)归并排序分配排序(箱排序、基数排序)所需辅助空间最多:归并排序所需辅助空间最少:堆排序平均速度最快:快速排序不稳定:快速排序,希尔排序,堆排序。
2)选择排序算法的时候要考虑数据的规模、数据的类型、数据已有的顺序。
⼀般来说,当数据规模较⼩时,应选择直接插⼊排序或冒泡排序。
任何排序算法在数据量⼩时基本体现不出来差距。
考虑数据的类型,⽐如如果全部是正整数,那么考虑使⽤桶排序为最优。
考虑数据已有顺序,快排是⼀种不稳定的排序(当然可以改进),对于⼤部分排好的数据,快排会浪费⼤量不必要的步骤。
数据量极⼩,⽽起已经基本排好序,冒泡是最佳选择。
我们说快排好,是指⼤量随机数据下,快排效果最理想。
⽽不是所有情况。
3)总结:——按平均的时间性能来分:时间复杂度为O(nlogn)的⽅法有:快速排序、堆排序和归并排序,其中以快速排序为最好;时间复杂度为O(n2)的有:直接插⼊排序、起泡排序和简单选择排序,其中以直接插⼊为最好,特别是对那些对关键字近似有序的记录序列尤为如此;时间复杂度为O(n)的排序⽅法只有,基数排序。
当待排记录序列按关键字顺序有序时,直接插⼊排序和起泡排序能达到O(n)的时间复杂度;⽽对于快速排序⽽⾔,这是最不好的情况,此时的时间性能蜕化为O(n2),因此是应该尽量避免的情况。
简单选择排序、堆排序和归并排序的时间性能不随记录序列中关键字的分布⽽改变。
——按平均的空间性能来分(指的是排序过程中所需的辅助空间⼤⼩):所有的简单排序⽅法(包括:直接插⼊、起泡和简单选择)和堆排序的空间复杂度为O(1);快速排序为O(logn ),为栈所需的辅助空间;归并排序所需辅助空间最多,其空间复杂度为O(n );链式基数排序需附设队列⾸尾指针,则空间复杂度为O(rd )。
——排序⽅法的稳定性能:稳定的排序⽅法指的是,对于两个关键字相等的记录,它们在序列中的相对位置,在排序之前和经过排序之后,没有改变。
数据结构(C语言)第八章 排序

直接插入排序过程
0 21 1 25 2 49 3 4 25* 16 5 08 temp
i=1
0 21
21
1 25
25 25
2 49
49 49
3 4 25* 16
25* 16 25* 16
5 08
08 08
temp 25
i=2
21
49
21
25
25 25
49
49 25*
25* 16
25* 16 49 16
希尔排序 (Shell Sort)
基本思想设待排序对象序列有 n 个对象, 首 先取一个整数 gap < n 作为间隔, 将全部对 象分为 gap 个子序列, 所有距离为 gap 的对 象放在同一个子序列中, 在每一个子序列中 分别施行直接插入排序。然后缩小间隔 gap, 例如取 gap = gap/2,重复上述的子序列划 分和排序工作。直到最后取 gap == 1, 将所 有对象放在同一个序列中排序为止。 希尔排序方法又称为缩小增量排序。
第八章 排序
概述
插入排序
交换排序 选择排序 归并排序 基数排序 各种内排方法比较
概 述
排序: 将一个数据元素的任意序列,重新
排列成一个按关键字有序的序列。
数据表(datalist): 它是待排序数据对象的
有限集合。
主关键字(key): 数据对象有多个属性域,
即多个数据成员组成, 其中有一个属性域可用 来区分对象, 作为排序依据,称为关键字。也 称为关键字。
直接插入排序 (Insert Sort)
基本思想 当插入第i (i 1) 个对象时, 前面的 R[0], R[1], …, R[i-1]已经排好序。这时, 用 R[i]的关键字与R[i-1], R[i-2], …的关键字顺 序进行比较, 找到插入位臵即将R[i]插入, 原 来位臵上的对象向后顺移。
排序的几种算法

排序的几种算法
一、冒泡排序
冒泡排序就是重复“从序列右边开始比较相邻两个数字的大小,再根据结果交换两个数字的位置”这一操作的算法。
在这个过程中,数字会像泡泡一样,慢慢从右往左“浮”到序列的顶端,所以这个算法才被称为“冒泡排序”。
二、选择排序
选择排序就是重复“从待排序的数据中寻找最小值,将其与序列最左边的数字进行交换”这一操作的算法。
在序列中寻找最小值时使用的是线性查找。
三、插入排序
插入排序是一种从序列左端开始依次对数据进行排序的算法。
在排序过程中,左侧的数据陆续归位,而右侧留下的就是还未被排序的数据。
插入排序的思路就是从右侧的未排序区域内取出一个数据,然后将它插入到已排序区域内合适的位置上。
四、堆排序
堆排序的特点是利用了数据结构中的堆。
五、归并排序
归并排序算法会把序列分成长度相同的两个子序列,当无法继续往下分时(也就是每个子序列中只有一个数据时),就对子序列进行归并。
归并指的是把两个排好序的子序列合并成一个有序序列。
该操作会一直重复执行,直到所有子序列都归并为一个整体为止。
总的运行时间为O,这与前面讲到的堆排序相同。
Java常用排序算法程序员必须掌握的8大排序算法

分类:1)插入排序(直接插入排序、希尔排序)2)交换排序(冒泡排序、快速排序)3)选择排序(直接选择排序、堆排序)4)归并排序5)分配排序(基数排序)所需辅助空间最多:归并排序所需辅助空间最少:堆排序平均速度最快:快速排序不稳定:快速排序,希尔排序,堆排序。
先来看看8种排序之间的关系:1.直接插入排序(1)基本思想:在要排序的一组数中,假设前面(n-1)[n>=2] 个数已经是排好顺序的,现在要把第n个数插到前面的有序数中,使得这n个数也是排好顺序的。
如此反复循环,直到全部排好顺序。
(2)实例(3)用java实现12345678911121314151617181920package com.njue;publicclass insertSort {public insertSort(){inta[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,2 5,53,51};int temp=0;for(int i=1;i<a.length;i++){int j=i-1;temp=a[i];for(;j>=0&&temp<a[j];j--){a[j+1]=a[j]; //将大于temp的值整体后移一个单位}a[j+1]=temp;}for(int i=0;i<a.length;i++){System.out.println(a[i]);}2. 希尔排序(最小增量排序)(1)基本思想:算法先将要排序的一组数按某个增量d(n/2,n为要排序数的个数)分成若干组,每组中记录的下标相差 d.对每组中全部元素进行直接插入排序,然后再用一个较小的增量(d/2)对它进行分组,在每组中再进行直接插入排序。
当增量减到1时,进行直接插入排序后,排序完成。
(2)实例:(3)用java实现123456789101112131415161718192122232425262728293031publicclass shellSort { publicshellSort(){int a[]={1,54,6,3,78,34,12,45,56,100}; double d1=a.length;int temp=0;while(true){d1= Math.ceil(d1/2);int d=(int) d1;for(int x=0;x<d;x++){for(int i=x+d;i<a.length;i+=d){int j=i-d;temp=a[i];for(;j>=0&&temp<a[j];j-=d){a[j+d]=a[j];}a[j+d]=temp;}}if(d==1){break;}for(int i=0;i<a.length;i++){System.out.println(a[i]);}}3.简单选择排序(1)基本思想:在要排序的一组数中,选出最小的一个数与第一个位置的数交换;然后在剩下的数当中再找最小的与第二个位置的数交换,如此循环到倒数第二个数和最后一个数比较为止。
数字的排序根据给定规则对数字进行排序

数字的排序根据给定规则对数字进行排序数字的排序是一项非常常见的任务,在日常生活和工作中经常用到。
而数字的排序可以通过不同的规则来进行,常见的包括升序和降序排序。
本文将根据给定的规则对数字进行排序,并介绍一些常见的排序算法。
一、升序排序升序排序是按照数字从小到大的顺序进行排序。
以下是一种简单的升序排序算法示例:1. 输入一组数字列表。
2. 从左到右遍历列表,选取当前位置的数字作为最小值。
3. 继续遍历列表,如果遇到比当前最小值更小的数字,则更新最小值。
4. 完成一次遍历后,将最小值与当前位置的数字交换位置。
5. 继续从下一个位置开始重复上述步骤,直到遍历完成。
这是一种简单但效率较低的排序算法,称为选择排序。
它的时间复杂度为O(n^2),其中n是数字的个数。
二、降序排序降序排序是按照数字从大到小的顺序进行排序。
以下是一种简单的降序排序算法示例:1. 输入一组数字列表。
2. 从左到右遍历列表,选取当前位置的数字作为最大值。
3. 继续遍历列表,如果遇到比当前最大值更大的数字,则更新最大值。
4. 完成一次遍历后,将最大值与当前位置的数字交换位置。
5. 继续从下一个位置开始重复上述步骤,直到遍历完成。
这也是一种简单但效率较低的排序算法,同样的时间复杂度为O(n^2)。
三、快速排序快速排序是一种常用的排序算法,它采用分治的策略来提高排序效率。
以下是快速排序的过程示例:1. 选择一个基准数,可以是列表中任意一个数字。
2. 将列表中比基准数小的数字放在左边,比基准数大的数字放在右边。
3. 对左右两边的子列表分别重复上述步骤,直到每个子列表只剩下一个数字。
4. 完成排序。
快速排序的时间复杂度为O(nlogn),具有较高的效率。
四、归并排序归并排序也是一种常用的排序算法,它通过将列表分成若干个子列表并分别排序,最后合并成一个有序的列表。
以下是归并排序的过程示例:1. 将列表分成两个子列表,分别进行排序。
2. 将排序好的子列表合并为一个有序的列表。
常用的内部排序方法

常用的内部排序方法有:交换排序(冒泡排序、快速排序)、选择排序(简单选择排序、堆排序)、插入排序(直接插入排序、希尔排序)、归并排序、基数排序(一关键字、多关键字)。
一、冒泡排序:1.基本思想:两两比较待排序数据元素的大小,发现两个数据元素的次序相反时即进行交换,直到没有反序的数据元素为止。
2.排序过程:设想被排序的数组R[1..N]垂直竖立,将每个数据元素看作有重量的气泡,根据轻气泡不能在重气泡之下的原则,从下往上扫描数组R,凡扫描到违反本原则的轻气泡,就使其向上"漂浮",如此反复进行,直至最后任何两个气泡都是轻者在上,重者在下为止。
【示例】:49 13 13 13 13 13 13 1338 49 27 27 27 27 27 2765 38 49 38 38 38 38 3897 65 38 49 49 49 49 4976 97 65 49 49 49 49 4913 76 97 65 65 65 65 6527 27 76 97 76 76 76 7649 49 49 76 97 97 97 97二、快速排序(Quick Sort)1.基本思想:在当前无序区R[1..H]中任取一个数据元素作为比较的"基准"(不妨记为X),用此基准将当前无序区划分为左右两个较小的无序区:R[1..I-1]和R[I+1..H],且左边的无序子区中数据元素均小于等于基准元素,右边的无序子区中数据元素均大于等于基准元素,而基准X 则位于最终排序的位置上,即R[1..I-1]≤X.Key≤R[I+1..H](1≤I≤H),当R[1..I-1]和R[I+1..H]均非空时,分别对它们进行上述的划分过程,直至所有无序子区中的数据元素均已排序为止。
2.排序过程:【示例】:初始关键字[49 38 65 97 76 13 27 49]第一次交换后[27 38 65 97 76 13 49 49]第二次交换后[27 38 49 97 76 13 65 49]J向左扫描,位置不变,第三次交换后[27 38 13 97 76 49 65 49]I向右扫描,位置不变,第四次交换后[27 38 13 49 76 97 65 49]J向左扫描[27 38 13 49 76 97 65 49](一次划分过程)初始关键字[49 38 65 97 76 13 27 49]一趟排序之后[27 38 13]49 [76 97 65 49]二趟排序之后[13]27 [38]49 [49 65]76 [97]三趟排序之后13 27 38 49 49 [65]76 97最后的排序结果13 27 38 49 49 65 76 97三、简单选择排序1.基本思想:每一趟从待排序的数据元素中选出最小(或最大)的一个元素,顺序放在已排好序的数列的最后,直到全部待排序的数据元素排完。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、交换排序1)气泡排序(bubble sorting)也是一种简单排序方法,T(n)=O(n2)算法:A[n],第一次排序区间为A[0]~A[n-1],第二次排序区间为A[1]~A[n-1,]…,最后一次排序区间为A[n-2]~A[n-1],每次排序轻者上浮,即排序区间最小者交换到排序区间的第一个位置,经n-1次排序。
完成排序过程。
Example 1#include<iostream>using namespace std;struct ET{int x;};void select(ET A[],int n){ET e;for(int i=0;i<n-1;i++){for(int j=i+1;j<n;j++){if(A[i].x>A[j].x){e=A[i];A[i]=A[j];A[j]=e;}}}}void display(ET a[],int n){for(int i=0;i<n;i++){cout<<a[i].x<<" ";}cout<<"\n";}void main(){ET a[10];/* a[0].x=100;a[1].x=20;a[2].x=15;a[3].x=50;a[4].x=200;a[5].x=80;a[6].x=300;a[7].x=10; */for(int i=0;i<10;i++){a[i].x=rand()/100;}cout<<"\n===========排序前====================\n\n";display(a,10);cout<<"\n===========排序后====================\n\n";select(a,10);display(a,10);cout<<endl;}Examplae 2#include<iostream>using namespace std; struct ET{int no;char* name;char* sex;double score;};void insertSort(ET A[],int n) {ET x;for(int i=0;i<n;i++){for(int j=i+1;j<n;j++){if(A[i].no>A[j].no){x=A[i];A[i]=A[j];A[j]=x;}}}}void insertSort1(ET A[],int n) {ET x;for(int i=0;i<n;i++){for(int j=i+1;j<n;j++){if(A[i].score>A[j].score){x=A[i];A[i]=A[j];A[j]=x;}}}}void display(ET e[8]){ for(int i=0;i<8;i++){cout.width(6);cout<<e[i].no<<" ";cout.width(12);cout<<e[i].name<<" ";cout.width(6);cout<<e[i].sex<<" ";cout.width(6);cout<<e[i].score<<endl;}}void main(){ET a[8];a[0].no=36;a[0].name="Bill Gates";a[0].sex="男";a[0].score=100;a[1].no=25;a[1].name="FF Gates";a[1].sex="女";a[1].score=98;a[2].no=48;a[2].name="Lucy Gates";a[2].sex="男";a[2].score=77;a[3].no=12;a[3].name="Jack Gates";a[3].sex="男";a[3].score=88;a[4].no=65;a[4].name="GG Gates";a[4].sex="女";a[4].score=66;a[5].no=43;a[5].name="BB Gates";a[5].sex="男"; a[5].score=99;a[6].no=20;a[6].name="KK Gates";a[6].sex="男";a[6].score=78;a[7].no=58;a[7].name="PP Gates";a[7].sex="男";a[7].score=99;cout<<"\n========排序前========================\n\n"; display(a);insertSort(a,8);cout<<"\n========排序后(按学号排序)==============\n\n"; display(a);insertSort1(a,8);cout<<"\n========排序后(按学分排序)==============\n\n"; display(a);}2)快速排序(quick sorting)(不稳定算法)是目前所有排序方法中速度最快的排序方法(但逼简单排序方法多占用n个栈空间)。
在最好的和一般的情况下,T(n)=O(nlog2n),但在最坏的情况下(原排序对象已经有序),T(n)=O(n2),与简单排序方法相当,且多占用n个栈空间,从而成为最差的排序方法。
所以,为了避免这种情况发生,1是实现判断,如果是这种情况,采用其它排序方法,2改进快速排序方法。
算法:在排序区间最后一个元素后边放一个“岗哨”;每次以待排序区间的第一个元素为基准元素,分成2个区间,前边的区间的元素值都小于基准元素,后边的区间的元素都大于基准元素,递归上边的过程,使得每个区间只有一个元素,排序完成。
A={45,53,18,36,72,30,48,93,15,36}[45,53,18,36,72,30,48,93,15,36]i j[45,36,18,36,72,30,48,93,15,53]i j[45,36,18,36,15,30,48,93,72,53] (i>j)j i[30,36,18,36,15],45,[48,93,72,53] (交换A[s]和A[j]) …………[15, 18, 36, 36, 45, 48, 53, 72, 93 ]Example 1#include<iostream>using namespace std;struct ET{int xx;};void quickSort(ET A[],int s,int t) {int i=s,j=t;ET x=A[s];do{do{i++;}while(A[i].xx<x.xx);do{j--;}while(A[j].xx>x.xx);if(i<j){ET temp=A[i];A[i]=A[j];A[j]=temp;}}while(i<j);A[s]=A[j];A[j]=x;if(s<j-1)quickSort(A,s,j);if(j+1<t)quickSort(A,j+1,t); }void display(ET s[],int n){for(int i=0;i<n;i++){cout.width(6);cout<<s[i].xx;}cout<<endl;}int posistion(ET a[],int first,int end) {int i=first;int j=end;ET x;while(i<j){while(i<j&&a[i].xx<=a[j].xx){i++;}while(i<j&&a[i].xx<=a[j].xx){j--;}if(i<j){x=a[i];a[i]=a[j];a[j]=x;}}return i;}void quickSort1(ET A[],int first,int end){if(first>end){return;}else{int p=posistion(A,first,end);quickSort1(A,first,p-1);quickSort1(A,p+1,end);}}void _print(char* s){cout<<"\n=============="<<s<<"==================\n"; }void main(){ET a[10];a[0].xx=100;a[1].xx=30;a[2].xx=300;a[3].xx=20;a[4].xx=100;a[5].xx=50;a[6].xx=100;a[7].xx=30;a[8].xx=100;a[9].xx=10;/*for(int i=0;i<10;i++){a[i].xx=rand()/100;}*/_print("排序前");display(a,10);_print("排序后");quickSort1(a,0,10);//quickSort(a,0,10);display(a,10);}Example 2#include<iostream>using namespace std;struct ST{int no;char* name;char* sex;int score;};void display(ST s[],int n){for(int i=0;i<n;i++){cout.width(3);cout<<s[i].no;cout.width(15);cout<<s[i].name;cout.width(5);cout<<s[i].sex;cout.width(6);cout<<s[i].score<<endl;}cout<<endl;}int posistion(ST a[],int first,int end) {int i=first;int j=end;ST x;while(i<j){while(i<j&&a[i].no<=a[j].no){i++;}while(i<j&&a[i].no<=a[j].no){j--;}if(i<j){x=a[i];a[i]=a[j];a[j]=x;}}return i;}void quickSort1(ST A[],int first,int end)if(first>end){return;}else{int p=posistion(A,first,end);quickSort1(A,first,p-1);quickSort1(A,p+1,end);}}int posistion2(ST a[],int first,int end){int i=first;int j=end;ST x;while(i<j){while(i<j&&a[i].score<=a[j].score){i++;}while(i<j&&a[i].score<=a[j].score){j--;}if(i<j){x=a[i];a[i]=a[j];a[j]=x;}}return i;}void quickSort2(ST A[],int first,int end){if(first>end){return;}else{int p=posistion2(A,first,end);quickSort2(A,first,p-1);quickSort2(A,p+1,end);}}void _print(char* s){cout<<"\n=============="<<s<<"==================\n";}void main(){ST a[8];a[0].no=100; a[0].name="Bill Gates"; a[0].sex="男"; a[0].score=100; a[1].no=21; a[1].name="FF Gates"; a[1].sex="女"; a[1].score=98; a[2].no=34; a[2].name="Lucy Gates"; a[2].sex="男"; a[2].score=77; a[3].no=56; a[3].name="Jack Gates"; a[3].sex="男"; a[3].score=88; a[4].no=12; a[4].name="GG Gates"; a[4].sex="女"; a[4].score=66; a[5].no=35; a[5].name="BB Gates"; a[5].sex="男"; a[5].score=99; a[6].no=11; a[6].name="KK Gates"; a[6].sex="男"; a[6].score=78; a[7].no=9; a[7].name="PP Gates"; a[7].sex="男"; a[7].score=99; _print("排序前");display(a,8);_print("按学号排序");quickSort1(a,0,8);display(a,8);_print("按学分排序");quickSort2(a,0,8);display(a,8);}2、归并排序(Merge Sorting)(稳定排序)二路归并排序:首先把排序区间A[0]~A[n-1]中的每一个元素看成是一个有序表,接着两两归并,等到新的有序表,如此进行,最后得到一个有序表,排序完成。
