弹性波动力学
弹性波动理论

四、波动方程 若应力体内两相邻质点应力相同,无相对运动,静止平衡状态
若二者之间有应力差,产生波动
为研究弹性波动形成的物理机制和传播规律,须建立波的运动方程(波动方程)
波动方程: 研究介质中质点位移随时间和空间的变化规律。
在弹性理论中,对于均匀、各向同性、理想弹性介质中的三维波动方程式为
(
)
x
2u
2u t 2
一个体积为V的立方体,在流体静压力P的挤压下所发生体积形变。即每个正
截面的压体变模量(压缩模量): 压力P与体积相对变化之比
P K=-
(1.7)
(4) 切变模量(μ)
切变模量(刚性模量):表示了物体切应力与切应变之比
μ=
(1.8)
对于液体: μ=0,不产生切应变,只有体积变化。
(5) 拉梅常数(λ、μ) 弹性力学中:受力物体内任意点受力 沿坐标轴分为三个分力,每个分力 都会引起纵向和横向沿三个轴的应力与应变。
因此:振动图是描述地震波质点位移随时间的变化规律的图像。 图中: t1――初至,质点刚开始振动 △t――波(质点振动)的延续时间,△t的大小直接影响地震勘探的分辨率。
1.8 (a) 振动图 (b)波形记录
体波:纵、横波,在整个空间
面波:弹性分界面附近 瑞利面波:自由界面,地滚波,R波 特点:低频、低速,能量大(强振幅),旋转(铅垂面,椭圆,逆转)
天然地震中,危害极大 勒夫面波:低速带顶底界面,平行界面的波动,振动方向垂直传播方向,
SH波 特点:对纵波勘探影响不大,对横波勘探严重干扰
图1.5 (a)瑞雷面波的传播 (b)勒夫面波的传播
自然界中绝大部分物体,在外力作用下,既可显弹,也可显塑
地震勘探,震源是脉冲式的,作用时间很短(持续十几~几十毫秒),岩土受 到的作用力很小,可把岩、土介质看作弹性介质,用弹性波理论来研究地震波。
弹性波的勘测

弹性波是应力波的一种,扰动或外力作用引起的应力和应变在弹性介质中传递的形式。
弹性介质中质点间存在着相互作用的弹性力。
某一质点因受到扰动或外力的作用而离开平衡位置后,弹性恢复力使该质点发生振动,从而引起周围质点的位移和振动,于是振动就在弹性介质中传播,并伴随有能量的传递。
在振动所到之处应力和应变就会发生变化。
弹性波理论已经广泛应用于地震、地质勘探、采矿、材料的无损探伤、工程结构的抗震抗爆、岩土动力学等方面。
弹性波频率分为瑞利波(R波)和拉夫波(L波),而R波在振动波组中能量最强、振幅最大、频率最低,容易识别也易于测量,所以弹性波频率勘探一般是指瑞利弹性波频率勘探。
R波在岩土工程勘察中的应用大致分为以下几个方面:查明工程区地下介质速度结构并进行地层划分;对岩土体的物理力学参数进行原位测试;工业与民用建筑的地基基础勘察;地下管道及埋藏物的探测;地下空洞、岩溶、古墓及废弃矿井的埋深、范围等探测;软土地基加固处理效果评价及饱和砂土层的液化判别;公路、机场跑道质量的无损检测;江河、水库大坝(堤)中软弱夹层的探测和加固效果评价等;场地土类别划分及滑坡调查等;断层及其它构造带的测定与追踪等。
二、勘探原理地震勘探,是用人工方法激发地震波(地壳的弹性振动),并且研究它们在地壳内传播的情况,来达到探查地壳地质结构的目的。
地震波由震源激发后,向各方传播,在存在密度差异的不同岩性地层的分界面上可能发生反射和折射,然后返回地面,引起地面的振动。
我们将专门的仪器设备(地震仪、检波器等)安置在地面上,记录地震的振动(地震记录),通过分析解释地震记录的特点(传播时间、振动的振幅、相位及频率等),就能确定地层的埋藏深度、岩石的组成成分和物理力学性质。
地震勘探依据的是弹性波传播原理。
弹性波理论分析表明,R波具有如下特点:在地震波形记录中振幅和波组周期最大,频率最小,能量最强;在不均匀介质中R波相速度(VR)具有频散特性,此点是弹性波频率勘探的理论基础;由P波初直到R波初至之间的1/3处为S波组初至,且VR与VS具有很好的相关性,其相关式为:VR=VS·(0.87 1.12μ)/(1 μ);式中:μ为泊松比;此关系奠定了R波在测定岩土体物理力学参数中的应用;R波在多道接受中具有很好的直线性,即一致的波震同相轴;质点运动轨迹为逆转椭圆,且在垂直平面内运动;R 波是沿地表传播的,且其能量主要集中在距地表一个波长(λR)尺度范围内。
弹性波动力学

学习意义:理解不同边界条件下的地震波波动方程的含义,理解各种弹性力学参数的物理意义并将参数和地下介质的岩性问题联系起来,最终为地震剖面的岩性解释服务。
刚体:变形忽略不计的物体弹性波:扰动在弹性介质中的传播波前面:波在介质中传播的某个时刻,介质内已扰动的区域和未扰动区域间的界面称为波前面地震波分类:纵波横波,平面波球面波柱面波,体波界面波表面波 哑指标:在同一项中重复两次从而对其应用求和约定的指标 自由指标:在同一项中出现一次因而不约定求和的指标各项同性张量:如果一个张量的每个分量都是坐标变换下的不变量,则称此张量为各项同性张量张量性质:二阶实对称张量的特征值都是实数:二阶实对称张量对应于不同特征值的两个特征向量垂直:二阶实对称张量总存在三个相互垂直的主方向:在主轴坐标系内二阶实对称张量的矩阵形式是对角形:三个相互垂直主方向的右手坐标系为主轴坐标系弹性:物体受外力时发生形变,外力消除时物体回到变形前的水平 弹性变形:在弹性范围内发生的可恢复原状的变形 弹性体:处于弹性变形阶段的物体弹性波动力学基本假设:物体是连续的:物体是线性弹性的:物体是均匀分布的:物体是各项同性的:小变形假设:无体物初应力假设 位形:弹性体在任意时刻所占据的空间区域参考位形:弹性体未受外力作用处在自然情况下的位形 运动:刚性平移,刚性转动,变形应变主方向:如果过p 点的某个方向的线源,在变形后只沿着他原来的方向产生相对伸缩主应变:沿着应变主方向的相对伸缩体力:连续分布作用于弹性体每个体元上的外力称为体力 面力:连续分布作用于弹性体表面上的力 运动微分方程的物理意义:表示应力张量在弹性体内部随点位置变化时应满足的关系式内能:弹性体在某个变形状态下,其内部分子的动能以及分子之间相互作用具有的势能总和应变能密度:单位体积内的弹性体所具有的应变能 广义胡克定律:线性弹性体内一点处的应力张量分量可以表示为该点处应变量张量的线性齐次方程动弹性模量:由介质的速度参数表达的弹性模量极端各向异性弹性体:过p 点任意方向都不同的弹性体粘滞力:实际流体中两层流体相互滑动流体间相互作用的阻力 理想流体介质:可以将粘滞力忽略的流体无旋波:无旋位移场的散度对应弹性体的涨缩应变场以波的形式传播(涨缩应变场)无散波:无散位移场的旋度对应弹性体的转动情况以波的形式运动平面波:波前面离开波源足够远时脉冲型和简谐型均匀和非均匀平面波 非频散波:波的传播速度仅仅依赖媒介密度拉美系数等而与波的频率无关 频散波:波的传播速度与频率有关频散:初始扰动的没一个简谐成分都以不同速度前进,从而初始波形在行进中发生了变化相速度:简谐波的传播速度群速度:由简谐波叠加而成的波其合成振幅的传播速度非均匀平面波:如果波的等位相面各点振幅不同,既等位相面和等振幅面不平行球面波:弹性媒质的位移矢量场具有球对称性,且只是空间变量和时间变量的函数 1、证明:kmjn kn jm im n ijk e e δδδδ-=;2、321321321n n n m m m i i i imne δδδδδδδδδ=3、321321321n n n m m m i i i ijkimn ijk e e e δδδδδδδδδ=4、kmjn kn jm knkm ki jn jm ji inim ii δδδδδδδδδδδδδ-==5、如果i i e a a =,ii e b b =,i i e c c=,证明:c b a b c a c b a )()()(∙-∙=⨯⨯;k ijk j i e e c b c b =⨯)()()(k ijk j i m m k ijk j i e e c b e a e e c b a c b a ⨯=⨯=⨯⨯n m kn ijk j i m k m ijk j i m e e e c b a e e e c b a=⨯=)(njn im jm in j i m n knm kij j i m e c b a e e e c b a)(δδδδ-==nn m m n m n m n n m m m n m e c b a e c b a e c b a c b a-=-=)(c b a b c a e c b a e b c a n n m m n n m m)()(∙-∙=-=分析:由于标量对坐标的选择无关,因此,如果证明了物理量在坐标变换前后相等,即可以认为此物理量是标量。
应用地球物理学原理第二章04弹性波的特征

03
弹性波在地壳中的传播
地壳的分层结构
地壳是地球最外层的硬壳,由 岩石和土壤组成,具有明显的 分层结构。
地球的地壳分为多个板块,板 块之间的相互作用可以产生地 震波。
地壳的分层结构对弹性波的传 播具有重要影响,不同层中的 波速和传播方向可能不同。
弹性波在不同介质中的传播
弹性波在固体、液体和气体中传播时具有不同的特征。
地下结构的不确定性可能导致弹性波传播模型的 误差,从而影响解释结果的准确性。
需要对地下结构进行详细调查和建模,以获得更 准确的弹性波传播特征。
数据处理与解释的复杂性
01
02
03
弹性波数据的处理涉及 多种算法和技术,如滤 波、反演、成像等,处
理过程较为复杂。
弹性波数据的解释需要 丰富的专业知识和经验 ,对解释人员的素质要
应用地球物理学原理第二章 04弹性波的特征
目录
• 弹性波的基本概念 • 弹性波的物理特性 • 弹性波在地壳中的传播 • 弹性波的应用 • 弹性波的局限性
01
弹性波的基本概念
弹性波的定义
弹性波
在弹性介质中传播的波动现象,由于介质的弹性性质,当 受到外力作用时,介质发生形变并产生恢复力,这种恢复 力会以波动的形式在介质中传播。
资源开发规划
通过分析地下岩层的弹性波特征,评 估资源的可开采性和开发风险,为资 源开发提供科学依据。
环境保护监测
利用弹性波技术监测环境变化,如土 壤污染、地下水污染等,为环境保护 提供技术支持。
05
弹性波的局限性
对地下结构的依赖性
弹性波的传播特性与地下结构密切相关,不同的 地下介质对弹性波的传播有显著影响。
弹性波的传播方式
弹性波可以通过反射、折射、散射等方式传播, 其传播路径和速度受到介质的不均匀性和边界条 件的影响。
地震波在分层介质中的反射、透射与...

第1章 绪论1.1 弹性波场论概述在普通物理的力学部分,我们曾经着重讨论过物体在外力作用下的机械运动规律。
在讨论时,由于物体变形影响很小,我们将其忽略,而将物体视为刚体或简化为质点,这是完全正确的。
然而,实际上任何物体在外力作用下不仅会产生机械运动,而且会产生变形。
由于变形物体内部将相互作用,产生内力、应力和应变。
当应力或应变达到一定极限时,物体就会破坏,这一点在研究材料和工程力学中尤其要考虑,地球介质也不例外,地壳运动或地震都会产生地质体的应力或应变。
在弹性力学中,主要讨论对物体作用时的变形效应,物体不再假定为刚体,而是弹性体、塑性体,应当视为可变形体,我们研究的视角也从外部整体过渡到内部局部。
长期的生产实际和科学实验均已表明,几乎所有的物体都具有弹性和塑性。
所谓的弹性是指物体的变形随外力的撤除而完全消失的这种属性。
所谓的塑性是指物体的变形在外力的撤除后仍部分残留的这种属性。
物体的弹性和塑性受诸多因素影响而发生改变,并在一定的条件下相互转化。
因此,确切地,应当说成物体处于弹性状态或塑性状态,而非简单地说物体是弹性体或塑性体。
在弹性力学中,只讨论物体处于弹性状态下的有关力学问题,这时物体可称为弹性体。
由上所述,弹性力学又称弹性理论,研究的对象是弹性体,其任务是研究弹性体在外界因素(包括外力,温度等)作用下的应力、应变和位移规律。
简单地说,弹性力学就是研究弹性体的应力、应变和位移规律的一门学科。
弹性力学是固体力学中很重要的一个分支。
而固体力学是从宏观观点研究固体在外力作用下的力学响应的科学,它主要研究固体由于受外力作用所引起的内力(应力)、变形(应变)以及与变形有直接关系的位移的分布规律及其随时间变化的规律。
可见,应力、应变和位移是空间和时间的函数。
与固体力学对应的还有流体力学等。
固体力学还包括材料力学,断裂力学等等。
弹性力学本身又分为弹性静力学(Elasticity Statics )和弹性动力学(Elasticity Dynamics )。
弹性波动力学2014

3 I2 II III 0
其中,
I Tii T 11 T 22 T 33
II 1 2 (Tii Tjj TijTij )
III det(Tij )
I,II,III 分别叫做二阶张量的第一、第二和第三不变量。 其特征向量满足的方程为:
(Tij ij )n j 0 n i n i 1
6.标量的梯度、向量的旋度、散度等的混合计算等。 第二章 1. 内力、附加内力、体应变、泊松比
2. 弹性波、波阵面、波速、纵波、横波、平面波、球面波、 柱面波、体波、面波 3. 弹性波动力学的基本假设: (连续性、线性弹性、均匀性、 各向同性、微小变形) 第三章 1.位形、参考位形、变形、运动; 2.位移、速度、加速度,空间点和质点的统一; 3.小变形应变张量( eij )及其各个分量的意义;
1. 弹性波(SV 波、SH 波、P 波)传播到介质和空气分界面, 入射波、反射波的类型及传播方向,垂直入射时各个波的(位 移)振幅系数。 2,弹性波(SV 波、SH 波、P 波)传播到弹性介质分界面, 入射波、反射波、透射波的类型及传播方向,垂直入射时各个 波的(位移)振幅系数等 3. 面波的基本概念。 第九章(本次考试不要求) 求解弹性波动力学问题的方法(理论推导,即解析解;数值方 法,如有限单元法、有限差分法、伪谱法等) ,一维有限差分 法合成地震记录的编程实现。 本次考试题型及分数分布: 一、名词解释 (每小题 5 分,共 30 分) 二、简答(每小题 8 分,共 32 分) 三、计算 (1 小题,共 15 分) 四、 (15 分)推导(一小题,共 15 分) 五、 (8 分)波场分析。
第一章 1.指标记号,求和约定,自由指标,哑指标 2.三个符号,克罗尼克尔符号( ij )排列符号( eijk ), 以及微分符号 ( ).
研究性教学模式在《弹性波动力学基础》课程中的实践

研究性教学模式在《弹性波动力学基础》课程中的实践作者:韩开锋来源:《中国科教创新导刊》2012年第28期摘要:研究性教学是教师为了使学生进行研究性学习而开展的一种课堂教学,具有教学形式与内容的开放性、教学方式的自主性、学生知识获得的实践性及素质提升的综合性等特点。
本文在探讨研究性教学特性和必要性的基础上,通过亲身实践创建了高校专业课程——《弹性波动力学基础》研究性教学的场景模式。
实践证明,该授课模式对提高专业课程的教学质量,培养学生的研究性思维和创新精神具有重要意义。
关键词:研究性教学特性弹性波动力学基础场景模拟中图分类号:G4 文献标识码:A 文章编号:1673-9795(2012)10(a)-0048-02研究性教学是教师以培养学生的研究意识和创新能力为目标,引导学生进行研究性学习,从而让学生掌握知识、培养研究能力和创新能力的教学,其目标在于让学生以类似于科学探究的形式进行学习。
目前,我国高校研究性教学更多集中在诸如“创新杯”、“挑战杯”之类的课外竞赛活动以及大学生科研计划等“第二课堂”来开展,而通过专门在“第一课堂”的教学中来实施研究性教学尚不普遍。
于是,大部分高校学生被排除在发现、探索、研究之外,继续接受着传统的以知识灌输型为主的教学,这严重抑制了学生的思维能力、创造能力以及科研兴趣等非智力因素的发展,已无法适应当代素质教育的需要。
因此,通过一门课程的研究性教学,让所有学生都能够独立的进行探究性学习,一直是我们教学过程中努力实践探索的目标。
1 研究性教学的特性所谓研究性教学,是指在教师的指导下,将课内讲授与课外实践、教师引导与学生自学、教材与课外阅读有机结合起来并达到完整、和谐、统一的教学。
[1]与传统的被动接受性教学相比,研究性教学具有以下特性。
1.1 教学形式与内容的开放性传统的接受性教学有一套规范的标准和预期的答案,而在研究性教学中,教师关注的是学生怎样找到解决问题的切入点,怎样进行论证,而不是要求得到统一的答案。
弹性波与结构动力学

弹性波与结构动力学引言:弹性波是物质中传播的一类波动现象,它在结构动力学中起着重要的作用。
通过研究弹性波的传播特性,我们可以深入了解结构的振动行为,进而为工程结构的设计和安全性评估提供理论支持。
一、弹性波的基本概念弹性波是一种沿着介质中传递的机械波,其传播过程中介质的形状和体积保持不变。
弹性波包括两种类型:纵波和横波。
纵波是沿传播方向的波动,介质中的粒子在波传播过程中沿波的传播方向振动。
而横波是垂直于传播方向的波动,介质中的粒子在波传播过程中垂直于传播方向振动。
二、弹性波的传播特性弹性波在传播过程中受到介质本身刚度和密度的影响。
根据介质的性质不同,弹性波的传播速度也不同。
例如,在固体中,纵波的传播速度大于横波的传播速度;而在液体中,纵波和横波的传播速度相等。
此外,弹性波的传播还受到外部条件的限制,如介质的边界条件和存在的障碍物。
这些因素会使波动的传播方向改变,产生反射、折射和散射现象。
三、结构动力学中的应用结构动力学旨在研究结构体在受到外界力作用下的响应行为。
通过研究弹性波的传播和结构的振动特性,我们可以了解结构在承受外力时的变形和应力分布情况,从而评估结构的安全性和稳定性。
1. 弹性波的成像技术利用弹性波的传播特性,我们可以将其应用于结构的成像技术中。
通过在结构表面上布置传感器,并采集传感器上的信号信息,可以获得结构内部的振动分布情况。
这对于检测结构的缺陷和损伤以及评估结构的健康状况具有重要意义。
2. 弹性波在地震工学中的应用地震是一种具有较高频率和较大能量的弹性波。
研究地震波的传播行为可以帮助我们了解地震的发生机理和地震波对结构的影响。
通过地震波的预测和分析,可以为建筑物的抗震设计和城市的抗震规划提供科学依据。
3. 结构动力响应的数值模拟结构动力学中的数值模拟是利用计算机模拟方法来分析结构体在受到外力激励下的响应行为。
其中,弹性波的传播特性被广泛应用于模拟结构的振动响应。
通过建立结构的有限元模型和适当的边界条件,可以计算结构在不同外力作用下的动态行为,为工程师提供设计和评估结构安全性的参考。
弹性波

斯通利波
在两种不同介质的半空间体的交界面上传播的波称为斯通利波,因斯通利首先发现并研究这种波而得名。它是一种波速与两个介质的性质有关的变态瑞利波。斯通利波的存在与介质的弹性拉梅常数和介质密度有关。在两个介质的拉梅常数λ1、G1和λ2、G2满足λ1/G1=λ2/G2=1的情况下,存在条件如图所示,如果两个介质的密度ρ1和ρ2之比ρ1/ρ2和G1/G2在图示坐标系中对应的点落在曲线A和曲线B之间,斯通利波就存在。在地震学中,理论上已证明斯通利波是存在的,但尚未观测到。
式中为拉普拉斯算符;α和β分别为纵波波速和横波波速;嗞=嗞(x,y,z,t)为标量势;ψx=ψx(x,y,z,t)、ψy=ψy(x,y,z,t)、ψz=ψz(x,y,z,t)为矢量势φ(x,y,z,t)的三个分量。ψx、ψy、ψz统称为波函数,它们和嗞同坐标系中的三个位移分量u、v、w的关系为:
上述波动方程是根据下面的假设导出的:①弹性介质中各质点间的相对位移为无穷小量;②介质是完全线弹性的,即应力和应变之间呈均匀线性关系,服从胡克定律;③介质是各向同性的;④不计外力(如重力、体积力、摩擦力等)。
在精确理论发展的同时,近似解理论也得到发展。有限差分方法先被用于解决短杆中弹性波的传播问题,后被推广到一些复杂结构中波的传播问题。有限元法逐步用于研究弹性波问题,开始用于分析细杆中弹性波的传播,后用于分析各种结构(柱、板、壳体)中的波的传播以及层状介质、正交异性介质中的波的传播等。非线性弹性波的传播问题的研究也取得初步成果。
声学基础

医学
大气地物球理和
生物 声学
大学地气震声学
生理学
听觉
心理 声学
通讯
音剧质声院室学内乐器乐律
音乐
2010/9/8
海洋学
水声 学
电工和 化工
工机程械
声声电工和声程超学噪声冲击振动
声学基础
建筑 工程
艺表术演
语言 心理学
次声学
¡ 研究次声的产生、传播、接收、作用试验检测的四种方法:次声、水声、
9
5
B超-B Mode (Cross Sectional 2 Dimensional) Imaging
2010/9/8
医学B超
工作在自发自收状态的超声波探头在空间一条线上 移动过程中测量的反射脉冲波所成图像。
Mechanical real-time scanners used for B mode scanning: (a) rectilinear, (b) sector, (c) spinner, and (d) oscillating reflector.
绪论课的教学内容
¡ 声学的各个分支;
¡ 声学在地球物理学中的地位; ¡ 关于本课程教学:
™本课程主要教学内容 ™本课程教学方法 ™本课程教学中对同学的要求
目的:开放视野、激发兴趣
声学的各个分支和应用
¡ 什么是声学?
™声学的定义 ™声学的分支
¡ 声学的应用
™A超、B超、C超、彩超 ™地震和海啸 ™声呐 ™声发射及其应用
显衰减;
声波
¡ 频率在20Hz~20kHz之间的机械波。 ¡ 也称为可闻声波,即人的耳朵可以感觉到的弹性波。 ¡ 我们生活在声波的海洋之中。
超声波
¡ 频率在20kHz以上的机械波。人耳听不到,但个别 动物(例如狗、蝙蝠等)可以感受到超声波的存在。
第六章弹性波波动方程及其解ppt课件

又 • u • uS 0
2
代入纳维方程 ( )( • u ) u f u
uS f uS
2 2
VS uS f uS
2
vs
结论:在均匀各向同性弹性体内,切变扰动以速度VS向
(4)
(5)
式u j , ji (ui , jj u j ,ij ) f i ui即为位移在弹性体
内传播时所满足的方程 .称为纳维 ( Navier)方程.
纳维方程是线性弹性假设条件下得到的各向同性弹性体中
的弹性波最基本方程。
指标表示的纳维方程 ( )u j , ji ui , jj f i ui
§6.1 线性弹性动力学的基本方程
1.
基本方程
➢
➢
运动微分方程 ji , j
几何方程
1
eij (ui , j u j ,i )
2
2 ui
f i 2
t
u1
e11
x1
u2
e22
x2
u
e33 3
x3
1 u1 u2
e12 (
)
2 x2 x1
v p t
上式表示波场是以速度VP向外传播的无旋场。
转动矢量表示的横波方程
2
( )( • u ) u f u两边取旋度
2
(
u
)
( )( ( • u )) 2 ( u ) ( f )
弹性动力学中的基本波

6、波动方程的定解问题
下面是本章要用到的第一章中的公式
xx 2 exx yy 2 eyy zz 2 ezz
u exx x
v eyy y
w ezz z
(1-74)
xz exz yz eyz xy exy
(2-19)
,并代入式(2-19),可得: 用E 和v 表示 、
2(1 ) 1 1 2
(2-20)
可见纵波速度大于横波速度。对自然界中常见的岩石 来说, = ,即 =0.25。具有这种性质的物体称为 =1.73; 泊松体。对泊松体而言,
总结:在均匀各向同性完全弹性介质中,纵波和横 波彼此独立存在和传播,在非均匀介质中,纵波和横波 彼此不能分开、独立传播,即纵波能产生横波,横波也 能产生纵波。 2 VS VP 拉梅方程
u u p us grad curl
(2 -3 )
其中 和 称为位移位, 为标量位, 为向量位。
up为标量位的梯度,其旋度为零,称为无旋场;us为向
量位的旋度,其散度为零,称为无散场;即
curl ( grad ) 0 div(curl ) 0
(2-4)
弹性力学 弹性波

u 0 (x,t) w 0
从而 e 0
而 2u 0
2
2
x 2
2w 0
代入不计体力的运动微分方程,可见其第一、第三式成为恒 等式,第二式简化为:
2
t 2
c22
2
x 2
E
c2 2(1 )
c2 为横波在弹性体中的传播速度。由于横波的体积应变
24
e 0 ,故横波为等容波。
横波的波动方程的通解为:
(x,t) f1(x c2t) f2(x c2t)
显然,整个通解表示朝相反两个方向传播的两个波,它的 位移沿着y方向,而传播方向是沿着x方向,传播速度等于
常量 c2 。
25
§11-4 球面波
如果弹性体具有圆球形的孔洞或具有圆球形的外表面, 则在圆球形孔洞或圆球形外表面上受到球对称的动力作用时 ,由孔洞向外传播或由外表面向内传播的弹性波,称为球面 波。
球面波是球对称的。利用球对称的基本微分方程:
E(1 ) (1 )(1 2)
(
d 2ur dr2
2 r2
dur dr
2 r2
ur )
kr
0
此时,ur ur (r, t) ,而不计体力时,用径向惯性力
2tu2r代替 kr ,
26
即得:
(1
E(1 )(1
) 2
)
(
2ur r 2
2 r
ur r
17
§11-3 纵波与横波
一、纵波 [定义] 弹性体的质点运动方向平行弹性波的传播方向(图示)
纵波的传播形式
18
将x轴取为波的传播方向,则弹性体内任取一点的位 移分量都有:
u u(x, t) 0 w 0
弹性波动力学概念

质点振动部分一 基本概念1) 构成振动系统的各部分都可看成是一个物理性质集中地元件,这种振动系统也称为质点振动系统。
OR 由物理性质集中的元件构成的振动系统。
2)单自由度系统A 简谐振动(无阻尼自由振动):物体在线性恢复力或线性恢复力矩的作用下的运动。
B 阻尼自由振动:因摩擦,声波辐射等原因阻碍震动的进行(阻尼),而导致震动幅度随时间衰减。
C 受迫振动:(策动力)在策动力作用下的振动称作受迫振动。
3)什么是3dB 带宽?在但自由度振动系统的震速振幅的频率特性曲线上,速度振幅比共振峰值处下降0.707倍所对应的两个频率分别为 和 ( > ),则3分贝带宽定义为 ,可以用3分贝带宽的大小表示频率特性曲线的平坦程度。
0.00.5 1.0 1.5 2.0012345678910B z z1z2二 基本原理与技能1) 简谐振动、阻尼振动和受迫振动表达式简谐振动:阻尼振动:欠阻尼状态:x(t)= cos( )过阻尼状态:x(t)=临界阻尼状态:x(t)=(受迫振动:2) 频率特性曲线的测量扫频法:将幅值相等但不同频率的简谐力加在振动系统上,测量每个频率的速度振幅,用描点法作出频率特性曲线。
脉冲法:将含有等幅值的各种频率成分的时域信号(强迫力)加在振动系统上,测量系统响应。
流体中声场部分一基本概念11)声压:设流体体积元受声扰动后压强由改变为P,则由声扰动产生的逾量压强(简称逾压)就称为声压,2)声场:媒质中有声波存在的区域。
3)声波传播速度:常数,温度为t(℃)时理想气体中的声速为(m/s)温度为20℃的空气中的声速约为334米/秒,常温下水中声速约为1500米/秒4)质点振动速度:5)声阻抗率:声场中某位置的声压与该位置的质点的速度的比值定义为该位置的声阻抗率。
== -26)声压级:声场中某点的声压级定义为该点的声压的有效值与参考声压的比值取常用对数,再乘以20。
空气中参考声压水中参考声压7)声强级:声场中某点的声强级定义为该点的声强与参考声强的比值取常用对数,再乘以10空气中参考声强一般取瓦米在空气中声压级与声强级数值上近于相等声强:通过垂直于声传播方向的单位面积上的平均能量流称为平均能量流密度或称为声强,即:I=38)临界角:光线从光密介质射向光疏介质时,折射角将大于入射角;当入射角为某一数值时,折射角等于90°,此入射角称临界角。
弹性波动力学复习提纲课件

04 弹性波的散射和干涉
弹性波的散射
弹性波散射的定义
弹性波在传播过程中遇到障碍物时,其传播方向和能量分布发生变化的现象。
弹性波散射的分类
瑞利散射、米氏散射、共振散射等。
弹性波散射的物理机制
波动与障碍物相互作用,产生反射、折射、吸收等现象。
弹性波散射的数学模型
散射波函数、散射系数等。
弹性波的干涉
三维波动方程
总结词
三维弹性波的波动方程是描述弹性波在三维空间介质中传播的基本方程。
详细描述
三维波动方程适用于描述任意方向传播的波,适用于各种复杂的三维介质结构。该方程全面考虑了波 在三维空间中的传播特性,包括波的传播方向、速度以及介质中质点的位移、速度和加速度。
边界条件和初始条件
总结词
边界条件和初始条件是确定弹性波波动方程解的重要约束条件。
随着入射角的增大,反射系数会发生变化。
弹性波的折射
1 2
折射系数
描述入射波与折射波之间振幅关系的系数。
斯涅尔定律
入射角等于折射角。
3
折射系数与入射角的关系
随着入射角的增大,折射系数也会发生变化。
全反射和透射
要点一
全反射
当入射角达到某一临界值时,折射波消失,只剩下反射波 。
要点二
透射
当入射角小于某一临界值时,折射波存在,且其振幅与入 射波相似。
详细描述
通过向物体内部发射弹性波并检测反射回来的波,可 以判断物体内部的缺陷、损伤等,如飞机、高铁等大 型机械的检测,确保其安全运行。
声呐探测
总结词
利用弹性波在水中传播的特性进行水下探测和通信。
详细描述
声呐系统通过向水下发送声波并接收回波,可以探测水 下目标的位置、大小、形状等信息,广泛应用于海洋科 学研究、水下考古等领域。同时,声呐技术还可用于水 下通信,实现水下设备之间的信息传递。
中国海洋大学《弹性波动力学》期末复习资料

一,名词解释1、 弹性:物体的变形随外力的撤除而完全消失的属性。
2、 塑性:物体的变形随外力的撤除后仍部分残留的属性。
3、 外力:是指其它物体作用在所研究物体上的力。
4、 面力:分布在物体表面上各点的外力,称为面力。
5、 应力:截面上任意点内力的集度称为应力。
6、 正应力:物体在某截面上一点的应力是矢量,这个矢量,一般来说不与截面垂直,也不与截面相切,通常把它分解为垂直于截面方向的分量σ和切于截面的分量τ,σ即为正应力。
7、 剪应力:物体在某截面上一点的应力是矢量,这个矢量,一般来说不与截面垂直,也不与截面相切,通常把它分解为垂直于截面方向的分量σ和切于截面的分量τ,τ即为剪应力。
8、 应力分量:垂直于三个坐标轴的平面上正应力和剪应力的投影。
9、 线应变:物体内一点沿某一方向线元受力后,该线元长度的改变量与原长度比值的极限称为该方向的线应变。
10、剪应变:过物体内任一点引两条相互垂直线段,变形后,这两个线段之间的夹角改变量(用弧度表示)定义为该点在这两个方向的剪应变,也称为角应变。
11、平面波:等相位面是平面,且波阵面与波的传播方向垂直的弹性波。
12、频散:不同谐波成分组成的波,虽然受同一起始扰动下,但各自以不同的速度传播,并且起始扰动的形状在传播中将产生变化。
扰动经传播以后将扩展成为一更长的波列,这种现象我们称之为频散。
13、群速度:产生频散时,波的传播速度与组成这个波的各个谐波成分的相速度是不同的,我们称这个波整体的传播速度为群速度。
14、相速度:指一定的相位移动的速度。
15、自由界面:地表应力为零的界面。
二,证明题1、 如果某一连续体内位移场是某一标量φ的梯度,即:φφ∇==grad U,证明:0=⨯∇=U U rot。
证明:)()()(),,(222222=∂∂∂-∂∂∂+∂∂∂-∂∂∂+∂∂∂-∂∂∂=∂∂∂∂∂∂⨯∇=∇⨯∇=⨯∇=k y x x y j x z z x i z y y z z y x U U rotφφφφφφφφφφ2、 如果连续体内位移场是某一矢量位移ψ的旋度,即ψψ⨯∇==rot U ,证明:0=∙∇=U U div证明:)()()(])()()[()(222222=∂∂∂-∂∂∂+∂∂∂-∂∂∂+∂∂∂-∂∂∂=∂∂-∂∂∂∂+∂∂-∂∂∂∂+∂∂-∂∂∂∂=∂∂-∂∂+∂∂-∂∂+∂∂-∂∂∙∇=⨯∇∙∇=∙∇=y z x z x y z y z x y x yx z x z y z y x k yx j x z i z y U U div x y z x y z xy z x y z x y z x y z ψψψψψψψψψψψψψψψψψψψ 3、 已知标量φ为空间坐标的函数,即),,(z y x φφ=,且二阶可导,证明: φφ2)(∇=∇∙∇; 证明:φφφφφφφφφφφ2222222)()()(),,()(∇=∂∂+∂∂+∂∂=∂∂∂∂+∂∂∂∂+∂∂∂∂=∂∂∂∂∂∂∙∇=∇∙∇z y x z z y y x x zy x4、在二维问题中,假设位移位ϕ及ψ都只与x ,y 和t 有关,即(,,)x y t ϕϕ=,(,,)x y t ψψ=,根据位移矢量公式证明二维问题的位移分量为:yx w x y v y x u x y zz ∂∂-∂∂=∂∂-∂∂=∂∂+∂∂=ψψψφψφ,,。
《弹性波动力学》固体中弹性波-05 声波在流体-固体界面上的反射和折射
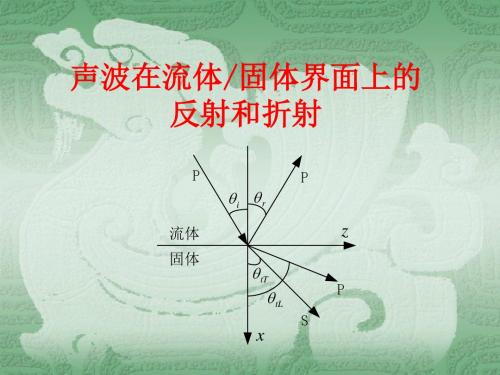
势函数的反射和折射系数的定义为
t t r r , t , t i i i
反射系数与折射系数
势函数的反射和折射系数为 r z2 L cos 2 2tT z2T sin 2 2tT z1L r , 2 2 i z2 L cos 2tT z2T sin 2tT z1L
上式应对所有的z都成立,因而式中指数因子部分必然应该恒等,即
k1L sin i k1L sin r k2 L sin tL k2T sin tT 波矢的界面分量相等
从此导得反射定律 i r
P P
与折射定律
sin i k2 L c1L , sin tL k1L c2 L sin i k2T c1L . sin tT k1L c2T
声波在流体/固体界面上的 反射和折射
P P
i r
流体 固体
z
折射
步骤(思路)
声学边界条件 写出波函数表达式 将波函数代入边界条件 定义和求解反射系数、透射系数 结果讨论
P P
i r
流体 固体
z
tT tL
S P
x
流固界面的边界条件
15
30
45
60
75
90
Incident Angle
Incident Angle
1.0 0.8
Amplitude
Tp R 第二临界角
f
第一临界角 0.6
0.4
1000.,1483 1700.0,1700.0,600.0
第一临界角 不存在第二临界角
t 1 2 z2 L cos 2tT t , 2 2 i 2 z2 L cos 2tT z2T sin 2tT z1L
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学习意义:理解不同边界条件下的地震波波动方程的含义,理解各种弹性力学参数的物理意义并将参数和地下介质的岩性问题联系起来,最终为地震剖面的岩性解释服务。
刚体:变形忽略不计的物体
弹性波:扰动在弹性介质中的传播
波前面:波在介质中传播的某个时刻,介质内已扰动的区域和未扰动区域间的界面称为波前面
地震波分类:纵波横波,平面波球面波柱面波,体波界面波表面波
哑指标:在同一项中重复两次从而对其应用求和约定的指标
自由指标:在同一项中出现一次因而不约定求和的指标
各项同性张量:如果一个张量的每个分量都是坐标变换下的不变量,则称此张量为各项同性张量
张量性质:二阶实对称张量的特征值都是实数:二阶实对称张量对应于不同特征值的两个特征向量垂直:二阶实对称张量总存在三个相互垂直的主方向:在主轴坐标系内二阶实对称张量的矩阵形式是对角形:三个相互垂直主方向的右手坐标系为主轴坐标系
弹性:物体受外力时发生形变,外力消除时物体回到变形前的水平
弹性变形:在弹性范围内发生的可恢复原状的变形
弹性体:处于弹性变形阶段的物体
弹性波动力学基本假设:物体是连续的:物体是线性弹性的:物体是均匀分布的:物体是各项同性的:小变形假设:无体物初应力假设
位形:弹性体在任意时刻所占据的空间区域
参考位形:弹性体未受外力作用处在自然情况下的位形
运动:刚性平移,刚性转动,变形
应变主方向:如果过p点的某个方向的线源,在变形后只沿着他原来的方向产生相对伸缩主应变:沿着应变主方向的相对伸缩
体力:连续分布作用于弹性体每个体元上的外力称为体力
面力:连续分布作用于弹性体表面上的力
运动微分方程的物理意义:表示应力张量在弹性体内部随点位置变化时应满足的关系式
内能:弹性体在某个变形状态下,其内部分子的动能以及分子之间相互作用具有的势能总和应变能密度:单位体积内的弹性体所具有的应变能
广义胡克定律:线性弹性体内一点处的应力张量分量可以表示为该点处应变量张量的线性齐次方程
动弹性模量:由介质的速度参数表达的弹性模量
极端各向异性弹性体:过p点任意方向都不同的弹性体
粘滞力:实际流体中两层流体相互滑动流体间相互作用的阻力
理想流体介质:可以将粘滞力忽略的流体
无旋波:无旋位移场的散度对应弹性体的涨缩应变场以波的形式传播(涨缩应变场)
无散波:无散位移场的旋度对应弹性体的转动情况以波的形式运动
平面波:波前面离开波源足够远时脉冲型和简谐型均匀和非均匀平面波
非频散波:波的传播速度仅仅依赖媒介密度拉美系数等而与波的频率无关
频散波:波的传播速度与频率有关
频散:初始扰动的没一个简谐成分都以不同速度前进,从而初始波形在行进中发生了变化相速度:简谐波的传播速度
群速度:由简谐波叠加而成的波其合成振幅的传播速度
非均匀平面波:如果波的等位相面各点振幅不同,既等位相面和等振幅面不平行
球面波:弹性媒质的位移矢量场具有球对称性,且只是空间变量和时间变量的函数
1、证明:;
2、
3、
4、
5、如果,,,证明:;
分析:由于标量对坐标的选择无关,因此,如果证明了物理量在坐标变换前后相等,即可以认为此物理量是标量。
原坐标系,原坐标系中距离为;新坐标系,原坐标系中距离为。
则:
又因为:,
分析:要证明是标量,而是为了证明与坐标选取无关。
原坐标系,,新坐标系,,。
例1:有个有序分量,如果对任意向量有,其中是向量。
证:为二阶张量。
设原坐标系为,新坐标系为
因为是任意向量,所以:所以为二阶张量。
例2:有个有序分量,如果对任意二阶张量都有,其中是二阶张量。
证明:是四阶张量。
设原坐标系为,新坐标系为
因为为任意二阶张量,所以:
所以是四阶张量。
