保角变换法求解定解问题
第6章保角变换-数学物理方法

f ( z0 ) 是经过映射Biblioteka f ( z ) 后通过点z0 的
的任何曲线C在 z0的伸缩率, 它与曲线C的形状及
方向无关. 所以这种映射又具有伸缩率的不变性.
5
2.共形映射(保角映射)
设函数w f ( z )在区域 D内解析, z0为 D内一点,
且 f ( z ) 0 , 那末映射w f ( z ) 在 z0 具有两个性 质: (1) 保角性; (2) 伸缩率不变性.
圆周的弧所围成的区域映射成一圆弧与一直线所 围成的区域. 3) 当二圆交点中的一个映射成无穷远点时, 这 二圆周的弧所围成的区域映成角形区域.
13
5. 几个初等函数所构成的映射
1) 幂函数 w z n ( n 2).
映射特点: 把以原点为顶点的角形域映射成以原
点为顶点的角形域, 但张角变成为原来的 n 倍.
故
b 1, a 1 i ,
(1 i ) z 1 ( i 1) z 1 所以 w 为所求. z (1 i ) z (1 i )
19
解3 利用典型区域映射公式
将所求映射设为 w e i
z z A , 1 z 1 z
保角变换
复变函数在几何意义上实际上相当于将平 面上的区域变成了平面上的另一个区域(简称 为映射). 应用:利用复变函数(特别是解析函数)所构 成的映射来实现复杂区域的简单化,这将给实 际问题的研究带来很大的方便.而利用保角变 换法求解数学物理方程边值问题.
1
本章内容: 1)保角射的概念; 2)分式线性映射和几个初等函数所构成的 映射; 3)典型实例描述保角映射的应用. 重点: 分式线性变换及其映射特点 难点:
保角变换法
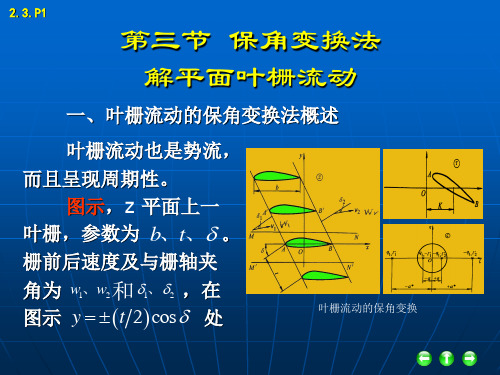
R R i c ln 2 wm t 1 R 1 R
式中
1 wm w1 w2 , c 2
平板叶栅的一般绕流
为绕一个翼型的环量。
2.3.P9
(五)平板叶栅一般流动中环量的确定
环量的确定依据是弧立翼型绕流中的库塔 —— 恰普雷金条件。而栅中翼型尾缘点 B 必然 是后驻点,此外速度是一有限值。 经换算得
a) b)
2.3.P6
其复势为
t W 2 i R 1 R i ie ln ie ln R 1 R
流动奇点强度为
q1 q2 t sin
1 2 t cos
(三)平板叶栅纯环量绕流 b) 图示,栅前后只有 列线方向速度 w1、w2 。
可见 L L t b , ,具体 数值见图示曲线。 由上述已解得的平板叶栅 流动,可以求解由任何翼型组 成的等价平面直列叶栅流动。
平板叶栅环量修正曲线
三、平面环列叶栅流动的解法
2.3.P11
设图示环列叶栅由 n 个翼型组成,流动自中心 向外。可见,只要确定一个扇形区域内的流动即可。
平板叶栅无环量平行绕流
2
2.3.P4
q t cos
t sin
Z 平面复势
W z zei
表示速度为 1 的均匀流复势。 变换为 平面为 R 处相应放置点源、点汇
q 和点涡 的绕圆流动。
其复势
t W 2 i R i 1 R e ln e ln R 1 R
变换为 平面绕单位圆流动,且有
R R i W ln 1 1 4 R R
数学物理方法 保角变换法共40页

1、战鼓一响,法律无声。——英国 2、任何法律的根本;不,不成文法本 身就是 讲道理 ……法 律,也 ----即 明示道 理。— —爱·科 克
3、法律是最保险的头盔。——爱·科 克 4、一个国家如果纲纪不正,其国风一 定颓败 。—— 塞内加 5、法律不能使人人平等,但是在法律 面前人 人是平 等的。 ——。 ——德 谟克利 特 67、今天应做的事没有做,明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生,以及整个命运 的,只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
数值保角变换的新算法

在图1中,C是z平面上任意的Jordan曲线,曲线C的区域外部作为D,灼j(j=1,2,…,N)是在区域内部配置的电荷点,zi(i=1,2,…,N)是边界C上的约束点,w=(f z)是从D軍(这里D軍=D胰C)到w平面上的单位圆外部w跃1(包括单位圆边界)的保角映射。在不失一般性的情况下,假定z=0在C的内部且(f 0)=0,保角变换函数w=(f z)满足正规化条件(f肄)=肄,f(忆肄)跃0时表示如下:f(z)=z酌exp(g(z)+ih(z))其中,酌是外部变换半径,g(z)是Dirichlet型场势问题:2g(z)=0,z沂Dg(z)=log酌-log z,z沂Cg(肄)=0扇墒设设设设缮设设设设的解。h(z)是g(z)的共轭调和函数,且h(肄)=0。以下文中均以G,H,祝表示g,h,酌的近似值。
数值保角变换的算法:淤给出模拟电荷法的模拟电荷和约束点数量N;于根据模拟电荷法的原理[11],给出电荷点灼1,…,灼N,约束点z1,…,zN;盂由模拟电荷点和约束点以及变换半径构造约束方程组(5);榆计算模拟电荷q1,…,qN和变换半径祝;虞根据(1)式和(2)式构造G(),H(z);愚构造近似保角变换函数F(z)=z祝exp(G(z)+iH(z))。
数值保角变换的新算法
摘要院保角变换理论在流体力学等许多领域中有着广泛的应用。但计算保角变换是个很困难的问题,因此寻求一种有效方法计算保角变换在实际应用中具有很大意义。本论文提出了一种数值保角变换的新算法,在这个新算法中我们在改进高斯消去法的基础上利用模拟电荷法计算新的电荷点,进而构造高精度的近似保角变换函数,并且通过典型图形的数值实验检验了新算法的有效性。
第十六保角变换法求解定解问题共37页文档

(u ,v)的拉普拉斯方程边值问题.
w = 同理可以证明,在单叶解析函数 f (z)
变换下,泊松方程
22(x,y)
x2 y2
(16.1.7a)
仍然变为泊松方程
2 u 2+ 2 v 2 |f(z)|2(x,y) (16.1.7b)
由上式可知,在保角变换下,泊松方程中的电荷密度
发生了变化.
同理可以证明,亥姆霍兹方程
2x2 2y2 k20 (16.1.8a)
经变换后仍然变为亥姆霍兹方程
22k2|f(z)|20 (16.1.8b) u2 v2
容易注意到方程要比原先复杂,且
能不是常系数.
前的系数可
下面将举例说明如何通过保角变换法来求解拉普拉斯方程.
保角变换法的优点不仅在于拉普拉斯方程、泊松方程 等方程的类型在保角变换下保持不变,更重要的是,能将 复杂边界问题变为简单边界问题,从而使问题得到解决.
(16.2.1)
作如下的保角变换.
(1)作分式线性变换
1
1
i1
za za
(16.2.2)
y
z 平面
1
1 平面
平面
πi
a
0
1
x
图图181.16.1
可以验证,考虑实轴 zx,(y0)的对应关系:
| (i)若 x | a ,则 axa,故
1
x x
a a
0 ,即有
1
0
(ii)若 | x | a 则 xa 或 xa
问题中的解析法――保角变换法,它是解决这类复杂边 界的最有效方法.它特别适合于分析平面场的问题,
例如静电场的问题,由于这种求解复杂边界的定解问 题具有较大的实用价值,所以有必要单独以一章的内 容进行介绍.复变函数论中已经系统介绍了保角变换
《流体力学》课件 3.9 保角变换

d w dW d d z d d z
在无穷远处,有:
d w d z
dW d
d dz
考虑到
dW d
kV
,
d dz
1 k
,有:
dw dz
V
三、环量的确定
1. 补充条件
dw 有限的常数
dz zB 2. 环量的确定
dz
d
E
0
dw 有限常数
dz zB
dw
d
E
w1 z
Q
2
lnz
i
h
Q
2
lnz
i
h
Q ln z2 h2 2
wz
w1 z
w1
a2 z
wz
Q
2
ln z2
a4 z2
h2
a4 h2
dz
d
k
;(其中:
k
是正的实数)
(根据黎曼定理这样的函数存在且是唯一的)
W
kV
w
z
kV R
kV
2
2 i
F z
ln
kV
F z
R
2
F z
ln
2 i
F
z
证明:1. 因W 是在 K D 上连续且在 D 内解析的函数, Fz是在 C D 上连续且在 D 内解析的函数。于是,根据复合函数的性质 wz W F z
一、保角变换的概念
w f z
V f lin w f ei Δz0 z
w wei f eiz f z ei
12
1 2
2 1` 2 1`
黎曼定理:
任何一个单连通区域必可通过某个保角变换 变为另一个任意给定的单连通区域。
144《高等渗流力学》—保角变换及应用

定义:平面 z = x + iy 上给出某个流动其复势是F ( z ) ,引 入新复变函数 w = u + iv
两者间关系: z = z ( w) 或则 w = w( z )
z 实部和虚部关系: ( w) = z (u + iv ) = x (u , v) + iy (u , v ) x = x (u , v ), y = y (u , v ) …………….....(1)
⎛ R1 ⎞ Re > R1 , m ≥ 5 时 ⎜ ⎟ ⎝ Re ⎠
<< 1
2π ( Φ e − Φ w ) q= R R m ln e + ln 1 R1 mrw
14
保角变换及应用
例五:
取变换: w = 直线无限井列的变换。
ρe ⋅ e
iπ z a
则
w = ρe ⋅ e
θ= πx
a
iπ ( x + iy ) a
上式是长轴为 a ,短轴为b的椭圆方程,给定一个 ρ 值,z平面上 给定一条等势线(圆)。因此,上式为z平面等势线方程。另 外,由于 a 2 − b 2 = c 2 ,故Z平面上所有等式椭圆共焦,焦距为c。 x2 y2 a 2 − b2 − 2 2 = =1 2 2 2 c cos θ c sin θ c W平面上给定一v值,相当于给定一流线,故上式为Z平面的 流线方程。
dL
dφ vn = − —— 法线渗流速度; dn
dz dn = dv dw
5
保角变换及应用
dz dL = dλ 和 dw
例一:
∫
dφ dL = dn
∫
dφ dz dφ dλ = ∫ dλ dz dw dv dv dw
保角变换数学物理方法

2
第3页/共31页
4)伸缩率
极限
f
(z0 )
lim
zz0
s
(s表示C上点z0与z间的
弧长, 表示上C在z0的伸缩率.
16
第17页/共31页
解2 利用不变对称点
因 z 1 i 时, w , 所以 w az b , z (1 i)
又 z 1时, w 1, 故 i a b,
由对称点的不变性知, z 1 对应 w 0, 1 i
故 b 1, a 1 i,
所以 w (1 i)z 1 (i 1)z 1 为所求. z (1 i) z (1 i)
1 i 据分式线性映射不变对称点的性质知
15
第16页/共31页
w 0在z平面上的逆象为z 1 (z 1 i对应w ). 1 i
由交比不变性知
(1,0,
w,)
1,
1
1
i
,
z,1
i
即
w w
1
z
z
1 1
1i
1 i 1 1i 1
z1 , zi z i
1 i
所以 w (i 1)z 1 为所求. z (1 i)
定义 设 w f (z)在 z0 的邻域内是解析的,在 z0 具有保角性和伸缩率不变性,那末 w f (z) 在 z0 是共形的,或称w f (z) 在 z0 是共形映射. 也称为第一类共形映射.仅保持夹角的绝对值不 变而方向相反的映射, 称为第二类共形映射
4
第5页/共31页
3.分式线性映射
10
保角变换

初等变换
其他初等函数构成的变换
正弦-反正弦变换对
一条为双曲线,一条为椭圆线,就如微带线的电力线和电位线 余弦-反余弦变换对
一条为双曲线,一条为椭圆线,就如微带线的电力线和电位线
初等变换
其他初等函数构成的变换 双曲正弦-反双曲正弦变换对
一条为双曲线,一条为椭圆线,就如微带线的电力线和电位线 双曲余弦-反双曲余弦变换对
复变函数、保角映射和初等变换
目录
复变函数
保角映射
初等变换
复变函数基本概念
自变量为复数
连续
可微
解析 奇异点
复变函数基本概念
柯西-黎曼条件(C-R条件)
共轭调和函数
������=const.和������=const。两组相互正交的曲线簇。一 般地,若其中某一曲线簇与平面二维场的等位面相 合,另一曲线簇同平面二维场电力线相合,则称前 者为电位函数,后者为通量函数。将通量函数������(������, ������) 和电位函数������(������,������)看作是复变函数的实部和虚 部。
复变函数基本概念
复变函数到保角变换
求解平面二维边值问题最有用的方法是保角变换法, 通常是通过分析,选取合适的解析函数,使得待求 边值问题的边界条件与该解析函数的实部和虚部的 变化曲线相吻合,从而得到复位函数的表达式,求 出简单边界问题的解,再求其逆变换,从而得到所 求问题的解。
保角变换基本概念
曲线切线倾角的复数表示
解析函数的导数的几何意义
保角变换基本概念
伸缩率不变性
旋转角不变性
保角变换基本概念
保角变换的概念
保角变换基本概念
保角变换的重要定理
保角变换基本概念
保角变换

dw b 容易验证:分式线性映射的逆映射 z , cw a (a)(d ) bc 0 也是分式线性映射,因此,我们通常也把分
式线性映射称为双线性映射.
dw ad bc 由于分式线性映射的导数 0 ,因而, 2 dz cz d
分式线性映射是保角映射. 容易验证 : 两个分式线性映射的复合仍是一个分式线性 映射. 事实上,设
定理 6.2.4 在 z 平面和 w 平面上任意给定三个相异的点 z1 ,
az b 【证明】 设 w cz d w k k 1, 2,3 ,即
2, 3 1,
wk
于是
az b azk b z zk ad bc w wk cz d czk d cz d czk d
azk b czk d
2, 3 , k 1,
k 1, 2
az3 b azk b z3 zk ad bc w3 w k cz3 d czk d cz3 d czk d
由此可得
2 k 1,
w w1 w 3 w 2 z z1 z3 z2 w w 2 w 3 w1 z z2 z3 z1
6.1 保角映射的概念
我们在讨论解析函数导数的几何意义时已经提到了保角映射这 一概念.
6.1.1 保角映射的概念
定义 6.1.1 为保角映射. 凡具有保角性(角度相同,旋转方向相同)和伸缩率不变性的映 射称为第一类保角映射. 凡具有保角性(角度相同但旋转方向相反 )和伸缩率不变性的映射 称为第二类保角映射. 保角映射 凡具有保角性和伸缩率不变性的映射称
az b 设w ,可以把它化为 cz d ad 1 a (6.2.1) w b c cz d c 1 B ( A , B 为复常数) 令 cz d , ,那么 w A .
习题19保角变换

=
π
4
+ tan −1
ρ sin ϕ ρ sin ϕ − a , − tan −1 ρ cos ϕ − a ρ cos ϕ
即 u1 ( ρ , ϕ ) =
ρ sin ϕ ρ sin ϕ − a ⎞ V ⎛π −1 − tan −1 。 ⎜ + tan π⎝4 ρ cos ϕ − a ρ cos ϕ ⎟ ⎠ ρ sin ϕ ρ sin ϕ + a ⎞ V ⎛π −1 − tan −1 ⎜ + tan π⎝4 ρ cos ϕ + a ρ cos ϕ ⎟ ⎠
显然 u2 ( ρ , ϕ ) = −u1 ( ρ , ϕ − π ) = −
所以 u = u1 + u2 =
ρ sin ϕ V ⎛ −1 ρ sin ϕ − tan −1 ⎜ tan π⎝ ρ cos ϕ − a ρ cos ϕ + a
+ tan −1
ρ sin ϕ + a ρ sin ϕ − a ⎞ − tan −1 ⎟ ρ cos ϕ ρ cos ϕ ⎠
2 2 2 iϕ iθ
2 2
r < cos θ ,即为圆内部 ζ −
1 1 < 。 2 2
362.若在分式线性变换 ζ = λ
z−μ 下, z1 , z2 , z3 各点分别变为 ζ 1 , ζ 2 , ζ 3 各点,试证: z −ν
ζ − ζ1 ζ −ζ2
ζ 3 − ζ 1 z − z1 = ζ 3 − ζ 2 z − z2
z 将单位圆内变换为上半单位圆内。
ζ1 +1 ,可看出该变换将 −1 变换为 0,1 变换为 ∞ ,所以 ζ 1 平面实轴上从-1 到 1 ζ1 −1
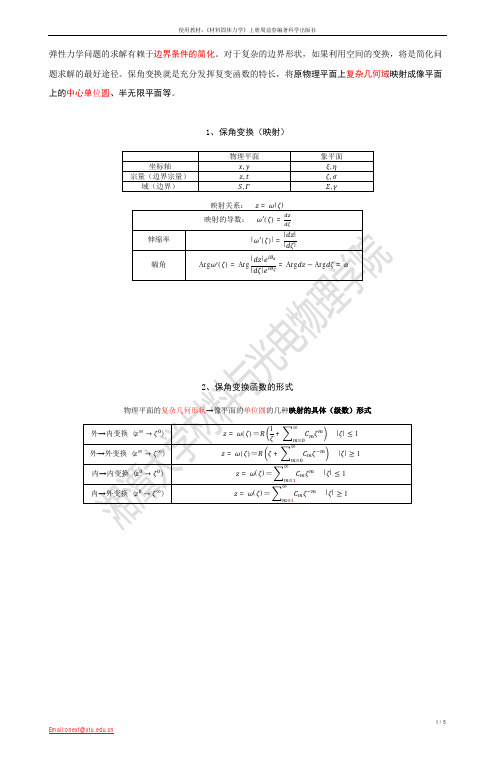
4.6 保角变换解法
1
()
1
() ()
1
()
1
2πi
−
+ 2πi
− ( ) + 2πi
−
= 2πi
−
l ( )=∑
在圆外域是解析的
l 位于圆内域
l ( )在圆内域是解析的 l 位于圆内域
1()2πi−源自= (∞) = +
∞ =0
1
()
2πi
−
= ()
(
)
=
−
1 2πi
() ()
1
− ( ) + 2πi
−
上表中的 ( )和 ( )的表达式的右端第一项与变换函数 ( )(即孔的形状)有关,称几何项。第二项与孔边和远 方的外力有关,称为载荷项。
B. 复杂情况求数值解 方法 1
→ →
(如:上面 4 种级数形式的映射关系就没办法逆映射):
(1) 先把应力组合转到像空间,
⎧ + = 2 ( ) + ( ) = 4Re[ ( )]
⎪ − +2
= ( ) 2[ ̅ ( ) + ( )]
(5)
⎨
⎪ ⎩
2
[
+
]=
( )−
() ()
( )− ( )
并利用像平面中解得的 ( ), ( )求解应力和位移分量,即分别得到了 (ξ, η)~
接下来就可以利用 4.5 节介绍的复数级数方法,来求解单位圆域的 ( )和 ( )。我们只需要用将 平面 K-M 函数的 级数代入(2)式左边,并把右边已知外力也在 平面展开成 F 级数,比较左右两边的系数就可求解。
2/5
Email:onexf@
保角变换法

式 中 t = 2 y max
式中b 式中 —— 弦长
1.4.P13
对于 ζ 平面绕圆流动有复位势
a 2 iα iΓ ζ + m W (ζ ) = ∞ (ζ + m ) e − iα + e − ln a ζ + m 2π
可由此求得 W ( z )。 环量为 Γ = −4π
∞
c (1 + ε ) sin α
ζ 平面上圆心在虚轴
上,距原点 m
c,
且过 ζ = ±c 两点的圆, 两点的圆, 可变换为 z 平面上的 圆弧,如图,方程为 圆弧,如图,
c c2 x2 + y + = c2 4 + 2 m m
2 2
1.4.P15
弦长为 b=4c ,顶点 f=2m。 。 在 z 平面上,以 b 和 f 表示其方程为 平面上,
2
平板升力为 升力系数为
L = πρ
2
∞
b sin α
Cl = 2π sin α
1.4.P11
(四)对称翼型(儒可夫斯基舵)绕流 对称翼型(儒可夫斯基舵)
ζ
平面上,圆心在横轴上原点左面,离原点 平面上,圆心在横轴上原点左面,
m<<c ,过 ζ = +c 的圆 ,经变换后得 z 平面上 的对称翼型。 的对称翼型。
dζ )
V
(z )
若 ζ 平面上来流复速度为
V (ζ ) =
∞ζ
e
− iα ζ
则 z 平面上来流复速度为
dz V ( z )( )ζ → ∞ = dζ
∞
e
− iα ζ
1.4.P4
(三)流动奇点强度在保角变换中的变化 作保角变换时,二平面上的点涡、 作保角变换时,二平面上的点涡、点源强度有 关系
保角变换法求解定解问题

2 u2
2 v 2
k2
|
f
( z )
|2
0
14.2 保角变换法求解定解问题
例14.2.1 设有半无限平板y>0,在边界y=0上,
|x|<a (a>0)范围内保持温度u=u0, |x|>a范围内保 持温度u=0。求平板上的稳定温度分布。
解:根据题意可得描述上述问题的定解问题
2u
x
2
2u y 2
0
ln1 ln | 1 | i arg1
ln z a za
把ζ1平面的上半平面变成ζ平面上平行于实轴,宽 为π的一个带型区域, ζ1平面的正实轴变换为ζ平 面的实轴(正实轴辐角为0,故对应于η=0,温度 u|y=0=0), ζ1平面的负实轴变换为ζ平面的平行于 实轴的直线(负实轴辐角为π,故对应于η=π,温度 u|y=0=u0)。
y u2 x
y v 2
+( 2u 2u ) ( 2v 2v ) x2 y2 u x2 y2 v
+2( u v + u v ) 2 x x y y uv
解析函数ω=f(z)=u+iv的C—R条件:
u v , v u x y x y
u v v u 0 x x y y
解析函数的实部和虚部分别满足拉普拉斯方程:
1
x x
a a
0
② 对于x>a (a>0),则x+a>2a>0、 x-a>0,因 此
1
x x
a a
0
如图所示,原定解问题中的边界条件中对应
于|x|<a范围温度为u0,变换后对应到ζ1平面的负 实轴(ξ1<0)温度为u0;而|x|>a温度为0则对应于变 换后的ζ1平面的正实轴温度保持为0。
保角变换基础理论

一、基础知识 1 定义在自变量域我们对同一个点从两个方向趋近,这两个趋近方向的夹角与在因变量上趋近的方向夹角一致,称为保角变换 2泊松方程与拉普拉斯方程对于泊松方程:20ρϕε∇=(在静电场中,可以表示电势与电荷的分布关系) 同时在没有电荷分布的地方满足拉普拉斯方程:20ϕ∇=3将在原来复杂的区域上的表达式通过一个变换,折射到宁一个区域上,使得某一分布函数得到简化变换的条件是泊松方程与拉普拉斯方程仍然成立22222x y∂∂∇=+∂∂,同时,我们定义x 、y 为ξ、η的函数:(,)x ξη、(,)y ξη 则x x x ξηξη∂∂∂∂∂=+∂∂∂∂∂2222222()x x x x x x x x x x ξηξξηηξηξξηη∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂=+=+++ ∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂ 其中:222x x x x x ξηξηξξξηξξηξ ∂∂∂∂∂∂∂∂∂∂∂∂=⋅+=+⋅∂∂∂∂∂∂∂∂∂∂∂∂∂ 同理:222x x x x x ηξηξηηηξηηξη∂∂∂∂∂∂∂∂∂∂∂∂=⋅+=+⋅ ∂∂∂∂∂∂∂∂∂∂∂∂∂ 所以:222222222222x x x x x x x ξηξηξηξηξηξη∂∂∂∂∂∂∂∂∂∂∂∂ =++++∂∂∂∂∂∂∂∂∂∂∂∂∂ 同理:222222222222y y y y y y y ξηξηξηξηξηξη∂∂∂∂∂∂∂∂∂∂∂∂=++++ ∂∂∂∂∂∂∂∂∂∂∂∂∂ 所以拉普拉斯方程变换为:22222222222222222222222x y x y x y xy xy x y y x ξξηηξξηηξηξηξηξηξη ∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂ ∇=+=+++++++++∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂要满足保角变换,其实部与虚部都需要满足拉普拉斯方程:20ξ∇=、20η∇= 将实部与虚部要满足的拉普拉斯方程代入上式:2222222222222x y x y x y ξξηηξη∂∂∂∂∂∂∂∂ ∇=+=+++∂∂∂∂∂∂∂∂ ()'f z ix xξη∂∂=+∂∂(对于趋近方向为:0,0x y ∆→∆=) 222222"()f z x x x y y x ξηξξηη ∂∂∂∂∂∂=+=+=+ ∂∂∂∂∂∂将其代入:22222222'()'()'f z f z ξη ∂∂∇=+=∇∂∂也就是说,原坐标下的拉普拉斯方程与泊松方程变换为:220'0ϕϕ∇=⇒∇=222001''()f z ρρϕϕεε∇=⇒∇= 那么对于一个线段,在原坐标系下长度为1,其在新的坐标系下长度为'()f z 二、常用的保角变换1. 线性变换f az b =+,显然'f a =,其几何效果如下:线性变换一般不单独使用:仅对原来的二位分布做了位似2.幂和根式n xn f z = i n in z Ae f A e ϕϕ=⇒=用来处理过原点的射线,原来的射线的长度ρ的取值范围为(0,+∞),求幂或根还是(0,+∞)将原来的自变量求幂次积,几何效果如下:假设有变换3f z =,其效果为:将原来的60°夹角变为180°,并且其中的点的分布也随之扩大角度,假设原来的函数为电势分布函数,求p 点的电势,则通过变换之后,在新的复平面得到了一个平行分布的电势图,设新的电势分布图中,边界上的电势为V 0,则空间中的电势分布为0u V C η=+⋅,其中,C 为常数,C 与介质表面的面密度σ相关,其正负与σ的正负相反我们在新的复平面中求出电势的表达式之后,再求逆变换得到在原来的复平面上的电势表达式:0u V C η=+⋅中,由原来的变换:()()()32332322333(3)(3)i x iy x x iy x iy iy x xy i x y y ξη+=+=+⋅++=−+−由实部对实部,虚部对虚部,得:233x y y η=− 将η代入电势表达式中:()2303u V C x y y =+⋅−得到电势关于x 、y 的表达式同理可以得到将原来的复平面上的表达式开根得到将原来的夹角缩小相应的倍数的变换方法3. 指对数变换(一)、对于指数函数:()z x iy x iy f e e e e +===⋅此处需要注意,这里使用了复变函数的幅角表示法,即:i z Ae ϕ=,所以此处的x e 为幅值,iy e 为幅角其几何空间意义如下: (1),复平面中平行于实轴的直线,其变换后的图像为过原点的射线对于原空间有一条平行于实轴的直线((,)y const x ∈−∞+∞,),原来的x 的值为幅角,y 的值为幅值。
§8.7保角变换和曲线坐标

§ 8.7 保角变换和曲线坐标学习思路:弹性力学问题的求解有赖于边界条件的简化。
对于复杂的边界形状,如果利用空间的变换,将是简化问题求解的最好途径。
保角变换就是充分发挥复变函数的特长,将孔口问题映射到平面的单位圆。
这一节将介绍保角变换和曲线坐标的概念。
由于应用保角变换,矢量-位移,张量-应力公式以及K-M 函数等均必须做出曲线坐标描述。
保角变换使得问题的公式复杂,但是边界条件的简化,以及柯西积分的应用将简化问题的分析。
在本节学习之前,请你先学习附录2,(有关保角变换的知识)学习要点:1.保角变换和曲线坐标;2.矢量的保角变换;3.位移分量的曲线坐标表达式;4.应力分量的曲线坐标表达式。
为了便于根据边界条件确定 K-M 函数,采取保角变换z = ()将物体在z 平面上所占的区域变为在平面所占的区域。
一般的说,通过保角变换可以将非圆边界映射为圆边界,使得问题得以简化。
假设将z 平面上的有限区域或者无限区域S 映射为平面的单位圆内的区域,并且将z 平面上的区域S的边界l 映射为单位圆,对应的关系如下表:由于平面上的任一点可以表示为,。
和是点的极坐标。
而根据保角变换公式z = ( ),则z平面任意一点也可以通过和表示。
因此,和又称为曲线坐标。
对于某些问题的描述中,采用曲线坐标形式表示位移和应力有利于问题的分析。
曲线坐标的概念:平面的一个圆周=const 和一条径向直线=const分别对应于z 平面的两条曲线,这两条曲线就记作=const和=const。
于是和可以看作z 平面上一点的曲线坐标。
由于变换的保角性,这个曲线坐标总是正交的,而且坐标轴和的相对位置和坐标轴Ox和Oy的相对位置相同,如图所示。
首先讨论矢量的保角变换。
设曲线坐标,即=const 与x 轴夹角,如果A 为z 平面上的任一矢量,设A 与曲线坐标夹角。
设A x, A y 分别表示矢量A 在x,y 轴的投影;A , A 表示在=const 和=const 上的投影,则上式的几何意义为,将矢量A 绕z 点顺时针方向转动角后,其在Oxy 坐标系的位置,相当于A 在曲线坐标系( , )中的位置,如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
xa xa
0
x a (b)再考虑
的情况, 则
x a 0 ,x a 2 a 0 ,
故
1
xa xa
0
如图16.1所示,根据(16.2.1)式中的边界条件,对应于
|
x
|
a
u 处温度为
,故
0
1
平面的负实轴(即 1
0
)
u 温度保持为 0 ;而在| x | a 处有 1 0 ,故
1 平面的正实轴温度保持为零.
是下列定解问题的解
(3)可证 (x ,y )1 (x ,y )2 (x ,y )
是下列定解问题的解:
V0 (x1)
0(y0,x),(x,0) V1 (1x1)
V2 (1x)
其中
V 0 V 1 V 1 , V 1 V 2 V 1 , V 2 V 2 V 2
( x, y)又可改写成
u 处保持温度 = 0.求平板上的稳定温度分布.
【解】根据题意可得出定解问题
2u
x
2
2u y 2
0
u
y0
u 0 , ( x a ) 0 , ( x a )
(16.2.1)
作如下的保角变换.
(1)作分式线性变换
1
1
i1
za za
(16.2.2)
y
z 平面
1
1 平面
平面
πi
a
0
第十六章 保角变换法求解定解问题
在许多物理问题中(如电学、热学、光学、流体 力学和弹性力学等)经常会遇到解平面场的拉普拉斯 方程或泊松方程的问题.尽管可用前几章的理论方法 如:分离变量法或格林函数法等来解决,但当边值问 题中的边界形状变得十分复杂时,分离变量法和格林 函数法却显得十分困难,甚至不能解决.对于复杂的
(16.1.7b)
由上式可知,在保角变换下,泊松方程中的电荷密度
发生了变化.
同理可以证明,亥姆霍兹方程
2x2 2y2 k20 (16.1.8a)
经变换后仍然变为亥姆霍兹方程
22k2|f(z)|20 (16.1.8b) u2 v2
容易注意到方程要比原先复杂,且
能不是常系数.
前的系数可
下面将举例说明如何通过保角变换法来求解拉普拉斯方程.
u v, v u x y x y
(16.1.4)
以及解析函数的实部和虚部分别满足拉普拉斯方程的性质
x2u2 y2u2 0,
x2v2 y2v2 0(16.1.5)
将式(16.1.4)和式(16.1.5)代入到式(16.1.3)化简后得到
2 2 [ ( u ) 2 ( v ) 2 ] ( 2 + 2 ) |f(z )|2 ( 2 + 2 )
理论,本章主要介绍利用保角变换法求解定解问 题。
16.1 保角变换与拉普拉斯方程边值问题的关系
w 在复变函数论中我们已经知道,由解析函数 f (z)
实现的从z平面到 w 平面的变换在 f (z) 0 的点具有保
角性质,因此这种变换称为保角变换.下面我们主要讨论一一
对应的保角变换,即假定 w f (z)和它的反函数都是单值
Im π ,如图16.3
所以,在变换 ln a z i之下,定解问题变换为
az
v
2v 0 0 v 1
v π v 2
定解问题的解(仿上例16.2.1)为
vv2π v1v1v2π v1Im
z 将变量回到 平面,则
v
v1
v2
v1 π
Im[ln(azi)] az
v1
v2
v1 π
1
x
图图181.16.1
可以验证,考虑实轴 zx,(y0)的对应关系:
| (i)若 x | a 0
,即有
1
0
(ii)若 | x | a 则 xa 或 xa
xa (a)首先讨论
a 的情况,考虑到题给条件 0
则 x a 0 ,x a 2 a 0 ;
故
1
Im{ln[yi(ax)]ln[(xa)iy]
v1
v2
v1 π
[arctanayxarctanxya]v1
v2
v1 π
a2 arctan
x2 y2 2ay
v1
v2
v1 π
π
[ arctan
2
a2
2ay x2 y2
]v1
v2 2
v1
v2 π
arctan a2
2 ay x2 y2
化成极坐标形式,则上式又改写成
d2u
d
2
0
u 0 0, u π u 0
(16.2.6)
方程的解是 uAB
考虑边界条件即得到
z 回到 平面,则
u u 0 (16.2.7) π
u(x,y)u0Im[ln(za)]u0Im[ln(za)ln(za)] π za π
u0[arctg y arctg y ]u0arctg 2ay π xa xa π x2y2a2
边界形状,拉普拉斯方程定解问题常采用保角变换 法求解.
保角变换法解定解问题的基本思想是:通过解析
函数的变换(或映射,这部分知识在复变函数论中已经学
z w 习过)将
平面上具有复杂边界形状的边值问题变换为
平面上具有简单形状(通常是圆、上半平面或带形域)的
边值问题,而后一问题的解易于求得.于是再通过逆变换
(x ,y ) V 0 π V 1 a r g (z 1 ) V 1 π V 2a r g (z 1 ) V 2
(4)进一步推广
( x ,y ) V 0 π V 1 a r g ( z x 1 ) V 1 π V 2 a r g ( z x 2 ) L V n 1 π V n a r g ( z x n ) V n
2(v)2 2 2 u v (16.1.2)
v2 y
uv y y
两式相加得到
22[(u)2 (u)2]2+[(v)2 (v)2]2
x2 y2 x
y u2 x
y v2
2u +(x2
2u y2 )
u (x2v2
y2v2 )
v
+2( u v + u v ) 2 x x y y uv
(16.1.3)
利用解析函数 wf(z)uiv的C-R条件
(2)作变换 ln1 ln| 1| ia rg1
(16.2.3)
把 1 平面的上半平面变成 平面上平行于实轴,宽为
π 的一个带形区域, 1 平面的正实轴变换为
0 平面的实轴(正实轴辐角为零,故对应于
),
1 平面的负实轴变换为 平面的平行于实轴的直线
π (负实轴辐角为 ,故对应于 = π ).
函数;或者如果它们之中有多值函数就规定取它的黎曼面的一 叶.
定律16.1.1 如果将由z x iy 到 wuiv
的保角变换看成为二元(实变)函数 ( x, y ) 的变换由 x , y
u , v z w 到
的变量代换,则 平面上的边界变成了
平面上的边界.我们能证明,如果 ( x, y ) 满足拉普拉斯方
(u,v) V1 V2 v (16.2.10)
π
v w平面
y z平面
πi v1
v2
O
v1
v2
x
u
图图118.2 6.2
O
而
w u ivlnzlnz iargz
所以 vargz
于是,作反变换便可求得所求问题的解为
(x ,y ) V 1 V 2 a r g z V 1 V 2 V 1 V 2 a r c ta n y
z ln z (3)再作变换
2
把
平面的上半平面变成
2
π 平面上平行于实轴,宽为
的一个带形区域,其边界的
y
z 平面
0 x
y1 z1 平面
x1
y2
z2 平面 x2
图图118.63 .3
πi
v2
平面
v1
z 变换是将 2 平面的正半实轴变换为 平面的实轴,
z 2 平面的负半实轴变换为 平面的平行于实轴的直线
就求得了原始定解问题的解.
这就是本章将要介绍的一种解决数学物理方程定解
问题中的解析法――保角变换法,它是解决这类复杂边 界的最有效方法.它特别适合于分析平面场的问题,
例如静电场的问题,由于这种求解复杂边界的定解问 题具有较大的实用价值,所以有必要单独以一章的内 容进行介绍.复变函数论中已经系统介绍了保角变换
x 2 y 2 x x u 2 v 2
u 2 v 2
注意到上式已经使用了:
wf(z)uiv x x
对于保角变换 wf(z)0, 因而只要
( x, y ) 满足拉普拉斯方程,则 (u , v )也满足拉
普拉斯方程,即为
22
22
0 x2 y2
(u2+v2)0(16.1.6)
这样我们就有结论:如果在 z x iy 平面上给定了
程,则经过保角变换后得到的 (u,v )也满足拉普拉斯方程.
【证明】 利用复合函数求导法则有
u v x u x v x
2 2u 2 (u )2 2v x2 u x2 u2 x v x2
2 ( v )2 2 2 u v
v 2 x
uv x x
(16.1.1)
同理
2 2u 2(u)2 2v y2 u y2 u2 y v y2
内的电场分布情况.
【解】即求解定解问题
2v 0
v
a
v1 v2
( a) (0 π) (π 2π)
作如下的保角变换
(1) 作变换
z1
z a
