(01) 第一章 量子力学基础3
量子力学课后习题答案

量子力学习题及解答第一章 量子理论基础1.1 由黑体辐射公式导出维恩位移定律:能量密度极大值所对应的波长m λ与温度T 成反比,即m λ T=b (常量);并近似计算b 的数值,准确到二位有效数字。
解 根据普朗克的黑体辐射公式dv e chv d kThv v v 11833-⋅=πρ, (1)以及 c v =λ, (2)λρρd dv v v -=, (3)有,118)()(5-⋅=⋅=⎪⎭⎫ ⎝⎛-=-=kThc v v ehc cd c d d dv λλλπλλρλλλρλρρ这里的λρ的物理意义是黑体内波长介于λ与λ+d λ之间的辐射能量密度。
本题关注的是λ取何值时,λρ取得极大值,因此,就得要求λρ 对λ的一阶导数为零,由此可求得相应的λ的值,记作m λ。
但要注意的是,还需要验证λρ对λ的二阶导数在m λ处的取值是否小于零,如果小于零,那么前面求得的m λ就是要求的,具体如下:01151186'=⎪⎪⎪⎭⎫⎝⎛-⋅+--⋅=-kT hc kThce kT hc ehcλλλλλπρ⇒ 0115=-⋅+--kThc ekThcλλ⇒ kThcekThc λλ=--)1(5 如果令x=kThcλ ,则上述方程为 x e x =--)1(5这是一个超越方程。
首先,易知此方程有解:x=0,但经过验证,此解是平庸的;另外的一个解可以通过逐步近似法或者数值计算法获得:x=4.97,经过验证,此解正是所要求的,这样则有xkhc T m =λ 把x 以及三个物理常量代入到上式便知K m T m ⋅⨯=-3109.2λ这便是维恩位移定律。
据此,我们知识物体温度升高的话,辐射的能量分布的峰值向较短波长方面移动,这样便会根据热物体(如遥远星体)的发光颜色来判定温度的高低。
1.2 在0K 附近,钠的价电子能量约为3eV ,求其德布罗意波长。
解 根据德布罗意波粒二象性的关系,可知E=hv ,λh P =如果所考虑的粒子是非相对论性的电子(2c E e μ<<动),那么ep E μ22= 如果我们考察的是相对性的光子,那么E=pc注意到本题所考虑的钠的价电子的动能仅为3eV ,远远小于电子的质量与光速平方的乘积,即eV 61051.0⨯,因此利用非相对论性的电子的能量——动量关系式,这样,便有ph=λnmm m E c hc E h e e 71.01071.031051.021024.1229662=⨯=⨯⨯⨯⨯===--μμ在这里,利用了m eV hc ⋅⨯=-61024.1以及eV c e 621051.0⨯=μ最后,对Ec hc e 22μλ=作一点讨论,从上式可以看出,当粒子的质量越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强;同样的,当粒子的动能越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强,由于宏观世界的物体质量普遍很大,因而波动性极弱,显现出来的都是粒子性,这种波粒二象性,从某种子意义来说,只有在微观世界才能显现。
(01) 第一章 量子力学基础

玻尔频率规则
Bohr的轨道角动量量子化
E h E E2 E1
h h
运用玻尔模型,结合经典物理学知识,玻尔计算了氢原子定态 的轨道半径及能量,圆满的解释了氢原子光谱。 1922年, Bohr
获诺贝尔物理学奖.
mv 2 e2 r 4 0 r 2
消去v,
2
r
h M mvr n 2
34
Js
这些不同能量的谐振子出现的几率之比为:
1: h / kT :2 hv / kT :…: nhv / kT e e e
的平均能量为
h e h / kT 1
因此频率为ν的振子的振动
,由此可得单位时间,单位表面积上辐
射的能量。公式计算值与实验结果非常吻合。
E 2h c
)
E总
me 4 1 R 2 2 2 2 8 0 r 8 0 h n n
e2
1 13.6 2 eV ( n 1,2,3 ) n
E总 E K 1 EV 2
当n=1,E=-R=-13.6eV,即为氢原子基态。
当电子从定态n1跃迁到n2时放出或吸收辐射。其频率满足于:
这样实物微粒若以大小为p=mv的动量运动时,伴随有 的波
h p h mv
例子:以1.0×106m.s-1 的速度运动的电子,求其de.Broglie波
长:
6.6 1034 J . s 7.0 1010 m (9.1 10 31 Kg) (1.0 106 m .s 1 )
在十九世纪末,人们利用传统的经典物理学对几个问题始终不能给予
解释, 这其中包括著名的黑体辐射、 光电效应、氢原子光谱和原子
结构等问题.
第一章 量子力学基础知识

《结构化学基础》讲稿第一章孟祥军第一章 量子力学基础知识 (第一讲)1.1 微观粒子的运动特征☆ 经典物理学遇到了难题:19世纪末,物理学理论(经典物理学)已相当完善: ◆ Newton 力学 ◆ Maxwell 电磁场理论 ◆ Gibbs 热力学 ◆ Boltzmann 统计物理学上述理论可解释当时常见物理现象,但也发现了解释不了的新现象。
1.1.1 黑体辐射与能量量子化黑体:能全部吸收外来电磁波的物体。
黑色物体或开一小孔的空心金属球近似于黑体。
黑体辐射:加热时,黑体能辐射出各种波长电磁波的现象。
★经典理论与实验事实间的矛盾:经典电磁理论假定:黑体辐射是由黑体中带电粒子的振动发出的。
按经典热力学和统计力学理论,计算所得的黑体辐射能量随波长变化的分布曲线,与实验所得曲线明显不符。
按经典理论只能得出能量随波长单调变化的曲线:Rayleigh-Jeans 把分子物理学中能量按自由度均分原则用到电磁辐射上,按其公式计算所得结果在长波处比较接近实验曲线。
Wien 假定辐射波长的分布与Maxwell 分子速度分布类似,计算结果在短波处与实验较接近。
经典理论无论如何也得不出这种有极大值的曲线。
• 1900年,Planck (普朗克)假定:黑体中原子或分子辐射能量时作简谐振动,只能发射或吸收频率为ν, 能量为 ε=h ν 的整数倍的电磁能,即振动频率为 ν 的振子,发射的能量只能是 0h ν,1h ν,2h ν,……,nh ν(n 为整数)。
• h 称为Planck 常数,h =6.626×10-34J •S•按 Planck 假定,算出的辐射能 E ν 与实验观测到的黑体辐射能非常吻合:●能量量子化:黑体只能辐射频率为 ν ,数值为 h ν 的整数倍的不连续的能量。
能量波长黑体辐射能量分布曲线 ()1/8133--=kt h c h eE ννπν1.1.2 光电效应和光子学说光电效应:光照射在金属表面,使金属发射出电子的现象。
-第1章-量子力学基础详细讲解汇总

第1章、 量子力学基础1.1 量子力学和量子光学发展简史1900,Planck (普朗克),黑体辐射,能量量子化:h εν=1905,Einstein (爱因斯坦), 光电效应,光量子–光子:E h ν=, h p λ= (h h E p c c νλ===)1913,Bohr (玻尔), 原子光谱和原子结构,定态、量子跃迁及跃迁频率:()/mn m n E E h ν=-1923, de Broglie (德布罗意), 物质粒子的波动性,物质波:E h ν=,h p λ=1925, Heisenberg (海森堡), 矩阵力学1926, Schrödinger (薛定谔), 波函数(),r t ψ,波动方程- Schrödinger 方程,波动力学:()(),,ir t H r t tψψ∂=∂ 1926, Born (波恩), 波函数的统计诠释:()2,r t ψ为概率密度,()2,1dr r t ψ=⎰1926, Dirac (狄拉克),狄拉克符号、态矢量ψ、量子力学的表象理论1927, Dirac ,电磁场的量子化 1928, Dirac ,相对论性波动方程至此,量子力学的基本架构已建立,起初主要用其处理原子、分子、固体等实物粒子问题。
尽管量子力学在处理实际问题中获得了巨大成功,但是关于量子力学的基本解释和适用范围一直存在争论,最著名的有: 1935, Schrödinger 猫态 1935, EPR 佯谬1960 前后,量子理论用于电磁场:量子光学 1956, Hanbury Brown 和Twiss ,强度关联实验 1963, Glauber (2005年诺奖得主),光的量子相干性1963, Jaynes & Cummings, J-C 模型:量子单模电磁场与二能级原子的相互作用 1962-1964, 激光理论(Lamb, Haken, Lax 三个主要学派) 1970’s, 光学瞬态、共振荧光、超荧光、超辐射 1980’s ,光学双稳态1990’s ,光场的非经典性质(反群聚效应、亚泊松分布、压缩态)、量子光学新发展:量子信息科学:量子通信、量子计算等。
第一章量子力学基础知识.doc

第一章 量子力学基础知识1.1 微观粒子的运动特征基本内容一、微观子的能量量子化1. 黑体辐射黑体:是理想的吸收体和发射体.Plank 假设:黑体中原子或分子辐射能量时作简谐振动,它只能发射或吸收频率为ν,数值为ε=hν整数倍的电磁波,及频率为ν的振子发射的能量可以等于:0hν,1 hν,2 hν,3 hν,…..,n hν.由此可见,黑体辐射的频率为ν的能量,其数值是不连续的,只能为hν的倍数,称为能量量子化。
2. 光电效应和光子光电效应:是光照射在金属样品表面上,使金属发射出电子的现象。
金属中的电子从光获得足够的能量而逸出金属,称为光电子。
光电效应的实验结果:(1) 只有当照射光的频率超过某个最小频率ν时金属才能发射光电子,不同金属的ν值也不同。
(2) 随着光强的增加,发射的电子数也增加,但不影响光电子的动能。
(3) 增加光的频率,光电子的动能也随之增加。
光子学说的内容如下:(1) 光是一束光子流,每一种频率的光的能量都有一个最小单位称为光子,光子的能量与光子的频率成正比即:νεh =0(2) 光子不但有能量,还有质量(m ),但光子的静止质量为零。
按相对论质能联系定律,20mc =ε,光子的质量为:c h c m νε==2,所以不同频率的光子有不同的质量。
(3) 光子具有一定的动量(p) p=mc=c h ν=λh(4) 光子的强度取决于单位体积内光子的数目即光子密度:ττρτd dNN =∆∆=→∆0lim将频率为ν的光照射到金属上,当金属中的一个电子受到一个光子撞击时,产生光电效应,并把能量hν转移给电子。
电子吸收的能量,一部分用于克服金属对它的束缚力,其余部分则表现为光电子动能。
2021mv h E w h k +=+=νν 当νh <w 时,光子没有足够的能量,使电子逸出金属,不发生光电效应,当νh =w 时,这时的频率时产生光电效应的临阈频率0ν,当νh >w 时从金属中发射的电子具有一定的动能,它随ν的增加而增加,阈光强无关。
第一章量子力学基础

RH 1 1 ~ 1 1 = 2 = RH 2 2 2 hc n1 n2 n n 2 1
~
实物微粒的波粒二象性
德布罗意假说: ε= hν=hu/λ p = h/λ ρ= K|Ψ|2 or ρ∝|Ψ|2
h/ p
h 2meT 1.226nm T / eV
ν/1014s-1
黑体辐射实验曲线
黑体辐射的解释
瑞利· 金斯公式 (麦克斯韦理论) : 8 2 kT E ( , T )d d 3
c
普朗克· 金斯公式:
左
8h 3 d E ( , T )d c 3 e h / kT 1
维恩公式
(统计热力学理论) :
第一章 量子力学基础
量子力学产生的背景 经典物理学的困难与旧量子论的诞生;实 物微粒的波粒二象性;不确定关系。 量子力学基本原理 波函数与微观粒子的状态;力学量和算符; 量子力学的基本方程;态叠加原理;电子自旋。 量子力学基本原理的简单应用 势箱中运动的粒子;线性谐振子;量子力 学处理微观体系的一般步骤与量子效应。
黑体辐射
黑体辐射模型
5 4
m-2 E (vT)/10-9J·
λБайду номын сангаас
2000K
3
维恩位移定律
T定,辐射频率:v v+dv 辐射能量:E(v,T)dv。辐射最强的 频率λmax随温度升高而发生位移: λmaxT=2.9×10-3 m· K
2
1500K
1
1000K
0 0 1 2 3
斯忒蕃公式
总辐射能量:E=σT4
爱因斯坦光子学说(1905年)
光是一束光子流。每一种频率的光能量都有一最小单位, 即为光子的能量ε: ε= hν 光的能量是量子化的,不连续的。 一束光的能量是hν的N微粒形式出现的集合体。 即: E = Nhν 光子密度: ρ= LinΔΝ/Δτ=dN/dτ Δτ→0 光子的能量和动量: 相对质能联系定律: εo = mc2,m = hν/c2 =h/cλ, 动量: p = mc = hν/c , p = h/λ 光子与电子相碰时服从能量守恒和动量守恒定律 hν=W + T = hνo + ½ mv2,T = ½ mv2 = hν- hνo 光波强度与光子密度的关系:I = ρhν, ρ= dN/dτ I = Eo2/8π+Ho2/8π=Ψ2/4π (麦克斯韦方程) ρhν= Ψ2/4π ρ= K|Ψ|2
01第一章量子力学基础

2
sin
n
x
a
(
x)
均所 值以
, 只 能 求 位 置 的 平
x
* ( x )x ( x )dx
0
2
0
x
sin
2
n
xdx
2
0
x
1
cos
2n
2
x dx
1
(
0
x
x
cos
2n
x )dx
1
[
x2 2
0
2n
0
xd
sin
2n
x]
1
[
2 2
2n
1
2n
( x sin 2
x
1 2n
cos 4
x) ]
E h
E E2 E1
h
h
实物粒子的波粒二象性
de Broglie关系式为: ν= E / h λ= h / p λ= h / mv
λ h/ 2mT
不确定原理
量子力学公设
公设1
微观体系的状态可用一个状态函数或波函 数Ψ(q, t)描述,Ψ(q, t)决定了体系的全部 可测物理量.
波函数应具有品优性: 单值性、 连续性、 平方可积性.
n=4
n=3 n=2 n=1
波函数
概率密度
1.3.2 三维无限深势阱中的粒子
1.3.2 三维无限深势阱中的粒子
能量本征方程为:
本 征 函 数 与 本 征 值
三维无限深正方体势阱中粒子的简并态
三维无限深正方体势阱中粒子的波函数
定理:
简并本征函数的任意线性组合仍是原算符的具有同样 本征值的本征函数.
(01) 第一章 量子力学基础

( 1 1 ), n n R 2 2 1 2 n1 n2 n1 1, Lyman 系 n1 2, Balmer 系 n1 3, Paschen 系 n1 4, Brackett系 n1 5, Pfund 系
原子光谱是原子结构的信使. 那么, 在此之前, 人们对 原子结构认识如何呢?
1903年,J.J.汤姆逊提出“葡萄布丁”原子模型.
1911年, 卢瑟福在α粒子散射实验基础上提出原子的
有核模型. 但问题是: 原子是一个电力系统, 电子如果像行
星绕太阳那样绕核运转, 就会在这种加速运动中发射电磁 波而损失能量, 从而沿螺旋线坠落到核上并发射连续光谱, 与原子稳定性和光谱分立性相矛盾:
结成经验公式(后被J.R.Rydberg表示成如下的波数形式),
并正确地推断该式可推广之(式中n1、n2均为正整数):
20 世 纪 初 , F.Paschen(1908 年 ) 、 F.S.Brackett (1922 年) 、H.A.Pfund (1924年)等在红外区, Lyman (1916年)在 远紫外区发现的几组谱线,都可用下列一般公式表示:
直认为是实物粒子的电子等物质, 也看作是波.
de Broglie关系式为:
ν= E / h
λ= h / p
尽管Einstein的光量子理论对de Broglie有重要影响, 但 实物微粒的波粒二象性并不能从光的波粒二象性经演绎推理 得出. de Broglie波的传播速度为相速度u, 不等于粒子运动速 度v; 它可以在真空中传播,因而不是机械波;它产生于所
匀速直线运动, 决不可能作圆周运动!
事实上, 按照经典物理学, Bohr模型中的电子只受一种向心力 mv2/r 作 用 , 才 产 生 了 圆 周 运 动 , 而 这 向 心 力 本 身 就 是 库 仑 引 力 e2/(4πε0r2) . 至于离心力和向心力, 它们是分别作用于原子核和电子的, 而不是 共同作用于电子.
-第1章-量子力学基础详细讲解

1.3.4 表象变换 设有两个表象A和B,其基矢分别为、。 (a)态矢的表象变换 在表象A中,可将任意态矢展开为 ,; 在表象B中,可将同一个态矢展开为 ,。 所谓态矢的表象变换,就是要建立和之间的关系。
(1.28) (1.29)
, (1.30) 其中
(1.31) 矩阵称为表象A和表象B之间的变换矩阵。(1.30)式可简写成
态矢量的归一化条件为 (1.23)
在连续变量表象中,完备性条件为 (1.24)
任意态矢量可展开为 (1.25a)
其中 (1.25b)
是态矢在表象中的表示,也就是通常讲的波函数。可见,态矢量在连续 表象中表现为一个普通函数。
态矢量的归一化条件为
(1.26) 可见,选定了一组基矢,就选定了一个表象;这类似于,选定了一 组单位矢量,就选定了一个坐标系。常用的连续表象有坐标表象和动量 表象;常用的离散表象有能量表象和角动量表象。
由于线性厄密算符的上述性质,在实验上可观测的力学量(如:坐 标、动量、能量、角动量、自旋等)均用线性厄密算符表示。不过,我 们也会遇到一些非常重要的非厄密算符,如光子产生算符、光子湮灭算 符等。
算符在量子态中的期望值(平均值)记为 (1.12a)
平均值为c数。若将态矢量按(1.11a)式用算符的本征态展开,则平均 值的计算如下:
1.4.2 纯态和混合态举例 (a) 纯态: 光子数态(photon-number state) ,其密度算符为 (1.51)
其中为光子数。 相干态(coherent state),其密度算符为 (1.52)
(1.18) 其中 。例如,坐标和动量的对易关系为
其不确定度关系为
(5) 全同粒子假设 作为量子力学的一条基本假设,认为所有的同一类粒子(例如所有 的电子、所有的光子等)的各种固有属性都是相同的,即同一类粒子是 全同的粒子。因而,在由全同粒子组成的系统中,交换其中任意两个粒 子不会改变系统的状态,这导致描述全同粒子系统的波函数对粒子的交 换要么是对称的,要么是反对称的。 研究发现,全同粒子可分为两大类,一类称为玻色子,其自旋为零 或正整数(,…);另一类称为费米子,其自旋为半奇数(,…)。玻 色子和费米子具有完全不同的性质,例如,描述玻色子系统的波函数对 粒子的交换是对称的,而描述费米子系统的波函数对粒子的交换是反对 称的;玻色子服从玻色-爱因斯坦统计,而费米子服从费米-狄拉克统 计。
第一章 量子力学基础知识

dx
(2)
d
2 2
(3x x )
3 2
d dx
(9 x 2 x) 18 x 2 (3x x )
2 3 2
dx
2013-3-22
3
第一章 量子力学基础知识
ˆ ˆ 将总能量算符 H 代入本征方程 A a , ˆ 则得方程 H E —— Schrodinger 方程
2
通解为: ( x) A cos x B sin x
2013-3-22
11
第一章 量子力学基础知识
根据边界条件确定方程的特解 边界条件为: (0) (l ) 0
(0) 0
A cos 0 B sin 0 0
A0 B0
( x) B sin x
2013-3-22 27
第一章 量子力学基础知识
掌握几重要个算符; 对于给定体系,会求: 本征态:物理量的确定值; 任意态:物理量的平均值;
A
2013-3-22
ˆ * A d
* d
或 A
ˆ * A d
28
第一章 量子力学基础知识
3. 掌握一维势相粒子的处理结果
2
] 0
B
2
l
2
B
2 l
( x)
2 l
Sin
nx l
一维势箱波函数
2013-3-22
14
第一章 量子力学基础知识
三、解的讨论
1、能级 A. 能量量子化 粒子的能量是不连续的,随n 不同,能量取一 系列不连续的分立值。
2013-3-22 15
E
n h 8ml
2
第01讲 量子力学基础
第01讲量子论基础1.1 经典物理学的困难毛泽东在《实践论》中指出:“在绝对宇宙发展过程中,各个具体过程的发展都是相对的。
因而在绝对真理的长河中,人们对于各个发展阶段的具体过程的认识只具有相对真理。
”量子力学的发展过程,是充满着矛盾和斗争的过程,一方面,新的现象的发现暴露了微观过程的内部矛盾,推动人们突破经典物理理论的限制,提出新的思想和新的理论;另一方面,也有一些人不愿承认经典物理理论的局限性,总是千方百计把这些新发现的现象提出新的思想,新的方法纳入经典物理理论的框架中。
19世纪末20世纪初,经典物理学,主要是经典力学、热力学和经典统计物理学、经典动力学,已经发展的相当完善。
比方说,速度远小于光速的物体的机械运动遵从牛顿力学规律;电磁现象满足麦克斯韦方程组;光的现象满足光的波动理论;特别是当时已认识到热辐射和光辐射都是电磁波,还提出了热辐射满足的基尔霍夫定律(Kirchhoff)定律和斯忒藩(Stefan)-波耳兹曼(Boltzmann)定律,证实黑体辐射场的能量密度与温度的四次方成正比。
对于热现象,除了已经有了非常系统的热力学理论外,还有波耳兹曼、吉布斯(Gibbs)等人提出的统计物理学。
经典物理学的大厦已经建立得相当完美了。
当时还有很多人都认为物理现象的基本规律完全被揭露了,剩下的工作只要把这些基本规律应用到具体的问题上进行一些计算就可以了。
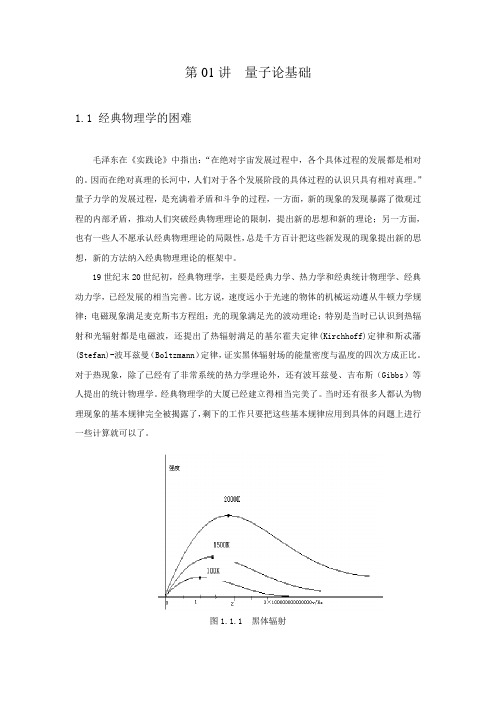
图1.1.1 黑体辐射但是,在和实验进一步对比的过程中,也出现了一些困难,而这些困难,在经典物理的范畴内是无法解释的。
这主要表现在: 1. 黑体辐射`任何物体总在吸收投射在它身上的辐射,物体吸收的辐射能量与投射到物体上的辐射能之比称为该物体的吸收系数,一般地讲,物体只吸收投射到它身上的部分能量,吸收系数小于1。
如果一个物体,能吸收投射到它表面上的全部辐射,即其吸收系数为1时,则称这个物体为黑体,一个开有小孔的空腔可近似为黑体。
因为一旦光线通过小孔射入空腔后,就很难在通过小孔反射过来。
第一章 量子力学基础-3

h2
h2
d ⎡ 2 nπ ⎛ nπ x ⎞ ⎤ =− 2 × cos ⎜ ⎢ ⎟⎥ l 8π m dx ⎣ l ⎝ l ⎠⎦ h2 h2 =− 2 nπ ⎡ nπ ⎛ nπ x ⎞ ⎤ sin × × − ⎜ ⎟⎥ l ⎢ l l 8π 2 m l ⎝ ⎠⎦ ⎣ h2
2 2 n 2π 2 2 ⎛ nπ x ⎞ n h ψn sin ⎜ = 2 × ⎟= 2 2 l 8π m l ⎝ l ⎠ 8ml
• 当x≤0,或者x≥l 此时,V = ∞ Hamiltonian算符:
Ⅰ V=∞ 0
Ⅱ V=0 l x
Ⅲ V=∞
2 2 2 d d ˆ =T ˆ +V ˆ =− H +∞ = − +∞ 2 2 2 8π m dx 2m dx
h2
Schrödinger方程:
⎛ ⎞ h2 d 2 + ∞ ⎟ψ = Eψ ⎜− 2 2 ⎝ 8π m dx ⎠
第一章 量子力学基础
2、花菁染料的吸收光谱 结构式: R2N (CH=CH )rCH=NR2 π电子总数:2r+2+2=2r+4 最高占据能级:ni=(2r+4)/2=r+2 最低空能级:nj=r+3
ΔE = En j − Eni = hν ⇒ ν =
n 2h2 E= 8ml 2
En j − Eni h
第一章 量子力学基础
− 根据品优函数的连续性和单值性以及边界条件: 当x=0时, ψ (0) = c1 cos(0) + c2 sin (0) = 0
∴c1 = 0
⎡⎛ 8π 2 mE ⎞ 12 ⎤ ⎡⎛ 8π 2 mE ⎞ 12 ⎤ ⎟ ⎟ ⋅ l ⎥ + c2 sin ⎢⎜ l⎥ = 0 当x=l 时, ψ (l ) = 0 ⋅ cos⎢⎜ 2 2 ⎜ ⎜ ⎟ ⎟ ⎢⎝ h ⎥ ⎢⎝ h ⎥ ⎠ ⎠ ⎣ ⎦ ⎣ ⎦
第01章量子力学基础

18
1.1.3 实物微粒的波粒二象性
实物微粒是指静止质量不为零的微观粒子(m0≠0) 如电子、质子、中子、原子、分子等。
(1)德布罗意(de Broglie)假设
实物微粒也具有波性。实物微粒所具 有的波就称为物质波或德布罗意波 (de Broglie Waves)。
1929年
De Broglie
E: 黑体辐射的能量
E
T=1500K T=1000K
Ed :频率在 到 d 范围 内、单位时间、单 位表面积上辐射的 能量
۞ 随温度的升高, E增 大,极大值也向高 频移动.
化学工程学院
6
Wien辐射波长分布类似于Maxwell分布
E( , T ) c1 exp(c2 / T )
化学工程学院
20
德布罗意波与光波不同:下列两式对于粒子正确吗?
p (m c) 1 2 E mc 2m 2m 2 hc 2 E h mc h mc hc
2
2
化学工程学院
21
(2)德布罗波波长的估算 动量为p的自由粒子,例如电子,当它的运动速度比光速小 得多时(v c) 1 2
汤姆逊实验——金-钒多晶 (G. P. Thomson)
G.P.Thomson 1937年
化学工程学院
24
戴维逊单晶电子衍射实验
电子在单晶金上的衍射
对Dovissn和Germer单晶电子衍射实验,由布拉格(Bragg)
方程 2dh k l sin hkl n 和
12.26 V
1921年
化学工程学院
13
光电效应的解释
将频率为v的光照射到金属上,当金属中的一个电 子受到一个光子的作用时,产生光电效应,光子消失, 并把它的能量传给电子。电子吸收的能量,一部分用 于克服金属对它的束缚力,其余部分则表现为电子的 动能 1
量子力学基础

i 2 i 2 xpx Et xpx Et A exp h x h
第一章 量子力学基础知识
i 2 i 2 i 2 xpx Et px A exp p x h h h
z
e2
第一章 量子力学基础知识
e1
不考虑核的运动
r1 r12 r2
z
2 p12 p2 2e 2 2e 2 e2 E 2m1 2m2 4 0 r1 4 0 r2 4 0 r12
e2
ˆ 2 2 2e 2e e H 1 2 2m1 2m2 4 0 r1 4 0 r2 4 0 r12
第一章 量子力学基础知识
合格(品优)波函数
由于波函数的概率性质,所以波函数必须满足下 列条件: • 单值的,即在空间每一点 只能有一个值;
• 连续的,即 的值不出现突跃; 对x, y, z的 一级微商也是连续函数;
• 平方可积的,即 在整个空间的积分
* d
为一个有限数,通常要求波函数归一化,即
态函数的形式与光波的方程类似,习惯上称之为 波函数。如: 平面单色光的波动方程: A exp i 2 x t E hv, p h 代人波粒二象性关系: i 2 得单粒子一维运动波函数: A exp xpx Et
h
定态波函数:当微观粒子的运动状态不随时 间而变时,其波函数可以写作:
x1 , y1 , z1 , x2 , y2 , z2 , x3 , y3 , z3 , t
or
or
1,2,3, t
q1 , q2 , q3 , t ,
<关于波函数的一些概念和说明> 波函数是体系中所有粒子的坐标和时间的函数。
第一章.量子力学基础知识-3

假设Ⅲ:自轭算符的第二项重要性质
• 自轭算符的本征函数y1, y2, y3,...正交归一。 • Consider these two eigen equations: • Multiply the left of the 1st eqn by ψm* and integrate, then take the complex conjugate of eqn 2, multiply by ψn and integrate
力学量与算符
• To every physical observable there corresponds a linear Hermitian operator. • To find this operator, write down the classical-mechanical expression for the observable in terms of Cartesian coordinates and corresponding linear-momentum components, • and then replace each coordinate x by the operator x. and each momentum component px by the operator -iћ∂/∂x.
假设Ⅰ:波函数
y一般是复数形式: y f+ig
y的共轭复数为: y *f-ig
那么:
y *y f2+g2
y *y是实数,有时也用y2来代替
假设Ⅰ:波函数
波函数y描述的波为概率波,在原子或分子Байду номын сангаас体系中, 称为原子轨道或分子轨道
第01章 量子力学基础(定稿)

从金属表面打出电子,临阈频率只与金 光的能量则是由光的强度(振幅) 属种类有关。 决定的。
光电流增大,但不影响光电子的动能。
● 随着光强的增加,发射的电子数目增加,
● 增加光的频率,光电子的动能也随之增加。
第一章
光电子动能mv 2/2
斜率为h
纵截距为-φ
光频率ν
第一章
Einstein 首先认识到 Planck 提出的能量量子化的重 要性,他将能量量子化的概念应用于电磁辐射。 1905年,Einstein提出了光子学说,内容如下: 1 光不是看成一种波,光是一束光子流。每一种频率的光的能量都有一个最
第一章
黑体
带有一个微孔的空心的 金属球,非常接近于黑 体,进入金属小孔的辐 射,经过多次吸收、反 射,使射入的辐射完全 被吸收,当空腔受热时 ,又能发射出各种波长 的电磁波。
第一章
5 4 3 2 1 1000K 0 1 2 3 14 -1 /10 s 1500K 2000K
E: 黑体辐射的能量,
Ed: 频率在到 +d范围内、单位 时间、单位表面积上辐射的能量。
E/(10-9J/m2)
以E对作图,得到能量分布曲线。
规律:
随着温度升高,
同一频率的E增大,
极大值向高频移动。
第一章
按照经典物理学的方法,Rayleigh-Jeans 及 Wien等分别作了很多 研究工作,但都不能满意地解释黑体辐射实验的能量分布曲线。
第一章
上式解释了光电效应实验的全部结果: 当hν<W 时,光子没有足够的能量使电子逸出金属,不发生 光电效应;
当hν=W 时,光子的频率是产生光电效应的临阈频率(ν0) ;
当hν>W 时,从金属中发射的电子具有一定的动能,它随ν的 增加而增加,与光强无关。 增加光的强度可增加光束中单位体积内的光子 数,因此增加发射电子的数目。
第一章:量子力学基础
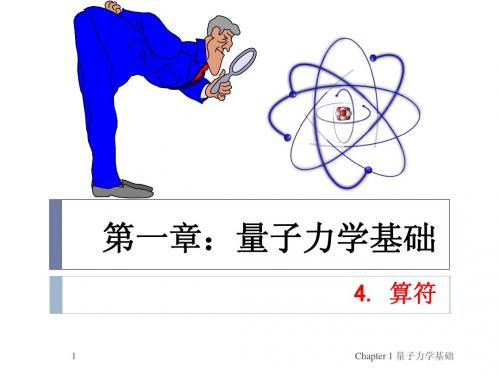
ˆ p n | pn 2 n d 2 n sin x ) * ( i ) sin xdx 0 a a dx a a a 2 n n n (i ) (sin x)( )(cos x)dx 0 a a a a 2 n 1 a 2 n (i )( ) sin xdx a a 2 0 a 0 (
1. 乘法与对易 满足结合律,一般不服从交换律
ˆ ˆ ˆ AB A( B )
ˆ ˆˆ ˆˆ ˆ A( BC ) ( AB)C
ˆ ˆ ˆˆ AB BA
ˆˆ 如: xDf ( x) xf ' ( x)
ˆ xf ( x) d xf ( x) f ( x) xf ' ( x) Dˆ dx ˆˆ ˆ ˆ ˆ ˆ ˆ Dx I xD xD
*
(m n ) m | n 0
因为
13
m n
所以
m | n 0
Chapter 1 量子力学基础
1.4 算符
厄米算符的本征函数与本征值 —— 性质 III
定理(3):厄米算符本征函数构成一完备集合,任何一个
品优函数可用它展开
f Cnn
n
其中展开系数:
1.4 算符 其它力学量表示法 动能
ˆ F (r ,i) ˆ F (r , p) F
p2 2 2 ˆ T T 2m 2m
势能 V(r ) V (r ) ˆ 角动量 L r p L r (i) H Hamilton 算符
1.4 算符
厄米算符 (Hermitian Operator)
对任意品优波函数,算符满足 则 F 是厄米算符
ˆ ˆ 定理:若两个厄米算符 A 和 B 对易,即 ˆ 是厄米的 。 ˆ 则乘积算符 AB
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
+
n=2
n=1
+
-
E2 E1
n=1
ψ22(x)
ψ12(x)
一维势箱中粒子的波函数、能级和概率率密度
势箱中自由粒子的波函数是正弦函数,基态 时, l长度势箱中只包含正弦函数半个周期,随着能 级升高,第一激发态包含一个周期,第二激发态包 含正弦波一个半周期……。随着能级升高,波函数 的节点越来越多。而概率分布函数告诉我们自由粒 l x 子在势箱中出现的概率大小。例如:基态时,粒子 2 在 处出现概率最大。而第一激发态,粒子在 l x 2 处出现几率为0,在 x l , 3l 处出现几率最大。
l nπ 1 nπ 2
2 l c 2 1 2
c 2
2 l
2 nx 箱中粒子的波函数 n ( x) sin l l
讨论:
ψ4(x)
+
n=4
n=4
-
+
+
E4
ψ42(x)
n=3
ψ32(x)
n=3
ψ3(x)
+
E3
n=2
ψ2(x)
一维无限深势阱中看不到的一种量子现象是隧道效 应. 当势垒为有限高度(V0) 和厚度时,入射到势垒上的粒 子能量E即使小于V0,也仍有一定的概率穿透势垒,似乎 是从隧道中钻出来的:
这种奇妙的量子现象是经典物理无法解释的. 量子力学 隧道效应是许多物理现象和物理器件的核心,如隧道二极 管、超导Josophson结、α衰变现象. 某些质子转移反应也 与隧道效应有关. 对于化学来讲,意义最大的恐怕是基于
ih l
nx nx d sin 0 sin l l
l
2 xl
ih sin (nx / l) 0 l 2 x 0
(3)粒子的动量平方px2值
2 2 2 nx h d 2 ˆ x n 2 2 p sin 4 dx l l h 2 d n 2 nx 2 cos 4 dx l l l 4 4ຫໍສະໝຸດ CC4/9E1
花菁燃料的吸收光谱
[R2N¨-(CH=CH-)r CH=N+R2] l l 定域键 l
1/9E1
3l 离域键
•势箱总长l=248r+565pm,共有2r+2+2个电子,基态时需占r+2个分子轨 道,当电子由第(r+2)个轨道跃迁到第(r+3)个轨道时,需吸收光的频率为 =△E/h=(h/8ml2)[(r+3)2-(r+2)2]=(h/8ml2)(2r+5), 由=c/,=8ml2c/(2r+5)h
隧道效应发明的扫描隧道显微镜(STM),放大倍数3千
万倍, 分辩率达0.01nm,它使人类第一次真实地“看见” 了单个原子!这是20世纪80年代世界重大科技成就之一.
第一章 作业
• P32 1.1 • P33 1.7,1.17,1.26,1.28,1.29,1.30, 1.31,1.33 • 1.35选择题写在书上
讨 论
(5) 体系的全部合理解构成正交归一完全集 .即:任何
一个波函数都是归一化的,任何两个不同波函数的乘积对 于坐标的积分都等于零;用这一本征函数系的线性组合可 以表示任一个具有相同自变量、定义域、边界条件的连续 函数.
(6) 能级差与粒子质量成反比,与粒子运动范围的平 方成反比.这表明量子化是微观世界的特征.
r 1 2 3 计算 311.6 412.8 514.0 实验 309.0 409.0 511.0 说明此体系可近似看做一维势箱。
(8) 基态能量 E1=h2/ ( 8ml2 ) , 表明体系有一份
永远不可剥夺的能量,即零点能.这是不确定关系的
必然结果.在分子振动光谱、同位素效应和热化学数 据理论计算等问题中,零点能都有实际意义.
通解为: ψ= c1cos (8π2m E / h2 )1/2 x + c2sin (8π2m E / h2 )1/2 x 根据品优波函数的连续性和单值条件, 当x = 0 和 x = l 时, ψ= 0 即 x = 0 时 ψ(0)= c1cos (0) + c2sin (0)= 0 则:c1 = 0
金属内的自由电子或共轭分子
的 π 电子,无限深势阱中的粒 子模型可以作为一种近似模型.
用量子力学处理微观体系的一般步骤
1. 写出体系势能函数,进而写出Hamilton算符;
2. 写出Schrö dinger 方程;
3. 解方程, 求出满足合格条件的解,得到体系的 波函数及相应的能量; 4. 对求解结果进行讨论,作出适当的结论。
h2 2 2 2 当a b c时,E ( n n n x y z) 2 8ma
三维无限深正方体势阱中粒子的波函数
这种现象就是所谓的“简并性”. 同一能级对应的状 态数为简并度 . 简并通常与对称性有关,对称性降低往往
会使简并度降低甚至完全解除 . 所以,正方体势阱中粒子
的简并现象, 在三维的一般矩形势阱中就被解除了. 过渡金属离子和具有C3轴以上对称性的分子常有简并 轨道,电子在这些简并轨道上按不成对的方式平行排列, 可设计成构建分子铁磁材料的基块;若除去某些基团而降 低分子对称性,轨道简并被解除,则铁磁性消失 . 在学过 第四章的群论基础知识后,对这一点将会有更深刻的理解.
abc a b c
2 2 2 n h nx n y z E n x,n y,n z均为非零整数 2 2 2 8m a b c h2 2 2 2 当a b c时,E ( n n n x y z) 2 8ma 2
三维势箱能级表达式:
简并态:能量相同的各个状态。
h n 2 nx 2 sin 4 l l l
2
2
nh 2 n 4l
2
2
2 2 n h 2 px 4l 2
E T V
1 1 n2h2 2 T px 2m 2m 4l 2 n2h2 8m l2
1.3.2
三维无限深势阱中的粒子
l * n l
粒子的平均位置在势箱的中央,说明它在势箱左、右 2 两个半边出现的几率各为0.5,即 图形对势箱 n 中心点是对称的。
(2)粒子动量的x轴分量px
ˆ 也无本征值,即 P ˆ a 可以验证, P x x n n
ˆ dx Px P n
0 * n x
l
2 l nx ih d nx sin sin dx l 0 l 2 dx l
其中三个量子数nx、ny、nz是独立变化的.
若a=b=c,势阱成为正方体,能级成为:
h2 2 2 2 E ( n n n 2 x y z ) 8ma
一维无限深势阱中的粒子未曾有过的新现象出现了: 具有不同量子数的态尽管是互不相同的独立的波函数,却 可能具有相同的能量:
三维无限深正方体势阱中粒子的简并态
c
2 2
2 2
sin
0
l
2
(nx / l)dx 1
1 1 2 sin ydy y sin 2 y 2 4
l c n
2 c2
nx 1 2nx 2nx nx 1 sin sin 1 l x l 2l 4 l x 0 2l 4
从这一规律定性地看更复杂的三维体系就不难理解:
普通金属费米能级附近的准连续能级在纳米颗粒中会变为
离散能级,而半导体中本来存在的窄能隙在纳米颗粒中会
变宽. 当这种能级差大于热能、电场能或者磁场能时,就 会呈现出与宏观物体不同的反常特性,即量子尺寸效应 . 例如,金属在超微颗粒时可变成绝缘体,光谱线向短波长 方向移动,等等.
非负的 . 概率密度为零的点或面(边界处除外)称
为节点或节面,一般说来,节点或节面越多的状态
,波长越短,频率越高,能量越高.
(4) 能量(或概率密度)不随时间变化的状态为 定态 . 若借用 de Broglie“ 定态与驻波相联系”的说 法,由de Broglie关系式λ=h/p和驻波条件n(λ/2)=l也 能得到能级公式:
由一维无限深势阱中粒子推广到三维无限深势阱中的 粒子,能量本征方程为:
三维势箱中粒子运动的Schrödinger方程:
2 2 2 h 2 2 2 E 2 8 m x y z 2
三维势箱中粒子运动的波函数: 1/ 2 n yy nxx nzz 8 sin sin sin
x = l 时 Ψ(l)= c2 sin (8π2m E / h2 )1/2 l = 0 c2 不能为 0
故必须是: (8π2m E / h2 )1/2 l = nπ n =1,2,3,… n≠ 0
∴ E= n2 h2 / 8m l2
***
***
Ψ(x)= c2 sin (nπx/ l )
C2可由归一化条件求出
(7) En=n2h2/(8ml2)表明:对于给定的 n, En与l2成反
比 , 即粒子运动范围增大,能量降低 . 这正是化学中大 π 键
离域能的来源(下图分别是苯和丁二烯大π 轨道中能量最低 的轨道,它们都有离域化特征):
一维势箱模型应用示例
C
C
C
C E1
C
C
丁二烯的离域效应: E定=22h28ml2=4E1 E离=2h2/8m(3l)2+222h2/8m(3l)2 =(10/9)E1 势箱长度的增加,使分子能量降低, 更稳定。
4 4
讨 论
( 1 )受束缚微观粒子的能量是量子化的,由量子数表征 . 最低能量状态为基态. n 称为量子数,只可能取正整数。
