第2章线性时不变系统
信号与系统课件:第二章 LTI系统

2.1 离散时间LTI系统: 卷积和
(1)用移位单位抽样信号表示离散时间信号 (2)卷积和在离散时间信号LTI系统中的表征 (3)卷积和的计算 (4) 离散时间信号LTI系统的性质
(1)用单位抽样信号表示离散时间信号
x[n] ... x[1] n 1 x[0] n x[1] n 1... x[n][0] x[n 1][1]
(1)初始条件为n<0时,y(n)=0,求其单位抽样响应;
(2)初始条件为n≥0时,y(n)=0,求其单位抽样响应。
解:(1)设x(n) (n),且 y(1) h(1) 0 ,必有
y(n) h(n) 0, n 0
依次迭代
y(0) h(0) (0) 1 y(1) 1 0 1
2
当系统的初始状态为零,单位抽样响应h(n)就 能完全代表系统,那么对于线性时不变系统,任意 输入下的系统输出就可以利用卷积和求得。
差分方程在给定输入和边界条件下,可用迭代 的方法求系统的响应,当输入为δ(n)时,输出 (响应)就是单位抽样响应h(n)。
例:常系数差分方程
y(n) x(n) 1 y(n 1) 2
x[n]u[n] x[k]u[n k] x[k]
k
k
(ii)交换律:
yn xnhn hn xn
例子: 线性时不变系统中的阶跃响应 sn
sn unhn hnun
阶跃输入
输 单位抽样信号 入 响应的累加
n
sn hk
k
(iii)分配律:
xnh1n h2 n xnh1n xnh2 n
y(1) h(1) (1) 1 y(0) 0 1 1
2
22
y(2) h(2) (2) 1 y(1) 0 1 1 (1)2
第2章-线性时不变系统

0
t
y(t)
d2Tt1T2
y(t)t2 T Td2T2 21(tT)2
tT
2
y(t) 0
1T2
2
t
0
T
2T
3T
例题:
f t 10u t etu t
u
t
t
0
f1
t
f2
d
10u t t e d 0
10 1 et u t
信号与系统
例: 计算 e 1 t u t * e 2 t u t
etut*ut 1ut 1
1[e(t1) 1]u(t 1) 1[e(t1) 1]u(t 1)
信号与系统
举例
❖ 已知某线性时不变系统的单位冲激响应和激
励信号分别为:e2tut ,ut 1ut2,则系
统的零状态响应为?
三. 卷积和的计算
计算方法:
有图解法、列表法、解析法(包括数值解法)。
运算过程: 将一个信号 x 不( k )动,另一个信号经反转后成
为h(k) ,再随参变量 n移位。在每个 值n 的情况
下,将 x ( k ) 与 h(nk) 对应点相乘,再把乘积的
各点值累加,即得到 n 时刻的 y ( n ) 。
otherwise
x(k )
1
0
4
h(nk)nk
k
n6
0
k
n
① n 0 时, y(n)0
n
n
② 0n4 时, y(n) nk n k
k0
k0
n
1(n1) 11
1n1 1
③
4n6 时,
y(n)
4
nk
k0
n
第二章 线性不变系统.

§1.7 傅里叶变换 Fourier Transform
常用傅里叶变换对
5. {d (x-a)}=exp(-j2pfxa) {exp(j2pfax)}= d (fx-fa)
6.
1 {cos (2pf 0 x) [d ( f x f 0 ) d ( f x f 0 )] 2 1 {sin(2pf 0 x) [d ( f x f 0 ) d ( f x f 0 )] 2j
0
圆对称函数的F.T. 仍是圆对称函数, 称为F-B (傅-贝)变 换,记为
-1{G()}
G() =
{g(r)}, g(r) =
§1-2 二维傅里叶变换 2-D Fourier Transform
傅里叶-贝塞尔变换
例: 利用F-B变换求圆域函数的F.T.
1, r 1 , 定义: circ(r ) 0, 其它 r x2 y 2
1
是圆对称函数
{circ(r )} 2p rJ 0 (2pr )dr
0
作变量替换, 令r’ =2pr, 并利用:
J
0
2p 0
x
0 ( )d
xJ1 ( x)
J1 (2p )
{circ(r )}
1 2p
2
r ' J 0 (r ' )dr'
§1.7 傅里叶变换 Fourier Transform
用算符表示系统
g(x, y) = ℒ{f(x, y)}
线性系统定义:
输入
f(x, y)
ℒ{
}
输出
g(x, y)
令 g1(x, y) = ℒ{f1(x, y)}, g2(x, y) = ℒ{f2(x, y)} 若对任意复常数a1, a2有: ℒ{a1 f1 (x, y) + a2 f2 (x, y) } = ℒ{a1 f1 (x, y)} + ℒ{a2 f2 (x, y) } = a1 ℒ{f1 (x, y)} + a2 ℒ{f2 (x, y) } = a1 g1 (x, y) + a2 g2 (x, y)
信号与系统王明泉版本~第二章习题解答
第2章 线性时不变连续系统的时域分析2.1 学习要求(1)会建立描述系统激励与响应关系的微分方程;(2)深刻理解系统的完全响应可分解为:零输入响应与零状态响应,自由响应与强迫响应,瞬态响应与稳态响应;(3)深刻理解系统的零输入线性与零状态线性,并根据关系求解相关的响应; (4)会根据系统微分方程和初始条件求解上述几种响应; (5)深刻理解单位冲激响应的意义,并会求解;(6)深刻理解系统起始状态与初始状态的区别,会根据系统微分方程和输入判断0时刻的跳变情况; (7)理解卷积运算在信号与系统中的物理意义和运算规律,会计算信号的卷积。
; 2.2 本章重点(1)系统(电子、机械)数学模型(微分方程)的建立; (2)用时域经典法求系统的响应; (3)系统的单位冲激响应及其求解;(4)卷积的定义、性质及运算,特别是()t δ函数形式与其它信号的卷积; (5)利用零输入线性与零状态线性,求解系统的响应。
2.3 本章的知识结构2.4 本章的内容摘要2.4.1系统微分方程的建立电阻:)(1)(t v Rt i R R =电感:dtt di L t v L L )()(= )(d )(1)(0t i v Lt i L tL L +=⎰∞-ττ 电容:dtt dv C t i C C )()(= ⎰+=tt L C C t i i Ct v 0)(d )(1)(0ττ 2.4.2 系统微分方程的求解 齐次解和特解。
齐次解为满足齐次方程t n t t h e c e c e c t y 32121)(λλλ+⋅⋅⋅++=当特征根有重根时,如1λ有k 重根,则响应于1λ的重根部分将有k 项,形如t k t k t k t k h e c te c e t c e t c t y 111112211)(λλλλ++⋅⋅⋅++=--- 当特征根有一对单复根,即bi a +=2,1λ,则微分方程的齐次解bt e c bt e c t y at at h sin cos )(21+= 当特征根有一对m 重复根,即共有m 重ib a ±=2,1λ的复根,则微分方程的齐次解bt e t c bt te c bt c t y at m m at h cos cos cos )(121-+⋅⋅⋅++= bt e t d bt te d bt e d at m m at at sin sin sin 121-+⋅⋅⋅+++ 特解的函数形式与激励函数的形式有关。
第二章 线性时不变系统的时域分析

基本内容: 基本内容: (1) 系统的定义及表示 ) (2) ) 系统的基本性质 (3) ) 线性时不变系统的时域描述 (4) ) 零输入响应和零状态响应 (5) ) 单位冲激响应
重点难点: 重点难点: 零状态响应的求解方法 响应的求解方法; (1) ) 零状态响应的求解方法; 冲激响应的求解方法; (2) ) 冲激响应的求解方法;
4.稳定性 稳定性
有界输入产生有界输出,则这个系统就 是稳定系统。 所谓有界,即输入或输出的最大幅值是 一个有限值。 例系统 y[n]=nx[n] 就是一个不稳定系统, 因为,当输入 x[n] 是有界时,系统的输 出却有界,它将随着 n 值的增加而增加, 直至无穷。
三、线性时不变系统的时域描述
线性时不变系统也简称为LTI系统,其 系统, 线性时不变系统也简称为 系统 分析方法建立在信号分解的基础之上。 分析方法建立在信号分解的基础之上。 线性时不变系统具有的线性和时不变性, 线性时不变系统具有的线性和时不变性, 其响应必然是系统对这些基本信号响应 的组合。 的组合。 连续时间LTI系统用微分方程描述; 系统用微分方程描述; 连续时间 系统用微分方程描述 离散时间LTI系统用差分方程描述。 系统用差分方程描述。 离散时间 系统用差分方程描述
这个常系数线性微分方程, 这个常系数线性微分方程,其完全解由 齐次解和特解两部分组成 。 齐次解是微分方程在输入为0时的齐次 齐次解是微分方程在输入为 时的齐次 方程的解( 方程的解(式2.111) ) 而特解则是在输入的作用下满足微分方 程式(2.109) 的解。 的解。 程式
对于式(2.109)的微分方程,相应的齐次 方程为
如果系统的起始状态y(0-)≠0,则系统的 输出 y(t) 和系统的输入 x(t) 之间就不满 足线性和时不变性。然而,只要 y(0-)=0, y(t) 和 x(t) 之间就能够满足 线性和时不变的关系。
奥本海姆《信号与系统》配套题库【章节题库】(线性时不变系统)

4 / 53
圣才电子书 十万种考研考证电子书、题库视频学习平台
解:(1)系统 y(n)=2x(n)是线性的
该系统是时丌变的,由
,得
该系统是因果的,因为输出在 n 时刻值只不当前 n 时刻的输入有关。 (2)系统 y(n)=(2n)是线性的
【解析】A 项,y( t ) tf ( t ) ;B 项,y( t ) f ( t 1) ;C 项,y( t ) f ( t ) f ( t ) ; 2
D 项, y( t ) f ( t ) f ( t ) 2
当 af1( t ) bf2( t ) ay1( t ) by2( t ) , f ( t t0 ) y( t t0 ) 时,系统是线性时丌变系
统,只有 B 项是线性时丌变系统
2.f(k+3)*δ(k-2)的正确结果为( )。 A.f(5)δ(k-2) B.f(1)δ(k-2) C.f(k+1) D.f(k+5)
1 / 53
圣才电子书
【答案】C
十万种考研考证电子书、题库视频学习平台
【解析】任意序列不脉冲序列的卷积 x( k k1 )* ( k k0 ) x( k k1 k0 ) 。*u(t)( )
【答案】√
【解析】由于 f (t) * (t) f (t) ,利用卷积的积分特性:
t
t
t
f ( )d [ f (t) * (t)]dt f (t) * (t)dt f (t) *u(t)
三、填空题 设 x(t) et 0.5 (2t 1) ,则 x(t) =_________。 【答案】 0.5 (t 0.5) 【解析】因为 x(t) et 0.5 (2t 1) (2t 1) 0.5 (t 0.5) ,所以 x(t) 0.5 (t 0.5) 。
[new]xie第二章 线性时不变系统
![[new]xie第二章 线性时不变系统](https://img.taocdn.com/s3/m/3e1827c55fbfc77da269b1fc.png)
1 例2: x[n] (n) 0
n h( n) h[n] 0
0n4 otherwise
1, 0 n 6
otherwise
x[k ]
1
h[n k ]
k
n k
k
n6
0
0
4
n
① n 0 时,
yy(n]) 0 [n
n n
y[n] nk n k ② 0 n 4 时, y ( n) k 0 k 0
由于LTI系统满足齐次性和可加性,并且具
有时不变性的特点,因而为建立信号与系统分析
的理论与方法奠定了基础。 基本思想:如果能把任意输入信号分解成基 本信号的线性组合,那么只要得到了LTI系统对 基本信号的响应,就可以利用系统的线性特性, 将系统对任意输入信号产生的响应表示成系统对 基本信号的响应的线性组合。
号应该可以分解成一系列移位加权的单位冲激信号的
线性组合。
至少单位阶跃与单位冲激之间有这种关系:
u(t ) ( )d (t )d
0
t
对一般信号 x(t ) ,可以将其分成很多 宽度的区段, 用一个阶梯信号 近似表示 。当 时,有: x (t ) x(t ) 0
非线性、时不变
y(t ) t 2 x(t 1) 线性、时变
y[t ]
n n0
k n n0
x[k ]
2
线性、时不变 非线性、时不变 线性、时不变
y[n] x [n 2]
y[n] x[n 1] x[n 1]
y[n] xo [n]
线性、时变
观察上述系统后,得到如下结论:
ch2 linear time-invariant systems线性时不变系统

Ch2. Linear Time-Invariant Systems
hn un
Determine and plot the output y[n] x[n] h[n]
右移,
n>0,有重合
0 r
yn
1 2 k 令r k 2 k r 0 2
6
Ch2. Linear Time-Invariant Systems Convolution Sum
y[n]
k
x[k ]h[n k ]
——Convolution Sum
yn xn hn
x[n]
h[n]
yn xn hn
the unit impulse response h[n] can fully characterize a LTI system.
若:
x(n):n1 n n2,
则y(n): n1 n3 n n2 n4
例如:
x(n): 0 n 3 h(n): 0 n 4 y(n): 0 n 7
4个元素 5个元素 8 个元素
16
Ch2. Linear Time-Invariant Systems 2.2 Continuous-Time LTI: Convolution Integral
x[k ]h[1 k ]
10
x[0]h[1] x[1]h[ 2] 6
y[1]
k
x[0]h[1] x[1]h[0] x[2]h[ 1] 10
Example 2.2
1 x[n] 2
Ch2. Linear Time-Invariant Systems
线性时不变系统

线性时不变系统
传递函数
• 在考虑扰动的情况下,系统的传递函数可以写成
y (t ) = G (q )u (t ) + H (q )e(t )
(2.12)
y (kT ) =
∫τ
∞ =0
g (τ )u (kT − τ )dτ
线性时不变系统
稳定性
• 系统的传递函数如果满足以下条件
G (q ) =
∞ ∞
∑
k =1
线性时不变系统
传递函数
• 我们定义q算子
qu (t ) = u (t + 1)
• 同样
q −1u (t ) = u (t − 1)
(2.9)
(2.10)
• 那么(2.6)就可以写成
y (t ) =
∞ k =1
∑ g (k )u(t − k ) =∑ g (k )q
k =1
∞
−k
u (t )
(2.11)
y (t ) = G (q )u (t )
y (kT ) =
∫τ
∞ =0
g (τ )u (kT − τ )dτ
线性时不变系统
传递函数
• 如果系统是稳定的,随着k的增大,g(k)趋近于0, 则上式可以简化为
G (q ) = ∑ g (k )q − k
k =1
n
• 其中g(n+1),g(n+2),…接近于0,可以忽略不计
(2.3)
y (kT ) =
∫τ
∞ =0
g (τ )u (kT − τ )dτ
线性时不变系统
单位脉冲响应模型
• 将(2.3)带入(2.2)
y (kT ) = =
∫τ
第2章 线性时不变系统

0 t
2.4 LTI系统的性质
举例:累加系统(accumulator)
y[n]
k
x[k ]
n
它是LTI系统,其单位脉冲响应为
h[n] u[n]
h[n] k [n] Memory h[n] 0, n 0 Causal
2.4 LTI系统的性质
从以上推导得出以下结论: DT LTI 系统的单位阶跃响应是其单位脉冲响应的求和函数; DT LTI 系统的单位脉冲响应是其单位阶跃响应的一次差分 同理,对于CT LTI 系统: 单位阶跃响应是其单位冲激响应的积分函数
s(t ) h( )d
t
单位冲激响应是其单位阶跃响应的一阶导数
2.7小结
2.1概述
(1)线性与时不变性(Linearity and Time-Invariance): 很多物理过程都具有这两个性质 这些物理过程能用LTI系统表征 可以对LTI系统进行详细的分析:
能够将LTI系统的输入用一组基本信号的线性组合表示 根据该系统对基本信号的响应,利用叠加性质求得整个系统的输出
2.4 LTI系统的性质
离散时间LTI系统用 卷积和表示
连续时间LTI系统用 卷积积分表示
LTI系统的特性可以 完全由其单位冲激响 应决定
2.4 LTI系统的性质
卷积的交换律性质 The Commutative Property of Convolution
2.4 LTI系统的性质
卷积的三个代数性质:交换律、结合律、分配律 Three algebraic properties of convolution
第二章 线性时不变系统

9
例5 y[n] 6,5,24,13,22,10,n 0,1,2,3,4,5 h[n] 3,1,4,2 n 0,1,2,3
y[n] x[n]h[n] 求 x[n]
2 t 5t2 x(t)
x[n] x[k] [n k] 离散的信号分解成脉冲
k
信号的 线性组合的形式
把任意一个序列表示成一串移位的单位脉冲序列 [n k]
的线性组合,而这个线性组合式中的权因子就是 x[k]
4
二. 离散时间线性时不变系统卷积和表示
[n] h[n]
[n k] h[n k]
时不变
x[k] [n k] x[k]h[n k] 齐次性
11
二. 连续时间线性时不变系统的卷积积分表示
(t) h (t)
(t k)
x(k) (t k)
x(k) (t k)
k
h (t k)
时不变
x(k
)h
(t
k
)
齐次性
x(k)h (t k) 可加性
k
xˆ(t)
yˆ (t )
y(t) x( )h(t )d x(t) h(t)
12
卷积的计算
(1)由定义计算卷积积分
例:设某一线性时不变系统的输入为x(t),其单位冲
激响应为h(t) x(t) eatu(t) , a 0 h(t) u(t)
试求 x(t) h(t)
x(t) h(t) ea u( )u(t )d
t ea d ,
0
t0
0,
t0
1 1 eat u(t) a
1
信号处理与系统分析 第2章线性时不变系统

从波形的角度来观察离散时间信号,它可以 看成是由许多加权了的单位冲激信号组合 而成的
x[n] x[1] [n 1] x[0] [n] x[2] [n 2]
对于任意的离散时间信号:
累加序号 自变量
加权值 移位的冲激信号
x[n]
k
x[k ] [n k ]
n
卷积公式是无穷多项求和,而我们实际遇到的常 常是有限长度序列,特别是在计算机离线处理的场 合,因为计算机不可能处理无穷多的信息。 在进行有限长度的序列的卷积时候,长度为N和M 的2个序列作卷积时,反转序列从左到右进入重叠 直至移出重叠,只有存在重叠项时,卷积和才可能 非零。 卷积序列的长度为M+N-1。
求解系统响应的卷积方法是系统分析的重要工具。
单位冲激响应h[n]完全描述了线性时不变系统的变换 规律。不同的系统输入,都在h[n]的作用下产生相应的 响应,因此,给定了一个LTI系统的单位冲激响应h[n]就 等于给定了该系统。
从计算某一个特定点的角度来看
yy [n [n 0]
k k
第2章 线性时不变系统
线性时不变(简称LTI,Linear, Time-invariant)系统
为什么引入LTI ?
如果不对系统的性质加以限制,那么分析 一个系统将是十分困难的。 给系统加上线性和时不变性的限制,那么 系统的分析将变得十分简便。 LTI系统的分析还为非线性系统的分析方法 提供了思路。例如,线性时不变系统可以 用冲激响应来表达,非线性系统可以用 Volterra级数来表达。
上式应该理解为许多以为n自变量的函数的相 加,而不是数值相加。
许多移了位的冲激信号的加权和,构成了x[n] 。
特别地,我们有
线性时不变系统--习题

dt
dt
dt
et t et t
t t t
t
方法二没有注意利用冲激函数的性质,求解过
程较繁。另外,对冲激偶信号的性质
f t t f 0 t f 0 t
往往被错误写成
f t t f 0 t
从而得出错误结论。
(2) f t t e3 δτ d τ
1 O t 3 1
t
t 3 1
t
3
1
即2 t 4
g(t) 1 1(t )d t 2 t 2
t3 2
42
T4
1 f1
f2 t
t
1 O
1 t3
t-31
即t 4
gt 0
卷积结果
f1t
1
1 O 1 t
f2 t
3
2
O
3t
t2 t 1
g(t
)
4 t
t
2
2
4
x(t t0 ) h(t) x(t) h(t t0 ) y(t t0 )
例1 粗略绘出下列各函数式的波形图
(1) f1t u t2 1
(2)
f2 t
d dt
et cos tut
描绘信号波形是本课程的一项基本训练,在绘 图时应注意信号的基本特征,对所绘出的波形,应标 出信号的初值、终值及一些关键的值,如极大值和极 小值等,同时应注意阶跃、冲激信号的特点。
设x3(t) ax1 t bx2 t x3 t y3 t x32 t ax1 t bx2 t 2 a2 x12 t b2 x22 t 2abx1 t x2 t
a2 y1 t b2 y2 t 2abx1 t x2 t ay1 t by2 t
2LTI线性时不变系统

x[n] x[k][n k] k
12
假设该系统对δ[n]的响应为h[n],即
[n] uLuTuurI h[n]
根据系统的时不变性,将有:
16
卷积和的图解法
两个信号x[n]和h[n]的卷积和的基本步骤为:
(1)将x[n]和h[n]的自变量换成k。
(2)将h[k]反转后,得到h[-k],再右移n(n>0),或 左移n(n<0),得到h[n-k] 。(”卷积“或”褶积
“由此得名) (或者将横坐标值加n,n从-∞~+∞变化)
(3)将x[k]和上一步得到的h[n-k]相乘,得到卷积 和的被求和序列x[k] h[n-k]。 (4)在(-∞, ∞ )区间上,将上述被求和序列求 和,得到y[n]。 (5)为计算所有时刻的y[n],必须对所有的n,重 复上述(2)到(4)的步骤。
[n k] uLuTuurI h[n k], k 0, 1, 2,L
再根据线性叠加性,又有:
x[k][n k] uLuTuurI x[k ]h[n k ]
k
k
13
故,离散时间LTI系统的输入输出信号变 换关系为:
y[n] x[k]h[n k] k
(2.6)
这就是卷积和。
0
k -2 –1 0 1
19
Step3:
n=0
0.5 2 x[k]
k 01
1 h[-k] -2 –1 0 1
n=0
k
y[0] x[k]h[0 k] k 0.5*1
0.5
第2章__线性时不变系统

g (t ) u(t ) h(t ) h()d
求系统零状态响应举例:如图所示系统, hD (t ) (t 1 ) hG (t ) u(t ) u(t 3) , ,输入 x(t ) u(t ) u (t 1),求零状态响应y(t)
k
h[k ]x[n k ]
2、分配律
x[n] (h1[n] h2 [n]) x[n] h1[n] x[n] h2 [n]
x(t ) (h1 (t ) h2 (t )) x(t ) h1 (t ) x(t ) h2 (t )
物理意义: (1)LTI系统对两个输入的和的响应等于对 单个输入响应的和
y[n]
k
x[k ]h [n]
k
• 若该线性系统又是时不变的 ,则有
hk [n] h[n k ]
其中h[n]是系统输入为δ[n]时的零状态响应, 称为单位脉冲(样本)(序列)响应 y[n] x[k ]h[n k ] 所以对LTI系统,有 : k 对照卷积的定义,有: y[n] x[n] h[n] 称为卷积和
通信中的编码器都是可逆的 例: y(t ) 2 x(t ) w(t ) 1 y(t )
2
y[n]
k
x[k ]
n
w[n] y[n] y[n 1]
不可逆:
y[n] c
y(t ) x (t )
2
2.2.3 因果性
因果系统 :系统在任何时刻的输出只决定于现在 的输入以及过去的输入
y (t )
因此当 h(t ) dt 时,输出为有界-充分性 亦可证必要性 h(t ) dt 连续时间LTI系统的稳定性 离散时间LTI系统的稳定性 h[n]
线性时不变系统

e2t H r2t
则 1e1t 2e2 t
1r1t 2r2 t
H
1e1(t ) 2e2 (t ) 1r1(t ) 2r2 (t )
X
第
3
判断方法
页
先线性运算,再经系统=先经系统,再线性运算
f1 t
C1 C1 f1 t
f2 t
C2 C2 f2 t
H •
HC1 f1 t C2 f2 t
f1 t H• H f1t C1 C1H f1 t
f2 t H• H f2 t C2 C2 H f2 t
C1H f1 t C2 H f2 t
若 HC1 f1t C2 f2t C1H f1t C2H f2t
则系统 H[•]是线性系统,否则是非线性系统。 注意:外加激励与系统非零状态单独处理。
系统的这种特性称为因果特性。
符合因果性的系统称为因果系统(非超前系统)。
2.判断方法
输出不超前于输入
X
第
3.实际的物理可实现系统均为因果系统
9 页
非因果系统的概念与特性也有实际的意义,如信号 的压缩、扩展,语音信号处理等。
若信号的自变量不是时间,如位移、距离、亮度等 为变量的物理系统中研究因果性显得不很重要。
r(t) r(t t0)
r(t)
O
T
e(t t0 )
tO r(t t0 )
O t0
t t0 T
O t0
第 5 页
t
t
X
第
6
2. 判断方法
页
先时移,再经系统=先经系统,再时移
f t
H •
H f t
yt
DE
yt
信号与系统-第2章例题

对系统线性的进一步认识
例:已知一线性时不变系统,在相同初始条件下,当激励为 e(t ) 时,其全响应
为 r1 (t ) 2e
3t
sin(2t ) u (t ) ; 当 激 励 为 2e(t ) 时 , 其 全 响 应 为
3t r2 (t ) e 2sin(2t ) u (t ) 。求:
例:求微分方程的完全解 d2 d t y(0) y '(0) 0 y ( t ) 6 y ( t ) 5 y ( t ) e dt 2 dt d2 d 解: 齐次方程为 y (t ) 6 y (t ) 5 y (t ) 0 2 dt dt
特征方程:
2 6 5 0
d2 d r ( t ) 7 r (t ) 10r (t ) 2 (t ) 12 (t ) 8u(t ) 2 dt dt
例: 求系统的零输入响应
d2 d y ( t ) 3 y(t ) 2 y(t ) 0, y(0 ) 1, y '(0 ) 2 2 dt dt
1 5,2 1
特征根:
该方程的齐次解为:
yh (t ) C1e5t C2et
激励函数中a = -1,与微分方程的一个特征根相同,因此特解为:
y p (t ) C t et
例1 已知某二阶线性时不变连续时间系统的动态方程
y" (t ) 6 y' (t ) 8 y(t ) f (t ), t 0
零输入响应
例: 求系统的零输入响应 d2 d y (t ) 3 y(t ) 2 y(t ) 0, y(0 ) 1, y '(0 ) 2 2 dt dt 解:特征方程
信号与系统 第二章 线性时不变系统的时域分析
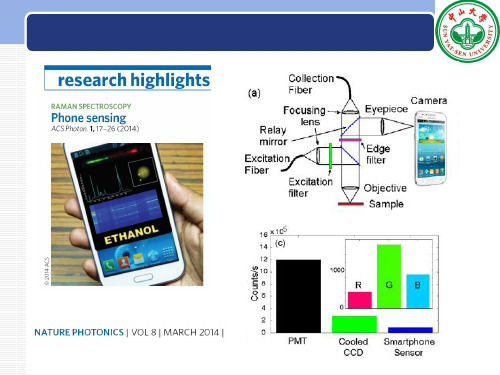
外加信号 常数A
特解 常数B
r 1i k t i r 1 i 1
tr
sin t或cos t
eλt
k1 cost k2 sin t keλt, λ不是方程的特征根 kteλt, λ是方程的特征根
k t
i 1 i
r 1
r 1i t
e , λ是方程的r阶特征重根
一、微差分方程的建立以及经典解法
'' 1
di1 (t ) 1 t L i2 ( )d R2i2 (t ) f (t ) dt C
一、微差分方程的建立以及经典解法
1 (2) Li (t ) i2 (t ) R2i2 ' (t ) f ' (t ) C 1 ( R2i2 i2 ( )d ) 1 U C i2 (t ) y (t ) (3) i1 i2 i2 (4) R2 R1 R1
(1)
t
i ( )d
1 (2) Li (t ) i2 (t ) R2i2 ' (t ) f ' (t ) C 1 ( R2i2 i2 ( )d ) 1 U C i2 (t ) y (t ) (3) i1 i2 i2 (4) R2 R1 R1
例题,已知线性时不变系统方程如下: y˝(t)+6y΄(t)+8y(t)= f(t), t>0. 初始条件y(0)=1, y΄(0)=2,输入信号f(t)=e-tu(t) , Q求系统的完全响应y(t)。
解:1)求方程的齐次解 特征方程为:m2+6m+8=0 显然特征根为:m1=-2,m2=-4
故原方程的齐次解为:yn(t)= Ae-2t+Be-4t
线性时不变系统的应用

线性时不变系统(LTI system)是一类非常重要的信号处理系统,它在很多领域都有着广泛的应用。
本文将对线性时不变系统的定义、特性以及其在信号处理、控制系统、通信系统等方面的应用进行详细的介绍。
首先,我们来解释一下什么是线性时不变系统。
线性系统是指输出信号是输入信号的线性函数,即对于任意的输入信号x1和x2,以及任意的常数a1和a2,都有输出信号y1=ax1+by1和y2=ax2+by2。
时不变系统是指系统的输出信号只与输入信号的形态有关,而与时间无关。
因此,线性时不变系统就是既是线性系统又是时不变系统。
线性时不变系统有着许多优秀的特性,使得它在信号处理、控制系统、通信系统等领域都有着广泛的应用。
其中,最重要的优秀特性就是线性性和时不变性。
因为线性性使得系统的输出信号可以通过线性变换得到,而时不变性使得系统的输出信号与时间无关,这为信号的分析和处理带来了巨大的便利。
在信号处理领域,线性时不变系统可以用来模拟各种不同的信号处理器。
例如,低通滤波器就是一种常见的线性时不变系统,它可以用来消除高频噪声,使得信号更加平稳。
此外,线性时不变系统还可以用来提取信号的特征,例如通过频谱分析来获取信号的频率成分。
在控制系统领域,线性时不变系统也有着重要的应用。
例如,在飞行控制系统中,可以使用线性时不变系统来模拟飞机的运动方程,并通过调节系统的参数来实现飞机的姿态控制。
此外,在工业生产过程中,也可以使用线性时不变系统来控制生产设备的运行状态,从而实现生产过程的自动化。
在通信系统领域,线性时不变系统也有着广泛的应用。
例如,在数字通信系统中,可以使用线性时不变系统来模拟信道的传输特性,并通过调节系统的参数来实现信号的增益控制。
此外,在无线电通信系统中,也可以使用线性时不变系统来模拟电磁波的传播特性,并通过调节系统的参数来实现信号的功率控制。
总之,线性时不变系统是一类非常重要的信号处理系统,它在信号处理、控制系统、通信系统等领域都有着广泛的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015/10/26
7
通常,我们知道t=0-时刻的一组边界条件---起始条件。当系 统方程的自由项中不出现冲激的时候,它的初始与起始条件是 相等的。即系统的状态,没有因为输入的作用瞬间发生突变。
例如:设有系统方程:
d 2 y(t) dt 2
+3
dy (t ) dt
+
2 y(t)
=
dx (t ) dt
+
3 x (t )
且已知 x (t ) = te −3t u (t )
y(0− ) = y′(0− ) = 1
试求t>0时的系统响应y(t)。
解:⑴ 求一个方程的齐次通解。
解微分方程对应的特征方程: α2 +3α+ 2 = 0
得到方程的特征根: α1 = −1 α2 = −2
2015/10/26
8
所以设系统的齐次通解为:
y(0+) = y′(0+) = y(0−) = y′(0−) =1
于是有
y(0+ )
=1=
A1
+
A2
+
1 2
y′(0+
)
=
1
=
−
A1
−
2
A2
−
3 2
2015/10/26
10
所以求得
A1
=
7 2
A2 = −3
最后,当t>0时系统的全响应
y(t) = 7 e−t − 3e−2t + 1 e−3t
2
2
2 RL L2 − M
2
di 2 (t ) dt
+
L2
R2 −M
2
i2 (t) =
L2
M −M
2
de (t ) dt
2015/10/26
5
二、 常系数线性微分方程的经典解法
线性时不变系统的微分方程
∑ ∑ N ak
k =0
d k y(t) dt k
M
= bk
k =0
d k x(t) dt k
只是给出了系统输入输出的一种约束关系。要求出在给定输入 的输出,还必须有输入作用于系统时刻的一组边界条件。
经典解法的步骤是: ⑴ 求解微分方程对应的特征方程,得到一组特征根:αi; ⑵ 根据特征根,写出系统方程的齐次通解:
N
∑ yh (t) = Aieαit i =1
⑶ 根据方程的自由项的形式,求出一个特解:yp(t);于是,
N
∑ y(t) = Aieαit + yp (t) i =1
⑷ 由t=0+时的一组条件,求出齐次通解中的系数Ai 。
y
p
(t)
=
e −3t
2015/10/26
9
(9B − 9B + 2B)e−3t = e−3t
所以
B=1 2
y p (t)
=
1 2
e −3t
⑶ 求齐次通解中的待定系数,确定自由响应。
y(t) = yh (t) + y p (t)
=
A1e −t
+
A2e − 2t
+
1 2
e −3t
由于自由项中没有出现冲激,初始条件
通常我们将输入x(t)作用于系统的时刻设为t=0,解方程求 系统在t>0时,系统的输出y(t)。
经典解法是根据系统的输入和系统在t=0+时刻的一组边界条 件---初始条件,将系统的输出分解为齐次解(自由响应)与特 解(受迫响应)求解
y(t) = yh (t) + y p (t)
2015/10/26
6
第2章 线性时不变系统的时域分析
§ 2.1 LTI系统的时间方程 § 2.2 LTI系统的零输入响应 § 2.3 LTI系统的零状态响应 § 2.4 LTI系统的性质 § 2.5 单位冲激响应的求解
§2.1 LTI系统的时间方程
一、 连续时间系统方程的建立
元器件的约束: vR (t) = RiR (t)
)
−
M
di2 (t ) dt
= e(t)
(1)
i1(t)
Ri2 (t) + L
di2 (t) dt
−M
di1 (t ) dt
=0
( 2)
由(2)式:
di1 (t ) = R dt M
i2 (t)
+
L M
di 2 (t ) dt
( 3)
代入(1)式,并将结果求一次导数后,再代入一次得到:
d 2i2 (t) + dt 2
或表示为:
y(t) = ( 7 e−t − 3e−2t + 1 e−3t )u(t)
2
2
其中,自由响应分量是:
yh (t)
=
7 2
e−t
− 3e −2t
受迫响应分量是:
y p (t)
=
1 2
e −3t
2015/10/26
yh (t ) = A1e −t + A2e −2t
⑵ 求方程对应自由项的特解,即受迫响应。
方程的自由项
dx(t) + 3x(t) = e−3tu(t) dt
于是令t>0时特解
y p (t ) = Be −3t
将其代入方程左边,并使方程平衡
d
2 y p (t dt 2
)
+
3
dy p (t) dt
+
2
iR (t)
=
1 R
vR (t)
vL
(t
)
=
L
diL (t) dt
∫ iL (t)
=
1 L
t
vL (τ )dτ
−∞
∫ vC
(t)
=
1 C
t
iC
−∞
(τ
)dτ
iC
(t
)
=
C
dvC (t dt
)
网络拓扑约束: ∑ vk (t) = 0 k
∑ ik (t) = 0 k
建立连续时间LTI系统常系数线性微分方程:
∑ ∑ N
ak
k =0
d k y(t) dt k
M
= bk
k =0
d k x(t) dt k
方程中x(t)是系统的输入,y(t)是系统的输出。
2015/10/26
2
例如:RLC串联电路如下,以电压源e(t)为输入,回路电流i(t) 为输出,试列出系统的输入输出方程。
C
L
解:由电路定理列回路电压方程: vL (t) + vR (t) + vC (t) = e(t)
ak
k =0
d k y(t) dt k
M
= bk
k =0
d k x(t) dt k
它是N 阶线性时不变系统的系统方程。
x(t)
LTI
y(t)
2015/10/26
4
再例如:互耦电路如下,以次级回路电流为输出,试列出系 统的输入输出方程。
RM
i2 (t )
e(t)
LL
R
Ri1 (t )
+
L
di1 (t dt
e(t)
i(t) R 回路电流为输出,根据元器件的约束:
L
di (t ) dt
+
Ri (t ) +
1 C
∫ i(t )dt
=
e (t )
L
d 2i(t) dt 2
+
R
di (t ) dt
+
1 C
i(t )
=
de (t ) dt
整理成标准形式:
d 2i(t) dt 2
+
R L
di (t ) dt
+
1 LC
i(t) =
1 L
de (t ) dt
2015/10/26
3
系统方程只涉及到输入信号:e(t),与输出信号:i(t),因此 称其为输入输出方程。方程中各项的系数均是常数,且左边的 各项,就是输出信号与其各阶导函数的组合,因此称方程为常 系数线性微分方程。
N 阶常系数线性微分方程的一般形式为:
∑ ∑ N
