2012高教社杯全国大学生数学建模竞赛b题
全国大学生数学建模竞赛题目B题

B题公交车调度
公共交通是城市交通的重要组成部分,作好公交车的调度对于完善城市交通环境、改进市民出行状况、提高公交公司的经济和社会效益,都具有重要意义。
下面考虑一条公交线路上公交车的调度问题,其数据来自我国一座特大城市某条公交线路的客流调查和运营资料。
该条公交线路上行方向共14站,下行方向共13站,第3-4页给出的是典型的一个工作日两个运行方向各站上下车的乘客数量统计。
公交公司配给该线路同一型号的大客车,每辆标准载客100 人,据统计客车在该线路上运行的平均速度为20公里/小时。
运营调度要求,乘客候车时间一般不要超过10分钟,早高峰时一般不要超过5分钟,车辆满载率不应超过120%,一般也不要低于50%。
试根据这些资料和要求,为该线路设计一个便于操作的全天(工作日)的公交车调度方案,包括两个起点站的发车时刻表;一共需要多少辆车;这个方案以怎样的程度照顾到了乘客和公交公司双方的利益;等等。
如何将这个调度问题抽象成一个明确、完整的数学模型,指出求解模型的方法;根据实际问题的要求,如果要设计更好的调度方案,应如何采集运营数据。
高教社杯全国大学生数学建模竞赛B题论文

碎纸片的拼接复原摘要本文利用Manhattan距离,聚类分析,图像处理等方法解决了碎纸片的拼接复原问题。
由于碎纸机产生的碎纸片是边缘规则且等大的矩形,此时碎纸片拼接方法就不能利用碎片边缘的尖角特征等基于边界几何特征的拼接方法,而要利用碎片内的字迹断线或碎片内的文字位置搜索与之匹配的相邻碎纸片。
拼接碎片前利用数学软件MATLAB软件对碎片图像进行数据化处理,得到对应的像素矩阵,后设置阈值对像素矩阵进行二值化处理,得到相应的0-1矩阵。
下面分别对三个问题的解决方法和算法实现做简单的阐述:问题一,分别对附件1和附件2的碎片数据进行处理得到相应的0-1矩阵,依次计算某个0-1矩阵最右边一列组成向量与其他所有0-1矩阵的最左边向量的Manhattan距离,可以得到某个最小距离值、说明最小距离值对应的碎片是可与基准碎片拼接的,最终得到碎片拼接完整的图像。
问题二,同样对于附件3和附件4中的碎片数据进行处理得到相应的数值矩阵,并计算得到每个碎片顶部空白高度和文字高度,即指每行像素点都为255的行数、一行中存在像素点为非255的行数,根据空白高度和文字高度对碎片进行聚类分类,聚类阀值取3像素,得到11组像素矩阵,进而得到11类可能在同一行的碎片类。
其中对附件4中的英文的处理中,我们还采用水平像素投影累积的方法,进一步分类出可能在同一行的碎片类。
用问题一的方法,计算Manhattan 距离可以对每一类碎片按次序排列好,得到11行已经排列好的碎片,再应用曼哈顿距离在竖直方向上进行聚合得到完整的图像。
问题三,首先,对于附件5中的碎片数据我们采用正反相接,本文将b面最左边的一列像素拼接到a面最右边的一列像素的下面,构成360×1的向量,再把其他的碎片采用相同的办法得到360×1的向量,再用问题一的方法,计算出各碎片之间的Manhattan距离。
其次,根据每个碎片顶部的空白高度或者文字高度对碎片进行区间分类,得到22组矩阵,然后应用曼哈顿距离将得到的22组矩阵聚成两类,每类各包含两面的11组矩阵,最后利用Manhattan距离在竖直方向上进行聚合得到完整的图像。
2012国赛B题

2012高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)B题太阳能小屋的设计在设计太阳能小屋时,需在建筑物外表面(屋顶及外墙)铺设光伏电池,光伏电池组件所产生的直流电需要经过逆变器转换成220V交流电才能供家庭使用,并将剩余电量输入电网。
不同种类的光伏电池每峰瓦的价格差别很大,且每峰瓦的实际发电效率或发电量还受诸多因素的影响,如太阳辐射强度、光线入射角、环境、建筑物所处的地理纬度、地区的气候与气象条件、安装部位及方式(贴附或架空)等。
因此,在太阳能小屋的设计中,研究光伏电池在小屋外表面的优化铺设是很重要的问题。
附件1-7提供了相关信息。
请参考附件提供的数据,对下列三个问题,分别给出小屋外表面光伏电池的铺设方案,使小屋的全年太阳能光伏发电总量尽可能大,而单位发电量的费用尽可能小,并计算出小屋光伏电池35年寿命期内的发电总量、经济效益(当前民用电价按0.5元/kWh计算)及投资的回收年限。
在求解每个问题时,都要求配有图示,给出小屋各外表面电池组件铺设分组阵列图形及组件连接方式(串、并联)示意图,也要给出电池组件分组阵列容量及选配逆变器规格列表。
在同一表面采用两种或两种以上类型的光伏电池组件时,同一型号的电池板可串联,而不同型号的电池板不可串联。
在不同表面上,即使是相同型号的电池也不能进行串、并联连接。
应注意分组连接方式及逆变器的选配。
问题1:请根据山西省大同市的气象数据,仅考虑贴附安装方式,选定光伏电池组件,对小屋(见附件2)的部分外表面进行铺设,并根据电池组件分组数量和容量,选配相应的逆变器的容量和数量。
问题2:电池板的朝向与倾角均会影响到光伏电池的工作效率,请选择架空方式安装光伏电池,重新考虑问题1。
问题3:根据附件7给出的小屋建筑要求,请为大同市重新设计一个小屋,要求画出小屋的外形图,并对所设计小屋的外表面优化铺设光伏电池,给出铺设及分组连接方式,选配逆变器,计算相应结果。
2012数学建模竞赛B优秀论文4

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): B我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):XXXX参赛队员(打印并签名) :1. XXX2. (隐去论文作者相关信息等)3. XXX指导教师或指导教师组负责人(打印并签名):XXXX日期: 2012 年 9 月 10 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):评阅人评分备注全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):太阳能小屋的设计摘要本文在太阳能应用与太阳能小屋设计的实际背景下,对逆变器与光伏电池的选择、配对,光伏电池的铺设以及房屋的设计建立了相关模型进行研究。
为了简化问题,首先我们定义了收益这一指标,并在每一问中都根据收益来剔除出不满足要求的光伏电池或组。
针对问题一,在仅考虑贴附安装方式情况下,对小屋部分表面铺设光伏电池,并选配相应逆变器要使得年发电量尽可能大,单位发电费用尽量低。
为此,本文建立了多目标规划模型,考虑到模型求解的复杂性,本文设计了一个启发式算法,利用Matlab软件构造0-1矩阵来模拟实际铺设,得到了一个优化的铺设方式,结果为:开头全年发电量为1580735kw·h,年发电量为497942kw·h,纯收入为73195元,投资的回报年限为23.7年,单位发电成本为0.353元。
浙江省2012年数学建模竞赛(B题)评审结果

雷春霞 徐晓乐 黄耀杰 苏爽爽 张梦夕 刘宏伟 周家程 杨裕文 秦芹 洪斌 程碧冠 魏旭 包天浩 何伟凡 娄屹川 周甲武 洪安 戚天兰 金梓 余濛濛 董炜 阚雅婷 蒋贤林 董镭刚 方ቤተ መጻሕፍቲ ባይዱ浩 陈咏志 沈丽琴 刘博文 朱晓青 王丽莉 李超 李梦 王鸿来 张佳梅 沈莉莉 林江峰 王林苗 陈茹萍 陈群云 石佳 雷晶 顾雯静 邱佳辉 虞上崇 王黎航 郑秀玲 王雪 王琳娜 吴欣怡 金勇胜 肖劲东 叶松 龚松挺
2012全国大学生数学建模竞赛浙江赛区评审结果(B题)
序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 队员1 刘栋 季康康 胡江泽 彭涛 俞少佳 高华岳 刘冬煜 余娜双 强芳芳 石珍妮 洪小茹 方舒梦 杨洁 李畅达 宫昊 金如梦 李向杰 汪文广 陈凯慧 黄晓春 王杰 常若菲 朱莎帅 吴铭 吴晓凤 徐涛 陈喻 朱芳丽 刘洋 金诚 李鹏飞 范登栋 郭伟君 厉洁 席晓丹 余佳益 侯良哨 徐申达 彭伟桃 胡秀文 莫凡琴 高勇 白植隆 葛人楷 蔡跃 罗旻 刘怡琳 伊燕瑛 陈盼庆 刘增明 谈凌浩 队员2 盛仲奎 朱月明 彭安妮 刘鹏 李瑞环 胡露 郑起 徐巧 陈修靖 张克林 王枫 汪凌珂 张巧 侯松岩 毛可安 刘喜勤 黄丽霞 孟祥飞 陈未 王力 金雯雯 王宁波 许丹桂 祝晓兰 朱胜 黄黎颖 华立锋 尤玮玮 陈祖现 倪紫京 徐一鸣 李丹 金秋琼 刘琦 赵润东 楼煜峰 陈建海 金俊树 章浩燕 孙小伦 郭红红 杨丙良 池海啸 邵祎雯 程菲菲 赵燕波 王振取 李可嘉 钟逸卓 李雨希 干梦迪 队员3 李欣格 严国丽 朱海鹏 盛若璇 卢维维 冯姗姗 谢宇 汪寒成 陈鹏 潘承丰 丁少婷 卓婧婧 周孝芳 周耀明 葛超俊 许晓燕 俞建军 汪嘉恒 姚琦峰 周嘉楠 杨旭光 任盘龙 姜程航 张翔翔 周世斌 方云哲 袁敏 栗志华 汪娜 郑涛 王伟 卢玉立 韩雄帅 叶建斌 傅嘉祎 陈厘蒙 龚德伟 孙佳丽 董少奇 冯任峰 徐统 杨丽娜 胡灵萍 潘阳阳 林剑 单丹婷 朱治亮 端木庆龙 颜刚 章坤 吴杰 指导教师 数模组 胡金杰 数模组 数模组 数模组 何颖俞 数模组 罗文昌 数模组 连新泽 数模组 数模组 数模组 数模组 李启会 吴宗大 数模组 数模组 数模组 胡金杰 数模组 数模组 数模组 胡金杰 数模组 数模组 罗文昌 杨宇博 数模组 数模组 数模组 王立洪 数模组 盛宝怀 数模组 祝汉灿 数模组 数模组 马飞遥 数模组 孙天川 数模组 姚燕云 数模组 鲁胜强 数模组 数模组 数模组 数模组 数模组 数模组 所属学校 中国计量学院 绍兴文理学院 浙江师范大学 中国计量学院 浙江工业大学 杭州师范大学 浙江大学 宁波大学 杭州电子科技大学 温州大学 中国计量学院 浙江师范大学 浙江工业大学 浙江大学 嘉兴学院 温州大学瓯江学院 浙江理工大学 浙江大学 杭州电子科技大学 绍兴文理学院 杭州电子科技大学 中国计量学院 浙江工业大学之江学院 绍兴文理学院 杭州电子科技大学信息工程学院 中国计量学院 宁波大学 嘉兴学院 中国计量学院 浙江理工大学 杭州电子科技大学 宁波大学 浙江外国语学院 绍兴文理学院 浙江大学 绍兴文理学院 浙江工业大学 宁波工程学院 宁波大学 浙江农林大学 湖州师范学院 杭州电子科技大学 绍兴文理学院 浙江工业大学 温州医学院 浙江师范大学 浙江工业大学 中国计量学院 浙江理工大学 中国计量学院 浙江工商大学 奖项 推荐全国一等 推荐全国一等 推荐全国一等 推荐全国一等 推荐全国一等 推荐全国一等 推荐全国一等 推荐全国一等 推荐全国一等 推荐全国一等 推荐全国一等 推荐全国一等 推荐全国一等 推荐全国一等 推荐全国二等 推荐全国二等 推荐全国二等 推荐全国二等 推荐全国二等 推荐全国二等 推荐全国二等 推荐全国二等 推荐全国二等 推荐全国二等 推荐全国二等 推荐全国二等 省一等 省一等 省一等 省一等 省一等 省一等 省一等 省一等 省一等 省一等 省一等 省一等 省二等 省二等 省二等 省二等 省二等 省二等 省二等 省二等 省二等 省二等 省二等 省二等 省二等
2012高教社杯全国大学生数学建模竞赛题目

2012高教社杯全国大学生数学建模竞赛题目
佚名
【期刊名称】《数学建模及其应用》
【年(卷),期】2012(001)004
【摘要】A题:葡萄酒的评价确定葡萄酒质量时一般是通过聘请一批有资质的评酒员进行品评。
每个评酒员在对葡萄酒进行品尝后对其分类指标打分,然后求和得到其总分,从而确定葡萄酒的质量。
酿酒葡萄的好坏与所酿葡萄酒的质量有直接的关系,葡萄酒和酿酒葡萄检测的理化指标会在一定程度上反映葡萄酒和葡萄的质量。
附件1给出了某一年份一些葡萄酒的评价结果,附件2和附件3分别给出了该年份这些葡萄酒的和酿酒葡萄的成分数据。
请尝试建立数学模型讨论下列问题:
【总页数】2页(P55-56)
【正文语种】中文
【相关文献】
1.雨量预报方法的模糊评价模型--2005高教社杯全国大学生数学建模竞赛题目之
一 [J], 杨金山;耿玉菊;马小女
2.2016年“高教社杯”全国大学生数学建模竞赛题目 [J],
3.NBA赛程的分析和评价——2008高教社杯全国大学生数学建模竞赛题目 [J], 马明远
4.2012高教社杯全国大学生数学建模竞赛题目 [J], ;
5.2016年“高教社杯”全国大学生数学建模竞赛题目 [J],
因版权原因,仅展示原文概要,查看原文内容请购买。
2012全国数学建模b题参考答案

太阳能设计的小屋方案摘要太阳能电池板方阵安装角度怎样计算由于太阳能发电系统的成本还是较高的,从我国现阶段的太阳能发电成本来看,其花费在太阳电池组件的费用大约为60~70%,因此,为了更加充分有效地利用太阳能,如何选取太阳电池方阵的方位角与倾斜角是一个十分重要的问题。
1.方位角太阳电池方阵的方位角是方阵的垂直面与正南方向的夹角(向东偏设定为负角度,向西偏设定为正角度)。
一般情况下,方阵朝向正南(即方阵垂直面与正南的夹角为0°)时,太阳电池在设计太阳能小屋时,需在建筑物外表面(屋顶及外墙)铺设光伏电池,光伏电池组件所产生的直流电需要经过逆变器转换成220V交流电才能供家庭使用,并将剩余电量输入电网。
不同种类的光伏电池每峰瓦的价格差别很大,且每峰瓦的实际发电效率或发电量还受诸多因素的影响,如太阳辐射强度、光线入射角、环境、建筑物所处的地理纬度、地区的气候与气象条件、安装部位及方式(贴附或架空)等。
因此,在太阳能小屋的设计中,研究光伏电池在小屋外表面的优化铺设是很重要的问题。
为了躲避太阳阴影时的方位角,以及布置规划、发电效率、设计规划、建设目的等许多因素都有关系。
如果要将方位角调整到在一天中负荷的峰值时刻与发电峰值时刻一致时,请参考下述的公式。
至于并网发电的场合,希望综合考虑以上各方面的情况来选定方位角。
方位角=(一天中负荷的峰值时刻(24小时制)-12)×15+(经度-116) 10月9日北京的太阳电池方阵处于不同方位角时,日射量与时间推移的关系曲线。
在不同的季节,各个方位的日射量峰值产生时刻是不一样的。
2.倾斜角倾斜角是太阳电池方阵平面与水平地面的夹角,并希望此夹角是方阵一年中发电量为最大时的最佳倾斜角度。
一年中的最佳倾斜角与当地的地理纬度有关,当纬度较高时,相应的倾斜角也大。
但是,和方位角一样,在设计中也要考虑到屋顶的倾斜角及积雪滑落的倾斜角(斜率大于50%-60%)等方面的限制条件。
【2012高教社杯全国大学生数学建模竞赛赛题B】cumcm2012B附件7_小屋的建筑要求

全国大学生数学建模竞赛真题试卷复习材料附件7:小屋的建筑要求
限定小屋使用空间高度为:建筑屋顶最高点距地面高度≤5.4m, 室内使用空间最低净空高度距地面高度为≥2.8m;建筑总投影面积(包括挑檐、挑雨棚的投影面积)为≤74m2;建筑平面体型长边应≤15m,最短边应≥3m;建筑采光要求至少应满足窗地比(开窗面积与房间地板面积的比值,可不分朝向)≥0.2的要求;建筑节能要求应满足窗墙比(开窗面积与所在朝向墙面积的比值)南墙≤0.50、东西墙≤0.35、北墙≤0.30。
建筑设计朝向可以根据需要设计,允许偏离正南朝向。
2012数学建模国赛评卷要点B题

2012数学建模国赛评卷要点B题
2012高教社杯全国大学生数学建模竞赛B题评阅要点[说明]本要点仅供参考,各赛区评阅组应根据对题目的理解及学生的解答,自主地进行评阅。
本题评阅时请注意:建模的准备工作、数学模型的建立、求解方法及过程、结果的表述、图示及分析和第三问的创新性。
建模的准备工作:这部分是建模及解答的基础(集中或分散描述)
(1)倾斜面总辐射强度的计算。
这里涉及到:太阳时、时角、赤纬角、太阳高度角和太阳方位角等
概念,还需要了解斜面的阳光直射辐射强度与散射辐射强度的计算。
(2)附件4提供的辐射强度是离散数据,需要将数据连续化, 计算光照辐射量。
问题1:只考虑贴附安装方式建立数学模型及求解
(1)建立模型: 单目标模型或多目标模型,可考虑发电总量、单位发电费用、经济效益和投资回收年
限等。
希望学生能够全面地分析问题,建立相应的优化模型。
(2)模型求解: 要求给出求解方法的详细描述。
(3)结果表述: 结果的表述、分析要清楚明确:要求给出电池铺设图及所配用的逆变器列表。
例如,
一种可行的铺设方式是:顶面可铺设40多块A3电池,南面可铺设30多块C10电池,西面可铺设C1和C10电池各10多块,东、北两面可不铺设(此例只是可行方案之一)。
问题2:考虑架空安装方式建立数学模型及求解
(1)重点考虑屋顶上架空的光伏电池平面的最佳倾角,约为30多度。
(2)其他要求同问题1.
问题3:小屋设计
(1)需要计算南墙的最佳朝向, 光伏电池板的最优铺设。
(2)根据计算结果,设计“最佳”小屋。
(3)本问题重点是考查学生的创造性。
高教社杯全国大学生数学建模竞赛题目 穿越沙漠

高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)B 题 穿越沙漠考虑如下的小游戏:玩家凭借一张地图,利用初始资金购买一定数量的水和食物(包括食品和其他日常用品),从起点出发,在沙漠中行走。
途中会遇到不同的天气,也可在矿山、村庄补充资金或资源,目标是在规定时间内到达终点,并保留尽可能多的资金。
游戏的基本规则如下:(1)以天为基本时间单位,游戏的开始时间为第0天,玩家位于起点。
玩家必须在截止日期或之前到达终点,到达终点后该玩家的游戏结束。
(2)穿越沙漠需水和食物两种资源,它们的最小计量单位均为箱。
每天玩家拥有的水和食物质量之和不能超过负重上限。
若未到达终点而水或食物已耗尽,视为游戏失败。
(3)每天的天气为“晴朗”、“高温”、“沙暴”三种状况之一,沙漠中所有区域的天气相同。
(4)每天玩家可从地图中的某个区域到达与之相邻的另一个区域,也可在原地停留。
沙暴日必须在原地停留。
(5)玩家在原地停留一天消耗的资源数量称为基础消耗量,行走一天消耗的资源数量为基础消耗量的2倍。
(6)玩家第0天可在起点处用初始资金以基准价格购买水和食物。
玩家可在起点停留或回到起点,但不能多次在起点购买资源。
玩家到达终点后可退回剩余的水和食物,每箱退回价格为基准价格的一半。
(7)玩家在矿山停留时,可通过挖矿获得资金,挖矿一天获得的资金量称为基础收益。
如果挖矿,消耗的资源数量为基础消耗量的3倍;如果不挖矿,消耗的资源数量为基础消耗量。
到达矿山当天不能挖矿。
沙暴日也可挖矿。
(8)玩家经过或在村庄停留时可用剩余的初始资金或挖矿获得的资金随时购买水和食物,每箱价格为基准价格的2倍。
请根据游戏的不同设定,建立数学模型,解决以下问题。
1. 假设只有一名玩家,在整个游戏时段内每天天气状况事先全部已知,试给出一般情况下玩家的最优策略。
求解附件中的“第一关”和“第二关”,并将相应结果分别填入Result.xlsx 。
2012数学建模国赛b题题目

2012数学建模国赛b题题目2012数学建模国赛B题题目解析摘要:本文是对2012年数学建模国赛B题的题目进行解析和讨论。
在本文中,我们将首先对题目进行解读,并确定所需解决的问题。
然后,我们将提供一个完整的解答方案,并进行详细的推导和分析。
最后,我们将总结解答的结果,并讨论可能的改进方向。
1. 题目解读2012年数学建模国赛B题涉及的主要内容是某高铁动车组列车的排队和调度问题。
根据题目提供的信息,我们需要解决以下几个问题:a) 列车的排队问题:给出不同车型列车的到达时间、停靠时间和出发时间,要求进行合理的排队,使得列车能够按时准确发出。
b) 列车的调度问题:对于不同的乘客流量需求,确定合适的车次数量以及发车间隔时间,以满足乘客的需求。
c) 最优调度方案:在满足列车发车要求和乘客需求的前提下,寻找最优的调度方案,使得列车的利用率最大化。
2. 解答方案a) 列车的排队问题:首先,我们需要根据到达时间、停靠时间和出发时间的要求,建立一个列车排队模型。
可以使用图论的方法,以列车作为节点,根据到达时间和出发时间的先后顺序建立有向边。
然后,通过拓扑排序算法,确定列车的排队顺序。
b) 列车的调度问题:对于不同的乘客流量需求,我们可以利用运筹学中的线性规划方法进行求解。
假设乘客流量的函数关系为f(t),其中t是时间变量。
我们可以建立一个约束条件,以保证乘客流量在规定时间范围内达到预期值。
c) 最优调度方案:在确定了列车的排队和调度方案之后,我们可以使用优化算法(如遗传算法或模拟退火算法)对调度方案进行优化。
通过调整车次数量和发车间隔时间,我们可以使得列车的利用率最大化。
3. 结果分析根据对题目所给信息和解答方案的分析,我们可以得出以下结论:a) 对于列车的排队问题,通过建立有向边和拓扑排序算法,我们可以得到一个合理的列车排队顺序。
b) 列车的调度问题可以通过线性规划方法进行求解,以满足乘客流量需求。
c) 使用优化算法对调度方案进行优化,可以最大化列车的利用率。
2012年全国大学生数学建模大赛B题--论文

二.问题的分析
图 1 流程图 首先, 根据附件给出的数据进行分析和运算。 已知山西大同市的地理条件 (经 纬度、海拔等等) 、全年每个小时水平面总辐射强度、水平面散射辐射强度、法 向直射辐射强度、各个方向总辐射强度等,建立太阳辐射几何模型,再由几何模 型建立数学模型, 得到各个表面每个小时太阳能光伏板表面的辐射量和中间参数
三型的假设
1.模型的建立 1.1 几何关系建立及基本参数的确定 S 东=S 总-S 门=24.23m^2 S 南=S 总-S 圆-S 窗-S 车库=21.78m^2 S 西=26.98m^2 S 北=S 总-S 窗-S 门=28.119m^2 S 南(顶)=60.785097m^2 S 北(顶)=14.031368m^2 以上全部根据题中给出数据计算。
2012 高教社杯全国大学生数学建模竞赛 B题 太阳能小屋的设计
摘要:
在太阳能小屋的设计中为实现太阳能光伏板最佳朝向、 倾角及排布阵列设计 及优化, 通过建立倾斜放置的光伏板表面接收太阳辐射能模型,计算到达光伏板 上的太阳辐射能量, 推导出光伏板的最佳朝向及倾角。为使光伏板最大限度地接 收太阳辐射的能量,在选择合适的朝向及倾角的基础上,对光伏电池排布阵列, 建立目标规划,并通过与实际逆变器的相互匹配,不断对目标进行优化,最终得 到一组最优解。通过上述研究,结合山西大同市本地情况,重新设计出一个更加 适合当地地理及气象条件的太阳能光能房屋并为其选择最优的阵列排布方案。 针对问题一: 电池板只是铺设房屋的表面, 没有涉及到电池板放的角度问题, 先求算出房屋的角度为 10.62 度,再根据角度,建立模型算出光伏板上太阳能辐 射量。 并用目标规划阵列排列方案计算出电池的排布。再通过排布计算出经济效 益,最后得出 35 年之内无法收回成本。 针对问题二:通过对角度建立模型,计算得出最佳角度 44.66 度,通过排布 计算出电池板排布最佳方案,建立模型计算出经济效益,在 28.5 年收回成本。 如考虑货币时间价值,35 年的经济效益是亏损的。 针对问题三: 要通过目标构建一个产电量尽量大, 而成本尽量小的理想模型。 假设小屋无挑檐、挑雨棚(即房顶的边投影与房体的长宽投影相等) ,建立模型 计算出最佳的图形,并画出模型图。
2012高教社杯全国大学生数学建模竞赛b题

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题.我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出.我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性.如有违反竞赛规则的行为,我们将受到严肃处理.我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等).我们参赛选择的题号是(从A/B/C/D中选择一项填写): B我们的参赛报名号为(如果赛区设置报名号的话): J2913 所属学校(请填写完整的全名):渭南师范学院参赛队员 (打印并签名) :1. 吕通2. 石法燕3. 王蓉指导教师或指导教师组负责人 (打印并签名):刘龙飞日期: 2012 年 9 月 10 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):太阳能小屋的设计摘 要讨论了太阳能小屋设计的优化问题,太阳能小屋就是利用在其房子的外围及其屋顶铺设光伏电池以接受太阳能从而获得太阳能量,用来供暖、供能以达到服务人们的目的.因为不同种类的光伏电池每峰瓦的价钱差别很大,且每峰瓦的实际发电效率还与太阳辐射强度,光线入射角,环境,建筑物所处的地理纬度,气候气象条件,安装部位及方式(贴附与架空)等因素有关,所以光伏电池的优化铺设是问题的核心.问题一:首先,对题目所给数据运用MATLAB 软件进行数据预处理,建立了小屋的全年太阳能光伏发电总量尽可能大的最优化模型:875924max 11*i j j j i j p m x A η===∑∑;然后,利用LINGO 编程求解该优化模型,从而得到电池组件的分组数量和容量;在此基础上进一步建立单位发电量的费用尽可能小的最优化模型:875924'111112n mi j j j l f i j l f S m x A s s η=====--∑∑∑∑从而选配出相应的逆变器的容量和数量;最后,根据电池不同使用年限的效率计算35年寿命期内的发电总量,根据不同型号光伏电池的价钱和逆变器的数量计算器经济效益和投资的回收年限.问题二:首先,在问题一所得到的铺设电池的数量、型号及其连接方式都不发生改变的条件下,仅仅考虑各个面上所对应的电池组件的架空角度,根据附件6中所给出来的有关概念,分别计算出各个时间所对应的太阳高度角α;然后,利用公式()s i n /s i n R S D θαθα=++⎡⎤⎣⎦,计算出各个面上的电池架空的最优角度θ;最后,计算出倾斜光伏阵面接受的太阳辐射强度.最终可以建立同问题一类似的最优化模型,利用LINGO 编程求解,最终达到题目所要求的最优结果.问题三:根据附件7中所给的限定条件,建立了小屋在所给范围内的最大有效面积的最优化模型:max log 22log log S wid wid hig hig w wwid =⨯+⨯⨯+⨯-⨯;然后利用LINGO 编程求解该优化模型得出小屋的有效面积.让房子与正南方向有一定夹角,运用Hay 模型求出最佳角度为045,这样该问题又回归到了问题二,运用问题二的计算方法进行进一步求解.得出,北向面经济效益为负值,所以我们在对小屋各面进行铺设时,只考虑其东南、西三面及顶面,这样才能达到经济效益最大. 且架空式铺设的经济效益大于贴附式铺设.关键词:太阳能小屋;光伏电池;Matlab 软件;Lingo 编程;太阳高度角.近年来,随着环境污染和能源的高消耗问题日益严峻,节能减排已势在必行.为此,国家积极倡导节能减排政策,维护我们赖以生存的家园.为响应政府的号召,某地需要设计太阳能小屋,即在建筑物的表面(屋顶及外墙)铺设光伏电池,光伏电池组件所产生的直流电需要经过逆变器转换成220V交流电才能供家庭使用,并将剩余电量输入电网.因为不同种类的光伏电池每峰瓦的价格差别很大,且每峰瓦的实际发电效率或发电量还受诸多因素的影响,如太阳辐射强度、光线入射角、环境、建筑物所处的地理纬度、地区的气候与气象条件、安装部位及方式(贴附或架空)等.因此,在太阳能小屋的设计中,研究光伏电池在小屋外表面的优化铺设是很重要的问题.附件1—7提供了相关的信息,根据所给的数据,对于下面的三个问题,分别给出它的铺设方案,使得小屋全年太阳能光伏发电量尽可能的大,而单位发电量的尽可能的小,并计算出小屋光伏电池35年寿命期内发电总量,经济效益(当前民用电价按0.5元/kWh 计算)及投资的回收年限.在求解每个问题时,都要求配有图示,给出小屋各外表面电池组件铺设分组阵列图形及组件连接方式(串、并联)示意图,也要给出电池组件分组阵列容量及选配逆变器规格列表.在同一表面采用两种或两种以上类型的光伏电池组件时,同一型号的电池板可串联,而不同型号的电池板不可串联.在不同表面上,即使是相同型号的电池也不能进行串、并联连接.应注意分组连接方式及逆变器的选配.问题一:请根据山西省大同市的气象数据,仅考虑贴附安装方式,选定光伏电池组件,对小屋(见附件2)的部分外表面进行铺设,并根据电池组件分组数量和容量,选配相应的逆变器的容量和数量.问题二:电池板的朝向与倾角均会影响到光伏电池的工作效率,请选择架空方式安装光伏电池,重新考虑问题1.问题三:根据附件7给出的小屋建筑要求,请为大同市重新设计一个小屋,要求画出小屋的外形图,并对所设计小屋的外表面优化铺设光伏电池,给出铺设及分组连接方式,选配逆变器,计算相应结果.二、问题分析问题一:第一小问要求我们根据山西省大同市的气象数据,仅考虑贴附安装方式,选定光伏电池组件,对小屋的部分外表面进行铺设.此问题属于优化问题,要想使小屋的全年太阳能光伏发电总量尽可能大,必须首先计算出小屋各个面的太阳辐射强度.首先对所给数据用MATLAB软件进行数据预处理,然后以铺设面积和块数为限定条件建立目标函数,用LINGO编程求解.最后用CAD制图.第二小问要求我们根据电池组件分组数量和容量,选配相应的逆变器的容量和数量.根据同型号电池可以串联,不同型号光伏电池组件在端电压相差不应超过10%的情况下可以并联的条件,对电池组间进行分组并选配相应的逆变器的容量和数量.问题二:同问题一一样是优化问题,只不过采用架空模式.架空铺设,电池板与墙面之间就有了一定的角度从而使得电池板接受的太阳辐射强度达到最大,可设此角度为θ建立一元函数,求出最适角度θ.再根据倾斜光伏阵面太阳辐射量计算公式,计算出倾斜光伏阵面接受的太阳辐射强度,建立同2.1的目标函数并用MATLAB编程求解.问题三:要求我们根据附件7给出的小屋建筑要求,重新设计一个小屋.充分利用题目所给条件,建立最优模型并根据所给限定条件用LINGO编程求解,得出小屋的最大有效面积,于是该题又变成了问题一,利用问题一的方法进行求解.1、假设题目所给数据都是正确的;2、假设每天都是晴天,不考虑阴雨天情况;3、假设附近没有高大建筑物;4、忽略光电池的内部消耗和分布效应;5、假设气候没有太大变化;6、假设温度对光伏电池的转换率没有影响.5.1问题一5.1.1模型一通过前面问题分析可以看出该问题属于优化问题,要想使小屋的全年太阳能光伏发电总量尽可能大,必须首先计算出小屋各个面的太阳辐射强度.首先对所给数据运用MATLAB编程进行数据预处理;根据年发电量公式:年发电量=年平均太阳辐射总量*电池总面积*光电转换效率,建立最优化模型:目标函数:875924max11i j j ji jP m x Aη===∑∑约束条件:241,1,2,......,24 j jjj jjx A Sx k jx Z=⎧≤⎪⎪⎪≤=⎨⎪∈⎪⎪⎩∑有效根据附件2计算出屋顶及东、西、南、北各面的有效面积如下表:屋顶东向面南向面西向面北向面有效面积/2m60.827792 24.230 19.235310 26.98 36.183东向面西向面南向面北向面最大发电量(W)3762775 5737500 6710314 1633202所选用型号及个数(个)东向面A1(6) A2(2) A3(18) A4(1)西向面A1(3) A2(2) A3(21) A4(1)南向面A1(9) A2(2) A3(15) A4(1)北向面A3(27) A4(1)经过优化后各面选用的光伏电池板型号、块数:所选用型号及个数(个)东向面A3(14) A1(2) C8(4)西向面A3(17) C3(9)南向面A1(2) A3(3) C7(12) C8(21) C9 (1) C10(2)北向面A3(24) C8(3) C9(5)图1 小屋北向面电池组件铺设分组阵列图图2 小屋东向面电池组件铺设分组阵列图图4 小屋南向面电池组件铺设分组阵列图由于题目没有给出屋顶的太阳辐射强度(屋顶为斜面),我们根据倾斜光伏阵面太阳辐射量计算公式:()sin /sin R S D βαβα=⋅++⎡⎤⎣⎦(屋顶倾斜角度为β)可计算出屋顶的辐射总强度.其中,sin sin sin cos cos cos αφδφδω=⋅+⋅⋅,由于α为正午时分太阳高度角,所以时角ω=0,cos ω=1.当地纬度φ=040.1,()228423.45sin 365n πδ+⎛⎫= ⎪⎝⎭(度).经过一系列的数据处理及计算得出屋顶的太阳总辐射强度为:116674797.42/W m .图5 各面太阳辐射强度比例如下饼形图建立如上最优模型:目标函数:875924max 11i j j j i j P m x A η===∑∑约束条件:241,1,2,......,24 j jjj jjx A Sx k jx Z=⎧≤⎪⎪⎪≤=⎨⎪∈⎪⎪⎩∑有效运用 LINGO编程得出屋顶最大发电量为:5684159.6W表1-6 屋顶铺设光伏电池板的优化结果铺设光伏电池型号A3 B7 C5 C6 C9铺设数量(个)28 6 4 28 14由此优化结果作出小屋顶面电池组件铺设分组阵列图如下:图6 小屋顶面电池组件铺设分组阵列图5.1.2 模型二通过以上求解及模型优化,得出了小屋各外表面电池组件铺设分组阵列图形.根据以上结果及附件1、3、5对各电池组件进行了最优链接并在经济投入最低的情况下为其安装了最优逆变器.建立了费用尽可能小的最优化模型:目标函数:875924'111112n mi j j j l fi j l fS m x A s sη=====--∑∑∑∑(S为经济效益,l s为电池板价格,f s为逆变器价格)约束条件:241,1,2,......,24j j j j j j x A S x k j x Z =⎧≤⎪⎪⎪≤=⎨⎪∈⎪⎪⎩∑有效电池组件连接方式图如下:图7 北向面所铺电池组件连接方式图8 南向面所铺电池组件连接方式图9东向面所铺电池组件连接方式图10 西向面所铺电池组件连接方式图11顶面所铺电池组件连接方式根据5.1.2中给出的小屋外表面光伏电池的铺设方案,参照附件3及5.1.2对小屋表面光伏电池板的年发电量计算的结果,计算出小屋光伏电池35年寿命期内的发电总量、经济效益(当前民用电价按0.5元/kWh计算)及投入如下表:表2-6东面西面南面北面顶面总和年发电量(千瓦)3762.775 5737.5 6710.314 1633.202 5684.159635年后总发电量118527.4125 180731.25 211374.891 51445.863 179051.0274 741130.4439 投入(元)21603.2 24295.5 34147.3 35696 42810 158552 经济效益37660.50625 66070.125 71540.1455 -9973.0685 46715.5137 212013.222有上表可知,北向面经济效益为负值,所以我们进一步优化不对小屋的背面进行铺设,只对其东、南、西面及顶面进行铺设.那么根据:投资回收年限=总投入/每年的经济效益,经过数据处理我们可得出投资的回收年限为:19年.5.2 问题二5.2.1 模型一:问题二与问题一的唯一区别是铺设方式不同,对于架空式安装,我们假设所有电池板的安装的角度相同(设为 ),我们需要计算出倾斜光伏电池面的光照强度才能建立同问题一一样的模型.倾斜光伏阵面太阳辐射量计算公式:()sin /sin R S D θαθα=++⎡⎤⎣⎦,其中α同5.1.2一样可以根据公式计算得出.因此次工时仅有θ一个自变量,为一一元函数.对此函数求导得:()'cos /sin R S θαθα=+⎡⎤⎣⎦ 令'0R θ= 得θ=036 ,则此θ值即为光伏电池板的最佳铺设角度.将θ代入公式()sin /sin R S D βαθα=++⎡⎤⎣⎦则可计算出各倾斜光伏阵面上的太阳辐射强度分别为:建立类似于5.1.1的目标函数:max 11i j j j i j P m x Aη===∑∑ 找出约束条件,并用LINGO编程计算出小屋各个面上的最大发电量如下表:5.2.2 模型二电池组件连接方式及逆变器的选择同5.1.2相同(见附录) 5.2.3 模型三架空安装情况下,小屋光伏电池35年寿命期内的发电总量、经济效益(当前民用电价按0.5元/kWh 计算)及投入如下表:表2—9由上表我们可得出架空是铺设投资的回收年限为:15 年,很显然,架空式铺设的经济效益大于贴附式铺设. 5.3 问题三 5.3.1 模型一:该问题要求我们根据附件7给出的小屋建筑要求,重新设计一个小屋。
全国大学生数学建模竞赛b题

“互联网+”时代的出租车资源配置摘要随着“互联网+”时代的到来,针对当今社会“打车难”的问题,多家公司建立了打车软件服务平台,并推出了多种补贴方案,这无论是对乘客和司机自身需求还是对出租车行业发展都具有一定的现实意义。
本文依靠ISM解释结构、AHP-模糊综合评价、价格需求理论、线性规划等模型依次较好的解决了三个问题。
对于问题一求解不同时空出租车资源“供求匹配”程度的问题,本文先将ISM模型里的层级隶属关系进行改进,将影响出租车供求匹配的12个子因素分为时间、空间、经济、其它共四类组合,然后使用经过改进的AHP-模糊综合评价方法建立模型,提出了出租车空载率这一指标作为评价因子的方案,来分析冬季某节假日哈尔滨市南岗区出租车资源“供求匹配”程度。
通过代入由1-9标度法确定的各因素相互影响的系数,得出各个影响因素的权重大小,利用无量纲化处理各影响因素,得出最终评判因子为0.3062,根据“供求匹配”标准,得出哈尔滨市南岗区出租车资源“供求匹配”程度处于供需合理状态的结论。
同理,也得到了哈尔滨市不同区县、不同时间的供求匹配程度,最后作出哈尔滨市出租车“供求匹配”程度图。
对于问题二我们运用价格需求理论建立模型,以补贴前后打车人数比值与空驶率变化分别对滴滴和快的两个公司的不同补贴方案进行求解,依次得到补贴后对应的打车人数及空驶率的变化,再和无补贴时的状态对比,最后得出结论:当各公司补贴金额大于5元时,打车容易,即补贴方案能够缓解“打车难”的状况;当补贴小于5元时,不能缓解“打车难”的状况。
对于问题三,在问题二的模型下,建立了一个寻找最优补贴金额的优化模型,利用lingo软件[1]进行求解算出最佳补贴金额为8元,然后将这个值带入问题二的模型进行验证,经论证合理后将补贴金额按照4种分配方案分配给司机乘客。
关键词:ISM解释结构模型;AHP-模糊综合评价;价格需求理论;线性规划一问题重述交通是社会生活众多产业当中的一项基础产业,不但和社会的经济发展关系紧密,与人们的生活也是息息相关。
全国大学生数学建模竞赛题目B题
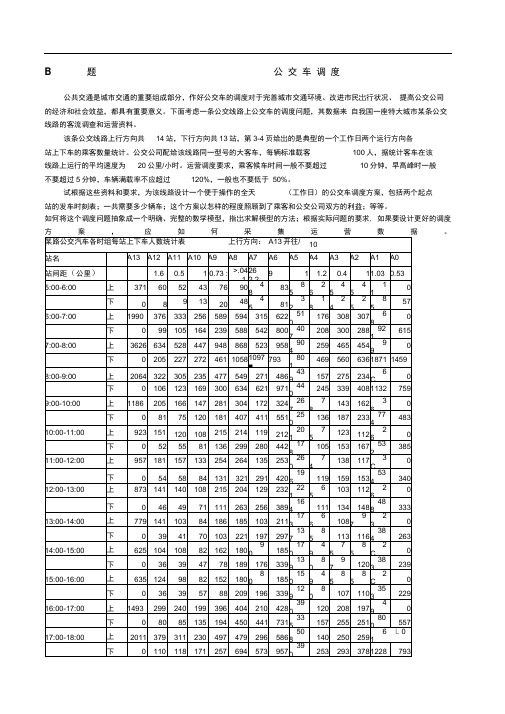
B 题公交车调度
公共交通是城市交通的重要组成部分,作好公交车的调度对于完善城市交通环境、改进市民岀行状况、提高公交公司的经济和社会效益,都具有重要意义。
下面考虑一条公交线路上公交车的调度问题,其数据来自我国一座特大城市某条公交线路的客流调查和运营资料。
该条公交线路上行方向共14站,下行方向共13站,第3-4页给岀的是典型的一个工作日两个运行方向各
站上下车的乘客数量统计。
公交公司配给该线路同一型号的大客车,每辆标准载客100人,据统计客车在该
线路上运行的平均速度为20公里/小时。
运营调度要求,乘客候车时间一般不要超过10分钟,早高峰时一般
不要超过5分钟,车辆满载率不应超过120%,一般也不要低于50%。
试根据这些资料和要求,为该线路设计一个便于操作的全天(工作日)的公交车调度方案,包括两个起点
站的发车时刻表;一共需要多少辆车;这个方案以怎样的程度照顾到了乘客和公交公司双方的利益;等等。
如何将这个调度问题抽象成一个明确、完整的数学模型,指岀求解模型的方法;根据实际问题的要求, 如果要设计更好的调度方案,应如何采集运营数据。
全国大学生数学建模竞赛题目B题

B题公交车调度公共交通是城市交通的重要组成部分,作好公交车的调度对于完善城市交通环境、改进市民出行状况、提高公交公司的经济和社会效益,都具有重要意义。
下面考虑一条公交线路上公交车的调度问题,其数据来自我国一座特大城市某条公交线路的客流调查和运营资料。
该条公交线路上行方向共14站,下行方向共13站,第3-4页给出的是典型的一个工作日两个运行方向各站上下车的乘客数量统计。
公交公司配给该线路同一型号的大客车,每辆标准载客100 人,据统计客车在该线路上运行的平均速度为20公里/小时。
运营调度要求,乘客候车时间一般不要超过10分钟,早高峰时一般不要超过5分钟,车辆满载率不应超过 120%,一般也不要低于50%。
试根据这些资料和要求,为该线路设计一个便于操作的全天(工作日)的公交车调度方案,包括两个起点站的发车时刻表;一共需要多少辆车;这个方案以怎样的程度照顾到了乘客和公交公司双方的利益;等等。
如何将这个调度问题抽象成一个明确、完整的数学模型,指出求解模型的方法;根据实际问题的要求,如果要设计更好的调度方案,应如何采集运营数据。
全国大学生数学建模B题解题思路

1、已知平板尺寸和高度,如何将抽象的描述动态变化过程这一问题数学化?
动态变化过程可以表述为曲线方程问题,其要点是参量的选取,哪些变量在整个折叠过程中是变化的?通过这些变量就能清晰的了解平板变化到桌子的过程。
在此基础上,给出设计加工参数。
开槽长度和桌角边缘线是肯定的描述的,同时可以引入其他变量,如角度等等,可以参照剪式铰的公式增加需要的参量。
第一问切记,要用数学模型和数学描述。
2、三个目标:稳固性好、加工方便、用材最少。
任意给定桌子高度和桌面直径,求平板尺寸和折叠桌的最优加工参数,切记,是最优加工参数;用哪些指标呢?简单举例:平板尺寸(材料最少)、钢筋位置(稳固性好)、开槽长度(加工方便),也可以根据需要自己增加;多目标规划问题,可以用很多方法来解,函数表达式要合理。
3、已知高度和桌面边缘线、桌角边缘线,求解平板尺寸和加工参数。
第三问需要在前两问的基础上进行整合,并建立数学模型。
自己设计的创意折叠桌就各凭本领了。
贯穿3个问题的主线是桌子的基本构架:长方形平板的尺寸和桌子的高度,这两个参量肯定存在着某种联系,而这两个参量的联系又与稳固性好、加工方便、用材最少密不可分。
具体到怎么做,就要看各个参赛队伍的想法了。
B题建模很重要,主要看模型,所以在模型上要多下功夫。
同时,也不要忽视了桌子本身的结构、角度、力学原理等问题,都可能扩展做题思路。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题.我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出.我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性.如有违反竞赛规则的行为,我们将受到严肃处理.我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等).我们参赛选择的题号是(从A/B/C/D中选择一项填写): B我们的参赛报名号为(如果赛区设置报名号的话): J2913 所属学校(请填写完整的全名):渭南师范学院参赛队员 (打印并签名) :1. 吕通2. 石法燕3. 王蓉指导教师或指导教师组负责人 (打印并签名):刘龙飞日期: 2012 年 9 月 10 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):太阳能小屋的设计摘 要讨论了太阳能小屋设计的优化问题,太阳能小屋就是利用在其房子的外围及其屋顶铺设光伏电池以接受太阳能从而获得太阳能量,用来供暖、供能以达到服务人们的目的.因为不同种类的光伏电池每峰瓦的价钱差别很大,且每峰瓦的实际发电效率还与太阳辐射强度,光线入射角,环境,建筑物所处的地理纬度,气候气象条件,安装部位及方式(贴附与架空)等因素有关,所以光伏电池的优化铺设是问题的核心.问题一:首先,对题目所给数据运用MATLAB 软件进行数据预处理,建立了小屋的全年太阳能光伏发电总量尽可能大的最优化模型:875924max 11*i j j j i j p m x A η===∑∑;然后,利用LINGO 编程求解该优化模型,从而得到电池组件的分组数量和容量;在此基础上进一步建立单位发电量的费用尽可能小的最优化模型:875924'111112n mi j j j l f i j l f S m x A s s η=====--∑∑∑∑从而选配出相应的逆变器的容量和数量;最后,根据电池不同使用年限的效率计算35年寿命期内的发电总量,根据不同型号光伏电池的价钱和逆变器的数量计算器经济效益和投资的回收年限.问题二:首先,在问题一所得到的铺设电池的数量、型号及其连接方式都不发生改变的条件下,仅仅考虑各个面上所对应的电池组件的架空角度,根据附件6中所给出来的有关概念,分别计算出各个时间所对应的太阳高度角α;然后,利用公式()s i n /s i n R S D θαθα=++⎡⎤⎣⎦,计算出各个面上的电池架空的最优角度θ;最后,计算出倾斜光伏阵面接受的太阳辐射强度.最终可以建立同问题一类似的最优化模型,利用LINGO 编程求解,最终达到题目所要求的最优结果.问题三:根据附件7中所给的限定条件,建立了小屋在所给范围内的最大有效面积的最优化模型:max log 22log log S wid wid hig hig w wwid =⨯+⨯⨯+⨯-⨯;然后利用LINGO 编程求解该优化模型得出小屋的有效面积.让房子与正南方向有一定夹角,运用Hay 模型求出最佳角度为045,这样该问题又回归到了问题二,运用问题二的计算方法进行进一步求解.得出,北向面经济效益为负值,所以我们在对小屋各面进行铺设时,只考虑其东南、西三面及顶面,这样才能达到经济效益最大. 且架空式铺设的经济效益大于贴附式铺设.关键词:太阳能小屋;光伏电池;Matlab 软件;Lingo 编程;太阳高度角.近年来,随着环境污染和能源的高消耗问题日益严峻,节能减排已势在必行.为此,国家积极倡导节能减排政策,维护我们赖以生存的家园.为响应政府的号召,某地需要设计太阳能小屋,即在建筑物的表面(屋顶及外墙)铺设光伏电池,光伏电池组件所产生的直流电需要经过逆变器转换成220V交流电才能供家庭使用,并将剩余电量输入电网.因为不同种类的光伏电池每峰瓦的价格差别很大,且每峰瓦的实际发电效率或发电量还受诸多因素的影响,如太阳辐射强度、光线入射角、环境、建筑物所处的地理纬度、地区的气候与气象条件、安装部位及方式(贴附或架空)等.因此,在太阳能小屋的设计中,研究光伏电池在小屋外表面的优化铺设是很重要的问题.附件1—7提供了相关的信息,根据所给的数据,对于下面的三个问题,分别给出它的铺设方案,使得小屋全年太阳能光伏发电量尽可能的大,而单位发电量的尽可能的小,并计算出小屋光伏电池35年寿命期内发电总量,经济效益(当前民用电价按0.5元/kWh 计算)及投资的回收年限.在求解每个问题时,都要求配有图示,给出小屋各外表面电池组件铺设分组阵列图形及组件连接方式(串、并联)示意图,也要给出电池组件分组阵列容量及选配逆变器规格列表.在同一表面采用两种或两种以上类型的光伏电池组件时,同一型号的电池板可串联,而不同型号的电池板不可串联.在不同表面上,即使是相同型号的电池也不能进行串、并联连接.应注意分组连接方式及逆变器的选配.问题一:请根据山西省大同市的气象数据,仅考虑贴附安装方式,选定光伏电池组件,对小屋(见附件2)的部分外表面进行铺设,并根据电池组件分组数量和容量,选配相应的逆变器的容量和数量.问题二:电池板的朝向与倾角均会影响到光伏电池的工作效率,请选择架空方式安装光伏电池,重新考虑问题1.问题三:根据附件7给出的小屋建筑要求,请为大同市重新设计一个小屋,要求画出小屋的外形图,并对所设计小屋的外表面优化铺设光伏电池,给出铺设及分组连接方式,选配逆变器,计算相应结果.二、问题分析问题一:第一小问要求我们根据山西省大同市的气象数据,仅考虑贴附安装方式,选定光伏电池组件,对小屋的部分外表面进行铺设.此问题属于优化问题,要想使小屋的全年太阳能光伏发电总量尽可能大,必须首先计算出小屋各个面的太阳辐射强度.首先对所给数据用MATLAB软件进行数据预处理,然后以铺设面积和块数为限定条件建立目标函数,用LINGO编程求解.最后用CAD制图.第二小问要求我们根据电池组件分组数量和容量,选配相应的逆变器的容量和数量.根据同型号电池可以串联,不同型号光伏电池组件在端电压相差不应超过10%的情况下可以并联的条件,对电池组间进行分组并选配相应的逆变器的容量和数量.问题二:同问题一一样是优化问题,只不过采用架空模式.架空铺设,电池板与墙面之间就有了一定的角度从而使得电池板接受的太阳辐射强度达到最大,可设此角度为θ建立一元函数,求出最适角度θ.再根据倾斜光伏阵面太阳辐射量计算公式,计算出倾斜光伏阵面接受的太阳辐射强度,建立同2.1的目标函数并用MATLAB编程求解.问题三:要求我们根据附件7给出的小屋建筑要求,重新设计一个小屋.充分利用题目所给条件,建立最优模型并根据所给限定条件用LINGO编程求解,得出小屋的最大有效面积,于是该题又变成了问题一,利用问题一的方法进行求解.1、假设题目所给数据都是正确的;2、假设每天都是晴天,不考虑阴雨天情况;3、假设附近没有高大建筑物;4、忽略光电池的内部消耗和分布效应;5、假设气候没有太大变化;6、假设温度对光伏电池的转换率没有影响.5.1问题一5.1.1模型一通过前面问题分析可以看出该问题属于优化问题,要想使小屋的全年太阳能光伏发电总量尽可能大,必须首先计算出小屋各个面的太阳辐射强度.首先对所给数据运用MATLAB编程进行数据预处理;根据年发电量公式:年发电量=年平均太阳辐射总量*电池总面积*光电转换效率,建立最优化模型:目标函数:875924max11i j j ji jP m x Aη===∑∑约束条件:241,1,2,......,24 j jjj jjx A Sx k jx Z=⎧≤⎪⎪⎪≤=⎨⎪∈⎪⎪⎩∑有效根据附件2计算出屋顶及东、西、南、北各面的有效面积如下表:屋顶东向面南向面西向面北向面有效面积/2m60.827792 24.230 19.235310 26.98 36.183东向面西向面南向面北向面最大发电量(W)3762775 5737500 6710314 1633202所选用型号及个数(个)东向面A1(6) A2(2) A3(18) A4(1)西向面A1(3) A2(2) A3(21) A4(1)南向面A1(9) A2(2) A3(15) A4(1)北向面A3(27) A4(1)经过优化后各面选用的光伏电池板型号、块数:所选用型号及个数(个)东向面A3(14) A1(2) C8(4)西向面A3(17) C3(9)南向面A1(2) A3(3) C7(12) C8(21) C9 (1) C10(2)北向面A3(24) C8(3) C9(5)图1 小屋北向面电池组件铺设分组阵列图图2 小屋东向面电池组件铺设分组阵列图图4 小屋南向面电池组件铺设分组阵列图由于题目没有给出屋顶的太阳辐射强度(屋顶为斜面),我们根据倾斜光伏阵面太阳辐射量计算公式:()sin /sin R S D βαβα=⋅++⎡⎤⎣⎦(屋顶倾斜角度为β)可计算出屋顶的辐射总强度.其中,sin sin sin cos cos cos αφδφδω=⋅+⋅⋅,由于α为正午时分太阳高度角,所以时角ω=0,cos ω=1.当地纬度φ=040.1,()228423.45sin 365n πδ+⎛⎫= ⎪⎝⎭(度).经过一系列的数据处理及计算得出屋顶的太阳总辐射强度为:116674797.42/W m .图5 各面太阳辐射强度比例如下饼形图建立如上最优模型:目标函数:875924max 11i j j j i j P m x A η===∑∑约束条件:241,1,2,......,24 j jjj jjx A Sx k jx Z=⎧≤⎪⎪⎪≤=⎨⎪∈⎪⎪⎩∑有效运用 LINGO编程得出屋顶最大发电量为:5684159.6W表1-6 屋顶铺设光伏电池板的优化结果铺设光伏电池型号A3 B7 C5 C6 C9铺设数量(个)28 6 4 28 14由此优化结果作出小屋顶面电池组件铺设分组阵列图如下:图6 小屋顶面电池组件铺设分组阵列图5.1.2 模型二通过以上求解及模型优化,得出了小屋各外表面电池组件铺设分组阵列图形.根据以上结果及附件1、3、5对各电池组件进行了最优链接并在经济投入最低的情况下为其安装了最优逆变器.建立了费用尽可能小的最优化模型:目标函数:875924'111112n mi j j j l fi j l fS m x A s sη=====--∑∑∑∑(S为经济效益,l s为电池板价格,f s为逆变器价格)约束条件:241,1,2,......,24j j j j j j x A S x k j x Z =⎧≤⎪⎪⎪≤=⎨⎪∈⎪⎪⎩∑有效电池组件连接方式图如下:图7 北向面所铺电池组件连接方式图8 南向面所铺电池组件连接方式图9东向面所铺电池组件连接方式图10 西向面所铺电池组件连接方式图11顶面所铺电池组件连接方式根据5.1.2中给出的小屋外表面光伏电池的铺设方案,参照附件3及5.1.2对小屋表面光伏电池板的年发电量计算的结果,计算出小屋光伏电池35年寿命期内的发电总量、经济效益(当前民用电价按0.5元/kWh计算)及投入如下表:表2-6东面西面南面北面顶面总和年发电量(千瓦)3762.775 5737.5 6710.314 1633.202 5684.159635年后总发电量118527.4125 180731.25 211374.891 51445.863 179051.0274 741130.4439 投入(元)21603.2 24295.5 34147.3 35696 42810 158552 经济效益37660.50625 66070.125 71540.1455 -9973.0685 46715.5137 212013.222有上表可知,北向面经济效益为负值,所以我们进一步优化不对小屋的背面进行铺设,只对其东、南、西面及顶面进行铺设.那么根据:投资回收年限=总投入/每年的经济效益,经过数据处理我们可得出投资的回收年限为:19年.5.2 问题二5.2.1 模型一:问题二与问题一的唯一区别是铺设方式不同,对于架空式安装,我们假设所有电池板的安装的角度相同(设为 ),我们需要计算出倾斜光伏电池面的光照强度才能建立同问题一一样的模型.倾斜光伏阵面太阳辐射量计算公式:()sin /sin R S D θαθα=++⎡⎤⎣⎦,其中α同5.1.2一样可以根据公式计算得出.因此次工时仅有θ一个自变量,为一一元函数.对此函数求导得:()'cos /sin R S θαθα=+⎡⎤⎣⎦ 令'0R θ= 得θ=036 ,则此θ值即为光伏电池板的最佳铺设角度.将θ代入公式()sin /sin R S D βαθα=++⎡⎤⎣⎦则可计算出各倾斜光伏阵面上的太阳辐射强度分别为:建立类似于5.1.1的目标函数:max 11i j j j i j P m x Aη===∑∑ 找出约束条件,并用LINGO编程计算出小屋各个面上的最大发电量如下表:5.2.2 模型二电池组件连接方式及逆变器的选择同5.1.2相同(见附录) 5.2.3 模型三架空安装情况下,小屋光伏电池35年寿命期内的发电总量、经济效益(当前民用电价按0.5元/kWh 计算)及投入如下表:表2—9由上表我们可得出架空是铺设投资的回收年限为:15 年,很显然,架空式铺设的经济效益大于贴附式铺设. 5.3 问题三 5.3.1 模型一:该问题要求我们根据附件7给出的小屋建筑要求,重新设计一个小屋。
