1-9届三年级小机灵杯真题答案

合集下载

数学竞赛小机灵杯三年级决赛解析

第十二届"小机灵杯"决赛试卷（三年级组）一、判断题（正确的打√，错误的打×）1、数字的希腊文原意就是"数字或计算"，早期数字的萌芽：结绳、粘珠、划道、木棒记事。

【分析】错2、在同一平面上，四边形不易于变形，有着稳定、坚固、耐压的特点。

【分析】错3、风的等级是1940年由美国气象机构制定的，他们建立了一套分级法，把风力分为19级。

【分析】错4、《几何原本》被广泛认为是历史上最成功的教科书，它的作者是古希腊最有影响的数学家之一的欧几里得。

【分析】对5、世界各国都有这样一条规定：军队过桥时一定要迈着整齐的步伐，这样可以抵消一部分振动，桥不会塌陷。

【分析】错【分析】7、有100个棋子，两人轮流取棋子，每次允许取其中1个或2个，谁最后把棋子取完就算获胜。

如果你先取，那么第一次你取（）个，才能保证获胜。

【分析】10012=331÷+ （），先取1个，使棋子变为99个，然后采取如下策略：若对手取2个，则取1个；若对手取1个，则取2个。

则每次都能使棋子变为3的倍数。

于是后手永远面对3的倍数，只能将其变为一个不是3的倍数的数，则后手无法使棋子变为0，先手胜。

8、三（1）班21名同学共做了69架纸飞机，女生每人做2架，男生每人做5架，那么男生有（）人，女生有（）人。

【分析】假设全是女生，共能做42架纸飞机，离实际69架纸飞机差27架，每将1名女生换为男生，可多做3架纸飞机，所以共有男生273=9÷名，女生为12名。

9、把12个小球分别标上数字1、2、3、……、12后放入一个纸盒中，甲、乙、丙三人各从纸盒中拿出4个球。

现知道他们三人所拿的球上所标的数之和都相等，甲有两个球标有数字6、11，乙有两个球标有数字4、8，丙有一个球标有数字1。

那么丙其他三个球上标有的数字是（）。

【分析】每人所拿4个球数字之和为123123=26++++÷ （），甲已有17，还差9，可从（1、8）（2、7）（3、6）（4、5）中选择1组，而其中1、4、6、8均已被取走，所以甲只能选（2、7）。

三年级小天才竞赛试题答案

三年级小天才竞赛试题答案三年级的同学们，欢迎参加小天才竞赛！以下是本次竞赛的试题答案，希望你们在竞赛中取得了好成绩。

1. 数学题目：- 第一题：计算下列各题的和：- 23 + 45 = 68- 32 + 56 = 88- 第二题：一个班级有48名学生，如果每4名学生分成一组，可以分成多少组？- 48 ÷ 4 = 12组2. 语文题目：- 第一题：填空题，用“和”、“或”填空：- 我喜欢吃苹果和（或）香蕉。

- 第二题：根据题目所给的成语，写出成语的反义词：- 一帆风顺的反义词是“坎坷不平”。

3. 英语题目：- 第一题：选择正确的单词填空：- I have a red __apple__.- 第二题：翻译句子：- 我有一个好朋友。

翻译为：I have a good friend.4. 科学题目：- 第一题：水的三个状态是什么？- 水的三个状态是固态（ice）、液态（water）、气态（steam）。

- 第二题：植物生长需要哪些基本条件？- 植物生长需要阳光、水分、土壤和适宜的温度。

5. 逻辑题目：- 第一题：如果所有的猫都怕水，而小明的宠物是一只猫，那么小明的宠物怕水吗？- 是的，小明的宠物怕水。

- 第二题：如果A大于B，B大于C，那么A、B、C三者的大小关系是什么？- A > B > C6. 常识题目：- 第一题：一年有多少个月？- 一年有12个月。

- 第二题：我国的首都是哪里？- 我国的首都是北京。

希望这份答案能帮助你们回顾竞赛的内容，也祝愿你们在未来的学习中不断进步，成为真正的小天才！。

小机灵杯1-14届试题及详解

2003年2004年2005年2006年2007年2008年2009年2010年2，4593，2284，35，306，43157，328，169，6610，11 11，10 12，2660 13，60 14，792 15，116，49/4 17，G18，44 19，12 20，1536，72012年2013年第十一届小机灵杯五年级初赛试题1、5.5×6.6＋6.6×7.7＋7.7×8.8＋8.8×9.92、五（1）班男生的平均身高是149cm，女生的平均身高是144cm，全班的平均身高是147cm。

那么，五（1）班的男生人数是女生人数的多少倍？3、甲、乙分别持有7张卡片，卡片上分别写有1、2、3、4、5、6、7七个数字。

如果两人各摸出一张卡片，那么两张卡片上数字和为8的可能性是多少？4、有一个圆形跑道，甲用40秒跑完一圈，乙跑的方向与甲相反，每15秒遇到甲一次。

乙跑完一圈需要几秒？5、50个各不相同的正整数，它们的和为2012，那么这些数里奇数最多有几个？6、把正整数排成下列数阵：1 2 5 10 …4 3 6 11 …9 8 7 12 …16 15 14 13 ………………第21行第21列的数是多少？7、有一叠卡片共200张，从上到下依次编号为1到200，从最上面的一张开始按如下次序进行操作：把最上面的第一张卡片拿掉，把下一张卡片放在这一叠卡片的最下面；再把最上面的第一张（原来的第三张）卡片拿掉，把下一张卡片放在这一叠卡片的最下面……依次重复这样做。

那么剩下的这张卡片是原来200张卡片里的第几张？8、某班有60人，其中42人会游泳，46人会骑车，50人会溜冰，55人会打乒乓球。

可以肯定至少有多少人四项运动都会？9、把既不是平方数也不是立方数的正整数（0除外）按从小到大的顺序排列，得到2，3,5,6,7,10，……，其中第1000个数是多少？10、如图所示，ABCD是梯形，三角形ADE的面积是1，三角形ABF的面积是9，三角形BCF的面积是27，那么三角形ACE的面积是多少？11、某学生漏看了写在两个三位数之间的乘号，将它们当成了一个六位数，而该六位数恰好是原来乘积的7倍，这两个三位数之和是多少？12、从1到900中选6个正整数，使这6个连续正整数的积的尾数恰好为4个0，有多少种选法？第十一届"小机灵"杯数学竞赛决赛五年级试题第一项，每题4分。

第九届“小机灵杯”四年级初赛试题

第九届“小机灵杯”小学生数学竞赛（初赛）试题（四年级）1．计算：()()2010200920101201020111+⨯+÷⨯-=⎡⎤⎣⎦（）。

2．选择填空：在一张9行9列的方格纸上，把每个方格所在的行数和列数加起来，填在这个方格中，例如538a =+=，在填入的81个数中，（）多。

A ：奇数 B ：偶数a 1234567899876543213．如图的竖式除法中，不同的字母表示不同的数字，竖式除法的商是（）。

A DB H E GG 9 9 9 9 9 9G B 9B H A 9 A D E 9 E F C 9 C E D 9 D I 04．甲、乙、丙三人过桥，桥上每次只能走两个人，每人过桥后再返回需要2分钟（往返各需1分钟），三人过桥后再返回一共至少需要（）分钟。

5．将九个连续正整数从小到大排列，最小的四个数的总和是58，那么最大的三个数的总和是（）。

6．某学校有学生1520人，每个班40名学生，每个班级一天上6节课，平均每个教师一天教3节课，那么这所学校至少需要配备（）名教师。

7．某地区有66条航空线路，每两个城市之间都设有一条直达的航空线，这66条航空线共连接这个地区（）个城市。

8．如图，线段12d=厘米，图形的周长是a=厘米，9c=厘米，6b=厘米，4（）厘米。

hb9．甲、乙、丙三条公路，甲公路的长度是乙公路的3倍，乙公路的长度比丙公路的2倍少25千米，甲公路的长度比丙公路长240千米，甲公路长（）千米，乙公路长（）千米，丙公路长（）千米。

10．小巧读一本小说，如果每天读30页，则比规定的日期迟一天读完全书；如果每天读35页，则最后一天要少读5页；如果每天读33页，最后一天要读（）页才能按规定的日期读完这本书。

11．如图，正方形ACEG的边上共有7个点：A、B、C、D、E、F、G，其中B、D、F分别在边AC、CE、EG上，那么以这7个点中任意4点为顶点组成的四边形有（）个。

三年级下册数学试题小机灵杯三年级初赛试题(解析版)

“小机灵杯”数学竞赛初赛（三年级组）时间：60 分钟总分：120 分（第1 题~第4 题，每题8 分）【第1 题】已知1050 -840 ÷□⨯8 =90 ，那么□=。

【分析与解】计算问题，易得□=7【第2 题】即将过去的一年中有连续的7 天，其日期数总和是100 ，那么这7 天的日期数分别是、、、、、、。

【分析与解】时间与日期。

如果这7 天在同一个月中，那么日期数总和是中间数⨯7 ；而100 不是7的倍数；故这7 天在相邻的两个月。

28 + 27 + 26 = 81，28 + 27 + 26 + 25 =106 >100 ；30 + 29 + 28 = 87 ，30 + 29 + 28 + 27 =114 >100 ；31+ 30 + 29 = 90 ，31+ 30 + 29 + 28 =118 >100 ；1+ 2 + 3 + 4 =10 ；所以只能是100 = 29 +30 +31+1+ 2 +3 + 4 ；即这7 天的日期数分别是29 、30 、31、1 、2 、3 、4 。

【第3 题】用5个相同的小正方形拼成一个轴对称图形，要求每个小正方形至少有一条边与另一个小正方形的边完全重合，共有种不同的拼法。

请你一一画出这些图形。

（通过旋转或翻折得到的图形算作同一种）【分析与解】图形剪拼。

考虑到对称图形，共有 6 种。

分别为“一字”形，“凹字”形，“T 字”形，“十字”形，“w 字”形, “L 字”形【第4 题】小明的弟弟是三胞胎，小明今年的年龄与3 个弟弟的年龄总和相等。

再过6 年，3 个弟弟的年龄总和是小明年龄的2 倍。

小明今年岁。

【分析与解】年龄问题，差倍问题。

（方法一）小明今年的年龄与3 个弟弟的年龄总和相等；故再过6 年，3 个弟弟的年龄总和比小明多6 ⨯3 - 6 =12 岁；而再过6 年，3 个弟弟的年龄总和是小明年龄的2 倍；则再过6 年，小明年龄为12 ÷(2 -1)=12 岁；小明今年12 - 6 = 6 岁。

第十二届“小机灵”杯初赛三年级详解

———————————————————————————————————————— 新舟同类型题目：
三年级超常班暑假班第五讲植树问题练习 6 小王要到大厦的 36 层去上班，一日因停电他步行上楼，他从一层到六层用了 100 秒。如果用同样的速度走到 36 层，还需要_________秒。 ——————————————————————————————————————————— 解析：从一楼到七楼需要走 6 层，而从 1 楼走到 7 楼走了 6 层，则下楼时也走了 6 层，走每一层用的时间 14 秒，则来回需要 2 6 14 168 秒。 ————————————————————————
三年级超常班秋季班第九讲例 5： 2 角和 5 角的硬币共 30 枚，总钱数是 102 角， 2 角硬币有（）枚， 5 角硬币有（）枚。 ———————————————————————————————————————————
解析：我们可以用假设法来解这道题目，如果假设 260 张都是二十元的人民币，那么有 260 20 5200 元，而实际是 100 100 10000 元，少了 10000 5200 4800 元，说明有 50 元的，而每出现一张 50 元的，
———————————————————————————————————————— 新舟同类型题目：三年级超常班秋季班第二讲趣味数字例 7 在 1-600 的自然数中，（ 1 ）出现________次数字 4 ；（ 2 ）含有数字 6 的数共有_______个。
———————————————————————————————————————————
考点：数字谜
———————————————————————————————————————— 新舟同类型题目：

第十三届小机灵杯初赛(三年级)—含答案

第十三届“小机灵杯”小学数学竞赛三年级组初赛试题一、判断题(正确的打“√”，错误的打“×”。

每题1分)1、路程÷时间=速度。

( ) √2．西方最早发现勾股定理的数学家之一是欧几里得。

( ) ×3．我们在数物理的时候，用来表示个数的1、2、3、……叫作自然数，一个物体也没有，用0表示，那说明“0”不是自然数。

( ) ×4．牛顿是17至18世纪的英国数学家，又被尊称为“物理学之父”。

( ) ×5．《九章算术》是中国古代最为著名的数学专著之一。

( ) √二、填空题(6~10题每题5分，11~15题每题8分，16~20题每题10分)6．2015－123－125－127－129－131＝( )。

13807．今年小兵7岁，小兵妈妈35岁。

( )年后妈妈的年龄是小兵的3倍。

78．95路公交车上午6点到7点从上海火车站(始发站)共发出11班车(6点整和7点整各有一班车开出)。

已知发出的相邻两班车的间隔时间相等。

那么每过( )分钟就会从始发站开出一辆95路公交车。

69．右图是一张道路图，图中每段路旁标注的数值表示走这段路所需的时间(单位：分钟)。

那么从A 出发走到B 最快需要( )分钟。

2110．有两个小数365和24，现将第一个数减去19，第二个数加12，这算一次操作。

那么操作( )次后，第一个数和第二个数相等。

1111．如图有12个点，相邻两个点之间的距离是1厘米，18 4 4 3 2 11 6 3 5 7 2 4 A B以这些点为顶点可以连成( )个长方形。

1212．某校三年级共有学生100人，其中68人爱看体育频道，55人爱看文艺频道，另有3人这两个频道都不爱看。

那么这两个频道都爱看的学生有( )人。

2613．将1、2、3、4、5、6、7、8、9填入下列方格中，使等式成立。

每个数字只能使用一次，那么四位数最大是( )。

1798□□□□+□□□+□□=211514．如右图，一只青蛙站在1号位置上，它第1次跳步，到达2号位置；第2次跳2步，到达4号位置；第3次跳 3步，到达1号位置；…；第n 次跳n 步。

行程问题(小机灵)

1 圈； 2
1 )＝48m＋24 2
因为速度相同，所以相同时内路程相同，起点相同，所以 30n＝48m＋24；即 5n＝8m＋4，有不定方城知识，解出有 n＝4，m＝2，所以小甲虫跑了 2 圈后，大小甲虫相距最远。【练习 3】【解析】
A
O B
C
当乙和丙相遇时，乙已经走了 30+15=45 千米。由于甲乙两人的速度比是 8：9，因此这时甲已经走了 45×8÷9=40 千米。当甲和丙相遇时，甲已经走了 30+20×2-6=64（千米），因此两次相遇之间的时间是全部时间的（64-40）÷64=
【例题突破】
【例 1】 A 、 B 两地相距 2400 米，甲从 A 地、乙从 B 地同时出发，在 A 、 B 两地间往返锻炼。甲每分钟跑 300 米，乙每分钟跑 240 米。在 30 分钟后停止运动，甲、乙两人第几次相遇时距 A 地最近？最近距离是多少？【例 2】甲乙二人从 A 、 B 两地同时出发相向而行，甲每分钟行 80 米，乙每分钟行 60 米. 出发一段时间后，二人在距离中点 120 米处相遇.如果甲出发后在途中某地停留了一会儿，二人还将在距中点 120 米处相遇.问：甲在途中停留了多少分钟？【例 3】一条小河流过 A 、 B 、 C 三镇， A 、 B 两镇之间有汽船来往，汽船在静水中的速
【例题突破】
【例 1】【解析】
B 乙
10
20 3
30
40 5
50
1 2 4 A 甲 10 20 30 40 50
利用折线图来讲解甲走一个全程需要 2400÷300＝8 （分钟），乙走一个全程需要 2400÷240 ＝10（分钟），通过画图如上知道第二次相遇离 A 点最近，此时甲乙共走了 3 个全程，乙走的路程为：2400×3÷（300＋240）×240＝3200（米），由图可知乙走了一个全程多距 A 的距离，所以距离 A 地为：3200－2400＝800（米）。【例 2】【解析】第一次，甲比乙多走的路程 S差 120 2 240 米，根据公式

中环杯、小机灵杯试题精选(题目)

中环杯、小机灵杯试题精选（题目）【1】1.四个球，编号为1，2，3，4，将他们分放到编号为1，2，3，4的四只箱子里，每箱一个，则至少有一箱恰使球号与箱号相同的放法有几种?2. 用数码1，2，3，4.....9各恰好两次，构成不同的质数，使它们的和尽可能小，则该和最小是几?【2】一班,二班,三班各有二人作为数学竞赛优胜者, 6人站一排照相, 要求同班同学不站在一起, 有( ) 种不同的站法?【3】一版邮票有20行20列,共400张邮票,称由3张同一行或同一列相连的邮票组成的纸块为"三联".小亮想剪出尽可能多的三联,他最多能得到几块三联?(五年级）【4】第一次在1，2两数之间写上3；第二次在1，3之间和3，2之间分别写上4，5；以后每一次都在已写上的两个相邻数之间，再写上这两个相邻数之和。

这样的过程共重复8次，那么所以数的和是多少？【5】一次测验共有5道试题，测试后统计如下：有81%的同学做对第1题，有85%的同学做对第2题，有91%的同学做对第3题，有74%的同学做对第4题，有79%的同学做对第5题。

如果做对3道或3道以上试题的同学为考试合格。

请问：这次考试的合格率最多达百分之几？最少达百分之几？【6】把156支铅笔分成n堆（n>等于2)，要求每堆一样多且为偶数支。

有（）种分法。

【7】七个相同的羽毛球,放在四个不同的盒子里, 每个盒子里至少放一个, 不同的放法有( ) 种.由甲城开往乙城的汽车每隔1小时一班逢整点出发，由乙城开往甲城的汽车每隔1小时一班但逢半点（30分）出发。

从一个城市到另一个城市需要6小时，假定汽车行驶在同一高速公路上，那么一辆开往乙城的汽车最多能遇到（）辆开往甲城的汽车。

【9】一群公猴、母猴和小猴共38只，每天共摘桃子266个。

已知每只公猴每天摘桃10个，每只母猴每天摘桃8个，每只小猴每天摘桃5个，并且公猴比母猴少4只，那么，这群猴子中小猴有多少只？这道题目除了设X做以外还有别的方法吗？【10】甲、乙两列车分别从A,B两站同时相向开出，已知甲车的速度与乙车速度的比为3：2，C站在A,B两站之间。

第十届小机灵杯三年级综合练习(2)详解

第十届小机灵杯数学竞赛综合练习（2）（三年级）1．计算：2222×17+3333×4+6666×9= 。

考点分析：速算与巧算。

1111×34+1111×12+1111×54=1111×（34+12+54）=1111×100=1111002．如果4*2=4+44=48，2*3=2+22+222=246，3*4=3+33+333+3333=3702，那么5*5= 。

考点分析：定义新运算。

5*5=5+55+555+5555+55555=5×（1+11+111+1111+11111）=5×12345=617253.顾客买15元的物品，付了一张50元，售货员无零钱，便向邻近柜台换，交易完毕后，邻近柜台的售货员发现这张50元纸币是假的。

于是又退了回来。

这样的售货员最多向公司赔偿元。

考点分析：等量代换。

售货员找给顾客35元，最终公司用15元得物品和35元人民币换得一张假币，所以售货员最多向公司赔偿50元。

4.如果，图1中共有个圆，把紧挨在一起的两个圆成为一对，例如图2中有3对（分别是A与B，B与C，C与A），图中这样的圆共有对。

考点分析：几何计数图1中共有1+2+3+4+5+6=21个圆按照每三个一组，图1中共有1+2+3+4+5=15组，15×3=45对5.将52只乒乓球放在9个盒子里，每个盒子放的乒乓球个数都不相同，每个盒子中至少放了一个乒乓球，那么最多的一个最多放了个乒乓球。

考点分析：等差数列按照第n个盒子放n个的理想状态,共需要1+2+3+4+5+6+7+8+9=45个52-45=7个，把多余的7个都放到第9个盒子里，最多一个放了16个。

6.小约翰做姜武每天可得3美元，做得特别好时每天可得5美元，有一个月（30天）他共得100美元，这个月他有天做得特别好。

考点分析：变形鸡兔同笼。

假设每天都得3美元，3×30=90（元）,100-90=10（元），10÷（5-3）=5（天）7在排列ABCDEDCBAABCDEDCBAABCDEDCBA…中，第1995个字母是，算到第1995个字母为止，共有该字母个。

第九届小机灵杯初赛(三年级)— 含答案

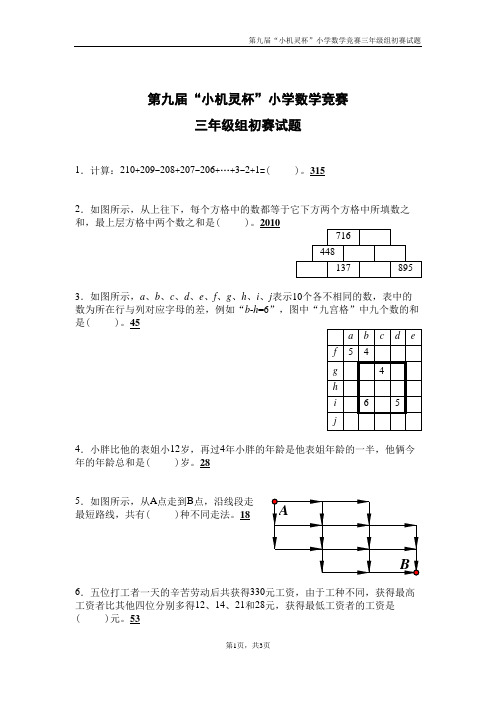
第九届“小机灵杯”小学数学竞赛三年级组初赛试题1．计算：210+209-208+207-206+…+3-2+1=()。

315 2．如图所示，从上往下，每个方格中的数都等于它下方两个方格中所填数之和，最上层方格中两个数之和是()。

20103．如图所示，a 、b 、c 、d 、e 、f 、g 、h 、i 、j 表示10个各不相同的数，表中的数为所在行与列对应字母的差，例如“b -h =6”，图中“九宫格”中九个数的和是()。

454．小胖比他的表姐小12岁，再过4年小胖的年龄是他表姐年龄的一半，他俩今年的年龄总和是()岁。

285．如图所示，从A 点走到B 点，沿线段走最短路线，共有()种不同走法。

186．五位打工者一天的辛苦劳动后共获得330元工资，由于工种不同，获得最高工资者比其他四位分别多得12、14、21和28元，获得最低工资者的工资是()元。

537．如图所示的图形的周长是()厘米。

2008．在数20468204682046820468中划去10个数字(不能改变原来数字的顺序)，得到一个最小的十位数，这个最小的十位数是()。

20004204689．右边的乘法算式中，只知道一个数字“8”，请你补全，那么这个算式的积最小是()。

106810．在1、2、3、4、5、6六个数中，选三个数，使它们的和能被3整除，那么，不同的选取共有()种。

811．有四袋糖，每袋糖的块数都不相同，任意三袋糖的块数总和都不少于60块，那么，这四袋糖的块数总和至少有()块。

8212．3根火柴可以摆成一个小三角形，用很多根火柴摆成了一个如图那样的大三角形，如果大三角形外沿的每条边都增加到10根火柴，那么摆成这样形状的大三角形需要用()根火柴。

30013．一次测验中，小胖答错了6道题，小亚答错了7道题，小丁丁答对的题的数量等于小胖和小亚答对题数量的总和，小丁丁答对了17道题，这次测验共有()道题。

1514．1997的数字和是1+9+9+7=26，小于2000的四位数中，数字和等于26的四位C B A × 8数共有()个。

中环杯、小机灵杯试题精选(题目)[1]

如果做对3道或3道以上试题的同学为考试合格。

请问：这次考试的合格率最多达百分之几？最少达百分之几？【6】把156支铅笔分成n堆（n>等于2)，要求每堆一样多且为偶数支。

有（）种分法。

【7】七个相同的羽毛球,放在四个不同的盒子里, 每个盒子里至少放一个, 不同的放法有( ) 种.【8】由甲城开往乙城的汽车每隔1小时一班逢整点出发，由乙城开往甲城的汽车每隔1小时一班但逢半点（30分）出发。

从一个城市到另一个城市需要6小时，假定汽车行驶在同一高速公路上，那么一辆开往乙城的汽车最多能遇到（）辆开往甲城的汽车。

【9】一群公猴、母猴和小猴共38只，每天共摘桃子266个。

1-9届三年级小机灵杯真题答案-图文

1-9届三年级小机灵杯真题答案-图文第一届............................................................. ............................................................... ..................2第二届............................................................. ............................................................... ..................3第三届............................................................. ............................................................... ..................4第四届............................................................. ............................................................... ..................5第五届复赛............................................................. ............................................................... ...........7第六届复赛............................................................. ............................................................... ...........7第七届复赛............................................................. ............................................................... ...........8第八届小机灵三年级初赛............................................................. ..................................................9第九届小机灵三年级复赛............................................................. .. (9)第1页共10页第一届答案1、4563672、23、88832964、32千克5、除数必定是9，商是36，所以被除数是3696、(33+3)38=33218887、(10+9+8+7+10)28、96(21)2649、有7种。

小晨精品9届小机灵杯决赛题及解析(优秀)

第九届“小机灵杯”小学生数学竞赛（决赛）试题（三年级）1、计算：12388294172009=（）。

【分析】速算与巧算。

原式=413841294172009=41(24187)2009=02、已知：*25，25，5221，则*代表的自然数是（）。

【分析】等量代换。

*=1。

3、父亲比儿子大30岁，明年父亲的年龄是儿子的3倍，那么儿子今年（）岁。

【分析】差倍型年龄问题。

以明年儿子的年龄作为“1”倍量，则根据差倍问题，儿子明年的年龄为：30(31)15（岁），所以儿子今年15114（岁）。

4、甲、乙两队进行篮球比赛，结果两队总分之和为86分。

现在知道甲队加上7分，就比乙队多1分，甲队得（）分。

【分析】和差问题。

甲队得分为：[86(71)]240分。

5、A、B、C、D、E五点在同一圆周上，任取其中的三点为顶点，可以得到一个三角形。

在这样的三角形中，以A、B两点中的至少一点为顶点的三角形共有（）个。

【分析】枚举法。

分成三类：（1）只包含A顶点的三角形有3个；（2）只包含B为顶点的三角形有3个；（3）同时包含A、B为顶点的三角形有3个，所以共有9个。

6、有10个数排成一排，每个数都是它前面一个数的一半，第四个数是64，这10个数的和是（）。

【分析】还原问题、数列规律。

和为：124816 (5121023)7、112233...20112011的末位数字是（）。

【分析】周期问题：尾数周期。

以10为一个周期，前10项的末位数字为112233...1010的末位数字，为5；因此2011项的末位数字为52011的末位数字，即为6.8、下面的乘法竖式中，不同的字母表示不同的数字，乘法竖式的乘积是（）。

F D1 39A98F G C10 4F F B117F E B C1274【分析】答案如又上图所示。

9、从1到100的整数中，有（）个数的各个数位中都不含数字1和2.【分析】页码问题、数字规律。

88163个。

10、下图中有（）个三角形。

11届小机灵杯三年级初赛解析

第十一届小机灵杯三年级初赛试题参考答案及分析1、【考点】计算——“山顶数列”【解析】1+2+3+……+49+50+49+……+3+2+1=50X50=25002、【考点】图形找规律【解析】观察图形规律的规律，我们发现3、【考点】还原问题【解析】最后书的数目相等为：450÷3=150（本）列表4、【考点】数字问题【解析】在919和920之间。

5、【考点】植树问题【解析】从第1根电线杆到第10根电线杆用了3分钟，共走了9个间隔，所以再走3分钟，还是走9个间隔。

10+9=19，即骑到第19根。

6、【考点】分步计数原理（乘法原理）【解析】6,7,8,9四个数字可以组成4×3×2×1=24（个）没有重复数字的四位数观察9768这个数比较大，从大到小排发现它是第4个数，所以从小到大排列，9768排在第21个。

7、【考点】周期问题，植树问题【解析】5×（20-1）=95（小时）95÷12=7 (11)倒推11个小时是时针指向108、【考点】计数【解析】9、【考点】归一问题【解析】先求出“单一量”135÷（5×2-1）=15，（735-135）÷5÷15=8（天）。

10、【考点】操作性问题【解析】如图所示：20+19+18+……+1+10=210+10=22011、【考点】等比数列求和【解析】1+3+9+27+81+243=（243×3-1）÷（3-1）=36412、【考点】巧填算符【解析】①1+2×3×4×5×6×7=5041②7-6-5+4+3-2÷1=15041-1=5040更多历年真题，敬请关注唯课数学公众号vclassedu。

1-9届5年级小机灵杯试题

第一届 (2)第二届 (4)第三届 (9)第四届 (13)第五届 (17)第六届“聪明小机灵”小学数学邀请赛（决赛）试题 (21)第七届“聪明小机灵”小学数学邀请赛（决赛）试题没有确定是否是 (24)第七届小机灵杯复赛 (27)第八届小机灵杯五年级决赛试题(含答案) (29)第九届小机灵杯五年级复赛试题 (31)第一届第二届第三届第四届第五届第六届“聪明小机灵”小学数学邀请赛（决赛）试题1、计算：0.02+0.04+0.06+……+20.04+20.06+20.08=（）。

2、已知N=95+195+1995+…+19999999995，那么，N的各位数字的和是（）。

3、有9个数，每次任意抽去一个数，计算剩下8个数的平均数，得到如下9个不同的平均数：101、102、103、104、105、106、107、108、109，这9个数的平均数是（）。

4、前2008个既能被2整除又能被3整除的正整数的和，除以9的余数是（）。

5、一本字典共有2008页，在这本字典的页码上，数字8共出现了（）次。

边长15分米的正方形分成两个高相等（AF=FD）的直角梯形与一个直角三角形，已知两个梯形面积的差是18平方分米，图中线段CG的长是（）分米。

7、文具店存有一批练习本，原定每本定价是20分。

现在决定把全部练习本按同一价格降价处理，但每本价格不能低于11分（降价后的价钱是整分数）。

如果把这批练习本全部卖出后可收得39.10元。

这批练习本一共有（）本，每本价钱比原定降价了（）元。

8、一个棱长都是正整数的长方体表面积是210平方厘米，已知它的六个面中有两个面积大于1平方厘米的正方形，则它的体积最大是（）立方厘米。

9、一次测验共有5道题，做对一题得1分，已知26人的平均分不少于4.8分，其中最低分得3分，并且至少有3人得4分，那么得5分的共有（）人。

10、M÷N÷P=6，M÷N-P=30，M-N=105，M=（）。