06第6章抽样调查1

合集下载

市场调查-第六章抽样技术

N = 721， n = 10, 721/10≈72
K =
用随机数表法，如果第一个确定的数字为102，则各样本单元编号依次为：102，174，246，318， 390，462，534，606，678，29。其中最后一个编号应为678 + 72 = 750。因大于N，故减去721,实际编号取为750- 721 = 29。
多级随机抽样是先把总体划分为若干一级单元，再把各个一级单元划分为若干个二级单元，直至不再划分的个体单元。在抽样时，先用简单随机抽样方法抽取部分一级单元，再在抽中的一级单元中抽取部分二级单元，依次操作，直到抽得个体单元为止。
多级随机抽样——demo
我国城市住户调查采用的就是多级抽样，先从全国各城市中抽取若干城市，再在城市中抽选街道，然后在各街道中抽选居民会，最后在各居委会中抽选居民户。
低收入 20%
高收入 20%
中收入 60%
高收入中收入低收入
分层比例抽样法
高收入层抽取的样本单元数为： 200×20%＝40（户）中收入层抽取的样本单元数为： 200×60%＝120（户）低收入层抽取的样本单元数为： 200×20%＝40（户）
在各层抽样时，只需采用简单随机抽样法即可。
2、分层最佳抽样法
二、分层随机抽样
分层随机抽样是先将总体所有单位按某一重要标志进行分层(类)，然后在各层(类)中采用简单随机抽样方式抽取样本单位的一种抽样技术形式。在划分层次时应注意，各层次内部保持确定的同质性，而各层次之间又应有明显的异质性。
分层比例抽样法分层最佳抽样法
1、分层比例抽样法
分层比例抽样法，指各层抽取的样本单元数是按各层单元数占总体单元数的比例加以确定。

第六章抽样调查习题答案

第六章抽样调查习题答案一、单项选择题1、 C2、 A3、 D4、 D5、C6、 D7、 C8、 A9、 D 10、A11、 D 12、C 13、B 14、 A 15、A16、 B 17、 B 18、D 19、 A 20、A21、 A 22、 D 23、 D 24、 B 25、A二、判断题1、CD2、AE3、BCD4、ABDE5、ABD6、AB7、ABCD8、AC9、ABCD三、判断题1、×2、√3、√4、√5、√6、×7、√8、×9、√10、√11、×12、√13、√14、×15、×16、√17、√18、×四、填空题1、随机、部分、总体2、计算、控制3、重复、不重复4、大于5、点估计、区间估计6、增加到4倍、减少三分之二、减少四分之三7、大样本、小样本8、正、反五、复习思考题1、影响抽样误差的主要因素有哪些？答：影响抽样误差大小的因素主要有：(1)总体单位的标志值的差异程度。

差异程度愈大则抽样误差愈大，反之则愈小。

(2)样本单位数的多少。

在其他条件相同的情况下，样本单位数愈多，则抽样误差愈小。

(3)抽样方法。

抽样方法不同，抽样误差也不相同。

一般说，重复抽样比不重复抽样，误差要大些。

(4)抽样调查的组织形式。

抽样调查的组织形式不同，其抽样误差也不相同，而且同一组织形式的合理程度也会影响抽样误差。

2、什么是抽样调查？它有哪些特点？答：抽样调查是根据部分实际调查结果来推断总体标志总量的一种统计调查方法，属于非全面调查的范畴。

它是按照科学的原理和计算，从若干单位组成的事物总体中，抽取部分样本单位来进行调查、观察，用所得到的调查标志的数据以代表总体，推断总体。

(1)只抽取总体中的一部分单位进行调查。

(2)用一部分单位的指标数值去推断总体的指标数值(3)调查样本是按随机的原则抽取的，在总体中每一个单位被抽取的机会是均等的，因此，能够保证被抽中的单位在总体中的均匀分布，不致出现倾向性误差，代表性强。

统计学原理-第六章抽样调查(复旦大学第六版)

全体。其单位数用N来表示。
2．样本总体：简称样本，是从全及总体中随机
抽取出来，代表全及总体部分单位的集合体。单位数用n表示。
5
二．全及指标和抽样指标
（一）全及指标
X 总体平均数： X N 总体成数：P
2
XF 或X F Q＝
2 2
N1 N N
（X－X）总体方差：＝总体标准差：＝（X－X）
（一）考虑顺序的不重复抽样数目
N! A N ( N 1)(N 2) ( N n 1) ( N n)! 4 3 2 1 2 例如A4 12 2 1
n N
（二）考虑顺序的重复抽样数目
B N
n N 2 4
n 2
例如 B 4 16
10
（三）不考虑顺序的不重复抽样数目
Ex X
28

2、一致性当抽样单位数充分大时，抽样指标和未知的总体指标之间的绝对离差为任意小的可能性也趋于必然性。
x X 任意小
3、有效性
即用抽样指标估计总体指标，要求作为优良估计量方差应该比其他估计量的方差小。

2
x X f
2
f

2
x X f
x
x E ( x)
2
18
说明：根据数理统计理论，在重复抽样条件下，抽样平均误差与全及总体的标准差成正比例关系。与抽样总体单位平方根成反比关系。
19
在不重复抽样情况下，抽样平均误差计算公式如下：
x x

N n 250 4－2 ( )＝（）＝9.13(件) n N 1 2 4－1
2
N
X X F 或 F X X F 或 F

统计学第六章抽样法

31
第六章抽样法
序号
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16 合计
样本变量x
40、40 40、50 40、70 40、80
50、40 50、50 50、70 50、80
70、40 70、50 70、70 70、80
80、40 80、50 80、70 80、80
－
x
x E(x)
总体
研究如何利用样本数据来推断总体特征。
内容包括：参数估计和假设检验。
目的：对总体
特征作出推
样本
断。
这是推断统计学研究的问题
5
第六章抽样法
描述统计与推断统计的关系
反映客观现象的数
据
概率论
（包括分布理论、大数定律和中心极限定
理等）
样本数
描述统计
推断统计
据
总体数据
（统计数据的搜集、整理、显示和分
13
第六章抽样法
第二节有关抽样的基本概念（2）
（二）抽样总体
也称子样，样本或样本总体，它是从全及总体中随机抽取出来的，代表全及总体的那部分单位的集合体。抽样总体的单位数称为样本容量，用n表示，对于N来说，n是很小的。
总体
样本
14
第六章抽样法
第二节有关抽样的基本概念（3）
• 二全及指标和抽样指标p.249 （一）全及指标
研究总体中的品质标志
总体成数 P N1
N
总体成数标准差 P
P1 P
17
第六章抽样法
第二节有关抽样的基本概念（5）
（二）抽样指标
抽样指标是由样本总体各单位标志值或标志特征计算的综合指标，也称统计量。与全及指标相对应有：样本平均数，样本标准差；样本成数，样本成数的标准差。

第六章抽样调查练习及答案

第六章抽样调查一、填空题1．抽选样本单位时要遵守原则，使样本单位被抽中的机会。

2．常用的总体指标有、、。

3．在抽样估计中，样本指标又称为量，总体指标又称为。

4．全及总体标志变异程度越大，抽样误差就；全及总体标志变异程度越小，抽样误差。

5．抽样估计的方法有和两种。

6．整群抽样是对被抽中群内的进行的抽样组织方式。

7．误差分为和代表性误差；代表性误差分为________和偏差；偏差是____________________________，也称为________________。

8．简单随机抽样的成数抽样平均误差计算公式是：重复抽样条件下：；不重复抽样条件下：。

9．误差范围△，概率度t 和抽样平均误差μ之间的关系表达式为。

10．抽样调查的组织形式有：。

二、单项选择题1．所谓大样本是指样本单位数在( )及以上A 30个B 50个C 80个 D100个2．抽样指标与总体指标之间抽样误差的可能范围是( )A 抽样平均误差B 抽样极限误差C 区间估计范围D 置信区间3．抽样平均误差说明抽样指标与总体指标之间的( )A 实际误差B 平均误差C 实际误差的平方D 允许误差4．是非标志方差的计算公式( )A P(1-P)B P(1-P)2C )1(P P -D P 2(1-P)5．总体平均数和样本平均数之间的关系是( )A 总体平均数是确定值，样本平均数是随机变量B 总体平均数是随机变量，样本平均数是确定值C两者都是随机变量 D两者都是确定值6．对入库的一批产品抽检10件，其中有9件合格，可以( )概率保证合格率不低于80％。

A 95．45％B 99．7396C 68．27％D 90％7．在简单随机重复抽样情况下，若要求允许误差为原来的2／3，则样本容量( )A 扩大为原来的3倍B 扩大为原来的2／3倍C 扩大为原来的4／9倍D 扩大为原来的2．25倍8.根据抽样调查得知：甲企业一等品产品比重为30%，乙企业一等品比重为50%一等品产品比重的抽样平均误差为（）A 甲企业大B 两企业相同C 乙企业大D 无法判断9．是非标志的平均数是（）A -P)1P(B P(1-P)C pD (1-P)210．重复抽样的误差一定（）不重复抽样的误差。

第6章抽样调查(1)

33
1、由于总体单位总数未知，因此采用重复抽样公式。又总体标准差未知，采用过去资料最大标准差作为估计值。
x

n

0.12 0.0219 （升） 30
n1 30 2 2、合格率p 93.3% n 30 S P p(1 p) 93.3% (1 93.3%) 6.25%
根据质量标准，使用寿命800小时及以上者为合格品，计算产品平均合格率和标准差。
14
全及指标
X XF X N F
P N1 N
X
2
( X X )2
N

( X X )2 F F
X
(X X )
N
2

(X X ) F F
2
P 2 P(1 P)
31
例上题中，如果寿命低于9000小时的产品是不合格品，计算不合格率（合格率）的抽样平均误差。
不合格率：
n1 90 x p 18% n 500
Sp
p(1 p)
Sp
0.18 (1 0.18) 38.4%
重复抽样下：
p
p
Sp n
0.384 1.7% n 500
3
特点
遵循随机原则抽取部分单位；
用样本推断总体；
会产生抽样误差，但误差可以计算和控制。
4
随机原则的实现
统计学概论
是将总体中每个单位的编号写在外形完全一致的签上，将其搅拌均匀，从中任意抽抽签法选，签上的号码所对应的单位就是样本单位。将总体中每个单位编上号码，然后使用随机数表，查出所要抽取的调查单随机数表法位。

统计学第六章抽样调查

n
N
例题2
xf
x
f
8400 200
42
s (x x)2 f 12200 7.81
f
200
2 (1 n ) 7.812 (1 200 ) 0.55
x
n
N
200
2000
例题3
❖某冷库的10万只冻鸡合格率为97%，如果按重复抽样与不重复抽样各抽取1000只和2000只，分别计算抽样平均误差。
A
B
较小的样本容量
X
成数
❖ 总体成数
每个总体单位标志值设为0或1 1：具有某种属性的总体单位标志值 0：不具有某种属性的总体单位标志值总体中具有某种特征的单位占全部总体单位
数的比例称为总体成数，记作P 成数总体方差：P(1-P)
总体成数和样本成数
❖ 样本成数
从成数总体中抽取样本容量为n的样本样本中具有此种特征的单位占全部样本单位
从1、2 、3、4中随机抽取2个的样本数
重复抽样考虑顺序
16
1、1 2、1 3、1 4、1
1、2 2、2 3、2 4、2
1、3 2、3 3、3 4、3
1、4 2、4 3、4 4、4
从1、2 、3、4中随机抽取2个的样本数
不重复抽样考虑顺序 12
2、1 3、1 4、1
1、2
3、2 4、2
1、3 2、3
- 2.58x
-1.65 x
+1.65x + 2.58x
x
-1.96 x
+1.96x
90%的样本
95% 的样本
99% 的样本
区间估计
❖ 根据一个样本的观察值给出总体参数的估计范围 ❖ 给出总体参数落在这一区间的概率 ❖ 例如: 总体均值落在50~70之间，置信度为 95%

第六章抽样调查习题

第六章抽样调查习题一、单项选择题1、抽样调查必须遵循的原则是（）。

A、准确性原则B、可靠性原则C、随机原则D、灵活性原则2、所谓小样本是指样本单位数在（）。

A、30个以下B、100个以下C、20个以下D、50个以下3、重复抽样误差和不重复抽样误差相比（）。

A、两者相等B、前者小于后者C、两者不定D、前者大于后者4、在纯随机重复抽样的情况下，要使抽样误差减少一半，（其它条件不变），则样本单位数必须（）。

A、增加2倍B、增加到2倍C、增加4倍D、增加到4倍5、某工厂连续生产，在一天中每隔半小时取出一分钟的产品进行全部检查，这是（）。

A、等距抽样B、类型抽样C、整群抽样D、纯随机抽样6、纯随机重复抽样条件下，抽样单位数扩大为原来的9倍，则（）。

A、抽样误差不变B、无法判断C、抽样误差缩小为原来的九分之一D、抽样误差缩小为原来的三分之一7、抽样推断的理论基础是概率论中的（）。

A、参数估计B、方差分析C、大数法则D、误差理论8、在抽样调查中（）。

A、既有登记误差，也有代表性误差B、只有登记误差，没有代表性误差C、没有登记误差，只有代表性误差D、既无登记误差，也无代表性误差9、在抽样调查中，无法避免的误差是（）。

A、登记性误差B、允许误差C、系统性误差D、抽样误差10、能够事先加以计算和控制的误差是（）。

A、抽样误差B、代表性误差C、登记误差D、系统性误差11、抽样误差与抽样极限误差的关系为（）。

A、前者小于后者B、前者大于后者C、前者等于后者D、不能断定大小12、抽样估计中，要概率保证程度为95%，则相应的概率度为（）。

A、2B、3C、1.96D、1.813、抽样单位数与抽样误差的关系为（）。

A、正比B、反比C、反向D、相等14、抽样误差与标准差的关系为（）。

A、正比B、反比C、反向D、相等15、抽样单位数与标准差的关系为（）。

A、正比B、反比C、反向D、相等16、抽样单位数与概率度的关系为（）。

A、反比B、正比C、反向D、相等17、一个全及总体（）。

6第六章抽样设计

分层
高收入层高高高高高高高中收入层中中中中中中低收入层低低低低低低低低
高
高
中
中
中
低
分群
第一群高高高中中中低低低
第二群高高高中中中低低低
第三群高高高中中中低低低
例
题
某市要进行啤酒需求量的调查，该市共有 30个街道，300个居民委，每个居民委有 200户居民，试采用分群抽样调查。
1、全及总体：简称总体或母体，是指所要调查对象的总体。 2、抽样总体：简称样本量或样本，是总体的一部分，是指从总体中抽选出所要直接观察的全部单位。每一个被抽到的个体或单位，就是一个样本。
三、指标和标志
1、标志：用来说明个体特征名称，如个人年龄、性别、职业等。标志可以是数量标志也可以是质量标志。一种标志是用数量来加以反映的，叫数量标志，有标志值。如，年龄、收入等；另一种是不可以用数值来加以反映的，叫品质标志，如职业、性别等。他们虽然可以用1，0来表示，但它只是一种代号，不代表数值。
六、抽样单元
为了便于实现抽样，常常将总体按某些特征划分成互不重叠的部分，每一个部分都叫做一个抽样单元。例如，对“北京市中高档商品房的市场需求调查，”就可以先按区域将北京划分为，东城区、西城区、崇文区、丰台区、海淀区、宣武区、潮阳区等。这是一级抽样单位，在案街道划分成二级抽样单位。
P+Q=1
3、总体（方差）标准差：是指说明总体数量特征离散程度的指标。用σ表示公式（1）简单式（2）加权式
五、重复抽样和不重复抽样
1、重复抽样：是指任何一个样本单位被抽出进行登记以后，再放回去参加下一次的抽取，总数始终不变。 2、不重复抽样：是指各样本单位被抽出登记信息，不再放回去参加第二次抽取。被抽中的样本不会在有第二次被抽中的可能性，抽样总体单位数减少。

第6章抽样

【观念应用4-3】仍以上述居民收入与购买力之间关系为例。各层样本标准差其中高收入为300元，中收入为200元，低收入为100元，为了便于观察，列表如表5-2所示。表4-2 调查单位数与样本标准差乘积计算表各层次（不同经济收入）
各层的调查单位数（户）Ni
4 000 12 000 4 000 20 000
47 74 76 56 59 22 11 26 21 60 28 62
43 24 62 85 56 77 17 63 12 17 17 37
73 67 27 99 35 94 53 78 86 34 12 35
86 62 66 26 64 39 71 59 29 44 13 18
36 42 56 96 37 49 57 16 78 09 40 98
各层的样本标准差（元）Si 300 200 100
高中低
∑NiSi
4.2.2

随机抽样技术的分类及技术特点
(3)等距离随机抽样技术抽样间隔计算公式为：抽样间隔=总体数（N）÷样本数（n） (4.2)

【观念应用4-4】某地区有零售店110户，采用等距离抽样方法抽选11户进行调查。【分析提示】等距离抽样，方法简单，省却了一个个抽样的麻烦，适用于大规模调查。还能使样本均匀地分散在调查总体中，不会集中于某些层次，增加了样本的代表性。
96 81 50 96 54 54 24 95 64 47 33 83
47 14 26 68 82 43 55 55 56 27 20 50
36 57 75 27 46 55 06 67 07 96 38 87
61 20 07 31 22 82 88 19 82 54 26 75

第六章抽样

册和登记表（抽样框）就可进行。
• 其局限是，只适用于总体单位数量不多，且分布
较均匀的调查总体，即单位间差异性不大的研究
对象，否则将无法保证样本的代表性。
• 练习请利用随机数表，从N=60总体中抽取15个样本。
系统抽样
• 系统抽样（等轴抽样、等距抽样、机械抽样）：把总体的单位进行编号排序，在计算出某中间隔，然后按这个固定的间隔抽取个体的号码来组成样本的方法。 • 基本和简单随机抽样一样，计算公式也一样。 • 需要完整的样本框，直接从总体中抽取个体。
• 获得完全正确的样本框几乎是不可能的。 • 制定抽样框是抽样的关键步骤之一。 • 当抽样是分段进行时，在几个不同的抽样层次上进行时，则要分别建立起几个不同的样本框。 • 比如：研究某市小学生的学习情况。从500所小学中抽取10所小学，再从这10所小学，每个小学抽取3个班级，被抽中的班级中再抽取10名同学。所以要有三个样本框：全市学校名单每所抽中学校班级名单每个被抽中班级学生的名单
抽样的概念
• 统计值（样本值）：样本中某一个变量的综合描述。 • 是从样本中计算出来的。 • 是作为总体值的估计值。
2 抽样的作用
• 用十分有限的人力、财力、时间去了解庞杂、广阔、纷繁、多变的社会现象。 • 比如：民意测验，要求迅速、准确。往往调查对象不到2000人。
3.抽样的类型
• 概论抽样 • 非概率抽样
决定抽样方案
• 对于具有不同研究目的、不同范围、不同对象和不同客观条件的社会研究，所使用的抽样方法是不一样的。 • 依据研究的目的的要求、依据各种抽样的特点，以及其他有关因素来觉得具体采用哪种抽样方法。 • 同时确定样本规模以及主要的精确程度。
实际抽取样本

第六章抽样调查

第六章抽样调查一、单项选择题1.随机抽样的基本要求是严格遵守（）①准确性原则；②随机原则；③代表性原则；④可靠性原则。

2.抽样调查的主要目的是（）①广泛运用数学的方法； ②计算和控制抽样误差；③修正普查的资料； ④用样本指标来推算总体指标。

3.抽样总体单位亦可称（）①样本； ②单位样本数； ③样本单位； ④总体单位。

4.反映样本指标与总体指标之间抽样误差可能范围的指标是（）①样本平均误差； ②抽样极限误差； ③可靠程度； ④概率程度。

5.在实际工作中，不重复抽样的抽样平均误差的计算，采用重复抽样的公式的场合是（）①抽样单位数占总体单位数的比重很小时；②抽样单位数占总体单位数的比重很大时；③抽样单位数目很少时； ④抽样单位数目很多时。

6.在其他条件不变的情况下，抽样单位数目和抽样误差的关系是（） ①抽样单位数目越大，抽样误差越大；②抽样单位数目越大，抽样误差越小；③抽样单位数目的变化与抽样误差的数值无关； ④抽样误差变化程度是抽样单位数变动程度的21。

7.用简单随机抽样（重复抽样）方法抽取样本单位，如果要使抽样平均误差降低50%，则样本容量需扩大到原来的（）①2倍； ②3倍； ③4倍； ④5倍。

8.事先将全及总体各单位按某一标志排列，然后依固定顺序和间隔来抽选调查单位的抽样组织形式，被称为（）①分层抽样；②简单随机抽样；③整群抽样；④等距抽样。

9.全及总体按其各单位标志性质不同，可以分为（）①有限总体和无限总体； ②全及总体和抽样总体；③可列无限总体和不可列无限总体；④变量总体和属性总体。

10.抽样指标是（）①确定性变量； ②随机变量； ③连续变量； ④离散变量。

11.用考虑顺序的重置抽样方法，从4个单位中抽选2个单位组成一个样本，则样本可能数目为（）①1642=； ②10!3!2!5=； ③12!2!4=； ④6!2!2!4=。

12.无偏性是用抽样指标估计总体指标应满足的要求之一，无偏性是指（） ①样本平均数等于总体平均数； ②样本成数等于总体成数；③抽样指标等于总体指标； ④抽样指标的平均数等于总体指标。

统计学相关单选题第6章题目及答案

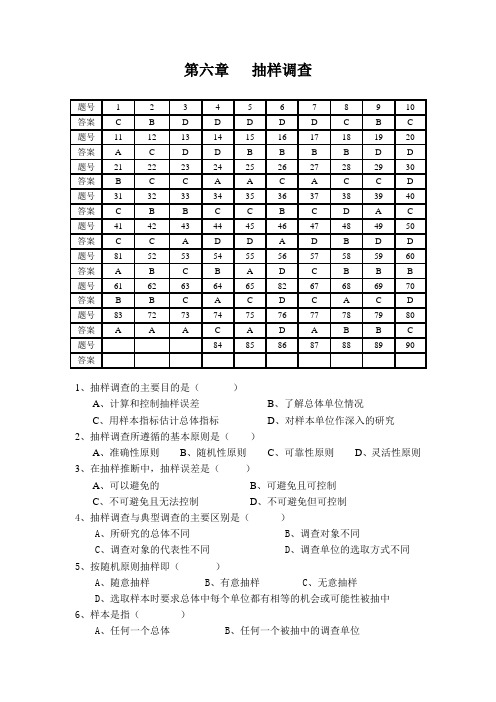
第六章抽样调查题号 1 2 3 4 5 6 7 8 9 10 答案 C B D D D D D C B C 题号11 12 13 14 15 16 17 18 19 20 答案 A C D D B B B B D D 题号21 22 23 24 25 26 27 28 29 30 答案 B C C A A C A C C D 题号31 32 33 34 35 36 37 38 39 40 答案 C B B C C B C D A C 题号41 42 43 44 45 46 47 48 49 50 答案 C C A D D A D B D D 题号81 52 53 54 55 56 57 58 59 60 答案 A B C B A D C B B B 题号61 62 63 64 65 82 67 68 69 70 答案 B B C A C D C A C D 题号83 72 73 74 75 76 77 78 79 80 答案 A A A C A D A B B C 题号84 85 86 87 88 89 90 答案1、抽样调查的主要目的是（）A、计算和控制抽样误差B、了解总体单位情况C、用样本指标估计总体指标D、对样本单位作深入的研究2、抽样调查所遵循的基本原则是（）A、准确性原则B、随机性原则C、可靠性原则D、灵活性原则3、在抽样推断中，抽样误差是（）A、可以避免的B、可避免且可控制C、不可避免且无法控制D、不可避免但可控制4、抽样调查与典型调查的主要区别是（）A、所研究的总体不同B、调查对象不同C、调查对象的代表性不同D、调查单位的选取方式不同5、按随机原则抽样即（）A、随意抽样B、有意抽样C、无意抽样D、选取样本时要求总体中每个单位都有相等的机会或可能性被抽中6、样本是指（）A、任何一个总体B、任何一个被抽中的调查单位C、抽样单元D、由被抽中的调查单位所形成的总体7、抽样框是指（）A、总体B、样本C、由总体单位组成的名单或地图D、全部抽样单位组成的名单或地图8、抽样误差是指（）A、在调查过程中由于观察、测量等差错所引起的误差B、在调查中违反随机原则出现的系统误差C、随机抽样而产生的代表性误差D、人为原因所造成的误差9、抽样极限误差是（）A、随机误差B、一定可靠程度下抽样误差的最大绝对值C、最小抽样误差D、最大抽样误差的绝对值10、反映样本指标与总体指标之间的平均误差程度的指标是（）A、抽样误差系数B、概率度C、抽样平均误差D、抽样极限误差11、抽样调查的误差包括（）A、登记性误差和代表性误差B、只有登记性误差，没有代表性误差C、没有登记性误差，只有代表性误差D、既没有登记性误差，也没有代表性误差12、抽样平均误差是指样本平均数或样本成数的（）A、平均数B、平均差C、标准差D、标准差系数13、抽样平均误差与极限误差的关系是（）A、抽样平均误差大于极限误差B、抽样平均误差小于极限误差C、抽样平均误差等于极限误差D、抽样平均误差可能大于、小于或等于极限误差14、下列事件中不属于严格意义上的随机事件的是（）。

统计学原理第六章随堂练习题 (1)

2
答案：
16.（2） 17.（1）
18．若总体服从正态分布，且总体方差已知，则通常选用统计量( )对总体平均数进行检验。
(1)
Z x X0 S n
(2)
Z
x X0

n
x X0 x X0 t t (3) (4) S n n 19．矿砂的5个样品中，测得其含铜量均值为
(
)
( )
10．假设检验和区间估计之间没有必然的联系。
答案： 6. × 7. √ 8. × 9. √ 10. ×
答案：
5.（4）
6.（3）
7．纯随机抽样(重复)的平均误差取决于( )。 (1)样本单位数 (2)总体方差 (3)样本单位数和样本单位数占总体的比重 (4)样本单位数和总体方差
N n 8．抽样平均误差公式中， N 1 这个因子总是( (1)大于1 (2)小于1 (3)等于1 (4)唯一确定值
变异程度的大小和抽样误差无关。 ( ) 7．正态分布总体有两个参数，一个是均值(期望值) X，一个是方差 2 ，这两个参数确定以后正态分布也就确定了。 ( ) 8．原假设的接受与否，与选择的检验统计量有关，与 (显著
水平)无关。
（）
9．单侧检验中，由于所提出的原假设不同，可分为左侧检验
和右侧检验。
( x x)
n
2
，这是( )。
答案：
3.（2）
4.（1）
5．抽样极限误差是指抽样指标和总体指标之间( (1)抽样误差的平均数 (2)抽样误差的标准差 (3)抽样误差的可靠程度 (4)抽样误差的最大可能范围
)。
6．抽样误差的定义是( )。 (1)抽样指标和总体指标之间抽样误差的可能范围 (2)抽样指标和总体指标之间抽样误差的可能程度 (3)样本指标与所要估计的总体指标之间数量上的差别 (4)抽样平均数的标准差