江苏省镇江市句容市天王中学七年级数学上册 2.3 数轴学案2

合集下载

新苏教版七年级数学上册2.3数轴学案

新苏教版七年级数学上册2.3数轴学案姓名【教学目标】1.进一步掌握数轴的三个要素，并正确画出数轴.2.能利用数轴比较两个有理数的大小.3.掌握在数轴上有理数是按照一定的顺序排列的，由数轴上两个数的位置关系，就可以判断这两个数的大小关系。

4.深化对数轴的理解，体会数形结合的思想.【旧知回顾】1.下列图形是数轴的是（）．2、利用数轴回答：（1）写出所有大于-3且不大于4的整数有；（2）数轴上，在原点左边且离原点3个单位长度的点表示的数是______；距离原点4个单位长度的点表示的数是_______；点A表示的数是112-，则距离A点2个单位长度的数是___________.(利用数形结合的思想来解决问题，有利于学生解题)3、一辆货车从超市出发，向东走了2km，到达小刚家，继续向东走了3km到达小红家，又向西走了9km到达小英家，最后回到超市.⑴请以超市为原点，以向东方向为正方向，用1cm单位长度表示1km，画出数轴；并在数轴上表示出小刚家、小红家、小英家的位置.⑵小英家距小刚家有多远？⑶货车一共行驶了多少千米？4、在数轴上画出表示下列各数的点：112 2,1,3,0,,4235 ---【新知探究】1、你会把上面第4小题中的数从小到大排列吗？请用“<”号将这些数连接起来。

2、请观察数轴上点的位置与它们所表示的数的大小有什么关系？【例题精讲】例1、利用数轴比较下列各组数的大小－３____－４0____ 5 -0.0001____ 0例2、在数轴上画出表示下列各数的点，并用“＞”号将这些数连接起来。

1,0,2,3,5, 1.52---【小结】有理数大小比较法则：（学生能够自己归纳出来比较好）练习：22p 习题3【当堂反馈】1、如图，根据有理数a,b,c 在数轴上的位置，下列关系正确的是（）A.、b>c>0>a B 、.a>0>c>b C 、.b>a>c>0 D 、.c<0<a<b2、在数轴上画出表示下列各数的点，并根据这些点的位置，用“<”号将这些数连接起来。

2.3数轴-苏科版七年级数学上册教案

2.3 数轴-苏科版七年级数学上册教案一、教学目标1.掌握数轴的基本概念及表示方法；2.掌握正数、负数在数轴上的位置；3.能够根据数值的大小在数轴上比较大小；4.能够将数轴上的点对应到数值上。

二、教学重难点重点：数轴的基本概念及表示方法。

难点：正数、负数在数轴上的位置。

三、教学过程1. 导入（5分钟）1.老师介绍数轴的基本概念，让学生了解数轴是什么，有什么作用。

2.老师让学生想想，在生活中我们经常用到数轴吗？有哪些地方用到数轴？2. 讲解（15分钟）1.老师介绍如何画数轴，怎样将数值对应到数轴上，以及如何表示正数、负数。

2.老师画一张简单的数轴，让学生模仿画一张。

3.老师在数轴上标出几个数，并让学生说出这些数在数轴上的位置。

4.老师介绍正数、负数在数轴上的位置，并让学生自己练习画出正数、负数所在的位置。

3. 练习（30分钟）1.老师出题让学生在数轴上标出一些数字并表示正数、负数。

2.老师出题让学生判断数轴上两点的大小关系。

3.老师出题让学生计算数轴上两点之间的距离。

4.老师出题让学生将数轴上的点对应到数值上。

4. 总结（5分钟）1.老师让学生回答几个关于数轴的问题，巩固学生的理解程度。

2.老师提醒学生要在课后复习并练习数轴相关的知识。

四、教学反思本节课的教学重点是讲解数轴的基本概念及表示方法。

在教学过程中，我通过讲解、演示和练习等方式帮助学生掌握了数轴的基本概念及表示方法，并让学生能够在数轴上表示数字并比较大小。

在教学中，我发现一些学生对数轴上正数、负数的位置还不够清晰，需要反复强调和练习。

此外，一些学生还不太熟练地将数轴上的点对应到数值上，也需要在课后继续练习。

总体来说，整节课的教学效果还不错。

在以后的教学中，我将注意加强对学生的巩固练习，并根据学生的实际情况适当调整教学策略，力争使每位学生都能够理解和掌握数轴相关的知识。

2.3数轴-苏科版七年级数学上册教学设计

2.3 数轴-苏科版七年级数学上册教学设计一、教学目标1.理解数轴的概念和作用；2.掌握数轴上数的表示方法；3.能够在数轴上画出给定数值的点；4.能够读取数轴上的数值；5.能够解决数轴上的简单问题。

二、教学准备1.教师准备：–数轴的模型或幻灯片；–钢笔和白板。

2.学生准备：–数学笔记本；–铅笔。

三、教学过程步骤一：引入1.教师拿出数轴模型或幻灯片，向学生展示，并简要解释数轴的定义和作用。

2.引导学生思考：数轴有什么作用？它是用来表示什么的？步骤二：认识数轴1.教师在白板上画出一个简单的数轴。

2.教师引导学生观察数轴，解释数轴上的刻度和标记。

3.教师提问：数轴上的刻度表示什么意思？标记的作用是什么？4.学生回答并讨论。

步骤三：数的表示方法1.教师解释数轴上数的表示方法：正数在原点的右侧，负数在原点的左侧。

2.教师在数轴上画出几个正数和负数的表示，并解释。

步骤四：标记给定数值1.教师在白板上画一个空的数轴，并给出一个数值。

2.学生根据给定的数值，在数轴上标记出相应的位置。

3.学生互相比较自己的标记，讨论是否一致。

4.教师给出正确的标记位置，并解释。

步骤五：读取数轴上的数值1.教师给出一个标记好的数轴，并提问：请读取数轴上的数值。

2.学生依次读取数轴上的数值，并进行核对。

3.教师在白板上画出几个带有标记的数轴图，学生读取数值并进行练习。

步骤六：解决数轴上的问题1.教师给出一个问题：在数轴上，0点与7点的距离是多少？请写出计算过程。

2.学生结合数轴的刻度和标记，回答问题并解释计算过程。

3.教师引导学生总结解决数轴上问题的方法和步骤。

四、教学总结1.教师向学生复习本节课的内容，并总结要点。

2.学生将笔记整理完善，并完成课后作业。

五、课后作业1.完成课后作业册中与数轴相关的练习题；2.思考：我们在生活中还能用到数轴吗？请举例说明。

苏科版-数学-七年级上册-2.3.2 数轴(2)教案

教学目标： 1.进一步掌握数轴的三个要素，并正确画出数轴.2.能利用数轴比较两个有理数的大小.3.掌握在数轴上有理数是按照一定的顺序排列的，由数轴上两个数的位置关系，就可以判断这两个数的大小关系。

4.深化对数轴的理解，体会数形结合的思想.教学重点：数轴上的已知点说出它所表示的数，能将有理数用数轴上的点表示出来.教学难点：会利用数轴比较有理数的大小.教学过程：（一）问题情境1把温度5℃、-2℃、-3℃、 0℃按从低到高的顺序排列；2在数轴上画出表示-3、-2、5、0的点，你能说出这几个数的大小吗？由此引入用数轴来比较两个有理数的大小。

数轴上的点的位置与所表示的数的大小有什么规律？学生讨论后归纳得出：数轴上两个点表示的数，右边的总比左边的大，正数都大于0，负数都小于0，正数大于负数。

例1、比较下列每组数的大小：（1）—3和—3.5 （2）－3.5，21 和－0.5 由（1）问：哪一个数大？哪一个点离原点的距离较近？那么3和3.5呢？哪个数大？哪一个点离原点的距离近？议一议：下列说法是否正确？说说你的理由。

最大的负数是-1；大于-6且小于-4的数是-5；-0.1>-10；（二）自学、相信自己1.课本21页：练一练2.课本22页：习题2.3 3、5、6.(三）应用探究1.在数轴上表示下列各数，并把它们按照从小到大．．．．的顺序排列： 2，94-，－1.5，0，132-2.如图，数轴上一点，把点A 向左移动3个单位长度到点B ，把点A 向右移动5个单位长度到点C. ⑴用“<”连结A 、B 、C 三点表示的数；⑵点3.观察数轴，回答下列问题（1）有没有最大或最小的整数？有没有最小的自然数？（2）不小于－3的负整数有哪些？（3）比－2小4的数是什么数？（4）－3比－9大多少？三、课堂小结1.在数轴上表示的两个数，右边的数总比左边的大；2.正数都大于零，负数都小于零，正数大于负数．四、作业布置数学补充习题板书设计教学反思：学生在用数轴比较大小时，数轴上的分数表示的时候错误较多。

七年级数学上册 2.3 数轴(第2课时)教学案 (新版)苏科版

2.3数轴（2）
教学内容
教材版本
苏科版
教学课时
共 2 课时第2 课时
课型
新授课
教学目标
教学重点
能利用数轴比较两个有理数的大小
教学难点
掌握在数轴上有理数是按照一定的顺序排列的，由数轴上两个数的位置关系，就可以判断这两个数的大小关系。
教学准备
教学过程
修注栏
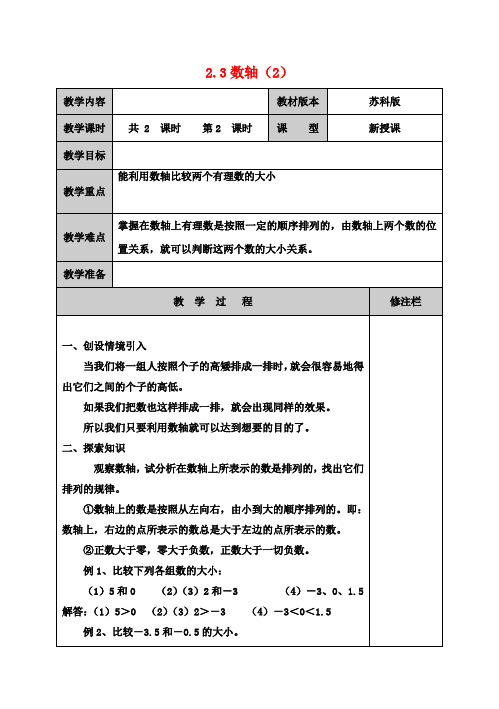
一、创设情境引入
当我们将一组人按照个子的高矮排成一排时，就会很容易地得出它们之间的个子的高低。
例1、比较下列各组数的大小：
（1）5和0 （2）（3）2和－3 （4）－3、0、1.5
解答：（1）5＞0 （2）（3）2＞－3 （4）－3＜0＜1.5
例2、比较－3.5和－0.5的大小。
解答：比较两个负数的大小时我们通常利用数轴进行比较：
由数轴可见：表示－3.5的点A在表示－0.5的点的左边，所以，－3.5＜－0.5
例3、在数轴上表示，并根据数轴指出所有大于的整数。
解答：整数有－3、－2、－1、0、1、2
例4、观察数轴，回答下列问题
（1）有没有最大或最小的整数？有没有最小的自然数？
（2）不小于－3的负整数有哪些？
（3）比－2小4的数是什么数？
（4）－3比Leabharlann 9大多少？解答：（1）没有最大或最小的整数，最小的自然数是0
（2）－3、－2、－1 （3）利用数轴：－6 （4）利用数轴：6
例5、在数轴上与数－2相距2个单位长度的点表示的数为＿＿＿＿，长为2个单位长度的木条放在数轴上，最少能覆盖＿＿个表示整数的点，最多能覆盖＿＿＿个表示整数的点。
解答：0或－4；2；3。
三、随堂练习
1、下列说法正确的是（）

江苏省镇江市句容市天王中学七年级数学上册 3.2 代数

3.2代数式课型：新授班级学生姓名: 执教人签名【学习目标】1.了解代数式，单项式，单项式的系数、次数，多项式，多项式的项、次数，整式的概念；2.能用代数式表示简单问题的数量关系；能解释一些简单代数式的实际背景或几何背景；【重点难点】1.单项式的系数、次数，多项式每一项的系数、次数；2.能解释一些简单代数式的实际背景或几何背景；【预习部分】1、一个长方形的长是 a m，宽是长的一半，这个长方形的宽是__________m ，面积是__________m22、钢笔每支2元，铅笔每支0.5元，n支钢笔和m支铅笔共____________元3、某农场有亩产a千克的水稻m亩，亩产b千克的水稻n亩，这个农场水稻的平均亩产为_ 千克。

日期教师评价家长签名【合作探究】1、我们把上述这些式子称为，单独的一个数或一个字母也是。

2、代数式的概念：代数式是用把和连接而成的式子。

3、数与_____的积组成的代数式叫单项式，单独一个_____或一个_____也是单项式。

4、单项式中的 _______叫做这个单项式的系数，单项式中的 ___ __ _ _叫做这个单项式的次数。

5、几个单项式的______叫做多项式。

在多项式中，每个单项式叫做多项式的_____ __，叫做多项式的次数。

6、_____ _和_____ __统称为整式。

7.书写代数式的注意点：（1）a×b通常写为或（乘号省略），但是数字与数字相乘乘号省略。

（2）1÷a通常写作（除号用表示）。

（3）写在的前面。

如2ab不写成ab2。

1【例题教学】例1、把下列式子填入相应的空格内（填序号） ⑴2.5, ⑵-35, ⑶2y , ⑷x5, ⑸2a+2b, ⑹yx 3223+, ⑺2x>-3 , ⑻y=ax 2+bx+c, ⑼kx+b. （10）0代数式:__________ . 单项式:___________ .多项式:_____ ___. 整式:____________ 例2、根据要求列代数式:⑴ a,b 两数的平方和表示为________. ⑵a,b 两数的和的平方表示为________. （3） a,b 两数的差的倒数表示为______.（4）n 表示任意一个整数,那么任意一个偶数可以表示为_____,任意一个奇数可以表示为______,任意一个被3除余2的数表示为______. 例3、请指出下列单项式的系数与次数。

2.3数轴-苏科版七年级数学上册导学案

第二章有理数课题：2.3数轴(1)【学习目标】:1、掌握数轴概念，理解数轴上的点和有理数的对应关系；2、会正确地画出数轴，利用数轴上的点表示有理数；3、领会数形结合的重要思想方法；【重点难点】：数轴的概念与用数轴上的点表示有理数；【导学指导】一、知识链接观察下面的温度计,读出温度.分别是5 °C、-10 °C、0 °C；二、自主探究1、由上面的两个问题，你受到了什么启发？能用直线上的点来表示有理数吗？答：能用直线上的点来表示有理数2、自己动手操作，看看可以表示有理数的直线必须满足什么条件？引导归纳：画数轴需要三个条件，即原点、正方向和单位长度。

例题评析例1.指出数轴上的点A,B,C,D分别表示什么数?A B E C D-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6答：A,B,C,D分别表示：-5,-1.5,2.5,63.用数轴上的点表示无理数做一做：怎样用数轴上的点表示圆周率π？(1)．画一个直径为1的圆片，将圆片上的点A放在原点处；(2)．把圆片沿数轴向右滚动一周，点A到达的位置点A′表示的数就是π．按要求画出表示π的点，如图．有理数和无理数都可以用数轴上的点表示；反过来，数轴上的任意一点都表示一个有理数或无理数．例 2.数轴是一个非常重要的数学工具，它使数和数轴上的点建立起对应关系，揭示了数与点之间的内在联系，它是“数形结合”的基础．请利用数轴回答下列问题：(1)在数轴上，到原点的距离为5的点有__2__个，它们表示的数是___5,-5____；(2)在数轴上，从表示2的点出发，先向右移动3个单位长度，再向左移动6个单位长度，最后的终点表示的数是_-1_(3)在数轴上，点A表示数2，那么与A点相距4个单位的点表示的数是__-2,6__三、巩固知识[典型问题]1.在数轴上,原点及原点左边所表示的数是 ( )A.正数B.负数C.不是负数D.不是正数2.下列语句中正确的是 ( )A.数轴上的点只能表示整数B.两个不同的有理数可以用数轴上的同一点表示C.数轴上的一个点,只能表示一个数D.数轴上到原点距离等于2个单位长度的点表示的数是23.数轴上表示－3的点在原点___ __侧,距原点的距离是___ ___;表示+4的点在原点的__ _侧,距原点的距离是__ ___.4.先画出数轴,并在数轴上画出表示下列各数的点:－1.5, 0, －3, 212, －2 再按数轴上从左到右的顺序,将这些数重新排列.5.指出数轴上的A 、B 、C 、D 、E 各点表示什么数.(注:如果这个点的位置不很明确,可估计) A B C D E-3 -2 -1 0 1 2 3【四基训练】6.数轴上与原点距离为3的点所表示的数是 ( )A. 3B. －3C. ±3D. 67.如下图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看出,终点表示的数是－2.-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6已知A,B 是数轴上的点,请参照上图,完成下列填空:(1)如果点A 表示－3,将A 向右移动7个单位长度,那么终点表示的数是_______;(2)如果点A 表示3,将A 向左移动7个单位长度,再向右移动5个单位长度,那么终点表示的数是_______;(3)如果将点B 向右移动3个单位长度,再向左移动5个单位长度,终点表示的数是0, 那么点B 所表示的数是__________8.一个点从原点开始,按下列条件移动两次后到达终点,说出它是表示什么数的点?(1)向右移动2个单位,再向左移动3个单位;(2)向左移动412个单位,再向右移动4个单位; (3)向左移动212 个单位,再向右移动212个单位.【拓展提升】9. 在数轴上,在－3右边,表示负数的点有_____个.10. 数轴上点A 所对应的数是+4,点B 所对应的数是－7,则A 、B 两点间的距离是________.11. 若在数轴上点A 所对应的数是2,那么在数轴上与点A 相距5个单位长度的点所表示的数是_______.12. 数轴上的点A、B分别表示－1和2, 点C在A、B两点之间且到A、B的距离相等,则点C表示的数是_______.13. 写出在数轴上到原点距离小于3的所有整数..答案:1. D2. C3. 左,3; 右,4-3 -2 －1.5 -1 0 1 2 2123 从左到右排列:－3, －2, －1.5, 0, 2125. A 、B 、C 、D 、E 各点分别表示：-2,-1.5,-0.5,0.8,1.2.(注:如果这个点的位置不很明确,可估计)6. C7.(1)如果点A 表示－3,将A 向右移动7个单位长度,那么终点表示的数是__4____;(2)如果点A 表示3,将A 向左移动7个单位长度,再向右移动5个单位长度,那么终点表示的数是__1_____;(3)如果将点B 向右移动3个单位长度,再向左移动5个单位长度,终点表示的数是0,那么点B 所表示的数是__2__8.(1) 它是表示-1的点; (2) 它是表示-12的点;(3) 它是表示0的点 9. 在数轴上,在－3右边,表示负数的点有__2__个.10. 数轴上点A 所对应的数是+4,点B 所对应的数是－7,则A 、B 两点间的距离是_11__.11. 若在数轴上点A 所对应的数是2,那么在数轴上与点A 相距5个单位长度的点所表示的数是__-3，7_____.12. 数轴上的点A 、B 分别表示－1和2,点C 在A 、B 两点之间且到A 、B 的距离相等,则点C 表示的数是__0.5_____.13.写出在数轴上到原点距离小于3的所有整数.答：有-2，-1，0，1，2课题：2.3数轴(2)【学习目标】:1．进一步巩固数轴上的点与数之间的关系．2．掌握利用点在数轴上的位置关系比较有理数的大小．【重点难点】：利用点在数轴上的位置关系比较有理数的大小．一、知识链接知识梳理：利用数轴比较有理数的大小(1)通过上节课的学习，我们知道了任意一个有理数或无理数都可以用数轴上唯一的__点__来表示．(2)观察数轴：我们发现：2>1，数轴上表示2的点在表示1的点的__右__边； 4>2，数轴上表示4 的点在表示2的点的_右_边．(3)归纳：①在数轴上表示的两个数，__右_边的数总比__右_边的数大；②数轴上表示正数的点都在原点的__右_边，说明正数___>____0；③数轴上表示负数的点都在原点的__右_边，说明负数___<____0；④正数__大于__负数．二、自主探究1. 两个同号的数中，较大的负数所表示的点离原点较__近_ ，较大的正数所表示的点离原点较__远_ _．（填“近”或“远”）2．用“>”或“<”填空：(1) －5__<___0；(2)－7__>__－9；(3)5__>__－10；(4) －4__<___4；(5)－0.5__>__－2.5.3．如图，如果点A、B、C、D所表示的数分别为a、b、c、d，则a、b、c、d的大小关系为( C )A．a<c<d<b B．b<d<a<c C．b<d<c<a D．a< b <c<d 4.例题评析例1：将有理数－4，3，0，－113，134，－3在数轴上表示出来，并用“<”号把这些数按从小到大的顺序连接起来．解：－4<－3<－113<0<134<3例2：下列各数是否存在？如果存在，把它找出来。

七年级数学上册 2.3 数轴(第2课时)学案(新版)苏科版

2.3 数轴学习目标：1.能进一步掌握数轴的三个要素，并正确画出数轴；2.学会由数轴上的已知点说出它所表示的数，能将有理数用数轴上的点表示出来；学习过程一、创设情境：1. 指出数轴上的点A 、B 、C 、D 分别表示什么数．2.（1）画出数轴，并在数轴上画出表示下列各数的点：二、新知讲解：1、在小学里，我们已学会比较两个正数的大小；那么，引进负数以后，怎样比较任意两个有理数的大小呢？例如，1与-2哪个大？-3与-4哪个大？想一想：（1）1℃与-2℃哪个温度高？（2）-1℃与0℃哪个温度高？（3）这个关系在温度计上为怎样的情形？把温度计横过来放，就好比一条数轴．从中能否发现在数轴上怎样比较两个有理数的大小？。

让学生从讨论中发现，在数轴上表示的两个数，．由此容易得到以下的比较法则：正数都零，负数都零，正数负数．2、实践应用：例1、将有理数3、0、165、-4按从小到大的顺序排列，用“<”连接起来.在数轴上画出表示这些数的点，再比较大小，结果怎样？例2、比较下列各数的大小：例3 观察数轴，能否找出符合下列要求的数：(1)最大的正整数和最小的正整数；(2)最大的负整数和最小的负整数；(3)最大的整数和最小的整数；(4)最小的正分数和最大的负分数．三、小结：通过这节课的学习，知道了四、练习：1. 比5小3的数是，比-3大4的数是，比3小5的数是，比-3小2的数是。

2.用“<”或“>”填空3. 如图，点A、B、C为数轴上的3点，填空：向左移动是。

4. 阅读下面的材料并完成填空：你能比较20052006与20062005的大小吗？为了解决这个问题，先把问题一般化．即比较n n+1与（n+1）n的大小（整数n≥1）．然后，从分析n=1，n=2，n=3，…这些简单情形入手，从中发现规律，经过归纳、猜想，得出结论．（1）通过计算，比较下列①到⑥各组中2个数的大小？①12 、21 ②23 、32 ③34 、43；④45 、54 ⑤56 、65 ⑥67 、76…”或“＜”）．。

苏教版数学七年级上册教学设计《2-3 数轴》第2课时

苏教版数学七年级上册教学设计《2-3 数轴》第2课时一. 教材分析《2-3 数轴》是苏教版数学七年级上册的教学内容，本节课主要让学生了解数轴的定义、特点以及数轴上的基本运算。

通过本节课的学习，使学生能够熟练运用数轴解决实际问题，培养学生的数学思维能力。

二. 学情分析学生在七年级上册已经学习了有理数的相关知识，对负数、正数、零有一定的了解。

但数轴作为一个新的概念，对学生来说还比较陌生。

因此，在教学过程中，教师需要从学生的实际出发，循序渐进地引导学生认识和理解数轴。

三. 教学目标1.知识与技能：使学生了解数轴的定义、特点，学会在数轴上表示数，掌握数轴上的基本运算。

2.过程与方法：通过观察、操作、思考、交流等活动，培养学生运用数轴解决问题的能力。

3.情感态度与价值观：激发学生学习数学的兴趣，培养学生的团队协作精神，使学生感受到数学在生活中的应用。

四. 教学重难点1.重点：数轴的定义、特点，数轴上的基本运算。

2.难点：理解数轴的概念，熟练运用数轴解决实际问题。

五. 教学方法采用问题驱动法、合作学习法、情境教学法等多种教学方法，引导学生主动探究、合作交流，提高学生的数学素养。

六. 教学准备1.教师准备：教材、PPT、数轴模型、黑板、粉笔等。

2.学生准备：笔记本、文具、数学知识基础相对扎实。

七. 教学过程1. 导入（5分钟）教师通过PPT展示生活中的实例，如火车时刻表、温度计等，引导学生观察并思考这些实例中是否存在数轴的影子。

从而引出数轴的概念，激发学生的兴趣。

2. 呈现（10分钟）教师简要讲解数轴的定义、特点，以及数轴上的基本运算。

通过PPT展示数轴的图像，让学生直观地感受数轴的魅力。

同时，教师可结合具体例子，如正数、负数、零在数轴上的位置，引导学生理解和掌握数轴的基本知识。

3. 操练（10分钟）教师提出一些关于数轴的问题，让学生独立思考和解答。

例如：“在数轴上，-3和2哪个更小？”、“已知数轴上A点表示的数是5，求B点表示的数。

七年级数学上册 2.3 数轴教学案(2) 苏科版

江苏省洪泽外国语中学2012-2013学年七年级数学上册 2.3 数轴教学案（2）苏科版学习目标：1. 进一步理解数轴概念，会利用数轴比较有理数的大小。

2. 培养发散思维能力，增强应用数学的意识，培养分析问题和解决问题的能力。

3. 渗透数形结合的数学思想，知道数学来源于实践，培养对数学的学习兴趣。

学习重点：会比较有理数的大小。

学习难点：如何比较两个负数(尤其是两个负分数)的大小。

一、预习：1.数轴的三要素：，和。

2. 正数都比零，负数都比零，正数都比负数；3. 零既不是，也不是；4、判断下列数轴是否正确,如不正确，在后面的括号内指出它的错误。

（1） ( )（2）（3）( )5、数轴上表示—3的点在原点的边个单位长度处；数轴上表示3的点在原点的边个单位长度处； -2 -1 0 1 2（2）在数轴上画出表示下列各数的点.并按从小到大的顺序排列。

-1， -2 ， -3 ，0 ，1，2，3（3）在数轴上，右边的点表示的数于左边的点表示的数；（填“大” “等” “小”）负数 0 正数（填“大于” “等于” “小于”）三．课堂练习（1）比较下列各组数的大小：①5和0 ②—21和0③2和—3 ④—3、0、1.5（2）利用数轴比较—3.5和—0.5的大小。

（3）在数轴上点A 表示的数是—2，那么与点A 相距4个单位的点表示的数是什么？它与121相比较大小关系如何？四．课堂小结五．板书设计六．教学反思2.3数轴（2）题人一．选择1. 在数轴上，原点及原点右边的点表示的数是（）A. 正数；B. 负数；C. 正整数；D. 非负数. 2. 不小于－2的负数有（）.A. 3个B. 2个C. 0个D. 无数个二．用“<”或“ 〉”填空：（1） 1 —2 （2）0 3 （3）0 —5 （4）—54 —34 （5）—0.5 —31三．填空：（1）数轴上与原点相距2个单位长度的点所表示的数据是（2）数轴上的点A 、B 、C 、D 分别表示—3、341、—3.5、287其中离原点最远的点是（3）通过数轴可以看出大于—3而不大于5的所有整数点有个：四．应用与拓展：2其中，年平均森林面积减少最多的国家是；减少最少的国家是。

2019-2020学年七年级数学上册《2.3 数轴》导学案苏科版.doc

2019-2020学年七年级数学上册《2.3 数轴》导学案苏科版章节与课题
本课时学习目标1、会正确画出数轴
2、会用数轴上的点表示有理数，能说出数轴上的点所表示的数。

3、知道有理数和无理数都可以在数轴上表示。

4、数轴上任意一个点都表示一个有理数或是无理数。

5、初步感受“数形结合”的思想
本课时重难点及学习建议重点：用数轴上的点表示有理数，能说出数轴上的点所表示的数
难点：知道有理数和无理数都可以在数轴上表示，数轴上任意一个点都表示一个有理数或是无理数
本课时教学
资源使用
教师教学参考资料、课件
学习过程学习要求或学法指导
一、情景创设：
1、在小学里我们会根据直线上一个点的位置写出合适的数，也会在直线上画出
表示一个数的点。

2、引入负数之后是否可以？
二、做一做
1、画一条水平直线，并在这条直线上取一点表示0，把这个点称为原点。

2、规定直线上从原点向右为正方向（画箭头表示），向左为负方向。

3、取适当长度（如1厘米）为单位长度，在直线向右每隔一个单位长度取一点，依次表示1,2,3……从原点向左每隔一个单位长度取一点，依次表示-1，-2，-3 …
三、基本知识
1、数轴：
2、注意点：
3、规定：
四、例题
例1
例2
五议一议
1面积是2的正方形的边长a能否在数轴上画出表示a的点？- a？圆周率呢？
五、作业
20页 2
六、小结回顾
给出固定数如何找点给出点表示何数
动手做
三要素
记忆理解
根据要求正确找点
写数
思考
理解
体会
学生小结课后反思与经验总结板书设计。

新苏科版七年级数学上册《2.3数轴(2)》学案

新苏科版七年级数学上册《2.3数轴(2)》学案【学习目标】1．会正确画出数轴.2．会利用数轴比较有理数的大小.3．初步感受“数形结合”的思想方法.【学习重点】初步理解数形结合的数学方法，能利用数轴比较有理数的大小.【学习难点】能正确理解有理数与数轴上的点的对应关系及如何比较负数的大小.【课前导学】1．把温度为－3℃、－2℃、0℃、5℃按从低到高的顺序排列；在数轴上画出表示－3、－2、0、5的点，你能说出这几个数的大小吗？2．任意给出几个数，并在数轴上画出表示这几个数的点，你能说出这些数的大小吗?3. 归纳：①在数轴上表示的两个数，右边的数总比左边的数 .②正数大于0，负数都小于0，正数负数.【演练展示】4. 利用数轴比较－3.5和－0.5的大小.5．在数轴上画出表示下列各数的点，并用“＜”号将这些数按从小到大的顺序连接起来: 21，0， 2，－3 ，5，－1.5－4－3 －2 －1 0 1 2 3 46．比较下列各组数的大小（1）5和0 （2）-0.5和0 （3）-3、0、1.5 (4) -3.5和-0.5【质疑拓展】7．如图，在数轴上有三个点A 、B 、C ，请回答：（1）将点B 向左移动3个单位后，三个点所表示的数谁最小？（2）将点A 向右移动4个单位后的数是多少？这时三个点所表示的数谁最小？（3）将C 点向左移动6个单位后，这时点B 所表示的数比点C 表示的数大多少？（4）移动A 、B 、C 中的两个点，使三个点表示的数相同，有几种移法？【当堂检测】1．在数轴上画出表示下列各数的点，并根据这些点的位置，用“＜”号将这些点表示的数按从小到大的顺序连接起来：-3.5，1.5，0，4.5，-0.5，-4，3．2．比较下列每组数的大小：（1）—3和—3.5 （2）－3.5，21 和－0.53．把数轴上表示4321--与的点分别记为A 和B ，那么哪一个点离原点的距离近？哪一个数较大？－2－1 0 1 2【总结评价】本节课我学到的知识点有：（1）；（2）．。

新苏教版七年级数学上册2.3《数轴》导学案

新苏教版七年级数学上册2.3《数轴》导学案学习目标：1.能根据构成数轴的三个要素正确画出数轴；2.学会由数轴上的已知点说出它所表示的数，能将有理数用数轴上的点表示出来；3. 学生通过对温度计的观察，探索有理数与数轴上的点的对应关系，初步感受“数形结合”思想。

学习重点：数轴的概念；学习难点：由数轴上的已知点说出它所表示的数。

一、课前预习：在小学里，我们会根据直线上一个点的位置写出合适的数，也会在直线上画出表示一个数的点。

1.能不能用直线上的点表示正数，零和负数？尝试用直线上的点来表示下列各数：2，3，-1，0．2.思考：用直线上的点能不能表示有理数和无理数？二、探索归纳要求：1.画一条水平直线，并在这条直线上取一点表示0，我们把这个点称为___2.规定直线上从原点向右为正方向（画箭头表示），向左为负方向．3.取适当长度（如1cm）为单位长度，在直线上，从原点向右每隔一个单位长度取一点，依次表示1、2、3……从原点向左每隔一个单位长度取一点，依次表示-1、-2、-3……如上图，像这样规定了_______、____________和___________的直线叫做数轴（number axis）．在数轴上画出表示有理数的点，可以先由这个数的符号确定它在数轴上原点的哪一边（正数在原点的右边，负数在原点的左边），再在相应的方向上确定它与原点相距几个单位长度，然后画上点．例如，表示-4.5的点，应在原点的______4.5个单位处．而数轴上的________就表示数零．记忆：构成数轴的三个要素 ______、________和____________，缺一不可．例1、指出数轴上A、B、C、D、E各点分别表示什么数．例2、画出数轴，并在数轴上画出表示下列各数的点：议一议：面积为2的正方形的边长a是无理数，如何在数轴上画出表示a的点？做一做：怎样用数轴上的点表示圆周率π？三、练一练1、数轴上表示3的点在原点的_______侧，距原点的距离是______,表示-4的点在原点的_____侧，距原点的距离是__________。

江苏省镇江市句容市华阳镇七年级数学上册 2.3 数轴学案2(无答案)(新版)苏科版

数轴班级_________组别姓名____________ 使用时间【知识网络图】：【学习目标】：1.能利用数轴比较两个有理数的大小.2.掌握在数轴上有理数是按照一定的顺序排列的，由数轴上两个数的位置关系，就可以判断这两个数的大小关系。

3.深化对数轴的理解，体会数形结合的思想.【学法指导】：1.认真看书本P20—P21页内容，独立完成“导读指南”的内容；2.将预习中不能解决的问题标出来，并填到“我的问题”处；3.建议完成时间为15分钟。

【导读指南】：一．利用数轴比较大小1、在数轴上画出表示0、5、-3、-2的点，并比较它们的大小。

（在横线上填“＞”或“＜”）0 5 ； 0 -3； 5 -2； -3 -22、数轴上点的位置与它们所表示数的大小有什么关系?（用红笔把正确答案再写一遍）3、仿照p20页的例3，比较—7和—8的大小（画出数轴）4、仿照P21页的例4，在下列空白处完成书本P21页“练一练”的第1题二．数轴上两点间的距离问题4、观察第3题的数轴，填空：（1）表示3的点在0的侧，表示3的点向左移动个单位所对应的数是0，也就是说表示3的点和0之间的距离为个单位长度。

（2）表示－4的点在表示３点的侧，这两个点相距个单位。

5、在数轴上，把表示3的点沿着数轴向负方向移5个单位，则与此位置相对应的数是。

我的问题：通过以上预习，你还有什么疑问？请写下来。

问题：个人评价 ____________ 组长评价 _____________ 教师评价____________练一练：1.比较下列各组数的大小(1) －３２（２）0 2（3）－35 －12 （4）-3 02.在数轴上，表示－5的数在原点的侧，它到原点的距离是个单位长度。

3.数轴上，点M表示－2，现从M点开始先向右移动3个单位到达P点，再从P点向左移动5个单位到达Q点.（1）点P、Q各表示什么数？（2）到达Q点后，再向哪个方向移动几个单位，才能回到原点？【课堂研讨】1．与原点距离为2.5个单位长度的点有个，它们表示的有理数是。

苏科版-数学-七年级上册-- 2.3 数轴教案(2)

例2：在数轴上画出表示下列各数的点，并用“<”号将这些数按从小到大的顺序连接起来：，0，2，-3，5，-1.5.
例3：下表记录的是某天我国8个城市的最低气温，请按气温从低到高的顺序，将这8个城市重新排列：
北京
哈尔滨
南京乌鲁木齐拉萨来自广州台北海口
-3℃
-9℃
0℃
-6℃
-4℃
4℃
2℃
5℃
分析：⑴在数轴上画出表示8个城市的最低气温的点。
4.比较大小，用“<”号连接：
(1)1，-3，-1.2 (2) ，- ，
5.课本22页第4题
5.小结
这节课你学到了什么？与同学们分享一下。
课后作业
课题：2.3数轴（第二课时）
学习目标
1.使学生进一步掌握数轴概念，会利用数轴比较有理数的大小；
2.使学生从数形两个侧面理解与解决问题，认识用形来解决数的问题的优越性，培养学生用数形结合的数学思想方法学习数学的理念。
学习重点
会比较有理数的大小．
学习难点
如何比较两个负数(尤其是两个负分数)的大小．
教学过程
⑵观察8个点的位置，按气温从低到高的顺序排列。
4、同步练习，巩固新知
1.课本21页练一练
2.根据数轴回答：在有理数的集合中，最大的负整数是，最小的正整数是，最小的非负数是。
（可以让学生想一想在数轴上能否找到最大的正整数和最小的负整数。）
3.如果数轴上的点A到原点的距离是2，点B到原点的距离是5.5，那么A、B两点之间的距离是。
归纳：在数轴上表示的两个数，右边的数总比左边的数大．
2. 做一做：
利用数轴比较下列各组数的大小：
⑴5和0；⑵ 和0；⑶2和-3；⑷ 和（5）-3、0、1.5

七年级数学上册 2.3 数轴(2)学案(无答案)苏科版(2021年整理)

江苏省镇江市石桥镇七年级数学上册2.3 数轴（2）学案（无答案）（新版）苏科版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（江苏省镇江市石桥镇七年级数学上册2.3 数轴（2）学案（无答案）（新版）苏科版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为江苏省镇江市石桥镇七年级数学上册2.3 数轴（2）学案（无答案）（新版）苏科版的全部内容。

2。

3 数轴（2）【学习目标】基本目标:会利用数轴比较有理数的大小.提升目标：利用数轴比较两个负数大小，即进一步感受数形结合思想【重点难点】重点：能利用数轴比较有理数的大小．难点：利用数轴比较两个负数大小【预习导航】1. 某日，北京，长春，江苏，黑龙江的最高气温分别是0°C,－2°C ，5°C ，－3°C① 你能直观地知道哪个温度高哪个低吗？对温度计来说,越是向上温度越大还是越小？② 在数轴上画出表示这些温度的点，你能得到什么结论？结论:____________________________________________________________2。

比较下列各组数的大小⑴ 5和3 ⑵ －31和2 ⑶ －1和03。

在数轴上表示下列各数的点，猜想它们的大小关系.1 －1 －4 0 531 －2 －214。

正数、负数和0 的大小关系。

【课堂导学】活动一:(1）在数轴上画出表示-5，3，−1，0，4的点.你能将这些数从小到大排列吗？说说你这样排列的理由。

（2）数轴上点的位置与它们所表示的数的大小有什么关系？例题：例1．比较-3.5和-0.5的大小例2.在数轴上画出表示下列个数的点,并用“〈"号将这些数按从小到大的顺序连接起来：—21,0，2，-3，5，—1.5【课堂检测】1. 用“＞”或“＜”填空：（1)−8 0; (2）−0.001 —0。

江苏省镇江市句容市华阳镇七年级数学上册 2.3 数轴(第1课时)学案(无答案)(新版)苏科版

数轴班级：姓名：【学习目标】1．会正确画出数轴，知道数轴的三要素；2．知道有理数和无理数都可以用数轴上的点表示，会用数轴上的点表示有理数，能说出数轴上的点所表示的数；3．会用数轴比较两个数的大小；4．初步感受数形结合的思想．【重、难点】重点：1．用数轴上的点表示有理数，能说出数轴上的点所表示的数；2．用数轴比较两个数的大小．难点：用数轴上的点表示有理数，用数轴比较两个数的大小【学习过程】试一试：在小学里，我们会根据直线上的一个点的位置写出合适的数，也会在直线上画出表示一个数的点．把图中直线上的点所表示的数写在相应的方框里．数轴做一做：1．画一条水平直线，并在这条直线上取一点表示0，我们把这点称为原点．2．规定直线上从原点向右为正方向（画箭头表示），向左为负方向．3．取适当长度（如1cm）为单位长度，在直线上，从原点向右每隔一个单位长度取一点，依次表示1，2，3……从原点向左每隔一个单位长度取一点，依次表示－1，－2，－3……像这样规定了原点、正方向和单位长度的直线叫做数轴．用数轴上的点表示有理数在数轴上，用原点右边且到原点的距离是1.5个单位长度的点表示1.5，用原点左边且到原点的距离是2.4个单位长度的点表示－2.4……例1 分别写出数轴上A、B、C表示的数：例2 在数轴上画出表示下列各数的点：31---1.5,3,,1.5,3.52有理数都可以用数轴上的点表示．用数轴上的点表示无理数无理数可以用数轴上的点表示吗？试一试：面积为2的正方形的边长a是无理数，如何在数轴上画出表示a的点？1．将边长为a的正方形放在数轴上（如图）；2．以原点为圆心，a为半径，用圆规画出数轴上的一个点A．点A就表示无理数a．做一做：怎样用数轴上的点表示圆周率π？1．画一个直径为1的圆片，将圆片上的点A放在原点处；2．把圆片沿数轴向右滚动一周，点A到达的位置点A′表示的数就是π．有理数和无理数都可以用数轴上的点表示；反过来，数轴上的任意一点都表示一个有理数或无理数．课堂小结：谈谈你这一节课有哪些收获．【课堂反馈】课本P20：“练一练”: 1~3【课后训练】《补充习题》P07~08: 1~6题【错题集选】。

苏教版七年级数学上册2-3 数轴2导学案

数学学科第二章第3节2.3《数轴2》学讲预案一、自主先学1. 把0℃、1℃、—3℃、—2℃按从低到高的顺序排列是_________________.2. 在数轴上画出表示0、1、—3、—2的点，并用“<”连这些数.3. 数轴上的点的位置与它们所表示的数的大小有什么关系？(1)_____________________________________________________________.(2)_____________________________________________________________.二、合作助学4. 比较—3.5和—0.5的大小.5.在数轴上画出表示下列各数的点，并用“<”号将这些数按从小到大的顺序连接起来：三、拓展导学6. 如图所示，在数轴上有三个点A 、B 、C ，请回答下列问题.5.1532021---，，，，，A BC(1) 将B 点向左移动3个单位长度后，三个点中_______表示的数最小，是_________.(2) 将A 点向右移动4个单位长度后，三个点中_______表示的数最小，是_________.(3) 将C 点向左移动6个单位长度后，点B 与点C 中_______表示的数大，大_________.四、检测促学7. 下列各数中，最小的数是 ( )A. 1B. 21 C. 0 D. —1 8. 下列说法错误的是 ( )A. 最小的正整数是1，最大的负整数是—1B. 在数轴上表示两个数，左边的数总比右边的数小C. 在数轴上表示211-的点在原点的左侧，距原点211个单位长度 D. 在数轴上，原点两边的数都比0大9. 比较大小(填写“>”或“<”).(1) —2.1_______1； (2) —3.2_______—4.3； (3) 21- _______ 31-； (4) 41- _______0.10.内含有的整数为________________.11. 某人从A 地向东走10 m ，然后折回向西走了3 m ，又折回向东走了6 m ，问此人最后在A 地哪个方向？距离A 地多少米？ ( 第10题 )五、反思悟学12. 数轴上点A、B的位置如图所示，若点A、B关于点A的对称点C，则点C表A示的数为_____________.( 第12题)考点综合专题：一元二次方程与其他知识的综合◆类型一一元二次方程与三角形、四边形的综合1．(雅安中考)已知等腰三角形的腰和底的长分别是一元二次方程x2－4x＋3＝0的根，则该三角形的周长可以是（）A．5 B．7 C．5或7 D．102．(广安中考)一个等腰三角形的两条边长分别是方程x2－7x＋10＝0的根，则该等腰三角形的周长是（）A．12 B．9C．13 D．12或93．(罗田县期中)菱形ABCD的一条对角线长为6，边AB的长是方程x2－7x ＋12＝0的一个根，则菱形ABCD的周长为（）A．16 B．12 C．16或12 D．244．(烟台中考)等腰三角形边长分别为a，b，2，且a，b是关于x的一元二次方程x2－6x＋n－1＝0的两根，则n的值为（）A．9 B．10C．9或10 D．8或105．(齐齐哈尔中考)△ABC的两边长分别为2和3，第三边的长是方程x2－8x ＋15＝0的根，则△ABC的周长是．6．(西宁中考)若矩形的长和宽是方程2x2－16x＋m＝0(0＜m≤32)的两根，则矩形的周长为．【方法8】7．已知一直角三角形的两条直角边是关于x的一元二次方程x2＋(2k－1)x ＋k2＋3＝0的两个不相等的实数根，如果此直角三角形的斜边是5，求它的两条直角边分别是多少．【易错4】◆类型二一元二次方程与函数的综合8．(泸州中考)若关于x的一元二次方程x2－2x＋kb＋1＝0有两个不相等的实数根，则一次函数y＝kx＋b的大致图象可能是（）9．(安顺中考)若一元二次方程x2－2x－m＝0无实数根，则一次函数y＝(m ＋1)x＋m－1的图象不经过（）A．第四象限B．第三象限C．第二象限D．第一象限10．(葫芦岛中考)已知k、b是一元二次方程(2x＋1)(3x－1)＝0的两个根，且k＞b，则函数y＝kx＋b的图象不经过（）A．第一象限B．第二象限C．第三象限D．第四象限11．(广元中考)从3，0，－1，－2，－3这五个数中抽取一个数，作为函数y＝(5－m2)x和关于x的一元二次方程(m＋1)x2＋mx＋1＝0中m的值．若恰好使函数的图象经过第一、三象限，且使方程有实数根，则满足条件的m的值是．12．(甘孜州中考)若函数y＝－kx＋2k＋2与y＝kx(k≠0)的图象有两个不同的交点，则k的取值范围是．.◆类型三一元二次方程与二次根式的综合13．(达州中考)方程(m－2)x2－3－mx＋14＝0有两个实数根，则m的取值范围为（）A．m＞52B．m≤52且m≠2C ．m ≥3D ．m ≤3且m ≠214．(包头中考)已知关于x 的一元二次方程x 2＋k －1x －1＝0有两个不相等的实数根，则k 的取值范围是．考点综合专题：一元二次方程与其他知识的综合1．B 2.A 3.A 4.B 5.86．16 解析：设矩形的长和宽分别为x 、y ，根据题意得x ＋y ＝8，所以矩形的周长为2(x ＋y)＝16.7．解：∵一元二次方程x 2＋(2k －1)x ＋k 2＋3＝0有两个不相等的实数根，∴Δ>0，∴(2k －1)2－4(k 2＋3)>0，即－4k －11>0，∴k<－114，令其两根分别为x 1，x 2，则有x 1＋x 2＝1－2k ，x 1·x 2＝k 2＋3，∵此方程的两个根分别是一直角三角形的两条直角边，且此直角三角形的斜边长为5，∴x 21＋x 22＝52，∴(x 1＋x 2)2－2x 1·x 2＝25，∴(1－2k)2－2(k 2＋3)＝25，∴k 2－2k －15＝0，∴k 1＝5，k 2＝－3，∵k<－114，∴k ＝－3, ∴把k ＝－3代入原方程得到x 2－7x ＋12＝0，解得x 1＝3，x 2＝4，∴直角三角形的两直角边分别为3和4.8．B9．D 解析：∵一元二次方程x 2－2x －m ＝0无实数根，∴Δ＜0，∴Δ＝4－4×1×(－m)＝4＋4m ＜0，∴m ＜－1，∴m ＋1＜1－1，即m ＋1＜0，m －1＜－1－1，即m －1＜－2，∴一次函数y ＝(m ＋1)x ＋m －1的图象不经过第一象限．故选D.10．B 11.－2 12.k>－12且k ≠013．B 14.k≥1。

江苏省句容市后白中学七年级数学上册《2.3绝对值和相反数》学案2 苏科版

江苏省句容市后白中学七年级数学上册《2.3绝对值和相反数》学案2 苏科版江苏省句容市后白中学七年级数学上册《2.3绝对值和相反数》学案2 苏科版学习目标：1.加深对绝对值的概念的理解，能借助数轴理解相反数的概念，能求一个数的相反数.2.理解相反数的两种概念，①只有符号不同的两个数是互为相反数；②符号不同，且到原点距离相等的两个数是互为相反数.3.通过对相反数的意义和求一个数的相反数的方法的究，培养观察、比较、分析、归纳、概括的逻辑思维能力以及动手实践能力，经历将实际题数学化的过程，感受数学与生活的关系.学习重点：理解相反数的意义，会求已知数的相反数.学习难点：理解相反数在生活中的实际意义，.掌握多重符号化简的规律学习过程：一、课前预习1.自学课本22页到23页，有哪些疑惑？2.填空⑴│2.3│= ，7，│6│=，4│0│=；⑵│5│= ，│10.5│= ，│ 2.3│= .3.有理数a、b满足│b│＜3，并且a＜b总成立，则a的取值范围是（）A.小于或等于3的有理数B.小于3的有理数C.小于或等于3的有理数D.小于3的有理数4.绝对值大于3而不大于6的负整数有5.已知│x3│+│y2│=0试求x、y的值.二、自学、合作探究（一）自学探究用心爱心专心31.小明的家在学校西边5㎞处，小丽的家在学校东边5㎞处.你能用我们刚学习的数轴的有关知识将小明、小丽家的相对位置表示出来吗？如何建立数轴？提问：如果小明、小丽分别以同样的速度从家到校，所用时间怎样？观察数轴上A、B二点位置及其到原点的距离，你们有什么发现？第1页2.在数轴上分别找到下列每一对数所表示的点；并指出它们与原点的距离的关系，再求它们的绝对值，你会发现一些什么共同点？符号不同，绝对值相等的两个数，叫做互为相反数（opposite number).规定，0的相反数还是0.3.求3，－4.5，，0的相反数.归纳：表示一个数的相反数，只要在这个数的前面添一个“－”号.用心爱心专心4如5的相反数是－5；而－5的相反数是－（－5）＝5，相反数的相反数是本身.4.化简下列符号：（二）自学、相信自己1.课本23页：练一练2.课本25页：习题2.3 2、3、4.(三）应用探究1.化简符号：（1）－｛－[＋（－8）]｝（2）[+（―︱―49︱）]2.在数轴上，如果点A、点B分别表示互为相反数的两个数，且A、B两点相距8个单位长度，问点A、点B分别表示什么数？3.由小到大排列的一组有理数x1,x2,x3,x4,x5,其用心爱心专心5中每个数都小于－1，请用“＜”将下列各数按大小顺序连接起来：1，x1,-x2,x3,-x4,x5.第2页三、学习体会1.相反数的意义.2.相反数的求法.四、自我练习A组⒈判断：⑴任何一个正数的相反数都是负数（）⑵互为相反数的两个数一定不相等（）⑶－3.25是3.25的相反数（）⑷符号不同的两个数是相反数（）2.填空：⑴－3是的相反数，⑵（7）是的相反数用心爱心专心64）是的相反数.3.填空：⑴（1－n）的相反数是，⑵（1＋n）与相反数⑶如果a＝―13，那么―a＝，⑷如果a＝＋5＝，4.化简：＋［―（―23）］＝，＋［－＝，―｛―［＋（－8）］｝＝，－︱＋＝ .5.下列说法错误的是（）A.－7与7互为相反数B.－8是－（－8）的相反数C.－（＋3）与＋（－3）是互为相反数D.－（－3）与＋（－3）是互为相反数6.下面各对数用心爱心专心7用心爱心专心8＋（－6）与＋6；－（＋6）与―6； ―（―6）―（＋6）与＋（－6）；＋（＋6）与―（―6）；＋6与其中，互为相反数的有（） A.3对 B.4对 C.5对 D.6对 7.下列说法正确的是( ) A.）与（2)21(+-互为相反数 B.5的相反数是5-C.数轴上表示-a 的点一定在原点的左边D.任何负数都小于它的相反数第3页8.下列说法正确的是 ( )①0是绝对值最小的有理数 ②相反数大于本身的数是负数③数轴上原点两侧的数互为相反数 ④两个数比较，绝对值大的反而小A.①②B.①③C.①②③D.①②③④B组9.a，b是有理数，它们在数轴上的对应点的位置如下图所示：a 0 b把a,-a,b,-b按照从小到大的顺序排列( )A .-b＜-a＜a＜b B.-a＜-b＜a＜bC.-b＜a＜-a＜bD.-b＜b＜-a＜a10.有A、B两点，在数轴上分别表示实数a、b，若a的绝对值是b的绝对值的4倍，且A、B两点间的距离是12，求a、 b出的值.探究1：若A、B两点在原点的同侧.①A、B两点都在原点的左侧时，a= ，b= .②A、B两点都在原点的右侧时，a= ，b= .探究2：若A、B两点在原点的两侧.用心爱心专心9①A在原点的左侧，B在原点的右侧，a= ，b= .②A在原点的右侧，B在原点的左侧，a= ，b= .五、学习札记用心爱心专心10。