同济大学 2000年运筹学 考研真题及答案
(精校版)同济大学交通运输工程历年真题

(完整word版)同济大学交通运输工程历年真题编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整word版)同济大学交通运输工程历年真题)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整word版)同济大学交通运输工程历年真题的全部内容。
同济大学2004交通工程学试题一简答题(6×8分)1 单向交通的设置条件?2 交通工程1后的习题.3 公共交通优先有什么措施?4出行分布的类型及其特点和适用条件。
5 给你道路1和道路2的时变图,如何确定是主干道还是次干道,并说明理由。
6 给你一个出行路线图,让你说明那条是基于家的出行HM和那条是非基于家的出行NHM,计算出行产生次数和出行吸引次数。
二计算题(18+8+8+18 )1 运用logit模型求两条道路所占的流量的比例。
2 计算高峰小时流量,PHF(15),给你日变系数,和月变系数让你求AADT.2005交通工程学试题1。
判断(10小题,每题3分)具体的回忆不起来了,都是些基本概念,大部分说的都很绝对,所以大部分都是错误的2。
简答(6道?8道?每题5分)这里面考察的都是比较理论的题目.有一题是考ITS,让你说下对ITS下面的几个子系统的看法等等。
有一题是问有关转移曲线的问题,基本概念。
还有考察设计车速的概念,信号配时方法等,具体的都记不清了,都是很基本的,不过有的题目出的有点偏,比如转移曲线的那道。
3.论述和计算(8道好像,每道都有10分左右)里面考察了时间平均车速和空间平均车速的概念,及其和交通量之间的关系;信号配时;排队论(很简单的排队);福来特迭代(这个比较费时间,两次迭代);泊松分布;交通网布局及其特点.(能想起来的就只有这些了)总的看来,05年的交通工程很偏重理论的,05年也是交通工程第一次作为专业课放在初试里考,第一次命题.计算题都比较简单,只是福来特迭代很麻烦,还要求迭代两次.同济大学2006年研究生入学考试考试一、判断题1交通工程学式关于道路、铁路、机场。
2000年全国硕士研究生入学统一考试数学一、二、三、四试题完整版附答案解析及评分标准

x y2
f12)
1 y2
f2
1 y
(xf21
x y2
f
22
)
1 x2
g
y x3
g
2000 年 • 第 2 页
f1
1 y2
f2 ' xyf11
x y3
f22
1 x2
g
y x3
g .
„„5 分
五、(本题满分 6 分)
计算曲线积分 I
L
xdy ydx 4x2 y2
,其中
L
是以点(1,0)为中心,R
三、(本题满分 5 分)
1
求
lim(
x0
2
ex
4
sin x
x) .
1 ex
1
4
3
解:因
lim
x0
(
2
ex
4
sin x
2e
) lim (
x
x0
x e
4
x
sin x) 1 x
,
1 ex
e x 1
1
1
2 ex
lim (
x0
4
sin x) x
2 ex
lim (
x0
4
sin x) 2 1 1, x
(5) 设二维随机变量 X ,Y 服从二维正态分布,则随机变量 X Y 与 X Y 不相关
的充分必要条件为
(B)
(A) E(X)=E(Y)
(B) E X 2 E X 2 E Y 2 E Y 2
(C) E X 2 E Y 2
(D) E X 2 E X 2 E Y 2 E Y 2
为半径的圆周(R>1).取逆时
2000数学一解析

2000年数学(一)真题解析一、填空题(1)【答案】7T方法一—x 2 dx = f a /1 — (jc — l)2 d(j? — 1)=J 0a /1 — x 2 dj?方法二1/----------帀x = sin tV 1 —无=o根据定积分的几何应用,「屆—工认即以曲线J 0y = Jlx — jc 2 (0 £工W 1)为曲边的曲边梯形的面积. 如图所示,显然[丿2工-工f =中.⑵【答案】千1_卄2_「2-46cos 2/d/=/2=£x Ko 2【解】"={F : ,F ; ,F ;} |(1,一2,2)= {2工,4y ,6z} |(i,_2,2)= {2, — 8,12},qr 1 yi —I — 2 N 2则曲面在点(1.—2,2)处的法线方程为、工占=乞丁.(3) 【答案】y =q + C2(C 】,C2为任意常数).X【解】 方法一 由xy" + 33/' = 0 ,得y"-----y' =0.X解得/hCojM =$,积分得原方程的通解为y =^ + C 2(C 15C 2为任意常数).XJC方法二 由砂"+ 3y f =0,得 x 7,y" + 3x 2y f =0 或(x 3y'Y =0.「 C于是工s ,=c 。
,解得y =-|,积分得原方程通解为^=4 + C 2(C.,C 2为任意常数).jc x (4) 【答案】 一1.【解】 因为原方程组无解,所以r (A ) <r (A ),而r (A )三3,所以r (A ) <3.于是|A 1 = 0,解得a =-1或a =3._ I 121/I 21 ! 1 \/I2 11当a = 3时,由A=”35Y -> 0 - 1-* °—131'13—2i o''o 1-3 - 1''00 00得r (A ) =r (A ) =2,原方程组有无数个解,所以a 工3 ,故a == -1.2(5)【答案】 y.【解】PCAB) =PCA) -F(AB), P CAB) = P (B) - P (AB),由P(AB)=P(AB),得P(A)=P(B).--------------1«由P(AB)=P(A+B)=l-P(A+B)=y,得P(A+B)=§.又P(A+B)=P(A)+P(B)-P(AB)=2P(A)-P2(A),o o得P2(A)-2P(A)+y=0,解得P(A)=y.二、选择题(6)【答案】(A).【解】由厂Q)gQ)TQ)g‘Q)<o,得&(工)」g(工)即牛¥为减函数,当a V工时,有牛牛>力黑>侏.gd g(工)g lb)于是/'(•z)g(b)>f(b)gO,应选(A).方法点评:本题考查函数单调性.若y'(H)>o或y'(_z)<o时,/•&)严格递增或严格递减.注意如下技巧:若题中出现/'(_r)g(>z)—/■(H)g'(_z)时,一般构造辅助函数;g(H)若题中出现f'(j;)+/(a-)g z(j:),一般构造辅助函数/(JC)g(J7).(7)【答案】(C).【解】由对面积的曲面积分的对称性质,得又因为s i x dS=JJ ydSs iF ds=.sjjj/dS=0,s』n dS9所以』n dS=4JJS]S S]zdS Z(1S9s】x dS9应选(C).方法点评:二重积分、三重积分、对弧长的曲线积分、对面积的曲面积分有类似的对称性,对面积的曲面积分的对称性如下:若》关于jrOy平面对称,其中工0夕平面上方为I】,则有]J/(z,z)dS=J0,12jJ/(jr,w)dS,I习f(.x,y,—z)=—f(工,y,z),f(a:,y,—2)=f{x,y,z).其他两种情形同上.(8)【答案】(D).【解】方法一令S”="]+“2------"”,因为工"”收敛,所以lim“”=0且limS…存在.”=]"-88设limS”=S,令S:=("]+“2)+("2+"3)+…+("”+«…+i)=2S”一"i+“卄i.OO因为limS:,=2S—-,所以级数工("”+"”+i)收敛,应选(D).心00”=1■(—1\H g/_1\W°°1方法二取U n=丄1、,级数工|/,1、收敛,而工丄1、发散,(A)不对;ln(z?+1)/z=1ln(n+1) z/=1n ln(7?+1)取"”=上?,级数》>7 =工丄发散,(B)不对;寸Tln = \” = 1"(—1 \n~l00 吕1取U ” =',级数工(“2”T — “2”)= Y —发散,(C)不对,应选(D).n n=\n=\ n(9) 【答案】(D).【解】 令 A =( a 1 .a?,…,a ”),B = (0i ,02,・"‘0,”).由 a i ,a 2, ,a m 线性无关,得 r (A ) =m .若山,卩-…仇线性无关,则r (B )=m,因为r(A) =r(B) 所以矩阵A.B 等价;反之,若矩阵A .B 等价,则r(A) — rCB ),因为r(A)—加,所以r(B)=加,又因为矩阵的秩与矩阵列向量组的秩相等,所以你,02,…,血的秩为加,即你心,…0”线性无关,应选(D).(10) 【答案】(E).【解】W 诃不相关的充分必要条件是Cov(f ,^) =0.而 Cov(Wq) =Cov(X + Y,X — Y) =Cov(X,X) -Cov(Y,Y) =D(X) -D(Y),又 D(X) =E(X 2) -[E(X )T , D(Y) =E(Y 2) ~[E(Y)]2,所以不相关的充分必要条件是D(X) =D(Y),即 E(X 2) ~[E(X)J 2 =E(Y 2) -[E(Y)]2,应选(E).三、解答题(11)【解】— . 1/2 + sin j - \ 2 -h e 7由 lim T + I I = lim -------r + lim z-o+'l+e ’ 1 1 ' 乂_°* 1 += 0 + 1=1,— . 1/2 + e J . sin jc \ 9 4- e 7 sin rlim ( T x I j = lim ------------lim --------=2 — 1 = 19/2 + e T sin x \得啸匚/ +甘)7(12)【解】由复合函数求偏导法则,得券= yf ; + —fi —气 g', dx y xdy=f\ + y (工咒y 〃-------gX1l —i £〃 无 〃〃 1 / y >—f 2 + ^yf 11 J 22 g s y yQ («Z 9』)=(13)【解】令 PCx.y) = , 2 24j ? + ydQ dp y 2 — 4 工23jc (4jc 2 + y 2 )2((乂,』)# (0,0)).如图所示,作L 0:4^2+y 2=r 2(r> 0且L 。
运筹学试题及答案解析

运筹学试题及答案一、填空题:(每空格2分,共16分)1、线性规划的解有唯一最优解、无穷多最优解、 无界解 和无可行解四种。
2、在求运费最少的调度运输问题中,如果某一非基变量的检验数为4,则说明 如果在该空格中增加一个运量运费将增加4 。
3、“如果线性规划的原问题存在可行解,则其对偶问题一定存在可行解”,这句话对还是错? 错4、如果某一整数规划: MaxZ=X 1+X 2X 1+9/14X 2≤51/14 -2X 1+X 2≤1/3 X 1,X 2≥0且均为整数所对应的线性规划(松弛问题)的最优解为X 1=3/2,X 2=10/3,MaxZ=6/29,我们现在要对X 1进行分枝,应该分为 X1≤1 和 X1≥2 。
5、在用逆向解法求动态规划时,f k (s k )的含义是: 从第k 个阶段到第n 个阶段的最优解 。
6. 假设某线性规划的可行解的集合为D ,而其所对应的整数规划的可行解集合为B ,那么D 和B 的关系为 D 包含 B7. 已知下表是制订生产计划问题的一张LP 最优单纯形表(极大化问题,约束条件均为“≤”型不等问:(1)写出B -1=⎪⎪⎪⎭⎫ ⎝⎛---1003/20.3/1312(2)对偶问题的最优解: Y =(5,0,23,0,0)T8. 线性规划问题如果有无穷多最优解,则单纯形计算表的终表中必然有___某一个非基变量的检验数为0______;9. 极大化的线性规划问题为无界解时,则对偶问题_ 无解_____;10. 若整数规划的松驰问题的最优解不符合整数要求,假设X i =b i 不符合整数要求,INT (b i )是不超过b i 的最大整数,则构造两个约束条件:Xi ≥INT (b i )+1 和 Xi ≤INT (b i ) ,分别将其并入上述松驰问题中,形成两个分支,即两个后继问题。
11. 知下表是制订生产计划问题的一张LP 最优单纯形表(极大化问题,约束条件均为“≤”型不等式)其中对偶问题的最优解: Y =(4,0,9,0,0,0) (2)写出B -1=⎪⎪⎪⎭⎫ ⎝⎛611401102二、计算题(60分)1、已知线性规划(20分) MaxZ=3X 1+4X 2X 1+X 2≤5 2X 1+4X 2≤12 3X 1+2X 2≤8X 1,X 2≥02)若C 2从4变成5,最优解是否会发生改变,为什么?3)若b 2的量从12上升到15,最优解是否会发生变化,为什么?4)如果增加一种产品X 6,其P 6=(2,3,1)T ,C 6=4该产品是否应该投产?为什么? 解:1)对偶问题为Minw=5y1+12y2+8y3 y1+2y2+3y3≥3y1+4y2+2y3≥4y1,y2≥02)当C 2从4变成5时, σ4=-9/8 σ5=-1/4由于非基变量的检验数仍然都是小于0的,所以最优解不变。
2000年全国硕士研究生入学统一考试数学一试题及解析

,其中
L 是以点
(1,0) 为中心,
R 为半径的圆周
(R
1)
取逆时针方向 . 【分析】 考查封闭曲线上第二类曲线积分。由于
R 1,故原点 (0,0) 包含在圆周 L 内,
而原点是被积函数的瑕点。 因此不满足格林公式条件, 须通过做一包含原点的闭曲线挖去原
点。在 L 所围域内做一有向闭曲线 C 挖去瑕点 (0,0) ,为了便于计算取 C : 4x2 y2 2 。
1, 2,
, m 线性无关
(A) 向量组 1, 2 , , m 可由向量组 1, 2, , m 线性表示
(B) 向量组 1, 2, , m 可由向量组 1, 2, , m 线性表示
(C)向量组 1, 2 , , m 与向量组 1, 2, , m 等价
(D) 矩阵 A ( 1, 2, , m ) 与矩阵 B ( 1, 2 , , m ) 等价
【分析】 考查线性表示、线性无关和等价的性质。
【详解】 (A) “充分非必要” 。向量组 1, 2 , , m 可由向量组 1, 2 , , m 线性表示,
则一定得到 1, 2, , m 线性无关(否则 1, 2 , , m 必线性相关了) 。但反之不真,如 1 (1 0 0 0 0)T , 2 (0 1 0 0 0)T ; 1 (0 0 0 1 0)T ,
(D) f ( x) g(x) f ( a) g(a)
【分析】 本题既可以用单调性来推出结论,也可以利用定积分保号性定理得到结论。
【详解】 法一:由于 f ( x) g(x) f ( x)g ( x) 0 ,所以
( f ( x) ) g( x)
f ( x) g (x) g ( x) f ( x) g 2 (x)
运筹学试题及答案

运筹学试题及答案大家不妨来看看小编推送的运筹学试题及答案,希望给大家带来帮助!《运筹学》复习试题及答案(一)一、填空题1、线性规划问题是求一个线性目标函数_在一组线性约束条件下的极值问题。
2、图解法适用于含有两个变量的线性规划问题。
3、线性规划问题的可行解是指满足所有约束条件的解。
4、在线性规划问题的基本解中,所有的非基变量等于零。
5、在线性规划问题中,基可行解的非零分量所对应的列向量线性无关6、若线性规划问题有最优解,则最优解一定可以在可行域的顶点(极点)达到。
7、线性规划问题有可行解,则必有基可行解。
8、如果线性规划问题存在目标函数为有限值的最优解,求解时只需在其基可行解_的集合中进行搜索即可得到最优解。
9、满足非负条件的基本解称为基本可行解。
10、在将线性规划问题的一般形式转化为标准形式时,引入的松驰数量在目标函数中的系数为零。
11、将线性规划模型化成标准形式时,“≤”的约束条件要在不等式左_端加入松弛变量。
12、线性规划模型包括决策(可控)变量,约束条件,目标函数三个要素。
13、线性规划问题可分为目标函数求极大值和极小_值两类。
14、线性规划问题的标准形式中,约束条件取等式,目标函数求极大值,而所有变量必须非负。
15、线性规划问题的基可行解与可行域顶点的关系是顶点多于基可行解16、在用图解法求解线性规划问题时,如果取得极值的等值线与可行域的一段边界重合,则这段边界上的一切点都是最优解。
17、求解线性规划问题可能的结果有无解,有唯一最优解,有无穷多个最优解。
18、19、如果某个变量Xj为自由变量,则应引进两个非负变量Xj , Xj,同时令Xj=Xj- Xj。
20、表达线性规划的简式中目标函数为ijij21、、(2、1 P5))线性规划一般表达式中,aij表示该元素位置在二、单选题1、如果一个线性规划问题有n个变量,m个约束方程(m<n),系数矩阵的数为m,则基可行解的个数最为_C_。
2000考研数二真题与解析

2000 年全国硕士研究生入学统一考试数学二试题一、填空题(本题共5小题,每小题3分,满分15分,把答案填在题中横线上) (1) 30arctan lim.ln(12)x x xx →-=+(2) 设函数()y y x =由方程2xyx y =+所确定,则0.x dy==(3)2.(7)2x x +∞=+-⎰(4) 曲线1(21)xy x e =-的斜渐近线方程为.(5) 设1000230004500067A ⎡⎤⎢⎥-⎢⎥=⎢⎥-⎢⎥-⎣⎦,E 为4阶单位矩阵,且1()()B E A E A -=+-则 1()E B -+=.二、选择题(本题共5小题,每小题3分,共15分,在每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.) (1) 设函数()bx xf x a e=+在(,)-∞+∞内连续,且lim ()0,x f x →-∞=则常数,a b 满足 ( ) (A)0,0.a b << (B)0,0.a b >> (C)0,0.a b ≤> (D)0,0.a b ≥<(2) 设函数()f x 满足关系式2()[()]f x f x x '''+=,且(0)0f '=,则 ( )(A)(0)f 是()f x 的极大值. (B)(0)f 是()f x 的极小值.(C)点(0,(0))f 是曲线()y f x =的拐点.(D)(0)f 不是()f x 的极值,点(0,(0))f 也不是曲线()y f x =的拐点.(3 ) 设(),()f x g x 是大于零的可导函数,且'()()()'()0,f x g x f x g x -<则当a x b << 时,有 ( )(A)()()()()f x g b f b g x > (B) ()()()()f x g a f a g x >(C)()()()()f x g x f b g b > (D) ()()()()f x g x f a g a >(4) 若30sin 6()lim 0x x xf x x →+⎛⎫=⎪⎝⎭,则206()lim x f x x →+为 ( ) (A)0. (B)6. (C)36. (D)∞.(5) 具有特解123,2,3x x xy e y xe y e --===的3阶常系数齐次线性微分方程是 ( )(A)0.y y y y ''''''--+= (B)0.y y y y ''''''+--= (C)61160.y y y y ''''''-+-= (D)220.y y y y ''''''--+=三、(本题满分5分)设ln(1)(ln )x f x x+=,计算()f x dx ⎰. 四、(本题满分5分)设xoy 平面上有正方形{}(,)01,01D x y x y =≤≤≤≤及直线:(0)l x y t t +=≥.若()S t 表示正方形D 位于直线l 左下方部分的面积,试求0(),(0)xS t dt x ≥⎰.五、(本题满分5分)求函数2()ln(1)f x x x =+在0x =处的n 阶导数(0)(3)nf n ≥.六、(本题满分6分)设函数0()|cos |xS x t dt =⎰,(1)当n 为正整数,且(1)n x n ππ≤≤+时,证明2()2(1)n S x n ≤<+; (2)求()limx S x x→+∞.七、(本题满分7分)某湖泊的水量为V ,每年排入湖泊内含污染物A 的污水量为6V,流入湖泊内不含A 的水量为6V ,流出湖泊的水量为3V,已知1999年底湖中A 的含量为05m ,超过国家规定指标.为了治理污染,从2000年初起,限定排入湖泊中含A 污水的浓度不超过0mV.问至多需要经过多少年,湖泊中污染物A 的含量降至0m 以内(注:设湖水中A 的浓度是均匀的) 八、(本题满分6分)设函数()f x 在[]0,π上连续,且()0,()cos 0f x dx f x xdx ππ==⎰⎰,试证明:在(0,)π内至少存在两个不同的点12,ξξ,使12()()0.f f ξξ== 九、(本题满分7分)已知()f x 是周期为5的连续函数,它在0x =的某个邻域内满足关系式(1sin )3(1sin )8()f x f x x x α+--=+其中()x α是当0x →时比x 高阶的无穷小,且()f x 在1x =处可导,求曲线()y f x =在点(6,(6))f 处的切线方程.十、(本题满分8分)设曲线2(0,0)y ax a x =>≥与21y x =-交于点A ,过坐标原点O 和点A 的直线与曲线2y ax =围成一平面图形.问a 为何值时,该图形绕x 轴旋转一周所得的旋转体体积最大?最大体积是多少? 十一、(本题满分8分)函数()f x 在[0,)+∞上可导,(0)1f =且满足等式01()()()0,1xf x f x f t dt x '+-=+⎰ (1)求导数()f x ';(2)证明:当0x ≥时,成立不等式()1xe f x -≤≤成立十二、(本题满分6分)设11012,,0,,2180T TA B αβγαββα⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪===== ⎪ ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭.其中T β是β的转置,求解方程22442B A x A x B x γ=++十三、(本题满7分)已知向量组12301,2,1110a b βββ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭与向量组1231392,0,6317ααα⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭具有相同的秩,且3β可由123,,ααα线性表出,求,a b 的值.2000 年全国硕士研究生入学统一考试数学二试题解析一、填空题 (1)【答案】16-【详解】()()()33ln 1222232322000011arctan arctan 11limlim lim lim 266ln 1261x x x x x x x x x x x x x x xx x +→→→→----+====-++:洛(2)设函数()y y x =由方程2xyx y =+所确定,则0.x dy==【答案】(ln 21)dx - 【详解】 方法1:对方程2xyx y =+两边求微分,有2ln 2().xy xdy ydx dx dy ⋅+=+由所给方程知,当0x =时1y =. 将0x =,1y =代入上式,有ln 2dx dx dy ⋅=+. 所以,0(ln 21)x dy dx ==-.方法2:两边对x 求导数,视y 为该方程确定的函数,有2ln 2()1.xy xy y y ''⋅+=+当0x =时1y =,以此代入,得ln 21y '=-,所以0(ln 21)x dy dx ==-. (3)【答案】3π【详解】由于被积函数在2x =处没有定义,则该积分为广义积分.对于广义积分,可以先按照不定积分计算,再对其求极限即可.22,22,x t x t dx tdt -=-==02202122arctan .(9)33323(7)2t t dt t t x x ππ+∞+∞+∞==⋅=⋅=++-⎰⎰(4)【答案】21y x =+【公式】y kx b =+为()y f x =的斜渐近线的计算公式:()()lim,lim [()]x x x x x x yk b f x kx x →∞→∞→+∞→+∞→-∞→-∞==-【详解】11lim lim (2)2,x x x y k e x x→+∞→+∞==-=10122lim (2)lim[(21)2]lim()u u xx u x e b y x x e x u e x u+→+∞→→+∞-=-=--= - 令 002(1)2lim()1lim()211u u u uu u e u e e u e uu ++→→-=- - -=-=: 所以,x →+∞方向有斜渐近线21y x =+. 当x →-∞时,类似地有斜渐近线21y x =+. 总之,曲线1(21)xy x e =-的斜渐近线方程为21y x =+.(5)【答案】1000120002300034⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥-⎣⎦【详解】先求出1()E B -+然后带入数值,由于1()()B E A E A -=+-,所以11111()()()()()()()12()()22000100024001200104600230200680034E B E E A E A E A E A E A E A E A E A -----⎡⎤+=++-⎣⎦⎡⎤=++++-⎣⎦⎡⎤=+=+⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥--⎢⎥⎢⎥ ==⎢⎥⎢⎥--⎢⎥⎢⎥--⎣⎦⎣⎦-1-1-1二、选择题 (1)【答案】D【详解】排除法:如果0a <,则在(,)-∞+∞内()f x 的分母bx a e +必有零点0x ,从而()f x 在0x x =处不连续,与题设不符.不选()A ,若0b >,则无论0a =还是0a ≠均有lim (),x f x →-∞=∞与题设lim ()0x f x →-∞=矛盾,不选()B 和()C .故选()D .(2)【答案】C【定理应用】判断极值的第二充分条件:设函数()f x 在0x 出具有二阶导数且0()0f x '=,0()0f x ''≠,那么:(1) 当0()0f x ''>时,函数()f x 在0x 处取得极大值;(2)当0()0f x ''<时,函数()f x 在0x 处取得极小值;【详解】令等式2()[()]f x f x x '''+=中0x =,得[]2(0)0(0)0f f '''=-=,无法利用判断极值的第二充分条件,故无法判断是否为极值或拐点.再求导数(因为下式右边存在,所以左边也存在):[]2()(())12()()f x x f x f x f x ''''''''=-=-以0x =代入,有(0)1f '''=,所以0()(0)()(0)limlim 10x x f x f f x f x x→→''''''-'''===-. 从而知,存在0x =去心邻域,在此去心邻域内,()f x ''与x 同号,于是推知在此去心邻域内当0x <时曲线()y f x =是凸的,在此去心临域内0x >时曲线()y f x =是凹的, 点(0,(0))f 是曲线()y f x =的拐点,选(C).(3)【答案】A【分析】由选项答案可知需要利用单调性证明,关键在于寻找待证的函数. 题设中已知'()()()'()0,f x g x f x g x -< 想到设函数为相除的形式()()f xg x . 【详解】设()()()f x F xg x =,则()2'()()()'()()0,()f x g x f x g x F x g x -'=< 则()F x 在a x b <<时单调递减,所以对a x b ∀<<,()()()F a F x F b >>,即()()()()()()f a f x f bg a g x g b >> 得 ()()()(),f x g b f b g x >a x b <<,()A 为正确选项.(4)【答案】()C【分析】本题有多种解法:(1)将含有()f x 的要求极限的表达式凑成已知极限的表达式,或反之;(2)利用极限与无穷小的关系,从已知极限中解出()f x 代入要求极限式中;(3)将具体函数用佩亚诺余项泰勒公式展开化简原极限. 【详解】方法1: 凑成已知极限2336()6()6sin 6sin 6()f x x xf x x x x xf x x x x ++-++==而 23222000012(6)6sin 666cos66(1cos6)2lim lim lim lim 3633x x x x x x x x x x x x x→→→→⋅---====洛 (由于211cos 2x x -:⇒211cos(6)(6)2x x -:)所以 2330006()6sin 6sin 6()lim lim lim 36036x x x f x x x x xf x x x x→→→+++=+=+= 方法2:由极限与无穷小关系,由已知极限式解出3sin 6()x xf x a x +=,0lim 0x a →=从而 3sin 6()x xf x ax +=⇒3sin 6()ax xf x x-=33223sin 666()6sin 6ax x f x ax x x x x x x -+++-== 所以 323300006()6sin 66sin 6lim lim lim lim x x x x f x ax x x x xa x x x →→→→++--==+极限的四则运算2220012(6)66cos620lim lim 3x x x xx x→→⋅-=+=36= 方法3: 将sin6x 在0x =处按佩亚诺余项泰勒公式展开至3x 项:3333(6)sin 66()636(),3!x x x x x x x οο=-+=-+于是 3333sin 6()6()36()x xf x x xf x x x x x ο++-+=3236()()36,f x x x x ο+=-+ 从而 32330006()sin 6()()limlim 36lim 036036.x x x f x x xf x x x x xο→→→++=+-=+-=(5)【答案】B【详解】由特解12,2x xy e y xe --==,对照常系数线性齐次微分方程的特征方程、特征根与解的对应关系知道,21r =-为特征方程的二重根;由33xy e =可知11r =为特征方程的单根,因此特征方程为232(1)(1)10,r r r r r -+=+--=由常系数齐次线性微分方程与特征方程的关系,得该微分方程为0.y y y y ''''''--+=三【详解】方法1:为了求不定积分,首先需要写出()f x 的表达式.为此,令ln x t =,有tx e =ln(1)ln(1)()(ln )t tx e f t f x x e ++===()ln(1)ln(1)xx x x f x dx ee dx e de --=+=-+⎰⎰⎰ln(1)1xxxxx e e e e dx e --=-+++⎰ 分部积分1ln(1)1x xxxxe e e e dx e-+-=-+++⎰ 拆项 ln(1)(1)1ln(1)111ln(1)111ln(1)1(1)1ln(1)ln(1)xxxxx x xxx x x xx x x xx x x e e e dx ee e e dx dxe e e dx de e e e dx d e ee e x e C-----=-++-+=-++-+=-++-+=-++-++=-++-++⎰⎰⎰⎰⎰⎰⎰ 方法2:作积分变量替换,命ln x t =,21ln(1)1()(ln )ln(1)t f x dx f t dt dt t d t t t +⎛⎫=⋅==-+ ⎪⎝⎭⎰⎰⎰⎰ ln(1)1[](1)t dt t t t +=--+⎰ 分部积分 ln(1)11()1t dt t t t+=-+-+⎰ 部分分式求和ln(1)11(1)1t dt d t t t t +=-+-++⎰⎰ln(1)ln ln(1)t t t C t +=-+--+ ln(1)ln(1).x x x e e x e C -=-++-++四【详解】先写出面积()S t 的(分段)表达式,当01t <<时,图形为三角形,利用三角形的面积公式:21()2S t t =;当12t <<时,图形面积可由正方形面积减去小三角形面 积,其中由于x y t +=与1y =交点的纵坐标为1t -,于是, 小三角形的边长为:1(1)2t t --=-,所以222111()1(2)1(44)21222S t t t t t t =--=--+=-+-;当2t >时,图形面积就是正方形的面积:()1S t =, 则221, 01,21()1(2), 12,21, 2.t t S t t t t ⎧≤≤⎪⎪⎪=--<≤⎨⎪<⎪⎪⎩当01x ≤≤时,3320011();2236xxxt x S t dt t dt ⎛⎫==⋅= ⎪⎝⎭⎰⎰当12x <≤时,1122010111()()()[1(2)]22xx x S t dt S t dt S t dt t dt t dt =+=+--⎰⎰⎰⎰⎰ 3321111(1)(2)66663x x x x x =+----=-+-+ 当2x >时,2022()()()11 1.xx xS t dt S t dt S t dt dt x =+=+=-⎰⎰⎰⎰因此 3320101611()126312x x x S t dt x x x x x x ⎧≤≤⎪⎪⎪=-+-+<≤⎨⎪->⎪⎪⎩⎰五【详解】方法1:按莱布尼茨高阶导数公式:S (t )x +y =t O11()()1(1)()()()().n n n k n k k n n n uv u v C u v C u v uv --'=+++++L L为了求ln(1)x +的n 阶导数,设ln(1)y x =+,11y x'=+; ()()221111y x x ''=-=-++;()()()33112211y x x ⋅'''=--⋅=++;()()(4)4412123311y x x ⋅⋅⋅=-=-++一般地,可得1()(1)(1)!(1)n n nn yx ---=+即 []1()(1)(1)!ln(1)(1)n n nn x x ---+=+ 设ln(1)u x =+,2v x =,利用上述公式对函数展开,由于对2x 求导,从三阶导数开始就为零,故展开式中只含有前三项.123()212(1)(1)!(1)(2)!(1)(1)!()2(1).(1)(1)(1)n n n n n n n n n n fx x nx n n x x x -----------=++-+++ 代入0x =,得:1()3(1)!(0)(1)(1)(3)!,3,4.2n n n n fn n n n n ---=---==-L方法2:()y f x =带佩亚诺余项的麦克劳林公式:()2(0)(0)()(0)(0)()2!!n nn f f f x f f x x x x n ο'''=+++++L求(0)(3)nf n ≥可以通过先求()y f x =的的麦克劳林展开式,则展开式中nx 项的系数与!n 的乘积就是()y f x =在点0x =处的n 阶导数值)0()(n f.由麦克劳林公式,23212ln(1)(1)(),232n n n x x x x x x n ο---+=-+++-+-L所以 452231ln(1)(1)().232n n n x x x x x x x n ο--+=-+++-+-L 对照麦克劳林公式()2(0)(0)(0)()(0)(),1!2!!n nn f f f f x f x x x x n ο'''=+++++L从而推知()1(0)(1)!2n n f n n --=- 得 1()(1)!(0),3,4.2n n n f n n --==-L六【详解】因为cos 0x ≥,且(1)n x n ππ≤<+, 所以(1)0cos cos cos .n x n x dx x dx x dx ππ+≤<⎰⎰⎰定积分的性质又因为cos x 具有周期π,所以在长度为π的积分区间上的积分值均相等:cos cos a ax dx x dx ππ+=⎰⎰,从而20(1)cos cos cos cos n n n x dx x dx x dx x dx ππππππ-=+++⎰⎰⎰⎰L202cos (cos cos )n x dx n xdx xdx ππππ==-⎰⎰⎰202(sin sin )(1(01))2n x x n n πππ=-=--= 所以(1)0cos 2(1).n xdx n π+=+⎰所以 02cos 2(1),x n xdx n ≤<+⎰即 2()2(1).n S x n ≤<+(2) 由(1)有,当(1)n x n ππ≤≤+时,2()2(1)(1)n S x n n x n ππ+<<+命n →∞取极限,222lim lim 1(1)(1)n n n n nπππ→∞→∞==++,12(1)2(1)2lim lim n n n n n πππ→∞→∞++==由夹逼定理,得()2limx S x x π→∞=.七【详解】设从2000年初(相应0t =)开始,第t 年湖泊中污染物A 的总量为m ,浓度为mV,则在时间间隔[,]t t dt +内,排入湖泊中A 的量为:00()66m mV t dt dt dt V ⋅+-=,流出湖泊的水中A 的量为33m V mdt dt V ⋅=. 因而时间从t 到t dt +相应地湖泊中污染物A 的改变量为:0()63m mdm dt =-. 由分离变量法求解:0()63dm dt m m =-两边求积分:001100()6333ln()63()()6363m m d m dm m dt t C t C m m m m -=⇔-=+⇔--=+--⎰⎰⎰ 10013ln()63363t C m m t C m m e +-+⇔-=⇔-=-103336C tm me e --⇔-=-+⋅110033333,(3)22C C t tm m m e e m C e C e ----⇔=-⋅⇔=-⋅=初始条件为0(0)5m m =,代入初始条件得092C m =-. 于是03(19)2tm m e -=+,要满足污染物A 的含量可降至0m 内,命0m m =,得6ln3t =. 即至多需经过6ln3年,湖泊中A 的含量降至0m 以内.八【证明】 方法1:令0()(),0xF x f t dt x π=≤≤⎰,有(0)0,F =由题设有()0F π=.又由题设()cos 0f x xdx π=⎰,用分部积分,有0()cos cos ()f x xdx xdF x ππ==⎰⎰()cos ()sin F x xF x xdx ππ=+⎰0()sin F x xdx π=⎰由积分中值定理知,存在(0,)ξπ∈使0()sin ()sin (0)F x xdx F πξξπ==⋅-⎰因为(0,)ξπ∈,sin 0ξ≠,所以推知存在(0,),ξπ∈使得()0F ξ=. 再在区间[0,]ξ与[,]ξπ上对()F x 用罗尔定理,推知存在1(0,)ξξ∈,2(,)ξξπ∈使12()0,()0F F ξξ''==,即 12()0,()0f f ξξ==方法2:由()0f x dx π=⎰及积分中值定理知,存在1(0,)ξπ∈,使1()0f ξ=. 若在区间(0,)π内()f x 仅有一个零点1ξ,则在区间1(0,)ξ与1(,)ξπ内()f x 异号. 不妨设在1(0,)ξ内()0f x >,在1(,)ξπ内()0f x <. 于是由()0,()cos 0f x dx f x xdx ππ==⎰⎰,有111101100()cos ()cos ()(cos cos )()(cos cos )()(cos cos )f x xdx f x dx f x x dxf x x dx f x x dxπππξπξξξξξ=-=-=-+-⎰⎰⎰⎰⎰当10x ξ<<时,1cos cos x ξ>,1()(cos cos )0f x x ξ->;当1x ξπ<<时,1cos cos x ξ<,仍有1()(cos cos )0f x x ξ->,得到:00>. 矛盾,此矛盾证明了()f x 在(0,)π仅有1个零点的假设不正确,故在(0,)π内()f x 至少有2个不同的零点.九【详解】为了求曲线()y f x =在点(6,(6))f 处的切线方程,首先需要求出()y f x =在6x =处的导数,即切线斜率. 而函数又是以周期为5的函数,且在1x =处可导,则在6x =处可导,且其导数值等于函数在1x =处的导数值.将(1sin )3(1sin )8()f x f x x x α+--=+两边令0x →取极限,由f 的连续性得(1)3(1)lim(8())0x f f x x α→-=+= ⇒ 2(1)0f -=故(1)0f =,又由原设()f x 在1x =处可导,两边同除sin x ,000(1sin )(1)(1sin )(1)8()lim3lim lim lim sin sin sin sin x x x x f x f f x f x x x xx x α→→→→+---+=+-根据导数的定义,得008()(1)3(1)limlim 8sin sin x x x x x x f f x x x xα→→''+=⋅+⋅= ⇒ 4(1)8f '= 所以(1)2f '=,又因(6)(51)(1)f f f '''=+=,所以(6)2f '=,由点斜式,切线方程为((6))(6)(6).y f f x '-=-以(6)(1)0,(6)2f f f '===代入得2(6).y x =- 即 2120.x y --=十【详解】首先联立两式,求直线与曲线的交点:221x ax -=,得:1x a=+,而0x ≥,则交点坐标为:(,))11a x y a a =++. 由点斜式,故直线OA 的方程为1y a=+由旋转体体积公式2()b aV f x dx π=⎰,要求的体积就是用大体积减去小体积:()2222224111000()11a a a a x V dx ax dx a x dx a a +++=-=-++123252152023(1)515(1)a a x a x a a a ππ+⎛=-=+⎝+为了求V 的最大值,对函数关于a 求导,225522221515(1)(1)dV a a da a a ππ''⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪++⎝⎭⎝⎭53222552(1)(1)2215(1)a a a a a π⋅+-⋅+=⋅+ 322275255(1)[2(1)][2(1)]222215(1)15(1)a a a a a a a a a ππ++-+-=⋅=⋅++ 222277722251[22][2]22[4]22151515(1)(1)(1)a a a a a a a a a a πππ+---=⋅=⋅=⋅+++ 0a > 命0,dVda=得唯一驻点4a =,所以4a =也是V 的最大值点,最大体积为4325a V ==.十一【详解】(1) 为了求()f x ',将01()()()01xf x f x f t dt x '+-=+⎰两边同乘(1)x +,得(1)()(1)()()0,xx f x x f x f t dt '+++-=⎰两边对x 求导,得()(1)()()(1)()()0f x x f x f x x f x f x ''''+++++-=即 (1)()(2)()0x f x x f x '''+++=.上述方程为二阶可降阶微分方程,令()u f x '=,化为(1)(2)0x u x u '+++=,即(2)(1)du x dx u x +=-+ 两边求积分:(2)1(1)(1)1du x dx dx u x x +=-=-+++⎰⎰⎰即 1ln (ln(1))u x x C =-+++ 所以 11(ln(1))1()1x x C C x u ee e x --++-=±=±⋅⋅+ 令1C C e =±,则1xCe u x -=+,于是()1x Ce f x u x -'==+.再以0x =代入原方程001(0)(0)()(0)(0)01f f f t dt f f ''+-=+=⎰,由(0)1f =,有(0)1f '=-,于是1,()1xe Cf x x -'=-=-+. (2)方法1:用积分证.()(0)()1.1tx xe f x f f t dt dt t -'=+=-+⎰⎰而 0-000011t t xx x t t x e dt e dt e e t ->---≤≤=-=-+⎰⎰牛莱公式两边同乘以(1)-,得:101txxe e dt t ---≤-≤+⎰, 即 0()111txxe ef x dt t --≤=-≤+⎰方法2 :用微分学方法证.因(0)1,()0f f x '=<,即()f x 单调递减,所以当0x ≥时()1f x ≤. 要证()xf x e-≥,可转化为证明()0xf x e--≥,令()()x x f x e ϕ-=-,则(0)110ϕ=-=,且()()()01xxe xf x ef x x ϕ--'''=+≥+=+ (0x ≥)所以,当0x ≥时()0x ϕ≥,即()xf x e -≥. 结合两个不等式,推知当0x ≥时,()1xef x -≤≤. 证毕.十二【详解】由题设得110121210210211102T A αβ⎡⎤⎢⎥⎛⎫⎢⎥⎡⎤ ⎪===⎢⎥⎢⎥ ⎪⎣⎦ ⎪⎢⎥⎝⎭⎢⎥⎣⎦,11102221T B βα⎛⎫⎡⎤ ⎪===⎢⎥ ⎪⎣⎦ ⎪⎝⎭. 所以 ()22T T T A A αβαβααββ===,48AA =;24B =,216B =代入原方程22442B A x A x B x γ=++中,得16816Ax Ax x γ=++,即()82A E x γ-=其中E 是三阶单位矩阵,令[]123Tx x ,x ,x =,代入上式,得线性非齐次方程组1212123102201212x x x x x x x ⎧-+=⎪⎪-=⎨⎪⎪+-=⎩(1) 显然方程组得同解方程为12123201212x x x x x -=⎧⎪⎨+-=⎪⎩ (2) 令自由未知量 1x k,=解得23122x k,x k ==- 故方程组通解为1231022011122x k x k k x k ⎡⎤⎡⎤⎢⎥⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦--⎢⎥⎢⎥⎣⎦⎣⎦,(k 为任意常数)十三【详解】方法1:先求()123,,,γααα将矩阵作初等行变换,得()123139139139206061201231701020000,,ααα⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=→--→⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦知()1232,,.γααα= 故()()1231232,,,,γβββγααα==,[]123,,βββ作初等行变换[]1230110121031110030a b ,,a b βββ-⎡⎤⎡⎤⎢⎥⎢⎥=→⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦因为()1232,,γβββ=,所以3a b =又3β可由123,,ααα线性表出,故()()12331232,,,,,γαααβγααα== 将[]1233,,,αααβ作初等行变换13913920610612123170110203b b b b ⎡⎤⎡⎤⎢⎥⎢⎥→---⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦M M M M M M()13912012600053123b b b b ⎡⎤⎢⎥⎢⎥-⎢⎥→⎢⎥-⎢⎥⎢⎥+-⎣⎦M MM 由()12332,,,γαααβ=,得()531203b b +-=,解得5b =,及315a b .== 方法2:由方法1中的初等变换结果可以看出12,αα线性无关,且31232ααα=+,故()1232,,γααα=,12,αα是123,,ααα的极大线性无关组. 又()()1231232,,,,γβββγααα==,123,,βββ线性相关. 从而得12301211310110100a ba b ,,,βββ===--计算三阶行列式得30a b -+=,得3a b =又3β可由123,,ααα线性表出 ,即可由12,αα线性表出,12,αα3β线性相关,有()123131313201061206120310010310003126b b b,,b b b b b ααβ==--=--=-+-行列式展开得()10631206b b ⎛⎫-+-= ⎪⎝⎭, 所以()531203b b +-=,得5b =及315a b .== 方法3:先利用3β可由123,,ααα线性表出,故方程组()123,,X αααβ=有解,即12313920613170x b x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦有解. 对其增广矩阵施行初等行变化13913920610612123170110203b b b b ⎡⎤⎡⎤⎢⎥⎢⎥→---⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦M M M M M M()13921012600053123b b b b ⎡⎤⎢⎥⎢⎥-⎢⎥→⎢⎥-⎢⎥⎢⎥+-⎣⎦M MM 由其次线性方程组有解的条件(系数矩阵的秩等于增广矩阵的秩),知()53123b b +-51033b =-= 解得5b .=又因为1α和2α线性无关,且31232ααα=+,所以向量组123,,ααα的秩为2 ,由题设条件知()1232,,γβββ=,从而123001211310110100a b a b ,,,βββ===--解得15a =。
《运筹学》习题与答案

《运筹学》习题与答案(解答仅供参考)一、名词解释1. 线性规划:线性规划是运筹学的一个重要分支,它主要研究在一系列线性约束条件下,如何使某个线性目标函数达到最大值或最小值的问题。
2. 动态规划:动态规划是一种解决多阶段决策问题的优化方法,通过把原问题分解为相互联系的子问题来求解,对每一个子问题只解一次,并将其结果保存起来以备后续使用,避免了重复计算。
3. 整数规划:整数规划是在线性规划的基础上,要求决策变量取值为整数的一种优化模型,用于解决实际问题中决策变量只能取整数值的情形。
4. 马尔可夫决策过程:马尔可夫决策过程是一种随机环境下的决策模型,其中系统的状态转移具有无后效性(即下一状态的概率分布仅与当前状态有关),通过对每个状态采取不同的策略(行动)以最大化期望收益。
5. 最小费用流问题:最小费用流问题是指在网络流模型中,每条边都有一个容量限制和单位流量的成本,寻找满足所有节点流量平衡的同时使得总成本最小的流方案。
二、填空题1. 运筹学的主要研究对象是系统最优化问题,其核心在于寻求在各种(约束条件)下实现(目标函数)最优的方法。
2. 在运输问题中,供需平衡指的是每个(供应地)的供应量之和等于每个(需求地)的需求量之和。
3. 博弈论中的纳什均衡是指在一个博弈过程中,对于各个参与者来说,当其他所有人都不改变策略时,没有人有动机改变自己的策略,此时的策略组合构成了一个(纳什均衡)。
4. 在网络计划技术中,关键路径是指从开始节点到结束节点的所有路径中,具有最长(总工期)的路径。
5. 对于一个非负矩阵A,如果存在一个非负矩阵B,使得AB=BA=A,则称A为(幂等矩阵)。
三、单项选择题1. 下列哪项不是线性规划的标准形式所具备的特点?(D)A. 目标函数是线性的B. 约束条件是线性的C. 决策变量非负D. 变量系数可以为复数2. 当线性规划问题的一个基解满足所有非基变量的检验数都非正时,那么该基解(C)。
A. 不是可行解B. 是唯一最优解C. 是局部最优解D. 不一定是可行解3. 下列哪种情况适合用动态规划法求解?(B)A. 问题无重叠子问题B. 问题具有最优子结构C. 问题不能分解为多个独立子问题D. 子问题之间不存在关联性4. 在运输问题中,如果某条路线的运输量已经达到了其最大运输能力,我们称这条路线处于(A)状态。
运筹学-总复习-同济

(1) max
z 3x1 x 2 x3
x1 2 x 2 x3 4 x 2 x 4 x 1 1 2 3 x1 x 2 3x3 1 x1 0, x 2 0, x3无约束
19
原问题的最优单纯形表中关于对偶问题 的最优解的信息:
31
原问题
可行解 可行解 非可行解 非可行解
对偶问题
可行解 非可行解 可行解 非可行解
结论或继续计算的 步骤 最优基不变
用单纯形法继续迭 代 用对偶单纯形法继 续迭代 引入人工变量,编 制新的单纯形表重 新计算
32
价值系数c发生变化:
1. c是非基变量的系数: 2. c是基变量的系数:
33
1. 若ck是非基变量的系数: 设 ck 变化为 ck + ck k’ = ck + ck -∑ci a’ik = k+ck 只要 k’ ≤ 0, 即 ck ≤ - k, 则最优解不变; 否则,将最优单纯形表中的检验数 k 用 k’ 取代,继续单纯形法的表格计算。
增加一个变量 增加变量 xn+1,由相应的Pn+1和cn+1计算: B-1Pn+1和n+1= cn+1 - ∑ci a’i n+1 填入最优单纯形表, 若 n+1 ≤ 0 则 最优解不变; 否则,进一步用单纯形法求解。
例2.8: :假设在例1中,该厂除了生产产品
I和II外,还有一种新产品III。已知生产 产品III每件需要消耗原材料A和B各为 6kg和3kg,使用设备2台时,每件可以获 利5元,问该厂是否应当生产该产品和生 产多少?
cB cB 0 xB xS b b xB B cB cN xN N cN 0 xS I 0
同济大学真题

历年真题同济大学2000年硕士经济学一.概念经济利润实证经济学帕雷托最有状态生产者剩余道德风险内在稳定器二.简答题1.一城市乘客对公共汽车票价需求的价格弹性为-0.6,票价1元,日乘客量为55万人,市政当局计划将提价后,净减少的日乘客量控制在10万人,新的票价应为多少。
2.消费者的效用函数为U=log aX+log a Y,预算约束为Px*X+Py*Y=M。
(1)求消费者均衡条件,(2)X与Y的需求函数3.在垄断竞争条件下一企业的需求函数为P=1264-8Q,其成本函数为TC =-10+64Q-8Q*Q+Q*Q*Q,求利润最大化的产量和利润。
4.请比较完全竞争和垄断竞争的劳动力市场上供求状况的差别5.间析哈罗德-多玛模型与新古典增长模型的异同。
三.论述分析1.政府对某产品实施最低限价,对消费者和厂商有何影响?请用几何图形和文字说明。
2. 用LS-LM工具分析通货紧缩的后果,并提出解决方案2004年同济研究生入学考试经济学一.名词解释6×5外显成本吉芬商品基尼系数奥肯定理国内生产总值二.计算1两个寡头垄断企业的成本函数分别为TC1=0.1Q*Q+20Q1+100000,TC2=0.4Q*Q+32Q2+2000,,两企业生产同质产品,其市场需求函数Q=4000-10P. 两企业遵从古若模型,求:(1)两企业的反映函数,(2)两企业的均衡价格,均衡产量。
(3)若两企业成卡特尔,求新的均衡价格,各自产量,总利润。
2某垄断企业的需求曲线位P=100-4Q,成本函数TC =50+20Q 求(1)利润最大时的价格,产量,消费者剩余,生产者剩余。
(2)什么是完全价格歧视(3)若实施完全价格歧视,利润最大化时的价格和产量。
3.一行业对劳动的需求曲线L=1200-10W ,供给曲线L=20W 求均衡工资,工人得到的经济租是多少?4. 设通货-存款比率0.1 定期存款活期存款比率0.5 ,活期存款的法定准备金率0.2,超额准备金率0.1,求(1)货币乘数(2)如果央行买进10亿人民币国债,货币供应量的变动是多少?5消费函数C=300+0.8Yd , Yd为可支配收入,投资I=200, 税收函数T=0.3Y,转移支付函数为TR =1.1Y,已知均衡收入为1800,求:(1)政府支出(2)预算盈余(赤字)三.证明:完全竞争市场上,企业短期供给曲线是边际成本曲线的一部分。
运筹学试题及答案4套汇总

《运筹学》试卷一一、(15分)用图解法求解下列线性规划问题二、(20分)下表为某求极大值线性规划问题的初始单纯形表及迭代后的表,、为松弛变量,试求表中到的值及各变量下标到的值。
-1311611 -2 002 -111/21/214 07三、(15分)用图解法求解矩阵对策,其中四、(20分)(1)某项工程由8个工序组成,各工序之间的关系为工序 a b c d e f g h —— a a b,c b,c,d b,c,d e 紧前工序试画出该工程的网络图。
(2)试计算下面工程网络图中各事项发生的最早、最迟时间及关键线路(箭线下的数字是完成该工序的所需时间,单位:天)五、(15分)已知线性规划问题其对偶问题最优解为,试根据对偶理论求原问题的最优解。
六、(15分)用动态规划法求解下面问题:七、(30分)已知线性规划问题用单纯形法求得最优单纯形表如下,试分析在下列各种条件单独变化的情况下,最优解将如何变化。
2-11 02311311111610-3-1-2(1)目标函数变为;(2)约束条件右端项由变为;(3)增加一个新的约束:八、(20分)某地区有A、B、C三个化肥厂向甲、乙、丙、丁四个销地供应同一种化肥,已知产地产量、销地需求量和各产地运往不同销地单位运价如下表,试用最小元素法确定初始调运方案,并调整求最优运输方案销地甲乙丙丁产量产地A 4 12 4 11 16B 2 10 3 9 10C 8 5 11 6 22 需求量8 14 12 14 48《运筹学》试卷二一、(20分)已知线性规划问题:(a)写出其对偶问题;(b)用图解法求对偶问题的解;(c)利用(b)的结果及对偶性质求原问题的解。
二、(20分)已知运输表如下:销地B1B2B3B4供应量产地A1 3 2 7 6 50A2 7 5 2 3 60A3 2 5 4 5 25需求量60 40 20 15(1)用最小元素法确定初始调运方案;(2)确定最优运输方案及最低运费。
2000年全国硕士研究生统一考试数学一真题及答案解析

.
(2)验证
η1
4
1
,
η2
1
1
是
A
的两个线性无关的特征向量,并求出相应的特征值.
1
(3)当
x1 y1
2 1 2
时,求
xn1 yn1
.
十二、(本题满分 8 分)
某流水线上每个产品不合格的概率为 p(0 p 1) ,各产品合格与否相对独立,当出现 1 个不合 格产品时即停机检修.设开机后第 1 次停机时已生产了的产品个数为 X ,求 X 的数学期望 E( X ) 和方 差 D(X ) .
S
S1
(C) zdS 4 xdS
S
S1
(3)设级数 un 收敛,则必收敛的级数为 n1
(B) ydS 4 xdS
S
S1
(D) xyzdS 4 xyzdS
S
S1
(A) (1)n un
n1
n
(B) un2 n1
(C) (u2n1 u2n ) n1
(D) (un un1) n1
2000 年全国硕士研究生入学统一考试
数学(一)试卷
一、填空题(本题共 5 小题,每小题 3 分,满分 15 分.把答案填在题中横线上)
(1) 1 2x x2 dx =_____________. 0
(2)曲面 x2 2 y2 3z2 21在点 (1, 2, 2) 的法线方程为_____________.
故正确选项为(B)。
三、(本题满分 6 分)
2
e
1 x
求
lxim0
1
e
4 x
sin x
x
.
【详解】因为
2
e
1 x
运筹学》习题答案运筹学答案汇总
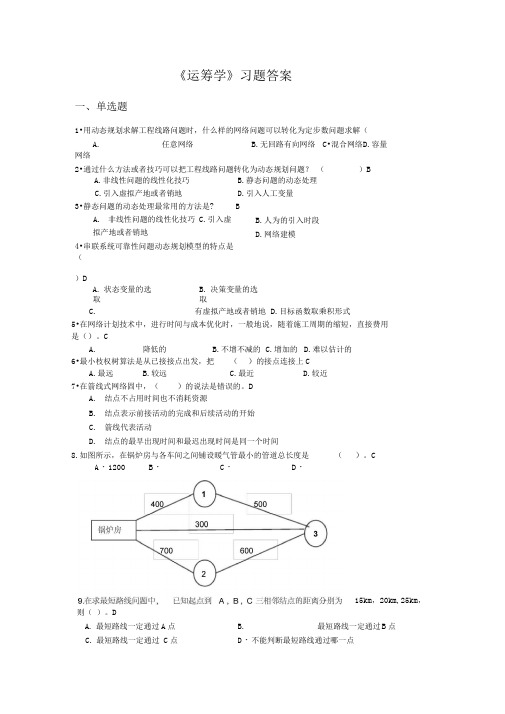
《运筹学》习题答案一、单选题1•用动态规划求解工程线路问题时,什么样的网络问题可以转化为定步数问题求解(A.任意网络B.无回路有向网络 C •混合网络 D .容量网络2•通过什么方法或者技巧可以把工程线路问题转化为动态规划问题? ()B3•静态问题的动态处理最常用的方法是?A. 非线性问题的线性化技巧 C.引入虚拟产地或者销地4•串联系统可靠性问题动态规划模型的特点是( )DA. 状态变量的选取B. 决策变量的选取C.有虚拟产地或者销地 D.目标函数取乘积形式5•在网络计划技术中,进行时间与成本优化时,一般地说,随着施工周期的缩短,直接费用 是()。
CA. 降低的B.不增不减的C.增加的D.难以估计的 6•最小枝权树算法是从已接接点出发,把 ( )的接点连接上CA.最远B.较远C.最近D.较近 7•在箭线式网络固中,( )的说法是错误的。
DA. 结点不占用时间也不消耗资源B. 结点表示前接活动的完成和后续活动的开始C. 箭线代表活动D. 结点的最早出现时间和最迟出现时间是同一个时间 8.如图所示,在锅炉房与各车间之间铺设暖气管最小的管道总长度是( )。
CA.非线性问题的线性化技巧B.静态问题的动态处理C.引入虚拟产地或者销地D.引入人工变量 BB.人为的引入时段 D.网络建模A. 最短路线一定通过A 点B. 最短路线一定通过 B 点C. 最短路线一定通过 C 点D ・不能判断最短路线通过哪一点A ・1200B ・C ・D ・则( )。
D15km ,20km,25km ,10・在一棵树中,如果在某两点间加上条边,则图一定()A A・存在一个圈B・存在两个圈C・存在三个圈D・不含圈11・网络图关键线路的长度()工程完工期。
CD・不一定等于12. 在计算最大流量时,我们选中的每一条路线 ( )。
CA. —定是一条最短的路线B. 一定不是一条最短的路线C.是使某一条支线流量饱和的路线D.是任一条支路流量都不饱和的路线13. 从甲市到乙市之间有 一公路网络,为了尽快从甲市驱车赶到乙市,应借用()CA. 树的逐步生成法B.求最小技校树法C.求最短路线法D.求最大流量法 14.为了在各住宅之间安装一个供水管道•若要求用材料最省,则应使用( )。
最全的运筹学复习题及答案-图文

最全的运筹学复习题及答案-图文5、线性规划数学模型具备哪几个要素?答:(1).求一组决策变量某i或某ij的值(i=1,2,…mj=1,2…n)使目标函数达到极大或极小;(2).表示约束条件的数学式都是线性等式或不等式;(3).表示问题最优化指标的目标函数都是决策变量的线性函数第二章线性规划的基本概念一、填空题1.线性规划问题是求一个线性目标函数_在一组线性约束条件下的极值问题。
2.图解法适用于含有两个变量的线性规划问题。
3.线性规划问题的可行解是指满足所有约束条件的解。
4.在线性规划问题的基本解中,所有的非基变量等于零。
5.在线性规划问题中,基可行解的非零分量所对应的列向量线性无关6.若线性规划问题有最优解,则最优解一定可以在可行域的顶点(极点)达到。
7.线性规划问题有可行解,则必有基可行解。
8.如果线性规划问题存在目标函数为有限值的最优解,求解时只需在其基可行解_的集合中进行搜索即可得到最优解。
9.满足非负条件的基本解称为基本可行解。
10.在将线性规划问题的一般形式转化为标准形式时,引入的松驰数量在目标函数中的系数为零。
11.将线性规划模型化成标准形式时,“≤”的约束条件要在不等式左_端加入松弛变量。
12.线性规划模型包括决策(可控)变量,约束条件,目标函数三个要素。
13.线性规划问题可分为目标函数求极大值和极小_值两类。
14.线性规划问题的标准形式中,约束条件取等式,目标函数求极大值,而所有变量必须非负。
15.线性规划问题的基可行解与可行域顶点的关系是顶点多于基可行解16.在用图解法求解线性规划问题时,如果取得极值的等值线与可行域的一段边界重合,则这段边界上的一切点都是最优解。
17.求解线性规划问题可能的结果有无解,有唯一最优解,有无穷多个最优解。
18.如果某个约束条件是“≤”情形,若化为标准形式,需要引入一松弛变量。
19.如果某个变量某j为自由变量,则应引进两个非负变量某j,某j,同时令某j=某j-某j。
《运筹学》试题及答案大全

《运筹学》试题及参考答案一、填空题(每空2分,共10分)1、在线性规划问题中,称满足所有约束条件方程和非负限制的解为可行解。
2、在线性规划问题中,图解法适合用于处理变量为两个的线性规划问题。
3、求解不平衡的运输问题的基本思想是设立虚供地或虚需求点,化为供求平衡的标准形式。
4、在图论中,称无圈的连通图为树。
5、运输问题中求初始基本可行解的方法通常有最小费用法、西北角法两种方法。
二、(每小题5分,共10分)用图解法求解下列线性规划问题:1)max z =6x 1+4x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤+≤+0781022122121x x x x x x x ,解:此题在“《运筹学》复习参考资料.doc ”中已有,不再重复。
2)min z =-3x 1+2x 2⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤-≤-≤+-≤+0,137210422422121212121x x x x x x x x x x 解:可行解域为abcda ,最优解为b 点。
⑴⑵⑶⑷⑸⑹、⑺由方程组⎩⎨⎧==+02242221x x x 解出x 1=11,x 2=0∴X *=⎪⎪⎭⎫⎝⎛21x x =(11,0)T∴min z =-3×11+2×0=-33三、(15分)某厂生产甲、乙两种产品,这两种产品均需要A 、B 、C 三种资源,每种产品的资源消耗量及单位产品销售后所能获得的利润值以及这三种资源的储备如下表所示:AB C 甲94370乙46101203602003001)建立使得该厂能获得最大利润的生产计划的线性规划模型;(5分)2)用单纯形法求该问题的最优解。
(10分)解:1)建立线性规划数学模型:设甲、乙产品的生产数量应为x 1、x 2,则x 1、x 2≥0,设z 是产品售后的总利润,则max z =70x 1+120x 2s.t.⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+0300103200643604921212121x x x x x x x x ,2)用单纯形法求最优解:加入松弛变量x 3,x 4,x 5,得到等效的标准模型:max z =70x 1+120x 2+0x 3+0x 4+0x 5s.t.⎪⎪⎩⎪⎪⎨⎧=≥=++=++=++5,...,2,1,03001032006436049521421321j x x x x x x x x x x j 列表计算如下:四、(10分)用大M 法或对偶单纯形法求解如下线性规划模型:min z =5x 1+2x 2+4x 3⎪⎩⎪⎨⎧≥≥++≥++0,,10536423321321321x x x x x x x x x 解:用大M 法,先化为等效的标准模型:max z /=-5x 1-2x 2-4x 3s.t.⎪⎩⎪⎨⎧=≥=-++=-++5,...,2,1,010********214321j y x x x x x x x x j增加人工变量x 6、x 7,得到:max z /=-5x 1-2x 2-4x 3-M x 6-M x 7s.t⎪⎩⎪⎨⎧=≥=+-++=+-++7,...,2,1,010*********2164321j x x x x x x x x x x x j大M 法单纯形表求解过程如下:五、(15分)给定下列运输问题:(表中数据为产地A i 到销地B j 的单位运费)B 1B 2B 3B 4s iA 1A 2A 312348765910119108015d j82212181)用最小费用法求初始运输方案,并写出相应的总运费;(5分)2)用1)得到的基本可行解,继续迭代求该问题的最优解。
2000考研数一真题解析

1全国硕士研究生入学统一考试数学一试题解析一、填空题 π(1)【答案】4【详解】 I =⎰= ⎰解法 1:用换元积分法:设 x -1 = sin t ,当 x = 0 时,s in t = -1,所以下限取 -π;当 x = 12时, s in t = 0 ,所以上限取0 .x -1=sin t 0所以I =⎰-πcost cos tdt2πππ由于在区间[-, 0],函数c os t 非负,则I = ⎰ πcos 2 tdt = ⎰ 2 cos 2 t = - 20 4解法 2:由于曲线 y ==是以点 (1, 0) 为圆心,以 1 为半径的上半圆周,它与直线 x = 1和 y = 0所围图形的面积为圆面积的 1,故答案是π44(2)【答案】x -1 = y + 2 = z - 2. 1 -4 6【详解】曲面方程 F (x , y , z ) = 0 在点(x 0 , y 0 , z 0 ) 的法矢量为:n = {F x (x 0 , y 0 , z 0 ), F y (x 0 , y 0 , z 0 ), F z (x 0 , y 0 , z 0 )}令 F (x , y , z ) = x 2+ 2 y 2 + 3z 2 - 21, 则有F x ' (1, -2, 2) = 2x |(1, -2, 2) = 2, F y ' (1, -2, 2) = 4 y |(1, -2, 2) = -8, F z ' (1, -2, 2) = 6z |(1, -2, 2) = 12.所以曲面在点(1, -2, 2) 处的法线方程为:x -1 = y + 2 = z - 2. 即 x - 1 = y + 2 = z - 2 .(3)【答案】 y =C 1+ C x22 2 -8 12 1 -4 6【分析】此方程为二阶可降阶的微分方程,属于 y " = f (x , y ')型的微分方程. 【详解】令 p = y ' ,有 y " =dp.原方程化为: xdp+ 3p = 0 , ⇒ dp + 3 p = 0 dxdx dxx2⎰ ⎰分离变量:两端积分:dp = -3 dx p xdp = -3 dx⇒ lnp xp = -3ln x + C 1从而p = e-3ln x +C 1= e C 1 e-3ln x= eC 1x -3= e C 1 1x3因记C 2 = e C 1> 0 是大于零的任意常数,上式可写成 p = ± C 2; x3记C = ±C , p = C 3 ,便得方程的通解 p = C x -3,3 2x 33 即 dy = C x -3 ⇒ dy = C x -3dx ,其中C 是任意常数dx 33 3对上式再积分,得:y = C x -3dx = -C 3x -2 + C=C 5 +⎛= -C 3 ⎫⎰324x2C 4 , C 52 ⎪ ⎝⎭所以原方程的通解为:y = C 1 + Cx22(4)【答案】 -1.【详解】化增广矩阵为阶梯形,有⎡1 2 1 1⎤ ⎡1 21 1 ⎤ ⎢23 a + 2 3⎥ → ⎢0 -1 a 1 ⎥ ⎢ ⎥ ⎢ ⎥ ⎢⎣1 a -2 0⎥⎦ ⎢⎣0 a - 2 -3 -1⎦⎥ ⎡1 21 1 ⎤ → ⎢0 -1 a 1 ⎥ ⎢ ⎥ ⎢⎣0 0 (a - 3)(a +1) a - 3⎥⎦当a = −1时,系数矩阵的秩为2,而增广矩阵的秩为3,根据方程组解的判定,其系数矩阵与增广矩阵的秩不同,因此方程组无解.当a = 3时,系数矩阵和增光矩阵的秩均为2,由方程组解的判定,系数矩阵的秩等于增广矩阵的秩,而且小于未知量的个数,所以方程组有无穷多解.(5)【答案】 2 3 (由 A , B 独立的定义: P (AB ) = P ( A )P (B ) ) 【详解】由题设,有 P (AB ) = 1, P ( AB ) = P ( AB )9因为 A 和 B 相互独立,所以 A 与 B , A 与 B 也相互独立.⎨ ⎨ ⎪⎪于是由 P ( AB ) = P ( AB ), 有 P (A )P (B ) = P ( A )P (B )即有 P ( A )[1- P (B )] = [1- P ( A )] P (B ) , 可得 P ( A ) = P (B ) , P (A ) = P (B )从而P (AB ) = P ( A )P (B ) = ⎡P ( A )⎤ 2 = [1- P ( A )]2 = 1 ,⎣ ⎦ 9解得P (A ) = 2.3二、选择题 (1)【答案】A【分析】由选项答案可知需要利用单调性证明,关键在于寻找待证的函数. 题设中已知f '(x )g (x ) - f (x )g '(x ) < 0,想到设函数为相除的形式 f (x ). g (x )【详解】设 F (x ) =f (x ) ,则(F (x ))' = f '(x )g (x ) - f (x )g '(x ) < 0,g (x )g 2 (x )则 F (x ) 在 a < x < b 时单调递减,所以对∀a < x < b , F (a ) > F (x ) > F (b ),即f (a ) > f (x ) >f (b )g (a ) g (x ) g (b )得 f (x )g (b ) > f (b )g (x ), a < x < b , ( A ) 为正确选项.(2)【答案】C【性质】第一类曲面积分关于奇偶性和对称性的性质有:性质 1:设 f (x , y , z ) 在分块光滑曲面 S 上连续, S 关于 y oz 平面对称,则⎧0 ⎰⎰ f (x , y , z )dS = ⎪2⎰⎰ f (x , y , z )dS 若f (x , y , z )关于x 为奇函数若f (x , y , z )关于x 为偶函数S其中 S 1 = S ⋂ {x ≥ 0}.⎩ S 1性质 2:设 f (x , y , z ) 在分块光滑曲面 S 上连续, S 关于 xoz 平面对称,则⎧0 ⎰⎰ f (x , y , z )dS = ⎪2⎰⎰ f (x , y , z )dS 若f (x , y , z )关于y 为奇函数若f (x , y , z )关于y 为偶函数S其中 S 1 = S ⋂ {y ≥ 0}.⎩ S 1⎨ n 性质 3:设 f (x , y , z ) 在分块光滑曲面 S 上连续, S 关于 x oy 平面对称,则⎧0 ⎰⎰f (x , y , z )dS = ⎪2⎰⎰ f (x , y , z )dS 若f (x , y , z )关于z 为奇函数若f (x , y , z )关于z 为偶函数S其中 S 1 = S ⋂ {z ≥ 0} .⎩ S 1【详解】方法 1:直接法:本题中 S 在 x oy 平面上方,关于 y oz 平面和 xoz 平面均对称,而 f (x , y , z ) = z 对 x , y均为偶函数,则⎰⎰ zdS性质1= 2 ⎰⎰zdS性质2= 4⎰⎰ zdSSS ⋂{x ≥0}S 1又因为在 S 1 上将 x 换为 y , y 换为 z , z 换为 x , S 1 不变(称积分区域 S 1 关于 x , y , z 轮换对称),从而将被积函数也作此轮换变换后,其积分的值不变,即有4⎰⎰ zdS = 4⎰⎰ xdS = 4⎰⎰ ydS . 选项(C ) 正确.S 1S 1S 1方法 2:间接法(排除法)曲面 S 关于 y oz 平面对称,x 为 x 的奇函数,所以 ⎰⎰ x dS = 0 ,而 ⎰⎰ xdS 中 x ≥ 0 且SS 1仅在 y oz 面上 x = 0 ,从而⎰⎰ xdS > 0 , ( A ) 不成立.S 1曲面 S 关于 zox 平面对称, y 为 y 的奇函数,所以 ⎰⎰ y dS = 0 ,而⎰⎰ xdS > 0 ,所以(B ) 不成立.SS 1曲面 S 关于 zox 平面对称,x yz 为 y 的奇函数,所以 ⎰⎰ x yzdS = 0 ,而 ⎰⎰ xyzdS > 0 ,SS 1所以(D ) 不成立.(3)设级数∑un 收敛,则必收敛的级数为( )n =1(A) ∑ n =1 (-1)n un.n(B)∑n =1 u 2.(C)∑(u2n -1- u 2n ).n =1【答案】D【详解】(D)∑(u n- u n +1).n =1∞ ∞ ∞ ∞ ∞n ∑ 1 1 1 1 ∞∞∞方法 1:直接法. 由∑un 收敛,所以∑un +1 也收敛.由收敛级数的性质(如果级数∑un 、n =1n =1n =1∑vnn =1分 别 收 敛 于 s 、 σ, 则 级 数∑(un± v n ) 也 收 敛 , 且 其 和 为 s ±σ). 知n =1∑(un+ u n +1 ) = ∑u n + ∑u n +1 . 选项(D ) 成立.n =1n =1n =1方法 2:间接法. 找反例:( A ):取u n= (-1)n1,级数ln(1 + n )∑ n =1u n 收敛,但∑(-1) n =1n u n = ∞n n =1(-1) n 1 n ln(1+ n )是发散的;(关于上述结束的敛散,有下述结果:∞1 ⎧收敛 当p > 1∑ (n +1) lnp(1+ n ) ⎨) 当p ≤ 1n =1(-1)n⎩发散∞∞2∞1(B) :取u n =,级数∑un 收敛,∑u n = ∑ n 发散;(-1)n -1n =1∞un =1n =1(C) :取u n =,级数∑n 收敛,但u - u n= 1 + 1 n =1= 4n -1 1 2 n -1 2n2n -1 2n 2n (2n -1) n由比较审敛法的极限形式知,级数∑(u2n -1- u 2n ) 发散.n =1(4)【答案】(D) 【详解】用排除法.(A)为充分但非必要条件:若向量组α1 ,⋅⋅⋅,αm 可由向量组β1 ,⋅⋅⋅, βm 线性表示,则一定 可推导β1 ,⋅⋅⋅, βm 线性无关,因为若β1 ,⋅⋅⋅, βm 线性相关,则r (α1 ,⋅⋅⋅,αm ) < m , 于是α1 ,⋅⋅⋅,αm 必线性相关,矛盾. 但反过来不成立,如当m =1时,α = (1, 0)T,β = (0,1)T均为单个非零 向量是线性相关的,但α1 并不能用β1 线性表示.(B)为既非充分又非必要条件:如当m = 1时,考虑α = (1, 0)T,β = (0,1)T均线性无关, 但并不能由α线性表示,必要性不成立;又如α = (1, 0)T,β = (0, 0)T , 可由α线性表示,1111∞ ∞ ∞ ∞∞∞ ∞ ∞x 但β1 并不线性无关,充分性也不成立.(C)为充分但非必要条件:若向量组α1 ,⋅⋅⋅,αm 与向量组β1 ,⋅⋅⋅, βm 等价,由α1 ,⋅⋅⋅,αm线性无关知, r (β1, ⋅⋅⋅, βm ) = r (α1,⋅⋅⋅,αm )= m , 因此β1 ,⋅⋅⋅, βm线性无关,充分性成立;当m= 1时,考虑α = (1, 0)T, β = (0,1)T均线性无关,但α与β并不是等价的,必要性不成立.1111(D) 剩下(D)为正确选项. 事实上,矩阵 A = (α1 ,⋅⋅⋅,αm )与矩阵B = (β1 ,⋅⋅⋅, βm )等价 ⇔r ( A )=r (B )⇔ r (β1, ⋅⋅⋅, βm ) = r (α1,⋅⋅⋅,αm ) = m , 条件. 因此是向量组β1 ,⋅⋅⋅, βm 线性无关的充要(5)【答案】B.【详解】ξ和η不相关的充分必要条件是它们的相关系数ρξη=Cov (ξ,η)= 0 ⇔ Cov (ξ,η) = 0由协方差的性质: c ov(aX + bY , Z ) = a cov( X , Z ) + b cov(Y , Z )故Cov (ξ,η) = Cov ( X + Y , X - Y )= Cov (X , X )- Cov (X ,Y )+ Cov (Y , X )- Cov (Y ,Y ) = Cov ( X , X ) - Cov (Y ,Y ) = D (X )- D (Y )可见Cov (ξ,η) = 0 ⇔ D ( X ) - D (Y ) = 0 ⇔ D ( X ) = D (Y )⇔ E ( X 2 ) - [E ( X )]2= E (Y 2 ) - [E (Y )]2(由方差定义 DX = EX 2 - (EX )2 )故正确选项为(B).1三【分析】由于极限中含有e x与 x ,故应分别求其左极限与右极限,若左极限与右极限相等,则极限值存在且等于其极限值,否则极限不存在. 【详解】⎛ 1⎫ ⎛1⎫ 2 + e x sin x ⎪2 + e x sin x ⎪ 2lim + x →0-4 = lim ⎪ x →0-4 - x = -1 = 1 ; ⎪1 ⎝ 1+ e x ⎭ ⎝ 1+ e x⎭1 24 4 ⎛ 1⎫ ⎛ 1⎫ lim 2 + e x + sin x ⎪ = lim 2 + e x + sin x ⎪ = 0 +1 = 1; x →0++4x ⎪ x →0+x ⎪ ⎝ 1 e x ⎭ ⎝ 1+ e x ⎭左极限与右极限相等,所以⎛ 1 ⎫ lim 2 + e x +sin x ⎪ = 1. x →0x ⎪ ⎝ 1+ e x ⎭四【详解】根据复合函数的求导公式,有∂z = f'⋅ y + f '⋅ 1 + g '⋅ ⎛ - y ⎫∂x 1 2yx 2 ⎪ ⎝ ⎭∂2 z = ⎡' + ' ⎛x ⎫⎤+ '+ ⎡ ' + ' ⎛ x ⎫⎤ 1于是∂x ∂y ⎢ f 11 x f 12 ⋅ - y 2 ⎪⎥ y f 1 ⎢ f 21 x f 22 ⋅ - y 2 ⎪⎥ y⎣ ⎝ ⎭⎦ ⎣ ⎝ ⎭⎦+ f ' ⎛ 1 ⎫ + g ' ⋅ 1 ⋅ ⎛ - y ⎫ + g ' ⋅ ⎛ - 1 ⎫2 ⋅ - y 2 ⎪ x x 2 ⎪x 2 ⎪ ⎝ ⎭⎝ ⎭ ⎝ ⎭= f '- 1 f '+ xyf ' - x f ' - 1 g '- yg " 1 y 2 2 11y 3 22 x 2 x 3五【详解】方法 1:(复连通条件下的封闭曲线积分)设:(1) L 1 与 L 2 是两条分段光滑的简单封闭曲线,具有相同的走向,(2)在 L 1 与 L 2 所包围的有界闭区域 D 1 与 D 2 的内部除一些点外, P (x , y ) 与Q (x , y ) 连续并具有连续的一阶偏导数,且∂Q ≡ ∂P . 则 ∂x ∂y⎰LP (x , y )dx + Q (x , y )dy = ⎰L P (x , y )dx + Q (x , y )dy解:以点(1, 0)为中心, R 为半径的圆周的参数方程是: x = 1+ R cos θ, y = R sin θ,逆 时针方向一周为从t = 0 到t = 2π,代入曲线积分I = ⎰ Lxdy - ydx 4x 2 + y 2由于分母很繁,计算不方便. 由曲线封闭,可以考虑使用格林公式,但在 L 所包围的区域内部有点O (0, 0) ,该点处分母为 0,导致被积函数不连续,格林公式不能用.- 2 ⎰2⎰⎰2 2⎰ L⎰- yx ∂Py 2- 4 x 2∂Q记 P =4 x 2+ y2, Q = 4 x 2 + y 2 , 且 P (x , y ) 与Q (x , y ) 满足 ∂x (x , y ) ≠ (0, 0) . 作足够小的椭圆:⎧x = ε os t= (4 x 2 + y 2 )2= ∂yL :ε⎪2c (t ∈[0, 2π], C 取逆时针方向), 1⎨ ⎪⎩ y = εsin t于是 L 与 L 1 及函数 P (x , y ) 与Q (x , y ) 满足“分析”中所述定理的一切条件,于是I = ⎰ xdy - ydx = 4x + y xdy - ydx 4x 2 + y 2 LL 1而后一积分可用参数法计算εε1 2I = xdy - ydx =cos t ⋅εcos t - εsin t ⋅ 2π2 2 (- s in t ) dt =2π2ε dt = π ⎰ 4x2+ y 2⎰ε21 ⎰ε2方法2:记 P =- y , Q =x, 则 ∂P - ∂Q= 0 ,(x , y ) ≠ (0, 0) . 在L 内加 L : 4 x 2 + y 24 x 2 + y 2∂x ∂y 1椭圆4x 2+ y 2 = ε2 的顺时针方向,则I = ⎰L + Lxdy - ydx 2 2 xdy - ydx L 2 21 4x + y 1 4x + y= ⎰⎰ 0dxdy - ⎰Lxdy - ydx 2 2( D 由 L 与 L 1 所围)D14x + y= -1Lxdy - ydx =12dxdy( D : 4x 2 + y 2 ≤ ε2) ε1=2 εε D1ε2⋅π⋅ 2⋅ε= π六【详解】由题设条件,可以用高斯公式:0 = ⎰⎰ xf (x )dydz - xyf (x )dzdx - e 2xzdxdy S= ±⎰⎰⎰ ⎡⎣ xf '(x ) + f (x ) - xf (x ) - e 2x ⎤⎦dvΩ其中Ω为S 所围成的有界闭区域,当 S 的法向量指向Ω 外时,“ ± ”中取“ + ”;当 S 的法向量指向Ω 内时,“ ± ”中取“ - ”. 由S 的任意性,知被积函数应为恒等于零的函数 即xf '(x ) + f (x ) - xf (x ) - e 2x = 0, (x > 0)1,⎰ ⎪ (e n ⎨ ⎰ ⎢ n变形后得f '(x ) + ⎭e 2x, (x > 0) 这是一阶线性非齐次微分方程,利用一阶线性非齐次微分方程 dy+ P (x ) y = Q (x ) 的通解公式:dx y = e - ⎰ P ( x )dx ⎛ Q (x ) ⋅ e ⎰ P ( x )dx dx + C ⎫ ⎝ ⎭其通解为(1-1)dx⎡ ⎛ 1 -1⎫dx ⎤ x x ⎰ 1 2 x ⎰ x ⎪e ⎡ 1 2 x - x ⎤ e xf (x ) = ex⎢ e ⎣x ⋅ e ⎝ ⎭ dx + C ⎥ = ⎥⎦ x ⎢⎣⎰ x e ⋅ xe dx + C ⎥⎦ = x (e + C )由于 lim ⎛ e 2x + Ce x ⎫ f (x ) = lim ⎪= 1, 故必有 l im (e 2x + Ce x)= 0, (否则不能满足极 x →0+x →0+⎝ x ⎭x →0+限值为1),即C +1 = 0, 从而C = −1.因此f (x ) = e x xx-1).七【定义概念】幂级数∑ n =0 a x n,若 lim n n →∞ = ρ,其中 a n , a n +1是幂级数∑ n =0 a x n 的相邻两项的系数,则该幂级数的收敛半径⎧ 1⎪ρ R = ⎪+∞⎪0 ⎪ ⎪⎩ρ≠ 0 ρ= 0ρ= +∞开区间(-R , R ) 叫做幂级数的收敛区间.【详解】nn⎡1+ ( -2)n ⎤ nlim = lim ⎡⎣3 + (-2) ⎤⎦ n = lim ⎣ 3 ⎥⎦ = 1 n →∞ x →∞ ⎣⎡3n +1 + (-2)n +1 ⎦⎤ (n +1) x →∞ 3 ⎡1+ ( -2)n +1 ⎤ (n +1) 3所以收敛半径为R = 3,相应的收敛区间为(-3, 3).当x =3时,因为⎣⎢3 ⎥⎦ 3 ⋅ 1=1 ⋅ 1 > 13n + (-2)n n⎛ -2 ⎫n n 2n1+ 3 ⎪ ⎝ ⎭∞ ∞ a n +1 a na n +1 a n⎛ 1 -1⎫ f (x ) = 1 ⎝ x ⎪ xn3 ⋅ ⋅ 0⋅ = - ⋅ = -1 - ⋅∞1且∑ 发散,由比较审敛法的极限形式,所以原级数在点x =3处发散; n =1当x = −3 时, 由于(-3)n 1 ⎛ (-3)n + 2n 2n ⎫ 1 ( )n 1 (2 )n 1 3n + (-2)nn3n + (-2)n 3n + (-2)n ⎪ n n 3n + (-2)n n ⎝ ⎭ ∞ n 1⎡ ⎛ 2 ⎫n ⎤ 分别考虑两个级数,级数∑(-1) n 是收敛的. 又因 lim ⎢1 + - 3 ⎪ ⎥ n = ∞ ,从而2n1n =1⎛ 2 ⎫n3 ⎪1 ⎛2 ⎫nn →∞ ⎢⎣ ⎝ ⎭ ⎥⎦⋅ = ⎝ ⎭ ⋅ < ⎪ 3n + (-2)nn ⎛ 2 ⎫n n ⎝ 3 ⎭∞ ⎛ 2 ⎫n1+ - ⎪ ⎝ ⎭∞ ⎛ (2)n 1 ⎫∞ ⎛ (-3)n 1 ⎫ 再由∑ ⎪ 收敛,根据比较审敛法知∑ n n ⎪ 收敛. 于是∑ n n ⎪ n =1 ⎝ 3 ⎭n =1 3 + (-2) n ⎪ n =1 3 + (-2) n ⎪ ⎝ ⎭ ⎝ ⎭收敛,所以原级数在点x = −3处收敛. 所以收敛域为[-3, 3) .八【详解】本题为一物理应用题,由于重心坐标是相对某一些坐标系而言的,因此本题的关 键是建立适当的坐标系,一般来说,可考虑选取球心或固定点 P 0 作为坐标原点,相应的有两种求解方法.方法1:记所考虑的球体为Ω,以Ω的球心为坐标原点O , 射线O P 0 为正 x 轴建立直角坐标系,则球面方程为: x 2+ y 2 + z 2 = R 2 , 点 P 的坐标为 (R , 0, 0), 设Ω 的重心位置为 (x , y , z ) , 由对称性, 得 y = 0, z = 0, 设 μ为 Ω 上点 (x , y , z ) 处的密度, 按题设,⎣ ⎦⎣ ⎦⎣ ⎦ ⎣ ⎦ π ⎣ ⎦ d d 0μ= k ⎡(x - R )2+ y 2 + z 2 ⎤ ,则⎰⎰⎰ x μdV ⎰⎰⎰ x ⋅ k ⎡(x - R )2 + y 2 + z 2 ⎤ dV x = Ω= Ω⎰⎰⎰μdV Ω而⎰⎰⎰ k ⎡(x - R )2+ y 2 + z 2 ⎤ dV Ω⎰⎰⎰ k ⎡(x - R )2+ y 2 + z 2 ⎤ dV Ω= ⎰⎰⎰ k (x 2 + y 2 + z 2 + R 2 )dV - 2kR ⎰⎰⎰ zdV Ω Ω= k ⎰⎰⎰ (x 2 + y 2 + z 2 )dV + k ⎰⎰⎰ R 2 dV - 0ΩΩ(利用奇函数的对称性)π πR= 8k ⎰ 2d θ⎰ 2d ϕ⎰r 2 ⋅ r 2 sin ϕdr + 4k πR 50 0 0 3(利用奇偶函数的对称性轮换对称性+ 球体体积公式)= 8k ⋅π⎰ 2sin ϕd ϕ⎰Rr 4dr + 4kπR 52 03π π⎛ r 5 ⎫ R4k= 8k ⋅ ⎰ 2 sin ϕd ϕ⋅ ⎪+ πR 5(牛-莱公式)2 0 ⎝ 5 ⎭3 π π R 5 4k = 8k ⋅ ⎰ 2 sin ϕd ϕ⋅ + πR 52 0= 4k πR 5 -5 3 ϕ π4k 5 ( cos52+πR3(牛-莱公式)= 4k πR 5+4k πR 5 = 32k πR 5 5 3 15 ⎰⎰⎰ kx ⎡( x - R )2 + y 2 + z 2 ⎤ dV Ω= k ⎰⎰⎰ x (x 2 + y 2 + z 2 + R 2 ) - 2kR ⎰⎰⎰ x 2dVΩΩ其中第一个积分的被积函数为 z 的奇函数, Ω 对称于 x Oy 平面,所以该积分值为零, 又由于Ω 关于 x , y , z 轮换对称,所以 ⎰⎰⎰ z 2dV = ⎰⎰⎰ x 2 dV = ⎰⎰⎰ y 2 dVΩΩΩ从而⎰⎰⎰ x 2dV = 1⎰⎰⎰(x2+ y 2 + z 2 )dV =1⎰ 2π θ⎰π ϕ⎰ Rr 2⋅ r 2sin ϕdr = 4πR 5Ω3 Ω3 0o15)⎣ ⎦ππr 00 0⎰ 于是⎰⎰⎰ kx ⎡( x - R )2 + y 2 + z 2 ⎤ dV= -2kR ⋅ 4 πR 5 = - 8kπR 6 15 15 Ω故 x = - R . 4因此,球体Ω的重心位置为(- R, 0, 0)4方法2:用Ω表示所考虑的球体, O 表示球心,以点 P 0 选为原点,射线 P 0 O为正z 轴建立直角坐标系,则球面的方程为 x 2+ y 2+ z 2= 2Rz ,设Ω的重心位置为(x , y , z ) ,由对称性,得 x = 0, y = 0 ,设μ为Ω 上点(x , y , z ) 处的密度,按题设μ= k ⎣⎡x 2 + y 2 + z 2 ⎦⎤ ⎰⎰⎰ z μdV ⎰⎰⎰ kz (x 2+ y 2 + z 2 )dV所以z= Ω= Ω⎰⎰⎰μdV Ω⎰⎰⎰ k (x2+ y 2 + z 2 )dVΩ因为⎰⎰⎰(x 2+ y 2 + z 2)dV = 4⎰ 2 d θ⎰ 2 d ϕ⎰2 R cos ϕ2⋅ r 2sin ϕdr = 32πR 5Ωπ π152R cos ϕ⎰⎰⎰ z (x 2 + y 2 + z 2 )dV = 4⎰ 2 d θ⎰ 2 d ϕ⎰ r 5 sin ϕcos ϕdrΩ= 64 3ππR 6 2 cos 7ϕsin ϕd ϕ= 08πR 63故 z = 5 R . 4 因此,球体Ω的重心位置为(0, 0, 5R ).4九【证明】⎰ππππξ1π1π方法1:令 F (x ) = xf (t )dt , 0 ≤ x ≤ π,有 F (0) = 0, 由题设有 F (π) = 0 .又由题设⎰f (x ) cos xdx = 0 ,用分部积分,有ππ0 = ⎰0 f (x ) cos xdx = ⎰0 cos xdF (x )π π = F (x ) cos x π + ⎰ F (x ) sin xdx = ⎰ (0 0由积分中值定理知,存在ξ∈ (0,π) 使πF x ) sin xdx 00 = ⎰0 F (x ) sin xdx = F (ξ) sin ξ⋅ (π- 0)因为ξ∈ (0,π) , s in ξ≠ 0 ,所以推知存在ξ∈ (0,π), 使得 F (ξ) = 0 . 再在区间[0,ξ] 与 [ξ,π] 上 对 F (x ) 用 罗 尔 定 理 , 推 知 存 在 ξ1 ∈(0,ξ) , ξ2 ∈(ξ,π) 使F '(ξ1 ) = 0,F '(ξ2 ) = 0 ,即 f (ξ1 ) = 0, f (ξ2 ) = 0方法2:由⎰f (x )dx = 0 及积分中值定理知,存在ξ1 ∈ (0,π) ,使 f (ξ1 ) = 0. 若在区间(0,π) 内 f (x ) 仅有一个零点ξ1 ,则在区间(0,ξ1 ) 与(ξ1 ,π) 内 f ( x ) 异号. 不妨设在(0,ξ1 ) 内π πf (x ) > 0 ,在(ξ1,π) 内 f (x ) < 0 . 于是由⎰f (x )dx = 0,⎰0f (x ) cos xdx = 0 ,有0 = f (x ) cos xdx -f (x ) cos ξdx =f (x )(cos x - cos ξ)dx⎰0⎰1⎰1=f (x )(cos x - cos ξ)dx +f (x )(cos x - cos ξ)dx⎰1⎰ξ1当 0 < x < ξ1 时 , c os x > cos ξ1 , f ( x )(cos x - cos ξ1 ) > 0 ;当 ξ1 < x < π时 ,c os x < cos ξ1 ,仍有 f ( x )(cos x - cos ξ1 ) > 0,得到:0 > 0. 矛盾,此矛盾证明了 f ( x ) 在(0,π) 仅有1个零点的假设不正确,故在(0,π) 内 f ( x ) 至少有2个不同的零点.十【分析】本题为解矩阵方程问题,相当于是未知矩阵,其一般原则是先简化,再计算,根 据题设等式,可先右乘A ,再左乘 A *,尽量不去计算 A-1【详解】方法1:由 AA * = A *A = A E , 知 A * = An -1,因此有8 = A * = A 3 ,于是 A = 2 ,所以 A * A = 2等式 ABA -1= BA -1+ 3E 两边先右乘 A ,得ABA -1A = BA -1 A + 3EA再左乘 A *,得A * ABA -1 A = A * BA -1 A + A * 3EA⎢ ⎥ ⎢⎥ 0 ⎤ ⎥化简⇒| A | BE = A * BE + 3A * A ⇒ 2B = A *B + 3 | A | E ⇒ 2B = A * B + 6E ⇒ (2E - A * )B = 6E ,于是B = (2E - A * )-1⎡ 1 0 0 0 ⎤-1 ⎢ ⎥⎡1 0 0 0 ⎤ ⎢0 1 00 ⎥ = 6 ⎢ 0 1 0 0 ⎥ ⎢⎥ 0 = 6 = ⎢-1 0 1 0 ⎥ ⎢1 0 1 0 ⎥ ⎢ ⎥⎢ 1 1 ⎥⎣ 03 0 -6⎦⎢0 0 - ⎥ ⎢⎣2 6 ⎥⎦ (由初等变换法求得)方法2: A = 2 (同解1),由 AA *= A * A = A E , 得-1 -1⎡ 1 0 0 0 ⎤ ⎢ 01 0 0 ⎥ ⎡2 0 0 0 ⎤⎢ 02 0 0 ⎥A = A (A * ) = 2 (A *) = 2 ⎢-10 1 0 ⎥ = ⎢-20 2 0 ⎥ ,⎢ 3 1 ⎥ ⎢3 1 ⎥⎢ 0 0 ⎥ ⎢0 ⎥ ⎢⎣(由初等变换法求得),可见 A − E 为逆矩阵.8 8 ⎥⎦ ⎢⎣ 4 4 ⎥⎦于是,由( A - E )BA -1= 3E ,-1 有B = 3(A - E )-1A , 而⎤-1⎥ ⎥ (A - E ) = ⎢-20 10 ⎥ = ⎢2 0 10 ⎥ , ⎢ 3 3 ⎥ ⎢3 ⎥ ⎢ 0 0 - ⎥ ⎢0 1⎣⎢4 4 ⎦⎥ ⎣⎢ 因此⎡1 0 0 0 ⎢0 1 00 ⎤ ⎡ 2 0 0 0 ⎤⎥ ⎢ 0 2 0 0 ⎥ ⎥ ⎢⎥ ⎢⎥ 0 B = 3 = ⎢2 0 1 0 ⎥ ⎢-20 2 0 ⎥ 0 ⎥ ⎢ 3 ⎥ ⎢ 3 1 ⎥ ⎥ ⎢0 1 0 - ⎥ ⎢ 0 0 ⎥ -1⎦⎣⎢4 ⎦⎥⎣⎢ 4 4 ⎦⎥ 方法3:由题设条件 ABA -1= BA -1+ 3E ,得( A - E ) BA -1= 3E .知: A - E , B 均是可逆矩阵,且⎛ * ⎫- 1B = 3(A - E )- 1A = 3 ⎡ A - 1 (A - E )⎤- 1= 3 (E - A-1 )- 1= 3 E - A ⎪⎣ ⎦A ⎪ ⎝ ⎭⎥ ⎡6 00 0 ⎤ ⎢ ⎢0 6 0 ⎥ ⎢60 6 0 ⎥ ⎢ ⎣0 3 0- ⎥ 1⎦⎡ 1 0 0 0 ⎢ 0 ⎢1 0 0 ⎡1 0 0 0 ⎤ ⎢0 ⎢ 1 0 0 ⎥ ⎥ 0 - ⎥4 ⎦⎥⎡6 00 ⎢ ⎢06 0 ⎢6 0 6 ⎢⎣0 3 0B = - * -1 ⎢ ( 1 0 1 0 0 0 6 0 0) ⎝ ⎭⎝ ⎩⎪ ⎪ 由 A *= An -1,其中n = 4 , A *= 8,得 A = 2 故⎛ 3 E A * ⎫-1⎪ ⎛ 2E - A * ⎫-1= 3⋅ ⎪= 6 (2E - A * )-1 ⎝ 2 ⎭ ⎝ 2 ⎭ 其中⎡1 0 0 0 ⎤ ⎢01 0 0 ⎥ 2E - A *= , (2E - A ) = 1 0 10 ⎥ , -1 0 1 0 ⎥ ⎥⎢ ⎥⎢ 1 1 ⎥⎣ 03 0-6⎦⎢0 0 - ⎥ ⎣⎢ 2 6 ⎥⎦⎡ 10 0 0 ⎤ ⎡60 0 0 ⎤⎢ ⎥ ⎢⎥所以B = 6 2E - A * - = 6 ⎢ ⎥ = ⎢ ⎥⎢-1 0 1 0 ⎥ ⎢6 0 6 0 ⎥0 3 0 -603 0 -⎣⎦ ⎣1⎦1 2 ⎛ 1 十一【详解】(1)由题意, x + y 是非熟练工人数, x+ y ⎫ 是年终由非熟练工人 6 n n 5 6 n n ⎪ 变成的熟练工人数, 5x 是年初支援其他部门后的熟练工人数,根据年终熟练工的人数列6 n出等式(1),根据年终非熟练工人人数列出等式(2)得⎧x = 5 x + 2 ⎛ 1 x + y ⎫ (1) ⎧x = 5 x + 1 x + 2 y ⎪ n +1 6 n5 6 n n ⎪ ⎪ n +1 n n n ⎝ ⎭ ⎨ 3 ⎛ 1 ⎫ ⎪ 6 15 5 ⎨1 3⎩⎪ y n +1 = 5 6 x n + y n ⎪ ⎭(2) ⎪ y n +1 = 10 x n + 5 y n⎧x = 9 x+ 2 y⎛ 9 2 ⎫⎪ n +1 10 n 5 n⎛ x n +1 ⎫ 10 5 ⎪ ⎛ x n ⎫ ⇒ ⎨ 1 3 ,即 y ⎪ = 1 3 ⎪ y ⎪ ⎪ y n +1 = x n + y n ⎩ 10 5 可见⎝ n +1 ⎭ ⎪ ⎝ n ⎭ ⎝ 10 5 ⎭ ⎛ 9 2 ⎫ A = 10 5 ⎪. 1 3 ⎪ ⎝ 105 ⎭(2) 把η1 ,η2 作为列向量写成矩阵的形式(η1,η2 ),因为其行列式(η,η) =4-1= 5 ≠ 0 121 1⇒ ⎪ ⎡ 10 0 0 ⎤ ⎢ ⎢ 01 0 0 ⎥ ⎥1 1 λ ⎪ λ ⎪ ⎭= ⎝矩阵为满秩,由矩阵的秩和向量的关系可见η1,η2线性无关. 又 ⎛ 9 2 ⎫ ⎛ - 1 ⎫A η = 105 ⎪ ⎛ 4 ⎫ = ⎛ 4 ⎫ = η, A η = 2 ⎪ = 1 η,11 3 ⎪ 1 ⎪ 1 ⎪ 12 1 ⎪ 2 2 ⎪⎝ ⎭ ⎝ ⎭⎪ ⎝ 105 ⎭ ⎝ 2 ⎭由特征值、特征向量的定义,得η1 为A 的属于特征值λ1 = 1的特征向量,η2 为A 的属于特征 值λ = 1特征向量.22(3)因为⎛ 1 ⎫⎛ x n +1 ⎫ = A ⎛ x n ⎫ = A 2 ⎛ x n -1 ⎫ = A n ⎛ x 1 ⎫= A n 2 ⎪ y ⎪ y ⎪ y ⎪ y ⎪1 ⎪⎝ n +1 ⎭ ⎝ n ⎭ ⎝ n -1 ⎭ ⎝ 1 ⎭ ⎪⎝ 2 ⎭因此只要计算 A n即可. 令P = (η,η) =⎛ 4-1⎫ , 12⎪ ⎝ ⎭则由 P -1AP = ⎛λ1⎝⎫, 有 A = P ⎛λ1 2 ⎭ ⎝⎫ P -1 , 2 ⎭于是⎡⎛ 1 ⎫n⎛ 1 ⎫n ⎤⎛λ ⎫n⎛ 4 -1⎫ ⎡1⎤ ⎛ 4 -1⎫-1 1 ⎢4 + 2 ⎪ 4 - 2 ⎪ ⎥ A n = P 1 ⎪ P -1 = ⎪ ⎢ n ⎥ ⎢ ⎛ 1 ⎫ ⎪ ⎝ ⎭ ⎝ ⎭ ⎥ ⎝ λ2 ⎭ ⎝1 1 ⎭ ⎢ ⎪ ⎥ ⎝1 1 ⎭5 ⎢ ⎛ 1 ⎫n ⎛ 1 ⎫n ⎥ ⎣⎢ ⎝ 2 ⎭ ⎥⎦⎢1- ⎪ 1+ 4 ⎪ ⎥其中求逆矩阵的过程为:⎣⎢ ⎝ 2 ⎭⎝ 2 ⎭ ⎥⎦ ⎛ 4 -1 1 0 ⎫ → ⎛ 1 1 0 1 ⎫ 1 1 0 1 ⎪ 4 -1 1 0 ⎪ ⎝ ⎭ ⎝ ⎭⎛ 1 1 0 1 ⎫ ⎛0 1 ⎫ ⎛ 4 4 ⎫→ ⎪ → 1 1 ⎪ → 1 0 5 5 ⎪ 0 - 1 1 1 ⎪ 0 1 - 4 1 ⎪ ⎪ 0 1 41 ⎝ 4 4 ⎭ ⎝ 5 5 ⎭ - 5 5 ⎪⎢ ⎛ 4 -1⎫-1⎡ 4 4 ⎤ ⎢ 55 ⎥1 ⎡ 4 4⎤ 所以1 1 ⎪= ⎢ 4 1 ⎥ = 5 ⎢-4 1⎥ ⎝ ⎭ ⎢-⎣ 因此⎥ ⎣ ⎦ 55 ⎥⎦⎛ 1 ⎫ ⎡ ⎛ 1 ⎫n⎤⎛ x ⎫ ⎪ 1 ⎢8 - 3 2 ⎪ ⎥ n +1 ⎪ = A n 2 ⎪ = ⎢ ⎝ ⎭ ⎥ ⎝ y n +1 ⎭ 1 ⎪ 10 ⎢⎛ 1 ⎫n ⎥⎪ ⎢2 + 3 ⎪ ⎥ ⎝ 2 ⎭ ⎢⎣ ⎝ 2 ⎭ ⎥⎦十二【分析】此分布为一典型分布——几何分布.【详解】显然 X 是一个离散型随机变量. 取值范围为 1,2,3,……现在关键在于建立 X 的分布律. 生产线上每个产品的生产可理解为一个试验. 各个产品合格与否是相互独立的,可以看成是各次试验是相互独立的.生产了个产品停机,应该理解为第 X 个产品是不合格产品,而前 X -1个产品则必为合格产品,这就不难写出分布律.记 q = 1- p , X 的概率分布为 P {X = k } = q k -1p , (k = 1, 2 ) . 由离散型随机变量的数学期望定义得, X 的数学期望为E ( X ) = ∑ kP {X = k } = ∑ kqk -1p = p ∑∞(q k)' = p ⎛ ∑∞ q k ⎫' = p ⎛ q ⎫' =1k =1k =1k =1⎪ k =1 1- q ⎪ p ⎝ ⎭ ⎝ ⎭因为∞∞⎡ ⎛ ∞ ⎫' ⎤' ⎡ q ⎤' 2 - p E (X 2 ) = ∑k 2 P {X = k }= ∑k 2q k -1 p = p ⎢q ∑q k ⎪ ⎥ = p ⎢ ⎥ =k =1 k =1 ⎢ ⎝ k =1 ⎭ ⎥ ⎢⎣(1- q )2 ⎦⎥ p 2⎣ ⎦(因为幂级数在其收敛区间内可逐项求导的性质,上面求 E ( X ) 和E (X 2) 时都用到了先求导化为易求和的级数,再积分还原的过程.)故 X 的方差为D ( X ) =E ( X 2) - [E ( X )]2=2 - p - 1= 1- pp 2 p 2p 2十三【概念】最大似然估计,实质上就是找出使似然函数最大的那个参数,问题的关键在于 构造似然函数. 似然函数的定义:设 x 1, x 2 ,..., x n 是相应于样本 X 1, X 2 ,..., X n 的一组观测值,则似然函数为:L (θ) =f (x 1 , x 2 , , x n ;θ) = ∏ f (x i ;θ) = i =1f (x 1;θ) f (x 2 ;θ) f (x n ;θ)【详解】似然函数为n ∞∞⎧ - n n L (θ) = L (x , x ,⋅⋅⋅, x ,θ) = f (x ;θ) = ⎪2ne 2∑(x i -θ) i =1, x ≥ θ(i = 1, 2, , n )1 2 n ∏ ii =1⎨ ⎪⎩0,其他当 x i ≥θ(i = 1, 2, , n )时, L (θ) > 0,所以ln L (θ) = n ln 2 - 2∑ (x i-θ).i =1(由于l n L 是单调递增函数, L 取最大与l n L 取最大取到的θ是一致的,而加对数后能把连乘转换成累加,这样求导,找极值比较方便)而d ln L (θ) = 2n > 0,d θ所以 L (θ) 单调增加. 要使得 L (θ) 值最大,θ是越大越好.又由于θ必须满足 x i ≥θ(i = 1, 2, , n ),因此当θ取 x 1 , x 2 ,⋅⋅⋅, x n 中的最小值时,x i ≥θ(i = 1, 2, , n )恒成立,且此时 L (θ) 取最大值,所以θ的最大似然估计值为θ = min(x 1, x 2 ,⋅⋅⋅, x n )n。
研究生运筹学考试题及其考试答案

一、 解: 121284x x x +=⎧⎨=⎩ ⇒ 1242x x =⎧⎨=⎩ *243214Z =⋅+⋅= 1212233x x x x +=⎧⎨+=⎩ ⇒ 123212x x ⎧=⎪⎪⎨⎪=⎪⎩ *33192224Z =+⋅=二、(10分)证明:若ˆX 、ˆY 分别是原问题和对偶问题的可行解。
那么ˆˆ0s s YX Y X ==,当且仅当ˆX、ˆY 为最优解。
证明:min ,0,0S S S S max z CX Yb AX X b YA Y C X X Y Y ω==+=-=≥≥设原问题和对偶问题的标准关系是原问题对偶问题将原问题目标函数中的系数向量C 用C=Y A-YS 代替后,得到 z =(YA − YS )X =YAX − YSX将对偶问题的目标函数中系数列向量b ,用b =AX +XS 代替后,得到 w =Y (AX +XS )=YAX +YXSˆˆˆˆˆˆˆˆ;,4,4ˆˆ2152160,0S SSSY X 0,YX 0Yb YAX CX X Y CX YAX YbYXY X ======--==若则由性质(),可知是最优解。
又若分别是原问题和对偶问题的最优解,根据性质(),则有由(),()式可知,必有三、1)(5分)写出下列线性规划问题的对偶问题123123123123123Min z x x 2x 2x 3x 5x 23x x 7x 3s.t x 4x 6x 5x ,x ,x 0=++++≥⎧⎪++≤⎪⎨++≤⎪⎪≥⎩解:123123123123123Max w 2y 3y 5y 2y 3y y 13y y 4y 1s.t 5y 7y 6y 2y 0,y ,y 0=++++≥⎧⎪++≥⎪⎨++≥⎪⎪≥≤⎩ 2)(5分)试写出下述非线性规划的Kuhn-Tucker 条件并求解2()(4)15Minf x x x =-≤≤解:先将该非线性规划问题写成以下形式212min ()(4)()10()50f x x g x x g x x ⎧=-⎪=-≥⎨⎪=-≥⎩写出其目标函数和约束函数的梯度:12()2(4),()1, ()1f x xg x g x ∇=-∇=∇=-对第一个和第二个约束条件分别引入广义拉格朗日乘子,设K-T 点为X*,则可以得到该问题的K-T 条件。
