24.2(2)比例线段 (黄金分割)

合集下载

沪教版(上海)九年级上册数学24.2：比例线段(2)导学案

学生编号学生姓名授课教师辅导学科数学所属年级九年级教材版本沪教版课题名称比例线段2课时进度授课时间月日教学目标如下重点难点如下24．2 比例线段（2）学习目标1、掌握黄金分割的含义；2、会找出一条线段的黄金分割点，找出一个图形中的黄金分割点；3、会运用同高（或等高）的两个三角形的面积之比等于对应底边的比,进行三角形的面积比与线段比的转化。

学习重点黄金分割的意义。

学习难点熟练并灵活运用黄金分割的意义解题。

学习过程一、学前准备已知a=2,b=4,c=6 ；若a，b，c，x 是成比例线段，则x= ；若a，x，b，c 是成比例线段，则x=小明的身高为 1.6m ，测得他的影长为1m，在同一时刻，旗杆的影长为5m，则旗杆的实际高度是若线段a、b、c满足a：b＝b： c ，则称线段 b 是线段 a 与 c 的实数b是 3 和8的比例中项，则b ＝已知线段a＝6cm，b＝24cm，那么线段 a 和、探究活动阅读材料：展示四个国家的国旗。

1、2、3、4、5、1、b 的比例中项c ＝cm。

新西兰人民共和国朝鲜这四面国旗中的共同图案是。

为什么都会选择这个图案呢？除了政治因素外，还有一个非常重要的原因就是：它本身是一个非常完美的图案。

古希腊数学家毕达哥拉斯有一句名言：“凡是美的东西，都具有共同的特征，这就是部分与部分以及部分与整体之1）2）间的协调一致。

”下面就让我们从数学的角度来探究此图案中部分与部分以及部分与整体之间存在着怎样的一种关系。

2、自主探究·解决问题五角星是我们常见的图形。

在右图中，度量点C到点A，B的距离，AC和BC相等吗？AB AC操作要求：请用直尺测量线段长度，再求比值。

B3、师生探究·合作交流BC AC如图，在线段 AB 上，点 C 把线段 AB 分成两条线段 AC 和 BC ，如果，那么称线段 AB 被点 C 黄金分割AC ABl 的代数式表示），即可找出上述的线段关系。

沪教版(上海)初中数学九年级第一学期 24.2 比例线段-黄金分割课件

比例的等比性质：
如果
a
,b
c d
k
(b,
d

0)
那么
ac a c _b___d___b____d_.
k
a k b a kb
c k d c kd
a c kb kd k bc bd
例1 在梯形ABCD中，对角线AC与BD相交于点
O，SAOD
SBOC ，求证：
DO OB
CO OA
想一想：将条件 SAOD SBOC 换成DC//AB，其它条件不变，能证明原来的结论正确吗？
AC AD
1.如图，在△ ABC中，点D、E分别在AB、AC
上，且 AD AE
DB EC
.已知S △ ADE=1，S △ DBC=12，
求S △ ABC.
H
3.已知四条线段长分别为1厘米， 2 厘米，2厘米，
x厘米，它们是成比例线段，则x=
厘米.
例2 如图，线段AB的长度为l，点P是线段AB上一点， PB AP (线段AP是PB、AB的比例中项）,
我们做过调查，如果市场上有的电视频主要有两种，一种是宽:长为3∶4的，另一种是 9∶16的.这两个比值都很接近0.618，也就是因为黄金矩形是最美的.
画家们发现，按 0.618∶1来设计腿长与身高的比例，画出的人体身材最优美，
现今的女性，腰身以下的长度平均只占身高的 0.58，因此古希腊维纳斯女塑像及太阳神阿波罗的形象都通过故意延长双腿，使之与身高的比值为0.618，
B P1
∵点P1称为AB的黄金分割点（点P1靠近B）
P1B AP1 5 1 0.618 (黄金数) AP1 AB 2
∵点P2称为AB的黄金分割点（点P2靠近B）

第6章《图形的相似》知识讲练(学生版)

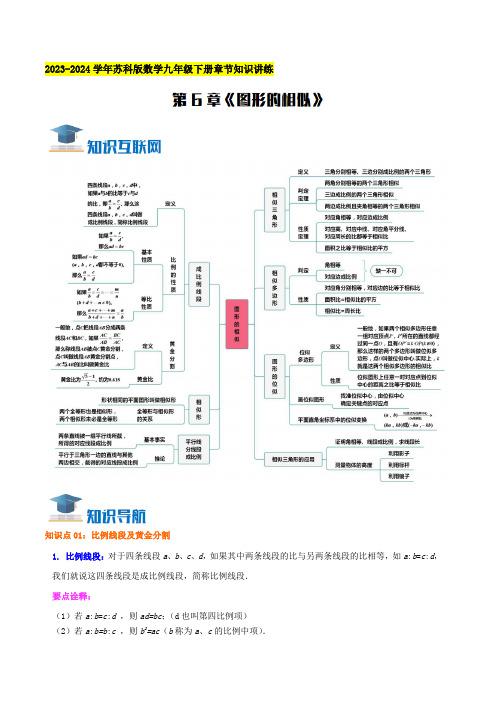
2023-2024学年苏科版数学九年级下册章节知识讲练知识点01：比例线段及黄金分割1.比例线段：对于四条线段a、b、c、d，如果其中两条线段的比与另两条线段的比相等，如a:b=c:d，我们就说这四条线段是成比例线段，简称比例线段．要点诠释：（1）若a:b=c:d，则ad=bc；（d也叫第四比例项）（2）若a:b=b:c，则b2=ac（b称为a、c的比例中项）．定义：如图，将一条线段AB 分割成大小两条线段AP 、PB ，若小段与大段的长度之比等于大段的长度与全长之比，即（此时线段AP 叫作线段PB 、AB 的比例中项），则P 点就是线段AB 的黄金分割点（黄金点），这种分割就叫黄金分割．3. 黄金矩形与黄金三角形：黄金矩形：若矩形的两条邻边长度的比值约为0.618，这种矩形称为黄金矩形.黄金三角形：顶角为36°的等腰三角形，它的底角为72°，恰好是顶角的2倍，人们称这种三角形为黄金三角形．黄金三角形性质：底角平分线将其腰黄金分割．知识点02：相似图形1．相似图形：在数学上，我们把形状相同的图形称为相似图形(similar figures).要点诠释：(1) 相似图形就是指形状相同，但大小不一定相同的图形；(2) “全等”是“相似”的一种特殊情况，即当“形状相同”且“大小相同”时，两个图形全等.各角分别相等，各边成比例的两个多边形，它们的形状相同，称为相似多边形．要点诠释：（1）相似多边形的定义既是判定方法，又是它的性质．（2）相似多边形对应边的比称为相似比.知识点03：相似三角形1. 相似三角形的判定:判定方法（一）：平行于三角形一边的直线与其他两边相交，所截得的三角形与原三角形相似.判定方法（二）：两角分别相等的两个三角形相似.要点诠释：要判定两个三角形是否相似，只需找到这两个三角形的两个对应角相等即可，对于直角三角形而言，若有一个锐角对应相等，那么这两个三角形相似.判定方法（三）：两边成比例夹角相等的两个三角形相似.要点诠释：ABAP AP PB此方法要求用三角形的两边及其夹角来判定两个三角形相似，应用时必须注意这个角必须是两边的夹角，否则，判断的结果可能是错误的.判定方法（四）：三边成比例的两个三角形相似.2.相似三角形的性质：（1）相似三角形的对应角相等，对应边的比相等；（2）相似三角形对应高，对应中线，对应角平分线的比都等于相似比；（3）相似三角形周长的比等于相似比；（4）相似三角形面积的比等于相似比的平方.3.相似多边形的性质：（1）相似多边形的对应角相等，对应边的比相等．（2）相似多边形的周长比等于相似比．（3）相似多边形的面积比等于相似比的平方．知识点04：图形的位似及投影1.位似多边形定义:如果两个相似多边形任意一组对应顶点所在的直线都经过同一个点O，且每组对应点与点O 点的距离之比都等于一个定值k，例如，如下图，OA′=k·OA（k≠0），那么这样的两个多边形叫做位似多边形，点O 叫做位似中心.要点诠释：位似图形与相似图形的区别：位似图形是一种特殊的相似图形，而相似图形未必能构成位似图形.2.位似图形的性质:（1）位似图形的对应点相交于同一点，此点就是位似中心；（2) 位似图形的对应点到位似中心的距离之比等于相似比；（3）位似图形中不经过位似中心的对应线段平行.3.作位似图形的步骤第一步：在原图上找若干个关键点，并任取一点作为位似中心；第二步：作位似中心与各关键点连线；第三步：在连线上取关键点的对应点，使之满足放缩比例；第四步：顺次连接各对应点.要点诠释：位似中心可以取在多边形外、多边形内，或多边形的一边上、或顶点，下面是位似中心不同的画法.在平行光的照射下，物体所产生的影称为平行投影.(1)等高的物体垂直地面放置时，如图1所示，在太阳光下，它们的影子一样长.(2)等长的物体平行于地面放置时，如图2所示，它们在太阳光下的影子一样长，且影长等于物体本身的长度.(3)在同一时刻，不同物体的物高与影长成正比例.即：=.甲物体的高甲物体的影长乙物体的高乙物体的影长利用上面的关系式可以计算高大物体的高度，比如旗杆的高度等.注意：利用影长计算物高时，要注意的是测量两物体在同一时刻的影长.在点光源的照射下，物体所产生的影称为中心投影.(1)等高的物体垂直地面放置时，如图1所示，在灯光下，离点光源近的物体它的影子短，离点光源远的物体它的影子长.(2)等长的物体平行于地面放置时，如图2所示.一般情况下，离点光源越近，影子越长；离点光源越远，影子越短，但不会比物体本身的长度还短.一．选择题（共10小题，满分20分，每小题2分）1．（2分）（2023春•仪征市校级月考）如图，△ABC∽△ADE，S△ABC：S四边形BDEC＝1：3，BC＝，则DE的长为（）A．B．C．D．2．（2分）（2023•靖江市一模）已知，则的值是（）A．B．C．3 D．3．（2分）（2023•姑苏区校级一模）如图，在△ABC中，AB＝4，，点D在AB的延长线上，∠A＝∠BCD＝45°，则△BCD的面积为（）B．C．74．（2分）（2023•盐都区三模）小明用地理中所学的等高线的知识在某地进行野外考察，他根据当地地形画出了“等高线示意图”，如图所示（注：若某地在等高线上，则其海拔就是其所在等高线的数值；若不在等高线上，则其海拔在相邻两条等高线的数值范围内），若点A，B，C三点均在相应的等高线上，且三点在同一直线上，则的值为（）A．B．C．D．25．（2分）（2023•锡山区校级四模）《墨子•天文志》记载：“执规矩，以度天下之方圆．”度方知圆，感悟数学之美．如图，正方形ABCD的面积为4，以它的对角线的交点为位似中心，作它的位似图形A′B′C′D′，若AB：A′B′＝1：2，则四边形A′B′C′D′的外接圆的半径为（）A．B．2 C．D．46．（2分）（2023•大丰区校级模拟）若4m＝5n（m≠0），则下列等式成立的是（）A．＝B．＝C．＝D．＝7．（2分）（2023•新吴区二模）如图，正方形ABCD中，AB＝4，E，F分别是边AB，AD上的动点，AE＝DF，连接DE，CF交于点P，过点P作PQ∥BC，且PQ＝2，在下列结论中：①DE＝CF；②AE2＝FP•FC；③在运动过程中，线段AP最小值为；④当∠CBQ的度数最大时，BQ的长为，其中正确的结论有（）A．1个B．2个C．3个D．4个8．（2分）（2023春•滨湖区期末）如图，矩形ABCD中，AB＝6，BC＝10，点E在边AD上，且AE＝2，F为边AB上的一个动点，连接EF，过点E作EG⊥EF交直线BC于点G，连接FG，若P是FG的中点，则DP的最小值为（）A．B．6 C．5 D．29．（2分）（2023•海州区校级三模）如图▱ABCD，F为BC中点，延长AD至E，使＝，连结EF交DC于点G，则＝（）A．2：3 B．3：2 C．9：4 D．4：910．（2分）（2023•沛县校级模拟）如图，“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．连接AC，若AH平分∠CAD，且正方形EFGH的面积为3，则正方形ABCD的面积为（）A．B．C．D．15二．填空题（共10小题，满分20分，每小题2分）11．（2分）（2023•宝应县二模）如图，五线谱是由等距离、等长度的五条平行横线组成的，同一条直线上的三个点A，B，C都在横线上．若线段AB＝3，则线段BC＝．12．（2分）（2023•青岛一模）如图，在平面直角坐标系中，△OAB的顶点分别为O（0，0），A（﹣3，0），B （﹣4，3），△ODC与△OAB是以原点为位似中心的位似图形，且位似比为1：3，则点C在第四象限的坐标为．13．（2分）（2023•姜堰区二模）如图，△AOB与△CDB关于点B位似，其中B（1，1），D（3，3），若S△AOB＝2，则S△CDB＝．14．（2分）（2023•梁溪区一模）如图，在平行四边形ABCD中，CE＝ED，BE交AC于点F，则EF：FB的比值是．15．（2分）（2023•张家港市校级二模）如图，点A、B、C、D在网格中小正方形的顶点处，AD与BC相交于点O，小正方形的边长为1，则AO的长等于．16．（2分）（2023•泉山区校级三模）如图，在△ABC中，点D、E分别在边AC、BC上，且，△CDE与四边形ABED的面积的比为．17．（2分）（2023•玄武区二模）如图，在矩形ABCD中，AB＝6，BC＝8，E是边BC上的动点，连接AE，过点E作EF⊥AE，与CD边交于点F，连接AF，则AF的最小值为．18．（2分）（2023•阜宁县二模）如图，小明同学用自制直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上．已知纸板的两条边DF＝50cm，DE＝40cm，测得边DF离地面的高度ACm，CD＝12m，则树高AB＝m．19．（2分）（2023•工业园区校级模拟）如图，正方形ABCD由16个边长为1的小正方形组成，形变后成为菱形A′B′C′D′，△AEF（E、F是小正方形的顶点）同时形变为△A′E′F′．当△AEF与△A′E′F′的面积之比等于2：时，则A′C′＝．20．（2分）（2023•海安市一模）已知点D（2，a）为直线y＝﹣x+3上一点，将一直角三角板的直角顶点放在D处旋转，保持两直角边始终交x轴于A、B两点，C（0，﹣1）为y轴上一点，连接AC，BC，则四边形ACBD面积的最小值为．三．解答题（共8小题，满分60分）21．（6分）（2023春•姑苏区校级期末）已知线段AB＝2，点P是线段AB的黄金分割点（AP＞BP）．（1）求线段AP的长；（2）以AB为三角形的一边作△ABQ，使得BQ＝AP，连接QP，若QP平分∠AQB，求AQ的长．22．（6分）（2023•沭阳县模拟）如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF持水平，并且边DE与点B在同一直线上，已知纸板的两条边DFm，EFm，测得边DF离地面的高度ACm，CD＝10m，求树高AB．23．（8分）（2023•滨湖区一模）如图，以AB为直径的⊙O经过△ABC的顶点C，D是的中点，连接BD、OD分别交AC于点E、F．（1）求证：△DEF∽△BEC；（2）若DE＝2，BE＝6，求⊙O的面积．24．（8分）（2023•江都区模拟）在数学活动课上，老师带领数学小组测量大树AB的高度．如图，数学小组发现大树离教学楼5m，大树的影子有一部分落在地面上，还有一部分落在教学楼的墙上，墙上的影子CD 长为2mm的竹竿在水平地面上的影子长1m，那么这棵大树高度是多少？25．（8分）（2023•海陵区校级二模）（1）如图1，在△ABC中，AB＞AC，请用无刻度的直尺和圆规在AB上确定一点P，使得△ACP∽△ABC．（保留作图痕迹，不要求写作法）（2）在（1）的条件下，若AC＝6，AB＝8，则AP的长为；（3）在如图2的正方形网格中，△DEF的三个顶点均为格点，请用无刻度的直尺，在边DF上确定一点M，使得DE2＝DM⋅DF．（保留作图痕迹，不要求写作法）26．（8分）（2023•宿城区校级模拟）问题提出如图（1），在△ABC中，∠BAC＝90°，∠ABC＝30°，D是△ABC内一点，AD⊥CD，∠ACD＝30°，若AD ＝1，连接BD，求BD的长．问题探究（1）请你在图（1）中，用尺规作图，在AB左侧作△ABE，使△ABE∽△ACD．（用直尺、圆规作图，保留作图痕迹，不写作法，不说明理由）（2）根据（1）中作图，你可以得到CD与BE的位置关系是；你求得BD的长为；问题拓展（3）如图（2），在△ABC中，∠BAC＝90°，∠ABC＝30°，D是△ABC内一点，若AD＝，BD＝2，CD＝4，求BC的长．27．（8分）（2023•启东市二模）如图，小红同学正在使用手电筒进行物理光学实验，地面上从左往右依次是墙、木板和平面镜．手电筒的灯泡在点G处，手电筒的光从平面镜上点B处反射后，恰好经过木板的边缘点F，落在墙上的点E处．点E到地面的高度DEm，点F到地面的高度CFm，灯泡到木板的水平距离ACm，墙到木板的水平距离为CD＝4m．已知光在镜面反射中的入射角等于反射角，图中点A、B、C、D在同一水平面上．（1）求BC的长．（2）求灯泡到地面的高度AG．28．（8分）（2023•邗江区校级模拟）定义：两个相似三角形共边且位于一个角的角平分线两边，则称这样的两个相似三角形为邻似三角形．（1）[初步理解]：如图1，四边形ABCD中，对角线AC平分∠BAD，∠BCD+∠BAD＝180°，求证：△ACB和△ADC为邻似三角形；（2）[尝试应用]：在（1）的基础上，如图2，若CD∥AB，AD＝4，AC＝6，求四边形ABCD的周长；（3）[拓展应用]：如图3，四边形ABCD中，△ACB和△ADC为邻似三角形，对角线AC平分∠BAD，且∠ADC＝∠ACB．若AB＝9，AD＝4，∠BAD＝60°，求△BCD的面积．。

成比例的线段黄金分割(复习整理)

成比例的线段黄金分割一、梳理知识1、线段的比的定义在同一单位长度下，两条线段的比叫做这两条线段的比。

2、比例线段的定义在四条线段中，如果其中两条线段的等于另外两条线段的，那么这四条线段叫做成比例线段，简称 .在a ：b=c ：d 中，a 、d 叫做比例的，b 、c 叫做比例的，称d 为a 、b 、c 的 . 3、比例的性质(1)比例的基本性质：如果a ∶b =c ∶d ，那么，特别地，若a ∶b=b ∶c ，即，则b 叫a ，c 的比例中项. (2)合(分)比性质：若dcb a =，则 . (3)等比性质：若nm f e d c b a ==== ，且，则 .4、黄金分割(1)黄金分割的意义：点C 把线段AB 分成两条线段AC 和BC ，如果，那么称线段AB 被点C 黄金分割.其中点C 叫做线段AB 的，AC 与AB 的比叫做 .二、典例解析例1 （1）已知线段a=2，b=3，c=5时，若a ，b ，c ，d 四条线段成比例，则d=_______．（2）已知1，5，5三个数，如果再添一个数，使之能与已知的三个数成比例，则这个数应该是 .（3）在比例尺为1：n 的某市地图上，规划出一块长5cm ×2cm 的矩形工业区，则该工业区的实际面积是平方米. 例2 比例的性质（1）若2a=3b ，则（a-b ）：（a+b ）的值是________．（2）在线段AB 上取一点P ，使AP ：PB=1：4，则AP ：AB=_____，AB ：PB=_______．（3）若5：2=（3-x ）：x ，则x=_______ 【仿练】1．如果a=15cm ，b=10cm ，且b 是a 和c 的比例中项，则c=________． 2．已知（a-b ）：b=2：3，则a ：b=_______．3．在比例尺为1：2 700 000的海南地图上量得海口与三亚间的距离约为8cm ，则海口与三亚两城间的实际距离为________km例3 已知P 是线段AB 上一点，且AP ：PB=3：5，求AB ：PB 的值．【仿练】若点P 在线段AB 上，点Q 在线段AB 的延长线上，AB =10，23==BQ ΑQ BP AP ，求线段PQ 的长．例4 (1)已知x ∶y ∶z =3∶4∶5，①求zyx +的值； ②若x +y +z =6，求x 、y 、z .【仿练】已知实数x ，y ，z 满足x+y+z=0，3x-y+2z=0，则x ：y ：z=________．(2)已知a 、b 、c 是非零实数，且k cb a dd a b c d c a b d c b a =++=++=++=++，求k 的值．【仿练】如果k cb a dd b a c d c a b d c b a =++=++=++=++，试求k 的值．(3)若a 、b 、c 是非零实数，并满足ac b a b c b a c c b a ++-=+-=-+，且a b c a c c b b a x ))()((+++=，求x 的值.【仿练】已知实数a ,b ,c 满足cb a b ac a c b +=+=+,求a cb +的值.例5 如图，若点P 是AB 的黄金分割点，则线段A P 、PB 、AB 满足关系式________，即AP 是________与________的比例中项.三、课堂练习1、如果53=-b b a ,那么b a =________.2、若a =2,b =3,c =33,则a 、b 、c 的第四比例项d 为________.3、若753z y x ==,则zy x z y x -++-=________. 4、已知dcb c=,则下列式子中正确的是（） A.a ∶b =c 2∶d 2 B.a ∶d =c ∶bC.a ∶b =（a +c ）∶（b +d ）D.a ∶b =（a －d ）∶（b －d ）5、如图，已知直角三角形的两条直角边长的比为a ∶b =1∶2,其斜边长为 45 cm ，那么这个三角形的面积是________cm 2.（）A.32B.16C.8D.46、若875c b a ==,且3a －2b +c =3,则2a +4b －3c 的值是（）A.14B.42C.7D.3147、如图，等腰梯形ABCD 的周长是104 cm ，AD ∥BC ，且AD ∶AB ∶BC =2∶3∶5，则这个梯形的中位线的长是________.cm.（）A.72.8B.51C.36.4D.288、已知四条线段a 、b 、c 、d 的长度，试判断它们是否成比例？（1）a =16 cm ，b =8 cm ，c =5 cm ，d =10 cm ；（2）a =8 cm ，b =5 cm ，c =6 cm ，d =10 cm ． 9、若65432+==+c b a ,且2a －b +3c =21，试求a ∶b ∶c ．10、已知线段AB=a ，在线段AB 上有一点C ，若AC=a 253-，则点C 是线段AB 的黄金分割点吗？为什么？四、课后作业1.等边三角形的一边与这边上的高的比是( )A.3∶2B.3∶1C.2∶3D.1∶32.下列各组中的四条线段成比例的是( )A.a =2，b =3，c =2，d =3B.a =4，b =6，c =5，d =10C.a =2，b =5，c =23，d =15D.a =2，b =3，c =4，d =13.已知线段a 、b 、c 、d 满足ab =cd ，把它改写成比例式，错误的是( )A.a ∶d =c ∶bB.a ∶b =c ∶dC.d ∶a =b ∶cD.a ∶c =d ∶b 4.若ac =bd ，则下列各式一定成立的是( )A.dc b a = B.c cb d d a +=+ C.cd ba =22D.da cd ab = 5.已知点M 将线段AB 黄金分割(AM ＞BM )，则下列各式中不正确的是( )A.AM ∶BM =AB ∶AMB.AM =215-AB C.BM =215-AB D.AM ≈0.618AB 6.在1∶500000的地图上，A 、B 两地的距离是64 cm ，则这两地间的实际距离是________. 7.正方形ABCD 的一边与其对角线的比等于________. 8.若2x －5y =0，则y ∶x =________，xyx +=________. 9.若53=-b b a ，则b a =________.10.若AEACAD AB =，且AB =12，AC =3，AD =5，则AE =________. 11.已知342=+x y x ，求yx.12.以长为2的线段AB 为边作正方形ABCD ，取AB 的中点P ，连结PD ，在BA 的延长线上取点F ，使PF =PD ，以AF 为边作正方形AMEF ，点M 在AD 上，如图。

黄金分割公式和计算

黄金分割公式和计算嘿，说起黄金分割，这可是个相当有趣又神秘的数学概念呢！咱们先来讲讲黄金分割到底是啥。

简单说，就是把一条线段分成两部分，较长部分与整体线段的比值等于较短部分与较长部分的比值。

这个比值约等于 0.618，这就是神奇的黄金分割比例。

那黄金分割公式是怎么来的呢？假设整条线段的长度是 a，较长部分的长度是 x，较短部分的长度就是 a - x 。

按照黄金分割的定义，就有 x / a = (a - x) / x 。

经过一番推导和计算，就能得出黄金分割的公式啦。

给您举个例子哈，比如说有一个长方形，咱想让它看起来符合黄金分割的美感。

假设这个长方形的长是 a，宽是 b ，要是满足 b / a =0.618 ，那这个长方形看起来就会特别舒服、顺眼。

我记得有一次去参观一个艺术展览，里面有好多画作和雕塑。

其中有一幅画，它的构图就巧妙地运用了黄金分割。

画面中主体部分的位置和大小，与整个画面的比例刚好接近黄金分割比例。

当时我就站在那幅画前，仔仔细细地观察，越看越觉得那种比例的安排简直太妙了。

整幅画的重心恰到好处，元素的分布既平衡又富有动感，让人的视线不自觉地就被吸引住，而且停留很久都不觉得腻。

再来说说在建筑中的黄金分割。

有些著名的建筑，比如古希腊的帕特农神庙，它的很多尺寸比例都接近黄金分割。

还有巴黎的埃菲尔铁塔，从某些角度去看，它的结构比例也蕴含着黄金分割的奥秘。

咱们在日常生活中也能发现黄金分割的影子。

比如拍照的时候，把主要的景物放在画面大约 0.618 的位置，拍出来的照片往往会更好看。

计算黄金分割也不难。

如果已知线段的长度是 10 厘米，要求出黄金分割点的位置，那就可以设较长部分的长度是 x 厘米，根据公式就有 x / 10 = (10 - x) / x ，通过解方程就能算出 x 的值啦。

总之，黄金分割这个概念虽然听起来有点神秘，但其实就在咱们身边，而且通过简单的公式和计算，咱们就能发现和运用它带来的美妙和神奇。

沪教版数学(上海)九年级第一24.2比例线段教学设计(2课时)

3.采用多元化的教学方法和评价方式：
-运用小组合作、讨论交流等形式，培养学生的合作意识和团队协作能力。
-采用课堂提问、课后作业、小组讨论等多种评价方式，全面了解学生的学习情况。
4.强化巩固，提高解题能力：
-设计具有代表性的例题和练习题，帮助学生巩固所学知识，形成解题思路。
-引导学生总结解题方法和技巧，提高学生的解题能力。
（二）讲授新知
1.比例线段的概念：讲解比例线段的定义，让学生明确什么是比例线段，以及如何表示比例线段。
2.比例线段的性质：通过具体实例，讲解比例线段的性质，如比例线段的分割性质、相似性质等，并引导学生运用性质解决实际问题。
3.比例尺的应用：介绍比例尺的概念，讲解如何根据比例尺进行地图上的距离计算和测量。
4.通过课堂练习和课后作业，巩固所学知识，提高学生的解题技巧。
（三）情感态度与价值观
1.培养学生对数学学科的兴趣，激发学生主动学习的热情，增强学生的自信心。
2.培养学生严谨、细致的学习态度，使学生养成良好的学习习惯。
3.培养学生运用数学知识解决实际问题的意识，增强学生的实践能力。
4.通过数学知识的学习，培养学生发现问题、分析问题、解决问题的能力，提高学生的综合素质。
1.学生对比例的概念已有初步了解，但部分学生对比例线段的性质和运用尚不熟练，需要教师在教学过程中进行引导和巩固。
2.学生在解决实际问题时，可能存在一定的困难。因此，在教学过程中，教师应注重培养学生的知识迁移能力，引导学生将所学知识运用到实际问题中。
3.学生的合作学习能力有待提高。在教学过程中，教师应充分利用小组合作、讨论交流等形式，培养学生的合作意识，提高学生的团队协作能力。
4.学生对数学学科的兴趣和自信心存在差异。教师应关注学生的个体差异，通过多样化的教学手段和评价方式，激发学生的学习兴趣，增强学生的自信心。

沪教版九年级(上)数学一课一练及单元测试卷和参考答案

16.如图，已知矩形ABCD，AB=1，四边形ABFE是正方形，若矩形ABCD与矩形CDEF相似，则AD的长为。
第16题图
三、解答题
17.若与是相似形，点A与点，点B与点，点C与点分别是对应顶点，，，AB=2, =5,BC=3, =6求的度数与边AC, 的长
18如图所示ቤተ መጻሕፍቲ ባይዱ相似四边形中，求未知边x，y的长度和角的大小
（A） 8 (B) 6 (C) 10 (D) 4
3．如图，已知梯形ABCD中，AB//CD，如果S△ODC: S△OBC=1:2,S△ODC：S△OBA（）
（A）1:2（B）1:3（C）1:4（D）1:6
第3题图第4题图第5题图
4.如图，已知AB⊥BD，ED⊥BD，垂足分别为B、D，AE与BD相交于点C，则下列各式错误的是（）
（A）1:7（B）1:6 (C). 1:5 (D). 1:3
第4题图第5题图第6题图
5.如图，在△ABC中，AD是角平分线，DE//AC，已知AB=12，AC=6,则DE的长（）
（A）3（B）4（C）5（D）6
6.在ABC中，AB//EF∥CD，AB=16，CD=48，则EF的长.为（）
（A）8（B）10 (C). 12 (D). 14
21、在梯形ABCD中，AD∥BC,点E在BD的延长线上，且CE∥AB，AC与BD相交于点O，求证：OB2=OD•OE。
数学九年级上第二十四章相似三角形
24.3 三角形一边的平行线第二课时（1）
一、选择题
1、在△ABC中，DE//BC，DF//AC， ,则等于（）
(A) (B) (C) (D)
24.6 实数与向量相乘第一课时（1）57
24.7向量的线性运算第一课时（1）62

黄金分割及比例线段

例2．若一个矩形的短边与长边的比值为（黄金分割数），我们把这样的矩形叫做黄金矩形。
（1）操作：请你在图2所示的黄金矩形ABCD（AB>AD）中，以短边AD为一边作正方形AEFD；
（2）探究：在（1）中的四边形EBCF是不是黄金矩形？若是，请予以证明；若不是，请说明理由；
（3）归纳：通过上述操作及探究，请概括出具有一般性的结论（不需要证明）。
④ 3个“黄金三角”（如外鼻正面观三角、外鼻侧面观三角、鼻根点至两侧口角点组成的三角等）．
此外，健美的人体（如古希腊雕塑《米罗的维纳斯》看上去健美漂亮就是典型的例子，19世纪以来，世界各国的选美标准大部分都依据《米罗的维纳斯》身材各部分的尺寸．她的体形符合希腊人关于美的理想与规范，身长比例接近利西普斯所追求的人体美标准，即身与头之比为8∶1．由于8为3加5之和，这就可以分割成1∶3∶5，这就是“黄金分割律”，这个比例成为后代艺术家创造人体美的准则．）亦有多组比例符合黄金分割比．如人的脐部到头顶的距离与脐部高度之比、头顶到举手指端的距离与脐部到头顶距离之比、膝盖到肚脐同膝盖到脚底之比，都符合黄金分割．
5、美妙的黄金分割和黄金数
任取一条线段AB,在AB上找一点C,使得，点C就叫做线段AB的黄金分割点.每条线段都有两个黄金分割点,若点C把线段AB分成AC，BC，如果，则点C是线段AB的黄金分割点，同样，若点D把线段AB分成AD，BD，如果，则点D也是线段AB的黄金分割点.那么黄金分割点到底在什么位置呢？让我们来算一算.
在日常生活中，还存在着许多令人费解的“黄金分割”之谜.科学家们发现，当外界环境的温度约为人体体温的0.618倍时，人会感到最舒适.我们的书本和窗户，其形状大都基本符合黄金分割.黄金分割留给我们的是永远的美和未解的谜，它到底反映了一个什么样的普遍规律呢？但愿你能有所发现！

24.2(2)比例线段

PB AP 点P是线段AB上的一点，且 AP AB
求线段AP的长.（用 l 表示）
x l-x
l
A
l
P
.
B
即线段 AP是AB 和PB的比例中项.
问1：由图可知，线段 AB、AP、PB之间有怎样的数量关系？
PB AP 问2：结合已知条件 AP AB
答1：AP+PB=AB，即AP+PB=l 设线段AP的长为x，则线段PB的长为l-x. PB AP 答2：由 AP AB
8
P1
B
线段AP是较长线段还是较短线段不确定，分析：所以要分类讨论. 解：（1）当AP＞PB时， ∴AP=
5 1 2 AB=
（2）当PB＞AP时， ∴AP=
3 5 2 AB=
5 1 ×8= 2
4 5 4 12 4 5
3 5 ×8= 2
A
P1
P2
B
两个一般地一条线段的黄金分割点有两个
1：已知线段MN的长为2厘米，点P 是线段MN的黄金分割点，则较长的线段MP的长是 ( 5 1) 厘米，较短的线段PN的长是 (3 5) 厘米. 2：已知点P是线段AB的黄金分割点，AP＞PB， AB=4厘米，那么线段AP、PB的长度分别是 (2 5 2)厘米和 (6 2 5) 厘米．
短= 3 5 全
5 1 3 5 全= 全 2 2
2
例题1：已知点P是线段AB的黄金分割点，若AB=8,
求较长线段AP和较短线段PB. ？分析：
？ 8
A
P
B
解：∵P是线段AB的黄金分割点，根据题意AP＞PB ∴AP= （或PB=
5 1 2 AB=
PB AB AP 8 (4 5 4) 12 4 5

黄金分割点比例公式初中

黄金分割点比例公式初中初三数学黄金分割公式：b2=a（a-b）=a2-ab；（√5-1）÷2。

公式中a为线段AB的长度，C点在靠近B点的黄金分割点上，b为AC的长度，b与a的比值就是黄金分割。

黄金分割线是一种古老的数学方法，黄金分割的创始人是古希腊的毕达哥拉斯，在当时十分有限的科学条件下大胆断言：一条线段的某一部分与另一部分之比，如果正好等于另一部分同整个线段的比即0.618。

黄金分割点AB÷a=a÷b=1.618拓展资料：1.条线段分割为两部分，使其中一部分与全长之比等于另一部分与这部分之比。

其比值是一个无理数。

2.这个分割点就叫做黄金分割点，通常用Φ表示。

这是一个十分有趣的数字，以0.618来近似表示。

3.黄金分割点美学价值：因为它在造型艺术中具有美学价值，在工艺美术和日用品的长宽设计中，采用这一比值能够引起人们的美感，在实际生活中的应用也非常广泛，建筑物中某些线段的比就科学采用了黄金分割。

4.舞台上的报幕员并不是站在舞台的正中央，而是偏在台上一侧，以站在舞台长度的黄金分割点的位置最美观，声音传播的最好。

5.就连植物界也有采用黄金分割的地方，如果从一棵嫩枝的顶端向下看，就会看到叶子是按照黄金分割的规律排列着的。

在很多科学实验中，选取方案常用一种0.618法，即优选法，它可以使我们合理地安排较少的试验次数找到合理的西方和合适的工艺条件。

6.正因为它在建筑、文艺、工农业生产和科学实验中有着广泛而重要的应用，所以人们才珍贵地称它为"黄金分割"。

黄金分割具有严格的比例性、艺术性、和谐性，蕴藏着丰富的美学价值。

应用时一般取0.618 ，就像圆周率在应用时取3.14一样。

7.黄金分割有着很多的应用。

如：最完美的人体：肚脐到脚底的距离/头顶到脚底的距离=0.618；最漂亮的脸庞：眉毛到脖子的距离/头顶到脖子的距离=0.618。

黄金分割线段公式(二)

黄金分割线段公式(二)黄金分割线段公式在数学和美学领域中，黄金分割线段公式是一种重要的比例关系。

这个公式是由著名的古希腊数学家欧几里得首次提出，被广泛应用于绘画、设计和建筑等领域。

黄金分割线段公式可以用于美学上的比例构图，使得作品更加平衡和谐。

下面是关于黄金分割线段公式的相关公式和解释。

1. 黄金分割比例黄金分割比例，也被称为黄金比例或黄金分割比，是指将一段物体分成两部分，使得整体与较大部分之间的比例等于较大部分与较小部分之间的比例。

公式表示如下：a /b = (a+b) / a = φ其中，a 代表较大部分，b 代表较小部分，φ 表示黄金分割比例，约等于。

例如，一根长度为 100 厘米的木棒，我们可以按照黄金分割比例将其分为厘米和厘米两部分。

2. 黄金分割线段黄金分割线段是一条将一段线段分成黄金分割比例的线。

根据黄金分割比例的定义，我们可以得到以下公式：(a + b) / a = a / b通过移项和化简，我们可以得到黄金分割线段的公式：a^2 = a * b + b^2这个公式可以用来计算黄金分割线段的长度。

例如，如果我们知道较大部分 a 的长度为 8 厘米，我们可以通过计算来确定较小部分 b 的长度：8^2 = 8 * b + b^264 = 9b + b^2b^2 + 9b - 64 = 0解这个二次方程可以得到 b 的值，进而确定黄金分割线段的长度。

3. 应用举例：黄金矩形黄金矩形是指长边和短边的比等于黄金分割比例的矩形。

根据黄金分割比例的定义，我们可以得到以下关系：长边 / 短边= φ黄金矩形具有很多美学特征，常常被用于画框、海报、广告和网页设计等领域。

黄金分割比例的使用可以带来视觉上的平衡和谐。

例如，一个黄金矩形的长边为 100 厘米，则其短边的长度为 100 / φ ≈ 厘米。

4. 应用举例：黄金螺旋黄金螺旋是一种特殊的螺旋曲线，其种子半径与黄金分割比例的关系可以用以下公式表示：r(n) = r0 * φ^n其中，r(n) 是第 n 个螺旋圈的半径，r0 是种子半径，φ 是黄金分割比例。

比例线段黄金分割相似三角形

学科教师辅导讲义六．三角形重心的定义：证（解）题规律、辅助线1．“等积”变“比例”，“比例”找“相似”。

2．找相似找不到，找中间比。

方法：将等式左右两边的比表示出来。

⑴)(,为中间比nm n m d c n m b a == ⑵'',,n n nm d c n m b a === ⑶),(,''''''nm n m n n m m n m d c n m b a =====或 3．添加辅助平行线是获得成比例线段和相似三角形的重要途径。

4．对比例问题，常用处理方法是将“一份”看着k;对于等比问题，常用处理办法是设“公比”为k 。

5．对于复杂的几何图形，采用将部分需要的图形（或基本图形）“抽”出来的办法处理。

例题分析：例1：如图 4－85． AB ⊥于l. CD ⊥l 于 C,E 为 AD 中点．求证：△EBC 是等腰三角形．例2：如图4－86，CB ⊥AB ，DA ⊥AB ，M 为CD 中点．求证：∠MAB ＝∠MBA ．例3：若25a c eb d f ===，求ac bd --，234234a ce b df +-+-4.已知：如图20□AB C D 中E 为AD 的中点，AF ：AB =1：6，EF 与AC 交于M 。

求：AM ：AC 。

5.已知：E 是正方形ABCD 的AB 边延长线上一点，DE 交CB 于M ，MN ∥AE ，求证：MN =MB6、已知线段AB 长为1cm ，P 是AB 的黄金分割点，则线段PA= ;7、已知：M 是线段AB 的黄金分割点，AM>BM. 求证：AMAB AB AB AM =+。

24.2比例线段(2)

24.4 比例线段（2）
复习：
1、比例线段的性质：
① 外项之积等于 ② 合比性 ③ 等比
内项之积
质
性质
2、解决比例计算问题常用方法：设K法
第1页，共8页。
例题讲解：
例1：已知：如图，四边形ABCD的对角线AC、BD交于
点O，
SAOD SBOC
D
C
求证： DO CO
O
OB OA
A
B
结论：同高或等高的三角形面积之比就等于
DB EC
S S 1,
12
ADE
DBC
S S 求：和 EDC
ABC

议一议：
同底或等底的两个三角形面积之比等于什么？
第4页，共8页。
回顾：比例中项
定义：如果比例的两个内项（或外项）相同，那么这个相同的项叫做比例中项
即： a b b就是a和c的比例中项 b2 ac bc
试一试：已知线段AB=4, CD=9,线段EF是AB、 CD的比例中项，（1）列出比例式（2）求出EF的长
例2：如图，已知线段AB的长是如l 果
点P是线段AB的黄金分割点，AP是较长
线段求线段AP的长和AP与AB的比值。
添问： PB与AP的比值是
5 1 2。
5 1
AP与AB的比值 2 叫做黄金分割数
5 1
简称：黄金数的倒数是
2叫做
第7页，共8页。
黄金比
想一想：一条线段有几个黄金分割点？两个
探讨：这条线段长度是 l 这两个黄金分割
所对应的底边之比,反之也成立
一题多变：条件 SAOD SBOC 改成DC∥AB
第2页，共8页。
发现规律：平行线三角形面积相等

八年级数学知识点黄金分割数

八年级数学知识点：黄金分割数黄金分割数：把一条线段分割为两部分，使其中一部分与全长之比等于另一部分与这部分之比。

其比值是一个无理数，取其前三位数字的近似值是0.618。

由于按此比例设计的造型十分美丽，因此称为黄金分割，也称为中外比。

黄金分割:黄金分割又称黄金律，是指事物各部分间一定的数学比例关系，即将整体一分为二，较大部分与较小部分之比等于整体与较大部分之比，其比值约为1∶0.618或1.618∶1，即长段为全段的0.618。

0.618被公认为最具有审美意义的比例数字。

上述比例是最能引起人的美感的比例，因此被称为黄金分割。

黄金分割线:黄金分割线是一种古老的数学方法。

黄金分割的创始人是古希腊的毕达哥拉斯，他在当时十分有限的科学条件下大胆断言：一条线段的某一部分与另一部分之比，如果正好等于另一部分同整个线段的比即0.618，那么，这样比例会给人一种美感。

后来，这一神奇的比例关系被古希腊著名哲学家、美学家柏拉图誉为“黄金分割律”。

黄金分割线的神奇和魔力，在数学界上还没有明确定论，但它屡屡在实际中发挥着意想不到的作用。

黄金分割线的最基本公式，是将1分割为0.618和0.382，它们有如下一些特点：(1)数列中任一数字都是由前两个数字之和构成。

(2)前一数字与后一数字之比例，趋近于一固定常数，即0.618。

(3)后一数字与前一数字之比例，趋近于1.618。

(4)1.618与0.618互为倒数，其乘积则约等于1。

(5)任一数字如与前面第二个数字相比，其值趋近于2.618;如与后面第二个数字相比，其值则趋近于0.382。

理顺下来，上列奇异数字组合除能反映黄金分割的两个基本比值0.618和0.382以外，尚存在下列两组神秘比值。

即： (1)0.191、0.382、0.5、0.618、0.809 (2)1、1.382、1.5、1.618、2、2.382、2.618黄金分割点:把一条线段分割为两部分，使其中一部分与全长之比等于另一部分与这部分之比。

数学相似三角形的知识点归纳

数学相似三角形的知识点归纳数学相似三角形的知识点归纳数学是人们认识自然、认识社会的重要工具。

它是一门古老而崭新的科学，是整个科学技术的基础。

随着社会的发展、时代的变化，以及信息技术的发展，数学在社会各个方面的应用越来越广泛，作用越来越重要。

以下是店铺整理的数学相似三角形的知识点归纳，希望帮助到您。

数学相似三角形的知识点归纳篇1本章有以下几个主要内容：一、比例线段1、线段比，2、成比例线段，3、比例中项————黄金分割，4、比例的性质：基本性质；合比性质；等比性质（1）线段比：用同一长度单位度量两条线段a，b，把他们长度的比叫做这两条线段的比。

（2）比例线段：在四条线段a，b，c，d中，如果线段a，b的比等于线段c，d的比，那么，这四条线段叫做成比例线段。

简称比例线段。

（3）比例中项：如果a：b=b：c，那么b叫做a，c的比例中项（4）黄金分割：把一条线段分成两条线段，如果较长线段是全线段和较短线段的比例中项，那么这种分割叫做黄金分割。

这个点叫做黄金分割点。

顶角是36度的等腰三角形叫做黄金三角形宽和长的比等于黄金数的矩形叫做黄金矩形。

（5）比例的性质基本性质：内项积等于外项积。

（比例=====等积）。

主要作用：计算。

合比性质，主要作用：比例的互相转化。

等比性质，在使用时注意成立的条件。

二、相似三角形的判定平行线等分线段——————平行线分线段成比例————————平行于三角形一边的直线截其他两边（或两边延长线），所截线段对应成比例——————（预备定理）平行于三角形一边的直线和其他两边（或两边延长线）相交，所截三角形与原三角形相似——————相似三角形的判定：类比于全等三角形的判定。

三、相似三角形的性质1、定义：相似三角形对应角相等对应边成比例。

2、相似三角形对应线段（对应角平分线、对应中线、对应高等）的比等于相似比3、相似三角形周长的比等于相似比4、相似三角形面积的比等于相似比的平方四、图形的位似变换1、几何变换：平移，旋转，轴对称，相似变换2、相似变换：把一个图形变成另一个图形，并保持形状不变的几何变换叫做相似变换。

黄金分割及答案

黄金分割（一）、主要知识点： 1.黄金分割的定义在线段AB 上，点C 把线段AB 分成两条线段AC 和BC ，如果ACBCAB AC =,那么称线段AB 被点C 黄金分割,点C 叫做线段AB 的黄金分割点，AC 与AB 的比叫做黄金比.其中215-＝AB AC ≈0.618. ABC推导黄金比过程。

设AB=1，AC=x ，则BC=1-x ，所以xxx -=11，即x x -=12，用配方法解得x=215-≈0.618 . 注意：（1）一条线段有2个黄金分割点。

（2）较长线段较短线段原线段较长线段黄金比==（3）宽与长的比等于黄金比的矩形称为黄金矩形（4）黄金分割点把线段分成一长一短，则较长线段较短线段原线段较长线段=，即：点C 是线段AB 的黄金分割点：①若AC>BC,则ACBCAB AC = ；②若AC<BC,则BCACAB BC = . 2．如何作一条线段的黄金分割点. 如图，已知线段AB ，按照如下方法作图：（1）经过点B 作BD ⊥AB ，使BD=21AB. （2）连接AD ，在DA 上截取DE=DB.（3）在AB 上截取AC=AE.则点C 为线段AB 的黄金分割点.作图原理：可设AB=1,，则BD=21,则由勾股定理可知25=AD .可进一步求出AE, AC.从而解决问题。

3.比例的基本性质：如果a b cd =,那么ad=bc ，逆命题也成立。

4.合比性质：如果a b c d =，那么a b b c d d +=+；如果a b c d =，那么a b b c dd -=-。

5.等比性质：如果a b c d ==……=mn（b ＋d ＋……＋n ≠0）；那么，a c m b d n ab ++++++=（二）、典型习题：一、选择题1．等边三角形的一边与这边上的高的比是_________． A ．3∶2 B ．3∶1 C ．2∶3 D ．1∶32．下列各组中的四条线段成比例的是_________． A ．a =2，b =3，c =2，d =3 B ．a =4，b =6，c =5，d =10 C ．a =2，b =5，c =23，d =15 D ．a =2，b =3，c =4，d =13．已知线段a 、b 、c 、d 满足ab =cd ，把它改写成比例式，错误的是_________． A ．a ∶d =c ∶b B ．a ∶b =c ∶dC ．d ∶a =b ∶cD ．a ∶c =d ∶b4．若ac =bd ，则下列各式一定成立的是_________．A ．d c b a =B ．c c b d d a +=+C ．c d b a =22D ．dacd ab =5．已知点M 将线段AB 黄金分割(AM ＞BM )，则下列各式中不正确的是_________．A ．AM ∶BM =AB ∶AM B ．AM =215-AB C ．BM =215-AB D ．AM ≈0．618AB 二、填空题6．在1∶500000的地图上，A 、B 两地的距离是64 cm ，则这两地间的实际距离是________．7．正方形ABCD 的一边与其对角线的比等于________． 8．若2x －5y =0，则y ∶x =________，xyx +=________． 9．若53=-b b a ，则b a=________． 10．若AE ACAD AB =，且AB =12，AC =3，AD =5，则AE =________．三、解答题 11．已知342=+x y x ，求y x ．12．在同一时刻物高与影长成比例，如果一古塔在地面上的影长为50 m ，同时高为1．5 m 的测杆的影长为2．5 m ，那么古塔的高是多少?13．在△ABC 中，D 是BC 上一点，若AB =15 cm ，AC =10 cm ，且BD ∶DC =AB ∶AC ，BD －DC =2 cm ，求B C ．14．如果一个矩形ABCD (AB ＜BC )中，215-=BC AB ≈0．618，那么这个矩形称为黄金矩形，黄金矩形给人以美感．在黄金矩形ABCD 内作正方形CDEF ，得到一个小矩形ABFE (如图1)，请问矩形ABFE 是否是黄金矩形？请说明你的结论的正确性．分式（一）、主要知识点： 1.分式的定义分母中含有字母的式子叫做分式，成立的条件：分母不为0 。