习题课一
工程流体力学习题课1-第2-3-4章-部分习题解答

2 2 d2
习题3-14解题示意图1
Dr W-X Huang, School of Chemical Engineering, Sichuan University, Chengdu 610065, P.R. China
工程流体力学——习题课(1)——第 2-3-4 章部分习题解答
Fx1 =
y x
H1
D
H2
图 3-26 习题 3-11 附图
1 1 ρ gH1 × ( DL) = × 1000 × 9.8 × 4 × (4 × 10) = 784000 N=784kN 2 2 1 D 1 4 Fx 2 = ρ gH 2 × ( L) = × 1000 × 9.8 × 2 × × 10 = 196000 N=196kN 2 2 2 2
H
h
由此得: H ≥ 122mm + h ≥ 244mm (2) 结合以上正负压操作时结果有:
p / ρ g ≤ h ≤ H − | p| / ρ g
图 3-23 习题 3-8 附图
→ 122mm ≤ h ≤ 178mm
Dr W-X Huang, School of Chemical Engineering, Sichuan University, Chengdu 610065, P.R. China
工程流体力学——习题课(1)——第 2-3-4 章部分习题解答
F1-6
习题 3-8 旋风除尘器如图 3-23 所示,其下端出灰口管段长 H,部分插入 水中,使旋风除尘器内部与外界大气隔开,称为水封;同时要求出灰管内液面 不得高于出灰管上部法兰位置。设除尘器内操作压力 ( 表 压 ) p = −1.2 kPa~ 1.2kPa。 净化空气 (1) 试问管段长 H 至少为多少 mm? (2) 若H=300mm,问其中插入水中的部分h应在 什么范围?(取水的密度 ρ =1000kg/m3) 含尘 解:(1) 正压操作时,出灰管内液面低于管外液 面,高差为 h′ = p / ρ g ;为实现水封,出灰管插入深 度 h 必须大于此高差,即
原子核物理习题课1 (1)

习题一:1. 试谈谈你对“格拉肖蛇”的理解。
物质科学体系——从“格拉肖蛇”蛇头到蛇尾,物质空间尺度依次减小,同时,“格拉肖蛇”首尾相衔,表明物理学中研究最大对象和最小对象的两个分支 宇宙学和粒子物理学就奇妙地衔接在一起,这并不意味着天体物理把粒子物理吞没,而是指在足够小和足够大的尺度下,两者具有统一的理论,即弱、电、强和引力相互作用“合四为一”。
2. 试论述中微子超光速实验测量原理。
意大利格兰萨索国家实验室下属的一个名为OPERA的实验装置接收了来自著名的欧洲核子研究中心的中微子,两地相距730公里,中微子“跑”过这段距离的时间比光速还快了60纳秒。
3. 试论述希格斯粒子对标准模型和超统一模型的作用。
杨振宁和米尔斯提出的杨-米尔斯非阿贝尔规范场理论,逐步构建完成了现代的标准模型理论。
但是杨-米尔斯方法无论应用到弱还是强相互作用中所遇到的主要障碍就是质量问题,由于规范理论规范对称性禁止规范玻色子带有任何质量,然而这一禁忌却与实验中的观测不相符合。
希格斯提出通过希格斯场产生对称性破缺,同时在现实世界留下了一个自旋为零的希格斯粒子,也称希格斯玻色子(Higgs boson )或“上帝粒子”。
可以说,希格斯粒子是整个标准模型的基石,也是标准模型中最后一种未被发现的粒子。
如果希格斯粒子不存在,将使整个标准模型失去效力。
4. 试绘出各层次物质的德布罗意波长变化曲线。
λ=p h =p 341062.6-⨯m=nm p251062.6-⨯以λ为纵坐标,p 为横坐标绘制曲线,λ与p 成反比关系。
5. 谈谈爱因斯坦质能方程(式1-1)的理解。
爱因斯坦狭义相对论中“质能关系式”进行质量能量转换:2E mc =,他是通过比例系数c 2将质量和能量联系起来,这也就表明物质质量和能量有一定对应关系。
6. 试绘出物质质量随运动速率变化(式1-2)的曲线。
提示:以速度υ运动着的物质的质量m 和它的静止质量0m之间有着关系:m =,当物质运动速率与光速可比拟时,必须要考虑相对论效应。
07 11.2 习题课(1)

边为角的邻边 找夹边的另一角(ASA)
找任一角 (AAS)
找夹边
已知两角
(ASA)
找任一边(AAS)
全等三角形,是证明两条线段或两个角 相等的重要方法之一,证明时应注意:
①要观察待证的线段或角,在哪两个可能全等的三 角形中; ②分析要证两个三角形全等,已有什么条件,还缺 什么条件; ③有公共边的,公共边一定是对应边;有公共角的, 公共角一定是对应角;有对顶角,对顶角也是对 应角。
已知一边一角
。
找任一角(AAS)
找夹角的另一边(SAS)
边为角的邻边 找夹边的另一角(ASA)
找任一角 (AAS)
B
E
A
C
5、(2007年山西模拟)下列各组条件,能
D
F
判定△ABC≌△DEF的是(
A、AB=DE,BC=EF,∠A=∠D
)
B、∠A=∠D,∠C=∠F,AC=EF
C、AB=DE,BC=EF,△ABC的周长=△DEF的周长 D、∠A=∠D,∠B=∠E,∠C=∠F
C
看谁方法多?
如图,已知AB= A′B′, 要说明
△ABC≌△A′B′C′,还需增加两个什么 条件?
A A′
B
C B′
C′
巩固练习
1、(2007年河北模拟)下列说法中:
①如果两个三角形可以依据“AAS”来判定全等,那么
一定也可以依据“ASA”来判定它们全等;
②如果两个三角形都和第三个三角形不全等,那么这
找夹边
已知两角
(ASA)
找任一边(AAS)
3、(2007沈阳)如图,AC、BD相交于点O,
∠A=∠D,请你再补充一个条件,使得
△AOB≌△DOC,你补充的条件是 。 D O
高中数学 习题课(一)新人教B版必修1-新人教B版高一必修1数学试题

习题课(一)C.{a|a≥2} D.{a|a>2}答案:C解析:由已知,得∁R B={x|x≤1或x≥2},又A∪(∁R B)=R,所以a≥2,故选C.6.定义集合运算:A⊙B={z|z=xy(x+y),x∈A,y∈B},设集合A={0,1},B={2,3},则集合A⊙B的所有元素之和为( )A.0 B.6C.12 D.18答案:D解析:x=0,y=2或y=3时z=0;x=1,y=2时z=6;x=1,y=3时z=12,∴A ⊙B={0,6,12},故选D.二、填空题(每小题5分,共15分)7.已知集合M={0,1,2},N={x|x=2a,a∈M},则集合M∩N=________.答案:{0,2}解析:N={0,2,4},∴M∩N={0,2}.8.设A={(x,y)|ax+y-3=0},B={(x,y)|x-y-b=0}.若A∩B={(2,1)},则a =________,b=________.答案:1 1解析:∵A∩B={(2,1)},∴(2,1)∈A,∴2a+1-3=0,a=1.(2,1)∈B,∴2-1-b =0,b=1.9.方程x2-px+6=0的解集为M,方程x2+6x-q=0的解集为N,且M∩N={2},那么以p、q为根的一元二次方程为________.答案:x2-21x+80=0解析:由M∩N={2},∴22-2p+6=0,p=5;22+12-q=0,q=16,p+q=21,p·q =80,所以以p、q为根的一元二次方程为x2-21x+80=0.三、解答题(本大题共4小题,共45分)10.(12分)已知集合A={-4,2a-1,a2},B={a-5,1-a,9},若9∈(A∩B),求a 的值.解:∵9∈(A∩B),∴9∈A,且9∈B,∴2a-1=9或a2=9,∴a=5或a=±3.当a=3时,B={-2,-2,9},违反了元素的互异性,故a=3(舍去).当a =-3时,A ={-4,-7,9},B ={-8,4,9}, 满足9∈(A ∩B ).当a =5时,A ={-4,9,25},B ={0,-4,9}, 满足9∈(A ∩B ).综上所述,a =-3或a =5时,有9∈(A ∩B ).11.(13分)已知集合A ={-3,4},B ={x |x 2-2ax +b =0},若B ≠∅且A ∩B =B ,求a ,b 的值.解:因为A ∩B =B ,所以B ⊆A .又因为A ={-3,4}且B ≠∅,所以B ={-3}或{4}或{-3,4}. 若B ={-3},则⎩⎪⎨⎪⎧ 2a =-3+-3=-6b =-3×-3=9,即⎩⎪⎨⎪⎧a =-3b =9;若B ={4},则⎩⎪⎨⎪⎧2a =4+4=8b =4×4=16,即⎩⎪⎨⎪⎧ a =4b =16;若B ={-3,4},则⎩⎪⎨⎪⎧2a =-3+4=1b =-3×4=-12,即⎩⎪⎨⎪⎧a =12b =-12.综上所述,a =-3,b =9或a =4,b =16或a =12,b =-12.能力提升12.(5分)设2 013∈{x ,x 2,x 2}则满足条件的所有x 组成的集合的真子集个数为( ) A .3 B .4 C .7 D .8 答案:A解析:由集合元素的不可重复性x =-2 013或x =- 2 013,∴满足条件的所有x 构成集合含有两个元素,其真子集有22-1=3个.13.(15分)若函数f (x )=ax 2-ax +1a的定义域是一切实数,某某数a 的取值X 围.解:函数y = ax 2-ax +1a 的定义域是一切实数,即对一切实数x ,ax 2-ax +1a≥0恒成立,即⎩⎪⎨⎪⎧a >0,Δ=-a 2-4×a ×1a≤0,∴⎩⎪⎨⎪⎧a >0,a 2≤4解得0<a ≤2.故所某某数a 的取值X 围是{a |0<a ≤2}.。
大学物理习题课1

v 0 与水平方向夹角
19.如图所示,小球沿固定的光滑的 1/4圆弧从A点由静止开始下滑,圆弧半 径为R,则小球在A点处的切向加速度 at =______________________,小球 在B点处的法向加速度 an =_______________________.
θ
A R
B
三.计算题
t 0 .96 0 mg , t 0 .20 1 9 .8 0 .96 1s
此后合力为 第2秒内冲量
I
t 0 .96 mg
t 0 .96 0 .14 1 9 .8 dt
2 1
1 t 0 .412 dt
2
1 2
t
2 2 1
(B)
(C)
a g sin
a g
a 4 g (1 cos ) g sin
2 2 2 2
(D) . [ ] 4. 将细绳绕在一个具有水平光滑轴的飞轮边缘上,现 在在绳端挂一质量为m的重物,飞轮的角加速度 为 .如果以拉力2mg代替重物拉绳时,飞轮的角加 速度将 (A) 小于 . (B) 大于 ,小于2 . (C) 大于2 . (D) 等于2 .[ ]
二.填空题 13.如图所示,质量为m的小球系在劲度系数为k 的轻弹簧一端,弹簧的另一端固定在O点.开始时弹 簧在水平位置A,处于自然状态,原长为l0.小球由 位置A释放,下落到O点正下方位置B时,弹簧的长度 为l,则小球到达B点时的速度大小为v=____
O l0 A k l m
O′
P
B m
Q R
R
F
F Ft
2 n
2
s 2 as 1 R
习题课1-5章

答案
(5)2008年12月31日 应确认的投资收益=(972.77+8.64) ×5%=49.07万元,“持有至到期投资—利息调 整”=49.07-1000×4%=9.07万元。 借:应收利息 40 持有至到期投资—利息调整 9.07 贷:投资收益 49.07 (6)2009年1月5日 借:银行存款 40 贷:应收利息 40
借:银行存款140.4 贷:主营业务收入 120 应交税费——应交增值税(销项 税额) 20.4 借:主营业务成本 140 贷:库存商品 140 借:存货跌价准备 10 贷:主营业务成本
存货计划成本法
华兴公司是增值税一般纳税人,采用计划成本 法对原材料进行日常成本核算。2007年8月1日, “原材料”账户的余额为40 000元,“材料成 本差异”账户的余额为1 700元(贷方),原材 料计划单位成本为80元。华兴公司本月材料收 入业务如下表所示:
答案
(5)2008年12月31日 借:应收利息 50 贷:投资收益 41.11 可供出售金融资产——利息调整 8.89 (6)借:资产减值损失 18.86 贷:可供出售金融资产——公允价值 变动 11.11 资本公积——其他资本公积 7.75
答案
(7)借:银行存款 50 贷:应收利息 50 (8)借:银行存款 995 可供出售金融资产——公允价值变动 18.86 投资收益 5 贷:可供出售金融资产——成本 1000 ——利息调整 18.86
答案
有合同约定部分: 可变现净值=10000×1.5-10000×0.1=14000万 元 账面成本=10000×1.4=14000万元 计提存货跌价准备金额为零 没有合同约定部分 可变现净值=3000×1.4-3000×0.1=3900万元 账面成本=3000×1.4=4200万元
第十二章 微分方程习题课 (一)(二)

(3) y′ =
3x + y − 6x + 3 2x y − 2 y
2 2
d y 3( x − 1)2 + y2 = 化方程为 dx 2y( x − 1)
dy dy dt dy = = 令t=x–1,则 dx d t dx d t dy 3t 2 + y2 (齐次方程 齐次方程) 齐次方程 = dt 2t y 令y=ut
y 方法 1 这是一个齐次方程 . 令 u = x 方法 2 化为微分形式
( 6x3 + 3x y2 )dx + ( 3x2 y + 2y3 )dy = 0
∂P ∂Q ∵ = 6x y = ∂y ∂x
故这是一个全微分方程 故这是一个全微分方程 .
5
求下列方程的通解: 例2. 求下列方程的通解 (1) x y′ + y = y( ln x + ln y )
22
为通解的微分方程 .
提示: 提示 由通解式可知特征方程的根为
(7) y′′ + 2 y′ + 5y = sin2x
特征根: 特征根 齐次方程通解 通解: 齐次方程通解 Y = e−x (C1 cos 2x + C2 sin 2x ) 令非齐次方程特解为 令非齐次方程特解为 特解 代入方程可得 A题1,2,3(1), (2), (3), (4), (5), (9), (10) , ,
(题3只考虑方法及步骤 题 只考虑方法及步骤 只考虑方法及步骤)
P326 题2 求以 为通解的微分方程. 为通解的微分方程 ( x + C )2 + y2 = 1 消去 C 得 提示: 提示 2( x + C )+ 2 y y′ = 0 P327 题3 求下列微分方程的通解 求下列微分方程的通解: 提示: 提示 令 u = x y , 化成可分离变量方程 : 提示: 提示 这是一阶线性方程 , 其中
物理化学习题课(一)

21. 在20℃和大气压力下,用凝固点降低法测物质的相对分 子质量。若所选的纯溶剂是苯,其正常凝固点为5.5℃,为 使冷却过程在比较接近于平衡状态的情况下进行,冷浴内的 恒温介质比较合适的是( ) (A)冰-水 (B)冰-盐水 (C)干冰-丙酮 (D)液氨
物理化学习题课(一)
热力学部分 何荣桓
假定气体为理想气体,计算下列过程的熵变: a) 将1mol N2 (T,p) 与 0.5mol N2 (T,p) 等温等压混合; b) 将1mol N2 (T,V)与 1 mol N2 (T,V) 等温等容混合 (Vmix=V) ;熵变与a)是否相同? c) 将1mol N2 (T,p)与 0.5mol O2 (T,p)等温等压混合,熵变与 a)是否相同?
21 答:A
22. 二组分理想液态混合物的蒸气总压( ) (A)与溶液的组成无关 (B)介于两纯组分的蒸气压之间 (C) 大于任一纯组分的蒸气压 (D)小于任一纯组分的蒸气压
22 答:B
23. A和B两组分在定温定压下混和形成理想液态混合物时,
则有:( )。
(A)ΔmixH=0 (C)ΔmixA=0 23 答:A
19 答:D
(C) Tb*> Tb, pA*< pA, ,μA* >μA
(D) Tb*< Tb, pA*> pA, ,μA* >μA
20. 已知环己烷、醋酸、萘、樟脑的凝固点降低系数 kf 分别是 20.2、9.3、6.9及39.7K•kg • mol-1。今有一未知物能在上述四 种溶剂中溶解,欲测定该未知物的相对分子质量,最适宜的溶 剂是( )
(A) 1 (B) 3/4 (C) 2/3 (D) 1/2
高一数学《基本初等函数习题课(一)》教学设计

芯衣州星海市涌泉学校根本初等函数习题课〔一〕一、内容与解析(一)内容:根本初等函数习题课〔一〕。
(二)解析:对数函数的性质的掌握,要先根据其图像来分析与记忆,这样更形像更直观,这是学习图像与性质的根本方法,在此根底上,我们要对对数函数的两种情况的性质做一个比较,使之更好的掌握.二、目的及其解析:(一)教学目的〔1〕掌握指数函数、对数函数的概念,会作指数函数、对数函数的图象,并能根据图象说出指数函数、对数函数的性质,理解五个幂函数的图象及性质.(二)解析(1)根本初等函数的学习重要是学习其性质,要掌握好性质,从图像上来理解与掌握是一个很有效的方法.〔2〕每类根本初类函数的性质差异比较大,学习时要有一个有效的区分.三、问题诊断分析在本节课的教学中,学生可能遇到的问题是不易区分各函数的图像与性质,不容易抓住其各自的特点。
四、教学支持条件分析在本节课一次递推的教学中,准备使用PowerPoint2021。
因为使用PowerPoint2021,有利于提供准确、最核心的文字信息,有利于帮助学生顺利抓住老师上课思路,节老师板书时间是是,让学生尽快地进入对问题的分析当中。
五、教学过程一、复习准备:1.提问:指数函数、对数函数、幂函数的图象和性质.2. 求以下函数的定义域:1218-=x y ;xy ⎪⎭⎫⎝⎛-=211;2log (1)(0,1)a y x a a =->≠且3.比较以下各组中两个值的大小:6log 7log 76与;8.0log log 23与π;5.37.201.101.1与二、典型例题:例1、函数y =的定义域为.例2、函数2321()2x x y -+=的单调区间为.例3、函数)10(11log )(≠>-+=a a xxx f a且.判断)(x f 的奇偶性并予以证明. 例4、按复利计算利息的一种储蓄,本金为a 元,每期利率为r ,设本利和为y 元,存期为x ,写出本利和y随存期x 变化的函数解析式.假设存入本金1000元,每期利率为5%,试计算5期后的本利和是多少〔准确到1元〕?〔复利是一种计算利息的方法,即把前一期的利息和本金加在一起算做本金,再计算下一期的利息.〕(二〕小结:掌握指数函数、对数函数、幂函数的图象与性质,会用函数性质解决一些简单的应用问题.六、 目的检测1.(2021-2021·岳口中学高一统测)44=() A .16aB .8aC .4aD .2a1.C 解析:由题意,0a ≥,那么9191919144444463366336[()][()]a a aa⨯⨯⨯⨯==⋅2.以下函数中,图象过定点)0,1(的是〔〕A .xy 2=B .x y 2log =C .21xy =D .2x y =2.B 解析:代入检验可得. 3.(2021·高一期末)集合2{|log (3)}M x y x ==-,{|32}x N y y ==+,那么MN =〔〕A .∅B .{|03}x x <<C .{|13}x x << D .{|23}x x <<3.D 解析:对M :30x ->,得3x <,那么{|3}M x x =<;对N :由30x >得,322x +>,即2y >,所以{|2}N y y =>.M N ={|23}x x <<.4.〔2021·上高二中高一期末〕设1m n >>,01a <<,那么以下关系正确的选项是〔〕 A .aa mn -->B .am an <C .m n a a <D .log log a a m n >4.C 解析:分别考察函数1a y x -=,2y ax =,3x y a =,4log a y x =.因为01a <<,函数1y ,3y ,4y 为减函数,2y 为增函数,又1m n >>,故a a m n --<,am an >,m n a a <,log log a a m n <.所以正确的选项是C.5.(2021·高一期末质检)假设函数2()log f x x =,那么下面必在()f x 反函数图象上的点是〔〕A.B .1(2)2-,C.D .1(2)2-, 5.C 解析:()f x 的反函数为()2x g x =,验证得C 满足.6.(2021-2021·六中学年高一期中)3log 2a =,那么33log 82log 6-用a 表示是〔〕A .52a -B .2a -C .23(1)a a -+ D .231a a--6.B 解析:原式333log 22log (32)=-⨯33log 22(1log 2)=-+333log 222log 2=--7.()x f x a =,()log ()a g x x =-(0,a >且1)a ≠,那么()f x 与()g x 在同一坐标系内的图象可能是(2)f -的值是()A .18-B .18C .27D .27-8.D 解析:13222(2)9927f -===,(2)(2)27f f -=-=-9.〔2021·同文中学高一下学期期初〕假设2008log 2009a=,2010log 2009b =,20091log 2010c =,那么〔〕A .a b c >>B .b a c >>C .c a b >>D .b c a >>9.A 解析:2008201020091log 20091log 20090log 2010>>>>. 10.以下函数中,同时具有性质:(1)图象过点(0,1);(2)在区间(0,)+∞上是减函数;(3)是偶函数.这样的函数是() A.11y x -=+ B.)2(log 2+=x y C.||2x y = D.||)21(x y =10.D 解析:11yx -=+图象不过点(0,1),在区间(0,)+∞上是减函数,但不是偶函数;)2(log 2+=x y 图象过点(0,1),但在区间(0,)+∞上是增函数,不是偶函数;||2x y =图象过点(0,1),是偶函数,但在区间(0,)+∞上是增函数;||)21(x y =图象过点(0,1),在区间(0,)+∞上是减函数,是偶函数.11.函数3log (45)y x =--的定义域为,值域为. 12.函数2322+--=x xy 的单调区间为.13.假设点)41,2(既在函数b ax y +=2的图象上,又在它的反函数的图象上,那么a =______,b =_______ 14.函数12+=-x a y (0>a ,且1≠a )的图象必经过点.15.计算()[]=++-+⎪⎭⎫ ⎝⎛-----2175.034303101.016254064.0.16.求以下函数的值域:xy -=215;xy -⎪⎭⎫ ⎝⎛=131;121-⎪⎭⎫ ⎝⎛=xy ;xy 21-=。
概率统计习题课1

大卫: 大卫:思索者
例1:设A,B是相互独立的事件,P(A∪B)=0.6,P(A)=0.4, 是相互独立的事件,P(A∪B)=0.6,P(A)=0.4, 求P(B). P(B).
P( A ∪ B ) = P( A) + P ( B ) P( AB )
P( A ∪ B) = P( A) + P( B) P( A) P( B)
∫
bHale Waihona Puke af ( x)dx = ∫ cos xdx = sin b sin a
a
b
练习5 下面那个函数不可作为随机变量X的分布函数? 练习5:下面那个函数不可作为随机变量X的分布函数?( )
0 x < 0 2 x ( A) F ( x) = 0 ≤ x <1 2 1 x ≥ 1
ln(1 + x) (C ) F ( x) = 1 + x 0
X 1 ~ b ( 20, 0.01) .
P{ X 1 ≥ 2} = 1 P{ X < 2} = 1 P{ X = 0} P{ X = 1} = 0.0169
80台设备不能得到及时维护 P"80台设备不能得到及时维护" 80台设备不能得到及时维护" = P( A ∪ A ∪ A ∪
1 2 3
(1 P( A) ) P( B) = P( A ∪ B) P( A)
P ( A ∪ B ) P ( A) 1 P( B) = = 1 P ( A) 3
习题课1

例15影响硅酸盐水泥水化热的因素有那些? 例 影响硅酸盐水泥水化热的因素有那些 影响硅酸盐水泥水化热的因素有那些? 水化热的大小对水泥的应用有何影响? 水化热的大小对水泥的应用有何影响? 例16.为什么流动的软水对水泥石有腐蚀作 例 为什么流动的软水对水泥石有腐蚀作 用? 例17 既然硫酸盐对水泥石具有腐蚀作用, 例 既然硫酸盐对水泥石具有腐蚀作用, 那么为什么在生产水泥时掺入的适量石膏对 水泥石不产生腐蚀作用? 水泥石不产生腐蚀作用? 例18何谓水泥的活性混合材料和非活性混合 例 何谓水泥的活性混合材料和非活性混合 材料?二者在水泥中的作用是什么? 材料?二者在水泥中的作用是什么? 例19 掺混合材的水泥与硅酸盐水泥相比, 例 掺混合材的水泥与硅酸盐水泥相比, 在性能上有何特点?为什么? 在性能上有何特点?为什么?
Ca (OH ) 2 + CO2 + nH 2Байду номын сангаасO = CaCO3 + (n + 1) H 2 O
由于氢氧化钙结晶速度慢且结晶量少,空气中 由于氢氧化钙结晶速度慢且结晶量少, 由于氢氧化钙结晶速度慢且结晶量少 二氧化碳稀薄,碳化速度慢。而且表面碳化后, 二氧化碳稀薄,碳化速度慢。而且表面碳化后, 形成紧密外壳, 形成紧密外壳,不利于二氧化碳的渗透和碳化 作用的深入。因而硬化石灰浆体具有以下特性: 作用的深入。因而硬化石灰浆体具有以下特性: (1)凝结硬化慢; )凝结硬化慢; (2)硬化后强度低; (2)硬化后强度低; (3)硬化时体积收缩大; )硬化时体积收缩大; (4)耐水性差,因为硬化石灰浆体的主要成分是 ( )耐水性差, 氢氧化钙,而氢氧化钙可微溶解于水。 氢氧化钙,而氢氧化钙可微溶解于水。 [评注 石灰浆体在空气中凝结硬化过程主要是依 评注] 评注 赖于浆体中Ca(OH)2的结晶析出和 赖于浆体中 的结晶析出和Ca(OH)2与空气 与空气 的结晶析出和 中的二氧化碳的碳化作用。 中的二氧化碳的碳化作用。
电路习题课(1-4)

Uoc= U1+ U2
U1= 456/9-45 2/10
b a
=30 - 9 = 21V
+
4
15A 4 2
U2 -
U2= (15 4/10) 2=12V Uoc= U1+ U2= 21+12 = 33V
b
3 6 4
a
求内阻Ri :
Ri 2 4
Ri=2+1.6=3.6
b
a
12V
U5
1
二、求电路中所有 的电压U 和 I 。
U1 a
U2
2 c
2 8V
d
40V
4
2
U3
I
1
U7 U6
b
2 U4
4 8 12 = = 0 .4 A I = 2 + 2 + 2 + 2 + 1 + 1 10 U 1 = U = 0.8V , U3 = U 4 = 0.8V , 2 = 0V U = 0.4V , U6 = 0.4V , U 7 5 Uab = U2 + 8 + U6 U4 = 0.8 + 8 + 0.4 + 0.8 = 10V
3
二、 求电流 I。
解: 用戴维南定理: 4
+ - 45V Is 15A 4 6 2 + 6 2
I
6.4
3 + - 45V Is 15A 4
a
Ri
a
4
Uoc -
+
Uoc -
b
b
3 + 4 - 45V 6 2 4 3 6
a 采用迭加定理求开路电压Uoc +
大一高数课件第十章 10-习题课-1

半圆周 ( x − a ) 2 + y 2 = a 2 , y ≥ 0 ,沿逆时针方向 .
三、证明: 证明:
xdx + ydy 在整个 xoy 平面除去 y 的负半轴及 2 2 x +y
内是某个二元函数的全微分, 原点的开区域 G 内是某个二元函数的全微分,并 求出一个这样的二元函数 .
测验题答案
(2) I2 = ∫ ( x2 − y+ y2)d x + ( y2 − x)d y L
= ∫ ( x2 − y)d x + ( y2 − x)dy + ∫ y2 dx
L L
L: x = acost, y = asint ,
t : 0 →π
= I − ∫ a sin3 t d t = −2a3
0
π 3
非闭
I = ∫ Pdx + Qdy =0
L
闭合
∂P ∂Q ∂P = ≠ ∂y ∂x ∂y ∂x非闭 补充曲线或用公式
∂Q ∂P 闭合 I = ∫∫ ( − )dxdy ∂x ∂y ∂Q D
解
由 I = ∫ ( x2 + 2xy)dx + ( x2 + y4 )dy
1
y
A
∂P ∂ 2 知 = ( x + 2 xy ) = 2 x ∂ y ∂y ∂Q ∂ 2 = ( x + y4 ) = 2 x x ∂x ∂x o 1 ∂P ∂Q 1 2 1 , 即 = 故原式 = ∫ x dx + ∫ (1 + y 4 )dy = 23 . ∂y ∂x 0 0
λ→0 i=1
n
∫ P( x, y)dx+ Q( x, y)dy
习题课1答案
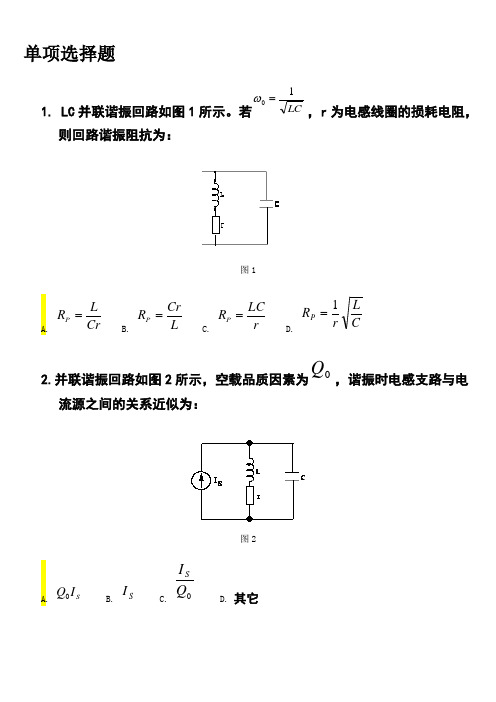
单项选择题1. LC 并联谐振回路如图1所示。
若LC 10=ω,r 为电感线圈的损耗电阻,则回路谐振阻抗为:图1 A. Cr L R P = B. L Cr R P = C. r LC R P = D. C L r R P 1=2.并联谐振回路如图2所示,空载品质因素为0Q ,谐振时电感支路与电流源之间的关系近似为:图2A. S I Q 0B. S IC. 0Q I SD. 其它3.串并联阻抗等效互换两支路(如图3所示)的品质因数分别为1L Q 、2L Q ,它们之间的关系为:图3A. 21L L Q Q >B. 21L L Q Q <C. 21L L Q Q =D. 不定4.回路抽头如图4所示,接入系数P 为:图4 A. 21N N B. 211N N N + C. 12N N D. 212N N N +5.非线性电路的重要特性之一是:A. 满足叠加原理;B. 不满足叠加原理;C.用传递函数描述;D.用线性微分方程描述;6. 并联谐振回路外加信号频率等于回路谐振频率时回路呈()A感性 B容性 C阻性 D容性或感性7. 小信号调谐放大器主要用于无线通信系统的()A.发送设备 B.接收设备 C.发送设备、接收设备8.LC单振荡回路的矩形系数值与电路参数的大小()A、有关B、成正比C、成反比D、无关9.高频小信号调谐放大器的级数愈多,其总的通频带()。
A、愈宽B、愈窄C、不变10.对于高频小信号放大,我们通常采用()和()相结合的方式来实现。
A、非线性放大器,集中选频放大器B、非线性放大器,LC谐振回路C、集成线性放大器,集中选频放大器D、集成线性放大器,LC谐振回路11.高频小信号谐振放大器不稳定的主要原因是:()A、增益太大B、通频带太宽C、晶体管集电结电容的反馈作用D、谐振曲线太尖锐12.在调谐放大器的 LC 回路两端并上一个电阻 R ,可以()A .提高回路的 Q 值。
B .加宽放大器的通频带。
高等数学习题课(1)函数极限与连续性

连续,
证明 f (x) 对一切 x 都连续 .
提示:
lim f (x x) lim [ f (x) f (x)]
x0
x0
f (x) f (0)
f (x 0) f (x)
P73 题5. 证明: 若 f (x) 在 (, )内连续, lim f (x)
x
存在, 则 f (x) 必在 (, )内有界.
III.课堂训练题 1. 求数列极限
1 lim[ n n n n ] n
2 lim 1 a1 a2 1 a2n ,( a 1) n
2. 求下列极限
1 lim x0
1 tan x 1 sin x sin3 x
2 lim sin x 1 sin x x
公式:sin A sin B 2cos A B sin A B
xx0
f (x)
f
(x0 )
6. 连续函数的性质
1) 有限个连续函数的和、差、积、商(分母不为 零),仍为连续函数;
2) 单值单调连续函数的反函数在对应区间上也为 单值单调的连续函数;
3) 连续函数的复合函数也是连续函数; 4) 一切初等函数在其定义区间内都是连续函数。
7. 闭区间上连续函数的性质
有 y f (x0 x) f (x0 )
如 果 lim y 0
①
x0
或
lim
x0
f
( x0
x)
f
(x0 )
②
或
lim
x x0
f (x)
f (x0 )
③
则 称 函 数y f (x) 在 点 x0 处 连 续 。
命题:lim xx0
f
(x)
f
计算机网络习题课1答案

第一章绪论一、选择题1. 世界上第一个计算机网络是( A )。
A. ARPANETB. ChinaNetC.InternetD.CERNET2. 计算机互联的主要目的是( D )。
A. 制定网络协议B. 将计算机技术与通信技术相结合C. 集中计算D. 资源共享3. 局部地区通信网络简称局域网,英文缩写为( B )。
A. WANB. LANC. SAND.MAN4. Internet的核心协议是(B)。
A. X.25B. TCP/IPC. ICMPD. UDP5. 在OSI参考模型的物理层、数据链路层、网络层传送的数据单位分别为( A )。
A.比特、帧、分组B.比特、分组、帧C.帧、分组、比特D.分组、比特、帧6. Internet服务提供者的英文简写是( D )。
A. DSSB. NIIC. IISD. ISP7. CSMA/CD总线网适用的标准( A )。
A. IEEE802.3B. IEEE802.5C. IEEE802.6D. IEEE802.118. 一座大楼内的一个计算机网络系统,属于(B )。
A. PANB. LANC. MAND. WAN9. 以下( B )不是一个网络协议的组成要素之一。
A.语法B.体系结构C.同步D.语义10. 在协议分层实现中,当数据分组从设备A传输到设备B时,在设备A的第3层加上首部分会在设备B的( B )层被读出。
A.2B.3C.4D.511.下列交换方式中实时性最好的是( C )A.数据报方式B.虚电路方式C.电路交换方式D.各种方法都一样12.计算机网络中为进行数据交换而建立的规则、标准或约定的集合称为( C )A.体系结构B.协议要素C.网络协议D.功能规范二、填空题1. 网络协议通常采用分层思想进行设计,OSI 开放系统体系结构中将协议分为7层,而TCP/IP系结构中将协议分为4层。
2. 因特网按工作方式可划分为边缘部分和核心部分。
主机位于网络的边缘部分,起作用是进行信息处理。
习题课1

u U ,
u 0 y
a sin b U ab cos b 0
u U sin
y 2
a U b 2
收缩管直径应限制在什么条件下,才能保证不出 现空化?(不考虑损失)
10m
解:水温40℃,汽化压强为7.38kPa 大气压强
pa 97.3 103 10m g 992.2 9.807
10m
汽化压强
pv 7.38103 0.76m g 992.2 9.807
1
1 10m
对液面V1=V2=0,p1=p2=0,由上式可得
l V2 H z1 z2 h f 1 h f 2 ( in v 2 b out ) d 2g
0.5 5.7 2
5.09m s 50 0.64 1.0 0.0173 0.1 2 9.81m s2
4
输油管道中安装一个收缩段以便测量流量Q ,管径从
d1 收缩到d2 。使用题图所示的缸套、活塞装置,活 塞直径 D,油的密度ρ ,如果固定活塞所要施加的力 F ,求管中油的体积流量 Q。
d1 260mm d 2 180mm D 300 mm 850kg / m3 F 75 N
t 0 1 x 0, y 0
C2
( x 1)( y 2) 2
例2:弦长为3m的机翼以300km/h的速度在温度为20℃、
压强为1at的静止空气中飞行,用λl=20的模型在风洞中 作试验:(1)如果风洞中空气的温度和压强不变,风 洞中空气速度应为多少? 解:风洞实验中粘性力是主要的——雷诺准则 υ相同
函数序列与函数项级数习题课(一)

(1) 当 1 1, 1 x 1, 1 x
即 x 0或x 2时, 原级数绝对收敛,所以收敛;
(2) 当 1 1, 1 x 1, 1 x
即 2 x 0时, 原级数发散.
(3) 当| 1 x | 1, x 0或x 2,
当 x 0时, 级数 (1)n收敛; n1 n
x
),
n1
⒊ un ( x)至少在一点x0处收敛,
n1
则 un ( x)在[a,b]上一致收敛,其和S'( x) C[a,b],
n1
且S'( x) g( x), 即有:
'
un
(
x)
un' (x)
n1
n1
逐项可导
典型例题
例1:求
n1
n x n nn x
收敛域
n xn
解:lim nn x
n
1
lim
n
1
x n
n
ex
nx
x 1
n x
n
收敛
n n1
n x
x 1,
n x n 发散
nnx
n1
例 判断 xn 1 x x2
1.
n0
和发散点集。
xn 的收敛点集
解:当 x 1时, 级数收敛; x 1时,级数发散.
收敛点集: (1,1);发散点集: (, 1] [1, ).
fn ( x), n 1,2, ...在I上连续,且{ fn( x)}在I上一致收敛 于f ( x),则f ( x)在I上连续.
定理4.2(函数项级数的和函数的连续性) 设级数
un ( x)在I上一致收敛于S( x), 且若un ( x) CI , 则
习题课1

ZJFC 32. 用108mm×4mm的管线每小时输送原油20t。原 油密度为900kg/m3,粘度为70mPa· s。已知管线总 长200km,管子最大许用压强为6.0Mpa(表压), 试定量分析输送途中至少需要几个加压站? 33 用风机通过内径为0.3m的圆形导管从大气中抽 取空气。导管壁开口接一U形管压差计,压差计 读数为245Pa(2.5cmH2O)(真空度)。已知空气的密 度为1.29kg/m3,求空气的流量(入口与管路的阻 力忽略不计)。
H=20m
H1=2m
ZHE JIANG FORESTRY UNIVERSITY
ZHE JIANG FORESTRY UNIVERSITY
ZJFC 27 有两种关于粘性的说法: (1) 无论是静止的流体还是运动的流体都具有粘性。 (2) 粘性只有在流体运动时才会表现出来。 正确的结论应是( )。 A.这两种说法都对; B.这两种说法都不对; C.第一种说法对,第二种说法不对; D.第二种说 法对,每一种说法不对 28利用因次分析法的目的在于( )。 A 使实验和关联工作简化; C. 建立数学表达式; B 增加实验结果的可靠性; D. 避免出现因次错误;
ZHE JIANG FORESTRY UNIVERSITY
ZJFC
31 在一定管路中,当孔板流量计的孔径和文丘里流量 计的喉径相同时,相同流动条件下,文丘里流量 计的孔流系数CV和孔板流量系数C0的大小为( )。 A.C0=CV B.C0>CV C. C0<CV D.不确定.
ZHE JIANG FORESTRY UNIVERSITY
1 1’
Z1 2 0 2’ 0’
ZHE JIANG FORESTRY UNIVERSITY
ZJFC
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
两个以上函数也可构成复合函数.例如,
y u, u0 u cot v , v k π (k 0, 1, 2 ,) x v , x (, ) 2 可定义复合函数:
k Z
x π x k π k π 时 , cot 0 2 2 2
5、复数的方根
设 z re i r (cos i si n ), 则 z 的n次 方 根 为
n
z r (cos
1 n
2k
n ( k 0,1,2, n 1)
i si n
2k
n
)
五、例题
1 0 x1 , 求函数 f ( x 3)的定义域. 例 设f ( x ) 2 1 x 2
True 1 0.8 0.6 0.4 0.2 -1 -0.5 0.5 1
(2) 符号函数
y
1 当x 0 y sgn x 0 当x 0 1 当x 0
1 o x
-1
x sgn x x
(3)取整函数 y=[x] [x]表示不超过 x 的最大整数
y
4 3 2 1 o
今后,当不需要指明 的具体数值时, N ( a , ) 简记为 N ( a ) ,
o
N ( a , ) 简记为 N ( a ) .
o
o
二. 确界
定义
设A R,且A ,若存在L R,使x A, 有x ( ) L, 则称L为A的一个上(下)界.
若数集A既有上界,又有下界,则称A有界,否则称A无界.
y f 1 ( x) , x f ( D)
性质: 1) y=f (x) 单调递增(减) , 其反函数 且也单调递增 (减) .
2) 函数 对称 .
与其反函数 的图形关于直线
y
Q(b, a)
y f 1 ( x )
yx
y f ( x)
例如 ,
指数函数 y e , x ( , )
点a叫做这邻域的中心,
叫做这邻域的半径.
去心邻域:
点 a 的 邻域去掉中心点 a 的集合称为 a 的去心 邻域, 记为 N (a , ) ,即
o
N (a, ) (a , a ) (a, a ) { x 0 x a }.
开区间 (a , a ) 称为 a 的左 邻域 , 开区间 (a , a ) 称为 a 的右 邻域 .
约定: 为简单计, 书写复合函数时不一定写出其定义域, 默认对应的函数链顺次满足构成复合函数的条件.
4. 初等函数
① 基本初等函数
(1)幂函数
y x
(是常数)
y
y x2
1
(1,1)
y x
y x
o
1 y x
1
x
(2)指数函数
y ax
(a 0, a 1)
1 x y( ) a
解
1 0 x1 f ( x) 2 1 x 2 1 0 x31 f ( x 3) 2 1 x 3 2 1 3 x 2 2 2 x 1
故 D f : [3,1]
e x , 例 设 f ( x) x, 求 f [( x )].
D( f ) ( , ), R( f ) Z
-4 -3 -2 -1
1 2 3 4 5 x -1 -2 -3 -4
阶梯曲线
四、复数
1、复数的表示法
1. z x iy 2. 复 平 面 上 的 点 ( x , y )或 向 量 P OP 3. z r (cos i si n ) ( 三 角 表 示 法 ) 4. z re i( 指 数 表 示 法 )
定义
设A R,且A ,若存在数 (或 )满足: (1)x A,有x (或x ), (2) 0,x0 A, 使x0 (或x0 ) 则称 为 A 的上确界,记为 sup A .
( 为 A 的下确界,记为 inf A .)
3、复数运算性质
z1 z1 z1 z2 z1 z2 , z1 z2 z1 z2, ( ) z2 z2 zz z ,
2
z1 z2 z1 z2 ,
z1 z2 z1 z2
4、复数的乘幂
设 z re i r (cos i si n ), 则 z 的n次 幂 为 z n ( re i )n r n (cosn i si nn )
arc sin x sin x
反余弦函数
y arccos x
定义域:[-1,1],值域: [0, ]
arc cos x
cos x
反正切函数
y arctan x
定义域(-∞, +∞ ),值域: ( , ) 2 2
tan x
arctan x
反余切函数
y arccot x
自变量
因变量
称为值域 函数图形:
y R f f ( D) y y f ( x), x D y
C ( x , y ) y f (x) , x D
O
a x b ( D [a, b] )
x
xD
(定义域)
f
y R f f ( D) y y f ( x), x D
如果一个数集存在上确界(下确界),则此确界是唯一的.
1 1 1 例:数集 A {1, , , , ,} ,则 inf A 0, sup A 1. 2 3 n
例:数集 A { x | x sin t ,
} ,则 inf A 1, 2 2 sup A 1. 1 n | n N } ,则 inf A , sup A 1. 例:数集 A { 2 n1
习题课一
一.邻域:
a 为给定的实数, 0 ,称区间 (a , a ) 为 a
的 邻域,记为 N (a , ) .
即 N (a , ) { x a x a } { x | x a | } a a a x
t
确界存在定理
有上(下)界的非空实数集必有上(下)确界.
例:数集 A { x | x 0, x 2, x Q} 在 Q 内有上界,
2
却没有上确界.
三、函数
1. 函数的概念
定义: 设数集D R , 则称映射 D 上的函数 , 记为 定义域 为定义在
y f ( x) , x D
(值域)
(对应规则)
函数的两要素:
定义域与对应法则.
约定: 定义域是自变量所能取的使算式有意义的 一切实数值.
例如, y 1 x 2
D : [1,1] D : ( 1,1)
例如, y
1 1 x2
分段函数:在自变量的不同变化范围中,对应法则 用不同的式子来表示的函数。
2 x 1, x 0 例如, f ( x ) 2 x 1, x 0
y x2 1
y 2x 1
2、函数的特性
(1)有界性:
若X D, M 0, x X , 有 f ( x ) M 成立,
则称函数f ( x )在X上有界.否则称无界 .
y
M y=f(x) o -M M
y
x
有界 X
x0
o -M X 无界
x
(2)单调性:
设函数 f ( x ) 的定义域为 D,区间 I D ,如果对于区间 I 上任意两点 x1 , x2 ,当 x1 x2 时,恒有 f ( x1 ) f ( x2 ) ,
y ax
(a 1)
(0,1)
(3)对数函数
y loga x (a 0, a 1)
y log a x
(1,0)
(a 1)
y log 1 x
a
(4) 三角函数 正弦函数 余弦函数 正切函数
y sin x
y cos x
y tan x
y cot x
余切函数
x1 x 2, , ( x ) 2 x1 x 1,
x0 , x0
解
10
e ( x ) , ( x ) 1 f [( x )] ( x ), ( x ) 1
( 或 f ( x1 ) f ( x2 ))
则称函数 f ( x ) 在区间 I 上是单调增加的。 (或单调减少的)
y
y f ( x)
f ( x2 )
y
y f ( x)
f ( x1 )
f ( x1 )
f ( x2 )
o
I
x
o
I
x
(3)奇偶性:
(原点对称) 设 D 关于 y 轴对称,对于 x D ,有 f ( x ) f ( x ) ,
2、幅角
arg z y arctan x y arctan x y arctan x y arctan x z在 第 一 象 限 z在 第 二 象 限 z在 第 三 象 限 z在 第 四 象 限
Arg ( z1 z 2 ) Argz1 Argz 2 z1 Arg Argz1 Argz 2 z2
称 f ( x ) 为偶函数。 (奇函数)
( f ( x ) f ( x ))
y
y f ( x)
-x f ( x)yy f ( x)f ( x)
f ( x )
