小学五年级精品数学(小哈弗)奥数教程(课后练习含答案)(专题3)一般应用题(三)

小学五年级奥数题练习及答案解析

一般应用题的解法（二）五年级奥数题：一般应用题的解法（二）一般应用题的解法（三）五年级奥数题：一般应用题的解法（三）一般应用题的解法（四）五年级奥数题：一般应用题的解法（四）一般应用题的解法（五）五年级奥数题：一般应用题的解法（五）分数数图形问题五年级奥数题：分数数图形问题长方形与正方形面积计算2010-03-26 15:49:17 来源：奥数网整理网友评论0条五年级奥数题：长方形与正方形面积计算长方形与正方形面积计算（二）2010-03-26 15:50:57 来源：奥数网整理网友评论0条五年级奥数题：长方形与正方形面积计算（二）长方形与正方形面积计算（三）2010-03-26 15:54:21 来源：奥数网整理网友评论0条五年级奥数题：长方形与正方形面积计算（三）长方形与正方形面积计算（四）2010-03-26 15:55:10 来源：奥数网整理网友评论0条长方形与正方形面积计算（五）2010-03-26 15:55:45 来源：奥数网整理网友评论0条小数的运算（一）2010-03-26 15:56:31 来源：奥数网整理网友评论0条五年级奥数题：小数的运算（一）小数的运算（二）2010-03-26 15:56:59 来源：奥数网整理网友评论0条五年级奥数题：小数的运算（二）小数乘法的计算2010-03-26 15:58:02 来源：奥数网整理网友评论0条五年级奥数题：小数乘法的计算小数除法的计算（一）2010-03-26 15:58:41 来源：奥数网整理网友评论0条五年级奥数题：小数除法的计算（一）小数除法的计算（二）2010-03-26 15:59:15 来源：奥数网整理网友评论0条五年级奥数题：小数除法的计算（二）小数除法的计算（三）2010-03-26 15:59:40 来源：奥数网整理网友评论0条五年级奥数题：小数除法的计算（三）。

五年级下册数学奥数题(含答案) 小学五年级奥数题大全及答案(更新版)-通用版

五年级奥数题问题+答案1、一块草地，可供24匹马吃6天；20匹马吃10天。

多少马12天吃尽？2、一块草地，可供5只羊吃40天；6只羊吃30天。

如果4只羊吃30天后又增加2只羊一起吃，那么这块草地还可以再吃多少天？3、每小时有3000人到书店买书。

如果设一个售书口，每分钟可以让50人买完离开；如果设2个售书口，1小时后就没有人排队了。

那么如果设4个口，多长时间后就没有人排队了？4、一口井，用3部抽水机40分钟可以抽干；6部抽水机16分钟可以抽干。

那么5部同样的抽水机，多少分钟可以抽干？5、一个水池，池内除原有的水外，每天都流入同样多的水。

如果用池中的水每天浇50亩地，10天用完；如果每天浇45亩地，20天用完。

那么，用这些水浇多少亩地，正好可用25天？6、一个大水坑，每分钟从四周流掉一定数量的水。

如果用5台水泵，6小时抽干；用10台，4小时抽干。

现在要2小时抽干，要多少水泵？7、仓库装满水泥时，可用30天。

现在仓库是空的，用大车运水泥，除每天供工地使用外，要装5天才可装满；用小车，除每天供工地使用外，要装10天才可装满。

如果大车小车一起用，除每天供工地使用外，要装几天才可装满？8、甲、乙、丙、丁四人加工同样的零件，甲先加工了一段时间，然后乙、丙、丁三人一起参加加工，6小时后乙和甲加工的一样多；9小时后丙和甲加工的一样多，12小时后丁和甲加工的一样多。

又知乙每小时加工27个零件，丙每小时加工23个零件。

那么，丁每小时加工零件多少个？答案1、假设草地单位为“1”，所以24*6=144 20*10=200 （200-144）/4=14 因此每天草地长草14个单位“1” 200-14*10=60，因此草地原有草60个单位"1"。

60/12+14=19 19马12天吃尽2、同理，40*5=200 30*6=180 （200-180）/（40-30）=2[每天草地长草] 200-2*40=120[原有草] 120-（4-2）*30=60 60/（6-2）=15（天）3、30分钟{每分钟有100人来，3000/（200-100）}4、20分钟{3*40-6*16=24 24/24=1 120-40*1=80 80/4=20}5、44亩地{45*20-50*10=400 400/10=40 500-40*10=100100/25+40=44}8、21个 {9*23-6*27=45 45/3=15 162-15*6=72 72/12+15=21}五年级奥数题有关行程问题的答案一环行跑道周长为240米，甲乙同向，丙与他们背向，都从同地点出发，每秒钟甲跑8米，乙跑5米，丙跑7米，出发后三人第一次相遇时，丙跑了多少圈？解：由题得知：甲比乙快8-5=3米/秒，也就是240/3=80秒后，甲会比乙多跑1圈且追上乙第一次相遇；要使甲、乙、丙同时相遇，则三者所用的时间必须是80秒的位数。

五年级下册数学奥数题及答案

五年级下册数学奥数题及答案导言数学是一门基础学科，也是五年级学生必修的科目之一。

在五年级下册的数学课程中，奥数题是一种常见的考核形式。

通过解答奥数题，可以提高学生的逻辑思维能力和创造性解决问题的能力。

本文将为你提供一些五年级下册数学奥数题以及相应的答案。

希望能够帮助你更好地理解和掌握数学奥数题的解题方法。

一、选择题1. 小图书馆里有10本科学书、6本文学书和4本历史书，请问从中任选一本书时，科学、文学和历史这三类书被选中的概率相同，这本书是科学书的概率是多少？A. 1/2B. 1/3C. 2/7D. 4/9答案：D解析：由题意可知，科学、文学和历史这三类书被选中的概率相同，即选中一本科学书的概率为1/3。

因此，答案为D。

2. 小明拥有4个红色的球和6个蓝色的球，现从中任选一个球，不看颜色，再随机从剩下的球中任选一个球。

求首次选中红色球并且第二次选中蓝色球的概率。

A. 1/6B. 2/15C. 1/5D. 4/15答案：B解析：首次选中一个红色球的概率为4/10，然后剩下的球中有6个蓝色球和3个红色球，因此第二次选中一个蓝色球的概率为6/9。

根据乘法原理，得到首次选中红色球并且第二次选中蓝色球的概率为(4/10) * (6/9) = 2/15。

因此，答案为B。

3. 有一段有10个小孩子的队伍，其中小明和小红不愿意站在同一侧，问在队伍的两侧各站4个小孩子的情况下，小明和小红不站在同一侧的方法数有多少种？A. 220B. 180C. 160D. 240答案：C解析：总的排列方法数为C(10, 4) = 210。

在这些排列方法中，小明和小红站在同一侧的情况有C(8, 2) = 28种。

因此，小明和小红不站在同一侧的方法数为210 - 28 = 182。

因此，答案为C。

二、填空题1. 把36用两个不同的质数相乘，得到的积是_________。

答案：2 \* 3 \* 2 \* 3 = 36解析：36可以分解为2 \* 3 \* 2 \* 3的形式。

小学奥数基础教程含练习题和答案五年级讲全册版

第1讲数字谜（一）数字谜的内容在三年级和四年级都讲过，同学们已经掌握了不少方法。

例如用猜想、拼凑、排除、枚举等方法解题。

数字谜涉及的知识多，思考性强，所以很能锻炼我们的思维。

这两讲除了复习巩固学过的知识外，还要讲述数字谜的代数解法及小数的除法竖式问题。

例1 把+，-，×，÷四个运算符号，分别填入下面等式的○内，使等式成立（每个运算符号只准使用一次）：（5○13○7）○（17○9）=12。

分析与解：因为运算结果是整数，在四则运算中只有除法运算可能出现分数，所以应首先确定“÷”的位置。

当“÷”在第一个○内时，因为除数是13，要想得到整数，只有第二个括号内是13的倍数，此时只有下面一种填法，不合题意。

（5÷13-7）×（17+9）。

当“÷”在第二或第四个○内时，运算结果不可能是整数。

当“÷”在第三个○内时，可得下面的填法：（5+13×7）÷（17-9）=12。

例2 将1～9这九个数字分别填入下式中的□中，使等式成立：□□□×□□=□□×□□=5568。

解：将5568质因数分解为5568=26×3×29。

由此容易知道，将 5568分解为两个两位数的乘积有两种：58×96和64×87，分解为一个两位数与一个三位数的乘积有六种：12×464， 16×348， 24×232，29×192， 32×174， 48×116。

显然，符合题意的只有下面一种填法：174×32=58×96=5568。

例3 在443后面添上一个三位数，使得到的六位数能被573整除。

分析与解：先用443000除以573，通过所得的余数，可以求出应添的三位数。

由443000÷573=773 (71)推知， 443000+（573-71）=443502一定能被573整除，所以应添502。

小学五年级奥数题大全及答案

班
姓名
得分
二、解答题
11、计算 172.4 6.2+2724 0.38
12、计算
0.00…0181 0.00…011 963 个 0 1028 个 0
13、计算 12.34+23.45+34.56+45.67+56.78+67.89+78.91+89.12+91.23
14、下面有两个小数: a=0.00…0105 1994 个 0 求 a+b,a-b,a b,a b. b=0.00…019 1996 个 0
13、在“改革”村的黑市上,人们只要有心,总是可以把两张任意的食品票换成 3 张其他票券,也可以反过来交换.试问,合作社成员瓦夏能否将 100 张黄油票换成 100 张香肠票,并且在整个交换过程中刚好出手了 1991 张票券？
14、试找出这样的最小自然数,它可被 11 整除,它的各位数字之和等于 13.
班
姓名
得分
二、解答题
1、173□是个四位数字.数学老师说：“我在这个□中先后填入 3 个数字, 所得到的 3 个四位数,依次可被 9、11、6 整除.”问：数学老师先后填入的 3 个数字的和是多少？
12、在 1992 后面补上三个数字，组成一个七位数，使它们分别能被 2、3、5、11 整除，这个七位数最小值是多少？
班
姓名
得分
二、解答题
11、计算 32.14+64.28 0.5378 0.25+0.5378 64.28 0.758 64.28 0.125 0.5378
12、计算 0.888 125 73+999 3
13、计算 1998+199.8+19.98+1.998

新人教版五年级小学数学全册奥数(含答案)

第2讲平均数（二）
精讲精练
【例题1】小明前几次数学测验的平均成绩是84分，这次要考100分，才能把平均成绩提高到86分。问这是他第几次测验？
练习1：
1.老师带着几个同学在做花，老师做了21朵，同学平均每人做了5朵。如果师生合起来算，正好平均每人做了7朵。求有多少个同学在做花？
2.一位同学在期中测验中，除了数学外，其它几门功课的平均成绩是94分，如果数学算在内，平均每门95分。已知他数学得了100分，问这位同学一共考了多少门功课？
练习5：
1.下面三个正方形的面积相等，剪去阴影部分的面积也相等，求原来正方形的周长发生了什么变化？（单位：厘米）
2.下面是一个零件的平面图，图中每条短线段都是5厘米，零件长35厘米，高30厘米。这个零件的周长是多少厘米？
三、课后作业
1.有6块边长是1厘米的正方形，如例题中所说的这样重叠着，求重叠后图形的周长。
【例题5】有一个周长是72厘米的长方形，它是由三个大小相等的正方形拼成的。一
1.五个同样大小的正方形拼成一个长方形，这个长方形的周长是36厘米，求每个正方形的面积是多少平方厘米？
2.有一张长方形纸，长12厘米，宽10厘米。从这张纸上剪下一个最大的正方形后，剩下部分的周长是多少厘米？
如何灵活运用平均数的数量关系解答一些稍复杂的问题呢？
下面的数量关系必须牢记：
平均数=总数量÷总份数总数量=平均数×总份数总份数=总数量÷平均数
二、精讲精练
【例题1】有4箱水果，已知苹果、梨、橘子平均每箱42个，梨、橘子、桃平均每箱36个，苹果和桃平均每箱37个。一箱苹果多少个？
练习1：
1.一次考试，甲、乙、丙三人平均分91分，乙、丙、丁三人平均分89分，甲、丁二人平均分95分。问：甲、丁各得多少分？

小学五年级精选奥数题及解析

小学五年级精选奥数题及解析1、算薪水有两个人在一家工地做工，由于一个是学徒，一个是技工，所以他们的薪水是不一样的。

技工的薪水比学徒的薪水多20美元,但两人的薪水之差是21美元。

你觉得他俩的薪水各是多少？2、100面彩旗某街道从东往西按照五面红旗、三面黄旗、四面绿旗、两面粉旗的规律排列，共悬挂1995面彩旗，你能算出从西往东数第100面彩旗是什么颜色的吗？3、时钟表盘时钟的表盘上按标准的方式标着1, 2, 3,…，11, 12这12个数，在其上任意做n 个120°的扇形，每一个都恰好覆盖4个数，每两个覆盖的数不全相同. 如果从这任做的n个扇形中总能恰好取出3个覆盖整个钟面的全部12个数，求n的最小值.4、两头猪有4头猪，这4头猪的重量都是整千克数，把这4头猪两两合称体重，共称5次，分别是99、113、125、130、144,其中有两头猪没有一起称过。

那么，这两头猪中重量较重那头有多重？5、三张卡片有三张卡片，它们上面各写着数字2, 3, 4,从中抽出一张、二张、三张, 按任意次序排列出来，可以得到不同的一位数、二位数、三位数，请你将其中的质数都写出来.6、数学竞赛要求的三个自然数分别是32、35和38。

9、答案与解析：此题需要求抽屉的数量，反用抽屉原理和最”坏”情况的结合，最坏的情况是只有10个同学来自同一个学校，而其他学校都只有9名同学参加，那么(1123-10)4-9=123......6 ,因此最多有：123+1=124个学校(处理余数很关键，如果有125个学校那么不能保证至少有10名同学来自同一个学校)10、答案与解析：120:2=60, 90:2=45,每两棵树之间的距离是它们的最大公约数。

(120, 60, 90, 45)=15, 一共要：(120+90)x24-15=28(棵)。

11、答案与解析：方法一：因为每班的平均成绩都是整数，且两班的总成绩相等，所以总成绩既是42的倍数，又是48的倍数,所以为[42, 48]=336的倍数.因为乙班的平均成绩高于80分，所以总成绩应高于48x80=3840分.乂因为是按百分制评卷，所以甲班的平均成绩不会超过100分，那么总成绩应不高于42x100=4200分.在3840〜4200之间且是336的倍数的数只有4032.所以两个班的总分均为4032 分.那么甲班的平均分为40324-42=96分，乙班的平均分为4032+48=84分.所以甲班的平均分比乙班的平均分高96-84=12分.方法二：甲班平均分x42=乙班平均分x48,即甲班平均分x7二乙班平均分x8, 因为7、8互质，所以甲班的平均分为某数的8倍，乙班的平均分为某数的7倍，乂因为两个班的平均分均超过80分，不高于100分，所以这个数只能为12.所以甲班的平均分比乙班的平均分高12x(8-7)=12分.12、答案与解析：小于20的质数有2, 3, 5, 7, 11, 13, 17, 19,其中5+19=7+17=11+13.每个木块掷在地上后向上的数可能是六个数中的任何一个，三个数的和最小是5+5+5=15,最大是19+19+19=57,经试验，三个数的和可以是从15到57的所有奇数，所有可能的不同值共有22个。

(完整)小学五年级奥数题及答案(附精讲)

小学五年级奥训练题及答案（精讲）一、工程问题1．一件工作，甲、乙合做需4小时完成，乙、丙合做需5小时完成。

现在先请甲、丙合做2小时后，余下的乙还需做6小时完成。

乙单独做完这件工作要多少小时？2．修一条水渠，单独修，甲队需要20天完成，乙队需要30天完成。

如果两队合作，由于彼此施工有影响，他们的工作效率就要降低，甲队的工作效率是原来的五分之四，乙队工作效率只有原来的十分之九。

现在计划16天修完这条水渠，且要求两队合作的天数尽可能少，那么两队要合作几天？3．甲乙两个水管单独开，注满一池水，分别需要20小时，16小时.丙水管单独开，排一池水要10小时，若水池没水，同时打开甲乙两水管，5小时后，再打开排水管丙，问水池注满还是要多少小时？4．一项工程，第一天甲做，第二天乙做，第三天甲做，第四天乙做，这样交替轮流做，那么恰好用整数天完工；如果第一天乙做，第二天甲做，第三天乙做，第四天甲做，这样交替轮流做，那么完工时间要比前一种多半天。

已知乙单独做这项工程需17天完成，甲单独做这项工程要多少天完成？5．师徒俩人加工同样多的零件。

当师傅完成了1/2时，徒弟完成了120个。

当师傅完成了任务时，徒弟完成了4/5这批零件共有多少个？6．一批树苗，如果分给男女生栽，平均每人栽6棵；如果单份给女生栽，平均每人栽10棵。

单份给男生栽，平均每人栽几棵？7．一个池上装有3根水管。

甲管为进水管，乙管为出水管，20分钟可将满池水放完，丙管也是出水管，30分钟可将满池水放完。

现在先打开甲管，当水池水刚溢出时，打开乙,丙两管用了18分钟放完，当打开甲管注满水是，再打开乙管，而不开丙管，多少分钟将水放完？8．某工程队需要在规定日期内完成，若由甲队去做，恰好如期完成，若乙队去做，要超过规定日期三天完成，若先由甲乙合作二天，再由乙队单独做，恰好如期完成，问规定日期为几天？9．两根同样长的蜡烛，点完一根粗蜡烛要2小时，而点完一根细蜡烛要1小时，一天晚上停电，小芳同时点燃了这两根蜡烛看书，若干分钟后来点了，小芳将两支蜡烛同时熄灭，发现粗蜡烛的长是细蜡烛的2倍，问：停电多少分钟？二．鸡兔同笼问题1．鸡与兔共100只，鸡的腿数比兔的腿数少28条，,问鸡与兔各有几只？三．数字数位问题1．把1至2005这2005个自然数依次写下来得到一个多位数123456789.....2005,这个多位数除以9余数是多少?2．A和B是小于100的两个非零的不同自然数。

小学五年级精品数学(小哈弗)奥数教程(课后练习含答案)(专题4)一般应用题(四)

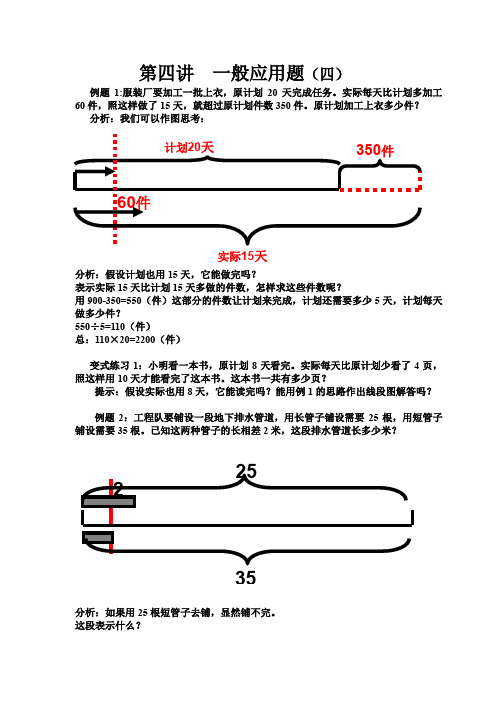
第四讲一般应用题（四）例题1:服装厂要加工一批上衣，原计划20天完成任务。

实际每天比计划多加工60件，照这样做了15天，就超过原计划件数350件。

原计划加工上衣多少件？分析：我们可以作图思考：实际15天分析：假设计划也用15天，它能做完吗？表示实际15天比计划15天多做的件数，怎样求这些件数呢？用900-350=550（件）这部分的件数让计划来完成，计划还需要多少5天，计划每天做多少件？550÷5=110（件）总：110×20=2200（件）变式练习1：小明看一本书，原计划8天看完。

实际每天比原计划少看了4页，照这样用10天才能看完了这本书。

这本书一共有多少页？提示：假设实际也用8天，它能读完吗？能用例1的思路作出线段图解答吗？例题2：工程队要铺设一段地下排水管道，用长管子铺设需要25根，用短管子铺设需要35根。

已知这两种管子的长相差2米，这段排水管道长多少米？35分析：如果用25根短管子去铺，显然铺不完。

这段表示什么？25根长管比25根短管长多少米：25×2=50（米）这段米数需要多少根短管去铺：35-25=10（根）每根短管的米数是：50÷10=5（米），排水管长：5×35=175（米）。

变式练习2：生产一批零件，甲单独生产要用6小时，乙单独生产要用8小时。

如果甲每小时比乙多生产10个零件，这批零件一共有多少个？提示：如果假设乙也单独做6小时。

那么甲6小时比乙单独6小时多做6×10=60（个），这60个乙还需要几小时？乙每小时做多少个？乙每小时做的个数求出后，这批零件一共有多少个自然会求出。

例题3：甲、乙、丙三人拿出同样多的钱买一批苹果，分配时甲、乙都比丙多拿24千克，结帐时，甲和乙都要付给丙32元，每千克苹果多少元？分析（1）甲、乙、丙三人拿出同样多的钱买一批苹果，那么它们分配的数量应怎样？（2）怎样才能让三人的苹果数量相同呢？24÷3=8（千克）（3）甲、乙都要付给丙32元，实际上是付几千克的钱？所以每千克多少元？32÷8=4（元）变式练习3：甲和乙拿出同样多的钱买相同的铅笔若干支，分铅笔时，甲拿了13支，乙拿了7支，因此，甲又给了乙6角钱。

小学奥数基础教程(含练习题和答案)五年级-30讲全册版.doc

第1讲数字谜（一）数字谜的内容在三年级和四年级都讲过，同学们已经掌握了不少方法。

例如用猜想、拼凑、排除、枚举等方法解题。

数字谜涉及的知识多，思考性强，所以很能锻炼我们的思维。

这两讲除了复习巩固学过的知识外，还要讲述数字谜的代数解法及小数的除法竖式问题。

例1 把+，-，×，÷四个运算符号，分别填入下面等式的○内，使等式成立（每个运算符号只准使用一次）：（5○13○7）○（17○9）=12。

分析与解：因为运算结果是整数，在四则运算中只有除法运算可能出现分数，所以应首先确定“÷”的位置。

当“÷”在第一个○内时，因为除数是13，要想得到整数，只有第二个括号内是13的倍数，此时只有下面一种填法，不合题意。

（5÷13-7）×（17+9）。

当“÷”在第二或第四个○内时，运算结果不可能是整数。

当“÷”在第三个○内时，可得下面的填法：（5+13×7）÷（17-9）=12。

例2 将1～9这九个数字分别填入下式中的□中，使等式成立：□□□×□□=□□×□□=5568。

解：将5568质因数分解为5568=26×3×29。

由此容易知道，将 5568分解为两个两位数的乘积有两种：58×96和64×87，分解为一个两位数与一个三位数的乘积有六种：12×464， 16×348， 24×232，29×192， 32×174， 48×116。

显然，符合题意的只有下面一种填法：174×32=58×96=5568。

例3 在443后面添上一个三位数，使得到的六位数能被573整除。

分析与解：先用443000除以573，通过所得的余数，可以求出应添的三位数。

由443000÷573=773 (71)推知， 443000+（573-71）=443502一定能被573整除，所以应添502。

(完整版)小学五年级奥数题及答案(附精讲)

小学五年级奥训练题及答案（精讲）一、工程问题1．一件工作，甲、乙合做需4小时完成，乙、丙合做需5小时完成。

现在先请甲、丙合做2小时后，余下的乙还需做6小时完成。

乙单独做完这件工作要多少小时？2．修一条水渠，单独修，甲队需要20天完成，乙队需要30天完成。

如果两队合作，由于彼此施工有影响，他们的工作效率就要降低，甲队的工作效率是原来的五分之四，乙队工作效率只有原来的十分之九。

现在计划16天修完这条水渠，且要求两队合作的天数尽可能少，那么两队要合作几天？3．甲乙两个水管单独开，注满一池水，分别需要20小时，16小时.丙水管单独开，排一池水要10小时，若水池没水，同时打开甲乙两水管，5小时后，再打开排水管丙，问水池注满还是要多少小时？4．一项工程，第一天甲做，第二天乙做，第三天甲做，第四天乙做，这样交替轮流做，那么恰好用整数天完工；如果第一天乙做，第二天甲做，第三天乙做，第四天甲做，这样交替轮流做，那么完工时间要比前一种多半天。

已知乙单独做这项工程需17天完成，甲单独做这项工程要多少天完成？5．师徒俩人加工同样多的零件。

当师傅完成了1/2时，徒弟完成了120个。

当师傅完成了任务时，徒弟完成了4/5这批零件共有多少个？6．一批树苗，如果分给男女生栽，平均每人栽6棵；如果单份给女生栽，平均每人栽10棵。

单份给男生栽，平均每人栽几棵？7．一个池上装有3根水管。

甲管为进水管，乙管为出水管，20分钟可将满池水放完，丙管也是出水管，30分钟可将满池水放完。

现在先打开甲管，当水池水刚溢出时，打开乙,丙两管用了18分钟放完，当打开甲管注满水是，再打开乙管，而不开丙管，多少分钟将水放完？8．某工程队需要在规定日期内完成，若由甲队去做，恰好如期完成，若乙队去做，要超过规定日期三天完成，若先由甲乙合作二天，再由乙队单独做，恰好如期完成，问规定日期为几天？9．两根同样长的蜡烛，点完一根粗蜡烛要2小时，而点完一根细蜡烛要1小时，一天晚上停电，小芳同时点燃了这两根蜡烛看书，若干分钟后来点了，小芳将两支蜡烛同时熄灭，发现粗蜡烛的长是细蜡烛的2倍，问：停电多少分钟？二．鸡兔同笼问题1．鸡与兔共100只，鸡的腿数比兔的腿数少28条，,问鸡与兔各有几只？三．数字数位问题1．把1至2005这2005个自然数依次写下来得到一个多位数123456789.....2005,这个多位数除以9余数是多少?2．A和B是小于100的两个非零的不同自然数。

小学五年级奥数题及答案(附精讲)

小学五年级奥训练题及答案（精讲）一、工程问题1．一件工作，甲、乙合做需4小时完成，乙、丙合做需5小时完成。

现在先请甲、丙合做2小时后，余下的乙还需做6小时完成。

乙单独做完这件工作要多少小时？2．修一条水渠，单独修，甲队需要20天完成，乙队需要30天完成。

如果两队合作，由于彼此施工有影响，他们的工作效率就要降低，甲队的工作效率是原来的五分之四，乙队工作效率只有原来的十分之九。

现在计划16天修完这条水渠，且要求两队合作的天数尽可能少，那么两队要合作几天？3．甲乙两个水管单独开，注满一池水，分别需要20小时，16小时.丙水管单独开，排一池水要10小时，若水池没水，同时打开甲乙两水管，5小时后，再打开排水管丙，问水池注满还是要多少小时？4．一项工程，第一天甲做，第二天乙做，第三天甲做，第四天乙做，这样交替轮流做，那么恰好用整数天完工；如果第一天乙做，第二天甲做，第三天乙做，第四天甲做，这样交替轮流做，那么完工时间要比前一种多半天。

已知乙单独做这项工程需17天完成，甲单独做这项工程要多少天完成？5．师徒俩人加工同样多的零件。

当师傅完成了1/2时，徒弟完成了120个。

当师傅完成了任务时，徒弟完成了4/5这批零件共有多少个？6．一批树苗，如果分给男女生栽，平均每人栽6棵；如果单份给女生栽，平均每人栽10棵。

单份给男生栽，平均每人栽几棵？7．一个池上装有3根水管。

甲管为进水管，乙管为出水管，20分钟可将满池水放完，丙管也是出水管，30分钟可将满池水放完。

现在先打开甲管，当水池水刚溢出时，打开乙,丙两管用了18分钟放完，当打开甲管注满水是，再打开乙管，而不开丙管，多少分钟将水放完？8．某工程队需要在规定日期内完成，若由甲队去做，恰好如期完成，若乙队去做，要超过规定日期三天完成，若先由甲乙合作二天，再由乙队单独做，恰好如期完成，问规定日期为几天？9．两根同样长的蜡烛，点完一根粗蜡烛要2小时，而点完一根细蜡烛要1小时，一天晚上停电，小芳同时点燃了这两根蜡烛看书，若干分钟后来点了，小芳将两支蜡烛同时熄灭，发现粗蜡烛的长是细蜡烛的2倍，问：停电多少分钟？二．鸡兔同笼问题1．鸡与兔共100只，鸡的腿数比兔的腿数少28条，,问鸡与兔各有几只？三．数字数位问题1．把1至2005这2005个自然数依次写下来得到一个多位数123456789.....2005,这个多位数除以9余数是多少?2．A和B是小于100的两个非零的不同自然数。

【K12学习】五年级全套(上下册)名校奥数教程教案及试题(含答案)

五年级全套(上下册)名校奥数教程教案及试题(含答案)文第一讲数的整除问题数的整除问题，内容丰富，思维技巧性强。

它是小学数学中的重要课题，也是小学数学竞赛命题的内容之一。

一、基本概念和知识1.整除——约数和倍数例如：15÷3=5，63÷7=9一般地，如a、b、c为整数，b≠0，且a÷b=c，即整数a除以整除b，除得的商c正好是整数而没有余数，我们就说，a能被b整除。

记作b｜a.否则，称为a不能被b整除，，记作ba。

如果整数a能被整数b整除，a就叫做b的倍数，b就叫做a的约数。

例如：在上面算式中，15是3的倍数，3是15的约数；63是7的倍数，7是63的约数。

2.数的整除性质性质1：如果a、b都能被c整除，那么它们的和与差也能被c整除。

即：如果c｜a，c｜b，那么c｜。

例如：如果2｜10，2｜6，那么2｜，并且2｜。

性质2：如果b与c的积能整除a，那么b与c都能整除a.即：如果bc｜a，那么b｜a，c｜a。

性质3：如果b、c都能整除a，且b和c互质，那么b 与c的积能整除a。

即：如果b｜a，c｜a，且=1，那么bc｜a。

例如：如果2｜28，7｜28，且=1, 那么｜28。

性质4：如果c能整除b，b能整除a，那么c能整除a。

即：如果c｜b，b｜a，那么c｜a。

文例如：如果3｜9，9｜27，那么3｜27。

3.数的整除特征①能被2整除的数的特征：个位数字是0、2、4、6、8的整数.“特征”包含两方面的意义：一方面，个位数字是偶数的整数，必能被2整除；另一方面，能被2整除的数，其个位数字只能是偶数.下面“特征”含义相似。

②能被5整除的数的特征：个位是0或5。

③能被3整除的数的特征：各个数位数字之和能被3整除。

④能被4整除的数的特征：末两位数能被4整除。

例如：1864=1800＋64，因为100是4与25的倍数，所以1800是4与25的倍数.又因为4｜64，所以1864能被4整除.但因为2564，所以1864不能被25整除.⑤能被8整除的数的特征：末三位数能被8整除。

小学五年级精品数学(小哈弗)奥数教程(课后练习含答案)(专题1)一般应用题(一)

小学五年级奥数教程第一讲一般应用题（一）解答一般应用题时，我们可以借助线段图，示意图、直观演示手段等手段帮助分析在分析应用题的数量关系时，我们可以从条件出发，逐步推出所求问题——综合法；也可以从问题出发，找出需要的两个条件——分析法。

在解决实际问题时，我们可以根据题目中的条件，灵活应用两种方法。

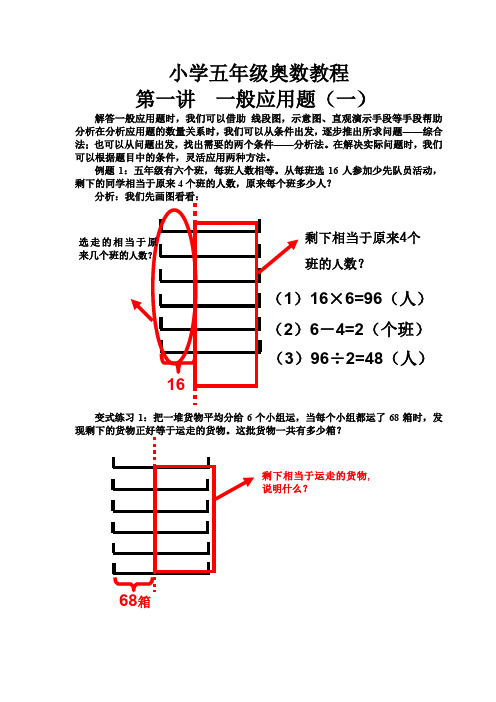
例题1：五年级有六个班，每班人数相等。

从每班选16人参加少先队员活动，剩下的同学相当于原来4个班的人数，原来每个班多少人？变式练习1：把一堆货物平均分给6个小组运，当每个小组都运了68箱时，发剩下相当于原来4个班的人数？选走的相16×6=96（人）6－4=2（个班）96÷2=48（人）剩下相当于运走的货物,说明什么？箱例题2：一个木器厂要生产一批课桌。

原计划每天生产60张，实际每天比计划多生产4张，结果提前1天完成任务。

这批课桌共多少张？那么原来最后一天需做的60张，现在要做它吗？这60张，现在应怎样处理？ 60÷4=15（天）60+4=64（张）64×15=960（张）变式练习2：修一条公路，计划每天修60米，实际每天多修15米，结果提前4天修完，一共修了多少米？提示：实际提前这4天，说明原来最后用的4天，现在需要吗？原来4天修的米数，应平均摊给前面这些天，每天摊15米，几天摊完？这个天数就是实际需要的天数，那么这条公路长多少米？例题3：有两盒玩具，甲有72个，乙有48个，每次从甲里拿3个给乙，多少次后两盒相等？甲拿到哪个位置时，甲、乙会相等？拿到甲比乙多的部分中一半时就会相等。

（72-48）÷2 ÷3=4（次）变式练习3：甲、乙两地相距200千米，汽车行完全程要5小时，步行要用40小时。

如果从甲到乙先步行8小时后改乘汽车，还需要几小时到达乙地？提示：汽车与步行的速度各是多少？步行8小时行多少千米？还剩多少千米？剩下路程乘车还需要几小时？变式练习4：某筑路队要修一条4200米的公路，原计划每人每天修4米，派21人来完成。

小学五年级精品数学(小哈弗)奥数教程(课后练习含答案)(专题2)一般应用题(二)

第二讲一般应用题（二）例题1：自行车厂计划每天生产自行车100辆，实际每天生产120辆，结果提前8天完成任务，这批自行车共有多少辆？分析：我们先画图看看：计划每天100辆实际每天120辆原来最后用的8天，现在还需要这几天时间吗？那么原来最后8天做的应平均摊给前面这些天，每天多摊几个？多少天就摊完了？100×8=800（辆）120-100=20（辆）800÷20=40（天）120×40=4800（辆）变式练习1：机械厂原计划30天生产一批机器，实际每天比计划多生产80台，结果提前25天就完成任务。

这批机器共多少台？提示：结果提前25天完成任务，说明实际不需要这25天，但是计划则需要这25天。

由题意我们可以知道，实际只需要几天？这几天每天多分摊了80台，总共多分摊了多少台？总共多分摊的台数是原来多少天做的？原来每天做多少台？这批机器多少台？例题2：甲、乙、丙三个公司到汽车厂订购18辆汽车，按照合同3个公司平均分配。

但付款时丙没有带钱，甲公司付出10辆的钱，乙付了8辆的钱，丙应付90万元。

甲、乙两公司应收回多少钱？分析：丙付90万元，是付几辆车的钱？18÷3=6每辆车的钱是多少？90÷6=15（万元）甲应收回多少钱？15×（10-6）=60（万元）乙应收回多少钱？15×（8-6）=30（万元）变式练习2：小华、小明和小强三人合用一些练习本，小华带来8本，小明带来7本，小强没有带练习本，他付出了10元。

小华应得几元？提示：小强应付几本的钱？每本练习本多少钱？小华应收回多少本的价钱？例题3：两个数的和是94，有人计算时将其中一个加数个位上的0漏掉了，结果算出的和是31。

求这两个数？分析：现在作图思考：3原来看漏掉0那个数有10份，现在只有几份，原来比现在多几份？10-1=9（份）原来看漏掉0那个数有比现在实际多多少？94-31=63多的64占几份，每份是多少？63÷（10-1）=7原来两个数：7×10=70，94-70=24。