C23_复数的定义-表示和实现-C语言程序

合集下载

复数详细

z1±z2=（a+bi）±（c+di）=（a±c）+（b±d）i，（a+bi）·（c+di）=（ac－bd）+（bc+ad）i，（a+bi）÷(c+di)=(ac+bd)/(c^2+d^2) +(bc-ad)i/(c^2+d^2) 其实两复数相除，完全可以转化为两复数相乘：（a+bi）÷(c+di)= （a+bi） /(c+di)，此时分子分母同时乘以分母 c+di 的共轭复数 c-di 即可。复数的加法乘法运算律 z1+z2=z2+z1 （z1+z2)+z3=z1+(z2+z3) z1z2=z2z1 z1(z2z3)=(z1z2)z3 z1(z2+z3)=z1z2+z1z3 虚数单位 i 的乘方 i^(4n+1)=i,i^(4n+2)=-1,i^(4n+3)=-i,i^4n=1(其中 n∈Z）加法法则复数的加法按照以下规定的法则进行：设 z1=a+bi,z2=c+di 是任意两个复数，则它们的和是 (a+bi)+(c+di)=(a+c)+(b+d)i. 两个复数的和依然是复数，它的实部是原来两个复数实部的和，它的虚部是原来两个虚部的和。复数的加法满足交换律和结合律，即对任意复数 z1,z2,z3,有： z1+z2=z2+z1; (z1+z2)+z3=z1+(z2+z3). 乘法法则规定复数的乘法按照以下的法则进行：设 z1=a+bi，z2=c+di(a、b、c、d∈R)是任意两个复数，那么它们的积 (a+bi)(c+di)=(ac－bd)+(bc+ad)i. 其实就是把两个复数相乘，类似两个多项式相乘，结果中 i^2 = −1，把实部与虚部分别合并。两个复数的积仍然是一个复数。除法法则复数除法定义：满足(c+di)(x+yi)=(a+bi)的复数 x+yi(x,y∈R)叫复数 a+bi 除以复数 c+di 的商

C#第三章习题

四、程序分析1.下面程序，输入不同参数，观察并分析运行结果。

using System;namespace Test{class Program{static void Main(string[] args){while (true){String s = Console.ReadLine();if (s == "exit") break;try{int i = 10 / Int32.Parse(s);Console.WriteLine("结果是" + i);}catch (IndexOutOfRangeException e){Console.WriteLine(e.Message);}catch (FormatException e){Console.WriteLine(e.Message);}catch (DivideByZeroException e){Console.WriteLine(e.Message); }catch (OverflowException e){Console.WriteLine(e.Message); }}Console.Read();}}}2.代码改为：using System;namespace Test{interface I1{void MyFunction1();}interface I2{void MyFunction2();}class Test : I1, I2{public void MyFunction1(){Console.WriteLine("Now I can say this here is I1 implemented!"); }public void MyFunction2(){Console.WriteLine("Now I can say this here is I2 implemented!"); }}class PavelTeskov{static void Main(string[] args){Test t = new Test();t.MyFunction1();t.MyFunction2();Console.Read();}}}3.用户自定义从 Digit 到 byte 的隐式转换using System;namespace Test{public class Digit{byte value;public Digit(byte value){if (value < 0 || value > 9)throw new ArgumentException();this.value = value;}public static implicit operator byte(Digit d){return d.value;}}class dig{static void Main(string[] args){Digit dig = new Digit(7);byte num = dig;Console.WriteLine("num={0}", num);Console.ReadLine();}}}五、编程题1.定义描述复数的类,并实现复数的输入和输出。

C2-3(顾元刚)

上一张下一张
3、关系运算符和关系表达式
所谓关系运算是对两个运算量进行比较的一种运算。进行关系运算的表达式称为关系表达式，他是用关系运算符和其他表达式连接而成的式子。关系运算是一种比较简单的逻辑运算。 C语言提供了6种关系运算符，其形式和作用详见表2.6。
上一张下一张
表2.6 关于运算符和关于表达式的基本形式
上一张下一张
⑤ 模运算,即是求余数运算，要求参与运算的量均为整型。其运算结果等于两数相除后的余数。例如：100%7的结果为2。 ⑥ 算术表达式的书写形式和数学公式的不同，例如，公式b2-4ac必须写成b*b4*a*c，这里的运算符“*”是不能省略的。另外还要注意运算的优先级，对于式子写成-b /(2*a)，绝不能写成-b/2*a。下面是一些合法的算术表达式的例子：
+
* / % ++ --
加法运算
减法运算乘法运算除法运算模运算（求余）自增1 自减1 取负
a+b a-b a*b
a/b a%b a++或++a a--或--a
√ √ √
√ √ √ √
√ √ √
√ × × ×
求a 与b的和求a 与b的差求a 与b的积
a 除以b的商求a 除以b的余数相当于a=a+1 相当于a=a-1
①
上一张下一张
②
在使用赋值表达式时，要注意以下几个问题：
① 赋值运算符“=”是右结合性运算符，即其运算次序应从右至左执行。 ② 由于赋值运算产生一个新的表达式，根据赋值运算的定义，他还可以赋给另一个变量，从而产生连续赋值的效果，非常适用于变量的初始化。例如： a=b=c=0 ③ 赋值表达式不是赋值语句，但按照Ｃ语言规定，任何表达式在其未尾加上分号就构成为语句。因此， a=b=c=0；才是一个是赋值语句。上一张下一张

c语言c23标准

c语言c23标准C23 是 C 语言的最新标准，它于 2022 年发布，带来了许多改进和新功能。

这些变化旨在提高 C 语言的可读性、可维护性和安全性。

本文将介绍 C23 标准的一些主要特性和改进。

一、可空类型（Nullable Types）：C23 引入了可空类型，使得我们能够在不使用指针的情况下，表示一个类型可以是空值。

这样可以减少错误和 crash 的风险，提高代码的可靠性。

可空类型通过在类型名称后面加上一个问号（?）来定义，例如`int?` 表示可空的整型变量。

二、泛型（Generics）：C23 支持泛型编程，使得我们可以编写可重用的通用算法和数据结构。

使用泛型，我们可以在运行时指定数据类型，从而减少代码的重复性和冗余性。

例如我们可以定义一个泛型的排序函数 `sort()`，然后在调用时传入不同的数据类型。

三、异常处理（Exception Handling）：C23 引入了异常处理机制，使得我们能够更好地处理错误和异常情况。

在出现错误时，我们可以抛出一个异常，并在适当的位置捕获和处理异常。

这有助于提高程序的健壮性和可靠性。

四、更严格的类型检查：C23 引入了更严格的类型检查机制，可以在编译时捕获更多的类型错误。

例如，不同类型之间的赋值或比较将会得到更严格的检查。

这有助于减少类型相关的错误，提高代码的正确性。

五、模块化编程：C23 支持模块化编程，使得代码的组织和管理更加方便。

我们可以将相关的函数、数据结构和常量放在一个独立的模块中，然后通过导入模块来使用其中的内容。

这有助于提高代码的可读性和可维护性。

六、更强大的标准库：C23 扩展了标准库，提供了更多的函数和数据结构，方便开发者使用。

例如，标准库新增了对日期时间的处理功能、正则表达式的支持等。

这样可以减少开发者的工作量，提高开发效率。

七、更好的内存管理：C23 引入了一些新的内存管理机制，使得内存的分配和释放更加安全和高效。

例如，新增了对内存空间的归还（reclaim）机制，可以在不再需要某块内存时，及时释放它，从而避免内存泄漏的问题。

c课程设计复数计算器源代码

//复数计算器#include<iostream.h>#include<math.h>#include<stdlib.h>#include<string.h>#include<fstream.h>#include<time.h>#include <windows.h>#define EPS 1e-5 //定义精度常数class CComplex ////定义一个CComplex类{private:double Real,Image;public:CComplex(double real=0,double image=0) //构造函数{Real=real;Image=image;}friend istream & operator>>(istream &is,CComplex &com); //重载输入friend ostream & operator<<(ostream &os,CComplex &com); //重载输出CComplex operator+(CComplex &com); //加法重载CComplex operator-(CComplex &com); //减法重载CComplex operator*(CComplex &com); //乘法重载CComplex operator/(CComplex &com); //除法重载CComplex operator+=(CComplex &com); //加法赋值重载CComplex operator-=(CComplex &com); //减法赋值重载CComplex operator*=(CComplex &com); //乘法赋值重载CComplex operator/=(CComplex &com); //除法赋值重载CComplex operator++(); //自加CComplex operator--(); //自减double mod(void); //求复数的模int operator>(CComplex &com);int operator<(CComplex &com);int operator!=(CComplex &com);int operator==(CComplex &com);};struct User //用户结构体类型定义{char szName[20]; //用户名int nTime; //使用次数int nTest; //测试次数double alAve; //平均成绩int nAdd; //加法次数int nSub; //减法次数int nMul; //乘法次数int nDiv;//除法次数int nMod;//求模次数double dlScore[3]; //3次测试得分}user; //定义全局变量CComplex CComplex::operator++() //重载运算符"++",实部与虚部均加1 { Real++;Image++;return *this;}CComplex CComplex::operator--() //重载运算符"--",实部与虚部均减1 {Real--;Image--;return *this;}double CComplex::mod() //求复数的模的平方,返回实部^2+虚部^2{return sqrt(Real*Real+Image*Image);}int CComplex::operator>(CComplex &com) //重载运算符">",比较模的大小{if(mod()>com.mod())return 1;elsereturn 0;}int CComplex::operator<(CComplex &com) {if(mod()<com.mod())return 1; //若大,则返回1elsereturn 0;}int CComplex::operator!=(CComplex &com) //重载运算符"!=",分别判断复数的实部和虚部{if(*this==com)return 0;elsereturn 1;}istream & operator>>(istream &is,CComplex &com) //重载输入,可以输入a+bi的形式{char s[80];is>>s; //用字符串的形式接受复数int len=strlen(s); //求出字符串的长度int n=0,sign=1;//n为当前从字符串中提取出来的数字,初始化为0;sign是难道符号,初始化为正com.Image=com.Real=0;for(int k=0;k<len;k++) //判断接受的字符串是否合法{if((s[k]<'0' || s[k]> '9') && (s[k]!='+' && s[k]!='-' && s[k]!='i')) {cout<<"error"<<endl;return is; //错误,输出出错信息并返回}}for(k=0;k<len;) //顺序识别字符串中各字符{if(n!=0 &&(s[k]=='-'||s[k]=='+')) //当前字符是否是符号位{com.Real=sign*n;//是符号位,且n!=0,即n已被赋值,表明当前读取的是虚部的符号n=0; //将原n*sign值赋给实部,将n清零,准备接受虚部的值} if(s[k]=='-') //当前字符为负号{sign=-1;k++; //给符号标志赋值}if(s[k]=='+') //当前字符为正号{sign=1;k++; //给符号标志赋值}if(s[k]=='i') //当前字符为'I'{if(k!=len-1) //判断字符'I'是否为字符串中作后一个字符cout<<"error\n"; //如果不是,说明复数数据格式错误elsecom.Image=sign*n;//是最后一个字符,复数对象已接受完,用sign*n为虚部赋值break; }while(s[k]>='0' && s[k]<='9')//当前字符在0~9之间,将数字字符转换成数字数值{n=n*10+s[k]-'0';k++;}}if(s[len-1]!='i' && n!=0)//如果最后一个字符不是'I',表示复数对象内只有实部,没有虚部{com.Real=n*sign;}return is;}ostream & operator<<(ostream &os,CComplex &com) //重载输入{if(fabs(com.Image)<EPS) // 如果虚部为0os<<com.Real; //只输出实部else if((fabs(com.Real)<EPS)) //如果实部为0os<<com.Image<<"i"; //只输出虚部else if(com.Image>0)os<<com.Real<<"+"<<com.Image<<"i"; //虚部为正elseos<<com.Real<<com.Image<<"i"; //虚部为负return os;}CComplex CComplex::operator+(CComplex &com) //加法重载{CComplex sum;sum.Real=Real+com.Real; //实部相加sum.Image=Image+com.Image; //虚部相加return sum;}CComplex CComplex::operator*(CComplex &com) //乘法重载{CComplex multi;multi.Real=Real*com.Real-Image*com.Image; //乘积实部multi.Image=Real*com.Image+Image*com.Real; //乘积虚部return multi;}CComplex CComplex::operator-(CComplex &com) //减法重载{CComplex sub;sub.Real=Real-com.Real;sub.Image=Image-com.Image;return sub;}CComplex CComplex::operator/(CComplex &com)//除法重载{CComplex div;div.Real=(Real*com.Real+Image*com.Image)/(com.Real*com.Real+com.Ima ge*com.Image);div.Image=(Image*com.Real-Real*com.Image)/(com.Real*com.Real+com.Image*com.Image);return div;}CComplex CComplex::operator+=(CComplex &com) //重载加法赋值{Real=Real+com.Real;Image=Image+com.Image;return *this;}CComplex CComplex::operator-=(CComplex &com) //重载减法赋值{Real=Real-com.Real;Image=Image-com.Image;return *this;}CComplex CComplex::operator*=(CComplex &com) //重载乘法赋值{double nReal=Real*com.Real-Image*com.Image;double nImage=Real*com.Image+Image*com.Real;Real=nReal;Image=nImage;return *this;}CComplex CComplex::operator/=(CComplex &com)//除法赋值重载{doublenReal=(Real*com.Real+Image*com.Image)/(com.Real*com.Real+com.Image* com.Image);doublenImage=(Image*com.Real-Real*com.Image)/(com.Real*com.Real+com.Image*com.Image);Real=nReal;Image=nImage;return *this;}int CComplex::operator==(CComplex &com) //重载等于{if(Real==com.Real && Image==com.Image)return 1;elsereturn 0;}void Test(void) //测试函数{user.nTest++;cout<<"共10道题,做100以内的加减运算,满分100分:\n";double real1,real2,image1,image2,real3,real4,image3,image4; CComplex answer,temp;int score=0;char op;for(int i=0;i<=9;i++){/////为复数产生随机值real1=rand()%200-100;image1=rand()%200-100;real2=rand()%200-100;image2=rand()%200-100;CComplex a(real1,image1),b(real2,image2);real3=rand()%20-10;image3=rand()%20-10;real4=rand()%20-10;image4=rand()%20-10;CComplex c(real3,image3),d(real4,image4);op=rand()%3; //产生随机加减乘法运算的三个值switch(op){case 0:answer=a+b;cout<<"( "<<a<<" )"<<" + "<<"( "<<b<<" )"<<" = "; break;case 1:answer=a-b;cout<<"( "<<a<<" )"<<" - "<<"( "<<b<<" )"<<" = "; break;case 2:answer=c*d;cout<<"( "<<c<<" )"<<" * "<<"( "<<d<<" )"<<" = "; break;}cin>>temp; //输入用户计算值if(answer==temp) //比较用户计算值{score+=10;cout<<"恭喜您答对了,加10分!\n\n";}else{cout<<"很遗憾,您答错了。

C++复数的实现

C++复数的实现在数字图像处理领域，复数这⼀类型会被经常使⽤到。

但是在C++和Qt中都没有可以使⽤的复数类。

为了今后的⽅便，我们可以⾃⼰定义⼀个C++复数类，以便将来使⽤。

⼀、复数的属性复数包含实数部分和虚数部分，如果直接使⽤ a + ib 的模式会使得后⾯的⼀系列操作变得较为复杂。

这⾥我们直接给复数定义两个成员变量 m_rl 和 m_im。

1public:2double m_rl,m_im;⼆、我们同样需要构造函数来初始化复数实例1public:2 ComplexNumber(double rl,double im);3 ComplexNumber();它们的实现如下：1 ComplexNumber::ComplexNumber()2 {3 m_rl = 0;4 m_im = 0;5 }67 ComplexNumber::ComplexNumber(double rl, double im)8 {9 m_rl = rl;10 m_im = im;11 }三、现在我们给复数加上算术运算的功能在复数的头⽂件中加⼊下述代码：1public:23// 重载四则运算符号45// 加6 ComplexNumber operator +(const ComplexNumber &c){7return ComplexNumber(m_rl+c.m_rl,m_im+c.m_im);8 }910// 减11 ComplexNumber operator -(const ComplexNumber &c){12return ComplexNumber(m_rl-c.m_rl,m_im-c.m_im);13 }1415// 乘16 ComplexNumber operator *(const ComplexNumber &c){17return ComplexNumber(m_rl*c.m_rl-m_im*c.m_im,18 m_rl*c.m_im+m_im*c.m_rl);19 }2021// 除22 ComplexNumber operator /(const ComplexNumber &c) {23if ((0==c.m_rl) && (0==c.m_im)) {24 qDebug()<<"ERROR: divider is 0!";25return ComplexNumber(m_rl, m_im);26 }2728return ComplexNumber((m_rl*c.m_rl + m_im*c.m_im) / (c.m_rl*c.m_rl + c.m_im*c.m_im), 2930 (m_im*c.m_rl - m_rl*c.m_im) / (c.m_rl*c.m_rl + c.m_im*c.m_im));3132 }四、其他函数1．设定复数值1void SetValue(double rl, double im); // 定义2void ComplexNumber::SetValue(double rl, double im) // 实现3 {4 m_rl = rl;5 m_im = im;6 }2．取模1double get_mold(); // 定义2double ComplexNumber::get_mold() // 实现3 {4double mold;5 mold = sqrt(m_rl*m_rl+m_im*m_im);6return mold;7 }⾄此，复数的实现就完成了。

c语言实现复数运算

c语言实现复数运算摘要：一、引言二、复数的定义与性质三、C 语言中复数的表示方法四、复数加法与减法五、复数乘法与除法六、共轭复数与模运算七、总结正文：一、引言复数在数学中占有重要地位，同时在工程和科学领域也有广泛应用。

C 语言作为一种通用的编程语言，实现复数运算具有重要意义。

本文将介绍如何使用C 语言实现复数运算。

二、复数的定义与性质复数，通常表示为a+bi，其中a 和b 为实数，i 为虚数单位（满足i^2=-1）。

复数具有加法、减法、乘法、除法等运算性质。

三、C 语言中复数的表示方法在C 语言中，我们可以使用结构体来表示复数，如下所示：```ctypedef struct {double real;double imag;} Complex;```四、复数加法与减法复数的加法和减法可以通过实部和虚部的对应相加或相减来实现。

具体实现如下：```cComplex add(Complex c1, Complex c2) {Complex result;result.real = c1.real + c2.real;result.imag = c1.imag + c2.imag;return result;}Complex subtract(Complex c1, Complex c2) {Complex result;result.real = c1.real - c2.real;result.imag = c1.imag - c2.imag;return result;}```五、复数乘法与除法复数的乘法和除法较为复杂，需要利用共轭复数和模运算来简化计算。

具体实现如下：```cComplex multiply(Complex c1, Complex c2) {Complex result;double temp = c1.real * c2.real + c1.imag * c2.imag;double angle = c1.real * c2.imag - c1.imag * c2.real;result.real = temp;result.imag = angle;return result;}Complex divide(Complex c1, Complex c2) {Complex result;double denominator = c2.real * c2.real + c2.imag * c2.imag;result.real = (c1.real * c2.real + c1.imag * c2.imag) / denominator;result.imag = (c1.imag * c2.real - c1.real * c2.imag) / denominator;return result;}```六、共轭复数与模运算共轭复数是指虚部取负的复数，如a-bi。

C++实现复数加减乘除实验报告

C++实现复数加减乘除实验报告实验 C++实现复数的加减乘除试用C语言的结构类型定义表示复数Complex的抽象数据类型。

（1）在复数内部用浮点数定义其实部与虚部；（2）设计实现复数的＋、－、×、÷等运算的函数。

基本操作函数接口：InitComplex( &Z, v1, v2 )：操作结果：构造复数Z,其实部和虚部分别被赋以参数v1和v2的值。

GetReal( Z, &realPart )：初始条件：复数已存在。

操作结果：用realPart返回复数Z的实部值。

GetImag( Z, &ImagPart )：初始条件：复数已存在。

操作结果：用ImagPart返回复数Z的虚部值。

Add( z1,z2, ∑ )：初始条件：z1,z2是复数。

操作结果：用sum返回两个复数z1,z2的和值。

Sub( z1,z2, &residue)：初始条件：z1,z2是复数。

操作结果：用res返回两个复数z1,z2的差值。

mul( z1,z2, &product )：初始条件：z1,z2是复数。

操作结果：用product返回两个复数z1,z2的积。

div( z1,z2, &quotient,&residue)：初始条件：z1,z2是复数。

操作结果：用quotient 返回两个复数z1除z2的商，用residue 返回它们的余数。

要求main函数中只能是基本的输入输出语句和函数调用语句，其运行界面如下：please input first complex number : a + bithe other one : c+ diplease choice operation: +, -, * or /:+(a + bi)+ (c+ di)=……其中a,b,c,d是用户从键盘上输入的实型值，分别代表两个复数的实部和虚部。

实验代码：#include //定义一个复数类typedef struct {float realpart;float imagpart;}Complex;Complex InitComplex(float v1,float v2) //初始化{ Complex z;z.realpart=v1;z.imagpart=v2;return z;}float Getreal(Complex z){return z.realpart;}float Getimagepart(Complex z){return z.imagpart;}Complex Add(Complex z1,Complex z2) //实现加法运算{z1.realpart=z1.realpart+z2.realpart;z1.imagpart=z1.imagpart+z2.imagpart;return z1;}Complex Sub(Complex z1,Complex z2) //实现减法运算{z1.realpart=z1.realpart-z2.realpart;z1.imagpart=z1.imagpart-z2.imagpart;return z1;}Complex Mul(Complex z1,Complex z2) //实现乘法运算{z1.realpart=z1.realpart*z2.realpart;z1.imagpart=z1.imagpart*z2.imagpart;return z1;}Complex Div(Complex z1,Complex z2) // 实现除法运算{z1.realpart=z1.realpart/z2.realpart;z1.imagpart=z1.imagpart/z2.imagpart;return z1;}int main (){ float a,b,c,d;char e;Complex z1,z2,z3;printf("please input first complex number a+bi:"); //只需输入实部a,虚部b scanf("%f %f",&a,&b);z1= InitComplex(a,b);printf("please input the other :");scanf("%f %f",&c,&d);z2=InitComplex(c,d);printf("please choice operation :+，-,*,/ :"); //选择运算符getchar();scanf("%c",&e);if (e=='+') //选择运算符z3= Add( z1,z2);if(e=='-')z3=Sub(z1,z2);if(e=='*')z3=Mul(z1,z2);if(e=='/')z3=Div(z1, z2);printf("%f+%fi",z3.realpart,z3.imagpart); return 0;}运行结果:。

（33条消息）C#实现复数运算类

（33条消息）C#实现复数运算类实现复数的加、减、乘、除，求实部、虚部、模和命令行输出。

源代码如下：///<summary>///复数类///</summary>public class Complex{///<summary>///默认构造函数///</summary>public Complex(): this(0, 0){}///<summary>///只有实部的构造函数///</summary>///<param name="real">实部</param>public Complex(double real): this(real, 0) { }///<summary>///由实部和虚部构造///</summary>///<param name="real">实部</param>///<param name="image">虚部</param>public Complex(double real, double image){this.real = real;this.image = image;}private double real;///<summary>///复数的实部///</summary>public double Real{get { return real; }set { real = value; }}private double image;///<summary>///复数的虚部///</summary>public double Image{get { return image; }set { image = value; }}///重载加法public static Complex operator +(Complex c1, Complex c2) {return new Complex(c1.real + c2.real, c1.image + c2.image);}///重载减法public static Complex operator -(Complex c1, Complex c2) {return new Complex(c1.real - c2.real, c1.image - c2.image);}///重载乘法public static Complex operator *(Complex c1, Complex c2) {return new Complex(c1.real * c2.real - c1.image * c2.image, c1.image * c2.real + c1.real * c2.image);}///<summary>///求复数的模///</summary>///<returns>模</returns>public double ToModul(){return Math.Sqrt(real * real + image * image);}///<summary>///重载ToString方法///</summary>///<returns>打印字符串</returns>public override string ToString(){if (Real == 0 && Image == 0){return string.Format("{0}", 0);}if (Real == 0 && (Image != 1 && Image != -1)) {return string.Format("{0} i", Image);}if (Image == 0){return string.Format("{0}", Real);}if (Image == 1){return string.Format("i");}if (Image == -1){return string.Format("- i");}if (Image < 0){return string.Format("{0} - {1} i", Real, -Image); }return string.Format("{0} + {1} i", Real, Image); }}。

C_语言的复数和常用复函数扩充

C++语言的复数和常用复函数扩充赖天树倪海鸣中山大学物理学系 (广州 510275) 广州电视台 (广州 510069)摘要本文利用C++语言的类概念,为C++语言扩充了复数型数据类型和常用复函数。

利用C++的运算符重载功能,实现了复数间和复数、实数间的四则运算,增强了C++语言的科学计算能力,使得开发集WINDOWS风格用户界面、含复数的科学计算和图形显示三位一体的应用软件变得非常容易。

关键词 C++语言复数类运算符重载1 引言80年代以来,随着科学计算可视化概念的形成和发展[1 3],要求以图形方式快速、方便地显示大量计算结果,实现计算与图形显示一体化。

此外,随着W IN DOWS操作系统的广泛流行和W IN DOWS风格的用户界面(菜单、对话框和消息框等)为用户所宠爱和推崇,也要求科学计算应用软件的用户界面WI NDOW S风格化。

这就要求编程语言既具有强的科学计算能力,又具有强大的图形和WIN DO WS风格界面资源开发功能。

然而,目前还没有任何一种编程语言能完全满足这些要求。

FORT RA N语言具有强大的科学计算能力,在科学计算中一直处于主导地位,但是它的图形功能较弱,更不具备W INDO WS风格的用户界面资源开发功能,因而难以满足W INDO WS风格的可视化科学计算应用软件的开发,除非用户自己开发一些图形功能和类似W IN DO WS界面的菜单、对话框等功能块。

文献[4]中进行了这一尝试。

但工作量是巨大的,并且还只是基于DOS操作系统。

要开发基于WI NDOW S操作系统的图形功能和界面资源则十分困难,甚至是不可能的,C++语言既具有较强的科学计算能力,又具有强大的图形功能和WIN DOWS风格界面资源开发功能(如V isual C++,Bor land C++),是一种能够较好地满足WI NDO WS风格的可视化科学计算应用软件开发的语言。

与F ORT RA N语言的计算能力相比,C++语言的计算能力仅弱在不能直接计算复数和复函数,而科学计算中复数和复函数又是常见的,也许正是这一缺点限制了C和C++语言在科学计算领域中的广泛应用。

CC++语言编程系列001——复数库complex用法

CC++语言编程系列001——复数库complex用法
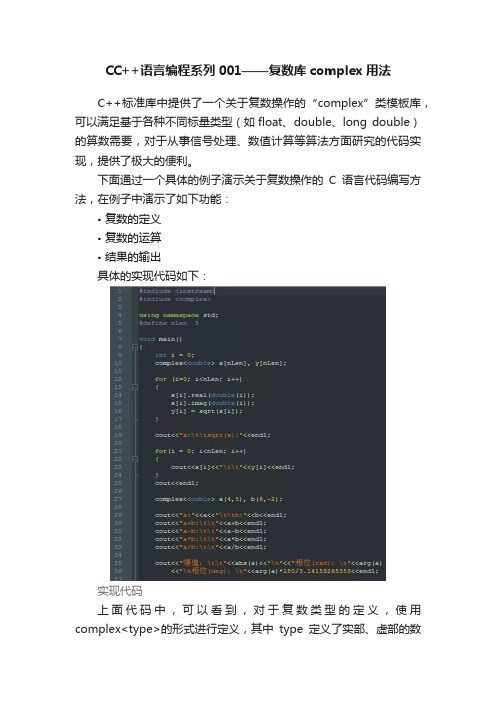
C++标准库中提供了一个关于复数操作的“complex”类模板库，可以满足基于各种不同标量类型（如float、double、long double）的算数需要，对于从事信号处理、数值计算等算法方面研究的代码实现，提供了极大的便利。

下面通过一个具体的例子演示关于复数操作的C语言代码编写方法，在例子中演示了如下功能：
▪复数的定义
▪复数的运算
▪结果的输出
具体的实现代码如下：
实现代码
上面代码中，可以看到，对于复数类型的定义，使用complex<type>的形式进行定义，其中type定义了实部、虚部的数
据类型；在给复数变量赋值方面，可以变量定义后再给实部、虚部分别单独赋值定义，也可以在变量定义时直接赋值。

其运行结果如下图所示：
运行结果
对于复数的运算，除例子中基本的加、减、乘、除、幅值、相位等计算外，该模板类中也提供了其它的运算函数，如real()、imag()、norml()、conj()、exp()、log()、log10()、pow()、sqrt()、sin()、sinh()、cos()、cosh()、tan()、tanh()、polar()等等函数，用法也相对比较简单。

数据结构复数的实现与操作

/*******************************************///文件名: * * *//作者:湖北科技学院计科院曹帅//日期：2013.10.28//功能：实现复数的基本操作/*******************************************///头文件#include<stdio.h>#include<malloc.h>#include<stdlib.h>#include<windows.h>#include<conio.h>//函数返回状态代码#define OK 1#define ERROR 0#define TRUE 1#define FALSE 0#define INFEASIBLE -1#define OVERFLOW -2//使用动态分配的顺序存储结构typedef int Status;typedef int ElemType;typedef ElemType * Complex;Status InitComplex(Complex &C,ElemType real,ElemType imag){ //初始化一个复数C=(ElemType *)malloc(2*sizeof(ElemType));if(!C) exit(OVERFLOW);C[0]=real;C[1]=imag;return OK;}//InitComplexStatus DestroyComplex(Complex &C){//销毁一个复数free(C);C=NULL;return OK;}//DestroyComplexStatus GetReal(Complex C,ElemType &real){//获取复数的实数部分real=C[0];return OK;}//GetRealStatus AddComplex(Complex C1,Complex C2,Complex &C3){ //两个复数相加C3=(ElemType *)malloc(2*sizeof(ElemType));if(!C3) exit(OVERFLOW);C3[0]=C1[0]+C2[0];C3[1]=C1[1]+C2[1];return OK;}//AddComplexStatus MultiplyComplex(Complex C1,Complex C2,Complex &C4){ //两个复数相乘C4=(ElemType *)malloc(2*sizeof(ElemType));if(!C4) exit(OVERFLOW);C4[0]=C1[0]*C2[0]-C1[1]*C2[1];C4[1]=C1[0]*C2[1]+C1[1]*C2[0];return OK;}//MutiplyComplexStatus SubComplex(Complex C1,Complex C2,Complex &C5){ //两个复数相减C5=(ElemType *)malloc(2*sizeof(ElemType));if(!C5) exit(OVERFLOW);C5[0]=C1[0]-C2[0];C5[1]=C1[1]-C2[1];return OK;}//SubComplexStatus DivComplex(Complex C1,Complex C2,Complex &C6){ //两个复数相除C6=(ElemType *)malloc(2*sizeof(ElemType));if(!C6) exit(OVERFLOW);C6[0]=(C1[0]*C2[0]+C1[1]*C2[1])/(C2[0]*C2[0]+C2[1]*C2[1]);C6[1]=(C1[0]*C2[1]-C1[1]*C2[0])/(C2[0]*C2[0]+C2[1]*C2[1]);return OK;}//AddComplexvoid main(){Complex C1,C2,C3,C4,C5,C6;ElemType real1,imag1,real2,imag2,temp;int select,i;while(1){printf("\n\t\t**********复数操作菜单***********\n\n");printf("\t\t 1.复数的输入;\n");printf("\t\t 2.复数的输出;\n");printf("\t\t 3.复数的四则运算;\n");printf("\t\t 4.复数的实部获取;\n");printf("\t\t 5.退出;\n\n");printf("\t\t*********************************\n");printf("\t\t您的选择是(1-5):");scanf("%d",&select);if(select > 5||select < 1)//限定输入选项{printf("\t\t输入错误!!!\n");printf("\t\t\t按任意键返回主菜单...\n");system("cls");getch();}switch(select){case 1:system("cls");//清屏;printf("\n\t*********输入操作界面***********\n");printf("\n\t\treal part: ");scanf("%d",&real1);printf("\t\timage part: ");scanf("%d",&imag1);printf("\n\t\treal part: ");scanf("%d",&real2);printf("\t\timage part: ");scanf("%d",&imag2);InitComplex(C1,real1,imag1);//创建复数InitComplex(C2,real2,imag2);//创建复数,若无该部则无法执行下一步AddComplex(C1,C2,C3);MultiplyComplex(C1,C2,C4);SubComplex(C1,C2,C5);DivComplex(C1,C2,C6);printf("\t\t\t按任意键返回主菜单...\n");system("cls");//清屏;getch();//返回主菜单;break;case 2:system("cls");//清屏;printf("\t *********输出操作界面***********\n");printf("\n\t\tComplex 1 is: (%d + %di)\n",C1[0],C1[1]);printf("\t\tComplex 2 is: (%d + %di)\n",C2[0],C2[1]);printf("\t\t\t按任意键返回主菜单...\n");getch();system("cls");//清屏system("cls");break;case 3:system("cls");//清屏printf("\t**************四则运算界面************\n");printf("\n\t\tThe Add : \n");printf("\t\t(%d+%di) + (%d+%di)= %d + %di\n",C1[0],C1[1],C2[0],C2[1],C3[0],C3[1]);printf("\n\t\tThe Mut : \n");printf("\t\t(%d+%di) * (%d+%di)= %d + %di\n",C1[0],C1[1],C2[0],C2[1],C4[0],C4[1]);printf("\n\t\tThe Sub : \n");printf("\t\t(%d+%di) - (%d+%di)= %d + %di\n",C1[0],C1[1],C2[0],C2[1],C5[0],C5[1]);printf("\n\t\tThe Div : \n");if(C6[1] == 0){printf("\t\t(%d+%di) / (%d+%di)= %d \n",C1[0],C1[1],C2[0],C2[1],C6[0]);}else{printf("\t\t(%d+%di) / (%d+%di)= %d + %di\n",C1[0],C1[1],C2[0],C2[1],C6[0],C6[1]);}printf("\t\t\t按任意键返回主菜单...\n");getch();system("cls");break;case 4:system("cls");//清屏printf("\t\t************实部获取界面**************\n");printf("\n\t\tWhich real part want to get(1 or 2) ? ");scanf("%d",&i);if(i!=1&&i!=2){printf("\t\tInput error!!!\n");}else if(i==1){GetReal(C1,temp);printf("\t\tFisrt complex's real part is: %d\n",temp);}else {GetReal(C2,temp);printf("\t\tSeconed complex's real part is: %d\n",temp);}printf("\t\t\t按任意键返回主菜单...\n");getch();system("cls");break;case 5:printf("\t\t成功退出!!!\n");DestroyComplex(C1);//销毁复数DestroyComplex(C2);DestroyComplex(C3);DestroyComplex(C4);//销毁复数DestroyComplex(C5);DestroyComplex(C6);return ;}}}。

cmath组合数

在C++的cmath库中，包含了一些用于处理复数（complex numbers）的函数。

复数是由实部和虚部组成的数，通常表示为a + bi，其中a是实部，b是虚部，而i是虚数单位，满足i² = -1。

在cmath库中，复数的表示采用std::complex类。

以下是一些与复数有关的cmath库的函数和操作：
1.std::complex类：该类用于表示复数。

它包含了一些常见的运算符，例如加
法、减法、乘法和除法。

使用该类可以方便地执行复数的基本运算。

2.std::abs函数：该函数用于计算复数的模（magnitude），即复数到原点的距
离。

3.std::arg函数：该函数用于计算复数的幅角（argument），即复数与实轴正
方向的夹角。

4.std::polar函数：该函数用于根据给定的模和幅角创建复数。

这些函数和操作使得在C++中处理复数变得更加方便。

需要注意的是，复数的运算与实数的运算有一些不同之处，例如幅角的处理，因此在使用这些函数时需要考虑到复数的特性。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

《数据结构》作业一
抽象数据类型一复数的定义、表示及其实现
1.抽象数据类型复数的定义:
ADT Comp lex{
数据对象：D={a,b|a,b R,R 为实数集}
数据关系：S={<a,b>|a 为复数实部，b 为复数虚部} 基本操你：
Comp lex( &z,a=0,b=0)
操作结果：
GetReal(x)
初始条件：操作结果：
Getlmag(x)
初始条件：操作结果：
Add(& z,x,y)
初始条件：操作结果： Sub( &z,x,y)
初始条件：操作结果： Mul( &z,x,y)
初始条件：操作结果： Div( &z,x,y)
初始条件：操作结果： Pow( &z,x ,n)
初始条件：操作结果：
Pow( &z,x,a)
初始条件：操作结果： Abs(x)
初始条件：操作结果： Comp lexA ng(x)
初始条件：操作结果：
Prin tImage(x) 初始条件：
操作结果：
ErrorExit(str)
构造复数 Z ,其实部和虚部分别为 a 和b ,不带参数时自动取 0。

返回返回
已存在; 的实部。

已存在;
的虚部。

复数x,y 已存在；将x 与y 的和存入
复数x,y 已存在；将x 与y 的差存入
复数x,y 已存在；将x
与y 的积存入
复数x,y 已存在；将x
与y 的商存入复数x 已存在；将x 的
n 次方存入
z。

z。

乙n 为非负整数。

复数x 已存在；
将x 的乘a 次幕存入z ，a 为实数。

复数x 已存在；返回复数 x 的模。

复数x 已存在；返回复数 x 的幅角。

复数x 已存在；以“ bi ”的形式显示复数 x 的虚部。

初始条件:
操作结果:
Prin t(x)
初始条件:
操作结果: }ADT Comp lex
str为字串常量；
遇到非法时(比如分母为0时)强形退出程序。

复数X已存在；
以“ a+bi ”的形式显示复数X。

2.抽象数据类型复数的表示与实现:
#in clude<c oni o.h> #in clude<iostream> //getch //cout
#in clude<cmath> using n ames pace std; //sqrt,pow
//std 命名空间
#defi ne eps 1.0e-10
#defi ne PI 3.1415926536 //
//
考虚计算精度
圆周率
class Comp
lex{ private:
double r,i; //
//
复数类的定义
私有变量：存取只能通过成员函数
public:
CompI ex(Co mp lex& z,double x=0,double y=0) {z.
r=x;z.i=y;}
double GetReal(Co mplex x){return x.r;}
double Getlmag(Co mp lex x){return x.i;} //
//
//
//
公有变量：可通过成员运算符存取构造函数：初始化
取实部
取虚部
void Add(Co mp lex &x,Co mp lex c1,Co mp lex c2) {
x.r=c1.r+c2.r;
x.i=c1.i+c2.i;
}
// 复数相加
void Sub(Co mplex &x,Co mp lex c1,Co mplex c2) {
x.r=c1.r-c2.r;
x.i=c1.i-c2.i;
}
// 复数相减
void Mul(Co mp lex &x,Com plex c1,Co mp lex c2) {
X.r=c1.r*c2.r-c1.i*c2.i;
X.i=c1.r*c2.i+c1.i*c2.r;
}
// 复数相乘double Abs(Co mplex x) // 复数求模
{
return sqrt(x.r*x.r+x.i*x.i);
}
void ErrorExit(char *s) { // 程序意外终止
cout<<s; getch(); exit(0); //
//
//
给出错误信息
等待按任意键
终止程序
void Div(Co mp lex &x,Com plex a,Com plex b) { double t;
if(Abs(b)<e ps)
ErrorExit("\nDivided by zero !");
t=b.r*b.r+b.i*b.i;
x.r=(a.r*b.r+a.i*b.i)/t; x.i=(a.i*b.r-
a.r*
b.i)/t;
} //
//
//
求数除法a/b
若分母为0
终止程序
double ComplexAn g(Co mplex x)
{
// 求复角
double r,a;
r=sqrt(x.r*x.r+x.i*x.i);
if(r<e ps)a=0;
else if(fabs(x.r)<e
ps){ if(x.i>0)a=(double)
PI/2; else a=-(double )P
1/2;
}
else{
a=ata n(x.i/x.r);
if(a>0&& x.r<0)a=Pl+a;
if(a<0&& x.r<0)a=Pl+a; }
return a; //
//
//
//
//
模与幅角
实-虚皆0
实部为0
同号：三象限
异号：二象限
void Pow(Co mp lex &x,Co mplex y,double n) {
double r,a;
if(n==0)x.i=0,x.r=1;
else{
if(Abs(y)<e ps)
if(* 0)ErrorExit(”\n
分母为
//
//
//
0!");//0
幕运算：实数幕
定义0的0次幕为1
模为0
负幕无意义
else x.r=0,x.i=0;
else{
110的正幕为0
a=Co mplexAn g(y); r=Abs(y); x.r =po w(r, n)*cos (n *a); x.i=po w(r, n)*sin(n *a);
r=Abs(x);
if(fabs(x.r/r)<e ps)x.r=0; if(fabs(x.i/r)<e ps)x.i=0; //
//
//
求辐角
求模
处理无穷小量
void Pow(Co mp lex &x,Co mplex a,un sig ned n) { x.r=1,x.i=0;
if(n==0)return;
for(i nt i=0;i< n; i++)Mul(x,x,a);
} // 重载Pow函数：乘方//0次幕为1
void Prin tlmag(Co mp lex x)
{
// 输出虚部if(x.i==1)cout<<"i"<<e ndl;
else if(x.i==-1)cout<<"-i"<<e ndl;
else cout<<x.i<<"i"<<e ndl;
void Prin t(Co mp lex x)
{
// 输出整个复数
} }; if(x.i&& x.r){
cout<<x.r;
if(x.i>=0)cout<<"+";
Prin tImag(x);
}
else if(x.i==0&& x.r==0)cout<<"0"<<e ndl; //
else if(x.i==0)cout<<x.r<<e ndl;
else Prin tImag(x);
//
//
//
//
实部虚部都不为0
实部虚部都为0
虚部为0
实部为0
类定义完毕
3.程序测试部分
void mai n()
{
Comp lex C,C1(1,1),C2(1,1); //C初始化（默认0,0）
C.Mul(C,C1,C2);
//
C.Prin t(C);
C.Div(C,C1,C2);
//
C.Prin t(C);
// 非负整数幕
C.Po w(C,C1,100u);
C.Prin t(C);
C.Po w(C,C1,100.0f);
// 实数幕
C.Prin t(C);
getch();
}。