轴队称变换----袁宝贞
用数学对称原理解决高考有关地球运动的问题

用数学对称原理解决地球运动的相关问题甘肃省兰州市外国语高级中学(730010) 鱼建英摘要:地球运动问题是高考中的重点、难点和高频考点,利用数学对称原理解决高考中有关地球运动的相关问题,是地理教学的偿试,是对传统教学方法的创新。
本文试图引导文科师生运用理科知识解决地理问题,培养文科学生的理科思维意识和能力。
关键词:对称原理;地球运动;地球运动的相关内容是高中地理教学的重点,也是难点,还是近年高考的高频考点,在全国卷和各地试卷中多有出现。
究其原因主要是地球运动能反映文科学生的理科素养,具有较强的区分度和选拔功能,符合高考选拔性的特点。
但是对学生而言,地球运动知识又是文科生的薄弱点、易错点和失分点。
教师针对文科生教学,更多采用一些机械的、生硬的传统教学方法,忽视了地球运动知识所蕴含的理科思维能力、运算能力和图形转换能力等,使学生没有掌握科学的方法,不能灵活应对高考,也不符合新一轮高考改革取消文理分科的大趋势。
因此,本人将可以运用数学对称原理解决的地球运动的典型问题归纳整理,与大家分享。
结论一:地球表面一点关于地心对称的另一点,与这个点的纬度数相同,南北纬度(半球)相反;经度数互补,东西经度相反。
例如:咸蛋超人在24ºS ,59ºW ,有一天他想要拜访住在地球另一端的面包超人,并决定(遁地)前去。
于是他从家中钻入地底,始终保持直线前进并穿越地心。
当他钻出地球另一端时,最可能看到图1所示的何种景观( )〖解析〗这是一道考查地球经纬网知识的试题。
学生是否对经纬网熟悉是判断这道题的前提和基础。
咸蛋超人位于24ºS ,59ºW ,利用结论一的对称原理可知:面包超人的纬度数是24º,南北半球相反即处于北半球;经度数与59º互补即为121º,东西经度相反即为东经度;则面包超人的地理坐标是24ºN ,121ºE 。
得出这个地理坐标,还要与四幅图片形成关联,即面包超人所在的位置是台湾岛,是亚热带季风气候,对图1 A C BD应的自然带是亚热带常绿阔叶林带。
4、3 坐标平面内的图形变换(1)

(-1.5,3) 点A2的坐标为____
y 4 (-a,b) 3 2 1 -4 -3 -2 -1 0 -1 -2 -3 -4
点(a,b)
(a,b)
1 2 3 4
x
关 于 x 轴 对 称
点(a,-b)
(a,-b)
点(-a,b)
关于y轴对称
点(a,b)
趁热打铁☞
A C
P126
在直角坐标系中,已知 点A(-1,2),B(1,- 3 ) C(0,1.5)
再做第二题
一个零件的横截面图
P127
单位:mm
100
150 400 100
500
1、按你自己所认为合适的比例,建立直角坐标系。
2、写出轮廓线各个转折点的坐标,在求这些点的坐标时,你运用了 怎样的坐标变化规律?
3.与你的同伴比较,你们写出的各转折点的坐标相同吗?为什么?
E' B' C'
D'
A(0,-2) O(0,0) B(3,2) C(2,2) D(2,3) E(1,3) F(0,5)
A'(0,-2) O'(0,0) B'(-3,2) C'(-2,2) D'(-2,3) E'(-1,3) F'(0,5)
O O' A A'
(2)利用坐标关系,求出它们关于y轴对称点的坐标。 (3)在同一坐标系中,描点A′,O′,B′,C′,D′,E′,F′,并用 线段依次将它们连接起来。
-------轴对称变换
龙港十四中 陈仁挺
y A2 4 3 2 1 -4 -3 -2 -1 0 -1 -2 -3 -4 A
作点A关于x轴、y轴 的对称点A1, A2
初中八年级数学教案- 轴对称与坐标变化-国赛一等奖
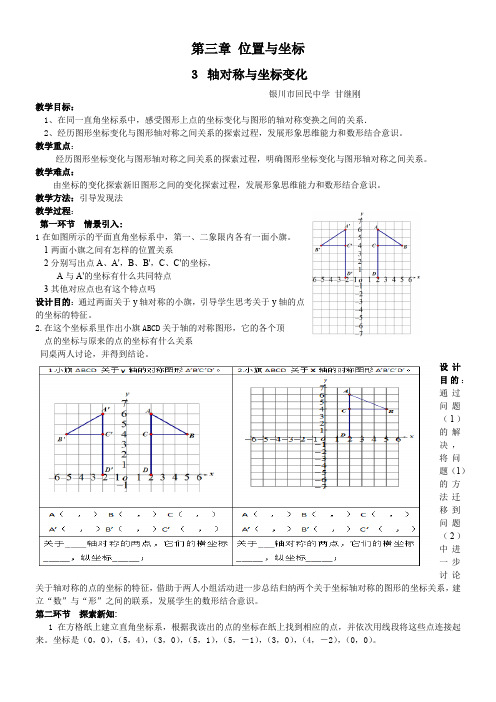
第三章位置与坐标3轴对称与坐标变化银川市回民中学甘继刚教学目标:1、在同一直角坐标系中,感受图形上点的坐标变化与图形的轴对称变换之间的关系.2、经历图形坐标变化与图形轴对称之间关系的探索过程,发展形象思维能力和数形结合意识。
教学重点:经历图形坐标变化与图形轴对称之间关系的探索过程,明确图形坐标变化与图形轴对称之间关系。
教学难点:由坐标的变化探索新旧图形之间的变化探索过程,发展形象思维能力和数形结合意识。
教学方法:引导发现法教学过程:第一环节情景引入:1在如图所示的平面直角坐标系中,第一、二象限内各有一面小旗。
1两面小旗之间有怎样的位置关系2分别写出点A、A',B、B',C、C'的坐标,A与A'的坐标有什么共同特点3其他对应点也有这个特点吗设计目的:通过两面关于y轴对称的小旗,引导学生思考关于y轴的点的坐标的特征。
2.在这个坐标系里作出小旗ABCD关于轴的对称图形,它的各个顶点的坐标与原来的点的坐标有什么关系同桌两人讨论,并得到结论。
设计目的:通过问题(1)的解决,将问题(1)的方法迁移到问题(2)中进一步讨论关于轴对称的点的坐标的特征,借助于两人小组活动进一步总结归纳两个关于坐标轴对称的图形的坐标关系,建立“数”与“形”之间的联系,发展学生的数形结合意识。
第二环节探索新知:1在方格纸上建立直角坐标系,根据我读出的点的坐标在纸上找到相应的点,并依次用线段将这些点连接起来。
坐标是(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)。
2将上图中的点(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)做以下变化:(1)纵坐标保持不变,横坐标分别乘以-1,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化(2)横坐标保持不变,纵坐标分别乘以-1,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化设计目的:通过四人小组的形式探索以上三种情况,培养学生合作学习的能力,在合作学习及小组分享的过程进一步感受轴对称与坐标变化之间的关系。
图形旋转——代玉臻

(△ABC) ,然后围绕旋转中心转动硬纸板,再 描出这个挖掉的三角形(△DEF) ,移开硬 纸板。 问题:请指出旋转中心和各对应点,哪一个角 是旋转角? B A
O ·
F
C
D E
1.从我们看到的旋转现象以及你所完成的实验中,你认为旋转主要因素是什么? 2.在图形的旋转过程中,哪些发生了改变?哪些没有发生改变? 图形的位置 图形的形状和大小
A
B
M
教师小结:帮助学生整理所学知识,引导学生进一步体会探究学习的过程和方法,领会数 学的思想。 【巩固练习】 1、下列现象中属于旋转的有( )个 ①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运 动;⑥荡秋千运动. A.2 B.3 C.4 D.5 2. 如图:P 是等边 ABC 内的一点,把 ABP 按不同的方向通过旋转得到 BQC 和 ACR, (1)指出旋转中心、旋转方向和旋转角度? (2) ACR 是否可以直接通过把 BQC 旋转得到?
A 抽象出线的旋转
F
B C (图 2) D E
图 1:在同一平面内,线段 AB 绕着定点 O 旋转某一角度得到线段 CD; 图 2:在同一平面内,三角形 ABC 绕着定点 O 旋转某一角度得到三角形 DEF。
观察了上面图形的运动后,引导学生进入本课第一个学习目标:图形旋转的概念: 把一个图形绕着某一点 O 转动一个角度的图形变换叫做旋转.点 O 叫做旋转中心, 转动的角 叫做旋转角。 重点突出旋转的三个要素:旋转中心、旋转方向和旋转角度。 【旋转应用】 (1) 如图,△ABO 绕点 O 旋转得到△CDO,则: 点B的对应点是点_____;线段OB的对应线段是线段______; 线段 AB 的对应线段是线段______;∠A 的对应角是______; ∠B 的对应角是______;旋转中心是点______; 旋转的角是 ______ 。 O D B C A
中考数学规律探索题分类评析__常平中学初中部周爱娇.doc

中考数学规律探索题分类评析广东东莞常平中学初中部周爱娇【摘要】:本文从分析近年中考数学题着手,通过题目给出的变化的数、式、图形等相关条件,了解其结构特点,通过比较、发现相互之间的内在联系,归纳出一為殳规律。
【关键词】:规律;新课标;中考;数学思想《新课程标准》指出:数学学习不仅包括数学的一些现成结果,还要包括这些结果的形成过程。
规律探索类题目,可以培养学生学会观察、比较、分析、猜想、类比、归纳等,发展学生直觉思维和合情推理能力。
如何发现规律,是解题的关键所在。
通过题目给出的变化的数、式、图形等相关条件,了解其结构特点,通过比较、发现相互之间的内在联系,归纳出一般规律。
这种由特殊到一般的思维方式,不仅是探索解决问题的重要思想方法,而且是数学创新的重要思想基础。
此外,规律探索类题还涵蕴了重要的数学思想如分类讨论思想、数形结合思想、方程思想等。
规律探索题是近年来广东中考的热点题目,它以“数字型”、“图形型”或“几何计算型” 为主,其解题方法主要是由特殊到一般,关注数据的变与不变,从而写出规律。
因此,在解题过程中,先要找(或计算)出特殊旳前二现:a},a2,a3;再由爭殊旳前二现:cz1,cz2,cz3的变与不变来发现规律,并用n的代数式表示通项a n o1数与式的规律探索通常根据给定一列数字、代数式、等式或者不等式,然后写出蕴含其中的一般规律,一般解法是根据数式的前三项,比较各式中相同的部分与不同的部分,找出共同的特征,改写成要求的规律的形式,并给了验证。
例1.1 观察下列等式:①、9 —1 = 2x4,② 25-1 = 4x6,③ 49-1 = 6x8, 按照这种规律写出第n个等式:分析经过观察发现式子的左边是奇数与1的平方差,等式的右边是两个连续偶数的积,因此,这组等式的一般规律是:(2/7+ 1)2 -1 = 277X(277 + 2)例1.2 (201K山州)我国古代数学的许多发现都曾位居世界前列,其屮“杨辉三角”就是一例。
2024届新高考一轮总复习人教版 第二章 第7节 函数的图象 课件(45张)

f(x)-k
f(x)-h
(2)伸缩变换 ①y=f(x)―a0―><1a―,<1―横,―坐横―标坐―缩标―短伸为―长原为―来原―的来―1a的―倍a1―,倍―纵,―坐纵―标坐不―标变不―变→ y=__f(_a_x_)__. ②y=f(x)―0―<a>a―<1,1―,纵―纵坐―坐标―标伸―缩长―短为为―原原―来来―的的―a倍a―倍,―,横―横坐―坐标―标不不―变变→ y=__a_f(_x_)__.
(2) (2022·全国乙卷)如图是下列四个函数中的某个函数在区间[-3,3]的大致图象, 则该函数是( )
x2-2x-1,x≥0, (3)y=x2+2x-1,x<0, 其图象如图③所示.
【思维升华】 作函数图象的两种常用方法 (1)直接法:当函数表达式(或变形后的表达式)是熟悉的基本初等函数时,就可根据 这些函数的特征直接作出; (2)图象变换法:若函数图象可由某个基本初等函数的图象经过平移、翻折、对称得 到,可利用图象变换作出,但要注意变换顺序.
(4)函数 y=f(x)与 y=2b-f(2a-x)的图象关于点(a,b)对称.
【小题热身】 1.思考辨析(在括号内打“√”或“×”) (1)函数 y=f(1-x)的图象可由 y=f(-x)的图象向左平移 1 个单位长度得到.( ) (2)当 x∈(0,+∞)时,函数 y=|f(x)|与 y=f(|x|)的图象相同.( ) (3)函数 y=f(x)与 y=-f(-x)的图象关于原点对称.( ) (4)若函数 y=f(x)满足 f(1+x)=f(1-x),则函数 f(x)的图象关于直线 x=1 对称.( ) 答案:(1)× (2)× (3)√ (4)√
2.将函数 y=log2(2x+2)的图象向下平移 1 个单位长度,再向右平移 1 个单位长度,
对称轴方程代换法

,
八1
3
= 一
元
“
目 习 ( 5k 5 +
一
4k
一
+
3k
。
3 +
k
5 6
n
`
+
(5
只)
I
, 十
(4
十
十
V
) 兽
U
十
(3
+
+
) 鲁
`
。
,
+
(:
一
粤)
U
, ,
十
(1
一
熹)
I
,
V
n`
+
n ,
+
n
`
n
, +
n ,
。
音
例 解
2
瓮
5。
譬
子
, ,
誓
,
品
, , ,
,
求习*
把例
1
中方程组 的常数 项
一
5 4 3 2 l O 换为 1 0 0 0 O 0
x 。,
0 ) 关 于 直线 y
(
,
,
y ;
)
由( 1 ) 得
,
,
}
l
`
`
’
一 `
一
“ , 刃不币蔺入
A
不
+
By
+
C
,
I V它 戈
-
=
V
一
以了 + 刀 , 月
十
`
C
一 乙力
一 一丁 ; 一一气二
A
初二数学函数图像对称变换分析

初二数学函数图像对称变换分析函数图像对称变换是数学中常见的基本概念,它能够帮助我们更好地理解函数的性质和变化。
在这篇文章中,我们将详细分析初二数学中函数图像的对称变换,包括关于x轴、y轴和原点的对称变换。
1. x轴对称变换当函数图像关于x轴对称时,我们可以观察到以下特点:首先,对于函数图像上任意一点P(x, y),其对称点P'关于x轴,其y坐标为-P的y坐标。
也就是说,如果点P的坐标为(x, y),则其对称点P'的坐标为(x, -y)。
其次,对于函数的方程,如果原方程为y=f(x),经过x轴对称变换后,新方程为y=-f(x)。
例如,如果原函数为y=x^2,经过x轴对称变换后新函数为y=-x^2。
2. y轴对称变换当函数图像关于y轴对称时,我们可以观察到以下特点:首先,对于函数图像上任意一点P(x, y),其对称点P'关于y轴,其x坐标为-P的x坐标。
也就是说,如果点P的坐标为(x, y),则其对称点P'的坐标为(-x, y)。
其次,对于函数的方程,如果原方程为y=f(x),经过y轴对称变换后,新方程为y=f(-x)。
例如,如果原函数为y=x^2,经过y轴对称变换后新函数还是y=x^2。
3. 原点对称变换当函数图像关于原点对称时,我们可以观察到以下特点:首先,对于函数图像上任意一点P(x, y),其对称点P'关于原点,其坐标为(-P的x坐标, -P的y坐标)。
也就是说,如果点P的坐标为(x, y),则其对称点P'的坐标为(-x, -y)。
其次,对于函数的方程,如果原方程为y=f(x),经过原点对称变换后,新方程为y=-f(-x)。
例如,如果原函数为y=x^2,经过原点对称变换后新函数为y=-x^2。
通过对函数图像的对称变换分析,我们可以更好地理解函数的性质和变化。
这种对称变换在数学和实际问题中都有广泛的应用。
例如,在几何中,我们可以利用对称变换来证明图形的性质;在物理中,对称变换可以帮助我们分析物体的运动轨迹。
信息技术课中学生创新精神和实践能力的培养

《轴对称变换》教案及教案说明-福建-福州一中-郭艺斌1

人教版数学八年级上册第十四章轴对称变换福建省福州第一中学数学教研组郭艺斌【一】教学目标1.知识目标:通过具体的实例认识轴对称变换,探索它的定义和基本性质。
能按要求作出简单平面图形经过一次或两次轴对称变换后的图形,能够利用轴对称变换进行简单的图案设计。
2.能力目标:用轴对称变换的方式去认识和构建几何图形,发展形象思维,并尝试用轴对称变换进行推理。
3.情感目标:结合教材内容,让学生体会数学来源于生活,数学美化生活,数学是我们生活中不可缺少的一部分,并培养学生空间想象能力,动手实践能力,以及善于合作、勇于创新的精神。
【二】教学重点、难点;教学重点:轴对称变换及轴对称作图;教学难点:利用轴对称变换认识和构建几何图形;突破重、难点的方法是设置问题,让学生观察思考、动手操作,合作探究,充分发挥他们的活力和创造力。
2、生活中人们办喜事时,都喜欢在门、窗上张贴大红的“囍”字,增添了很多喜庆的气氛。
让学生观察上面的“囍”字剪纸作品。
提问1:这些“囍”字有什么特点?一半图形,再展开就可以了。
【四】教案设计说明在初中的教学中,我崇尚并践行这样的教学理念:数学来源于现实,存在于现实,且应用于现实,数学教师的任务之一就是帮助学生构造数学现实,把现实“数学化”,积极引导学生通过探索、实践、思考,获得知识,形成技能,发展思维,学会学习。
这个理念来源于两个方面:一是世界著名数学家和数学教育家弗赖登塔尔在他的著作《作为教育任务的数学》中提到的:“数学来源于现实,存在于现实,且应用于现实,而且每个学生有各自不同的“数学现实”。
数学教师的任务是帮助学生构造数学现实,并在此基础上发展他们的数学现实;引导他们把现实“数学化”,最终实现数学的“再创造”。
另一个是在《数学课程标准》中提到“数学教学应从学生的实际出发,创设有助于学生自主学习的问题情境,引导学生通过实践、思考、探索、交流获得知识,形成技能,发展思维,学会学习。
在这个理念的指导下,我对这节课的教材进行了详细的分析。
巧用圆转化轴对称中的最值问题

巧用圆转化轴对称中的最值问题
苏国东
【期刊名称】《中学数学:初中版》
【年(卷),期】2022()5
【摘要】轴对称中的最值问题常出现在动态几何压轴题中,其中一类最值问题可通过构造辅助圆,转化为圆上一点到圆外一点或一直线的距离最值问题进行解决.【总页数】2页(P59-60)
【作者】苏国东
【作者单位】广州市真光中学
【正文语种】中文
【中图分类】G63
【相关文献】
1.巧用转化法解最值问题
2.另辟蹊径,圆中自有新天地r——巧用"隐圆"模型求解线段最值问题
3.巧用“隐圆”求一类几何最值问题
4.巧用隐形圆解决线段的最值问题
5.巧用微专题,提高复习效率--以“与圆有关的最值问题”为例
因版权原因,仅展示原文概要,查看原文内容请购买。
广义轴对称变换与三角形的不动点

广义轴对称变换与三角形的不动点
龚智发;文家金
【期刊名称】《湖南数学通讯》
【年(卷),期】1998(000)004
【总页数】3页(P14-16)
【作者】龚智发;文家金
【作者单位】四川安岳中学;安岳一中
【正文语种】中文
【中图分类】O181
【相关文献】
1.基于不动点法研究阶三角形电阻网络的等效电阻 [J], 嵇英华;胡菊菊;蔡十华
2.b-似度量空间中广义(ψ,Φ)-弱压缩映射的公共不动点 [J], 关洪岩;李健菊
3.广义渐近伪非扩张半群不动点Cesaro平均黏滞迭代逼近 [J], 张树义;张芯语
4.广义度量空间上(ψ,Ф,φ(φ^(*)))-弱收缩映射的重合点和公共不动点 [J], 朴勇杰
5.不完全偏好下非连续增算子的不动点与广义不动点定理 [J], 张金清
因版权原因,仅展示原文概要,查看原文内容请购买。
新人教版初中数学八年级数学上册第三单元《轴对称》检测题(答案解析)(3)

一、选择题1.如图,在边长为9的等边△ABC 中,CD ⊥AB 于点D ,点E 、F 分别是边AB 、AC 上的两个点,且AE=CF=4cm ,在CD 上有一动点P ,则PE +PF 的最小值是( )A .4B .4.5C .5D .82.以下尺规作图中,点D 为线段BC 边上一点,一定能得到线段AD BD =的是( ) A . B .C .D .3.如图,在ABC 中,6AB =,8AC =,10BC =,EF 是BC 的垂直平分线,P 是直线EF 上的一动点,则PA PB +的最小值是( ).A .6B .8C .10D .114.已知点A 是直线l 外的一个点,点B ,C ,D ,E 是直线l 上不重合的四个点,再添加①AB AC =;②AD AE =;③BD CE =中的两个作为题设,余下的一个作为结论组成一个命题,组成真命题的个数为( ).A .0B .1C .2D .3 5.已知123n A A A A 、、中,1A 与2A 关于x 轴对称,2A 与3A 关于y 轴对称,3A 与4A 关于x 轴对称,4A 与5A 关于y 轴对称……,如果1A 在第二象限,那么100A 在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限6.如图所示,已知ABC 和DCE 均是等边三角形,点B 、C 、E 在同一条直线上,连接AE 、BD 、FG ,AE 与BD 交于点O ,AE 与CD 交于点G ,AC 与BD 交于点F ,则下列结论中:①AE BD =; ②AG BF =; ③FG//BE ; ④CF CG =,以上结论正确的有( )A .1个B .2个C .3个D .4个7.如图,ABC ∆和CDE ∆都是等边三角形,且62EBD ∠=,则AEB ∠的度数是( )A .124B .122C .120D .1188.若a ,b 为等腰ABC 的两边,且满足350a b -+-=,则ABC 的周长为( )A .11B .13C .11或13D .9或15 9.如图,在ABC 中,AB AC =,108BAC ∠=︒,72ADB ∠=︒,DE 平分ADB ∠,图中等腰三角形的个数是( )A .3B .4C .5D .610.如图,已知AD 为ABC 的高线,AD BC =,以AB 为底边作等腰Rt ABE △,且点E 在ABC 内部,连接ED ,EC ,延长CE 交AD 于F 点,下列结论:①EBD DAE ∠=∠;②ADE BCE ≌△△;③BD AF =;④BDE ACE S S =△△,其中正确的结论有( )A .1个B .2个C .3个D .4个11.平面直角坐标系中,已知()1,1A ,()2,0B .若在x 轴上取点C ,使ABC 为等腰三角形,则满足条件的点C 的个数是( )A .2个B .3个C .4个D .5个12.如图,△ABC 中,∠ABC =45°,CD ⊥AB 于D ,BE 平分∠ABC ,且BE ⊥AC 于E ,与CD 相交于点F ,DH ⊥BC 于H ,交BE 于G ,下列结论:①BD =CD ;②AD +CF =BD ;③CE =12BF ;④AE =BG .其中正确的是( )A .①②B .①③C .①②③D .①②③④二、填空题13.平面直角坐标系xOy 中,先作出点P (2,3)-关于y 轴的对称点,再将该对称点先向下平移1个单位,再向左平移2个单位得到点P 1,称为完成一次图形变换,再将点P 1进行同样的图形变换得到点P 2,以此类推,则点P 2020的坐标为___________.14.如图,在ABC 中,90ACB ︒∠=,30B ,6AC =,P 为BC 边的垂直平分线DE 上一个动点,则ACP △周长的最小值为________.15.如图,点D 、E 是ABC 的边BC 上的点,且AED n ∠=︒,::1:3:2CAD DAE BAE ∠∠∠=,若点D 在边AC 的垂直平分线上,点E 在边AB 的垂直平分线上,则n =________.16.若等腰三角形的顶角为30°,腰长为10,则此等腰三角形的面积为_________. 17.如图,已知30MON ∠=︒,点1A ,2A ,3A ,…在射线ON 上,1B ,2B ,3B ,…在射线OM 上,112A B A △,223A B A △,334A B A △,…均为等边三角形;若48OA =,则1n n n A B A +△的边长为______.18.如图,30MON ∠=︒,点1234,,,A A A A ,…在射线ON 上,点123,,B B B ,…在射线OM 上,且112223334,,A B A A B A A B A △△△,…均为等边三角形,以此类推,若11OA =,则202120212022A B A △的边长为_______.19.给出如下三个图案,它们具有的公共特点是:________.(写出1个即可)20.如图,在正方形网格中,分别将①②③④四个网格涂上阴影,能与原阴影部分构成一个轴对称图形的有____________.(填网格序号)三、解答题21.小明遇到这样一个问题:如图①,在ABC 中,12AB =,8AC =,AD 是中线,求AD 的取值范围.她的做法是:过点B 作//BE AC 交AD 的延长线于点E ,证明BED CAD △≌△,经过推理和计算就可以使问题得到解决.按照上面的思路,请回答:(1)小红证明BED CAD △≌△的判定定理是:______;(2)AD 的取值范围是______;方法运用:(3)如图②,AD 是ABC 的中线,在AD 上取一点F ,连接BF 并延长交AC 于点E ,使AE EF =,求证:BF AC =.22.如图,在平面直角坐标系中,每个小方格的边长为1,ABC 的三个顶点分别为()()4,3,3,()3,1,1A B C -.请在坐标系中标出,,A B C 三点,画出ABC ∆,并画出ABC ∆关于y 轴对称的图形111A B C ∆,写出点111,,A B C 的坐标.23.如图:已知ABC 中AB AC =:(1)尺规作图:过A 点作//AE BC (不写作法,保留作图痕迹);(2)求证:AE 是ABC 的一个外角角平分线.24.在平面直角坐标系中,点(0,)A a ,点(,0)B b ,点(3,0)C -,且a 、b 满足269||0a a a b -++-=.(1)点A 坐标为______,点B 坐标为______,ABC 是______三角形.(2)如图,过点A 作射线l (射线l 与边BC 有交点),过点B 作BD l ⊥于点D ,过点C 作CE l ⊥于点E ,过点E 作EF DC ⊥于点F 交y 轴于点G .①求证:BD AE =;②求点G 的坐标.(3)如图,点P 是x 轴正半轴上一动点,APO ∠的角平分线交y 轴于点Q ,点M 为线段OP 上一点,过点M 作//MN PQ 交y 轴于点N ;若45AMN ∠=︒,请探究线段AP 、AN 、PM 三者之间的数量关系,并证明你的结论.25.如图,在ABC ∆中,,AB AC =过点A 作//AD BC 交ABC ∠的平分线BD 于点D ,求证:AC AD =.26.在平面直角坐标系中,△ABC 的位置如图所示,已知点A 、B 的坐标为(-4,3)(3,0).(1)点C关于x对称的点的坐标(,);(2)在图中作出△ABC关于y轴的对称图形△A′B′C′;(3)△ABC的面积为.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】作点E关于AD的对称点G,所以连接FG,与CD的交点即为P点.此时PF+PE=FG最小,通过计算证明△AFG是等边三角形,从而得出结果.【详解】作点E关于AD的对称点G,连接FG与CD的交点即为P点,如图:∴PG=PE,此时PF+PE=PF+ PG有最小值,最小值为FG,∵△ABC是边长为9等边三角形,且CD⊥AB,AE=CF=4,∴AD=BD=1AB=4.5,AF=AC-CF=9-4=5,∠A=60 ,2∴ED=GD= AD- AE =4.5-4=0.5,∴AG=AE+ED+GD=5= AF ,∴△AFG 是等边三角形,∴FG= AF=5,∴PF+PE 的最小值是5,故选:C .【点睛】本题主要考查了轴对称-最短路径问题,等边三角形的判定和性质,掌握轴对称-最短路径的确定方法是解题的关键.2.D解析:D【分析】点D 到点A 、点B 的距离相等可知点D 在线段AB 的垂直平分线上,据此可得答案.【详解】解:∵点D 到点A 、点B 的距离AD=BD ,∴点D 在线段AB 的垂直平分线上,故选择:D .【点睛】本题主要考查作图−复杂作图,解题的关键是掌握线段中垂线的性质与尺规作图. 3.B解析:B【分析】根据题意,设EF 与AC 的交点为点P ,连接BP ,由垂直平分线的性质,则BP=CP ,得到PA PB PA PC AC +=+=,即可得到PA PB +的最小值.【详解】解:根据题意,设EF 与AC 的交点为点P ,连接BP ,如图:∵EF 是BC 的垂直平分线,∴BP=CP ,∴8PA PB PA PC AC +=+==,∴PA PB +的最小值为8;故选:B .【点睛】本题考查了垂直平分线的性质,解题的关键是正确找出点P 的位置,使得PA PB +有最小值.4.D解析:D【分析】写出所组成的三个命题,然后根据等腰三角形的判断与性质对各命题进行判断.【详解】解:根据题意吧,如图:由等腰三角形的性质和全等三角形的判定定理,易证△ABD≌△ACE;命题1:若AB=AC,AD=AE,则BD=CE,此命题为真命题;命题2:若AB=AC,BD=CE,则AD=AE,此命题为真命题;命题3:若AD=AE,BD=CE,则AB=AC,此命题为真命题.故选:D.【点睛】本题考查了等腰三角形的性质,全等三角形的判定和性质,以及命题真假的判断,解题的关键是熟练掌握所学的知识,正确的判断命题的真假.5.A解析:A【分析】根据关于x轴对称的点,横坐标相同,纵坐标互为相反数;关于y轴对称的点,纵坐标相同,横坐标互为相反数;关于原点对称的点,横坐标与纵坐标都互为相反数,以及循环的规律就可以得到.【详解】解:A1与A2关于x轴对称,A2与A3关于y轴对称,A3与A4关于x轴对称,A4与A5关于y 轴对称,A1与A5是同一个点,四次一循环,100÷4=25,A100与A4重合,即第一象限,故选:A.【点睛】本题考查了关于x轴、y轴对称的点的坐标,关于x轴对称的点,横坐标相同,纵坐标互为相反数;关于y轴对称的点,纵坐标相同,横坐标互为相反数;关于原点对称的点,横坐标与纵坐标都互为相反数.6.D解析:D【分析】首先根据等边三角形性质得出BC=AC,CD=CE,∠ACB=∠ECD=60°,即可证明△BCD与△ACE全等、△BCF与△ACG全等以及△DFC与△EGC全等,最后利用全等三角形性质以及等边三角形性质证明即可.【详解】∵△ABC与△CDE为等边三角形,∴BC=AC,CD=CE,∠ACB=∠ECD=60°,∴∠ACB+∠ACD=∠ACD+∠ECD,∠ACD=60°,即:∠ACE=∠BCD,在△BCD与△ACE中,∵BC=AC,∠ACE=∠BCD,CD=CE,∴△BCD≌△ACE(SAS),∴AE=BD,即①正确;在△BCF与△ACG中,由①可知∠CBF=∠CAG,又∵AC=BC,∠BCF=∠ACG=60°,∴△BCF≌△ACG(ASA),∴AG=BF,即②正确;在△DFC与△EGC中,∵△BCF≌△ACG,∴CF=CG.即④正确;∵∠GCF =60°,∴△CFG为等边三角形,∴∠CFG=∠FCB=60°,∴FG∥BE,即③正确;综上,①②③④都正确.故选:D.【点睛】本题考查了等边三角形的性质,全等三角形的判定和性质以及平行线的判定,解题的关键是正确寻找全等三角形来解决问题,.7.B解析:B【分析】由等边三角形的性质,得到AC=BC ,CE=CD ,∠ACB=∠ECD=60°,然后证明△ACE ≌△BCD ,则∠CAE=∠CBD ,由角的关系,求出∠ABE+∠BAE=58°,即可得到答案.【详解】解:如图:∵ABC ∆和CDE ∆都是等边三角形,∴AC=BC ,CE=CD ,∠ACB=∠ECD=60°,∴∠ACE+∠BCE=∠BCD+∠BCE=60°,∴∠ACE=∠BCD ,∴△ACE ≌△BCD ,∴∠CAE=∠CBD ,即6062BAE EBC ︒-∠=︒-∠,∵60EBC ABE ∠=︒-∠,∴6062(60)BAE ABE ︒-∠=︒-︒-∠,∴58ABE BAE ∠+∠=︒,∴18058122AEB ∠=︒-︒=︒;故选:B .【点睛】本题考查了等边三角形的性质,全等三角形的判定和性质,三角形的内角和定理,以及角的和差关系,解题的关键是掌握所学的知识,正确求出58ABE BAE ∠+∠=︒. 8.C解析:C【分析】根据非负数的意义列出关于a 、b 的方程并求出a 、b 的值,再根据b 是腰长和底边长两种情况讨论求解.【详解】解:根据题意得a-3=0,b-5=0,解得a=3,b=5,(1)若3是腰长,则三角形的三边长为:3、3、5,能组成三角形,周长为:3+3+5=11;(2)若3是底边长,则三角形的三边长为:3、5、5,能组成三角形,周长为3+5+5=13.故选:C .【点睛】本题考查了等腰三角形的性质、非负数的性质及三角形三边关系;解题主要利用了非负数的性质,分情况讨论求解时要注意利用三角形的三边关系对三边能否组成三角形作出判断.9.C解析:C【分析】利用等腰三角形的性质“等边对等角”,求出角的度数,再根据“等角对等边”证明三角形是等腰三角形.【详解】解:∵AB AC =,∴ABC 是等腰三角形,∵108BAC ∠=︒, ∴180108362B C ︒-︒∠=∠==︒, ∵72ADB ∠=︒,∴18072BAD B ADB ∠=︒-∠-∠=︒,∴ADB BAD ∠=∠,∴AB BD =,∴ABD △是等腰三角形,∵1087236DAC BAC BAD ∠=∠-∠=︒-︒=︒,∴DAC C ∠=∠,∴AD CD =,∴ACD △是等腰三角形,∵DE 平分ADB ∠, ∴1362ADE BDE ADB ∠=∠=∠=︒, ∴18072AED ADE DAE ∠=︒-∠-∠=︒,∴AED DAE ∠=∠,∴DE DA =,∴ADE 是等腰三角形,∵BDE B ∠=∠, ∴BE DE =, ∴BED 是等腰三角形,一共有5个等腰三角形.故选:C .【点睛】本题考查等腰三角形的性质和判定,解题的关键是掌握等腰三角形的性质和判定. 10.D解析:D【分析】由AD 为△ABC 的高线,可得∠CBE+∠ABE+∠BAD=90°,Rt △ABE 是等腰直角三角形, 可得90ABE BAD DAE ∠+∠+∠=︒,从而可判断①;由等腰Rt ABE △可得AE BE =,结合AD BC =,∠DAE=∠CBE ,可判断②;由△ADE ≌△BCE ,可得,ADE BCE ∠=∠ 再证明∠BDE=∠AFE ,结合EBD DAE ∠=∠,AE BE =, 证明△AEF ≌△BED ,可判断③;由△ADE ≌△BCE ,可得,DE CE = 由△AEF ≌△BED ,,EF DE = 证明,EF CE =从而可判断④.【详解】解:∵AD 为△ABC 的高线,∴∠CBE+∠ABE+∠BAD=90°,∵Rt △ABE 是等腰直角三角形,∴90ABE BAD DAE ∠+∠+∠=︒,∴∠DAE=∠CBE ,即EBD DAE ∠=∠,故①正确;∵Rt △ABE 是以AB 为底等腰直角三角形,∴AE=BE ,在△ADE 和△BCE 中,AE BE DAE CBE AD BC =⎧⎪∠=∠⎨⎪=⎩,∴△ADE ≌△BCE (SAS ); 故②正确;△ADE ≌△BCE ,,ADE BCE ∴∠=∠∵∠BDE=∠ADB+∠ADE ,∠AFE=∠ADC+∠ECD ,90ADB ADC ∠=∠=︒,∴∠BDE=∠AFE ,在△AEF 和△BED 中,FAE DBE AFE BDE AE BE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AEF ≌△BED (AAS ),∴AF BD =; 故③正确;∵△ADE ≌△BCE ,∴,DE CE =△AEF ≌△BED ,,,AEF BED EF DE S S ∴==,EF CE ∴=∴,AEF ACE SS = ∴ ,BDE ACES S =故④正确; 综上:正确的有①②③④.故选:D .【点睛】本题考查的是三角形的内角和定理,三角形的中线与高的性质,三角形全等的判定与性质,等腰直角三角形的性质,掌握以上知识是解题的关键.11.C解析:C【分析】分三种情况:当AB=AC 时,当BA=BC 时,当AC=AB 时,根据等腰三角形两边相等的性质分别作图即可得解.【详解】当AB=AC 时,点C 与点O 重合;当BA=BC 时,以点B 为圆心,AB 长为半径画弧,与x 轴有两个交点;当AC=AB 时,作线段AB 的垂直平分线,与x 轴有一个交点,共有4个点C ,故选:C ..【点睛】此题考查等腰三角形的性质,直角坐标系中作等腰三角形的方法,熟记等腰三角形的性质并利用其作图是解题的关键.12.C解析:C【分析】根据∠ABC=45°,CD ⊥AB 可得出BD=CD ,利用ASA 判定Rt △DFB ≌Rt △DAC ,从而得出DF=AD ,BF=AC .则CD=CF+AD ,即AD+CF=BD ;再利用ASA 判定Rt △BEA ≌Rt △BEC ,得出CE=AE=12AC,又因为BF=AC所以CE=12AC=12BF,连接CG.因为△BCD是等腰直角三角形,即BD=CD.又因为DH⊥BC,那么DH垂直平分BC.即BG=CG.在Rt△CEG中,CG是斜边,CE是直角边,所以CE<CG.即AE<BG.【详解】解:∵CD⊥AB,∠ABC=45°,∴△BCD是等腰直角三角形.∴BD=CD.故①正确;在Rt△DFB和Rt△DAC中,∵∠DBF=90°﹣∠BFD,∠DCA=90°﹣∠EFC,且∠BFD=∠EFC,∴∠DBF=∠DCA.又∵∠BDF=∠CDA=90°,BD=CD,∴△DFB≌△DAC.∴BF=AC;DF=AD.∵CD=CF+DF,∴AD+CF=BD;故②正确;在Rt△BEA和Rt△BEC中∵BE平分∠ABC,∴∠ABE=∠CBE.又∵BE=BE,∠BEA=∠BEC=90°,∴Rt△BEA≌Rt△BEC.∴CE=AE=12AC.又由(2),知BF=AC,∴CE=12AC=12BF;故③正确;连接CG.∵△BCD是等腰直角三角形,∴BD=CD又DH⊥BC,∴DH垂直平分BC.∴BG=CG 在Rt△CEG中,∵CG是斜边,CE是直角边,∴CE<CG.∵CE=AE,∴AE<BG.故④错误.∴正确的选项有①②③;故选:C.【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、AAS、ASA、HL.在复杂的图形中有45°的角,有垂直,往往要用到等腰直角三角形,要注意掌握并应用此点.二、填空题13.【分析】按程序先作y轴对称求出点坐标横坐标-2纵坐标-1完成一次图形变换求出P变换后的坐标找出几次变换后规律奇次变换点的横坐标x=0偶次变换点的横坐标x=-2纵坐标变一次下移一个单位【详解】解:完成--解析:(2,2017)【分析】按程序先作y轴对称,求出点坐标,横坐标-2,纵坐标-1,完成一次图形变换求出P变换后的坐标,找出几次变换后规律奇次变换点的横坐标x=0,偶次变换点的横坐标x=-2,纵坐标变一次下移一个单位.【详解】-关于y轴的对称点(2,3),横坐标2-2=0,纵坐标3-解:完成1次图形变换,点P (2,3)1=2,P1(0,2),完成2次图形变换,点P1(0,2)关于y轴的对称点(0,2),横坐标0-2=-2,纵坐标2-1=1,P2(-2,1),完成3次图形变换,点P2(-2,1)关于y轴的对称点(2,1),横坐标3-3=0,纵坐标1-1=0,P3(0,0),完成4次图形变换,点P3(0,0)关于y轴的对称点(0,0),横坐标0-2=-2,纵坐标0-1=-1,P4(-2,-1),……,完成2020次图形变换,点P2019(0,3-2019)关于y轴的对称点(0,-2016),横坐标0-2=-2,纵坐标-2016-1=-2017,P2020(-2,-2017).故答案为:(-2,-2017).【点睛】本题考查图形规律探索问题,掌握图形程序变换的轴对称性质和平移特征,关键是找到变换规律奇次变换点的横坐标x=0,偶次变换点的横坐标x=-2,纵坐标变一次下移一个单位.14.18【分析】因为BC的垂直平分线为DE所以点C和点B关于直线DE对称所以当点动点P 和E 重合时则△ACP 的周长最小值再结合题目的已知条件求出AB 的长即可【详解】解:如图∵P 为BC 边的垂直平分线DE 上一解析:18【分析】因为BC 的垂直平分线为DE ,所以点C 和点B 关于直线DE 对称,所以当点动点P 和E 重合时则△ACP 的周长最小值,再结合题目的已知条件求出AB 的长即可.【详解】解:如图,∵P 为BC 边的垂直平分线DE 上一个动点,∴点C 和点B 关于直线DE 对称,∴当点动点P 和E 重合时则△ACP 的周长最小值,∵∠ACB=90°,∠B=30°,AC=6,∴AB=2AC=12,∵AP+CP=AP+BP=AB=12,∴△ACP 的周长最小值=AC+AB=18,故答案为:18.【点睛】本题考查了轴对称-最短路线的问题以及垂直平分线的性质,正确确定P 点的位置是解题的关键,确定点P 的位置这类题在课本中有原题,因此加强课本题目的训练至关重要. 15.80【分析】先根据垂直平分线的性质和等边对等角可得∠DAC=∠C ∠BEA=∠B 再根据比例关系设根据三角形内角和定理可求得x 再根据三角形外角的性质可得∠AED 【详解】解:∵点D 在边AC 的垂直平分线上点 解析:80【分析】先根据垂直平分线的性质和等边对等角可得∠DAC=∠C ,∠BEA=∠B ,再根据比例关系设,3,2CAD x DAE x BAE x ∠=∠=∠=,根据三角形内角和定理可求得x ,再根据三角形外角的性质可得∠AED .【详解】解:∵点D 在边AC 的垂直平分线上,点E 在边AB 的垂直平分线上,∴AD=CD ,AE=BE ,∴∠DAC=∠C ,∠BAE=∠B ,∵::1:3:2CAD DAE BAE ∠∠∠=,∴设,3,2CAD x DAE x BAE x ∠=∠=∠=,∴,2C x B x ∠=∠=,∵∠B+∠C+∠BAC=180°,∴322180x x x x x ++++=︒,解得20x =︒,∴22480AED BAE B x x x ∠=∠+∠=+==︒,即n=80,故答案为:80.【点睛】本题考查垂直平分线的性质,等边对等角,三角形内角和定理和三角形外角的性质.理解线段垂直平分线上的点到线段两端距离相等是解题关键.16.25【分析】依据含30°角的直角三角形的性质即可得到该等腰三角形腰上的高再根据三角形面积计算公式进行计算即可【详解】解:如图所示AB=AC=10∠A =30°过B 作BD ⊥AC 于D ∵∠A =30°AB =1解析:25【分析】依据含30°角的直角三角形的性质,即可得到该等腰三角形腰上的高,再根据三角形面积计算公式进行计算即可.【详解】解:如图所示,AB=AC=10,∠A =30°,过B 作BD ⊥AC 于D ,∵∠A =30°,AB =10,∴BD =12AB =5, ∴S △ABC =12AC ×BD =12×10×5=25, 故答案为:25.【点睛】本题主要考查了等腰三角形的性质以及含30°角的直角三角形的性质,作出腰上的高并根据30°角求出高是解题关键.17.【分析】根据等边三角形的性质以及含30度角的直角三角形得出OA2=A2B2=OA3OA3=A3B3=OA4…再将解得OA3==OA2==OA1=找到规律进而得出答案【详解】解:∵△A1B1A2是等边解析:12n -【分析】根据等边三角形的性质以及含30度角的直角三角形得出OA 2=A 2B 2=12OA 3,OA 3=A 3B 3=12OA 4…,再将48OA =解得OA 3=1842⨯==312-,OA 2=1422⨯==212-,OA 1=1112122-⨯==,找到规律,进而得出答案. 【详解】解:∵△A 1B 1A 2是等边三角形,∴A 1B 1=A 2B 1,∠B 1A 1A 2=∠A 1B 1A 2=60°∵∠MON=30°,∴∠OB 1A 1=30°,∠OB 1A 2=90°∴OA 1=A 1B 1=12OA 2, 同理可得OA 2=A 2B 2=12OA 3,OA 3=A 3B 3=12OA 4 ∵48OA =∴OA 3=1842⨯==312-,OA 2=1422⨯==212-,OA 1=1112122-⨯==, 以此类推△A n B n A n+1的边长为2n-1.故答案为2n-1.【点睛】本题考查了等边三角形的性质及含30°角的直角三角形的性质,根据得出的数值找到规律是解题的关键.18.【分析】根据是等边三角形得进而得可得以此类推即可求解【详解】解:∵是等边三角形∴∴∴∴同理:…均为等边三角形…则的边长为故答案是:【点睛】本题考查了规律型-图形的变化类解决本题的关键是观察图形的变化 解析:20202.【分析】根据30MON ∠=︒,11OA =,112A B A △是等边三角形,得11260∠=︒B A A ,进而得1130∠=︒OB A ,1111AO B A ,可得22OA =,以此类推即可求解.【详解】 解:∵30MON ∠=︒,11OA =,112A B A △是等边三角形,∴11260∠=︒B A A∴1130∠=︒OB A∴1111AO B A∴22OA =同理:223A B A △,334A B A △,…均为等边三角形,2222B A OA ==,233342B A OA…则202120212022A B A △的边长为20202.故答案是:20202.【点睛】本题考查了规律型-图形的变化类,解决本题的关键是观察图形的变化寻找规律. 19.都是轴对称图形【分析】利用已知图形的特征分别得出其公共特征【详解】解:答案不唯一例如:都是轴对称图形故答案为:都是轴对称图形【点睛】本题考查了轴对称图形解题的关键是正确把握轴对称图形的特征 解析:都是轴对称图形【分析】利用已知图形的特征分别得出其公共特征.【详解】解:答案不唯一,例如:都是轴对称图形,故答案为:都是轴对称图形.【点睛】本题考查了轴对称图形,解题的关键是正确把握轴对称图形的特征.20.②③【分析】根据轴对称图形的概念求解【详解】解:有2个使之成为轴对称图形分别为:②③故答案是:②③【点睛】此题主要考查了轴对称图形的概念正确把握轴对称图形的概念是解题关键解析:②③.【分析】根据轴对称图形的概念求解.【详解】解:有2个使之成为轴对称图形,分别为:②,③.故答案是:②③.【点睛】此题主要考查了轴对称图形的概念,正确把握轴对称图形的概念是解题关键.三、解答题21.(1)角角边或者角边角(AAS 或ASA );(2)210AD <<;(3)见解析【分析】(1)由“ASA”或“AAS”可证△BED ≌△CAD ;(2)由全等三角形的性质可得AC=BE=8,由三角形的三边关系可求解;(3)延长AD 至H ,使AD=DH ,连接BH ,由“SAS”可证△BHD ≌△CAD ,可得AC=BH ,∠CAD=∠H ,由等腰三角形的性质可得∠H=∠BFH ,可得BF=BH=AC ;【详解】解:(1)∵AD 是中线,∴BD=CD ,又∵∠ADC=∠BDE ,∵//BE AC ,∴EBD C ∠=∠,E CAD ∠=∠,∴△BED ≌△CAD (ASA ),或△BED ≌△CAD (AAS ),故答案为:SAS 或AAS ;(2)∵△BED ≌△CAD ,∴AC=BE=8,在△ABE 中,AB-BE <AE <AB+BE ,∴4<2AD <20,∴2<AD <10,故答案为:2<AD <10;(3)过点B 作//BG AC 交AD 的延长线于点G ,则CAD BGD ∠=∠∵AD 是中线,∴BD CD =在ADC 和GDB △中∵CAD BGD ∠=∠,ADC GDB ∠=∠,BD CD =,∴ADC GDB ≌△△∴BG CA =∵AE EF =∴EAF AFE ∠=∠又∵CAD BGD ∠=∠,AFE BFG ∠=∠∴BGD BFG ∠=∠∴BG BF =,又∵BG CA =,∴BF AC =;【点睛】本题考查了等腰三角形的性质,全等三角形的判定和性质,三角形的三边关系,添加恰当辅助线构造全等三角形是本题的关键.22.图见解析;点111,,A B C 的坐标分别为()()–4,3,3,3--,()1,1-【分析】先在平面直角坐标系中画出,,A B C 三点,顺次连接即可;再按照轴对称的性质,画出它们的对称点即可.【详解】解:如图所示,111,ABC A B C ∆∆,即为所求;点111,,A B C 的坐标分别为()()–4,3,3,3--,()1,1-【点睛】本题考查了在平面直角坐标系中描点和画轴对称图形,关于y 轴对称点的坐标变化规律,解题关键是正确描点和画对称点.23.(1)见解析;(2)见解析.【分析】(1)作∠CAE=∠C 即可;(2)延长BA ,根据两直线平行,同位角相等,有∠EAF=∠B ,由(1)可知∠CAE=∠C ,再根据AB=AC ,可得∠B=∠C ,等量替换之后即可得证.【详解】(1)射线AE 为所求;(2)证明:如图所示,延长BA ,∵//AE BC ,∴∠EAF=∠B ,∠CAE=∠C ,∵AB=AC ,∴∠B=∠C ,∴∠EAF=∠CAE ,∴AE 是ABC 的一个外角角平分线.【点睛】本题考查了平行线的性质和判定,等腰三角形的性质和角平分线的判定等知识,掌握相关知识是解题的关键.24.(1)(0,3)A ,(3,0)B ,等腰直角;(2)①见解析;②点 (0,3)G -;(3)AP AN PM =+,证明见解析.【分析】(1)根据偶次方与绝对值的非负性,解得a b 、的值,即可解得点A 、B 的坐标,继而根据等腰直角三角形的判定方法解题;(2)①由等角的余角相等,解得BAD ACE =∠∠,结合(1)中结论,进而证明AEC BDA ≌△△(AAS),即可解题;②由AEC BDA ≌△△可证CAE ABD ∠=∠,继而得到GAE CBD ∠=∠,设CF 交y 轴于点H ,根据等角的余角相等,得到HGE OCH ∠=∠,继而证明AGE BCD ≌△△(AAS)解得AG 、OG 的长即可解题;(3)在AP 上截取AH AN =,连接MH ,设NMO α∠=,分别解得45AMO α∠=︒+,=45NAM α∠︒-,由角平分线的性质解得2APO α∠=,45HAM α∠=︒-,进而得到NAM HAM ∠=∠,即可证明AMN AMH ≌(SAS),继而证明PMH PHM ∠=∠,PH PM =即可解题.【详解】(1)269||0a a a b -++-=2(3)||0a a b ∴-+-=3,3a b a ∴===(0,3)A ∴,(3,0)B ,(3,0)C -,AO OB CO AO ∴==90AOB AOC ∠=∠=︒45ACO ABO ∴∠=∠=︒90CAB ∴∠=︒()AOC AOB SAS ∴≅AC AB ∴=ABC ∴为等腰直角三角形,故答案为:(0,3)A ,(3,0)B ,等腰直角;(2)①BD l ⊥,CE l ⊥90BDA AEC ∴∠=∠=︒90,90BAD CAE CAE ACE ∠+∠=︒∠+∠=︒BAD ACE ∴∠=∠AC AB =AEC BDA ∴≌(AAS),∴BD AE =.②AEC BDA ≌ CAE ABD ∴∠=∠45CAO ABO ∠=∠=︒GAE CBD ∴∠=∠,设CF 交y 轴于点HEF DC ⊥90CFG ∴∠=︒90FGH FHG ∴∠+∠=︒90COH ∠=︒90OCH CHO ∴∠+∠=︒∴CHO FHG ∠=∠HGE OCH ∴∠=∠又∵AE BD =∴AGE BCD ≌△△(AAS)∴6AG BC ==又∵3AO =,∴3OG =∴点(0,3)G -.(3)AP AN PM =+.证明过程如下:在AP 上截取AH AN =,连接MH ,设NMO α∠=,45AMN ∠=︒45AMO α∴∠=︒+,∴()904545NAM αα∠=︒-︒+=︒-,又∵//MN PQ∴QPO NMO α∠=∠=,∵PQ 平分APO ∠∴2APO α∠=∴45245HAM ααα∠=︒+-=︒-∴NAM HAM ∠=∠又∵AN AH =,AM AM =∴AMN AMH ≌(SAS)∴45AMH AMN ∠=∠=︒∴90PMH α∠=︒-, 又∵()454590PHM αα∠=︒+︒-=︒-∴PMH PHM ∠=∠∴PH PM ==+=+.∴AP AH PH AN PM【点睛】本题考查全等三角形的判定与性质、等腰直角三角形、角平分线的性质、平行线的性质、绝对值的非负性、偶次方的非负性等知识,是重要考点,难度一般,掌握相关知识是解题关键.25.见解析【分析】由已知可得∠ABD=∠D,从而得到AB=AD,进而得到AC=AD.【详解】证明:∵BD是∠ABC 的平分线,∴∠ABD=∠CBD,又AD//BC,∴∠CBD=∠D,∴∠ABD=∠D,∴AB=AD,∵AB=AC,∴AC=AD.【点睛】本题考查等腰三角形的性质与判定,熟练掌握平行线的性质、角平分线的定义、等腰三角形的判定与性质是解题关键.26.(1)-2,-5;(2)见解析;(3)10【分析】(1)根据轴对称的性质解答;(2)根据轴对称的性质作图;(3)利用割补法求解.【详解】(1)根据坐标系知点C坐标为(-2,5),∴点C关于x对称的点的坐标(-2,-5),故答案为:-2,-5;(2)如图,△A′B′C′即为所求;(3)1117537225510222ABCS=⨯-⨯⨯-⨯⨯-⨯⨯=,故答案为:10.【点睛】此题考查关于坐标轴对称的性质:关于x轴对称的点的横坐标相等,纵坐标互为相反数;关于y轴对称的点的横坐标互为相反数,纵坐标相等.。
初中数学北师大版八年级上册3 轴对称与坐标变化

如右图所示的平面直角坐标系中, 第一、二象限内各有一面小旗。
( -2,6)
1、两面小旗之间有怎样的位置关系?
关于y轴对称
2、对应点A与A1的坐标有什么特点?
纵坐标相同,横坐标互为相反数
3、其它对应的点也有这个特点吗?
同样具有
( 2,6)
4、在这个坐标系里面画 出小旗ABCD关于x轴的对称 图形,它的各个“顶点” 的坐标与原来的点的坐标 有什么关系?
北师大版数学八年级(上) 第三章 位置与坐标
学校:黑山县第三初级中学 教师:史春辉
1、掌握在平面直角坐标系中,关于x 轴和y轴对称点的坐标特点,并能运用它解 决简单的问题。
2、能在平面直角坐标系中画出一些简 单的关于x轴和y轴的对称图形。
内容:课本68页“小旗”问题。
要求:1、独立思考完成课本问题(1)(2)。 2、思考:图形关于x轴对称时, 对应点的坐标有何特点? 关于y轴对称呢?
顶点坐标的变化:
(x,y–)4 (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x,-y–)5 (0,0) (5,-4) (3,0) (5,-1) (5, 1) (3,0) (4, 2) (0,0)
点的坐标变化
图形变化
横坐标不变,纵坐标乘以-1,即横同纵反时,
对应点的横坐标保持不变,纵坐标都乘以-1, 两图形位置关系如何? 对应点的纵坐标保持不变,横坐标都乘以-1, 两图形位置关系如何?
y
(1)在直角坐
5
标系中描出以下
4
各点:(0,0) (5,4)
(3,0) (5,1) (5,-1)
3
(3,0) (4,-2) (0,0)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教材:人民教育出版社《义务教育课程标准实验教材》八年级上册第14章
《轴对称变换(一)》教学设计
单位:广东省江门市恩平市年乐夫人学校设计者:袁宝贞
一、教学背景:
1、面向学生:中学学科:数学
2、课时:1课时
3、学生分析:
此阶段的学生已经熟知了轴对称图形以及轴对称的性质,并且会用垂直平分线的性质定理和判定定理证明,但学生平时画出来的轴对称图形仍然处于初级阶段还很不规范,这节课就是要教会学生画好轴对称图形,并会利用轴对称变换设计图案。
二,教材分析与学生分析:
(一)、内容:《轴对称变换》是新人教版八年级教材第14章
(二)、教材分析:《新课程标准》对本部分知识的要求是:了解轴对称变换并能用轴对称变换设计图案。
前一节学习的是轴对称图形、垂直平分线的性质定理和判定定理以及垂直平分线的画法。
为后面轴对称变换的学习提供了理论基础,也让学生更好地理解如何找出作轴对称变换图案的解题方法。
(三)、教学目标:(一)知识与技能
1.通过实际操作,了解什么叫轴对称变换。
2.能按要求作出简单平面图形经过一次或2次轴对称后的图形。
3.能利用轴对称变换进行图案设计。
(二)过程与方法
经历实际操作,认真体验的探究过程,发展学生的空间思维,并从实践中体会轴对称变换在实际生活中的应用。
(三)情感态度与价值观
1.鼓励学生积极参与数学活动,培养学生的数学兴趣。
2.初步认识数学和人类生活的密切联系,体验活动过程充满着探索与创造,从中感受数学的应用意识。
3.在数学活动中获得成功的体验,锻炼克服困难的意志,培养创新精神。
(四)、教学重点:
轴对称及轴对称变换作图,
(五)、教学难点:
1.作出简单图形关于直线对称的轴对称图形。
2.利用轴对称进行一些图案设计。
三、教法:
根据本节教材内容和编排特点,为了更有效地突出重点,突破难点,将现代信息技术与数学课程加以整合,构建了以学生为主体、教师为主导、学生自主探索为主线,以自我评价为主要评价方式的教学理念。
教学中,精心设计一些带有启发性和思考性的问题,创设问题情景,诱导学生思考、操作,教师适时地演示,并运用多媒体课件化静为动,激发学生探求知识的欲望,逐步推导归纳得出结论,使学生始终处于主动探索问题的积极状态,从而培养思维能力。
四、学法:
根据学法指导自主性和差异性原则,让学生在“观察----操作----概括----检验-----应用”的学习过程中,自主参与知识的发生、发展、形成的过程,使学生掌握知识。
五、教材处理:
本节课尽量创设与学生生活环境、知识背景相关的教学情境,以生动活泼的形式呈现有关内容。
重视动手操作,实践探究,但如果只有操作,而没有数学体验,数学课又很容易上成劳技课,所以,本节课的设计在重视活动的同时,又重视知识的获取,因为动手操作的目的本身就是在于更直观地发现新知识。
数学知识、数学方法要与实际生活密切联系,使学生体会数学在现实生活中的重要性,让学生能够从数学的角度考察和解决身边的事物现象,提高学生运用数学知识和方法解决问题的能力。
本节课的许多素材都来源于生活,使学生感受数学的现实性、趣味性,体验数学离不开生活,数学就在我们身边。
练习的设计具有一定的层次性,体现不同的学生在数学上得到的不同的发展。
六,教学方法:
实验、观察、归纳、讨论、练习等。
七,教具准备:
多媒体课件,视频, 纸板,剪刀。
八,教学过程:
(一)创设情境,引入新课:/showzipdown.php?id=69758
给出一些生活中的美丽的图片,让学生体会到轴对称图形的美。
并用几幅几何图形复习轴对称图形的相应知识,引入课题。
设计意图:欣赏图片,陶冶情操,引发兴趣,引入问题。
(二) 动手操作,感受变换:首先,动手操作画出左脚印和右脚印,初步感受轴对称变换。
其次,(视频展示)给出两组用轴对称变换设计出的美丽图案,归纳出它们的一些特征。
再次,在上面的基础上引导学生得出轴对称变换的概念。
最后,提出问题让学生思考:假如给出一个轴对称图形的一半,设疑让学生思考如何画出它的另一半。
设计意图:让学生动手、动脑经历实际操作,认真体验,猜想验证的过程,培养学生的动手能力,想象能力;发展空间思维。
并使学生和上节轴对称图形联系起来,形成知识,自然过渡,符合建构主义的从学生原有知识和经验出发,建构新知识的理论。
(三)研究图形,探究图形的轴对称变换的作法。
图形中的点A与点A`什么关系?若已知点A和对称轴l,你能作出点A的对称点A`吗?
作法:作A`A⊥l,并延长AH至A`,使AH=A`H,则点A`就是所求作的点。
如图中△ABC和折痕l,你能作出△ABC关于直线l的轴对称图形吗?
作法:①作点A关于直线l的对称点A`
②同理作点B、C关于直线l的对称点B`、C`
③连结A`B`、B`C`、C`A`,则△A`B`C`就是所求作的图形。
首先,让学生理解一个点关于某条直线轴对称之后的点怎么画。
其次,让学生理解一条直线关于某条直线轴对称之后的直线怎么画。
再次,让学生理解一个三角形关于某条直线轴对称之后的三角形怎么画。
最后,让学生理解一个复杂的平面几何图形关于某条直线轴对称之后的图形怎么画,并总结出轴对称变换的解题规律。
设计意图:由点扩大到面,进而启发诱导学生作出三角形关于直线的对称图形,进而可以用同样方法把整个图形的轴对称图形做出来,在此过程中,不仅培养了作图能力,也渗透了由特殊到一般的思想方法,总结出,要想作图形的轴对称图形,可以先确定关键点的对称点,再连结这些对称点,
(四)运用变换,设计图案:让学生有针对性地做一些轴对称变换的练习,再加上例题扩展,变式练习,让知识得到延伸,由简到繁,由易到难。
变式练习,熟悉新知。
已知△ABC 与直线l ,作出△ABC 关于直线l 轴对称的图形。
学生作图,教师通过演示当对称轴变化时,图形的位置、形状变化情况。
(多媒体课件)
多次轴对称变换后可得到连续的可用来装饰的图案,通过多媒体演示让学生体会轴对称变换在生活中的应用。
设计意图:通过作图,强化本节课重点,提高作图能力,加深对轴对称变换性质的理解,多次变换丰富了变换的内涵,让学生认识到数学在生活中广泛应用,这一系列设计能够强化重点,突破难点。
(五)归纳小结:
1、对本节课的重点内容进行小结。
布置适量的相应练习。
并借助多媒体欣赏一些精美图片,你能利用本节课知识设计一些生活中常见的图案吗?如花坛、板报、像框等,可以和平移结合起来,效果更好,同学之间交流成果,体验成功乐趣。
设计意图:充分调动课堂学习主动性,培养创新意识,加强数学和生活实际的联系
2、收获成果,巩固新知。
设计意图:活跃课堂气氛,提高学习效率,巩固新知,加深对轴对称变换的A B C l A B C l
理解。
3、学习小结,自主评价。
学生自主小结,交流在本课学习中的体会、收获,交流学习过程中体验与感受,以及可能存在的困惑,师生合作共同完成课堂小结。
设计意图:体现教学民主性,同时培养学生归纳,概括能力,有助于学生理清脉络,引导学生反思学习过程,帮助学生认清自我,增强信心,提高兴趣。
(六)布置作业
1.必做题P135-136 1、5
2.选做题P137 8、9
3,预习P131-134
设计意图:为了适应各层次学生需要,进行分层次作业,让学生带着问题走出课堂,从而把学生的思维引向一个更加广阔的空间。
八,教学反思:
本节课的知识比较简单,再加上有很多和实际生活相关的图案,学生对这部分知识的理解比较容易。
而且可以用本节知识设计出很多美丽的图案,易于提高学生的学习兴趣和学习热情。
板书设计:
§14.2.1.1 轴对称变换(一)
一轴对称变换
由一个平面图形得到它的轴对称图形叫做轴对称变换
二利用轴对称变换设计图案
三随堂练习。
