3画出轴对称图形的对称轴
《轴对称图形》教案

《轴对称图形》教案《轴对称图形》教案(通用6篇)作为一名优秀的教育工作者,常常要根据教学需要编写教案,教案是备课向课堂教学转化的关节点。
那么大家知道正规的教案是怎么写的吗?以下是店铺整理的《轴对称图形》教案,仅供参考,大家一起来看看吧。
《轴对称图形》教案篇1教材简析:《轴对称图形》是六年《数学》中继“认识圆的特征”,“计算圆的周长和面积”之后的一个学习内容。
在本章教材的编排顺序中起着承上启下的作用。
把它放在圆的后面,一方面可以更好地说明轴对称图形的特点,另一方面可以对所学的各种平面图形中轴对称的情况作全面的了解。
从而更好地发展学生的空间观念。
教学重点:掌握轴对称图形的概念。
教学难点:能找出轴对称图形的对称轴。
学生分析:学生已学过简单平面图形,对平面图形已有一定的认识,且初步了解研究平面图形的方式方法。
高年级的学生具有好胜,好强的特点,班级中已初步形成合作交流,敢于探索与实践的良好学风,学生间相互讨论的气氛较浓。
设计理念:根据基础教育课程改革的具体目标以及鼓励学生在具体、直观操作中发现知识是《数学课程标准》的一个特点。
改变课程过于注重知识传授的倾向,强调形成积极主动的学习态度,关注学生的学习兴趣和经验,实施开放式教学,让学生主动参与学习活动,并引导学生在课堂活动中感悟知识的生成、发展与变化。
教学目标:1、通过教学向学生渗透事物的特殊性存在于普遍性之中,体会对称美。
2、通过操作活动培养学生观察能力,概括能力。
3、使学生直观的认识轴对称图形,在操作中理解掌握轴对称的概念,并能找出轴对称图形的对称轴。
教学流程:一、创设问题情境,导入课题。
1、(屏幕出示相关图片)观察下面的图形,(折一折,看一看)这些图形有什么特点?2、指出:像前三个这样的图形,我们把它叫轴对称图形。
3、引入课题:轴对称图形二、学生通过直观感知,操作确认等实践活动,加强对图形的认知和感受。
【实施动手操作,合作交流方式教学,让学生主动参与学习活动,经历和体验检验轴对称图形的方法。
人教版初二上册第2课时画对称轴教案

人教版初二上册第2课时画对称轴教案体会活动一:概念构成二、探求新知【活动1】效果:我们曾经学过,假设两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线,所以我们只需找到两个图形的一对对应点,然后画出以对应点为端点的线段的垂直平分线即可,如何作线段的垂直平分线呢?效果1如图(1),点A和点B关于某条直线成轴对称,你能作出这条直线吗?剖析:我们只需衔接点A和点B,作出线段AB的垂直平分线,就可以失掉点A和点B的对称轴,为此作出到点A,B距离相等的两点,即线段AB的垂直平分线上的两点,从而作出线段AB的垂直平分线.教员详细剖析画法、写出画法,依据画法作出图形.先生模拟教员的画法,边写画法,边引出新课。
———————教员解说对称轴的作法.先生回忆轴对称的性质:对称轴是任何一对对应点所连线段的垂直平分线。
思索所作直线与A,B两点的关系:是线段AB的垂直平分线。
教员给出结论:作线段AB的垂直平分线即可.————————先生自学教材第63页线段的垂直平分线的画法,并在练习本上自己画线段AB的垂直平分线.图进一步稳固轴对称的性质,同时展现出轴对称的性质对作图题的作用.—————充沛调动先生学习的积极性,把先生能自己完成的事交给先生.新旧知识及时融合构成体系.增强线段的垂直平分线的画法的练习.活动二:实际探求交流新知画图.作法:如图(2).(1)区分以点A,B为圆心,以大于12AB的长为半径作弧(想一想,为什么),两弧相交于C,D两点;(2)作直线CD.CD就是所求作的直线.这个作法实践上就是线段的垂直平分线的尺规作图.教员引导先生思索:(1)在作法中为什么有CA=CB,DA=DB?(2)可以用这种方法找线段的中点吗?四等分点呢?2.你能作出∠AOB的对称轴吗?【活动2】效果1.图(1)是一个五角星,你能画出它的对称轴吗?有几条?教学方法:引导先生思索五角星有几条对称轴,点A可以和哪些点成对应点?最后化归到例2,由先生自己完成.2.你能画出以下图形的对称轴吗?(1)正方形;(2)圆;(3)长方形;(4)等边三教员依据先生画的状况准确板书线段的垂直平分线的画法.让先生练习线段的画法,教员引导启示,先生自己完成。
画轴对称图形

E C F
相等。 ③连接BE,CF与MN的位置关 系是 垂直 。
N
四、课堂练习(P90的习题)
1. 在图中分别画出点A关于两条直线的对称点A′和 点A″。
2. 画出所示图形关于直线的对称图形.
A
五、课堂小结:
1.如何画轴对称图形? ①画已知图中各点关于直线l的对称点, ②将对称点连结得到对称线段, ③对称线段组成的图形就是对称图形.
B A
C P M
b
D
如图,O是∠APB内的一点,点M,N分别是点O关 于PA,PB的对称点,MN与PA,PB的交点分别是E, F,若MN=18cm,则△OEF的周长是多少?
解:∵点M,O关于直线PA的对称点
M
E O
∴ 直线PA垂直平分线段MO
(对称点的连线被对称轴垂直平分) 即 直线PA是线段MO的垂直平分线 ∴ EM=EO(垂直平分线上的点
2.因为整个图形是轴对称图形,所以要作的那 一半与已知图形是成轴对称的.
课外 作业
P109--110 习题10.1
例2 把下列各图形补成以直线m为对称轴的轴 对称图形。
对称轴上的 点的对称点 A 就是它本身
C′ B B′ m m D C B′
A′
E
例3. 如下图,草原上两个居民点A、B在河流的同旁. 一汽车从点A出发到B,途中需要到河边加水.汽车在 哪一点加水,可使行驶的路程最短?在图上画出这点 并说明理由。 解: 画法:
书上P105的图形
(2)
二、交流合作,探索新知
l
1.如图,已知点A和直线l ,试画出
画法:Biblioteka 点A关于直线的对称点A′。 1)从点A出发画直线l的垂线,垂 足为点O; A O A′
初中数学轴对称图形知识点加习题总结

知识点1 轴对称图形如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;这时,我们也说这个图形关于这条直线的轴对称。
知识点2 对称轴的性质1.对称轴是一条直线。
2.在轴对称图形中,对称轴两侧的对应点到对称轴两侧的距离相等。
3.在轴对称图形中,沿对称轴将它对折,左右两边完全重合。
4.图形对称例1下面哪些图形是轴对称图形?画出轴对称图形的对称轴。
例2.推理游戏:下面应该是什么图形?知识点3线段垂直平分线定义及其性质定义:经过某一条线段的中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线。
性质1.垂直平分线垂直且平分其所在线段。
2.垂直平分线上任意一点,到线段两端点的距离相等。
逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
3.如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线。
例3.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=6,则线段PB的长度为〔〕A.3 B.5 C.6 D.8解析:∵直线CD是线段AB的垂直平分线,∴PB=PA,∵PA=6,∴PB=6.答案C.例4如以下图,DE是线段AB的垂直平分线,以下结论一定成立的是〔〕A.ED=CDB.∠DAC=∠BC.∠C>2∠BD.∠B+∠ADE=90°分析:∵DE是线段AB的垂直平分线,∴AD=BD.∴∠B=∠BAD,∠ADE=∠BDE.∴∠B+∠ADE=90°答案D课堂练习11.点A,B关于直线a对称,P是直线a上的任意一点,以下说法不正确的选项是〔〕A.直线AB与直线a垂直B.直线a是点A和点B的对称轴C.线段PA与线段PB相等D.假设PA=PB,则点P是线段AB的中点2.三角形中到三边的距离相等的点是〔〕A.三条边的垂直平分线的交点B.三条高的交点C.三条中线的交点D.三条角平分线的交点3.已知A和B两点在线段EF的中垂线上,且∠EAF=100°,∠EBF=70°,则∠AEB等于( )A、95°B、15°C、95°或15°D、170°或30°4.已知:如图,线段AB垂直平分线段CD则AC=。
《图形的对称》教案8篇

《图形的对称》教案优秀8篇作为一名老师,往往需要进行教案编写工作,教案是备课向课堂教学转化的关节点。
那么应当如何写教案呢?本文范文为朋友们整理了8篇《《图形的对称》教案》,希望能够对困扰您的问题有一定的启迪作用。
对称图形篇一轴对称图形教学目标1.通过观察和操作认识轴对称图形和轴对称的含义。
2.会画出轴对称图形的对称轴。
3.使学生在操作中加深对图形的认识,建立空间观念。
教学重点认识轴对称图形,并能正确画对称图。
教学难点认识图形,建立空间观念。
教学过程一、复习准备口算二、新授教学(一)出示图片:树叶、蜻蜓、天平(二)分组讨论1.这些图形有什么特点?2.找出一些生活中实例图形。
(三)学生汇报图形左右部分一样(四)出示图片:实验先把一张纸对折,在折好的一侧画出图形,剪下来,再把纸打开,看一看能得到一个什么样的图形?(五)小结:这个图形就是轴对称图形,折痕所在的这条直线叫做对称轴。
(六)练习1.下面哪些图形是轴对称图形?找出它们的对称轴。
(出示图片:练习一)2.画出下面图形的对称轴。
(出示图片:练习二)3.下面的图形,哪些是轴对称图形?(出示图片:练习三)(七)分组实验。
1.出示图片:几何图形2.哪些图形是轴对称图形?画出它们的对称轴。
3.小结:正方形、长方形、等腰三角形、等腰梯形、圆,都是轴对称图形。
有的轴对称图形有不止一条对称轴。
三、课堂练习1.下面的数字,哪些是轴对称图形?它们各有几条对称轴?(出示图片:练习五)2.画出下面每组图形的对称轴。
各能画几条?(出示图片:练习六)3.把一张纸对折后,剪下一个图形,把剪下的图形展开,所得的图形是不是轴对称图形?(出示图片:练习四)四、课后作业运用学过的知识,用纸剪去一个对称图形,可以怎样剪?五、板书设计轴对称图形轴对称图形:如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形是轴对称图形。
对称轴:折痕所在的这条直线叫做对称轴。
教案点评:该教学设计体现了以学生为主体,通过让学生动手画、折、剪、量、比等方法,引导学生主动探索,启发调动了学生全部心理活动的积极性,使情感、意志、兴趣、注意、动机都趋于积极化,使学习知识和提高能力同步得到发展。
冀教版数学三年级上册《第三课时 轴对称》教案

第三课时轴对称教学内容:冀教版小学数学三年级上册第40、41页轴对称。
教学提示:在自然界和日常生活中具有轴对称性质的图形很多。
学生已认识了一些基本图形特征。
学生学习这些知识,一方面可以加深对一些已学过的图形特征的认识,另一方面,可以认识自然界和日常生活具有轴对称性质的一些事物,并为以后进一步学习数学研究一些问题的基本性质打下基础。
教学目标:1、知识与技能:初步认识轴对称图形,理解轴对称图形的含义,能找出对称图形的对称轴,并能用自己的方法创造出轴对称图形。
2、过程与方法:通过观察、思考和动手操作,培养学生探索与实践能力,发展学生的空间观念。
3、情感态度与价值观:引导学生领略自然世界的美妙与对称世界的神奇,激发学生的数学审美情趣。
重点、难点教学重点:(1)认识轴对称图形的特点,建立轴对称图形的概念;(2)准确判断生活中哪些物体是轴对称图形。
教学难点:找轴对称图形的对称轴。
教具准备:多媒体教学课件等。
学具准备:白纸、彩纸、剪刀等学习材料一份。
教学过程一、创设情境,导入新课。
拿出一张彩纸,对折后描出“爱心”图的一半。
谈话:老师把这张彩纸对折一下,沿着这条边剪一个图形,你能猜出老师剪的是什么图形吗?(演示:剪出图形并展开),原来是一个“爱心”图。
我希望同学们每人都有一颗爱心。
(把“爱心”图贴在黑板上)请你们仔细观察一下,这个图形的左右两边是怎样的?生:(1)左右两边是一样的;(2)左右两边是对称的……小结:像这样的图形,两边是对称的。
有趣吗?今天我们就来学习像这样的图形。
(板书:轴对称图形)【设计意图:同学在日常的学习生活中已经接触到一些对称的物体,对对称现象有了一定的感性认识。
在课的开头,用剪纸的形式导入,容易吸引同学的注意,营造愉悦的课堂氛围,为认识轴对称图形的教学作好铺垫。
】二师生互动、探究新知。
1、教学轴对称图形。
师:现在请同学们认真观察这些图形,看看有什么发现?(出示教材第40页的图片课件)生:我发现蝴蝶的左右两边是一样的。
几何画板怎么画轴对称图形

几何画板怎么画轴对称图形
反射是指将选中的对象按标记的镜面(即对称轴,可以是直线、射线或线段)构造轴对称关系。
以下教程通过举例讲解如何使用几何画板反射命令作轴对称图形。
注意:并不是所有的对象都可以反射,如构造出来的轨迹和函数图像都不能反射。
反射命令不会弹出对话框,反射前必须标记镜面,否则系统会随机标记一个线段、射线或直线作为标记镜面。
举例:构造△ABC关于一条直线的轴对称图形
构造△ABC关于一条直线的轴对称图形示例
具体的操作步骤如下:
1.单击多边形工具,在画板的适当位置绘制一个△ABC。
2.单击直线工具,在画板的适当位置绘制一条直线DE。
3.选中直线DE,执行“变换”菜单下的“标记镜面”命令,标记直线DE为一个镜面,此时直线DE会有一个短暂的闪动,说明标记成功。
4.选中△ABC,执行“变换”菜单下的“反射”命令,得到与△ABC轴对称的新△A’B’C’。
5.执行“文件”—“保存”命令,并以“构造△ABC关于一条直线的轴对称图形”为文件名保存。
提示:轴对称图形从左到右演示了拖动三角形顶点改变其位置和形状,可以观察到动态保持的对称关系和相关性质。
学习了以上教程,相信大家都对使用几何画板反射命令作轴对称变换有了更深的了解,从而学会构造轴对称图形。
轴对称图形新课标版(【最新版推荐下载】

1.初步认识轴对称图形,知道轴对称图形的含义, 能判断一个图形是不是轴对称图形;
2.能够找出轴对称图形的对称轴,并画出对称轴; 3.培养同学们观察、操作实践和抽象、概括的能 力。
观察下面的图形,这些图形有什么特点?
这些图形左右都是对称的
我们再来看一看其它的对称图Fra bibliotek。先把一张纸对折,在折好的一侧画出图形, 用剪刀剪下来,再把纸打开,看一 看能得到一个什么样的图形?
功地把自己推销给别人之前,你必须百分之百的把自己推销给自己。即使爬到最高的山上,一次也只能脚踏实地地迈一步。
用微笑告诉别人,今天的我,比昨天更强。瀑布跨过险峻陡壁时,才显得格外雄伟壮观。勤奋可以弥补聪明的不足,但聪明无法弥补懒惰的缺陷。孤独是 每个强者必须经历的坎。有时候,坚持了你最不想干的事情之后,会得到你最想要的东西。生命太过短暂,今天放弃了明天不一定能得到。只有经历人生 的种种磨难,才能悟出人生的价值。没有比人更高的山,没有比脚更长的路学会坚强,做一只沙漠中永不哭泣的骆驼!一个人没有钱并不一定就穷,但没 有梦想那就穷定了。困难像弹簧,你强它就弱,你弱它就强。炫丽的彩虹,永远都在雨过天晴后。没有人能令你失望,除了你自己人生舞台的大幕随时都 可能拉开,关键是你愿意表演,还是选择躲避。能把在面前行走的机会抓住的人,十有八九都会成功。再长的路,一步步也能走完,再短的路,不迈开双 脚也无法到达。有志者自有千计万计,无志者只感千难万难。我成功因为我志在成功!再冷的石头,坐上三年也会暖。平凡的脚步也可以走完伟大的行程。 有福之人是那些抱有美好的企盼从而灵魂得到真正满足的人。如果我们都去做自己能力做得到的事,我们真会叫自己大吃一惊。只有不断找寻机会的人才 会及时把握机会。人之所以平凡,在于无法超越自己。无论才能知识多么卓著,如果缺乏热情,则无异纸上画饼充饥,无补于事。你可以选择这样的“三 心二意”:信心恒心决心;创意乐意。驾驭命运的舵是奋斗。不抱有一丝幻想,不放弃一点机会,不停止一日努力。如果一个人不知道他要驶向哪个码头, 那么任何风都不会是顺风。行动是理想最高贵的表达。你既然认准一条道路,何必去打听要走多久。勇气是控制恐惧心理,而不是心里毫无恐惧。不举步, 越不过栅栏;不迈腿,登不上高山。不知道明天干什么的人是不幸的!智者的梦再美,也不如愚人实干的脚印不要让安逸盗取我们的生命力。别人只能给 你指路,而不能帮你走路,自己的人生路,还需要自己走。勤奋可以弥补聪明的不足,但聪明无法弥补懒惰的缺陷。后悔是一种耗费精神的情绪,后悔是 比损失更大的损失,比错误更大的错误,所以,不要后悔!复杂的事情要简单做,简单的事情要认真做,认真的事情要重复做,重复的事情要创造性地做。 只有那些能耐心把简单事做得完美的人,才能获得做好困难事的本领。生活就像在飙车,越快越刺激,相反,越慢越枯燥无味。人生的含义是什么,是奋 斗。奋斗的动力是什么,是成功。决不能放弃,世界上没有失败,只有放弃。未跌过未识做人,不会哭未算幸运。人生就像赛跑,不在乎你是否第一个到 达终点,而在乎你有没有跑完全程。累了,就要休息,休息好了之后,把所的都忘掉,重新开始!人生苦短,行走在人生路上,总会有许多得失和起落。 人生离不开选择,少不了抉择,但选是累人的,择是费人的。坦然接受生活给你的馈赠吧,不管是好的还是坏的。现在很痛苦,等过阵子回头看看,会发 现其实那都不算事。要先把手放开,才抓得住精彩旳未来。可以爱,可以恨,不可以漫不经心。我比别人知道得多,不过是我知道自己的无知。你若不想 做,会找一个或无数个借口;你若想做,会想一个或无数个办法。见时间的离开,我在某年某月醒过来,飞过一片时间海,我们也常在爱情里受伤害。1、 只有在开水里,茶叶才能展开生命浓郁的香气。人生就像奔腾的江水,没有岛屿与暗礁,就难以激起美丽的浪花。别人能做到的事,我一定也能做到。不 要浪费你的生命,在你一定会后悔的地方上。逆境中,力挽狂澜使强者更强,随波逐流使弱者更弱。凉风把枫叶吹红,冷言让强者成熟。努力不不一定成 功,不努力一定不成功。永远不抱怨,一切靠自己。人生最大的改变就是去做自己害怕的事情。每一个成功者都有一个开始。勇于开始,才能找到成功的 路。社会上要想分出层次,只有一个办法,那就是竞争,你必须努力,否则结局就是被压在社会的底层。后悔是一种耗费精神的情绪后悔是比损失更大的 损失,比错误更大的错误所以不要后悔。每个人都有潜在的能量,只是很容易:被习惯所掩盖,被时间所迷离,被惰性所消磨。与其临渊羡鱼,不如退而结网。 生命之灯因热情而点燃,生命之舟因拼搏而前行。世界会向那些有目标和远见的人让路。不积跬步,无以至千里;不积小流,无以成江海。骐骥一跃,不 能十步;驽马十驾,功在不舍。锲而舍之,朽木不折;锲而不舍,金石可镂。若不给自己设限,则人生中就没有限制你发挥的藩篱。赚钱之道很多,但是 找不到赚钱的种子,便成不了事业家。最有效的资本是我们的信誉,它小时不停为我们工作。销售世界上第一号的产品——不是汽车,而是自己。在你成
画对称轴的三种方法

画对称轴的三种方法对称轴是图形学中重要的概念之一,它指的是平面上一条直线,将图形沿着这条直线进行翻转后,两边的图形完全一样。
在绘画、制图、设计等领域,对称轴的运用十分广泛,因此学会如何准确地画出对称轴是非常必要的。
本文将介绍三种画对称轴的方法,希望能为读者提供帮助。
一、用工具画对称轴第一种方法是使用直尺和铅笔来画对称轴。
具体步骤如下:1.用直尺在图形中心位置画一条直线,这条直线必须经过图形的中心点。
2.用铅笔将这条直线延长,直到它超出图形的边缘。
3.将图形沿着这条直线进行翻转,如果两边的图形重合,则说明这条直线是对称轴。
4.用橡皮擦去多余的线条,保留对称轴即可。
这种方法简单易行,适合于对称轴较简单的图形。
二、用纸板画对称轴第二种方法是使用纸板来画对称轴。
具体步骤如下:1.将纸板对折,使两边完全重合。
2.将需要画对称轴的图形放在纸板的一侧,使它与纸板的折痕对齐。
3.用铅笔沿着图形的边缘,在纸板上画出图形的轮廓。
4.将纸板展开,将图形沿着纸板的折痕进行翻转,如果两边的图形重合,则说明这条折痕是对称轴。
5.用剪刀将纸板沿着对称轴剪开,保留对称轴即可。
这种方法适用于对称轴较复杂的图形,可以通过对纸板的折叠来快速确定对称轴的位置。
三、用数学方法画对称轴第三种方法是使用数学方法来画对称轴。
具体步骤如下:1.找到图形的中心点,可以通过计算或者直观感觉来确定。
2.找到图形上每一个点和中心点之间的连线。
3.将每一个点和中心点之间的连线进行翻转,得到一条新的线段。
4.将所有新的线段连接起来,得到一条直线,这条直线就是对称轴。
这种方法需要一定的数学基础,但是可以准确地画出对称轴,适用于对称轴的位置比较重要的情况。
总结以上是三种画对称轴的方法,它们分别是用工具画对称轴、用纸板画对称轴和用数学方法画对称轴。
不同的方法适用于不同的情况,读者可以根据自己的需要选择合适的方法。
在实际应用中,画出准确的对称轴可以帮助我们更好地完成绘画、制图、设计等任务,因此掌握这些方法是非常有用的。
盐津县六月上旬七年级数学下册第10章轴对称平移与旋转10.1轴对称3画轴对称图形教案新版华东师大版3

10.1.3 画轴对称图形1.使学生能够按要求作出简单平面图形经过一次对称后的图形.2.通过画轴对称图形,增强学生学习几何的趣味感,培养审美情操.重点让学生识别轴对称图形与画轴对称图形的对称轴.难点画轴对称图形.一、创设情境,问题引入1.如图,作出它们的对称轴.2.如图,给出一个图形和一条直线,那么如何画出这个图形关于这条直线的对称图形呢?二、探索问题,引入新知如图,实线所构成的图形为已知图形,虚线为对称轴,请画出已知图形的轴对称图形.思考下面两个问题:(1)你可以通过什么方法来验证你画的是否正确.(2)和其他同学比较一下,你的方法是最简单吗?在格点图中,很容易画出已知图形的轴对称图形,如果没有格点图,我们还能比较准确地画出已知图形的轴对称图形吗?你能画出点A关于直线L的对称点吗?画法:(1)过点A向直线L画垂线段AO,垂足点O;(2)延长AO至OA1,使OA1=OA.则点A1就是点A关于直线L的对称点.做一做:你能画出线段AB关于直线L的对称线段吗?画法:(1)画点A,点B关于直线L的对称点A1,B1;(2)连结A1,B1.则线段A1 B1就是线段AB关于直线L的对称线段.做一做:你能画出三角形ABC关于直线L的对称图形吗?画法:(1)画出点A,点B和点C关于直线L的对称点A1,B1和C1;(2)连结A1 B1,B1 C1,A1 C1,则△A1 B1 C1就是△ABC关于直线L的对称三角形.从上面的例子可以知道,如果图形是由直线、线段或射线组成时,那么只要画出图形中的特殊点的对称点,然后连结对称点,就可以画出关于这条直线的对称图形.结论:先画点的对称点,再画线段的对称图形,最后画三角形的对称图形.由易到难,这样学生就很容易的知道了知识的形成过程.【例1】如图,方格图中每个小正方形的边长为1,点A,B,C都是格点.画出△ABC 关于直线BM对称的△A1B1C1.分析:画出图形中的特殊点的对称点,然后连结对称点,就可以画出关于这条直线的对称图形.解:如图所示,△A1B1C1即为所求【例2】如图,请把△ABC和△A′B′C′图形补充完整,使得它们关于直线l对称.(保留作图痕迹)分析:过点C,点B′作关于直线l的对称点,连结AB,BC,B′C及A′C′即可.解:如图所示:三、巩固练习1.下面是四位同学作△ABC关于直线MN的轴对称图形,其中正确的是( )2.下列各图都是一个汉字的一半,你能想像出它的另一半并能确定它是什么字吗?(有几个字的笔划在对称轴上).3.如图,先画△ABC关于直线l1的对称△A1B1C1,(直线l1过点C),再画出△A1B1C1,关于直线l2的对称△A2B2C2.4.如图,在网格中有两个大小、形状一样的图形(阴影部分),用这两个图形拼成轴对称图形,试分别在图中画出两种不同的拼法.四、小结与作业小结先小组内交流收获和感想,然后以小组为单位派代表进行总结.教师加以补充.作业1.教材第110页“习题10.1”中第6 题.2.完成练习册中本课时练习.学生是学习的主体,要让学生成为真正的主人,就必须在数学活动中学习数学,也就是在创造中学习数学.本课从最基本的图形中,让学生自己动手画,体验探索成功的快乐;通过动手操作,小组讨论来解决自己提出的问题;通过有层次的练习,提高学生解决问题的能力,巩固所学知识.巧用幂的乘方分解因式幂的乘方公式:m n n m a a )()(==nm a , 它的逆向公式是:nm a =mn n m a a )()(=。
轴对称知识点总结

轴对称知识点总结一、轴对称1.轴对称图形的定义:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.这时,我们也说这个图形关于这条直线(成轴)对称.2.判断一个图形是不是轴对称图形,可利用轴对称图形的定义,将图形对折,看是否能够完全重合,若能够完全重合,则这个图形是轴对称图形,否则这个图形不是轴对称图形.注意:(1)对称轴是一条直线,而不是射线或线段.(2)一个轴对称图形的对称轴可以有1条,也可以有多条,还可以有无数条.(3)轴对称图形是对于一个图形而言的,它表示具有一定特性(轴对称性)的某一类图形.3.把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.4.轴对称和轴对称图形的区别与联系5.轴对称的性质:(1)两个图形成轴对称的性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.(2)轴对称图形的性质:轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线.(3)轴对称图形(或关于某条直线对称的两个图形)的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等.(4)成轴对称的两个图形全等;轴对称图形被对称轴分成的两部分也全等,但全等的两个图形不一定是轴对称图形.二、线段垂直平分线的性质和判定1.线段垂直平分线的定义:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也叫线段的中垂线.2.线段垂直平分线的性质:线段垂直平分线上的点与这条线段两个端点的距离相等.如下图所示,点P在线段AB 的垂直平分线上,则P A=PB.3.线段垂直平分线的判定:与线段两个端点距离相等的点在这条线段的垂直平分线上.如上图所示,若P A=PB,则点P在线段AB的垂直平分线上三、尺规作图(线段的垂直平分线)1.作图步骤:(1)以A为圆心,以大于线段AB一半的长度画弧(2)再以B为圆心,以相同长度为半径画弧,交前弧于C、D两点(3)连接CD,直线CD即为线段AB的垂直平分线四、尺规作图(轴对称)1.轴对称图形或成轴对称的两个图形的对称轴的画法,步骤如下:(1)找出轴对称图形或成轴对称的两个图形的任意一对对应点;(2)连接这对对应点;(3)画出对应点所连线段的垂直平分线.这条垂直平分线就是该轴对称图形或成轴对称的两个图形的对称轴.注意:对于轴对称图形或两个图形成轴对称,它们的对应点有一个共同的特征——对应点所连的线段被对称轴垂直平分,这是我们画图形的对称轴的依据.2.在坐标系中画轴对称图形的方法:(1)计算——计算对称点的坐标;(2)描点——根据对称点的坐标描点;(3)连接——依次连接所描各点得到成轴对称的图形五、关于坐标轴对称的点的坐标1.关于坐标轴对称的点的坐标特点:(1)点(x,y)关于x轴对称的点的坐标为(x,-y);(2)点(x,y)关于y轴对称的点的坐标为(-x,y).2.已知两个点的坐标分别为P1(x1,y1),P2(x2,y2),若x1=x2,y1+y2=0,则点P1,P2关于x轴对称;若x1+x2=0,y1=y2,则点P1,P2关于y轴对称.反之也成立。
画轴对称图形教案

画轴对称图形教案认识对称现象,初步理解对称轴和轴对称图形的含义,掌握判断一个图形是否是轴对称图形的方法。
经历观察、操作、想象、交流等活动,感知现实世界中普遍存在的对称现象,发展空间观念。
一起看看画轴对称图形教案!欢迎查阅! 画轴对称图形教案1教学目标:1、认识对称现象,初步理解对称轴和轴对称图形的含义,掌握判断一个图形是否是轴对称图形的方法。
2、经历观察、操作、想象、交流等活动,感知现实世界中普遍存在的对称现象,发展空间观念。
3、体验到生活中处处有数学,获得成功的喜悦,培养学生的探究精神和美感。
教学重点:认识对称现象和轴对称图形的特点。
教学难点:掌握识别轴对称图形的方法。
教具准备:多媒体课件、实物图片等。
教学过程:一、谈话引入,激发兴趣1、说说在游乐场喜欢玩的项目,出示主题图,引导学生观察。
2、从蝴蝶形状的风筝引出“对称”二、合作探究,学习新知(一)观察图形,认识对称1、观察几幅对称图形,引导学生感悟对称。
2、说一说生活中的对称现象(二)动手操作,认识轴对称图形1、猜一猜:出示几幅轴对称图形,猜一猜它们是怎么来的。
2、动手操作,剪出轴对称图形(1)师示范剪一件上衣的过程:折一折、画一画、剪一剪。
(2)生动手剪出自己喜欢的轴对称图形。
(3)交流展示学生的作品3、认识对称轴(1)看一看,摸一摸,说一说(2)画一画:师示范画出对称轴,然后学生自己画,再交流。
4、初步理解轴对称图形(1)说一说轴对称图形的特点,初步理解轴对称图形。
(2)议一议:讨论判断轴对称图形的方法(对折后完全重合才是轴对称图形)。
(3)举一举身边的轴对称图形的例子。
三、巩固练习,拓展延伸1、判一判:哪些是轴对称图形。
2、猜一猜:出示轴对称图形的一半,猜出它是什么图形。
3、折一折、画一画、数一数:长方形、正方形、圆形各有几条对称轴。
四、课堂总结通过这节课的学习,你有什么收获五、欣赏轴对称图形的美丽画轴对称图形教案2教学目标:1、知识与技能:通过观察和操作活动,初步认识轴对称图形。
四年级下册数学课件第1单元3 轴对称图形及其对称轴苏教版

如下图,想要由图形A 得到图形B,不可以单独进行( )。
A.旋转 (1)下面图形不是轴对称图形的是( )。
三条边长度相等的三角形 画出下面每个图形的另一半,使它们成B.平移 用两个完全相同的等边三角形摆成有一条对称轴的图形,怎样摆?如果摆成有两条对称轴的图形呢?画出简单的示意图。
折一折,画一画略。它有4条对称轴。
知识点2:画出轴对称图形的所有对称轴 2.画出下面轴对称图形的所有对称轴。
知识点3:在方格纸上补全一个简单的轴对称图形 3.画出下面图形的另一半,使它成为轴对称图形。
4.下面的图形中,哪些是轴对称图形?在括号里画 “√”,并画出它们所有的对称轴。
√
√
√
5.填一填。 (1)在口,日,民,晶这几个汉字中,不是轴对称图形 的有( 民 )。 (2)有两条边长度相等的三角形有( 1 )条对称轴, 长方形有( 2 )条对称轴。
有一条对称轴的摆法如图(1)(2)所示。
三条边长度相等的三角形
对折4次后有15条折痕。
画出下面轴对称图形的所有对称轴。
(1)下面图形不是轴对称图形的是( )。
350-(24+76)×2=
(230-215÷5)×6=
知识点1:认识轴对称图形及其对称轴 1.拿出一张正方形纸,折一折,画一画,它有几条对称轴?
江苏版-四年级-下
第1单元
3 轴对称图形及其对称轴
有两条对称轴的摆法如图(3)所示。
350-(24+76)×2=
(230-215÷5)×6=
三条边长度相等的三角形
三条边长度相等的三角形
350-(24+76)×2= 150 在方格纸上设计一个轴对称图形,并画出它的对称轴。
画出下面轴对称图形的所有对称轴。
轴对称图形 基础知识复习讲义

【知识点 11】 实数概念: 】 实数概念:
有理数
正有理数
实数的分类: 实数的分类:
实数 正无理数 负无理数
〖基础回顾〗 基础回顾〗 1.与数轴上的点一一对应的数是 . 。 的点到原点的距离是_________ _________。 2. 数轴上表示 − 6 的点到原点的距离是_________。 点M在数轴上与原点相距 5 个单位,则点 表示的实数为 在数轴上与原点相距 个单位,则点M表示的实数为 3. −7.2 5
·北师大版
4、在△ABC中, AB=15,AD=12,BD=9,AC=13,求 、 中 , , 求 的周长和面积。 △ABC的周长和面积。 的周长和面积
·北师大版
【知识点 4】 勾股定理与方程的综合运用 】 〖基础回顾〗 基础回顾〗 1.AC=6cm,BC=8cm,现将直角边AC沿直线 折叠,使它落 , ,现将直角边 沿直线AD折叠, 沿直线 折叠 在斜边AB上 且与AE重合 你能求出CD的长吗 重合, 的长吗? 在斜边 上,且与 重合,你能求出 的长吗?
. M N
【知识点 7】等腰三角性是
等腰三角形的性质: 等腰三角形的性质 等腰三角形的判定: 等腰三角形的判定
图形,它的对称轴是 图形 它的对称轴是
〖基础回顾〗 基础回顾〗
1.等腰三角形ABC中,AB=AC,AD是角平分线,则“①AD⊥BC,②BD=DC, .等腰三角形 是角平分线, 中 , 是角平分线 ⊥ , , ③∠B=∠C,④∠BAD=∠CAD”中,结论正确的个数是( ) ∠ , ∠ 中 结论正确的个数是( A、4 B、3 C、2 D、1 、 、 、 、 2.如果等腰三角形的一个底角为 °,那么其余两个角为 .如果等腰三角形的一个底角为50° 那么其余两个角为______和___ __ 和 如果等腰三角形的一个角为80° 那么它的一个底角为__________ 如果等腰三角形的一个角为 °,那么它的一个底角为 已知等腰三角形的一个角是110° 已知等腰三角形的一个角是 °,则其余两角为 3.一个等腰三角形的两边分别为8cm和6cm,则它的周长为 .一个等腰三角形的两边分别为8 4.已知:如图1.5-20,点D、E在△ABC的边 上,AD=AE,BD=EC. 1.5的边BC上 .已知:如图1.5 20, 、 在 的边 = = 求证: = 求证:AB=AC
三年级下册数学轴对称复习

三年级下册数学轴对称复习小学数学三年级下册《轴对称》整理复习一、知识要点1、定义:把一个图形沿着某一条直线对折,如果直线两边的图形能完全重合,那么这个图形就叫轴对称图形。
这条直线叫对称轴。
特征:对折后左右两边完全重合的图形是轴对称图形。
注意:物体的对称性与轴对称图形这两个概念是不同的。
“对称性”是某些物体的特征,“轴对称”是部分平面图形的特征。
2、轴对称图形概念的几种表述:(1)如果一个图形沿着一条直线对折,折痕两侧的图形能够完全重合,这个图形就是轴对称图形。
(2)一个图形可以用一条直线平分成两半,并且这两半完全相同,这个图形就是轴对称图形。
(3)对折后能完全重合的图形就是轴对称图形。
以上三种概念表述说明:轴对称图形是一个两部分能完全重合的图形。
3、类型:左右对称或上下对称的图形,都是轴对称图形。
常见的轴对称图形有:长方形、正方形、圆形、等边三角形。
字母是轴对称图形的有:A、B、C、D、E、H、I、 K、M、O、T、V、U、W、X、Y。
4、画图:根据轴对称图形的一半,画出它的另一半。
A.画对称轴的方法:左右对称的图形,在它左右两边的最上端找到一组相对称的点,并量出这两个点的中点。
然后在最下端量出一组对称点的中点。
最后经过这两个中点划出一条虚线。
(上下对称的图形画法相似)B.根据对称轴画出轴对称图形的另一半的方法:先将已知图形的每个角的顶点,在对称轴的另一端,以对称轴为中点量出与它们的相对称的点。
最后将这些点用已知图形的连接方法一一连接起来。
(记住:找对称点时,必须以对称轴为中心。
)二、自主练习单元测试(一)题号一二三四五卷面总分得分温馨提示:1、请你注意卷面的干净!!2、聪明的你认真思考、仔细读题,你一定会成功!!一、填空我最棒。
1、一个正方形有()条对称轴。
2、李阳左手拿本,右手拿笔站在镜子前,镜子中的李阳()手拿本,()手拿笔。
3、风扇叶片转动属于()现象。
4、物体在做平移和旋转运动时,它的()、()不变。
第3课时画图形的对称轴

第3课时画图形的对称轴
教学目的
使学生掌握用“连结对称点的线段被对称轴垂直平分”验证一个图形是不是轴对称图形,并请熟练画出轴对称图形的对称轴。
重点、难点
重点:画轴对称图形的对称轴。
难点:归纳总结画轴对称图形对称轴的方法。
教学过程
一、复习
1.轴对称图形以及它的对称点是怎么定义的?
2.看以下两个图形是否是轴对称图形?你能否画出它的对称轴?
二、新课
1.试着画出下边两个图形的对称轴。
用折叠的方法检验所画的对称轴是否准确,如果准确的话,请你总结方法,并说出如何判断对称轴的位置。
2.对称轴的画法
首先找出轴对称图形的任意一组对称点,连结对称点,其次画对称点所连线段的垂直平分线,就得到该图形的对称轴。
3.画轴对称图形的对称轴举例
例1:画出以下图形的对称轴
例2:下面的虚线,哪些是图形的对称轴,哪些不是?
4.如果图形关于某一条直线对称,那么连结对称点的线段被对称轴垂直平分。
三、课堂练习
课本P88练习第1、2题。
四、课堂小结
要能熟练地画出轴对称图形的对称轴,知道如果图形关于某条直线对称,那么连结对称点的线段被对称轴垂直平分。
五、作业
课本P93习题10.2第1题。
小学数学三年级下册《轴对称图形》知识要点
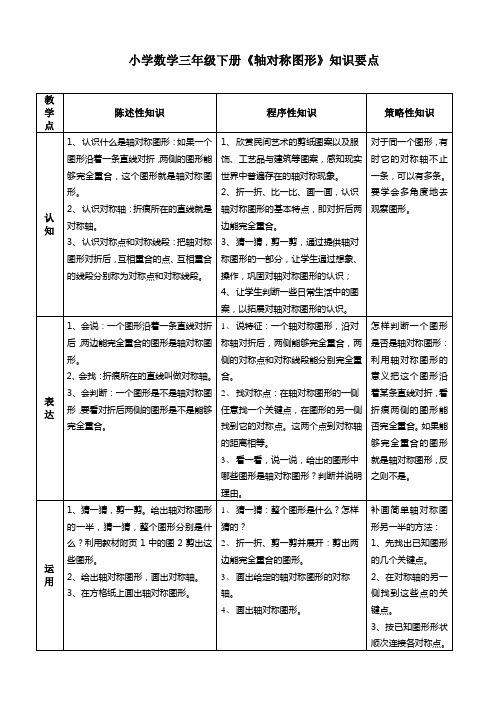
表达
1、会说:一个图形沿着一条直线对折后,两边能完全重合的图形是轴对称图形。
2、会找:折痕所在的直线叫做对称轴。
3、会判断:一个图形是不是轴对称图形,要看对折后两侧的图形是不是能够完全重合。
1、说特征:一个轴对称图形,沿对
称轴对折后,两侧能够完全重合,两侧的对称点和对称线段能分别完全重合。
2、找对称点:在轴对称图形的一侧
任意找一个关键点,在图形的另一侧找到它的对称点。这两个点到对称轴的距离相等。
3、看一看,说一说,给出的图形中
哪些图形是轴对称图形?判断并说明理由。
怎样判断一个图形是否是轴对称图形:利用轴对称图形的意义把这个图形沿着某条直线对折,看折痕两侧的图形能否完全重合。如果能够完全重合的图形就是轴对称图形,反之则不是。
渗透化繁为简的数学思想。
补画简单轴对称图形另一半的方法:
1、先找出已知图形的几个关键点。
2、在对称轴的另一侧找到这些点的关键点。源自3、按已知图形形状顺次连接各对称点。
创新
1、感受生活中轴对称图形的美,愿意主动去寻找生活中哪些是轴对称图形,并运用它去美化生活。
1、一组图形是怎样通过对称得到
的?
2、找出其中最基本的图形。
3、用对称的方法创作自己喜欢的图形。
运用
1、猜一猜,剪一剪。给出轴对称图形的一半,猜一猜,整个图形分别是什么?利用教材附页1中的图2剪出这些图形。
2、给出轴对称图形,画出对称轴。
3、在方格纸上画出轴对称图形。
1、猜一猜:整个图形是什么?怎样
猜的?
2、折一折、剪一剪并展开:剪出两
边能完全重合的图形。
3、画出给定的轴对称图形的对称
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五年级上册数学导学案(三)
课题:画出轴对称图形的对称轴课型:新授课
主备人: 牛玉美班级: 姓名:
学习目标:1.体会轴对称图形的基本特征。
2.掌握在方格纸上画轴对称图形的对称轴的方法,能在方格纸上画出轴对称图形的对称轴。
一、自学指导
自学课本34页例2的内容,回答以下问题:
1、判断一个图形是不是轴对称图形的方法有哪些?
2、观察例2找出轴对称图形,并画出对称轴,你能总结画对称轴的方法吗?
二、尝试练习
1、先判断下面是不是轴对称图形,如果是的,请画出对称轴。
2、下面各图形是轴对称图形吗?如果是,共有几条对称轴,请画出来。
三、精讲点拨
轴对称图形的对称轴的画法:
(1)找出轴对称图形的一组(或多组)对应点。
(2)找出对应点所在线段的中点,过中点做垂直于这条线段的垂线就是轴对
称图形的对称轴。
提醒:有的轴对称图形的对称轴不止一条,对称轴要画成虚线。
因为对称轴是一条直线,所以两端都要超出原图形。
四、自我检测
一、填空。
1.如果一个图形沿着一条()对折,直线两边的部分能够(),则这个图形叫做轴对称图形,折痕所在的直线是它的()。
2.轴对称图形的()、对应线段到对称轴的()相等。
3.长方形有()条对称轴,等腰三角形有()条对称轴,等边三角形有()条对称轴,正方形有()条对称轴,菱形有()条对称轴。
二、判断题。
1.正方形的对角线是它的对称轴。
()
2.线段不是轴对称图形。
()
3.等腰三角形和等边三角形都只有一条对称轴。
()
4.长方形的对称轴是长方形的对角线所在的直线。
()
三、画出下面各图形的对称轴,并标明对称轴的条数。
得分:------- 整洁:--------- 日期:-------月-------日
错题更正:。
