用两步Hough变换检测圆
Hough变换检测圆坐标源代码

Hough变换检测圆坐标源代码HOUHG 变换检测圆坐标源代码(原创)我们用HOUGH检测直线的时候是两个未知量,因为轴半径和相角可以确定一条直线,在HOUGH域出现累计最大点就可能是原域中的直线。
现在回到圆的检测上来,确定一个圆需要什么:X坐标,Y坐标,半径三个未知量吧,好了,现在,你做一个三维空间的HOUGH域,以这三个未知量作为三个轴,现在按照一定步长进行三重循环,在最内层循环是这样的,X,Y确定,以不同的半径进行搜索,如果你的X,Y 刚好就是实际图像的X,Y处,半径又搜索到实际真实的半径,那么是不是在这个三维空间e-mail :bigwangenglish@/doc/5912227014. html,void HoughCircle(){/*原图数据区指针宽= 100 高= 100 ,二值灰白图片(只有0 和255)*/BYTE gData_Buff[100*100*3];/*宽= 100*/int wide = 100;/* 高= 100*/int height = 100;unsigned char * m_temp;m_temp=new unsigned char [wide*height];/*中间变量*/int i,j,cx,cy1,cy2;memset(m_temp,0,sizeof(m_temp));/*以离散点位中心画圆*/for(i=0;i<wide*height;i++)< p="">m_temp[i]=0;/* 计数数组,图象上的每一个像素点对应一个计数值,用来确定该点是否是某个圆的圆心。
*/int* pCount;/* X坐标数组,其中的元素是圆环上点的X坐标。
*/int* ixCor;/* Y坐标数组,其中的元素是圆环上点的Y坐标。
*/int* iyCor;int* ixCalCor;int* iyCalCor;int iPointNum;int ixBegin, iyBegin;int iMinRadius;int iMaxRadius;int iRadius;int iNumOfCircle;iMinRadius = 16; /* 要检测的圆环的内半径*//* 要检测的圆环的外半径,即圆环的检测宽度为3,像素在这个圆环内,都视作圆上的*/ iMaxRadius = 18;int Count1;Count1 = 0;for (i=iMinRadius;i<=iMaxRadius;i++){Count1 +=i;}/* 圆环上点的个数? 2*PI*16 + 2*PI*15 + 2*PI*14 =2*3.14*45 = 282 ,每个点占4个字节,共8*3.14*45 = 1128个字节*/ iPointNum = (int)( 8 * 3.14 * Count1 * 1.5 );/* 图像上的每一个像素对应一个计数值。
hough变换圆拟合

hough变换圆拟合
Hough变换圆拟合(Hough transform circle fitting)是一种用于从图像中检测圆的技术。
它是从Hough变换(Hough transform)算法演变而来的。
Hough变换圆拟合算法使用梯度信息来检测圆,并且它能够检测出各种大小、位置和形状的圆。
算法步骤如下:
1. 首先对图像进行预处理,如灰度化、边缘检测等。
2. 选择一组圆心候选点,可以采用图像中的各种特征点,例如边缘点、角点、中心点等。
3. 对于每个候选点,设定一个半径范围,然后在这个半径范围内搜索圆。
4. 对于每个搜索到的圆,计算出它的梯度值。
如果梯度值大于设定的阈值,则将这个圆作为候选圆。
5. 重复步骤3和步骤4,直到所有的候选点都被搜索完毕。
6. 统计所有候选圆的得票数,并根据得票数高低进行排序。
7. 选取得票数最高的圆作为最终检测结果。
Hough变换圆拟合算法的优点是可以检测出各种大小、位置和形状的圆,它的缺点是计算量大,需要较长的运行时间。
Python下opencv使用hough变换检测直线与圆
Python下opencv使⽤hough变换检测直线与圆在数字图像中,往往存在着⼀些特殊形状的⼏何图形,像检测马路边⼀条直线,检测⼈眼的圆形等等,有时我们需要把这些特定图形检测出来,hough变换就是这样⼀种检测的⼯具。
Hough变换的原理是将特定图形上的点变换到⼀组参数空间上,根据参数空间点的累计结果找到⼀个极⼤值对应的解,那么这个解就对应着要寻找的⼏何形状的参数(⽐如说直线,那么就会得到直线的斜率k与常熟b,圆就会得到圆⼼与半径等等)。
关于hough变换,核⼼以及难点就是关于就是有原始空间到参数空间的变换上。
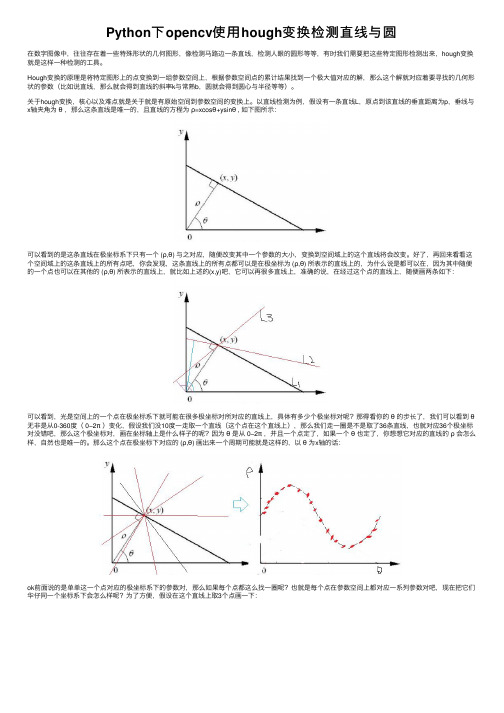
以直线检测为例,假设有⼀条直线L,原点到该直线的垂直距离为p,垂线与x轴夹⾓为θ,那么这条直线是唯⼀的,且直线的⽅程为ρ=xcosθ+ysinθ , 如下图所⽰:可以看到的是这条直线在极坐标系下只有⼀个 (ρ,θ) 与之对应,随便改变其中⼀个参数的⼤⼩,变换到空间域上的这个直线将会改变。
好了,再回来看看这个空间域上的这条直线上的所有点吧,你会发现,这条直线上的所有点都可以是在极坐标为 (ρ,θ) 所表⽰的直线上的,为什么说是都可以在,因为其中随便的⼀个点也可以在其他的 (ρ,θ) 所表⽰的直线上,就⽐如上述的(x,y)吧,它可以再很多直线上,准确的说,在经过这个点的直线上,随便画两条如下:可以看到,光是空间上的⼀个点在极坐标系下就可能在很多极坐标对所对应的直线上,具体有多少个极坐标对呢?那得看你的θ的步长了,我们可以看到θ⽆⾮是从0-360度( 0−2π)变化,假设我们没10度⼀⾛取⼀个直线(这个点在这个直线上),那么我们⾛⼀圈是不是取了36条直线,也就对应36个极坐标对没错吧,那么这个极坐标对,画在坐标轴上是什么样⼦的呢?因为θ是从 0−2π,并且⼀个点定了,如果⼀个θ也定了,你想想它对应的直线的ρ会怎么样,⾃然也是唯⼀的。
那么这个点在极坐标下对应的 (ρ,θ) 画出来⼀个周期可能就是这样的,以θ为x轴的话:ok前⾯说的是单单这⼀个点对应的极坐标系下的参数对,那么如果每个点都这么找⼀圈呢?也就是每个点在参数空间上都对应⼀系列参数对吧,现在把它们华仔同⼀个坐标系下会怎么样呢?为了⽅便,假设在这个直线上取3个点画⼀下:那么可以看到,⾸先对于每⼀个点,在极坐标下,会存在⼀个周期的曲线来表⽰通过这个点,其次,这三个极坐标曲线同时经过⼀个点,要搞清楚的是,极坐标上每⼀个点对 (ρ,θ) 在空间坐标上都是对应⼀条直线的。
Hough变换对圆的检测

Hough变换对圆的检测Hough变换的基本原理在于,利用点与线的对偶性,将图像空间的线条变为参数空间的聚集点,从而检测给定图像是否存在给定性质的曲线。
Hough对圆的检测程序如下% p:阈值,0,1之间的数% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% output% hough_space:参数空间,h(a,b,r)表示圆心在(a,b)半径为r的圆上的点数% hough_circl:二值图像,检测到的圆% para:检测到的圆的圆心、半径[m,n] = size(BW);size_r = round((r_max-r_min)/step_r)+1;size_angle = round(2*pi/step_angle);hough_space = zeros(m,n,size_r);[rows,cols] = find(BW);ecount = size(rows);% Hough变换% 将图像空间(x,y)对应到参数空间(a,b,r)% a = x-r*cos(angle)% b = y-r*sin(angle)for i=1:ecountfor r=1:size_rfor k=1:size_anglea = round(rows(i)-(r_min+(r-1)*step_r)*cos(k*step_angle));b = round(cols(i)-(r_min+(r-1)*step_r)*sin(k*step_angle));if(a>0&a<=m&b>0&b<=n)hough_space(a,b,r) = hough_space(a,b,r)+1;endendendend% 搜索超过阈值的聚集点max_para = max(max(max(hough_space)));index = find(hough_space>=max_para*p);length = size(index);hough_circle = false(m,n);for i=1:ecountfor k=1:lengthpar3 = floor(index(k)/(m*n))+1;par2 = floor((index(k)-(par3-1)*(m*n))/m)+1;par1 = index(k)-(par3-1)*(m*n)-(par2-1)*m;if((rows(i)-par1)^2+(cols(i)-par2)^2<(r_min+(par3-1)*step_r)^2+5&...(rows(i)-par1)^2+(cols(i)-par2)^2>(r_min+(par3-1)*step_r)^2-5) hough_circle(rows(i),cols(i)) = true;endendend% 打印检测结果for k=1:lengthpar3 = floor(index(k)/(m*n))+1;par2 = floor((index(k)-(par3-1)*(m*n))/m)+1;par1 = index(k)-(par3-1)*(m*n)-(par2-1)*m;par3 = r_min+(par3-1)*step_r;fprintf(1,'Center %d %d radius %dn',par1,par2,par3);para(:,k) = [par1,par2,par3];end。
hough 变换检测圆的一般步骤

hough 变换检测圆的一般步骤霍夫变换是一种图像处理算法,可用于检测图像中的圆形。
下面是霍夫变换检测圆的一般步骤:1.导入图像:首先,将要检测圆的图像导入到计算机中。
图像可以来自于摄像机、存储设备或是从其他算法的输出中获得。
2.灰度化处理:将彩色图像转换为灰度图像。
这是因为灰度图像只有一个通道,可以简化后续处理步骤。
3. 边缘检测:使用边缘检测算法(如Canny算子)对灰度图像进行处理,提取图像中的边缘。
这一步骤可以帮助找到圆形的边界。
4.霍夫变换:将边缘图像输入到霍夫变换中。
霍夫变换将边缘点从笛卡尔坐标系转换到霍夫空间,形成二维投票器矩阵。
在投票器矩阵中,每个圆形都有一个对应的概率值,用于表示该圆形的可能性。
5.阈值设置:在霍夫变换之后,需要设置一个阈值来确定哪些圆形应被认为是检测到的圆形。
根据应用的需求和图像的噪声程度,可以调整阈值的大小。
较高的阈值会产生较少的圆形,而较低的阈值会产生较多的圆形。
6.圆形检测:根据阈值从投票器矩阵中选择可能的圆形。
这些圆形可能包含噪声或重叠的圆形。
因此,需要进行圆形重叠或去噪的处理。
7.圆形参数提取:从霍夫空间中获取每个候选圆形的参数,如圆心的坐标和半径长度。
8.绘制圆形:根据提取的参数,在原始图像上绘制检测到的圆形。
这样一来,圆形就会在图像中展示出来。
9.输出结果:最后,将包含检测到的圆形的图像保存或显示出来。
可以使用不同的颜色或标记形式来区分不同的圆形。
霍夫变换是一种广泛应用于图像处理和计算机视觉领域的算法。
通过这一变换,我们可以快速准确地检测图像中的圆形,为后续的分析和应用提供基础。
基于HOUGH变换的圆检测

基于HOUGH变换的圆检测摘要:我们知道,圆是一个简单的几何图形,是构成图像的一个基本要素。
因此,在数字图像处理技术不断发展的今天,能够快速,准确地对圆进行检测,在图像处理特别是工业图像处理中显得尤位重要。
本文所要研究的是基于HOUGH变换的圆检测,即通过HOUGH变换提取出被检测圆的一些特征值,如圆的半径及圆心所在的坐标。
本次设计在圆检测中的HOUGH变换前增加预处理过程。
结果表明,使用我们提出的算法仍能基本保留传统HOUGH变换的优点,并且对图像场景中的干扰不敏感,在圆周残缺不全的情况下仍能进行正确检测。
关键字:图像处理圆检测 HOUGH变换abstract:We know that circle is an simple sketch, and is also an essential element that constitutes the picture. Therefore, can carry on the detection to the circle accurately quickly, seem to be an importance in picture detection, especially the industry picture processing. What this text to study is according to an detection by the transformation of HOUGH, some round characteristics value will bi found, like the round radius and the center of a circle. then withdraw be examined through a transformation of HOUGH.At this time we add a process of preparation before circle detection with transformation of HOUGH. As the result express that the method that we used can still reserve the advantage of the traditional transformation of HOUGH, and is not sensitive to the interference in the picture , still can carry on the right detection when the circumference is incomplete.Keywords: picture processing, detection of circle , HOUGH transformation目录第一章概述 (4)1.1研究意义 (4)1.2研究现状 (4)1.3文本的组织 (4)第二章数字图像处理概述 (5)2.1数字图像处理的概念 (5)2.2数字图像处理技术的应用 (5)2.3数字图像处理的前景及展望 (6)小结 (6)第三章系统开发工具介绍 (7)3.1V ISUAL C++6.0介绍 (7)3.2MFC类库介绍 (7)3.3V ISUAL C++6.0的优点 (9)3.4V ISUAL C++6.0不足 (10)小结 (10)第四章基于HOUGH变换的圆检测 (11)4.1研究意义 (11)4.2曲线检测方法综述 (11)4.3基于HOUGH变换的圆检测 (11)4.3.1 HOUGH变换的原理 (11)4.3.2基于HOUGH变换的圆检测的算法实现 (12)4.3.2.1 预处理 (13)4.3.2.2 HOUGH变换 (14)4.3.2.3 流程图 (15)4.4对结果的分析 (16)4.5HOUGH变换的应用 (16)小结 (16)第五章不足和展望 (18)5.1目前存在的不足 (18)5.2对未来的展望 (18)致谢 (19)参考文献 (20)附录 (21)(一)中英文文摘: (21)(1)Edge Detection (21)(2)HOUGH TRANSFORM FOR CIRCLE (22)(1)边缘检测 (23)(2)基于HOUGH变换的圆周检测 (24)(二)计算程序及说明 (25)第一章概述1.1研究意义当人在观察外面的世界时,反映在脑海的并不是杂乱无章的图像的分布,而是可分离的物体的集合.这是因为人的视觉系统会对景物进行自动提取.随着数字图像的产生,我们也希望把图像分解成可辨识的景物,这一过程就称为景物提取。
hough变换检测圆原理

hough变换检测圆原理
Hough变换是一种常用的图像处理算法,用于检测图像中的圆形目标。
其原理是将图像中的每个像素点转换为极坐标系下的参数空间,并在该空间中寻找圆心和半径相对应的峰值。
具体实现步骤如下:
1. 对图像进行边缘检测,得到一系列边缘点。
2. 在极坐标系下,将每个边缘点表示为一个三元组(r,θ,a),
其中r表示边缘点到图像原点的距离,θ表示边缘点与x轴的夹角,a表示圆心坐标在x轴上的投影。
3. 在参数空间中建立一个二维数组,表示每个可能的圆心(a,b)和半径r对应的计数值。
4. 遍历所有的边缘点,在参数空间中对应的位置上增加计数值。
5. 在参数空间中寻找计数值最大的位置,该位置所对应的圆心
和半径即为检测到的圆形目标。
通过Hough变换,我们可以快速高效地检测图像中的圆形目标。
该算法在计算复杂度和空间复杂度上相对较高,但其检测精度和鲁棒性较为优秀,广泛应用于计算机视觉和机器人领域。
- 1 -。
霍夫变换圆形检测
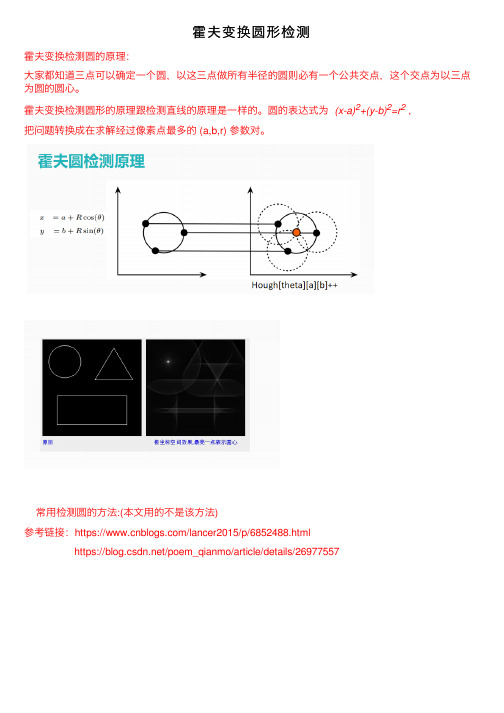
霍夫变换圆形检测霍夫变换检测圆的原理:⼤家都知道三点可以确定⼀个圆,以这三点做所有半径的圆则必有⼀个公共交点,这个交点为以三点为圆的圆⼼。
霍夫变换检测圆形的原理跟检测直线的原理是⼀样的。
圆的表达式为(x-a)2+(y-b)2=r2,把问题转换成在求解经过像素点最多的 (a,b,r) 参数对。
常⽤检测圆的⽅法:(本⽂⽤的不是该⽅法)参考链接:https:///lancer2015/p/6852488.htmlhttps:///poem_qianmo/article/details/26977557代码如下:#include <opencv2/opencv.hpp> #include <iostream>#include <math.h>using namespace cv;using namespace std;int main(int argc, char** argv) {Mat src, dst;src = imread("L:/8.png");if (!src.data){printf("could not load image...\n");return -1;}char INPUT_TITLE[] = "input image";char OUTPUT_TITLE[] = "hough circle demo";namedWindow(INPUT_TITLE, CV_WINDOW_AUTOSIZE);namedWindow(OUTPUT_TITLE, CV_WINDOW_AUTOSIZE);imshow(INPUT_TITLE, src);//中值滤波Mat moutput;//GaussianBlur(src, moutput,Size(5,5),0,0);medianBlur(src, moutput, 3);cvtColor(moutput, moutput, CV_BGR2GRAY);//霍夫圆检测vector<Vec3f>pcircles;HoughCircles(moutput,pcircles, CV_HOUGH_GRADIENT, 1, 10, 100, 30, 5, 50); src.copyTo(dst);for (size_t i = 0; i < pcircles.size(); i++){Vec3f cc = pcircles[i];circle(dst, Point(cc[0], cc[1]), cc[2], Scalar(0, 0, 255), 1.5, LINE_AA); //画圆形 //参数:1.要画的图像 2.圆⼼ 3.半径 4.颜⾊ 5.线的粗细 6.线条类型circle(dst, Point(cc[0], cc[1]), 2, Scalar(0, 255, 0), 2, LINE_AA); //画圆⼼ }imshow(OUTPUT_TITLE, dst);waitKey(0);return0;}实验结果:原图检测图:。
霍夫变换检测同心圆

霍夫变换检测同心圆引言霍夫变换是一种图像处理技术,用于检测图像中的特定形状。
本文将介绍如何使用霍夫变换来检测同心圆。
首先,我们将简要介绍霍夫变换的原理和应用领域。
然后,我们将详细讨论如何在图像中检测同心圆,并提供相关代码示例和实验结果。
霍夫变换原理霍夫变换是由Paul Hough于1962年提出的一种图像处理技术。
它可以用来检测图像中的直线、圆等特定形状。
霍夫变换的基本思想是将图像空间中的点映射到参数空间中,从而使特定形状在参数空间中对应于一个明显的峰值。
以检测直线为例,对于每个图像空间中的点(x, y),我们可以通过一条直线方程ρ = x cos(θ) + y sin(θ)来表示。
其中,ρ是直线到原点的距离,θ是直线与x轴之间的角度。
通过遍历所有可能的ρ和θ值,并统计通过每个点(x, y)的直线数量,在参数空间中找到峰值点即可得到最终检测到的直线。
类似地,我们可以将同心圆表示为一组参数(a, b, r),其中(a, b)是圆心坐标,r 是半径。
通过遍历所有可能的(a, b, r)值,并统计通过每个点(x, y)的圆数量,在参数空间中找到峰值点即可得到最终检测到的同心圆。
霍夫变换检测同心圆步骤以下是使用霍夫变换检测同心圆的步骤:1.读取图像:首先,我们需要从文件或其他数据源中读取待处理的图像。
2.预处理图像:为了提高检测效果,我们通常需要对图像进行预处理。
常见的预处理操作包括灰度化、平滑滤波、边缘检测等。
3.参数空间初始化:根据待检测同心圆的半径范围,初始化参数空间。
参数空间通常以三维数组形式表示,其中第一维表示圆心x坐标,第二维表示圆心y坐标,第三维表示半径r。
4.遍历图像空间:对于每个图像空间中的点(x, y),计算其对应于参数空间中所有可能(a, b, r)值的投票。
投票操作可以简单地增加对应(a, b, r)位置的计数器。
5.寻找峰值点:在参数空间中找到投票数量最多的点,该点对应于检测到的同心圆。
hough变换圆检测程序

BW2(ii,jj)=BW2(ii,jj)+1;
% BW1为输入的需检测的圆图象的矩阵,[x0,y0]为估算的定位中心的位置,r0为估算的定位的半径,rr是检测范围的外扩值
[m,n]=size(BW1);
%确定搜索范围,搜索的矩形的四个定点为[e3,e1],[e3,e2],[e4,e1],[e4,e2]
e1=floor(x0-r0)-rr;
if e1<1
e1=1;
end
e2=ceil(x0+r0)+rr;
if e2>n
e2=n;
end
e3=floor(y0-r0)-rr;
if e3<1
n=length(y);
if n>1 %最大值的位置坐标不唯一时取所有位置的算术平均值
yy=sum(y)/n;
r0=r0-1;
BW3=BW2;
flag=1;
end
end
[y,x]=find(BW3==count); %最大值的位置坐标
end
end
end
end
A=max(BW2); %BW2中的各列最大值组成向量A
if k>-1600&k<1600 %这个点在有效区内
real=j-x0;imag=y0-i;
xx=sum(x)/n;
y=yy;
x=xx;
end
r=r0+1; %定位的半径
return;
e3=1;
end
e4=ceil(y0+r0)+rr;
用Hough变换检测直线和圆.

特殊图像变换1、 HoughLines功能:利用 Hough 变换在二值图像中找到直线格式:CvSeq* cvHoughLines2( CvArr* image, void* line_storage, int method, double rho, double theta, int threshold,double param1=0, double param2=0 ;参数:image:输入 8-比特、单通道 (二值图像,其内容可能被函数所改变line_storage:检测到的线段存储仓. 可以是内存存储仓 (此种情况下,一个线段序列在存储仓中被创建,并且由函数返回),或者是包含线段参数的特殊类型(见下面)的具有单行/单列的矩阵(CvMat*。
矩阵头为函数所修改,使得它的cols/rows将包含一组检测到的线段。
如果line_storage是矩阵,而实际线段的数目超过矩阵尺寸,那么最大可能数目的线段被返回(线段没有按照长度、可信度或其它指标排序.method:Hough 变换变量,是下面变量的其中之一:CV_HOUGH_STANDARD - 传统或标准 Hough 变换. 每一个线段由两个浮点数(ρ, θ 表示,其中ρ 是点与原点 (0,0 之间的距离,θ 线段与 x-轴之间的夹角。
因此,矩阵类型必须是CV_32FC2 type.CV_HOUGH_PROBABILISTIC - 概率 Hough 变换(如果图像包含一些长的线性分割,则效率更高. 它返回线段分割而不是整个线段。
每个分割用起点和终点来表示,所以矩阵(或创建的序列)类型是 CV_32SC4.CV_HOUGH_MULTI_SCALE - 传统 Hough 变换的多尺度变种。
线段的编码方式与CV_HOUGH_STANDARD 的一致。
rho:与象素相关单位的距离精度theta:弧度测量的角度精度threshold:阈值参数。
如果相应的累计值大于threshold,则函数返回的这个线段. param1:第一个方法相关的参数:∙对传统 Hough 变换,不使用(0.∙对概率 Hough 变换,它是最小线段长度.∙对多尺度 Hough 变换,它是距离精度rho的分母 (大致的距离精度是rho而精确的应该是rho / param1 .param2:第二个方法相关参数:∙对传统 Hough 变换,不使用 (0.∙对概率 Hough 变换,这个参数表示在同一条直线上进行碎线段连接的最大间隔值(gap, 即当同一条直线上的两条碎线段之间的间隔小于param2时,将其合二为一。
(标准)Hough变换检测圆

Hough变换检测圆(附:MATLAB程序)分类:图像处理Hough圆2011-12-11 21:37 12587人阅读评论(33) 收藏举报matlab算法图像处理internetfunction任务Hough变换的基本原理在于,利用点与线的对偶性,将图像空间的线条变为参数空间的聚集点,从而检测给定图像是否存在给定性质的曲线。
圆的方程为:(x-a)^2+(y-2)^2=r^2,通过Hough变换,将图像空间对应到参数空间。
附录中的MATLAB程序为网上比较常见的,实际运行中存在一些问题,这里进行些修改。
原理:霍夫变换是图像处理中从图像中识别几何形状的基本方法之一,应用很广泛,也有很多改进算法。
最基本的霍夫变换是从黑白图像中检测直线(线段)。
我们先看这样一个问题:设已知一黑白图像上画了一条直线,要求出这条直线所在的位置。
我们知道,直线的方程可以用y=k*x+b 来表示,其中k和b是参数,分别是斜率和截距。
过某一点(x0,y0)的所有直线的参数都会满足方程y0=kx0+b。
即点(x0,y0)确定了一族直线。
方程y0=kx0+b在参数k--b平面上是一条直线,(你也可以是方程b=-x0*k+y0对应的直线)。
这样,图像x--y平面上的一个前景像素点就对应到参数平面上的一条直线。
我们举个例子说明解决前面那个问题的原理。
设图像上的直线是y=x, 我们先取上面的三个点:A(0,0), B(1,1), C(22)。
可以求出,过A点的直线的参数要满足方程b=0, 过B点的直线的参数要满足方程1=k+b, 过C点的直线的参数要满足方程2=2k+b, 这三个方程就对应着参数平面上的三条直线,而这三条直线会相交于一点(k=1,b=0)。
同理,原图像上直线y=x上的其它点(如(3,3),(4,4)等) 对应参数平面上的直线也会通过点(k=1,b=0)。
这个性质就为我们解决问题提供了方法:首先,我们初始化一块缓冲区,对应于参数平面,将其所有数据置为0.对于图像上每一前景点,求出参数平面对应的直线,把这直线上的所有点的值都加1。
用两步Hough变换检测圆

Usn o s e s H o g r n f r o de e to l p e i g t w- t p u h t a s o m t t c i n el s
t e o e ai f ce c n dv nc o d t c n e l e. h p rtng e in y a d a a e t e e ta li i ps Ke y wor : Ho g r n f r s cr l tci ; so e; me h d ds u h ta so m ; ice dee t on lp to
当点数很多时 , 算法 的性能 急剧下降 。为此 , 有学者提出了改 进的 R T用于圆检测 。 。例如 , H J 利用两不平行 弦的中垂线 必交于圆心” , 利用 内接 直角 三角形 的斜边 必过 圆心 j利 , 用边缘图上各点梯 度所 在的直线过 圆心 的特点 , 对选取 的 任意三点进行 约束 , 文献 [ ] 7 则采 用多级约束 来减少 R T的 H
(colfMahm ta c ne N r a nvrt,Q Sau n 7 15 hn) Sho o te ai l i c,Q c Se om lU i sy h tog2 36 ,C ia ei t
Abs r t Ho gh rnso m p a s n mpo tn pa i t e ma e r c si g I i a efci e pp o c f r c V tac : u ta fr l y a i ra t r n h i g p o e sn . t s n fe tv a r a h o ure t
0 引言
H g …变换是利用图像 空 间到参数 空 间的 映射来 进行 uh 直线检测 。它的基本思想是利 用点与线 的对偶性 : 图像 空间 中共线 的点对应参数空 间中相 交的直线 ; 参数 空间 中相 交于 同一点的直线对应于图像空 间中共线 的点 , 过统计参 数空 通
用点Hough变换实现圆检测的方法

图像中圆的检测及其参数确定是计算机视觉和模式识 别中一项重要任务。常用的圆检测技术有形状分析法、环路 积分微分法[1]、圆Hough变换(CHT)[2]等。CHT是目前应用 最为广泛的圆检测方法,该方法的最大特点是可靠性高,在 噪声、变形、甚至部分区域丢失的状态下仍然能取得理想的 结果。但该方法的缺点是计算复杂,资源需求大。 Davies[3] 利用过圆周一点且与该点切线垂直的线通过圆心的特点,将 CHT转变成直线Hough变换(SLHT )。但由于噪声的影响 及圆周的数字化误差,难以保证梯度方向的准确性,在信噪 比低的情况下该方法难以实用。Ioannou等[4]根据弦的中垂线 通过圆心的性质,用SLHT确定圆的参量。目前的方法将传 统CHT三维搜索空间降低到二维,但在二维空间搜索时计算 复杂度仍然较高。为此,我们对CHT进行了改进,利用圆周 上任意两条不平行弦的中垂线相交与圆心的性质,同时选取 3 点,将搜索空间从三维减低到一维——我们称之为点 Hough变换(PHT),进一步降低了计算复杂性。另外,在 统计时只包括已计算出的交点,而不是整个变量取值范围, 提高了效率。以下将详细阐述PHT方法。
设图像中有N个待分析点,如果选择所有的组合,则有
N ( N − 1)( N − 2) 个点组。应用中,先去除噪声和无效点, 后选 6
∆ = x − xc + y − yc + r − rc 。图4中分别列出了比较结果。
为了便于观察,图4中I-SLHT和PHT的时间值已乘以 1000。 从图中可见,随着噪声点的增加, CHT处理的点增多, 处理速 度近似反比下降,但I-SLHT和PHT的速度与噪声点数无关, PHT速度最快。在检测精度上,当噪声和信号点数比小于 22 时,PHT 和其他两种方法具有同样的精度,且检测结果稳 定。但噪声继续增强时,PHT和I-SLHT一样结果急剧变坏, 无法实用。 一般情况下,实际图像中的噪声强度远小于上述使PHT 变坏的情形。图 5 中用PHT做眼睛瞳孔检测的结果说明了 PHT的实用性。图像的大小为256×256。
hough拟合圆弧

hough拟合圆弧圆弧检测之前都需要对数据进行分割,将一系列的点分割成不同的区域,然后计算圆弧的位置。
Hough变换不需要知道某区域是否有圆弧,以类似于投票的机制,某参数获得的票数越多,则存在圆弧的可能性越大,大于某阈值时,则可以认为该处存在圆弧。
x - a = r*cos(theta)y - b = r*sin(theta)对于每一个点x y,有无数个点满足上式,即有无数个圆在经过该点的,每个圆对应一组(a,b,r)参数,设立一个票箱,里面有所有可能的(a,b,r)参数,当某组参数出现一次,就将该票箱中的票数加1,所有的点都扫描之后,查看票箱,票数最多的点即是圆出现概率最大的情况。
此时应该设定一个阈值,如果最多的票数小于该阈值,则认为不存在圆,否则认为有圆存在。
//这是一个简化的Hough圆算法,假设半径已知的情况,1.int HoughArc(int X[] , int Y[] , int Cnt ,int r, ArcPara * Arc) {2.vector<iPoint>center;3.vector<int>VoteCnt;4.double theta;5.int a,b;6.int minA,maxA,minB,maxB;7.int VotedFlag = 0;8.double deltaTheta = PI/180;//间隔1度9.double startAngle = 150.0*PI/180;10.double endAngle = PI*2 + PI/6;11.center.clear();12.VoteCnt.clear();13.minA = maxA = X[0] - r;14.minB = maxB = X[0]; //theta = 015.//计算a,b的最小和最大值16.for (int i = 0; i < Cnt;i++)17.{18.for (theta = startAngle; theta < endAngle;theta += de ltaTheta)19.{20. a = (int)(X[i] - r*cos(theta) + 0.5);21. b = (int)(Y[i] - r*sin(theta) + 0.5);22.if (a > maxA)23.{24.maxA = a;25.}else if (a < minA)26.{27.minA = a;28.}29.30.if (b > maxB)31.{32.maxB = b;33.}else if (b < minB)34.{35.minB = b;36.}37.38.}39.}40.//确定a,b的范围之后,即确定了票箱的大小41.int aScale = maxA - minA + 1;42.int bScale = maxB - minB + 1;43.44.int *VoteBox = new int[aScale*bScale];45.//VoteBox初始化为046.for (int i = 0; i < aScale*bScale;i++)47.{48.VoteBox[i] = 0;49.}50.//开始投票51.for (int i = 0; i < Cnt;i++)52.{53.//printf("%d ",i);54.for (theta = startAngle; theta < endAngle;theta += de ltaTheta)55.{56.57. a = (int)(X[i] - r*cos(theta) + 0.5);58. b = (int)(Y[i] - r*sin(theta) + 0.5);59.VoteBox[(b - minB)*aScale + a - minA] = VoteBox[(b - minB)*aScale + a - minA] + 1;60.}61.}62.63.//筛选票箱64.int VoteMax = 0;65.int VoteMaxX,VoteMaxY;66.for (int i = 0; i < bScale ;i++)67.{68.for (int j = 0; j < aScale ;j++)69.{70.if (VoteBox[i*aScale + j] > VoteMax)71.{72.VoteMax = VoteBox[i*aScale + j];73.VoteMaxY = i;74.VoteMaxX = j;75.}76.}77.}78.79.int Count = 0;80.printf("VoteMax: %d",VoteMax);81.for (int i = 0; i < bScale ;i++)82.{83.for (int j = 0; j < aScale ;j++)84.{85.if (VoteBox[i*aScale + j] >= VoteMax)86.{87.Count++;88.}89.}90.}91.printf(" %d \n",Count);92.//释放内存93.delete [] VoteBox;94.if (VoteMax > 3)95.{96.Arc->center.x = VoteMaxX + minA;97.Arc->center.y = VoteMaxY + minB;98.Arc->r = r;99.return 1;100.}else { 101.return 0; 102.}103.return 1; 104.}。
用Hough变换检测直线和圆

特殊图像变换1、HoughLines功能:利用Hough 变换在二值图像中找到直线格式:CvSeq* cvHoughLines2( CvArr* image, void* line_storage, int method, double rho, double theta, int threshold,double param1=0, double param2=0 );参数:image:输入8-比特、单通道(二值) 图像,其内容可能被函数所改变line_storage:检测到的线段存储仓. 可以是内存存储仓(此种情况下,一个线段序列在存储仓中被创建,并且由函数返回),或者是包含线段参数的特殊类型(见下面)的具有单行/单列的矩阵(CvMat*)。
矩阵头为函数所修改,使得它的cols/rows将包含一组检测到的线段。
如果line_storage是矩阵,而实际线段的数目超过矩阵尺寸,那么最大可能数目的线段被返回(线段没有按照长度、可信度或其它指标排序).method:Hough 变换变量,是下面变量的其中之一:∙CV_HOUGH_STANDARD- 传统或标准Hough 变换. 每一个线段由两个浮点数(ρ, θ) 表示,其中ρ 是点与原点(0,0) 之间的距离,θ 线段与x-轴之间的夹角。
因此,矩阵类型必须是CV_32FC2 type.∙CV_HOUGH_PROBABILISTIC - 概率Hough 变换(如果图像包含一些长的线性分割,则效率更高). 它返回线段分割而不是整个线段。
每个分割用起点和终点来表示,所以矩阵(或创建的序列)类型是CV_32SC4.∙CV_HOUGH_MULTI_SCALE- 传统Hough 变换的多尺度变种。
线段的编码方式与CV_HOUGH_STANDARD 的一致。
rho:与象素相关单位的距离精度theta:弧度测量的角度精度threshold:阈值参数。
如果相应的累计值大于threshold,则函数返回的这个线段.param1:第一个方法相关的参数:∙对传统Hough 变换,不使用(0).∙对概率Hough 变换,它是最小线段长度.∙对多尺度Hough 变换,它是距离精度rho的分母(大致的距离精度是rho而精确的应该是rho / param1 ).param2:第二个方法相关参数:∙对传统Hough 变换,不使用(0).∙对概率Hough 变换,这个参数表示在同一条直线上进行碎线段连接的最大间隔值(gap), 即当同一条直线上的两条碎线段之间的间隔小于param2时,将其合二为一。
