第章气体动理论
合集下载
气体动理论
（答案：前者是由于分子碰撞次数增加导致,后者是由于运动 加剧导致）
2.两种不同种类的理想气体,压强相同,温度相同,体积不同, 试
问单位体积内的分子数是否相同?
（答案:相同）
3.两瓶不同种类的气体,分子平均平动动能相同,但气体的分 子数密度不同,试问他们的压强是否相同? （答案:不同）
4.两瓶不同种类的气体,体积不同,但温度和压强相同,问气体 分子的平均平动动能是否相同?单位体积中的分子的总平动 动能是否相同?方均根速率是否相同？（答案:相同,相同,不同）
2. 理想气体的内能包括哪些？ 理想气体的内能=所有气体分子动能量的总和;
3. 内能与机械能有什么区别？
机械能可以为零，而内能永不为零。
一摩尔理想气体的内能:
Emol N
i KT i RT
2
2
M千克理想气体的内能: E M i RT i vRT
M mol 2
2
问题：
1.三个容器内分别储有1mol氦气(He),1mol氢气(H2),1mol氨 气(NH3)( 三种气体均 视为刚性分子的理想气体),若它们的 温度都升高 1K , 则三种气体内能的增加分别是多少？ (答案:12.5J, 20.8J, 24.9J) 2.写出下列各量的表达式：
(2) 分子沿各个方向运动的机会是均等的，没有任何一个 方向上气体分子的运动比其它方向更占优势。即沿着各 个方向运动的平均分子数应该相等;
(3) 分子速度在各个方向的分量的各种平均值相等。
五、气体动理论的统计方法 (statistical metheds)
用对大量分子的平均性质的了解代替个别分子的 真实性质。对个别分子（或原子）运用牛顿定律求 出其微观量，如:质量、速度、能量等，再用统计的 方法，求出大量分子关于微观量的统计平均值，并 用来解释在实验中直接观测到的物体的宏观性质， 如:温度、压强、热容等。
2.两种不同种类的理想气体,压强相同,温度相同,体积不同, 试
问单位体积内的分子数是否相同?
（答案:相同）
3.两瓶不同种类的气体,分子平均平动动能相同,但气体的分 子数密度不同,试问他们的压强是否相同? （答案:不同）
4.两瓶不同种类的气体,体积不同,但温度和压强相同,问气体 分子的平均平动动能是否相同?单位体积中的分子的总平动 动能是否相同?方均根速率是否相同？（答案:相同,相同,不同）
2. 理想气体的内能包括哪些？ 理想气体的内能=所有气体分子动能量的总和;
3. 内能与机械能有什么区别？
机械能可以为零，而内能永不为零。
一摩尔理想气体的内能:
Emol N
i KT i RT
2
2
M千克理想气体的内能: E M i RT i vRT
M mol 2
2
问题：
1.三个容器内分别储有1mol氦气(He),1mol氢气(H2),1mol氨 气(NH3)( 三种气体均 视为刚性分子的理想气体),若它们的 温度都升高 1K , 则三种气体内能的增加分别是多少？ (答案:12.5J, 20.8J, 24.9J) 2.写出下列各量的表达式：
(2) 分子沿各个方向运动的机会是均等的，没有任何一个 方向上气体分子的运动比其它方向更占优势。即沿着各 个方向运动的平均分子数应该相等;
(3) 分子速度在各个方向的分量的各种平均值相等。
五、气体动理论的统计方法 (statistical metheds)
用对大量分子的平均性质的了解代替个别分子的 真实性质。对个别分子（或原子）运用牛顿定律求 出其微观量，如:质量、速度、能量等，再用统计的 方法，求出大量分子关于微观量的统计平均值，并 用来解释在实验中直接观测到的物体的宏观性质， 如:温度、压强、热容等。
气体动理论
第十三章 气体动理论本章从理想气体的微观组成出发，假以统计性假设，推出理想气体的压强和温度公式，揭示了压强和温度的本质；提出了理想气体内能的概念，介绍了理想气体能量按自由度均分原理；阐述了理想气体的麦克斯韦速率分布率。
这称为气体动理论。
气体动理论的产生和发展凝聚了众多物理学家的智慧和心血。
早在1678年，胡克就提出了气体压强是由大量气体分子与器壁碰撞的结果的观点。
之后，在1738年，伯努利根据这一观点推导出压强公式，并且解释了玻意耳定律。
1744年，俄国的罗蒙诺索夫提出了热是分子运动表现的观点。
在19世纪中叶，气体动理论经克劳修斯、麦克斯韦和玻耳兹曼的努力而有了重大发展。
1858年，克劳修斯提出气体分子平均自由程的概念并导出相关公式。
1860年，麦克斯韦指出，气体分子的频繁碰撞并未使它们的速度趋于一致，而是达到稳定的分布，导出了平衡态气体分子的速率分布和速度分布。
之后，麦克斯韦又建立了输运过程的数学理论。
1868年，玻耳兹曼在麦克斯韦气体分子速率分布律中又引进重力场。
第一节理想气体状态方程一、状态参量1．状态参量概念如何描述系统的冷热变化规律，这就需要一些物理量。
假设气体的质量为 m ，其宏观状态一般可以用气体的压强p 、体积V 和温度T 三个物理量来描述。
如果在热力学过程中伴随着化学反应，还需要物质的量、摩尔质量 、物质各组分的质量等物理量来描述。
如果热力学系统处于磁场中，还需要电场强度E 、电极化矢量P 、磁场强度H 和磁化强度M 等物理量来描述。
选择几个描写系统状态的参量，称为状态参量。
2．状态参量分类按照不同的划分标准，状态参量可作如下划分：（1）按状态参量描写系统的性质划分可分为：V P E P H M几何参量：描述系统的空间广延性。
如体积 。
力学参量：描述系统的强度。
如压强 。
化学参量：描述系统的化学组分。
如各组分的质量，物质的量。
电磁参量：描述系统的电磁性质。
如电场强度 ，电极化强度 ，磁场强度 ，磁化强度 。
大学物理-气体动理论
为漏气,经过若干时间后,压力降到原来的 5 8 ,温度降到 270c。
求: (1) 容器的容积,
(2) 漏去了多少氧气?
解: (1)
pv M RT
VM P RT8.21(升)
(2) 设漏气后的压力、温度、质量分别为 p' T' M'
p'V M' RT'
M' p'V0.06K 7 g
RT'
M 0 .1 0 0 .0 6 0 .0 7 K 3 3 g
平衡态: 在不受外界影响的条件下,一个系统的宏观性质不随时间
改变的状态。热动平衡
平衡过程:气体从一个状态变化到另一个状态,其间所经历的
过渡方式称为状态变化的过程.
如果过程所经历的所有中间状态都无限接近平衡状态,
该过程称为平衡过程.
2020/5/2
2
二、状态参量:
1、气体所占的体积 V: m 3
2、压强 P:
总的分子数密度为
n
n i
i
设 dA 法向为 x 轴
dA
一次碰撞单分子动量变化
vi dt
2 mvix
x 在 dt 时间内与dA碰撞的分子数
2020/5/2
ni vix dt dA 斜柱体体15积
dt 时间内传给 dA 的冲量为
dI = 2 mnivix2 dt dA
(vix>0)vx2= Nhomakorabeai
ni
vxi2
第三章 气体动理论
理想气体状态方程
麦克斯韦速率分布律
气体动理论的压强公式 玻耳兹曼分布律
气体动理论的温度公式
能量均分定理
2020/5/2
1
求: (1) 容器的容积,
(2) 漏去了多少氧气?
解: (1)
pv M RT
VM P RT8.21(升)
(2) 设漏气后的压力、温度、质量分别为 p' T' M'
p'V M' RT'
M' p'V0.06K 7 g
RT'
M 0 .1 0 0 .0 6 0 .0 7 K 3 3 g
平衡态: 在不受外界影响的条件下,一个系统的宏观性质不随时间
改变的状态。热动平衡
平衡过程:气体从一个状态变化到另一个状态,其间所经历的
过渡方式称为状态变化的过程.
如果过程所经历的所有中间状态都无限接近平衡状态,
该过程称为平衡过程.
2020/5/2
2
二、状态参量:
1、气体所占的体积 V: m 3
2、压强 P:
总的分子数密度为
n
n i
i
设 dA 法向为 x 轴
dA
一次碰撞单分子动量变化
vi dt
2 mvix
x 在 dt 时间内与dA碰撞的分子数
2020/5/2
ni vix dt dA 斜柱体体15积
dt 时间内传给 dA 的冲量为
dI = 2 mnivix2 dt dA
(vix>0)vx2= Nhomakorabeai
ni
vxi2
第三章 气体动理论
理想气体状态方程
麦克斯韦速率分布律
气体动理论的压强公式 玻耳兹曼分布律
气体动理论的温度公式
能量均分定理
2020/5/2
1
气体动理论
压强是大量分子对器壁冲量的统计平均效果，单个 分子的压强没有意义。
17
§2.1.3理想气体的温度
1.宏观意义：冷热程度，是决定某一系统 与另一系统是否处于热平衡的宏观标志。
2.微观意义：由状态方程可得
pV = N RT NA
状态方程：
p=
N V
R NA
T = nkBT
波尔兹曼常数：
kB
=
R NA
= 1.38 10-23 J
K -1
18
温度的统计意义
p = 2 nω 3
p = nkT
ω = 3 kT 2
此式称为理想气体分子温度公式. 温度的统计意义：
（1）温度是分子平均平动动能的量度，反映无 规则热运动的剧烈程度；
（2）温度是大量分子集体表现，对个别分子 温度没有意义。
相等。
2.气体分子沿各方向运动的概率相等 即分子速度在各方向上分量的各种平均值相
等。
在直角坐标系中有： vx2 = vy2 = vz2
vx2 + vy2 + vz2 = v2
vx2
=
vy2
=
vz2
=
1 v2 3
11
§2.1.2理想气体的压强
1.产生
固体、液体的 ：重力原因 气体压强：大量分子不断碰撞的结果。
单个分子碰撞器壁的作用力是不 连续的、偶然的、不均匀的。从 总的效果上来看，分子碰撞对器 壁产生一个持续的平均作用力。
PA=F/SA
12
2 .理想气体压强公式的导出
公式导出 见图：
PA=F/SA
长方形容器内分子总数为N。
设分子质量为m，速率为vx、vy、vz；
17
§2.1.3理想气体的温度
1.宏观意义：冷热程度，是决定某一系统 与另一系统是否处于热平衡的宏观标志。
2.微观意义：由状态方程可得
pV = N RT NA
状态方程：
p=
N V
R NA
T = nkBT
波尔兹曼常数：
kB
=
R NA
= 1.38 10-23 J
K -1
18
温度的统计意义
p = 2 nω 3
p = nkT
ω = 3 kT 2
此式称为理想气体分子温度公式. 温度的统计意义：
（1）温度是分子平均平动动能的量度，反映无 规则热运动的剧烈程度；
（2）温度是大量分子集体表现，对个别分子 温度没有意义。
相等。
2.气体分子沿各方向运动的概率相等 即分子速度在各方向上分量的各种平均值相
等。
在直角坐标系中有： vx2 = vy2 = vz2
vx2 + vy2 + vz2 = v2
vx2
=
vy2
=
vz2
=
1 v2 3
11
§2.1.2理想气体的压强
1.产生
固体、液体的 ：重力原因 气体压强：大量分子不断碰撞的结果。
单个分子碰撞器壁的作用力是不 连续的、偶然的、不均匀的。从 总的效果上来看，分子碰撞对器 壁产生一个持续的平均作用力。
PA=F/SA
12
2 .理想气体压强公式的导出
公式导出 见图：
PA=F/SA
长方形容器内分子总数为N。
设分子质量为m，速率为vx、vy、vz；
大学物理 气体动理论
三、 温 度
决定一个系统是否与其它系统达到热平衡的宏观性质。
处于热平衡的多个系统具有相同的温度
具有相同温度的几个系统放在一起必然处于热平衡。
温度测量
酒精或水银
A
B
A 和 B 热平衡，TA = TB
热胀冷缩特性，标准 状态下，冰水混合， B 上留一刻痕， 水沸 腾，又一刻痕，之间 百等份，就是摄氏温 标（Co）。
生碰撞的�数目为：Ni = nivix dt d A 速度为 vi 分子在 dt 时间对 dA 的冲量为：
�
x
vxi
dA
vidt
nivixdAdt ⋅ (2mvix )
∑ 所有分子在
dt
时间内对
dA 产生的总冲量为：dI = 1 2
i
2mni
v
2
ix
dAdt
∑ ∑ 气体对器壁的宏观压强为：
p=
mni
T0
273.15
= 8.31(Jmol⋅K)
若写成 ν = N NA
N A = 6.023 × 1023 / mol
N为气体分子总数 阿伏伽德罗常量
µN
R
pV = RT = N T
µNA
NA
令
k
≡
R NA
=
1.38 × 10−23
J
K
玻耳兹曼常数
pV = NkT
p = N kT = nkT V
n：气体分子数密度
2
三、气体分子的平均总动能
设分子有： 平动自由度 t 转动自由度 r
分子平均总动能：
1 εk = (t + r) 2 kT
单原子分子 刚性双原子分子
3
第5章 气体动理论
x x + ∆x
17
x
5.3 气体分子热运动的速率分布规律
概率 wx = lim 统计分布的基本方法 分间隔 坐标分布 速率分布 能量分布
∆Nx dNx = N→∞ N N
dNx N
x − x + dx
υ −υ + dυ
ε − ε + dε
dNυ N dNε N
18
5.3 气体分子热运动的速率分布规律
20
υ 附近
Nf (υ )dυ = dN υ
5.3 气体分子热运动的速率分布规律
2）f (υ ) 的性质
∞
= ∫ f (υ)dυ= 1
0
(υ =∞)
∞
∫) (υ
(
=0)
dNυ N
归一性质
∫ f (υ)dυ =1 几何意义
0
∆ Nυ dNυ f (υ) = N∆ υ Ndυ
f (υ)dυ
曲线下面积恒为1 曲线下面积恒为1
7
Nmi NAkT → PV = NAmi
N → P = kT V
→ P = nkT
5.1 理想气体状态方程
热力学系统由大量粒子组成 1) 标况
T = 273K
P = 1atm = 1.013×105 Pa
1.013×105 P = 2.69×1025 / m3 = n= kT 1.38×10−23 × 273
19
速率分布函数
dNυ = f (υ) Ndυ
5.3 气体分子热运动的速率分布规律
1）f (υ) 的意义 分子速率在
dNυ f (υ) = Ndυ
f (υ)dυ
dNυ = N
单位速率间隔内的分子数 占总分子数的百分比 分子速率在 υ −υ +dυ 间隔内的分子数占 总分子数的百分比 分子速率在 υ −υ +dυ 间隔内的分子数 可以求平均值
17
x
5.3 气体分子热运动的速率分布规律
概率 wx = lim 统计分布的基本方法 分间隔 坐标分布 速率分布 能量分布
∆Nx dNx = N→∞ N N
dNx N
x − x + dx
υ −υ + dυ
ε − ε + dε
dNυ N dNε N
18
5.3 气体分子热运动的速率分布规律
20
υ 附近
Nf (υ )dυ = dN υ
5.3 气体分子热运动的速率分布规律
2）f (υ ) 的性质
∞
= ∫ f (υ)dυ= 1
0
(υ =∞)
∞
∫) (υ
(
=0)
dNυ N
归一性质
∫ f (υ)dυ =1 几何意义
0
∆ Nυ dNυ f (υ) = N∆ υ Ndυ
f (υ)dυ
曲线下面积恒为1 曲线下面积恒为1
7
Nmi NAkT → PV = NAmi
N → P = kT V
→ P = nkT
5.1 理想气体状态方程
热力学系统由大量粒子组成 1) 标况
T = 273K
P = 1atm = 1.013×105 Pa
1.013×105 P = 2.69×1025 / m3 = n= kT 1.38×10−23 × 273
19
速率分布函数
dNυ = f (υ) Ndυ
5.3 气体分子热运动的速率分布规律
1）f (υ) 的意义 分子速率在
dNυ f (υ) = Ndυ
f (υ)dυ
dNυ = N
单位速率间隔内的分子数 占总分子数的百分比 分子速率在 υ −υ +dυ 间隔内的分子数占 总分子数的百分比 分子速率在 υ −υ +dυ 间隔内的分子数 可以求平均值
第1章_气体
第一章 气 体
解： 对混合气体有
pH2O nH2O
pmix
nB
或 pH2O
pH2O
nH2O
p干烃 pmix pH2O n干烃
25.51000
nH2O
104365
760
mol 25.5
33.7mol
101325
第一章 气 体
Vmix
nH2O n干烃 RT pm ix
第一章 气 体
图上显示：273K等温线可分为三段： D(气体)→F(饱和气体)， F(饱和气体)→H(饱和液体)， H(饱和液体)→ 液体
饱和蒸气压： 从F→H，体系始终保持气、液两相平衡，称一定
温度压力下气、液平衡为饱和，气相称为饱和气体，液 相称为饱和液体，气相的平衡压力称为液体在该温度下 的饱和蒸气压。
k
pmix p1 p2 pk pB B1 适用条件：理想混合气
第一章 气 体
理想混合气中B组分的分压力：
pB pmix xB
k
理想混合气 pmix pB B1
pg
nBRTmix nB nB RTmix
：
pΑ xΑ nΑ pΒ xΒ nΒ
pΒ
第一章 气 体
图1-8 液体饱和蒸气压动画演示图
第一章 气 体
(2) 当T<304.5K时，实际气体可以液化‚当T>304.5K 时， 实际气体不能液化； 温度升高，水平线变短，饱和蒸气压增大。
(3) T=304.5K，图上出现拐点Ｃ，在Ｃ点处，气液不分‚ 水平段消失。 304.5K 称为CO2的临界温度，C点称为临界点； C点对应的温度、压力、体积分别称为CO2的临界温 度、临界压力、临界体积。
一定条件下，宏观物质处于何种状态，主要取决于
气体动理论基础
dt
dt
•dt时间内能遇到dA上旳分子数为：
ni ixdtdA
•这些分子在dt时间内对dA总旳冲量：
dIi niixdtdA(2mix )
dA x
•全部分子对器壁旳总冲量：
dI 1 2
2mni
2 ix
dAdt
i
dF
mni
2 ix
dA
i
i dt ix dt
4.理想气体旳压强公式 p dF dA
A
C
若 A 和 B、B 和 C 分别热平衡，
则 A 和 C 一定热平衡。
B
（热力学第零定律）
处于相互热平衡状态旳多种系统拥有某一 共同旳宏观物理性质
——温度 温标：温度旳数值表达措施。
摄氏温标、热力学温标
T t 273.15
8-3 温度旳统计解释
一、温度旳统计解释
pV m RT M
p 1 N RT n R T
p
mni
2 ix
m
ni
2 ix
i
i
2 x
ni 2ix
n
p
nm
2 x
平衡态下
x2
y2
z2123源自p 1 nm 23
t
1 m 2
2
分子旳平均平动动能
p
2 3
n
t
温度旳宏观定义：
表征物体旳冷热程度
初
A
绝热板
A、B 两体系互不影响
态
B
各自到达平衡态
末
A
导热板
A、B 两体系到达共同
态
B
旳热平衡状态
v 8kT 8RT 1.60 RT
m M
第四章 气体动理论
§4-1
分子动理论的基本观点
一、物质微观结构的物理图象 1、物质是由大量的微观粒子——原子或分子组 成的； 2、分子在作永不停息的无规则运动； 3、分子之间有相互作用力。 综上所述，一切宏观物体（不论它是气体、 液体、还是固体）都是由大量的原子或分子组 成的；所有分子都在不停的、无规则运动中； 分子之间有相互作用力。这就是关于物质微观 结构的三个基本观点。
(s t )
C2 引力： f1 t , C2、t均 0 r 斥力： f C 1 , C 、s均 0 2 1 s r t:4 ~ 7 s : 9 ~ 13
2、图线
（f—r图线）
三、分子间的势能曲线（Ep—r图线）
1、分子间的势能： dE p fdr
C1 C2 E p fdr ( s t )dr r r C1 C2 s 1 t 1 ( s 1)r (t 1)r
N pV RT NA
p nkT
温度 T 的物理意义
1 2 3 平 m v kT 2 2
1） 温度是分子平均平动动能的量度 平 T （反映热运动的剧烈程度）.
2）温度是大量分子的集体表现，个别分子无意义.
3）在同一温度下，各种气体分子平均平动动能均 相等。 注意 热运动与宏观运动的区别：温度所反 映的是分子的无规则运动，它和物体的整 体运动无关，物体的整体运动是其中所有 分子的一种有规则运动的表现.
由于热力学方法的局限性，我们对平衡态下系统内 部的情况不了解，从而对温度和理想 气体的理解 也很肤浅，对气体的压强更是一无所知，因此，为 了全面了解平衡态下的基本热学信息，我们必须用 分子物理学的方法从微观本质上加以认识。
• 气体动理论是统计物理学的基础； • 气体动理论是从微观的观点来研究气体的热学 性质； • 解释气体的温度、压强、热容、内能等的微观 本质； • 建立统计的概念。
大学物理教程 第18章 气体动理论
大学物理教程
光程: n r 的乘积称为与路程 r 相应的光程。
2. 光程差
2 2
r2
2 1
r1
2
n2 r2
2
n1r1
2
(n2r2
n1r1 )
光程差： n2r2 n1r1
相位差和光程差的关系：
2
S1*
n1 n2
S2*
r1
P
●
r2
2024/4/13
8
哈尔滨工业大学(威海)
18.1 相干光 Harbin Institute of Technology at Weihai
第18章 气体动理论 哈尔滨工业大学(威海) Harbin Institute of Technology at Weihai
大学物理教程
§ 18.1 相干光 § 18.2 杨氏双缝干涉 § 18.3 薄膜干涉
本章要点：理解掌握光的干涉条件、相干光获得的传统方法及干涉分析的一般方 法，掌握光程概念的实质及引入光程概念的意义；熟练掌握杨氏双缝 干涉、劈尖干涉、牛顿环干涉等倾干涉的具体分析方法及应用。
子发光相互独立，不一定同步，原子跃迁发射的波列在传播方向、振动方向
及初相上具有随机性，难以满足相干条件。
2024/4/13
4
哈尔滨工业大学(威海)
18.1 相干光 Harbin Institute of Technology at Weihai
大学物理教程
非相干(不同原子发的光)
非相干(同一原子先后发的光)
2024/4/13
2
哈尔滨工业大学(威海)
18.1 相干光 Harbin Institute of Technology at Weihai
第2章气体动理论
第2章气体动理论◆本章学习目标了解：玻耳兹曼分布率；范德瓦耳斯方程和输运过程。
理解：理想气体的压强，温度的微观意义；能量均分定理，麦克斯韦速率分布律及其统计意义；麦克斯韦速率分布律的实验验证，实际气体等温线；气体分子的平均自由程的概念。
掌握：理想气体的压强，能量均分定理，麦克斯韦速率分布律及其统计意义；实际气体等温线；气体分子的平均自由程的概念。
◆本章教学内容1、理想气体压强公式2、温度的微观意义3、能量均分定理4、麦克斯韦速率分布律5、麦克斯韦速率分布律的实验验证*6、玻尔兹曼分布率◆本章重点压强和温度的微观实质和意义、理想气体的内能、速率分布函数以及理想气体平衡态的特征速率等。
◆本章难点压强和温度的微观实质和意义。
速率分布函数的物理意义以及相关的计算。
2.1 理想气体的压强一、理想气体模型1. 关于单个分子的力学性质的假设在宏观上我们知道，理想气体是一种在任何情况下都遵守玻意耳定律、盖-吕萨克定律和查理定律的气体。
但从微观上看什么样的分子组成的气体才具有这种宏观特性呢？气体分子的运动是肉眼看不见的，所以理想气体的微观模型是通过对宏观实验结果的分析和综合提出的一个假说。
通过这个假说得到的结论与宏观实验结果进行比较来判断模型的正确性。
通过前人多年的努力，我们现在知道理想气体的微观模型具有以下特征：（1）分子与容器壁和分子与分子之间只有在碰撞的瞬间才由相互作用，其它时候的相互作用可以忽略不计。
（2）分子本身的体积在气体中可以忽略不计，即对分子可采用质点模型。
（3）而分子与容器壁以及分子与分子之间的碰撞属于牛顿力学中的完全弹性碰撞。
实验证明，实际气体中分子本身占的体积约只占气体体积的千分之一，在气体中分子之间的平均距离远大于分子的几何尺寸，所以将分子看成质点是完全合理的。
从另一个方面看，对已达到平衡态的气体如果没有外界影响，其温度、压强等态参量都不会因分子与容器壁以及分子与分子之间的碰撞而发生改变，气体分子的速度分布也保持不变，因而分子与容器壁以及分子与分子之间的碰撞是完全弹性碰撞也是理所当然的。
第十一章 气体动理论
2020/3/5
6
§11.1 平衡态 • 状态参量 • 理想气体
四、理想气体状态方程
理想气体：对于能准确遵守玻意耳-马略特、盖-吕萨克和 查理定律这三个实验定律的气体。
质量为M、摩尔质量为的理想气体，应用上述三定
律，得到理想气体在平衡态下，三个参量p、V、T之 间满足的关系：
理想气体状态方程
M
y
A2 i o
- mmvvvxx
z l1
A1 l2
l3 x
2020/3/5
14
§11.2 理想气体的压强和温度
i分子一次碰撞施予A1面的冲量
第i个分子，它的速度为vi，在直角坐标系中的三个分量为 vix，viy，viz。碰撞后，i分子的速度变为vix，viy，viz。
A1面受到的冲量 Ii 2mvix
理想气体状态方程的另一形式 p nkT
上式表明在相同的温度和压强下，各种气体的分子数 密度n都相等，实际上就是阿伏伽德罗定律。
2020/3/5
8
§11.2 理想气体的压强和温度
一、分子及其运动假设
分子永不停息地、无规则地运动
气体、液体、固体中都有扩散现象，这是分子运动的 有力证明。
分子间有相互作用力
1 2
mv2
3 2
kT
可以计算气体分子
速率平方的开方根，称为方均根速率
v 2 3kT 3RT
M
方均根速率反映的是分子的平均平动动能的大小，
与分子的平均运动速率 不同v 。
2020/3/5
20
§11.3 能量均分定理理想气体的热力学能
理想气体分子作为一个弹性质点，因此分子的运动只有 平动。实际上分子具有比较复杂的内部结构，还有转动及振 动，气体分子热运动的能量应包括这些运动所具有的所有能 量。
气体动理论
上一张 下一张 返回
三Hale Waihona Puke 、 压 强 推 导上一张 下一张
返回
具有速度 vi 的Ni 个分子作用：
上一张 下一张 返回
上一张 下一张 返回
压强公式的推导过程：
• 对象：理想气体的微观模型。
• 状态：平衡态。
• 方法：个别分子服从力学规律，
•
大量分子服从统计规律。
• 结论：P = n m v 2/ 3
即:
（1） f (v) dN Ndv
f (v)表示在速率v 附近 单位速率间隔内的分子数 占总分子数的比率.
（2） f (v)dv dN N
表示速率在 v~v+dv 区间 内的分子数占总分子数的比 率，即阴影1 面积。
（3） v2 f (v)dv N
v1
N
表示速率在 v1~ v2 区间 内的分子数占总分子数的 比率， 即阴影2 面积。
• Q：系统与外界的热交换。 Q>0表示系统从外界吸热；Q<0表示系统向外 界放热。
• E：系统内能的改变量。 E>0表示系统内能增加（若是理想气体，则 温度升高)；E<0表示系统内能减少。
• A：系统对外界的做功情况。 A>0表示系统对外界作正功，如体积膨胀的过 程；A<0表示系统对外界作负功，亦即外界对 系统做功。
不可逆 可逆.
上一张 下一张 返回
有关物质结构与运动规律的 三条基本定理
• 宏观物体有大量微粒组成。 • 分子间存在相互作用力。 • 分子永不停息地无规运动。
上一张 下一张 返回
气体分子运动的特点：
• 看作是惯性支配下的自由运动。 • 分子间存在频繁碰撞。 • 服从统计规律。
三Hale Waihona Puke 、 压 强 推 导上一张 下一张
返回
具有速度 vi 的Ni 个分子作用：
上一张 下一张 返回
上一张 下一张 返回
压强公式的推导过程：
• 对象：理想气体的微观模型。
• 状态：平衡态。
• 方法：个别分子服从力学规律，
•
大量分子服从统计规律。
• 结论：P = n m v 2/ 3
即:
（1） f (v) dN Ndv
f (v)表示在速率v 附近 单位速率间隔内的分子数 占总分子数的比率.
（2） f (v)dv dN N
表示速率在 v~v+dv 区间 内的分子数占总分子数的比 率，即阴影1 面积。
（3） v2 f (v)dv N
v1
N
表示速率在 v1~ v2 区间 内的分子数占总分子数的 比率， 即阴影2 面积。
• Q：系统与外界的热交换。 Q>0表示系统从外界吸热；Q<0表示系统向外 界放热。
• E：系统内能的改变量。 E>0表示系统内能增加（若是理想气体，则 温度升高)；E<0表示系统内能减少。
• A：系统对外界的做功情况。 A>0表示系统对外界作正功，如体积膨胀的过 程；A<0表示系统对外界作负功，亦即外界对 系统做功。
不可逆 可逆.
上一张 下一张 返回
有关物质结构与运动规律的 三条基本定理
• 宏观物体有大量微粒组成。 • 分子间存在相互作用力。 • 分子永不停息地无规运动。
上一张 下一张 返回
气体分子运动的特点：
• 看作是惯性支配下的自由运动。 • 分子间存在频繁碰撞。 • 服从统计规律。
气体分子动理论'
例. 扔硬币
单个小球落入位置 少量小球按位置的分布 大量小球按位置的分布 偶然事件 规律不明显 确定的规律 伽尔顿板实验
随机试验： 在相同条件下可重复进行； 每次试验有多种可能结果； 试验结果事先不可预测；
不同试验之间无关联。
（随机试验的每一个可能结果称为一个随机事件。） 伽耳顿板实验中粒子落入的位置 掷色子出现的点数 气体分子的速率、动量、动能等
y
vix
O
z
a
A1
c
I
i 1
N
t
a
v
2 ix
t
a
v
i 1
N
x
b
2 ix
F I t N 2 N 2 p vix V vix S A1 bc abc i 1 i 1
p
V
2 vix i 1
N
1 2 vx N
2 vix i 1
2
例 一容积为 V = 1.0 m3 的容器内装有 N1 = 1.0×1024 个氧分子 N2 = 3.0×1024 个氮分子的混合气体， 混合气体的压强 P = 2.58×104 Pa 。 求 解
(1) 分子的平均平动动能； (2) 混合气体的温度。
(1) 由压强公式 ,有
3 p 3 p 9.68 1021 J 2 n 2 ( N1 N 2 ) V
分子间有相互作用力 f
r0 10
10
m (
平衡位置 )
斥力
r r0 r r0
r0 结论
分子力表现为引力 分子力表现为斥力
合力
O
r0
引力
r
势能
分子有效直径
大学物理学(下册)第10章 气体动理论
➢ 对单个分子的力学性质的假设 理想气体分子本身的线度可以忽略不计 除了碰撞的瞬间外，分子之间以及分子与容器壁之 间的相互作用力可以忽略不计 分子之间以及分子与容器器壁之间的碰撞都是完全 弹性碰撞
➢ 处于平衡态下的理想气体的统计假设 每一分子在容器中任意位置出现的 概 率都是相等的 分子沿各个方向运动的概率都相同
自由度上也具有相同的平均动能，大小也为kT/2。
平方项的平均值
k
i 2
kT
平动自由度
结论：分子的每一个平动自由度上具有相
同的平均平动动能，都是kT/2
10.5.3 理想气体的内能 一个系统内分子热运动能量的总和称为系统的内能。系统的 内能包括系统内所有分子的动能和势能。
理想气体内能是分子动能之和 说明：
Nv
f (v) dN
此式的物理意义：速率在v附近，单位速率 区间内的分子数占总分子数的百分比。称为
Ndv 分子速率分布函数。
速率分布函数归一化条件
由： f (v) dN Ndv
f (v)dv
dN dv
0
0 Ndv
N dN
0 N
1
0.45 0.4
0.35 0.3
0.25 0.2
0.15 0.1
yz xyz
vi2x
P 1 nmv2 3
p
nmv
2 x
等概率原理：
v
2 x
v
2 y
v
2 z
统计平均的概念：
v
2 x
v12x
v22x
v
2 Nx
＝
N
vi2x N
v2
v
2 x
v
2 y
vz2
10.3.3 压强公式的统计意义及微观本质
➢ 处于平衡态下的理想气体的统计假设 每一分子在容器中任意位置出现的 概 率都是相等的 分子沿各个方向运动的概率都相同
自由度上也具有相同的平均动能，大小也为kT/2。
平方项的平均值
k
i 2
kT
平动自由度
结论：分子的每一个平动自由度上具有相
同的平均平动动能，都是kT/2
10.5.3 理想气体的内能 一个系统内分子热运动能量的总和称为系统的内能。系统的 内能包括系统内所有分子的动能和势能。
理想气体内能是分子动能之和 说明：
Nv
f (v) dN
此式的物理意义：速率在v附近，单位速率 区间内的分子数占总分子数的百分比。称为
Ndv 分子速率分布函数。
速率分布函数归一化条件
由： f (v) dN Ndv
f (v)dv
dN dv
0
0 Ndv
N dN
0 N
1
0.45 0.4
0.35 0.3
0.25 0.2
0.15 0.1
yz xyz
vi2x
P 1 nmv2 3
p
nmv
2 x
等概率原理：
v
2 x
v
2 y
v
2 z
统计平均的概念：
v
2 x
v12x
v22x
v
2 Nx
＝
N
vi2x N
v2
v
2 x
v
2 y
vz2
10.3.3 压强公式的统计意义及微观本质
大学物理第十章 气体动理论
分子间的相互作用力,
f
称分子力。此力为短程力,
引力、斥力视距离而定
斥
力
当 r = r0（r0 10-10 m）时 f = 0
当 r < r0 时 f 为斥力 当 r > r0 时 f 为引力 当 r > 10-9 m 时，分子力可忽略。
o
引 r0
力
r
§6-2气体的状态参量、平衡状态、理想气体状态方程
p
F A1
F l2l3
m l1 l 2 l 3
N
v
2 ix
i 1
1 mN V
v
2 ix
N
1 V
mN
v
2 x
v
2 x
1 v2
3
1
N
mv 2
3V
分子数密度n
理想气体压强公式
p 1 nmv 2 3
p 1 nmv 2 3
2 3
1 n(
2
mv2 )
2 3
得 P M RT Nm RT N R T nkT
V
VN 0 m
V N0
N0m
波尔兹曼常数
由压强公式
p nkT
p
2 3
n
k
k
3 kT 2
可见：从微观角度看，温度是分子
大小的量度,表征大
k
量气体分子热运动剧烈程度,是一统计平均值,对个别分子无
意义。
§6—5 能量按自由度均分原则、理想气体的内能
一、运动自由度：
确定运动物体在空间位置所需要的独立坐标数目，称为 该物体的自由度
第4章气体动理论
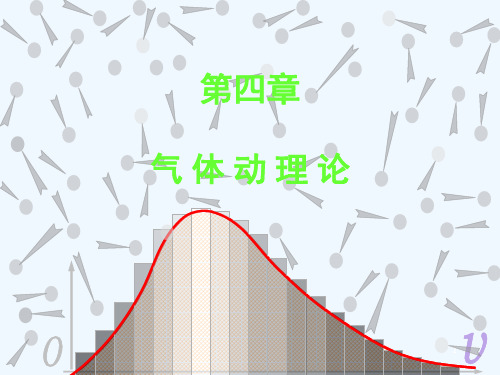
小球每次落入哪个狭槽是不
完全相同的，这表明在一次
实验中小球落入哪个狭槽中 是偶然的。 尽管一个小球落入哪个槽中 是偶然的，但大量小球的分 布规律则是确定的，即遵从
统计分布规律。
7
统计规律：当小球数N 足够大时小球的分布具有统计规律。
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
子，如果分子有 t 个平动自由度，r 个转动自由度，则气体分 子的平均动能为
1 i ( t r ) kT kT 2 2
单原子分子
双原子分子
多原子分子
3 kT 2
5 kT 2
6 kT 2
27
★ 理想气体的内能 实际气体的内能 气体分子热运动的各种形式的动能和势能的总和。 平动动能 分子动能 转动动能 振动动能 分子振动势能
i i
于1，称为概率的归一化条件。
6
小球在伽尔顿板中的分布规律
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
单位： 8.31J · mol-1 · K-1
4
★ 统计规律
一定条件下，大量偶然随机事件的整体具有确定的规律
性，这种规律称为统计规律。
对单个分子运用力学规律，对大量分子求统计平均值， 从而建立大量分子微观量的统计平均值与系统宏观量之 间的关系。这种关系就是所要寻求的统计规律。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
º C (代号t)
t=T-273.15
T:热力学温标 ; t:摄氏温标
第十章 气体动理论 6
p 、V、T 的单位
1、气体的体积V 气体的体积V是指气体分子无规则热运动所能到达 的空间。对于密闭容器中的气体，容器的体积就是 气体的体积。 单位：m3 2、压强p 压强P是大量分子与容器壁相碰撞而产生的，它等 于容器壁上单位面积所受到的正压力。 p=F/S 单位： 1Pa=1N.m-2 标准大气压 1atm=76cm.Hg=1.013×105Pa
第十章 气体动理论 7
3、温度T 100º C 温度的高低反映分子热运 动激烈程度。 (1)热力学温标T，单位：K (2)摄氏温标t ，单位：0C 00C——水的三相点温度 50º C 0 100 C——水的沸腾点温度 (3)华氏温标F， 单位0F 320F ——水的三相点温度 2120F——水的沸腾点温度 关系： 0º C T=273.15+t -17.8º C F=9t/5+32
P V1 P 1 2V2 T1 T2 6 P V 4 . 2 10 22 T T ( 273 47 ) 930 K 2 1 4 P V 8 . 5 10 17 1 1
这一温度超过了柴油的燃点,所以喷入柴油会立即燃烧.
第十章 气体动理论 14
第十章 气体动理论 13
例1 某种柴油机汽缸容量为0.827103m3.设压缩前其中气体的温度是47C,压 强为8.5 104Pa,当活塞急剧上升时.可把 空气压缩到原体积的1/17,压强增加到 4.2 106Pa.求此时空气的温度,这时将柴 油喷入汽缸将发生怎样的情况?(空气可 视为理想气体) 解:将空气看作理想气体,有
第十章 气体动理论
4
§10-1
热力学第零定律
热力学第零定律或热平衡定律
如果两个系统分别与处于确定状态的第三个系统 达到热平衡，则这两个系统彼此也将处于热平衡。
热力学第零定律表明，处在同一平衡态的 所有热力学系统都有一个共同的宏观性质， 这个决定系统热平衡的宏观性质的物理量 可以定义为温度。
第十章 气体动理论 5
第十章 气体动理论
212º F 200º F
122º F 100º F
32º F 0º F
8
二、系统与外界
1. 热力学系统（简称系统）
在给定范围内，人们所研究的由大量微观粒子 所组成的宏观客体。本课程中主要研究气体系统。
2.系统的外界（简称外界）
能够与所研究的热力学系统发生相互作用的其 它物体。
第十章 气体动理论
第十章 气体动理论 10
热平衡态的图示，p-V图
热力学平衡状态(热动平衡态), 用一组(P、V、T)表示
P
P1
I(P 1,V !,T 1)
II ( P ,V ,T ) 2 2 2
O
状态变化的过程,
平衡过程
V1
V2
V
第十章 气体动理论
11
四 理想气体的状态方程
状态方程：在平衡态下，状态参量间的函数关系。 理想气体：同时满足三个气体定律的气体。 是一个理想模型。实际气体在温度不太低， 压强不太大的情况下可以近似为理想气体。 理想气体的状态方程 P
按照研究方法的不同，热学可分为两门学科， 即热力学和统计物理学。它们从不同角度研 究热运动，二者相辅相成，彼此联系又互相 补充。
第十章 气体动理论
3
第六章 气体动理论
§10-1 热力学第零定律 §10-2 气体的状态参量 理想气体物态方程 平衡状态 §10-3 气体动理论的基本概念 §10-3 气体动理论的压强公式 §10-4 气体分子的平均平动动能与温度的关系 §10-5 能量按自由度均分原则 理想气体的内能 §10-6 麦克斯韦速率分布律 §10-7 玻尔兹曼分布律 §10-8 分子的平均自由程和平均碰撞次数 §10-9 气体内的迁移现象 §10-10 实际气体的范德瓦尔斯方程
§10-2 气体的状态参量 理想气体物态方程 平衡状态
一
状态参量
气体的状态参量（State Parameter ）
状态参量
标准单位 常用单位
பைடு நூலகம்
主要换算关系
体积(代号V) m 3 压强(代号P) Pa 温 度
K (代号 T)
3 3 3 升( dm 3 ) 1 dm 10 m atm 1atm=101325Pa
9
三 平衡态(equilibrium state)和平衡过程
一个系统在不受外界影响的条件下，如果它的宏观性质不 再随时间变化，我们就说这个系统处于热力学平衡态。 （1）不受外界影响和系统的所有宏观性质不随时间变 化，这是判别一个系统是否处于平衡态的两个重要依据， 二者缺一不可。 （2）在不存在外力或外力作用可以忽略的情况下、一个均 匀系统在达到平衡态时，它内部的各种宏观性质处处一样。 在外力的作用不可忽略的情况下,一个系统达到平衡态时， 它内部的某些宏观性质就不是均匀的。 （3）平衡是相对的。这有两方面的含义，一是指平衡态 是一个理想的概念．二是指当一个系统处于平衡态时， 组成系统的分子仍在不停地运动着.
M PV RT Mmol
摩尔气体常量 R=8.31 J/mol.K
第十章 气体动理论
T T T 1 2 3
O
T3 T2
T1
V
12
在温度不太低(与室温相比)和压强不太大(与大气压相 比)时，有三条实验定律 Boyle-Mariotte定律 等温过程中 pV=const Gay-Lussac定律 等体过程中 p/T=const Charles定律 等压过程中 V/T=const Avogadro定律：在同样的温度和压强下，相同体积的 气体含有相同数量的分子。在标准状态下，1摩尔任 何气体所占有的体积为22.4升。 理想气体的定义：在任何情况下都遵守上述三个实验 定律和Avogadro定律的气体称为理想气体。
• 平衡态与平衡过程 • • • •
章气体动理论
1
第三篇
气体动理论和热力学基础
第十章 气体动理论 第十一章 热力学基础
第十章 气体动理论
2
引言：热学的研究对象和两种研究方法
热学是以研究热运动的规律及其对物质宏观性 质的影响，以及与物质其他运动形态之间的转 化规律为任务的。所谓热运动即组成宏观物体 的大量微观粒子的一种永不停息的无规运动。